26.2锐角三角函数的计算

合集下载

锐角三角函数特殊公式锐角三角函数例题解析锐角三角函数诱导公式

锐角三角函数的定义•锐角三角函数：锐角角A的正弦（sin）,余弦（cos）和正切（tan）,余切（cot）以及正割（sec），余割（csc）都叫做角A的锐角三角函数。

初中学习的锐角三角函数值的定义方法是在直角三角形中定义的，所以在初中阶段求锐角的三角函数值，都是通过构造直角三角形来完成的，即把这个角放到某个直角三角形中。

所谓锐角三角函数是指：我们初中研究的都是锐角的三角函数。

初中研究的锐角的三角函数为：正弦（sin），余弦（cos），正切（tan）。

正弦：在直角三角形中，锐角A的对边与斜边的比叫做∠A的正弦，记作sinA，即；余弦：在直角三角形中，锐角A的邻边与斜边的比叫做∠A的余弦，记作cosA，即；正切：在直角三角形中，锐角A的对边与邻边的比叫做∠A的正切，记作tanA，即，锐角A的正弦、余弦、正切都叫做A的锐角三角函数。

•锐角三角函数的增减性：°～90°°≤A≤90°间变化时，0≤sinA≤1, 1≥cosA≥0；当角度在0°<A0, cotA>0。

•锐角三角函数的关系式：同角三角函数基本关系式tanα·cotα=1sin2α·cos2α=1cos2α·sin2α=1sinα/cosα=tanα=secα/cscαcosα/sinα=cotα=cscα/secα(sinα)2+(cosα)2=11+tanα=secα1+cotα=cscα诱导公式sin（－α）=－sinαcos（－α）=cosαtan（－α）=－tanαcot（－α）=－cotαsin（π/2－α）=cosαcos（π/2－α）=sinαtan（π/2－α）=cotαcot（π/2－α）=tanαsin（π/2+α）=cosαcos（π/2+α）=－sinαtan（π/2+α）=－cotαcot（π/2+α）=－tanαsin（π－α）=sinαcos（π－α）=－cosαtan（π－α）=－tanαcot（π－α）=－cotαsin（π+α）=－sinαcos（π+α）=－cosαtan（π+α）=tanαcot（π+α）=cotαsin（3π/2－α）=－cosαcos（3π/2－α）=－sinαtan（3π/2－α）=cotαcot（3π/2－α）=tanαsin（3π/2+α）=－cosαcos（3π/2+α）=sinαtan（3π/2+α）=－cotαcot（3π/2+α）=－tanαsin（2π－α）=－sinαcos（2π－α）=cosαtan（2π－α）=－tanαcot（2π－α）=－cotαsin（2kπ+α）=sinαcos（2kπ+α）=cosαtan（2kπ+α）=tanαcot（2kπ+α）=cotα(其中k∈Z)二倍角、三倍角的正弦、余弦和正切公式Sin(2α)=2sinαcosαCos(2α)=（cosα）2－(sinα)2=2(cosα)2－1=1－2(sinα)2Tan(2α)=2tanα/(1tanα)sin(3α)=3sinα4sin3α=4sinα·sin(60°+α)sin(60°α)cos(3α)=4cos3α3cosα=4cosα·cos(60°+α)cos(60°α)tan(3α)=(3tanαtan3α)/(13tan2α)=tanαtan(π/3+α)tan(π/3α) 和差化积、积化和差公式sinα+sinβ=2sin[(α+β)/2]·cos[(αβ)/2]sinαsinβ=2cos[(α+β)/2]·sin[(αβ)/2]cosα+cosβ=2cos[(α+β)/2]·cos[(αβ)/2]cosαcosβ=2sin[(α+β)/2]·sin[(αβ)/2]sinαcosβ=[sin（α+β）+sin（α－β）]sinαsinβ=[1][cos（α+β）cos（αβ）]/2cosαcosβ=[cos（α+β）+cos（αβ）]/2sinαcosβ=[sin（α+β）+sin（αβ）]/2cosαsinβ=[sin（α+β）sin（αβ）]/2。

锐角三角函数(公式、定理、结论图表) --中考数学知识必备

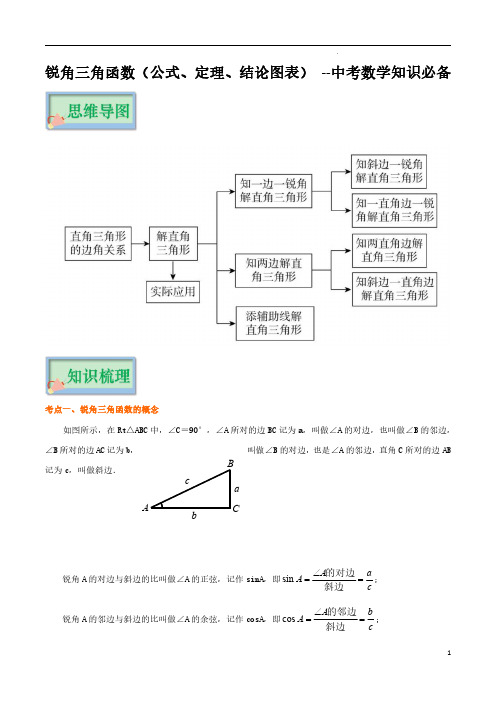
锐角三角函数（公式、定理、结论图表）--中考数学知识必备考点一、锐角三角函数的概念如图所示，在Rt△ABC 中，∠C＝90°，∠A 所对的边BC 记为a，叫做∠A 的对边，也叫做∠B 的邻边，∠B 所对的边AC 记为b，叫做∠B 的对边，也是∠A 的邻边，直角C 所对的边AB记为c，叫做斜边．锐角A 的对边与斜边的比叫做∠A 的正弦，记作sinA，即sin A aA c ∠==的对边斜边；锐角A 的邻边与斜边的比叫做∠A 的余弦，记作cosA，即cos A bA c∠==的邻边斜边；BCa c锐角A的对边与邻边的比叫做∠A的正切，记作tanA，即tanA a AA b∠==∠的对边的邻边.同理sinB bBc∠==的对边斜边；cosB aBc∠==的邻边斜边；tanB bBB a∠==∠的对边的邻边．要点诠释：(1)正弦、余弦、正切函数是在直角三角形中定义的，反映了直角三角形边与角的关系，是两条线段的比值．角的度数确定时，其比值不变，角的度数变化时，比值也随之变化．(2)sinA，cosA，tanA分别是一个完整的数学符号，是一个整体，不能写成，，，不能理解成sin与∠A，cos与∠A，tan与∠A的乘积．书写时习惯上省略∠A的角的记号“∠”，但对三个大写字母表示成的角(如∠AEF)，其正切应写成“tan∠AEF”，不能写成“tanAEF”；另外，、、常写成、、．(3)任何一个锐角都有相应的锐角三角函数值，不因这个角不在某个三角形中而不存在．(4)由锐角三角函数的定义知：当角度在0°＜∠A＜90°之间变化时，，，tanA＞0．典例1：（2022•扬州）在△ABC中，∠C＝90°，a、b、c分别为∠A、∠B、∠C的对边，若b2＝ac，则sin A的值为．．【分析】根据勾股定理和锐角三角函数的定义解答即可．【解答】解：在△ABC中，∠C＝90°，∴c2＝a2+b2，∵b2＝ac，∴c2＝a2+ac，等式两边同时除以ac得：＝+1，令＝x，则有＝x+1，∴x2+x﹣1＝0，解得：x1＝，x2＝（舍去），当x＝时，x≠0，∴x＝是原分式方程的解，∴sin A＝＝．故答案为：．【点评】本题主要考查了锐角三角函数，熟练掌握勾股定理和锐角三角函数的定义是解答本题的关键．考点二、特殊角的三角函数值利用三角函数的定义，可求出0°、30°、45°、60°、90°角的各三角函数值，归纳如下：要点诠释：(1)通过该表可以方便地知道0°、30°、45°、60°、90°角的各三角函数值，它的另一个应用就是：如果知道了一个锐角的三角函数值，就可以求出这个锐角的度数，例如：若，则锐角．(2)仔细研究表中数值的规律会发现：sin0︒、、、、sin90︒的值依次为0、、、、1，而cos0︒、、、、cos90︒的值的顺序正好相反，、、的值依次增大，其变化规律可以总结为：当角度在0°＜∠A＜90°之间变化时，①正弦、正切值随锐角度数的增大(或减小)而增大(或减小)②余弦值随锐角度数的增大(或减小)而减小(或增大)．典例2：（2022•天津）tan45°的值等于（）A．2B．1C．D．【分析】根据特殊角的三角函数值，进行计算即可解答．【解答】解：tan45°的值等于1，故选：B．【点评】本题考查了特殊角的三角函数值，熟练掌握特殊角的三角函数值是解题的关键．考点三、锐角三角函数之间的关系如图所示，在Rt△ABC中，∠C=90°．(1)互余关系：，；(2)平方关系：；(3)倒数关系：或；(4)商数关系：．要点诠释：锐角三角函数之间的关系式可由锐角三角函数的意义推导得出，常应用在三角函数的计算中，计算时巧用这些关系式可使运算简便．考点四、解直角三角形在直角三角形中，由已知元素(直角除外)求未知元素的过程，叫做解直角三角形.在直角三角形中，除直角外，一共有5个元素，即三条边和两个锐角.设在Rt△ABC中，∠C=90°，∠A、∠B、∠C所对的边分别为a、b、c，则有：①三边之间的关系：a2+b2=c2(勾股定理).②锐角之间的关系：∠A+∠B=90°.③边角之间的关系：，，，，，.④，h为斜边上的高.要点诠释：(1)直角三角形中有一个元素为定值(直角为90°)，是已知的值.(2)这里讲的直角三角形的边角关系指的是等式，没有包括其他关系(如不等关系).(3)对这些式子的理解和记忆要结合图形，可以更加清楚、直观地理解.考点五、解直角三角形的常见类型及解法已知条件解法步骤Rt△ABC两边两直角边(a，b)由求∠A，∠B=90°－∠A，斜边，一直角边(如c，a)由求∠A，∠B=90°－∠A，一边一角一直角边和一锐角锐角、邻边(如∠A，b)∠B=90°－∠A，，锐角、对边(如∠A，a)∠B=90°－∠A，，斜边、锐角(如c，∠A)∠B=90°－∠A，，要点诠释：1．在遇到解直角三角形的实际问题时，最好是先画出一个直角三角形的草图，按题意标明哪些元素是已知的，哪些元素是未知的，然后按先确定锐角、再确定它的对边和邻边的顺序进行计算.2．若题中无特殊说明，“解直角三角形”即要求出所有的未知元素，已知条件中至少有一个条件为边.典例3：（2022•丹东）如图，AB是⊙O的直径，点E在⊙O上，连接AE和BE，BC平分∠ABE交⊙O于点C，过点C作CD⊥BE，交BE的延长线于点D，连接CE．（1）请判断直线CD与⊙O的位置关系，并说明理由；（2）若sin∠ECD＝，CE＝5，求⊙O的半径．【分析】（1）结论：CD是⊙O的切线，证明OC⊥CD即可；（2）设OA＝OC＝r，设AE交OC于点J．证明四边形CDEJ是矩形，推出CD＝EJ＝4，CJ＝DE＝3，再利用勾股定理构建方程求解．【解答】解：（1）结论：CD是⊙O的切线．理由：连接OC．∵OC＝OB，∴∠OCB＝∠OBC，∵BC平分∠ABD，∴∠OBC＝∠CBE，∴∠OCB＝∠CBE，∴OC∥BD，∵CD⊥BD，∴CD⊥OC，∵OC是半径，∴CD是⊙O的切线；（2）设OA＝OC＝r，设AE交OC于点J．∵AB是直径，∴∠AEB＝90°，∵OC⊥DC，CD⊥DB，∴∠D＝∠DCJ＝∠DEJ＝90°，∴四边形CDEJ是矩形，∴∠CJE＝90°，CD＝EJ，CJ＝DE，∴OC⊥AE，∴AJ＝EJ，∵sin∠ECD＝＝，CE＝5，∴DE＝3，CD＝4，∴AJ＝EJ＝CD＝4，CJ＝DE＝3，在Rt△AJO中，r2＝（r﹣3）2+42，∴r＝，∴⊙O的半径为．【点评】本题考查解直角三角形，切线的判定，垂径定理，矩形的判定和性质，勾股定理等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型考点六、解直角三角形的应用解直角三角形的知识应用很广泛，关键是把实际问题转化为数学模型，善于将某些实际问题中的数量关系化归为直角三角形中的边角关系是解决实际应用问题的关键.解这类问题的一般过程是：(1)弄清题中名词、术语的意义，如仰角、俯角、坡度、坡角、方向角等概念，然后根据题意画出几何图形，建立数学模型.(2)将已知条件转化为几何图形中的边、角或它们之间的关系，把实际问题转化为解直角三角形的问题.(3)根据直角三角形(或通过作垂线构造直角三角形)元素(边、角)之间的关系解有关的直角三角形.(4)得出数学问题的答案并检验答案是否符合实际意义，得出实际问题的解.拓展：在用直角三角形知识解决实际问题时，经常会用到以下概念：(1)坡角：坡面与水平面的夹角叫做坡角，用字母表示.坡度(坡比)：坡面的铅直高度h和水平距离的比叫做坡度，用字母表示，则，如图，坡度通常写成=∶的形式.(2)仰角、俯角：视线与水平线所成的角中，视线中水平线上方的叫做仰角，在水平线下方的叫做俯角，如图.(3)方位角：从某点的指北方向线按顺时针转到目标方向的水平角叫做方位角，如图①中，目标方向PA，PB，PC的方位角分别为是40°，135°，245°.(4)方向角：指北或指南方向线与目标方向线所成的小于90°的水平角，叫做方向角，如图②中的目标方向线OA，OB，OC，OD的方向角分别表示北偏东30°，南偏东45°，南偏西80°，北偏西60°.特别如：东南方向指的是南偏东45°，东北方向指的是北偏东45°，西南方向指的是南偏西45°，西北方向指的是北偏西45°.要点诠释：1．解直角三角形实际是用三角知识，通过数值计算，去求出图形中的某些边的长或角的大小，最好画出它的示意图.2．非直接解直角三角形的问题，要观察图形特点，恰当引辅助线，使其转化为直角三角形或矩形来解.例如：3．解直角三角形的应用题时，首先弄清题意(关键弄清其中名词术语的意义)，然后正确画出示意图，进而根据条件选择合适的方法求解.典例4：（2022•黑龙江）小明去爬山，在山脚看山顶角度为30°，小明在坡比为5：12的山坡上走1300米，此时小明看山顶的角度为60°，山高为（）米A．600﹣250B．600﹣250C．350+350D．500【分析】设EF＝5x米，根据坡度的概念用x表示出BF，根据勾股定理求出x，根据正切的定义列出方程，解方程得到答案．【解答】解：设EF＝5x米，∵斜坡BE的坡度为5：12，∴BF＝12x米，由勾股定理得：（5x）2+（12x）2＝（1300）2，解得：x＝100，则EF＝500米，BF＝1200米，由题意可知，四边形DCFE为矩形，∴DC＝EF＝500米，DE＝CF，在Rt△ADE中，tan∠AED＝，则DE＝＝AD，在Rt△ACB中，tan∠ABC＝，∴＝，解得：AD＝600﹣750，∴山高AC＝AD+DC＝600﹣750+500＝（600﹣250）米，故选：B．【点评】本题考查的是解直角三角形的应用—坡度坡角问题，掌握坡度是坡面的铅直高典例5：（2022•湖北）如图，有甲乙两座建筑物，从甲建筑物A点处测得乙建筑物D点的俯角α为45°，C 点的俯角β为58°，BC为两座建筑物的水平距离．已知乙建筑物的高度CD为6m，则甲建筑物的高度AB为16m．（sin58°≈0.85，cos58°≈0.53，tan58°≈1.60，结果保留整数）．【分析】过点D作DE⊥AB于点E，则BE＝CD＝6m，∠ADE＝45°，∠ACB＝58°，在Rt△ADE中，∠ADE＝45°，设AE＝xm，则DE＝xm，BC＝xm，AB＝AE+BE＝（6+x）m，在Rt△ABC中，tan∠ACB ＝tan58°＝≈1.60，解得x＝10，进而可得出答案．【解答】解：过点D作DE⊥AB于点E，如图．则BE＝CD＝6m，∠ADE＝45°，∠ACB＝58°，在Rt△ADE中，∠ADE＝45°，设AE＝xm，则DE＝xm，∴BC＝xm，AB＝AE+BE＝（6+x）m，在Rt△ABC中，tan∠ACB＝tan58°＝≈1.60，解得x＝10，∴AB＝16m．故答案为：16．【点评】本题考查解直角三角形的应用﹣仰角俯角问题，熟练掌握锐角三角函数的定义是解答本题的关键典例6：（2022•资阳）小明学了《解直角三角形》内容后，对一条东西走向的隧道AB进行实地测量．如图所示，他在地面上点C处测得隧道一端点A在他的北偏东15°方向上，他沿西北方向前进100米后到达点D，此时测得点A在他的东北方向上，端点B在他的北偏西60°方向上，（点A、B、C、D在同一平面内）（1）求点D与点A的距离；（2）求隧道AB的长度．（结果保留根号）【分析】（1）根据方位角图，易知∠ACD＝60°，∠ADC＝90°，解Rt△ADC即可求解；（2）过点D作DE⊥AB于点E．分别解Rt△ADE，Rt△BDE求出AE和BE，即可求出隧道AB的长．【解答】解；（1）由题意可知：∠ACD＝15°+45°＝60°，∠ADC＝180°﹣45°﹣45°＝90°，在Rt△ADC中，∴（米），答：点D与点A的距离为300米．（2）过点D作DE⊥AB于点E，∵AB是东西走向，∴∠ADE＝45°，∠BDE＝60°，在Rt△ADE中，∴（米），在Rt△BDE中，∴（米），∴（米），答：隧道AB的长为米．【点评】本题考查了解直角三角形的应用﹣方向角问题，掌握方向角的概念，掌握特殊角的三角函数值是解题的关键．考点七、解直角三角形相关的知识如图所示，在Rt△ABC 中，∠C＝90°，(1)三边之间的关系：222a b c +=；(2)两锐角之间的关系：∠A+∠B＝90°；(3)边与角之间的关系：sin cos a A B c ==，cos cos a A B c ==，cos sin b A B c ==，1tan tan a A b B==．(4)如图，若直角三角形ABC 中，CD⊥AB 于点D，设CD＝h，AD＝q，DB＝p，则由△CBD∽△ABC，得a 2＝pc；由△CAD∽△BAC，得b 2＝qc；由△ACD∽△CBD，得h 2＝pq；由△ACD∽△ABC 或由△ABC 面积，得ab＝ch．(5)如图所示，若CD 是直角三角形ABC 中斜边上的中线，则①CD＝AD＝BD＝12AB；②点D 是Rt△ABC 的外心，外接圆半径R＝12AB．(6)如图所示，若r 是直角三角形ABC 的内切圆半径，则2a b c ab r a b c +-==++．直角三角形的面积：①如图所示，111sin 222ABC S ab ch ac B === △．（h 为斜边上的高）②如图所示，1()2ABCS r a b c=++△．典例7：（2022•黄石）我国魏晋时期的数学家刘徽首创“割圆术”：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体，而无所失矣”，即通过圆内接正多边形割圆，从正六边形开始，每次边数成倍增加，依次可得圆内接正十二边形，内接正二十四边形，…．边数越多割得越细，正多边形的周长就越接近圆的周长．再根据“圆周率等于圆周长与该圆直径的比”来计算圆周率．设圆的半径为R，图1中圆内接正六边形的周长l6＝6R，则π≈＝3．再利用圆的内接正十二边形来计算圆周率，则圆周率π约为（）A．12sin15°B．12cos15°C．12sin30°D．12cos30°【分析】利用圆内接正十二边形的性质求出A6A7＝2A6M＝2R×sin15°，再根据“圆周率等于圆周长与该圆直径的比”，即可解决问题．【解答】解：在正十二边形中，∠A6OM＝360°÷24＝15°，∴A6M＝sin15°×OA6＝R×sin15°，∵OA6＝OA7，OM⊥A6A7，∴A6A7＝2A6M＝2R×sin15°，∴π≈＝12sin15°，故选：A．【点评】本题主要考查了圆内接多边形的性质，解直角三角形等知识，读懂题意，计算出正十二边形的周长是解题的关键．。

锐角三角函数公式和面积公式

锐角三角函数公式正弦：sin α=∠α的对边/∠α的斜边余弦：cos α=∠α的邻边/∠α的斜边正切：tan α=∠α的对边/∠α的邻边余切：cot α=∠α的邻边/∠α的对边面积公式长方形，正方形以及圆的面积公式面积公式包括扇形面积共式，圆形面积公式，弓形面积公式，菱形面积公式，三角形面积公式，梯形面积公式等多种图形的面积公式。

扇形面积公式在半径为R的圆中，因为360°的圆心角所对的扇形的面积就是圆面积S＝πR^2，所以圆心角为n°的扇形面积：S＝nπR^2÷360比如：半径为1cm的圆，那么所对圆心角为135°的扇形的周长：C＝2R＋nπR÷180＝2×1＋135×3.14×1÷180＝2＋2.355＝4.355(cm)＝43.55(mm)扇形的面积：S＝nπR^2÷360＝135×3.14×1×1÷360＝1.1775(cm^2)=117.75(mm^2)扇形还有另一个面积公式S=1/2lR其中l为弧长，R为半径三角形面积公式任意三角形的面积公式（海伦公式）：S=√p(p-a)(p-b)(p-c), p=（a+b+c）/2,a.b.c,为三角形三边。

证明：证一勾股定理分析：先从三角形最基本的计算公式S△ABC = aha入手，运用勾股定理推导出海伦公式。

证明：如图ha⊥BC，根据勾股定理，得: x = y = ha = = = ∴S△ABC = aha= a× = 此时S△ABC为变形④，故得证。

证二：斯氏定理分析：在证一的基础上运用斯氏定理直接求出ha。

斯氏定理:△ABC边BC上任取一点D，若BD=u，DC=v,AD=t.则t 2 = 证明：由证一可知，u = v = ∴ha 2 = t 2 = －∴S△ABC = aha = a × = 此时为S△ABC的变形⑤，故得证。

锐角三角形计算公式

锐角三角形计算公式在咱们的数学世界里，锐角三角形那可是个有趣的存在！说起锐角三角形的计算公式，这可得好好唠唠。

先来说说什么是锐角三角形吧。

它呀，就是三个角都小于 90 度的三角形。

那对于锐角三角形，有不少计算公式能帮咱们更好地了解它的特性呢。

咱先瞅瞅面积的计算。

说到面积，常见的公式就是 S = 1/2 ×底 ×高。

就拿我曾经给学生讲这个知识点的时候发生的一件事来说。

有一次课堂上，我画了一个锐角三角形在黑板上，底边标了个 6 厘米，高是 4厘米。

我就问同学们：“那这个三角形的面积是多少呀？”结果好多同学都一脸懵。

我就引导他们：“想想咱们的公式呀！”终于，有个聪明的小家伙举起手说：“老师，是 12 平方厘米！”我笑着问他：“怎么算出来的呀？”他大声回答：“底乘高除以 2，6 乘 4 除以 2 就是 12 ！”那一刻，我心里可美了，感觉自己的努力没白费。

除了面积，还有正弦定理和余弦定理也和锐角三角形息息相关。

正弦定理是 a/sinA = b/sinB = c/sinC ，余弦定理是 a² = b² + c² - 2bc×cosA 。

这两个定理在解决锐角三角形的边长和角度问题时，那可太有用了。

记得有一回，我给学生们出了一道题，一个锐角三角形，已知两条边和一个夹角，让他们求另外一条边。

一开始大家都抓耳挠腮的，我就一点点带着他们分析，从已知条件入手，运用余弦定理，一步一步算出结果。

当最后得出正确答案的时候，同学们都露出了恍然大悟的表情，那种满足感，真的让人特别开心。

还有啊，在实际生活中，锐角三角形的计算公式也大有用处。

比如说，建筑工人在搭建屋顶的时候，如果屋顶的形状是个锐角三角形，那他们就得用这些公式来计算材料的用量和角度，确保屋顶既牢固又美观。

总之，锐角三角形的计算公式虽然看起来有点复杂，但只要咱们用心去学，多做练习，就一定能掌握得牢牢的。

就像咱们解决生活中的其他难题一样，只要有耐心、有方法，啥都能搞定！希望大家都能在数学的海洋里畅游，把锐角三角形的计算公式运用得炉火纯青！。

26.2 锐角三角函数的计算课件(共16张PPT)

例1 用计算器求三角函数值：(精确到0.000 1)．(1)sin 10°； (2) cos 50°18' ．
例题示范
解：（1） ∴ sin 10°≈ 0.173 6．（2） ∴ cos 50°18' ≈ 0. 638 8．
例2 用计算器求下列各锐角的度数：（结果精确到1"）（1）已知cosα=0.523 7，求锐角α.
第二十六章解直角三角形
26.2 锐角三角函数的计算
学习目标
学习重难点
重点
难点
1.会用计算器求锐角的三角函数值．2.会用计算器根据一个锐角三角函数的值求对应的锐角．
会用计算器求锐角的三角函数值．
正确使用计算器求锐角的三角函数值．
回顾复习
根据前面学习的特殊角的三角函数值，完成下面的表格．
问题引入
我们已经知道30°，45°，60°的三角函数值，那么，怎样计算任意锐角的函数值呢？反过来，已知一个锐角的三角函数值，怎样求出这个锐角呢？如何求它的三角函数值呢？
新知引入
思考如何用计算器求锐角的三角函数值呢？

计算器上只要有sin,cos,tan键，就可以用来求锐角的三角函数值．
不同计算器的按键方法各有不同，现在介绍一种计算器，先按ON/C键，再按MODE键，使显示器屏幕出现“DEG”，然后再按有关三角函数的键．
拓展练习
1.用计算器求sin 16°，cos 42°，tan 85°，sin 72°38′25″的值.
按键顺序
显示结果
sin 16°
0.275 637 355
cos 42°
0.743 144 825
tan 85°
11. 430 052 3
sin72°38′25″

锐角三角函数基本公式

1
余弦(cos)
1
√3/2
√2/2
1/2
0
正切(tan)
0
√3/3
1
√3
不存在
余切(cot)
不存在
√3
1
√3/3
0
取值范围(θ是锐角,简单的图像画法）
0<sinθ<10<cosθ<1tanθ>0cotθ>0
变化情况
1.锐角三角函数值都是正值。
2.当角度在0°～90°间变化时，
正弦值随着角度的增大而增大，减小而减小，余弦值随着角度的增大而减小，减小而增大；
锐角三角函数
基本三角函数：
正弦（sin）等于对边比斜边；sinA=a/c
余弦（cos）等于邻边比斜边；cosA=b/c
正切（tan）等于对边比邻边；tanA=a/b
余切（cot）等于邻边比对边；cotA=b/a
特殊角的三角函数值如下：
角度
0°
30°
45°
60°
90°
正弦(sin)
0
1/2
√2/2
√3/2
正切值随着角度的增大而增大，减小而减小，余切值随着角度的增大而减小，减小而增大；
3.当角度在0°≤A≤90°间变化时，0≤sinA≤1, 1≥cosA≥0；当角度在0°<A0, cotA>0。
同角三角函数基本关系式
tanα·cotα=1
sinα/cosα=tanα cosα/sinα=cotα
sin（90Байду номын сангаас－α）=cosα cos（90°－α）=sinα
tan（90°－α）=cotα cot（90°－α）=tanα
tanα* tan（90°－α）=1

锐角三角函数公式

锐角三角函数公式 sin α=∠α的对边 / 斜边 cos α=∠α的邻边 / 斜边 tan α=∠α的对边 / ∠α的邻边 cot α=∠α的邻边 / ∠α的对边三倍角公式推导 sin3a =sin(2a+a)=sin2acosa+cos2asina 辅助角公式Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t)，其中sint=B/(A^2+B^2)^(1/2)cost=A/(A^2+B^2)^(1/2)tant=B/AAsinα+Bcosα=(A^2+B^2)^(1/2)cos(α-t)，tant=A/B 降幂公式sin^2(α)=(1-cos(2α))/2=versin(2α)/2 cos^2(α)=(1+cos(2α))/2=covers(2α)/2tan^2(α)=(1-cos(2α))/(1+cos(2α))倍角公式Sin2A=2SinA?CosACos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-1 tan2A=（2tanA ）/（1-tanA^2）（注：SinA^2 是sinA 的平方 sin2（A ））三倍角公式sin3α=4sinα·sin(π/3+α)sin(π/3-α) cos3α=4cosα·cos(π/3+α)cos(π/3-α) tan3a = tan a · tan(π/3+a)· tan(π/3-a)半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))两角和差cos(α+β)=cosα·cosβ-sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβ tan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)和差化积sinθ+sinφ = 2 sin[(θ+φ)/2] cos[(θ-φ)/2]sinθ-sinφ = 2 cos[(θ+φ)/2] sin[(θ-φ)/2]cosθ+cosφ = 2 cos[(θ+φ)/2] cos[(θ-φ)/2]cosθ-cosφ = -2 sin[(θ+φ)/2] sin[(θ-φ)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB) tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)诱导公式奇变偶不变，符号看象限积化和差sinαsinβ = [cos(α-β)-cos(α+β)] /2cosαcosβ = [cos(α+β)+cos(α-β)]/2sinαcosβ = [sin(α+β)+sin(α-β)]/2cosαsinβ = [sin(α+β)-sin(α-β)]/2(3)对于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC证:A+B=π-C tan(A+B)=tan(π-C)(tanA+tanB)/(1-tanAtanB)=(tanπ-tanC)/(1+tanπtanC)同样可以得证,当x+y+z=nπ(n∈Z)时,该关系式也成立由tanA+tanB+tanC=tanAtanBtanC可得出以下结论(5)cotAcotB+cotAcotC+cotBcotC=1(6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2)(7)(cosA）^2+(cosB）^2+(cosC）^2=1-2cosAcosBcosC(8)（sinA）^2+（sinB）^2+（sinC）^2=2+2cosAcosBcosC(9)sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1)/n]=0。

锐角三角函数公式大全

锐角三角函数公式　sin α=∠α的对边 / 斜边 cos α=∠α的邻边 / 斜边 tan α=∠α的对边 / ∠α的邻边 cot α=∠α的邻边 / ∠α的对边倍角公式 Sin2A=2SinA?CosA Cos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-1 tan2A=（2tanA）/（1-tanA^2）（注：SinA^2 是sinA的平方 sin2（A））三倍角公式 sin3α=4sinα·sin(π/3+α)sin(π/3-α) cos3α=4cosα·cos(π/3+α)cos(π/3-α) tan3a = tan a · tan(π/3+a)· tan(π/3-a) 三倍角公式推导 sin3a =sin(2a+a) =sin2acosa+cos2asina 辅助角公式 Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t)，其中 sint=B/(A^2+B^2)^(1/2) cost=A/(A^2+B^2)^(1/2) tant=B/AAsinα+Bcosα=(A^2+B^2)^(1/2)cos(α-t)，tant=A/B 降幂公式 sin^2(α)=(1-cos(2α))/2=versin(2α)/2 cos^2(α)=(1+cos(2α))/2=covers(2α)/2 tan^2(α)=(1-cos(2α))/(1+cos(2α)) 推导公式 tanα+cotα=2/sin2α tanα-cotα=-2cot2α 1+cos2α=2cos^2α 1-cos2α=2sin^2α 1+sinα=(sinα/2+cosα/2)^2 =2sina(1-sin²a)+(1-2sin²a)sina =3sina-4sin³a cos3a =cos(2a+a) =cos2acosa-sin2asina =(2cos²a-1)cosa-2(1-sin²a)cosa =4cos³a-3cosa sin3a=3sina-4sin³a =4sina(3/4-sin²a) =4sina[(√3/2)²-sin²a] =4sina(sin²60°-sin²a) =4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°-a)/2] =4sinasin(60°+a)sin(60°-a) cos3a=4cos³a-3cosa =4cosa(cos²a-3/4) =4cosa[cos²a-(√3/2)²] =4cosa(cos²a-cos²30°) =4cosa(cosa+cos30°)(cosa-cos30°) =4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°)/2]} =-4cosasin(a+30°)sin(a-30°)　=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)] =-4cosacos(60°-a)[-cos(60°+a)] =4cosacos(60°-a)cos(60°+a) 上述两式相比可得 tan3a=tanatan(60°-a)tan(60°+a) 半角公式 tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA); cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA. sin^2(a/2)=(1-cos(a))/2 cos^2(a/2)=(1+cos(a))/2　tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a)) 三角和sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγ cos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγ tan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα) 两角和差 cos(α+β)=cosα·cosβ-sinα·sinβ cos(α-β)=cosα·cosβ+sinα·sinβ sin(α±β)=sinα·cosβ±cosα·sinβ tan(α+β)=(tanα+tanβ)/(1-tanα·tanβ) tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ) 和差化积　sinθ+sinφ = 2 sin[(θ+φ)/2] cos[(θ-φ)/2]　sinθ-sinφ = 2 cos[(θ+φ)/2] sin[(θ-φ)/2]　cosθ+cosφ = 2 cos[(θ+φ)/2] cos[(θ-φ)/2] cosθ-cosφ = -2 sin[(θ+φ)/2] sin[(θ-φ)/2] tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB) tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB) 积化和差 sinαsinβ = [cos(α-β)-cos(α+β)] /2 cosαcosβ = [cos(α+β)+cos(α-β)]/2 sinαcosβ = [sin(α+β)+sin(α-β)]/2 cosαsinβ = [sin(α+β)-sin(α-β)]/2 诱导公式 sin(-α) = -sinα cos(-α) = cosα tan (—a)=-tanα sin(π/2-α) = cosα cos(π/2-α) = sinα sin(π/2+α) = cosα cos(π/2+α) = -sinα sin(π-α) = sinα cos(π-α) = -cosα sin(π+α) = -sinα cos(π+α) = -cosα tanA= sinA/cosA tan（π/2＋α）＝－cotα tan（π/2－α）＝cotα tan（π－α）＝－tanα tan（π＋α）＝tanα 诱导公式记背诀窍：奇变偶不变，符号看象限万能公式 sinα=2tan(α/2）/［1+tan＾(α/2)］ cosα=［1-tan＾(α/2)］/1+tan＾(α/2)］ tanα=2tan(α/2)/［1-tan＾(α/2)］。

锐角三角形函数公式表

锐角三角形函数公式表锐角三角形是指三角形中最大角度小于90度的三角形。

在数学中，锐角三角形函数是指正弦、余弦和正切等函数，它们是三角函数的一种。

这些函数在数学、物理、工程和其他领域中都有广泛的应用。

正弦函数（sin）正弦函数是指在锐角三角形中，对于一个角度θ，其对边与斜边的比值。

正弦函数的值域在-1到1之间，当θ等于0度时，正弦函数的值为0，当θ等于90度时，正弦函数的值为1。

余弦函数（cos）余弦函数是指在锐角三角形中，对于一个角度θ，其邻边与斜边的比值。

余弦函数的值域也在-1到1之间，当θ等于0度时，余弦函数的值为1，当θ等于90度时，余弦函数的值为0。

正切函数（tan）正切函数是指在锐角三角形中，对于一个角度θ，其对边与邻边的比值。

正切函数的值域在负无穷到正无穷之间，当θ等于0度时，正切函数的值为0，当θ等于45度时，正切函数的值为1。

余切函数（cot）余切函数是指在锐角三角形中，对于一个角度θ，其邻边与对边的比值。

余切函数的值域也在负无穷到正无穷之间，当θ等于0度时，余切函数的值为正无穷，当θ等于45度时，余切函数的值为1。

正割函数（sec）正割函数是指在锐角三角形中，对于一个角度θ，其斜边与邻边的比值。

正割函数的值域在-1到1之间，当θ等于0度时，正割函数的值为1，当θ等于90度时，正割函数的值为正无穷。

余割函数（csc）余割函数是指在锐角三角形中，对于一个角度θ，其斜边与对边的比值。

余割函数的值域在-1到1之间，当θ等于0度时，余割函数的值为正无穷，当θ等于90度时，余割函数的值为1。

总结锐角三角形函数公式表是数学中的重要内容，它们在各个领域中都有广泛的应用。

掌握这些函数的定义和性质，可以帮助我们更好地理解和应用数学知识。

锐角三角形函数值

锐角三角形函数值
锐角三角形是指三个角都小于90度的三角形。

我们常用的函数sin、cos和tan都可以用来计算锐角三角形的
函数值。

sin函数的值代表三角形中对边与斜边的比值，即sinθ = 对边
/斜边。

cos函数的值代表三角形中邻边与斜边的比值，即cosθ = 邻边/斜边。

tan函数的值代表三角形中对边与邻边的比值，即tanθ = 对边/邻边。

这些函数值可以帮助我们计算出锐角三角形的边长或角度。

例如，如果我们知道一个锐角三角形的斜边长度为5，邻边长度
为4，我们可以使用cos函数来计算出其中一个角的值：
cosθ = 4/5，即θ = arccos(4/5)。

同样地，我们可以使用sin和tan函数来计算出其余两个角的值，以及对边的长度。

锐角三角形的函数值在数学和物理中有广泛的应用，例如在测量
角度、距离和速度等方面。

锐角三角形的三角函数

锐角三角形的三角函数三角函数是数学中的重要概念，它们在几何、物理学等领域中具有广泛的应用。

其中，锐角三角函数是指以锐角为自变量的三角函数。

本文将介绍锐角三角形的三角函数，并探讨其性质和应用。

一、正弦函数正弦函数是将一个锐角的相对边长度与斜边长度的比值定义为该锐角的正弦。

用符号表示为 sin，其计算公式如下：sin A = 相对边长度 / 斜边长度正弦函数的定义域为(0°, 90°)，值域为[0, 1]。

正弦函数具有周期性，即 sin(A + 180°) = -sinA。

二、余弦函数余弦函数是将一个锐角的邻边长度与斜边长度的比值定义为该锐角的余弦。

用符号表示为 cos，其计算公式如下：cos A = 邻边长度 / 斜边长度余弦函数的定义域为(0°, 90°)，值域为(0, 1]。

余弦函数也具有周期性，即 cos(A + 180°) = -cosA。

三、正切函数正切函数是将一个锐角的相对边长度与邻边长度的比值定义为该锐角的正切。

用符号表示为 tan，其计算公式如下：tan A = 相对边长度 / 邻边长度正切函数的定义域为(0°, 90°)，值域为(0, +∞)。

正切函数也具有周期性，即 tan(A + 180°) = tanA。

四、余切函数余切函数是将一个锐角的邻边长度与相对边长度的比值定义为该锐角的余切。

用符号表示为 cot，其计算公式如下：cot A = 邻边长度 / 相对边长度余切函数的定义域为(0°, 90°)，值域为(0, +∞)。

余切函数也具有周期性，即 cot(A + 180°) = cotA。

五、正割函数和余割函数正割函数是将一个锐角的斜边长度与邻边长度的比值定义为该锐角的正割。

用符号表示为 sec，其计算公式如下：sec A = 斜边长度 / 邻边长度正割函数的定义域为(0°, 90°)，值域为(1, +∞)。

求锐角三角函数值的几种常用方法

求锐角三角函数值的几种常用方法锐角三角函数是初中数学的重要内容，也是中考的热点之一．求锐角的三角函数值方法较多，下面举例介绍求锐角三角函数值的几种常用方法，供参考．一、定义法当已知直角三角形的两条边，可直接运用锐角三角函数的定义求锐角三角函数的值．例1 如图1，在△ABC 中，∠C =90°，AB =13，BC =5，则sin A 的值是( )(A )513 (B )1213 (C )512 (D )135分析题目中已知乞A 的对边BC 和斜边AB 的长，可直接运用锐角三角函数的定义求解．解 ∵在△ABC 中，∠C =90°，AB =13，BC =5，∴sin A 513BC AB =故选A 二、参数法锐角三角函数值实质是直角三角形两边的比值，所以解题中有时需将三角函数转化为线段比，通过设定一个参数，并用含该参数的代数式表示出直角三角形各边的长，然后结合相关条件解决问题．例2 在△ABC 中，∠C =90°，如果tan A =512，那么sin B 的值是．分析由已知条件∠A 的正切，可知直角三角形中两边的比值，据此可用参数法将第三边表示出来，进而求出sin B 的值．解如图2 ∵tan A =512BC AC =， ∴设BC =5k ，AC =12k (k >O )．由勾股定理，得AB =13k ，∴1212sin 1313AC k B AB k === 三、等角代换法当一个锐角的三角函数不能直接求解或锐角不在直角三角形中时，可将此角通过等角转换到能够求出三角函数值的直角三角形中，利用“两锐角相等，则三角函数值也相等” 来解决．例3 如图3，在Rt △ABC 中，∠BCA =90°，CD 是AB 边上的中线，BC =5，CD =4，则cos ∠ACD 的值为．分析由已知条件，不难知道∠ACD 与∠A 相等，所以欲求cos ∠ACD ，只要求cos A 即可．解在Rt △ABC 中，∵CD 是AB 边上的中线，∴CD =AD =BD ，∴∠ACD =∠A ．又∵CD =4，∴AB =2 CD =8，由勾股定理，得AC =∴cos A =AC AB =∴cos ∠ACD =cos A =8 四、构造法直角三角形是求解或运用三角函数的前提条件，故当题目中已知条件并非直角三角形时，需通过添加辅助线构造直角三角形，然后求解．例4 在△ABC 中，∠A =120°，AB =4，AC =2，则sinB 的值是( )(A (B (C (D 分析由于∠B 不在直角三角形中，因此需添加辅助线构造直角三角形，从而求解．解如图4，过点C 作CD ⊥BA ，交BA 的延长线于点D ．∵∠BAC =120°，∴∠DA C =180°一∠BAC=180°一120°=60°．在Rt △ABC 中，∵A C =2，∠DAC =60°，∴CD =AC ·sin ∠DAC =2=∴AD =1．又∵AB =4 ∴BD =AB +AD =5，在Rt △ABC 中，由勾股定理，得BC =∴sin CD B BC === 故选D ．。

锐角三角函数的计算教学PPT课件

(1) 33，1， 3， 33，1， 3
sin cos
αα＝tan
α
(2)试用计算器计算，并将结果直接填入表中，(结果精确到0.000 1)
α
sin α cos α
10° 20° 50° 70° 80° …
tan α
比较表中数值，它能验证你的猜想吗？
(3)请利用直角三角形证明你的猜想． (2)0.176 3，0.364 0，1.191 8，2.747 5，5.671 3， 0.1763 ，0.364 0，1.191 8，2.747 5，5.671 3
【错解】原式＝sin 248°＋sin 242°－tan 44°·tan 46°.
【错因分析】错解没有解答完，还可继续解答下去．因为 48°＋42° ＝90°，44°＋46°＝90°，所以有：sin 42°＝cos 48°，sin 248°＋cos 248°＝1， tan 44°·tan 46°＝1.
19．(10分)地震发生后，一支专业搜救队驱车前往灾区救援．如图，汽车在一条南北走向的公路上向北行驶，当在A处时，车
载GPS(全球卫星定位系统)显示村庄C在北偏西26°方向，汽车以35 km/h的速度前行2 h到达B处，GPS显示村庄在北偏西 52°方向．
(1)求B处到村庄C的距离； (2)求村庄C到该公路的距离．(结果精确到0.1km/h)参考数据： sin 26°≈0.4384，cos 26°≈0.8988，sin 52°≈0.7880，cos 52°≈0.6157)
A．tan 26°＜cos 27°＜sin 28° B．tan 26°＜sin 28°＜cos 27° C．sin 28°＜tan 26°＜cos 27° D．cos 27°＜sin 28°＜tan 26°

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

450 600
1 2 2 2 3 2
3 2 2 2 1 2
3 3
1
3
1
3
3 3
这张表还可以看出许多知识之间的内在联系?
新乐市实验学校
补充讲解：
0 Sin0° =___ 1 Cos0°=___ 1 sin90°=___ 0 cos90°=___ 无意义 tan90° =___ 0 cot90°=___
新乐市实验学校
三角函数正弦sinα 锐角α
余弦 cosα
正切tanα 余切cotα
回顾:
300 450 600
1
2
45
60
2
30
1
1
3
新乐市实验学校
特殊角的三角函数值表
三角函数正弦sinα 锐角α 余弦 cosα
驶向胜利的彼岸
正切tanα 余切cotα
300
要能记住有多好
新乐市实验学校
26.2锐角三角函数的计算
主备人甄俊芬九年级数学备课组
2014年10月20日
新乐市实验学校
锐角三角函数的意义回顾:
B
a c
在Rt△ABC中，∠C=90°， sinA=
tanA=
a b
，cosA=
，cotA=
b c
a
，
C 。
c b
A
b a
在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半。
D
新乐市实验学校
练习
2 3 1.在ABC中, 若 sin B , cos A , 2 2 求A, B, C的度数 B 2.已知 B为锐角，且 tan B 3, 则 cos ____ 2
3. 已知x为锐角 3 cot (x 10 )
0
3,
则 cos(x 20 ) _________
新乐市实验学校
例3:
已知A、B、C是ABC的三个内角，且 2 sin A 1 t an B 1 0, 求C的度数
新乐市实验学校
拓展
例4.在RtABC中, C 90, b 6, A的平分线AD长为4 3, 求BAC及a, c的值.
A
4 3 B
b=6 C
新乐市实验学校
知识的运用
1. 计算: (1)sin300+cos450;(2) sin2600+cos2600+tan450. 解: (1)sin300+cos450 1 2 1 2 . 温馨提示: 2 2 2 2600表示 Sin 2600+cos2600-tan450 (2) sin 0)2, 怎样 (sin 60 2 2
0
新乐市实验学校
拓展探究求已知锐角的三角函数值：
1.求sin63゜52′41″的值. 2.求cot70゜45′的值.（精（精确到0.0001）确到0.0001）先用如下方法将角度单位状态设定为“度” 在角度单位状态为“度” 的情况下:屏幕显示出
显示
再按下列顺序依次按键
按下列顺序依次按键
新乐市实验学校
解答
?
3 1 1 2 2
0.
3 1 1 4 4
cos2600表示 (cos600)2, 其余类推.
新乐市实验学校
例2 根据下列条件，求出相应的锐角A：
2 3 (1) sin A ; (2) cos A 0; 2 2 (3)3 cot A 3 0; (4) tan(A 20) 1.
新乐市实验学校
2. 如图:一个小孩荡秋千,秋千链子的长度为2.5m, 当秋千向两边摆动时,摆角恰好为600,且两边摆动的角度相同,求它摆至最高位置时与其摆至最低位置时提示:将的高度之差(结果精确到0.01m).
?
咋办
解:如图,根据题意可知,
1 0 0 ∠AOD 60 30 , OD=2.5m, OC 2 cos 30 0 , OD 3 0 OC OD cos30 2.5 2.165(m). 2
Tan0° =___ 0
无意义 Cot0°值:
(1)2cos60゜+2sin30゜+4tan45゜ ;
(2) sin30゜+sin245゜-tan260゜;
2 (3) cos 45 1
(4)
(4 sin 30 tan60)(cot30 4 cos60)
实际问题数学化.
O
●
∴AC=2.5-2.165≈0.34(m).
2.5
┌C D B ∴最高位置与最低位置的高度差约为0.34m. A
新乐市实验学校
小结
拓展
c
• 直角三角形中的边角关系
看图说话: 直角三角形三边的关系. 直角三角形两锐角的关系. 直角三角形边与角之间的关系.
A
B
a
b ┌ C
在直角三角形中，如果一个锐角等于30゜，那么它所对的直角边等于斜边的一半
互余两角之间的三角函数关系. 同角之间的三角函数关系
特殊角300,450,600角的三角函数值.
450 450
300
┌
600
┌
新乐市实验学校
1.特殊角的三角函数值 1 2 sin30°= 2 sin45°= 2
新乐市实验学校
同角三角函数关系式
sin A tan A cos A
2 2
回顾:
1 cot A tan A
sin A cos A 1
互为余角的三角函数之间的关系
sin(90－A）＝cosA, tan(90 －A）＝cotA, cos(90 －A）＝sinA, cot(90 －A）＝tanA.
cos30 °=
小结
sin60°=
3 2
3 2
cos45 °=
cos60 °=
1 2
2 2
2、已知一个锐角的正弦、余弦或正切、
余切的特殊值能说出这个角的度数。
中考连接：
新乐市实验学校
1、(２００３.北京 )（1）在△ABC中，
∠B=90º，BC=3，AC=4，则tanA= ＿＿＿ cosA=＿＿＿＿（2）tanA· cot20º =1，则锐角∠A = ＿＿＿＿