L^2(R^n)上的半正交多小波框架
小波包、多小波及第二代小波

M
因此,很容易得到小波子空间的各种分解如下: jW
3121++⊕=jjjUUW
72625242++++⊕⊕⊕=jjjjjUUUUW
M
121221.
+
+
++
+⊕⊕⊕=lllljljljjUUUWL 4.14
M
文本框:
jW空间分解的子空间序列可以写作,;mljlU+
+
212,,1,0.ቤተ መጻሕፍቲ ባይዱlmLjl,,2,1L=;。子空间
序列的标准正交基为:
L,2,1=jmljlU+
+
2
{}Znntwljmljl∈.+.
+
+.:)2(2)(
22/)( 4.15
当和时,子空间序列简化为,相应的正交基简化为0=l0=mmljlU+
+
2jjWU=1{})2(2)2(22/
在感兴趣的频率点上尽可能地提高频域分辨率,在感兴趣的时间点上尽可能地提高时间分辨率,这样当用
滤波器组对信号进行分解时,短时Fourier变换的等带宽或小波变换的恒-Q带宽都不一定合适,应该按信
号特性选择相应组合的滤波器组,这就是小波包(Wave1et Packet)。
小波包的概念是由M.V.WickerhaMser,R.R.Coifman等人在小波变换的基础上,根据实际应用的需求
()()0,122=.+ktWtwll
4.1.2 小波包分解
现在令、L,2,1=lL,2,1=j,并对式(4.11)进行迭代分解,有
第六章小波分析基础ppt课件

由母小波按如下方式的伸缩平移可构成L2(R)空间的标准正交基
j
j,k (t) 2 2 (2 j t k),j, k Z,t R
(3.1)
如何构造母小波呢?1989年,Mallat和Meyer提出了按多分辨分析 的思想来构造母小波,其基本思想是:
现构造一个具有特定性质的层层嵌套的闭子空间序列{Vj}jZ, 这个闭子空间序列充满了整个L2(R)空间。 在V0子空间找一个函数g(t),其平移{g(t-k)}k Z构成V0子空间的 Riesz基。
如图1所示的LENA图像f(x,y),假设图像的大小是512x512,量 化级是256,即
0 f (x, y) 255 0 x, y 511
y
x
2、L2(R)空间的正交分解和变换[1] 对 f(t)L2(R) , 存 在 L2(R) 的 一 组 标 准 正 交 基 gi(t) , t R ,
一、认识小波
1、预备知识 从数学的角度讲,小波是构造函数空间正交基的基本单元,
是在能量有限空间L2(R) 上满足允许条件的函数,这样认识小波 需要L2(R) 空间的基础知识,特别是内积空间中空间分解、函数 变换等的基础知识。
从信号处理的角度讲,小波(变换)是强有力的时频分析(处理) 工具,是在克服傅立叶变换缺点的基础上发展而来的,所以从信 号处理的角度认识小波,需要傅立叶变换、傅立叶级数、滤波器 等的基础知识。
小波变换有效地克服了傅立叶变换的这一缺点,信号变换到 小波域后,小波不仅能检测到高音与低音,而且还能将高音 与低音发生的位置与原始信号相对应,如图所示。
例2、信号逼近:如图(a)和(b)是原始信号,其余的是逼近信号。
因此我们需要这样一个数学工具:既能在时域很好地刻画信号的局部性,
小波分析简述

第一篇:小波分析发展历史简述1910年,Haar提出了L2(R)中第一个小波规范正交基,即Haar正交基。
1936年,Littlewood和Paley对傅立叶级数建立了二进制频率分量分组理论,(即L-P理论:按二进制频率成分分组,其傅立叶变换的相位并不影响函数的大小和形状),这是多尺度分析思想的最早起源。
1952年~1962年,Calderon等人将L-P理论推广到高维,建立了奇异积分算子理论。
1965年,Calderon发现了著名的再生公式,给出了抛物型空间上H1的原子分解。
1974年,Coifman实现了对一维空间和高维空间的原子分解。
1976年,Peetre在用L-P理论对Besov空间进行统一描述的同时,给出了Besov空间的一组基。
1981年,Stromberg引入了Sobolev空间Hp的正交基,对Haar正交基进行了改造,证明了小波函数的存在性。
1981年,法国地球物理学家Morlet提出了小波的正式概念。
1985年,法国数学家Meyer提出了连续小波的容许性条件及其重构公式。
1984年~1988年,Meyer、Battle和Lemarie分别给出了具有快速衰减特性的小波基函数:Meyer小波、Battle-Lemarie样条小波。
1987年,Mallat将计算机视觉领域中的多尺度分析思想引入到小波分析中,提出了多分辨率分析的概念,统一了在此前的所有具体正交小波的构造,给出了构造正交小波基的一般方法,提出了快速小波变换(即Mallat算法)。
1988年,Daubechies基于多项式方式构造出具有有限支集的光滑正交小波基(即Daubechies基)。
Chui和中国学者王建忠基于样条函数构造出单正交小波函数,并提出了具有最优局部化性能的尺度函数和小波函数的一般性构造方法。
1988年,Daubechies在美国NSF/CBMS 主办的小波专题研讨会上进行了10次演讲,引起了广大数学家、物理学家、工程师以及企业家的重视,将小波理论发展与实际应用推向了一个高潮。
一类三元多重向量值双正交小波包的研究

绵 阳师范学院学报
J ur a o in a g Nom a ie s o n l fM a y n r lUnv ri
— — — —
F b2 1 e . 01 V0 . 0 No 2 13 .
一
类 三 元 多 重 向量 值 双 正 交 小 波 包 的 研 究
1 预 备知 识
首先介绍下文用到的记号。用 z和 z+ 分别记为整数集和非负整数集 , (。 2 , : ∈ , Z ={z, , )z z A=l Z ^ 、 2 3 , ={ , , )z 、} ( ZZ : 2 3 ∈Z+A=123 , , 、、 }R 表示 了三维欧几 里得空 间 , 于 V Y∈R , M 对 , 。记 X={ : Mx
f I, )… g ( I g( 1£ 1 l ,)1 s 己 R, : {( : 1… … … Ig ( E2 。 )=G£ = ( c ) } £ ( ) ,。 ) L R 。
【 f () … g t f g t () J
m { .
定 义 3 两 个 向量 值 函数的 内积称为符 号 内积 。 [ 定义如 下 :
V ( ,( , , ()H t t H t L( c) <Gt,( G ) )E )>=f () ( ’t式中, 表示复共轭转置。 tH t d G ) 。 “ ”
定 义 4 定义空 间 ( , ) [ 为所有 的三元多 重 向量值 函数 c t的集合 , : () 即
=
( £ , t, , t) () ) :l2 … ,} g()g() … g() : t EL( , ,, z。其 中 f 0常数且 Z 2 为 。 定 义 2 向量值 函数 的积分 定义 为各个分 量 的积分 , : 即
《小波分析概述》PPT课件

Heisenberg不等式表明窗口Fourier变换的时 窗半径和频窗半径, 一个减小必然引起另一个的 增大, 不能同时减小.
窗口Fourier变换的窗函数选定以后, 其时-频 窗就固定不变了, 这样就限制了窗口Fourier变换 的实际应用. 为了提取高频分量的信息, 时窗应该 尽量地窄, 而允许频窗适当地宽; 对于低频分量, 时窗则应适当加宽, 以保证至少能包含一个周期的 过程, 频窗应当尽量缩小, 保证有较高的频率分辨率.
§4.2 窗口Fourier变换简介
窗口Fourier变换是在 Fourier 变换的框架内, 将非平稳过程看成是一系列短时平稳信号的叠加, 通过在时域上加上窗口来实现短时性. 通常选择在 有限区间外恒等于零或迅速趋于零的钟形函数g(t) 作为窗函数, 用平移滑动的窗函数g(t-t)与信号f (t) 相乘, 有效地抑制了t=t 邻域以外的信号, 在t 附近 开窗, 通过平移来覆盖整个时间域. 再进行Fourier 变换, 所得的结果反映了t=t 时刻附近的频谱信息, 从而产生了时域局部化的作用.
设 f , g Lk12, k(2R是)任,意常数, 则
W (k1 f k2g) (a,b) k1 W f (a,b) k2 W g (a,b).
(2) 平移性质
设 f L2则(R),
W f (t t0 ) (a,b) W f (t) (a,b t0).
(3) 尺度法则
第四章 小波变换基础
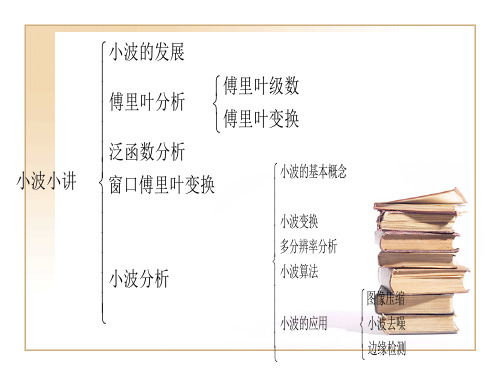
§4.1 小波变换的背景 §4.2 窗口Fourier变换简介 §4.3 连续小波变换 §4.4 二进小波变换和离散小波变换 §4.5 多分辨分析 §4.6 Mallat分解与重构算法
主要内容
小波分析是当前数学中一个迅速发展的 新领域,它也是一种积分变换,是一个时间和 频率的局域变换,因而能有效地从信号中提 取信息,通过伸缩和平移等运算功能对函数 或信号进行多尺度细化分析,解决了Fourier 变换不能解决的许多困难问题.本章简单介绍 小波变换的基本理论和应用.
关于L~2(R~d)中仿射子空间小波标架的一个注记

摘要:研究了 L
)的有 限生成仿射子 空间中小波标架的构造.证 明了任意有限生成仿射子
空间都容许一个具有有限多个 生成 元的 P a r s e v a l 小波标架,并且得到了仿射子 空间是约化子 空间的一个 充分条件 . 对其傅里 叶变换是 一个特征函数的单个 函数生成的仿射子空间, 得到了 与小波 标架构造相关 的投影算 子在傅里 叶域上 的明确表达式,同时也给 出了一些例子. 关键词 : 仿射子 空间; P a r s e v a l 标架;小波标架.
i CI
z .同余 的 ,若 存在 s 1的一个 分 划 { s 1 , : J∈z )使得 f 1 , +J: J∈z ) 是 的一个 分 划 .对可 测 函数 。 厂 , 定义 其支 撑为
s u p p ( f ) ={ ∈ 碾 : . , ( ) ≠0 }
收稿 日 期: 2 0 1 i - 0 3 — 1 1 ; 修订 日 期: 2 0 1 2 0 8 一 l 7
E — ma i l : y z l e e @b j u t . e d u . c n
基金项 目:国家 自然科学基金 ( 1 1 2 7 1 0 3 7 )、北京 市 自 然科学基金 ( 1 1 2 2 0 0 8 ) 和北京市教育委员会科技计划面
数学物理学报
h t t p : / / a c t a ms . w i p m. a c . c n
关于 2 ( d )中仿射子空间小波标架的一个注记
周 凤英 李 云章
( 东华理工大 学理学院 南昌 3 3 0 0 1 3 ; 北京工业大学应用 数理 学院 北京 1 0 0 1 2 4 )
容易验证它们都是酉算子.给定 ( ) 的一个闭子空间 , 称 x 为一个平移不变子空间, 若对 每个 k E z , T k X= ; 称 为 。 ( ) 的一个 约化子 空 间,若 DX = X, 并且对 任意 k ∈z , T k X= ; 称 为 ( ) 的一个仿射子空间,若存在一个至多可数集 c L 。 ( ) ,
偶对称双尺度因数的Daubechies双正交小波简捷构造法

L n I Ya
( o e eo r C l g f t S i c , h n h i r i eU i. h n h i 0 1 5 hn ) l A s& c n e S a g a Maim nv ,S a g a 2 0 3 ,C ia e t
的, 它在 时一 频局 部化 方面 具有很 强 的灵 活性 , 已广
泛应 用 于信号 处理 、 图像 处 理 、 式识 别 和语 音 识别 模 等领 域 . 多分 辨 分 析 ( l.eoui nl i,MR MutR sltnA a s i o ys A) 是构 造 小 波 的 统 一 框 架 , 西( 设 )∈L ( R)为
维普资讯
第2 9卷 第 2期
20 0 8年 6月
上
海
海
事 大 学 学
报
Vo . No. 129 2
J u n l fS a g a Mai me Un v ri o r a h n h i r i ie 海高校选拔培养优 秀青年教师科研专项基金 ( 37 1 ; 上 o 2O ) 上海市教 育委 员会 自然科 学项 目(5 Z 2 0 F3 )
作者简介 :李 艳( 97 ), , 17 一 女 山东莒南人 , 师, 讲 硕士 , 究方 向为 小波理论及其应用 , Ema ) al b -h t-d -l 研 ( - i yni c smu eu C l @d ' l
c r i g t h o re o i e ta f r o c l q t n o u e h e irh no a v lt n ag — o d n o te F u ir c sn r nso m f s ae e uai fDa b c i s b o t o r lwa ee ,a l o o m
瞎扯数学分析3、泛函分析简介

瞎扯数学分析3、泛函分析简介先声明一下,这篇帖子对数学基础不好或者抽象能力不强的人不友好,建议不要浪费时间。
不过希望工程师们看看,也许有启发,因为泛函分析现在是高水平工程师混饭吃的标配,傅立叶变换,小波分析,最优控制,数学规划,资源最优配置,偏微分方程数值求解,有限元分析,弹性力学数值计算等等等等,基础都是泛函分析。
这是介绍数学思维方式的最后一部分。
主要介绍抽象思维的强大。
由于泛函分析是古典数学和现代数学的桥梁,是古典数学分析,代数和几何以现代观念交叉在一起发展起来的学科,是数学承先启后的门槛,又有广泛的应用,既是所有优化资源配置技术的基础,又是所有控制技术的基础,更是化繁为简的利器。
我在实际工作中体会是几门数学学科在实际应用上的地位是:微积分就像是钢丝钳,粗活细活都能干,凡是能够定义连续因果关系的问题,用微积分试一下没错;线性代数就像是螺丝刀,凡是离散问题,定义线性关系,就能试图找一下构造基(特征根),把问题分解投影到基上,就能分而治之;数理统计就象是扳手,碰到没有明显因果关系的糊涂乱麻问题,先寻找一下趋势外推或线性拟合,找一下统计相关性;实在碰到无法下嘴的问题,只能是数值逼近或数值模拟了。
不过泛函分析是很特殊的工具,类似电钻,可以把困难问题彻底击穿,找到本质。
当然数理方程是工程师的电锯,有招没招锯一下,大卸八块找原理。
作为一个现代工程师,如果工具箱里没钢丝钳,螺丝刀,扳手,榔头,电钻,电锯,可能心中没底,觉得自己全身赤裸,裸奔的工程师,没法见人。
其实现在工程师会不会计算并不重要,因为现在都有现成的计算软件包,关键是在一堆现象中发现问题,定义问题关键因素,并对解决问题知道用什么工具。
泛函分析是把代数(泛函分析有人就称为无穷维空间线性代数),分析(泛函就是把函数当成自变量的广义函数),几何(泛函分析的主要对象之一就是函数组成的赋范空间)整合在一体的学科,是现代数学的门槛,学过泛函分析,基本就算看到现代数学大门了。
紧支撑半正交小波的构造

() ∑ ( 1 。 ( 一) ・= 一 ) 2・ , I
则 { . )n∈ z) ( 一n : 是 的一 个标准 正交基 , 时 , 此 我们 称 是 一个小 波.但 当 { . )n∈z) ( 一n : 是
的一 个 Rez i 基而不 是一个 标准 正交基 时 , 却 不 一定 是 一个 半正 交 小波 ,这 是 因为 它可 能包 含有 s
洛 阳 大 学 学报
J 0URN U AL OF L OYANG UNI R I Y VE S T
Vo . 122 No. 2
J n 2 0 u. 07
紧支 撑半 正 交 小 波 的构 造 术
李云章 , 刘慧敏
( 北京工业大学 应 用数 学系,北京 10 2 ) 00 2
1 引 言
对 1≤ P < ∞ , L( 表示 R上 p次可 积 函数 全体组 成 的 Bnc 以 p R) aah空间 , ,∈L ( ) 以 表示 对 PR , 其 范数
=
(x, ・ f 2l e
对 ,EL ( , 义其 Fuir R) 定 or 变 e
( )= ( 仃) 蚴 一 . 2 一
紧支撑 半正 交小 波 的方 法 , 给出 了紧支 撑半 正交对 称 或反对称 样条 小波 的构造 例 子 也 引.但这
种方法依赖于一个多项式零点的确定 , 在大多数情况下这不是很容易的【 引 .本文在某多项式没有零
点 的条件 下 ,给 出了一个 构造 半正交小 波 的方 法. 种构 造 继 承 了来 源于 尺度 函数 及其 符 号 的对称 性 和 这
中的分量 .于是 , 一个 自然 的 问题是 在这种 情况 下如 何构造 半正 交小波 , 文将 讨论 这一 问题. 本 我 们知 道 , 在相 差一 个整数 平移及 ±1因子的意 义下 ,除 H a 小 波 外 , 存 在其 他 紧支 、正 交 、对 ar 不 称或反 对称 的实 值 MR A小波 [.但对半 正交小 波来 讲 , 况不 是这样 的.C u 与 Wag给 出 了一个 构造 1 】 情 hi n
小波分析及其应用(精品教程)

A c j ,k
2 l
2Βιβλιοθήκη j k c
2 j ,k
j ,k
2
B c j ,k
2 l2
2 l2
对所有二重双无限平方可和序列 c j ,k 成立, 即对于 c j ,k 立。
j k
c
2 j ,k
k
c e
k
ikx
(8.1-1)
1 2 (8.1-2) f x e ikx dx 0 2 然而,被分析函数的性质并不能完整地由傅里叶系数来刻划,这里有一个例子来说 [3] 明 :从任一个平方可和的函数 f ( x) 出发,为了得到一个连续函数 g ( x) ,只需或者增大 f(x)的傅里叶系数的模,或者保持它不变并适当地改变系数的位相。因此,不可能仅根 据傅里叶系数大小的阶就预知函数的性质(如大小、正则性) 。 傅里叶变换的定义如式(8.1-3)、(8.1-4) ck
为了能重构信号 f t ,要求 j ,k j ,kZ 是 L2 R 的 Riesz 基。 定义 8.2-1 一个函数 L2 R 称为一个 R 函数,如果 j ,k j ,kZ 在下述意义上是一个
Risez 基: j ,k , j , k Z 的线性张成在 L2 R 中是稠密的,并且存在正常数 A 与 B ,
16
第八章 小波分析理论及应用 间。一个适当的表示应结合这两者互补描述的优点,并用一个离散的刻划来表示,以适 应通讯理论[3]。 ” 为此,人们提出了短时傅里叶变换(STFT)的概念: ˆ 满足: 定义 8.1-1 若 W L2 R 选择得使 W 与它的傅里叶变换 W
小波分析全章节讲解
3.从泛函角度描述傅里叶变换 (1)用内积表示傅里叶变换 内积空间中的函数,其傅里叶变换可 用内积表示为
F () f( t ) e j td t f( t ) ,e j t
(2)用基底表示函数的展开
f f,en en n
三、窗口傅里叶变换(傅里叶→小波)
由于传统傅里叶分析只适用于平稳信号 ,在进行非平稳信号的分析时通常采用 时频处理方法,它将一维时域信号分解 为二维时域—频域联合分布表示。传统 傅里叶分析不适用于时变信号的分析, 但是可以在时域和频域内进行加窗处理 ,窗内的信号认为是准平稳的,对它们 可以采用平稳信号的分析方法,如频谱 分析和功率谱分析。这就是窗口傅里叶 变换。
但是现实世界中的很多信号,例如,脑电波信号、地震信号 、语音信号等,都是非平稳的。这些信号的频率是时变的。 对于这种信号的准确描述,必须使用具有局部 性能的时域和频域的二维 ( t , )联合表示, 或者说必须提取特定时间段和频率段内的信号 特性。这时,传统的傅里叶分析就显得无能为力了。 傅里叶变换所描述的是整个时间段内频率 的特性,或者说它是一种全局的变换而没有 刻画出特定时间段或频率段的特性。
其中 b 为时间位移。平移后的窗函数分别
与原信号相乘,其结果就等效于提取了 原信号的不同时间段内的信息而屏蔽了 段外的信号。
f (t)Hale Waihona Puke 0tg (t)
0
t
f(t)g(t)
0
t
最简单的时间窗是矩形窗函数,如上图所示。但 是也可以根据需要选择其他的窗函数,如Gauss窗、 Hanning窗、Blackman窗等。其中,矩形窗函数具有 非常良好的时域局部化性质: (1)具有时域紧支集。 (2)窗内信号保持原样。 (3)窗外信号完全衰减为0,完全地屏蔽了窗外信号 。 (4)窗的过渡带为“陡”的阶跃跳变,
小波变换原理与应用

3.小波变换的基本原理与性质
离散小波变换DWT( discrete wavelet transform,DWT ) 定义
对尺度参数按幂级数进行离散化处理,对时间进行均 匀离散取值 (要求采样率满足尼奎斯特采样定理)
m
DWTx(m, n) x(t), m,n (t) 2 2
x(t) (2m t n)dt
数学中的显微镜小波
小波变换原理及其应用案例介绍
Wavelet Transform Theory and Applications Introduction
饶利强 电机与电器
1
主要内容
1. 小波的发展历史 2.小波变换与傅里叶变换的比较 3.小波变换的基本原理与性质 4.几种常用的小波简介 5.小波变换的应用领域 6.小波分析应用前景 7.小波变换的去噪应用 8.小波分析面临的主要问题
x(t)
a
1
2
(t
b表示为平移因子a和伸 缩因子b的函数
20
3.小波变换的基本原理与性质——多分辨 分析
FT
信号
连续正弦波或余弦波
傅立叶分解过程
CWT
信号
不同尺度和平移因子的小波
小波分解过程
21
3.小波变换的基本原理与性质——多分辨 分析
伸缩因子对小波的作用
出了小波变换的概念,20世纪80年代开发出了连续小 波变换CWT( continuous wavelet transform ) 1986:Y.Meyer——提出了第一个正交小波Meyer小波 1988: Stephane Mallat——Mallat快速算法(塔式分解和 重构算法)
4
1.小波的发展历史——工程到数学
6
2.小波变换与傅里叶变换的比较
半双正交小波Riesz基的构造及性质

第12卷 第2期 红河学院学报 Vol.12 No.22014年4月 Journal of Honghe University Apr.2014半双正交小波Riesz基的构造及性质冯祖针(红河学院数学学院,云南 蒙自 661199) 摘 要:根据方括号积多尺度分析对的基本理论,探讨了半双正交小波Riesz基的构造方法,并将该方法应用到基数B-样条,具体构造了一对半双正交样条小波Riesz基,同时研究了其支撑和对称性质. 关键词:方括号积;半双正交小波;基数B-样条;紧支撑;对称性 中图分类号:O174.2 文献标识码:A 文章编号:1008-9128(2014)02-0024-03收稿日期:2013-04-27项目基金:云南省应用基础研究计划项目(2013FZ118);云南省应用基础研究计划青年项目(2012FD054);云南省教育厅 科学研究基金项目(2011Y297);红河学院博硕专项科研基金项目(10BSS135)作者简介:冯祖针(1985-),男,硕士,助教,研究方向:算子理论与小波分析、Hilbert-Huang变换及其在信号处理中的应用。
1 引言利用小波变换(WT)对信号进行多尺度分析,实际上是对信号的一种特殊滤波处理. 从信号重构的角度来说,总是希望这种滤波运算产生的附加失真越小越好,这就要求滤波器具有线性相位性,即具有对称性或反对称性[1].尽管紧支撑正交小波基具有很多优良性质,但除Haar小波外,实紧支撑小波均不存在对称性或反对称性[2],即其对应滤波器不存在线性相位性;此外,Haar小波基的局部化性能很差,很少用于实际应用. 所以为了获得性质相对优良的小波,需要适当放松对正交性的限制.基于这一设想,1992年,Chui和Wang在尺度函数紧支对称的前提下,在文献[3,4]中提出了一个构造紧支撑对称半正交小波的方法,由此得到的小波具有了对称性. 与此同时,基于完全重构滤波器的思想,用于信号分解和重构的滤波器可以不同,Cohen、Daubechies和Feauveau于文献[5,6]中提出了双正交小波及其设计方法,由该方法可构造对称或反对称的紧支撑样条双正交小波基. 该类小波对应的是一个双正交多尺度分析. 2003年,Jia、Wang和Zhou 在文献[7]中对满足更弱条件(不要求是双正交或半正交)的尺度函数 和 ,提出了构造Sobolev空间中紧支撑小波Riesz基的方法,由该方法构造得到的小波性质十分良好.在以上研究工作基础上,本文将探讨L 2(R)空间中半双正交小波Riesz基的构造方法,并将该方法应用到基数B-样条,具体构造一对半双正交样条小波Riesz基,同时研究其支撑和对称性质.2 半双正交小波Riesz基的构造记平方可和序列空间为 .R上的平方可积函数空间为 ,则L 2(R)在下面内积定义下是一个Hilbert空间:,式中,g *(x )表函数g(x )的复共轭.L 2(R)中函数f (x )的范数定义为 .可积函数f (x )的Fourier变换定义为 ,其中i为虚数单位. Fourier变换可以很自然地扩展到整个L 2(R)中的函数.记 L 2(R)中函数f ,g 的方括号积为:, 很明显,方括号积[f ,g ]是 上的一个 周期函数.L 2(R )中的函数序列 称为一个R i e s z 序列当且仅当存在两个正常数C 1和C 2,满足0<C 1<C 2<∞,使得对任意仅含有限非零项的序列成立:此外,若序列 的线性张成在L 2(R)中稠密,即 ,则称序列 为L 2(R)的一个Riesz基.设函数 ,记 .若函数列 构成L 2(R)中的一个Riesz基,则称f 为L 2(R)的一个R-函数.设 , 为Hilbert空间L 2(R)中的一对紧支撑函数,满足条件:(1) (1)(2) 双尺度方程:(2)其中尺度序列 具有有限支撑且 .25冯祖针:半双正交小波Riesz基的构造及性质记且令(4)在文献[8]中已经得到论证,对上面给出的 和 ,若还满足方括号积 ,则 和 构成L2(R)的一对方括号积多尺度分析.类似正交、半正交和双正交性的定义,此处引入半双正交性的定义.定义2.1 设ψ, 均为R-函数,而如式(3)所给出. 对 ,若(5)则称ψ和 为L2(R)的一对半双正交函数,并称式(5)为半双正交条件式.记 ,其中 .半双正交小波的构造基于下面两个引理.引理2. 1[7]记 和v为由以下方式给出的序列:(6)且令ψ, 为由以下形式定义的函数:(7)则下面两个结果成立:(1) 且 ;(2) 且 .设 ,对 是 的线性组合.由引理2.1, 因此,(8)而对 是 的线性组合.但 .因此,当 时,式(8)总是成立的,即其满足半双正交性.引理2. 2[7]设ψ和 均为L2(R)上的紧支撑函数,且 . 若 满足以下两个条件:(1) 半双正交性: ;(2) 方括号积不为零,即 ,则序列 均为L2(R)的Riesz序列.可推得由引理2.1构造得到的ψ和 满足 ,且 , . 由于 ,故 . 此外,由上述方式定义的函数ψ和 是紧支撑的,从而由ψ和 生成的函数序列 及 在满足半双正交性条件(8)下,按引理2.2均为L2(R)的Riesz序列.进一步地,令 , ,则 和 均在L2(R)中稠密,故 和 均为 的小波Riesz基,从而 和 构成 L2(R)的一对半双正交小波Riesz基.归纳上述讨论,可得如下命题.命题2.1若Hilbert空间L2(R)中的一对紧支撑函数和 满足方括号积 , 及条件式(1)和(2),则由引理2.1定义的函数ψ和 为L2(R)的一对半双正交小波,且其函数列 和 构成L2(R)的一对半双正交小波Riesz基.3 半双正交样条小波Riesz基的构造及性质下面将上述构造方法应用到基数B-样条(有关知识可参阅文献[9,10]),具体构造一对半双正交样条小波Riesz基,并对其一些性质作探讨.m阶B-样条B m是特征函数x[0,1]的m次卷积,它的支撑为[0,m]并且关于 对称,即对任意 ,B m(m-x)=B m(x). 此外,B m是m-1阶可导的. 对正整数m和n,有B m+n=B m*B n,故有 , . 特别地,有很明显,B m满足性质 及如下频域双尺度方程:对任何整数对m与j,而 ,令则 是具有Riesz界 和C2=1的V j m的一个Riesz基,而且这些界是最优的.对于每个j,因为 和 ,由上述推论,有(9)其中 ,且有(10)显然 是具有有限支撑的,且 ,所以公式(9)可以用(11)精确给出,这个公式称为m阶基数B-样条的(时域)双尺度方程.若令尺度函数 , ,其中m,n均为奇数或偶数,尺度空间序列 及 ,则 , 且和 构成L2(R)的一对方括号积多尺度分析[8].下面例子进一步说明,在此前提下由引理2.1得到的ψ, 的函数列 和 构成L2(R)的一对半双正交样条小波Riesz基.例子 设尺度函数 , ,均为基数B-样条,其中m,n均为奇数或偶数,令(12)(13)则 和 按命题2.1构成L2(R)的一对半双正交样条小波Riesz基,且(1)当m,n均为奇数时,ψ和 的支撑分别为[0,m]和[0,n],并分别关于m/2和n/2反对称;(2)当m,n均为偶数时,ψ和 的支撑分别为 [0,m+1]和[0,n+1],并分别关于(m+1)/2和(n+1)/2对称.证明 例子中给出的ψ和 是满足上述关于基数B-样条的一切条件结果的,此处不再对其贽述.由引理2.1可得,(3)26红河学院学报 2014.2/物理学·数学研究同理可得, .从而再由引理2.1可得式(12)和(13). 从而和 按命题2.1构成L 2(R)的一对半双正交样条小波Riesz基.显然,当m ,n 均为奇数时,ψ和 的支撑分别为[0,m ]和[0,n ];而当m ,n 均为偶数时,ψ和 的支撑分别为[0,m+1]和[0,n+1]. 相比之下,文献[3,4]构造得到的半正交m 阶光滑样条小波的支撑至少为2m ,而由文献[5,6]构造得到的双正交m 阶光滑样条小波的支撑大于4m .往下证明当m ,n 均为奇数时,ψ和 分别关于 2/m 和2/n 反对称.由于从而ψ关于m /2反对称. 同理可证得 关于n /2反对称.类似可证得当m ,n 均为偶数时,ψ和 分别关于(m +1)/2和(n +1)/2对称.4 结论由多尺度分析构造小波是目前构造小波的流行方法. 本文在方括号积多尺度分析对的基础上,探讨了L 2(R)空间中半双正交小波Riesz基的构造方法,并将该方法应用到基数B-样条,具体构造了一对半双正交样条小波Riesz基,同时研究了其支撑和对称性质.参考文献:[1]唐向宏,李齐良.时频分析与小波变换[M].北京:科学出版 社,2008.[2]Daubechies I. Ten Lectures on Wavelets[M].Philadephia:SIAM, 1992.[3]Chui C K,Wang J Z.On compactly supported spline wavelets and a duality principle[J].Trans Amer Math Soc,1992,330:903-916.[4]Chui C K, Wang J Z.A general framework of compactly supported splines and wavelets[J].J Approx Theory,1993,71:263-304.[5]Cohen A, Daubechies I,Feauveau J C.Bi-orthogonal bases of compactly supported wavelets[J].Comm Pure Appl Math,1992, 45(5):485-560.[6]Cohen A,Daubechies I. A stability criterion for bi-orthogonal wavelet bases and their related subband coding scheme[J].Duke Math J,1992,68:313-335.[7]Jia R Q,Wang J Z, Zhou D pactly supported wavelet bases for Sobolev spaces[J].Appl Comput Harmon Anal,2003,15(3): 224-241.[8]冯祖针,崔向照,龙瑶. 一类方括号积多尺度分析的构造[J]. 云南民族大学学报(自然科学版),2013,22(5):337-340.[9]Chui C K. An Introduction to Wavelets[M].北京:人民邮电出 版社,2009.[10]Schoenberg I J. Cardinal Spline Interpolation[M].Philadelphia: SIAM,1973.[责任编辑 张灿邦]The Construction and Properties of Semi-Biorthogonal Wavelet Riesz BasesFENG Zu-zhen(College of Mathematics, Honghe University, Yunnan Mengzi 661199, China) Abstract:By the basic theory of bracket products multi-resolution analysis, the construction of semi-biorthogonal wavelet Riesz bases have been discussed. Then the method has been applied to the cardinal B-spline to construct a pair of semi-biorthogonal spline wavelet Riesz bases, and the support and symmetry are studied. Key words:bracket products;semi-biorthogonal wavelets;cardinal B-spline;compact support;symmetry。
正交多小波消噪变异的浮点数编码遗传算法

异 , 能对 奇数长度 染色体 编码 消噪 变异 , 也 基于这一 结论提 出了基 于正 交多小波 消噪 变异的浮 点数 编码遗传 算法 (GA F WDM) ,
并进行 了实验 。研 究和 实验 的结 果表 明, 该方 法理论 上是可靠 的, 方法上是可行 的, 于拓展浮 点数编码遗传 算法的应 用空 间具 对
摘
要: 编码是遗传 算法研究的难点 问题之 一。浮点数编码在 函数 优化 和约束优化领 域明显有效 于其他 编码 。但消除浮 点数 编
码 在遗传算法运行环境 中产 生的噪音 , 以提 高遗传算法性 能的理论 和方法 尚不被人们 所认 识 。在用正 交多小波对浮点数编码遗
传 算法消噪变异 的基础 上 , 针对染 色 编码 长度 的奇偶数 问题 , 体 从理论 上证 明 了 交多 小波既能对偶数 长度 染 色体编 码消噪 变 正
S h o f Co u e c o l o mp t r& I f r t n E g n e i g He a i e st f Fi a c & Ec n m is Zh n z o 5 0 2, i a n o ma i n i e rn . n n Un v r i o n n e o y o o c , e g h u 4 0 0 Ch n
e e . n t f c rmo o n o e a l b tt t v l e os gT e Fo t C d A ( C v n 1 gh o h o s me e c d d c n a e mua d wi wa e t d n i n .h la o e G F GA) wi r o o . e l e h e i t ot n r h h
基于小波分析的低压电弧特性识别模型的研究

hk、gk———尺度函数和小波函数对应的低通与 带通滤波器响应系数。
当 j=1时,为原始输入信号。其中,g0 =-2, g1 =2;h-1 =h2 =0.125;h0 =h1 =0.375。
由式(5),利用 LabVIEW 数组函数和运算函
数设计迭代程序,构建了二进小波模型。
Key words: wavelet recognition model; series fault arc; switching arc; voltage waveform characteristics;energyspectrum
郑 昕(1976—),男,副教授,研究方向为电器及其智能化技术。 基金项目:国家自然科学基金资助项目(51707039);福州市科技成果转移转化项目(2020GX25);晋江市福大科 教园发展中心科研项目(2019JJFDKY05)
1 小波识别模型的构建
1.1 正交小波识别模型
db小波是 一 种 有 限 长 度 的 具 有 紧 支 撑 结 构
的正交小波,广泛应用于离散小波变换中,本文采
用该小波函数建立正交小波模型。对于有限长度
的小波,进行快速转换时会产生两个实数组成的
数列,称为尺度 函 数 (低 通 滤 波 )及 小 波 函 数 (高
离散小波变换与框架ppt

(F F )1 f , F F (F F )1 f (F F )1 f , f
利用式3-16,有:
B1 f , f , (F F )1 f , f A1 f , f
将以上两式合并,有:
B1 f 2 f ,~j 2 A1 f 2
(式3-19)
jJ
上式表明, ~j jJ 就是H空间得一个框架。
2 A
(FF) f B
Rf N 1
(将R表达式代入)
f N 1
2 (F F )( f A B
f N 1)
最后得到迭代公式
f N
f N 1
2 A B
[
jJ
f , j
f N 1, j
] j
f0
2 (FF) f A B
2 A B
jJ
f , j
j
(式3-30) (式3-31)
三、小波框架(本节定理证明参见《小波十讲》) 现在我们再回到利用离散小波系数重构原函数f(t)得问题
令:c Ff ,即c j f , j ,则上式变为:
F Ff f , j j jJ
f (F F )1 f , j j f , j (F F )1 j
jJ
jJ
同理:
f f , j ~j jJ
f f ,~j j jJ
(式3-21) (式3-22)
以上两式就就是 f 得重构公式,由<f, φj >重构 f 需要求出框架
c j0 ,k0 f (t), j0 ,k0 (t) f (t) j0 ,k0 (t)dt
c j,k~j,k (t) j0,k0 (t)dt
R
c j,k
~j,k (t) j0,k0 (t)dt
L^2(R^2)空间上的正交小波基

L^2(R^2)空间上的正交小波基
杨守志;谢长珍;张少武
【期刊名称】《信阳师范学院学报:自然科学版》
【年(卷),期】1999(12)2
【摘要】本文构造出L2(R2)空间的一组正交小波基。
它们是L2R空间4尺度正交小波基通过张量积的方法产生的。
【总页数】3页(P139-141)
【关键词】多分辨分析;正交小波基;高维空间;小波分析
【作者】杨守志;谢长珍;张少武
【作者单位】西安交通大学理学院;信阳师范学院物理系
【正文语种】中文
【中图分类】O174.22
【相关文献】
1.有限区间上正交小波基 [J], 杨守志;韩德志
2.具有周期正交拟小波基空间的逼近性质 [J], 覃跃海;乙了
3.四进正交小波基在图像压缩上的应用 [J], 郑果;张平柯;王国秋
4.S—空间中正交小波基的一种构造法 [J], 陈基明;彭瑞仁
5.L^2[0,1]上的正交小波基 [J], 杨守志;韩德志
因版权原因,仅展示原文概要,查看原文内容请购买。
双正交小波介绍

j
W
j
V j V j 1 W
W
j 1
( 5) 双 尺 度 方 程 变 为 :
(x) (x)
kZ
2 hk ( 2 x k ) 2 g k (2 x k )
(x) (x)
kZ
2 h k (2 x k ) 2 g k (2 x k )
k
2 g k 2l
j ,k
2 g k 2l f j ,
k
j ,k
2 g k 2 l c j ,k
k
双正交小波的分解与重构
重 构 : c j ,k f j ,
j ,k
j 1, l
c
l
j 1, l
对比
• 正交多分辨分析中
| P ( z ) | | P ( z ) | 1 Q ( z ) z P ( z )
2 2
| Z | 1
紧支撑双正交小波的构造
• 必要条件
有限滤波器 h , h , g , g 使得尺度函数 , 和对偶小波 ,
d
l j ,k
j 1, l
j 1, l
,
j ,k
,
c
l
j 1, l
j 1, l ,
d
l
j 1, l
j 1, l
j ,k
c
l
j 1, l
k
2 h k 2 l j ,k ,
j ,k
d
l
j 1, l
第12章 双正交小波及小波包

- 352 -第12章 双正交小波及小波包我们在上一章给出了正交小波的构造方法。
正交小波有许多好的性质,如)()(),(',,'k k t t k j k j -=δφφ,)()(),(',,'k k t t k j k j -=δψψ,0)(),(',,=t t k j k j ψφ ,此外,尺度函数和小波函数都是紧支撑的,有着高的消失矩等等。
Daubechies 给出的正交小波的构造方法可以方便的构造出所需要的小波(如DBN ,SymN ,CoifN)。
但是,正交小波也有不足之处,即)(t φ和)(t ψ都不是对称的,尽管SymN 和CoifN 接近于对称,但毕竟不是真正的对称,因此,这在实际的信号处理中将不可避免地带来相位失真。
)(t φ和)(t ψ的不对称性来自所使用的共轭正交滤波器组)(0z H 和)(1z H 的不对称性。
我们已在7.8节讨论了具有线性相位的双正交滤波器组的基本概念,给出了可准确重建的双正交滤波器组的设计方法。
本章,我们把这些内容引入到小波分析,给出适合小波变换的双正交滤波器组准确重建的条件,给出双正交条件下的多分辨率分析及双正交小波的构造方法,最后简要讨论小波包的基本概念12.1 双正交滤波器组现在,我们结合小波变换的需要来研究双正交滤波器组的内在关系及实现准确重建的条件。
所谓“小波变换的需要”是指在用)(0z H 对)(0z a 分解时需要将)(0z H 和)(1z H 的系数作时间上的翻转,即用的是)(10-z H 及)(11-z H ,或)()(00n h n h -=,)()(11n h n h -=,见(10.6.1)式及图10.6.2。
将图10.6.2的正变换和图10.6.3的反变换结合起来,我们可得到如图12.1.1所示的一级分解和重建的类似于两通道滤波器组的信号流图。
注意,图中用于重建的滤波器不再是图10.6.3中的)(0z H 和)(1z H ,而是)(ˆ0z H 和)(ˆ1z H ,它们分别是)(0z H 和)(1z H 的对偶滤波器。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
≠( j 2 , 1 2 ) , V 1 , 2∈z 成立 , 则称 是严 格半 正交 的. 特别 地 , 若 函数系 {
… ,
, J∈z, 尼∈z , f =1 ,
)构 成 L 。 ( )中 的一个 正交 系, 则称 是 正交 的 .
对一个 P a r s e v a l 多小波框架 =( 妒 1 …. , 砂 L ) L ( ) 而言, 它具备一个类似于标准正交基 的 性质, 即对 于任 意 的 f∈L ( ) ,
给 出了一个 紧小 波框架 能 由多分 辨分 析 ( MR A) 构造 生成 的等价 条件 . B a k i d[ 6 ] 证 明了高维情 形 下, 当 l d e t Al :2 , A∈ ( z )时, GMR A P a r s e v a l 小波框 架类 与半 正 交 P a r s e v a l 小 波框 架类 是相 互等价 的 ; ( z )情 形下 的半 正交 P a r s e v a l 小波 框 架进 行 了刻画 .K i m 等人 [ 0 ] 研究了 B a k i d [ r l同时证 明 了每 个 严格 半 正交 P a r s e v a l多小波 框架 都 是 G MR A P a r s e v a l多小波 框架 .L i u等 人[ 8 ] 对 l d e t Al =2 , A∈
E— m ai l : s z y a ng  ̄s t u. e du. c n,0 9 xwz h e ng  ̄s t u. e du. c n
收 稿 日期 : 2 0 1 3 — 0 5 — 0 8 ; 接 受 日期 : 2 0 1 3 — 0 7 — 2 1 ; 通信 作 者
国家 自然科学基金 ( 批准号: 1 1 0 7 1 1 5 2 ) 和广 东省 自然科学基金 ( 批准号: ¥ 2 0 1 1 0 1 0 0 0 4 5 1 1和 ¥ 2 0 1 3 0 1 0 0 1 3 1 0 1 )资助 项 目
关键词 多小波框架 ( 严格)半正交 多小波框架 小波集
MS C( 2 0 1 0 )主题 分类 4 2 C 1 5 , 4 2 C 4 0
1 引言
半正交小波的概念分别是由 A u s c h e r [ 1 】 . C h u i 和 Wa n g [ 2 - 4 ] 独立引入的, 这个研究领域在理论上很 快 发展 到关于 半正 交小波框 架 的研究 . 目前 依然有 许多学 者继续着 这方 面 的工作, 其 中以关于 P a r s e v a l 小波框 架 的研 究 最为重 要 . P a l u s z y i f s k i 等人【 5 】 揭示 了半 正交 紧小波 框架 与小波 维 函数 之 间的关 系, 并
m& x ∈ I . 厂 ( ∈ ) l <。 。的 函数 构成 的 函数空 间. 记 ,的支 撑为 s u p p f=
中子集 S 的 L e b e s g u e测 度 .
3 半正交 多小波刻画
本节 将着重 于刻 画半正 交和严 格 半正交 多小波框 架 . 本节前 半部 分从 时域和频 域对半 正交 多小波 框 架进 行 刻 画, 后 半部 分则 着重 于讨 论 P a r s e v a l 多小 波框架 与 GMR A P a r s e v a l 多小波框 架 之 间的关 系. 为 方便 起见 , 记 f , = DJ , B =AT . 下面 , 首先对 正 交和严 格 半正 交多 小波框 架 的时频特 性 进行刻 画 , 特 别 是频域 紧支 撑 多小波 .
( i ) + 1 , V ∈z ; ( i i ) D = + 1 , V J∈z ; ( i i i ) n ∈ z ={ 0 ) ; Uj ∈ z =L ( ) ; ( i v ) 空 间 是平 移不变 的, 即 f∈ = = > f∈ , V ∈Z n . 对于 所 有 的 J∈z ,定义
交小 波集 , 构造 若干 半正 交小 波框架 的例 子 .
2 基本概念及记号
在 讨论 。 ( )中小波 框架 时 , 需要用 到两 组 酉算 子:平 移 算子 ( T k f ) ( ・ ) =_ 厂 ( ・ 一 )和伸 缩 算子
杨守志等 : L 。 ( ) 上 的半正交多小波框架
厂 l = ∑( . 厂 , D j )
l , j .
( 2 . 1 )
事 实 上, 对 于 一般 的 Hi l b e r t空 间 P a r s e v a l 框 架是 一类很 重 要 的框 架 , 在理 论和 应用 上都 有 很广泛 的 应用 . 关于 H i l b e r t空 问上 的框 架理 论可 参见 文献 『 1 6 1 .
框 架.
本文用 表示 n 维方体 [ 一 百 1 , ) R , 对于函数 f ∈ L 2 ( ” ) , 记号 . 厂 ( ∈ ) : f ( x ) e 丌 i ∈ d 表
示 . 厂的  ̄u r i e r 变换, 其 中 . ∈表示 n中的 内积 . 注 意到
对于 咖∈L ( ) , 记 ( ) : ={ , ∈z ) , 并用 ( ) 表示 生成的平移不变子空 间, 即( ) 是 由 ( ) 生成的闭线性空间. 对于 f , g∈L 。 ( R ) , 定义方框积函数如下:
[ f , g ] ( ) ∑ , ( + ) 9 ( + ) ,a _ e . z ∈
半正 交小 波框 架 与框架 多分 辨分 析 的关系 . 作 为形 式上 最简 单 的小波 , 小波 集 的研 究吸 引 了很 多学 者
的注 意,目前 已经 有 许多相 关 的文献 , 如文 献 『 1 0 1 5 ] . 本文 研 究高 维半 正 交多 小波 框架 的刻 画 , 特 别 是对 于半 正 交 P a r s e v a l 多 小波 框架 的刻 画 .为 此 , 从频 域和 时域 两方 面对 半正 交多小 波框 架进 行刻 画, 并 给 出半正 交 P a r s e v a l 多小波 框架 与 G MRA 多 小波 框架 之 问的 关系 ; 进而 利用 高维 形式 的半 正交 化过 程, 给 出严 格 半正 交多 小波框 架 的一个 等价 刻 画: 最 后, 本 文给 出高 维半 正交 多 小波 P a r s e v a l 框 架集 的一 个等 价 条件 , 并 利用 己知 的一 维形 式 的正
∈Zn
特别地, 对于 . 厂∈ L 2 ( 碾 ) ,记 ,= 都 以 1为周 期) , 且 满 足 l f ( x ) l
. 另 外,用 L P (  ̄ r )表 示 所有 的 z 一周 期 ( 即对 每 一变 量 <。 。 的 函数 f 全 体 所构 成 的 函数 空 间 . ( T )表 示满 足 , 记 为
蔚( ∈ ) = e - 2  ̄ i k . ∈ ) ,厨 ( ∈ ) :I d e t A I — J / 2  ̄ B 一 ∈ ) 氟 7 ( f ) :l a e t A I — j / 2 e i B — j
25 0
中 国科 学 : 数学
第 4 4卷
第 3期
其 中 B= T , 上标 T 表示 矩 阵的转 置 .
( 肽 ) , 如果函数系 {
, J∈z , ∈z , l =1 ,
A I I f l l ≤ ∑∑ ∑ I I f , D
/ =1 J ∈Z ∈Z他
≤ B U l l 。 ,v f ∈ L 2 ( ” )
则 称其 为 。 ( )的一 个 多小波框 架 ; 如果 A= B, 则称 为紧 多小波 框架 ; 如果 A= B = 1 , 则称 其
… ,
定义 3 对于一个 P  ̄ r s e v a l 多小波框架 ={ 1 , …, 饥) , 如果 { ( ) , f =1 …. , ) 构成 = e 的一个 P a r s e v a l 框架, 则称 与一个 GMR A f )相 关, 或称 是 一个 G MRA 多小波
( J [ ) ' 厂 ) ( . ) =l d e t AI / 。 f ( A. ) , 其 中 A∈Mn ( Z ) 是 任 意的一 个扩 张矩 阵. 扩 张矩 阵是 指 的所 有 的特 征值
的绝对 值都 大于 1.
…
,
定义 1 对于有限集 = { 1 , …, L ) }满 足如 下条件 :
定 理 1 假 设 有 限集 = < …. , e L } L ( )是 。 ( ) 的 一个 多小波 框架 .{ ) 在频 率 域上都是紧支撑的, 同时, < ( ) , f =1 …. , ) 构成子空间 ={ _ 厂: s u p p f M)的一个 P a r s e v a l
摘要
本文研 究 ( ) 上 伸缩矩 阵 满 足 l d eห้องสมุดไป่ตู้t AI >1的半正 交多小 波框 架. 本 文得 到半 正交和 严格
半正 交框 架 的一 系列 性质 及 刻 画.本文 证 明半 正交 P a r s e v a l多小 波框 架与广 义 多分 辨分 析 f GMR A) P a r s e v a l多小 波框 架是 等价 的.特别 地 , 本文 利 用最小 频 率支 撑 ( MS F )多小波框 架 和小 波集 , 构造 若 干半 正交 多小 波框 架的例 子.
框架, 其中 M =【 J L _ s u p p  ̄ z . 则有
一
般 来说 , 构 造小 波基 的主 要 方法 是著 名 的 MRA. B a g g e t t 等人 [ ”】 为 了得 到构 造 小波框 架 的方
法 将 MR A 的概念 推广 为 GMRA .
定义 2 L 。 ( R ) 的一组闭子空间族 { ) J ∈ z称为是一个 G MR A , 如果 { ) j ∈ z满足:
中 国科 学 : 数 学 2 0 1 4年
