2014年江门一模理科数学
广东省十校2014届高三上学期第一次联考数学(理)试题(含答案)

广东“十校”2013—2014学年度高三第一次联考理科数学试题本试卷共6页,21小题, 满分150分.考试用时120分钟.注意事项:1.答卷前,考生务必用黑色字迹钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上. 2.选择题每小题选出答案后,用黑色字迹钢笔或签字笔将答案填写在答题卡上对应题目的序号下面,如需改动,用橡皮擦干净后,再选填其他答案,答案不能答在试卷上.3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效.4.作答选做题时,请先用2B 铅笔填涂选做题的题号对应的信息点,再作答。
漏涂、错涂、多涂的,答案无效.5.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回.第Ⅰ卷 (选择题 共4 0分)一.选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设集合{}23,log P a =,{},Q a b =,若{}0P Q =,则P Q =( ) A .{}3,0 B .{}3,0,2 C . {}3,0,1D .{}3,0,1,2 2.如图,在复平面内,复数1z ,2z 对应的向量分别是OA ,OB ,则复数12z z 对应的点位于( ) A.第一象限 B.第二象限C.第三象限D.第四象限3.已知等差数列{}n a 中,25a = ,411a =,则前10项和=10S ( )A . 55B . 155C . 350D . 400 4.学校为了解学生在课外读物方面的支出情况,抽取了n 个同学进行调查,结果显示这些同学的支出都在[10,50) (单 位:元),其中支出在[)30,50(单位:元)的同学 有67人,其频率分布直方图如右图所示,则n 的值为( ) A .100 B .120 C .130 D .390 5.平面四边形ABCD 中0AB CD +=,()0AB AD AC -=⋅,则四边形ABCD 是 ( )A .矩形B .梯形C .正方形D .菱形6. 一个四棱锥的三视图如图所示,其中主视图是腰长为1的等腰 直角三角形,则这个几何体的体积是 A .21 B .1 C .23D .2 7.下列命题:①函数22()sin cos f x x x =-的最小正周期是π;②函数()(1f x x =- ③若111(1)adx a x=>⎰,则a e =; ④椭圆)0(3222>=+m m y x 的离心率不确定。
江门市2014年初中毕业生学业水平调研测试(数学)试题及答案

江门市2014年初中毕业生学业水平调研测试(数学)试题及答案江门市2014年初中毕业生学业水平调研测试数学试卷共25小题,满分120分,考试时间100分钟。
注意事项包括:填写姓名、考生号等信息,选择题用铅笔涂黑答题卡上对应的选项,非选择题用黑色字迹钢笔或签字笔作答,保持答题卡整洁,不使用铅笔和涂改液。
一、选择题共10小题,每小题3分,共30分。
每小题给出四个选项,只有一个是正确的。
例如,第一题的正确答案是C,即-2的相反数是2.二、非选择题包括15小题,共90分。
其中,第三题是关于方差的问题,给出了甲、乙两个芭蕾舞团女演员的平均身高和方差,要求选择哪个团演员身高更整齐。
正确答案是D,即无法确定谁更整齐。
第九题是一个关于长方形面积的问题,给出了一根1m长的铁丝和要围成的长方形面积,要求设长方形的长为x,列出方程并解出x。
正确答案是C,即x(.5-x)=.06.其余题目没有明显错误,不需要改写。
二、选择题11.B12.(x-1)^213.3/814.命题:两个角互为对顶角。
结论:这两个角相等。
15.S = 1/216.-2.3.1/2.2/3三、解答题17.化简后得到:x/(x+1) + (x+1)/x = 4x/(x^2-1),代入x=3得到左边等于12/5,因此答案为12/5.18.⑴⑵根据勾股定理得到AB=13,因此BC=5.由于AC=5,所以BB'=5,根据相似三角形得到BB'=BC/AC*AB=13/5,因此BB=BB'-BC=8.19.⑴ x/(x+y)⑵ 3/8 = x/(x+10+y),解得x=15,代入得到y=20.四、解答题20.⑴由于AB=BC=CD,DE=EF=FG,因此XXX=CG。
⑵因为AB=BC,DE=EF,所以AE和CG平行。
又因为AE=CG,所以AE和CG垂直。
21.⑴教师每小时植树的速度为120/3=40颗,因此学校原计划每小时植树40颗。
江门市2014届高三调研测试理科数学试题及答案

图1江门市2014届高三调研测试理科数学一、选择题:本大题共8小题,每小题5分,满分40分.⒈已知集合{}21|<<-=x x A ,{}31|<<=x x B ,则=B A A .) 3 , 1(- B .) 2 , 1 ( C .] 3 , 1[- D .] 2 , 1 [ ⒉若复数 i m m m m )3()65(22-++- 是纯虚数( i 是虚数单位),则实数=m A .2=m B .3=m C .0=m D .2=m 或3=m ⒊已知平面向量)3 , ( -=λa ,)2 , 4( -=b ,若 b a ⊥,则实数=λ A .23-B .23C .6-D .6⒋已知点)2 , 1(A ,)1 , 2(B ,则线段AB 的垂直平分线的方程是A .03=-+y xB .01=+-y xC .0=-y xD .0=+y x ⒌设a 、R b ∈,若0|| <+b a ,则下列不等式中正确的是A .0>-b aB .033>+b aC .022<-b a D .0 <+b a⒍如图1,E 、F 分别是正方体1111D C B A ABCD -中1AD 、C B 1上的动点(不含端点),则四边形FDE B 1的俯视图可能是A .B .C .D .⒎已知函数⎪⎩⎪⎨⎧<-≥-=-,0 , 12,0 ,21)(x x x f x x,则该函数是A .偶函数,且单调递增B .偶函数,且单调递减C .奇函数,且单调递增D .奇函数,且单调递减⒏平面直角坐标系中,抛物线x y 212=与函数x y ln =图象的交点个数为 A .0 B .1 C .2 D .3二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分. (一)必做题(9~13题)⒐3log 2 2log 3(填“>”或“<” ). ⒑在ABC ∆中,3=c ,045=A ,075=B ,则=a .⒒若双曲线的渐近线方程为x y 3±=,它的一个焦点是)0 , 10(,则双曲线方程是 .BCMN1A 1B 1C ⒓若x ,y 满足约束条件⎪⎩⎪⎨⎧≤+≥+≥43430y x y x x ,则y x z -=的最大值是 .⒔若α、β是不重合的平面,a 、b 、c 是互不相同的空间直线,则下列命题中为真命题的是 .(写出所有真命题的序号) ① 若α//a ,α//b ,则b a // ② 若α//c ,α⊥b ,则b c ⊥ ③ 若α⊥c ,β//c ,则βα⊥④ 若α⊂b ,α⊂c 且b a ⊥,c a ⊥,则α⊥a (二)选做题(14、15题,考生只能从中选做一题)⒕直线x y =和抛物线2x y =所围成封闭图形的面积=S . ⒖在数列{}n a 中,11=a ,nn n a a a +=+11(*∈N n ),试归纳出这个数列的通项=n a .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. ⒗(本小题满分12分)已知1)2cos 2sin 3(2cos2)(-+=xx x x f ,R x ∈. ⑴ 求)(x f 的最小正周期;⑵ 设α、)2, 0(πβ∈,2)(=αf ,58)(=βf ,求)(βα+f 的值.⒘(本小题满分13分)如图2,直三棱柱111C B A ABC -中,CB CA ⊥,1==CB CA ,棱21=AA ,M 、N 分别是11B A 、A A 1的中点.⑴ 求证:⊥N C 1平面BCN ;⑵ 求直线C B 1与平面MN C 1所成角θ的正弦值.⒙(本小题满分13分)为配制一种药液,进行了三次稀释,先在体积为V 的桶中盛满纯药液,第一次将桶中药液倒出10升后用水补满,搅拌均匀第二次倒出8升后用水补满,然后第三次倒出10升后用水补满.⑴ 求第一次稀释后桶中药液的含量;⑵ 若第二次稀释后桶中药液含量不超过容积的60%,求V 的取值范围; ⑶ 在第⑵问的条件下,第三次稀释后桶中的药液能否达到容积的50%,为什么?⒚(本小题满分14分)如图3,椭圆Γ的中心在坐标原点O ,过右焦点)0 , 1(F 且垂直于椭圆对称轴的弦MN 的长为3.⑴ 求椭圆Γ的方程;⑵ 直线 l 经过点O 交椭圆Γ于P 、Q 两点,NQ NP =,求直线 l 的方程.⒛(本小题满分14分)已知正项等比数列{}n a (*∈N n ),首项31=a ,前n 项和为n S ,且33a S +、55a S +、44a S +成等差数列.图3⑴ 求数列{}n a 的通项公式; ⑵ 求数列{}n nS 的前n 项和n T .21(本小题满分14分)已知函数)()(b ax e x f x +=,曲线)(x f y =经过点)2 , 0(P ,且在点P 处的切线为l :24+=x y .⑴ 求常数a ,b 的值;⑵ 求证:曲线)(x f y =和直线 l 只有一个公共点;⑶ 是否存在常数k ,使得]1 , 2[--∈x ,)24()(+≥x k x f 恒成立?若存在,求常数k 的取值范围;若不存在,简要说明理由.参考答案一、选择题 BAAC DBCD二、填空题9.> 10.2 11.1922=-y x 12.0 13.②③(对1个3分,错1个2-分) 14.61 15.n 1三、解答题16.解:⑴x x x f cos sin 3)(+=……2分,)6sin(2π+=x ……4分,)(x f 的最小正周期π2=T ……5分⑵因为2)6sin(2=+πα,1)6sin(=+πα,3266ππαπ<+<……6分,所以26ππα=+,3πα=……7分,58)6sin(2=+πβ,54)6sin(=+πβ,3266ππβπ<+<……8分,因为2354<,所以266ππβπ<+<,53)6cos(=+πβ……9分,所以ββππβαβαcos 2)2sin(2)6sin(2)(=+=++=+f ……10分,6sin )6sin(26cos )6cos(2]6)6cos[(2ππβππβππβ+++=-+=……11分,5433+=……12分。
广东版2014届高三名校数学(理)试题分省分项汇编:专题05 平面向量(解析版)

一.基础题组1.【广东省惠州市2013届高三第一次模拟考试(理)】已知向量(1,1)a =- ,(3,)b m =,//()a a b +,则m =( )A .错误!未找到引用源。
2B .2-C .3-D .32.【广东省汕头四中2014届高三上学期第一次月考(理)】已知平面向量a ,b 的夹角为60°,=a ,||1=b ,则|2|+=a b ( )A.2 C. D.3.【广东省东莞市2013届高三模拟考试一(理)】已知(1,2)= a ,(0,1)= b ,(,2)k =- c ,若(2)+⊥a b c ,则k =( )A .2B .8C .2-D .8- 【答案】B4.【广东省湛江市2014届高三普通高考调研测试(理)】向量()1,2a =-- ,()0,1b =,则a b +=( )A.()1,1--B.()1,3--C.()1,3-D.()0,2-5.【广东省珠海一中等六校2014届高三第一次联考(理)】已知单位向量,i j满足(2)j i i -⊥ ,则,i j夹角为( )A .4π B .6πC .3π D .23π二.能力题组1.【广东省韶关市20914届高三摸底考试(理)】若||2||||a b a b a=-=+,则向量a b+( ) A .6πB.3πC.32π D.65π2.【广东省佛山市南海区2014届高三8月质检(理)】若a ,b 是两个非零向量,则“+=-a b a b ”是“⊥a b ”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件 【答案】C 【解析】b a b a b a b a ⊥⇔=⋅⇔-=++0)()(22. 考点:向量运算,充分必要条件判断.3.【广东省十校2014届高三第一次联考(理)】平面四边形ABCD 中0AB CD +=,()0AB AD AC -=⋅,则四边形ABCD 是 ( )A .矩形B .梯形C .正方形D .菱形 【答案】D 【解析】试题分析:0AB CD += AB CD DC ⇒=-=ABCD ⇒是平行四边形,()0AB AD AC DB AC -∙=∙=DB AC ⇒⊥,所以平行四边形ABCD 是菱形.考点:向量的加减运算和向量的垂直.4.【广东省珠海市2014届高三9月摸底考试(理)】如图,在ABC ∆中,点D 是BC 边上靠近B 的三等分点,则AD =( )ABCDA .2133AB AC - B .1233AB AC +C .2133AB AC +D .1233ABAC -5.【广东省广州市越秀区2014届高三入学摸底考试(理)】在△ABC 中,3sin 5A =,8AB AC ⋅=,则△ABC 的面积为 ( )A.3B.4C.6D.125【答案】A 【解析】试题分析:cos 80AB AC AB AC A ⋅=⋅⋅=> ,由于0AB > ,0AC > ,故c o s 0A >,cos A ∴=45==,85810cos 4AB AC A ∴⋅==⨯= ,1sin 2ABC S AB AC A ∆∴=⋅⋅1310325=⨯⨯=,即ABC ∆的面积为3. 考点:平面向量的数量积、同角三角函数之间的关系、三角形的面积三.拔高题组1.【广东省十校2014届高三第一次联考(理)】已知函数1()sin πcos π22f x x x =+, x ∈R .(1)求函数()f x 的最大值和最小值;(2)设函数()f x 在[1,1]-上的图象与x 轴的交点从左到右分别为,M N ,图象的最高点为P ,求PM 与PN的夹角的余弦.∴3cos ,5||||PM PN PM PN PM PN ∙<>==∙. ………12分。
2014年高考试题(全国课标Ⅰ卷)数学(理科)试卷及答案

2014年普通高等学校招生全国统一考试全国课标Ⅰ理科数学注意事项:1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答题前,考生务必将自己的姓名、准考证号填写在答题卡上.2.回答第Ⅰ卷时,选出每个小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮搽干净后,再选涂其他答案标号,写在本试卷上无效.3. 回答第Ⅱ卷时,将答案写在答题卡上,答在本试题上无效.4. 考试结束,将本试题和答题卡一并交回.第Ⅰ卷一.选择题:共12小题,每小题5分,在每个小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={x |2230x x --≥},B={x |-2≤x <2=,则A B ⋂= ( )A .[-2,-1]B .[-1,2)C .[-1,1]D .[1,2)2.32(1)(1)i i +-= ( ) A .1i + B .1i - C .1i -+ D .1i --3.设函数()f x ,()g x 的定义域都为R ,且()f x 时奇函数,()g x 是偶函数,则下列结论正确的是( )A .()f x ()g x 是偶函数B .|()f x |()g x 是奇函数C .()f x |()g x |是奇函数D .|()f x ()g x |是奇函数4.已知F 是双曲线C :223(0)x my m m -=>的一个焦点,则点F 到C 的一条渐近线的距离为( )A .3B .3C .3mD .3m5.4位同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率 ( )A .18B .38C .58D .786.如图,圆O 的半径为1,A 是圆上的定点,P 是圆上的动点,角x 的始边为射线OA ,终边为射线OP ,过点P 作直线OA 的垂线,垂足为M ,将点M 到直线OP 的距离表示为x 的函数()f x ,则y =()f x 在[0,π]上的图像大致为 ( )7.执行下图的程序框图,若输入的,,a b k 分别为1,2,3,则输出的M = ( )A .203 B .165 C .72 D .1588.设(0,)2πα∈,(0,)2πβ∈,且1sin tan cos βαβ+=,则 ( ) A .32παβ-=B .22παβ-=C .32παβ+=D .22παβ+=9.不等式组124x y x y +≥⎧⎨-≤⎩的解集记为D .有下面四个命题:1p :(,),22x y D x y ∀∈+≥-,2p :(,),22x y D x y ∃∈+≥, 3P :(,),23x y D x y ∀∈+≤,4p :(,),21x y D x y ∃∈+≤-.其中真命题是 ( )A .2p ,3PB .1p ,4pC .1p ,2pD .1p ,3P10.已知抛物线C :28y x =的焦点为F ,准线为l ,P 是l 上一点,Q 是直线PF 与C 的一个焦点,若4FP FQ =,则||QF = ( )A .72 B .52C .3D .2 11.已知函数()f x =3231ax x -+,若()f x 存在唯一的零点0x ,且0x >0,则a 的取值范围为 ( )A .(2,+∞)B .(-∞,-2)C .(1,+∞)D .(-∞,-1)12.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的个条棱中,最长的棱的长度为 ( )A .62B .42C .6D .4第Ⅱ卷本卷包括必考题和选考题两个部分。
2014年广东高考试卷理科数学(含全部答案)

2014年普通高等学校招生全国统一考试(广东卷)数学(理)一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{1,0,1},{0,1,2},M N =-=则M N ⋃=A .{1,0,1}- B. {1,0,1,2}- C. {1,0,2}- D. {0,1} 答案:B2.已知复数Z 满足(34)25,i z +=则Z=A .34i - B. 34i + C. 34i -- D. 34i -+ 答案:A 2525(34)25(34):=34,.34(34)(34)25i i z i i i i --===-++-提示故选A 3.若变量,x y 满足约束条件121y xx y z x y y ≤⎧⎪+≤=+⎨⎪≥-⎩且的最大值和最小值分别为M 和m ,则M-m=A .8 B.7 C.6 D.5:(),(2,1)(1,1)3,3,6,.CM m M m C --==-∴-=答案:提示画出可行域略易知在点与处目标函数分别取得最大值与最小值选4.若实数k 满足09,k <<则曲线221259x y k -=-与曲线221259x y k -=-的 A .离心率相等 B.虚半轴长相等 C. 实半轴长相等 D.焦距相等09,90,250,(9)34(25)9,k k k k k k <<∴->->+-=-=-+答案:D提示:从而两曲线均为双曲线,又25故两双曲线的焦距相等,选D.5.已知向量()1,0,1,a =-则下列向量中与a 成60︒夹角的是A .(-1,1,0) B.(1,-1,0) C.(0,-1,1) D.(-1,0,1)0222222:(1,0,1)(1,1,0)11:,,60,.2210(1)1(1)0B B -⋅-=∴++-⋅+-+答案提示即这两向量的夹角余弦值为从而夹角为选6、已知某地区中小学生人数和近视情况分别如图1和图2所示,为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为 A. 200,20 B. 100,20 C. 200,10 D. 100,10::(350045002000)2%200,20002%50%20,.AA ++⋅=⋅⋅=∴答案提示样本容量为抽取的高中生近视人数为:选7.若空间中四条两两不同的直线1234,,,l l l l ,满足122334,,l l l l l l ⊥⊥⊥,则下列结论一定正确的是 A.14l l ⊥ B.14//l l C.14,l l 既不垂直也不平行 D.14,l l 的位置关系不确定 答案:D 8.设集合(){}12345=,,,,{1,0,1},1,2,3,4,5i A x x x x xx i ∈-=,那么集合A 中满足条件“1234513x x x x x ≤++++≤”的元素个数为A.60B.90C.120D.130答案: D1234511122252551311225254:1,2,31:C 10;:C 40;:C C C 80.104080130,D .x x x x x C C A C C ++++=+=+=++=提示可取和为的元素个数为和为2的元素个数为和为3的元素个数为故满足条件的元素总的个数为选二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分.(一)必做题(9~13题)9.不等式521≥++-x x 的解集为 .(][)(][),32,:12532,,32,.-∞-+∞---∞-+∞答案:提示数轴上到与距离之和为的数为和故该不等式的解集为:10.曲线25+=-xe y 在点)3,0(处的切线方程为 .'5'0:530:5,5,35,530.xx x y y eyy x x y -=+-==-∴=-∴-=-+-=答案提示所求切线方程为即11.从0,1,2,3,4,5,6,7,8,9中任取七个不同的数,则这七个数的中位数是6的概率为 .367101:6:67,36,136,.6C C =答案提示要使为取出的个数中的中位数则取出的数中必有个不大于另外个不小于故所求概率为12.在ABC ∆中,角C B A ,,所对应的边分别为c b a ,,,已知b B c C b 2cos cos =+, 则=ba. 2222222:2::cos cos ,2, 2.sin cos sin cos 2sin ,sin()2sin ,sin 2sin ,2, 2.::2,24,222, 2.ab Cc B a a b bB C C B B B C B aA B a b ba b c a c b b b a ab ab ac aa b b+==∴=+=+=∴==∴=+-+-⋅+==∴==答案提示解法一由射影定理知从而解法二:由上弦定理得:即即解法三由余弦定理得即即13.若等比数列{}n a 的各项均为正数,且512911102e a a a a =+,则1220l n l n l n a a a +++= .51011912101112202019151201011:100:,,ln ln ln ,ln ln ln ,220ln 20ln 20ln 100.a a a a a a e S a a a S a a a S a a a a e =∴==+++=+++∴====答案提示设则(二)选做题(14~15题,考生从中选做一题)14.(坐标与参数方程选做题)在极坐标系中,曲线C 1和C 2的方程分别为2sincos ρθθ=和sin ρθ=1,以极点为平面直角坐标系的原点,极轴为x 轴的正半轴,建立平面直角坐标系,则曲线C 1和C 2的交点的直角坐标为__221212:(1,1):(sin )cos ,,:1,(1,1).C y x C y C C ρθρθ===∴答案提示即故其直角坐标方程为:的直角坐标方程为与的交点的直角坐标为15.(几何证明选讲选做题)如图3,在平行四边形ABCD 中,点E 在AB 上且EB =2AE ,AC 与DE 交于点F ,则CDF AEF ∆∆的面积的面积=___22:9:,()()9.CDFAEF CDF CD EB AE AEF AE AE∆∆∴∆+===∆答案提示显然的面积的面积三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和 演算步骤.16、(12分)已知函数R x x A x f ∈+=),4sin()(π,且23)125(=πf , (1)求A 的值; (2)若23)()(=-+θθf f ,)2,0(πθ∈,求)43(θπ-f . 552332:(1)()sin()sin , 3.121243223(2)(1):()3sin(),4()()3sin()3sin()443(sin cos cos sin )3(sin()cos cos()sin )444423cos sin 46cos 326cos ,(0,),42f A A A f x x f f πππππππθθθθππππθθθθπθθπθθ=+==∴=⋅==+∴+-=++-+=++-+-===∴=∈解由得10sin 4331030()3sin()3sin()3sin 3.44444f θπππθθπθθ∴=∴-=-+=-==⨯=17、(13分)随机观测生产某种零件的某工厂25名工人的日加工零件数(单位:件),获得数据如下:根据上述数据得到样本的频率分布表如下:(1)确定样本频率分布表中121,,n n f 和2f 的值; (2)根据上述频率分布表,画出样本频率分布直方图;(3)根据样本频率分布直方图,求在该厂任取4人,至少有1人的日加工零件数落在区间(30,50]的概率.(](]12120044472:(1)7,2,0.28,0.08;2525(2);(3),30,50:10.120.88,130,503:1(0.88)(0.12)1().25n n f f C ======-=-=-解略根据频率分布直方图可得工人们日加工零件数落在区间的概率为故至少有人的日加工零件数落在区间的概率为18.(13分)如图4,四边形ABCD 为正方形,PD ⊥平面ABCD ,∠DPC =030,AF ⊥PC 于点F ,FE ∥CD ,交PD 于点E.(1)证明:CF ⊥平面ADF ;(2)求二面角D -AF -E 的余弦值.:(1):,,,,A ,,,,,,,,,,.(2):E EG//CF DF G,,,G GH AF H,EH,PD ABCD PD PCD PCD ABCD PCD ABCD CD D ABCD AD CD AD PCD CF PCD CF AD AF PC CF AF AD AF ADF ADAF A CF ADF CF DF EG DF ⊥⊂∴⊥=⊂⊥∴⊥⊂∴⊥⊥∴⊥⊂=∴⊥⊥∴⊥⊥∠解证明平面平面平面平面平面平面平面平面又平面平面解法一过作交于平面A 平面A 过作于连则0022,CD 2,30,130,==1,213324,,,=,,,3,2222333319322EG .,7,,42231933193193622,()()474747EHG D AF E DPC CDF CF CD DE CF DE CP EF DC DE DF DP CP DE EF AE AF EF DF AE EF EH HG AF --=∠=∴∠==∴=∴==⋅⋅======⋅⋅∴====-=为二面角的平面角设从而∥即还易求得EF=从而易得故3,476347257cos .1947319GH EHG EH ∴∠==⋅=12:,,,,,2,1(0,0,2),C(0,2,0),P(23,0,0),,(23,22,0),,,43331(,,0),(,0,0),ADF CP (3,1,0),2222AEF (x DP DC DA x y z DC A CF CP F DF CF F E n n λλλλ==-⊥===-=解法二分别以为轴建立空间直角坐标系设则设则可得从而易得取面的一个法向量为设面的一个法向量为2212212,y,z),0,0,43257(4,0,3),.19||||219n AE n AF n n n n n ⋅=⋅=⋅==⋅⨯利用且得可以是从而所求二面角的余弦值为19.(14分)设数列{}n a 的前n 和为n S ,满足2*1234,n n S na n n n N +=--∈,且315S =. (1)求123,,a a a 的值; (2)求数列{}n a 的通项公式;211222122331212121331221232121:(1)2314127+=432424()204(15)20,+83,,1587,53,5,7,(2)2342,2(1)3(1)4(n n n n a S a a a a S a S a a a a a a a a S a a a a a a S na n nn S n a n n +-==-⨯-⨯=-=-⨯-⨯=---=---∴==⎧∴=--=-=⎨=⎩====--∴≥=-----解①②联立①②解得综上③当时11121)2161,22(1)21,:()(1),1,3211,;(),,21,21611,22211(21)322411322232(1)11n n n k k k n n a a n na n i n a ii n k a k k k n k a a k k k k k k k k k k k n k ++-+-=+=+===⨯+==+-+=+=+-=⋅+++-=++=+=++=+④③④并整理得:由猜想以下用数学归纳法证明由知当时猜想成立假设当时猜想成立即则当时这就是说,,,2 1.n n N a n *∈=+时猜想也成立从而对一切20.(14分)已知椭圆2222:1(0)x y C a b a b +=>>的一个焦点为(5,0),离心率为53,(1)求椭圆C 的标准方程;(2)若动点00(,)P x y 为椭圆外一点,且点P 到椭圆C 的两条切线相互垂直,求点P 的轨迹方程.222220022002255:(1)5,,3,954,31.94(2),,4(3,2),(3,2).(),(),194(94)18(c c e a b a c a a x y C x y y y k x x x y y k x x y k x k y ====∴==-=-=∴+=-±±-=-=-++=++解椭圆的标准方程为:若一切线垂直轴则另一切线垂直于轴则这样的点P 共个,它们的坐标分别为若两切线不垂直于坐标轴,设切线方程为即将之代入椭圆方程中并整理得:2000022222200000022220000012202200)9()40,,0,(18)()36()4(94)0,4()4(94)0,4(9)240,,1,:1,913,(3,2),(3,2)kx x y kx k y kx y kx k y kx k y x k x y k y k k x x y ⎡⎤-+--=∆=⎣⎦⎡⎤----+=--+=⎣⎦-∴--+-=∴=-=--∴+=-±±依题意即:即两切线相互垂直即显然这四点也满足以上方22,13.P x y ∴+=程点的轨迹方程为21.(本题14分)设函数2221()(2)2(2)3f x x x k x x k =+++++-,其中2k <-,(1)求函数()f x 的定义域D (用区间表示); (2)讨论()f x 在区间D 上的单调性;(3)若6k <-,求D 上满足条件()(1)f x f >的x 的集合(用区间表示). .解:(1)可知222(2)2(2)30x x k x x k +++++->,22[(2)3][(2)1]0x x k x x k ∴+++⋅++->, 223x x k ∴++<-或221x x k ++>,2(1)2x k ∴+<--(20)k -->或2(1)2x k +>-(20)k ->,|1|2x k ∴+<--或|1|2x k +>-,12k ∴----<12x k <-+--或12x k <---或12x k >-+-, 所以函数()f x 的定义域D 为(,12)k -∞---(12,k ----12)k -+--(12,)k -+-+∞; (2)232222(2)(22)2(22)'()2(2)2(2)3x x k x x f x x x k x x k +++++=-+++++-23222(21)(22)(2)2(2)3x x k x x x k x x k ++++=-+++++-, 由'()0f x >得2(21)(22)0x x k x ++++<,即(1)(1)(1)0x k x k x +++-+<,1x k ∴<---或11x k -<<-+-,结合定义域知12x k <---或112x k -<<-+--, 所以函数()f x 的单调递增区间为(,12)k -∞---,(1,12)k --+--,同理递减区间为(12,1)k -----,(12,)k -+-+∞;(3)由()(1)f x f =得2222(2)2(2)3(3)2(3)3x x k x x k k k +++++-=+++-,2222[(2)(3)]2[(2)(3)]0x x k k x x k k ∴++-++++-+=, 22(225)(23)0x x k x x ∴+++⋅+-=,(124)(124)(3)(1)0x k x k x x ∴++--+---⋅+-=, 124x k ∴=----或124x k =-+--或3x =-或1x =, 6k <-,1(1,12)k ∴∈--+--,3(12,1)k -∈-----,12412k k ----<---,12412k k -+-->-+-, 结合函数()f x 的单调性知()(1)f x f >的解集为(124,12)k k -------(12,3)k -----(1,12)k -+--(12,124)k k -+--+--..。
2014年高考广东理科数学试题及答案(word解析版)

2014年高考广东理科数学试题及答案(word解析版)2014年普通高等学校招生全国统一考试(广东卷)数学(理科)一、选择题:本大题共8小题,每小题5分,满分40分,在每小题给出的四个选项中,只有一项是符合题目要求的. (1)【2014年广东,理1,5分】已知集合{1,0,1}M =-,{0,1,2}N =,则M N =U ( ) (A ){1,0,1}- (B ){1,0,1,2}- (C ){1,0,2}- (D ){0,1} 【答案】B【解析】{1,0,1,2}M N =-U ,故选B . (2)【2014年广东,理2,5分】已知复数z 满足(34i)25z +=,则z =( ) (A )34i - (B )34i + (C )34i -- (D )34i -+ 【答案】A【解析】2525(34i)25(34i)=34i 34i (34i)(34i)25z --===-++-,故选A . (3)【2014年广东,理3,5分】若变量,x y 满足约束条件121y xx y z x y y ≤⎧⎪+≤=+⎨⎪≥-⎩且的最大值和最小值分别为M 和m ,则M m -=( ) (A )8 (B )7 (C )6 (D )5 【答案】C 【解析】画出可行域,易知在点(2,1)与(1,1)--处目标函数分别取得最大值3M =,与最小值3m =-,6M m ∴-=,故选C .(4)【2014年广东,理4,5分】若实数k 满足09k <<,则曲线221259x y k-=-与曲线221259x y k -=-的( ) (A )离心率相等 (B )虚半轴长相等 (C )实半轴长相等 (D )焦距相等 【答案】D【解析】09k <<Q ,90k ∴->,250k ->,从而两曲线均为双曲线,又25(9)34(25)9k k k +-=-=-+,两双曲线的焦距相等,故选D .(5)【2014年广东,理5,5分】已知向量()1,0,1a =-,则下列向量中与a 成60︒夹角的是( ) (A )()1,1,0- (B )()1,1,0- (C )()0,1,1- (D )()1,0,1- 【答案】B【解析】2222221210(1)1(1)0=++-⋅+-+,即这两向量的夹角余弦值为12,从而夹角为060,故选A . (6)【2014年广东,理6,5分】已知某地区中小学生人数和近视情况分别如图1和图2所示,为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为( ) (A )200,20 (B )100,20 (C )200,10 (D )100,10 【答案】A【解析】样本容量为(350045002000)2%200++⋅=,抽取的高中生近视人数为:20002%50%20⋅⋅=,故选A .(7)【2014年广东,理7,5分】若空间中四条两两不同的直线1234,,,l l l l ,满足12l l ⊥,23l l ⊥,34l l ⊥则下列结论一定正确的是( )(A )14l l ⊥ (B )14//l l (C )14,l l 既不垂直也不平行 (D )14,l l 的位置关系不确定 【答案】D【解析】平面中的四条直线,14l l ⊥,空间中的四条直线,位置关系不确定,故选D .(8)【2014年广东,理8,5分】设集合(){}12345=,,,,{1,0,1},1,2,3,4,5iA x x x x x x i ∈-=,那么集合A 中满足条件“1234513x x x x x ≤++++≤”的元素个数为( )(A )60 (B )90 (C )120 (D )130 【答案】D【解析】12345x x x x x ++++可取1,2,3,和为1的元素个数为:1125C 10C =;和为2的元素个数为:122255C 40C A +=;和为3的元素个数为:1311225254C C C 80C C +=,故满足条件的元素总的个数为104080130++=,故选D .二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分.(一)必做题(9~13) (9)【2014年广东,理9,5分】不等式125x x -++≥的解集为 .【答案】(][),32,-∞-+∞U【解析】数轴上到1与2-距离之和为5的数为3-和2,故该不等式的解集为:(][),32,-∞-+∞U . (10)【2014年广东,理10,5分】曲线52xy e -=+在点(0,3)处的切线方程为 .【答案】530x y +-=【解析】'55xy e -=-,'5x y =∴=-,∴所求切线方程为35y x -=-,即530x y +-=.(11)【2014年广东,理11】,5分从0,1,2,3,4,5,6,7,8,9中任取七个不同的数,则这七个数的中位数是6的概率为 . 【答案】16【解析】要使6为取出的7个数中的中位数,则取出的数中必有3个不大于6,另外3个不小于6,故所求概率为3671016C C=. (12)【2014年广东,理12,5分】在ABC ∆中,角,,A B C 所对应的边分别为,,a b c ,已知cos cos 2b C c B b +=,则a b = . 【答案】2【解析】解法一:由射影定理知cos cos b C c B a +=,从而2a b =,2ab ∴=. 解法二:由上弦定理得:sin cos sin cos 2sin B C C B B +=,即sin()2sin B C B +=,sin 2sin A B ∴=,即2a b =,2ab ∴=. 解法三:由余弦定理得:222222222a b c a c b b bab ac+-+-⋅+=,即224a ab=,2a b ∴=,即2ab =.(13)【2014年广东,理13,5分】若等比数列{}na 的各项均为正数,且510119122a a a a e +=,则1220ln ln ln a a a +++=L L .【答案】50【解析】1011912a a a a =Q ,51011a a e ∴=,设1220ln ln ln S a a a =+++L ,则20191ln ln ln S a a a =+++L , 51201011220ln 20ln 20ln 100S a a a a e ∴====,50S ∴=.(二)选做题(14-15题,考生只能从中选做一题)(14)【2014年广东,理14,5分】(坐标系与参数方程选做题)在极坐标系中,曲线1C 和2C 的方程分别为2sin cos ρθθ=和sin 1ρθ=,以极点为平面直角坐标系的原点,极轴为x 轴的正半轴,建立平面直角坐标系,则曲线1C 和2C 的交点的直角坐标为 .【答案】(1,1)【解析】1C 即2(sin )cos ρθρθ=,故其直角坐标方程为:2y x =,2C 的直角坐标系方程为:1y =,1C ∴与2C 的交点的直角坐标为(1,1).(15)【2014年广东,理15,5分】(几何证明选讲选做题)如图3,在平行四边形ABCD 中,点E 在AB 上且2EB AE =,AC 与DE 交于点,则CDF AEF ∆=∆的面积的面积. 【答案】9【解析】显然CDF AEF ∆∆:,∴22()()9CDF CDEB AE AEF AEAE∆+===∆的面积的面积.三、解答题:本大题共6题,共80分.解答应写出文字说明,证明过程或演算步骤. (16)【2014年广东,理16,12分】已知函数()sin(),4f x A x x R π=+∈,且53()122f π=. (1)求A 的值;(2)若3()()2f f θθ+-=,(0,)2πθ∈,求3()4f πθ-. 解:(1)5523()sin()sin 1212432f A A ππππ=+==,3323A ∴=⋅=. (2)由(1)得:()3sin()4f x x π=+,()()3sin()3sin()44f f ππθθθθ∴+-=++-+33(sin cos cos sin )3(sin()cos cos()sin )23cos sin 6cos 444442πππππθθθθθθ=++-+-===,6cos θ∴=,(0,)2πθ∈Q ,10sin θ∴=,331030()3sin()3sin()3sin 3444f πππθθπθθ∴-=-+=-==⨯=.(17)【2014年广东,理17,12分】随机观测生产某种零件的某工厂25名工人的日加工零件数(单位:件),获得数据如下:30,42,41,36,44,40,37,37,25,45,29,43,31,36,49,34,33,43,38,42,32,34,46,39,36.根据上述数据得到样本的频率分布表如下:分组 频数 频率 [25,30] 3 0.12 (30,35] 5 0.20 (35,40] 8 0.32 (40,45] 1n 1f (45,50] 2n 2f(1)确定样本频率分布表中121,,n n f 和2f 的值;(2)根据上述频率分布表,画出样本频率分布直方图;(3)根据样本频率分布直方图,求在该厂任取4人,至少有1人的日加工零件数落在区间(]30,35的概率.解:(1)17n =,22n =,170.2825f ==,220.0825f ==. (2)频率分布直方图如下所示:(3)根据频率分布直方图,可得工人们日加工零件数落在区间(]30,35的概率为0.2,设日加工零件数落在区间(]30,35的人数为随机变量ξ,则(4,0.2)B ξ:,故4人中,至少有1人的日加工零件数落在区间(]30,35 的概率为:0441(0.2)(0.8)10.40960.5904C -=-=.(18)【2014年广东,理18,14分】如图4,四边形ABCD 为正方形,PD ⊥平面ABCD ,30DPC ∠︒=,AF PC ⊥于点F ,//FE CD ,交PD 于点E . (1)证明:CF ⊥平面ADF ;(2)求二面角D AF E --的余弦值. 解:(1)PD ⊥平面ABCD ,PD PCD ⊂,∴平面PCD ⊥平面ABCD ,平面PCD I 平面ABCD CD =,AD ⊂平面ABCD ,AD CD ⊥,AD ∴⊥平面PCD ,CF ⊂平面PCD ,CF AD ∴⊥,又AF PC ⊥,CF AF ∴⊥,,AD AF ⊂平面ADF ,AD AF A =I ,CF ∴⊥平面ADF .(2)解法一:过E 作//EG CF 交DF 于G ,CF ⊥Q 平面ADF ,EG ∴⊥平面ADF ,过G 作GH AF ⊥于H ,连EH则EHG ∠为二面角D AF E --的平面角,设2CD =,030DPC ∠=Q ,30CDF ∴∠=,从而1==12CF CD , 4CP =,EF DC Q ∥,DE CFDP CP∴=,即12=223,3DE ∴=,还易求得32EF =,3DF =,从而3332243DE EF EG DF ⋅⋅===,易得19AE =,7AF =,32EF =,19331922747AE EF EH AF ⋅⋅∴===,故22319363()()44747HG =-=,6347257cos 47319GH EHG EH ∴∠==⋅=.解法二:分别以DP ,DC ,DA 为x ,y ,z 轴建立空间直角坐标系,设2DC =,则(0,0,2)A ,(0,2,0)C ,(23,0,0)P ,设CF CP λ=u u u r u u u r ,则(23,22,0)F λλ-,DF CF ⊥u u u r u u u r Q ,可得14λ=,从而33(,0)2F ,易得 3(E ,取面ADF 的一个法向量为11(3,1,0)2n CP ==-u u r u u u r,设面AEF的一个法向量为2(,,)nx y z =u u r, 利用20n AE ⋅=u u r u u u r ,且20n AF ⋅=u u r u u u r ,得2n u u r可以是3),从而二面角的余弦值为121243257||||219n n n n ⋅==⋅⨯u u r u u r u u r u u u r . (19)【2014年广东,理19,14分】设数列{}na 的前n 和为nS ,满足2*1234,n n S na n n n N +=--∈,且315S =. (1)求123,,a a a 的值;(2)求数列{}na 的通项公式.解:(1)211222314127a S a a ==-⨯-⨯=- ①2122331212+=432424()204(15)20a a S a S a a a a =-⨯-⨯=---=---,12+8a a ∴= ②联立①②解得1235a a =⎧⎨=⎩,33121587a S a a ∴=--=-=,综上13a =,25a =,37a =.(2)21234nn Sna n n +=-- ③ ∴当2n ≥时,212(1)3(1)4(1)n n Sn a n n -=----- ④-③④并整理得:1216122n n n n aa n n+-+=+,由(1)猜想21nan =+,以下用数学归纳法证明:(ⅰ)由(1)知,当1n =时,13211a ==⨯+,猜想成立; (ⅱ)假设当n k =时,猜想成立,即21ka k =+,则当1n k =+时,212161211411(21)33232(1)1222222k k k k k k a a k k k k k k k k k+-+--=+=⋅+++=++=+=++,这就是说1n k =+时,猜想也成立,从而对一切n N *∈,21na n =+.(20)【2014年广东,理20,14分】已知椭圆2222:1(0)xy C a b ab+=>>的一个焦点为(5,0)5.(1)求椭圆C 的标准方程;(2)若动点0(,)P x y 为椭圆外一点,且点P 到椭圆C 的两条切线相互垂直,求点P 的轨迹方程.解:(1)5c =,55c e a ==3a ∴=,222954b a c =-=-=,∴椭圆C 的标准方程为:22194x y +=.(2)若一切线垂直x 轴,则另一切线垂直于y 轴,则这样的点P 共4个,它们的坐标分别为(3,2)-±,(3,2)±.若两切线不垂直与坐标轴,设切线方程为()y y k x x -=-,即0()y k x x y =-+,将之代入椭圆方程22194x y+=中并整理得:222(94)18()9()40k x k y kx x y kx ⎡⎤++-+--=⎣⎦,依题意,0∆=,即222200(18)()36()4(94)0k y kx y kx k ⎡⎤----+=⎣⎦,即224()4(94)0y kx k--+=, 2220000(9)240x k x y k y ∴--+-=,Q 两切线相互垂直,121k k∴=-,即2020419y x -=--,220013xy ∴+=,显然(3,2)-±,(3,2)±这四点也满足以上方程,∴点P 的轨迹方程为2213x y +=.(21)【2014年广东,理21,14分】设函数222()(2)2(2)3f x x x k x x k =+++++-2k <-.(1)求函数()f x 的定义域D (用区间表示);(2)讨论()f x 在区间D 上的单调性;(3)若6k <-,求D 上满足条件()(1)f x f >的x 的集合(用区间表示).解:(1)222(2)2(2)30x x k x x k +++++->,则221x x k ++> ① 或 223x x k ++<- ②由①得:2210x x k ++->,144(1)4(2)0k k ∆=--=->(2)k <-Q , ∴方程2210x x k ++-=的解为12k --,∴由2210x x k ++->得12x k <--12x k >--由②得2230x x k +++<,方程2230x x k +++=的判别式244(3)4(2)0k k ∆=-+=-->(2)k <-Q ,∴该方程的解为12k ---,由2230x x k +++<得1212k x k ----<-+--2k <-Q ,121211212k k k k ∴--<-----<-----(,12)(12,12)(12,)D k k k k ∴=-∞--------+---+-+∞U U .(2)设222(2)2(2)30u x x k x x k +++++->, 则3'221()2(2)(22)2(22)2f x u x x k x x -⎡⎤=-⋅⋅++⋅+++⎣⎦ 3222(1)(21)u x x x k -=-+⋅+++, (ⅰ)当(,12)x k ∈-∞--时,10x +<,221110x x k +++>+>,'()0f x ∴>;(ⅱ)当(12,1)x k ∈-----时,10x +<,221310x x k +++<-+<,'()0f x ∴<; (ⅲ)当(1,12)x k ∈--+--时,10x +>,221310x x k +++<-+<,'()0f x ∴>; (ⅳ)当(12,)x k ∈-+-+∞时,10x +>,221110x x k +++>+>,'()0f x ∴<. 综上,()f x 在D 上的单调增区间为:(,12),(1,12)k k -∞-----+--,()f x 在D 上的单调减区间为:(12,1),(12,)k k -----+-+∞.(3)设222(x)(2)2(2)3g x x k x x k =+++++-,由(1)知,当x D ∈时,()0g x >; 又2(1)(3)2(3)3(6)(2)g k k k k =+++-=++,显然,当6k <-时,(1)0g >, 从而不等式()(1)()(1)f x f g x g >⇔<,2222()(1)[(2)2(2)3][(3k)2(3)3]g x g x x k x x k k -=+++++--+++-22222[(2)(3k)]2[(2)(3)](3)(1)(225)x x k x x k k x x x x k =++-++++-+=+-+++,6k <-, 1421212311212142k k k k k k ∴--------<-<<----+--+--(ⅰ)当12x k <--时,(3)(1)0x x +->,∴欲使()(1)f x f >,即()(1)g x g <,亦即22250x x k +++<,即142142k x k ---<<---14212k x k ∴---<---(ⅱ)123k x ---<-时,(3)(1)0x x +->,22225(2)(5)3(5)0x x k x x k k k +++=++++<-++<,此时()(1)g x g <,即()(1)f x f >;(ⅲ)31x -<<时,(3)(1)0x x +-<,22253(5)0x x k k +++<-++<()(1)g x g ∴>不合题意;(ⅳ)112x k <<-+--时,(3)(1)0x x +->,22253(5)0x x k k +++<-++<,()(1)g x g ∴<,不合题意;(ⅴ)12x k >--时,(3)(1)0x x +->,∴欲使()(1)g x g <,则22250x x k +++<,即142142k x k ---<<---,从而12142k x k --<-+--.综上所述,()(1)f x f >的解集为: (()()(142,1212,31,1212,142k k k k k k ----------+-----+--U U U .。
2014届江门市高考模拟考试一模理科数学

1A BCDE1A 1B 1C 1D 2图江门市2014年高考模拟考试数学(理科)本试卷共4页,21小题,满分150分,考试用时120分钟。
参考公式:锥体的体积公式Sh V 31=,其中S 是锥体的底面积,h 是锥体的高. 如果事件A 、B 互斥,那么)()()(B P A P B A P +=+.符合题目要求的.1.在复平面内,复数i z 21+-=( i 是虚数单位)对应的点在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限2.从2、3、5、7这四个质数中任取两个相乘,可以得到不相等的积的个数是( ) A .4 B .5 C .6 D .83.已知函数)(x f 为奇函数,且当0<x 时,x x x f 2)(2+=,则=)1(f ( ) A .1 B .1- C .3 D .3- 4.将甲、乙两个篮球队10场比赛的得分数据整理成如图1所示的茎叶图,由图1可知( )A .甲、乙两队得分的平均数相等B .甲、乙两队得分的中位数相等C .甲、乙两队得分的极差相等D .甲、乙两队得分在) 39 , 30 [分数段的频率相等5.在平面直角坐标系xOy 中,已知) , 1(t -=,)2 , 2(=,若090=∠ABO ,则=t ( ) A .2 B .4 C .5 D .86.已知两条不重合直线1 l 、2l 的斜率分别为1 k 、2k ,则“21//l l ”是“21k k =”成立的( ) A .充分非必要条件 B .必要非充分条件 C .非充分非必要条件 D .充要条件 7.如图2,在正方体1111D C B A ABCD -中,E 是棱1CC 的中点,F 是侧面11BCC B 上的动点,并且//1F A 平面1AED ,则动点F 的轨迹是( )A .圆B .椭圆C .抛物线D .线段8.设函数2sin )(-+=x x x f ,2ln )(-+=x e x g x ,若实数a ,b 满足0)(=a f ,0)(=b g ,则( )A .)(0)(b f ag << B .)(0)(a g b f << C .)()(0b f a g << D .0)()(<<a g b f2二、填空题:本大题共7小题,考生作答6小题,每小题5(一)必做题(9~13题)9.已知命题p :R x ∈∀,0222>++x x .则命题p 的否定p ⌝: . 10.执行如图3的程序框图,输出的=S . 11.定积分=⎰-11|| dx x .12.已知直线 l 过点)1 , 2(A 和) , 1(2m B (R m ∈),则直线 l 斜率的取值范围是 , 倾斜角的取值范围是 .13.某个部件由三个元件如图4方式连接而成,元件A或元件B 正常工作,且元件C 正常工作,则部件正 常工作.若3个元件的次品率均为31,且各个元件 相互独立,那么该部件的次品率为 . (二)选做题(14、15题,考生只能从中选做一题)三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)已知函数16sin(cos 4)(-+=πx x x f ,R x ∈.⑴求)0(f 的值;⑵若将)(x f y =的图象向右平移ϕ(0>ϕ)个单位,所得到的曲线恰好经过坐标原点,求ϕ的最小值.3BD随机询问某大学40名不同性别的大学生在购买食物时是否读营养说明,得到如下列联表: 性别与读营养说明列联表⑴营养说明之间有关系?⑵从被询问的16名不读营养说明的大学生中,随机抽取2名学生,求抽到男生人数ξ的分布列及其均值(即数学期望).(注:))()()(()(22d b c a d c b a bc ad n K ++++-=,其中d c b a n +++=为样本容量.)18.(本小题满分14分)如图6,四棱锥ABCD P -的底面ABCD 是平行四边形,⊥PA 底面ABCD ,3=PA ,2=AD ,4=AB ,060=∠ABC .⑴求证:PC AD ⊥;⑵E 是侧棱PB 上一点,记λ=,是否存在实数λ,使⊥PC 平面ADE ?若存在,求λ的值;若不存在,说明理由. 19.(本小题满分12分)已知数列{}n a 的首项11=a ,*∈∀N n ,nnn a a a +=+221. ⑴求数列{}n a 的通项公式; ⑵求证:*∈∀N n ,312<∑=ni i a .4已知椭圆Γ的焦点为)0 , 1(1-F 、)0 , 1(2F ,点)23, 1(M 在椭圆Γ上. ⑴求椭圆Γ的方程;⑵设双曲线∑:12222=-by a x (0>a ,0>b )的顶点A 、B 都是曲线Γ的顶点,经过双曲线∑的右焦点F 作x 轴的垂线,与∑在第一象限内相交于N ,若直线MN 经过坐标原点O ,求双曲线∑的离心率.21.(本小题满分14分)已知函数)ln ()(2x x a x x f ++=,0>x ,R a ∈是常数.试证明: ⑴R a ∈∀,)12)(1(-+=x a y 是函数)(x f y =的图象的一条切线; ⑵R a ∈∀,存在) , 1(e ∈ξ,使1)1()()(/--=e f e f f ξ.5评分参考一、选择题 BCAA CDDB二、填空题 ⒐ R x ∈∃0(3分),022020≤++x x (0x 写作x 亦可,但要统一,否则只计1处得分;≤写作<扣1分)⒑ 3 ⒒ 1 ⒓ ]1 , (-∞(3分),) , 2(]4 , 0[πππ (1分+1分)⒔2711 ⒕ 22⒖ 15 三、解答题⒗⑴11211416s i n 0co s 4)0(=-⨯⨯=-=πf ……4分(代入1分,三角函数值2分,结果1分) ⑵向右平移ϕ个单位,所得到的曲线为1)6sin()cos(4-+--=πϕϕx x y ……6分曲线经过坐标原点,得01)6sin()cos(4=-+--πϕϕ……7分 化简(和差化积或积化和差),得0)62sin(=-πϕ(或332tan =ϕ)……10分ππϕk =-62,Z k ∈……11分,122ππϕ+=k ,ϕ的最小正值为12πϕ=……12分.(若学生在第⑴问化简函数,则相应的分值仍然计入第⑵问)⒘⑴由表中数据,得635.667.620201624)481216(402>≈⨯⨯⨯⨯-⨯⨯=k ……4分 因此,能在犯错误的概率不超过0.01的前提下,认为性别与读营养说明有关……5分 ⑵ξ的取值为0,1,2……6分2011)0(216212===C C P ξ,52)1(21614112=⨯==C C C P ξ,201)2(21624===C C P ξ……12分 ξ的分布列为……13分ξ的均值为21201252120110=⨯+⨯+⨯=ξE ……14分. ⒙⑴连接AC ,则32cos 222=∠⨯⨯⨯-+=ABC BC AB BC AB AC ……1分(方法一)⊥PA 底面ABCD ,所以AB PA ⊥,AC PA ⊥……2分522=+=AB PA PB ,2122=+=AC PA PC ……3分222BC PC PB +=,所以090=∠PCB ,PC BC ⊥……4分因为BC AD //,所以PC AD ⊥……5分6(方法二)222AC AD CD +=,所以090=∠CAD ,AC AD ⊥……2分⊥PA 底面ABCD ,所以AD PA ⊥……3分因为A AC PA = ,所以⊥AD 平面PAC ……4分 因为⊂PC 平面PAC ,所以PC AD ⊥……5分⑵(方法一)过C 作AB CF ⊥于F ,则⊥CF 平面PAB ……6分 连接PF ,由⑴知⊥PC 平面ADE 当且仅当AE PC ⊥……7分 又AE CF ⊥,所以⊥AE 平面PCF ……8分,PF AE ⊥……9分 依题意,121==BC BF ,所以3=AF ,PA AF =……10分,AE 是PAF ∠的平分线, 从而也是PAB ∠的平分线……11分 在PAE ∆和ABE ∆中,PEA PA PAE PE ∠=∠sin sin ,BEAABBAE BE ∠=∠sin sin ……12分所以43==AB PA BE PE ……13分,73=PB PE ,即所求λ的值为73……14分. (方法二)在平面ABCD 内过点A 作CD AF ⊥,以A 为原点,AF 、AB 、AP 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系……6分则)0 , 0 , 0(A ,)0 , 4 , 0(B ,)3 , 0 , 0(P ……7分,)0 , 3 , 3(C ……8分 设) , , (c b a E ,由λ=得,)3 , 4 , 0()3 , , (-=-λc b a ……9分 解得0=a ,λ4=b ,λ33-=c ……10分由⑴知⊥PC 平面ADE 当且仅当AE PC ⊥……11分,即0=⋅……12分 所以0)33(343)33 , 4 , 0()3 , 3 , 3(=--⨯=-⋅-λλλλ……13分 解得73=λ……14分. (方法三)过E 作BC EF //,交PC 于F ,连接DF ,则平面ADE 即平面ADFE ……6分,由⑴知⊥PC 平面ADE 当且仅当DF PC ⊥……7分由⑴及余弦定理得 211392cos 222⨯=⨯⨯-+=∠PD PC CD PD PC CPD ……9分 所以219cos =∠⨯=CPD PD PF ……12分7321219=⨯=PCPF……13分,又BC EF //,所以73===PC PF PB PE λ……14分.7⒚⑴由nn n a a a +=+221,得21111+=+n n a a ……1分,21111=-+n n a a ……2分所以⎭⎬⎫⎩⎨⎧n a 1是首项11=n a ,公差21=d 的等差数列……3分 212111+=-+=n n a n ……4分,所以*∈∀N n ,12+=n a n ……5分 ⑵(方法一)nn n n n a n 24124)1(42222+<++=+=……6分,222+-=n n ……7分 4>n 时,由以上不等式得 )222()1212()5232()4222()3212(12+-++--++-+-+-<∑=n n n n a ni i……9分 22122212+-+-+=n n ……10分,3<……11分 因为⎭⎬⎫⎩⎨⎧∑=n i i a 12是递增数列,所以*∈∀N n ,312<∑=ni n a ……12分.(方法二))1(4)1(422+<+=n n n a n ……6分,244+-=n n ……7分 2>n 时,由以上不等式得 )144()4434()3424(112212+-++-+-+<+=∑∑==n n a a ni in i i ……9分 14241+-+=n ……10分,3<……11分因为⎭⎬⎫⎩⎨⎧∑=n i i a 12是递增数列,所以*∈∀N n ,312<∑=ni n a ……12分.⒛⑴椭圆Γ的焦距2||2211==F F c ……1分长轴423492||||22211=++=+=MF MF a ……4分 椭圆Γ的短轴3221=b ……5分,所以椭圆Γ的方程为13422=+y x ……6分 ⑵设双曲线∑焦距为c 2,依题意,1||2222=-b FN a c ……7分,a b FN 2||=……8分(方法一)) , (2ab c N ……9分,直线OM 的方程为x y 23=……10分O 、M 、N 共线,所以c a b 232=……11分,即2322=-ac a c ……12分,231=-e e ,02322=--e e ……13分,解得双曲线∑的离心率2=e (21-=e 舍去)……14分.(方法二)依题意,M OF 2∆~OFN ∆……9分,||||||||22OF FN OF M F =……10分 所以acb 223=……11分,即2322=-ac a c ……12分,231=-e e ,02322=--e e ……13分,8解得双曲线∑的离心率2=e (21-=e 舍去)……14分.21.⑴)11(2)(/xa x x f ++=……1分,直线)12)(1(-+=x a y 的斜率)1(2+=a k ……2分,由)1(2)11(2+=++a xa x ,取1=x ……3分22)1(/+=a f ,曲线)(x f y =在点))1( , 1(f 的切线为)1)(22()1(-+=-x a f y , 即)12)(1(-+=x a y ,所以)12)(1(-+=x a y 是曲线)(x f y =的一条切线……4分⑵直接计算知111)1()(-+++=--e aa e e f e f ……5分 设函数1)1(21)1()()()(/--++-=---=e ax a e x e f e f x f x g ……6分 1)1()2(11)1(2----=--+-=e e e a e a a e g ……7分 )1()1(11)(2---=--+-=e e ae e e a e a e e g ……8分 当2)1(->e e a 或2)1(2--<e e a 时,222)1(])1(][)1()2([)()1(-------=e e e e a e e a e g g 0<……10分,因为)(x g y =的图象是一条连续不断的曲线,所以存在) , 1(e ∈ξ,使0)(=ξg ,即) , 1(e ∈ξ,使1)1()()(/--=e f e f f ξ……11分;当22)1(2)1(-≤≤--e e a e e 时,)1(g 、0)(≥e g ,而且)1(g 、)(e g 之中至少一个为正……12分,由均值不等式知,1122)(2--+-≥e e a a x g ,等号当且仅当) , 1(2e ax ∈=时成立,所以)(x g 有最小值1)1(2)1(2112222----+-=--+-=e e a e a e e a a m , 且01)3)(1()]1(2[1)1(2)1(222<---+---=----+-=e e e e a e e a e a m ……13分,此时存在) , 1(e ∈ξ()2 , 1(a ∈ξ或) , 2(e a∈ξ),使0)(=ξg 。
2014年高考真题——数学理(全国Ⅰ卷)+Word版含答解析

2014年高招全国课标1(理科数学word 解析版)第Ⅰ卷一.选择题:共12小题,每小题5分,共60分。
在每个小题给出的四个选项中,只有一项是符合题目要求的一项。
1.已知集合A={x |2230x x --≥},B={}22x x -≤<,则A B ⋂=A .[-2,-1]B .[-1,2)C .[-1,1]D .[1,2)【答案】:A【解析】:∵A={x |2230x x --≥}={}13x x x ≤-≥或,B={}22x x -≤<,∴A B ⋂={}21x x -≤≤,选A..2.32(1)(1)i i +-= A .1i + B .1i - C .1i -+ D .1i --【答案】:D【解析】:∵32(1)(1)i i +-=2(1)12i i i i +=---,选D..3.设函数()f x ,()g x 的定义域都为R ,且()f x 是奇函数,()g x 是偶函数,则下列结论正确的是A .()f x ()g x 是偶函数B .|()f x |()g x 是奇函数C .()f x |()g x |是奇函数D .|()f x ()g x |是奇函数【答案】:C【解析】:设()()()F x f x g x =,则()()()F x f x g x -=--,∵()f x 是奇函数,()g x 是偶函数,∴()()()()F x f x g x F x -=-=-,()F x 为奇函数,选C.4.已知F 是双曲线C :223(0)x my m m -=>的一个焦点,则点F 到C 的一条渐近线的距离为A .B .3CD .3m【答案】:A【解析】:由C :223(0)x my m m -=>,得22133x y m -=,233,c m c =+=设)F,一条渐近线y x =,即0x =,则点F 到C 的一条渐近线的距离d = A. .5.4位同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率A .18B .38C .58D .78【答案】:D【解析】:4位同学各自在周六、周日两天中任选一天参加公益活动共有4216=种,周六、周日都有同学参加公益活动有两种情况:①一天一人一天三人有11428C A =种;②每天2人有246C =种,则周六、周日都有同学参加公益活动的概率为867168+=;或间接解法:4位同学都在周六或周日参加公益活动有2种,则周六、周日都有同学参加公益活动的概率为1627168-=;选D.6.如图,圆O 的半径为1,A 是圆上的定点,P 是圆上的动点,角x 的始边为射线OA ,终边为射线OP ,过点P 作直线OA 的垂线,垂足为M ,将点M 到直线OP 的距离表示为x 的函数()f x ,则y =()f x 在[0,π]上的图像大致为【答案】:B【解析】:如图:过M 作M D ⊥OP 于D,则 PM=sin x ,OM=cos x ,在Rt OMP ∆中,MD=cos sin 1x xOM PM OP =cos sin x x =1sin 22x =,∴()f x 1sin 2(0)2x x π=≤≤,选B. .7.执行下图的程序框图,若输入的,,a b k 分别为1,2,3,则输出的M =A .203 B .165 C .72 D .158【答案】:D【解析】:输入1,2,3a b k ===;1n =时:1331,2,222M a b =+===; 2n =时:28382,,3323M a b =+===;3n =时:3315815,,28838M a b =+===;4n =时:输出158M = . 选D.8.设(0,)2πα∈,(0,)2πβ∈,且1sin tan cos βαβ+=,则 A .32παβ-=B .22παβ-=C .32παβ+=D .22παβ+=【答案】:B【解析】:∵sin 1sin tan cos cos αβααβ+==,∴sin cos cos cos sin αβααβ=+ ()sin cos sin 2παβαα⎛⎫-==- ⎪⎝⎭,,02222ππππαβα-<-<<-<∴2παβα-=-,即22παβ-=,选B9.不等式组124x y x y +≥⎧⎨-≤⎩的解集记为D .有下面四个命题:1p :(,),22x y D x y ∀∈+≥-,2p :(,),22x y D x y ∃∈+≥, 3P :(,),23x y D x y ∀∈+≤,4p :(,),21x y D x y ∃∈+≤-.其中真命题是A .2p ,3PB .1p ,4pC .1p ,2pD .1p ,3P【答案】:C【解析】:作出可行域如图:设2x y z +=,即122zy x =-+,当直线过()2,1A -时,min 220z =-+=,∴0z ≥,∴命题1p 、2p 真命题,选C.10.已知抛物线C :28y x =的焦点为F ,准线为l ,P 是l 上一点,Q 是直线PF 与C 的一个交点,若4FP FQ =,则||QF =A .72 B .52C .3D .2 【答案】:C【解析】:过Q 作Q M ⊥直线L 于M ,∵4FP FQ = ∴34PQPF =,又344QM PQ PF ==,∴3QM =,由抛物线定义知3QF QM == 选C11.已知函数()f x =3231ax x -+,若()f x 存在唯一的零点0x ,且0x >0,则a 的取值范围为A .(2,+∞)B .(-∞,-2)C .(1,+∞)D .(-∞,-1)【答案】:B【解析1】:由已知0a ≠,2()36f x ax x '=-,令()0f x '=,得0x =或2x a=, 当0a >时,()22,0,()0;0,,()0;,,()0x f x x f x x f x a a ⎛⎫⎛⎫'''∈-∞>∈<∈+∞> ⎪ ⎪⎝⎭⎝⎭;且(0)10f =>,()f x 有小于零的零点,不符合题意。
江门一模数学试题及答案

江门一模数学试题及答案一、选择题1. 若函数f(x) = 2x^2 - 4x + 3的图象关于直线x = 1对称,则该函数的最小值为:A. 2B. 1C. 0D. -12. 已知数列{an}满足a1 = 1,an+1 = 2an + 1,求数列{an}的通项公式:A. an = 2^n - 1B. an = 2^n + 1C. an = 2^(n-1) - 1D. an = 2^(n-1) + 13. 若直线l的方程为y = kx + b,且直线l与圆x^2 + y^2 = 1相切,则k的取值范围为:A. -√3 ≤ k ≤ √3B. -1 ≤ k ≤ 1C. -√2 ≤ k ≤ √2D. -2 ≤ k ≤ 24. 已知函数f(x) = x^3 - 3x^2 + 2,求f'(x)的零点个数:A. 1B. 2C. 3D. 4二、填空题5. 计算定积分∫[0,1] (2x - x^2) dx的值为______。
6. 若复数z满足|z - 1| = 1,且|z| = √2,则z的值可以是______。
三、解答题7. 已知函数f(x) = x^2 - 4x + 5,求证f(x) ≥ 1。
证明:首先求导f'(x) = 2x - 4,令f'(x) = 0,解得x = 2。
当x < 2时,f'(x) < 0,说明f(x)在(-∞, 2)上单调递减;当x > 2时,f'(x) > 0,说明f(x)在(2, +∞)上单调递增。
因此,f(x)的最小值出现在x = 2处,即f(2) = 2^2 - 4*2 + 5 = 1。
所以,对于所有x∈R,都有f(x) ≥ 1。
8. 已知三角形ABC中,角A、B、C的对边分别为a、b、c,且a = 2,b = 3,A = π/3,求边c的长度。
解:由余弦定理得,a^2 = b^2 + c^2 - 2bc*cosA,代入已知条件得4 = 9 + c^2 - 3c,解得c = 1 或 c = 5。
2014年高考数学全国I卷(理)真含答案

绝密★启封并使用完毕前2014年普通高等学校招生全国统一考试理科数学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至2页,第Ⅱ卷3至4页。
全卷满分150分。
考试时间120分钟。
注意事项:1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至3页,第Ⅱ卷3至5页。
2. 答题前,考生务必将自己的姓名、准考证号填写在本试题相应的位置。
3. 全部答案在答题卡上完成,答在本试题上无效。
4. 考试结束,将本试题和答题卡一并交回。
第Ⅰ卷A 卷一.(1)已知集合A={}032|2≥--x x x ,B={}22|<≤-x x ,则=B A A []1,2-- B [)2,1- C []1,1- D [)2,1(2) 23)1()1(i i -+=A i +1B i -1C i +-1D i --1(3)设函数)(x f ,)(x g 的定义域都为R ,且)(x f 是奇函数,)(x g 是偶函数,则下列结论中正确的是 A )()(x g x f 是偶函数 B )(|)(|x g x f 是奇函数 C |)(|)(x g x f 是奇函数 D |)()(|x g x f 是奇函数(4)已知F 为双曲线C:)0(322>=-m m my x 的一个焦点,则点F 到C 的一条渐近线的距离为 A 3 B 3 C m 3 D m 3(5)4位同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率为 A81 B 83 C 85 D 87 (6)如图,圆O 的半径为1,A 是圆上的定点,P 是圆上的动点,角x 的始边为射线OA ,终边为射线OP ,过点P 作直线OA 的垂线,垂足为M ,将点M 到直线OP 的距离表示成x 的函数)(x f ,则)(x f y =在[]π,0的图像大致为A BC D (7)执行右图的程序框图,若输入的k b a ,,分别为1,2,3,则输出的M= A320 B 27 C 516 D 815(8)设)2,0(πα∈,)2,0(πβ∈,且ββαcos sin 1tan +=,则A 23πβα=- B 23πβα=+ C 22πβα=-D2α(9)不等式组⎩⎨⎧≤-≥+421y x y x 的解集记为D 22,),(:1-≥+∈∀y x D y x P22,),(:2≥+∈∃y x D y x P32,),(:3≤+∈∀y x D y x P 12,),(:4-≤+∈∃y x D y x P 其中的真命题是A 32p pB 21p pC 41p pD 31p p(10)已知抛物线C :x y 82=的焦点为F ,准线为l ,P 上一点,Q 是直线PF 与C 的一个交点。
2014届高三理科数学江门一模和广州一模考试总结
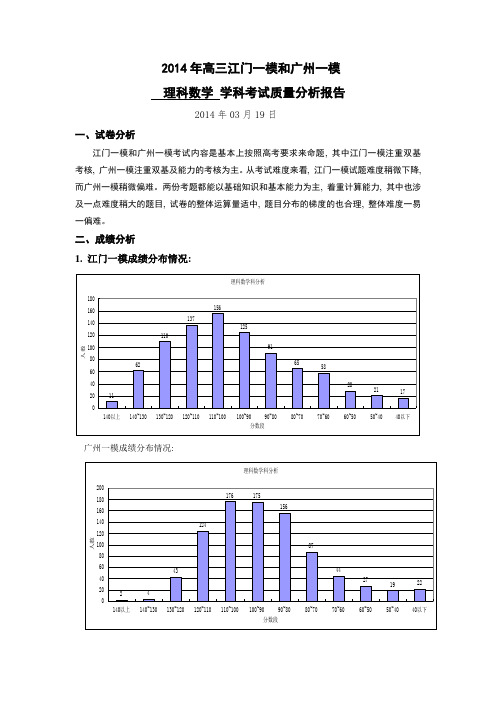
2014年高三江门一模和广州一模理科数学学科考试质量分析报告2014年03月19日一、试卷分析江门一模和广州一模考试内容是基本上按照高考要求来命题, 其中江门一模注重双基考核, 广州一模注重双基及能力的考核为主。
从考试难度来看, 江门一模试题难度稍微下降, 而广州一模稍微偏难。
两份考题都能以基础知识和基本能力为主, 着重计算能力, 其中也涉及一点难度稍大的题目, 试卷的整体运算量适中, 题目分布的梯度的也合理, 整体难度一易一偏难。
二、成绩分析1. 江门一模成绩分布情况:广州一模成绩分布情况:2. 各层次班分差分布合理:1)江门一模:尖子班分差: 2.56分;重点班分差: 3.4分;普通班分差: 4.02分;复读班分差: 5.32分2)广州一模:尖子班分差: 0.88分;重点班分差: 1.88分;普通班分差: 5.93分;复读班分差: 5.3分3. 各层次学生成绩情况:1)江门一模:平均分:98.45分, 最高分146分, 140分以上人数有11人, 120分以上人数有183人;60分以下人数有67人。
2)广州一模:平均分:91.86分, 最高分140分, 140分以上人数有2人, 107分以上人数有220人;60分以下人数有118人。
三、测试试题中得分较低的试题的统计与分析四、存在的主要问题及对策从两次模考成绩来看, 整体的成绩基本保持稳定。
特别是重点班的数学成绩稳中带升, 但是从广州一模成绩分布情况来看, 中下层生的数学成绩略有下降, 尖子层学生人数还有待提高。
对于存在问题, 我们在下一阶段在教学和课后安排上做如下调整:1)认真抓好课堂教学, 向课堂教学要质量。
争取在课堂中能集中解决学生必须解决的问题, 然后通过课后作业来巩固和提高。
2)加强集体备课, 在备课中集中讨论和挖掘学生集中出现的问题, 在课堂分析和课后通过练习的形式来巩固和提高。
3)利用坐班时间加强各班中、下层生的学法和心理辅导工作, 特别是各课任教师所负责的临界生的辅导工作。
【2014江门一模】广东省江门市2014届高考模拟考试数学文试题-Word版含答案

江门市2014年高考模拟考试数学(文科)本试卷共4页,21小题,满分150分,考试用时120分钟。
注意事项:1. 答题前,考生务必把自己的、考生号等填写在答题卡相应的位置上。
2. 做选择题时,必须用2B 铅笔把答题卷上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
3. 非选择题必须使用黑色字迹钢笔或签字笔,将答案写在答题卡规定的位置上。
4. 所有题目必须在答题卡上指定位置作答,不按以上要求作答的答案无效。
5. 考生必须保持答题卡的整洁。
考试结束后,将答题卡交回。
参考公式:锥体的体积公式Sh V 31=,其中S 是锥体的底面积,h 是锥体的高. 如果事件A 、B 互斥,那么)()()(B P A P B A P +=+.一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1. i 是虚数单位,=+-)21(i iA .2+iB .2-iC .i --2D .i -2 2.已知x x f -=1)(定义域为M ,x e x g =)(值域为N ,则=N M A .]1 , 0[ B .]1 , 0( C .) , 0(∞+ D .) , 1 [∞+ 3.已知函数)(x f 为奇函数,且当0>x 时,x x x f 2)(2+=,则=-)1(f A .1 B .1- C .3 D .3- 4.已知)2 , 1(-=a ,52||=b ,且//,则=A .)4 , 2(-B .)4 , 2(-C .)4 , 2(-或)4 , 2(-D .)8 , 4(- 5.将甲、乙两个篮球队10场比赛的得分数据整理成如右所示的茎叶图,由图可知 A .甲、乙两队得分的中位数相等 B .甲、乙两队得分的平均数相等 C .甲、乙两队得分的极差相等 D .甲、乙两队得分的方差相等6.若l ,m ,n 是互不相同的空间直线,α,β是不重合的平面,则下列命题中为真命题的是A .若βα//,α⊂l ,β⊂n ,则n l //B .若βα⊥,α⊂l ,则β⊥lC .若n l ⊥,n m ⊥,则m l //D .若α⊥l ,β//l ,则βα⊥图27.设a ,R b ∈,则“0)(2>-a b a ”是“b a >”的 A .充分非必要条件 B C .非充分非必要条件 D .充要条件 8.执行如图1所示的程序框图,输出的=S A .2013 B .2014 C .1 D .29.已知抛物线x y 82=的焦点F 也是双曲线12222=-by a x 的一个焦点,P 是抛物线与 双曲线的一个交点,若5||=PF ,则此 双曲线的离心率=e A .2 B .3 C .2 D .12+10.设a ,R b ∈,定义运算“⊗”和“⊕”如下:⎩⎨⎧>≤=⊗b a b b a a b a , , ,⎩⎨⎧>≤=⊕b a a ba b b a , , .若2≥⊗n m ,2≤⊕q p ,则 A .4≥mn 且4≤+q p B .4≥+n m 且4≤pq C .4≤mn 且4≥+q p D .4≤+n m 且4≤pq二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分. (一)必做题(11~13题)11.某厂对一批产品进行抽样检测,图2是抽检产品净重(单位:克)数据的频率 分布直方图,样本数据分组为[76,78)、[78,80)、…、[84,86]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1A BCDE1A 1B 1C 1D 2图江门市2014年高考模拟考试数学(理科)班级 姓名 座号 成绩一、选择题:本大题共8小题,每小题5分,满分40分.1.在复平面内,复数i z 21+-=( i 是虚数单位)对应的点在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限2.从2、3、5、7这四个质数中任取两个相乘,可以得到不相等的积的个数是( ) A .4 B .5 C .6 D .83.已知函数)(x f 为奇函数,且当0<x 时,x x x f 2)(2+=,则=)1(f ( ) A .1 B .1- C .3 D .3- 4.将甲、乙两个篮球队10场比赛的得分数据 整理成如图1所示的茎叶图,由图1可知( ) A .甲、乙两队得分的平均数相等 B .甲、乙两队得分的中位数相等 C .甲、乙两队得分的极差相等D .甲、乙两队得分在) 39 , 30 [分数段的频率相等5.在平面直角坐标系xOy 中,已知) , 1(t OA -=,)2 , 2(=OB ,若090=∠ABO 则=t ( )A .2B .4C .5D .8 6.已知两条不重合直线1 l 、2l 的斜率分别为1 k 、2k ,则 “21//l l ”是“21k k =”成的( )A .充分非必要条件B .必要非充分条件C .非充分非必要条件D .充要条件 7.如图2,在正方体1111D C B A ABCD -中,E 是 棱1CC 的中点,F 是侧面11BCC B 上的动点,并且//1F A 平面1AED ,则动点F 的轨迹是( )A .圆B .椭圆C .抛物线D .线段8.设函数2sin )(-+=x x x f ,2ln )(-+=x e x g x,若实数a ,b 满足0)(=a f ,0)(=b g ,则( )A .)(0)(b f a g <<B .)(0)(a g b f <<C .)()(0b f a g << D .0)()(<<a g b f2二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分. (一)必做题(9~13题)9.已知命题p :R x ∈∀,0222>++x x .则命题p 的否定p ⌝: . 10.执行如图3的程序框图,输出的=S . 11.定积分=⎰-11|| dx x .12.已知直线 l 过点)1 , 2(A 和) , 1(2m B (R m ∈),则直线 l 斜率的取值范围是 , 倾斜角的取值范围是 .13.某个部件由三个元件如图4方式连接而成,元件A或元件B 正常工作,且元件C 正常工作,则部件正已知函数16sin(cos 4)(-+=πx x x f ,R x ∈.⑴求)0(f 的值;⑵若将)(x f y =的图象向右平移ϕ(0>ϕ)个单位,所得到的曲线恰好经过坐标原点,求ϕ的最小值.3BD随机询问某大学40名不同性别的大学生在购买食物时是否读营养说明,得到如下列联表: 性别与读营养说明列联表0.01的前提下认为性别与是否读营养说明之间有关系?⑵从被询问的16名不读营养说明的大学生中,随机抽取2名学生,求抽到男生人数ξ的分布列及其均值(即数学期望).(注:)(22bc ad n K -=,其中d c b a n +++=为样本容量.)18.(本小题满分14分)如图6,四棱锥ABCD P -的底面ABCD 是平行四边形,⊥PA 底面ABCD ,3=PA ,2=AD ,4=AB ,060=∠ABC .⑴求证:PC AD ⊥;⑵E 是侧棱PB 上一点,记λ=,是否存在实数λ,使⊥PC 平面ADE ?若存在,求λ的值;若不存在,说明理由. 19.(本小题满分12分)已知数列{}n a 的首项11=a ,*∈∀N n nnn a a a +=+221. ⑴求数列{}n a 的通项公式;⑵求证:*∈∀N n ,312<∑=ni i a .4已知椭圆Γ的焦点为)0 , 1(1-F 、)0 , 1(2F ,点)23, 1(M 在椭圆Γ上. ⑴求椭圆Γ的方程;⑵设双曲线∑:12222=-by a x (0>a ,0>b )的顶点A 、B 都是曲线Γ的顶点,经过双曲线∑的右焦点F 作x 轴的垂线,与∑在第一象限内相交于N ,若直线MN 经过坐标原点O ,求双曲线∑的离心率.21.(本小题满分14分)已知函数)ln ()(2x x a x x f ++=,0>x ,R a ∈是常数.试证明: ⑴R a ∈∀,)12)(1(-+=x a y 是函数)(x f y =的图象的一条切线; ⑵R a ∈∀,存在) , 1(e ∈ξ,使1)1()()(/--=e f e f f ξ.5评分参考一、选择题 BCAA CDDB二、填空题 ⒐ R x ∈∃0(3分),022020≤++x x ⒑ 3 ⒒ 1 ⒓ ]1 , (-∞,[0 , ]( , )42πππ⋃ ⒔ 2711 ⒕ 22 ⒖ 15三、解答题⒗⑴11211416sin0cos 4)0(=-⨯⨯=-=πf ……4分 ⑵向右平移ϕ个单位,所得到的曲线为1)6sin()cos(4-+--=πϕϕx x y ……6分曲线经过坐标原点,得01)6sin()cos(4=-+--πϕϕ……7分 化简(和差化积或积化和差),得0)62sin(=-πϕ(或332tan =ϕ)……10分ππϕk =-62,Z k ∈……11分,122ππϕ+=k ,ϕ的最小正值为12πϕ=……12分.⒘⑴由表中数据,得635.667.620201624)481216(402>≈⨯⨯⨯⨯-⨯⨯=k ……4分 因此,能在犯错误的概率不超过0.01的前提下,认为性别与读营养说明有关……5分 ⑵ξ的取值为0,1,2……6分2011)0(216212===C C P ξ,52)1(21614112=⨯==C C C P ξ,201)2(21624===C C P ξ……12分 ξ的分布列为ξ的均值为220251200=⨯+⨯+⨯=ξE ……14分. ⒙⑴222AC AD CD +=,所以090=∠CAD ,AC AD ⊥……2分⊥PA 底面ABCD ,所以AD PA ⊥……3分因为A AC PA = ,所以⊥AD 平面PAC ……4分 因为⊂PC 平面PAC ,所以PC AD ⊥……5分⑵(方法一)过C 作AB CF ⊥于F ,则⊥CF 平面PAB ……6分6连接PF ,由⑴知⊥PC 平面ADE 当且仅当AE PC ⊥……7分 又AE CF ⊥,所以⊥AE 平面PCF ……8分,PF AE ⊥……9分 依题意,121==BC BF ,所以3=AF ,PA AF =……10分, AE 是PAF ∠的平分线,从而也是PAB ∠的平分线……11分在PAE ∆和ABE ∆中,PEA PA PAE PE ∠=∠sin sin ,BEAABBAE BE ∠=∠sin sin ……12分所以43==AB PA BE PE ……13分,73=PB PE ,即所求λ的值为73……14分. (方法二)在平面ABCD 内过点A 作CD AF ⊥,以A 为原点,AF 、AB 、AP 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系……6分则)0 , 0 , 0(A ,)0 , 4 , 0(B ,)3 , 0 , 0(P ……7分,)0 , 3 , 3(C ……8分 设) , , (c b a E ,由PB PE λ=得,)3 , 4 , 0()3 , , (-=-λc b a ……9分 解得0=a ,λ4=b ,λ33-=c ……10分由⑴知⊥PC 平面ADE 当且仅当AE PC ⊥……11分,即0=⋅……12分 所以0)33(343)33 , 4 , 0()3 , 3 , 3(=--⨯=-⋅-λλλλ……13分 ⒚⑴由nn n a a a +=+221,得21111+=+n n a a ……1分,21111=-+n n a a ……2分所以⎭⎬⎫⎩⎨⎧n a 1是首项11=n a ,公差21=d 的等差数列……3分212111+=-+=n n a n ……4分,所以*∈∀N n ,12+=n a n ……5分 ⑵(方法一)nn n n n a n 24124)1(42222+<++=+=222+-=n n ……7分 4>n 时,由以上不等式得212222222222()()()()()132435112nii a n n n n =<-+-+-++-+--++∑K 22122212+-+-+=n n 3<……11分7因为⎭⎬⎫⎩⎨⎧∑=n i i a 12是递增数列,所以*∈∀N n ,312<∑=ni n a ……12分.(方法二))1(4)1(422+<+=n n n a n ……6分,244+-=n n ……7分 2>n 时,由以上不等式得)144()4434()3424(112212+-++-+-+<+=∑∑==n n a a ni in i i ……9分 14241+-+=n ……10分,3<……11分 因为⎭⎬⎫⎩⎨⎧∑=n i i a 12是递增数列,所以*∈∀N n ,312<∑=ni n a ……12分.⒛ ⑴椭圆Γ的焦距2||2211==F F c ……1分长轴423492||||22211=++=+=MF MF a ……4分 椭圆Γ的短轴3221=b ……5分,所以椭圆Γ的方程为13422=+y x ……6分 ⑵设双曲线∑焦距为c 2,依题意,1||2222=-b FN a c ……7分,a b FN 2||=……8分(方法一)) , (2ab c N ……9分,直线OM 的方程为x y 23=……10分O 、M 、N 共线,所以c a b 232=……11分,即2322=-ac a c ……12分,231=-e e ,02322=--e e ……13分,解得双曲线∑的离心率2=e (21-=e 舍去)……14分. (方法二)依题意,M OF 2∆~OFN ∆……9分,||||||||22OF FN OF M F =……10分 所以acb 223=……11分,即2322=-ac a c ……12分,231=-e e ,02322=--e e , 解得双曲线∑的离心率2=e (21-=e 舍去)……14分821.⑴)11(2)(/xa x x f ++=……1分,直线)12)(1(-+=x a y 的斜率)1(2+=a k , 由)1(2)11(2+=++a xa x ,取1=x 22)1(/+=a f ,曲线)(x f y =在点))1( , 1(f 的切线为)1)(22()1(-+=-x a f y ,即)12)(1(-+=x a y ,所以)12)(1(-+=x a y 是曲线)(x f y =的一条切线⑵直接计算知111)1()(-+++=--e aa e e f e f ……5分 设函数1)1(21)1()()()(/--++-=---=e ax a e x e f e f x f x g ……6分1)1()2(11)1(2----=--+-=e e e a e a a e g ……7分 )1()1(11)(2---=--+-=e e ae e e a e a e e g 当2)1(->e e a 或2)1(2--<e e a 时,222)1(])1(][)1()2([)()1(-------=e e e e a e e a e g g 0<,因为)(x g y =的图象是一条连续不断的曲线,所以存在) , 1(e ∈ξ,使0)(=ξg ,即) , 1(e ∈ξ,使1)1()()(/--=e f e f f ξ;当22)1(2)1(-≤≤--e e a e e 时,)1(g 、0)(≥e g ,而且)1(g 、)(e g 之中至少一个为正,由均值不等式知,1122)(2--+-≥e e a a x g ,等号当且仅当) , 1(2e ax ∈=时成立,所以)(x g 有最小值1)1(2)1(2112222----+-=--+-=e e a e a e e a a m ,且01)3)(1()]1(2[1)1(2)1(222<---+---=----+-=e e e e a e e a e a m ,此时存在) , 1(e ∈ξ()2, 1(a ∈ξ或) , 2(e a∈ξ),使0)(=ξg 。
