2018年长郡理科实验班数学招生试题(1)及答案
湖南省长沙市长郡中学2018-2019学年高一下学期入学考试数学试题(带答案解析)

13.《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验方式为:弧田面积= ,弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”指半径长与圆心到弦的距离之差.现有圆心角为 ,半径等于4米的弧田.下列说法不正确的是( )
A.“弦” 米,“矢” 米
(2)当 时,函数 的最大值与最小值的和为 ,求实数 的值.
24.已知函数f(x)=log4(4x+1)+kx(k∈R)是偶函数.
(1)求k的值;
(2)设g(x)=log4 ,若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
25.设函数 是定义域为 的奇函数.
(1)若 ,求使不等式 对一切 恒成立的实数 的取值范围;
B.按照经验公式计算所得弧田面积( )平方米
C.按照弓形的面积计算实际面积为( )平方米
D.按照经验公式计算所得弧田面积比实际面积少算了大约0.9平方米(参考数据 )
14.已知函数 设 表示 中的较大值, 表示 中的较小值,记 得最小值为种新运算: ,已知函数 ,若函数
恰有两个零点,则 的取值范围为()
A. B. C. D.
第II卷(非选择题)
评卷人
得分
二、填空题
16.已知函数 的图象如图所示,则 _____.
17.若 的图象过点 ,则 ______.
18. _____.
19.已知函数 的定义域是 ,且满足 , ,如果对于 ,都有 ,则不等式 的解集为_____.
12.B
【解析】
【分析】
由分段函数的解析式作出 的图象,由题意得出 为奇函数,根据函数关于原点对称作出 的图象,由数形结合得出答案.
长郡中学理科实验班招生考试—数学试题

长郡中学 理科实验班招生考试数学试卷满分:100 时量:70min一、选择题(本题有8小题,每小题4分,共32分)1.函数y =1x -图象的大致形状是 ( )A B C D2.小明随机地在如图所示的正三角形及其内部区域投针,则针扎到其内切圆(阴影)区域的概率为( )A 、21B 、π63C 、π93 D 、π33 3.满足不等式3002005<n 的最大整数n 等于 ( )(A )8 (B )9 (C )10 (D )114.甲、乙两车分别从A ,B 两车站同时开出相向而行,相遇后甲驶1小时到达B 站,乙再驶4小时到达A 站. 那么,甲车速是乙车速的 ( )(A )4倍 (B )3倍 (C )2倍 (D )1.5倍5.图中的矩形被分成四部分,其中三部分面积分别为2,3,4,那么,阴影三角形的面积为 ( )(A )5 (B )6 (C )7 (D )86.如图,AB ,CD 分别是⊙O 的直径和弦,AD ,BC 相交于点E ,∠AEC=α,则△CDE 与△ABE的面积比为 ( )(A )cos α (B )sin α (C )cos 2α (D )sin 2α7.两杯等量的液体,一杯是咖啡,一杯是奶油. 舀一勺奶油到咖啡杯里,搅匀后舀一勺混合液注入到奶油杯里. 这时,设咖啡杯里的奶油量为a ,奶油杯里的咖啡量为b ,那么a 和 b 的大小为 ( )(A )b a > (B )b a < (C )b a = (D )与勺子大小有关8.设A ,B ,C 是三角形的三个内角,满足B C B A 23,53<>,这个三角形是 ( )(A )锐角三角形 (B )钝角三角形 (C )直角三角形 (D )都有可能二、填空题(本题有6小题,每小题5分,共30分)9. 用数字1,2,3,4,5,6,7,8不重复地填写在下面连等式的方框中,使这个连等式成立:1+□+□=9+□+□=8+□+□=6+□+□10.如图,正三角形与正六边形的边长分别为2和1,正六边形的顶点O 是正三角形的中心,则四边形OABC 的面积等于 ______ .y x O y x O y x O yx O11.计算:622633++++= ________ .12.五支篮球队举行单循坏赛(就是每两队必须比赛1场,并且只比赛一场),当赛程进行到某天时,A 队已赛了4场,B 队已赛了3场,C 队已赛了2场,D 队已赛了1场,那么到这天为止一共已经赛了 __ 场,E 队比赛了 ___ 场.13.已知∠AOB=30°,C 是射线OB 上的一点,且OC=4,若以C 为圆心,半径为r 的圆与射线OA 有两个不同的交点,则r 的取值范围是_____________14.如图,△ABC 为等腰直角三角形,若 AD=31AC ,CE=31BC ,则∠1 __ ∠2 (填“>”、“<”或“=”)(第14题)。
湖南省长沙市长郡中学2017-2018学年高三上学期入学考试理数试题 Word版含解析

2017-2018学年普通高等学校招生全国统一考试(长郡中学高三入学考试)理科数学 第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合{|A x y ==,{|1}B x a x a =≤≤+,若A B A = ,则实数a 的取值范围为( )A .(,3][2,)-∞-+∞B .[1,2]-C .[2,1]-D .[2,)+∞ 【答案】C 【解析】试题分析:{}{||22A x y x x ===-≤≤,又因为A B A = 即B A ⊆,所以122a a +≤⎧⎨≥-⎩,解之得21a -≤≤,故选C. 考点:1.集合的表示;2.集合的运算.2. 设复数2()1a i z i+=+,其中a 为实数,若z 的实部为2,则z 的虚部为( ) A .12- B .12i - C .32- D . 32i -【答案】C考点:1.复数数的概念;2.复数的运算.3. “0a <”是“函数()|(1)|f x x ax =+在区间(,0)-∞内单调递减”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要 【答案】A 【解析】试题分析:当0a <时,在区间(,0)-∞上,1()|(1)|()f x x ax ax x a=+=--单调递减,但()|(1)|f x x ax =+区间(,0)-∞上单调递减时,0a ≤,所以“0a <”是“函数()|(1)|f x x ax =+在区间(,0)-∞内单调递减”的,故选A.考点:1.函数的单调性;2.充分条件与必要条件.4. 设函数()(21)x f x e x ax a =--+,其中1a <,若存在唯一的整数0x ,使得0()0f x <,则a 的取值范围为( ) A .3[,1)2e -B .33[,)24e -C .33[,)24eD .3[,1)2e【答案】D考点:函数与不等式.【名师点睛】本题考查函数与不等式,中档题;函数与不等式是高考考查的重要内容,数形结合是解决函数与不等式的重要途径,通常可把所有的数学表达式移到不等式的一边,构造一个函数作图解决不等式问题,也可象本题这样把变量放在不等式的两边,构造两个函数,在同一坐标系内作出两个函数的图象,通过图象求解. 5. 将函数sin()cos()22y x x ϕϕ=++的图象沿x 轴向右平移8π个单位后,得到一个偶函数的图象,则ϕ的取值不可能是( ) A .54π-B .4π-C .4π D .34π【答案】C考点:1.三角函数的图象与性质;2.函数图象平移变换.6. 已知点(1,0)M ,,A B 是椭圆2214x y +=上的动点,且0MA MB ∙= ,则MA BA ∙ 的取值范围是( )A .2[,1]3B .[1,9]C .2[,9]3D . 【答案】C 【解析】试题分析:设1122(,),(,)A x y B x y ,则11221212(1,),(1,),(,)MA x y MB x y BA x x y y =-=-=--,由题意有1212(1)(1)0MA MB x x y y ∙=--+=,所以21121121112112(1)()()(1)(1)MA BA x x x y y y x x x x y y y ∙=--+-=---+-[]22221111212111111(1)(1)(1)114x x y x x y y x x x x x =-+---++-=-+--+ 221111334222(),[2,2]4433x x x x =-+=-+∈- 所以,当2x =-时,MA BA ∙ 有最大值9,当43x =时,MA BA ∙ 有最小值23,故选C.考点:1.椭圆的标准方程与几何性质;2.向量的运算. 7. 如图所示程序框图中,输出S =( ) A .45 B .-55 C .-66 D .66【答案】B【解析】试题分析:该程序框图所表示的算法功能为:222222222212345678910(12345678910)55 S=-+-+-+-+-=-+++++++++=-,故选B.考点:程序框图.8. 如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数1(0)y xx=>图象下方的区域(阴影部分),从D内随机取一个点M,则点M取自E内的概率为()A.ln22B.1ln22-C.1ln22+D.2ln22-【答案】C 【解析】试题分析:如下图所示,四边形OABC 的面积122S =⨯=,阴影部分的面积可分为两部分,一部分是四边形OEDC 的面积11212S =⨯=,另一部分是曲边梯形的面积11121221ln ln 2S dx x x ===⎰,所以点M 来自E 内的概率为121ln 22S S P S ++==,故选C.考点:1.几何概型;2.积分的几何意义.【名师点睛】本题考查几何概型、积分的几何意义,属中档题.概率问题是高考的必考见容,概率问题通常分为古典概型与几何概型两种,几何概型求概率是通过线段的长度比或区域的面积比、几何体的体积比求解的,本题是用的区域的面积比,但求面积是通过积分运算来完成的,把积分运算与几何概型有机的结合在一起是本本题的亮点.9. 在棱长为3的正方体1111ABCD A BC D -中,P 在线段1BD 上,且112BP PD =,M 为线段11B C 上的动点,则三棱锥M PBC -的体积为( )A .1B .32C .92D .与M 点的位置有关 【答案】B 【解析】考点:1.正方体的性质;2.多面体的体积.10. 已知点A 是抛物线2:2(0)C x py p =>上一点,O 为坐标原点,若,A B 是以点(0,10)M 为圆心,||OA 的长为半径的圆与抛物线C 的两个公共点,且ABO ∆为等边三角形,则P 的值是( ) A .52 B .53 C .56 D .59【答案】C 【解析】试题分析:由抛物线的性质及题意可知,,A B 两点关于y 轴对称,所以可设1111(,),(,)A x y B x y -,则2222211111(10)4x y x y x +=+-=,解之得2112535x y ⎧=⎪⎨⎪=⎩,又因为点A 在抛物线上,所以25253p =⨯,解得56p =,故选C. 考点:抛物线的标准方程与几何性质.11. 设,x y 满足约束条件1210,0y x y x x y ≤+⎧⎪≥-⎨⎪≥≥⎩,则目标函数(0,0)z abx y a b =+>>的最大值为11,则a b +的最小值为( )A .2B .4C .6D .8 【答案】B 【解析】试题分析:在直角坐标系中作出可行域,如下图所示,因为0,0a b >>,所以目标函数z abx y =+取得最大值时的最优解为(2,3)B ,所以1123ab =⨯+,即4ab =,所以4a b +≥=,当且仅当2a b ==时取等号,故选B.考点:1.线性规划;2.基本不等式.12.设函数61(),0()0x x x f x x ⎧-<⎪=⎨⎪≥⎩,则当0x >时,[()]f f x 表达式的展开式中常数项为( )A .-20B .20C .-15D .15 【答案】A考点:1.分段函数的表示;2.二项式定理.【名师点睛】本题考查分段函数的表示与二项式定理,属中档题;分段函数的表示与二项式定理是最近高考的常考内容,但两者很少在同一个题目中出现,本题在考查分段函数的同时,考查二项式定理的应用,可谓立意新颖、思维独特.第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 若423401234(12)x a a x a x a x a x -=++++,则013||||||a a a ++等于 . 【答案】41 【解析】试题分析: 4234(12)18243216x x x x x -=-+-+,所以0131,8,32a a a ==-=-,013||||||41a a a ++=.考点:二项式定理.14.给定双曲线22:1C x -=,若直线l 过C 的中心,且与C 交于,M N 两点,P 为曲线C 上任意一点,若直线,PM PN 的斜率均存在且分别记为,PM PN k k ,则PM PN k k ∙= .【解析】试题分析:设直线l 的方程为y k x =,1122(,),(,)M x y N x y ,00(,)P x y ,则01020102,,PM PNy y y y k k x x x x --==--由221x y kx⎧-=⎪⎨⎪=⎩得,222)1)0k x -=,所以有12120,x x x x +==, 2220102001212001212220102001212001212()()()()PM PNy y y y y y y y y y y ky x x k x x k k x x x x x x x x x x x x x x x x ---++-++⋅=⨯==---++-++2012x +===. 考点:1.双曲线的标准方程与几何性质;2.直线与双曲线的位置关系;3.斜率公式.15. 已知点(,)P x y的坐标满足0200y x y -<+<⎨⎪≥⎪⎩的取值范围为 .【答案】[ 【解析】0y +=,如下图所示,过点P 作PF ⊥直0y +=于点F ,表示可行域内的点(,)P x y0y +=的距离PF表示可行域内的点P到原点O的距离PO,所以sinPFPOFPO==∠,当点Py+=上时,222sin0POF===∠=,当点Py+=r222sin POF===∠的取值范围为,当点Py+=r在左下方时,222sin POF==-=-∠的取值范围为[的取值范围为[.考点:1.线性规划;2.点到直线距离、两点间的距离;3.直角三角形中正弦函数定义.【名师点睛】本题考查线性规划、两点间的距离公式、点到直线距离公式、直角三角形中正弦函数定义,属难题;对线性规划问题,先作出可行域,在作出目标函数,利用z的几何意义,结合可行域即可找出取最值的点,通过解方程组即可求出做最优解,代入目标函数,求出最值,要熟悉相关公式,确定目标函数的意义是解决最优化问题的关键,目标函数常有距离型、直线型和斜率型.本题利用两个距离的比构成了一个角的三角函数值,再数形结合求解,可谓是匠心独运,视角独特.16. 在数列{}na中,11a=,122133232(2)n n nn na a n----=-∙+≥,nS是数列1{}nan+的前n 项和,当不等式*1(31)()1()3()m n mn S m m N S m ++-<∈-恒成立时,mn 的所有可能取值为 . 【答案】1或2或4 【解析】试题分析:由122133232(2)n n n n n a a n ----=-∙+≥得1212213(1)3(1)33232(2)n n n n n n n a a n ------+=++--∙+≥,即1213(1)3(1)2(2)n n n n a a n ---+=++≥,所以数列{}13(1)n n a -+是以1113(1)2a -+=为首项、2为公比的等比数列,所以13(1)2n n a n -+=,由1123n n a n -+=,12(1)133(1)1313nn nS ⨯-==--,所以1111(31)[3(1)](31)()(3)33(3)33(3)323331113()(3)33(3)333[3(1)]3m mm n m n n m n n m m n m m n mmn n m S m m m m S m m m m +++++++--+---+----⋅-===+<-------即(3)32330(3)33n m m n mm m +--⋅-<--,当3m =时,该不等式不成立,当3m ≠时有233330133m nn m m⋅+--<--恒成立,当1m =时,19322n<<,1n =,这时1mn =,当2m =时,1321n <<,1,2n =,这时2mn =或4mn =,当4m ≥时,233330133m nn m m⋅+--<--不成立,所以mn 的所有可能取值为1或2或4. 考点:1.数列的递推公式;2.等差数列的定义与求和公式;3.不等式恒成立问题. 【名师点睛】本题考查数列的递推公式、等差数列的定义与求和公式、不等式恒成立问题,属难题;数列的递推公式一直是高考的重点内容,本题给出的递推公式非常复杂,很难看出其关系,但所要求的数列的和给出了我们解题思路,即在解题中强行构造数列{}13(1)n n a -+是解题的关键,然后根据不等式恒成立分类讨论求解,体现的应用所学数学知识去解决问题的能力.三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. (本小题满分12分)已知函数2()2sin (0)2xf x x ωωω=->的最小正周期为3π.(1)求函数()f x 在区间3[,]4ππ-上的最大值和最小值;(2)已知,,a b c 分别为锐角三角形ABC 中角,,A B C 的对边,且满足2,()1b f A ==,2sin b A =,求ABC ∆的面积.【答案】(1)min ()1f x =,max ()1f x =;. 【解析】试题分析:(1)利用三角恒等变换相关公式化简函数解析式得()2sin()16f x x πω=+-,由周期为3π,可求ω的值,由三角函数性质可求函数的最值.(2)2sin b A =及正弦定理可求得sin 2B =,从而是求出解B 的值,由()1f A =可求出角4A π=及角51246C πππ==+,由正弦定理求出边a ,即可求三角形面积. 考点:1.三角恒等变换;2.三角函数的图象与性质;3.正弦定理与余弦定理.【名师点睛】本题考查三角恒等变换、三角函数的图象与性质、正弦定理与余弦定理,属中档题;此类题目是解三角形问题中的典型题目,可谓相当经典.解答本题,关键在于能利用三角公式化简函数解析式从而达到求最值的目的,三角形中的求角问题,往往要利用余弦定理用边表示角的函数.本题覆盖面较广,能较好的考查考生的基本运算求解能力及复杂式子的变形能力等.18. (本小题满分12分)某城市城镇化改革过程中最近五年居民生活用水量逐年上升,下表是2011年至2015年的统计数据:(1)利用所给数据求年居民生活用水量与年份之间的回归方程y bx a =+;(2)根据改革方案,预计在2020年底城镇改革结束,到时候居民的生活用水量将趋于稳定,预测该城市2023年的居民生活用水量.参考公式:^1221()ni ii nii x y nx yb xn x ==-=-∑∑,^^^a yb x =-.【答案】(1) 13(2013)260.2y x =-+ ;(2)351.2万吨. 【解析】试题分析:(1)由公式先求出,x y ,再利用公式求出 ,ba 即可求回归方程;(2)将2020x =代入所求回归方程求出y 的值即可. 试题解析:(1)解法一:容易算得:2013,260.2x y ==,121()()13()niii nii x x y y b x x ==--==-∑∑,260.2132013a y bx =-=-⨯,故所求的回归直线方程为13260.213201313(2013)260.2y x x =+-⨯=-+解法二:由所给数据可以看出,年需求量与年份之间的是近似值直线上升,为此时数据预处理如下表:对预处理后的数据,容易算得:110n i i x x n ===∑,11 3.2ni i y y n ===∑,12211301310()ni ii nii x y nx yb xn x ==-===-∑∑, 3.2a y bx =-= 所求的回归直线方程为257(2013)13(2013) 3.2y b x a x -=-+=-+, 即13(2013)260.2y x =-+.(2)根据题意,该城市2023年的居民生活用水量与该城市2020年的居民生活用水量相当, 当2020x =时,满足(1)中所求的回归直线方程,此时13(2013)260.2351.2y x =-+=(万吨)考点:线性回归方程及其应用. 19. (本小题满分12分)如图,在等腰梯形ABCD 中,//AB CD ,1AD DC CB ===,60ABC ∠= ,四边形ACFE为矩形,平面ACFE ⊥平面ABCD ,1CF =. (1)求证:BC ⊥平面ACFE ;(2)点M 在线段EF 上运动,设平面MAB 与平面FCB 二面角的平面角为(90)θθ≤ ,试求cos θ的取值范围.【答案】(1)由余弦定理求出2AC ,由勾股定理的逆定理证明BC AC ⊥即可;(2)分别以直线,,CA CB CF 为x 轴,y 轴,z 轴建立所示空间直角坐标系,令(0FM λλ=≤≤,求出平面MAB 与平面FCB 的法向量(用λ表示)即可求cos θ的范围. 【解析】 试题分析:试题解析:(1)证明:在梯形ABCD 中,∵//AB CD ,1AD DC CB ===,60ABC ∠=,∴2AB =,∴2222cos603AC AB BC AB BC =+-∙∙=,∴222AB AC BC =+,∴BC AC ⊥,∴平面ACFE ⊥平面ABCD ,平面ACFE 平面ABCD AC =,BC ⊂平面ABCD , ∴BC ⊥平面ACFE .(2)由(1)分别以直线,,CA CB CF 为x 轴,y 轴,z 轴发建立如图所示空间直角坐标系,令(0FM λλ=≤≤,则(0,0,0),(0,1,0),(,0,1)C A B M λ,∴(,0),(,1,1)AB BM λ==-.设1(,,)n x y z =为平面MAB 的一个法向量,由1100n AB n BM ⎧∙=⎪⎨∙=⎪⎩,得00y x y z λ⎧+=⎪⎨-+=⎪⎩, 取1x =,则1(1)n λ=,∵2(1,0,0)n =是平面FCB 的一个法向量,∴1212||cos ||||n n n n θ∙=== .∵0λ≤≤0λ=时,cos θ,当λ=cos θ有最大值12,∴1cos ]2θ∈. 考点:1.空间直线与直线垂直的判定;2.空间向量的应用. 20. (本小题满分12分)已知椭圆:C 22221(0)x y a b a b+=>>的两个焦点分别为1(F,2F ,以椭圆短轴为直径的圆经过点(1,0)M . (1)求椭圆C 的方程;(2)过点M 的直线l 与椭圆C 相交于,A B 两点,设直线,AN BN 的斜率分别为12,k k ,问12k k +是否为定值?并证明你的结论.【答案】(1) 2213x y += ;(2) 12k k +为定值2.试题解析:(1)由已知得:222c a b -=,由已知易得||1b OM ==,解得a =椭圆C 的方程为2213x y +=. (2)①当直线l 的斜率不存在时,由22113x x y =⎧⎪⎨+=⎪⎩,解得1,x y ==,设(1,A B,122233222k k +=+=. ②当直线l 的斜率存在时,设直线l 的方程为(1)y k x =-,将(1)y k x =-代入2213x y +=整理化简,得2222(31)6330k x k x k +-+-=,依题意,直线l 与椭圆C 必相交于两点,设1122(,),(,)A x y B x y ,则2122631k x x k +=+,21223331k x x k -=+,又11(1)y k x =-,22(1)y k x =-, 所以12122112121222(2)(3)(2)(3)33(3)(3)y y y x y x k k x x x x ----+--+=+=---- 12211212[2(1)](3)[2(1)](3)93()k x x k x x x x x x ---+---=-++1212121212122()[24()6]93()x x k x x x x x x x x -++-++=-++2212222222336122()[246]3131633933131k k x x k k k k k k k --++⨯-⨯+++=--⨯+++ 2212(21)26(21)k k +==+ 综上得:12k k +为定值2.(说明:若假设直线l 为1x my =+,按相应步骤给分) 考点:1.椭圆的标准方程与几何性质;2.直线与椭圆的位置关系.【名师点睛】本题考查椭圆的标准方程与几何性质、直线与椭圆的位置关系,属难题;高考解析几何解答题大多考查直线与圆锥曲线的位置关系,直线与圆锥曲线的位置关系是一个很宽泛的考试内容,主要由求值、求方程、求定值、最值、求参数取值范围等几部分组成, .其中考查较多的圆锥曲线是椭圆与抛物线,解决这类问题要重视方程思想、函数思想及化归思想的应用.21. (本小题满分12分)设1()1xxa f x a +=-(0a >且1a ≠),()g x 是()f x 的反函数.(1)设关于x 的方程2log ()(1)(7)atg x x x =--在区间[2,6]上有实数解,求t 的取值范围;(2)当a e =(e为自然对数的底数)时,证明:22()nk g k =>∑(3)当102a <≤时,试比较1|()|nk f k n =-∑与4的大小,并说明理由.【答案】(1) [5,32] ;(2)见解析;(3) 1|()|4nk f k n =-<∑.【解析】试题分析:(1) 由反函数的定义先求出()g x 的解析式,代入已知条件可得2(1)(7)t x x =--,[2,6]x ∈,求导,研究函数2(1)(7)t x x =--的单调性,即可求t 的取值范围;(2)21231(1)()ln ln ln ln ln 34512nk n n n g k n =-+=++++=-+∑ ,构造函数2211()ln 2ln ,0z u z z z z z z z-=--=-+->,求导研究其单调性可得()u z 在(0,)+∞上是增函数,从而(1)0u u >=,即(1)12ln 0(1)n n n n +->+,可证结论成立;(3)当1n =时易得2|(1)1|24f p-=≤<,当2n ≥时,由122(1)122()11(1)1(1)1k k k k kk k k p f k p p C p C p C p ++==+=++-+-+++ 可得1224441()111(1)1k k f k C C k k k k <≤+===+-+++,求和可得1()(1)14nk n f k f n n =<<++≤+∑,即可得到1|()|4nk f k n =-<∑.试题解析:(1)由题意,得101xy a y -=>+, 故1()log 1a x g x x -=+,(,1)(1,)x ∈-∞-+∞ , 由21log log (1)(7)1aa t x x x x -=--+,得2(1)(7)t x x =--,[2,6]x ∈. 则'2318153(1)(5)t x x x x =-+-=---,令'0t >,得25x ≤<,知2(1)(7)t x x =--在区间[2,5)上递增; 令'0t <,得56x <≤,知2(1)(7)t x x =--在区间(5,6]上递减,所以当5t =时,32t =最大值,有当2x =时,5t =;6x =时,25t =,所以5t =最小值, 所以t 的取值范围为[5,32].(2)212311231(1)()ln ln ln ln ln()ln 345134512nk n n n n g k n n =--+=++++=⨯⨯⨯⨯=-++∑ 令2211()ln 2ln ,0z u z z z z z z z-=--=-+->则'22211()1(1)0u z z z z=-++=-≥,所以()u z 在(0,)+∞上是增函数, 又因为当2n ≥10>>,所以(1)0u u >=即(1)12ln0(1)n n n n +->+,即22()nk g k =>∑(3)设11a p=+,则1p ≥,121(1)131a f a p +<==+≤-当1n =时,2|(1)1|24f p-=≤<, 当2n ≥时,设*2,k k N ≥∈时,则122(1)122()11(1)1(1)1k k k k kk k k p f k p p C p C p C p ++==+=++-+-+++ , 所以1224441()111(1)1k k f k C C k k k k <≤+===+-+++ 从而24441()111211nk n f k n n n n n =-<≤-+-=+-<+++∑ 所以1()(1)14nk n f k f n n =<<++≤+∑,综上所述,总有1|()|4nk f k n =-<∑.考点:1.反函数的定义与求法;2.导数与函数的单调性;3.函数与不等式. 请考生在22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分. 22. (本小题满分10分)选修4-1:几何证明选讲已知AD 是ABC ∆的外角EAC ∠的平分线,交BC 的延长线于点D ,延长DA 交ABC ∆的外接圆于点F ,连接,FB FC . (1)求证:FB FC =;(2)若AB 是ABC ∆外接圆的直径,120EAC ∠=,BC =AD 的长.【答案】(1)见解析;(2)6.试题解析:(1)证明:∵AD 平分EAC ∠,∴EAD DAC ∠=∠,因为四边形AFBC 内接于圆,∴DAC FBC ∠=∠,又∵EAD FAB FCB ∠=∠=∠,∴FBC FCB ∠=∠,∴FB FC =. (2)∵AB 是圆的直径,∴90ACD ACB ∠=∠=,∵120EAC ∠=,∴60DAC BAC ∠=∠= ,∴30D ∠= ,在Rt ACB ∆中,∵BC =60BAC ∠= ,∴3AC =,又在Rt ACD ∆中,30D ∠= ,3AC =,∴6AD =.考点:1.三角形外角平分线性质;2.圆的性质. 23. (本小题满分10分)选修4-4:坐标系与参数方程已知曲线C的参数方程为31x y αα⎧=⎪⎨=⎪⎩(α为参数),以直角坐标系原点为极点,x 轴正半轴为极轴建立极坐标系.(1)求曲线C 的极坐标方程,并说明其表示什么轨迹; (2)若直线的极坐标方程为1sin cos θθρ-=,求直线被曲线C 截得的弦长.【答案】(1) C 的极坐标方程为6cos 2sin ρθθ=+,表示圆;【解析】试题分析:(1)将曲线C 的参数方程化为普通方程,再利用直角坐标与极坐标的互化公式进行转换即可; (2)将1sin cos θθρ-=转换为直角坐标方程,求出圆心C 到直线的距离,由勾股定理求弦长即可.(2)∵直线的直角坐标方程为1y x -=∴圆心C到直线的距离为2d ==. 考点:1.参数方程与普通方程的互化;2.直线坐标与极坐标的互化;3.直线与圆的位置关系. 24. (本小题满分10分)选修4-5:不等式选讲 已知函数1()||||f x x a x a=+++(0)a >. (1)当2a =时,求不等式()3f x >的解集;(2)证明:1()()4f m f m +-≥. 【答案】(1) 111{|}44x x x <->或;(2)见解析.【解析】试题分析:(1)当2a =时,分区间去绝对值,分别解不等式即可;(2)由绝对值不等式的性质及基本不等式可得111111()()||||||||2||4f m f m a a m m m m a m a m+-=++-++++-+≥+≥. 试题解析: (1)当2a =时,1()|2|||2f x x x =+++,原不等式等价于21232x x x <-⎧⎪⎨---->⎪⎩或1221232x x x ⎧-≤≤-⎪⎪⎨⎪+-->⎪⎩或121232x x x ⎧>-⎪⎪⎨⎪+++>⎪⎩ 解得:114x <-或φ或14x >. 不等式的解集为111{|}44x x x <->或.考点:1.绝对值不等式的解法;2.绝对值不等式的性质.。
湖南省长郡中学高三下学期第一次模拟考试数学(理)试题及答案

长郡中学2018届高考模拟卷(一)数学(理科)第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}|||2A x x =<,{}|13B x x =<<,则A B 等于( )A .{}|21x x -<<B .{}|23x x -<<C .{}|23x x <<D .{}|12x x <<2.若(1)z i i +=,则||z 等于( )A .1B .32 C .22D .123.下列函数中,既是偶函数,又是在区间(0,)+∞上单调递减的函数为( ) A .3y x = B .1ln||y x = C .||2x y = D .cos y x = 4.执行如图所示的算法,则输出的结果是( )A .2B .43 C .54D .1 5.某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,两条虚线互相垂直,则该几何体的体积是( )A .203 B .163 C .86π- D .83π- 6.将函数()sin(2)3f x x π=+的图象向右平移ϕ个单位,得到的图像关于原点对称,则ϕ的最小正值为( ) A .6π B .3π C .512π D .712π7.某赛季甲、乙两名篮球运动员各13场比赛得分情况用茎叶图表示如图:( )A .甲运动员得分的极差大于乙运动员得分的极差B .甲运动员得分的中位数大于乙运动员得分的中位数C .甲运动员的得分平均值大于乙运动员的得分平均值D .甲运动员的成绩比乙运动员的成绩稳定 8.已知等比数列{}n a 的各项都是正数,且13a ,312a ,22a 成等差数列,8967a aa a +=+( ) A .6 B .7 C .8 D .99.在ABC ∆中,内角A ,B ,C 的对边分别为a ,b ,c ,若ABC ∆的面积为S ,且222()S a b c =+-,则tan C =( ) A .34-B .43-C .34D .4310.已知双曲线22221x y a b-=的左右焦点分别为1F ,2F ,O 为双曲线的中心,P 是双曲线的右支上的点,12PF F ∆的内切圆的圆心为I ,且圆I 与x 轴相切于点A ,过2F 作直线PI 的垂线,垂足为B ,若e 为双曲线的离心率,则( )A .||||OB e OA = B .||||OA e OB =C .||||OB OA =D .||OA 与||OB 关系不确定 11.如图,在OMN ∆中,A 、B 分别是OM 、ON 的中点,若OP xOA yOB =+(x ,y R ∈),且点P 落在四边形ABNM 内(含边界),则12y x y +++的取值范围是( )A .12,33⎡⎤⎢⎥⎣⎦ B .13,34⎡⎤⎢⎥⎣⎦ C .13,44⎡⎤⎢⎥⎣⎦ D .12,43⎡⎤⎢⎥⎣⎦12.在实数集R 中,我们定义的大小关系“>”为全体实数排了一个“序”,类似的,我们这平面向量集合{}|(,),,D a a x y x R y R ==∈∈上也可以定义一个称为“序”的关系,记为“>”.定义如下:对于任意两个向量111(,)a x y =,222(,)a x y =,12a a >当且仅当“12x x >”或“12x x =且12y y >”,按上述定义的关系“>”,给出下列四个命题:①若1(1,0)e =,2(0,1)e =,0(0,0)=,则120e e >>; ②若12a a >,23a a >,则13a a >;③若12a a >,则对于任意的a D ∈,12a a a a +>+;④对于任意的向量0a >,其中0(0,0)=,若12a a >,则12a a a a ⋅>⋅. 其中正确的命题的个数为( )A .4B .3C .2D .1第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.若251()ax x+的展开式中5x 的系数是80-,则实数a = . 14.已知直线l 过抛物线C 的焦点,且与C 的对称轴垂直,l 与C 交于A 、B 两点,||12AB =,P 为C 的准线l 上一点,则ABP ∆的面积为 .15.已知14C 的半衰期为5730年(是指经过5730年后,14C 的残余量占原始量的一半).设14C 的原始量为a ,经过x 年后的残余量为b ,残余量b 与原始量a 的关系如下:kxb ae-=,其中x 表示经过的时间,k 为一个常数.现测得湖南长沙马王堆汉墓女尸出土时14C 的残余量约占原始量约占原始量的76.7%.请你推断一下马王堆汉墓的大致年代为距今 年.(已知2log 0.7670.4≈-)16.已知()|2018||2017||1||1||2017||2018|f x x x x x x x =-+-++-+++++++……(x R ∈),且满足2(32)(1)f a a f a -+=-的整数a 共有n 个,222sin cos22()3cos sin 22x xg x kx x x =-+(0x ≥)的最大值为m ,且3m n +=,则实数k 的取值范围为 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知数列{}n a ,{}n b 满足12a =,121n n n a a a +=+,1n n b a =-,0n b ≠. (1)求证:数列1n b ⎧⎫⎨⎬⎩⎭是等差数列,并求数列{}n a 的通项公式; (2)令12n nn c b =,求数列{}n c 的前n 项和n T .18.如图,ABCD 是边长为3的正方形,DE ⊥平面ABCD ,//AF DE ,且6DE =,2AF =.(1)试在线段BD 上确定一点M 的位置,使得//AM 平面BEF ; (2)求二面角A BE C --的余弦值.19.为了引导居民合理用水,某市决定全面实施阶梯水价.阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价,具体划分标准如表:阶梯级别第一阶梯水量第二阶梯水量第三阶梯水量月用水量范围(单位:立方米)(0,10](10,15](15,)从本市随机抽取了10户家庭,统计了同一月份的月用水量,得到如图茎叶图:(1)现要在这10户家庭中任意选取3家,求取到第二阶梯水量的户数X的分布列与数学期望;(2)用抽到的10户家庭作为样本估计全市的居民用水情况,从全市依次随机抽取10户,若抽到n户月用水量为二阶的可能性最大,求n的值.20.已知1F ,2F 是椭圆22221(0)x y a b a b +=>>的左、右焦点,点2(1,)2P -在椭圆上,线段2PF 与y 轴的交点M 满足2PM MF =. (1)求椭圆的标准方程;(2)过点2F 作不与x 轴重合的直线l ,设l 与圆2222x y a b +=+相交于A ,B 两点,与椭圆相交于C ,D 两点,当11F A FB λ⋅=且2,13λ⎡⎤∈⎢⎥⎣⎦时,求1FCD ∆的面积S 的取值范围.21.已知函数()x x f x e e -=+,其中e 是自然对数的底数.(1)若关于x 的不等式()1x mf x e m -≤+-在(0,)+∞上恒成立,求实数m 的取值范围; (2)已知正数a 满足:存在0[1,)x ∈+∞,使得3000()(3)f x a x x <-+成立.试比较1a e -与1e a-的大小,并证明你的结论.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.选修4-4:坐标系与参数方程在直角坐标系xOy 中,圆C 的方程为22(6)25x y ++=.(1)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,求C 的极坐标方程; (2)直线l 的参数方程是cos ,sin x t y t αα=⎧⎨=⎩(t 为参数),l 与C 交于A 、B 两点,||10AB =,求直线l 的斜率.23.选修4-5:不等式选讲已知函数()||f x x a =-,其中1a >.(1)当2a =时,求不等式()4|4|f x x ≥--的解集;(2)已知关于x 的不等式|(2)2()|2f x a f x +-≤的解集为{}|12x x ≤≤,求a 的值.长郡中学2018届高考模拟卷(一)数学(理科)答案一、选择题1-5:DCBDA 6-10:ADDBC 11、12:CB二、填空题13.2- 14.36 15.2292 16.13k ≥三、解答题17.解:(1)∵1n n b a =-,∴1n n a b =+,由121n n n a a a +=+, ∴12(1)1(1)(1)n n n b b b ++=+++,化简得11n n n n b b b b ++-=, ∵0n b ≠, ∴+1111n n n n n n b b b b b b ++-=,即+1111n n b b -=(*n N ∈), 而111111121b a ===--, ∴数列1n b ⎧⎫⎨⎬⎩⎭是以1为首项,1为公差的等差数列. ∴11(1)1nn n b =+-⨯=,即1(*)n b n N n =∈,∴111n n a n n +=+=(*n N ∈). (2)由(1)知,2n n n c =,∴1212222n n n T =+++…,∴2311122222n n n T +=+++…, 两式相减得,1211111(1)111122211222222212n n n n n n n n n T +++-+=+++-=-=--…, 故222n n n T +=-.18.(1)证明:取BE 的三等分点K (靠近点B ),过K 作KM BD ⊥交BD 于M ,则有123KM DE ==,由DE ⊥平面ABCD ,//AF DE ,可知AF ⊥平面ABCD , ∴AF BD ⊥,∴//FA KM ,且FA KM =.∴四边形FAMK 为平行四边形,可知//AM FK ,∴//AM 平面BEF ,∵13MK BM ED BD ==,∴M 为BD 的一个三等分点(靠近点B ).(2)如图建立空间直角坐标系:则(3,0,0)A ,(3,3,0)B ,(0,0,6)E ,(0,3,0)C ,(3,3,6)EB =-,(0,3,0)AB =,(3,0,0)BC =-,设平面AEB 的法向量为11(,,1)n x y =,由1113360,30,x y y +-=⎧⎨=⎩可得(2,0,1)n =.设平面BCE 的法向量为22(,,1)m x y =,由2223360,30,x y x +-=⎧⎨=⎩可得(0,2,1)m =,因为二面角A BE C --为钝二面角,可得22200211cos ||52121θ⨯+⨯+=-=-+⋅+,所以二面角A BE C --余弦值为15-.19.解:(1)由茎叶图可知抽取的10户中用水量为一阶的有2户,二阶的有6户,三阶的有2户. 第二阶段水量的户数X 的可能取值为0,1,2,3,30463101(0)30C C P X C ===,21463103(1)10C C P X C ===,12463101(2)2C C P X C ===,03463101(3)6C C P X C ===,所以X 的分布列为X 0 1 2 3P130310 12 1613119()01233010265E X =⨯+⨯+⨯+⨯=.(2)设Y 为从全市抽取的10户中用水量为二阶的家庭户数,依题意得3~(10,)5Y B , 所以101032()()()55kkkP Y k C -==,其中k =0,1,2, (10)设101011111032()()()3(11)5532(1)2()()55k k k k k k C P Y k k t P Y k kC ----=-====-, 若1t >,则 6.6k <,(1)()P Y k P Y k =-<=; 若1t <,则 6.6k >,(1)()P Y k P Y k =->=.所以当6k =或7,()P Y k =可能最大,664107731032()()(6)75532(7)6()()55C P Y P Y C ====1>,所以n 的取值为6. 20.解:(1)∵2PM MF =,则M 为线段2PF 的中点,∴OM 是12PF F ∆的中位线, 又12OM F F ⊥,∴112PF F F ⊥,于是1c =,且221112a b+=,解得22a =,221b c ==, ∴椭圆的标准方程为2212x y +=. (2)由(1)知1(1,0)F -,2(1,0)F ,由题意,设直线l 的方程为1x ty =+,11(,)A x y ,22(,)B x y ,由221,3,x ty x y =+⎧⎨+=⎩得22(1)220t y ty ++-=,则12221t y y t +=-+,12221y y t =-+. 111122(1,)(1,)F A FB x y x y ⋅=+⋅+1112(1)(1)x x y y =+++1212(2)(2)ty ty y y =+++ 21212(1)2()4t y y t y y =++++22224222411t t t t -=--+=++.∵112,13F A F B ⎡⎤⋅∈⎢⎥⎣⎦,∴22222131t t -≤≤+,解得211,32t ⎡⎤∈⎢⎥⎣⎦. 由221,1,2x ty x y =+⎧⎪⎨+=⎪⎩消x 得22(2)210t y ty ++-=,设33(,)C x y ,44(,)D x y , 则12123434341||||()42F CDS F F y y y y y y ∆=⋅-=+-22224()22t t t =-+++2228(1)(2)t t +=+. 设21t m +=,则2881(1)2m S m m m==+++,其中43,32m ⎡⎤∈⎢⎥⎣⎦, ∵S 关于m 在43,32⎡⎤⎢⎥⎣⎦上为减函数,∴4346,57S ⎡⎤∈⎢⎥⎣⎦,即1FCD ∆的面积S 的取值范围为4346,57⎡⎤⎢⎥⎣⎦. 21.解:(1)由条件知(1)1x x x m e e e --+-≤-在(0,)+∞上恒成立,令xt e =(0x >),则1t >,所以21111111t m t t t t -≤-=--+-++-对于任意1t >成立. 因为11112(1)131(1)t t t t -++≥-⋅+=--,∴1113111t t -≥--++-, 当且仅当2t =,即ln 2x =时等号成立. 因此实数m 的取值范围是1(,]3-∞-. (2)令函数31()(3)xx g x e a x x e =+--+,则21'()3(1)xx g x e a x e=-+-, 当1x ≥时,10xx e e->,210x -≥,又0a >,故'()0g x >, 所以()g x 是[1,)+∞上的单调递增函数,因此()g x 在[1,)+∞上的最小值是1(1)2g e e a -=+-. 由于存在0[1,)x ∈+∞,使00300(3)0xx e ea x x -+--+<成立,当且仅当最小值(1)0g <,故120e e a -+-<,即12e e a -+>.1a e -与1e a -均为正数,同取自然底数的对数,即比较(1)ln a e -与(1)ln e a -的大小,试比较ln 1e e -与ln 1aa -的大小. 构造函数ln ()1x h x x =-(1x >),则211ln '()(1)xx h x x --=-,再设1()1ln m x x x =--,21'()xm x x-=,从而()m x 在(1,)+∞上单调递减, 此时()(1)0m x m <=,故'()0h x <在(1,)+∞上恒成立,则ln ()1xh x x =-在(1,+)∞上单调递减.综上所述,当1(,)2e e a e -+∈时,11a e e a --<; 当a e =时,11a e ea --=;当(,)a e ∈+∞时,11a e ea -->.22.解:(1)由cos x ρθ=,sin y ρθ=可得C 的极坐标方程212cos 110ρρθ++=. (2)在(1)中建立的极坐标系中,直线l 的极坐标方程为θα=(R ρ∈),由A ,B 所对应的极径分别为1ρ,2ρ,将l 的极坐标方程代入C 的极坐标方程得212cos 110ρρα++=, 于是1212cos ρρα+=-,1211ρρ=,22121212||||()4144cos 44AB ρρρρρρα=-=+-=-,由||10AB =得23cos 8α=,15tan 3α=±, 所以l 的斜率为153或153-.23.解:(1)当2a =时,26,2,()|4|2,24,26,4,x x f x x x x x -+≤⎧⎪+-=<<⎨⎪-≥⎩当2x ≤时,由()4|4|f x x ≥--得264x -+≥,解得1x ≤;当24x <<时,由()4|4|f x x ≥--得无解;当4x ≥时,由()4|4|f x x ≥--得264x -≥,解得5x ≥, 故不等式的解集为{}|15x x x ≤≥或.(2)令()(2)2()h x f x a f x =+-,则2,0,()42,0,2,,a x h x x a x a a x a -≤⎧⎪=-<<⎨⎪≥⎩由|()|2h x ≤,解得1122a a x -+≤≤, 又知|()|2h x ≤的解集为{}|12x x ≤≤,所以11,212,2a a -⎧=⎪⎪⎨+⎪=⎪⎩于是解得3a =.。
高三数学实验班选拔考试试题文(含解析)

长郡中学2017~2018学年新高三实验班选拔考试文科数学试卷本试卷分第I卷和第Ⅱ卷两部分,时量120分钟,满分150分。
第Ⅰ卷(60分)一、选择题(本大题共12小题,毎小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1、已知集合,若,则符合条件的集合的个数为A、 1 B、 2 C、 4 D。
8【答案】C【解析】设为集合的子集,由题意可得:,结合自己个数公式可得:符合条件的集合的个数为个、本题选择C选项、2、已知复数在复平面内对应的点在第三象限,则在复平面上对应的点在A。
第一象限 B。
第二象限 C、第三象限D、第四象限【答案】A、。
、、、、、、。
、。
、。
、、。
、。
则,结合题意可得:,即在复平面上对应的点在第一象限、本题选择A选项、3、长郡中学将参加摸底测试的1200名学生编号为1,2,3,…,1200,从中抽取一个容量为50的样本进行学习情况调查,按系统抽样的方法分为50组,假如第一组中抽出的学生编号为20,则第四组中抽取的学生编号为A、 68B、92C、82 D。
170【答案】B【解析】依照系统抽样的方法结合题意可得:第四组中抽取的学生编号为、本题选择B选项、4、在菱形中,,则A、 5 B、-5 C。
D、【答案】B【解析】设BD交AC于点E,且,由题意可得:、本题选择B选项。
5、已知椭圆与圆交于两点,若四边形(为原点)是菱形,则椭圆的离心率为A、 B。
C、 D、【答案】B【解析】圆的方程即:,结合对称性可得点A的横坐标,不妨设点A位于第一象限,则,代入椭圆方程有:,整理可得:,则:。
本题选择B选项、6、1927年德国汉堡大学的学生考拉兹提出一个猜想:关于每一个正整数,假如它是奇数,对它乘3再加1,假如它是偶数,对它除以2,如此循环,最终结果都能得到1、该猜想看上去特别简单,但有的数学家认为“该猜想任何程度的解决都是现代数学的一大进步,将开辟全新的领域至于如此简单明了的一个命题为什么能够开辟一个全新的领域,这大概与它其中蕴含的奇偶归一思想有关。
湖南省长沙市长郡中学2018届高三数学实验班选拔考试试题理(含解析)

长郡中学2017~2018学年新高三实验班选拔考试理科数学试卷本试卷分第I卷和第Ⅱ卷两部分,时量120分钟,满分150分第Ⅰ卷(60分)一、选择题(本大题共12小题,毎小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1. 若复数(其中,为虚数单位)的虚部为1,则A. 1B. 2C.D.【答案】C【解析】,的虚部为,,故选C.2. 已知集合,集合,则A. B. C. D.【答案】B【解析】,,故选B.3. 长郡中学要从师生推荐的参加说课比赛的3位男教师和2名女教师中,任选2人参加说课比赛,则选取的2人恰为一男一女的概率为A. B. C. D.【答案】B【解析】由古典概型概率公式,可得选取的人恰为一男一女的概率为,故选B.4. 已知等差数列的前项和为,若,则A. 23B. 96C. 224D. 276【答案】D【解析】是等差数列,可设首项为,公差为,由,可得,,故选D.5. 已知为双曲线的一个焦点,其关于双曲线的一条渐近线的对称点在另一条渐近线上,则双曲线的离心率为A. B.C. 2D.【答案】C【解析】设右焦点关于渐近线:的对称点为,则在上交于,由点到直线距离公式可得,为直角三角形,三边分别为,由对称性知,,,故选C.6. 下列函数在其定义域上既是增函数又是奇函数的是A. B.C. D.【答案】C【解析】对于.函数是奇函数,在为整数)上递增,则不满足;对于.函数为奇函数,由于,则在上递增,则满足;对于.函数为偶函数,则不满足;对于.函数既不是奇函数,也不是偶函数,则不满足,故选C.。
2017-2018学年湖南省长郡中学高一入学分班考试数学试题(解析版)

湖南省长郡中学2017-2018学年高一入学分班考试数学试题一、选择题1.已知方程组7{13x y ax y a+=---=+的解x 为非正数,y 为非负数,则a 的取值范围是( ) A. 23a -<≤ B. 23a -≤< C. 23a -<< D. 2a ≤- 【答案】D【解析】由方程组7{ 13x y a x y a +=---=+可解得3{ 28x a y a =-=--,由题设可得30{ 2280a a a -≤⇒≤---≥,应选答案D 。
2.已知226a b ab +=,且0a b >>,则a ba b+-的值为( )A.B. C. 2 D. 2±【答案】A【解析】由226a b ab +=可解得3a b -=±,又0a b >>,故(3a b =+,则(4a b b +=+, (2a b b -=+,故a ba b+=-,应选答案A 。
3.经过某十字路口的汽车,它可能继续直行,也可能向左或向右转,若这三种可能性大小相同,则两辆汽车经过该十字路口全部继续直行的概率为( ) A.13 B. 23 C. 19 D. 16【答案】C【解析】由题设每辆汽车的直行的概率是13,因此两辆汽车行驶彼此独立,故两辆汽车经过该十字路口全部继续直行的概率为111339⨯=,应选答案C 。
4.在日常生活中如取款、上网等都需要密码,有一种用“因式分解”法产生的密码记忆方便,原理是:如对于多项式44x y -,因式分解的结果是()()()22x y x y x y -++,若取9x =, 9y =时,则各个因式的值是: 0x y -=, 18x y +=, 22162x y +=,于是就可以把“018162”作为一个六位数的密码,对于多项式32x xy -,取20x =,10y =时,用上述方法产生的密码不可能是( )A. 201010B. 203010C. 301020D. 201030 【答案】A【解析】由于()()32x xy x x y x y -=+-,所以取20x =, 10y =,则30,10x y x y +=-=,所以用上述方法产生的密码可以是203010, 301020, 201030,应选答案A 。
长郡理科实验班招生 考试数学试卷(一)

最全长郡理科实验班招生考试数学试卷(一)时量:60分钟满分:100分一选择题(每题5分,共30分)l.已知α为实数,则代数式27−12α+2a2的最小值为()A.0B.3C.33D.92.若n为整数,则能使n+1n−1也为整数的n的个数有()A.1个B.2个C.3个D.4个·3.已知α,b为实数,且αb=1,设M=a a+1+b b+1,N=1a+1+1b+1,则M、N的大小关系是A..M>NB.M=NC.M<N.D.无法确定4.一张圆桌旁有四个座位如图,A,B,C,D四人随机坐在四个座位上,则A与D相邻的概率是()A.23B12C14 D.295.如图,∠ACB=60°,半径为2的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离为()A.2πB.πC.23D.46.如图,平面中两条直线l1,和l2相交子点0,对于平面上任意一点M,若P,q分别是M到直线l1和l2的距离,则称有序非负实数对(p1,q)是点M的“距离坐标”,根据上述定义,有以下几个结论:①“距离坐标”是(0,1)的点有1个;②“距离坐标”是(5,的的点有4个;③“距离坐标”是(α,α),(α为非负实数)的点有4个.其中正确的有其中正确的有()A.0个B.1个C.2个D.3个二、填空题(每题5分,共30分)7.已知α,b,C是实数,且α2+6b=-17,b2+8c=-23,c2+2α=14,则α+b+c=.8.已知关于 的不等式(2α-b)>b的解集是 棨−12,则a b b+-36a3=.9.对正实数α,b作定义a∗b=ab−a+b,若4*x=44,则x的值是.10.在△ABC中,AB=4C,∠A=45°,AC的垂直平分线分别交AB、AC于D、E 两点,连结CD,如果AD=l,则tan∠BCD的值为.11.已知:如图,在直角△ABC中,AD=DE=EB,且CD2+CE2=1,则斜边AB的长为12.小明、小林和小颖共解出100道数学题,每人都解出了其中的60道,如果将其中只有1人解出的题叫做难题,2人解出的是基叫做中裆题,3人都解出的题叫做容易题,那么难题比容易题多道.三、解答题(每题10分,共40分)13.某商场将进价为2600元的彩电以3000元售出,平均每天能销售出6台.为丁配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种彩电的售价每降低50元,平均每天就能多售出3台.(1)商场要想在这种彩电销售中每天盈利3600元,同时又要使百姓得到最卢大实惠,每台彩电应降价多少元?(2)每告彩电降价多少元时,商场每天销售这种彩电的利润最高?最高利润是多少?14.已知点M,N的坐标分别为(0,1),(0,-1),点P是抛物线y=14x2上的一个动点.(1)求证:以点P为圆心,PM为半径的圆与直线y=-1的相切;(2)设直线PM与抛物线y=14x2的另一个交点为点Q,连接NP、NQ,求证:∠PNM=∠QNM.15、已知关于x的方程(m2−1)x2−33m−1+18=0有两个正整数根(m是整数),△ABC的三边a、b、c满足c=23,m2+a2m−8a=0,m2+b2m−8b=0,求:(1)m的值;(2)△ABC的面积;16.直线y=x−10与x轴交于A点,点B在第一象限,且AB=35,以cos∠OAB=25 (1)若点C是点B关于x轴的对称点,求过0、C、A三点的抛物线的表达式(2)在(1)中的抛物线上是否存在点P(P点在第一象限),使得以点P、0、C、A为顶点的囚边形是梯形?若存在,求出点O的坐标;若不存在,请说明理由.(3)若将点O、A分别变换为点Q(-4m,0),R(6m,0)(m 0且为常数)),设过Q、R两点且以QR的垂直平分线为对称轴的抛物线(开口向上)与y轴的交点为N,其顶点为M,记△QNM的面积为S∆QNM,△QNR的面积为S∆QNR,求S∆QNM:S∆QNR的数学试卷(一)参考答案一、选择题(每题5分,共30分)1.B2.D3.B4.A5.C6.B二、填空题(每题5分,共30分)7.-88.-39.3610.12 11.55312.20三、解答题(每题10分,共40分)13.解:设每台彩电降价x 元(0<x<400),商场销售这种彩电平均每天的利润为y 元,则有y =3000−2600−x 6+=350(x 2−−4000)……………………4分(1)因为要每天盈利3600元,则y=36002−300x −4000=3600所以x 2−300x +2000=0,解得x=100或俨200,又因为要使百姓得到最大实惠,则每台要降价200元.…………………………7分(2)∵y =350x 2−300x −4000=350(x −150)2+3750∴当x=150时,y 取得最大值为3750,所以每台彩电降价150元时,商场的利润最高为3750元.………………10分14.解:(1)设点P 的坐标为(x 0,14x 02),则PM===14x02+1;……………………4分(2)如图,分别过点P,Q作直线y=-1的垂线,垂足分别为H、R,由(1)知PH=PM,MN、QR都垂直于直线y=-1,所以PH//MH//QR,于是QM EN=MP NH,所以QR RN=PH HN,因此,Rt∆PHN∽Rt∆QNM.………………………………9分于是∠HNP=∠RNQ,从而∠PNM=∠QNM。
湖南省长沙市长郡中学2018年高中理实班招生拔尖试题(含答案)

2018年湖南省长沙市长郡中学高中理实班招生拔尖试题(时间:90分钟满分:120分)一、选择题(本大题共6小题,每小题5分,共30分)1.对于任意的有理数a ,方程0)43()1(222=+--++b a a x a x 的根总是有理数,则b 的值为( )A .1B .-1C .2D .02.如图,平面中两条直线1l 和2l 相交于点O ,对于平面上任意一点M ,若p ,q 分别是M 到直线1l 和2l 的距离,则称有序非负实数对(p ,q )是点M 的“距离坐标”根据上述定义,有以下几个结论:①“距离坐标”是(0,1)的点有1个;②“距离坐标”是(5,6)的点有4个;iM (p ,q )③“距离坐标”是(a ,a )(a 为非负实数)的点有4个其中正确的有( )A .0个B .1个C .2个D .3个 3.一张等腰三角形纸片,底边长13cm ,底边上的高为32.5cm .现沿底边依次从下往上裁剪宽度均为5cm 的矩形纸条,如图所示已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )A .第3张B .第4张C .第5张D .第6张 4.如图,正方形ABCD 的边长为1,点M ,N 分别在BC ,CD 上,且△CMN 的周长为2,则△MAN的面积的最小值为 ( )A .12-B .222-C .22D .122-5.如图,将一张三角形纸片沿虚线剪成甲、乙、丙三块,其中甲、丙为梯形,乙为三角形,根据图中标示的边长数据,比较甲、乙、丙的面积大小,下列判断正确的是( )A .乙>丙>甲B .丙>乙>甲C .甲>丙>乙D .无法判断6.将一枚六个面编号分别为1,2,3,4,5,6的质地均匀的正方体骰子先后投掷两次,记第一次掷出的点数为a 第二次掷出的点数为b ,则使关于x ,y 的方程组⎩⎨⎧=+=+223y x by ax ,只有正数解的概率为( ) A .121 B .92 C .185 D .3613 二、填空题(本大题共6小题,每小题5分,共30分)7.计算:24066312305941--+++= .8.已知||x-2|-b |=a 有四个不同的解,则||||||||b b a a a b a b b a b a ++--+++= . 9.若抛物线1422++-=p px x y 中不管p 取何值时都通过定点,则定点坐标为 .10.如图,半径为r 的圆O 沿折线ABCDE 作无滑动的滚动,如果AB =BC =CD =DE =r π2,∠ABC =∠CDE =150°,∠BCD=120°,那么,圆O 自点A 至点E 转动了 周.11.二次函数a ax x y ++=22在21≤≤-x 上有最小值-4,则a 的值为.12.在平面直角坐标系中,已知P 1的坐标为(1,0),将其绕着原点按逆时针方向旋转30°得到P 2,延长OP 2到P 3使OP 3=2OP 2,再将P 3绕原点按逆时针方向旋转30°得到P 4,延长OP 4到P 5,使OP 5=2OP 4,如此继续下去,则点P 2010的坐标为 .三、解答题(本大题共5小题,第13题10分,第14-16题各12分,第17题14分,共60分)13.已知m ,n 是方程0132=++x x 的两根.(1)求mm m m m 23102)5165(---⋅--+的值; (2)求mn n m 33+的值.14.甲、乙两人从A 地到B 地,甲骑自行车,乙步行,已知甲每小时比乙每小时多走8千米,甲、乙同时出发,甲比乙早到5小时,若甲到B 地后立即沿原路返回,则在距B 地15千米处与乙相遇,求A ,B 两地间的距离及甲、乙两人的速度.15.如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D,P分别是AC,BC的中点,△ADE是等腰三角形,∠AED=90°,连接BE,EC.(1)判断线段BE和EC的关系,并证明你的结论;(2)连接P A,PE,过点A作AM∥PE,过点E作EM∥P A,AM和EM相交于点M,在图中先补充图形,再判断四边形P AME的形状,并证明你的结论.16.如图,在 ABCD 中,E 为对角线BD 上一点,且满足∠ECD =∠ACB ,AC 的延长线与△ABD的外接圆交于点F ,证明:∠DFE =∠AFB .17.如图,在平面直角坐标系中,直角梯形OABC 的顶点A ,B 的坐标分别是(5,0),(3,2),点D在线段OA 上,BD =BA ,点Q 是线段BD 上一个动点,点P 的坐标是(0,3),设直线PQ 的解析式为y =kx +b(1)求k 的取值范围;(2)当k 为取值范围内的最大整数时,若抛物线ax ax y 52-=的顶点在直线PQ ,OA ,AB ,BC围成的四边形内部,求a 的取值范围.。
湖南省长沙市长郡中学2018-2019学年高二下学期入学考试数学(理)试题含答案

长郡中学2018-2019学年度高二第二学期入学考试数学(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共8页.时量90分钟.满分150分.第Ⅰ卷一、选择题:每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若222x y +>,则1x >或1y >的否命题是( ) A. 若222x y +<,则1x ≤或1y ≤ B. 若222x y +<,则1x ≤且1y ≤ C. 若222x y +<,则1x <或1y <D. 若222x y +≤,则1x ≤且1y ≤2.在复平面内,复数(1)(1)z a a i =-++(a R ∈,i 为虚数单位),对应的点在第四象限的充要条件是( ) A. 1a ≥- B. 1a >-C. 1a ≤-D. 1a <-3.已知{}n a 等差数列,1010a =,其前10项和1070S =,则其公差为( )A.23B.32C. 23-D. 32-4.设函数()sin (0)f x x ωω=>,将()y f x =的图象向左平移3π个单位长度后,所得图象与原函数的图象重合,则ω的最小值是( ) A.13B. 3C. 6D. 95.已知x y 、满足2213xy +=,则2432u x y x y =+-+--的取值范围为( )A. []112, B. []06,C. []012, D. []113, 6.已知点P 是椭圆221168x y +=上非顶点的动点,1F ,2F 分别是椭圆的左、右焦点,O 是坐标原点,若M是12F PF ∠的平分线上一点,且10F M MP ⋅=u u u u r u u u r,则OM u u u u r 的取值范围是( ) A. [)0,3B. (0,C. )⎡⎣D. (]0,4 7.执行如图所示的程序框图,若输出的S 的值为2670,则判断框中的条件可以为( )是A. 5?i <B. 6?i <C. 7?i <D. 8?i <8.已知点P ,Q 为圆C :x 2+y 2=25上任意两点,且|PQ|<6,若PQ 中点组成的区域为M ,在圆C 内任取一点,则该点落在区域M 上的概率为( )A.35 B.925 C. 1625D. 259.某几何体的三视图如图所示,则这个几何体的体积为 ( )A. 4B.203C.263D. 810.已知函数224log ,02(){1512,22x x f x x x x <<=-+≥,若存在实数a b c d 、、、,满足()()()()f a f b f c f d ===,其中0d c b a >>>>,则abcd 的取值范围是( ) A. (16,21)B. (16,24)C. (17,21)D. (18,24)11.三角形ABC 中,5BC =,G ,O 分别为三角形ABC 重心和外心,且5GO BC ⋅=u u u r u u u r,则三角形ABC的形状是( ) A. 锐角三角形B. 钝角三角形C. 直角三角形D. 上述均不的12.设函数2()ln 2f x x x x =-+,若存在区间1[,][,)2a b ⊆+∞,使得()f x 在[,]a b 上的值域为[(2),(2)]k a k b ++,则k 的取值范围是( )A. 92ln 2[1,]4+ B. 92ln 2(1,)4+ C. 92ln 2[1,]10+ D. 92ln 2(1,]10+ 第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共20分.将答案填在答题纸上.13.设{}1,0,1,3a ∈-,{}2,4b ∈-,则以(),a b 为坐标的点落在第四象限的概率为___________.14.已知向量,a b rr 满足:13a =r ,1b =r ,512a b -≤r r ,则b r 在a r 上的投影的取值范围是 .15.曲线sin y x =与直线,32x x ππ=-=及x 轴所围成的图形的面积是________.16.如图所示,将平面直角坐标系的格点(横、纵坐标均为整数的点)按如下规则标上数字标签:原点处标数字0,点()1,0处标数字1,点(11)-,处标数字2,点(01)-,处标数字3,点(11),--处标数字4,点(10)-,处标数字5,点()11-,处标数字6,点(01),处标数字7,…以此类推:记格点坐标为()m n ,的点(m n ,均为正整数)处所标的数字为()f m n =,,若n m >,则()f m n =, .三、解答题:本大题共70分.解答应写出文字说明、证明过程或演算步骤.17.通过市场调查,得到某种产品的资金投入x (单位:万元)与获得的利润y (单位:万元)的数据,如表所示: 资金投入x 2 3 4 5 6 利润y 23569(1)画出数据对应的散点图;(2)根据上表提供的数据,用最小二乘法求线性回归直线方程y bx a =+$$$; (3)现投入资金10万元,求获得利润的估计值为多少万元?参考公式:1122211ˆ()ˆ)(()nni i i ii i n nii i i x x y y x y nxyax x x nx b y bx====⎧---⎪⎪==⎪⎨--⎪⎪=-⎪⎩∑∑∑∑ 18.在数列{}n a 中,11a =,()1121n n n a ca c n ++=++()n *∈N ,其中实数0c ≠.(1)求23,a a ,并由此归纳出{}n a 的通项公式; (2) 用数学归纳法证明(Ⅰ)的结论.19.已知(2cos ,1),(cos ,)m x x n x y =+=-v v,且m n ⊥u v v. (1)将y 表示为x 的函数()f x ,并求()f x 的单调递增区间;(2)已知,,a b c 分别为ABC ∆的三个内角A,B,C 的对边,若()32Af =,且2a =,4b c +=,求ABC ∆的面积..20.如图,在四棱锥P ABCD -中,底面ABCD 是平行四边形,PG ⊥平面ABCD ,垂中为G ,G 在AD 上,且14,,,23PG AG GD BG GC GB GC ==⊥==,E 是BC 的中点.(1)求异面直线GE 与PC 所成角余弦值;(2)若F 点是棱PC 上一点,且DF GC ⊥,求PFFC的值. 21.已知抛物线C 的顶点为原点,其焦点()()0,0F c c >到直线的距离为322.设P 为直线l 上的点,过点P 作抛物线C 的两条切线,PA PB ,其中,A B 为切点.(1) 求抛物线C 的方程;(2) 当点()00,P x y 为直线l 上的定点时,求直线AB 的方程;(3) 当点P 在直线l 上移动时,求AF BF ⋅的最小值. 22.已知函数21()ln ,2f x x ax x a R =-+∈. (1)若(1)0f =,求函数()f x 的单调递减区间;(2)若关于x 的不等式()1f x ax ≤-恒成立,求整数a 的最小值数学(理科)参考答案本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共8页.时量90分钟.满分150分.第Ⅰ卷一、选择题:每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.D2.D3.A4.C5.D6.B7.B8.B9.B10.B11.B12.D第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共20分.将答案填在答题纸上..13. 14,1]14 [51315 3216. (2n+1)2+m−n−1三、解答题:本大题共70分.解答应写出文字说明、证明过程或演算步骤.17.(1)依次画出图中所对应的五个点,(2)根据上表提供数据,先求平均数和,然后根据所给的第二个公式,计算,和,代入公式求出以后,再根据回归直线过点,代入直线方程求,得到回归直线方程;(3)当时,代入回归直线方程,得到利润的预报值.试题解析:(1)(2)x̅=2+3+4+5+65=4,y̅=2+3+5+6+95=5b=∑x i y i−nx̅y̅ni=1∑x i2−nx̅2ni=1=2×3+3×3+4×5+5×6+6×9−5×4×54+9+16+25+36−5×16=1.7∴a=y̅−bx̅=−1.8,∴ŷ=1.7x−1.8(3)当x=10(万元),ŷ=15.2(万元)18.(1) 由a1=1,及a n+1=ca n+c n+1(2n+1)(n∈N∗)得a2=ca1+c2⋅3=(22−1)c2+c,a3=ca2+c3(2×2+1)=c[(22−1)c2+c]+c3(2×2+1)=(32−1)c3+c2于是猜测:a n=(n2−1)c n+c n−1(n∈N∗)(2)下面用数学归纳法予以证明:10当n=1时,由a1=1=(12−1)c+c1−1显然结论成立.20假设n=k时结论成立,即a k=(k2−1)c k+c k−1那么,当n=k+1时,由a k+1=ca k+c k+1(2k+1)=c[(k2−1)c k+c k−1]+c k+1(2k+1)=(k2+2k)c k+1+c k=[(k+1)2−1]c k+1+c k显然结论成立.由10、20知,对任何n∈N∗都有a n=(n2−1)c n+c n−1(n∈N∗)19.(1)∵,∴,,由,得kπ−π3≤x≤kπ+π6,k∈Z,∴函数的递增区间为[kπ−π3,kπ+π6],k∈Z.(2)由(1)得,∴,,,∴.在中,由余弦定理得,,∴,∴.20.(1)以G点为原点,、、分别为x轴、y轴、z轴建立空间直角坐标系,则B(2,0,0),C(0,2,0),P(0,0,4),故∵,∴GE与PC所成角的余弦值为√1010.(2)解:设F(0,y,z),则,∵,∴,即(32,y −32,z)⋅(0,2,0)=2y −3=0,∴y =32, 又,即(0,32,z −4)=λ(0,2,−4),∴z =1,故F(0,32,1),,∴PFFC =3√52√52=321.解:(1)依题意,设拋物线C 的方程为x 2=4cy ,由√2=3√22结合c >0,解得c =1,所以拋物线C 的方程为x 2=4y .(2)拋物线C 的方程为x 2=4y ,即y =14x 2,求导得y ′=12x , 设A(x 1,y 1),B(x 2,y 2)(其中y 1=x 124,y 2=x 224)则切线PA,PB 的斜率分别为12x 1,12x 2,所以切线PA 的方程为y −y 1=x 12(x −x 1),即y =x 12x −x 122+y 1,即x 1x −2y −2y 1=0,同理可得切线PB方程为x 2x −2y −2y 2=0,因为切线PA,PB 均过点P(x 0,y 0),所以x 1x 0−2y 0−2y 1=0,x 2x 0−2y 0−2y 2=0, 所以(x 1,y 1),(x 2,y 2)为方程x 0x −2y 0−2y =0的两组解, 所以直线AB 的方程为x 0x −2y −2y 0=0.(3)由拋物线定义可知|AF|=y 1+1,|BF|=y 2+1,联立方程{x 0x −2y −2y 0=0x 2=4y,消去x 整理得y 2+(2y 0−x 02)y +y 02=0. 由一元二次方程根与系数的关系可得y 1+y 2=x 02−2y 0,y 1y 2=y 02, 所以|AF|⋅|BF|=y 1y 2+(y 1+y 2)+1=y 02+x 02−2y 0+1又点P(x 0,y 0)在直线l 上,所以x 0=y 0+2,所以y 02+x 02−2y 0+1=2y 02+2y 0+5=2(y 0+12)2+92, 所以当y 0=−12时,|AF|⋅|BF|取得最小值,且取得最小值为92. 22.(1)因为f(1)=1−a2=0,的所以a=2,故f(x)=lnx−x2+x,x>0,所以f′(x)=1x −2x+1=−2x2+x+1x=−(x−1)(2x+1)x(x>0),由f′(x)<0,解得x>1,所以f(x)的单调减区间为(1,+∞).(2)令g(x)=f(x)−(ax−1)=lnx−12ax2+(1−a)x+1,x>0,由题意可得g(x)<0在(0,+∞)上恒成立.又g′(x)=1x −ax+(1−a)=−ax2+(1−a)x+1x.①当a≤0时,则g′(x)>0.所以g(x)在(0,+∞)上单调递增,又因为g(1)=ln1−12a×12+(1−a)+1=−32a+2>0,所以关于x的不等式f(x)≤ax−1不能恒成立.②当a>0时,g′(x)=−ax2+(1−a)x+1x =−a(x−1a)(x+1)x,令g′(x)=0,得x=1a.所以当x∈(0,1a)时,g′(x)>0,函数g(x)单调递增;当x∈(1a,+∞)时,g′(x)<0,函数g(x)单调递减.故当x=1a 时,函数g(x)取得极大值,也为最大值,且最大值为g(1a)=ln1a−12a×(1a)2+(1−a)×1a+1=12a−lna.令ℎ(a)=12a−lna,a>0,则ℎ(a)在(0,+∞)上单调递减,因为ℎ(1)=12>0,ℎ(2)=14−ln2<0.所以当a≥2时,ℎ(a)<0,所以整数a的最小值为2.。
数学---湖南省长沙市长郡中学实验班2018届高三(上)选拔考试试卷(理)(解析版)

湖南省长沙市长郡中学实验班2018届高三(上)选拔考试数学试卷(理科)一、选择题(本大题共12小题,毎小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(5分)若复数z=(其中a∈R,i为虚数单位)的虚部为1,则|z|=()A.1 B.2C.D.2.(5分)已知集合A={x|x2+2x﹣3≤0,x∈Z},集合B={x|ln x<2},则A∩B=()A.{0} B.{1}C.{0,1} D.∅3.(5分)长郡中学要从师生推荐的参加说课比赛的3位男教师和2名女教师中,任选2人参加说课比赛,则选取的2人恰为一男一女的概率为()A.B.C.D.4.(5分)已知等差数列{a n}的前n项和为S n,若a4+a12﹣a8=8,a10﹣a6=4,则S23=()A.23 B.96C.224 D.2765.(5分)已知F为双曲线C:﹣=1(a>0,b>0)的一个焦点,其关于双曲线C 的一条渐近线的对称点在另一条渐近线上,则双曲线C的离心率为()A.B.C.2 D.6.(5分)下列函数在其定义域上既是增函数又是奇函数的是()A.f(x)=sin x B.f(x)=x3+1C.f(x)=log2(+x)D.f(x)=7.(5分)执行如图所示的程序框图,若输入i=1,S=0,则输出的结果为()A.7 B.9 C.10 D.118.(5分)若二项式(x2+)7展开式的各项系数之和为﹣1,则含x2项的系数为()A.560 B.﹣560 C.280 D.﹣2809.(5分)某几何体的三视图如图,其俯视图中的曲线部分为半圆,则该几何体的体积是()A.192+96πB.256+96πC.192+100πD.256+100π10.(5分)已知椭圆C:+=1,若直线l经过M(0,1),与椭圆交于A、B两点,且=﹣,则直线l的方程为()A.y=±x+1 B.y=±x+1 C.y=±x+1 D.y=±x+111.(5分)已知三棱锥S﹣ABC的每个顶点都在球O的表面上,SA⊥底面ABC,AB=AC=4,BC=2,且二面角S﹣BC﹣A的正切值为4,则球O的表面积为()A.240πB.248πC.252πD.272π12.(5分)已知函数f(x)=x2﹣x ln x﹣k(x+2)+2在区间[,+∞)上有两个零点,则实数k的取值范围为()A.B.C.D.二、填空题(本大题共4小题,每小题5分,共20分.)13.(5分)若实数x,y满足,则z=3x+y的最小值为.14.(5分)设=(,m),=(m,),且•=1,则||=.15.(5分)已知cos(﹣α)+sin(π﹣α)=﹣,﹣<α<0,则cos(2α+)=.16.(5分)在数列{a n}中,首项不为零,且a n=a n﹣1(n∈N*,n≥2),S n为{a n}的前n项和,令T n=,n∈N*,则T n的最大值为.三、解答题(本大题共7小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(8分)在锐角△ABC中,a,b,c分别为角A,B,C的对边,且4sin A cos2A﹣cos(B+C)=sin3A+.(Ⅰ)求A的大小;(Ⅱ)若b=2,求△ABC面积的取值范围.18.(8分)如图,在直三棱柱ABC﹣A1B1C1中,BA=BC=5,AC=8,D为线段AC的中点.(Ⅰ)求证:BD⊥A1D;(Ⅱ)若直线A1D与平面BC1D所成角的正弦值为,求AA1的长.19.(8分)某地4个蔬菜大棚顶部,阳光照在一棵棵茁壮生长的蔬菜上.这些采用水培、无土栽培方式种植的各类蔬菜,成为该地区居民争相购买的对象.过去50周的资料显示,该地周光照量X(小时)都在30以上.其中不足50的周数大约有5周,不低于50且不超过70的周数大约有35周,超过70的大约有10周.根据统计某种改良黄瓜每个蔬菜大棚增加量y(百斤)与每个蔬菜大棚使用农夫1号液体肥料x(千克)之间对应数据为如图所示的折线图:(Ⅰ)依据数据的折线图,用最小二乘法求出y关于x的线性回归方程=x+;并根据所求线性回归方程,估计如果每个蔬菜大棚使用农夫1号肥料10千克,则这种改良黄瓜每个蔬菜大棚增加量y是多少斤?(Ⅱ)因蔬菜大棚对光照要求较大,某光照控制仪商家为应对恶劣天气对光照的影响,为该基地提供了部分光照控制仪,该商家希望安装的光照控制仪尽可能运行,但每周光照控制仪最多可运行台数受周光照量X限制,并有如下关系:若某台光照控制仪运行,则该台光照控制仪周利润为5000元;若某台光照控制仪未运行,则该台光照控制仪周亏损800元,欲使商家周总利润的均值达到最大,应安装光照控制仪多少台?附:回归方程系数公式:=,=﹣.20.(12分)已知P是抛物线E:y2=2px(p>0)上一点,P到直线x﹣y+4=0的距离为d1,P到E的准线的距离为d2,且d1+d2的最小值为3.(Ⅰ)求抛物线E的方程;(Ⅱ)直线l1:y=k1(x﹣1)交E于点A,B,直线l2:y=k2(x﹣1)交E于点C,D,线段AB,CD的中点分别为M,N,若k1k2=﹣2,直线MN的斜率为k,求证:直线l:kx﹣y﹣kk1﹣kk2=0恒过定点.21.(12分)已知函数f(x)=﹣1(b∈R,e为自然对数的底数)在点(0,f(0))处的切线经过点(2,﹣2).(Ⅰ)讨论函数F(x)=f(x)+ax(a∈R)的单调性;(Ⅱ)若∀x∈R,不等式e x f(x)≤c(x﹣1)+1恒成立,求实数c的取值范围.22.(14分)设a1,a2,a3,a4,a5是5个正实数(可以相等).证明:一定存在4个互不相同的下标i,j,k,l,使得|﹣|<.[选修4-4:坐标系与参数方程]23.(8分)在直角坐标系中,已知曲线M的参数方程为(β为参数),在极坐标系中,直线l1的方程为:α1=θ,直线l2的方程为α2=θ+.(Ⅰ)写出曲线M的直角坐标方程,并指出它是何种曲线;(Ⅱ)设l1与曲线M交于A,C两点,l2与曲线M交于B,D两点,求四边形ABCD面积的取值范围.【参考答案】一、选择题1.C【解析】由复数z==的虚部为1,得,即a=2.∴z=1+i.则|z|=.故选:C.2.B【解析】集合A={x|x2+2x﹣3≤0,x∈Z}={x|﹣3≤x≤1,x∈Z}={﹣3,﹣2,﹣1,0,1},集合B={x|ln x<2}={x|0<x<e2},则A∩B={1}.故选:B.3.B【解析】长郡中学要从师生推荐的参加说课比赛的3位男教师和2名女教师中,任选2人参加说课比赛,基本事件总数n==10,选取的2人恰为一男一女包含的基本事件个数m==6,选取的2人恰为一男一女的概率为p==.故选:B.4.D【解析】设等差数列{a n}的公差为d,∵a4+a12﹣a8=8,a10﹣a6=4,∴a1+7d=8,4d=4,解得d=1=a1.则S23=23+=276.故选:D.5.C【解析】双曲线C:﹣=1的左焦点为F(﹣c,0),渐近线方程为y=±x,设F关于y=x的对称点为(m,﹣m),由题意可得=﹣,(*)且(0﹣m)=•(m﹣c),可得m=c,代入(*)可得b2=3a2,c2=a2+b2=4a2,则离心率e==2.故选:C.6.C【解析】逐一考查所给选项中函数的性质:A.f(x)=sin x是定义域上的奇函数,函数不具有单调性,不合题意;B.f(x)=x3+1是定义域上的非奇非偶函数,函数单调递增,不合题意;C.是定义域上的奇函数,函数单调递增,符合题意;D.是定义域上的奇函数,函数单调递减,不合题意;故选:C.7.B【解析】模拟程序的运行,可得i=1,S=0,满足条件S<2,执行循环体,S=ln3,i=3满足条件S<2,执行循环体,S=ln3+ln=ln5,i=5满足条件S<2,执行循环体,S=ln5+ln=ln7,i=7满足条件S<2,执行循环体,S=ln7+ln=ln9>2,i=9此时,不满足条件S<2,退出循环,输出i的值为9.故选:B.8.A【解析】令x=1,可得:(1+a)7=﹣1,解得a=﹣2.∴的通项公式:T r+1==(﹣2)r x14﹣3r,令14﹣3r=2,解得r=4.∴含x2项的系数==560.故选:A.9.C【解析】根据几何体的三视图知,该几何体是半圆柱体与直三棱柱的组合体,且组合体的底面积与俯视图相同;如图所示,∴俯视图的面积为S底=π•52+×8×6=+24,∴该几何体的体积是V几何体=(+24)×8=100π+192.故选:C.10.B【解析】设直线l的方程为m(y﹣1)=x.A(x1,y1),B(x2,y2).联立,化为:(9+5m2)y2﹣10m2y+5m2﹣45=0,∴y1+y2=,y1y2=,∵=﹣,∴y1﹣1=﹣.联立解得m=±3.则直线l的方程为:y=x+1.故选:B.11.D【解析】由题意,AB=AC=4,BC=2,底面是等腰三角形,过A作BC垂直交于D,AD⊥BC,且D是BC中点.可得AD=1.底面外接圆半径r=8.SA⊥底面ABC,AB=AC=4∴SC=SB.D是BC中点.∴SD⊥BC.平面S﹣BC﹣A的二面角是∠SDA,二面角正切值为4,∴AS=4AD.可得AS=4.外接球R2=解得:R2=68球O的表面积S=4πR2=272π.故选:D.12.A【解析】令f(x)=0可得:,令,则,令t(x)=x2+3x﹣4﹣2ln x,则,据此可得函数t(x)在区间上单调递增,且t(1)=0,故当x∈(0,1)时,t(x)<0,h’(x)<0,当x∈(1,+∞)时,t(x)>0,h’(x)>0,则函数h(x)在区间上单调递减,在区间(1,+∞)上单调递增,而:,据此可得:实数k的取值范围为.故选:A.二、填空题13.﹣2【解析】作出不等式表示的平面区域(如图示:阴影部分):由得A(﹣2,4),由z=3x+y得y=﹣3x+z,平移y=﹣3x,易知过点A时直线在y上截距最小,所以z=3x+y的最小值:﹣2.故答案为:﹣2.14.【解析】∵=(,m),=(m,),且•=1,∴==1,解得m=1,∴=(1,),∴||==.故答案为:.15.【解析】由cos(﹣α)+sin(π﹣α)=﹣,可得cos cosα+sin sinα+sinα=.即cosα+sinα=.∴sin(α+)=.∵﹣<α<0,∴﹣<α+<,∴cos(α+)=则cos(2α+)=cos2(α+)﹣sin2(α+)=故答案为:.16.2+2【解析】数列{a n}中,首项不为零,且a n=a n﹣1(n∈N*,n≥2),∴数列{a n}为等比数列,首项为a1,公比为.∴,.S n=,S2n=,T n====≤=2(),当且仅当n=2时取等号.∴T n的最大值为2+2.故答案为:2+2.三、解答题17.解:(Ⅰ)∵4sin A cos2A﹣cos(B+C)=sin3A+,∴4sin A cos2A+cos A=sin3A+,∴2cos A sin2A+cos A=sin2A cos A+cos2A sin A+,整理可得:cos A+sin A=,∴可得:sin(A+)=,∵A∈(0,),可得:A+∈(,),∴A+=,可得:A=.(Ⅱ)∵A=,b=2,∴S△ABC=sin A==c.又∵由正弦定理,可得:,∴c===+1,∵B,C为锐角,可得:B∈(30°,90°),可得:tan B∈(,+∞),可得:∈(0,3),可得:c=+1∈(1,4),∴S△ABC=c∈(,2).18.(Ⅰ)证明:∵三棱柱ABC﹣A1B1C1是直三棱柱,∴AA1⊥平面ABC,又BD⊂平面ABC,∴BD⊥AA1,∵BA=BC,D是AC的中点,∴BD⊥AC,又AC∩AA1=A,AC⊂平面ACC1A1,AA1⊂平面ACC1A1,∴BD⊥平面ACC1A1,又A1D⊂平面ACC1A1,∴BD⊥A1D.(Ⅱ)过A1作A1E⊥C1D于E,由(I)可知BD⊥平面ACC1A1,∴BD⊥A1E,又BD∩C1D=D,∴A1E⊥平面BC1D,∴∠A1DE为直线A1D与平面BC1D所成角,即sin∠A1DE=,∴cos∠A1DE=±.设AA1=x,则A1D=C1D=,在△A1DC1中,由余弦定理得:=±,解得x=2或x=8.∴AA1=2或8.19.解:(Ⅰ)由题意可得:,则:,所以y关于x的线性回归方程为,当x=10时,百斤=550斤,所以估计如果每个蔬菜大棚使用农夫1号肥料10千克,则这种改良黄瓜每个蔬菜大棚增加量y是550斤.(Ⅱ)记商家总利润为Y元,由已知条件可知至少需安装1台,①安装1台光照控制仪可获得周利润5000元,②安装2台光照控制仪的情形:当X>70时,一台光照控制仪运行,此时Y=5000﹣800=4200元,当30<X≤70时,两台光照控制仪都运行,此时Y=5000+5000=10000元,故Y的分布列为所以EY=4200×0.2+10000×0.8=8840元,③安装3台光照控制仪的情形:当X>70时,一台光照控制仪运行,此时Y=5000﹣1600=3400元,当50≤X≤70时,两台光照控制仪运行,此时Y=5000+5000﹣800=9200元,当30<X<50时,三台光照控制仪都运行,此时Y=5000+5000+5000=15000元,故Y的分布列为所以EY=3400×0.2+9200×0.7+15000×0.1=8620元,综上,为使商家周总利润的均值达到最大应该安装2台光照控制仪.20.解:(Ⅰ)根据题意,抛物线E:y2=2px,则其焦点为,由抛物线的定义可得d2=|PF|,则d1+d2=d1+|PF|,其最小值为点F到直线x﹣y+4=0的距离,∴,解得p=4(舍去负值),∴抛物线E的方程为y2=8x;证明:(Ⅱ)设A(x1,y1),B(x2,y2),由可得,则,所以y1+y2=k1(x1﹣1)+k1(x2﹣1);∴AB的中点M的坐标为,同理可得点N的坐标为,则直线MN的斜率,则k=(k1+k2)=﹣2,则直线l的方程kx﹣y﹣kk1﹣kk2=0可化为y=kx﹣k(k1+k2),即y=kx+2,令x=0可得y=2,∴直线l恒过定点(0,2).21.解:(Ⅰ)因为f(0)=b﹣1,所以过点(0,b﹣1),(2,﹣2)的直线的斜率为k=﹣,而f′(x)=﹣,由导数的几何意义可知,f′(0)=﹣b=﹣,所以b=1,所以f(x)=﹣1,则F(x)=ax+﹣1,F′(x)=a﹣,当a≤0时,F′(x)<0,函数F(x)在R上单调递减;当a>0时,由F′(x)=a﹣=0,得x=﹣ln a,当x∈(﹣∞,﹣ln a)时,F′(x)<0,函数F(x)单调递减,当x∈(﹣ln a,+∞)时,F′(x)>0,函数F(x)单调递增.(Ⅱ)不等式e x f(x)≤c(x﹣1)+1恒成立,即不等式e x+cx﹣c≥0恒成立,设g(x)=e x+cx﹣c,g(x)=e x+c,若c≥0,则g′(x)>0,函数g(x)单调递增且不存在最小值,不满足题意;当c<0时,由g′(x)=e x+c=0,得x=ln(﹣c),当x∈(﹣∞,ln(﹣c))时,g′(x)<0,g(x)单调递减;当x∈(ln(﹣c),+∞)时,g′(x)>0,g(x)单调递增,所以g(x)≥g(ln(﹣c))=﹣2c+c ln(﹣c),要使得g(x)≥0恒成立,只需﹣2c+c ln(﹣c)≥0恒成立,由于c<0,所以有ln(﹣c)≤2,解得﹣e2≤c<0,即当c∈[﹣e2,0)时,g(x)≥0恒成立,即e x+cx﹣c≥0恒成立,也即不等式e x f(x)≤c(x﹣1)+1恒成立,所以实数c的取值范围为[﹣e2,0).22.证明:不妨设a1≤a2≤a3≤a4≤a5,考虑以下5个分数:,,,,,①它们都属于区间(0,1],把区间(0,1]分成两个区间:和,由抽屉原理知,区间或中一定有一个区间至少包含①中的3个数(记这3个数依次为a,b,c),将①中的5个数依次围成一个圆圈,则①中任意三个数中都有两个数是相邻的(与是相邻的),即a,b,c中至少有两个数是相邻的,假设a与b相邻,则另一方面,由①中5个分数的分子、分母的下标特征知,围成的圆圈中,任意相邻两个分数的分子、分母的4个下标互不相同.于是,a、b对应的分数的分子、分母的4个下标符合要求.因此,一定存在4个互不相同的下标i,j,k,l,使得|﹣|<.23.解:(Ⅰ)由(β为参数)消去参数β得:(x﹣1)2+(y﹣1)2=8,∴曲线M是以(1,1)为圆心,为半径的圆.(Ⅱ)设|OA|=ρ1,|OC|=ρ2,∵O,A,C三点共线,则①,将曲线M的方程化成极坐标方程得:ρ2﹣2ρ(sinθ+cosθ)﹣6=0,∴,代入①得:,用代θ得:又∵l1⊥l2,∴,∴,∵sin22θ∈[0,1],∴.。
湖南省长沙市长郡中学2018届高三实验班选拔考试理数试题(解析版)

绝密★启用前长郡中学2017~2018学年新高三实验班选拔考试理科数学试卷本试卷分第I卷和第Ⅱ卷两部分,时量120分钟,满分150分第Ⅰ卷(60分)一、选择题(本大题共12小题,毎小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.若复数(其中,为虚数单位)的虚部为1,则A. 1B. 2C.D.【答案】C【解析】,的虚部为,,故选C.2.已知集合,集合,则A. B. C. D.【答案】B【解析】,,故选B.3.长郡中学要从师生推荐的参加说课比赛的3位男教师和2名女教师中,任选2人参加说课比赛,则选取的2人恰为一男一女的概率为A. B. C. D.【答案】B【解析】由古典概型概率公式,可得选取的人恰为一男一女的概率为,故选B.4.已知等差数列的前项和为,若,则A. 23B. 96C. 224D. 276【答案】D【解析】是等差数列,可设首项为,公差为,由,可得,,故选D.5.已知为双曲线的一个焦点,其关于双曲线的一条渐近线的对称点在另一条渐近线上,则双曲线的离心率为A. B.C. 2D.【答案】C【解析】设右焦点关于渐近线:的对称点为,则在上交于,由点到直线距离公式可得,为直角三角形,三边分别为,由对称性知,,,故选C.6.下列函数在其定义域上既是增函数又是奇函数的是A. B.C. D.【答案】C【解析】对于.函数是奇函数,在为整数)上递增,则不满足;对于.函数为奇函数,由于,则在上递增,则满足;对于.函数为偶函数,则不满足;对于.函数既不是奇函数,也不是偶函数,则不满足,故选C.7.执行如图所示的程序框图,若输,则输出的结果为()A. 7B. 9C. 10D. 11【答案】B【解析】执行程序框图,第一次循环,;第二次循环,;第三次循环,;第四次循环,;结束循环,输出,故选B.【方法点睛】本题主要考查程序框图的循环结构流程图,属于中档题. 解决程序框图问题时一定注意以下几点:(1) 不要混淆处理框和输入框;(2) 注意区分程序框图是条件分支结构还是循环结构;(3) 注意区分当型循环结构和直到型循环结构;(4) 处理循环结构的问题时一定要正确控制循环次数;(5) 要注意各个框的顺序,(6)在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算,直到达到输出条件即可.8.若二项式展开式的各项系数之和为,则含项的系数为A. 560B.C. 280D.【答案】A【解析】因为二项式展开式的各项系数之和为,所以,的通项为,令项的系数为,故选A.9.某几何体的三视图如图,其俯视图中的曲线部分为半圆,则该几何体的体积是A. B.C. D.【答案】C【解析】依题意,由几何体的三视图可知,此几何体为一个直三棱柱和一个半圆柱组成的组合体,且直三棱柱底面为两直角边为和的直角三角形,高为,半圆柱的底面半径为,高为,所以该几何体的体积为,故选C.10.已知椭圆,若直线经过,与椭圆交于两点,且,则直线的方程为A. B. C. D.【答案】B【解析】设直线斜率为,,,由与联立可得,,则,解得,故选B.11.已知三棱锥的每个顶点都在球的表面上,底面,且二面角的正切值为4,则球的表面积为A. B. C. D.【答案】D【解析】设中点为,可得,则是“二面角”的平面角,由于“二面角” 的正切值为,,由余弦定理知,,由正弦定理知,外接圆直径,设外接球半径为,则,球的表面积为,故选D. 【方法点睛】本题主要考查三棱锥外接球表面积的求法,属于难题.要求外接球的表面积和体积,关键是求出求的半径,求外接球半径的常见方法有:①若三条棱两垂直则用(为三棱的长);②若面(),则(为外接圆半径);③可以转化为长方体的外接球;④特殊几何体可以直接找出球心和半径.12.已知函数在区间上有两个零点,则实数的取值范围为A. B. C. D.【答案】A【解析】函数在区间上有两个零点,等价于与的图象有两个交点,设与的图象相切,切点为,则,解得,因为关于的方程,与有两个交点,,故选A.【方法点睛】判断方程零点个数的常用方法:①直接法:可利用判别式的正负直接判定一元二次方程根的个数;②转化法:函数零点个数就是方程根的个数,结合函数的图象与性质(如单调性、奇偶性、周期性、对称性) 可确定函数的零点个数;③数形结合法:一是转化为两个函数的图象的交点个数问题,画出两个函数的图象,其交点的个数就是函数零点的个数,二是转化为的交点个数的图象的交点个数问题 .本题的解答就利用了方法③.第Ⅱ卷(90分)二、填空题(本大题共4小题,每小题5分,共20分)13.若实数满足,则的最小值为__________.【答案】【解析】画出表示的可行域如图,由图知,直线平移经过点时,有最小值为,故答案为.【方法点晴】本题主要考查线性规划中利用可行域求目标函数的最值,属简单题.求目标函数最值的一般步骤是“一画、二移、三求”:(1)作出可行域(一定要注意是实线还是虚线);(2)找到目标函数对应的最优解对应点(在可行域内平移变形后的目标函数,最先通过或最后通过的顶点就是最优解);(3)将最优解坐标代入目标函数求出最值.14.设,,且,则__________.【答案】【解析】由,可得,故答案为.15.已知,,则__________.【答案】【解析】,,故答案为.16.在数列中,首项不为零,且,为的前项和.令,则的最大值为__________.【答案】【解析】数列首项,所以数列是公比为的等比数列,,,,所以,设,令,当且时取等号,,即的最大值为,故答案为.三、解答题(本大题共7小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.在锐角中,分别为角的对边,且.(Ⅰ)求的大小;(Ⅱ)若,求面积的取值范围.【答案】(1) ;(2).【解析】试题分析:(Ⅰ)由,根据二倍角的正弦、余弦公式以及辅助角公式化简可得,从而可得结果;(Ⅱ)在中,由正弦定理得,又,∴,∴,又∵,从而可得结果.试题解析:(Ⅰ)∵,∴①,又∵,∴②,又③,将①,②,③代入已知得:,整理得,即,又∵,∴,即.(Ⅱ)由(Ⅰ)得,∴,∵为锐角三角形,∴且,解得,在中,由正弦定理得:,∴,又,∴,∴,又∵,∴.18.如图,在直三棱柱中,,为线段的中点.(Ⅰ)求证:;(Ⅱ)若直线与平面所成角的正弦值为,求的长.【答案】(1)证明见解析;(2)或.【解析】【详解】试题分析:(Ⅰ)由直棱柱的性质可得,由等腰三角形的性质可得,由线面垂直的判定定理可得平面,进而由面面垂直的判定定理可得结论;(Ⅱ)以为原点,为轴,为轴,过点平行于的直线为轴建立空间直角坐标系,设,求出平面的一个法向量及,利用空间向量夹角余弦公式可得结果.试题解析:(Ⅰ)∵三棱柱是直三棱柱,∴平面,又平面∴,∵,是的中点,∴,又平面平面,∴平面,又平面,∴.(Ⅱ)由(Ⅰ)知平面,故以为原点,为轴,为轴,过点平行于的直线为轴建立空间直角坐标系(如图所示),设,则,∴,· 设平面的一个法向量,则,即,则,令可得,,故,设直线与平面所成角为,则,解得或,即或.19.某地4个蔬菜大棚顶部,阳光照在一棵棵茁壮生长的蔬菜上.这些采用水培、无土栽培方式种植的各类蔬菜,成为该地区居民争相购买的对象.过去50周的资料显示,该地周光照量(小时)都在30以上.其中不足50的周数大约有5周,不低于50且不超过70的周数大约有35周,超过70的大约有10周.根据统计某种改良黄瓜每个蔬菜大棚增加量(百斤)与每个蔬菜大棚使用农夫1号液体肥料(千克)之间对应数据为如图所示的折线图:(Ⅰ)依据数据的折线图,用最小二乘法求出关于的线性回归方程;并根据所求线性回归方程,估计如果每个蔬菜大棚使用农夫1号肥料10千克,则这种改良黄瓜每个蔬菜大棚增加量是多少斤?(Ⅱ)因蔬菜大棚对光照要求较大,某光照控制仪商家为应对恶劣天气对光照的影响,为该基地提供了部分光照控制仪,该商家希望安装的光照控制仪尽可能运行,但每周光照控制仪最多可运行台数受周光照量限制,并有如下关系:周光照量若某台光照控制仪运行,则该台光照控制仪周利润为5000元;若某台光照控制仪未运行,则该台光照控制仪周亏损800元,欲使商家周总利润的均值达到最大,应安装光照控制仪多少台?附:回归方程系数公式:.【答案】(1) ;(2).【解析】试题分析:(Ⅰ)算出样本中心点的坐标,利用公式求得,由可得,即可得回归方程,再将时代入即可得结果;(Ⅱ)分别求出安装2台光照控制仪的周利润的均值、安装3台光照控制仪的均值,与安装1台光照控制仪可获得周利润进行比较即可得结果.试题解析:(Ⅰ),,,,所以关于的线性回归方程为,当时,百斤=550斤,所以估计如果每个蔬菜大棚使用农夫1号肥料10千克,则这种改良黄瓜每个蔬菜大棚增加量是500斤.(Ⅱ)记商家总利润为元,由已知条件可知至少需安装1台,①安装1台光照控制仪可获得周利润5000元,②安装2台光照控制仪的情形:当时,一台光照控制仪运行,此时元,当时,两台光照控制仪都运行,此时元,故的分布列为所以元,③安装3台光照控制仪的情形:当时,一台光照控制仪运行,此时元,当时,两台光照控制仪运行,此时元,当时,三台光照控制仪都运行,此时元,故的分布列为所以元,综上,为使商家周总利润的均值达到最大应该安装2台光照控制仪.【方法点晴】本题主要考查线性回归方程及离散型随机变量的分布列与数学期望,属于难题.求回归直线方程的步骤:①依据样本数据确定两个变量具有线性相关关系;②计算的值;③计算回归系数;④写出回归直线方程为;(2) 回归直线过样本点中心是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.20.已知是抛物线上一点,到直线的距离为,到的准线的距离为,且的最小值为.(Ⅰ)求抛物线的方程;(Ⅱ)直线交于点,直线交于点,线段的中点分别为,若,直线的斜率为,求证:直线恒过定点.【答案】(1) ;(2)证明见解析.【解析】试题分析:(Ⅰ)的最小值等价于点到直线的距离,∴,解得,从而可得结果;(Ⅱ)设,由可得,由中点坐标公式以及斜率公式可得的斜率,直线的方程可化为,从而可得结果.试题解析:(Ⅰ)抛物线的焦点为,由抛物线的定义可得,则,其最小值为点到直线的距离,∴,解得(舍去负值),∴抛物线的方程为.(Ⅱ)设,由可得,则,所以∴的中点的坐标为,同理可得点的坐标为,则直线的斜率,则,则直线的方程可化为,即,令可得,∴直线恒过定点.【方法点睛】本题主要考查待定系数法求抛物线方程及韦达定理、直线和抛物线的位置关系、最值问题及直线过定点问题.属于难题. 探索曲线过定点的常见方法有两种:① 可设出曲线方程,然后利用条件建立等量关系进行消元,借助于曲线系的思想找出定点(直线过定点,可以根据直线的各种形式的标准方程找出定点). ② 从特殊情况入手,先探求定点,再证明与变量无关.21.已知函数(,为自然对数的底数)在点处的切线经过点.(Ⅰ)讨论函数的单调性;(Ⅱ)若,不等式恒成立,求实数的取值范围.【答案】(1) 当时,函数在上单调递减;当时,函数在上递减,函数在上单调递增;(2).【解析】试题分析:(Ⅰ)求出,由过点的直线的斜率为可得,讨论两种情况,分别由得增区间,得减区间;(Ⅱ)原不等式等价于不等式恒成立,利用导数研究的单调性,求其最小值,令其最小值不小于零即可得结果.试题解析:(Ⅰ)因为,所以过点的直线的斜率为,而,由导数的几何意义可知,,所以,所以.则,当时,,函数在上单调递减;当时,由得,当时,,函数单调递减,当时,,函数单调递增.(Ⅱ)不等式恒成立,即不等式恒成立,设,若,则,函数单调递增且不存在最小值,不满足题意;当时,由得,当时,单调递减;当时,单调递增,所以,要使得恒成立,只需恒成立,由于,所以有,解得,即当时,恒成立,即恒成立,也即不等式恒成立,所以实数的取值范围为.22.设,,,,是5个正实数(可以相等).证明:一定存在4个互不相同的下标,,,,使得.【答案】证明见解析.【解析】试题分析:可设,则,,,,都属于区间,由抽屉原理知,区间或中一定有一个区间至少包含其中的3个数,5个分数的分子、分母的下标特征知,围成的圆圈中,任意相邻两个分数的分子、分母的4个下标互不相同.、对应的分数的分子、分母的4个下标符合要求.因此,结论成立.试题解析:不妨设,考虑以下5个分数:,,,,,①它们都属于区间.把区间分成两个区间:和,由抽屉原理知,区间或中一定有一个区间至少包含①中的3个数(记这3个数依次为,,).将①中的5个数依次围成一个圆圈,则①中任意三个数中都有两个数是相邻的(与是相邻的),即,,中至少有两个数是相邻的.假设与相邻,则.另一方面,由①中5个分数的分子、分母的下标特征知,围成的圆圈中,任意相邻两个分数的分子、分母的4个下标互不相同.于是,、对应的分数的分子、分母的4个下标符合要求.因此,结论成立.23.选修4-4:坐标系与参数方程在直角坐标系中,已知曲线的参数方程为(为参数),在极坐标系中,直线的方程为:,直线的方程为.(Ⅰ)写出曲线的直角坐标方程,并指出它是何种曲线;(Ⅱ)设与曲线交于两点,与曲线交于两点,求四边形面积的取值范围.【答案】(1) 以为圆心,为半径的圆;(2).【解析】试题分析:(Ⅰ)利用平方法可消去参数,从而可得曲线的直角坐标方程,进而得它是何种曲线;(Ⅱ)设,,曲线的方程化成极坐标方程,将曲线的方程化成极坐标方程得:,∴,,从而可得结果.试题解析:(Ⅰ)由(为参数)消去参数得:,∴曲线是以为圆心,为半径的圆.(Ⅱ)设,,∵三点共线,则①,将曲线的方程化成极坐标方程得:,∴,代入①得:,用代得:又∵,∴,∴,∵,∴。
长郡中学理科实验班招生考试数学试卷
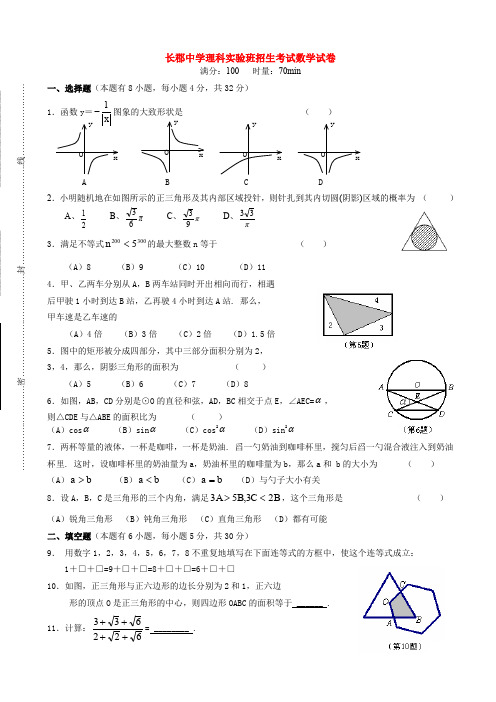
长郡中学理科实验班招生考试数学试卷满分:100 时量:70min一、选择题(本题有8小题,每小题4分,共32分) 1.函数y =1x -图象的大致形状是 ( ) A B C D 2.小明随机地在如图所示的正三角形及其内部区域投针,则针扎到其内切圆(阴影)区域的概率为 ( ) A 、21 B 、π63 C 、π93 D 、π33 3.满足不等式3002005<n 的最大整数n 等于 ( ) (A )8 (B )9 (C )10 (D )11 4.甲、乙两车分别从A ,B 两车站同时开出相向而行,相遇 后甲驶1小时到达B 站,乙再驶4小时到达A 站. 那么, 甲车速是乙车速的 (A )4倍 (B )3倍 (C )2倍 (D )1.5倍 5.图中的矩形被分成四部分,其中三部分面积分别为2, 3,4,那么,阴影三角形的面积为 ( ) (A )5 (B )6 (C )7 (D )8 6.如图,AB ,CD 分别是⊙O 的直径和弦,AD ,BC 相交于点E ,∠AEC=α, 则△CDE 与△ABE 的面积比为 ( ) (A )cos α (B )sin α (C )cos 2α (D )sin 2α 7.两杯等量的液体,一杯是咖啡,一杯是奶油. 舀一勺奶油到咖啡杯里,搅匀后舀一勺混合液注入到奶油杯里. 这时,设咖啡杯里的奶油量为a ,奶油杯里的咖啡量为b ,那么a 和 b 的大小为 ( ) (A )b a > (B )b a < (C )b a = (D )与勺子大小有关8.设A ,B ,C 是三角形的三个内角,满足B C B A 23,53<>,这个三角形是 ( )(A )锐角三角形 (B )钝角三角形 (C )直角三角形 (D )都有可能二、填空题(本题有6小题,每小题5分,共30分)9. 用数字1,2,3,4,5,6,7,8不重复地填写在下面连等式的方框中,使这个连等式成立:1+□+□=9+□+□=8+□+□=6+□+□10.如图,正三角形与正六边形的边长分别为2和1,正六边形的顶点O 是正三角形的中心,则四边形OABC 的面积等于 ______ .11.计算:622633++++= ________ .y x O y x O y x O y x O ……………..………….密………………..…………….封……………………………..线…………………….12.五支篮球队举行单循坏赛(就是每两队必须比赛1场,并且只比赛一场),当赛程进行到某天时,A 队已赛了4场,B 队已赛了3场,C 队已赛了2场,D 队已赛了1场,那么到这天为止一共已经赛了 __ 场,E 队比赛了 ___ 场.13.已知∠AOB=30°,C 是射线OB 上的一点,且OC=4,若以C 为圆心,半径为r 的圆与射线OA 有两个不同的交点,则r 的取值范围是_____________14.如图,△ABC 为等腰直角三角形,若 AD=31AC ,CE=31BC ,则∠1 __ ∠2 (填“>”、“<”或“=”)三.解答题(共38分) 15. (12分)今年长沙市筹备60周年国庆,园林部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配A B ,两种园艺造型共50个摆放在五一大道两侧,已知搭配一个A 种造型需甲种花卉80盆,乙种花卉40盆,搭配一个B 种造型需甲种花卉50盆,乙种花卉90盆.(1)某校九年级(1)班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来.(2)若搭配一个A 种造型的成本是800元,搭配一个B 种造型的成本是960元,试说明(1)中哪种方案成本最低?最低成本是多少元?16.(12分)如图,ABC △是O 的内接三角形,AC BC =,D 为O 中AB 上一点,延长DA 至点E ,使CE CD =.(1)求证:AE BD =;(2)若AC BC ⊥,求证:2AD BD CD +=.(第14题)C E A O D B17.(14分)如图,在等腰梯形ABCD中,AD∥BC,AB=DC=50,AD=75,BC=135.点P从点B出发沿折线段BA-AD-DC以每秒5个单位长的速度向点C匀速运动;点Q从点C出发沿线段CB方向以每秒3个单位长的速度匀速运动,过点Q向上作射线QK⊥BC,交折线段CD-DA-AB于点E.点P、Q同时开始运动,当点P与点C重合时停止运动,点Q也随之停止.设点P、Q运动的时间是t秒(t>0).(1)当点P到达终点C时,求t的值,并指出此时BQ的长;(2)当点P运动到AD上时,t为何值能使PQ∥DC ?(3)设射线QK扫过梯形ABCD的面积为S,分别求出点E运动到CD、DA上时,S与t的函数关系式;(不必写出t的取值范围)(4)△PQE能否成为直角三角形?若能,写出t的取值范围;若不能,请说明理由.参考答案选择题 D C D C C C C B9. 1+8+6=9+5+1=8+3+4=6+7+210. 33 11. 26 12. 6场,2场 13.223r <≤ 14.=15.(1)解:设搭配A 种造型x 个,则B 种造型为(50)x -个,依题意,得:8050(50)34904090(50)2950x x x x +-⎧⎨+-⎩≤≤ ,解这个不等式组,得:3331x x ⎧⎨⎩≤≥,3133x ∴≤≤ x 是整数,x ∴可取313233,,,∴可设计三种搭配方案:①A 种园艺造型31个 B 种园艺造型19个②A 种园艺造型32个 B 种园艺造型18个③A 种园艺造型33个 B 种园艺造型17个.(2)应选择方案③,成本最低,最低成本为42720元16.证明:(1)在ABC △中,CAB CBA ∠=∠.在ECD △中,CAB CBA ∠=∠.CBA CDE ∠=∠,(同弧上的圆周角相等),ACB ECD ∴∠=∠. ACB ACD ECD ADE ∴∠-∠=∠-∠.ACE BCD ∴∠=∠.在ACE △和BCD △中,ACE BCD CE CD AC BC ∠=∠==;;ACE BCD ∴△≌△.AE BD ∴=.(2)若AC BC ACB ECD ∠=∠⊥,.9045ECD CED CDE ∴∠=∴∠=∠=,.2DE CD ∴=,又AD BD AD EA ED +=+= 2AD BD CD ∴+=17.解:(1)t =(50+75+50)÷5=35(秒)时,点P 到达终点C .此时,QC=35×3=105,∴BQ 的长为135-105=30.(2)如图8,若PQ ∥DC ,又AD ∥BC ,则四边形PQCD为平行四边形,从而PD=QC ,由QC=3t ,BA+AP=5t得50+75-5t=3t ,解得t=1258. 经检验,当t=1258时,有PQ ∥DC . (3)①当点E 在CD 上运动时,如图9.分别过点A 、D作AF ⊥BC 于点F ,DH ⊥BC 于点H ,则四边形ADHF 为矩形,且△ABF ≌△DCH ,从而FH= AD=75,于是BF=CH=30.∴DH=AF=40. DK P QH Q CDH=4t.又QC=3t,从而QE=QC·tanC=3t·CH(注:用相似三角形求解亦可)QE·QC=6t2;∴S=S⊿QCE =12②当点E在DA上运动时,如图8.过点D作DH⊥BC于点H,由①知DH=40,CH=30,又QC=3t,从而ED=QH=QC-CH=3t-30.(ED+QC)DH =120 t-600.∴S= S梯形QCDE =12(4)△PQE能成为直角三角形.。
2018年湖南省长沙市长郡中学高中理实班招生拔尖试题

2018年湖南省长沙市长郡中学高中理实班招生拔尖试题(时间:90分钟满分:120分)一、选择题(本大题共6小题,每小题5分,共30分)1.对于任意的有理数a ,方程0)43()1(222=+--++b a a x a x 的根总是有理数,则b 的值为( )A .1B .-1C .2D .02.如图,平面中两条直线1l 和2l 相交于点O ,对于平面上任意一点M ,若p ,q 分别是M 到直线1l 和2l 的距离,则称有序非负实数对(p ,q )是点M 的“距离坐标”根据上述定义,有以下几个结论: ①“距离坐标”是(0,1)的点有1个;②“距离坐标”是(5,6)的点有4个;iM (p ,q ) ③“距离坐标”是(a ,a )(a 为非负实数)的点有4个其中正确的有 ( )A .0个B .1个C .2个D .3个3.一张等腰三角形纸片,底边长13cm ,底边上的高为32.5cm .现沿底边依次从下往上裁剪宽度均为5cm 的矩形纸条,如图所示已知剪得的纸条中有一张是正方形,则这张正方形纸条是( ) A .第3张 B .第4张C .第5张D .第6张4.如图,正方形ABCD 的边长为1,点M ,N 分别在BC ,CD 上,且△CMN 的周长为2,则△MAN 的面积的最小值为( )A .12-B .222-C .22D .122-5.如图,将一张三角形纸片沿虚线剪成甲、乙、丙三块,其中甲、丙为梯形,乙为三角形,根据图中标示的边长数据,比较甲、乙、丙的面积大小,下列判断正确的是 ( )A .乙>丙>甲B .丙>乙>甲C .甲>丙>乙D .无法判断6.将一枚六个面编号分别为1,2,3,4,5,6的质地均匀的正方体骰子先后投掷两次,记第一次掷出的点数为a 第二次掷出的点数为b ,则使关于x ,y 的方程组⎩⎨⎧=+=+223y x by ax ,只有正数解的概率为( )A .121 B .92C .185 D .3613 二、填空题(本大题共6小题,每小题5分,共30分)7.计算:24066312305941--+++=.8.已知||x-2|-b |=a 有四个不同的解,则||||||||b ba a ab a b b a b a ++--+++=. 9.若抛物线1422++-=p px x y 中不管p 取何值时都通过定点,则定点坐标为. 10.如图,半径为r 的圆O 沿折线ABCDE 作无滑动的滚动,如果AB =BC =CD =DE =r π2,∠ABC =∠CDE =150°,∠BCD=120°,那么,圆O 自点A 至点E 转动了周.11.二次函数a ax x y ++=22在21≤≤-x 上有最小值-4,则a 的值为.12.在平面直角坐标系中,已知P 1的坐标为(1,0),将其绕着原点按逆时针方向旋转30°得到P 2,延长OP 2到P 3使OP 3=2OP 2,再将P 3绕原点按逆时针方向旋转30°得到P 4,延长OP 4到P 5,使OP 5=2OP 4,如此继续下去,则点P 2010的坐标为.三、解答题(本大题共5小题,第13题10分,第14-16题各12分,第17题14分,共60分)13.已知m ,n 是方程0132=++x x 的两根.(1)求mm m m m 23102)5165(---⋅--+的值; (2)求m n n m 33+的值.14.甲、乙两人从A 地到B 地,甲骑自行车,乙步行,已知甲每小时比乙每小时多走8千米,甲、乙同时出发,甲比乙早到5小时,若甲到B 地后立即沿原路返回,则在距B 地15千米处与乙相遇,求A ,B 两地间的距离及甲、乙两人的速度.15.如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D,P分别是AC,BC的中点,△ADE是等腰三角形,∠AED=90°,连接BE,EC.(1)判断线段BE和EC的关系,并证明你的结论;(2)连接P A,PE,过点A作AM∥PE,过点E作EM∥P A,AM和EM相交于点M,在图中先补充图形,再判断四边形P AME的形状,并证明你的结论.16.如图,在 ABCD 中,E 为对角线BD 上一点,且满足∠ECD =∠ACB ,AC的延长线与△ABD 的外接圆交于点F ,证明:∠DFE =∠AFB .17.如图,在平面直角坐标系中,直角梯形OABC 的顶点A ,B 的坐标分别是(5,0),(3,2),点D 在线段OA 上,BD =BA ,点Q 是线段BD 上一个动点,点P 的坐标是(0,3),设直线PQ 的解析式为y =kx +b(1)求k 的取值范围;(2)当k 为取值范围内的最大整数时,若抛物线ax ax y 52-=的顶点在直线PQ ,OA ,AB ,BC 围成的四边形内部,求a 的取值范围.。
