等腰梯形的性质判定复习
等腰梯形的性质和判定

1.4 等腰梯形的性质和判定一、操作:请你在下图中的每个三角形中画一条线段,使线段的两个端点分别在三角形的两边上。
1、怎样画才能得到一个梯形?2、在你得到的梯形中,有特殊梯形吗?腰梯形的判定定理:在同一底上的两个角相等的梯形是等腰梯形已知:如图梯形ABCD ,AD ∥BC ,∠B=∠C 求证:梯形ABCD 是等腰梯形等腰梯形性质定理:1、等腰梯形同一底上的两底角相等。
2、等腰梯形的两条对角线相等。
已知:在等腰梯形ABCD 中,AD ∥BC ,AB=CD ,对角线AC 和BD 相交于点O 。
求证:(1)∠ABC=∠DCB (2)AC=BD例1:判断下列说法是否正确。
(1)一组对边平行的四边形是梯形.(2)等腰梯形的对角线相等. (3)等腰梯形的两个底角相等. (4)等腰梯形有一条对称轴.例2、如图,等腰梯形ABCD 中,AD ∥BC ,点E 是AD 延长线上一点,DE =BC .(1)求证:∠E =∠DBC ;(2)判断△ACE 的形状C B A C B A C B AD C BA D CB A ED C B A练习:1、将两个形状相同的三角板放置在一张矩形纸片上,按图示画线得到四边形ABCD ,则四边形ABCD 的形状是 .依据: .2.如图,在等腰梯形ABCD 中,AB=CD=8,BC=15,∠B=60°,则AD= .3、已知如图,等腰梯形ABCD 的面积是4㎝2,M 为CD 中点,连AM ,BM ,则△ABM 的面积是_______4、如图,在等腰梯形ABCD 中,AD ∥BC ,对角线AC ⊥BD ,AC =6, AD +BC = .5、如图2,在梯形ABCD 中,AD∥BC,点E 是BC 边的中点,EM ⊥AB ,EN ⊥CD ,垂足分别为M 、N 且 EM =EN .求证:梯形ABCD 是等腰梯形。
6.如图,在梯形ABCD 中,AD ∥BC ,B=900,AD=24cm ,AB=8cm ,BC=26cm ,动点P 从A 点开始沿AD 边以1cm/秒的速度向D 运动,动点Q 从C 点开始沿CB 边以3cm/秒的速度向B 运动,P 、Q 分别从A 、C 同时出发,当其中一点到端点时,另一点也随之停止运动。
二十七讲 等腰梯形复习

易 错 防 范 课 时 跟 踪 检 测
上 页
下 页
返 回
中考步步高
课 前 必 读 对 接 中 考
考情分析 年份 考查点 梯形中位线性质(3分) 等腰梯形的性质(3分) 等腰梯形的判定(8分) 题型 填空题 填空题 解答题 难易度 容易 中等 中等
网 络 构 建 考 点 梳 理
近三 2010年 年浙 江省 2011年 中考 情况 2012年
求证:梯形ABCD是等腰梯形.
易 错 防 范 课 时 跟 踪 检 测
上 页
下 页
返 回
中考步步高
课 前 必 读 对 接 中 考
证明
∵AD∥BC,∴∠ADB=∠DBC,
网 络 构 建 考 点 梳 理
∵BD平分∠ABC,∴∠ABD=∠CBD,
∴∠ADB=∠ABD,∴AB=AD,
∵AD=DC,∴AB=CD, ∵四边形ABCD是梯形, ∴梯形ABCD是等腰梯形.
上 页
下 页
返 回
中考步步高
解析
课 前 必 读
过 E 点作 EG⊥DF,
对 接 中 考
∵E 是 AB 的中点, AB=6,∴AE=DG=3, ∵EG=AD= DG 3,tan∠DEG= = 3 EG
网 络 构 建 考 点 梳 理
∴∠DEG=60°,∵∠DEF=120°, GF ∴tan 60°= , 3 解得 GF=3,∴DF=6.
易 错 防 范 课 时 跟 踪 检 测
上 页
下 页
返 回
中考步步高
课 前 必 读 对 接 中 考
对接点三:梯形的中位线
常考角度
运用梯形中位线的性质进行相关的计算.
网 络 构 建 考 点 梳 理
等腰梯形的性质与判定

等腰梯形的性质与判定等腰梯形是指具有两条平行边且两组对边相等的四边形。
在几何学中,等腰梯形是一种特殊的多边形,具有一些独特的性质和判定方法。
本文将探讨等腰梯形的性质以及如何判定一个四边形是否为等腰梯形。
一、等腰梯形的性质1.等腰梯形的两底角相等:等腰梯形的两底角(非对顶角)相等。
证明如下:连接等腰梯形的两个非平行边,可以得到两个全等的三角形,根据三角形的性质可知,两个三角形的对应角相等,因此两底角相等。
2.等腰梯形的对顶角互补:等腰梯形的两对顶角互补(角的和为180度)。
证明如下:连接等腰梯形的两个对角,可以得到两个对顶的全等三角形,根据全等三角形的性质可知,两个对顶角互补。
3.等腰梯形的对边平行:等腰梯形的两条对边平行。
证明如下:连接等腰梯形的两个对顶点和两个底边的中点,可以得到一对全等的三角形和一对等腰三角形。
根据全等三角形的性质可知,两个底边的中点连线平行于顶点连线,即证得两对边平行。
二、判定一个四边形是否为等腰梯形1.判定条件一:两底边相等且两腰边相等。
如果一个四边形的两条底边相等且两条腰边相等,那么这个四边形就是等腰梯形。
这个判定条件基于等腰梯形的定义,即两组对边相等。
2.判定条件二:两底角相等。
如果一个四边形的两个底角相等,那么这个四边形可能是等腰梯形。
这个判定条件基于等腰梯形的性质之一,即两底角相等。
但需要注意的是,仅满足该条件并不能确定一个四边形为等腰梯形,因为它可能是其他类型的四边形,如矩形或平行四边形。
3.判定条件三:对角线平分一个角。
如果一个四边形的对角线能够平分其中一个角,那么这个四边形就是等腰梯形。
这个判定条件基于等腰梯形的性质之一,即对角线平分一个角。
总结起来,判定一个四边形为等腰梯形的充分条件是:两底边相等且两腰边相等,或者两底角相等,或者对角线能够平分一个角。
但需要注意的是,这些条件并不一定都是必要条件,因为其他类型的四边形也可能满足这些条件。
结论等腰梯形是具有两条平行边且两组对边相等的四边形。
八年级数学等腰梯形的判定1

性质一:等腰梯形同一底上的两个角相等。 性质二:等腰梯形的对角线相等。 逆命题: 同一底上的两个角相等的梯形
是等腰梯形。
逆命题:对角线相等的梯形是等腰梯形。
逆命题: 同一底上的两个角相等的梯形 是等腰梯形。 A D
已知: 在梯形ABCD 中, AD//BC,
∠ B= ∠ C.
B (3) C
(2 )
3、已知: 在梯形ABCD 中,AD//BC, E为BC中点,EF 垂直 A B, EG垂直CD,EF=EG。 求证: 梯形ABCD为等腰梯形? A F B E D G C
逆命题:对角线相等的梯形为等腰梯形。
已知: 在梯形ABCD 中, AD//BC,AC=BD
求证: 梯形ABCD为等腰梯形。 A D
∠ACB= ∠DBC.
求证: 梯形ABCD是等腰梯形
A O B C D
请把你的收获告诉大家,
让我们一起分享!
判定一:同一底上的两角相等的梯形为
等腰梯形。
判定二:对角线相等的梯形为等腰梯形.
A B
D C
A B
A B
D
C D C B
A
D
C A B D B
A
D C
C
请各位老师提出宝贵意见
三寸人间 / 三寸人间
求证 : 梯形ABCD为等 腰梯形. (1) (2)
已知:
在梯形ABCD 中,AD//BC, ∠ B= ∠ C.
求证 :
梯形ABCD为等腰梯形.Fra bibliotekA DB
E
C
已知:
在梯形ABCD 中,AD//BC, ∠ B= ∠ C.
求证 :
梯形ABCD为等腰梯形.
A
等腰梯形的性质与判定

直角梯形
A
DBC来自(1)定义法:两条腰相等的梯形是等腰梯形。 (2)定理:同一底上的两个内角相等的梯形是等腰梯形。 (3)定理:对角线相等的梯形是等腰梯形。
A A D B B
图1
D
C
图2
C
一组对边平行而
四边形
等腰梯形
梯形
另一组对边不平行
直角梯形
二、等腰梯形的性质 (1)两底平行,两腰相等 AD∥BC, AB=CD (2)同底上两角相等 ∠A= ∠D, ∠B= ∠C (3)对角线相等 AC=BD B A D
C
(4)是轴对称图形
证明:等腰梯形同一底上两个角相等
C
等腰梯形的判定方法
1、定义法:两条腰相等的梯形是等腰梯形。
2、定理:同一底上的两个内角相等的梯形是等腰梯形。 3、定理:对角线相等的梯形是等腰梯形。
同一底上的两个内角相等的梯形是等腰梯形
已知:如图, 在梯形ABCD中,AD∥BC,∠B=∠C。 求证:梯形ABCD是等腰梯形。 证明:如图,过点D作DE//AB,交BC于点E,则 ∠1=∠B. ∵AD//BC, DE//AB. ∴四边形ABED是平行四边形. ∴AB=DE(平行四边形对边相等). ∵ ∠B =∠C ∴∠1=∠C ∴DE=DC(等角对等边) ∴ AB=DC(等量代换) ∴梯形ABCD是等腰梯形
D
B
E
F
C
辅助线:作高
E
证明3:延长BA,CD相交点E. ∵ ∠B =∠C ∴ BE=CE(等角对等边) ∴ ∠1 =∠B, ∠2 =∠C (两直线平行,同位角相等) ∴ ∠1 =∠2 (等量代换) ∴ AE=DE(等角对等边) ∴ BE -AE=DE-CE 即AB=DC ∴梯形ABCD是等腰梯形
等腰梯形的性质定理和判定定理及其证明

等腰梯形的性质定理和判定定理及其证明等腰梯形是指具有两边边长相等的梯形。
在等腰梯形的性质定理和判定定理中,我们会探讨一些关于其边长,角度,和对角线的性质。
下面,我将解释等腰梯形的性质定理和判定定理,并给出它们的证明。
性质定理1:等腰梯形的两个底角是相等的。
证明:考虑一个等腰梯形ABCD,其中AB和CD是底边,BC和AD是斜边。
假设∠A和∠B是两个底角。
首先,我们可以根据等腰梯形的性质,得到AB=CD。
接着,我们可以通过等边三角形来证明∠BAD≌∠CBA。
因为AB=CD,所以三角形ABC和三角形DCA是等边三角形。
因此,∠ABC≌∠CDA和∠CAB≌∠DAC。
我们可以通过相邻角的和等于180度的原理,得到∠BAD+∠ABC+∠CAB=180度和∠CBA+∠CDA+∠DAC=180度。
由于∠ABC≌∠CDA和∠CAB≌∠DAC,所以∠BAD+∠ABC+∠CAB=∠BAD+∠CDA+∠DAC。
因此,根据相等的角度和等于相等的角度之和,我们得到∠BAD+∠ABC+∠CAB=∠CBA+∠CDA+∠DAC。
将等腰梯形的性质AB=CD和∠BAD+∠ABC+∠CAB=∠CBA+∠CDA+∠DAC代入其中,我们可以得到∠BAD=∠CBA。
因此,等腰梯形的两个底角是相等的。
性质定理2:等腰梯形的两个对角线相等。
证明:考虑一个等腰梯形ABCD,其中AB和CD是底边,BC和AD是斜边。
我们需要证明AC=BD。
我们已经知道∠BAD=∠CBA。
因此,∠BAD和∠CBA是等腰梯形的两个底角,根据性质定理1,我们可以知道∠A=∠D和∠B=∠C。
我们可以通过相同边上的相等角来证明∠BAD≌∠BCD和∠ABD≌∠ACD。
因为∠A=∠D和∠B=∠C,所以AB//CD。
根据平行线的性质,我们得到∠ABD≌∠CDA和∠ACD≌∠BDA。
因此,根据等腰三角形的定义,我们可以知道三角形ABD和三角形CAD是等腰三角形。
因此,AD=BD和AC=CD。
等腰梯形的性质和判定

等腰梯形的性质和判定适用精选文件资料分享等腰梯形的性质和判断§1.4 等腰梯形的性质和判断一、预习导学 1 、______________ _________________的图形叫做等腰梯形。
2 、____________相等的____________ ___叫做等腰梯形 ; 3 、依据等腰梯形的定义,一个图形要成为等腰梯形 , 第一它一定是 _____, 还要具备 _____相等 ; 4 、由等腰三角形的判判定理猜想等腰梯形的判断定理:定理的证明:已知:求证:(解析:本题可以从以下的三个角度着手证明(附三种方法的图形)。
)证法一:证法二:证法三:5、定理的书写格式∵∴_________________________ 6、等腰梯形的性质 1 、定理 1、等腰梯形同一底上的两底角相等。
定理 2 、等腰梯形的两条对角线相等。
2 、证明等腰梯形的性质二、自主研究如图,已知在梯形 ABCD中, AD∥BC,AB=DC,对角线AC和 BD订交于点 O,E 是 B C边上的一个动点(点E 不于 B、C 两点重合),EF∥BD交 AC于点 F。
EG∥AC交 BD于点 G。
(1)、求证:四边形 EFOG的周长等于 2OB;(2)、请将上述题目的条件“梯形A BCD 中, AD∥B C,AB=DC”改为另一种四边形,其余条件不变,使得结论“四边形EFOG的周长等于2OB”仍成立,并将改编后的题目画出图形,写出已知、求证,不用证明。
三、反响练习1、如图,等腰梯形 ABCD中, AD∥BC,AB=CD。
点 E 是 AD延长线上一点,DE=B C.(1)求证:∠ E=∠ DBC;(2)判断△ ACE的形状(不需要说明原由).2.如图2,在梯形ABCD中,AD∥BC,点 E 是BC边的中点,EM⊥AB,EN⊥CD,垂足分别为M、N且EM=EN.求证:梯形ABCD 是等腰梯形。
3.证明等腰梯形一底边的中点到另一底两端的距离相等。
§1.4等腰梯形的的性质与判定
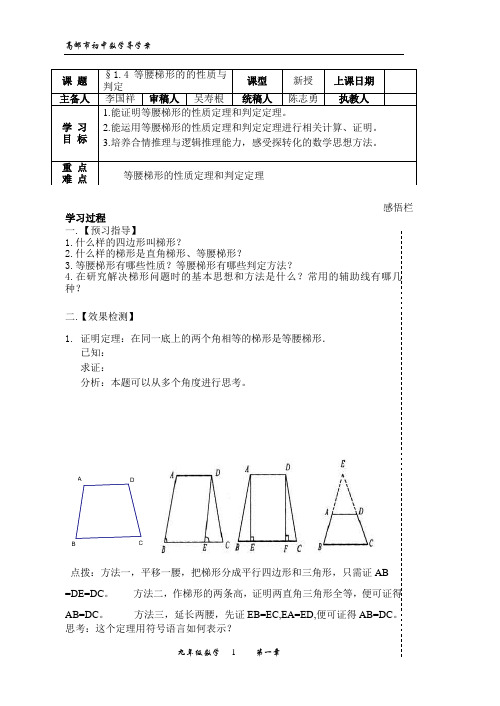
学习过程一.【预习指导】1.什么样的四边形叫梯形?2.什么样的梯形是直角梯形、等腰梯形?3.等腰梯形有哪些性质?等腰梯形有哪些判定方法?4.在研究解决梯形问题时的基本思想和方法是什么?常用的辅助线有哪几种?二.【效果检测】1. 证明定理:在同一底上的两个角相等的梯形是等腰梯形. 已知:求证:分析:本题可以从多个角度进行思考。
点拨:方法一,平移一腰,把梯形分成平行四边形和三角形,只需证AB=DE=DC 。
方法二,作梯形的两条高,证明两直角三角形全等,便可证得AB=DC 。
方法三,延长两腰,先证EB=EC,EA=ED,便可证得AB=DC 。
思考:这个定理用符号语言如何表示?感悟栏DC B A三.【小组检查】感悟栏小组内成员就上述习题进行讨论、修正。
四.【布置任务】师生互动探究问题1. “在同一底上的两个角相等的梯形是等腰梯形”的逆命题是什么?证明:等腰梯形同一底上的两底角相等。
思考:这个定理用符号语言如何表示?问题2. 等腰梯形的两条对角线相等。
思考:这个定理用符号语言如何表示?五.【小组交流】学生展示1.证明:等腰梯形同一底上的两底角相等。
2.证明:两条对角线相等的梯形是等腰梯形六.【课堂训练】拓展延伸问题3.如图等腰梯形ABCD 中,AD ∥BC ,AB=DC ,M 是AD 的中点, 求证:BM=CM思考:你能够用一个命题概括吗?拓展:(1)如图等腰梯形ABCD 中,AD ∥BC ,BM=CM 。
求证: M 是AD 的中点(2)如图梯形ABCD 中,AD ∥BC ,M 是AD 的中点,BM=CM 。
求证:四边形ABFE 是等腰梯形;七.【课堂小结】1.梯形性质和判定定理是什么?2.解决梯形问题的基本思想和方法有哪些?3.解决梯形问题时,常用的辅助线有哪几种?.4.你还有哪些困惑?B C A M D感悟栏八.【课堂反馈】 班级____________ 姓名________ 成绩____________1.四边形的四个内角的度数比是2∶3∶3∶4,则这个四边形是( )A.等腰梯形B.直角梯形C.平行四边形D.不能确定2.在等腰梯形ABCD 中,AD ∥BC ,AE ⊥BC 于E ,且AE=AD ,BC=3AD ,则∠B 等于( )A.30°B.45°C.60°D.135°3.梯形的上底长为6 cm ,将一腰平移到上底的另一端点位置后与另一腰和 下底所构成的三角形的周长为20 cm ,那么梯形的周长为_______.4.梯形ABCD 中,AD ∥BC ,∠B=50°,∠C=80°,AD=8,BC=11,则CD=____。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B
C
E
例5 : 如图, 梯形ABCD中,AD//BC,EF//AB 2.5cm 且E为CD中点,AB=5cm,则EF=_________
A B M F D E C
例6 : 如图, 梯形ABCD中,AD//BC,B C 90 AD 1
0
1 BC 3, E, F分别为AD, BC的中点, 则EF __________
C
• 答:梯形的面积为6.8.
• 误点剖析 要注意灵活应用梯形面积的求 法. • 评注(1)当梯形(或任意四边形)对角线 互相垂直时,它们的面积等于对角线乘积 的一半. • (2)本题也可以利用等量关系 D A • S梯形ABCD=S△ABC+S△ADC来解答.
如图,等腰梯形ABCD中,AD∥BC,点E是线段AD上的一个 动点(E与A、D不重合),G、F、H分别是BE、BC、CE的 中点. (1)试探索四边形EGFH的形状,并说明理由; (2)当点E运动到什么位置时,四边形EGFH是菱形? 并加以证明; (3)若(2)中的菱形EGFH是正方形,请探索线段EF与 线段BC的关系,并证明你的结论.
距离叫做梯形的高.
两腰不相等的梯形; 等腰梯形:两腰相等的梯形叫做等腰梯形; (2)分类:梯形: 直角梯形:一腰与底垂直的梯形叫做直角 梯形.
1 (3)面积:S 梯形= (上底+下底)×高=中位线×高. 2
2.梯形的中位线 定义:连接梯形两腰中点的线段叫做梯形中位线. 判定: (1)经过梯形一腰中点与底平行的直线必平分另一腰; (2)定义法. 性质:梯形的中位线平行于两底,并且等于两底和的一半.
A
E
D
B
M
F
N
C
例7 : 梯形ABCD中, AD / / BC, AB 7, BC 8
1<CD<3 AD 2, 则另一腰CD的范围______________
A
D
B
E
C
例8 : 等腰梯形ABCD中, AB / / CD, AD BC 5, DC 7 P从A点出发以3个单位/秒的速度沿AD DC向终点C 运动,同时Q从B以1个单位 / 秒的速度沿BA向终点A运动
等腰梯形的性质定理2:
等腰梯形的两条对角线相等
有效训练:
如图:已知在等腰梯形ABCD中, AD ∥ BC, AB=DC,对角线AC⊥ BD,垂足为O,BD =8cm,则 梯形ABCD的面积为 32cm2 .
平行移对角线
1.梯形的定义
分类及面积
(1)定义:一组对边平行,而另一组对边不平行的
四边形叫做梯形.其中,平行的两边叫做底,两底间的
A O
D
B
E
F
C
典型例题:
例1、如图甲,四边形ABCD是等腰梯形,AB∥DC.由4个这样
的等腰梯形可以拼出图乙所示的平行四边形. (1)求梯形ABCD最小的角为 度; (2)试探梯形ABCD四条边之间存在的数量关系,并说明理由.
五、当堂检测 1、梯形ABCD中,AD∥BC, 135 ∠A:∠B=3:1,则∠A=
• 解:∵AC⊥BD 1 1 • ∴S△ABD= AO· BD S△BCD= CO· BD 2 2 • S梯形ABCD=S△ABD+S△BCD •
1 =2
1 AO· BD+ CO· BD 2
A O B
D
• • 即S梯形ABCD= AC· BD= ×4×3.4=6.8
2 2
1 = (AO+CO)· BD 2 1 1
(1)(2)(3)
A
D F C
E B H
例10 : 等腰梯形ABCD中, AD / / BC , AD 3cm, BC 7cm B 600 , 点P为BC (不与B, C重合)上一动点, 连接AP, 过 P作PE交CD于E使APE=B (1)求证:ABP~PCE (2)求AB长 (3)在BC上是否存在一点P使DE:EC=5:3? 若存在求出BP的长,若不存在说明理由.
A
D
B
C
小试牛刀: 2.如图,在等腰梯形ABCD中,AD∥BC, 对角线AC⊥BD,AD=3cm,BC=7cm, 则梯形的高是 cm.
A D
B
C
小试牛刀:
3、(2010山东)已知等腰梯形的底角为45o,高为2, 上底为2,则其面积为( ) A. 2 B.6 C.8 D.12
小试牛刀:
4、如图,在等腰梯形ABCD中,AD∥BC,对角线 AC⊥BD于点O,AE⊥BC,DF⊥BC,垂足分别为E、F, 设AD=a,BC=b,则四边形AEFD的周长是( ) A.3a+b B.2(a+b) C.2b+a D.4a+b
B
A
D C
第1,2,3题图
AD,下底是BC,腰是AB、CD. AB 时, CD =
3、如图,梯形ABCD中,AD∥BC,当 梯形ABCD是等腰梯形.
典型例题: 例2、如图,在等腰梯形ABCD中,∠C=60°,AD∥BC,
且AD=DC,E、F分别在AD、DC的延长线上,且DE=CF, AF、BE于点P. (1)求证:AF=BE; (2)请你猜测∠BPF的度数,并证明你的结论.
A D E
B
P
C
解 :∵APC PAB B EPC APE 且APE B PAB EPC 又∵B C ABP~PCE
B
A
D E
F
P
C
1 (2)作AF BC于F , 则BF ( BC AD) 2cm 2 又∵B 600 AB 4cm
(1)∵在梯形 ABCD 中,AD∥BC,AB=CD, ∴∠BAD=∠CDA. ∵△ABE,△CDF 均为等边三角形, ∴∠EAB=∠FDC,AB=AE,DC=DF, ∴∠EAD=∠FDA,AE=DF. 又 AD 为公共边, ∴△AED≌△DFA(SAS), ∴AF=DE.
(2)如图,过点 B 作 BH⊥AD 于点 H,过 点 C 作 CK⊥AD 于点 K.∵∠BAD=45°,AB 2 =a,∴AH=BH= a.∵四边形 ABCD 是等 2 2 1 腰梯形, ∴DK= a, HK=BC.∴S 梯形 ABCD= 2 2 2 3 2 2 2× 2 a+2BC · 2 a.∵S△ABE=S△CDF= 4 a , 3 2 1 2 2 ∴2× a = 2× a+2BC · a,解得 BC 4 2 2 2 6- 2 = a. 2
还有其它的 ∴ AB∥DE,AB=DE 方法吗? ∴ 四边形ABED是平行四边形 ∴ BE=AD=2,AB=DE=CD ∴ EC=BC – BE = 4 – 2 = 2 在等腰△DEC中,DF是高 ∴CF= ½ EC=1 在Rt △DFC中, 根据勾股定理得 CF² +DF² =CD² 即 CD² = 1² + 2² =5 ∴ CD=
A
D
B
E
C
例4 : 等腰梯形ABCD中,AD//BC,AC BD且 AD BC 16, 则S梯形 ________________ 64
析 : 作DE / / AC , 证BE 16, 则BD DE 8 2 1 S梯形 8 2 8 2 64 2
A D
度.
2、梯形ABCD中,AD∥BC,AB=DC, 若AC=3cm,则BD= 3 cm 3、在梯形ABCD中,AD∥BC, ∠B=90°,∠C=30°, 则∠A= 90 ° , ∠D=150 ° 4、在等腰梯形ABCD中,AD∥BC, AB ∥ DE,DF是高,则CF = EF.
有效训练:
1、如图,四边形ABCD中,当AD∥BC , 且AB不平行于CD时,四边形ABCD是梯形. 2、如图,梯形ABCD中,AD∥BC, 则上底是
• 例. 如图,梯形ABCD中,AD∥BC,AC与BD交 于O,且AC⊥BD,AC=4,BD=3.4,求梯形 D ABCD的面积 A •. O
B C
思路点拨:求梯形的面积常用公式 S= 底、下底、高都是未知数,故不能用此公式 ,但S梯形ABCD=S△ABD+S△BCD,利用这一等量 关系可求.
1 (上底+下底) 高 来计算,而此题上 2
等腰梯形有哪些性质?
A O B C D
等腰梯形的判定方法有哪些?
一般地,对于梯形问题,我们通过分割、 拼接,把它转化为三角形或平行四边形问题.
作 高
平行移腰
平行移腰
平行移对角线
延长两腰
小试牛刀:
1、如图,在等腰梯形ABCD中,AD∥BC, ∠B=60°,AD=AB=DC=6cm,则等腰梯 形ABCD的周长是 cm.
B
E
F
C
小结: 四边形的问题 我们经常转化为特 殊三角形(Rt △)的问 题,再利用勾股定理 解决.
5
挑战自我
1、已知:在梯形ABCD中,AD∥BC,M、N分别是AD、 BC的中点,且∠B+∠C=90°.
1 求证:M
E
N
F
C
挑战自我
2、(2010沈阳市)若等腰梯形ABCD的上、下底之 和为2,并且两条对角线所成的锐角为60°,则等腰 梯形ABCD的面积为 .
3.解决梯形问题的基本思路及辅助线的作法 (1)基本思路:梯形问题―→转化分割,拼接三角形 或平行四边形. (2)常见辅助线的作法:
梯形辅助线的作法 : 要么作出高,要么平移腰. 有时平移对角线,有时延长到相交 腰上遇中点赶快作旋转,构造全等形 数学真简单.
4.等腰梯形的性质与判定
定 有两腰________ 相等 的梯形叫做等腰梯形. 义
24cm SAEF 6cm则S梯形 = _______________________
A D F
2
E B
C
M
例2 : 梯形ABCD中,AD//BC,AD=4,AB=3 3且 B 30 , C 60 则BC _____________ 10
