复变函数和积分变换-3.2 柯西积分定理
第三章 复变函数的积分 第一节、柯西定理

第三章复变函数的积分(Integration of function of thecomplex variable)第一讲授课题目:§3.1复积分的概念§3.2柯西积分定理教学内容:复变函数的积分的定义、复变函数积分的计算问题、复变函数积分的基本性质、柯西积分定理.学时安排:2学时教学目标:1、了解复变函数积分的定义和性质,会求复变函数在曲线上的积分2、会用柯西积分定理和复合闭路定理计算积分,了解不定积分的概念教学重点:复变函数积分的计算问题教学难点:柯西积分定理教学方式:多媒体与板书相结合P思考题:1、2、习题三:1-10作业布置:7576板书设计:一、复变函数积分的计算问题二、柯西积分定理三、举例参考资料:1、《复变函数》,西交大高等数学教研室,高等教育出版社.2、《复变函数与积分变换学习辅导与习题全解》,高等教育出版.3、《复变函数论》,(钟玉泉编,高等教育出版社,第二版)2005年5月.4、《复变函数与积分变换》苏变萍陈东立编,高等教育出版社,2008年4月.课后记事:1、会求复变函数在曲线上的积分2、用柯西积分定理和复合闭路定理计算积分计算方法掌握不理想3、利用课余时间多和学生交流教学过程:§3.1 复积分的概念(The conception of complex integration)一、复变函数的积分的定义(Complex function of theintegral definition )定义(Definition )3.1设在复平面上有一条连接A 及B 两点的光滑简单曲线C 设),(),()(y x iv y x u z f +=是在C 上的连续函数.其中),(y x u 及),(y x v 是)(z f 的实部及虚部.把曲线C 用分点B z z z z z A n n ==-,...,,,1210分成n 个小弧段,其中),...,2,1,0(n k y x z k k k =+=在每个狐段上任取一点k k k ηξς+=,作和式))((11-=-∑k n k k k z z f ς(1) 令|}{|max 11-≤≤-=k k n k z z λ,当0→λ时,若(1)式的极限存在,且此极限值不依赖于k k k ηξς+=的选择,也不依赖于曲线C 的分法,则就称此极限值为)(z f 沿曲线C 的积分.记作=⎰C z z f d )())((lim 110-=→-∑k nk k k z z f ςλ当)(z f 沿曲线C 的负方向(从B 到A )积分,记作⎰-C z z f d )(当)(z f 沿闭曲线C 的积分,记作()dz z f C⎰ 定理(Theorem)3.1 若),(),()(y x iv y x u z f +=沿光滑简单曲线C 连续,则)(z f 沿C 可积,且,d ),(d ),(d ),(d ),(d )(y y x u x y x v i y y x v x y x u z z f CC C ++-=⎰⎰⎰(2) 证明:))((11-=-∑k n k k k z z f ς)]())][(,(),([111k k nk k k k k k k y y i x x iv u -+-+=+=+∑ηξηξ],))(,())(,([))(,())(,(1111111111∑∑∑∑-=+=+-=+=+-+-+---=n k k k k k n k k k k k n k k k k k n k k k k k y y u x x v i y y v x x u ηξηξηξηξ由),(),()(y x iv y x u z f +=沿光滑简单曲线C 连续,可知),(),,(y x v y x u 沿光滑简单曲线C 也连续,当0→λ时,有0|}{|max 11→--≤≤k k n k x x 0|}{|max 11→--≤≤k k nk y y 于是上式右端的极限存在,且有,d ),(d ),(d ),(d ),(d )(y y x u x y x v i y y x v x y x u z z f CC C ++-=⎰⎰⎰ 二、复变函数积分的计算(Complex integration of computational problems) 设有光滑曲线C : ()()()t iy t x t z z +== ()βα≤≤t ,即()t z '在[]βα,上连续且有不为零的导数()()()t y i t x t z '+'='.又设()z f 沿C 连续.由公式(2)我们有[()()()()()()()()]dtt y t y t x v t x t y t x u y y x u x y x v i y y x v x y x u z z f CC C '-'=++-=⎰⎰⎰⎰βα,,),(),(),(),()(d d d d d [()()()()()()()()]dt t y t y t x u t x t y t x v i '+'+⎰βα,,即()()[](),dt t z t z f dz z f c '⎰=⎰βα (3) 或 ()Re βα⎰=⎰dz z f c ()[]{()}()[]{()}dt t z t z f i dt t z t z f '⎰+'Im βα (4)用公式(3)或(4)计算复变函数的积分,是从积分路径C 的参数方程着手,称为参数方程法.注:当是分段光滑简单曲线时,我们仍然可以得到这些结论. 例1 计算dz z C⎰,其中C 是 (1) 从点1到i 的直线段1C ;(2) 从点1到0的直线段2C ,再从点0到i 得直线段3C 所连接成的折线段32C C C +=.解:(1))()(;1011≤≤+-==t it t t z C C ,有:⎰⎰⎰⎰=+-=+---=101010)12()1)(1(i dt i dt t dt i it t dz z c (2)).10()(:),10(1)(:2312≤≤=≤≤-=t it t z C t t t z C ,有:⎰⎰⎰⎰⎰=+--=+=10100)1(32tdt dt t dz z dz z dz z c c c例2 计算dz z ii I ⎰-=其中C 是 (1)连接i i 到-的直线段;(2)连接i i 到-的单位圆的左半圆(3)连接i i 到-的单位圆的右半圆解: i t i tdt i idt it dz z i i I t it z i =⋅==-=-=≤≤-=-⎰⎰⎰1221201211,11,)1( 于是程为:到i的直线段的参数方 ie de idt e e dz z i i I ,t e z it it it it it 2232232223,)2(223===⋅=-==⎰⎰⎰ππππππππ于是到从方程为单位圆的左半圆的参数 i e e d e dz z I ,t e z it it it i i it 2)(20,)3(2222=====---⎰⎰πππππ到从方程为单位圆的右半圆的参数上述二例说明:复变函数的积分与积分路径有关例3()0n Cdz z z -⎰,其中n 为任意整数,C 为以0z 为中心,r 为半径的圆周.解 C 的参数方程为0,02i z z re θθπ=+≤≤,由公式得()22(1)1000221100cos(1)sin(1)2,1,0, 1.i i n n n in n Cn n dz ire i d e d r e r z z i i n d n d r ri n n θππθθππθθθθθθπ-----==-=-+-=⎧=⎨≠⎩⎰⎰⎰⎰⎰ 此例的结果很重要,以后经常要用到.以上结果与积分路径圆周的中心和半径没有关系,应记住这一特点.例4 计算Czdz ⎰,其中C 为从原点到点34i +的直线段. 解: 此直线方程可写作3,4,01x t y t t ==≤≤ 或 34,01z t i t t =+≤≤. 在C 上,(34),(34)z i t dz i dt =+=+,于是()()()112220013434342C zdz i tdt i tdt i =+=+=+⎰⎰⎰. 因()()C CC C zdz x iy dx idy xdx ydy i ydx xdy =++=-++⎰⎰⎰⎰易验证,右边两个线积分都与路线C 无关,所以C zdz ⎰的值,不论是对怎样的连接原点到34i +的曲线,都等于()21342i +. 例5 设C 是圆ρα=-||z ,其中α是一个复数,ρ是一个正数,则按逆时针方向所取的积分i z dz C πα2=-⎰ 证明:令 θραi e z =-,于是 θρθd d i ie z =,从而 i id z dz Cπθαπ220⎰⎰==- 三、复变函数积分的基本性质(Complex integration of the basic nature)设)(z f 及)(z g 在简单曲线C 上连续,则有(1)是一个复常数其中k z z f k z z kf C C,d )(d )(⎰⎰= (2);d )(d )(d )]()([⎰⎰⎰±=±C C C z z g z z f z z g z f(3)⎰⎰⎰⎰+++=n C C C C z z f z z f z z f z z f d )(...d )(d )(d )(21其中曲线C 是有光滑的曲线n C C C ,...,,21连接而成;(4)⎰⎰-=-C C z z f z z f d )(d )( 定理3.2(积分估值) 如果在曲线C 上,()M z f ≤,而L 是曲线C 的长度,其中M 及L 都是有限的正数,那么有()ML dz z f z z f CC ≤≤⎰⎰|d )(|, (5) 证明:因为ML z z M z z f k n k k k n k k k ≤-≤-∑∑-=+-=+|||))((|111111ζ两边取极限即可得:()ML dz z f z z f CC ≤≤⎰⎰|d )(| 例6 试证:⎰=→=+r z r dz z z 01lim 230 证:不妨设1<r ,我们用估值不等式(5)式估计积分的模,因为在r z =上,⎰⎰==-≤+≤+r z r z r r dz z z dz z z 24232312||1|1π上式右端当0→r 时极限为0,故左端极限也为0,所以⎰=→=+r z r dz z z 01lim 230 本节重点掌握: (1)复变函数积分的计算;(2)复变函数积分的基本性质§3.2 柯西积分定理(Cauchy integral theorem)下面讨论复变函数积分与路径无关问题定理(Theorem)3.3设)(z f 是在单连通区域D 内的解析函数,则)(z f 在D 内沿任意一条闭曲线C 的积分0d )(=⎰C z z f ,在这里沿C 的积分是按反时针方向取的.此定理是1825年Cauchy 给出的.1851年Riemann 在)(z f '连续的假设下给出了简单证明如下 证明:已知)(z f 在单连通区域D 内解析,所以)(z f '存在,设)(z f '在区域D 内连续,可知u 、v 的一阶偏导数在区域D 内连续,有0d )(=⎰Cz z f ⎰⎰⎰++-=⊂∀C C c udyvdx i vdy udx dz )z (f D C ,,又⎰⎰⎰⎰⎰⎰=-=+=--=-Dy x c D y x c dxdy v u udy vdx dxdy u v vdy udx Green 0)(,0)(公式由注1: 此定理证明假设“)(z f '在区域D 内连续”,失去定理的真实性,法国数学家古萨(E.Goursat )在1900年给出了真实证明,但比较麻烦.注2: 若C 是区域D 的边界,)(z f 在单连通区域D 内解析,在D 上连续,则定理仍成立.定理(Theorem)3.4若)(z f 是在单连通区域D 内的解析函数,1C 、1C 是在D 内连接0z 及z 两点的任意两条简单曲线,则=⎰1)(C dz z f ⎰2)(C dz z f证明:由柯西积分定理-⎰1)(C dz z f ⎰2)(C dz z f ()021==⎰+dz z f C C将柯西积分定理推广到多连通区域上定理(Theorem)3.5(复合围线积分定理)设有n +1条简单闭曲线,,...,,n C C C 1曲线n C C ,...,1中每一条都在其余曲线的外区域内,而且所有这些曲线都在的C 内区域,n C C C ,...,,1围成一个有界多连通区域D ,D 及其边界构成一个闭区域D .设f (z )在D 上解析,那么令Γ表示D 的全部边界,我们有0=⎰Γdz z f )(其中积分是沿Γ按关于区域D 的正向取的.即沿C 按逆时针方向,沿n C C ,...,1按顺时针方向取积分;或者说当点沿着C 按所选定取积分的方向一同运动时,区域D 总在它的左侧.因此0 1=+++=⎰⎰⎰⎰--ΓnC C Cdz z f dz z f dz z f dz z f )()()()(即 ⎰⎰⎰++=nC C Cdz z f dz z f dz z f )(...)()(1例7 计算dz z z e zz ⎰-=)1(23,其中C 是包含0与1、-1的简单闭曲线.解:作互不相交的互不包含的三个小圆周321,,c c c 分别包含0,1,-1,且都在3=z 内,应用复合围线积分定理,有)2()22(21)1(1)1(11)1()1()1()1(111222223321321-+=++=+⋅-+-⋅++⋅-=-+-+-=---=⎰⎰⎰⎰⎰⎰⎰e e i e e e i z dzz z e z dz z z e z dz z dz z z e dz z z e dz z z e dz z z e z cz c c zc z c z c z z ππ由柯西积分定理可知:若)(z f 是在单连通区域D 内的解析函数,则沿着区域D 内的简单闭曲线C 的积分⎰Cd f ςς)(与路径无关,只与起点0z 及终点z 有关,此时也可写成⎰zz d f 0)(ζζ在单连通区域D 内固定0z ,当z 在区域D 内变动时,⎰zz d f 0)(ζζ确定了上限z 的一个函数,记作⎰=z z d f z F 0)()(ζζ定理(Theorem)3.6 设)(z f 是单连通区域D 的解析函数,则⎰=zz d f z F 0)()(ζζ也是区域D 内的解析函数,且)()('z f z F =证明: D z z ∈∆+∀,得⎰zz d f 0)(ζζ与路径无关,则⎰⎰-=-∆+∆+z z zz z d f d f z F z z F 0)()()()(ζζζζ=⎰∆+zz zd f ζζ)(其中积分路径取z 到z z ∆+得直线段,有()()()zz f z z F z z F ∆=-∆-∆+1(())⎰∆+-zz zd x f f ζζ)(因)(z f 在D 内连续,δδε<∆>∃>∀z ,0,0,有()()()ε<-∆-∆+z f zz F z z F即)()('z f z F =定义(Definition)3.2设在是单连通区域D 内,有)()('z f z F =,则称()z F 是)(z f 的原函数.定理(Theorem)3.7若)(z f 是在单连通区域D 内的解析函数,()z F 是)(z f 的一个原函数.则⎰=zz dz z f 0)(()z F -()0z F其中D z D z ∈∈,0注3: 此定理说明,如果某一个区域内的连续函数有原函数,那么它沿这个区域内曲线的积分可以用原函数来计算,这是数学分析中牛顿-莱布尼茨公式的推广. 例8 ( 重要积分)) 试证明:⎩⎨⎧Z ∈≠==-⎰n n n i a z dzc n ,1012)(π 这里 C 表示绕行a 一周的简单闭曲线.证明: 作圆周 1C : |z-a | = ρ, 使得 C 在 1C 的内区域中. 则有=-⎰c n a z dz )(⎰-1)(c n a z dz由例5结果即得证.例9 计算⎰+cdz z )1ln(,其中C 是从-i 到i 的直线段解 因为)1ln(z +是在全平面除去负实轴上一段1-≤x 的区域D 内为(单值)解析,又因为区域D 是单连通的,在D 内有[]ii i i i i i i z z i i i i dzzi i i i dzzzz z dz z iii i ii ii c )22ln 2()1ln()1ln(2)1ln()1ln()1ln()1ln()1ln()111()1ln()1ln(1|)1ln()1ln(π++-=--++--++=+---++=+---++=+-+=+----⎰⎰⎰本节重点掌握:1、柯西积分定理 2、柯西积分定理的推广 内容小结:1、复变函数的积分的定义2、复变函数积分的计算问题()()[](),dt t z t z f dz z f c '⎰=⎰βα3、复变函数积分的基本性质4、柯西积分定理5、柯西积分定理的推广2 1§3.3柯西积分公式§3.4解析函数的高阶导数柯西积分公式、解析函数的无穷可微性、柯西不等式与刘维尔定理、莫勒拉定理.1、掌握用柯西积分公式及高阶导数的求导公式计算积分的方法2、理解刘维尔定理与莫勒拉定理柯西积分公式解析函数的无穷可微性讲授法多媒体与板书相结合P思考题:1、2、习题三:11-157576一、柯西积分公式二、解析函数的无穷可微性三、举例[1]《复变函数》,西交大高等数学教研室,高等教育出版社.[2]《复变函数与积分变换学习辅导与习题全解》,高等教育出版社.[3]《复变函数论》,(钟玉泉编,高等教育出版社,第二版)2005.[4]《复变函数与积分变换》,苏变萍陈东立编,高等教育出版社,2008.1、掌握用柯西积分公式及高阶导数的求导公式计算积分的方法2、解析函数的无穷可微性理解很好3、利用课余时间对学生进行答疑第二讲授课题目:§3.3柯西积分公式§3.4解析函数的高阶导数教学内容:柯西积分公式、解析函数的无穷可微性、柯西不等式与刘维尔定理、莫勒拉定理.学时安排:2学时教学目标:1、掌握用柯西积分公式及高阶导数的求导公式计算积分的方法2、理解刘维尔定理与莫勒拉定理教学重点:柯西积分公式教学难点:解析函数的无穷可微性教学方式:多媒体与板书相结合作业布置:习题三:11-15板书设计:一、柯西积分公式二、解析函数的无穷可微性三、举例参考资料:1、《复变函数》,西交大高等数学教研室,高等教育出版社.2、《复变函数与积分变换学习辅导与习题全解》高等教育出版.3、《复变函数论》,(钟玉泉编,高等教育出版社,第二版).4、《积分变换》,南京工学院数学教研室,高等教育出版社.课后记事:1、掌握用柯西积分公式及高阶导数的求导公式计算积分的方法2、解析函数的无穷可微性理解很好3、利用课余时间对学生进行答疑教学过程:§3.3 柯西积分公式 (Cauchy integral formula )柯西积分公式(Cauchy integral formula )设)(z f 在以圆)0(|:|000+∞<<=-ρρz z C 为边界的闭圆盘上连续,C 的内部D 上解析,由柯西积分定理0d )(=⎰Cz z f 考虑⎰-C d z f ζζζ)(设D z ∈,显然函数在zf -ζζ)(满足z D ≠∈ζζ,的点ζ处解析. 以z 为心,作一个包含在D 内的圆盘,设其半径为ρ,边界为圆ρC .在D 上,挖去以ρC 为边界的圆盘,余下的点集是一个闭区域ρD .在ρD 上,函数)(ζf 以及zf -ζζ)(解析,所以有 ⎰⎰-=-ρζζζζζζC C d z f d z f )()(于是又如下定理定理(Theorem)3.8设)(z f 在在简单闭曲线C 所围成的区域D 内解析在C D D ⋃=上连续,0z 是区域D 内任一点,则有dzz z z f i z f C ⎰-=0)(21)(π (1)其中,沿曲线C 的积分是按反时针方向取的,(1)式就是柯西积分公式.它是解析函数的积分表达式,因而是今后我们研究解析函数的重要工具. 说明:1、有界闭区域上的解析函数,它在区域内任一点所取的值可以用它在边界上的值表示出来.2、柯西公式是解析函数的最基本的性质之一,可以帮助我们研究解析函数的许多重要性质.推论1(平均值公式)设)(z f 在)(z f R z z C <-|:|0内解析,在R z z C =-|:|0上连续,则π21)(0=z f ⎰+πθθ200)Re (d z f i推论 2 设)(z f 在由简单闭曲线1C 、2C 围成的二连通区域D 内解析,并在曲线1C 、2C 上连续,2C 在1C 的内部,0z 为区域D 内一点,则⎰-=100)(21)(C dz z z z f i z f π⎰--20)(21C dz z z z f i π例1 求下列积分的值(1)()⎰⎰==+-222.))(9(2;sin z z dz i z z zdz zz 解:(1)0|sin 2sin 02====⎰z z z i dz zzπ (2)⎰⎰=-===-=---=+-2122225|92)(9))(9(z z z z z i dz i z z z dz i z z z ππ 由平均值公式还可以推出解析函数的一个重要性质,即解析函数的最大模原理.解析函数的最大模原理,是解析函数的一个非常兆耀的原理,它说明了一个解析函数的模,在区域内部的任何一点都达不到最大值,除非这个函数恒等于常数.定理(Theorem)3.9(最大模原理) 设)(z f 在区域D 内解析,)(z f 不是常数,则在区域D 内()z f 没有最大值. 推论1在区域D 内的解析函数,若其模在区域D 内达到最大值,则此函数必恒等于常数推论2设)(z f 在有界区域D 内解析,在D 上连续,则()z f 必在区域D 的边界上达到最大值.证明:若)(z f 在区域D 内为常数,显然成立,若)(z f 在区域D 内不恒为常数,有连续函数的性质及本定理即可得证. 本节重点掌握:柯西积分公式§3.4 解析函数的高阶导数(The higher order derivative of analytic function) 一、解析函数的无穷可微性(Analytic functions ofinfinitely differentiable)定理(Theorem)3.10 设函数)(z f 在简单闭曲线C 所围成的区域D 内解析,在D 上连续,则)(z f 的各阶导数均在区域D 内解析,对区域D 内任一点z ,有,...)3,2,1( )()(2!)(1)(=-=⎰+n d z f i n z f C n n ζζζπ,证明:先证明1=n 时的情形.对区域D 内任一点z ,设D h z ∈+.⎰---=Cd z h z f ih ζζζζπ2))(()(2 现在估计上式右边的积分.设以z 为心,以δ2为半径的圆盘完全在D 内,并且在这个圆盘内取h z +,使得δ<<h 0,那么当D ∈ζ时,,||,||δζδζ>-->-h z z设()z f 在C 上的最大值是M ,并且设C 的长度是L ,于是由积分估值定理有,2|||))(()(2|22δπζζζζπMLh d z h z f i hC ⋅≤---⎰ ])()(2)(21)(21[1)()(21)()(22⎰⎰⎰⎰------=---+C C C C d z f i h d z f i d h z f i h d z f i h z f h z f ζζζπζζζπζζζπζζζπ这就证明了当h 趋近于0时,积分⎰---Cd z h z f i hζζζζπ2))(()(2趋于0.即当1=n 时定理成立.设k n =时定理成立.当1+=k n 时,对区域D 内任一点z ,设D h z ∈+.仿1=n 时的证明方法,可推得定理成立.证毕例2 计算下列各积分)())()()⎰⎰⎰>==>=-+-1223221511121cos 1r z z zr z dzz z dzze dzz zπ解:)()()()()⎰>=-==-=-1545121cos !1521cos 1r z i z z i dz z zππππ)()()()()()⎰⎰⎰+-+-+=+>=12222212212CCzzr z zdz i z i z e dz i z i z e dz z e()()⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-+='⎪⎪⎭⎫ ⎝⎛+=41sin 2222πππi i z i z e i z i z e i z z3)被积函数22)1(1-z z 有两个奇点:01=z 和12=z ,都在2=z 内,2)1(1-z 在31=z 内解析,21z在311=-z 内解析,作圆周3113121=-=z c z c :,:,利用复合围线积分定理, ⎰⎰⎰⎰⎰=-==-==-+--=-+-=-311233132311233123223)1(1)0()1(1)1()1()1(z z z z z dz z z dz z z z z dz z z dz z z dz由高阶导数公式,得()0661!1211!22)1(1302223=-='⎪⎭⎫ ⎝⎛+"⎪⎪⎭⎫ ⎝⎛-=-===⎰i i z i z i z z dzz z z ππππ应用上述定理可得出解析函数的无穷可微性定理(Theorem)3.11 设函数)(z f 在区域D 内解析,那么)(z f 在D 内有任意阶导数.并且它们也在区域D 内解析注3: 任意阶导数公式是柯西公式的直接推论;二、柯西不等式与刘维尔定理(Cauchy inequality and Liouville's theorem)柯西不等式(Cauchy inequality ) 设函数)(z f 在以R z z <-||0内解析,在以R z z <-||0内()M z f ≤,则,...)2,1,0(!!|)(|0)(=≤n RMn n z fn n 证明:令1R C 是圆)0(||110R R R z z <<=-,)(z f 在以10||R z z ≤-上解析,由高阶导数公式,有,2,1,0!22|)()(2!||)(|1111100)(1==⋅⋅≤-=++⎰n R M n R R M n!dz z z z f in z fnn C n n R πππ令R R →1,得 ,2,1,0!|)(|10)(=≤n R Mn z fn n上述的不等式称为柯西不等式.如果函数)(z f 在整个复平面上解析,那么就称)(z f 为一个整函数,例如z e z z ,cos ,sin 都是整函数.关于整函数,我们有下面的刘维尔定理:定理3.12(刘维尔Liouvlle 定理) 有界整函数一定恒等常数.证明:设)(z f 是有界整函数,即存在),0(+∞∈M ,使得M z f z <∈∀|)(|C,.),0(,C 0+∞∈∀∈∀R z ,)(z f 在R z z <-||0内解析.由柯西公式,有RM z f ≤|)('|0, 令+∞→R , 0)(',C 00=∈∀z f z ,由此可知)(z f 在C 上恒等于常数.三、莫勒拉定理(Mole La Theorem):应用解析函数有任意阶导数,可以证明柯西定理的逆定理,称为莫勒拉定理.定理(Theorem)3.13如果函数)(z f 在区域D 内连续,并且对于D 内的任一条简单闭曲线C ,我们有0)(=⎰Cdz z f那么)(z f 在区域D 内解析.本节重点掌握:(1) 解析函数的无穷可微性;(2)柯西不等式 内容小结: 1、柯西积分公式 2、解析函数的无穷可微性3、柯西不等式与刘维尔定理4、莫勒拉定理5、柯西定理的逆定理。
§1 复变函数的积分§2 柯西定理及其推广
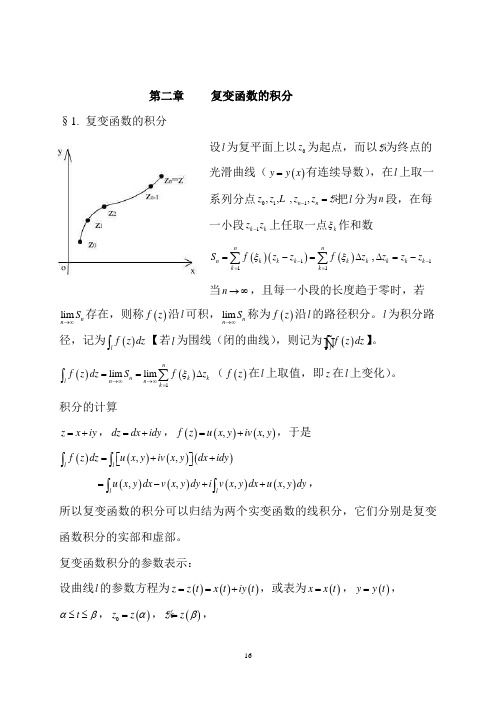
第二章 复变函数的积分§1. 复变函数的积分设l 为复平面上以0z 为起点,而以z为终点的光滑曲线(()y y x =有连续导数),在l 上取一系列分点011,,,,n n z z z z z-= 把l 分为n 段,在每一小段1k k z z -上任取一点k ξ作和数()()()111nnn k k k k k k k S f z z f z ξξ-===-=∆∑∑,1k k k z z z -∆=-当n →∞,且每一小段的长度趋于零时,若lim n n S →∞存在,则称()f z 沿l 可积,lim n n S →∞称为()f z 沿l 的路径积分。
l 为积分路径,记为()l f z dz ⎰【若l 为围线(闭的曲线),则记为()l f z dz ⎰ 】。
()()1lim lim nnk k ln n k f z dz Sf z ξ→∞→∞===∆∑⎰(()f z 在l 上取值,即z 在l 上变化)。
积分的计算z x iy =+,dz dx idy =+,()()(),,f z u x y iv x y =+,于是()()()(),,llf z dz u x y iv x y dx idy =++⎡⎤⎣⎦⎰⎰ ()()()(),,,,llu x y dx v x y dy i v x y dx u x y dy =-++⎰⎰,所以复变函数的积分可以归结为两个实变函数的线积分,它们分别是复变函数积分的实部和虚部。
复变函数积分的参数表示:设曲线l 的参数方程为()()()z z t x t iy t ==+,或表为()x x t =,()y y t =,t αβ≤≤,()0z z α=,()zz β= ,记 ()()(),u x t y t u t =⎡⎤⎣⎦,()()(),v x t y t v t =⎡⎤⎣⎦,于是()dx x t dt '=,()dy y t dt '=,()dz z t dt '=,()()()z t x t iy t '''=+,则()()()()()()()()()cf z dz u t x t v t y t dt i v t x t u t y t dt ββαα''''=-++⎡⎤⎡⎤⎣⎦⎣⎦⎰⎰⎰ ()()()()()()u t iv t x t iy t dt f z t z t dt ββαα'''=++=⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦⎰⎰。
复变函数-柯西积分定理

显然, F(z)
z
f ( )d
是 f (z)的一个原函数。
z0
利用原函数的概念, 可以得出复积分的牛顿— 莱布 尼兹公式 :
定理 设 f (z) 在单连通区域D 内解析, F (z) 是 f (z) 的 一个原函数, 则对 a, b D, 有
b a
f
( z )dz
F(z)
b a
F(b)
F (a)
注:
(1) 本公式只用于计算与积分路径无关的积分;
(2) 在求原函数时, 实函数的换元积分法和分步 积分法仍成立。
例 计算积分 24i z 2dz 1 i
解:
z2
在 整 个 复 平 面 上 解 析, 且
1
z3
z2
3
24i z2dz 1 z3 24i 1 (86 18i)
1 i
3 1i
§3.2 柯西积分定理
问题 : f (z) 在什么条件下, C f (z)dz 仅与积分路径的起点
和终点有关, 而与积分路径无关呢?
定理(柯西积分定理) 若 f (z) 在单连通域 D 内处处解析, 那么 函数 f (z) 沿 D 内任意一条闭曲线C 的积分为零, 即
C f (z)dz 0
推论 如果 f (z) 在单连通域 D 内处处解析, 则 C f (z)dz
f (z0 ) 2i
dz or C z z0
1 f ( )
f (z)
d
2 i C z
称之为柯西积分公式。
说明: (1) 通过柯西积分公式, 可以把函数在C 内部任 一点z 的值用它在边界C 上的值通过积分来表示;
(2) 给出了解析函数的一个积分表达式:
C
复变函数和积分变换第二版本-3.3 柯西积分公式-文档资料

推出一些理论结果,从而进一步认识解析函数。 5
§3.3 柯西积分公式
cos z 第 例 计算 I d z, 其中 C 为: C z 三 章 : | z 2 | 1 . (1) C :|z | 1 ; (2) C 2 1
7
§3.3 柯西积分公式 第 三 章
C P67 例3.10 部分
3 复 变 解 I | z| 2 函 数 z π 的 2πi . 2 9 z zi 积 5 分 试考虑积分路径为 | z| 4 的情况。
z ( ) 2 9 z dz . z (i)
0
2
3
i
8
§3.3 柯西积分公式
换句话说,解析函数可用其解析区域边界上的值以一种
特定的积分形式表达出来。 4
§3.3 柯西积分公式 第 一、柯西积分公式 z 三 注意 柯西积分公式中的区域 D 可以 D 章 C2 P67 是多连域。比如对于二连域 D , C1 推论 z0 复 2 C C 其边界为 C 变 1 2,则 函 1 f( z ) 数 f( z ) d z 0 C 2 π i z z 0 的 积 1 f ( z ) 1 f ( z ) d z d z , ( z D ) . 分 0 C C 2 π i1 z z 2 π i 2 z z 0 0 应用
§3.3 柯西积分公式 第 例 三 章 解 复 变 函 数 的 积 分 计算 I
C
2 z1 d z, 其中 C 如图所示。 2 z z
C
C1 0 1 C2 2
2 z1 2z 1 , 令 f (z) 2 , 则 f (z) z(z1 ) z z
复变函数柯西定理

复变函数柯西定理
柯西定理(Cauchy's Theorem)是复变函数论里极为重要的定理,其联系的柯西积分(Cauchy's Integral)应用于复平面单连通和复连通区域分别导致复变函数在某点附近的泰勒展开(Taylor Expansion)和洛朗展开(Laurent Expansion)。
柯西定理说:解析函数在复平面解析区域里的积分是路径独立的。
另一种表达是解析函数在其解析区域里的环路积分为零。
(I) 柯西定理的证明一般是结合联系面积分与线积分的格林定理(Green's Theorem):
[注:格林定理可以直接证明,亦可由联系面-线积分的旋度(Curl)公式给出。
]
以及解析函数的柯西-黎曼方程(Cauchy-Riemann Equation):
具体而言:
现在:1. 利用(1),对于实部和虚部分别取(P,Q)=(u,-v)和(P,Q)=(v,u); 2. 利用(2),环路积分为零得证。
(II) 另一个角度,可证明如下:
对于解析函数,由柯西-黎曼方程可知:(3)中的实部:udx-vdy 和虚部:vdx+udy 分别是全微分形式,可写作某实函数的全微分:
而实函数全微分的环路积分为零。
3.2柯西积分定理

C = C0 + C1 + C2 +L+ Cn
C1
C2 Cn
C0
D
C = C0 + C + C + L + C
− 1 − 2 − n
C = C0 + C + C + L + C 所围的n + 1连通区域,f ( z)在
定理3.10 设D是由复周线
− 1 − 2 − n
D内解析且连续到边界,则 内 f ( z )dz = 0. ∫
C1 Cn
∫
C0
f (z)dz = ∫ f (z)dz + ∫ f (z)dz +L+ ∫ f (z)dz.
C1 C2 Cn
C1
C2
C0
Cn
D
特例:如图,若f ( z )在二连通 区域D内解析,连续到边界,则
∫
C
f ( z)dz =∫ f ( z)dz.
Γ
可 作用: 把 积
Γ
D
分路径规范化!
C
更 一 般 的 情 形
由格林定理, 由格林定理,有
∫
C
udx − vdy = 0, vdx + udy = 0. ∫
故
∫
C
f ( z )dz = 0
C
柯西 柯西积分定理的严格证明 是古莎给出的,证明过程比较 长,我们略去不予介绍。有兴 趣的同学自己阅读。
定理3.4 设f(z)是单连通区域 的 是单连通区域D的 定理 是单连通区域 解析函数, 解析函数,设C是D内任一闭曲线 是 内任一闭曲线 不必是简单曲线), ),那么 (不必是简单曲线),那么
由定理3.9,得
复变函数-柯西积分定理

z
1
i
dz
C
1 z
dz
1 2
C
zБайду номын сангаас
1
i
dz
1 2
C
z
1
dz i
2i 0 0 2i
(2)
I
C
1 z
dz
1 2
C
z
1
i
dz
1 2
C
z
1
i
dz
0 0 2 i
2
i
| z | 1 2
| z i | 1 2
例 不经计算, 验证下列积分值为零, 其中, C 为| z | 1。
1
1
(1) C z2 5z 6 dz (2) C (z2 2)( z3 3) dz
i(12z
2 0
2)
2(6z
2 0
1)i
Morera 定理 : 若函数 f (z) 在单连通域 D 内连续,且对 D 内任意封闭
曲线 C 有 ÑC f (z)dz 0,则 f (z) 在区域 D 内解析。
Liouville 定理 : 若 f (z) 在复平面上解析且有界,则 f (z) 恒为常数。
当 f (z) 有奇点时,不能直接应用该定理。
例 计算
1 C z(z2 1) dz
(1) C 为| z | 1 ; (2) C 为| z i | 1
2
2
解
:
由于
1 z(z2
1)
1 z
1 2
z
1
i
1 2
z
1
i
所以
| z | 1 2
| z i | 1 2
复变函数第3节:柯西积分公式及高阶导数公式

第3节 柯西积分公式
柯西积分公式 高阶导数公式
一、柯西积分公式
设B为单连通域, f(z)在B内解析, z0∈B, 设C为B内
绕z0的任一正向简单闭曲线, 则
f (z) z z0
在z0不解析.
z0
在C内部作CR: |zz0|=R (取其正向)
C
f (z) d z
f
(z)
d
R
z
D
说明: 1) 解析函数具有任意阶导数;
2) f (n)(z0 ) 可用函数 f(z)在边界上的值通过积分唯一 确定。
说明:
3)
高阶导数公式的应用: 可求积分
C
f (z) (z z0 )n1 d z
要注意:a) f(z)在简单闭曲线C及其内部解析,
b) z0在C的内部.
高阶导数公式的作用: 不在于通过积分来求导,
若
C2
f((zz)2
1)2
dz.
n
f (z)dz
f (z)dz,
C
k 1 Ck
C
C1
C2 C3
• •
C1 i
o
C2 i
C
x
ez
C1
(
z
2
ez
1)2
dz
C1
( (
z z
i i
)2 )2
dz
y
C1 i
C
• •
2i (2 1)!
(
z
ez i
)2
(1 i)ei .
2
o
C2 i
z1 z1
sin z
dz
2i 4
2 i.
z1 2
复变函数与积分变换第3章复变函数的积分

C f( z ) d z C u d x v d y i C v d x u d y .
b
a{u[x(t),y(t)]x(t)v[x(t),y(t)]y(t)}dt
容易验证,右边两个线积分都与路线C 无关,
所以
的zd值z 无论
1 3 4i2 c
2
是C怎样的曲线都等于
例 3求 证 lri m 0 |z|rz2z 31dz0.
例 4求 Cz1 idz的 积 分 的 一 个 绝 对 上 界 , 其 中 C
为 从 原 点 到 34i的 直 线 段 .
区 域 包 含 于 D . 若 f(z)在 区 域 D 内 解 析 , 则
D
n
i) f(z)dz f(z)dz;
C
k1Ck
Ci
ii) f(z)dz0其 中 为 C 与 C k
围 成 的 复 合 闭 路 ,C 与 C k均 取 正 方 向
例 3.7计 算2z1dz,其 中 C是 包 含 0和 1的 Cz2z
定 理 3 . 6设 f(z)在 单 连 通 区 域 D 解 析 , F (z)为 f(z)的 一 个 原 函 数 , 则 对 任 意 z0,z1 D , 有
z1 z0
f(z)dzF(z1)F(z0)
例 8计 算 bznd z,其 中 n是 正 整 数 。 a
例9计算izcoszdz. 0
为f (z)沿曲线C的积分,记为
n
Cf(z)dz=ln→ i∞ mk=1f(ζ k)Δ zk
沿 曲 线 C 的 负 方 向 的 积 分 记 为 f( z ) d z C
复变函数与积分变换 第三章第五节 柯西积分公式

C
f( z
z) z0
dz
将接近于
C
f (z0 )dz. z z0
( 缩小)
C
f (z0 )dz z z0
f (z0 ) C
z
1 z0
dz
2if
( z0
).
二、柯西积分公式
定理
如果 f(z) 在区域 D 内处处解析,C 为 D
的边界曲线(正向简单闭), z0 为 C 内任一点,
f(z0 )
第五节 柯西积分公式
一、问题的提出 二、柯西积分公式 三、典型例题 四、小结与思考
一、问题的提出
复习:柯西-古萨基本定理
设曲线 C 是单连通区域 B 的边界 f(z)在B上解析
B
C
c f(z)dz 0.
问题:设z0是B内的一点, 求C
f(z) dz z z0
z0
C
B
分析:
如果
f
(z) 在 B内解析, 那末
R K
ds
2π .
上不等式表明, 只要 R 足够小, 左端积分的模就
可以任意小,
根据闭路变形原理知, 左端积分的值与 R 无关,
所以只有在对所有的 R 积分值为零时才有可能.
f
(z0 )
1 2i
f (z) dz
C z z0
柯西积分公式
[证毕]
关于柯西积分公式的说明:
(1) 把函数在C内部任一点的值用它在边界上的
1 2i sin z
2i
z0
0;
(2)
z
4
z
1
1
z
2
3
dz.
1 dz
2 dz 2i 1 2i 2
复变函数(3.2.2)--柯西-古萨定理及其推广

定义 3.2 如果函数在区域内导数等于,即,且在内连续,那么称为在区域内的一个 原
函数。
F (z) = f D(z zf)( )d z0
定理 3.4 表明,是在单连域内的一个原函数。
5
FFf (z)
易得,的任何两个原函数之间只相差一个复常数。事实上,设和是的任意两个原函数 , 那么
▎ 注记:在上式的证明中,因为复变函数本身不能比较大小,所以高等数学中拉格朗日中值 定理在复变函数积分不成立. 易见,定理 3.4 非常类似于实变函数中的变上限积分的求导定理(微积分第一基本定 理)。由此,我们还可以进一步得到类似实变函数中的另一个微积分基本定理和牛顿-莱布 尼茨公式。为此,先引入原函数的概念。
C
因此,为了研究复变函数延闭路经的积分,只要研究相应的两个线积分
ᆴ vuddxx+-uv d y = 0
C
与
1
u, v, ux ,CDuy , vx , vy
因此,若在复平面上由简单闭曲线围城的单连域内连续,并且上述两个线积分沿内任一闭曲线积分等于零,即由格林公式得
�u
C
d
x
-
v
d
y
=
��(-
D
ᆴv ᆴx
-
ᆴu ᆴy
)dxdy
=
0
,
�v
C
d
x
+
u
d
y
=
�D�( ᆴᆴux
-
ᆴv ᆴy
)dxdy
=
0
.
f
(z)
=
u
B x
+fff (D(izzv))xd=z
第三章 复变函数的积分

连接.设想将D沿割线割破,于是D就被分成两个单连
通区域(图3.10是 n 2的情形),其边界各是一条围线, 分别记为1和 2 .而由定理3.9,我们有
1
f
zdz
0, 2
f
zdz
0,
将这两个等式相加,并注意到沿着 L0 , L1, , Ln 的积分, 各从相反的两个方向取了一次,在相加的过程中互相 抵消.于是,由复积分的基本性质(3)就得到
下,我们称区域D的边界是一条复围线
C C0 C1 C2 Cn
它包括取正方向的C0 ,以及取负方向的 C1,C2 , ,Cn .换句话 说,假如观察者沿复围线C的正方向绕行时,区域D的点总 在它的左手边(图3.10是 n 2的情形).
D
C2
C1
C0
L2
D
L1
L0
C1
C2
C0
图3.10
定理3.10 设D是由复围线
适合 C. R. 条件 ,
由格林定理, C udx vdy 0, C vdx udy 0,
故得
f (z)dz 0.
C
由柯西积分定理,可以得到
定理3.4 设f (z) 在 z 平面上的单连通区域 D 内解析,C 为D
内任一闭曲线(不必是简单的),则
C f (z)dz 0.
证 因为D总可以看成区域 C 内有限多条围线衔接而
f (z) 1 za
只以z a 为奇点,即在“z 平面除去一点a ”的非单连通区域内处处解
析,但是积分
C
dz za
2i
0,
其中 C 表圆周 z a 0 ,即在此区域内积分与路径有关;
复变函数与积分变换3.2柯西积分定理

C
1 dz dz dz 2 C z C z 1 z z
(由闭路变形原理) dz dz C2 z 1 C1 z 2 i 2 i 0
C
C1
0
1
C2
(2) (由复合闭路定理)
C
1 dz dz dz 2 2 C2 z 2 z C1 z z z z
问题:复变函数f(z)=u(x,y)+iv(x,y)满足什么条件在单连 通区域D内沿闭路径的积分为零?
要使 只要
f ( z) d z 0.
C
C
udx vdy 0且 vdx udy 0.
C
这只须u与v具有一阶连续偏导数且ux=vy, uy=-vx. Cauchy: 若f(z)在单连通区域D内解析,且f'(z)连续, 则对D内任意闭曲线C有
c
z0 z1 。 其中C:
固定z0,z1=z在D内变化,于是 C 于z的单值函数:
z C C z0
f ( z )dz
在D内确定了关
f z dz f d f d : F ( z )
F z f d
z0 z
变上限积分。
解析函数的原函数仍为解析函数
1 例题1 求 C 2 dz , C 如图所示: z 解:存在 f (z)的解析单连通域D包含
i
i
3 i
曲线 C ,故积分与路径无关,仅与起
点和终点有关。
0,i 0,i
从而
C
1 1 4 1 1 1 dz d i 2 z z 0,3i i 3i 3 0, 3i z
(完整版)柯西定理及其应用

(完整版)柯西定理及其应用柯西定理及其应用柯西定理是分析数学中的一个重要定理,它在复变函数理论中有着广泛的应用。
本文将介绍柯西定理的原理以及它在几个具体问题中的应用。
柯西定理的原理柯西定理是指在复平面上,如果一个函数在一个简单闭合曲线内是全纯的(即在该曲线内的每个点上有定义且可导),那么该函数在这个曲线内的任何一点的复积分都等于零。
具体来说,设函数f(z)在曲线C内是全纯函数,则对于曲线C内任意一点z0,有以下公式成立:∮C f(z)dz = 0其中∮C表示沿曲线C的积分,f(z)dz表示f(z)乘以dz的积分。
柯西定理的应用柯西定理在许多问题的求解中起着关键作用。
下面将介绍其中几个经典的应用。
1. 柯西积分公式柯西积分公式是柯西定理的一个重要推论。
它表明,如果函数f(z)在一个围绕点z0的简单闭合曲线内是全纯的,那么函数f(z)在该曲线内的任意一点z的导数可以通过曲线上的积分来计算。
具体来说,如果函数f(z)在简单闭合曲线C内是全纯的,那么对于曲线C内任意一点z,有以下公式成立:f^(n)(z0) = \frac{n!}{2\pi i} \int_{C} \frac{f(z)}{(z -z0)^{n+1}}dz其中f^(n)(z0)表示f(z)在z0处的n阶导数。
2. 柯西积分定理柯西积分定理是柯西定理的另一个重要推论。
它表明,如果函数f(z)在一个简单闭合曲线内是全纯的,那么函数f(z)在该曲线内的积分只取决于曲线C所围成的区域,而与曲线C的具体形状无关。
具体来说,如果函数f(z)在简单闭合曲线C内是全纯的,那么对于曲线C内的两条等价曲线C'和C'',有以下公式成立:\int_{C'} f(z)dz = \int_{C''} f(z)dz其中C'和C''是等价曲线,即它们由于同一个简单闭合曲线而围成的区域相同。
3. 柯西不等式柯西不等式是柯西定理的一个重要推论。
复变函数课件3.2复变函数的积分 柯西公式(2)

柯西公式:
f (z) dz f (z) f (z0 ) f (z0 ) dz
C z z0
Cr
z z0
f (z0 ) Cr
1 dz z z0
Cr
f (z) f (z0 ) dz z z0
由于由f(z)在点z0的连续性,所以
0, 0( r0 )
令, z z0 ei
柯西公式:
则有
I i C f (z0 ei )d
由于I的值只f(z)与在z0点附近的值有关, 与r无关,由f(z)在点z0的连续性,应该有
I 2if (z0 ),
即
f
( z0
)
1
2i
f (z) dz C z z0
事实上,当r趋近于0时,有
f
(k ) (z
h) h
f
(k) (z)
(k 1)!
2i
C
(
f ( )
z)k2
d
1[ k!
h 2i
C (
f (
z
) h)
k
1
d
k!
2i
C
(
f ( )
z)k
1
d
]
(k 1)!
2i
C
(
f ( )
z)k2
d
z
h
2i
C (
f ( ) z h)(
z)2 d
h
2i
C
f
(
( )
z)2
d
]
高阶导数公式:
现在估计上式右边的积分。设以z为心,以2d为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C 1 f ( z ) d z C 2 f ( z ) d z C 2 f ( z ) d z .
可见,解析函数在单连域内的积分只与起点和终点有关,
13
§3.2 柯西积分定理
第 三 章
例 计算 ICsinzdz, 其中 C 为如图所示的一个半圆。
P61 例3.6
y
解 设 G 如图所示,由于 sinz在复平面上 i
C 1
C 2
Γ
在区域内的一个解析函数沿闭曲线的积分,不因闭曲线在
区域内作连续变形而改变它的值,称此为闭路变形原理。
6
§3.2 柯西积分定理
第▲
三 章
P57 例3.2
解 曲线 C 的参数方程为 zz0rei, :0 2π,
复 变 函
I
2π 0
rei i (rei)n
dθ
y
数 的 积
rni1
2πei(1n)dθ,
0
分
当n1时,
C
1
(z z0 )n dz i
2π d 2i;
0
o
z
z0 r
x
当n1时,
C
(z
1 z0
)n
dz
i rn 1
2π(cn o 1 s ) (isin n 1 )()d
0
0;
所
以
zz0
r
1 (zz0)n
dz
2i,
0,
n 1, n 1.
注:此例说明积分与半径r无关,与中心z0也无关
|f() f(z)|d s ,
z
| z| z
16
§3.2 柯西积分定理
第 五、原函数
三 章
2. 由变上限积分构成的原函数
直线段
D
复 定理 若 f (z)在单连域 D 内处处解析,
变 函
令
F(z) z f()d, z0
z,z0D,
z zz
z0
数
则 F(z)在 D 内解析,且 F (z)f(z).
上述定理又称为柯西-古萨(Cauchy-Goursat)基本定理。
2
§3.2 柯西积分定理
第 一、柯西基本定理
三 章 定理 设函数 f (z) 在单连通域 D 内解析,
D
复
G 为 D 内的任意一条简单闭曲线,
G
G
变 函
则有 Γf(z)dz0.
数
的
积
注: 定理中的条件还可以进一步减弱。
分
定理 设单连域 D的边界为C,函数 f (z)
变 3.2 则有 f(z)dz0.
函
Γ
G
G
数 的
证明
Γ f ( z ) d z Γ ( u d x v d y ) i Γ ( v d x u d y )
积
分
Green公式 (?)
G ( x v u y)d x d y iG ( u x v y)d x d y
C R方程 0 .
的
积
分
证明 (2)
(思路)
F f(z)1
z Δ z
|f() f(z)|d s ,
z
| z| z
1 |Δz|, (当|Δ z |充分小时)
|Δz|
lim ΔFf(z)0, 即 F (z)f(z). Δz 0 Δz 17
§3.2 柯西积分定理
第 例 求 1i z2dz .
三
0
章 解 1i z2dz 1 z 3 1i 1 (1 i)3.
i
章
解:存在 f (z)的解析单连通域D包含曲线 C ,
复 故积分与路径无关,仅与起点和终点有关。 i
变 函 数 的
从而 Cz12dz3iid1z1zi3i
3i
积
分
1 i
1 3i
4 3
i
20
§3.2 柯西积分定理
第 三 章
复 变 函 数 的 积 分
休息一下 ……
21
,
则 f(z) 1 1 , 奇点为 z0,1. z z1
的
积 分
(2) 当 C 为
x2 22
y2 1
1 时,令 C1:| z
|
1, 3
C2:| z 1|
1 3
,
则 I1 d z 1d z1 d z 1d z
C 1z C 1z 1 C 2z C 2z 1
2 π i 0 0 2 π i 4 π i.
变
函
P63 定理 3.5
令
F(z) z f()d, z0
z,z0D,
z0
数
则 F(z)在 D 内解析,且 F (z)f(z).
的
z zz
积
分
证明
(思路)
(1)
FF(zΔz)F(z) 1 zΔz f()d,
z
z
z z
(跳过?)
f(z)1 zΔz f(z)d,
z z
F f(z)1
z Δ z
P60 [注]
在 D内解析,在 D D C上连续,
则有 Cf(z)dz0.
C D
3
§3.2 柯西积分定理
第
三例
计算积分 1 dz.
章
z12z3
复 变
解: 函数 1 在z1内解 , 析 2z3
函 数 的
根据柯西积分定理,
有
1 dz0. z1 2z3
积
分 注:以上讨论中D为单连通域。
f
(z)
z
1
0
30 3
复
变
函
例
求
b
coszdz.
a
数
的解 积
b
b
coszdz sin z sibn sian .
a
a
分
例求
i
zcoszdz.
0
解
i
i
ii
zcoszdz zdsinz zsizn sizndz
0
0
00
i
(zsin zcozs) isi n cio 1 s . 0
18
§3.2 柯西积分定理
7
§3.2 柯西积分定理
Ñ Ñ 第
三 章
例如
dz
z a 3 z a 2 i,
dz
za 3 (z a)2 0 ,
复
dz
变 函
Ñ z z 2 3 0 ,
Ñ z d z z 4
0,
数
的 积 分
Ñ Ñ d z z1 z
2 iei d
0
0
dz
2 ei d 0
z 1 z
0
8
§3.2 柯西积分定理
第▲
三 重要 章
解 如图以 z 0 为圆心 r为半径作圆,
复 变 函
则函数
f(z)
1 (zz0)n
在
r
G
C z0
D
数 的
D D ΓC 上解析,
积 分
因此有
I
Γ
dz (zz0)n
C
dz (z z0)n
2πi ,
当
n1时,
0 , 当 n1时。
9
§3.2 柯西积分定理
第 三、复合闭路定理
三 章
将柯西积分定理推广到多连域
复 定理 设多连域 D的边界为 C C 0 C 1 C 2 C n (如图),
变 函
P62 推论
函数 f (z)在 D内解析,
数
在 C 上连续,则
的
积 分
Cf(z)dz0
Cn C0
C3
…
C1 D C2
或 f ( z ) d z f ( z ) d z f ( z ) d z f ( z ) d z .
的
积 分
(1) 当 C 为 | z 3 |
1 2
时,I C 2z2z1zdz0.
11
§3.2 柯西积分定理
第
三
例 计算 I C 2z2z1z dz, 其中 C 为:
章 复
(1)
| z 3|
1 2
;
(2)
x2 22
y2 1. 1
C
C1 C2 01 2
C
3
变
函 数
解
令
f (z)
2z1 z2 z
第
P65 例3.9
三
章 解
i
i
i
ln1(z)dz zln1 (z)
z dz
i
i i 1z
复
变 函
i
zln 1 (z)
i
z11dz
i i 1z
数
i
的
[zln 1z ()z ln 1z ()]
积
i
分
(2ln2)iπi.
2
19
§3.2 柯西积分定理
第 例: 求
三
1 C z 2 d z , C 如图所示:
§3.2 柯西积分定理
第 三
§3.2
柯西积分定理
章 一、柯西基本定理
复 变
二、闭路变形原理
函 数
三、复合闭路定理
的 四、路径无关性
积
分 五、原函数
1
§3.2 柯西积分定理
第 一、柯西基本定理
三 章 定理 设函数 f (z) 在单连通域 D 内解析,
D
复
P60 定理
G 为 D 内的任意一条简单闭曲线,
a
在区域
D 0za 内解析,
Ñ 1 dz2i0 za1za
这里D为复连通域。
4
§3.2 柯西积分定理
第 二、闭路变形原理
