江苏省无锡市崇安区2012-2013学年八年级上学期期中考试数学试题
2012-2013学年度八年级上学期期中考试数学试题

2012—2013学年度上学期期中考试八年级数学试卷一、精心选一选,慧眼识金(每小题3分,共30分) 1、下列实数中,无理数是( )A 、0B 、3C 、-21 D 、3.142、38-的相反数是( )A 、2B 、-2C 、±2D 、22-3、函数1+=x y 中自变量x 的取值范围是( )A 、x ≥1B 、x ≥0C 、x ≤-1D 、x ≥-14、已知点A (2,3)在函数12+-=x ax y 的图象上,则a 等于( )A 、1B 、-1C 、-2D 、25、已知,如图∠A=∠D, ∠1=∠2,那么要得到△AB C ≌△DEF , 还应给出的条件是( ) A 、∠E=∠B B 、ED=BCC 、AB=EFD 、AF=CD6、△AB C 中,∠C=90°,AD 平分∠BAC 交BC 于D , BD :DC=3:2,点D 到AB 的距离是6,则BC 长为( ) A 、10 B 、15 C 、20D 、257、已知点P (-2,3)关于y 轴的对称点为Q (b a ,),则b a +的值是( )A 、1B 、-1C 、-5D 、58、等腰三角形的周长为20,则某底边BC 的取值范围是( )A 、0<BC <5B 、0<BC <10C 、5<BC <10D 、10<BC <209、如图,△AB C 中,∠C=90°,∠B=15°,AB 的垂直平分线 交BC 于D ,垂足于E ,若BD+AC=24,则B D -AC 等于( ) A 、8B 、7C 、6D 、5DDD10、如图所示,I 是△AB C 三内角平分线的交点,I E ⊥BC 于E ,AI 延长线交BC 于D ,CI 的延长线交AB 于F ,下列结论:①CID BIE ∠=∠;②)(21AC BC AB IE S ABC ++=∆;③)(21AC BC AB BE -+=;④DC AF AC +=,其中正确的结论是( )A 、①②③B 、①②④C 、②③④D 、①②③④二、耐心填一填,一锤定音(每小题3分,共18分)11、若0≠x ,则xx 33-=.12、如图,在△AB C 中,AB=AD=DC ,∠BAD=26°,则∠C= . 13、如图,已知等腰ABC Rt ∆中,∠BAC=90°,D 为AC 中点,C E ⊥BD 于E,交BA 的延长线于F ,若BF=18,则△FBC 的面积为 . 14、如图,△ABC 中,DE 是AC 的垂直平分线,AE=3cm ,△ABD 的周长为13cm ,则△ABC 的周长是 .15、已知某一次函数当自变量取值范围是2≤x ≤6时,函数值的取值范围是5≤y ≤9,则此一次函数的解析式为 .16、如图,在△ACB 中,∠ACB=90°,AC=BC ,BC 与y 轴交于D 点,点C 的坐标为(-2,0),点A 的坐标为(-6,3),则B 点的坐标是 .┐ CAFBD E I CD BA第12题图B 第13题图CD B AE第14题图第16题图三、用心做一做,马到成功(共52分)17、(本题5分)计算:)22(221)2(2+--+- 18、(本题6分)求下列各式“x ”值 ①0492=-x②0125)1(3=+-x19、(本题6分)如图,点B 、F 、C 、E 在一条直线上, FB=CE ,A B ∥ED ,A C ∥FD ,求证AC=DF.20、(本题6分)如图,直线22+=x y 交x 轴于A ,交y 于B 点.(1)将直线AB 向上平移1个单位长度,再向左平移2个单位长度后得到的直线解析式为 .(2)直线AB 关于x 轴的对称的直线解析式为 .(3)求直线AB 关于直线y =x 对称的直线解析式.21、(本题6分)如图,已知△ABC 的三个顶点分别为A (2,3),B (3,1),C (-2,-2) (1)请在图中作出△ABC 关于直线x =-1的轴对称图形△DEF (A 、B 、C 的对应点分别是D 、E 、F ),并直接写出D 、E 、F 的坐标.(2)求四边形ABED 的面积. 22、(本题6分),如图在△ABC 中,AB=AC ,∠BAC=120°,D 为BC 中点,D E ⊥AB 于E ,求EB :EA 的值.BFECAxA DEB23、(本题7分)如图,已知等腰ABC Rt ∆和等腰CDE Rt ∆,D 、E 分别在BC ,AC 上,C N ⊥BE 交AD 于M.(1)求证:DM=AM(2)将△CDE 绕C 点旋转,如图,求证:AM=DM.AECNM BDAECN MBD24、(本题10分)如图(1)在平面直角坐标系中,A 点的坐标为(a ,0),B 点坐标为(0,b ),a 、b 满足06364212=--+-b b a ,C 在x 轴负半轴上,且OB OC1=.(1)求直线BC 的解析式(2)已知AB=10,求CBOABO∠∠(3)平面直角坐标系中,是否存在点P (a ,3a +1),使ABC PBC S S ∆∆=?若存在求a 的值,若不存在,请说明理由.。
2012-2013八年级期中试题及答案

2012~2013学年度第一学期期中教学质量监测八年级数学试卷(考试时间:100分钟,总分:100分)一、选择题(本题共10小题,每小题2分,共20分.下列各题都有代号为A 、B 、C 、D 的四个结论供选择,其中只有一个结论是正确的,请把正确结论的代号填入题后的括号内.) 1.在以下永洁环保、绿色食品、节能、绿色环保四个标志中,是轴对称图形是( )A .B .C .D .2.64的立方根是( )A .8B .±8C .4D .±4310.323232π,,…中,无理数有( )个A .1B .2C .3D .44.等腰三角形两边长分别为4和8,则这个等腰三角形的周长为( ) A .16 B .18 C .16或20 D .205.如图,点P 是等边△ABC 的边上的一个作匀速运动的动点,其由点A 开始沿AB 边运动到B 再沿BC 边运动到C 为止,设运动时间为t ,△ACP 的面积为S ,S 与t 的大致图象是( )A .B .C .D .6.对于一次函数24y x =-+,下列结论错误的是( )A . 函数值随自变量的增大而减小B .函数的图象与x 轴的交点坐标是(0,4)C .函数的图象不经过第三象限D .函数的图象向下平移4个单位长度得2y x =-的图象 7.若实数a b c 、、满足0a b c ++=,且a b c <<,则函数y ax c =+的图象可能是( )A .B .C .D .8.在如图所示的数轴上,点B 与点C 关于点A 对称,A 、B和1-,则点C 所对应的实数是( ) A .1+ B.2+C.1 D.19.如图,函数2y x =和4y ax =+的图象相交于点A (m ,3),则不等式24x ax <+的解集为( ) A .32x <B . 3x <C . 32x >D . 3x >10.如图,四边形ABCD 中,∠BAD =120°,∠B =∠D =90°,在BC 、CD 上分别找一点M 、N ,使△AMN 周长最小时,则∠AMN +∠ANM 的度数为( ) A .130° B .120° C .110° D .100°二、填空题(本题共8小题,每小题3分,共24分.把最后的结果填在题中横线上.) 11.函数y =x 的取值范围是______________..小明从镜子里看到对面电子钟示数是 ,小数部分为b ,则代数式b -的值为_____________.15.如图,在Rt △ABC 中,∠C =90°,∠B =15°,AB 的垂直平分线MN 交BC 于D ,且BD =6,则AC = .16.已知一次函数的图象经过点(0,1),且满足y 随x 的增大而增大,则该一次函数的解析式可以为__________________. 17.已知x y 、为实数,且满足5y =,则x y +的平方根为_____________.18.如图,已知A (-1,2),B (0,-2),点P 是直线x =1上的一动点,当点P 的坐标为_________时,△ABP 的周长最短.第18题P第8题第9题第10题三、解答题(本题共7小题,共56分.解答时应写出文字说明、证明过程或演算步骤.) 19.(本题满分8分)(1)解方程:24250x -= (22-+20.(本题满分6分)如图,在平面直角坐标系xOy 中,点A (6,0),点B (6,8).(1)只用直尺(没有刻度)和圆规,求作一个点P ,使点P 同时满足下列两个条件①点P 到A ,B 两点的距离相等; ②点P 到∠xOy 的两边的距离相等.(要求保留作图痕迹,不必写出作法)(2)在(1)作出点P 后,点P 的坐标为_____________.21.(本题满分8分)如图,在△ABC 中,AB =AC 点D 、E 、F 分别在AB 、BC 、CA 上,且BE =CF ,BD =CE .⑴求证△DEF 是等腰三角形;⑵当∠A =40°时,求∠DEF 的度数; ⑶△DEF 可能是等腰直角三角形吗?为什么?22.(本题满分8分)甲、乙两地距离300km ,一辆货车和一辆轿车先后从甲地出发驶向乙地.如图,线段OA 表示货车离甲地的距离y (km )与时间x (h )之间的函数关系,折线BCDE 表示轿车离甲地的距离y (km )与时间x (h )之间的函数关系,根据图象,解答下列问题:(1)线段CD 表示轿车在途中停留了___________小时 (2)求线段DE 对应的函数解析式;(3)求轿车从甲地出发后经过多长时间追上货车.x .. O y B A23.(本题满分8分)如图,直线24y x =-+与x 轴相交于点A ,与y 轴相交于点B ,以线段AB 为边在第一象限内作等腰直角△ABC ,∠BAC =90°,求直线BC 的解析式.24.(本题满分8分)如图,等边△ABC 中,D 、E 分别为BC 、AC 边上的两个动点,且总有BD=CE , AD 与BE 交于点F ,AG ⊥BE 于点G ,试探究A F 与FG 的数量关系,并说明理由.25.(本题满分10分)如图,在平面直角坐标系xOy 中,A 、B 、C 三点的坐标分别为A (8,0),B (8,11), C (0,5),点D 为线段BC 上一点且D 点的横坐标为4,动点P 从点O 出发,以每秒1个单位的速度,沿折线OAB 的路线移动,至点B 停止.设点P 移动的时间为t 秒,△OPD 的面积为S .(1)求直线BC 的解析式及点D 的坐标;(2)请求出S 与t 的函数关系式,并写出自变量t 的取值范围;(3)当点P 运动到何处时△OPD 的面积S 最大,最大值是多少?(直接写出答案)GF EDCBA2012~2013学年度第一学期期中教学质量监测八年级数学参考答案一、选择题二、填空题11. x ≥12; 12.(3,4); 13. 21:05; 14. 9- 15. 3;16.例y =x +1; 17.3±; 18.(1,32-)三、解答题 19.(1)解:52x =±(2分+2分)(2)解:原式=323--+……………………3分=2-+………………… 4分20.解:(1)图略.(图2分,痕迹2分)(2)P (4,4).(2分)21.(1)证明:∵AB =AC ∴∠B =∠C ,……………………1分在△BDE 与△CEF 中 BD =CE ∠B =∠CBE =CF∴△BDE ≌△CEF .∴DE =EF ,即△DEF 是等腰三角形.……………………3分 (2)解:由(1)知△BDE ≌△CEF ,∴∠BDE =∠CEF∵∠CEF +∠DEF =∠BDE +∠B ∴∠DEF =∠B ………………… …5分∵AB =AC ,∠A =40° ∴∠DEF =∠B =(180°-40°)÷ 2 =70°.……………………6分 (3)解:△DEF 不可能是等腰直角三角形.……………………7分 ∵AB =AC ,∴∠B =∠C ≠90°∴∠DEF =∠B ≠90°,∴△DEF 不可能是等腰直角三角形.……………………8分22.(1)利用图象可得:线段CD 表示轿车在途中停留了:2.5-2=0.5小时;……………2分(2)根据D 点坐标为:(2.5,80),E 点坐标为:(4.5,300),代入y=kx+b ,得: 2.5804.5300k b k b +=⎧⎨+=⎩解得:110195k b =⎧⎨=-⎩,故线段DE 对应的函数解析式为:y=110x-195;……………………5分 (3)∵A 点坐标为:(5,300),代入解析式y=ax 得,300=5a ,解得:a =60,故y =60x ,当60x =110x-195,解得:x =3.9小时,故3.9-1=2.9(小时), 答:轿车从甲地出发后经过2.9小时追上货车.……………………8分23. 求出A 的坐标是(2,0),B 的坐标是(0,4).……………………2分作CD ⊥x 轴于点D .∵∠BAC =90°,∴∠OAB +∠CAD =90°,又∵∠CAD +∠ACD =90°,∴∠ACD =∠BAO 又∵AB =AC ,∠BOA =∠CDA =90°∴△ABO ≌△CAD ,∴AD =OB =4,CD =OA =2,OD =OA +AD =6.则C 的坐标是(6,2). ……………………6分设BC 的解析式是y=kx+b ,根据题意得: 624k b b +=⎧⎨=⎩,解得134k b ⎧=-⎪⎨⎪=⎩.则BC 的解析式是:143y x =-+ ……………………8分24. AF =2FG ……………………1分证得△ABD ≌△BCE ……………………4分 求得∠AFG =60°∠F AG =30° ……………………7分 ∴AF =2FG ……………………8分25.(1)设BC 的解析式为y =kx +b 根据题意得:05811b k b +=⎧⎨+=⎩ 解得 345k b ⎧=⎪⎨⎪=⎩∴BC 的解析式为y =43x +5 ………………… 3分当4x =时,8y = ∴D (4,8)………………… 4分(2)当0<t ≤8时,S=4t ………………… 6分 当8<t ≤19时,S=48-2 t …………………… 8分(3)当点P 运动到点A 处△OPD 的面积S 最大,最大值是32.…………………10分。
2012—2013学年度上学期八年级数学期中考试试卷 (考试时间120

2012—2013学年度上学期八年级数学期中考试试卷(考试时间:120分钟 满分:150分)一、选择题(每题3分,共24分)1、若直角三角形两边长为12和5,则第三边长为( )A 、13B 、15C 、13或15D 、13或119 2、下列说法正确的是( )A 、8的立方根是±2B 、负数没有立方根C 、互为相反数的两个数的立方根也互为相反数D 、立方根是它本身的数是03、如图,在平行四边形ABCD 中,对角线AC 、BD 相交于O ,将△AOB 平移至△DEC 的位置,则图中与OA相等的其他线段有( ) A 、1条 B 、2条 C 、3条 D 、4条4、已知平行四边形的一边长是14,下列各组数中能分别作为它的两条对角线的是( ) A 、10与16 B 、12与16 C 、20与22 D 、10与405、已知菱形较大的角是较小角的3倍,并且高为4cm ,则这个菱形的面积是( ) A 、82cm ² B 、162cm ² C 、3323 cm ² D 、32 cm ²6、下各数:(35)³,0.2323……,π,0,32)1(-,3.7842,-3,722,其中无理数有( ) A 、2个 B 、3个 C 、4个 D 、5 7、如果a 200是一个整数,那么正整数a 最小应取( ) A 、8 B 、5 C2 D 、18、下列给出的条件中,能判定一个四边形是菱形的是( ) A 、有一组对边平行且相等,有一个角是直角B 、有一组对边平行且相等,一组邻角相等评卷人 得分AODBCEC 、有一组对边平行,一组对角相等,两条对角线相等D 、一组对边平行,一组对角相等,有一组邻边相等二、填空(每题3分,共24分)9、已知直角三角形两直角边的比是3︰4,斜边长为20cm ,则斜边上的高是( )。
10、如图,有一个高12cm ,底面直径为10cm 的圆锥,现有一只蚂蚁在圆锥的顶部M 处,它想吃圆锥底部N 处的食物,需要爬行的最短路程是( )cm 。
2012——2013八年级数学第一学期期中考试卷

2012——2013学年八年级第一学期期中考试数学试卷(问卷)(时间:90分钟,满分:100分)注意事项:1. 本试卷分两部分:第一卷选择题10题,共30分。
第二卷非选择题12题,填空题5题;18分,解答题7题,52分,共70分。
共100分。
2.答卷前务必将自己的姓名,考号等填写在装订线内规定位置。
3.将解答过程填写在答卷规定位置。
第1卷 (选择题10题 30分)一、选择题(本大题共10小题,每小题3分,共30分,每题只有一个答案)1.如图所示,图中不是轴对称图形的是( ).2.下列数中是无理数的是( ).A .31B .9-C .0.4102•D 23.下列运算正确的是( )A .4=±2B .2)2(-=-2C .38-=-2D .2--=24.点P (一2,1)关于x 轴的对称点的坐标为( ) A .(-2 ,-1) B.(2 , 1) C .(2 ,-l) D .(1 ,-2)5.等腰三角形的周长是18cm,其中一边长为4cm ,其它两边长分别为( )A . 4cm ,l0cmB . 7cm , 7cmC .4cm,l0cm 或7cm,7cmD .无法确定 6-下列三角形不一定全等的是( )A 、面积相等的两个三角形B 、斜边和一条直角边分别对应相等的两个直角三角形C 、周长相等的两个等边三角形D 、有一个角是100°,腰长相等的两个等腰三角形 7.如图:已知∠1=∠2,AC=AD ,增加下列条件:(1)AB=AE ;(2)BC=ED ;(3)∠C=∠D (4)∠B=∠E ,其中能使△ABC ≌△AED 的条件有( )A .1个B . 2个C .3个D .4个12C EBD A第7题8.如图,△ABC 与△A ’B ’C ’关于直线l 对称,则∠B 的度数为( ) A .30° B . 50° C .90° D .100°9.如图,已知,在△ABC 中,AB=AC ,D 是BC 中点,DE ⊥AB 于E ,DF ⊥AC 于F ,那么图中全等的三角形有( )对。
2012—2013学年度第一学期期中考试八年级数学试卷

2012—2013学年度第一学期期中考试八年级数学试卷(100分钟,100分)2012.111、下列说法正确的是( )A.064.0-的立方根是0.4B.9-的平方根是3±C. 16的立方根是316D. 0.01的立方根是0.0000012、 如图(1):Rt △ABC 中,∠ACB=900,CD 是高,AC=4cm ,BC=3cm ,则CD=( )A. 5cmB.512cm C.125cm D.34cm3、在菱形ABCD 中,∠ADC=120°则BC:AC ( )A 、2:3B 、3:3C 、2:1D 、1:34、以下列各组数为边长,能组成直角三角形的是( )A.8、15、7B. 8、10、6C. 5、8、10D. 8、39、385)二.填空题。
(每题3分,共15分)6、算术平方根和立方根都等于本身的数是 ,81的算数平方根是 。
7、菱形有一个内角是120度,有一条对角线长为 6 cm ,此菱形的边长是 。
8、一个多边形内角和是540°,那么从一个顶点引出的对角线的条数是 。
9、 如图(2),△ABC 经过平移后到△GMN 的位置,BC 上一点D 也同时平移到点H的位置,若AB=8cm 。
∠HGN=25°,则GH= ,∠DAC= 。
10、如图(3)矩形ABCD 的对角线AC 、BD 相交于点0,过点0的直线交AB 、CD 于E 、F ,AB=6,BC=10,则图中阴影部分的面积为 。
三.解答题。
(共70分)11、计算:(每题5分,共20分)(1) 200320042)2)+ (2)()()131381672-++-(3) 40)52(2-+. (4)2101.036813-+-CBDA图(1)E12、(6分)规律探求,观察522-=58=524⨯=252,即522-=252;1033-=1027=1039⨯=3103,即1033-=3103(1)猜想2655-等于什么,并通过计算验证你的猜想;(2)写出符合这一规律的一般等式。
江苏省无锡市八年级上学期期中考试数学试题 新人教版

江苏省无锡市2012-2013学年八年级上学期期中考试数学试题新人教版注意事项:本试卷满分100分考试时间:100分钟一、选择题:(本大题共8小题,每小题3分,共24分)1.立方根等于本身的数是……………………………………………………………()A.-1 B.0 C.±1 D.±1或02.下列图形中,是中心对称图形但不是轴对称图形的是()A.B.C.D.3.在数0、2.0、3π、722、1010010001.0、11131、27中,无理数有…( )A.1个 B.2个 C.3个 D.4个4.已知等腰三角形的一内角为40º,则这个等腰三角形的顶角为………………( )A.40º B.100º C.40º或70º D.40º或100º5.如图,OAB△绕点O逆时针旋转80o到OCD△的位置,已知35AOBo,则AOD等于…………………………()A.55o B.45o C.40o D.35o6.有下列说法:①等腰梯形同一底上的两个内角相等;②等腰梯形的对角线相等;③等腰梯形是轴对称图形,且只有一条对称轴;④有两个内角相等的梯形是等腰梯形.其中正确的有……………………………………………………………………()A.1个 B.2个 C.3个 D.4个7.下列性质中,等腰三角形具有而直角三角形不一定具有的是………………()A.有一个角的平分线垂直于这个角的对边 B.外角和等于360°C.有两个锐角的和等于90°D.两条边的平方和等于第三条边的平方8.勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为…………………()A.90 B.110 C.121 D.144二.填空:(本大题共有15空,每空2分,共30分.)9.如图,在数轴上表示实数15的点可能是点10.94的平方根是,27的立方根是.11.比较大小:3253,(-16)2(16)2 (用“﹥、=、﹤”号连结)10 2 3 4NMQP第9题图MNCBA 12.2012年中秋、国庆黄金周无锡市的旅游总收入约为5176900000元,此数据保留四个有效数字的近似数为 元,此近似数精确到 位. 13.观察下列各式: 11111112,23,34334455,请你将发现的规律用含正整数n 的等式表达 .14.已知正数x 的两个不同的平方根为a +2和2a -8,则x 的值为 . 15.已知22 c b +(b -c +1)2=0,则32b c .16.如图,△ABC 中,AB =AC ,D 在BC 上,且BD =AD ,DC =AC ,则∠B = °.17.如图,在等腰梯形ABCD 中,上底为6㎝,下底为8㎝,高为3㎝,则腰长为 ㎝.18.如图,在直角△ABC 中,∠C =90,AD 平分∠BAC ,CD :BD =1:2,点D 到AB 的距离DE =4厘米,则BC = 厘米.19.如图,点A 的正方体左侧面的中心,点B 是正方体的一个顶点,正方体的棱长为2,一蚂蚁从点A 沿其表面爬到点B 的最短路程是 .20.如图,在等边△ABC 中,AB =6,N 为AB 上一点,且AN =2,∠BAC 的平分线交BC 于点D ,M 是AD 上的动点, 连结 BM 、MN ,则BM +MN 的最小值是 三.解答题:(本大题共7小题,共46分.)21.求下列各式中的x (每小题3分,共计6分)(1) 036)2(2x (2) 364(1)27x22.计算:(每小题4分,共计8分)⑴ 13232(8)(2) ⑵ 20(2)12(2)23.利用网格线用三角尺画图,(本题5分) (1)在图中找一点O ,使得OA =OB =OC ;(1分) (2)画出△ABC 绕点O 逆时针旋转90°后的三角形;(2分) (3) 求点B 经过的路径长.(结果保留精确值)(2分)第20题24.如图,等腰梯形ABCD中,AD∥BC,AB=CD,对角线BD平分∠ABC,且BD⊥DC,上底AD=3cm,对角线BD=27cm. (本题6分)(1)求∠ABC的度数;(3分)(2)求梯形ABCD的周长. (3分)25、小王剪了两张直角三角形纸片,进行了如下的操作:(本题7分)操作一:如图1,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.(1)如果AC=6cm,BC=8cm,可求得△ACD的周长为;(2分)(2)如果∠CAD:∠BAD=4:7,可求得∠B的度数为;(2分)操作二:如图2,小王拿出另一张Rt△ABC纸片,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,若AC=9cm,BC=12cm,请求出CD的长.(3分)26.如图(1),△ACB和△ECD均为等腰直角三角形,∠ACB=∠ECD=90º,把△ECD绕点C逆时针旋转,使点 D在AB上,如图(2),连结AE.(6分)(1)求证:△ACE≌△BCD;(3分)(2)如图(2),若AB=4,ED=10,求△ADE的面积.(3分)B27.(本题8分)如图,在梯形ABCD中,AD∥BC,∠B=90º,AD=8cm,AB=6cm,BC=10 cm,点Q从点A出发以1 cm/s的速度向点D运动,点P从点B出发以2cm/s的速度在线段BC间往返运动,P、Q两点同时出发,当点Q到达点D时,两点同时停止运动。
2012-2013年八年级数学上册期中考试试题及答案

2012-2013 学年度第一学期期中质量监测八年级数学试题2012.11.【注意事项】本试卷共8页,全卷共三大题28小题,满分150分,考试时间120分钟.一、用心选一选,将你认为正确的答案填入下表中。
(每题3分,共24分)1、下列几种图案中,既是中心对称又是轴对称图形的有()A.1个B.2个C.3个 D.4个2、在实数4.21⋅⋅,π,-722,0)21(-中无理数的个数是()A.1个B.2个C.3个 D.4个3).A.点P B.点Q C.点M D.点N4、如图,O A B△绕点O逆时针旋转80 到O C D△的位置,已知45AOB∠= ,则A O D∠等于().A.55 B.45 C.40 D.355、下列说法: ①无限小数都是无理数;②无理数都是无限小数;③带根号的数都是无理数;④不带根号的数一定是有理数;⑤有理数和数轴上的点一一对应;⑥负数没有立方根。
其中正确的有( )A.1个B.2个C.3个D.4个6、等腰三角形两边长为2和5,则此三角形的周长为()A.7B.9C.12D.9或1210 2 3 4NMP第4题7、如图在平行四边形A B C D 中C E AB ⊥,E 为垂足.如果 ∠A=115°,则B C E =∠( ) A.55 B.358、如图,已知△ABC 中,∠ABC =90°,AB =BC ,三角形的顶点在相互平行的三条直线l 1,l 2,l 3上,且l 1,l 2之间的距离为1 , l 2,l 3之间的距离为2 ,则AC 的长是( )A .13B .20C .26D .5 二、细心填一填:(每题3分,共30分)9、 9的平方根是_____________。
10、定义运算“@”的运算法则为: x@y ,则 (2@6)@8=____。
11、据统计,2011年十²一期间,某市某风景区接待中外游客的人数为86740人次,将这个数字保.留三个有效数字.......,用科学记数法可表示为 12、小明有两条长分别是3厘米和4厘米的小木棒,当他再找一根长度为 厘米的小木棒时,可以使这三根木棒刚好拼成一个直角三角形. 13、已知梯形的中位线长为6 cm ,高为3 cm ,则此梯形的面积为_______cm 2. 14、直角三角形两直角边长分别为3和4,则它斜边上的高为__________. 15、平行四边形ABCD 中,AB=6cm ,BC=8cm ,对角线AC 、BD 相交于点O ,则:△BCO 与△ABO 的周长之差为 。
2012-2013学年八年级(上)期中数学试卷

2012-2013学年八年级(上)期中数学试卷一、选择题(每题2分,满分20分)1.(2分)在实数,0.3,,,,﹣3,中,无理数有()A.1个B.2个C.3个D.4个分析:根据无理数的定义即可判定选择项.解答:解:在实数,0.3,,,,﹣3,中,根据无理数的定义可得,无理数有,,三个.故选C.点评:此题主要考查了无理数的定义.注意带根号的要开不尽方的才是无理数,无限不循环小数为无理数.如π,,0.8080080008…(每两个8之间依次多1个0)等形式..1的平方根是±1 B.﹣1的立方根是﹣1.是2的平方根D.﹣3是的平方根D、根据平方根的定义即可判定.解答:解:A、1的平方根是±1,故选项正确;B、﹣1的立方根是﹣1,故选项正确;C、是2的平方根,故选项正确;D、=3,故选项D错误.故选D.点评:本题考查了平方根的定义.注意一个正数有两个平方根,它们互为相反数;0的平方3.(2分)(2011•呼伦贝尔)如图,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为()4.(2分)如图,△ABC中,AB=AC,D是BC中点,下列结论中不正确的是()A.∠B=∠C B.A D⊥BC C.A D平分∠BAC D.A B=2BD5.(2分)已知A,B两点的坐标分别是(﹣2,3)和(2,3),则下面四个结论:①A,B 关于x轴对称;②A,B关于y轴对称;③A,B关于原点对称;④A,B之间的距离为4,6.(2分)(2013•黔西南州)如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x<ax+4的解集为()A.x<B.x<3 C.x>D.x>3的坐标,再根据函数的图象即可得出不等式2x<ax+4的解集.解答:解:∵函数y=2x和y=ax+4的图象相交于点A(m,3),∴3=2m,m=,∴点A的坐标是(,3),∴不等式2x<ax+4的解集为x<;故选A.点评:此题考查的是用图象法来解不等式,充分理解一次函数与不等式的联系是解决问题的7.(2分)(2011•衢州)如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=2,则PQ的最小值为()A.1B.2C.3D.4∴PA=PQ=2,故选B.点评:此题主要考查了角平分线的性质,本题的关键是要根据直线外一点与直线上各点连接8.(2分)若点(x1,y1)和(x2,y2)都在直线y=﹣3x+5上,且x1>x2,则下列结论正确9.(2分)如图,∠A=15°,AB=BC=CD=DE=EF,则∠DEF等于()10.(2分)(2008•枣庄)如图,点A的坐标为(1,0),点B在直线y=﹣x上运动,当线段AB最短时,点B的坐标为().(,﹣)C.(,﹣)D.(﹣,):计算题;压轴题.分析:线段AB最短,说明AB此时为点A到y=﹣x的距离.过A点作垂直于直线y=﹣x 的垂线AB,由题意可知:△AOB为等腰直角三角形,过B作BC垂直x轴垂足为C,则点C为OA的中点,有OC=BC=,故可确定出点B的坐标.解答:解:过A点作垂直于直线y=﹣x的垂线AB,∵点B在直线y=﹣x上运动,∴∠AOB=45°,∴△AOB为等腰直角三角形,过B作BC垂直x轴垂足为C,则点C为OA的中点,则OC=BC=.作图可知B在x轴下方,y轴的右方.∴横坐标为正,纵坐标为负.所以当线段AB最短时,点B的坐标为(,﹣).故选B.点评:动手操作很关键.本题用到的知识点为:垂线段最短.二、填空题(每小题3分,共30分)11.(3分)(2013•沛县一模)函数y=中自变量x的取值范围是x≤5.分析:根据二次根式的性质列出不等式,求出不等式的取值范围即可.解答:解:若使函数y=有意义,∴5﹣x≥0,即x≤5.故答案为x≤5.点评:本题主要考查了函数自变量取值范围的知识点,注意:二次根式中的被开方数必须是12.(3分)点P(5,﹣3)关于x轴对称的点的坐标为(5,3).13.(3分)△ABC≌△DEF,且△ABC的周长为18.若AB=5,EF=6,则AC=7.14.(3分)(2011•嘉兴)如图,在△ABC中,AB=AC,∠A=40°,则△ABC的外角∠BCD= 110度.∵∠A=40°,∴∠B=∠ACB=(180°﹣∠A)=70°,∴∠BCD=∠A+∠B=40°+70°=110°,故答案为:110.点评:本题主要考查对等腰三角形的性质,三角形的内角和定理,三角形的外角性质等知识15.(3分)若m+3与m﹣1是同一个正数的两个平方根,则m的值是﹣1.16.(3分)一个等腰三角形有两边分别为5和8厘米,则周长是18或21厘米.17.(3分)Rt△ABC中,∠C=90°,∠B=2∠A,BC=3cm,AB=6cm.分析:根据直角三角形的性质即可解答.解答:解:如图:∵Rt△ABC中,∠C=90°,∠B=2∠A∴∠A+∠B=90°∴∠A=30°,∠B=60°∴=,∵BC=3cm,∴AB=2×3=6cm.故填空答案:6.点评:此题较简单,只要熟记30°角所对的直角边等于斜边的一半即可解答.18.(3分)(2012•衡阳)如图,一次函数y=kx+b的图象与正比例函数y=2x的图象平行且经过点A(1,﹣2),则kb=﹣8.19.(3分)(2011•衡阳)如图,一次函数y=kx+b的图象与x轴的交点坐标为(2,0),则下列说法:①y随x的增大而减小;②b>0;③关于x的方程kx+b=0的解为x=2.其中说法正确的有①②③(把你认为说法正确的序号都填上).20.(3分)(2007•烟台)观察下列各式:…请你将发现的规律用含自然数n(n≥1)的等式表示出来(n≥1).:压轴题;规律型.分析:观察分析可得:=(1+1);=(2+1);…则将此题规律用含自然数n(n≥1)的等式表示出来是=(n+1)(n≥1).解答:解:=(n+1)(n≥1).点评:本题考查学生通过观察、归纳、抽象出数列的规律的能力,要求学生首先分析题意,找到规律,并进行推导得出答案.本题的关键是根据数据的规律得到=(n+1)(n≥1).三、解答题(共50分)21.(6分)(1)计算:.(2)解方程:4(x﹣3)2=9.:计算题.分析:(1)根据二次根式的性质、立方根与算术平方根得到原式=3﹣4﹣2,然后进行加减运算;(2)先变形为(x﹣3)2=,根据平方根定义得到x﹣3=±,然后解一次方程即可.解答:解:(1)原式=3﹣4﹣2=﹣3;(2)∵(x﹣3)2=,∴x﹣3=±,∴x=或x=.22.(6分)如图所示,△ABC在正方形网格中,若点A的坐标为(0,5),按要求回答下列问题:(1)在图中建立正确的平面直角坐标系;(2)根据所建立的坐标系,写出点B和点C的坐标;(3)作出△ABC关于x轴的对称图形△A′B′C′.(不用写作法)即为所求.解答:解:(1)所建立的平面直角坐标系如下所示:(2)点B和点C的坐标分别为:B(﹣3,1)C(1,3);(3)所作△A'B'C'如上图所示.点评:本题考查了轴对称变换作图,作轴对称后的图形的依据是轴对称的性质,基本作法是:23.(4分)如图,小明在完成数学作业时,遇到了这样一个问题,AB=CD,BC=AD,请说明:∠A=∠C的道理,小明动手测量了一下,发现∠A确实与∠C相等,但他不能说明其中的道理,你能帮助他说明这个道理吗?试试看.把他们放到两个三角形中,作为对应边.解答:解:∵AB=CD,BC=AD,又∵BD=DB,在△ABD和△CDB中,∴△ABD≌△CDB,∴∠A=∠C.24.(5分)如图,折线ABC是甲地向乙地打长途电话所需要付的电话费y(元)与通话时间t(分钟)之间关系的图象(注意:通话时间不足1分钟按1分钟计费).(1)通话1分钟,要付电话费多少元?通话5分钟要付多少电话费?(2)通话多少分钟内,所支付的电话费一样多?(3)通话3.2分钟应付电话费多少元?案.解答:解:(1)根据图象可知,通话1分钟时,要付电话费2.5元,通话5分钟时,要付费4.5元;(2)根据图象可知,通话3分钟内,所支付的电话费一样多;(3)当t>3时,设y=kt+b把B(3,2.5),C(5,4.5)代入得解得,y=t﹣0.5当t=4时,y=3.5.点评:此题比较复杂,关键是正确理解题意,然后分析图形要分清不同时间段,电话费的不25.(5分)已知2a+1的平方根是±3,5a+2b﹣2的算术平方根是4,求:3a﹣4b的平方根.分析:根据已知得出2a+1=9,5a+2b﹣2=16,求出a b,代入求出即可.解答:解:根据题意得:2a+1=32=9,5a+2b﹣2=16,即a=4,b=﹣1,∴3a﹣4b=16,∴3a﹣4b的平方根是±=±4.答:3a﹣4b的平方根是±4.点评:本题考查了平方根和算术平方根的应用,关键是根据题意列出算式.26.(7分)已知直线y=kx+6经过点C(3,0).(1)求k的值;(2)点A(﹣2,a)、B(0.5,b)在直线y=kx+6的图象上,试比较a、b的大小.(3)求S△BCO.(3)首先计算出B点坐标,再根据三角形的面积公式计算出答案即可.解答:解:(1)把点(3,0)代入y=kx+6,得:0=3k+6,解得:k=﹣2;(2)∵k=﹣2,∴函数值y随x的增大而减小,又∵﹣2<0.5,∴a>b;(3)把B(0.5,b)代入函数y=﹣2x+6中,解得:b=5,则B(0.5,5),S△BOC=×CO×5=×3×5=7.5.点评:此题主要考查了待定系数法求一次函数解析式,以及一次函数的性质,关键是掌握待27.(7分)A、B两所学校在一条东西走向公路的同旁,以公路所在直线为x轴建立如图所示的平面直角坐标系,且点A的坐标是(2,2),点B的坐标是(7,3).一辆汽车由西向东行驶,在行驶过程中是否存在一点C,使C点到A、B两校的距离之和最小,如果有?请用尺规作图找出该点,保留作图痕迹,并求出它的坐标.出直线与x轴的交点坐标即可.解答:解:(1)如图所示,作A关于x轴的对称点A′,连接A′B交x轴于C,则点C为所求;(2)由图可知,点A'(2,﹣2),设直线A'B的解析式为y=kx+b,则有,解得,∴直线A'B的解析式为y=x﹣4,设点C坐标为(a,0),并代入y=x﹣4,得:0=a﹣4,解得:a=4,∴点C坐标为(4,0).点评:本题考查了解二元一次方程组,作图与基本作图,用待定系数法求一次函数的解析式,28.(10分)如图,一次函数的图象分别与x轴、y轴交于点A、B,以线段AB 为边在第一象限内作等腰Rt△ABC,∠BAC=90°.求过B、C两点直线的解析式.C点坐标,再用待定系数法即可求出直线BC的解析式.解答:解:∵一次函数中,令x=0得:y=2;令y=0,解得x=3.∴B的坐标是(0,2),A的坐标是(3,0).作CD⊥x轴于点D.∵∠BAC=90°,∴∠OAB+∠CAD=90°,又∵∠CAD+∠ACD=90°,∴∠ACD=∠BAO又∵AB=AC,∠BOA=∠CDA=90°∴△ABO≌△CAD,∴AD=OB=2,CD=OA=3,OD=OA+AD=5.则C的坐标是(5,3).设BC的解析式是y=kx+b,根据题意得:,解得.则BC的解析式是:y=x+2.。
2012-2013学年度上学期期中八年级数学试卷
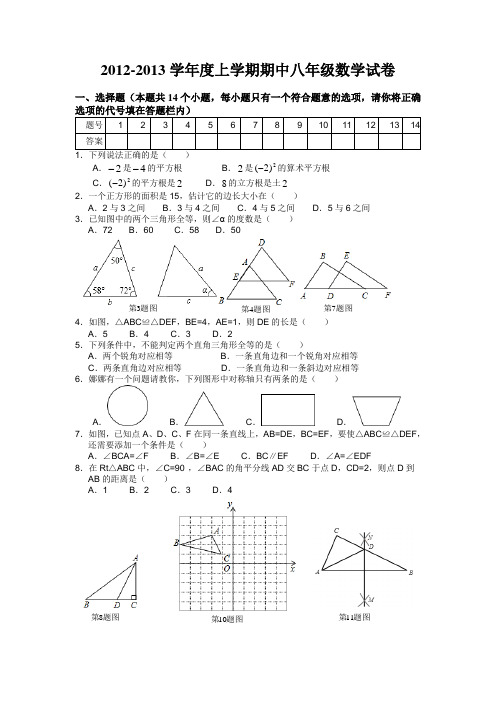
2012-2013学年度上学期期中八年级数学试卷一、选择题(本题共14个小题,每小题只有一个符合题意的选项,请你将正确A .2-是4-的平方根B .2是2)2(-的算术平方根C .2)2(-的平方根是2 D .8的立方根是土2 2.一个正方形的面积是15,估计它的边长大小在( )A .2与3之间B .3与4之间C .4与5之间D .5与6之间 3.已知图中的两个三角形全等,则∠α的度数是( ) A .72° B .60° C .58° D .50°4.如图,△ABC ≌△DEF ,BE=4,AE=1,则DE 的长是( ) A .5 B .4 C .3 D .25.下列条件中,不能判定两个直角三角形全等的是( )A .两个锐角对应相等B .一条直角边和一个锐角对应相等C .两条直角边对应相等D .一条直角边和一条斜边对应相等 6.娜娜有一个问题请教你,下列图形中对称轴只有两条的是( )A .B .C .D .7.如图,已知点A 、D 、C 、F 在同一条直线上,AB=DE ,BC=EF ,要使△ABC ≌△DEF ,还需要添加一个条件是( )A .∠BCA=∠FB .∠B=∠EC .BC ∥EFD .∠A=∠EDF 8.在Rt △ABC 中,∠C=90°,∠BAC 的角平分线AD 交BC 于点D ,CD=2,则点D 到AB 的距离是( )A .1B .2C .3D .4题图第3题图第4题图第7题图第8题图第10题图第119.等腰三角形两边长分别为4和8,则这个等腰三角形的周长为( ) A .16 B .18 C .20 D .16或2010.如图,△ABC 在平面直角坐标系中第二象限内,顶点A 的坐标是(2-,3),先把△ABC 向右平移4个单位得到△A 1B 1C 1,再作△A 1B 1C 1关于x 轴对称图形△A 2B 2C 2,则顶点A 2的坐标是( )A .(3-,2)B .(2,3-)C .(1,2-)D .(3,1-) 11.如图,在△ABC 中,分别以点A 和点B 为圆心,大于21AB 的长为半径画孤,两弧相交于点M ,N ,作直线MN ,交BC 于点D ,连接AD .若△ADC 的周长为10,AB=7,则△ABC 的周长为( )A .7B .14C .17D .2012.如图,在平面直角坐标系中,在x 轴、y 轴的正半轴上分别截取OA 、OB ,使OA=OB ;再分别以点A 、B 为圆心,以大于21AB 长为半径作弧,两弧交于点C .若点C 的坐标为(1-m ,n 2),则m 与n 的关系 为( )A .12=+n mB .12=-n mC .12=-m nD .12=-m n13.光线以如图所示的角度α,照射到平面镜I 上, 然后在平面镜I 、II 之间来回反射,已知∠α=50°,∠β=60°,则∠ν等于( ) A .40° B .50° C .60° D .70°14.如图,在△ABC 中,∠ABC 和∠ACB 的平分线交于点E ,过点E 作MN ∥BC 交AB于M ,交AC 于N ,若BM+CN=9,则线段MN 的长为( ) A .6 B .7 C .8 D .9二、填空题(本题5个小题,请你将答案填写在题目中的横线上)15.若x ,y 为实数,且满足|3-x |3++y 0= ,则(yx)2012的值是 .16.尺规作图中的平分已知角,其根据是构造两个三角形全等.由作法知,判定所构造的两个三角形全等的依据是 . 17.如图,△ABC 中,AB=AC ,AD ⊥BC ,垂足为D ,若∠BAC=70°,则∠BAD= °.18.如图,将正方形ABCD 沿BE 对折,使点A 落在对角线BD 上的A′处,连接A′C ,则∠BA′C= 度.19.在Rt △ABC 中,∠ACB=90°,BC=2cm ,CD ⊥AB ,在AC 上取一点E ,使EC=BC ,过点E 作EF ⊥AC 交CD 的延长线于点F ,若EF=5cm ,则AE= cm .题图第12题图第13题图第14题图第19题图第18题图第17三、解答题(本题共7个小题,请将解答过程写在每题规定的区域内)20.计算:1-21.已知:如图,AB=AE ,∠1=∠2,∠B=∠E .求证:BC=ED .题图第2122.我们在学习“实数”时,画了这样一个图,即“以数轴上的单位长为…1‟的线段作一个正方形,然后以原点O 为圆心,正方形的对角线长为半径画弧交x 轴于点A”,请根据图形回答下列问题:(1)线段OA 的长度是多少?(要求写出求解过程) (2)这个图形的目的是为了说明什么?(3)这种研究和解决问题的方式,体现了 的数学思想方法. (将下列符合的选项序号填在横线上)A 、数形结合;B 、转化;C 、函数;D 、方程.23.如图所示,△ABC 在正方形网格中,若点A 的坐标为(0,3),按要求回答下列问题: (1)在图中建立正确的平面直角坐标系;(2)根据所建立的坐标系,写出点B 和点C 的坐标; (3)作出△ABC 关于x 轴的对称图形△A'B'C'.(不用写作法)题图第22题图第2324.如图,点E 、F 分别是AD 上的两点,AB ∥CD ,AB=CD ,AF=DE .问:线段CE 、BF有什么数量关系和位置关系?并加以证明.25.如图,△ABC 中,AB=AC ,∠A=36°,AC 的垂直平分线交AB 于E ,D 为垂足,连接EC .(1)求∠ECD 的度数; (2)若CE=5,求BC 长.题图第24题图第2526.如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.(1)求证:△ADE≌△BFE;(2)连接EG,判断EG与DF的位置关系并说明理由.第26题图2012-2013学年度上学期期中八年级数学试卷答案一、选择题(本题共14个小题,每小题3分,共42分)1.B 2.B 3.D 4.A 5.A 6.C 7.B 8.B 9.C 10.B 11.C 12.B 13.D 14.D二、填空题(本题5个小题,每小题3分,共15分)15.1 16.边边边(sss )17.35 18.5.67 19.3三、解答题(本题共7个小题,共63分)20.解:原式=2314=24.CE 和BF 的数量关系是CE=BF ,位置关系是CE ∥BF ,证明:∵AB ∥CD ,∴∠A=∠D ,∵在△ABF 和△DCE 中⎪⎩⎪⎨⎧=∠=∠=DE AF D A CD AB ,∴△ABF ≌△DCE ,∴CE=BF ,∠AFB=∠DEC , ∴CE ∥BF ,即CE 和BF 的数量关系是CE=BF ,位置关系是CE ∥BF . 25.解:(1)∵DE 垂直平分AC ,∴CE=AE ,∴∠ECD=∠A=36°; (2)∵AB=AC ,∠A=36°,∴∠B=∠ACB=72°,∴∠BEC=∠A+∠ECD=72°, ∴∠BEC=∠B , ∴BC=EC=5.答:(1)∠ECD 的度数是36°; (2)BC 长是5.26.(1)证明:∵AD ∥BC ,∴∠ADE=∠BFE ,∵E 为AB 的中点,∴AE=BE ,在△AED 和△BFE 中,⎪⎩⎪⎨⎧=∠=∠∠=∠BE AE BEF AED EFB ADE ,∴△AED ≌△BFE (AAS );(2)解:EG 与DF 的位置关系是EG ⊥DF ,理由为:连接EG ,∵∠GDF=∠ADE ,∠ADE=∠BFE , ∴∠GDF=∠BFE ,由(1)△AED ≌△BFR 得:DE=EF ,即GE 为DF 上的中线, ∴GE ⊥DF .。
江苏省无锡市2012-2013学年八年级数学上学期期中试题 苏科版

八年级数学期中考试卷一、选择题(每小题3分,共24分)1.下列各数是无理数的是 ( )A .722 B .38 C .32 D .0.4144144145 2.在下列长度的各组线段中,能组成直角三角形的是 ( )A .5,6,7B .5,12,13C .1,4,9D .5,11,123.已知如图1所示的四张牌,若将其中一张牌旋转180°后得到图2.则旋转的牌是( )4.已知一直角三角形的木版,三边的平方和为1800cm 2,则斜边长为 ( )A .120cmB .90cmC .80cmD .30cm5. 正方形具有而菱形不一定具有的性质是 ( )A .对角线互相垂直B .对角线互相平分C .对角线相等 D. 对角线平分一组对角6.如图,数轴上点N 表示的数可能是 ( )A .10B .17C .3D .5(第6题图) (第7题图)7. 如图,某公园有一块矩形草地ABCD ,矩形草地的边及对角线BD 是小路,BC 长40米,CD 长30米,妈妈站在A 处,亮亮沿着小路B-C-D-B 跑步,在跑到95米处时,此时亮亮与妈妈之间的距离为 ( )A .22米B .23米C .24米D .25米8.如图是一个长、宽都是30cm ,高是50cm 的长方体无盖纸箱,一只蚂蚁在纸箱外部的A 点,而在纸箱里面B 点处有一滴蜜(B 离纸箱口30cm ),蚂蚁想吃到这一滴蜜,它从A 点沿纸箱爬到B 点,那么图1 图2 A B C D它所爬行的最短路线的长是( )A. 100B. 140C. 10D. 80 二、选择题(每空2分,共24分)9. 4的算术平方根是 。
-64的立方根是 。
10. ABCD 中,若AB=3cm ,A D=5cm ,则ABCD 的周长为 。
11. 若2m -1没有平方根,则m 的取值范围是 。
12. 长城总长约为6700010米,用科学记数法表示是 。
(保留三个有效数字)13. 如图,在△ABC 中,AB =AC =32cm ,DE 是AB 的垂直平分线,分别交AB 、AC 于D 、E两点.(1)若∠C =700,则∠BEC = ;(2)若BC =21cm ,则△BCE 的周长是cm 。
2012~2013学年度(上)学期八年级期中测试数学试卷(五四分段)

13 y 34x y 2y 34 xy 3 2x 5y 0.6 2y x x ==+==-=+=2012~2013学年度(上)学期八年级期中测试数学试卷一.选择题(每题3分,共30分)1. 在下列各电视台的台标图案中,是轴对称图形的是( )A B C D2. 下列函数中,y 是x 的一次函数的是( ) A.3个 B.4个 C.5个 D.2个3. 在下列说法中,正确的是( )A .如果两个三角形全等,则它们必是关于直线成轴对称的图形;B .如果两个三角形关于某直线成轴对称,那么它们是全等三角形;C .等腰三角形是关于底边中线成轴对称的图形;D .一条线段是关于经过该线段中点的直线成轴对称的图形4. 一次函数y =—2x +3的图象与x 轴、y 轴的交点分别是( ) A .(-2,0)、(0,3) B .(23,0)、(0,3) C .(3,0)、(0,-2) D .(3,0)、(0,23)5. 将两块全等的直角三角形(有一锐角为30︒)拼成一个四边形,其中轴对称图形的四边形有多少个( ) A 、1 B 、2 C 、3 D 、46.一次函数y=ax+b 的图像如图所示,则下面结论中正确的是( ) A .a <0,b <0 B .a <0,b >0 C .a >0,b >0 D .a >0,b <07.等腰三角形的一个内角是50°,则另外两个角的度数分别是( )A.65°、65°B.50°、80°C.65°、65°或50°、80°D.50°、50°8.在平面直角坐标系中,函数1y x =-+的图象经过( )A .一、二、三象限B .二、三、四象限C .一、三、四象限D .一、二、四象限9.如图,△ABC 中,∠ABC 与∠ACB 的平分线交于点F ,过点F 作DE ∥BC 交AB 于点D ,交AC 于点E ,那么下列结论:①△BDF 和△CEF 都是等腰三角形;②DE=BD+CE ;•③△ADE 的周长等于AB 与AC 的和;④BF=CF .其中正确的有( )A .①②③B .①②③④C .①②D .①10.已知函数y kx b =+的图象如图,则2y kx b =+的图象可能是( )二.填空题(每题3分,共30分) 11.已知A (2,b ),B (a,-4),若A ,B 关于x 轴对称,那么a ,b 为 和 ; 12.若一次函数y=x+b 的图象过点A (1,-1),则b=__________。
2012-2013学年八年级上学期数学期中考试试题

2012-2013学年八年级上学期期中考试数学试题(本试卷三大题共24个小题,考试时间:120分钟;试卷满分:100分)一.选择题(下列各小题均有四个选项, 其中只有一个正确的, 请把它选出来填在题后的括号内, 每小题3分, 满分24分)1.下列图形:①三角形,②线段,③正方形,④直角其中是轴对称图形的个数有()A.4个B.3个C.2个D.1个2. 2-1的绝对值是()A.2-1 B.1-2C.-1-2D.-2-1 3.如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM ≌△CDN的是()A.∠M=∠NB. AM∥CNC.AB=CDD. AM=CN4.AD是△ABC的角平分线且交BC于D,过点D作DE⊥AB于E,DF⊥AC于F•,则下列结论不一定正确的是()A.DE=DF B.BD=CD C.AE=AF D.∠ADE=∠ADF 5.9的算术平方根是()A. 3B.-3C.3D.36.一定能确定△ABC≌△DEF的条件是()A、∠A=∠D,∠B=∠E,∠C=∠FB、∠A=∠E,AB=EF,∠B =∠DC、∠A=∠D,AB=DE,∠B=∠ED、AB=DE,BC=EF,∠A =∠D7.下列说法中,正确的是()A.有理数都是有限小数 B.无限小数就是无理数C.实数包括有理数、无理数和零D.无论是有理数还是无理数,都可以用数轴上的点来表示。
8. 在下列各数:3.1415926;10049;0.2;π1;7;11131;327;2中,无理数的个数 ( ) A 、2 B 、3 C 、4 D 、5二、填空题(每小题3分,共21分).9. 等腰三角形的一个角为40°,则它的底角为 。
10. ︱35-︳的相反数是______________。
11. 若x y ,为实数,且0x +=,则2011⎪⎪⎭⎫⎝⎛y x 的值为 。
12. 16的平方根是_______________ 。
13. 已知点P (-3,4),关于x 轴对称的点P′的坐标为 。
2012-2013学年度第一学期期中考试八年级数学试卷

2012~2013学年度第一学期期中考试八年级数 学 试 题时间 120分钟 满分 150分第Ⅰ卷(本卷满分100分)一、选择题:(共8小题,每小题3分,共24分)下面每小题给出的四个选项中, 有且只有一个是正确的, 请把正确选项前的代号填在答卷指定位置.1.点A (-3,-4)关于x 轴的对称点是( ).A .(3,-4)B .(-3,4)C .(3,4)D .(-4,3) 2.对称现象无处不在,请你观察下面的四个图形,它们体现了中华民族的传统文化,其中,可以看作是轴对称图形的有( ).A .1个B .2个C .3个D .4个3.如图,△ACE ≌△DBF ,若AD =8,BC =2,则AB 的长度等于( ). A .6 B .4 C .2 D .34.如果等腰三角形两边长分别是10cm 和4cm ,那么它的周长是( ). A .14cm B .18cm C .24cm 或18cm D .24cm 5.下列运算正确的是( ). A .632a a a =⋅B .532)(a a = C .a a a 532=+D .23a a a =-6.等腰三角形中有一个角是40︒,则另外两个角的度数是( ).A .70︒ , 70︒B .40︒, 100︒C .70︒, 40︒D .70︒, 70︒或40︒,100︒7.若412++kx x 是完全平方式,则常数k 的值为( ). A .21 B .21± C .1 D .1±8.如图,O 是△ABC 的两条边AB 、BC 的垂直平分线的交点,∠BAC =70°,则∠BOC =( ).A .120°B .125°C .130°D .140°第3题图OCBA第8题图A二、填空题(共8小题,每小题3分,共24分)下列各题不需要写出解答过程,请将结果直接填写在答卷指定的位置.9.已知如图,AD =BC ,要得到△ABD ≌△CDB ,可以添加角的条件:∠_______=∠_______.第9题图10.如图,△ABC 中,已知AB =AC ,BD =DC ,则∠ADB =_______.11.如图,△ABC 的两条高CD 与BE 交于O ,若CD=BE ,则图中共有_______对全等三角形. 12.计算:()()12+-x x = .13.一个正方形的边长增加3cm ,它的面积就增加39cm 2,则这个正方形的边长为 cm .14.如图,在Rt △ABC 中,∠ACB =90°, ∠A =30°, CD ⊥AB 于D 点,若1=BD ,则=AD .第14题图15.如图,等边△ABC 的边长为3cm ,D 、E 分别是AB 、AC 上的两点,将△沿直线DE 折叠,点A 落在点A ' 处,且点A '在△ABC 周长为________ cm .16.命题:①有一条边相等的两个等边三角形全等;②两条直角边对应 相等的两个直角三角形全等;③有两边和一角分别相等的两个三角形全等;④底边相等的两个等腰三角形全等. 以上命题正确的有_________.(填序号)三、解答题(共52分)下列各题需要在答题卷指定位置写出文字说明、证明过程或计算步骤.17.(本题满分10分)计算: (1) xy x 362⋅ (2) ()()b b a 242--DB C 第11题图第15题图A18.(本题满分10分)先化简,再求值: ()()()b a b a b a -+-+522,其中31=a ,61-=b .19.(本题满分10分)如图,△ABC 中,AC =BC ,∠BAC =50°,延长CB 至D ,使DB =BA ,延长BC 至E ,使CE =CA ,连接AD 、AE ,求∠D ,∠E 的度数.20. (本题满分10分)如图,BD 是∠ABC 的平分线,AB =BC ,点E 在BD 上,连接AE ,CE ,DF ⊥AE ,DG ⊥CE ,垂足分别是F 、G ,求证:DF =DG .第19题图 第20题图B21.(本题12分)如图,在平面直角坐标系,直线l 过点T (0,2),且平行于x 轴. (1)如果△ABC 三个顶点的坐标分别是A (1-,1),B(0,2-),C (3-,1-) . △ABC 关于y 轴的对称图形是△A 1B 1C 1,△A 1B 1C 1关于直线l 的对称图形是△A 2B 2C 2,在所给坐标系中画出△A 1B 1C 1与△A 2B 2C 2,A 2的坐标为________;B 2的坐标为________;C 2的坐标为________.(2)如果点F 的坐标是(m ,n -),其中0<n <2,点F 关于x 轴的对称点是F 1,点F 1关于直线l 的对称点是F 2,求FF 2的长.第Ⅱ卷(本卷满分50分)四、选择题(共2小题,每小题4分,共8分)下面每小题给出的四个选项中, 有且只有一个是正确的, 请把正确选项前的代号填在答卷指定位置.22.若63=m ,34=n ,则2412的值(用含m 、n 的式子表示)为( A .mn B .2118n m C .42n m D .84n m 23.如图,△ABC 是等腰直角三角形,∠EDF 是一个直角,将顶点D BC 的中点上,转动∠EDF ,设DE ,DF 分别交AC ,BA 的延长线于E 则下列结论:①AG =CE ;② DG =DE ;③CE AC BG =-; ④ 2S △BDG -2S △CDE =S △ABC . .其中总是成立的是( ). A .①②③ B .①②③④ C .②③④ D .①②④C第21题图第23题图DCBA五、填空题(共2小题,每小题4分,共8)下列各题不需要写出解答过程,请将结果直接填写在答卷指定的位置.24.若0132=+-x x ,则221x x += .25. 如图,将长方形ABCD 沿EF 折叠,使CD 落在GH 的位置,GH 交BC 于M ,若∠HMB =52°,则HEF ∠的度数为________.六、解答题(共34分)下列各题需要在答题卷指定位置写出文字说明、证明过程或计算步骤.26.(本题满分10分)五边形ABCDE 中,AB =AE ,BC +DE =CD ,∠ABC +∠AED =180°,求证:AD 平分∠CDE .27.(本题满分12分)如图,△ABC 是等边三角形,D 是三角形外一动点.(1)若∠ADB =600,当D 点在AC 的垂直平分线上时,请直接写出线段DA ,DC ,DB 的数量关系;(2)若∠ADB =600,当D 点不在AC 的垂直平分线上时,(1)中的结论是否仍然成立?请说明理由;DCBAM HGF EDCB A第25题图第26题图D CBA(3)当D 点在如图的位置时,∠ADC =600,请直接写出线段AD 、BD 和CD 之间的数量关系.28.(本题满分12分) 如图,直角坐标系中,点B (a ,0),点C (0,b ),点A 在第一象限.若a ,b 满足(t >0) . (1)证明:OB =OC ;(2)如图1,连接AB ,过A 作AD ⊥AB 交y 轴于D ,在射线AD 上截取AE =AB ,连接CE ,F 是CE 的中点,连接AF ,OA ,当点A 在第一象限内运动(AD 不过点C )时,证明:∠OAF 的大小不变;(3)如图2,B ′与B 关于y 轴对称,M 在线段BC 上,N 在CB ′的延长线上,且BM =NB ′,连接MN 交x 轴于点T ,过T 作TQ ⊥MN 交y 轴于点Q ,求点Q 的坐标.()02=-+-tb t a 图1 图 22012~2013学年度第一学期期中考试八年级数学试题 答案第Ⅰ卷(本卷满分100分)一、选择题1.B 2.D 3.D 4.D 5.C 6.D 7.D 8.D 二、填空题9.ADB ; CBD 10. 90° 11. 3 12.22--x x 13.5 14..3 15. 9 16. ①② 三、解答题17. ①y x 318 ②328b ab +- 18. 原式=()22225444bab a b ab a -+-++ ┄┄┄┄┄4´=2263b a + ┄┄┄┄┄6´当31=a ,61-=b 时,原式=6561-631322=⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛ ┄┄┄┄┄10´19. 证明: ∵AC =BC∴∠ABC =∠BAC =50°,∠ACB =180°-50°-50°=80° ┄┄┄┄┄2´ ∵BD =AB∴∠BAD =∠D ´ 又∠BAD +∠D =∠ABC =50° ∴∠D =25° ┄┄┄┄┄6´ 同理:∠E =40° ┄┄┄┄┄10´20.证明: ∵BD 平分∠ABC∴∠ABD =∠DBC ┄┄┄┄┄2´ 在△ABD 和△CBD 中, ∵BD =CB∠ABD =∠DBC BD =BD∴△ABD ≌△CBD∴∠ADB =∠BDC ┄┄┄┄┄6´ ∴∠AED =∠CED又∵DF ⊥AE , DG ⊥EC ∴DF =DG ┄┄┄┄10´21. (1) (1,3); (0,6); (3,5) ┄┄┄┄┄3´画图△A 1B 1C 1与△A 2B 2C 2 ┄┄┄┄┄6´ (2) FF 2=4 ┄┄┄┄┄12´ 方法1:根据坐标求长度方法2:根据轴对称的性质求长度第Ⅱ卷(本卷满分50分)22. D 23. B 24. 7 25.71° 26. 证明:延长DE 至T ,使ET =BC ,连接AT 、AC ┄┄┄┄┄1´证明△AET ≌△ABC ┄┄┄┄┄5´ 再证明△ACD ≌△ATD ┄┄┄┄┄9´∴∠CDA =∠TDA即:AD 平分∠CDE. ┄┄┄┄┄10´27. (1)BD =AD +AC ┄┄┄2´ (2)延长DA 到E ,使得∠EBD =600,∵∠ADB =60°∴△EBD 是一个等边三角形, ∴BE =ED =BD ,∠EBD =60°, ┄┄┄┄┄4´ ∵△ABC 是等边三角形, ∴AB =BC ,∠ABC =60°,∴∠EBA =∠DBC ┄┄┄┄┄6´ 在△EBA 与△DBC 中,BE BD EBA DBC AB BC =⎧⎪∠=∠⎨⎪=⎩∴△EBD ≌△CBD , ┄┄┄┄┄8´ ∴EA =DC ┄┄┄┄┄9´ ∴BD =ED =EA +AD =DC +AD ;. ┄┄┄┄┄10´ (3)DC <DA +DB ┄┄┄┄┄12´ 28.(1)易得t a =,t b =,B (t ,0),点C (0,t )∴OB =OC ┄┄┄┄┄3´ (2)延长AF 至T ,使TF =AF ,连接TC ,TO ,F , 证明△TCF ≌△AEF ┄┄┄┄┄4´ 再证明△TCO ≌△ABO ┄┄┄┄┄6´得到△TAO 为等腰直角三角形,从而△F AO 为等腰直角三角形,故∠OAF=45°┄┄┄┄┄7´(3)连接MQ ,NQ ,BQ ,B ’Q ,过M 作MH ‖CN 交x 轴于H. 证明△NTB ’≌△MTH ,∴TN=MT,又TQ⊥MN∴MQ=NQ∵CQ垂直平分BB’∴BQ=B’Q∴△NQB’≌△MQB∴∠NB’Q=∠CBQ┄┄┄┄┄10´而∠NB’Q+∠CB’Q=180°∴∠CBQ+∠CB’Q=180°∴∠B’CB+∠B’QB=180°,又∠B’CB=90°∴∠B’QB=90°∴△BQB’是等腰直角三角形,∴OQ=OB=t∴Q(0,-t) ┄┄┄┄┄12´N。
2012-2013学年度第一学期期中考试八年级数学试题

2012—2013学年度第一学期八年级期中数学参考答案一、选择题(本题共有12小题,每小题3分,共36分)1、B2、A3、A4、C5、B6、A7、B8、C9、D 10、C 11、B 12、A二、填空题(本题共有4题,每小题3分,共12分) 13、(2,3) 14、9 15、1, 3 16、80°,50° 三、解答题(本题共有9小题,共72分)17、解:原式=-4+2 ……4分 18、解:(a-6)+(3a-2)=0 ……4分=-2 ……6分 a =2 ……6分19、证明:在△ABO 和△CDO 中∵OA=OC, ∠AOB=∠COD, OB=OD, ……3分∴△ABO ≌△CDO, ……4分 ∴∠A=∠B, ……5分 ∴AB ∥DC. ……6分 20、解:∵∠CAN=∠C+∠A ∴∠C=∠CAN -∠A =86°-43°=43°, ……3分 ∴∠C=∠A , ……4分 ∴BC=AB , ……5分∵BC=15╳2=30(海里), ……6分 ∴AB=30海里. ……7分 21、(1)图略, A 1(1,-3);……4分 (2)S△A 1B 1C 1=8.5; ……6分 (3)略. ……7分22、(1)证明:∵△ABC 和△ADF 都是等边三角形∴AB=AC ,AD=AF , ∠BAC=∠DAF =∠ACB=60°, ……2分 ∴∠BAD=∠FAC, ……4分 在△ABD 和△ACF 中AB=AC , ∠BAD=∠FAC , AD=AF,∴△ABD ≌△ACF, ……5分 ∴BD=CF ……6分(2)解:∵△ABD ≌△ACF∴∠ACF=∠ABD=60° ……7分 ∴∠FCD=60°-(∠ACB +∠ACF )= 60° ……8分23、(1)解:∵BM 是∠ABC 的平分线,CN 是∠ACB 的平分线,∴∠ABM=∠CBM ,∠CAN=∠BCN ……1分 ∵∠A=60° ∴∠OBC+∠BCN=60°……2分 ∴∠BOC=120°……3分(2)证明:∵ OB =OC ,∴ ∠OBC=∠OCB , ……4分 又∠OBC=21∠ABC , ∠OCB=21∠ACB , ∴∠ABC =∠ACB , ∴ AB =AC , ……5分 而∠A=60°, ∴△ABC 是等边三角形 ……6分(3)在BC 上截取BD =BN,连接OD ,又∠OBD =∠OBN ,BO =BO ,∴△OBD ≌△OBN , ……7分∴∠BON =∠BOD ,而∠BOC ==120°,∴∠BON =∠BOD =∠COM =60°,∴∠COD =60°,∴∠COM =∠COD , ……8分又∠OCM =∠OCD ,CO =CO , ∴△COM ≌△COD , ……9分 ∴CM =CD , ∴CM+BN =CD+BD =BC ……10分24、(1)解:CF=MF=EB . ……2分证明如下:∵AB=BC , ∠ABC=90° , ∴∠BAC=∠C=45°,∵MF ⊥BC ,∴∠FMC=45°=∠C , ∴MF=FC ; ……3分∵EM=EA , ∴∠EAM=∠EMA , ∴ ∠EAB=∠MEC , ……4分∵∠ABE=∠EFM=90° , AE=EM ,∴△AEB ≌△EMF , ∴MF=BE. ……5分(2)过B 作BD ⊥AC 于D , ……6分∵ AB=BC , ∠ABC=90°, ∴ ∠BAC=∠C=45°,∵ME=MB, ∴∠MEB=∠MBE, ……7分 ∴∠MEF=∠BME,∵∠MEF=∠MDB=90°,∴△EMF ≌△BMD, ……8分 ∴MF=BD,∵AB=BC, ∴AC=2BD, ……9分 ∴AC=2MF. ……10分 25、(1)解:△ABO 是等腰直角三角形 ……1分 证明如下:过A 作AH ⊥OB,∵A (2,2), ∴OH=2 ,AH=2, ……2分 ∵B (4,0), ∴OB=4,∴BH=2, ∴BH=AH=OH, ……3分 ∵∠AHO=∠AHB=90°,∴∠AOH=∠OAH=∠HAB=∠ABH=45°, ……4分 ∴△ABO 是等腰直角三角形.(2)过C 作CF ⊥OB ,∵C (a ,2),∴CF=2, ……5分 ∵∠COB=30°, ∠CFO=90°, ∴CF=21OC ,OC=4 , ∴OB=OC, ……6分 ∴∠OBC=∠OCB=75°, ……7分 ∴∠ABC=∠OBC - ∠ABO =75°-45°=30°. ……8分(3)过C 作CK ⊥AB,∵A (2,2) , C (a ,2), ∴AC ∥OB, ……9分 ∴∠CAB=∠ABO=45°,∵CE ⊥AC, ∴CK=21AE , ……10分 ∵∠ABC=30°, ∴CK=21BC , ……11分∴AE=BC. ……12分。
最全面江苏省无锡八年级上学期期中考试数学试卷有答案(精华版)

19.( 8 分)( 1)计算: 3 - 27-|1- 3|+ 2013 0 ( 2)求 x 的值: (x+ 1)2= 36
20.( 6 分) 如图,已知△ ABC,求作一点 P,使 P 到∠ A 的两边的距离相等,且 PA=PB.
C
A
B
21. ( 7 分)如图,在四边形 ABCD 中, AB= DC ,延长线段 CB 到 E,使 BE= AD ,连接 AE、 AC,且 AE= AC,求证:( 1)△ ABE≌△ CDA ;( 2) AD∥EC .
( 3 分) ( 4 分) ( 5 分) ( 6 分)
26. 作 DH ⊥ AB 于 H…………………………………………… ( 1 分)
A
可得等腰 Rt △DBH ,由 AB= 4,可知 BC= 2 2……… ( 2 分)
于是 BD = 2, BH = DH =1……………………………… ( 3 分)
)
A.
B.
C.
D.
3.下列每一组数据中的三个数值分别为三角形的三边长,不能构成直角三角形的是(
)
A . 3、 4、 5
B. 6、 8、 10
C. 5、 12、 13
D. 3、 2、 5
4. 如图,在数轴上表示实数 15的点可能是 ……………………………………… (
)
P
Q MN
?
? ??
0 1 2 34
综上所述,符合要求的 x 值为 7或 2……………………………………………… 6
( 8 分)
25. 作点 P 关于 OA 的对称点 P1,点 P 关于 OB 的对称点 P2,连结 P1P2, 与 OA 的交点即为点 M ,与 OB 的交点即为点 N……………………………… ( 2 分)
2012-2013年八年级上期中数学试题含答案

为
;
14.比较大小:
5 1 2
0.5;
15.如右图,在 Rt△ABC中,∠C=90°,沿过 点 B 的一条直线 BE折叠△ABC,使点 C 恰好落 在 AB边的中点 D 处,则∠A 的度数是 ____________;
16.阅读下列解题过程:
1 5
4(
1( 5 4) 5 4)( 5 4)
C. a 无意义;
D.0.4的算术平方根是 0.2.
3.下列实数中,无理数是(
)
A.272
B. 8
C. 3 8
D. 16
4.如右图所示,在 RtΔACB中,∠C=90°,AD平分∠BAC,若
BC=16,BD=10,则点 D 到 AB的距离是( )
C
A.9
B.8
D
C.7
D.6
5.下列各组数中互为相反数的是( )
理由:___________________;
_________________________.
19.计算(每小题 4 分,共 8 分).
⑴
38
0
1 4
⑵ | 3 2 | + | 32|
20.求下列各式中 x 的值(每小题 4 分,共 8 分).
⑴ 4x2 9
⑵ (x 1)2 25
21.(4 分)若 2x 3 + 2x y =0,求 4 x - y2
22.(4 分)如图,点 B、D、C、F 在一条直线上,BD=CF,AB=EF, 且 AB∥EF.求证:AC=ED.
23.(5 分)如图,在等腰△ABC中,点 D、E
是 BC边上两点,且 AD=AE.求证 :BD=CE.
A
5
江苏省无锡市崇安区八年级(上)期中数学试卷(含答案)

(第5题图)AB DE C(第7题图)(第8题图)无锡市××中学2012~2013学年第一学期期中试卷初二数学(考试时间:100分钟 满分:100分)一.选择题(本大题共8小题,每题3分,共24分.)1.下列各图是选自历届世博会会徽中的图案,其中是中心对称图形的是………( )A B C D 2.在-9,π2,349,227,1.414,(1-2)0,2.121121112中,无理数有………( )A .2个B .3个C .4个D .5个3.下面几组条件中,能判断一个四边形是平行四边形的是 ……………………( ) A. 一组对边相等,一组对边平行 B. 两条对角线互相平分 C. 一组对边平行,一组邻角相等 D. 两条对角线互相垂直4.以a 、b 、c 为边,不能组成直角三角形的是…………………………………( )A .a =6,b =8,c =10B .a =1,b =3,c =2C .a =24,b =7,c =25D .a =13,b =14,c =155.如图,等腰△ABC 的周长为21,底边BC =5,AB 的垂直平分线DE 交AB 于点D ,交AC 于点E ,则△BEC 的周长为……………………………………………( ) A .13 B .14 C .15 D .16 6.平行四边形的对角线长为x 、y ,一边长为12,则x 、y 的值可能是………( ) A .8和14B .10和14C .18和20D .10和347.如图,在□ABCD 中,∠A =70°,将□ABCD 折叠,使点D 、C 分别落在点F 、E 处(点F 、E 都在直线AB 所在的直线上),折痕为MN ,则∠AMF 等于………( ) A .70º B .40º C .30º D .20º8.如图,是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A 、B 、C 、D 的边长分别是3、5、2、3,则最大正方形E 的面积是………………………………………………………………………………( ) A .13 B .47 C . 26 D .94二.填空题(本大题共10小题,每空2分,共24分.)9.9的算术平方根是 ,—27的立方根是 . 10.(-2) 2= ,3(-6) 3= . 11.若2a -b +||b +2=0,则a -b = .12.若一正数的两个平方根分别是2a -1与2a +5,则这个正数等于 . 13.正五边形绕着它的中心至少旋转 度后能与自身重合. 14.已知等腰三角形的一个外角等于100°,则它的顶角为 . 15.如图,将□ABCD 的一边BC 延长至E ,若∠A =70º,则∠DCE = .16.如图,在△ABC 中,∠A =∠B ,D 是AB 上任意一点,DE ∥BC ,DF ∥AC ,AC =4cm ,则四边形DECF 的周长是 .17.已知在梯形ABCD 中,AD ∥BC ,AB =CD ,∠B =60°,AD =3cm ,梯形ABCD 的周长为18cm ,则BC 的长为_________.18.如图,在□ABCD 中,AB =6,AD =12,∠BAD 的平分线交BC 于点E ,交DC 的延长线于点F ,BG ⊥AE ,垂足为G ,BG =42,则△CEF 的周长为 .三.解答题(本大题共8小题,共52分. 解答需写出必要的文字说明或演算步骤)19.(6分)(1)计算:3-8-||1-2+(1-2)0 (2)求x 的值:4x 2=4920.(7分)下面网格图中,每个小正方形的边长均为1,每个小格的顶点叫做格点. (1)请在图1中,画一个格点三角形,使它的三边长都是有理数; (2)请在图2中,画一个有一边长为5的格点直角三角形;(3)图3中的△ABC 的面积为 ,画出它绕点A 逆时针旋转90º后的图形.21.(6分)已知:如图,在等边△ABC 的AC 边上取中点D ,在BC 的延长线上取一点E ,使 CE =CD . 求证:BD =DE .ABCDEDAB GEC F (第18题图) A B C E D(第15题图) A B D C E F (第16题图) 图1 图2图3ACB22.(5分)(1)如图1,等边△ABC 中,AB =2,点E 是AB 的中点,AD 是高,P 为AD 上一点,则BP +PE 的最小值等于 .(2)如图2,在四边形ABCD 的对角线AC 上找一点P ,使∠APB =∠APD .23.(6分)如图,将□ABCD 的对角线BD 向两个方向延长至点E 和点F ,使BE =DF ,求证:四边形AECF 是平行四边形.24.(7分)如图,在□ABCD 中,E 为BC 边上一点,且AB =AE . (1)求证:△ABC ≌△EAD ;(2)若AE 平分∠DAB ,∠EAC =25º,求∠AED 的度数.25.(6分)强台风过境时,斜坡上一棵6m 高的大树被刮断,已知斜坡中α=30º,大树顶端A 与底部C 之间为2m ,求这棵大树的折断处与底部的距离BC ?ABCD·A DE BC图1图2A FC E B DABCα=30º26.(9分)如图,在梯形ABCD 中,AD ∥BC ,AB =5,AD =6, DC =42,∠C =45º.动点M 从B 点出发沿线段BC 以每秒1个单位长度的速度向终点C 运动;动点N 同时从C 点出发沿C →D →A 运动,在CD 上的速度为每秒2个单位长度,在DA 上的速度为每秒1个单位长度,当其中一个点到达终点是另一个点也随之停止运动.设运动的时间为t 秒. (1)求BC 的长.(2)当四边形ABMN 是平行四边形时,求t 的值. (3)试探究:t 为何值时,△ABM 为等腰三角形.ADCBMN•初二数学期中考试参考答案与评分标准 2012.11一、选择题(每题3分)C A B D A C B B 二、填空题(每空2分)9. 3,3 10. 2,-6 11. 1 12. 9 13. 72 14. 20º或50º 15. 110º 16. 8cm 17. 7cm 18. 16 三、解答题19.(1)原式=-2+1-2+1=- 2(2)x 2=494,x =±72………………………………………(每小题3分,分步酌情给分)20. 画图略,……………………(每图2分); 面积32,……………………(1分)21. 证明:∵△ABC 是等边三角形,∴∠ABC =∠ACB =60º……………………(2分)又∵D 是AC 边的中点,且CE =CD∴∠DBC =12∠ABC =30º,∠E =12∠ACB =30º………………………(4分)∴∠DBC =∠E ………………(5分) ∴BD =DE ……………………(6分)22.(1)3………………………………………………………………………………(3分) (2)作点D 关于AC 的对称点D ’,连结D ’B ,并延长与AC 的交点即为点P (5分) 23. 连结AC ,与BD 交于点O ………………………………………………………(1分)∵四边形ABCD 是平行四边形 ∴OA =OC ,OB =OD ……………………(3分) 又∵点E 、F 在BD 上,且BE =DF ,∴OB +BE =OD +DF ,即OE =OF …………………………………………… (5分) ∴四边形AECF 是平行四边形.……………………………………………… (6分) 注:其它正确的证明方法,按类似原则分步酌情给分. 24.(1)∵在□ABCD 中,AD ∥BC ,BC =AD …………(1分) ∴∠1=∠2………………………………………(2分)又∵AB =AE ,∴∠B =∠2, ∴∠B =∠1……(3分) ∴△ABC ≌△EAD (SAS )……………………(4分)(2)先证△ABE 为等边三角形,得∠BAE =60º…………………………………(5分) ∴∠AED =∠BAC =∠BAE +∠EAC =60º+25º=85º………………………(7分) 25. 作AH ⊥BC 于点H …………………………………(1分)在Rt △ACH 中,AC =2,∠CAH =30º∴CH =1,AH =3………………………………(2分) 设BC =x ,则BH =x -1,AB =6-x ……………(3分) 在Rt △ABH 中,(6-x )2-(x -1)2=(3)2………(5分)解得:x =3.2m ……………………………………(6分) 答:这棵大树的折断处与底部的距离BC 为3.2m. 26.(1)BC =13 ………………………………………(2分)(2)由题意,点N 必在DA 上,且BM =AN ……………………………………(3分) 从t =6-(t -4)解得t =5 ………………………………………………………(5分)1 2ABCα=30ºH(3)当BA =BM 时,t =5……………(6分);当AB =AM 时,t =6……………(7分)当MA =MB 时,由t 2=(t -3)2+42,得t =256………………………………(9分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5题图)(第7题图)(第8题图)无锡市³³中学2012~2013学年第一学期期中试卷初二数学(考试时间:100分钟 满分:100分)一.选择题(本大题共8小题,每题3分,共24分.)1.下列各图是选自历届世博会会徽中的图案,其中是中心对称图形的是………( )A B C D 2.在-9,π2,349,227,1.414,(1-2)0,2.121121112中,无理数有………( )A .2个B .3个C .4个D .5个3.下面几组条件中,能判断一个四边形是平行四边形的是 ……………………( ) A. 一组对边相等,一组对边平行 B. 两条对角线互相平分 C. 一组对边平行,一组邻角相等 D. 两条对角线互相垂直4.以a 、b 、c 为边,不能组成直角三角形的是…………………………………( )A .a =6,b =8,c =10B .a =1,b =3,c =2C .a =24,b =7,c =25D .a =13,b =14,c =155.如图,等腰△ABC 的周长为21,底边BC =5,AB 的垂直平分线DE 交AB 于点D ,交AC 于点E ,则△BEC 的周长为……………………………………………( ) A .13 B .14 C .15 D .166.平行四边形的对角线长为x 、y ,一边长为12,则x 、y 的值可能是………( ) A .8和14B .10和14C .18和20D .10和347.如图,在□ABCD 中,∠A =70°,将□ABCD 折叠,使点D 、C 分别落在点F 、E 处(点F 、E 都在直线AB 所在的直线上),折痕为MN ,则∠AMF 等于………( )A .70ºB .40ºC .30ºD .20º8.如图,是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A 、B 、C 、D 的边长分别是3、5、2、3,则最大正方形E 的面积是………………………………………………………………………………( ) A .13 B .47 C . 26 D .94二.填空题(本大题共10小题,每空2分,共24分.)9.9的算术平方根是 ,—27的立方根是 . 10.(-2) 2= ,3(-6) 3= . 11.若2a -b +||b +2=0,则a -b = .12.若一正数的两个平方根分别是2a -1与2a +5,则这个正数等于 .13.正五边形绕着它的中心至少旋转 度后能与自身重合.14.已知等腰三角形的一个外角等于100°,则它的顶角为 . 15.如图,将□ABCD 的一边BC 延长至E ,若∠A =70º,则∠DCE = .16.如图,在△ABC 中,∠A =∠B ,D 是AB 上任意一点,DE ∥BC ,DF ∥AC ,AC =4cm ,则四边形DECF 的周长是 .17.已知在梯形ABCD 中,AD ∥BC ,AB =CD ,∠B =60°,AD =3cm ,梯形ABCD 的周长为18cm ,则BC 的长为_________.18.如图,在□ABCD 中,AB =6,AD =12,∠BAD 的平分线交BC 于点E ,交DC 的延长线于点F ,BG ⊥AE ,垂足为G ,BG =42,则△CEF 的周长为 .三.解答题(本大题共8小题,共52分. 解答需写出必要的文字说明或演算步骤)19.(6分)(1)计算:3-8-||1-2+(1-2)0(2)求x 的值:4x 2=4920.(7分)下面网格图中,每个小正方形的边长均为1,每个小格的顶点叫做格点. (1)请在图1中,画一个格点三角形,使它的三边长都是有理数; (2)请在图2中,画一个有一边长为5的格点直角三角形;(3)图3中的△ABC 的面积为 ,画出它绕点A 逆时针旋转90º后的图形.21.(6分)已知:如图,在等边△ABC 的AC 边上取中点D ,在BC 的延长线上取一点E ,使 CE =CD . 求证:BD =DE .22.(5分)(1)如图1,等边△ABC 中,AB =2,点E 是AB 的中点,AD 是高,P 为AD 上一点,则BP +PE 的最小值等于 .ABCDEDABG ECF(第18题图)A BD(第15题图)AB DCEF(第16题图)图1图2图3ACB(2)如图2,在四边形ABCD 的对角线AC 上找一点P ,使∠APB =∠APD .23.(6分)如图,将□ABCD 的对角线BD 向两个方向延长至点E 和点F ,使BE =DF ,求证:四边形AECF 是平行四边形.24.(7分)如图,在□ABCD 中,E 为BC 边上一点,且AB =AE . (1)求证:△ABC ≌△EAD ;(2)若AE 平分∠DAB ,∠EAC =25º,求∠AED 的度数.25.(6分)强台风过境时,斜坡上一棵6m 高的大树被刮断,已知斜坡中α=30º,大树顶端A 与底部C 之间为2m ,求这棵大树的折断处与底部的距离BC ?26.(9分)如图,在梯形ABCD 中,AD ∥BC ,AB =5,AD =6,DC =42,∠C =45º.动点M 从B 点出发沿线段BC 以每秒1个单位长度的速度向终点C 运动;动点N 同时从C 点出发沿C →D →A 运动,在CD 上的速度为每秒2个单位长度,在DA 上的速度为每秒1个单位长度,当其中一个点到达终点是另一个点也随之停止运动.设运动的时间为t 秒. (1)求BC 的长.(2)当四边形ABMN 是平行四边形时,求t 的值.ABCD²A DE BC图1图2A F C EB DABCα=30º(3)试探究:t为何值时,△ABM为等腰三角形.初二数学期中考试参考答案与评分标准 2012.11一、选择题(每题3分)C A B D A C B B 二、填空题(每空2分)9. 3,3 10. 2,-6 11. 1 12. 9 13. 72 14. 20º或50º 15. 110º 16. 8cm 17. 7cm 18. 16 三、解答题19.(1)原式=-2+1-2+1=- 2(2)x 2=494,x =±72………………………………………(每小题3分,分步酌情给分)20. 画图略,……………………(每图2分); 面积32,……………………(1分)21. 证明:∵△ABC 是等边三角形,∴∠ABC =∠ACB =60º……………………(2分)又∵D 是AC 边的中点,且CE =CD∴∠DBC =12∠ABC =30º,∠E =12∠ACB =30º………………………(4分)∴∠DBC =∠E ………………(5分) ∴BD =DE ……………………(6分)22.(1)3………………………………………………………………………………(3分) (2)作点D 关于AC 的对称点D ’,连结D ’B ,并延长与AC 的交点即为点P (5分) 23. 连结AC ,与BD 交于点O ………………………………………………………(1分)∵四边形ABCD 是平行四边形 ∴OA =OC ,OB =OD ……………………(3分) 又∵点E 、F 在BD 上,且BE =DF ,∴OB +BE =OD +DF ,即OE =OF …………………………………………… (5分) ∴四边形AECF 是平行四边形.……………………………………………… (6分) 注:其它正确的证明方法,按类似原则分步酌情给分.24.(1)∵在□ABCD 中,AD ∥BC ,BC =AD …………(1分)∴∠1=∠2………………………………………(2分)又∵AB =AE ,∴∠B =∠2, ∴∠B =∠1……(3分) ∴△ABC ≌△EAD (SAS )……………………(4分)(2)先证△ABE 为等边三角形,得∠BAE =60º…………………………………(5分) ∴∠AED =∠BAC =∠BAE +∠EAC =60º+25º=85º………………………(7分) 25. 作AH ⊥BC 于点H …………………………………(1分)在Rt △ACH 中,AC =2,∠CAH =30º ∴CH =1,AH =3………………………………(2分) 设BC =x ,则BH =x -1,AB =6-x ……………(3分)在Rt△ABH 中,(6-x )2-(x -1)2=(3)2………(5分)解得:x =3.2m ……………………………………(6分)答:这棵大树的折断处与底部的距离BC 为3.2m. 26.(1)BC =13 ………………………………………(2分)(2)由题意,点N 必在DA 上,且BM =AN ……………………………………(3分) 从t =6-(t -4)解得t =5 ………………………………………………………(5分) (3)当BA =BM 时,t =5……………(6分);当AB =AM 时,t =6……………(7分)当MA =MB 时,由t 2=(t -3)2+42,得t =256………………………………(9分)1 2 A B C α=30º H。
