高等数学竞赛报名表
高中数学竞赛报名模板

高中数学竞赛报名模板
尊敬的组委会:
我校学生愿参加贵校举办的高中数学竞赛。
我们将按照规定的格式和要求报名参赛,特向贵校提交以下报名信息:
1. 报名学校信息:
学校名称:(填写学校名称)
学校地址:(填写学校地址)
联系人:(填写联系人姓名)
联系电话:(填写联系人电话)
电子邮箱:(填写联系人邮箱)
2. 参赛学生信息:
参赛学生姓名:(填写学生姓名)
性别:(填写学生性别)
年级:(填写学生所在年级)
学号:(填写学生学号)
联系电话:(填写学生电话)
电子邮箱:(填写学生邮箱)
3. 指导教师信息:
指导教师姓名:(填写指导教师姓名)
学科:(填写指导教师所教学科)
联系电话:(填写指导教师电话)
电子邮箱:(填写指导教师邮箱)
4. 参赛类别:
(请在以下选项中选择适用的类别,并在括号内填写序号)
- 个人赛(1)
- 团体赛(2)
若选择团体赛,请填写团体队员信息:
- 团体队员1姓名:(填写团体队员1姓名)
- 团体队员2姓名:(填写团体队员2姓名)
- 团体队员3姓名:(填写团体队员3姓名)
- 团体队员4姓名:(填写团体队员4姓名)
5. 其他信息补充:
(请在下方填写其他需要补充的信息,如特殊需求、备注等)
我们将按照比赛规定及时缴纳报名费用,配合贵校的组织工作,遵守竞赛规则,共同营造良好的竞赛氛围。
如需进一步确认信息或有其他问题,请随时与我们联系。
谢谢!
此致
敬礼
(学校名称)(联系人签名)(年月日)。
浙江海洋学院上报浙江省大学生高等数学(微积分)竞赛报名表

学校: 浙江海洋学院 数学类:4 6 人; 工科类:4 准考号 姓 名 性别 3610001 陈亚菲 女 3610002 吕礼渊 女 3610003 沈阳 女 3610004 尹琪 男 3610005 于祥雨 男 3610006 迟云强 男 3610007 白杰 男 3610008 刘嘉仑 男 3610009 闫雨 男 3610010 申东洋 男 3610011 蔡培焱 男 3610012 王徐炜 男 3610013 谢陈龙 男 3610014 赵建忠 男 3610015 陈如达 男 3610016 方羡 女 3610017 杜慧 女 3610018 邵霞倩 女 3610019 诸爱萍 女 3610020 陈李莎 女 3610021 叶依上 女 3610022 施芳 女 3610023 陆凤尧 女 3610024 池旗旗 女 3610025 陆秋夏 女 3610026 林俊 男 3610027 胡存亮 男 3610028 应超 男 3610029 钟裕翔 男 3610030 詹熠楠 男 3610031 邵永明 男 3610032 陈正 男 3610033 陈华丰 男 3610034 邱佳泺 男 3610035 杨建孝 男 3610036 龚航俊 男 3610037 盛楚楚 女 3610038 杨茜茜 女 3610039 张志勇 男 3610040 蔡锦澄 男 3610041 冯炫 男 3610042 黄吴彬 男 3610043 聂士娟 女 第 一考场 人; 经管类:0 人 ; 文专科:0 人。 专业、年级 类 别 考场 数学与应用数学 10级 数学 东105 数学与应用数学 10级 数学 东105 数学与应用数学 10级 数学 东105 数学与应用数学 10级 数学 东105 数学与应用数学 10级 数学 东105 数学与应用数学 10级 数学 东105 数学与应用数学 11级 数学 东105 数学与应用数学 11级 数学 东105 数学与应用数学 11级 数学 东105 数学与应用数学 11级 数学 东105 数学与应用数学 11级 数学 东105 数学与应用数学 11级 数学 东105 数学与应用数学 11级 数学 东105 数学与应用数学 11级 数学 东105 数学与应用数学 11级 数学 东105 数学与应用数学 11级 数学 东105 数学与应用数学 11级 数学 东105 数学与应用数学 11级 数学 东105 数学与应用数学 11级 数学 东105 数学与应用数学 11级 数学 东105 数学与应用数学 12级 数学 东105 数学与应用数学 12级 数学 东105 数学与应用数学 12级 数学 东105 数学与应用数学 12级 数学 东105 数学与应用数学 12级 数学 东105 信息与计算科学 10级 数学 东105 信息与计算科学 10级 数学 东105 信息与计算科学 10级 数学 东105 信息与计算科学 11级 数学 东105 信息与计算科学 11级 数学 东105 信息与计算科学 11级 数学 东105 信息与计算科学 11级 数学 东105 信息与计算科学 11级 数学 东105 信息与计算科学 11级 数学 东105 信息与计算科学 11级 数学 东105 信息与计算科学 11级 数学 东105 信息与计算科学 11级 数学 东105 信息与计算科学 11级 数学 东105 信息与计算科学 12级 数学 东105 信息与计算科学 12级 数学 东105 信息与计算科学 12级 数学 东105 信息与计算科学 12级 数学 东105 信息与计算科学 12级 数学 东105 考试时间
全国大学生数学竞赛数学类比赛大纲

数学分析占50%,高等代数占35%,解析几何占15%,具体内容如下:Ⅰ、数学分析部分一、集合与函数1. 实数集、有理数与无理数的稠密性,实数集的界与确界、确界存在性定理、闭区间套定理、聚点定理、有限覆盖定理.2. 上的距离、邻域、聚点、界点、边界、开集、闭集、有界(无界)集、上的闭矩形套定理、聚点定理、有限复盖定理、基本点列,以及上述概念和定理在上的推广.3. 函数、映射、变换概念及其几何意义,隐函数概念,反函数与逆变换,反函数存在性定理,初等函数以及与之相关的性质.二、极限与连续1. 数列极限、收敛数列的基本性质(极限唯一性、有界性、保号性、不等式性质).2. 数列收敛的条件(Cauchy准则、迫敛性、单调有界原理、数列收敛与其子列收敛的关系),极限及其应用.3.一元函数极限的定义、函数极限的基本性质(唯一性、局部有界性、保号性、不等式性质、迫敛性),归结原则和Cauchy收敛准则,两个重要极限及其应用,计算一元函数极限的各种方法,无穷小量与无穷大量、阶的比较,记号O与o的意义,多元函数重极限与累次极限概念、基本性质,二元函数的二重极限与累次极限的关系.4. 函数连续与间断、一致连续性、连续函数的局部性质(局部有界性、保号性),有界闭集上连续函数的性质(有界性、最大值最小值定理、介值定理、一致连续性).三、一元函数微分学1.导数及其几何意义、可导与连续的关系、导数的各种计算方法,微分及其几何意义、可微与可导的关系、一阶微分形式不变性.2.微分学基本定理:Fermat定理,Rolle定理,Lagrange定理,Cauchy定理,Taylor公式(Peano 余项与Lagrange余项).3.一元微分学的应用:函数单调性的判别、极值、最大值和最小值、凸函数及其应用、曲线的凹凸性、拐点、渐近线、函数图象的讨论、洛必达(L'Hospital)法则、近似计算.四、多元函数微分学1. 偏导数、全微分及其几何意义,可微与偏导存在、连续之间的关系,复合函数的偏导数与全微分,一阶微分形式不变性,方向导数与梯度,高阶偏导数,混合偏导数与顺序无关性,二元函数中值定理与Taylor公式.2.隐函数存在定理、隐函数组存在定理、隐函数(组)求导方法、反函数组与坐标变换.3.几何应用(平面曲线的切线与法线、空间曲线的切线与法平面、曲面的切平面与法线).4.极值问题(必要条件与充分条件),条件极值与Lagrange乘数法.五、一元函数积分学1. 原函数与不定积分、不定积分的基本计算方法(直接积分法、换元法、分部积分法)、有理函数积分:型,型.2. 定积分及其几何意义、可积条件(必要条件、充要条件:)、可积函数类.3. 定积分的性质(关于区间可加性、不等式性质、绝对可积性、定积分第一中值定理)、变上限积分函数、微积分基本定理、N-L公式及定积分计算、定积分第二中值定理.4.无限区间上的广义积分、Canchy收敛准则、绝对收敛与条件收敛、非负时的收敛性判别法(比较原则、柯西判别法)、Abel判别法、Dirichlet判别法、无界函数广义积分概念及其收敛性判别法.5. 微元法、几何应用(平面图形面积、已知截面面积函数的体积、曲线弧长与弧微分、旋转体体积),其他应用.六、多元函数积分学1.二重积分及其几何意义、二重积分的计算(化为累次积分、极坐标变换、一般坐标变换).2.三重积分、三重积分计算(化为累次积分、柱坐标、球坐标变换).3.重积分的应用(体积、曲面面积、重心、转动惯量等).4.含参量正常积分及其连续性、可微性、可积性,运算顺序的可交换性.含参量广义积分的一致收敛性及其判别法,含参量广义积分的连续性、可微性、可积性,运算顺序的可交换性.5.第一型曲线积分、曲面积分的概念、基本性质、计算.6.第二型曲线积分概念、性质、计算;Green公式,平面曲线积分与路径无关的条件.7.曲面的侧、第二型曲面积分的概念、性质、计算,奥高公式、Stoke公式,两类线积分、两类面积分之间的关系.七、无穷级数1. 数项级数级数及其敛散性,级数的和,Cauchy准则,收敛的必要条件,收敛级数基本性质;正项级数收敛的充分必要条件,比较原则、比式判别法、根式判别法以及它们的极限形式;交错级数的Leibniz 判别法;一般项级数的绝对收敛、条件收敛性、Abel判别法、Dirichlet判别法.2. 函数项级数函数列与函数项级数的一致收敛性、Cauchy准则、一致收敛性判别法(M-判别法、Abel判别法、Dirichlet判别法)、一致收敛函数列、函数项级数的性质及其应用.3.幂级数幂级数概念、Abel定理、收敛半径与区间,幂级数的一致收敛性,幂级数的逐项可积性、可微性及其应用,幂级数各项系数与其和函数的关系、函数的幂级数展开、Taylor级数、Maclaurin级数.4.Fourier级数三角级数、三角函数系的正交性、2及2周期函数的Fourier级数展开、Beseel不等式、Riemanm-Lebesgue定理、按段光滑函数的Fourier级数的收敛性定理.Ⅱ、高等代数部分一、多项式1. 数域与一元多项式的概念2. 多项式整除、带余除法、最大公因式、辗转相除法3. 互素、不可约多项式、重因式与重根.4. 多项式函数、余数定理、多项式的根及性质.5. 代数基本定理、复系数与实系数多项式的因式分解.6. 本原多项式、Gauss引理、有理系数多项式的因式分解、Eisenstein判别法、有理数域上多项式的有理根.7. 多元多项式及对称多项式、韦达(Vieta)定理.二、行列式1. n级行列式的定义.2. n级行列式的性质.3. 行列式的计算.4. 行列式按一行(列)展开.5. 拉普拉斯(Laplace)展开定理.6. 克拉默(Cramer)法则.三、线性方程组1. 高斯(Gauss)消元法、线性方程组的初等变换、线性方程组的一般解.2. n维向量的运算与向量组.3. 向量的线性组合、线性相关与线性无关、两个向量组的等价.4. 向量组的极大无关组、向量组的秩.5. 矩阵的行秩、列秩、秩、矩阵的秩与其子式的关系.6. 线性方程组有解判别定理、线性方程组解的结构.7. 齐次线性方程组的基础解系、解空间及其维数四、矩阵1. 矩阵的概念、矩阵的运算(加法、数乘、乘法、转置等运算)及其运算律.2. 矩阵乘积的行列式、矩阵乘积的秩与其因子的秩的关系.3. 矩阵的逆、伴随矩阵、矩阵可逆的条件.4. 分块矩阵及其运算与性质.5. 初等矩阵、初等变换、矩阵的等价标准形.6. 分块初等矩阵、分块初等变换.五、双线性函数与二次型1. 双线性函数、对偶空间2. 二次型及其矩阵表示.3. 二次型的标准形、化二次型为标准形的配方法、初等变换法、正交变换法.4. 复数域和实数域上二次型的规范形的唯一性、惯性定理.5. 正定、半正定、负定二次型及正定、半正定矩阵六、线性空间1. 线性空间的定义与简单性质.2. 维数,基与坐标.3. 基变换与坐标变换.4. 线性子空间.5. 子空间的交与和、维数公式、子空间的直和.七、线性变换1. 线性变换的定义、线性变换的运算、线性变换的矩阵.2. 特征值与特征向量、可对角化的线性变换.3. 相似矩阵、相似不变量、哈密尔顿-凯莱定理.4. 线性变换的值域与核、不变子空间.八、若当标准形1.矩阵.2. 行列式因子、不变因子、初等因子、矩阵相似的条件.3. 若当标准形.九、欧氏空间1. 内积和欧氏空间、向量的长度、夹角与正交、度量矩阵.2. 标准正交基、正交矩阵、施密特(Schmidt)正交化方法.3. 欧氏空间的同构.4. 正交变换、子空间的正交补.5. 对称变换、实对称矩阵的标准形.6. 主轴定理、用正交变换化实二次型或实对称矩阵为标准形.7. 酉空间.Ⅲ、解析几何部分一、向量与坐标1. 向量的定义、表示、向量的线性运算、向量的分解、几何运算.2. 坐标系的概念、向量与点的坐标及向量的代数运算.3. 向量在轴上的射影及其性质、方向余弦、向量的夹角.4. 向量的数量积、向量积和混合积的定义、几何意义、运算性质、计算方法及应用.5. 应用向量求解一些几何、三角问题.二、轨迹与方程1.曲面方程的定义:普通方程、参数方程(向量式与坐标式之间的互化)及其关系.2.空间曲线方程的普通形式和参数方程形式及其关系.3.建立空间曲面和曲线方程的一般方法、应用向量建立简单曲面、曲线的方程.4.球面的标准方程和一般方程、母线平行于坐标轴的柱面方程.三、平面与空间直线1.平面方程、直线方程的各种形式,方程中各有关字母的意义.2.从决定平面和直线的几何条件出发,选用适当方法建立平面、直线方程.3.根据平面和直线的方程,判定平面与平面、直线与直线、平面与直线间的位置关系.4. 根据平面和直线的方程及点的坐标判定有关点、平面、直线之间的位置关系、计算他们之间的距离与交角等;求两异面直线的公垂线方程.四、二次曲面1.柱面、锥面、旋转曲面的定义,求柱面、锥面、旋转曲面的方程.2.椭球面、双曲面与抛物面的标准方程和主要性质,根据不同条件建立二次曲面的标准方程.3.单叶双曲面、双曲抛物面的直纹性及求单叶双曲面、双曲抛物面的直母线的方法.4.根据给定直线族求出它表示的直纹面方程,求动直线和动曲线的轨迹问题.五、二次曲线的一般理论1.二次曲线的渐进方向、中心、渐近线.2.二次曲线的切线、二次曲线的正常点与奇异点.3.二次曲线的直径、共轭方向与共轭直径.4.二次曲线的主轴、主方向,特征方程、特征根.5.化简二次曲线方程并画出曲线在坐标系的位置草图.。
(扬州大学)第十一届江苏省高等数学竞赛电子报名表

吴夏丽女
陆海峰男机械10丁方静女信息10庄静女信息10王潍潍女信息10沙金烨女信息10田闯男信息10汤兰兰女信息10王宁宁女信息10冯晶晶女信息10程会芳女信息10魏晓盈女信息10包玉霞女信息10王洋男水利10付浩雁男水利10郁怀光男水利10张玉坚男水利10王碗琴女水利10郁杨天男水利10孙鹏明男水利10周荔女建工10陆丽洁女建工10郑孝青男建工10仇晶晶女建工10王鹏男建工10蔡文华女建工10朱怡婷女建工10武言哲男能动10徐松男能动10张俊男能动10袁亚男能动10姚东男环境10张爱阳男环境10卓猛男环境10李欢女环境10曹春红女物理10罗强男物理10徐柳女物理10王露男物理10徐威男物理10倪楷茗男物理10葛海峰男物理10谷专元男物理10过恒荣男物理10李彦涛男物理10李其兆男化学10
陆遥男化学10刘文旭男化学10朱建新女化学10周亮男化学10余宽男化学10沈榴女物理11徐琼婷女物理11包志佳女物理11李国文男物理11张远辉男物理11严德洋男物理11孙正亮男物理11姚雨婷女化学11张静女化学11冯林男化学11王磊女化学11徐佳女化学11王新亚男化学11王宇男化学11殷凯男机械11苗胜男机械11李犇男机械11郑金燕女信息11张明凯男信息11刘学男信息11明新春男信息11张炜男信息11谢琳莹女信息11张玉女信息11王恺男信息11 乔科男信息11王洁女水利11王延召男水利11李兴霞女水利11袁满女水利11肖俊男水利11杨涛男水利11严岳同男水利11戚瑞宇男建工11韦中华男建工11周玲女建工11薛栋杨男建工11冯海春女建工11李秋子女建工11李敏男建工11姜伟男能动11王梦成男能动11
陆世明男能动11汤嘉欣男能动11周树青女能动11胡凯男能动11李增海男能动11尤光朝男能动11鲁波男能动11吴晗女能动11沈俊妍女环境11陈芸芸女环境11。
赛事报名登记表

赛事报名登记表报名表姓名:年龄:性别:联系电话:电子邮件:参赛项目:比赛经历:个人介绍:照片上传:请将以上信息填写完整,并发送至以下邮箱:[邮箱地址]赛事报名登记表尊敬的各位参赛者,感谢您对本次赛事的关注与参与。
为了更好地了解您的个人情况和报名信息,我们制定了本报名登记表。
请您仔细填写以下内容,确保信息的准确性。
一、个人信息1. 姓名:请填写您的真实姓名,确保与身份证或护照上的姓名一致。
2. 年龄:请填写您的年龄,确保符合参赛要求。
3. 性别:请填写您的性别,确保与身份证或护照上的性别一致。
4. 联系电话:请填写您的联系电话,确保及时获取赛事相关通知。
5. 电子邮件:请填写您常用的电子邮件地址,确保能接收到赛事组委会的邮件通知。
二、参赛项目请根据本次赛事的要求选择您希望参加的项目。
请确保您具备参加该项目的能力和条件。
三、比赛经历请简要描述您过去的比赛经历,包括参加过的比赛以及相关获奖情况(如有)。
这将有助于我们更好地了解您的能力和水平。
四、个人介绍请简要自述您的个人背景、爱好、特长或其他相关信息。
这将有助于我们更全面地了解您的个人特点。
五、照片上传请将您的个人照片上传至以下地址:[文件上传链接]。
请确保照片清晰、真实,以便用于参赛者名单、展示或宣传等用途。
请将填写完整的报名登记表发送至以下邮箱:[邮箱地址],并在邮件标题中注明“报名登记表”。
感谢您的支持和参与,祝您在本次赛事中取得优异成绩!注:本报名登记表将作为报名参赛者的必备资料,请务必填写完整、准确。
如发现填写虚假信息或不符合赛事要求的行为,将取消参赛资格。
同时,我们将对您的个人信息予以保密,并严格按照相关法律法规进行处理。
全国数学竞赛非数学类准考证

全国数学竞赛非数学类准考证
亲爱的参赛者,
感谢您参与本次全国数学竞赛非数学类。
以下是您的准考证:
[准考证编号]
请您仔细核对以上信息,确认无误后,请在参加比赛时携带此证。
准考证是您参加比赛的重要凭证,请妥善保管。
请注意以下几点事项:
1. 请在比赛当天携带此证,以便工作人员核实身份。
2. 请确保准考证上的个人信息准确无误,如姓名、身份证号等。
3. 请按照比赛当天的安排,准时到达比赛现场,以免耽误比赛。
4. 如有特殊情况需要调整比赛时间或地点,请及时与组委会联系。
5. 请在比赛结束后将准考证归还至指定地点,以便我们进行后续工作。
本次全国数学竞赛非数学类将于[具体日期]在[具体地点]举行。
请您提前做好行程安排,确保按时到达比赛现场。
如有疑问,请随时联系组委会工作人员,我们将竭诚为您解答。
祝您在比赛中取得优异成绩,为学校、为家乡争光!
再次感谢您参与本次比赛,期待在比赛中与您相见!
敬请妥善保管您的准考证,祝您一切顺利!
敬上!
[您的名字]
[组委会代表]。
比赛报名表word模板竞赛报名表格通用版

学校
院系
地址
团队名称
我
领队
教师
联系电话
(务必确认)
QQ/邮箱
(务必确认)
指导
教师
联系电话
(务必确认)
QQ/邮箱
(务必确认)
参赛
学生
姓名
性别
大赛
赛项
联系ห้องสมุดไป่ตู้话
(务必确认)
QQ/邮箱
(务必确认)
1(队长)
2
3
4
5
学校
意见
盖院/系公章
备注:
1.本次比赛以团队形式报名,指导教师限1-2人,参赛学生限3-5人。
2.参赛队伍可根据大赛模块及专业实际情况,从提供的赛项表中选择【I】、【口】、【HI】、
【IV】、[V]5个赛项中的任一赛项报名参赛。
3.参赛学生第1位默认为队长,且不可变更,请大家填表时注意。
4.指导教师和参赛学生人员报名确定后,原则上不得更改。
5.团队名称将在大赛期间频繁使用,报名提交后原则上不得更改,请认真审慎对待。
报名表和评分细则
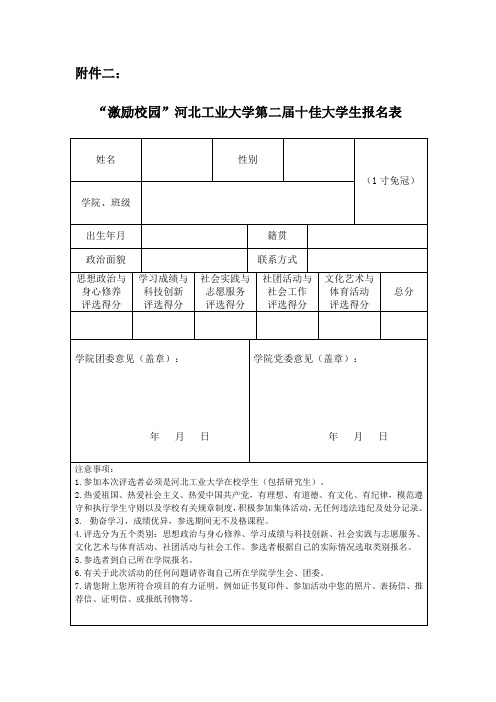
附件二:“激励校园”河北工业大学第二届十佳大学生报名表注①:学术知识竞赛类参加评选范围如下:全国“挑战杯”竞赛全国大学生数学建模竞赛全国大学生英语竞赛全国大学生节能减排社会实践与科技竞赛全国大学生电子设计竞赛全国大学生“飞思卡尔”杯智能汽车竞赛全国大学生结构设计竞赛全国高等学校人工环境工程学科奖全国高等学校城市规划本科学生课程社会调查作业评优全国高等学校城市规划专业本科学生城市规划设计课程作业评优河北省高等学校网络技能大赛2008年美国交叉学科建模竞赛(ICM)河北省高校“世纪之星”英语演讲大赛天津市大学生化学实验邀请Revit杯大学生建筑设计作业观摩赛天津市大学生数学竞赛天津市大学生计算机应用能力竞赛(“高新区希望”杯创新成果竞赛)校级“大学数学竞赛”注②科技发明及科研课题类得分须根据获奖等级和完成人顺序乘以相应系数特等奖*1,一等奖*0.9,二等奖*0.8,三等奖*0.7。
同时,第一作者*1,第二作者*0.8,第三作者*0.6,第四作者*0.4,第五作者*0.3注②发表学术论文类得分须根据作者顺序乘以相应系数第一作者*1,第二作者*0.8,第三作者*0.6,第四作者*0.4,第五作者*0.31. 参选人所参加活动均为大学期间参加,且参加本年度评选的各奖项获得的截止时间为2011年4月8日。
2.参加本次评选的人在以上五方面的评选除特殊注明外,均可以无上限累计加分。
3. 若您符合以上内容中的若干项目,请您附上您所符合项目的有力证明(有证明单位签章的证明)。
例如证书复印件、参加活动中您的照片、表扬信、推荐信、证明信、或报纸刊物等,若无有力证明,将会取消您在该项目中的加分。
4.评选过程将坚持公开、透明,随时接受广大师生的监督。
5.如违反法律法规或校纪校规,学校有权取消其称号。
比赛报名表范文3篇

比赛报名表范文3篇比赛报名表范文1个人信息- 姓名:[姓名]- 性别:[性别]- 年龄:[年龄]- 联系[联系电话]- 邮箱:[邮箱]比赛信息- 比赛名称:[比赛名称]- 比赛日期:[比赛日期]- 比赛地点:[比赛地点]- 参赛项目:[参赛项目]个人简介[在这里简要介绍你自己,包括教育背景、比赛经历、获奖情况等]比赛经验[在这里描述你参加过的类似比赛经历,包括参赛项目、比赛成绩等]目标和期望[在这里说明你参加本次比赛的目标和期望,以及你为此做了哪些准备工作]其他补充信息[在这里可以提供其他和比赛相关的信息,如特长、团队合作能力等]比赛报名表范文2个人信息- 姓名:[姓名]- 年龄:[年龄]- 性别:[性别]- 联系[联系电话]- 邮箱:[邮箱]比赛信息- 比赛名称:[比赛名称]- 比赛日期:[比赛日期]- 比赛地点:[比赛地点]- 参赛项目:[参赛项目]个人简介[在这里简要介绍你自己,包括个人特点、兴趣爱好等]比赛经历[在这里描述你参加过的类似比赛经历,包括参赛项目、比赛成绩等]参赛动机[在这里说明你为什么想参加本次比赛,以及你对比赛的期望]相关技能[在这里列举你相关的技能和知识,比如学过的课程、参加过的培训等]比赛报名表范文3个人信息- 姓名:[姓名]- 性别:[性别]- 年龄:[年龄]- 联系[联系电话]- 邮箱:[邮箱]比赛信息- 比赛名称:[比赛名称]- 比赛日期:[比赛日期]- 比赛地点:[比赛地点]- 参赛项目:[参赛项目]个人简介[在这里简要介绍你自己,包括教育背景、工作经历、个人特长等]比赛经验[在这里描述你参加过的类似比赛经历,包括参赛项目、比赛成绩等]目标和期望[在这里说明你参加本次比赛的目标和期望,以及你为此做了哪些准备工作]预期效益[在这里说明你希望通过参加本次比赛能够获得的效益,如提升自身能力、拓展人脉等]推荐信[在这里提供推荐人的联系信息,如姓名、联系电话、邮箱等]。
中国大学生数学竞赛竞赛大纲初稿为了进一步推动高等学校数学课程

中国大学生数学竞赛竞赛大纲(初稿)为了进一步推动高等学校数学课程的改革和建设,提高大学数学课程的教学水平,激励大学生学习数学的兴趣,发现和选拔数学创新人才,更好地实现“中国大学生数学竞赛”的目标,特制订本大纲。
一、竞赛的性质和参赛对象“中国大学生数学竞赛”的目的是:激励大学生学习数学的兴趣,进一步推动高等学校数学课程的改革和建设,提高大学数学课程的教学水平,发现和选拔数学创新人才。
“中国大学生数学竞赛”的参赛对象为大学本科二年级及二年级以上的在校大学生。
二、竞赛的内容“中国大学生数学竞赛”分为数学专业类竞赛题和非数学专业类竞赛题。
(一)中国大学生数学竞赛(数学专业类)竞赛内容为大学本科数学专业基础课的教学内容,即,数学分析占50%,高等代数占35%,解析几何占15%,具体内容如下:Ⅰ、数学分析部分一、集合与函数1. 实数集 、有理数与无理数的稠密性,实数集的界与确界、确界存在性定理、闭区间套定理、聚点定理、有限覆盖定理.2. 2 上的距离、邻域、聚点、界点、边界、开集、闭集、有界(无界)集、2 上的闭矩形套定理、聚点定理、有限复盖定理、基本点列,以及上述概念和定理在n 上的推广.3. 函数、映射、变换概念及其几何意义,隐函数概念,反函数与逆变换,反函数存在性定理,初等函数以及与之相关的性质.二、极限与连续1. 数列极限、收敛数列的基本性质(极限唯一性、有界性、保号性、不等式性质).2. 数列收敛的条件(Cauchy 准则、迫敛性、单调有界原理、数列收敛与其子列收敛的关系),极限1lim(1)n n e n →∞+=及其应用. 3.一元函数极限的定义、函数极限的基本性质(唯一性、局部有界性、保号性、不等式性质、迫敛性),归结原则和Cauchy 收敛准则,两个重要极限sin 10lim 1,lim(1)xx x x x x e →→∞=+=及其应用,计算一元函数极限的各种方法,无穷小量与无穷大量、阶的比较,记号O 与o 的意义,多元函数重极限与累次极限概念、基本性质,二元函数的二重极限与累次极限的关系.4. 函数连续与间断、一致连续性、连续函数的局部性质(局部有界性、保号性),有界闭集上连续函数的性质(有界性、最大值最小值定理、介值定理、一致连续性).三、一元函数微分学1.导数及其几何意义、可导与连续的关系、导数的各种计算方法,微分及其几何意义、可微与可导的关系、一阶微分形式不变性.2.微分学基本定理:Fermat 定理,Rolle 定理,Lagrange 定理,Cauchy 定理,Taylor 公式(Peano 余项与Lagrange 余项).3.一元微分学的应用:函数单调性的判别、极值、最大值和最小值、凸函数及其应用、曲线的凹凸性、拐点、渐近线、函数图象的讨论、洛必达(L'Hospital )法则、近似计算.四、多元函数微分学1. 偏导数、全微分及其几何意义,可微与偏导存在、连续之间的关系,复合函数的偏导数与全微分,一阶微分形式不变性,方向导数与梯度,高阶偏导数,混合偏导数与顺序无关性,二元函数中值定理与Taylor 公式.2.隐函数存在定理、隐函数组存在定理、隐函数(组)求导方法、反函数组与坐标变换.3.几何应用(平面曲线的切线与法线、空间曲线的切线与法平面、曲面的切平面与法线).4.极值问题(必要条件与充分条件),条件极值与Lagrange 乘数法.五、一元函数积分学1. 原函数与不定积分、不定积分的基本计算方法(直接积分法、换元法、分部积分法)、有理函数积分:(cos ,sin )R x x dx ⎰型,()R x dx ⎰型.2. 定积分及其几何意义、可积条件(必要条件、充要条件:i i x ωε∆<∑)、可积函数类. 3. 定积分的性质(关于区间可加性、不等式性质、绝对可积性、定积分第一中值定理)、变上限积分函数、微积分基本定理、N-L 公式及定积分计算、定积分第二中值定理.4.无限区间上的广义积分、Canchy 收敛准则、绝对收敛与条件收敛、()f x 非负时()a f x dx +∞⎰的收敛性判别法(比较原则、柯西判别法)、Abel 判别法、Dirichlet 判别法、无界函数广义积分概念及其收敛性判别法.5. 微元法、几何应用(平面图形面积、已知截面面积函数的体积、曲线弧长与弧微分、旋转体体积),其他应用.六、多元函数积分学1.二重积分及其几何意义、二重积分的计算(化为累次积分、极坐标变换、一般坐标变换).2.三重积分、三重积分计算(化为累次积分、柱坐标、球坐标变换).3.重积分的应用(体积、曲面面积、重心、转动惯量等).4.含参量正常积分及其连续性、可微性、可积性,运算顺序的可交换性.含参量广义积分的一致收敛性及其判别法,含参量广义积分的连续性、可微性、可积性,运算顺序的可交换性.5.第一型曲线积分、曲面积分的概念、基本性质、计算.6.第二型曲线积分概念、性质、计算;Green 公式,平面曲线积分与路径无关的条件.7.曲面的侧、第二型曲面积分的概念、性质、计算,奥高公式、Stoke 公式,两类线积分、两类面积分之间的关系.七、无穷级数1. 数项级数级数及其敛散性,级数的和,Cauchy 准则,收敛的必要条件,收敛级数基本性质;正项级数收敛的充分必要条件,比较原则、比式判别法、根式判别法以及它们的极限形式;交错级数的Leibniz 判别法;一般项级数的绝对收敛、条件收敛性、Abel 判别法、Dirichlet 判别法.2. 函数项级数函数列与函数项级数的一致收敛性、Cauchy 准则、一致收敛性判别法(M-判别法、Abel 判别法、Dirichlet 判别法)、一致收敛函数列、函数项级数的性质及其应用.3.幂级数幂级数概念、Abel 定理、收敛半径与区间,幂级数的一致收敛性,幂级数的逐项可积性、可微性及其应用,幂级数各项系数与其和函数的关系、函数的幂级数展开、Taylor 级数、Maclaurin 级数.4.Fourier 级数三角级数、三角函数系的正交性、2π及2l 周期函数的Fourier 级数展开、 Beseel 不等式、Riemanm-Lebesgue 定理、按段光滑函数的Fourier 级数的收敛性定理.Ⅱ、高等代数部分一、多项式1.数域与一元多项式的概念2.多项式整除、带余除法、最大公因式、辗转相除法3.互素、不可约多项式、重因式与重根.4.多项式函数、余数定理、多项式的根及性质.5.代数基本定理、复系数与实系数多项式的因式分解.6.本原多项式、Gauss引理、有理系数多项式的因式分解、Eisenstein判别法、有理数域上多项式的有理根.7.多元多项式及对称多项式、韦达(Vieta)定理.二、行列式1.n级行列式的定义.2.n级行列式的性质.3.行列式的计算.4.行列式按一行(列)展开.5.拉普拉斯(Laplace)展开定理.6.克拉默(Cramer)法则.三、线性方程组1. 高斯(Gauss)消元法、线性方程组的初等变换、线性方程组的一般解.2. n维向量的运算与向量组.3. 向量的线性组合、线性相关与线性无关、两个向量组的等价.4. 向量组的极大无关组、向量组的秩.5. 矩阵的行秩、列秩、秩、矩阵的秩与其子式的关系.6. 线性方程组有解判别定理、线性方程组解的结构.7. 齐次线性方程组的基础解系、解空间及其维数四、矩阵1. 矩阵的概念、矩阵的运算(加法、数乘、乘法、转置等运算)及其运算律.2. 矩阵乘积的行列式、矩阵乘积的秩与其因子的秩的关系.3. 矩阵的逆、伴随矩阵、矩阵可逆的条件.4. 分块矩阵及其运算与性质.5. 初等矩阵、初等变换、矩阵的等价标准形.6. 分块初等矩阵、分块初等变换.五、双线性函数与二次型1.双线性函数、对偶空间2.二次型及其矩阵表示.3.二次型的标准形、化二次型为标准形的配方法、初等变换法、正交变换法.4.复数域和实数域上二次型的规范形的唯一性、惯性定理.5.正定、半正定、负定二次型及正定、半正定矩阵六、线性空间1.线性空间的定义与简单性质.2.维数,基与坐标.3.基变换与坐标变换.4.线性子空间.5.子空间的交与和、维数公式、子空间的直和.七、线性变换1.线性变换的定义、线性变换的运算、线性变换的矩阵.2.特征值与特征向量、可对角化的线性变换.3.相似矩阵、相似不变量、哈密尔顿-凯莱定理.4.线性变换的值域与核、不变子空间.八、若当标准形λ矩阵.1.-2. 行列式因子、不变因子、初等因子、矩阵相似的条件.3. 若当标准形.九、欧氏空间1.内积和欧氏空间、向量的长度、夹角与正交、度量矩阵.2.标准正交基、正交矩阵、施密特(Schmidt)正交化方法.3.欧氏空间的同构.4.正交变换、子空间的正交补.5.对称变换、实对称矩阵的标准形.6.主轴定理、用正交变换化实二次型或实对称矩阵为标准形.7.酉空间.Ⅲ、解析几何部分一、向量与坐标1. 向量的定义、表示、向量的线性运算、向量的分解、几何运算.2. 坐标系的概念、向量与点的坐标及向量的代数运算.3. 向量在轴上的射影及其性质、方向余弦、向量的夹角.4. 向量的数量积、向量积和混合积的定义、几何意义、运算性质、计算方法及应用.5. 应用向量求解一些几何、三角问题.二、轨迹与方程1.曲面方程的定义:普通方程、参数方程(向量式与坐标式之间的互化)及其关系.2.空间曲线方程的普通形式和参数方程形式及其关系.3.建立空间曲面和曲线方程的一般方法、应用向量建立简单曲面、曲线的方程.4.球面的标准方程和一般方程、母线平行于坐标轴的柱面方程.三、平面与空间直线1.平面方程、直线方程的各种形式,方程中各有关字母的意义.2.从决定平面和直线的几何条件出发,选用适当方法建立平面、直线方程.3.根据平面和直线的方程,判定平面与平面、直线与直线、平面与直线间的位置关系.4. 根据平面和直线的方程及点的坐标判定有关点、平面、直线之间的位置关系、计算他们之间的距离与交角等;求两异面直线的公垂线方程.四、二次曲面1.柱面、锥面、旋转曲面的定义,求柱面、锥面、旋转曲面的方程.2.椭球面、双曲面与抛物面的标准方程和主要性质,根据不同条件建立二次曲面的标准方程.3.单叶双曲面、双曲抛物面的直纹性及求单叶双曲面、双曲抛物面的直母线的方法.4.根据给定直线族求出它表示的直纹面方程,求动直线和动曲线的轨迹问题.五、二次曲线的一般理论1.二次曲线的渐进方向、中心、渐近线.2.二次曲线的切线、二次曲线的正常点与奇异点.3.二次曲线的直径、共轭方向与共轭直径.4.二次曲线的主轴、主方向,特征方程、特征根.5.化简二次曲线方程并画出曲线在坐标系的位置草图.(二)中国大学生数学竞赛(非数学专业类)竞赛内容为大学本科理工科专业高等数学课程的教学内容,具体内容如下:一、函数、极限、连续1. 函数的概念及表示法、简单应用问题的函数关系的建立.2. 函数的性质:有界性、单调性、周期性和奇偶性.3. 复合函数、反函数、分段函数和隐函数、基本初等函数的性质及其图形、初等函数.4. 数列极限与函数极限的定义及其性质、函数的左极限与右极限.5. 无穷小和无穷大的概念及其关系、无穷小的性质及无穷小的比较.6. 极限的四则运算、极限存在的单调有界准则和夹逼准则、两个重要极限.7. 函数的连续性(含左连续与右连续)、函数间断点的类型.8. 连续函数的性质和初等函数的连续性.9. 闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理).二、一元函数微分学1. 导数和微分的概念、导数的几何意义和物理意义、函数的可导性与连续性之间的关系、平面曲线的切线和法线.2. 基本初等函数的导数、导数和微分的四则运算、一阶微分形式的不变性.3. 复合函数、反函数、隐函数以及参数方程所确定的函数的微分法.4. 高阶导数的概念、分段函数的二阶导数、某些简单函数的n 阶导数.5. 微分中值定理,包括罗尔定理、拉格朗日中值定理、柯西中值定理和泰勒定理.6. 洛必达(L ’Hospital )法则与求未定式极限.7. 函数的极值、函数单调性、函数图形的凹凸性、拐点及渐近线(水平、铅直和斜渐近线)、函数图形的描绘.8. 函数最大值和最小值及其简单应用.9. 弧微分、曲率、曲率半径.三、一元函数积分学1. 原函数和不定积分的概念.2. 不定积分的基本性质、基本积分公式.3. 定积分的概念和基本性质、定积分中值定理、变上限定积分确定的函数及其导数、牛顿-莱布尼茨(Newton-Leibniz )公式.4. 不定积分和定积分的换元积分法与分部积分法.5. 有理函数、三角函数的有理式和简单无理函数的积分.6. 广义积分.7. 定积分的应用:平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力及函数的平均值.四.常微分方程1. 常微分方程的基本概念:微分方程及其解、阶、通解、初始条件和特解等.2. 变量可分离的微分方程、齐次微分方程、一阶线性微分方程、伯努利(Bernoulli )方程、全微分方程.3. 可用简单的变量代换求解的某些微分方程、可降阶的高阶微分方程:),()n (x f y = ),,(y x f y '=''),(y y f y '=''.4. 线性微分方程解的性质及解的结构定理.5. 二阶常系数齐次线性微分方程、高于二阶的某些常系数齐次线性微分方程.6.简单的二阶常系数非齐次线性微分方程:自由项为多项式、指数函数、正弦函数、余弦函数,以及它们的和与积7.欧拉(Euler)方程. 8. 微分方程的简单应用五、向量代数和空间解析几何1.向量的概念、向量的线性运算、向量的数量积和向量积、向量的混合积.2.两向量垂直、平行的条件、两向量的夹角.3.向量的坐标表达式及其运算、单位向量、方向数与方向余弦.4.曲面方程和空间曲线方程的概念、平面方程、直线方程.5.平面与平面、平面与直线、直线与直线的夹角以及平行、垂直的条件、点到平面和点到直线的距离.6.球面、母线平行于坐标轴的柱面、旋转轴为坐标轴的旋转曲面的方程、常用的二次曲面方程及其图形.7.空间曲线的参数方程和一般方程、空间曲线在坐标面上的投影曲线方程.六、多元函数微分学1.多元函数的概念、二元函数的几何意义.2.二元函数的极限和连续的概念、有界闭区域上多元连续函数的性质.3.多元函数偏导数和全微分、全微分存在的必要条件和充分条件.4.多元复合函数、隐函数的求导法.5.二阶偏导数、方向导数和梯度.6.空间曲线的切线和法平面、曲面的切平面和法线.7.二元函数的二阶泰勒公式.8.多元函数极值和条件极值、拉格朗日乘数法、多元函数的最大值、最小值及其简单应用.七、多元函数积分学1.二重积分和三重积分的概念及性质、二重积分的计算(直角坐标、极坐标)、三重积分的计算(直角坐标、柱面坐标、球面坐标).2.两类曲线积分的概念、性质及计算、两类曲线积分的关系.3.格林(Green)公式、平面曲线积分与路径无关的条件、已知二元函数全微分求原函数.4.两类曲面积分的概念、性质及计算、两类曲面积分的关系.5.高斯(Gauss)公式、斯托克斯(Stokes)公式、散度和旋度的概念及计算.6.重积分、曲线积分和曲面积分的应用(平面图形的面积、立体图形的体积、曲面面积、弧长、质量、质心、转动惯量、引力、功及流量等)八、无穷级数1.常数项级数的收敛与发散、收敛级数的和、级数的基本性质与收敛的必要条件.2.几何级数与p级数及其收敛性、正项级数收敛性的判别法、交错级数与莱布尼茨(Leibniz)判别法.3.任意项级数的绝对收敛与条件收敛.4.函数项级数的收敛域与和函数的概念.5.幂级数及其收敛半径、收敛区间(指开区间)、收敛域与和函数.6.幂级数在其收敛区间内的基本性质(和函数的连续性、逐项求导和逐项积分)、简单幂级数的和函数的求法.7.初等函数的幂级数展开式.8.函数的傅里叶(Fourier)系数与傅里叶级数、狄利克雷(Dirichlei)定理、函数在[-l,l]上的傅里叶级数、函数在[0,l]上的正弦级数和余弦级数。
全国大学生数学竞赛文件

1全国大学生数学竞赛文件关于举办第四届全国大学生数学竞赛的通知各省、市、自治区数学会、解放军院校协作中心数学联席会:为了培养人才、服务教学、促进高等学校数学课程的改革和建设,增加大学生学习数学的兴趣,培养分析、解决问题的能力,发现和选拔数学创新人才,为青年学子提供一个展示基础知识和思维能力的舞台,经中国数学会批准,第四届全国大学生数学竞赛将由电子科技大学数学学院承办。
4月初,中国数学会普及工作委员会(奥林匹克委员会)在重庆召开工作会议,决定成立全国大学生数学竞赛工作小组,具体领导、协调、组织全国大学生数学竞赛工作。
本届比赛预赛在2012年10月27日(星期六)上午9:00—11:30举行,决赛于2013年3月份的第三周周六上午在电子科技大学(成都)举行。
现将竞赛的具体事宜通知如下:(1)参赛对象:大学本科二年级或二年级以上的在校大学生。
竞赛分为非数学专业组和数学专业组(含数学与应用数学、信息与计算科学专业的学生)。
数学专业学生不得参加非数学专业组的竞赛。
(2)竞赛内容:非数学专业组竞赛内容为本科高等数学内容(高等数学内容为理工科本科教学大纲规定的高等数学的教学内容)。
数学专业组竞赛内容含数学分析、高等代数和解析几何(均为数学专业本科教学大纲规定的教学内容),所占比重分别为50%、35%及15%左右。
(3)报名办法:2012年9月30日前按所在省、直辖市、自治区数学会或学会委托的承办大学的要求报名。
(4)竞赛组织工作:分区预赛由各省(市、区、军队院校)数学会负责组织选拔,使用全国统一试2题,在同一时间内进行考试。
决赛由全国大学生数学竞赛工作小组和承办单位负责组织实施。
(5)竞赛收费标准:每个参赛学生要向参赛单位交报名费60元,其中50元用于分赛区,10元交给全国大学生数学竞赛组委会,分别用于分区预赛和决赛阶段竞赛工作的组织、命题、评奖、颁奖以及召开竞赛工作领导小组会议的费用。
(6)奖项的设立:设预赛(以省、市、自治区作为赛区,军队院校为一个独立赛区)奖与决赛奖。
2014年校第十二届大学生高等数学竞赛考场安排表
Z139 Z140 Z141 Z142 Z143 Z144 Z145 Z146 Z147 Z148 Z149 Z150 Z151 Z152 Z153 Z154 Z155 Z156 Z157 Z158 Z159 Z160 Z161 Z162 Z163 Z164 Z165 Z166 Z167 Z168 Z169 Z170 Z171 Z172 Z173 Z174 Z175 Z176 Z177 Z178 Z179 G001 G002 G003 G004 G005 G006
专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组 专业组
理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院
理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院
竞赛参赛报名模板

竞赛参赛报名模板尊敬的组织者:我自愿报名参加您组织的竞赛活动。
特此填写本报名表,详细说明我的个人信息和参赛意向,希望能够取得机会展示自己的才华和技能。
一、个人信息1. 姓名:2. 性别:3. 年龄:4. 联系电话:5. 电子邮箱:6. 学校/单位名称:7. 年级/职务:二、竞赛项目选择请在下列项目中选择一个您希望参加的竞赛项目,并填写相关信息:项目名称:项目简介:参赛动机:参赛经验(若有):个人特长:个人期望(获奖、提升技能等):三、参赛宣言根据您所提供的参赛项目信息,以及您的个人特长和参赛期望,请在此部分撰写一段参赛宣言,用于展示您的热情和决心。
在宣言中,您可以表达对参赛项目的热爱,以及参赛所带来的个人成长和收获。
(这部分请根据具体情况自行撰写)四、其他相关信息请在此部分填写您认为需要告知组织者的其他相关信息,例如特殊需要、技能证书等。
如果您有任何可以证明您参赛能力的相关文件,请在此附上副本。
附件清单:1.2.3.五、参赛须知请您阅读以下参赛须知,并确保您已经了解并同意遵守:1. 所有参赛者必须按照比赛规则参加,确保公平竞争。
2. 所有参赛者必须遵守竞赛组织方的安排和管理。
3. 如有违反比赛规则和行为规范的情况,将取消参赛资格。
4. 在活动期间,组织者有权使用参赛者的相关照片、视频等素材进行宣传和报道。
5. 如有任何问题或变动,会尽快通知参赛者。
六、签名请在此处签名确认以上填写的信息准确无误,并表示自愿参赛。
日期:签名:感谢您的耐心填写本报名表,如果您的报名被接受,我们将会尽快通知您的下一步参赛安排。
祝您取得优异的成绩!致敬!(正文结束)。
全国大学生数学竞赛考纲

中国大学生数学竞赛(非数学专业类)竞赛内容为大学本科理工科专业高等数学课程的教学内容,具体内容如下:一、函数、极限、连续1.函数的概念及表示法、简单应用问题的函数关系的建立.2.函数的性质:有界性、单调性、周期性和奇偶性.3.复合函数、反函数、分段函数和隐函数、基本初等函数的性质及其图形、初等函数.4.数列极限与函数极限的定义及其性质、函数的左极限与右极限.5.无穷小和无穷大的概念及其关系、无穷小的性质及无穷小的比较.6.极限的四则运算、极限存在的单调有界准则和夹逼准则、两个重要极限.7.函数的连续性(含左连续与右连续)、函数间断点的类型.8.连续函数的性质和初等函数的连续性.9.闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理).二、一元函数微分学1. 导数和微分的概念、导数的几何意义和物理意义、函数的可导性与连续性之间的关系、平面曲线的切线和法线.2. 基本初等函数的导数、导数和微分的四则运算、一阶微分形式的不变性.3. 复合函数、反函数、隐函数以及参数方程所确定的函数的微分法.4. 高阶导数的概念、分段函数的二阶导数、某些简单函数的n阶导数.5. 微分中值定理,包括罗尔定理、拉格朗日中值定理、柯西中值定理和泰勒定理.6. 洛必达(L’Hospital)法则与求未定式极限.7. 函数的极值、函数单调性、函数图形的凹凸性、拐点及渐近线(水平、铅直和斜渐近线)、函数图形的描绘.8. 函数最大值和最小值及其简单应用.9. 弧微分、曲率、曲率半径.三、一元函数积分学1. 原函数和不定积分的概念.2. 不定积分的基本性质、基本积分公式.3. 定积分的概念和基本性质、定积分中值定理、变上限定积分确定的函数及其导数、牛顿-莱布尼茨(Newton-Leibniz)公式.4. 不定积分和定积分的换元积分法与分部积分法.5. 有理函数、三角函数的有理式和简单无理函数的积分.6. 广义积分.7. 定积分的应用:平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力及函数的平均值.四.常微分方程1. 常微分方程的基本概念:微分方程及其解、阶、通解、初始条件和特解等.2. 变量可分离的微分方程、齐次微分方程、一阶线性微分方程、伯努利(Bernoulli)方程、全微分方程.3. 可用简单的变量代换求解的某些微分方程、可降阶的高阶微分方程: .4. 线性微分方程解的性质及解的结构定理.5. 二阶常系数齐次线性微分方程、高于二阶的某些常系数齐次线性微分方程.6. 简单的二阶常系数非齐次线性微分方程:自由项为多项式、指数函数、正弦函数、余弦函数,以及它们的和与积7. 欧拉(Euler)方程.8. 微分方程的简单应用五、向量代数和空间解析几何1. 向量的概念、向量的线性运算、向量的数量积和向量积、向量的混合积.2. 两向量垂直、平行的条件、两向量的夹角.3. 向量的坐标表达式及其运算、单位向量、方向数与方向余弦.4. 曲面方程和空间曲线方程的概念、平面方程、直线方程.5. 平面与平面、平面与直线、直线与直线的夹角以及平行、垂直的条件、点到平面和点到直线的距离.6. 球面、母线平行于坐标轴的柱面、旋转轴为坐标轴的旋转曲面的方程、常用的二次曲面方程及其图形.7. 空间曲线的参数方程和一般方程、空间曲线在坐标面上的投影曲线方程.六、多元函数微分学1. 多元函数的概念、二元函数的几何意义.2. 二元函数的极限和连续的概念、有界闭区域上多元连续函数的性质.3. 多元函数偏导数和全微分、全微分存在的必要条件和充分条件.4. 多元复合函数、隐函数的求导法.5. 二阶偏导数、方向导数和梯度.6. 空间曲线的切线和法平面、曲面的切平面和法线.7. 二元函数的二阶泰勒公式.8. 多元函数极值和条件极值、拉格朗日乘数法、多元函数的最大值、最小值及其简单应用.七、多元函数积分学1. 二重积分和三重积分的概念及性质、二重积分的计算(直角坐标、极坐标)、三重积分的计算(直角坐标、柱面坐标、球面坐标).2. 两类曲线积分的概念、性质及计算、两类曲线积分的关系.3. 格林(Green)公式、平面曲线积分与路径无关的条件、已知二元函数全微分求原函数.4. 两类曲面积分的概念、性质及计算、两类曲面积分的关系.5. 高斯(Gauss)公式、斯托克斯(Stokes)公式、散度和旋度的概念及计算.6. 重积分、曲线积分和曲面积分的应用(平面图形的面积、立体图形的体积、曲面面积、弧长、质量、质心、转动惯量、引力、功及流量等)八、无穷级数1. 常数项级数的收敛与发散、收敛级数的和、级数的基本性质与收敛的必要条件.2. 几何级数与p级数及其收敛性、正项级数收敛性的判别法、交错级数与莱布尼茨(Leibniz)判别法.3. 任意项级数的绝对收敛与条件收敛.4. 函数项级数的收敛域与和函数的概念.5. 幂级数及其收敛半径、收敛区间(指开区间)、收敛域与和函数.6. 幂级数在其收敛区间内的基本性质(和函数的连续性、逐项求导和逐项积分)、简单幂级数的和函数的求法.7. 初等函数的幂级数展开式.8. 函数的傅里叶(Fourier)系数与傅里叶级数、狄利克雷(Dirichlei)定理、函数在[-l,l]上的傅里叶级数、函数在[0,l]上的正弦级数和余弦级数。
2013年高等数学竞赛结果通知 A

常州大学2012-2013年度数学竞赛获奖名单本部机类(高等数学A)一等奖(共34人)谢敬涛(信管101)刘浩浩(机械教改121)陈圆圆(机制101) 夏阳春(热能122) 宗文浩(储运113) 周伟(储运103) 唐归源(石工122) 徐丽娜(信管101) 邓吕(装备102) 周军勇(储运103) 陈春龙(建环101) 王明敏(土木121) 戚中一(计算机121) 魏婷婷(电科121) 华松杰(华院121) 郑国峰(装备102) 黄佳佳(电科121) 李洋(给水121) 朱绪跃(华院122) 陈龙海(装备122) 朱晓云(信科教改122) 卞雷(机械教改121) 苏聪(电科121) 万根(华院121) 樊姜威(土木122) 陈雪慧(电科121) 荆斌(电科122) 郁秋华(华院122)孙涛(机制103) 陈继雨(土木121) 殷啸林(土木122) 夏威威(机制122) 刘锐(装备101) 郑张笑(电科111)二等奖(共50人)蒋斌(储运121)郭雪萍(石工101)江晓栋(给水121)卓优(热能121)王雪冰(石工101)刘朝阳(储运123)张涵机(械教改121)王抄(电科121)李益凡(安全121)王盛(热能121)田志娟(建环122)宦敏(电科121)吕留新(储运123)郭新光(成型102)盛丽(机制101)盛哲(土木122)李磊(土木122) 杨伟建(机械教改121)刘志强(成型121)吴永祥(土木122)陈晟(华院122)王金德(热能122)邢扬(机制102)朱礼(装备101)占婷婷(计算机121)张涛(建环122)杨杨(石工101)邱航(土木122)张勤勤(华院121)管旭(华院121)王俊彦(华院122)唐鑫鑫(华院122)周行洁(华院122)徐慧(储运121)魏雪芹(储运103)王小忠(电科121)何亚峰(自动化121)李如洲(自动化121)杜沄燕(安全121)潘晓菲(安全121)谈志超(华院122)陈智伟(信科教改121)耿勇强(软件121)吴国邦(石工101)张柏杨(石工102)吴和军(机械教改122)杜蔚(软件122)尹展翅(热能121)曹松泽(电子121)朱晓莉(安全122)三等奖高振(机械教改121) 何于阎(成型121) 韩凯文(热能122) 张小兵(石工121) 冯聪聪{机制103) 王嘉(装备102) 黄明(土木122) 张玮(电子121)钱静(安全122) 魏鹏飞(华院121) 陈广泽(机制101) 衡威(土木122) 周松松(电科122) 沈田(给水121) 丁超颖(华院121) 杨通(华院121) 周逸鸣(信科教改121)叶茂凯(信科教改122)王玉文(软件122) 杨健(热能122) 冯志刚(机制122) 付立志(热能122) 徐沛扬(储运111) 张国彪(土木122) 徐定兴(软件121) 施巧(装备122) 宗永迪(储运121) 王殷浩(热能122) 谈刚(机制101) 马达(装备102) 黄健(安全121) 钱斌(给水121) 陈璐(华院121) 钱文荣(机械教改122) 朱奇(石工122) 俞贵琴(电子121) 华乾(华院122) 赵成胤(建环122) 鞠焱(机械教改121)周艳红(储运111) 王鑫(储运103) 章建森(电气123) 姜晓雨(安全122) 许重阳(给水121) 陆敏(华院121) 孙萌(华院121) 汪凯(华院121) 咸苹苹(华院122) 施奕(华院122) 胡琪(华院122) 张威(华院122) 张建(信科教改121) 向太鑫(信科教改122)蔡森林(成型121) 李良妹(石工121) 秦慧芳(机制103) 崔莹莹(土木122) 朱柯鑫(电科122) 王慧(电子121) 袁文晶(电子122) 张鸿(华院121) 刘园(华院122) 闫盼盼(信科教改122)曹岩斌(软件122) 吕游(储运111) 王俊梁(成型102) 张贤(电气121) 常慧(给水121) 唐剑(安全121) 冷成龙(给水121) 唐烨栋(给水121) 姬进豹(热能122) 周运(机械教改122) 张镇(机械教改122) 张国花(机制103) 孙劲飞(石工101) 付强(电科122) 杨建(华院122) 纪加超(华院122) 陈菲(信科教改121) 石友义(自动化122) 王伟(石工101) 邱曙(石工101) 李晨治(土木121) 朱文垚(电气121) 张娟(电气123) 赵华强(给水122) 徐秀(华院122) 赵雅(信科教改121) 谈美萍(软件122)化工类(高等数学B)一等奖葛敏(无机121) 陈博文(化工121) 杨信李(无机122) 曹少博(化工122)王乾(化工教改121)邵家虎(无机121) 戎春勇(应化122) 高泽华(化工121)梁佩(无机121) 谢伟伟(化工123) 屈寒寒(化工123) 郑世福(化工124)苏鹏霄(制药121) 石红兵(材料122) 赵笑(材化112) 李文(高分子122) 朱含枪(化工124) 张振香(环工111) 段沙沙(高分子121) 王春萍(化工121)贾正材(化工121) 张敬文(高分子122) 吴殷琦(生工121) 朱峥嵘(环工123) 张世平(复材121) 马光明(化工121) 宋璐(无机122) 翟鹏(材料121) 二等奖孙乾(制药121) 单涛(制药121) 邵宁宁(复材121) 高延成(化工121) 段华玲(化工123) 陈慧贤(金材122) 丁佳颖(制药121) 张霄敏(化工122)刘云忠(轻化121) 黄家驹(材料122) 张培盈(环工123) 朱相红(化工121) 陶圣然(化工122) 赵鑫(金材122) 王静(金材122) 刘海韵(材料121) 尹翔(应化123) 周冲(复材121) 张丽(高分子121) 许斌(高分子122) 蔡峰(化工124) 唐立朋(环工123) 丁琪(应化122) 刘玉姣(化工121) 吴贤(化工123) 陈天翔(金材122) 王伟(轻化121) 钱婷婷(应化122) 柏至伟(复材121) 陈浩(高分子122) 符饲铨(化工121) 杨清清(高分子121) 周建荣(高分子122) 丛田田(化工121) 吕辉(化工121) 王硕(金材122) 经青(无机122) 姚福达(材料121) 高旭(材料121) 吉得文(食品121)卫梦露(应化123) 师旷(应化123) 尹锴(化改121) 周雅静(材料122) 张婷(食品121)三等奖梁宇春(应化123) 曹钰(高分子122) 文江福(高分子122) 陈恒恒(化改121) 陈俊杰(应化122) 周必航(化改121) 徐逸琦(化工123) 梁爽(金材122) 李文林(化工121) 冯桂林(化工123) 钱程(金材122) 王青(环工122) 崔万稳(应化122) 申洁(高分子121) 张铎(无机122) 孙淑珍(生工121) 储凯强(环工122) 陈世娟(材化121) 凌志鹏(材化122) 王子初(制药121) 陈丹彬(应化122) 葛宇凯(应化122) 成非凡(应化123) 吴建民(化改121) 陆程 (金材122) 刘来娣(食品121) 恽倩妍(环工123) 王勃(应化122) 李庆刚(金材121) 高晓羽(金材122) 丁琳(材化122) 陈圣宇(应化123) 竺宝玉(应化123) 梁红维(高分子121) 刘莉(化工123) 钱瀚杨(金材121) 周志强(轻化121) 庄艳(材料121) 刘广明(材料122) 黄佟莉(环工123) 吴西林(制药121) 李鑫材(化工122) 孔德欣(化工121) 沈梦芸(材料121) 邓逸凡(材料122) 华恋琦(环工123) 翟樱玉(环工123) 杨健(材化121) 夏德勇(材化122) 张杏雯(制药122) 杨嫣然(应化122) 潘必越(应化123)王文杰(高分子121) 陈情(生工121) 朱青(环工122 ) 董琰(环工121) 黄兴(环工121) 陈治孚(应化122) 王伟(应化123) 李平(化工122) 梁正午(材料122) 李梦萍(环工122) 陈柏祥(材化121) 常成(材化122) 刘雅婷(制药122) 侯楚珺(应化122) 胡猛男(应化122) 陈中京(应化123) 赵丽琴(化工123) 苗雨(金材121) 包梦洁(制药121) 李静(高分子121) 山炯(金材122) 张如月(材料122)经管类(高等数学C)一等奖史璟文(会计107) 陈姝彤(会计122) 彭秀秀(国贸122) 翟清仪(国贸121) 汤勤玲(会计121) 徐桂霞(物流122) 马雪娇(人力122) 封翠(物流121) 高智慧(物流121) 朱敏(营销121) 葛翔(会计126) 奚珊珊(物流121) 霍姝(金融121) 蒋国卫(营销121) 罗敏仪(会计124) 薛冬梅(物流122) 二等奖刘佳雯国贸121) 姜芹(财务121) 张葛琴(金融121) 韩於憬(财务121) 朱美玲(财务121) 凌如婳(会计123) 金逸馨(会计122) 卢艳(人力122) 刘易萌(人力122) 李玥(工商121) 卞桂锋(国贸122) 李慧(人力122) 陈茗(金融121) 毛律欣(会计123) 姜秀(金融121) 王莲(会计121) 高珍(会计125) 王晓嫄(会计123) 李响(会计122) 付倩雯(会计124) 居文静(国贸122) 朱萍(物流121) 刘春春(物流122) 许英杰(会计121) 蒋喃(会计123)三等奖庞静怡(物流122) 李嘉佳(国贸121) 许斌(会计127) 王嘉诚(营销121) 朱书研(物流122) 王楚煜(国贸121) 徐宜丰(会计121) 蔡倩(国贸121) 江丽君(财务121) 黄思捷(财务121) 倪敏(人力122) 植玉凤(财务121) 张露洁(财务121) 居紫嫣(物流121) 蒋盼盼(财务121) 孔德佩(财务121) 羌银(物流122) 张康康(物流121) 程渝涵(会计124) 孙淼(会计125) 付东祥(财务121) 王雪蒙(金融121) 辛倩倩(财务121) 房玲玲(工商121) 葛梅云(工商121) 李思晴(人力122) 张杰(人力122) 黄宵(国贸121)刘争秋(金融121) 姜慧敏(国贸121) 缪晨磊(物流121) 陈月(金融121) 陈佳仁(金融121) 张祖华(会计125) 郑文俊(营销121) 周月雯(会计124) 季盈萍(财务121) 唐伟仁(物流121)数学分析类二等奖张跃(信息121)顾泽洲(应数101)三等奖邵晨宇(应数111)张伟(应数111)石喜霞(信息121)怀德学院(高等数学C)一等奖王亚萍(会计105)庄浏镭(土木101) 郑猛(土木101)曹兵兵(土木101)张晔(土木101)蒋庆(土木101) 王晨(会计105) 谭笑(电子121) 吴晓(会计103) 吴昊(计算机122) 李寒冰(机制121) 束婷婷(给水122) 朱苠江(装备102)二等奖蔡杨(会计124) 杨晶(会计103) 赵生淦(电子102) 潘旻贇(电子102) 杨中校(电子102) 张刚刚(化工121) 戴强(化工123) 丁宇(自动化102) 吴灯(自动化122) 王宏苡(自动化121) 章文晋(化工121) 赵静(高分子121) 王浩(会计125) 乔广明(装备102) 王宇(给水121) 丁静文(电子122) 沈新霞(电子122) 朱荟锦(机制121) 程进(化工101) 高翔(制药101) 杨帧(艺设121) 吉娜(会计104) 唐琥程(电气111) 邓东旭(电子123) 顾迪(机制122)三等奖许城(化工122) 陈媛媛(国贸123) 范学成(装备102) 邱飞(机制121) 陈刚(化工101) 张月(制药121) 李颖(电子102) 王佩佩(电子123) 包盛辉(电气122) 张羽(化工123) 周炴(会计124) 李凯尚(装备121) 陈伟(装备121) 李俊杰(装备122) 范恕领(储运121) 章志阳(机制121)陈志立(制药121) 何汶晓(制药121) 马怡冰(会计105) 范镇(电子102) 柏锦程(自动化112) 赵梦华(自动化121) 周天(机制121) 陈明(给水121) 汤超(高分子122) 归小燕(会计121) 金艺冉(会计104) 郑敏(自动化112) 徐婷(会计125) 李小珍(会计123) 钮妍(会计103) 王浩(机制122) 邹金烨(机制121)。
关于举办我校第二十届高等数学竞赛.

关于举办我校第二十届高等数学竞赛暨首届全国大学生数学竞赛选拔赛的通知接中国数学会通知,将举办首届全国大学生数学竞赛。
而我校延续了二十一年的高度数学竞赛——第二十届高等数学竞赛也将举行,为使二者有效地衔接,组委会决定:我校第二十届高等数学竞赛同时作为首届全国大学生数学竞赛的选拔赛。
本次竞赛由教务处、学生工作部、理学系联合主办。
现将竞赛工作有关事项通知如下:一、第二十届高度数学竞赛1.报名对象:我院本科二年级及二年级以上的在校大学生(包括科技学院)2.报名时间:2009年9月9日~9月14日3.报考办法:以班为单位集体报名,各班班长持本班报名表在上述期限内到所在系辅导员处报名。
各系辅导员于9月14日下午5点前将报名表(报盘)送理学系办公室王老师处汇总。
理学系不受理个人报名。
由于本次校内赛将为全国赛选拔人才,建议有考研意向的同学、高等数学成绩好的同学、有意为我院争得荣誉的同学踊跃报名。
3.考试时间:2009年9月21日下午3:00~5:004.考试范围:同济大学编《高等数学》(第五版或第六版)上、下册全部内容。
5.授奖办法:(1)团体奖励:各系前五名分数之和为该系团体总分。
团体第一名将获得获奖证书。
(2)个人奖励:一等奖二名(奖金200元),二等奖四名(奖金120元),三等奖十二名(奖金50元),优胜奖二十名。
以上奖项获得者将同时获得获奖证书。
6.考试分数不予公布。
二、首届全国大学生数学竞赛1.竞赛形式:竞赛分为两个阶段进行。
在当年10月份的第三个周六举行分区(省、直辖市、自治区)赛;在次年5月份的第三个周六举行全国决赛。
各分区由省(市、区)数学会负责组织进行竞赛、评奖和选拔决赛选手,使用全国统一賽题,在同一时间进行竞赛。
湖北省赛区决定于2009年10月24日在武汉大学组织“第一届全国大学生数学竞赛湖北赛区竞赛”。
2.参赛名额:湖北赛区为我院分配参赛名额为10人。
我们将主要依据本次校内数学竞赛的成绩选拔优秀学生参加湖北赛区的竞赛。
全国高等院校数学能力挑战赛

全国高等院校数学能力挑战赛本文旨在介绍全国高等院校数学能力挑战赛的背景和目的。
本次全国高等院校数学能力挑战赛将考察以下题目类型、数学领域和难度级别:选择题:考察学生对数学基础知识的掌握程度,包括代数、几何、概率与统计等方面的题目。
解答题:要求学生通过分析、推理和解决实际问题的能力来回答问题,其中包括数学建模和证明等方面的题目。
计算题:要求学生运用数学计算方法来解决问题,包括数值计算、函数计算、积分和微分等方面的题目。
考试内容将涵盖高等数学、线性代数、概率论与数理统计等数学领域,难度级别将覆盖从基础知识应用到较为复杂的问题解决的各个层次。
在本次比赛中,我们将以简化的策略进行设计,避免引入法律复杂性的问题,确保以公正、公平和公开的原则进行比赛评判和结果确认。
请各位参赛选手提前做好充分准备,熟悉以上题目类型和数学领域,以应对本次全国高等院校数学能力挑战赛的考验。
了解比赛信息:参赛者需要先了解比赛的相关信息,包括时间、地点、报名截止日期等。
填写报名表格:参赛者需要下载并填写比赛的报名表格,准确填写个人信息和联系方式。
提交报名表格:参赛者需要按照指定的方式将填写好的报名表格提交给组委会。
考试形式:比赛采用笔试方式进行,参赛者需要准时到达考试地点,按照指定座位进行考试。
题目类型:比赛包括一系列数学能力挑战题目,涵盖多个数学领域,包括代数、几何、概率等。
考试时间:每道题目有指定的答题时间限制,参赛者需要根据题目要求合理安排时间,高效完成答题。
答题方式:参赛者需要使用提供的答题卡,按照题目要求在答题卡上作答,包括填空、解答等。
答题准确性:参赛者的答案需要准确无误,按照标准答案进行评判。
解题思路:除了答案准确性外,参赛者的解题思路也会得到评判,创新和合理的解题思路将获得额外加分。
时间管理:参赛者需要合理安排时间,高效完成答题,时间使用得当也会得到一定的评分加分。
以上是《全国高等院校数学能力挑战赛》的比赛流程,包括报名流程、答题方式和评分标准。
全国大学生数学竞赛

19:56 2011-9-28Ⅰ、数学分析部分一、集合与函数 1. 实数集、有理数与无理数的稠密性,实数集的界与确界、确界存在性定理、闭区间套定理、聚点定理、有限覆盖定理.2. 上的距离、邻域、聚点、界点、边界、开集、闭集、有界(无界)集、上的闭矩形套定理、聚点定理、有限覆盖定理、基本点列,以及上述概念和定理在上的推广.3. 函数、映射、变换概念及其几何意义,隐函数概念,反函数与逆变换,反函数存在性定理,初等函数以及与之相关的性质. 二、极限与连续 1. 数列极限、收敛数列的基本性质(极限唯一性、有界性、保号性、不等式性质). 2. 数列收敛的条件(Cauchy准则、迫敛性、单调有界原理、数列收敛与其子列收敛的关系),极限及其应用. 3.一元函数极限的定义、函数极限的基本性质(唯一性、局部有界性、保号性、不等式性质、迫敛性),归结原则和Cauchy收敛准则,两个重要极限及其应用,计算一元函数极限的各种方法,无穷小量与无穷大量、阶的比较,记号O与o的意义,多元函数重极限与累次极限概念、基本性质,二元函数的二重极限与累次极限的关系.4. 函数连续与间断、一致连续性、连续函数的局部性质(局部有界性、保号性),有界闭集上连续函数的性质(有界性、最大值最小值定理、介值定理、一致连续性). 三、一元函数微分学 1.导数及其几何意义、可导与连续的关系、导数的各种计算方法,微分及其几何意义、可微与可导的关系、一阶微分形式不变性. 2.微分学基本定理:Fermat定理,Rolle定理,Lagrange定理,Cauchy定理,Taylor公式(Peano余项与Lagrange余项). 3.一元微分学的应用:函数单调性的判别、极值、最大值和最小值、凸函数及其应用、曲线的凹凸性、拐点、渐近线、函数图象的讨论、洛必达(L'Hospital)法则、近似计算. 四、多元函数微分学 1. 偏导数、全微分及其几何意义,可微与偏导存在、连续之间的关系,复合函数的偏导数与全微分,一阶微分形式不变性,方向导数与梯度,高阶偏导数,混合偏导数与顺序无关性,二元函数中值定理与Taylor公式. 2.隐函数存在定理、隐函数组存在定理、隐函数(组)求导方法、反函数组与坐标变换. 3.几何应用(平面曲线的切线与法线、空间曲线的切线与法平面、曲面的切平面与法线). 4.极值问题(必要条件与充分条件),条件极值与Lagrange乘数法.五、一元函数积分学 1. 原函数与不定积分、不定积分的基本计算方法(直接积分法、换元法、分部积分法)、有理函数积分:型,型. 2. 定积分及其几何意义、可积条件(必要条件、充要条件:)、可积函数类. 3. 定积分的性质(关于区间可加性、不等式性质、绝对可积性、定积分第一中值定理)、变上限积分函数、微积分基本定理、N-L公式及定积分计算、定积分第二中值定理. 4.无限区间上的广义积分、Canchy收敛准则、绝对收敛与条件收敛、非负时的收敛性判别法(比较原则、柯西判别法)、Abel判别法、Dirichlet判别法、无界函数广义积分概念及其收敛性判别法. 5. 微元法、几何应用(平面图形面积、已知截面面积函数的体积、曲线弧长与弧微分、旋转体体积),其他应用. 六、多元函数积分学 1.二重积分及其几何意义、二重积分的计算(化为累次积分、极坐标变换、一般坐标变换). 2.三重积分、三重积分计算(化为累次积分、柱坐标、球坐标变换).3.重积分的应用(体积、曲面面积、重心、转动惯量等).4.含参量正常积分及其连续性、可微性、可积性,运算顺序的可交换性.含参量广义积分的一致收敛性及其判别法,含参量广义积分的连续性、可微性、可积性,运算顺序的可交换性.5.第一型曲线积分、曲面积分的概念、基本性质、计算.6.第二型曲线积分概念、性质、计算;Green公式,平面曲线积分与路径无关的条件.7.曲面的侧、第二型曲面积分的概念、性质、计算,奥高公式、Stoke公式,两类线积分、两类面积分之间的关系. 七、无穷级数 1. 数项级数级数及其敛散性,级数的和,Cauchy准则,收敛的必要条件,收敛级数基本性质;正项级数收敛的充分必要条件,比较原则、比式判别法、根式判别法以及它们的极限形式;交错级数的Leibniz判别法;一般项级数的绝对收敛、条件收敛性、Abel判别法、Dirichlet 判别法. 2. 函数项级数函数列与函数项级数的一致收敛性、Cauchy准则、一致收敛性判别法(M-判别法、Abel判别法、Dirichlet判别法)、一致收敛函数列、函数项级数的性质及其应用. 3.幂级数幂级数概念、Abel定理、收敛半径与区间,幂级数的一致收敛性,幂级数的逐项可积性、可微性及其应用,幂级数各项系数与其和函数的关系、函数的幂级数展开、Taylor级数、Maclaurin级数. 4.Fourier级数三角级数、三角函数系的正交性、2及2周期函数的Fourier级数展开、Beseel不等式、Riemanm-Lebesgue 定理、按段光滑函数的Fourier级数的收敛性定理. Ⅱ、高等代数部分一、多项式 1. 数域与一元多项式的概念 2. 多项式整除、带余除法、最大公因式、辗转相除法 3. 互素、不可约多项式、重因式与重根. 4. 多项式函数、余数定理、多项式的根及性质. 5. 代数基本定理、复系数与实系数多项式的因式分解. 6. 本原多项式、Gauss引理、有理系数多项式的因式分解、Eisenstein判别法、有理数域上多项式的有理根. 7. 多元多项式及对称多项式、韦达(Vieta)定理. 二、行列式 1. n级行列式的定义. 2. n级行列式的性质. 3. 行列式的计算. 4. 行列式按一行(列)展开. 5. 拉普拉斯(Laplace)展开定理. 6. 克拉默(Cramer)法则. 三、线性方程组 1. 高斯(Gauss)消元法、线性方程组的初等变换、线性方程组的一般解. 2. n维向量的运算与向量组. 3. 向量的线性组合、线性相关与线性无关、两个向量组的等价.4. 向量组的极大无关组、向量组的秩.5. 矩阵的行秩、列秩、秩、矩阵的秩与其子式的关系.6. 线性方程组有解判别定理、线性方程组解的结构.7. 齐次线性方程组的基础解系、解空间及其维数四、矩阵 1. 矩阵的概念、矩阵的运算(加法、数乘、乘法、转置等运算)及其运算律. 2. 矩阵乘积的行列式、矩阵乘积的秩与其因子的秩的关系. 3. 矩阵的逆、伴随矩阵、矩阵可逆的条件. 4. 分块矩阵及其运算与性质.5. 初等矩阵、初等变换、矩阵的等价标准形.6. 分块初等矩阵、分块初等变换. 五、双线性函数与二次型 1. 双线性函数、对偶空间 2. 二次型及其矩阵表示. 3. 二次型的标准形、化二次型为标准形的配方法、初等变换法、正交变换法. 4. 复数域和实数域上二次型的规范形的唯一性、惯性定理. 5. 正定、半正定、负定二次型及正定、半正定矩阵六、线性空间 1. 线性空间的定义与简单性质. 2. 维数,基与坐标. 3. 基变换与坐标变换. 4. 线性子空间. 5. 子空间的交与和、维数公式、子空间的直和. 七、线性变换 1. 线性变换的定义、线性变换的运算、线性变换的矩阵. 2. 特征值与特征向量、可对角化的线性变换. 3. 相似矩阵、相似不变量、哈密尔顿-凯莱定理. 4. 线性变换的值域与核、不变子空间. 八、若当标准形 1.矩阵. 2. 行列式因子、不变因子、初等因子、矩阵相似的条件. 3. 若当标准形.九、欧氏空间 1. 内积和欧氏空间、向量的长度、夹角与正交、度量矩阵. 2. 标准正交基、正交矩阵、施密特(Schmidt)正交化方法. 3. 欧氏空间的同构. 4. 正交变换、子空间的正交补. 5. 对称变换、实对称矩阵的标准形. 6. 主轴定理、用正交变换化实二次型或实对称矩阵为标准形. 7. 酉空间. Ⅲ、解析几何部分一、向量与坐标 1. 向量的定义、表示、向量的线性运算、向量的分解、几何运算. 2. 坐标系的概念、向量与点的坐标及向量的代数运算. 3. 向量在轴上的射影及其性质、方向余弦、向量的夹角. 4. 向量的数量积、向量积和混合积的定义、几何意义、运算性质、计算方法及应用. 5. 应用向量求解一些几何、三角问题. 二、轨迹与方程 1.曲面方程的定义:普通方程、参数方程(向量式与坐标式之间的互化)及其关系. 2.空间曲线方程的普通形式和参数方程形式及其关系. 3.建立空间曲面和曲线方程的一般方法、应用向量建立简单曲面、曲线的方程. 4.球面的标准方程和一般方程、母线平行于坐标轴的柱面方程. 三、平面与空间直线 1.平面方程、直线方程的各种形式,方程中各有关字母的意义. 2.从决定平面和直线的几何条件出发,选用适当方法建立平面、直线方程. 3.根据平面和直线的方程,判定平面与平面、直线与直线、平面与直线间的位置关系. 4. 根据平面和直线的方程及点的坐标判定有关点、平面、直线之间的位置关系、计算他们之间的距离与交角等;求两异面直线的公垂线方程. 四、二次曲面 1.柱面、锥面、旋转曲面的定义,求柱面、锥面、旋转曲面的方程. 2.椭球面、双曲面与抛物面的标准方程和主要性质,根据不同条件建立二次曲面的标准方程. 3.单叶双曲面、双曲抛物面的直纹性及求单叶双曲面、双曲抛物面的直母线的方法. 4.根据给定直线族求出它表示的直纹面方程,求动直线和动曲线的轨迹问题. 五、二次曲线的一般理论1.二次曲线的渐进方向、中心、渐近线. 2.二次曲线的切线、二次曲线的正常点与奇异点. 3.二次曲线的直径、共轭方向与共轭直径. 4.二次曲线的主轴、主方向,特征方程、特征根. 5.化简二次曲线方程并画出曲线在坐标系的位置草图. (二)中国大学生数学竞赛(非数学专业类)竞赛内容为大学本科理工科专业高等数学课程的教学内容,具体内容如下:一、函数、极限、连续1.函数的概念及表示法、简单应用问题的函数关系的建立. 2.函数的性质:有界性、单调性、周期性和奇偶性. 3.复合函数、反函数、分段函数和隐函数、基本初等函数的性质及其图形、初等函数. 4.数列极限与函数极限的定义及其性质、函数的左极限与右极限. 5.无穷小和无穷大的概念及其关系、无穷小的性质及无穷小的比较. 6.极限的四则运算、极限存在的单调有界准则和夹逼准则、两个重要极限. 7.函数的连续性(含左连续与右连续)、函数间断点的类型. 8.连续函数的性质和初等函数的连续性. 9.闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理). 二、一元函数微分学 1. 导数和微分的概念、导数的几何意义和物理意义、函数的可导性与连续性之间的关系、平面曲线的切线和法线. 2. 基本初等函数的导数、导数和微分的四则运算、一阶微分形式的不变性.3. 复合函数、反函数、隐函数以及参数方程所确定的函数的微分法.4. 高阶导数的概念、分段函数的二阶导数、某些简单函数的n阶导数.5. 微分中值定理,包括罗尔定理、拉格朗日中值定理、柯西中值定理和泰勒定理.6. 洛必达(L’Hospital)法则与求未定式极限.7. 函数的极值、函数单调性、函数图形的凹凸性、拐点及渐近线(水平、铅直和斜渐近线)、函数图形的描绘.8. 函数最大值和最小值及其简单应用.9. 弧微分、曲率、曲率半径. 三、一元函数积分学 1. 原函数和不定积分的概念. 2. 不定积分的基本性质、基本积分公式. 3. 定积分的概念和基本性质、定积分中值定理、变上限定积分确定的函数及其导数、牛顿-莱布尼茨(Newton-Leibniz)公式. 4. 不定积分和定积分的换元积分法与分部积分法. 5. 有理函数、三角函数的有理式和简单无理函数的积分. 6. 广义积分. 7. 定积分的应用:平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力及函数的平均值.四.常微分方程 1. 常微分方程的基本概念:微分方程及其解、阶、通解、初始条件和特解等. 2. 变量可分离的微分方程、齐次微分方程、一阶线性微分方程、伯努利(Bernoulli)方程、全微分方程. 3. 可用简单的变量代换求解的某些微分方程、可降阶的高阶微分方程:. 4. 线性微分方程解的性质及解的结构定理. 5. 二阶常系数齐次线性微分方程、高于二阶的某些常系数齐次线性微分方程. 6. 简单的二阶常系数非齐次线性微分方程:自由项为多项式、指数函数、正弦函数、余弦函数,以及它们的和与积7. 欧拉(Euler)方程. 8. 微分方程的简单应用五、向量代数和空间解析几何 1. 向量的概念、向量的线性运算、向量的数量积和向量积、向量的混合积. 2. 两向量垂直、平行的条件、两向量的夹角. 3. 向量的坐标表达式及其运算、单位向量、方向数与方向余弦. 4. 曲面方程和空间曲线方程的概念、平面方程、直线方程. 5. 平面与平面、平面与直线、直线与直线的夹角以及平行、垂直的条件、点到平面和点到直线的距离. 6. 球面、母线平行于坐标轴的柱面、旋转轴为坐标轴的旋转曲面的方程、常用的二次曲面方程及其图形.7. 空间曲线的参数方程和一般方程、空间曲线在坐标面上的投影曲线方程. 六、多元函数微分学 1. 多元函数的概念、二元函数的几何意义. 2. 二元函数的极限和连续的概念、有界闭区域上多元连续函数的性质. 3. 多元函数偏导数和全微分、全微分存在的必要条件和充分条件. 4. 多元复合函数、隐函数的求导法. 5. 二阶偏导数、方向导数和梯度. 6. 空间曲线的切线和法平面、曲面的切平面和法线. 7. 二元函数的二阶泰勒公式. 8. 多元函数极值和条件极值、拉格朗日乘数法、多元函数的最大值、最小值及其简单应用. 七、多元函数积分学 1. 二重积分和三重积分的概念及性质、二重积分的计算(直角坐标、极坐标)、三重积分的计算(直角坐标、柱面坐标、球面坐标). 2. 两类曲线积分的概念、性质及计算、两类曲线积分的关系. 3. 格林(Green)公式、平面曲线积分与路径无关的条件、已知二元函数全微分求原函数. 4. 两类曲面积分的概念、性质及计算、两类曲面积分的关系. 5. 高斯(Gauss)公式、斯托克斯(Stokes)公式、散度和旋度的概念及计算. 6. 重积分、曲线积分和曲面积分的应用(平面图形的面积、立体图形的体积、曲面面积、弧长、质量、质心、转动惯量、引力、功及流量等) 八、无穷级数 1. 常数项级数的收敛与发散、收敛级数的和、级数的基本性质与收敛的必要条件.2. 几何级数与p级数及其收敛性、正项级数收敛性的判别法、交错级数与莱布尼茨(Leibniz)判别法.3. 任意项级数的绝对收敛与条件收敛.4. 函数项级数的收敛域与和函数的概念.5. 幂级数及其收敛半径、收敛区间(指开区间)、收敛域与和函数.6. 幂级数在其收敛区间内的基本性质(和函数的连续性、逐项求导和逐项积分)、简单幂级数的和函数的求法.7. 初等函数的幂级数展开式.8. 函数的傅里叶(Fourier)系数与傅里叶级数、狄利克雷(Dirichlei)定理、函数在[-l,l]上的傅里叶级数、函数在[0,l]上的正弦级数和余弦级数编辑本段试卷及解答编辑本段获奖名单第一届全国大学生数学竞赛决赛获奖名单第二届全国大学生数学竞赛决赛获奖名单(非数学类)第二届全国大学生数学竞赛决赛获奖名单(数学类)编辑本段最新通知关于举办第三届全国大学生数学竞赛的通知各省、市、自治区数学会、解放军院校协作中心数学联席会:为了培养人才、服务教学、促进高等学校数学课程的改革和建设,增加大学生学习数学的兴趣,培养分析、解决问题的能力,发现和选拔数学创新人才,为青年学子提供一个展示基础知识和思维能力的舞台,经中国数学会批准,第三届全国大学生数学竞赛由上海同济大学承办。
