辽宁省大连市枫叶国际学校九年级数学上册 24.1.2 垂径定理学案(1)
人教版九年级数学24.1.2:垂径定理(教案)

在今天的教学中,我发现学生们对垂径定理的理解普遍较好,他们能够通过观察和实验操作,发现直径与弦的关系。但在定理的证明部分,有些学生显得有些吃力,需要我通过图示和步骤分解来逐步引导。这让我意识到,在今后的教学中,我应该更加注重培养学生的逻辑推理能力和几何直观。
在讲授垂径定理的应用时,我尽量用生活中的实例来说明,让学生感受到数学知识在实际生活中的重要性。这一点从学生的反馈来看,效果还是不错的,他们能够主动思考定理在生活中的应用。但我也注意到,部分学生在解决综合性较强的题目时,还是显得有些力不从心。这说明在今后的教学中,我需要进一步加强学生对知识综合运用能力的培养。
(一)导入新课(用时5分钟)
同学们,今天我们将要学习的是《垂径定理》这一章节。在开始之前,我想先问大家一个问题:“你们在画圆或者观察圆的时候,有没有注意过直径与弦的关系?”这个问题与我们将要学习的内容密切相关。通过这个问题,我希望能够引起大家的兴趣和好奇心,让我们一同探索垂径定理的奥秘。
(二)新课讲授(用时10分钟)
3.成果分享:每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上,以便全班都能看到。
(五)总结回顾(用时5分钟)
今天的学习,我们了解了垂径定理的基本概念、重要性和应用。同时,我们也通过实践活动和小组讨论加深了对垂径定理的理解。我希望大家能够掌握这些知识点,并在解决与圆相关的几何问题时灵活运用。最后,如果有任何疑问或不明白的地方,请随时向我提问。
3.重点难点解析:在讲授过程中,我会特别强调垂径定的证明,我会通过图示和步骤分解来帮助大家理解。
(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与垂径定理相关的实际问题。
2.实验操作:为了加深理解,我们将进行一个简单的实验操作。通过实际画圆和测量,学生可以直观地看到直径和弦的关系。
数学人教版九年级上册24.1.2垂直于弦的直径(第1课时)教学设计

活动 3:定理的基础应用 1、如图,AB 是⊙O 的直径,CD 为弦,CD⊥AB 于 E,则下列结论中不成立的是( )
3
2、如图,OE⊥AB 于 E,若⊙O 的半径为 10cm,OE=6cm,则 AB=
cm。
3、如图,在⊙O 中,弦 AB 的长为 8cm,圆心 O 到 AB 的距离为 3cm,求⊙O 的半径
教学内容 分析
理第 1 课的定理,为考察 重点,所以至少需要 2 课时来探究。垂径定理的推论(知二推三)和灵活运 用及更深入的应用和拓展将在第 2 课时进行研究、探讨。
知识能力目标:探索圆的对称性,进而得到垂直于弦的直径所具有的性质及证明, 能够利用垂径定理的性质求线段的长、证明线段相等、角相等等问题 过程与方法:在探索问题的过程中培养学生的动手操作能力,使学生感受圆的对称性,
反馈评价
做的不太好,需要老师评讲才会。
评价量规
1、本节课在课堂教学中采取了自主、合作、探究学习的方式,由学生动手操 作、讨论观察得结果从而激发学生学习的兴趣。 2、将问题抛出引导学生进一步思考、小组讨论发现证明垂径定理的方法,从而归纳得 出垂径定理加深对垂径定理的理解,突出了重点。 3、基本应用的 3 题简单且典型,引导学生联系弦、半径、弦心距等条件通过做辅助线构造 直角三角形解决问题,第 4 题主要利用垂径定理、勾股定理、方程的知识进行综合应用,通 过这种有梯度的训练加强了学生对垂径定理,突破了难点。
1
2
图1 图2
在完成上述的操作过程后,观察图形你能发现有相等的线段和相等的弧吗?如有, 能证明吗?(探究垂径定理) 学生活动设计:如图 2 所示,连接 OA、OB,得到等腰△OAB,即 OA=OB.因 CD ⊥AB,故△OAM 与△OBM 都是直角三角形,又 OM 为公共边,所以两个直角三角形全 等,则 AM=BM.所以 CD 是 AB 的垂直平分线,就是说圆上的任意一点 A 在圆上都有 关于直线 CD 的对称点 B,因此⊙O 关于直径 CD 对称。由于⊙O 关于直径 CD 对称,所 以 A 点和 B 点关于 CD 对称, 当圆沿着直径 CD 对折时, 点 A 与点 B 重合, AC 与 BC
2024年人教版九年级数学上册教案及教学反思第24章24.1.2 垂直于弦的直径

24.1 圆的有关性质24.1.2 垂直于弦的直径一、教学目标【知识与技能】1.通过观察实验,使学生理解圆的轴对称性.2.掌握垂径定理及其推论.理解其证明,并会用它解决有关的证明与计算问题.【过程与方法】通过探索垂径定理及其推论的过程,进一步体会和理解研究几何图形的各种方法.【情感态度与价值观】1.结合本课特点,向学生进行爱国主义教育和美育渗透.2.激发学生探究、发现数学问题的兴趣和欲望.二、课型新授课三、课时1课时。
四、教学重难点【教学重点】垂径定理及其推论,会运用垂径定理等结论解决一些有关证明,计算和作图问题.【教学难点】垂径定理及其推论.五、课前准备课件、图片、直尺等.六、教学过程(一)导入新课你知道赵州桥吗?它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37m,拱高(弧的中点到弦的距离)为7.23m,你能求出赵州桥主桥拱的半径吗?(出示课件2)(二)探索新知探究一圆的轴对称性教师问:把一个圆沿着它的任意一条直径对折,重复几次,你发现了什么?由此你能得到什么结论?(出示课件4)学生通过自己动手操作,归纳出结论:圆是轴对称图形,任何一条直径所在直线都是它的对称轴.出示课件5:教师问:圆是轴对称图形吗?如果是,它的对称轴是什么?你能找到多少条对称轴?学生答:圆是轴对称图形,任意一条直径所在直线都是圆的对称轴.思考:如何来证明圆是轴对称图形呢?出示课件6:已知:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为E.教师问:此图是轴对称图形吗?学生答:是轴对称图形.教师问:满足什么条件才能证明圆是轴对称图形呢?师生共同解答如下:(出示课件7)证明:连结OA、OB.则OA=OB.又∵CD⊥AB,∴直径CD所在的直线是AB的垂直平分线.∴对于圆上任意一点,在圆上都有关于直线CD的对称点,即⊙O关于直线CD对称.师生进一步认知:圆是轴对称图形,任何一条直径所在直线都是圆的对称轴.探究二垂径定理及其推论出示课件8:如图,AB是⊙O的一条弦, 直径CD⊥AB, 垂足为E.你能发现图中有哪些相等的线段和劣弧?为什么?学生独立思考后口答:线段:AE=BE弧:AC⌒=BC⌒,AD⌒=BD⌒学生简述理由:把圆沿着直径CD折叠时,CD两侧的两个半圆重合,点A 与点B重合,AE与BE重合,重合.教师总结归纳:(出示课件9)垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.推导格式:∵CD是直径,CD⊥AB,∴AE=BE, AC⌒=BC⌒,AD⌒=BD⌒教师强调:垂径定理是圆中一个重要的定理,三种语言要相互转化,形成整体,才能运用自如.想一想:下列图形是否具备垂径定理的条件?如果不是,请说明为什么?(出示课件10)学生独立思考后口答:1图是;2图不是,因为没有垂直;3图是;4图不是,因为CD没有过圆心.教师强调:垂径定理的几个基本图形:(出示课件11)出示课件12:如果把垂径定理(垂直于弦的直径平分弦,并且平分弦所对的两条弧)结论与题设交换一条,命题是真命题吗?①过圆心;②垂直于弦;③平分弦;④平分弦所对的优弧;⑤平分弦所对的劣弧.上述五个条件中的任何两个条件都可以推出其他三个结论吗?学生思考后教师总结:深化认知:(出示课件13)如图,①CD是直径;②CD⊥AB,垂足为E;③AE=BE;④AC⌒=BC⌒;⑤AD⌒=BD⌒.举例证明其中一种组合方法.学生思考后独立解决,并加以交流,教师加以指导,并举例.(出示课件14)如图,AB是⊙O的一条弦,作直径CD,使AE=BE.(1)CD⊥AB吗?为什么?⑵AC⌒与BC⌒相等吗?AD⌒与BD⌒相等吗?为什么?证明:⑴连接AO,BO,则AO=BO,又AE=BE,OE=OE∴△AOE≌△BOE(SSS),∴∠AEO=∠BEO=90°,∴CD⊥AB.(2)由垂径定理可得AC⌒=BC⌒,AD⌒=BD⌒教师归纳总结:(出示课件15)垂径定理的推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.思考:“不是直径”这个条件能去掉吗?如不能,请举出反例.教师强调:圆的两条直径是互相平分的.出示课件16:例1 如图,OE⊥AB于E,若⊙O的半径为10cm,OE=6cm,则AB=cm.学生思考后师生共同解答:连接OA,∵OE⊥AB,巩固练习:(出示课件17)如图,⊙O的弦AB=8cm,直径CE⊥AB于D,DC=2cm,求半径OC的长.学生自主思考后,独立解答如下:解:连接OA,∵CE⊥AB于D,,∴设OC=xcm,则OD=x-2,根据勾股定理,得x2=42+(x-2)2,∴22221068AE OA OE=-=-=cm.1184(cm)22AD AB==⨯=解得x=5,即半径OC的长为5cm.出示课件18:例2 已知:⊙O中弦AB∥CD,求证:学生思考后师生共同解答.证明:作直径MN⊥AB.∵AB∥CD,∴MN⊥CD.则(垂直于弦的直径平分弦所对的弧)教师强调:平行弦夹的弧相等.师生共同归纳总结:(出示课件19)解决有关弦的问题,经常是过圆心作弦的弦心距(垂线段),或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件.巩固练习:(出示课件20)如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,求证: 四边形ADOE是正方形.学生独立解答,一生板演.证明:∵OE⊥AC,OD⊥AB,AB⊥AC,∴∠OEA=∠EAD=∠ODA=90°.∴四边形ADOE为矩形,AE=12AC,AD=12AB.又∵AC=AB,∴AE=AD.∴四边形ADOE为正方形.出示课件21:例3 根据刚刚所学,你能利用垂径定理求出导入中赵州桥主桥拱半径的问题吗?教师引导学生分析题意,先把实际问题转化为数学问题,然后画出图形进行解答.解:如图,用AB表示主桥拱,设AB所在圆的圆心为O,半径为R.经过圆心O作弦AB的垂线OC垂足为D,与弧AB交于点C,则D是AB的中点,C 是弧AB的中点,CD就是拱高.∴AB=37m,CD=7.23m.AB=18.5m,OD=OC-CD=R-7.23.∴AD=12OA2=AD2+OD2,R2=18.52+(R-7.23)2,解得R≈27.3.即主桥拱半径约为27.3m.巩固练习:(出示课件23)如图a、b,一弓形弦长为,弓形所在的圆的半径为7cm,则弓形的高为_______.学生独立思考后解答:如图,分两种情况,弓形的高为5cm或12cm.教师归纳:1.涉及垂径定理时辅助线的添加方法(出示课件24)在圆中有关弦长a,半径r, 弦心距d(圆心到弦的距离),弓形高h的计算题时,常常通过连半径或作弦心距构造直角三角形,利用垂径定理和勾股定理求解.2.弓形中重要数量关系弦a,弦心距d,弓形高h,半径r之间有以下关系:⑴d+h=r;⑵2 222ar d⎛⎫=+ ⎪⎝⎭.(三)课堂练习(出示课件25-29)1.2.已知⊙O中,弦AB=8cm,圆心到AB的距离为3cm,则此圆的半径为.3.⊙O的直径AB=20cm, ∠BAC=30°则弦AC= .4.(分类讨论题)已知⊙O的半径为10cm,弦MN∥EF,且MN=12cm,EF=16cm,则弦MN和EF之间的距离为.5.已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点.你认为AC和BD有什么关系?为什么?6.如图,一条公路的转弯处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD,垂足为F,EF=90m.求这段弯路的半径.参考答案:1.C2.5cm3.4.14cm或2cm5.证明:过O作OE⊥AB,垂足为E,则AE=BE,CE=DE.∴AE-CE=BE-DE.即AC=BD.6.解:连接OC.设这段弯路的半径为Rm,则OF=(R-90)m.,OE CD ⊥11600300(m)22CF CD ∴==⨯=,根据勾股定理,得222,OC CF OF =+ ()22230090.R R =+- 解得R=545.∴这段弯路的半径约为545m.(四)课堂小结通过这节课的学习,你有哪些收获和体会?(五)课前预习预习下节课(24.1.3)的相关内容.七、课后作业配套练习册内容八、板书设计:九、教学反思:1.这节课的教学从利用垂径定理来解决赵州桥桥拱半径问题开始,引入课题从实验入手,得到圆的轴对称性,进而推出垂径定理及推论.教学设计中,从具体、简单、特殊到抽象、复杂、一般,层层递进,以利于提高学生的数学思维能力,同时,注意加强对学生的启发和引导,培养学生们大胆猜想,小心求证的科学研究素质.2.本课的教学方法是将垂径定理和勾股定理有机结合,将圆的问题转化为直角三角形,常作的辅助线是半径或垂直于弦的直径.。
人教版数学九年级上册24.1.2《垂径定理》教学设计2

人教版数学九年级上册24.1.2《垂径定理》教学设计2一. 教材分析《垂径定理》是人教版数学九年级上册第24章第1节的内容,本节课主要介绍圆中的垂径定理。
垂径定理是指:圆中,如果一条直线垂直于直径,那么这条直线平分这条直径,并且平分直径所对的圆周角。
教材通过生活中的实例引入垂径定理的概念,然后通过证明和应用来巩固这个定理。
二. 学情分析学生在学习本节课之前,已经掌握了圆的基本概念和性质,如圆的周长、直径、半径等。
同时,学生也掌握了平行线和相交线的性质。
但是,学生对于圆中的垂径定理可能比较难以理解和证明,因此需要通过生活中的实例和图形的直观展示,帮助学生理解和掌握这个定理。
三. 教学目标1.知识与技能:让学生理解和掌握圆中的垂径定理,能够运用垂径定理解决相关问题。
2.过程与方法:通过观察、操作、证明等过程,培养学生的几何思维和解决问题的能力。
3.情感态度与价值观:激发学生对数学的兴趣,培养学生的团队合作意识。
四. 教学重难点1.教学重点:理解和掌握垂径定理,能够运用垂径定理解决相关问题。
2.教学难点:垂径定理的证明和运用。
五. 教学方法1.情境教学法:通过生活中的实例引入垂径定理,激发学生的学习兴趣。
2.演示法:通过图形的直观展示,帮助学生理解和证明垂径定理。
3.问题驱动法:通过提出问题和解决问题,引导学生主动探索和学习。
4.小组合作学习:鼓励学生分组讨论和合作,培养学生的团队合作意识。
六. 教学准备1.教具准备:多媒体教学设备、圆规、直尺、黑板等。
2.教学素材:教材、课件、练习题等。
七. 教学过程1.导入(5分钟)通过展示生活中的实例,如自行车轮子、时钟等,引导学生观察和思考圆中的垂径定理。
让学生感受到数学与生活的紧密联系,激发学生的学习兴趣。
2.呈现(10分钟)展示垂径定理的定义和性质,通过图形的直观展示,让学生理解和掌握垂径定理。
同时,引导学生思考如何证明这个定理。
3.操练(10分钟)让学生分组讨论和合作,尝试证明垂径定理。
九年级上册数学 24.1.2 垂直于弦的直径学案

24.1.2 垂直于弦的直径学案【学习目标】1.使学生理解圆的轴对称性 .2.掌握垂径定理及其推论,学会运用垂径定理及其推论解决有关的证明、计算问题.【重点难点】重点:垂径定理、推论及它们的应用.难点:对垂径定理的探索和证明,并能应用垂径定理进行简单计算或证明.【课堂探究】一、自主探究问题一用纸剪一个圆,将圆对折、打开,再重复做几次,你发现了什么?由此你能得到什么结论?问题二1、观察、思考并回答:(1)在含有一条直径AB的圆上再增加一条直径CD,两条直径的位置关系怎样?(2)把直径AB向下平移,变成非直径的弦,弦AB是否一定被直径CD平分?(3)猜想:弦AB在怎样情况下会被直径CD平分?(4)思考:直径CD两侧相邻的两条弧是否也相等?如何证明?2、你能给上题中这条特殊的直径命名吗?这条特殊的直径有哪些性质?请用一句话概括出来.例1 看下列图形,是否能使用垂径定理?问题三命题“平分弦的直径一定垂直于这条弦,并且平分这条弦所对的两条弧.”这个命题正确吗?画图说明.如果不正确,错在哪里?你认为应该怎样修改?二、尝试运用1、如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,求⊙O 的半径.2、已知:如图1,若以O为圆心作一个⊙O的同心圆,交大圆的弦AB于C,D两点.求证:AC=BD.变式1:隐去(图1)中的大圆,连接OA,OB,设OA=OB,求证:AC=BD.变式2:再添加一个同心圆,得(图2)则AC BD(写出答案,不证明).3、请用所学知识解决求赵州桥拱半径的问题.三、补偿提高1、已知⊙O的半径为13,弦AB=24,P是弦AB上任意一点,求OP的取值范围.2、见教材第90页习题24.1第9题.四、小结与作业学生小结:1、必做题教材第83页练习1,2题2、选做题教材第90页习题24.1第10题。
人教版数学九年级上册24.1.2《垂径定理》说课稿1

人教版数学九年级上册24.1.2《垂径定理》说课稿1一. 教材分析《垂径定理》是人教版数学九年级上册第24章圆的一部分,它是圆的性质中的重要定理之一。
本节课的主要内容是引导学生探究并证明圆中垂径定理,即圆中垂直于弦的直径平分弦,并且平分弦所对的弧。
这个定理在解决圆的相关问题时具有重要作用,为学生进一步学习圆的性质和圆的方程打下基础。
二. 学情分析九年级的学生已经学习了平面几何的基本知识,对图形的性质和证明有一定的理解。
他们对圆的概念和性质有一定的了解,但可能对垂径定理的理解还不够深入。
在学习本节课时,学生需要通过观察、思考、探究、证明等过程,理解和掌握垂径定理。
三. 说教学目标1.知识与技能目标:学生能够理解垂径定理的内容,并能够运用垂径定理解决相关问题。
2.过程与方法目标:学生通过观察、思考、探究、证明等过程,培养逻辑思维能力和解决问题的能力。
3.情感态度与价值观目标:学生通过对垂径定理的学习,增强对数学的兴趣和自信心,培养坚持不懈、严谨治学的态度。
四. 说教学重难点1.教学重点:学生能够理解并掌握垂径定理的内容。
2.教学难点:学生能够通过证明过程,理解并掌握垂径定理的证明方法。
五. 说教学方法与手段1.教学方法:采用问题驱动的教学方法,引导学生观察、思考、探究、证明。
2.教学手段:利用多媒体演示和实物模型,帮助学生直观地理解垂径定理。
六. 说教学过程1.导入:通过展示一些与圆相关的实际问题,引发学生对圆的性质的思考,激发学生的学习兴趣。
2.新课引入:介绍垂径定理的概念,引导学生观察和思考垂径定理的性质。
3.探究与证明:学生分组进行探究,通过观察、实验、推理等方法,引导学生自己发现并证明垂径定理。
4.讲解与解释:教师对学生的探究结果进行讲解和解释,帮助学生理解和掌握垂径定理。
5.练习与巩固:学生进行一些相关的练习题,巩固对垂径定理的理解和运用。
6.总结与拓展:学生总结垂径定理的内容和证明方法,并进行一些拓展问题的讨论。
人教版数学九年级上册24.1.2《垂径定理》教案2

人教版数学九年级上册24.1.2《垂径定理》教案2一. 教材分析《垂径定理》是人教版数学九年级上册第24章第一节的一部分,主要介绍了圆中垂径定理的内容。
垂径定理是指:圆中,如果一条直径的两端点分别连接圆上两点,那么这条直径垂直于连接这两点的弦。
这一定理是九年级学生学习圆的基础知识,对于培养学生的空间想象能力和逻辑思维能力具有重要意义。
二. 学情分析学生在学习本节课之前,已经掌握了圆的基本概念和性质,如圆的周长、直径等。
但是,对于垂径定理的理解和运用还需要进一步引导。
此外,学生对于几何图形的观察和分析能力有待提高,因此需要通过实例讲解和动手操作来帮助学生理解和掌握垂径定理。
三. 教学目标1.让学生理解垂径定理的内容,并能够运用垂径定理解决实际问题。
2.培养学生的空间想象能力和逻辑思维能力。
3.提高学生的观察和分析能力,培养学生的合作意识和解决问题的能力。
四. 教学重难点1.重点:理解并掌握垂径定理的内容。
2.难点:如何运用垂径定理解决实际问题。
五. 教学方法1.实例讲解:通过具体的图形和实例,讲解垂径定理的内容和运用。
2.动手操作:让学生亲自动手画图和验证垂径定理,提高学生的实践能力。
3.小组讨论:学生进行小组讨论,分享学习心得和解决问题的方法。
4.问题解决:引导学生运用垂径定理解决实际问题,培养学生的解决问题的能力。
六. 教学准备1.教学PPT:制作相关的教学PPT,展示垂径定理的图形和实例。
2.教学素材:准备一些相关的几何图形和题目,用于讲解和练习。
3.教学工具:准备黑板、粉笔等教学工具。
七. 教学过程1.导入(5分钟)教师通过提问方式引导学生回顾圆的基本概念和性质,为新课的学习做好铺垫。
2.呈现(10分钟)教师通过PPT展示垂径定理的图形和实例,引导学生观察和分析,然后讲解垂径定理的内容和证明过程。
3.操练(10分钟)教师给出一些相关的题目,让学生亲自动手画图和验证垂径定理,提高学生的实践能力。
九年级数学上册 24.1.2 垂径定理学案(1)

24.1.2 垂径定理(1)教学目标:1、使学生通过观看实验明白得圆的轴对称性;2、把握垂径定理,明白得垂径定理的推证进程;重点:明白得圆的轴对称性难点:垂径定理的推证进程教学进程一、知识频道(交流与发觉)1创设情境观看赵州桥及所给数据,你能求出赵州桥拱的半径吗?这需要用到一个重要的定理:垂径定理2想一想1)若是一个图形沿着一条直线折叠,直线的两旁的部份能够相互重合,那么那个图形叫做________;这条直线叫做________.2)等腰三角形是轴对称图形吗?答:3 试一试用纸剪一个圆,沿着圆的任意一条直径对折,重复做几回,你发觉了什么?答:4 悟一悟:“圆”是不是轴对称图形?它的对称轴是什么?答:例已知:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为E.求证:AE=EB,= ,=C O A B M N 证明:连结OA ,OB ,那么OA=OB .又CD ⊥AB ,∴直线CD 是等腰△OAB 的对称轴,又是 ⊙O 的对称轴.因此沿着直径CD 折叠时,CD 双侧的两个半圆重合,A 点和B 点重合,AE 和BE 重合,、 别离和 、 重合. 因此, 从而取得圆的一条重要性质.5总一总:垂径定理垂直于弦的直径平分这条 ,而且平分弦所对的两条 。
反过来取得推论:平分弦(不是直径)的直径垂直于 ,而且平分弦所对的 。
二 、 方式频道1、以下命题错误的选项是( )A 垂直于弦的直径平分这条弦B 弦的中垂线必通过圆心C 平分弧的直径平分这条弧所对的弦D 平分弦的直径平分这条弦所对的弧二、如图,在⊙O 中(填写你以为正确的结论)①假设MN ⊥AB ,垂足为C ,MN 为直径,那么 , ,②假设AC =BC,MN 为直径,A B 不是直经,那么 , ,.三、利用垂径定明白得决问题 例1:如图7-10,已知在⊙O 中,弦AB 的长为8cm ,圆心O 到AB 的距离为3cm.求⊙O 的半径分析:要求⊙O 的半径,连结OA ,只要求出OA 的长就能够够了,因为已知条件点O 到AB 的距离为3cm ,因此作OE ⊥AB 于E ,由 定理解:连结OA ,作OE ⊥AB ,垂足为E∵OE⊥AB,∴().∵AB=8cm,∴AE=又∵OE=3cm,在Rt△AOE中,OA=因此⊙O的半径为.。
九年级数学上册24-1-2垂直于弦的直径学案(新版)新人教版

九年级数学上册24-1-2垂直于弦的直径学案(新版)新人教版1.圆的对称性.2.通过圆的轴对称性质的学习,理解垂径定理及其推论.3.能运用垂径定理及其推论进行计算和证明.重点:垂径定理及其推论.难点:探索并证明垂径定理.一、自学指导.(10分钟)自学:研读课本P81~83内容,并完成下列问题.1.圆是轴对称图形,任何一条直径所在的直线都是它的对称轴,它也是中心对称图形,对称中心为圆心.2.垂直于弦的直径平分弦,并且平分弦所对的两条弧,即一条直线如果满足:①AB经过圆心O且与圆交于A,B两点;②AB⊥CD交CD于E,那么可以推出:③CE =DE;④=;⑤=.3.平分弦(非直径)的直径垂直于弦,并且平分弦所对的两条弧.点拨精讲:(1)画图说明这里被平分的弦为什么不能是直径.(2)实际上,当一条直线满足过圆心、垂直弦、平分弦、平分弦所对的优弧、平分弦所对的劣弧,这五个条件中的任何两个,就可推出另外三个.二、自学检测:学生自主完成,小组内展示,点评,教师巡视.(6分钟)1.在⊙O中,直径为10 cm,圆心O到AB的距离为3 cm,则弦AB的长为 __8_cm__.2.在⊙O中,直径为10 cm,弦AB的长为8 cm,则圆心O到AB的距离为__3_cm__.点拨精讲:圆中已知半径、弦长、弦心距三者中的任何两个,即可求出另一个.3.⊙O的半径OA=5 cm,弦AB=8 cm,点C是AB的中点,则OC的长为__3_cm__.点拨精讲:已知弦的中点,连接圆心和中点构造垂线是常用的辅助线.4.某公园的一石拱桥是圆弧形(劣弧),其跨度为24米,拱的半径为13米,则拱高为多少米?(8米)点拨精讲:圆中已知半径、弦长、弦心距或弓形高四者中的任何两个,即可求出另一个.一、小组合作:小组讨论交流解题思路,小组活动后,小组代表展示活动成果.(6分钟)1.AB是⊙O的直径,弦CD⊥AB,E为垂足,若AE=9,BE=1,求CD的长.解:6.点拨精讲:常用辅助线:连接半径,由半径、半弦、弦心距构造直角三角形.2.⊙O的半径为5,弦AB的长为8,M是弦AB上的动点,则线段OM的长的最小值为__3__.最大值为__5__.点拨精讲:当OM与AB垂直时,OM最小(为什么),M在A(或B)处时OM最大.3.如图,线段AB与⊙O交于C,D两点,且OA=OB.求证:AC=BD.证明:作OE⊥AB于E.则CE=DE.∵OA=OB,OE⊥AB,∴AE=BE,∴AE-CE=BE-DE.即AC=BD.点拨精讲:过圆心作垂线是圆中常用辅助线.二、跟踪练习:学生独立确定解题思路,小组内交流,上台展示并讲解思路.(10分钟)1.在直径是20 cm的⊙O中,∠AOB的度数是60°,那么弦AB的弦心距是__5__cm.点拨精讲:这里利用60°角构造等边三角形,从而得出弦长.2.弓形的弦长为6 cm,弓形的高为2 cm,则这个弓形所在的圆的半径为____cm.3.如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点.求证:AC=BD.证明:过点O作OE⊥AB于点E.则AE=BE,CE=DE.∴AE-CE=BE-DE.即AC=BD.点拨精讲:过圆心作垂径.4.已知⊙O的直径是50 cm,⊙O的两条平行弦AB=40 cm,CD=48 cm,求弦AB与CD之间的距离.解:过点O作直线OE⊥AB于点E,直线OE与CD交于点F.由AB∥CD,则OF⊥CD.(1)当AB,CD在点O两侧时,如图①.连接AO,CO,则AO=CO=25 cm,AE=20 cm,CF=24 cm.由勾股定理知OE=15 cm,OF=7 cm.∴EF=OE+OF=22 (cm).即AB与CD之间距离为22 cm.(2)当AB,CD在点O同侧时,如图②,连接AO,CO.则AO=CO=25 cm,AE=20 cm,CF=24 cm.由勾股定理知OE=15 cm,OF=7 cm.∴EF=OE-OF=8 (cm).即AB与CD之间距离为8 cm.由(1)(2)知AB与CD之间的距离为22 cm或8 cm.点拨精讲:分类讨论,①AB,CD在点O两侧,②AB,CD在点O同侧.(学生总结本堂课的收获与困惑).(3分钟)1.圆是轴对称图形,任何一条直径所在直线都是它的对称轴.2.垂径定理及其推论以及它们的应用.学习至此,请使用本课时对应训练部分.(10分钟)。
人教版九年级上册数学学案:24.1.2垂径定理

word 版 初中数学1 / 1 24.1.2 垂直于弦的直径 第1课时主备人 备课组长: 年级主任: 时间:10,20学材分析:本节是这一章重要定理,是圆证明的基础 学习目标:1、理解圆的轴对称性; 2、了解拱高、弦心距等概念; 3、使学生掌握垂径定理,并能应用它解决有关弦的计算和证明问题。
学习重难点:重点:“垂径定理”及其应用 难点:垂径定理的题设和结论以及垂径定理的证明。
一、自主学习(看书81页-82页) ①在找圆心的过程中,把圆纸片折叠时,两个半圆 _______ ②刚才的实验说明圆是____________,对称轴是经过圆心的每一条_________。
⒈在找圆心的过程中,折叠的两条相交直径可以是哪样一些位置关系呢?垂直是 一种特殊情况,你能得出哪些等量关系?⒉若把AB 向下平移到任意位置,变成非直径的弦,观察一下,还有与刚才相类似的结论吗?3、垂径定理:4、推论:平分弦( )的直径垂直于弦,并且5、知识归纳: 垂径定理及推论实际是:在①经过圆心;②垂直于弦;③平分弦;④平分优弧;⑤平分劣弧;这五个条件中,已知两个条件就可以推出其它三个条件。
二、课堂反馈 1.如图1,如果AB 为⊙O 的直径,弦CD ⊥AB ,垂足为E ,那么下列结论中,错误的是( ). A .CE=DE B .弧BC=弧BD C .∠BAC=∠BAD D .AC>AD 2.如图2,⊙O 的直径为10,圆心O 到弦AB 的距离OM 的长为3,则弦AB 的长 是( ) A .4 B .6 C .7 D .8 3.如图3,已知⊙O 的半径为5mm ,弦AB=8mm ,则圆心O 到AB 的距离是( ) A .1mm B .2mmm C .3mm D .4mm 4.P 为⊙O 内一点,OP=3cm ,⊙O 半径为5cm ,则经过P 点的最短弦长为________;•最长弦长为_______.5.如图4,OE ⊥AB 、OF ⊥CD ,如果OE=OF ,那么_______(只需写一个正确的结论)6、一条排水管的截面如图所示.已知排水管的截面圆半径OB=10,截面圆圆心O 到水面的距离OC 是6,则水面宽AB 是( )A .16B .10C .8D .67、问题1:如图1,AB 是两个以O 为圆心的同心圆中大圆的直径,AB 交小圆交于C 、D 两点,求证:AC=BD问题2:把圆中直径AB 向下平移,变成非直径的弦AB ,如图2,是否仍有AC=BD 呢?、问题3:在图2中连结OC ,OD ,将小圆隐去,得图4,设OC=OD ,求证:AC=BD问题4:在图2中,连结OA 、OB ,将大圆隐去,得图5,设AO=BO ,求证:AC=BD三、反思:你收获了什么?还有哪些困惑?BA C E D OB A O M B AC ED OF 图1 图2 图3 图4 A BC D O A B C O A B C O E。
人教版九年级数学上册优秀教学案例:24.1.2垂径定理

2.解决教师提出的实际问题,如计算圆的半径、直径和弦长等。
3.交流各自的学习心得,分享解题技巧。
小组合作有助于培养学生的团队精神和协作能力,同时,通过讨论交流,学生可以相互学习,提高自己的几何素养。
(四)反思与评价
在教学活动结束后,教师组织学生进行反思与评价,主要包括以下几个方面:
3.通过几何学习,培养学生严谨、细致的学习态度,增强他们的自信心和自主学习能力。
4.培养学生之间的互助、合作精神,使他们学会倾听、尊重他人意见,形成良好的人际交往能力。
本章节教学目标旨在帮助学生在掌握垂径定理相关知识的基础上,提高几何素养,培养空间想象能力和逻辑思维能力,同时注重培养学生的情感态度与价值观,使他们在轻松愉快的氛围中学习数学,真正体会到数学的魅力。
为了巩固所学知识,教师布置以下作业:
1.完成教材中的练习题,特别是涉及到垂径定理的相关题目。
2.结合生活实例,自己设计一道运用垂径定理解决的问题,并给出解答过程。
3.写一篇学习心得,总结自己在学习垂径定理过程中的收获和困惑。
五、案例亮点
1.生活化情景导入,激发学生兴趣
本案例以校园内的圆形花坛为背景,将生活实际与几何知识紧密结合,让学生在轻松愉快的氛围中自然导入新课。这种生活化的情景导入方式,有助于激发学生的学习兴趣,使他们感受到数学与现实生活的紧密联系。
本案例注重学科知识与现实生活的紧密结合,倡导以学生为主体的教学理念,强调动手实践与思维训练的重要性,力求使学生在轻松愉快的氛围中掌握垂径定理,为后续几何知识的学习打下坚实基础。
二、教学目标
(一)知识与技能
1.理解并掌握垂径定理的概念及其在几何图形中的应用,能够准确描述定理的内容及其证明过程。
24.1.2-垂径定理(学案1)

永宁中学九年级数学(上)导学案备课组长:教研组长:教科室:课题垂径定理第 1 课时共3 课时设计人唐伟文学习目标:1、探究垂径定理及推论; 2、会用符号语言描述垂径定理。
学习重点:探究垂径定理及推论、学习过程:一、知识点回顾(知识准备):圆的对称性:二、探究新知:如图:AB是圆形纸片的一条弦,作直径CD,使CD⊥AB,垂足为E。
沿CD对折纸片,发现:①这个图形是对称图形吗②图中有哪些相等的线段和弧请说明理由。
③你能用一句话概括这些结论吗垂直于弦的直径______________________________(垂径定理)④你能用符号语言表达这个结论吗符号语言:∵CD为⊙O的直径,且CD⊥AB于E∴_____________,__________________,________________⑤由对折以上纸片我们还进一步发现:平分弦(不是直径)的直径__________于弦,并_________弦所对的两条弧(垂径定理推论)符号语言:∵CD为⊙O的直径,且AE = BE∴_____________,__________________,_______________三、教师引导:垂径定理的题设和结论关系较复杂,从以上探究我们可进一步将其并归结为:一条直线(1)过圆心;(2)垂直于弦;(3)平分弦;(4)平分弦所对的优弧;(5)平分弦所对的劣弧。
垂径定理就是满足条件(1)、(2)而推出其他结论;推论是满足条件(1)、(3)而推出其他结论。
四、归纳小结:梳理本节所学知识点五、检测与反馈:1、判断下列图形,是否能使用垂径定理(a)AB⊥CD于E (b)E是AB中点 (c)OC⊥AB于E (d)OE⊥AB于E2、如图,AB为⊙O的直径,且AB⊥CD于E。
请用符号语言描述垂径定理及其推论。
A OBCDEO BA CEODCBAEODCBAEOBA E1。
人教版九年级数学上册学案:24.1.2垂径定理(1)

课题:24.1.1垂直于弦的直径(1)【学习目标】1.掌握垂径定理及相关结论,2.运用这些结论解决一些有关证明、计算和作图问题。
重点:垂径定理、垂径定理的推论以及它们的应用。
难点:垂径定理及推论的条件和结论的区分,垂径定理的证明。
【学习过程】自主学习阅读课本第80页至 81页的部分,完成以下问题.圆是轴对称图形吗?如果是,它的对称轴是什么?你能找到多少条对称轴?探究合作 展示评价问题1:在⊙O 中,作弦AB ,并作直径CD ⊥AB 于点E 。
你发现图中有哪些相等的线段和弧(不包括半径)?说一说你的理由.相等的线段:相等的弧:由此可得垂径定理:___________________________________________________________请结合图形,写出它的推理形式.∵∴ 精讲拓展例1 已知AB 是⊙O 的一条弦,且AB=8cm ,圆心O 到AB 的距离为OE=3cm,求⊙O的半径.探究合作展示评价问题2:若将问题1中的直径CD⊥AB改为CD平分AB,你又能得到结论:______________________________________________ _O ( 图中弦AB是否可为直径?)请结合图形,写出它的推理形式. ∵∴训练巩固1.下列命题正确的是 (请填上序号)(1)平分弦的直径垂直这条弦. (2)圆有无数条对称轴.(3)直径是圆的对称轴. (4)过圆心的直线必定垂直平分弦(5)垂直于弦的直径必定平分这条弦所对的两条弧2.已知AB是⊙O的一条弦,且AB=8cm,⊙O的半径为5cm,求圆心到弦AB的距离小结提升课后作业A BO。
九年级数学上册24.1.2垂直于弦的直径教案(新版)新人教版
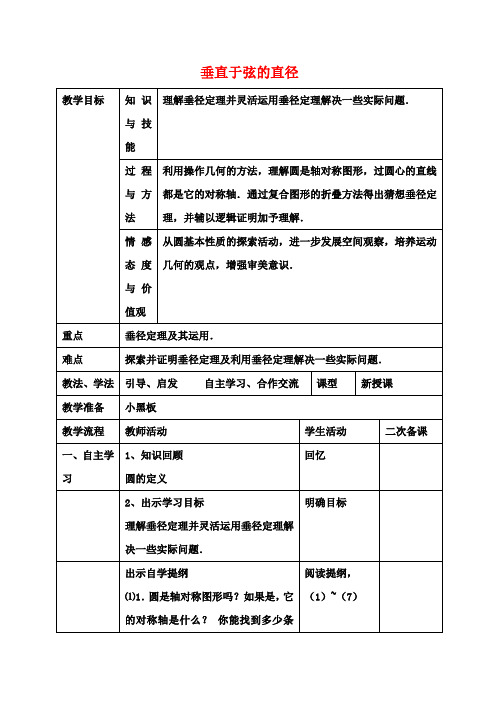
BE 构成的两个三角形全等.因此,只
要连结 OA、•OB 或 AC、BC 即可.
证明:如图,连结 OA、OB,则 OA=OB
在 Rt△OAM 和 Rt△OBM 中
OA=OA
OE=OE
∴Rt△OAE≌Rt△OBE
∴AE=BE
∴点 A 和点 B 关于 CD 对称
∵⊙O 关于直径 CD 对称
∴当圆沿着直线 CD 对折时,点 A
垂直于弦的直径
教学目标 知 识 理解垂径定理并灵活运用垂径定理解决一些实际问题.
与技
能
过 程 利用操作几何的方法,理解圆是轴对称图形,过圆心的直线
与 方 都是它的对称轴.通过复合图形的折叠方法得出猜想垂径定
法 理,并辅以逻辑证明加予理解.
情 感 从圆基本性质的探索活动,进一步发展空间观察,培养运动
态 度 几何的观点,增强审美意识.
与价
值观
重点
垂径定理及其运用.
难点
探索并证明垂径定理及利用垂径定理解决一些实际问题.
教法、学法 引导、启发 自主学习、合作交流 课型 新授课
教学准备 小黑板
教学流程 教师活动
学生活动
二次备课
一、自主学 1、知识回顾
回忆
习
圆的定义
2、出示学习目标
明确目标
理解垂径定理并灵活运用垂径定理解
决一些实际问题.
出示自学提纲
阅读提纲,
⑴1.圆是轴对称图形吗?如果是,它 (1)~(7)
的对称轴是什么?•你能找到多少条
对称轴? ⑵你是用什么方法解决上述问题的? ⑶如图,AB 是⊙O 的一条弦,作直径 CD,使 CD⊥AB,垂足为 E.
你能发现图中有哪些等量关系?说一
数学人教版九年级上册24.1.2垂径定理 导学案

新人教版义务教育教科书九年级上册24.1.2《垂直于弦的直径》导学案一、学习目标:1、理解圆的轴对称性,掌握垂径定理及其推论。
2、学会运用垂径定理及其推论解决计算,证明和作图问题。
二、预习内容(自学课本81页至83页)复习:1、什么叫做轴对称图形?把一个平面图形沿一条直线______,直线两旁的部分能够互相_________,这个图形就叫做轴对称图形。
圆是轴对称图形吗?对称轴是什么?2、什么叫等弧?在同圆或等圆中,能够互相______的弧叫做等弧。
三、探究学习活动一:自主探究把一个圆沿着它的任意一条直径对折,重复几次,你发现了什么?由此你能得到什么结论?结论:圆是___________图形,_________________________是它的对称轴.活动二:小组合作交流(要求:小组每个成员积极发言,记录员填写,每组派一名同学汇报)1、做一做:在⊙O上作的一条弦AB,做直径CD,使CD⊥AB,垂足为E.(1)这个图形是轴对称图形吗?如果是,它的对称轴是什么?答:_______________________________________________________(2)你能发现图中有那些相等的线段和弧?为什么?答:相等的线段:______=_____相等的弧:______=______________=________证明:(方法1)如图,连接OA、OB ,则OA=OB在Rt△OAE和Rt△OBE中,(方法2):连接OA、OB ,则OA=___∴△OAB是______三角形∴Rt△OAE≌Rt△OBE()又AB CD∴AE= ∴AE =____(等腰三角形“三线合一”) ∴点和点关于CD对称∵⊙O关于CD对称∴当圆沿着直线CD对折时,点A与点B重合,弧AC与BC重合,AD与CD重合.∴,,2、进一步,我们还可以得到垂径定理推论:四、巩固测评1、2、3题(看课件直接说出答案)4、如图,在⊙O 中,弦AB 的长为8cm ,圆心O 到AB 的距离为3cm ,求⊙O 的半径.5、如图,CD 是⊙O 的直径,弦AB ⊥CD 于E ,CE=1,AB=10,求半径的长6、赵州桥的桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4m ,拱高(弧的中点到弦的距离)为7.2m ,你能求出赵州桥的主桥拱的半径吗?五、学习心得 _ _____________________________________________________________________________. · OAB EC DO。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
24.1.2垂径定理(1)
【学习目标】通过探索、归纳、验证得出垂直于弦的直径的性质和推论,并能初步应用它解
决一些简单的计算、证明和作图问题。
【学习重点】垂直于弦的直径的性质、推论及其应用。
【学习难点】垂直于弦的直径的性质、推论及其应用。
【学习内容】教材第80~81页
【活动一】 (独立思考,认真完成,2分钟)
1.圆是轴对称图形,对称轴是____________________________________
【活动二】 (合作交流,8分钟)
2.如图1,AB 是⊙O 的一条弦,作直径C D ,使CD ⊥AB 于E.
可以得出:相等的线段有:_____________________________
相等的弧有: _______________________________ 请说明理由:
C
图1
归纳垂直定理: 垂直于弦的直径______________,并且平分__________
_________. 符号语言叙述:∵直径CD ⊥弦AB
∴_________________________________________
4.如图3,在⊙O 中,直径为10cm ,弦CD=6,AB ⊥CD 于点,求BE 的长.
B
A 图3
5.如图4,在⊙O 中,AB 、AC 为互相垂直且相等的两条弦,OD ⊥AB 于D ,OE ⊥AC 于E 。
求
证:四边形ADOE 是正方形。
图4
【活动四】(交流探究,10分钟)
6.已知CD 是直径,且平分弦AB ,如图5,能否得到使CD ⊥AB 于点M ,且平分弧ACB 及弧AB?
图5
归纳垂径定理推论:
平分弦(不是直径)的直径____________,并且平分________________.
符号语言叙述:∵CD 是直径,且平分弦AB ,AB 不是直径________
∴________________________________________
附加:7.⊙O 的直径为10,弦AB 的长为8,P 是弦AB 上的一个动点,则OP 长的取值范围为__________________
【课后反思】____________ ____________________________
垂直于弦的直径(1) 课堂检测
完成时间:8分钟
1.圆既是____________对称图形,又是___________对称图形;
它的对称中心是
____________,对称轴是________________________,圆有_______条对称轴。
2.下列判断中不正确的是:()
A.平分弦的直径垂直于弦
B.垂直于弦的直径也必平分弦
C.弦的垂直平分线必平分弦所对的两条弧
D.平分一条弧的直径必平分这条弧所对的弦
3.如图,AB是⊙O的弦,OC⊥AB于点P,若AB=8cm,OP=3cm,求⊙O的半径。
C。
