雨花统计

雨花统计第十九期（总第74期）长沙市雨花区统计局二○○七年七月十日积极引导健康发展——雨花区房地产业市场调查报告之一伴随着城市化发展进程加快，户籍制度改革、城市扩容等城市人口增长方式的改变、住房制度的改革和城市经济实力的增强，雨花区房地产市场快速发育，并逐步成长为国民经济的重要支柱。

针对房地产结构性过热，中央和地方先后出台了一系列严厉调控房地产市场的措施，从紧缩信贷到提高房贷利率，从土地市场整顿到户型比例控制，从自有开发资金门槛设定到税收政策的完善，房地产市场在抑制中进一步规范和发展。

为贯彻国家宏观调控政策，积极引导全区房地产业持续健康发展，进一步加强对房地产市场管理，发挥房地产在经济社会发展中的积极作用，区统计局根据区委、区政府精神，历时两个月，对全区房地产进行了一次全面调查。

现将调查情况报告如下：一、房地产业对经济社会发展作用重大房地产业逐步成长为区域经济的支柱产业，在全区经济社会发展中起着举足轻重的作用。

1、房地产业是投资的生力军。

房地产业是投资增长的主动力。

从全区房地产投资额看，2004年实现房地产投资33.64亿元、2005年39.07亿元、2006年55.55亿元，2007年1-6月实现投资47.29亿元。

房地产投资已成为全区投资的重要组成部分，且年均增长高于全社会固定资产的增长速度。

特别是近两年，无论是项目数量、项目规模、项目品质还是投资总规模都有明显增大或提高。

从房地产投资占全社会固定资产投资的比重看，2004年占35%，2005年占36%，2006年上升到40%，2007年1-6月更是达到了60%。

房地产业投资的比重快速增大，一方面是全区基础设施和生活环境不断改善，吸引了大批房地产投资商和购房者，旺盛需求刺激投资欲望，促使房地产投资额增加；另一方面是随着全区大规模基础设施率先完成，我区投资方向逐渐向工业、服务业等产业项目转移，产业项目建设年逐步启动和推进，但较多大型产业项目尚未完全启动，导致除房地产外的其他投资偏少，显现出房地产投资占比的“过快”增长。

2、房地产业是区级财税的重要来源。

房地产企业应纳税种涵盖了营业税（销售不动产）、企业所得税、土地增值税、土地使用税、印花税、契税、个人所得税、房产税等较多税目。

房地产业具有投资周期短、见效快、税额较大等特点，在现有的财税体制下表现为区级税收为主，因此房地产业的迅速发展为我区财税快速增长奠定了坚实基础。

2006年全区房地产开发企业实际上缴营业税（销售不动产）3.3亿元，共计缴纳各种税收3.56亿元。

若考虑房地产承建企业所缴纳的建安营业等税，房地产行业对全部区级财税的贡献在50%以上。

2007年1-5月我区完成房地产投资额30.72亿元，同比增长131.09%。

实现房地产税收32523万元，其中：销售不动产（营业税）22314万元，区级销售不动产营业税20933万元。

今年税务机关加大了对房地产企业税收征管力度，表现最明显的是强力征缴土地增值税和预征企业所得税。

2007年1-5月已入库土地增值税1019万，2006年全年仅征20万元；今年1-5月入库房地产企业所得税6137万元，比去年全年的505万元多出5632万元。

这为全区今年税收任务的完成提供了有力保障。

根据此次调查，乡（镇）、街道预计今年可实现房地产业税收6亿左右。

2007年1-5月房产、建安税收明细表3、房地产业对经济社会发展起着较大作用。

近三年来全区房地产业增加值占GDP的比重一直稳定在3.5%左右（不包含商品房建筑形成的增加值），在雨花区GDP基数较大基础上房地产业占比仍达到了全市平均水平，说明雨花区的房地产业目前优于长沙各兄弟区县的发展，但与全国平均水平及房地产业发展成熟的发达地区比尚有一定差距。

全国2004年房地产增加值占GDP比重即达到4.5%，上海、北京2005年的占比分别为7.3%、6.2%，说明房地产业在长沙的发展仍有较大空间。

房地产业健康发展，不仅有力拉动了经济增长，更有效推动了城市化进程，提高了城市品味和人民生活水平。

2006年全区城镇居民人均住房建筑面积达28.88平方米，已基本达到人均30平方米的全面小康标准。

从雨花区城市开发进程看，是基础设施率先完善，房地产企业积极跟进有效凝聚人气后，带动区域商业、服务业发展。

沃尔玛、购宝乐（原华银旺和）等大型超市选址落户就充分考虑了周边众多商业楼盘所凝聚的人气和购买力。

房地产楼盘品质不断提升，基础设施改善和楼盘开发形成相互促进的良性循环，较好地改善、美化了区域环境，同升湖山庄、奥林匹克花园等知名楼盘已成为区域名片,有效提高了城市品味。

二、房地产业运行特点1、房地产开发度居市内五区前列注：“四县”为之和。

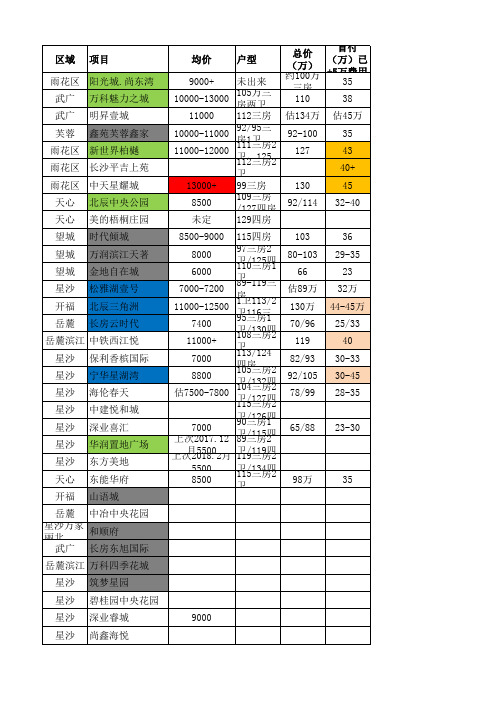
从上表看,全区2006年房地产开发的投资额居市内五区第二，销售面积和房地产项目数均为市内五区之首。

雨花区以完善的市政设施和便利的交通网络，成为了房地产开发的热土。

特别是去年下半年以来,由于新开工项目较多,雨花区房地产投资更是呈现快速增长之势。

据产业办统计，截止6月底登记在册的产业项目达189个，其中房地产项目120个，占总项目数的63%，计划投资额更是占全部项目投资额的70%。

新签约项目中房地产项目仍多于工业和服务业。

另据长沙房地产信息中心公布的数据，2006年我区房地产销售额最大，当年批准预售面积也较多，尤其是第二、三季度。

由于去年推向市场的商品房较多，今年上半年雨花区商品房销售继续一路走高。

2、商品房地域分布向外扩散全区房地产的开发目前多集中在韶山路、万家丽路和芙蓉路两厢，并逐渐向城郊结合区域扩散。

内城区以工业企业“退二进三”、外城区以农民拆迁让地为主。

这种以全区道路主干道为轴线，向四周辐射的房地产项目分布，为全区老城区的改造和新城区的发展，提供了广阔的平台。

从房地产项目分布来看，外街、乡（镇）因拥有较多的土地资源及良好的生态环境吸引了众多的房地产商。

注：上图中统计数据为已开工并报送了统计报表的房地产项目，左纵轴为项目数，右纵轴为投资额。

3、价格不断上扬近两年来，长沙房地产销售价格呈现快速上扬趋势。

今年1-5月长沙房屋销售价格同比上涨6%，土地交易价格同比上涨34%，房屋租赁价格同比上涨2.4%。

近两年房价上扬主要是三方面的因素所至：一是低位补涨。

长沙市商品房价格在全国37个省会及重点城市中一直处于较低水平，与中部省会城市相比，2005年我市价格都处于最低水平，这与我市人民生活水平并不相称，价格洼地积蓄了上涨空间和动能。

二是楼盘品质提高。

随着浙江、广东、福建等外地品牌企业纷纷进驻，不仅带来了新的设计理念和家居文化，也快速提升了楼盘品质和商品房价格。

如“倾力铸造城市生活全新标杆”、有“中国创新示范楼盘”之称的融科三万英尺，其销售价格在4000元/㎡以上，且销售一路看好，2006年四季度、2007年一季度禅联长沙房地产销售金额十强排行榜冠军，今年一季度销售面积、销售套数分别名列十强榜的第三、第五位。

楼盘品质提升、别墅等高档住宅增加、小户型精装修等因素推动了房价的上涨。

三是开发成本增加。

随着土地成本、节能环保要求带来的建筑成本、人工成本等上涨，加之报建费、配套费、相关税收增加，也一定程度上助推了房价上涨。

从本次调查看，雨花区在建的房地产项目除龙吉湾等个别经济适用房项目外，对外宣传报价基本在3000元/㎡以上，市中心、高品质楼盘报价在4000元/㎡左右，别墅项目报价为5000-6000元/㎡。

预计房地产价格近期内仍将稳中有升。

4、商品房结构以住宅为主左图显示：全区商品房以住宅为主，而支撑后续财源的办公楼（写字楼）和商业营业用房则相对偏少。

虽然大量的住宅可以为全区聚集人流、物流和资金流，但也增添了教育、治安、计生等许多社会问题和社会成本。

住宅是一种典型的快餐经济，投资回报快、一次性收入大，但后期支出多。

所以通过合理规划和引导，利用住宅开发带来的资源，大力发展办公楼（写字楼）和商业营业用房，为我区经济持续增长增添新的动力源。

从市场供应的住宅户型结构看，120-144㎡的户型在雨花区所占的比重最大，占到调查总量的28%。

据长沙房地产信息中心公布的数据，120-144㎡的户型也是最畅销的，今年一季度销售占比为29.78%。

90-120㎡、90㎡以下供应占比仅随其后。

全区户型结构与全市比较，小户型占比略小，这与雨花区房地产地域分布有关。

5、资金状况良好今年以来央行连续两次加息、五次提高存款准备金率，中央政府控制过度投资和抑制过度流动性的决心可见一斑。

作为资金密集性的房地产企业在国家的宏观调控中也受到一定影响。

本次调查问卷的82家房地产企业，有33 家反映资金困难。

从目前全区房地产企业资金来源结构看，近三成来源于房地产企业向银行的贷款，近四成来源于购房者Array交纳的定金、预收款和银行按揭购房款，企业自筹资金仅占三成左右。

三、走势分析雨花区由于区位、自然环境、基础设施等比较优势的共同作用，房地产开发一直走在兄弟区县前列。

未来两年预计全区房地产业在各级政府的积极引导下，将继续积极应对国家宏观调控政策实现持续、健康发展，为全区经济转型作出积极贡献。

1、区位优势明显。

随着“中部崛起”战略深入推进及泛珠区域合作、协同发展，长沙的城市地位日益提升。

作为长株潭一体化的桥头堡，南城越来越被商人和消费者青睐。

据《2007长沙楼市万人全景调查报告》显示，最受消费者欢迎的区域是省政府周边，其次是五一广场、湘江大道沿线、市政府周边，我区东塘广场名列第五，新火车站板块名列第七。

雨花区良好的区位优势、完善的配套设施及优美的生态环境，仍将吸引众多的消费者，凝聚实力雄厚的房地产开发商，继续保持房地产开发的热度。

2、房地产储备项目较多。

据产业办统计，全区截止6月底登记在册在谈的产业项目达251个，在册的产业项目189个，其中房地产项目120个，计划总投资过5亿元的项目在25个以上。

区统计局房地产调查结果显示，本次调查的94个项目中，有22个尚未完全启动，包括新世界、泰禹二期、锦锈世纪、中城丽景香山二期、现代华都等，以上项目的建筑面积在200万平方米以上，还不包括完全未启动没有列入本次调查范围的项目，如华盛世纪新城、恒隆国际花园等。

94个项目中，预计2007年将完工的项目30个，建筑面积近200万平方米；预计2008年完工的项目31个，包括华雅生态园、丽星景园、山水城市风景、美洲故事、上河国际等，建筑面积近300万平方米；预计在2009年及以后完工的项目20个左右，包括新世界、锦锈世纪、茂华、奥林匹克二期、鄱阳小区、国中星城等，其建筑面积在300万平方米以上，还有近10个项目在2007年底基本完成投资。

3、保有一定的土地储备。

本次调查的94个项目中，本年完成土地开发面积近70万平方米（约1000亩），正在开发的土地面积50万平方米（约750亩），待开发土地面积达190万平方米（约2800亩）（注：已完成七通一平、开始建筑安装工程投资的不计土地开发面积，只计算投资额，故未列入储备）。