北京各区2018高三一模立体几何汇编

合集下载

2018-2022五年全国高考数学立体几何真题分类汇编(试卷版)

2018-2022五年全国各省份高考数学真题分类汇编专题21立体几何解答题一、解答题1．(2022高考北京卷·第17题)如图，在三棱柱111ABC A B C -中，侧面11BCC B 为正方形，平面11BCC B ⊥平面11ABB A ，2AB BC ==，M ，N 分别为11A B ，AC 的中点．(1)求证：MN ∥平面11BCC B ；(2)再从条件①、条件②这两个条件中选择一个作为已知，求直线AB 与平面BMN 所成角的正弦值．条件①：AB MN ⊥；条件②：BM MN =．注：如果选择条件①和条件②分别解答，按第一个解答计分．2．(2022年高考全国甲卷数学(理)·第18题)在四棱锥P ABCD -中，PD ⊥底面,,1,2,ABCD CD AB AD DC CB AB DP =====∥．(1)证明：BD PA ⊥；(2)求PD 与平面PAB 所成的角的正弦值．3．(2022年浙江省高考数学试题·第19题)如图，已知ABCD 和CDEF 都是直角梯形，//AB DC ，//DC EF ，5AB =，3DC =，1EF =，60BAD CDE ∠=∠=︒，二面角F DC B --的平面角为60︒．设M ，N 分别为,AE BC 的中点．(1)证明：FN AD ⊥；(2)求直线BM 与平面ADE 所成角的正弦值．4．(2022新高考全国II 卷·第20题)如图，PO 是三棱锥P ABC -的高，PA PB =，AB AC ⊥，E 是PB 的中点．(1)证明：//OE 平面PAC ；(2)若30ABO CBO ∠=∠=︒，3PO =，5PA =，求二面角C AE B --的正弦值．5．(2022新高考全国I 卷·第19题)如图，直三棱柱111ABC A B C -的体积为4，1A BC 的面积为．(1)求A 到平面1A BC 的距离；(2)设D 为1A C 的中点，1AA AB =，平面1A BC ⊥平面11ABB A ，求二面角A BD C --的正弦值．6．(2022年高考全国乙卷数学(理)·第18题)如图，四面体ABCD 中，,,AD CD AD CD ADB BDC ⊥=∠=∠，E 为AC 的中点．(1)证明：平面BED ⊥平面ACD ；(2)设2,60AB BD ACB ==∠=︒，点F 在BD 上，当AFC △的面积最小时，求CF 与平面ABD 所成的角的正弦值．-中，底面ABCD是平行四边7．(2021年高考浙江卷·第19题)如图，在四棱锥P ABCDBC PC的中点，形，120,1,4,∠=︒===M，N分别为,ABC AB BC PA⊥⊥．PD DC PM MD,(1)证明：AB PM⊥；(2)求直线AN与平面PDM所成角的正弦值．-中，底面ABCD是正方形，若8．(2021年新高考全国Ⅱ卷·第19题)在四棱锥Q ABCD===．AD QD QA QC2,3(1)证明：平面QAD⊥平面ABCD；--的平面角的余弦值．(2)求二面角B QD A9．(2021年新高考Ⅰ卷·第20题)如图，在三棱锥A BCD -中，平面ABD ⊥平面BCD ，AB AD =，O 为BD 的中点．(1)证明：OA CD ⊥；(2)若OCD 是边长为1的等边三角形，点E 在棱AD 上，2DE EA =，且二面角E BC D --的大小为45︒，求三棱锥A BCD -的体积．10．(2021年高考全国乙卷理科·第18题)如图，四棱锥P ABCD -的底面是矩形，PD ⊥底面ABCD ，1PD DC ==，M 为BC 的中点，且PB AM ⊥．(1)求BC ；(2)求二面角A PM B --的正弦值．11．(2021年高考全国甲卷理科·第19题)已知直三棱柱111ABC A B C -中，侧面11AA B B 为正方形，2AB BC ==，E ，F 分别为AC 和1CC 的中点，D 为棱11A B 上的点．11BF A B ⊥(1)证明：BF DE ⊥；(2)当1B D 为何值时，面11BB C C 与面DFE 所成的二面角的正弦值最小?12．(2021高考北京·第17题)如图：在正方体1111ABCD A B C D -中，E 为11A D 中点，11B C 与平面CDE 交于点F．(1)求证：F 为11B C 的中点；(2)点M 是棱11A B 上一点，且二面角M FC E --的余弦值为53，求111A M A B 的值．13．(2020年高考课标Ⅰ卷理科·第18题)如图，D为圆锥的顶点，O是圆锥底面的圆心，=．ABC是底面的内接正三角形，P为DO上一点，AE为底面直径，AE ADPO=．(1)证明：PA⊥平面PBC；--的余弦值．(2)求二面角B PC E14．(2020年高考课标Ⅱ卷理科·第20题)如图，已知三棱柱ABC-A1B1C1的底面是正三角形，侧面BB1C1C是矩形，M，N分别为BC，B1C1的中点，P为AM上一点，过B1C1和P的平面交AB于E，交AC于F．(1)证明：AA1∥MN，且平面A1AMN⊥EB1C1F；(2)设O为△A1B1C1的中心，若AO∥平面EB1C1F，且AO=AB，求直线B1E与平面A1AMN所成角的正弦值．15．(2020年高考课标Ⅲ卷理科·第19题)如图，在长方体1111ABCD A B C D -中，点,E F分别在棱11,DD BB 上，且12DE ED =，12BF FB =．(1)证明：点1C 在平面AEF 内；(2)若2AB =，1AD =，13AA =，求二面角1A EF A --的正弦值．16．(2020年新高考全国Ⅰ卷(山东)·第20题)如图，四棱锥P -ABCD 的底面为正方形，PD⊥底面ABCD ．设平面PAD 与平面PBC 的交线为l ．(1)证明：l ⊥平面PDC ；(2)已知PD =AD =1，Q 为l 上的点，求PB 与平面QCD 所成角的正弦值的最大值．17．(2020年新高考全国卷Ⅱ数学(海南)·第20题)如图，四棱锥P-ABCD的底面为正方形，PD⊥底面ABCD．设平面PAD与平面PBC的交线为l．(1)证明：l⊥平面PDC；(2)已知PD=AD=1，Q为l上的点，QB，求PB与平面QCD所成角的正弦值．18．(2020年浙江省高考数学试卷·第19题)如图，三棱台DEF—ABC中，面ADFC⊥面ABC，∠ACB=∠ACD=45°，DC=2BC．(I)证明：EF⊥DB；(II)求DF与面DBC所成角的正弦值．19．(2020天津高考·第17题)如图，在三棱柱111ABC A B C -中，1CC ⊥平面,,2ABC AC BC AC BC ⊥==，13CC =，点,D E 分别在棱1AA 和棱1CC 上，且12,AD CE M ==为棱11A B 的中点．(Ⅰ)求证：11C M B D ⊥；(Ⅱ)求二面角1B B E D --的正弦值；(Ⅲ)求直线AB 与平面1DB E 所成角的正弦值．20．(2020江苏高考·第24题)在三棱锥A BCD -中，已知CB CD ==,2BD =，O 为BD的中点，AO ⊥平面BCD ，2AO =，E 为AC 的中点．(1)求直线AB 与DE 所成角的余弦值；(2)若点F 在BC 上，满足14BF BC =，设二面角F DE C --的大小为θ，求sin θ的值．21．(2020江苏高考·第15题)在三棱柱111ABC A B C -中，AB AC ⊥，1B C ⊥平面ABC ，,E F分别是1,AC B C 的中点．(1)求证：EF 平面11AB C ；(2)求证：平面1AB C ⊥平面1ABB ．22．(2020北京高考·第16题)如图，在正方体1111ABCD A B C D -中，E 为1BB 的中点．(Ⅰ)求证：1//BC 平面1AD E ；(Ⅱ)求直线1AA 与平面1AD E 所成角的正弦值．23．(2019年高考浙江·第19题)如图，已知三棱柱111ABC A B C -，平面11A ACC ⊥平面ABC ，90ABC ∠=︒，30BAC ∠=︒，11A A A C AC ==，E ，F 分别是AC ，11A B 的中点．(Ⅰ)证明：EF BC ⊥；(Ⅱ)求直线EF 与平面1A BC 所成角的余弦值．24．(2019年高考天津理·第17题)如图，AE ⊥平面ABCD ，//,//CF AE AD BC ，,1,2AD AB AB AD AE BC ⊥====．(Ⅰ)求证：BF ∥平面ADE ；(Ⅱ)求直线CE 与平面BDE 所成角的正弦值；(Ⅲ)若二面角E BD F --的余弦值为13，求线段CF 的长．25．(2019年高考上海·第17题)如图，在长方体1111ABCD A BC D -中，M 为1BB 上一点，已知2BM =，4AD =，3CD =，15AA =.(1)求直线1AC 与平面ABCD 的夹角；(2)求点A 到平面1AMC 的距离.26．(2019年高考全国Ⅲ理·第19题)图1是由矩形ADEB ，Rt △ABC 和菱形BFGC 组成的一个平面图形，其中AB =1，BE =BF =2，∠FBC =60°，将其沿AB ，BC 折起使得BE 与BF 重合，连结DG ，如图2．(1)证明：图2中的A ，C ，G ，D 四点共面，且平面ABC ⊥平面BCGE ；(2)求图2中的二面角B−CG−A 的大小．27．(2019年高考全国Ⅱ理·第17题)如图，长方体1111ABCD A B C D -的底面ABCD 是正方形，点E 在棱1AA 上，1BE EC ⊥．()1证明：BE ⊥平面11EB C ；()2若1AE A E =，求二面角1B EC C --的正弦值．28．(2019年高考全国Ⅰ理·第18题)如图，直四棱柱1111ABCD A B C D -的底面是菱形，14,2,60,,,AA AB BAD E M N ==∠=︒分别是BC ，1BB ，1A D 的中点．(1)证明：//MN 平面1C DE ；(2)求二面角1A MA N --的正弦值．29．(2019年高考江苏·第16题)如图，在直三棱柱111ABC A B C -中，,D E 分别为BC ，AC 的中点，AB BC =．求证：(1)11A B ∥平面1DEC ；(2)1BE C E ⊥．30．(2019年高考北京理·第16题)如图，在四棱锥P –ABCD 中，PA ⊥平面ABCD ，AD ⊥CD ，AD ∥BC ，PA =AD =CD =2，BC =3．E 为PD 的中点，点F 在PC 上，且13PF PC =．(Ⅰ)求证：CD ⊥平面PAD ；(Ⅱ)求二面角F–AE–P 的余弦值；(Ⅲ)设点G 在PB 上，且23PG PB =．判断直线AG 是否在平面AEF 内，说明理由．31．(2018年高考数学江苏卷·第25题)(本小题满分10分)如图，在正三棱柱ABC -A 1B 1C 1中，AB =AA 1=2，点P ，Q 分别为A 1B 1，BC 的中点．(1)求异面直线BP 与AC 1所成角的余弦值；(2)求直线CC 1与平面AQC 1所成角的正弦值．32．(2018年高考数学江苏卷·第15题)(本小题满分14分)在平行六面体1111ABCD A B C D -中，1111,AA AB AB B C =⊥．求证：(1)11AB A B C 平面∥；(2)111ABB A A BC ⊥平面平面．33．(2018年高考数学浙江卷·第19题)(本题满分15分)如图，已知多面体111ABCA B C ，111,,A A B B C C 均垂直于平面ABC ，120ABC ∠=︒，14A A =，11C C =，12AB BC B B ===．(1)证明：1AB ⊥平面111A B C ；(2)求直线1AC 与平面1ABB 所成角的正弦值．34．(2018年高考数学上海·第17题)(本题满分14分，第1小题满分6分，第2小题满分8分)已知圆锥的顶点为P ，底面圆心为O ，半径为2，(1)设圆锥的母线长为4，求圆锥的体积；(2)设4PO =，OA OB 、是底面半径，且90AOB ∠=︒，M 为线段AB 的中点，如图，求异面直线PM 与OB 所成的角的大小．35．(2018年高考数学天津(理)·第17题)(本小题满分13分)如图，//AD BC 且2AD BC =，AD CD ⊥，//EG AD 且EG AD =，//CD FG ，且2CD FG =，DG ⊥平面ABCD ，2DA DC DG ===．(1)若M 为CF 的中点，N 为EG 的中点，求证：//MN 平面CDE ；(2)求二面角E BC F --的正弦值；(3)若点P 在线段DG 上，且直线BP 与平面ADGE 所成的角为60︒，求线段DP 的长．36．(2018年高考数学课标Ⅲ卷(理)·第19题)(12分)如图，边长为2的正方形ABCD 所在平面与半圆弧CD 所在的平面垂直，M 是弧CD 上异于,C D 的点．(1)证明：平面AMD ⊥平面BMC ；(2)当三棱锥M ABC -体积最大时，求面MAB 与面MCD 所成二面角的正弦值．37．(2018年高考数学课标Ⅱ卷(理)·第20题)(12分)如图，在三棱锥P ABC -中，AB BC ==，4PA PB PC AC ====，O 为AC 的中点．(1)证明：PO ⊥平面ABC ；(2)若点M 在棱BC 上，且二面角M PA C --为30︒，求PC 与平面PAM 所成角的正弦值．PAB M CO 38．(2018年高考数学课标卷Ⅰ(理)·第18题)(12分)如图，四边形ABCD 为正方形，,E F 分别为,AD BC 的中点，以DF 为折痕把DCF ∆折起，使点C 到达点P 的位置，且PF BF ⊥．(1)证明:平面PEF ⊥平面ABFD ；(2)求DP 与平面ABFD 所成角的正弦值．39．(2018年高考数学北京(理)·第16题)(本小题14分)如图，在三棱柱111ABC A B C -中，1CC ⊥平面ABC ,,,,D E F G 分别为1111,,,AA AC A C BB 的中点，AB BC ==，12AC AA ==．(Ⅰ)求证：AC ⊥平面BEF ；(Ⅱ)求二面角1B CD C --的余弦值；(Ⅲ)证明：直线FG 与平面BCD 相交．。

北京市丰台区2018年高三年级一模数学试题(理)(精编含解析)

三、解答题共 6 小题，共 80 分。解答应写出文字说明，演算步骤或证明过程。
15. 己知函数 (Ⅰ)求 f(x)的定义域及最小正周期；
(Ⅱ)求 f(x)的单调递减区间．
【答案】(1)
, ;(2) 的单调递减区间为
【解析】试题分析：（Ⅰ）根据三角恒等变换的公式，化简期；（Ⅱ）根据三角函数的图象与性质，即可得到函数的单调区间．试题解析：
点睛：本题考查了平面向量的线性运算法则和向量的数量积的运算，对于平面向量的计算问题，往往有两种形式，一是利用数量积的定义式，二是利用数量积的坐标运算公式，涉及几何图形的问题，先建立适当的平面直角坐标系，可起到化繁为简的妙用，利用向量夹角公式、模公式及向量垂直的充要条件，可将有关角度问题、线段长问题及垂直问题转化为向量的数量积来解决．
证：以为直径的圆被直线截得的弦长是定值．
【答案】（Ⅰ）
．（Ⅱ）见解析．
【解析】试题分析：（Ⅰ）依题意，得到，利用定义得到
（Ⅱ）设
，
，根据直线方程，求解
即可得到弦长为定值．
的坐标，可得
试题解析：
，即可求解椭圆的标准方程；
，利用
，求得的值，
（Ⅰ）依题意，椭圆的另一个焦点为
，且．
因为所以，
C. x <1,
D. x ≥1,
【答案】C
【解析】根据全称命题与存在性命题之间的关系，
可知命题
的否定为
，故选 C．
3. 设不等式组 A. 原点 O 在内
表示的平面区域为 .则
B. 的面积是 1
C. 内的点到 y 轴的距离有最大值 D. 若点 P(x0,y0) ，则 x0+y0≠0 【答案】A

2018全国高考立体几何(完整答案)

2018全国高考立体几何（完整答案）一．解答题（共40小题）1．已知圆锥的顶点为P，底面圆心为O，半径为2．（1）设圆锥的母线长为4，求圆锥的体积；（2）设PO=4，OA、OB是底面半径，且∠AOB=90°，M为线段AB的中点，如图．求异面直线PM与OB所成的角的大小．2．如图，矩形ABCD所在平面与半圆弧所在平面垂直，M是上异于C，D 的点．（1）证明：平面AMD⊥平面BMC；（2）在线段AM上是否存在点P，使得MC∥平面PBD？说明理由．3．在平行六面体ABCD﹣A1B1C1D1中，AA1=AB，AB1⊥B1C1．求证：（1）AB∥平面A1B1C；（2）平面ABB1A1⊥平面A1BC．4．如图，在四棱锥P﹣ABCD中，底面ABCD为矩形，平面PAD⊥平面ABCD，PA ⊥PD，PA=PD，E，F分别为AD，PB的中点．（Ⅰ）求证：PE⊥BC；（Ⅱ）求证：平面PAB⊥平面PCD；（Ⅲ）求证：EF∥平面PCD．5．如图，在平行四边形ABCM中，AB=AC=3，∠ACM=90°，以AC为折痕将△ACM 折起，使点M到达点D的位置，且AB⊥DA．（1）证明：平面ACD⊥平面ABC；（2）Q为线段AD上一点，P为线段BC上一点，且BP=DQ=DA，求三棱锥Q ﹣ABP的体积．6．如图，四棱锥P﹣ABCD中，底面ABCD为菱形，PA⊥平面ABCD，BD交AC 于点E，F是线段PC中点，G为线段EC中点．（Ⅰ）求证：FG∥平面PBD；（Ⅱ）求证：BD⊥FG．7．如图所示，在四棱锥P﹣ABCD中，平面PAB⊥平面ABCD，AD∥BC，AD=2BC，∠DAB=∠ABP=90°．（Ⅰ）求证：AD⊥平面PAB；（Ⅱ）求证：AB⊥PC；（Ⅲ）若点E在棱PD上，且CE∥平面PAB，求的值．8．如图，在三棱锥P﹣ABC中，PA=PB=AB=2，BC=3，∠ABC=90°，平面PAB⊥平面ABC，D，E分别为AB，AC中点．（1）求证：DE∥平面PBC；（2）求证：AB⊥PE；（3）求三棱锥P﹣BEC的体积．9．如图，在四棱锥P﹣ABCD中，底面ABCD为直角梯形，AD∥CB，∠ADC=90°，平面PAD⊥底面ABCD，Q为AD的中点，，M是棱PC上的点．（Ⅰ）求证：平面PQB⊥平面PAD；（Ⅱ）若PA=PD=2，BC=1，，异面直线AP与BM所成角的余弦值为，求的值．10．如图，梯形ABCD中，AD=BC，AB∥CD，AC⊥BD，平面BDEF⊥平面ABCD，EF∥BD，BE⊥BD．（1）求证：平面AFC⊥平面BDFE；（2）若AB=2CD=2，BE=EF=2，求BF与平面DFC所成角的正弦值．11．如图，在三棱锥P﹣ABC中，AB⊥PC，CA=CB，M是AB的中点．点N在棱PC上，点D是BN的中点．求证：（1）MD∥平面PAC；（2）平面ABN⊥平面PMC．12．如图，已知PA垂直于矩形ABCD所在的平面，M，N分别是AB，PC的中点，若∠PDA=45°，（1）求证：MN∥平面PAD；（2）求证：MN⊥平面PCD．13．如图，正三棱柱ABC﹣A1B1C1中，AA1=AB，D为BB1的中点．（1）求证：A1C⊥AD；（2）若点P为四边形ABB1A1内部及其边界上的点，且三棱锥P﹣ABC的体积为三棱柱ABC﹣A1B1C1体积的，试在图中画出，P点的轨迹．并说明理由．14．如图，在三棱柱ABC﹣A1B1C1中，底面ABC为边长为2等边三角形，BB1=4，A1C1⊥BB1，且∠A1B1B=45°．（I）证明：平面BCC1B1⊥平面ABB1A1；（Ⅱ）求B﹣AC﹣A1二面角的余弦值．15．已知三棱柱ABC﹣A1B1C1的侧棱垂直于底面，∠BAC=90°，AB=AA1=2，AC=1，M，N分别是A1B1，BC的中点．（Ⅰ）证明：MN∥平面ACC1A1；（II）求二面角M﹣AN﹣B的余弦值．16．已知空间几何体ABCDE中，△BCD与△CDE均为边长为2的等边三角形，△ABC为腰长为3的等腰三角形，平面CDE⊥平面BCD，平面ABC⊥平面BCD．（1）试在平面BCD内作一条直线，使得直线上任意一点F与E的连线EF均与平面ABC平行，并给出详细证明；（2）求三棱锥E﹣ABC的体积．17．如图，在四棱锥P﹣ABCD中，∠ADB=90°，CB=CD，点E为棱PB的中点．（1）若PB=PD，求证：PC⊥BD；（2）求证：CE∥平面PAD．18．如图，长方体ABCD﹣A1B1C1D1中，AB=BC=2，A1C与底面ABCD所成的角为60°，（1）求四棱锥A1﹣ABCD的体积；（2）求异面直线A1B与B1D1所成角的大小．19．如图，四棱锥P﹣ABCD的底面ABCD是边长为2的菱形∠BAD=60°．已知PB=PD=2，PA=．（Ⅰ）证明：PC⊥BD；（Ⅱ）若E为PA上一点，记三棱锥P﹣BCE的体积和四棱锥P﹣ABCD的体积分别为V1和V2，当V1：V2=1：8时，求的值．20．如图，正方体ABCD﹣A1B1C1D1的棱长为2，E，F分别是CB，CD的中点，点M在棱CC1上，CM=tCC1（0＜t＜1）．（Ⅰ）三棱锥C﹣EFM，C1﹣B1D1M的体积分别为V1，V2，当t为何值时，V1•V2最大？最大值为多少？（Ⅱ）若A1C∥平面B1D1M，证明：平面EFM⊥平面B1D1M．21．如图，直角梯形ABEF中，∠ABE=∠BAF=90°，C、D分别是BE、AF上的点，且DA=AB=BC=a，DF=2CE=2a．沿CD将四边形CDFE翻折至CDPQ，连接AP、BP、BQ，得到多面体ABCDPQ，且AP=a．（Ⅰ）求多面体ABCDPQ的体积；（Ⅱ）求证：平面PBQ⊥平面PBD．22．如图，已知四棱锥P﹣ABCD的底面ABCD是菱形，∠BAD=60°，PA=PD，O 为AD边的中点．（1）证明：平面POB⊥平面PAD；（2）若，求四棱锥P﹣ABCD的体积．23．如图，在四棱锥P﹣ABCD中．底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD．Q为AD的中点，M是棱PC上的点，PA=PD=2．BC=AD=1，CD=．（I）求证：平面PBC⊥平面PQB；（Ⅱ）若平面QMB与平面PDC所成的锐二面角的大小为60°，求PM的长．24．在如图所示的几何体中，面CDEF为正方形，面ABCD为等腰梯形，AB∥CD，，AB=2BC=2，AC⊥FB．（Ⅰ）求证：AC⊥平面FBC；（Ⅱ）求四面体FBCD的体积；（Ⅲ）线段AC上是否存在点M，使EA∥平面FDM？证明你的结论．25．如图所示的几何体中，平面PAD⊥平面ABCD，△PAD是直角三角形，∠APD=90°，四边形ABCD是直角梯形，AB∥DC，AB⊥AD，PQ∥DC，PQ=PD=DC=1，PA=AB=2．（I）求证：PD∥平面QBC；（Ⅱ）求证：QC⊥平面PABQ；（Ⅲ）在线段QB上是否存在点M，使得AM⊥BC，若存在，求QM的值；若不存在，请说明理由．26．如图1，△ABC是边长为3的等边三角形，D在边AC上，E在边AB上，且AD=BE=2AE．将△ADE沿直线DE折起，得四棱锥A'﹣BCDE，如图2（1）求证：DE⊥A'B；（2）若平面AD'E⊥底面BCDE，求三棱锥D﹣A'CE的体积．27．如图，在三棱锥P﹣ABC中，PA⊥AC，AB⊥BC，PA=BC=2，PB=AC=2，D 为线段AC的中点，将△CBD折叠至△EBD，使得平面EDB⊥平面ABC且PC交平面EBD于F．（1）求证：平面BDE⊥平面PAC．（2）求三棱锥P﹣EBC的体积．28．如图1，在矩形ABCD中，AD=2AB=4，E是AD的中点．将△ABE沿BE折起使A到点P的位置，平面PEB⊥平面BCDE，如图2．（Ⅰ）求证：PB⊥平面PEC；（Ⅱ）求三棱锥D﹣PEC的高．29．如图1，ABCD是一个直角梯形，∠ABC=∠BAD=90，E为BC边上一点，AE、BD相交于O，AD=EC=3，BE=1，AB=．将△ABE沿AE折起，使平面ABE⊥平面ADE，连接BC、BD，得到如图2所示的四棱锥B﹣AECD．（Ⅰ）求证：CD⊥平面BOD；（Ⅱ）求直线AB与面BCD所成角的余弦值．30．如图，四棱柱ABCD﹣A1B1C1D1为长方体，点P是CD中点，Q是A1B1的中点．（I）求证：AQ∥平面PBC1；（l）若BC=CC1，求证：平面A1B1C⊥平面PBC1．31．如图，在四棱锥P﹣ABCD中，AD∥BC，AD=3BC=6，，点M在线段AD上，且DM=4，AD⊥AB，PA⊥平面ABCD．（1）证明：平面PCM⊥平面PAD；（2）当∠APB=45°时，求四棱锥P﹣ABCM的表面积．32．已知等腰梯形ABCD中，AD∥EC，EC=2AD=2AE=4，B为EC的中点，如图1，将三角形ABE沿AB折起到ABE′（E′⊄平面ABCD），如图2．（1）点F为线段AE′的中点，判断直线DF与平面BCE′的位置关系，并说明理由；（2）当平面ABE′与平面DE′C所成的二面角的大小为时，证明：平面ABE′⊥平面ABCD．33．如图，在四棱锥P﹣ABCD中，△PAD和△BCD都是等边三角形，平面PAD ⊥平面ABCD，且AD=2AB=4，．（I）求证：CD⊥PA；（II）E，F分别是棱PA，AD上的点，当平面BEF∥平面PCD时，求四棱锥C﹣PEFD的体积．34．如图，在四棱锥P﹣ABCD中，底面ABCD是平行四边形，AB=AC=2，AD=2，PB=，PB⊥AC．（1）求证：平面PAB⊥平面PAC；（2）若∠PBA=45°，试判断棱PA上是否存在与点P，A不重合的点E，使得直线CE与平面PBC所成角的正弦值为，若存在，求出的值；若不存在，请说明理由．35．如图，四棱锥P﹣ABCD中，PA⊥平面ABCD，四边形ABCD为直角梯形，AD ∥BC，∠BAD=∠CBA=90°，PA=AB=BC=1，AD=2，E，F，G分别为BC，PD，PC的中点．（1）求EF与DG所成角的余弦值；（2）若M为EF上一点，N为DG上一点，是否存在MN，使得MN⊥平面PBC？若存在，求出点M，N的坐标；若不存在，请说明理由．36．如图所示，在多面体ABC﹣A1B1C1中，D，E，F分别是AC，AB，CC1的中点，AC=BC=4，，CC1=2，四边形BB1C1C为矩形，平面ABC⊥平面BB1C1C，AA1∥CC1（1）求证：平面DEF⊥平面AA1C1C；（2）求直线EF与平面ABC所成的角的正切值．37．如图，在三棱柱ABC﹣A1B1C1中，BC⊥平面AA1B1B，AB=AA1=2，∠A1AB=60°．（Ⅰ）证明：平面AB1C⊥平面A1BC；（Ⅱ）若四棱锥A﹣BB1C1C的体积为，求该三棱柱的侧面积．38．如图，在四棱锥P﹣ABCD中，PD⊥底面ABCD，底面ABCD为正方形，E，F，G分别是AB，PB，PC的中点．（1）求证：CD∥平面PAB；（2）求证：CD⊥平面EFG．39．如图，在四棱锥P﹣ABCD中，底面ABCD是平行四边形，平面ABP⊥平面BCP，∠APB=90°，BP=BC，M为CP的中点．求证：（1）AP∥平面BDM；（2）BM⊥平面ACP．40．已知梯形ABCD中，AD∥BC，，AB=BC=2AD=4，E、F分别是AB、CD上的点，EF∥BC，AE=x．沿EF将梯形ABCD翻折，使平面AEFD⊥平面EBCF（如图）．G是BC的中点，以F、B、C、D为顶点的三棱锥的体积记为f （x）．（1）当x=2时，求证：BD⊥EG；（2）求f（x）的最大值；（3）当f（x）取得最大值时，求异面直线AE与BD所成的角的余弦值．2018全国高考立体几何（完整答案）参考答案与试题解析一．解答题（共40小题）1．【解答】解：（1）∵圆锥的顶点为P，底面圆心为O，半径为2，圆锥的母线长为4，∴圆锥的体积V===．（2）∵PO=4，OA，OB是底面半径，且∠AOB=90°，M为线段AB的中点，∴以O为原点，OA为x轴，OB为y轴，OP为z轴，建立空间直角坐标系，P（0，0，4），A（2，0，0），B（0，2，0），M（1，1，0），O（0，0，0），=（1，1，﹣4），=（0，2，0），设异面直线PM与OB所成的角为θ，则cosθ===．∴θ=arccos．∴异面直线PM与OB所成的角的为arccos．2．【解答】（1）证明：矩形ABCD所在平面与半圆弦所在平面垂直，所以AD⊥半圆弦所在平面，CM⊂半圆弦所在平面，∴CM⊥AD，M是上异于C，D的点．∴CM⊥DM，DM∩AD=D，∴CM⊥平面AMD，CM⊂平面CMB，∴平面AMD⊥平面BMC；（2）解：存在P是AM的中点，理由：连接BD交AC于O，取AM的中点P，连接OP，可得MC∥OP，MC⊄平面BDP，OP⊂平面BDP，所以MC∥平面PBD．3．【解答】证明：（1）平行六面体ABCD﹣A1B1C1D1中，AB∥A1B1，AB∥A1B1，AB⊄平面A1B1C，A1B1⊂∥平面A1B1C⇒AB∥平面A1B1C；（2）在平行六面体ABCD﹣A1B1C1D1中，AA1=AB，⇒四边形ABB1A1是菱形，⊥AB1⊥A1B．在平行六面体ABCD﹣A1B1C1D1中，AA1=AB，AB1⊥B1C1⇒AB1⊥BC．∴⇒AB1⊥面A1BC，且AB1⊂平面ABB1A1⇒平面ABB1A1⊥平面A1BC．4．【解答】证明：（Ⅰ）PA=PD，E为AD的中点，可得PE⊥AD，底面ABCD为矩形，可得BC∥AD，则PE⊥BC；（Ⅱ）由于平面PAB和平面PCD有一个公共点P，且AB∥CD，在平面PAB内过P作直线PG∥AB，可得PG∥CD，即有平面PAB∩平面PCD=PG，由平面PAD⊥平面ABCD，又AB⊥AD，可得AB⊥平面PAD，即有AB⊥PA，PA⊥PG；同理可得CD⊥PD，即有PD⊥PG，可得∠APD为平面PAB和平面PCD的平面角，由PA⊥PD，可得平面PAB⊥平面PCD；（Ⅲ）取PC的中点H，连接DH，FH，在三角形PCD中，FH为中位线，可得FH∥BC，FH=BC，由DE∥BC，DE=BC，可得DE=FH，DE∥FH，四边形EFHD为平行四边形，可得EF∥DH，EF⊄平面PCD，DH⊂平面PCD，即有EF∥平面PCD．5．【解答】解：（1）证明：∵在平行四边形ABCM中，∠ACM=90°，∴AB⊥AC，又AB⊥DA．且AD∩AC=A，∴AB⊥面ADC，∴AB⊂面ABC，∴平面ACD⊥平面ABC；（2）∵AB=AC=3，∠ACM=90°，∴AD=AM=3，∴BP=DQ=DA=2，由（1）得DC⊥AB，又DC⊥CA，∴DC⊥面ABC，∴三棱锥Q﹣ABP的体积V==××==1．6．【解答】证明：（Ⅰ）连接PE，G、F为EC和PC的中点，∴FG∥PE，FG⊄平面PBD，PE⊂平面PBD，∴FG∥平面PBD…（6分）（Ⅱ）∵菱形ABCD，∴BD⊥AC，又PA⊥面ABCD，BD⊂平面ABCD，∴BD⊥PA，∵PA⊂平面PAC，AC⊂平面PAC，且PA∩AC=A，∴BD⊥平面PAC，FG⊂平面PAC，∴BD⊥FG…（14分）7．【解答】（Ⅰ）证明：因为∠DAB=90°，所以AD⊥AB．……………………（1分）因为平面PAB⊥平面ABCD，……………………（2分）且平面PAB∩平面ABCD=AB，……………………（3分）所以AD⊥平面PAB．……………………（4分）（Ⅱ）证明：由已知得AD⊥AB因为AD∥BC，所以BC⊥AB．……………………（5分）又因为∠ABP=90°，所以PB⊥AB．……………………（6分）因为PB∩BC=B……………………（7分）所以AB⊥平面PBC……………………（8分）所以AB⊥PC．……………………（9分）（Ⅲ）解：过E作EF∥AD交PA于F，连接BF．……………………（10分）因为AD∥BC，所以EF∥BC．所以E，F，B，C四点共面．……………………（11分）又因为CE∥平面PAB，且CE⊂平面BCEF，且平面BCEF∩平面PAB=BF，所以CE∥BF，……………………（13分）所以四边形BCEF为平行四边形，所以EF=BC．在△PAD中，因为EF∥AD，所以，……………………（14分）即．8．【解答】证明：（1）∵D，E分别为AB，AC的中点，∴DE∥BC，又DE⊄平面PBC，BC⊂平面PBC，∴DE∥平面PBC．（2）连接PD，∵DE∥BC，又∠ABC=90°，∴DE⊥AB，又PA=PB，D为AB中点，∴PD⊥AB，又PD∩DE=D，PD⊂平面PDE，DE⊂平面PDE，∴AB⊥平面PDE，又PE⊂平面PDE，∴AB⊥PE．（3）∵平面PAB⊥平面ABC，平面PAB∩平面ABC=AB，PD⊥AB，PD⊂平面PAB，∴PD⊥平面ABC，∵△PAB是边长为2的等边三角形，∴PD=，∵E是AC的中点，∴．9．【解答】证明：（Ⅰ）∵AD∥BC，，Q为AD的中点∴四边形BCDQ为平行四边形，∴CD∥BQ．∵∠ADC=90°，∴∠AQB=90°，即QB⊥AD．又∵平面PAD⊥平面ABCD，且平面PAD∩平面ABCD=AD．∵BQ⊥平面PAD∵BQ⊂平面PQB，∴平面PQB⊥平面PAD．解：（Ⅱ）∵PA=PD，Q为AD的中点，∴PQ⊥AD．∵平面PAD⊥平面ABCD，且平面PAD∩平面ABCD=AD．∵PQ⊥平面ABCD．以Q为原点分别以、、为x轴、y轴、z轴的正方向建立空间直角坐标系，则Q（0，0，0），A（1，0，0），，，，设M（x0，y0，z0），∴，，．由M是PC上的点，设，化简得．设异面直线AP与BM所成角为θ，则．∴，解得或，故或．10．【解答】解：（1）证明：∵平面BDFE⊥平面ABCD，平面BDFE∩平面ABCD=BD，AC⊂平面ABCD，AC⊥BD，∴AC⊥平面BDFE．又AC⊂平面AFC，∴平面AFC⊥平面BDFE．（2）设AC∩BD=O，∵四边形ABCD为等腰梯形，AC⊥BD，AB=2CD=2，∴OD=OC=1，OB=OA=2，∵EF∥OB且EF=OB，∴四边形FEBO为平行四边形，∴OF∥BE，且OF=BE=2，又∵BE⊥平面ABCD，∴OF⊥平面ABCD．以O为原点，向量的方向分别为x轴，y轴，z轴的正方向，建立如图所示的空间直角坐标系，则B（0，2，0），D（0，﹣1，0），F（0，0，2），C（﹣1，0，0），∴=（0，1，2），=（1，﹣1，0），=（0，﹣2，2），设平面DFC的一个法向量为=（x，y，z），则有，即，不妨设z=1，得x=y=﹣2．即=（﹣2，﹣2，1），于是cos＜，＞===．设BF与平面DFC所成角为θ，则sinθ=|cos＜，＞|=．∴BF与平面DFC所成角的正弦值为．11．【解答】证明：（1）在ABN中，∵M是AB的中点，D是BN的中点，∴MD∥AN，又AN⊂平面PAC，MD⊄平面PAC，∴MD∥平面PAC．（2）在△ABC中，∵CA=CB，M是AB的中点，∴AB⊥MC，又∵AB⊥PC，PC⊂平面PMC，MC⊂平面PMC，PC∩MC=C，∴AB⊥平面PMC．又∵AB⊂平面ABN，∴平面ABN⊥平面PMC．12．【解答】证明：（1）如图，取PD的中点E，连接AE，NE．∵E、N分别为PD，PC的中点，∴EN CD，又M为AB的中点，∴AM CD，∴EN AM，∴四边形AMNE为平行四边形．∴MN∥AE，∴MN∥平面PAD．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（5分）（2）∵PA⊥平面ABCD，∠PDA=45°，∴△PAD为等腰直角三角形，∴AE⊥PD，又∵CD⊥AD，CD⊥PA，AD∩PA=A，∴CD⊥平面PAD，∵AE⊂平面PAD，∴CD⊥AE，又CD∩PD=D，∴AE⊥平面PCD，∴MN⊥平面PCD．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（10分）13．【解答】（1）证明：取AB的中点F，连接CF，A1F，∵A1A⊥平面ABC，CF⊂平面ABC，∴所以A1A⊥CF．∵△ABC为正三角形，F为AB的中点，∴BA⊥CF，又∵AA1，AB⊂平面AA1B1B，AA1∩AB=A，∴CF⊥平面AA1B1B，又∵AD⊂平面AA1B1B，所以CF⊥AD，正方形AA1B1B中，∵Rt△A1AF≌Rt△ABD，∴∠DAB=∠FA1A，又∵∠AFA1+∠FA1A=90°，∴∵∠AFA1+∠DAB=90°，，故AD⊥A1F，又∵CF∩A1F=F，CF，A1F⊂平面A1FC，∴AD⊥平面A1FC，又∵A1C⊂平面A1FC，∴A1C⊥AD．（2）取AA1中点E，连接DE，则线段DE为点P的运动轨迹．理由如下：∵DE∥AB，DE⊄平面ABC，AB⊂平面ABC，∴ED∥平面ABC，∴P到平面ABC的距离为．所以V==．14．【解答】证明：（Ⅰ）过点A1在平面ABB1A1内作BB1的垂线，垂足为O，连结C1O，∵A1C1⊥B1B，A1O⊥B1B，A1C1∩A1O=A1，∴B1B⊥平面A1OC1，∵OC1⊂平面A1OC1，∴B1B⊥OC1，由题可知A1B1=A1C1=B1C1=2，在B△A1OB1中，∵A1O⊥OB1，∠A1B1B=45°，A1B1=2，∴OA1=OB1=2，在△OB1C1中，∵C1O⊥OB1，B1C1=2，OB1=2，∴OC1=2，∴=A1C12，∴OC1⊥OA1，∵OA1∩OB1=O，∵OC1⊂平面BCC1B1，∴平面BCC1B1⊥平面ABB1A1．解：（Ⅱ）由（Ⅰ）知OC1、OA1、OB1两两垂直，以O为坐标原点，OA1为x轴，OB1为y轴，OC1为z轴，建立空间直角坐标系，∵AB=2，BB1=4，OC1=2，OA1=2，OB1=2，∴A1（2，0，0），B1（0，2，0），C1（0，0，2），B（0，﹣2，0），A（2，﹣4，0），C（0，﹣4，2），=（2，﹣2，0），=（0，﹣2，2），=（﹣2，0，2），=（0，4，0），设=（x，y，z）是平面ABC的法向量，则，取x=1，得=（1，1，1），设=（x，y，z）是平面A1AC的法向量，则，取x=1，得=（1，0，1），∴cos＜＞==．∴二面角B﹣AC﹣A1的余弦值为．15．【解答】解：解法一：依条件可知AB、AC，AA1两两垂直，如图，以点A为原点建立空间直角坐标系A﹣xyz．根据条件容易求出如下各点坐标：A（0，0，0），B（0，2，0），C（﹣1，0，0），A1（0，0，2），B1（0，2，2），C1（﹣1，0，2），M（0，1，2），（I）证明：∵是平面ACCA1的一个法向量，且，所以又∵MN⊄平面ACC1A1，∴MN∥平面ACC1A1（II）设=（x，y，z）是平面AMN的法向量，因为，由得解得平面AMN的一个法向量=（4，2，﹣1）由已知，平面ABC的一个法向量为=（0，0，1）∴二面角M﹣AN﹣B的余弦值是解法二：（I）证明：设AC的中点为D，连接DN，A1D∵D，N分别是AC，BC的中点，∴又∵，∴，∴四边形A 1DNM是平行四边形∴A1D∥MN∵A1D⊂平面ACC1A1，MN⊄平面ACC1A1∴MN∥平面ACC1A1（II）如图，设AB的中点为H，连接MH，∴MH∥BB1∵BB1⊥底面ABC，∵BB1⊥AC，BB1⊥AB，∴MH⊥AC，MH⊥AB∴AB∩AC=A∴MH⊥底面ABC在平面ABC内，过点H做HG⊥AN，垂足为G 连接MG，AN⊥HG，AN⊥MH，HG∩MH=H ∴AN⊥平面MHG，则AN⊥MG∴∠MGH是二面角M﹣AN﹣B的平面角∵MH=BB1=2，由△AGH∽△BAC，得所以所以∴二面角M﹣AN﹣B的余弦值是16．【解答】解：（1）∵平面CDE⊥平面BCD，平面ABC⊥平面BCD．∴过E作EQ⊥平面BCD，交CD于Q，过A作AP⊥平面BCD，交BC于P，∴EQ∥AP，过Q作QO∥BC，交BD于O，则直线OQ就是在平面BCD内所求的直线，使得直线OQ上任意一点F与E的连线EF均与平面ABC平行．证明如下：∵EQ∥AP，QO∥BC，EQ∩QO=Q，AP∩BC=P，EQ、QO⊂平面EQO，AP、BC⊂平面ABC，∴平面EQO∥平面ABC，∴直线OQ上任意一点F与E的连线EF均与平面ABC平行．（2）∵△BCD与△CDE均为边长为2的等边三角形，△ABC为腰长为3的等腰三角形，平面CDE⊥平面BCD，平面ABC⊥平面BCD，∴AP==2，∴S==2，△ABC点E到平面ABC的距离d===，∴三棱锥E﹣ABC的体积V E===．﹣ABC17．【解答】证明：（1）取BD的中点O，连结CO，PO，因为CD=CB，所以△CBD为等腰三角形，所以BD⊥CO．因为PB=PD，所以△PBD为等腰三角形，所以BD⊥PO．又PO∩CO=O，所以BD⊥平面PCO．因为PC⊂平面PCO，所以PC⊥BD．解：（2）由E为PB中点，连EO，则EO∥PD，又EO⊄平面PAD，所以EO∥平面PAD．由∠ADB=90°，以及BD⊥CO，所以CO∥AD，又CO⊄平面PAD，所以CO∥平面PAD．又CO∩EO=O，所以平面CEO∥平面PAD，而CE⊂平面CEO，所以CE∥平面PAD．18．【解答】解：（1）∵长方体ABCD﹣A1B1C1D1中，AB=BC=2，∴AA1⊥平面ABCD，AC==2，∴∠A1CA是A1C与底面ABCD所成的角，∵A1C与底面ABCD所成的角为60°，∴∠A1CA=60°，∴AA1=AC•tan60°=2•=2，=AB×BC=2×2=4，∵S正方形ABCD∴四棱锥A1﹣ABCD的体积：V===．（2）∵BD∥B1D1，∴∠A1BD是异面直线A1B与B1D1所成角（或所成角的补角）．∵BD=，A1D=A1B==2，∴cos∠A1BD===．∴∠A1BD=arccos．∴异面直线A1B与B1D1所成角是arccos．19．【解答】证明：（Ⅰ）连接BD、AC交于O点，∵PB=PD，∴PO⊥BD，又∵ABCD是菱形，∴BD⊥AC，而AC∩PO=O，∴BD⊥平面PAC，且PC⊂平面PAC，∴BD⊥PC．解：（Ⅱ）由条件可知△ABD≌△PBD，∴AO=PO=，∵PA=，∴PA2=OA2+OP2，∴PO⊥AC，由（Ⅰ）知，BD⊥平面PAC，PO⊂平面PAC，∴PO⊥BD，∴PO⊥平面ABCD，∴平面APC⊥平面ABCD，过E点作EF⊥AC，交AC于F，则EF⊥平面ABCD，∴EF∥PO，∴EF、PO分别是三棱锥E﹣ABC和四棱锥P﹣ABCD的高．又V1=V P﹣ABC﹣V E﹣ABC=，，由=，得4（PO﹣EF）=PO，∴，又由△AEF∽△APO，=，∴=．20．【解答】解：（Ⅰ）由题可知，CM=2t，C1M=2﹣2t，∴V1=S△ECF•CM==，=S•C1M=（2﹣2t）=（1﹣t），V2∴V1•V2=≤•（）2=．当且仅当t=1﹣t，即t=时等号成立．所以当t=时，V1•V2最大，最大值为．（Ⅱ）连接A1C1交B1D1于点O，则O为A1C1的中点，∵A1C∥平面B1D1M，平面A1CC1∩平面B1D1M=OM，∴A1C∥OM，∴M为CC1的中点，连接BD，∵E，F为BC、CD的中点，∴EF∥BD，又AC⊥BD，∴AC⊥EF．∵AA1⊥平面ABCD，EF⊂平面ABCD，∴AA1⊥EF，又AA1∩AC=A，∴EF⊥平面A1AC，又A1C⊂平面A1AC，∴EF⊥A1C．同理可得：EM⊥A1C，又EF∩EM=E，∴A1C⊥平面EFM．又A1C∥平面B1D1M，∴平面EFM⊥平面B1D1M．21．【解答】解：（Ⅰ）∵DA=AB=BC=a，∠ABE=∠BAF=90°，∴四边形ABCD是正方形，∴CD⊥AD，CD⊥DP，又AD∩DP=D，∴CD⊥平面ADP．∵AD2+DP2=AP2，∴AD⊥DP，又CD⊥AD，CD∩DP=D，∴AD⊥平面CDPQ，又AD∥BC，∴BC⊥平面CDPQ．∴V B﹣CDPQ==（a+2a）×a×a=a3，V B﹣ADP===．∴多面体ABCDPQ的体积为V B﹣CDPQ +V B﹣ADP=．（Ⅱ）取BP的中点G，连接GQ、DG、DQ，在△ABP中，BP==2a，∴BG=BP=a，在△BCQ中，BQ==a，PQ==a，∴PQ=BQ，∴GQ⊥BP．∴QG==a，又BD==2a=DP，∴DG⊥BP，∴DG==a，又DQ==a，∴DQ2=QG2+DG2，即QG⊥DG．又BP∩DG=G，∴QG⊥平面PBD，又QG⊂平面PBQ，∴平面PBQ⊥平面PBD．22．【解答】（1）证明：连接BD，因为底面ABCD是菱形，∠BAD=60°，所以△ABD 是正三角形，所以AD⊥BO，因为O为AD的中点，PA=PD，所以AD⊥PO，且PO∩BO=O，所以AD⊥平面POB，又AD⊂平面PAD，所以平面POB⊥平面PAD；（2）解：因为是正三角形，所以OB=3，在Rt△PAO中，，所以PO=2，又，所以OB2+PO2=PB2，所以∠POB=90°，即PO⊥OB，又AD⊥PO，且OB∩AD=O，所以PO⊥平面ABCD，因为，所以四棱锥P﹣ABCD的体积为．23．【解答】（I）证明：∵PA=PD，Q是AD的中点，∴PQ⊥AD，又平面PAD⊥底面ABCD，平面PAD∩底面ABCD=AD，PQ⊂平面PAD，∴PQ⊥平面ABCD，∴BC⊥PQ，∵BC=AD=DQ，BC∥AD，∠ADC=90°，∴四边形BCDQ是矩形，∴BC⊥BQ，又PQ∩BQ=Q，∴BC⊥平面PBQ，又BC⊂平面PBC，∴平面PBC⊥平面PQB．（II）过M作MN∥CD交PD与N，则平面BMQ∩平面PCD=MN，∵平面PAD⊥底面ABCD，平面PAD∩底面ABCD=AD，BQ⊥AD，BQ⊂平面PAD，∴BQ⊥平面PAD，又BQ∥CD∥MN，∴MN⊥平面PAD，∴MN⊥NQ，MN⊥PD，∴∠DNQ为平面BMQ与平面PCD所成角，即∠DNQ=60°，∵PD=PA=2，AD=2BC=2，∴∠PDO=60°，∴△DNQ是等比三角形，∴DN=DQ=1，即N是PD的中点，∴M是PC的中点，∵PD=2，CD=，∴PC=，∴PM==．24．【解答】（Ⅰ）证明：在△ABC中，∵，AB=2，BC=1，∴AC2+BC2=AB2．∴AC⊥BC．又∵AC⊥FB，BF∩CB=B，∴AC⊥平面FBC．（Ⅱ）解：∵AC⊥平面FBC，∴AC⊥FC．∵CD⊥FC，∴FC⊥平面ABCD．在Rt△ACB中，，∴∠CAB=30°，∴在等腰梯形ABCD中可得∠ABD=∠CDB=∠CBD=30°，∴CB=DC=1，∴FC=1．∴△BCD的面积S==．∴四面体FBCD的体积为：．（Ⅲ）解：线段AC上存在点M，且M为AC中点时，有EA∥平面FDM，证明如下：连接CE与DF交于点N，连接MN．由CDEF为正方形，得N为CE中点．∴EA∥MN．∵MN⊂平面FDM，EA⊄平面FDM，∴EA∥平面FDM．所以线段AC上存在点M，使得EA∥平面FDM成立．25．【解答】（Ⅰ）证明：∵PQ∥DC，PQ=PD=DC=1，∴四边形PQCD是平行四边形，∴PD∥CQ，∵PD⊄平面QBC，CQ⊂平面QBC，∴PD∥平面QBC．（Ⅱ）证明：∵∠APD=90°，∴PD⊥PA，∵平面PAD⊥平面ABCD，△PAD是直角三角形，四边形ABCD是直角梯形，AB ∥DC，AB⊥AD，∴AB⊥平面PAD，∴AB⊥PD，∵PD∥QC，∴PA⊥QC，AB⊥QC，∵PA∩AB=A，∴QC⊥平面PABQ．（Ⅲ）解：存在．由（Ⅱ）可知QC⊥平面PABQ；作AM⊥BQ，交BQ于M，可知AM⊥CQ，BQ∩CQ=Q，所以AM⊥平面BCQ，BC⊂平面BCQ，∴AM⊥BC．QB=，cosB=，BM=2=，QM==．26．【解答】解：（1）证明：在图1中，由题意知AE=1，AD=BE=2，在△ADE中，由余弦定理知：DE2=AE2+AD2﹣AE×AD=12+22﹣1×2=3，所以：AE2+DE2=AD2，所以：DE⊥AE，DE⊥BE，在△ADE沿直线DE折起的过程中，DE与AE，BE的垂直关系不变，故在图2中有DE⊥A'E，DE⊥BE，又A'E∩BE=E，所以DE⊥平面A'EB，所以DE⊥A'B．（2）如图2，因为平面A'DE⊥底面BCDE，由（1）知DE⊥A'E，且平面A'DE∩底面BCDE=DE，所以A'E⊥底面BCDE，所以A'E为三棱锥A'﹣EDC的高，且A'E=AE=1，又因为在图1中，S△ECD=S△ABC﹣S△AED﹣S△BEC=，所以：，故三棱锥D﹣A'CE的体积为．27．【解答】（1）证明：∵PA⊥AC，PA=2，AC=2，∴，又∵，BC=2，∴PB2+BC2=PC2，则BC⊥PB．又∵AB⊥BC，∴BC⊥平面PAB，则BC⊥PA，又PA⊥AC，AC∩BC=C，∴PA⊥平面ABC．又∵BD⊂平面PAC，∴PA⊥BD，在Rt△ABC中，由BC=2，AC=2，可得AB=2，又∵D为AC的中点，∴BD⊥AC，而PA∩AC=A，∴BD⊥平面PAC，则平面BDE⊥平面PAC；=V E﹣PBC=V B﹣APCE﹣V P﹣ABC．（2）解：V P﹣EBC由已知，DE∥AP，∴．∴=，．∴．28．【解答】解：（Ⅰ）证明：∵AD=2AB，E为线段AD的中点，∴AB=AE，取BE中点O，连接PO，则PO⊥BE，又平面PEB⊥平面BCDE，平面PEB∩平面BCDE=BE，∴PO⊥平面BCDE，则PO⊥EC，在矩形ABCD中，∴AD=2AB，E为AD的中点，∴BE⊥EC，则EC⊥平面PBE，∴EC⊥PB，又PB⊥PE，且PE∩EC=E，∴PB⊥平面PEC．（Ⅱ）以OB所在直线为x轴，以平行于EC所在直线为y轴，以OP所在直线为z轴建立空间直角坐标系，∵PB=PE=2，则B（，0，0），E（﹣，0，0），P（0，0，），D（﹣2，，0），C（﹣，2，0），∴=（﹣，0，﹣），=（﹣，2，﹣），∴cos∠EPC===，可得：sin∠EPC==，可得：S△EPC=||•||•sin∠EPC=2×2×=2，=V D﹣EPC，设三棱锥D﹣PEC的高为h，则可得：S△ECD•OP=S△EPC•h，可∵V P﹣ECD得：=2×h，∴解得：三棱锥D﹣PEC的高h=1．29．【解答】解：（Ⅰ）在Rt△BEB中，BE=1，AB=，所以∠BAE=30°……（1分）同理∠BDA=30°，从而∠AOD=90°，AF⊥BD……（2分）又因为AD∥EC，AD=EC，所以ADCE是平行四边形，∠CDO=∠AOD=90°，CD⊥DO……（3分）因为平面ABE⊥平面ADE，平面ABE∩平面ADE=AE，BO⊥AE，所以BO⊥平面ADE……（4分）又CD⊂平面ADE，所以BO⊥CD，BO∩DO=O，BO⊂平面BOD，OD平面BOD．所以CD⊥平面BOD……（6分）（Ⅱ）由（Ⅰ）可知，四边形AECD的面积S=CD•OD=3……（7分）连接AC，则△ACD的面积S1=，三棱锥B=ACD的体积V=……（9分）△BCD的面积S2=……（10分）设A到平面BCD的距离为h，则h=，h=……（11分）直线AB与面BCD所成角的正弦值为，余弦值为……（12分）30．【解答】证明：（1）取AB中点为R，连接PR，B1R∵点P是CD中点，Q是A1B1的中点，∴四边形AQB1R，PRB1C1都为平行四边形，∴AQ∥B1R，B1R∥PC1，∴AQ∥PC1．∵AQ⊄平面PBC1，PC1⊂平面PBC1，∴AQ∥平面PBC1．（Ⅱ）∵四棱柱ABCD﹣A1B1C1D1为长方体，BC=CC1，∴B1C⊥BC1．∵A1B1⊥平面BB1C1C，∴A1B1⊥BC1．∵A1B1∩B1C=B1，A1B1⊂平面A1B1C，B1C⊂平面A1B1C，∴BC1⊥平面A1B1C，BC1⊂平面PBC1，∴平面A1B1C⊥平面PBC1．31．【解答】（1）证明：由AD=6，DM=4可得AM=2，则BC=AM，又AD∥BC，则四边形ABCM是平行四边形，则CM∥AB，∵AD⊥AB，∴CM⊥AD．又PA⊥平面ABCD，CM⊂平面ABCD，∴PA⊥CM，∵PA∩AD=A，PA，AD⊂平面PAD，∴CM⊥平面PAD，又CM⊂平面PCM，∴平面PCM⊥平面PAD．（2）解：∵PA⊥平面ABCD，∴PA⊥AB，∵∠APB=45°，∴AP=AB=6．∵，∴．∴四棱锥P﹣ABCM的表面积为．32．【解答】（本小题满分12分）解：（1）直线DF与平面BCE'相交，理由如下：因为E'⊄平面ABCD，所以D⊄平面BCE'．若DF∥平面BCE'，设平面DCE'∩平面BCE'=CM，则DF∥CM．CM与CB不重合．又因为AD∥BC，所以平面ADE'∥平面BCE'，矛盾．所以直线DF与平面BCE'相交．…………………………（4分）证明：（2）取AB的中点O，连接E'O，BD，由等腰梯形ADCE中，AD∥EC，EC=2AD=2AE=4，，所以E'O⊥AB，DO⊥AB，…………………………（6分）分别以BA，OD所在的直线为x轴，y轴，过O垂直于平面ABCD的直线为z轴建立如图所示的空间直角坐标系，设二面角E'﹣AB﹣D的大小为α．则．过E'作E'G⊥OD于点G．因为E'O⊥AB，DO⊥AB，所以AO⊥平面E'OD，∠E'OD=α．所以E'G⊥AO．所以E'G⊥平面ABCD．…………………………（8分）所以．设平面E'AB的法向量为n=（x，y，z），则，即令y=1，得平面E'AB的一个法向量为n=（0，1，﹣cotα）．…………………………（10分）同理可求平面E'DC的一个法向量为．所以．解得：．所以二面角E'﹣AB﹣D的大小为，即平面ABE'⊥平面ABCD．…………………………（12分）33．【解答】证明：（I）因为AD=4，AB=2，，所以AB2+BD2=AD2，AB⊥BD，且∠ADB=30°．又△BCD是等边三角形，所以∠ADC=90°，即CD⊥AD．…（3分）因为平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，CD⊂平面ABCD，所以CD⊥平面PAD．所以CD⊥PA．……（6分）解：（II）因为平面BEF∥平面PCD，所以BF∥CD，EF∥PD，且BF⊥AD．……（8分）又在直角三角形ABD中，DF=，所以AE=AF=1．所以．……（10分）由（I）知CD⊥平面PAD，故四棱锥C﹣PEFD的体积．…（12分）34．【解答】解：（1）四边形ABCD是平行四边形，AD=2，∴BC=AD=2，又AB=AC=2，∴AB2+AC2=BC2，∴AC⊥AB，又PB⊥AC，且AB∩PB=B，∴AC⊥平面PAB，∵AC⊂平面PAC，∴平面PAB⊥平面PAC；（2）由（1）知AC⊥AB，AC⊥平面PAB，分别以AB、AC所在直线为x轴、y轴，平面PAB内过点A且与直线AB垂直的直线为z轴，建立空间直角坐标系A﹣xyz，如图所示；则A（0，0，0），B（2，0，0），C（0，2，0），=（0，2，0），=（﹣2，2，0）；由∠PBA=45°，PB=，可得P（1，0，1），∴=（1，0，1），=（﹣1，0，1）；假设棱PA上存在点E，使得直线CE与平面PBC所成角的正弦值为，设=λ（0＜λ＜1），则=λ=（λ，0，λ），=﹣=（λ，﹣2，λ），设平面PBC的法向量为=（x，y，z），则，即，令z=1，可得x=y=1，∴平面PBC的一个法向量为=（1，1，1），设直线CE与平面PBC所成的角为θ，则sinθ=|cos＜，＞|===，解得λ=或λ=（不合题意，舍去），∴存在=，使得直线CE与平面PBC所成角的正弦值为．35．【解答】解：（1）以A为坐标原点，AB为x轴，AD为y轴，AP为z轴，建立空间直角坐标系，则A（0，0，0），B（1，0，0），C（1，1，0），D（0，2，0），P（0，0，1），∵E、F、G分别为BC、PD、PC的中点，∴，F（0，1，），G（），∴=（﹣1，），=（），设EF与DG所成角为θ，则cosθ==．∴EF与DG所成角的余弦值为．（2）设平面PBC的法向量为=（x，y，z），∵=（0，1，0），=（1，0，﹣1），∴，取x=1，得=（1，0，1），M为EF上一点，N为DG上一点，若存在MN，使得MN⊥平面PBC，则∥，设M（），N（x2，y2，z2），则，①∵点M，N分别是线段EF与DG上的点，∴，∵=（），=（x2，y2﹣2，z2），∴，且，②把②代入①，得，解得，∴M（），N（）．36．【解答】解：（1）∵D，E分别是AC，AB的中点，∴DE∥BC，∵四边形BB1C1C为矩形，∴BC⊥CC1．∵AC=BC=4，AB=4，∴AC2+BC2=AB2，∴BC⊥AC，又AC∩CC1=C，∴BC⊥平面AA1C1C，∴DE⊥平面AA1C1C．。

新编北京市各区高三一模试题分类汇编：3立体几何(含答案解析)

北京市各区高三一模试题分类汇编03立体几何(理科)1 (东城一模理科)2 (西城一模理科)如图，设P为正四面体A BCD-表面（含棱）上与顶点不重合的一点，由点P到四个顶点的距离组成的集合记为M，如果集合M中有且只有2个元素，那么符合条件的点P有（ C ）（A）4个（B）6个（C）10个（D）14个3 (西城一模理科)已知一个正三棱柱的所有棱长均等于2，它的俯视图是一个边长为2的正三角形，那么它的侧（左）视图面积的最小值是__4 (海淀一模理科)一个空间几何体的三视图如图所示，该几何体的体积为__96__．5 (某三棱锥的三视图如图所示，则这个三棱锥的体积为______，表面积为______）6 (中，SB⊥底面ABCD．底面ABCD为梯形，AB AD⊥，AB∥CD，．若点E是线段AD上的动点，则满足90SEC∠=︒的点E的个数是__2_7 (丰台一模理科)棱长为2的正方体被一平面截成两个几何体，其中一个几何体的三视图如图所示，那么该几何体的体积是（B）（A）143（B）4 （C）103（D）38 (石景山一模理科)右图是某个三棱锥的三视图，其中主视图是等边三角形，左视图是直角三角形，俯视图是等腰直角三角形，则该三棱锥的体积是（B ）A．12B．3C．4D．69 (顺义一模理科)一个几何体的三视图如图所示，则这个几何体的体积是_________10 (延庆一模理科)右图是一个几何体的三视图，则该几何体的体积是(A)A．3B．34C．1D．3211 (东城一模理科)侧视图俯视图BC DESA侧视图俯视图主视图1主视图左视图俯视图主视图左视图俯视图BADC. P主视图侧视图12 (西城一模理科)如图，在四棱柱1111ABCD A B C D -中，底面ABCD 和侧面11BCC B 都是矩形，E 是CD 的中点，1D E CD ⊥，22AB BC ==.（Ⅰ）求证：1⊥BC D E ；（Ⅱ）求证：1B C // 平面1BED ；（Ⅲ）若平面11BCC B 与平面1BED 所成的锐二面角的大小为π3，求线段1D E 的长度.13 (海淀一模理科) 如图1，在Rt △ABC 中，∠ACB =30°，∠ABC =90°，D 为AC 中点，AE BD ⊥于E ，延长AE 交BC 于F ，将∆ABD 沿BD 折起，使平面ABD ⊥平面BCD ，如图2所示．（Ⅰ）求证：AE ⊥平面BCD ；（Ⅱ）求二面角A –DC –B 的余弦值．（Ⅲ）在线段AF 上是否存在点M 使得//EM 平面ADC ？若存在，请指明点M 的位置；若不存在，请说明理由．14 (朝阳一模理科)如图，四棱锥P ABCD -的底面为正方形，侧面PAD ⊥底面ABCD ．PAD △为等腰直角三角形，且PA AD ⊥．E ，F 分别为底边AB 和侧棱PC 的中点．（Ⅰ）求证：EF ∥平面PAD ；（Ⅱ）求证：EF ⊥平面PCD ；（Ⅲ）求二面角E PD C --的余弦值．15 (丰台一模理科)如图，在棱长为1的正方体ABCD-A1B1C1D1中，点E 是棱AB 上的动点.（Ⅰ）求证：DA1⊥ED1 ；（Ⅱ）若直线DA1与平面CED1成角为45o ，求AEAB的值；（Ⅲ）写出点E 到直线D1C 距离的最大值及此时点E 的位置（结论不要求证明）.16 (石景山一模理科)如图，正三棱柱111ABC A B C -的底面边长是2，D 是AC 的中点．（Ⅰ）求证：1B C∥平面1A BD；（Ⅱ）求二面角1A BD A--的大小；（Ⅲ）在线段1AA 上是否存在一点E ，使得平面11B C E ⊥平面1A BD ，若存在，求出AE 的长；若不存在，说明理由．17 (顺义一模理科) 如图在四棱锥P ABCD -中，底面ABCD 是菱形，060BAD ∠=，平面PAD ⊥平面ABCD ，2PA PD AD ===，Q 为AD 的中点，M 是棱PC 上一点，且13PM PC =.1BFA E BCDPFA1A1B1CCDB（Ⅰ）求证：PQ ⊥平面ABCD ；（Ⅱ）证明：PA ∥平面BMQ （Ⅲ）求二面角M BQ C --的度数.18 (延庆一模理科) 在四棱锥ABCD P -中，⊥PA 平面ABCD ，底面ABCD 是正方形，且2==AD PA ，F E ，分别是棱PC AD ,的中点．（Ⅰ）求证：//EF 平面PAB ；（Ⅱ）求证：⊥EF 平面PBC ；（Ⅲ）求二面角D PC E --的大小．北京市各区高三一模试题汇编--立体几何(理科)答案1．；2．C ；3．；4．96 ；5．13，；6．2 ；7．B ；8． B ；9．；10．A ；11.吧12（Ⅰ）证明：因为底面ABCD 和侧面11BCC B 是矩形，所以 BC CD ⊥，1BC CC ⊥，又因为 1=CDCC C ，所以 BC ⊥平面11DCC D ， ………………2分因为 1D E ⊂平面11DCC D ，所以1BC D E ⊥. …………4分（Ⅱ）证明：因为 1111//, BB DD BB DD =，所以四边形11D DBB 是平行四边形. 连接1DB 交1D B 于点F ，连接EF ，则F 为1DB 的中点.在1∆B CD 中，因为DE CE =，1DF B F =，所以 1//EF B C .……………6分又因为 1⊄B C 平面1BED ，⊂EF 平面1BED ，所以 1//B C 平面1BED . ………8分（Ⅲ）解：由（Ⅰ）可知1BC D E ⊥，又因为 1D E CD ⊥，BCCD C =，所以 1D E ⊥平面ABCD . ………………9分设G 为AB 的中点，以E 为原点，EG ，EC ，1ED 所在直线分别为x 轴，y 轴，z 轴 A BA 1B 1D C ED 1 C 1zyxF GFA BEPDC如图建立空间直角坐标系，设1D E a =，则11(0,0,0), (1,1,0), (0,0,), (0,1,0), (1,2,), (1,0,0)E B D a C B a G . 设平面1BED 法向量为(,,)x y z =n ，因为1(1,1,0), (0,0,)EB ED a ==，由10,0,EB ED ⎧⋅=⎪⎨⋅=⎪⎩n n 得0,0.x y z +=⎧⎨=⎩ 令1x =，得(1,1,0)=-n . …………11分设平面11BCC B 法向量为111(,,)x y z =m ，因为1(1,0,0), (1,1,)CB CB a ==，由10,0,CB CB ⎧⋅=⎪⎨⋅=⎪⎩m m得11110,0.x x y az =⎧⎨++=⎩令11z =，得(0,,1)a =-m .…………12分由平面11BCC B 与平面1BED 所成的锐二面角的大小为π3，得||π|cos ,|cos 3⋅<>===m n m n m n ， ……………13分解得1a =. ………………14分13（Ⅰ）因为平面ABD ⊥平面BCD ，交线为BD ，又在ABD ∆中，AE BD ⊥于E ，AE ⊂平面ABD所以AE ⊥平面BCD ．————————————————3分（Ⅱ）由（Ⅰ）结论AE ⊥平面BCD 可得AE EF ⊥．由题意可知EF BD ⊥，又AE ⊥BD ．如图，以E 为坐标原点，分别以,,EF ED EA 所在直线为x 轴，y 轴，z 轴，建立空间直角坐标系E xyz -——4分不妨设2AB BD DC AD ====，则1BE ED ==．由图1条件计算得，AE =BC =BF =则(0,0,0),(0,1,0),(0,1,0),2,0)E D B A F C -———————5分(3,1,0),(0,1,DC AD ==．由AE ⊥平面BCD 可知平面DCB 的法向量为EA ．———————6分设平面ADC 的法向量为(,,)x y z =n ，则0,0.DC AD ⎧⋅=⎪⎨⋅=⎪⎩n n即0,0.y y +=-=⎪⎩令1z =，则1y x ==，所以1)=-n ．——————————8分平面DCB的法向量为EA 所以cos ,||||EA EA EA ⋅<>==⋅n nn ，所以二面角A DC B --—————————————9分（Ⅲ）设AM AFλ=，其中[0,1]λ∈．由于3(AF =，所以(AM AF λλ==，其中[0,1]λ∈————————————10分所以3,0,(13EM EA AM λλ⎛=+=-⎝————————————11分由0EM ⋅=n 0λ=-(1-———12分解得3=(0,1)4λ∈．————13分所以在线段AF 上存在点M 使EM ADC ∥平面，且34AM AF =．————————14分 14（Ⅰ）证明：取PD 的中点G ，连接FG ，AG ．因为F ，G 分别是PC ，PD 的中点，所以FG 是△PCD 的中位线．所以FG ∥CD ，且12FG CD =．又因为E 是AB 的中点，且底面ABCD 为正方形，所以1122AE AB CD ==，且AE ∥CD ．所以AE ∥FG ，且AE FG =．所以四边形AEFG 是平行四边形．所以EF ∥AG ．又EF ⊄平面PAD ，AG ⊂平面PAD ，所以EF 平面PAD ．…………………4分（Ⅱ）证明：因为平面PAD ⊥平面ABCD ，PA AD ⊥，且平面PAD I 平面ABCD AD =，所以PA ⊥平面ABCD ．所以PA AB ⊥，PA AD ⊥．又因为ABCD 为正方形，所以AB AD ⊥，所以,,AB AD AP 两两垂直．以点A 为原点，分别以, , AB AD AP 为, , x y z 轴，建立空间直角坐标系（如图）．由题意易知AB AD AP ==，设2AB AD AP ===，则(0,0,0)A ，(2,0,0)B ，(2,2,0)C ，(0,2,0)D ，(0,0,2)P ，(1,0,0)E ，(1,1,1)F ．因为(0,11)EF =uu u r ，，(022)PD =-uu u r ，，，(200)CD =-uu u r，，，且(0,11)(0,2,2)0EF PD ⋅=⋅-=uu u r uu u r，， A E B CDPFyxz(0,11)(2,00)0EF CD ⋅=⋅-=uu u r uu u r，，所以EF PD ⊥，EF CD ⊥．又因为PD ，CD 相交于D ，所以EF ⊥平面PCD ．…………… 9分（Ⅲ）易得(102)EP =-uu r ，，，(0,22)PD =-uu u r,．设平面EPD 的法向量为(, , )x y z =n ，则0,0.EP PD ⎧⋅=⎪⎨⋅=⎪⎩uu ruu u r n n 所以20,220. x z y z -+=⎧⎨-=⎩即2,. x z y z =⎧⎨=⎩ 令1z =，则(2,1,1)=n ．由（Ⅱ）可知平面PCD 的法向量是(0,11)EF =uu u r，，所以cos ,EF EF EF⋅〈〉===⋅uu u ruu u r uu u r n n n E PD C --的大小为锐角，所以二面角E PD C --．…………14分 15.解：以D 为坐标原点，建立如图所示的坐标系，则D(0,0,0),A （1，0，0）， B(1,1,0)，C(0,1,0),D1(0,1,2),A1(1,0,1)，设E(1,m,0)（0≤m≤1）（Ⅰ）证明：1(1,0,1)DA =，1(1,,1)ED m =-- 111(1)0()110DA ED m ⋅=⨯-+⨯-+⨯=所以DA1⊥ED1. ----4分（Ⅱ）设平面CED1的一个法向量为(,,)v x y z =,则10v C D v C E ⎧⋅=⎪⎨⋅=⎪⎩，而1(0,1,1)CD =-，(1,1,0)CE m =-所以0,(1)0,y z x m y -+=⎧⎨+-=⎩取z=1,得y=1,x=1-m ，得(1,1,1)v m =-.因为直线DA1与平面CED1成角为45o ，所以1sin 45|cos ,|DA v ︒=<> 所以11||22||||DA v DA v ⋅=⋅=m=12.-----11分（Ⅲ）点E 到直线D1C E 在A 点处.------14分 16（Ⅰ）证明：连结1AB 交1A B 于M ，连结1B C DM ，，因为三棱柱111ABC A B C -是正三棱柱，所以四边形11AA B B 是矩形，所以M 为1A B 的中点．因为D 是AC 的中点，所以MD 是三角形1AB C 的中位线，…………………………2分所以MD ∥1B C ．…………………………3分因为MD ⊂平面1A BD ，1B C ⊄平面1A BD ，所以1B C ∥平面1A BD ．……………4分（Ⅱ）解：作CO AB ⊥于O ，所以CO ⊥平面11ABB A ，所以在正三棱柱111ABC AB C -中如图建立空间直角坐标系O xyz -．因为2AB =，1AA =D 是AC 的中点．所以(100)A ，，，(100)B -，，，(00C ，，1(10)A …………5分所以1(02D ，，3(02BD =，， 1(20)BA =．设()n x y z =，，是平面1A BD 的法向量，所以100n BD n BA ⎧⋅=⎪⎨⋅=⎪⎩，，即30220xx ⎧=⎪⎨⎪=⎩，，令x =2y =，3z =，所以(323)n =-，，是平面1A BD 的一个法向量．……………6分由题意可知1(00)AA =是平面ABD 的一个法向量，………7分所以121cos 2n AA <>==，．………………8分所以二面角1A BD A --的大小为3．…………………………9分xyzOBDA 1A1B1CCMA1A1B1CBCD（Ⅲ）设(10)E x ，，，则1(1C E x =-，11(10C B ，，=-设平面11B C E 的法向量1111()n x y z ，，=，所以111100n C E n C B ，，⎧⋅=⎪⎨⋅=⎪⎩即11111)00x x y x ，，⎧-+=⎪⎨-=⎪⎩令1z =13x =，1y =，1(3n =，…………………12分又10n n ⋅=，即0-=，解得x = 所以存在点E ，使得平面11B C E ⊥平面1A BD且AE =．…………………………14分结BD ，Q 底面ABCD 是菱形，且060BAD ∠=，∴BAD 是等边三角形，∴BQ AD ⊥由（Ⅰ）PQ ⊥平面ABCD . ∴PQ AD ⊥.以Q 为坐标原点，,,QA QB QP 分别为x 轴y 轴z 轴建立空间直角坐标系则(0,0,0),(1,0,0),Q A B P .————10分设平面BMQ 的法向量为(,,)m x y z =，∴00m QB m MN ⎧⋅=⎪⎨⋅=⎪⎩，注意到MN ∥PA∴0m QB m PA ⎧⋅=⎪⎨⋅=⎪⎩，解得(3,0,1)m =是平面BMQ 的一个法向量——12分（Ⅰ）证明：设G 是PB 的中点，连接GF AG , ∵F E ,分别是PC AD ,的中点，∴BC GF 21//，BC AE 21// ∴AE GF //，∴AEFG 是平行四边形，∴AG EF //………………2分 ∵⊄EF 平面PAB ⊂AG 平面PAB ，∴//EF 平面PAB ………………3分（Ⅱ）∵AB PA =，∴PB AG ⊥，………………4分∵ABCD PA ⊥，∴BC PA ⊥，又∵AB BC ⊥，∴⊥BC 平面PAB ， ∴AG BC ⊥，………………6分∵PB 与BC 相交，∴⊥AG 平面PBC ， ∴⊥EF 平面PBC ．………………7分（Ⅲ）以AP AD AB ,,分别为x 轴、y 轴、z 轴，建立空间直角坐标系xyz A -，…8分 ∵2==AD PA ，∴)0,1,0(E ，)0,2,2(C ，)2,0,0(P ，)1,1,1(F 设H 是PD 的中点，连接AH ∵⊥AG 平面PBC ，∴同理可证⊥AH 平面PCD ，∴AH 是平面PCD 的法向量，)1,1,0(=………………9分)0,1,2(=，)2,1,0(-=设平面PEC 的法向量),,(z y x m = ，则0,0=⋅=⋅m∴02,02=+-=+z y y x 令2=y ，则1,1=-=z x ∴)1,2,1(-=m …………12分∴23263||||,cos =⋅=<AH m m．………………13分∴二面角D PC E --的大小为︒30………………14分。

2018北京各区数学一模试题分类汇编——立体几何精品

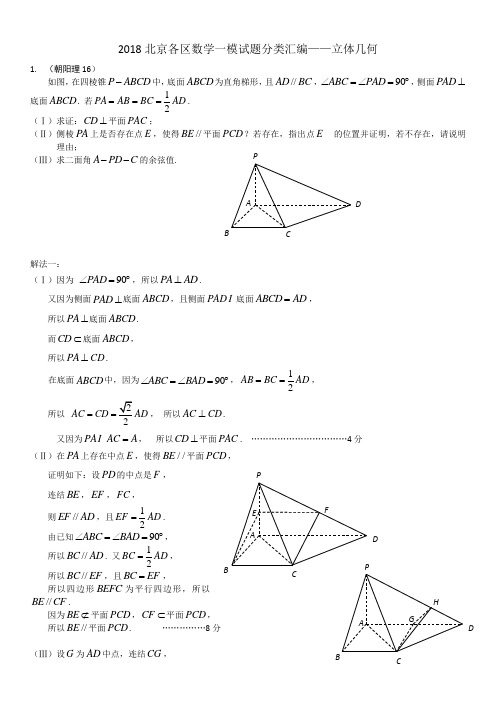
2018北京各区数学一模试题分类汇编——立体几何1. （朝阳理16）如图，在四棱锥P ABCD -中，底面ABCD 为直角梯形，且//AD BC ，90ABC PAD ∠=∠=︒，侧面PAD ⊥底面ABCD . 若12PA AB BC AD ===. （Ⅰ）求证：CD ⊥平面PAC ；（Ⅱ）侧棱PA 上是否存在点E ，使得//BE 平面PCD ？若存在，指出点E 的位置并证明，若不存在，请说明理由；（Ⅲ）求二面角A PD C --的余弦值.解法一：（Ⅰ）因为 90PAD ∠=︒，所以PA AD ⊥.又因为侧面PAD ⊥底面ABCD ，且侧面PAD 底面ABCD AD =，所以PA ⊥底面ABCD . 而CD ⊂底面ABCD ，所以PA ⊥CD .在底面ABCD 中，因为90ABC BAD ∠=∠=︒，12AB BC AD ==，所以2AC CD AD ==，所以AC ⊥CD . 又因为PA AC A = ，所以CD ⊥平面PAC . ……………………………4分（Ⅱ）在PA 上存在中点E ，使得//BE 平面PCD ，证明如下：设PD 的中点是F ，连结BE ，EF ，FC ，则//EF AD ，且12EF AD =.由已知90ABC BAD ∠=∠=︒，所以//BC AD . 又12BC AD =，所以//BC EF ，且BC EF =，所以四边形BEFC 为平行四边形，所以//BE CF .因为BE ⊄平面PCD ，CF ⊂平面PCD所以//BE 平面PCD . (8)（Ⅲ）设G 为AD 中点，连结CG ，则 CG ⊥AD .又因为平面ABCD ⊥平面PAD ，所以 CG ⊥平面PAD . 过G 作GH PD ⊥于H ，连结CH ，由三垂线定理可知CH PD ⊥. 所以GHC ∠是二面角A PD C --的平面角.设2AD =，则1PA AB CG DG ====, DP =. 在PAD ∆中，GH DG PA DP =，所以GH =. 所以tan CG GHC GH ∠==，cos GHC ∠=. 即二面角A PD C --………………………………13分解法二：因为 90PAD ∠=︒，所以PA AD ⊥.又因为侧面PAD ⊥底面ABCD ，且侧面PAD 底面ABCD AD =，所以 PA ⊥底面ABCD . 又因为90BAD ∠=︒，所以AB ，AD ，AP 两两垂直. 分别以AB ，AD ，AP 为x 轴， y 轴，z 轴建立空间直角坐标系，如图.设2AD =，则(0,0,0)A ，(1,0,0)B ，(1,1,0)C ，(0,2,0)D ，(0,0,1)P .（Ⅰ）(0,0,1)AP = ，(1,1,0)AC = ，(1,1,0)CD =-,所以 0AP CD ⋅= ，0AC CD ⋅=，所以AP ⊥CD ，AC ⊥CD .又因为AP AC A = ，所以CD ⊥平面PAC . ………………………………4分（Ⅱ）设侧棱PA 的中点是E ，则1(0, 0, )2E ，1(1, 0, )2BE =- .设平面PCD 的一个法向量是(,,)x y z =n ，则0,0.CD PD ⎧⋅=⎪⎨⋅=⎪⎩n n 因为(1, 1, 0)CD =- ，(0, 2,1)PD =-，所以0,20.x y y z -+=⎧⎨-=⎩ 取1x =，则(1, 1, 2)=n .所以1(1, 1, 2)(1, 0, )02BE ⋅=⋅-= n ，所以BE ⊥ n .因为BE ⊄平面PCD ，所以BE 平面PCD . ………………………………8分（Ⅲ）由已知，AB ⊥平面PAD ，所以(1, 0, 0)AB =为平面PAD 的一个法向量.由（Ⅱ）知，(1, 1, 2)=n 为平面PCD 的一个法向量. 设二面角A PD C --的大小为θ，由图可知，θ为锐角，所以cos AB ABθ⋅===n n . 即二面角A PD C --的余弦值为6………………………………13分2. （朝阳文17）如图，在四棱锥P ABCD -中，底面ABCD 为直角梯形，且//AD BC ，90ABC ∠=︒，侧面PAD ⊥底面ABCD ，90PAD ∠=︒. 若12AB BC AD ==. （Ⅰ）求证：CD ⊥平面PAC ；（Ⅱ）设侧棱PA 的中点是E ，求证：BE 平面PCD .解：（Ⅰ）因为 90PAD ∠=︒，所以PA AD ⊥.又因为侧面PAD ⊥底面ABCD ，且侧面PAD 底面ABCD AD =，所以PA ⊥底面ABCD . 而CD ⊂底面ABCD ，所以PA ⊥CD . 在底面ABCD 中，因为90ABC BAD ∠=∠=︒，12AB BC AD ==，所以AC CD AD ==，所以AC ⊥CD . 又因为PA AC A = ，所以CD ⊥平面PAC . ……………………………6分PA B CD QM（Ⅱ）设侧棱PD 的中点为F ，连结BE ，EF ，FC ，则EF AD ，且12EF AD =. 由已知90ABC BAD ∠=∠=︒，所以BC AD . 又12BC AD =，所以BC EF . 且BC EF =.所以四边形BEFC 为平行四边形，所以BE CF . 因为BE ⊄平面PCD ，CF ⊂平面PCD ，所以BE 平面PCD . ………………………………………………………13分3. （丰台理16）如图，在四棱锥P -ABCD 中，底面ABCD 为直角梯形，AD //BC ，∠ADC =90°，平面PAD ⊥底面ABCD ，Q 为AD 的中点，M 是棱PC 上的点，PA =PD =2，BC =12AD =1，CD （Ⅰ）若点M 是棱PC 的中点，求证：PA // 平面BMQ ；（Ⅱ）求证：平面PQB ⊥平面PAD ；（Ⅲ）若二面角M -BQ -C 为30°，设PM =tMC ，试确定t 的值．证明：（Ⅰ）连接AC ，交BQ 于N ，连接MN ．∵BC ∥AD 且BC =12AD ，∴四边形BCQA 为平行四边形，且N 为AC 中点，又∵点M 在是棱PC 的中点，∴ MN // PA ∵ MN ⊂平面MQB ，PA ⊄平面MQB ， ∴ PA // 平面MBQ ．（Ⅱ）∵AD // BC ，BC =12AD ，Q 为AD 的中点， ∴四边形BCDQ 为平行四边形，∴CD // BQ ． ∵∠ADC =90° ∴∠AQB =90° 即QB ⊥AD ．又∵平面PAD ⊥平面ABCD 且平面PAD ∩平面ABCD=AD ， ∴BQ ⊥平面PAD ．∵BQ ⊂平面PQB ，∴平面PQB ⊥平面PAD ． …………………9分另证：AD // BC ，BC =12AD ，Q 为AD 的中点， ∴ 四边形BCDQ 为平行四边形，∴CD //∵ ∠ADC =90° ∴∠AQB =90°． ∵ PA =PD ， ∴PQ ⊥AD ．∵ PQ ∩BQ =Q ， ∴AD ⊥平面PBQ ． ∵ AD ⊂平面PAD ，∴平面PQB PAD ．……9分（Ⅲ）∵PA =PD ，Q 为AD 的中点， ∴PQ ⊥AD ．∵平面PAD ⊥平面ABCD ，且平面PAD ∩平面ABCD=AD ， PA BCDQM∴PQ ⊥平面ABCD ．如图，以Q 为原点建立空间直角坐标系．则平面BQC 的法向量为(0,0,1)n =；(0,0,0)Q，P ，B，(1C -．设(,,)M x y z，则(,,PM x y z =，(1,)MC x y z =---， ∵PM tMC = ，∴(1))(x t x y t y z t z =--⎧⎪=⎨⎪=-⎩）， ∴11t x t y t z ⎧=-⎪+⎪⎪=⎨+⎪⎪=⎪⎩ …………………12分在平面MBQ中，QB =，(1t QM t =-+ ，∴ 平面MBQ法向量为)m t =．∵二面角M -BQ -C 为30°，c o s 30n m n m ︒⋅===∴ 3t =． ……………………14分4. （丰台文16）如图，在四棱锥P ABCD -中，底面ABCD 为直角梯形，AD //BC ，∠ADC =90°，BC =12AD ，PA =PD ，Q 为AD 的中点．（Ⅰ）求证：AD ⊥平面PBQ ；（Ⅱ）若点M 在棱PC 上，设PM =tMC ，试确定t 的值，使得PA //平面BMQ ．证明：（Ⅰ）AD // BC ，BC =12AD ，Q 为AD 的中点， ∴ 四边形BCDQ 为平行四边形， ∴CD // BQ ． ∵ ∠ADC =90° ∴∠AQB =90° 即QB ⊥AD ． ∵ PA =PD ，Q 为AD 的中点， ∴PQ ⊥AD ． ∵ PQ ∩BQ =Q ，∴AD ⊥平面PBQ ． ……………………6分C（Ⅱ）当1t =时，PA //平面BMQ ．连接AC ，交BQ 于N ，连接MN ． ∵BC //12DQ ， ∴四边形BCQA 为平行四边形，且N 为AC 中点， ∵点M 是线段PC 的中点， ∴ MN // PA ．∵ MN ⊂平面BMQ ，PA ⊄平面BMQ ，∴ PA // 平面BMQ ． ……………………13分5. （门头沟理16）已知四棱锥P ABCD -的底面ABCD 为菱形，且060,ABC ∠=2PB PD AB ===，PA PC =，AC 与BD 相交于点O .（Ⅰ）求证：⊥PO 底面ABCD ；（Ⅱ）求直线PB 与平面PCD 所成角的正弦值；（Ⅲ）若M 是PB 上的一点，且PB CM ⊥，求PM MB的值．（Ⅰ）证明：因为ABCD 为菱形，所以O 为,AC BD 的中点……………………………1分因为,PB PD PA PC ==,所以,PO BD PO AC ⊥⊥所以⊥PO 底面 ABCD …………3分（Ⅱ）因为ABCD 为菱形，所以AC BD ⊥建立如图所示空间直角坐标系又060,2ABC PB AB ∠===得1,1OA OB OP === ……………………………4分所以(0,0,1),(0,(1,0,0),P B C D(0,1)PB =- ,(1,0,1)PC =-,1)PD =-……………………5分设平面PCD 的法向量(,,)m x y z =APDCOB有00m PC m PD ⎧=⎪⎨=⎪⎩所以00x z z -=⎧⎪-=解得x z y z =⎧⎪⎨=⎪⎩所以m =……………………………8分cos ,m PB m PB m PB =cos ,7m PB ==- ……………………………9分 PB 与平面PCD…………………10分（Ⅲ）因为点M 在PB 上,所以(0,1)PM PB λλ==-所以(0,,1)M λ-+, (1,,1)CM λ=--+因为PB CM ⊥所以 0CM PB = , 得310λλ+-= 解得14λ=所以13PMMB = ……………………………14分6. （门头沟文16）如图所示，PA 垂直矩形ABCD 所在的平面， F E 、分别为PC AB 、的中点。

北京各区2018年高中高三一模解析几何汇编

.【海淀一模】(19) （本小题14分）x 2 y 2 1 （ab 0）的离心率为 3 ，且点T(2,1)在椭圆C 上，设已知椭圆C ：2 b 2 2 a与OT 平行的直线l 与椭圆C 订交于P ，Q 两点，直线TP ，TQ 分别与x 轴正半轴交于M ，两点．求椭圆C 的标准方程； (Ⅱ)判断OM ON 的值能否为定值，并证明你的结论．（19）（本小题 14分） 4 11 a2b 2（Ⅰ）由题意a 2b 2c 2，c 3e2a解得：a 22，b2，c6 故椭圆C 的标准方程为 x 2 y 21·······························5分8 2（Ⅱ）假定直线 TP 或TQ 的斜率不存在，则P 点或Q 点的坐标为(2，－1)，直线l 的方程为112(x2)，即y 2x2.y1x 2 y 218 2联立方程，得x 2 4x40，y1 2x2此时，直线 l 与椭圆C 相切，不合题意 .故直线TP 和TQ 的斜率存在.方法1：设P(x 1,y 1)，Q(x 2,y 2)，则直线TP:y1y 1 1(x2)，x 1 2直线TQ:y1y 2 1(x2)x 2 2x 12x 2 2故|OM|2，|ON|21y 11 y 2;...由直线OT:y1x ，设直线PQ:y1x t （t 0）22x 2 y 2 182x 22tx 2t 24 0联立方程，1xy t2当0时，x 1 x 22t ，x 1x 22t 24|OM||ON|4(x12x 2 2)y 11 y2 14 (x 1 2x 2 21x)1xt1 t12 12 24x 1x 2 (t 2)(x 1 x 2) 4(t1)1124 x 1x 2 2 (t1)(x 1x 2)(t1)42t 2 4 (t2)(2t) 4(t1)1(t1)(1(2t 24)2t)(t1)242···································14分方法2：设P(x 1,y 1)，Q(x 2,y 2)，直线 TP 和TQ的斜率分别为k1和k2由OT:y1x ，设直线PQ:y1x t （t 0）22x 2 y 218222联立方程，x 2tx 2t 401xy t2当0时，x 1 x 22t ，x 1x 22t 24k 1 k 2y 1 1 y 2 1x 1 2x 2 21x 1 t 1 1x 2 t 12 2 x 1 2x 2 2x 1x 2 (t2)(x 1 x 2) 4(t 1)(x 1 2)(x 22);...2t 24 (t 2)(2t) 4(t 1)(x 1 2)(x 2 2)故直线TP 和直线TQ 的斜率和为零故 TMN TNM故TMTN故T 在线段MN 的中垂线上，即MN 的中点横坐标为2故|OM| |ON| 4···································14分【东城一模】(18)（本小题13分）已知椭圆C ：x 2y 21（ab0）的离心率为3，且过点A(2,0).a 2b 22（Ⅰ）求椭圆C 的方程；(II ）设M,N 是椭圆C 上不一样于点A 的两点，且直线AM ，AN 斜率之积等于1 ，试问直4线MN 能否过定点？假如，求出该点的坐标；若不是，请说明原因．（19）（本小题14分）411a 2b 2（Ⅰ）由题意a 2b 2c 2 ，ec 3a2解得：a2 2，b2，c6故椭圆C 的标准方程为x 2 y 2 1·······························5分8 2（Ⅱ）假定直线 TP 或TQ 的斜率不存在，则 P 点或Q 点的坐标为(2，－1)，直线l 的方程为y11(x2)，即y1x2 .22x 2 y 218 2联立方程，得x 24x40，y 1x 22此时，直线 l 与椭圆C 相切，不合题意 .故直线TP 和TQ 的斜率存在.;...方法1：设P(x1,y1)，Q(x2,y2)，则直线TP:y1y11(x2)，x12直线TQ:y1y21 (x2)x22故|OM|2x12，|ON|2x22 y11y21由直线OT:y 1x，设直线PQ:y1x t（t0）22x2y218222联立方程，x2tx2t401xy t2当0时，x1x22t，x1x22t24|OM||ON|4(x12x22)y11y214(x12x221x2) 1x1t1t1 224x1x2(t2)(x1x2)4(t1) 1xx1(t1)(x x)(t1)2 41221242t24(t2)(2t)4(t1) 1(2t24)1(t1)(2t)(t1)2 42···································14分方法2：设P(x1,y1)，Q(x2,y2)，直线TP和TQ的斜率分别为k1和k2由OT:y 1x，设直线PQ:y1x t（t0）22x2y218222联立方程，x2tx2t401xy t2;..当0时，x1x22t，x1x22t24k1k2y11y21x12x221x1t11x2t122x12x22x1x2(t2)(x1x2)4(t1)(x12)(x22)2t24(t2)(2t)4(t1)(x12)(x22)故直线TP和直线TQ的斜率和为零故TMN TNM故TMTN故T在线段MN的中垂线上，即MN的中点横坐标为2故|OM| |ON|4···································14分【西城一模】19．（本小题满分14分）已知圆O:x2y24和椭圆C:x22y24，F是椭圆C的左焦点．（Ⅰ）求椭圆C的离心率和点F的坐标；（Ⅱ）点P在椭圆C上，过P作x轴的垂线，交圆O于点Q（P,Q不重合），l是过点Q的圆O的切线．圆F的圆心为点F，半径长为|PF|．试判断直线l与圆F的地点关系，并证明你的结论．解：（Ⅰ）由题意，椭圆C的标准方程为x2y21．[1分] 42所以a24，b22，进而c2a2b22．所以a2，c2．故椭圆C的离心率e c2．[3分]a2椭圆C的左焦点F的坐标为(2,0)．[4分]（Ⅱ）直线l与圆F相切．证明以下：[5分]设P(x0,y0)，此中2x02，则x022y024，[6分] ;..依题意可设Q(x 0,y 1)，则x 02y 124．[7 分]直线l的方程为y y 1x 0(x x 0)，y 1整理为 x 0xy 1y 4 0．[ 9分]所以圆F 的圆心F 到直线l的距离d| 2x 04| | 2x 2|．[11分]x 02 y 122由于|PF|2(x2)2y2(x2)21(4x2) 1x 2 22x4．[13分]0 022所以|PF|2 d 2，即|PF|d ，所以直线l 与圆F 相切．[14分]【旭日一模】19．(本小题满分 14分)222，且过点(1,已知椭圆C:x2y 2 1(a b 0)的离心率为2 )．ab22（Ⅰ）求椭圆C 的方程；（Ⅱ）过椭圆C 的左焦点的直线l 1 与椭圆C 交于A,B 两点，直线l 2 过坐标原点且与直线l 1的斜率互为相反数．若直线l 2 与椭圆交于E,F 两点且均不与点A,B 重合，设直线AE 与x 轴所成的锐角为 1，直线BF 与x 轴所成的锐角为2，判断1与2大小关系并加以证明．19．(本小题满分 14分)c2,a2解：（Ⅰ）由题意得a 2b 2 2 ,解得a 2， b1 ，c．c 11 1 1.a22b22故椭圆C 的方程为xy 2 1．..5分2（Ⅱ）1=2．证明以下：由题意可设直线 l 1的方程为yk(x 1)，直线l 2 的方程为y kx ，设点A(x 1,y 1)，;..B(x 2,y 2) ，E(x 3,y 3)， F(x 3, y 3)．要证1=2，即证直线 AE 与直线BF 的斜率之和为零，即k AE k BF 0．由于k AEkBFy 1 y 3 y 2 y 3x 1 x 3 x 2x 3k(x 1 1)kx 3k(x 2 1)kx 3x 1 x 3 x 2 x 3k[2xx(xx) 2x 2]12 12x 3)3．(x 1 x 3)(x 2yk(x1),由x 2y2得(1 2k 2 )x 24k 2 x 2k 22 0 ，1,222所以x 1x 21 4k ，x 1x 22k2 ．2k 2 1 2k 2ykx,2由 x 2得(1 2k 2)x 22，所以 22．y2 1,x 31 2k2所以2x 1x 2(x 1 2 4k 244k 24．x 2)2x 3 121 2k 21202k2kkAEkBFk[2x 1x 2 (x 1 x 2) 2x 32]0 ．(x 1 x 3)(x 2 x 3)所以1=2．..14分【丰台一模】（19）（本小题共 14分）3x 2 y 21(ab0)上，F(1,0)是椭圆的一个焦点．已知点P(1,)在椭圆C ：b 2 2a 2（Ⅰ）求椭圆C 的方程；（Ⅱ）椭圆C 上不与P 点重合的两点D ，E 对于原点O 对称，直线PD ，PE 分别交y 轴于M ，N 两点．求证：以MN 为直径的圆被直线 y3 截得的弦长是定值．2（19）（本小题共14分）解：（Ⅰ）依题意，椭圆的另一个焦点为F(1,0)，且c1．1分由于2a22(3)22(3)24，22;..所以a 2，ba 2 c 23，⋯⋯⋯⋯⋯⋯⋯⋯3分所以C 的方程x 2y 2 1．⋯⋯⋯⋯⋯⋯⋯⋯4分4 3（Ⅱ）明：由意可知D ，E 两点与点P 不重合．因D ，E 两点对于原点称，所以D(m,n)，E( m, n)，(m1)．⋯⋯⋯⋯⋯⋯⋯⋯5分以MN 直径的与直y3 交于G(t,3),H(t,3)(t0)两点，所以GM GN ．222⋯⋯⋯⋯⋯⋯⋯⋯6分3n直PD ：y32(x1)．2m1当x 0，y3 直PE ：y2n33 n 32 ，所以M(0, 2 m 1 2 m 1n 32 (x1)． m13)．⋯⋯⋯⋯⋯⋯7分2 n 33n当x0，y2 m 13，所以N(0,22m13)．⋯⋯⋯⋯⋯⋯⋯⋯8分2n33n所以GM (t,2)，m1GN(t,2)，m 1⋯⋯⋯⋯⋯⋯⋯⋯ 9分因GMGN ，所以GMGN0，⋯⋯⋯⋯⋯⋯⋯⋯10分2所以GM GNt 24n 2 9 0． ⋯⋯⋯⋯⋯⋯⋯⋯11分4(m 1)因m 2n 2 1，即3m 2 4n 212，4n 2 93 3m 2，⋯⋯⋯⋯⋯⋯12分43所以t23 0，所以t3⋯⋯⋯⋯⋯⋯⋯⋯13分4．2所以G(3,3)，H(3,3)，所以GH3．2 2 2 2所以以MN 直径的被直y3 3．⋯⋯⋯⋯14分截得的弦是定2【石景山一模】18．（本小共 13分）;...在平面直角坐标系xOy中，动点E到定点(1,0)的距离与它到直线x1的距离相等．（Ⅰ）求动点E的轨迹C的方程；（Ⅱ）设动直线 l:y kx b与曲线C相切于点P，与直线x1订交于点Q．证明：以PQ为直径的圆恒过x轴上某定点．18．（本小题共13分）（Ⅰ）解：设动点E的坐标为(x,y)，由抛物线定义知，动点E的轨迹是以(1,0)为焦点，x1为准线的抛物线，所以动点E的轨迹C的方程为y24x．5分y kxb4y4b0．（Ⅱ）证明：由，消去x得：ky2y24x由于直线l与抛物线相切，所以16-16kb0，即b 1．8分k所以直线l的方程为y kx 1．k令x1，得y k1．k所以Q1,k1．10分k设切点坐标P(x0,y0)，则ky024y0+40，k12解得：P( , )，11分设M(m,0)，MQMP 1m(1m)21)2m1 k2k(k=m m2k2k所以当m2m2=0，即m1时，MQMP0m-10所以MQ MP所以以PQ为直径的圆恒过x轴上定点M(1,0)．13分;..。

2018届北京市西城区高三第一次模拟考试卷数学(理)附答案

2018届北京市西城区高三第一次模拟考试卷数学（理）附答案第Ⅰ卷（选择题共40分）一、选择题：本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．若集合，，则（）A．B．C．D．2．执行如图所示的程序框图，输出的值为（）A．2 B．3 C．4 D．53．已知圆的方程为．以原点为极点，轴正半轴为极轴建立极坐标系，该圆的极坐标方程为（）A．B．C．D．4．正三棱柱的三视图如图所示，该正三棱柱的表面积是（）A ．B ．C ．D ．5．已知是正方形的中心．若，其中，，则（）A ．B ．C ．D ．6．设函数．则“有两个不同的零点”是“，使”的（）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件7．函数，则的图象上关于原点对称的点共有（）A ．0对B ．1对C ．2对D ．3对8．某计算机系统在同一时间只能执行一项任务，且该任务完成后才能执行下一项任务．现有三项任务，，，计算机系统执行这三项任务的时间（单位：）依次为，，，其中．一项任务的“相对等待时间”定义为从开始执行第一项任务到完成该任务的时间与计算机系统执行该任务的时间之比．下列四种执行顺序中，使三项任务“相对等待时间”之和最小的是（） A ．B ．C ．D ．U V W s U V W →→V W U →→W U V →→U W V→→第Ⅱ卷（非选择题共110分）二、填空题：本大题共6小题，每小题5分，共30分．9．若复数的实部与虚部相等，则实数____．10．设等差数列的前项和为，若，，则____；____．11．已知抛物线的焦点与双曲线的一个焦点重合，则____；双曲线的渐近线方程是____________．12．设，若函数的最小正周期为，则____．13．安排甲、乙、丙、丁4人参加3个运动项目，每人只参加一个项目，每个项目都有人参加．若甲、乙2人不能参加同一个项目，则不同的安排方案的种数为____．（用数字作答）14．如图，在长方体中，，，点在侧面上．若点到直线和的距离相等，则的最小值是____．三、解答题：本大题共6小题，共80分．解答应写出必要的文字说明、证明过程或演算步骤．15．（13分）在△中，已知．（1）求的大小；（2）若，，求△的面积．16．（13分）某企业2017年招聘员工，其中、、、、五种岗位的应聘人数、录用人数和录用比例（精确到1%）如下：（1 （2）从应聘岗位的6人中随机选择2人．记为这2人中被录用的人数，求的分布列和数学期望；（3）表中、、、、各岗位的男性、女性录用比例都接近（二者之差的绝对值不大于5%），但男性的总录用比例却明显高于女性的总录用比例．研究发现，若只考虑其中某四种岗位，则男性、女性的总录用比例也接近，请写出这四种岗位．（只需写出结论）A B C D E E A B C D E17．（14分）如图1，在△中，，分别为，的中点，为的中点，，．将△沿折起到△的位置，使得平面平面，如图2．（1）求证：；（2）求直线和平面所成角的正弦值；（3）线段上是否存在点，使得直线和所成角的余弦值为？若存在，求出的值；若不存在，说明理由．图1 图218．（13分）已知函数，其中．（1）若曲线在处的切线与直线垂直，求的值；（2）当时，证明：存在极小值．19．（14分）已知圆和椭圆，是椭圆的左焦点．（1）求椭圆的离心率和点的坐标；（2）点在椭圆上，过作轴的垂线，交圆于点（不重合），是过点的圆的切线．圆的圆心为点，半径长为．试判断直线与圆的位置关系，并证明你的结论．20．（13分）数列：满足：．记的前项和为，并规定．定义集合．（1）对数列：，，，，，求集合；（2）若集合，证明：；（3）给定正整数．对所有满足的数列，求集合的元素个数的最小值．2018届北京市西城区高三第一次模拟考试卷数学（理）答案一、选择题：本大题共8小题，每小题5分，共40分．1-5．DCBDB 6-8．CCA二、填空题：本大题共6小题，每小题5分，共30分．9．10．6，11．，12．213．30 14．注：第10，11题第一空3分，第二空2分．三、解答题：本大题共6小题，共80分．其他正确解答过程，请参照评分标准给分．15．【答案】（1）；（2）见解析．【解析】（1）因为，所以．在△中，由正弦定理得，所以．因为，所以．（2）在△中，由余弦定理得，所以，整理得，解得，或，均适合题意．当时，△的面积为．当时，△的面积为．16．【答案】（1）；（2）分布列见解析，；（3）、、、．【解析】（1）因为表中所有应聘人员总数为，被该企业录用的人数为，所以从表中所有应聘人员中随机选择1人，此人被录用的概率约为．（2）X 可能的取值为0，1，2．因为应聘E 岗位的6人中，被录用的有4人，未被录用的有2人，所以；；．所以X 的分布列为：．（3）这四种岗位是：、、、．17．【答案】（1）见解析；（2）；（3）存在，．【解析】（1）因为在△中，，分别为，的中点，()43E X =B C DE B C D E所以，．所以，又为的中点，所以．因为平面平面，且平面，所以平面，所以．（2）取的中点，连接，所以．由（1）得，．如图建立空间直角坐标系．由题意得，，，，．所以，，．设平面的法向量为，则，即，令，则，，所以．设直线和平面所成的角为，则．所以直线和平面所成角的正弦值为．（3）线段上存在点适合题意．设，其中．设，则有，所以，从而，所以，又，所以．令，整理得．解得，舍去．所以线段上存在点适合题意，且．18．【答案】（1）；（2）见解析．【解析】（1）的导函数为．依题意，有，解得．（2）由及知，与同号．令，则．所以对任意，有，故在单调递增．因为，所以，，故存在，使得．与在区间上的情况如下：↘极小值↗所以在区间上单调递减，在区间上单调递增．所以存在极小值．19．【答案】（1），；（2）相切，证明见解析．【解析】（1）由题意，椭圆的标准方程为．所以，，从而．因此，．故椭圆的离心率，椭圆的左焦点的坐标为．（2）直线与圆相切．证明如下：设，其中，则，依题意可设，则．直线的方程为，整理为．所以圆的圆心到直线的距离．因为．所以，e =()F即，所以直线与圆相切．20．【答案】（1）；（2）见解析；（3）．【解析】（1）因为，，，，，，所以．（2）由集合的定义知，且是使得成立的最小的k，所以．又因为，所以，所以．（3）因为，所以非空．设集合，不妨设，则由（2）可知，同理，且．所以．因为，所以的元素个数．取常数数列：，并令，则，适合题意，且，其元素个数恰为．综上，的元素个数的最小值为．。

2018北京六区高三一模数学(文)汇编--立体几何

2018北京六区高三一模数学（文）汇编--立体几何【海淀一模】(18)（本小题14分）如图，四棱锥E ABCD -中，1//,12AD BC AD Ab AE BC ====，且BC ⊥平面ABE ，M 为棱CE 的中点．(I)求证：DM ∥平面ABE ; (Ⅱ)求证：平面CDE ⊥平面CBE ;(Ⅲ)当四面体D ABE -的体积最大时，判断直线AE 与直线CD 是否垂直，并说明理由．18．（Ⅰ）证明：取线段EB 的中点N ，连接,MN AN .DABCMEN因为M 为棱CE 的中点，所以在CBE ∆中//MN BC ，12MN BC =. 又//AD BC ，12AD BC =, 所以//,MN AD MN AD =.所以四边形DMNA 是平行四边形, 所以//DM AN . 又DM ⊄平面ABE , AN ⊂平面ABE ,所以//DM 平面ABE . （Ⅱ）因为AE AB =,N 为EB 中点,所以AN BE ⊥. 又BC ⊥平面ABE ,AN ⊂平面ABE ,所以BC AN ⊥ 又BCBE B =,所以AN ⊥平面BCE . 又//DM AN ，所以DM ⊥平面BCE . 因为DM⊂平面CDE ,所以平面CDE ⊥平面CBE . .…………………….…9分（Ⅲ）AE CD ⊥. 设EAB θ∠=，1AD AB AE ===则四面体D ABE -的体积 sin V AE AB AD θ⨯⋅⋅⋅11=321sin 6θ=. 当90θ=︒，即AE AB ⊥时体积最大. 又BC ⊥平面ABE ,AE ⊂平面ABE ,所以AE BC ⊥. 因为BCAB B =,所以AE ⊥平面ABC . 因为CD ⊂平面ABCD ，所以AE CD ⊥. .…………………….…14分【西城一模】18．（本小题满分14分）如图1，在△ABC 中，D ，E 分别为AB ，AC 的中点，O 为DE 的中点，AB AC ==，4BC =．将△ADE 沿DE 折起到△1A DE 的位置，使得平面1A DE ⊥平面BCED ，F 为1A C 的中点，如图2．（Ⅰ）求证：//EF 平面1A BD ；（Ⅱ）求证：平面1A OB ⊥平面1A OC ；（Ⅲ）线段OC 上是否存在点G ，使得OC ⊥平面EFG ？说明理由．图1 图218．（本小题满分14分）解：（Ⅰ）取线段1A B 的中点H ，连接HD ，HF ．[1分]因为在△ABC 中，D ，E 分别为AB ，AC 的中点，所以 //DE BC ，12DE BC =．因为 H ，F 分别为1A B ，1A C 的中点，所以 //HF BC ，12HF BC =，所以 //HF DE ，HF DE =，所以四边形DEFH 为平行四边形，[3分] 所以 //EF HD ．[ 4分]因为 EF ⊄平面1A BD ， HD ⊂平面1A BD ，所以 //EF 平面1A BD ．[ 5分]（Ⅱ）因为在△ABC 中，D ，E 分别为AB ，AC 的中点，所以 AD AE =．所以11A D A E =，又O 为DE 的中点，所以 1A O DE ⊥．[ 6分]因为平面1A DE ⊥平面BCED ，且1A O ⊂平面1A DE ，所以 1A O ⊥平面BCED ，[ 7分] 所以 1CO A O ⊥．[ 8分]在△OBC 中，4BC =，易知 OB OC == 所以 CO BO ⊥，所以 CO ⊥平面1A OB ，[ 9分] 所以平面1A OB ⊥平面1A OC ．[10分]（Ⅲ）线段OC 上不存在点G ，使得OC ⊥平面EFG ．[11分] 否则，假设线段OC 上存在点G ，使得OC ⊥平面EFG ，连接 GE ，GF ，则必有 OC GF ⊥，且OC GE ⊥．A在Rt △1A OC 中，由F 为1A C 的中点，OC GF ⊥，得G 为OC 的中点．[12分] 在△EOC 中，因为OC GE ⊥，所以EO EC =，这显然与1EO =，EC 矛盾！所以线段OC 上不存在点G ，使得OC ⊥平面EFG ．[14分]【东城一模】（18）（本小题14分）如图，四边形ABCD 为菱形，60DAB ∠=o ，ED ⊥平面ABCD ，22ED AD EF ===，EF ∥AB ，M 为BC 中点．（Ⅰ）求证：FM ∥平面BDE ；（Ⅱ）求证：AC BE ⊥；（Ⅲ）若G 为线段BE 上的点，当三棱锥G BCD -的体积为9时，求BGBE的值．（18）（共14分）解：（Ⅰ）设，连结．因为分别是的中点，因为EF //AB ，且12EF=AB ，因为OM //AB ，且12OM=AB ， AC BD O =I ,EO MO ,M O ,BC BD所以EF //OM ，且EF=OM ．所以四边形EOMF 为平行四边形．所以∥．又因为平面，平南，所以FM ∥平面BDE ． ………5分（Ⅱ）因为ABCD 为菱形，所以．因为平面ABCD ，所以．因为，所以平面．又因为平面，所以AC BE ⊥． ………10分（Ⅲ）过作ED 的平行线交BD 于．由已知ED ⊥平面ABCD ，所以平面ABCD ．所以为三棱锥的高．因为三棱锥G BCD -的体积为9，所以三棱锥G BCD -的体积11sin 6032V BD BC GH =⨯⋅⋅⋅⋅=o ．所以． FM EO EO ⊂BDE FM ⊄BDE AC BD ⊥ED ⊥ED AC ⊥BD ED D =I AC ⊥BDE BE ⊂BDE G H GH ⊥GH G BCD -23GH =A所以21323GH BG ED BE ===．所以13BG =BE ． ………14分【朝阳一模】18.（本小题满分14分）如图1，在梯形ABCD 中，//BC AD ，1BC =，3AD =，BE AD ⊥于E ，1BE AE ==．将ABE ∆沿BE 折起至A BE '∆，使得平面A BE '⊥平面BCDE （如图2），M 为线段A D '上一点．（Ⅰ）求证：A E CD '⊥；（Ⅱ）若M 为线段A D '中点，求多面体A BCME '与多面体MCDE 的体积之比；（Ⅲ）是否存在一点M ，使得A B '//平面MCE ？若存在，求A M '的长．若不存在，请说明理由．18. （本小题满分14分）证明：（Ⅰ）如图1，在梯形中，因为，所以（如图2）．因为平面平面，且平面平面，所以平面．又因为平面，所以． ……………… 4分（Ⅱ）解：由（Ⅰ）可知平面，所以，．过点作于，则，所以平面．因为为中点，，所以． ABCD BE AD ⊥BE A E '⊥A BE '⊥BCDE A BE 'BCDE BE =A E '⊥BCDE CD ⊂BCDE A E CD '⊥A E '⊥BCDE A E BE '⊥A E DE '⊥M MH DE ⊥H //MH A E 'MH ⊥BCDE M A D '1A E '=12MH =图1EABC D图2C BMDA 'ECBMDA ′EH设四棱锥的体积为，则．设三棱锥的体积为，则．所以12111263A BCME V V V '=-=-=多面体所以11::2:136A BCME MCDE V V '==多面体多面体． ……………… 9分（Ⅲ）解：存在一点M ，使得平面MCE ．理由如下：连结交于，连结，则平面平面．由平面，得．所以．在梯形中，因为，所以∽．又因为，，所以．于是12A M MD '=，所以13A M AD '=．又因为1A E '=，，所以A D '=．故A M '…………14分【丰台一模】（17）（本小题共14分）如图所示，在四棱锥P ABCD -中，平面PAB ⊥平面ABCD ，//AD BC ，=2AD BC ，90DAB ABP ∠=∠=︒．（Ⅰ）求证：AD ⊥平面PAB ；（Ⅱ）求证：AB ⊥PC ；A BCDE '-1V 111111()(12)1133262BCDE V S A E BC DE BE A E ''=⋅⋅=⨯+⋅⋅=+⨯⨯=四边形M CDE -2V 211111121332626CDE V S MH DE BE MH ∆=⋅⋅=⨯⋅⋅=⨯⨯⨯=//A B 'BD CE N MN A BD'MCE MN =//A B 'MCE //A B MN '::A M MD BN ND '=BCDE //BC DE BNC ∆DNE ∆1BC =2DE =::1:2BN ND BC DE ==2DE =（Ⅲ）若点E 在棱PD 上，且CE ∥平面PAB ，求PEPD的值．（17）（本小题共14分）（Ⅰ）证明：因为90DAB ∠=︒，所以AD ⊥AB ． ……………………1分因为平面PAB ⊥平面ABCD ， ……………………2分且平面PAB I 平面=ABCD AB ， ……………………3分所以AD ⊥平面PAB ． ……………………4分（Ⅱ）证明：由已知得AD ⊥AB因为AD BC ∥，所以BC ⊥AB ． ……………………5分又因为90ABP ∠=︒，所以PB ⊥AB ． ……………………6分因为=PB BC B I ……………………7分所以AB ⊥平面PBC ……………………8分所以AB ⊥PC ． ……………………9分（Ⅲ）解：过E 作EF AD ∥交PA 于F ，连接BF ． ……………………10分因为AD BC ∥，所以EF BC ∥．所以E ，F ，B ，C 四点共面． ……………………11分又因为CE ∥平面PAB ，且CE ⊂平面BCEF ，且平面BCEF I 平面=PAB BF ，所以CE BF ∥， ……………………13分所以四边形BCEF 为平行四边形，所以=EF BC ．在△PAD 中，因为//EF AD ，所以1===2PE EF BC PD AD AD ， ……………………14分即1=2PE PD ．【石景山一模】18．（本小题共14分）如图，在三棱锥D ABC -中，已知BCD △是正三角形，AB ⊥平面BCD ，AB BC a ==，E 为BC 的中点，F 在棱AC 上，且3AF FC =．（Ⅰ）求三棱锥D ABC -的体积；（Ⅱ）求证：AC ⊥平面DEF ；（Ⅲ）若M 为DB 中点，N 在棱AC 上，且38CN CA =，求证：MN //平面DEF ． 18.（本小题14分）解：（Ⅰ）因为BCD △是正三角形，且AB BC a ==，所以24BCD S =△．………………2分又AB ⊥平面BCD ，………………3分故13D ABC A BCD V V AB --==⋅⋅S △BCD 2134a =⋅312a =．………………4分（Ⅱ）在底面ABC 中，取AC 的中点H ，连接BH ，因AB BC =，故BH AC ⊥．因3AF FC =，故F 为CH 的中点．又E 为BC 的中点，故EF ∥BH ，ABCDNFM EABDN M E HO故EF AC ⊥．……5分因AB ⊥平面BCD ，AB ⊂平面ABC ，故平面ABC ⊥平面BCD ．BCD △是正三角形，E 为BC 的中点，故DE BC ⊥，故DE ⊥平面ABC ．………………7分AC ⊂平面ABC ，故DE ⊥AC ．………………8分又DE EF E ⋂=，故AC ⊥平面DEF ．………………9分（Ⅲ）当38CN CA =时，连CM ，设CM DE O ⋂=，连OF ．因E 为BC 的中点，M 为DB 中点，故O 为△BCD 的重心，23CO CM =．………………10分因3AF FC =，38CN CA =，故23CF CN =，所以MN ∥OF ．………………12分又OF ⊂平面DEF ，MN ⊄平面DEF ，所以MN ∥平面DEF ．……14分。

2018北京六区高三一模数学(理)解答题分类汇编--立体几何

ቤተ መጻሕፍቲ ባይዱ2y
2z
0,
y 2z 0.
n A1 D 0,
令 x 1，则 y 2 ， z 1 ，所以 n (1,2, 1) ． [7 分 ]
设直线 A1C 和平面 A1BD 所成的角为，
则 sin
| cos n, A1C | | n A1C | | n || A1C |
2 2． 3
所以直线 A1C 和平面 A1 BD 所成角的正弦值为
（Ⅲ）在线段 A C 上是否存在点 P ，使得 OP // 平面 A DE ? 若存在，求出 A P 的值；若不存在，请说明理由． AC
A
E
D
O
A
E D
O
B
C
B
C
图
图
1
2
证明：（Ⅰ）由已知 AB AE 2 ，
因为 O 为 BE 中点，所以 A O BE ．因为平面 A BE 平面 BCDE ，且平面 A BE 平面 BCDE
所以 DE // BC ， AD AE ．
所以 A1D A1E ，又 O 为 DE 的中点，所以 A1O DE ． [1 分 ] 因为平面 A1DE 平面 BCED ，且 A1O 平面 A1DE ，所以 A1O 平面 BCED ， [3 分] 所以 A1O BD ． [ 4 分 ] （Ⅱ）取 BC 的中点 G ，连接 OG ，所以 OE OG ．由（Ⅰ）得 A1O OE ， A1O OG ．如图建立空间直角坐标系 O - xyz ． [5 分]
由题意得， A1 (0,0,2) ， B(2, 2,0) ， C (2,2,0) ， D(0, 1,0) ．
1 / 11
所以 A1B (2, 2, 2) ， A1D (0, 1, 2) ， A1C (2,2, 2) ．设平面 A1BD 的法向量为 n (x , y , z) ，

高考文科数学总复习——真题汇编之立体几何含参考答案

高考文科数学总复习——真题汇编之立体几何（含参考答案）一、选择题1.【2018全国一卷5】已知圆柱的上、下底面的中心分别为1O ，2O ，过直线12O O 的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为 A ．122πB ．12πC ．82πD ．10π2.【2018全国一卷9】某圆柱的高为2，底面周长为16，其三视图如图．圆柱表面上的点M 在正视图上的对应点为A ，圆柱表面上的点N 在左视图上的对应点为B ，则在此圆柱侧面上，从M 到N 的路径中，最短路径的长度为 A ．172B ．52C ．3D ．23.【2018全国一卷10】在长方体1111ABCD A B C D -中，2AB BC ==，1AC 与平面11BB C C 所成的角为30︒，则该长方体的体积为 A ．8B ．62C ．82D ．834.【2018全国二卷9】在正方体中，为棱的中点，则异面直线与所成角的正切值为 A ．B ．C ．D ．5.【2018全国三卷3】中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是1111ABCD A B C D -E 1CC AE CD 23576.【2018全国三卷12】设是同一个半径为4的球的球面上四点，为等边三角形且其面积为，则三棱锥体积的最大值为A ．B ．C ．D ．7.【2018北京卷6】某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为A.1B.2C.3D.4第7题图第8题图8.【2018浙江卷3】某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：cm 3）是 A ．2B ．4C ．6D ．8A B C D ，，，ABC△D ABC俯视图正视图22119.【2018浙江卷8】已知四棱锥S −ABCD 的底面是正方形，侧棱长均相等，E 是线段AB 上的点（不含端点），设SE 与BC 所成的角为θ1，SE 与平面ABCD 所成的角为θ2，二面角S −AB −C 的平面角为θ3，则 A ．θ1≤θ2≤θ3B ．θ3≤θ2≤θ1C ．θ1≤θ3≤θ2D ．θ2≤θ3≤θ110.【2018上海卷15】《九章算术》中，称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马.设AA ₁是正六棱柱的一条侧棱，如图，若阳马以该正六棱柱的顶点为顶点，以AA ₁为底面矩形的一边，则这样的阳马的个数是（）（A ）4 （B ） 8（C ）12 （D ）16二、填空题1.【2018全国二卷16】已知圆锥的顶点为，母线，互相垂直，与圆锥底面所成角为，若的面积为，则该圆锥的体积为__________．2.【2018天津卷11】如图，已知正方体ABCD –A 1B 1C 1D 1的棱长为1，则四棱锥A 1–BB 1D 1D 的体积为__________．3.【2018江苏卷10】如图所示，正方体的棱长为2，以其所有面的中心为顶点S SA SB SA 30 SAB △8的多面体的体积为．三、解答题1.【2018全国一卷18】如图，在平行四边形ABCM 中，3AB AC ==，90ACM =︒∠，以AC 为折痕将△ACM 折起，使点M 到达点D 的位置，且AB DA ⊥．（1）证明：平面ACD ⊥平面ABC ；（2）Q 为线段AD 上一点，P 为线段BC 上一点，且23BP DQ DA ==，求三棱锥Q ABP -的体积．2.【2018全国二卷19】如图，在三棱锥中，，，为的中点．（1）证明：平面；（2）若点在棱上，且，求点到平面的距离．P ABC-AB BC ==4PA PB PC AC ====O AC PO ⊥ABC M BC 2MC MB =CPOM3.【2018全国三卷19】如图，矩形所在平面与半圆弧所在平面垂直，是上异于，的点．（1）证明：平面平面；（2）在线段上是否存在点，使得平面？说明理由．4.【2018北京卷18】如图，在四棱锥P −ABCD 中，底面ABCD 为矩形，平面PAD ⊥平面ABCD ，PA ⊥PD ，PA =PD ，E ，F 分别为AD ，PB 的中点.（Ⅰ）求证：PE ⊥BC ；（Ⅱ）求证：平面PAB ⊥平面PCD ；（Ⅲ）求证：EF ∥平面PCD .5.【2018天津卷17】如图，在四面体ABCD 中，△ABC 是等边三角形，平面ABC ⊥平面ABD ，点M 为棱AB 的中点，AB =2，AD=BAD =90°．（Ⅰ）求证：AD ⊥BC ；（Ⅱ）求异面直线BC 与MD 所成角的余弦值；（Ⅲ）求直线CD 与平面ABD 所成角的正弦值．ABCD CD M CD C D AMD ⊥BMC AM P MC ∥PBD6.【2018江苏卷15】在平行六面体1111ABCD A B C D -中，1111,AA AB AB B C =⊥．求证：（1）AB ∥平面11A B C ；（2）平面11ABB A ⊥平面1A BC ．7.【2018江苏卷22（附加题）】如图，在正三棱柱ABC -A 1B 1C 1中，AB =AA 1=2，点P ，Q 分别为A 1B 1，BC 的中点．（1）求异面直线BP 与AC 1所成角的余弦值；（2）求直线CC 1与平面AQC 1所成角的正弦值．8.【2018浙江卷19】如图，已知多面体ABCA1B1C1，A1A，B 1B，C1C均垂直于平面ABC，∠ABC=120°，A1A=4，C 1C=1，AB=BC=B1B=2．（Ⅰ）证明：AB1⊥平面A1B1C1；（Ⅱ）求直线AC1与平面ABB1所成的角的正弦值．9.【2018上海卷17】已知圆锥的顶点为P，底面圆心为O，半径为2（1）设圆锥的母线长为4，求圆锥的体积；（2）设PO=4，OA，OB是底面半径，且∠AOB=90°，M为线段AB的中点，如图，求异面直线PM与OB所成的角的大小.参考答案一、选择题1.B2.B3.C4.C5.A6.B7.C8.C9.D 10.D 二、填空题1.π82.31 3.43三、解答题1.解：（1）由已知可得，BAC ∠=90°，BA AC ⊥．又BA ⊥AD ，所以AB ⊥平面ACD ．又AB ⊂平面ABC ，所以平面ACD ⊥平面ABC ．（2）由已知可得，DC =CM =AB =3，DA =32．又23BP DQ DA ==，所以22BP =．作QE ⊥AC ，垂足为E ，则QE =13DC ．由已知及（1）可得DC ⊥平面ABC ，所以QE ⊥平面ABC ，QE =1．因此，三棱锥Q ABP -的体积为1111322sin 451332Q ABP ABP V QE S -=⨯⨯=⨯⨯⨯⨯︒=△．2解：（1）因为AP =CP =AC =4，O 为AC 的中点，所以OP ⊥AC ，且OP =．连结OB ．因为AB =BC =，所以△ABC 为等腰直角三角形，且OB ⊥AC ，OB ==2．2322AC 12AC由知，OP ⊥OB ．由OP ⊥OB ，OP ⊥AC 知PO ⊥平面ABC ．（2）作CH ⊥OM ，垂足为H ．又由（1）可得OP ⊥CH ，所以CH ⊥平面POM ．故CH 的长为点C 到平面POM 的距离．由题设可知OC ==2，CM ==，∠ACB =45°．所以OM =，CH ==．所以点C 到平面POM 的距离为．3.解：（1）由题设知，平面CMD ⊥平面ABCD ，交线为CD ．因为BC ⊥CD ，BC 平面ABCD ，所以BC ⊥平面CMD ，故BC ⊥DM ．因为M 为上异于C ，D 的点，且DC 为直径，所以DM ⊥CM ．又BC ∩CM =C ，所以DM ⊥平面BMC ．而DM 平面AMD ，故平面AMD ⊥平面BMC ．（2）当P 为AM 的中点时，MC ∥平面PBD ．证明如下：连结AC 交BD 于O ．因为ABCD 为矩形，所以O 为AC 中点．连结OP ，因为P 为AM 中点，所以MC ∥OP ．MC 平面PBD ，OP 平面PBD ，所以MC ∥平面PBD ．222OP OB PB +=12AC 23BC 42325sin OC MC ACB OM ⋅⋅∠4545⊂CD ⊂⊄⊂4.解：（Ⅰ）∵PA PD=，且E为AD的中点，∴PE AD⊥.∵底面ABCD为矩形，∴BC AD∥，∴PE BC⊥.（Ⅱ）∵底面ABCD为矩形，∴AB AD⊥.∵平面PAD⊥平面ABCD，∴AB⊥平面PAD.∴AB PD⊥.又PA PD⊥，∴PD⊥平面PAB，∴平面PAB⊥平面PCD.（Ⅲ）如图，取PC中点G，连接,FG GD.∵,F G分别为PB和PC的中点，∴FG BC∥，且12FG BC=.∵四边形ABCD为矩形，且E为AD的中点，∴1,2ED BC DE BC=∥，∴ED FG∥，且ED FG=，∴四边形EFGD为平行四边形，∴EF GD∥.又EF⊄平面PCD，GD⊂平面PCD，∴EF∥平面PCD.5.解：（Ⅰ）证明：由平面ABC⊥平面ABD，平面ABC∩平面ABD=AB，AD⊥AB，可得AD⊥平面ABC，故AD⊥BC．（Ⅱ）解：取棱AC的中点N，连接MN，ND．又因为M为棱AB的中点，故MN ∥BC．所以∠DMN（或其补角）为异面直线BC与MD所成的角．在Rt△DAM中，AM=1，故DMAD⊥平面ABC，故AD⊥AC．在Rt△DAN中，AN=1，故DN在等腰三角形DMN中，MN=1，可得12cosMNDMNDM∠==．所以，异面直线BC与MD（Ⅲ）解：连接CM．因为△ABC为等边三角形，M为边AB的中点，故CM⊥AB，CM又因为平面ABC⊥平面ABD，而CM⊂平面ABC，故CM⊥平面ABD．所以，∠CDM为直线CD与平面ABD所成的角．在Rt△CAD中，CD=4．在Rt△CMD中，sin CMCDMCD∠==．所以，直线CD与平面ABD．6.证明：（1）在平行六面体ABCD -A 1B 1C 1D 1中，AB ∥A 1B 1．因为AB ⊄平面A 1B 1C ，A 1B 1⊂平面A 1B 1C ，所以AB ∥平面A 1B 1C ．（2）在平行六面体ABCD -A 1B 1C 1D 1中，四边形ABB 1A 1为平行四边形．又因为AA 1=AB ，所以四边形ABB 1A 1为菱形，因此AB 1⊥A 1B ．又因为AB 1⊥B 1C 1，BC ∥B 1C 1，所以AB 1⊥BC ．又因为A 1B ∩BC =B ，A 1B ⊂平面A 1BC ，BC ⊂平面A 1BC ，所以AB 1⊥平面A 1BC ．因为AB 1⊂平面ABB 1A 1，所以平面ABB 1A 1⊥平面A 1BC ．7.解：如图，在正三棱柱ABC −A 1B 1C 1中，设AC ，A 1C 1的中点分别为O ，O 1，则OB ⊥OC ，OO 1⊥OC ，OO 1⊥OB ，以1,{},OB OC OO 为基底，建立空间直角坐标系O −xyz ．因为AB =AA 1=2，所以1110,1,0,3,0,0,0,1,0,0,1,()()()()(2,3,0,2,0,1,2)()A B C A B C --．（1）因为P 为A 1B 1的中点，所以1,2)2P -，从而131(,,2)(0,2,22),BP AC ==--，故111|||cos ,|||||5BP AC BP AC BP AC ⋅==⋅．因此，异面直线BP 与AC 1所成角的余弦值为．（2）因为Q 为BC 的中点，所以1,0)2Q ，因此33(,0)2AQ =，11(0,2,2),(0,0,2)AC CC ==．设n =（x ，y ，z ）为平面AQC 1的一个法向量，则10,0,AQ AC ⎧⎪⎨⎪⎩⋅=⋅=n n 即30,2220.x y y z +=⎪+=⎩不妨取1,1)=-n ，设直线CC 1与平面AQC 1所成角为θ，则111||sin|cos|,|||CCCCCC|θ==⋅⋅==nnn，所以直线CC1与平面AQC1所成角的正弦值为．8.解：方法一：（Ⅰ）由11112,4,2,,AB AA BB AA AB BB AB===⊥⊥得111AB A B==，所以2221111A B AB AA+=.故111AB A B⊥.由2BC=，112,1,BB CC==11,BB BCCC BC⊥⊥得11B C=，由2,120AB BC ABC==∠=︒得AC=由1CC AC⊥，得1AC=2221111AB B C AC+=，故111AB B C⊥.因此1AB⊥平面111A B C.（Ⅱ）如图，过点1C作111C D A B⊥，交直线11A B于点D，连结AD.由1AB ⊥平面111A B C 得平面111A B C ⊥平面1ABB ，由111C D A B ⊥得1C D ⊥平面1ABB ，所以1C AD ∠是1AC 与平面1ABB 所成的角.由111111BC A B AC ===111111cos C AB C A B ∠=∠=，所以1C D =，故111sin C D C AD AC ∠==. 因此，直线1AC 与平面1ABB方法二：（Ⅰ）如图，以AC 的中点O 为原点，分别以射线OB ，OC 为x ，y 轴的正半轴，建立空间直角坐标系O -xyz .由题意知各点坐标如下：111(0,(1,0,0),(0,(1,0,2),A B A B C因此11111(1,3,2),(1,3,2),(0,23),AB A B AC ==-=-[来源:学#科#网Z#X#X#K]由1110AB A B ⋅=得111AB A B ⊥.由1110AB AC ⋅=得111AB AC ⊥. 所以1AB ⊥平面111A B C .（Ⅱ）设直线1AC 与平面1ABB 所成的角为θ.由（Ⅰ）可知11(0,23,1),(1,3,0),(0,0,2),AC AB BB === 设平面1ABB 的法向量(,,)x y z =n .由10,0,AB BB ⎧⋅=⎪⎨⋅=⎪⎩n n 即0,20,x z ⎧=⎪⎨=⎪⎩可取(=n.所以111|sin |cos ,||||AC AC AC θ⋅===⋅n |n n |因此，直线1AC 与平面1ABB 所成的角的正弦值是13.9.解：(1)依题意可知：圆锥的高度为322422=-=OP ，所以其体积为：πππ338322313122=⨯⨯⨯==h r V 。

北京各区2018分类汇编立体几何

北京各区2018分类汇编立体几何1、( 海淀2018.1 )2、( 海淀文2018.1 )3、( 朝阳2018.1 ) (本小题满分14 分)如图，在三棱柱ABC A1B1C1 中，ACB 90 ，A1 C1 D是线段AC 的中点，且A1D 平面ABC ．B1（Ⅰ）求证：平面A1BC 平面AA1C1C ；（Ⅱ）求证：B1C // 平面A1BD ； DA C（Ⅲ）若A B AC ，A C BC 2，1 1B求二面角A A1B C 的余弦值.4、( 西城2018.1 ) （本小题满分14 分）如图，三棱柱A BC A B C 中，AB 平面AA1C1C ，AA1 AB AC 2 ，A1 AC 60 .1 1 1过A A 的平面交B1C1 于点E ，交BC 于点F .1（Ⅰ）求证：A C 平面ABC1 ；1（Ⅱ）求证：四边形AA1 EF 为平行四边形；（Ⅲ）若B FBC 23，求二面角 B AC1 F 的大小.5、( 人大附2017.12.3 )6、（2017 北京高考）（本小题15 分）如图，在四棱锥P-ABCD中，底面ABCD为正方形，平面PAD⊥平面ABCD，点M 在线段PB 上，PD// 平面MAC,PA=PD= ,AB=4.6(I)求证：M 为PB的中点；(II)求二面角B-PD-A的大小；(III)求直线MC 与平面BDP所成角的正炫值.7、（2016 年北京高考）如图，在四棱锥P-ABCD中，PC⊥平面ABCD，AB∥DC, DC AC（I）求证：；DC 平面PACPAB PAC（II）求证：平面平面；（III）设点 E 为AB 的中点，在棱PB 上是否存在点F，// C F使得平面?说明理由.8、（2015 年北京高考）如图，在三棱锥V C 中，平面V 平面 C ，V 为等边三角形， C C 且C C 2 ，，分别为，V 的中点．（Ⅰ）求证：V // 平面 C ；（Ⅱ）求证：平面 C 平面V ；（Ⅲ）求三棱锥V C 的体积．39、（2014 年北京高考）如图，在三棱柱A BC A B C中，侧棱垂直于底面，AB BC ，1 1 1AA1 AC 2，E 、F 分别为A1C1 、BC 的中点.（Ⅰ）求证：平面ABE 平面B BCC ；1 1（Ⅱ）求证：C1F // 平面ABE ；（Ⅲ）求三棱锥 E ABC 的体积.P10、（昌平区2016 届高三二模）如图，P 是菱形ABCD 所在平面外一点，BAD 60 , PCD 是等MG边三角形，AB 2，PA 2 2 , M 是PC 的中点，点G 为线段DM 上一点（端点除外），平面APG 与D H C BD 交于点H .（I ）求证：PA / /GH ；OA B（II ）求证：平面PAC 平面BDM ；（III ）求几何体M BDC 的体积.11、（朝阳区2016 届高三二模）在四棱锥 A BCDE 中，底面BCDE 为菱形，侧面ABE 为等边三角形，且侧面ABE 底面BCDE ，O, F 分别为BE, DE 的中点．（Ⅰ）求证：AO CD ；（Ⅱ）求证：平面AOF 平面ACE ；（Ⅲ）侧棱AC 上是否存在点P ，使得BP // 平面AOF ?A P的值；若不存在，请说明理由．若存在，求出PC选填训练1、（2017 北京高考）某四棱锥的三视图如图所示，则该四棱锥的最长棱的长度为（A）3 （B）22 3（C）2 （D）222、（2016 年北京高考）四棱柱的三视图如图所示，则该四棱柱的体积为___________.3、（2015 年北京高考）某四棱锥的三视图如图所示，该四棱锥最长棱的棱长为（）A．1B． 2C． 3 D． 24、（朝阳区2016 届高三二模）已知m，n，l 为三条不同的直线，α，β，γ为三个不同的平面，则下列命题中正确的是A．若m⊥l ，n⊥l ，则m∥n B．若m∥α，n∥α，则m∥nC．若m⊥α，n⊥α，则m∥n D．若α⊥γ，β⊥γ，则α∥β5、（东城区2016 届高三二模）已知一个三棱锥的三视图如图所示，其中俯视图是等腰直角三角形，则该三棱锥的四个面中，最大面积为________.56、（丰台区2016 届高三一模）如图，已知三棱锥P-ABC 的底面是等腰直角三角形，且O∠ACB=90 ，侧面PAB⊥底面ABC，AB=PA=PB=4. 则这个三棱锥的三视图中标注的尺寸x, y, z 分别是zP （A）23, 2 2 , 2x（B）4,2, 2 2主视图侧视图Ay（C）2 3, 2，2CBy（D）23, 2, 2 2俯视图7、（海淀区2016 届高三二模）正方体ABCD A1B1C1D1 的棱长为1，点P，Q，R分别是棱A A，A B，A D的中点，以PQR 为底面1 1 1 1 1作正三棱柱，若此三棱柱另一底面的三个顶点也都在该正方体的表面上，则这个正三棱柱的高为A.22B. 2C.33D.328、（石景山区2016 届高三一模）某四面体的三视图如图所示，该四面体四个面的面积中最大的是( )A．8B．6 2C．10 D．8 29、（西城区2016 届高三二模）某四棱锥的三视图如图所示，该四棱锥最长棱的棱长为_____.10、（朝阳区2016 届高三上学期期末）已知m，n 表示两条不同的直线，，表示两个不同的平面，且m ，n ,则下列说法正确的是A．若/ / ，则m / /n B．若m ，则611、（大兴区2016 届高三上学期期末）某几何体的三视图如图所示，其中俯视图为扇形，则该几何体的体积为（A）2π（B）316π（C）9π（D）32π9421正视图侧视图2俯视图第11 题第12 题12、（顺义区2016 届高三上学期期末）已知某三棱锥的三视图尺寸（单位cm ）如右上图，则这个三棱锥的体积是（）（A）833cm （B）433cm （C）233cm （D）133cmWORD文档专业资料。

北京市各区高三一模试题分类汇编3立体几何含答案解析

2019年北京市各区高三一模试题分类汇编03立体几何(理科)1 (2019年东城一模理科)2 (2019年西城一模理科)如图，设P为正四面体A BCD-表面（含棱）上与顶点不重合的一点，由点P到四个顶点的距离组成的集合记为M，如果集合M中有且只有2个元素，那么符合条件的点P有（ C ）（A） 4个（B）6个（C）10个（D）14个3 (2019年西城一模理科)已知一个正三棱柱的所有棱长均等于2，它的俯视图是一个边长为2的正三角形，那么它的侧（左）视图面积的最小值是__4 (2019年海淀一模理科)一个空间几何体的三视图如图所示，该几何体的体积为__96__．5 (2019某三棱锥的三视图如图所示，则这个三棱锥的体积为______，表面积为______）6 (2019S ABCD-中，SB⊥底面ABCD．底面ABCD为梯形，AB AD⊥，AB∥CD，E是线段AD上的动点，则满足90SEC∠=︒的点E的个数是__2_7 (2019年丰台一模理科)棱长为2的正方体被一平面截成两个几何体，其中一个几何体的三视图如图所示，那么该几何体的体积是（B）（A）143（B）4 （C）103（D）38 (2019年石景山一模理科)右图是某个三棱锥的三视图，其中主视图是等边三角形，左视图是直角三角形，俯视图是等腰直角三角形，则该三棱锥的体积是（B ）A9 (2019年顺义一模理科)一个几何体的三视图如图所示，则这个几何体的体积是_________10 (2019年延庆一模理科)右图是一个几何体的三视图，则该几何体的体积是(A)A．3 B．34C．1 D．3211 (2019年东城一模理科)12 (2019年西城一模理科)如图，在四棱柱1111ABCD A B C D-中，底面ABCD和侧面11BCC B都是矩形，E是CD的中点，1D E CD⊥，22AB BC==.（Ⅰ）求证：1⊥BC D E；侧视图俯视图BC DESA侧视图俯视图主视图1主视图左视图俯视图主视图左视图俯视图BADC. P主视图侧视图A1 B1ED1 C1（Ⅱ）求证：1B C // 平面1BED ；（Ⅲ）若平面11BCC B 与平面1BED 所成的锐二面角的大小为π3，求线段1D E 的长度. 13 (2019年海淀一模理科) 如图1，在Rt △ABC 中，∠ACB=30°，∠ABC=90°，D 为AC 中点，AE BD ⊥于E ，延长AE 交BC 于F ，将∆ABD 沿BD 折起，使平面ABD ⊥平面BCD ，如图2所示．（Ⅰ）求证：AE ⊥平面BCD ；（Ⅱ）求二面角A –DC –B 的余弦值．（Ⅲ）在线段AF 上是否存在点M 使得//EM 平面ADC ？若存在，请指明点M 的位置；若不存在，请说明理由．14 (2019年朝阳一模理科)如图，四棱锥P ABCD -的底面为正方形，侧面PAD ⊥底面ABCD ．PAD △为等腰直角三角形，且PA AD ⊥．E ，F 分别为底边AB 和侧棱PC 的中点．（Ⅰ）求证：EF ∥平面PAD ；（Ⅱ）求证：EF ⊥平面PCD ；（Ⅲ）求二面角E PD C --的余弦值．15 (2019年丰台一模理科)如图，在棱长为1的正方体ABCD-A1B1C1D1中，点E 是棱AB 上的动点.（Ⅰ）求证：DA1⊥ED1 ；（Ⅱ）若直线DA1与平面CED1成角为45o ，求AEAB的值；（Ⅲ）写出点E 到直线D1C 距离的最大值及此时点E 的位置（结论不要求证明）.16 (2019年石景山一模理科)如图，正三棱柱111ABC A B C -的底面边长是2D 是AC 的中点．（Ⅰ）求证：1B C ∥平面1A BD；（Ⅱ）求二面角1A BD A--的大小；（Ⅲ）在线段1AA 上是否存在一点E ，使得平面11B C E ⊥平面1A BD ，若存在，求出AE 的长；若不存在，说明理由．17 (2019年顺义一模理科) 如图在四棱锥P ABCD -中，底面ABCD 是菱形，060BAD ∠=，平面PAD ⊥平面ABCD ，2PA PD AD ===，Q 为AD 的中点，M 是棱PC上一点，且13PM PC =. （Ⅰ）求证：PQ ⊥平面ABCD ；（Ⅱ）证明：PA ∥平面BMQ（Ⅲ）求二面角M BQ C --的度数.18 (2019年延庆一模理科) 在四棱锥ABCD P -中，⊥PA 平面ABCD ，底面ABCD 是正方形，且2==AD PA ，F E ，分别是棱PC AD ,的中点．（Ⅰ）求证：//EF 平面PAB ；（Ⅱ）求证：⊥EF 平面PBC ；（Ⅲ）求二面角D PC E --的大小．2019年北京市各区高三一模试题汇编--立体几何(理科)答案 1．；2．C ；3．；4．96 ；5．13，；6．2 ；7．B ；8． B ；9．；10．A ；11.B FA EBCDP F1A AA1A1B1CCDBFAB EP DC吧12（Ⅰ）证明：因为底面ABCD 和侧面11BCC B 是矩形，所以 BC CD ⊥，1BC CC ⊥，又因为 1=CDCC C ，所以 BC ⊥平面11DCC D ， ………………2分因为 1D E ⊂平面11DCC D ，所以 1BC D E ⊥. …………4分（Ⅱ）证明：因为 1111//, BB DD BB DD =，所以四边形11D DBB 是平行四边形.连接1DB 交1D B 于点F ，连接EF ，则F 为1DB 的中点.在1∆B CD 中，因为DE CE =，1DF B F =，所以 1//EF B C .……………6分又因为 1⊄B C 平面1BED ，⊂EF 平面1BED ，所以 1//B C 平面1BED . ………8分（Ⅲ）解：由（Ⅰ）可知1BC D E ⊥，又因为 1D E CD ⊥，BC CD C =，所以 1D E ⊥平面ABCD . ………………9分设G 为AB 的中点，以E 为原点，EG ，EC ，1ED如图建立空间直角坐标系，设1D E a =，则1(0,0,0), (1,1,0), (0,0,), E B D a C 设平面1BED 法向量为(,,)x y z =n ，因为 1(1,1,0), (0,0,)EB ED a ==，由10,0,EB ED ⎧⋅=⎪⎨⋅=⎪⎩n n 得0,0.x y z +=⎧⎨=⎩ 令1x =，得(1,1,0)=-n . …………11分设平面11BCC B 法向量为111(,,)x y z =m ，因为 1(1,0,0), (1,1,)CB CB a ==，由10,0,CB CB ⎧⋅=⎪⎨⋅=⎪⎩m m得11110,0.x x y az =⎧⎨++=⎩令11z =，得(0,,1)a =-m .…………12分由平面11BCC B 与平面1BED 所成的锐二面角的大小为π3，得 ||π|cos ,|cos 3⋅<>===m n m n m n ， ……………13分解得1a =. ………………14分13（Ⅰ）因为平面ABD ⊥平面BCD ，交线为BD ，又在ABD ∆中，AE BD ⊥于E ，AE ⊂平面ABD 所以AE ⊥平面BCD ．————————————————3分（Ⅱ）由（Ⅰ）结论AE ⊥平面BCD 可得AE EF ⊥．由题意可知EF BD ⊥，又AE ⊥BD ．如图，以E 为坐标原点，分别以,,EF ED EA 所在直线为x 轴，y 轴，z轴，建立空间直角坐标系E xyz -——4分不妨设2AB BD DC AD ====，则1BE ED ==．由图1条件计算得，AE =BC =BF = 则(0,0,0),(0,1,0),(0,1,0),2,0)3E D B AF C -———————5分 (3,1,0),(0,1,DC AD ==．由AE ⊥平面BCD 可知平面DCB 的法向量为EA ．———————6分设平面ADC 的法向量为(,,)x y z =n ，则0,0.DC AD ⎧⋅=⎪⎨⋅=⎪⎩n n 即0,0.y y +==⎪⎩令1z =，则1y x ==，所以1)=-n ．——————————8分平面DCB 的法向量为EA 所以cos ,5||||EA EA EA ⋅<>==-⋅n n n ，所以二面角A DC B --—————————————9分（Ⅲ）设AM AF λ=，其中[0,1]λ∈．由于3(AF =，所以(AM AF λλ==，其中[0,1]λ∈————————————10分所以3,0,(13EM EA AM λλ⎛=+=- ⎝————————————11分由0EM ⋅=n 0λ=-(1-———12分解得3=(0,1)4λ∈．————13分所以在线段AF 上存在点M 使EM ADC ∥平面，且34AM AF =．————————14分 14（Ⅰ）证明：取PD 的中点G ，连接FG ，AG ．因为F ，G 分别是PC ，PD 的中点，所以FG 是△PCD 的中位线．1所以FG ∥CD ，且12FG CD =．又因为E 是AB 的中点，且底面ABCD 为正方形，所以1122AE AB CD ==，且AE ∥CD ．所以AE ∥FG ，且AE FG =．所以四边形AEFG 是平行四边形．所以EF ∥AG ．又EF ⊄平面PAD ，AG ⊂平面PAD ，所以EF 平面PAD ．…………………4分（Ⅱ）证明：因为平面PAD ⊥平面ABCD ，PA AD ⊥，且平面PAD I 平面ABCD AD =，所以PA ⊥平面ABCD ．所以PA AB ⊥，PA AD ⊥．又因为ABCD 为正方形，所以AB AD ⊥，所以,,AB AD AP 两两垂直．以点A 为原点，分别以, , AB AD AP 为, , x y z 轴，建立空间直角坐标系（如图）．由题意易知AB AD AP ==，设2AB AD AP ===，则(0,0,0)A ，(2,0,0)B ，(2,2,0)C ，(0,2,0)D ，(0,0,2)P ，(1,0,0)E ，(1,1,1)F ．因为(0,11)EF=uu u r ，，(022)PD =-uu u r ，，，(200)CD =-uu u r，，，且(0,11)(0,2,2)0EF PD ⋅=⋅-=uu u r uu u r，， (0,11)(2,00)0EF CD ⋅=⋅-=uu u r uu u r，，所以EF PD ⊥，EF CD ⊥．又因为PD ，CD 相交于D ，所以EF ⊥平面PCD ．…………… 9分（Ⅲ）易得(102)EP =-uu r ，，，(0,22)PD =-uu u r,．设平面EPD 的法向量为(, , )x y z =n ，则0,0.EP PD ⎧⋅=⎪⎨⋅=⎪⎩uu r uu u r n n 所以20,220. x z y z -+=⎧⎨-=⎩即2,. x z y z =⎧⎨=⎩令1z =，则(2,1,1)=n ．由（Ⅱ）可知平面PCD 的法向量是(0,11)EF =uu u r，，所以cos ,EF EF EF⋅〈〉===⋅uu u ruu u r uu u r n n n ．由图可知，二面角E PD C --的大小为锐角，所以二面角E PD C --．…………14分 15.解：以D 为坐标原点，建立如图所示的坐标系，则D(0,0,0),A （1，0，0）， B(1,1,0)，C(0,1,0),D1(0,1,2),A1(1,0,1)，设E(1,m,0)（0≤m≤1）（Ⅰ）证明：1(1,0,1)DA =，1(1,,1)ED m =-- 111(1)0()110DA ED m ⋅=⨯-+⨯-+⨯=所以DA1⊥ED1. ----4分（Ⅱ）设平面CED1的一个法向量为(,,)v x y z =,则10v CD v CE ⎧⋅=⎪⎨⋅=⎪⎩，而1(0,1,1)CD =-，(1,1,0)CE m =-所以0,(1)0,y z x m y -+=⎧⎨+-=⎩取z=1,得y=1,x=1-m ，得(1,1,1)v m =-.因为直线DA1与平面CED1成角为45o ，所以1sin 45|cos ,|DA v ︒=<> 所以11||22||||DA v DA v ⋅=⋅=m=12.-----11分（Ⅲ）点E 到直线D1C E 在A 点处.------14分 16（Ⅰ）证明：连结1AB 交1A B 于M ，连结1B C DM ，，因为三棱柱111ABC A B C -是正三棱柱，所以四边形11AA B B 是矩形，所以M 为1A B 的中点．因为D 是AC 的中点，所以MD 是三角形1AB C 的中位线，…………………………2分所以MD ∥1B C ．…………………………3分因为MD ⊂平面1A BD ，1B C ⊄平面1A BD ，所以1B C ∥平面1A BD ．……………4分（Ⅱ）解：作CO AB ⊥于O ，所以CO ⊥平面11ABBA ，所以在正三棱柱111ABC ABC -中如图建立空间直角坐标系O xyz -．因为2AB =，1AAD 是AC 的中点．所以(100)A ，，，(100)B -，，，(00C ，，1(10)A …………5分所以1(022D ，，，3(022BD =，，，1(20)BA =．设()n x y z =，，是平面1A BD 的法向量，所以100n BD n BA ⎧⋅=⎪⎨⋅=⎪⎩，，即30220x x ⎧=⎪⎨⎪=⎩，，令3x =-，则2y =，3z =，所以(323)n =-，，是平面1A BD 的一个法向量．……………6分由题意可知1(00)AA =是平面ABD 的一个法向量，………7分所以121cos 2n AA <>==，．………………8分所以二面角1A BD A --的大小为3π．…………………………9分（Ⅲ）设(10)E x ，，，则1(1C E x =-，11(10C B ，，=-设平面11B C E 的法向量1111()n x y z ，，=，所以111100n C E n C B ，，⎧⋅=⎪⎨⋅=⎪⎩ 即11111)00x x y x ，，⎧-+=⎪⎨--=⎪⎩ xyzOBDA 1A1B1CCMA 1A1B1CB CD令1z =13x =，1y =，1(3n =，…………………12分又10n n ⋅=，即0-=，解得x = 所以存在点E ，使得平面11B C E ⊥平面1A BD且AE =分结BD ，Q 底面ABCD 是菱形，且060BAD ∠=，∴BAD 是等边三角形，∴BQ AD ⊥由（Ⅰ）PQ ⊥平面ABCD . ∴PQ AD ⊥.以Q 为坐标原点，,,QA QB QP 分别为x 轴y 轴z 轴建立空间直角坐标系则(0,0,0),(1,0,0),(0,0,3)Q A B P .————10分设平面BMQ 的法向量为(,,)m x y z =，∴00m QB m MN ⎧⋅=⎪⎨⋅=⎪⎩，注意到MN ∥PA∴0m QB m PA ⎧⋅=⎪⎨⋅=⎪⎩，解得(3,0,1)m =是平面BMQ 的一个法向量——12分（Ⅰ）证明：设G 是PB 的中点，连接GF AG ,∵F E ,分别是PC AD ,的中点，∴BC GF 21//，BC AE 21//∴AE GF //，∴AEFG 是平行四边形，∴AG EF //………………2分∵⊄EF 平面PAB ⊂AG 平面PAB ，∴//EF 平面PAB ………………3分（Ⅱ）∵AB PA =，∴PB AG ⊥，………………4分∵ABCD PA ⊥，∴BC PA ⊥，又∵AB BC ⊥，∴⊥BC 平面PAB ， ∴AG BC ⊥，………………6分∵PB 与BC 相交，∴⊥AG 平面PBC ， ∴⊥EF 平面PBC ．………………7分（Ⅲ）以AP AD AB ,,分别为x 轴、y 轴、z 轴，建立空间直角坐标系xyz A -，…8分∵2==AD PA ，∴)0,1,0(E ，)0,2,2(C ，)2,0,0(P ，)1,1,1(F 设H 是PD 的中点，连接AH ∵⊥AG 平面PBC ，∴同理可证⊥AH 平面PCD ，∴是平面PCD 的法向量，)1,1,0(=………………9分)0,1,2(=，)2,1,0(-=设平面PEC 的法向量),,(z y x m =，则0,0=⋅=⋅m∴02,02=+-=+z y y x 令2=y ，则1,1=-=z x ∴)1,2,1(-=m…………12分∴23263||||,cos =⋅=<AH m m．………………13分∴二面角D PC E --的大小为︒30………………14分。

2018年北京市高考期末理科数学试题分类汇编之立体几何

十二、三视图（一）试题细目表区县+题号类型考点思想方法2018•西城期末·13填空三视图、几何体表面积2018•海淀区期末•7选择三视图、三棱锥2018•石景山期末•7选择三视图、几何体体积2018·丰台期末·6选择三视图2018•通州期末•13填空三视图2018·房山区期末·7选择三视图、几何体体积2018·朝阳区期末·5选择三视图、几何体体积2018·东城区期末·7 选择三视图、几何体体积（二）试题解析1.（2018•西城期末·13）．从一个长方体中截取部分几何体，得到一个以原长方体的部分顶点为顶点的凸多面体，其三视图如图所示．该几何体的表面积是____．【答案】362.（2018·海淀区期末·7）某三棱锥的三视图如图所示，则下列说法中：①三棱锥的体积为②三棱锥的四个面全是直角三角形③三棱锥的四个面的面积最大的是所有正确的说法是A. ①B. ①②C. ②③D. ①③【答案】D2.（2018·石景山期末·7）《九章算术》卷五商功中有如下问题：今有刍甍（底面为矩形的屋脊状的几何体），下广三丈，袤四丈，上袤二丈，无广，高一丈，问积几何．下图网格纸中实线部分为此刍甍的三视图，设网格纸上每个小正方形的边长为1丈，那么此刍甍的体积为（）A. 3立方丈B. 5立方丈C. 6立方丈D. 12立方丈【答案】B3.（2018·丰台期末·6）某三棱锥的三视图如图所示，则该三棱锥最长的棱的棱长为（）A．2 B．5 C．22 D．3【答案】D4.（2018·通州区期末·13）在正方形网格中，某四面体的三视图如图所示．已知小正方形网格的边长为1，那么该四面体的四个面中，面积最大的面的面积是_______.【答案】125.（2018·昌平区期末·5）某四棱锥的三视图如图所示，则该四棱锥的四个侧面中，面积的最小值为A. 1B.C. 2D.【答案】B6.（2018·房山区期末·7）如图，网格纸上小正方形的边长为1，粗实线画出的是一个几何体的三视图，则这个几何体的体积是120（B）60（A）（D）20（C）24【答案】B7.（2018·朝阳区期末·5）某四棱锥的三视图如图所示，网格纸上小正方形的边长为1，则该四棱锥的体积为A. 4B. 4 3C.42D.42【答案】A2222主视图左视图俯视图1128.（2018·东城区期末·7）某三棱锥的三视图如图所示，该三棱锥的体积为A.16B.13C.12D.1【答案】A十三、立体几何（一）试题细目表线与平面平行、二面角2018•东城期末•17解答直线与平面平行、直线和平面所成的角、平面和平面垂直（二）试题解析1.（2018·朝阳区期末·8）如图1，矩形ABCD 中，3AD =.点E 在AB 边上， CE DE⊥且1AE =. 如图2，ADE △沿直线DE 向上折起成1A DE △．记二面角1A DE A --的平面角为θ，当θ()00180∈o ，时， ① 存在某个位置，使1CE DA ⊥； ② 存在某个位置，使1DE AC ⊥；③ 任意两个位置，直线DE 和直线1A C 所成的角都不相等. 以上三个结论中正确的序号是A . ① B. ①② C. ①③ D. ②③ 【答案】C2.（2018•海淀区期末·13）．已知正方体的棱长为，点是棱的中点，点在底面内，点在线段上，若，则长度的最小值为 . 【答案】3.（2018·通州区期末·8）如图，各棱长均为1的正三棱柱111ABC A B C -，M ，N 分别为线段1A B ，1B C 上的动点，若点M ，N 所在直线与平面11ACC A 不相交，点Q 为MN 中点，则点的轨迹的长度是1111ABCD A B C D -42M BC P ABCD Q 11A C 1PM =PQ 33Q 图1BA DCCDA图2A ．2 B ． 2C ．1D 【答案】B4.（2018•丰台区期末·17）在四棱锥P ABCD -中，底面ABCD 是矩形，侧棱PA ⊥底面ABCD ，,E F 分别是,AB PC 的中点，2PA AD ==，CD =（Ⅰ）求证：EF ∥平面PAD ；（Ⅱ）求PC 与平面EFD 所成角的正弦值；（Ⅲ）在棱BC 上是否存在一点M ，使得平面PAM ⊥平面EFD ？若存在，求出BMBC的值；若不存在，请说明理由.【答案】解：（Ⅰ）证明：取PD 中点G ，连接,AG FG . 因为,F G 分别是,PC PD 的中点，所以FG CD ∥，且12FG CD =. 因为ABCD 是矩形，E 是AB 中点，所以AE FG ∥，AE FG =. 所以AEFG 为平行四边形. 所以EF AG ∥.又因为AG ⊂平面PAD ，EF ⊄平面PAD ，所以EF ∥平面PAD .（Ⅱ）因为PA ⊥平面ABCD ，所以PA AB ⊥，PA AD ⊥.因为四边形ABCD 是矩形，所以AB AD ⊥. 如图建立直角坐标系Axyz ，所以E ⎫⎪⎪⎝⎭，F ⎫⎪⎪⎝⎭，()0,2,0D ，所以()0,1,1EF =uu u r，2,0DE ⎫=-⎪⎪⎝⎭uuu r .设平面EFD 的法向量为(),,n x y z =r，因为00n EF n DE ⎧⋅=⎪⎨⋅=⎪⎩r uu u r r uuu r，所以0202y z x y +=⎧-=⎩. 令1y =，所以1z x =-⎧⎪⎨=⎪⎩()1n =-r .又因为)2,2PC =-uu u r，设PC 与平面EFD 所成角为θ，所以sin cos ,PC n PC n PC nθ⋅===⋅uu u r r uu u r r uu u rr 45=. 所以PC 与平面EFD 所成角的正弦值为45.（Ⅲ）因为侧棱PA ⊥底面ABCD ，所以只要在BC 上找到一点M ，使得DE AM ⊥，即可证明平面PAM ⊥平面EFD . 设BC 上存在一点M ，则()[]()2,,00,2Mt t ∈，所以()2,,0AM t =uuu r .因为2,2,0ED ⎛⎫=- ⎪ ⎪⎝⎭uu u r ，所以令0AM ED ⋅=uuu r uu u r ，即120t -+=，所以12t =.所以在BC 存在一点M ，使得平面PAM ⊥平面EFD ，且14BM BC =.5.（2018·西城区期末·17）如图，三棱柱中，平面，，.过的平面交于点，交于点. （Ⅰ）求证：平面；（Ⅱ）求证：四边形为平行四边形；（Ⅲ）若，求二面角的大小.111ABC A B C -AB ⊥11AA C C 12AA AB AC ===160A AC ︒∠=1AA 11B C E BC F 1A C ⊥1ABC 1AA EF 1B AC F --【答案】解：（Ⅰ）因为平面，所以． [ 1分]因为三棱柱中，，所以四边形为菱形，所以． [ 3分]所以平面． [ 4分]（Ⅱ）因为，平面，所以平面． [ 5分]因为平面平面，所以． [ 6分] 因为平面平面，平面平面，平面平面，所以． [ 7分]所以四边形为平行四边形． [ 8分] （Ⅲ）在平面内，过作．因为平面，如图建立空间直角坐标系． [ 9分] 由题意得，，，，，．因为，所以，所以．由（Ⅰ）得平面的法向量为．设平面的法向量为，则即令，则，，所以． [11分]所以． [13分]AB ⊥11AA C C 1A C AB ⊥111ABC A B C -1AA AC =11AA C C 11A C AC ⊥1A C ⊥1ABC 11//A A B B 1A A ⊄11BB C C 1//A A 11BB C C 1AA EF I 11BB C C EF =1//A A EF //ABC 111A B C 1AA EF I ABC AF =1AA EF I 1111A B C A E =1//A E AF 1AA EF 11AA C C A Az AC ⊥AB ⊥11AA C C A xyz -(0,0,0)A (2,0,0)B (0,2,0)C 1(0,1,3)A 1(0,3,3)C 1ABC 1AC F (,,)x y z =n 1y =2x =-3z =-(2,1,3)=--n由图知二面角的平面角是锐角，所以二面角的大小为． [14分]6.（2018·海淀区期末·17）如题1，梯形中，为中点.将沿翻折到的位置，如图2.（Ⅰ）求证：平面平面；（Ⅱ）求直线与平面所成角的正弦值；（Ⅲ）设分别为和的中点，试比较三棱锥和三棱锥（图中未画出）的体积大小，并说明理由.【答案】（Ⅰ）证明：因为，，，，平面 ……………..1分所以平面……………..2分因为平面，所以平面平面 ……………..3分（Ⅱ）解：在平面内作，由平面，建系如图. ……………..4分1B AC F --1B AC F --45︒ABCD //,,1,2,AD BC CD BC BC CD AD E ⊥===AD ABE ∆BE 1A BE ∆1A DE ∆⊥BCDE 1A B 1A CD ,M N 1A E BC 1M A CD -1N A CD -1BE A E ⊥BE DE ⊥1A E DE E =I 1A E DE ⊂1A DE BE ⊥1A DE BE ⊂BCDE 1A DE ⊥BCDE 1A DE EF ED ⊥BE ⊥1A DE则，，，，.，， ……………..7分设平面的法向量为，则，即，令得，，所以是平面的一个方向量. ……………..9分……………..10分所以与平面所成角的正弦值为. ……………..11分（Ⅲ）解：三棱锥和三棱锥的体积相等.……………..12分理由如: 方法一：由，，知，则因为平面，所以平面. ……………..13分故点、到平面的距离相等，有三棱锥和同底等高，所以体积相等. ……………..14分方法二：如图，取中点，连接，，.因为在中，，分别是，的中点，所以因为在正方形中，，分别是，的中点，所以因为，，平面，，平面(1,0,0)B (1,1,0)C (0,1,0)D (0,0,0)E (1,0,0)DC =u u u r1A CD (,,)n x y z =r1z =3y=n =r1A CD 1A B 1ACD 1M A CD -1N A CD -0MN n ⋅=uuu r rMN ⊂1A CD //MN 1A CD M N 1A CD 1M A CD -1N A CD -DE P MP NP MN 1A DE ∆M P 1A E DE 1//MP A D BCDE N P BC DE //NP CD MP NP P =I MP NP ⊂MNP 1A D CD ⊂1A CD所以平面平面因为平面，所以平面 ……………..13分故点、到平面的距离相等，有三棱锥和同底等高，所以体积相等. ……………..14分法二法三方法三：如图，取中点，连接，，.因为在中，，分别是，的中点，所以且因为在正方形中，是的中点，所以且所以且，故四边形是平行四边形，故因为平面，平面，所以平面. ……………..13分故点、到平面的距离相等，有三棱锥和同底等高，所以体积相等. ……………..14分MNP //1A CD MN ⊂MNP //MN 1A CD M N 1A CD 1M A CD -1N A CD-1A D Q MN MQ CQ 1A DE ∆M Q 1A E 1A D //MQ ED BCDE N BC //NC ED //MQ NC MQ NC =MNCQ //MN CQ CQ ⊂1A CD MN ⊂1A CD //MN 1A CD M N 1A CD 1M A CD -1N A CD -7.（2018·石景山期末·17）如图，在四棱锥P ABCD -中，底面ABCD 为矩形，平面PCD ⊥平面ABCD ，1BC =，2AB =，2PC PD ==，E 为PA 中点．（Ⅰ）求证：//PC BED 平面；（Ⅱ）求二面角A PC D --的余弦值；（Ⅲ）在棱PC 上是否存在点M ，使得BM AC ⊥？若存在，求PMPC的值；若不存在，说明理由．【答案】解：（Ⅰ）证明：设AC 与BD 的交点为F ，连接EF . 因为ABCD 为矩形，所以F 为AC 的中点，在PAC ∆中，由已知E 为PA 中点，所以//EF PC ， ……………2分又EF ⊂平面BED ，PC ⊄平面BED ， ……………3分所以//PC 平面BED . ……………4分（Ⅱ）解：取CD 中点O ，连接PO . 因为PCD ∆是等腰三角形，O 为CD 的中点，所以PO CD ⊥，又因为平面PCD ⊥平面ABCD ，因为PO ⊂平面PCD ，PO CD ⊥，所以PO ⊥平面ABCD ． ……………5分取AB 中点G ，连接OG ，由题设知四边形ABCD 为矩形，所以OF CD ⊥，所以PO OG ⊥．如图建立空间直角坐标系O xyz -，则(1,1,0)A -，(0,1,0)C ，(0,0,1)P ，(0,1,0)D -，(1,1,0)B ，(0,0,0)O ，(1,0,0)G .(1,2,0)AC =-u u u r ，(0,1,1)PC =-uu u r. ……………6分设平面PAC 的法向量为(,,)n x y z =r，则0,0,n AC n PC ⎧⋅=⎪⎨⋅=⎪⎩r uuu r r uu u r 即20,0.x y y z -=⎧⎨-=⎩ 令1z =，则1y =，2x =，所以.平面的法向量为，设，的夹角为，所以. ……………9分由图可知二面角为锐角，所以二面角的余弦值为. ……………10分（Ⅲ）设是棱上一点，则存在使得．因此点，，． ……12分由，即．因为，所以在棱上存在点，使得，此时． ……………14分8.（2018·通州区期末·17）如图，在四棱柱PCD n r OG uuu rαA PC D --A PC B --M PC PM PC λ=uuu r uu u r (0,,1)M λλ-0BM AC ⋅=uuu r uuu rPC M BM AC ⊥1111ABCD A B C D -A x DCE Pyz O BMFG中，平面,底面为梯形，，，，点，分别为，的中点. （Ⅰ）求证：平面；（Ⅱ）求二面角的余弦值；（Ⅲ）在线段上是否存在点，使与平面所成角的正弦值是，若存在，求的长；若不存在，请说明理由. 【答案】解：（Ⅰ）连接，因为点，分别为，的中点，所以，. 所以四边形是平行四边形. 所以因为平面，平面，所以平面……………………4分（Ⅱ）因为平面,，所以平面.……………………5分所以以为坐标原点，分别以直线，为轴，轴建立空间直角坐标系，则轴在平面内．所以，，，，所以，. ……………………7分设平面的法向量为，所以即所以. ……………………8分设平面的法向量为，所以1AA ⊥ABCD ABCD //AD BC 2AB DC ==P Q 11A D AD //CQ 1PAC 1C AP D --BC E PE 1PAC BE PQ P Q 11A D AD 1//PQ C C 1PQ C C =PQCC 11//.CQ C P CQ ⊄1PAC 1C P ⊂1PAC //CQ 1.PAC 1AA ⊥ABCD 1//AA PQ PQ ⊥ABCD Q QA QP x z Qxyz y ABCD (),,C -12121PAC PAD又二面角为锐角，所以二面角的余弦值是……………………10分（Ⅲ）存在. 设点，所以设与平面所成角为，所以所以，解得所以……………………14分9.（2018·昌平区期末·18）如图，在四棱锥P －ABCD 中，底面ABCD 是边长为2的菱形，∠ABC ＝60°，为正三角形，且侧面PAB ⊥底面ABCD ，为线段的中点，在线段上.（I ）当是线段的中点时，求证：PB // 平面ACM ；（II ）求证：；（III ）是否存在点，使二面角的大小为60°，若存在，求出的值；若不存在，请说明理由．【答案】（I ）证明：连接BD 交AC 于H 点，连接MH ，因为四边形ABCD 是菱形，所以点H 为BD 的中点. 又因为M 为PD 的中点，所以MH // BP .又因为 BP 平面ACM , 平面ACM . 所以 PB // 平面ACM . ……………4分（II ）证明：因为为正三角形，E 为AB 的中点，所以PE ⊥AB .因为平面P AB ⊥平面ABCD ，平面P AB ∩平面ABCD=AB ，PE 平面P AB ，所以PE ⊥平面ABCD .1C AP D --1C AP D --PE 1PAC θ 1.a =1.BE =PAB ∆E AB M PD M PD PE AC ⊥M M EC D --⊄MH ⊂PAB ∆⊂又因为平面，所以. ……………8分(Ⅲ) 因为ABCD 是菱形，∠ABC ＝60°，E 是AB 的中点，所以CE ⊥AB .又因为PE ⊥平面ABCD ，以为原点，分别以为轴，建立空间直角坐标系，则，，，，． ………10分假设棱上存在点，设点坐标为，，则，所以，所以，，设平面的法向量为，则，解得．令，则，得．因为PE ⊥平面ABCD ，所以平面ABCD 的法向量，所以．因为二面角的大小为60°，所以，即，解得，或（舍去）所以在棱PD 上存在点，当时，二面角的大小为60°．…………………14分10.（2018·房山区期末·18）如图几何体ADM -BCN 中，是正方形，，，，，.（Ⅰ）求证：；AC ⊂ABCD PE AC ⊥3(1)x λ=-M EC D --23210λλ+-=1λ=-M EC D --ABCD NM //CD CN CD MD AD ⊥⊥,=∠MDC o 120ο30=∠CDN 42==MD MN CDMN AB 平面//（Ⅰ）求证：；（Ⅲ）求二面角的余弦值.【答案】解：（Ⅰ）在正方形中，；又，；…………………5分（Ⅰ）四边形是正方形，，，，，…………………10分（Ⅲ）法1：以点D 为坐标原点，建立空间直角坐标系，如图所示；由（Ⅱ）；设面的法向量，AMD DN 平面⊥D AM N --ABCD CD AB //ΘMNCD 面⊂CD MNCD 面⊄AB MNCD //面AB ∴ΘABCD ⊥∴AD DC Θ⊥AD MD I CD D MD =CD MNCD MD 平面⊂⊥∴AD MNCD 平面ΘMNCD DN ⊂⊥∴AD DN Θ=∠MDC o 120ο30=∠CDN ο90=∠∴MDN ∴MD ND ⊥ΘD MD AD =I AMD MD AD 平面，⊂AMD DN 面⊥∴xyz D -3,3,32===CN CD DN )0,32,0(),0,0,2(),3,0,0(),0,0,0(N M A D ∴)0,32,0(),3,32,0(),3,0,2(=-=-=∴DN AN AM AMN ),,(z y x n =ϖx令，由图可知二面角为锐角二面角的余弦值为…………………14分法2：以点C 为坐标原点，建立空间直角坐标系，如图所示；由（Ⅱ）；设面的法向量，令，由图可知二面角为锐角二面角的余弦值为. …………………14分11.（2018·朝阳区期末·17）如图，在三棱柱中，，是线段的中点，且平面．（Ⅰ）求证：平面平面；3,3,2===y x z 则)2,3,3(=∴nϖD AM N --∴D AM N --xyz D -3,3,32===CN CD DN )0,3,0(),0,3,4(),3,0,3(),0,0,3(),0,0,0(N M A D C ∴)0,3,3(),3,3,3(),3,3,1(-=--=-=∴AMN ),,(z y x n =ϖ3,1==y z 则)1,3,0(=∴nϖD AM N --∴D AM N --111ABC A B C -90ACB ∠=oD AC 1A D ⊥ABC 1A BC ⊥11AAC C ACBB 1C 1A 1D（Ⅱ）求证：平面；（Ⅲ）若，，求二面角的余弦值.【答案】（Ⅰ）证明：因为，所以．根据题意，平面，平面，所以．因为，所以平面．又因为平面，所以平面平面． ………………4分（Ⅱ）证明：连接，设，连接．根据棱柱的性质可知，为的中点，因为是的中点，所以．又因为平面，平面，所以平面．………………8分（Ⅲ）如图，取的中点，则，因为，所以，又因为平面，所以两两垂直．以为原点，分别以为轴建立空间坐标系（如图）. 由（Ⅰ）可知，平面, 所以．又因为，,1//B C 1A BD 11A B AC ⊥2AC BC ==1A A B C--90ACB ∠=oBC AC ⊥1A D ⊥ABC BC ⊂ABC 1A D BC ⊥1A D AC D =I BC ⊥11AAC C BC ⊂1A BC 1A BC ⊥11AAC C 1AB 11AB A B E =I DE E 1AB D AC 1//DE B C DE ⊂1A BD 1B C ⊄1A BD 1//B C 1A BD AB F //DF BC BC AC ⊥DF AC ⊥1A D ⊥ABC 1,,DF DC DA D 1,,DF DC DA ,,x y z BC ⊥11AAC C 1BC AC ⊥11A B AC ⊥1BC A B B =I ACB B 1C 1A 1DEA所以平面，所以，所以四边形为菱形．由已知，则，，，．设平面的一个法向量为，因为，，所以，即设，则．再设平面的一个法向量为，因为，，所以，即设，则．故．由图知，二面角的平面角为锐角，所以二面角的余弦值为． …………14分11.（2018·东城区期末·17）如图，在四棱锥E ABCD -中，平面ADE ⊥平面ABCD ，,O M 为线段,AD DE 的中点，四边形BCDO 是边长为1的正方形，,AE DE AE DE =⊥. （Ⅰ）求证：CM ∥平面ABE ；（Ⅰ）求直线DE 与平面ABE 所成角的正弦值；（Ⅰ）点N 在直线AD 上，若平面BMN ⊥平面ABE ，求线段AN 的长.1AC ⊥1A BC 11AC AC ⊥11AAC C 2AC BC ==1A AB 1z =1A BC 11z =1A A B C --1A A B C --【答案】解：（Ⅰ）如图取线段AE 中点P ，连接BP 、MP ，∵M 为DE 中点，∴MP//AD ，MP ＝12AD ，又∵四边形BCDO 是边长为1的正方形，∴BC//CO ，BC=CO,∴BC//MP,BC ＝MP ．∴四边形BCMP 为平行四边形，∴CM//BP∵CM ⊄面ABE ，BP ⊂面ABE ，∴CM ∥平面ABE ；（Ⅰ）连接EO ，∵AE=DE ，O 为AD 中点，∴EO ⊥AD ．∵EO ⊂面ADE ，面ADE ⊥面ABCD ，面ADE∩面ABCD=AD ．∴EO ⊥面ABCD ．又∵OB ⊂面ABCD ，OD ⊂面ABCD ，∵EO ⊥BO ，EO ⊥OD ，如图建立空间直角坐标系．A （0，-1，0），B （1，0，0），C （1，1，0），D （0，1，0），E （0，0，1），11(0,,)22M设面ABE 的法向量为(,,),(1,1,0),(0,1,1)m x y z AB AE ===u r u u u r u u u r由00AB m x y AE m y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩u u u r u r u u u r u r ，可取(1,1,1)m =-u r .(0,1,1),cos ,DE m DE m DE DE m⋅=-<>=u u u r u r u u u r u r u u u r u u u r u r . ∴直线DE 与平面ABE（Ⅰ）设11,(0,,0),(1,,0),(1,,)22ON OD N NB MB λλλ==-=--u u u r u u u r u u u r u u u r . 设面BMN 的法向量为(,,)n a b c =r 则有011022n NB a b n MB a b c λ⎧⋅=-=⎪⎨⋅=--=⎪⎩r u u u r r u u u r 可得(,1,21)n λλ=-r∵平面BMN ⊥平面ABE ，∴0m n ⋅=u r r ，解得2=3λ. ∴53AN =.。

2018东城区高中数学理一模及答案

市东城区2017-2018学年度第二学期高三综合练习高三数学〔理科〕2018.4本试卷共4页,150分.考试时长120分钟.考生务必将答案答在答题卡上,在试卷上作答无效.考试结束后,将本试卷和答题卡一并交回.第一部分〔选择题共40分〕一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.〔1〕若集合{|31}A x x =-<<,{|1B x x =<-或2}x >,则A B =〔A 〕{|32}x x -<< 〔B 〕{|31}x x -<<- 〔C 〕{|11}x x -<< 〔D 〕{|12}x x <<〔2〕复数i1iz =-在复平面上对应的点位于〔A 〕第一象限〔B 〕第二象限〔C 〕第三象限〔D 〕第四象限〔3〕已知,a b R ∈,且a b >,则下列不等式一定成立的是〔A 〕220a b ->〔B 〕cos cos 0a b -> 〔C 〕110a b-< 〔D 〕0a b e e ---< 〔4〕在平面直角坐标系xOy 中,角θ以Ox 为始边,终边与单位圆交于点34(,)55,则tan()θπ+的值为〔A 〕43 〔B 〕34〔C 〕43- 〔D 〕34- 〔5〕设抛物线24y x =上一点P 到y 轴的距离是2,则P 到该抛物线焦点的距离是〔A 〕1 〔B 〕2〔C 〕3〔D 〕4〔6〕故宫博物院五一期间同时举办"戏曲文化展"、"明代御窑瓷器展"、"历代青绿山水画展"、"赵孟頫书画展".某同学决定在五一当天的上、下午各参观其中的一个,且至少参观一个画展,则不同的参观方案共有〔A 〕6种〔B 〕8种〔C 〕10种〔D 〕12种〔7〕设{}n a 是公差为d 的等差数列,n S 为其前n 项和,则"0d>"是"{}n S 为递增数列"的〔A 〕充分而不必要条件〔B 〕必要而不充分条件〔C 〕充分必要条件〔D 〕既不充分也不必要条件〔8〕某次数学测试共有4道题目,若某考生答对的题大于全部题的一半,则称他为"学习能手",对于某个题目,如果答对该题的"学习能手"不到全部"学习能手"的一半,则称该题为"难题".已知这次测试共有5个"学习能手",则"难题"的个数最多为〔A 〕4 〔B 〕3 〔C 〕2 〔D 〕1第二部分〔非选择题共110分〕二、填空题共6小题,每小题5分,共30分.〔 9 〕在ABC △中,角,,A B C 所对的边分别为,,a b c . 若222a c b ac +=+,则B =．〔10〕在极坐标系中,圆2cos ρθ=的圆心到直线sin 1ρθ=的距离为．〔11〕若,x y 满足410,,,x y x y x ≤≤≥-⎧⎪+⎨⎪⎩则2z x y =+的最大值为．〔12〕某几何体的三视图如图所示,该几何体的表面积为____________.〔13〕设平面向量,,a b c 为非零向量．能够说明"若a b =a c ,则b =c "是假命题的一组向量,,a b c 的坐标依次为．〔14〕单位圆的内接正(3)n n ≥边形的面积记为()f n ,则(3)f =_________；下面是关于()f n 的描述:①2()sin2n f n nπ=； ②()f n 的最大值为π；③()(1)f n f n <+；④()(2)2()f n f n f n <≤.其中正确结论的序号为__________.〔注：请写出所有正确结论的序号〕三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 〔15〕〔本小题13分〕已知函数22()sin 2sin cos cos f x x x x x =+-. <Ⅰ> 求()f x 的最小正周期；<Ⅱ>求()f x 在[0,]2π上的最大值和最小值. 〔16〕〔本小题13分〕从高一年级随机选取100名学生,对他们的期中考试的数学和语文成绩进行分析,成绩如图所示.〔Ⅰ〕从这100名学生中随机选取一人,求该生数学和语文成绩均低于60分的概率；〔Ⅱ〕从语文成绩大于80分的学生中随机选取两人,记这两人中数学成绩高于80分的人数为,求的分布列和数学期望()E ；〔Ⅲ〕试判断这100名学生数学成绩的方差a 与语文成绩的方差b 的大小.〔只需写出结论〕〔17〕〔本小题14分〕如图1,在边长为2的正方形ABCD 中,P 为CD 中点,分别将PAD ,PBC 沿PA ,PB 所在直线折叠,使点C 与点D 重合于点O ,如图2.在三棱锥P OAB -中,E 为PB 的中点．〔Ⅰ〕求证：PO AB ⊥；〔Ⅱ〕求直线PB 与平面POA 所成角的正弦值；〔Ⅲ〕求二面角P AO E --的大小.图1 图2 〔18〕〔本小题13分〕已知椭圆22221(0)x y C a b a b +=>>：的离心率为2,且过点A <2,0>．<Ⅰ> 求椭圆C 的方程；<Ⅱ> 设M ,N 是椭圆C 上不同于点A 的两点,且直线AM ,AN 的斜率之积等于－错误!.试问直线MN 是否过定点？若是,求出该点的坐标；若不是,请说明理由．〔19〕〔本小题14分〕已知函数()e (1)xf x a x =-+.〔I 〕若曲线()y f x =在(0,(0))f 处的切线斜率为0,求a 的值；〔II 〕若()0f x ≥恒成立,求a 的取值范围；〔III 〕证明：当0a =时,曲线()(0)y f x x =>总在曲线2ln y x =+的上方. 〔20〕〔本小题13分〕在(2)n n n ⨯≥个实数组成的n 行n 列的数表中,ij a 表示第i 行第j 列的数,记12i i i in r a a a =+++(1)in ,12(1)j j j nj c a a a j n =+++≤≤.若{1,0,1}ij a ∈-(1,)i jn .且1212,,,,,,,n n r r r c c c 两两不等,则称此表为"n 阶H 表".记{}1212,,,,,,,n n n H r r r c c c =.〔I 〕请写出一个"2阶H 表"；〔II 〕对任意一个"n 阶H 表",若整数[,]n n λ∈-,且n H λ∉,求证：λ为偶数；〔III 〕求证：不存在"5阶H 表".市东城区2017-2018学年度第二学期高三综合练习〔一〕高三数学参考答案与评分标准〔理科〕一、选择题〔共8小题,每小题5分,共40分〕〔1〕B 〔2〕B 〔3〕D 〔4〕A〔5〕C 〔6〕C 〔7〕D 〔8〕D 二、填空题〔共6小题,每小题5分,共30分〕〔9〕3π〔10〕1〔11〕6 〔12〕12+〔13〕(1,0),(0,1),(0,-1)〔答案不唯一〕〔14〕4；①③④ 三、解答题〔共6小题,共80分〕〔15〕〔共13分〕解：〔Ⅰ〕因为22()sin 2sin cos cos f x x x x x =+-)4x π=-.所以()f x 的最小正周期为22π=π. ……………………………………7分 <Ⅱ>因为02x .所以32444x.当242x ,即38x 时,()f x 当244x,即0x时,()f x 取得最小值1.所以()f x 在[0,]2π,最小值为1.………………………13分〔16〕〔共13分〕解：〔I 〕由图知,在被选取的100名学生中,数学和语文成绩均低于60分的有9人,所以从100名学生中随机选取一人,该生数学和语文成绩均低于60分的概率为90.09100=. ……………………………………………………………………………………3分〔Ⅱ〕由图知,语文成绩大于80分的学生优10人,这10人中数学成绩高于80分的有4人,所以的所有可能取值为0,1,2.262101(0)3C P C ,11462108(1)15C C P C ,242102(2)15C P C ,所以的分布列为故的数学期望1824()012315155E .……………………………10分〔Ⅲ〕由图判断,a b . …………………………………………13分〔17〕〔共14分〕证明：〔Ⅰ〕在正方形ABCD 中,P 为CD 中点,PD AD ⊥,PC BC ⊥, 所以在三棱锥P OAB -中,PO OA ⊥,PO OB ⊥. 因为OA OB O =,所以PO ⊥平面OAB .因为AB ⊂平面OAB ,所以PO AB ⊥.……………………4分〔Ⅱ〕取AB 中点F ,连接OF ,取AO 中点M ,连接BM . 过点O 作AB 的平行线OG .因为PO ⊥平面OAB ,所以PO ⊥OF ,PO ⊥OG . 因为OA ＝OB ,F 为AB 的中点, 所以OF ⊥AB . 所以OF ⊥OG . 如图所示,建立空间直角坐标系O －xyz . A 错误!,B 错误!,P 错误!,M <错误!,错误!,0>．因为BO ＝BA ,M 为OA 的中点,所以BM ⊥OA .因为PO ⊥平面OAB ,PO ⊂平面POA ,所以平面POA ⊥平面OAB . 因为平面POA ∩平面OAB ＝OA ,BM ⊂平面OAB , 所以BM ⊥平面POA .因为BM ＝<错误!,－错误!,0>．所以平面POA 的法向量m ＝错误!.BP ＝<1,－错误!,1>．设直线BP 与平面POA 所成角为α,则15sin cos 5BP BPBPm m,m .所以直线BP 与平面POA 所成角的正弦值为错误!.………………10分〔Ⅲ〕由<Ⅱ>知1122E ⎛⎫- ⎪ ⎪⎝⎭,1122OE ⎛⎫=- ⎪ ⎪⎝⎭,()1,OA =. 设平面OAE 的法向量为n ,则有 0,0.OA OE ⎧⋅=⎪⎨⋅=⎪⎩n n即0,0.x x z ⎧=⎪⎨-++=⎪⎩令1y =-,则x =z =即=-n .所以21cos ,242⋅===⋅⨯m n m n m n .由题知二面角P －AO －E 为锐角,所以它的大小为3.……………………………14分〔18〕〔共13分〕解：〔I〕由已知有2,2a a =⎧=⎩解得2,1.a b =⎧⎨=⎩ 椭圆C 的方程为2214x y +=.……………………………4分〔II 〕若直线MN 斜率存在,设直线MN 方程为y kx n =+.由22,1,4y kx n x y =+⎧⎪⎨+=⎪⎩消去y ,得222(14)8440k x knx n +++-=. 当0∆>,设1122(,),(,)M x y N x y ,则122814kn x x k +=-+………..①,21224414n x x k -=+………..②.由12121224AM AN y y k k x x ⋅=⋅=---以与11y kx n =+,22y kx n =+整理,得 221212(14)(42)()(44)0k x x nk x x n ++-+++=.将①,②代入上式,整理,得220n kn +=,解得0n =或2n k =-.当0n =时,直线y kx n =+过(0,0)；当2n k =-时,直线y kx n =+过(2,0)〔舍〕. 若直线MN 斜率不存在,则直线,AM AN 斜率互为相反数.不妨设11,22AM AN k k =-=,于是直线1:(2)2AM y x =--与椭圆交于(0,1)M , 由对称性可知直线AN 与椭圆交于(0,1)N -. 所以直线MN 也过(0,0).综上,直线MN 过定点(0,0).……………………………13分19〕〔共14分〕解：〔I 〕函数()e (1)xf x a x =-+的定义域为R . 因为()e (1)xf x a x =-+,所以'()e xf x a =-.由'(0)10f a =-=得1a =.……………………………4分〔II 〕'()e (R)x f x a x =-∈. ①当0a >时,令'()0f x =得ln x a =.ln x a <时,'()0f x <；ln x a >时,'()0f x >.()f x 在(,ln )a -∞上单调递减,在(ln ,+)a ∞上单调递增.所以当ln x a =时,()f x 有最小值(ln )(1ln )ln f a a a a a a =-+=-. "()0f x ≥恒成立"等价于"()f x 最小值大于等于0",即ln 0a a -≥. 因为0a >,所以01a <≤.②当0a =时,()e 0xf x =>符合题意；③当0a <时,取011x a=-+,则111101()e (11)e 10a a f x a a -+-+=--++=-<,不符合题意.综上,若()0f x ≥对x R ∈恒成立,则a 的取值范围为[0,1].……………………9分〔III 〕当0a =时,令()()(2ln )e ln 2(0)xh x f x x x x =-+=-->,可求1'()e xh x x=-. 因为121'()e 1002h =-<,'(1)e 10h =->,且1'()e xh x x=-在(0,)+∞上单调递增,所以在〔0,〕上存在唯一的0x ,使得0001'()e 0xh x x =-=,即001e x x =,且112x .当x 变化时,()h x 与'()h x 在〔0,〕上的情况如下：则当0x x =时,()h x 存在最小值0()h x ,且000001()e ln 22xh x x x x =--=+-. 因为01(,1)2x ∈,所以0001()220h x x x =+->=. 所以当0a =时,()2ln (0)f x x x >+>所以当0a =时,曲线()(0)y f x x =>总在曲线2ln y x =+的上方. .. …………14分〔20〕〔共13分〕解：〔I 〕……………………3分〔II 〕对任意一个"n 阶H 表",i r 表示第i行所有数的和,j c 表示第j 列所有数的和〔1,i j n ≤≤〕.1nii r=∑与1njj c=∑均表示数表中所有数的和,所以1n i i r =∑1njj c==∑.1212,,,,,,,n n r r r c c c 只能取[,]n n -内的整数.因为{1,0,1}ij a ∈-,所以又因为1212,,,,,,,n n r r r c c c 互不相等,[,]n n λ∈-且n H λ∉, 所以1212{,,,,,,,,}{,1,,1,0,1,,1,}n n r r r c c c n n n n λ=--+--,所以λ+1ni i r =∑1njj c=+∑(1)(1)01++(1)0n n n n =-+-+++-++-+=.所以λ12ni i r ==-∑为偶数.………………………………………8分〔III 〕假设存在一个"5阶H 表",则由〔II 〕知55,5,3,3H --∈,且54H ∈和54H -∈至少〔答案不唯一〕有一个成立,不妨设54H ∈.设125,5r r ==-,则121,1(15)j j a a j ==-≤≤,于是3(15)j c j ≤≤≤,因而可设34r =,313233341a a a a ====,350a =.①若3是某列的和,由于52c ≤,故只能是前四列某列的和,不妨设是第一列,即41511a a ==.现考虑3-,只能是4r 或5r ,不妨设43r =-,即424344451a a a a ====-,由234,,c c c 两两不等知525354,,a a a 两两不等,不妨设5253541,0,1a a a =-==,若551a =-则530r c ==；若550a =则541r c ==；若551a =则530c c ==,均与已知矛盾.②若3是某行的和,不妨设43r =,则第4行至少有3个1,若这3个1是前四个中某三个数,不妨设4142431a a a ===,则第五行前三个数只能是3个不同的数,不妨设5152531,0,1a a a =-==,则343c r ==矛盾,故第四行只能前四个数有2个1,第五个数为1,不妨设41424344450,1a a a a a =====,所以53r =-,第五行只能是2个0,3个1-或1个1,4个1-.则515255,,a a a 至少有两个数相同,不妨设5152a a =,则12c c =与已知矛盾. 综上,不存在"5阶H 表".………………………………………13分。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

【海淀一模】( 17)（本小题14分）已知三棱锥P ABC -（如图1）的平面展开图（如图2）中，四边形ABCD的正方形，△ABE 和△BCF 均为正三角形，在三棱锥P ABC -中： (I)证明：平面PAC ⊥平面ABC ; (Ⅱ)求二面角A PC B --的余弦值； (Ⅲ)若点M 在棱PC 上，满足CM PM λ=，12[,]33λ∈，点N 在棱BP 上，且BM AN ⊥，求BNBP的取值范围．17.（本题满分14分）（Ⅰ）方法1：OPCA设AC 的中点为O ，连接BO ，PO . 由题意PA PB PC ===1PO =，1AO BO CO ===因为在PAC ∆中，PA PC =，O 为AC 的中点所以PO AC ⊥，因为在POB ∆中，1PO =，1OB =，PB =所以PO OB ⊥ 因为ACOB O =，,AC OB ⊂平面ABC所以PO ⊥平面ABC因为PO ⊂平面PAC ·································································· 4分所以平面PAC ⊥平面ABC 方法2：OPCA B设AC 的中点为O ，连接BO ，PO .因为在PAC ∆中，PA PC =，O 为AC 的中点所以PO AC ⊥，因为PA PB PC ==，PO PO PO ==，AO BO CO ==所以POA ∆≌POB ∆≌POC ∆ 所以90POA POB POC ∠=∠=∠=︒ 所以PO OB ⊥ 因为ACOB O =，,AC OB ⊂平面ABC所以PO ⊥平面ABC因为PO ⊂平面PAC ·································································· 4分所以平面PAC ⊥平面ABC 方法3：OPCA Q设AC 的中点为O ，连接PO ，因为在PAC ∆中，PA PC =，所以PO AC ⊥设AB 的中点Q ，连接PQ ，OQ 及OB . 因为在OAB ∆中，OA OB =，Q 为AB 的中点所以OQ AB ⊥.因为在PAB ∆中，PA PB =，Q 为AB 的中点所以PQ AB ⊥. 因为PQOQ Q =，,PQ OQ ⊂平面OPQ所以AB ⊥平面OPQ 因为OP ⊂平面OPQ 所以OP AB ⊥因为AB AC A =，,AB AC ⊂平面ABC所以PO ⊥平面ABC因为PO ⊂平面PAC ·································································· 4分所以平面PAC ⊥平面ABC（Ⅱ）由PO ⊥平面ABC ，OB AC ⊥，如图建立空间直角坐标系，则(0,0,0)O ，(1,0,0)C ，(0,1,0)B ，(1,0,0)A -，(0,0,1)P由OB ⊥平面APC ，故平面APC 的法向量为(0,1,0)OB = 由(1,1,0)BC =-，(1,0,1)PC =- 设平面PBC 的法向量为(,,)n x y z =，则由00BC PC ⎧⋅=⎨⋅=⎩n n 得：0x y x z -=⎧⎨-=⎩ 令1x =，得1y =，1z =，即(1,1,1)n =cos ,||||3n OB n OB n OB ⋅<>===⋅由二面角A PC B --是锐二面角，所以二面角A PC B --·········································· 9分（Ⅲ）设BN BP μ=，01μ≤≤，则(1,1,0)(1,0,1)(1,1,)BM BC CM BC CP λλλλ=+=+=-+-=-- (1,1,0)(0,1,1)(1,1,)AN AB BN AB BP μμμμ=+=+=+-=-令0BM AN ⋅=得(1)1(1)(1)0λμλμ-⋅+-⋅-+⋅= 即1111λμλλ==-++，μ是关于λ的单调递增函数，当12[,]33λ∈时，12[,]45μ∈，所以12[,]45BN BP ∈ ········································································ 14分【东城一模】(17)（本小题14分）如图1，在边长为2的正方形ABCD 中，P 为CD 中点，分别将△PAD, △PBC 沿 PA,PB 所在直线折叠，使点C 与点D 重合于点O ，如图2．在三棱锥P-OAB 中，E 为 PB 中点． (Ⅰ)求证：PO ⊥AB;(II ）求直线BP 与平面POA 所成角的正弦值； (Ⅲ）求二面角P-AO-E 的大小．（17）（共14分）证明：（Ⅰ）在正方形ABCD 中，P 为CD 中点，PD AD ⊥,PC BC ⊥，所以在三棱锥P OAB -中，PO OA ⊥，PO OB ⊥. 因为OA OB O =，所以PO ⊥平面OAB .因为AB ⊂平面OAB ,所以PO AB ⊥. ……………………4分（Ⅱ）取AB 中点F ，连接OF ，取AO 中点M ，连接BM . 过点O 作AB 的平行线OG .因为PO ⊥平面OAB ，所以PO ⊥OF ，PO ⊥OG . 因为OA ＝OB ，F 为AB 的中点，所以OF ⊥AB . 所以OF ⊥OG .如图所示，建立空间直角坐标系O －xyz .A ()1，3，0，B ()－1，3，0，P ()0，0，1，M (12，32，0)．因为BO ＝BA ，M 为OA 的中点，所以BM ⊥OA .因为PO ⊥平面OAB ，PO ⊂平面POA ，所以平面POA ⊥平面OAB . 因为平面POA ∩平面OAB ＝OA ，BM ⊂平面OAB ，所以BM ⊥平面POA .因为BM uuu r ＝(32，－32，0)．所以平面POA 的法向量m ＝()3，－1，0.BP uu r＝(1，－3，1)．设直线BP 与平面POA 所成角为α，则sin cos BP BP BPa ×=<>==uu r uu ruu r m m,m . 所以直线BP 与平面POA 所成角的正弦值为155. ………………10分（Ⅲ）由(Ⅱ)知1122E ⎛⎫- ⎪ ⎪⎝⎭，1122OE ⎛⎫=- ⎪ ⎪⎝⎭，()OA =. 设平面OAE 的法向量为n ，则有 0,0.OA OE ⎧⋅=⎪⎨⋅=⎪⎩n n即0,0.x x z ⎧+=⎪⎨-++=⎪⎩ 令1y =-，则xz =即=-n .所以21cos ,242⋅===⋅⨯m n m n m n .由题知二面角P －AO －E 为锐角，所以它的大小为3p. ……………………………14分【西城一模】17．（本小题满分14分）如图1，在△ABC 中，D ，E 分别为AB ，AC 的中点，O 为DE的中点，AB AC ==4BC =．将△ADE 沿DE 折起到△1A DE 的位置，使得平面1A DE ⊥平面BCED ，如图2．（Ⅰ）求证：1AO BD ⊥；（Ⅱ）求直线1A C 和平面1A BD 所成角的正弦值；（Ⅲ）线段1A C 上是否存在点F ，使得直线DF 和BC求出11A FA C的值；若不存在，说明理由．图1 图2解：（Ⅰ）因为在△ABC 中，D ，E 分别为AB ，AC 的中点，所以 //DE BC ，AD AE =．所以11A D A E =，又O 为DE 的中点，所以 1AO DE ⊥．[1分]因为平面1A DE ⊥平面BCED ，且1AO ⊂平面1A DE ，所以 1AO ⊥平面BCED ，[3分] 所以 1AO BD ⊥．[ 4分]（Ⅱ）取BC 的中点G ，连接OG ，所以OE OG ⊥．由（Ⅰ）得1A O OE ⊥，1A O OG ⊥．如图建立空间直角坐标系O xyz -．[5分]由题意得，1(0,0,2)A ，(2,2,0)B -，(2,2,0)C ，(0,1,0)D -．所以1(2,2,2)A B −−→=--，1(0,1,2)A D −−→=--，1(2,2,2)A C −−→=-．设平面1A BD 的法向量为(,,)x y z =n ，则110,0,A B A D −−→−−→⎧⋅=⎪⎨⎪⋅=⎩n n 即2220,20.x y z y z --=⎧⎨--=⎩令1x =，则2y =，1z =-，所以(1,2,1)=-n ．[7分] 设直线1A C 和平面1A BD 所成的角为θ，则111||sin |cos ,|3||||A C A C A C θ−−→−−→−−→⋅=〈〉==n n n ．所以直线1A C 和平面1A BD．[9分] （Ⅲ）线段1A C 上存在点F 适合题意．设11A F A C λ−−→−−→=，其中[0,1]λ∈．[10分]设111(,,)F x y z ，则有111(,,2)(2,2,2)x y z λλλ-=-，所以1112,2,22x y z λλλ===-，从而(2,2,22)F λλλ-，所以(2,21,22)DF λλλ−−→=+-，又(0,4,0)BC −−→=，所以|||cos ,|||||DF BC DF BC DF BC −−→−−→−−→−−→−−→−−→⋅〈〉=[12分]，整理得23720λλ-+=．[13分]解得13λ=，舍去2λ=．所以线段1A C上存在点F适合题意，且1113A FA C=．[14分]【朝阳一模】16．(本小题满分14分)如图1，在矩形ABCD中，2AB=，4BC=，E为AD的中点，O为BE中点．将ABE∆沿BE折起到A BE'，使得平面A BE'⊥平面BCDE（如图2）．（Ⅰ）求证：A O CD'⊥；（Ⅱ）求直线A C'与平面A DE'所成角的正弦值；（Ⅲ）在线段A C'上是否存在点P，使得//OP平面A DE'? 若存在，求出A PA C''的值；若不存在，请说明理由．证明：（Ⅰ）由已知2AB AE==，因为O为BE中点，所以A O BE'⊥．因为平面A BE'⊥平面BCDE，且平面A BE'平面BCDE BE=，A O'⊂平面A BE'，所以A O'⊥平面BCDE．又因为CD⊂平面BCDE，所以A O CD'⊥．………….5分（Ⅱ）设F为线段BC上靠近B点的四等分点，G为CD中点．由已知易得OF OG⊥．由（Ⅰ）可知，A O'⊥平面BCDE，所以A O OF'⊥，A O OG'⊥.以O为原点，,,OF OG OA'所在直线分别为,,x y z轴建立空间直角坐标系（如图）．因为2A B'=，4BC=，图1EAB CDOA'图2DEO所以(00(110),(130),(130),(110)A B C D E ,，，，，，，，'---．设平面A DE '的一个法向量为111(,,)x y z =m ，因为(132),(020)A D DE ，，，，'=--=-，所以 0, 0,A D DE ⎧'⋅=⎪⎨⋅=⎪⎩m m 即111130, 20. x y y ⎧-+=⎪⎨-=⎪⎩取11z =-，得1)=-m ．而A C '=(1,3,.所以直线A C '与平面A DE '所成角的正弦值sin 3θ== ……….10分（Ⅲ）在线段A C '上存在点P ，使得//OP 平面A DE '. 设000(,,)P x y z ，且(01)A PA Cλλ'=≤≤'，则A P A C λ''=，[0,1]λ∈．因为(00(130)A C ，，'，所以000(,,(,3,)x yz λλ=，所以000,3,x y zλλ===，所以(,3)P λλ，(,3)OP λλ=．若//OP 平面A DE '，则OP ⊥m .即0OP ⋅=m .由（Ⅱ）可知，平面A DE '的一个法向量1)=-m，0=，解得1[0,1]2λ=∈，所以当12A P A C '='时，//OP 平面A DE '． ……….14分【丰台一模】（16）（本小题共14分）如图，在四棱锥P ABCD -中，平面PAB ⊥平面ABCD ，AB BC ⊥，AD BC ∥，3AD =，22PA BC AB ===，PB =（Ⅰ）求证：BC PB ⊥；（Ⅱ）求二面角P CD A --的余弦值；（Ⅲ）若点E 在棱PA 上，且BE ∥平面PCD ，求线段BE 的长．（16）（本小题共14分）（Ⅰ）证明：因为平面PAB ⊥平面ABCD ，且平面PAB 平面=ABCD AB ，因为BC ⊥AB ，且BC ⊂平面ABCD所以BC ⊥平面PAB ． ……………………3分因为PB ⊂平面PAB ，所以BC ⊥PB ． ……………………4分（Ⅱ）解：在△PAB 中，因为=2PA，=PB =1AB ，所以222=+PA AB PB ，所以PB ⊥AB ． ……………………5分所以，建立空间直角坐标系B xyz -，如图所示．所以(1,0,0)A -，(0,0,0)B ，(0,2,0)C ，(1,3,0)D -，P ，(1,1,0)CD =-，(0,2,PC =．易知平面ABCD 的一个法向量为=(0,0,1)n ． ……………………6分设平面PCD 的一个法向量为=(,,)x y z m ，则00CD PC ⎧⋅=⎪⎨⋅=⎪⎩m m ，即2x y y =⎧⎪⎨=⎪⎩，令=2z，则=m ． ……………………8分设二面角P CD A --的平面角为α，可知α为锐角，则cos cos ,α⋅=<>===⋅n m n m n m ，即二面角P CD A --……………………10分（Ⅲ）解：因为点E 在棱PA ，所以AE AP λ=，[0,1]λ∈． ……………………11分因为=1AP （，所以=)AE λ（，(1)BE BA AE λ=+=-．………12分又因为//BE 平面PCD ，m 为平面PCD 的一个法向量，所以0BE ⋅=m1)20λλ-+=，所以1=3λ． ………………13分所以2(,0,33BE =-，所以7==BE BE ． …………………14分【石景山一模】17．（本小题共14分）如图，四边形ABCD 是正方形，PA ⊥平面ABCD ，EB //PA ，4AB PA ==，2EB =，F 为PD 的中点．（Ⅰ）求证：AF PC ⊥；（Ⅱ）求证：BD //平面PEC ；（Ⅲ）求二面角D PC E --的大小． 17．（本小题共14分）（Ⅰ）证明：依题意，PA ⊥平面ABCD ．如图，以A 为原点，分别以AD 、AB 、AP 的方向为x 轴、y 轴、z 轴的正方向建立空间直角坐标系． ……2分依题意，可得(0,0,0)A ，(0,4,0)B ，(4,4,0)C ，(4,0,0)D ，(0,0,4)P ，(0,4,2)E ，(2,0,2)F ．因为(2,0,2)AF =，(4,4,4)PC =-，所以80(8)0AF PC ⋅=++-=． ……5分所以AF PC ⊥. ……6分（Ⅱ）证明：取PC 的中点M ，连接EM ．因为(2,2,2)M ，(2,2,0)EM =-，(4,4,0)BD =-，所以2BD EM =，所以//BD EM ． ……8分又因为EM ⊂平面PEC ，BD ⊄平面PEC ，所以//BD 平面PEC ． ……9分（Ⅲ）解：因为AF PD ⊥，AF PC ⊥，PD PC P =，所以AF ⊥平面PCD ，故(2,0,2)AF =为平面PCD 的一个法向量．……10分设平面PCE 的法向量为(,,)n x y z =，因为(4,4,4)PC =-，(0,4,2)PE =-，所以0,0,n PC n PE ⎧⋅=⎪⎨⋅=⎪⎩即4440,420,x y z y z +-=⎧⎨-=⎩ 令1y =-，得1x =-，2z =-，故(1,1,2)n =---． ……12分所以cos ,AF n <>==……13分所以二面角D PC E --的大小为5π6． ……14分。