第四版电路孙立山第7章频率特性和谐振现象
数字电子技术 7-3多谐振荡器

uI1
显然: 任何≥3 奇 首尾接 可形成环
(uO)
(a)
tPd
数个反相器 在一起 形振荡器
振荡频率: f 1
O
uI2
tPd
t
2ntPd
---式中n为串联门的个数,n=3、5、7、…
uIO3 tPd
t
优点:电路简单
O
缺点:频率太高不可调不实用 tPd只有几十纳秒到一二百纳秒
t (b)
工作波形图
R
R1 Rs
R1 R
UOL1
R u13
UOH2
RS
C
uI3
可求得电容C充电时间T1
T1
RECln
UE
UTH UOH UE UTH
U OL
RECln
2UOH UTH UOH UTH
O
VCC R1
G3
UE
RE
u13
C UOL
UTH+(UOH UOL)
UTH t
UTH (UOH UOL )
7.3.1
获得较大电
VDD
压放大倍数
uI1
uI2
uO2
使uO1↓到UOL ,而uO2↑至UOH,电路进入暂稳态
1/2VDD
直线uO1=uI1
O
P
G1静态
工作点
1/2VDD
uI
电压传输特性
7.3.1
用门电路构 成的振荡器
➢ 随着C放电uI1↓=UTH时: 另一正反馈过程发生
uI1
uI2
uO2
使uO1↓UOH,
品质因数高 选频特性好
由阻抗频率特性知:
当外加电压 信号的频率
等于
清华电工课件第5讲 电路中的谐振现象与频率特性

∙ ������ሶ
复导纳的虚部为0
并联谐振条件
������
+
������������ L ������������
������ C
R
−
������������
������0������ + ������0������
������
− ������0������
=
������
得:������������ =
������������ + ������������ ������ − ������(������������ + ������������ ������ − ������������)
∙ ������ሶ
=
������ ������������ + ������������ ������
∙ ������ሶ
即在电感和电容上可以产生比总电压 大很多的交流电压。
������������ = ������������ ≫ ������
������������ ������������
������
t
������������ + ������������ = ������
谐振时的相量图
������ሶ ������
=
������0������ ������
=
1 ������0������������
Q 则体现了在谐振状态下电容或电 感上电压比电源电压高出的倍数。若 R<<XL、R<<XC ,则品质因数很大。
串联谐振特性曲线
������
������ =
������2 +
������������
电路理论基础第四版 孙立山 陈希有主编 第7章习题答案详解

《电路理论基础》习题7答案答案7.1解:由阻抗并联等效公式得:Ω+=+=---33636310j 110)10j /(110)10j /(10)j (ωωωωZ 阻抗模及幅角分别为:233)10(110)j (ωω-+=Z ,)10arctan()(3ωωθ--=令2/1)j (c=ωZ 求得截止角频率rad/s 103c=ω,故通带及阻带分别为: 通带=ω0~rad/s 103,阻带=ωrad/s 103~∞。
幅频特性和相频特性如图(b)和(c)所示。
1234O(b)|)j (|ωZ 10.7(c)1234O)(ωθο45-ο90-c/ωωc/ωω答案7.2解: RC 并联的等效阻抗RC RC R C R Z RCωωωj 1j /1j /+=+= RCRC Z L Z U U H +==ωωj /)j (12&& RL LC RC L R R /j 11)j 1(j 2ωωωω+-=++= 幅频特性222)/()1(1)j (R L LC H ωωω+-=当0→ω时, 1)j (=ωH ;当∞→ω时,0)j (=ωH所以它具有低通特性。
答案7.3解:设1111111j j 1//C R R R C R Z ωω+==, 2222222j j 1//C R R R C R Z ωω+== 由分压公式得:12122U Z Z Z U &&+= )j 1()j 1()j 1()j (11222111212C R R C R R C R R U U H ωωωω++++==&& 当R 1C 1=R 2C 2时,得212)j (R R R H +=ω,此网络函数模及辐角均不与频率无关。
答案7.4解:因为电路处于谐振状态,故电感与电容串联电路相当于短路,因此有50S12121==+I U R R R R Ω代以Ω=1001R ,解得Ω=1002R 又因为电路处于谐振状态 , 所以 Ω==100C L X X 故有V 5021S12=⨯+==L L L X R R I R X I U 答案7.5解:(1)根据题意,电路发生谐振时,存在下列关系:⎪⎩⎪⎨⎧======V10A1/rad/s 10/14LI U R U I LC L ωω 解得 ⎪⎩⎪⎨⎧==Ω=F 10mH 11.0μC L R 品质因数 1001.010===U U Q L(2)V 9010V 901001)(j ︒-∠=︒-∠⨯︒∠==C I U Cω&& 即有V )90cos(210︒-=t u Cω 答案9.9解:由串联谐振规律得:⎪⎪⎩⎪⎪⎨⎧===∆==Ω=RL Q Q LC R /rad/s 100/rad/s 10/1100030ωωωω 解得 ⎪⎩⎪⎨⎧==Ω=1μμC H 1100L R答案7.6解:(1)F 10034.132.0)8752(117220-⨯=⨯⨯==πωL C Qωω=∆ , 5.3250/875/0==∆=ωωQ R L Q /0ω=, Ω=⨯⨯==65.5025.3/32.08752/0πωQ L R 谐振频率为Hz 759)14121(021c ≈⨯++-=f Q Q f Hz 1009)14121(02c2≈⨯++=f QQ f(2) 谐振时电路的平均功率为:W 071.165.502)65.502/2.23(2200=⨯==R I P 在截止频率处,电流下降至谐振电流0I 的2/1,故功率减小到0P 的一半,所以当Hz 759=f 和Hz 1009=f 时,电路平均功率均为W 535.02/0==P P (3)V 2.812.235.3=⨯===QU U U CL 答案7.7解:由谐振时阻抗为Ω310得 Ω=1000RRLC 并联电路带宽:Q/0ωω=∆(参考题9.16) 由带宽与谐振角频率及品质因数的关系得:10/0=∆=ωωQ RLC 并联电路的品质因数为10/0==G C Q ω 由上式求得:μF10)10001000/(10/100=⨯==ωG C 由C L 00/1ωω=得 H1.0H )1010/(1/15620=⨯==-C L ω答案7.8略 答案7.9解:当两线圈顺接时,等效电感H 05.0221=++=M L L L 谐振角频率s rad 10102005.011361=⨯⨯==-LC ω 取V06︒∠=U &,则谐振时的电流 A 04.0A 1050621︒∠=+︒∠=+=R R U I && 由互感的元件方程得: j124(0.4]V j100.4j20)10[(j )j (j8)V 2(0.4]V j100.4j10)5[(j )j (1212211111+=⨯+⨯+=++=+=⨯+⨯+=++=I M I L R U I M I L R U &&&&&&ωωωω两线圈电压的有效值分别为V 24.882221=+=U ,V 65.12124222=+=U 当两线圈反接时,等效电感H 01.0221'=-+=M L L L 谐振角频率rad/s 10236.2102001.01362⨯=⨯⨯=-ω j8.94(0.4A j22.36)10(j )j (2V A 4.05j )j (2222221211+=⨯Ω+=-+==⨯Ω=-+=I M I L R U I M I L R U &&&&&&ωωωω此时两线圈电压的有效值分别为V 21=U ,V 8.995.84222=+=U 答案7.10略答案7.11图示电路,V )cos(22S t u ω=,角频率rad/s 100=ω,Ω=1R ,F 1021-=C ,F 105.022-⨯=C 。
高频电子线路第四版第7章正弦波振荡器

Av
Av 0 1
1
jQL
0
0
arc
tanQ
0
0
图 7.5.4 并联谐振回路的 相频特性
7.6.1 互感耦合振荡器 7.6.2 电感反馈式三端振荡器
(哈特莱振荡器)
7.6.3 电容反馈式三端振荡器 (考毕兹振荡器)
7.6.4 LC三端式振荡器相位平衡条件 的判断准则
放大器与振荡器本质上都是将直流电能转化为交 流电能,不同之处在于:放大器需要外加控制信号而 振荡器不需要。因此,如果将放大器的输出正反回输 入端,以提供控制能量转换的信号,就可能形成振荡 器。
被保留,成为等幅振荡输出信号。(从无到有)
然而,一般初始信号很微弱,很容易被干扰信号淹没,不 能形成一定幅度的输出信号。因此,起振阶段要求
起振条件 A(0 ) F (0 ) 1 (由弱到强)
A (0 ) F (0 ) 2nπ
当输出信号幅值增加到一定程度时,就要限制它继续增加。 稳幅的作用就是,当输出信号幅值增加到一定程度时,
如果由LC谐振回路通过互感耦合将输出信号送
回输入回路,所形成的是互感耦合振荡器。
由互感耦合同名端定义可判知,反馈网络形成 正反馈,满足相位平衡条件。如果再满足起振条件, 就符合基本原理。射基(集)同名
三极管,LC谐振回路
变压器
如果正反馈网络由LC谐振回路中的电感分压电路将输出信号
送回输入回路,所形成的是电感反馈式三端振荡器。
而对于基频和3次泛音频率来 说,回路呈感性,振荡器不满足相 位平衡条件,不能产生振荡。而对 于7次及其以上的泛音频率,回路 呈容性,但其电容量过大,负载阻 抗过小,以致电压增益下降太多, 不能起振。
图 7.8.5 泛音晶体振荡器 交流等效电路
电路理论基础第四版孙立山陈希有主编

电路理论基础第四版孙立山陈希有主编1. 引言电路理论是电子工程的核心内容之一,其基础理论对于电子工程师的培养至关重要。
《电路理论基础》是一本经典的教材,在第四版中由孙立山和陈希有主编。
本文将介绍该教材的主要内容和特点,并对其在电子工程教育中的应用进行讨论。
2. 内容概述《电路理论基础》第四版按照电路理论的基本概念和原理进行组织和讲解。
全书共分为十章内容,主要包括以下内容:1.电路基本概念:介绍电路的基本概念,如电流、电压、电阻等。
解释了电路中的基本元件和参数的含义及其相互关系。
2.Ohm定律与基本电路定律:介绍了Ohm定律和基本电路定律,如基尔霍夫定律、毕奥-萨伐尔定律等。
解释了这些定律的原理和应用。
3.串联与并联电路:讲解了串联和并联电路的特点和计算方法。
分析了在串联和并联电路中电流和电压的分布情况。
4.电路的戴维南定理与戴证神定理:详细介绍了电路的戴维南定理和戴证神定理,分析了这两个定理在电路分析中的重要作用。
5.交流电路:讲解了交流电路的基本概念和特点。
介绍了正弦波电压和电流的表达方式及其相关的计算方法。
6.电路的幅频特性:详细介绍了电路的幅频特性,包括电路的增益、相位和频率响应等概念。
解释了幅频特性在电路分析与设计中的重要性。
7.滤波器电路:介绍了滤波器电路的基本原理和分类。
讲解了低通滤波器、高通滤波器、带通滤波器和带阻滤波器的设计与应用。
8.放大电路:详细介绍了放大电路的基本概念和原理。
解释了放大电路的输入阻抗、输出阻抗和增益等重要参数及其影响因素。
9.模拟电路:讲解了模拟电路的基本概念和特点。
介绍了放大电路、振荡电路、多级放大电路等模拟电路的设计和分析方法。
10.数字电路:介绍了数字电路的基本概念和分类。
讲解了数字电路的逻辑门、触发器和计数器等重要元件的工作原理和应用。
3. 特点分析《电路理论基础》第四版在内容安排上注重基础理论的系统性和层次性,既注重理论概念的讲解,又注重实际电路应用的分析。
电机的谐振频率-概述说明以及解释

电机的谐振频率-概述说明以及解释1.引言1.1 概述电机的谐振频率是指在特定条件下,电机产生谐振现象所对应的频率。
谐振是一种物理现象,当系统受到外力激励时,如果其固有频率与外力频率完全或接近地匹配,系统会发生共振现象,这种共振所对应的频率即为谐振频率。
对于电机而言,谐振频率的研究对于了解其工作特性和性能具有重要意义。
电机作为一种能够将电能转换为机械能的装置,在各个行业和领域中起着不可或缺的作用。
然而,由于电机的运行过程中会受到各种因素的干扰,如电压变化、负载波动等,导致电机可能产生谐振现象。
当电机处于谐振状态时,其振动幅度会迅速增大,严重影响了电机的正常运行和稳定性。
本文旨在对电机的谐振频率进行详细介绍和分析。
首先,我们将探讨电机谐振现象的特点和机制,了解电机在何种情况下容易发生谐振。
其次,我们将给出谐振频率的定义和计算方法,以便于更好地理解和研究电机的谐振现象。
最后,我们还将讨论影响谐振频率的因素,并探讨电机谐振频率的应用和意义。
通过对电机谐振频率的研究,我们可以更好地了解电机的工作原理和特性,帮助我们设计和选择适合的电机,提高其工作效率和稳定性。
同时,对于电机维护和故障诊断方面也有一定的指导意义。
因此,深入研究电机的谐振频率对于电机相关行业和领域具有重要的理论意义和应用价值。
1.2 文章结构文章结构部分旨在介绍本文的整体组织结构和各个章节之间的逻辑关系。
通过清晰地呈现文章的架构,读者能够更好地理解和掌握文章的内容。
本文共分为引言、正文和结论三个部分。
在引言部分,我们会提供概述、文章结构和目的的内容介绍。
正文部分将详细讨论电机的谐振现象和谐振频率的定义。
结论部分将总结影响谐振频率的因素,并探讨谐振频率在实际应用中的意义。
首先,在引言部分的概述中,我们将简要介绍电机的谐振频率是什么以及为什么它很重要。
同时,我们还会提及电机谐振频率的实际应用和研究背景,为读者建立起对这一主题的基本认识。
接下来,在引言部分的文章结构中,我们将简要描述整个文章中各个章节的内容组成。
电路理论基础第四版孙立山陈希有主编第7章习题答案详解

《电路理论基础》习题7答案答案解:由阻抗并联等效公式得:Ω+=+=---33636310j 110)10j /(110)10j /(10)j (ωωωωZ 阻抗模及幅角分别为:233)10(110)j (ωω-+=Z ,)10arctan()(3ωωθ--=令2/1)j (c=ωZ 求得截止角频率rad/s 103c=ω,故通带及阻带分别为: 通带=ω0~rad/s 103,阻带=ωrad/s 103~∞。
幅频特性和相频特性如图(b)和(c)所示。
--答案解: RC 并联的等效阻抗RCRC R C R Z RCωωωj 1j /1j /+=+= RCRC Z L Z U U H +==ωωj /)j (12&& RL LC RC L R R /j 11)j 1(j 2ωωωω+-=++= 幅频特性222)/()1(1)j (R L LC H ωωω+-=当0→ω时, 1)j (=ωH ;当∞→ω时,0)j (=ωH所以它具有低通特性。
答案解:设1111111j j 1//C R R R C R Z ωω+==, 2222222j j 1//C R R R C R Z ωω+== 由分压公式得:12122U Z Z Z U &&+= )j 1()j 1()j 1()j (11222111212C R R C R R C R R U U H ωωωω++++==&& 当R 1C 1=R 2C 2时,得212)j (R R R H +=ω,此网络函数模及辐角均不与频率无关。
答案解:因为电路处于谐振状态,故电感与电容串联电路相当于短路,因此有50S12121==+I U R R R R Ω代以Ω=1001R ,解得Ω=1002R 又因为电路处于谐振状态 , 所以Ω==100C L X X 故有V 5021S12=⨯+==LL L X R R I R X I U 答案解:(1)根据题意,电路发生谐振时,存在下列关系:⎪⎩⎪⎨⎧======V10A1/rad/s 10/14LI U R U I LC L ωω 解得 ⎪⎩⎪⎨⎧==Ω=F 10mH 11.0μC L R 品质因数 1001.010===U U Q L (2)V 9010V 901001)(j ︒-∠=︒-∠⨯︒∠==C I U Cω&& 即有V )90cos(210︒-=t u Cω答案解:由串联谐振规律得:⎪⎪⎩⎪⎪⎨⎧===∆==Ω=R L Q Q LC R /rad/s 100/rad/s10/1100030ωωωω 解得 ⎪⎩⎪⎨⎧==Ω=1μμC H 1100L R答案解:(1)F 10034.132.0)8752(117220-⨯=⨯⨯==πωL C Qωω=∆ , 5.3250/875/0==∆=ωωQ R LQ /0ω=, Ω=⨯⨯==65.5025.3/32.08752/0πωQ L R 谐振频率为Hz 759)14121(021c ≈⨯++-=f Q Q f Hz 1009)14121(02c2≈⨯++=f QQ f(2)谐振时电路的平均功率为:W 071.165.502)65.502/2.23(2200=⨯==R I P 在截止频率处,电流下降至谐振电流0I 的2/1,故功率减小到0P 的一半,所以当Hz 759=f 和Hz 1009=f 时,电路平均功率均为W 535.02/0==P P (3)V 2.812.235.3=⨯===QU U U CL 答案解:由谐振时阻抗为Ω310得 Ω=1000RRLC 并联电路带宽:Q/0ωω=∆(参考题) 由带宽与谐振角频率及品质因数的关系得:10/0=∆=ωωQ RLC 并联电路的品质因数为10/0==G C Q ω 由上式求得:μF10)10001000/(10/100=⨯==ωG C 由C L 00/1ωω=得 H1.0H )1010/(1/15620=⨯==-C L ω答案略 答案解:当两线圈顺接时,等效电感H 05.0221=++=M L L L 谐振角频率rad 10102005.011361=⨯⨯==-LC ω 取V06︒∠=U &,则谐振时的电流 A 04.0A 1050621︒∠=+︒∠=+=R R U I && 由互感的元件方程得: j124(0.4]V j100.4j20)10[(j )j (j8)V 2(0.4]V j100.4j10)5[(j )j (1212211111+=⨯+⨯+=++=+=⨯+⨯+=++=I M I L R U I M I L R U &&&&&&ωωωω两线圈电压的有效值分别为V 24.882221=+=U ,V 65.12124222=+=U 当两线圈反接时,等效电感H 01.0221'=-+=M L L L 谐振角频率rad/s 10236.2102001.01362⨯=⨯⨯=-ω j8.94(0.4A j22.36)10(j )j (2V A 4.05j )j (2222221211+=⨯Ω+=-+==⨯Ω=-+=I M I L R U I M I L R U &&&&&&ωωωω此时两线圈电压的有效值分别为V 21=U ,V 8.995.84222=+=U 答案略答案图示电路,V )cos(22S t u ω=,角频率rad/s 100=ω,Ω=1R ,F 1021-=C ,F 105.022-⨯=C 。
电工电子技术--谐振电路及其频率特性

若用户:cos 0.6则电源可发出的有功功率为:
P UN INcos 600kW
而需提供的无功功率为:
Q U I sin 800kvar NN
所以提高 cos可使发电设备的容量得以充分利用。
(2)增加线路和发电机绕组的功率损耗 设输电线和发电机绕组的电阻为 : r
要求: P U I cos (P、U定值)时
Ucos 220 0.5
电源的额定电流为:
IN
SN UN
10 103 220
A 45.45A
例2:
该电源供出的电流超过其额定电流。
(2)如将cos 提高到0.9后,电源提供的电流为:
I P 6103 A 30.3A
Ucos 220 0.9
该电源还有富裕的容量。即还有能力再带负载; 所以提高电网功率因数后,将提高电源的利用率。
u1
_ +
L L=250H, R=20, C=150pF(调好),
u2
U1=U2= U3 =10V, 0=5.5106 rad/s,
_ +
C f0=820 kHz.则能收到哪个台?
u3
_
北京台 中央台
北京经济台
f (kHz) 820
640
1026
L
1290
1000
1611
1
ωC
1290
1660
1034
I( )
路对非谐振频率下的电流具有较强的 0.707 抑制能力,所以选择性好。
Q=0.5
Q=1
在I / I0 1/ 2 0.707处作一水平线, 与每一谐振曲线交于两点, 对应横坐
0 1 1 2
Q=10
第7章习题解答哈工大习题册
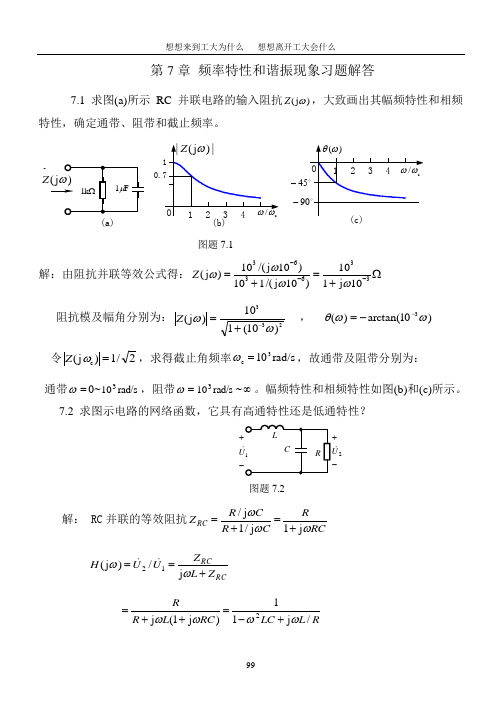
第7章 频率特性和谐振现象习题解答7.1 求图(a)所示RC 并联电路的输入阻抗)j (ωZ ,大致画出其幅频特性和相频特性,确定通带、阻带和截止频率。
(a)Z (b)--图题7.1解:由阻抗并联等效公式得:36336310/(j 10)10(j )101/(j 10)1j 10Z ωωωω---==Ω++ 阻抗模及幅角分别为:233)10(110)j (ωω-+=Z , )10arctan()(3ωωθ--=令2/1)j (c =ωZ ,求得截止角频率rad/s 103c =ω,故通带及阻带分别为: 通带=ω0~rad/s 103,阻带=ωrad/s 103~∞。
幅频特性和相频特性如图(b)和(c)所示。
7.2 求图示电路的网络函数,它具有高通特性还是低通特性?2图题7.2解: RC 并联的等效阻抗RCRC R C R Z RC ωωωj 1j /1j /+=+=RCRCZ L Z U U H +==ωωj /)j (12RL LC RC L R R /j 11)j 1(j 2ωωωω+-=++=幅频特性222)/()1(1)j (R L LC H ωωω+-=当0→ω时, 1)j (=ωH ;当∞→ω时,0)j (=ωH所以它具有低通特性。
7.3求图示电路的转移电压比21(j )/H U U ω=,当1122R C R C =时,此网络函数有何特性?2图 题7.3解:设1111111j j 1//C R R R C R Z ωω+==, 2222222j j 1//C R R R C R Z ωω+==由分压公式得:12122U Z Z Z U += )j 1()j 1()j 1()j (11222111212C R R C R R C R R U U H ωωωω++++== 当R 1C 1=R 2C 2时,得212)j (R R R H +=ω,此网络函数模及辐角均不与频率无关。
7.4设图示电路处于谐振状态,其中S 1A I =,150V U =,1100C R X ==Ω。
谐振电路的频率特性
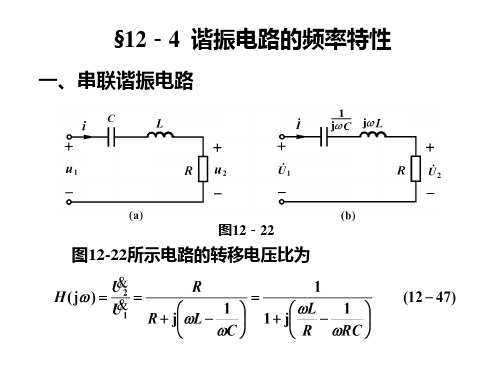
一、串联谐振电路
图12-22
图12-22所示电路的转移电压比为
代入
, 将上式改为
其振幅为
由此式可见,当=0或=时,|H(j)|=0; 当 时,电路发生谐振,|H(j)|=1达到
最大值,说明该电路具有带通滤波特性。为求出通频带的 宽度,先计算与 (即-3dB)对应的频率+和
此式说明并联谐振电路的幅频特性曲线和计算频带宽 度等公式均与串联谐振电路相同,不再重述。
例12-8 RLC并联谐振电路中,已知R=10k,L=1H, C=1F。试求电路的谐振角频率、品质因数和3dB 带宽。 解:
图12-23
例12-7 欲接收载波频率为10MHz的某短波电台的信号,试 设计接收机输入谐振电路的电感线圈。要求带宽 f=100kHz,C=100pF。 解:由 求得:
由此得到电感线圈的参数为 L=2.53H和R=1.59。
二、并联谐振电路
图12-24
图示电路的转移电流比为
代入
将上式改为
-,为此令
求解得到
由此求得3dB带宽
或
这说明带宽与品质因数Q成反比,Q越大,越小, 通带越窄,曲线越尖锐,对信号的选择性越好。
对不同Q值画出的幅频特性曲线,如图12-24所示。此
曲线横坐标是角频率与谐振角频率之比(即相对频率),纵 坐标是转移电压比,也是相对量,故该曲线适用于所有串 联谐振电路,因而被称为通用谐振曲线。当=+或 =- 时, |H(j)|=0.707 (对应-3dB),=45。
电路基础原理概述电路的共振和谐振频率

电路基础原理概述电路的共振和谐振频率电路是现代生活中不可或缺的一部分,从简单的电子玩具到复杂的计算机系统,都离不开电路的设计和应用。
在电路中,共振和谐振频率是一项重要的概念和实践,对于电路的稳定性和性能起着至关重要的作用。
共振是指在电路中,当感性元件(如电感、变压器等)和容性元件(如电容)相互耦合时,电路中的电流和电压呈现出特定的增加或减小的现象。
共振频率是指在某一频率下,电路中的电流或电压达到最大或最小值。
共振频率的计算可以通过电路的参数和元件来实现。
共振频率的计算涉及到电路中的电感和电容的数值。
有一个简单的公式可以用来计算共振频率:共振频率= 1 / (2π√(LC)),其中π是圆周率,L是电感的值,C是电容的值。
通过这个公式,我们可以根据电路中的元件数值来计算出共振频率。
共振频率的计算对于电路的设计和优化至关重要。
在很多应用中,我们希望电路在特定频率下能够达到最佳的性能和效果。
例如,在无线通信中,我们希望电路能够在特定的频率下实现信号的传输和接收。
通过计算共振频率,我们可以根据需要选择合适的电感和电容数值,来实现电路对特定频率的敏感度和增益。
谐振频率是共振频率的一种特殊情况,指的是在电路中只有一个频率能够实现共振现象。
在谐振频率下,电路中的电流和电压达到最大或最小值,能够实现最佳的传输和转换效果。
谐振频率的计算方法和共振频率类似,通过电感和电容的数值来计算。
共振和谐振频率的实际应用非常广泛。
在无线通信中,共振和谐振频率的设计能够提高信号的传输质量和距离。
在调频电台和调幅电台中,通过调整电感和电容的数值,可以使电路在特定频率范围内实现最佳传输效果。
在音频系统中,谐振频率的调整可以实现音量和音质的优化。
总之,电路的共振和谐振频率是电路设计和应用中不可或缺的一部分。
通过计算和调整电感和电容的数值,可以实现电路对特定频率的增益和敏感度。
这对于提高电路的性能和稳定性有着重要的作用。
因此,对于电路设计者和工程师来说,了解和掌握共振和谐振频率的原理和计算方法是至关重要的。
频率特性

U2( jω) 1 G( jω) = = = A(ω)e jϕ(ω) U1( jω) 1+ jωT
A(ω) =
1 1+ (Tω)2
幅值A(ω 幅值A(ω)随着频率升高而衰减 A( 对于低频信号 (ωT << 1) 对于高频信号 (ωT >> 1)
A(ω) ≈ 1
1 A(ω) ≈ ≈0 ωT
频率特性的定义
什么是频率特性? 什么是频率特性? 对于确定的角频率ω,输出与输入之间有确定的关系。 对于确定的角频率 ,输出与输入之间有确定的关系。
x(t ) = X sinωt
& X = X∠0o
ys (t) = Y sin(ωt +ϕ) & Y =Y∠ϕ
频率特性的定义
频率特性的定义
频率特性与传递函数的关系
y(t ) = be− jωt + be jωt + a1e−s1t + a2e−s2t ... + ane−snt
X(s)
t ≥0
对于稳定的所有的闭环极点都在左半s平面,所以, 对于稳定的所有的闭环极点都在左半 平面,所以,输 平面 出的稳态值为: 出的稳态值为:
G( jω) = U(ω) + jV (ω) −112×0.02ω U(ω) = 0.4×10−3ω3 + ω − 112 V(ω) = 0.4×10−3ω3 + ω
频率特性的图示方法
G( jω) = A(ω)e jϕ(ω) lg G( jω) = lg A(ω) + jϕ(ω)lg e
幅值相乘变为相加,简化作图。 幅值相乘变为相加,简化作图。 对数幅频+对数相频 对数幅频 对数相频 为了拓宽频率范围, 为了拓宽频率范围,通常 将对数幅频特性绘在以10 将对数幅频特性绘在以 为底的半对数坐标中。 为底的半对数坐标中。
高频电子线路第7章参考答案第四版

高频电子线路习题参考答案
(2) 若υΩ(t)=20sin(2π*103t),则: AM调幅时,信号带宽仍然B=2F=2ⅹ1000=2000Hz。 但在FM调制时,Δfm=20kf=20Hz, 则调频信号带宽为 BS=2(Δfm+F)= 2(20+1)=42kHz. (3)比较(1)和(2)的结果,可以看到,AM调幅时的信号带宽 只取决于调制信号的频率,而与调制信号的大小无关。对于 FM调制,在窄带调制时,信号带宽基本上等于AM信号带宽, 但在宽带调制时,主要取决于调制灵敏度和调制信号的振幅, 带宽基本不随调制信号频率而变化,可以看作是恒定带宽。
题7—8图
高频电子线路习题参考答案
解7-8 ( 1 )该电路是一个变容二极管部分接入的直接调频电路, C1、C2、Cj 和L组成谐振回路,并与晶体管组成一个电容 三点式振荡器。调制信号经Lc加到二极管上,形成随调制 信号变化的反向偏压。当调制信号随时间改变时,振荡器 的频率也随之改变,达到了调频的目的。Lc为高频扼流圈, C3 、 C4 和 C5 为高频旁路电容。 Lc 、 C5 和 Lc 、 C4 组成的低 通滤波器保证了高频正弦信号不会影响直流偏置,并避免 了给电源带来高频干扰,C3对高频信号相当短路,从而提 高了振荡器的环路增益。调节R2,可改变变容二极管的静 态偏置电压,达到调整中心载波频率的目的。
高频电子线路习题参考答案
高频电子线路习题参考答案
7-4 频率为 100 MHz的载波被频率被 5 kHz的正弦信号调 制, 最大频偏为 50 kHz。,求此时FM波的带宽。若 UΩ加倍, 频率不变,带宽是多少?若UΩ不变,频率 增大一倍,带宽 如何?若UΩ和频率都增大一倍,带宽又如何 解7-4
根据题意,已知
电路理论基础第四版-孙立山-陈希有主编-第7章习题答案详解Word版

《电路理论基础》习题7答案答案7.1解:由阻抗并联等效公式得:Ω+=+=---33636310j 110)10j /(110)10j /(10)j (ωωωωZ 阻抗模及幅角分别为:233)10(110)j (ωω-+=Z ,)10arctan()(3ωωθ--=令2/1)j (c=ωZ 求得截止角频率rad/s 103c =ω,故通带及阻带分别为: 通带=ω0~rad/s 103,阻带=ωrad/s 103~∞。
幅频特性和相频特性如图(b)和(c)所示。
(b)--答案7.2解: RC 并联的等效阻抗RCRC R C R Z RCωωωj 1j /1j /+=+= RCRC Z L Z U U H +==ωωj /)j (12 RL LC RC L R R /j 11)j 1(j 2ωωωω+-=++= 幅频特性222)/()1(1)j (R L LC H ωωω+-=当0→ω时, 1)j (=ωH ;当∞→ω时,)j (=ωH所以它具有低通特性。
答案7.3解:设1111111j j 1//C R R R C R Z ωω+==, 2222222j j 1//C R R R C R Z ωω+== 由分压公式得:12122U Z Z Z U += )j 1()j 1()j 1()j (11222111212C R R C R R C R R U U H ωωωω++++== 当R 1C 1=R 2C 2时,得212)j (R R R H +=ω,此网络函数模及辐角均不与频率无关。
答案7.4解:因为电路处于谐振状态,故电感与电容串联电路相当于短路,因此有50S12121==+I U R R R R Ω代以Ω=1001R ,解得Ω=1002R 又因为电路处于谐振状态 , 所以 Ω==100C L X X 故有V 5021S12=⨯+==LL L X R R I R X I U 答案7.5解:(1)根据题意,电路发生谐振时,存在下列关系:⎪⎩⎪⎨⎧======V10A1/rad/s 10/14LI U R U I LC L ωω 解得 ⎪⎩⎪⎨⎧==Ω=F 10mH 11.0μC L R 品质因数 1001.010===U U Q L(2)V 9010V 901001)(j ︒-∠=︒-∠⨯︒∠==C I U Cω即有V )90cos(210︒-=t u Cω 答案9.9解:由串联谐振规律得:⎪⎪⎩⎪⎪⎨⎧===∆==Ω=R L Q Q LC R /rad/s 100/rad/s10/1100030ωωωω 解得 ⎪⎩⎪⎨⎧==Ω=1μμC H 1100L R答案7.6解:(1)F 10034.132.0)8752(117220-⨯=⨯⨯==πωL C Qωω=∆ , 5.3250/875/0==∆=ωωQ R L Q /0ω=, Ω=⨯⨯==65.5025.3/32.08752/0πωQ L R 谐振频率为Hz 759)14121(021c ≈⨯++-=f Q Q f Hz 1009)14121(02c2≈⨯++=f QQ f(2) 谐振时电路的平均功率为:W 071.165.502)65.502/2.23(2200=⨯==R I P 在截止频率处,电流下降至谐振电流0I 的2/1,故功率减小到0P 的一半,所以当Hz 759=f 和Hz 1009=f 时,电路平均功率均为W 535.02/0==P P (3)V 2.812.235.3=⨯===QU U U CL 答案7.7解:由谐振时阻抗为Ω310得 Ω=1000RRLC 并联电路带宽:Q/0ωω=∆(参考题9.16) 由带宽与谐振角频率及品质因数的关系得:10/0=∆=ωωQ RLC 并联电路的品质因数为10/0==G C Q ω 由上式求得:μF10)10001000/(10/100=⨯==ωG C 由C L 00/1ωω=得 H1.0H )1010/(1/15620=⨯==-C L ω答案7.8略 答案7.9解:当两线圈顺接时,等效电感H 05.0221=++=M L L L 谐振角频率rad 10102005.011361=⨯⨯==-LC ω 取V06︒∠=U ,则谐振时的电流 A 04.0A 1050621︒∠=+︒∠=+=R R U I 由互感的元件方程得: j124(0.4]V j100.4j20)10[(j )j (j8)V 2(0.4]V j100.4j10)5[(j )j (1212211111+=⨯+⨯+=++=+=⨯+⨯+=++=I M I L R U I M I L R U ωωωω两线圈电压的有效值分别为V 24.882221=+=U ,V 65.12124222=+=U 当两线圈反接时,等效电感H 01.0221'=-+=M L L L 谐振角频率rad/s 10236.2102001.01362⨯=⨯⨯=-ω j8.94(0.4A j22.36)10(j )j (2V A 4.05j )j (2222221211+=⨯Ω+=-+==⨯Ω=-+=I M I L R U I M I L R U ωωωω此时两线圈电压的有效值分别为V 21=U ,V 8.995.84222=+=U 答案7.10略答案7.11图示电路,V )cos(22S t u ω=,角频率rad/s 100=ω,Ω=1R ,F 1021-=C ,F 105.022-⨯=C 。
电阻对理想RLC串联谐振电路频率特性的影响

姓名班级学号实验日期 5.28 节次7.8 教师签字成绩电阻对理想RLC串联谐振电路频率特性的影响1.实验目的1.测量分析由于信号源内阻、电容及电感电阻存在所导致的实验常用简单无源滤波器滤波性能变化。
2.分析电阻值大小会对无源滤波器的滤波影响变化趋势并尝试提出实际缩小误差的方案。
2.总体设计方案或技术路线1. 在实际中由于电源内阻、电感电阻、电容阻值的影响,谐振电路的频率特性会受到各种各样的的影响,本实验期望通过对于带通滤波器仿真及实际实验测量分析电阻在各个元件中以及电源中的存在对于频率特性的影响。
2.在仿真实验中,由于各元件都是理想状态,因而可以直接将相应原件与一适宜大小的电阻进行串联3.实验电路图4.仪器设备名称、型号交直流实验箱示波器数字万用表函数信号发生器直流稳压电源、各型号电感电容以及导线等5.电感内阻电容内阻FrequencyV(R2:1)+ V(C1:1)FrequencyV(R2:1)+ V(L1:1)3.0V2.0V1.0V0V1.0Hz 3.0Hz10Hz30Hz100Hz300Hz 1.0KHz 3.0KHz10KHz30KHz100KHz V(R1:1)+ V(R2:1)Frequency电阻增加V(R1:1)Frequency电源内阻其中所有电阻变化在图线下标中均为从左向右依次增加,第一个为1nΩ,模拟0内阻的时候,其余四个为10Ω,100Ω,1kΩ,10kΩ6.详细实验步骤及实验结果数据记录(包括各仪器、仪表量程及内阻的记录)测量电源内阻影响1.按照电路图连接电路,并检查个部分工作是否正常。
2.对电源进行串连一个电阻箱,并调节相应电阻值。
3.调节信号源频率,使获得最大信号强度,记录此时频率f0。
4.在此频率基础上测量获得两个截止频率,并在其中选取相应频率值记数。
5.改变电阻值,再次测量。
信号源频率/Hz 10 80 149 180 210 f0 223 输出电压/mv 30.9 266 582 726 810 821信号源频率/Hz 260 310 340 400 1k 电阻值Ω输出电压/mv 777 652 581 469 160 0信号源频率/Hz 10 40 144 170 210 f0 223 输出电压/v 30.9 126 536 645 750 758 信号源频率/Hz 270 290 352 500 2k 电阻值Ω输出电压/v 705 663 535 349 77.1 100信号源频率/Hz 20 80 110 150 190 f0 223 输出电压/v 61.8 239 316 394 437 446 信号源频率/Hz 280 340 464 600 1k 电阻值Ω输出电压/v 430 392 315 251 155 1k 相应修正:信号源电压Vrms=1v,C=5uF,L=1H,Rl=146Ω测量电感内阻影响1.按照电路图连接电路,并检查个部分工作是否正常。
正弦交流电路的频率特性(精)

1 RC 2
T
其中: T --- 幅频特性:输出与输入有效值
之比与频率的关系。
---相频特性:输出与输入相位差 与频率的关系。
低通滤波器的频率特性
T
幅频特性
1
T()
1
1 2
1 RC2
0 :截止频率 0 ~ 0 :带宽
Z0
Zmax
L RC
并联谐振 电路总阻抗:
L Z0 Zmax RC
当 R 0时 Z0
所以,纯电感和纯电容并联谐振时,相当于断路。
U
U
ZO Zmax
外加电压一定时,
总电流最小。
IS
I
U ZO
I
min
I U IL
外输加出恒电流 压源 最大IS。时,
f
关于谐振曲线的讨论
I
I
I
I0
I0
I0
0
(a) 0 不变,
I 0 变化。
01 02
(b) I 0 不变,
0 变化。
0
(c) I 0 不变,
0 不变,
f 变化。
I
I0
I 0
0
谐振曲线讨论(之一)
(1)
不变
0
R小
0
1 LC
即LC不变
R大
(2)
I0
U R
R改变
Ui
2
3dB
T 三分
1
贝点
1
2
0
1 RC
(二)高通滤波器
第7讲正弦稳态电路的谐振

相量图:
UL UR = U
UC
+
IR
+ UR
-
+
I
U
L UL
-
电压谐振 -
+ UX
C -UC
2.串联谐振的特点: (1) u、i 同相
(2) L 和 C 串联部分相当于短路
Z = R =│Z│,最小
——电路呈现纯电阻特性
(3) UL = UC →电压谐振
(4) 品质因数: Q =
UL = U
UC U
7.1.1 串联谐振
一、RLC串联谐振电路条件
I•
+
•+ UR–
•
U
•+ UL–
•+
– UC–
按谐振的一般定义: U与I同相
R
UI
R
j(L
1
C
)
Z
j L
则: u i
tg 1
XL XC R
0
即:
–
j
1
C
L 1 C
谐振频率为: 0
1 LC
or
f0
2
1 LC
当外加频率一定,则可以调整L或C使之发生谐振。
=
+
U
-
XLI = RI
IR
+ UR
-
+
L UL -
+ UX
C -UC
XL = Xc RR
Q是无量纲的物理量
谐振在电力系统中应
尽量避免。
串联谐振在电力工
程中的应用例子:
L
200V
LC
uo
几十万伏
10kV
