普通计算器用计算器解方程的方法
计算器怎么解二元一次方程

计算器怎么解二元一次方程在数学中,二元一次方程是一种常见的方程形式,通常表示为ax + by = c。
其中,a、b、c都是已知的常数,而x和y则是未知数。
解决这种方程可以使用多种方法,例如代数法、图形法和矩阵法等。
但是,如果您不想手动计算,那么使用计算器可以更快速和准确地解决问题。
本文将介绍如何使用计算器解二元一次方程,以及如何处理可能出现的错误。
第一步:输入方程首先,您需要打开计算器并输入方程。
在大多数计算器中,您可以使用“Shift”和“=”键输入“+”和“-”符号。
例如,对于方程2x - 3y = 4和3x + 4y = 5,您应该输入:2x-3y=43x+4y=5请确保您输入的方程正确无误。
如果您输入了错误的方程,那么计算器将给出错误的答案。
第二步:选择求解方法接下来,您需要选择计算器使用的求解方法。
大多数计算器都提供了多种求解方法,例如消元法、行列式法和克拉默法等。
不同的方法可能需要不同的输入格式,因此请仔细查看计算器的使用说明。
在本文中,我们将以消元法为例进行讲解。
消元法是一种基于代数运算的方法,通过消去一个未知数,将二元一次方程转化为一元一次方程,从而求解未知数的值。
第三步:求解方程现在,您可以按下计算器上的“=”键,让计算器求解方程。
在消元法中,您需要使用计算器的加减乘除功能,将两个方程消元,从而求解未知数的值。
对于方程2x - 3y = 4和3x + 4y = 5,我们可以按以下步骤求解:1. 将第一个方程乘以3,得到6x - 9y = 12。
2. 将第二个方程乘以2,得到6x + 8y = 10。
3. 将两个方程相减,得到17y = -2。
4. 解出y的值为y = -2/17。
5. 将y的值代入第一个方程,解出x的值为x = 14/17。
这样,我们就求出了方程的解为x = 14/17,y = -2/17。
第四步:检查答案最后,您需要检查计算器给出的答案是否正确。
您可以将x和y 的值代入原方程,看看是否满足方程的条件。
如何使用自己的计算器解决数学问题

如何使用自己的计算器解决数学问题在现代社会中,计算器已经成为数学学习和工作中必不可少的工具。
虽然现在的手机也具备计算器的功能,但使用专门的计算器更加方便,尤其是在考试时。
在本文中,我们将讨论如何使用自己的计算器解决数学问题,包括基本的运算、解方程、微积分等。
一、基本的运算使用计算器进行基本的运算非常简单。
包括加减乘除,指数和根号等。
一般来说,计算器的操作符和数字键位很容易理解。
例如,在大多数计算器中,加号是“+”,减号是“-”,乘号是“×”,除号是“÷”,指数键是“×y”,根号键是“√”。
例如,要计算“3+4”,只需按下数字键“3”、“+”、“4”和“=”即可。
对于一些较大的运算,也可以使用括号键“()”来进行分组。
二、解方程对于方程的求解,计算器也提供了一些辅助功能。
例如,方程求根功能。
对于形如“ax²+bx+c=0”的二次方程,只需按键“a”、“x ²”、“+”、“b”、“x”、“+”、“c”、“=”、“x”、“=”即可得到方程的根。
一般来说,计算器会显示出两个根:一个是解析解,另一个是数字近似解。
对于更加复杂的方程,看起来似乎无法使用计算器进行计算时,可以尝试使用计算器的图形功能来帮助解决问题。
例如,对于形如“y=sin(x)”或“y=x²”的函数,可以根据名为绘图函数的功能在平面直接上进行图形绘制。
通过观察图形,我们可以获得一些粗略的解析结果,甚至可以用图形进行验证。
三、微积分实际上,许多计算器都提供微积分的计算功能,包括导数和积分等。
例如,对于函数“y =x²”,我们要求它在点“x =3”的导数,只需按键“y = x ²”、“=”、按下“2nd”、“x”、“d/dx”、“=>”、“3”、“=”即可得到它在点“x =3”的导数。
同样,我们也可以使用计算器的积分功能来解决问题。
例如,对于形如“y = sin(x)”的函数,我们要求它在一个区间“[0,π]”内的积分,只需按键“y = sin x”、“=”、“2nd”、“quad”、“=>”、“0”、“,”、“π”、“)”、“=”,即可得到所求区间的积分。
万能计算器解方程

万能计算器解方程解方程是数学中的一项重要内容,它涉及到的知识点有很多,要解决一个方程,我们需要使用各种方法和技巧。
在本篇文章中,我将为大家介绍一种用万能计算器解方程的方法。
万能计算器通常有很多不同的功能,其中就包括求解方程的功能。
使用万能计算器解方程的优势在于它可以帮助我们快速地计算出方程的解,不需要手动进行繁琐的计算过程。
下面我将详细介绍使用万能计算器解方程的步骤和注意事项。
步骤一:打开计算器并进入求解方程的功能页面。
通常,你可以在计算器的功能菜单中找到求解方程的选项,选择它即可进入求解方程的界面。
步骤二:输入方程。
在方程的输入框中输入待解方程,确保输入的格式和语法正确。
通常,方程的形式如下:ax+b=c。
其中,a、b、c是给定的常数,x是未知数。
你需要将方程中的系数和常数都正确地输入进去。
步骤三:点击“求解”按钮。
一旦你输入好了方程,点击求解按钮即可开始计算方程的解。
计算器会自动进行运算,找出方程的解,并将解显示在屏幕上。
步骤四:检查答案的合理性。
得到方程的解之后,我们不应该只是简单地接受答案,还需要检查答案的合理性。
我们可以将解代入原方程中验证,看看方程两边是否相等。
如果方程两边相等,说明我们得到的解是正确的。
在使用万能计算器解方程时,还需要注意一些细节。
注意一:输入方程的格式。
方程的格式应该是正确的,否则计算器可能无法识别你输入的方程。
你需要保证方程的各个项之间使用适当的符号连接,以及各项的系数和常数都被正确地输入。
注意二:保持计算器的正确设置。
不同的计算器可能有不同的设置选项,你需要确认计算器的设置是正确的。
特别是对于小数精度和方程求解的方法,你需要确认它们与你的要求相符。
注意三:根据方程的特性选择求解方法。
在解方程时,我们可以使用各种不同的方法,如代入法、配方法、分离变量法等等。
你需要根据方程的特性选择合适的方法,在万能计算器中进行对应的设置和操作。
总结起来,使用万能计算器解方程可以帮助我们快速地计算出方程的解,而不需要进行繁琐的手算过程。
计算器怎么解一元一次方程

计算器怎么解一元一次方程
一元一次方程是数学中的基础知识,如果不熟悉解一元一次方程的方法,很多数学问题也会变得非常棘手。
而计算器正是一种方便、快捷的工具,可以帮助我们解决各种数学问题。
本文将介绍如何使用计算器来解一元一次方程,让你轻松掌握这一技巧。
首先,我们需要知道什么是一元一次方程。
一元一次方程是形如ax+b=c的一种方程,其中a、b、c是已知数,x是未知数。
这种方程的解法很简单,只需要将方程中的x求出来即可。
那么,如何用计算器求解一元一次方程呢?很简单,只需要按照下面的步骤操作:
1. 打开计算器并选择“计算”模式;
2. 将方程的形式改写为x=(c-b)/a的形式;
3. 将a、b、c的值输入计算器;
4. 按下“=”键,计算器会自动计算并显示出x的值。
这样,你就可以在不用手写计算的情况下,轻松求解一元一次方程了。
需要注意的是,当a=0时,方程就变成了bx=c的形式,此时要特别小心,因为这个方程的根可能是零或无穷大。
为了避免这种情况出
现,我们建议在使用计算器时,如果a=0,就手动计算x的值,或者使用其他方法解决问题。
此外,还需要注意计算器的精度问题。
计算器的精度可能不够高,这时我们需要手动计算,确保答案的准确性。
总之,使用计算器解一元一次方程是一种方便、快捷的方法。
只
需要按照上述步骤操作,即可轻松求解一元一次方程。
当然,也需要
注意方程的形式和计算器的精度等问题。
希望本文对你解决数学问题
有所帮助。
万能计算器解方程

万能计算器解方程万能计算器解方程是指一种能够解决各种类型方程的计算器,无论是一元一次方程、一元二次方程还是高次方程都能够解答。
通过使用这种计算器,我们可以方便快捷地得到方程的解答,省去了手工计算的麻烦。
下面将以一元二次方程和高次方程为例,介绍万能计算器解方程的过程。
首先,我们来介绍一下一元二次方程的解法。
一元二次方程的一般形式为ax^2 + bx + c = 0,其中a、b、c为实数且a≠0。
在万能计算器中,我们输入方程的系数a、b、c,计算器会自动求解出方程的根。
例如,我们输入方程2x^2+3x-2=0,计算器将计算出方程的根为x=0.5和x=-2接下来,我们继续介绍高次方程的解法。
高次方程是指次数大于等于3的方程,如三次方程、四次方程等。
万能计算器同样可以解决这些方程。
对于高次方程的求解,万能计算器通常使用数值方法,如牛顿法、二分法等。
这些方法通过不断逼近方程的根,最终求得方程的解。
例如,我们输入一个三次方程x^3+2x^2-4x-8=0,计算器将通过迭代逼近的方式求解出方程的根为x=1例如,我们输入一个二元一次方程2x+3y=5和x+y=2,计算器将计算出方程的解为x=1和y=1通过以上的介绍,我们可以看出万能计算器解方程的过程是非常简单和高效的。
只需要输入方程的系数,计算器会自动求解出方程的根。
无论是一元还是多元,一次还是高次,方程的解都能够通过万能计算器得到。
然而,值得注意的是,万能计算器无法解决一些特殊类型的方程,如无解方程、恒等式方程等。
这些方程需要其他方法进行求解。
总结起来,万能计算器是一种便捷高效的工具,能够解决各种类型的方程。
通过输入方程的系数,计算器可以快速求解出方程的根,无论是一元还是多元,一次还是高次。
但在使用计算器时,我们需要注意方程的特殊情况,以免得到错误的结果。
卡西欧计算器列方程

卡西欧计算器列方程卡西欧计算器是学生们常用的工具之一,不仅可以进行基本的计算,还能用来列方程。
下面是一些列方程的方法:1. 列一元一次方程假设有一个问题是这样描述的:小明有10元钱,他买了一些苹果,每个苹果2元,问他最多能买几个苹果?解决这个问题,可以先设他买了x个苹果,那么他花费的钱就是2x元,根据题目中的条件,可以列出方程:2x <= 10化简后得:x <= 5因此,小明最多能买5个苹果。
2. 列二元一次方程假设有一个问题是这样描述的:小王和小李一共有20元钱,他们一共买了10个苹果,小王买了x个苹果,小李买了y个苹果,每个苹果的价格相同,问小王和小李分别买了几个苹果?解决这个问题,可以设小王买了x个苹果,小李买了y个苹果,则有:x + y = 102x + 2y = 20化简后得:x + y = 10x + y = 10可见,这两个方程是等式,因此无法用这种方法解决。
这时,可以将其中一个方程进行变形,比如将第二个方程化为:x = 10 - y代入第一个方程中,得:10 - y + y = 10化简后得:y = 0再将y = 0代入x + y = 10中,得:x = 10因此,小王买了10个苹果,小李没有买。
3. 列多元一次方程假设有一个问题是这样描述的:小明、小红、小李一共有100元钱,他们一共买了30个苹果,小明比小红多买了5个苹果,小红比小李多买了3个苹果,每个苹果的价格相同,问小明、小红、小李分别买了几个苹果?解决这个问题,可以设小明买了x个苹果,小红买了y个苹果,小李买了z个苹果,则有:x + y + z = 30x - y = 5y - z = 3x + y + z = 100化简后得:x + y + z = 30x - y = 5y - z = 3x + y + z = 100可见,这四个方程是等式,因此无法用这种方法解决。
这时,可以使用消元法或代入法等其他方法解决。
用计算器解方程(牛顿法)

【教程】用计算器解方程(牛顿法)(转自土木论坛)一、前言很多计算器都自带利用标准式解方程的功能,解方程式,需要手动输入abc的值。
但这样往往需要化简出abc到底是多少,这样容易计算错误,还加大了计算量,往往在注册考试中不实用。
下面我介绍一个直接的方法,无需化简公式,就可以解出结果的方法。
二、利用此方法的好处可解决所有公式变形问题,利用牛顿法解方程,一元方程可直接出结果,一元多次方程无需化简成标准形式,直接求解,大大节省化简、变形公式时间。
提高做题效率,解决重复简单计算的厌恶感。
提高做题准确率。
三、牛顿法解方程具体步骤1、你的计算器是否有此功能大多数科学计算器都长的差不多,但是考友们手里的计算器是否有该功能那就不一定了。
无论是手算解方程还是计算器自动解方程,只要是方程,就有两个必不可少的元素:“等号=”,“未知数x”。
以卡西欧fx-991es plus型号计算器举例,此型号计算器如图所示。
只要带“等号=”、“未知数x”的科学计算器,就有解方程功能。
需要注意的是,这里说的“等号=”并不是如图所示右下角的“=”,而是左上角那个红色的“=”。
细心的同学会发现,黄色的1号上档键SHIFT,对应的都是标志有黄色字体的功能;红色的2号上档键ALPHA,对应的都是标志有红色字体的功能。
2、输入方程以解5x-9=3为例,这是一个简单的一元一次方程。
而我们只需要把方程输入到计算器中,即可解出x。
具体输入方法如下:(1)按数字“5”(2)按“2号上档键”,再按“方程中的未知数x键”。
即:红色的ALPHA和白色的右半边括号。
这样我们就输入了未知数x(3)按“-”,再按“9”(4)按“2号上档键”,再按“方程中的等号键”。
即:红色的ALPHA和白色的CALC。
这样我们就输入了“=”(5)按数字“3”3、解方程做到这里,我们的方程就已经输入好了。
接下来我们解方程。
(1)按“1号上档键”,再按“方程中的等号键”。
即:黄色的SHIFT和白色的CALC。
计算器solve的使用方法

计算器solve的使用方法
计算器是我们日常生活中必不可少的工具之一,它可以帮助我们进行各种数学计算,如加减乘除、开方、求幂等等。
而在计算器中,solve功能则是一个非常实用的工具,它可以帮助我们解方程、求根等问题。
下面就来介绍一下计算器solve的使用方法。
我们需要打开计算器。
在Windows系统中,计算器可以通过开始菜单中的“计算器”选项来打开。
在Mac系统中,计算器可以通过“应用程序”文件夹中的“实用工具”选项来打开。
接着,我们需要选择“科学”模式。
在Windows系统中,可以通过计算器窗口中的“查看”菜单来选择“科学”模式。
在Mac系统中,可以通过计算器窗口中的“视图”菜单来选择“科学”模式。
然后,我们需要输入要解决的方程。
在计算器中,方程的输入格式为“solve(方程, 变量)”。
例如,要解决方程“2x + 3 = 7”,可以输入“solve(2x + 3 = 7, x)”来求解x的值。
我们需要按下“等于”键来得到方程的解。
计算器会自动计算出方程的解,并将其显示在屏幕上。
如果方程有多个解,计算器会将所有解都显示出来。
除了解方程外,计算器solve还可以用来求根、求极值等问题。
例
如,要求函数“y = x^2 - 2x + 1”的极值,可以输入“solve(dy/dx = 0, x)”来求解x的值,然后再将x的值代入函数中求出y的值。
计算器solve是一个非常实用的工具,可以帮助我们解决各种数学问题。
只要掌握了它的使用方法,就可以轻松地解决各种方程、求根、求极值等问题。
普通计算器用计算器解方程的方法

普通计算器用计算器解方程的方法用计算器解方程的方法高中时发现一个用计算器来解方程的方法,前一阵用到计算器就想起来了,习惯性地谷歌之、百度之,居然没有发现类似的方法,于是就想把它写下来。
说明下对计算器的要求,只要是个带有"Ans"键的计算器就行,一般我们用的都是这种计算器。
对于要解的方程,无论是超越方程还是高次方程,基本上都一样。
先来初步尝试一下。
如果要解的方程是:exp(x)=-x+3 (注:exp(x) 是表示e的x次方) ,你要按的键就像下面一样:0 =ln ( - Ans + 3 ) = = = = ??如你所知,Ans键有保存上一次计算结果的功能,所以第一条语句就是给Ans赋初值的意思,初值要选在解的附近,大概估计下就可以。
第二条我没有打错,你在连续按了十几次"=" 后,是不是发现再按的时候屏幕上的数值不变了?这就是方程的解。
看起来好像很晕,还是解释解释这样做的原因:看见上面的图了吗?小赵(高一数学老师)曾经给我们介绍过一种有趣的现象,一般情况下两函数图象在交点附近有这种类似螺旋的收敛特性。
灵感正是来自这里。
是不是有点眉目了?假设上面的图中两个图象分别是y=f(x) 和 y=g(x) ,而我们要解的方程是f(x)=g(x)。
为了方便,这里把F(x)和G(x)分别记做f(x)和g(x)的反函数。
于是这个方程可以等价变换为 x=F(g(x)) 和x=G(f(x)) 。
这两个式子的右半边就是我们要输入计算器然后不断按"="的,当然,输入计算器的时候所有的x都用Ans代替。
再看看上面的图,其实这两个式子中,一个的代表顺时针螺旋,另一个代表逆时针螺旋;一个能使螺旋收敛于交点,另一个会使螺旋扩张。
不幸滴是,我们不知道哪个式子能使螺旋扩张,哪个能使收敛,所以两个式子都得试试,在我们按了若干次"=" 后如果屏幕上数值稳定了,就说明这是收敛式,并且这个稳定的值就是解。
如何利用Casio计算器解方程、不等式(solve)

按等号,再输入初值 6,得到 x=8.913. Note:本例一元三次方程,有是个实数根,一个负数,两个正数。 合理的是 Ld=8.913m. 991ES PLUS 也有相同6-107
6.12x3+21.42x2+64*(10+x)*1.6, 移动光标到分母,输入 4.41*(7.62+x)3/3 得到下面式子
移动光标到分式 的最右测,按 按 , ,再按 ,在等号右侧输入 1.2,
,输入初值 0, 得到 x=1.10466,这个答案不正确。
如何利用casio计算器解方程不等式solve举案例说明华南虎案例一本通上册6107612x32142x26410x16移动光标到分母输入441762x33得到下面式子移动光标到分式的最右测按按再按在等号右侧输入12输入初值0得到x110466这个答案不正确
如何利用 Casio 计算器解方程、不等式(solve)
卡西欧计算器解方程组

卡西欧计算器解方程组
在高中数学学习中,解方程组是一个重要的知识点。
而在解方程组的过程中,计算器也能够为我们提供很大的帮助。
特别是卡西欧计算器,它不仅能够解常数项为整数的方程组,还能够解复数方程组和含参数的方程组。
卡西欧计算器解方程组的步骤非常简单,只需要按照以下步骤即可:
1.将方程组写成矩阵形式,即将系数、未知数和常数分别写成矩阵的形式。
2.从计算器中选择矩阵求逆功能,求得系数矩阵的逆矩阵。
3.将逆矩阵与常数矩阵相乘,得到未知数矩阵。
4.最后,将未知数矩阵中的数值代入原方程组中,验证是否正确。
需要注意的是,在使用卡西欧计算器求解方程组时,要保证输入的矩阵形式正确,否则计算结果会出现错误。
此外,对于含参数的方程组,需要先对参数进行赋值,再进行计算。
总的来说,卡西欧计算器解方程组的操作简单、快捷,能够为我们省去很多繁琐的手工计算,提高解题效率。
- 1 -。
利用计算器建立二次曲线回归方程的方法

利用计算器建立二次曲线回归方程的方法在进行统计学习和科学研究的过程中,二次曲线回归的技术被用于分析两组数据之间的关系。
这种方法有助于我们更好地了解数据,并为进一步的研究奠定坚实的基础。
本文介绍了如何利用计算器建立二次曲线回归方程的方法。
首先,为了建立二次曲线回归方程,我们必须准备好一组数据。
数据中应当包括两组数据,分别是自变量和因变量,并且应该尽量多地收集数据,以便我们能够建立准确的模型。
其次,我们需要使用计算器来进行分析。
可以使用数学软件或计算器来计算出自变量和因变量之间的相关性。
我们可以首先将所有数据用计算器进行算术运算,得出回归方程,这就是我们将要构建的二次曲线回归方程。
再次,我们需要使用计算器计算出回归方程的参数和系数。
回归方程的参数有助于确定自变量和因变量之间的关系。
确定回归方程的参数也可以帮助我们了解这两组数据之间的趋势和相互影响的方式。
最后,我们使用由计算器获得的回归方程和参数,来分析自变量和因变量之间的关系。
将回归方程输入到计算器中,可以迅速计算出自变量与因变量之间的关系,并得出曲线图。
最后,我们可以针对不同的值输出不同的曲线结果,从而得出正确的结论。
总之,利用计算器建立二次曲线回归方程是一个非常有效的方法,在数据分析的过程中,它可以帮助我们了解自变量和因变量之间的关系,并从其中获取有用的信息,为后续研究奠定基础。
二元一次方程组计算器

二元一次方程组计算器简介二元一次方程组是一个包含两个未知数和两个等式的方程组。
在数学中,我们经常需要解二元一次方程组来求解未知数的值。
为了简化计算过程,我们可以使用二元一次方程组计算器来自动求解方程组。
本文档将介绍如何使用二元一次方程组计算器来求解二元一次方程组,并提供一些实例来帮助读者理解计算器的使用方法。
使用方法使用二元一次方程组计算器求解二元一次方程组的步骤如下:1.打开二元一次方程组计算器。
2.在计算器界面中,输入待求解的方程组。
3.点击“求解”按钮,计算器将自动求解方程组并显示结果。
4.查看计算器的输出,得到方程组的解。
实例实例1待求解的方程组为:2x + 3y = 74x - 5y = -1使用二元一次方程组计算器求解该方程组的步骤如下:1.打开二元一次方程组计算器。
2.在计算器界面中,输入方程组:2x + 3y = 74x - 5y = -13.点击“求解”按钮,计算器将自动求解方程组并显示结果。
4.计算器的输出为:x = 1y = 2因此,方程组的解为 x = 1,y = 2。
实例2待求解的方程组为:3x - 2y = 8x + 4y = 7使用二元一次方程组计算器求解该方程组的步骤如下:1.打开二元一次方程组计算器。
2.在计算器界面中,输入方程组:3x - 2y = 8x + 4y = 73.点击“求解”按钮,计算器将自动求解方程组并显示结果。
4.计算器的输出为:x = 2y = 1因此,方程组的解为 x = 2,y = 1。
总结本文介绍了二元一次方程组计算器的使用方法,并提供了两个实例来帮助读者理解计算器的使用。
通过使用二元一次方程组计算器,我们可以更快地求解二元一次方程组,提高计算效率。
希望本文能够对读者有所帮助。
用计算器解一元二次方程的方法
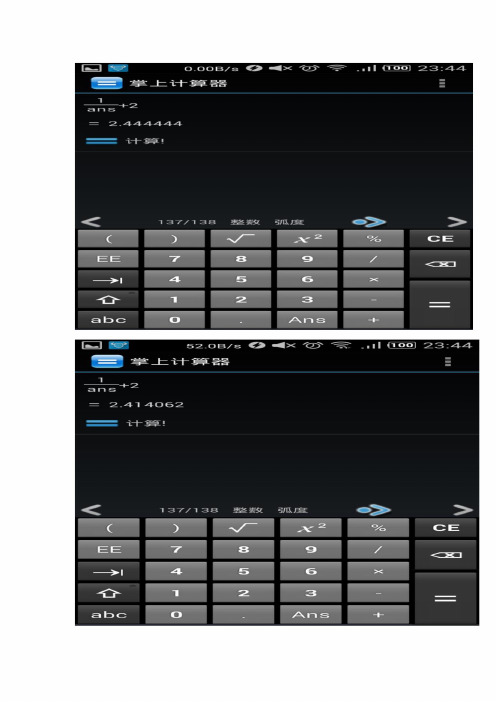
计算器解一元二次方程的方法用计算器解一元二次方程的方法我们假设某个一元二次方程为a*x^2+b*x+c=0;我们可以把它化成(-c)/(a*x)-b/a=x的形式,这时好玩的事情就发生了,我们能在科学计算器上找到一个叫ans 的按键,这就是解这个方程的关键了,我们可以利用这个ans按键的功能来接某一个一元二次方程,我们在计算器按键上按下式子(-c)/(ans*a)-b/a=的时候你就一直的按等于,等于,就会计算出一堆奇怪的小数,你只要一直的按下去,你会发现这个数字会从最高位开始数字逐渐的趋于稳定,如下图所示这里稳定的值2.414214就是我们想要的答案之一了,将x^(-1)+2=x化成方程x^2-2x-1=0,把答案2.414214带入x^2-2x-1=0中,发现成立,其实这里就是方程x^2-2x-1=0的一个解1+2^0.5,还有另外的一个解1-2^0.5,这里它却不能给出另外的一个答案,当然了,上次计算的结果可以是除了0以外的任一值都能得出我们的1+2^0.5,如果上次的值刚好在某一范围内的话,还会计算出1-2^0.5这个解,但是却无法得到1+2^0.5这个解了。
你把最后稳定下来的数值带入到原方程你会发现就是我们所想要的答案了,但是这个方程总的有两个根,用这种方法却只能求得其中的某一个根,这也是这个方法的不足之处,如果你把没有实数根的式子化成了这种的形式的话,你就会发现无论你按了有多久的等于号你也无法得到一个稳定的值,还有就是两个根相等的话也就无法用这种方法来解方程的,至于为什么呢?其实我也不知道这是为什么,我也是偶然的发现这个奇葩的方法的。
是不是很神奇呢,你还能用这种方法来解一元三次,四次,五次,n次呢!例如用它来解一元三次方程,a*x^3+b*x^2+c*x+d=0,这样子的方程呢,像这样的方程我就把它化成(-d)/(a*x^2)-c/(a*x)-b/a=x的形式时,我们就把这个式子中的x代换成ans,然后在计算器中输入这个式子,然后就一直的按等于号,如下图所示:n次的方程的话也就把式子化成XX/(XX*ans^n)-XX/(XX*ans^(n-1))-XX/(XX*an s^(n-2)).........-XX/XX=ans就可以了,这里的ans就相当于方程中的x,这里我就不演示了,这里我们还能用这种方法解决别的方程,例如:cos(x)=x,这里就很简单了,我们直接在计算器上输入cos(ans)=,然后我们就一直的按等于号就行了,你就会发现等到数值稳定的时候,这个值就是我们所想要的解了,,用这种方法可以算很多的一元有解得方程,但是也会有某一些的方程无法用这种方法,目前我还没有发现这种方法的某个切确的规律。
【教程】用计算器解方程(牛顿法)

【教程】⽤计算器解⽅程(⽜顿法)⼀、前⾔很多计算器都⾃带利⽤标准式解⽅程的功能,解⽅程式,需要⼿动输⼊abc的值。
但这样往往需要化简出abc到底是多少,这样容易计算错误,还加⼤了计算量,往往在注册考试中不实⽤。
下⾯我介绍⼀个直接的⽅法,⽆需化简公式,就可以解出结果的⽅法。
⼆、利⽤此⽅法的好处可解决所有公式变形问题,利⽤⽜顿法解⽅程,⼀元⽅程可直接出结果,⼀元多次⽅程⽆需化简成标准形式,直接求解,⼤⼤节省化简、变形公式时间。
提⾼做题效率,解决重复简单计算的厌恶感。
提⾼做题准确率。
三、⽜顿法解⽅程具体步骤1、你的计算器是否有此功能⼤多数科学计算器都长的差不多,但是考友们⼿⾥的计算器是否有该功能那就不⼀定了。
⽆论是⼿算解⽅程还是计算器⾃动解⽅程,只要是⽅程,就有两个必不可少的元素:“等号=”,“未知数x”。
以卡西欧fx-991es plus型号计算器举例,此型号计算器如图所⽰。
只要带“等号=”、“未知数x”的科学计算器,就有解⽅程功能。
需要注意的是,这⾥说的“等号=”并不是如图所⽰右下⾓的“=”,⽽是左上⾓那个红⾊的“=”。
细⼼的同学会发现,黄⾊的1号上档键SHIFT,对应的都是标志有黄⾊字体的功能;红⾊的2号上档键ALPHA,对应的都是标志有红⾊字体的功能。
2、输⼊⽅程以解5x-9=3为例,这是⼀个简单的⼀元⼀次⽅程。
⽽我们只需要把⽅程输⼊到计算器中,即可解出x。
具体输⼊⽅法如下:(1)按数字“5”(2)按“2号上档键”,再按“⽅程中的未知数x键”。
即:红⾊的ALPHA和⽩⾊的右半边括号。
这样我们就输⼊了未知数x(3)按“-”,再按“9”(4)按“2号上档键”,再按“⽅程中的等号键”。
即:红⾊的ALPHA和⽩⾊的CALC。
这样我们就输⼊了“=”(5)按数字“3”3、解⽅程做到这⾥,我们的⽅程就已经输⼊好了。
接下来我们解⽅程。
(1)按“1号上档键”,再按“⽅程中的等号键”。
即:黄⾊的SHIFT和⽩⾊的CALC。
计算器解方程组

计算器解方程组
计算器解方程组是数学学科中的一项技能,是运用计算器帮助我们计算方程组的未知量,从而解决一系列问题。
在本文中,我们将深入探讨计算器解方程组的方法和步骤。
一、基本概念
方程组是将多个方程联立起来,求出多个未知数的值。
在数学中,方程组有线性方程组、二次方程组等等。
在此我们着重介绍线性方程组。
二、计算器解方程组的步骤
1.进入计算器,点击“函数”选项卡,打开“方程求解器”。
2.在“线性方程组”中输入已知的方程,形如:
3x + 2y + z = 15
2x + 3y - z = 10
x - y + 2z = 7
键入完成后,点击“求解”。
3.计算器将根据输入的方程进行求解,得出未知量的值。
x=2, y=4, z=3
4.将解出的未知量代入原方程中检验,确保计算的准确性。
例如代入第一式:
3x+2y+z=15
3(2)+2(4)+3=15
6+8+3=15
15=15
检查通过。
三、注意事项
1.计算器只能计算较为简单的线性方程组,对于较长或较复杂的方程组,计算器可能会出现计算错误。
2.在输入方程时要注意每个方程的位置和符号,以免造成计算混
乱。
3.在代入未知值检验时,要仔细核对符号和计算过程,以确保答案的正确性。
总之,计算器是一个方便快捷解决方程组问题的工具,但也要注意其应用的限制。
如果遇到较为复杂的问题,建议使用手工计算方法辅助计算器求解。
计算器解方程原理

计算器解方程原理
计算器解方程的原理是基于数学方程的性质和计算机编程算法的结合。
首先,计算器能够通过键盘输入数学表达式,包括各种运算符和数字。
当用户输入一个方程时,计算器可以通过检测方程的等号并提取方程中的表达式,将其存储为一个数学问题。
接下来,计算器会使用一系列算法和规则来解决这个数学问题。
其中一个常用的解方程算法是二分法。
这个算法通过不断逼近解的范围来找到方程的解。
计算器将根据方程的类型,使用不同的算法来解决方程。
例如,对于一元一次方程,可以使用简单的代数运算来计算解,而对于高阶方程,则需要更复杂的算法,如牛顿迭代法或拉格朗日插值法等。
在计算器执行解方程的算法之后,它会返回方程的解作为输出并在显示屏上显示。
用户可以通过读取计算器的输出来获得方程的解。
需要注意的是,计算器解方程的精确度是有限的。
由于计算器使用有限的计算资源和算法,它可能无法找到一些复杂方程的解,或者仅能找到近似解。
在解方程时,用户需要谨慎使用计算器的结果,并在必要时使用更精确的方法来验证解的准确性。
计算器解多元方程

计算器解多元方程
在数学中,多元方程是一种含有两个或两个以上未知数的方程。
解决多元方程通常需要进行一系列复杂的运算和代数操作。
然而,借助计算器的帮助,我们可以更轻松地解决这类问题。
本文将介绍如何使用计算器解多元方程,并通过示例演示具体步骤。
计算器解多元方程的步骤
为了使用计算器解多元方程,我们需要遵循以下步骤:
1.输入方程:将多元方程的各项系数和未知数输入计算器内部。
2.选择求解方式:根据方程的类型和计算器的功能,选择适当的求解
方式,如代数解法或数值解法。
3.获取解:计算器将自动执行计算过程,并给出多元方程的解。
示例
让我们通过一个具体的示例来演示如何使用计算器解多元方程。
假设我们有以下两元一次方程组:
2x + 3y = 8
3x - y = 1
我们可以将这个方程组输入到计算器中,并选择使用高斯消元法求解。
计算器将给出如下解:
x = 2
y = 1
通过计算器的帮助,我们很容易地得出了方程组的解。
这种方法不仅节省了时间,还减少了人为错误的可能性。
结论
计算器是解决多元方程的强大工具,它可以帮助我们在短时间内得出准确的解答。
通过本文介绍的步骤和示例,相信读者对如何使用计算器解多元方程有了更清晰的认识。
希望本文能够对你的学习和工作有所帮助!。
casio解方程

casio解方程
(实用版)
目录
1.解方程的重要性
2.Casio 计算器的功能和应用
3.使用 Casio 计算器解方程的步骤
4.实际案例:解一元二次方程
5.总结
正文
解方程是数学学习中非常重要的一部分,无论是在学校教育还是在实际生活工作中,都有着广泛的应用。
而在众多的数学工具中,Casio 计算器以其强大的功能和易用的操作,成为了许多学生和专业人士的首选。
Casio 计算器不仅能进行基本的四则运算,还能进行复杂的代数运算、三角函数、对数函数等运算。
此外,它还有着数据统计、图形绘制等功能,可以满足各种数学需求。
对于解方程这一问题,Casio 计算器同样有着出色的表现。
下面,我将详细介绍一下如何使用 Casio 计算器解一元二次方程。
一元二次方程的标准形式是 ax+bx+c=0,其中 a、b、c 是常数,且 a ≠0。
解一元二次方程的常用方法有求根公式法、配方法、因式分解法等。
其中,求根公式法是最直接、最常用的方法。
使用 Casio 计算器解一元二次方程的步骤如下:
1.首先,将方程 ax+bx+c=0 输入到计算器中,其中 a、b、c 分别代表方程中的系数。
2.然后,按下计算器上的“=”键,计算器会自动给出方程的解。
3.如果需要,可以继续按下“=”键,计算器会显示详细的解法过程。
以方程 x-3x+2=0 为例,我们可以将系数代入计算器中,得到解 x1=1,x2=2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用计算器解方程的方法
高中时发现一个用计算器来解方程的方法,前一阵用到计算器就想起来了,习惯性地谷歌之、百度之,居然没有发现类似的方法,于是就想把它写下来。
说明下对计算器的要求,只要是个带有"Ans"键的计算器就行,一般我们用的都是这种计算器。
对于要解的方程,无论是超越方程还是高次方程,基本上都一样。
先来初步尝试一下。
如果要解的方程是:exp(x)=-x+3 (注:exp(x) 是表示e的x次方) ,你要按的键就像下面一样:
0 =
ln ( - Ans + 3 ) = = = = ⋯⋯
如你所知,Ans键有保存上一次计算结果的功能,所以第一条语句就是给Ans赋初值的意思,初值要选在解的附近,大概估计下就可以。
第二条我没有打错,你在连续按了十几次"=" 后,是不是发现再按的时候屏幕上的数值不变了?这就是方程的解。
看起来好像很晕,还是解释解释这样做的原因:
看见上面的图了吗?小赵(高一数学老师)曾经给我们介绍过一种有趣的现象,一般情况下两函数图象在交点附近有这种类似螺旋的收敛特性。
灵感正是来自这里。
是不是有点眉目了?
假设上面的图中两个图象分别是y=f(x) 和 y=g(x) ,而我们要解的方程是f(x)=g(x)。
为了方便,这里把F(x)和G(x)分别记做f(x)和g(x)的反函数。
于是这个方程可以等价变换为 x=F(g(x)) 和x=G(f(x)) 。
这两个式子的右半边就是我们要输入计算器然后不断按"="的,当然,输入计算器的时候所有的x都用Ans代替。
再看看上面的图,其实这两个式子中,一个的代表顺时针螺旋,另一个代表逆时针螺旋;一个能使螺旋收敛于交点,另一个会使螺旋扩张。
不幸滴是,我们不知道哪个式子能使螺旋扩张,哪个能使收敛,所以两个式子都得试试,在我们按了若干次 "=" 后如果屏幕上数值稳定了,就说明这是收敛式,并且这个稳定的值就是解。
比如前面的例子,方程可以变成 x=ln(-x+3) 和 x=-exp(x) +3 ,其中-exp(x)+3使值扩散,而ln(-x+3)使值收敛,就想一开始做的那样。
如果这个方程有好几个解呢?那你就使用不同的初值,一般来说,它总会收敛于离初值比较近的那个解。
要注意的是,使方程各个解收敛的螺旋方向可能不同,也就是说对于每个解,你还是需要代两个式子。
上面说的是理想情况,比如遇到x^5+x^2 = x^4-x+5 这样的方程,总不可能去求两边的反函数吧,累都累死。
这时候,提取两边最能体现原本特征的一部分就可以了,比如这里就是x^5 和x^4 ,变换后的式子是 x=5次根号下的(x^4-x+5-x^2) 和 x=4次根号的(x^5+x^2+x-5) 。
最后不得不说,比如x=-x+3 这种情况,这种方法无效。
