Color Constancy from Hyper-Spectral Data

合集下载

spectracolours-AmazonWebServices：光谱的颜色-亚马逊网络服务

spectra coloursN ATURALI NSPIRATIONOCEAN914Blue green infinity.The ocean’s depths containcountless mysteries thatcontinue to intrigue mankind.Subtle droplets of silverrain revitalize the green innature’s most diverseenvironment.Nature’s seasons; areminder of the circle of life,from spring fresh green tobrown-red autumn.spectra coloursAMAZON916spectra coloursAUTUMN915spectra coloursW ARM M ETALStoic grey refines itself intopolished gold; moderndesign is celebrated, butinspired by tradition.A powerful fusion of red andgold represents a decorativematerial for a powerfuldesign.Red, orange and yellow melttogether to form history’senduring symbol of wealthand commerce.ANTIQUE 911RED BRASS 912CUPRAL913spectra coloursspectra coloursN EWL UXURYAn amazing shift of freshleaves and blossoms on theJapanese cherry tree, asymbol of feminine beautyand elegant luxury.Emerald glitters on ruby, anextraordinary combination ofprecious luxury goods.Brilliant Gold sparkles on aluxurious blue-violet tapestryas wide as the summer sky.SAKURA917JEWEL909SUNSET910•Continuous colour shift over whole colour SPECTRUM (from colour 1 to colour 2)•Irrespective of the viewing angle•Your eyes see various coloursFascinating WorldsThroughout history, mankind has had an enduringappreciation of colour. From the discovery of organic purple dyes before 1900 B.C to the development of colour TV and movies after 1900 A.D, the world we live in is saturated in colour. Colour conveys emotion, it inspires and motivates.And now… colour has evolved.ALUCOBOND ®spectra colours celebrate the natural colour shifts that occur in materials that affect everyday life: The subtle nuances and colour contrasts found readily in nature, the glowing luster and sheen in modern metals and the colour shifts found in today’s luxury goods. Colour adds fascination to the world, ALUCOBOND ®spectra colours add fascination to architectural design.Fascinating SurfacesALUCOBOND ®spectra colours operate on the same principals as natural colour shifting surfaces. Depending upon the pigment type and viewing angle, different wavelengths of light are reflected back to the audience resulting in an ever-changing colour gradient with iridescent highlights. With ALUCOBOND ®spectracolours , architects can create a truly memorable experience that will fascinate the audience and provide a lasting personal impression. The use of high-quality Fluorocarbon paint systems applied in a continuous coil-coating process ensures that the original design isn’t compromised.RemarkALUCOBOND ®spectra colours can be applied on ALUCOBOND ®,ALUCOBOND ®plus and ALUCOBOND ®A2. Minimum order quantity applies. For details and available specification please refer to the manufacturer or your nearest ALUCOBOND ®representative.To avoid possible reflection differences, it is recommended to install the panels in the same direction as marked on the protective peel-off-foil. Colour variations may occur between panels originating from different production batches. To ensure colour consistency, the total requirement for a project must be placed in one order.spectra coloursspectra colours P r i n t e d i n G e r m a n y G &02/09/2010 G BG International Contacts Europe / Middle East / Africa 3A Composites GmbHAlusingenplatz 1D-78224 Singen, GermanyPhone: +49 77 31 80 23 47Fax: +49 77 31 80 28 45*********************Asia / PacificAlucobond (Far East) Pte Ltd.300 Beach RoadThe Concourse #20-02Singapore 199555Phone:+65 6501 1160Fax:+65 6501 1165*********************.sq3A Composites – A true …global player“•Sales offices and production plants in Europe,North and South America and Asia •Wide range of available panels •Partnerships with leading distributors •Professional sales teams 3A Composites GmbHAlusingenplatz 1D-78224 Singen, Germany*********************。

可见光光谱英文

可见光光谱英文The visible light spectrum, encompassing wavelengths ranging from approximately 400 nanometers (nm) to 700 nm,is a narrow slice of the electromagnetic radiation that our eyes are capable of perceiving. This band of wavelengths, although relatively small compared to the vast expanse of the electromagnetic spectrum, plays a pivotal role in our daily lives, shaping our perception of the world around us. At the shorter wavelength end of the visible spectrum, we encounter violet light. Violet waves, with their frequencies exceeding 668 THz, are the highest in energy among all visible colors. As we move towards the red end of the spectrum, wavelengths increase, resulting in lower frequencies and consequently, lower energy levels. Red light, with wavelengths exceeding 700 nm, has the lowest energy among all visible colors.The visible spectrum is not just a random assortment of colors; it is a carefully crafted array of hues that enables us to perceive a wide range of colors. The human eye is equipped with photoreceptors called cones, which are sensitive to specific wavelengths within the visiblespectrum. These cones are primarily sensitive to blue, green, and red light, allowing us to perceive the full range of colors visible to the naked eye.The importance of the visible light spectrum extends beyond our ability to see colors. It plays a crucial role in photosynthesis, the process by which plants convert light energy into chemical energy. Chlorophyll, the green pigment found in plants, is highly absorbent of blue and red light wavelengths, which are essential for photosynthesis. Without the visible light spectrum, photosynthesis would not be possible,严重影响着整个生态系统的运转。

Colour fastness to Perspiration

Color fading and alteration can be caused by the reaction between dyes on garments and the constituents of human perspiration, such as skin waste. It varies for different individuals and conditions. Methods for testing fastness levels of dyed materials against perspiration have been established by ISO, AATCC and various other standards. There are cases where more color fading and alteration is caused by depending on the conditions under which garments are worn. Coupled with the eventual accumulation and concentration of perspiration, the reaction with sunlight is regarded as the cause for such occurrences, casting an influence on certain elements in the dye structure. To forecast such occurrences, methods for examining the components of perspiration under different conditions (acid and alkaline pH values) have been suggested by these standards.Colour fastness to Perspiration - Standard Test Methods:This test is designed for use in assessing the fastness of the dyed, printed, or otherwise colored textile yarns and fabrics of all kinds to the effects of human perspiration. The following standard methods are generally employed to assess the perspiration fastness.•ISO 105 – EO4 1994 (Acid and Alkaline perspiration)•AATCC 15:2002 (only Acid perspiration)Summary:Specimens of the textile in contact with the standard multifibre fabric (for colour transfer) are immersed in simulated alkaline and acid solution (see table below for liquor composition), drained and placed between two plates under a specific pressure, temperature and time in a testing device (perspirometer). Any change in colour of the specimens and staining of the multifibre is then assessed with the corresponding Grey scales for colour change and staining.ISO 105 – E04 AATCC 15 – 2002(1994) Chemical compositionAlkaline solution Acid solution Acid solution L- histidine monohydrochloride monohydrate (C 6H 9O 2N 3.HCl.H 2O) 0.5 g 0.5 g 0.25 ± 0.001 g Sodium chloride (NaCl)5.0 g 5.0 g 10 ± 0.01 g5.0 g - - Disodium hydrogen orthophosphate dodecahydrate (Na 2HPO 4 .12H 2O) or Disodium hydrogen orthophosphate dihydrate (Na 2HPO 4.2 H 2O) 2.5 g 2.2 g - Sodium dihydrogen orthophosphate, anhydrous (Na 2HPO 4) --1 ± 0.01 g Lactic acid (85%) - - 1 ± 0.01 g Total volume 1 litre 1 litre 1 litre pH8.0 5.5 4.3 ± 0.2 Specimen size 100 x 40 mm 60 x 60 mm Test conditions37 ± 2º C for 4 hours undera pressure of 5 kg38 ± 1º C for 6 hours under a pressure of4.54 kgProcedure in brief:Reagents:• Alkaline Solution - Freshly prepared, composition as given in Table above • Acid Solution - Freshly prepared, composition as given in Table aboveTest Specimens• Cut two specimens 100mm x 40mm (one specimen of 60 x 60 cm in AATCC method)along the length or width direction. For multi-coloured fabrics, prints or stripes, all colours of the design should be in contact with all components of the multifibre.• Where it is not possible for all colours to be in contact with all components, more thanone test specimen may need to be prepared.• For fabrics of different shade or fibre composition on face and back, both sides should betested.• Avoid samples within 50 mm of the selvedge.• Cut two pieces of multifibre 40mm wide. The multifibre has selvedges and isapproximately 100mm long. For AATCC method 60 x 60 cm size multifibre fabric is cut.•Align the test specimens and multifibre and sew together along one short edge to forma composite specimen.Test Procedure•Weigh each specimen. Calculate the amount of test solution according to a liquor ratio of 50:1, i.e. 50 ml test solution per 1g of specimen.•Immerse one composite specimen in the alkaline solution and the other in the Acid solution for 30 minutes at room temperature to ensure that the specimens arethoroughly wetted out. (In AATCC method, place the test specimen in a 9 cm diameter and 2 cm deep Petri dish. Add only acid perspiration solution to a depth of 1.5 cm andsoak for 30 min.)•Place each specimen onto a resin plate and draw across with the stirring rod to remove any air bubbles. Place another resin plate on top of the specimen to fully enclose it.Place a maximum of ten specimens into the perspirometer ensuring that each specimen is separated by one resin plate. Use a separate perspirometer for each solution.•(In AATCC method, pass the specimen through the wringer so that it weighs 2.25 ±0.05 times the original weigh. To obtain consistent results all specimens of a givenconstruction in a test series should have identical pickup, as the degree of stainingincreases with the amount of retained solution. Assemble the plates in the perspirometer with the specimens evenly distributed between the plates. Place all 21 plates into theunit regardless of the number of specimens)•Bring the upper pressure plate of the perspirometer down to rest on top of the resin plates and place the weight onto the pressure plate and tighten the securing screws.This is equal to a pressure of 12.5 KPa (5 kg) in between being applied on thespecimens.•Drain off any excess solution.•Place the specimens into the oven at 37 ± 2°C, for 4 hours (38 ± 1ºC, for 6 hours in AATCC method), set a timer for this.•On completion of the test remove the specimens from the oven and separate them from the resin plates.•Open out the specimens, so that they are only in contact at the line of stitching.•Dry the specimens in an incubator or by laying on a screen at a temperature not exceeding 60°CEvaluation of results•After drying, assess the specimens in a colour matching cabinet under D65, artificial daylight.•Assess colour staining of all components on the multifibre using the grey scale for assessing staining.•For multi-coloured prints only assess the worst area of staining on each component.•Assess the change of shade on the original specimen compared to the tested specimen, using the grey scales for assessing change.Some notes on testing•It is sometimes advised that a complete different set of Perspirometers / plates be used for alkaline and acidic perspiration tests. This is recommended so that there is nocontamination between the two.•Some laboratories use different sets of equipment for ISO and AATCC testing for thesame reasons.Case studies:Photograph for representationalpurposes onlyCase 1Gold coloured printing is quite popular due to the unique effects that it can offer to garments. Typically, gold prints are done using inorganic metallic pigments. There was a case where a woven shirt with gold coloured motif print was exported to Europe for a summer season. This article had passed the normal colourfastness tests as specified by the buyer.Unfortunately, the garments were returned by customers with a complaint that the gold motif changed colour to green after use in areas such as the armhole, back where perspiration is excessive. The colour change was irreversible. This problem was investigated and it was found that the print was sensitive to perspiration, possibly because it was a copper based compound. On testing, the print failed colourfastness to perspiration – a test that was not performed as part of the quality control protocol.Investigation revealed the use of a poor quality cheap gold powder which was sensitive to perspiration and turned green. The problem was solved only when the goods were redone using standard gold paste for the printing.Other casesColourfastness to perspiration is often a problem for sportswear. There have been cases where articles for use in sports with poor colourfastness to perspiration have led to staining of undergarments.Similar issues have been seen for industrial work wear where the users often work in conditions where perspiration is a natural occurrence, especially in hot environments such as India.We have also seen problems with ladies undergarments such as brassieres being stained due to poor colourfastness to perspiration of outer garments.These cases show that Colourfastness to perspiration is an important criterion in garment quality evaluation.Squeezing excess liquor from sampleLoading the perspirometer Loaded Perspirometer。

The von Kries Hypothesis and a Basis for Color Constancy

sjg@
Todd Zickler Harvard University
zickler@
Abstract
Color constancy is almost exclusively modeled with diagonal transforms. However, the choice of basis under which diagonal transforms are taken is traditionally ad hoc. Attempts to remedy the situation have been hindered by the fact that no joint characterization of the conditions for {sensors, illuminants, reﬂectances} to support diagonal color constancy has previously been achieved. In this work, we observe that the von Kries compatibility conditions are impositions only on the sensor measurements, not the physical spectra. This allows us to formulate the von Kries compatibility conditions succinctly as rank constraints on an order 3 measurement tensor. Given this, we propose an algorithm that computes a (locally) optimal choice of color basis for diagonal color constancy and compare the results against other proposed choices.

光谱仪色温英文缩写

光谱仪色温英文缩写Spectral Instrument and Colour Temperature: An In-Depth Analysis.Spectral instruments and colour temperature are two concepts that play a pivotal role in the understanding and measurement of light. Spectral instruments are devices that are used to measure and analyze the spectral components of light, while colour temperature is a metric that characterizes the colour of a light source based on its spectral distribution.Spectral Instruments.Spectral instruments are precision devices that are designed to measure the spectral properties of light. These instruments can be used to determine the wavelength, intensity, and other characteristics of light sources. Spectral analysis is crucial in various fields, including physics, chemistry, and astronomy, as it allows researchersto identify and understand the properties of matter by examining the interaction of light with matter.One common type of spectral instrument is the spectrometer, which is used to measure the intensity of light at different wavelengths. Spectrometers can be divided into several categories based on their operating principles, including dispersive spectrometers, Fourier transform spectrometers, and grating spectrometers. Each type of spectrometer has its unique advantages and disadvantages, making it suitable for different applications.Colour Temperature.Colour temperature is a metric that is used to describe the colour of a light source. It is measured in units of Kelvin (K) and is based on the comparison of the spectral distribution of the light source to that of a blackbody radiator at a particular temperature. A blackbody radiator is an idealized emitter that absorbs all incident radiation and emits radiation solely based on its temperature.The colour temperature of a light source is determined by the relative intensities of the different wavelengths of light emitted by the source. Light sources with a lower colour temperature emit more energy at longer wavelengths, resulting in a warmer, redder appearance. Conversely, light sources with a higher colour temperature emit more energy at shorter wavelengths, resulting in a cooler, bluer appearance.Spectral Instruments and Colour Temperature.Spectral instruments play a crucial role in the measurement of colour temperature. By analyzing thespectral distribution of a light source, spectral instruments can provide information about the colour temperature of the source. This information can be used to characterize the light source, compare it to other sources, and ensure that it meets specific requirements for applications such as photography, cinematography, and lighting design.In addition to measuring colour temperature, spectral instruments can also be used to analyze the quality oflight sources. By examining the spectral components of light, spectral instruments can reveal the presence of unwanted artefacts such as colour casts or colour shifts. This information can be used to improve the performance of light sources or to select the most suitable source for a particular application.Applications of Spectral Instruments and Colour Temperature.Spectral instruments and colour temperature have a wide range of applications across multiple industries and fields. In the field of photography, for example, spectral instruments can be used to measure the spectraldistribution of light sources to ensure accurate colour reproduction in photographs. This is particularly important for professional photography, where accurate colour representation is crucial.In the field of lighting design, spectral instrumentsand colour temperature play a key role in creating comfortable and visually appealing environments. By analyzing the spectral properties of light sources and adjusting their colour temperatures, designers can create spaces that are both visually pleasing and functional. This is particularly important in spaces such as museums, galleries, and theatres, where accurate colour representation is essential for displaying art and other visual media.In the field of astronomy, spectral instruments are used to analyze the spectra of stars and other celestial objects. By examining the spectral lines emitted by these objects, astronomers can determine their composition, temperature, and other physical properties. This information can then be used to understand the evolution and structure of the universe.Conclusion.Spectral instruments and colour temperature are two fundamental concepts in the understanding and measurementof light. Spectral instruments provide a precise and accurate way to measure the spectral properties of light sources, while colour temperature provides a metric to describe the colour of these sources. Together, they play a crucial role in various fields such as physics, chemistry, astronomy, photography, cinematography, and lighting design. As technology continues to advance, spectral instrumentsand colour temperature will continue to play anincreasingly important role in our understanding and utilization of light.。

Miscellaneous Topics regarding colour

What is colour constancy?Colour constancy is the phenomenon that most colour surfaces appear to retain their approximate daylight appearance even when viewed under light sources that differ markedly from daylight. Colour constancy is surprising since the spectral distribution of light entering the eye from a surface can vary markedly from one light source to another. The phenomenon of colour constancy is only approximate, however, and surfaces do not retain their daylight colours when viewed under certain fluorescent light sources or when viewed under monochromatic radiation. Certain surfaces appear to change markedly from one light source to another and such surfaces are said to lack colour constancy; this phenomenon must not be confused with metamerism which is a phenomenon associated with at least two samples.What is metamerism?Metamerism refers to the situation where two colour samples appear to match under one condition but not under another; the match is said to be conditional. Metamersim is usually discussed in terms of two illuminants (illuminant metamerism) whereby two samples may match under one illuminant but not under another. Other types of metamerism include geometrical metamerism and observer metamerism. Two samples that conditionally match are said to be a metameric pair. If two samples have identical reflectance spectra then they cannot be metameric - they are an unconditional match.How do I measure whiteness?Whiteness is a complex perceptual phenomenon that depends not only the luminance of a sample but also on the chromaticity. To promote uniformity of practice in the evaluation of whiteness the CIE has recommended that the formula for whiteness, W or W10, be used for comparisons of the whiteness of samples evaluated for CIE Standard Illuminant D65:W = Y + 800(x n - x) + 1700(y n - y),orW10 = Y + 800(x n,10 - x10) + 1700(y n,10 - y10),where x n and y n refer to the chromaticities of the illuminant (D65), and the subscript 10 distinguishes the 10 degree observer data from the 2 degree data.The higher the value of W or W10 the greater the whiteness: the formulae, however, are only valid for samples that would commercially considered white and within certain other constraints.If the measurement of whiteness is important, and if samples may be fluorescent, then it is very important that the light source in the spectrophotometer be a close approximation to the D65 illuminant.How do I measure yellowness?The preferential absorption of light in the short wavelength region (380-440nm) by a nominally white substance usually causes an appearance of yellowness. A number of yellowness scales have been developed over the years. The simplest, though not necessaril best, index for quantifying yellowness is simply the difference between the Y and Z tristimulus values, thus Y-Z.What can I do if my sample is not uniform?It must be realised that a spectrophotometer (or a colorimeter) spatially averages the light reflected by a sample: thus it is possible that a uniform grey sample and a black-and-white checkerboard sample could give rise to identical measurements. The CIE system is strictly limited to the measurement of uniform colour stimuli.Digital colour camera devices are beginning to be used for colour measurement - especially for textured samples. They measure colour at many thousands of spatial locations on the sample but currently provide relatively poor colour resolution and precision.What is device-independent colour space?There is an increasing need to be able to communicate colour from one device (such as a VDU screen) to another (such as a colour printer) with no loss in colour fidelity. One way to achieve this is if all devices are calibrated in terms of a device-independent colour space. The CIE system for colour specification is being adopted by industry as a device-independent space.。

3B Scientific 透光光谱实验说明书

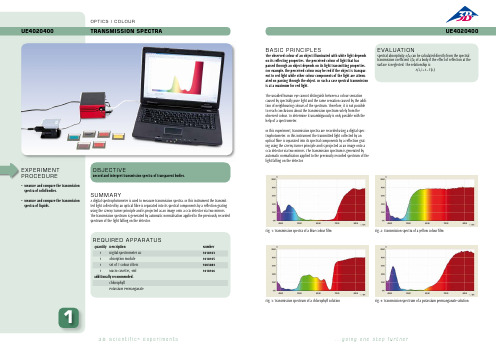
...g o i n g o n e s t e p f u r t h e r3B S c i e n t i f i c ® E x p e r i m e n t s1UE4020400OP T IC S / COLOUR Transmission spEcTra OB JEC T I V ERecord and interpret transmission spectra of transparent bodies.SUMM A RYA digital spectrophotometer is used to measure transmission spectra. In this instrument the transmit-ted light collected by an optical fibre is separated into its spectral components by a reflection grating using the Czerny-Turner principle and is projected as an image onto a CCD detector via two mirrors. The transmission spectrum is generated by automatic normalisation applied to the previously recorded spectrum of the light falling on the detector.E X PERIMEN T PROCEDURE• M easure and compare the transmission spectra of solid bodies.• M easure and compare the transmission spectra of liquids.UE4020400BASIC PRINCIPL ESThe observed colour of an object illuminated with white light dependson its reflecting properties. The perceived colour of light that has passed through an object depends on its light transmitting properties. For example, the perceived colour may be red if the object is transpar -ent to red light while other colour components of the light are attenu -ated on passing through the object. In such a case spectral transmission is at a maximum for red light.The unaided human eye cannot distinguish between a colour sensation caused by spectrally pure light and the same sensation caused by the addi-tion of neighbouring colours of the spectrum. Therefore, it is not possible to reach conclusions about the transmission spectrum solely from the observed colour. To determine it unambiguously is only possible with the help of a spectrometer.In this experiment, transmission spectra are recorded using a digital spec-trophotometer. In this instrument the transmitted light collected by an optical fibre is separated into its spectral components by a reflection grat-ing using the Czerny-Turner principle and is projected as an image onto a CCD detector via two mirrors. The transmission spectrum is generated by automatic normalisation applied to the previously recorded spectrum of the light falling on the detector.E VA LUAT IONSpectral absorptivity A (λ) can be calculated directly from the spectral transmission coefficient T (λ) of a body if the effect of reflection at the surface is neglected. The relationship is:()λ−=λT )(A 1Fig. 1: Transmission spectra of a blue colour filmFig. 2: Transmission spectra of a yellow colour filmFig. 3: Transmission spectrum of a chlorophyll solution Fig. 4: Transmission spectrum of a potassium permanganate solutionREqUIRED A PPA R AT USQuantity DescriptionNumber 1Digital-Spectrometer LD 10181031Absorption module 10181051Set of 7 Colour Filters 10030841Macro cuvettes, 4ml1018106Additionally recommended:ChlorophyllPotassium Permanganate。

高光谱英文缩写

高光谱英文缩写Hyperspectral imaging, often referred to as HSI, is a powerful and versatile technology that has revolutionized the way we perceive and analyze the world around us. This advanced imaging technique goes beyond the capabilities of traditional digital cameras by capturing a vast array of spectral information from the electromagnetic spectrum, providing a wealth of data that can be used in a wide range of applications.At its core, hyperspectral imaging involves the acquisition of high-dimensional data cubes, where each pixel in the image contains a detailed spectral signature. This signature represents the unique reflectance or emission characteristics of the target material, allowing for the identification and classification of a wide variety of substances and materials. Unlike conventional RGB (red, green, blue) imaging, which captures only three color channels, hyperspectral sensors can record hundreds or even thousands of narrow spectral bands, creating a rich and detailed spectral profile.The power of hyperspectral imaging lies in its ability to revealinformation that is invisible to the human eye or traditional imaging techniques. By capturing the subtle nuances of the electromagnetic spectrum, HSI can detect and analyze a diverse range of materials, from minerals and vegetation to man-made objects and even chemical compounds. This capability has made it an indispensable tool in a variety of fields, including remote sensing, environmental monitoring, agriculture, and even medical diagnostics.In the realm of remote sensing, hyperspectral imaging has revolutionized the way we study and manage our natural resources. By analyzing the spectral signatures of different materials, researchers can map and monitor the distribution of minerals, identify areas of vegetation stress, and detect the presence of pollutants or contaminants in the environment. This information is invaluable for a wide range of applications, from mineral exploration and forestry management to environmental impact assessments and disaster response.In the agricultural sector, hyperspectral imaging has become a crucial tool for precision farming and crop monitoring. By analyzing the spectral signatures of plants, farmers can detect early signs of disease, nutrient deficiencies, or water stress, allowing them to take targeted action to improve crop yields and reduce the environmental impact of their operations. Additionally, HSI can be used to map soil composition, monitor crop growth, and even detect the presence ofpests or weeds, enabling more efficient and sustainable farming practices.The medical field has also benefited greatly from the advances in hyperspectral imaging technology. In the area of diagnostics, HSI has shown promise in the early detection of various diseases, such as skin cancer, breast cancer, and cardiovascular conditions. By analyzing the unique spectral signatures of diseased tissues, healthcare professionals can identify subtle changes that may not be visible to the naked eye, enabling earlier intervention and improved patient outcomes.Beyond these applications, hyperspectral imaging has found its way into numerous other industries, including art conservation, forensics, and even aerospace engineering. In the field of art conservation, HSI can be used to identify pigments, detect forgeries, and monitor the condition of valuable artworks, while in forensics, it has been employed to analyze trace evidence and identify illicit substances.As the technology continues to evolve, the potential applications of hyperspectral imaging are virtually limitless. With advancements in sensor technology, data processing, and analytical algorithms, the future of HSI looks increasingly bright, promising new discoveries and innovations that will shape our understanding of the world around us.However, the widespread adoption of hyperspectral imaging technology is not without its challenges. The sheer volume of data generated by HSI systems, coupled with the complexity of the spectral analysis, can pose significant computational and storage challenges. Additionally, the cost of the specialized equipment and the expertise required to interpret the data can be barriers to entry for some organizations and individuals.Despite these challenges, the benefits of hyperspectral imaging are clear, and the technology continues to gain traction across a wide range of industries and disciplines. As researchers and engineers work to overcome the technical hurdles, the future of HSI looks increasingly promising, with the potential to unlock new insights and discoveries that will shape our understanding of the world around us.In conclusion, hyperspectral imaging is a transformative technology that has the power to revolutionize the way we perceive and interact with our environment. By capturing the rich spectral information that lies beyond the visible spectrum, HSI has opened up new frontiers of scientific exploration and practical applications, from remote sensing and precision agriculture to medical diagnostics and forensic analysis. As the technology continues to evolve and become more accessible, the potential of hyperspectral imaging to drive innovation and improve our understanding of the world around us is truly limitless.。

Colorimetry

Measuring diffuse reflectance
• Instruments measuring the color of reflecting objects consist of an illuminator, a sample holder, and a receiver • The CIE recommends four illuminating and viewing geometries for making reflectance measurements: 45/0, 0/45, d/0, and 0/d • The most common instrument for measuring diffuse reflectance is the integrating sphere • Another type of technique, which is getting more popular, is the angular integration of gonioreflectometric measurement results
பைடு நூலகம்
Color perception
• 92 % of men and 99,5 % of women have “normal” color vision • The retina comprises rod cells (night vision) and cone cells (color vision) • Majority of the cells are rod cells • There are three types of cone cells: one has peak sensitivity to blue light, one to green light and one to red light

Color Rendering and Luminous Efficacy of White LED Spectra

88
Fourth International Conference on Solid State Lighting, edited by Ian T. Ferguson, Nadarajah Narendran, Steven P. DenBaars, John C. Carrano, Proc. of SPIE Vol. 5530 (SPIE, Bellingham, WA, 2004) · 0277-786X/04/$15 · doi: 10.1117/12.565757
studying the CRI, some people are led to believe that white LED spectra should mimic the spectrum of the sun or a blackbody. While such spectra would give high CRI values no doubt, they would suffer significantly from low LER. The challenge in creating LEDs for use as illumination sources is to provide the highest possible energy efficiency while achieving best color rendering possible. As such, an accurate metric of color rendering is of importance. If the metric is incorrect, energy will be wasted. To analyze the possible performance of white LEDs and also the problems in the CRI, a simulation program has been developed. Various white LED spectra, multi-chip type and phosphor type, were modeled and analyzed in comparison to conventional lamps. The results of the simulation are presented, and the problems and expected improvements of the CRI are discussed. 2. COLOR RENDERING INDEX (CRI) The CRI is currently the only internationally agreed metric for color rendering evaluation. The procedure for the calculation is, first, to calculate the color differences ∆Ei (on the 1964 W*U*V* uniform color space – now obsolete) of 14 selected Munsell samples when illuminated by a reference illuminant and when illuminated by a given illumination. The first eight samples are medium saturated colors, and the last six are highly saturated colors (red, yellow, green, and blue), complexion, and leaf green. The reference illuminant is the Planckian radiation for test sources having a correlated color temperature (CCT) < 5000 K, or a phase of daylight‡ for test sources having CCT ≥ 5000 K. The process incorporates the von Kries chromatic adaptation transformation. The Special Color Rendering Indices Ri for each color sample is obtained by Ri = 100 – 4.6 ∆Ei ; (i =1, …, 14). (1)

Color Dependence in the Spatial Distribution of Satellite Galaxies

a r X i v :0711.0989v 2 [a s t r o -p h ] 8 A p r 2008Astronomy &Astrophysics manuscript no.chen cESO 2008April 8,2008Color Dependence in the Spatial Distribution of Satellite GalaxiesJacqueline Chen 1Argelander-Institut f¨u r Astronomie,Universit¨a t Bonn,Auf dem H¨u gel 71,D-53121Bonn,Germany;jchen@astro.uni-bonn.de Preprint online version:April 8,2008ABSTRACTAims.We explore the color dependence of the radial proﬁle of satellite galaxies around isolated parent galaxies.Methods.Samples of potential satellites selected from large galaxy redshift surveys are signiﬁcantly contaminated by interlopers –objects not bound to the parent galaxy.We use the Sloan Digital Sky Survey to estimate the interloper fraction in samples of candidate satellite galaxies.Results.We show that samples of red and blue satellites have di ﬀerent interloper populations:a larger fraction of blue galaxies are likely to be interlopers compared to red galaxies.Both with and without interloper subtraction,the radial proﬁle of blue satellites is signiﬁcantly shallower than that of red satellites.In addition,while red and blue primaries have di ﬀerent interloper fractions,the slope of the corrected radial proﬁles are consistent after interloper correction.We discuss the implications of these results for galaxy formation models.Key words.cosmology:theory –dark matter –galaxies:formation –galaxies:fundamental parameters –galaxies:structure1.IntroductionIn cold dark matter (CDM)models of the universe,large num-bers of dark matter (DM)subhalos lie within the virial radius of larger dark matter halos.In some halos and subhalos,bary-onic material has cooled and formed stars,resulting in a central galaxy and satellite galaxies.The spatial distribution of satel-lite galaxies in galaxy-sized halos,then,reﬂects the evolution of satellite galaxies and the mass accretion history of their par-ent halos.For example,dark matter simulations suggest that the angular distribution of subhalos follows the shape of the DM halo,which is indicative of infall of subhalos along ﬁlaments (e.g.,Zentner et al.2005;Libeskind et al.2005),while observa-tions suggest that satellites lie along the major axis of the light distribution for early-type galaxies (e.g.,Sales &Lambas 2004;Brainerd 2005;Yang et al.2006;Azzaro et al.2007).In dark matter simulations,the radial distribution of subhalos is biased with respect to the density proﬁle of DM halos;at small separations from the center of the halo (within ∼20−50%of the virial radius),the distribution of DM subhalos has a lower con-centration,but it follows the dark matter density proﬁle at larger radii (Ghigna et al.1998;Col´ın et al.1999;Ghigna et al.2000;Springel et al.2001;De Lucia et al.2004;Diemand et al.2004;Gao et al.2004;Nagai &Kravtsov 2005;Macci`o et al.2006).Studies that include baryons,star formation and cooling,how-ever,show that the distribution of galaxies associated with sub-halos has a steeper inner proﬁle than the subhalo distribution,both at cluster and at galaxy scales (Nagai &Kravtsov 2005;Macci`o et al.2006).For samples of subhalos selected by tidally-truncated mass,objects near the halo center lose a greater per-centage of their dark matter mass than objects near the virial radius.Stellar mass selected samples of satellite galaxies are resistant to this e ﬀect since baryonic components are located in the centers of dark matter subhalos and are tightly bound.The observed radial proﬁle of satellites in galaxy-sized halos is generally more centrally concentrated than the subhalo dis-tribution (Chen et al.2006)but consistent with the dark matter proﬁle (van den Bosch et al.2005;Chen et al.2006),although Sales &Lambas (2005)have contrary results.The color dependence in the spatial distribution of satellite galaxies has been studied extensively in angular distributions.The angular distribution of satellites is anisotropic and aligned with the major axis for red host galaxies and is consistent with isotropic for blue hosts (Yang et al.2006;Agustsson &Brainerd 2008;Azzaro et al.2007).These results are consistent with the picture where the orientation of the major axis of elliptical galax-ies is determined by the direction along which subhalos are falling into the galaxy –along ﬁlaments.The orientation of spiral galaxies is determined by the angular momentum vector,which,in simulations,has shown only poor alignment with the mi-nor axis of the dark matter halo.A secondary result found in these studies is that red satellites of red hosts show a stronger anisotropy than blue satellites.This result might be explained by a scenario where satellite color is determined by accretion time;red satellites were accreted earlier,while blue satellites represent recent infall.If the major axis of the host galaxy is set early and the orientation of infalling subhalos with respect to the host galaxy changes over time,then objects which accreted early would show a stronger alignment with respect to the host galaxy.These observational results have been analyzed by com-parison to mock galaxy catalogs derived from semi-analytic models –simulating galaxies using the mass accretion histo-ries of dark matter halos in a simulation and a variety of as-sumption about the physics of galaxy formation and evolution.Agustsson &Brainerd (2008)use mock galaxy catalogs to sug-gest that the di ﬀerence in degree of anisotropy between blue and red host galaxies is real and not due to di ﬀerences in the inter-loper populations,while Kang et al.(2007)come to an oppo-site conclusion using a very di ﬀerent technique –the color de-pendence is due to interlopers in the group catalog.Kang et al.(2007)also conclude that the di ﬀerence in alignment between red and blue satellites is due to the masses of the satellites;red satellites are larger and associated with subhalos which were2Jacqueline Chen:Color Dependence in the Spatial Distribution of Satellite Galaxiesmore massive at the epoch of accretion and which in simula-tions are accreted more preferentially along the major axis of the halo(Libeskind et al.2005;Wang et al.2005).The semi-analytic model of Agustsson&Brainerd(2008)suggests that the amount of interloper contamination is much greater for blue satellites than red satellites(∼50%to∼15%,deﬁning inter-lopers as objects with a physical separation greater than500kpc from the parent galaxy),although the color dependence in the anisotropy of satellites is still observed after subtracting inter-lopers.The color dependence in the radial distribution of satel-lites has been studied by Sales et al.(2007)using semi-analytic galaxy catalogs constructed from the Millennium Simulation. They note that the radial distribution of red satellites is signif-icantly more centrally concentrated than the distribution of blue satellites.This trend is attributable to accretion time in a scenario similar to one explanation for greater anisotropy in the angular distribution of red satellites compared to blue satellites:early ac-creting satellites are stripped of hot gas,stop forming stars,and become redder.Early accreters are also likely to orbit closer to the center.Observationally,the eﬀects of color selection on the radial distribution of satellite galaxies has been previously examined by Sales&Lambas(2004)using data from the Two Degree Field Galaxy Redshift Survey(2dFGRS).Theyﬁnd a steeper outer slope for satellites of blue parent galaxies than for red pri-maries.In addition,red satellites have a distribution that requires a larger core radius than blue satellites and they attribute this result to correlations between the primary and satellite prop-erties.However,in observational searches for satellites,candi-date satellites are chosen based upon their projected separation and velocity diﬀerence from the parent galaxy.Samples of ob-jects chosen in this manner are heavily contaminated by ob-jects which are not satellites–interlopers.In Chen et al.(2006), we discussed the importance of interlopers in making relatively unbiased estimates of the projected radial distribution of satel-lite galaxies and developed a reliable method of interloper sub-traction.Other methods to account for interlopers have been investigated.For example,van den Bosch et al.(2004)exclude interlopers using an iterative,adaptive selection criterion for satellites,and Chen(2008)model satellites and interlopers to-gether using a halo occupation distribution(HOD)based ana-lytic model for the galaxy correlation function.The Chen et al. (2006)approach has the advantage that it may easily be com-pared to previous results.In this paper,we add color selection to the interloper estima-tion method described in Chen et al.(2006)and apply it to data from the Sloan Digital Sky Survey(SDSS)spectroscopic sam-ple.We show that samples of red and blue candidate satellites have diﬀerent levels of contamination by interlopers,while the model interloper samples for red and blue primaries are similar in color distribution.We discuss these results in terms of the en-vironmental dependence of satellite galaxies and wider applica-tions to the angular distribution of satellite galaxies and to galaxy formation models.2.Observational Data2.1.The Sloan Digital Sky SurveyThe Sloan Digital Sky Survey(SDSS)includes imaging of the the northern Galactic cap inﬁve bands,u,g,r,i,z,down to r∼22.5using a dedicated2.5m telescope at Apache Point Observatory in New Mexico in addition to spectro-scopic observations for a subsample of objects from the imag-ing catalog(York et al.2000;Fukugita et al.1996;Gunn et al. 1998;Hogg et al.2001;Smith et al.2002;Strauss et al.2002; Blanton et al.2003;Gunn et al.2006;Tucker et al.2006).The SDSS spectroscopy is carried out using opticalﬁbers posi-tioned in pre-drilled holes on a circular plate,with mini-mum separation betweenﬁbers of55′′,theﬁber collision dis-tance.Reobservations of aﬁeld can result in observed spec-tra with separations less than theﬁber collision distance,down to theﬁber diameter of3′′.The spectroscopic targets are se-lected with r-band Petrosian magnitudes r≤17.77and r-band Petrosian half-light surface brightnessesµ50≤24.5mag arcsec−2.An automated pipeline measures the redshifts and classiﬁes the reduced spectra(Stoughton et al.2002;Pier et al. 2003;Ivezi´c et al.2004,D.J.Schlegel et al.2008,in prepara-tion).1We use the spectroscopic Main galaxy catalog available as Data Release Six(DR6;Adelman-McCarthy et al.2008),cov-ering an area of7425deg2.Because the SDSS spectroscopy is taken through circular plates with aﬁnite number ofﬁbers ofﬁnite angular size,the spectroscopic completeness varies across the survey area.The resulting spectroscopic mask is represented by a combination of disks and spherical polygons (Tegmark et al.2004).Each polygon also contains the com-pleteness,a number between0and1based on the fraction of targeted galaxies in that region which were observed.We ap-ply this mask to the spectroscopy and include only galaxies from regions where completeness is at least90%.We use r-band magnitudes in DR6,built from the NYU Value-Added Galaxy Catalog(Blanton et al.2005),normalized to h=1,such that M r=M0.1r−5log10h,where M0.1ris the absolute magni-tude K-corrected to z=0.1(kcorrect v4.1.4)as described in Blanton&Roweis(2007).2.2.Volume-Limited Galaxy SamplesFollowing the procedure in Chen et al.(2006),we use a volume-limited galaxy sample with a depth of13,500km s−1,corre-sponding to the limiting redshift of z=0.045.This limit is cho-sen as a trade-oﬀbetween the volume of the sample and the ab-solute magnitude limit for our satellites,which would need to be decreased to brighter magnitudes for more distant primaries.In addition,the limiting magnitude sets a minimum separation at whichﬁber collisions become important,which increases with distance.To include more distant primaries we would have to sacriﬁce the ability to probe density distributions at small sepa-rations.From our volume-limited sample,we construct a primary sample of isolated host galaxies and a sample of potential satel-lites that are projected close to primaries and refer to these two samples as the primary sample and the satellite sample.Isolated host galaxies are chosen in order to reduce the number of galaxy groups selected and eliminate the contamination from satellites of galaxy group members.Parameters for the criteria follow Prada et al.(2003)and Chen et al.(2006)and are listed in Table 1.The isolation criterion requires that a primary have only neigh-bors at least two magnitudes fainter within∆R=0.5h−1MpcJacqueline Chen:Color Dependence in the Spatial Distribution of Satellite Galaxies3 Table1.Selection&Isolation CriteriaParameters Valueand∆V=1000km s−1.2Potential satellites of any isolated pri-mary must be at least2magnitudes fainter than the primaryand withinδr=0.5h−1Mpc andδv=500km s−1.The max-imum absolute magnitude for satellites is set by M r,lim−5log h=17.77−DM−K0.1in the r-band,where the17.77is theﬂuxlimit in this band,DM is the distance modulus,and K0.1is theK-correction at z=0.1.This gives a limiting absolute magnitudeof M r=−17.77.The satellites are thus limited to the bright-est satellite galaxies,∼0.1L∗.In order to avoid biasing froma deﬁcit of close pairs of objects,the minimum separation be-tweenﬁbers is32.9h−1kpc–theﬁber collision separation at theredshift of the furthest point in our sample.Finally,we choosegalaxies that are in areas that are at least90%complete.For therange−23<M r<−20,there are1602primary galaxies and690objects in the satellite sample with projected radii greaterthan the minimum separation and less than0.5h−1Mpc.2.3.Interloper SubtractionThere is a fraction of objects in our satellite samples that arenot gravitationally bound to the primaries but are included inthe sample because of projection eﬀects.Throughout this pa-per,we call such objects interlopers(in turn,satellites sampleswithout interloper contamination are referred to as true satellitesamples).Interloper subtraction is discussed in greater detail inChen et al.(2006).In semi-analytic galaxy catalogs and in dark matter simula-tions,interlopers are signiﬁcant in samples of satellites or DMsubhalos.For example Agustsson&Brainerd(2008)ﬁnd in asemi-analytic galaxy catalog constructed from the MillenniumSimulation–using a stricter isolation criteria than we use–thatthe interloper contamination fraction is∼30%.In DM-only sim-ulations,the fraction of interlopers as a function of projected ra-dius rises from a few percent at R∼50h−1kpc to nearly100%atR=0.5h−1Mpc(see Fig.1,Chen et al.2006).Chen et al.(2006)developed and tested several methods ofsubtracting interlopers from the satellite sample statistically.Theprojected surface density of candidate satellites, Σ(R) sat is es-timated in bins and normalized by the total number of primarygalaxies in the sample.Simple methods of interloper subtractionestimate the corresponding projected surface density in interlop-3In our data there is a total of3325model interlopers.4Jacqueline Chen:Color Dependence in the Spatial Distribution of SatelliteGalaxiesFig.1.The color distribution for the primary sample (solid),satellite sample (dotted),and model interloper sample (dashed).Red satellites are deﬁned to have M g −M r >0.65,while red primaries have colors M g −M r >0.9.Poisson errors are shown for the primary and satellite sample.The corresponding Poisson errors for the model interloper sample are signiﬁcantly smaller than for the satellite sample.our parent galaxy halos,making ﬁtting for the scale radius im-practical.3.ResultsThe M g −M r color distributions for theprimary,satellite,and model interloper samples are shown in Fig.1.The primary sam-ple is redder than the satellite sample with a large red peak and a bluer tail,while the satellite sample has a vaguely bimodal distri-bution,split at M g −M r ∼0.65.The model interloper distribution appears tilted to bluer objects compared with the distribution of the satellite sample.3.1.Red and Blue SatellitesThe di ﬀerences in color distribution between the satellite sample and the model interloper sample suggests that a greater fraction of blue objects in the satellite sample will be interlopers than of red objects.Deﬁning red satellites to M g −M r >0.65,of the 690objects in the satellite sample,285are red and 405are blue.By comparison to the model interloper sample,the fraction of the objects that are interlopers in the whole sample is 24%,while the percentages for the red and blue satellite sample are 16%and 30%,respectively.This di ﬀerence a ﬀects the estimates of the slope of the power-law ﬁt to the radial distribution.In Figure 2,the biasing of the best-ﬁt power-law is shown for all satellites and blue and red satellites.The distribution of blue satellites is signiﬁcantly ﬂatter than the distribution of red satellites,and the distribution of blue satellites is more e ﬀected by interlopers than the distribution of red satellites.In the interloper-contaminated satellite samples,the best-ﬁt slopes for blue and red satellites (shown in Table 2and Figure 3)are inconsistent,with a much shallower slope for blue satellites.After interloper subtraction,although the di ﬀerence in slopes isFig.2.The surface density of the satellite sample (squares)and the interloper-subtracted satellite sample (circles)for all satel-lites (top),blue satellites (center),and red satellites (bottom).The best ﬁt power-laws are also plotted with solid lines for the satellite sample and dotted lines for the interloper-subtracted sample.smaller,the blue slope is still signiﬁcantly shallower than the red slope,and the slopes are inconsistent given both the marginal-ized errors and their 1σconﬁdence intervals (see Fig.3).The projected radial distribution of red satellites is as steep as might be expected for the dark matter density distribution in halos which host galaxies such as are found in our primary sample.The distribution of blue satellites,on the other hand,is as shal-low as might be expected for the subhalo distribution in the same host halos (see,for comparison,Chen et al.2006).Jacqueline Chen:Color Dependence in the Spatial Distribution of Satellite Galaxies5 Table2.Best-Fit Power-Law Slopes to the Surface DensityProﬁle of SatellitesInput Data Satellite Sample InterloperSubtracted Fig.3.The68%conﬁdence intervals for the normalization(A)and slope(α)of the power-law,Σ(R)=ARα.Shaded contours are for blue satellites;solid line contours are for red satellites. The contour for interloper-subtracted samples are in each case atsteeper slopes than their satellite sample counterparts.In general,we expect blue satellites to be fainter than red satellites,so it is useful to attempt todisentangle the eﬀects of luminosity from those of color.While Chen et al.(2006)tests luminosity dependence(which is further discussed in Section 4),they do not have suﬃcient numbers of objects to test color and luminosity together.Figure4shows the luminosity distri-butions for the blue and red satellites and primaries.We split each color sample of satellites into a faint and a bright sample at M r=−18.3.Table2shows that the interloper-subtracted sur-face density proﬁles of faint and bright samples are consistent for color-selected samples,i.e.,color is the dominant attribute in the radial distribution of satellites.3.2.Red and Blue PrimariesWe split the1602primary galaxies by color at M g−M r=0.9. The591red primary galaxies have358objects in their satellite sample,while the1011blue primary galaxies have332candi-Fig.4.The luminosity distribution with corresponding Poisson errors of primaries(top)and objects in the satellite sample(bot-tom),where red objects and blue objects are shown separately, in dotted and solid lines respectively.Bright and faint satellites are split at M r=−18.3,while bright and faint primaries are split at M r=−20.8.date satellites.The interloper percentages for the red and blue primary sample are21%and28%,respectively.Red primaries of M g−M r>0.9have a larger fraction of red objects in their satellite sample than than blue primaries(52%to30%)and,sub-sequently,more true satellites(see Fig.5).This can also be seen in Fig.6,where the amplitude of the satellite proﬁle of red pri-maries is greater than that of the blue primary proﬁle.After inter-loper subtraction,the slopes of the density proﬁles of satellites for blue and red primaries are consistent.Figure4additionally shows that red primaries are in gen-eral brighter than blue primaries.Splitting the color-selected pri-maries into faint and bright samples at M r=−20.8,Table2 shows signiﬁcant diﬀerences for the distribution of satellites of faint and bright primaries,depending on the color of the primary. Red,brighter primaries have an interloper-subtracted satellite proﬁle that is shallower than the distribution of satellites in red, fainter primaries,α=−1.34±0.11toα=−1.82+0.15−0.14.This is not unexpected;from numerical simulations we expect the satel-lite distribution to scale with the mass distribution of the primary,6Jacqueline Chen:Color Dependence in the Spatial Distribution of SatelliteGalaxiesFig.5.The color distribution for the satellite sample and model interloper sample for red primaries (thick and thin solid lines,respectively)and the color distribution for the satellite sample and model interloper sample for blue primaries (thick and thin dashed lines,respectively).and larger primaries have smaller concentrations leading to shal-lower slopes at the radii at which we measure.Interestingly,blue primaries show the opposite dependence:the distribution of satellites around brighter primaries seems to have a steeper slope than around fainter primaries.This trend is accompanied by a change in the fraction of red satellites:38%of the satel-lite sample for bright,blue primaries are red,while 23%of the corresponding sample for faint,blue primaries are red.The er-rors,however,are nearly as large as the discrepancy between the samples,and larger samples will be required to conﬁrm this re-sult.In addition,the slope for satellites of bright,blue primaries is steeper than that for bright,red primaries,which may reﬂect color dependence in using luminosity as a proxy for mass.Similar results can be seen if wesplit both the primary and the satellite samples by color.In Table 3,we show that red satel-lites around blue primaries have a larger interloper fraction and a steeper power-law slope than found for red satellites of red primaries.The di ﬀerence in power-law slope can be attributed to the same luminosity dependence discussed previously:red primaries are more massive and have mass and satellite dis-tributions described by smaller concentrations.Interloper con-tamination increases from small separations to large,and for larger primaries,the range of radii we probe preferentially sam-ple areas with smaller level of interloper contamination.On the other hand,for blue satellites of red and blue primaries,we ﬁnd very similar interloper fractions and shallow power-law slopes.Unfortunately,in all cases,statistics are poor and future larger samples will be required for statistical signiﬁcance to be as-cribed.3.3.Environmental DependenceDespite the di ﬀerence in satellite samples,the color distribution of the model interloper samples of red and blue primaries are similar to each other and to the color distribution of the satel-lite sample of blue primaries (see Fig.5).Restated,although red primaries are found in more clustered environments,the envi-Fig.6.The surface density of the satellite sample (squares)and the interloper-subtracted satellite sample (circles)for satellites of blue primaries (top)and of red primaries (bottom).The best ﬁt power-laws are also plotted with solid lines for the satellite sample and dotted lines for the interloper-subtracted sample.Table 3.Primaries and Satellites Selected by ColorInput DataNumber in Interloper Power-Law (Primary-Satellite)Satellite SampleFractionSloperonments of red and blue primaries are not noticeably di ﬀerent as measured by the color distribution of model interlopers.Red primaries live in more clustered environments than blue primaries as measured in the average surface number density of model interlopers:0.159h 2Mpc −2for red primaries and 0.117h 2Mpc −2for blue primaries.In the previous section,we noted that these slightly di ﬀerent environments have similar color dis-tributions of faint objects,even though we do not use ﬁxed lumi-nosity criteria for these objects.We test one less clustered envi-ronment,sampling isolated points that lie outside of a 2h −1Mpc radius from our isolated galaxies (outside the criteria for our in-terloper subtraction method).Here,the average surface density is 0.042h 2Mpc −2.All three model interloper distributions are plotted in Fig.7,in which all environments have similar colorJacqueline Chen:Color Dependence in the Spatial Distribution of Satellite Galaxies7Fig.7.The color distribution for the model interloper samples for red primaries (solid),blue primaries (dashed),and for sam-pling isolated points greater than 2h −1Mpc from primaries (dot-ted).The average surface number density of objects in these samples is 0.159,0.117,and 0.0415h 2Mpc −2.dependences with a possible trend to bluer objects in less dense ﬁelds.4.ConclusionsIn Chen et al.(2006),we constrained the projected radial dis-tribution for isolated galaxies and found that their power-law slopes are steeper than the expected slopes for the distribution of dark matter subhalos and may be as steep as the density pro-ﬁle of the host dark matter halos.We reproduce this result with a survey area that is ∼50%larger.However,the distribution of satellite galaxies shows some signiﬁcant dependence on color.When samples of candidate satellites are split by color,we see that blue objects are more likely to be interlopers than red objects.The observed estimated interloper contamination of red objects in the satellite sample is 16%,while that of blue ob-jects is 30%.Agustsson &Brainerd (2008)produce a di ﬀer-ence of 15%and 50%,respectively,in the interloper contami-nation of red and blue satellites samples,using a semi-analytic galaxy formation model.It is,then,not appropriate to assume that red and blue satellites have the same level of interloper con-tamination and this must be taken into account in testing the color dependence in the angular distribution of satellite galaxies.This result also suggests that the prevalence of faint red galax-ies could be developed into a method to ﬁnd small groups of galaxies in a manner similar to the method by which the red se-quence of early-type galaxies is used to ﬁnd galaxy clusters (e.g.,Gladders &Yee 2000).Both with and without interloper subtraction,the radial pro-ﬁle of blue satellites is signiﬁcantly shallower than that of red satellites.The best-ﬁt power-law slope of interloper-subtracted blue satellites is α=1.34±0.10and the that of red satellites is α=−1.80±0.10.This result is consistent with the trend found by Sales et al.(2007)who test color dependence in semi-analytic galaxy catalogs constructed from the Millennium Simulation,ﬁnding a more centrally concentrated radial distribution of red satellites than of blue satellites.This trend is repeated when theyselect by a proxy for accretion time –whether the satellite retains a DM halo or whether it has been tidally destroyed.Blue satellites are generally fainter than red satellites.Correspondingly,Chen et al.(2006)found that the best-ﬁt power-law slope for bright satellites is steeper than that of faint satellites (cut at M r =−18.28)–although without statistical sig-niﬁcance –in a volume-limited sample.In a ﬂux-limited sample,the reverse relation was found;however,this sample used a lu-minosity cut as faint as the faintest satellites in our sample,at M r =−17.76,and so is not directly comparable.When we cut the satellites samples by color and luminosity,we ﬁnd that the dominant e ﬀect is from color;the best-ﬁt power-law slopes of bright and faint samples of red satellites are consistent as are those of bright and faint blue satellites.The power-law slope for red satellites is as steep as might be expected for the dark matter density distribution of halos which host galaxies like those found in our primary sample.On the other hand,the power-law slope for blue satellites is as shal-low as the expected subhalo distribution.The shallowness of the subhalo proﬁle is attributed to tidal stripping.This is unlikely to e ﬀect satellite galaxies,since they are located at the centers of the dark matter subhalos.The shallower proﬁle for blue satel-lites as compared to red satellites,then,might be interpreted as consistent with the scenario where satellite color is determined by accretion time:red satellites were accreted earlier,while blue satellites represent more recent infall.Satellites are expected to be redder in the inner regions of parent halos due to environ-mental processes that shut o ﬀstar formation (ram pressure strip-ping,strangulation,etc.).This morphological segregation has also been observed in more massive clusters and in the fainter satellites found in the Local Group.When splitting the satellite sample by primary color,red primaries have a signiﬁcantly larger fraction of red satellites and somewhat smaller interloper fractions than blue primaries.After interloper subtraction,the best-ﬁt power-law slopes of satellites of red and blue primaries are consistent within errors.Red primaries are,on average,more luminous than blue galax-ies.Correspondingly,Chen et al.(2006)found that the best-ﬁt power-law slope for satellites bright primaries is consistent with that of satellites of faint primaries (cut at M r =−21).When we cut the primary sample by luminosity and color,the trend with luminosity is di ﬀerent for red and blue primaries.The slope of satellites of bright,red primaries is shallower than that of faint,red primaries,a relation probably dominated by the mass of the parent halo as brighter primary galaxies reside in bigger par-ent halos which have mass distributions characterized by smaller concentrations.The slope of satellites of bright,blue primaries is steeper than that of faint,blue primaries,as the fraction of red satellites drops with primary luminosity.The color distribution of objects in model interloper sam-ples are similar,regardless of their environment (as measured by average surface density).While robust conclusions cannot be drawn as to how similar these distributions are,it suggests that there are fundamental di ﬀerences between satellite galax-ies and faint galaxies in the ﬁeld.Intriguingly,this blue-tilted color distribution also resembles that of the satellites sample of blue primaries.Better understanding of the processes that e ﬀect the color of faint objects and the radial distribution of satellite galaxies will require further studies.Acknowledgements.We would like to thank Andrey Kravtsov,Francisco Prada,Michael Blanton,and Erin Sheldon for their suggestions and invaluable contri-butions to understanding interloper contamination and systematics in the data.In addition,we would like to acknowledge the anonymous referee for many helpful suggestions.。

7彩色图像处理PPT课件

Color matching functions x,y,andz
16
600 nm 550 nm 450 nm (1931)
R:700 nm G:546.1 nm B:435.8 nm (1931)
R:575 nm G:535 nm B:445 nm (1965)
CIE standard color matching functions
5
Physical Nature of Color
The color spectrum can be divided into six regions violet, blue, green, yellow, orange and red
The visible light is composed of a narrow band frequencies with wavelengths from 400 to 700 nm (10-9 m) in the electromagnetic energy spectrum.
6
7
Physical Nature of Color
White light consists of a continuous spectrum of colors ranging from violet to red.
8
三基色与生物成像原理
9
Three Perception Cones
R:575 nm G:535 nm B:445 nm (1965)
Color Image Processing
Color Fundamentals Color Models Basics of Full-Color Image Processing Color Transformations

unparalleled color performance

unparalleled color performance Unparalleled Color Performance: Exploring the Art and Science of ColorColor is an essential aspect of our visual world. It impacts how we perceive our surroundings, engages our emotions, and communicates meaning. In a world where digital media continues to transform our content consumption patterns, color performance has never been more critical. With the rise ofhigh-definition displays, virtual and augmented reality, and advanced imaging and printing technologies, the ability to deliver accurate, consistent and captivating color performance is paramount.The term "unparalleled color performance" refers to the ability of a device or system to deliver superior color accuracy, precision, and consistency at all times. Achieving unparalleled color performance across various devices and platforms requires a multi-layered approach that combines the art and science of color. It involves careful calibration, color management, processing,and rendering to ensure that colors are reproduced precisely as intended.Understanding the Science of Color PerformanceThe science of color performance is complex and multidisciplinary. It involves the physical properties of light and color vision, human perception, digital imaging and processing, and color reproduction technologies. Accurate color reproduction requires precise measurement, control, and correction of color deviations at every stageof the imaging chain.One of the key challenges of color reproduction is that our visual system is highly adaptable and can compensate for significant color deviations. Therefore, color measurements need to be standardized, calibrated, and verified against industry standards and reference materials to ensure consistent and accurate results. Some of the tools and techniques used for color measurement and calibration include colorimeters, spectrophotometers, color targets, and software color management systems.The Art of Color PerformanceThe art of color performance is equally crucial in delivering unparalleled color accuracy and consistency. It involves understanding the role of color in visual storytelling, design, and branding, and how to leverage color to enhance emotional engagement and convey meaning.Color is essential in creating a brand identity and differentiating products from competitors. It can signify luxury, quality, innovation, or humor, depending on the context and target audience. Effective use of color requires a keen understanding of color theory, cultural associations, and audience preferences. Designers and marketers need to tailor color choices and combinations to reflect the message and values they want to convey.The Role of Unparalleled Color Performance in IndustriesUnparalleled color performance is essential in several industries, including printing, imaging, photography, cinematography, and gaming. Inprinting, accurate color reproduction is essential for producing high-quality images, logos, packaging designs, and marketing materials. Printers need to ensure that the colors match the intended hue, saturation, and brightness levels.In imaging and photography, accurate color reproduction is essential for capturing and preserving the natural colors of the subject. Cameras and displays need to have precise color calibration, white balance, and gamma adjustments to achieve accurate results. Accurate color reproduction is also essential in cinematography, where color grading and timing are critical in creating the desired mood and atmosphere.In gaming, unparalleled color performance is essential in delivering an immersive and engaging experience. The colors need to be vibrant, consistent across different platforms, and accurately reflect the intended mood and atmosphere of the game. Color performance is particularly crucial in virtual and augmented reality applications, where the color accuracy andconsistency can significantly impact the user experience.ConclusionIn conclusion, achieving unparalleled color performance is a multi-faceted endeavor that requires a combination of art and science. Accurate color reproduction is essential for conveying meaning, enhancing emotional engagement, creating a brand identity, and delivering an immersive experience. Achieving unparalleled color performance requires precision, attention to detail, and a thorough understanding of color theory, human perception, and color reproduction technologies. By mastering the art and science of color performance, companies and individuals can unlock new avenues of creativity, enhance their brand value, and improve the user experience.。

AATCC EP6(评定程序)-2003(2007)仪器测色方法(英文)

Copyright © 2006 American Association of Textile Chemists and Colorists 384EP 6AATCC Technical Manual/2007Developed in 1995 by AATCC Commit-tee RA36; reaffirmed 1996, 1997, 2003;reaffirmed and editorially revised 1998.Technically equivalent to ISO 105-J01.1.General Description of Instrumental Color Measurement1.1 Purpose1.1.1 This evaluation procedure is a reference document to support the proper measurement of the color (or colored ap-pearance) of specimens by instrumental means as required in many of the current AATCC test methods. The document contains three major subsections cover-ing reflectance measurement , transmit-tance measurement and related calcula-tions . In addition, an appendix is supplied which details specific techniques and specimen handling procedures.1.2 Terminology1.2.1 area-of-view, n.—of color mea-suring instrument , the dimensions of the surface area that a color measuring in-strument is capable of covering in a sin-gle color measurement.1.2.2 color measuring instrument,n.— any device, such as a colorimeter or spectrophotometer, used to measure the relative amounts of energy reflected from (or transmitted through) a specimen in the visible region of the energy spectrum (comprising the wavelengths from 360-780 nm, and including as a minimum the region from 400-700 nm).1.2.3color measurement, n.—a nu-merical representation of the color of an object obtained by use of a color measur-ing instrument. A single measurement may represent an average of multiple readings of a specimen.1.2.4 fluorescence, n.—a phenomenon in which radiant flux of certain wave-lengths is absorbed and re-emitted non-thermally at other, usually longer, wave-lengths.1.2.5 geometry, n.—of a color mea-suring instrument , one of the following terms (diffuse/0, 0/diffuse, 0/45 or 45/0)which describe the angle or manner in which a color measuring instrument:(1) illuminates the specimen (diffuse,0, 45).(2) views the resulting reflected light (0 [0°-10°], diffuse, 45, 0).Diffuse/0 and 0/diffuse geometry instru-ments contain a sphere used to diffuse the light illuminating [or reflected from] the specimen, while 0/45 and 45/0 geometry instruments generally use mirrors or fiber optics to direct the illumination [or view-ing] at a 45 angle to the specimen.NOTE: Instruments of different geo-metrics may produce different colorimet-ric results on most textile materials.1.2.6 reflectance, n.—the ratio of the reflected radiant or luminous energy (light) to the incident energy in the given conditions.1.2.7 reflectance factor, n.—the ratio of the light reflected from the specimen to the light reflected from the perfect reflecting diffuser under the same geometric and spectral conditions of measurement.1.2.8 specular reflection, n.—the re-flection without diffusion, in accordance with the laws of optical reflection, as in a mirror.1.2.9 standardization, n.—of color measuring instrument , the act of measur-ing one or more standard materials with a color measuring instrument for the purpose of calculating a set of correction factors to be applied to all subsequent measurements.1.2.10 transmittance, n.—the ratio of transmitted light to incident light under specified geometric and spectral conditions.NOTE: Regular transmittance (of trans-parent materials) is the ratio of undiffused transmitted light to incident light.1.2.11 transmittance factor, n.—the ratio of the light transmitted by a speci-men and evaluated by a receiver to the light passing through the same optical sys-tem and evaluated by the receiver when the specimen is removed from the system.1.2.12 verification standard, n.—in color measurement , any stable material which is used for the purpose of con-firming (or verifying) the validity of an instrument standardization. Color mea-surements, which are made immediately following a standardization, are compared to original measurements of the standard to detect improper standardization.1.3 Safety Precautions1.3.1 Normal safe laboratory practices should be observed during sample prepa-ration and color measurement proce-dures. The operation of color measuring instruments should be done in accordance with specific manufacturer’s instructions and precautions concerning operation and maintenance procedures.1.4 General Guidelines1.4.1 In general, instrumental color measurement procedures are dictated by the type of specimen to be measured and the instrument with which it will be mea-sured. Many types of color measuring in-struments are available, differing in suchfeatures as area-of-view, illumination method and geometry. The user is cau-tioned that conflicting results may be obtained by comparing data acquired on instruments of different designs.1.5 Procedure1.5.1 Operators who utilize Evaluation Procedure 6 as a reference for color mea-surement should generally conduct such measurements as follows:1.5.2 Refer to the appropriate section (Reflectance or Transmittance) for speci-men to be measured.1.5.3 Standardize instrument according to section titled Standardization . Maintain a record of the procedure and of the results for any verification standards measured.1.5.4 Obtain and prepare specimen,noting any special sampling and/or con-ditioning procedures that may be required (see Appendix A.1.2).1.5.5 Present specimen to color measur-ing instrument, again following any spe-cial techniques required for the type of ma-terial being measured (see Appendix A).1.5.6 Measure the color of the speci-men, obtaining the appropriate spectral reflectance or transmittance factors or colorimetric values.1.5.7 Perform any appropriate numeri-cal calculations as specified in Section 4 or as is required by the specific test method.2.Measurement of Color by Reflectance Methods2.1 Principle2.1.1 Materials of an opaque or nearly opaque nature (but not translucent) are measured by reflectance methods to ob-tain a numerical representation of the color of the specimen. Proper equipment setup, standardization of the color mea-suring instrument, and proper presenta-tion of the test specimens to the instru-ment are required to achieve consistent,reliable, and meaningful reflectance mea-surement results. In addition, calculation of the colorimetric values required for evaluating the results must be performed in the prescribed manner.2.2 Uses and Limitations2.2.1 This section is restricted to the measurement of the color of opaque and nearly opaque specimens by reflectance spectrophotometers or reflectance color-imeters. The use of special procedures and/or aids to the presentation of speci-mens is covered in the appendix.2.3 Apparatus and Materials2.3.1 Reflectance color measuring in-strumentation illuminates a specimen and measures the amount of light which is re-AATCC Evaluation Procedure 6Instrumental Color MeasurementCopyright The American Association of Textile Chemists and ColoristsProvided by IHS under license with AATCCLicensee=Hong Kong Polytechnic Univ/9976803100Not for Resale, 03/24/2007 04:07:53 MDTNo reproduction or networking permitted without license from IHS--`````,``````,,``,`,,,```,,``-`-`,,`,,`,`,,`---Copyright © 2006 American Association of Textile Chemists and Colorists AATCC Technical Manual/2007EP 6385flected from the surface of the specimen.Illumination is normally done in a poly-chromatic manner (white light), however monochromatic mode is acceptable for nonfluorescent specimens. Reflectance color measuring instruments may be broadly divided between two groups:Spectrophotometers and Colorimeters.2.3.2 Spectrophotometers (typically diffuse/0°, using polychromatic illumina-tion) separate and measure the spectrum of light reflected from the specimen, rela-tive to a reference, white at regular inter-vals (wavelength intervals of 5 nm, 10nm, and 20 nm are most common). This data may be used to calculate the needed tristimulus values (X ,Y ,Z ) for any given il-luminant and observer. Some spectropho-tometers (typically 0/diffuse) illuminate the sample with monochromatic light,and measure the amount of light reflected from the surface as the sample is illumi-nated at regular wavelength intervals.2.3.3 Colorimeters measure the tristim-ulus values (X ,Y ,Z ) directly through broadband filters which are designed to produce colorimetric values for one illu-minant and observer (typically C/2°).Measurement of reflectance factors at specific wavelengths is not possible with a colorimeter.2.3.4 Within these two categories, the instruments are further defined by their geometry. Two types of geometries are prevalent: Sphere (also referred to as dif-fuse/0° [d/0°] or 0/diffuse [0°/d]) and 45/0 or 0/45. The first term in each geometry type refers to the method (or angle) by which the sample is illuminated (ex: 45degrees in a 45/0 instrument). The second term refers to the angle at which the in-strument views the illuminated specimen (ex: 0 degrees in a 45/0 instrument).2.3.5 Diffuse/0 (sphere) instruments il-luminate the specimen indirectly when the specimen is placed against a port opening into a diffusely illuminated sphere, and view the specimen at an angle between 0and 10 degrees from the perpendicular.This arrangement is designed to capture all light reflected from the specimen.Some sphere instruments with a viewing angle greater than 0 include a specular port which allows for the inclusion or ex-clusion of the specular reflectance .2.3.6 0/diffuse (sphere) instruments are similar, but the path of illumination and viewing are reversed. This method illu-minates the sample at an angle between 0and 10 degrees, and measures the amount of light reflected from the surface into the sphere.2.3.7 Instruments with 45/0 or (0/45)geometry illuminate the specimen at the first angle and view the specimen at the second. These two geometries can be ei-ther circumferential (viewing or illumi-nating at 45 to the specimen in a com-plete circle) or directional. For most textile samples, either 45/0 or 0/45 yield equivalent results.2.3.8 All color measuring instruments require a white calibrated standard with which to standardize the instrument. The colorimetric values for this calibration standard are stored in the instrument or the software and require only that a spe-cific standard be used to standardize the instrument. The correct white standard is usually identified with a serial number.2.4 Standardization2.4.1 Proper standardization of any color measuring instrument is absolutely necessary to achieve uniform, accurate results. While different types of instru-ments require varying methods of stan-dardization, there are common principles which must be observed.2.4.2 In general, an instrument stan-dardization involves measuring a clean white surface of known reflectance fac-tors (referenced to a perfect reflecting diffuser) and calculating (through soft-ware built into the instrument or com-puter program) a series of correction fac-tors which will be applied to all subsequent measurements. Some instru-ments also require a black tile (or light trap), and possibly a gray tile. Each of these materials must be maintained in its original clean, unscratched condition. Re-fer to manufacturer’s recommendations for cleaning instructions.2.4.3 The frequency with which this standardization must be performed depends on many factors including the type of in-strument, the environmental conditions in which the instrument operates, and the re-quired accuracy of the results. For most ap-plications, an interval of 2-4 h is typical.2.4.4 Once the standardization step has been performed, it is important to verify the success of the procedure by measur-ing some colored materials (verification standards ) and comparing the resulting colorimetric values to the original values for these materials. If the measured val-ues do not fall within an acceptable varia-tion from their original values, the stan-dardization is not considered valid. The number of verification standards and the acceptability limits depend on user re-quirements, but are typically 1-3 stan-dards and an acceptance limit of 0.20∆E CMC (2:1) (D 65/10°) units.2.5 Sampling2.5.1 All measurements taken on color measuring instrumentation involve “sampling .” The area-of-view of the in-strument, the number of presentations averaged to produce a single measure-ment, the difficulty of presenting the specimen to the instrument, and the accu-racy with which the sample represents the object of concern (garment, roll, dye lot,etc.) all play important parts in achieving meaningful and reproducible results. Re-fer to ASTM Test Method E 1345 (see 7.1) and SAE Test Method J1545 (see 7.3) for techniques in establishing sam-pling procedures.2.6 Specimen Preparation2.6.1 The ideal specimen to measure is a rigid, non-textured, inert, opaque speci-men of uniform color. Such ideal speci-mens do not exist in textiles, so it be-comes necessary to employ techniques and practices when measuring most tex-tile materials which eliminate or reduce the effect any objectionable characteris-tics have on the instrumental color mea-surement. Specific procedures and tech-niques for handling specimens which meet the following characteristics are presented in the Appendix.2.6.2 Fluorescence of the specimen (from dyes or fluorescent whitening agents [FWAs]) will influence the results depending on the amount of fluorescing material present and the amount and quality of ultraviolet and visible energy in the instrument light source. Results may be particularly hard to duplicate be-tween instruments. Example materials are white or lightly colored materials treated with FWAs.2.6.3 Moisture Content of textile mate-rials can affect their color and appearance characteristics. The amount of condition-ing time necessary to achieve a stable moisture state varies with fiber, fabric construction, dyes and surrounding con-ditions. Examples of materials which are typically affected by moisture content are cotton and rayon fabrics.2.6.4 Non-Rigid specimens tend to pro-trude (or “pillow”) into the viewing port of instruments which contact the speci-men at the measurement port. The amount of intrusion may vary depending on number of layers, softness of material and the backing pressure applied to mount the specimen. Variations in the amount of intrusion will result in signifi-cant deviations in the resulting color measurement which are both unpredict-able and non-reproducible. Examples of these materials are fiber, yarn, knits and layers of lightweight fabric.2.6.5 Non-Opaque specimens allow some light to pass through the material during measurement. Most textile materi-als, by nature of their structure, fit this cat-egory. During measurement, any light which passes through the material to reach the backing plate (or escape from the in-strument) will yield false and unpredict-able results. Examples of these materials are knits, lightweight materials, and fiber.2.6.6 Sensitivity of the specimen to light (photochromism) and/or heat (ther-mochromism) will result in unpredictable and nonreproducible results, depending on the degree of sensitivity and the amount of time the specimen is exposed to objectionable conditions.2.6.7 Size of the specimen is importantCopyright The American Association of Textile Chemists and Colorists Provided by IHS under license with AATCCLicensee=Hong Kong Polytechnic Univ/9976803100Not for Resale, 03/24/2007 04:07:53 MDTNo reproduction or networking permitted without license from IHS--`````,``````,,``,`,,,```,,``-`-`,,`,,`,`,,`---Copyright © 2006 American Association of Textile Chemists and Colorists 386EP 6AATCC Technical Manual/2007in obtaining a representative measure-ment by the instrument. When the speci-men is too small for normal measure-ment, special techniques may be required to achieve a proper color measurement.2.6.8 Surface Texture of the specimen (including pile lay, twill, gloss, and lus-ter) will affect the results of the color measurement. The color measurement of specimens with such physical character-istics will be affected in different ways depending on the geometry of the instru-ment. Results between instruments may be non-reproducible. Examples of these specimens are carpet, corduroy and wound yarn.2.6.9 Variation in Color (non-uniformity) within the specimen, as related to the area-of-view of the instru-ment can cause inaccurate and non-reproducible results. Examples are denim and heathers.3.Measurement of Color by Transmittance Methods3.1 Principle3.1.1 Materials of a transparent nature are measured by transmittance methods to obtain a numerical representation of their color and/or strength. The most common application is the measurement of solutions of dyes in clear solvents contained in a glass cuvette or flow cell for the purposes of determining col-orant identity, relative strength or color difference.3.2 Uses and Limitations3.2.1 This method is generally suitable for the measurement of true solutions which are transparent and void of particu-late matter. Although translucent or tur-bid liquids are sometimes measured by transmittance methods, such methods are beyond the scope of this evaluation procedure.3.3 Apparatus, Reagents, and Materials 3.3.1 Transmittance instruments may be dedicated instruments (capable only of measuring transmittance specimens), or may be combined with a sphere for an in-strument capable of performing both re-flectance and transmittance measure-ments. Most transmittance instruments are spectrophotometers, although a few are colorimeters.3.3.2 Transmittance cells (used to hold the solution during measurement) are typically made of glass or quartz, and are designed for specific pathlengths (nor-mally 10 mm) suitable for measurement of most textile related solutions (usually requiring some dilution steps to be taken before measurement). Flow-through cells, which allow the solution to be pumped or fed through them, are more efficient for high volume applications and usually result in better reproducibil-ity of results.3.3.3 When using volumetric procedures,volumetric glassware (pipettes and flasks)is absolutely required for proper prepara-tion of specimens, and only glassware which is rated at class A should be used.3.3.4 Balances which are capable of accurate results within 0.1% of the quan-tity being weighed must be used when weighing specimens used to prepare the solution for measurement.3.4 Standardization3.4.1 Before measuring specimen(s),the instrument must be standardized ac-cording to the manufacturer’s directions.Normally this requires measuring a clear solution of the solvent used for dissolu-tion (usually distilled water) in a clean transmittance cell to produce a 100% ref-erence line. Some instruments require the measurement of a “blocked beam” to set a 0% reference. This procedure produces a set of correction factors which are ap-plied to all subsequent measurements.The use of one or more colored filters as a verification standard to check both photometric and wavelength accuracy is recommended.3.5 Sampling3.5.1 Sampling procedures for trans-mission methods depend on the nature of the material and the type of specimen col-lected. Powder and paste specimens should be taken from enough locations to ensure a reproducible sample within the population being sampled and thoroughly mixed prior to proceeding with weighing and dissolving.3.6 Specimen Preparation3.6.1 Specimens must be prepared by prescribed laboratory procedures using analytical balances and volumetric glass-ware. Solutions should be prepared at a concentration at which the percent trans-mittance of the solution in the transmit-tance cell is between 10% and 50% at the wavelength of maximum absorbance (see 7.4). Each specimen must be in true solu-tion, not in suspension, dispersion or as-sociation. When preparing specimens where solubility is unknown, it is neces-sary to let the prepared solution stand for a period of time to observe any settling of contents. If such settling is observed, a true solution does not exist and other sol-vent systems are required. All specimens should be allowed to reach room temper-ature prior to presenting the specimen to the instrument.4. CalculationsMost calculations of colorimetric nature are performed by the software being used to operate the color measuring instru-ment. In normal cases of reference to this Evaluation Procedure it will not be neces-sary for the user to perform these calcula-tions; however they are described in this Evaluation Procedure as a means of refer-ence and standardization for those who may need to perform such calculations.4.1 Tristimulus Values4.1.1 The tristimulus values (X ,Y ,Z ) are derived from spectral data and are the ba-sis for all colorimetric calculations. The exact X ,Y ,Z values derived from a set of spectral data depend on several factors in-cluding the wavelength range (and inter-val) of measurement and the user’s choice of illuminant/observer functions used in the calculation. While most calculations of tristimulus values are performed by com-puter programs, interested persons should refer to ASTM Method E 308 (see 7.1)for definitive procedures (see 7.2).4.2 1976 CIE L*,a*,b*, C*, and hue angle (h ab )4.2.1 Calculate the L *, a *, b *, C *ab , h ab values from the X ,Y ,Z tristimulus values for both the reference and specimen as follows:L * = 116(Y /Y n )1/3 – 16ifY /Y n > 0.008856butL * = 903.3 (Y /Y n )ifY /Y n ≤ 0.008856a * = 500[f (X /X n ) – f (Y /Y n )]b * = 200[f (Y /Y n ) – f (Z/Z n )]where:f (X /X n ) = (X /X n )1/3ifX /X n > 0.008856orf (X /X n ) = 7.787(X /X n ) + 16/116ifX /X n ≤ 0.008856f (Y /Y n ) = (Y /Y n )1/3ifY /Y n > 0.008856orf (Y /Y n ) = 7.787(Y /Y n ) + 16/116ifY /Y n ≤ 0.008856f (Z /Z n ) = (Z /Z n )1/3ifZ /Z n > 0.008856orf (Z /Z n ) = 7.787(Z /Z n ) + 16/116ifZ /Z n ≤ 0.008856C*ab = (a *2 + b *2)1/2h ab = arctan(b */a *) expressed on a 0° to 360° scale with the a * positive axis be-ing 0° and the b * positive axis at 90°.For these equations, X n , Y n and Z n are the tristimulus values of the illuminant.For daylight the preferred illuminant/observer combination is D 65/10°. Table I gives the values for all combinations in ASTM Method E 308.4.3 Color Strength Value using Re-flectance Measurement4.3.1 Color Strength V alue is a single numerical value related to the amount of color absorbing material (colorant) con-tained in a specimen. It is most often usedCopyright The American Association of Textile Chemists and ColoristsProvided by IHS under license with AATCCLicensee=Hong Kong Polytechnic Univ/9976803100Not for Resale, 03/24/2007 04:07:53 MDTNo reproduction or networking permitted without license from IHS--`````,``````,,``,`,,,```,,``-`-`,,`,,`,`,,`---Copyright © 2006 American Association of Textile Chemists and Colorists AATCC Technical Manual/2007EP 6387to calculate the difference in strength (%strength) between two colored speci-mens. Color Strength Value may be cal-culated by any one of four acceptable methods. The value which results from one method may not agree with any other method. The choice of method is usually dependent on the nature of the specimen and the need for obtaining a color strength value. Colorimeters must calcu-late this value using a tristimulus function method. The methods used are labeled as SWL, SUM, WSUM and TSVSTR, and are calculated as follows:4.3.2 Color Strength Value of speci-mens measured on a spectrophotometer most often involves calculation of a K/S value at one or more wavelength inter-vals. The commonly used equation for calculation of the K/S value for opaque specimens (i.e., textiles) at a specified wavelength (λ) is:K /S = ((1.0 – R λ)2)/(2.0R λ)where:R λ is the absorption coefficient of the specimen (the %R value normally mea-sured by a spectrophotometer and nor-malized to 1.0 [i.e., 100% = 1.0]).4.3.3 For applications where the Pineo correction form of the equation is re-quired (generally for deeply dyed tex-tiles), the formula used is:K/S = (1.0 – (R λ – s)2)/2.0(R λ – s)where:s is the minimum reflectance achiev-able in the deepest dyed shade and is used for all wavelengths.4.3.4 The four types of Color Strength Value calculations that are most com-monly used are:(SWL) K/S at single wavelength (usu-ally wavelength of maximum absor-bance). Use equation 4.3.2 and calcu-late K/S for a single wavelength.(SUM) K/S summed over wavelength interval within the visible e equation 4.3.2, calculate K/S at each desired wavelength interval and sum. The resulting value may be nor-malized by dividing it by the number of intervals summed.(WSUM) K/S weighted by visual function (such as the x,y,z functions and the D 65 illuminant energy function)and summed over a wavelength inter-val within the visible spectrum, then divided by the number of wavelength intervals summed.WSUM = Σλ [(K/S λ * x λ * E λ)+ (K/S λ + y λ * E λ)+ (K/S λ * z λ * E λ)]/nwhere:K/S = K/S as calculated in equation4.3.2 aboveE =Energy of selected illuminant(normally D 65)x,y,z tristimulus weighting valuesfor selected observer (normally 10°)n =number of wavelength inter-vals used(TSVSTR) tristimulus color strength value (X ,Y ,Z function). Normally the Y value is used as a gross color strength value related to the visual lightness function, although either the X or Z may be chosen for measurement of components where the absorption characteristics are known and fall intowidely separated regions of the visible spectrum. In most applications, the smallest of the 3 tristimulus values (X ,Y or Z ) is chosen and is used in place of the %R value in equation in 4.3.2above. While the TSVSTR equation is used in the textile industry, no specific scientific support of it can be found in normally accepted reference books.NOTE: See 4.5 below to calculate the relative difference in strength between two specimens using one of these calcu-lation methods.4.4 Color Strength Value using Transmittance Measurement4.4.1 Color Strength V alue is a single numerical value related to the amount of color absorbing material (colorant) con-tained in a solution. It is most often used to calculate the difference in strength (%strength) between two colored solutions.Color Strength Value may be calculated by any one of four acceptable methods.The value which results from one method may not agree with any other method.The choice of method is usually depen-dent on the nature of the specimen and the need for obtaining a color strength value. Colorimeters must calculate this value using a tristimulus function method. The methods used are labelled as SWL, SUM, WSUM and TSVSTR, and are calculated as follows:4.4.2 Color Strength V alue of specimens measured on a spectrophotometer most of-ten involves calculating an absorbance value at one or more wavelengths. The equation for calculating the absorbance value at a specified wavelength (λ) is:A λ = log 10 (1.0/τλ)where:τλ is the internal transmittance of the specimen (the %T value normally mea-sured by a spectrophotometer and nor-malized to 1.0 [i.e., 100% = 1.0]).4.4.3 The four types of Color Strength Value calculations that are most com-monly used are:(SWL) absorbance at single wave-length (usually wavelength of max-imum absorbance). Use equation in 4.4.2 and calculate A for a single wavelength.(SUM) absorbance summed over wavelength interval within the visible spectrum. Use equation in 4.4.2, calcu-late A at each desired wavelength in-terval and sum. The resulting value may be normalized by dividing it by the number of intervals summed.(WSUM) absorbance weighted by visual function (such as the x,y,z func-tions and the D 65 illuminant energy function) and summed over a wave-length interval within the visible spec-trum, then divided by the number of wavelength intervals summed.Table I—Tristimulus Values for Illuminant/Observer CombinationsIlluminant/Observer Combinations Tristimulus ValuesX n Y nZ n(Ten degree observer)A/10°111.146100.00035.203C/10°97.285100.000116.145D 50/10°96.720100.00081.427D 55/10°95.799100.00090.926D 65/10°94.811100.000107.304D 75/10°94.416100.000120.641F2/10° (Cool White Fluorescent)103.279100.00069.027F7/10° (Daylight Fluorescent)95.792100.000107.686F11/10° (Ultralume 4000, TL84)103.863100.00065.607(Two degree observer)A/2°109.850100.00035.585C/2°98.074100.000118.232D 50/2°96.422100.00082.521D 55/2°95.682100.00092.149D 65/2°95.047100.000108.883D 75/2°94.972100.000122.638F2/2°(Cool White Fluorescent)99.186100.00067.393F7/2°(Daylight Fluorescent)95.041100.000108.747F11/2°(Daylight Fluorescent)100.962100.00064.350Copyright The American Association of Textile Chemists and Colorists Provided by IHS under license with AATCCLicensee=Hong Kong Polytechnic Univ/9976803100Not for Resale, 03/24/2007 04:07:53 MDTNo reproduction or networking permitted without license from IHS--`````,``````,,``,`,,,```,,``-`-`,,`,,`,`,,`---。

色差原理介绍

CIE標準觀察者
為了建立一個標準，以作為數值化色彩之參考。 1931年 CIE建立 2 Degree Standard Observer.— 標準觀察者。（67人的色彩感覺之測量平均值）
1964年—10°標準觀察者
1964年，10° 觀察者為商業顏色的組合提供更好的關連
三激值
將觀察到的顏色狀態，反射率、光源能量、以及人眼的三原色刺激量等要件，以數據量化，並經過轉換成所謂的三激值。物體的物裡反射率（或穿透率）能被量測，並記錄成光譜曲線。
CIE Lab
a 為紅—綠座標軸紅色在正的方向綠色在負的方向
b 為黃—藍座標軸黃色在正的方向藍色在負的方向
L* Lightness
L*= 100 white
L*= 50 grey
L*= 0 black
a* red - green b* yellow - blue
b*= + xx yellow
色差原理介紹
DSC 林慕雄
如何感受到顏色？
有三個重要的因素必須同時存在，才能觀察到色彩的發生。
光源 light source
物體 object
觀察者 observer
光
光被定義為一輻射能，並被表示為電磁輻射表中的一小部分。人類僅能感受到整個光能量帶的極小部分，稱為可見光。. 可見光的波長範圍約為 400-700 nanometer (nm.).
a*= - xx green
a*= + xx red
b*= + xx blue
C* Chroma h hue angle
h=90?
h=180?
h=0?
C* = + x low chroma

色温（Colortemperature）

色温（Color temperature）Color temperatureColor temperatureEnglish Name: color temperatureDefinition 1: determine the temperature by comparing the shape of the emission spectrum of the projectile with the shape of the best fitted blackbody emission spectrum.Definition 2: absolute temperature and full radiator measured radiation of the same color.Color temperature (colo (U) r temperature) is the measure of light source light and color, the unit is K (Kelvin). Color temperature is an important application in photography, video, publishing and other fields. The temperature of the light is by comparing the color and thermal theory to determine the blackbody radiator. To match the heat and light color blackbody radiator when the Kelvin temperature is the temperature of the light, and it is directly linked to the Planck blackbody radiation law.SummaryColor temperature is the most common indicator of the spectral quality of light sources. Usually expressed in Tc. The color temperature is defined in terms of absolute black bodies. The radiation of the light source is exactly the same as the radiation of the blackbody in the visible region, and thetemperature of the blackbody is called the color temperature of the source. The characteristic of low color temperature light source is the energy distribution. The red radiation is relatively more. It is usually called "warm light". After the increase of color temperature, the energy distribution is concentrated, and the proportion of blue radiation is increased, which is usually called "cold light"". Some of the commonly used light source color temperature: standard candle is 1930K (Kelvin temperature unit); tungsten lamp for 2760-2900K fluorescent lamp; 3000K; flash 3800K; midday sun 5600K; electronic flash 6000K; blue sky 12000-18000K.In discussing the problem of light in color photography, photographers often refer to the concept of color temperature. What exactly does color temperature mean?We know that the light normally seen by the human eye consists of the spectrum of 7 colored lights. But some of the light is blue, some partial red, color method is specially used to measure and calculate the color components of light, is at the end of nineteenth Century by the British physicist Lord? Created by Kelvin, he worked out a set of color temperature calculation method, and the specific standard is a blackbody radiator made based on the wavelength.Color temperature (ColorTemperature) is a performance indicator for high-end displays. We know that when a light source glows, it produces a set of spectra, a temperature that is needed to produce the same spectrum in a pure black body, which is the color temperature of the light source. Now more than 15 inches of numerical control display must have colortemperature adjustment function, through this function (generally has 9300K, 6500K, 5000K three choices), can make the color of the monitor can meet the high standard work requirements. Some of the high quality products also support linear color temperature adjustment.The color of a light source is represented by the concept of color temperature. When the light emitted by a light source is the same as that of a blackbody at a certain temperature, the temperature of the blackbody is called the color temperature of the source. In blackbody radiation, with different temperature, light of different colors, red, orange, black presented by yellow - white and yellow - white - blue and white gradualchange. The color of a light emitted by a light source looks the same as that of a black body at a certain temperature. The temperature of the blackbody is called the color temperature of the source. The higher the temperature of the blackbody, the more blue the spectrum is, and the less red there is.For example, the color of an incandescent lamp is warm white, and its color temperature is expressed as 2700K, while the color temperature of the fluorescent lamp is represented by 6000K.Some discharge light sources that emit light with different colors than black bodies emit at various temperatures. So, in this case, the concept of "relative color temperature" is used. The color of the light emitted by the light source is closest to the color of the light emitted by the blackbody at a certain temperature, and the temperature of the blackbody is referred to as the relative color temperature of the light source.Light source color temperature is different, light color is different, bring the feeling is not the same:<3300K warm (reddish white) steady and warm30005000K middle (white) readily>5000K cool (bluish white) coldColor temperature and brightness: high color temperature light source irradiation, such as brightness is not high, it gives people a bleak atmosphere; low color temperature light source irradiation, the brightness is too high, people will have a sultry feeling. Comparison of color and light: in the same space, use two kinds of light sources with great color difference, and their contrast will have the effect of gradation. When the contrast of color and light is large, the level of light and color can be obtained at the same time of obtaining brightness level.principleKelvin think, assuming a black object, will fall on all of its heat absorption, and no losses, while the heat energy generated by all the "light" in the form of release, it produces a radiation wavelength of maximum intensity with temperature changes. For example, when the blackbody is subjected to a heat equivalent of 500 - 550 DEG C, it becomes dark red (the maximum intensity of radiation at a red wavelength) reaches 1050 and becomes yellow at 1150 degrees centigrade...... Accordingly,the color component of the light source corresponds to the temperature of the blackbody. Color temperature is expressed by the Kelvin temperature (K) rather than by centigrade temperature units. In the process of iron, black iron in the furnace temperature gradually turns red, this is the best example of blackbody theory. Usually the tungsten filament in the bulb we use is equivalent to this black body. Color temperature calculation is based on the above principle, using K to correspond to the object at the specified temperature radiation when the maximum wavelength of color.According to this principle, the color temperature of any light is equivalent to the "temperature" when the black body emits the same color". The color is actually a kind of psychological and physical effect on all color impression, is due to intermittent reaction spectrum in the eyes, so that the color of the color is used for visual impression.EffectIn the color preferences vary from person to person, this with our daily see scenery scenery, such as near the equator, the average daily temperature is seen in 11000K (8000K (Huang Hun) to 17000K (noon)), so relatively high color temperature (love looks real), on the contrary, in the high latitude the area (average color temperature 6000K) love people relatively low color temperature (5600K or 6500K), that is to say if you are using a high temperature TV to show Arctic scenery, looks feel slightly green; on the contrary if you use the TV to see the low color temperature subtropical style, you will feel a little red,Color temperature is the sensation of the human eye towards a luminous body or white reflector, which is physics.A feeling of complex and complex factors in physiology and psychology, and also varies from person to person. In color TV (light) or photography (reflector) is can be changed by artificial way, for example in photography we use incandescent lamp 3200K (3200K), but we add a red filter filter through a red light to make photos look a little on the lens color temperature is low; the same the reason, we can also reduce a little red on TV (but less too much will affect the normal performance of the red color) make the picture look a little higher.use casePhotographyThe design of color film is usually based on the illumination of a light source which can record a certain color temperature in real time. It is divided into 5500K type, 3400K type, strong light type and 3200K tungsten lamp type. Therefore, photographers must know how to use the color film with the same color temperature as the light source to obtain accurate color reproduction. If the color temperature of the light source and the color temperature of the film are not in balance with each other, it is necessary to rely on the filter to enhance or reduce the color temperature of the light source, and to match the color temperature of the film, so that the accurate color reproduction can be achieved.Typically, two types of filters are used to balance color temperature. One is a red 81 series filter, and the other is a 82 color filter with a bluish color. The former is used when the light is too blue (that is, when the color temperature is too high): the latter is used to deal with red light to increase the color temperature. The 82 series filters do not have the better chance of using the 81 series. In fact, the experience of many photographers is to increase color temperature as much as possible, not to reduce the color temperature. The most common sunset phenomenon, with a yellowish filter, can produce spectacular results.The experience of a photographer in the United States is that using a micro red filter can reduce the color temperature when the color temperature is as high as 8000K, while the blue filter can make daylight films suitable for up to 4400K color temperature conditions. Usually by using these filters, they can be photographed almost at any time of the day, with natural hues. However, in exceptional circumstances, when the color temperature goes beyond this range, a color conversion filter, such as an amber colored 85B filter, is needed to allow up to 19000K of color temperature to be suitable for daylight films. Instead, the use of light film with a 82 series of filters can reduce the color temperature to 2800K.You can also use a 80 filter if you want to use daylight film to shoot under the condition of tungsten filament lighting. If the TTL exposure meter is not used at that time, a 2 stage aperture shall be added to compensate for the loss of light. When the light type film is taken in daylight, the 85B filteris required and the 2/3 aperture is added.However, the current filter codes on the market are very confusing and difficult to identify, and not all manufacturers use standard codes and designs. Therefore, in many filters, it is not easy to choose a suitable filter. In order to systematize the chaotic state of the filter classification and simplify the work of the selection filter, Canadian photographer Schwartz introduced a new method for calibrating the color temperature of the light source internationally.DisplayTV or display color is how to define? Because in the China scenery throughout the year the average color temperature in 8000K ~ 9500K,Therefore, the television program in the production of the audience to the color temperature of 9300K to photography. Europe and the United States but because the usual temperature and we have differences, the average color temperature of 6000K throughout the year for the production of reference, so we look at those foreign movies, you will find the most suitable 5600K ~ 6500K watch. Of course, this difference makes us feel that suddenly see Europe's computer or TV screen when feeling color is red, warm, some do not meet.Color temperature locationHow to accurately locate color temperature? This requires the use of a color thermometer. In general, 10 noon to 2 pm,cloudless sky, in the absence of direct sunlight conditions, standard sunlight at about 5200~5500 ~ K. News photography light color temperature at 3200 DEG K; general tungsten, photo studio shooting black and white photos using a tungsten lamp and ordinary light bulb temperature at about 2800 DEG K; the lower color temperature, so in this case the shooting photos enlarged will feel the color yellow. The color temperature of the average fluorescent lamp is about 7200~8500 degrees K, so the photos taken under the fluorescent lamp will be blue. This is because the color of the shooting environment and the shooting machine set the color temperature caused by wrong. General can be adjusted in enlargers. But if there is a fluorescent lamp and a tungsten filament lamp in the shooting scene, we become a mixed light source, which is hard to adjust.To sum up, it is very important to consider and set up and adjust the color temperature during the shooting. Whether you use traditional cameras or digital cameras and camcorders. Attention must be paid to color temperature!Color temperature selectionColor temperature is the sensation of the human eye towards a luminous body or white reflector, which is physics. A feeling of complex and complex factors in physiology and psychology, and also varies from person to person. In color TV (light) or photography (reflector) is can be changed by artificial way, for example in photography we use incandescent lamp 3200K (3200K), but we add a red filter filter through a red light to make photos look a little on the lens color temperature is low; the same the reason, we can also reduce a little red on TV (butless too much will affect the normal performance of the red color) make the picture look a little higher.In the color preferences vary from person to person, this with our daily see scenery scenery, such as near the equator, the average daily temperature is seen in 11000K (8000K (Huang Hun) to 17000K (noon)), so relatively high color temperature (love looks real), on the contrary, in the high latitude the area (average color temperature 6000K) love people relatively low color temperature (5600K or 6500K), that is to say if you are using a high temperature TV to show Arctic scenery, looks feel slightly green; on the contrary if you use the TV to see the low color temperature subtropical style, you will feel a little red.TV or display color is how to define? Because in the China scenery throughout the year the average color temperature in 8000K ~ 9500K, so in the television program production to the audience to photograph the color temperature is 9300K. But Europe and the United States because of the usual color temperature and we have differences,The average color temperature of 6000K throughout the year for the production of reference, so we look at those foreign movies, you will find the most suitable 5600K ~ 6500K watch. Of course, this difference makes us feel that suddenly see Europe's computer or TV screen when feeling color is red, warm, some do not meet. Is the color temperature, dark eyes of people, 9300K is white, but the blue eyes of the people are blue, 6500K blue eyes look at the white, we Chinese people are yellow.Color temperature effectColor temperature is a physical quantity used in illumination optics to define the color of a light source. When a blackbody is heated to a temperature, the color of its emitted light is the same as the color of the light emitted by a light source. The temperature of the black body is called the color temperature of the source, or color temperature. The units are represented by "K". Low color temperature light yellow, such as incandescent lamp, 2800K or so, high temperature color light blue, such as purple light, 9000K or more. Generally, the standard white light color temperature is 6500K CRT, the white light is about 5500K, so the mixing ratio changed slightly three colors, can be simulated by the subtractive temperature effect, the color temperature of the principle of photography, camera, display and other process equipment changes is known as color effect.Color BalancingIn the shooting of film and television lens, more than two kinds of lighting are usually used, and the color temperature is consistent in most cases. On location or photographing, in daylight lighting conditions, such as light as common auxiliary light, if the low color temperature lamp (3200K) to the sun (5600k) color temperature adjustment, commonly used method is used for color temperature light paper or the direct use of high color temperature lamp, sometimes deliberately two color lights are lighting the same scenery is not balanced, in order to obtain the temperature and lighting effect. The color temperature coordination relationship between a light sourceand a color film or video camera. Solar panels can only be taken in 5600k color temperature conditions; light films can only be taken under 3200K color temperature conditions. Camera in the sunlight and 5600k filter, 3200K filter and shooting in 3200K light.。

英语三级笔译综合能力2004年试卷、答案及解析

英语三级笔译综合能力2004年试卷Section 1 Vocabulary and Grammar (25 points)This section consists of three parts. Bead the directions for each part before answering the questions. The time for this section is 25 minutes.Part 1 Vocabulary SelectionIn this party there are 20 incomplete sentences. Below each sentence, there are four choices respectively marked by letters A, B, C and D. Choose the word or phrase which best completes each sentence. There is only ONE right answer. Then blacken the corresponding letter with a single bar across the square brackets on your Machine-scoring ANSWER SHEET.1. Grover Cleveland was the first president ______ in the White House.A. got marriedB. to get marriedC. has got marriedD. was married2. If cauliflowers are not _____ from extreme temperatures, the heads get discolored.A. protectedB. shelterC. shadeD. saved3. The gas ______ from the tank is dangerous.A. given offB. giving outC. giving awayD. given up4. When it started to snow, we turned round and _____ the hotel.A. got byB. searched forC. made forD. cleared up5. Since writing home to their parents for money, they had lived _____ hope.A. inB. forC. onD. through6. Rice is the ______ food of most Southeast Asians.A. commonB. generalC. stapleD. popular7. William Byrd was the owner of the largest library in colonial ______.A. periodB. timeC. timesD. periods8. Exobiology is the study of life ______ other planets.A. inB. atC. onD. to9. The Declaration of Independence, _______ the Constitution of the United States,was drawn up with the help of Benjamin Franklin.A. andB. alsoC. as well asD. so too10. It was from the Lowell Laboratory that the ninth ______, Pluto, was sighted in1930.A. planetB. constellationC. stardomD. satellite11 .The rodent, _______ the mouse, rat, guinea pig, and porcupine, are mammals withincisor-like teeth in both jaws.A. made upB. includingC. consistingD. constitute12. ______ into oceans and rivers is a serious form of pollution.A. Pouring sewageB. Emptying litterC. Throwing garbageD. Dumping sewage13. Products which are made from dirts and are _____ high temperatures are knownas ceramics.A. tempered inB. subjected toC. exposed toD. baked in14. A pigment called melanin protects the _____ layers of skin from sun rays.A. underB. belowC. underlyingD. underneath15. Oranges are a ______ source of vitamin C.A. wellB. betterC. goodD. very16. Even after having their grandchildren live with them for ten years, the couple feltthat ______ children these days was the most difficult of all family matters.A. risingB. raisingC. caringD. taking care17. The most important ______ of the farmers in Iraq is dates, of which Iraq is theworld's leading exporter.A. economic cropB. cash cropC. money cropD. staple18. More has been learned about the Moon than any other of the Earth's neighbors inspace because of the Apollo program, which enabled men to walk on the Moon and bring back hundreds of pounds of _____.A. rocksB. rockC. stoneD. stones19. _____ the variety that the average family has in beef, fish, poultry, and vegetarianrecipes, they find most meals unexciting.A. InspiteB. InspiteC. Despite ofD. Despite20. The speaker _____ have criticized the paraprofessionals, knowing full well thatthey were seated in the audience.A. should not toB. must notC. ought not toD. may notPart 2 Vocabulary ReplacementThis part consists of 15 sentences in which one word or phrase is underlined. Below each sentence, there are four choices respectively marked by letters A, By C and D. Choose the word or phrase that can replace the underlined part without causing any grammatical error or changing the basic meaning of the sentence. There is only ONE right answer. Blacken the corresponding letter with a single bar across the square brackets on your Machine-scoring ANSWER SHEET.21. Iceland has the oldest parliament, which goes as far back to 930 A. D. whenAlthing, the legislative organization, was established.A. officeB. adobeC. assemblyD. building22. The only problem with the debate last week was that the beginning sounded morelike a personal attack than a dispassionate, intellectual arguing.A. discussionB. argumentC. talkD. speech23. Susan Jones was at the bus stop well on time to take the 7:01 bus, but she had tomiss her breakfast to do it.A. catch up withB. catchC. run up toD. be catching24. Since her father could not drive her to the airport, she requested her uncle to driveher instead.A. takeB. bringC. dispatchD. deliver25. A famous collection of Persian, Indian, and Arabian folktales, the Arabian Nightswas supposedly told by the legendary queen Scheherazade to her husband every night for 1,001 days.A. imaginaryB. imageryC. fabledD. legend26. What may be the oldest fossil footprint yet found was discovered in June 1968 byWilliam J. Meister, a non-professional fossil collector.A. a part-timeB. a spare-timeC. an untrainedD. an amateur27. Most of us think of sharks as dangerous, owing to lack of information rather thanfear.A. due toB. becauseC. asD. for28. Double Eagle D, the first trans-Atlantic balloon, was greeted by avid crowds inFrance.A. eagerB. surgingC. appreciativeD. vigorous29. The discovery of the connection between aspirin and Reyessyndrome, a rare anddeadly ailment, is a recent example of the caution with which drugs must be used, even for medical purposes.A. diseaseB. sickC. illD. illness30. My parents moved out of their old home sometime last year after they hadcelebrated their 50th year there.A. anniversaryB. years oldC. ageD. wedding31. The library she worked in lent books, magazines, audio-cassettes and maps to itscustomers, who could keep them for four weeks.A. borrowersB. lendersC. patronsD. clients32. A common question that people ask a story writer is whether or not he hasexperienced what he has written about.A. fictionB. scienceC. imaginaryD. literary33. At the World literacy Center, an organization that works to help people read, thehelpers work hard, enabling them to successfully reach their goals.A. assistantsB. volunteersC. part-timersD. amateurs34. The officers made it clear that they were letting her go only because that she wasold and not because she was above suspicion.A. for reasonB. due toC. because ofD. on the grounds35. The book, which is a useful guide for today's young people, deals with manyquestions and problems that face them at school and at home as well as in society.A. are facedB. confrontC. in oppositionD. meetPart 3 Error CorrectionThis part consists of 75 sentences in which there is an underlined part that indicates a grammatical error. Below each sentence, there are four choices respectively marked by letters A, B, C and D. Choose the word or phrase that can replace the underlined part so that the error is corrected. There is only ONE right answer. Blacken the corresponding letter with a single bar across the square brackets on your Machine-scoring ANSWERSHEET.36. All don't have a free ticket must pay the admission fee.A. Everyone who doesn't have a free ticketB. No one who doesn't have a free ticketC. No one who has free ticketsD. Anyone who has free tickets37. When I last saw them, the police had chased the robbers down Columbus Street.A. were chasingB. was chasingC. chasedD. were on a chase38. Erosion that is a slow process, but it constantly changes the features on the surfaceof the earth.A. which isB. althoughC. beingD. is39. When an organism is completely encapsulated and preserved, it becomes a fossil,therefore turning into evidence of things that once lived.A. therebyB. as a result ofC. soD. in the end40. The pictures of the Loch Ness Monster show a remarkable resemblance to aplesiosaur, a large water reptile of the Mesozoic era presuming extinct for more than 70 million years.A. supposedB. presumablyC. presumptuousD. is presumed41. In our own galaxy, the Milky Way, there are perhaps 200 billion stars, a small partof them probably have planets on which life is feasible.A. a small fraction in whichB. a small fraction of whichC. a small fraction whichD. which a fraction of42. "But you'll be able to come, won’t you?" "Yes, I think such."A. thatB. itC. soD. this43. The professor is quite difficult pleased.A. to pleaseB. to be pleasedC. for pleasingD. pleasing44. Because everyone knows, facts speak louder than words.A. SinceB. ThatC. ItD. As45. The trapeze artist who ran away with the clown broke up the lion tamer's heart.A. broke awayB. broke downC. brokeD. broken down46. His heavy drinking and fond of gambling makes him a poor role model.A. and fact that he gamblesB. and that he gamblesC. and he gambles whichD. and gambling47. Depression that inflicts people who believe their lives lack content when the rushof the busy week stops referred to by a prominent psychiatrist as Sunday Neurosis.A. has been referred to by a prominent psychiatristB. has been referred to as by a prominent psychiatristC. a prominent psychiatrist has referred to itD. it has been referred to by a prominent psychiatrist48. Just as there are occupations that require college degrees also there areoccupations for which technical training is necessary.A. so to there areB. so too there areC. so there areD. so too are there49. Most of the older civilizations which flourished during the fifth century B. C. aredied out.A. they have died outB. has died outC. have died outD. they had died out50. The student asked her professor if he would have gone on the spaceship he didknow earlier.A. if he knewB. if he knowsC. he had knownD. had he known Section 2 Reading Comprehension (55 points)In this section you will find after each of the passages a number of questions or unfin-ished statements about the passage, each with four (A, B, C and D) choices to com-plete the statement. You must choose the one which you think fits best. Then blacken the corresponding letter with a single bar across the square brackets on your Machine-scoring ANSWER SHEET.Passage OneQuestions 51 - 56 are based on die following passage.Awarded the Nobel Prize for physics in 1918, German physicist Max Planck is best remembered as the originator of the quantum theory. His work helped usher in a new era in theoretical physics and revolutionized the scientific community’s understanding of atomic and subatomic processes.Planck introduced an idea that led to the quantum theory, which became the foundation of twentieth century physics. In December 1900, Planck worked out an equation that described the distribution of radiation accurately over the range of low to high frequencies. He had developed a theory which depended on a model of matter that seemed very strange at the time. The model required the emission of electromagnetic radiation in small chunks or particles. These particles were later called quantums. The energy associated with each quantum is measured by multiplying the frequency of the radiation, v, by a universal constant, h. Thus, energy, or E, equals hv. The constant, h, is known as Planck's constant. It is now recognized as one of the fundamental constants of the world.Planck announced his findings in 1900, but it was years before the full consequences of his revolutionary quantum theory were recognized. Throughout his life, Planck made significant contributions to optics, thermodynamics and statistical mechanics, physical chemistry, among other fields.51. In which of the following fields did Max Planck NOT make a significantcontribution?A. Optics.B. Thermodynamics.C. Statistical mechanics.D. Biology.52. The word "revolutionary" as used in Line 15 means_.A. radicalB. extremistC. momentousD. militaristic53. It can be inferred from the passage that Planck’s work led to the development of________.A. The rocketB. The atomic bombC. The internal combustion engineD. The computer54. The particles of electromagnetic radiation given off by matter are known as ____.A. quantumsB. atomsC. electronsD. valences55. The implication in this passage is that ______.A. only a German physicist could discover such a theoryB. quantum theory, which led to the development of twentieth century physics, isbasically a mathematical formulaC. Planck's constant was not discernible before 1900D. radiation was hard to study56. ―An idea‖ as used in line 5, refers to _____.A. a model of matterB. emission of electromagnetic radiationC. quantumsD. the equation that described the distribution of radiation accurately over the range of low to high frequenciesPassage TwoQuestions 57 ~ 62 are based on the following passage.There has been much speculation about the origin of baseball. In 1907 a special commission decided that the modern game was invented by Abner Doubleday in 1839. One hundred years later the National Baseball Museum was opened to honor Doubleday. Historians, however, disagree about the origin of baseball. Some say that baseball comes from bat-and-ball games of ancient times. It is a matter of record that in the 1700s English boys played a game they called ―baseball‖. Americans have played a kind of baseball since about 1800. At first the American game had different rules and different names in various parts of the country —―town ball‖, ―rounders‖, or ―one old cat‖. Youngsters today still play some of these simplified forms of the game.Baseball did not receive a standard set of rules until 1845, when Alexander Cartwright organized the Knickerbocker Baseball Club of New York City. The rules Cartwright set up for his nine-player team were widely adopted by other clubs and formed the basis of modern baseball. The game was played on a "diamond" infield with the bases 90 feet apart. The first team to score 21 runs was declared the winner. By 1858 the National Association of Baseball Players was formed with 25 amateur teams. The Cincinnati Red Stockings began to pay players in 1869.57. Which of the following is true about the origins of baseball?A. Historians agree that baseball was invented by Abner Doubleday.B. Baseball, as played in the early 19th century, differed very little from today'sgame.C. As early as the 1700s, English boys played a game called "baseball".D. The first standard set of baseball rules was established at the turn of the century.58. What was the first professional baseball team called?A. New York Knickerbockers.B. Milwaukee Braves.C. Cincinnati Red Stockings.D. Brooklyn Dodgers.59. Who first gave baseball a standard set of rules?A. Abner Doubleday.B. Alexander Cartwright.C. Albert Spalding.D. Babe Ruth.60. Which of the followings was not a predecessor of baseball?A. Rounders.B. Town ball.C. Cricket.D. One old cat.61. The tone of the passage is ______.A. persuasiveB. informativeC. biasedD. argumentative62. The passage implies that until 1869, baseball was played for all of the followingreasons except _______.A. exerciseB. leisureC. profitD. socializingPassage ThreeQuestions 63-68 are based on the following passage.The blue of the sea is caused by the scattering of sunlight by tiny particles suspended in the water. Blue light, being of short wavelength, is scattered more efficiently than light of longer wavelengths. Although waters of the open ocean are commonly some shade of blue, green water is commonly seen near coasts, especially in tropical or subtropical regions. This is caused by yellow pigments being mixed with blue water. Phytoplankton are one source of the yellow pigment. Other microscopic plants may color the water brown or brownish-red. Near the shore, silt or sediment in suspension can give water a brownish hue. Outflow of large rivers can often be observed many miles offshore by the coloration of suspended soil particles.Marine phytoplankton (Greek for "plant wanderers") are microscopic single-celled plants that include diatoms, dinoflagellates, coccolithophorids, green algae, and blue-green algae, among others. The growth of these organisms, which photogynthesize light, depends on a delicate balance of nutrient enrichment via vertical mixing, which is often limited by the availability of nitrogen and light. Diatoms are one-celled plants with patterned glass coverings. Each glass, or silicon dioxide box, is ornamented with species-specific designs, pits, and perforations making them popular with microscopists and, more recently, electron scanning microscopists.63. Green water near coastlines is almost always caused by _____.A. sand colorB. red pigments in coastal watersC. blue pigmentD. reflected light and yellow pigment from plant life64. Phytoplankton are the source of which color pigment?A. Red.B. Green.C. Yellow.D. Blue.65. What can give waters a brownish hue near the shore?A. Sediment.B. Phytoplankton.C. Blue pigment.D. Diatoms.66. Which of the following is NOT a type of phytoplankton?A. Green algae.B. Diatoms.C. Blue-green algae.D. Amoeba.67. The growth of phytoplankton is often limited by the availability of _____.A. oxygenB. hydrogenC. nitrogenD. carbon dioxide68. The main idea of this passage is that _____.A. light causes sea colorB. sea coloration is varied because of a combination of length of light waves andmicroscopic plant life and siltC. microscopic plant life causes sea colorD. water composition causes sea colorPassage FourQuestions 69 - 75 are based on the following passage.The United States government publishes guidelines for appropriate nutrient intakes. These are known as the Recommended Dietary Allowances (RDAs) and are updated regularly based on new research in nutrition. RDAs are suggested amounts of calories, protein, and some minerals and vitamins for an adequate diet. For other dietary substances, specific goals must await further research. However, for the U.S. population as a whole, increasing starch and fiber in one's diet and reducing calories (primarily from fats, sugar, and alcohol) is sensible. These suggestions are especially appropriate for people who have other factors for chronic diseases due to family history of obesity, premature heart disease, diabetes, high blood pressure, and high blood cholesterol, or for those who use tobacco.Snacks can furnish about one-fourth of the calorie requirements among teenagers. Those snacks should also provide much of the day's allowances for protein, minerals, and vitamins. Sandwiches, fruit, and milk make good snacks for active teenagers. Food from the food pyramid may be part of any meal. A grilled cheese sandwich or a bowl of whole-grain cereal is just as nutritious in the morning as it is at noon. In addition, a good breakfast consists of any foods that supply about one-fourth of the necessary nutrients for the day.69. The passage directly states that most of the U. S. population should increase theirintake of ______.A. proteinB. fatsC. starch and fiberD. sandwiches70. A good breakfast should supply about what percentage of the necessary nutrientsfor the day?A. One-half.B. One-third.C. One-fourth.D. Less than one-fourth.71. The passage implies which of the following?A. The rime of day when food is consumed affects its nutritive value.B. Different foods can be combined to increase total nutrition value.C. It can be detrimental to your health to eat breakfast foods later in the day.D. When food is eaten has no bearing on its nutritive effects.72. Why are RDAs regularly updated?A. New discoveries in the science of nutrition are constantly being made.B. Americans' diets are constantly changing.C. As people age, their nutritional needs change.D. Very little is currently known about nutrition.73. In this passage RDAs refers to___.A. types of vitaminsB. types of proteinC. types of mineralsD. amounts of energy, protein, vitamins, and minerals74. One implication in this passage is that _____.A. all RDAs have been establishedB. not all RDAs have been established yetC. it's not important to know RDAsD. RDAs are necessary only for sick people75. The reduction of calories in the diet is particularly good for people who sufferfrom ________.A. obesityB. premature heart disease and diabetesC. high blood pressure and cholesterol levelsD. all of the abovePassage FiveQuestions 76 - 81 are based on the following passage.The most popular organic gem is the pearl. A pearl is the response of a marine mollusk to the presence of an irritating impurity accidentally introduced into its body;a cultured pearl is the result of the intentional insertion of a mother-of-pearl bead into a live mollusk. Whether introduced accidentally or intentionally, the pearl-making process is the same: the mollusk coats the irritant with a substance called nacre. Nacre is composed chiefly of calcium carbonate. Because very few natural pearls are now on the market, most pearls used in fine jewelry are cultured. These include "Biwa" pearls and most other freshwater pearls. Cultured pearls are not easily distinguished from natural pearls except by an expert.76. Which of the following people could tell the difference between a cultured pearland an organic pearl?A. Scuba diver.B. Fisherman.C. Jeweler.D. Clerk.77. What is the chief component of nacre?A. Sand.B. Bead.C. Calcium carbonate.D. Biwa.78. The difference between a pearl and a cultured pearl is the nature of the ____.A. colorB. introduction of the irritating impurityC. coating materialD. irritating impurity79. Nacre is a substance that is ______.A. mechanically manufacturedB. the result of laboratory testingC. organically secreted by the molluskD. present in the chemical composition of freshwater pounds80. The main idea of this passage is that ______.A. most marketable pearls are cultured because nature does not produce enough ofits own to satisfy the marketB. cultured pearls are of a higher quality than natural pearlsC. there are two major methods of pearl-makingD. a natural ―drought‖ of pearl production is taking place81. Cultured pearl is formed by ____.A. insertion of a pearl into a live molluskB. an oyster into which a piece of grit has been placedC. putting in a live molluskD. placing a bead into culturePassage SixQuestions 82-87 are based on the following passage.Stress is with us all the time. It comes from mental or emotional activity as well as physical activity. It is unique and personal to each of us. So personal, in fact, that what may be relaxing to one person may be stressful to another. For example, if you're a busy executive who likes to keep occupied all of the time, "taking it easy" at the beach on a beautiful day may be extremely frustrating, nonproductive, and upsetting. You may be emotionally distressed from "doing nothing." Too much emotional stress can cause physical illnesses such as high blood pressure, ulcers, or even heart disease. Physical stress from work or exercise is not likely to cause such ailments. The truth is that physical exercise can help you to relax and to better handle your mental or emotional stress.82. Which of the following people would find ―taking it easy‖ stressful?A. Construction workers.B. Business executives.C. Farm workers.D. Truck drivers.83. Which of the following would be a determinant as to what people find stressful?A. Personality.B. Education.C. Marital status.D. Shoe size.84. This article, published by the Department of Health and Human Services,probably came from the ______.A. Federal Bureau of InvestigationB. Alcohol, Drug Abuse, and Mental Health AdministrationC. Education AdministrationD. Communicable Diseases Administration85. A source of stress NOT specifically mentioned in this passage is _____.A. educational activityB. physical activityC. mental activityD. emotional activity86. Physical problems caused by emotional stress can appear as all of the followingEXCEPT _____.A. ulcersB. pregnancyC. heart diseaseD. high blood pressure87. One method mentioned to help handle stress is ____.A. physical exerciseB. tranquilizersC. drugsD. taking it easy Passage SevenQuestions 88 ~ 92 are based on the following passage.With the sudden onset of severe psychotic symptoms, the individual is said to be experiencing acute schizophrenia (精神分裂症) - "Psychotic" means out of touch with reality, or unable to separate real from unreal experiences. Some people have only one such psychotic episode. Others have many episodes during a lifetime but lead relatively normal lives during interim periods. The individual with chronic (continuous or recurring) schizophrenia often does not fully recover normal functioning and typically requires long-term treatment, generally including medication, to control the symptoms. These symptoms may include hallucinations (幻觉), incoherence, delusions, lack of judgment, deterioration of the abilities to reason and feel emotion, and a lack of interaction between the patient and his environment. The hallucinations may be a visual, auditory, or tactile. Some chronic schizophrenic patients may never be able to function without assistance of one sort or another.88. Which of the following is not a symptom of schizophrenia?A. Hallucinations.B. Delusions.C. Incoherence.D. Vertigo.89. It can be inferred from the passage that a person experiencing acute schizophreniamost likely ______.A. cannot live without medicationB. cannot go on livingC. can hold a full-time jobD. cannot distinguish real from unreal90. According to this passage, thinking that one can fly might be an example of ____.A. medicine overdoseB. being out of touch with realityC. recovering normal functioningD. symptom control91. The passage suggests that the beginning of severe psychotic symptoms of acuteschizophrenia may be any of the following EXCEPT_____.A. debilitatingB. sudden occurrenceC. occurring after a long period of normalcyD. drug-induced92. The passage implies that normal life may be possible for the chronicschizophrenic with the help of ______.A. medicinesB. neurotic episodesC. psychotic episodesD. time Passage EightQuestions 93 ~ 100 are based on the following passage.Aspirin is one of the safest and most effective drugs invented by man. The most popular medicine in the world today, it is an effective pain reliever. Its bad effects are relatively mild. It is also cheap.For millions of people suffering from arthritis, it is the only thing that works. Aspirin, in short, is truly the 20th-century wonder drug. It is also the second largest suicide drug and is the leading cause of poisoning among children. It has side effects that, although relatively mild, are largely unrecognized among users.Although aspirin was first sold by a German company in 1899, it has been around much longer than that. Hippocrates, in ancient Greece, understood the medical value of tree barks and leaves which today are known to contain a chemical found in aspirin. During the 19th century, there was a great deal of experimentation in Europe with this。

Cosmology with High-redshift Galaxy Survey Neutrino Mass and Inflation

a r X i v :a s t r o -p h /0512374v 3 5 J u n 2006Cosmology with High-redshift Galaxy Survey:Neutrino Mass and InﬂationMasahiro Takada 1,Eiichiro Komatsu 2and Toshifumi Futamase 11Astronomical Institute,Tohoku University,Sendai 980-8578,Japan and 2Department of Astronomy,The University of Texas at Austin,Austin,TX 78712High-z galaxy redshift surveys open up exciting possibilities for precision determinations of neu-trino masses and inﬂationary models.The high-z surveys are more useful for cosmology than low-z ones owing to much weaker non-linearities in matter clustering,redshift-space distortion and galaxy bias,which allows us to use the galaxy power spectrum down to the smaller spatial scales that are inaccessible by low-z surveys.We can then utilize the two-dimensional information of the linear power spectrum in angular and redshift space to measure the scale-dependent suppression of matter clustering due to neutrino free-streaming as well as the shape of the primordial power spectrum.To illustrate capabilities of high-z surveys for constraining neutrino masses and the primordial power spectrum,we compare three future redshift surveys covering 300square degrees at 0.5<z <2,2<z <4,and 3.5<z <6.5.We ﬁnd that,combined with the cosmic microwave background data expected from the Planck satellite,these surveys allow precision determination of the total neutrino mass with the projected errors of σ(m ν,tot )=0.059,0.043,and 0.025eV,respectively,thus yielding a positive detection of the neutrino mass rather than an upper limit,as σ(m ν,tot )is smaller than the lower limits to the neutrino masses implied from the neutrino oscillation experiments,by up to a factor of 4for the highest redshift survey.The accuracies of constraining the tilt and running index of the primordial power spectrum,σ(n s )=(3.8,3.7,3.0)×10−3and σ(αs )=(5.9,5.7,2.4)×10−3at k 0=0.05Mpc −1,respectively,are smaller than the current uncertainties by more than an or-der of magnitude,which will allow us to discriminate between candidate inﬂationary models.In particular,the error on αs from the future highest redshift survey is not very far away from the prediction of a class of simple inﬂationary models driven by a massive scalar ﬁeld with self-coupling,αs =−(0.8−1.2)×10−3.PACS numbers:95.55.Vj,98.65.Dx,98.80.Cq,98.70.Vc,98.80.EsI.INTRODUCTIONWe are living in the golden age of cosmology.Vari-ous data sets from precision measurements of tempera-ture and polarization anisotropy in the cosmic microwave background (CMB)radiation as well as those of matter density ﬂuctuations in the large-scale structure of the universe mapped by galaxy redshift surveys,Lyman-αforests and weak gravitational lensing observations are in a spectacular agreement with the concordance ΛCDM model [1,2,3,4].These results assure that theory of cos-mological linear perturbations is basically correct,and can accurately describe the evolution of photons,neu-trinos,baryons,and collisionless dark matter particles [5,6,7],for given initial perturbations generated during inﬂation [8,9].The predictions from linear perturbation theory can be compared with the precision cosmological measurements,in order to derive stringent constraints on the various basic cosmological parameters.Future obser-vations with better sensitivity and higher precision will continue to further improve our understanding of the uni-verse.Fluctuations in diﬀerent cosmic ﬂuids (dark matter,photons,baryons,and neutrinos)imprint characteristic features in their power spectra,owing to their interac-tion properties,thermal history,equation of state,and speed of sound.A remarkable example is the acoustic oscillation in the photon-baryon ﬂuid that was generated before the decoupling epoch of photons,z ≃1088,which has been observed in the power spectrum of CMB tem-perature anisotropy [10],temperature–polarization cross correlation [11],and distribution of galaxies [12,13].Yet,the latest observations have shown convincingly that we still do not understand much of the universe.The standard model of cosmology tells us that the universe has been dominated by four components.In chronolog-ical order the four components are:early dark energy (also known as “inﬂaton”ﬁelds),radiation,dark mat-ter,and late-time dark energy.The striking fact is that we do not understand the precise nature of three (dark matter,and early and late-time dark energy)out of the four components;thus,understanding the nature of these three dark components has been and will continue to be one of the most important topics in cosmology in next decades.Of which,one might be hopeful that the next generation particle accelerators such as the Large Hadron Collider (coming on-line in 2007)would ﬁnd some hints for the nature of dark matter particles.On the other hand,the nature of late-time dark energy,which was dis-covered by measurements of luminosity distance out to distant Type Ia supernovae [14,15],is a complete mys-tery,and many people have been trying to ﬁnd a way to constrain properties of dark energy (see,e.g.,[16]for a review).How about the early dark energy,inﬂaton ﬁelds,which caused the expansion of the universe to accelerate in the very early universe?We know little about the nature of inﬂaton,just like we know little about the nature of late-time dark energy.The required property of inﬂa-ton ﬁelds is basically the same as that of the late-time2dark energy component:both must have a large negativepressure which is less than−1/3of their energy density. To proceed further,however,one needs more informationfrom observations.Diﬀerent inﬂation models make spe-ciﬁc predictions for the shape of the power spectrum[8](see also Appendix B)as well as for other statistical prop-erties[17]of primordial perturbations.Therefore,one ofthe most promising ways to constrain the physics of in-ﬂation,hence the nature of early dark energy in the uni-verse,is to determine the shape of the primordial power spectrum accurately from observations.For example,theCMB data from the Wilkinson Microwave Anisotropy Probe[1],combined with the large-scale structure datafrom the Two-Degree Field Galaxy Redshift Survey[18], have already ruled out one of the popular inﬂationarymodels driven by a self-interacting massless scalarﬁeld [19].Understanding the physics of inﬂation better willlikely provide an important implication for late-time dark energy.“Radiation”in the universe at around the matter-radiation equality mainly consists of photons and neu-trinos;however,neutrinos actually stop being radiationwhen their mean energy per particle roughly equals the temperature of the universe.The physics of neutrinoshas been revolutionized over the last decade by solar, atmospheric,reactor,and accelerator neutrino experi-ments having provided strong evidence forﬁnite neutrino masses via mixing between diﬀerent neutrinoﬂavors,theso-called neutrino oscillations[20,21,22,23,24].These experiments are,however,only sensitive to mass squarediﬀerences between neutrino mass eigenstates,implying ∆m221≃7×10−5eV2and∆m232≃3×10−3eV2;thus, the most fundamental quantity of neutrinos,the abso-lute mass,has not been determined yet.Cosmologicalneutrinos that are the relic of the cosmic thermal his-tory have distinct inﬂuences on the structure formation.Their large energy density,comparable to the energy den-sity of photons before the matter-radiation equality,de-termines the expansion history of the universe.Even after the matter-radiation equality,neutrinos having be-come non-relativistic aﬀect the structure formation by suppressing the growth of matter densityﬂuctuations at small spatial scales owing to their large velocity disper-sion[25,26,27,28,29,30](see Sec.II and Appendix A for more details).Therefore,the galaxy redshift surveys, combined with the CMB data,provide a powerful,albeit indirect,means to constraining the neutrino properties [31,32,33,34,35].This approach also complements the theoretical and direct experimental eﬀorts for under-standing the neutrino physics.In fact,the cosmological constraints have placed the most stringent upper bound on the total neutrino mass,mν,tot<∼0.6eV(2σ)[36], stronger than the direct experiment limit<∼2eV[37].In addition,the result obtained from the Liquid Scintillator Neutrino Detector(LSND)experiment,which implies¯νµto¯νe oscillations with∆m2>∼0.2eV2[38]in an apparent contradiction with the other neutrino oscillation experi-ments mentioned above,potentially suggests the need for new physics:the cosmological observations will provide independent tests of this hypothesis.In this paper we shall study the capability of future galaxy surveys at high redshifts,combined with the CMB data,for constraining(1)the neutrino properties,more speciﬁcally the total neutrino mass,mν,tot,and the num-ber of non-relativistic neutrino species,N nrν,and(2)the shape of the primordial power spectrum that is parame-terized in terms of the spectral tilt,n s,and the running index,αs,motivated by inﬂationary predictions(see Ap-pendix B).For the former,we shall pay particular at-tention to our ability to simultaneously constrain mν,tot and N nrν,as they will provide important clues to resolv-ing the absolute mass scale as well as the neutrino mass hierarchy.The accuracy of determining the neutrino pa-rameters and the power spectrum shape parameters will be derived using the Fisher information matrix formal-ism,including marginalization over the other cosmologi-cal parameters as well as the galaxy bias.Our analysis diﬀers from the previous work on the neutrino parameters in that we fully take into account the two-dimensional nature of the galaxy power spec-trum in the line-of-sight and transverse directions,while the previous work used only spherically averaged,one-dimensional power spectra.The geometrical distortion due to cosmology and the redshift space distortion due to the peculiar velocityﬁeld will cause anisotropic features in the galaxy power spectrum.These features help to lift degeneracies between cosmological parameters,sub-stantially reducing the uncertainties in the parameter de-terminations.This is especially true when variations in parameters of interest cause modiﬁcations in the power spectrum shape,which is indeed the case for the neutrino parameters,tilt and running index.The usefulness of the two-dimensional power spectrum,especially for high-redshift galaxy surveys,has been carefully investigated in the context of the prospected constraints on late-time dark energy properties[39,40,41,42,43,44,45].We shall show the parameter forecasts for future wide-ﬁeld galaxy surveys that are already being planned or seriously under consideration:the Fiber Multiple Object Spectrograph(FMOS)on Subaru telescope[46],its sig-niﬁcantly expanded version,WFMOS[47],the Hobby–Ebery Telescope Dark Energy eXperiment(HETDEX) [48],and the Cosmic Inﬂation Probe(CIP)mission[49]. To model these surveys,we consider three hypothetical galaxy surveys which probe the universe over diﬀerent ranges of redshift,(1)0.5≤z≤2,(2)2≤z≤4and (3)3.5≤z≤6.5.Weﬁx the sky coverage of each sur-vey atΩs=300deg2in order to make a fair compari-son between diﬀerent survey designs.As we shall show below,high-redshift surveys are extremely powerful for precision cosmology because they allow us to probe the linear power spectrum down to smaller length scales than surveys at low redshifts,protecting the cosmological in-formation against systematics due to non-linear pertur-bations.We shall also study how the parameter uncertainties3 are aﬀected by changes in the number density of sam-pled galaxies and the survey volume.The results wouldgive us a good guidance to deﬁning the optimal surveydesign to achieve the desired accuracies in parameter de-terminations.The structure of this paper is as follows.In Sec.II,wereview the physical pictures as to how the non-relativistic(massive)neutrinos lead to scale-dependent modiﬁca-tions in the growth of mass clustering relative to thepure CDM model.Sec.III deﬁnes the parameterization of the primordial power spectrum motivated by inﬂation-ary predictions.In Sec.IV we describe a methodology to model the galaxy power spectrum observable from aredshift survey that includes the two-dimensional nature in the line-of-sight and transverse directions.We thenpresent the Fisher information matrix formalism that is used to estimate the projected uncertainties in the cos-mological parameter determination from statistical errors on the galaxy power spectrum measurement for a givensurvey.After survey parameters are deﬁned in Sec.V, we show the parameter forecasts in Sec.VI.Finally,wepresent conclusions and some discussions in Sec.VII.We review the basic properties of cosmological neutrinos inAppendix A,the basic predictions from inﬂationary mod-els for the shape of the primordial power spectrum in Ap-pendix B,and the relation between the primordial powerspectrum and the observed power spectrum of matter densityﬂuctuations in Appendix C.In the following,we assume an adiabatic,cold dark matter(CDM)dominated cosmological model withﬂatgeometry,which is supported by the WMAP results [1,36],and employ the the notation used in[51,52]:the present-day density of CDM,baryons,and non-relativistic neutrinos,in units of the critical density,aredenoted asΩc,Ωb,andΩν,respectively.The total mat-ter density is thenΩm=Ωc+Ωb+Ων,and fνis theratio of the massive neutrino density contribution toΩm: fν=Ων/Ωm.II.NEUTRINO EFFECT ON STRUCTUREFORMATIONThroughout this paper we assume the standard ther-mal history in the early universe:there are three neutrinospecies with temperature equal to(4/11)1/3of the photon temperature.We then assume that0≤N nrν≤3species are massive and could become non-relativistic by thepresent epoch,and those non-relativistic neutrinos have equal masses,mν.As we show in Appendix A,the den-sity parameter of the non-relativistic neutrinos is given byΩνh2=N nrνmν/(94.1eV),where we have assumed 2.725K for the CMB temperature today[50],and h is the Hubble parameter deﬁned as H0=100h km s−1Mpc−1. The neutrino mass fraction is thus given byfν≡Ων0.658eV 0.141eVΩm h21+z 1/2.(2)Therefore,non-relativistic neutrinos with lighter masses suppress the growth of structure formation on larger spa-tial scales at a given redshift,and the free-streaming length becomes shorter at a lower redshift as neutrino velocity decreases with redshift.The most important property of the free-streaming scale is that it depends on the mass of each species,mν,rather than the total mass,N nrνmν;thus,measurements of k fs allow us to dis-tinguish diﬀerent neutrino mass hierarchy models.For-tunately,k fs appears on the scales that are accessible by galaxy surveys:k fs=0.096−0.179Mpc−1at z=6−1 for mν=1eV.On the spatial scales larger than the free-streaming length,k<k fs,neutrinos can cluster and fall into gravi-tational potential well together with CDM and baryonic matter.In this case,perturbations in all matter com-ponents(CDM,baryon and neutrinos,denoted as‘cbν’hereafter)grow at the same rate given byD cbν(k,z)∝D(z)k≪k fs(z),(3) where D(z)is the usual linear growth factor(see,e.g., Eq.(4)in[53]).On the other hand,on the scales smaller than the free-streaming length,k>k fs,perturbations in non-relativistic neutrinos are absent due to the large ve-locity dispersion.In this case,the gravitational potential well is supported only by CDM and baryonic matter,and the growth of matter perturbations is slowed down rela-tive to that on the larger scales.As a result,the matter power spectrum for k>k fs is suppressed relative to that for k<k fs.In this limit the total matter perturbations grow at the slower rate given byD cbν(k,z)∝(1−fν)[D(z)]1−p k≫k fs(z),(4) where p≡(5−√4FIG.1:Suppression in the growth rate of total matter per-turbations(CDM,baryons and non-relativistic neutrinos), D cbν(a),due to neutrino free-streaming.(a=(1+z)−1is the scale factor.)Upper panel:D cbν(a)/Dν=0(a)for the neutrino mass fraction of fν=Ων/Ωm=0.05.The number of non-relativistic neutrino species is varied from N nrν=1,2,and3 (from thick to thin lines),respectively.The solid,dashed,and dotted lines represent k=0.01,0.1,and1h Mpc−1,respec-tively.Lower panel:D cbν(a)/Dν=0(a)for a smaller neutrino mass fraction,fν=0.01.Note that the total mass of non-relativistic neutrinos isﬁxed to mν,tot=N nrνmν=0.66eV and0.13eV in the upper and lower panels,respectively. Eq.(2).It is thus expected that a galaxy survey with diﬀerent redshift slices can be used to eﬃciently extract the neutrino parameters,N nrνand mν.The upper and middle panels of Figure2illustrate how free-streaming of non-relativistic neutrinos suppresses the amplitude of linear matter power spectrum,P(k), at z=4.Note that we have normalized the primordial power spectrum such that all the power spectra match at k→0(see§III).To illuminate the dependence of P(k) on mν,weﬁx the total mass of non-relativistic neutri-nos,N nrνmν,by fν=0.05and0.01in the upper and middle panels,respectively,and vary the number of non-relativistic neutrino species as N nrν=1,2and3.The suppression of power is clearly seen as one goes from k<k fs(z)to k>k fs(z)(see Eq.[2]for the value of k fs).The way the power is suppressed may be easily un-derstood by the dependence of k fs(z)on mν;for example,linear power spectrum at z=4due to free-streaming of non-relativistic neutrinos.Weﬁx the total mass of non-relativistic neutrinos by fν=Ων/Ωm=0.05,and vary the number of non-relativistic neutrino species(which have equal masses, mν)as N nrν=1(solid),2(dashed),and3(dot-dashed). The mass of individual neutrino species therefore varies as mν=0.66,0.33,and0.22eV,respectively(see Eq.[1]).The shaded regions represent the1-σmeasurement errors on P(k) in each k-bin,expected from a galaxy redshift survey observ-ing galaxies at3.5≤z≤4.5(see Table I for deﬁnition of the survey).Note that the errors are for the spherically averaged power spectrum over the shell of k in each bin.Diﬀerent N nrνcould be discriminated in this case.Middle panel:Same as in the upper panel,but for a smaller neutrino mass fraction, fν=0.01.While it is not possible to discriminate between diﬀerent N nrν,the overall suppression on small scales is clearly seen.Lower panel:Dependences of the shape of P(k)on the other cosmological parameters.P(k)at smaller k is more suppressed for a smaller mν,as lighter neutrinos have longer free-streaming lengths.Onvery small scales,k≫k fs(z)(k>∼1and0.1Mpc−1for fν=0.05and0.01,respectively),however,the amountof suppression becomes nearly independent of k,and de-pends only on fν(or the total neutrino mass,N nrνmν) as∆P5 ≈8fν.(5)We therefore conclude that one can extract fνand N nrνseparately from the shape of P(k),if the suppression “pattern”in diﬀerent regimes of k is accurately measured from observations.5Are observations good enough?The shaded boxes in the upper and middle panels in Figure2represent the1-σmeasurement errors on P(k)expected from one of the ﬁducial galaxy surveys outlined in Sec.V.Weﬁnd thatP(k)will be measured with∼1%accuracy in each k bin. If other cosmological parameters were perfectly known,the total mass of non-relativistic neutrinos as small as mν,tot=N nrνmν>∼0.001eV would be detected at more than2-σ.This limit is much smaller than the lower mass limit implied from the neutrino oscillation exper-iments,0.06eV.This estimate is,of course,unrealistic because a combination of other cosmological parameters could mimic the N nrνor fνdependence of P(k).The lower panel in Figure2illustrates how other cosmolog-ical parameters change the shape of P(k).In the fol-lowing,we shall extensively study how well future high-redshift galaxy surveys,combined with the cosmic mi-crowave background data,can determine the mass of non-relativistic neutrinos and discriminate between diﬀerent N nrν,fully taking into account degeneracies between cos-mological parameters.III.SHAPE OF PRIMORDIAL POWER SPECTRUM AND INFLATIONARY MODELSInﬂation generally predicts that the primordial power spectrum of curvature perturbations is nearly scale-invariant.Diﬀerent inﬂationary models make speciﬁc predictions for deviations of the primordial spectrum from a scale-invariant spectrum,and the deviation is of-ten parameterized by the“tilt”,n s,and the“running index”,αs,of the primordial power spectrum.As the pri-mordial power spectrum is nearly scale-invariant,|n s−1| and|αs|are predicted to be much less than unity. This,however,does not mean that the observed mat-ter power spectrum is also nearly scale-invariant.In Ap-pendix C,we derive the power spectrum of total matter perturbations that is normalized by the primordial cur-vature perturbation(see Eq.[C6])k3P(k,z)5H20Ωm 2×D2cbν(k,z)T2(k) k2αs ln(k/k0),(6)where k0=0.05Mpc−1,δ2R=2.95×10−9A,and A is the normalization parameter given by the WMAP collaboration[1].We adopt A=0.871,which gives δR=5.07×10−5.(In the notation of[63,64]δR=δζ.) The linear transfer function,T(k),describes the evolu-tion of the matter power spectrum during radiation era and the interaction between photons and baryons be-fore the decoupling of photons.Note that T(k)depends only on non-inﬂationary parameters such asΩm h2and Ωb/Ωm,and is independent of n s andαs.Also,the eﬀects of non-relativistic neutrinos are captured in D cbν(k,z); thus,T(k)is independent of time after the decoupling epoch.We use theﬁtting function found in[51,52]for T(k).Note that the transfer function and the growth rate are normalized such that T(k)→1and D cbν/a→1 as k→0during the matter era.In Appendix B we describe generic predictions on n s andαs from inﬂationary models.For example,inﬂation driven by a massive,self-interacting scalarﬁeld predicts n s=0.94−0.96andαs=(0.8−1.2)×10−3for the num-ber of e-foldings of expansion factor before the end of inﬂation of50.This example shows that precision deter-mination of n s andαs allows us to discriminate between candidate inﬂationary models(see[8]for more details). IV.MODELING GALAXY POWER SPECTRUMA.Geometrical and Redshift-Space DistortionSuppose now that we have a redshift survey of galax-ies at some redshift.Galaxies are biased tracers of the underlying gravitationalﬁeld,and the galaxy power spec-trum measures how clustering strength of galaxies varies as a function of3-dimensional wavenumbers,k(or the inverse of3-dimensional length scales).We do not measure the length scale directly in real space;rather,we measure(1)angular positions of galax-ies on the sky,and(2)radial positions of galaxies in redshift space.To convert(1)and(2)to positions in 3-dimensional space,however,one needs to assume a ref-erence cosmological model,which might be diﬀerent from the true cosmology.An incorrect mapping of observed angular and redshift positions to3-dimensional positions produces a distortion in the measured power spectrum, known as the“geometrical distortion”[54,55,56].The geometrical distortion can be described as follows.The comoving size of an object at redshift z in radial,r ,and transverse,r⊥,directions are computed from the exten-sion in redshift,∆z,and the angular size,∆θ,respec-tively,asr =∆zH(z′),(8) where H(z)is the Hubble parameter given byH2(z)=H20 Ωm(1+z)3+ΩΛ .(9)6 HereΩm+ΩΛ=1,andΩΛ≡Λ/(3H20)is the present-daydensity parameter of a cosmological constant,Λ.A trickypart is that H(z)and D A(z)in Eq.(7)depend on cosmo-logical models.It is therefore necessary to assume someﬁducial cosmological model to compute the conversionfactors.In the following,quantities in theﬁducial cos-mological model are distinguished by the subscript‘ﬁd’.Then,the length scales in Fourier space in radial,kﬁd ,and transverse,kﬁd⊥,directions are estimated from theinverse of rﬁd and rﬁd⊥.Theseﬁducial wavenumbers arerelated to the true wavenumbers byk⊥=D A(z)ﬁdH(z)ﬁdkﬁd .(10)Therefore,any diﬀerence between theﬁducial cosmolog-ical model and the true model would cause anisotropicdistortions in the estimated power spectrum in(kﬁd⊥,kﬁd )space.In addition,shifts in z due to peculiar velocities ofgalaxies distort the shape of the power spectrum alongthe line-of-sight direction,which is known as the“redshiftspace distortion”[57].From azimuthal symmetry aroundthe line-of-sight direction,which is valid when a distant-observer approximation holds,the linear power spectrumestimated in redshift space,P s(kﬁd⊥,kﬁd ),is modeled in[39]asP s(kﬁd⊥,kﬁd )=D A(z)2ﬁd H(z)k2⊥+k22×b21P(k,z),(11)where k=(k2⊥+k2)1/2andβ(k,z)≡−1d ln(1+z),(12)is a function characterizing the linear redshift space distortion,and b1is a scale-independent,linear biasparameter.Note thatβ(k,z)depends on both red-shift and wavenumber via the linear growth rate.Inthe infall regime,k≪k fs(z),we have b1β(k,z)≈−d ln D(z)/d ln(1+z),while in the free-streaming regime, k≫k fs(z),we have b1β(k,z)≈−(1−p)d ln D(z)/d ln(1+ z),where p is deﬁned below Eq.(4).One might think that the geometrical and redshift-space distortion eﬀects are somewhat degenerate in the measured power spectrum.This would be true only if the power spectrum was a simple power law.For-tunately,characteristic,non-power-law features in P(k) such as the broad peak from the matter-radiation equal-ity,scale-dependent suppression of power due to baryons and non-relativistic neutrinos,the tilt and running of the primordial power spectrum,the baryonic acoustic os-cillations,etc.,help break degeneracies quite eﬃciently [39,40,41,42,43,44,47,55,56].ments on Baryonic OscillationsIn this paper,we employ the linear transfer function with baryonic oscillations smoothed out(but includes non-relativistic neutrinos)[51,52].As extensively in-vestigated in[39,44,47],the baryonic oscillations can be used as a standard ruler,thereby allowing one to precisely constrain H(z)and D A(z)separately through the geo-metrical distortion eﬀects(especially for a high-redshift survey).Therefore,our ignoring the baryonic oscillations might underestimate the true capability of redshift sur-veys for constraining cosmological parameters.We have found that the constraints on n s andαs from galaxy surveys improve by a factor of2–3when baryonic oscillations are included.This is because the baryonic os-cillations basicallyﬁx the values ofΩm,Ωm h2andΩb h2, lifting parameter degeneracies betweenΩm h2,Ωb h2,n s, andαs.However,we suspect that this is a rather opti-mistic forecast,as we are assuming aﬂat universe dom-inated by a cosmological constant.This might be a too strong prior,and relaxing our assumptions about geom-etry of the universe or the properties of dark energy will likely result in diﬀerent forecasts for n s andαs.In this paper we try to separate the issues of non-ﬂat universe and/or equation of state of dark energy from the physics of neutrinos and inﬂation.We do not include the bary-onic oscillations in our analysis,in order to avoid too optimistic conclusions about the constraints on the neu-trino parameters,n s,andαs.Eventually,the full analysis including non-ﬂat uni-verse,arbitrary dark energy equation of state and its time dependence,non-relativistic neutrinos,n s,andαs, using all the information we have at hand including the baryonic oscillations,will be necessary.We leave it for a future publication(Takada and Komatsu,in prepara-tion).C.Parameter Forecast:Fisher Matrix Analysis In order to investigate how well one can constrain the cosmological parameters for a given redshift survey de-sign,one needs to specify measurement uncertainties of the galaxy power spectrum.When non-linearity is weak, it is reasonable to assume that observed density perturba-tions obey Gaussian statistics.In this case,there are two sources of statistical errors on a power spectrum measure-ment:the sampling variance(due to the limited number of independent wavenumbers sampled from aﬁnite sur-vey volume)and the shot noise(due to the imperfect sampling ofﬂuctuations by theﬁnite number of galax-ies).To be more speciﬁc,the statistical error is given in [58,59]by∆P s(k i)N k 1+1。

The Chemical Abundances of Tycho G in Supernova Remnant 1572

a r X i v :0809.0601v 1 [a s t r o -p h ] 3 S e p 2008The Chemical Abundances of Tycho G in SupernovaRemnant 1572Jonay I.Gonz´a lez Hern´a ndez 1,2,Pilar Ruiz-Lapuente 3,4,Alexei V.Filippenko 5,Ryan J.Foley 5,Avishay Gal-Yam 6,7,and Joshua D.Simon 6ABSTRACTWe present an analysis of the chemical abundances of the star Tycho G in the direction of the remnant of supernova (SN)1572,based on Keck high-resolution optical spectra.The stellar parameters of this star are found to be those of a G-type subgiant with T eﬀ=5900±100K,log(g/cm s2)=3.85±0.30dex,and [Fe /H]=−0.05±0.09.This determination agrees with the stellar parameters derived for the star in a previous survey for the possible companion star of SN 1572(Ruiz-Lapuente et al.2004).The chemical abundances follow the Galactic trends,except for Ni,which is overabundant relative to Fe,[Ni /Fe]=0.16±0.04.Co is slightly overabundant (at a low signiﬁcance level).These enhancements in Fe-peak elements could have originated from pollution by the supernova ejecta.We ﬁnd a surprisingly high Li abundance for a star that has evolved away from the main sequence.We discuss these ﬁndings in the context of companion stars of supernovae.Subject headings:stars:abundances —supernovae:general —stars:evolution3411:alex@,rfo-ley@ .6Department of Astronomy,California In-stitute of Technology,MS 105-24,Pasadena,CA 91125:avishay@,jsi-mon@ .7Benoziyo Center for Astrophysics,Weiz-mann Institute of Science,76100Rehovot,Israel:avishay.gal-yam@weizmann.ac.il .1.IntroductionType Ia supernovae(SNe Ia)are the best known cosmological distance indica-tors at high redshifts.Their use led to the discovery of the currently accelerating ex-pansion of the Universe(Riess et al.1998; Perlmutter et al.1999);see Filippenko (2005)for a review.They were also used to reveal an early era of deceleration,up through about9billion years after the big bang(Riess et al.2004,2007).Larger, higher-quality samples of SNe Ia,together with other data,are now providing increas-ingly accurate and precise measurements of the dark energy equation-of-state parame-ter,w=P/(ρc2)(e.g.,Astier et al.2006; Riess et al.2007;Wood-Vasey et al.2007; Kowalski et al.2008).Though the increase in the empirical knowledge of SNe Ia has led to an enor-mous advance in their cosmological use, the understanding of the explosion mecha-nism still requires careful evaluation(e.g., Hillebrandt&Niemeyer2000;Wheeler 2007).While in Type II SNe we have the advantage that the explosion leaves a com-pact star to which surviving companions (if they exist)often remain bound,thus enabling a large number of studies(e.g., Mart´ın et al.1992;Israelian et al.1999), in SNe Ia the explosion almost certainly does not produce any compact object.To investigate how the explosion takes place,we examine the rates of SNe Ia at high redshifts,or we can take a more direct approach and survey theﬁeld of histori-cal SNe Ia.The latter strategy has been followed since1997in a collaboration that used the observatories at La Palma,Lick, and Keck(Ruiz-Lapuente et al.2004).The stars appearing within the15%in-nermost area of the remnant of SN1572 (0.65′)were observed both photometrically and spectroscopically at multiple epochs over seven years.The proper motions of these stars were measured as well using im-ages obtained with the WFPC2on board the Hubble Space Telescope(HST)(GO–9729).The results revealed that many properties of any surviving companion star of SN1572were unlike those predicted by hydrodynamical models.For example,the surviving companion star(if present)could not be an overluminous object nor a blue star,as there were none in thatﬁeld.Red giants and He stars were also discarded as possible companions.A subgiant star(G2IV)with metal-licity close to solar and moving at high speed for its distance was suggested as the likely surviving companion of the explod-ing white dwarf(WD)that produced SN 1572(Ruiz-Lapuente et al.2004).This star,denoted Tycho G,has coordinates α=00h25m23.7s andδ=+64◦08′02′′(J2000.0).Comparisons with a Galactic model showed that the probability ofﬁnd-ing a rapidly moving subgiant with solar metallicity at a location compatible with the distance of SN1572was very low.A viable scenario for the Tycho SN1572 progenitor would be a system resembling the recurrent nova U Scorpii.This sys-tem contains a white dwarf of M WD= 1.55±0.24M⊙and a secondary star with M2=0.88±0.17M⊙orbiting with a pe-riod P orb≈1.23d(Thoroughgood et al. 2001).On the other hand,based on analysis of low-resolution spectra,Ihara et al.(2007) recently claimed that the spectral type ofTycho G is not G2IV as found by Ruiz-Lapuente et al.(2004),but rather F8V. In addition,Ihara et al.(2007)suggested the star Tycho E as the companion star of the Tycho SN1572,but we consider their conclusion to be unjustiﬁed.They base it on a single Fe I feature at3720˚A in a spec-trum having a signal-to-noise ratio(SNR) of only∼13.The short spectral range of their data(3600–4200˚A)and the low res-olution(λ/∆λ≈400,with a dispersion of 5˚A/pixel)add to our concern.The present work resolves questions re-garding the metallicity and spectral clas-siﬁcation of Tycho G.We concentrate on providing both the chemical composition of the star and the stellar parameters as derived from new data.In addition,we present a detailed chemical analysis of Ty-cho G aimed at examining the possible pol-lution of the companion star by the su-pernova.Although more data are still re-quired to deﬁnitively settle this issue,the overall properties of this star remain con-sistent with being the surviving companion of SN1572.2.ObservationsIn order to perform an abundance anal-ysis of Tycho G,spectra of it were ob-tained with the High Resolution Echelle Spectrometer(HIRES;Vogt et al.1994) on the Keck I10-m telescope(Mauna Kea, Hawaii).Nine spectra(with individual ex-posure times of1200s and1800s)were obtained on10September2006(UT dates are used throughout this paper)and four spectra(with exposure times of1800s) on11October2006,covering the spectral regions3930–5330˚A,5380–6920˚A,and 6980–8560˚A at resolving powerλ/∆λ≈50,000.The spectra were reduced in a stan-dard manner using the makee package. We checked in each individual spectrumthe accuracy of the wavelength calibra-tion using the[O I]λ6300.3andλ5577.4night-sky lines and found it to be within0.2km s−1.After putting each individ-ual spectrum into the heliocentric frame,we combined all of the spectra from eachnight.Then,each night’sﬁnal spectrum was cross-correlated with the solar spec-trum(Kurucz et al.1984)properly broad-ened with the instrumental resolution of∼6.6km s−1.Theﬁnal HIRES spectrum of Tycho G has a SNR of∼20at5200˚A,∼30at6500˚A,and∼50at7800˚A.This spectrum was not corrected from telluriclines since it was unnecessary for the chem-ical analysis(see§3.3).With the aim of determining the spec-tral classiﬁcation of several targets in theTycho SN1572ﬁeld,on12December2007 we obtained spectra with the Low Resolu-tion Imaging Spectrometer(LRIS;Oke et al.1995)on the Keck I telescope.We used the400/3400grism,the400/8500grat-ing,and the D560dichroic,covering the range3180–9150˚A.The full width at half-maximum(FWHM)resolution was6.4˚A in the red part(λ 5500˚A)and6.3˚A in the blue,with respective dispersions of 1.86˚A pixel−1and1.09˚A pixel−1.Ty-cho E,F,G,and D were observed in single exposures of700,200,400,and450s,re-spectively;see Ruiz-Lapuente et al.(2004) for star identiﬁcations.The SNR of the individual spectra is21,37,31,and25 at4600˚A for Tycho E,F,G,and D,re-spectively.These spectra were reduced us-ing standard techniques(e.g.,Foley et al.4000500060007000λ (ANGSTROMS)0.00.51.01.52.02.5N O R M A L I Z E D F L U XF6VF8IG2IVTycho G4000500060007000λ (ANGSTROMS)123456N O R M A L I Z E D F L U XF9VTycho G: E(B-V)=0.86G2IVTycho G: E(B-V)=0.76G4VTycho G: E(B-V)=0.66Fig.1.—Left panel:Keck LRIS spectrum of Tycho G compared with three template spectra having spectral types G2IV,F8I,and F6V taken from a library of low-resolution stellar spectra (Jacoby et al.1984).The absorption feature near 6900˚A in the template spectra is the telluric B band.Another,weaker telluric feature is visible near 7200˚A .Right panel:LRIS spectrum of Tycho G dereddened with E (B −V )=0.66,0.76,and 0.86mag,compared with spectra from the low-resolution library of Jacoby et al.(1984).The best ﬁts to the diﬀerent dereddened spectra of Tycho G are also shown.2003),including removal of telluric absorp-tion lines.The spectrum of Tycho G is shown in Figure 1;spectra and classiﬁcations of the other stars are available in Appendix A.In general,our results do not support the spectral classiﬁcations suggested by Ihara et al.(2007),which are based on low-resolution (λ/∆λ≈400),low-SNR spec-tra obtained with the instrument FOCAS at the Subaru Telescope over a short spec-tral range (3600–4200˚A ).Moreover,their relative ﬂux calibrations are questionable since they apply a correction to the slope of each spectrum that is ﬁtted when com-paring with a template.Thus,we consider their spectral classiﬁcations to be unreli-able.3.Stellar Parameters 3.1.Low-Resolution SpectraThe blue and red parts of the LRIS spec-tra were merged and then rebinned at a scale of 2˚A pixel −1.We compared the spectra of the four targets with a library of low-resolution stellar spectra from Jacoby,Hunter,&Christian (1984).We chose this library because the spectra have a similar resolution (∼4.5˚A ),with a dispersion of 1.4˚A pixel −1,and cover a similar spectral region (3510–7427˚A )as our LRIS obser-vations.The low-resolution comparison with template spectra depends on the color excess applied to the LRIS spectra.We dereddened the calibrated spectra accord-ing to the parameterization of Cardelli,Clayton,&Mathis (1989),including the update for the near-ultraviolet given byO’Donnell(1994).Moreover,there is un-certainty in the spectral classiﬁcation of each template.Thus,the spectral classi-ﬁcation of stars using low-resolution spec-tra must always be considered only as an initial guess.The bestﬁt is found for a reddening E(B−V)=0.76mag,with χ2ν=3.68(see below for details).This value of reddening was used in the com-parison shown in Figure1.In the library of Jacoby et al.(1984),there are not many spectra with luminosity class IV(only F0, F3,G2,G5IV),whereas luminosity class V is very well sampled with several tem-plates for each spectral type.If only low-resolution spectra are used to derive the spectral and luminosity classes,the results may be erroneous,since they depend on reddening and on theﬂux calibration of the observed spectra.Nonetheless,as aﬁrst step,we com-pare the LRIS spectrum of Tycho G with the low-resolution spectra of three tem-plate stars having diﬀerent spectral types (Fig.1).To evaluate the goodness ofﬁt, we employ a reducedχ2statistic,χ2ν=1σi 2,(1)where N is the number of wavelength points,M is the number of free param-eters(here one),f i is the templateﬂux,F i is the targetﬂux(in this case,Tycho G), andσi=1/SNR.The SNR was estimated as a constant average value in the contin-uum over the range4610–4630˚A;this re-gion was also used to normalize both target and template spectra.The spectral regions used to evaluateχ2are3850–6800˚A and 7000–7400˚A,avoiding strong telluric lines near6900˚A present only in the template spectra.The bestﬁt is found for the G2IV tem-plate withχ2ν=3.68,whereas the F8I and F6V templates provideχ2ν=6.39 and9.66,respectively.Ihara et al.(2007) have claimed that the spectral type of Ty-cho G could be either F8I,F8V,or F6V,rather than G2IV as found by Ruiz-Lapuente et al.(2004).However,our anal-ysis shows that those other spectral types provide worseﬁts than the G2IV template.In the following sections we use more ac-curate classiﬁcation methods,which are in-dependent of reddening,to derive not only the spectral type of Tycho G but actually the eﬀective temperature and surface grav-ity,using a high-resolution spectrum.3.2.HαProﬁleThe wings of Hαare a very good tem-perature indicator(e.g.,Barklem et al. 2002).Adopting the theory of Ali&Griem (1965,1966)for resonance broadening and Griem(1960)for Stark broadening,we computed Hαproﬁles for several eﬀective temperatures,using the code SYNTHE (Kurucz et al.2005;Sbordone et al.2005). For further details on the computations of hydrogen lines in SYNTHE,see Castelli &Kurucz(2001)and Cowley&Castelli (2002).Figure2compares these synthetic Hαproﬁles with the observed proﬁle for sev-eral temperatures.To evaluate the good-ness ofﬁt,we employ the same method as in the previous section.However,in this case M=1(the eﬀective tempera-ture T eﬀ),f i is the synthetic normalized ﬂux,F i is the observed normalizedﬂux, andσi=1/SNR.The SNR was estimated as a constant average value in continuum65556560656565700.600.700.800.901.001.10N O R M A L I Z E D F L UXT EFF = 5800K T EFF = 6050K T EFF = 6300KTycho GT EFF∆χν2T EFF∆χν2T EFF∆χν2Fig.2.—Upper panel:Synthetic H αproﬁles for three eﬀective temperatures compared to the observed spectrum of Tycho G (SNR ≈30)and normalized to the level of the observed spectrum of Tycho G at 6540˚A .We also display the ﬁtting regions at the top.Lower panel:Results of χ2νanalysis for three continuum positions separated by ±1/SNR =0.03: 1.03(left),1.00(middle),and 0.97(right).regions close to the observed H αproﬁle.The ﬁtting regions are indicated in Fig-ure 2,which contains all of the spectral regions close the center of the H αpro-ﬁle where there are no stellar lines and where the normalized ﬂux is greater than ∼0.7.The best ﬁt provided a temperature of T eﬀ=6050±250K,with the error bars estimated from the best ﬁts after displac-ing the observed continuum up and down by 1/SNR =0.03.In the following section,we adopt the currently most reliable method for the de-termination of the stellar parameters.3.3.Ionization Equilibrium of IronThe best determination of the atmo-spheric parameters of Tycho G can be ob-tained from the ionization equilibrium of iron.We measured the equivalent widths of 32Fe I and 10Fe II isolated lines using an automatic line-ﬁtting procedure which performs both line detection and Gaus-sian ﬁts to unblended lines (Fran¸c ois et al.2003).The analysis was done us-ing the 2002version of the code MOOG (Sneden 1973)and a grid of local ther-modynamic equilibrium (LTE)model at-mospheres (Kurucz 1993).We adoptedχl (eV)l o g ε (F e I )χl (eV)l o g ε (F e I)χl (eV)l o g ε (F e I )log(EW/λ)l o gε (F e I )log(EW/λ)l o g ε(F e I )log(EW/λ)l o g ε (F e I )χl(eV)l o g ε (F e I I )χl(eV)l o g ε (F e I I )χl (eV)l o g ε (F e I I )Fig.3.—Fe I and Fe II abundances computed using the best-ﬁt atmospheric parameters of Tycho G (left panels)and two sets of stellar parameters:T eﬀ=5900K and log(g/cm s2)=2dex (middle panels),T eﬀ=6200K and log(g/cm s2)=4.35dex (right panels).Upper panels:Fe I abundance vs.excitation potential;middle panels:Fe I abundance vs.reduced equivalent widths;bottom panels:Fe II abundance vs.excitation potential.The dashed lines in the upper and middle panels represent the ﬁts to the points,and in the bottom panels the mean abundance.the atomic data from Santos,Israelian,&Mayor (2004),where the log gf values are adjusted until the solar atlas (Kurucz et al.1984)is reproduced with a Kurucz model for the Sun having T eﬀ=5777K,log(g/cm s2)=4.44dex,ξt =1.00km s −1,and log ⊙ǫ(F e )=7.47dex.This line list was designed to determine stellar parame-ters of planet-host stars with roughly the same atmospheric parameters and metal-licity as Tycho G;it provides a compila-tion of 42completely unblended Fe lines ideal for the determination of stellar atmo-spheric parameters.Note that none of the stellar lines used in this work for chemical analysis is aﬀected by telluric lines.The atmospheric parameters were de-termined by iterating until correlation co-eﬃcients between log ǫ(Fe I )and χl ,as well as between log ǫ(Fe I )and log(W λ/λ),were zero,and the mean abundances from Fe I and Fe II lines were the same (see leftpanels of Fig.3).The derived parameters were T eﬀ=5900±100K,log(g/cm s2)= 3.85±0.30dex,ξt=1.23±0.23km s−1,and [Fe/H]=−0.05±0.09.The uncertainties in the stellar parameters were estimated as described by Gonzalez&Vanture(1998). Thus,the uncertainties inξt and T eﬀtake into account the standard deviation of the slope of the least-squaresﬁts,logǫ(Fe I) versus log(Wλ/λ)and logǫ(Fe I)versusχl. The uncertainty in log g considers the uncertainty on T eﬀin addition to the scat-ter of the Fe II abundances.Finally,the uncertainty in Fe abundance is estimated from a combination of the uncertainties in ξt and T eﬀ,in addition to the scatter of the Fe I abundances,all added in quadrature.In Figure3,we also show two set of stellar parameters,T eﬀ=5900K and log(g/cm s2)=2dex(middle panels),and T eﬀ=6200K and log(g/cm s2)=4.35dex (right panels),corresponding to the spec-tral types F8I and F6-7V(Gray1992). The lower-middle and upper-middle panels show inconsistent abundances between Fe I and Fe II,whereas the upper-right panel shows a negative slope for iron abundance versus excitation potentialχl of the spec-tral lines Fe I.Therefore,these two sets of parameters cannot be the stellar parame-ters of Tycho G.According to the spectral classiﬁcation provided by Gray(1992),the stellar parameters of Tycho G correspond to a spectral type of G0-1IV.Non-LTE(NLTE)corrections for stars with similar stellar parameters and metal-licity have been estimated at 0.07dex for Fe I lines,while Fe II seems to be insen-sitive to NLTE eﬀects(Th´e venin&Idiart 1999).In addition,Santos et al.(2004) compared spectroscopic surface gravities with log g using Hipparcos parallaxes and found an average diﬀerence of∼+0.03 dex,which might in fact reﬂect NLTE ef-fects on Fe I lines.Our assumption of LTE seems to be accurate enough to determine the surface gravity of the star within the error bars.Note that ionization equilib-rium also holds for Si and Cr(see§4).This determination of eﬀective tempera-ture is consistent within the error bars with that derived from the Hαproﬁle(T eﬀ= 6050±250K).However,echelle spectro-graphs are not ideally suited for measur-ing the shape of broad features such as the wings of Balmer lines(Allende Prieto et al.2004),and the SNR of∼30is not high enough for the determination of eﬀective temperature from the Hαproﬁle with great accuracy.For this reason,we will adopt the T eﬀ=5900±100K value for the de-termination of the chemical abundances.4.Chemical AbundancesUsing the derived stellar parameters,we determine the element abundances from the absorption-line equivalent width(EW) measurements of the elements given in Ta-ble4,except for lithium and sulfur for which we use aχ2procedure toﬁnd the bestﬁt to the observed features(e.g., Gonz´a lez Hern´a ndez et al.2004,2005, 2006).The atomic data for O,C,S,and Zn are taken from Ecuvillon,Israelian,& Santos(2004,2006),those of Na,Mg,Al, Si,Ca,Sc,Ti,V,Cr,Mn,Co,and Ni are from Gilli,Israelian,&Ecuvillon(2006), and those for Sr,Y,and Ba are from Reddy et al.(2003).In Figures4,5,and6we display sev-eral spectral regions of the observed spec-trum of Tycho G in comparison with syn-64306440645064606470λ (ANGSTROMS)0.20.40.60.81.0N O R M A L I Z E D F L U XTycho GFeIFeII CaI MnI CaICoI CaI FeIICaI FeI CrI FeI655065556560656565706575λ (ANGSTROMS)0.00.20.40.60.81.0N O R M A L I Z E D F L U XTycho GH αFig.4.—Best synthetic spectral ﬁts (solid lines)to the Keck HIRES spectrum of Tycho G for two spectral regions.The core of the H αline suﬀers from NLTE eﬀects that are not taken into account in our LTE synthetic spectrum.thetic spectra computed using the derived element abundances.Uncertainties in the abundances of all elements were then de-termined,adding in quadrature the er-rors due to the sensitivities of the result-ing abundances to changes in assumed at-mospheric parameters and the dispersion of the abundances from individual lines of each element.In Table 1we provide the average abun-dance of each element together with the er-rors.The errors in the element abundances show their sensitivity to the uncertainties in the eﬀective temperature (∆T eﬀ),surfacegravity (∆log g ),microturbulence (∆ξ),and the dispersion of the measurements from diﬀerent spectral features (∆σ).The er-rors ∆σwere estimated as ∆σ=σ/√Table1Chemical Abundances of Tycho G∆log g∆ξ∆[X/H]∆[X/Fe]n b Species logǫ(X)⊙a[X/H][X/Fe]σ∆σ∆TeffNote.—Chemical abundances of Tycho G and uncertainties produced by∆(T eﬀ)=+100K,∆(log g)=+0.3 dex,and∆(ξ)=+0.23km s−1.a The solar element abundances were adopted from Santos et al.(2004),Ecuvillon et al.(2004,2006),Gilli et al.(2006),and Reddy et al.(2003).b Number of spectral lines of this element analyzed in the star,or if there is only one,its wavelength.c These abundances were determined byﬁtting the observed spectra with synthetic spectra computed with the LTE code MOOG.61606165617061756180618561906195λ (ANGSTROMS)0.20.40.60.81.0N O R M A L I Z E D F L U XTycho GCaI CaI NiI CaIFeI C aI CaI CaI FeI FeIFeINiIFeINiI FeINiI FeI66256630663566406645665066556660λ (ANGSTROMS)0.40.60.81.0N O R M A L I Z E D F L U XTycho GFeIFeIFeI FeINiIFig.5.—Same as Fig.4,but for other spectral regions.average value if we consider the intrinsic dispersion ([Ni/Fe]=−0.07±0.04,see Fig.9)for the stars with similar metallic-ity of Tycho G ([Fe/H]=−0.05±0.09).In Figure 5we display several spectral ranges where some Ni I lines are well repro-duced.Generally,Ni tracks Fe throughout the [Fe/H]range down to [Fe/H]=−1.The average value and scatter found by Reddy,Lambert,&Allende Prieto (2006)is [Ni/Fe]=−0.05±0.02for thin-disk stars and [Ni/Fe]=−0.01±0.04for thick-disk stars.Bensby et al.(2005)found [Ni/Fe]=−0.06±0.04for thin-disk stars and [Ni/Fe]=−0.02±0.02for thick-disk stars.This suggests pollution in Ni by Ty-cho SN 1572ejecta.We ﬁnd in general solar or slightly above solar abundances of heavy elements,while the αelements are consistent with the solar value or below.The binary companions of black holes or neutron stars show a diﬀerent enhance-ment of metals with respect to the so-lar values.These stars exhibit signiﬁ-cant enrichment in αelements.For in-stance,the black hole binary Nova Scor-pii 1994([Fe/H]=–0.1)shows enhance-ments of [α/Fe]=4–8in Mg,S,Si,and O (Gonz´a lez Hern´a ndez et al.2008a).The pollution seems to be related to the fall-back of the ejected material of the super-nova.In SNe Ia,one does not expect fall-67006705671067156720λ (ANGSTROMS)0.40.60.81.0N O R M A L I Z E D F L U XTycho GFeIFeI LiIFeIFeIFeI TiICaI77707772777477767778778077827784λ (ANGSTROMS)0.40.60.81.0N O R M A L I Z E D F L U XTycho GOI OI OIFeI Fig.6.—Same as Fig.4,but for other spectral regions.back of material onto the companion star since the compact object (the white dwarf in this case)is destroyed and the gravita-tional potential well is not suﬃciently deep to retain the ejected material.Therefore,one expects to have a low contamination in intermediate-mass elements.The material captured by the companion should consist of heavy elements;they are less likely to es-cape the companion star since they move at lower velocities in the supernova ejecta.A discussion of this is given in §8.1.Another feature of interest in Tycho G is its high lithium abundance;the Li line at 6708˚A is pronounced.Modeling the Li abundance gives A (Li)=2.50±0.09.The lithium abundance is provided here as A (Li)=log[N (Li)/N (H)]+12and takes into account NLTE eﬀects.The NLTE abundance correction,∆NLTE =log ǫ(X)NLTE −log ǫ(X)LTE ,for Li was de-rived from the theoretical LTE and NLTE curves of growth in Pavlenko &Magazz`u (1996).The high Li abundance in Tycho G is intriguing since Li is easily destroyed in the convective envelopes of stars that have evolved away from the main se-quence.Subgiants with A (Li)>2.2are rare.Thor´e n,Edvardsson,&Gustafsson (2004)found that subgiants with detected Li divide into two groups:the stars with-0.6-0.4-0.20.00.20.4[Fe/H]-0.4-0.20.00.20.40.6[O /F e ]O-0.6-0.4-0.20.00.20.4[Fe/H]-0.4-0.20.00.20.40.6[N a /F e ]Na-0.6-0.4-0.20.00.20.4[Fe/H]-0.4-0.20.00.20.40.6[M g /F e ]Mg -0.6-0.4-0.20.00.20.4[Fe/H]-0.4-0.20.00.20.40.6[A l /F e ]AlFig.7.—Abundance ratios of Tycho G (wide cross)in comparison with the abundances of G and K metal-rich dwarf stars.Galactic trends were taken from Ecuvillon et al.(2004),Ecuvillon et al.(2006),and Gilli et al.(2006).The size of the cross indicates the 1σuncertainty.For the abundance of oxygen in metal-rich dwarfs,we have only considered abundance measurements in NLTE for the triplet O I 7771–5˚A .The dashed-dotted lines indicate solar abundance values.T eﬀ<5500K have A (Li)≤1.5,and a warmer group of stars have higher abun-dances,although still much lower than their primordial abundances,with A (Li)≤2.2.This seems to go in the direction of conﬁrming post-main-sequence evolution toward lower amounts of Li as expected from stellar models.Tycho G shares a high Li content with a known sample of binary companions of neutron stars and black holes (Mart´ın et al.1994a;Gonz´a lez Hern´a ndez et al.2004,2005).However,we know that cataclysmicvariables,whose compact objects are white dwarfs,do not show such high Li abun-dances (Mart´ın et al.1995).We discuss this further in §8.2.5.DistanceOne can estimate the distance of Ty-cho G from diﬀerent photometric colors and stellar parameters.We use the photo-metric magnitudes in ﬁve diﬀerent ﬁlters:-0.6-0.4-0.20.00.20.4[Fe/H]-0.4-0.20.00.20.40.6[S i /F e ]Si-0.6-0.4-0.20.00.20.4[Fe/H]-0.4-0.20.00.20.40.6[S /F e ]S-0.6-0.4-0.20.00.20.4[Fe/H]-0.4-0.20.00.20.40.6[C a /F e ]Ca -0.6-0.4-0.20.00.20.4[Fe/H]-0.4-0.20.00.20.40.6[T i /F e ]TiFig.8.—Same as Fig.7,but for diﬀerent elements.m V =18.71±0.04and m R =17.83±0.03mag from Ruiz-Lapuente et al.(2004),and m J =15.84±0.07,m H =15.16±0.11,and m K =15.03±0.12mag from the 2MASS catalog 1.We derived the radius of the star from the surface gravity,log(g/cm s2)=3.85±0.3dex,and assuming a mass of 1M ⊙.This radius,together with the spectroscopic estimate of the eﬀective tem-perature,T eﬀ=5900±100K,provides an intrinsic bolometric luminosity of 1.9<-0.6-0.4-0.20.00.20.4[Fe/H]-0.4-0.20.00.20.40.6[C r /F e ]Cr-0.6-0.4-0.20.00.20.4[Fe/H]-0.4-0.20.00.20.40.6[M n /F e ]Mn-0.6-0.4-0.20.00.20.4[Fe/H]-0.4-0.20.00.20.40.6[C o /F e ]Co -0.6-0.4-0.20.00.20.4[Fe/H]-0.4-0.20.00.20.40.6[N i /F e ]NiFig.9.—Same as Fig.7,but for diﬀerent elements.in the distance due to the uncertainty in the stellar parameters of Tycho G.Note that the relatively small formal error in the distance estimate for each ﬁlter is cal-culated by assuming that the magnitudes equal m i +∆m i .In Table 2,we also show for each set of parameters the average distance de-terminations weighted by the uncertainty of each individual distance determination.These values cover a distance range 2.48–4.95kpc with errors of 0.21–0.52kpc.We have also considered the possibility that Tycho G lost part of its envelope,∆M =−0.2M ⊙,due to the impact of the supernova shock wave (Marietta,Bur-rows,&Fryxell 2000;Pakmor et al.2008).However,a lower mass does not produce a signiﬁcant change in the derived aver-age distance.In all cases,we have as-sumed that the companion star is able to almost completely recover thermal equi-librium between ∼102and ∼103yr after the white dwarf explosion (Podsi-adlowski 2003).The distance to the SN 1572remnant inferred from the expansion of the radio shell and by other methods is 2.83±0.79kpc (Ruiz-Lapuente 2004).Such a distance is in good agreement with the derived distances of Tycho G.。

2019-Beyond Fluorescence Line Height – Making sense of - Ocean Color除了荧光线高度–了解海洋的颜色

– Iron stress – Photocompensation / acclimation with growth irradiance that incorporates hydrodynamics
OCRT 5/5/2009
Fluorescence
JRM & MB
What Fluorescence can’t do
F f a ph Eo
JRM & MB
The Fluorescence Paradox
• Two potential and mutually incompatible uses
– Abundance - need constant fluorescence efficiency – Physiology - need variable fluorescence efficiency.
OCRT 5/5/2009 Fluorescence JRM & MB
Changing the odds - 2019
Quantum Yield of Fluorescence
PQ NPQ
NPQ Dominates in Satellite Derived measurements Energy Dependent Quenching – decreases φf with increasing irradiance PSII downregulation (photoinhibition) – suppresses φf at all irradiances
OCRT 5/5/2009
Hale Waihona Puke FluorescenceJRM & MB
Gulf of Maine case Study Climatologies (2019-2019)