2.6节多种资源限制最优方案选择-案例正文

合集下载

面对资源限制时的模板专项施工方案范文使用技巧与建议

面对资源限制时的模板专项施工方案范文使用技巧与建议在现代社会，资源的有限性成为了一个不可忽视的问题。

无论是在建筑、工程还是其他领域，都需要面对资源有限的挑战。

为了更好地应对这一问题，模板专项施工方案应运而生。

本文将探讨面对资源限制时，如何使用模板专项施工方案，并提供一些实用的技巧和建议。

一、了解模板专项施工方案的基本概念模板专项施工方案是指根据特定的施工需求和条件，提前设计好的一套施工方案模板。

它可以帮助施工人员在资源有限的情况下，更高效地完成工作。

模板专项施工方案通常包括施工流程、材料选用、施工要点等内容。

二、选择适合的模板专项施工方案在面对资源限制时，选择适合的模板专项施工方案至关重要。

首先，要根据具体的施工需求和条件，选择与之相匹配的模板方案。

其次，要考虑方案的可行性和实用性。

一个好的模板专项施工方案应该能够在资源有限的情况下，提高工作效率，减少资源浪费。

三、合理利用现有资源在使用模板专项施工方案时，合理利用现有资源是非常重要的。

首先，要充分了解现有资源的情况，包括材料、设备和人力资源等。

其次，要根据实际情况，合理配置资源，避免浪费和不必要的消耗。

例如，在材料选用上，可以选择更加环保和节能的材料，以减少资源的使用量。

四、优化施工流程模板专项施工方案的一个重要组成部分就是施工流程。

通过优化施工流程，可以提高工作效率，减少资源的浪费。

在优化施工流程时，可以考虑以下几点。

首先，要合理安排施工顺序，避免重复工作和资源的重复使用。

其次，要提前做好施工准备工作，减少临时性的资源调配。

最后，要加强施工过程的监控和管理，及时发现和解决问题，避免资源的浪费。

五、培养团队合作意识在使用模板专项施工方案时，团队合作是非常重要的。

只有团队成员之间相互配合，才能更好地利用有限的资源。

因此，要培养团队合作意识，加强沟通和协作。

团队成员之间要互相支持和帮助，共同完成施工任务。

六、持续改进和创新面对资源限制，持续改进和创新是必不可少的。

多种资源限制最优方案选择案例正文

案例名称：多种资源限制最优方案选择专业领域/方向：管理会计适用课程：《高级管理会计》选用课程：《高级管理会计》编写目的：本案例要实现的教学目标在于：在追求短期边际利润最大化的生产计划中，当存在多种限制性资源时，单一限制理论所遵循的充分利用这种限制性资源直到它被用光为止的方案已经不再适用。

所以本节主要探讨的是存在多种限制性资源的情况下，如何优化限制性资源，实现利润最大化的问题。

知识点：企业短期计划经营预算关键词：多种限制性资源、短期预算、利润最大化中文摘要：弹性资源是企业根据其需要量购买和使用的诸如原材料和辅助材料之类的资源。

它的成本大小等于企业消耗的资源数量。

相反地，约束性资源在短期的供应是不变的。

它可以为企业开展各项活动提供必要的生产能力。

与变动成本不同，约束性资源成本的大小取决于企业资源的拥有量，而不是实际的耗用量。

由于约束性资源生产能力在短期不会发生改变，而当一项约束性资源限制了企业进一步进行短期扩，即进一步利用弹性资源时，就会造成企业因不能进一步扩大产量而造成机会损失。

所以短期规划主要考虑如何以最优的生产方式利用它。

我■W们将通过塞恩维橱柜厂的案例来充分解释其中的要点，然后试图将这些要点与短期资源的分配相结合来预测相关的财务效应。

多种资源限制下从两种方案分析如何实现利润最大化一、背景简介塞恩维橱柜厂（一）生产情况介绍1. 橱柜厂生产销售5种大型电子橱柜，具体每种型号橱柜生产和销售月份（如图）；2•橱柜厂采用适时生产模式，除型号c5全年生产，只在6月和12月销售;3.该厂作业流程包括6步，每个部门消耗工作量（如图:）（二）资金情况介绍1•该公司保持最小现金余额为50000美元，且任何短期营运资金都可用信贷筹集，每月利息按期初信贷额度的0.5%计算；2•该公司按销售收入5%计提坏账准备；3•假定该公司销售收入回收如下：销售收入在本月回收：65%，销售收入在下月回收：20%，销售收入在下两个月回收：10%。

2.6节多种资源限制最优方案选择-案例正文

2.6节多种资源限制最优方案选择-案例正文案例名称：多种资源限制最优方案选择专业领域/方向：管理会计适用课程：《高级管理会计》选用课程：《高级管理会计》编写目的：本案例要实现的教学目标在于：在追求短期边际利润最大化的生产计划中，当存在多种限制性资源时，单一限制理论所遵循的充分利用这种限制性资源直到它被用光为止的方案已经不再适用。

所以本节主要探讨的是存在多种限制性资源的情况下，如何优化限制性资源，实现利润最大化的问题。

它的成本大小等于企业消耗的资源数量。

相反地，约束性资源在短期内的供应是不变的。

它可以为企业开展各项活动提供必要的生产能力。

与变动成本不同，约束性资源成本的大小取决于企业资源的拥有量，而不是实际的耗用量。

由于约束性资源生产能力在短期内不会发生改变，而当一项约束性资源限制了企业进一步进行短期扩张，即进一步利用弹性资源时，就会造成企业因不能进一步扩大产量而造成机会损失。

所以短期规划主要考虑如何以最优的生产方式利用它。

我们将通过塞恩维橱柜厂的案例来充分解释其中的要点，然后试图将这些要点与短期资源的分配相结合来预测相关的财务效应。

多种资源限制下从两种方案分析如何实现利润最大化一、背景简介塞恩维橱柜厂（一）生产情况介绍1.橱柜厂生产销售5种大型电子橱柜，具体每种型号橱柜生产和销售月份（如图）；2.橱柜厂采用适时生产模式，除型号c5全年生产，只在6月和12月销售；3.该厂作业流程包括6步，每个部门消耗工作量（如图:）4.该厂每年与生产能力无关设备维护成本为12000000美元，该成本按月均摊。

（二）资金情况介绍1.该公司保持最小现金余额为50000美元，且任何短期营运资金都可用信贷筹集，每月利息按期初信贷额度的0.5%计算；2.该公司按销售收入5%计提坏账准备；3.假定该公司销售收入回收如下：销售收入在本月回收：65%，销售收入在下月回收：20%，销售收入在下两个月回收：10%。

多种资源受限多项目排序问题的两层决策方法

2001年2月系统工程理论与实践第2期　文章编号:100026788(2001)022*******多种资源受限多项目排序问题的两层决策方法谈　烨1,仲伟俊2,徐南荣2(1.上海大学上海市机械自动化及机器人重点实验室,上海200072;2.东南大学经济管理学院,江苏南京210096)摘要:　分析了多种资源受限多项目排序问题的性质和特点,提出用两层决策方法建立这类问题的数学模型Λ将基于直接搜索法的随机全局优化方法用于求解该问题的全局最优解,给出了具体的算法步骤Λ计算示例表明,本文建立的模型和给出的算法能有效地求解多种资源受限多项目排序问题Λ关键词:　项目排序;两层决策;随机全局优化方法中图分类号:　C934 αB i2level D ecisi on M ethod fo r M u lti2R esou rceCon strained M u lti2p ro ject Schedu lingTAN Ye1,ZHON G W ei2jun2,XU N an2rong2(1.Shanghai Enhanced L abo rato ry of M anufactu ring A u tom ati on&Robo tics,Shanghai U n iversity, Shanghai200072;2.Schoo l of Econom ics and M anagem en t,Sou theast U n iversity,N an jing210096)Abstract　In th is paper,the characteristics of m u lti2resou rce con strained m u lti2p ro jectschedu ling p rob lem is analyzed.A b i2level decisi on m ethod is u sed to con struct them athem atical model of th is p rob lem.A stochastic global op ti m izati on m ethod based ondirect search is in troduced to so lve the global op ti m al so lu ti on of the p rob lem,and thep rocess is also discu ssed in detail.T he resu lts of m athem atical examp les indicate thatthe m athem atical model and the op ti m izati on m ethod p ropo sed in th is paper can so lvethe m u lti2resou rce con strained m u lti2p ro ject schedu ling p rob lem effectively.Keywords　m u lti2p ro ject schedu ling;b i2level decisi on m ak ing;stochastic globalop ti m izati on m ethod1　引言在制造业、加工业和建筑业中经常存在资源有限多项目排序的问题Ζ比如,某大型制造厂几乎同时承接了p种产品的生产任务,分别交给p个下属分厂完成Ζ每个分厂除拥有自己的资源外,共同需要用到m 种属总厂控制的资源Ζ总厂怎样将这m种资源分给p个分厂,才能使p个分厂都能在要求的预定交货期内完成产品的生产任务且消耗的资源量最小,或者当资源紧缺无法按期交货时,实际交货期相对于预定交货期的拖期最小?对于总厂给出的每个资源分配方案,p个分厂就有各自相应的一个网络计划最短工期与之对应Ζ问题是怎样在诸多的资源分配方案中求出一个能使p种产品都能在要求的预定交货期内完成的分配方案?这是一个典型的需要将总厂拥有的多种有限资源在多个分厂间进行最优分配,以使得各分厂的生产进度计划能很好地执行的问题Ζ该问题具有内在目标不一致性Ζ因为总厂将共享资源分配给各分厂时,各分厂间的目标是互相冲突的,一个分厂获得的资源多了,别的分厂获得的资源就少了Ζ当总厂给定一个资源分配方案,各分厂都以工期最短为各自的目标,这与总厂的目标又不尽一致Ζ各决策目标间的不一致性给问题的描述和求解带来很大困难Ζα2系统工程理论与实践2001年2月目前,国内外对资源受限单项目排序问题研究得比较多,且取得了丰富的成果[1～4]Λ而对资源受限多项目排序问题的研究成果还比较少ΛP ritsker(1969)[5]等提出了用021线性规划模型描述该问题,并用021整数线性规划编码法求解该问题Λ当项目个数及每个项目中包含的活动数增加,供分配的资源种类增加时,描述模型的变量个数和约束条件将大大增加,给问题的求解带来困难ΛKu rtu lu s和D avis(1982)[6]没有用数学模型描述问题,而是根据项目的特性将多项目排序的启发式规则分类,提出基于两种衡量标准的分类方法Λ第一种衡量标准是找出项目中资源需求总量的峰值;第二种衡量标准是求出每种资源的利用率Λ根据这两个衡量标准值的不同将启发式排序规则在多项目环境中的作用进行分类ΛSperanza(1993)[7]提出通过加入虚工序将多个项目的网络计划图合并成一个总网络计划图,并用分枝定界法求解多模式多项目的排序问题,而H artm ann(1996)[8]则指出了该算法的明显缺陷,它有可能找不到存在的可行解Λ同时进行的多个项目之间在时间上虽然会有先后,但并不象一个项目内部的各活动那样存在不可违反的紧前关系,所以资源在多个项目间分配与在单个项目内部各活动间分配是不同的,即所需满足的约束条件不同Λ将资源受限单项目排序问题的求解方法用于研究资源受限多项目排序问题存在缺陷Λ由于资源受限多项目排序问题决策过程的复杂性,过去还没有很有效的解决该问题的模型和方法Λ两层决策方法是一种具有递阶结构的系统优化方法Λ它包含一个上层问题和多个下层问题,上层问题和下层问题都有各自的目标函数和约束条件Λ上层问题的目标函数和约束条件不仅与上层决策变量有关,而且还依赖于下层问题的最优解,而下层问题的最优解又受上层决策变量的影响Λ一般上层决策者处于一个领导和协调下层各执行部门的地位,而下层各决策者处于执行地位Λ在决策中,上层决策者有权首先确定他的决策方案,并将该信息传递给下层各执行部门Λ决策方案的满意与否是由上层决策者根据其自身的目标函数决定的Λ两层决策方法所描述决策问题的决策过程是上层决策者首先宣布它的决策,这一决策将影响下层决策问题的约束集和目标函数Λ然后下层各决策者在这种限制下选取使自己的目标函数最优的决策,它也影响上层决策问题的目标函数,上层决策者再调整它的决策变量的取值,该过程不断进行,直至上层目标函数达到最优为止[9,10]Λ由于两层决策模型的结构和决策过程可以恰如其分地描述资源受限多项目排序问题,因此本文提出用两层决策方法研究资源受限多项目排序问题,针对资源可连续变化的情况,建立了数学模型,并给出相应的求解方法Λ仿真示例表明,本文建立的模型和提出的算法能有效地求解资源受限多项目排序问题Λ2　多项目排序问题的两层决策模型为建立多种资源受限多项目排序问题的模型,我们设上层(总厂)有m种可连续变化的资源要分配给下层p个项目,下层每个项目还拥有各自的独立资源Ζ下层各项目的进度计划分别用网络计划表示,设第k 个项目中共有N个活动,用双代号法表示有M个节点,其中有m个活动用到m种共享资源,且每个活动只用到一种共享资源Ζ为简化问题,在此不考虑每个项目中独立资源的分配Ζ假定下层各项目中使用独立资源的活动所需独立资源量均能满足,且活动持续时间固定不变,使用共享资源的活动持续时间由所分配到的资源量决定Ζ设使用共享资源的活动持续时间与资源分配量成反比关系(如2台机器干6天,4台机器就干3天)Ζ那么活动持续时间=活动工作量÷资源量Ζ上层以p个项目均在各自的预定工期内完成,消耗的共享资源总量最小为目标,下层p个项目都以工期最短为目标Ζ由此描述多种资源受限多项目排序问题的数学模型如下:m in F(R)=6p k=1(m ax(T k-T3k,0))+Ε′6m l=16p k=1R k l(1a)s.t.6p k=1R k lΦs l l=1,2,…,m(1b) R k lΕ0　k=1,2,…,p;　l=1,2,…,m(1c) m inT k=w k M-w k1 k=1,2,…,p(1d) ks.t.x k ij(w k j-w k i)Εx k ij D k ij　i=1,…,M;j=1,…,M;k=1,…,p(1e)x k ij D k ij =U k ijR k l t k ij l =1,2,…,m ;i =1,…,M ;j =1,…,M(1f )x k ij =01　i =1,…,M ;j =1,…,M ;k =1,…,p (1g )式中,(1a )式为上层决策者的目标函数,该式中第一项代表各个项目的生产周期相对于指定完工期的拖期;第二项为一辅助目标,Ε′为一任意小的正数(如10-4)Ζ在目标函数中加上该项是由于下层决策问题的目标函数是工期最短,那么存在这样一种情况,当网络计划中使用共享资源的m 个活动有一个或几个不在网络的关键路线上时,该活动所分配到的资源在一定范围内变化将不影响整个工期,出现解的不唯一性Ζ为了克服解的不唯一性,在上层目标函数中加入要求资源消耗量最小的辅助目标ΖT k 为第k 个项目的网络计划最短工期;T 3k 为第k 个项目要求的预定工期;R k l 为分配给第k 个项目的第l 种共享资源量;S l 为第l 种共享资源总量;(1b )、(1c )式表示共享资源约束;(1d )式为下层第k 个决策者的目标函数[11];w k i 为第k 个项目中事项i 的实现时间;D k ij 为第k 个项目中活动i -j 的持续时间,x k ij 为021变量,当第k 个项目存在活动i -j 时为1,否则为0;U k ij 为第k 个项目中使用共享资源的活动i -j 工作量;t k ij 为第k 个项目中独立资源确定的时间Ζ(1e )式表示第k 个项目网络计划中紧前关系约束;(1f )式表示第k 个项目中各活动的持续时间Ζ 在上述模型中,式(1a )～(1c )是上层决策者面对的决策问题Ζ他们所要解决的问题是在m 种资源总量一定的情况下Ζ将它们分配给p 个项目,使p 个项目都能在预定工期内完成,且消耗的共享资源总量最小Ζ式(1d )～(1g )是下层第k 个项目负责人面临的问题,它所解决的问题是根据上层决策者给定的资源量来制定自己的进度计划,其目标是使自己的项目工期尽可能短Ζ整个模型描述的决策过程是上层决策者首先给出一个资源分配方案,下层p 个决策者利用所分配到的资源求出各自的最短工期,并将结果返回给上层决策者Ζ上层决策者根据其目标函数的要求调整资源分配方案,该过程持续进行,直到上层决策者的目标函数达到最优为止Ζ3　基于直接搜索法的随机全局优化算法求解两层决策问题的全局最优解存在极大的困难Ζ因为对于一般的两层规划问题,即使上、下层问题中的目标函数和约束函数都是线性的,它一般也是一个非凸问题,存在多个局部最优解Ζ从数学角度看,可以有多种求取非凸优化问题全局最优解的方法Ζ随机全局优化方法[12]是一种比较适合于求解两层规划问题的方法Ζ该方法求解问题分为两个阶段,即全局阶段和局部阶段Ζ在全局阶段,以一定的分布随机采样一定数量的初始点,并计算其相应的目标函数值Ζ在局部阶段,利用局部寻优技术求取该采样点领域内的局部最优解,产生全局最优解的候选解Ζ随机全局优化方法虽然不能确保求得问题的全局最优解,但它是以概率1保证的Ζ基于直接搜索法的随机全局优化法是将直接搜索法用于求取两层规划问题局部最优解的一种随机全局优化方法Ζ由于直接搜索法求解问题时不要求完全信息,即上层决策者只要知道下层各个决策者对他的反应即可,无需了解下层决策问题的所有信息Ζ因此我们采用基于直接搜索法的随机全局优化方法求解模型(1)描述的多种资源受限多项目排序问题Ζ直接搜索法求解问题(1)的过程是:上层决策者首先宣布一个满足共享资源约束的分配方案R ,并送给下层p 个决策者Ζ对给定的R ,下层决策者面临的是一个求网络计划最短工期问题,有唯一最优解T k ,k =1,…,p Ζ将T k 返回上层,以这点作为初始基点求出相应的上层目标值F Ζ然后对R 中的某一分量沿正方向以某一步长∆探测,计算并比较在点R 和R +∆i 处的T k 值,若在点R 和R +∆i 处的T k 值比在点R 处的T k 值小,则取R +∆i 为临时点,计算目标函数F 的值;若T k 的值不变,说明使用R 中这一分量资源的活动不在网络的关键路线上,此时沿该分量的负方向探测,求得不使T k 增加的该资源分量的最小值R -∆i ,并以R -∆i 为临时点,计算目标函数F 的值,再由此点沿另一分量进行同样的搜索,如能得到比以前更好的3第2期多种资源受限多项目排序问题的两层决策方法点,即目标函数值小的点,就以该点代替前面的点作为新的临时点Ζ如此沿R中的各个分量轮流搜索一遍,最后一轮得到的点为最好的临时点,它也成为一个新的基点Ζ注意在探测过程中每次都要判断是否满足共享资源约束,若不满足则放弃在该方向上的探测Ζ由上述搜索过程可归纳出利用直接搜索法求解问题(1)的局部最优解的算法步骤如下:Step1　上层决策者确定一初始的可行基点R(0)=R=(R11,…,R k l)和初始探测步长∆=(∆1,…,∆k×l)T及精度要求Ε,设计数器i=1;Step2　由给定的R计算出相应的T k,k=1,…,p的值,计算F(R)的值ΖStep3　计算尝试点R(i)=(R11,…,R ij+∆i×j,…,R k l)T判断是否满足式(1b)、(1c),若不满足转step5;若满足,计算对应T(i)k,k=1,…,p的值,转step4;Step4　计算F(R(i)),若F(R(i))<F(R),令R=R(i),F(R)=F(R(i)),转step6;否则转step5;Step5　令R(i)=(R11,…,R ij-∆i×j,…,R k l)T,计算对应的T(i)k,k=1,…,p的值Ζ若T(i)k=T k,且F (R(i))<F(R),令R=R(i),F(R)=F(R(i)),转step6;若T(i)k>T k则保留R和F(R)的原值,转step6;Step6　判断i是否等于k3l,如是转step7;否则,令i=i+1,返回step3继续计算;Step7　判别F(R(k3l))<F(R(0)),是否成立,若成立转step9;否则转step8;Step8　判别∆i×jΦΕΠi×j=1,…,k3l是否成立,如成立转step9;否则令∆=∆ 10,转step1继续计算;Step9　求得局部最优解为F(R)=F(R(k3l)),计算过程结束Ζ结合前述直接搜索法,在此采用随机全局优化方法中的多级单连接算法[12]求解多种资源受限多项目排序问题Ζ该算法先按一定的随机分布如均匀分布确定多个初始点,然后对每个初始点,若该点距已搜索的点距离大于一定的值,从该初始点出发利用直接搜索法求其对应的局部最优解,并将其最优的局部最优解作为全局最优解的候选点Ζ该方法也是以概率1保证获得问题的全局最优解的Ζ具体算法步骤如下: Step1　以均匀分布随机产生L个满足共享资源约束的初始点,令计数器i=1;Step2　选择第i个初始点R i;Step3　计算第i个初始点R i与已利用直接搜索法进行局部最优解搜索的初始点之间的距离,如果其距离小于阈距离d,令i=i+1,返回step2Λ否则转step4继续计算ΖStep4　从R i出发,利用上述直接搜索法求取局部最优解ΖStep5　将具有最优目标函数的局部最优解作为全局最优解的候选解Ζ如果有充分高的置信度确认所有局部最优解已获得,输出计算结果,终止计算过程Ζ否则令i=i+1,返回step2继续计算Ζ在算法的第3步中,阈距离d可用下式计算:d=V(X)#1+n12log(L)L1 n1(2)式中,V(x)是搜索空间X的体积;#是gamm a函数,它被定义为#(a)=∫∞0z b-1e-z d z其它(a-1)!如果a是奇数算法第5步中的置信度有两种表示方法Ζ一种是局部最优解的期望总数E:E=W(N-1)N-W-2(3)另一种是局部最优解的吸收空间占整个搜索空间的比例B:B=(N-W-1)(N+W)N(N-1)(4)式中,W是已发现的不同局部最优解的数量,N是实际进行的求取局部最优解即执行算法中第4步的次数Ζ置信度是否充分高即全局最优解是否已获得用下列二式判别:E<W+0.5(5) 4系统工程理论与实践2001年2月B Ε0.995(6)式(5)的含义是已发现的不同局部最优解的数量W 非常接近于局部最优解的期望值;式(6)的含义是已发现局部最优解的吸收空间覆盖了整个搜索空间的99.5%Ζ如果式(5)和式(6)成立,结束计算过程Ζ4　算例本文所建立的模型和提出的算法已在多个示例上进行了仿真计算,获得了比较满意的结果Ζ由于受文章篇幅的限制,在此我们给出一个较简单的三种资源在两个项目中的分配算例用于说明本文提出的方法求解多种资源受限多项目排序问题的有效性Ζ具体算例如下(图1,图2):图1　项目一图2　项目二例　项目一要求的预定工期T 31=20天,项目二要求的预定工期T 32=19天Ζ上层供分配的三种共享资源总量分别为s 1=8,s 2=10,s 3=6Ζ按式(1a )～(1g )建立模型,用基于直接搜索法的随机全局优化方法求解该问题Ζ 在计算过程中令L =10,∆=(∆1,∆2,…,∆6)T =(0.1,0.1,…,0.1)T ,Ε=10-6Ζ计算所得的最优解为:R 11=2.532361;R 12=3.859884;R 13=2.076309;R 21=2.696442;R 22=6.125422;R 23=3.908997上层目标函数值为:V a l =2.119941310-3相应下层目标函数值为:T 1=19.9973 T 2=18.9876从计算结果可以看出,项目一和项目二的生产周期均未超过各自的预定工期,且共享资源使用量s 1达到最小,s 2和s 3的使用量均未超过资源总量Ζ这说明用基于直接搜索法的随机全局优化方法求解多种资源受限多项目排序问题能得到从工程角度上足够满意的最优解,算法有良好的收敛性,但算法所需计算时间会随着最优解的精确度的提高而大大增加Ζ由于从(3)式可以估计出局部最优解的数目,因而在实际应用中采用本算法能在最优解的精确度和所需计算时间之间进行折衷处理Ζ5　结束语多种资源受限多项目排序问题是一个比较复杂的问题Λ为描述该问题内在的目标间的不一致性,本文用两层决策方法建立了数学模型Λ该问题本身特有的非凸性给求解其全局最优解带来极大的困难Λ在此用基于直接搜索法的随机全局优化方法求解问题的全局最优解Λ计算实例表明,运用本文提出的方法基本可以得到问题的全局最优解Λ由于求解多种资源受限多项目排序问题的算法复杂度随着资源种类和项目数的增加会大大增加,因此更加简便、有效的算法还有待进一步研究Λ参考文献:[1]　Patterson J H ,T ab lo t F B .Slow in sk i R et al .Compu tati onal experience w ith a back track ingalgo rithm fo r so lving a general class of p recedence and resou rce 2con strained schedu ling p rob lem s [J ].Eu ropean Jou rnal of the Operati onal R esearch ,1990,49:68～79.(下转第16页)5第2期多种资源受限多项目排序问题的两层决策方法61系统工程理论与实践2001年2月6　结论由于在群决策中群成员的期望水平和保留水平可能随着群决策过程中群成员之间相互作用发生变化,本文提出了可期望水平和可期望保留水平的概念,给出了一种间接估计群成员的期望水平和保留水平方法,用这种方法估计群成员的期望水平和保留水平,可以避免决策人直接提供保留水平和期望水平的不真实和不现实Ζ本文算例证明了该方法的有效性和可操作性Ζ参考文献:[1]　宜家骥,方爱群.目标规划及其应用[M].合肥,安徽教育出版社,1987.[2]　Kersten G E,M ichalow sk iW,Gray D,et al.A n analytic basic fo r decisi on suppo rt in nego tiati on s[A].D ecisi on analysis labo rato ry schoo l of bu siness[C],Carleton U n iv,中国,天津大学学术交流论文,1996.[3]　R aiffa H.T he art of nego tiati on s[M].Cam b ridge:H arvard U n iv,P ress,1982.[4]　王仁超,孙惠,顾培亮.不精确偏好与非传递偏好[J].系统工程学报,1997,12(3):31～38.[5]　王仁超.面向过程的群决策理论、方法与应用研究[D]Λ天津大学博士论文,1997.(上接第5页)[2]　E rik L.D em eu lem eester,W illy S.H erroelen.A b ranch2and2bound p rocedu re fo r the generalizedresou rce2con strained p ro ject schedu ling p rob lem[J].Operati on s R esearch.1997,45(2):201～212. [3]　Bocto r F F.A new and efficien t heu ristic fo r schedu ling p ro jects w ith resou rce restricti on s andm u lti p le execu ti on modes[J].Eu ropean Jou rnal of Operati onal R esearch,1996,90:349～361. [4]　Ko lisch R.D rex l A.L ocal search fo r nonp reemp tive m u lti2mode resou rce2con strained p ro jectschedu ling[J].IIE T ran sacti on s,1997,29(11):987～999.[5]　P ritsker A.B.M u ti2p ro ject schedu ling w ith li m ited resou rces:A zero2one p rogramm ing app roach[J].M anagem en t Science,1969,16:93～108.[6]　Ku rtu lu s I.D avis E.W.M u lti p ro ject schedu ling:Catego risati on of heu ristic ru les perfo rm ance[J].M anagem en t Science,1982,28:161～172.[7]　Speranza M G.V ercellis C.H ierarch ical models fo r m u lti2p ro ject p lann ing and schedu ling[J].Eu ropean Jou rnal of Operati onal R esearch,1993,64:312～325.[8]　H artm ann S.Sp recher A.A no te on"H ierarch ical models fo r m u lti2p ro ject p lann ing andschedu ling"[J].Eu ropean Jou rnal of Operati onal R esearch,1996,94,:377～383.[9]　徐南荣,仲伟俊.科学决策理论与方法[M].南京:东南大学出版社,1996.[10]　仲伟俊,徐南荣.具有合作关系的多人递阶资源分配问题研究[J].系统工程理论与实践,1993,13(2):11～16.[11]　冯允成.活动网络分析[M].北京:北京航空航天大学出版社,1991.[12]　R innooy A H G.T i m m er GT.Stochastic global op ti m izati on m ethods[J].M athem aticalP rogramm ing,1987,39(1):27～58.。

选择最优方案说明

选择最优方案说明引言在进行任何项目或决策时，选择最优方案是至关重要的环节。

无论是在商业领域、科学研究还是个人生活中，选择最优方案可以有效地提高效率、降低成本、最大化利益。

本文将介绍选择最优方案的一般步骤以及一些常用的方法和工具。

步骤1. 定义问题和目标在选择最优方案之前，首先需要明确问题和目标。

明确问题将有助于我们理解需要解决的核心难题，而明确目标则有助于我们评估不同方案对目标的贡献程度。

通过明确问题和目标，我们能够在选择最优方案时更加专注和有针对性。

2. 收集信息收集信息是选择最优方案的重要一步。

信息可以来自多个渠道，例如市场调研、数据分析、专家意见等。

通过收集信息，我们可以更好地了解当前的情况和趋势，并为选择最优方案提供有力的依据。

3. 制定评估标准在选择最优方案时，我们需要制定评估标准来进行有针对性的评估。

评估标准应该与问题和目标密切相关，并且应该是可量化的。

例如，如果目标是降低成本，我们可以制定评估标准为每年可节省的成本金额。

制定评估标准可以帮助我们更加客观地比较不同方案的优劣。

4. 评估备选方案在收集信息和制定评估标准之后，我们可以开始评估备选方案了。

评估备选方案应该基于制定的评估标准，并且应该考虑到各种因素的权重。

一种常用的评估方法是决策矩阵，它可以帮助我们将各个评估标准以及备选方案的得分进行系统化的比较和综合。

5. 决策和执行在评估备选方案之后，我们需要进行决策并执行选择最优方案。

在做决策时，我们应该综合考虑评估结果、可行性、风险等因素，并权衡利弊。

一种常用的决策方法是决策树，它可以帮助我们逐步分析各个备选方案的优点与缺点，并最终确定最优方案。

常用方法和工具决策矩阵决策矩阵是一种常用的评估工具，它可以帮助我们将各个评估标准以及备选方案的得分进行综合和比较。

决策矩阵可以将主观的评估转化为可量化的指标，并为选择最优方案提供有力的支持。

决策矩阵可以通过Excel等软件进行制作和分析。

决策树决策树是一种常用的决策方法，它基于树状结构进行分析和判断。

价值工程中最优方案的选择

价值工程中最优方案的选择价值工程是一个系统的、组织性的方法，以最经济、最有效的方式实施项目。

它包括对项目目标、需求和约束的分析，以及对不同方案的评估和比较。

最终目的是为了确保项目以最少的成本、最高的效益实现。

在价值工程中，最优方案的选择通常需要通过多方面的分析和决策来确定。

首先，需要对项目的目标和需求进行充分的了解和分析。

这包括识别出项目的关键目标和约束条件，以及明确项目的各项需求和要求。

针对这些目标和需求，需要考虑不同的技术和经济方案，以找出最适合的方案。

在选择最优方案的过程中，需要进行综合评估和比较。

这包括对不同方案的成本、效益、风险和可行性进行评估分析。

在考虑成本时，需要包括项目阶段、预算限制以及资源限制等。

在考虑效益时，需要充分考虑项目的长期效益和可持续性。

在考虑风险和可行性时，需要充分考虑项目的技术难度和可行性，以及可能出现的风险和变数。

在综合评估和比较的基础上，需要制定一个决策方案。

这包括对不同方案的优势和劣势进行权衡分析，并决定是否采取某个方案或某些方案。

在制定决策方案时，需要充分考虑项目的整体目标和需求，以确保最终选择的方案能够最大限度地满足这些目标和需求。

在价值工程中，最优方案的选择还需要考虑到项目的整体效益和风险。

这包括对不同方案的长远效益和可持续性进行评估，以及对可能出现的风险和变数进行风险管理。

在考虑整体效益时，需要考虑项目的长期价值和可持续性，以确保选择的方案能够最大限度地实现项目的长期目标。

最终，在价值工程中选择最优方案需要进行决策和实施。

这包括对决策方案进行推广和实施，以确保最终选择的方案能够得到有效实施和执行。

在实施过程中，需要确保项目的整体目标和需求得到有效满足，以确保项目最终实现。

总之，在价值工程中选择最优方案是一个非常重要的决策过程，需要充分考虑项目的整体目标和需求，并通过系统的分析和决策来确定最优方案。

只有通过整体评估和比较，明智的决策和有效的实施，才能够最大限度地实现项目的目标和价值。

对于多方案择优

对于多方案择优在面对问题时，人们往往会提出多种解决方案。

然而，不同的方案可能会有各自的优劣之处。

如何在多个方案之间进行选择，从而择优取舍，是一个需要深思熟虑的问题。

本文将讨论对于多方案择优的一些方法和策略，帮助读者在面对选择时做出明智的决策。

首先，了解每个方案的细节和要求是做出决策的基础。

例如，在解决一个项目管理问题时，我们可能有多个时间和资源预算的方案可供选择。

为了择优，我们需要仔细研究每个方案的具体时间安排、成本分配和资源需求。

只有全面了解每个方案的情况，我们才能在选择时做出明智的判断。

其次，评估方案的优劣利弊是决策过程中不可或缺的一步。

我们可以根据一些指标来进行评估，比如效率、成本、实施难度等。

对于特定问题，不同的评估指标可能有所不同。

我们可以给每个指标设定权重，根据权重对每个方案进行打分和排名。

通过这种评估方法，我们可以量化地比较不同方案之间的优劣，帮助我们做出选择。

除了定量评估，我们还可以考虑一些定性因素。

有时候，方案的可行性、风险程度、可持续性等因素也会对我们的选择产生重要影响。

因此，我们需要对这些因素进行全面的分析和权衡。

比如，在选择一种市场营销策略时，我们除了要考虑各种指标的数据，还需要考虑市场环境、竞争对手的反应等因素，以确保我们的选择是可行且有效的。

此外，我们还可以借鉴过去的经验和案例来进行决策。

有些问题可能在过去已经出现过类似的情况，我们可以通过借鉴他人的经验来减少错误和风险。

人们常说“站在巨人的肩膀上”，这意味着我们可以利用他人的智慧和经验来指导我们的选择。

通过研究过去的案例，我们可以学习别人的成功或失败教训，从而更好地做出决策。

最后，决策是一个动态的过程。

我们不能期望一次选择就能解决所有问题。

有时候，我们需要采取试错的策略，选择一个方案并进行实施，然后根据实际情况做出调整和改善。

这就需要我们保持灵活性和适应性，不断重新评估和调整我们的决策。

只有在实施和反馈的过程中，我们才能真正了解各个方案的效果和可行性。

精益求精优化资源配置的实用策略与案例

精益求精优化资源配置的实用策略与案例在当今竞争激烈的商业环境中，企业如何优化资源配置以实现更高效、更可持续的发展已成为一个关键问题。

精益求精是一种管理理念，它强调不断优化和改进的重要性。

本文将探讨精益求精优化资源配置的实用策略，并通过一些实际案例进一步说明其有效性。

一、全面分析资源需求在优化资源配置之前，首先需要全面分析企业的资源需求。

这包括对生产、销售、人力、财务等各个方面的需求进行深入了解。

只有了解了资源需求的具体情况，企业才能有针对性地进行优化。

比如，一家电子产品制造商在市场需求分析的基础上，确定了各个产品的产能需求，从而优化了生产线的资源配置，并提高了生产效率。

二、精细管理资源使用精益求精的核心思想是避免浪费和优化效率。

在实践中，企业可以通过精细管理资源使用来实现这一目标。

一方面，可以对生产流程进行不断优化，避免重复劳动和资源浪费。

另一方面，可以通过数据分析和技术创新来提高资源利用效率。

例如，一家物流公司利用物联网和人工智能技术，优化了货物配送的路线和时间，减少了资源消耗和运营成本。

三、跨部门协作与资源共享优化资源配置离不开不同部门之间的协作和资源共享。

企业应通过建立有效的沟通渠道和协调机制，使各个部门能够更好地协同工作，避免资源浪费和重复投入。

例如，一家跨国零售企业实行集中采购和分布式存储的模式，通过统一的供应链管理，实现了企业各个部门之间的资源共享和协调，提高了整体运营效率。

四、持续改善和创新精益求精要求企业持续改善和创新，不断寻求资源配置的完善和优化。

企业应该建立一个持续改进的机制，鼓励员工提出问题和改进的建议，并及时对其进行评估和实施。

另外，企业应鼓励创新思维和实践，不断探索新的资源配置模式和方法。

例如，一家制造业企业引入了机器人生产线，通过自动化和智能化的方式，实现了资源的高效利用和生产效率的提升。

综上所述，精益求精是一种优化资源配置的实用策略。

通过全面分析资源需求、精细管理资源使用、跨部门协作与资源共享、持续改善和创新等方法，企业可以实现资源配置的优化，提高运营效率。

最优方案选择

最优方案选择在日常生活中，我们往往面临各种各样的决策。

无论是在个人生活中还是在工作场合，我们都需要在不同的选择中找到最优的方案。

最优方案选择是一个有挑战性的任务，需要综合考虑各种因素，包括成本、时间、资源和效益等。

本文将探讨如何进行最优方案选择，并提供一些实用的方法和策略。

在进行最优方案选择之前，首先需要明确目标和需求。

明确目标和需求可以帮助我们更好地理解和定义问题，从而更有针对性地选择合适的方案。

例如，如果我们的目标是节约成本，那么我们就需要寻找成本低廉的方案；如果我们的目标是提高效率，那么我们就需要寻找能够快速完成任务的方案。

其次，我们需要收集和评估各种可能的方案。

收集方案的来源可以包括个人经验、专业知识、咨询意见和市场调研等。

评估方案时，我们可以通过制定评估标准来进行比较。

评估标准可以是各种指标，例如成本、时间、质量、风险和可行性等。

通过评估标准的比较，我们可以得出各种方案的优缺点，进而找到最优的方案。

除了评估标准，我们还可以使用决策矩阵来帮助进行最优方案选择。

决策矩阵是一种将各种方案按照不同指标进行打分的方法。

在使用决策矩阵时，我们需要将各种方案列在矩阵的行上，将评估标准列在矩阵的列上，然后按照评估标准对各个方案进行打分。

最后，我们可以将各个方案的得分相加，得出最优的方案。

决策矩阵可以帮助我们更系统地比较和评估各种方案，从而做出更理性的决策。

此外，我们还可以使用决策树来进行最优方案选择。

决策树是一种将决策过程可视化的方法。

在使用决策树时，我们需要将不同的选择和结果以树的形式展示出来。

通过对不同选择和结果的权衡，我们可以找到最优的方案。

决策树可以帮助我们更清晰地理解问题，并在决策过程中观察到各种可能的结果，从而做出更明智的选择。

最后，我们还可以考虑使用模型和数据分析来进行最优方案选择。

模型和数据分析可以帮助我们更客观地评估和预测各种方案的效果。

通过模型和数据分析，我们可以通过对过去数据的分析和对未来的预测来辅助决策过程。

面对资源有限时的模板专项施工方案范文使用技巧

面对资源有限时的模板专项施工方案范文使用技巧在建筑施工过程中，专项施工方案的编制是非常重要的一环。

然而，面对资源有限的情况下，如何编制出高效、经济、可行的专项施工方案，成为了每个建筑从业者需要面对的挑战。

本文将分享一些使用技巧，帮助建筑从业者在面对资源有限时编制出优质的专项施工方案。

首先，明确目标和需求是编制专项施工方案的基础。

在资源有限的情况下，我们需要明确工程的核心目标和需求，以确保专项施工方案的编制符合项目的整体要求。

例如，如果项目的核心目标是快速完成，那么我们可以在施工方案中注重提高工程进度的措施，如采用预制构件等方式，以减少现场施工时间。

如果项目的核心目标是节约成本，那么我们可以在施工方案中注重优化材料的使用，选择更经济的施工方法等。

其次，合理利用现有资源是编制专项施工方案的关键。

在资源有限的情况下，我们需要充分考虑现有资源的利用效率。

例如，可以通过调整工程进度，合理安排施工队伍，减少闲置时间，最大限度地提高资源利用率。

此外，我们还可以考虑与其他项目的资源共享，如共用设备、共用人员等，以减少资源的浪费。

第三，技术创新是编制专项施工方案的重要手段。

在资源有限的情况下，我们需要通过技术创新来提高施工效率和质量。

例如，可以采用先进的建筑技术和设备，如BIM技术、机器人施工等，以提高施工效率和减少资源消耗。

此外，我们还可以通过优化施工工艺，减少材料浪费，提高资源利用率。

技术创新不仅可以提高施工效率，还可以降低施工成本，提高工程质量。

最后，风险管理是编制专项施工方案的重要环节。

在资源有限的情况下，我们需要充分考虑各种风险，并采取相应的措施进行管理。

例如，可以通过提前预测和评估风险，制定相应的应对方案，以减少风险对施工进度和质量的影响。

此外，我们还可以通过与供应商的合作，确保材料的供应和质量，以降低施工风险。

综上所述，面对资源有限时的模板专项施工方案的编制，需要明确目标和需求，合理利用现有资源，通过技术创新提高效率，以及进行风险管理。

资源管理的最佳实践与效率提升案例

资源管理的最佳实践与效率提升案例在当今高度竞争的商业环境中，资源管理对于企业的成功至关重要。

有效的资源管理可以帮助企业提高效率、减少浪费，并为持续增长和发展奠定坚实的基础。

本文将介绍一些资源管理的最佳实践，并结合一个案例来说明如何通过资源管理提升效率。

一、资源规划与分配资源规划是确保资源合理利用的重要步骤。

企业应进行全面的资源评估，并制定明确的资源规划策略。

这包括确定资源的需求，分配资源的优先级和时序，并制定相应的预算计划。

合理的资源规划可以避免资源浪费，提高资源利用率。

以某汽车制造企业为例，该企业在进行新产品开发时，通过资源规划和分配确保项目顺利进行。

首先，他们对各个项目的资源需求进行评估，包括人力、物料、设备等。

然后，根据项目的优先级和时程要求，将资源进行合理分配，保证各个项目的资源需求得到满足，同时避免资源的过度使用和拥挤。

二、资源优化与流程改进资源管理也涉及到流程改进和资源优化。

企业应该不断寻找优化资源配置的机会，并对现有流程进行改进以提高效率。

以某电子制造公司为例，该公司通过优化生产线上的资源配置，实现了显著的效率提升。

首先，他们对生产线上各个工序的资源使用情况进行分析，并通过重新规划资源的配置，减少了资源浪费和重复劳动。

同时，他们还改进了流程，并采用了先进的自动化设备，进一步提高了生产效率。

三、信息技术支持信息技术在资源管理中发挥着重要作用。

现代企业可以利用信息技术来跟踪和管理资源的使用情况，并进行及时的监控和调整。

以某零售企业为例，该企业利用先进的供应链管理系统，实现了对库存和销售数据的实时监控和分析。

这使得企业能够更好地预测市场需求，避免过量的库存或供应不足的情况，并通过及时调整资源的分配来提高效率。

四、人力资源管理人力资源是企业最重要的资源之一，有效的人力资源管理对于提高企业效率至关重要。

企业应该注重员工激励和培训，通过提供良好的工作环境和发展机会，吸引和留住优秀人才。

以某IT服务公司为例，该公司实施了灵活的工作制度和激励机制，提高了员工的工作满意度和积极性。

2.6-运筹学应用实例汇总

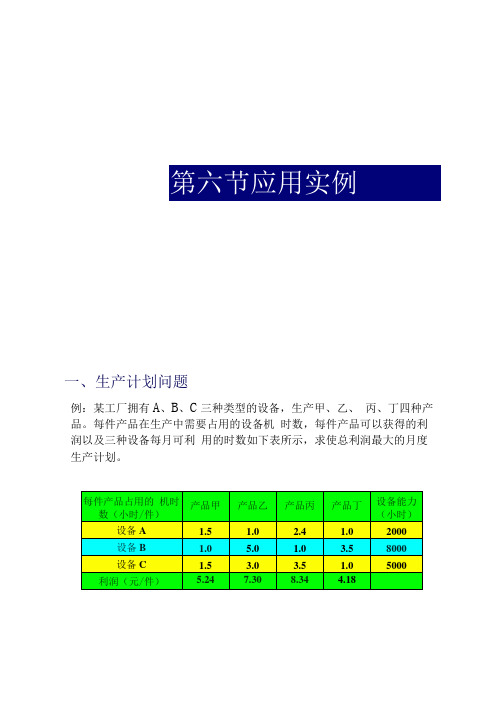
一、生产计划问题例：某工厂拥有A、B、C三种类型的设备，生产甲、乙、丙、丁四种产品。

每件产品在生产中需要占用的设备机时数，每件产品可以获得的利润以及三种设备每月可利用的时数如下表所示，求使总利润最大的月度生产计划。

建模思路■用线性规划制订使总利润最大的生产计划。

■设变量X1为第i种产品的生产件数(i=1, 2, 3, 4),目标函数z为相应的生产计划可以获得的总利润。

在加工时间以及利润与产品产量成线性关系的假设下，可以建立如下的线性规划模型：建模max z= 5.24X1 +7.30x2 +8.34x3 +4.18x4目标函数1.5Xj +1.0x2+2.4X3+1.0X4<2000LOX1 +5.0X2+1.0X3+3.5X4<8000 约束条件1・5X] +3.0X2+3.5X3+1.0X4<5000Xp X2, X3, X4 >0 变量非负约束练习：某公司面临一个是外包协作还是自行生产的问题。

该公司生产甲、乙、丙三种产品，都需要经过铸造、机加工和装配三个车间。

甲、乙两种产品的铸件可以外包协作，亦可以自行生产，但产品丙必须本厂铸造才能保证质量。

数据如下表。

问：公司为了获得最大利润，甲、乙、丙三种产品各生产多少件？甲、乙两种产品的铸造中，由本公司铸造和由外包协作各应多少件？甲 .乙丙资源限制铸造工时（小时/件）51078000机加工工时（小时/件）64812000装配工时（小时/件）32210000自产铸件成本（兀/件）354外协铸件成本（兀/件）56一机加工成本（元/件）213装配成本（元/件）322产品售价（元/件）231816解：设孙孙寺分别为三道工序都由本公司加工的甲、乙、丙三种产品的件数，同，幅分别为由外协铸造再由本公司加工和装配的甲、乙两种产品的件数。

求占的利润：利润二售价-各成本之和产品甲全部自制的利润产品甲铸造外协，其余自制的利润产品乙全部自制的利润产品乙铸造外协，其余自制的利润产品丙的利润可得到毛（i = 1,2, 3,4,5）的利润分别为15、10、7、13、9=23-（3+2+3）=15 =23-（5+2+3）=13 =18-（5+1+2）=10 =18-（6+1+2）=9 =16-（4+3+2）=7通过以上分析,可建立如下的数学模型：目标函数：Max 15百+ 10电+ 7两+ 13题+ 9不约束条件：5为+ 10西+ 7玛＜80006为+ 4出+ 8^ + 6々+ 4不3百+ 2X2 + 2均+ 3局+ 2不毛，演，传，演，与12000 10000二、混合配料问题例：某工厂要用四种合金T1, T2, T3和T4为原料，经熔炼成为一种新的不锈钢G。

如何在工程项目中应对资源限制和优化利用

如何在工程项目中应对资源限制和优化利用在工程项目中，资源限制和优化利用是一个至关重要的问题。

合理管理和利用资源不仅可以提高项目的效率和成果，还可以减少成本和资源浪费。

本文将探讨如何在工程项目中应对资源限制并优化利用。

一、资源限制的背景和原因在工程项目中，资源限制指的是物质、资金、人力等方面的限制条件。

这些限制条件不仅会影响项目进展和质量，还会对项目目标的实现产生影响。

导致资源限制的原因多种多样，包括预算不足、人力不足、时间紧迫等。

二、资源限制应对策略为了应对资源限制，工程项目可以采取以下策略：1. 资源评估与规划：首先需要对项目所需资源进行评估和规划。

根据项目的需求和可用资源的情况，明确各项资源的优先级和配比，合理安排资源的分配和利用。

2. 优化任务分配：在资源有限的情况下，将任务合理分配给项目团队成员。

根据各自的专长和能力，合理分工，提高工作效率，避免资源浪费和冗余。

3. 合理调配资源：在项目执行过程中，根据项目进展和需求的变化，及时调整资源的分配和利用。

对于临时性的资源短缺，可以考虑外部资源的补充，如租赁、借用等。

4. 优化资源利用方式：通过技术手段和工艺改进，优化资源的利用方式。

比如，引入节能设备、采用新材料等，降低资源消耗，提高资源利用效率。

三、资源优化利用的方法为了实现资源的优化利用，可以采取以下方法：1. 采用先进的技术和工艺：选择性能更好、能耗更低的技术和工艺方案，提高资源的利用率。

2. 节能减排：在项目实施中，应注重节能减排，减少能源消耗和对环境的影响。

通过提高电器设备的能效、优化建筑设计等手段，实现资源的节约利用。

3. 循环利用与回收再利用：对于可循环利用的资源，应采取措施进行回收再利用。

例如，在建筑工程中，可以对废弃材料进行分类回收，降低资源浪费。

4. 资源共享：在一个工程项目中，可以通过资源共享的方式，减少资源的重复投入。

比如，多个子项目可以共享一部分设备和人力资源，提高资源利用效率。

优化资源使用的规划方案设计

优化资源使用的规划方案设计一、引言在当今社会，资源的有限性成为了制约社会发展的一个重要问题。

为了实现可持续发展，我们需要制定合理的规划方案来优化资源的使用。

本文将探讨如何设计一套有效的规划方案，以实现资源的最大化利用和保护。

二、资源评估与分析在制定规划方案之前，我们首先需要对现有资源进行评估和分析。

这包括对各类资源的数量、分布、质量等方面的调查和研究。

通过对资源的评估，我们可以了解到资源的状况和潜力，为后续的规划提供依据。

三、资源利用目标的确定在评估和分析的基础上，我们需要确定资源利用的目标。

这些目标应当符合可持续发展的原则，既要满足当前的需求，又要保证未来世代的需求得到满足。

例如，我们可以制定减少能源消耗、提高资源回收率等目标，以促进资源的可持续利用。

四、资源利用的规划策略为了实现资源利用目标，我们需要制定一系列的规划策略。

这些策略应当包括从资源获取、利用到回收再利用的全过程。

例如，我们可以通过提高资源利用效率、加强资源管理和监控等方式来实现资源的优化利用。

1. 提高资源利用效率提高资源利用效率是实现资源优化利用的关键。

我们可以通过技术创新、工艺改进等方式来提高资源的利用效率。

例如，采用先进的节能设备和生产工艺，减少资源的浪费和损耗。

2. 加强资源管理和监控加强资源管理和监控是确保资源优化利用的重要手段。

我们可以建立完善的资源管理体系，包括资源调度、监测和评估等环节。

通过对资源的全面管理和监控，可以及时发现和解决资源利用中存在的问题，提高资源利用效率。

3. 推动资源回收再利用资源回收再利用是实现资源优化利用的重要途径。

我们可以通过建立废物回收体系、制定相关政策和法规等方式来推动资源的回收再利用。

例如，建立废物分类收集系统，鼓励企业和个人参与废物回收，将废物转化为可再利用的资源。

五、资源利用规划的实施规划的实施是资源优化利用的关键环节。

在实施过程中，我们需要充分调动各方的积极性和参与度。

这包括政府、企业、社会组织和个人等各方的共同努力。

有效的问题解决方法与实战案例分析

策划方案资源分配策略随着社会发展进步，各行各业对于资源的需求越来越迫切。

而在策划方案的实施过程中，资源的分配策略显得尤为重要。

下面本文将通过分析现有问题和提出解决方案，介绍一种合理的策划方案资源分配策略。

一、问题分析资源分配策略的关键问题在于如何在有限的资源下实现最大化的效益。

目前，我们面临的主要问题有以下几个方面：1.资源不均衡。

在策划方案中，有些资源相对稀缺，而有些资源相对丰富。

如何合理利用稀缺资源，达到平衡资源分配的目的是一个亟需解决的问题。

2.资源浪费。

由于缺乏资源规划和管理机制，很多资源被浪费在无效的地方上。

如何避免资源的浪费，提高资源的利用效率是需要解决的难题。

3.资源优先级。

在资源分配中，如何确定资源的优先级是一个需要权衡和考虑的问题。

不同的资源在不同的环境下具有不同的优先级，因此需要建立一套合理的评估机制。

二、解决方案为了解决上述问题，需要采取一系列的策略措施来进行资源的分配。

下面将提出几点具体的解决方案：1.资源均衡分配。

首先，需要建立一个资源统计和管理系统，全面了解和掌握各种资源的情况。

同时，要根据实际需求和优先级，合理安排和分配资源，以达到均衡和合理利用的目的。

2.资源规划和管理。

建立资源规划和管理机制，制定资源的使用计划和方案。

通过对资源的有序分配和调度，避免资源浪费和过度使用的问题。

3.资源优先级评估。

建立一套合理科学的资源评估机制，可以根据不同资源的重要性、稀缺程度和周期性等因素，对资源进行评估和排序。

以便在资源分配过程中，科学合理地确定资源优先级。

4.资源协同应用。

通过资源协同应用，可以促进资源共享和互补。

不同资源之间可以进行合作和协同，实现资源的最大化利用效益。

5.资源的再生利用。

实施资源的再生利用是一个重要的环节。

通过技术手段和科学管理方法，对废旧资源进行再造和再利用，可以实现资源的经济化利用。

6.资源监管和保护。

建立资源监管和保护机制，加强对资源的管理和保护工作。

有限资源：如何做出最佳选择

有限资源：如何做出最佳选择在生活中，我们常常面临着各种各样的选择。

然而，资源是有限的，我们无法一次性获得所有我们想要的东西。

因此，如何在有限的资源下做出最佳选择成为了一个重要的问题。

在这篇文章中，我将探讨有限资源下如何做出最佳选择的一些方法和策略。

首先，要做出最佳选择，我们需要清晰地了解自己的需求和目标。

在资源有限的情况下，我们需要优先考虑自己最需要的东西是什么，以及达成目标所需的资源是哪些。

这样一来，我们就可以有针对性地选择最符合自己需求和目标的资源，避免浪费在不必要的东西上。

其次，要做出最佳选择，我们需要对可选资源进行评估和比较。

在资源有限的情况下，我们需要权衡各种资源之间的优劣势，包括价格、质量、效用等方面。

通过对资源进行全面的评估和比较，我们可以更好地选择出对自己最有利的资源，从而实现最佳选择。

另外，要做出最佳选择，我们需要考虑资源的长期效益。

有时候，一时的选择可能会给我们带来短期的满足，但长远来看却可能不是最佳选择。

因此，在选择资源时，我们需要考虑其长期效益，避免只顾眼前利益而忽视了资源的长期潜力。

此外，要做出最佳选择，我们还需要考虑资源的可持续性。

资源有限，我们需要在选择资源时考虑到资源的可持续性，避免选择那些对环境或者社会造成不可逆转的损害的资源。

只有选择了可持续的资源，我们才能够在长期内实现最佳选择。

最后，要做出最佳选择，我们需要不断学习和调整。

在资源有限的情况下，我们可能会犯错，选择了不合适的资源。

这时，我们需要及时总结经验教训，不断学习和调整，以便在下一次选择时做出更好的决策，实现最佳选择。

综上所述，有限资源下如何做出最佳选择是一个复杂而又重要的问题。

通过清晰了解需求和目标、评估和比较资源、考虑长期效益和可持续性，以及不断学习和调整，我们可以更好地做出最佳选择，实现个人和社会的可持续发展。

希望以上内容能够帮助大家在面对有限资源时做出更明智的选择。

最优方案问题的题

最优方案问题的题问题背景在日常生活中，我们经常会遇到各种各样的问题，例如如何选择最佳目的地旅行、如何找到最佳购物方案、如何规划最佳工作流程等。

在这些问题中，最优方案的选择对于我们的生活和工作有着重要的影响。

但是，如何寻找最优方案却是一个非常具有挑战性的问题。

问题描述最优方案问题是指在给定一定的限制条件和目标的情况下，寻找到满足条件且使目标最大或最小的方案。

例如，在选择旅行目的地的问题中，我们需要考虑到预算、时间、旅游景点等因素，从中选择一个最佳的方案。

问题解决方法为了解决最优方案问题，我们可以采用多种方法，下面介绍几种常见的方法：1.贪心算法：贪心算法是一种简单而有效的方法，它通过每一步选择当前状态下的最优解，最终得到全局的最优解。

贪心算法适用于那些具有贪心选择性质的问题，即通过局部最优选择达到全局最优解。

然而，贪心算法并不是适用于所有最优方案问题，有时会导致得到次优解甚至不可行解。

2.动态规划：动态规划是一种将问题拆分为一个个子问题，并使用递归的方式解决的方法。

动态规划具有重叠子问题和最优子结构的特性，通过将已解决的子问题的解存储起来，避免了重复计算，提高了计算效率。

动态规划适用于那些存在着重叠子问题和最优子结构的问题，可以得到正确的最优解。

3.数学建模：数学建模是一种将实际问题抽象为数学模型，并通过数学工具来分析和解决问题的方法。

数学建模可以将复杂的问题简化为数学模型，通过数学方法求解得到最优解。

数学建模需要具备数学建模的基本知识和技能，适用于各种最优方案问题。

案例分析以下通过一个具体案例来演示如何解决最优方案问题。

问题描述小明计划去旅行，他有一个预算限制和一些旅游景点的评分，他希望在预算允许范围内选择旅游景点使得评分最高。

解决方法为了解决这个问题，我们可以使用贪心算法来选择旅游景点：1.首先，将所有的旅游景点按照评分从高到低排序。

2.然后，从评分最高的旅游景点开始选择，直到预算用完或者没有可选景点为止。

最佳施工方案的筛选与推广案例分析

最佳施工方案的筛选与推广案例分析探索最佳施工方案的筛选与推广案例分析随着社会的发展和科技的进步，建筑施工行业日益发展，各类施工方案层出不穷。

然而，在众多方案中如何选择最佳的施工方案成为一个重要问题。

本文将从多个角度分析最佳施工方案的筛选与推广案例，探讨如何通过对比研究、优化设计、经验总结等手段来确定最佳施工方案。

一、成本与效益的平衡在施工方案筛选过程中，成本与效益是首要考虑的因素。

以一座大型高层建筑的外墙装修方案为例，传统的砖瓦施工方式需要大量人工和材料投入，施工周期长，且难以保证质量。

而现代化的装饰板材施工方案则具备施工速度快、质量可控、材料使用量少等优势。

通过对成本及效益进行综合评估，赢得了业主的认可。

二、施工质量与安全保障施工质量与安全是施工方案的关键关注点。

在一家核工厂的修建工程中，核心施工方案的选择至关重要。

在施工方案的筛选过程中，需要综合考虑施工过程中的安全保障措施、质检手段等。

通过与其他方案的比较，选定了一套安全、高效的方案，并取得了良好的工程效果。

三、环境影响与可持续发展环境影响评价是施工方案筛选中的必要环节。

以一个垃圾处理厂的建设为例，方案的筛选需要综合考虑噪音、污染、能耗等方面的影响。

通过与环保方案进行对比，选定了一套既能够实现垃圾处理的功能，又能够减少环境污染的施工方案。

四、技术创新与优化设计技术创新与优化设计是推广最佳施工方案的重要手段。

在一项铁路建设工程中，传统的路基施工方式需要大量人力物力，效率低下。

通过引入机械化装备、自动化监控等技术创新，打造了一套高效、低耗的施工方案，取得了良好的经济和环境效益。

五、经验总结与案例分享经验总结与案例分享是推广最佳施工方案的重要手段之一。

通过总结与分析施工过程中的问题、挑战和解决方法，可以形成一套标准操作流程，并与行业内其他企业进行案例分享。

这种方式不仅能够提高自身的施工效率和质量，同时也能够推广最佳施工方案的应用。

六、全球案例分析与借鉴全球案例分析与借鉴是寻找最佳施工方案的重要途径。

资源优化管理的策略与成功案例分享

资源优化管理的策略与成功案例分享在当今快速发展的社会中，资源的优化管理变得至关重要。

针对这一挑战，本文将探讨资源优化管理的策略，并分享一些成功案例。

一、资源优化管理的策略在资源优化管理中，以下几个策略被广泛应用，并取得了显著成效。

1. 数据驱动决策资源优化管理的第一步是收集和分析相关数据。

只有通过了解资源的使用情况和效益，我们才能够制定相应的优化策略。

通过使用业务智能工具、大数据分析和预测模型，可以有效地帮助企业做出明智的决策，从而最大化资源的效用。

2. 合理配置资源资源的合理配置是资源优化管理的关键一环。

企业需要评估各种资源的需求，并合理分配给不同的部门和项目。

通过优化资源配置，可以最大化资源的利用率，降低浪费，并提高整体效率。

同时，资源的配置还需要灵活变通，以适应市场变化和企业战略调整。

3. 提高资源利用效率提高资源利用效率是资源优化管理的核心目标之一。

这包括优化生产过程，减少能源和物料的浪费，提高生产效率。

同时，也包括提高人力资源的利用效率，通过培训和激励措施，提高员工的产出和工作效率。

4. 推行绿色环保资源优化管理的策略还应该关注环境可持续发展。

企业应该积极采取措施，减少对自然资源的消耗，降低对环境的影响。

此外，推广绿色生产和循环经济模式也是资源优化管理的一部分。

这不仅有助于企业的可持续发展，也符合社会的期望和法规的要求。

二、成功案例分享下面分享两个成功案例，展示了资源优化管理策略的实际应用效果。

1.电能资源优化管理案例：某工厂通过数据分析和监测系统，实时掌握了电能的使用情况，并利用节能技术降低了能源浪费。

通过合理调整设备运行时间和电力负荷，该工厂成功降低了电费支出，提高了生产效率，同时还起到了环保减排的效果。

2.人力资源优化管理案例：某公司引入了人力资源管理系统，对员工进行综合评估，并根据评估结果合理分配岗位和培训资源。

同时，该公司还实行了弹性工作制和奖励制度，激励员工发挥出更大的潜力。

2.6节 多种资源限制最优方案选择-案例正文

面对资源限制时的模板专项施工方案范文使用技巧与建议

多种资源限制最优方案选择案例正文

2.6节多种资源限制最优方案选择-案例正文

多种资源受限多项目排序问题的两层决策方法

选择最优方案说明

价值工程中最优方案的选择

对于多方案择优

精益求精优化资源配置的实用策略与案例

最优方案选择

面对资源有限时的模板专项施工方案范文使用技巧

资源管理的最佳实践与效率提升案例

2.6-运筹学应用实例汇总

如何在工程项目中应对资源限制和优化利用

优化资源使用的规划方案设计

有效的问题解决方法与实战案例分析

有限资源：如何做出最佳选择

最优方案问题的题

最佳施工方案的筛选与推广案例分析

资源优化管理的策略与成功案例分享

2.6节多种资源限制最优方案选择-案例正文