七年级数学下册-5.3《平行线的性质》习题精选-(新版)新人教版

合集下载

2022-2023学年人教版七年级数学下册《5-3平行线的性质》同步练习题(附答案)

2022-2023学年人教版七年级数学下册《5.3平行线的性质》同步练习题（附答案）一．选择题1．如图，AB∥EC，则下列结论正确的是（）A．∠A＝∠ECD B．∠A＝∠ACE C．∠B＝∠ACE D．∠B＝∠ACB 2．如图，已知AB∥EF，DE∥BC，则与∠1相等的角有（）A．1个B．2个C．3个D．4个3．已知直线m∥n，将一块含30°角的直角三角板ABC按如图方式放置（∠ABC＝30°），其中A，B两点分别落在直线m，n上，若∠1＝20°，则∠2的度数为（）A．20°B．30°C．45°D．50°4．如图，在△ABC中，∠ACB＝90°，CD∥AB，∠ACD＝40°，则∠B的度数为（）A．40°B．50°C．60°D．70°5．如图，直线a∥b，直线c与a、b相交，∠1＝55°，则∠2＝（）6．如图，将矩形ABCD沿GH折叠，点C落在点Q处，点D落在AB边上的点E处，若∠AGE＝32°，则∠GHC等于（）A．112°B．110°C．108°D．106°7．如图，直线a，b，a∥b，点C在直线b上，∠DCB＝90°，若∠1＝70°，则∠2的度数为（）A．20°B．25°C．30°D．40°8．如图，一条公路修到湖边时，需拐弯绕湖而过，如果第一次拐弯处的∠A是66°，第二次拐弯处的角是∠B，第三次拐弯处的∠C是153°，这时道路恰好和第一次拐弯之前的道路平行，则∠B是（）A．87°B．93°C．39°D．109°9．一艘轮船从A港出发，沿着北偏东63°的方向航行，行驶至B处时发现前方有暗礁，所以转向北偏西27°方向航行，到达C后需要把航向恢复到出发时的航向，此时轮船航行的航向向顺时针方向转过的度数为（）10．一把直尺与一块直角三角板按如图方式摆放，若∠1＝47°，则∠2＝（）A．40°B．43°C．45°D．47°二．填空题（共6小题）11．如图，已知AB∥CD，CE平分∠ACD，交AB于点B，∠ABE＝150°，则∠A为．12．如图，AB∥DE，FC⊥CD于点C，∠ABC＝107°，∠CDE＝130°，点G在BC的延长线上，则∠FCG的度数是．13．如图，直线a∥b，直线c与直线a，b分别交于点A，B．若∠1＝45°，则∠2＝．14．如图，直线a∥b，一块含60°角的直角三角板ABC（∠A＝60°），按如图所示放置，若∠1＝55°，则∠2的度数为．15．如图，已知l1∥l2，直线l与l1、l2相交于C、D两点，把一块含30°角的三角尺按如图位置摆放．若∠1＝130°，则∠2＝．16．如图1是我们常用的折叠式小刀，图2中刀柄外形是一个矩形挖去一个小半圆，其中刀片的两条边缘线可看成两条平行的线段，转动刀片时会形成如图2所示的∠1与∠2，则∠1与∠2的度数和是度．三．解答题（共6小题）17．如图：已知AB∥DE∥CF，若∠ABC＝70°，∠CDE＝130°，求∠BCD的度数．18．如图，MN∥BC，BD⊥DC，∠1＝∠2＝60°．（1）AB与DE平行吗？请说明理由；（2）若DC是∠NDE的平分线．①试说明∠ABC＝∠C；②试说明BD是∠ABC的平分线．19．如图所示，已知AB∥CD，分别探讨下面四个图形中，∠APC，∠P AB与∠PCD的关系．20．如图所示，直线a∥b，AC丄AB，AC交直线b于点C，∠1＝60°，求∠2的度数．21．如图，∠BAP+∠APD＝180°，∠1＝∠2，求证：∠E＝∠F．22．如图，已知AB∥ED，∠C＝90°，∠ABC＝∠DEF，∠D＝130°，∠F＝100°，求∠E的大小．参考答案一．选择题1．解：∵AB∥EC，∴∠A＝∠ACE，∠B＝∠ECD．故选：B．2．解：如图所示，与∠1相等的角有∠B、∠DEF、∠EFC共3个，故选：C．3．解：∵直线m∥n，∴∠2＝∠ABC+∠1＝30°+20°＝50°，故选：D．4．解：∵CD∥AB，∠ACD＝40°，∴∠A＝∠ACD＝40°，∵在△ABC中，∠ACB＝90°，∴∠B＝90°﹣∠A＝50°．故选：B．5．解：∵a∥b，∴∠1＝∠3，∵∠1＝55°，∴∠3＝55°，又∵∠2＝∠3，∴∠2＝55°，故选：A．6．解：∵∠AGE＝32°，∴∠DGE＝148°，由折叠可得，∠DGH＝∠DGE＝74°，∵AD∥BC，∴∠GHC＝180°﹣∠DGH＝106°，故选：D．7．解：∵∠1＝70°，∠1与∠3是对顶角，∴∠3＝∠1＝70°．∵a∥b，点C在直线b上，∠DCB＝90°，∴∠2+∠DCB+∠3＝180°，∴∠2＝180°﹣∠3﹣∠DCB＝180°﹣70°﹣90°＝20°．故选：A．8．解：如图：过B作直线b平行于拐弯之前的道路a，由平行线的传递性得a∥b∥c，∵a∥b，∴∠A＝∠1＝66°，∵b∥c，∴∠2＝180°﹣∠C＝180°﹣153°＝27°，∴∠ABC＝∠1+∠2＝66°+27°＝93°．故选：B．9．解：根据题意，得AE∥BF，AM∥CN；∠A＝63°，∠FBC＝27°．∵AE∥BF，∴∠1＝∠A＝63°．∵AM∥CN，∴∠DCN＝∠DBM＝∠1+∠FBC＝63°+27°＝90°．故选：C．10．解：方法1：如图，∵∠1＝47°，∠4＝45°，∴∠3＝∠1+∠4＝92°，∵矩形对边平行，∴∠5＝∠3＝92°，∵∠6＝45°，∴∠2＝180°﹣45°﹣92°＝43°．方法2：如图，作矩形两边的平行线，∵矩形对边平行，∴∠3＝∠1＝47°，∵∠3+∠4＝90°，∴∠4＝90°﹣47°＝43°∴∠2＝∠4＝43°．故选：B．二．填空题11．解：∠ABC＝180°﹣∠ABE＝180°﹣150°＝30．∵AB∥CD，∴∠BCD＝∠ABC＝30°．∵CE平分∠ACD，∴∠ACD＝2∠BCD＝60°．∴∠A＝180°﹣∠ACD＝180°﹣60°＝120°．故答案为：120°．12．解：过点C作CH∥AB∴∠GCH＝∠ABC＝107°∴∠HCD+∠CDE＝180°∴∠HCD＝180°﹣130°＝50°∴∠GCD＝∠GCH﹣∠HCD＝107°﹣50°＝57°∴∠FCG＝90°﹣57°＝33°．故答案为33°．13．解：∵直线a∥b，∠1＝45°，∴∠3＝45°，∴∠2＝180°﹣45°＝135°．故答案为：135°．14．解：∵∠1＝55°，∠A＝60°，∴∠3＝∠4＝65°，∵a∥b，∴∠4+∠2＝180°，∴∠2＝115°．故答案为：115°．15．解：∵∠1＝130°，∴∠3＝50°，又∵l1∥l2，∴∠BDC＝50°，又∵∠ADB＝30°，∴∠2＝20°，故答案为：20°．16．解：如图2，AB∥CD，∠AEC＝90°，作EF∥AB，则EF∥CD，所以∠1＝∠AEF，∠2＝∠CEF，所以∠1+∠2＝∠AEF+∠CEF＝∠AEC＝90°．故答案为90．三．解答题17．解：∵AB∥CF，∠ABC＝70°，∴∠BCF＝∠ABC＝70°，又∵DE∥CF，∠CDE＝130°，∴∠DCF+∠CDE＝180°，∴∠DCF＝50°，∴∠BCD＝∠BCF﹣∠DCF＝70°﹣50°＝20°．18．解：（1）AB∥DE，理由如下：∵MN∥BC，（已知）∴∠ABC＝∠1＝60°．（两直线平行，内错角相等）又∵∠1＝∠2，（已知）∴∠ABC＝∠2．（等量代换）∴AB∥DE．（同位角相等，两直线平行）；（2）①∵MN∥BC，∴∠NDE+∠2＝180°，∴∠NDE＝180°﹣∠2＝180°﹣60°＝120°．∵DC是∠NDE的平分线，∴∠EDC＝∠NDC＝∠NDE＝60°．∵MN∥BC，∴∠C＝∠NDC＝60°．∴∠ABC＝∠C．②∠ADC＝180°﹣∠NDC＝180°﹣60°＝120°，∵BD⊥DC，∴∠BDC＝90°．∴∠ADB＝∠ADC﹣∠BDC＝120°﹣90°＝30°．∵MN∥BC，∴∠DBC＝∠ADB＝30°．∴∠ABD＝∠DBC＝∠ABC．∴BD是∠ABC的平分线．19．解：图1：∠APC＝∠P AB+∠PCD．理由：过点P作PE∥AB，∵AB∥CD，∴AB∥PE∥CD（平行线的传递性），∴∠1＝∠A，∠2＝∠C，∴∠APC＝∠1+∠2＝∠P AB+∠PCD，即∠APC＝∠P AB+∠PCD；图2：∠APC+∠P AB+∠PCD＝360°．理由：过点P作PE∥AB．∵AB∥CD，∴AB∥PE∥CD（平行线的传递性），∴∠A+∠1＝180°，∠2+∠C＝180°，∴∠A+∠1+∠2+∠C＝360°，∴∠APC+∠P AB+∠PCD＝360°；图3：∠APC＝∠PCD﹣∠P AB．理由：延长DC交AP于点E．∵AB∥CD，∴∠1＝∠P AB（两直线平行，同位角相等）；又∵∠PCD＝∠1+∠APC，∴∠APC＝∠PCD﹣∠P AB；图4：∴∠P AB＝∠APC+∠PCD．理由：∵AB∥CD，∴∠1＝∠P AB（两直线平行，内错角相等）；又∵∠1＝∠APC+∠PCD，∴∠P AB＝∠APC+∠PCD．20．解：∵AC丄AB，∴∠BAC＝90°，∵∠1＝60°，∴∠B＝180°﹣∠1﹣∠BAC＝30°，∵a∥b，∴∠2＝∠B＝30°．21．证明：∵∠BAP+∠APD＝180°（已知），∴AB∥CD（同旁内角互补，两直线平行）．∴∠BAP＝∠APC（两直线平行，内错角相等）．又∵∠1＝∠2（已知），∴∠FP A＝∠EAP，∴AE∥PF（内错角相等，两直线平行）．∴∠E＝∠F（两直线平行，内错角相等）．22．解：延长DC、AB交于G，∵ED∥AB，∠D＝130°，∴∠G＝50°，又∵∠BCD＝90°，∠BCD＝∠G+∠CBG，∴∠CBG＝40°，∴∠ABC＝140°，∴∠E＝∠ABC＝140°．。

人教版数学七年级下册《5.3平行线的性质》基础训练(含答案)

人教版数学七年级下册5.3 平行线的性质基础训练一、选择题1.如图，直线a∥b,∠1=60°，则∠2=( B )A.30°B.60°C.45°D.120°2.下列命题是真命题的有( B )①有一条公共边的角叫做邻补角；②若两个角是直角，则这两个角相等;③直线外一点到这条直线的垂线段的长度，叫做点到直线的距离.A.0个B.1个C.2个D.3个3. 如图,BD平分∠ABC,DE∥BC,则图中相等的角共有( D )A. 2对B. 3对C. 4对D. 5对4.下列命题：①若|a|＞|b|，那么a2＞b2；②两点之间，线段最短；③对顶角相等；④内错角相等．其中真命题的个数是(C)A．1个B．2个C．3个D．4个5.如图，把一个直角三角尺的直角顶点放在直尺的一边上，若∠1=50°,则∠2=( C )A.20°B.30°C.40°D.50°6.下列说法不正确的是( C )A.证实命题正确与否的推理过程叫做证明B.定理是命题,而且是真命题C.“对顶角相等”是命题，但不是定理D.要证明一个命题是假命题只要举出一个反例即可7. 如图,AB∥EF,CD⊥EF,∠BAC=50°,则∠ACD=( B )A. 120°B. 130°C. 140°D. 150°8. 如图，直线l1∥l2，l3⊥l4，∠1＝44°，那么∠2的度数为( A )A．46° B．44° C．36° D．22°9.如图，已知c⊥a,c⊥b，直线b，c，d交于一点，若∠1=50°，则∠2等于( B )A.60°B.50°C.40°D.30°10.如图，AB∥CD∥EF，AC∥DF，若∠BAC=120°，则∠CDF=(A )A.60°B.65°C.50°D.45°11.对于命题“若a2＞b2,则a＞b”，下面四组关于a,b的值中，能说明这个命题是假命题的是( C )A.a=3,b=2B.a=-3,b=2C.a=3,b=-1D.a=-1,b=312.如图，点A在直线BG上,AD∥BC，AE平分∠GAD，若∠CBA=80°,则( C )A.60°B.50°C.40°D.30°二、填空题13.如图AC∥DF,AB∥EF，点D，E分别在AB，AC上，若∠2=50°，则∠1的度数为 .【答案】50°14.把命题“对顶角相等”改写成“如果……那么……”的形式: .【答案】如果两个角是对顶角，那么这两个角相等15. 如图，AB∥EF，BC∥DE，则∠E+∠B的度数为________．【答案】180°16.如图，点D,E分别在AB，BC上，DE∥AC，AF∥BC，∠1=70°，则∠2= °.【答案】1017.用一组a，b，c的值说明命题“若 a＜b，则ac＜bc”是错误的，这组值可以是a=,b=,c=. __【答案】23 -1(答案不唯一）18.如图，若∠∠，，则∠与∠的关系是________．【答案】相等三、解答题19.如图，已知直线AB∥DF,∠D+∠B=180°.(1)试说明DE∥BC；(2)若∠AMD=75°，求∠AGC的度数.解析：(1)∵AB∥DF,∴∠D+∠BHD= 180°,∵∠D+∠B=∠DHB,∴DE∥BC.(2)由（1)知 DE∥BC,∴∠AGB=∠AMD=75°,∴AGC=180°-∠AGB =180°-75°= 105°.20.如图，现有以下三个条件：①AB∥CD,②∠B=∠C,③∠E=∠F.请你以其中两个作为题设，另一个作为结论构造命题.(1)你构造的是哪几个命题？(2)你构造的命题是真命题还是假命题？若是真命题，请给予证明;若是假命题，请举出反例.解析：(1)如果①②，那么③;如果①③，那么②;如果②③，那么①.(2)“如果①②,那么③”是真命题.证明如下：AB CD,B CDF.BC C=CDF,CE BF,E= F.,.AB CD,:. B CDF.E F,CE BF, C CDF,AB CD.∴∠=∠∠=∠∴∠∠∴∴∠∠∠=∠∠=∠∴∴∠=∠∴∥又，∥“如果①③那么②”是真命题证明如下：∥∥∥E=F CE BF C=CDF.B= C B=CDF AB CD∠∠∴∴∠∠∠∠∴∠∠∴“如果②③，那么①”是真命题.证明如下：， ∥，又，，∥21.如图，直线AB ∥CD ，BC 平分∠ABD ，∠1＝65°，求∠2的度数．解：∵直线AB ∥CD ，∠1＝65°，∴∠ABC ＝∠1＝65°.∵BC 平分∠ABD ，∴∠ABD ＝2∠ABC ＝130°.∵直线AB ∥CD ，∴∠ABD ＋∠BDC ＝180°.∴∠2＝∠BDC ＝180°－∠ABD ＝180°－130°＝50°.22.如图，在四边形ABCD,若AB ∥CD,点P 为BC 上一点，设∠CDP=∠α,∠DPC=∠3，当点P 在BC 上运动时，∠α，∠β的和与∠B之间有何关系？请证明你的结论.解析：B.P PQ CD AD Q,DPQ=(.AB CD(PQ AB(B=CPQ CPQ DPQ ,a B(αβαββ∠+∠=∠∠∠∠∠∠=∠+∠∠+∠=∠证明如下：过点作∥交于点则两直线平行，内错角相等）因为∥已知)，所以∥平行公理的推论)，所以(两直线平行，同位角相等）.又所以等量代换).。

七年级数学人教版下册 5.3平行线的性质作业(含答案)

人教版七年级数学下册 5.3平行线的性质一、选择题1．如图，已知直线a ∥b ，直线c 与直线a ，b 分别交于点A ，B ．若∥1＝54°，则∥2等于（）A ．126°B ．134°C ．136°D ．144°2．如图，有,,A B C 三个地点，且AB BC ⊥，从A 地测得B 地的方位角是北偏东43︒，那么从C 地测B 地的方位角是（）A ．南偏东47︒B ．南偏西43︒C ．北偏东43︒D ．北偏西47︒3．如图，AB ∥CD ，∥1＝∥2，∥3＝130°，则∥2等于（）A ．30°B ．25°C ．35°D ．40°4．如图，//AB CD ，EC 分别交,AB CD 于点,F C ，链接DF ，点G 是线段CD 上的点，连接FG ，若13∠=∠，24∠∠=，则结论∥C D ∠=∠，∥FG CD ⊥，∥EC FD ⊥，正确的是（）A ．∥∥B ．∥∥C ．∥∥D ．∥∥∥5．已知，如图，点D 是射线AB 上一动点，连接CD ，过点D 作//DE BC 交直线AC 于点E ，若84ABC ∠=︒，20CDE ∠=︒，则ADC ∠的度数为（）A ．104︒B ．76︒C ．104︒或76︒D ．104︒或64︒6．一艘船停留在海面上，如果从船上看灯塔位于北偏东30°，那么从灯塔看船上位于灯塔的（）A ．北偏东30°B ．北偏东60°C ．南偏西30°D ．南偏西60°7．如图，a ，b 是两条平行的小路，小何沿与小路b 的夹角为55°的方向前进，到点O 处时，向左拐60°继续前进，则他拐弯后的路线与小路a 的夹角（∥1）的度数是（）A ．50°B ．55°C ．65°D ．75°8．小明和小亮在研究一道数学题，如图EF AB ⊥，CD AB ⊥，垂足分别为E 、D ，G 在AC 上．小明说：“如果CDG BFE ∠=∠，则能得到AGD ACB ∠=∠”；小亮说：“连接FG ，如果//FG AB ，则能得到GFC ADG ∠=∠”．则下列判断正确的是（）A ．小明说法正确，小亮说法错误B ．小明说法正确，小亮说法正确C ．小明说法错误，小亮说法正确D ．小明说法错误，小亮说法错误9．已知，//AB CD ，且2CD AB =，ABE △和CDE △的面积分别为2和8，则ACE △的面积是（）A ．3B ．4C ．5D ．610．下列命题中，真命题是（）A ．同位角相等B ．同旁内角相等的两直线平行C ．同旁内角互补D ．平行于同一条直线的两直线平行二、填空题11．如图，直线//AB CD ，BC 平分ABD ∠，若162∠=︒，则2∠=________．12．把一张对边互相平行的纸条，折成如图所示，EF 是折痕，若32EFB ∠=︒，则下列结论：（1）'32C EF ∠=︒；（2）148AEC ∠=︒；（3）64BGE ∠=︒；（4）116BFD ∠=︒．正确的有________个．13．一副直角三角板叠放如图∥，90C E ∠=∠=︒．现将含45︒角的三角板ADE 固定不动，把含30角的三角板ABC（其中30CAB ∠=︒）绕顶点A 顺时针旋转角()0180αα︒<<︒．（1）如图∥，当α=______度时，边BC 和边AE 所在的直线互相垂直；（2）当旋转角α在30180α︒<<︒的旋转过程中，使得两块三角板至少有一组对应边（所在的直线）互相平行，此时符合条件的α=______．14．如图，a ∥b ，∥1＝68°，∥2＝42°，则∥3＝_____________．15．在平面直角坐标系中，点A 在x 轴负半轴上，点B 在y 轴正半轴上，且60ABO ∠=︒，射线BA 以每秒9︒的速度绕B 点顺时针方向旋转至射线1BA ，M 为x 轴正半轴上一点，射线MO 以每秒6︒的速度绕M 点逆时针方向旋转至射线1MO ，设运动时间为t 秒()030t <<，当t =______秒时，11//BA MO ．三、解答题16．如图，已知∥1=∥2，AD =2BC ，三角形ABC 的面积为3，求三角形CAD 的面积．17．如图，已知//AD EF ，250∠=︒．（1）求3∠的度数：（2）若12∠=∠，问：//DG BA 吗？请说明理由；（3）若12∠=∠，且20DAG ∠=︒，求AGD ∠的度数．18．如图，已知直线AB //EF ，AB //CD ，∥ABE =50°，EC 平分∥BEF ，求∥DCE 的度数．19．如图，13180∠+∠=︒，CD AD ⊥于D ，CM 平分DCE ∠．求4∠的度数．20．如图，AE BC ⊥，DF BC ⊥，且12∠=∠．（1）判断AB 与CD 是否平行，并请说明理由；（2）若BC 平分ABD ∠，且390BDC ∠=∠+︒，求C ∠的度数．21．如图，AB//CD ，点M 为两直线之间一点．（1）如图1，若∥AEM 与∥CFM 的平分线交于点N ，若∥EMF=88°，求∥ENF 的度数．（2）如图2，若∥AEM 与∥CFM 的平分线交于点N ，∥EMF 与∥ENF 有何数量关系？并证明你的结论．（3）如图3，若∥AEM 的平分线与∥DFM 的平分线所在的直线交于点N ，请直接写出∥EMF 与∥ENF 之间的数量关系：．22．如图，已知直线//AB CD ，100A C ∠=∠=︒，E 、F 在CD 上，且满足DBF ABD ∠=∠，BE 平分CBF ∠．（1）直线AD 与BC 有何位置关系？请说明理由．（2）求DBE ∠的度数．（3）若平行移动AD ，在平行移动AD 的过程中，存在使BEC ADB ∠=∠的情况，求ADB ∠的度数．23．为了安全起见在某段铁路两旁安置了两座可旋转探照灯．如图1所示，灯A 射线从AM 开始顺时针旋转至AN 便立即回转，灯B 射线从BP 开始顺时针旋转至BQ 便立即回转，两灯不停交又照射巡视．若灯A 转动的速度是每秒2度，灯B 转动的速度是每秒1度．假定主道路是平行的，即//PQ MN ，且:3:2BAM BAN ∠∠=．（1）填空：BAN ∠=_________；（2）若灯B 射线先转动30秒，灯A 射线才开始转动，在灯B 射线到达BQ 之前，A 灯转动几秒，两灯的光束互相平行？（3）如图2，若两灯同时转动，在灯A 射线到达AN 之前．若射出的光束交于点C ，过C 作ACD ∠交PQ 于点D ，且126ACD ∠=︒，则在转动过程中，请探究BAC ∠与BCD ∠的数量关系是否发生变化？若不变，请求出其数量关系；若改变，请说明理由．【参考答案】1．A 2．A 3．B 4．B 5．D 6．C 7．C 8．A 9．B 10．D11．56°12．313．15 60°或105°或135°14．110°15．2秒或14秒或26秒16．617．（1）50°；（2）平行；（3）110°18．∥DCE =155°19．45°20．（1）平行；（2）30C ∠=︒．21．（1）44°；（2）∥EMF +2∥ENF =360°；（3）∥ENF +12EMF ∠=90°． 22．（1）直线AD 与BC 互相平行；（2）40DBE ∴∠=︒（3）存在，60BEC ADB ∠=∠=︒． 23．（1）72°；（2）30秒或110秒；（3）不变，∥BAC =2∥BCD。

人教版初中数学七年级下《5.3平行线的性质》同步练习题(含答案)

人教版初中数学七年级下《5.3平行线的性质》同步练习题《平行线的性质》同步练习1课堂作业1．下列图形表示平面内直线AB∥CD的是()A．B．C．D．2．下列说法正确的是()A．同一平面内没有公共点的两条线段平行B．两条不相交的直线是平行线C．同一平面内没有公共点的两条线平行D．同一平面内没有公共点的两条射线平行3．经过直线外一点画直线，下列说法错误的是()A．可以画无数条直线与这条直线相交B．可以画无数条直线与这条直线平行C．能且只能画一条直线与这条直线平行D．能且只能画一条直线与这条直线垂直4．如图，写出图中所有的平行线：________．5．根据下列要求画图：(1)如图①，过点A画MN∥BC；(2)如图②，过点P画PE∥OB，交OA于点E；(3)如图③，过点C画CE∥DA，交AB于点E，交DB于点H；过点C画CF∥DB，交AB的延长线于点F．课后作业6．在同一平面内，一条直线与另外两条平行直线的位置关系是()A．一定与两条平行直线相交B．与两条平行直线中的一条平行，而与另一条相交C．一定与两条平行直线平行D．与两条平行直线都平行或都相交7．下列说法：①一条直线的平行线只有一条；②过一点与已知直线平行的直线只有一条；③因为a∥b，c∥d，所以a∥d；④经过直线外一点，有且只有一条直线与这条直线平行．其中，正确的有() A．1个B．2个C．3个D．4个8．a、b、c是平面上的任意三条直线，它们的交点可以有()A．1个或2个或3个B．0个或1个或2个或3个C．1个或2个D．以上都不正确9．已知直线a、b都过点M，且直线a∥l，b∥l，那么直线a、b是同一条直线，根据是________．10．将一张长方形的硬纸片ABCD对折后打开，折痕为EF，把长方形ABEF平摊在桌面上．另一面CDFE无论怎样改变位置，总有CD∥AB，理由是________．11．如图，P为直线AB外一点，读下列语句画图形：(1)过点P画PC⊥AB，垂足为C；(2)过点P画PD∥AB；(3)观察图形，猜想PC与PD的位置关系(不要求说明理由)．12．如图，直线AB、CD是一条河的两岸，并且AB∥CD，E为直线AB、CD外一点，现想过点E画岸CD的平行线，只需过点E画岸AB的平行线即可．画图，并说明理由．13．如图，AD∥BC，AE＝BE．(1)过点E画EF∥BC，交DC于点F．(2)AD与EF平行吗？为什么？(3)通过测量，试判断等式DF＝CF与1()2EF AD BC=+是否成立．答案[课堂作业]1．B2．C3．B4．AB∥CD，EF∥BH5．略[课后作业]6．D7．A8．B9．经过直线外一点，有且只有一条直线与已知直线平行10．如果两条直线都与第三条直线平行，那么这两条直线也互相平行11．(1)如图所示(2)如图所示(3)PC⊥PD12．图略理由：如果两条直线都与第三条直线平行，那么这两条直线也互相平行．13．(1)略(2)略(3)两个等式都成立《平行线的性质》同步练习21．平面内两条________的直线叫平行线，如果直线a与直线b平行可记为______，读作_________．2．经过直线外一点，__________与这条直线平行．3．如果两条直线和第三条直线______，那么这两条直线平行；若a∥b，b•∥c，•则_______．4．在同一平面内，•不互相重合的两条直线位置关系有_____•种，•它们是____，______．5．在同一平面内L1与L2没有公共点，则L1______L2．6．在同一平面内L1和L2有一个公共点，则L1与L2______．7．在同一平面内，不重合的两条直线的位置关系有_______种，分别是________．8．（经典题）设a，b，c为平面内三条不同直线：（1）若a∥b，c⊥a，则b与c的位置关系是______；（2）若a∥b，b∥c，则a与c的位置关系是______．9．（合作探究题）在同一平面内三条直线交点有多少个？甲：同一平面三直线相交交点的个数为0个，因为a∥b∥c，如图（1）所示．乙：同一平面内三条直线交点个数只有1个，因为a，b，c交于同一点O，如图（2）所示．以上说法谁对谁错？为什么？10．请举出一例生活中平行线的例子，如笔直铁路上铁轨是互相平行的直线．举例：__________________参考答案1．不相交，a∥b，a平行于b2．有且只有一条直线3．都平行，a∥c4．2，相交，平行5．∥6．相交7．2，相交，平行8．（1）b⊥C（2）a∥c（点拨：画图来判定）9．甲，乙说法都不对，各自少了三种情况．a∥b，c与a，b相交如图（1），a，b，•c两两相交如图（2），所以三条直线互不重合，交点有0个或1个或2个或3个，共四种情况．解题规律：三条直线在同一平面的位置关系有四种情况，有1个交点，2个交点，•3个交点和0个交点．10．窗户的柱子《平行线的性质》同步练习31．公路两旁的两根电线杆位置关系是________．2．练习本中的横线格中的横线段是_______，如图所示．3．如图所示，AB∥CD，EF与AB，CD相交，EF与AB交于点_____，•EF•与CD•交于______．4．下列说法不正确的是（）A．过马路的斑马线是平行线B．100米跑道的跑道线是平行线C．若a∥b，b∥d，则a⊥dD．过直线外一点有且只有一条直线与已知直线平行5．下列说法正确的是（）A．同一平面内不相交的两线段必平行B．同一平面内不相交的两射线必平行C．同一平面内不相交的一条线段与一条直线必平行D．同一平面内不相交的两条直线必平行6．如图所示，在这些四边形AB不平行于CD的是（）7．（原创题）如图所示，在∠AOB内有一点P．（1）过P画L1∥OA；（2）过P画L2∥OB；（3）用量角器量一量L1与L2相交的角与∠O的大小有怎样关系？8．如图所示，在5×5的网格中，AC是网格中最长的线段，请画出两条线段与AC平行并且过网格的格点．9．（教材变式题）“垂直于同一条直线的两直线平行”，•运用这一性质可以说明铺设铁轨互相平行的道理．如图所示，已知∠2是直角，再度量出∠1或∠3就会知道铁轨平行不平行？方案一：若量得∠3=90°，结合∠2情况，说明理由．方案二：若量得∠1=90°，结合∠2情况，说明理由．10．（原创题）如图所示，在书写艺术字时，常常运用画“平行线段”这种基本作图方法，此图是在书写字“M”：（1）请从正面，上面，右侧三个不同方向上各找出一组平行线段，并用字母表示出来；（2）EF与A′B′有何位置关系？CC′与DH有何位置关系？参考答案1．平行关系2．互相平行的线段3．M，N4．C（点拨：用平行线定义来判定）5．D（点拨：A，B，C都有可能相交）．6．D（点拨：A是平行四边形，B是梯形，C是正方形．）7．（1），（2）如图所示，（3）L1与L2夹角有两个，∠1，∠2，∠1=∠O，∠2+∠O=•180°，所以L1和L2夹角与∠O相等或互补．思路点拨：注意∠2与∠O是互补关系，易漏掉．8．如图所示：EF∥AC，PQ∥AC，MN∥AC，且它们都过格点．解题技巧：过网格格点，EF，PQ，MN与竖直线AB都成45°角，AC与AB成45°，由同位角相等得两直线平行．9．方案一：如果量∠3=90°，而∠2=90°∴两铁轨都与枕木垂直，那么两铁轨就平行．方案二：如果量得∠1=90°，而∠2=90°，∴两铁轨都与枕木垂直，那么两铁轨就平行．思路点拨：运用已知定理及垂直的定义来说明．10．（1）正面：AB∥EF，AE∥MF等等；上面：A′B′∥AB，C′D′∥CD等等；右侧：•DD′∥HR，DH∥D′R（2）EF∥A′B′，CC′⊥DH思路点：（1）在同一平面的两线段平行，假设延长看有无交点；（2）•不在同一平面的线段位置关系判断，可通过两个平面的交线来判定．。

人教版七年级数学下册5.3《平行线的性质》课时练习(简单答案)

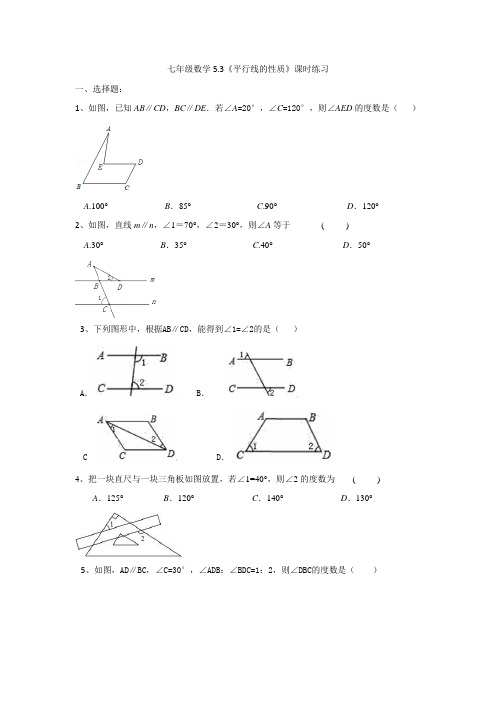
七年级数学5.3《平行线的性质》课时练习一、选择题：1、如图，已知AB∥CD，BC∥DE．若∠A=20°，∠C=120°，则∠AED的度数是（）A.100°B．85°C.90°D．120°2、如图，直线m∥n，∠1＝70°，∠2＝30°，则∠A等于( )A.30°B．35°C.40°D．50°3、下列图形中，根据A B∥CD，能得到∠1=∠2 的是（）A．B．C D．4、把一块直尺与一块三角板如图放置，若∠1=40°，则∠2的度数为( )A．125°B．120°C．140°D．130°5、如图，AD∥B C，∠C=30°，∠AD B：∠BDC=1：2，则∠DBC 的度数是（）A．30° B．36° C．45° D．50°6、如图，若AB∥CD，BF平分∠ABE，DF平分∠CDE，∠BED=80°，则∠BFD的度数是（）A．20°B．30°C．40°D．45°7、将一副直角三角板ABC和DEF如图放置(其中∠A=60︒，∠F=45︒)，使点E落在AC边上，且ED∥BC，则∠CEF的度数为（）A.15°B．35°C.20°D．22.5°8、如图，把一块三角板的直角顶点放在一直尺的一边上，若∠1=50°，则∠2 的度数为（）A．55° B．50° C．45° D．40°二、填空题：9、如图，AB∥CD，AD平分∠BAC，若∠BAD=70°，那么∠ACD的度数为。

DCBA10、如图，AB∥CD，点E在CB的延长线上，若∠ABE=60º，则∠ECD的度数为。

七年级数学下册53平行线的性质教材习题解析素材(新版)新人教版.docx

平行线的性质教材习题解析习题5・3（P22）1.解析：本题考查平行线的性质2.解答木题的关键是，要理解“两次转弯后，和原来的方向相同“的意义，即两次转弯前后的公路所在的直线平行，根据“两直线平行，内错角相等”得，第二次的拐角ZB应等于135*.2.解析：本题考查平行线的性质3.已知AD〃BC,厶・fiT,根据“两直线平行，同旁内角互补”可得，^B-I8（r-Z4-12T;不用度量方法，仅根据平行线的性质，不能求得ZD的度数.因为ZD 与ZA是同旁内角，而直线AB与CD是否平行不得而知，因此不能用平行线的性质來求解.3.解析：本题考查了平行线的三个性质.解题时要弄清楚直线和角的位置关系.（1）由4・1师，根据平行线的性质2 “两直线平行，内错角相等”得，乂2・11叭（2）由zi・mr,根据平行线的性质1 “两直线平行，同位角相等”得，（3）由，根据平行线的性质3“两直线平行，同旁内角互补”得，z<-i8（r-ii（r-7r■4.解析：本题考查平行线的性质2,性质3及性质1（或邻补角定义）.由性质2可求得Z2,由性质3可求得Z3,由性质1（或邻补角定义）可求得Z4.因为。

〃内，根据“两直线平行，内错角相等”，可得因为根据“两直线平行，同旁内角互补”，可得Z3=i8（r-Z5=iior;因为Z4与Z5互为邻补角，所以&・wr-z5・iir （或根据“两直线平行，同位角相等”，可得Z4-Z3-UF）.5.解析：本题考查平行线的性质3的应用.木题求解时，可以把公路两侧的管道看成平行线，对接的管道看作截线，应用“两直线平行，同旁内角互补”可得，另一侧应以iar-iar=«r 的角铺设.6.解析：本题考查平行线的性质和判定的综合应用，以及分析推理能力.解题时，应对照图形区分每一步推理是使用平行线的判定，还是使用平行线的性质，然后再填写理由.答案依次是:内错角相等，两直线平行；两直线平行，内错角相等.7.解析：本题考查平行线的性质2和性质3•第（1）题关键是寻找其中的同位角或内错角.注意到AB〃CD, AC是截线，因此只有Z1和Z4是内错角，它们相等；其他角中没有同位角，不存在相等的关系；第（2）题屮ZACE被CD分为ZACD和ZECD两个角，运用平行线的性质3,由AB〃CD 得到ZBAC+ZACD--W,由CD〃EF 得到ZECD+ZCEF-IW ,所以ZBAC+ ZACE+ ZCEF= ZBAC+ ZACD+ ZECD+ ZCEF-3HT ,本题答案应为（1） C；（2） C.8.解析：本题考查平行线的性质1和性质3的实际运用.解答本题的关键是已知光线平行，同吋水面与水底面也是平行的，然后根据平行线的性质可以求出各角.由“两直线平行，同位角相等”得，Z4-Z2-m.由“两直线平行，同旁内角互补”得，心・1抄-/4・瑚，Z7-18T -Zl-137 , ZB-I80T -0・BT9.解析：本题考查文字语言与符号语言的互相转化，及平行线的判定与性质.用式子表示一些三段论推理的句子，一方面可以培养学生儿何不同语言相互转化的能力，另一方面, 通过用符号表示一些简单的推理过程，为后面学习证明做准备.（1） VZ1=Z2（已知），・・・AB〃EF（内错角相等，两直线平行）；（2）・・・DE〃BC（已知）,AZ1=ZB, Z3=ZC（两直线平行，同位角相等）.10.解析：本题考查平行线、垂线在生活中的运用，涉及如何画平行线、垂线的问题.答案略.11.解析：本题考查相交线、垂线、平行线在生活中的应用.画好一个篮球场地，需要用到许多垂线、平行线的知识，通过解决这样一个问题，让学生感受到平行线知识在实际生活中的应用.第（1）题答案不唯一，比如操场上的单杠与立柱垂直，双杠中的两根杠子平行等等；第（2）题在纸上画篮球场地，可以用直角三角板或平行线的性质来保证垂直.画平行线可以用推三角尺的方法或用平行线的判定方法来操作.画图略.12.解析：本题考查真、假命题的概念和判断，以及如何说明一个命题是假命题，体会反例的作用.（1）假命题，比如：冊和70•都是锐角，但它们的和1处不是锐角;(2)真命题；(3)假命题，只要作出一对不互补的同旁内角即可，例如一个三角形中，任意两个内角都可以看作是同旁内角，但它们不互补.13.解析：本题考查分析推理能力和对证明过程的理解，主要是填写证明过程川的关键步骤和理由，涉及平行线的性质、角平分线的定义、等量代换等知识.答案依次是：(1)ZC；两直线平行，内错角相等；两直线平行，同旁内角互补.(2)2 ；角平分线的定义；等量代换(或等式的性质).14.解析：本题考查平行线的性质、平角的定义等.本题是证明三角形内角和定理的另一种方法.(1)ZDAB二44°,因为DE〃BC,根据“两直线平行,内错角相等”可得,ZDAB=ZB=44°；(2)ZEAC=57°,因为DE〃BC,根据“两直线平行，内错角相等”可得,ZEAC=ZC=57°；(3)ZBAC=79°，因为ZDAE 是平角，所以ZBAC=180° -ZDAB-ZEAC=180° -44° -57° =79°・由以上结论可得：ZB+ZC+ZBAC二180°,这实际上说明了三角形三个内角和为180° .15.解析：本题考查平角的定义、平行线的性质和判定的综合应用等•解答时关键要认识到两面镜子是平行的，从而Z2与Z3是一对内错角，所以它们相等.本题要求说明两条光线平行，需要分析这两条光线是被哪一条直线所截，形成了哪些角？这些角有什么数量关系，进而发现形成的Z5与Z6是一对内错角，只要Z5与Z6相等，就能说明这两条光线平行.因为两而镜子是平行放置的，根据“两直线平行，内错角相等”可得，由平角等于1ST 可得，Z5-IW-Z1-Z2 , ZB-l8(r-z3-Z4 .因为Z1-Z2,厶所以又由“内错角相等，两直线平行”可以判断，进入潜望镜的光线与离开潜望镜的光线是平行的.。

七年级数学下册5.3平行线的性质典型例题素材新人教版(new)

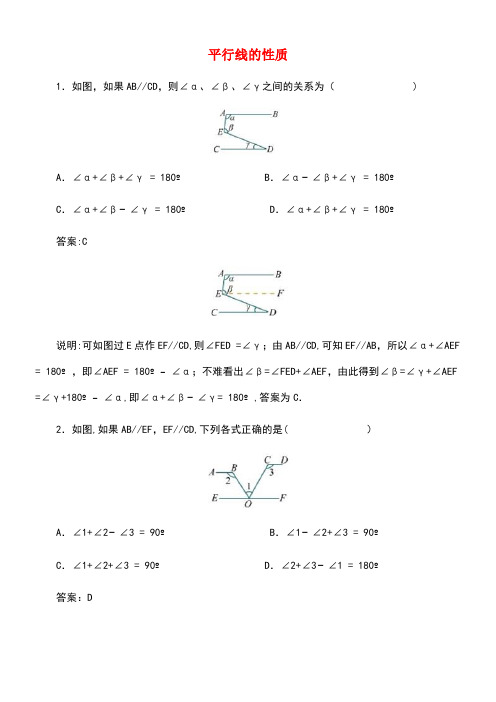
平行线的性质1．如图，如果AB//CD，则∠α、∠β、∠γ之间的关系为（ )A．∠α+∠β+∠γ = 180ºB．∠α−∠β+∠γ = 180ºC．∠α+∠β−∠γ = 180ºD．∠α+∠β+∠γ = 180º答案:C说明:可如图过E点作EF//CD,则∠FED =∠γ；由AB//CD,可知EF//AB，所以∠α+∠AEF = 180º，即∠AEF = 180º−∠α；不难看出∠β=∠FED+∠AEF，由此得到∠β=∠γ+∠AEF =∠γ+180º−∠α,即∠α+∠β−∠γ= 180º,答案为C．2．如图,如果AB//EF，EF//CD,下列各式正确的是( ）A．∠1+∠2−∠3 = 90ºB．∠1−∠2+∠3 = 90ºC．∠1+∠2+∠3 = 90ºD．∠2+∠3−∠1 = 180º答案：D说明：由AB//EF,得到∠2 =∠BOF，再由CD//EF,得到∠3+∠COF = 180º，因为∠COF = ∠BOF−∠1,所以有∠3+∠BOF−∠1 = 180º，即∠3+∠2−∠1 = 180º，答案为D．3．如图所示．已知:AD∥BC，∠AEF=∠B，求证：AD∥EF．分析：(执果索因)从图直观分析,欲证AD∥EF，只需∠A+∠AEF=180°，(由因求果）因为AD∥BC,所以∠A+∠B=180°,又∠B=∠AEF，所以∠A+∠AEF=180°成立．于是得证．证明：因为 AD∥BC，（已知）所以∠A+∠B=180°．（两直线平行,同旁内角互补）因为∠AEF=∠B，(已知)所以∠A+∠AEF=180°，(等量代换)所以 AD∥EF．（同旁内角互补，两条直线平行）4．如图所示,AB∥CD，AC∥BD．找出图中相等的角与互补的角．A B此题一定要强调，哪两条直线被哪一条直线所截．答：相等的角为:∠1=∠2，∠3=∠4，∠5=∠6，∠7=∠8．互补的角为：∠BAC+∠ACD=180°，∠ABD+∠CDB=180°，∠CAB+∠DBA=180°，∠ACD+∠BDC=180°．相等的角还有：∠ACD=∠ABD，∠BAC=∠BDC．(同角的补角相等)尊敬的读者：本文由我和我的同事在百忙中收集整编出来，本文档在发布之前我们对内容进行仔细校对，但是难免会有不尽如人意之处，如有疏漏之处请指正，希望本文能为您解开疑惑,引发思考。

(新人教版)数学七年级下册：5.3.1《平行线的性质》同步练习两套(含答案)

平行线的性质习题一、填空题.1.用式子表示下列句子:用∠1与∠2互为余角,又∠2与∠3互为余角,根据“同角的余角相等”，所以∠1和∠3相等_________________.2.把命题“直角都相等”改写成“如果……，那么……”形式___________.3.命题“邻补角的平分线互相垂直”的题设是_____________, 结论是____________.4.两条平行线被第三条直线所截,同旁内角的度数的比为2:7, 则这两个角分别是____________度.二、选择题.1.设a、b、c为同一平面内的三条直线,下列判断不正确的是( )A.设a⊥c,b⊥c,则a⊥bB.若a∥c,b∥c,则a∥bC.若a∥b,b⊥c,则a⊥cD.若a⊥b,b⊥c,则a⊥c2.若两条平行线被第三条直线所截,则互补的角但非邻补角的对数有( )A.6对B.8对C.10对D.12对3.如图,已知AB∥DE,∠A=135°,∠C=105°,则∠D的度数为( )A.60°B.80°C.100°D.120°E D CBA4.两条直线被第三条直线所截,则一组同位角的平分线的位置关系是( )A.互相平行B.互相垂直;C.相交但不垂直D.平行或相交三、解答题.1.已知,如图1,∠AOB纸片沿CD折叠,若O′C∥BD,那么O′D与AC平行吗?请说明理由.O '4321ODCBA2.如图,已知B 、E 分别是AC 、DF 上的点,∠1=∠2,∠C=∠D. (1)∠ABD 与∠C 相等吗?为什么.(2)∠A 与∠F 相等吗?请说明理由.FE21DCBA3.如图,已知EAB 是直线,AD ∥BC,AD 平分∠EAC,试判定∠B 与∠C 的大小关系,并说明理由.E D CBA4.如(图4),DE∥AB,DF∥AC,∠EDF=85°,∠BDF=63°. (1)∠A 的度数; (2)∠A+∠B+∠C 的度数.F EDCBA答案:一、1.因为∠2+∠1=90° 又∠2+∠3=90°,所以∠1=∠3(同角的余角相等)2.如果两个角是直角,那么这两个角相等3.两个角是邻补角,这两个角的平分线互相垂直4.40°,140°二、1.D 2.B 3.D 4.D三、1.平行因为O′C∥BD所以∠2=∠3(两直线平行,内错角相等)又∠1=∠2,∠3=∠4所以∠1=∠4所以AC∥O′D(内错角相等,两直线平行)2.(1)相等.因为∠1=∠2,所以BD∥CE(内错角相等,两直线平行)所以∠ABD=∠C(两直线平行,同位角相等)(2)相等因为∠ABD= ∠C 又∠D=∠C所以∠D=∠ABD所以DF∥AC(内错角相等,两直线平行)所以∠A=∠F( 两直线平行,内错角相等)3.∠B=∠C 因为AD∥BC所以∠B=∠EAD(两直线平行, 同位角相等),∠C=∠CAD(两直线平行,内错角相等)又∠EAD=∠CAD(角平分线定义)所以∠B=∠C平行线的性质检测评估1.(2004江苏无锡)如图，已知a∥b，∠2=140°，则∠1= °2.如图1：当AD∥BC时,∠DAC＝∠________.图1 图2 图33.如图2：AB∥CD , A＝98°,∠C＝75°,∠B=_____度,∠D＝_____°.4.如图3：AB∥CD,∠A＝80°,∠B＝60°,则∠ACB＝____________度.5.如图4, 已知: AP∥CQ, PB∥QD, ∠P＝80°则∠Q＝________°图4 图66.一个人在公路上东行, 两次拐弯后仍向东行, 第一次拐的角是90度. 那么第二次拐的角应为_____°.7.如图6, 已知ED∥AB, 则: ∠DCB＋∠D＋∠B＝___________度.8.两条平行线被第三条直线所截,一组同旁内角的平分线的位置关系是相交成__角.9.在同一平面内如果a⊥b, c⊥b, 则直线a, c的位置关系为（）．A.平行B.垂直C.相交但不垂直D.无法确定10. 若两个角的一边在同一条直线上, 另一边互相平行, 那么这两个角的关系是（）．A.相等B.互补C.相等且互补D.相等或互补11.如右图：∠1=∠2 你能用两种方法说明∠3=∠4相等吗?12.观察探索题如图，已知三角形ABC，延长BC到D，过点C作CE∥AB．由于AB∥CE，所以可得到∠B＝∠3和∠A＝∠2．又因为∠1＋∠2＋∠3组成一ABC的三个内角的和为180°，即∠A＋∠B＋∠ACB＝180°．试根据以上叙述，写出已知、求证及说明∠A＋∠B＋∠ACB＝180°的过程．已知：延长三角形ABC的边BC到D，过C作CE∥AB．求证：∠A＋∠B＋∠ACB＝180°说明：检测评估答案 1.400 2.∠ACB 3. 105 82 4. 40 5. 80 6 . 90 7360 8.直角9.A 10.C 11.略 12.略。

人教版七年级数学下学期《5.3 平行线的性质》同步练习

5.3 平行线的性质一．选择题1．下列语句是命题的是（）A．画直线AB B．直线a∥bC．如果a∥b，b∥c，则a∥c D．点M与点N都在直线AB上2．下列命题中，真命题的个数是（）①过一点有且只有一条直线与已知直线平行；②过一点有且只有一条直线与已知直线垂直；③图形平移的方向一定是水平的；④内错角相等；⑤相等的角是对顶角；⑥垂线段最短A．3B．2C．1D．03．下列五个命题：①如果两个数的绝对值相等，那么这两个数的平方相等；②内错角相等；③在同一平面内，垂直于同一条直线的两条直线互相平行；④两个无理数的和一定是无理数；⑤坐标平面内的点与有序数对是一一对应的．其中真命题的个数是（）A．2个B．3个C．4个D．5个4．下列选项中a，b的取值，可以说明“若a＞b，则|a|＞|b|”是假命题的反例为（）A．a＝﹣5 b＝﹣6B．a＝6 b＝5C．a＝﹣6 b＝5D．a＝6 b＝﹣5 5．下列命题中，逆命题为真命题的是（）A．对顶角相等B．邻补角互补C．两直线平行，同位角相等D．互余的两个角都小于90°6．如图是婴儿车的平面示意图，其中AB∥CD，∠1＝120°，∠3＝40°，那么∠2的度数为（）A．80°B．90°C．100°D．102°7．如图，直线a，b被直线m所截，若a∥b，∠2＝62°，则∠1＝（）A．62°B．108°C．118°D．128°8．能说明“锐角α，锐角β的和是锐角”是假命题的例证图是（）A．B．C．D．9．如图，将直尺与含30°角的三角尺摆放在一起，若∠1＝20°，则∠2的度数是（）A．30°B．40°C．50°D．60°10．若直线a∥b，点M到直线a的距离是5cm，到直线b的距离是3cm，那么直线a，b间的距离是（）cm．A．2B．8C．2或8D．4二．填空题11．若a2＝b2，那么a＝b；请举出一个反例，说明该命题是假命题；12．把命题“两直线平行，同位角相等”改写成“如果…那么…”的形式是：．13．“同角的余角相等”，这个命题改写成如果…那么…形式应该为．三．解答题14．已知：如图，AD∥BE，∠1＝∠2，求证：∠A＝∠E．15．如图，已知∠ABC+∠ECB＝180°，∠P＝∠Q．求证：∠1＝∠2．参考答案一．选择题1．解：C是用数学式子表达的可以判断真假的陈述句，是命题；A、B、D均不是可以判断真假的陈述句，没有题设和结论之分，都不是命题．故选：C．2．解：过直线外一点有且只有一条直线与已知直线平行，①是假命题；在同一平面内，过一点有且只有一条直线与已知直线垂直，②是假命题；图形平移的方向不一定是水平的，③是假命题；两直线平行，内错角相等，④是假命题；相等的角不一定是对顶角，⑤是假命题；垂线段最短，⑥是真命题，故选：C．3．解：①如果两个数的绝对值相等，那么这两个数的平方相等，是真命题；②两直线平行，内错角相等，原命题是假命题；③在同一平面内，垂直于同一条直线的两条直线互相平行，是真命题；④两个无理数的和不一定是无理数，原命题是假命题；⑤坐标平面内的点与有序数对是一一对应的，是真命题；故选：B．4．解：当a＝﹣5，b＝﹣6时，a＞b，但|a|＜|b|，∴“若a＞b，则|a|＞|b|”是假命题，故选：A．5．解：A、对顶角相等的逆命题是相等的角是对顶角，逆命题是假命题；B、邻补角互补的逆命题是互补的角是邻补角，逆命题是假命题；C、两直线平行，同位角相等逆命题是同位角相等，两直线平行，逆命题是真命题；D、互余的两个角都小于90°的逆命题是都小于90°的角互余，逆命题是假命题；故选：C．6．解：∵AB∥CD，∴∠A＝∠3＝40°，∵∠1＝120°，∴∠2＝∠1﹣∠A＝80°，故选：A．7．解：如图，∵a∥b，∴∠3＝∠2＝62°，∵∠3+∠1＝180°，∴∠1＝180°﹣62°＝118°．故选：C．8．解：例如C选项图中：三角形三个内角都是锐角，则∠α+∠β＞90°．故选：C．9．解：如图，∵∠BEF是△AEF的外角，∠1＝20°，∠F＝30°，∴∠BEF＝∠1+∠F＝50°，∵AB∥CD，∴∠2＝∠BEF＝50°，故选：C．10．解：分为两种情况：如图1，直线a，b间的距离是5cm﹣3cm＝2cm，如图2，直线a，b间的距离是5cm+3cm＝8cm，故选：C．二．填空题11．解：若a2＝b2，那么a＝b，是假命题．例如：22＝（﹣2）2＝4但是2≠﹣2．所以答案可以是：若22＝（﹣2）2＝4，但是2≠﹣2．12．解：“两直线平行，同位角相等”的条件是：“两直线平行”，结论为：“同位角相等”，∴写成“如果…，那么…”的形式为：“如果两直线平行，那么同位角相等”，故答案为：如果两直线平行，那么同位角相等．13．解：根据命题的特点，可以改写为：“如果两个角是同一个角的余角，那么这两个角相等”，故答案为：如果两个角是同一个角的余角，那么这两个角相等．三．解答题14．证明：∵AD∥BE，∴∠A＝∠3，∵∠1＝∠2，∴DE∥AC，∴∠E＝∠3，∴∠A＝∠EBC＝∠E．15．证明：∵∠ABC+∠ECB＝180°，∴AB∥DE，∴∠ABC＝∠BCD，∵∠P＝∠Q，∴PB∥CQ，∴∠PBC＝∠BCQ，∵∠1＝∠ABC﹣∠PBC，∠2＝∠BCD﹣∠BCQ，∴∠1＝∠2．。

人教版七年级数学下册《5.3.1平行线的性质》同步练习(含答案)

1 =命题点1两直线平行，同位角相等 [热度：92%]4. 2018襄阳如图5 — 3 — 4,把一个三角尺的直角顶点放在一直尺的一边上，若/50 °则/ 2的度数为（A . 55 °B . 50°)C . 5.③如图5— 3 — 5, 直线图 5 — 3 — 4AB // CD , BC 平分/ ABD.若/ 1 = 54° 则/ 2 =基础自我诊断关键问答① 三线八角”图形中，有些角不是同位角、内错角、同旁内角，那么可以通过什么方法把它们转化成同位角、内错角或同旁内角？② 由平行线可以得到哪些角的数量关系？5 — 3 — 1,直线a // b ,直线c 与直线a, b 相交，若/ 1= 56°则/ 2等于（）考向提升训练5.3平行线的性质 5.3.1平行线的性质①如图 C . 2. 的度数为（24 ° 56 °2018 B . 34°D . 124黔南州如图 5— 3— 2，已知 AD // BC ,Z B = 30 °, DB 平分/ ADE ，则/ DEC )A . 30 ° 3.②如图 ABD 的度数为B . 60°5— 3 — 3,C . 90°BD 平分/ D . 120° ABC ，点 E 在 BC 上且 EF // AB ,若/ FEB = 80°,则/ A . 50 ° B . 65°C. 30°图 5— 3—3D . 80 ° 1.D£图 5— 3—245° D .40 °图 5 — 3 — 5图 5— 3— 95 — 3—9所示的方式摆放，两个三角尺的一直角边重合，含 30°角的三角尺的斜边与纸条一边重合，含 45°角的三角尺的一个顶点在纸条的另一边上，则/ 1的度数是_解题突破④/ ABD ，/ CDB 分别是多少度？不是，如何添加辅助线可以使这些角成为10.⑤如图 5 — 3— 10，AB // DE //方法点拨⑤有关角的比例问题，先设每一份为 x ,然后根据题意，转化为方程求解命题点4平行线的性质与判定的综合应用[热度：96%]11. 已知：如图 5— 3— 11,/ B =解题突破③在能用图中字母表示的角中， / 1的同位角是哪个角？/ 2的同位角是哪个角？它们之间有什么关系？命题点2两直线平行，内错角相等 [热度：92%]6. 2018自贡在平面内，将一个直角三角尺按如图5— 3— 6所示方式摆放在一组平行线上.若/ 1 = 55°则/ 2的度数是（）A . 50 C . 40°B . 45° D . 35°7.如图命题点 & 2018 A . 42 ° 图 5— 3 — 7 AB // CD // EF ，若/ A = 30 °, / AFC = 15 °,贝 C = ___________ [热度：92%] ，/ CBA = 64。

人教版七年级数学下学期 5.3 平行线的性质同步练习卷

5.3 平行线的性质一．选择题（共12小题，满分36分，每小题3分）1．（3分）如图，直线a，b被直线m所截，若a∥b，∠2＝62°，则∠1＝（）A．62°B．108°C．118°D．128°2．（3分）如图，将一张长方形纸片ABCD沿AE折叠，若∠BAD′＝26°，则∠AED′等于（）A．68°B．64°C．58°D．26°3．（3分）如图，直线a∥b，直角三角形如图放置，∠DCB＝90°，若∠1+∠B＝65°，则∠2的度数为（）A．20°B．25°C．30°D．35°4．（3分）将一副三角板（∠A＝30°）按如图所示方式摆放，使得AB∥EF，则∠1等于（）A．75°B．90°C．105°D．115°5．（3分）已知如图DC∥EG，∠C＝40°，∠A＝70°，则∠AFE的度数为（）A．140°B．110°C．90°D．30°6．（3分）如图，若∠1＝40°，∠2＝40°，∠3＝116°30′，则∠4＝（）A．63°30′B．53°30′C．73°30′D．93°30′7．（3分）如图，如果∠1＝∠3，∠2＝60°，那么∠4的度数为（）A．60°B．100°C．120°D．130°8．（3分）如图，AD，CE是△ABC的高，过点A作AF∥BC，则下列线段的长可表示图中两条平行线之间的距离的是（）A．AB B．AD C．CE D．AC9．（3分）如图，AB∥DC，ED∥BC，AE∥BD，那么图中和△ABD面积相等的三角形（不包括△ABD）有（）A．1个B．2个C．3个D．4个10．（3分）小柔要榨果汁，她有苹果、芭乐、柳丁三种水果，且其颗数比为9：7：6，小柔榨完果汁后，苹果、芭乐、柳丁的颗数比变为6：3：4，已知小柔榨果汁时没有使用柳丁，关于她榨果汁时另外两种水果的使用情形，下列叙述何者正确？（）A．只使用苹果B．只使用芭乐C．使用苹果及芭乐，且使用的苹果颗数比使用的芭乐颗数多D．使用苹果及芭乐，且使用的芭乐颗数比使用的苹果颗数多11．（3分）若∠A和∠B是两条平行线中的同旁内角，且∠A比∠B的2倍少30°，则∠B 的度数是（）A．30°B．110°C．70°D．30°或70°12．（3分）下列语句中，不是命题的是（）A．等角的余角相等B．对顶角相等C．过直线l外一点P作直线l的垂线D．如果a＝b，则二．解答题（共6小题，满分36分，每小题6分）13．（6分）如图，AD平分∠EAC，若∠C＝55°，∠EAC＝110°，AD与BC平行吗？为什么？请根据解答过程填空（理由或数学式）解：AD∥BC．理由：∵AD平分∠EAC（已知）∴∠DAC＝∠EAC（）∵∠EAC＝110°（已知）∴∠DAC＝∠EAC＝°∵∠C＝55°（已知）∴∠C＝∠∴AD∥BC（）14．（6分）如图，直线CD、EF被直线OA、OB所截，∠1+∠2＝180°．求证：∠3＝∠4．15．（6分）如图，在四边形ABCD中，AD∥BC，∠1＝∠2，∠2与∠3互余，以点C为顶点，CD为一边，在四边形ABCD的外部作∠5，使∠5＝∠4，交DE于点F，试探索DE 和CF的位置关系，并说明理由．16．（6分）如图，已知∠4＝∠B，∠1＝∠3，求证：AC平分∠BAD．17．（6分）如图，把一个长方形纸片沿EF折叠后，点D、C分别落在D′、C′的位置，若∠EFB＝65°，求∠AED′的度数．18．（6分）已知：如图，AE⊥BC，FG⊥BC，∠1＝∠2（1）求证：AB∥CD（2）若∠D＝∠3+50°，∠CBD＝70°，求∠C的度数．参考答案一．选择题（共12小题，满分36分，每小题3分）1．C．2．C．3．B．4．C．5．B．6．A．7．C．8．B．9．B．10．B．11．C．12．C．二．解答题（共6小题，满分36分，每小题6分）13．解：AD∥BC．理由：∵AD平分∠EAC（已知）∴∠DAC＝∠EAC（角平分线的定义）∵∠EAC＝110°（已知）∴∠DAC＝∠EAC＝55°∵∠C＝55°（已知）∴∠C＝∠DAC，∴AD∥BC（内错角相等，两直线平行）故答案为：角平分线的定义；55°；∠DAC；内错角相等；两直线平行．14．证明：∵∠2与∠5是对顶角，∴∠2＝∠5，∵∠1+∠2＝180°，∴∠1+∠5＝180°，∴∠3＝∠4．15．解：DE⊥CF，理由如下：∵AD∥BC，∠1＝∠2，∴∠1＝∠4＝∠2，又∵∠5＝∠4，∴∠5＝∠2，又∵∠2与∠3互余，∴∠3与∠5互余，∴∠5+∠3＝90°，∴DE⊥CF．16．解：∵∠4＝∠B，∴CD∥AB，∴∠3＝∠2，又∠1＝∠3，∵∠1＝∠2，AC平分∠BAD，∴AC平分∠BAD．17．解：∵AD∥BC，∠EFB＝65°，∴∠DEF＝65°，又∵∠DEF＝∠D′EF，∴∠D′EF＝65°，∴∠AED′＝50°．18．（1）证明：∵AE⊥BC，FG⊥BC，∴∠AMB＝∠GNM＝90°，∴∠A＝∠2；又∵∠2＝∠1，∴∠A＝∠1，∴AB∥CD；（2）解：∵AB∥CD，∴∠D+∠CBD+∠3＝180°，∵∠D＝∠3+50°，∠CBD＝70°，∴∠3＝30°，∵AB∥CD，∴∠C＝∠3＝30°．。

(新人教版)七年级数学下册：5.3.1《平行线的性质》习题(含答案)

图254321l ba 平行线的性质习题1、如图1所示，直线a b ，被直线c 所截，若a b ∥，160∠=°，则2∠= °． (20XX 年双柏县)2、如图2所示，直线l 截两平行直线a 、b ，则下列式子不一定成立的是（）（20XX 年郴州市）A ．∠1=∠5 B． ∠2=∠4C ． ∠3=∠5 D． ∠5=∠23、如图3所示，AB ∥CD ，∠C ＝65o ，CE ⊥BE ，垂足为E ，则∠B 的度数为．（20XX 年湖北省咸宁市）4、如图4所示，直线l 1//l 2，AB ⊥CD ，∠1=34°，那么∠2的度数是．5、如图5所示，AB ∥CD ，直线PQ 分别交AB 、CD 于点E 、F ，EG 是∠FED 的平分线，交AB 于点G . 若∠QED=40°，那么∠EGB 等于（）A. 80°B. 100°C. 110°D.120XX （20XX 年宜宾市）6、.如图6所示, 已知直线 25,115,//=∠=∠A C CD AB ,则=∠E ( )(A) 70 (B) 80 (C) 90 (D) 1007、将一直角三角板与两边平行的纸条如图7所示放置，下列结论：（1）∠1＝∠2；（2）∠3＝∠4；（3）∠2+∠4＝90°；（4）∠4+∠5＝180°，其中正确的个数是（）（20XX年荆州市）A.1B.2C.3D.4参考答案1分析：∠1的对顶角与∠2是一对同位角，根据条件a∥b，可以得到，∠2与∠1的对顶角相等，根据对顶角相等，得到：∠2=∠1，因为∠1=60°，所以，∠2=60°。

解：∠2=60°。

2分析:两直线平行，同位角相等，所以，∠1=∠ 5 ，因此，A是成立的；两直线平行，内错角相等，所以，∠2=∠ 4 ，因此，B是成立的；对顶角是相等的，所以，∠3=∠ 5 因此，C是成立的；这样，只有D是不一定成立的了。

人教版七年级数学下册 5.3平行线的性质单元测试题有答案

5.3平行线的性质一选择题1、有下列四个命题：①对顶角相等；②等角的补角相等；③如果b∥a，c∥a，那么b∥c；④如果一个角的两边分别平行于另一个角的两边，那么这两个角相等或互补．其中是真命题的有（）A．4个B．3个C．2个D．1个2、如图，AB∥CD，CD⊥EF，若∠1=125°，则∠2=（）A．25°B．35°C．55°D．65°3、如图，小明课间把老师的三角板的直角顶点放在黑板的两条平行线a、b上，已知∠1=55°，则∠2的度数为（）A．45°B．35°C．55°D．125°4、如图，直线l1∥l2，l3⊥l4．有三个结论：①∠1+∠3=90°；②∠2+∠3=90°；③∠2=∠4．下列说法中，正确的是（）A．只有①正确B．只有②正确C．①和③正确D．①②③都正确5、如图，△ABC中，BD是∠ABC的角平分线，DE∥BC交AB 于点E,，∠A=60º,∠BDC=95º，则∠BED的度数是（）A．35 º B．70º C．100 º D．110 º6、如图，AD∥EF∥BC,EG∥BD,和∠1相等的角有（）A. 4个B.5个C.6个D.7个7、如图，将三角尺的直角顶点放在直尺的一边上，∠1=30°，∠2=50°，则∠3的度数等于（）A．50°B．30°C．20°D．15°二填空题1、填空：如图所示，已知∠1+∠2=180°，∠3=∠B，求证：∠AED=∠ACB证明：∵∠1+∠2=180°（已知）∠1+__=180°（邻补角的定义）∴∠2=_____（同角的补角定义）∴AB∥EF（）∴∠3=___（已知）∴∠B=____（等量代换）∴DE∥BC（）∴∠AED=∠ACB（）2、完成下面的证明．如图，E点为DF上的点，B为AC上的点，∠1=∠2，∠C=∠D，求证：DF∥AC．证明：∵∠1=∠2（已知），∠1=∠3，∠2=∠4 （）∴∠3=∠4（等量代换）．∴_________∥_______（）∴∠C=∠ABD （）∵∠C=∠D （）∴∠D=∠ABD （）∴AC∥DF （）3、小明在学习三角形知识时，发现如下三个有趣的结论：在直角△ABC中，∠A ＝90°，BD平分∠ABC，M为直线AC上一点，ME⊥BC，垂足为E，∠AME的平分线交直线AB于点F．（1）如图①，M为边AC上一点，则BD、MF的位置关系是_______；如图②，M为边AC反向延长线上一点，则BD、MF的位置关系是 ________ ；如图③，M为边AC延长线上一点，则BD、MF的位置关系是______________ （2）请在图①、图②、或图③中任选两种情况，给出证明.我选图___________来证明.三解答题1、将下列命题改写成“如果……那么……”的形式（1）直角都相等；（2）等量代换；（3）末位数是5的整数能被5整除；（4）三角形的内角和是180°.2、判断下列命题是真命题还是假命题，并说明理由.（1）两个锐角的和是钝角；（2）点P到A、B两点的距离相等，则P是线段AB的中点；（3）不相等的角不是对顶角；（4）若∠1+∠2=90°，∠3+∠2=90°，则∠1=∠3.3、如图，AD∥BC，BD平分∠ABC．求证：AB=AD．4、如图，AD⊥BC于D，EG⊥BC于G，∠E=∠1，求证：AD平分∠BAC。

七年级数学下册平行线的性质习题新版新人教版

5.3.1 平行线的性质基础题知识点1平行线的性质1．(重庆中考)如图.直线AB∥CD.直线EF分别与直线AB.CD相交于点G.H.若∠1＝135°.则∠2的度数为(C)A．65° B．55° C．45° D．35°2．(宁波中考)如图.在△ABC中.∠ACB＝90°.CD∥AB.∠ACD＝40°.则∠B的度数为(B) A．40° B．50° C．60° D．70°3．(重庆中考)如图.AB∥CD.AD平分∠BAC.若∠BAD＝70°.那么∠ACD的度数为(A) A．40° B．35° C．50° D．45°4．(黔东南中考)如图.直线a.b与直线c.d相交.已知∠1＝∠2.∠3＝110°.则∠4＝(A) A．70° B．80° C．110° D．100°5．(广州中考)如图.AB∥CD.直线l分别与AB.CD相交.若∠1＝50°.则∠2的度数为50°．6．(宜宾中考)如图.直线a.b被第三条直线c所截.如果a∥b.∠1＝70°.那么∠3的度数是70°.知识点2平行线性质的应用7．某商品的商标可以抽象为如图所示的三条线段.其中AB∥CD.∠EAB＝45°.则∠FDC的度数是(B)A．30°B．45°C．60°D．75°8．一只因损坏而倾斜的椅子.从背后看到的形状如图所示.其中两组对边的平行关系没有发生变化.若∠1＝76°.则∠2的大小是(C)A．76° B．86° C．104° D．114°9．如图.在A.B两地挖一条笔直的水渠.从A地测得水渠的走向是北偏西42°.A.B两地同时开工.B地所挖水渠走向应为南偏东42°.10．某次考古发掘出的一个梯形残缺玉片.工作人员从玉片上量得∠A＝115°.∠D＝100°.已知梯形的两底AD∥BC.请你帮助工作人员求出另外两个角的度数.并说明理由．解：∵AD∥BC.∠A＝115°.∠D＝100°.中档题11．(昆明中考)如图.在△ABC中.∠B＝40°.过点C作CD∥AB.∠ACD＝65°.则∠ACB的度数为( D)A．60° B．65° C．70° D．75°12．(滨州中考)如图.AB∥CD.直线EF与AB.CD分别交于点M.N.过点N的直线GH与AB交于点P.则下列结论错误的是(D)A．∠EMB＝∠END B．∠BMN＝∠MNCC．∠CNH＝∠BPG D．∠DNG＝∠AME13．(黄冈中考)如图.AB∥CD∥EF.AC∥DF.若∠BAC＝120°.则∠CDF＝(A)A．60°B．120°C．150°D．180°14．一大门的栏杆如图所示.BA垂直于地面AE于A.CD平行于地面AE.则∠ABC＋∠BCD＝270°.15．如图.一只船从点A出发沿北偏东60°方向航行到点B.再以南偏西25°方向返回.则∠ABC ＝35°．16．(益阳中考)如图.直线AB∥CD.BC平分∠ABD.∠1＝65°.求∠2的度数．解：∵直线AB∥CD.∠1＝65°.∴∠ABC＝∠1＝65°.∵BC平分∠ABD.∴∠ABD＝2∠ABC＝130°.∵直线AB∥CD.∴∠ABD＋∠BDC＝180°.∴∠2＝∠BDC＝180°－∠ABD＝180°－130°＝50°.17．如图.已知AB∥DE∥CF.若∠ABC＝70°.∠CDE＝130°.求∠BCD的度数．解：∵AB∥CF.∠ABC＝70°.∴∠BCF＝∠ABC＝70°.又∵DE∥CF.∠CDE＝130°.∴∠DCF＋∠CDE＝180°.∴∠DCF＝50°.∴∠BCD＝∠BCF－∠DCF＝70°－50°＝20°.综合题18．阅读下列解答过程：如图甲.AB∥CD.探索∠P与∠A.∠C之间的关系．解：过点P作PE∥AB.∵AB∥CD.∴PE∥AB∥CD(平行于同一条直线的两条直线互相平行)．∴∠1＋∠A＝180°(两直线平行.同旁内角互补).∠2＋∠C＝180°(两直线平行.同旁内角互补)．∴∠1＋∠A＋∠2＋∠C＝360°.又∵∠APC＝∠1＋∠2.∴∠APC＋∠A＋∠C＝360°.如图乙和图丙.AB∥CD.请根据上述方法分别探索两图中∠P与∠A.∠C之间的关系．解：如图乙.过点P作PE∥AB.∵AB∥CD(已知).∴PE∥AB∥CD(平行于同一直线的两条直线平行)．∴∠A＝∠EPA.∠EPC＝∠C(两直线平行.内错角相等)．∵∠APC＝∠EPA＋∠EPC.。