球杆系统控制器设计及MATLAB仿真
matlab大作业-平衡杆小球位置控制系统-华中科技大学

MATLAB语言、控制系统分析与设计大作业平衡杆小球位置控制系统设计与仿真专业:电气工程及其自动化班级:设计者:学号:华中科技大学电气与电子工程学院2008年1月平衡杆小球位置控制系统设计与仿真一、问题描述与实验要求A ball is placed on a beam, see figure below, where it is allowed to roll with 1 degree of freedom along the length of the beam. A lever arm is attached to the beam at one end and a servo gear at the other. As the servo gear turns by an angle theta, the lever changes the angle of the beam by alpha. When the angle is changed from the vertical position, gravity causes the ball to roll along the beam. A controller will be designed for this system so that the ball's position can be manipulated.For this problem, we will assume that the ball rolls without slipping and friction between the beam and ball is negligible. The constants and variables for this example are defined as follows:M mass of the ball 0.11 kgR radius of the ball 0.015 mD lever arm offset 0.03 mG gravitational acceleration 9.8 m/s^2L length of the beam 1.0 mJ ball's moment of inertia 9.99e-6 kgm^2R ball position coordinateAlpha beam angle coordinateTheta servo gear angleSystem EquationsThe Lagrangian equation of motion for the ball is given by thefollowing:Linearization of this equation about the beam angle, alpha = 0, gives usthe following linear approximation of the system:The equation which relates the beam angle to the angle of the gear canbe approximated as linear by the equation below:Substituting this into the previous equation, we get:Design requirementsThe design criteria for this problem are: ∙Settling time less than 3 seconds ∙ Overshoot less than 5%1.数学模型的建立将上面推导的简化式做拉普拉斯变换,得到: 22()()()J d m R s s m gs RLθ+=- 变化后得到:22()()()d m gR s lJ s m sRθ=-+化简为:222()()()R s m gdRs J m R lsθ=-+2.设计目标希望能精确小球的位置,即要求小球的稳态误差为零,同时希望因扰动引起的稳态误差也能为零。
球杆控制系统设计与仿真XS07012040禹志

控制系统实践大作业球杆控制系统设计与仿真学号:XS07012040姓名:禹志球杆控制系统设计与仿真一球杆系统的数学模型球杆系统的物理模型如下图所示:图1:球杆系统模型在这个模型里,我们假设球在杆上只有纯滚动而没有滑动并且我们忽略球和杆之间的摩擦力。
我们定义这个模型中的变量和常量如下:m 球的质量0.1 kgR 球的半径0.02 md 轮的半径0.05 mg 重力加速度9.8 m/s^2L 杆长 1.0 mJ 球的转动惯量 1.0e-5 kgm^2r 球的位置α杆与水平的夹角θ伺服机构与水平的夹角表1:模型的变量和常量球杆系统的数学建模:系统的动能:222])r L [(m 21rm 21)R r(J 21T α-++= 系统的势能:α-=sin mgr U该系统的拉格朗日方程为:0rUr T )r T (dt d =∂∂+∂∂-∂∂ 通过拉格朗日法得到球的运动方程:0))(r L (m sin mg r)m RJ(22=α-+α-+ 若我们假设杆与水平的夹角是小角度且0≈α ,对上面的方程进行线性化,我们得到:α=+mg r)m RJ(2 杆的角度与伺服机构的角度的关系可以近似的线性化为:θ=αLd综合上面几个方程我们得到:θ=+Ldmg r)m R J (2对方程两边做拉普拉斯变换:)s (Ld mg s )s (R )m R J (22Θ=+ 整理后我们得到系统线性化后的开环传递函数:22s1)mRJ(Lmgd)s()s(R+=Θ二控制器的设计在这里,我们采用普遍使用的PID控制器。
整个系统的闭环框图可以表达为:图2:线性化后的控制框图令)S()S(R)S(HΘ=,得:)S(R)s(HSKSKSK))S(R)S(r(IP2D=⋅++-我们取pK=21,IK=0,DK=14,将球稳定在杆的中点,仿真结果如下图所示:图3:仿真结果通过仿真结果表明将系统线性化后,该系统的超调量小于1%,上升时间3秒。
实验5--球杆系统的数字PID控制实验

学生实验报告开课学院及实验室:学院机电年级、专业、班姓名学号实验课程名称计算机控制技术成绩实验项目名称实验5 球杆系统的数字PID控制实验指导教师一、实验目的1.熟悉Matlab\simulink软件;2.通过试凑法确定球杆系统的PID参数;3.在球杆系统上验证PID参数的控制效果。
二、使用仪器、材料1.球杆系统装置。
2.装有matlab2012b的计算机。
三、实验步骤1.现场实验前先用Matlab\simulink软件进行仿真。
给出球杆装置的理想传递函数(1)用Simulink设计出该系统的模型。
输入信号为阶跃信号,控制器选择PID。
(2)用试凑法确定出合适的PID参数。
(3)比较设置不同参数时系统的响应特性。
2.进行现场实验。
测试好现场装置后,试着将仿真后得出的几个PID参数输入到控制系统中,观察球杆装置的运行情况。
在现场调整参数使系统取得良好的控制效果。
(1)打开球杆系统电控箱上的电源按钮,在MATLAB/Current Folder 中打开文件系统自带程序“PID_ Control_Modify.slx”,会弹出如图所示的实时控制界面(2)双击“PID Controller”模块,设置Kp、Ki、Kd的参数,参数为仿真过程得出的参数。
双击“Step”模块,设置阶跃信号参数:step time=0,initial value=0,final value=0.25。
(3) 点击编译程序,待编译成功后,点击连接程序,点击运行程序,观察球杆和小球的运动现象。
待小球静止后,点击停止程序,打开示波器scope观察响应曲线的超调量,调节时间。
若能达到理想的控制效果,说明所设置的PID参数合理。
否则,根据波形呈现的超调量,调节时间,以及最终稳定后呈现的静差,调整PID参数,继续调试系统,最终达到理想的控制效果。
四、实验过程原始记录(程序、数据、图表、计算等)1.Simulink仿真程序框图如下:系统输入为阶跃信号,阶跃时间为0,初始值为0,终值定为1,采样时间为0.1。
1球杆系统
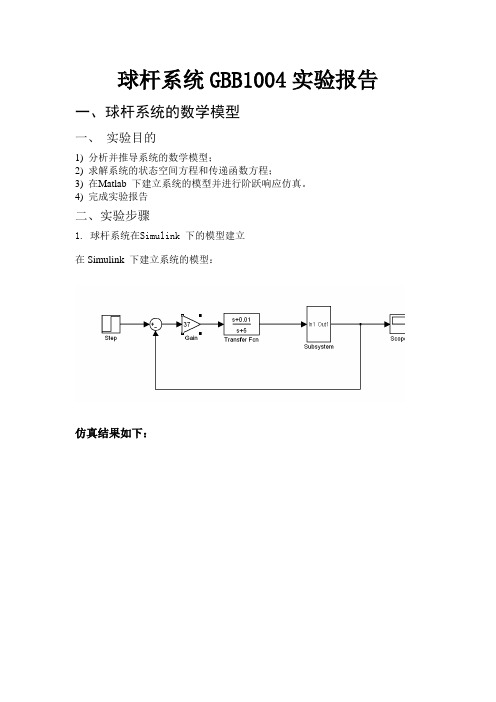
球杆系统GBB1004实验报告一、球杆系统的数学模型一、实验目的1) 分析并推导系统的数学模型;2) 求解系统的状态空间方程和传递函数方程;3) 在Matlab 下建立系统的模型并进行阶跃响应仿真。
4) 完成实验报告二、实验步骤1. 球杆系统在Simulink 下的模型建立在Simulink 下建立系统的模型:仿真结果如下:二、球杆系统的数字控制器实验报告一、实验目的学习使用根轨迹法设计一个稳定的系统,进一步理解根轨迹的基本概念和根轨迹图所代表的含义,通过实验来验证增加零、极点以及开环增益对系统性能有何影响。
二、实验步骤1、开环根轨迹实验程序:m=0.028;R=0.0145;g=-9.8;L=0.40;d=0.045;J=0.4*m*R^2;K=(m*g*d)/(L*(J/R^2+m));num=[-K]; den=[1 0 0];plant=tf(num,den);rlocus(plant)运行结果:2、可以看到系统在原点有两个极点沿虚轴伸向无穷远处使用sgrid 命令可以将设计目标也显示在根轨迹上m=0.028;R=0.0145;g=-9.8;L=0.40;d=0.045;J=0.4*m*R^2;K=(m*g*d)/(L*(J/R^2+m));num=[-K];den=[1 0 0];plant=tf(num,den);rlocus(plant)sgrid(0.7,1.9)axis([-5 5 -2 2])运行结果:3、超前补偿器;在上面那个程序前添加以下程序:zo=0.01;po=5;contr=tf([1 zo],[1 po])rlocus(contr*plant)sgrid(0.7,1.9)运行结果:4、现在,根轨迹的分支已经在设计目标范围内。
使用rlocfind 命令来确定系统的增益。
在m文件中加入以下几行[k,poles]=rlocfind(contr*plant)到图形显示窗口选择用十字形光标一点。
自动控制球杆系统实验指导书-2016资料

自动控制综合实验2 实验指导书Part 1球杆系统GBB1004北京邮电大学自动化学院林雪燕2016.5.24前言自动控制是一门理论与实践并重的技术,在成功掌握了理论知识(经典控制、现代控制)的同时再配合做一些经典的自动控制实验,从而加深对自动控制的理解与掌握,为今后从事自动控制的设计和研究工作打下扎实的基础。
为了更好地配合理论教学,达到理论与实践完美的结合,将自动控制相关的实验独立设置成一门实验课:自动控制综合实验。
自动控制理论实验主要目的是通过实验进一步理解自动控制理论的基本概念,熟悉和掌握控制系统的分析方法和设计方法,掌握常用工程软件使用,如MATLAB、LabVIEW 等。
上学期开设的自动控制综合实验(1)主要内容为控制系统的Matlab/simulink 仿真和基于实验箱的硬件模拟,以电路系统为研究对象。
本学期开始的自动控制综合实验(2)的内容是基于典型控制理论实验设备(球杆系统和倒立摆系统),熟悉和掌握控制系统的分析和设计方法。
球杆系统机械简单,结构紧凑,安全性高,采用智能伺服驱动模块和Windows 程序界面,可用于教学或科研。
对于自动控制理论等课程来说,针对设备的非线性与不稳定性特点,设计有效的控制系统是项有意义的工作。
球杆系统要完成的实验有:实验一:小球位置的数据采集处理实验二:球杆系统的PID法控制实验三:球杆系统的根轨迹法控制实验四:球杆系统的频率响应法控制倒立摆是一个典型的不稳定系统,同时又具有多变量、非线性、强耦合的特性,是自动控制理论中的典型被控对象。
运用控制手段可使之具有一定的稳定性和良好的性能。
许多抽象的控制概念如控制系统的稳定性、可控性、系统收敛速度和系统抗干扰能力等,都可以通过倒立摆系统直观的表现出来。
倒立摆系统要完成的实验有:实验五:倒立摆的数学建模及稳定性分析实验六:倒立摆的状态反馈控制实验七:不同状态下状态反馈控制效果比较实验八:倒立摆的LQR 控制同学们完成实验后,要完成相应的实验报告,并及时提交。
球杆实验指导

球杆系统GBB1004实验指导书1.2011年球杆系统简介1.1 要点球杆系统是为学习与研究自动控制和运动控制等专业课程而专门开发的,对于经典控制理论和现代控制理论等课程,是一个非常便于基础实验和研究的研究平台。
1.2 球杆系统的特点球杆系统是一个典型的非线性系统,理论上而言,它是一个真正意义上的非线性系统,其执行机构还具有很多非线性特性,包括:♦死区♦直流马达和带轮的传动非线性。
♦位置测量的不连续性。
♦导轨表面不是严格的光滑表面,产生非线性阻力。
这些非线性因素对于传统意义上的测量和建模造成很大的影响,并对系统的控制性能造成非常大的影响,怎样去设计一个鲁棒的控制系统,是现代控制理论的一个重要问题。
固高科技提供的球杆系统既可以用于研究控制系统运行的非线性动力学,也可以用于研究控制系统的非线性观测器等,是一个较为通用的实验设备。
因为系统机械结构的特点,球杆系统具有一个最重要的特性——不稳定性,对于传统的实验方法,存在一些实验的难处,不稳定的系统容易对实验人员产生危险或是不可预料的伤害,球杆系统相对而言,机械比较简单,结构比较紧凑,安全性也比较高,是一个可以避免这些危险和伤害的实验设备。
采用智能伺服驱动模块和直观的Windows程序界面,是控制系统实验的一个理想的实验设备。
1.3 主要组成部分球杆系统主要由以下几部分组成,如图所示。
♦球杆系统组成:包含直流伺服马达和直流电源的机械部分IPM100智能伺服驱动♦控制计算机1.3.1 机械部分机械部分包括底座、小球、横杆、减速皮带轮、支撑部分、马达等。
小球可以在横杆上自由的滚动,横杆的一端通过转轴固定,另一端可以上下转动,通过控制直流伺服电机的位置,带动皮带轮转动,通过传动机构就可以控制横杆的倾斜角。
直流伺服电机带有增量式编码器(1000P/R),可以检测电机的实际位置,在横杆上的凹槽内,有一线性的传感器用于检测小球的实际位置,两个实际位置的信号都被传送给控制系统,构成一个闭环反馈系统。
基于MATLAB环境下球杆系统PID控制器设计
的时 间 。 A LB在 数 值 计 算 中 , 有 开 发 程 序 简 练 , MTA 具 提 供 控 制 工 具 箱 和 与 系 统 标 准 信 号 相 应 函数 等 优 点 。为 此 , 文 使 用 M T A 本 A L B调 整球 杆 系统 P D控 制 I
器参数值 ,能够快速地求 出最佳 的参数分析 。
维普资讯
20 06年 5月
农 机 化 研 究
第 5期
基 于 M TL 境 下 球 杆 系 统 P A AB环 I D控 制 器 设 计
张 志 勇 ,何 东 健 ,张 建锋 ,张 军 辉
( . 北 农 林 科 技 大 学 信 息 工 程 学 院 ,陕 西 杨 凌 7 2 0 ;2 陕 西 广 电 网 络 杨 凌分 公 司 ,陕 西 杨 凌 7 2 0 1西 110 . 1 10) 摘 要 :在 机 械控 制 系 统 中 ,不 稳 定 系统 的控 制 问 题 是 公 认 的 控 制 难 点 ,由于 不稳 定 控 制 系 统 具 有 一 定 的
压 信号获得钢球在轨道上 的位 置 。电机转动带 动 齿 轮 系 驱 动 杠杆 臂 ( e e r 转 动 , 道 ( em) L v r m) A 轨 Ba
随 杠杆 臂 的 转 动 与 水 平 方 向 有 一 偏 角 ,钢 球 的 重 力 分 量 使 钢 球 沿 着 轨 道 滚 动 。设 计 一 个 控 制 系 统 通 过 调 节 伺 服 角 度 , 得 钢 球 保 持 在 轨 道 上 预 定 位 置 。 使
典 和 现 代 的 设 计 方法 ,具有 一 个 重 要 的 性 质一 开 环
球 杆
装 置
竺竺兰J 竺 卜
直 线 位 移 传 感 器
建模仿真_球杆实验_实验报告

《建模仿真与相似原理》課程实验报告第一章简化模型的建立和稳定性分析一、实验目的1.了解机理法建模的基本步骤;2.会用机理法建立球杆系统的简化数学模型;3.掌握控制系统稳定性分析的基本方法;二、实验要求1.采用机理法建立球杆系统的数学模型;2.分析的稳定性,并在 matlab 中仿真验证;三、实验设备1.球杆系统;2.计算机 matlab 平台;四、实验分析及思考题Simulink模型:Matlab仿真结果:思考题:1.根据建模的过程,总结机理法建模的基本步骤:1)根据系统运动的物理规律建立方程;2)化简为微分方程;3)根据小偏差线性化的理论化简为线性系统的传递函数;2.实验结果分析、讨论和建议。
答:影响系统稳定的因素是闭环系统的极点位置,闭环极点为[i,-i],在虚轴上,所以其阻尼为0,则系统震荡。
测量系统稳定性的方法之一是加入大小合适的阶跃信号,根据其输出的阶跃响应分析系统的稳定性和其他性能。
第二章仿真及实物模拟仿真实验2.1 PID仿真及实物模拟仿真实验一、实验目的1.会用 PID 法设计球杆系统控制器;2.设计并验证校正环节;二、实验要求1.根据给定的性能指标,采用凑试法设计 PID 校正环节,校正球杆系统,并验证之。
2.设球杆系统的开环传递函数为:设计 PID 校正环节,使系统的性能指标达到: St ≤10s,δ≤30%。
三、实验设备1.球杆系统;2.计算机 matlab 平台;四、实验过程1.未校正系统仿真Simulink模型及仿真结果如第一章所示;2.PID校正法仿真Simulink模型:Matlab仿真结果:参数设定:Kp=10 Ki=0 Kd=103.PID实时控制Simulink模型:实时控制结果:Step参数设定:Step time=1 Final value=0.25PID参数设定:P=3 I=1 D=1.54.实验记录五、实验分析1.怎样确定PID 控制器的参数?答:由于ID 控制器各校正环节的作用如下:比例环节:成比例地反映控制系统的偏差信号e(t),偏差一旦产生,控制器立即产生作用,以减少偏差;积分环节:主要用于消除稳态误差,提高系统的型别。
球杆系统控制器设计实验报告(北京理工大学)

球杆系统控制器设计实验报告学院:自动化学院组号:5成员:球杆系统控制器设计实验一、实验目的和要求1.1 实验目的(1)通过本设计实验,加强对经典控制方法(PID控制器)和智能控制方法(神经网络、模糊控制、遗传算法等)在实际控制系统中的应用研究。
(2)提高学生有关控制系统控制器的程序设计、仿真和实际运行能力.(3)熟悉MATLAB语言以及在控制系统设计中的应用。
1.2 实验要求(1)每两人一组,完成球杆系统的开环系统仿真、控制器的设计与仿真以及实际运行结果;(2)认真理解设计内容,独立完成实验报告,实验报告要求:设计题目,设计的具体内容及实验运行结果,实验结果分析、个人收获和不足,参考资料。
程序清单文件。
二、实验内容本设计实验的主要内容是设计一个稳定的控制系统,其核心是设计控制器,并在MATLAB/SIMULINK环境下进行仿真实验,并在球杆实验平台上实际验证。
算法实现:设计模糊控制器控制球杆系统,达到要求目标。
三、实验原理3.1 球杆系统的特点球杆系统是一个典型的非线性系统,理论上而言,它是一个真正意义上的非线性系统,其执行机构还具有很多非线性特性,包括:死区,直流马达和带轮的传动非线性,位置测量的不连续性,导轨表面不是严格的光滑表面,产生非线性阻力,这些非线性因素对于传统意义上的测量和建模造成很大的影响,并对系统的控制性能造成非常大的影响,怎样去设计一个鲁棒的控制系统,是现代控制理论的一个重要问题。
因为系统机械结构的特点,球杆系统具有一个最重要的特性——不稳定性,对于传统的实验方法,存在一些实验的难处,不稳定的系统容易对实验人员产生危险或是不可预料的伤害,球杆系统相对而言,机械比较简单,结构比较紧凑,安全性也比较高,是一个可以避免这些危险和伤害的实验设备。
3.2 球杆系统的数学模型对小球在导轨上滚动的动态过程的完整描述是非常复杂的,设计者的目的是对于该控制系统给出一个相对简单的模型,如图3.1所示为实验使用球杆系统简化图。
球杆系统控制器设计及MATLAB仿真

摘要以球杆系统作为主体,系统中的小球作为被控对象,设计一个模糊控制器,控制小球在装置导轨上的运行状态,分析小球在导轨上的运行状态,以此来反映模糊控制器的控制性能。
设计首先对球杆系统组成结构及其基本原理进行分析之后,建立一个相对简化后的球杆系统模型;运用相关的模糊控制原理,建立球杆系统模糊控制规则,再对球杆系统进行模糊控制器设计。
并在MATLAB仿真环境下建立控制器的仿真模型,对球杆系统进行仿真,测试模糊控制器的控制性能。
针对球杆系统自身存在的不稳定特性,在进行仿真时加入闭环反馈控制环节,这样不但可以提高系统的稳定性,还可以提高控制的精度,相较于其他一般控制,它更具有独特优势,更符合人类思维。
球杆系统作为如今研究控制理论的经典案例,与模糊控制融合之后,能更好地表现模糊控制在自动控制方面的优良特性。
关键词:球杆系统;模糊控制;MATLAB建模ABSTRACTIn the ball and beam system as the main body, the ball as a controlled object,design a fuzzy controller , to control the ball in the guide rail device running status. Analysis the ball movement on the guide rail, in order to reflect the fuzzy controller performance. First,the design analysis the composition structure and the basic principle of the ball and beam system , then establish a relatively simplified of the ball and beam system model; using the principle of fuzzy control, to establish fuzzy control rules of the ball and beam system, design a fuzzy controller to the ball and beam system. And in the MATLAB simulation environment, establish the simulation model of the controller, simulate the club system and test the control performance of the fuzzy controller.For the ball and beam system own existence the instability characteristics, in the simulation by adding closed loop feedback control link, which can not only improve the system stability, but also can improve the control accuracy, compared with other general control, it is more unique advantages, more in line with human thinking.Club system as a classic case in study control theory, and after fusion with fuzzy control, can performance the excellent characteristics of fuzzy control in the automatic control .Key words: the ball and beam system;fuzzy control;MATLAB modeling目录1 绪论 (1)1.1 课题背景和研究意义 (1)1.1.1 课题背景 (1)1.1.2 课题的研究意义 (1)1.2 模糊控制的发展及研究状况 (2)1.2.1 模糊控制论的产生与发展 (2)1.2.2 模糊控制论的研究和现状 (3)2 球杆系统建模及仿真 (5)2.1 球杆系统介绍 (5)2.1.1 系统简述 (5)2.1.2 系统组成 (5)2.2 球杆系统建模 (6)2.2.1 球杆系统数学模型建立 (6)2.3 MATLAB建模 (7)2.3.1 MATLAB软件介绍 (7)2.3.2 球杆系统在MATLAB的模型建立 (7)3 模糊控制器设计 (13)3.1 模糊控制器概述及原理 (13)3.2 模糊控制器结构 (13)4 球杆系统的模糊控制器设计 (15)4.1 模糊控制的实现 (16)4.1.1 各个变量个论域 (16)4.1.2 隶属度划分 (16)4.1.3 模糊规则的建立 (18)4.2 模型仿真 (20)结束语 (22)参考文献 (23)致谢 (24)1 绪论1.1 课题背景和研究意义1.1.1 课题背景如今的世界已经迎来一场重要的信息革命了,而模糊理论的发展正好充分的印证了这次革命的必要。
自动控制球杆系统实验指导书-2016教材

自动控制综合实验2 实验指导书Part 1球杆系统GBB1004北京邮电大学自动化学院林雪燕2016.5.24前言自动控制是一门理论与实践并重的技术,在成功掌握了理论知识(经典控制、现代控制)的同时再配合做一些经典的自动控制实验,从而加深对自动控制的理解与掌握,为今后从事自动控制的设计和研究工作打下扎实的基础。
为了更好地配合理论教学,达到理论与实践完美的结合,将自动控制相关的实验独立设置成一门实验课:自动控制综合实验。
自动控制理论实验主要目的是通过实验进一步理解自动控制理论的基本概念,熟悉和掌握控制系统的分析方法和设计方法,掌握常用工程软件使用,如MATLAB、LabVIEW 等。
上学期开设的自动控制综合实验(1)主要内容为控制系统的Matlab/simulink 仿真和基于实验箱的硬件模拟,以电路系统为研究对象。
本学期开始的自动控制综合实验(2)的内容是基于典型控制理论实验设备(球杆系统和倒立摆系统),熟悉和掌握控制系统的分析和设计方法。
球杆系统机械简单,结构紧凑,安全性高,采用智能伺服驱动模块和Windows 程序界面,可用于教学或科研。
对于自动控制理论等课程来说,针对设备的非线性与不稳定性特点,设计有效的控制系统是项有意义的工作。
球杆系统要完成的实验有:实验一:小球位置的数据采集处理实验二:球杆系统的PID法控制实验三:球杆系统的根轨迹法控制实验四:球杆系统的频率响应法控制倒立摆是一个典型的不稳定系统,同时又具有多变量、非线性、强耦合的特性,是自动控制理论中的典型被控对象。
运用控制手段可使之具有一定的稳定性和良好的性能。
许多抽象的控制概念如控制系统的稳定性、可控性、系统收敛速度和系统抗干扰能力等,都可以通过倒立摆系统直观的表现出来。
倒立摆系统要完成的实验有:实验五:倒立摆的数学建模及稳定性分析实验六:倒立摆的状态反馈控制实验七:不同状态下状态反馈控制效果比较实验八:倒立摆的LQR 控制同学们完成实验后,要完成相应的实验报告,并及时提交。
自动控制实验报告——球杆系统倒立摆bupt概要

球杆系统实验实验一小球位置的数据采集处理一、实验目的:学会用Simulink仿真与硬件连接并获得小球位置。
二、实验任务:1、在MatLab Simulink中通过添加功能模块完成球杆系统模型的建立;2、正确获得小球位置数据;三、实验原理:小球的位置通过电位计的输出电压来检测,它和IPM100的AD转换通道AD5相连,AD5(16位)的范围为0-65535,对应的电压为0-5V,相应的小球位置为0-400mm。
MatLab Simulink环境下的数据采集处理工具箱提供了强大的功能。
可以编写扩展名为mdl的图形文件,采集小球的位置信号,并进行数字滤波。
四、实验设备及仪器:1、球杆系统;2、计算机MATLAB平台;五、实验步骤:将MatLab主窗口的Current Directory文本框设置为球杆控制程序的系统文件夹;在MatLab主窗口点击进入Simulink Library Brower窗口,打开工具箱Googol Education Products\4. Ball & Beam\A. Data Collection and Filter Design,运行Data Collection and Filter Design程序,确认串行口COM Port为1后,双击Start Real Control模块,打开数据采集处理程序界面;已有的模块不需再编辑设置,其中Noise Filter1模块是专门设计的滤波器,用来抑制扰动。
请参考以下步骤完成剩余部分:1、添加、设置模块:添加User-Defined Functions组中的S-Function模块,双击图标,设置name为AD5;parameters为20.添加Math Operations组中的Gain模块,双击图标,设置Gain为0.4/65535.0.添加Sinks组中的Scope模块,双击图标,打开窗口,点击(Parameters),设置General 页中的Number of axes为2,Time Range为20000,点击OK退出,示波器屏成双;分别右击双屏,选Axes properties,设置Y-min为0,Y-max为0.4.2、连接模块:顺序连接AD5、Gain、Noise Filter1、Scope模块,完成后的程序界面如图所示:图1.1.1 完成后的数据采集处理程序界面点击运行程序,双击Scope模块,显示滤波前后的小球位置-时间图,拨动小球在横杆上往返滚动,可得如下实验结果:图1.1.2 小球位置的数据采集处理六、实验总结通过这个实验、我学会了球杆系统模型的建立以及小球位置的获取。
球杆系统控制器设计及matlab仿真

球杆系统控制器设计及matlab仿真本文旨在讨论《球杆系统控制器设计及matlab仿真》的主要内容和目标。
图论主要是介绍球杆系统控制器的设计原理和matlab仿真的应用,以及探索如何在该系统中实现强大的控制功能。
通过理论分析和数值模拟,我们将展示该系统的稳定性和性能优势。
这篇文档将提供给工程师和研究人员一个深入探讨球杆系统控制器设计与matlab仿真的指南。
通过这些工作,我们的目标是进一步推动该领域的发展,并提供实用、可靠的解决方案。
目标:球杆系统控制器的设计原理Matlab仿真在球杆系统控制中的应用探索如何实现强大的控制功能展示球杆系统的稳定性和性能优势提供工程师和研究人员指南引言本文旨在介绍球杆系统控制器设计及Matlab仿真的研究背景和目的。
球杆系统是指用于击球的高尔夫球杆,而控制器是指控制球杆运动和力量输出的设备。
设计合适的控制器可以帮助高尔夫球手提高球杆的稳定性和精准度。
高尔夫球运动具有一定的技术要求,其中球杆的使用对于取得高分尤为重要。
然而,球杆击球时的运动状态及力量输出是一个相对复杂的控制过程,需要综合考虑多个因素,如包括杆身材料、空气阻力、击球力量等。
为了改善球杆的控制性能,减少误差并提高击球精度,研究人员开始关注球杆系统的控制器设计及Matlab仿真。
Matlab是一种强大的数学建模和仿真工具,可以帮助工程师进行系统分析和设计。
通过Matlab仿真,可以模拟球杆系统的运动状态及力量输出,根据不同的参数和控制策略进行优化。
因此,利用Matlab进行球杆系统控制器设计及仿真,可以辅助研究人员深入了解球杆系统的控制原理,并提供有效的设计方案。
本文的目的是为了探讨球杆系统控制器设计及Matlab仿真的可行性和优势。
通过系统地分析和仿真,我们希望能够指导高尔夫球杆控制器的改进和优化,提高球手的击球技术和成绩。
同时,本文也为后续相关研究提供了理论基础和方法参考。
综上所述,本文将通过研究和分析球杆系统的控制器设计及Matlab仿真,为高尔夫球杆控制技术的发展做出贡献,并为相关研究提供参考和启示。
自动控制原理实验报告——球杆系统

1系统建模连线(连杆和同步带轮的连接点与齿轮中心的连线)和水平线的夹角为(的角度存在一定的限制,在最小和最大的范围之间),它作为连杆的输入,横杆的倾斜角和之间的有如下的数学关系:角度和电机轴之间存在一个减速比n=4的同步带,控制器设计的任务是通过调整齿轮的角度,使得小球在某一位置平衡。
小球在横杆上滚动的加速度如下式:其中:小球在横杆上的位置r为输出小球的质量m = 0.11kg;小球的半径R = 0.015m;重力加速度g = -9.8m/s2;横杆长L = 0.4m;连杆和齿轮的连接点与齿轮中心的距离为d = 0.04(m);小球的转动惯量J = 2*m*R^2/5(N/m2)。
我们假设小球在横杆上的运动为滚动,且摩擦力可以忽略不计。
因为我们期望角度在0附近,因此我们可以在0附近对其进行线性化,得到近似的线性方程:Laplace变换得:2实验步骤【主要方法】:通过球杆系统仿真,与理想传递函数下的反馈系统的对比,深刻理解系统的调节以及稳定性特征。
2.1PID控制法2.1.1P控制1.含有控制器、球杆系统结构和小球位置反馈的系统框图如下所示:其中,Xd(s)为小球目标位置的拉普拉斯变换,P控制器为:GP(s)=K P 闭环系统的传递函数为:其中,。
2.MATLAB仿真程序代码:m=0.11; R=0.015; g=-9.8; L=0.4; d=0.04;J=2*m*R^2/5;K=(m*g*d)/(L*(J/R^2+m));num=[-K]; den=[1 0 0];plant=tf(num,den);kp=3;sys_cl=feedback(kp*plant,1);step(0.2*sys_cl)(1)当Kp=3时(2)当Kp=6时(3)当Kp=10时3.在Simulink环境下仿真(1)当Kp=3时(2)当Kp=6时(3)当Kp=10时分析:从仿真图和实验图中可以看出,他们的大致波形是一致的,但由于实验受环境影响,如用手抓取小球,桌面收到碰撞震荡等,使波形出现很多毛刺,但系统是不稳定的,出现等幅振荡。
用matlab和admas模拟小球杠杆平衡

13.根据matlab中生成的AAA,BBB,CCC,DDD四个矩阵来创建。将四个文件中的数据复制到新建的数组中。如图12所示:
图12
14.创建控制信号,创建变量:Build-System Elements-State Variable-New,修改变量:Build-System Elements-State Variable-Modify。在Database Nagivator中选择ball_beam-Torque_In,在弹出的窗口中选择Data Element,先选择Algebraic Variable Value,输入变量名control_signal。再选择Array Element Value,数组名输入ARRAY_Y,元素数输入1。如图13所示:
图5
7.将两个LTI System的名称修改为SS和rsys如图6所示:
图6
8.双击示波器Scope,将Data history中的Limit data points to last去掉,仿真,在示波器Scope中的显示结果如图7左图所示,将显示结果沿Y轴局部放大,可以看到其趋近于-0.0177。
图7
图10
12.在adams的模型中,创建数组:Build-Data Element-Array-New。通过Tools-Database Navigator-tmp_MDI_POUTPUT中的Variables查看U数组中输入变量的顺序,这里是先Angle后Position。创建U,X,Y数组。如图11所示:
9.将Math Operation中的Gain添加到Step和Sum之间,并修改Gain中的参数为-1|0.0177。如图8所示:
图8
10.再次对模型进行仿真,并在示波器上显示仿真结果。如图9所示:
球杆系统控制器设计实验报告(北京理工大学).

球杆系统控制器设计实验报告学院:自动化学院组号:5成员:球杆系统控制器设计实验一、实验目的和要求1.1 实验目的(1)通过本设计实验,加强对经典控制方法(PID控制器)和智能控制方法(神经网络、模糊控制、遗传算法等)在实际控制系统中的应用研究。
(2)提高学生有关控制系统控制器的程序设计、仿真和实际运行能力.(3)熟悉MATLAB语言以及在控制系统设计中的应用。
1.2 实验要求(1)每两人一组,完成球杆系统的开环系统仿真、控制器的设计与仿真以及实际运行结果;(2)认真理解设计内容,独立完成实验报告,实验报告要求:设计题目,设计的具体内容及实验运行结果,实验结果分析、个人收获和不足,参考资料。
程序清单文件。
二、实验内容本设计实验的主要内容是设计一个稳定的控制系统,其核心是设计控制器,并在MATLAB/SIMULINK环境下进行仿真实验,并在球杆实验平台上实际验证。
算法实现:设计模糊控制器控制球杆系统,达到要求目标。
三、实验原理3.1 球杆系统的特点球杆系统是一个典型的非线性系统,理论上而言,它是一个真正意义上的非线性系统,其执行机构还具有很多非线性特性,包括:死区,直流马达和带轮的传动非线性,位置测量的不连续性,导轨表面不是严格的光滑表面,产生非线性阻力,这些非线性因素对于传统意义上的测量和建模造成很大的影响,并对系统的控制性能造成非常大的影响,怎样去设计一个鲁棒的控制系统,是现代控制理论的一个重要问题。
因为系统机械结构的特点,球杆系统具有一个最重要的特性——不稳定性,对于传统的实验方法,存在一些实验的难处,不稳定的系统容易对实验人员产生危险或是不可预料的伤害,球杆系统相对而言,机械比较简单,结构比较紧凑,安全性也比较高,是一个可以避免这些危险和伤害的实验设备。
3.2 球杆系统的数学模型对小球在导轨上滚动的动态过程的完整描述是非常复杂的,设计者的目的是对于该控制系统给出一个相对简单的模型,如图3.1所示为实验使用球杆系统简化图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
摘要以球杆系统作为主体,系统中的小球作为被控对象,设计一个模糊控制器,控制小球在装置导轨上的运行状态,分析小球在导轨上的运行状态,以此来反映模糊控制器的控制性能。
设计首先对球杆系统组成结构及其基本原理进行分析之后,建立一个相对简化后的球杆系统模型;运用相关的模糊控制原理,建立球杆系统模糊控制规则,再对球杆系统进行模糊控制器设计。
并在MATLAB仿真环境下建立控制器的仿真模型,对球杆系统进行仿真,测试模糊控制器的控制性能。
针对球杆系统自身存在的不稳定特性,在进行仿真时加入闭环反馈控制环节,这样不但可以提高系统的稳定性,还可以提高控制的精度,相较于其他一般控制,它更具有独特优势,更符合人类思维。
球杆系统作为如今研究控制理论的经典案例,及模糊控制融合之后,能更好地表现模糊控制在自动控制方面的优良特性。
关键词:球杆系统;模糊控制;MATLAB建模ABSTRACTIn the ball and beam system as the main body, the ball as a controlled object,design a fuzzy controller , to control the ball in the guide rail device running status. Analysis the ball movement on the guide rail, in order to reflect the fuzzy controller performance. First,the design analysis the composition structure and the basic principle ofthe ball and beam system , then establish a relatively simplified of the ball and beam system model; using the principle of fuzzy control, to establish fuzzy control rules of the ball and beam system, design a fuzzy controller to the ball and beam system. And in the MATLAB simulation environment,establish the simulation model of the controller, simulate the club system and test the control performance of the fuzzy controller.For the ball and beam system own existence the instability characteristics, in the simulation by adding closed loop feedback control link, which can not only improve the system stability, but also can improve the control accuracy, compared with other general control, it is more unique advantages, more in line with human thinking.Club system as a classic case in study control theory, andafterfusion with fuzzy control, canperformance the excellent characteristics of fuzzy control in the automatic control .Key words: the ball and beam system;fuzzy control;MATLAB modeling目录1 绪论 (1)1.1 课题背景和研究意义 (1)1.1.1 课题背景 (1)1.1.2 课题的研究意义 (1)1.2 模糊控制的发展及研究状况 (2)1.2.1 模糊控制论的产生及发展 (2)1.2.2 模糊控制论的研究和现状 (3)2 球杆系统建模及仿真 (5)2.1 球杆系统介绍 (5)2.1.1 系统简述 (5)2.1.2 系统组成 (5)2.2 球杆系统建模 (6)2.2.1 球杆系统数学模型建立 (6)2.3 MATLAB建模 (7)2.3.1 MATLAB软件介绍 (7)2.3.2 球杆系统在MATLAB的模型建立 (7)3 模糊控制器设计 (13)3.1 模糊控制器概述及原理 (13)3.2 模糊控制器结构 (13)4 球杆系统的模糊控制器设计 (15)4.1 模糊控制的实现 (16)4.1.1 各个变量个论域 (16)4.1.2 隶属度划分 (16)4.1.3 模糊规则的建立 (18)4.2 模型仿真 (20)结束语 (22)参考文献 (23)致谢………………………………………………………………………… (24)1 绪论1.1 课题背景和研究意义1.1.1 课题背景如今的世界已经迎来一场重要的信息革命了,而模糊理论的发展正好充分的印证了这次革命的必要。
第一次提出完全相异于传统数学和控制理论的模糊集合理论的是美国控制理论学者L.A.Zadeh,到后来的第一块包含模糊逻辑的智能芯片研发成功,只用了20年这短短的时间。
这样的事实充分表明了模糊控制理论具有相当的可挖掘性和前瞻性。
正是因为模糊控制理论这门科学为如今这场信息革命提供了一种强有力的数学工具及手段,才使得它具有如此大的应用前景。
模糊控制理论具有许多优点。
模糊控制理论用相对简单的可以让机器变得更灵活的软件或者硬件,使机器更具有智能性。
如今已经加入模糊控制理论元素的许多产品和工业控制系统都提供了充分的证据。
模糊控制理论能为心理,教育,管理等许多学科的研究和发展提供更加合理化,具体化的数学语言和工具,这一点将会为软科学的研究提供最大程度的帮助。
这也将决定模糊控制理论比其他的数学理论的应用程度更普遍。
模糊控制理论作为模糊控制的基础,在经过几十年的发展之后,它已经将人类实践操作经验完美的加入到自动控制的策略当中。
1.1.2课题的研究意义在如今,人们对于工业制造过程中机器的控制智能和精度的要求不断提高,对非线性不稳定系统及复杂大系统等越来越看重,对其投入的研究资源也越来越多。
正因为任何实际系统都具有非线性的特性,参数和结构都具有不确定性。
非线性系统作为控制系统中一般的系统,相对于一般系统而言,除了强弱程度不同以外,它的特性致使它的局限性越来越明显。
而模糊控制就是解决这一矛盾的重要手段之一。
它在进行控制的过程中,切入点并不是系统的数学模型,而是将现场操作人员的经验及专家知识纳入其中,这将使它更具有人类思维,更易于实现人的控制。
球杆系统作为一个经典的研究控制的平台,可以很方便的在实验室里研究关于非线性不稳定系统的建模和控制器的设计方面等很多需要解决的难点,所以,这个课题具有非常高的研究价值和研究前景。
球杆系统作为一个研究经典控制理论和现代控制理论的经典的教学实验平台之一,它是研究控制技术方面的重要的实验研究对象。
球杆系统除了跟普通控制系统有相同或相类似的性质之外,在实际实验过程中,小球在水平导轨上运动时,运动的状态是不稳定的,我们无法实施有效的操作可以让小球停留在人为指定的位置,这就是球杆系统相对于其他一般系统的不同之处的特性之一:开环不稳定性。
由于球杆系统特有的不稳定性,球杆系统可以应用到很多领域当中,具有很大的通用性,不但可以直观的观察自动控制方面许多控制器的控制性能,还可以验证以前的研究成果的准确性甚至可以发现和研究还未被证实的科学定理。
这些先天具有的优势都极大地促进了球杆系统研究的发展和控制理论的蓬勃发展。
1.2 模糊控制的发展及研究状况1.2.1 模糊控制论的产生及发展现代控制理论在近几十年来,在工业、农业、军事、航空方面的应用越来越普遍,都取得了成功的应用。
比如极小值原理应用于最优控制,预测控制应用于大滞后过程等,但这些控制过程都必须有一个基本要求:建立被控对象的精确数学模型。
伴随科学技术飞速发展的同时,科技生活等各个领域对自动控制系统的控制精度、响应速度、系统稳定性等的要求也愈加提高,研究涉及的系统也更加复杂多变。
但在实际研究过程中,会遇到一列的难点瓶颈,例如被控对象的非线性、时变性、外界环境因素的干扰、运行过程的复杂性、实际情况的不确定性等因素致使在实际研究过程中难以建立被控对象的精确模型。
在遇到难以建立适合数学模型的复杂对象,传统的数学控制方法反倒不如一个有实际操作经验的人员对其进行手动控制。
这一点是基于人脑有能力对模糊事物有一定的识别能力和判决能力,那些看起来不确定的模糊手段往往可以很轻松的达到预想的目的。
人因为具有天生的学习能力,所以在实际操作过程中可以不断的积累经验,利用已有的操作经验对被控对象进行控制,这些经验信息往往是用自然语言表达的,所以是定性的描述,具有模糊性。
因为这种特性不能采用已有的定量控制理论对其进行处理,所以必须得研究出一种新的理论和方法。
事实上,模糊现象的存在已经是人们无法回避的了。
早在100多年前,就已经有人在研究如何将客观上存在的模糊现象用语言描述出来。
1923年,B.Russell有一篇关于“含糊性”的论文,其中提到了关于含糊和精确其实是语言的属性,都不是现实中存在的东西。
语言都是模糊的,就像“红色的”和“新的”都不是清晰地。
1937年M.Black发表的一篇文章当中就说过“轮廓一致”的概念,这一观点可以当成是后来扎德提出隶属函数的启蒙,他还提出模糊集合和子集合的定义。
所以,事实上他既是模糊集合的最开始的鼻祖。
在当时,也有其他人意识到模糊现象是普遍存在在现实中的,爱因斯坦就提出过这类思想观点。
而且在这个时候还有人发觉传统的二值逻辑有很大的局限性,它并不能真实的反映现实世界。
传统逻辑并不能适用在现实生活,它只适合在想象中的理想状态。
L.A.Zadeh发表的模糊集合理论,它的核心部分是对复杂的系统使用一种语言分析的数学模式,让自然语言在正常情况下转化成电脑能接收的算法语言。
正是模糊集合理论的产生,为人们在处理一些客观性的模糊性问题时提供有力的工具,也正是这一理论的产生为自适应科学的发展解决了难题。
在这种情况下,模糊控制理论作为模糊数学的一个分支便产生了。
