陕西省西安市高新一中等五校2013届高三第一次联考数学文(附答案) (23)

合集下载

陕西省西安市高新一中等五校2013届高三第一次联考文科综合试题

文科综合能力试题第Ⅰ卷（选择题共140分）本卷共35个小题，每小题4分，共140分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

某中学地理兴趣小组在2012年9月23日对该校5米高的旗杆的影子进行测量，并绘制了旗杆影长随时间变化曲线。

据图回答1～2题。

1．该地的农业地域类型为A．商品谷物农业B．水稻种植业C．种植园农业D．混合农业2．该地区农业发展最主要的不利条件是A．洪涝灾害频繁B．农业生产机械落后C．纬度较高，热量不足D．灌溉水源不足郑（州）西（安）高铁是我国中长期铁路规划中10条客运专线中的徐兰客运专线中最先开工的一段。

2005年9月2 5日正式开工，2009年6月28日，郑西客运专线全线铺通，2010年2月6日，郑西高速铁路客运专线正式投入商业运营。

右图为郑（州）西（安）铁路客运专线示意图。

据此回答第3题。

3．下列关于郑西客运专线走向的解释，最合理的是西太平洋副热带高压（简称副高）是影响我国大陆的重要天气系统。

我国东部的主要锋面雨带，通常位于副高脊线以北5～8个纬度距离处，并随副高的北进南退而移动，下图是某同学绘制的副高对我国天气影响示意图。

读图回答4～5题。

4．该同学绘制的示意图中有一处明显错误，其错误点及理由分别是A．北方的冷空气——这个季节不存在B．暖湿气流——气流方向错误C．副高控制下天气——晴朗少雨D．锋面雨带——锋面雨带在副高北侧5．以下地理现象最可能出现于图示季节的是A．我国西北地区黄沙漫天B．澳大利亚森林火险等级高C．法国地中海沿岸海水浴场人满为患D．前往波斯湾地区的日本货船经过阿拉伯海时顺风顺水下图为2009年我国和美国人口迁移年龄分布图，读图，完成6～7题。

6．下列有关两国人口的叙述正确的是A．中国人口迁移率峰值比美国早与农村早婚有关B．美国老年人口迁移率较高主要因为和子女团聚C．美国老年人口迁移的方向自南部向东北部D．中国与美国10岁儿童的迁移量相当7．针对我国人口迁移的特点，迁入地今后应重点做好A．加强法制和道德建设B．加大城市幼儿园建设C．加大医疗、卫生事业建设D．加强户籍管理制度建设下图是两区域一月平均气温分布图，读图回答8~9题。

陕西省西安市高新一中等五校2013届高三第一次联考语文试题

长安一中、高新一中、交大附中、师大附中、西安中学2013届第一次模拟考试语文试题注意事项：1．本试题卷分第1卷（阅读题）和第Ⅱ卷（表达题）两部分，其中第1卷第三、四题为选考题，其它题为必考题．总分1 50分，考试时间150分钟．2．答题前，考生须将自己的学校、班级、姓名、考号填写在本试题卷指定的位置上。

3．选择题的每小题选出答案后，用2B铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，不能答在试题卷上．4．非选择题必须按照题号顺序在答题卡上各题目的答题区域内作答．超出答题区域或在其他题的答题区域内书写的答案无效；在草稿纸、本试题卷上答题无效．5．考试结束，将本试题卷和答题卡一并交回．第Ⅰ卷阅读题甲必考题一、现代文阅读（9分，每小题3分）阅读下面的文字，完成1—3题。

《现代汉语词典》对‚大师‛的释义是‚在学问或艺术上有很深的造诣，为大家所尊崇的人‛。

简言之，成为大师，有两项条件：有造诣、被尊崇。

于是，大师的存在，便不仅仅是一种个体的存在，而是具有社会学意义的存在。

他们的存在，遮蔽着他人与群体，同时也遮蔽着历史。

他们是以人类代言人的身份存在的。

芸芸众生死去，只有他们永生。

思想的不朽与伟大愈发令人深刻地感受到个体生命的短暂与渺小。

人们确立了大师的话语权的同时，也丧失了自我的话语权．当人们试图透过对大师的解读逼近原始的历史，更发现历史已经被他们垄断。

大师是山峰，也是鸿沟。

当我们站立在国家图书馆望不到首尾的书柜旁，我们会感到一种阅读的恐惧，读书越多，恐惧便越深，因为我们发现所有的思想都被表达过，所有的情感都被倾诉过了。

当文学家面对曹雪芹和托尔斯泰，当哲学家面对庄子和尼采，当经济学家面对马克思和萨缪尔森，他们都可能染上一种疑难杂症——失语。

像孔子说的‚予欲无言‛．大师的存在足以令后人乱了方寸，就像婆婆怒目之下的小媳妇，不知什么该说，什么不该说。

我们实在不能断定大师的存在是成全了我们还是妨碍了我们。

陕西省长安一中高新一中交大一中师大附中高三数学五校第一次模拟考试试题理(含解析)北师大版

11．设F1、F2是双曲线的两焦点，点P在双曲线上．若点P到焦点F1的距离等于9，则点P到焦点F2的距离等于。
【答案】1或17
【解析】由双曲线的定义知：，即点P到焦点F2的距离等于1或17。
12．已知向量的最小值为。
【答案】6
【解析】因为，。所以的最小值为6。
13．若函数在（0，1）内有极小值，则实数b的取值范围是。
④若定义在R上的函数则6是函数的周期。
以上四种说法，其中正确说法的序号为。
【答案】①③④
【解析】①若p或q为真，p且q为假，则p与q必为一真一假，正确；
②若数列，错误。；
③若实数t满足的一个次不动点，设函数与函数为自然对数的底数）的所有次不动点之和为m，则m=0，正确。由函数的性质知：方程和方程的两个互为相反数，所以此命题正确；
（II）若过点T（3，0）的直线与椭圆D相交于两点M、N，设P为椭圆上一点，且满足
（O为坐标原点），求实数t取值范围．
21．（本小题满分13分）已知函数
（I）求函数的单调区间；
（II）是否存在实数m，使不等式时恒成立？若存在，求出实数m的取值范围；若不存在，请说明理由。
（III）已知正整数列中的最大项。
【答案】
【解析】因为函数在（0，1）内有极小值，所以在（0，1）内有根，且是的两根中较大的那个，所以，解得实数b的取值范围是。
14．以下有四种说法：①若p或q为真，p且q为假，则p与q必为一真一假；
②若数列；
③若实数t满足的一个次不动点，设函数与函数为自然对数的底数）的所有次不动点之和为m，则m=0
A．10个B．15个C．16个D．18个
【答案】B
【解析】当a，b都为正偶数时：，共有5种情况；

陕西省高三数学上学期第一次模拟考试试题文新人教A

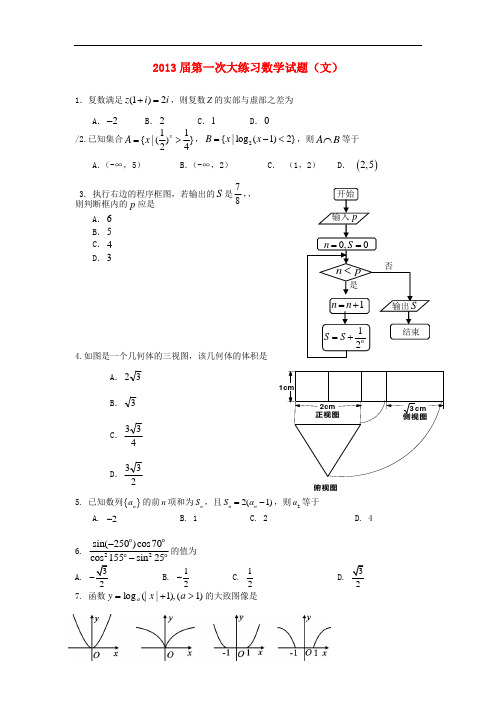
俯视图侧视图正视图3cm 1cm2cm 开始n p <是输入p结束输出S 否12nS S =+1n n =+0,0n S ==2013届第一次大练习数学试题（文）1．复数满足(1)2z i i +=，则复数Z 的实部与虚部之差为A ．2-B ．2C ．1D ．0/2.已知集合11{|()}24x A x =>，2{|log (1)2}B x x =-<，则A B ⋂等于A ．（-∞，5）B ．（-∞，2）C ．（1，2）D ． ()2,5 3. 执行右边的程序框图，若输出的S 是78，，则判断框内的p 应是A ．6B ．5C ．4D ．34.如图是一个几何体的三视图，该几何体的体积是A ．32B ．3C ．433 D ．233 5. 已知数列{}n a 的前n 项和为n S ，且2(1)n n S a =-，则2a 等于A. 2-B. 1C. 2D. 46. 22sin(250)cos70cos 155sin 25--o o o o的值为A. 3-B. 12-C. 12D. 37. 函数)1(),1|(|log >+=a x y a 的大致图像是A B C D8.设()cos sin f x x x =-，把()f x 的图象按向量(,0)(0)a m m =>r平移后，图象恰好为函数cos sin y x x =+的图象，则m 的值可以为 A ．4π B ．34π C ．π D. 2π 9.过点P(4,2)作圆224x y +=的两条切线，切点分别为A 、B ，0为坐标原点，则OAB ∆的外接圆方程是A ．22(2)(1)5x y -+-= B ．22(4)(2)20x y -+-=C ．22(2)(1)5x y +++= D ．22(4)(2)20x y +++=10. 已知()f x 、()g x 都是定义在R 上的函数，'()()()'()0f x g x f x g x +<，()()xf xg x a =，5(1)(1)(1)(1)2f g f g +--=．在区间[3,0]-上随机取一个数x ，()()f x g x 的值介于4到8之间的概率是A. 38B.13C.23D.12二、填空题：本大题共5小题，每小题5分，共25分，把答案填在答题卡的相应位置。

2013年陕西省高考文科数学试卷(有答案)(word版)

2013年普通高等学校招生全国统一考试(陕西卷)
文科两部分,第一部分为选择题,第二部分为非选择题.
2.考生领到试卷后,须按规定在试卷上填写姓名、准考证号，并在答题卡上填涂对应的试卷类型信息.
3.所有解答必须填写在答题卡上指定区域内.考试结束后,将本试卷和答题卡一并交回.
第一部分(共50分)
8.已知点M(a,b)在圆外,则直线ax+by= 1与圆O的位置关系是
(A)相切(B)相交(C)相离(D)不确定
9.设△ABC的内角A,B,C所对的边分别为a,b,c,若 ,则△ABC的形状为
(A)直角三角形(B)锐角三角形(C)钝角三角形(D)不确定
10.设[x]表示不大于x的最大整数,则对任意实数x,y,有
(A)0.09(B) 0.20(C) 0.25(D) 0.45
6.设z是复数,则下列命题中的假命题是
(A)若 ,则z是实数(B)若 ,则z是虚数
(C)若z是虚数,则 (D)若z是纯虚数,则
7.若点(x,y)位于曲线y= |x|与y= 2所围成的封闭区域,则2x－y的最小值为
(A)－6(B)－2(C)0(D) 2
15. A【答案】R
B【答案】
C【答案】(1, 0)
16【解】 = 。
最小正周期。
所以最小正周期为。
(Ⅱ) .
.
所以，f (x)在上的最大值和最小值分别为 .
17【解】(Ⅰ)设公差为d,则
.
(Ⅱ) 。
.
所以, 是首项 ,公比的等比数列。
18【解】(Ⅰ)设 .
.
.(证毕)
(Ⅱ) .
在正方形AB CD中,AO = 1.
三、解答题:解答应写出文字说明、证明过程及演算步骤（本大题共6小题，共75分）

陕西省西安市第一中学高三上学期期末考试数学文试题.pdf

西安市第一中学 2012-2013学年度第一学期期末高三年级数学（文科）一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的（本大题共1小题，每小题5分，共0分）．，，则=（） A． B． C．D． 2．已知为等差数列,若,则的值为 ( ) A． B． C．- D． 3．若椭圆的离心率为，则双曲线的渐近线方程为 ( ) A． B． C． D． 4．函数（其中）的图象如图所示，为了得到的图像，则只要将的图像 ( ) A．向右平移个长度单位 B．向右平移个长度单位 C．向左平移个长度单位 D．向左平移个长度单位 5．设p∶，q∶，则p是q的 ( ) A充要条件. B.必要不充分条件C.充分不必要条件D.既不充分也不必要条 6．，…则的末两位数字为（） A．01 B．43 C．07 D．49 7．平面向量=（） A．1B．2C．3D． 8．在等差数列中，已知,那么A．-30 B．15 C．-60 D．-15 9．设、为两个不同的平面，l、m为两条不同的直线，且l，m，有如下的两个命题：①若∥，则l∥m；②若l⊥m，则⊥．那么A．①是真命题，②是假命题 B．①是假命题，②是真命题 C．①②都是真命题 D．①②都是假命题何体的体积为( ) A．6 B．5.5 C．5 D．4.5 二、填空题：本大题共小题，每小题5分，满分25分．，且是第二象限的角，则 ___________. 12．=12, 则输出的= ； 13．函数若则的值为：； 14．在椭圆的焦点为，点p在椭圆上，若，则____=_______ 15.设函数若，则的取值范围是 . 三、解答题：解答应写出文字说明，证明过程或演算步骤（本答题共6小题，共75分） 16，（本题满分12分）已知函数在时取得最大值4．　(1)?求的最小正周期； (2)?求的解析式； (3)?若(α?+)=,求sinα． 17．（本小题12分）. （1）若从集合中任取一个元素，从集合中任取一个元素，求方程y=0有两个不相等实根的概率；（2）若从区间中任取一个数，从区间中任取一个数，求方程y=0 没有实根的概率. 18．（本小题12分）在平面直角坐标系xoy中，已知四点 A(2，0)， B(－，0)，C(0，－)，D(－，－)，把坐标系平面沿y轴折为直二面角. 求证：BC⊥AD；求三棱锥C—AOD的体积. 19．（本小题12分）数列的前n项和为满足, 求数列 (3) 若求数列的前n项和. y 2= x与直线 y=k ( x + 1 )相交于A、B两点, 点O是坐标原点. (1) 求证: OA(OB; (2) 当△OAB的面积等于时, 求k的值. 21、（本题满分14分）已知函数 (1) 若曲线在处的切线平行于直线，求函数的单调区间； (2) 若，且对时，恒成立，求实数的取值范围. 文科数学参考答案与评分标准一、选择题：题号12345678910答案ACBA C BBA DC 二、填空题: 11．； 12．4.； 13．1或 14. 2, 15．．．三、解答题：，，，，． 17．解：（1）a取集合｛0，1，2，3｝中任一元素，b取集合｛0，1，2｝中任一元素 ∴a、b的取值情况有（0，0），（0，1）（0，2）（1，0）（1，1）（1，2）（2，0），（2，1），（2，2），（3，0）（3，1）（3，2）其中第一个数表示a的取值，第二个数表示b的取值，基本事件总数为12. 设“方程有两个不相等的实根”为事件A，当时方程有两个不相等实根的充要条件为当时，的取值有（1，0）（2，0）（2，1）（3，0）（3，1）（3，2）即A包含的基本事件数为6. ∴方程有两个不相等的实根的概率 ……………………………………………………（6分）（2）∵a从区间［0，2］中任取一个数，b从区间［0，3］中任取一个数则试验的全部结果构成区域这是一个矩形区域，其面积设“方程没有实根”为事件B 则事件B构成的区域为即图中阴影部分的梯形，其面积由几何概型的概率计算公式可得方程没有实根的概率 ………………………………………………（12分） 18．解法一：（1）∵BOCD为正方形， ∴BC⊥OD， ∠AOB为二面角B-CO-A的平面角 ∴AO⊥BO ∵AO⊥CO 且BO∩CO=O ∴AO⊥平面BCO 又∵ ∴AO⊥BC 且DO∩AO=O ∴BC⊥平面ADO ∴BC⊥AD …………(6分) （2）…………………………（12分） 19．解：（1）因为，令，解得 ……1分再分别令，解得 …………………3分（2）因为，所以，两个代数式相减得到 ……………………5分所以，又因为，所以构成首项为2，公比为2的等比数列…7分（3）因为构成首项为2，公比为2的等比数列所以，所以 ……………………8分因为，所以所以令因此 ……………………………11分所以 ………………………12分 20. (本小题满分13分) 解: (1) 当k=0时直线与抛物线仅一个交点, 不合题意, ………… 2分 ∴k ( 0由y=k (x+1)得x=1 代入y 2= x 整理得: y 2 +y 1=0 ， 2分设A (x 1 , y 1), B (x 2 , y 2) 则y 1 + y 2=, y 1y 2=1. ………… 2分 ∵A、B在y 2= x上, ∴A (, y 1 ), B (, y 2 ) ， ∴ kOA·kOB=== 1 . ∴ OA(OB. ……………………… 3 分 (2) 设直线与x轴交于E, 则 E ( 1 , 0 ) ∴|OE|=1 ， S△OAB=|OE|(| y 1| + | y 2| )=| y 1 y 2|==, 解得k=( 4分 21．（本小题满分14分）解: (1) 定义域为直线的斜率为, ………………………3分所以由; 由所以函数的单调增区间为, 减区间为 …………………………………………6分 (2) ，且对时，恒成立 . 即设 ……………………………10分当时, , 当时, , …………………………12分所以当时,函数在上取到最大值,且所以所以所以实数的取值范围为 …………………………………14分．。

2013年陕西高考文科数学试题及答案

2013年陕西高考文科数学试题及答案2013年普通高等学校招生全国统一考试(陕西卷)文科数学注意事项:1. 本试卷分为两部分, 第一部分为选择题, 第二部分为非选择题.2. 考生领到试卷后, 须按规定在试卷上填写姓名、准考证号，并在答题卡上填涂对应的试卷类型信息.3. 所有解答必须填写在答题卡上指定区域内. 考试结束后, 将本试卷和答题卡一并交回.第一部分(共50分)一、选择题：在每小题给出的四个选项中，只有一项符合题目要求（本大题共10小题，每小题5分，共50分）1. 设全集为R , 函数()1f x x =-的定义域为M ，则C M R 为 (A) (－∞,1) (B) (1, + ∞) (C) (,1]-∞ (D) [1,)+∞2. 已知向量(1,),(,2)a m b m ==，若a //b ，则实数m 等于 (A) 2- (B) 2 (C) 2-或2 (D) 03. 设a , b , c 均为不等于1的正实数, 则下列等式中恒成立的是 (A) ·log log log a c c b a b = (B) ·log lo log g a a a b a b = (C) ()log og g l lo a a a b c bc = (D) ()log g og o l l a a a b b c c +=+4. 根据下列算法语句, 当输入x 为60时, 输出y 的值为(A) 25(B) 30 (C) 31 (D) 614. 对一批产品的长度(单位: 毫米)进行抽样检测, 下图为检测结果的频率分布直方图. 根据标准, 产品长度在区间[20,25)上为一等品, 在区间[15,20)和区间[25,30)上为二等品, 在区间[10,15)和[30,35)上为三等品. 用频率估计概率, 现从该批产品中随机抽取1件, 则其为二等品的概率为(A) 0.09 (B) 0.20 (C) 0.25 (D) 0.45 6. 设z 是复数, 则下列命题中的假．命题是 (A) 若20z ≥, 则z 是实数 (B) 若20z <, 则z 是虚数 (C) 若z 是虚数, 则20z ≥ (D) 若z 是纯虚数, 则20z < 7. 若点(x ,y )位于曲线y = |x |与y = 2所围成的封闭区域, 则2x －y 的最小值为 (A) －6 (B) －2 (C) 0 (D) 2输入xIf x ≤50 Theny = 0.5 * x Else y = 25 + 0.6*(x -50) End If 输出y17. (本小题满分12分)设S n表示数列{}na的前n项和.(Ⅰ) 若{}na为等差数列, 推导S n的计算公式;(Ⅱ) 若11,0a q=≠, 且对所有正整数n, 有11nnqSq-=-. 判断{}na是否为等比数列.18. (本小题满分12分)如图, 四棱柱ABCD－A1B1C1D1的底面ABCD是正方形, O为底面中心, A1O⊥平面ABCD,12AB AA==O D1B1C1D AC A1(Ⅰ) 证明: A1BD // 平面CD1B1;(Ⅱ) 求三棱柱ABD－A1B1D1的体积.19. (本小题满分12分)有7位歌手(1至7号)参加一场歌唱比赛, 由500名大众评委现场投票决定歌手名次, 根据年龄将大众评委分为5组,组别A B C D E人数51015155(Ⅰ) 为了调查评委对7, 其中从B组中抽取了6人. .组别A B C D E人数50 1015155抽取人数6(Ⅱ) 在(Ⅰ)中, 若A, B, 现从这两组被抽到的评委中分别任选1人, 求这2人都支持1号歌手的概率.20. (本小题满分13分)已知动点M (x ,y )到直线l :x = 4的距离是它到点N (1,0)的距离的2倍. (Ⅰ) 求动点M 的轨迹C 的方程;(Ⅱ) 过点P (0,3)的直线m 与轨迹C 交于A , B 两点. 若A 是PB 的中点, 求直线m 的斜率.21. (本小题满分14分) 已知函数()e ,x f x x =∈R .(Ⅰ) 求f (x )的反函数的图象上图象上点(1,0)处的切线方程; (Ⅱ) 证明: 曲线y = f (x) 与曲线2112y x x =++有唯一公共点. (Ⅲ) 设a <b , 比较2a b f +⎛⎫ ⎪⎝⎭与()()f b f a b a --的大小, 并说明理由.答案：1.B2. C3. B4. C5. D6. C7. A8. B9. A 10. D 11.45 12.π313. (1)(2)(3)()213(21)nn n n n n n ++++=⨯⨯⨯⋅-14. 2015. (－∞,﹢∞)B .6C (1, 0)16【解】()·f x =a b =)62sin(2cos 212sin 232cos 21sin 3cos π-=-=-⋅x x x x x x 。

陕西长安一中高新一中交大一中师大附中、西安中学2013届高三五校第一次模拟考试理综试题

陕西长安一中高新一中交大一中师大附中、西安中学2013届高三五校第一次模拟考试理综试题本试卷分第I卷（选择题）和第II卷（非选择题）两部分，150分钟，共300分。

以下数据可供解题时参考，可能用到的相对原子质量：H 1 N 14 O 16 S 32第I卷（选择题共126分）一、选择题：本大题共13小题，每小题6分。

在每小题给出的四个选项中，只有一项是符合题目要求的．1．现有一种含催产素的新药，它能使人们对陌生人产生信赖感．这一新药可能有助于治疗孤独症等疾病．催产素是由下丘脑合成、垂体后叶释放的一种九肽荷尔蒙．下列有关叙述正确的是A．催产素一定含有C、H、O、N四种元素，含有9个肽键B．孤独症患者直接口服适量该药可以有效地缓解症状C．下丘脑中有些细胞不仅能够分泌激素，而且能传导兴奋D．催产素参与的调节过程具有作用范围比较局限、作用时间比较长等特点2．下列关于生物科学研究方法和相关实验的叙述中，正确的是A．摩尔根运用类比推理的方法证明了基因位于染色体上B．模型方法就是指借助具体的实物，对认识的对象进行形象化描述C．用于观察质壁分离与复原的紫色洋葱表皮细胞同样可用来观察植物细胞有丝分裂D．标志重捕法调查种群密度时，部分标志物脱落，实验所得到数值与实际数值相比偏大3．正常情况下，下列四个图若改变自变量或因变量，则曲线变化最大的是A．图①将“光照强度”改为“CO2浓度”B．图②将“胰岛素相对含量”改为“胰高血糖素相对含量”C．图③将“有丝分裂各时期”改为“减数第二次分裂各时期”D．图④将“酶活性”改为有氧呼吸释放CO2量”4．下图①l②③④分别表示不同的变异类型，其中图③中的基因2由基因l变异而来。

有关说法正确的是A．图①②都表示易位，发生在减数分裂的四分体时期B．图③中的变异属于染色体结构变异中的缺失C．图④中的变异属于染色体结构变异中的缺失或重复D．图中4种变异能够遗传的是①③5．下图为人体某一反射弧的示意图，a、b为微型电流计F的两极，下列叙述错误．．的是A．兴奋从细胞B传到细胞D，存在化学信号与电信号的转换B．从a处切断神经纤维，刺激b赴，效应器能产生反射活动C．刺激皮肤细胞A，电流计指针将发生两次方向相反的偏转D．神经元静息时，细胞膜对K+的通透性增加以维持电位差6．下图l、2为实验的初始状态，以下关于生长素调节的叙述正确的是A．图1和图2实验结果都能体现生长素的促进生长作用，而图3则能说明生长素作用有两重性B．图l的实验结果A、B都不弯曲，但原因不相同C．图2中的实验结果是放M的胚芽鞘弯向一侧而放N的不弯曲D．图3茎卷须中生长素含量外侧比内侧少7．下列说法正确的是A．光导纤维、蚕丝、棉花、涤纶的主要成分都是纤维素B．CO2、NO2或SO2都会导致酸雨的形成C．氨基酸、淀粉、蛋白质均属于高分子化合物D．实验室制各氢氧化亚铁是用新制的硫酸亚铁溶液与氢氧化钠溶液反应，制备氢氧化铝是用硫酸铝溶液与氨水反应8．分子式为C11H16的单取代芳烃，其可能的结构有A．5种B．6种C．7种D．8种9．下列表示对应化学反应的离子方程式正确的是A．氢氧化钡溶液与硫酸铜溶液反应：Ba2++SO2—4=BaSO4↓B．向10mLlmol/LNa2CO3溶液中逐滴加入5mL lmol/L盐酸：2H++CO2—3=CO2↑+H2OC．将过量SO2通入冷氨水中：SO2+NH3·H2O =HSO—3+NH+4D．用稀硝酸洗涤试管内壁的银镜：Ag+2H++NO—3=Ag++NO↑+H2O10．下列与有机物的结构、性质有关的叙述正确的是A．苯、甲苯均不能使酸性KMnO4溶液褪色B．乙醇、苯酚均能与Na反应放出H2，二者分子中官能团相同C．淀粉、纤维素的分子式均可表示为（C6H10O5）n，二者互为同分异构体D．甲烷和Cl2的反应与乙烯和Br2的反应属于同一类型的反应11．下列说法正确的是A．常温下，将pH =11的氨水稀释到原体积的10倍后，溶液的pH=10B．为确定某酸H2A是强酸还是弱酸．可测NaHA溶液的pH，若pH>7，则H2A是弱酸；若pH<7，则H2A是强酸C．用0.2000 mol/L NaOH标准溶液滴定HCl与CH3COOH的混合溶液（混合液中两种酸的浓度均约为0.l mol/L），至中性时，溶液中的酸未被完全中和D．相同温度下，将足量氯化银固体分别放入相同体积的①蒸馏水、②0.1 mol/L盐酸、③0.1 mol/L 氯化镁溶液、④0.1 moI/L硝酸银溶液中，Ag+浓度：①>④=②>③12．现有含Fe（NO3）3、Cu（NO3）2、HNO3的某稀溶液，若向其中逐步加入铁粉，溶液中Fe2+浓度与加入铁粉的物质的量之间的关系如图所示，则该溶液中Fe（NO3）3、Cu（NO3）2、HNO3物质的量浓度之比为A．1:1:3 B．1:2:4C．1:1:4 D．l:3:113．下列说法错误的是A．原子最外层电子数为2的元素一定处于周期表IIA族B．主族元素X、Y能形成XY2型化合物，则X与Y的原子序数之差可能为2或5C．L层电子为奇数的所有元素所在族的序数与该元素原子的L层电子数相等D．M层电子为奇数的所有主族元素所在族的序数与该元素原子的M层电子数相等二、选择题．本题共8小题，每小题6分。

陕西省西安市高新一中等五校2013届高三第一次联考数学文(附答案) (2)

长安一中、高新一中、交大附中、师大附中、西安中学高2013届第一次模拟考试数学（文）试题第Ⅰ卷（选择题共50分）一、选择题（本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．已知集合M={x|一3<x<3，x ∈Z ），N={x|x<1}，则M N=A ．{|3x x -<<1}B ．{|02}x x <<C ．{-3，-2，-1，0,1）D ．{-2，一1，0）2．已知直线a 和平面α，那么a//α的一个充分条件是A ．存在一条直线b ，a//b 且b ⊂αB ．存在一条直线b ，a ⊥b 且b ⊥αC ．存在一个平面β，a ⊂β∥且α//βD ．存在一个平面β，α//β且α//β3．如果数列321121,,,,,n n a a a a a a a -…是首项为1，公比为2-的等比数列，则a 5等于 A ．32 B ．64C ．—32D ．—64 4．设实数x ，y 满足11,11x y x y -≤+≤⎧⎨-≤-≤⎩则点（x,y ）在圆面2212x y +≤内部的概率为A ．8πB ．4πC ． 34πD ．2π 5．过抛物线22(0)y px p =>的焦点作直线交抛物线于1122(,),(,)P x y Q x y 两点，若122,||4x x PQ +==，则抛物线方程是A ．24y x =B ．28y x =C ．22y x =D ．26y x =6．若某空间几何体的三视图如图所示，则该几何体的表面积是 A ．226++ B ．2(12)6++C ．23D ．32262++7．给出15个数：1，2，4，7，1 l ，…，要计算这15个数的和，现给出解决该问题的程序框图（如右图所示），那么框图中判断框①处和执行框②处应分别填入A ．16?;1i p p i ≤=+-B ．14?;1i p p i ≤=++C ．15?;1i p p i ≤=++D ．15?;i p p i ≤=+8．已知函数()sin(2)f x A x ϕ=+的部分图象如图所示，则f （0）=A ．12-B ．—1C ．32-D ．—39．台风中，C,A 地以每小时20千米的速度向东北方向移动，离台风中心30千米内的地区为危险区。

数学_2012-2013学年陕西省西安市某校高三(上)第一次质量检测数学试卷(文科)(含答案)

2012-2013学年陕西省西安市某校高三（上）第一次质量检测数学试卷（文科）一、选择题（5×14=70分）1. 已知集合A ={1, 2, 3, 4, 5}，B ={(x, y)|x ∈A, y ∈A, x −y ∈A}，则B 中所含元素的个数为( )A 3B 6C 8D 102. 若P ={x|x <1}，Q ={x|x >1}，则( )A P ⊆QB Q ⊆PC ∁R P ⊆QD Q ⊆∁R P3. 在集合{a, b, c, d}上定义两种运算⊕和⊗如下：那么b ⊗(a ⊕c)=( )A aB bC cD d4. 若a ∈R ，则“a =1”是“|a|=1”的( )A 充分而不必要条件B 必要而不充分条件C 充要条件D 既不充分又不必要条件5. 下列命题中，真命题是（）A ∃m ∈R ，使函数f(x)=x 2+mx(x ∈R)是偶函数B ∃m ∈R ，使函数f(x)=x 2+mx(x ∈R)是奇函数C ∀m ∈R ，使函数f(x)=x 2+mx(x ∈R)都是偶函数D ∀m ∈R ，使函数f(x)=x 2+mx(x ∈R)都是奇函数6. 已知α，β角的终边均在第一象限，则“α>β”是“sinα>sinβ”的（）A 充分不必要条件B 必要不充分条件C 充要条件D 既不充分也不必要条件7. 函数f(x)=11−x +lg(1+x)的定义域是（）A (−∞, −1)B (1, +∞)C (−1, 1)∪(1, +∞)D (−∞, +∞)8. 已知函数f(x)={log 3x ，x >02x ，x ≤0，则f[f(19)]=( ) A 4 B 14 C −4 D −149. 已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线y ＝2x 上，则cos2θ=（）A −45B −35C 35D 45 10. 已知m <−2，点(m −1, y 1)，(m, y 2)，(m +1, y 3)都在二次函数y =x 2−2x 的图象上，则（）A y 1<y 2<y 3B y 3<y 2<y 1C y 1<y 3<y 2D y 2<y 1<y 311. 若log a 2<log b 2<0，则（）A 0<a <b <1B 0<b <a <1C a >b >1D b >a >112. l 1，l 2，l 3是空间三条不同的直线，则下列命题正确的是( )A l 1⊥l 2，l 2⊥l 3⇒l 1 // l 3B l 1⊥l 2，l 2 // l 3⇒l 1⊥l 3C l 1 // l 2 // l 3⇒l 1，l 2，l 3共面D l 1，l 2，l 3共点⇒l 1，l 2，l 3共面13. 方程|x 2−2x|=a 2+1 (a ∈R +)的解的个数是（）A 1B 2C 3D 414. 曲线y =sinx sinx+cosx −12在点M(π4, 0)处的切线的斜率为（） A −12 B 12 C −√22 D √22二、填空题（共6小题，每小题5分，满分30分）15. 设f(x)是定义在R 上的奇函数，当x ≤0时，f(x)=2x 2−x ，则f(1)=________．16. 在△ABC 中，若a =3，b =√3，∠A =π3，则∠C 的大小为________．17. 函数y =x 2−2ax −3在(2, +∞)上单调递增，则a 的取值范围是________．18. 函数y =2cos 2x +sin2x 的最小值是________．19. 已知函数f(x)=e x −2x +a 有零点，则实数a 的取值范围是________．20. 已知抛物线y 2=4x 的焦点为F ，过点F 作一条直线交抛物线于A ，B 两点，若|AF|=3，则|BF|=________．三、解答题（共4小题，满分50分）21. 已知等差数列{a n }中，a 1=1，a 3=−3．（1）求数列{a n }的通项公式；（2）若数列{a n }的前k 项和S k =−35，求k 的值．22. 在△ABC 中，内角A ，B ，C 所对的边分别是a ，b ，c ，已知a =2，c =√2，cosA =−√24．（1）求sinC 和b 的值；（2）求cos(2A +π3)的值． 23. 某旅店有客房120间，每间房间的日租金为50元，每天都客满．旅店装修后要提高租金，经市场调查，如果一间客房的日租金每增加5元，则客房每天出租数会减少6间．不考虑其它因素，旅店将每间客房的日租金提高到多少元时，客房日租金的总收入最高？比装修前的日租金总收入增加多少元？（须有必要的文字说明）24. 已知函数f(x)=lnx+ke x （k 为常数，e =2.71828…是自然对数的底数），曲线y =f(x)在点(1, f(1))处的切线与x 轴平行．(1)求k 的值；(2)求f(x)的单调区间．2012-2013学年陕西省西安市某校高三（上）第一次质量检测数学试卷（文科）答案1. D2. D3. C4. A5. A6. D7. C8. B9. B10. B11. B12. B13. B14. B15. −316. π2 17. (−∞, 2]18. 1−√219. (−∞, 2ln2−2]20. 32 21. 解：（1）设等差数列{a n }的公差为d ，则a n =a 1+(n −1)d由a 1=1，a 3=−3，可得1+2d =−3，解得d =−2，从而，a n =1+(n −1)×(−2)=3−2n ；（2）由（1）可知a n =3−2n ，所以S n =n[1+(3−2n)]2=2n −n 2，进而由S k =−35，可得2k −k 2=−35，即k 2−2k −35=0，解得k =7或k =−5，又k ∈N +，故k =7为所求．22. 解：(1)△ABC 中，由cosA =−√24 可得sinA =√144．再由a sinA =c sinC 以及a =2、c =√2，可得sinC =√74．由a 2=b 2+c 2−2bc ⋅cosA 可得b 2+b −2=0，解得b =1．（2）由cosA =−√24、sinA =√144 可得cos2A =2cos 2A −1=−34，sin2A =2sinAcosA =−√74．故cos(2A+π3)=cos2Acosπ3−sin2Asinπ3=−3+√218．23. 解：设每间房的日租金提高x个5元，日租金总收入为y元，则由一间客房的日租金每增加5元，则客房每天出租数会减少6间，可得日租金为(50+5x)元，房间数为(120−6x)间，由利润=日租金×房间数，可得y=(50+5x)(120−6x)，即y=−30(x−5)2+6750，当x=5时，y max=6750，即旅社将每间客房将日租金提高到75元时，客房日租金的总收入最高，∴ 日租金总收入多6750−120×50=750（元）．24. 解：(1)因为函数f(x)=lnx+ke x ，所以f′(x)=1x−lnx−ke x，因为曲线y=f(x)在点(1, f(1))处的切线与x轴平行，所以f′(1)=0，即1−ln1−ke=0，解得k=1.(2)函数f(x)的定义域为(0, +∞)，由f′(x)=(1x−lnx−1)e xe2x，令g(x)=1x−lnx−1，此函数只有一个零点1，且当x>1时，g(x)<0，当0<x<1时，g(x)>0，所以当x>1时，f′(x)<0，所以原函数在(1, +∞)上为减函数；当0<x<1时，f′(x)>0，所以原函数在(0, 1)上为增函数．故函数f(x)的单调递增区间为(0, 1)，单调递减区间为(1, +∞)．。

西安市第一中学2013届高三上学期期末考试文科数学试卷

西安市第一中学2013届高三上学期学期期末数学试卷（文科）一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的（本大题共10小题，每小题5分，共50分）1．已知集合}{11A x x x =<->或，}{2log 0B x x =>，则A B ⋂= （）A ．}{1x x >B ．}{0x x >C ．}{1x x <-D ．}{11x x x <->或2．已知{}n a 为等差数列,若1598a a a π++=,则28cos()a a +的值为 ( )A ． 23-B ．12C ．-21 D ．233．若椭圆22221(0)x y a b ab+=>>2，则双曲线12222=-bx ay 的渐近线方程为( )A ．12y x =±B ．2y x =±C ．4y x =±D ．14y x=±4．函数()sin()f x A x ωϕ=+（其中0,||2A πϕ><）的图象如图所示，为了得到x x g 2sin )(=的图像，则只要将()f x 的图像 ( )A ．向右平移6π个长度单位 B ．向右平移12π个长度单位 C ．向左平移6π个长度单位 D ．向左平移12π个长度单位5．设p ∶10||2x <-，q ∶260x x +-<，则p 是q 的 ( )A 充要条件. B.必要不充分条件 C.充分不必要条件 D.既不充分也不必要条6．观察下列各式234749,7343,72401===，…则20117的末两位数字为（）A ．01B ．43C ．07D ．49 7．平面向量|2|,1||),0,2(,120b a b a b a +==︒则的夹角为与=（）A ．1B ．2C ．3D ．38．在等差数列{}n a 中，已知14812152a a a a a ---+=,那么15S 的值为（）A ．-30B ．15C ．-60D ．-159．设α、β 为两个不同的平面，l 、m 为两条不同的直线，且l ⊂α，m ⊂β，有如下的两个命题：①若α∥β，则l ∥m ；②若l ⊥m ，则α⊥β．那么（） A ．①是真命题，②是假命题 B ．①是假命题，②是真命题 C ．①②都是真命题 D ．①②都是假命题10，已知一个几何体的三视图如图（由左至右依次为主，左，俯）所示，则该几何体的体积为( )A ．6B ．5.5C ．5D ．4.5二、填空题：本大题共5小题，每小题5分，满分25分．11．已知5cos 13α=-，且α是第二象限的角，则tan(2)πα-=___________.12．执行右边的程序框图，若p =12, 则输出的n = ；13．函数21(10)sin()()(0)x x x f x x e π--<<⎧=⎨≥⎩若 (1)()2,f f a +=则a 的值为：；15.设函数()()[)22,,1,,1,.x x f x x x -⎧∈-∞⎪=⎨∈+∞⎪⎩ 若()4f x >，则x 的取值范围是 .三、解答题：解答应写出文字说明，证明过程或演算步骤（本答题共6小题，共75分） 16，（本题满分12分）已知函数()sin(3)(0,,0)f x A x A x R ϕϕπ=+>∈<<在12x π=时取得最大值4． (1) 求()f x 的最小正周期； (2) 求()f x 的解析式； (3) 若f (23α +12π)=125,求sin α．17．（本小题12分）已知函数222-b ax x y +=.（1）若a 从集合{0,1,2,3}中任取一个元素，b 从集合{0,1,2}中任取一个元素，求方程y=0有两个不相等实根的概率；（2）若a 从区间[0,2]中任取一个数，b 从区间[0,3]中任取一个数，求方程y=0 没有实根的概率.18．（本小题12分）在平面直角坐标系xoy 中，已知四点 A(2，0)， B(－2，0)，C(0，－2)，D(－2，－2)，把坐标系平面沿y 轴折为直二面角. （1）求证：BC⊥AD；（2）求三棱锥C —AOD 的体积.19．（本小题12分）已知数列{}n a 的前n 项和为n S , 且满足n 2-=n n a S ,(1,2,3,.....)n = (1) 求321,,a a a 的值;(2) 求证:数列}1{+n a 是等比数列； (3) 若n n b na =, 求数列{}n b 的前n 项和n T . 20、（本小题满分13分）已知抛物线 y 2 = – x 与直线 y = k ( x + 1 )相交于A 、B 两点, 点O 是坐标原点. (1) 求证: OA ⊥OB; (2) 当△OAB 的面积等于10时, 求k 的值.21、（本题满分14分）已知函数()ln 1,.a f x x a R x=+-∈(1) 若曲线()y f x =在0(1,)P y 处的切线平行于直线1y x =-+，求函数()y f x =的单调区间；(2) 若0a >，且对(0,2]x e ∈时，()0f x >恒成立，求实数a 的取值范围.文科数学参考答案与评分标准一、选择题：题号 1 2 3 4 5 6 7 8 9 10 答案 ACBA CB BA DC二、填空题:11．125； 12．4.； 13．1或2-14. 2,23π 15．()(),22,-∞-⋃+∞．．三、解答题：3sin(2)25πα+=，3cos 25α=，2312sin 5α-=，21sin 5α=，sin 5α=±17．解：（1）a 取集合｛0，1，2，3｝中任一元素，b 取集合｛0，1，2｝中任一元素∴a 、b 的取值情况有（0，0），（0，1）（0，2）（1，0）（1，1）（1，2）（2，0），（2，1），（2，2），（3，0）（3，1）（3，2）其中第一个数表示a 的取值，第二个数表示b 的取值，基本事件总数为12.设“方程()0f x =有两个不相等的实根”为事件A ，当0,0a b ≥≥时方程()0f x =有两个不相等实根的充要条件为a b >当a b >时，a 的取值有（1，0）（2，0）（2，1）（3，0）（3，1）（3，2）即A 包含的基本事件数为6.∴方程()0f x =有两个不相等的实根的概率61()122P A == ……………………………………………………（6分）（2）∵a 从区间［0，2］中任取一个数，b 从区间［0，3］中任取一个数则试验的全部结果构成区域{(,)|02,03}a b a b Ω=≤≤≤≤ 这是一个矩形区域，其面积236S Ω=⨯= 设“方程()0f x =没有实根”为事件B则事件B 构成的区域为{(,)|02,03,}M a b a b a b =≤≤≤≤≤ 即图中阴影部分的梯形，其面积162242M S =-⨯⨯=由几何概型的概率计算公式可得方程()0f x =没有实根的概率42()63M S P B S Ω=== ………………………………………………（12分）18．解法一：（1）∵BOCD 为正方形，∴BC ⊥OD ， ∠AOB 为二面角B-CO-A 的平面角 ∴AO ⊥BO ∵AO ⊥CO 且BO ∩CO=O ∴AO ⊥平面BCO 又∵BCO BC 平面⊆ ∴AO ⊥BC 且DO ∩AO=O ∴BC ⊥平面ADO ADO AD 平面⊆ ∴BC ⊥AD …………(6分) （2）114(22)2323C A OD A C O D V V --==⨯⨯⨯=…………………………（12分）19．解：（1）因为n 2-=n n a S ，令1=n ，解得,11=a ……1分再分别令3,2==n n ，解得233,7a a == …………………3分（2）因为n a S n n -=2，所以)1(211--=--n a S n n ， (1,)n n N >∈两个代数式相减得到121+=-n n a a ……………………5分所以）（1211+=+-n n a a ， (1,)n n N >∈ 又因为211=+a ，所以}1{+n a 构成首项为2，公比为2的等比数列…7分（3）因为}1{+n a 构成首项为2，公比为2的等比数列所以n n a 21=+，所以12-=n n a ……………………8分因为n n na b =，所以n n b n n -⋅=2所以)...21(22)1(......2322211321n n n T n n n +++-⋅+-++⋅+⋅+⋅=-令 1231122232...(1)22 (1)n n n H n n -=⋅+⋅+⋅++-+⋅ 23412122232...(1)22 (2)n n n H n n +⋅=⋅+⋅+⋅++-+⋅123111212(1)(2)222 (22)2(1)2212nnn n n n H n n n +++---=++++-⋅=-⋅=-⋅--（）得：因此12)1(2 +⋅-+=n n n H ……………………………11分所以 .2)1(2)1(21+-⋅-+=+n n n T n n ………………………12分20. (本小题满分13分)解: (1) 当k = 0时直线与抛物线仅一个交点, 不合题意, ………… 2分∴k ≠ 0由y = k (x+1)得x = ky–1 代入y 2 = – x 整理得: y 2 +k1y – 1 = 0 ，2分设A (x 1 , y 1), B (x 2 , y 2) 则y 1 + y 2 = –k1, y 1y 2 = –1. …………2分∵A 、B 在y 2 = – x 上, ∴A (–21y , y 1 ), B (–22y , y 2 ) ， ∴ k OA ·k OB =)y (y )y (y 222211-⋅-=21y y 1= – 1 .∴ OA ⊥OB. ………………………3 分(2) 设直线与x 轴交于E, 则 E ( – 1 , 0 ) ∴|OE| = 1 ，S △OAB =21|OE|(| y 1| + | y 2| ) =21| y 1 – y 2| =214k12+=10, 解得k = ±614分 21．（本小题满分14分）解: (1) ()ln 1,.a f x x a R x=+-∈)(x f 定义域为),0(+∞直线1y x =-+的斜率为1-,xxa x f 1)('2+-= 11)1('-=+-=a f 2=∴a ………………………3分所以22212)('xx xxx f -=+-=由20)('>>x x f 得; 由200)('<<<x x f 得所以函数()y f x =的单调增区间为)2(∞+，,减区间为(0,2) …………………………………………6分 (2) 0a >，且对(0,2]x e ∈时，()0f x >恒成立ln 10(0,2]a x x e x+->∈在恒成立. 即恒成立对]2,0()ln 1(e x x x a ∈->设]2,0(,ln )ln 1()(e x x x x x x x g ∈-=-= ……………………………10分]2,0(,ln 1ln 1)('e x x x x g ∈-=--=当10<<x 时, 0)('>x g ,为增函数)(x g当e x 20≤<时, 0)('<x g ,为减函数)(x g …………………………12分所以当1=x 时,函数)(x g 在]2,0(e x ∈上取到最大值,且11ln 1)1(=-=g 所以1)(≤x g 所以1a >所以实数a 的取值范围为),1(+∞ …………………………………14分。

陕西省长安一中、高新一中、交大附中、师大附中、西安中学2013届第五次模拟考试数学(文)(解析版)

陕西省长安一中、高新一中、交大附中、师大附中、西安中学2013届高三第二次模拟考试数学（文）试题（解析版）第Ⅰ卷（选择题共50分）一、选择题（本大题共10小题，每小题5分，共50分．（在每小题给出的四个选项中，只有一项是符合题目要求的）1．已知集合2{|(1)}(,),A x x a a i a R i A R ==+-∈⊆是虚数单位若，则a=A ．1B ．-1C ．±1D ．0【答案】C【解析】因为2{|(1)}(,),A x x a a i a R i A R==+-∈⊆是虚数单位若，所以210,1a a -==±即。

2．某程序框图如图所示，现输入如下四个函数，其中可以输出的函数是． A ．2()f x x =B ．1()f x x=C ．()ln 26f x x x =+-D ．()sin f x x =【答案】D【解析】可以输出的函数应具有的性质为：是奇函数且有零点。

A 是偶函数，排除；B 不存在零点，排除；C 不是奇函数，是非奇非偶函数，排除；D 即是奇函数又有零点，因此选D 。

3．命题“若220,,,0a b a b R a b +=∈==则”的逆否命题是 A ．若0a ≠或0b ≠，22,,0.a b R a b ∈+≠则B ．若a=b 0≠，22,,0.a b R a b ∈+≠则 C ．若0a ≠或0b ≠，22,,0.a b R a b ∈+≠则D ．若a ≠b 0≠，22,,0.a b R a b ∈+=则【答案】A【解析】命题“若220,,,0a b a b R a b +=∈==则”的逆否命题是“若0a ≠或0b ≠，22,,0.a b R a b ∈+≠则”。

4．已知()f x 是定义在R 上的偶函数，且对2为周期，则“()]f x 为[0,1上的增函数”是“()[3,4]f x 为上的减函数”的A ．既不充分也不必要的条件B ．充分而不必要的条件C ．必要而不充分的条件D ．充要条件【答案】D【解析】因为()f x 是定义在R 上的偶函数，且对2为周期，，所以由“()]f x 为[0,1上的增函数”可以得到“()]f x 为[-1,0上的间函数”，所以可以得到“()[3,4]f x 为上的减函数”，反之也正确，因为“()]f x 为[0,1上的增函数”是“()[3,4]f x 为上的减函数”的充要条件。

陕西省西安市2013届高三第一次质检数学(文)试题Word版含答案

陕西省西安市2013届高三第一次质检数学（文）试题本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分，全卷满分150分，考试时间120分钟。

第I 卷（选择题共50分）一、选择题（本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．若向量(23),(47),BA CA ==，，则BC = A ．（－2，－4）B ．（3．4）C ．（6，10）D ．（－6．－10）2．设集合{}|3213A x x =-≤-≤，集合B 为函数1(1)y g x =-的定义域，则A B =A ．（1，2）B ．[l ，2]C ．[1．2）D ．（1，2] 3．复数z 满足：（z －i ）i=2+1则z= A ．一l －i B ．1－i C ．—1+3i D ．1－2i 4．右图是一个算法的流程图，最后输出的W= A ．12 B ．18 C ．22 D ．265．要得到函数y= cos （2x+1）的图象，只要将函数y=cos2x 的图象 A ．向左平移1个单位 B ．向右平移1个单位 C ．向左平移12个单位 D ．向右平移12个单位 6．设函数1,()0,x D x x ⎧=⎨⎩为有理数为无理数，则下列结论错误的是A ．()D x 的值域为{0，1}B ．()D x 是偶函数C ．()D x 不是周期函数D ．()D x 不是单调函数7．若直线10x y -+=与圆22()2x a y -+=有公共点，则实数a 取值范围是 A ．[－3，－1] B ．[－1，3]C ．[－3,l ]D ．（－∞，－3] ⋃ [1．+∞）8．设ϕ∈R ．则“0ϕ≠”是“()cos()()f x x x R ϕ=+∈为偶函数”的A ．充分而不必要条件B 必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件 9．一个空间几何体的三视图如图所示，则该几何体的表面积为 A 48B ．32十C ．48 + D ． 8010．函数1(0,1)xy a a a a=->≠的图象可能是第II 卷（非选择题共100分）二、填空题（本大题共5小题，每小题5分，共25分）11．若x ，y 满足约束条件02323x x y x y ≥⎧⎪+≥⎨⎪+≤⎩，则z=x －y ，的最小值是。

【Word版解析】陕西省西安市2013届高三第一次质检数学(文)试题

陕西省西安市2013届高三第一次质检数学（文）试题本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分，全卷满分150分，考试时间120分钟。

第I 卷（选择题共50分）一、选择题（本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．若向量(23),(47),BA CA ==，，则BC =A ．（－2，－4）B ．（3．4）C ．（6，10）D ．（－6．－10）【答案】A【解析】因为(23),(47),BA CA == ，，所以()2,4BC BA AC =+=--.2．设集合{}|3213A x x =-≤-≤，集合B 为函数1(1)y g x =-的定义域，则A B = A ．（1，2）B ．[l ，2]C ．[1．2）D ．（1，2]【答案】D【解析】集合{}{}|3213|12A x x x x =-≤-≤=-≤≤，集合B 为函数1(1)y g x =-的定义域，所以{}|1B x x =>，所以A B = （1，2]。

3．复数z 满足：（z －i ）i=2+i ，则z= A ．一l －i B ．1－i C ．—1+3i D ．1－2i【答案】B【解析】设()z a bi a b R =+∈、，因为（z －i ）i=2+1，所以()12a bi i i ai b i +-=-+=+，1=21=11b a a b -+=⎧⎧⎨⎨=-⎩⎩所以，解得：，所以1z i =-。

4．右图是一个算法的流程图，最后输出的W=A ．12B ．18C ．22D ．26【答案】C【解析】开始循环：21,S T S =-=≥不满足S 10，T=T+2=3；再次循环：28,S T S =-=≥不满足S 10，T=T+2=5；再次循环：217,S T S =-=≥满足S 10，此时输出的=17+5=22W S T =+，因此选C 。

5．要得到函数y= cos （2x+1）的图象，只要将函数y=cos2x 的图象 A ．向左平移1个单位 B ．向右平移1个单位 C ．向左平移12个单位 D ．向右平移12个单位【答案】C【解析】把函数y=cos2x 的图象向左平移12个单位，得()1c o s 2,c o s 212y x y x ⎛⎫=+=+⎪⎝⎭即，因此选C 。

【Word版解析】陕西省西安市第一中学2013届高三上学期期中考试数学(文)试题

西安市第一中学2012-2013学年度第一学期期中高三年级数学（文科）试题命题人：张莲生审题人：一．选择题(本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的.)1．设集合}02|{2<-=x x x M ，},11|{≤≤-=x x N 则=N M （）A ．}10|{<<x xB ．}21|{<≤x xC ．}10|{≤<x xD ．}21|{<<x x【答案】C【解析】因为}02|{2<-=x x x M ={}|02x x <<，},11|{≤≤-=x x N ，所以=N M }10|{≤<x x 。

2．若R a ∈，则“2=a ”是“0)2)(1(=--a a ”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【答案】A【解析】若2=a ，则0)2)(1(=--a a ；若0)2)(1(=--a a ，则21a a ==或，所以“2=a ”是“0)2)(1(=--a a ”的充分不必要条件。

3．设n S 为等差数列}{n a 的前n 项和，公差2-=d ，若1110S S =，则=1a ( )A ．18B ．20C ．22D ．24【答案】B【解析】因为1110S S =，所以110a =，即11110a a d =+，又2-=d ，所以=1a 20。

4．设复数z 满足2)1(=+z i ，其中i 为虚数单位，则=z （）A ．i +1B ．i -1C ．i 22+D ．i 22-【答案】B【解析】因为2)1(=+z i ，所以()()()2121111i z i i i i -===-++-。

5．函数233x x y +-=在点（1,2）处的切线方程为（）A ．13-=x yB ．53+-=x yC ．53+=x yD ．x y 2=【答案】A【解析】因为233x x y +-=，所以()''36,13y x x k f =-+==所以，所以切线方程为()231y x -=-，即13-=x y 。

陕西省西安市高新一中等五校2013届高三第一次联考历史

陕西省长安一中、高新一中、交大附中、师大附中、西安中学2013 届第一次模拟考试文科综合能力试题命题学校：交大附中审题学校：长安一中注意事项：1．本试题卷分第Ⅰ卷（选择题）和第II 卷（非选择题）两部分，总分300 分，考试时间150 分钟．2．答题前，考生须将自己的学校、班级、姓名、学号填写在本试题卷指定的地点上。

3．选择题的每题选出答案后，用2B 铅笔将答题卡上对应题目的答案标号涂黑，如需变动，用橡皮擦洁净后，再选涂其余答案，不可以答在试题卷上，4．非选择题一定依照题号次序在答题卡上各题目的答题地区内作答，高出答题地区或在其余题的答题地区内书写的答案无效；在底稿纸、本试题卷上答题无效。

5．考试结束，将本试题卷和答题卡一并交回。

第Ⅰ卷（选择题共140 分）本卷共 35 个小题，每题 4 分，共 140 分。

在每题给出的四个选项中，只有一项为哪一项切合题目要求的。

24．我国古代的“族田义庄”常常是宗族中官僚士绅所置的主要赡济族人的田庄。

它是我国古代宗族宗法制度的产物。

族田义庄必定程度上能够起到社会保障功能作用。

因而可知，族田义庄A．有助于稳固和保护封建统治B．确定了社会保障系统C．有益于防备宗族内部的权益纷争D．阻挡了田庄经济的发展25．荀子《天论》一文：“列星随旋，日月递熠，四时代御，阴阳大化，风雨博施，万物各得其和以生，各得其养以成，不见其事而见其功，夫是之谓神；皆知其所以成，莫知其无形，夫是之谓天。

据资料可知是荀子的A．天人相分的思想B．天行有常的思想C．制天数而用之的思想D．唯物主义的思想26．据《汉书》记录：“文翁 ,, 景帝末为蜀郡守。

仁喜好教化，见蜀地辟陋，有夷狄风。

文翁欲诱进之，乃选郡县小吏开敏有材者张叔等十余人，亲身饬厉，遣诣京师，受业博士， ,, 又修起学官于成都市中，招下县子弟认为学官弟子。

”上述资料表示A．汉景帝时开始在蜀设郡B．文翁从教育下手，来改变蜀郡落伍状况C．文翁在蜀郡创办选官的新式制度D．汉代用官学教育的形式培育人材27．明朝推行严苛的“海禁”政策后，向来到嘉靖期间，海禁政策时松时紧，整体上说是以紧为主。

西安市高新届高考一模考试数学试题(文)含答案

数学试题(文科)一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知复数z 满足()3425i z +=，则z =（） A.34i -B.34i +C.34i --D.34i -+ 2.已知全集U R =，{}112,0,,22A x x B x x C x x ⎧⎫⎧⎫=-<<=≤=≥⎨⎬⎨⎬⎩⎭⎩⎭则集合C =（） A.A B B. ()U C A B C. ()U A C BD.()U C A B3. 在等差数列{}n a 中，前n 项和为n S ，31S S 42=，则84S S等于（）A.103 B. 81 C.91 D. 314. 设()f x 是定义在R 上的周期为3的函数，当x∈[－2，1)时，242,20(),01x x f x x x ⎧--≤≤=⎨<<⎩，则5()2f ＝（）A ．0B ． 1C ．12D ．1-5. 命题:p 若1,01,y x a <<<<，则 11yxa a <，命题:q 若1,0y x a <<<，则a a x y <.在命题①p q 且 ②p q 或 ③非p ④非q 中，真命题是（）A ．①③ B.①④ C.②③ D.②④6.在如右所示的程序框图中,输入5N ,则输出的数等于( )A. 54B. 45C. 65D. 567. 下列说法正确的是（）A.存在0x R ∈，使得30211cos log 10x -=B.函数sin 2cos 2y x x =的最小正周期为πC. 函数cos 23y x π⎛⎫=+ ⎪⎝⎭的一个对称中心为,03π⎛⎫- ⎪⎝⎭D. 角α的终边经过点()()()cos 3,sin 3--，则角α是第三象限角8. 一个样本容量为10的样本数据，它们组成一个公差不为0的等差数列{}n a ，若38a =，且137,,a a a 成等比数列，则此样本的平均数和中位数分别是（）A ．13,12B ．13,13C ．12,13D ．13,149. 如右下图所示是一个三棱锥的三视图，则此三棱锥的外接球的体积为（）A．43πB.2C.610．若x、y满足2020x ykx yy+-≥⎧⎪-+≥⎨⎪≥⎩，且g z y x=-的最小值为-6，则k的值为（）A．3 B．-3 C．13D．13-11. 设抛物线28y x=的焦点为F，准线为l，P为抛物线上一点，PA l⊥，A为垂足,如果直线AF斜率为PF=（）A. B. 8 C. D. 1612.设)0(25)(,12)(2>-+=+=aaaxxgxxxf，若对于任意]1,0[1∈x，总存在]1,0[∈x，使得)()(1xfxg=成立，则a的取值范围是 ( )A.),4[+∞B．]25,0(C.]4,25[D．),25[+∞二、填空题：本大题共4小题，每小题5分，共20分.把答案填在对应题号后的横线上.13. 已知向量()cos,sinaθθ=，()1,2b=-,若//a b，则代数式θθθθcossincossin2+-的值是；14.若直线260ax y++=和直线()2110x a a y a+++-=垂直，则a= ；15．已知数列{}n a的通项公式()*1log2Nnnnan∈+=，设其前n项和为nS，则使4-<nS成立的自然数n的最小值为.16．设函数)(xf是定义在R上的以5为周期的奇函数，若33)3(,1)2(2-++=>aaaff，则a的取值范围是.三、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17. （本题满分12分）在ABC∆中，角,,A B C的对边分别是,,a b c，已知.coscoscos2CbBcAa+=（Ⅰ）求Acos的值；（Ⅱ）若221,cos cos122B Ca=+=+，求边c的值．18. （本小题满分12分）某地区农科所为了选择更适应本地区种植的棉花品种，在该地区选择了5块土地，每块土地平均分成面积相等的两部分，分别种植甲、乙两个品种的棉花，收获时测得棉花的亩产量如右图所示：（Ⅰ）请问甲、乙两种棉花哪种亩产量更稳定，并说明理由；（Ⅱ）求从种植甲种棉花的5块土地中任选2块土地，这两块土地的亩产量均超过种植甲种棉花的5块土地的总平均亩产量的概率．19. （本小题满分12分）等腰ABC ∆的底边66=AB ，高3=CD ，点E 是线段BD 上异于点D B ,的动点.点F 在BC 边上，且AB EF ⊥.现沿EF 将BEF ∆折起到PEF ∆的位置，使AE PE ⊥. (Ⅰ)证明⊥EF 平面PAE ；（Ⅱ）记x BE =，)(x V 表示四棱锥ACFE P -的体积,求)(x V 的最值。