matlab实验五
(完整版)实验五用matlab求二元函数的极值

实验五 用matlab 求二元函数的极值1.计算二元函数的极值对于二元函数的极值问题,根据二元函数极值的必要和充分条件,可分为以下几个步骤: 步骤1.定义二元函数),(y x f z =.步骤2.求解方程组0),(,0),(==y x f y x f y x ,得到驻点.步骤3.对于每一个驻点),(00y x ,求出二阶偏导数22222,,.z z z A B C x x y y ∂∂∂===∂∂∂∂ 步骤4. 对于每一个驻点),(00y x ,计算判别式2B AC -,如果02>-B AC ,则该驻点是极值点,当0>A 为极小值, 0<A 为极大值;如果02=-B AC ,需进一步判断此驻点是否为极值点; 如果02<-B AC 则该驻点不是极值点.2.计算二元函数在区域D 内的最大值和最小值设函数),(y x f z =在有界区域D 上连续,则),(y x f 在D 上必定有最大值和最小值。
求),(y x f 在D 上的最大值和最小值的一般步骤为:步骤1. 计算),(y x f 在D 内所有驻点处的函数值;步骤2. 计算),(y x f 在D 的各个边界线上的最大值和最小值;步骤3. 将上述各函数值进行比较,最终确定出在D 内的最大值和最小值。
3.函数求偏导数的MATLAB 命令MATLAB 中主要用diff 求函数的偏导数,用jacobian 求Jacobian 矩阵。
可以用help diff, help jacobian 查阅有关这些命令的详细信息例1 求函数32824-+-=y xy x z 的极值点和极值. 首先用diff 命令求z 关于x,y 的偏导数>>clear; syms x y;>>z=x^4-8*x*y+2*y^2-3;>>diff(z,x)>>diff(z,y)结果为ans =4*x^3-8*yans =-8*x+4*y即.48,843yxyzyxxz+-=∂∂-=∂∂再求解方程,求得各驻点的坐标。
MATLAB(实验五)

实验五1、 编写程序,该程序在同一窗口中绘制函数在[]0,2π之间的正弦曲线和余弦曲线,步长为200/π,线宽为 2 个象素,正弦曲线设置为蓝色实线,余弦曲线颜色设置为红色虚线,两条曲线交点处,用红色星号标记,并通过函数方式在生成的图形中添加注释,至少应包括:标题,文本注释,图例和坐标轴标注。
x=0:pi/200:2*pi;sinx = sin(x); cosx = cos(x);k=find(abs(sinx-cosx)<1e-2); x1=x(k);figure,plot(x,sinx,'LineWidth',2) hold on ,plot(x,cosx,'r:','LineWidth',2)hold on ,plot(x(find(cosx==sinx)),cosx(find(cosx==sinx)),'r*','LineWidth',2)hold on ,plot(x1,sin(x1),'r*') xlabel('x:(0-2\pi)'); ylabel('y:sin(x)/cos(x)');title('正弦曲线和余弦曲线');text(x1+0.1,sin(x1),'sin(x)=cos(x)');gtext('sin(x)') gtext('cos(x)')legend('sin(x)','cos(x)')2、 绘制图像:双曲抛物面:22164x y z =-,1616x -<<,44y -<<,并对绘制的双曲抛物面尝试进行视点控制。
[X,Y] = meshgrid(-16:0.4:16,-4:0.1:4); Z = X.^2/16 - Y.^2/4;subplot(1,3,1),plot3(X,Y,Z),view(0,180),title('azimuth = 0,elevation = 180'); subplot(1,3,2),plot3(X,Y,Z),view(-37.5,-30),title('azimuth = -37.5,elevation = -30');subplot(1,3,3),plot3(X,Y,Z),view([3,3,2]),title('viewpoint=[3,3,1]');3、 表中列出了4个观测点的6次测量数据,将数据绘制成为分组形式和堆叠形式的条形图。
matlab实验内容答案

实验报告说明:matlab 课程实验需撰写8个实验报告,每个实验报告内容写每次实验内容中标号呈黑体大号字显示的题目。
第一次实验内容:实验一 MATLAB 运算基础一、实验目的1.熟悉启动和退出MATLAB 的方法。
2.熟悉MATLAB 命令窗口的组成。
3.掌握建立矩阵的方法。
|4.掌握MATLAB 各种表达式的书写规则以及常用函数的使用。
二、实验内容1.先求下列表达式的值,然后显示MATLAB 工作空间的使用情况并保存全部变量。
(1)22sin 8511z e︒=+ (2)12ln(2z x =,其中2120.455i +⎡⎤=⎢⎥-⎣⎦(3)0.30.33sin(0.3), 3.0, 2.9, 2.8,,2.8,2.9,3.02a ae e z a a --=+=--- 提示:利用冒号表达式生成a 向量,求各点的函数值时用点乘运算。
(4)2220141122123t t z t t t t t ⎧≤<⎪=-≤<⎨⎪--≤<⎩,其中t =0::】提示:用逻辑表达式求分段函数值。
2.已知12344347873657A -⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,131203327B -⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦求下列表达式的值:(1) A+6=B 和A-B+I(其中I 为单位矩阵)。
(2) A*B 和A.*B 。
(3) A^3和A^.3 。
(4) A/B 和B\A 。
(5)[A ,B]和[A([1,3],;);B^2] 。
!3.设有矩阵A 和B12345678910111213141516171819202122232425A ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦, 30161769023497041311B ⎡⎤⎢⎥-⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎣⎦(1) 求它们的乘积C 。
(2) 将矩阵C 的右下角3×2子矩阵赋给D(3) 查看MATLAB 工作空间使用情况。
4.完成下列操作:(1)求[100,999]之间能被21整除的数的个数。
MATLAB实验指导书(附答案)

MATLAB基础实验指导书漳州师范学院物电系2010年10月目录实验一MATLAB环境的熟悉与基本运算 (2)实验二MATLAB数值运算 (8)实验三MATLAB语言的程序设计 (12)实验四MATLAB的图形绘制 (16)实验五采用SIMULINK的系统仿真 (20)实验六MATLAB在电路中的应用 (25)实验七MATLAB在信号与系统中的应用 (27)实验八MATLAB在控制理论中的应用 (29)实验一 MATLAB环境的熟悉与基本运算一、实验目的:1.熟悉MATLAB开发环境2.掌握矩阵、变量、表达式的各种基本运算二、实验基本知识:1.熟悉MATLAB环境:MATLAB桌面和命令窗口、命令历史窗口、帮助信息浏览器、工作空间浏览器文件和搜索路径浏览器。
2.掌握MATLAB常用命令3.MATLAB变量与运算符变量命名规则如下:(1)变量名可以由英语字母、数字和下划线组成(2)变量名应以英文字母开头(3)长度不大于31个(4)区分大小写MATLAB中设置了一些特殊的变量与常量,列于下表。
MATLAB运算符,通过下面几个表来说明MATLAB的各种常用运算符表2 MATLAB算术运算符表3 MATLAB关系运算符表4 MATLAB逻辑运算符表5 MATLAB特殊运算4.MATLAB的一维、二维数组的寻访表6 子数组访问与赋值常用的相关指令格式5.MATLAB的基本运算表7 两种运算指令形式和实质内涵的异同表6.MATLAB的常用函数表8 标准数组生成函数表9 数组操作函数三、实验内容1、学习使用help命令,例如在命令窗口输入help eye,然后根据帮助说明,学习使用指令eye(其它不会用的指令,依照此方法类推)2、学习使用clc、clear,观察command window、command history和workspace等窗口的变化结果。
3、初步程序的编写练习,新建M-file,保存(自己设定文件名,例如exerc1、exerc2、exerc3……),学习使用MATLAB的基本运算符、数组寻访指令、标准数组生成函数和数组操作函数。
matlab实验五

实验五 基于matlab 的数据拟合与回归分析一、 实验类型验证性实验二、 实验学时2学时三、 实验目的1、掌握利用MATLAB 中实现单因变量的多元线性回归分析(经典多元线性回归分析)的方法;2、掌握利用MATLAB 中实现多因变量的多元线性回归分析(多对多线性回归分析)的方法。
3、掌握MATLAB 有关逐步回归的命令。
四、 实验内容及要求 实验内容:1 学习MATLAB 中有关经典多元线性回归分析的命令;(1) [b,bint,r,rint,stats] = regress(y,X,alpha)建立回归分析模型01122,i i i ip ip i y b b x b x b x ε=+++++其中()()2E 0,D i i εεσ==,1,2,,i n =.注:在该命令中,设计矩阵()(1)ij n p X x ⨯+=(X 的第1列全为1 ) 或响应值向量()1i n y y ⨯=中的无效值Nan 将被免忽略。
输入参数至少有2个,alpha 是检验的显著性水平,默认值为0.05。
输出参数至少有1个,b 是回归系数的估计值;bint 是各回归系数的置信度为1-alpha 的置信区间(第1列是它们的下界,第2列是它们的上界);r 是残差,rint 是残差的置信区间;stats 给出一个1*4的向量,依次是判定系数2R ,F 统计量的观测值及检验的p 值,以及误差的方差的估计值2ˆσ. 这里//(1)U p MMSF Q n p MSE==-- 是检验回归模型是否显著的检验统计量,当012:0p H b b b ====成立时, ~(,1)F F p n p --.可以通过分析残差的置信区间来观察原始数据是否存在异常点,若残差的置信区间不包括0,则可认为对应的观测值是异常值,将异常值全部去掉,重新建立的回归模型将更加精确。
可以调用命令rcoplot(r,rint)按观测顺序逐个画出各组观测值对应的残差和残差置信区间,从而观测异常值的位置。
实验五 MATLAB二维、三维图形的绘制

实验五 MATLAB二维、三维图形的绘制一、实验目的1.掌握二维、三维图形的绘制;2.掌握特殊二维图形的绘制;3.掌握绘图参数的设置;4.了解并学习简单动画的制作。
二、实验内容1.运行下列程序,学会并掌握标题、坐标轴标签和网格线的设置方法x=0:1:10;y=x.^2-10*x+6;plot(x,y);title ('Plot of y=x.^2-10*x+6');xlabel ('x');ylabel ('y');grid on;2.运行下列程序,学会并掌握线型、点型、颜色的设置方法x = -pi:pi/20:pi;y1 = sin(x);y2 = cos(x);plot(x,y1,'bo',x,y2,'r:');title('线型、点型和颜色');xlabel('时间'),ylabel('Y');grid on;3.同一坐标系内多条曲线的绘制1)使用 plot(x,[y1;y2;…])x = -pi:pi/20:pi;y1 = sin(x);y2 = cos(x);plot(x,[y1;y2]);legend('sin x','cos x');2)使用hold命令x = -pi:pi/20:pi;y1 = sin(x);y2 = cos(x);plot(x,y1);hold on;plot(x,y2,‘r’);3)在plot后使用多输入变量x = -2*pi:pi/20:2*pi;y1 = 2*sin(x);y2 = 2*cos(x);plot(x,y1,'ro',x,y2,'b:');title('线型、点型和颜色');xlabel('时间'),ylabel('Y');4) 使用plotyy命令x = -pi:pi/20:pi;y1 = sin(x);y2 = 5*cos(x);plotyy(x,y1,x,y2);grid on;gtext(‘sinx’) ; gtext(‘5cosx’) ;4.子图形窗口的绘制subplot(2,1,1);x= -pi:pi/20:pi;y=sin(x);plot(x,y) ; grid on;title('正弦曲线');subplot(2,1,2);x= -pi:pi/20:pi;y=cos(x);plot(x,y); grid on;title('余弦曲线');5.对数坐标图形x=0:0.1:10;y=x.^2 -10.*x +25;subplot(2,2,1);plot(x,y); grid on;xlabel('a) x、y轴线性刻度');subplot(2,2,2);semilogx(x,y); grid on;xlabel('b) x轴对数刻度、y轴线性刻度');subplot(2,2,3);semilogy(x,y); grid on;xlabel('c) x轴线性刻度、y轴对数刻度');subplot(2,2,4);loglog(x,y); grid on;xlabel(‘d) x、y轴对数刻度');6.极坐标下的绘图theta = 0:pi/20:2*pi;r = 0.5+cos(theta);polar(theta,r);7.复数的绘图,并比较下面几种情况的不同1)t = 0:pi/20:6*pi;y = exp(0.1*t) .* (cos(t) + i * sin(t));plot(y);grid on ;title('Plot of Complex Function vs Time');xlabel('Real Part');ylabel('Imaginary Part');2)t = 0:pi/20:6*pi;y = exp(0.1*t) .* (cos(t) + i * sin(t));plot(t, y);grid on ;title('Plot of Complex Function vs Time');xlabel('t');ylabel('y(t)');3)t = 0:pi/20:6*pi;y = exp(0.1*t) .* (cos(t) + i * sin(t));plot(t, real(y),'b-');grid on;hold on;plot(t, imag(y),'r-');title('Plot of Complex Function vs Time');xlabel('t');ylabel('y(t)');legend('real','imaginary');hold off;4)t = 0:pi/20:6*pi;y = exp(0.1*t) .* (cos(t) + i * sin(t));polar(angle(y),abs(y));title('Plot of Complex Function');8.特殊二维图形的绘制1)x = [1 2 3 4 5 6];y = [2 6 8 7 8 5];stem(x,y);title('Example of a Stem Plot');xlabel('x');ylabel('y');axis([0 7 0 10]);将上述程序中的stem语句换为stairs、bar、barh和compass,即可实现阶梯图、条形图、罗盘图的绘制。
matlab实验五循环结构程序设计实验报告

实验五:循环结构程序设计实验报告一、实验目的1. 了解循环结构的基本概念和原理;2. 掌握使用Matlab进行循环结构程序设计的方法;3. 提高编程能力和问题解决能力。
二、实验内容1. 学习while循环和for循环的基本语法和用法;2. 设计并编写一些基于循环结构的Matlab程序;3. 分析程序运行结果并进行总结。
三、实验原理循环结构是程序设计中的重要组成部分,它可以让一段代码重复执行多次,从而简化程序的编写。
在Matlab中,循环结构主要有while 循环和for循环两种形式。
while循环在执行循环体前判断条件是否为真,只有条件为真时才会执行循环体;for循环则是指定循环的次数,每次迭代时执行一次循环体。
四、实验步骤与结果1. 编写一个使用while循环的程序,实现1~100的累加。
程序代码如下:```matlabsum = 0;i = 1;while i <= 100sum = sum + i;i = i + 1;enddisp(sum);```运行程序后,得到的结果为5050。
2. 编写一个使用for循环的程序,实现1~10的阶乘。
程序代码如下:```matlabresult = 1;for i = 1:10result = result * i;enddisp(result);```运行程序后,得到的结果为xxx。
五、实验总结通过本次实验,我深刻理解了循环结构的基本概念和原理,掌握了使用Matlab进行循环结构程序设计的方法。
在编写循环程序的过程中,我发现循环结构可以大大简化程序的编写,并且能够高效地处理重复性任务。
我也进一步提高了自己的编程能力和问题解决能力。
本次实验使我对Matlab中的循环结构有了更加深入的了解,我相信这对我的编程能力和日后的学习工作都将大有裨益。
六、实验感想和改进意见通过本次实验,我深刻认识到循环结构在程序设计中的重要性和灵活性。
循环结构能够帮助我们简化程序的编写,提高代码的重用性和可读性,因此在实际的程序设计中,合理地运用循环结构能够大大提高程序的效率和逻辑清晰度。
实验五+MATLAB数值计算(含实验报告)

实验五 MATLAB 数值计算一、实验目的1.掌握求数值导数和数值积分的方法。
2.掌握代数方程数值求解的方法。
3.掌握常微分方程数值求解的方法。
二、实验的设备及条件计算机一台(带有MATLAB7.0以上的软件环境)。
设计提示1.参考本节主要内容,学习并理解相关函数的含义及调用方法。
三、实验内容1.线性系统方程:分别使用左除(\)和求逆(inv )求解下面系统方程的解:⎪⎩⎪⎨⎧=+=+=++377251463c b b a c b a2. 数值积分:使用quad 和trapz 求解⎰-503/dx xe x 的数值积分,并与其解析解9243/5+--e 相比较;3. 请完成教材P154页中实验指导环节的实验内容第2题4. 请完成教材P155页中思考练习的第3题(1),并绘制解在该求解区间(即[0,5])上的图像;。
5、请完成教材P164页实验指导环节的实验内容第5题。
(提示:该函数的符号导数,可以通过函数diff 求得。
首先定义符号变表达式,如求sin(x)的一阶符号导数,可以先定义f=’sin(x)’;df=diff(f);可求得df=cos(x)。
其中df 即为函数f 的一阶符号导数)。
四、实验报告要求(包含预习报告要求和最终报告要求)1.实验名称2.实验目的3.实验设备及条件4.实验内容及要求5.实验程序设计指程序代码。
6.实验结果及结果分析实验结果要求必须客观,现象。
结果分析是对实验结果的理论评判。
7.实验中出现的问题及解决方法8. 思考题的回答五、实验报告的提交方式Word文档,命名方式:实验号_你的学号_姓名例如本次实验:实验一_000000001_张三.doc(信息101提交报告邮箱):E_mail: *******************(网络工程101提交作业邮箱):E_mail: *******************(注意网络班的M是大写的)下一次课前提交,过期不收!六、参考文献参考教材和Matlab帮助文件。
MATLAb与数学实验 第五章习题解答

1 3 2 4 1 3 5 2 4 3 5
j=
1 1 2 2 3 3
3 4 4 5 5
s=
1 3 1 3 2 1 3 2 1 2 1 A1 =
10200 01020 30102 03010 00301 (2) n=nnz(A)
n=
13 ans =
1 2 -1 3 -2 4 1 -3 5 2
-4 3 -5
>> nx=nzmax(A)
nx =
35
>> [i,j,s]=find(A)
i=
1 2 1 3 2 4 1 3 5 2 4 3 5
j=
1 2 3 3 4 4 5 5 5 6 6 7 7
s=
1 2 -1 3 -2 4 1 -3 5 2 -4 3 -5
A1 =
1 0 -1 0 1 0 0
0 2 0 -2 0 2 0
C=
11 11 11
>> B=[3 5 7;0 1 0]
B=
357 010
>> D=[0 0 0;0 0 0]
D=
000 000
2.随机生成:(1)一个含有五个元素的列向量. (2)一个数值在 0~100 之间的三行四列的矩阵.
答 (1) rand(5,1)
ans =
0.9501
0.2311 0.6068 0.4860 0.8913
0 0 3 0 -3 0 3
0 3 0 1 0
0 0 0
4
0
4
0
0 0 3 0 1
0 0 0 0 5 0 5
答(1) n=nnz(A)
n=
11
>> nonzeros(A)
实验五 用Matlab数据拟合

2. 已知观测数据点如表所示 x 1.6 2.7 1.3 4.1 3.6 2.3 y 17.7 49 13.1 189.4 110.8 34.5
0.6
4
4.9
409.1
3
65
2.4
36.9
求a, b, c的值, 使得曲线 f(x)=aex+bsin x+c lnx 与已知数据 点在最小二乘意义上充分接近.
例4 已知观测数据点如表所示
x 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 y 3.1 3.27 3.81 4.5 5.18 6 7.05 8.56 9.69 11.25 13.17 求三个参数 a, b, c的值, 使得曲线 f(x)=aex+bx2+cx3 与 已知数据点在最小二乘意义上充分接近.
1.55
500 106
2.47
2. 93
3. 03
2.89
1000 106 1500 106 2000 106 2375 106
3 1.953 103 1.517 103 1.219 10
/ / N / m 2 3.103 103 2.465 103
解: 描出散点图, 在命令窗口输入: t=[0:1:16] y=[30.0 29.1 28.4 28.1 28.0 27.7 27.5 27.2 27.0 26.8 26.5 26.3 26.1 25.7 25.3 24.8 24.0] plot(t,y,'*')
a=polyfit(t,y,1) a= -0.3012 29.3804 hold on
beta
= 3.0022 4.0304 0.9404
(完整版)Matlab实验5选择结构程序结构

实验五、选择与循环结构一、实验目的:1、 掌握建立和执行M 文件的方法。
2、 掌握利用if 语句实现选择结构的方法。
3、 掌握利用switch 语句实现多分支选择结构的方法。
4、 掌握try 语句的使用。
5、 掌握利用for 语句实现循环结构的方法。
6、 掌握利用while 语句实现循环结构的方法。
7、 熟悉利用向量运算来代替循环的操作方法。
二、实验内容:1、 列分段函数的值。
⎪⎩⎪⎨⎧--≠≠<≤+--≠<-+=其他且且,632,100,6530,6222x x x x x x x x x x x y要求:(1) 用if 语句实现,分别输出x =-0.5,-3.0,1.0,2.0,2.5,3.0,5.0时的y 值。
提示:x 的值从键盘输入,可以是向量。
%homework_5_1_1.mx=input('请输入x 的值:x=');if (x<0 & x~=-3)y= x.*x + x - 6elseif (x>=0 & x<10 & x~=2 & x~=3)y=x.*x-5.*x+6elsey=x.*x-x-6end>> homework_5_1请输入x 的值:x=[-0.5 -3.0 1.0 2.0 2.5 3.0 5.0]y =-5.2500 6.0000 -6.0000 -4.0000 -2.2500 0 14.0000(2) 用逻辑表达式实现上述函数。
%homework_5_1_2.mx=input('请输入x 的值:x=')y=(x<0 & x~=-3).*(x.*x+x-6)...+(x>=0 & x<10 &x~=2 &x~=3).*(x.*x-5.*x+6)...+(x>=10 | x==-3 | x==3 | x==2).*(x.*x-x-6)>> homework_5_1_2请输入x=[-0.5 -3.0 1.0 2.0 2.5 3.0 5.0]x =-0.5000 -3.0000 1.0000 2.0000 2.5000 3.0000 5.0000 y =-6.2500 6.0000 2.0000 -4.0000 -0.2500 0 6.00002、输入一个百分制成绩,要求输出成绩的等级为A,B,C,D,E。
matlab实验报告(实验5)

一、 实验目的
开课学院及实验室:机电学院
2012 年 12 月 28 日
机电学
学院
院
实验课程名称
年级、专 业、班
1、 掌握 M 脚本文件和函数文件的创建方法,理解两者在形式上和运行上的区别; 2、 理解基本空间和函数空间的含义。 3、 掌握以控制流进行 MATLAB 程序设计的方法以及向量化程序设计方法,了解两者之间的异同; 二、
为频域抽样间隔, 2 1 为带宽。 K
四、实验报告要求
1、简述实验目的、实验原理及其要点; 2、把所有实验内容涉及的指令都以 M 文件方式创建并运行,保存实验结果图形。 3、总结实验中的主要结论。
按照实验内容 1 定义的 f(t)及时域采样方式,并取频域抽样点数 K=100,利用 MATLAB 编程,使用 for 循 环结构计算 F ( ) 在 [8 ,8 ] 在各个频域采样点的值,并画出其频谱图形。
T N 1 F (1 k ) f (t1 nt )e j (1 k )(t1 nt ) N n 0
其中,
(2.1)
根据以上两个等式,利用 MATLAB 编程,使用向量化计算的方法重新完成实验内容 2 和实验内容 3,并把计算结 果与实验内容 2 和实验内容 3 的结果进行比较是否相同(通过计算两者之间的最大绝对误差,观察其值是否接 近 0) 。 6、利用实验内容 5 的代码,把傅里叶变换和傅里叶逆变换分别写为两个 M 函数文件,函数定义形式为: function [F, w] = Fourier_lab2(f, N, T, K) function [f, t] = iFourier_lab2(F, K, W, N) 其中,f 为时域信号,t 为对时域信号 f 的采样点(即采样时刻) 为对时域信号 f 的采用点数,T 为 f 的 ,N 持续时间,K 为频域采样点数,F 为 f 的傅里叶变换,w 为对 F 的频域采样点,W 为 F 的频域带宽。 利用以上两个函数,写出 M 脚本文件重新完成实验内容 5。
实验五 matlab基础知识(简单)

本次实验注意:《实验五MALTAB基础知识(简单)》《实验五基于Matlab的信号频谱分析(复杂)》选作一个即可实验五MALTAB基础知识(一)实验目的 (2)(二)实验设备 (2)(三)实验要求 (2)(四)实验内容 (2)1.1 MATLAB基础知识 (2)1.1.1 MATLAB程序设计语言简介 (2)1.1.2 MA TLAB界面及帮助 (2)1.2 MA TLAB基本运算 (4)1.2.1 MA TLAB内部特殊变量和常数 (4)1.2.2 变量类型 (4)1.2.3 内存变量管理 (5)1.2.4 MA TLAB常用数学函数 (5)1.2.5 MA TLAB矩阵生成 (5)1.2.6 MA TLAB矩阵运算 (8)1.2.7 MA TLAB中的矩阵分析 (10)1.3 MA TLAB程序设计 (10)1.3.1 M文件 (10)1.3.2 程序控制结构 (12)实验五MALTAB基础知识(一)实验目的●了解MA TLAB 程序设计语言的基本特点,熟悉MA TLAB软件运行环境●掌握创建、保存、打开m文件及函数的方法●掌握变量等有关概念,具备初步的将一般数学问题转化为对应的计算机模型并进行处理的能力(二)实验设备计算机,Matlab软件(三)实验要求本实验属于验证实验,请根据(四)实验内容的步骤,运行相应的指令或例子,并将仿真结果截图至文档(请自己新建一个word文档,注意,并不一定所有指令或例子的实验结果都要截图,截图数目大于等于5个即可,自己选择性截图,答案不唯一,自由发挥)请在页眉处填写班级、学号、姓名,并将实验报告命名为“实验五_学号_姓名”,并通过FTP上传至指定文件夹。
(四)实验内容1.1 MATLAB基础知识1.1.1 MATLAB程序设计语言简介MA TLAB,Matrix Laboratory的缩写,是由MathWorks公司开发的一套用于科学工程计算的可视化高性能语言,具有强大的矩阵运算能力。
MATLAB数值分析实验五(欧拉法,荣格-库塔法解常微分方程)

佛山科学技术学院实 验 报 告课程名称 数值分析 实验项目 常微分方程问题初值问题数值解法 专业班级 姓 名 学 号 指导教师 陈剑 成 绩 日 期一. 实验目的1、理解如何在计算机上实现用Euler 法、改进Euler 法、Runge -Kutta 算法求一阶常微分方程初值问题⎩⎨⎧=∈='1)(],[),,()(y a y b a x y x f x y 的数值解。
2、利用图形直观分析近似解和准确解之间的误差。
二、实验要求(1) 按照题目要求完成实验内容; (2) 写出相应的Matlab 程序;(3) 给出实验结果(可以用表格展示实验结果); (4) 分析和讨论实验结果并提出可能的优化实验。
(5) 写出实验报告。
三、实验步骤1、用Matlab 编写解常微分方程初值问题的Euler 法、改进Euler 法和经典的四阶Runge-Kutta 法。
2、给定初值问题⎪⎩⎪⎨⎧=≤≤-=;1)1(,21,1')1(2y x xy x y⎪⎩⎪⎨⎧=≤≤++-=31)0(10,25050')2(2y x x x y y 要求:(a )用Euler 法和改进的Euler 法(步长均取h=0.05)及经典的四阶Runge-Kutta 法(h=0.1)求(1)的数值解,并打印)10,....2,1,0(1.01=+=i i x 的值。
(b) 用经典的四阶Runge-Kutta 方法解(2),步长分别取h=0.1, 0.05,0.025,计算并打印)10,....2,1,0(1.0==i i x 个点的值,与准确解25031)(x e x y x +=-比较,并列表写出在x=0.2,0.5,0.8处,对于不同步长h 下的误差,讨论同一节点处,误差随步长的变化规律。
(c )用Matlab 绘图函数绘制(2)的精确解和近似解的图形。
四、实验结果 %Euler.mfunction y = Euler(x0,xn,y0,h) %Euler 法解方程f_xy ; %x0,y0为初始条件; %x0,xn 为求值区间; %h 为步长; %求区间个数: n = (xn-x0)/h;%矩阵x 存储n+1个节点: x = [x0:h:xn]';%矩阵y 存储节点处的值: y = [y0;zeros(n,1)];%矩阵y_存储节点处导数值: y_(1)= f_xy(x0,y0); y_ = [y_(1);zeros(n,1)];%进行迭代(欧拉法迭代;求导数): for i = 2:n+1y (i) = y(i-1)+h*y_(i-1); y_(i) = f_xy(x(i),y(i)); end%Imp_Euler.mfunction y = Imp_Euler(x0,xn,y0,h)%改进的Euler法解方程f_xy;%x0,y0为初始条件;%x0,xn为求值区间;%h为步长;%求区间个数:n = (xn-x0)/h;%矩阵x存储n+1个节点:x = [x0:h:xn]';%矩阵y存储节点处的值:y = [y0;zeros(n,1)];%矩阵y_存储节点处导数值:y_(1)= f_xy(x0,y0);y_ = [y_(1);zeros(n,1)];%使用改进Euler法求值(欧拉法求近似;近似点导数;梯形校正;求导):for i = 2:n+1y_l = y(i-1) + h*y_(i-1);y_l = f_xy(x(i),y_l);y(i) = y(i-1) + (h/2)*(y_(i-1)+y_l);y_(i)= f_xy(x(i),y(i));end%R_Kutta4.mfunction y = R_Kutta4(x0,xn,y0,h)%Runger_Kutta法解方程f_xy;%x0,y0为初始条件;%x0,xn为求值区间;%h为步长;%求区间个数:n = (xn-x0)/h;%矩阵x存储n+1个节点:x = [x0:h:xn]';%矩阵y存储节点处的值:y = [y0;zeros(n,1)];%矩阵k1,k2,k3,k4存储各节点(中点)数值:k1(1)= f_xy(x0,y0);k1 = [k1(1);zeros(n,1)];k2(1)= f_xy(x0+h/2,y0+h*k1(1)/2);k2 = [k2(1);zeros(n,1)];k3(1)= f_xy(x0+h/2,y0+h*k2(1)/2);k3 = [k3(1);zeros(n,1)];k4(1)= f_xy(x0+h,y0+h*k3(1));k4 = [k4(1);zeros(n,1)];for i= 2:n+1y(i) = y(i-1)+(h/6)*(k1(i-1)+2*k2(i-1)+2*k3(i-1)+k4(i-1));k1(i)= f_xy(x(i),y(i));k2(i)= f_xy(x(i)+h/2,y(i)+h*k1(i)/2);k3(i)= f_xy(x(i)+h/2,y(i)+h*k2(i)/2);k4(i)= f_xy(x(i)+h,y(i)+h*k3(i));end(a):%f_xy.mfunction y_=f_xy(x,y)%求解第五次作业第一题的点(x,y)处的导数;y_ = 1/(x^2) - y/x;%run521.mclc,clear;x0 = 1;xn = 2;h = 0.05;y0 = 1;%便于显示出x,与y对应:x = [x0:h:xn]';y = Euler(x0,xn,y0,h);YE =[x,y];y = Imp_Euler(x0,xn,y0,h); YIE= [x,y];h = 0.1;x = [x0:h:xn]';y = R_Kutta4(x0,xn,y0,h); YRK= [x,y];(b): %f_xy.mfunction y_=f_xy(x,y) %求第二个方程的导数: y_ = -50*y+50*(x^2)+2*x;%run522.mclc,clear; x0 = 0; xn = 1; y0 = 1/3; %步长0.1: h = 0.1; x = [x0:h:xn]';y = R_Kutta4(x0,xn,y0,h); y_r= f_Real(x); Y1 = [x,y,y_r];%步长0.05: h = 0.05; x = [x0:h:xn]';y = R_Kutta4(x0,xn,y0,h); y_r= f_Real(x); Y2 = [x,y,y_r]; %步长0.025: h = 0.025; x = [x0:h:xn]';y = R_Kutta4(x0,xn,y0,h); y_r= f_Real(x); Y3 = [x,y,y_r];五、讨论分析(a)从结果可以看出使用RK 方法,步长较大但是结果也更加精确; (b)分析求值结果的误差,可以发现当步长取0.1时,误差是超级大的(10^8数量级),但是当步长缩小一半取0.05时,误差就很小了,再缩小一半,误差就更小了。
实验5 基于Matlab的数字滤波器设计

实验五 基于Matlab 的数字滤波器设计实验目的:加深对数字滤波器的常用指标和设计过程的理解。
实验原理:低通滤波器的常用指标如下所述,其典型规格如下:⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧≤≤≤≤+≤≤-πδδδw w e G w w e G s s jw p p jw p ,)(,1)(1 通带边缘频率:p ϖ阻带边缘频率:s ϖ 通带起伏:p δ 通带峰值起伏:))(1(log 2010dB p p δα--=阻带起伏: s δ 最小阻带衰减:))((log 2010dB s s δα-=数字滤波器有IIR 和FIR 两种类型,他们的特点和设计方法不同。
一、窗函数法设FIR 滤波器在Matlab 中产生窗函数十分简单:(1) 矩形窗调用格式:w=boxcar(n) ,根据长度n 产生一个矩形窗w 。
(2) 三角窗调用格式:w=triang(n) ,根据长度n 产生一个三角窗w 。
(3)汉宁窗调用格式:w=hanning(n) ,根据长度n 产生一个汉宁窗w 。
(4)汉明窗调用格式:w=hamming(n) ,根据长度n 产生一个汉明窗w 。
(5)布莱克曼窗调用格式:w=Blackman(n) ,根据长度n 产生一个布莱克曼窗w 。
基于窗函数的FIR 滤波器设计利用Matlab 提供的函数firl 来实现。
调用格式:firl(n,wn,’ftype ’,Window),n 为阶数,wn 是截止频率(如果输入是形如[w1 w2]的矢量时,本函数将设计带通滤波器,其通带为w1<w<w2)、ftype 是滤波器的类型(底通——省略该参数、高通——ftype=high 、带阻——ftype=stop )、Window 是窗函数。
1、设计一个长度为8的线性相位FIR 滤波器。
Window=boxcar(8); b=fir1(7,0.4,Window); freqz(b,1); Window=blackman(80;b=fir1(7,0.4,Window); freqz(b,1);2、设计线性相位带通滤波器,其长度N=15,上下边带截止频率分别为w1=0.3π,w2=0.5π Window=blackman(16); B=firl(15,[0.3 0.5],Window); Freqz(b,1);3、设计指标为,dB A dB R s a p p 50,3.0,25.0,2.0====πϖπϖ的底通滤波器。
matlab实验五

实验五曲面绘图【实验目的】1.了解二元函数图形的制作。
2.空间曲面等高线的制作。
3.学习掌握MATLAB软件有关的命令。
【实验内容】画出函数22y=的图形,并画出其等高线。
xz+【实验准备】1.曲线绘图的MATLAB命令MATLAB中主要用mesh,surf命令绘制二元函数图形。
可以用help mesh, help surf查阅有关这些命令的详细信息【实验方法与步骤】练习1画出函数22y=的图形,不妨将区域限制在z+x⨯-x。
用MATLAB作图的程序代码为:(-y∈)]3,3,[]3,3[>>clear;>>x=-3:0.1:3; %x的范围为[-3,3]>>y=-3:0.1:3; %y的范围为[-3,3]>>[X,Y]=meshgrid(x,y); %将向量x,y指定的区域转化为矩阵X,Y>>Z=sqrt(X.^2+Y.^2); %产生函数值Z>>mesh(X,Y,Z)结果如图5.1。
图5.1是网格线图,如果要画完整的曲面图,只需将上述的MATLAB 代码mesh(X,Y,Z)改为surf(X,Y,Z), 结果如图5.2图5.1 锥面图5.2 锥面要画等高线,需用contour,contour3命令.其中contour为二维等高线, contour3为三维等高线,如画图5.1的三维等高线, MATLAB代码为:>>clear;>>x=-3:0.1:3;>>y=-3:0.1:3;>>[X,Y]=meshgrid(x,y);>>Z=sqrt(X.^2+Y.^2);>>contour3(X,Y,Z,10) %画10条等高线>>xlabel('X-axis'),ylabel('Y-axis'),zlabel('Z-axis') %三个坐标轴的标记>>title('Contour3 of Surface') %标题>>grid on %画网格线结果如图5.3.图5.3 等高线如画图5.1的二维等高线, MATLAB代码为:>>clear; x=-3:0.1:3; y=-3:0.1:3;>>[X,Y]=meshgrid(x,y); Z=sqrt(X.^2+Y.^2);>> contour(X,Y,Z,10)>>xlabel('X-axis'),ylabel('Y-axis')>>title('Contour of Surface')>>grid on结果如图5.4.图5.4 等高线如果要画1=z 的等高线,则用命令>>clear; x=-3:0.1:3; y=-3:0.1:3;>>[X,Y]=meshgrid(x,y); Z=sqrt(X.^2+Y.^2);>> contour(X,Y,Z,[1 1])结果如图5.5。
控制系统计算机仿真(matlab)实验五实验报告
实验五 控制系统计算机辅助设计一、实验目的学习借助MATLAB 软件进行控制系统计算机辅助设计的基本方法,具体包括超前校正器的设计,滞后校正器的设计、滞后-超前校正器的设计方法。
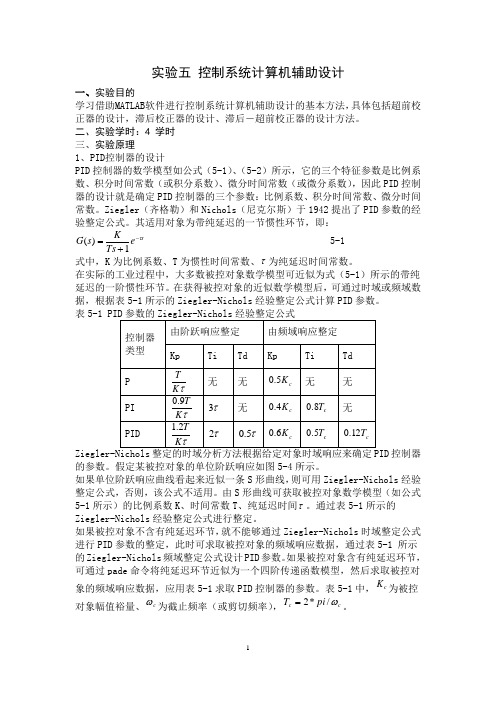
二、实验学时:4 学时 三、实验原理1、PID 控制器的设计PID 控制器的数学模型如公式(5-1)、(5-2)所示,它的三个特征参数是比例系数、积分时间常数(或积分系数)、微分时间常数(或微分系数),因此PID 控制器的设计就是确定PID 控制器的三个参数:比例系数、积分时间常数、微分时间常数。
Ziegler (齐格勒)和Nichols (尼克尔斯)于1942提出了PID 参数的经验整定公式。
其适用对象为带纯延迟的一节惯性环节,即:s e Ts Ks G τ-+=1)( 5-1式中,K 为比例系数、T 为惯性时间常数、τ为纯延迟时间常数。
在实际的工业过程中,大多数被控对象数学模型可近似为式(5-1)所示的带纯延迟的一阶惯性环节。
在获得被控对象的近似数学模型后,可通过时域或频域数据,根据表5-1所示的Ziegler-Nichols 经验整定公式计算PID 参数。
表控制器的参数。
假定某被控对象的单位阶跃响应如图5-4所示。
如果单位阶跃响应曲线看起来近似一条S 形曲线,则可用Ziegler-Nichols 经验整定公式,否则,该公式不适用。
由S 形曲线可获取被控对象数学模型(如公式5-1所示)的比例系数K 、时间常数T 、纯延迟时间τ。
通过表5-1所示的Ziegler-Nichols 经验整定公式进行整定。
如果被控对象不含有纯延迟环节,就不能够通过Ziegler-Nichols 时域整定公式进行PID 参数的整定,此时可求取被控对象的频域响应数据,通过表5-1 所示的Ziegler-Nichols 频域整定公式设计PID 参数。
如果被控对象含有纯延迟环节,可通过pade 命令将纯延迟环节近似为一个四阶传递函数模型,然后求取被控对象的频域响应数据,应用表5-1求取PID 控制器的参数。
【MATLAB】实验五:数值微积分与方程数值求解

实验五 数值微积分与方程数值求解一、实验目的1. 掌握求数值导数和数值积分的方法。
2. 掌握代数方程数值求解的方法。
3. 掌握常微分方程数值求解的方法。
二、实验内容要求:命令手工 ( )输入1. 求函数在指定点的数值导数。
232()123,1,2,3026x x x f x x x x x==2. 用数值方法求定积分。
(1) 210I π=⎰的近似值。
(2) 2220ln(1)1x I dt xπ+=+⎰3. 分别用三种不同的数值方法解线性方程组。
6525494133422139211x y z u x y z u x y z u x y u +-+=-⎧⎪-+-=⎪⎨++-=⎪⎪-+=⎩4. 求非齐次线性方程组的通解。
1234123412342736352249472x x x x x x x x x x x x +++=⎧⎪+++=⎨⎪+++=⎩解:先建立M 函数文件,然后命令窗口中写命令。
121/119/112/115/111/1110/11100010X k k --⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥=++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,其中12,k k 为任意常数。
5. 求代数方程的数值解。
(1) 3x +sin x -e x =0在x 0=1.5附近的根。
(2) 在给定的初值x 0=1,y 0=1,z 0=1下,求方程组的数值解。
23sin ln 70321050y x y z x z x y z ⎧++-=⎪+-+=⎨⎪++-=⎩ans =1289/6826. 求函数在指定区间的极值。
(1) 3cos log ()xx x x x f x e ++=在(0,1)内的最小值。
(2) 33212112122(,)2410f x x x x x x x x =+-+在[0,0]附近的最小值点和最小值。
(以下选作题,是微分方程的数值解)7. 求微分方程的数值解。
x 在[1.0e-9,20]2250(0)0'(0)0xd y dy y dx dx y y ⎧-+=⎪⎪⎪=⎨⎪=⎪⎪⎩解:M 文件:运行结果:8. 求微分方程组的数值解,并绘制解的曲线。
MATLAB与控制系统仿真及实验 2016(五)

一个 Simulink 仿真模型的基本模块包括信源、信宿以及系统三个部分。其中,信源 可以是常数、正弦波、阶梯波等信号源,信宿可以是示波器、图形记录仪等,系统则 是被研究系统的 SIMULINK 方框图。系统、信源、信宿,可以从 SIMULINK 模块库中 直接获得,也可以根据用户意愿用库中的模块构建而成。
2
2、 连续系统的建模与仿真 连续系统指的是可以用微分方程来描述的系统。用于建模连续系统的模块:
Simulink 模块组中的 Continous、Math 以及 Nonlinear 模块库中。 利用 Simulink 进行系统仿真的步骤如下: (1) 建立系统仿真模型,这包括添加模块、设置模块参数以及进行模块连接等操
作。 (2) 设置仿真参数。 (3) 启动仿真并分析仿真结果。
四、实验内容
1. 建立单位负反馈二阶系统的 SIMULINK 仿真模型,当输入信号源分别为阶跃信号、 斜坡信号、正弦信号时,给出系统输出的波形图。开环传递函数如下所示
3
2. 利用 SIMULINK 仿真下列曲线并给出结果,取 2 ,
MATLAB 与控制系统仿真及实验 实验报告
(五) 2015- 2016 学年第 2 学期
专业: 班级: 学号: 姓名:
2016 年 5 月 18 日
实验五 SIMULINK 系统仿真设计 一、实验目的
MATLAB第五章实验报告

MATLAB数值计算班级:11电信一班姓名:何得中学号:20111060108实验目的:1.了解MATLAB提供的标准多项式的常用函数;2.掌握用MATLAB创建多项式;3.学会用MATLAB对数据的分析;实验仪器:MATLAB软件,电脑实验数据:>> poly2sym([1 2 6 -5 3 9])ans =x^5+2*x^4+6*x^3-5*x^2+3*x+9 >> A=[7 8 9;4 5 6;1 2 3];>> B=poly(A)B =1.0000 -15.0000 18.00000.0000>> poly2sym(B)ans=x^3-15*x^2+18*x+422583449577050 7/633825300114114700748351602688 >> v=[0.5 0.6i -0.4 -0.6i]v =0.5000 0 + 0.6000i -0.4000 0 - 0.6000i>> p=poly(v)p =1.0000 -0.1000 0.1600 -0.0360 -0.0720>> pr=poly2sym(p)pr=x^4-1/10*x^3+4/25*x^2-9/250*x-9/12 5>> p=poly([1 2 3 4 5]);>> polyval(p,6)ans =120>> p=[1 3 1 2 1];>> polyvalm(p,[3 6;8 4])ans = 7186 66668888 8297>> polyvalm(p,7)ans =3494>> p=[1 4 2];>> x=0:0.8:4;>> y=polyval(p,x)y = 2.0000 5.8400 10.9600 17.3600 25.0400 34.0000>> a=[1 -1 4 10];>> r=roots(a);r = 1.1879 + 2.4202i1.1879 -2.4202i-1.3758>> pp=poly(r)pp =1.0000 -1.0000 4.0000 10.0000>> p1=[1,0,1,1];>> p2=[0,1,-1,2];>> p1+p2ans =1 1 0 3>> p1-p2ans =1 -1 2 -1>> c=conv([1 1 2 2],[1 2 5 4])c = 1 3 9 15 18 18 8>> p1=[1,0,1,1]; >> p2=[1,-1,2];>> [q,r]=deconv(p1,p2) q = 1 1 r = 0 0 0 -1 >> g=[1 5 4 6 20 48 27 72 39 ]; >> h=polyder(g) h = 8 35 24 30 80 144 54 72 >> q=polyint(h) q =1 5 4 6 20 48 27 72 0 >> b=[4,9]; >> a=[1,7,8]; >> [r,p,k]=residue(b,a) r = 3.2127 0.7873 p = -5.5616 -1.4384 k = [] >> [b,a]=residue(r,p,k) b = 4.0000 9.0000 a = 1 7 8 x=linspace(0,2*pi,50); >> y=sin(x); >> [p,s]=polyfit(x,y,3) p = 0.0912 -0.8596 1.8527 -0.1649 s = R: [4x4 double] df: 46 normr: 0.5055>> plot(x,y,'r:*',x,polyval(p,x),'-o')>> a=ceil(rand(4,4)*12) a = 12 11 10 12 3 10 6 9 8 6 8 3 6 1 10 5 >> b=ceil(rand(4,4)*10) b = 10 1 2 3 10 4 3 2 5 9 2 1 9 1 7 8 >> x=a\b x = -0.6400 -0.3800 -0.5800 -0.3600 0.0814 1.4697 -0.2959 -0.7021 0.9883 1.0679 0.9748 0.7876 0.5752 -1.7738 0.2055 0.5972 >> x=[1 1.5 2 2.5 3 3.5 4 4.5 5]'; >> y=[-1.4 2.7 3 5.9 8.4 12.2 16.6 18.8 26.2]'; >> e=[ones(size(x)) x.^2]; >> c=e\y c = -1.0685 1.0627>> x1=[1:0.1:5]'; >> y2=[ones(size(x1)),x1.^2]*c;>> plot(x,y,'ro',x1,y2,'k')>> a=[2 4 7 4;9 3 5 6]; >> b=[8 5]'; >> x=pinv(a)*bx = -0.21510.44590.79490.2707>> x=0:0.02*pi:2*pi;>> y=sin(x);>> ymax=max(y)ymax = 1>> ymin=min(y)ymin = -1>> ymean=mean(y)ymean =2.2995e-017>> ystd=std(y)ystd =0.7071>> score=[90 80 78 98 79;100 90 68 78 69;88 77 99 87 100];>> score_sum=sum(score)score_sum = 278 247 245 263 248>> score_avg=score_sum/3.score_avg =92.6667 82.3333 81.6667 87.6667 82.6667>> score_max=max(score)score_max=100 90 99 98 100>>[score_max,score_max_student]=max(s core)score_max =100 90 99 98 100score_max_student = 2 2 3 1 3>> score_min=min(score)score_min = 88 77 68 78 69>>[score_min,score_min_student]=min(sc ore)score_min = 88 77 68 78 69score_min_studen t=3 3 2 2 2>> score_student_sum=sum(score) score_student_sum=278 247 245 263 248>>score_student_savg=score_student_sum. /3score_student_savg =92.6667 82.3333 81.6667 87.6667 82.6667>> std(score)ans =6.4291 6.8069 15.8219 10.0167 15.8219>> var(score)ans =41.3333 46.3333 250.3333 100.3333 250.3333>> x=linspace(0,2*pi,10)x =0 0.6981 1.3963 2.0944 2.7925 3.4907 4.1888 4.8869 5.5851 6.2832>> y=sin(x)y=0 0.6428 0.9848 0.8660 0.3420 -0.3420 -0.8660 -0.9848 -0.6428 -0.0000>> dy=diff(y)dy=0.6428 0.3420 -0.1188 -0.5240 -0.6840 -0.5240 -0.1188 0.3420 0.6428>> d2y=diff(y,2)d2y= -0.3008 -0.4608 -0.4052 -0.1600 0.1600 0.4052 0.4608 0.3008>> d3y=diff(y,3)d3y= -0.1600 0.0556 0.2452 0.3201 0.2452 0.0556 -0.1600>> x=[1 2 3 4 5];>> y=[4 5 6 7 8];>> cx=cov(x)cx = 2.5000>> cy=cov(y)cy = 2.5000>> cxy=cov(x,y)cxy =2.5000 2.50002.5000 2.5000>> x=-1:0.2:1;>> z=exp(x.^2);>> fx=gradient(z)fx= -0.8218 -0.6425 -0.3615 -0.1963 -0.0868 0 0.0868 0.1963 0.3615 0.6425 0.8218function ex=ex(x)ex=exp(-x.^2)return>> format long>> quad('ex',0,1,1e-6)ex = 1.00000000000000 0.981730032806080.928898599395100.778800783071400.588254444230630.473852624646280.36787944117144ex = 0.99540087747802 0.95936125127772ex =0.86171221264734 0.68574192538547ex = 0.53040332078406 0.41944631668514ans = 0.74682418072642>> quadl('ex',0,1,1e-6)ex=1.000000000000000.999184727905840.991616959101330.968441445328330.926451851978820.864349866175970.778800783071400.682385279905670.592380095006350.509706301048790.438272262810980.389185953389380.36787944117144ex = 0.99161695910133 0.926451851978820.778800783071400.592380095006350.43827226281098ans = 0.74682413398845>> quad8('ex',0,1,1e-6) ex =1.00000000000000 0.999184727905840.991616959101330.968441445328330.92645185197882 0.86434986617597 0.778800783071400.682385279905670.592380095006350.509706301048790.438272262810980.389185953389380.36787944117144ex= 0.99161695910133 0.926451851978820.778800783071400.592380095006350.43827226281098ans = 0.74682413398845x0=0:pi/5:4*pi;y0=sin(x0).*exp(-x0/10);xi=0:pi/20:4*pi;yi=interp1(x0,y0,xi,'spline');plot(x0,y0,'or',xi,yi,'--b');Untitled2>> t=0:5:65;>> x=2:5:57;>>f=[3.1025,2.256,879.5,1835.9,2968.8,41 36.2,5237.9,6152.7,6725.3,6848.3,6403. 5,6824.7,7328.5,7857.6];>> f1=interp1(t,f,x)f1 = 1.0e+003 *0.002763900000000.353153600000001.262060000000002.289060000000003.435760000000004.576880000000005.603820000000006.381740000000006.774500000000006.670380000000006.571980000000007.02622000000000>> f2=interp1(t,f,x,'nearext') f2 = 1.0e+003 *0.003102500000000.002256000000000.879500000000001.835900000000002.968800000000004.136200000000005.237900000000006.152700000000006.725300000000006.848300000000006.403500000000006.82470000000000>> f3=interp1(t,f,x,'spline') f3 = 1.0e+003 *-0.170259056484550.306978324423981.256000890788642.269771808421483.439603875525464.589619889476705.637043766567756.422853844252316.859291256423016.653528330055636.481654623354457.04407557652658 >> f4=interp1(t,f,x,'cubic')f4 = 1.0e+003 *0.002438844000000.223194994900141.248358437730492.273647289639383.436483654858934.591276133775775.636234122067276.436239461848896.797756124209326.691730400000006.507716445924327.01855707680041[x,y,z]=peaks(6);mesh(x,y,z)[xi,yi]=meshgrid(-3:0.2:3,-3:0.2:3); z1=interp2(x,y,z,xi,yi,'nearest');z2=interp2(x,y,z,xi,yi,'linear');z3=interp2(x,y,z,xi,yi,'spline');z4=interp2(x,y,z,xi,yi,'cubic'); subplot(2,2,1)mesh(xi,yi,z1)title('nearest插值的网络图') subplot(2,2,2)mesh(xi,yi,z2)title('linear插值的网络图') subplot(2,2,3)mesh(xi,yi,z3)title('spline插值的网络图') subplot(2,2,4)mesh(xi,yi,z4)title('cubic插值的网络图')。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
密度函数值就是某个特定值的概率,即利用函数pdf
求输入分布的概率。
9
概率密度函数值
通用概率密度函数pdf,计算特定值的概率命令格式
为:Y = pdf (‘name’, k, A)
Y = pdf (‘name’, k, A, B) Y = pdf (‘name’, k, A, B, C) 说明:返回以name为分布,在随机变量X = k处,参数 为A、B、C的概率密度值;对离散型随机变量X,返回X
设随机变量X的分布律为:
P {X = k } = Cnk p ^k *(1-p) ^(n – k)
k = 0, 1, 2, …, n
其中:0< p <1,n为独立重复试验的总次数,k为n次重复 试验中事件A发生的次数,p为每次试验事件A发生的概 率。则称X服从二项分布,记为X~B (n, p)。
6
几个常见的概率分布
min (n, M))可由下列命令求得: 命令格式:pdf (‘hyge’, k, N, M, n)或hygepdf (k, N, M, n) 2. 累积概率值的求法: 命令格式:cdf(‘hyge’, k, N, M, n)或hygecdf(k, N, M, n)
说明:该函数的功能是返回次品数X≤k的概率之和。
15
2.在n次独立重复试验中,事件A至少发生k次的概率P_s。
命令格式:cdf (‘bino’, k, n, p)或 binocdf (k, n, p)
说明:该命令的功能是返回随机变量X≤k的概率之和(即累 积概率值)。其中cdf为通用函数,binocdf为专用函数,n为 试验总次数,k为n次试验中,事件A发生的次数,p为每次试 验事件A发生的概率。所以,至少发生k次的概率为
= k处的概率值,name为分布函数名。
常见的分布有:name = bino(二项分布),hyge(超 几何分布),geo(几何分布),poiss(Poisson分布)
10
专用概率密度函数计算特定值的概率
(1)二项分布的概率值
命令格式:binopdf (k,n,p)
说明:等同于pdf (‘bino’, k, n, p)。n:试验总次 数;p:每次试验事件A发生的概率;k:事件A发生k次。 (2)Poisson分布的概率值 命令格式: poisspdf (k, Lambda)
解法二:由于呼叫次数X≤0就是呼叫0次,即X = 0。因此,此题也可用
poisspdf求解。 即:poisspdf (0, 1.5)和1-poisspdf (0, 2.5)。
25
3 超几何分布
1. 设N为产品总数,M为其中次品总数,n为随机抽取件数
(n≤N),则次品数X恰为k件的概率p_k(k = 0, 1, 2, …,
求随机变量的最大值元素。
求随机变量的忽略NaN的最大值元素。 求随机变量的最小值元素。 求随机变量的忽略NaN的最小值元素。 生成均值为mu ,标准差
注 normrnd(mu,sigma,m,n)
为sigma的m行n列的正态分布矩阵。
3
数据比较
median
求随机变量的中值。
nanmedian
(2)求1-P{X≤0}。
24
解法一:在Matlab命令窗口键入:
>> poisscdf (0,1.5) %X = 0表示0次呼叫,Lambda = t/2 = 1.5
ans = 0.2231 即(1)中没sscdf (0,2.5)
ans = 0.9179 即(2)中至少收到1次呼叫的概率为0.9179。
说明:等同于pdf (‘poiss’, k, Lambda),参数Lambda = np。
11
(3)超几何分布的概率值
命令格式:hygepdf (k, N, M, n)
说明:等同于pdf (‘hyge’, k, N, M, n),N:产品总数,M: 次品总数,n:抽取总数(n≤N),k:抽得次品数。
1. 求n次独立重复试验中事件A恰好发生k次的概率P。
命令格式:pdf (‘bino’, k, n, p)或binopdf (k, n, p)
说明:该命令的功能是计算二项分布中事件A恰好发生k次
的概率。pdf为通用函数,bino表示二项分布,binopdf为专 用函数,n为试验总次数,k为n次试验中,事件A发生的次 数,p为每次试验事件A发生的概率。
26
例 设盒中有5件同样的产品,其中3件正品,2件次 品,从中任取3件,求不能取得次品的概率。
解:在Matlab编辑器中编辑M文件:LX04.m N=input('input N=') M=input('input M=') n=input('input n=') for k=1:M+1 p_k=hygepdf(k-1,N,M,n) end
12
用函数cdf计算随机变量X≤k的概率之和(累积概率值) 命令格式:
cdf (‘name’, k, A)
cdf (‘name’, k, A, B) cdf (‘name’, k, A, B, C) 说明:返回以name为分布、随机变量X≤k的概率之和(即 累积概率值),name为分布函数名。
13
回一个数值;若X为矩阵,sum (X)为X中各列元素之和, 返回一个行向量。
nansum
prod
忽略NaN求向量或矩阵元素的累和。
若X为向量,prod (X)为X中各元素之积,返回
一个数值;若X为矩阵,prod (X)为X中各列元素之积,
返回一个行向量。
5
离散型随机变量的概率及概率分布
二项分布
超几何分布
设一批同类产品共N件,其中有M件次品,从中任取n (n≤N)
件,其次品数X恰为k件的概率分布为:
k n C M C N kM P{ X k} , n CN
k 0,1,2, , min( n, M )
则称次品数X服从参数为 (N, M, n)的超几何分布。超
M 几何分布用于无放回抽样,当N很大而n较小时,次品率 p N
19
2.n次独立重复试验中,事件A至少发生k次的概率P
(1)累积概率值 命令格式:cdf (‘poiss’, k, Lambda)或 poisscdf (k, Lambda)
说明:该函数返回随机变量X≤k的概率之和,Lambda = np
(2)A至少发生k次的概率P_k P_k = 1- cdf (‘poiss’, k-1, Lambda) 或 P_k = 1- poisscdf (k-1, Lambda)
23
例
某市公安局在长度为t的时间间隔内收到的呼叫次数服从 参数为t/2的Poisson分布,且与时间间隔的起点无关(时 间以小时计)。求: (1)在某一天中午12时至下午3时没有收到呼叫的概率; (2)某一天中午12时至下午5时至少收到1次呼叫的概率。
解:在此题中,Lamda = t/2
设呼叫次数X为随机变量,则该问题转化为: (1)求P{X = 0};
mad
求随机变量的忽略NaN的中值。
求随机变量的绝对差分平均值。
sort
sortrows range
对随机变量由小到大排序。
对随机矩阵按首行进行排序。 求随机变量的值的范围,即最大值与最小值
的差(极差)。
4
累和与累积
在Matlab中,求向量或矩阵的元素累和或累积运算,可由 以下函数实现。
sum
若X为向量,sum (X)为X中各元素之和,返
(1)恰有1件次品的概率 在Matlab命令窗口键入:
>> p=pdf('bino',1,100,0.01) %利用通用函数计算恰好发生k次的概率
p= 0.3697
或在Matlab命令窗口键入:
>> p=binopdf(1,100,0.01) %利用专用函数计算恰好发生k次的概率 p=
0.3697
17
在抽取前后差异很小,就用二项分布近似代替超几何分
布,其中二项分布的 p M 。而且在一定条件下,也可用
Poisson分布近似代替超几何分布。
8
N
概率密度函数值
无论是离散分布还是连续分布,在Matlab中,都用通用
函数pdf或专用函数来求概率密度函数值。而对于离散
型随机变量,取值是有限个或可数个,因此,其概率
22
在Matlab的命令窗口键入LX02,回车后按提示输入p和n的值,显示如下:
input p=180/(63*153) p= 0.0187 input n=153 n= 153 lamda = 2.8571 p_k = Columns 1 through 7 0.0574 0.1641 0.2344 0.2233 0.1595 0.0911 0.0434 Columns 8 through 9 0.0177 0.0063 注意:在Matlab中,p_k (0)被认为非法,因此应避免。
P_s = 1- cdf (‘bino’, k-1, n, p) 或 P_s = 1- binocdf (k-1, n, p)
16
例 某机床出次品的概率为0.01,求生产100件产品中: (1)恰有1件次品的概率;(2)至少有1件次品的概率。
解:此问题可看作是100次独立重复试验,每次试验出次品的概率为0.01
实验五 概率统计
实验目的
利用Matlab来解决常见的数据分析问题。
利用Matlab来解决概率统计学中的概率分布、数
字特征问题。
1
数据分析
在Matlab中,对给定的一组数据中进行各种均值的计算,是
由以下函数实现的:
