数字图像处理课件第五章
合集下载
第5章 图像变换技术 MATLAB 数字图像处理课件
5.6.2 Hough变换的MATLAB实现
hough函数用于实现Hough变换。其调用格式为： （1）[H, theta, rho]=hough(BW) （2）[H, theta, rho]=hough(BW, param1,
val1, param2, val2)
【例5-15】用hough函数检测图像中的直线。
（2）B = idct2(A,m,n)或B = idct2(A,[m n])：在对图 像A进行二维离散余弦逆变换前，先将图像A补零到m×n。 如果m和n比图像A的尺寸小，则在进行变换前，将图像A进 行剪切。
【例5-9】对图像进行二维离散余弦逆变换。
（a）原始图像
（b）逆DCT变换
3．dctmtx函数 在MATLAB图像处理工具箱中提供了dctmtx函数用
于计算二维离散DCT矩阵。 其调用格式为：D = dctmtx(n)。
返回n×n的DCT变换矩阵，如果矩阵A的大小为 n×n，D*A为A矩阵每一列的DCT变换值，A*D'为A 每一列的DCT变换值的转置（当A为n×n的方阵） 。
【例5-10】计算二维离散DCT矩阵。
（a）原始图像
（b）离散DCT矩阵
5.4 离散余弦变换
5.4.1 一维离散余弦变换 5.4.2 二维离散余弦变换 5.4.3 快速离散余弦变换
5.4.4 离散余弦变换的MATLAB实现
1．dct2函数 在MATLAB图像处理工具箱中提供了dct2函数用于实现二维
离散余弦变换。该函数常用于图像压缩，最常见的便是用 于JPEG图像压缩。其调用格式为： （1）B = dct2(A)：返回图像A的二维离散余弦变换值，其 大小与A相同，且各元素为离散余弦变换的系数B(k1,k2)。 （2）B = dct2(A,m,n)或B = dct2(A,[m n])：在对图像A 进行二维离散余弦变换前，先将图像A补零到m×n。如果m 和n比图像A的尺寸小，则在进行变换前，将图像A进行剪切 。
数字图像处理的课件
第五章数字图像的预处理技术5.1图像退化模型与噪声分类 5.2图像噪声的空间域滤波方法5.2.1针对加性噪声的空间域滤波方法 (1)自适应均值滤波器 2．自适应中值滤波器3．自适应梯度倒数加权滤波器5.2.2空间域滤波方法的MATLAB 实现 5.3图像空间域滤波新方法探索5.3.1中值滤波算法的研究 1 噪声检测 2基于1数据逼近和细节保护规则函数的凸面代价函数与噪声恢复3方法性能的仿真实验评价 5.3.2均值滤波算法的研究1基于RADON 变换的图像主纹理方向分析 2概率统计模型3方法性能的仿真实验评价 5.4周期噪声与频域滤波 5.5小波滤波5.5.1 小波域去噪模型 5.5.2阈值的估计5.5.3小波滤噪的MA TLAB 实现 5.6偏微分方程图像去噪 5.7边缘检测5.7.1边缘检测的梯度算子 1Roberts 算子1(,)(,)0(,)g x y T d x y g x y T≥⎧⎪=⎨<⎪⎩ （5-116）2 Prewitt 算子3 Sobel 算子4 LOG 算子5 Canny 算子5.7.2基于梯度算子的边缘检测MATLAB 编程 5.7.3Hough 变换与线检测第五章数字图像的预处理技术数字图像的预处理技术是图像处理与分析的基础，其处理结果对后序图像的处理与分析结果有非常大的影响。
图像的预处理技术主要包括图像复原、图像增强两种操作，图像复原是通过使用退化现象的先验知识试图重建或恢复一幅退化图像，主要包括几何畸变的修正、图像滤噪等，本书在第三章介绍了几何畸变的修正的基本内容。
本章主要介绍图像滤噪的相关内容。
图像增强是根据图像处理或分析的主要目标，以增强图像中相关的部分信息为主要目标的操作，主要包括图像锐化、边缘检测及基于图像直方图的图像增强等。
在第三章介绍了基于图像直方图的图像增强技术。
本章主要介绍图像图像锐化、边缘检测的相关内容。
5.1图像退化模型与噪声分类在图像生成与传输过程中，由于成像系统与通讯信道各种因素的影响，可能使图像质量降低。
数字图像处理(Photoshop)模块五 教学PPT6.2.2 演示PPT
1、通道的概念
• 通道就是用灰度图来保存图像颜色信息以及选区 的一个载体。
• 首先是存储图像所有的颜色信息，如：RGB颜色通 道 、CMYK颜色通道 。另外还有一些专色通道。
• 其次是用来保存选区，也叫alpha通道。
数字图像处理 （Photoshop）
RGB颜色模式的通道显示
CMYK颜色模式的通道显示
数字图像处理 （Photoshop）
模块五
图像高级合成技巧
——图层、通道的特性及其运用技巧
数字图像处理 （Photoshop）
任课教师：张 磊
实例1 给建筑物制作倒影
一、图层的艺术Layer
实例2 公益广告设计
• 重点： • 1. 图层的概念 • 2. 图层的类型 • 3. 图层面板 • 4. 图层的基本操作
数字图像处理 （Photoshop）
数字图像处理 （Photoshop）
图层混合模式是选择的图层和其下面图层的混合所产生的效果。 其中常用的有： 将图像白色部分去掉的如：变暗、正片叠底、颜色加深和线性加深。 将图像黑色部分去掉的如：变亮、滤色、颜色减淡和线性减淡。
实例1 给建筑物制作倒影
填充图层
实例2 公益广告设计
数字图像处理 （Photoshop）
数字图像处理 （Photoshop）
实例1 给建筑物制作倒影 实例2 公益广告设计
二、通道的艺术
• 重点： • 1. 通道的概念 • 2. 通道的分类 • 3. 通道的操作
• 难点：
• 利用通道对半透明素材（如烟雾、云彩、 火焰等）进行抠图
数字图像处理 （Photoshop）
实例1 给建筑物制作倒影 实例2 公益广告设计
数字图像处理 （Photoshop）
数字图像处理(冈萨雷斯)
✓脉冲噪声（椒盐噪声）
均匀噪声
高斯噪声
瑞利噪声
噪声
指数噪声
椒盐噪声
第14页，共62页。
①高斯噪声
高斯噪声的概率密度函数(PDF)
p(z) 1 e(z )2 /2 2 (5.2 1)
2
灰度值
✓ 当z服从上式分布时，其值有70%落在 , ， 有 95%落在
范围内。 2 , 2
✓ 高斯噪声的产生源于电子电路噪声和由低照明度或高温带来的 传感器噪声。
其中zi值是像素的灰度值, p(zi )表示相应的归一化直方图.
第30页，共62页。
5.3 空间域滤波复原（唯一退化是噪声）
当唯一退化是噪声时，则退化系统H(u,v) 1
g( x, y) f ( x, y) ( x, y) (5.3 1)
G(u, v) F (u, v) N (u, v) (5.3 2)
的开关操作）
第22页，共62页。
例5.1 样本噪声图像和它们的直方图
✓ 用于说明噪声模型的测试图
✓ 由简单、恒定的区域组成 ✓ 仅仅有3个灰度级的变化
第23页，共62页。
例5.1 样本噪声图像和它们的直方图
高斯噪声
瑞利噪声
伽马噪声
图像
直方图
第24页，共62页。
例5.1 样本噪声图像和它们的直方图
➢在图像获取中从电 力或机电干扰中产生.
➢是空间相关噪声.
➢周期噪声可以通过 频率域滤波显著减少.
周期噪声
被不同频率的 正弦噪声干扰 了的图像
呈圆形分布 的亮点为噪 声频谱
第27页，共62页。
典型的周期噪声---正弦噪声
• Sinusoidal （单 一频率）
均匀噪声
高斯噪声
瑞利噪声
噪声
指数噪声
椒盐噪声
第14页，共62页。
①高斯噪声
高斯噪声的概率密度函数(PDF)
p(z) 1 e(z )2 /2 2 (5.2 1)
2
灰度值
✓ 当z服从上式分布时，其值有70%落在 , ， 有 95%落在
范围内。 2 , 2
✓ 高斯噪声的产生源于电子电路噪声和由低照明度或高温带来的 传感器噪声。
其中zi值是像素的灰度值, p(zi )表示相应的归一化直方图.
第30页，共62页。
5.3 空间域滤波复原（唯一退化是噪声）
当唯一退化是噪声时，则退化系统H(u,v) 1
g( x, y) f ( x, y) ( x, y) (5.3 1)
G(u, v) F (u, v) N (u, v) (5.3 2)
的开关操作）
第22页，共62页。
例5.1 样本噪声图像和它们的直方图
✓ 用于说明噪声模型的测试图
✓ 由简单、恒定的区域组成 ✓ 仅仅有3个灰度级的变化
第23页，共62页。
例5.1 样本噪声图像和它们的直方图
高斯噪声
瑞利噪声
伽马噪声
图像
直方图
第24页，共62页。
例5.1 样本噪声图像和它们的直方图
➢在图像获取中从电 力或机电干扰中产生.
➢是空间相关噪声.
➢周期噪声可以通过 频率域滤波显著减少.
周期噪声
被不同频率的 正弦噪声干扰 了的图像
呈圆形分布 的亮点为噪 声频谱
第27页，共62页。
典型的周期噪声---正弦噪声
• Sinusoidal （单 一频率）
数字图像处理课件第五章.
ii. 把这个符号的概率与其余符号的概率按从大到 小进行排列，然后再把最末两个符号的概率加 起来，合成一个概率。
iii. 重复上述做法，直到最后剩下两个概率为止。
iv. 从最后一步剩下的两个概率开始逐步向前进行
编码。每步只需对两个分支各赋予一个二进制
码，如对概率大的赋予码0，对概率小的赋予
码1。
28
37
第五章 图像编码
Huffman编码
输入 输入概率第一步第二步第三步第四步 S1 0.4 0.4 0.4 0.4 0.6 0 S2 0.3 0.3 0.3 0.3 0 0.4 1 S3 0.1 0.1 0.2 0 0.3 1 S4 0.1 0.1 0 0.1 1 S5 0.06 0 0.1 1 S6 0.04 1 S4=0100
I = D － du
I — 信息量 D — 数据量 du — 冗余量，包含在D中
● 冗余举例 播音员—— 180字/分钟，2Byte一个字，360Byte (合0.35KB/分钟) 音频数据——8kHz采样×8bit×60秒 = 3840KBit (合480KB/分钟)
6
第五章 图像编码
[1] 空间冗余—— 规则物体的物理相关性 [2] 时间冗余—— 视频与动画画面间的相关性 [3] 统计冗余—— 具有空间冗余和时间冗余 [4] 结构冗余—— 规则纹理、相互重叠的结构表面 [5] 信息熵冗余—— 编码冗余，数据与携带的信息 [6] 视觉冗余—— 视觉、听觉敏感度和非线性感觉 [7] 知识冗余—— 凭借经验识别 [8] 其他冗余—— 上述7种以外的冗余
8
第五章 图像编码
图像数据压缩技术的重要指标
（1）压缩比：图像压缩前后所需的信息存储量之比， 压缩比越大越好。 （2）压缩算法：利用不同的编码方式，实现对图像 的数据压缩。
DIP5国科大数字图像处理第5章PPT
s4 448 0.11
32
例
步骤5：计算p(sk)。
计算 n1
：（见表） n n 64 64， n1 790, n3 1023, n5 850, n 6 985, n7 448 n 0.19, n3 n 0.25, n5 n 0.21, n6 n 0.24, n7 n 0.11
直方图均衡化
直方图均衡化是将原图像的直方图通过 变换函数修正为均匀的直方图，然后按均衡 直方图修正原图像。 图像均衡化处理后，图像的直方图是平 直的，即各灰度级具有相同的出现频数。
15
直方图均衡化
连续灰度的直方图-非均匀分布
16
直方图均衡化
连续灰度的直方图-均匀分布
17
直方图均衡化
直方图均衡化
40
直方图均衡化
直方图均衡化技术是图像增强的实质： 直方图均衡化实质上是减少图象的灰度级以换取对 比度的加大。在均衡过程中，原来的直方图上频数较小 的灰度级被归入很少几个或一个灰度级内。 若这些灰度级所构成的图象细节比较重要，则需采 用局部区域直方图均衡。
41
直方图均衡化
直方图均衡化技术是图像增强的实质： （1）两个占有较多像素的灰度变换后，灰度之间的差距 增大。一般，背景和目标占有较多的像素，这种技 术实际上加大了背景和目标的对比度。 （2）占有较少像素的灰度变换后需要归并。一般，目标 与背景的过渡处像素较少，由于归并，其或者变为 背景点或者变为目标点，从而使边界变得陡峭。
s4 448
30
例
步骤4：计算nsk 。
计 算 对 应 每 个 s k的 像 元 数 目 n k： r0 0 s 0 1, 所 以 有 790 个 像 元 取 s 0 1这 个 灰 度 值 ； r1 s1 , 所 以 有 1023 个 像 元 取 s1 3 这 个 灰 度 值 ； r2 s 2 , 所 以 有 850 个 像 元 取 s 2 5 这 个 灰 度 值 ； 而 r3 和 r4 都 映 射 到 s 3 s 4 6, 所 以 有 656 329 985 个 像 元 取 s3,4 6 这 个 灰 度 值 ； 同 理 r5 , r6 , r7 都 映 射 到 s 5 ,6 ,7 1, 所 以 有 245 122 81 448 个 像 元 取 s 5 ,6 ,7 1这 个 灰 度 值 。
数字图像处理第五章
Digital Image Processing
Image Enhancement: Filtering in the Frequency Domain
Course Website: p.dit.ie/bmacnamee Luguangm@
2 of 66
| F (u , v) | R 2 (u , v) I 2 (u , v) I (u , v) (u, v) arct an R (u , v) P (u , v) R 2 (u , v) ቤተ መጻሕፍቲ ባይዱI 2 (u , v)
5 of 66
Introduction to Fourier Transform
f(x): continuous function of a real variable x Fourier transform of f(x):
F [ f ( x)] F (u )
1
f ( x)e j 2ux dx F (u )e j 2ux du
Contents
In this lecture we will look at image enhancement in the frequency domain
– The Fourier series级数 & the Fourier transform – DFT Properties – Steps of Filtering in the Frequency Domain – Some Basic Frequency Domain Filters
coefficients is equal to 1/N.
7 of 66
The Discrete Fourier Transform (DFT)
Image Enhancement: Filtering in the Frequency Domain
Course Website: p.dit.ie/bmacnamee Luguangm@
2 of 66
| F (u , v) | R 2 (u , v) I 2 (u , v) I (u , v) (u, v) arct an R (u , v) P (u , v) R 2 (u , v) ቤተ መጻሕፍቲ ባይዱI 2 (u , v)
5 of 66
Introduction to Fourier Transform
f(x): continuous function of a real variable x Fourier transform of f(x):
F [ f ( x)] F (u )
1
f ( x)e j 2ux dx F (u )e j 2ux du
Contents
In this lecture we will look at image enhancement in the frequency domain
– The Fourier series级数 & the Fourier transform – DFT Properties – Steps of Filtering in the Frequency Domain – Some Basic Frequency Domain Filters
coefficients is equal to 1/N.
7 of 66
The Discrete Fourier Transform (DFT)
第 05 章 图像分割——数字图像处理及应用北航谢凤英课件PPT
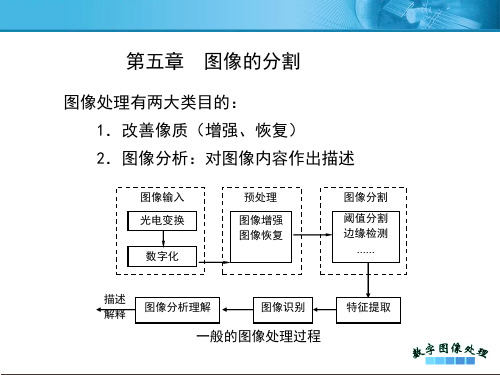
灰度
目标
边界
背景
梯度
c 多波段：
R、G、B可分别组成R-B, G-B, R-B两维直方图， 图上强的地方反映一个区。
5.2 边缘检测
1 边缘检测原理 其导数在边缘方向取得极值
0
0
(a) 一幅纵向 0 边缘的图像
(b) 每行像素的 灰度剖面图
(c) 一阶导数 (d) 二阶导数
从数学上看，图像的模糊相当于图像被平均或积分，为实现图象的 锐化，必需用它的反运算“微分”－－加强高频分量作用，使轮廓清晰。
图像分割：将图像中有意义的特征或需要应用的特征提 取出来。
（简单而又难于实现的最基础的识别工作。人的视觉系统对图像分 割是十分复杂的，也是相当有效的。但分割原理和模型都未搞清 楚。）
第五章 图像的分割
5.1 阈值分割 5.2 边缘检测 5.3 区域分割 5.4 Hough变换 5.5 近邻法分割 5.6 基于动态聚类的分割 5.7 基于神经网络的分割 5.8 其它分割方法
2 (1,2 ) w0,1[w0 (0 0,1)2 w1(1 0,1)2 ]
w12[w1(1 1,2 )2 w2 (2 1,2 )2 ] w0,2[w0 (0 0,2 )2 w2 (2 0,2 )2 ]
概率统计的阈值选取法 如:目标占整幅图像面积百分比
3 影响因素 噪音、照度不均匀，结构特征等。
-1 -c -1 -1 1 -c c
1 c 1 -1 1
c1 1 -1
-1 -c
1c -1 1 -c -1
注意：边缘检测对噪声敏感，常在作边缘检测前对图
像进行某些预处理，如平滑处理等。
2 典型算子 f) 二阶微分算子--- laplace算子
2
matlab《数字图像处理》第5章 算术运算(计科)
非线性点运算对应与非线性映射函数，典 型的映射函数包括平方函数、对数函数、 截取（窗函数）、阈值函数等
6
7
5.2、图像的算术运算
算术运算是指两幅或多幅输入图像之间进 行点对点的加、减、乘、除运算得到输出 图像的过程。
算术运算可以简单理解成数组的运算。
8
算术运算是指两幅或多幅输入图像之间。 算术运算的结果很容易超出数据类型允许 的范围。如uint8能够存储最大数是255， 乘法运算很容易超过这个数值；还有除法 运算会产生分数结果。所以超过范围的都 按数据范围的极值截取，分数结果将被四 舍五入。 无论哪一种代数运算都要保证两幅输入图 像的大小相等，且类型相同
4
5.1.1 线性点运算
在线性点运算中，灰度变换函数在数学上 就是线性函数：f(r)=ar+b
a>1时，输出图像对比度增大；
a<1时，输出图像对比度降低；
a=1,b~=0时，仅使输出图像的灰度值上 移或下移，其效果是使整个图像更亮或更暗。
线性点运算的典型应用是灰度分布标准化。
5
5.1.2 非线性点运算
10
在 Matlab图像处理工具箱中，imadd函数 实现图像相加运算。可以是一副图像与另 一幅图像相加；也可以是一副图像加上一 个常数。 Z=imadd(X, Y)
11
注意类型处理
X=uint8([255 0 75; 44 225 100]); Y=uint8([50 50 50; 50 50 50]); Z=imadd(X,Y)
k=imsubtract(I,J);
k1=255-k;
figure(),imshow(I)
6
7
5.2、图像的算术运算
算术运算是指两幅或多幅输入图像之间进 行点对点的加、减、乘、除运算得到输出 图像的过程。
算术运算可以简单理解成数组的运算。
8
算术运算是指两幅或多幅输入图像之间。 算术运算的结果很容易超出数据类型允许 的范围。如uint8能够存储最大数是255， 乘法运算很容易超过这个数值；还有除法 运算会产生分数结果。所以超过范围的都 按数据范围的极值截取，分数结果将被四 舍五入。 无论哪一种代数运算都要保证两幅输入图 像的大小相等，且类型相同
4
5.1.1 线性点运算
在线性点运算中，灰度变换函数在数学上 就是线性函数：f(r)=ar+b
a>1时，输出图像对比度增大；
a<1时，输出图像对比度降低；
a=1,b~=0时，仅使输出图像的灰度值上 移或下移，其效果是使整个图像更亮或更暗。
线性点运算的典型应用是灰度分布标准化。
5
5.1.2 非线性点运算
10
在 Matlab图像处理工具箱中，imadd函数 实现图像相加运算。可以是一副图像与另 一幅图像相加；也可以是一副图像加上一 个常数。 Z=imadd(X, Y)
11
注意类型处理
X=uint8([255 0 75; 44 225 100]); Y=uint8([50 50 50; 50 50 50]); Z=imadd(X,Y)
k=imsubtract(I,J);
k1=255-k;
figure(),imshow(I)
数字图像处理课件第五章
图像复原是针对图像退化的原因做出补偿， 使恢复后的图像尽可能接近原始图像。 评判图像复原质量好坏的是客观标准。
返回
第5章 图像复原
连续图像退化模型
n(x,y) f(x,y)
H +
g(x,y)
第5章 图像复原
连续图像退化的模型
第5章 图像复原
连续图像退化模型
第5章 图像复原
连续图像退化模型
第5章 图像复原
第5章 图像复原
图像退化机理
4. 什么是图像复原？
图像复原是将图像退化的过程加以估计,并 补偿退化过程造成的失真,以便获得未经干扰退 化的原始图像或原始图像的最优估值，从而改善 图像质量的一种方法。 图像复原是图像退化的逆过程。
典型的图像复原方法是根据图像退化的先验知 识建立一个退化模型以此模型为基础，采用滤波 等手段进行处理，使得复原后的图像符合一定的 准则，达到改善图像质量的目的。
第5章 图像复原
离散图像退化模型
为便于计算机实现，需将退化模型离 散化。
(1) 先讨论一维卷积 对f(x)及h(x)均匀采样,样本数分别为A及 B,即
f ( x) x=0,1,---,A-1 h (x) x=0,1,---,B-1
离散循环卷积是针对周期函数定义的，
第5章 图像复原
离散图像退化模型
第5章 图像复原
图像退化机理
3.图像退化的处理方法？
无论是由光学、光电或电子方法获得的图像 都会有不同程度的退化；退化的形式多种多样， 如传感器噪声、摄像机未聚焦、物体与摄像设备 之间的相对移动、光学系统的相差、成像光源或 射线的散射等； 如果我们对退化的类型、机制和过程都十分 清楚，那么就可以利用其反过程来复原图像。
数字图像处理第5章-46页PPT文档资料
解压缩时（224 224+1 224+1-2）
f k e k f k
2019/11/16
26
5.4 无损预测编码
利用预测器，可以将对原始图像序列的编码转换成对预测 误差的编码。
由于在预测比较时，预测误差的动态范围会远小于原始图 像序列的动态范围，所以对预测误差的编码所需的比特数 会大大减少，这是预测编码可以获得数据压缩结果的原因。
224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224
5
5.1 引言（图像压缩的基本概念）
压缩后图像数据 234 1 1 1 1 1 -2
2019/11/16
3
5.1 引言（图像压缩的基本概念）
2.时间冗余 视频图像序列中的不同帧之间的相关性所造成的冗余。
3.视觉冗余 是指人眼不能感知或不敏感的那部分图像信息。人的眼
睛对图像细节和颜色的辨认受到人的视觉特性的限制，人类 最多能分辨 216种颜色，而彩色图像用24表示，即 224种颜色， 这种数据冗余称为视觉冗余。
第5章 图像编码与压缩
5.1 引言（图像压缩的基本概念） 5.2 图像保真度准则（图像评价） 5.3 无损压缩技术 5.4 无损预测编码 5.5 有损预测编码 5.6 图像变换编码基本原理 5.7 视频图像编码简介
2019/11/16
1
5.1 引言（图像压缩的基本概念）
例如：输入（224 225 223）则经预测器后需传输（224
f k e k f k
2019/11/16
26
5.4 无损预测编码
利用预测器，可以将对原始图像序列的编码转换成对预测 误差的编码。
由于在预测比较时，预测误差的动态范围会远小于原始图 像序列的动态范围，所以对预测误差的编码所需的比特数 会大大减少，这是预测编码可以获得数据压缩结果的原因。
224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224 224
5
5.1 引言（图像压缩的基本概念）
压缩后图像数据 234 1 1 1 1 1 -2
2019/11/16
3
5.1 引言（图像压缩的基本概念）
2.时间冗余 视频图像序列中的不同帧之间的相关性所造成的冗余。
3.视觉冗余 是指人眼不能感知或不敏感的那部分图像信息。人的眼
睛对图像细节和颜色的辨认受到人的视觉特性的限制，人类 最多能分辨 216种颜色，而彩色图像用24表示，即 224种颜色， 这种数据冗余称为视觉冗余。
第5章 图像编码与压缩
5.1 引言（图像压缩的基本概念） 5.2 图像保真度准则（图像评价） 5.3 无损压缩技术 5.4 无损预测编码 5.5 有损预测编码 5.6 图像变换编码基本原理 5.7 视频图像编码简介
2019/11/16
1
5.1 引言（图像压缩的基本概念）
例如：输入（224 225 223）则经预测器后需传输（224
第5章_数字图像处理技术(上)
三维色彩空间
图像处理中的色彩学知识
• 色彩模型：色彩空间是三维的，作为色彩空间
三维坐标的三个独立参数可以是色彩心理的三 属性，用不同的三个色彩参数就代表不同的色
彩模型
图像处理中的色彩学知识
• 色域
–一个色彩系统能够显示或打印的色彩范围 –色域由宽到窄的顺序： 人眼所看到的色谱 Lab色域
RGB色域
– RGB模式是一种发光屏幕的加色模式，CMYK 模式是一种颜色反光的印刷减色模式。而Lab 模式既不依赖光线，也不依赖于颜料，它是 CIE组织确定的一个理论上包括了人眼可以看
见的所有色彩的色彩模式。Lab模式弥补了
RGB和CMYK两种色彩模式的不足。
图像处理中的色彩学知识
④ LAB模型
– Lab模式由三个通道组成，但不是R、G、B通道。它的 一个通道是亮度，即L。另外两个是色彩通道，用A和
音频类似，数字图像的数据量一般都比较
大，在存储时会占用大量的空间，因此需
要对图像进行压缩编码。
数字图像处理概述
• 现代图像的范围
① 可见光范围内的图像，不可见光范围内的图 像（红外成像技术） ② 可见图像和不可见图像 – 可见图像：照片、图、画
– 不可见图像：主要是物理图像，如温度、气 压、地势图等，还包括医学影像
图像数字化的途径 特点
扫描仪扫描 数码相机拍摄 网上搜索并下载 抓图工具抓拍 方便快捷，需用扫描仪 方便快捷，需用数码相机 方便快捷 方便快捷
利用图像编辑软件 专业性强，较慢 自己加工或创作
图像处理中的色彩学知识
1. 色彩
– 单色光：通过三棱镜也不会再分解为其它 的色光
– 由单色光所混合的光称为复色光
图像处理中的色彩学知识
数字图像处理chap5课件
找退化原因→建立退化模型→反向推演→恢复图像
可见，图像复原主要取决于对图像退化过程的先验知识 所掌握的精确程度，体现在建立的退化模型是否合适。
图像复原和图像增强的区别： 图像增强不考虑图像是如何退化的，而是试图采用各种 技术来增强图像的视觉效果。因此，图像增强可以不顾增强 后的图像是否失真，只要看得舒服就行。 而图像复原就完全不同，需知道图像退化的机制和过程 等先验知识，据此找出一种相应的逆处理方法，从而得到复 原的图像。 如果图像已退化，应先作复原处理，再作增强处理。 二者的目的都是为了改善图像的质量。
5.3 频率域恢复方法
5.3.1 逆滤波恢复法
对于线性移不变系统而言
g(x, y) f (, )h(x , y )dd n(x, y) f (x, y) h(x, y) n(x, y)
对上式两边进行傅立叶变换得
G(u,v) F(u,v)H (u,v) N(u,v)
H(u,v)称为系统的传递函数。从频率域角度看，它使图像 退化，因而反映了成像系统的性能。
H(u,v);
(3)逆滤波计算 (4)计算
F (u, v) G(u, v) /
的逆傅立叶变换，求得
H (u, v)
。
F (u, v)
f (x, y)
但实际获取的影像都有噪声，因而只能求F(u,v)的估
计值 Fˆ (u, v) 。
Fˆ (u, v) F (u, v) N (u, v) H (u, v)
因此还有
f (x , y ) f (x, y) (x , y )
二维线性位移不变系统 如果对二维函数施加运算T[·] ，满足
⑴ T f1x, y f2 x, y T f1x, y T f2 x, y
⑵ Taf x, y aT f x, y
可见，图像复原主要取决于对图像退化过程的先验知识 所掌握的精确程度，体现在建立的退化模型是否合适。
图像复原和图像增强的区别： 图像增强不考虑图像是如何退化的，而是试图采用各种 技术来增强图像的视觉效果。因此，图像增强可以不顾增强 后的图像是否失真，只要看得舒服就行。 而图像复原就完全不同，需知道图像退化的机制和过程 等先验知识，据此找出一种相应的逆处理方法，从而得到复 原的图像。 如果图像已退化，应先作复原处理，再作增强处理。 二者的目的都是为了改善图像的质量。
5.3 频率域恢复方法
5.3.1 逆滤波恢复法
对于线性移不变系统而言
g(x, y) f (, )h(x , y )dd n(x, y) f (x, y) h(x, y) n(x, y)
对上式两边进行傅立叶变换得
G(u,v) F(u,v)H (u,v) N(u,v)
H(u,v)称为系统的传递函数。从频率域角度看，它使图像 退化，因而反映了成像系统的性能。
H(u,v);
(3)逆滤波计算 (4)计算
F (u, v) G(u, v) /
的逆傅立叶变换，求得
H (u, v)
。
F (u, v)
f (x, y)
但实际获取的影像都有噪声，因而只能求F(u,v)的估
计值 Fˆ (u, v) 。
Fˆ (u, v) F (u, v) N (u, v) H (u, v)
因此还有
f (x , y ) f (x, y) (x , y )
二维线性位移不变系统 如果对二维函数施加运算T[·] ，满足
⑴ T f1x, y f2 x, y T f1x, y T f2 x, y
⑵ Taf x, y aT f x, y
数字图像处理第5章PPT课件
(m ,n ) ; 0 m A 1 且 0 n B 1 e(m ,n ) 0 ; A m M 1 或 B n N 1
Digital Image Processing
5.1 退化模型
g (m ,n ) ; 0 m A 1 且 0 n B 1 g e(m ,n ) 0 ; A m M 1 或 B n N 1 所以线性时不变系统的离散退化模型为：
模型，由于退化过程是卷积过程，线性卷积后点数变长，为 了方便计算，需要将各函数进行延拓，具体如下所示：
f(m ,n ) ; 0 m A 1 且 0 n B 1 fe (m ,n ) 0 ; A m M 1 或 B n N 1
h (m ,n ) ; 0 m C 1 且 0 n D 1 h e (m ,n ) 0 ; C m M 1 或 D n N 1
wM(M1,M-1)
w M (i,m )ex p (j2 im /M ) i,m 0 ,1 ,2 , ,M 1
w N (k,n )ex p (j2 kn/N ) k,n0,1 ,2, ,N 1
Digital Image Processing
5.1 退化模型
从而
W W M W N{ w M (i,m )} { w N (k,n )}
f e (1 , 0 )
f e (1 ,1 )
f e ( M 1 , N 1 )
g e(0,0 )
g e (0 ,1)
g
g e(0, N 1) g e (1 , 0 )
g e (1 ,1 )
g e ( M 1 , N 1 )
Digital Image Processing
H1
H2
H3
he(i,0)
Hi
Digital Image Processing
5.1 退化模型
g (m ,n ) ; 0 m A 1 且 0 n B 1 g e(m ,n ) 0 ; A m M 1 或 B n N 1 所以线性时不变系统的离散退化模型为：
模型，由于退化过程是卷积过程，线性卷积后点数变长，为 了方便计算，需要将各函数进行延拓，具体如下所示：
f(m ,n ) ; 0 m A 1 且 0 n B 1 fe (m ,n ) 0 ; A m M 1 或 B n N 1
h (m ,n ) ; 0 m C 1 且 0 n D 1 h e (m ,n ) 0 ; C m M 1 或 D n N 1
wM(M1,M-1)
w M (i,m )ex p (j2 im /M ) i,m 0 ,1 ,2 , ,M 1
w N (k,n )ex p (j2 kn/N ) k,n0,1 ,2, ,N 1
Digital Image Processing
5.1 退化模型
从而
W W M W N{ w M (i,m )} { w N (k,n )}
f e (1 , 0 )
f e (1 ,1 )
f e ( M 1 , N 1 )
g e(0,0 )
g e (0 ,1)
g
g e(0, N 1) g e (1 , 0 )
g e (1 ,1 )
g e ( M 1 , N 1 )
Digital Image Processing
H1
H2
H3
he(i,0)
Hi
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
he ( j , N 1) he ( j , N 2) he ( j ,0) h ( j ,1) h ( j ,0) h ( j , N 1) e e e H j he ( j , 2) he ( j ,1) he ( j ,0) he ( j , N 1) he ( j , N 2) he ( j , N 3)
T ˆ T ˆ J ( f ) 2Q Qf 2H ( g Hfˆ ) 0 ˆ f
ˆ (H H f
T
1
Q Q) H g
T
1
T
第5章 图像复原
令γ=1/λ
T T 1 T ˆ f ( H H Q Q) H g
常数γ必须反复迭代调整直到满足约束条 件 || n || 2 || g Hfˆ || 2 。求解式(7-33)的关键就是如何 选用一个合适的变换矩阵Q。
1. 什么是图像退化？
在景物成像过程中，由于目标的高速运动、散 射、成像系统畸变和噪声干扰，致使最后形成的 图像存在种种恶化， 称之为“ 退化”。
退化的形式有图像模糊或图像有干扰等。
第5章 图像复原
第5章 图像复原
第5章 图像复原
2. 图像退化原因
成像系统镜头聚焦不准产生的散焦； 相机与景物之间的相对运动； 成像系统存在的各种非线性因素以及系统 本身的性能 ； 射线辐射大气湍流等因素造成的照片畸变； 成像系统的像差、畸变、有限带宽等； 底片感光图像显示时会造成记录显示失真； 成像系统中存在的各种随机噪声 ；
也即
f ( x) 0 x A 1 f e ( x) A x M 1 0 h( x ) 0 x B 1 he ( x) B x M 1 0
第5章 图像复原
f e (x)、 he(x)均是长度为M的周期性离散 函数，其卷积为
g e ( x) f e (m)he ( x m)
he ( M 1) he ( M 2) he ( M 3) he (0)
利用周期性：he(x)=he(x+M)
第5章 图像复原
he ( M 1) he ( M 2) he (0) h (1) h ( 0 ) h ( M 1 ) e e e H he (2) he (1) he (0) he ( M 1) he ( M 2) he ( M 3)
g ( x, y ) H
f ( , ) ( x, ; y, )dd
f ( , ) H ( x, ; y, )dd
f ( x, y )
， 因而造成图 像模糊。 通常把成像系统考虑成为线性位移不变 系统，即
he ( j ,1) he ( j , 2) he ( j ,3) he ( j ,0)
第5章 图像复原
(3) n是MN 维噪声向量，则退化模型
g Hf n
第5章 图像复原
第5章 图像复原
退化参数的确定
退化参数： h(x,y), n(x,y) 图像恢复： 对原始图像作出尽可能好的估计。 已知退化图像，要作这种估计，须知 道退化参数的有关知识。
第5章 图像复原
则循环卷积为
g ( x, y ) f e (m, n)he ( x m, y n)
m 0 n 0
M 1 N 1
x 0,1,2...... M 1 y 0,1,2...... N 1
第5章 图像复原
矩阵形式 :
g Hf f、g是MN维向量，H是MN MN矩阵。
H是分块循环矩阵。
第5章 图像复原
H 0 H M 1 H M 2 H H H 1 0 M 1 H H2 H1 H0 H M 1 H M 2 H M 3
H1 H2 H3 H0
第5章 图像复原
为了不致使离散循环卷积的周期性序列 之间发生相互重叠现象（卷绕效应），必 须把函数 f (x)和h (x)周期性地延拓成
f e ( x), x 0,1,2, , M 1 he ( x), x 0,1,2, , M 1 其中， M A B 1
第5章 图像复原
离散图像退化模型
循环卷积写成矩阵形式：
g Hf
H是M*M的矩阵。
第5章 图像复原
第5章 图像复原
he (1) he (2) he (0) h (1) he (0) he (1) e H he (2) he (1) he (0) he ( M 1) he ( M 2) he ( M 3)
返回
第5章 图像复原
图像复原的方法 代数复原方法 逆滤波复原方法 中值滤波复原方法
第5章 图像复原
代数复原方法
图像复原的主要目的是当给定退化的 图像g(x,y)及系统h(x,y)和噪声n(x,y)的 某种了解或假设，估计出原始图像f(x,y)。 其代数表达式即为g=Hf+n，此时可用线性 代数中的理论解决复原问题。
第5章 图像复原
离散图像退化模型
为便于计算机实现，需将退化模型离 散化。
(1) 先讨论一维卷积 对f(x)及h(x)均匀采样,样本数分别为A及 B,即
f ( x) x=0,1,---,A-1 h (x) x=0,1,---,B-1
离散循环卷积是针对周期函数定义的，
第5章 图像复原
离散图像退化模型
he (1) he (2) he (3) he (0)
循环矩阵：方阵，每一行是前一行循环右 移一位的结果。
第5章 图像复原
(2)推广到二维空间 f (x,y)、h (x,y)均匀采样，样本数分别为 A*B，C*D。周期性地延拓成M*N样本
f ( x, y ) 0 x A 1和0 y B 1 f e ( x, y ) A x M 1和B y N 1 0 h( x, y ) 0 x C 1和0 y D 1 he ( x, y ) C x M 1和D y N 1 0
m 0
M 1
x 0,1,2,, M 1
g e (x)也是长度为M的周期性离散函数。
第5章 图像复原
若把f e (x)、 g e (x) 表示成向量形式：
f [ f e (0), f e (1),, f e ( M 1)]
T T
g [ g e (0), g e (1),, g e ( M 1)]
第5章 图像复原
连续图像退化模型
第5章 图像复原
连续图像退化模型
第5章 图像复原
连续图像退化模型
第5章 图像复原
连续图像退化模型
第5章 图像复原
连续图像退化模型
(1) 如果线性成像系统的冲击响应是理想 的 ， 即 Hδ(x-α,y-β)=δ(x-α,y-β) ， 那么形成的图象g(x,y)就和原始图象一样， 不产生模糊。
第5章 图像复原
点扩展函数的确定
（一）运用先验知识: 大气湍流 光学系统散焦 照相机与景物相对运动 根据导致模糊的物理过程（先验知 识）来确定h(x,y)或H(u,v)。
第5章 图像复原
点扩展函数的确定
（1）长时间曝光下大气湍流造成的转移 函数
H (u , v ) exp[ c u v
第5章 图像复原
噪声的确定
当噪声与图像不相关时，噪声是加性 的。 在有些情况下噪声大小确实与图像信 号有关。如以下的乘性白噪声
g ( x, y ) f ( x, y ) ( x , y ) f ( x, y ) f ( x, y )[1 ( x, y )] f ( x, y ) n ( x, y )
2
2 5/ 6
]
C是与湍流性质有关的常数。
第5章 图像复原
点扩展函数的确定
（2）光学散焦
H (u , v)
J1 (d )
d
(u 2 v 2 )1/ 2
d 是散焦点扩展函数的直径 ,J1(•) 是第一 类贝塞尔函数。
第5章 图像复原
点扩展函数的确定
（3）照相机与景物相对运动 设T为快门时间，x0(t)，y0(t)是位移的 x分量和y分量
第5章 图像复原
图像退化机理
3.图像退化的处理方法？
无论是由光学、光电或电子方法获得的图像 都会有不同程度的退化；退化的形式多种多样， 如传感器噪声、摄像机未聚焦、物体与摄像设备 之间的相对移动、光学系统的相差、成像光源或 射线的散射等； 如果我们对退化的类型、机制和过程都十分 清楚，那么就可以利用其反过程来复原图像。
第5章 图像复原
第5章 图像复原
图像退化机理
4. 什么是图像复原？
图像复原是将图像退化的过程加以估计,并 补偿退化过程造成的失真,以便获得未经干扰退 化的原始图像或原始图像的最优估值，从而改善 图像质量的一种方法。 图像复原是图像退化的逆过程。
典型的图像复原方法是根据图像退化的先验知 识建立一个退化模型以此模型为基础，采用滤波 等手段进行处理，使得复原后的图像符合一定的 准则，达到改善图像质量的目的。
第5章 图像复原
第五章
图像复原
图像退化机理 连续图像退化的数学模型 离散图像退化的数学模型 图像复原的方法
第5章 图像复原
图像退化机理
什么是图像的退化 图像退化原因 图像退化的处理方法 什么是图像复原 图像增强和图像复原的区别
返回