三角函数对照表
三角函数表

三角函数表你没有看错,这是一个关于紧固件的企业网站,却在讲述三角函数这风牛马不相及的故事.因为......三角函数表用于计算角度和边长的关系,在产品零件的绘图和设计中经常用到,所以我们整理了下表。
此表不仅可供我们机械工人参考,也可供其他工人或学生参考。
先来个定义正弦函数 sin(A)=a/h余弦函数 cos(A)=b/h正切函数 tan(A)=a/b余切函数 cot(A)=b/a正割函数 sec (A) =h/b余割函数 csc (A) =h/a注:a—所研究角的对边b—所研究的邻边h—所研究角的斜边以下是具体的对应参数表:1,正弦函数表 sinsin1=0. sin2=0. sin3=0.sin4=0. sin5=0. sin6=0.sin7=0. sin8=0. sin9=0.sin10=0. sin11=0. sin12=0. sin13=0. sin14=0. sin15=0. sin16=0. sin17=0. sin18=0. sin19=0. sin20=0. sin21=0. sin22=0. sin23=0. sin24=0. sin25=0. sin26=0. sin27=0. sin28=0. sin29=0. sin30=0. sin31=0. sin32=0. sin33=0. sin34=0. sin35=0. sin36=0. sin37=0. sin38=0. sin39=0. sin40=0. sin41=0. sin42=0. sin43=0. sin44=0. sin45=0. sin46=0. sin47=0. sin48=0. sin49=0. sin50=0. sin51=0. sin52=0. sin53=0. sin54=0. sin55=0. sin56=0. sin57=0. sin58=0. sin59=0. sin60=0. sin61=0. sin62=0. sin63=0. sin64=0. sin65=0. sin66=0. sin67=0. sin68=0. sin69=0. sin70=0. sin71=0. sin72=0. sin73=0. sin74=0. sin75=0. sin76=0. sin77=0. sin78=0. sin79=0. sin80=0. sin81=0. sin82=0. sin83=0. sin84=0. sin85=0. sin86=0. sin87=0. sin88=0. sin89=0.sin90=12,余弦函数表 coscos1=0. cos2=0. cos3=0.cos4=0. cos5=0. cos6=0.cos7=0. cos8=0. cos9=0.cos10=0. cos11=0. cos12=0. cos13=0. cos14=0. cos15=0. cos16=0. cos17=0. cos18=0. cos19=0. cos20=0. cos21=0. cos22=0. cos23=0. cos24=0. cos25=0. cos26=0. cos27=0. cos28=0. cos29=0. cos30=0. cos31=0. cos32=0. cos33=0. cos34=0. cos35=0. cos36=0. cos37=0. cos38=0. cos39=0. cos40=0. cos41=0. cos42=0. cos43=0. cos44=0. cos45=0. cos46=0. cos47=0. cos48=0. cos49=0. cos50=0. cos51=0. cos52=0. cos53=0. cos54=0. cos55=0.2 cos56=0. cos57=0.2 cos58=0. cos59=0. cos60=0. cos61=0. cos62=0.6 cos63=0. cos64=0.6 cos65=0. cos66=0. cos67=0. cos68=0.2 cos69=0. cos70=0. cos71=0.5 cos72=0.5cos73=0.7 cos74=0. cos75=0. cos76=0. cos77=0. cos78=0. cos79=0. cos80=0. cos81=0. cos82=0. cos83=0. cos84=0. cos85=0. cos86=0. cos87=0. cos88=0. cos89=0.cos90=03,正切函数表 tantan1=0. tan2=0. tan3=0.tan4=0. tan5=0. tan6=0.tan7=0. tan8=0. tan9=0.tan10=0. tan11=0. tan12=0. tan13=0. tan14=0. tan15=0. tan16=0. tan17=0. tan18=0. tan19=0. tan20=0. tan21=0. tan22=0. tan23=0. tan24=0. tan25=0. tan26=0. tan27=0. tan28=0. tan29=0. tan30=0. tan31=0. tan32=0. tan33=0. tan34=0. tan35=0. tan36=0. tan37=0. tan38=0. tan39=0. tan40=0. tan41=0. tan42=0. tan43=0. tan44=0. tan45=0. tan46=1. tan47=1. tan48=1. tan49=1. tan50=1. tan51=1. tan52=1. tan53=1. tan54=1.tan58=1. tan59=1. tan60=1. tan61=1. tan62=1. tan63=1. tan64=2. tan65=2. tan66=2. tan67=2. tan68=2. tan69=2. tan70=2. tan71=2. tan72=3. tan73=3. tan74=3. tan75=3. tan76=4. tan77=4. tan78=4. tan79=5. tan80=5. tan81=6. tan82=7. tan83=8. tan84=9. tan85=11. tan86=14. tan87=19. tan88=28. tan89=57.tan90=(无限)4,余切函数 cotcot89=0. cot88=0. cot87=0. cot86=0. cot85=0. cot84=0. cot83=0. cot83=0. cot81=0. cot80=0. cot79=0. cot78=0. cot77=0. cot76=0. cot75=0. cot74=0. cot73=0. cot72=0. cot71=0. cot70=0. cot69=0. cot68=0. cot67=0. cot66=0. cot65=0. cot64=0. cot63=0. cot62=0. cot61=0. cot60=0. cot59=0. cot58=0. cot57=0. cot56=0. cot55=0. cot54=0.cot50=0. cot49=0. cot48=0. cot47=0. cot46=0. cot45=0. cot44=1. cot43=1. cot42=1. cot41=1. cot40=1. cot39=1. cot38=1. cot37=1. cot36=1. cot35=1. cot34=1. cot33=1. cot32=1. cot31=1. cot30=1. cot29=1. cot28=1. cot27=1. cot26=2. cot25=2. cot24=2. cot23=2. cot22=2. cot21=2. cot20=2. cot19=2. cot18=3. cot17=3. cot16=3. cot15=3. cot14=4. cot13=4. cot12=4. cot11=5. cot10=5. cot9=6. cot8=7. cot7=8. cot6=9. cot5=11. cot4=14. cot3=19. cot228. cot1=57.cot0=(无限)咨询与留言。
常用三角函数值对照表图

常用三角函数值对照表
在学习三角函数的过程中,掌握常用角度对应的三角函数
值是非常重要的。
下表列出了常用角度的正弦、余弦和正切值,帮助我们更好地理解和记忆这些数值。
角度
(度)030456090180270360正弦值01/2√2/2√3/210-10
余弦值1√3/2√2/21/20-101
正切值0√3/31√3不存
在0不存
在
通过以上对照表,我们可以得出以下结论: - 在0度和360度时,正弦值为0,余弦值为1,正切值为0,注意到余弦值在这两个角度上的正弦值均是最大的; - 在90度时,正弦值最大为1,余弦值为0,正切值不存在,因为在这个角度余弦为0; - 在180度时,正弦值为0,余弦值最小为-1,正切值为0; - 在270度时,正弦值为-1,余弦值为0,正切值不存在,因为在这个角度正弦为-1。
通过这张对照表,我们可以更快更准确地计算各种角度的三角函数值,加深对三角函数的理解,也为解决相关数学问题提供了重要的参考依据。
三角函数是数学中一个重要的分支,深入理解三角函数对于数学学习和应用都具有重要意义。
特殊三角函数值对照表(特殊角的三角函数值)

特殊三角函数值对照表(特殊角的三角函数值)《特殊角的三角函数值》是人教版数学九年级下册第二十八章的内容,特殊三角函数值一般指在0,30°,45°,60°,90°,180°角下的正余弦值。
这些角度的三角函数值是经常用到的。
并且利用两角和与差的三角函数公式,可以求出一些其他角度的三角函数值。
具体的三角函数值如下表:扩展资料:黄金三角函数介绍:α=18°(π/10) sinα=(√5-1)/4 cosα=√(10+2√5)/4tαnα=√(25-10√5)/5cscα=√5+1 secα=√(50-10√5)/5 cotα=√(5+2√5)α=36°(π/5) sinα=√(10-2√5)/4 cosα=(√5+1)/4tαnα=√(5-2√5)cscα=√(50+10√5)/5 secα=√5-1 cotα=√(25+10√5)/5α=54°(3π/10) sinα=(√5+1)/4 cosα=√(10-2√5)/4 tαnα=√(25+10√5)/5是数学中属于初等函数中的超越函数的一类函数。
它们的本质是任意角的集合与一个比值的集合的变量之间的映射。
通常的三角函数是在平面直角坐标系中定义的,其定义域为整个实数域。
另一种定义是在直角三角形中,但并不完全。
扩展资料:三角函数在复数中有重要的应用。
三角函数也是物理学中的常用工具。
它有六种基本函数函数名正弦余弦正切余切正割余割符号 sin cos tan cot sec csc正弦函数sin(A)=a/c余弦函数cos(A)=b/c正切函数tan(A)=a/b余切函数cot(A)=b/a其中a为对边,b为邻边,c为斜边特殊角的值如下表:在直角三角形中,任意一锐角∠A的对边与斜边的比叫做∠A 的正弦,记作sinA(由英语sine一词简写得来),即sinA=∠A的对边/斜边。
扩展资料:sinα = tanα × cosα(即sinα / cosα = tanα )cosα = cotα × sinα (即cosα / sinα = cotα)tanα = sinα × secα (即tanα / sinα = secα)sin ( α ± β ) = sinα · cosβ ± cosα · sinβsin ( α + β + γ ) = sinα · cosβ · cosγ +cosα · sinβ · cosγ + cosα · cosβ · sinγ - sinα · sinβ · sinγcos ( α ± β ) = cosα cosβ ∓ sinβ sinαtan ( α ± β ) = ( tanα ± tanβ ) / ( 1 ∓ tanα tanβ )完整初中三角函数值表如下图所示:常见的三角函数有正弦函数、余弦函数和正切函数。
常用三角函数值对照表兀表示度数

常用三角函数值对照表及表示度数三角函数是数学中重要的概念,在解决几何问题和物理问题中有着广泛应用。
常见的三角函数包括正弦函数、余弦函数和正切函数。
这些函数在不同的角度下具有不同的数值,下面将介绍它们在特定角度下的取值,并给出一个简单的对照表。
正弦函数正弦函数通常记作sin,表示一个角的对边与斜边的比值。
在不同角度下,正弦函数的取值如下:•sin(0°) = 0•sin(30°) = 1/2•sin(45°) = √2/2•sin(60°) = √3/2•sin(90°) = 1余弦函数余弦函数通常记作cos,表示一个角的邻边与斜边的比值。
在不同角度下,余弦函数的取值如下:•cos(0°) = 1•cos(30°) = √3/2•cos(45°) = √2/2•cos(60°) = 1/2•cos(90°) = 0正切函数正切函数通常记作tan,表示正弦和余弦的比值。
在不同角度下,正切函数的取值如下:•tan(0°) = 0•tan(30°) = √3/3•tan(45°) = 1•tan(60°) = √3•tan(90°) = 无穷大根据以上对照表,我们可以方便地计算不同角度下三角函数的值。
在实际问题中,这些数值可以帮助我们解决各种复杂的三角关系,为数学和物理的研究提供重要依据。
深入了解三角函数的性质和应用,有助于我们更好地理解数学的美妙之处。
综上所述,常用三角函数值对照表及表示度数为数学中一个重要的概念,通过这些数值我们可以更好地理解三角函数在不同角度下的取值规律。
希望本文能够帮助读者更好地掌握三角函数的知识,提升数学水平。
三角函数正弦余弦表

三角函数正弦余弦表
正弦和余弦是三角函数中最基本的两个函数,它们在数学、物理、工程等领域都有广泛的应用。
下面是正弦和余弦表:一、正弦表角度0°30°45°60°90°
sinθ0 1/2 √2/2√3/2 1二、余弦表角度 0° 30°45° 60° 90°
cosθ 1 √3/2 √2/2 1/2 0
从上述表格可以看出,当角度为0时,正弦值为0,余弦值为1;当角度为30时,正弦值为1/2,余弦值为√3/2;当角度为45时,正弦值和余弦值均为√( ) / ( ) ,即根号二分之一;当角度为60时,正弦值和余弧值分别是√( ) / ( ) 和半径的一半;而当角底等于90时,则正弧值等于半径长(即单位圆的直径),而其餘则无定义。
需要注意的是,在三维空间中存在着双曲线函数tanh(x)与双曲线反函数arctanh(x),这些也被称作“超越函数”,但它们并不属于三角函数的范畴。
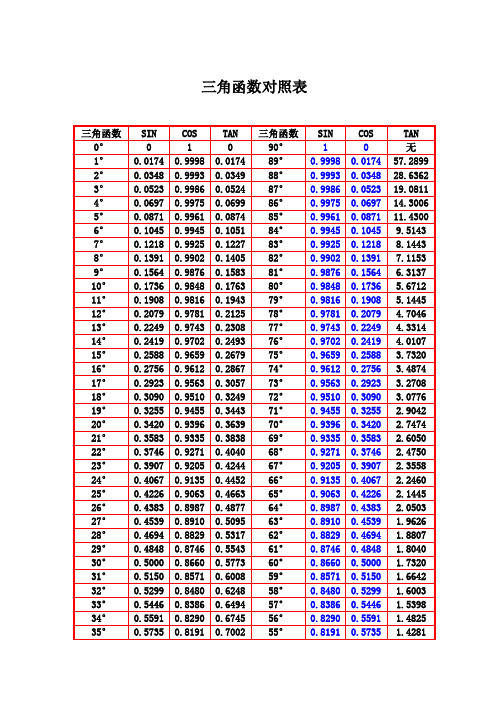
三角函数对照表
商的关系
sin tan sec
cos
csc
cos cot csc
sin
sec
平方关系
2
2
sin cos 1
2
2
1 tan sec
2
2
1 cot csc
诱导公式
sin() sin
cos( ) cos tan() tan
cot() cot
sin( ) cos 2
cos( ) sin 2
0.9998 0.9993 0.9986 0.9975 0.9961 0.9945 0.9925 0.9902 0.9876 0.9848 0.9816 0.9781 0.9743 0.9702 0.9659 0.9612 0.9563 0.9510 0.9455 0.9396 0.9335 0.9271 0.9205 0.9135 0.9063 0.8987 0.8910 0.8829 0.8746 0.8660 0.8571 0.8480 0.8386 0.8290 0.8191
36° 37° 38° 39° 40° 41° 42° 43° 44° 45°
0.5877 0.6018 0.6156 0.6293 0.6427 0.6560 0.6691 0.6819 0.6946 0.7071
0.8090 0.7986 0.7880 0.7771 0.7660 0.7547 0.7431 0.7313 0.7193 0.7071
TAN 0
0.0174 0.0349 0.0524 0.0699 0.0874 0.1051 0.1227 0.1405 0.1583 0.1763 0.1943 0.2125 0.2308 0.2493 0.2679 0.2867 0.3057 0.3249 0.3443 0.3639 0.3838 0.4040 0.4244 0.4452 0.4663 0.4877 0.5095 0.5317 0.5543 0.5773 0.6008 0.6248 0.6494 0.6745 0.7002
常见三角函数值对照表

常见三角函数值对照表
三角函数的本质是任意角的集合与一组比值的变量之间的映射。
接下来分享常见的三角函数值对照表。
三角函数值对照表
三角函数值口诀
30°,45°,60°这三个角的正弦值和余弦值的共同点是:分母都是2,若把分子都加上根号,则被开方数就相应地变成了1,2,3.正切的特点是将分子全部都带上根号,令分母值为3,则相应的被开方数就是3,9,27。
记忆口诀一
三十,四五,六十度,三角函数记牢固;
分母弦二切是三,分子要把根号添;
一二三来三二一,切值三九二十七;
递增正切和正弦,余弦函数要递减.
记忆口诀二
一二三三二一,戴上根号对半劈。
两边根号三,中间竖旗杆。
分清是增减,试把分母安。
正首余末三,好记又简单。
零度九十度,斜线z形连。
端点均为零,余下竖横填。
判断三角函数值的符号
记忆公式是:奇变偶变,符号看象限。
对于π/2*k±α(k∈Z)的三角函数值,
①当k是偶数时,得到α的同名函数值,即函数名不改变;
②当k是奇数时,得到α相应的余函数值,即
sin→cos;cos→sin;tan→cot,cot→tan.(奇变偶不变),然后在前面加上把α看成锐角时原函数值的符号。
(符号看象限)
示例:
sin(2π-α)=sin(4·π/2-α),k=4为偶数,所以取sinα。
当α是锐角时,2π-α∈(270°,360°),sin(2π-α)<0,符号为“-”。
所以sin(2π-α)=-sinα。
三角函数对照表(转)

sin90=1
cos1=0.9998476951563913 cos2=0.9993908270190958 cos3=0.9986295347545738
cos4=0.9975640502598242 cos5=0.9961946980917455 cos6=0.9945218953682733
sin4=0.0697564737441253 sin5=0.08715574274765816 sin6=0.10452846326765346
sin7=0.12186934340514747 sin8=0.13917310096006544 sin9=0.15643446504023087
(1)特殊角三角函数值
sin0=0
sin30=0.5
sin45=0.7071 二分之根号2
sin60=0.8660 二分之根号3
sin90=1
cos0=1
cos30=0.866025404 二分之根号3
cos45=0.707106781 二分之根号2
cos58=0.5299192642332049 cos59=0.5150380749100544 cos60=0.5000000000000001
cos61=0.4848096202463371 cos62=0.46947156278589086 cos63=0.4539904997395468
cos16=0.9612616959383189 cos17=0.9563047559630355 cos18=0.9510565162951535
cos19=0.9455185755993168 cos20=0.9396926207859084 cos21=0.9335804264972017
三角函数对照表

三角函数对照表
三角函数的和差化积公式 三角函数的积化和差公式
sin sin 2sin
cos
22sin sin 2cos sin
22
cos cos 2cos cos
22cos cos 2sin sin
22
αβ
αβ
αβαβαβ
αβαβαβ
αβαβαβ
αβ+-+=⋅+--=⋅+-+=⋅+--=-⋅
[][]
[]
[]
1
sin cos sin()sin()21
cos sin sin()sin()2
1
cos cos cos()cos()21
sin sin cos()cos()2αβαβαβαβαβαβαβαβαβαβαβαβ⋅=
++-⋅=+--⋅=++-⋅=-+--
化asinα ±bcosα为一个角的一个三角函数的形式(辅助角的三角函数的公式)
22sin cos sin()a x b x a b x φ±=+±
其中φ角所在的象限由a 、b 的符号确定,φ角的值由tan b
a
φ=确定
六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
”。
常见三角函数表

常见三角函数表
在数学中,三角函数是研究角和三角形关系的函数。
常见
的三角函数包括正弦函数、余弦函数、正切函数等。
这些函数在数学、物理、工程等领域中都有广泛的应用。
下面是常见三角函数的表格:
正弦函数(Sine Function)
正弦函数通常用sin表示,定义域为实数集,值域为[-1, 1]。
其在圆上一条弧对应角的正弦值等于这个角的对边长与斜边长的比值。
具体如下:
角度(度)角度(弧度)正弦值
000
30π/61/2
45π/4√2/2
60π/3√3/2
90π/21
余弦函数(Cosine Function)
余弦函数通常用cos表示,定义域为实数集,值域为[-1, 1]。
其在圆上一条弧对应角的余弦值等于这个角的邻边长与斜边长的比值。
具体如下:
角度(度)角度(弧度)余弦值
001
30π/6√3/2
45π/4√2/2
60π/31/2
90π/20
正切函数(Tangent Function)
正切函数通常用tan表示,定义域为实数集,其在圆上一条弧对应角的正切值等于这个角的正弦值与余弦值的商。
具体如下:
角度(度)角度(弧度)正切值
000
30π/6√3/3
45π/41
60π/3√3
90π/2不存在
以上是常见三角函数表,这些函数在几何、三角、物理等领域中都有着重要的作用。
深入理解这些函数的性质和应用,对于提高数学水平和解决实际问题都有着重要的意义。
0到360度三角函数值对照表

0到360度三角函数值对照表度数sin cos tan0°0 1 030°1/2 √3/21/√345°√2/2√2/2 160°√3/21/2 √390° 1 0 无穷120°√3/2-1/2 -√3135°√2/2-√2/2-1150°1/2 -√3/2-1/√3180°0 -1 0210°-1/2 -√3/21/√3225°-√2/2-√2/21240°-√3/2-1/2 -√3270°-1 0 无穷300°-√3/21/2 √3315°-√2/2√2/2-1330°-1/2 √3/2-1/√3360°0 1 0由于三角函数中的数度数与它们的函数值之间具有固定的联系,我们可以根据上面列举的表格来查看不同的角度的三角函数的值:以弧度为0°、30°、45°、60°、90°、120°、135°、150°、180°、210°、225°、240°、270°、300°、330°和360°为例,分别来看它们的sin值、cos值和tan值:0°:sin为0,cos为1,tan为0;30°:sin为1/2,cos为√3/2,tan为1/√3;45°:sin为√2/2,cos为√2/2,tan为1;60°:sin为√3/2,cos为1/2,tan为√3;90°:sin为1,cos为0,tan为无穷;120°:sin为√3/2,cos为-1/2,tan为-√3;135°:sin为√2/2,cos为-√2/2,tan为-1;150°:sin为1/2,cos为-√3/2,tan为-1/√3;180°:sin为0,cos为-1,tan为0;210°:sin为-1/2,cos为-√3/2,tan为1/√3;225°:sin为-√2/2,cos为-√2/2,tan为1;240°:sin为-√3/2,cos为-1/2,tan为-√3;270°:sin为-1,cos为0,tan为无穷;300°:sin为-√3/2,cos为1/2,tan为√3;315°:sin为-√2/2,cos为√2/2,tan为-1;330°:sin为-1/2,cos为√3/2,tan为-1/√3;360°:sin为0,cos为1,tan为0。
常见三角函数值表

数据处理技巧
• 数据筛选与排序
• 数据拟合与插值
• 数据可视化
数据存储与查询
• 建立数据文件
• 设计数据查询接口
• 提供数据查询服务
⌛️
三角函数值表的应用场景与优势
应用场景
• 教育与教学
• 科学研究
• 工程与产品设计
优势
• 提高计算效率
• 减少误差
• 方便数据查询与共享
04
三角函数值表的比较与评估
不同来源的三角函数值表的比较
纸质三角函数值表
⌛️
• 传统方法与工具
• 信息量有限
• 查询速度慢
网络三角函数值表
• 实时更新与维护
电子三角函数值表
• 便捷访问与共享
• 丰富的应用场景
• 数字化方法与工具
• 信息量大
• 查询速度快
三角函数值表的准确性评估
01
误差来源分析
• 测量误差
• 计算误差
• 数据处理误差
01
计算机技术
• 数据处理与计算
• 数据存储与查询
• 数据可视化
02
信息技术
• 网络传输与共享
• 数据库建设与维护
• 信息系统开发与应用
03
人工智能技术
• 数据分析与挖掘
• 误差分析与控制
• 智能计算与优化
未来三角函数值表的发展趋势与前景
发展趋势
• 更高的计算精度
• 更广泛的应用场景
• 更智能化的数据处理
三角函数值表在实际应用中的案例
测量问题
• 测量建筑物的高度
• 测量物体的距离
• 测量角度的大小
物理学问题
三角函数常用值对照表

三角函数常用值对照表
在数学中,三角函数是代数学中最基础的概念之一。
学习
三角函数的过程中,熟悉常用值是非常重要的,因为这些常用值可以帮助我们快速计算各种三角函数的值,从而简化数学运算。
下表列出了常用的三角函数数值,让我们一起来看看吧:
角度(°)正弦余弦正切余切正割余割
0010无穷1无穷
301/2√3/21/√3√322/√3
45√2/2√2/211√2√2
60√3/21/2√31/√32/√32
9010无穷0无穷1
从这个对照表中,我们可以看出不同角度下三角函数的值,对于解题和计算来说非常有帮助。
对于初学者来说,熟悉这些常用值可以提高解题的效率,对于高级应用来说,这些常用值也是基础中的基础。
希望大家多多掌握这些常用值,提高自己的数学水平!。
三角函数对照表
45°
1
同角基本关系式
倒数关系
商的关系
平方关系
诱导公式
(其中k∈Z)
两角和与差的三角函数公式
万能公式
半角的正弦、余弦和正切公式
三角函数的降幂公式
二倍角的正弦、余弦和正切公式
三倍角的正弦、余弦和正切公式
三角函数的和差化积公式
三角函数的积化和差公式
化asinα ±bcosα为一个角的一个三角函数的形式(辅助角的三角函数的公式)
70°
21°
69°
22°
68°
23°
67°
24°
66°
25°
65°
26°
64°
27°
63°
28°
62°
29°
61°
30°
60°
31°
59°
32°
58°
33°
57°
34°
56°
35°
55°
36°
54°
37°
53°
38°
52°
39°
51°
40°
50°
41°
49°
42°
48°
43°
47°
44°
46°
45°
其中 角所在的象限由 、 的符号确定, 角的值由 确定
六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。”
三角函数对照表
三角函数
SIN
COS
TAN
三角函数
SIN
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角函数对照表
三角函数
SIN
COS
TAN
三角函数
SIN
COS
TAN
0°
0
1
0
90°
1
0
无
1°
89°
2°
88°
3°
87°
4°
86°
5°
85°
6°
84°
7°
83°
8°
82°
9°
81°
10°
80°
11°
79°
12°
78°
13°
77°
14°
76°
15°
75°
16°
74°
17°
73°
18°
72°
44°
46°
45°
1
45°
1同角基Biblioteka 关系式倒数关系商的关系
平方关系
诱导公式
(其中k∈Z)
两角和与差的三角函数公式
万能公式
半角的正弦、余弦和正切公式
三角函数的降幂公式
二倍角的正弦、余弦和正切公式
三倍角的正弦、余弦和正切公式
三角函数的和差化积公式
三角函数的积化和差公式
化asinα±bcosα为一个角的一个三角函数的形式(辅助角的三角函数的公式)
其中 角所在的象限由 、 的符号确定, 角的值由 确定
六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。”
19°
71°
20°
70°
21°
69°
22°
68°
23°
67°
24°
66°
25°
65°
26°
64°
27°
63°
28°
62°
29°
61°
30°
60°
31°
59°
32°
58°
33°
57°
34°
56°
35°
55°
36°
54°
37°
53°
38°
52°
39°
51°
40°
50°
41°
49°
42°
48°
43°
47°
