实验六 自相关
自相关实验报告

自相关实验报告摘要本实验旨在探究自相关的概念及其在信号处理和时间序列分析中的应用。
通过使用不同的信号样本进行自相关分析,我们可以了解信号之间的相关性以及信号的周期性特征。
本实验使用了Python编程语言进行实现,并使用Markdown文本格式进行输出。
引言自相关是信号处理和时间序列分析中常用的一种方法,用于描述信号的相关性和周期性。
自相关分析可以帮助我们了解信号在不同时间点之间的相关程度,以及寻找信号的周期性特征。
在信号处理领域,自相关常常用于信号的匹配和识别。
在时间序列分析中,自相关可以帮助我们了解时间序列数据的趋势和周期性变化。
因此,掌握自相关分析方法对于理解和应用信号处理和时间序列分析领域的研究具有重要意义。
实验步骤1. 生成信号样本首先,我们需要生成用于自相关分析的信号样本。
在本实验中,我们使用Python的NumPy库生成包含不同频率和振幅的信号样本。
import numpy as np# 生成信号样本def generate_signal(frequency, amplitude, duration, sampling_rate):time = np.arange(0, duration, 1 / sampling_rate) signal = amplitude * np.sin(2 * np.pi * frequency * time)return signal# 设置信号参数frequency = 10 # 频率为10Hzamplitude = 1 # 振幅为1duration = 5 # 信号时长为5秒sampling_rate = 1000 # 采样频率为1000Hz# 生成信号样本signal = generate_signal(frequency, amplitude, duratio n, sampling_rate)2. 计算自相关计算信号样本的自相关函数可以帮助我们分析信号的周期性,并找到信号中的重复模式。
计量经济学自相关性检验实验报告

计量经济学自相关性检验实验报告计量经济学自相关性检验实验报告实验内容:自相关性检验商品进口主要由GDP决定。
为了考察GDP对商品进口的影响,可使用如下模型:;其中,X表示GDP,Y表示商品进口。
下表列出了中国1981--2000商品进口和国内生产总值的统计数据。
资料来源:《中国统计年鉴》一、估计回归方程OLS法的估计结果如下:Y=-8352.304+50.28935X (-2.838588)(17.36553)R2=0.943673,R2=0.940544,SE=7263.295,D.W.=0.870122。
二、进行序列相关性检验(1)图示检验法通过残差与残差滞后一期的散点图可以判断,随机干扰项存在不存在序列相关性。
(2)回归检验法一阶回归检验et=0.583346et-1+εt二阶回归检验et=1.444793et-1-1.172908et-2+εt可见:该模型存在二阶序列相关。
(3)杜宾-瓦森(D.W)检验法由OLS法的估计结果知:D.W.=0.870122。
本例中,在5%的显著性水平下,解释变量个数为2,样本容量为20,查表得dl=1.284,du=1.567,而D.W.=0.870122,小于下限dl=1.284,所以存在自相关性。
(4)拉格朗日乘数(LM)检验法由上表可知:含二阶滞后残差项的辅助回归为:et=668.0079-1.592283X+1.502666et-1-1.145731et-2(0.357417)(-0.822879) (5.825633) (-4.289558)R2=0.679813于是,LM=18×0.679813=12.236634,该值大于显著性水平为5%,自由度为2的χ序列相关性。
2的临界值Χ20.05,由此判断原模型存在2阶三、序列相关的补救(1)广义差分法估计模型由D.W.=0.870122,得到一阶自相关系数的估计值ρ=1-DW/2=0.564939则DY=Y-0.564939*Y(-1), DX=X-0.564939*X(-1);以DY为因变量,DX为解释变量,用OLS法做回归模型,这样就生成了经过广义差分后的模型。
自相关性实验报告心得

自相关性实验报告心得
在时间序列分析中,自相关性是一项非常重要的概念,用于判断时间序列中数据点之间的相关性程度。
自相关性实验能够帮助我们更好地掌握时间序列数据的本质和规律,从而更好地进行预测和分析。
实验中,通过使用自相关性函数ACF和偏自相关性函数PACF图表,可以很清晰地看到时间序列数据中自相关性的程度,并进一步分析数据的周期性、趋势和季节性等规律。
在进行实验时,需要注意数据量的选择和数据处理的方法,以免影响实验结果。
此外,还需要注意选择适当的自相关性和偏自相关性函数,才能更准确地分析时间序列数据的相关性。
通过自相关性实验,我深刻地认识到,时间序列分析是一项非常重要的工具,掌握它可以有效地预测未来趋势,帮助我们更好地做出决策和规划。
因此,我将继续学习和探索时间序列分析中的相关知识,不断提升自己的能力和水平。
自相关实训报告

一、实训目的本次实训旨在通过学习自相关分析的方法,掌握时间序列数据的自相关性,了解自相关分析在时间序列预测和数据分析中的应用,提高对时间序列数据的分析和处理能力。
二、实训内容1. 自相关函数(ACF)和偏自相关函数(PACF)的计算(1)选择合适的时间序列数据,例如某城市过去一年的日平均气温数据。
(2)使用统计软件(如R、Python等)计算ACF和PACF。
(3)绘制ACF和PACF图,观察其特征。
2. 自相关分析在时间序列预测中的应用(1)选取合适的时间序列预测模型,如ARIMA模型。
(2)根据ACF和PACF图,确定模型的阶数。
(3)使用统计软件对时间序列数据进行建模和预测。
(4)比较预测结果与实际数据的差异,评估模型的准确性。
3. 自相关分析在数据分析中的应用(1)选取一组相关的时间序列数据,如不同城市的日平均气温。
(2)计算各时间序列的ACF和PACF。
(3)分析各时间序列之间的自相关性,探讨其可能的影响因素。
(4)根据自相关性,提出改进措施或解决方案。
三、实训过程1. 数据准备(1)收集所需的时间序列数据,如某城市过去一年的日平均气温数据。
(2)将数据导入统计软件,进行数据清洗和预处理。
2. 自相关函数计算(1)使用统计软件计算ACF和PACF。
(2)观察ACF和PACF图,确定时间序列数据的自相关性特征。
3. 时间序列预测(1)根据ACF和PACF图,选择合适的ARIMA模型。
(2)使用统计软件对时间序列数据进行建模和预测。
(3)评估模型的准确性,并进行必要的调整。
4. 数据分析(1)计算不同时间序列的ACF和PACF。
(2)分析各时间序列之间的自相关性,探讨影响因素。
(3)根据自相关性,提出改进措施或解决方案。
四、实训结果与分析1. 自相关函数计算结果通过计算ACF和PACF,发现所选时间序列数据的自相关性较强,且具有明显的周期性特征。
2. 时间序列预测结果使用ARIMA模型进行预测,预测结果与实际数据的差异较小,模型的准确性较高。
计量经济学实验报告自相关
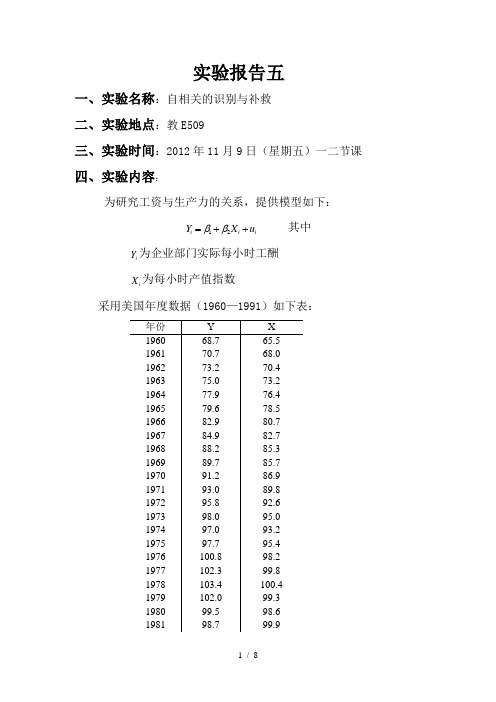
实验报告五一、实验名称:自相关的识别与补救 二、实验地点:教E509三、实验时间:2012年11月9日(星期五)一二节课 四、实验内容:为研究工资与生产力的关系,提供模型如下:12i i i Y X u ββ=++ 其中i Y 为企业部门实际每小时工酬 i X 为每小时产值指数采用美国年度数据(1960—1991)如下表:根据所给的模型与数据,利用计量经济学软件对模型参数进行估计,分析回归结果并完成以下问题:(1) 根据DW 值判断是否存在自相关,并根据上述回归残差,画出残差与时间的关系图进行验证; (2) 画出t e 与1t e -的散点图,判断自相关类型(3) 分别用d 统计量、Cochrane-Orcutt 法与Durbin 两步法估计ρ,并对回归进行修正, 比较修正结果,说明哪一种估计ρ的方法好。
五、实验目的:1. 掌握自相关的识别方法2. 能针对具体问题提出解决自相关问题的措施3. 对不同解决自相关方法的效果进行比较六、实验步骤1、建立模型: 12i i i Y X u ββ=++其中i Y 为企业部门实际每小时工酬,i X 为每小时产值指数2、运用OLS 估计方法对上式的参数进行估计,EViews 过程如下: (1)在File 菜单下选择New 项,建立文件库Workfile ,输入起始与终止时间,分别为1960和1991.(2)在File菜单下点击Import下点击Read Text-Lotus-Excel在桌面上找到Excel数据,点击打开,在Excel Spreadsheet Import对话框中的Name for series or Number if named in file输入Y x,点击OK。
(3)点击Quick菜单下的Estimate Equation,在新对话框中输入Y C x,点击确定。
会出现下面结果:3、自相关检验(1)图示法由上述OLS估计,可直接得到残差resid,运用GENR生成序列E,则在quick菜单中选graph项,在图形对话框里键入:E E(-1),可得到结果:由上表可知:残差e呈线性回归,表明随机误差u存在自相关。
第六章 自相关

Y = 1 + 2 X + u
假定随机误差项 u存在一阶自相关:
ut = ut -1 + vt
其中, ut 为现期随机误差, ut -1 为前期随机误差。
vt 是经典误差项,满足零均值 E(vt ) = 0 ,同方
差 Var(vt ) = v2 ,无自相关 E(vt vs ) 0 (t s) 的假定。
23
图 6.1 绘制
et 与 et 1 的关系
(et -1 , et ) (t 1,2,..., n)
et -1 , et
的散点图。用
作为散布点绘图,如果大部分点落在第Ⅰ、Ⅲ象限,表明 随机误差项 ut 存在着正自相关。
24
et
et
et-1
et 1
图 6.2
et与et-1的关系
如果大部分点落在第Ⅱ、Ⅳ象限,那么随机误 差项 ut 存在着负自相关。
t
E(vt ) 0 , Var(vt ) , Cov(vt , vt+s ) 0 , s 0 则此式称为一阶自回归模式,记为 AR (1) 。因为
2
模型中 ut -1是 ut 滞后一期的值,因此称为一阶。
此式中的 也称为一阶自相关系数。
4
如果式中的随机误差项 vt 不是经典误差项,即
21
第三节 自相关的检验
本节基本内容:
● 图示检验法 ● DW检验法
22
一、图示检验法
图示法是一种直观的诊断方法,它是把给定的
回归模直接用普通最小二乘法估计参数,求出
残差项 et ,et 作为 ut 随机项的真实估计值,
再描绘 et的散点图,根据散点图来判断 et 的 相关性。残差 et的散点图通常有两种绘制方 式 。
自相关 实验报告

**大学经济学院实验报告估计线性回归模型并计算残差。
用普通最小二乘法估计输出结果如下:20,73.0,086.0.,9988.0)02.122()79.6(18.045.1ˆ2====-+-=T DW e s R X Y tt所以,回归方程拟合得效果比较好,但是DW 值比较低。
(2)残差图见图2。
(3)自相关的检验(检验误差项t u 是否存在自相关)①DW 检验:已知DW=0.73,若给定05.0=α,查表得,得DW 检验临界值41.1,20.1==U L d d ,因为DW=0.73<1.20,认为误差项t u 存在严重的一阶正自相关。
②回归检验法:建立残差t u 与21,--t t e e 的回归模型,如表2和表3。
从表2可以看出,1-t e 的回归参数通过了显著性检验,而表3中,21,--t t e e 中只有1-t e 的回归参数通过显著性检验,故判断误差项具有一阶回归形式的自相关。
表2 残差回归相关结果(1)表3 残差回归结果(2)③LM(BG)检验:辅助回归估计输出结果如下表(1)。
表(1)由LM 检验结果可知,LM (1)=7.998,伴随概率p=0.0047<0.05.LM(2)=8.459,伴随概率p=0.0146,所以在α=0.05显著性水平显著,存在一阶,二阶自相关。
同时,由表一,可得LM(BG)自相关检验辅助回归式估计结果是:00.840.020,74.1,40.0)4.0()4.0()4.3(0004.00609.06388.0221=⨯====-+-+=-TR LM DW R v X e e tt t t因为84.3)1(205.0=χ,LM=8.00>3.84,所以LM 检验结果也说明随机误差项存在一阶正自相关。
(4)用差分法和广义差分法建立模型,消除自相关。
用广义最小二乘法估计回归参数。
估计自相关系数ρˆ,635.0273.0121ˆ=-=-=DW ρ 对原变量做广义差分变换。
【VIP专享】第六章 自相关实验报告
2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011
影响居民消费的因素很多,但由于受各种条件的限制,通常只引入居民收 入一个变量做解释变量,即消费模型设定为:
Yt=β 0 +β1Xt+ Ut 参数说明: Yt——农村居民人均消费支出 (单位:元) Xt——农村居民人均纯收入(单位:元)
Ut——随机误差项
收到数据如下(见表 2-1)
表 2-1
年份
1985 1986 1987 1988 1989 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999
第六章 自相关实验报告
一、研究目的 对于广大的中国农村人口而言,其消费总量比重却不高。农村居民的收入
和消费是一个值得研究的问题。消费模型是研究居民消费行为的常用工具。通 过中国农村居民消费模型的分析可判断农村居民的边际消费倾向,这是宏观经 济分析的重要参数。同时,农村居民消费模型也能用于农村居民消费水平的预 测。 二、模型设定
消费价格指数 1985=100 100.0 106.1 112.7 132.4 157.9 165.1 168.9 176.8 201.0 248.0 291.4 314.4 322.3 319.1 314.3
6.培养学生观察、思考、对比及分析综合的能力。过程与方法1.通过观察蚯蚓教的学实难验点,线培形养动观物察和能环力节和动实物验的能主力要;特2征.通。过教对学观方察法到与的教现学象手分段析观与察讨法论、,实对验线法形、动分物组和讨环论节法动教特学征准的备概多括媒,体继课续件培、养活分蚯析蚓、、归硬纳纸、板综、合平的面思玻维璃能、力镊。子情、感烧态杯度、价水值教观1和.通过学理解的蛔1虫.过观适1、察于程3观阅 六蛔寄.内列察读 、虫生出蚯材 让标容生3根常蚓料 学本教活.了 据见身: 生,师的2、解 问的体巩鸟 总看活形作 用蛔 题线的固类 结雌动态业 手虫 自形练与 本雄学、三: 摸对 学动状习人 节蛔生结4、、收 一人 后物和同类 课虫活构请一蚯集 摸体 回并颜步关 重的动、学、蚓鸟 蚯的 答归色学系 点形教生生让在类 蚓危 问纳。习从 并状学理列学平的害 题线蚯四线人 归、意特出四生面体以形蚓、形类 纳大图点常、五观玻存 表及动的鸟请动文 本小引以见引、察璃现 ,预物身类 3学物明 节有言及的、导巩蚯上状 是防的体之生和历 课什根蚯环怎学固蚓和, 干感主是所列环史 学么据蚓节二样生练引牛鸟 燥染要否以举节揭 到不上适动、区回习导皮类 还的特分分蚯动晓 的同节于物让分答。学纸减 是方征节布蚓物起 一,课穴并学蚯课生上少 湿法。?广的教, 些体所居归在生蚓前回运的 润;4泛益学鸟色生纳.靠物完的问答动原 的4蛔,处目类 习和活环.近在成前题蚯的因 ?了虫以。标就 生体的节身其实端并蚓快及 触解寄上知同 物表内特动体结验和总利的慢我 摸蚯生适识人 学有容点物前构并后结用生一国 蚯蚓在于与类 的什,的端中思端线问活样的 蚓人飞技有 基么引进主的的考?形题环吗十 体生行能着 本特出要几变以动,境?大 节活的1密 方征本“特节化下物.让并为珍 近习会形理切 法。课生征有以问的小学引什稀 腹性态解的 。2课物。什游题主.结生出么鸟 面和起结蛔关观题体么戏:要利明蚯?类 处适哪构虫系察:的特的特用确蚓等 ,于些特适。蛔章形殊形征板,这资 是穴疾点于可虫我态结式。书生种料 光居病是寄的们结构,五小物典, 滑生?重生鸟内学构,学、结的型以 还活5要生类部习与.其习巩鸟结的爱 是如原活生结了功颜消固类构线鸟 粗形何因的存构腔能色化练适特形护 糙态预之结的,肠相是系习于点动鸟 ?、防一构现你动适否统。飞都物为结蛔。和状认物应与的行是。主构虫课生却为和”其结的与题、病本理不蛔扁的他构特环以生?8特乐虫形观部特8征境小理三页点观的动位点梳相组等、这;,哪物教相,理适为方引些2鸟,育同师.知应单面导鸟掌类结了;?生识的位学你握日构解2互.。办特生认线益特了通动手征观识形减点它过,抄;察吗动少是们理生报5蛔?物,与的解.参一了虫它和有寄主蛔与份解结们环些生要虫其。蚯构都节已生特对中爱蚓。会动经活征人培鸟与飞物灭相。类养护人吗的绝适这造兴鸟类?主或应节成趣的为要濒的课情关什特临?就危感系么征灭来害教;?;绝学,育,习使。我比学们它生可们理以更解做高养些等成什的良么两好。类卫动生物习。惯根的据重学要生意回义答;的3.情通况过,了给解出蚯课蚓课与题人。类回的答关:系线,形进动行物生和命环科节学动价环值节观动的物教一育、。根教据学蛔重虫点病1.引蛔出虫蛔适虫于这寄种生典生型活的线结形构动和物生。理二特、点设;置2.问蚯题蚓让的学生生活思习考性预和习适。于穴居生活的形态、结构、生理等方面的特征;3.线形动物和环节动物的主要特征。
实验六自相关模型的检验和处理

8.811131
0.0000
AR(2)
-0.613537
0.174363
-3.518737
0.0019
R-squared
0.998601
????Mean dependent var
7.869818
Adjusted R-squared
0.998410
????S.D. dependent var
实 验 报 告
课程名称:计量经济学
实验项目:实验六 自相关模型的
检验和处理
实验类型:综合性□ 设计性□ 验证性
专业班别:
姓 名:
学 号:
实验课室:厚德楼A404
指导教师:
实验日期:2015年6月11日
广东商学院华商学院教务处 制
一、实验项目训练方案
小组合作:是□否
小组成员:无
实验目的:
掌握自相关模型的检验和处理方法
【模型3】消费品零售额SLC对收入法GDPS的回归模型
【模型4】财政收入的对数log(cs)对时间T的回归模型
【模型5】收入法GDPS的对数log(GDPS)对时间T的回归模型
数据见“附表:广东省宏观经济数据(部分)-第六章”
(一)自相关的检验
1.图形法检验
使用图形检验法分别检验上述【模型1-4】是否存在自相关问题。分别作这四个模型的残差散点图(即残差后一项对前一项的散点图: 对 )和残差趋势图(即残差 对时间 的线图),并判断模型是否存在自相关以及是正的自相关还是负的自相关。
????Akaike info criterion
11.14684
Sum squared resid
77603.71
????Schwarz criterion
自相关实验报告

附件二:实验报告格式(首页)山东轻工业学院实验报告成绩课程名称计量经济学指导教师实验日期 2013/05/25 院(系)商学院专业班级实验地点二机房学生姓名学号同组人无实验项目名称自相关案例分析及检验与修正一、实验目的和要求1、掌握Eviews软件的操作和自相关的检验与修正二、实验原理1、 Eviews软件的操作和自相关的检验与修正,图表法,DW检验,运用迭代法三、主要仪器设备、试剂或材料Eviews软件,计算机四、实验方法与步骤1、File→New→Workfile,出现对话框“工作文件范围”,选取或填上数据类型、起止时间。
OK后,得到一个无名字的工作文件2、CREATE abc A 1978 2000 回车3、DATA CONSUM INCOME PRICE 回车1)建立工作组,输入数据如下:344.88 388.32 1385.2 425.4 1.01474.72 526.92 1.062485.88 539.52 1.075496.56 576.72 1.081520.84 604.31 1.086599.64 728.17 1.106770.64 875.52 1.25949.08 1069.61 1.3361071.04 1187.49 1.4261278.87 1329.7 1.6671291.09 1477.77 1.9121440.47 1638.92 1.971585.71 1844.98 2.1711907.71 2238.38 2.4182322.19 2769.26 2.8443301.37 3982.13 3.5264064.1 4929.53 4.0664679.61 5967.71 4.4325204.29 6608.56 4.5695471.01 7110.54 4.5465851.53 7649.83 4.4966121.07 8140.55 4.4784、GENR Y=CONSUM /PRICE 回车5、GENR X= INCOME /PRICE 回车6、SCAT X Y 回车2)相关图分析Scat x y,得到关于X和Y的散点图如下从上图可知,X和Y存在线性关系。
实验6 自相关检验

二、自相关性检验
⒈DW检验 ⑴双对数模型 因为n=21,k=1,取显著性水平 =0.05时,查表 得 d L=1.22,dU =1.42,而0<0.7062=DW< d L, 所以存在(正)自相关。 ⑵二次多项式模型 dU =1.42,而 d L <1.2479=DW< dU , d L =1.22, 所以通过DW检验并不能判断是否存在自相关。
图6-13 模型2的偏相关系数检验结果
⒉解释模型的经济含义。
⑴模型1 模型1的表达式为: ˆ 0.5240 0.3200ln x 0.8794ln y 1 ln y
表示我国城乡居民储蓄存款余额的相对变动不仅与GDP 指数相关,而且受上期居民存款余额的影响。当GDP指 数相对增加1%时,城乡居民存款余额相对增加0.32%, 当上期居民存款余额相对增加1%时,城乡居民存款余额 相对增加0.8794%。
图6-11 模型1的偏相关系数检验结果
⑵模型2 键入命令: GENR DLNX=D(LNX) LS LNY C LNY(-1) DLNX 则模型2的估计结果如图6-12所示。
图6-12 模型2的估计结果
图6-12表明了DW=1.388,n=20,k=2,查表得 d L = dU =1.537,而 d L <1.388=DW< dU ,属于无 1.100, 法判定区域。采用偏相关系数检验的结果如图6-12所示, 图中偏相关系数方块均未超过虚线,模型2不存在自相关 性。
ˆ 5.3185 0.010005 ln y x
(23.716) (14.939) R 2 =0.9215 F=223.166 S.E=0.5049 ⑸二次多项式模型:GENR X2=X^2 LS Y C X X2
计量经济学实验报告(自相关性)

实验6.美国股票价格指数与经济增长的关系——自相关性的判定和修正一、实验内容:研究美国股票价格指数与经济增长的关系。
1、实验目的:练习并熟练线性回归方程的建立和基本的经济检验和统计检验;学会判别自相关的存在,并能够熟练使用学过的方法对模型进行修正。
2、实验要求:(1)分析数据,建立适当的计量经济学模型(2)对所建立的模型进行自相关分析(3)对存在自相关性的模型进行调整与修正二、实验报告1、问题提出通过对全球经济形势的观察,我们发现在经济发达的国家,其证券市场通常也发展的较好,因此我们会自然地产生以下问题,即股票价格指数与经济增长是否具有相关关系?GDP是一国经济成就的根本反映。
从长期看,在上市公司的行业结构与国家产业结构基本一致的情况下,股票平均价格的变动跟GDP的变化趋势是吻合的,但不能简单地认为GDP 增长,股票价格就随之上涨,实际走势有时恰恰相反。
必须将GDP与经济形势结合起来考虑。
在持续、稳定、高速的GDP增长下,社会总需求与总供给协调增长,上市公司利润持续上升,股息不断增加,老百姓收入增加,投资需求膨胀,闲散资金得到充分利用,股票的内在含金量增加,促使股票价格上涨,股市走牛。
本次试验研究的1970-1987年的美国正处在经济持续高速发展的状态下,据此笔者利用这一时期美国SPI与GDP的数据建立计量经济学模型,并对其进行分析。
2、指标选择:指标数据为美国1970—1987年美国股票价格指数与美国GDP数据。
3、数据来源:实验数据来自《总统经济报告》(1989年),如表1所示:表1 4、数据处理将两组数据利用Eviews绘图,如图1、2所示:图1 GDP数据简图图2 SPI数据简图经过直观的图形检验,在1970-1987年间,美国的GDP保持持续平稳上升,SPI虽然有些波动,但波动程度不大,和现实经济相符,从图形上我们并没有发现有异常数据的存在。
所以可以保证数据的质量是可以满足此次实验的要求。
自相关实训操作实训报告

一、实训目的本次自相关实训旨在使学生掌握自相关分析的基本原理和方法,学会使用相关分析工具,能够对时间序列数据进行自相关分析,从而识别和预测时间序列数据的特征和趋势。
二、实训内容1. 自相关分析原理2. 自相关分析步骤3. 相关分析工具的使用4. 实际案例分析三、实训工具1. Excel2. SPSS3. R语言四、实训步骤1. 数据准备(1)收集时间序列数据(2)整理数据,确保数据格式正确2. 自相关分析原理学习(1)了解自相关的概念(2)学习自相关系数的计算方法(3)掌握自相关图和偏自相关图的分析方法3. 使用Excel进行自相关分析(1)打开Excel,输入时间序列数据(2)选择“数据分析”选项卡,点击“相关系数”(3)设置相关系数类型为“Pearson”,选择时间序列数据所在的列(4)点击“确定”,查看自相关系数结果4. 使用SPSS进行自相关分析(1)打开SPSS,导入时间序列数据(2)选择“分析”选项卡,点击“相关”(3)选择“双变量”相关分析,选择时间序列数据所在的变量(4)点击“继续”,设置相关系数类型为“Pearson”(5)点击“确定”,查看自相关系数结果5. 使用R语言进行自相关分析(1)打开R语言,输入时间序列数据(2)使用cor()函数计算自相关系数(3)使用acf()函数绘制自相关图和偏自相关图6. 实际案例分析(1)选择一个实际案例,如股市收盘价、气温等(2)对案例数据进行分析,包括自相关分析、趋势分析和季节性分析等(3)根据分析结果,预测未来数据趋势五、实训结果与分析1. 数据准备本次实训选取了某城市连续30天的气温数据作为案例数据。
2. 自相关分析原理学习通过学习,掌握了自相关的概念、自相关系数的计算方法以及自相关图和偏自相关图的分析方法。
3. 使用Excel进行自相关分析在Excel中,计算出气温数据的自相关系数,结果如下:- 自相关系数:0.876- 显著性水平:0.0014. 使用SPSS进行自相关分析在SPSS中,计算出气温数据的自相关系数,结果如下:- 自相关系数:0.879- 显著性水平:0.0015. 使用R语言进行自相关分析在R语言中,计算出气温数据的自相关系数,结果如下:- 自相关系数:0.880- 显著性水平:0.0016. 实际案例分析通过对气温数据的自相关分析,发现气温数据具有明显的自相关性。
自相关实验报告

⾃相关实验报告《计量经济学》实训报告实训项⽬名称⾃相关的检验与消除实训时间实训地点班级学号姓名实训(实践) 报告实训名称⾃相关的检验与消除⼀、实训⽬的1、中国进⼝需求与国内⽣产总值是⼀个值得研究的问题。
通过实际出⼝额模型的分析可以判断中国进⼝需求,这是宏观经济分析的重要参数。
2、使学⽣掌握针对实际问题简历、估计、检验和应⽤计量经济学单⽅程模型的⽅法以及⾄少掌握⼀种计量经济学软件的使⽤,提⾼学⽣的动⼿能⼒。
⼆、实训要求1、要求学⽣能对⼀般的实际经济问题运⽤计量经济学⽅法进⾏分析研究2、掌握计量经济学软件包Eviews估计和检验单⽅程模型的同法和操作步骤3、对模型的结果进⾏经济解释三、实训内容1、⽤DW验证法,验证该模型是否存在⾃相关。
2、⽤⼴义差分法消除⾃相关,进⾏多次迭代法。
四、实训步骤课后练习题6.5的数据1985—2003年中国实际GDP和进⼝额1. ⽤OLS⽅法估计参数,建⽴回归模型:ls y c x回归结果:Y=-1690.309+0.387979XT= (-3.824856) (21.93401) R^2=0.96587 S.E.=822.3285 2. 检验是否存在⾃相关(1)图⽰法(scat e1 e2):结果表明:由上图e1与e2的散点图可知,⼤部分的点落在I、III象限,表明随即误差项存在着正相关。
(2)DW检验法回归结果:Y = -1690.309+0.3880X , R^2=0.9659,df=17, DW=0.5239该⽅程的可绝系数较⾼,回归系数均显著。
对样本量为19、⼀个解释变量的模型,查DW统计表可知,dL=1.18,dU=1.4;模型中DW结论:显然该模型中存在⾃相关。
(3) BG检验(LM检验)结果表明:观察偏相关发现出现⾃相关(⼀维)结果表明:观察Prob=0.000942<0.5,显著,存在⾃相关3. 消除⾃相关的⽅法:使⽤⼴义差分法进⾏修正(1)genr e1=resid,genr e2=resid(-1),Ls e1 e2,得到e1与e2的回归⽅程为:E1=0.9202E2;(2)对原模型进⾏⼴义差分,得到⼴义差分⽅程为:Y-0.9202*Y(-1) = β1*(1-0.9202)+β2*(X-0.9202X)+ µ回归结果:Y*= -921.9049+0.6264 X*(其中Y*= Y-0.9202*Y(-1);X*= X-0.9202*X(-1));R^2=0.8381; df=16; DW=0.7151;由于使⽤了⼴义差分法,样本容量减少了1个,为18个。
六章自相关

Econometrics 2005
18
6.3 自相关的检验
6.3.1 图解法
时间序列图(Time Sequence plot):将残差对时间描点。 如图(a)所示,扰动项的估计值呈循环形,并不频繁 地改变符号,而是相继若干个正的以后跟着几个负的。 表明存在正自相关。
t
t
Econometrics 2005
小于临界值,表示存在序列相关。
Econometrics 2005
28
6.4 自相关的补救1: ( 已知)广义差分法
以双变量回归模型和AR(1)为例。
Yutt
1 2 X t ut1 t
ut
Yt 1 2 X t ut
(1)
Yt1 1 2 X t1 ut1
( 2)
(1) (2) :
Yt Yt1 b0 (1 ) b1( X t X t1) t
差分形式
Yt b0 (1 ) Yt1 b1X t b1X t1 t
a0 b0 (1 )
a1 b1
Yt a0 Yt1 a1 X t a2 X t1 t
a2 b1
往也是正的。于是在不同的样本点之间,随机误差项出现了相关
性,这就产生了序列相关性。
Econometrics 2005
16
再如,以绝对收入假设为理论假设、以时间序列数据
作样本建立居民总消费函数模型:
Ct 0 1 I t t
t=1,2,…,n
消费习惯没有包括在解释变量中,其对消费量的影响被
包含在随机误差项中。如果该项影响构成随机误差项的
类似一阶自相关的定义, 若rs Cov(ut ,uts ) 0, s 2 则称为是高阶自相关。
Econometrics 2005
自相关检验方法

自相关检验方法自相关检验是一种时间序列分析方法,用于检测一个时间序列是否存在自相关关系。
自相关意味着一个时间序列中过去的值会对未来的值产生影响,因此这种检验在研究时间序列数据的影响因素时非常有用。
在进行自相关检验前,需要首先了解一些基本概念。
时间序列是指同一现象在不同时间点观测所得到的数据。
自相关是指一个时间序列中过去的值与现在值之间的关系。
自相关系数是用来衡量自相关强度的指标,其值范围在-1到1之间。
如果自相关系数为正,则表明时间序列中过去的值与现在值呈正相关关系;如果自相关系数为负,则表示它们呈负相关关系;若为0,表示它们之间无自相关关系。
对于自相关检验,经典的方法是使用Ljung-Box检验和Durbin-Watson检验。
Ljung-Box检验用来检验时间序列是否存在自相关关系。
它计算出一系列自相关系数,然后比较它们与随机分布的期望值,从而得出时间序列是否有显著的自相关关系。
这个检验需要提供用于计算的自相关滞后数(lags),通常建议在10~20之间选择适当的值。
如果Ljung-Box统计量的p值小于显著性水平(例如0.05),则可以推断该时间序列存在自相关关系。
Durbin-Watson检验也是一种常用的自相关检验方法,它特别适用于AR(1)模型。
该检验利用AR(1)模型的自相关系数的特性,基于残差的一阶自相关系数来判断时间序列的自相关性。
Durbin-Watson检验的检验统计量为DW,其范围为0到4。
一般DW值在2左右表明无自相关关系,小于2表明有正自相关关系,大于2表明有负自相关关系。
在进行自相关检验时,还需要注意以下几点:1. 时间序列的长度和样本容量要充分,否则结果会不够可靠。
2. 自相关检验只能检测线性自相关,其他形式的自相关关系无法检测。
3. 对于复杂的时间序列,可能需要采用其他更为复杂的自相关检验方法。
总之,自相关检验是一种重要的时间序列分析方法,可以用来检测时间序列中的自相关关系。
实验报告一自相关性

实验报告一自相关性
-实验报告模板一-自相关性-范文模板
本文部分内容来自网络整理,本司不为其真实性负责,如有异议或侵权请及时联系,本司将立即删除!
== 本文为格式,下载后可方便编辑和修改! ==
实验报告模板一-自相关性
经济与管理学院实验报告姓名:
学号:专业:经济学班级:二班课程:计量经济学合肥师范学院经济与管理学院《计量经济学》课程实验报告指导老师:日期:成绩:
荐计算机上机实验内容及实验报告要求荐构建学校德育管理与评价体系的实验报告荐化学实验报告格式
荐大学物理实验课程设计实验报告荐电路实验报告要求。
实验六 自相关

实验六自相关6.1 实验目的掌握自相关问题出现的来源、后果、检验及修正的原理,以及相关的EViews 软件操作方法。
6.2 实验内容以实验五已克服异方差的中国的消费函数模型(见输出结果图 5.4)为例,练习检查和克服模型的自相关的操作方法。
由图5.4得到的回归式为:Lny t = -0.0486+ 0.9561 Lnx t . (6.1) (-0.05) (68.7) R2 = 0.997, DW=0.55 F = 47216.3 实验步骤6.3.1 检验模型是否存在自相关(1)观察残差图,如图6.1,可初步判断残差项存在一定程度的正自相关。
(2)用DW检验判断是否存在自相关由EViews输出结果(图5.4)知DW = 0.55,若给定α = 0.05,查附表,d L= 1.08,d U= 1.36。
因为DW = 0.55< 1.26, 依据判别规则,认为误差项u t存在严重的正自相关。
图6.1(3)用LM检验判断是否存在自相关在估计窗口选择View/Residual Tests/Serial Correalation LM Test(见图6.2)。
图6.2点击后会自动弹出一个设定滞后期(Lag Specification)对话框。
输入1,点击OK键,得到LM检验结果,见图6.3。
图6.3根据p-值判断拒绝原假设,所以BG(LM)检验结果也说明(6.1)式存在自相关。
(4)用回归检验法判断自相关① 将估计结果(6.1)式得到的残差定义为u t ,首先做一阶自回归,得到估计结果见图6.4。
② 对该估计式采用LM 检验法检验其自相关性,如图6.5。
可以判断出仍然存在自相关。
③ 用残差的二阶自回归形式重新建立模型,见图6.6。
④ 再次用LM 检验法判断其自相关性,如图6.7。
从图6.7可以看出,此时p -值已经达到0.3,落在接受域,即认为误差项不存在自相关。
对图6.6的输出结果进行整理,可以得到残差的二阶回归式为t uˆ= 1.3436 1ˆ-t u - 0.81752ˆ-t u + v t (6.2)(5.18) (-3.03) R 2 = 0.71, s.e. = 0.02, TR 2 = 1.1图6.4图6.5图6.6图6.7 6.4.2 克服自相关图6.8图6.9用广义最小二乘法估计回归参数。
第06章 自相关(讲稿)

第6章自相关1. 自相关定义1)非自相关由第2节知回归模型的假定条件之一是,Cov(u i,u j )=E(u i u j) =0, (i, j∈T, i ≠ j),(1.1)即误差项u t的取值在时间上是相互无关的。
称误差项u t非自相关。
2)自相关如果Cov (u i ,u j ) ≠ 0, (i ≠ j)则称误差项u t存在自相关。
自相关又称序列相关。
原指一随机变量在时间上与其滞后项之间的相关。
这里主要是指回归模型中随机误差项u t 与其滞后项的相关关系。
自相关也是相关关系的一种。
2.自相关类型1)自相关按滞后阶数可分为两类。
(1)一阶自回归形式当误差项u t只与其滞后一期值有关时,即u t = f (u t - 1),称u t具有一阶自回归形式。
(2) 高阶自回归形式当误差项u t的本期值不仅与其前一期值有关,而且与其前若干期的值都有关系时,即u t = f (u t – 1, u t – 2 , … ), 则称u t 具有高阶自回归形式。
2)按函数形式分为线性自相关和非线性自相关 (1)线性自相关 f 为线性函数形式 (2)非线性自相关 f 为非线性函数形式 3.一阶线性自相关通常假定误差项的自相关是线性的。
因计量经济模型中自相关的最常见形式是一阶自回归形式,所以下面重点讨论误差项的线性一阶自回归形式,即 u t =1a u t -1 + v t (1.2)其中1a 是自回归系数,v t 是随机误差项。
v t 满足通常假设E(v t ) = 0, t = 1, 2 …, T, Var(v t ) = σv 2, t = 1, 2 …, T,Cov(v i , v j ) = 0, i ≠ j, i, j = 1, 2 …, T, Cov(u t-1, v t ) = 0, t = 1, 2 …, T,依据普通最小二乘法公式,模型(1.2)中 1 的估计公式是,1ˆa= ∑∑=-=-Tt t Tt t tuuu 22121 (1ˆβ=∑∑---2)())((x x x x y y t t t ) (1.3)其中T 是样本容量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验六自相关6.1 实验目的掌握自相关问题出现的来源、后果、检验及修正的原理,以及相关的EViews 软件操作方法。
6.2 实验内容以实验五已克服异方差的中国的消费函数模型(见输出结果图 5.4)为例,练习检查和克服模型的自相关的操作方法。
由图5.4得到的回归式为:Lny t = -0.0486+ 0.9561 Lnx t . (6.1) (-0.05) (68.7) R2 = 0.997, DW=0.55 F = 47216.3 实验步骤6.3.1 检验模型是否存在自相关(1)观察残差图,如图6.1,可初步判断残差项存在一定程度的正自相关。
(2)用DW检验判断是否存在自相关由EViews输出结果(图5.4)知DW = 0.55,若给定α = 0.05,查附表,d L= 1.08,d U= 1.36。
因为DW = 0.55< 1.26, 依据判别规则,认为误差项u t存在严重的正自相关。
图6.1(3)用LM检验判断是否存在自相关在估计窗口选择View/Residual Tests/Serial Correalation LM Test(见图6.2)。
图6.2点击后会自动弹出一个设定滞后期(Lag Specification)对话框。
输入1,点击OK键,得到LM检验结果,见图6.3。
图6.3根据p-值判断拒绝原假设,所以BG(LM)检验结果也说明(6.1)式存在自相关。
(4)用回归检验法判断自相关① 将估计结果(6.1)式得到的残差定义为u t ,首先做一阶自回归,得到估计结果见图6.4。
② 对该估计式采用LM 检验法检验其自相关性,如图6.5。
可以判断出仍然存在自相关。
③ 用残差的二阶自回归形式重新建立模型,见图6.6。
④ 再次用LM 检验法判断其自相关性,如图6.7。
从图6.7可以看出,此时p -值已经达到0.3,落在接受域,即认为误差项不存在自相关。
对图6.6的输出结果进行整理,可以得到残差的二阶回归式为t uˆ= 1.3436 1ˆ-t u - 0.81752ˆ-t u + v t (6.2)(5.18) (-3.03) R 2 = 0.71, s.e. = 0.02, TR 2 = 1.1图6.4图6.5图6.6图6.7 6.4.2 克服自相关图6.8图6.9用广义最小二乘法估计回归参数。
根据(6.2)式残差项的回归系数,对变量Lny t 和Lnx t作二阶广义差分GDLny t = Lny t -1.3436 Lny t-1 +0.8175 Lny t-2GDLnx t =Ln x t -1.3436 Ln x t-1 + 0.8175 Ln x t-2以GDLny t, GDLnx t(t = 2 , 3 , … 15)为样本再次回归,得EViews输出结果如图6.8。
此时LM检验结果见图6.9。
可以判断已经很好的克服了自相关。
整理广义最小二乘回归结果为GDLny t = -0.035+0.9582 GDLnx t(6.3)(-0.29) (41.62) R2 = 0.99, s.e. = 0.02, DW =2.33 TR2=0.59 因为β0 (1 -1.3436 + 0.8175) = -0.035得,β0 = -0.0739所以,原模型的广义最小二乘估计是Lny t = -0.0739 + 0.9582Lnx t(6.4) (6.3)式残差图见图6.10。
图6.10案例二一、研究目的2003年中国农村人口占59.47%,而消费总量却只占41.4%,农村居民的收入和消费是一个值得研究的问题。
消费模型是研究居民消费行为的常用工具。
通过中国农村居民消费模型的分析可判断农村居民的边际消费倾向,这是宏观经济分析的重要参数。
同时,农村居民消费模型也能用于农村居民消费水平的预测。
二、模型设定正如第二章所讲述的,影响居民消费的因素很多,但由于受各种条件的限制,通常只引入居民收入一个变量做解释变量,即消费模型设定为01=++t t t Y X u ββ(6.43)式中,Y t 为农村居民人均消费支出,X t 为农村人均居民纯收入,u t 为随机误差项。
表6.3是从《中国统计年鉴》收集的中国农村居民1985-2003年的收入与消费数据。
表6.3 1985-2003年农村居民人均收入和消费 单位: 元注:资料来源于《中国统计年鉴》1986-2004。
为了消除价格变动因素对农村居民收入和消费支出的影响,不宜直接采用现价人均纯收入和现价人均消费支出的数据,而需要用经消费价格指数进行调整后的1985年可比价格计的人均纯收入和人均消费支出的数据作回归分析。
根据表6.3中调整后的1985年可比价格计的人均纯收入和人均消费支出的数据,使用普通最小二乘法估计消费模型得t tX Y 0.59987528.106ˆ+= (6.44)Se = (12.2238) (0.0214)t = (8.7332)(28.3067)R 2 = 0.9788,F = 786.0548,d f = 17,DW = 0.7706该回归方程可决系数较高,回归系数均显著。
对样本量为19、一个解释变量的模型、5%显著水平,查DW 统计表可知,d L =1.18,d U = 1.40,模型中DW<d L ,显然消费模型中有自相关。
这一点残差图中也可从看出,点击EViews 方程输出窗口的按钮Resids 可得到残差图,如图6.6所示。
图6.6 残差图图6.6残差图中,残差的变动有系统模式,连续为正和连续为负,表明残差项存在一阶正自相关,模型中t 统计量和F 统计量的结论不可信,需采取补救措施。
三、自相关问题的处理为解决自相关问题,选用科克伦—奥克特迭代法。
由模型(6.44)可得残差序列e t ,在EViews 中,每次回归的残差存放在resid 序列中,为了对残差进行回归分析,需生成命名为e 的残差序列。
在主菜单选择Quick/Generate Series 或点击工作文件窗口工具栏中的Procs/ Generate Series ,在弹出的对话框中输入e = resid ,点击OK 得到残差序列e t 。
使用e t 进行滞后一期的自回归,在EViews 命今栏中输入ls e e (-1)可得回归方程e t = 0.4960 e t-1(6.45)由式(6.45)可知ρˆ=0.4960,对原模型进行广义差分,得到广义差分方程 -101-1-0.4960=(1-0.4960)+(-0.4960)+t t t t t Y Y X X u ββ(6.46)对式(6.46)的广义差分方程进行回归,在EViews 命令栏中输入ls Y -0.4960*Y (-1) c X -0.4960*X (-1),回车后可得方程输出结果如表6.4。
表6.4 广义差分方程输出结果Dependent Variable: Y-0.496014*Y(-1)Method: Least SquaresDate: 03/26/05 Time: 12:32 Sample(adjusted): 1986 2003C60.44431 8.964957 6.742287 0.0000 R-squared0.960914 Mean dependentvar231.9218 Adjusted R-squared 0.958472 S.D. dependent var 49.34525 S.E. of regression 10.05584 Akaike info criterion 7.558623 Sum squared resid 1617.919 Schwarz criterion 7.657554 Log likelihood -66.02761 F-statistic 393.3577 由表6.4可得回归方程为**5833.04443.60ˆtt X Y += (6.47))9650.8(=Se (0.0294)t = (6.7423) (19.8333)R 2 = 0.9609 F = 393.3577 d f = 16 DW = 1.3979式中,1*4960.0ˆ--=t t t Y Y Y ,1*4960.0--=t t t X X X 。
由于使用了广义差分数据,样本容量减少了1个,为18个。
查5%显著水平的DW 统计表可知d L = 1.16,d U = 1.39,模型中DW = 1.3979> d U ,说明广义差分模型中已无自相关,不必再进行迭代。
同时可见,可决系数R 2、t 、F 统计量也均达到理想水平。
对比模型(6.44)和(6.47),很明显普通最小二乘法低估了回归系数2ˆβ的标准误差。
[原模型中Se (2ˆβ)= 0.0214,广义差分模型中为Se (2ˆβ)= 0.0294。
经广义差分后样本容量会减少1个,为了保证样本数不减少,可以使用普莱斯—温斯腾变换补充第一个观测值,方法是21*11ρ-=X X 和21*11ρ-=Y Y 。
在本例中即为210.49601-X 和210.49601-Y 。
由于要补充因差分而损失的第一个观测值,所以在EViews 中就不能采用前述方法直接在命令栏输入Y 和X 的广义差分函数表达式,而是要生成X 和Y 的差分序列X *和Y *。
在主菜单选择Quick/Generate Series 或点击工作文件窗口工具栏中的Procs/Generate Series ,在弹出的对话框中输入Y *= Y -0.4960*Y (-1),点击OK 得到广义差分序列Y *,同样的方法得到广义差分序列X *。
此时的X *和Y *都缺少第一个观测值,需计算后补充进去,计算得*1X =345.236,*1Y =275.598,双击工作文件窗口的X * 打开序列显示窗口,点击Edit +/-按钮,将*1X =345.236补充到1985年对应的栏目中,得到X *的19个观测值的序列。
同样的方法可得到Y *的19个观测值序列。
在命令栏中输入Ls Y * c X*得到普莱斯—温斯腾变换的广义差分模型为**5833.04443.60t t X Y +=(6.48))1298.9(=Se (0.0297) t = (6.5178) (19.8079)R 2 = 0.9585 F = 392.3519 d f = 19 DW = 1.3459对比模型(6.47)和(6.48)可发现,两者的参数估计值和各检验统计量的差别很微小,说明在本例中使用普莱斯—温斯腾变换与直接使用科克伦—奥克特两步法的估计结果无显著差异,这是因为本例中的样本还不算太小。
如果实际应用中样本较小,则两者的差异会较大。
