柱下条形基础计算书

合集下载

柱下条基设计(倒梁法)

某框架结构柱下条形基础设计（倒梁法）一、设计资料1、某建筑物为7层框架结构，框架为三跨的横向承重框架，每跨跨度为7.2m ；边柱传至基础顶部的荷载标准值和设计值分别为：Fk=2665KN 、Mk=572KN •M 、Vk=146KN ，F=3331KN 、M=715KN •M 、V=182KN ；中柱传至基础顶部的荷载标准值和设计值分别为：Fk=4231KN 、Mk=481KN •M 、Vk=165KN ，F=5289KN 、M=601KN •M 、V=206KN 。

2、根据现场观察描述，原位测试分析及室内试验结果，整个勘察范围内场地地层主要由粘性土、粉土及粉砂组成，根据土的结构及物理力学性质共分为7层，具体层位及工程特性见附表。

勘察钻孔完成后统一测量了各钻孔的地下水位，水位埋深平均值为0.9m ，本地下水对混凝土无腐蚀性，对钢筋混凝土中的钢筋无腐蚀性。

3、根据地质资料，确定条基埋深d ＝1.9m ；二、内力计算1、基础梁高度的确定取h ＝1.5m 符合GB50007-2002 8.3.1柱下条形基础梁的高度宜为柱距的11~48的规定。

2、条基端部外伸长度的确定据GB50007-2002 8.3.1第2条规定外伸长度宜为第一跨的0.25倍考虑到柱端存在弯矩及其方向左侧延伸0.250.257.2 1.8l m m =⨯=为使荷载形心与基底形心重合，右端延伸长度为ef l ，ef l 计算过程如下：a . 确定荷载合力到E 点的距离o x ：333137.2528927.271526012182 1.52206 1.523331252892o x ⨯⨯+⨯⨯-⨯-⨯-⨯⨯-⨯⨯=⨯+⨯得18239610.5817240o x m ==b . 右端延伸长度为ef l ：(1.8 2.77.2210.58)2 1.87.23 2.24ef l m =++⨯-⨯--⨯= 3、地基净反力j p 的计算。

柱下独立基础计算书

J—1、一、基础设计（f ak=180kPa）1.基础上荷载N k=3116kN.m N=3852kN。

mM xk=—6kN.m M x=-8kN.mM yk=—41kN。

m M y=—51kN.mQ xk=—82kN Q x=-101kNQ yk=49kN Q y=61kN轴向力最大标准组合轴向力最大基本组合基础埋深为2.5m,地下水位为未知，不考虑。

2.确定基础底面尺寸及地基承载力验算查规范,粉质黏土的承载力修正系数为：ηb=0，ηd=1.6 (只进行深度修正)f a=f ak+ηbγ(b—3）+ηdγm（d-0。

5)=180+1。

6×18×（2.5—0.5）=237。

6kPa(1)基础底面尺寸的确定在轴力荷载F作用下,基础底面积A´为：A´=N k/（f a—γm d)=3116/（237.6—18×2.5)=16。

17m2选取基础尺寸为:A=4.1×4.1=16.81m²,取基础高度为700mm。

(2)地基承载力验算W=bl2/6=4.13/6=13。

25m3基础底面的压力为:p k=(F k+G k）/A±M xk/W x=（3116+16.81×2。

5×18)/ 16。

81±(6+82×0.7)/11.49=230.37±5.52p kmax=235。

89kPa<1.2f a=1。

2×237。

6=285.12kPaP kmin=224。

85kPa〉0，均满足要求。

(3)受冲切承载力验算进行冲切计算式,按由柱边起成45°的冲切角椎体的斜面进行验算。

p=（F+G）/A±M x/W x=(3852+1。

35×16。

81×2。

5×18）/ 16。

81±（8+101×0。

7）/13.25=289。

柱下条形基础计算书

1. 工程概况及设计资料某柱下条形基础，所受外荷载大小及位置如图1.1所示。

柱采用C40混凝土，截面尺寸800800mm mm ⨯。

地基为均质粘性土，地基承载力特征值160ak a f KP =，土的重度319/KN m γ=。

地基基础等级：乙级。

地下防水等级：二级。

图1.12. 基础宽度计算基础埋深定为2m 。

总竖向荷载值1000180014004000kiNKN KN KN KN =++=∑180********.5 5.334000N KN m KN me m KN⨯+⨯==假设两端向外延伸总长度为3m ，则 4.56313.5L m m m m =++= 地基底面以上土的加权重度319/m KN m γ=查得《地基规范》中对于粘性土： 1.6d η=，0.3b η= 持力层经深度修正后的地基承载力特征值3(0.5)160 1.619/(20.5)205.6a ak d m a af f d m KP KN m m m KP ηγ=+-=+⨯⨯-=()()34000 1.789205.620/ 2.013.5kia G a NKNb m f d lKP KN m m mγ≥==--⨯⨯∑取 2.0b m =3. 两端外伸长度验算即地基承载力验算320/ 2.013.5 2.01044k G KN m m m m KN =⨯⨯⨯=400010445044kik NG KN KN KN +=+=∑ 80kiMKN m =⋅∑ 800.0155244N G KN me m KN+⋅==113.5 5.445 1.3052l m m ⎛⎫=-= ⎪⎝⎭213.5 5.055 1.6952l m m ⎛⎫=-= ⎪⎝⎭5244194.22205.62.013.5kikk a a a NG KNp KP f KP blm m +===<=⨯∑,max ,min6195.58 1.2246.7524460.015(1)(1)2.013.513.5192.860kikk N G a a ak a NG p e KP f KP KN p bll m m KP ++>=⨯=±=±=⨯>∑图1.24. 计算基础内力（倒梁法）（1）求基地净反力基础高度定为1.5m ，1.516.04i h l ==，满足要求。

柱下条形基础计算

二.计算图式1.上部结构荷载和基础剖面图2.静力平衡法计算图式3.倒梁法计算图式三.设计前的准备工作在采用上述两种方法计算基础梁之前,需要做好如下工作:1.确定合理的基础长度为使计算方便,并使各柱下弯矩和跨中弯矩趋于平衡,以利于节约配筋,一般将偏心地基净反力(即梯形分布净反力)化成均布,需要求得一个合理的基础长度.当然也可直接根据梯形分布的净反力和任意定的基础长度计算基础.基础的纵向地基净反力为:式中Pjmax,Pjmin—基础纵向边缘处最大和最小净反力设计值.∑Fi—作用于基础上各竖向荷载合力设计值(不包括基础自重和其上覆土重,但包括其它局部均布qi).∑M—作用于基础上各竖向荷载(Fi ,qi),纵向弯矩(Mi)对基础底板纵向中点产生的总弯矩设计值.L—基础长度,如上述.B—基础底板宽度.先假定,后按第2条文验算.当Pjmax与Pjmin相差不大于10％,可近似地取其平均值作为均布地基反力,直接定出基础悬臂长度a1=a2(按构造要求为第一跨距的1/4~1/3),很方便就确定了合理的基础长度L；如果Pjmax与Pjmin相差较大时，常通过调整一端悬臂长度a1或a2，使合力∑Fi的重心恰为基础的形心(工程中允许两者误差不大于基础长度的3%),从而使∑M为零,反力从梯形分布变为均布,求a1和a2的过程如下:先求合力的作用点距左起第一柱的距离:式中,∑Mi—作用于基础上各纵向弯矩设计值之和.xi—各竖向荷载Fi距F1的距离.当x≥a/2时,基础长度L=2(X+a1), a2=L-a-a1.当x<a/2时,基础长度L=2(a-X+a2), a1=L-a-a2.按上述确定a1和a2后,使偏心地基净反力变为均布地基净反力,其值为:式中, pj—均布地基净反力设计值.由此也可得到一个合理的基础长度L.2.确定基础底板宽度b.由确定的基础长度L和假定的底板宽度b,根据地基承载力设计值f,一般可按两个方向分别进行如下验算,从而确定基础底板宽度b.基础底板纵向边缘地基反力:应满足基础底板横向边缘地基反力:应满足式中, pmax, pmin—基础底板纵向边缘处最大和最小地基反力设计值p'max, p'min—基础底板横向边缘处最大和最小地基反力设计值G—基础自重设计值和其上覆土重标准值之和,可近似取G=20bLD,D为基础埋深,但在地下水位以下部分应扣去浮力.∑M'—作用于基础上各竖向荷载、横向弯矩对基础底板横向中点产生的总弯矩设计值.其余符号同前述当∑M'=0时,则只须验算基础底板纵向边缘地基反力当∑M=0时,则只须验算基础底板横向边缘地基反力.当∑M=0且∑M'=0时(即地基反力为均布时),则按下式验算,很快就可确定基础底板宽度b式中, p—均布地基反力设计值.3.求基础梁处翼板高度并计算其配筋先计算基础底板横向边缘最大地基净反力pmax和最小地基净反力pmin,求出基础梁边处翼板的地基净反力pj1,如图,再计算基础梁边处翼板的截面弯矩和剪力,确定其厚度h1和抗弯钢筋面积.图中, p—翼板悬挑长度, b1 =(b- b0)/2h1—基础梁边翼板高度b0,h—基础梁宽和梁高基础底板横向边缘处地基净反力式中, S—从基础纵向边缘最大地基反力处开始到任一截面的距离. 其余符号同前述基础梁边处翼板地基净反力基础梁边处翼板每米宽弯矩基础梁边处翼板每米宽剪力若∑M'=0时,则上述M,V表达式为若∑M=0时,则上述M,V表达式为但p'j1和p'j2公式中的p'jmax和p'jmin可简化为若∑M=0和∑M'=0时,则上述M,V表达式为基础梁边处翼板有效高度基础梁边处翼板截面配筋式中, fc—混凝土轴心抗压强度设计值.fy—钢筋抗拉强度设计值.其余符号同前述4.抗扭当上述∑M'≠0时,对于带有翼板的基础梁,一般可以不考虑抗扭计算,仅从构造上将梁的箍筋做成闭合式;反之,则应进行抗扭承载力计算.四.静力平衡法和倒梁法的应用在采用净力平衡法和倒梁法分析基础梁内力时,应注意以下六个问题:第一,由于基础自重和其上覆土重将与它产生的地基反力直接抵消,不会引起基础梁内力,故基础梁的内力分析用的是地基净反力.第二,对a1和a2悬臂段的截面弯矩可按以下两种方法处理: 1.考虑悬臂段的弯矩对各连续跨的影响,然后两者叠加得最后弯矩; 2.倒梁法中可将悬臂段在地基净反力作用下的弯矩,全由悬臂段承受,不传给其它跨.第三,两种简化方法与实际均有出入,有时出入很大,并且这两种方法同时计算的结果也不相同.建议对于介于中等刚度之间且对基础不均匀沉降的反应很灵敏的结构,应根据具体情况采用一种方法计算同时,采用另一种方法复核比较,并在配筋时作适当调整.第四,由于建筑物实际多半发生盆形沉降,导至柱荷载和地基反力重新分布.研究表明:端柱和端部地基反力均会加大.为此,宜在边跨增加受力纵筋面积,并上下均匀配置.第五,为增大底面积及调整其形心位置使基底反力分布合理,基础的端部应向外伸出,即应有悬臂段.第六,一般计算基础梁时可不考虑翼板作用.(一)静力平衡法静力平衡法是假定地基反力按直线分布不考虑上部结构刚度的影响根据基础上所有的作用力按静定梁计算基础梁内力的简化计算方法1.静力平衡法具体步骤:先确定基础梁纵向每米长度上地基净反力设计值,其最大值为pjmax*b,最小值为pjmin*b,若地基净反力为均布则为pj*b,如图中虚线所示:对基础梁从左至右取分离体,列出分离体上竖向力平衡方程和弯矩平衡方程,求解梁纵向任意截面处的弯矩MS和剪力VS,一般设计只求出梁各跨最大弯矩和各支座弯矩及剪力即可.2.静力平衡法适用条件:地基压缩性和基础荷载分布都比较均匀,基础高度大于柱距的1/6或平均柱距满足l,£1.75/l,且上部结构为柔性结构时的柱下条形基础和联合基础,用此法计算比较接近实际.上式中lm—基础梁上的平均柱距其中ks—基床系数,可按ks= p0/S0计算(p0为基础底面平均附加压力标准值,S0为以p0计算的基础平均沉降量),也可参照各地区性规范按土类名称及其状态已给出的经验值.b0,IL—基础梁的宽度和截面惯性矩.Ec—混凝土的弹性模量.3.对静力平衡法的一些看法(仅供参考评议):由于静力平衡法不考虑基础与上部结构的相互作用,因而在荷载和直线分布的基底反力作用下可能产生整体弯曲.与其它方法比较,这样计算所得的基础梁不利截面的弯矩绝对值一般还是偏大.上述适用条件中要求上部结构为柔性结构.如何判断上部结构为柔性结构,从绝大多数建筑的实际刚度来看均介于绝对刚性和完全柔性之间,目前还难以定量计算.在实践中往往只能定性地判断其比较接近哪一种极端情况,例如,剪力墙体系的高层建筑是接近绝对刚性的,而以屋架--柱--基础为承重体系的排架结构和木结构以及一般静定结构,是接近完全柔性的.具体应用上,对于中等刚度偏下的建筑物也可视为柔性结构,如中、低层轻钢结构;柱距偏大而柱断面不大且楼板开洞又较多的中、低层框架结构以及体型简单,长高比偏大(一般大于5以上)的结构等等.(二)倒梁法倒梁法是假定上部结构完全刚性,各柱间无沉降差异,将柱下条形基础视为以柱脚作为固定支座的倒置连续梁,以线性分布的基础净反力作为荷载,按多跨连续梁计算法求解内力的计算方法.1.倒梁法具体步骤:先用弯矩分配法或弯矩系数法计算出梁各跨的初始弯矩和剪力.弯矩系数法比弯矩分配法简便,但它只适用于梁各跨度相等且其上作用均布荷载的情况,它的计算内力表达式为:M=弯矩系数* pj * b * lª ; V=剪力系数* pj * b * l如前述，pj*b即是基础梁纵向每米长度上地基净反力设计值。

柱下条形基础内力计算(zhang)

一、柱下条形基础的计算1. 倒梁法倒梁法假定上部结构是刚性的，柱子之间不存在差异沉降，柱脚可以作为基础的不动铰支座，因而可以用倒连续梁的方法分析基础内力。

这种假定在地基和荷载都比较均匀、上部结构刚度较大时才能成立。

此外，要求梁截面高度大于1/6柱距，以符合地基反力呈直线分布的刚度要求。

倒梁法的内力计算步骤如下：(1).按柱的平面布置和构造要求确定条形基础长度L ，根据地基承载力特征值确定基础底面积A ，以及基础宽度B=A/L 和截面抵抗矩6/2BL W =。

(2).按直线分布假设计算基底净反力n p ：minmaxn n p p W M A F ii ∑±∑=（4-12）式中 ∑i F 、∑i M −相应于荷载效应标准组合时，上部结构作用在条形基础上的竖向力（不包括基础和回填土的重力）总和，以及对条形基础形心的力矩值总和。

当为轴心荷载时，nn n p p p ==min max 。

(3).确定柱下条形基础的计算简图如图4-13，系为将柱脚作为不动铰支座的倒连续梁。

基底净线反力B p n 和除掉柱轴力以外的其它外荷载（柱传下的力矩、柱间分布荷载等）是作用在梁上的荷载。

(4).进行连续梁分析，可用弯矩分配法、连续梁系数表等方法。

(5).按求得的内力进行梁截面设计。

(6).翼板的内力和截面设计与扩展式基础相同。

倒连续梁分析得到的支座反力与柱轴力一般并不相等，这可以理解为上部结构的刚度对基础整体挠曲的抑制和调整作用使柱荷载的分布均匀化，也反映了倒梁法计算得到的支座反力与基底压力不平衡的缺点。

为此提出了“基底反力局部调整法”，即将不平衡力（柱轴力与支座反力的差值）均匀分布在支座附近的局部范围（一般取1/3的柱跨）上再进行连续梁分析，将结果叠加到原先的分析结果上，如此逐次调整直到不平衡力基本消除，从而得到梁的最终内力分布。

由图4-14，连续梁共有n 个支座，第i 支座的柱轴力为i F ，支座反力为i R ，左右柱跨分别为1-i l 和i l ，则调整分析的连续梁局部分布荷载强度i q 为：边支座)1(n i i ==或 3/)(1)1(0)(1)(1)(1n n n n n l l R F q +-=+ （4-13a ）中间支座)1(n i <<i i i i i l l R F q +-=-1)(3 （4-13b ）当i q 为负值时，表明该局部分布荷载应是拉荷载,例如图4-14中的2q 和3q 。

条形基础设计计算书

一、设计资料：1、本设计的任务是设计一多层办公楼的钢筋混凝土柱下条形基础，框架柱的截面尺寸均为b×h=500mm×600mm，柱的平面布置如下图所示：2、办公楼上部结构传至框架柱底面的荷载值标准值如下表所示：注：表中轴力的单位为KN，弯矩的单位为；所有1、2、3轴号上的弯矩方向为逆时针、4、5、6轴号上的弯矩为顺时针，弯矩均作用在h方向上。

3、该建筑场地地表为一厚度为1.5m的杂填土层（容重为17kN/m3），其下为粘土层，粘土层承载力特征值为F ak=110kPa，地下水位很深，钢筋和混凝土的强度等级自定请设计此柱下条形基础并绘制施工图。

二、确定基础地面尺寸：1、确定合理的基础长度：设荷载合力到支座A的距离为x，如图1：则：x=∑∑∑+i iiiF Mx F=300700700700700350)5.17300147005.1070077005.37000(++++++⨯+⨯+⨯+⨯+⨯+=8.62mG图1因为x=〈21=⨯，所以,由《建筑地基基础设计规范》（GB50007-2002）8.3.1第2条规定条形基础端部应沿纵向从两端边柱外伸，外伸长度宜为边跨跨距的倍取a 2=(与41l=⨯相近)。

为使荷载形心与基底形心重合，使基底压力分布较为均匀，并使各柱下弯矩与跨中弯矩趋于均衡以利配筋，得条形基础总长为：L=2(a+a 2-x)=2⨯+19.36m ≈19.4m 121.1m 、确定基础底板宽度b ：竖向力合力标准值:∑KiF=350+700+700+700+700+300=3450kN选择基础埋深为，则m γ=（⨯+⨯）÷=m 3深度修正后的地基承载力特征值为：()5.0-+=d f f m d ak a γη=110+⨯⨯由地基承载力得到条形基础b 为： b ≥)20(d f L Fa Ki-∑=)8.120529.132(4.193450⨯-⨯=1.842m取b=2m ，由于b 〈3m ，不需要修正承载力和基础宽度。

柱下条形基础计算方法与步骤(全)

柱下条形基础简化计算及其设计步骤提要:本文对常用的静力平衡法和倒梁法的近似计算及其各自的适用范围和相互关系作了一些叙述,提出了自己的一些看法和具体步骤，并附有柱下条基构造表,目的是使基础设计工作条理清楚,方法得当,既简化好用,又比较经济合理.一适用范围:柱下条形基础通常在下列情况下采用:1.多层与高层房屋无地下室或有地下室但无防水要求,当上部结构传下的荷载较大,地基的承载力较低,采用各种形式的单独基础不能满足设计要求时.2.当采用单独基础所需底面积由于邻近建筑物或构筑物基础的限制而无法扩展时.3.地基土质变化较大或局部有不均匀的软弱地基,需作地基处理时.4.各柱荷载差异过大,采用单独基础会引起基础之间较大的相对沉降差异时.5.需要增加基础的刚度以减少地基变形,防止过大的不均匀沉降量时.其简化计算有静力平衡法和倒梁法两种,它们是一种不考虑地基与上部结构变形协调条件的实用简化法,也即当柱荷载比较均匀,柱距相差不大,基础与地基相对刚度较大,以致可忽略柱下不均匀沉降时,假定基底反力按线性分布,仅进行满足静力平衡条件下梁的计算.二计算图式1.上部结构荷载和基础剖面图2.静力平衡法计算图式3.倒梁法计算图式三.设计前的准备工作在采用上述两种方法计算基础梁之前,需要做好如下工作:1.确定合理的基础长度为使计算方便,并使各柱下弯矩和跨中弯矩趋于平衡,以利于节约配筋,一般将偏心地基净反力(即梯形分布净反力)化成均布,需要求得一个合理的基础长度.当然也可直接根据梯形分布的净反力和任意定的基础长度计算基础.基础的纵向地基净反力为:式中 P jmax,P jmin —基础纵向边缘处最大和最小净反力设计值.∑F i —作用于基础上各竖向荷载合力设计值(不包括基础自重和其上覆土重,但包括其它局部均布q i).∑M —作用于基础上各竖向荷载(F i ,q i),纵向弯矩(M i)对基础底板纵向中点产生的总弯矩设计值.L —基础长度,如上述.B —基础底板宽度.先假定,后按第2条文验算.j j i pF bL MbL min max =±∑∑62当P jmax 与P jmin 相差不大于10％,可近似地取其平均值作为均布地基反力,直接定出基础悬臂长度a 1=a 2(按构造要求为第一跨距的1/4~1/3),很方便就确定了合理的基础长度L ；如果P jmax 与P jmin 相差较大时，常通过调整一端悬臂长度a 1或a 2，使合力∑F i 的重心恰为基础的形心(工程中允许两者误差不大于基础长度的3%),从而使∑M 为零,反力从梯形分布变为均布,求a 1和a 2的过程如下:先求合力的作用点距左起第一柱的距离:式中,∑M i —作用于基础上各纵向弯矩设计值之和.x i —各竖向荷载F i 距F 1的距离.当x ≥a/2时,基础长度L=2(X+a 1), a 2=L-a -a 1.当x <a/2时,基础长度L=2(a-X+a 2), a 1=L-a -a 2.按上述确定a 1和a 2后,使偏心地基净反力变为均布地基净反力,其值为:式中, p j —均布地基净反力设计值.由此也可得到一个合理的基础长度L.2.确定基础底板宽度b.由确定的基础长度L 和假定的底板宽度b,根据地基承载力设计值f,一般可按两个方向分别进行如下验算,从而确定基础底板宽度b.基础底板纵向边缘地基反力:应满足基础底板横向边缘地基反力:x F x M F i iii =+∑∑∑j ip F bL =∑2max min 6bL M bL G F i p ∑∑±+=2max min '6'bL M bL G F i p ∑∑±+=()fp p f p≤+≤22.1min max max min 及应满足式中, p max, p min —基础底板纵向边缘处最大和最小地基反力设计值p'max, p'min —基础底板横向边缘处最大和最小地基反力设计值G —基础自重设计值和其上覆土重标准值之和,可近似取G=20bLD,D 为基础埋深,但在地下水位以下部分应扣去浮力.. ∑M '—作用于基础上各竖向荷载、横向弯矩对基础底板横向中点产生的总弯矩设计值.其余符号同前述当∑M '=0时,则只须验算基础底板纵向边缘地基反力当∑M=0时,则只须验算基础底板横向边缘地基反力.当∑M=0且∑M '=0时(即地基反力为均布时),则按下式验算,很快就可确定基础底板宽度b:式中, p —均布地基反力设计值.3.求基础梁处翼板高度并计算其配筋先计算基础底板横向边缘最大地基净反力p max 和最小地基净反力p min ,求出基础梁边处翼板的地基净反力p j1,如图,再计算基础梁边处翼板的截面弯矩和剪力,确定其厚度h 1和抗弯钢筋面积.右图中, p —翼板悬挑长度, b 1 =(b- b 0)/2h 1—基础梁边翼板高度b 0,h —基础梁宽和梁高基础底板横向边缘处地基净反力式中, S —从基础纵向边缘最大地基反力处开始到任一截面的距离.p F G bL f b F L f D ii=+≤⇒≥-∑∑()20()2min max max maxmin '6'bL M p p L S p j j j j j p ∑±⎥⎦⎤⎢⎣⎡--=()fp p f p ≤+≤2''2.1min max max '及其余符号同前述基础梁边处翼板地基净反力基础梁边处翼板每米宽弯矩基础梁边处翼板每米宽剪力若∑M'=0时,则上述M,V 表达式为若∑M=0时,则上述M, V 表达式为但p'j1和p'j2公式中的p'jmax 和p'jmin 可简化为若∑M=0和∑M'=0时,则上述M,V 表达式为基础梁边处翼板有效高度基础梁边处翼板截面配筋式中, f c —混凝土轴心抗压强度设计值.()min max 1max 1''''j j j j p p bb p p --=1max 22112''2'3''j j j j j p p b p p M p -=⎪⎪⎭⎫ ⎝⎛+=112'2'b p p V j j ⎪⎪⎭⎫ ⎝⎛+=()()1min max max 21min max ,21b p p L S p V b p p L S p M j j j j j jnax ⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡--=1122112'2',2'3'b p P V b p p M j j j j ⎪⎪⎭⎫ ⎝⎛+=⎪⎪⎭⎫ ⎝⎛+=2maxmin '6'bL M bL F i j j p ∑∑±=bp V b p M j j ==,2121bL F i j p ∑=()mm f V c h ⨯⨯≥100007.001()2019.0mm f h M y s A =f y—钢筋抗拉强度设计值.其余符号同前述4.抗扭当上述∑M'≠0时,对于带有翼板的基础梁,一般可以不考虑抗扭计算,仅从构造上将梁的箍筋做成闭合式;反之,则应进行抗扭承载力计算.四.静力平衡法和倒梁法的应用在采用净力平衡法和倒梁法分析基础梁内力时,应注意以下六个问题:第一,由于基础自重和其上覆土重将与它产生的地基反力直接抵消,不会引起基础梁内力,故基础梁的内力分析用的是地基净反力.第二,对a1和a2悬臂段的截面弯矩可按以下两种方法处理: 1.考虑悬臂段的弯矩对各连续跨的影响,然后两者叠加得最后弯矩; 2.倒梁法中可将悬臂段在地基净反力作用下的弯矩,全由悬臂段承受,不传给其它跨.第三,两种简化方法与实际均有出入,有时出入很大,并且这两种方法同时计算的结果也不相同.建议对于介于中等刚度之间且对基础不均匀沉降的反应很灵敏的结构,应根据具体情况采用一种方法计算同时,采用另一种方法复核比较,并在配筋时作适当调整.第四,由于建筑物实际多半发生盆形沉降,导至柱荷载和地基反力重新分布.研究表明:端柱和端部地基反力均会加大.为此,宜在边跨增加受力纵筋面积,并上下均匀配置.第五,为增大底面积及调整其形心位置使基底反力分布合理,基础的端部应向外伸出,即应有悬臂段.第六,一般计算基础梁时可不考虑翼板作用.(一)静力平衡法静力平衡法是假定地基反力按直线分布不考虑上部结构刚度的影响根据基础上所有的作用力按静定梁计算基础梁内力的简化计算方法1.静力平衡法具体步骤:先确定基础梁纵向每米长度上地基净反力设计值,其最大值为p jmax*b,最小值为p jmin*b,若地基净反力为均布则为p j*b,如图中虚线所示:❷对基础梁从左至右取分离体,列出分离体上竖向力平衡方程和弯矩平衡方程,求解梁纵向任意截面处的弯矩M S 和剪力V S ,一般设计只求出梁各跨最大弯矩和各支座弯矩及剪力即可.2.静力平衡法适用条件:地基压缩性和基础荷载分布都比较均匀,基础高度大于柱距的1/6或平均柱距满足l,≤1.75/λ,且上部结构为柔性结构时的柱下条形基础和联合基础,用此法计算比较接近实际.上式中 l m —基础梁上的平均柱距其中 k s —基床系数,可按k s = p 0/S 0计算(p 0为基础底面平均附加压力标准值,S 0为以p 0计算的基础平均沉降量),也可参照各地区性规范按土类名称及其状态已给出的经验值.b 0,I L —基础梁的宽度和截面惯性矩.E c —混凝土的弹性模量.3.对静力平衡法的一些看法(仅供参考评议):❶由于静力平衡法不考虑基础与上部结构的相互作用,因而在荷载和直线分布的基底反404IE b k c s =λ力作用下可能产生整体弯曲.与其它方法比较,这样计算所得的基础梁不利截面的弯矩绝对值一般还是偏大.❷上述适用条件中要求上部结构为柔性结构.如何判断上部结构为柔性结构,从绝大多数建筑的实际刚度来看均介于绝对刚性和完全柔性之间,目前还难以定量计算.在实践中往往只能定性地判断其比较接近哪一种极端情况,例如,剪力墙体系的高层建筑是接近绝对刚性的,而以屋架--柱--基础为承重体系的排架结构和木结构以及一般静定结构,是接近完全柔性的.具体应用上,对于中等刚度偏下的建筑物也可视为柔性结构,如中、低层轻钢结构;柱距偏大而柱断面不大且楼板开洞又较多的中、低层框架结构以及体型简单,长高比偏大(一般大于5以上)的结构等等.(二)倒梁法倒梁法是假定上部结构完全刚性,各柱间无沉降差异,将柱下条形基础视为以柱脚作为固定支座的倒置连续梁,以线性分布的基础净反力作为荷载,按多跨连续梁计算法求解内力的计算方法.1.倒梁法具体步骤:❶先用弯矩分配法或弯矩系数法计算出梁各跨的初始弯矩和剪力.弯矩系数法比弯矩分配法简便,但它只适用于梁各跨度相等且其上作用均布荷载的情况,它的计算内力表达式为:M=弯矩系数* p j * b * l ; V=剪力系数* p j * b * l如前述，p j*b即是基础梁纵向每米长度上地基净反力设计值。

基础工程课程设计柱下条形基础设计

柱下条形基础设计一、总则1.本设计依据《建筑地基基础设计规范》（GB5007-2002）和《混凝土结构设计规范》(GB5010-2002)。

2.上部结构资料上部为四层框架，层高为 4.5m，框架柱、主梁、次梁、板都为现浇整体式，主梁截面2⨯，楼板厚10cm，柱子截面2⨯，楼4050cm2560cm⨯，次梁截面23080cm屋面活荷载2kN m。

8/①轴线荷载（基本组合）3、结构平面图和剖面图柱网平面图结构剖面图4.地基资料地基持力层承载力特征值155ak f kPa =，地基下卧层承载力特征值70ak f kPa =。

根据地质情况，基础室外埋深定为 1.5d m =。

建筑物位于非地震区，不考虑地震影响。

本地基基础设计的等级属可不作地基变形计算的丙级的建筑物范围。

二、决定柱下条形基础底面尺寸，并验算持力层和软弱下卧层承载力（一）确定基础梁的外挑长度0l 与基础梁总长。

原则：基础底面的形心应尽可能与上部荷载的合力作用线重合。

()() 3.5(13891463)9.2(18111814) 3.59 5.4 6.710.9681.11A DBC A B C Dp x p p p p M M M M ⨯=-+-⨯+++-=-⨯+-⨯+++-=-681.11681.110.11(1389181118141463)x m F --∴===-+++∑ 假设左边伸出0.5m,则为保证合力在基底形心，右边伸出0.72m ，为了简便计算，暂取左边及右边均伸出0.5m 。

（二）确定基底尺寸，并验算持力层和软弱下卧层得承载力。

（按荷载标准组合计算）1.按持力层的承载力决定宽度b 。

（先填土再施工上部结构）()ka Fb L f d γ>-⨯∑因为 1.50.5d m m =>，ak f 应当进行深度修正，根据持力层粘土性质查规范承载力修正系数表得：0.3b η= 1.6d η=00.717.00.818.8(0.5)155 1.6(1.50.5)183.74()1.5a ak d f f d kPa ηγ⨯+⨯=+-=+⨯-=(1389181118141463)/1.351.67()19.4(183.7420 1.8)b m +++≥=⨯-⨯取 2.0b m =（考虑地基基础共同工作时边跨处基底反力有所增大）。

柱下条形基础设计计算书

0.78mm 0.025 si 1.02mm
（3）确定沉降经验系数 ①计算
s
Es
Es
A E
i
Ai si

z
i i
i 1 i 1
z

据
i z i i 1 z i 1 E si

1617.6 765 121.2 42.92 5.77 MPa 1617.6 765 121.2 42.92 6.91 4.44 4.71 4.71
（mm）
s
i
（mm）
0 1 2 3 4
1.6176 0.7650 0.1212 0.0429
21.26 15.60 2.34 0.82 40.8
5.5 7.333 4 0.1038 6.5 8.667 4 0.0963 6.8 9.067 4 0.0936
确定沉降计算深度 s n
下卧层顶面处的自重应力值为：
pcz 17 0.7 18.0 0.9 18.8 0.5 (18.8 10) 1.9 (18.5 10) 3.1
80.57 kPa
下卧层承载力特征值为：
f az f azk d m (d z 0.5) 130 1.0 130.57 (7.1 0.5) 8.4 251.37 kPa
Fk
650 7 650 0.5 2 0.8 125.49kN 33.15 (80 25) 8 0.8 20.27 kN m 33.15
基础底面在单位 1m 长度内受平均弯矩 M k 基础平均埋深为1.825m
b
Fk 125.49 0.91m f a G d 181.32 20 1.825

基础工程课程设计任务书另附计算书(柱下条形基础)

土木工程专业《基础工程》课程设计指导书一、设计目的《基础工程》是土木工程专业重要的专业技术课之一，具有很强的理论性和实际应用性。

通过课程设计，可以使学生较系统地掌握基础的设计理论和计算方法，培养学生综合利用所学的理论知识分析解决实际问题的能力、利用和查阅资料的能力、独立工作的能力以及计算机应用能力，为使学生成为合格的工程师或设计师打下扎实的基础。

二、设计任务完成某工业厂房○B 轴线柱下条形基础设计，并绘制基础施工图一张。

三、设计内容及步骤：（一）根据建筑物荷载大小、地基土质情况等，合理选择基础类型和材料。

（二）根据工程地质条件、建筑物使用要求以及地下水影响等因素、确定基础埋深。

首先根据工程地质条件，可初步选择基础持力层，建筑地基基础设计规范规定，基础埋深不得小于0.5 m 。

对于寒冷地区，确定外墙基础埋深时，应考虑地基土冻胀的影响。

主要根据持力层土质情况、冻前天然含水量、及冻结期间地下水位距冻结面的最小距离、平均冻胀率等因素，确定地基土的冻胀性。

再根据土的冻胀性、基础形式、采暖情况、基底平均压力，确定基底下容许残留冻土层厚度max h ，然后计算基础最小埋深（还需考虑土的类别、环境对冻深等因素的影响）即：m ax m in h z d d -=选择外基础埋深时，要求基础埋深d ＞min d ，内墙基础埋深不必考虑地基土冻胀的影响，可以适当浅埋。

（三）根据工程地质条件，计算地基持力层和下卧层的承载力。

如果地基下卧层是软弱土层（淤泥或淤泥质土），必须进行软弱下卧层承载力验算，并要求满足：az cz z f p p ≤+（四）根据修正后的地基承载力特征值a f 以及相应于荷载效应标准组合上部结构传至基础顶面的竖向力K F ，按下式计算柱下条形基础宽度：Ld f F B G a K).(γ-∑≥（五）对于柱下钢筋混凝土条形基础，通常根据抗弯刚度条件确定基础梁高度h ，取41(=h ~l )81，l 为柱距，同时还要考虑其构造要求。

[建筑土木]柱下条形基础

软土好土
软土好土
弯矩图
三、地基、基础与上部结构共同作用概念
♠ 地基、基础与上部结构的共同作用(小结)
♦基础沉降、内力和基底反力分布与上部结构刚度、基础刚度、地基的刚度（土层的压缩性及非均匀性）有关
♧ 基础相对于地基刚度较大，则驾越作用大，基底反力直线分布
♦地基、基础与上部结构的共同作用
♧ 地基、基础与上部结构作为一个整体产生受力和变形，各部分之间变形协调
的轴力、弯矩和剪力
H H
∑ Mi Fi R = Fi
Ti A B OC D
x0
a1
ai ei a
a2
Mi
Fi Ti
A BC
p j max
L
D p j min
一、倒梁法及计算步骤
♦确定竖向力合力作用点及基础梁长度
♧ 竖向力合力作用点 ♧ 设荷载合力作用点距A点x0，基础梁外伸长
度为a1、a2，两边柱间轴线距离为a ♧ 以A点为参考点，用合力矩定理，则有
♦基础梁两端外伸长度确定
♧ 在基础平面布置允许的情况下，基础梁两端应有适当长度伸出边柱外，目的是增大底板的面积及调整底板形心的位置，使其合力作用点与底面形心相重合或接近
H H
∑ Mi Fi R = Fi
Ti A B OC D
x0
a1
ai ei a
a2
Mi
Fi Ti
A BC
p j max
L
D p j min
∑∑ x0 =
MA Fi
∑ ∑ ∑ ∑ M A = Fiai + Mi + Ti ⋅ H
H H
∑ Mi Fi R = Fi
Ti A B OC D

条形基础计算范例

条形基础计算范例5.1设计资料已知底层柱组合内力如下表所示：5.2埋深的确定根据上部结构要求柱截面尺寸拟采用400×400mm。

初选基础埋深为2.5m。

5.3确定地基承载力地下水位取-1.50m γm=（18×1.5+0.45×14+0.55×18）/ 2 .5=17.3kN/m3先假定b≤3m 则fa =fak+ηdγm（d-0.5）=103+1.2×17.3×（2.5-0.5）=144.5kPa5.4确定底板尺寸1）外伸长度：C左=C右=7000×1/4=1750mmL=2×1750+3×7000=24500mm2）宽度B：B≥∑F k/（fa-20d+10h w）L=（1426+1839+1927+1329）/（144.5-20×2.5+10×1）×24.5=2.55m取B=2.70m设计由于偏心荷载较小，故不考虑偏心荷载作用。

即使考虑偏心荷载Pmax =（∑Fk+Gk+Gwk）/ lb+6∑Mk/bl2= （6521+24.5×2.7×2.5×20+10×24.5×2.7×1）/（24.5×2.7）+（1329×10.5+1927×3.5-1426×10.5-1839×3.5-2.5-1）/（2.7×24.52）= 136kPa<1.2 f a 满足要求5.5按构造要求选取翼板尺寸初选翼板厚度为500mm,采用变厚度翼板，坡度取1/45.6基础梁尺寸h=1/6×L=1/6×7000≈1200mmb=1/2.4×h=500mm翼板及肋梁尺寸见下图5.7验算底板厚度基础采用C20混凝土，f t =1.10N/ mm2P j=F/bl=（1927+1426+1839+1329）×1.35/（2.7×24.5）=133.1kPab1=1/2×（2.7-0.5）=1.1mh0≥（P j ×b1）/（0.7 f t）=（133.1× 1.1）/（0.7×1100）=190mm取a s=40mm，h= h0+a s=190+40=230mm<500mm 满足要求5.8验算软弱下卧层强度基础持力层下为淤泥，低压缩性均匀性好，fak=70kPa需要进行软弱下卧层强度验算z=1.95+3.65-2.5=3.1mz/b=3.1/2.7>0.50取θ=23o tan θ=0.424P k=（F k+G k）/ A=（F k+γG Ad-γw Ah w）/ A=（6521+24.5×2.7×2.5×20-10×24.5×2.7×1）/（24.5×2.7）=138.6kPaσz =b（P k-σcd）/（b+2ztanθ）=2.7（138.6-18×1.5-0.45×14-0.55×18）/（2.7+2×3.1×0.424）=48.3kPa下卧层顶面处的自重应力：σcz =18×1.5+0.45×（24-10）+3.65×（28-10）=99kPa下卧层承载力特征值：γm=σcz/（d+z）=99/（2.5+3.1）=17.7 kN/ m3faz=70+1.2×17.7×（5.6-0.5）=178.3kPa验算：σcz+σz=99+48.3=147.3kPa<faz（可以）5.9配筋计算a．翼板配筋计算1）计算地基净反力Pj =F/bl=（6521×1.35）/（2.7×24.5）= 133.1kPa2）最不利位置I-I弯矩M =1/2×Pjb12=1/2×133.1×（（2.7-0.5）/2）2=80.5kN·m3）沿基础长度方向取L=1m ，则每米长As≥M/（0.9f y h 0）主受力筋用I 级钢筋 f y =210 N/ mm 2h 0=500-40=460mmAs≥（80.5×106）/（0.9×210×460）=926 mm 2配筋12Φ120，As=942 mm 2 可以 b ．基础梁配筋计算1）计算地基沿基础纵向净反力，用弯矩分配法计算肋梁弯矩b p j =∑F /L=（6521×1.35）/24.5=359kN/m 边跨固端弯矩为：M BA =1/12×bp j l 12=1/12×359×72 =1467kN·m中跨固端弯矩为：M BC =1/12×bp j l 22=1/12×359×72 =1467kN·mA 截面（左边）伸出端弯矩 M A l =221l b pj =275.135921⨯⨯=550kN·m A （3） B （9） C （15） D （21）传递与分配 917 -917 458.5 -458.5-1.3 -1.6 1.6 1.33）肋梁剪力计算 A 截面左边的剪力为：kN l b V pj lA 3.62875.13590=⨯== 取OB 段作脱离体，计算A 截面的支座反力m kN M l l b l R B pj A ⋅=-+⨯⨯=-+=2.1728]8.1645)775.1(35921[71])(21[122101 A 截面右边的剪力为：kN R l b V A pj rA 11002.172875.13590-=-⨯=-=kN R l l b R A pj B 1.14132.1728)775.1(359)(10'=-+⨯=-+=取BC 段作为脱离体)21(1222"C B pj B M M l b l R -+==kN 5.1256)8.16458.1645735921(712=-+⨯⨯ kN R R R B B B 6.26695.12561.1413"'=+=+= kN R V B l B 1.1413'== kN R V B r B 5.1256"-=-=按跨中剪力为零的条件来求跨中最大负弯矩： OB 段：02.1728359=-=-x R x b A pjm x 8.4=所以 m kN R x b M A pj ⋅-=⨯-⨯⨯=⨯-=3.113505.32.17288.43592105.321221 BC 段对称，最大负弯矩在中间截面m kN M l b M B pj ⋅-=+⨯⨯-=+-=5538.1645735981812222由以上的计算结果可做出条形基础的弯矩图和剪力图。

柱下独立基础结构计算书

柱下独立基础结构设计1、设计题目：基础埋深按2.0m 计算地基承载力f ak =180kPa1）混凝土标号，钢筋级别自己确定2）柱尺寸为400×6003）计算出地基承载力4）验算基础抗冲切选用C20混凝土f t =1.1×103kN/mm 2,钢筋采用HRB400，f y =360kN/mm 2,地基土质按粉土计算，b η=0.3，d η=1.5，钢筋混凝土重度c γ=25kN/m,土的重度m γ=20kN/m.1、地基承载力验算：1）荷载计算：标准值设计值N k =2000kN N=1.35N k =2700kNM k =60kN.m M=1.35M k =81kN.mV k =12.5kN V=1.35V k =16.88kNf a =f ak +b ηr(b-3)+d η(d-0.5)m γ假定基础宽度为3~6m则： f a =180+1.5×1.5×2.0=225kPaA ’≥d f N m a Kγ-=2202252000⨯-=10.8m 2选用l=b=3.6mA=l ×b=12.96m 2>10.08m 2 W=62bl =7.82)基底净反力平均值：P s =A N =26.32700=208.33kPa 柱截面尺寸：400×600系数：C1=s t t P f b b /6.0122+-=33.208/11006.016.06.322⨯+-=3.02 C1=st t P f b b /6.0122+-=3.07 基础有效高度：h 0=21(-b t +C b t +2) 解得：h 01=0.62 h 02=0.7h=h 0+保护层厚度故去h=800mm3)采用两级台阶，每阶高400mm,台阶宽度分别为800、750mm 则剪力产生弯矩M V =Vh=10kN.m∑M k =70kN.m ∑M=94.5kN.mG k =m γAd=518.4kN G=1.35G k =699.84kN e=k k F M ∑∑=0.035<6b 故 P max =W M A G N k k k ∑++=203.3kPa,P min =WM A G N k k k ∑-+=185.4kPa P max <f a =225kPa,满足地基承载力要求2、抗冲切验算：1)x 方向：柱与基础交界处（第二级台阶处） h 0=h-40=760mmA l =3.6×(0.8-0.7)+(3.6+2.2)×0.7/2=2.39m 2地基净反力：P max =W M A N -=8.75.946.327002+=220.5kPa Fl =P max A L =527kNa m =(a t +ab )/2=(0.6+0.6+2×0.76)/2=1.360.70h a f m t hp β=795.82kN>F l 满足抗冲切要求2)Y 方向柱与基础交接处（第二级台阶处） h 0=800-40=760mmA l =(b t +2h 0)(02h L L t --)+(02h L L t --)2=1.89m 2 a m =(a t +a b )/2=(0.4+0.4+2×0.76)÷2=1.160.70h a f m t hp β=0.7×1100×1.16×0.76=678.32kNF l =P max A L =416.75kN<0.70h a f m t hp β=678.32kN 满足抗冲切要求3）x 方向：第一级台阶处h 0=400-40=360mma m =(a t +ab )/2=(2.1+2.1+2×0.36)÷2=2.46A l =1.31m 2F l =P max A L =228.9kN0.70h a f m t hp β=0.7×1×1100×2.46×0.36=681.912kN>F l =228.9kN故满足抗冲切要求。

建筑物柱下条形基础结配筋设计及地基梁设计计算书

这些内容都是对我们土力学浅基础设计和钢筋混凝土设计的复习与巩固，使我们对AutoCAD等制图软件的运用更加熟练，锻炼了我们独立思考和自主创新的能力，同时本设计为我们今后在工作中对浅基础的设计和施工建立了扎实的基础。
第二章柱下十字交叉条形基础设计
2.1 场地工程地质条件
2.1.1 工程上部结构概况
本论文阐述了某烟酒公司商场工程地质条件和水文条件，确定了相关工程地质参数，在此基础上按规范进行地基基础设计。上部为四层框架，层高4.5m,框架、主梁、次梁、板都为现捣整体式。主梁截面30×80cm²,次梁25×60cm²,楼板厚10cm,柱子截面40×50 cm²,楼屋面活载8KN/m²。
18世纪欧洲工业革命开始以后，随着资本主义工业化的发展，城建、水利、桥梁、道路等建筑规模也在不断地扩大，从而促使人们对基础工程加以重视并开展研究。当时在作为本学科理论基础的土力学方面，砂土抗剪强度公式、土压力理论等相继提出，基础工程也随之得到了发展。到了2 0世纪20年代，太沙基归纳了以往主要在土力学方面的成就，分别发表了《土力学》和《工程地质学》等专著，从而也带动了各国学者对基础工程各方面进行研究和探索，井取得不断进展。例如：举世闻名的意大利比萨斜塔，始建于1173年，竣工于1372年，施工历时整整200年，是世界建筑史上绝无仅有的一项“大胡子工程”；自1992年以后，斜塔经采用堆载促沉及钻孔取土相结合的方法，边施工、边监测，历经8年至2000年6月，其倾斜度回复到了130年前一样；又经约一年工作，斜塔的倾斜度达到了与250年前一样；2001年6月17日，斜塔重新开放供游人参观。上述比萨斜塔的罕见实例，既说明了纠偏托底技术发展的缓慢，也说明了此类技术的难度和风险远远大于正常的基础施工技术。20世纪初，英国对Winchester大教堂的基础进行加固，它可能是世界上最早的大型托底工程之一。该教堂在加固前已下沉历900年。加固工作是依靠一位潜水工潜入水下在原有墙基下掏土挖坑，挖穿其下的泥炭层和粉砂层而达到砾石层，然后在砾石层上用包装的混凝土往上砌筑，一直接至原来的墙基。这种托底方法今称为“坑式”托底。从而该教堂至今完好无恙。

条形基础计算程序兼计算书

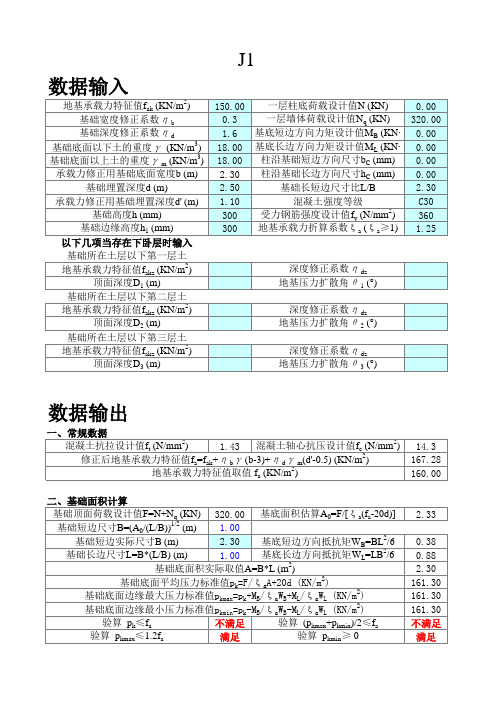
2.33 0.38 0.88 2.30 161.30 161.30 161.30 不满足满足
三、抗冲切验算基础底面净反力最大值pSmax=F/A+MB/WB+ML/WL (KN/m2) 基础有效高度h0=h-40 (mm) 受冲切承载力截面高度影响系数β 260 2 2 冲切面积Al=[(L-hC)/2-h0]*B-[(B-bC)/2-h0] (m ) （当(B-bC)/2-h0＜0时，取0）冲切力Fl=pSmaxAl (KN) -33.4 抗冲切面积At=(bC+h0)h0 (m2) 抗冲切力Ft=0.7β hpftAt (KN) 验算 Fl≤ Ft 67.7 四、抗剪切验算抗剪切面积AV=Bh0-(h-h1)(B-bC)/2 (m2) 0.60 抗剪切力0.7β hsftAV (KN) 598.60
hp
139.13 1.000 -0.24 0.07 满足
Hale Waihona Puke 受剪承载力截面高度影响系数β 剪切力V=pSmax(L-hC)B/2 (KN) 验算 V≤ 0.7β hsftAV
hs
1.000 160.00 满足
五、软弱下卧层验算修正后下卧层地基承载力特征值faz=fakz+11η dz(D-0.5) (KN/m2) 基底所在土层以下各土层顶面至上一土层顶面或基底的距离z1=D1-d；zn+1=Dn+1-Dn (m) 下卧层顶面附加压力标准组合值pz=F/ξ a(B+∑2ztgθ )(L+∑2ztgθ ) (KN/m ) 下卧层顶面土自重压力标准值pcz=11D (KN/m2) pz+pcz (KN) 验算 pz+pcz≤faz 六、基础配筋计算 139.13 0.24 1.21 2 67.90 基础短边方向弯矩M1=pSa1 (2L+hC)/6 (KN· m) 2 806.03 基础短边方向配筋AS1=M1/(0.9fyLh0) (mm ) 基础长边方向弯矩计算长度a2=(L-hC)/2 (m) 0.50 2 26.67 基础长边方向弯矩M2=pSa2 (2B+bC)/6 (KN· m) 2 137.63 基础长边方向配筋AS2=M2/(0.9fyBh0) (mm ) 2 基础全截面折算高度h' (mm) 300.0 最小配筋量ASmin=0.15%h*1000 (mm ) 450.00 短边选用钢筋直径d (mm) 长边选用钢筋直径d (mm) 12 10 钢筋间距s (mm) 钢筋间距 s (mm) 150 150 2 2 753.98 523.60 短边实配钢筋 (mm ) 长边实配钢筋 (mm ) 短边是否满足不满足长边是否满足满足基础底面净反力平均值pS=F/A (KN/m2) 砖长(m) 基础短边方向弯矩计算长度a1=b1+1/4砖长 (m)

条形基础计算书

条形基础计算书
项目名称_____________构件编号_____________日期_____________ 设计_____________校对_____________审核_____________
一、设计资料
基础类型：刚性基础计算形式：验算截面尺寸已知尺寸： B1 = 1000(mm), B = 400(mm) H1 = 200(mm) 埋深 d = 2000(mm) as = 80 mm 折减系数:Ks = 1.35 荷载数据(每延长米)：竖向荷载 F = 200.00kN M = 0.00kN· m V = 0.00kN
五、刚性基础放大角验算
计算公式：按《建筑地基基础设计规范》（GB 50007--2002）下列公式验算： H0 (b - b0)/2tan (8.1.2) 混凝土刚性基础宽高比：
pk = 114.07 kPa ≤ 200 kPa
tan = 1.00
(b - b0) / (2× tan) = (2.00-0.40 )/(2× 1.00) = 0.80 m ＞h = 0.20m 不满足要求！
二、作用在基础底部的弯矩设计值
M0 = M + V× d = 0.00 + 0.00× 2.00 = 0.00kN· m
三、修正地基承载力
修正后的地基承载力特征值 fa = 118.00 kPa
四、轴心荷载作下地基承载力验算
按《建筑地基基础设计规范》(GB 50007--2002) pk = Fk + G k A (5.2.2-1)
其中：A = 1.00× 2.00 = 2.00m2 Fk = F/Ks = 200.00/1.35 = 148.15kN Gk = 20.0 × A × d = 20.0 × 2.00 ×2000 = 80.00kN pk = (Fk + Gk)/A = ( 148.15 + 80.00 ) / 2.00 = 114.07 kPa ≤ fa = 118.00 kPa 满足要求