2014年5月11日上午
2014年-工作月历(新节假日)-A4直接打印版-样式A

十九
20
二十
21
春分
22
廿二
23
廿三
24
廿四
25
廿五
26
廿六
27
廿七
28
廿八
29
廿九
30
三十
31
3月小
1
初二
2
初三
3
初四
4
初五
5
清明节
6
初七
2014年4月April
星期一
星期二
星期三
星期四
星期五
星期六
星期日
31
3月小
1
初二
2
初三
3
初四
4
初五
5
清明节
6
初七
7
初八
8
初九
9
初十
10
十一
11
十二
12
十三
23
廿四
24
廿五
25
廿六
26
廿七
27
廿八
28
廿九
1
2月大
2
初二
2014年3月March
星期一
星期二
星期三
星期四
星期五
星期六
星期日
24
廿五
25
廿六
26
廿七
27
廿八
28
廿九
1
2月大
2
初二
3
初三
4
初四
5
惊蛰
6
初六
7
初七
8
妇女节
9
初九
10
初十
11
十一
12
2014年日历(记事可打印完美版_年历 月历 月计划).

星期三
星期四
星期五
30
初四
1
儿童节
2
端午节
3
初六
4
初七
5
初八
6
芒种
7
初十
8
十一
9
十二
10
十三
11
十四
12
十五
13
十六
14
十七
15
父亲节
16
十九
17
二十
18
廿一
19
廿二
20
廿三
21
夏至
22
廿五
23
廿六
24
廿七
25
廿八
26
廿九
27
6月大
28
初二
29
初三
2014年7月July
重要计划
星期一
星期二
星期三
星期四
星期五
1
建党节
2
初六
3
初七
4
初八
5
初九
6
初十
7
小暑
8
十二
9
十三
10
十四
11
十五
12
十六
13
十七
14
十八
15
十九
16
二十
17
廿一
18
廿二
19
廿三
20
廿四
21
廿五
22
廿六
23
大暑
24
廿八
25
廿九
26
三十
27
7月小
28
初二
29
初三
30
2014年5月全省部分媒体违法药品广告监测汇总041019185246
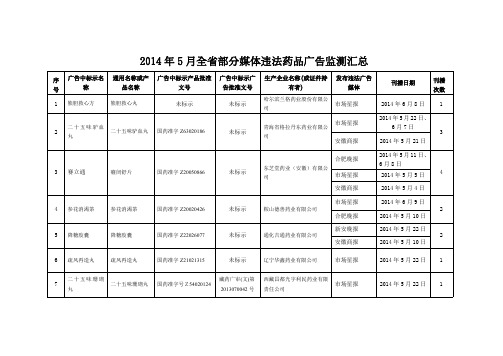
2014-5-30 至 30 10 2014-5-1 至 4
45
霍氏益气聪明 丸
益气聪明丸
国药准字 Z20054552
陕西中医学院制药厂
合肥晚报
2014-5-18 至 18
1
淮北公共频道 宁波大红鹰药业股份有 限公司
2014-5-1 至 18
46
耆鹿逐痹胶囊
耆鹿逐痹胶囊
国药准字 Z20010052
刊播日期
刊播 次数
2014 年 6 月 8 日 2014 年 5 月 22 日、 6月7日 2014 年 5 月 21 日 2014 年 5 月 11 日、 6月8日 2014 年 5 月 5 日 2014 年 5 月 4 日 2014 年 6 月 9 日
1
2
二十五味驴血 丸
二十五味驴血丸
国药准字 Z63020186
淮北教育频道 淮北新闻综合 频道
2014-5-1 至 8
42
2014-5-1 至 18
47
安芙康
百癣夏塔热胶 囊
国药准字 Z20050139
陕西东泰制药有限公司
淮南新闻综合 频道(1) 淮南经济生活
2014-5-2 至 15
14
48
黄花杜鹃油胶 丸
黄花杜鹃油胶 丸
青药广审(文) 国药准字 Z20026103 第 2013030044 号
26
56
风湿灵仙液
风湿灵仙液
国药准字 Z22026236
吉林省长中制药有限公 司
铜陵新闻综合 频道 铜陵影视娱乐 频道 芜湖新闻综合
26
57
宏微除障片
除障则海甫片
国药准字 Z20053328
陕西省科学院制药厂
2014年重大节日时间表

8月7星期四农历七月十二:立秋
8月10星期日农历七月十五:中元节
8月23星期六农历七月廿八:处暑
2014年9月节日:
9月8星期一农历八月十五:中秋节
9月10星期三农历八月十七:教师节
9月18星期四农历八月二十五:九一八事变83周年{1931年9月18日}
9月20星期六农历八月二十七:第12个公民道德宣传日,《公民道德建设实施纲要》印发13周年{2001年9月20日}
10月8星期三农历九月十五:寒露
10月15星期三农历闰九月二十二:第7个全农历闰九月初八:第9个世界勤俭日
2014年11月节日:
11月1星期六农历闰九月初九:万圣节
11月7星期五农历闰九月十五:立冬
11月9星期日农历闰九月十七:第24个消防宣传日。
2月4日农历一月初五:立春
2月14日农历一月十五:元宵节
2月19星期三农历一月二十:雨水
2014年三月节日:
3月2星期日农历二月初二:龙抬头
3月6星期四农历二月初六:惊蛰
3月8星期六农历二月初八:妇女节
3月12星期三农历二月十二:植树节
3月21星期五农历二月廿一:春分
2014年四月节日:
4月1星期二农历三月初二:愚人节
4月5星期六农历三月初六:清明节
4月20星期日农历三月廿一:谷雨
2014年5月节日:
5月1星期四农历四月初三:劳动节
5月4星期日农历四月初六:青年节
5月5日星期一农历四月初七:立夏
5月11星期日农历四月十三:母亲节
5月12星期一农历四月十四:护士节
5月21星期三农历四月廿三:小满
2014年6月节日:
2014年重大节日教育查询
2014年黄道吉日

2014年黄道吉日2014年01月01日农历12月(大)01日星期三冲虎(丙寅)煞南2014年01月08日农历12月(大)08日星期三冲鸡(癸酉)煞西2014年01月10日农历12月(大)10日星期五冲猪(乙亥)煞东2014年01月11日农历12月(大)11日星期六冲鼠(丙子)煞北2014年01月13日农历12月(大)13日星期一冲虎(戊寅)煞南2014年01月20日农历12月(大)20日星期一冲鸡(乙酉)煞西2014年01月22日农历12月(大)22日星期三冲猪(丁亥)煞东2014年01月23日农历12月(大)23日星期四冲鼠(戊子)煞北2014年01月25日农历12月(大)25日星期六冲虎(庚寅)煞南2014年01月31日农历01月(小)01日星期五冲猴(丙申)煞北2014年02月01日农历01月(小)02日星期六冲鸡(丁酉)煞西2014年02月03日农历01月(小)04日星期一冲猪(己亥)煞东2014年02月05日农历01月(小)06日星期三冲牛(辛丑)煞西2014年02月10日农历01月(小)11日星期一冲马(丙午)煞南2014年02月14日农历01月(小)15日星期五冲狗(庚戍)煞南2014年02月17日农历01月(小)18日星期一冲牛(癸丑)煞西2014年02月22日农历01月(小)23日星期六冲马(戊午)煞南2014年02月25日农历01月(小)26日星期二冲鸡(辛酉)煞西2014年02月28日农历01月(小)29日星期五冲鼠(甲子)煞北2014年03月01日农历02月(大)01日星期六冲牛(乙丑)煞西2014年03月06日农历02月(大)06日星期四冲马(庚午)煞南2014年03月09日农历02月(大)09日星期日冲鸡(癸酉)煞西2014年03月12日农历02月(大)12日星期三冲鼠(丙子)煞北2014年03月14日农历02月(大)14日星期五冲虎(戊寅)煞南2014年03月16日农历02月(大)16日星期日冲龙(庚辰)煞北2014年03月18日农历02月(大)18日星期二冲马(壬午)煞南2014年03月19日农历02月(大)19日星期三冲羊(癸未)煞东2014年03月21日农历02月(大)21日星期五冲鸡(乙酉)煞西2014年03月24日农历02月(大)24日星期一冲鼠(戊子)煞北2014年03月25日农历02月(大)25日星期二冲牛(己丑)煞西2014年03月26日农历02月(大)26日星期三冲虎(庚寅)煞南2014年03月31日农历03月(小)01日星期一冲羊(乙未)煞东2014年04月05日农历03月(小)06日星期六冲鼠(庚子)煞北2014年04月13日农历03月(小)14日星期日冲猴(戊申)煞北2014年04月17日农历03月(小)18日星期四冲鼠(壬子)煞北2014年04月25日农历03月(小)26日星期五冲猴(庚申)煞北2014年04月28日农历03月(小)29日星期一冲猪(癸亥)煞东2014年04月29日农历04月(大)01日星期二冲鼠(甲子)煞北2014年05月08日农历04月(大)10日星期四冲鸡(癸酉)煞西2014年05月09日农历04月(大)11日星期五冲狗(甲戍)煞南2014年05月17日农历04月(大)19日星期六冲马(壬午)煞南2014年05月23日农历04月(大)25日星期五冲鼠(戊子)煞北2014年05月25日农历04月(大)27日星期日冲虎(庚寅)煞南2014年05月27日农历04月(大)29日星期二冲龙(壬辰)煞北2014年05月29日农历05月(小)01日星期四冲马(甲午)煞南2014年06月01日农历05月(小)04日星期日冲鸡(丁酉)煞西2014年06月02日农历05月(小)05日星期一冲狗(戊戍)煞南2014年06月04日农历05月(小)07日星期三冲鼠(庚子)煞北2014年06月05日农历05月(小)08日星期四冲牛(辛丑)煞西2014年06月17日农历05月(小)20日星期二冲牛(癸丑)煞西2014年06月18日农历05月(小)21日星期三冲虎(甲寅)煞南2014年06月19日农历05月(小)22日星期四冲兔(乙卯)煞东2014年06月20日农历05月(小)23日星期五冲龙(丙辰)煞北2014年06月27日农历06月(大)01日星期五冲猪(癸亥)煞东2014年06月29日农历06月(大)03日星期日冲牛(乙丑)煞西2014年07月02日农历06月(大)06日星期三冲龙(戊辰)煞北2014年07月05日农历06月(大)09日星期六冲羊(辛未)煞东2014年07月13日农历06月(大)17日星期日冲兔(己卯)煞东2014年07月18日农历06月(大)22日星期五冲猴(甲申)煞北2014年07月19日农历06月(大)23日星期六冲鸡(乙酉)煞西2014年07月21日农历06月(大)25日星期一冲猪(丁亥)煞东2014年07月23日农历06月(大)27日星期三冲牛(己丑)煞西2014年07月25日农历06月(大)29日星期五冲兔(辛卯)煞东2014年07月26日农历06月(大)30日星期六冲龙(壬辰)煞北2014年07月30日农历07月(小)04日星期三冲猴(丙申)煞北2014年07月31日农历07月(小)05日星期四冲鸡(丁酉)煞西2014年08月01日农历07月(小)06日星期五冲狗(戊戍)煞南2014年08月02日农历07月(小)07日星期六冲猪(己亥)煞东2014年08月13日农历07月(小)18日星期三冲狗(庚戍)煞南2014年08月15日农历07月(小)20日星期五冲鼠(壬子)煞北2014年08月21日农历07月(小)26日星期四冲马(戊午)煞南2014年08月24日农历07月(小)29日星期日冲鸡(辛酉)煞西2014年08月26日农历08月(大)02日星期二冲猪(癸亥)煞东2014年08月27日农历08月(大)03日星期三冲鼠(甲子)煞北2014年08月29日农历08月(大)05日星期五冲虎(丙寅)煞南2014年08月31日农历08月(大)07日星期日冲龙(戊辰)煞北2014年09月02日农历08月(大)09日星期二冲马(庚午)煞南2014年09月06日农历08月(大)13日星期六冲狗(甲戍)煞南2014年09月07日农历08月(大)14日星期日冲猪(乙亥)煞东2014年09月08日农历08月(大)15日星期一冲鼠(丙子)煞北2014年09月10日农历08月(大)17日星期三冲虎(戊寅)煞南2014年09月12日农历08月(大)19日星期五冲龙(庚辰)煞北2014年09月18日农历08月(大)25日星期四冲狗(丙戍)煞南2014年09月20日农历08月(大)27日星期六冲鼠(戊子)煞北2014年09月24日农历09月(大)01日星期三冲龙(壬辰)煞北2014年09月30日农历09月(大)07日星期二冲狗(戊戍)煞南2014年10月01日农历09月(大)08日星期三冲猪(己亥)煞东2014年10月06日农历09月(大)13日星期一冲龙(甲辰)煞北2014年10月13日农历09月(大)20日星期一冲猪(辛亥)煞东2014年10月14日农历09月(大)21日星期二冲鼠(壬子)煞北2014年10月15日农历09月(大)22日星期三冲牛(癸丑)煞西2014年10月16日农历09月(大)23日星期四冲虎(甲寅)煞南2014年10月17日农历09月(大)24日星期五冲兔(乙卯)煞东2014年10月23日农历09月(大)30日星期四冲鸡(辛酉)煞西2014年10月26日农历09月(润)03日星期日冲鼠(甲子)煞北2014年10月28日农历09月(润)05日星期二冲虎(丙寅)煞南2014年10月29日农历09月(润)06日星期三冲兔(丁卯)煞东2014年11月04日农历09月(润)12日星期二冲鸡(癸酉)煞西2014年11月07日农历09月(润)15日星期五冲鼠(丙子)煞北2014年11月13日农历09月(润)21日星期四冲马(壬午)煞南2014年11月15日农历09月(润)23日星期六冲猴(甲申)煞北2014年11月16日农历09月(润)24日星期日冲鸡(乙酉)煞西2014年11月19日农历09月(润)27日星期三冲鼠(戊子)煞北2014年11月22日农历10月(大)01日星期六冲兔(辛卯)煞东2014年11月23日农历10月(大)02日星期日冲龙(壬辰)煞北2014年11月25日农历10月(大)04日星期二冲马(甲午)煞南2014年11月28日农历10月(大)07日星期五冲鸡(丁酉)煞西2014年11月29日农历10月(大)08日星期六冲狗(戊戍)煞南2014年12月08日农历10月(大)17日星期一冲羊(丁未)煞东2014年12月20日农历10月(大)29日星期六冲羊(己未)煞东2014年12月24日农历11月(小)03日星期三冲猪(癸亥)煞东2014年12月27日农历11月(小)06日星期六冲虎(丙寅)煞南。
2014年重大节日表

2014年重大节日2014年3月节日:3月1日:国际民防日/国际海豹日3月2日:龙抬头3月3日:全国爱耳日3月5日:学习雷锋日/中国青年志愿日3月6日:惊蛰3月7日:女生节3月8日:妇女节3月12日:中国植树节/孙中山逝世89周年3月21日:春分3月22日:世界水日3月23日:世界气象日3月30日:地球一小时(20:30~21:30)3月31日:复活节2014年4月节日:4月1日:愚人节4月5日:清明节4月7日:世界卫生日4月14日:黑色情人节4月20日:谷雨4月22日:世界地球日/世界法律日4月23日:世界读书日4月26日:世界知识产权日2014年5月节日:5月1日:国际劳动节日5月4日:五四青年节5月5日:立夏5月8日:世界微笑日/世界红十字日5月11日:母亲节5月12日:护士节/汶川大地震六周年/全国防灾减灾日5月19日:中国旅游日/全国助残日5月21日:小满5月31日:世界无烟日2014年6月节日:6月1日:国际儿童节6月2日:端午节6月5日:世界环境日6月6日:芒种6月12日:端午节6月15日:父亲节6月21日:夏至6月25日:全国土地日6月26日:国际禁毒日2014年7月节日:7月1日:香港回归日、建党日2014年9月节日:9月8日:中秋节9月10日:教师节9月12日:示爱日9月14日:世界清洁地球日9月18日:九一八事变83周年{1931年9月18日}9月20日:第12个公民道德宣传日,《公民道德建设实施纲要》印发13周年{2001年9月20日}9月21日:第14个全民国防教育日9月23日:秋分9月28日:孔子诞辰2565周年{公元前551年9月28日}2014年10月节日:10月1日:国庆节10月2日:重阳节10月5日:第21个世界教师节《关于教师地位的建议书》通过48周年10月8日:寒露10月15日:第7个全球洗手日10月23日:霜降10月31日:第9个世界勤俭日2014年11月节日:11月1日:万圣节11月7星期五农历闰九月十五:立冬11月9日:第24个消防宣传日。
2014年西安日出日落时间表 (纬度:34.09 经度: 108.55)

日期日出日中日落2014年1月1日7:51:2312:49:1717:47:11 2014年1月2日7:51:3412:49:4517:47:57 2014年1月3日7:51:4312:50:1317:48:43 2014年1月4日7:51:5012:50:4017:49:30 2014年1月5日7:51:5612:51:0717:50:19 2014年1月6日7:52:0012:51:3417:51:08 2014年1月7日7:52:0212:52:0017:51:58 2014年1月8日7:52:0212:52:2617:52:50 2014年1月9日7:52:0012:52:5117:53:42 2014年1月10日7:51:5612:53:1517:54:34 2014年1月11日7:51:5012:53:3917:55:28 2014年1月12日7:51:4312:54:0317:56:22 2014年1月13日7:51:3412:54:2517:57:17 2014年1月14日7:51:2212:54:4717:58:12 2014年1月15日7:51:0912:55:0917:59:08 2014年1月16日7:50:5512:55:3018:00:05 2014年1月17日7:50:3812:55:5018:01:02 2014年1月18日7:50:1912:56:0918:01:59 2014年1月19日7:49:5912:56:2818:02:57 2014年1月20日7:49:3712:56:4618:03:55 2014年1月21日7:49:1312:57:0318:04:54 2014年1月22日7:48:4712:57:2018:05:52 2014年1月23日7:48:1912:57:3518:06:51 2014年1月24日7:47:5012:57:5018:07:50 2014年1月25日7:47:1912:58:0418:08:49 2014年1月26日7:46:4712:58:1818:09:49 2014年1月27日7:46:1212:58:3018:10:48 2014年1月28日7:45:3612:58:4218:11:47 2014年1月29日7:44:5912:58:5318:12:47 2014年1月30日7:44:2012:59:0318:13:46 2014年1月31日7:43:3912:59:1218:14:45 2014年2月1日7:42:5612:59:2118:15:45 2014年2月2日7:42:1312:59:2818:16:44 2014年2月3日7:41:2712:59:3518:17:43 2014年2月4日7:40:4012:59:4118:18:42 2014年2月5日7:39:5212:59:4618:19:40 2014年2月6日7:39:0212:59:5118:20:39 2014年2月7日7:38:1112:59:5418:21:37 2014年2月8日7:37:1912:59:5718:22:35 2014年2月9日7:36:2512:59:5918:23:33 2014年2月10日7:35:3013:00:0018:24:31 2014年2月11日7:34:3313:00:0118:25:28 2014年2月12日7:33:3613:00:0018:26:25 2014年2月13日7:32:3712:59:5918:27:21 2014年2月14日7:31:3712:59:5718:28:18 2014年2月15日7:30:3612:59:5518:29:14 2014年2月16日7:29:3412:59:5218:30:10 2014年2月17日7:28:3012:59:4818:31:05 2014年2月18日7:27:2612:59:4318:32:00 2014年2月19日7:26:2012:59:3818:32:55 2014年2月20日7:25:1412:59:3218:33:492014年2月26日7:18:1612:58:4218:39:08 2014年2月27日7:17:0312:58:3218:40:00 2014年2月28日7:15:5012:58:2118:40:52 2014年3月1日7:14:3612:58:1018:41:43 2014年3月2日7:13:2112:57:5818:42:34 2014年3月3日7:12:0612:57:4518:43:25 2014年3月4日7:10:5012:57:3218:44:15 2014年3月5日7:09:3312:57:1918:45:05 2014年3月6日7:08:1612:57:0618:45:55 2014年3月7日7:06:5912:56:5118:46:44 2014年3月8日7:05:4012:56:3718:47:33 2014年3月9日7:04:2212:56:2218:48:22 2014年3月10日7:03:0312:56:0718:49:11 2014年3月11日7:01:4312:55:5118:49:59 2014年3月12日7:00:2312:55:3518:50:47 2014年3月13日6:59:0312:55:1918:51:35 2014年3月14日6:57:4212:55:0318:52:23 2014年3月15日6:56:2212:54:4618:53:10 2014年3月16日6:55:0112:54:2918:53:58 2014年3月17日6:53:3912:54:1218:54:45 2014年3月18日6:52:1812:53:5518:55:31 2014年3月19日6:50:5612:53:3718:56:18 2014年3月20日6:49:3412:53:1918:57:05 2014年3月21日6:48:1212:53:0218:57:51 2014年3月22日6:46:5012:52:4418:58:37 2014年3月23日6:45:2812:52:2618:59:23 2014年3月24日6:44:0612:52:0819:00:09 2014年3月25日6:42:4412:51:5019:00:55 2014年3月26日6:41:2212:51:3119:01:41 2014年3月27日6:40:0012:51:1319:02:27 2014年3月28日6:38:3812:50:5519:03:13 2014年3月29日6:37:1612:50:3719:03:58 2014年3月30日6:35:5412:50:1919:04:44 2014年3月31日6:34:3312:50:0119:05:29 2014年4月1日6:33:1112:49:4319:06:15 2014年4月2日6:31:5012:49:2519:07:00 2014年4月3日6:30:3012:49:0819:07:46 2014年4月4日6:29:0912:48:5019:08:32 2014年4月5日6:27:4912:48:3319:09:17 2014年4月6日6:26:2912:48:1619:10:03 2014年4月7日6:25:1012:47:5919:10:48 2014年4月8日6:23:5012:47:4219:11:34 2014年4月9日6:22:3212:47:2619:12:19 2014年4月10日6:21:1412:47:0919:13:05 2014年4月11日6:19:5612:46:5319:13:51 2014年4月12日6:18:3912:46:3819:14:37 2014年4月13日6:17:2212:46:2219:15:22 2014年4月14日6:16:0612:46:0719:16:08 2014年4月15日6:14:5112:45:5319:16:542014年4月21日6:07:3312:44:3219:21:32 2014年4月22日6:06:2312:44:2019:22:18 2014年4月23日6:05:1312:44:0919:23:05 2014年4月24日6:04:0412:43:5819:23:52 2014年4月25日6:02:5712:43:4719:24:38 2014年4月26日6:01:5012:43:3719:25:25 2014年4月27日6:00:4412:43:2819:26:12 2014年4月28日5:59:3912:43:1919:26:59 2014年4月29日5:58:3512:43:1019:27:46 2014年4月30日5:57:3212:43:0219:28:32 2014年5月1日5:56:3012:42:5519:29:19 2014年5月2日5:55:2912:42:4819:30:06 2014年5月3日5:54:3012:42:4119:30:53 2014年5月4日5:53:3112:42:3519:31:40 2014年5月5日5:52:3412:42:3019:32:27 2014年5月6日5:51:3712:42:2519:33:13 2014年5月7日5:50:4212:42:2119:34:00 2014年5月8日5:49:4912:42:1819:34:47 2014年5月9日5:48:5612:42:1519:35:33 2014年5月10日5:48:0512:42:1219:36:19 2014年5月11日5:47:1512:42:1019:37:06 2014年5月12日5:46:2612:42:0919:37:52 2014年5月13日5:45:3912:42:0819:38:37 2014年5月14日5:44:5312:42:0819:39:23 2014年5月15日5:44:0812:42:0819:40:08 2014年5月16日5:43:2512:42:0919:40:53 2014年5月17日5:42:4312:42:1119:41:38 2014年5月18日5:42:0312:42:1319:42:22 2014年5月19日5:41:2412:42:1519:43:07 2014年5月20日5:40:4712:42:1919:43:50 2014年5月21日5:40:1112:42:2219:44:33 2014年5月22日5:39:3712:42:2719:45:16 2014年5月23日5:39:0412:42:3119:45:59 2014年5月24日5:38:3312:42:3719:46:40 2014年5月25日5:38:0312:42:4219:47:22 2014年5月26日5:37:3512:42:4919:48:03 2014年5月27日5:37:0812:42:5519:48:43 2014年5月28日5:36:4312:43:0319:49:22 2014年5月29日5:36:2012:43:1019:50:01 2014年5月30日5:35:5812:43:1819:50:39 2014年5月31日5:35:3812:43:2719:51:16 2014年6月1日5:35:1912:43:3619:51:53 2014年6月2日5:35:0212:43:4519:52:29 2014年6月3日5:34:4612:43:5519:53:04 2014年6月4日5:34:3312:44:0519:53:38 2014年6月5日5:34:2012:44:1619:54:11 2014年6月6日5:34:1012:44:2619:54:43 2014年6月7日5:34:0112:44:3719:55:14 2014年6月8日5:33:5312:44:4919:55:442014年6月14日5:33:4212:46:0219:58:22 2014年6月15日5:33:4512:46:1419:58:44 2014年6月16日5:33:5012:46:2719:59:04 2014年6月17日5:33:5712:46:4019:59:24 2014年6月18日5:34:0512:46:5319:59:42 2014年6月19日5:34:1412:47:0619:59:58 2014年6月20日5:34:2512:47:1920:00:14 2014年6月21日5:34:3712:47:3320:00:28 2014年6月22日5:34:5112:47:4620:00:40 2014年6月23日5:35:0612:47:5920:00:51 2014年6月24日5:35:2212:48:1120:01:01 2014年6月25日5:35:4012:48:2420:01:09 2014年6月26日5:35:5912:48:3720:01:15 2014年6月27日5:36:1912:48:5020:01:20 2014年6月28日5:36:4112:49:0220:01:23 2014年6月29日5:37:0312:49:1420:01:25 2014年6月30日5:37:2712:49:2620:01:25 2014年7月1日5:37:5212:49:3820:01:24 2014年7月2日5:38:1812:49:4920:01:21 2014年7月3日5:38:4512:50:0020:01:16 2014年7月4日5:39:1312:50:1120:01:10 2014年7月5日5:39:4212:50:2220:01:02 2014年7月6日5:40:1212:50:3220:00:52 2014年7月7日5:40:4312:50:4220:00:41 2014年7月8日5:41:1412:50:5120:00:28 2014年7月9日5:41:4712:51:0020:00:14 2014年7月10日5:42:2112:51:0919:59:58 2014年7月11日5:42:5512:51:1719:59:40 2014年7月12日5:43:3012:51:2519:59:20 2014年7月13日5:44:0612:51:3219:58:59 2014年7月14日5:44:4212:51:3919:58:37 2014年7月15日5:45:1912:51:4619:58:12 2014年7月16日5:45:5712:51:5119:57:46 2014年7月17日5:46:3512:51:5719:57:19 2014年7月18日5:47:1412:52:0219:56:50 2014年7月19日5:47:5312:52:0619:56:19 2014年7月20日5:48:3312:52:1019:55:46 2014年7月21日5:49:1312:52:1319:55:13 2014年7月22日5:49:5412:52:1519:54:37 2014年7月23日5:50:3512:52:1719:54:00 2014年7月24日5:51:1612:52:1919:53:22 2014年7月25日5:51:5812:52:2019:52:42 2014年7月26日5:52:4012:52:2019:52:00 2014年7月27日5:53:2212:52:2019:51:17 2014年7月28日5:54:0412:52:1919:50:33 2014年7月29日5:54:4712:52:1719:49:47 2014年7月30日5:55:3012:52:1519:49:00 2014年7月31日5:56:1312:52:1219:48:11 2014年8月1日5:56:5612:52:0919:47:212014年8月7日6:01:1812:51:3619:41:54 2014年8月8日6:02:0112:51:2819:40:55 2014年8月9日6:02:4512:51:2019:39:55 2014年8月10日6:03:2912:51:1119:38:54 2014年8月11日6:04:1212:51:0219:37:51 2014年8月12日6:04:5612:50:5219:36:48 2014年8月13日6:05:3912:50:4219:35:44 2014年8月14日6:06:2312:50:3119:34:38 2014年8月15日6:07:0612:50:1919:33:32 2014年8月16日6:07:5012:50:0719:32:24 2014年8月17日6:08:3312:49:5419:31:16 2014年8月18日6:09:1612:49:4119:30:06 2014年8月19日6:09:5912:49:2819:28:56 2014年8月20日6:10:4212:49:1419:27:45 2014年8月21日6:11:2512:48:5919:26:33 2014年8月22日6:12:0812:48:4419:25:20 2014年8月23日6:12:5112:48:2819:24:06 2014年8月24日6:13:3312:48:1319:22:52 2014年8月25日6:14:1612:47:5619:21:37 2014年8月26日6:14:5812:47:3919:20:21 2014年8月27日6:15:4012:47:2219:19:04 2014年8月28日6:16:2212:47:0519:17:47 2014年8月29日6:17:0512:46:4719:16:29 2014年8月30日6:17:4712:46:2919:15:11 2014年8月31日6:18:2812:46:1019:13:52 2014年9月1日6:19:1012:45:5119:12:32 2014年9月2日6:19:5212:45:3219:11:12 2014年9月3日6:20:3412:45:1319:09:52 2014年9月4日6:21:1512:44:5319:08:31 2014年9月5日6:21:5712:44:3319:07:09 2014年9月6日6:22:3812:44:1319:05:48 2014年9月7日6:23:1912:43:5219:04:25 2014年9月8日6:24:0112:43:3219:03:03 2014年9月9日6:24:4212:43:1119:01:40 2014年9月10日6:25:2412:42:5019:00:17 2014年9月11日6:26:0512:42:2918:58:53 2014年9月12日6:26:4612:42:0818:57:30 2014年9月13日6:27:2812:41:4718:56:06 2014年9月14日6:28:0912:41:2518:54:42 2014年9月15日6:28:5012:41:0418:53:18 2014年9月16日6:29:3212:40:4318:51:54 2014年9月17日6:30:1312:40:2118:50:29 2014年9月18日6:30:5512:40:0018:49:05 2014年9月19日6:31:3612:39:3818:47:40 2014年9月20日6:32:1812:39:1718:46:16 2014年9月21日6:33:0012:38:5618:44:51 2014年9月22日6:33:4212:38:3418:43:27 2014年9月23日6:34:2412:38:1318:42:03 2014年9月24日6:35:0612:37:5218:40:382014年9月30日6:39:2312:35:5018:32:17 2014年10月1日6:40:0712:35:3118:30:55 2014年10月2日6:40:5112:35:1218:29:32 2014年10月3日6:41:3512:34:5318:28:10 2014年10月4日6:42:1912:34:3418:26:49 2014年10月5日6:43:0412:34:1618:25:28 2014年10月6日6:43:4912:33:5818:24:07 2014年10月7日6:44:3412:33:4018:22:47 2014年10月8日6:45:1912:33:2318:21:27 2014年10月9日6:46:0512:33:0718:20:08 2014年10月10日6:46:5112:32:5018:18:50 2014年10月11日6:47:3812:32:3518:17:32 2014年10月12日6:48:2412:32:1918:16:15 2014年10月13日6:49:1112:32:0518:14:58 2014年10月14日6:49:5912:31:5118:13:42 2014年10月15日6:50:4712:31:3718:12:27 2014年10月16日6:51:3512:31:2418:11:13 2014年10月17日6:52:2312:31:1118:09:59 2014年10月18日6:53:1212:30:5918:08:46 2014年10月19日6:54:0112:30:4818:07:34 2014年10月20日6:54:5112:30:3718:06:23 2014年10月21日6:55:4112:30:2718:05:13 2014年10月22日6:56:3112:30:1818:04:04 2014年10月23日6:57:2212:30:0918:02:56 2014年10月24日6:58:1312:30:0118:01:49 2014年10月25日6:59:0512:29:5418:00:43 2014年10月26日6:59:5712:29:4717:59:37 2014年10月27日7:00:4912:29:4117:58:34 2014年10月28日7:01:4112:29:3617:57:31 2014年10月29日7:02:3412:29:3217:56:29 2014年10月30日7:03:2812:29:2817:55:29 2014年10月31日7:04:2112:29:2517:54:29 2014年11月1日7:05:1512:29:2317:53:31 2014年11月2日7:06:0912:29:2217:52:35 2014年11月3日7:07:0412:29:2117:51:39 2014年11月4日7:07:5912:29:2217:50:45 2014年11月5日7:08:5412:29:2317:49:52 2014年11月6日7:09:4912:29:2517:49:01 2014年11月7日7:10:4512:29:2817:48:11 2014年11月8日7:11:4012:29:3217:47:23 2014年11月9日7:12:3612:29:3617:46:36 2014年11月10日7:13:3312:29:4217:45:51 2014年11月11日7:14:2912:29:4817:45:07 2014年11月12日7:15:2512:29:5517:44:25 2014年11月13日7:16:2212:30:0317:43:44 2014年11月14日7:17:1812:30:1217:43:05 2014年11月15日7:18:1512:30:2117:42:27 2014年11月16日7:19:1212:30:3217:41:52 2014年11月17日7:20:0812:30:4317:41:182014年11月23日7:25:4612:32:0817:38:30 2014年11月24日7:26:4212:32:2517:38:09 2014年11月25日7:27:3712:32:4317:37:49 2014年11月26日7:28:3212:33:0217:37:31 2014年11月27日7:29:2712:33:2117:37:15 2014年11月28日7:30:2112:33:4117:37:01 2014年11月29日7:31:1412:34:0117:36:48 2014年11月30日7:32:0812:34:2317:36:38 2014年12月1日7:33:0012:34:4517:36:30 2014年12月2日7:33:5212:35:0817:36:23 2014年12月3日7:34:4312:35:3117:36:18 2014年12月4日7:35:3412:35:5517:36:16 2014年12月5日7:36:2412:36:1917:36:15 2014年12月6日7:37:1312:36:4417:36:16 2014年12月7日7:38:0112:37:1017:36:19 2014年12月8日7:38:4812:37:3617:36:24 2014年12月9日7:39:3412:38:0217:36:30 2014年12月10日7:40:2012:38:2917:36:39 2014年12月11日7:41:0412:38:5717:36:50 2014年12月12日7:41:4712:39:2417:37:02 2014年12月13日7:42:2912:39:5317:37:16 2014年12月14日7:43:1012:40:2117:37:32 2014年12月15日7:43:5012:40:5017:37:50 2014年12月16日7:44:2812:41:1917:38:10 2014年12月17日7:45:0512:41:4817:38:31 2014年12月18日7:45:4112:42:1717:38:54 2014年12月19日7:46:1512:42:4717:39:19 2014年12月20日7:46:4812:43:1717:39:45 2014年12月21日7:47:2012:43:4617:40:13 2014年12月22日7:47:4912:44:1617:40:43 2014年12月23日7:48:1812:44:4617:41:14 2014年12月24日7:48:4512:45:1617:41:47 2014年12月25日7:49:1012:45:4617:42:21 2014年12月26日7:49:3412:46:1517:42:57 2014年12月27日7:49:5612:46:4517:43:34 2014年12月28日7:50:1612:47:1417:44:13 2014年12月29日7:50:3412:47:4417:44:53 2014年12月30日7:50:5112:48:1317:45:34 2014年12月31日7:51:0612:48:4217:46:17。
2014十大国际事件

一、MH370航班失联事件2014年3月8日凌晨2点40分,马来西亚航空公司称与一架载有239人的波音777-200飞机与管制中心失去联系的,该飞机航班号为MH370,原定由吉隆坡飞往北京。
二、中国成为世界第一大经济体据国际货币基金组织(IMF)的数据估计,按照购买力平价(PPP)的计算方式,中国的经济规模在2014年超过美国,成为世界第一大经济体。
三、昆明恐怖袭击3·1昆明火车站暴力恐怖案,指的是2014年3月1日21时20分左右,在云南省昆明市昆明火车站发生的一起以阿不都热依木·库尔班为首的新疆分裂势力一手策划组织的严重暴力恐怖事件事件。
四、韩国岁月号客轮沉没事故4·16韩国客轮沉没事故,即4.16韩客轮沉没事件,指的是当地时间2014年4月16日上午8时58分许,一艘载有470人的“世越(SEWOL)号”客轮在韩国西南海域发生浸水事故而下沉。
船上有325名中学生,15名教师,30名船务人员,以及89名其他乘客。
此外还载有150-180辆汽车和1157吨货物。
五、埃博拉肆虐2014年西非埃博拉病毒疫情是自2014年2月开始爆发于西非的疫情,截至2014年11月30日,世界卫生组织关于埃博拉疫情报告称,几内亚、利比里亚、塞拉利昂、美国、西班牙、马里以及已结束疫情的尼日利亚与塞内加尔累计出现埃博拉确诊、疑似和可能感染病例17145例,其中6070人死亡。
2014年西非埃博拉病毒疫情爆发的感染及死亡人数都达到历史最高,并仍处于恶化状态中。
七、乌克兰危机乌克兰危机是由2013年底乌克兰亲俄派总统亚努科维奇中止和欧洲联盟签署政治和自由贸易协议,欲强化和俄罗斯的关系导致。
2013年11月22日,乌克兰亲欧洲派在基辅展开反政府示威,抗议群众要求政府和欧盟签署协议、亚努科维奇下台、提前举行选举。
2014年2月22日,亚努科维奇被议会罢免其总统职务,并宣布提前于同年5月25日举行总统大选。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
认识三角形
1、已知△ABC的一个外角为50°,则△ABC一定是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.锐角三角形或钝角三角形
2、三角形三条高所在直线的交点一定在( )
A.三角形的内部 B.三角形的外部
C.三角形的内部或外部 D.三角形的内部、外部或顶点
3、若三角形的两边长分别为6cm,9cm,则其第三边的长可能为( )
A.2cm B.3cm C.7cm D.16cm
4、一个三角形的三边长分别为4,7,x,那么x的取值范围是( )
A.3<x<11 B.4<x<7 C.-3<x<11 D.x>3
5、设△ABC的三边为a、b、c,化简:|a-b-c|+|b-c-a|+|c-a-b|=__________
6、如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B=______
7、直角三角形中,两锐角的角平分线所夹的锐角是___________度
8、在△ABC中,高BD和CE所在的直线相交于O,若△ABC不是直角三角形,且∠A=60°,
则∠BOC= 度。
9、一副三角板叠在一起如图放置.最小锐角的顶点D恰好放在等腰直角三角板的斜边AB
上,BC与DE交于点M.如果∠ADF=100°,那么∠BMD为________度
10、一副三角板如图所示叠放在一起∠a度数为: 度。
11、如图,在△ABC中,∠A=80°,剪去∠A 后得到四边形BCDE,则∠1+∠2= 度。
12、等腰△ABC中,AB=AC,一腰上的中线BD将这个等腰三角形的周长分为21和12两部
分,则该三角形的底长是: 。
13、如图,BP平分∠ABC交CD于点F,DP平分∠ADC交AB于点E,AB于CD相交于
点O,若∠A=40°,∠C=36°,则∠P= 度。
14、多边形内角中最多有 个锐角。
15、凸多边形恰好有三个内角是钝角,这样的多边形
边数的最大值是:( )A、4 B、5 C、6 D、7
16、有一个凸n边形,除去一个内角以外的所有其他内角之和为2570°,则n= 。
17、如图,已知∠BGF=150°,那么∠A+∠B+∠C+∠D+∠E+∠F的度数是: 度。
18、如图(1),在△ABC中,∠C>∠B,AD⊥BC于点D,AE平分∠BAC,你能找出
∠EAD与∠B、∠C之间的数量关系吗?并说明理由.
(2)如图(2),AE平分∠BAC,F为直线AE上一点,FM⊥BC于点M,这时∠EFM与
∠B、∠C之间又有何数量关系?请你直接说出它们的关系,不需要证明.
(3)若∠C为钝角,则(1)中的结论成立吗?请说明理由
第6题 第9题 第10题 第11题 第13题
第16题
DE
C
B
A
19、下面是有关三角形内外角平分线的探究,阅读后按要求作答:
探究1:如图(1),在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通
过分析发现:1902BOCA
探究2:如图(2)中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠
BOC与∠A有怎样的数量关系?请说明理由.
探究3:如图(3)中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,
则∠BOC与∠A有怎样的数量关系?请说明理由.
.
20、如图,在△BCD中,BE平分∠DBC交CD于F,延长BC至G,CE平分∠DCG,且
EC、DB的延长线交于A点,若∠A=33°,∠DFE=63°.
(1)求证:∠DFE=∠A+∠D+∠E; (2)求∠E的度数;
(3)若在上图中作∠CBE与∠GCE的平分线交于E1,作∠CBE1与∠GCE1的平分线交于
E2,作∠CBE2与∠GCE2的平分线于E3,以此类推,∠CBEn与∠GCEn的平分线交于En+l,
请用含有n的式子表示∠En+l的度数(直接写答案).
21、如图,已知∠MON=90°,点A,B分别在射线OM,ON上移动,∠OAB的角平分线
与∠ABO的外角平分线交于点C.①当∠OAB=60°时,求∠ACB的度数;
②试猜想,随着点A,B的移动,∠ACB的度数是否变化?说明理由.
22、探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一
个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD
的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图2,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数
量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论
探究∠P与∠A+∠B的数量关系.探究四:若将上题中的四边形ABCD改为六边形ABCDEF
(图4)呢?请直接写出∠P与∠A+∠B+∠E+∠F的数量关系:
23、已知:线段AB、CD相交于点O,连接AB、CD、∠CAB和∠CDB的平分线AP和
DP相交于点P,试解答下列问题:
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系: ____________________
(2)如果图2中∠D和∠B为任意角,其他条件不变,试写出∠P与∠D、∠B之间数量关
系.并说明理由。
(3)点E在CA的延长线上,∠BAE的平分线和∠CDB的平分线交于点N,Q且∠C=24°,
∠B=42°,求∠APC度数
24、如图1,我们不妨把这样的图形叫作“燕尾形”,那么这个简单的图形中,到底隐藏了那
些数学知识呢?下面就请发挥你的聪明才智解决一下问题:
(1)观察“燕尾形”,试探究∠BDC与∠A,∠B,∠C之间的关系,并证明.
(2)请你直接利用以上的结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY,XZ恰好经
过点B,C.若∠A=50°,则∠ABX+∠ACX= °.
②如图3,BG平分∠ABD,GC平分∠ACD.若∠BAC=50°,∠CDB=140°,求∠BGC
的度数.
③如图4,∠ABD,∠ACD的10等分线相交于点G1,G2,…,G9.若∠BDC=160°,
∠BG1C=70°,求∠A的度数.
D
CB
A
P
D
CB
A
N
M
E
P
D
CB
A
25、(1)如图1,这是一个五角星ABCDE,你能计算出∠A+∠B+∠C+∠D+∠E的度数吗?
为什么?(必须写推理过程)
(2)如图2,如果点B向右移动到AC上,那么还能求出∠A+∠DBE+∠C+∠D+∠E的大
小吗?若能结果是多少?(可不写推理过程)
(3)如图,当点B向右移动到AC的另一侧时,上面的结论还成立吗?
(4)如图4,当点B、E移动到∠CAD的内部时,结论又如何?根据图3或图4,说明你
计算的理由.
26、观察并探求下列各问题,写出你所观察得到的结论.
(1)如图①,在△ABC中,P为边BC上一点,则BP+PC AB+AC(填“>”、“<”或“=”)
(2)将(1)中点P移到△ABC内,得图②,试观察比较△BPC的周长与△ABC的周长
的大小,并说明理由.
(3)将(2)中点P变为两个点P1、P2得图③,试观察比较四边形BP1P2C的周长与△ABC
的周长的大小,并说明理由.
27、将纸片△ABC沿DE折叠使点A落在A′处的位置.
1)如果A′落在四边形BCDE的内部(如图1),∠A′与∠1+∠2之间存在怎样的数量关系?
并说明理由.
(2)如果A′落在四边形BCDE的BE边上,这时图1中的∠1变为0°角,则∠A′与∠2之
间的关系是 .
(3)如果A′落在四边形BCDE的外部(如图2),这时∠A′与∠1、∠2之间又存在怎样的
数量关系?并说明理由.
