基于 MATLAB 的变频器整流侧输入电流的谐波分析

合集下载

基于MATLAB的电力谐波分析

基于MATLAB的电力谐波分析电力谐波是电力系统中常见的问题，可以导致电力设备故障、能耗增加以及电压波形失真等不良效果。

因此，对电力谐波进行分析和处理具有重要意义。

MATLAB是一种功能强大的工具，可以用于电力谐波分析。

一、电力谐波的概念和原理电力谐波是指在电力系统中，超过基波频率的功率频率成分。

它们是由非线性负载引起的，如电弧炉、变频器等。

谐波会导致电压和电流波形变形，使得电压谐波、电流谐波和功率谐波产生，严重时会导致设备损坏。

电力谐波分析的主要原理是通过傅里叶级数展开，将非线性负载引起的电压和电流信号分解为基波和谐波成分。

然后，可以计算谐波分量的谐波电流、谐波电压、相角等信息。

根据这些信息，可以评估电力系统中谐波的程度，并采取适当的措施进行补偿和抑制。

二、MATLAB工具箱的使用MATLAB有多个工具箱可以用于电力谐波分析，包括基本的波形分析工具箱、信号处理工具箱和工具箱的傅里叶分析工具。

1.使用波形分析工具箱进行谐波分析在波形分析工具箱中，有多种函数可以用于谐波分析，如fft、ifft、spectrogram等。

通过调用这些函数，可以对电压和电流信号进行傅里叶变换，得到频率和幅值谱。

然后，可以从频谱中提取出谐波分量的频率、幅值等信息。

2.使用信号处理工具箱进行谐波分析信号处理工具箱提供了更多用于谐波分析的函数，如stft、wavelet 等。

通过调用这些函数，可以对电压和电流信号进行时频分析，得到谐波分量的时频特性。

此外，还可以通过滤波等方法对谐波信号进行补偿和抑制。

3.使用傅里叶分析工具进行谐波分析MATLAB的傅里叶分析工具提供了多种方法进行谐波分析，如离散傅里叶变换（DFT）、快速傅里叶变换（FFT）等。

通过调用这些函数，可以对电压和电流信号进行频域分析，得到谐波分量的频谱特性。

然后，可以计算谐波电流、谐波电压、相角等信息。

三、电力谐波分析的步骤进行电力谐波分析时，可以按照以下步骤进行：1.数据采集：使用合适的传感器采集电压和电流信号数据。

基于MATLAB仿真的方波信号谐波分析

Value Engineering0引言谐波分析在控制系统、电能质量监控、精密机械、电子产品生产检验、输电线路设备监控等领域被广泛应用；而准确、快速、有效的谐波分析方法是进行相关检测、监控、分析的技术基础。

目前，信号谐波分析存在的运算量大、计算时间长、实时性差等技术瓶颈。

信号频谱和信号本身同样是现实可以观测的，可以通过频谱分析仪来观测信号的频谱。

比如图像颜色不同是由于频率的差异，声音音调不同，也是因为频率的差异。

而用正交函数集表示任意信号可以得到比较简单而又足够精确的表示式，因此，把信号表示为一组不同频率的复指数函数或正弦信号的加权和，对信号进行频谱分析，为基于MATLAB 仿真的FFT （快速傅里叶变换）提供理论依据。

1周期信号傅里叶级数与傅里叶变换把信号表示为一组不同频率的复指数函数或正弦信号的加权和，称为信号的频谱分析或傅里叶分析，简称信号的谱分析。

用频谱分析的观点分析系统，称为系统的傅里叶分析。

如果一个信号x （t ）是周期性的，那么对一切t 有一个非零正值T 使得下式成立：（1）x （t ）的基波周期T 0就是满足T 中的最小非零正值，而基波角频率（2）正弦函数cos ω0t 和复指数函数ej ω0t都是周期信号，其角频率为ω0，周期为（3）呈谐波关系的复指数函数集（4）也是周期信号，其中每个分量的角频率是ω0的整数倍。

用这些函数加权组合而成的信号（5）也是以T 0为周期的周期信号。

其中n=0的项c 0为常数项或者直流分量；n=+1或者n=-1这两项的周期都是基波周期T 0，两者合在一起称为基波分量或者一次谐波分量；n=+2或者n=-2这两项的周期是基波周期的一半，频率是基波周期的两倍，称为二次谐波分量，以此类推n=+N ，或者n=-N 的分量称为N 次谐波分量。

将周期信号表示成式（5）的形式，即一组成谐波关系的复指数函数的加权和，即为傅里叶级数表示。

对于周期性矩脉冲，（6）周期性函数的傅里叶级数等效于把函数分解成它的各频率正（余）弦分量，简称为频率分量。

基于MATLAB的谐波分析FFT概要

基于MATLAB的谐波分析FFT概要谐波分析是一种用于分析信号频谱的方法，主要用于确定信号中存在的谐波成分。

在MATLAB中，谐波分析可以通过使用快速傅里叶变换（FFT）来实现。

本文将详细介绍基于MATLAB的谐波分析FFT的概要。

首先，快速傅里叶变换（FFT）是一种用于将时域信号转换为频域信号的数学技术。

它能够将信号分解为一系列频率成分，并显示每个成分的幅度和相位。

因为FFT算法在计算上非常高效，所以它成为了谐波分析的主要工具。

在MATLAB中进行谐波分析FFT时，首先需要准备要分析的信号。

信号可以是实际测量到的数据，也可以是经过仿真或计算得到的数据。

通常，信号是一个包含多个周期的数据序列。

然后，为了进行谐波分析，需要对信号进行预处理。

这包括对信号进行采样和量化。

采样是将连续信号转换为离散数据点的过程，而量化是将连续数据转换为离散数值的过程。

在MATLAB中，可以使用内置的函数来执行这些操作。

接下来，将使用MATLAB的FFT函数对预处理后的信号进行频谱分析。

FFT函数将信号转换为复数数组表示形式，并将其分解为频率成分。

它返回一个包含信号频率谱的长度为N的向量，其中N是输入信号的长度。

在得到频谱后，可以使用MATLAB的plot函数来可视化频谱。

可以将频谱以线性刻度或对数刻度绘制，以便更好地显示信号的谐波成分。

通过分析频谱中的峰值，可以确定信号中存在的谐波频率和对应的幅度。

谐波分析不仅可以用于确定信号中存在的谐波成分，还可以用于分析信号的频率特性和频带宽度。

通过对谐波分析结果进行进一步处理和计算，可以得到信号的功率谱密度、频谱峰值等相关信息。

在进行谐波分析FFT时，还需要注意一些常见的问题和注意事项。

例如，由于FFT是一种离散傅里叶变换方法，它要求输入信号的长度必须是2的幂。

如果信号长度不符合这个要求，可以使用MATLAB的补零技术进行填充。

此外，为了改善谐波分析的准确性，还可以对信号进行窗函数处理。

基于MATLAB的谐波分析FFT概要

基于MATLAB的谐波分析FFT概要谐波分析是一种用于研究信号频谱及频率成分的技术。

它可以通过将信号分解为不同频率的谐波分量，来揭示信号的频率结构和频率成分之间的关系。

谐波分析可以在多个领域中得到广泛应用，包括音频处理、振动分析、机械故障诊断等。

快速傅里叶变换（Fast Fourier Transform，FFT）是一种常用的谐波分析方法，它通过对信号进行频域离散傅里叶变换（Discrete Fourier Transform，DFT）来实现。

FFT算法是一种高效的计算DFT的方法，其时间复杂度为O(N log N)，相较于直接计算DFT的O(N^2)时间复杂度更加高效。

因此，FFT方法广泛应用于信号处理领域中。

谐波分析的基本思想是，将时域信号转换为频域信号，并通过对频域信号的分析，得出信号的频率分量和振幅。

谐波分析的关键步骤包括：数据预处理、信号转换、频谱分析和结果可视化。

在MATLAB中，进行谐波分析主要涉及以下几个函数：1. fft(x)：该函数用于计算信号x的FFT，返回信号的频域表示。

2. abs(X)：该函数用于计算X的幅度谱，即频域信号的振幅值。

3. angle(X)：该函数用于计算X的相位谱，即频域信号的相位角度。

4. fftshift(X)：该函数用于将频域信号X的零频分量移动到频谱的中心。

在进行谐波分析时，可以按照以下步骤进行：1.载入信号数据并进行预处理。

预处理可以包括去除直流分量、去除噪声等。

2. 使用fft(函数计算信号的FFT，得到频域信号X。

3. 使用abs(函数计算频谱的幅度谱，得到信号的频率分量和振幅。

4. 使用angle(函数计算频谱的相位谱，得到信号的相位信息。

5. 使用fftshift(函数将频域信号X的零频分量移动到频谱的中心，以便于结果的可视化。

6. 可视化频谱分析结果。

可以使用plot(函数绘制频率-振幅图，也可以使用stem(函数绘制频谱，以直观地展示信号的频域特征。

基于MATLAB谐波电流检测仿真研究

式中，φ＝φe －φi 。
以三相电路瞬时无功功率理论为基础，计算 ip、iq 为出发点，即可得出三相电路谐波和无功电流检测的方法，即 ip、iq 运算方式。［2－3］该方法原理如图 2 所示，图中：
ω ω 姨 sinωt －cosωt
C＝－cosωt －sinωt
，C32 ＝
2 3
ω1 ωω ω0
e＝eα ＋eβ ＝e∠φe
（3）
i＝iα ＋iβ ＝i∠φi
（4）
式中 e、i 为矢量 e、i 的模，ψe、ψi 分别为矢量 e、i 的幅角。
瞬时有功电流 ip 和瞬时无功电流 iq 如图 1 所示，分别为矢
量 i 在矢量 e 及其法线上的投影。即：
ip ＝icosφ
（5）
iq ＝isinφ
（6）
时功率理论及其在电力调节中的应用［M］．徐政，译．北京：机械工业出版社，2009
［收稿日期：2011．6．19 ］
图9 由上述仿真结果可见，基于瞬时无功功率理论的谐波电流检测方法能够较好地检测出系统中的谐波电流。 3 结束语
基于瞬时无功功率理论的 pq 法自提出以来，在谐波电流的检测中获得了广泛应用，但也有一些局限性。要求系统三相对称，当系统电压畸变时，按该方法算出的基波电流中包含谐波分量，从而影响检测精度。此外，该方法无法反映零序分量的大小，因此不适合于三相四线制系统的谐波电流检测，这需要更进一步的改进和研究。
本文针对电力系统非线性设备给电网造成的谐波污染问题，采用 ip－iq 运算方式，基于 MATLAB 软件建立仿真模型，对电流信号检测分析，结果表明本文采用的方法能够迅速准确地检测出系统谐波电流，为谐波抑制和无功补偿提供了条件。

基于Matlab的加窗FFT电力系统谐波分析

基于Matlab的加窗FFT电力系统谐波分析目录摘要： (1)1绪论............................................................................................. 错误!未定义书签。

1.1课题背景、研究意义....................................................... 错误!未定义书签。

1.2 谐波的危害与来源.......................................................... 错误!未定义书签。

1.2.1 谐波来源................................................................... 错误!未定义书签。

1.2.2 电力系统谐波的危害 (3)1.3 谐波检测.......................................................................... 错误!未定义书签。

1.4 谐波的标准与指标.......................................................... 错误!未定义书签。

1.5 国内外关于谐波的研究现状 (5)2谐波分析测量............................................................................. 错误!未定义书签。

2.1 傅里叶级数与系数.......................................................... 错误!未定义书签。

2.2 傅里叶级数的复指数形式.............................................. 错误!未定义书签。

多重化整流电路的MATLAB仿真和谐波分析

464
电
力
学
报
第 23 卷
15° , 可构成串联 4 重联结电路, 此电路为 24 脉冲整
流电路。这里不再给出具体电路
[ 1, 5 ]
。
具 ( Pow erSystem B lock set ) 可用于电力电子电路和系统仿真, 文中的模型就是基于该工具箱建立的。
当负载为阻性负载, 负载电流的谐波含量与输出电压相同, 当负载为感性时, 由于电感的滤波作用, 负载电流的波动更小, 谐波含量更少。

© 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved.
2 多重化整流电路的仿真
由于 2 重并联联接和 2 重串联联接波形完全相同, 而3 重、 4 重等多重联结时的谐波规律雷同。限于篇幅的原因, 只给出 2 重串联联接的 12 脉冲整流电路的仿真模型。本文在M A TLAB 环境下对 12 脉波整流路进行仿真,M a t lab6. 5 版本中的电力系统工
图 1 并联联结的 12 脉冲整流电路的原理图
1 多重化整流电路的结构
整流电路的多重连结有并联多重连接和串联多重联结。图 1 给出了将两个整流电路并联联接而成的电路原理图。图 2 给出了将两个三相全控桥整流电路串联联结而成的电路原理图。图 1 的并联联结电路与图 2 的串联联结电路相比, 多使用了一个平衡电抗器, 其作用为平衡两组整流器的电流, 保证任一瞬间每组三相桥电路同时工作。在整流 2 重联结时, 利用变压器二次绕组接法的不同, 使两组三相交流电源间相位错开 30° , 从而使输出整流电压在一个电源周期中脉动 12 次, 故两电路均为 12 脉冲整流电路。整流变压器二次绕组分别采用星形和三角形接法, 为保证两组电压的大小相等, 变压器一次绕组和二次绕组的匝数比为

基于MatlabSimulink的变频系统仿真毕业设计(论文)

基于Matlab/Simulink的变频系统仿真<a target='_blank'href='/www/delivery/ck.php?n=826cd67'><img border='0' alt='' src='/www/delivery/avw.php?zoneid=212&n=826cd67' /></a>0 引言节能减排对于保护环境和国民经济的可持续发展有着巨大作用，己得到世界各国政府和人民的重视，为节省工业用户中使用电动机时消耗的大量的电能，交流变频器调速用得愈来愈多，特别是在风机，泵类的调速中。

不仅如此，在一些可再生能源的装置中也要大量采用变频装置。

例如在风力发电利用永磁发电机发电的直驱发电系统中，其产生的低频电压须经变频后向工频电网送电；又如风力发电中目前广泛采用双馈感应发电机（DFIG），允许转子异步运行，但又要和电网联接，稳定运行，这时必须要向转子输入滑差频率的电流，因滑差可正可负，要求变频器既能送出电能到转子，又能将转子能量反馈到电网。

众所周知，变频器最主要的部件是逆变器，早期的逆变器，比如三相桥式逆变器常采用6脉冲运行方式，其输出电压为方波或阶梯波，谐波含量很大。

近年来，随着开关频率允许很高的全控型电力电子器件，如IGBT，GTR，IGCT等的问世，逆变器的控制大多被脉宽调制PWM代替，其中以正弦波脉宽调制SPWM用得最多。

PWM 的优点是可以同时完成调频、调压的任务，使输出电压中谐波含量极大地减少，此外由于开关频率高，所以有利于快速电流控制。

在设计和研究变频器时，最方便的方法，无疑是利用仿真工具，应该说经过近三十年发展起来的MATHWORKS公司的Matlab软件，特别是它提供的Simulink仿真工具，应是最佳选择之一，它是功能十分强大而齐全的仿真软件，有许多工具箱，用户可以从工具箱中取出所需的元器件，通过联接等操作，建立与实物相对应的数学模型，从而对它进行测试，所得仿真结果可供设计研究参考。

基于MATLAB谐波电流检测仿真研究

随着电力电子器件的广泛应用，系统电流发生畸变，网中电
的谐波污染日益严重，响了供电质量并且造成了电能的浪费，影所以电网中的谐波问题的解决备受关注。本文基于瞬时无功功
真研究。建立电流检测系统的仿真模型，别检测系统电流、分电
Ｌ
…
…
…
一
图１ｏＢ坐标系中的电压、流矢量ｃ — 电
淮阴工学院青年教师基金项目（ＨＧＣ９５００）
图３
系统电流波形
ＡｂｔａｃｓｒｔＴｈｍｅｈｏｒｃｉｅｅｔｏｄｆｅａｔｃｕｒｔｖｒｅｎｄｅｅｃｉｉｏｎｏｔｅｅｔｃｈｏｌｇｙｎａｒｏｃｕｔｔｏｎｓｅｆｈｋｙｅｎｏｉｈｍｎｉｓｐｐｒｓｓｏｎｎｒａｉｐｏｒｅｉａｄｅｃｔｖｅｗｅ
设三相电路各相电压和电流的瞬时值分别为ｅ、ｂｅ和ｉｅ、。、ｉｃ变换到ｏ１相正交的坐标系上，到ｄ、＿，．ｒ３两一得１相瞬时电压３两和电流分别为ｅ；ＢｅＩ。
１
ｃｉｔ－Ｏ｝＝ｓｅＣＳ［ｅｎ
ｃｏｍｐｅｎａｉａｅａＴｈｓａｐａｎｌｚｓｓｔｏｎｒｓ．ｉｐｅｒａｙｅｐｒｃｉｅｏｔｅｐｑｈｉｐｌｓｆｈｉ－ｉｅｏｒｔａｌｉｃｉｅｓａｄｎｔｅｉｐｒｐｌ，ｎｇｉｓｄｉｒｍｏｆｈｅｃｎｖｅａａｇａｔｄｅｅｃｉｎｔｔｏｓｓｅｍ．ｍｕａｔｎｎｙｓｓｙｔＳｉｌｉａａｌｓｉａｃｅｅｄｎａｌ／ｍｕｉｐｌｔｏｒ，ｎｄｕｒｅｔｏｉｈｉｖｉＭｔａｂＳｉｌｎｋａｆｍａｃｒｎｗａｅｏｍｉｇｉｅｎ．ｅｎｙｓｅｓｌｓｏｗｖｆｒｓｖＴｈａａｌｓｉｒｕｔｈｓ

基于MATLAB的交-交变频器谐波分析

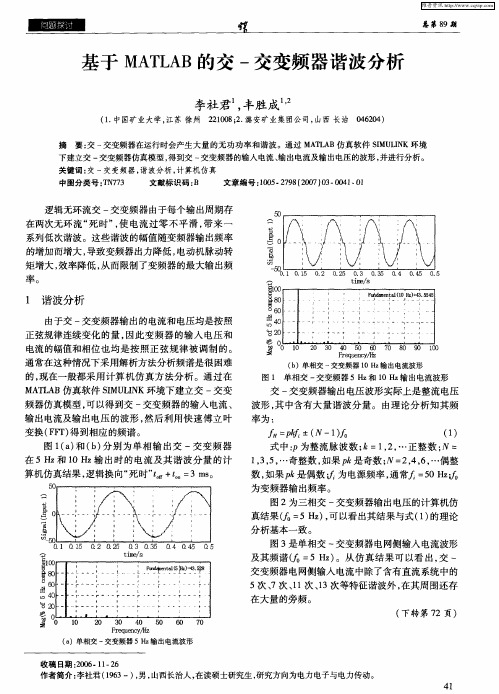
逻辑无环流交一交变频器由于每个输出周期存在两次无环流 “ 死时” 使电流过零不平滑，，带来一系列低次谐波。这些谐波的幅值随变频器输出频率的增加而增大，导致变频器出力降低，电动机脉动转矩增大，效率降低，从而限制了变频器的最大输出频率。
１谐波分析
下建立交一交变频器仿真模型，到交一变频器的输入电流、出电流及输出电压的波形，得交输并进行分析。
关键词：一交变频器，交谐波分析，计算机仿真
中图分类号：Ｎ７Ｔ７３文献标识码：Ｂ文章编号：０５２９（０７０．０１１１０．７８２０）３０４Ｏ
由于交一交变频器输出的电流和电压均是按照正弦规律连续变化的量，此变频器的输入电压和因
电流的幅值和相位也均是按照正弦规律被调制的。通常在这种情况下采用解析方法分析频谱是很困难
的，在一般都采用计算机仿真方法分析。通过在现ＭＡＬＢ仿真软件ＳＭＵＩＫ环境下建立交一交变ＴＡＩＬＮ频器仿真模型，以得到交一交变频器的输入电流、可
维普资讯
总第８９期
基于ＭＴＡＡＬＢ的交一交变频器谐波分析
李社君丰胜成， ’
（．１中国矿业大学，江苏徐州２１０；．２０８２潞安矿业集团公司，山西长治０６０）４２４摘要：一交交变频器在运行时会产生大量的无功功率和谐波。通过ＭＡＬＢ仿真软件ＳＭＵＩＫ环境ＴＡＩＬＮ

12脉波整流电路MATLAB_Simulink仿真及谐波分析

图 5 移相 30°串联 2重联结电路电流波形
将 iA 进行傅里叶分析 ,展开见式 (1)
iA
=
43 π
Id
[
sinωt
-
1 11
sin11ωt
-
1 13
sin13ωt
+
1 sin23ωt + 1 sinωt -
23
25
…
=
43 π Id
sinωt
+
∑ 4 3
π
Id
n = 12k ±1
(-
1) i sinnωt
12 脉动整流电路的与 6 脉动整流电路的 THD (谐波失真 )对比见图 6。
4 结论
从以上分析可以看出 ,采用 12脉波整流的联结方法可以很好地抑制 6脉波整流电路中某些特定次数的高次谐波 ,有效的提高系统的功率因数 , 因此在大容量整流电路中特别是在钢厂电力系统中有着重要的应用。
摘要 :以 12脉波整流电路为研究对象 ,利用 M atlab2Simulink建立模型对其进行仿真 ,并对其产生谐波电流进行分析和计算 ,阐述了其消谐原理。并将其与 6脉波整流电路进行了分析对照 ,证明了 12脉波整流电路消谐的有效性。关键词 :整流装置 ;谐波 ;谐波失真 ;仿真作者简介 :张文斌 ,从事机电工程与自动化研究。中图分类号 : TM762 文献标识码 : A 文章编号 : 100129529 (2008) 0420070203
整流变压器一次侧a2之和其波形见图5c30串联2重联结电路电流波形11sin11t13sin13t23sin23t25sintth17th19th谐波因相互抵消而被消除a相电流只含有12k1次谐波电流可以消除6脉动整流电路中的7等次数的谐波大大减少了电网中的谐波含量其与6脉动整流电路中的各次谐波幅值对比见表16脉动与12脉动整流电路各次谐波含量对比harmonics1113171923251412pluse1712脉动整流电路的与脉动整流电路的thd谐波失真对比见图612脉动与6脉动整流电路的thd对比由仿真波形和表1的对比关系看出由于采用了移相变压器th17th19th谐波相互抵消只剩下11th13th23th25th谐波相比6脉动整流电路而言12脉动整流电路可以很好的抑制某些特定次数的谐波同时由图6可得12脉动较6脉动的谐波失真更小12脉动整流电路的优势更为明显

基于MATLAB的电力谐波分析

目录摘要 (2)Abstract (2)1：绪论 (2)1.1课题背景 (2)1.2谐波的产生 (3)1.3电网中谐波的危害 (5)1.4研究谐波的重要性 (5)2：谐波的限制标准和常用措施 (7)2.1国外谐波的标准和规定 (8)2.1.1谐波电压标准 (8)2.1.2谐波电流的限制 (9)2.2我国谐波的标准和规定 (9)2.2.1谐波电压标准 (10)2.2.2谐波电流的限制 (11)2.3谐波的限制措施 (12)3：谐波的检测与分析 (15)3.1电力系统谐波检测的基本要求 (15)3.2国内外电力谐波检测与分析方法研究现状 (15)3.3谐波的分析 (18)3.3.1电力系统电压（或电流）的傅立叶分析 (19)3.3.2基于连续信号傅立叶级数的谐波分析 (19)4：电力谐波基于FFT的访真 (21)4.1快速傅立叶变换的简要和计算方法 (21)4.1.1快速傅立叶变换的简要 (21)4.1.2快速傅立叶变换的计算方法 (21)4.2 FFT应用举例 (22)5：结论 (28)附录： (28)参考文献： (30)致谢： (30)基于MATLAB的电力谐波分析学生：指导老师：电气信息工程学院摘要：电力系统的谐波问题早在20世纪20年代就引起人们的注意，到了50年代和60年代，由于高压直流输电技术的发展，发表了有关换流器引起电力系统谐波问题的大量论文。

70年代以来，由于电力电子技术的飞速发展，各种电力电子装置在电力系统、工业、交通及家庭中的应用日益广泛，谐波所造成的危害也日趋严重。

世界各国都对谐波问题予以充分的关注。

本文首先对目前国内外电力谐波检测与分析方法进行了综述与展望，并对电力谐波的基本概念、性质和特征参数进行了详细的分析，给出了谐波抑制的措施。

并得出基于连续信号傅立叶级数的各次谐波系数的计算公式，推导了该计算公式与MATLAB函数FFT计算出的谐波系数的关系。

实例证明：准确测量各次谐波参数，对电力系统谐波分析和抑制具有很大意义，可确保系统安全、可靠、经济地运行。

MATLAB仿真的谐波治理方法的探讨

基于MAT LAB仿真的谐波治理方法的探讨王琮泽1　王春光2　杨　佳1　魏立明1(1.吉林建筑工程学院,吉林长春　130021; 2.空军航空大学航空理论系,吉林长春　130022)【摘　要】随着智能建筑及智能小区的迅速发展,电子类电器负荷比重逐渐增大,谐波污染影响日趋严重。

由于谐波源负荷单个容量小,数量多、分布广,尚未引起足够的重视,亦无成熟的防治办法、但这类谐波负荷增长迅猛,其污染影响已不容忽视,采取必要的治理措施已是必然。

针对楼宇电气系统的特点,本文采用了一种混合补偿器进行建筑电气谐波治理的方案,提出控制策略。

并且在此基础上利用M AT LAB提供的仿真平台建立了仿真模型,仿真结果表明所提出的补偿方案有良好的滤波效果。

【关键词】谐波治理;有源电力滤波器;混合补偿法中图分类号:TH132143文献标识码:A1　引　言近年来,智能建筑将向智能建筑群、智能街区、智能城市迅速发展,成为新的经济增长点,智能建筑也成为一个地区、一座城市、一个国家经济和科技实力的象征。

但是,智能建筑由大量的电气设备与电子设备等非线性负荷形成的谐波源,产生谐波和无功功率,对电力系统造成严重污染,使电能质量下降,不仅给智能建筑中的电气设备、电子设备及楼宇智能化系统带来严重的危害和不良影响,并且对智能建筑配电系统以外的电气与电子设备带来危害。

由谐波引发的各种事故和故障,给国民经济和生活造成巨大的损失。

虽然智能建筑技术和谐波抑制技术是当今国内外的研究热点,但对于智能建筑中谐波的危害和不良影响及治理问题没有受到足够的重视,目前已引起国内外有关学者的关注。

2　几种常见的谐波治理方法抑制谐波的总体思路有三个:(1)装置谐波补偿装置来补偿谐波;(2)对电力系统装置本身1;(3)在电网系统中采用适当的措施来抑制谐波[1]。

具体方法有以下几种:211　选用适当的电抗器(1)输入电抗器。

(2)串联直流电抗器[2]。

(3)输出电抗器(电机电抗器)。

基于Matlab的电容滤波型整流电路的谐波分析及电路设计

In the power system, various harmonic source of power system harmonics on the environmental pollution caused by, affect the entire electrical power system environment ， including the power system itself and the majority of users, and the scope of pollution, from far away.
Key words：harmonic；capacitor-filter；rectifier circuit；harmonic analysis；Simulink model
基于 Matlab 的电容滤波型整流电路的谐波分析及电路设计
目录
1 绪论................................................................................................................................. 1 1.1 课题背景及目的..................................................................................................... 1 1.2 国内外研究状况..................................................................................................... 1 1.3 课题研究方法......................................................................................................... 2 1.4 论文构成及研究内容..............................................................................................3

基于MATLAB的变频器谐波抑制的仿真研究(下)

第三章变频器谐波对电网和电动机的影响3.1 变频器对电网的影响3.1.1 变频器输入谐波对电网的影响随着变频器的应用越来越广泛，变频调速系统所占电网负荷也愈来愈大，所以对电网产生的谐波危害也不容忽视。

变频器一般都大量使用了晶闸管或二极管等非线性电力电子元件，不管采用哪种整流方式，变频器从电网中吸取能量的方式均不是连续的正弦波，而是以脉动的断续方式向电网索取电流，这种脉动电流和电网的沿路阻抗共同形成脉动电压降叠加在电网的电压上，使电压发生畸变，经傅立叶分析可知，这种非同期正弦波电流是由于频率相同的基波和频率大于基波频率的谐波组成。

变频器等谐波源设备接入电网后，会向电网注入谐波电流，谐波电流在电网中产生谐波电压，谐波电压叠加在在正弦基波上，通过电网的传递，谐波会影响到整个电网。

主要体现在以下几方面:(l)降低电网电力质量谐波使电网电压、电流波形发生畸变，可能造成中性线电流升高，甚至超过相线电流，可能造成线路过载、发热。

谐波电流、电压必然产生有功消耗和无功消耗，增加线路压降，降低电网效率。

(2)影响自动装置，威胁安全运行线路中电流、电压受谐波影响，不但波形畸变，电流、电压值也会发生变化，导致第二章中高压变频器对电网和电动机的影响测量和计量不准确，很有可能造成电网保护误动或拒动，给电网安全运行留下隐患。

3.1.2 变频器输入侧谐波抑制方法解决谐波污染有两种办法:一是装设谐波补偿装置来补偿谐波，这对各种谐波源都适用。

二是对电力电子装置本身进行改造。

采用产生谐波电流较小的变频器，使其不产生谐波，且功率因数可控制为1。

谐波抑制具体方法如下:(1)谐波滤波装置的传统方法就是采用LC滤波器，既可补偿谐波，又可补偿无功功率，且结构简单，一直被广泛使用，但其存在诸多问题。

谐波抑制的另一个趋势是采用有源电力滤波器，其基本原理是从补偿对象中检测出谐波电流，由补偿装置产生一个与该谐波电流大小相等而极性相反的补偿电流，从而使电网电流中只含有基波分量。

基于Matlab的整流装置谐波分析

, , 由以上仿真结果可以看出，电流中主要含有基波、& 次、% 次、$$ 次、$) 次和 $% 次等各次谐波，表 ( 中各次谐波含量和用理论推导出的谐波含量（见表 $ ）相符，且特征谐波电流幅值和谐波次 ! 6 & # ! ）基本一数的近似关系也与式 " ! 4 "$ # $" ( （致，说明本文所建立的仿真模型及仿真结果正确。整流负荷在实际运行中除产生特征谐波外，还产生非特征谐波，即谐波次数不是 3 % G $ 次的谐波电流，如对于三相六脉动整流桥，产生 ) 次、’ 次和 $& 次等非特征谐波。非特征谐波是由于整流设备触发延迟角不均匀、供电电压不平衡、系统三相阻抗不对称及负荷波动等因素引起的，其谐波次数不能像特征谐波那样由脉动数来决定。非特征谐波电流的计算比较复杂，而且许多因素和参数难以确定，所以非特征谐波一般采用估计的方法。
谌贵辉
整流装置的电气系统模型
— —三相六脉动整以大型整流装置— 流器为例，分析其在电力系统中的谐波问题。图 $ 所示为三相可控整流的电气模型。三相整流桥详细的整流过程分析与供电电流表达式非常复杂，从配电网使
[ 23-" 1 !4& ] 1 "
% !9 %-
（ %）（ 6）
4 !$ + ! ! 9 !’$
用谐波计算的角度看，详细的整流负荷
3 3 3 3 3 3 3 3 图 43 三相可控整流模型
西南石油大学自然科学基金资助（编号： %&&’()*$$% ）。
# !"
・石化电气・*++, 年第 *- 卷第 ** 期

基于MATLAB的谐波分析

基于MATLAB的谐波分析谐波分析在信号处理和电力系统中非常重要，它可以帮助我们理解信号的频率成分以及电力系统中的谐波问题。

MATLAB是一个功能强大的工具，可以用来进行谐波分析，下面将介绍基于MATLAB的谐波分析方法，并说明其在实际应用中的作用。

首先，我们需要知道什么是谐波。

在信号处理中，谐波是指信号中频率为整数倍于基频的成分。

在电力系统中，谐波是指频率为60Hz或50Hz的交流电中的非整数倍成分。

谐波分析的目的是确定信号中的谐波频率和幅值。

在MATLAB中，我们可以使用FFT（快速傅里叶变换）来进行谐波分析。

FFT可以将时域信号转换为频域信号，从而可以获得信号的频率成分。

首先，我们需要准备一个信号，并将其表示为MATLAB中的向量。

然后，我们可以使用FFT函数对信号进行变换，得到信号的频率成分。

```matlabt = 0:1/fs:1-1/fs; % 时间向量f=1000;%信号频率x = sin(2*pi*f*t); % 正弦波信号```接下来，我们可以使用FFT函数对信号进行变换，并计算信号的幅频响应。

然后，我们可以选择性地显示特定频率范围内的幅频响应。

```matlabX = fft(x); % 对信号进行傅里叶变换Mag_X = abs(X); % 计算傅里叶变换的幅频响应frequencies = (0:length(X)-1)*(fs/length(X)); % 计算频率向量%选择显示特定频率范围内的幅频响应f_min = 0; % 最小频率f_max = 2000; % 最大频率indices = find(frequencies >= f_min & frequencies <= f_max);plot(frequencies(indices), Mag_X(indices))xlabel('Frequency (Hz)')ylabel('Amplitude')```上述代码将生成频率范围在0Hz到2000Hz之间的幅频响应图。

基于MATLAB的谐波分析FFT教材

目录（1）Matlab6.5以上版本软件； ....................................................... 错误！未定义书签。

绪论. (1)1 公式分析及计算 (2)1.1傅里叶变换的原理 (2)1.2傅里叶变换的证明 (3)1.3 周期信号的分解 (3)1.4 方波的分解 (5)2 建模与仿真 (7)2.1建模 (7)2.2仿真 (8)3 仿真结果分析 (10)4 小结 (11)参考文献 (13)绪论方波是一种非正弦曲线的波形，通常会于电子和讯号处理时出现。

由于一般电子零件只有“高(1)”和“低(0)”两个值，方波就自然产生，所以理想方波只有“高”和“低”这两个值。

电流的波形为矩形的电流即为方波电流。

不论时间轴上下是不是对称的，只要是矩形就可叫方波，必要时，可加“对称”，“不对称”加以说明。

而在现实世界，方波只有有限的带宽。

因为方波可以快速从一个值转至另一个(即0→1或1→0)，所以方波就用作时钟讯号来准确地触发同步电路。

但是如果用频率定义域来表示方波，就会出然一连串的谐波。

所以方波可用相应频率的基波及其奇次谐波合成。

在电路信号系统的分析中，随着电路规模的加大，微分方程的阶数以及联立后所得的方程的个数也随之加大，加上电器元件的多样化，这些都给解题运算分析电路系统带来了一定的困难。

传统的计算机编程语言，如FORTRAN、C语言等，虽然都可以帮助计算，但在处理高阶微分方程和大规模的联立方程组的问题时大量的时间和精力都花在矩阵处理和图形的生成分析等繁琐易错的细节上。

而MATLAB凭借其强大的矩阵运算能力、简便的绘图功能、可视化的仿真环境以及丰富的算法工具箱，已成为科研和工程技术人员的有力开发工具。

利用MATLAB不仅可以简单快速的求解电路方程，同时，MAYLAB提供的Simulink工具还可以直接建立电路模型，随意改变模型的参数，并且还可以快速得到仿真拟结果，进一步省去了编程的步骤。