砀山五中八年级一元一次不等式培优专题训练
初中八年级数学一元一次不等式及一元一次不等式组专题练习

一元一次不等式及一元一次不等式组(一)一、填空:(每小题2分,共32分) 1.若a>b,则不等式级组x ax b <⎧⎨≤⎩的解集是 ( )A .x ≤b B.x<a C.b ≤x<aD.无解2.在方程组221x y my x -=⎧⎨-=⎩ 中,x,y 满足x+y>0,m 的取值范围是 ( )A . B. C.D.3.下列按要求列出的不等式中错误的是 ( ) A.m 是非负数,则m ≥0 B.m 是非正数,则m ≦0 C.m 不大于-1,则m<-1 D.2倍m 为负数,则2m<04.不等式9-114x>x+23的正整数解的个数是 ( ) A.1 B.2C.3D.45.已知a>b>0,那么下列不等式中错误的是 ( ) A.1a >1b >0 B.a b >b aC.-a<-bD.a-b>b-a 6.如果b<a<0,则下列结论中正确的是 ( ) A.b 2<ab B.b 2>ab>a2C.b 2<a2D.b 2>a 2>ab7.a<0,b>0,a+b<0,则下列关系中正确是 ( ) A.a>b>-b>-a B.a>-a>b>-b C.-a>b>-b>a D.b>a>-b>-a 8.如果a>b,那么下列不等式中正确的是 ( ) A.a-2>b+2 B.8a <8bC.ac<bcD.-a+3<-b+3 9.若a<0,下列式子不成立的是 ( ) A.-a+2<3-a B.a+2<a+3 C.-2a <-3aD.2a>3a 10. 若a 、b 、c 是三角形三边的长,则代数式a 2+ b 2—c 2—2ab 的值 ( ). A.大于0 B.小于0 C.大于或等于0 D.小于或等于011.若方程7x+2m=5+x 的解在-1和1之间,则m 的取值范围是 ( )A.3>m>12 B.3>m>-12 C.112>m>-12 D.12>m>-112 12.若方程35x a -=26b x-的解是非负数,则a 与b 的关系是 ( )A.a ≤56bB.a ≥56bC.a ≥-56bD.a ≥528b13.下列不等式中,与不等式2x+3 ≤7有相同解集的是 ( )A. 1+22x -≥3x B. 722x - -23x -≥2(x+1) C. 3x -2(2)3x -≤6 D.1-13x -≤12x- 14.如果不等式(m+1)x>m+1的解集是x<1,那么m 必须满足 ( ) A.m ≤-1 B.m<-1 C.m ≥1D.m>1.15.若方程组3133x y k x y +=+⎧⎨+=⎩ 的解x 、y 满足01x y <+<,则k 的取值范围是 ( )A .40k -<< B. 10k -<< C.08k << D. 4k >-16.设a 、b 、c 的平均数为M ,a 、b 的平均数为N ,N 、c 的平均数为P ,若a >b >c ,则M 与P 的大小关系是( ).A. M = PB. M > PC. M < PD. 不确定 二、填空:(每小题2.5分,共40分)17. 用不等式表示“7与m 的3倍的和是正数“就是____ _. 18.不等式组3231x x -≥⎧⎨->⎩的解集是 .19.当x ________ 时,代数式354x -的值是非正数,当x _______时,代数式3(2)5x -的值是非负数.20.关于x 的方程3x+2m=x-5的解为正数,则m 的取值范围是 .21.关于x 的方程kx+15=6x+13的解为负数,则k 的取值范围是 . 22.能使代数式12×(3x-1)的值大于(5x-2)+14的值的最大整数x 是 . 23. 已知x >0,y <0.且x + y <0,那么有理数x , y ,- x ,- y 的大小关系为 .24.若关于x 的不等式组41320x xx a +⎧>+⎪⎨⎪-<⎩ 解集为x<2,则a 的取值范围是 .25. 在一次“人与环境”知识竞赛中,共有25个题,每题四个答案,其中只有一个答案正确,每选对一题得4分,不选或选错倒扣2分,如果一个学生在本次竞赛中得分不低于60分,那么他至少要答对________题.26.已知机器工作时,每小时耗油9kg,现油箱中存油多于38kg但少超过45kg,问这油箱中的油可供这台机器工作时间t的范围为___________ 。
初中数学一元一次不等式专项练习

初中数学一元一次不等式专项练习(总38页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除初中数学一元一次不等式专项练习题号 一二三四五总分得分1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明评卷人 得分一、选择题(题型注释) 1.若不等式a x x ≤-+-3312有解,则实数a 最小值是( ) A 、1 B 、2 C 、4 D 、62.关于x 的不等式组⎪⎪⎩⎪⎪⎨⎧+<+->+a x x x x 3223215只有5个整数解,则a 的取值范围是( )3.若不等式组⎩⎨⎧<-<+022m x mx 的解集为x <2m -2,则m 的取值范围是( )A .m≤2B .m≥2C .m >2D .m <24.(2011山东济南,6,3分)不等式组2324x x +<⎧⎨-<⎩的解集是( )A .x >﹣2B .x <1C .﹣2<x <1D .x <﹣25.若b a >,则下列不等式成立的是( )A .33-<-b aB .b a 22->-C .44ba < D .1->b a6.(11·贺州)已知⊙O 1和⊙O 2的半径分别为2和5,如果两圆的位置关系为外离,那么圆心距O 1O 2的取值范围在数轴上表示正确的是7.不等式组211420x x ->⎧⎨-⎩,≤的解在数轴上表示为( ▲ )8.如果a >b ,c <0,那么下列不等式成立的是( ). (A) a +c >b +c ; (B) c -a >c -b ; (C) ac >bc ; (D)a b c c> . 9.(2011•湛江)不等式的解集x≤2在数轴上表示为( )10.(2011•金华)不等式组的解在数轴上表示为( )A 、B 、C 、D 、11.不等式组⎩⎨⎧+≤3123>x x 的解集在数轴上表示正确的是( )12. 解集在数轴上表示为如图1所示的不等式组是( )A.⎩⎨⎧≥->23x xB.⎩⎨⎧≤-<23x xC.⎩⎨⎧≥-<23x xD.⎩⎨⎧≤->23x x13.已知关于x的不等式组20xx a+>⎧⎨-≤⎩的整数解共有4个,则a的最小值为()A.2B.2.1C.3D.114.若不等式组⎩⎨⎧->+<+1472,03xxax的解集为0<x,则a的取值范围为()A. a>0 B. a=0 C. a>4 D.a=415.不等式组2030xx-<⎧⎨-≥⎩的正整数解的个数是()A.1个B.2个C.3个D.4个16.不等式组⎩⎨⎧≤-->542xx的解集是()A.2->x B.52≤<-x C.5≤x D.无解17.. 如果不等式(a+1)x>a+1的解集为x<1,那么a的取值范围是. ()A .a>0 B.a<0 C.a>-1 D.a<-118.如果不等式组⎩⎨⎧><mxx3有解,那么m的取值范围是()A.m>3B.3≥m C.m<3 D.3≤m19.不等式组213351xx+>⎧⎨-⎩≤的解集在数轴上表示正确的是()20.若不等式组0,122x ax x+⎧⎨->-⎩≥有解,则a的取值范围是()A.a >-1.B.a ≥-1. C a ≤1. D.a <1.21.不等式组24,241x x x x +⎧⎨+<-⎩≤的正整数解有:(A)1个 (B)2个(C)3个 (D)4个22.若不等式ax 2+7x-1>2x+5对-1≤a≤1恒成立,则x 的取值范围是( ).(A)2≤x≤3 (B)2<x<3 (C)-1≤x≤1 (D)-1<x<123.不等式组⎩⎨⎧≥->+125523x x 的解在数轴上表示为( )24.某校团委与社区联合举办“保护地球,人人有责”活动,选派20名学生分三组到120个店铺发传单,若第一、二、三小组每人分别负责8、6、5个店铺,且每组至少有两人,则学生分组方案有【 】 A. 6种 B. 5种 C. 4种 D. 3种 25.-3x<-1的解集是( )A 、x<31B 、x<-31C 、x>31D 、x>-3126.点P (x-1,x+1)不可能在( )A 、第一象限B 、第二象限C 、第三象限D 、第四象限27.不等式组⎩⎨⎧2x -4≤x +2x ≥3的解集是( )A .x ≥3B .x ≤6C .3≤x ≤6D .x ≥6 28.下列不等式组中,解集在数轴上表示出来如图所示的不等式组为( )A. ⎩⎨⎧-≥<;1,2x xB. ⎩⎨⎧-><;1,2x xC. ⎩⎨⎧-≤>;1,2x x D. ⎩⎨⎧-≤<.1,2x x29.若a<b ,则下列不等式中正确的是()(A) -a> -b (B)a+b<0 (C)ac<bc (D) a-b>030.在一条笔直的公路边,有一些树和路灯,每相邻的两盏灯之间有3棵树,相邻的树与树,树与灯间的距离是10cm,如图,第一棵树左边5cm处有一个路牌,则从此路牌起向右510m~550m之间树与灯的排列顺序是【】0 1 2 3 4-1-2-3第II卷(非选择题)请点击修改第II卷的文字说明评卷人得分二、填空题(题型注释)31.若不等式3x-a≤0的正整数解是1,2,3,则a的取值范围是32.关于x的不等式3x-2a≤-2的解集如图所示,则a=______.33.写出含有解为x=1的一元一次不等式__ __(写出一个即可).34.某班级为筹备运动会,准备用365元购买两种运动服,其中甲种运动服20元/套,乙种运动服35元/套,在钱都用尽的条件下,有种购买方案. 35.不等式2-x≤1的解集为____________.36.不等式组⎩⎨⎧-<+<212mxmx的解集是x<m-2,则m的取值应为_________。
2019-2020初中数学八年级上册《一元一次不等式》专项测试(含答案) (1047)
2019-2020年八年级数学上册《一元一次不等式》测试卷学校:__________题号一 二 三 总分 得分评卷人得分 一、选择题1.(2分)不式式组324235x x ->⎧⎨+<⎩的解是( ). A . 12x << B . 2x >或1x < C .无解 D .01x <<2.(2分)若2a a >,则a 应满足( )A .0a <B .01a <<C .11a -<<D .1a >或0a < 3.(2分)不等式组475(1)22463x x x x -<-⎧⎨->-⎩的解在数轴上表示为( )A .B .C .D . 4.(2分)如果不等式组731x x x n +<-⎧⎨>⎩的解集是4x >,那么n 的取值范围是( ) A .4n ≥B .4n ≤C .4n =D .64n < 5.(2分)不等式组2130x x ≤⎧⎨+>⎩的解在数轴上可表示为( )A .B .C .D .6.(2分)亮亮准备用自己节省的零花钱买一台英语复读机,他现在已存有45元,计划从现在起以后每个月节省30元,直到他至少..有300元.设x 个月后他至少有300元,则可以用于计算所需要的月数x 的不等式是( )A .3045300x -≥B .3045300x +≥C .3045300x -≤D .3045300x +≤7.(2分)关于不等式22x a -+≥的解集如图所示,a 的值是( )A .0B .2C .-2D .-48.(2分)若方程3(1)1(3)5m x m x x ++=--的解是负数,则 m 的取值范围是( )A .54m >- B .54m > C .54m <- D .54m < 9.(2分)晨晨准备用自己节省的零花钱买一台英语复读机,她现在已有 65 元,计划从现在起 以后每个月节省 25 元,直到她至少有 320元钱,设x 个月她至少有 320 元,则可以用于计算她所需要的月数x 的不等式是( )A .2565320x -≥B .2565320x +≥C .2565320x -≤D .2565320x +≤10.(2分)设221P y y =++,21Q y =+,如果P Q >,那么必有( )A .0y >B .0y <C .0y ≥D .0y ≤11.(2分)下列属于一元一次不等式的是( )A .10>8B .2132x y +>+C .12(1)12y y +>- D .235x +> 12.(2分)如果x y x ->,x y y +<,那么下列式子中,正确的是( )A .0x y +> 0x y -< C .0xy < D .0x y> 13.(2分)小宝和爸爸、妈妈三人在操场上玩跷跷板,爸爸体重为69千克,坐在跷跷板的一端,体重只有妈妈一半的小宝和妈妈同坐在跷跷板的一端,这是爸爸的一端仍然着地.后来小宝借来一副质量为6千克的哑铃,加在他和妈妈坐的一端,结果爸爸被跷起离地.小宝体重可能是( )A .23.3千克B .23千克C .21.1千克D .19.9千克二、填空题14.(2分) 若0a b +<,0ab <,a b <,,则a 、a -、b 、b -的大小关系用“<”连接起来是 .15.(2分)如果不等式组05x a x ->⎧⎨>⎩的解为5x >,那么a 的取值范围是 . 16.(2分)如果不等式2(1)3x a --≤的正整数解是 1、2、3,那么a 的取值范围是 .17.(2分)不等式组42x x >-⎧⎨<⎩的解集是 . 18.(2分)已知2(34)|1|0x y a x --+-=中,2y <,则a 的取值范围是 .19.(2分)不等式322104x x --+>的所有整数解的积为 .三、解答题20.(7分) 某公司为了扩大经营,决定购进 6台机器用于生产某种活塞.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产活塞的数量如下表所示. 经过预算,本次购买机器所耗资金不能超过34万元.问:(1)按该公司要求,可以有哪几种购买方案?(2)如果该公司要求购进的 6 台机器的日生产能力不能低于380个,那么为了节约资金应选择哪种购买方案?21.(7分)下表为北京奥运会官方票务网站公布的几种球类比赛的门票价格,某球迷准备用8000 元预订 10 张下表中比赛项目的门票.(1)若全部资金用来预订男篮门票和乒乓球门票,问他可以订男篮门票和乒乓球门票各多少张?(2)若在现有资金 8000 元允许的范围内和总票数不变的前提下,他想预订下表中三种球类门票,其中男篮门票数与足球门票数相同,且乒乓球门票的费用不超过男篮门票的费用,求他能预订三种球类门票各多少张?22.(7分)某种植物适宜生长在温度为18℃~20℃的山区,已知山区海拔每升高100 m,气温下降 0.5℃,现在测出山脚下的平均气温为22℃,问该植物种在山的哪一部分为宜(假设山脚海拔为 0 m)?23.(7分)解不等式组523483x x x x -<+⎧⎪+⎨≥-⎪⎩,并写出它的非负整数解.24.(7分)解不等式组12512x x x +≤⎧⎪⎨->⎪⎩,并写出它的所有整数解.25.(7分)已知关于x 的不等式424233x x a +<+的解也是不等式12162x -<的解,求a 的值.26.(7分)某班 34 个同学去春游,共收款 80 元,由小军去买点心,要求每人1 包.已知有 3元一包和 2 元一包两种点心,试问 3 元一包的点心最多能买几包?27.(7分)已知方程21|28|(5)02x x y a -+--=.(1)当0y >时,求a 的取值范围;(2)当0y <时,求a 的取值范围.28.(7分)已知3(21)23x x b -=-的解不大于2,求b 的取值范围.53b ≥-29.(7分)若x y<,比较32x-与32y-的大小,并说明理由.30.(7分)(1)你能找出几个使不等式2 2.515x-≥⋅成立的x的值吗?(2)x=3,5,7 能使不等式225 1.5x-⋅≥成立吗?【参考答案】***试卷处理标记,请不要删除一、选择题1.C2.D3.A4.B5.A6.B7.A8.A9.B10.A11.C12.D13.C二、填空题14.a b b a<-<<-15.5a≤16.13a ≤<17.-4<x<218.5a >-19.0三、解答题20.(1)3种:方案一:选购甲机器2台,乙机器4台;方案二:选购甲机器1 台,乙机器5 台;方案三:选乙机器6台 (2)选购甲机器 1台,乙机器 5 台21.(1)可以订男篮门票6张,乒乓球门票4张;(2)可以订男篮门票3张,足球门票3张,乒乓球门票4张22.400 m 到800m23.-2≤x<3,x=0,l ,224.1≤x<3,1,225.726.12包27.(1)a<20;(2)a>2028.53b ≥-29.3-2x>3-2y30.(1)能,x=2,3,4,…;(2)成立。
八年级一元一次不等式练习题(经典版)

一元一次不等式1、下列不等式中,是一元一次不等式的是 ( )A012>-x ; B 21<-; C 123-≤-y x ; D 532>+y ;2.下列各式中,是一元一次不等式的是( ) A.5+4>8 B.2x -1 C.2x ≤5D.1x-3x ≥0 3. 下列各式中,是一元一次不等式的是( ) (1)2x<y (2)(3)(4)4.用“>”或“<”号填空.若a>b,且c ,则:(1)a+3______b+3; (2)a-5_____b-5; (3)3a____3b; (4)c-a_____c-b (5); (6)5.若m >5,试用m 表示出不等式(5-m )x >1-m 的解集______. 二、填空题(每题4分,共20分) 1、不等式122x >的解集是: ;不等式133x ->的解集是: ; 2、不等式组⎩⎨⎧-+0501>>x x 的解集为 . 不等式组3050x x -<⎧⎨-⎩>的解集为 .3、不等式组2050x x ⎧⎨-⎩>>的解集为 . 不等式组112620x x ⎧<⎪⎨⎪->⎩的解集为 .三. 解下列不等式,并在数轴上表示出它们的解集.(1) 8223-<+x x 2. x x 4923+≥-(3). )1(5)32(2+<+x x (4). 0)7(319≤+-x (5) 31222+≥+x x (6) 223125+<-+x x(7) 7)1(68)2(5+-<+-x x (8))2(3)]2(2[3-->--x x x x (9)1215312≤+--x x (10) 215329323+≤---x x x(11)11(1)223x x -<- (12) )1(52)]1(21[21-≤+-x x x(13) 41328)1(3--<++x x (14) ⋅->+-+2503.0.02.003.05.09.04.0x x x三、解不等式组,并在数轴上表示它的解集 1. ⎩⎨⎧≥-≥-.04,012x x2.⎩⎨⎧>+≤-.074,03x x4⎪⎩⎪⎨⎧+>-<-.3342,121x x x x 5.-5<6-2x <3.6.⎪⎩⎪⎨⎧⋅>-<-322,352x x x x7.⎪⎩⎪⎨⎧->---->-.6)2(3)3(2,132x x xx8⎪⎩⎪⎨⎧+>-≤+).2(28,142x x x9..234512x x x -≤-≤-10.532(1)314(2)2x x x -≥⎧⎪⎨-<⎪⎩ 11.⎪⎩⎪⎨⎧≥--+.052,1372x x x12.⎪⎩⎪⎨⎧---+.43)1(4,1321x x x x13.14321<--<-x四.变式练习 1不等式组⎩⎨⎧+>+<+1,159m x x x 的解集是x >2,则m 的取值围是( ).(A)m ≤2 (B)m ≥2(C)m ≤1(D)m ≥12. k 满足______时,方程组⎩⎨⎧=-=+4,2y x k y x 中的x 大于1,y 小于1.3. 若m 、n 为有理数,解关于x 的不等式(-m 2-1)x >n .4. .已知关于x ,y 的方程组⎩⎨⎧-=++=+134,123p y x p y x 的解满足x >y ,求p 的取值围.5. 已知方程组⎩⎨⎧-=++=+②①m y x m y x 12,312的解满足x +y <0,求m 的取值围.6. 适当选择a 的取值围,使1.7<x <a 的整数解:(1) x 只有一个整数解; (2) x 一个整数解也没有.7. 当310)3(2k k-<-时,求关于x 的不等式k x x k ->-4)5(的解集.8. 已知A =2x 2+3x +2,B =2x 2-4x -5,试比较A 与B 的大小.9. 当k 取何值时,方程组⎩⎨⎧-=+=-52,53y x k y x 的解x ,y 都是负数.10. 已知⎩⎨⎧+=+=+122,42k y x k y x 中的x ,y 满足0<y -x <1,求k 的取值围.11. 已知a 是自然数,关于x 的不等式组⎩⎨⎧>-≥-02,43x a x 的解集是x >2,求a 的值.12. 关于x 的不等式组⎩⎨⎧->-≥-123,0x a x 的整数解共有5个,求a 的取值围.13. k 取哪些整数时,关于x 的方程5x +4=16k -x 的根大于2且小于10?14. 已知关于x ,y 的方程组⎩⎨⎧-=-+=+34,72m y x m y x 的解为正数,求m 的取值围.15. 若关于x 的不等式组⎪⎪⎩⎪⎪⎨⎧+<+->+a x x x x 322,3215只有4个整数解,求a 的取值围.探究: 1、 如果不等式组x a x b >⎧⎨<⎩无解,问不等式组11y a y b +≥⎧⎨+≤⎩的解集是怎样的?2、已知()()3525461x x x ++<-+,化简3113x x +--。
八年级数学上册一元一次不等式专题卷(附答案)

八年级数学上册一元一次不等式专题卷(附答案)评卷人得分一、选择题(题型注释)1.如果不等式组无解,那么m 的取值范围是()A.m>5 B.m≥5 C.m<5 D.m≤52.不等式组840312xx-⎩≤-⎧⎨>的解集在数轴上表示为()3.如果不等式无解,则b的取值范围是()A.b>﹣2 B.b<﹣2 C.b≥﹣2 D.b≤﹣24.不等式2x﹣6<0的解集是()A.x>3 B.x<3 C.x>﹣3 D.x<﹣35.已知不等式组,其解集在数轴上表示正确的是()6.关于x的不等式x-b>0恰有两个负整数解,则b的取值范围是()A.-3<b<-2 B.-3<b≤-2C.-3≤b≤-2 D.-3≤b<-27.不等式组的解集在数轴上表示为()A. B .C . D.8.在数轴上表示不等式组202(1)1xx x+>⎧⎨-≤+⎩的解集,正确的是()A. B. C . D.9.不等式2x﹣6>0的解集是()A.x>1 B.x<﹣3 C.x>3 D.x<310.如果不等式组有解,那么m的取值范围是()A.m>8 B.m<8 C.m≥8 D.m≤811.已知不等式组1x a x >⎧⎨≥⎩的解集是x ≥1,则a 的取值范围是( ) A .a <1 B .a ≤1 C .a ≥1 D .a >1 评卷人得分二、填空题(题型注释) 12.学校举行百科知识抢答赛,共有20道题,规定每答对一题记10分,答错或放弃记﹣4分,八年级一班代表的得分目标为不低于88分,则这个队至少要答对 道题才能达到目标要求.13.不等式组⎩⎨⎧-≤->+x x x 81212的最大整数解是 .14.不等式组的解集为 .15.不等式组10241x x x +⎧⎨+-⎩>≥的解集为 . 16.定义新运算:对于任意实数a ,b 都有:a ⊕b=a (a ﹣b )+1,其中等式右边是通常的加法、减法及乘法运算.如:2⊕5=2×(2﹣5)+1=2×(﹣3)+1=﹣5,那么不等式3⊕x <13的解集为 。
八年级一元一次不等式练习题(经典版)

一元一次不等式1、下列不等式中,是一元一次不等式的是 ( )A012>-x ; B 21<-; C 123-≤-y x ; D 532>+y ;2.下列各式中,是一元一次不等式的是( ) A.5+4>8 B.2x -1 C.2x ≤5D.1x-3x ≥0 3. 下列各式中,是一元一次不等式的是( ) (1)2x<y (2)(3)(4)4.用“>”或“<”号填空.若a>b,且c ,则:(1)a+3______b+3; (2)a-5_____b-5; (3)3a____3b; (4)c-a_____c-b (5); (6)5.若m >5,试用m 表示出不等式(5-m )x >1-m 的解集______. 二、填空题(每题4分,共20分) 1、不等式122x >的解集是: ;不等式133x ->的解集是: ; 2、不等式组⎩⎨⎧-+0501>>x x 的解集为 . 不等式组3050x x -<⎧⎨-⎩>的解集为 .3、不等式组2050x x ⎧⎨-⎩>>的解集为 . 不等式组112620x x ⎧<⎪⎨⎪->⎩的解集为 .三. 解下列不等式,并在数轴上表示出它们的解集.(1) 8223-<+x x 2. x x 4923+≥-(3). )1(5)32(2+<+x x (4). 0)7(319≤+-x (5) 31222+≥+x x (6) 223125+<-+x x(7) 7)1(68)2(5+-<+-x x (8))2(3)]2(2[3-->--x x x x (9)1215312≤+--x x (10) 215329323+≤---x x x(11)11(1)223x x -<- (12) )1(52)]1(21[21-≤+-x x x(13) 41328)1(3--<++x x (14) ⋅->+-+2503.0.02.003.05.09.04.0x x x三、解不等式组,并在数轴上表示它的解集 1. ⎩⎨⎧≥-≥-.04,012x x2.⎩⎨⎧>+≤-.074,03x x4⎪⎩⎪⎨⎧+>-<-.3342,121x x x x 5.-5<6-2x <3.6.⎪⎩⎪⎨⎧⋅>-<-322,352x x x x7.⎪⎩⎪⎨⎧->---->-.6)2(3)3(2,132x x xx8⎪⎩⎪⎨⎧+>-≤+).2(28,142x x x9..234512x x x -≤-≤-10.532(1)314(2)2x x x -≥⎧⎪⎨-<⎪⎩ 11.⎪⎩⎪⎨⎧≥--+.052,1372x x x12.⎪⎩⎪⎨⎧---+.43)1(4,1321x x x x13.14321<--<-x四.变式练习 1不等式组⎩⎨⎧+>+<+1,159m x x x 的解集是x >2,则m 的取值围是( ).(A)m ≤2 (B)m ≥2(C)m ≤1(D)m ≥12. k 满足______时,方程组⎩⎨⎧=-=+4,2y x k y x 中的x 大于1,y 小于1.3. 若m 、n 为有理数,解关于x 的不等式(-m 2-1)x >n .4. .已知关于x ,y 的方程组⎩⎨⎧-=++=+134,123p y x p y x 的解满足x >y ,求p 的取值围.5. 已知方程组⎩⎨⎧-=++=+②①m y x m y x 12,312的解满足x +y <0,求m 的取值围.6. 适当选择a 的取值围,使1.7<x <a 的整数解:(1) x 只有一个整数解; (2) x 一个整数解也没有.7. 当310)3(2k k-<-时,求关于x 的不等式k x x k ->-4)5(的解集.8. 已知A =2x 2+3x +2,B =2x 2-4x -5,试比较A 与B 的大小.9. 当k 取何值时,方程组⎩⎨⎧-=+=-52,53y x k y x 的解x ,y 都是负数.10. 已知⎩⎨⎧+=+=+122,42k y x k y x 中的x ,y 满足0<y -x <1,求k 的取值围.11. 已知a 是自然数,关于x 的不等式组⎩⎨⎧>-≥-02,43x a x 的解集是x >2,求a 的值.12. 关于x 的不等式组⎩⎨⎧->-≥-123,0x a x 的整数解共有5个,求a 的取值围.13. k 取哪些整数时,关于x 的方程5x +4=16k -x 的根大于2且小于10?14. 已知关于x ,y 的方程组⎩⎨⎧-=-+=+34,72m y x m y x 的解为正数,求m 的取值围.15. 若关于x 的不等式组⎪⎪⎩⎪⎪⎨⎧+<+->+a x x x x 322,3215只有4个整数解,求a 的取值围.探究: 1、 如果不等式组x a x b >⎧⎨<⎩无解,问不等式组11y a y b +≥⎧⎨+≤⎩的解集是怎样的?2、已知()()3525461x x x ++<-+,化简3113x x +--。
八年级的下册列一元一次不等式组解应用题专项练习.doc

八年级下册列一元一次不等式组解应用题专项练习1.某学校组织八年级学生参加社会实践活动,若单独租用35 座客车若干辆,则刚好坐满;若单独租用55 座客车,则可以少租一辆,且余45 个空座位.(1)求该校八年级学生参加社会实践活动的人数;(2)已知 35 座客车的租金为每辆320 元, 55 座客车的租金为每辆400 元.根据租车资金不超过1500 元的预算,学校决定同时租用这两种客车共 4 辆(可以坐不满).请你计算本次社会实践活动所需车辆的租金.2.某渔场计划购买甲、乙两种鱼苗共6000 尾,甲种鱼苗每尾0.5 元,乙种鱼苗每尾0.8 元.相关资料表明:甲、乙两种鱼苗的成活率分别为90%和 95%.(1)若购买这批鱼苗共用了 3600 元,求甲、乙两种鱼苗各购买了多少尾?(2)若购买这批鱼苗的钱不超过4200 元,应如何选购鱼苗?(3)若要使这批鱼苗的成活率不低于93%,且购买鱼苗的总费用最低,应如何选购鱼苗?3. 为支持玉树搞震救灾,某市A、 B、 C 三地现分别有赈灾物资100 吨、 100 吨、 80 吨,需全部运往玉树重灾地区 D、 E 两县,根据灾区情况,这批赈灾物资运往 D 县的数量比运往 E 县的数量的 2 倍少 20 吨 .(1)求这赈灾物资运往D、 E 两县的数量各是多少?(2)若要求 C 地运往 D 县的赈灾物资为60 吨, A 地运往 D 的赈灾物资为x吨(x为整数),B地运往D 县的赈灾物资数量小于 A 地运往 D县的赈灾物资数量的 2 倍,其余的赈灾物资全部运往E 县,且 B 地运往 E 县的赈灾物资数量不超过25 吨,则 A、 B 两地的赈灾物资运往D、 E 两县的方案有几种?(3)已知 A、 B、 C三地的赈灾物资运往D、 E 两县的费用如下表:A地B地C地运往 D 县的费用(元/220 200 200吨)运往 E 县的费用(元/吨)250 220 210为即时将这批赈灾物资运往D、 E 两县,某公司主动承担运送这批赈灾物资的总费用,在(2)问的要求下,该公司承担运送这批赈灾物资的总费用最多是多少?4.某花农培育甲种花木 2 株,乙种花木 3 株,共需成本1700 元;培育甲种花木 3 株,乙种花木 1 株,共需成本 1500 元.( 1)求甲、乙两种花木每株成本分别为多少元?( 2)据市场调研, 1 株甲种花木售价为760 元, 1 株乙种花木售价为540 元.该花农决定在成本不超过 30000 元的前提下培育甲乙两种花木,若培育乙种花木的株数是甲种花木的 3 倍还多 10 株 ,那么要使总利润不少于21600 元,花农有哪几种具体的培育方案?5. 近期以来,大蒜和绿豆的市场价格离奇攀升,网民戏称为“蒜你狠”、“豆你玩”.以绿豆为例, 5 月上旬某市绿豆的市场价已达16 元 / 千克.市政府决定采取价格临时干预措施,调进绿豆以平抑市场价格.经市场调研预测,该市每调进100 吨绿豆,市场价格就下降 1 元/ 千克.为了即能平抑绿豆的市场价格,又要保护豆农的生产积极性,绿豆的市场价格控制在8 元/ 千克到 10 元/ 千克之间(含8 元/ 千克和 10 元 / 千克).问调进绿豆的吨数应在什么范围内为宜?6. 郑老师想为希望小学四年(3)班的同学购买学习用品,了解到某商店每个书包价格比每本词典多8 元.用 124 元恰好可以买到 3 个书包和 2 本词典.( 1)每个书包和每本词典的价格各是多少元?( 2)郑老师计划用l000 元为全班 40 位学生每人购买一件学习用品( 一个书包或一本词典) 后.余下不少于 l OO元且不超过120 元的钱购买体育用品.共有哪几种购买书包和词典的方案?7.某企业在生产甲、乙两种节能产品时需用A、 B 两种原料,生产每吨节能产品所需原料的数量如下表所示:原料A 原料(吨)B 原料(吨)节能产品甲种产品 3 3乙种产品 1 5m(万元 )甲乙6O 2 3 n(吨) 销售甲、乙两种产品的利润m(万元)与销售量n(吨)之间的函数关系如图所示.已知该企业生产了甲种产品x吨和乙种产品y吨,共用去 A 原料 200 吨.(1)写出x与y满足的关系式;(2)为保证生产的这批甲种、乙种产品售后的总利润不少于220 万元,那么至少要用 B原料多少吨?列不等式(组)解应用题专项练习参考答案1.解:( 1)设单独租用35 座客车需 x 辆,由题意得:35x 55( x 1) 45 ,解得: x 5 .∴35x 35 5 175(人).答:该校八年级参加社会实践活动的人数为175 人. 3 分( 2)设租35 座客车 y 辆,则租 55 座客车(4 y )辆,由题意得:35y 55(4 y) ≥175320 y 400(4 y) ≤1500 , 6 分11≤ y ≤ 21解这个不等式组,得4 4 .∵ y 取正整数,∴y = 2.∴4- y = 4 - 2 = 2.∴320× 2+ 400× 2 = 1440(元) .所以本次社会实践活动所需车辆的租金为1440 元.8 分2.解:( 1) 甲种 苗x 尾, 乙种 苗(6000 x) 尾,由 意得:0.5x 0.8(6000 x) 3600⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1分)解 个方程,得:x4000∴6000 x 2000答:甲种 苗4000 尾,乙种 苗 2000 尾. ⋯⋯⋯⋯⋯⋯⋯ (2分) ( 2)由 意得:0.5x0.8(6000 x) 4200 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(3分) 解 个不等式,得: x2000即 甲种 苗 不少于 2000 尾. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(4 分)( 3) 苗的 用y ,y0.5x 0.8(6000 x) 0.3x 4800 ( 5 分)90 x95(6000 x)93 6000由 意,有 100 100100⋯⋯⋯⋯⋯⋯⋯⋯⋯(6 分) 解得: x2400⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(7 分)在y0.3x 4800 中∵ 0.3 0 ,∴ y 随 x 的增大而减少∴当x2400 ,y最小4080 .即 甲种 苗2400 尾,乙种 苗 3600 尾 , 用最低. ⋯⋯⋯ (9 分)3. 【答案】( 1) 180, 100( 2)五种( 3)当x 41, 用有最大60390 元4.【答案】 ( 1)解:( 1) 甲、乙两种花木的成本价分x 元和 y 元.2x 3y 1700 由 意得:3x y1500x 400解得:y 300( 2) 种植甲种花木a 株, 种植乙种花木 ( 3a+10)株.400a 300(3a 10) 30000160270(760 400)a (540 300)(3a 10) 21600 解得:9a( 3) 有:13由于 a整数,∴ a 可取 18 或 19 或 20, 所以有三种具体方案:①种植甲种花木 18 株,种植乙种花木 3a+10=64 株; ②种植甲种花木 19 株,种植乙种花木 3a+10=67 株;③种植甲种花木 20 株,种植乙种花木 3a+10=70 株 .5. 【答案】 豆 x 吨,根据 意,得x 8,16100x10.16100 解得 600≤ x ≤800.答: 豆的吨数 不少于600 吨,并且不超 800 吨.6.【答案】( 1)解: 每个 包的价格x 元, 每本 典的价格( x -8)元.根据 意得:3 x +2(x - 8)= 124解得: x = 28.∴ x - 8= 20.答:每个书包的价格为28 元,每本词典的价格为20 元.( 2)解:设昀买书包y 个,则购买词典(40- y)本.根据题意得:1000 [23 y ()≥100,20 40 y ]1000 [28 y ()≤120.20 40 y ]解得: 10≤ y≤ 12.5.因为 y 取整数,所以y 的值为 10 或 11 或 12.所以有三种购买方案,分别是:①书包 10 个,词典30 本;②书包 11 个,词典29 本;③书包 12 个,词典28 本.7. 【答案】解:(1) 3x+y=200.( 2)销售每吨甲种产品的利润为 3 万元,销售每吨乙种产品的利润为 2 万元,由题意,得3x+2y≥220,200- y+2y≥220,∴ y≥20 ∴B 原料的用量为3x+5y=200- y+5y=200+4y≥ 280答:至少要用B原料 280 吨.。
八年级数学一元一次不等式组练习.doc

13.3一元一次不等式组练习(A)卷一、填空1、不等式组21xx>-⎧⎨>⎩的解集是2、不等式组12xx<⎧⎨>-⎩的解集是3、不等式组12xx<⎧⎨<-⎩的解集是4、不等式组21xx<-⎧⎨>⎩的解集是5、将下列数轴上的x的范围用不等式表示出来⑴⑵⑶⑷6、不等式组235324xx+<⎧⎨->⎩的解集为7、34125x+-<≤的整数解为8、三角形三边长分别为4,1-2a,7,则a的取值范围是二、选择题:9、当x>4时,代数式4-x的值一定()A、大于-8B、大于0C、小于-8D、小于010、已知xy23-=且12-x>y,则x的取值范围是()A、x>1 B、x<1 C、x>2 D、x<211、已知一元一次不等式组()x a a b x b <⎧≠⎨<⎩的解集为x a <,则( ) A .a b > B .a b < C .0a b >> D .0a b <<12、一元一次不等式组x a x b>⎧⎨>⎩的解集是x>a,则a 与b 的关系为( )...0.0A a b B a b C a b D a b ≥≤≥>≤<13、不等式15.0+-y ≥0的正整数解有( )A、1个 B、2个 C、3个 D、无数个14、已知等腰三角形的周长为12,腰长为x ,要确定x 的取值范围,可列出的不等式组是( )A 、x >0B 、x >0C 、x >0D 、以上都不对x ->0 x x +>x 212- x -12>0x x +>x 212-三、解下列不等式组(1) ⎪⎩⎪⎨⎧<->+x x x 987121 (2) ⎩⎨⎧+>++<-145123x x x x(3)⎪⎩⎪⎨⎧-≤-+>-x x x x 237121)1(325 (4) ⎩⎨⎧<>-621113x x13.3一元一次不等式组练习 (B )卷一、填空 1、不等式组()122431223x x x x ⎧--≥⎪⎪⎨-⎪>+⎪⎩的解集为 2、若m<n ,则不等式组12x m x n >-⎧⎨<+⎩的解集是3.若不等式组2113x ax <⎧⎪-⎨>⎪⎩无解,则a 的取值范围是 . 4.已知方程组2420x ky x y +=⎧⎨-=⎩有正数解,则k 的取值范围是 .5.若关于x 的不等式组61540x x x m +⎧>+⎪⎨⎪+<⎩的解集为4x <,则m 的取值范围是 .6.不等式723x x +--<的解集为 .二、选择题:7、若关于x 的不等式组12x x m -≤<⎧⎨>⎩有解,则m 的范围是( )A .2m ≤B .2m <C .1m <-D .12m -≤<8、不等式组2.01x x x >-⎧⎪>⎨⎪<⎩的解集是( ).1.0.01.21A x B x C x D x >-><<-<<9、如果关于x 、y 的方程组322x y x y a +=⎧⎨-=-⎩的解是负数,则a 的取值范围是( )A.-4<a<5B.a>5C.a<-4D.无解三、解答题10、解下列不等式组,并在数轴上表示解集。
八年级数学《一元一次不等式(组)》测试卷1

八年级数学《一元一次不等式(组)》测试卷一、选择题(每题3分,共30分)1.已知b a <,下列不等式中错误的是( )A.z b z a +<+B.c b c a ->-C.b a 22<D.b a 44->-2.不等式53>-x的解集是( )A.15-<xB.15->xC.35-<x D.35->x 3.把不等式组 ⎩⎨⎧->≤12x x 的解集表示在数轴上,正确的是 ( )A. B. C. D. 4.已知三角形的两边长分别是3、5,则第三边a 的取值范围是( )A.2≤a ≤ 8B.82<<aC.2>aD.8<a 5.“x 的2倍与3的差不大于8”列出的不等式是( )A.2x -3≤8;B.2x -3≥8;C.2x -3<8;D.2x -3>86.不等式3312-≥-x x 的正整数解的个数是( )A.1个B.2个C.3个D.4个 7.⎩⎨⎧>+<-01312x x 的解集是( )A.2<xB.1->xC.21<<-xD.无解8.无论x 取什么数,下列不等式总成立的是( )A.x+5>0B.x+5<0C.x 2<0 D.x 2≥09.在平面直角坐标系内,点P (3-m ,5-m )在第四象限,则m 的取值范围是( )A.35<<-mB.53<<-mC.53<<mD.35-<<-m10.不等式组⎩⎨⎧>>mx x 4的解集是4>x ,那么m 的取值范围是( )A.4=mB.4<mC.4≥mD.4≤m 二.填空题(每小题3分,共15分)11.用适当的符号表示:m 的2倍与n 的差是非正数:12.已知a 、b 两个实数在数轴上的对应点如下图所示:请你用“>”或“<”完成填空:(1)a b ;(2)a b ; (3)b a + 0; 13.一次函数y=kx+b 的图象如图所示,当y<0时,x 的取值范围是 ,当y >3时,x 的取值范围是 14.用“<”、“>”号填空: 如果x <y ,则3x -1________3y -1; 如果a >b ,则1-a________1-b .15.已知关于x 的不等式2)1(>-x a 的解集为ax -<12,则a 的取值范围是_____. 三、 解答题(共55分)16.解下列不等式(组),并把解集在数轴上表示出来((1,2题)每题6分,(3、4题每题7分,共26分):(1)x x 4923-<+ (2)1132x x --≤;13题图(3)3521≤+-≤x (4)⎪⎪⎩⎪⎪⎨⎧>+<-312013x x x17.已知3,3221+-=-=x y x y ,当x 取何值时,(1)2121)2(,y y y y >≤(7分)18.小明准备用21元钱买笔和笔记本,已知每枝笔3元,每个笔记本2.2元,他买了2个笔记本,请你帮她算一算,他还可能买几枝笔?(7分)19.某种商品的进价为15元,出售是标价是22.5元。
八年级数学一元一次不等式练习题

一元一次不等式(组)一、知识点1.判断不等式是否成立:关键是分析判定不等号的变化,变化的依据是不等式的性质,特别注意的是,不等式两边都乘以(或除以)同一个负数时,要改变不等号方向;反之,若不等式的不等号方向发生改变,则说明不等式两边同乘以(或除以)了一个负数。
因此,在判断不等式成立与否或由不等式变形求某些字母的范围时,要认真观察不等式的形式与不等号方向。
2.解一元一次不等式(组):解一元一次不等式的步骤与解一元一次方程的步骤大致相同,应注意的是,不等式两边所乘以(或除以)的数的正负,并根据不同情况灵活运用其性质。
一元一次不等式(组)常与分式、根式、一元二次方程、函数等知识相联系,解决综合性问题。
3.求不等式(组)的特殊解:不等式(组)的解往往是有无数多个,但其特殊解在某些范围内是有限的,如整数解、非负整数解,要求这些特殊解,首先是确定不等式(组)的解集,然后再找到相应的答案。
注意应用数形结合思想。
二、典型例题例1 下列四个命题中,正确的...有()①若a>b,则a+1>b+1;②若a>b,则a-1>b-1;③若a>b,则-2a<-2b;④若a>b,则2a<2b.A .1个B .2个C .3个D .4个 例2解不等式x>13x-2,并将其解集表示在数轴上.例3 (淄博市)解不等式组,并在数轴上表示解集.338,213(1)8.x x x -⎧+≥⎪⎨⎪--<-⎩ 【点评】先求每个不等式的解集,再借助数轴求不等式组的解集.三、应知应会1.已知a>b>0,则下列不等式不一定...成立的是( ) A .ab>b 2 B .a+c>b+c C .1a<1bD .ac>bc 2.不等式2-x>1的解集是( )A .x>1B .x<1C .x>-1D .x<-1 3.如图,数轴上所表示的不等式组的解集是( ) A .x>-1 B .-1<x ≤2 C .-1≤x ≤2 D .x ≤2 4.下列不等式组的解集,在数轴上表示为如图所示的是( )5.不等式组20,11x x +≥⎧⎨-<⎩的解集在数轴上表示正确的是( )6.不等式组533(1),13822x x x x ->-⎧⎪⎨≤-⎪⎩的解集是( ) A .0<x ≤4 B .3<x<4 C .1<x ≤4 D .2<x ≤87.关于x 的不等式组153,2223x x x x a +⎧>-⎪⎪⎨+⎪<+⎪⎩只有4个整数解,则a 的取值范围是( ) A .-5≤a ≤-143 B .-5≤a ≤-143 C .-5<a ≤-143D .-5<a<-1438.不等式组110210x x ⎧+>⎪⎨⎪-≥⎩的整数解是_______. 三、 中考链接1.(08无锡)不等式112x ->的解集是( ) A.12x >-B.2x >- C.2x <- D.1x <-2.(08河北)把某不等式组中两个不等式的解集表示在数轴上,如图)40 图1 4A .41x x >⎧⎨-⎩,≤ B .41x x <⎧⎨-⎩,≥C .41x x >⎧⎨>-⎩,D .41x x ⎧⎨>-⎩≤,3.(08南昌)不等式组2131x x -<⎧⎨-⎩≥,的解集是( )A .2x <B .1x -≥C .12x -<≤D .无解 4.(08天津)不等式组322(1)841x x x x +>-⎧⎨+>-⎩,的解集为 .5.(08北京)解不等式5122(43)x x --≤,并把它的解集在数轴上表示出来.6、(08济南)解不等式组24036x x +>⎧⎨+<⎩①②,并把解集在数轴上表示出来.7.(08成都)解不等式组10223x x x +>⎧⎪-⎨+⎪⎩≤,,并写出该不等式组的最大整数1 2 3解.一元一次不等式(组)的应用总第节一、知识点列不等式(组)解应用题:注意分析题目中的不等量关系,考查的热点是与实际生活密切相联的不等式(组)应用题。
北师大版八年级数学下册 2.4.1一元一次不等式及其解法 培优训练(含答案)

北师版八年级数学下册2.4.1 一元一次不等式及其解法培优训练一、选择题(共10小题,3*10=30)1.下列不等式,不是一元一次不等式的是( )A .x>3B .-y +1>yC .1x >2D .2x>12.下列不等式是一元一次不等式的是( )A .2(1-y)+y>4y +2B .x 2-2x -1<0C .12+13>16D .x +1<x +23.若不等式(m +1)xm 2>3是一元一次不等式,则m 的值为() A .±1 B .1 C .-1 D .04. 不等式3x -1≥x +3的解集是( )A .x ≤4B .x ≥4C .x ≤2D .x ≥25.下列不等式2+x 3>2x -15的变形过程:①去分母,得5(2+x)>3(2x -1);②去括号,得10+5x>6x -3;③移项,得5x -6x>-3-10;④系数化为1,得x>13.其中错误的步骤是( )A .①B .②C .③D .④6.不等式3(x -2)≤x +4的非负整数解有( )A .4个B .5个C .6个D .无数个7.不等式13(x -m)>2-m 的解集为x>2,则m 的值为( )C .32D .128.若实数3是不等式2x -a -2<0的一个解,则a 可取的最小正整数为( )A .2B .3C .4D .59. 不等式5x +1≥3x -1的解集在数轴上表示正确的是( )10.(荆门中考)已知关于x 的不等式3x -m +1>0的最小整数解为2,则实数m 的取值范围是( )A .4≤m <7B .4<m <7C .4≤m ≤7D .4<m ≤7二.填空题(共8小题,3*8=24)11.下列不等式:① -2<0;② 3x -5>0;③ x 2-x >1;④ x >1;⑤ 1x-2>0;⑥ x +2>y +1,其中一元一次不等式有_________(填序号)12. 不等式2x +9≥3(x +2)的解集是____________.13.若(m +1)x |m|+2>0是关于x 的一元一次不等式,则m 的取值是________.14. 不等式x -1≤2的非负整数解有____________.15. 若实数3是不等式2x -a -2<0的一个解,则a 可取的最小正整数为___________.16.使不等式-6x -23≤3x 2+12成立的最小整数解是__________. 17. 已知关于x 的不等式3x -m +1>0的最小整数解为2,则实数m 的取值范围是__________.18. 若不等式2x +53-1≤2-x 的解集中x 的每一个值,都能使关于x 的不等式3(x -1)+5>5x +2(m +x)成立,则m 的取值范围是_____________.三.解答题(共7小题, 46分)19.(6分)解不等式:(1)4x -3>x=6.(2)-5x -1<x +17.20.(6分21.(6分) 解下列不等式:(1) 3x -1≥2(x -1);(2)5(x -4) <3(3x -16)22.(6分) 若关于x ,y 的二元一次方程组⎩⎪⎨⎪⎧x -3y =4m +3,x +5y =5的解满足x +y≤0,求m 的取值范围.23.(6分) 求不等式5(x +2)≤28-2x 的非负整数解.24.(8分) 解下列不等式:(1) x +12≥3(x -1)-4.(2) 2x -13≤3x +24-1.25.(8分) 阅读理解:我们把⎪⎪⎪⎪⎪⎪a bc d 称为二阶行列式,其运算法则为⎪⎪⎪⎪⎪⎪a bc d =ad -bc.如:⎪⎪⎪⎪⎪⎪2345=2×5-3×4=-2.如果有⎪⎪⎪⎪⎪⎪23-x 1x >0,求x 的取值范围.参考答案1-5CABDD 6-10 CBDBA11. ②④12. x ≤313. 414. 0,1,2,315.516.017.4≤m <718.m <-3519. 解:(1) 移项,得4x -x >6+3.合并同类项,得3x >9.系数化为1,得x >3.(2) 移项,得-5x -x <17+1,合并同类项,得-6x <18,系数化为1,得x >-3.20. 解:去分母得x -m >3(3-m),去括号、移项、合并同类项得x >9-2m.又∵不等式的解集为x >1,∴9-2m =1,解得m =4.21. 解:(1)去括号,得3x -1≥2x -2,移项,得3x -2x ≥-2+1,合并同类项,得x ≥-1,(2)去括号,得5x -20<9x -48,移项,得5x -9x <-48+20,合并同类项,得-4x <-28,系数化为1,得x >7.22. 解:⎩⎪⎨⎪⎧x -3y =4m +3,①x +5y =5.②则x +y =2m +4.根据题意,得2m +4≤0,解得m≤-2.23. 解:5(x +2)≤28-2x ,5x +10≤28-2x ,5x +2x≤28-10,7x≤18,x≤187. ∴不等式5(x +2)≤28-2x 的非负整数解为0,1,2.24. 解:去分母,得(1) x +1≥6(x -1)-8,去括号,得x +1≥6x -6-8,移项,得x -6x ≥-6-8-1,合并同类项,得-5x ≥-15.两边都除以-5,得x ≤3.(2))去分母,得4(2x -1)≤3(3x +2)-12.去括号,得8x -4≤9x +6-12.移项,得8x -9x ≤4+6-12.合并同类项,得-x ≤-2.两边都除以-1,得x ≥2.25. 解:由题意,得2x -(3-x)>0,去括号,得2x -3+x >0,移项,合并同类项,得3x >3,系数化为1,得x >1.∴x 的取值范围为x >1.。
八年级数学-一元一次不等式及一元一次不等式组--提高训练[1]2
![八年级数学-一元一次不等式及一元一次不等式组--提高训练[1]2](https://img.taocdn.com/s3/m/109c5c25b307e87100f6961b.png)
一元一次不等式及一元一次不等式组【典型例题】例1、若关于x 的不等式组⎪⎩⎪⎨⎧<++>+01456m x x x 的解集为x<4,求m 的取值范围。
变式练习:已知关于x 的不等式组⎩⎨⎧>--≥-0125a x x 无解,求a 的取值范围;$例2、已知关于x 的不等式组010x a x ->⎧⎨->⎩,的整数解共有3个,求:a 的取值范变式练习:(1)若不等式组x-a 03-2x>-1≥⎧⎨⎩有5个整数解,则a 的取范围是_______ (2) 若不等式组240,20x x a ->⎧⎨-+<⎩无解,则a 的取值范围是_______. 例3、已知方程组⎩⎨⎧-=-+=+172652y x k y x 的解为负数,求k 的取值范围. ?例4、已知x ,y ,z 为非负实数,且满足x+y+z=30,3x+y-z=50.求u=5x+4y+2z 的最大值和最小值!【课后练习】一. 填空题1. 若211852m x -->是关于x 的一元一次不等式,则m =_________. 2. 不等式6120x -<的解集是____________.3. 当x _______时,代数式423x +的值是正数. 4. 当2a <时,不等式25ax x >+的解集时________.5. 已知22231k k x+->是关于x 的一元一次不等式,那么k =_______,不等式的解集是_______. 6. }7. 若不等式组2123x a x b -<⎧⎨->⎩的解集为11x -<<,则()()11-+b a 的值为_________.8. 小于88的两位正整数,它的个位数字比十位数字大4,这样的两位数有_______个.9. 小明用100元钱去购买笔记本和钢笔共30件,如果每枝钢笔5元,每个笔记本2元,那么小明最多能买________枝钢笔.二. 选择题9.下列不等式,是一元一次不等式的是 ( )A.2(1)42y y y -+>+B.2210x x --< C.111236+> D.2x y x +<+ 与某数的7倍的和不大于6与该数的5倍的差,若设某数为x ,则x 的最大整数解是( ) (D011.若代数式72+a 的值不大于3,则a 的取值范围是( )A.4≤aB.2-≤aC.4≥aD.2-≥a12.某种商品的进价为800元,出售时标价为1200元,后来由于商品积压,商品准备打折出售,但要保证利润率不低于5%,则至多可打( )折13.如果,2323,11--=++=+x x x x 那么x 的取值范围是( ) A.321-≤≤-x B.1-≥x C.32-≤x D.132-≤≤-x 三. 解答题)17.解下列不等式组 1)13232334x x x x x +>-⎧⎪--⎨<+⎪⎩ 2)()2532.123x x x x ⎧+≤+⎪⎨-<⎪⎩~18.当m 在什么范围内取值时,关于x 的方程()()x m x m --=-+4122有:(1)正数解; (2)不大于2的解.19.如果关于x 的不等式60k x --+>正整数解为1,2,3,正整数k 应取怎样的值!【能力训练】1、关于x 的不等式组12x m x m >->+⎧⎨⎩的解集是1x >-,则m =. 2、已知2ab =.(1)若3-≤b ≤1-,则a 的取值范围是____________.(2)若0b >,且225a b +=,则a b +=____________.4、如果不等式组2223xa xb ⎧+⎪⎨⎪-<⎩≥的解集是01x <≤,那么a b +的值为~5、已知关于x 的不等式组0521x a x -⎧⎨->⎩≥,只有四个整数解,则实数a 的取值范围是. 6、已知关于x 的不等式(3a -2)x +2<3的解集是x >-41,则a =______.7、若a <0,则不等式⎪⎪⎩⎪⎪⎨⎧<<32a x ax 的解集是_______.8、如果一元一次不等式组3x x a >⎧⎨>⎩的解集为3x >.则a 的取值范围是( )A .3a >B .a ≥3C .a ≤3D .3a <9、若不等式组0,122x a x x +⎧⎨->-⎩≥有解,则a 的取值范围是( )A .1a >-B .1a -≥C .1a ≤D .1a <~10、如果a <0,ab <0,则|b -a +4|-|a -b -6|化简的结果为…………………………()(A )2 (B )-10 (C )-2 (D )2b -2a -211、解关于x 的不等式组()02114x k x k->⎧⎪⎨+>-⎪⎩1 2x a-≥a都成立,试求a的取值范围.12、对于x≥1的一切实数,不等式()。
2019-2020初中数学八年级上册《一元一次不等式》专项测试(含答案) (315)

27.(7 分)某服装商店出售一种优惠购物卡,花 200 元买这种卡后,凭卡可以在这家商店按 8 折购物,什么情况下买卡购物合算?
28.(7 分) k 为何值时,代数式 2(k −1) 的值不大于代数式 1− 5k 的值.
3
6
k5 9
29.(7 分) 4(x + 2) − 5 = 3a + 2 的解小于 3a +1 x = a(2x + 3) 的解,求 a 的取值范围.
21.(2
分)不等式组
x −4
x
2
的解集是
.
22.(2 分)不等式 3x − 2 − 2x +1 0 的所有整数解的积为 . 4
评卷人 得分
三、解答题
23.(7 分)解下列不等式组,并把它的解在数轴上表示 出来:
(1)
2(4 − 2x) 4x 2x −1 3(1− 3x)
(2)
2(x + 3) 3 − 5(x
3
2
a− 1 15
30.(7 分)利用不等式性质,将下列不等式化成“ x a ” 或“ x aL ”的形式:
(1) x + 5 −2 ;(2) 4x 36 ;(3) − 1 x 3 ;(4) x + 1 0
4
2
【参考答案】***试卷处理标记,请不要删除
评卷人 得分
一、选择题
1.B 2.A 3.D 4.A 5.B 6.A 7.A 8.A 9.A 10.C 11.B 12.D 13.D 14.C
A.
B.
C.
D.
12.(2 分)如果 x − y x , x + y y ,那么下列式子中,正确的是( )
A. x + y 0 x − y 0 C. xy 0
2019-2020初中数学八年级上册《一元一次不等式》专项测试(含答案) (980)

【参考答案】***试卷处理标记,请不要删除
评卷人 得分
一、选择题
1.A 2.D 3.C 4.B 5.A 6.B 7.D 8.C 9.A 10.B 11.D 12.C 13.A
评卷人
得分
二、填空题
14. x = 2、3、4 15. 3x −1 1 (2 + x)
3.(2 分)若 a<b,有下列不等式:① a + m b + m ;② a − m b − m ;③ ma mb ;④ a b mm
( m 0 ).
其中恒成立的不等式的个数为( )
A.1
B.2
C.3
D. 4
4.(2
分)在方程组
2x − y = m
2y
−
x
=1
中,
x
、
y
满足
x
+
y
0
,则
m
27.(7 分)宏志高中高一年级近几年来招生人数逐年增加,去年达到 550 名,其中有面向全 省招 收的“宏志班”学生,也有一般普通班学生.由于场地、师资等限制,今年的招生 人数最多比去年增加 100 人,其中普通班学生,可多招 20%,“宏志班”学生可多招 10%,问今年最少可招收“宏志班”学生多少名?
体重可能是( )
A.23.3 千克 B.23 千克 C.21.1 千克 D.19.9 千克
13.(2 分)不等式 5 − 2x>0 的解集是( )
A. x< 5 2
B. x> 5 2
C. x< 2 5
评卷人 得分
二、填空题
D. x< − 5 2
2019-2020初中数学八年级上册《一元一次不等式》专项测试(含答案) (525)
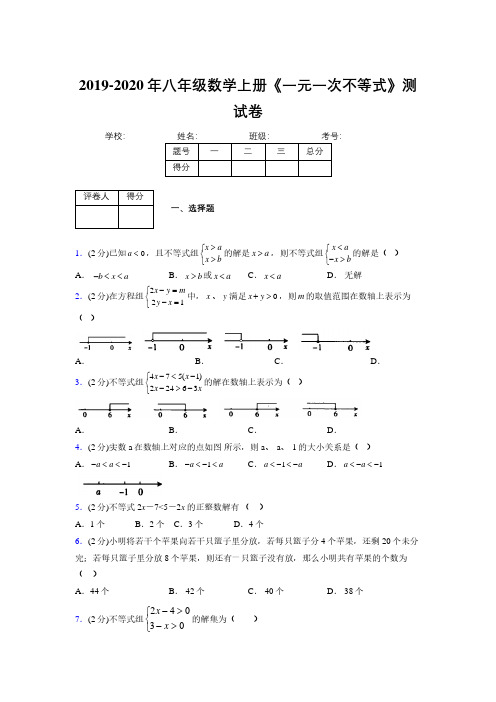
14.(2 分)当 x a 0 时, x2 与 ax 的大小关系是 .
15.(2 分) 10 在两个连续整数 a 和 b 之间,a< 10 <b, 那么 a , b 的值分别是 .
16.(2 分)乐天借到一本有 72 页的图书,要在 10 天之内读完,开始两天每天只读 5 页,那
么以后几天里每天至少要读多少页?设以后几天里每天至少要读 x 页,所列不等式
9.(2 分)已知关于 x 的一元一次方程 4x − m = 3x +1 的解是负数,则 m 的取值范围是( )
A. m −1
B. m −1
C. m −1
D. m −1
10.(2 分)某种奶制品的包装盒上注明“蛋白质≥2.9%”,它的含义是( )
A.蛋白质的含量是 2.9%
B.蛋白质的含量高于 2. 9%
的解是(
)
A. −b x a
B. x b 或 x a C. x a
D. 无解
2.(2
分)在方程组
2x − y = m
2y
−
x
=1
中,
x
、
y
满足
x
+
y
0
,则
m
的取值范围在数轴上表示为
()
A.
B.
C.
D.
3.(2
分)不等式组
4x 2x
− −
7 5(x −1) 24 6 − 3x
的解在数轴上表示为(
为.
17.(2
分)已知不等式组
x −1 x Biblioteka − k,当k=
1
时,它的解集为
为.
;当 k = 2 时,它的解集
18.(2 分)三角形三边长分别为 4,1− 2a ,9,则 a 的取值范围是 .
2019-2020初中数学八年级上册《一元一次不等式》专项测试(含答案) (599)

台;方案三:选乙机器 6 台 (2)选购甲机器 1 台,乙机器 5 台
22. x −2 23. a 2
24.-2≤x<3,x=0,l,2
25.13 km/h 到 15 kmn/h
26. − 3 m 3
4
4
27.-l<x<3
28.超过 1000 元
29.7
30.12 包
A.41
B.42
C.43
D.44
7.(2 分)使代数式 x − 9 +1的值不小于代数式 x +1 −1 的值的 x 应为( )
2
3
A. x 17
B. x 17
C. x 17
D. x 29
8.(2 分)不等式 4(x − 2) 2(3x − 5) 的正整数解的个数为( )
A.0 个
B.1 个
C.无解
D. 0 x 1
2.(2 分)不等式 x − 2 3(x +1) 的负整数有( )
A. 0 个
B. 1 个
C.2 个
D.3 个
3.(2 分)已知关于 x 的不等式 2x − m −3 的解的解如图所示,则 m 的值等于( )
A.2
B.1
C. -1
D.0
4.(2 分) 已知三角形的两边长分别为 3,5,则第三边上的中线 m 的取值范围是( )
18.(2 分)和小于 15 的最大的三个连续正整数是 . 19.(2 分)若 x = a +1 是不等式 1 x −1 2 的解,则 a .
2 评卷人 得分
三、解答题
20.(7 分)某校为了奖励获奖的学生,买了若干本课外读物. 如果每人送 3 本,还余 8 本; 如果每人送 5 本,则最后一人能得到课外物,但不足 3 本.设该校买了 m 本课外读物,有 x 名学生获奖,试解:
2019-2020初中数学八年级上册《一元一次不等式》专项测试(含答案) (1053)

D. x 0 y
评卷人 得分
二、填空题
15.(2 分)已知 等腰三角形的周长是 12,则腰长 x 的取值范围是 .
16. a b ,则 a + 5 b + 5 , −2a −2b .
18.(2 分) 根据“ x 的相反数的 1 不大于 x 的 2 倍与 10 的和”,列出不等式:
5x +1 3(x +1)
28.(7
分)解不等式组
1 2
x
−1
1
−
3 2
x
,并写出不等式组的正整数解.
29.(7 分)用不等式表示下列语句,并写出解集. (1)x 与 3 的差不大于 2;
(2)y 的 3 倍与 2 的和大于 5.
30.(7 分)根据下列条件,,写出仍能成立的不等式. (1) 7 −2 ,两边都加 2; (2) −3 5 ,两边都减 1; (3) 2 3 ,两边都乘以 4; (4) 3 −9 ,两边都除以 3; (5) −2 −4 ,两边都乘以 −3 ; (6) −16 −8 ,两边都除以一 4. 观察以上各题的结果,你有什么发现吗?
足的不等式是
.
评卷人 得分
三、解答题
22.(7 分)某公司甲、乙两座仓库分别有运输车 12 辆和 6 辆,要调往 A 地 10 辆,调往 B 地 8 辆. 已知从甲仓库调运一辆到 A 地和 B 地的费用分别为 40 元与 80 元;从乙仓库调运一辆到 A 地和 B 地的费用分别为 30 元与 50 元. 设从乙仓库调到入地 x 辆车. (1)用含 x 的式子表示调运车辆的总费用; (2)若要求总费用不超过 900 元,共有几种运方案? (3)求出总费用最低的方案,最低费用是多少元?
A.10
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
砀山五中八年级一元一次不等式培优专题训练1
姓名 ______ 班级______
一、选择题:
1、下列不等式一定成立的是( )
A.5a >4a
B.x +2<x +3
C.-a >-2a
D.a
a 24
> 2、某数的2倍加上5不大于这个数的3倍减去4,那么该数的范围是( )
A .9>x
B .9≥x
C .9<x
D .9≤x
3、 如果10<<x ,则下列不等式成立的( )
A 、x x x 12<<
B 、x x x 12<<
C 、21x x x <<
D 、x x x
<<21 4、在数轴上与原点的距离小于8的点对应的x 满足( )
A.-8<x <8
B.x <-8或x >8
C.x <8
D.x >8
5、在平面直角坐标系内,点P (3-m ,5-m )在第四象限,则m 的取值范围是( )
A 、
35<<-m B 、53<<-m C 、53<<m D 、35-<<-m 6、若不等式(a +1)x >a +1的解集是x <1,则a 必满足 ( ).
(A)a <0
(B)a >-1 (C)a <1 (D)a <-1 7、不等式组⎩⎨
⎧+>+<+1,159m x x x 的解集是x >2,则m 的取值范围是( ). (A)m ≤2 (B)m ≥2 (C)m ≤1 (D)m ≥1
8、若不等式组⎩
⎨⎧>≤<k x x ,21有解,则k 的取值范围是 ( ). (A)k <1 (B)k ≥2 (C)k <2 (D)1≤k <2
9、若不等式组⎩⎨
⎧>≤11x m x 无解,则m 的取值范围是( ) A.m <11 B.m >11 C.m ≤11 D.m ≥11
10、现用 甲、乙两种运输车将46吨抗旱物资运往灾区,甲种运输车载重5吨,乙种运输车载重4吨,安排车辆不超过10辆,则甲种运输车至少应安排.( )
A .4辆
B .5辆
C .6辆
D .7辆
二、填空题
11、若x 是非负数,则5231x -≤
-的解集是______. 12、若11
|1|-=--x x ,则x 的取值范围是_______ 13、 如果关于x 的不等式5)1(+<-a x a 和42<x 的解集相同,则a 的值为________.
14、若不等式组⎩⎨
⎧>-<-3212b x a x 的解集为11<<-x ,那么)3)(3(+-b a 的值等于_______.
15、已知不等式03≤-a x 的正整数解恰好是1、2、3,则a 的取值范围是___________。
16、已知关于x 的不等式组⎩⎨
⎧>-≥-0025a x x 无解,则a 的取值范围是是___________。
17、已知6<a <10,2
a ≤
b ≤a 2,b a
c +=,则c 的取值范围是 。
18、满足不等式组﹣5<6﹣2x <3的所有整数解的和是 。
三、解答题:
1.解下列不等式(组):
(1)
13
12523-+≥-x x ; (2) 0415212<---x x
(3)⎪⎩⎪⎨⎧-<-+≤-3314)3(265x x x x (4)⎪⎩⎪⎨⎧<--+->++-.,021331215)1(2)5(7x x x x
2、已知A =2x 2+3x +2,B =2x 2-4x -5,试比较A 与B 的大小
3、已知不等式
42213x a x +-〉的解集是x>2,求()a x a -〉-23
1的解集。
4、已知关于x ,Y 的方程组⎩⎨⎧-=+-=-1331k y x k y x 的解满足x+y >3k+2,求k 的取值范围
5、不等式组12,3 5.
a x a x -<<+⎧⎨
<<⎩的解集是3<x <a +2,则a 的取值范围
6、已知不等式()()716825+-<+-x x 的最小整数解为方程32=-ax x 的解,求代数式a
a 144-的值。
7、若干个小朋友,若每人分3件,则剩余4件;若每人分4件,则最后一人得到的玩具不足3件,求小朋友的人数和玩具数。
8. 某工厂有甲种原料360kg ,乙种原料290kg ,计划用这两种原料生产A 、B 两种产品共50件。
已知生产一件A 种产品,需用甲种原料9kg ,乙种原料3kg ,可获利润700元:生产一件B 种产品,需用甲种原料4kg ,乙种原料10kg ,可获利润1200元。
(1)按要求安排A 、B 两种产品的生产件数,有哪几种方案?请你设计出来。
(2)设生产A 、B 两种产品获总利润W (元),采用哪种生产方案获总利润最大?最大利润为多少?。
