1.2库伦定律
课件12:1.2库仑定律

[特别提醒] (1)从宏观意义上讨论电子、质子等带电粒子时,完全可以把它们视为点电 荷. (2)带电的物体能否看成点电荷,有时还要考虑带电体的电荷分布情况.
[例 1] 下面关于点电荷的说法正确的是( ) A.只有体积很小的带电体才能看成点电荷 B.体积很大的带电体一定不是点电荷 C.当两个带电体的大小、形状等因素对它们相互作用力的影响可忽略时, 这两个带电体可看成点电荷 D.任何带电球体,都可看成电荷全部集中于球心的点电荷
第一章 静电场
2 库仑定律
18世纪中叶以后,在已认识同种电荷相斥,异种电荷相吸基 础上,不少学者对电荷间的相互作用力规律进行了猜测和实验探索.
牛顿力学取得很大的成功,当时的电学家米谢尔、普里斯特 利、卡文迪许和库仑等人类比引力定律猜测电力亦遵循平方反比定 律.
法国科学家库仑通过扭力称实验给予平方反比律严格的实验 基础.库仑以其精妙的实验技巧和对物理学的贡献名垂科学史.
(1)两小球电性相同:相互接触时两小球电荷量平分,每个小球带的电荷量 为7q2+q=4q,放回原处后相互作用力大小为 F1=k4qr·24q=k16r2q2,故FF1=176. (2)两小球电性不同:相互接触时电荷量先中和后平分,每个小球带的电荷 量为7q- 2 q=3q,放回原处后相互作用力大小为 F2=k3qr·23q=k9rq22,故FF2=97. 所以选项 C、D 正确. 答案:CD
约1750年,德国柏林科学院院士爱皮努斯发现两带电体之间的距 离缩短时,两者之间的吸引力或排斥力明显增加,但没有继续研究下去.
大约1760年,丹尼尔·伯努利从牛顿力学自然观出发,猜测电力跟 万有引力一样,服从平方反比定律.其想法具有一定的代表性,引力平方 反比定律早已确立,对人们的自然观具有深刻的影响。
1.2库仑定律

F3 + c F1
F2 F4
小
结
1、内容:真空中两个点电荷之间的相互作用力, 跟它们的电荷量的乘积成正比,跟它们的距离的 二次方成反比,作用力的方向在它们的连线上.
q1q 2 F k 2 2、公式: r
k=9.0×109N· m2/C2
3、适用条件:⑴ 真空(空气中近似成立)
⑵ 点电荷 4、点电荷:是一种力的影响可以忽略不 计时,带电体可视为点电荷.
答案:AD.
思考: 当带电球体的大小、形状不能忽略时,是否可以看 做是集中在球心位置的点电荷? 1、如果是两个电荷分布均匀的带电球体:两球心间距离r0
r r0
r r0
2、如果是两个球形带电导体:两球心间的距离为r0
r r0
r r0
课堂训练
2、两个半径为0.3m的金属球,球心相距1.0m放置,当他 们都带1.5×10−5 C的正电时,相互作用力为F1 ,当它 们分别带+1.5×10−5 C和−1.5×10−5 C的电量时,相互 作用力为F2 , 则( ) A .F1 = F2 B.F1 <F2 C.F1 > F2 D.无法判断
讨论: 库仑力(静电力)
与万有引力
相同点 (1)两种力都与距离的二次方成反比 (2)两种力都与和作用力有关的物理量的乘积成正比. (3)两种力的方向都在两物体的连线上. 不同点 (1)描述了两种作用.(性质不同) 库仑力是由于物体带电引起的作用, 万有引力是由于物体具有质量引起的作用.
(2)力的大小与相关的物理量不全相同; 库仑力是电荷量,万有引力是质量 (3)静电力可以是引力,也可以是斥力, 万有引力只能是引力.
§1、2库仑定律
复习
1、电荷
1.2 库仑定律

实验表明:电荷之间的作用力 (1)随电荷量的增大而增大
(2)随距离的增大而减少
2、定量研究
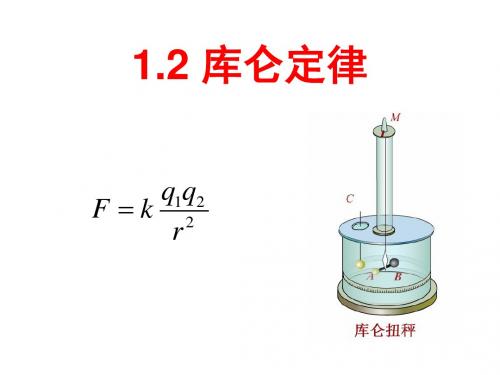
库仑扭秤实验
实验结论:真空中两个点电荷之间的相 互作用力,与它们的电荷量的乘积成正 比,与它们的距离的二次方成反比,作 用力的方向在它们的连线上,同种电荷相 互排斥,异种电荷相互吸引。
二、库仑定律
1、内容:真空中两个点电荷之间的相互作用力,与它们的电荷量的
1.2 库仑定律
同种电荷相互排斥
异种电荷相互吸引 -qB
思考:A、B均为形状不规则的带电体,A带正电,B带负 电,如图所示,求两带电体之间的电荷相互作用力。
+qA
A
B
由于A、B均为形状不规则的带电体,它们所带电荷之间 相互作用力是很复杂的,为了方便研究,我们把两个带电 体形状理想化,用点模型来代替这两个带电体,即等效成 求两个点电荷之间的相互作用力。 +qA A -qB B 这种忽略物体形状和大 小而用一个点来代替的 带电体叫做点电荷。
一、点电荷
点电荷
实质 条件
有电量、无形状、无 大小的点 当带电体本身的尺寸比 起它到其它带电体的距 离小得多时 理想化模型 实际不存在
质点
有质量、无形状、无大小 的点 当物体本身的形状和大小 对所研究的物体没有影响 或影响较小时 理想化模型 实际不存在
共同点 注:
1、点电荷是带电体;元电荷不是带电体,是电量单位。 2、点电荷的电量、体积可以很大也可以很小;质点的质量、体积 可以很大也可以很小。 3、理想模型是物理学常用的研究方法。在研究过程中抓住主要因素,忽 略次要因素,将研究对象抽象为理想模型。这样可以使问题的处理大为简 化。
q2 F 36k 2 L
(2)C球所带电量为多少?带何种电荷?
1.2 库仑定律
仍然小于B球的悬线与竖直方向的夹角
12.如图所示,把质量为2.0g的带负电的小球A用绝缘细绳悬 挂起来,若将带电量为qB=4.0×10-6 C的带电小球B靠近小 球A,当两个带电小球在同一高度相距30cm时,绳与竖直
方向恰成450角.(小球A、B可看成点电荷)g取10m/s2,求:
(1)A球所受的库仑力大小;(2)A球所带电荷量. 13.如图所示,悬挂在O点的一根不可伸长的绝缘细线下端 有一个带电量不变的小球A,在两次实验中,通过绝缘手 柄缓慢的移动另一带同种电荷的小球B,当B到达悬点O的 正下方并与A在同一水平线上时,A处于静止状态,此时 悬线偏离竖直方向的角度为θ,若在两次实验中B的电量分 别为q1和q2,θ分别为300和450,求q2/q1
时 1、2 之间作用力的大小仍为 F,方向不变.由此可知( )
A.n=3
B.n=4
C .n = 5
D.n=6
6.关于库仑定律的公式
F
k
q1q2 r2
,下列说法正确的是(
)
A.当真空中的两个点电荷间的距离 r →∞时,F→0
B.当真空中的两个点电荷间的距离 r →0 时,F→∞
7.如图所示,两个质量均为 m 的完全相同的金属球壳 a 与 b,
同时将小球B的质量增大到原来的2倍
11.如图所示,把大小可以不计的带有同种电荷的小球A和
B各用丝线悬挂在同一点,静止时,绝缘等长细线与竖直
方向的夹角分别为α和β,且α<β,由此可知( )
A.B球的电荷量较大,受到的库仑力较大
B.B球的质量较大
αβ
C.B球受到细线的拉力较大
A
B
D.两球接触后,再静止时,A球的悬线与竖直方向的夹角
1.2库仑定律

图 1- 2- 2
库仑定律和力学规律的综合应用 如图1- 2-4所示,悬挂在O 点的一根不可伸长的绝缘细线下端 有一个带电荷量不变的小球 A.在两 次实验中,均缓慢移动另一带同种 电荷的小球 B. 当 B 到达悬点 O 的正 下方并与 A 在同一水平线上, A 处 于受力平衡时,悬线偏离竖直方向 的角度为θ,若两次实验中B的电荷 量分别为 q1 和 q2 , θ 分别为 30°和 45°.则q2/q1为( )
q· Q Q· 4Q 以 A 为研究对象,则 k 2=k 2 , r r′ q· 4Q Q· 4Q 以 B 为研究对象,则 k 2 , 2=k r r+r′ Q· q 4Q· q 以 C 为研究对象,则 k 2=k 2, r′ r+r′ 由以上任意两个方程可得出 q=4Q,r′=r=3 m.
F qQ tanθ=mg,其中 F=k 2 lsinθ mgtanθsin2θl2 两式整理得:q= kQ 将题干中的两种情况代入得: q2 tan 45° sin 45° = =2 3 . 2 q1 tan30° sin 30°
【答案】 C
2
图 1- 2- 5
课堂训练
3、 三个相同的金属小球a、b和c,原来c不 带电,而a和b带等量异种电荷,相隔一定 距离放置,a、b之间的静电力为F 。现将c 球分别与a、b接触后拿开,则a、b之间的 静电力将变为( C )。 A.F/2 B.F/4 C.F/8 D.3F/8
r
二、库仑定律的说明
• 1、适用范围:
– ①真空点电荷
r
q1q2 F k 2 r
R
• 点电荷(理想模型):当带电体间距离比它 们自身的大小大很多,带电体的形状、大小 及电荷分布状况对它们间作用力的影响可忽 略不计时,可将其看作有电荷量的点(R<<r)
1.2库仑定律

F q1q 2 r
2
(1.2)
当q1=q2=1及r=1时,且规定k=1,由上式F=1。 即: 当两个电荷相等的点电荷相距1厘米,而它们 之间的电性力为1达因时,这两个点电荷的电荷均 为1静库。
2、国际制(MKSA制) 基本量为: 长度、质量、时间、电流强度 基本单位为:米、千克、秒、安培 (1)在国际单位制中,电荷的单位是库仑,库仑 的定义为: 如果导线中载有1安培的稳恒(恒定)电流,则在 1秒内通过导线横截面的电荷定义为1库仑,即: 1库仑=1安培· 1秒
因此在国际单位制中,库仑定律表述为:
F 1 4
0
q1 q 2 r
2
(1.3)
四 库仑定律的矢量形式 1、矢量的表示(本书中矢量的表示法)
ˆ ˆ a a a aa
ˆ 推广: r r e
2、库仑定律的矢量形式
F12 q1 q 2 4 0 r
ˆ e r 12
F12
q1
q2
图1 q1、q2同号(排斥力)
ˆ 如果:q1、q2异号,q1 *q2<0,则 F12 与 e r 12 反向,
为吸引力,如图2。
q1
ˆ e r 12
F 21
ˆ e r 21
F12
q2
图2 q1、q2异号(吸引力)
五 (力的)叠加原理 当空间有两个以上的点电荷时,作用于每一个电 荷上的总静电力等于其它点电荷单独存在时作用于该 电荷的静电力的矢量和,这就叫做叠加原理。 叠加原理说明: (1)一个点电荷作用于另一点电荷的力,总是服从 库仑定律的,不论其周围是否存在其它电荷。 (2)任何宏观带电体都可以分成无限多个带电元, 将这些带电元视为点电荷,利用库仑定律和力的叠加 原理,原则上可以解决静电学的全部问题。
1.2 库仑定律
2.关于点电荷的下列说法中正确的是( ABD ) A.真正的点电荷是不存在的 B.点电荷是一种理想化模型 C.足够小的电荷就是点电荷 D.一个带电体能否看成点电荷,不是看它的尺寸大 小,而是看它的形状和大小对所研究的问题的影响 是否可以忽略不计
3.两个半径均为1cm的导体球,分别带+Q和-3Q的电
量,两球心相距90cm,相互作用力大小为F,现将它们碰
一下后,放在两球心相距3cm处,则它们的相互作用力
大小变为 ( D )
A.3000F
B.1200F
C.900F
D.无法确定
练习1.(库仑力作用下的平衡)如图所示,悬挂在O点的
一根不可伸长的绝缘细线下端有一个带电荷量不变的小
球A.在两次实验中,均缓慢移动另一带同种电荷的小球
解:氢核与电子所带的电荷量都是 1.61019c 氢核与电子之间的库仑力F库
电子和质子的库
F库 F引
2.3 1039
仑力远大于它们
间万有引力。研
F库
k
q1q2 r2
9.0 109
(1.61019 )2 (5.31011 )2
N
8.2108 N
究带电微粒间相 互作用时,经常 忽略万有引力.
库仑
氢核与电子之间的万有引力 F 引
B -2Q,在A左侧距A为L/2处
C -4Q,在B右侧距B为L处
D + 2Q,在A右侧距A为3L/2处
A
L
B
-4Q
+Q
由库仑定律得:
“两大夹小、两同夹异、近小远大” 解得:q=4Q 带负电
1.库仑定律的适用范围是( CD ) A.真空中两个带电球体间的相互作用 B.真空中任意带电体间的相互作用 C.真空中两个点电荷间的相互作用 D.真空中两个大小远小于它们之间的距离的带电体
1.2库仑定律

1.2 库仑定律简介库仑定律是电磁学中的基本定律之一,描述了带电物体之间相互作用力的大小与它们之间距离、电荷量的关系。
该定律是由法国物理学家库仑于18世纪末提出的,被认为是电磁学的基石之一,对于理解电荷之间的相互作用以及电磁现象的发生和演化具有重要意义。
定义库仑定律可以表述如下:两个电荷之间的静电力的大小与它们之间直线距离的平方成反比,在恒定吸引或排斥力的情况下,与这两个电荷的数量成正比。
公式表示为:F = k * (q1 * q2) / r^2其中,F表示两个电荷之间的静电力,k是库仑常数,q1和q2分别表示两个电荷的电荷量,r表示它们之间的距离。
库仑常数库仑常数是一个物理常数,用于计算两个电荷之间的静电力。
它的数值约为9.0 x 10^9 Nm2/C2,其中Nm2/C2是国际单位制中的单位。
电荷的性质根据库仑定律,电荷有两种性质:正电荷和负电荷。
正电荷尽可能地排斥彼此,而负电荷也尽可能地排斥彼此。
正电荷和负电荷之间会产生吸引力,这是导致电荷之间相互作用的原因。
实例分析下面我们通过一个实例来分析和应用库仑定律。
假设有两个电荷,电荷q1的电荷量为2C,电荷q2的电荷量为-4C,它们之间的距离r为1m。
我们可以使用库仑定律来计算它们之间的静电力。
根据库仑定律的公式,我们有:F = k * (q1 * q2) / r^2代入具体数值得到:F = (9.0 x 10^9 Nm2/C2) * (2C * -4C) / (1m)^2简化计算得到:F = -7.2 x 10^9 N由此可见,这两个电荷之间的静电力是-7.2 x 10^9 N(牛顿)。
负号表示这两个电荷之间的力是吸引力,而不是排斥力。
应用库仑定律在众多领域中都有广泛的应用。
以下是一些常见的应用场景:1.静电学:库仑定律对于描述静电现象和静电力的大小提供了基本的理论基础。
2.电荷的分布与运动:在电荷的分布和运动方面,库仑定律有很多应用,比如计算静电场的大小、电荷在电场力作用下的运动等。
1.2库仑定律
库仑的扭秤实验
研究方法: 控制变量法
思想方法: 1、小量放大思想
2、电量均分原理
实验方案:
1、q1、q2一定时,探究F与r的关系 F∝1/r2
2、r一定时,探究F与的q1、q2关系 F ∝q1q2
二、库仑定律
1、定律内容 真空中两个静止点电荷之间的相互作用力,与
它们的电荷量的乘积成正比,与它们的距离的二次 方成反比,作用力的方向在它们的连线上。
(1)核实适用条件:相互作用的电荷能否看成点电荷
在两电荷之间距离接近为零时,由于两个电荷已经失去 了点电荷的前提条件,因此不能根据库仑定律得到库仑力无 穷大的结论
两个带电的导体球若靠近,电荷分布不再均匀,不能 当成电荷集中在球心处的点电荷处理。
(2)Q1、Q2只需用绝对值带入即可,求出的F为库仑力的 大小;F的方向,需通过Q1、Q2的电性来判断 (3)两个电荷间的作用力不因为第三个点电荷的存在而有 所改变。当一个点电荷受到多个点电荷的作用,可以根据 力的独立作用原理进行力的合成的矢量运算。
maaa mbab mcac 0
ab (aa ac ) 2m/s 2
三、例题 1、用等效思想处理电荷间的库仑力 例1、如图所示,是半径为r的圆内接正五边形,在 其顶点a、b、c、d处各固定有电荷量为+Q的点电荷, 在e处固定有电荷量为−3Q的点电荷,则放置在圆心 O处的点电荷−q所受到的静电力的大小为_______, 方向为________。
从e指向O
例2、半径为R的绝缘球壳上,均匀带有电量+Q,另 有电量+q的点电荷A放在球心处。由于对称性,A受 力为0。现在球壳上挖去半径为r(r<<R)的小圆孔, 则此时A受力大小和方向如何?
1.2 库仑定律

q2 +
平行四边形定则
F3
F1
F= 2F1 cos 30 = 0.25N
方向沿q1与q2连线的垂直平分线
课堂训练
1、关于点电荷的下列说法中正确的是:( ) ABD A .真正的点电荷是不存在的. B .点电荷是一种理想模型. C .足够小的电荷就是点电荷. D .一个带电体能否看成点电荷,不是看它的尺 寸大小,而是看它的形状和大小对所研究的问 题的影响是否可以忽略不计
第二节 库仑定律
同种电荷相互排斥,异种电荷相互吸引
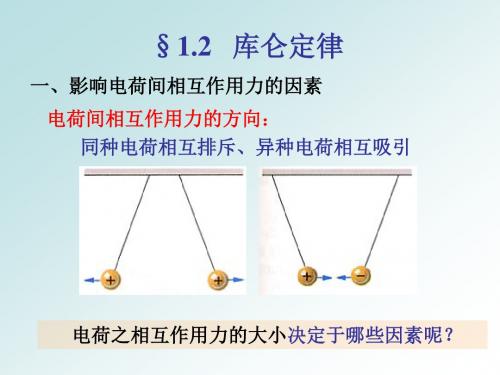
既然电荷之间存在相互作用,那么电荷 之间相互作用力的大小决定于那些因素呢?
猜想
电荷电量 两个电荷间的距离
一、探究影响电荷间相互作用力的因素
1.F与r有关
电荷间相互作用力随距离的增大而 减少
2.F与q有关 电荷之间的相互作用力随电荷量的增 大而增大。
4、两个半径为0.3m的金属球,球心相 距1.0m放置,当他们都带1.5×10−5 C 的正电时,相互作用力为F1 ,当它们 分别带+1.5×10−5 C和−1.5×10−5 C的 电量时,相互作用力为F2 , 则( B) A .F 1 = F 2 B. F 1 < F 2 C.F 1 > F2 D.无法判断
若上题中a、b两点放-Q和4Q,其它条件不变,试确定点 电荷c的位置、电性及它的电荷量。
答案:c应放在a、b连线上两点间的外侧,距a为l处,带正 电,带电量为4Q
小结:三个自由的电荷只受库仑力的平衡规律 两同夹异,两大夹小,近小远大。 7.真空中有两个点电荷,分别带电q1=5×10-3C, q2=-2×10-2C,它们相距15cm,现引入第三个 点电荷,它应带电量为________,放在________位置 才能使三个点电荷都处于静止状态.
1.2库仑定律
0.1
5.3 108 C
q1q2 F库 k 2 r 9
8
解:氢核与电子所带的电荷量都是1.6×10-19C
8.2 10 N
1.6 10 1.6 10 9.0 10 N 5.3 10
19 19 11 2
m1m2 F引 G 2 r
6.7 10 11
3.6 10
1.67 10 9.1 10 N 5.1 10 47
27 31 11 2
N
F库 2.3 1039 F引
可见,微观粒子间的万有引力小于库伦力, 因此在研究微观带电粒子相互作用时,可以把 万有引力忽略掉。
课堂小结
一、库仑定律
Q1Q2 公式: F k 2 r
代入数据得: r
T
F
A θ B
mg
3kQq mg
教材习题答案
1.答:根据库伦的发现,两个相同的带点金属 球接触后所带的电荷量相等。所以,先把A球
q 与B球接触,此时,B球带电 ;再把B球与C球 2 q 接触,则B、C球分别带电 ;最后,B球再次与 4
3q q q A球接触,B球带电qB 。 2 8 2 4
导入新课
力的大 + + 小可以 求吗? 同种电荷相互排斥异种电荷相互吸引
第一章 静电场
1.2 库伦定律
内容解析
一、库仑定律
二、库伦的实验
探究
影响电荷间相互作用力的因素
实 验 装 置 图
通过实验你观察到了什么现象?你能总结出 都有哪些因素在影响电荷间的相互作用了吗?这 些因素对作用力的大小有什么影响?
结论
影响电荷间的相互作用的因素有电荷量 的多少和电荷之间距离的长短。
专题1.2 库仑定律

第一章 静电场课时2 库仑定律一、库仑定律 1.内容真空中两个静止 之间的相互作用力,与它们的电荷量的 成正比,与它们的距离的二次方成 ,作用力的方向在它们的连线上。
电荷间的这种相互作用力叫做静电力或库仑力。
2.适用范围(1)真空中 (2)静止的 (3)点电荷 二、点电荷当带电体间的距离比它们自身的大小 得多,以致带电体的形状、大小及电荷分布状况对它们之间的作用力的影响可以 时,这样的带电体就可以看作带电的点,叫做 。
注意:点电荷类似于力学中的质点,也是一种 的模型。
库仑定律的表达式 。
式中的k 是比例系数,叫做静电力常量。
k = 。
注意:计算大小时只需将电荷量的绝对值代入。
静电力与万有引力的比较1.相同点:公式形式相同,应用时都有条件 都是不接触力,且与距离的二次方成反比2.不同点:万有引力只是相互吸引,而静电力可以是引力,也可以是斥力 3.在求静电力时,万有引力可以忽略点电荷 乘积 反大 忽略 点电荷 理想化 122=q q F kr9229.010N m C ⨯⋅一、对库仑定律的理解和应用库仑定律的适用条件是真空中的静止点电荷。
点电荷是一种理想化的物理模型,当带电体间的距离远大于带电体的自身大小时,可以视其为点电荷,可以用库仑定律,否则不能用。
【例题1】如图所示,两个质量均为m的完全相同的金属球壳a与b,其壳层的厚度和质量分布均匀,将它们固定于绝缘支架上,两球心间的距离为l,为球壳外半径r的3倍,若使它们带上等量的异种电荷,使其所带电荷量的绝对值均为Q,那么a、b两球间的万有引力F1与库仑力F2为A.212mF Gl=,222QF kl=B.212mF Gl≠,222QF kl≠C.212mF Gl≠,222QF kl=D.212mF Gl=,222QF kl≠参考答案:D二、三个自由点电荷仅在它们系统的静电力作用下处于平衡状态时,满足的规律1.“三点共线”——三个点电荷分布在同一直线上。
1.2 库仑定律

1 1、当电量不变时,F与距离r的二次方成反比:F∝ 2 r
Q1 Q2 的乘积成正比: 2、当之间距离不变时,F与、
四、库仑定律 1、内容:真空中两个静止的点电荷之间的作用 力(斥力或引力)与这两个电荷所带电荷量的 乘积成正比,跟它们之间距离的二次方成反比, 作用力的方向沿着这两个点电荷的连线。
如图所示,真空中有两个点电荷A、B, 它们固定在一条直线上相距l=0.3 m的两点, 它们的电荷量分别为QA=1.44×10-16 C, QB=3.6×10-17 C,现引入第三个点电荷C. • (1)若要使C处于平衡状态,试求C的电荷量和放 置的位置. •
如图所示,真空中有两个点电荷A、B, 它们固定在一条直线上相距l=0.3 m的两点, 它们的电荷量分别为QA=1.44×10-16 C, QB=3.6×10-17 C,现引入第三个点电荷C. (2)若点电荷A、B不固定,而使三个点电荷在库仑 力作用下都能处于平衡状态,试求C的电荷量和 放置的位置. •
三个共线自由点电荷的平衡问题 规律:三点共线,两同夹异, 两大夹小,近小远大。 [针对训练] • 4.在例4中,若A、B为相距l的异种电荷且不 固定,QA=-4Q,QB=Q.引入第三个点电荷 C,使三个点电荷在库仑力作用下都能处于平 衡状态,试求C的电荷量和放置的位置.
小结:
一个模型: 一个定律: 一个公式: 理想模型—点电荷 库仑定律
[针对训练] 3.如图所示,悬挂在 O 点的一根不可伸长的绝缘细线下端有一 个带电荷量不变的小球 A.在两次实验中,均缓慢移动另一带同 种电荷的小球 B.当 B 到达悬点 O 的正下方并与 A 在同一水平 线上,A 处于受力平衡时,悬线偏离竖直方向的角度为 θ,若两 次实验中 B 的电荷量分别为 q1 和 q2, θ 分别为 30˚ 和 45˚ .则 q2/q1 为( ) A.2 B.3 C.2 3 D.3 3
1.2库仑定律

C:
qq qq k 1 2 2 k 2 23 r1 r2 qq q1q3 k 322 k r2 (r1 r2 ) 2
两同夹一异;两大夹一小;近小远大
二、库仑定律的应用
4、库仑力作用下的力学问题
绝缘竖直墙面上固定一个带电小球A, o 带电量为+Q,另一个带电小球B,电 L 荷量为+q,用绝缘轻绳悬挂在竖直 T H 墙面上的o点,并保持平衡状态。两 +q 小球均可看作点电荷。由于空气潮湿, +Q 两小球的电荷量均在缓慢的减少,以 B A d 致小球B的位置缓慢移动。分析在此 过程中,轻绳的拉力和AB间的库仑力 mg 大小如何变化?
Q2 F库 k 2 r Q F库 k 2 r
如果AB两个小球是两个 质量分布均匀,电荷分布 均匀的绝缘小球呢?
二、库仑定律的应用
2、非点电荷库仑定律的使用
一个电荷分布均匀的的半球壳C,半径为r,带电量为+Q, AB两点的连线过球心O,并且距球心的距离均为2r。在B 点放一个电荷量也为+Q的点电荷,已知点电荷受到的库 仑力为F,若把点电荷放至A点,求它受到的库仑力。已知 静电力常量为k。 +Q C A r r o
+Q
B
常用方法: 添补法; 对称法;
二、库仑定律的应用
3、库仑力的叠加
真空中有两个带电量分别为+Q、-Q的两个静止的点电荷, AB是它们连线上的两点,分居连线中点O点的两侧。现将 一个带电量为+q的点电荷放至A点,在从A点移动到B点的 过程中,它所受到的库仑力如何变化? A
+Q
o B
-Q
二、库仑定律的应用
静电场
复习
一、库仑定律
1.2库仑定律

= 9×10 9 ×
= 9×10 -13 N
(斥力)
注意:计算时,电荷的正负号可不要代入!
知识拓展
一、两导体接触后电荷分配规律:
• 1、完全相同的金属小球接触后电荷分配
•
•
同种电荷:先相加再平分 异种电荷:先中和再平分
2、不完全相同的金属物体接触后电荷分配
不一定均分,电荷尽量分布在导体的外
表面
• 例3:三个相同的金属小球,原来有两个小球带
+
Q
A
QC
-
+
B
4Q
kQ1q kQ2 q 2 r (L r )2 2L r 3 kQ1Q2 kQ2 q 2 L (L r)2 Q1 q 9
三个自由点电荷平衡:
Q1 第三电荷带电量为 ,且为负电 9
三点共线,两同夹异,两大夹小,近小远大
练习1: A、B两个点电荷,相距为L,A带电 量为9Q,B带电量为4Q (1)如果A和B固定,应如何放置第三个点电 荷C,才能使此电荷处于平衡状态?此时对 C的电性及电量q有无要求? (2)如果A和B是自由的,又应如何放置第三 个点电荷,使系统处于平衡状态?此时对第 三个点电荷 C 的电量 q 的大小及电性有无要 求?
• •
A、X2=2X1 C、X2<4X1
B、X2=4X1 D、X2>4X1
【例题9】
mg F T
三、含库仑力的动力学问题
• 思路:运用牛顿第二定律结合运动学公式求解
• 例10 如图,质量均为 m的两个带电小球 A、B,放置在 光滑的绝缘水平面上,彼此相隔的距离为 L ,( L 比球 半径 r 大的多), B 球带电量为 QB=-3q , A 球带电量为 QA=6q, 若在 B 上加一水平向右的恒力 F ,要使 A 、 B 两球 始终保持L的间距运动,求
课件11:1.2 库仑定律

第2节 库仑定律
学习目标
1. 知道点电荷的概念,了解带电体能被看作点电荷 的条件. 2.掌握库仑定律,理解库仑定律的含义及其公式, 知道静电力常量. 3.会用库仑定律的公式进行有关的计算. 4.知道库仑扭秤的实验原理.
一、对点电荷的正确理解
1.点电荷是物理模型 只有电量,没有大小、形状的理想化的模型,类似于力 学中的质点,实际中并不存在. 2.带电体看成点电荷的条件 如果带电体间的距离比它们自身的大小大得多,以至于 带电体的形状和大小对相互作用力的影响很小,就可以 忽略形状、大小等次要因素,带电体就能看成点电荷.
4.适用范围:真空、静止、点电荷
想一想
1.现有一个半径为20 cm的带电圆盘,问能否把它看 做点电荷?
【答案】能否把带电圆盘看做点电荷,不能只看 大小,要视具体情况而定.若另一带电体离它很 远(如10 m),完全可以将它视为点电荷;若另一 带电体离它很近(如1cm),带电圆盘的大小不能 忽略,则不能视为点电荷.
(已知质子的质量为1.67× 10-27 kg,电子的质量为
9.1×10-31 kg)
解:氢原子核与电子之间的库仑力 F电为:
F电
k
q1q2 r2
9.0109 (1.61019 )2 (5.3 1011 )2
N 8.2108
N
氢原子核与电子之间的万有引力F引为:
F引
G
m1 r
m
2
2
6.67 1011
【解析】带电体能否看成点电荷,和带电体的 体积无关,主要看带电体的体积相对所研究的 问题是否可以忽略,如果能够忽略,则带电体 可以看成点电荷,否则就不能.
【答案】C
例2 在氢原子中,原子核只有1个质子, 核外只有1个 电子, 它们之间的距离 r = 5.3×10-11 m .求氢原子核与 电子之间的库仑力 F电及它们之间的万有引力F引 ?
1.2 库仑定律

二、库仑定律
1. 真空中两个静止点电荷之间的相互作用力, 与它们的电荷量的乘积成正比,与它们的距离的 二次方成反比,作用力的方向在它们的连线上。
2.大小:
q1q2 F k 2 r
K----静电力常量:k=9.0×109N· m2/C2
3.适用范围:1.真空中 2.静止的点电荷.
F ----- 叫做静电力或库仑力.
q1q2 F k r2
2.大小:
K----静电力常量:k=9.0×109N· m2/C2
3.适用范围:1.真空中 2.静止的点电荷.
4、库伦定律的说明
r
R
(1)点电荷(理想模型):当带电体间距 离比它们自身的大小大很多,可将其看作有 电荷量的点(R<<r) (2)使用库伦定律计算时,点电荷电量用绝 对值代入公式进行计算,然后根据同性相 斥、异性相吸判断方向
1.两个电荷之间的库伦力为F,若电 荷量大小不变,距离变为原来的2倍, F/4 库伦力变为______________
2.两个半径相同的金属小球其球心间距r远远 大于球半径R,带电荷量之比为1:7,两 者相互接触后再放回原来位置上,则相互 作用力可能为原来的( C) D
A. 4/7 B. 3/7 C. 9/7 D. 16/7
思维严密,考虑多种情况
总结:库仑定律
1. 真空中两个静止点电荷之间的相互作用力, 与它们的电荷量的乘积成正比,与它们的距离的 二次方成反比,作用力的方向在它们的连线上。
第二节
库仑定律
同种电荷相互排斥 异种电荷相互吸引
猜想
电荷之间相互作用力的大小源自决定于那些因素呢?探究影响电荷间相互作用的因素 •猜想:
电荷量 间距
•实验装置
1.2 静电力--库仑定律

解:q3共受F1和F2两个力的作用,q1=q2=q3=q,相互间的距离 r 都相同,
q1
所以
F2
q2
9.0 109 2 106 2 N
F1=F2=K
=
r2
0.52
q3
30 ° F
=0.144 N
F1 q2
根据平行四边形定则,合力是:
F 2F1 cos30 0.25 N
合力的方向沿q1与q2连线的垂直平分线向外.
当堂提升
例. A、B两个点电荷,相距为r,A带有9Q 的正电荷,B带有4Q的正电荷.如果A和B 固定,应如何放置第三个点电荷q,才能 使此电荷处于平衡状态?
9Q
+
A
-
+ 4Q
B
C
Q
口诀:两同夹一异 两大夹一小 近小远大
例 两个放在绝缘上的相同金属球A、B,相距d,球 1 的半径比d小得多,分别带有电荷3q和-q,A球
其中k:静电力常量
k=9.0×109N·m2
计算时,若电荷是负电荷只需它的绝对值代入 /C2
3.方向:在两电荷的连线上,同种电荷相互排斥,异种电荷相互吸引.
4.适用条件: ⑴真空(空气中近似成立) ⑵点电荷
解题 库仑定律的适用是什么条件? 提醒
点电荷:物理模型,即如果满足相互之间距离远大
于带电体大小则带电体便可看做点电荷.
)2
F电为
N
(5.31011 )2
8.2108 N
质子F引与6.电6G7子m1之0r1m21间1 2的9.万1有10引31力1.F67引
为
1027
N
(5.3 1011 )2
3.6 1047 N
库仑力与万有引力 的比值为
1.2 库仑定律讲解

思考题
两个靠近的带电球体,是否可 以看出是集中在球心位置的点电荷?
不可以
课堂训练
1、两个半径为0.3m的金属球,球心相距 1.0m放置,当他们都带1.5×10−5 C的 正电时相互作用力为F1 ,当它们分 别带+1.5×10−5 C和−1.5×10−5 C的电 量时,相互作用力为F2 , 则( ) A.F1 = F2 B.F 1 <F2 C.F1 > F2 D.无法判断
A.4/7 B. 3/7
C. 9/7
D. 16/7
课堂训练
4、两个半径为0.3m的金属球,球心相 距1.0m放置,当他们都带1.5×10−5 C 的正电时,相互作用力为F1 ,当它们 分别带+1.5×10−5 C和−1.5×10−5 C的 电量时,相互作用力为F2 , 则( B ) A .F 1 = F 2 B. F 1 < F 2 C.F 1 > F 2 D.无法判断
1.2 库仑定律
同种电荷相互排斥 异种电荷相互吸引
既然电荷之间存在相互作用,那么电 荷之间相互作用力的大小决定于那些因素 呢?
猜想:力F与两电荷的电荷量q、距离r有关。
用控制变量法来研究
+Q +q
带电量相同,带 电小球偏转角不 同 ,可见其受力 大小不同。
结论:电荷之间的作用力F随着q的增大而 增大,随着r的增大而减小。
√
课堂训练
2、关于点电荷的下列说法中正确的是: ABD A .真正的点电荷是不存在的. B .点电荷是一种理想模型. C .足够小的电荷就是点电荷. D .一个带电体能否看成点电荷,不是看它 的尺寸大小,而是看它的形状和大小对 所研究的问题的影响是否可以忽略不计
课堂训练
3、下列说法中正确的是: D A .点电荷就是体积很小的电荷. B .点电荷就是体积和带电量都很小 的带电体. C .根据公式可知F=k(q1q2)/r2, 当 间距r→0时,静电力F→∞ D .静电力常量的数值是由实验得到 的.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课堂检测
1.下列说法中正确的是()
A.点电荷是一种理想模型,真正的点电荷是不存在的
B.点电荷就是体积和带电量都很小的带电体
C.根据F=k可知,当r趋近于0时,F趋近于∞
D.一个带电体能否看成点电荷,不是看它的尺寸大小,而是看它的形状和大小对所研究的问题的影响是否可以忽略不计
2.有两个半径为r的带电金属球中心相距为L(L=4r),对于它们之间的静电作用力(设每次各球带电量绝对值相同)()
A.带同号电荷时大于带异号电荷时
B.带异号电荷时大于带同号电荷时
C.带等量负电荷时大于带等量正电荷时
D.大小与带电性质无关,只取决于电荷量
3.三个相同的金属小球a、b和c,原来c不带电,而a和b带等量异号电荷,相隔一定距离放置,a、b之间的静电力为F.现将c球分别与a、b接触后拿开,则a、b之间的静电力将变为()
A. B. C. D.
4.如图所示,两个带电小球A、B分别用细丝线悬吊在同一点O,静止后两小球在同一水平线上,丝线与竖直方向的夹角分别为α、β(α>β),关于两小球的质量m1、m2和带电荷量q1、q2,下列说法中正确的是()
A.一定有m1<m2,q1<q2
B.可能有m1<m2,q1>q2
C.可能有m1=m2,q1=q2
D.可能有m1>m2,q1=q2
5.两个完全相同的带电小球,质量均为m且带有等量同号电荷,用两根长度相同的绝缘细线悬挂于同一点,如图所示,静止后两条细线张角为2θ,若细线长度为L,两个小球所带电荷量大小均为,悬线张力大小为.
6.如图所示,把质量为0.2g的带电小球A用丝线吊起,若将带电荷量为4×10-8C的小球B靠近它,当两小球在同一高度且相距3cm时,丝线与竖直方向夹角为45°,此时小球B受到库仑力F=.小球A带的电荷量q A=.
7.如图所示,等边三角形ABC,边长为L,在顶点A、B处有等量异号点电荷
Q A,Q B,Q A=+Q,Q B=-Q,求在顶点C处的点电荷+Q C所受的静电力.
课堂检测
1.AD
2.B解析:由于两电荷距离太近,不能看作是点电荷,又因为同号电荷互相排斥,则它们的中心距离大于L.而异号电荷互相吸引,则它们的中心距离小于L.由此可知,异号电荷间的作用力大于同号电荷间的作用力.
3.C解析:a、b带等量异号电荷,用不带电的c分别与其接触后,a的带电量为原来的,b的带电量为原来的,所以a、b间的静电力为原来的.
4.B解析:A、B两球的静电力F大小相等,方向相反,但带电量的大小不能确定.根据受力平衡可知m1g=,m2g=,α>β,所以m1<m2.
5.2L sinθ
6.解析:根据题给条件,可知小球A处于平衡状态,分析小球A受力情况如图所示.mg:小球A的重力、F T:丝线的张力、F库:小球B对小球A的静电力,三个力的合力为零.F库
=mg tan45°=0.2×10-3×10×1=2×10-3N.题中小球A,B都视为点电荷,它们之间相互吸引,其作用力大小F库=k.
由k=mg tan45°,则q A=--
C=5.0×10-9C.
-
小球B受到库仑力与小球A受到库仑力为作用力与反作用力,所以小球B受到的库仑力大小为2×10-3N.小球A与小球B相互吸引,B带正电,小球A带负电.
答案:2×10-3N-0.5×10-8C
7.答案:F=k方向:水平向右.。
