23.2中心对称(1)
23.2.1中心对称图形课件

如图:过□ABCD的对角线交点O作两条互相垂
直的直线分别交□ABCD各边于点E、F、G、H,
求证:四边形EFGH是菱形 A
GD
证明:∵O是□ABCD的对称中心
EF、GH经过点O
E
F
O
∴E、F和G、H分别关于点O对称 B H
C
∴ OE=OF,OG=OH
∵EF⊥GH
∴四边形EGFH是菱形
y 5
4
②3 ① 2
1
-5 -4 -3 -2 -1 O -1
③ -2 -3 -4 -5
1 2 3 4 5x
④
练习(见学案例2):在如图的方格纸中,每个小正方形 的边长都是为1. (1)画出点C关于点O的对称点C1 (2)画出线段BC关于点O的对称线段B1C1 (3)画出将A △ABC关于点O对称△A1B1C1;
判断下列说法是否正确 (1)轴对称图形也是中心对称图形。(×)
(2)旋转对称图形也是中心对称图形。( ×)
(3)平行四边形、长方形和正方形都是中心对称图 形,对角线的交点是它们的对称中心。( √ )
(4)角是轴对称图形也是中心对称图形。( × )
(5)在成中心对称的两个图形中,对应线段平行
(或在同一直线上)且相等。
如果将中心对称图形,对称的部分看成 两个图形,则它们是关于中心对称。
轴对称图形与中心对称图形:
轴对称图形
中心对称图形
有一条对称轴—直线 有一个对称中心—点 图形沿轴对折 图形绕这个点旋转180O
对折部分与另一部分 旋转后与原图形重合 重合
想一想
下面哪些图形是中心对称图形? o
在下列图形中,是中心对称图形的是
( C)
23.2 中心对称(第1课时)教学设计

23.2 中心对称(1)第一课时教学内容两个图形关于这个点对称或中心对称、对称中心、关于中心的对称点等概念及其运用它们解决一些实际问题.教学目标1.知识与技能了解中心对称、对称中心、关于中心的对称点等概念及掌握这些概念解决一些问题.复习运用旋转知识作图,•旋转角度变化,•设计出不同的美丽图案来引入旋转180°的特殊旋转──中心对称的概念,并运用它解决一些实际问题.2.过程与方法复习对称轴和轴对称图形的有关概念,•通过知识迁移讲授中心对称图形和对称中心的有关内容,并附加练习巩固这个内容.通过几何操作题,探究猜测发现规律,并给予证明,附加例题进一步巩固.3.情感、态度与价值观让学生经历观察、操作等过程,了解图形旋转的概念,从事图形旋转基本性质的探索活动,进一步发展空间观察,培养运动几何的观点,增强审美意识.让学生通过独立思考,自主探究和合作交流进一步体会旋转的数学内涵,获得知识,体验成功,享受学习乐趣.让学生从事应用所学的知识进行图案设计的活动,享受成功的喜悦,激发学重难点、关键1.重点:利用中心对称、对称中心、关于中心对称点的概念解决一些问题.2.难点与关键:从一般旋转中导入中心对称.教具、学具准备小黑板、三角尺教学过程一、复习引入请同学们独立完成下题.如图,△ABC 绕点O 旋转,使点A 旋转到点D 处,画出旋转后的三角形,•并写出简要作法.老师点评:分析,本题已知旋转后点A 的对应点是点D ,且旋转中心也已知,所以关键是找出旋转角和旋转方向.显然,逆时针或顺时针旋转都符合要求,•一般我们选择小于180°的旋转角为宜,故本题选择的旋转方向为顺时针方向;•已知一对对应点和旋转中心,很容易确定旋转角.如图,连结OA 、OD ,则∠AOD 即为旋转角.接下来根据“任意一对对应点与旋转中心的连线所成的角都是旋转角”和“对应点到旋转中心的距离相等”这两个依据来作图即可.作法:(1)连结OA 、OB 、OC 、OD ;(2)分别以OB、OB为边作∠BOM=∠CON=∠AOD;(3)分别截取OE=OB,OF=OC;(4)依次连结DE、EF、FD;即:△DEF就是所求作的三角形,如图所示.二、探索新知问题:作出如图的两个图形绕点O旋转180°的图案,并回答下列的问题:1.以O为旋转中心,旋转180°后两个图形是否重合?2.各对称点绕O旋转180°后,这三点是否在一条直线上?老师点评:可以发现,如图所示的两个图案绕O旋转180°都是重合的,即甲图与乙图重合,△OAB与△COD重合.像这样,把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心.这两个图形中的对应点叫做关于中心的对称点.例1.如图,四边形ABCD绕D点旋转180°,请作出旋转后的图案,写出作法并回答.(1)这两个图形是中心对称图形吗?如果是对称中心是哪一点?如果不是,请说明理由.(2)如果是中心对称,那么A、B、C、D关于中心的对称点是哪些点.分析:(1)根据中心对称的定义便直接可知这两个图形是中心对称图形,•对称中心就是旋转中心.(3)旋转后的对应点,便是中心的对称点.解:作法:(1)延长AD,并且使得DA′=AD(2)同样可得:BD=B′D,CD=C′D(3)连结A′B′、B′C′、C′D,则四边形A′B′C′D为所求的四边形,如图23-44所示.答:(1)根据中心对称的定义便知这两个图形是中心对称图形,对称中心是D 点.(2)A 、B 、C 、D 关于中心D 的对称点是A ′、B ′、C ′、D ′,这里的D ′与D 重合.例2.如图,已知AD 是△ABC 的中线,画出以点D 为对称中心,与△ABD•成中心对称的三角形.分析:因为D 是对称中心且AD 是△ABC 的中线,所以C 、B 为一对的对应点,因此,只要再画出A 关于D 的对应点即可.解:(1)延长AD ,且使AD=DA ′,因为C 点关于D 的中心对称点是B (C ′),B•点关于中心D 的对称点为C (B ′)(2)连结A ′B ′、A ′C ′.则△A ′B ′C ′为所求作的三角形,如图所示.C(B ')B(C ')AA 'D 三、巩固练习教材P74 练习2.。
2021年人教版数学九年级上册23 中心对称(第一课时)课件

A.点 E C.点 G
B.点 F D.点 H
8
3.如图,△ABC 与△A′B′C′关于点 O 成中心对称,则下列结论不成立的是 ( D)
A.点 A 与点 A′是对称点 C.AB∥A′B′
B.BO=B′O D.∠ACB=∠C′A′B′
9
4.如图,在△ABC 中,AB=AC,△ABC 与△FEC 关于点 C 成中心对称,连 接 AE、BF.若四边形 ABFE 为矩形,则∠ACB 为( C )
另外两个矩形,得到连接各自中心
的第二条线段,两条线段交于点G,
点G即为重心.
22
图2
►在有欢声笑语的校园里,满地都是雪,像一块大地毯。房檐上挂满了冰凌 ,一根儿一根儿像水晶一样,真美啊!我们一个一个小脚印踩在大地毯上 ,像画上了美丽的图画,踩一步,吱吱声就出来了,原来是雪在告我们: 和你们一起玩儿我感到真开心,是你们把我们这一片寂静变得热闹起来。 对了,还有树。树上挂满了树挂,有的树枝被压弯了腰,真是忽如一夜春 风来,千树万树梨花开。真好看呀! ►冬天,一层薄薄的白雪,像巨大的轻软的羊毛毯子,覆盖摘在这广漠的荒 原上,闪着寒冷的银光。
B.(- 3,2),( 3,-2)
C.(- 3,2),(2,- 3)
D.- 27,
221, 27,-
21 2
14
8.如图,四边形 ABCD 是中心对称图形,对称中心为点 O,过点 O 的直线与 AD、BC 分别交于点 E、F,则图中相等的线段有( C )
A.3 对 C.5 对
B.4 对 D.6 对
►走进颐和园,眼前是繁华的苏州街,现在依稀可以想象到当年的热闹场面, 苏州街围着一片湖,沿着河岸有许多小绿盘子里装着美丽的荷花。这里是 仿照江南水乡--苏州而建的买卖街。当年有古玩店、绸缎店、点心铺等, 店铺中的店员都是太监、宫女妆扮的,皇帝游览的时候才营业。我正享受 着皇帝的待遇,店里的小贩都在卖力的吆喝着。 ►走近一看,我立刻被这美丽的荷花吸引住了,一片片绿油油的荷叶层层叠 叠地挤在水面上,是我不由得想起杨万里接天莲叶无穷碧这一句诗。荷叶 上滚动着几颗水珠,真像一粒粒珍珠,亮晶希望对您有帮助,谢谢 晶的。 它们有时聚成一颗大水珠,骨碌一下滑进水里,真像一个顽皮的孩子!
23.2.1 中心对称(共43张PPT)
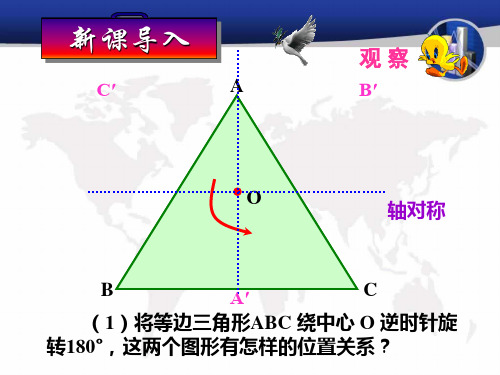
15 8
2
OF
15 8
同理OE 15 ,即 OF OE OF 15
8
4
A
D
C′
D′
O 重合
B′
A′
B
C
(4)将平行四边形ABCD绕中心O逆时针旋 转180°,这两个图形有怎样的位置关系?
有的轴对称, 有的重合。
绕中心旋转180°,旋转后的图 形与原图的位置关系有什么不同?
教学目标
【知识与能力】
了解中心对称、对称中心、关于中心的对称 点等概念。 通过具体实例认识两个图形关于某一点成中 心对称的本质:就是一个图形绕一点旋转180° 而成。 作出中心对称的图形。
它是轴对称图形吗? 不是轴对称图形。
这个图形是否能够通过某种图形运动与自 身重合?
探究
下列图形是否能够通过某种图形运动与自
身重合?图旋Biblioteka 形转绕后中与
线段绕中点旋转180°
心原 旋图
旋转后与原图重合
转重
180 合
°
知识要点
把一个图形绕着某一个点旋转180°, 如果它能够与另一个图形重合,那么就说 这两个图形关于这个点对称或中心对称 (central symmetry),这个点叫做对称中 心。这两个图形中的对应点叫做关于中心 的对称点。
经历对日常生活中与中心对称有关的图形进行 观察、分析、欣赏、动手操作、画图等过程,发 展审美能力,增强对图形的欣赏意识。
从图形变化过程中,树立正确的辩证唯物主义 观点。
认识几何图形的对称美,培养学生热爱数学, 热爱生活。
教学重难点
利用中心对称、对称中心、关于中心的 对称点的概念解决一些问题。 从一般旋转中导入中心对称。 中心对称的性质及初步应用。 中心对称与旋转之间的关系。
23.2.1 中心对称

23.2.1 中心对称
基础通关 能力突破 素养达标
1 2 3 4 5 6 7 8 9 10 11 12 13 14
23.2.1 中心对称
基础通关 能力突破 素养达标
1 2 3 4 5 6 7 8 9 10 11 12 13 14
1 2 3 4 5 6 7 8 9 10 11 12 13 14
23.2.1 中心对称
基础通关 能力突破 素养达标
3.
如图,已知 O 是▱ ABCD 对角线的交点,则图中关于点 O 对
称的三角形有 4 对.
【解析】图中关于点 O 对称的三角形有△ AOD 和△ COB ,△ ABO 与△ CDO ,△ ACD 与△ CAB ,△ ABD 和△ CDB ,共4对.
1 2 3 4 5 6 7 8 9 10 11 12 13 14
23.2.1 中心对称
基础通关 能力突破 素养达标
2. 下列各组图形中,△A'B'C'与△ ABC 成中心对称的是( D )
【解析】A. 是平移变换图形,故本选项错误;B. 是轴对称图形,故本 选项错误;C. 是旋转变换图形,故本选项错误;D. 是中心对称图形, 故本选项正确.
A. 1个
B. 2个
C. 3个
D. 4个
第10题图
1 2 3 4 5 6 7 8 9 10 11 12 13 14
23.2.1 中心对称
基础通关 能力突破 素养达标
【解析】△ ABC 与△ CDA 关于点 O 对称,则 AB = CD , AD = BC , ∴四边形 ABCD 是平行四边形,即点 O 就是▱ ABCD 的对称中心,则有 ①点 E 和点 F , B 和 D 是关于点 O 的对称点,正确; ②直线 BD 必经过点 O ,正确; ③四边形 DEOC 与四边形 BFOA 的面积必相等,正确; ④△ AOE 与△ COF 成中心对称,正确; 其中正确的有4个.
人教版九年级数学上册:23.2.1中心对称(教案)

-理解中心对称的实质:学生往往容易将中心对称与轴对称混淆,需要通过实例讲解和练习,使学生明确两者的区别。
-判断中心对称图形:学生可能在判断复杂图形是否为中心对称图形时遇到困难,需要教授一些识别技巧和辅助方法。
-应用中心对称解决实际问题:将中心对称应用于实际问题解决时,学生可能不知如何下手,需提供具体的案例和指导。
-中心对称在图案设计中的应用:学生可能缺乏创新意识,难以独立设计出具有中心对称美的图案。
举例:
-对于难点的突破,可以通过以下方法:
1.对比中心对称和轴对称,通过直观演示和图例分析,强化学生对中心对称实质的理解。
2.提供一系列图形,指导学生通过观察、折叠、标记等方法判断其是否为中心对称图形。
3.设计一些实际问题,如平面坐标系的图形变换、建筑物布局等,指导学生运用中心对称的性质进行求解。
-掌握中心对称的性质:中心对称图形的每一点关于对称中心都有对应的另一点,且两点之间的线段被对称中心平分。
-学会识别中心对称图形:能够识别常见的中心对称图形,如正方形、圆形、线段等。
-应用中心对称进行图形变换:掌握如何利用中心对称对图形进行旋转、翻折等变换。
举例:讲解中心对称的定义时,可以通过实际操作教具或多媒体演示,让学生直观感受中心对称的过程。
3.重点难点解析:在讲授过程中,我会特别强调中心对称的定义和性质这两个重点。对于难点部分,如中心对称与轴对称的区别,我会通过举例和比较来帮助大家理解。
(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与中心对称相关的实际问题,如如何在坐标平面上找到对称中心。
2.实验操作:为了加深理解,我们将进行一个简单的实验操作。比如,通过折叠和旋转正方形,观察中心对称的基本原理。
02-第二十三章23.2.1中心对称

23.2.1 中心对称
(2)点D的位置共有三种可能.如图:
栏目索引
23.2.1 中心对称
栏目索引
1.点A和点B的坐标分别为(0,2),(1,0),若将△OAB绕点B顺时针旋转180° 后,得到△O'A'B,则点A的对应点A'的坐标是 ( ) A.(0,2) B.(2,2) C.(-2,2) D.(2,-2)
图23-2-1-6
23.2.1明中的应用 例2 如图23-2-1-7,在△ABC中,∠A=90°,D为BC的中点,DE⊥DF,DE交 AB于点E,DF交AC于点F,试探索线段BE,EF,FC之间的数量关系.
图23-2-1-7
23.2.1 中心对称
解析 FC2+BE2=EF2.理由如下: ∵D为BC的中点, ∴BD=DC. 作△BDE关于点D对称的△CDM,如图23-2-1-8所示, 由中心对称的性质可得△BDE≌△CDM. ∴CM=BE,MD=DE,∠DCM=∠B. 又∵∠B+∠ACB=90°, ∴∠DCM+∠ACB=90°,即∠FCM=90°. 连接FM,在△FME中,MD=DE,FD⊥ME, ∴FM=FE. 又∵在Rt△FCM中,FC2+CM2=FM2,
答案 D 如图所示,点A和点B的坐标分别为(0,2),(1,0),∴OA=2,OB=1, ∠AOB=90°.将△OAB绕点B顺时针旋转180°后,得到△O'A'B,∴O'B=OB =1,O'A'=OA=2,∠A'O'B=90°,∴点A的对应点A'的坐标为(2,-2).
23.2.1 中心对称
栏目索引
图23-2-1-3
23.2.1 中心对称
人教版九年级数学上册23.2.2.1《中心对称》教案

人教版九年级数学上册23.2.2.1《中心对称》教案一. 教材分析人教版九年级数学上册第23章《中心对称》是学生在学习了平面几何相关知识的基础上,进一步引导学生探索中心对称的性质和运用。
本节内容通过具体的实例,让学生了解中心对称的定义,掌握中心对称图形的性质,并能够运用中心对称解决实际问题。
教材通过丰富的图片和实例,激发学生的学习兴趣,培养学生动手操作和观察分析的能力。
二. 学情分析九年级的学生已经具备了一定的几何知识基础,对平面几何图形有一定的了解。
但学生在学习过程中,可能对中心对称的概念和性质理解不够深入,需要通过大量的练习和操作来巩固。
此外,学生对实际问题的解决能力有待提高,需要通过具体的例子来引导和培养。
三. 教学目标1.了解中心对称的定义,掌握中心对称图形的性质。
2.能够运用中心对称解决实际问题,提高学生的应用能力。
3.培养学生的动手操作和观察分析能力,激发学生学习几何的兴趣。
四. 教学重难点1.中心对称的定义和性质。
2.中心对称在实际问题中的应用。
五. 教学方法采用问题驱动法、案例教学法和小组合作学习法。
通过具体的实例和问题,引导学生探索中心对称的性质,培养学生的动手操作和观察分析能力。
同时,学生进行小组合作学习,鼓励学生发表自己的观点和思考,提高学生的合作能力和沟通能力。
六. 教学准备1.准备相关的图片和实例,用于引导学生探索中心对称的性质。
2.准备一些实际问题,用于巩固学生对中心对称的应用。
3.准备黑板和粉笔,用于板书重要的概念和性质。
七. 教学过程1.导入(5分钟)通过展示一些图片,如天安门、蝴蝶等,引导学生观察这些图片的共同特点,引发学生对中心对称的思考。
让学生发表自己的观点,教师总结并引入中心对称的概念。
2.呈现(10分钟)教师通过展示一些实例,如将一张纸折叠后,对折线两侧的图形完全重合,引导学生探索中心对称的性质。
教师引导学生动手操作,观察分析中心对称图形的性质,如对称轴的性质、对称点的性质等。
《23.2.1中心对称》学历案-初中数学人教版12九年级上册

《中心对称》学历案(第一课时)一、学习主题本节课的学习主题是“初中数学课程《中心对称》”。
中心对称是初中数学中关于图形变换的重要概念,是理解几何图形性质和规律的基础。
本节课将通过学习中心对称的定义、性质和实例,培养学生的空间想象能力和几何思维。
二、学习目标1. 理解中心对称的定义,掌握中心对称图形的特点。
2. 能够判断给定的图形是否为中心对称图形,并找出其对称中心。
3. 通过实例分析,培养学生的空间想象能力和几何思维。
4. 提高学生的数学学习兴趣和自主学习能力。
三、评价任务1. 口头回答问题:学生能够准确阐述中心对称的定义和特点,以及如何判断一个图形是否为中心对称。
2. 书面作业:学生能够独立完成一系列关于中心对称的判断题和简答题,并能够准确找出给定图形的对称中心。
3. 小组讨论:学生能够与小组成员合作,通过讨论和交流,加深对中心对称概念的理解和应用。
四、学习过程1. 导入新课:通过展示一些中心对称的实例,引导学生感受中心对称的概念,并激发学生的学习兴趣。
2. 讲解定义:教师讲解中心对称的定义,让学生明确概念,理解其含义。
3. 探究性质:通过具体的图形,让学生探究中心对称图形的性质,如对称点的性质、对称轴的性质等。
4. 实例分析:教师给出一些中心对称的图形,让学生判断是否为中心对称,并找出其对称中心。
5. 小组合作:学生分组进行讨论,加深对中心对称概念的理解和应用,教师巡视指导,及时解答学生的疑问。
6. 总结归纳:教师总结本节课的学习内容,强调中心对称的概念和性质,让学生形成完整的知识体系。
五、检测与作业1. 课堂检测:通过一系列关于中心对称的判断题和简答题,检测学生对中心对称概念的理解和应用能力。
2. 课后作业:布置一些关于中心对称的练习题,让学生巩固所学知识,并提高解题能力。
六、学后反思1. 学生反思:学生应反思自己在本次学习中的收获和不足,如何改进自己的学习方法,提高学习效率。
2. 教师反思:教师应对本次教学进行反思,总结教学经验,找出教学中存在的问题和不足,为今后的教学提供参考。
23.2.1中心对称的概念与性质

巩固练习
课本第66页:练习.
归纳小结
(1)中心对称的概念与性质 (2)画一个图形关于一个点的对称图形
测试作业
课本第69页:第1题.
九年级
上册
23.2 中心对称(第1课时)
情景引入
(1)如图,把其中一个图案绕点 O 旋转180°, 你有什么发现? 两个图案能够完全重合在一起.
情景引入
(2)如图,线段 AC,BD 相交于点 O,OA=OC, OB=OD.把 △OCD 绕点 O 旋转 180°,你 有什么发现? 两个图案能够完全重合在一起.
A O D
B
C
归纳定义
swf样,把一个图形绕着某一点旋转 180°,如果 它能够与另一个图形重合,那么就说这两个图形关 于这个点对称或中心对称.这个点叫做对称中心.
这两个图形在旋转后能重合的对应点叫做关于对称 中心的对称点.
归纳定义
C A B O B′ C' A′
巩固练习
1.指出下图中的对称点,对称中心是如何确定的? D A O C
B
巩固练习
2.如图,已知△ABC 与△DEF 中心对称,点 A 和点 D 是对称点,画出对称中心 O.
F
E
A
B
D C
典型例题
例1(1)如左图,选择点 O 为对称中心,画出点 A 关于 点 O 的对称点 A';
典型例题
例1(2)如右图,选择点 O 为对称中心,画出与 △ABC关于点O 对称的△A'B'C'.
23.2:中心对称(解答题专练)(解析版)

23.2:中心对称(解答题专练)1.下图是一个风车图案的一部分,风车图案是一个关于点O的中心对称图形,请你把它补全.【答案】详见解析.【解析】易得旋转中心是O,旋转角度为45°,旋转方向顺时针,按此作图即可.【解答】如图,【点评】旋转作图的关键是得到旋转中心,旋转方向.2.华丰木器加工厂需加工一批矩形木门,为了安装的需要,在木门的中心要钻一个小孔,假如你是工人师傅,你应该如何确定小孔的位置.【答案】两对角线的交点即为小孔的位置【解析】矩形的两条对角线可以看作是两对对应点的连线,中心对称图形上的每一对对应点所连成的线段,都过对称中心,且被对称中心平分,而矩形的两条对角线互相平分,故两条对角线的交点,必为对称中心.【解答】解:只要画出矩形木门的两条对角线,两对角线的交点即为小孔的位置(•如答图所示的O点).【点评】本题考查了中心对称及矩形的性质,难度不大,熟练掌握矩形是中心对称图形,其对角线的交点是对称中心是解答本题的关键.3.如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,2)请解答下列问题:(1)画出△ABC关于原点O成中心对称的△A1B1C1,并写出A1的坐标;(2)画出△ABC绕点B逆时针旋转90°后得到的△A2B2C2,并求出点C在旋转过程中经过的路径长是多少?【答案】(1)画图见解析,A1(-2,-2);(2)画图见解析,5 2π【解析】【解析】根据题意画出相应的三角形, 确定出所求点坐标和弧长即可.【解答】解: (1)画出△ABC关于y轴对称的△A1B1C1,如图所示, 此时A1的坐标为(-2,2);(2) 画出△ABC绕点B逆时针旋转90后得到的△A2B2C2,易得5此时C点旋转过程中经过的路程l为:l=9025360oo)5.【点评】本题主要考查图形的轴对称、尺规作图和弧长公式.4.如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;(2)请画出△ABC关于原点对称的△A2B2C2;并写出点A2、B2、C2坐标;(3)请画出△ABC绕O逆时针旋转90°后的△A3B3C3;并写出点A3、B3、C3坐标.【答案】(1)见解析;(2)见解析,A2(﹣1,﹣1)、B2(﹣4,﹣2)、C2(﹣3,﹣4);(3)见解析,A3(﹣1,1)、B3(﹣2,4)、C3(﹣4,3).【解析】(1)利用平移的性质得出对应点的位置进而得出答案(2)利用关于原点对称点的性质得出对应点的位置进而得出答案(3)利用旋转的性质得出旋转后的点的坐标进而得出答案【解答】解:(1)如图,△A1B1C1即为所求;(2)如图,△A2B2C2即为所求,A2(﹣1,﹣1)、B2(﹣4,﹣2)、C2(﹣3,﹣4);(3)如图,△A3B3C3即为所求,A3(﹣1,1)、B3(﹣2,4)、C3(﹣4,3).【点评】本题主要考查了二次函数平移旋转等图形变换的基本性质,掌握前后变换规律是解题关键5.如图,ABC与ADE关于点A成中心对称.(1)点A,B,C的对应点分别是什么?(2)点C,A,E的位置关系是怎样?(3)指出图中相等的线段和相等的角.【答案】(1)点A ,B ,C 的对应点分别是点A ,D ,E ;(2)点C ,A ,E 在同一条直线上;(3)AB AD =,AC AE =,BC DE =,B D ∠=∠,C E ∠=∠,BAC DAE ∠=∠.【解析】(1)根据两个图形成中心对称即可得出答案;(2)根据两个图形成中心对称即可得出答案;(3)分别找到成中心对称的两个图形对应的线段和对应角即可得出答案.【解答】(1)∵ABC 与ADE 是成中心对称的两个图形,∴点A ,B ,C 的对应点分别是点A ,D ,E .(2)根据中心对称的性质,可知点C ,A ,E 在同一条直线上.(3)AB AD =,AC AE =,BC DE =,B D ∠=∠,C E ∠=∠,BAC DAE ∠=∠.【点评】本题主要考查两个图形成中心对称,掌握中心对称的性质是解题的关键.6.画出如图所示的四边形ABCD 关于点O 成中心对称的四边形A B C D ''''.【答案】如图所示,四边形A B C D ''''即为所求;见解析.【解析】根据旋转的性质即可画出四边形ABCD 关于点O 成中心对称的四边形A B C D ''''.【解答】如图所示,四边形A B C D ''''即为所求:.【点评】本题考查了作图−旋转变换,解决本题的关键是掌握旋转的性质.7.如图,在Rt △OAB 中,∠OAB =90°,且点B 的坐标为(4,2).(1)画出OAB 关于点O 成中心对称的11OA B ,并写出点B 1的坐标;(2)求出以点B 1为顶点,并经过点B 的二次函数关系式.【答案】(1)图见解析,点()142B --,;(2)()214216y x =+-. 【解析】(1) 先由条件求出A 点的坐标, 再根据中心对称的性质求出1A 、 1B 的坐标, 最后顺次连接1OA 、1OB , △OAB 关于点O 成中心对称的△11OA B 就画好了,可求出B 1点坐标.(2) 根据 (1) 的结论设出抛物线的顶点式, 利用待定系数法就可以直接求出其抛物线的解析式.【解答】(1)如图,点()142B --,.(2)设二次函数的关系式是()242y a x =+-,把(4,2)代入上式得()22442a =+-,116a ∴=, 即二次函数关系式是()214216y x =+-. 【点评】本题主要考查中心对称的性质,及用待定系数法求二次函数的解析式,难度不大.8.如图,△ABC 的三个顶点和点O 都在正方形网格的格点上,每个小正方形的边长都为1.(1)将△ABC先向右平移4个单位,再向上平移2个单位得到△A1B1C1,请画出△A1B1C1;(2)请画出△A2B2C2,使△A2B2C2和△ABC关于点O成中心对称.【答案】解:(1)所画△A1B1C1如图所示.(2)所画△A2B2C2如图所示.【解析】(1)图形的整体平移就是点的平移,找到图形中几个关键的点,也就是A,B,C点,依次的依照题目的要求平移得到对应的点,然后连接得到的点从而得到对应的图形;(2)在已知对称中心的前提下找到对应的对称图形,关键还是找点的对称点,找法是连接点与对称中心O 点并延长相等的距离即为对称点的位置,最后将对称点依次连接得到关于O点成中心对称的图形。
23.2-1 中心对称(解析版)
23.2-1 中心对称建议用时:45分钟总分50分一选择题(每小题3分,共18分)1.(2020•金牛区模拟)在平面直角坐标系xOy中,点A(﹣2,3)关于点O中心对称的点的坐标是()A.(2,3)B.(﹣2,﹣3)C.(2,﹣3)D.(﹣2,3)【答案】C【解析】∵点A(﹣2,3)与点A关于原点O中心对称,∴点B的坐标为:(2,﹣3).故选:C.2.(2020•延庆区一模)下列各组图形中,△A'B'C'与△ABC成中心对称的是()A.B.C.D.【答案】D【解析】A、是平移变换图形,故本选项错误;B、是轴对称图形,故本选项错误;C、是旋转变换图形,故本选项错误;D、是中心对称图形,故本选项正确.故选:D.3.(2020•武汉模拟)下列四组图形中,左边的图形与右边的图形成中心对称的有()A.1组B.2组C.3组D.4组【答案】C【解析】根据中心对称的概念,知②③④都是中心对称.故选:C.4.(2020•任丘市期末)已知下列命题,其中正确的个数是()(1)关于中心对称的两个图形一定不全等;(2)关于中心对称的两个图形是全等形;(3)两个全等的图形一定关于中心对称.A.0个B.l个C.2个D.3个【答案】B【解析】关于中心对称的两个图形一定全等,两个全等的图形不一定关于中心对称.故只有(2)说法正确,故选:B.5.(2020•东营区一模)如图,将△ABC绕点C(0,√3)旋转180°得到△A'B'C,设点A的坐标为(a,b),则点A'的坐标为()A.(﹣a,﹣b)B.(a,﹣b+2√3)C.(﹣a,﹣b+√3)D.(﹣a,﹣b+2√3)【答案】D【解析】将点A的坐标为(a,b)向下平移√3个单位,得到对应点坐标为(a,b−√3),再将其绕原点旋转180°可得对称点坐标为(﹣a,﹣b+√3),然后再向上平移√3个单位可得点A'的坐标为(﹣a,﹣b+2√3),故选:D.6.(2020•永康市一模)如图,将等边△AOB放在平面直角坐标系中,点A的坐标为(0,4),点B在第一象限,将等边△AOB绕点O顺时针旋转180°得到△A′OB′,则点B的对应点B′的坐标是()A.(2√3,2)B.(2√3,−2)C.(−2√3,−2)D.(0,﹣4)【答案】C【解析】作BH⊥y轴于H,如图,∵△OAB为等边三角形,∴OH=AH=2,∠BOA=60°,∴BH=√3OH=2√3,∴B点坐标为(2√3,2),∵等边△AOB绕点O顺时针旋转180°得到△A′OB′,∴点B′的坐标是(﹣2√3,﹣2).故选:C.二、填空题(每小题3分,共9分)7.(2020•武汉模拟)在平面直角坐标系中,点P(4,1)关于点(2,0)中心对称的点的坐标是.【答案】(0,﹣1)【解析】如图所示:点P(4,1)关于点(2,0)中心对称的点的坐标是:(0,﹣1).故答案为:(0,﹣1).8.(2020•定西期末)如图,△ABC与△DEC关于点C成中心对称,若AB=2,则DE=2.【答案】2【解析】∵△ABC与△DEC关于点C成中心对称,∴CA=CD,CB=CE,∵∠ACB=∠DCE∴△ABC≌△DEC(SAS),∴AB=DE,∵AB=2,∴DE=2,故答案为2.9.如图,如果△ABC和△DEF关于点G成中心对称,那么△ABC绕点G旋转°后能与△DEF 重合.【答案】180【解析】∵△ABC和△DEF关于点G成中心对称,∴△ABC绕点G旋转180°后能与△DEF重合.故答案为:180.三、解答题(7分+8分+8分=23分)10.(2020 •灌云县期中)如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE =AD,连接BE.(1)图中哪两个图形成中心对称?(2)若△ADC的面积为4,求△ABE的面积.解:(1)图中△ADC和三角形EDB成中心对称;(2)∵△ADC和三角形EDB成中心对称,△ADC的面积为4,∴△EDB的面积也为4,∵D为BC的中点,∴△ABD的面积也为4,所以△ABE的面积为8.11.(2020•莫旗期末)如图,△ABO与△CDO关于O点中心对称,点E,F在线段AC上,且AF=CE,求证:FD=BE.证明:∵△ABO与△CDO关于O点中心对称,∴BO=DO,AO=CO,∵AF=CE,∴AO﹣AF=CO﹣CE,∴FO=EO,在△FOD和△EOB中{FO=EO∠FOD=∠EOB BO=DO,∴△FOD≌△EOB(SAS),∴DF=BE.12.(2020•合浦县期中)如图,△ABC与△DEF关于点O对称,请你写出两个三角形中的对称点,相等的线段,相等的角.解:对称点为:A和D、B和E、C和F;相等的线段有AC=DF、AB=DE、BC=EF;相等的角有:∠A=∠D,∠B=∠E,∠C=∠F.。
《23.2.1 中心对称》教学设计教学反思-2023-2024学年初中数学人教版12九年级上册

《中心对称》教学设计方案(第一课时)一、教学目标1. 理解中心对称的概念,掌握其定义和性质。
2. 能够识别中心对称图形,并确定其对称中心。
3. 通过观察、分析和讨论,培养学生的观察能力和抽象思维能力。
二、教学重难点1. 教学重点:理解中心对称的概念,掌握其定义和性质。
2. 教学难点:能够识别中心对称图形,并确定其对称中心。
三、教学准备1. 准备教学PPT,包含图片、动画和相关概念的解释。
2. 准备中心对称的实例,如钟表、风扇、旋转门等。
3. 准备小组讨论的材料,以便学生交流和讨论。
4. 准备练习题,用于学生巩固所学知识。
四、教学过程:(一)课前准备1. 学生复习相关知识,为新课学习做好准备。
2. 教师准备教学用具,如黑板、白板、中心对称图形等。
(二)导入新课1. 提问学生:大家还记得我们之前学过的图形对称吗?你能举出一些例子吗?2. 引导学生回顾轴对称图形,并让学生讨论和总结轴对称和中心对称的区别。
3. 教师解释中心对称的概念,并引导学生了解中心对称在实际生活中的应用。
(三)探究学习1. 教师出示一些中心对称图形,如正方形、矩形、平行四边形等,让学生观察它们的特征,并讨论它们如何通过旋转和反射实现中心对称。
2. 教师引导学生探究中心对称图形的性质,如对应点连线交于对称中心,图形沿对称中心翻折180度后能够完全重合等。
3. 学生分组讨论和总结中心对称的性质,教师给予指导和帮助。
(四)课堂活动1. 完成课后习题和相关练习题,巩固学生对中心对称知识的掌握。
2. 进行小组讨论和展示,让学生分享自己的学习成果和经验,教师给予评价和反馈。
3. 引导学生运用中心对称知识解决实际问题,如设计图案、测量实物等。
(五)小结作业1. 教师总结本节课的重点和难点,强调中心对称的性质和应用。
2. 布置与中心对称相关的作业,让学生回家后继续思考和实践。
希望中心对称的性质:1. 中心对称的两个图形,交换对称点,可以重合。
2. 中心对称不改变图形的形状和大小。
23.2中心对称

关于y轴对称 关于原点对称
(x,-y)
(-x,y)
(-x,-y)
课堂练习
利用关于原点对称的点的坐标的特点, 作出与线段AB关于原点对称的图形。
解:点P(x,y)关于原点的对称点为 P′(-x,-y),因此,线段AB的两个端 点A(2,6),B(-6,-5)关于原点的 对称点分别为A′(-2,-6),B ′ (6, 5)。 连结A′B′。 则就可得到与线段AB关于原点对称的 线段A′B′。
你知道这个图形的对称中心和关于中心的对称点是什么吗?
旋转和中心对称的联系和区别
中心对称 一般旋转
联系
区别
都是绕着某一点进行 旋转
旋转角度都是180° 旋转角度不固定
因此,中心对称是特殊的旋转。
轴对称和中心对称的联系和区别
比较
轴对称
中心对称
区别
有一条对称轴--直线 图形沿轴对折180°
有一个对称中心--点 图形绕中心旋转180°
将线段AB绕它的中点旋转180°,你有什么发现? 重合
A
O
B
情景思考
将▱ABCD绕它的两条对角线的交点O旋转180°,你有什么发现?
A B
D
O C
重合
中心对称图形概念
如果一个图形绕一个点旋转180°后,能和原来的图形互相重合,那么这个图形 叫做中心对称图形;这个点叫做它的对称中心;互相重合的点叫做对称点.
A’(-4, 0) B’( 0, 3) C’(-6,-5) D’( 3,-4)
D(-3,4)
A’(-4,0)
横坐标互为相反数 在坐标系上找一些点验证上述结论?
C’(-6,5)
C(6,5)
B’(0,3)
A(4,0)
23.2.1中心对称 课件2024-2025学年人教版数学九上

证明:∵△ABO与△CDO关于O点中心对称,
∴BO=DO,AO=CO,
∵AF=CE,∴AO-AF=CO-CE,∴FO=EO,
FO EO ,
在△FOD和△EOB中,∠FOD ∠EOB,
DO BO ,
∴△FOD≌△EOB(SAS), ∴DF=BE.
随堂练习
3. 如图,已知AD是△ABC的中线,画出以点D为对称中心,与△ABD
称中心平分.(即对称点与对称中心三点共线)
2.中心对称的两个图形是全等形.
知识讲解
知识点1 中心对称的定义及性质
【例 1】如下图所示的四组图形中,左边图形与右边图形成中心对称的
有(
A.1组
)
B.2组
C.3组
D.4组
知识讲解
知识点1 中心对称的定义及性质
解析:将选项中左边图形沿着某一点旋转180°能与右边图形重合的
②同样可得:BD=B′D,CD=C′D;
③连接A′B′、B′C′、C′D,则四边形A′B′C′D为所
求的四边形,如图所示.
知识讲解
知识点2 中心对称作图
(1)这两个图形是否成中心对称?如果是,对称中心是哪一点?如果不
是,请说明理由.
(2)如果是中心对称,那么A、B、C、D关于中心的对称点是哪些点?
数量关系,并说明理由.
∴∠F=∠CPM﹣∠PMF=α﹣β,
∠MCD=∠CDE﹣∠DMC=α﹣β,
∴∠F=∠MCD.
课后小结
中心对称的定义
及性质
定义
定义相关
性质
中心对称
中心对称作图
作图形关于某点对
称的图形
找出对称中心
数量关系,并说明理由.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A O
D O
B
C
1.了解中心对称的概念
像这样,把一个图形绕着某一点旋转 180°,如果 它能够与另一个图形重合,那么就说这两个图形关于这 个点对称或中心对称.这个点叫做对称中心. 这两个图形在旋转后能重合的对应点叫做关于对称 中心的对称点.
1.了解中心对称的概念
问题3 中心对称与一般的旋转的联系和区别? 联系:中心对称和一般的旋转都是绕着某一点进行 旋转; 区别:中心对称的旋转角度都是180°,一般的 旋转的旋转角度不固定,中心对称是特殊的旋转.
(2)如图,已知△ABC 与△DEF 中心对称,点 A 和点 D 是对称点,画出对称中心 O.
F
E
A
B
D C
4.应用中心对称性质画图
例1 (1)如左图,选择点 O 为对称中心,画出点 A 关于点 O 的对称点 A'; (2)如右图,选择点 O 为对称中心,画出与 △ABC关于点 O 对称的△A'' B C' . C
问题1 (2)如图,线段 AC,BD 相交于点 O,OA =OC,OB=OD.把 △OCD 绕点 O 旋转 180°,你有什 么发现? 两个图案能够完全重合在一起.A O DBC1.了解中心对称的概念
问题2 你能说说上述两个旋转的共同点吗? (1)图形中旋转中心是哪一点? (点 O) (180°) (2)旋转的角度是多少? (重合) (3)两个图形的关系?
A
B
O B′ C' A′
2.探究中心对称的性质
(1)中心对称的两个图形, 对称点所连线段都经 过对称中心,而且被对称中心所平分; (2)中心对称的两个图形是全等图形.
3.练习、巩固中心对称性质
(1)如图,以顶点 A 为对称中心,画一个与已知 四边形 ABCD 成中心对称的图形.
D C
A
B
3.练习、巩固中心对称性质
九年级
上册
23.2 中心对称(第1课时)
课件说明
• 本节课从旋转变换引入中心对称的概念,先让学生从 旋转的角度观察两个图形之间的关系,类比旋转得出 中心对称的定义,渗透了从一般到特殊的思想方法. 在此基础上,通过探究成中心对称的两个图形的对称 中心与对应点所连线段之间的关系得到中心对称的性 质,并能运用中心对称的性质画出一个图形关于某一 点中心对称的对称图形.
A O A
B
O
5.小结
(1)本节课学了哪些主要内容? (2)怎样画一个图形关于一个点的对称图形?
6.布置作业
教科书第 66 页,练习 1,2 题.
1.了解中心对称的概念
问题4 对称中心和对称点是如何确定的? 你能指 出下图中的对称点吗?
D A O C
B
2.探究中心对称的性质
问题5 中心对称是特殊的旋转,它有哪些性质?
C A B O B′ C' A′
2.探究中心对称的性质
画好图形后思考: (1)点 O 在线段 AA'上吗?如果在,在什么位置? (2)△ABC 和△A' B' C' 有什么关系? (3)你能从这个探究中得到什么结论?
课件说明
• 学习目标: 1.知道中心对称的概念,能正确表述中心对称的性 质; 2.会画一个图形关于某一点中心对称的对称图形. • 学习重点: 中心对称的概念和性质.
1.了解中心对称的概念
问题1 (1)如图,把其中一个图案绕点 O 旋转 180°,你有什么发现?
两个图案能够完全重合在一起.
O
1.了解中心对称的概念
