山东省德州市2014届高三第二次模拟检测理科综合试题
【解析】【2014德州市一模】小题解析:山东省德州市2014届高三3月模拟考试 数学(理)试题

德州市高中三年级模拟检测数学(理科)试题一、选择题:本大题共l0小题,每小题5分,共50分把正确答案涂在答题卡上.1.已知全集为R ,集合A={1|()12xx ≤},B={|2x x ≥},R A B ð= A .[0,2) B .[0,2] C .(1,2) D .(1,2]2.设复数21i z i=-+,则复数2z 的实部与虚部的和为 A .0 B .2 C .-2 D .43.对具有线性相关关系的变量x ,y ,有一组观测数据(i x ,i y )(i =1,2,…,8),其回归直线方程是:16y x a =+,且12381238...3(...)6x x x x y y y y ++++=++++=,则实数a 的值是 A .116 B .18 C .14 D .11164.若a ,b 均为实数,且方程222(1)20x a x b b -+-+=无实根,则函数()log a b y x +=是增函数的概率是 A .1142π- B .142π- C .12π D .1124π-5.∆ABC 中内角A ,B ,C 的对边分别是a ,b ,c.若223sin 23sin a b bc C B -==,,则A= A .56π B .23π C .3π D .6π6.已知变量x ,y 满足约束条件11x y x y x a +≤⎧⎪-≤⎨⎪≥⎩,若25x y +≥-恒成立,则实数a 的取值范围为A .(-∞,-1]B .[-1,+∞)C .[-1,1]D .[-1,1)7.函数sin ,[,]y x x x ππ=+∈-的大致图象是【答案】A 【解析】试题分析:考察函数的性质,函数sin y x x =+是奇函数,图象关于原点对称,只有A D 、符合要求,又'1cos 0y x =+≥,即函数sin y x x =+在R 上是增函数,符合条件的只有A ,因此选A .考点:函数的性质与图象.8.已知双曲线2222:1(0,0)x y C a b a b-=>>的焦距为25,抛物线21116y x =+与双曲线C 的渐近线相切,则双曲线C 的方程为A .22182x y -=B .22128x y -= C .2214y x -= D .2214x y -=9.已知平面内点A ,B ,O 不共线,AP OA OB λμ=+,则A ,P ,B 三点共线的必要不充分条件是A .=λμB .||=||λμC .=-λμD .=1-λμ10.已知函数()y f x =是定义在R 上的奇函数,对x R ∀∈都有(1)(1)f x f x -=+成立,当(0,1]x ∈且12x x ≠时,有2121()()0f x f x x x -<-。
2014年高考山东德州市2014届高三第二次模拟检测

2014年高考(435)山东德州市2014届高三第二次模拟检测高考模拟2014-03-21 2237山东省德州市2014届高三第二次模拟检测语文试题第I卷(选择题,共36分)一、(15分,每小题3分)1.下列词语中加点的字,每耐凄音都相同的一组是A.纤绳/翩跹果脯/相辅幅成旖旎/倚马可待B.苛求/沉疴船舷/弦外之音怠慢/春风骀荡C.娉婷/伶俜自诩/栩栩如生裨益/稗官野史D.缟素/枯槁逡巡/怙恶不俊讣告/赴汤蹈火2.下列各句中,没有错别字的一句是A.和放开中小城市的户籍限制一样,城乡养老并轨也是破除制度壁垒、助推资源流动的关键性举措。
B.让我们留住文化记忆,在历史传统与现代文明的有机溶台中铸造城镇之魂,谱写城镇化新篇章。
C.依靠拾荒的微簿收入,烟台“五保”老人刘盛兰15年捐助百余位学生,只为一个炽热的“助学梦”。
D.党中央“八项规定”约束的都是违规违纪的行为,整肃的都是歪风斜气,叫停的都是不应得的福利。
3.下列各句中,标点符号使用不正确的一句是A.多加强引导,确保候乘秩序良好;多检查维护,确保变通设备状态正常;多采取措施,确保餐饮及时供应……这些不仅是相关部门的责任,更是义务。
B.“血脉偾张”是个成语,现在多用来形容激动、亢奋。
“血脉偾张”能不能写成“血脉喷张”呢,不能,汉语中没有这种写法,也讲不通。
C.南极泰山站与昆仑站一样,同属于度夏站,即仅在南极的夏天——12月下旬至第二年3月中旬使用,可满足20人度夏考察、生活的需要。
D.《左传》是我国第一部详细完整的编年体历史著作,因为它和《公羊传》《谷梁传》都是为解说《春秋》而作,所以它们叉被称作《春秋三传》。
4.下列各句中,加点的词语使用恰当的一项是A.一次普通的胆部手术和几份病例中的签名,让一对江西夫妇陷入与西安交大第一附属医院长达l3年的医疗纠纷中。
B.新赛季亚冠联赛首轮,坐镇天河体育场的广州恒大在上半场连丢两球的情况下,下半场连扳四球,战胜澳洲的墨尔本胜利队,取得了满堂红。
2014年高考理综试题及答案全国卷2

2014年普通高等学校招生全国统一考试理科综合能力测试一、选择题:本题共13小题,每小题6分。
在每小题给出的四个选项中,只有一项是符合题目要求的.1. 关于细胞的叙述,错误的是A。
植物细胞的细胞连丝具有物资运输的作用B. 动物细胞间的粘着性细胞膜上的糖蛋白有关C. A TP水解释放的能量可用于细胞内的吸能反应D. 哺乳动物的细胞可以合成蔗糖,也可以合成乳糖2.同一动物个体的神经细胞与肌细胞在功能上是不同的,造成这种差异的主要原因是A.二者所处的细胞周期不同B。
二者合成的特定蛋白不同C。
二者所含有的基因组不同D。
二者核DNA的复制方式不同3.关于在正常情况下组织液生成与回流的叙述,错误的是A.生成与回流的组织液中氧气的含量相等B。
组织液不断生成与回流,并保持动态平衡C。
血浆中的有些物质经毛细血管动脉端进入组织液D。
组织液中的有些物质经毛细血管静脉端进入血液4.讲某植物花冠切成大小和形状相同的细条,分为a、b、c、d、e和f组(每组的细条数相等),取上述6组细条数分别置于不同浓度的蔗糖溶液中,浸泡相同时间后测量各组花冠细条的长度,结果如图所示.假如蔗糖溶液与花冠细胞之间只有水分交换则A.试验后,a组液泡中的溶质浓度比b组的高B.浸泡导致f组细胞中液泡的失水量小于b组的C.A组细胞在蔗糖溶液中失水或吸水所耗ATP大于b组D.使细条在浸泡前后长度不变的蔗糖浓度介于0.4~0。
5mol—L—1之间5.关于核酸的叙述,错误的是A.细胞核中发生的转录过程有RNA聚合酶的参与B.植物细胞的线粒体和叶绿素体中均可发生DNA的复制C.双链DNA分子中一条链上的磷酸和核糖是通过氨键链接的D.用甲基绿和吡罗红染色可观察DNA和RNA在细胞中的分布6.关于光合作用和呼吸作用的叙述,错误的是A.磷酸是光反应中合成A TP所需的反应物B.光合作用中叶绿素吸收光能不需要酶的参与C.人体在剧烈运动时所需要的能量由乳酸分解提供D.病毒核酸的复制需要宿主细胞的呼吸作用提供能量7.下列过程没有发生化学反应的是A.用活性炭去除冰箱中的异味B.用热碱水清除炊具上残留的污垢C.用浸泡过高锰酸钾溶液的硅藻土保鲜水果D.用含硅胶、铁粉的透气小袋与食品一起密封包装8.四联苯的一氯代物有A。
2014年东三省三校高三二模理综试题及答案

可能用到的相对原子质量:H 1 C 12 N 14 O 16 S 32 K 39 Mn 55 Fe 56 一、选择题:本题共13小题,每小题6分,在每小题给出的四个选项中,只有一个是符合题目要求的。
1.下列有关生物体组成元素和化合物的叙述,正确的是 A.严重缺铁的人容易产生乳酸中毒B.一个DNA 分子彻底水解后能得到4种脱氧核苷酸C.蛋白质和DNA 分子的多样性都与它们的空间结构密切相关D.淀粉、糖原、纤维素和麦芽糖彻底水解后,得到的产物是不同的 2.下列关于实验条件或现象的描述,完全正确的是 A.使用双缩脲试剂鉴定蛋白质时,需要水浴加热B.纸层析法分离绿叶中色素时,滤纸条自上而下的第三条色素带最宽,颜色为蓝绿色C.用溴麝香草酚蓝水溶液检测CO 2时,颜色变化为蓝色→黄色→绿色D.观察细胞中的染色体数目,实验材料为人的口腔上皮细胞 3.A.该病毒的遗传物质不是双链DNAB.该病毒的遗传信息流动过程不遵循中心法则C.以该病毒DNA 为模板,复制出的DNA 不是子代病毒的遗传物质D.该病毒DNA 的突变频率较高4.下图一是真核细胞DNA 复制过程的模式图,图二是大肠杆菌DNA 复制过程模式图,箭头表示复制方向。
对此描述错误的是A.真核细胞DNA 有多个复制起点,而大肠杆菌只有一个B.两者均具有双向复制的特点C.真核细胞DNA复制时,在起点处不都是同时开始的 D.两者的遗传物质均是环状的 5.下列关于下丘脑的叙述正确的是A.下丘脑通过释放促甲状腺激素来促进垂体分泌相关激素B.下丘脑控制生物节律,同时呼吸中枢也位于下丘脑C.出现尿量异常增大的可能原因是下丘脑或垂体受损D.下丘脑体温调节中枢可感受到寒冷或炎热6.如图是人类睾丸横切片示意图,其中①→⑤为精子发生过程中各阶段的细胞,下列有关说法正确的是 A.①为精原细胞,它只能进行减数分裂B.②为初级精母细胞,②所指细胞内有染色体92条图一 ① ②③图二 图二C.③为次级精母细胞,细胞内可能有2条X 染色体 8.下列关于氯水的说法正确的是A.向氯水中通入少量二氧化硫,氯水的漂白性增强B.氯水中加入NaCl 固体,对溶液的pH 无影响C.常温下,pH=2的氯水中:c(Cl -)+c(ClO -)+c(OH -)=0.01mol/L D.向氯水中滴加少量NaHCO 3溶液的离子反应方程式为:Cl 2+2HCO 3-2CO 2↑+Cl -+ClO -+H 2O9.相对分子质量为100的有机物A 能与钠反应,且完全燃烧只生成CO 2和H 2O 。
2014年山东省高考理综试题及答案(全)

2014年普通高等学校招生全国统一考试 (山东卷)理科综合 物理试题(110分/300分)第Ⅰ卷(必做,共42分)二、选择题(本题包括7小题,每小题给出四个选项中,有的只有一个选项正确,有的有多个选项正确,全部选对的得6分,选对但不全的得3分,有选错的得0分)14.如图,用两根等长轻绳将木板悬挂在竖直木桩上等高的两点,制成一简易秋千,某次维修时将两轻绳各剪去一小段,但仍能保持等长且悬挂点不变。
木板静止时,1F 表示木板所受合力的大小,2F 表示单根轻绳对木板拉力的大小,则维修后 A .1F 不变,2F 变大 B .1F 不变,2F 变小 C .1F 变大,2F 变大 D .1F 变小,2F 变小15.一质点在外力作用下做直线运动,其速度v 随时间t 变化的图像如图.在图中标出的时刻中,质点所受合外力的方向与速度方向相同的有 A .1t B .2t C .3tD .4t16.如图,一端接有定值电阻的平行金属轨道固定在水平面内,通有恒定电流的长直绝缘导线垂直并紧靠轨道固定,导体棒与轨道垂直且接触良好.在向右匀速通过N M 、两区的过程中,导体棒所受安培力分别用M F 、N F 表示。
不计轨道电阻,以下叙述正确的是 A .M F 向右 B .N F 向左 C .M F 逐渐增大 D .N F 逐渐减小17.如图,将额定电压为60V 的用电器,通过一理想变压器接在正弦交变电源上。
闭合开关S 后,用电器正常工作,交流电压表和交流电流表(均为理想电表)的示数分别为220V 和2.2A 。
以下判断正确的是 A .变压器输入功率为484WB .通过原线圈的电流的有效值为6。
6AC .通过副线圈的电流的最大值为2。
2AD .变压器原、副线圈的电流匝数比3:11:21=n n18.如图,场强大小为E 、方向竖直向下的匀强电场中有一矩形区域abcd ,水平边ab 长为s ,竖直边ad 长为h 。
质量均为m 、带电量分别为q +和q -的两粒子,由c a 、两点先后沿ab 和cd 方向以速率0v 进入矩形区(两粒子不同时出现在电场中).不计重力,若两粒子轨迹恰好相切,则0v 等于 A .mh qE s 22 B .mh qE s 2 C .mh qE s 24 D .mhqEs 419.如图,半径为R 的均匀带正电薄球壳,其上有一小孔A .已知壳内的场强处处为零;壳外空间的电场与将球壳上的全部电荷集中于球心O 时在壳外产生的电场一样。
2014年高考真题——理科综合(新课标Ⅰ卷)解析版.pdf

本实验中加入过量乙酸的目的是:实验中加入少量无水硫酸镁的目的是:在蒸馏操作中,仪器选择及安装都正确的
是:(填标号)
本实验的产率是:A.30
B.40
C.50
D.60
(8)在进行蒸馏操作时,若从130 ℃开始收集馏分,产率偏
(填高或者低)原因是
27、(15分)
次磷酸(H3PO)是一种精细化工产品,具有较强还原性,回答下列问题:
反应的速率与I-的浓度有关 B. IO-也是该反应的催化剂
C反应活化能等于98KJ·mol-1 D.v(H2O2)=v(H2O)=v(O2)
10.W、X、Y、Z均是周期元素,X、Y处于同一周期,X、Z的最低价离子分别为X2-和Z- ,Y+和Z-离子具有相同
的电子层结构。下列说法正确的是( )
氨气会降低肥效DFeCl3溶液可用于铜质印刷线路板制作FeCl3能从含有Cu2+的溶液中置换出铜9.已知分解1 mol H2O2
放出热量98KJ,在含少量I-的溶液中,H2O2的分解机理为:
H2O2+ I- →H2O +IO-
慢H2O2+ IO-→H2O +O2+ I- 快
下列有关反应的说法正确的是( )
分泌抗A抗体的杂交瘤细胞。
回答下列问题:
(1)制备融合所需的B淋巴细胞时,所用免疫小鼠的血清抗体效价需达到16000以上,则小鼠最少需要经过
次免疫后才能有符合要求的。达到要求的X、Y、Z这3只免疫小鼠中,最适合用于制备B淋巴细胞的是
小
鼠,理由是
。
(2)细胞融合实验完成后,融合体系中除含有未融合的细胞和杂交细胞外,可能还有 ,体系中出现多种类型
细胞的原因是
。
(3)杂交瘤细胞中有
个细胞核,染色体数目最多是
德州市2014届高三4月模拟考试 数学(理)

高中三年级模拟检测 数学(理科)试题2014.4本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,第I 卷1-2页,第II 卷3-5页,共150分,测试时间120分钟.注意事项:山东中学联盟选择题为四选一题目,每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑如需改动,用橡皮擦干净后,再选涂其它答案,不能答在测试卷上.第I 卷(共50分)一、选择题:本大题共10小题,每小题5分,共50分.把正确答案涂在答题卡上. 1.若复数z 满足()255z i i +=+(i 为虚数单位),则z 为 A.35i +B.35i -C.35i -+D. 35i --2.设集合(){}{}1lg 2,2,,x R A x y x B y y x A C A B -==-==∈⋃则A.()2+∞,B.[)2+∞,C.∅D.R3.下列命题错误的是A.命题“若2320x x x d -+==,则”的逆否命题为“若21320x x x ≠-+≠,则” B.若p q ∧为假命题,则,p q 均为假命题C.对于命题22:1010p x R x x p x R x x ∃∈++<⌝∀∈++≥,使得,则为:,均有D.“2x >”是“2320x x -+>”的充分不必要条件4.已知()y f x =是定义在R 上的偶函数,且在[)0,+∞上单调递增,则满足()()1f m f <的实数m 的范围是 A.10m -<< B.01m << C.11m -<<D.11m -≤≤5.右图是函数()sin 0,0,2y A x A πωϕωϕ⎛⎫=+>>≤⎪⎝⎭图象的一部分.为了得到这个函数的图象,只要将()sin y x x R =∈的图象上所有的点A.向左平移3π个单位长度,再把所得各点的横坐标缩短到原来的12,纵坐标不变B.向左平移3π个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 C.向左平移6π个单位长度,再把所得各点的横坐标缩短到原来的12倍,纵坐标不变D.向左平移6π个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变6.已知12e e 、是两个单位向量,若向量12122,346a e e b e e a b =-=+=-,且,则向量12e e 、的夹角是 A.6πB.4π C.3π D.2π 7.函数()()[]1sin ,,f x x x x ππ=-∈-的图象为8.执行如图所示的程序框图,则输出的a 值是 A. 2 B.3- C.12- D.139.过椭圆()222210x y a b a b+=>>左焦点F 斜率为1的直线交椭圆于A ,B 两点,向量OA OB +与向量()3,1α=-共线,则该椭圆的离心率为C.D.10.若函数()f x 满足()()[]110,11f x x f x +=∈+,当时,()f x x =,若在区间(]1,1-上,方程()20f x mx m --=有两个实数角,则实数m 的取值范围是A.103m <≤ B.103m << C.113m <≤D.113m <<第II 卷(共100分)二、填空题:本大题共5小题,每小题5分,共25分.把答案填在答题卡的相应位置.11.已知变量,x y 满足约束条件,1,22,y x x y z x y x ≤⎧⎪+≥=-⎨⎪≤⎩则的最大值为_________.12.已知()4220322a x x dx ax ⎛=- ⎝⎰,则的展开式中x 的系数为________.13.一个几何体的三视图如图所示,其侧(左)视图是一个等边三角形,则这个几何体的体积是_________. 14.以下四个命题中:①为了解600名学生对学校某项教改试验的意见,打算从中抽取一个容量为30的样本,考虑和系统抽样,则分段的间隔k 为30; ②直线()()22x-cos sin 1y kx y θθ=+-=与圆恒有公共点;③在某项测量中,测量结果ξ服从正态公布()()()22,0.1N σσξ>-∞若在,内取值的概率为0.15,则ξ在(2,3)内取值的概率为0.7;④若双曲线224x y k -=的渐近线方程为12y x =±,则k=1. 其中正确命题的序号是__________. 15.对任意实数,a b 定义()()1,2F a b a b a b =+--,如果函数()()()2ln ,3f x e x g x x ==-,那么()()()(),G x F f x g x =的最大值为_______.三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.16.(本小题满分12分)如图在,3ABC BC D AB π∆∠=中,已知A=为上一点.(I )若CD=2,BDC S ∆BD 长; (II )若AC=AD ,求BCD ∆周长的最大值. 17.(本小题满分12分)如图,DA ⊥平面ABC,DA//PC,90,12ACB AC AD BC PC ∠=====,,E 为PB 的中点. (I )求证:DE//平面ABC ;(II )求二面角E —CD —B 的余弦值.18.(本小题满分12分)某公司招聘工作人员,有甲、乙两组题目,现有A 、B 、C 、D 四人参加招聘,其中A 、B 两人独自参加甲组测试,C 、D 两人独自参加乙组测试;已知A 、B 两人各自通过的概率均为23,C 、D 两人各自通过的概率均为14. (I )求参加甲组测试通过的人数多于参加乙组测试通过人数的概率; (II )记甲乙两组测试通过的总人数为X ,求X 的分布列和期望. 19.(本小题满分12分) 已知数列{}11,1,1nn n n a a a a a +==+中. (I )求{}n a 的通项公式; (II )证明:对一切正常整数n ,有31271234n a a a a n +++⋅⋅⋅+<. 20.(本小题满分13分)已知函数()()()2ln 20f x a x x a x a =-+->.(I )当2a =时,求曲线()1y f x x ==在处的切线方程; (II )若函数()f x 的最大值是12,求a 的值; (III )令()()()()21,g x f x a x y g x =+-=若在区间()0,2上不单调,求a 的取值范围. 21.(本小题满分14分)已知点()()4,0P a a >在抛物线()2:20C y px p =>上,P 点到抛物线C 的焦点F 的距离为5.(I )求抛物线C 的方程;(II )已知圆22:2E x y x +=,过圆心E 作直线l 与圆E 和抛物线C 自上而下依次交于A 、B 、C 、D ,如果2AB CD BC +=,求直线l 的方程;(III )过点()4,2Q 的任一直线(不过P 点)与抛物线C 交于A 、B 两点,直线AB 与直线4y x =+交于点M ,记直线PA 、PB 、PM 的斜率分别为123k k k 、、,问是否存在实数λ,使得123k k k λ+=,若存在,求出 的值,若不存在,说明理由.。
山东省2014届理科数学一轮复习试题选编7:函数的综合问题(学生版)

山东省2014届理科数学一轮复习试题选编7:函数的综合问题一、选择题 1 .(山东省潍坊市2013届高三第二次模拟考试理科数学)某学校要召开学生代表大会,规定根据班级人数每10人给一个代表名额,当班级人数除以10的余数大于6时,再增加一名代表名额.那么各班代表人数y与该班人数x 之间的函数关系用取整函数[]y x =([x]表示不大于*的最大整数)可表示为 ( )A .[]10x y = B .3[]10x y += C .4[]10x y += D .5[]10x y += 2 .(山东省寿光市2013届高三10月阶段性检测数学(理)试题)已知函数321,,1,12()111,0,.362x x x f x x x ⎧⎛⎤∈ ⎪⎥+⎪⎝⎦=⎨⎡⎤⎪-+∈⎢⎥⎪⎣⎦⎩函数π()sin()22(0)6g x a x a a =-+ ,若存在[]12,0,1x x ∈,使得12()()f x g x =成立,则实数a 的取值范围是 ( )A .14,23⎡⎤⎢⎥⎣⎦ B .10,2⎛⎤⎥⎝⎦ C .24,33⎡⎤⎢⎥⎣⎦D .1,12⎡⎤⎢⎥⎣⎦3 .(山东省德州市2013届高三第二次模拟考试数学(理)试题)若对于定义在R 上的函数f(x),存在常数()t t R ∈,使得f(x+t)+tf(x)=0对任意实数x 均成立,则称f(x )是阶回旋函数,则下面命题正确的是( )A .f(x)=2x是12-阶回旋函数 B .f(x)=sin(πx)是1阶回旋函数C .f (x)=x 2是1阶回旋函数D .f(x)=log a x 是0阶回旋函数4 .(山东省2013届高三高考模拟卷(一)理科数学)已知c b a ,,为互不相等的三个正实数,函数)(x f 可能满足如下性质:①)(a x f -为奇函数;②)(a x f +为奇函数;③)(b x f -为偶函数;④)(b x f +为偶函数;⑤()()f x c f c x +=-.类比函数2013sin y x =的对称中心、对称轴与周期的关系,某同学得到了如下结论:(i)若满足①②,则)(x f 的一个周期为4a ;(ii)若满足①③;则)(x f 的一个周期为||4b a -;(iii)若满足③④,则)(x f 的一个周期为||3b a -;(iv)若满足②⑤;则)(x f 的一个周期为||4c a +. 其中正确结论的个数为 ( ) A .1 B .2 C .3 D .45 .(山东省枣庄市2013届高三3月模拟考试数学(理)试题)已知函数2()1f x x =+的定义域为[,]()a b a b <,值域为[1,5],则在平面直角坐标系内,点(a,b)的运动轨迹与两坐标轴围成的图形的面积是 ( ) A .8 B .6 C .4 D .2 6 .(山东省德州市2013届高三3月模拟检测理科数学)已知函数(1)y f x =-的图象关于直线1x =对称,且当(,0),()'()0x f x xf x ∈-∞+<成立若a=(20.2)·0.2(2),(12)f b n =·121(12),(1)4f n c og =·121(1)4f og ,则a,b,c 的大小关系是 ( ) A .a b c >>B .b a c >>C .c a b >>D .a c b >>7 .(2012年山东理)(12)设函数f (x)=,g(x )=ax 2+bx 若y=f(x)的图像与y=g(x)图像有且仅有两个不同的公共点A(x 1,y 1),B(x 2,y 2),则下列判断正确的是 ( ) A .当a<0时,x 1+x 2<0,y 1+y 2>0 B .当a<0时, x 1+x 2>0, y 1+y 2<0 C .当a>0时,x 1+x 2<0, y 1+y 2<0 D .当a>0时,x 1+x 2>0, y 1+y 2>0 8 .(山东省2013届高三高考模拟卷(一)理科数学)我们定义若函数)(x f 为D 上的凹函数须满足以下两条规则:(1)函数在区间D 上的任何取值有意义;(2)对于区间D 上的任意n 个值n x x x ,,,21 ,总满足)()()()(2121nx x x nf x f x f x f n n +++≥+++ ,那么下列四个图象中在]2,0[π上满足凹函数定义的是9 .(山东省夏津一中2013届高三4月月考数学(理)试题)函数y=f(x),x∈D,若存在常数C,对任意的x l ∈D,仔在唯一的x 2∈D,使得C =,则称函数f(x)在D 上的几何平均数为C .已知f(x)=x 3,x∈[1,2],则函数f(x)=x 3在[1,2]上的几何平均数为 ( )AB .2C .4D . 10.(山东省威海市2013届高三上学期期末考试理科数学)对于函数(f x ,如果存在锐角θ使得()f x 的图象绕坐标原点逆时针旋转角θ,所得曲线仍是一函数,则称函数()f x 具备角θ的旋转性,下列函数具有角4π的旋转性的是 ( )A .y =B .ln y x =C .1()2x y =D .2y x =11.(山东省实验中学2013届高三第一次诊断性测试数学(理)试题)已知定义在R 上的函数()y f x =满足以下三个条件:①对于任意的x R ∈,都有(4)()f x f x +=;②对于任意的121212,,02,()();x x R x x f x f x ∈≤<≤<且都有③函数(2)y f x =+的图象关于y 轴对称,则下列结论中正确的是( )A .(4.5)(7)(6.5)f f f <<B .(7)(4.5)(6.5)f f f <<C .(7)(6.5)(4.5)f f f <<D .(4.5)(6.5)(7)f f f <<12.(山东省青岛市2013届高三上学期期中考试数学(理)试题)已知定义在R 上的奇函数()f x 满足(4)()f x f x -=-,且[]0,2x ∈时,2()log (1)f x x =+,甲、乙、丙、丁四位同学有下列结论:甲:()31f =;乙:函数()f x 在[]6,2--上是减函数;丙:函数()f x 关于直线4x =对称;丁:若()0,1m ∈,则关于x 的方程()0f x m -=在[]8,8-上所有根之和为8-,其中正确的是( )A .甲、乙、丁B .乙、丙C .甲、乙、丙D .甲、丙二、填空题:本大题共4小题,每小题4分,共16分.13.(山东省夏津一中2013届高三4月月考数学(理)试题)函数y = 1n|x-1|的图像与函数y=-2 cosπx(-2≤x≤4)的图像所有交点的横坐标之和等于( )A .8B .6C .4D .2 14.(山东省文登市2013届高三3月二轮模拟考试数学(理))对于正实数α,记M α为满足下述条件的函数()f x 构成的集合:12,x x R ∀∈且21x x >,有212121()()()()x x f x f x x x αα--<-<-.下列结论中正确的是( )A .若12(),()f x M g x M αα∈∈,则12()()f x g x M αα++∈B .若12(),()f x M g x M αα∈∈且12αα>,则12()()f x g x M αα--∈C .若12(),()f x M g x M αα∈∈,则12()()f x g x M αα⋅⋅∈D .若12(),()f x M g x M αα∈∈且()0g x ≠,则12()()f x M g x αα∈ 15.(2013年山东临沂市高三教学质量检测考试理科数学)已知集合M={(x,y )|y f (x )=},若对于任意11(x ,y )M ∈,存在22(x ,y )M ∈,使得12120x x y y +=成立,则称集合M 是“垂直对点集”.给出下列四个集合:①M={1(x,y )|y x=};②M={1(x,y )|y sin x =+}; ③M={2(x,y )|y log x =};④{(,)2}x M x y y e ==-.其中是“垂直对点集”的序号是 ( )A .①②B .②③C .①④D .②④二、填空题 16.(山东省枣庄三中2013届高三上学期1月阶段测试理科数学)已知()f x 为R 上的偶函数,对任意x R ∈都有(6)()(3)f x f x f +=+且当[]12,0,3x x ∈, 12x x ≠ 时,有1212()()0f x f x x x ->-成立,给出四个命题:①(3)0f = ② 直线6x =-是函数()y f x =的图像的一条对称轴③ 函数()y f x =在[]9,6--上为增函数 ④ 函数()y f x =在[]9,9--上有四个零点 其中所有正确命题的序号为______________17.(山东省潍坊市2013届高三上学期期末考试数学理(A ))若函数)(x f 满足0,≠∈∃m R m ,对定义域内的任意)()()(,m f x f m x f x +=+恒成立,则称)(x f 为m 函数,现给出下列函数: ①xy 1=; ②x y 2=; ③x y sin =; ④nx y 1=其中为m 函数的序号是.(把你认为所有正确的序号都填上)18.(2009高考(山东理))已知定义在R 上的奇函数)(x f ,满足(4)()f x f x -=-,且在区间[0,2]上是增函数,若方程f(x)=m(m>0)在区间[]8,8-上有四个不同的根1234,,,x x x x ,则1234_________.x x x x +++=19.(山东省济宁市2013届高三第一次模拟考试理科数学 )函数(x)f 的定义域为D,若存在闭区间[a,b]⊆D,使得函数f (x )满足:(1) f (x )在[a,b]内是单调函数;(2)f (x )在[a,b]上的值域为[2a,2b],则称区间[a,b]为y=f (x )的“和谐区间”.下列函数中存在“和谐区间”的是_______ (只需填符合题意的函数序号) ①20f (x )x (x )=≥;②xf (x )e (x R )=∈; ③10f (x )(x )x =>;④2401xf (x )(x )x =≥+. 20.(山东省烟台市2013届高三上学期期中考试数学试题(理科))函数()f x 的定义域为A ,若12,x x A ∈且12()()f x f x =时总有12x x =,则称()f x 为单函数.例如:函数)(12)(R x x x f ∈+=是单函数.给出下列命题:①函数)()(2R x x x f ∈=是单函数; ②指数函数)(2)(R x x f x∈=是单函数;③若()f x 为单函数,12,x x A ∈且12x x ≠,则12()()f x f x ≠; ④在定义域上具有单调性的函数一定是单函数,其中的真命题是 ______________.(写出所有真命题的序号)21.(山东济南外国语学校2012—2013学年度第一学期高三质量检测数学试题(理科))具有性质:1()()f f x x=-的函数,我们称为满足“倒负”交换的函数,下列函数:①1;y x x =-②1;y x x=+ ③,(01)0,(1)1(1)x x y x x x⎧⎪<<⎪==⎨⎪⎪->⎩中满足“倒负”变换的函数是________________.22.(山东省日照市2013届高三12月份阶段训练数学(理)试题)定义在R 上的函数()yf x =,若对任意不等实数12,x x 满足()()12120f x f x x x -<-,且对于任意的,x y R ∈,不等式()()22220f x x f y y -+-≤成立.又函数()1y f x =-的图象关于点()1,0对称,则当14x ≤≤时,yx的取值范围为_______________. 23.(山东省青岛市2013届高三上学期期中考试数学(理)试题)已知函数()f x 的定义域为R ,若存在常数0m >,对任意R x ∈,有()f x m x ≤,则称函数()f x 为F -函数.给出下列函数:①2()f x x =;②2()1x f x x =+;③()2xf x =;④()sin 2f x x =. 其中是F -函数的序号为_________________.24.(山东省淄博市2013届高三复习阶段性检测(二模)数学(理)试题)已知函数()f x 在实数集R 上具有下列性质:①直线1x =是函数()f x 的一条对称轴;②()()2f x f x +=-;③当1213x x ≤<≤时,()()()21f x f x -⋅()210,x x -<则()2012f 、()2013f 从大到小的顺序为_______.25.(山东省莱芜市莱芜二中2013届高三4月模拟考试数学(理)试题)如图,已知边长为8米的正方形钢板有一个角锈蚀,其中4AE =米,6CD =米. 为了合理利用这块钢板,将在五边形ABCDE 内截取一个矩形块BNPM ,使点P 在边DE 上. 则矩形BNPM 面积的最大值为_________平方米 .A MEPDCB N F三、解答题26.(2009高考(山东理))两县城A 和B 相距20km ,现计划在两县城外以AB 为直径的半圆弧上选择一点C 建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A 和城B 的总影响度为城A 与城B 的影响度之和,记C 点到城A 的距离为x km ,建在C 处的垃圾处理厂对城A 和城B 的总影响度为y,统计调查表明:垃圾处理厂对城A 的影响度与所选地点到城A 的距离的平方成反比,比例系数为4;对城B 的影响度与所选地点到城B 的距离的平方成反比,比例系数为k ,当垃圾处理厂建在的中点时,对城A 和城B 的总影响度为0.065.(1)将y 表示成x 的函数;(11)讨论(1)中函数的单调性,并判断弧上是否存在一点,使建在此处的垃圾处理厂对城A 和城B 的总影响度最小?若存在,求出该点到城A 的距离;若不存在,说明理由。
山东省2014届理科数学一轮复习试题选编6:方程的解与函数的零点及二分法(学生版)

山东省2014届理科数学一轮复习试题选编6:方程的解与函数的零点及二分法一、选择题1 .(山东省枣庄市2013届高三3月模拟考试数学(理)试题)设函数4()(0)f x x ax a =->的零点都在区间[0,5]上,则函数1()g x x=与函数3()h x x a =- 的图象的交点的横坐标为正整数时实数a 的取值个数为( )A .3B .4C .5D .无穷个2 .(山东省德州市乐陵一中2013届高三十月月考数学(理)试题)设函数)0(ln 31)(>-=x x x x f ,则)(x f y =( )A .在区间),1(),1,1(e e 内均有零点B .在区间),1(),1,1(e e 内均无零点C .在区间)1,1(e 内有零点,在区间),1(e 内无零点D .在区间)1,1(e内无零点,在区间),1(e 内有零点3 .(山东省莱芜市第一中学2013届高三12月阶段性测试数学(理)试题)已知函数21(0)(),()(1)(0)x x f x f x x a f x x -⎧-≤==+⎨->⎩若方程有且只有两个不相等的实数根,则实数a 的取值范围为( )A .(,0]-∞B .[0,1)C .(,1)-∞D .[0,)+∞4 .(山东省青岛市2013届高三第一次模拟考试理科数学)已知函数2, 0(), 0x x f x x x x ≤⎧=⎨->⎩,若函数()()g x f x m =-有三个不同的零点,则实数m 的取值范围为( ) A .1[,1]2- B .1[,1)2- C .1(,0)4- D .1(,0]4-5 .(山东省济南市2012届高三3月高考模拟题理科数学(2012济南二模))偶函数f (x )满足f (x -1)=f (x +1),且在x ∈[0,1]时,f (x )=x ,则关于x 的方程f (x )= 110x⎛⎫⎪⎝⎭,在x ∈[0,4]上解的个数是( )A .1B .2C .3D .46 .(山东省曲阜市2013届高三11月月考数学(理)试题)如果若干个函数图象经过平移后能够重合,则称这些函数为“同族函数”.给出下列函数:①()sin cos f x x x =; ②()2sin 4f x x π⎛⎫=+ ⎪⎝⎭;③()sin f x x x =; ④()21f x x =+其中“同族函数”的是 ( )A .①②B .①④C .②③D .③④ 7 .(山东省实验中学2013届高三第三次诊断性测试理科数学)函数x x x f ln )1()(+=的零点有 ( )A .0个B .1个C .2个D .3个8 .(2013年山东临沂市高三教学质量检测考试理科数学)函数1f (x )lg x x=-的零点所在的区间是( )A .(3,4)B .(2,3)C .(1,2)D .(0,1)9 .(山东省烟台市2013届高三上学期期末考试数学(理)试题)设()338x f x x =+-,用二分法求方程3380x x +-=在(1,2)x ∈内近似解的过程中得(1)0,(1.5)0,(1.25)0f f f <><,则方程的根落在区间( )A .(1,1.25)B .(1.25,1.5)C .(1.5,2)D .不能确定10.(山东省寿光市2013届高三10月阶段性检测数学(理)试题)函数223,0()2ln ,0x x x f x x x ⎧+-≤=⎨-+⎩ 的零点个数为 ( )A .3B .2C .1D .011.(山东省凤城高中2013届高三4月模拟检测数学理试题 )若定义在R 上的偶函数()f x 满足(2)()f x f x +=,且当[0,1]x ∈时,()f x x =,则方程3()log ||f x x =的解个数是( )A .0个B .2个C .4个D .6个 12.(山东济南外国语学校2012—2013学年度第一学期高三质量检测数学试题(理科))函数23)(3+-=x x x f 的零点为 ( )A .1,2B .±1,-2C .1,-2D .±1, 2 13.(山东省青岛市2013届高三上学期期中考试数学(理)试题)若函数a ax x f 213)(-+=在区间)1,1(-上存在一个零点,则a 的取值范围是 ( )A .51>a B .51>a 或1-<a C .511<<-a D .1a <-14.(山东省曲阜市2013届高三11月月考数学(理)试题)函数223,0()2ln ,0x x x f x x x ⎧+-≤=⎨-+>⎩的零点个数是( )A .0B .1C .2D .315.(山东省滨州市2013届高三第一次(3月)模拟考试数学(理)试题)定义在R 上的奇函数()f x ,当x ≥0时, ))12log (1),0,1,()1|3|,1,,x x f x x x ⎧+∈⎡⎣⎪=⎨⎪--∈+∞⎡⎣⎩则关于x 的函数()()F x f x a =-(0<a <1)的所有零点之和为( )A .1-2aB .21a-C .12a--D .21a--16.(山东省潍坊市2013届高三上学期期末考试数学理( )A .)已知函数⎩⎨⎧>≤+=0,10,2)(x nx x kx x f ()k R ∈,若函数()y f x k =+有三个零点,则实数k 的取值范围是( )A .2k ≤B .10k -<<C .21k -≤<-D .2k ≤-17.(山东省菏泽市2013届高三5月份模拟考试数学(理)试题)已知定义在R 上的函数()f x 的对称轴为3x =-,且当3x ≥-时,()23xf x =-,若函数()f x 在区间(1,)()k k k Z -∈上有零点,则K 的值为 ( )A .2或-7B .2或-8C .1或-7D .1或-818.(山东省日照市2013届高三12月份阶段训练数学(理)试题)设函数()f x 的零点为1x ,函数()422x g x x =+-的零点为2x ,若1214x x ->,则()f x 可以是 ( )A .()122f x x =-B .()214f x x x =-+- C.()110xf x =-D .()()ln 82f x x =-19.(山东省潍坊市四县一校2013届高三11月期中联考(数学理))已知0x 是xx f x1)21()(+=的一个零点,)0,(),,(0201x x x x ∈-∞∈,则 ( )A .0)(,0)(21<<x f x fB .0)(,0)(21>>x f x fC .0)(,0)(21<>x f x fD .0)(,0)(21><x f x f 20.(山东省临沂市2013届高三5月高考模拟理科数学)已知定义在R 上的函数()y f x =对任意的x 都满足(1)()f x f x +=-,当11x -≤< 时,3()f x x =,若函数()()log a g x f x x =-至少6个零点,则a 取值范围是( )A .10,5,5+∞ (]()B .10,[5,5+∞ ())C .11,]5,775(()D .11,[5,775())21.(山东省莱芜市莱芜十七中2013届高三4月模拟数学(理)试题)已知()f x 是定义在R 上的奇函数,满足33()()22f x f x -+=+,当3(0,)2x ∈时, 2()ln(1)f x x x =-+,则函数()f x 在区间[0,6]上的零点个数是 ( )A .3B .5C .7D .922.(山东省莱芜市莱芜十七中2013届高三4月模拟数学(理)试题)已知函数x x f x 21log 2)(-=,且实数a >b >c >0满足0)()()(<⋅⋅c f b f a f ,若实数0x 是函数y =)(x f 的一个零点,那么下列不等式中不可..能.成立的是 ( )A .a x <0B .a x >0C .b x <0 D .c x <0二、填空题 23.(山东省文登市2013届高三3月二轮模拟考试数学(理))函数12()3sin log f x x x π=-的零点的个数是__________.24.(2011年高考(山东理))已知函数()log a f x x x b =+-(0a >,且1a ≠).当234a b <<<<时,函数()f x 的零点()0,1x n n ∈+,*n N ∈,则n =_________.25.(2013届山东省高考压轴卷理科数学)给定方程:1()sin 102x x +-=,下列命题中:①该方程没有小于0的实数解;②该方程有无数个实数解;③该方程在(–∞,0)内有且只有一个实数解;④若0x 是该方程的实数解,则0x >–1.则正确命题是___________.26.(山东省烟台市2013届高三上学期期中考试数学试题(理科))函数2221()431x x f x x x x -≤⎧=⎨-+>⎩, , 的图象和函数()()ln 1g x x =-的图象的交点个数是 ____________.27.(山东省烟台市莱州一中2013届高三第二次质量检测数学(理)试题)若函数()33f x x x a =-+有三个不同的零点,则实数a 的取值范围是__________.28.(山东省济南市2013届高三3月高考模拟理科数学)()()()()()()()121116()|21|,(),,,n n f x x f x f x f x f f x f x f f x -=-=== .则函数()4y f x =的零点个数为______________.29.(2009高考(山东理))若函数f(x)=a x-x-a(a>0且a ≠1)有两个零点,则实数a 的取值范围是 . 30.(山东省威海市2013届高三上学期期末考试理科数学)已知|||lg |,0()2,0x x x f x x >⎧=⎨≤⎩,则函数22()3()1y f x f x =-+的零点的个数为_______个.31.(山东省寿光市2013届高三10月阶段性检测数学(理)试题)若函数()(01)xf x a x a a a =--≠ 且有两个零点,则实数a 的取值范围是________.山东省2014届理科数学一轮复习试题选编6:方程的解与函数的零点及二分法参考答案一、选择题1. 【答案】B43()()0f x x ax x x a =-=-=,解得0x =或x =即函数的零点有两个,要使零点都在区间[0,5]上,则有05<≤,解得0125a <≤.由()()h x g x =得31x a x-=,即41x ax -=有正整数解.设4()m x x ax =-,当1x =时,(1)11m a =-=,解得0a =,不成立.当2x =时,4(2)221621m a a =-=-=,解得151252a =<成立.当3x =时,4(3)338131m a a =-=-=,解得2551254a =<成立.当5x =时,4(5)5562551m a a =-=-=,解得6241255a =<成立.当6x =时,4(6)66129661m a a =-=-=,解得12951256a =>,不成立.所以满足条件的实数a 的取值为2,3,4,5,共有4个.选B.2. D 【解析】111()10(1)=0()10333e f e f f e e =->>=+>,,,根据根的存在定理可知,选D.3. C 【解析】做出函数)(x f 的图象如图,,由图象可知当直线为1+=x y 时,直线与函数)(x f 只要一个交点,要使直线与函数有两个交点,则需要把直线1+=x y 向下平移,此时直线恒和函数)(x f 有两个交点,所以1<a ,选C.4. 【答案】 C 由()()=0g x f x m =-得()f x m =,作出函数()y f x =的图象,,当0x >时,2211()()024f x x x x =-=--≥,所以要使函数()()g x f x m =-有三个不同的零点,则104m <<,即1(,0)4-,选C.5. 【答案】D【解析】由)1()1(+=-x f x f ,知)()2(x f x f =+,周期为2,又函数为偶函数,所以)1()1()1(x f x f x f -=+=-,函数关于1=x 对称,在同一坐标内做出函数x y x f y )101(),(==的图象,由图象知在]4,0[内交点个数为个.选D.6. C7. B 【解析】由()(1)ln 0f x x x =+=得1ln 1x x =+,做出函数1ln ,1y x y x ==+的图象,如图由图象中可知交点个数为1个,即函数的零点个数为1个,选B.8. 【答案】B 因为1(2)lg 202f =-<,1(3)lg 303f =->, 所以函数的零点在区间(2,3)上,选B. 9. 【答案】B【解析】因为(1.5)0,(1.25)0f f ><,所以根据根的存在定理可知方程的根落在区间(1.25,1.5)上,所以选B. 10. B 11. C12. C 【解析】由3()320f x x x =-+=得3(22)0x x x ---=,即2(1)(2)0x x -+=,解得1x =或2x =-,选C. 13. B 14. C15. 【答案】A当01x ≤<时,()0f x ≤.当1x ≥时,函数()1|3|f x x =--,关于3x =对称,当1x ≤-时,函数关于3x =-对称,由()()0F x f x a =-=,得(),y f x y a ==.所以函数()()F x f x a =-有5个零点.当10x -≤<,时,01x <-≤,所以122()log (1)log (1)f x x x -=-+=--,即2()log (1)f x x =-,10x -≤<.由2()log (1)f x x a =-=,解得12a x =-,因为函数()f x 为奇函数,所以函数()()F x f x a =-(0<a <1)的所有零点之和为12a x =-,选A. 16. 【答案】D【解析】由()0y f x k =+=,得()f x k =-,所以0k ≤.做出函数()y f x =的图象如图,要使函数()y f x k =+有三个零点,则由2k -≥,即2k ≤-,选D. 17. A18. C 【解析】113()2220422g =+-=-<,1()212102g =+-=>,则11()()024g g ⋅<,所以 21142x <<.若为 A.()122f x x =-,则()122f x x =-的零点为114x =,所以211044x <-<,所以121||4x x -<,不满足题意.如为 B.()214f x x x =-+-的零点为112x =,211024x <-<,所以121||4x x -<,不满足题意.若为 C.()110x f x =-的零点为10x =,所以211042x <-<,所以满足121||4x x ->.若为D.()()ln 82f x x =-的零点为138x =,23133182884x -<-<-,即2131888x -<-<,所以121||8x x -<,不满足题意,所以选C.19. C 【解析】在同一坐标系下做出函数11()(),()2x f x f x x==-的图象由图象可知当0(,)x x ∈-∞时,11()2x x >-,0(,0)x x ∈时,11()2x x<-,所以当)0,(),,(0201x x x x ∈-∞∈,有0)(,0)(21<>x f x f ,选C20. 【答案】A 由(1)()f x f x +=-得,(2)()f x f x +=,所以函数的周期是2. 由()()log =0a g x f x x =-.得()=log a f x x ,分别作出函数(),()=log a y f x y m x x ==的图象,因为(5)=log 5(5)a m m =-.所以若1a >,由图象可知要使函数()()log a g x f x x =-至少6个零点,则满足(5)=log 51a m <.此时5a >.若01a <<,由图象可知要使函数()()log a g x f x x =-至少6个零点,则满足(5)=log 51a m -≥-,此时105a <≤.所以a 取值范围是10,5,5+∞ (](),选A.21. D22. D二、填空题 23. 924.解析:根据(2)log 22log 230a a f b a =+-<+-=,(3)log 32log 340a a f b a =+->+-=,而函数()f x 在(0,)+∞上连续,单调递增,故函数()f x 的零点在区间(2,3)内,故2n =.答案应填:2.25. ②③④【解析】由1()sin 102x x +-=得1sin 1()2x x =-,令()f x =sin x ,()g x =11()2x-,在同一坐标系中画出两函数的图像如右,由图像知:①错,③、④对,而由于()g x =11()2x-递增,小于1,且以直线1=y 为渐近线,()f x =sin x 在-1到1之间振荡,故在区间(0,+∞)上,两者图像有无穷多个交点,所以②对,故选填②③④.26. 2 【解析】画出图象知交点个数为2.27. (2,2)- 【解析】函数的导数为()22'333(1)f x x x =-=-,所以1x =和1x =-是函数的两个极值,由题意知,极大值为(1)2f a -=+,极小值为(1)2f a =-+,所以要使函数()f x 有三个不同的零点,则有20a +>且20a -+<,解得22a -<<,即实数a 的取值范围是(2,2)-. 28. 【答案】8由43()(())0f x f f x ==,即32()10f x -=,解得31()2f x =.又3221()(())2()12f x f f x f x ==-=,解得23()4f x =或21()4f x =.当23()4f x =时,2113()(())2()14f x f f x f x ==-=,解得17()8f x =或11()8f x =,当21()4f x =时,2111()(())2()14f x f f x f x ==-=,解得15()8f x =或13()8f x =,由17()()218f x f x x ==-=,所以1511616x =或.由13()()218f x f x x ==-=,所以1151616x =或.由15()()218f x f x x ==-=,所以1331616x =或.由13()()218f x f x x ==-=,所以1151616x =或.所以共有8个零点.29. 【解析】: 设函数(0,x y a a =>且1}a ≠和函数y x a =+,则函数f(x)=a x-x-a(a>0且a ≠1)有两个零点,就是函数(0,xy a a =>且1}a ≠与函数y x a =+有两个交点,由图象可知当10<<a 时两函数只有一个交点,不符合,当1>a 时,因为函数(1)xy a a =>的图象过点(0,1),而直线y x a =+所过的点一定在点(0,1)的上方,所以一定有两个交点.所以实数a 的取值范围是1>a 答案: 1>a30. 【答案】5 由22()3()10y f x f x =-+=解得()1f x =或1()2f x =.若()1f x =,当0x >时,由lg 1x =,得lg 1x =±,解得10x =或110x =.当0x ≤时,由21x =得0x =.若1()2f x =,当0x >时,由1lg 2x =,得1lg 2x =±,解得x =或x =.当0x ≤时,由122x=得1x =-,此时无解.综上共有5个零点.31. {|1}a a。
【市级联考】山东省德州市2024届高三第二次模拟考试理科综合全真演练物理试题
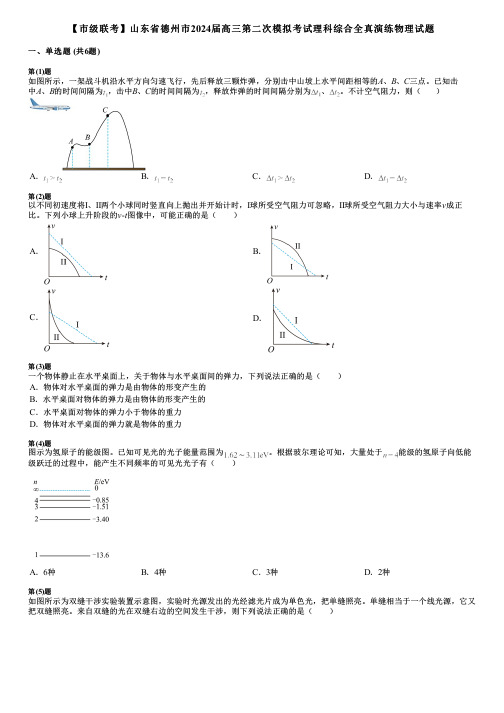
【市级联考】山东省德州市2024届高三第二次模拟考试理科综合全真演练物理试题一、单选题 (共6题)第(1)题如图所示,一架战斗机沿水平方向匀速飞行,先后释放三颗炸弹,分别击中山坡上水平间距相等的A、B、C三点。
已知击中A、B的时间间隔为,击中B、C的时间间隔为,释放炸弹的时间间隔分别为、。
不计空气阻力,则()A.B.C.D.第(2)题以不同初速度将Ⅰ、Ⅱ两个小球同时竖直向上抛出并开始计时,Ⅰ球所受空气阻力可忽略,Ⅱ球所受空气阻力大小与速率v成正比。
下列小球上升阶段的v-t图像中,可能正确的是( )A.B.C.D.第(3)题一个物体静止在水平桌面上,关于物体与水平桌面间的弹力,下列说法正确的是( )A.物体对水平桌面的弹力是由物体的形变产生的B.水平桌面对物体的弹力是由物体的形变产生的C.水平桌面对物体的弹力小于物体的重力D.物体对水平桌面的弹力就是物体的重力第(4)题图示为氢原子的能级图。
已知可见光的光子能量范围为。
根据玻尔理论可知,大量处于能级的氢原子向低能级跃迁的过程中,能产生不同频率的可见光光子有( )A.6种B.4种C.3种D.2种第(5)题如图所示为双缝干涉实验装置示意图,实验时光源发出的光经滤光片成为单色光,把单缝照亮。
单缝相当于一个线光源,它又把双缝照亮。
来自双缝的光在双缝右边的空间发生干涉,则下列说法正确的是( )A.组装实验仪器时,应将单缝和双缝垂直放置B.若想增加在目镜中观察到的条纹个数,应将单缝向双缝靠近C.若将滤光片去掉,则毛玻璃上将呈现黑白相间条纹D.若将红色滤光片换成绿色滤光片,则毛玻璃上的干涉条纹间距将变窄第(6)题安培定律的建立过程中,安培设计了一个无定向秤,如图所示,由同一根导线作成两个大小相等、电流方向相反的平面回路1和2,两回路固定连在一起。
线圈的两端A、B通过水银槽和固定支架相连。
这样,线圈既可通入电流,又可自由转动。
下列说法正确的是( )A.当处于非匀强磁场中,线圈可能会发生转动B.当处于平行线圈平面的匀强磁场中,线圈可能会发生转动C.当处于垂直线圈平面的匀强磁场中,线圈可能会发生转动D.当有一条形磁铁靠近线圈时候,线圈不可能会发生转动二、多选题 (共4题)第(1)题匀强电场中,一带电粒子受重力和电场力作用在竖直平面内的运动轨迹如图所示。
山东省2014届理科数学一轮复习试题选编7:函数的综合问题

山东省2014届理科数学一轮复习试题选编7:函数的综合问题一、选择题错误!未指定书签。
.(山东省潍坊市2013届高三第二次模拟考试理科数学)某学校要召开学生代表大会,规定根据班级人数每10人给一个代表名额,当班级人数除以10的余数大于6时,再增加一名代表名额.那么各班代表人数y 与该班人数x 之间的函数关系用取整函数[]y x =([x]表示不大于*的最大整数)可表示为 ( ) A .[]10xy = B .3[]10x y += C .4[]10x y += D .5[]10x y += 【答案】B 法一:特殊取值法,若x=56,y=5,排除 C .D,若x=57,y=6,排除A,所以选B法二:设)90(10≤≤+=ααm x ,,时⎥⎦⎤⎢⎣⎡==⎥⎦⎤⎢⎣⎡++=⎥⎦⎤⎢⎣⎡+≤≤10103103,60x m m x αα 1101103103,96+⎥⎦⎤⎢⎣⎡=+=⎥⎦⎤⎢⎣⎡++=⎥⎦⎤⎢⎣⎡+≤<x m m x αα时当,所以选B 错误!未指定书签。
.(山东省寿光市2013届高三10月阶段性检测数学(理)试题)已知函数321,,1,12()111,0,.362x x x f x x x ⎧⎛⎤∈ ⎪⎥+⎪⎝⎦=⎨⎡⎤⎪-+∈⎢⎥⎪⎣⎦⎩函数π()s i n ()22(0)6g x a x a a =-+ ,若存在[]12,0,1x x ∈,使得12()()f x g x =成立,则实数a 的取值范围是( )A .14,23⎡⎤⎢⎥⎣⎦ B .10,2⎛⎤⎥⎝⎦C .24,33⎡⎤⎢⎥⎣⎦ D .1,12⎡⎤⎢⎥⎣⎦【答案】B错误!未指定书签。
.(山东省德州市2013届高三第二次模拟考试数学(理)试题)若对于定义在R 上的函数f(x),存在常数()t t R ∈,使得f(x+t)+tf(x)=0对任意实数x 均成立,则称f(x )是阶回旋函数,则下面命题正确的是 ( ) A .f(x)=2x是12-阶回旋函数 B .f(x)=sin(πx)是1阶回旋函数 C .f (x)=x 2是1阶回旋函数 D .f(x)=log a x 是0阶回旋函数【答案】B错误!未指定书签。
山东省2014届理科数学一轮复习试题选编16:平面向量的综合问题(学生版)

山东省2014届理科数学一轮复习试题选编16:平面向量的综合问题一、选择题1 .(山东省凤城高中2013届高三4月模拟检测数学理试题 )已知||||2OA OB ==u u u r u u u r,点C 在线段AB 上,且||OC uuu r 的最小值为1,则||(OA tOB t -∈u u u r u u u rR)的最小值为( )ABC .2D2 .(2012年普通高等学校招生全国统一考试预测卷 理科数学1)设()()1212,,,a a a b b b ==r r,定义一种向量积()()()12121122,,,a b a a b b a b a b ⊗=⊗=r r.已知12,,,023m n π⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭u r r ,点P (x ,y )在y=sin x 的图象上运动,点Q 在y=f (x )的图象上运动,且满足OQ m OP n =⊗+u u u r u r u u u r r(其中O 为坐标原点),则y=f (x )的最大值为( )A .1B .3C .5D .213 .(山东省德州市2013届高三3月模拟检测理科数学)若,,a b c r r r均为单位向量,且0a b ⋅=r r ,则a b c +-r r r 的最小值为 ( )A1-B .1C1+D4 .(2012年高考(广东文))(向量、创新)对任意两个非零的平面向量α和β,定义⋅⋅=⋅αβαβββ,若平面向量a 、b 满足0≥>a b ,a 与b 的夹角0,4πθ⎛⎫∈ ⎪⎝⎭,且o a b 和o b a 都在集合2n n Z ⎧⎫∈⎨⎬⎩⎭中,则=o a b ( )A .12B .1C .32D .525 .(山东省济南市2012届高三3月高考模拟题理科数学(2012济南二模))在△ABC 中,E 、F 分别为AB ,AC中点.P 为EF 上任一点,实数x ,y 满足PA u u u r +x PB u u u r+y PC u u u r =0.设△ABC ,△PBC ,△PCA ,△PAB 的面积分别为S ,1S ,2S ,3S ,记11S S λ=,22SS λ=,33S Sλ=,则23λλg 取最大值时,2x +y 的值为( )A .-1B .1C .-32D .326 .(山东省莱钢高中2013届高三4月模拟检测数学理试题 )定义域为[a,b]的函数()y f x =图像的两个端点为 ( )A .B,M(x ,y )是()f x 图象上任意一点,其中(1)[,]=+-∈x a b a b λλ,已知向量(1)ON OA OB λλ=+-u u u r u u u r u u u r ,若不等式||MN k ≤u u u u r恒成立,则称函数()[,]f x a b 在上“k 阶线性近似”.若函数1y x x=-在[1,2]上“k 阶线性近似”,则实数k 的取值范围为 ( )A .[0,)+∞B .1[,)12+∞C .3[2,)2++∞D .3[2,)2-+∞7 .(北京市东城区2012届高三上学期期末教学统一检测(数学文))在平面直角坐标系xOy 中,已知向量OA u u u r 与OB u u u r关于y 轴对称,向量)0,1(=a ,则满足不等式20OA AB +⋅≤u u u r u u u r a 的点),(y x A 的集合用阴影表示为8 .(哈尔滨市第六中学2011-2012学年度上学期期末高三理科考试卷)已知点G 是ABC ∆重心,),(R ∈+=μλμλ,若2,120-=⋅=∠AC AB A ο,AG 的最小值是( )A .33 B .22 C .32 D .43 9 .(2013届山东省高考压轴卷理科数学)定义平面向量之间的一种运算“⊙”如下:对任意的a=(m,n),b=(p,q),令a ⊙b= mq-np,下面说法错误的是( )A .若a 与b 共线,则a ⊙b =0B .a ⊙b =b ⊙aC .对任意的λ∈R,有(λa)⊙b =λ(a ⊙b)D .(a ⊙b)2+(a·b)2= |a|2|b|210.(山东省淄博市2013届高三复习阶段性检测(二模)数学(理)试题)定义域为[],a b 的函数()y f x =的图象的两个端点为A,B,M()(),x y x 是f 图象上任意一点,其中()()()1,1x a b R ON OA OB λλλλλ=+-∈=+-u u u r u u u r u u u r向量,若不等式MN k ≤u u u u r 恒成立,则称函数()[],f x a b 在上“k 阶线性近似”.若函数[]112y x x=+在,上“k 阶线性近似”,则实数k 的取值范围为 ( )A .[)0+∞,B .[)1+∞,C.32⎡⎫+∞⎪⎢⎣⎭ D.32⎡⎫++∞⎪⎢⎣⎭11.(2012年高考(安徽理))在平面直角坐标系中,(0,0),(6,8)O P ,将向量OP uuu r 按逆时针旋转34π后,得向量OQ uuu r则点Q 的坐标是 ( )A.(- B.(-C.(2)--D.(2)-12.(山东省烟台市2013届高三上学期期中考试数学试题(理科))在ABC ∆中,P 是BC 边中点,角A ,B ,C的对边分别是a ,b ,c ,若0cAC aPA bPB ++=u u u r u u u r u u u r r,则ABC ∆的形状为( )A .等边三角形B .钝角三角形C .直角三角形D .等腰三角形但不是等边三角形.13.(2010昌平二模试题(理科)正式稿)设向量1212(,),(,)a a a b b b ==r r,定义一种向量积:12121122(,)(,)(,)a b a a b b a b a b ⊗=⊗=r r .已知1(,3),(,0),26m n π==u r r 点P 在sin y x =的图像上运动,点Q 在()y f x =的图像上运动,且满足OQ m OP n =⊗+u u u r u r u u u r r(其中O 为坐标原点),则()y f x =的最大值及最小正周期分别是 ( )A .1,2π B .1,42π C .3,πD .3,4π二、填空题14.(山东省菏泽市2013届高三第二次模拟考试数学(理)试题)下列命题中,正确的是____________________(1)平面向量a ρ与b ρ的夹角为060,)0,2(=a ρ,1=b ρ,则=+b a ρρ(2)已知((sin ,a b θ==r r ,其中θ∈⎝⎛⎭⎪⎫π,3π2,则a b ⊥r r(3)O 是ABC ∆所在平面上一定点,动点P 满足:sin sin AB AC OP OA C B λ⎛⎫=++ ⎪ ⎪⎝⎭u u u r u u u ru u u r u u u r ,()0,λ∈+∞,则直线AP 一定通过ABC ∆的内心15.(山东省滨州市2013届高三第一次(3月)模拟考试数学(理)试题)定义平面向量的一种运算:||||sin ,⊗=⋅a b a b a b ,则下列命题:①⊗=⊗a b b a ;②()()λλ⊗=⊗a b a b ;③()()()+⊗=⊗+⊗a b c a c b c ; ④若a =11221221(,),(,),||x y x y x y x y =⊗=-则b a b .其中真命题是_________(写出所有真命题的序号).16.(山东省莱钢高中2013届高三4月模拟检测数学理试题 )已知O 为锐角△ABC 的外心,10,6==AC AB 若AO =x AB +y AC ,且5102=+y x ,则BAC ∠cos 的值是________17.(山东省烟台市莱州一中2013届高三第二次质量检测数学(理)试题)已知点P 是△ABC 的中位线EF 上任意一点,且EF//BC,实数x,y 满足0.,,,PA xPB yPC ABC PBC PCA PAB ++=∆∆∆∆u u u r u u u r u u u r r设的面积分别为S,S 1,S 2,S 3,记312123,,S S SS S Sλλλ===,则23λλ⋅取最大值时,2x+y 的值为________. 18.(山西省实验中学仿真演练试卷文)对于命题:若O 是线段AB 上一点,则有0OB OA OA OB ⋅+⋅=u u u r u u u r u u u r u u u r r.将它类比到平面的情形是:若O 是△ABC 内一点,则有0OBC OCA OBA S OA S OB S OC ⋅+⋅+⋅=u u u r u u u r u u u r r.将它类比到空间的情形应该是:若O 是四面体ABCD 内一点,则有______________________________________.19.(山东师大附中2013届级高三12月第三次模拟检测理科数学)下列命题中,正确的是____________________①平面向量a ρ与b ρ的夹角为060,)0,2(=a ρ,1=b ρ,则=+b a ρρ②已知((sin ,a b θ==r r ,其中θ∈⎝⎛⎭⎪⎫π,3π2,则a b ⊥r r③O 是ABC ∆所在平面上一定点,动点P 满足:sin sin AB AC OP OA C B λ⎛⎫=++ ⎪ ⎪⎝⎭u u u r u u u ru u u r u u u r ,()0,λ∈+∞,则直线AP 一定通过ABC ∆的内心20.(安徽寿县一中2012年高三第四次月考试卷)关于非零平面向量,,a b c .有下列命题:①若(1,),(2,6)k ==-a b ,∥a b ,则3k =-; ②若||||||==-a b a b ,则a 与+a b 的夹角为60o; ③||||||+=+a b a b ⇔a 与b 的方向相同; ④||||||+>-a b a b ⇔a 与b 的夹角为锐角; ⑤若(1,3),(2,4),(4,6)---a =b =c =,则表示向量4,32,-a b a c 的有向线段首尾连接能构成三角形.其中真命题的序号是____________(将所有真命题的序号都填上).三、解答题21.(湖北黄冈中学高三五月适应训练)已知ABC ∆中,90C ∠=︒,D 为斜边AB 上靠近顶点A 的三等分点.(I)设,CA a CB b ==u u u r r u u u r r,求CD uuu r ;(II)若1CA CB ==,求CD uuu r 在AB u u u r方向上的投影.山东省2014届理科数学一轮复习试题选编16:平面向量的综合问题参考答案一、选择题 1. B 2. D3. 【答案】A 222222232()a b c a b c a b a c b c a b c +-=+++⋅-⋅-⋅=-+⋅r r r r r r r r r r r r r r r,因为0a b ⋅=r r ,且1a b c ===r r r ,所以2a c +=r r ,所以()cos ,2cos ,a b c a b c a b c a b c +⋅=+<+>=<+>r r r r r r r r r r r r,所以2322cos (),a b c a b c +-=-<+>r r r r r r ,所以当cos (),1a b c <+>=r r r时,2a b c +-r r r 最小为22322(21)a b c +-=-=-r r r ,所以21a b c +-=-r r r ,即a b c +-r r r 的最小值为21-.选A.4. 解析:C.⋅==⋅o a a b a b b b b 1cos 2k θ=,=o b b a a 2cos 2k θ=,两式相乘,可得212cos 4k kθ=.因为0,4πθ⎛⎫∈ ⎪⎝⎭,所以1k 、2k 都是正整数,于是2121cos 124k k θ<=<,即1224k k <<,所以123k k =.而0≥>a b ,所以13k =,21k =,于是32=o a b . 5. 【答案】D【解析】由题意知2111==λS S ,即S S 211=.,所以S S S S 211132=-=+,两边同除以S ,得2132=+S S S ,即2132=+λλ,所以3232221λλλλ≥+=,所以16132≤⋅λλ,当且仅当4132==λλ,此时点P 位EF 的中点,延长AP 交BC 于D,则D 为中点,由0=++PC y PB x PA ,得AP PA PC y PB x =-=+, PC PB PC PB PD AP 2121)(21+=+==,所以21,21==y x ,所以232=+y x ,选D.6. D7. B8. C9. B 【解析】由定义知:a ⊙b= mq-np:所以选项A 正确;又b ⊙a=pn-mq≠a⊙b= mq-np,所以选项B 错误;(λa)⊙b=mq np λλ-,λ(a ⊙b)= λ( mq-np)= mq np λλ-,所以 对任意的λ∈R,有(λa)⊙b =λ(a ⊙b),选项C 正确;(a ⊙b)2+(a·b)2=( mq-np)2+( mp+nq)2=22222222m q n p m p n q +++,|a|2|b|2=()()222222222222m n p q m q n p m p n q ++=+++,所以(a ⊙b)2+(a·b)2= |a|2|b|2,因此D 正确.10. 【答案】C 由题意知1,2a b ==,所以5(1,2),(2,)2A B .所以直线AB 的方程为1(3)2y x =+.因为()()1212M x a b λλλλλ=+-=+-=-,()()551(1,2)1(2,)(2,)222ON OA OB λλλλλλ=+-=+-=--u u u r u u u r u u u r ,所以2N x λ=-,,M N 的横坐标相同.且点N 在直线AB 上.所以1113(3)222M N x MN y y x x x x =-=+-+=+-u u u u r ,因为112222x x x x +≥⋅=,且1322x x +≤,所以13313()222222x x MN x x =+-=-+≤-u u u u r ,即MN u u u u r 的最大值为322-,所以322k ≥-,选C. 11. 【解析】选A【方法一】设34(10cos ,10sin )cos ,sin 55OP θθθθ=⇒==u u u r则33(10cos(),10sin())(72,2)44OQ ππθθ=++=--u u u r【方法二】将向量(6,8)OP =u u u r 按逆时针旋转32π后得(8,6)OM =-u u u u r则()(72,2)2OQ OP OM =-+=--u u u r u u ur u u u u r 12.A【解析】如图由AC c +aPA bPB +=u u u r u u u r r 知PC b c PA c a PC b PA a PA PC c )()()(-+-=-+-0=,而PA 与PC 为不共线向量,0=-=-∴b c c a ,.c b a ==∴故选A.13. C 二、填空题 14. ①②③15. 【答案】①④由定义可知||||sin ,⊗=⋅=⊗b a b a a b a b ,所以①正确.②当λ<时,,,a b a b λπ<>=-<>r r r r,所以()||||sin ,||||sin ,λλλλ⊗=⋅=-⋅a b a b a b a b a b ,而()||||sin ,λλ⊗=⋅a b a b a b ,所以②不成立.③因为a b +r r 的长度不一定等于a b +r r,所以③不成立.④2222222()||||sin ,||||(1cos ,)⊗=⋅<>=⋅-<>a b a b a b a b a b 22222||||||||cos ,=⋅-⋅<>a b a b a b222222222112212121221||||()()()()()a b x y x y x x y y x y x y =⋅-⋅=++-+=-r r a b ,所以1221||x y x y ⊗=-a b ,所以④成立,所以真命题是①④.16.3117. 32 【解析】由题意知12312S S S S ==+,223232322()1216S S S S S S λλ+=≤=,当且仅当23S S =时取等号,此时点P 在EF 的中点,所以0PF PE +=u u u r u u u r r,由向量加法的四边形法则可得,2PA PB PE +=u u u r u u u r u u u r ,2PA PC PF +=u u u r u u u r u u u r ,所以20PA PB PC ++=u u u r u u u r u u u r r ,即11022PA PB PC ++=u u u r u u u r u u u r r,又0PA xPB yPC ++=u u u r u u u r u u u r r ,所以12x y ==,所以322x y +=.18. 0O BCD O ACD O ABD O ABC V OA V OB V OC V OD ----+++=u u u r u u u r u u u r u u u r r19. ①②③ 【解析】①中,2a =r ,所以1cos 60212a b a b ==⨯=o r r r r g ,所以22221427a b a b a b +=++=++=r r r r r r g ,所以a b +=rr ,正确.②中,sin sin a b θθ==r rg ,即sin sin sin a b θθθ=+=+r r g ,因为3(,)2πθπ∈,所以sin 0θ<,所以sin sin sin sin 0a b θθθθ=+=-=r r g ,即a b ⊥r r ,正确.③中,根据正弦定理可知2sin sin AB AC RC B ==,所以sin ,sin 22AB ACC B R R==,即()2()sin sin AB AC AB AC R C B AB ACλλ+=+u u u r u u u r u u u r u u u r,即2()AB ACOP OA R APAB AC λ-=+=u u u r u u u ru u u r u u u r u u u r ,即AP u u u r 与BAC ∠的角平分线共线,所以直线AP 一定通过ABC∆的内心,正确,所以正确的命题为①②③.20. ①③⑤三、解答题21. (1) ∵ 3AB AD =u u u r u u u r 即()3CB CA CD CA -=-u u u r u u u r u u u r u u u r∴32CD CB CA =+u u u r u u u r u u u r 故 2133CD a b =+u u u r r r(2)过C 作CE AB ⊥于E ,则由射影定理得83AE =∴53DE = 又因为CD uuu r 在AB u u u r 方向上的投影为负,故CD uuu r 在AB u u u r 方向上的投影为53-。
山东省德州市2014届高三4月模拟考试(2014德州市二模)文综政治 Word版含答案

高中三年级模拟检测文科综合试题2014.4 本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,共12页。
满分300分,考试时间150分钟。
考试结束后,将本试卷和答题纸一并交回。
答卷前,考生务必将自己的姓名、准考证号、考试科目填涂在答题纸规定的地方。
第I卷(必做,共l40分)注意事项:1.每小题选出答案后,用2B铅笔把答题纸上对应题目的答案标号涂黑。
如需改动。
用橡皮擦干净后。
再选择其他答案标号。
不能答在试卷上。
2.第I卷共35小题,每小题4分,共140分。
在每题给出的四个选项中。
只有一项是最符合题目要求的。
24.近年来,水污染问题日益引发关注,越来越多的居民开始选购净水器。
净水器售价上涨的走势成为该行业发展的催化剂。
不考虑其他因素,能正确反映这种变动传导效应的是(注:D为需求曲线,S为供给曲线,D、S为变动前,D1、S1为变动后)A.①→③B.①→④C.②→③D.②→④25.三条小鬣狗能捕杀一匹大斑马,其秘诀在于分工明确,合作紧密,分工优势激发出合作的巨大能量。
这种经济活动模式被称为“小狗经济”。
“小狗经济”对我国经济发展的启示有①鼓励和支持中小企业兼并、重组,追求规模效益②中小企业应以市场为导向,制定正确的经营战略③促进社会分工和生产专业化,增强中小企业活力④发挥中小型企业对经济发展的主导作用A.①②B.②③C.①④D.②④26.2014年我国继续实施积极的财政政策,适当扩大财政赤字和国债规模。
在风险可控的前提下,适当扩大财政赤字会①扩大社会总需求,促进经济增长②减轻企业的税负,改善经济结构③增加货币流通量,引发通货膨胀④带动企业投资,增加就业机会A.①②B.②③C.①④D.②④27.2014年4月4日,国家铁路局对环渤海地区山东省城际轨道交通网规划方案调整及青藏铁路格尔木至拉萨段扩能改造等项目建设问题提出行业意见和建议,支持、鼓励和引导社会资本投资铁路,加快推进项目建设。
这说明A.各种所有制经济公平参与市场竞争B.统一开放竞争有序的市场体系已经建立C.我国鼓励和支持混合所有制经济发展D.政府通过经济手段对资源配置起决定性作用28.随着微博、微信等的广泛使用,公民的意见表达和利益诉求日益快速、便捷和多样化。
山东省2014届理科数学一轮复习试题选编19:等差与等比的综合问题(学生版)

山东省2014届理科数学一轮复习试题选编19:等差与等比的综合问题一、选择题 1 .(山东省实验中学2013届高三第三次诊断性测试理科数学)已知等差数列{}n a 的公差d 不为0,等比数列{}n b 的公比q 是小于1的正有理数.若d a =1,,21d b =且321232221b b b a a a ++++是正整数,则q 的值可以是( )A .71 B .-71 C .21 D .-21 2 .(山东省莱芜五中2013届高三4月模拟数学(理)试题)已知数列{},{}n n a b 满足113a b ==,113n n n nb a a b ++-==,n N +∈,若数列{}n c 满足n n a c b =,则2013c = ( )A .20129B .201227C .20139D .2013273 .(山东省烟台市莱州一中2013届高三第二次质量检测数学(理)试题)已知各项均不为零的数列{}n a ,定义向量()()1,,,1,n n n n c a a b n n n N *+==+∈ .下列命题中真命题是( )A .若n N *∀∈总有n n c b ⊥成立,则数列{}n a 是等比数列B .若n N *∀∈总有//n n c b 成立,则数列{}n a 是等比数列C .若n N *∀∈总有n n c b ⊥成立,则数列{}n a 是等差数列D .若n N *∀∈总有//n n c b 成立,则数列{}n a 是等差数列二、填空题 4 .(山东省莱芜市第一中学2013届高三12月阶段性测试数学(理)试题)已知等差数列{}n a 中,有11122012301030a a a a a a ++++++=成立.类似地,在正项等比数列{}n b 中,有_____________________成立.三、解答题 5 .(山东省济南市2013届高三4月巩固性训练数学(理)试题)已知数列{}n a 满足13a =,*133()n n n a a n N +-=∈,数列{}n b 满足3nn na b =. (1)证明数列{}n b 是等差数列并求数列{}n b 的通项公式; (2)求数列}{n a 的前n 项和n S .6 .(山东省济宁市2013届高三第一次模拟考试理科数学 )已知数列{n a }的前n 项和1122n *n n S a ()(n N )-=--+∈,数列{n b }满足n b =2n n a .(I)求证数列{n b }是等差数列,并求数列{n a }的通项公式;(Ⅱ)设2n n n c log a =,数列{22n n c c +}的前n 项和为T n ,求满足2521*n T (n N )<∈的n 的最大值.7 .(山东省莱芜五中2013届高三4月模拟数学(理)试题)在等差数列{}n a 中,345842,30a a a a ++==.(1)求数列{}n a 的通项公式; (2)若数列{}n b满足2n a n b λ+=+(R λ∈),则是否存在这样的实数λ使得{}n b 为等比数列;(3)数列{}n c 满足112,1,2n n n n n c T a n --⎧⎪=⎨⎪⎩为奇数,为偶数为数列{}n c 的前n 项和,求2n T .8 .(山东省凤城高中2013届高三4月模拟检测数学理试题 )设等比数列{}n a 的前项和为n S ,已知122n n a S +=+,(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)在n a 与1n a +之间插入n 个数,使这2+n 数组成公差为n d 的等差数列,求1{}nd 的前n 项和n T .9 .(山东省莱芜市莱芜十七中2013届高三4月模拟数学(理)试题)已知数列{}n a 的前n 项和n S 满足21n n S a =-,等差数列{}n b 满足11b a =,43b S =.(1)求数列{}n a 、{}n b 的通项公式; (2)设11n n n c b b +=,数列{}n c 的前n 项和为n T ,问n T >10012012的最小正整数n 是多少?10.(山东省青岛即墨市2013届高三上学期期末考试数学(理)试题)等差数列}{n a 中,9,155432==++a a a a .(Ⅰ)求数列}{n a 的通项公式; (Ⅱ)设213+=n a n b ,求数列n n a 1{,b }2+的前n 项和n S .11.(山东省德州市2013届高三上学期期末校际联考数学(理))数列{a n }的前n 项和为1,2(1)n n n S S n +=-+,等差数列{}n b 的各项为正实数,其前n 项和为31122339,,,n T T a b a b a b =+++,且又成等比数列. (I)求数列{a n }、{}n b 的通项公式;(2)若.n n n c a b =,当n≥2时,求数列{}n c 的前n 项和A n .12.(山东省泰安市2013届高三第二次模拟考试数学(理)试题)已知等差数列{}n a 的首项13,0a d =≠公差,其前n 项和为n S ,且1413,,a a a 分别是等比数列{}n b 的第2项,第3项,第4项. (I)求数列{}n a 与{}n b 的通项公式;(II)证明1211113.34n S S S ≤++⋅⋅⋅+< 13.(山东省泰安市2013届高三第一轮复习质量检测数学(理)试题)设等比数列{}n a 的前n 项和为,415349,,,n S a a a a a =-成等差数列.(I)求数列{}n a 的通项公式;(II)证明:对任意21,,,k k k R N S S S +++∈成等差数列.14.(山东师大附中2013届高三第四次模拟测试1月理科数学)已知数列{}n a 是等差数列,{}n b 是等比数列,且112a b ==,454b =,12323a a a b b ++=+.(1)求数列{}n a 和{}n b 的通项公式(2)数列{}n c 满足n n n c a b =,求数列{}n c 的前n 项和n S .15.(山东省烟台市莱州一中2013届高三第二次质量检测数学(理)试题)已知{}n a 是公差为2的等差数列,且317111a a a +++是与的等比中项.(1)求数列{}n a 的通项公式;(2)令()12n n na b n N *-=∈,求数列{}n b 的前n 项和Tn. 16.(2012年山东理)(20)在等差数列{}n a 中,345984,73a a a a ++==.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)对任意*m ∈N ,将数列{}n a 中落入区间2(9,9)m m 内的项的个数记为{}n b ,求数列{}n b 的前m 项和m S .17.(山东省枣庄三中2013届高三上学期1月阶段测试理科数学)已知数列{}n a 的前n 项和为1,3n n n S a S n +=-+且,1,2n a ∈=+N .(Ⅰ)求数列{}n a 的通项; (Ⅱ)设()2n n nb n S n =∈-++N 的前n 项和为n T ,证明:n T <34. 18.(山东省日照市2013届高三12月份阶段训练数学(理)试题)已知{}n a 是公差不为零的等差数列,11391,,,a a a a =成等比数列.求: (I)数列{}n a 的通项公式; (II)数列{}2an n a ⋅的前n 项和n S19.(山东省莱钢高中2013届高三4月模拟检测数学理试题 )设数列{}n a 为等差数列,且145=a ,720a =,且132(2,)n n S S n n N -=+≥∈;, (Ⅰ(Ⅱ为数列{}n c 的前n 项和. T n <m 恒成立对N n *∈,求m 的最小值.20.(山东省莱芜市第一中学2013届高三12月阶段性测试数学(理)试题)已知数列n a 满足222121na a a n n =+⋅⋅⋅++- (Ⅰ)求数列{}n a 的通项; (Ⅱ)若nn a nb =,求数列{}n b 的前n 项的和n S .21.(山东师大附中2013届级高三12月第三次模拟检测理科数学)数列{}n a 的前n 项的和为n S ,对于任意的自然数0n a >,()241n n S a =+(Ⅰ)求证:数列{}n a 是等差数列,并求通项公式 (Ⅱ)设3nn na b =,求和12n n T b b b =+++ 22.(山东省兖州市2013高三9月入学诊断检测数学(理)试题)设等比数列{}n a 的前n 项和为n S ,已知122(n n a S n +=+∈N *).(1)求数列{}n a 的通项公式;(2)在n a 与1n a +之间插入n 个数,使这n+2个数组成公差为n d 的等差数列,求数列1n d ⎧⎫⎪⎨⎬⎪⎭⎩的前n 项和n T . 23.(山东省潍坊市四县一校2013届高三11月期中联考(数学理))已知各项均为正数的数列{}n a 前n 项和为n S ,首项为1a ,且n n S a ,,21等差数列. (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)若n b n a )21(2=,设n n n a b c =,求数列{}n c 的前n 项和n T .24.(山东省夏津一中2013届高三4月月考数学(理)试题)在等比数列}{n a 中,412=a ,512163=⋅a a .设22122log 2log 2nn n a a b +=⋅,n T 为数列{}n b 的前n 项和.(Ⅰ)求n a 和n T ;(Ⅱ)若对任意的*∈N n ,不等式n n n T )1(2--<λ恒成立,求实数λ的取值范围.25.(山东省济南市2013届高三3月高考模拟理科数学)数列{}n a 的前n 项和为n S ,11a =,121n n a S +=+*()n N ∈,等差数列{}n b 满足 353,9b b ==.(1)分别求数列{}n a ,{}n b 的通项公式; (2)设*22()n n n b c n N a ++=∈,求证113n n c c +<≤.26.(山东省济南市2013届高三上学期期末考试理科数学)已知等差数列{}n a 的前n 项和为n S ,365,36a S ==,(1)求数列{}n a 的通项公式;(2) 设2n an b =,求数列{}n b 的前n 项和n T .27.(山东省潍坊市2013届高三上学期期末考试数学理(A ))设数列{}n a 为等差数列,且9,553==a a ;数列{}n b 的前n 项和为n S ,且2=+n n b S .(I)求数列{}n a ,{}n b 的通项公式; (II)若()+∈=N n b a c nnn ,n T 为数列{}n c 的前n 项和,求n T .28.(山东威海市2013年5月高三模拟考试数学(理科))已知{}n a 为等差数列,n S 为其前n 项和,且222n n S a n =+.(Ⅰ)求,n n a S ;(Ⅱ)若2221,,k k k a a a -+成等比数列,求k 的值及公比.山东省2014届理科数学一轮复习试题选编19:等差与等比的综合问题参考答案一、选择题1. C 【解析】由题意知21312,23a a d d a a d d =+==+=,22222131,b b q d q b b q d q ====,所以2222221232222212349141a a a d d d b b b d d q d q qq++++==++++++,因为321232221b b b a a a ++++是正整数,所以令2141t q q=++,t 为正整数.所以2114t q q ++=,即21014t q q ++-=,解得5613t q +-+===,因为t 为正整数,所以当8t =时,12122q -+===.符合题意,选C2. D3. D 【解析】由//nn c b 得,1(1)n n na n a +=+,即11n n a a n n +=+,所以11n n a n a n ++=,所以1n a na =,故数列{}n a 是等差数列,选D.二、填空题4. 由算术平均数类比几何平均数,容易得出30302110201211b b b b b b =. 三、解答题5. 解(1)证明:由3n n n a b =,得1113n n n a b +++=, ∴1111333n n n n n n a a b b +++-=-=所以数列{}n b 是等差数列,首项11b =,公差为13∴121(1)33n n b n +=+-=(2)13(2)3n n n n a b n -==+⨯n n a a a S +++=∴ 2113)2(3413-⨯+++⨯+⨯=n n ----① n n n S 3)2(343332⨯+++⨯+⨯=∴ -------------------②①-②得n n n n S 3)2(33313212⨯+-++++⨯=--n n n 3)2(3331212⨯+-+++++=-n n n 3)2(233⨯+-+=23)2(433nn n n S +++-=∴6. 解:(Ⅰ)在2)21(1+--=-n n n a S 中,令n=1,可得1121a a S n =+--=,即211=a . 当2≥n 时,2)21(211+--=---n n n a S ∴111)21(---++-=-=n n n n n n a a S S a ,∴11)21(2--+=n n n a a ,即12211+=--n n n n a a .∵n n n a b 2=,∴11+=-n n b b ,即当2≥n 时,11=--n n b b . 又1211==a b ,∴数列{b n }是首项和公差均为1的等差数列.于是n n n a n n b 21)1(1==⋅-+=,∴nn n a 2= (Ⅱ)∵nn a nc 2log ==n n =2log 2, ∴22211(2)2n n+==-c c n n+n n+, ∴)211()1111()5131()4121()311(+-++--++-+-+-=n n n n T n =2111211+-+-+n n 由n T 2125<,得2111211+-+-+n n 2125<,即42132111>+++n n , =)(n f 2111+++n n 单调递减,∵4213)5(,209)4(==f f , ∴n 的最大值为47. 解:(1)因为{}n a 是一个等差数列,所以34544342,14a a a a a ++==∴=.设数列{}n a 的公差为d ,则84416d a a =-=,故4d =;故4(4)42n a a n d n =+-=-(2)29n a n n b λλ+=+=+.假设存在这样的λ使得{}n b 为等比数列,则212n n n b b b ++=⋅,即122(9)(9)(9)n n n λλλ+++=+⋅+,整理可得0λ=. 即存在0λ=使得{}n b 为等比数列(3)∵12,23,n n n c n n -⎧=⎨-⎩为奇数为偶数,∴242221(223)2(243)22(223)n n T n -=+⨯-++⨯-++++⨯- 242212224(12)3n n n -=++++++++-214(1)414321423n n n n n n n -+-=+⨯-=+-- 8. 解:(Ⅰ)由122(n n a S n +=+∈ N +)得122(n n a S n -=+∈N +,2n ≥), 两式相减得:12n n n a a a +-=, 即13(n n a a n +=∈N +,2n ≥),∵{}n a 是等比数列,所以213a a = ; 又2122,a a =+则11223a a +=,∴12a =, ∴132-⨯=n n a(Ⅱ)由(1)知132-⨯=n n a ,则nn a 321⨯=+∵1(1)n n n a a n d +=++ , ∴1341+⨯=-n d n n∵123111n T d d d =+++1nd + ∴1210341344343342-⨯+++⨯+⨯+⨯=n n n T ① nn n n n T 34134344343342311321⨯++⨯++⨯+⨯+⨯=- ② ①-②得nn n n T 3413413413413413423213210⨯+-⨯++⨯+⨯+⨯+⨯=-n n n 3413113113141211⨯+--⎪⎭⎫ ⎝⎛-⨯+=-n n 385285⨯+-= ∴1316521615-⨯+-=n n n T 9. 解:(1)当1n =时,11121a S a ==-,∴11a =当2n ≥时,111(21)(21)22n n n n n n n a S S a a a a ---=-=---=-, 即12nn a a -= ∴数列{}n a 是以11a =为首项,2为公比的等比数列,∴12,21n n n n a S -==- 设{}n b 的公差为,d 111b a ==,4137b d =+=,∴2d = ∴1(1)221n b n n =+-⨯=-(2)111111()(21)(21)22121n n n c b b n n n n +===--+-+ ∴11111111(1...)(1)2335212122121n n T n n n n =-+-++-=-=-+++ 由n T >10012012,得21n n +>10012012,解得n >100.1∴n T >10012012的最小正整数n 是10110.解:(Ⅰ)设数列{}由题意得首项的公差为,1a d a n且⎩⎨⎧=+=+⎩⎨⎧==++941563915115432d a d a a a a a 即 解得⎩⎨⎧==211d a所以数列{}12-=n a a n n 的通项公式为 (Ⅱ)由(Ⅰ)可得n n n ab 3231==+所以n n n n b a3..21=+所以+++=323.33.23.11n S 13.+n n两式相减得++++-=433333(22n S 13.)3+++n n n 10 分43).12(323..1233.31313111+++-+=-+=+---=n n n n n n S n n n 即)()(11.12.13.14. 【解析】:(Ⅰ)设{}n a 的公差为d ,{}n b 的公比为q由341b b q =,得354272q ==,从而3q = 因此11132--⋅=⋅=n n n q b b又123223361824a a a a b b ++==+=+=,28a ∴= 从而216d a a =-=,故466)1(1-=⋅-+=n n a a n (Ⅱ)13)23(4-⋅-⋅==n n n n n b a c令122103)23(3)53(373431--⋅-+⋅-++⨯+⨯+⨯=n n n n n Tn n n n n T 3)23(3)53(37343131321⋅-+⋅-++⨯+⨯+⨯=-两式相减得13)13(3313)23(333333331211321--⨯+=⋅--⨯++⨯+⨯+⨯+=---n nn n n Tnn 3)23(⋅--n 1n 9(31)13n 2)32--=+--⋅(73(67)44n n n T -∴=+,又n n n S 4T 7(6n 7)3==+-⋅15.16. (20)解:(Ⅰ)因为{}n a 是一个等差数列,所以3454384a a a a ++==,即428a =. 所以,数列{}n a 的公差9473289945a a d --===-, 所以,*4(4)289(4)98()n a a n d n n n =+-=+-=-∈N (Ⅱ)对*m ∈N ,若 299m m n a <<,则 298998m m n +<<+,因此 121919m m n --+≤≤, 故得 2199m m m b -=-(lb ylfx) 于是 123...m m S b b b b =++++35212121(999...9)(199...9)9(181)19181199109180m m m m m m --+=++++-++++⨯--=----⨯+=17.解:(Ⅰ)()113,213n n n n a S n n a S n +-=-+≥=--+ 时, ,,12,111-=-=-∴++n n n n n a a a a a 即 112(1),(2,),n n a a n n +∴-=-≥∈N* 2221(1)232n n n a a --∴-=-=∙=n a ⎩⎨⎧≥+∙=-2,1231,22n n n (Ⅱ)113322n n n S a n n -+=+-=∙+- ,123-∙=∴n n nb⎪⎭⎫⎝⎛++++=∴-1222322131n n n T⎪⎭⎫ ⎝⎛++++=n n n T 2232221312132 相减得,⎪⎭⎫⎝⎛-++++=-n n n n T 22121211312112 ,n n n nT 23221134∙-⎪⎭⎫ ⎝⎛-=∴﹤34∴结论成立.18.解:(Ⅰ)设等差数列{}n a 的公差为d ,由题设知0d ≠,由11391,,,a a a a =成等比数列,得1218112d dd++=+ 解得1,0d d ==(舍去).故{}n a 的通项公式为11)1=+(n a n n -⨯=(Ⅱ)由(I)知22n a n n a n ⋅=⋅,1231122232(1)22n n n S n n -=⨯+⨯+⨯++-⨯+⨯ , (1)23412122232(1)22n n n S n n +⨯=⨯+⨯+⨯++-⨯+⨯ ,(2) (1)(2)-,得123122222n n n S n +-=++++-⨯所以11222.12n n n S n ++--=-⨯-从而1(1)2 2.=nS n +-⨯+19.∵T n <m 恒成立对N n *∈∴2≥m ∴m 的最小值是220.解:(Ⅰ)2111==a n 时222213221na a a a n n =+++- (1)21222123221-=+++--n a a a a n n (2) (1)-(2)得2121=-n n a 即n n a 21=(n 2≥),又211=a 也适合上式∴n n a 21=21.解 :(1)令(2)-(1)是等差数列(2)---①---②①-②所以22. (1)由122(n n a S n +=+∈ Z *)得122(n n a S n -=+∈ Z *,2n ≥),两式相减得:12n n n a a a +-=, 即13(n n a a n +=∈ Z *,2n ≥),∵{}n a 是等比数列,所以213a a = ; 又2122,a a =+则11223a a +=,∴12a =, ∴132-⨯=n n a(2)由(1)知132-⨯=n n a ,则n n a 321⨯=+ ∵1(1)n n n a a n d +=++ ,∴1341+⨯=-n d n n∵123111n T d d d =+++1nd +∴1210341344343342-⨯+++⨯+⨯+⨯=n n n T ① nn n n n T 34134344343342311321⨯++⨯++⨯+⨯+⨯=- ② ①-②得nn n n T 3413413413413413423213210⨯+-⨯++⨯+⨯+⨯+⨯=- n n n 3413113113141211⨯+--⎪⎭⎫ ⎝⎛-⨯+=-nn 385285⨯+-= ∴1316521615-⨯+-=n n n T 23.解(1)由题意知0,212>+=n n n a S a当1=n 时,21212111=∴+=a a a当2≥n 时,212,21211-=-=--n n n n a S a S两式相减得1122---=-=n n n n n a a S S a整理得:21=-n n a a∴数列{}n a 是以21为首项,2为公比的等比数列.211122212---=⨯=⋅=n n n n a a(2)42222--==n b n n a∴n b n 24-=,nn n n n nn a b C 28162242-=-==-nn n nn T 28162824282028132-+-⋯+-++=- ① 13228162824202821+-+-+⋯++=n n n n n T ② ①-②得1322816)212121(8421+--+⋯++-=n n n nT 1112816)211442816211)2112184+-+----=----⋅-=n n n nn (( n n 24= .28n n n T =∴24.解:(Ⅰ)设}{n a 的公比为q ,由5121161552263==⋅=q q a a a 得21=q , ∴n n n q a a )21(22=⋅=-22211211()2122()2log 2log 2=log 2log 21111()(21)(21)22121n n nn n a a b n n n n -++=⋅⋅==--+-+∴)1211215131311(21+--++-+-=n n T n 111)22n 121nn =-=++( (Ⅱ)①当n 为偶数时,由2-<n T n λ恒成立得,322)12)(2(--=+-<nn n n n λ恒成立,即m in )322(--<nn λ, 而322--n n 随n 的增大而增大,∴2=n 时0)322(m in =--nn ,∴0<λ; ②当n 为奇数时,由2+<n T n λ恒成立得,522)12)(2(++=++<nn n n n λ恒成立,即m in )522(++<n n λ,而95222522=+⋅≥++n n n n ,当且仅当122=⇒=n nn 等号成立,∴9<λ综上,实数λ的取值范围0∞(-,)25.解:(1)由121n n a S +=+----① 得121n n a S -=+----②,①-②得112()n n n n a a S S +--=-,13n n a a +∴=13n n a -∴=;5326,3b b d d ∴-==∴= 36n b n ∴=-(2)因为 1223,3n n n a b n +++==所以 1333n n nn nc+==所以032111<-=-++n n n nc c1113n n c c c +<<⋅⋅⋅<=所以113n n c c +<≤26.解: (1)设{}n a 的公差为d , 36535a S =⎧∴⎨=⎩;则1125656362a d a d +=⎧⎪⎨⨯+=⎪⎩即112556a d a d +=⎧⎨+=⎩,解得112a d =⎧⎨=⎩,*12(1)21,()n a n n n N ∴=+-=-∈(2) 2122na n nb -==135212222n n T -∴=++++2(14)2(41)143n n --==-27.28.解:(Ⅰ)∵{}n a 为其等差数列,设公差为d1n =,则有11112a a =+,∴12a = 2n =,有122142a a a +=+,∴24a =,∴21422d a a =-=-=∴2+2(1)2n a n n =-=,(22)(1)2n n n S n n +==+ (Ⅱ)若2221,,k k k a a a -+成等比数列,则有22221k k k a a a -+= 即24(22)22(21)k k k -=⋅+,整理得22940k k -+=, 解得4k =或12k =(舍) ∴469,,a a a 成等比数列,6432a q a ==。
【解析】【2014德州市一模】山东省德州市2014届高三3月模拟 文综地理

德州市高中三年级模拟检测文科综合试题——地理2014.3 本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分。
共12页。
满分300分,考试时间150分钟。
考试结束后,将本试卷和答题纸一并交回。
答卷前,考生务必将自己的姓名、准考证号、考试科目填涂在答题纸规定的地方。
第I卷 (必做,共l40分)注意事项:1.每小题选出答案后,用2B铅笔把答题纸上对应题目的答案标号涂黑。
如需改动。
用橡皮擦干净后。
再选择其他答案标号。
不能答在试卷上。
2.第I卷共35小题,每小题4分,共140分。
在每题给出的四个选项中。
只有一项是最符合题目要求的。
读图,图中L表示洋流,M为晨昏线,a为最冷月等温线。
完成l~2题。
1.有关图中地理现象叙述,正确的是A.此时甲地地方时可能是17时45分 B.洋流L为向南流动的寒流C.此时甲地盛行东北风 D.甲地植被类型为常绿硬叶林2.图示月份中,下列现象正确的是A.此时索契正在举办冬奥会 B.南半球夜渐长、昼渐短C.新加坡正午太阳高度大于海口 D.北京日出时刻早于6点读“城市雨水利用系统示意图”,完成3~4题。
3.图中右侧的深井,所发挥的作用是A.滴灌 B.漫灌 C.回灌地下水 D.抽取地下水4.该雨水利用系统的意义在于①可以缓解城市用水紧张②有利于大气降水的直接下渗③减少城市污水排放④提高城市防洪能力A.①② B.②③ C.②④ D.①③读“某地等高线地形图”,完成5~6题。
5.图中P—Q两地间有一座桥梁,该桥下溪流的正常水位最接近A.55米 B.65米 C.85米 D.95米6.当地环保部门在桥下采样检测水质量,发现有高浓度的农药残留。
这些农药最有可能来自下列哪一个地区A.甲 B.乙 C.丙 D.丁读“我国两城市的甲乙两家庭(人口、住房、收入等条件相当)各月用电量比较图”。
完成7~8题。
7.家庭用电量与所在地气候状况存在一定的相关性。
下列说法正确的是A.两地气温最高都在7月份 B.两地气温最低都在1月份C.甲所在地区大陆性强 D.乙所在地区大陆性强8.我国是能源消费大国,而核电所占比重小。
2014年全国2卷高考理科综合(物理部分)试题及答案

2014年普通高等学校招生全国统一考试理综物理部分 (全国2-甲卷)二、选择题:本题共8小题,每小题6分。
在每小题给出的四个选项中,第14~18题只有一项符合题目要求,第19~21题有多项符合题目要求。
全部选对的得6分,选对但不全的得3分,有选错的得0分。
14.甲乙两汽车在一平直公路上同向行驶。
在t =0到t=t 1—t 图像如图所示。
在这段时间内 A .汽车甲的平均速度比乙大B .汽车乙的平均速度等于221v v + C .甲乙两汽车的位移相同 D .汽车甲的加速度大小逐渐减小,汽车乙的加速度大小逐渐增大【答案】A【解析】由于图线与坐标轴所夹的面积表示物体的位移,在0-t 1时间内,甲车的位移大于乙车,由x v t=可知,甲车的平均速度大于乙车,A 正确, C 错误;因为乙车做变减速运动故平均速度不等于122v v +,B 错误;又图线的切线的斜率等于物体的加速度,则甲乙两车的加速度均逐渐减小,选项D 错误。
15.取水平地面为重力势能零点。
一物块从某一高度水平抛出,在抛出点其动能与重力势能恰好相等。
不计空气阻力,该物块落地时的速度方向与水平方向的夹角为A .6πB .4πC .3πD .125π 【答案】 B【解析】设物体水平抛出的初速度为v 0,抛出时的高度为h ,则2012mv mgh =,故0v =竖直速度y v =则落地时速度方向与水平方向的夹角0tan 1y y x v v v v θ===,则4πθ=,选项B 正确.16.一物体静止在粗糙水平地面上,现用一大小为F 1的水平拉力拉动物体,经过一段时间后其速度变为v ,若将水平拉力的大小改为F 2,物体从静止开始经过同样的时间后速度变为2v ,对于上述两个过程,用1F W 、2F W 分别表示拉力F 1、F 2所做的功,1f W 、2f W 分别表示前后两次克服摩擦力所做的功,则A .214F F W W >,212f f W W >B .214F F W W >,122f f W W =C .214F F W W <,122f f W W =D .214F F W W <,212f f W W <【答案】C【解析】由于物体两次受恒力作用做匀加速运动,由于时间相等,末速度之比为1:2,则加速度之比为1:2,位移之比为1:2。
山东省2014届理科数学一轮复习试题选编23:线性规划

山东省2014届理科数学一轮复习试题选编23:线性规划一、选择题1 .(山东省济南市2013届高三3月高考模拟理科数学)已知实数y x ,满足1218y y x x y ≥⎧⎪≤-⎨⎪+≤⎩,则目标函数y x z-=的最小值为 ( ) A .2- B .5 C .6 D .7 【答案】A由z x y =-得y x z =-.作出不等式对应的平面区域BCD,平移直线y x z =-,由平移可知,当直线y x z =-经过点C 时,直线的截距最大,此时z 最小.由218y x x y =-⎧⎨+=⎩,解得35x y =⎧⎨=⎩,即(3,5)C ,代入z x y =-得最小值为352z =-=-,选A .2 .(山东省德州市2013届高三上学期期末校际联考数学(理))已知变量x 、y,满足202300x y x y x -≤⎧⎪-+≥⎨⎪≥⎩,则41(24)z og x y =++的最大值为( )A .23B .1C .32D .2【答案】C【解析】设2t x y =+,则2y x t =-+.做出不等式组对应的可行域如图为三角形OBC 内.做直线2y x =-,平移直线2y x =-,当直线2y x t =-+经过点C 时,直线2y x t =-+的截距最大,此时t 最大,对应的z 也最大,由20230x y x y -=⎧⎨-+=⎩,得1,2x y ==.即(1,2)C 代入2t x y =+得4t =,所以41(24)z og x y =++的最大值为44431(24)(44)82z og x y log log =++=+==,选 C .3 .(山东省烟台市2013届高三3月诊断性测试数学理试题)实数x,y 满足⎪⎩⎪⎨⎧≤->≤≥0)1(1y x a a y x ,若函数z=x+y 取得最大值4,则实数a 的值为 ( )A .2B .3C .4D .23 【答案】A,由z x y =+得y x z =-+,作出不等式对应的区域,平移直线y x z =-+,由图象可知当直线经过点D 时,直线的截距最大为4,由40x y x y +=⎧⎨-=⎩,解得22x y =⎧⎨=⎩,即D(2,2),所以2a =,选A .4 .(山东省菏泽市2013届高三5月份模拟考试数学(理)试题)已知x,y 满足线性约束条件1020,(,2),(1,)410x y x y a x b y x y -+≥⎧⎪+-≤=-=⎨⎪++≥⎩若向量,则z=a·b 的最大值是 ( )A .-1B .52-C .5D .7【答案】C5 .(山东省莱芜五中2013届高三4月模拟数学(理)试题)已知变量,x y 满足约束条件2823y x x y x y ≤⎧⎪-≤⎨⎪+≥⎩,则目标函数62z x y =-的最小值为 ( )A .32B .4C .8D .2【答案】B6 .(山东省济南市2012届高三3月高考模拟题理科数学(2012济南二模))已知实数x ,y 满足|2x +y +1|≤|x +2y +2|,且11≤≤-y ,则z =2x +y 的最大值( )A .6B .5C .4D .-3【答案】B【解析】)1(2)1(2++≤++y x y x ,平方得22)1(+≤y x ,因为11≤≤-y ,所以210≤+≤y ,所以1+≤y x ,即11+≤≤--y x y ,所以y x ,满足⎪⎩⎪⎨⎧≤--+≤≤≤-x y y x y 1111,做出可行域,由图象知,当直线经过⎩⎨⎧==--11y y x 的交点为)1,2(时,z 取最大值,此时5122=+⨯=z ,选 B .7 .(山东省淄博市2013届高三复习阶段性检测(二模)数学(理)试题)已知x,y 满足条件020x y x x y k ≥⎧⎪≤⎨⎪++≤⎩(k为常数),若目标函数3z x y =+的最大值为8,则k= ( )A .16-B .6-C .83-D .6【答案】B 由3z x y =+得133zy x =-+.先作出0x y x≥⎧⎨≤⎩的图象,,因为目标函数3z x y =+的最大值为8,所以38x y +=与直线y x =的交点为C,解得(2,2)C ,代入直线20x y k ++=,得6k =-,选B . 8 .(山东省2013届高三高考模拟卷(一)理科数学)已知点),(y x P 满足⎪⎩⎪⎨⎧≥≥≤+,1,,4x x y y x 过点P 的直线与圆1422=+y x 相交于A,B 两点,则AB 的最小值为( )A .2B .62C .52D .4【答案】D 【解析】当P 点同时满足(1)P 为AB 的中点;(2)P 点到D 点的距离最大时,AB 取得最小值.P 点的可行域如图所示,因为直线x y =和直线+x 4=y 垂直,故P 点的坐标是(1,3)时,OP 最大.易知此时AB=4,故选 D .9 .(山东省青岛即墨市2013届高三上学期期末考试数学(理)试题)设变量y x ,满足约束条件⎪⎩⎪⎨⎧≤-+≤+-≥+-08010502y x y x y x ,则目标函数y x z 34-=的最小值和最大值分别为 ( )A .-6,11B .2,11C .-11,6D .-11,2【答案】A【 解析】由y x z 34-=得433z y x =-.做出可行域如图阴影部分,平移直线433zy x =-,由图象可知当直线433z y x =-经过点C 时,直线433z y x =-的截距最小,此时z 最大,当433zy x =-经过点B 时,直线433zy x =-的截距最大,此时z 最小.由510080x y x y -+=⎧⎨+-=⎩得53x y =⎧⎨=⎩,即(5,3)C ,又(0,2)B ,把(5,3)C 代入y x z 34-=得43209=11z x y =-=-,把(0,2)B 代入y x z 34-=得4332=6z x y =-=-⨯-,所以函数y x z 34-=的最小值和最大值分别为6,11-,选 ( )A .10.(山东省莱芜市第一中学2013届高三12月阶段性测试数学(理)试题)已知实数,x y 满足220,2,1,x y x y +-≥⎧⎪≤⎨⎪≤⎩,则342z x y =+-的最大值为( )A .8B .6C .5D .1【答案】A11.(山东师大附中2013届级高三12月第三次模拟检测理科数学)若实数,x y 满足不等式组0,2100,0,x y x y y ⎧->⎪--<⎨+-≥ 则2x y +的最大值是 ( ) A .11 B .23 C .26 D .30 【答案】D 【解析】做出可行域如图,设2z x y =+,即2y x z =-+,平移直线2y x z =-+,由图象可知当直线经过点D 时,直线2y x z =-+的截距最大,此时z 最大.由0,2100,x y x y -=⎧⎨--=⎩解得10,10,x y =⎧⎨=⎩,即(10,10)D ,代入得230z x y =+=,所以最大值为30,选D .12.(山东省枣庄市2013届高三3月模拟考试数学(理)试题)设z x y =+,其中实数x,y 满足200,0x y x y y k +≥⎧⎪-≤⎨⎪≤≤⎩若z 的最大值为6,则z 的最小值为 ( )A .—3B .—2C .—1D .0【答案】A由z x y =+得y x z =-+,作出20,0x y x y +≥⎧⎨-≤⎩的区域BCD,平移直线y x z =-+,由图象可知当直线经过C 时,直线的截距最大,此时6z =,由6y x y x =⎧⎨=-+⎩解得33x y =⎧⎨=⎩,所以3k =,解得(6,3)B -代入z x y =+的最小值为633z =-+=-,选( ) A .13.(山东省枣庄三中2013届高三上学期1月阶段测试理科数学)设x , y 满足约束条件⎪⎩⎪⎨⎧≥≥≥+-≤--0,002063y x y x y x ,若目标函数z ax by =+(a .>0,b >0),最大值为12,则ba 32+ 的最小值为 ( )A .724B .625 C .5 D .4【答案】B【解析】做出可行域,由z ax by =+得a z y x b b =-+,因为0,0a b >>,所以直线斜率0ab-<,直线截距越大,z 越大,做出直线a z y x b b=-+,,由图象可知当直线a zy x b b =-+经过点B 时,截距做大,此时12z =,由36020x y x y --=⎧⎨-+=⎩得46x y =⎧⎨=⎩,代入直线z ax by =+得4612a b +=,即132a b +=.所以2323232325()()23232326a b a b a b a b b a +=++=+++≥++=,当且仅当a bb a=,即a b =时取等号,所以选 B . 14.(2013山东高考数学(理))在平面直角坐标系xoy 中,M 为不等式组220,210,380,x y x y x y --≥⎧⎪+-≥⎨⎪+-≤⎩所表示的区域上一动点,则直线OM 斜率的最小值为 ( )A .2B .1C .13-D .12-【答案】C 【解析】作出可行域如图由图象可知当M 位于点D 处时,OM 的斜率最小.由210380x y x y +-=⎧⎨+-=⎩得31x y =⎧⎨=-⎩,即(3,1)D -,此时OM 的斜率为1133-=-,选 C . 15.(山东师大附中2013届高三第四次模拟测试1月理科数学)已知x y 、满足5030x y x x y -+≥⎧⎪≤⎨⎪+≥⎩,则24z x y=+的最小值为 ( ) A .5B .-5C .6D .-6【答案】D 【解析】做出可行域如图:由24z x y =+,得124zy x =-+,平移直线,由图象可知当直线124z y x =-+经过点C 时,直线124zy x =-+的截距最小,此时z 最小.C 点坐标为(3,3)-,代入24z x y =+得234(3)6z =⨯+⨯-=-,选D ..16.(山东省兖州市2013高三9月入学诊断检测数学(理)试题)变量y x ,满足约束条件⎪⎩⎪⎨⎧-≥-≤+≥+144222y x y x y x ,则目标函数y x z -=3的取值范围是( )A .⎥⎦⎤⎢⎣⎡-6,23 B .⎥⎦⎤⎢⎣⎡--1,23C .[]6,1-D .⎥⎦⎤⎢⎣⎡-23,6【答案】A 解析:作出可行域,直线03=-y x ,将直线平移 至点)0,2(处有最大值,点)3,21(处有最小值, 即623≤≤-z .答案应选 ( )A .17(理)试题)设变量,x y 满足约束条件2201220,110x y y x y x x y --≤⎧+⎪-+≥⎨+⎪+-≥⎩则s=的取值范围是 ( )A .31,2⎡⎤⎢⎥⎣⎦B .1,12⎡⎤⎢⎥⎣⎦C .1,22⎡⎤⎢⎥⎣⎦D .[]1,2【答案】C 【解析】做出约束条件表示的可行域如图,由图象可知(0,1),(1,0)B C .11y x ++s=的几何意义是区域内的任一点到定点(1,1)M --的斜率的变化范围,由图象可知,10111,211210MC MB k k ----====----,所以MC MB k s k ≤≤,即122s ≤≤,所以取值范围是1[,2]2,选C .18.(山东省烟台市2013届高三上学期期末考试数学(理)试题)若实数x y 、满足2400 0x y x y +-≤⎧⎪≥⎨⎪≥⎩,则21y z x +=-的取值范围为( )A .2(,4][,)3-∞-⋃+∞ B .2(,2][,)3-∞-⋃+∞C .2[2,]3-D .2[4,]3-【答案】A【解析】做出不等式组对应的平面区域OBC.因为21y z x +=-,所以z 的几何意义是区域内任意一点(,)x y 与点(1,2)P -两点直线的斜率.所以由图象可知当直线经过点,P C 时,斜率最小,经过点,P B 时,直线斜率最大.由题意知(0,2),(4,0)B C ,所以22410PB k --==--,202143PC k --==-,所以21y z x +=-的取值范围为23z ≥或4z ≤-,即2(,4][,)3-∞-⋃+∞,选( ) A . 由40x y x y +=⎧⎨-=⎩,得22x y =⎧⎨=⎩,即(2,2)A ,此时321523AM k -==-,所以35n z m -=-的最小值是13,选 D .19.(山东省泰安市2013届高三上学期期末考试数学理)已知不等式组210y x y kx y ≤-+⎧⎪≤-⎨⎪≥⎩所表示的平面区域为面积等于14的三角形,则实数k 的值为 ( )A .1-B .12-C .12D .1【答案】D【解析】由图象知0k >.当0y =时,1B x k =.2C x =.,所以12k <,即12k >由21y x y kx =-+⎧⎨=-⎩,得211A k y k -=+,所以11211(2)214ABC k S k k ∆-=-⨯=+,解得1k =或2172k =<(舍去),所以1k =,选 D .20.(山东省济宁邹城市2013届高三上学期期中考试数学(理)试题)设x,y 满足条件20360,(0,0)0,0x y x y z ax by a b x y -+≥⎧⎪--≤=+>>⎨⎪≥≥⎩若目标函数的最大值为12,则32a b +的最小值为( )A .256B .83C .113D .4【答案】D21.(山东省枣庄市2013届高三4月(二模)模拟考试数学(理)试题)已知实数,x y 满足1000x y x y x +-≤⎧⎪-≤⎨⎪≥⎩,则2x y-的最大值为 ( )A .12 B .0C .1-D .12-【答案】A22.(2009高考(山东理))设x ,y 满足约束条件⎪⎩⎪⎨⎧≥≥≥+-≤--0,002063y x y x y x ,若目标函数z=ax+by (a>0,b>0)的是最大值为12,则23a b+的最小值为 ( )A .625 B .38 C .311 D .4【答案】【解析】:不等式表示的平面区域如图所示阴影部分,当直线ax+by= z (a>0,b>0)过直线x-y+2=0与直线3x-y-6=0的交点(4,6)时, 目标函数z=ax+by (a>0,b>0)取得最大12, 即4a+6b=12,即2a+3b=6, 而23a b +=2323131325()()26666a b b a a b a b ++=++≥+=,故选 ( ) A . 答案:A23.(山东省曲阜市2013届高三11月月考数学(理)试题)已知向量(,1),(2,),a x z b y z =-=+且a b ⊥ ,若变量,x y 满足约束条件1,,32 5.x y x x y ≥-⎧⎪≥⎨⎪+≤⎩则z 的最大值为( )A .4B .3C .2D .1【答案】B24.(山东省实验中学2013届高三第一次诊断性测试数学(理)试题)设x 、y 满足24,1,22,x y x y x y +≥⎧⎪-≥-⎨⎪-≤⎩则z x y=+( )A .有最小值2,最大值3B .有最小值2,无最大值C .有最大值3,无最大值D .既无最小值,也无最大值【答案】B【解析】做出可行域如图(阴影部分).由z x y =+得y x z =-+,做直线y x =-,平移直线y x =-由图可知当直线经过点C(2,0)时,直线y x z =-+的截距最小,此时z 最小为2,没有最大值,选 B .25.(山东省德州市2013届高三第二次模拟考试数学(理)试题)已知变量x,y 满足约束条件221x y x y x +≤⎧⎪-≤⎨⎪≥⎩,若2x y a +≥恒成立,则实数a 的取值范围为( )A .(-∞,-1]B .(-∞,2]C .(-∞,3]D .[-1,3]【答案】A二、填空题26.(山东省莱芜市莱芜十七中2013届高三4月模拟数学(理)试题)已知点A ,O 为坐标原点,点(,)P x y满足0200y x y ⎧-≤⎪⎪+≥⎨⎪≥⎪⎩,则||OA OP Z OA ⋅=的最大值是___________27.(山东济南外国语学校2012—2013学年度第一学期高三质量检测数学试题(理科))已知x 和y 是实数,且满足约束条件y x z x y x y x 32,72210+=⎪⎩⎪⎨⎧≥≤-≤+则的最小值是_________.【答案】223做出不等式对应的可行域如图,由23z x y =+得233z y x =-+,做直线23y x =-,平移直线23y x =-,由图象可知当直线经过C 点时,直线233z y x =-+的截距最小,此时z 最小,此为73(,)22C ,代入目标函数得73232323222z x y =+=⨯+⨯=.28.(山东省实验中学2013届高三第三次诊断性测试理科数学)当实数y x ,满足约束条件⎪⎩⎪⎨⎧≤++≤≥0220a y x x y x (a为常数)时y x z 3+=有最大值为12,则实数a 的值为_______________.【答案】-12 【解析】y x z 3+=的最大值为12,即312x y +=由图象可知直线220x y a ++=也经过点B.由312x y y x +=⎧⎨=⎩,解得33x y =⎧⎨=⎩,即点(3,3)B ,代入直线220x y a ++=得12a =-.29.(山东省德州市2013届高三3月模拟检测理科数学)若x,y 满足约束条件1122x y x y x y +≥⎧⎪-≥-⎨⎪-≤⎩,目标函数2z x y=+最大值记为a,最小值记为b,则a-b 的值为_________.【答案】10由2z x y =+得122zy x =-+.作出不等式组对应的区域,,平移直线122z y x =-+,由平移可知,当直线122zy x =-+经过点D 时,直线的截距最小,此时z 最小.经过点B时,直线的截距最大,此时z 最大.由122x y x y +=⎧⎨-=⎩,解得10x y =⎧⎨=⎩,即(1,0)D 代入2z x y =+得1b =.由122x y x y -=-⎧⎨-=⎩解得34x y =⎧⎨=⎩,即(3,4)B ,代入2z x y =+得11a =,所以11110a b -=-=. 30.(山东省烟台市莱州一中2013届高三第三次质量检测数学(理)试题)设x 、y 满足约束条件23023400-+≥⎧⎪-+≤⎨⎪≥⎩x y x y y ,若目标函数z ax by =+(其中a>0,b>0)的最大值为3,则12a b +的最小值为________【答案】3 【解析】做出可行域,由z ax by =+得a zy x b b=-+,因为0,0a b >>,所以直线斜率0a b -<,直线截距越大,z 越大,做出直线a z y x b b =-+,由图象可知当直线a zy x b b=-+经过点A 时,截距做大,此时3z =,由2302340x y x y -+=⎧⎨-+=⎩得12x y =⎧⎨=⎩,代入直线z ax by =+得23a b +=,即2133a b+=.所以12122142252254()()2333333333333a b a b a b a b a b b a b a +=++=+++≥+⨯=+=,当且仅当2233a b b a =,即a b =时取等号,所以12a b+的最小值为1.31.(山东省滨州市2013届高三第一次(3月)模拟考试数学(理)试题)设实数x ,y 满足约束条件2220,20,220,x y x y x y x y ⎧-≤⎪-≥⎨⎪+--≤⎩,则目标函数z x y =+的最大值为_________. 【答案】4 由z x y =+得y x z =-+.作出不等式对应的区域,平移直线y x z =-+,由图象可知,当直线y x z =-+与圆在第一象限相切时,直线y x z =-+的截距最大,此时z 最大.直线与圆的距离22z d ==即4z =±,所以目标函数z x y =+的最大值是4.32.(山东省潍坊市四县一校2013届高三11月期中联考(数学理))若实数y x ,满足⎪⎩⎪⎨⎧≤≥+≥+-,0,0,01x y x y x ,则yx z 23+=的值域是____________.【答案】[1,9] 【解析】令2t x y =+,则122t y x =-+,做出可行域平移直线12y x =-,由图象知当直线经过O 点是,t 最小,当经过点(0,1)D 时,t 最大,所以02t ≤≤,所以19z ≤≤,即yx z 23+=的值域是[1,9].33.(山东省青岛市2013届高三第一次模拟考试理科数学)已知,x y 满足约束条件224200x y x y y ⎧+≤⎪-+≥⎨⎪≥⎩,则目标函数2z x y =+的最大值是___________【答案】由2z x y =+得,2y x z =-+.作出不等式对应的区域,,平移直线2y x z =-+,由图象可知,当直线2y x z =-+与圆在第一象限相切时,直线2y x z =-+的截距最大,此时z 最大.直线与圆的距离2d ==,即z =±,所以目标函数2z x y =+的最大值是34.(山东省潍坊市2013届高三上学期期末考试数学理(A ))已知y x ,满足⎪⎩⎪⎨⎧≤--≥-+≥+-0330101y x y x y x ,则y x -2的最大值为.【答案】2【解析】设2z x y =-,则2y x z =-.作出可行域如图作直线2y x =,平移直线2y x z =-,由图象可知当直线2y x z =-经过点D 时,直线2y x z =-的截距最下,此时z 最大,把(1,0)D 代入直线2z x y =-得2z =,所以y x -2的最大值为2. 35.(2013年山东临沂市高三教学质量检测考试理科数学)已知O 是坐标原点,点M 的坐标为(2,1),若点N(x ,y )为平面区域212x y x y x +≤⎧⎪⎪≥⎨⎪≥⎪⎩上的一个动点,则OM ON的最大值是_________ . 【答案】32OM ON x y =+,设2z x y =+,则2y x z =-+.不等式对应的区域为BCD,平移直线2y x z =-+,由图象可知当直线2y x z =-+经过点C 时,直线2y x z =-+的截距最大,此时z 最大,由2x y y x +=⎧⎨=⎩,解得11x y =⎧⎨=⎩,即(1,1)C ,代入2z x y =+得23z x y =+=,所以OM ON的最大值是3. 36.(山东省莱钢高中2013届高三4月模拟检测数学理试题 )设实数,x y 满足2025020x y x y y --≤⎧⎪+-≥⎨⎪-≤⎩,的取值范围是 _______【答案】⎥⎦⎤⎢⎣⎡3102,37.(山东省济南市2013届高三4月巩固性训练数学(理)试题)不等式组2000x x y x y -≤⎧⎪+≥⎨⎪-≥⎩表示平面区域为Ω,在区域Ω内任取一点(),P x y ,则P 点的坐标满足不等式222x y +≤的概率为_________.【答案】.8π。
烃和烃的衍生物

烃和烃的衍生物1.(2014届内蒙古鄂尔多斯市高三第一次模拟考试理综化学试卷)有机物R的分子式为C12H18,经测定数据表明,分子中除含苯环外不再含有其他环状结构,且苯环上只有两个侧链(分别是-C2H5和-C4H9),符合此条件的烃的结构有A.6种B.9种C.12种D.15种2.(2014届广东省揭阳市高中毕业班高考第一次模拟考试理综化学试卷)下列说法正确的是( )A.乙烷和乙烯均可使酸性KMnO4溶液褪色B.纤维素、淀粉和蛋白质都是高分子化合物C.煤的干馏和石油的分馏均属化学变化D.酯类和糖类均能发生水解反应3.(2014届广东省江门市高三一模理综化学试卷)下列说法正确的是()A.蛋白质、油脂、糖类都是高分子化合物B.甲烷、乙烯和苯在工业上都可通过石油分馏得到C.苯、乙醇和乙酸都能发生取代反应D.汽油、煤油、卤代烃均为烃4.(2014届山东省烟台市高三3月模拟化学试卷)下列关于有机物的叙述不正确的是A.淀粉、纤维素都属于糖类且互为同分异构体B.戊烷(C5H12)有三种同分异构体C.乙醇、乙酸、葡萄糖均能发生酯化反应D.福尔马林、医用酒精均能使蛋白质变性,可用作消毒剂5.(2014届山东省青岛市高三3月第一次模拟考试理综化学试卷)有关物质性质及用途的说法,正确的是A.甲烷与氯气在光照的条件下可以制取纯净的一氯甲烷B.将溴水加入苯中,溴水的颜色变浅,这是由于发生了加成反应C.牡丹籽油是一种优良的植物油脂,它可使酸性高锰酸钾溶液褪色D.等质量的乙烯和聚乙烯充分燃烧所需氧气的量不相等6.(2014届江西省重点中学盟校十校联考高三第一次联考理综化学试卷)相对分子质量为100的烃完全燃烧后,生成CO2和H2O的物质的量之比以及分子结构中有四个甲基的同分异构体的数目分别是A.6:7和2 B.6:7和3 C.7:8和3 D.7:8和47.(2014届福建省漳州市高三3月质检理综化学试卷)下列关于有机物的说法中不正确的是A.苯与氯气在一定条件下可发生取代反应B.塑料、纤维都是合成高分子材料C.乙烯、氯乙烯均可使酸性高锰酸钾溶液褪色D.油脂、纤维紊和蛋白质在一定条件下都能发生水解反应8.(2014届山东省德州市高三模拟检测理综化学试卷)萜品醇可作为消毒剂、抗氧化剂和溶剂。
山东德州一中2014高三高考二轮模拟题

德州市高中三年级模拟检测理科综合试题2014.3 本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分。
共16页,满分300分,考试用时150分钟。
考试结束后,将本试卷和答题纸一并交回。
答卷前,考生务必将自己的姓名、准考证号、考试科目填涂在试卷和答题纸规定的地方。
第I卷(选择题共l07分)注意事项:山东中学联盟每小题选出答案后,用2B铅笔把答题纸上对应的答案标号涂黑。
如需改动,用橡皮擦于净以后,再涂写其他答案标号。
在试卷上答题无效。
以下数据可供答题时参考:可能用到的相对原子质量:H:1 C:l2 O:16 Na:23 C1:35.5 Fe:56Cu:64 Zn:65一、选择题(本题包括l3小题,每小题5分,共65分,每小题给出的四个选项中。
只有一项最符合题目要求)1.下列关于细胞结构的叙述,正确的是A.有线粒体的细胞一定是真核细胞B.高尔基体能合成和分泌多种消化酶C.细胞内的酶都分布在生物膜上D.细胞膜上的蛋白质都与物质运输有关2.下列关于生物学实验的说法,正确的是A.检测酵母菌培养过程中是否产生CO2可判断其呼吸方式B.用健那绿染液对解离后的细胞染色可观察其线粒体分布C.滤纸条上色素带的宽窄可反映叶绿体中各色素含量的多少D.以H2O2溶液作为底物可用于探究温度对酶活性的影响3.下列叙述符合现代生物进化理论观点的是A.只有生殖隔离能阻止种群间的基因交流B.自然选择导致突变并对有利变异进行定向积累C.人为因素和物种入侵不改变进化的速度和方向D.种群基因频率的变化趋势能反映生物进化的方向4.下图为温特研究植物向光性的实验设计,①~⑥是在黑暗环境中对切去尖端的胚芽鞘进行的不同处理。
下列分析错误的是A.温特猜想尖端产生的化学物质可以扩散到琼脂块中B.若在单侧光照下进行该实验,不能得到相同的实验结果C.④和⑥结果表明胚芽鞘向光弯曲与尖端产生的物质有关D.设置⑤和⑥组的目的是排除琼脂块对胚芽鞘生长的影响5.研究发现,秀丽隐杆线虫有两种性别:性染色体组成为XX的是雌雄同体,XO(缺少Y染色体)为雄体;在发育过程中,一个受精卵分裂形成l090个细胞,但成体只含有959个细胞。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
山东省德州市2014届高三第二次模拟检测理科综合试题2014.4本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,共16页。
满分300分。
考试用时150分钟。
考试结束后,将本试卷和答题纸一并交回。
答卷前,考生务必将自己的姓名、准考证号、考试科目填涂在试卷和答题纸规定的地方。
第I卷(选择题共107分)注意事项:每小题选出答案后,用2B铅笔把答题纸上对应的答案标号涂黑。
如需改动,用橡皮擦干净以后,再涂写其他答案标号。
在试卷上答题无效。
以下数据可供答题时参考:可能用到的相对原子质量:H:1 C:12 O:16 Na:23 C1:35.5 Fe:56Cu:64 Zn:65一、选择题(本题包括l3小题,每小题5分,共65分,每小题给出的四个选项中。
只有一项最符合题目要求)1.下列有关生物进化的叙述中,正确的是A.基因频率的改变标志着新物种的产生B.基因频率的改变决定了生物进化的方向C.基因频率的改变仅与可遗传的变异有关D.长期地理隔离可使不同种群的基因库发生显著差异2.颜色变化常作为生物实验结果观察的一项重要指标,下列叙述正确的是A.甲基绿一吡罗红试剂可将口腔上皮细胞大部分染成红色B.加入酸性重铬酸钾出现灰绿色说明酵母菌只进行无氧呼吸C.新鲜豆浆中加入双缩脲试剂,需水浴加热才呈现紫色D.烘干的口腔上皮细胞经健那绿染液染色后,线粒体呈蓝绿色3.吞噬细胞可将侵人人体的病原体吞噬并降解,之后细胞表面出现抗原与MHC蛋白结合形成的复合物,该复合物可被某些淋巴细胞识别。
相关叙述正确的是A.降解病原体的过程需要溶酶体参与B.淋巴细胞识别复合物后立即增殖分化C.复合物能被浆细胞识别D.上述过程属于非特异性免疫4.下图为细胞质基质中合成的前体蛋白进入线粒体基质并成为成熟蛋白的过程。
下列有关判断正确的是A.高尔基体是前体蛋白加工的主要场所B.肽酶切割信号肽的过程中产生水C.成熟蛋白可催化脱氢反应及CO2的产生D.有氧呼吸有关的酶均以图示方式进入线粒体5.下图为某单基因遗传病的家系图。
下列有关分析不合理的是A.该遗传病最可能是显性遗传B.该病一定不是伴X染色体隐性遗传C.Ⅲ一1与Ⅲ一3基因型相同的概率为100%D.若Ⅱ—5不携带致病基因,则其子代中男女患病概率不同6.原癌基因导致细胞癌变的几种方式如下图所示。
有关叙述不正确的是A.原癌基因存在于正常的细胞中B.癌细胞一定含有异常的蛋白质C.染色体变异可能导致细胞癌变D.癌细胞中不一定都存在癌基因7.化学与社会、生产、生活密切相关。
下列说法正确的是A.碳纤维是一种新开发的材料,它属于合成有机高分子化合物B.对“地沟油”进行分馏可得到汽油C.漂白粉长期暴露在空气中最后会变质失效D.氯气溶于水生成次氯酸有强氧化性,可以起到除去水中杂质和杀菌消毒作用8.下列有关叙述不正确的是A.MgO、Al2O3熔点高,可用于制作耐火材料B.用浓氢氧化钠溶液可除去乙酸乙酯中混有的乙酸、乙醇杂质C.除去NaCl溶液中的Na2CO3,应选择试剂为盐酸,而不是硝酸D.油脂在碱性条件下易发生水解,可用于制作肥皂9.下列说法中,正确的是A.利用铁加入硫酸铜溶液中的反应可以比较Cu、Fe2+的还原性B.足量的铜跟一定量的浓硝酸反应只产生一种气体C.氮的固定只有在高温、高压、催化剂的条件下才能实现D.以铁为阴极、铜片为阳极、硫酸铜为电镀液可以实现铁制品镀铜10.某有机物的结构简式如右图所示,下列说法正确的是A.可使溴的四氯化碳溶液或酸性KMnO4溶液褪色B.含有两种官能团C.与乙酸互为同系物D.可以发生取代反应和加成反应,但不能发生聚合反应11.主族元素M、R形成的简单离子M2-离子与R+离子的核外电子数之和为20,下列说法正确的是A.M原子的质子数一定大于R原子的质子数B.M可能存在16M、18M两种核素C.M2-的离子与R+的电子层结构不可能相同D.两种离子结合形成的化合物中可能含有共价键12.下列说法中,正确的是A.已知25℃时NH4CN水溶液显碱性,则25℃时的电离常数K(NH3·H2O)>K(HCN) B.25℃时,Mg(OH)2固体在20 mL0.01 mol·L-1氨水中的K sp比在20 mL0.01 mol·L-1NH4Cl溶液中的K sp小C.pH试纸测得新制氯水的pH为4.5D.FeCl3溶液和Fe2(SO4)3溶液加热蒸干、灼烧都得到Fe2O313.利用右图装置进行实验,甲乙两池均为l mol·L-1的AgNO3溶液,A、B均为Ag电极。
实验开始先闭合K1,断开K2。
一段时间后,断开K1,闭合K2,形成浓差电池,电流计指针偏转(Ag+浓度越大氧化性越强)。
下列说法不正确的是A.闭合K1,断开K2后,A电极增重B.闭合K1,断开K2后,乙池溶液浓度上升C.断开K1,闭合K2后,A电极发生氧化反应D.断开K1,闭合K2后,NO3-向B电极移动二、选择题(本题包括7小题,每小题给出的四个选项中,有的只有一个选项正确。
有的有多个选项正确,全部选对的得6分,选对但不全的得3分。
有选错的得0分) 14.以下叙述正确的是A.伽利略根据理想斜面实验,否定了“力是维持物体运动状态的原因”这一观点B.库仑在研究电荷间相互作用时,提出了“电场”的概念C.欧姆定律UIR采用比值定义法定义了电流强度这一物理量D.用质点来代替实际物体是等效替代的方法15.如图所示,三个重均为100N的物块,叠放在水平桌面上,各接触面水平,水平拉力F=20N 作用在物块2上,三条轻质绳结于O点,与物块3连接的绳水平,与天花板连接的绳与水平方向成45o角,竖直绳悬挂重为20N的小球P。
整个装置处于静止状态。
则A.物块1和2之间的摩擦力大小为20NB.水平绳的拉力大小为20NC.桌面对物块3的支持力大小为320ND.物块3受5个力的作用16.如图所示,A为置于地球赤道上的物体,B为绕地球做椭圆轨道运行的卫星,C为绕地球做圆周运动的卫星,P为B、C两卫星轨道的交点。
已知A、B、C绕地心运动的周期相同。
相对于地心,下列说法中正确的是A.卫星C的运行速度大于物体A的速度B.物体A和卫星C具有相同大小的加速度C.卫星B运动轨迹的半长轴与卫星C运动轨迹的半径相等D.卫星B在P点的加速度大小与卫星C在该点加速度大小相等17.如图甲为远距离输电示意图,变压器均为理想变压器。
升压变压器原副线圈匝数比为l:100,其输入电压如图乙所示,远距离输电线的总电阻为100 。
降压变压器右侧部分为一火警报警系统原理图,其中R1为一定值电阻,R2为用半导体热敏材料制成的传感器,当温度升高时其阻值变小。
电压表V显示加在报警器上的电压(报警器未画出)。
未出现火警时,升压变压器的输入功率为750kW。
下列说法中正确的有A.降压变压器副线圈输出的交流电频率为50HzB.远距离输电线路损耗功率为180kwC.当传感器R2所在处出现火警时,电压表V的示数变大所在处出现火警时,输电线上的电D.当传感器R流变大18.如图所示,菱形的三个顶点有三个等量的正点电荷,另一顶点为M,其所在的角为120o,O为菱形对角线的交点。
A、B为其中一条对角线上的两点,且AO=BO=MO。
下列说法正确的是A.A、B两点的电场强度相同B.A、B两点的电势相等C.M点的电场强度小于O点的电场强度D.负电荷在O点的电势能小于在M点的电势能19.如图甲所示,在坐标系xOy中,有边长为L的正方形金属线框abcd,其对角线ac和y轴重合,顶点a位于坐标原点O处。
在y轴右侧的第I象限内有一等腰直角三角形区域,直角边边长为L,底边的左端位于坐标原点O处,内有垂直纸面向里的匀强磁场。
t=0时刻,线圈从图示位置沿cb方向,匀速穿过磁场区域。
取a→b→c→d→a为感应电流的正方向,则在线圈穿越磁场区域的过程中,感应电流i、ab间的电势差U ab。
随时间t变化的图线应是乙图中的20.如图所示,竖直轻质弹簧,下端固定在地面,上端固定一质量为M的木板,木板上方放一质量为m的物块,木板和物块间不粘连,一竖直向下的力F作用在物块上,整个系统处于静止状态。
在撤去F,木板和物块向上运动的过程中,下列说法正确的是A.物块先处于超重状态,再处于失重状态B.木板对物块做正功,物块的机械能增加C.木板和物块组成的系统机械能守恒D.当弹簧处于自然状态时,物块克服重力做功的功率最大第Ⅱ卷(非选择题,共l93分)注意事项:1.第Ⅱ卷共18个题。
其中21—30题为必做部分。
31—38题为选做部分。
考生必须从中选择1个物理、l个化学和l个生物题作答。
不按规定选做者。
阅卷时将根据所选科目题号的先后顺序只判前面的l个物理题、1个化学题和1个生物题,其他作答的题目答案无效。
2.第Ⅱ卷所有题目的答案考生须用黑色签字笔答在答题纸上,在试题卷上答题无效。
【必做部分】21.(18分)(1)(6分)某同学设计了如图甲的实验装置测定一个物块的质量,他将一端带有定滑轮的长木板水平放置,物块一端通过细线与力传感器和重物连接,一端连接穿过打点计时器的纸带。
他通过改变重物的质量使物块在不同的拉力作用下运动,物块所受拉力F的大小由力传感器读出,物块运动的加速度a由纸带上打点计时器打出的点计算出,该同学通过多次实验测得的数据画出了物块加速度a与所受拉力F的关系图线如图乙。
①该同学测得物块的质量m= kg②利用该同学的数据还可得出物块和长木板之间的动摩擦因数μ= (已知当地重力加速度g=10m/s2)③下面做法可以减小物块质量的测量误差的是A.尽量减小定滑轮处的摩擦B.尽量使重物的质量远小于物块的质量C.实验前将长木板右侧适当抬高来平衡摩擦力D.改变重物的质量进行多次实验(2)(12分)如图甲所示,是某同学设计的一个测电源电动势和内阻的原理图,待测电源电动势E、内阻r,电压表V的量程为3V,内阻非常大(可视为理想电压表),电阻箱R,一段电阻未知的电阻丝R0,单刀单掷开关K1,单刀双掷开关K2,实验步骤如下①调节电阻箱的阻值为20Ω,K2接到a,闭合K1,记下电压表的读数为2.00V,断开K1;②保持电阻箱的阻值不变,K2切换到b,闭合K1,记下图乙所示电压表的读数为V,断开K1。
由此可以算出电阻丝的电阻R0为Ω;③将K2再切换到a,闭合K1,多次调节电阻箱,读出多组电阻箱的示数和对应的电压表的示数,断开K1。
由测得的数据,绘出如图丙所示的11U R-图象。
根据图象可以求得电源电动势E= V,电源内阻r= Ω。
(结果保留两位有效数字)④根据原理图连接实物图22.(18分)如图所示,B、C、D在同一水平面,CED为半径R=lm的圆形光滑圆弧,O 为其圆心,其圆心角α=74o,E为圆弧的最低点,圆弧与传送带相切于D点,传送带与水平面的夹角β=37o。
