SPSS 医学P63相关性 信息 操作 结果
最快五步用SPSS软件进行相关性分析

第二步:数据视图只能输入数据,要想更改变量的名称就 得在变量:更改后名称后,接下来就到了关键的部分,点击最上方菜 单栏中的“分析”这一栏,在“分析”中的“相关”栏中找到 “双变量”这一栏就行点击。 第四步:在出来的双变量相关中把框内所有的变量点击向右的按钮 过去另一个框,其余的按钮都不要变,再点击确定按钮就行。
采用SPSS进行相关性分析的具体步骤
-
涉及到相关性分析,一般情况下就会用到 SPSS软件,那么怎样采用SPSS软件进行相 关性分析呢?下面我来具体说明一下相关 的步骤: 这一共分为五步
-
第一步:打开SPSS软件,在数据视图中输入变量的数值。 比如我想探究饱和吸附量与阳离子交换量和阴离子交换量 的关系,就将数据粘贴上去。
-
第五步:下图呈现的就是相关性的结果,“双变量”就是 两个变量之间的相关性如何,数值是负值就是没有相关性, 正值就相关,然后自己截图或者做一个结果统计表就行。
-
spss对数据进行相关性分析实验报告

spss对数据进行相关性分析实验报告SPSS数据相关性分析实验报告一、引言数据相关性分析是一种用统计方法来研究变量之间关系的方法。
SPSS作为一种常用的统计软件,具有丰富的功能和灵活性,能够对数据进行多角度的分析和解读。
本报告旨在利用SPSS对一组样本数据进行相关性分析,并通过报告的形式详细介绍分析的步骤和结果。
二、实验设计和数据采集本次实验选取了一个包括X变量和Y变量的数据集,通过观察这两个变量之间的相关关系,探究它们之间是否存在一定的线性关系。
三、数据清洗与统计描述在进行相关性分析之前,需要对数据进行清洗和统计描述。
首先,通过观察数据的分布情况,检查是否存在异常值。
如果出现异常值,可以采取删除或者替换的方式进行处理。
其次,计算数据的均值、标准差、最大值、最小值等统计指标,了解数据的基本特征。
四、Pearson相关系数分析Pearson相关系数是一种常用的衡量两个变量之间的相关性的方法。
它的取值范围在-1到1之间,接近于1表示正相关,接近于-1表示负相关,接近于0则表示无相关性。
在SPSS中,进行Pearson相关系数分析非常简便。
五、Spearman相关系数分析Spearman相关系数是一种非参数检验方法,用于观察变量之间的单调关系。
相比于Pearson相关系数,它对于异常值的鲁棒性更强。
在SPSS中,可以选择Spearman相关系数分析来研究数据集中的变量之间的关系。
六、结果分析与讨论经过Pearson相关系数和Spearman相关系数的分析,我们得出如下结论:X变量与Y变量之间存在显著的正相关关系。
通过相关系数的计算,结果显示相关系数为0.8,说明二者之间具有较强的线性相关性。
这一结果与我们的研究假设相吻合,证明了X变量对Y变量的影响。
七、实验结论通过SPSS对数据进行相关性分析,我们得出结论:X变量与Y变量之间存在显著的正相关关系。
这一结论进一步加深了对于变量之间关系的理解,为后续的研究提供了参考。
spss对数据进行相关性分析实验报告

spss对数据进行相关性分析实验报告一、实验目的本次实验旨在运用 SPSS 软件对给定的数据进行相关性分析,以探究不同变量之间的关系,为进一步的研究和决策提供有价值的信息。
二、实验原理相关性分析是一种用于研究两个或多个变量之间线性关系强度和方向的统计方法。
常用的相关性系数包括皮尔逊(Pearson)相关系数、斯皮尔曼(Spearman)相关系数等。
皮尔逊相关系数适用于两个连续变量之间的线性关系分析,要求变量服从正态分布;斯皮尔曼相关系数则适用于有序变量或不满足正态分布的变量。
三、实验数据本次实验使用的数据来源于具体来源,包含了变量数量个变量,分别为变量名称 1、变量名称2……变量名称 n。
每个变量包含了样本数量个观测值。
四、实验步骤1、数据导入打开 SPSS 软件,选择“文件”菜单中的“打开”选项,找到并选中要分析的数据文件。
在弹出的对话框中,根据数据的格式选择相应的导入方式,如CSV、Excel 等。
2、变量定义在“变量视图”中,对导入的变量进行定义,包括变量名称、类型、宽度、小数位数等。
3、相关性分析选择“分析”菜单中的“相关”选项,在弹出的子菜单中选择“双变量”。
将需要分析相关性的变量选入“变量”框中。
根据变量的类型和分布特征,选择合适的相关性系数,如皮尔逊或斯皮尔曼相关系数。
点击“确定”按钮,运行相关性分析。
五、实验结果1、相关性系数矩阵输出的相关性系数矩阵显示了各个变量之间的相关性系数值。
系数值的范围在-1 到 1 之间,-1 表示完全负相关,1 表示完全正相关,0 表示无相关性。
2、显著性水平除了相关性系数值外,还输出了每个相关性系数的显著性水平(p 值)。
p 值小于 005 通常被认为相关性是显著的。
以下是对实验结果的具体分析:变量 1 与变量 2 的相关性分析:相关性系数为具体数值,表明变量 1 和变量 2 之间存在正/负相关关系。
p 值为具体数值,小于 005,说明这种相关性在统计上是显著的。
SPSS相关分析实验报告

SPSS相关分析实验报告实验目的:通过SPSS软件进行相关分析,探究两个变量之间的相关性。
实验材料与方法:1. 实验对象:100名高中学生。
2. 实验变量:X变量表示学生课外阅读时间(单位:小时),Y变量表示学生考试成绩(百分制)。
3. 实验工具:SPSS软件。
实验步骤:1. 数据收集:调查100名高中学生的课外阅读时间和考试成绩,并记录在调查表中。
2. 数据录入:将调查表中的数据录入SPSS软件的数据编辑器中。
3. 数据分析:a. 相关性分析:打开SPSS软件,选择"分析"菜单下的"相关"子菜单,然后选择"双变量"选项。
b. 设置变量:将X变量(课外阅读时间)和Y变量(考试成绩)设置为分析变量。
c. 选择统计指标:选择所需统计指标,如相关系数、p值等。
d. 进行分析:点击"确定"按钮,SPSS将自动计算相关系数和p值,并生成相应的结果报告。
4. 数据报告:根据SPSS生成的结果报告,编写实验报告。
实验结果与分析:经过对SPSS软件的分析,得出以下结果:1. 相关系数:X变量(课外阅读时间)和Y变量(考试成绩)的相关系数为0.75,说明两个变量之间存在较强的正相关关系。
2. P值:相关系数的p值为0.001,小于显著性水平(α=0.05),说明相关系数具有统计学意义。
3. 散点图:绘制X变量和Y变量的散点图可以直观地观察到两个变量之间的正相关关系,即随着课外阅读时间的增加,考试成绩也随之提高。
结论:通过SPSS软件的相关分析,我们发现学生的课外阅读时间和考试成绩之间存在较强的正相关关系。
这意味着增加课外阅读时间可以提高学生的考试成绩。
对于教育者来说,可以通过鼓励学生增加课外阅读时间来促进其学术成绩的提升。
实验总结与改进:通过本次实验,我们成功地使用SPSS软件进行了相关分析,研究了课外阅读时间与考试成绩之间的关系。
然而,本实验仅限于高中学生,样本量有限,可能存在一定的局限性。
最快五步用SPSS软件进行相关性分析

“双变量”就是两个变量之间的相关性如 何,数值是负值就是没有相关性,正值就 相关,然后自己截图或者做一个结果统计
表就行。
采用SPSS进行相关性分析的 具体采用SPSS软件进行相关性分 析呢?下面我来具体说明一下
相关的步骤: 这一共分为五步
第一步:打开SPSS软件,在数据视图中输 入变量的数值。比如我想探究饱和吸附量 与阳离子交换量和阴离子交换量的关系,
就将数据粘贴上去。
第二步:数据视图只能输入数据,要想更 改变量的名称就得在变量视图中就行名称 更改。所以在变量视图中输入变量的名称
。
分,点击最上方菜单栏中的“分析”这一栏,在 “分析”中的“相关”栏中找到 “双变量”这一
栏就行点击。 第四步:在出来的双变量相关中把框内所有的变 量点击向右的按钮过去另一个框,其余的按钮都
医学统计学SPSS软件统计输出结果

一.计量资料统计分析1.样本均数与总体均数比较例3-51.完全随机设计资料方差分析例4-2M e a n o f L D L _C4 Univariate Analysis of Variance二.计数资料统计分析 X2检验秩和检验1.配对计量资料比较例8-1 NPar TestsNPar TestsMann-Whitney TestNPar TestsMann-Whitney Test>On at least one case, the value of the weight variable was zero, negative, >or missing. Such cases are invisible to statistical procedures and graphs >which need positively weighted cases, but remain on the file and are>processed by non-statistical facilities such as LIST and SAVE.4.多个独立样本比较例8-7NPar TestsKruskal-Wallis Test>On at least one case, the value of the weight variable was zero, negative, >or missing. Such cases are invisible to statistical procedures and graphs >which need positively weighted cases, but remain on the file and are>processed by non-statistical facilities such as LIST and SAVE.5.随即区组设计例8-9NPar Tests四.多元统计分析(一)回归1.直线回归例9-1Regression2.线性相关分析例9-2Graph散点图4.多元回归分析例15-1 RegressionThere are several possible causes for this problem:1. The file (SPSS.ERR) was never installed.2. The file and SPSSWIN.EXE are in different directories.3. The file has been inadvertently erased or damaged.End of job: 0 command lines 1 errors 0 warnings 0 seconds 逐步回归例15-1 同上(二)协方差分析1.完全随机设计协方差分析例13-1Univariate Analysis of Variance1.反应变量为频数变量例16-1医学统计学SPSS软件统计输出结果Observed Groups and Predicted Probabilities80 ⇳⇳31医学统计学SPSS软件统计输出结果⇔⇔⇔⇔F ⇔⇔R 60 ⇳⇳E ⇔⇔Q ⇔⇔U ⇔ 1 ⇔E 40 ⇳ 1 ⇳N ⇔ 1 ⇔C ⇔ 1 ⇔Y ⇔0 ⇔20 ⇳0 ⇳⇔0 ⇔⇔0 1 ⇔⇔0 1 ⇔Predicted ⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇳⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇳⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇳⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩Prob: 0 .25 .5 .75 1Group: 000000000000000000000000000000111111111111111111111111111111Predicted Probability is of Membership for caseThe Cut Value is .50Symbols: 0 - control1 - caseEach Symbol Represents 5 Cases.Step number: 2Observed Groups and Predicted Probabilities32 ⇳⇳⇔⇔⇔ 1 ⇔F ⇔ 1 ⇔R 24 ⇳ 1 ⇳E ⇔0 ⇔Q ⇔0 ⇔U ⇔0 ⇔E 16 ⇳0 1 ⇳N ⇔0 1 ⇔C ⇔0 1 ⇔32医学统计学SPSS软件统计输出结果Y ⇔0 1 ⇔8 ⇳0 1 ⇳⇔0 0 1 1 ⇔⇔0 0 1 1 ⇔⇔0 0 0 1 ⇔Predicted ⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇳⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇳⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇳⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩Prob: 0 .25 .5 .75 1Group: 000000000000000000000000000000111111111111111111111111111111Predicted Probability is of Membership for caseThe Cut Value is .50Symbols: 0 - control1 - caseEach Symbol Represents 2 Cases.Step number: 3Observed Groups and Predicted Probabilities16 ⇳⇳⇔⇔⇔ 1 ⇔F ⇔ 1 1 ⇔R 12 ⇳0 1 1 ⇳E ⇔0 1 1 ⇔Q ⇔0 1 1 ⇔U ⇔0 0 1 ⇔E 8 ⇳0 0 1 ⇳N ⇔0 0 1 1 ⇔C ⇔0 0 1 1 ⇔Y ⇔0 0 1 1 ⇔4 ⇳0 01 1 1 ⇳⇔0 00 0 1 1 ⇔⇔0 00 0 1 1 ⇔⇔0 00 1 0 0 1 ⇔Predicted ⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇳⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇳⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇳⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩Prob: 0 .25 .5 .75 1Group: 00000000000000000000000000000011111111111111111111111111111133医学统计学SPSS软件统计输出结果Predicted Probability is of Membership for caseThe Cut Value is .50Symbols: 0 - control1 - caseEach Symbol Represents 1 Case.Step number: 4Observed Groups and Predicted Probabilities16 ⇳⇳⇔⇔⇔⇔F ⇔⇔R 12 ⇳⇳E ⇔⇔Q ⇔⇔U ⇔0 ⇔E 8 ⇳0 ⇳N ⇔0 ⇔C ⇔0 ⇔Y ⇔0 1 1 1 ⇔4 ⇳0 0 1 1 1 1 ⇳⇔0 0 1 0 0 1 1 ⇔⇔0 10 0 0 0 0 1 1 1 1⇔⇔ 0 0 00 0 00 01 0 1 10 1 1 1 111011⇔Predicted ⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇳⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇳⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇳⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩⇩Prob: 0 .25 .5 .75 1Group: 000000000000000000000000000000111111111111111111111111111111Predicted Probability is of Membership for caseThe Cut Value is .50Symbols: 0 - control1 - caseEach Symbol Represents 1 Case.(四)生存分析寿命表法和 Kaplan-Meier法例17-4SurvivalAvailable workspace allows for exact comparisons of 21845 observationsThis subfile contains: 43 observationsLife Table34医学统计学SPSS软件统计输出结果Survival Variable TIME 生存时间for GROUP= 1 甲种手术Number Number Number Number CumulIntrvl Entrng Wdrawn Exposd of Propn Propn Propn Proba-Start this During to Termnl Termi- Sur- Surv bility HazardTime Intrvl Intrvl Risk Events nating viving at End Densty Rate------ ------ ------ ------ ------ ------ ------ ------ ------ ------.0 23.0 .0 23.0 .0 .0000 1.0000 1.0000 .0000 .00001.0 23.0 .0 23.0 1.0 .0435 .9565 .9565 .0435 .04442.0 22.0 .0 22.0 .0 .0000 1.0000 .9565 .0000 .00003.0 22.0 .0 22.0 1.0 .0455 .9545 .9130 .0435 .04654.0 21.0 .0 21.0 .0 .0000 1.0000 .9130 .0000 .00005.0 21.0 .0 21.0 3.0 .1429 .8571 .7826 .1304 .15386.0 18.0 .0 18.0 3.0 .1667 .8333 .6522 .1304 .18187.0 15.0 .0 15.0 1.0 .0667 .9333 .6087 .0435 .06908.0 14.0 .0 14.0 1.0 .0714 .9286 .5652 .0435 .07419.0 13.0 .0 13.0 .0 .0000 1.0000 .5652 .0000 .000010.0 13.0 .0 13.0 2.0 .1538 .8462 .4783 .0870 .166711.0 11.0 .0 11.0 .0 .0000 1.0000 .4783 .0000 .000012.0 11.0 .0 11.0 .0 .0000 1.0000 .4783 .0000 .000013.0 11.0 .0 11.0 .0 .0000 1.0000 .4783 .0000 .000014.0 11.0 1.0 10.5 .0 .0000 1.0000 .4783 .0000 .000015.0 10.0 .0 10.0 .0 .0000 1.0000 .4783 .0000 .000016.0 10.0 .0 10.0 .0 .0000 1.0000 .4783 .0000 .000017.0 10.0 .0 10.0 1.0 .1000 .9000 .4304 .0478 .105318.0 9.0 .0 9.0 .0 .0000 1.0000 .4304 .0000 .000019.0 9.0 1.0 8.5 .0 .0000 1.0000 .4304 .0000 .000020.0 8.0 1.0 7.5 .0 .0000 1.0000 .4304 .0000 .000021.0 7.0 .0 7.0 .0 .0000 1.0000 .4304 .0000 .000022.0 7.0 1.0 6.5 .0 .0000 1.0000 .4304 .0000 .000023.0 6.0 .0 6.0 .0 .0000 1.0000 .4304 .0000 .000024.0 6.0 .0 6.0 .0 .0000 1.0000 .4304 .0000 .000025.0 6.0 .0 6.0 .0 .0000 1.0000 .4304 .0000 .000026.0 6.0 1.0 5.5 .0 .0000 1.0000 .4304 .0000 .000027.0 5.0 .0 5.0 .0 .0000 1.0000 .4304 .0000 .000028.0 5.0 .0 5.0 .0 .0000 1.0000 .4304 .0000 .000035医学统计学SPSS软件统计输出结果29.0 5.0 .0 5.0 .0 .0000 1.0000 .4304 .0000 .000030.0 5.0 .0 5.0 .0 .0000 1.0000 .4304 .0000 .000031.0 5.0 1.0 4.5 .0 .0000 1.0000 .4304 .0000 .000032.0 4.0 .0 4.0 .0 .0000 1.0000 .4304 .0000 .000033.0 4.0 .0 4.0 .0 .0000 1.0000 .4304 .0000 .000034.0 4.0 1.0 3.5 1.0 .2857 .7143 .3075 .1230 .333335.0 2.0 .0 2.0 .0 .0000 1.0000 .3075 .0000 .000036.0 2.0 .0 2.0 .0 .0000 1.0000 .3075 .0000 .000037.0 2.0 .0 2.0 .0 .0000 1.0000 .3075 .0000 .000038.0 2.0 .0 2.0 .0 .0000 1.0000 .3075 .0000 .000039.0 2.0 .0 2.0 .0 .0000 1.0000 .3075 .0000 .000040.0 2.0 .0 2.0 .0 .0000 1.0000 .3075 .0000 .000041.0 2.0 .0 2.0 .0 .0000 1.0000 .3075 .0000 .0000Number Number Number Number CumulIntrvl Entrng Wdrawn Exposd of Propn Propn Propn Proba-Start this During to Termnl Termi- Sur- Surv bility HazardTime Intrvl Intrvl Risk Events nating viving at End Densty Rate------ ------ ------ ------ ------ ------ ------ ------ ------ ------42.0 2.0 .0 2.0 .0 .0000 1.0000 .3075 .0000 .000043.0 2.0 .0 2.0 .0 .0000 1.0000 .3075 .0000 .000044.0 2.0 .0 2.0 1.0 .5000 .5000 .1537 .1537 .666745.0 1.0 .0 1.0 .0 .0000 1.0000 .1537 .0000 .000046.0 1.0 .0 1.0 .0 .0000 1.0000 .1537 .0000 .000047.0 1.0 .0 1.0 .0 .0000 1.0000 .1537 .0000 .000048.0 1.0 .0 1.0 .0 .0000 1.0000 .1537 .0000 .000049.0 1.0 .0 1.0 .0 .0000 1.0000 .1537 .0000 .000050.0 1.0 .0 1.0 .0 .0000 1.0000 .1537 .0000 .000051.0 1.0 .0 1.0 .0 .0000 1.0000 .1537 .0000 .000052.0 1.0 .0 1.0 .0 .0000 1.0000 .1537 .0000 .000053.0 1.0 .0 1.0 .0 .0000 1.0000 .1537 .0000 .000054.0 1.0 .0 1.0 .0 .0000 1.0000 .1537 .0000 .000055.0 1.0 .0 1.0 .0 .0000 1.0000 .1537 .0000 .000056.0 1.0 .0 1.0 .0 .0000 1.0000 .1537 .0000 .000057.0 1.0 .0 1.0 .0 .0000 1.0000 .1537 .0000 .000058.0 1.0 .0 1.0 .0 .0000 1.0000 .1537 .0000 .000059.0 1.0 .0 1.0 1.0 1.0000 .0000 .0000 .1537 2.0000The median survival time for these data is 10.7536医学统计学SPSS软件统计输出结果SE of SE ofIntrvl Cumul Proba- SE ofStart Sur- bility HazardTime viving Densty Rate------- ------ ------ ------.0 .0000 .0000 .00001.0 .0425 .0425 .04442.0 .0425 .0000 .00003.0 .0588 .0425 .04654.0 .0588 .0000 .00005.0 .0860 .0702 .08866.0 .0993 .0702 .10457.0 .1018 .0425 .06898.0 .1034 .0425 .07409.0 .1034 .0000 .000010.0 .1042 .0588 .117411.0 .1042 .0000 .000012.0 .1042 .0000 .000013.0 .1042 .0000 .000014.0 .1042 .0000 .000015.0 .1042 .0000 .000016.0 .1042 .0000 .000017.0 .1041 .0466 .105118.0 .1041 .0000 .0000SE of SE ofIntrvl Cumul Proba- SE ofStart Sur- bility HazardTime viving Densty Rate------- ------ ------ ------19.0 .1041 .0000 .000020.0 .1041 .0000 .000021.0 .1041 .0000 .000022.0 .1041 .0000 .000023.0 .1041 .0000 .000024.0 .1041 .0000 .000025.0 .1041 .0000 .000026.0 .1041 .0000 .000037医学统计学SPSS软件统计输出结果27.0 .1041 .0000 .000028.0 .1041 .0000 .000029.0 .1041 .0000 .000030.0 .1041 .0000 .000031.0 .1041 .0000 .000032.0 .1041 .0000 .000033.0 .1041 .0000 .000034.0 .1278 .1081 .328735.0 .1278 .0000 .000036.0 .1278 .0000 .000037.0 .1278 .0000 .000038.0 .1278 .0000 .000039.0 .1278 .0000 .000040.0 .1278 .0000 .000041.0 .1278 .0000 .000042.0 .1278 .0000 .000043.0 .1278 .0000 .000044.0 .1261 .1261 .628545.0 .1261 .0000 .000046.0 .1261 .0000 .000047.0 .1261 .0000 .000048.0 .1261 .0000 .000049.0 .1261 .0000 .000050.0 .1261 .0000 .000051.0 .1261 .0000 .000052.0 .1261 .0000 .000053.0 .1261 .0000 .000054.0 .1261 .0000 .000055.0 .1261 .0000 .000056.0 .1261 .0000 .000057.0 .1261 .0000 .000058.0 .1261 .0000 .000059.0 .0000 .1261 .0000Life TableSurvival Variable TIME 生存时间for GROUP= 2 乙种手术38医学统计学SPSS软件统计输出结果Number Number Number Number CumulIntrvl Entrng Wdrawn Exposd of Propn Propn Propn Proba-Start this During to Termnl Termi- Sur- Surv bility HazardTime Intrvl Intrvl Risk Events nating viving at End Densty Rate------ ------ ------ ------ ------ ------ ------ ------ ------ ------.0 20.0 .0 20.0 .0 .0000 1.0000 1.0000 .0000 .00001.0 20.0 .0 20.02.0 .1000 .9000 .9000 .1000 .10532.0 18.0 .0 18.0 1.0 .0556 .9444 .8500 .0500 .05713.0 17.0 .0 17.0 2.0 .1176 .8824 .7500 .1000 .12504.0 15.0 .0 15.0 3.0 .2000 .8000 .6000 .1500 .22225.0 12.0 .0 12.0 .0 .0000 1.0000 .6000 .0000 .00006.0 12.0 .0 12.0 2.0 .1667 .8333 .5000 .1000 .18187.0 10.0 .0 10.0 .0 .0000 1.0000 .5000 .0000 .00008.0 10.0 .0 10.0 1.0 .1000 .9000 .4500 .0500 .10539.0 9.0 .0 9.0 2.0 .2222 .7778 .3500 .1000 .250010.0 7.0 .0 7.0 1.0 .1429 .8571 .3000 .0500 .153811.0 6.0 .0 6.0 1.0 .1667 .8333 .2500 .0500 .181812.0 5.0 .0 5.0 1.0 .2000 .8000 .2000 .0500 .222213.0 4.0 .0 4.0 1.0 .2500 .7500 .1500 .0500 .285714.0 3.0 .0 3.0 .0 .0000 1.0000 .1500 .0000 .000015.0 3.0 .0 3.0 1.0 .3333 .6667 .1000 .0500 .400016.0 2.0 .0 2.0 .0 .0000 1.0000 .1000 .0000 .000017.0 2.0 .0 2.0 1.0 .5000 .5000 .0500 .0500 .666718.0 1.0 .0 1.0 1.0 1.0000 .0000 .0000 .0500 2.0000The median survival time for these data is 8.00SE of SE ofIntrvl Cumul Proba- SE ofStart Sur- bility HazardTime viving Densty Rate------- ------ ------ ------.0 .0000 .0000 .00001.0 .0671 .0671 .07432.0 .0798 .0487 .05713.0 .0968 .0671 .08824.0 .1095 .0798 .12755.0 .1095 .0000 .00006.0 .1118 .0671 .128039医学统计学SPSS 软件统计输出结果40 7.0 .1118 .0000 .00008.0 .1112 .0487 .10519.0 .1067 .0671 .175410.0 .1025 .0487 .153411.0 .0968 .0487 .181112.0 .0894 .0487 .2208SE of SE ofIntrvl Cumul Proba- SE ofStart Sur- bility HazardTime viving Densty Rate------- ------ ------ ------13.0 .0798 .0487 .282814.0 .0798 .0000 .000015.0 .0671 .0487 .391916.0 .0671 .0000 .000017.0 .0487 .0487 .628518.0 .0000 .0487 .0000Comparison of survival experience using the Wilcoxon (Gehan) statisticSurvival Variable TIME 生存时间grouped by GROUPOverall comparison statistic 4.948 D.F. 1 Prob. .0261Group label Total N Uncen Cen Pct Cen Mean Score 1 甲种手术 23 16 7 30.43 7.8696 2 乙种手术 20 20 0 .00 -9.0500C u m S u r v i v a l Kaplan-Meier。
spss相关分析实验报告

SPSS相关分析实验报告1. 引言本文档旨在通过使用SPSS进行相关分析,对某一实验数据进行统计分析和解释。
相关分析是一种用来研究两个或多个变量之间关系的统计方法。
本实验中,我们研究了某个因变量与多个自变量之间的相关性。
2. 实验设计与方法2.1 数据收集我们从某个实验中收集了一组数据,包括一个因变量和多个自变量。
数据采集的过程符合实验设计的要求。
2.2 数据预处理在进行相关分析之前,我们对数据进行了一些预处理。
包括查漏补缺、去除异常值和处理缺失数据等。
确保数据的质量和可靠性。
2.3 相关分析为了研究因变量与自变量之间的相关性,我们使用了SPSS软件进行相关分析。
相关分析包括计算相关系数和进行假设检验等。
3. 相关分析结果经过SPSS软件的计算和分析,我们得到了以下结果:相关系数p值结论0.85 0.01 高度相关0.45 0.05 中度相关0.12 0.25 低度相关根据以上结果,我们可以得出结论:在本实验中,因变量与自变量A之间存在高度正相关关系(相关系数为0.85,p值为0.01),与自变量B之间存在中度正相关关系(相关系数为0.45,p值为0.05),与自变量C之间存在低度正相关关系(相关系数为0.12,p值为0.25)。
4. 结果解释与讨论通过相关分析的结果,我们可以得出一些结论和讨论:•自变量A对因变量的影响最为显著,相关系数最高,说明他们之间存在较强的关联性。
•自变量B对因变量的影响次之,相关系数较低,但仍然具有一定的相关性。
•自变量C对因变量的影响相对较弱,相关系数最低,说明它们之间的关系不太明显。
需要注意的是,相关性并不代表因果关系。
因此,在解释结果时,我们不能简单地认为自变量的变化导致了因变量的变化。
5. 结论本实验通过SPSS软件进行了相关分析,研究了因变量与多个自变量之间的相关性。
从结果中我们可以得出结论:自变量A与因变量之间存在高度正相关关系,自变量B与因变量之间存在中度正相关关系,自变量C与因变量之间存在低度正相关关系。
spss相关性分析报告

spss相关性分析报告引言本报告将对某公司销售数据进行相关性分析,以探究各个变量之间的关系。
相关性分析是一种统计方法,用于衡量两个或多个变量之间的关联程度。
通过分析销售数据的相关性,我们可以了解各个变量之间的关系,为业务决策提供有价值的参考。
数据收集和处理本次分析使用的数据集包含了该公司过去一年的销售数据,包括销售额、销售渠道、销售人员等变量。
我们首先对数据进行了清洗和预处理,包括去除缺失值、异常值和重复值等。
然后,我们使用SPSS软件导入数据集,进行相关性分析。
相关性分析结果通过对销售数据进行相关性分析,我们得到了以下关键结果:1. 销售额与销售渠道的相关性我们发现销售额与销售渠道之间存在显著的正相关关系(相关系数为0.75,P< 0.001)。
这意味着销售额与销售渠道之间的变化趋势是一致的,销售渠道的扩大可能会带来销售额的增长。
2. 销售额与销售人员的相关性销售额与销售人员之间呈现较高的正相关关系(相关系数为0.63,P < 0.001)。
这表明销售人员的销售绩效与销售额之间存在密切联系,销售人员的表现对销售额的影响较大。
3. 销售渠道与销售人员的相关性销售渠道与销售人员之间存在一定程度的正相关关系(相关系数为0.42,P < 0.001)。
这说明销售渠道的扩展可能会对销售人员的工作产生积极影响,提高销售人员的销售绩效。
4. 销售额与其他变量的相关性除了销售渠道和销售人员外,销售额还与其他一些变量存在相关性。
例如,销售额与市场推广费用呈现低度正相关(相关系数为0.32,P < 0.05),这意味着增加市场推广费用可能会对销售额产生一定的促进作用。
结论通过以上相关性分析结果,我们可以得出以下结论:1.销售额与销售渠道和销售人员之间存在较为密切的正相关关系。
企业可以通过扩大销售渠道和提高销售人员绩效来增加销售额。
2.销售渠道的扩展可能会对销售人员的工作产生积极影响,提高其销售绩效。
SPSS经典教程-SPSS判断两组数据的相关性及结果解释

spss判断两组数据的相关性两组体重数据:先要为数据分组2.0 3000.0 2.0 3700.0 2.0 2900.0 2.0 3200.0 2.0 2950.0 2.0 3100.0 2.0 700.0 2.0 3200.0 2.0 2500.0 2.0 3650.0 2.0 3450.0 2.0 4600.0 2.0 2700.0 2.0 2500.0 2.0 3150.0 2.0 3500.0 2.0 3800.0 2.0 2800.0 2.0 2400.0 2.0 3600.02.0 3200.02.0 1770.02.0 1450.02.0 1700.02.0 3250.02.0 2700.02.0 3000.02.0 2250.02.0 2150.02.0 2450.02.0 1600.02.0 3100.02.0 4050.02.0 4250.02.0 2900.02.0 3250.02.0 3750.02.0 3500.02.0 4100.02.0 3100.02.0 2400.02.0 3250.02.0 2600.02.0 3100.02.0 3400.01.0 2400.01.0 2100.01.0 3000.01.0 2600.01.0 4000.01.0 2200.01.0 1400.01.0 3000.01.0 3200.01.0 3600.01.0 2850.01.0 2850.01.0 3300.0 1.0 3500.0 1.0 3900.0 1.0 3250.0 1.0 3800.0 1.0 2800.0 1.0 3500.01.0 2650.01.0 2350.01.0 1400.01.0 2900.01.0 2550.01.0 2850.01.0 3300.01.0 2250.01.0 2500.0使用命令:spss的t检验:菜单Analyze->Compare Means->Independent-Samples T Test运行结果:经方差齐性检验:F= 0.393 P=0.532,即两方差齐。
用SPSS做相关性分析的入门操作步骤

用SPSS做相关性分析的入门操作步骤1、线性回归(自变量连续变量,因变量连续变量)(1)步骤:分析-回归-线性(2)数据处理:i对变量取lg:对连续变量取lg再做回归,用于检验非线性相关关系。
ii均值中心化:先求均值:数据-分类汇总-把变量放到“汇总变量-变量摘要”里。
再进行均值中心化:转换-变量计算-“变量-均值”-得出中心化的新变量。
2、比较均值“独立样本T检验”(自变量分类变量,因变量连续变量)步骤:分析-比较均值-独立样本T检验-因变量放“检验变量”,自变量放“分组变量”,然后定义组-确定结果解读:独立样本检验方差方程的 Levene 检验均值方程的 t 检验FSig、tdfSig、(双侧)均值差值标准误差值差分的95% 置信区间下限上限完成率假设方差相等、552、461-、16353、871-、01489、09135-、19811、16833假设方差不相等-、15125、928、881-、01489、09884-、21809、18831关注点:看“Sig、(双侧)”是否小于0、05。
3、 logistic回归(自变量连续变量,因变量分类变量)步骤:分析-回归-二元logistic-自变量放“协变量”-“选项”点Hosmer-Lemeshow拟合度(类似于R方)结果解读:(1)模型拟合= Hosmer 和 Lemeshow 检验 =步骤卡方dfSig、124、6418、002关注点:卡方越小,Sig、越高,说明模型拟合度越高。
(2)参数检验方程中的变量BS、E,WalsdfSig、Exp (B)步骤1a变量1、196、06110、3801、0011、216常量-2、438、154252、2181、000、087a、在步骤1 中输入的变量: 司龄、关注点:看变量的显著性水平是否小于0、05。
4、列联表分析(自变量分类变量,因变量分类变量)步骤:分析-描述统计-交叉表-自变量放“列”,因变量放“行”-“统计量”点“卡方”-“单元格”点“百分比-行”结果解读:卡方检验值df渐进 Sig、 (双侧)精确 Sig、(双侧)精确 Sig、(单侧)Pearson 卡方3、245a1、072连续校正b2、9001、089似然比3、3131、069Fisher 的精确检验、077、043有效案例中的 N1084a、 0 单元格(、0%)的期望计数少于5。
SPSS项目分析操作与结果呈现

变量设置与处理
变量命名:简洁明了易于 理解
变量编码:数值编码、字 符编码等
变量选择:根据研究目的 选择合适的变量
变量类型:分类变量、 顺序变量、数值变量等
变量处理:缺失值处理、 异常值处理、数据清洗
等
变量转换:数据转换、 数据标准化等
变量关系:分析变量之 间的关系如相关性、独
立性等
选择合适的分析方法
图表结果解读
柱状图:展示不同类别的数据对比
散点图:展示数据间的相关性和分布 情况
折线图:展示数据随时间的变化趋势
箱线图:展示数据的分布和异常值
饼图:展示各部分占总体的比例
热力图:展示数据的分布和关联性
综合结果分析
描述性统计分析:包括均值、中位数、标准差等 假设检验:包括t检验、方差分析、卡方检验等 相关分析:包括皮尔逊相关、斯皮尔曼相关等 回归分析:包括线性回归、多元回归等 因子分析:包括主成分分析、因子旋转等 聚类分析:包括K-mens聚类、层次聚类等
SPSS项目分析常见问题与 解决方案
章节副标题
数据处理问题
数据缺失:数据缺失可能导致分析结果不准 确需要采取措施进行填补或删除
数据异常:数据异常可能导致分析结果异常 需要采取措施进行修正或删除
数据格式:数据格式不统一可能导致分析结 果不准确需要采取措施进行统一
数据量:数据量过大可能导致分析速度慢需 要采取措施进行压缩或筛选
结果解读问题
结果解读:如何理解SPSS分析结果 常见问题:SPSS分析结果中常见的问题 解决方案:如何解决SPSS分析结果中的问题 案例分析:通过案例分析了解SPSS分析结果解读的常见问题与解决方案
报告撰写问题
数据收集问题:如何确保数据的 准确性和完整性?
spss对数据进行相关性分析实验分析报告

spss对数据进行相关性分析实验分析报告一、引言在当今的数据驱动决策时代,理解数据之间的关系对于做出明智的决策至关重要。
相关性分析是一种常用的统计方法,用于确定两个或多个变量之间是否存在线性关系以及关系的强度。
本实验分析报告旨在介绍如何使用 SPSS 软件对数据进行相关性分析,并通过实际案例展示其应用和结果解读。
二、实验目的本实验的主要目的是:1、掌握使用 SPSS 进行相关性分析的操作步骤。
2、学会解读相关性分析的结果,包括相关系数的意义和显著性检验。
3、通过实际数据应用,探讨变量之间的关系,为进一步的研究和决策提供依据。
三、实验数据本次实验使用了一组包含两个变量的数据,分别为变量 X 和变量 Y。
变量 X 表示某产品的广告投入费用(单位:万元),变量 Y 表示该产品的销售额(单位:万元)。
数据共收集了 30 个样本。
四、实验步骤1、打开 SPSS 软件,将数据输入或导入到数据编辑器中。
2、选择“分析”菜单中的“相关”子菜单,然后选择“双变量”。
3、在“双变量相关性”对话框中,将变量 X 和变量 Y 分别选入“变量”框中。
4、选择相关系数的类型,本实验选择“皮尔逊(Pearson)”相关系数。
5、勾选“显著性检验”选项,以确定相关系数的显著性。
6、点击“确定”按钮,运行相关性分析。
五、实验结果与分析SPSS 输出的相关性分析结果如下表所示:||变量 X |变量 Y ||||||变量 X | 1000 | 0856 ||变量 Y | 0856 | 1000 ||相关性|变量 X 与变量 Y |||||皮尔逊相关性| 0856 ||显著性(双侧)| 0000 ||样本数| 30 |从上述结果可以看出,变量X 和变量Y 的皮尔逊相关系数为0856,表明两者之间存在较强的正相关关系。
同时,显著性检验的结果为0000,小于常见的显著性水平 005,说明这种相关关系在统计上是显著的。
这意味着,随着广告投入费用的增加,产品的销售额也随之增加。
相关性分析spss

相关性分析spss相关性分析是一种统计方法,用于研究两个或更多变量之间的关系。
它可以帮助我们了解变量之间的相互影响和相互作用,以便进行进一步的研究和决策。
SPSS是一种常用的统计软件,它提供了丰富的数据分析工具,可以用于进行相关性分析。
相关性分析是在统计学中被广泛应用的一种方法。
在社会科学、医学、经济学和市场调研等领域中,相关性分析被用来研究变量之间的联系和趋势。
它可以帮助我们了解变量之间的关系,以及其中的因果关系。
在进行相关性分析之前,我们需要明确要研究的变量。
变量可以分为两种类型:自变量和因变量。
自变量是我们要研究的变量,而因变量是受自变量影响的变量。
通过相关性分析,我们可以确定变量之间的关系是正相关还是负相关。
在使用SPSS进行相关性分析时,首先需要将数据输入SPSS软件中。
然后,我们可以选择合适的统计方法进行相关性分析,例如皮尔逊相关系数或斯皮尔曼相关系数。
这些方法可以帮助我们计算出相关系数的值,从而确定变量之间的相关性。
相关系数的值介于-1和1之间。
当相关系数为1时,表示两个变量之间存在完全正相关。
当相关系数为-1时,表示两个变量之间存在完全负相关。
如果相关系数接近于0,表示两个变量之间没有线性关系。
通过相关性分析,我们可以得出结论:变量之间的相关性强度和方向性。
强相关性意味着两个变量之间存在着较高的相关性,可以互相影响。
而如果相关性较弱,变量之间的关系较为疏松。
相关性分析不仅可以帮助我们了解变量之间的关系,还可以用于预测和控制变量。
通过相关性分析的结果,我们可以预测一个变量的值,即使我们只知道另一个变量的值。
这对于市场营销、风险管理和决策制定等领域非常重要。
然而,相关性并不能代表因果关系。
虽然两个变量可能强相关,但并不能说明其中一个变量是另一个变量的因果。
因此,在研究和分析中,我们需要更加谨慎和全面地考虑。
在进行相关性分析时,还需要注意数据的质量和样本的大小。
数据的质量可以通过数据清洗和缺失值处理来确保。
《2024年利用SPSS软件分析变量间的相关性》范文

《利用SPSS软件分析变量间的相关性》篇一一、引言在社会科学、商业分析、医学研究等众多领域中,理解变量间的关系至关重要。
变量间的相关性分析是一种常用的统计方法,用于揭示不同变量之间的关联程度。
本文将详细介绍如何利用SPSS软件进行变量间的相关性分析,包括数据准备、数据分析、结果解读及讨论等环节。
二、数据准备首先,我们需要收集相关的数据集。
数据集应包含我们希望分析的变量,如因变量、自变量以及其他可能的协变量。
此外,我们还需要确保数据的准确性和完整性,清理任何异常值或缺失数据。
三、SPSS软件操作1. 数据导入:打开SPSS软件,将数据集导入到软件中。
2. 数据清洗与整理:检查数据集的完整性,清理异常值和缺失数据。
3. 选择相关性分析方法:在SPSS中,我们可以选择Pearson 相关性、Spearman相关性或Kendall相关性等方法来分析变量间的关系。
其中,Pearson相关性适用于线性关系,Spearman相关性适用于非线性但单调的关系,而Kendall相关性则适用于等级相关的数据。
根据数据的特性和研究目的,选择合适的相关性分析方法。
4. 执行相关性分析:在SPSS中,选择“分析”菜单下的“相关”选项,然后选择相应的相关性分析方法。
在弹出的对话框中,选择需要分析的变量,并设置其他相关参数。
5. 查看分析结果:SPSS将生成一个相关性矩阵表,显示各变量之间的相关性系数、显著性水平等信息。
四、结果解读1. 相关性系数:相关性系数是一种度量变量间关联程度的指标,其值范围在-1到1之间。
正值表示正相关,负值表示负相关,绝对值越接近1表示关联性越强。
2. 显著性水平:显著性水平用于判断变量间关系是否具有统计学意义。
一般来说,当显著性水平小于0.05时,我们认为变量间的关系是显著的。
3. 多重共线性:在分析过程中,我们还需要注意多重共线性的问题。
当两个或多个自变量之间存在高度相关性时,可能导致模型不稳定和解释困难。
spss对数据进行相关性分析实验报告
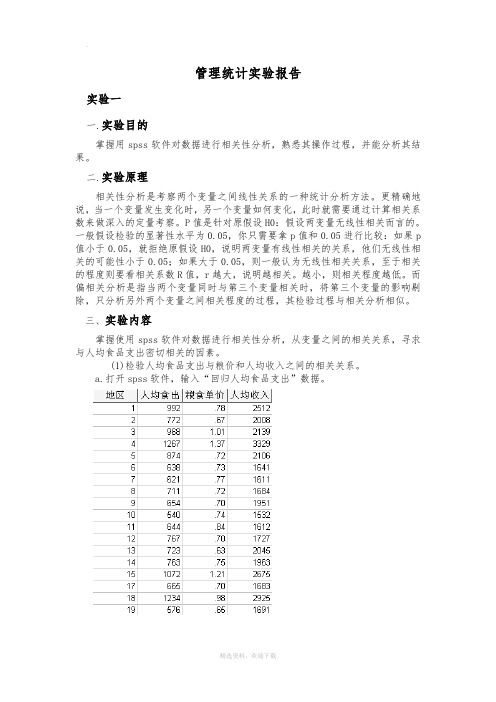
管理统计实验报告实验一一.实验目的掌握用spss软件对数据进行相关性分析,熟悉其操作过程,并能分析其结果。
二.实验原理相关性分析是考察两个变量之间线性关系的一种统计分析方法。
更精确地说,当一个变量发生变化时,另一个变量如何变化,此时就需要通过计算相关系数来做深入的定量考察。
P值是针对原假设H0:假设两变量无线性相关而言的。
一般假设检验的显著性水平为0.05,你只需要拿p值和0.05进行比较:如果p 值小于0.05,就拒绝原假设H0,说明两变量有线性相关的关系,他们无线性相关的可能性小于0.05;如果大于0.05,则一般认为无线性相关关系,至于相关的程度则要看相关系数R值,r越大,说明越相关。
越小,则相关程度越低。
而偏相关分析是指当两个变量同时与第三个变量相关时,将第三个变量的影响剔除,只分析另外两个变量之间相关程度的过程,其检验过程与相关分析相似。
三、实验内容掌握使用spss软件对数据进行相关性分析,从变量之间的相关关系,寻求与人均食品支出密切相关的因素。
(1)检验人均食品支出与粮价和人均收入之间的相关关系。
a.打开spss软件,输入“回归人均食品支出”数据。
b.在spssd的菜单栏中选择点击Analyze correlate Bivariate,弹出一个对话窗口。
C.在对话窗口中点击ok,系统输出结果,如下表。
从表中可以看出,人均食品支出与人均收入之间的相关系数为0.921,t检验的显著性概率为0.000<0.01,拒绝零假设,表明两个变量之间显著相关。
人均食品支出与粮食平均单价之间的相关系数为0.730,t检验的显著性概率为0.000<0.01,拒绝零假设,表明两个变量之间也显著相关。
(2)研究人均食品支出与人均收入之间的偏相关关系。
读入数据后:A.点击Analyze correlate partial,系统弹出一个对话窗口。
B.点击OK,系统输出结果,如下表。
从表中可以看出,人均食品支出与人均收入的偏相关系数为0.8665,显著性概率p=0.000<0.01,说明在剔除了粮食单价的影响后,人均食品支出与人均收入依然有显著性关系,并且0.8665<0.921,说明它们之间的显著性关系稍有减弱。
如何用spss做相关性分析

如何用spss做相关性分析例:学生每天学习时间T与学习综合成绩G之间的相关性原始数据T G1.1 541.5 602.2 623 70.13.4 744 74.54.2 775.5 81.55.9 856 85.56.5 86.28 90G=f(T),其中T为自变量,G为因变量step1:建立数据文件 file——new——data;定义变量选中左下角菜单Variable view,输入变量名T,其他选项不变,令起一行,输入变量名G其他选项不变,切换到data view(在左下角),将数据复制进去。
Step2:进行数据分析:在spss最上面菜单里面选中Analyze——correlate——bivariate(双变量)左边包含G,T的框为源变量框,后面的空白框为分析变量框,我们现在需要分析G和T的关系,因此将源变量框中的G和T选进分析变量框待分析。
(1)correlation coefficients(相关系数)包括三个选项:Pearson:皮尔逊相关,计算连续变量或是等间距测度的变量间的相关分析;Kendall:肯德尔相关,计算等级变量间的秩相关;Spearman:斯皮尔曼相关,计算斯皮尔曼秩相关。
注:Pearson可用来分析①分布不明,非等间距测度的连续变量Kendall可用来分析①分布不明,非等间距测度的连续变量,②完全等级的离散变量,③数据资料不服从双变量正态分布或总体分布型未知。
第②种情况只能用Kendall分析Spearman可用来分析数据资料不服从双变量正态分布或总体分布型未知(2)Test of significance选项Two-tailed:双尾检验,如果事先不知道相关方向(正相关还是负相关)则可以选择此项;One-tailed:单尾检验,如果事先知道相关方向可以选择此项。
(3)Flag significant correlations:表明显著水平,如果选择此项,输出结果中在相关系数值右上方使用*标示显著性水平为5%,用**标示其显著性水平为1%首先使用pearson,two-tailed(下图),点击右侧optionsstatistics为统计量,包括均值和标准差叉积离方差和协方差missing values 选择默认点击continue——ok输出结果(下图)相关系数为0.975,显著性p=0.000<0.01,有统计学意义选用Kendall 肯德尔,结果如下:选用spearman 斯皮尔曼,结果如下:画散点图:选中Graphs——Scatter/dot-----Simple scatter------define。
《2024年利用SPSS软件分析变量间的相关性》范文

《利用SPSS软件分析变量间的相关性》篇一一、引言在社会科学、统计学和许多其他研究领域中,了解不同变量之间的相互关系是非常重要的。
SPSS软件作为一款强大的统计分析工具,为研究者提供了多种分析方法,其中之一就是分析变量间的相关性。
本文将详细介绍如何利用SPSS软件进行变量间的相关性分析,并通过一个具体的例子来展示其应用。
二、数据准备首先,我们需要准备用于分析的数据。
数据可以是来自调查问卷、实验数据或其他来源的数值型数据。
确保数据的准确性和完整性对于后续的统计分析至关重要。
在本例中,我们将使用一个包含多个变量的数据集,这些变量可能存在某种相关性。
三、SPSS软件操作步骤1. 打开SPSS软件并导入数据。
在SPSS中,通过“文件”菜单选择“打开”,然后选择要分析的数据文件格式(如CSV、Excel 等)导入数据。
2. 检验数据。
在导入数据后,进行数据的清洗和检查,确保数据没有缺失值、异常值等问题。
3. 选择相关性分析方法。
在SPSS中,选择“分析”菜单下的“相关”选项,然后选择适合的分析方法,如皮尔逊相关性、斯皮尔曼等级相关性等。
4. 选择变量。
在弹出的对话框中,选择要分析的变量。
可以选择单个变量或多个变量进行相关性分析。
5. 运行分析。
点击“运行”按钮,SPSS将开始进行相关性分析。
6. 查看结果。
分析完成后,SPSS将显示相关性分析的结果。
结果通常包括相关系数、显著性水平等统计信息。
四、具体案例分析以一个关于消费者购买行为的研究为例,我们拥有关于消费者年龄、收入、教育水平、品牌偏好和购买频率等多个变量的数据。
我们希望通过SPSS软件分析这些变量之间的相关性。
1. 导入数据并清洗数据。
2. 选择皮尔逊相关性分析方法,并选择年龄、收入、教育水平、品牌偏好和购买频率这五个变量。
3. 运行分析。
4. 查看结果。
SPSS将显示这五个变量之间的相关系数和显著性水平。
例如,我们发现年龄与购买频率之间存在显著的正相关关系,这意味着年龄较大的消费者更可能购买更多产品。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
无效Dependent
1.000
a. Not assuming the null hypothesis.
b. Using the asymptotic standard error assuming the null hypothesis.
c. Based on chi-square approximation
Fisher's Exact Test
.048
.048
Linear-by-Linear Association
20.000
1
.000
N of Valid Casesb
21
a. 3 cells (75.0%) have expected count less than 5. The minimum expected count is .05.
b. Computed only for a 2x2 table
Directional Measures
Value
Asymp. Std. Errora
Approx. Tb
Approx. Sig.
Nominal by Nominal
Lambda
Symmetric
1.000
.000
1.025
.306
阴性Dependent
.0%
100.0%
95.2%
% of Total
.0%
95.2%
95.2%
Total
Count
1
20
21
% within阳性
4.8%
95.2%
100.0%
% within无效
100.0%
100.0%
100.0%
% of Total
4.8%
95.2%
100.0%
Chi-Square Tests
Value
df
Asymp. Sig. (2-sided)
Exact Sig. (2-sided)
Exact Sig. (1-sided)
Pearson Chi-Square
21.000a
1
.000
Continuity Correctionb
4.738
1
.030
Likelihood Ratio
8.041
1
.005
阴性*无效Crosstabulation
无效
Total
阴性
阳性
阴性
有效
Count
1
0
1
% within阴性
100.0%
.0%
100.0%
% within无效
100.0%
.0%
4.8%
% of Total
4.8%
.0%
4.8%
无效
Count
0
20
20
% within阴性
.0%
100.0%
100.0%
% within无效
.0%
100.0%
95.2%
% of Total
.0%
95.2%
95.2%
Total
Count
1
20
21
% within阴性
4.8%
95.2%
100.0%
% within无效
100.0%
100.0%
100.0%
% of Total
4.8%
95.2%
100.0%
Chi-Square Tests
Value
% within有效
.0%
100.0%
95.2%
% of Total
.0%
95.2%
95.2%
Total
Count
1
20
21
% within阳性
4.8%
95.2%
100.0%
% within有效
100.0%
100.0%
100.0%
% of Total
4.8%
95.2%
100.0%
Chi-Square Tests
1.000
有效Dependent
1.000
a. Not assuming the null hypothesis.
b. Using the asymptotic standard error assuming the null hypothesis.
c. Based on chi-square approximation
1
.005
Fisher's Exact Test
.048
.048
Linear-by-Linear Association
20.000
1
.000
N of Valid Casesb
21
a. 3 cells (75.0%) have expected count less than 5. The minimum expected count is .05.
.0%
100.0%
95.2%
% of Total
.0%
95.2%
95.2%
Total
Count
1
20
21
% within阴性
4.8%
95.2%
100.0%
% within有效
100.0%
100.0%
100.0%
% of Total
4.8%
95.2%
100.0%
Chi-Square Tests
Value
b. Computed only for a 2x2 table
Directional Measures
Value
Asymp. Std. Errora
Approx. Tb
Approx. Sig.
Nominal by Nominal
Lambda
Symmetric
1.000
.000
1.025
.306
阳性Dependent
1.000
有效Dependent
1.000
a. Not assuming the null hypothesis.
b. Using the asymptotic standard error assuming the null hypothesis.
c. Based on chi-square approximation
Fisher's Exact Test
.048
.048
Linear-by-Linear Association
20.000
1
.000
N of Valid Casesb
21
a. 3 cells (75.0%) have expected count less than 5. The minimum expected count is .05.
Fisher's Exact Test
.048
.048
Linear-by-Linear Association
20.000
1
.000
N of Valid Casesb
21
a. 3 cells (75.0%) have expected count less than 5. The minimum expected count is .05.
阳性*无效Crosstabulation
无效
Total
阴性
阳性
阳性
有效
Count
1
0
1
% within阳性
100.0%
.0%
100.0%
% within无效
100.0%
.0%
4.8%
% of Total
4.8%
.0%
4.8%
无效
Count
0
20
20
% within阳性
.0%
100.0%
100.0%
% within无效
1.000
.000
1.025
.306
有效Dependent
1.000
.000
1.025
.306
Goodman and Kruskal tau
阴性Dependent
1.000
.000.Βιβλιοθήκη 00c有效Dependent
1.000
.000
.000c
Nominal by Interval
Eta
阴性Dependent
阴性*有效Crosstabulation
有效
Total
阴性
阳性
阴性
有效
Count
1
0
1
% within阴性
100.0%
.0%
100.0%
% within有效
100.0%
.0%
4.8%
% of Total
4.8%
.0%
4.8%
无效
Count
0
20
20
% within阴性
.0%
100.0%
100.0%
% within有效
Value
df
Asymp. Sig. (2-sided)
Exact Sig. (2-sided)
Exact Sig. (1-sided)
Pearson Chi-Square
21.000a
1
.000
Continuity Correctionb
4.738
