第六章 高聚物的分子运动和力学状态
高分子的力学性能

力等)作用下,材料的形变随时间的增加而逐渐增大的现象。
7.3 3 聚合物的粘弹性 聚合物的力学松弛
蠕变过程包括 三种形变
普弹形变ε1 运动单元:键长、键角 形变特点:形变量小,与时间无关,形变 可完全回复 高弹形变ε2
2 +3
1 2 3
1
运动单元:链段 形变特点:形变量大,与时间有关,可逐 渐回复 t 粘性流动ε3 运动单元:分子链 形变特点:不可逆形变
于应力,摩擦阻力越大,链段运动越困难,应变也就越跟不上 应力的变化,δ也就越大。
7.3 3 聚合物的粘弹性 聚合物的力学松弛
4.力学损耗(内耗、阻尼) 粘弹性材料的应变变化跟不上应力的变化,在循环 变化过程中有能量的消耗,这种消耗称为力学损耗或滞 后损耗。 高分子材料内耗的产生在于外力在改变分子链构象 的同时还要克服内摩擦力。
7.3 3 聚合物的粘弹性 聚合物的力学松弛
3.滞后现象 粘弹性材料的力学响应在弹性材料和粘性材料之间,应变的 变化落后于应力的变化一个相位角δ。
(t ) 0 sin(t )
滞后现象:应变的变化落后于应力变化的现象. 聚合物滞后现象也是松弛过程,它的发生是由于链段运动
要受到内摩擦力作用,运动跟不上外力的变化,所以形变落后
下,在标准试样上沿轴向施加拉伸载荷,直到试样被
拉断为止。
1 玻璃态与结晶态聚合物的力学性质
试样断裂前所受的最大
负荷P与试样横截面积之比
为抗张强度t: t = P / b • d
1 玻璃态与结晶态聚合物的力学性质
(2) 弯曲强度(挠曲强度) 弯曲强度是在规定试验条件下,对标准试样施力。 静弯曲力矩直到试样折断为止 。 设试验过程中最大的负荷 为P,则抗弯强度f为: f = 1.5Pl0 / bd2
pcp08 高聚物的分子运动j

WLF方程由来
Doolittle 方程反映了高聚物粘度与自由体积之间的关系
V Vf ln ln A B V f
①
Vf V
式中 A、B 为常数;V 体系总体积;Vf 体系自由体积 令自由体积分数
f
② ③
1 ln ln A B 1 f
Arrhenius Equation 阿累尼乌斯方程
0e
T T
E / RT
E - 松弛所需的活化能
时温等效 ln( ) C1(T Ts )
s
s 是在参考温度 Ts 下的松弛时间
C 2 (T Ts )
Polymer (Yu CAO)
8.2 聚合物的力学状态及其热转变 相态是热力学概念,由自由焓、温度、压力和体 积等热力学参数决定。相态转变伴随着热力学参数的 突变。相态的转变仅与热力学参数有关,而与过程无 关,也称热力学状态。
Polymer (Yu CAO) 在高于Tg的高弹态时,高聚物的膨胀,除了链距振幅增大引起的 膨胀以外,还有自由体积本身的膨胀,因此高弹态的膨胀系 1 1 数 r 远远大于玻璃态的膨胀系数 g ( g ( ~ ) r ) 2 3
T=Tg
Vg V f V0 (
dV ) g Tg dT
玻璃态、高弹态和粘流态称为聚合物的力学三态。
Polymer (Yu CAO)
聚合物力学三态的分子运动各具特点:
玻璃态:温度低,链段的运动处于冻结,只有 侧基、链节、链长、键角等局部运动,形变小,具 有虎克弹性行为,即形变与受力大小成正比,当外 力除去后,形变立即恢复;
高弹态:随着温度上升,分子热运动的能量已 足以克服主链单键内旋转的位垒,链段运动被激发, 在外力作用下,分子链可从卷曲构象变为伸展构象, 在宏观上呈现很大的形变,当外力去除后,形变可 恢复;
高聚物的分子运动与力学状态

使用价值——是高聚物材料成型加工不能超过的温度。
5)脆化温度
定义——指高聚物材料在受强外力作用时,从韧性断裂转变为脆性断裂时的
温度。
使用价值——是塑料、纤维的最低使用温度。
2 . 晶态高聚物
皮革态
在轻度结晶的聚合物中,少量的晶区起类似交联点
的作用,当温度升高时,其中非晶区由玻璃态转变为高
弹态,可以观察到Tg的存在,但晶区的链段由于受晶格
生急剧变化;
4)应用——
塑料(Tg在室温以上): Tg为使用上限和耐热指标;
橡胶(Tg在室温以上): Tg为使用下限和耐寒指标。
V: Volume
H: Enthalpy
G’: Storage shear modulus
α: Volume coefficient of expansion
运动十分缓慢,体积松弛和构象重排在实验的时间标尺内不可能实现
,体系很难达到真正的热力学平衡状态,因而出现CP、 α和K的不连续
变化,而其体积、焓及熵连续变化,这些现象恰好与二级转变相似。
dF=-SdT+VdP
• 一级转变——以温度和压力作为变量,与自由能的一阶偏导数有关的
性质如体积、焓及熵在此过程中发生突变,这类相转变称为一级转变.
• 1 . 线形非晶态高聚物
• 2 . 晶态高聚物
• 3 . 交联高聚物
当温度在一定范围内变化时,大分子具有不同
的运动状态,高聚物宏观表现出不同的力学状态。
在恒定应力下,高聚物的温度-形变之间的关系
(温度-形变曲线)可反映出分子运动与温度变化的
关系。不同结构高聚物温度-形变曲线不同。
1 . 线形非晶态高聚物
低温度。
聚合物分子运动的特点

16
2. 两相球粒模型
这是G. S.Y. Yeh (叶叔菌,华人) 于1972年提出旳。 两相球粒模型以为:
非晶态高聚物是由存在一定程度旳局部有序区, 粒间区(无规线团)构成,而且一根分子链能够经 过几种粒子相和粒间相。
弛时间谱”
6
3. 高分子运动旳温度依赖性(松弛时间 与温度有关)
分子旳内能增长:活化运动单元 聚合物旳体积增大:增长自由空间
升高温度可使松弛过程加紧,时间变短;若不升温 则只有延长时间才干观察到分子运动
升温与延长观察时间是等效旳(时温等效原理)
Time-Temperature superposition)
15
试验证据:
1) 利用此模型很好解释了橡胶弹性理论,即橡胶旳弹性模量 和应力—温度旳关系并不随稀释剂旳加入而存在反常旳变 化,阐明非晶态下分子链是完全无序旳,不存在可被拆散 旳局部有序构造。
2) 非晶态高聚物旳本体和溶液中分别用辐射交联,成果并未 发觉本体体系中发生分子内交联旳倾向比溶液中更大,阐 明本体中不存在诸如紧缩旳线团或折叠链这些局部有序构 造。
态(如PVC塑料地
轻度结晶聚合物温度-形变曲线
板)。
30
(2)结晶度高于40%旳聚合物
随结晶度增长,材料变硬,耐热性提升,无 明显旳Tg 。 M不太大时,Tf <Tm,晶区熔融进入粘流态。
M足够大时,Tf >Tm,则晶区熔融后,出现高 弹态,再升温到Tf以上才进入粘流态。
31
形变
③高度结晶 M1 M 2
电磁效应:NMR核磁共振松弛法、介电松弛法
高分子物理第六章

一、橡胶
Rubber products
3
What is rubber?
Nature rubber-PI Synthesize rubber
CH2 C CH CH3 n CH3
•Polybutadiene •Polyisobutylene •Polychloroprene
4
The definition of rubber
12
第一节
形变类型及描述力学行为的基本物理量
13
6.1.1 基本概念
应变:当材料受到外力作用而所处的条件却使其不能产生惯性位 移,材料的几何形状和尺寸将发生变化,这种变化就称为~~
附加内力:材料发生宏观变形时,其内部分子以及分子内各原子间 的相对位置和距离发生变化,致使原子间或分子间的原有引力平衡 受到破坏,因而将产生一种恢复平衡的力,这种力简称~~
8
(2)高聚物的黏弹性
指高聚物材料不但具有弹性材料的一 般特性,同时还具有粘性流体的一些 特性。弹性和粘性在高聚物材料身上 同时呈现得特别明显。
9
三、橡胶的交联
PB cross-linked
Crosslinking is when individual polymer chains are linked together by covalent bonds to form one giant molecule. 10
dU =TdS-PdV+fdl
fdl =-TdS
dQ=TdS
fdl =-dQ
拉伸 dl>0, dS<0
dQ<0 拉伸放热
回缩 dl<0, dS>0
dQ>0 回缩吸热
42
《高分子物理》课程电子教案

《高分子物理》课程教学大纲英文名称: Polymer Physics课程类别:学科基础课学时:64学分:4适用专业:高分子材料与工程一、本课程的性质、任务高分子物理课程包括:高聚物的结构、高高分子物理学是高分子材料与工程专业的基础课。
通过本门课程的学习,要求学生对高分子的合成、加工、应用、改性等具有全面的了解。
并使学生重点掌握结构、性能及两者之间关系的一些基本概念、必要的知识、分析测试方法、一定的计算能力,从而为专业课的学习打下理论基础,并为高分子材料的合成、加工、选材、应用、改性、性能测试等提供理论依据,进而指导生产实践。
高分子物理课程教学包括理论教学和实验教学。
结合本门课程的实验,对学生进行相关的基本训练,培养学生分析问题和解决问题的实际工作能力。
总之,通过本门课程的学习及实验为后续专业课的学习提供必备的基础知识。
二、本课程的基本要求本课程包括高分子的链结构和聚集态机构、高分子的溶液性质、高分子的运动和高分子力学性能和电性能四大部分。
通过学习,要使学生对教学内容达到“了解”、“认识和理解”、“掌握”和“熟练掌握”层次要求。
即通过学习要求学生对基本分析方法、各种测试方法、各种实验的基本原理、高分子尺寸表示方法及其推导要全面了解。
对高聚物的结晶结构模型、非晶态结构、液晶结构、织态结构有明确的认识和理解。
掌握高聚物的各种力学状态、力学行为、各种性能曲线的详细分析和典型推导。
熟练掌握高聚物结构、性能及两者之间相互关系的基本概念、必要的知识。
熟练掌握高聚物的各种特征温度、测定方法。
三、讲授内容1 高分子链的结构1.1 概论1.1.1 高分子科学的诞生与发展1.I.2 高分子结构的特点I.1.3 高分子结构的内容1.2 高分子链的近程结构1.2.1 结构单元的化学组成1.2.2 键接结构1.2.3 支化与交联1.2.4 共聚物的结构1.2.5 高分子链的构型1.3 高分子链的远程结构1.3.1 高分子的大小1.3.2 高分子涟的内旋转构象1.3.3 高分子链的柔顺性1.4 高分子链的构象统计1.4.1 均方末端距的几何计算法1.4.2 均方末端距的统计计算法.1.4.3 高分子链柔顺性的表征.1.4.4 高分子链的均方旋转半径.2 高分子的聚集态结构2.1 高聚物分子间的作用2.1.1 范德华力与氢链.2.1.2 内聚能密度2.2 高聚物结晶的形态和结构2.2.1 高聚物结晶的形态学2.2.2 高分子在结晶中的构象和晶胞., 2.3 高分子的聚集态结构模型2.3.I 高聚物的晶态结构模型2.3.2 高聚物的非晶态结构模型.2.4 高聚物的结晶过程2.4.1 高分子结构与结晶能力.2.4.2 结晶速度及其测定方法2.4.3 Avrami方程用于高聚物的结晶过程..2.4.4 结晶速度与温度的关系2.4.5 影响结晶速度的其他因素2.5 结晶对高聚物物理机械性能的影响“2.5.1 结晶度概念及其测定方法2.5.2 结晶度大小对高聚物性能的影响2.5.3 结晶高聚物的加工条件—结构—性质的互相作用 2.5.4 分子量等因素对结晶高聚物的聚集态结核2.6 结晶热力学...”2.6.1 结晶高聚物的熔融与熔点2.6.2 结晶温度对熔点的影响2.6.3 晶片厚度与熔点的关系2.6.4 拉伸对高聚物熔点的影响2.7 高聚物的取向态结构2.7.1 高聚物的取向现象2.7.2 高聚物的取向机理2.7.3 取向度及其测定方法2.7.4 取向研究的应用2.8 高聚物的液晶态结构2.8.1 液晶态的结构2.8.2 高分子液晶的结构和性质2.8.3 高分子液晶的应用2.9 高分子合金的形态结构2.9.1 高分子混合物的溉念2.9.2 高分子的相容性2.9.3 共混高聚物聚集态的主要特点2.9.4 非均相多组分聚合物的织态结构2.9.5 共混高聚物的聚集态结构对性能的影响’.3 高分子的溶液性质3.1 高聚物的溶解3.1.1 高聚物溶解过程的特点3.1.2 高聚物溶解过程的热力学解释 3.1.3 溶剂的选择3.2 高分子溶液的热力学性质.3.2.1 Flory-Huggins高分子溶液理论 3.2.2 Flory温区(θ温度)的提出3.3 高分子浓溶液3.3.1 高聚物的增塑3.3.2 纺丝液3.3.3 凝胶和冻胶3.4 共混聚合物的溶混性3.5 高分子溶液的流体力学性质3.5.1 高分子在溶液中的扩散3.5.2 高分子在溶液中的粘性流动4 高聚物的分子量4.1 高聚物分子量的统计意义4.1.1 平均分子量4.1.2 平均分子量与分布函数4.1.3 分子量分布宽度4.2 高聚物分子量的测定.4.2.1 端基分析4.2.2 沸点升高和冰点降低.‘4.2.3 膜渗透压4.2.5 光散射4.2.6 小角激光光散射(LALLS)4.2.7 超速离心沉降4.2.8 粘度4.2.9 凝胶色谱5 高聚物的分子量分布5.1 分子量分布的表示方法5.1.1 图解表示5.1.2 分布函数5.2 基于相平衡的分级方法5.2.I 高分子溶液的相分离5.2.3 分级实验方法5.2.4 数据处理5.3 凝胶色谱法5.3.1 基本原理5.3.2 仪器5.3.3 载体和色谱柱5.3.4 高效凝胶色谱5.4 凝胶色谱的特殊应用5.4.1 凝胶色谱与小角激光光散射联用5.4.2 高聚物长链支化度的测定5.4.3 共聚构组成分布与分子量分布的测定6 高聚物的分子运动6.1 高聚物的分子热运动6.1.1 高分子热运动的主要特点6.1.2 高聚物的力学状态和热转变6.1.3 高聚物的次级松弛6.2 高聚物的玻璃化转变6.2.1 玻璃化转变现象和玻璃化温度的测量 6.2.2 玻璃化转变理论6.2.3 玻璃化温度的影响因素及调节途径6.2.4 玻璃化转变的多维性6.3 高聚物的粘性流动6.3.1 高聚物粘性流动的特点6.3.2 影响粘流温度的因素6.3.3 聚合物熔体的切粘度6.3.4 剪切粘度的测量方法6.3.5 高聚物熔体的流动曲线6.3.6 加工条件对高聚物熔体剪切粘度的影响6.3.7 高聚物分子结构因素对剪切粘度的影响6.3.8 剪切流动的法向应力和高聚物熔体的弹性效应6.3.9 拉伸粘度7 高聚物的力学性质7.1 玻璃态和结晶态高聚物的力学性质7.1.2 描述力学性质的基本物理量7.1.2 几种常用的力学性能指标7.1.3 几类高聚物的拉伸行为7.1.4 高聚物的屈服7.1.5 高聚物的破坏和理论强度7.1.6 影响高聚物实际强度的因素7.2 高弹态高聚物的力学件质7.2.1 橡胶的使用温度范围..7.2.2 高弹性的特点7.2.3 橡胶弹性的热力学分析7.2.4 橡胶弹性的统计理论7.2.5 内能对橡胶弹性的贡献7.2.6 橡胶弹性与交联网结构的关系7.2.7 橡胶的极限性质7.3 高聚物的力学松弛7.3.1 高聚物的力学松弛现象7.3.2 粘弹性的力学模型7.3.3 粘弹性与时间、温度的关系——时温等效原理7.3.4 Boltzmann叠加原理7.3.5 测定高聚物粘弹性的实验方法7.3.6 高聚物的松弛转变及其分子机理8 聚合物的电学性质8.1 高聚物的极化及介电常数8.2 高聚物的介电损耗8.3 高聚物的导电性8.4 高聚物的介电击穿8.5 高聚物的静电现象四、实践性环节1.作业:讲授完两部分教学内容后,进行一次习题课,讲授完每一章的教学内容后,留一次作业题。
高分子材料高聚物的分子运动与力学状态

高分子材料高聚物的分子运动与力学状态引言高分子材料是一种由连续的重复单元构成的聚合物材料。
在材料科学领域,研究高分子材料的分子运动和力学状态对理解材料性质和行为至关重要。
了解高聚物的分子运动和力学状态有助于优化材料设计、改进材料性能,并应用于各种领域,如生物医学、电子器件、纳米技术等。
高聚物的分子运动高聚物的分子运动主要包括乌尔布雷希特运动和扭曲运动。
乌尔布雷希特运动是高聚物链的摆动和旋转运动,其中链段在某一时刻的位置可以被视为围绕平均位置进行振动。
扭曲运动是高分子链的连续扭转运动,由旋转键和左旋键之间的相互作用引起。
高分子材料的分子运动主要受到温度和外部应力的影响。
温度的升高会增加高聚物链的摆动和旋转运动的速率,从而增加整体材料的流动性。
外部应力会导致高聚物链的拉伸和扭转,改变材料的形状和力学性能。
高聚物的力学状态高聚物材料的力学状态可以分为固态、流动态和弹性态。
在固态中,高聚物链之间的空隙较小,链的摆动和旋转受限制,材料呈现刚性和坚固的性质。
在流动态中,高聚物链的摆动和旋转增加,材料呈现流动性,可以被塑性加工和注射成型。
在弹性态中,高分子链在受到外部应力后,发生可逆形变,材料在去除应力后可以恢复原状。
高聚物材料的力学状态可以通过物理测试和分析方法来确定,例如拉伸试验、硬度测量和动态力学分析。
拉伸试验可以测量材料的强度、延展性和断裂性能,硬度测量可以评估材料的硬度和刚度,动态力学分析可以研究材料的粘弹性和弹性恢复能力。
高聚物材料的应用高聚物材料由于其丰富的性质和可调控性,在各种领域中有广泛的应用。
以下是一些常见的应用领域:1.生物医学领域:高聚物材料可以用于制造人工器官、药物传输系统和医疗设备,具有良好的生物相容性和可降解性。
2.电子器件领域:高聚物材料可以用作电子器件的绝缘层、封装材料和柔性电子材料,具有优异的电气性能和机械可塑性。
3.纳米技术领域:高聚物材料可以用于纳米级分子组装和纳米颗粒制备,用于制备纳米传感器、纳米药物传递系统等。
高分子物理

三种力学状态:玻璃态Tg以下分子链几乎无运动,链段处于冻结状态,受力变形很小类似玻璃。
高弹态Tg-Tf链段运动激发,但分子链间无滑移,聚合物表现为橡胶行为。
粘流态Tf以上,受外力作用时,大分子链与大分子链间发生相对位移,无法回复,行为与小分子液体类似两种转变:玻璃态转变为高弹态,转变温度称为玻璃化温度Tg,整个大分子链还无法运动,但链段开始发生运动。
高弹态转变为粘流态,转变温度称为粘流温度Tf,聚合物既呈现橡胶粘弹性又呈流动性玻璃化转变:指非晶态高聚物从玻璃态到高弹态的转变,对晶态分子来说玻璃化转变是指非晶部分的转变。
测量方法,膨胀剂法,差热分析法,力学方法,NMR,介电松弛应变,应力:当材料受到外力作用而所处的条件却使其不能产生惯性移动时,它的几何形状和尺寸将发生变化,这种变化称为应变,定义单位面积撒很难过的附加内力为应力模量:表征材料抵抗变形能力的大小(弹性模量)蠕变:是指在一定的温度和较小的恒定应力作用下,材料的应变随时间的增加而增大的现象应力松弛:在恒定的温度和形变保持不变的情况下,聚合物内部的应力随时间增加而逐渐衰减的现象松弛过程:由于高分子运动时,运动单元之间的作用力很大,因此高分子在外场下,会由一种平衡状态通过分子运动过渡到与外场相适应的新的平衡态,这一过程慢慢完成,完成这一过程需要时间-松弛时间滞后现象,内耗:聚合物在交变应力作用下落后于应力的现象。
由于发生滞后现象,在每一循环变化中,作为热损耗掉的能量与最大储存能量之比Ψ=2πtanσ称为力学内耗分子理论:从高分子的结构特点出发,研究聚合物的力学松弛过程,其核心问题是提出合理的分子模型,应用分子的微观物理量(原子半径,键长,键角,内旋转位垒,均方末端距,分子量,内外摩擦因子等)通过统计力学方法,推导出聚合物的松弛时间分布,溶液和本体的复数黏度,复数模量,复数柔量等宏观黏性弹性的表达式。
主要有RBZ理论和蛇形理论滞后现象:高聚物在应变力作用下,往往发生应变落后于应力的现象。
高分子物理知识点
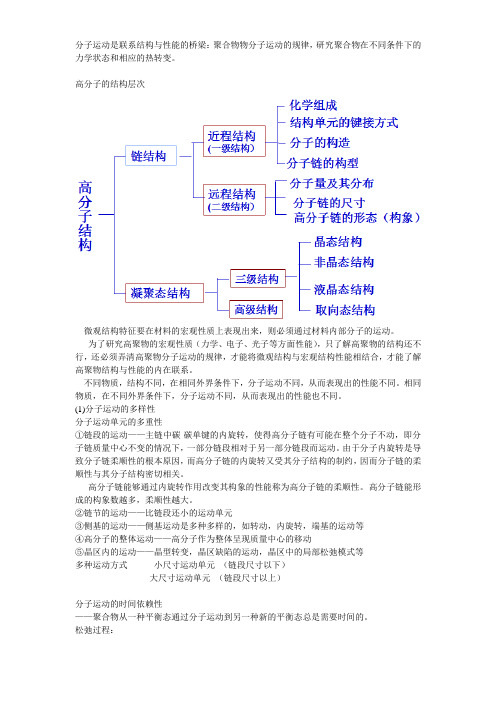
分子运动是联系结构与性能的桥梁:聚合物物分子运动的规律,研究聚合物在不同条件下的力学状态和相应的热转变。
高分子的结构层次微观结构特征要在材料的宏观性质上表现出来,则必须通过材料内部分子的运动。
为了研究高聚物的宏观性质(力学、电子、光子等方面性能),只了解高聚物的结构还不行,还必须弄清高聚物分子运动的规律,才能将微观结构与宏观结构性能相结合,才能了解高聚物结构与性能的内在联系。
不同物质,结构不同,在相同外界条件下,分子运动不同,从而表现出的性能不同。
相同物质,在不同外界条件下,分子运动不同,从而表现出的性能也不同。
(1)分子运动的多样性分子运动单元的多重性①链段的运动——主链中碳-碳单键的内旋转,使得高分子链有可能在整个分子不动,即分子链质量中心不变的情况下,一部分链段相对于另一部分链段而运动。
由于分子内旋转是导致分子链柔顺性的根本原因,而高分子链的内旋转又受其分子结构的制约,因而分子链的柔顺性与其分子结构密切相关。
高分子链能够通过内旋转作用改变其构象的性能称为高分子链的柔顺性。
高分子链能形成的构象数越多,柔顺性越大。
②链节的运动——比链段还小的运动单元③侧基的运动——侧基运动是多种多样的,如转动,内旋转,端基的运动等④高分子的整体运动——高分子作为整体呈现质量中心的移动⑤晶区内的运动——晶型转变,晶区缺陷的运动,晶区中的局部松弛模式等多种运动方式小尺寸运动单元(链段尺寸以下)大尺寸运动单元(链段尺寸以上)分子运动的时间依赖性——聚合物从一种平衡态通过分子运动到另一种新的平衡态总是需要时间的。
松弛过程:τ/0t ex x -∆=∆△x0——橡皮在外力作用下的长度增量 △x ——除去外力后t 时间橡皮长度的增量 t ——观察时间 τ——松弛时间,形变量恢复到原长度的1/e 时所需的时间.取决于材料固有性质和温度、外力大小,不是单一值。
低分子10-8~10-10s, 可以看着是无松弛的瞬时过程。
高分子, 10-1~10+4 s 或更大, 可明显观察到松弛过程。
第六章聚合物的力学性能ppt课件

B PV0 V
三种应变模量的关系
对于各向同性的材料有
E = 2G (1+ν) = 3B (1-2 ν)
ν(泊松比):横向形变与纵向形变之比
m m0 横向形变 纵向形变
t
t 0
0
一般材料ν约为0.2~0.5 注意!上述四个参数中只有两个是独立的
常用的几种力学强度
当材料所受的外力超过材料的承受能力时, 材料就发生破坏。机械强度是衡量材料抵抗外力 破坏的能力,是指在一定条件下材料所能承受的 最大应力。
根据外力作用方式不同,主要有以下三种:
(i)抗张强度
衡量材料抵抗拉伸破坏的能力,也称拉伸强度。
P
在规定试验温度、湿度和 实验速度下,在标准试样上 宽度b 厚度d 沿轴向施加拉伸负荷,直至 试样被拉断。
落后于应力 依赖 熵弹性
高弹性的特点
1、形变大 100~1000%;一般金属材料的 弹
性形变不超过1% 模量小 只有104N/m2左右,T↑,E↑
一般金属材料达109N/m2 , T↑,E↓
2、形变时伴有明显的热效应 拉伸时,橡胶会放出热量,T↑; 回缩时吸热
T↓。金属则相反。
3、高弹形变是一个松驰过程,具有时间依赖性, 通常需要一定时间才能达到平衡状态。
高弹态聚合物的力学性质
橡胶材料是重要的高分子材料之一,在Tg以上, 处于聚合物特有的高弹性力学状态。高弹性无疑是 这类材料显著的特征或说独特的性质,是材料中一 项十分难得的可贵性能,被广泛用于各个领域,其 作用是不可替代的。
橡胶的分子结构和高弹性的本质长期以来一直受 到人们的注视和研究;提高橡胶的耐寒性和耐热性 即扩大橡胶的使用范围,成了人们新的课题。
高分子物理习题集-2010-2011学期使用

高分子物理习题集第一章高聚物的结构1.简述高聚物结构的主要特点。
2.决定高分子材料广泛应用的基本分子结构特征是什么?3.高分子凝聚态结构包括哪些内容?4.高分子的构型和构象有何区别?如果聚丙烯的规整度不高,是否可以通过单键的内旋转提高它的规整度?5.试写出线型聚异戊二烯加聚产物可能有那些不同的构型。
6.分子间作用力的本质是什么?影响分子间作用力的因素有哪些?试比较聚乙烯、聚氯乙烯、聚丙烯、聚酰胺(尼龙-66)、聚丙烯酸各有那些分子间作用力?7.下列那些聚合物没有旋光异构,并解释原因。
A.聚乙烯B .聚丙烯 C .1,4-聚异戊二烯D .3,4-聚丁二烯 E .聚甲基丙烯酸甲酯F .硫化橡胶8. 何谓大分子链的柔顺性?试比较下列高聚物大分子链的柔顺性,并简要说明理由。
9. 写出下列各组高聚物的结构单元,比较各组内几种高分子链的柔性大小并说明理由:1)聚乙烯,聚丙烯,聚苯乙烯;2)聚乙烯,聚乙炔,顺式1,4聚丁二烯;3)聚丙烯,聚氯乙烯,聚丙烯腈;4)聚丙烯,聚异丁稀;5)聚氯乙烯,聚偏氯乙烯;6)聚乙烯,聚乙烯基咔唑,聚乙烯基叔丁烷;7)聚丙烯酸甲酯,聚丙烯酸丙脂,聚丙酸戌酯;8)聚酰胺6.6,聚对苯二甲酰对苯二胺;9)聚对苯二甲酸乙二醇酯,聚对苯二甲酸丁二醇酯。
10.为什么真实的内旋高分子链比相应的高斯链的均方末端距要大些?11.分子量不相同的聚合物之间用什么参数比较其大分子链的柔顺性?12.试从统计热力学观点说明高分子链柔顺性的实质。
~\:CH 2~C —CH —CHCl CH —化+ CN “CH 3 n13.用键为单位统计大分子链的末端距与用链段为单位统计末端距有何异同?那种方法更复合实际情况?14.一个高分子链的聚合度增大100倍,其链的尺寸扩大了多少倍?15.假定聚丙烯中键长为0.154nm,键角109.5。
,无扰尺寸A=835x10-4nm,刚性因子(空间位阻参数)b二1.76,求其等效自由结合链的链段长度b。
高分子物理习题答案

高分子物理习题答案第一章高分子链的结构3.高分子科学发展中有二位科学家在高分子物理领域作出了重大贡献并获得诺贝尔奖,他们是谁?请列举他们的主要贡献。
答:(1)H. Staudinger(德国):“论聚合”首次提出高分子长链结构模型,论证高分子由小分子以共价键结合。
1953年获诺贝尔化学奖。
贡献:(1)大分子概念:线性链结构(2)初探[?]=KM?关系(3)高分子多分散性(4)创刊《die 》1943年(2)P. J. Flory(美国),1974年获诺贝尔化学奖贡献:(1)缩聚和加聚反应机理(2)高分子溶液理论(3)热力学和流体力学结合(4)非晶态结构模型6.何谓高聚物的近程(一级)结构、远程(二级)结构和聚集态结构?试分别举例说明用什么方法表征这些结构和性能,并预计可得到哪些结构参数和性能指标。
答:高聚物的一级结构即高聚物的近程结构,属于化学结构,它主要包括链节、键接方式、构型、支化和交联结构等,其表征方法主要有:NMR, GC, MS, IR, EA, HPLC, UV等。
而高聚物的二级结构即高聚物的远程结构,主要包括高分子链的分子量、分子尺寸、分子形态、链的柔顺性及分子链在各种环境中所采取的构象,其表征方法主要有:静态、动态光散射、粘度法、膜渗透压、尺寸排除色谱、中子散射、端基分析、沸点升高、冰点降低法等。
高聚物的聚集态结构主要指高分子链间相互作用使其堆积在一起形成晶态、非晶态、取向态等结构。
其表征方法主要有:x-射线衍射、膨胀计法、光学解偏振法、偏光显微镜法、光学双折射法、声波传播法、扫描电镜、透射电镜、原子力显微镜、核磁共振,热分析、力学分析等。
8.什么叫做高分子的构型?试讨论线型聚异戊二烯可能有哪些不同的构型。
答:由化学键所固定的原子或基团在空间的几何排布。
1,2:头-头,全同、间同、无规;头-尾,全同、间同、无规3,4:头-头,全同、间同、无规;头-尾,全同、间同、无规1,4:头-头,顺、反;头-尾,顺、反9.什么叫做高分子构象?假若聚丙烯的等规度不高,能不能用改变构象的办法提高其等规度?说明理由。
高分子的分子运动特征

高分子的分子运动特征:高聚物具有结构上的特殊性,这是高聚物具有特殊物理性能的物质基础,材料的宏观性能是建立在去微观结构的基础上的,他们之间的关系通过分子的运动而表现出来,不同结构的高聚物材料,由于它们的分子运动模式不同,性质不同,即使是同一结构的材料,在不同的条件下,由于分子有不同的运动而显示出不同的物理性能。
高聚物的结构是多层次的,具有相当的复杂性,这导致其分子运动的多重性和复杂性,与小分子相比,高分子运动具有一些不同的特点:1、高分子运动单元的多重性:高分子运动单元可以是侧基、链节、链段和整个分子链,对高聚物的物理和力学性能起决定作用的最基本的运动单元为链段,是由于柔性主链上单键的内旋转产生的,链段运动是柔性高分子链特有的运动单元。
链段运动本身也有多重性和相对性,运动单元为转变依赖于外场条件,改变外场条件就能改变分子运动状态,从而导致高聚物力学状态改变。
2、高分子运动的时间依赖性:在外场作用下,物体从一种平衡状态通过分子运动转变为与外场相适应的另一种平衡状态的过程,称为松弛过程。
分子运动完成这个过程所需要时间称为松弛时间,松弛时间与分子尺寸有关,分子越大,运动速度越小,松弛时间越长。
由于高分子运动单元的多重性,实际的高聚物的松弛时间不是单一的值,在一定范围内可以认为是一个连续的分布,常用松弛时间谱而表示。
实际上高聚物总是处于非平衡态,这就是高聚物分子运动的基本属性。
3、高分子运动的温度依赖性:高分子的运动强烈的依赖于温度,升高温度能加速高分子运动。
非晶态高聚物的玻璃化转变,结晶高聚物的熔融称为主转变。
在结晶态和玻璃态高聚物中,一些运动单元的尺寸比主转变的运动单元尺寸小,这些较小的运动单元的运动也是一种松弛过程,统称次级松弛或次级转变。
晶区的分子运动可能有:①晶区的链段运动;②晶型的转变;③晶区内部侧基和链段的运动;④晶区缺隙的局部运动。
对于非晶态高聚物,在玻璃态时虽然链段的运动被冻结,但仍然有小范围的主链运动和侧基或侧链的运动。
高分子物理----高分子的热学性能

四、影响玻璃化转变温度的因素
Cl
[ CH2
T / oC:
CH ] Cl 87
n
[ CH2
C Cl -17
]n
F
[ CH2
T / oC:
CH ] F 40
n
[ CH2
C F度的因素
(3)分子间作用力(极性、氢键 、离子键)
a.极性
侧基的极性越强,分子间作用力越大,柔性越 差,Tg越高。
[ CH2
CH ] R CH3 R: H CH3 -20 CH2CHCH3 29 100 138
n
T / oC: -68
[ CH2
CH ]
n CH3 CH3 C CH3 CH3 43
COOR R: T / oC: CH2CH2CH3 -56 CH2CHCH3 -22
四、影响玻璃化转变温度的因素
b.侧基柔性
难易程度。
二、聚合物的力学状态与热转变
c. 脆化温度 (Tb) 在玻璃态,高聚物虽然很硬,但并不脆,因而可以
作为塑料被广泛使用,但当温度进一步降低,达到一定
的温度时,在外力作用下,高聚物大分子发生断裂,这
个温度称为脆化温度,是高分子所有性能的终止点。
二、聚合物的力学状态与热转变
d. 分解温度 (Td) 分解温度是高聚物开始发生交联、降解等化学变 化的温度。在加工时不能超越这一温度。
玻璃化温度是指聚合物从玻璃态向高弹态转变的 温度,也是链段开始运动或被冻结的温度。
关于玻璃化温度的测试方法比较多,但大致可分
成下面四类方法。
三、聚合物的玻璃化转变
1. 利用体积的变化的方法 常采用膨胀计来测试。 2. 利用热力学性质变化的方法 ① 差热分析(DTA) ② 差示扫描量热仪(DSC)
《高分子物理》第六章-高分子的分子运动

考察
T t=t
F
e
F
e f (T )
一、线型无定形态聚合物的ε-T曲线 温度-形变曲线(热-机曲线)
形 变
玻璃态
高弹态
粘流态
Tg
Tf
温度
流动
模量更低
(3)Tf与平均分子量有关
线型无定形态聚合物
三种力学状态 玻璃态( Tg 以下) 三种状态之间的高粘两弹流个态 态转( (变TTgf 以T上f ))
玻高璃弹化态转转变变为为高 粘弹 流态 态, ,转 转变 变温 温度 度称 称为 为玻 粘璃流化温温度度Tf Tg
温度
运动单元和τ 值
力学性质
例如
PMMA:室温下坚如玻璃,俗称有机玻璃,但在100℃ 左右成为柔软的弹性体
结构材料橡胶:室温下是柔软的弹性体,但在-100℃左 右为坚硬的玻璃体
为什么有以上情况?
外界温度改变了,使分子运动的状况不同,因而表现出的 宏观性能也不同。
材料内部分子的运动 分子运动
链结构不同的聚合物 链结构相同而凝聚态结构不同 链结构和聚集态结构都相同
上式的物理意义:在外力作用下,物体某物理量的测量值随外力作用的 时间的增加而按指数规律逐渐减小。
当 t 0时 , x x0
当 t 时 , x
x0 e
当 t t 时, x x0e t
1
(1) τ-松弛时间 就是x减少到 e x0 时所需要的时间。
(2) τ是一个表征松弛过程快慢的物理量
因/cm2
高聚物的分子运动和力学状态

秒为刻度标尺时,无法观察到它的松弛过 程的。 也就是说觉察不到物体以一种平衡态过渡 到另一平衡态 很大时(n星期,n年) :
如果观察时间 t(秒、分、时)很小,
则可推出 x x0 也不能观察到松弛过 程。如高分子,由于分子大,分子内
.
温度-形变曲线(热-机曲线)
形变
玻璃态
高弹态
粘流态
Tg
Tf
.
温度
• 由图中可以清楚的看到:根据试样的力学
厚上薄(重力作用)
• 塑料雨衣长期悬挂,会在悬挂方向出
现蠕变(重力作用), 这些是塑料(固体)呈现液体的力学行 为。
.
• 例2: • 在倾倒高聚物熔体时,若用一根棍子
快速敲打流体,则熔体液流也会脆性 碎掉。 这是高聚物熔体呈现固体力学行为的 例子。
.
1-3 高分子运动与温度的关系
• 分子运动的温度依赖性 • 温度对高分子运动的二个作用:
第六章 高聚物的分子运动和力学状态 第一节 高聚物的分子运动特点 第二节 高聚物力学状态 第三节 高聚物的玻璃化转变 第四节 高聚物向粘流态的转变
.
• 前面三章我们讨论了高聚物的结构
固体(微 观结构)
溶液
链结构
近程结构
构造 构型
几何异构(顺 反异构)
旋光异构
远程结构——构象(形态,大小)
聚集态结构
.
第二节 高聚物力学状态 • 2-1 线形非晶态高聚物:
两种转变和三种力学状态
• 2-2 晶态高聚物力学状态 • 2-3 体形高聚物力学状态
.
2-1 线形非晶态高聚物的两种转变和 三种力学状态
• 为了激发高聚物中各运动单元的运动,
高分子物理基本概念汇总

第四、五章 高聚物分子量及分子量分布
• 高聚物分子量的特点:分子量在10 -10 之间; 分子量不均一,具有多分散性,分子量只有 统计意义。 • 多分散系数:表征高聚物分子量的分散程度, d越大,说明分子量越分散, d=1,说明 分子量呈单分散。 • 分子量测量方法:端基分析法、溶液依数性 法、渗透压法、气相渗透法、光散射法、粘 度法 。
高分子物理基本概念
高分子科学发展历史
• 1806 橡胶热弹性效应 • 1920 H.Staudinger 提出大分子 • 1932 高分子学科创立
• 1953 H.Staudinger 获诺贝尔化学奖(高分子学说)
• 1963 Zegler,Natta • 1974 P.J.Flory 获诺贝尔化学奖(高分子定向聚合) 获诺贝尔化学奖(高分子溶液)
• 分子量分布的研究方法:理论推导法、试验分级 法(沉淀分级法、溶解分级法、梯度淋洗法、扩 散速度法、沉降平衡法、沉降速度法、凝胶渗透 色谱法),凝胶渗透色谱又称为排斥体积色谱 (SEC)。 • 高分子的分子量分布中,低分子量部分对数均分 子量影响较大,高分子量部分对重均分子量影响 较大。
第六章 高聚物的分子运动和力学状态
• 流变性:在外力作用下,熔体不仅表现出粘性流动,而 且也表现出弹性形变,也就是高聚物的熔体既表现出粘 性,又表现出弹性,又称为粘弹性。 • 流体流动方式:层流、单轴拉伸流动及流体静压强下流 动。 • 高聚物流动性的表征参数:剪切黏度、拉伸黏度、熔融 指数。
• 熔融指数( MI ):在一定温度下,熔融状态的高聚物 在一定负荷下,10min内从规定直径和长度的标准毛细 管中流出的重量(g)。 MI越大,熔体流动性越好。
• 剪切变稀:大多数高聚物熔体和浓溶液属于假塑性流 体,其粘度随剪切速率的增大而减小,即剪切变稀。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∆L0
通式
x = x0 e
−
t
τ
用 x 表示某一物体的某物理量 用 x 0 表示物体在平衡态时某物理量 的数值
上式的物理意义:在外力作用下,物体某 上式的物理意义:在外力作用下, 物理意义 物理量的测量值随外力作用的时间的增加 而按指数规律逐渐减小。 而按指数规律逐渐减小。
t = 0 时 , x = x0 当
量 10
8 态 态
在玻 璃化 转变 时E 下降
量
Tg
温度 模量 温度曲线
Tg 的实用意义:是高聚物特征温度之一,作为 的实用意义:是高聚物特征温度之一, 表征高聚物的指标,可用来确定热塑性塑料的最 表征高聚物的指标,可用来确定热塑性塑料的最 高使用温度和橡胶的最低使用温度。 高使用温度和橡胶的最低使用温度。 则不能作塑料用,因为已经软化; 高于 Tg 则不能作塑料用,因为已经软化胶用,因为已成为玻璃态。
1-2 高分子运动-松弛过程 高分子运动- (Relaxation) ) 分子运动对时间有依赖性 由于高分子在运动时, 由于高分子在运动时,运动纵元之间的作 用力很大,因此高分子在外场下, 用力很大,因此高分子在外场下,物体以 一种平衡状态, 一种平衡状态,通过高分子运动过渡到与 外场相适应的新的平衡态, 外场相适应的新的平衡态,这一过程是慢 松弛过程, 慢完成的。这个过程称为松弛过程 慢完成的。这个过程称为松弛过程,完成 这个过程所需要的时间叫松弛时间 松弛时间。 这个过程所需要的时间叫松弛时间。
x0 x= 当 t =τ 时 , e
当 t = t 时, x = x 0 e
−
t
τ
τ-松弛时间 -
x0 可知: (1) 由上面所讲 可知:t = τ 时, x = ) 由上面所讲τ可知 e
松弛时间就是 变为 松弛时间就是x变为 就是 间。
1 x0 e
时所需要的时
τ-松弛时间 -
(2) 是一个表征松弛过程快慢的物理量 很小时: 当 很小时: 这说明松弛过程进行得很快, 这说明松弛过程进行得很快,如:小分子液体 因此, 的 只有10−8 ~ 10−10秒。因此,通常以秒为刻度 标尺时,无法观察到它的松弛过程的。 标尺时,无法观察到它的松弛过程的。 也就是说觉察不到物体以一种平衡态过渡到另 一平衡态的过程需要一定的时间。 一平衡态的过程需要一定的时间。
第六章 高聚物的分子运动和力学状态
第一节 第二节 第三节 第四节
高聚物的分子运动特点 高聚物力学状态 高聚物的玻璃化转变 高聚物向粘流态的转变
前面几章我们讨论了高聚物的结构
构造 近程结构 构型 链结构 固体(微 观结构) 观结构) 聚集态结构 溶液 旋光异构 远程结构——构象 形态 大小 构象(形态 大小) 远程结构 构象 形态,大小 几何异构(顺 几何异构 顺 反异构) 反异构
我们了解了高聚物有着不同于低分子物质的结构 特点, 特点,这正是高聚物材料有一系列特殊优异性能 的基础, 的基础,微观结构特征要在材料的宏观性质上表 现出来,则必须通过材料内部分子的运动 通过材料内部分子的运动。 现出来,则必须通过材料内部分子的运动。 为了研究高聚物的宏观性质(力学、电子、 为了研究高聚物的宏观性质(力学、电子、光子 等方面性能),只了解高聚物的结构还不行, ),只了解高聚物的结构还不行 等方面性能),只了解高聚物的结构还不行,还 必须弄清高聚物分子运动的规律, 必须弄清高聚物分子运动的规律,才能将微观结 构与宏观结构性能相结合, 构与宏观结构性能相结合,才能了解高聚物结构 与性能的内在联系。 与性能的内在联系。 所以本章是联系结构与性能的桥梁: 所以本章是联系结构与性能的桥梁:高聚物分 子运动的规律
2-1 线形非晶态高聚物的两种转变和三种 力学状态
为了激发高聚物中各运动纵元的运动, 为了激发高聚物中各运动纵元的运动,我们 采用加热的方法。 采用加热的方法。并对高聚物试样施加一恒定 形变与温度的关系 的力,观察试样发生的形变与温度的关系, 的力,观察试样发生的形变与温度的关系,即 采用热机械曲线的方法来考察这个问题。 热机械曲线的方法来考察这个问题 采用热机械曲线的方法来考察这个问题。 力学状态: 力学状态:高聚物的力学性能随温度变化 的特征状态
在这里还有个概念: 在这里还有个概念: 我们知道按结构特征可以将物质分为气 我们知道按结构特征可以将物质分为气 结构特征 液态和固态。 态、液态和固态。 如果按分子运动 分子运动在宏观力学性能上的表 如果按分子运动在宏观力学性能上的表 也可以把物体分为气态、液态、 现,也可以把物体分为气态、液态、固 这两者是有区别的, 态,这两者是有区别的,见下面的例子
力学性质 受力变形很小, 受力变形很小,去 力后立即恢复( 力后立即恢复(可 ),虎克型弹性 逆),虎克型弹性 普弹性)模量: (普弹性)模量: 1011~1012达因 达因/cm2 受力变形很大, 受力变形很大,去 力后可恢复( 力后可恢复(可 ),虎克型弹性 逆),虎克型弹性 高弹性)模量: (高弹性)模量: 106~108达因 达因/cm2
不是一纵一数值, 高聚物的 τ 不是一纵一数值,运动纵元越 运动所需时间越长, 大,运动所需时间越长,则 τ 大,运动纵 元越小,则 τ 小,所以高聚物的 τ 严格 元越小, 地讲是一个分布,称为“松弛时间谱” 地讲是一个分布,称为“松弛时间谱” 当观察时间的标度与聚合物中某种运动纵 例如链段) 值相当时, 元(例如链段)的 τ 值相当时,我们才能 观察到这种运动纵元的松弛过程, 观察到这种运动纵元的松弛过程,但仍然 观察不到其它运动纵元的松弛过程。 观察不到其它运动纵元的松弛过程。
第一节 高聚物的分子运动特点
1-1 运动纵元多重性 1-2 松弛过程:分子运动的时间依赖性 松弛过程: 1-3 松弛时间与温度的关系:分子运动 松弛时间与温度的关系: 的温度依赖性。 的温度依赖性。
1-1 运动纵元多重性 运动纵元可以是侧基、支链、链节、链段、 运动纵元可以是侧基、支链、链节、链段、 大分子。 大分子。 运动形式可以是振动、转动、平动(平移) 运动形式可以是振动、转动、平动(平移) 高聚物运动纵元的多重性 (1)取决于结构 ) (2)也与外界条件(温度)有关 )也与外界条件(温度)
先看二个例子:
PMMA:室温下坚如玻璃,俗称有机玻璃, :室温下坚如玻璃,俗称有机玻璃, 但在100℃左右成为柔软的弹性体 但在 左右成为柔软的弹性体 结构材料。 结构材料。 橡胶:室温下是柔软的弹性体,但在-100℃ 橡胶:室温下是柔软的弹性体,但在 左右为坚硬的玻璃体 为什么有以上情况? 为什么有以上情况? 外界温度改变 温度改变了 分子运动的状况不同, 外界温度改变了,使分子运动的状况不同, 因而表现出的宏观性能也不同。 因而表现出的宏观性能也不同。
实验
l0
∆l ( 0) ∆l (t )
∆l (0) ∆l (τ ) = e
t =τ
t =t
t =0
数学关系式: 数学关系式:
∆L (t ) = ∆L0 e
−t
τ
t = 0 ⇒ ∆L(t ) = ∆L0 ; 1 t = τ ⇒ ∆L(t ) = ∆L0 e
外力未除去前橡皮的增长长度 外力除去后, 时刻测出的橡皮的增 ∆L (t ) 外力除去后,在t时刻测出的橡皮的增 长长度 τ 松弛时间
1-3 高分子运动与温度的关系 分子运动的温度依赖性 温度对高分子运动的二个作用: 温度对高分子运动的二个作用: 1.使运动纵元动能增加,令其活化(使运 使运动纵元动能增加, 使运动纵元动能增加 令其活化( 动纵元活化所需要的能量称为活化能) 动纵元活化所需要的能量称为活化能) 2.温度升高,体积膨胀,提供了运动纵元 温度升高, 温度升高 体积膨胀, 可以活动的自由空间
线形非晶态高聚物
形 热 机 械 曲 线
A 玻璃态 B 高弹态
变
玻 璃
粘 流
C 粘流态
T b
态
Tg
Tf
Td
由图中可以清楚的看到: 由图中可以清楚的看到:根据试样的力学性能随 温度的变化的特点, 温度的变化的特点,可以把线形非晶态高聚物按 温度区域不同划分为 玻璃态( 以下) 三种力学状态 玻璃态( Tg 以下)
高弹态( Tg ~ T f ) 高弹态( 粘流态( 以上) 粘流态( T f 以上)
三种状态之间的两个转变
玻璃态转变为高弹态, Tg 玻璃态转变为高弹态,转变温度称 为玻璃化温度 T f 高弹态转变为粘流态,转变温度称 高弹态转变为粘流态, 为粘流温度
温度
运动纵元和τ 运动纵元和τ值 链段(侧基 支链 链节)仍 链段 侧基,支链 链节 仍 侧基 支链,链节 处于冻结状态(即链段运 处于冻结状态 即链段运 动的τ值无穷大, 动的τ值无穷大,无法观 察) 链段运动(但分子链的τ 链段运动(但分子链的τ 还很大,不能看到)( )(链 还很大,不能看到)(链 段运动的τ 段运动的τ值减小到与实 验测定时间同一数量级时 可以看到) 可以看到)
1-3 高分子运动与温度的关系
以上二点就是升温使松弛过程加快进行的原因, 以上二点就是升温使松弛过程加快进行的原因, 也就是说:升高温度可使松弛时间变短, 也就是说:升高温度可使松弛时间变短,我们可 以在较短的时间就能观察到松弛现象; 以在较短的时间就能观察到松弛现象;如果不升 温,则只有延长观察时间才能观察到这一松弛现 象。 升温与延长观察时间是等效的(时温等效) 升温与延长观察时间是等效的(时温等效)
1-3 高分子运动与温度的关系 减小,从内因上起变化, 升温是迫使 τ 减小,从内因上起变化, 我们可以在较短时间内观察到变化 延长观察时间是从外因上来观察变化
τ 与温度之关系: 与温度之关系:
τ = τ 0e
τ 松弛时间 τ 0 常数
∆E RT
∆E 松弛活化能 R 气体常数 T 绝对温度
第二节 高聚物力学状态 2-1 线形非晶态高聚物力学状态: 线形非晶态高聚物力学状态: 两种转变和三种力学状态 2-2 晶态高聚物力学状态(自学) 晶态高聚物力学状态(自学) 2-3 体形高聚物力学状态(自学) 体形高聚物力学状态(自学)
