2014届高三理科数学江门一模和广州一模考试总结
2014广东高考理科数学分析及历年知识点对比

2014广东高考数学理科试题分析纵观2014 年广东高考理科数学试题,我们发现高考试题整体的结构没有大的变化,知识点和往年有些出入,另外对知识的考查今年更灵活。
总之,今年广东理科数学是考点变化比例加大,上手易高分难。
一、总体趋势变化较大:思路灵活、运算量上升从总体情况看,试卷结构没有变化(8+6+6),但题目没有 13 年基础。
选择、填空题中考查了去年没有涉及的空间向量和解三角形,而且其中中档题的比例也加大了。
解答题中,考察内容除最后一题外,基本不变。
前三道难度与去年相比变化不大。
后三道解答题的思路不是很常规,计算量较大,且与去年不同的是,最后一道大题的求解并不需要导数。
二、试卷难度上升从整张试卷看,相较 2013 年广东高考理科数学试题而言,整体难度上升不少。
试题中中高档题目比例增大,且对计算的要求非常高,要求考生具备极强的耐心进行细致的运算。
尤其是后面三道大题,难度增加颇大。
三、考点分析:中档题比例增加以下表格是对广东省2014年高考理科数学考点的统计:题号考点难度题号考点难度1 集合低 16 (1)三角函数求值低2 复数低 (2)三角公式中3 线性规划中17 (1)频数、频率低4 圆锥曲线中 (2)直方图低5 空间向量低 (3)概率低6 概率统计低 18 (1)线面垂直低7 立体几何低 (2)二面角中8 集合创新题中 19 (1)数列基本概念中9 绝对值不等式低 (2)数列通项公式中11 概率中20 (1)圆锥曲线方程低12 解三角形中 (2)圆锥曲线切线难13 等比数列中 21 (1)函数的定义域中14 参数方程与极坐标中 (2)函数的单调性难15 平面几何低 (3)函数综合难从上表可以看出,1—18 题中,中档题的比例增加,而且考查了去年未涉及到的空间向量及解三角形。
这就要求考生在平时备考时,知识点必须悉数复习到位,不能有所遗漏。
以下对后三大题逐题点评:第 19 题:和去年考察内容一样,均为数列知识,但思路不太相同。
2014年高考理科数学广东卷答案及解析(word精教版)

绝密★启用前 试卷类型:B2014年普通高等学校招生全国统一考试(广东卷)数学(理科)本试卷共4页,21小题,满分150分.考试用时120分钟.注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、考场号、座 位号填写在答题卡上.用2B 铅笔将试卷类型A 填涂在答题卡相应位置上.将条形 码横贴在答题卡右上角“条形码粘贴处”. 2. 选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑, 如需改动,用橡皮擦干净后,再选涂其他答案.答案不能答在试卷上.3. 非选择题必须用黑色字迹钢笔或签字笔作答,答案必须填写在答题卡各题目指定区 域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用 铅笔和涂改液.不按以上要求作答的答案无效.4.作答选做题时,请先用2B 铅笔填涂选做题的题号(或题组号)对应的信息点,再 作答.漏涂、错涂、多涂的,答案无效.5.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回.一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{1,0,1}M =-,{0,1,2}N =,则M N = A.{1,0,1}- B.{1,0,1,2}- C.{1,0,2}-D.{0,1}2.已知复数Z 满足(34)25i z +=,则Z= A.34i - B.34i +C.34i --D.34i -+3.若变量,x y 满足约束条件121y x x y z x y y ≤⎧⎪+≤=+⎨⎪≥-⎩且的最大值和最小值分别为m 和n ,则m n -=A.8B.7C.6D.54.若实数k 满足09k <<,则曲线221259x y k-=-与曲线221259x y k -=-的A.离心率相等B.虚半轴长相等C.实半轴长相等D.焦距相等5.已知向量()1,0,1a =-,则下列向量中与a 成60︒夹角的是A.(-1,1,0)B.(1,-1,0)C.(0,-1,1)D.(-1,0,1)6.已知某地区中小学生人数和近视情况分别如图1和图2所示,为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别是图1 图2A.200,20B.100,20C.200,10D.100,107.若空间中四条两两不同的直线1234,,,l l l l ,满足122334,,l l l l l l ⊥⊥⊥,则下面结论一定正确的是A.14l l ⊥B.14//l lC.14,l l 既不垂直也不平行D.14,l l 的位置关系不确定8.设集合(){}12345=,,,,{1,0,1},1,2,3,4,5iA x x x x x x i ∈-=,那么集合A 中满足条件“1234513x x x x x ≤++++≤”的元素个数为A.60B.90C.120D.130二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分. (一)必做题(9~13题)9.不等式521≥++-x x 的解集为 。
2014届高三“一模”数学科成绩分析及后一阶段备考建议

2014届高三“一模”数学科成绩分析及后一阶段备考建议1 近年来我市数学高考情况科目年份全省平均分我市平均分对比我市平均分在全省排名全省前100名我市所占人数备注200777.8581.27+3.42第7名最高148分;最低137分。
共129人。
2人从2011年起,顺德从佛山市分离出来,单独排名。
200870.5871.86+1.28第8名最高149分;最低139分。
共149人.5人最高文科数学200968.7473.03+4.29第7名149分;最低139分。
共129人。
25人201081.6287.53+5.91第5名最高146分;最低140分。
共141人。
18人201168.1877.68+9.5第1名最高136分;最低125分。
共137人。
13人201274.1987.53+13.34第1名最高150分;最低144分。
共118人。
16人201377.55约92.1约+14.55年报上未公布理科数学200784.7384.83+0.1第10名最高150分;最低138分。
共131人3人从2011年起,顺德从佛山市分离出来,单独排名。
200884.4384.17-0.26第8名最高149分;最低145分。
共120人2人200971.8873.80+1.92第8名最高149分;最低141分。
共125人。
7人201094.2596.53+2.28第6名最高148分;最低141分。
共179人。
7人第7最高147分;最低131201179.3883.47+4.09名分。
共109人。
8人201292.5698.06+5.5第5名最高150分;最低142分。
共139人。
8人201390.72约97.72约+7年报上未公布2 2014届高三“一模”情况文科数学(全体)序号学校考生数最高分平均分离均率>=140>=130>=120>=110>=100>=901东莞中学318142106.945.95118611462242822东莞一中42013597.633.270728972033133实验中学44913390.623.640118801742924高级中学47713493.828.0404291122193365松山湖学校27613592.125.650264497167石6中学38112180.810.330018451157常平中学47713476.8 4.8701536851688万江中学45012968.7-6.220013179虎门中学43014762.4-14.8423351110厚街中学47211569.3-5.4600053210311塘厦中学44411862.8-14.330002912东莞二中29311465.5-10.6300021313东莞四中53411266.4-9.400031314东莞五中50310956.1-23.380000615莞六中50412173.1-0.2300163016东莞七中46611468.2-6.8500041917东莞八中25311463.5-13.340001818东莞十中2799754.9-25.020000019麻涌中学40611467.6-7.70003620长安中学2609946.4-36.650000021济川中学26410762.1-15.230000522南城中学13211165-11.2500012大朗中23学24010854.3-25.850000424大岭山中学16011561-16.80002225东华高级63714588.120.274388113521531526光明中学49814580.810.32212235511218127虎门外语10414499.836.171721395528英才学校10211372.9-0.560001729翰林学校18913474.4 1.570210172630南开实验10413073.30.101141431光正实验15911957.7-21.2700049明32学校10612869-5.760013633石竹学校16012561-16.720013934水霖学校14210552.5-28.320000335全市1136414773.3 109930184617313127理科数学(全体)序号学校考生数最高分平均分离均率>=140>=130>=120>=110>=100>=901东莞中学584148.0110.329.684451543234585362东莞一中662135.0102.620.65010762474155303实验中学667136.096.613.5608391553374754高级中学580138.0104.522.910965215394514松山湖5校371137.0102.520.5207331152223086石龙中学545141.083.0-2.431111541102147常平中学539132.085.10.11029561422528万江中学502119.079.9-6.020*********9虎门中学450128.066.8-21.390018328110厚街中学295124.077.7-8.66004135110411塘厦中学458117.071.1-16.390005259512东莞二中268118.068.8-19.060005134413东莞四中473127.077.0-9.40002652125东14五中299122.066.0-22.330014154315东莞六中577129.083.8-1.4200114713125016东莞七中234117.071.3-16.210003205117东莞八中426123.068.8-19.130017297618东莞十中164115.059.6-29.900001319麻涌中学389117.073.7-13.2900012409520长安中学150115.063.3-25.590002112821济川中学190118.070.0-17.6800010174122南城中学144117.069.8-17.86000192723朗中学232117.052.0-38.83000251624大岭山中学155116.063.9-24.870004122325东华高级857147.0103.721.91137018635152166226光明中学716138.091.77.820124214428141827虎门外语191142.0103.321.5317378111714528英才学校142125.085.10.0700414316729翰林学校320134.085.90.9906175010815830南开实验240134.089.8 5.590182877133光正31实验165130.073.5-13.6201515325532明珠学校155126.075.4-11.380018295733石竹学校195127.075.5-11.240037306034水霖学校181125.067.3-20.82001102843 全市13028148.085.0 201917472112406962033 对下一阶段备考工作的几点建议3.1 下阶段备考的指导思想巩固——巩固前阶段复习成果,把巩固“三基”放在首位.完善——通过专题复习,查漏补缺,进一步完善知识与方法的网络体系.综合——在训练上,减少单一知识点大训练,增强知识的连接点,增加知识交汇点的题目,加大题目的综合性和灵活性.提高——培养思维能力、概括能力、探究能力、分析问题、解决问题的能力,尤其要进一步提升读题能力、运算能力(数据处理能力,尤其是字母运算和分类讨论)、空间想象能力、逻辑推理能力.3.2 具体建议3.2.1 狠抓落实,加强跟踪,及时反馈▲课堂教学中,应根据学生的接受情况,及时调整教学策略与方式,并及时解决学生在课堂学习中出现的问题。
2014届高三数学一模分析

2014届高三数学一模分析张向农 2014.3.26于三中1、本次考试的难易度这届考生进入总复习后共参加了3次全市组织的考试,摸底、质检、一模。
摸底考试理科数学18333人文科数学11648人12月份质检理科数学18110人文科数学10691人3月份一模考试理科数学18889人文科数学14497人三次考试的区分度均在0.4之上,0.4以上的区分度意味着区分度很好。
本次一模考试数据理科数学区分度达到0.48,文科数学区分度更是达到0.53。
说明试卷的区分度很好,可以有效检测一轮复习过后,考生对知识的掌握、方法的落实和技能的提高情况。
希望各校用好这次统计数据,详细分析本校,本班学生数学各块复习的效果。
2、两次高考的基本难度2012年全省难度文科数学 0.36, 理科数学 0.502013年全省难度文科数学0.44 理科数学0.52一模考试有效分理科一本108 二本91 三本49文科一本110 二本91 三本553、本次考试数学命题原则遵循考试说明,注重考查学生的基础知识基本技能和基本思想方法方法,尽量增大覆盖面,适度创新。
4、对本次一模考试的基本数据评价(1)基本数据本次考试,比较好地反映出我市一轮复习结束后学生的真实底数,也就是说,反映了在知识、方法和能力三方面学生的层次,特别是学校整体的层次。
我们可以从平均分、有效分率、区分度、难度等指标进行学校之间的对比,进行学校和全市的对比,从中发现学校的优势和不足。
比如,理科数学平均分全市76.01,学校均分超过这一分数的学校共有7所,接近这一分数的5所。
从有效分率来看,理科全市有效分率为36.44%,高于这一比例的有6所学校,接近这个比例的学校有3所。
最高的有效分率为79%。
然而有些省示范性高中的有效分率仅仅是个位数。
这次考试从难度上看,与高考的难度持平,文科略大一些。
如果考虑到还有76天这个因素,难度应该和高考相当。
(2)、本次考试的意义通过阅卷发现到目前为止存在的薄弱问题,举例如下基础知识不扎实。
2014年广州市数学“一模”分析

命题背景分析
二、考查内容分布
“一模”数学试卷考查的知识点涉及集合与常用逻辑用语,函数、导数与不等式(含指定选考 内容) ,数列、推理与证明,平面向量与三角函数,概率与统计,立体几何,解析几何,复数,计数 原理(理科)等必考知识板块,以及坐标系与参数方程、几何证明选讲等选考内容.具体分值分布 与得分情况见表 1、2. 表 1:广州市 2014 年“一模”文科数学试卷考点分布及得分情况 内容 集合与常用逻辑用语 题号 7 9 1 函数、导数与不等式 5 6 20 题型 选择题 选择题 选择题 选择题 选择题 解答题 分值 5 5 5 5 5 14
5 14 5 5 12 5 5 12 5 14 5 5 14 5 5 150 分
2.17 2.73 3.38 1.66 8.35 2.2 3.79 10.54 3.02 4.96 3.90 0.56 1.85 4.14 1.97 72.7
周期数列的前 n 项和 等差数列、分组求和 正弦定理、二倍角的正弦 平面向量与充要条件 特殊角的三角函数、三角函数的图象 与性质 几何概型 程序框图 古典概型 三视图、几何体的体积 线线垂直、共面问题、几何体的体积 圆关于直线对称 空间向量、模的最值 双曲线的几何性质、直线与圆锥曲线 的位置关系、定值问题 复数相等的条件 极坐标下直线与圆的位置关系 圆中切割线定理、相似比
2
立体几何
11 18 3
填空题 解答题 选择题 解答题 选择题 填空题 填空题
5 14 5 14 5 5 150 分
3.95 9.71 4.67 3.39 4.71 2.48 85.4
三视图、几何体的体积 线线垂直、共面问题、二面角的计算 圆关于直线对称 双曲线的几何性质、直线与圆锥曲线的 位置关系、定值问题 复数相等的条件 极坐标下直线与圆的位置关系 圆中切割线定理、相似比
广东省十校2014届高三上学期第一次联考数学理试题汇总

“十校”2013—2014学年度高三第一次联考理科数学试题本试卷共6页,21小题, 满分150分.考试用时120分钟.注意事项:1.答卷前,考生务必用黑色字迹钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上.2.选择题每小题选出答案后,用黑色字迹钢笔或签字笔将答案填写在答题卡上对应题目的序号下面,如需改动,用橡皮擦干净后,再选填其他答案,答案不能答在试卷上.3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效.4.作答选做题时,请先用2B 铅笔填涂选做题的题号对应的信息点,再作答。
漏涂、错涂、多涂的,答案无效.5.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回.第Ⅰ卷 (选择题 共4 0分)一.选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设集合{}23,log P a =,{},Q a b =,若{}0P Q =,则P Q =( )A .{}3,0B .{}3,0,2C . {}3,0,1D .{}3,0,1,22.如图,在复平面内,复数1z ,2z 对应的向量分别是OA ,OB ,则复数12z z 对应的点位于( )A.第一象限B.第二象限C.第三象限D.第四象限3.已知等差数列{}na 中,25a = ,411a =,则前10项和=10S ( ) A . 55 B . 155 C . 350 D . 400 4.学校为了解学生在课外读物方面的支出情况,抽取了n 个同学进行调查,结果显示这些同学的支出都在[10,50) (单 位:元),其中支出在[)30,50(单位:元)的同学有67人,其频率分布直方图如右图所示,则n 的值为( ) A .100 B .120 C .130 D .390 5.平面四边形ABCD 中0AB CD +=,()0AB AD AC -=⋅,则四边形ABCD 是 ( )A .矩形B .梯形C .正方形D .菱形6. 一个四棱锥的三视图如图所示,其中主视图是腰长为1的等腰 直角三角形,则这个几何体的体积是A .21 B .1 C .23 D .27.下列命题:①函数22()sin cos f x x x =-的最小正周期是π;②函数()(1f x x =-③若111(1)adx a x=>⎰,则a e =; ④椭圆)0(3222>=+m m y x 的离心率不确定。
广东省2014.04高三数学惠一模考试试题(理)

广东省惠州市2014届高三4月模拟考试 数 学 试 题 (理科) 2014.04本试卷共4页,21小题,满分150分。
考试用时120分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.考生必须保持答题卡的整洁.考试结束后,将答题卡一并交回. 参考公式:①如果事件B A 、互斥,则P(B)P(A)B)P(A +=+ ②如果事件B A 、相互独立,则P(B)P(A)B)P(A ⋅=⋅一、选择题:本大题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有一项符合题目要求. 1.设集合A ={0,1},则集合A 的子集的个数为( )A .1B .2C .3D .42.不等式0x2x1≥+-的解集为( ). A .]1,2[- B .]1,2(- C .),1()2,(+∞--∞ D .),1(]2,(+∞--∞3.若抛物线)0p (px 2y 2>=的焦点坐标为)0,1(,则p 的值为( )A .1B .2C .4D .84.“1a =”是“函数ax sin ax cos y 22-=的最小正周期为π”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件5.如图,一个空间几何体的主视图、左视图、俯视图为全等的等腰直角三角形,如果学科网直角三角形的直角边长为1那么这个几何体的体积为 ( )A .1B .21 C .31 D .616.程序框图的运算结果为 ( )A .12B .24C .16D .48左视图主视图P7.椭圆1by ax 22=+与直线x 1y -=交于A 、B 两点,过原点与线段AB 中点的直线的斜率为23,则ab值为( )A .23 B .332 C .239 D .2732 8.已知y ,x 满足,2)2y (x ,0x 22=-+≥则 2222y x y 3xy 2x 3w +++=的最大值为( )A .4B .5C .6D .7二、填空题(本大题共7小题,分为必做题和选做题两部分.每小题5分,满分30分) (一)必做题:第9至13题为必做题,每道试题考生都必须作答. 9.复数)i 1(i +(i 为虚数单位)的虚部等于__________. 10.二项式6)x1x (-的展开式的常数项是__________.(用数字作答) 11. 已知变量y ,x 满足约束条件⎪⎩⎪⎨⎧≤-+≥≤+-07y x 1x 02y x , 则x y 的最大值是__________.12.已知j ,i 为互相垂直的单位向量,j 2i a -=, j i b λ+=,且a 与b 的夹角为锐角,则实数λ的取值范围是 .13. 已知数列}a {n 是正项等差数列,若n321na a 3a 2a b n321n ++++++++=,则数列}b {n 也为等差数列. 类比上述结论,已知数列}c {n 是正项等比数列,若n d = ,则数列{n d }也为等比数列.(二)选做题:第14、15题为选做题,考生只选做其中一题,两题全答的,只计前一题的得分.14.(极坐标与参数方程)若圆C 的方程为:⎩⎨⎧+=+=,,θθsin 1y cos 1x (θ为参数),以原点O 为极点,以x 轴正半轴为极轴建立极坐标系,则圆C 的圆心极坐标为_________ .(极角范围为)2,0[π)15.(几何证明选讲)如右图,P 是圆O 外一 点,过P 引圆O 的两条割线PAB 、PCD ,PA =AB =5,CD =3,则PC =____________.三、解答题:本大题共6小题,满分80分,解答应写出文字说明,证明过程或演算步骤.16.(本题满分12分)已知函数R x x x x x f ∈+=,cos sin cos )(2(1)求)6(πf 的值;(2)若53sin =α,且),2(ππα∈,求)242(πα+f .17.(本题满分12分)在一个盒子中,放有标号分别为1,2,3的三张卡片,现从这个盒子中,有放回...地先后抽得两张卡片的标号分别为x 、y ,记x y 2x -+-=ξ.(1)求随机变量ξ的最大值,并求事件“ξ取得最大值”的概率; (2)求随机变量ξ的分布列和数学期望.18.(本题满分14分)如图,已知正三棱柱ABC —111C B A 的底面边长是2,D 是侧棱1CC 的中点,直线AD 与侧面C C BB 11所成的角为︒45.(1)求此正三棱柱的侧棱长;(2)求二面角C BD A --的余弦值大小.ABCD1A 1B 1C19.(本题满分14分)设等比数列}a {n 的前n 项和为n S ,已知2S 2a n 1n +=+(+∈N n ) (1)求数列}a {n 的通项公式;(2)在n a 与1n a +之间插入n 个数,使这2n +个数组成一个公差为n d 的等差数列. 求证:1615d 1d 1d 1n 21<+⋅⋅⋅++(+∈N n ).20.(本题满分14分)平面直角坐标系xoy 中,直线01y x =+-截以原点O 为圆心的圆所得的弦长为6(1)求圆O 的方程;(2)若直线l 与圆O 切于第一象限,且与坐标轴交于D 、E ,当DE 长最小时,求直线l 的方程;(3)设M 、P 是圆O 上任意两点,点M 关于X 轴的对称点为N ,若直线MP 、NP 分别交于X 轴于点(0,m )和(0,n ),问mn 是否为定值?若是,请求出该定值;若不是,请说明理由.21.(本题满分14分)已知函数.ln )(,2)23ln()(x x g x x x f =++=(1)求函数()f x 的单调区间;(2)如果关于x 的方程m x x g +=21)(有实数根,求实数m 的取值集合; (3)是否存在正数k ,使得关于x 的方程)()(x kg x f =有两个不相等的实数根?如果存在,求k 满足的条件;如果不存在,说明理由.数学 (理科)参考答案与评分标准一.选择题:共8小题,每小题5分,满分40分1.【解析】集合{0,1}A =的子集有φ、}0{、}1{、}2,1{.选D .2.【解析】⇔≥+-0x2x1⎩⎨⎧≠+≥+-0x 20)x 2)(1x (得:1x 2≤<-.选B . 3.【解析】2p ,12p),0,2p (px 2y 2==∴=即的焦点坐为.选B . 4.【解析】当1a =时,函数可化为x 2cos y =,故周期π;反之,函数可化为ax 2cos y =,若周期为π,则1a ±=.选A .5.【解析】可知该几何体是三棱锥,底面面积为21,高为1,故6121131V =⨯⨯=.选D .6.【解析】当5=n 时,244321s =⨯⨯⨯=,选B .7.【解析】设交点分别为A ),(11y x 、B ),(22y x ,代入椭圆方程:12121=+by ax ,12222=+by ax 由两式得:0121212121=++⋅--⋅+x x y y x x y y a b ,即,∴00-0-12121=⋅--⋅+中中x y x x y y a b ,可化简为:0231-1=⋅⋅+)(a b ,即332=a b .选B . 8.【解析】已知y ,x 满足,2)2y (x 22=-+则2222yx y 3xy 2x 3w +++=可化为 22y x xy 23w ++=;要求22y x xy 23w ++=最大值,即求22y x xy2+的最值,由基本不等式可知 22y x xy 2+≤,∴1y x xy222≤+,当且仅当⎩⎨⎧=-+=2)2y (x y x 22取等号,即1y x ==或 1y x -==时,2222yx y 3xy 2x 3w +++=的最大值为4W max =.选A. 二.填空题:共7小题,每小题5分,满分30分.其中14~15题是选做题,考生只能选做一题. 9.1 10.20- 11.6 12.)21,2()2,(---∞13.n n nc c c c ++++⋅⋅⋅⋅⋅ 321133221)( 14.)4,2(π15. 29.【解析】 )i 1(i +=i 1+-,所以虚部等于1. 10.【解析】 6)x1x (-=61)]x (x [--+,r 1r 6r 61r )x (x C T --+-==r )1(-r26r 6x C -,当0r 26=-则3r =,常数项为=4T 3)1(-36C =20-..11【解析】先画出可行域(如图),xy是可行域内的点M )y ,x ( 与原点O )0,0(连线的斜率,当直线OM 过点)6,1(时,xy取得最大值6..12【解析】 215)2(1cos λλθ+⋅⋅-+==)1(5212λλ+-,又θ为锐角,1)1(52102<+-<λλ解得:221-≠<λλ且,)21,2()2,(---∞∈∴ λ. 13. 【解析】由等差数列}a {n 的n 21na a 2a +⋅⋅⋅++的和,则等比数列}c {n 可类比为1c ﹒⋅⋅⋅22)c (n n )c (的积;对n 21na a 2a +⋅⋅⋅++求算术平均值,所以对 1c ﹒⋅⋅⋅22)c (nn )c (求几何平均值,所以类比结果为n 3211n n33221)c c c c (++++⋅⋅⋅⋅⋅ .14.【解析】圆的圆心为)1,1(,,21122=+=ρ))2,0[(11tan πθθ∈=,又圆心在第一象限,故4πθ=.圆心的极坐标为)4,2(π.15.【解析】如右图,P 是圆O 外一点,过P 引圆O 的两条割线PAB 、PCD ,PA = AB =5由圆的割线定理)PD PC (PC )PB PA (PA +⋅=+⋅,即)3x (x )55(5+=+,化简为 010x 3x 2=-+,解得:2x =或5-x =(舍去).三.解答题16.(本题满分12分)本小题考查三角函数的化简与求值。
2014年广州一模数学试题及答案

试卷类型:A2014年广州市普通高中毕业班综合测试(一)数学(理科)2014.3本试卷共4页,21小题, 满分150分.考试用时120分钟 注意事项:1.答卷前,考生务必用2B 铅笔在“考生号”处填涂考生号。
用黑色字迹钢笔或签字笔将自己所在的市、县/区、学校以及自己的姓名和考生号、试室号、座位号填写在答题卡上。
用2B 铅笔将试卷类型(A )填涂在答题卡相应位置上。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.作答选做题时,请先用2B 铅笔填涂选做题题号对应的信息点,再作答。
漏涂、错涂、多涂的,答案无效。
5.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
参考公式:锥体的体积公式Sh V 31=,其中S 是锥体的底面积,h 是锥体的高. ()()22221211236n n n n ++++++=()*n ∈N . 一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知i 是虚数单位,若()2i 34i m +=-,则实数m 的值为A .2-B .2±C .D .22.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若2C B =,则c b为 A .2sin C B .2cos B C .2sin B D .2cos C 3.圆()()22121x y -+-=关于直线y x =对称的圆的方程为A .()()22211x y -+-= B .()()22121x y ++-= C .()()22211x y ++-= D .()()22121x y -++=4.若函数()f x =R ,则实数a 的取值范围为A .()2,2-B .()(),22,-∞-+∞C .(][),22,-∞-+∞D .[]2,2-5.某中学从某次考试成绩中抽取若干名学生的分数,并绘制2成如图1的频率分布直方图.样本数据分组为[)50,60,[)60,70,[)70,80,[)80,90,[]90,100.若用分层抽样的方法从样本中抽取分数在[]80,100范围内的数据16个, 则其中分数在[]90,100范围内的样本数据有A .5个B .6个C .8个D .10个 6.已知集合32A x x x ⎧⎫=∈∈⎨⎬-⎩⎭Z Z 且,则集合A 中的元素个数为 A .2 B .3 C .4D .57.设a ,b 是两个非零向量,则使a b =a b 成立的一个必要非充分条件是A .=a bB .⊥a bC .λ=a b ()0λ>D .ab8.设a ,b ,m 为整数(0m >),若a 和b 被m 除得的余数相同,则称a 和b 对模m 同余,记为()mod a b m ≡.若0122202020202020C C 2C 2C 2a =+⋅+⋅++⋅,()mod10a b ≡,则b 的值可以是A .2011B .2012C .2013D .2014 二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分. (一)必做题(9~13题)9.若不等式1x a -<的解集为{}13x x <<,则实数a 的值为 . 10.执行如图2的程序框图,若输出7S =,则输入k ()*k ∈N 的值为 . 11.一个四棱锥的底面为菱形,其三视图如图3所示,则这个四棱锥的体积是 .12.设α为锐角,若cos 65α⎛⎫+= ⎪⎝⎭,则sin 12απ⎛⎫-= ⎪⎝⎭. 侧(左)视图图3俯视图爱迪教育 D 爱迪个性化教育发展中心D Idea Personalized Education Development C 313.在数列{}n a 中,已知11a =,111n n a a +=-+,记n S 为数列{}n a 的前n 项和,则2014S = .(二)选做题(14~15题,考生只能从中选做一题) 14.(坐标系与参数方程选做题)在极坐标系中,直线()sin cos a ρθθ-=与曲线2cos 4sin ρθθ=-相交于A ,B 两点,若AB =3a 的值为 .15.(几何证明选讲选做题)如图4,PC 是圆O 的切线,切点为C ,直线PA 与圆O 交于A ,B 两点,APC ∠的平分线分别交弦CA ,CB 于D ,E两点,已知3PC =,2PB =,则PEPD的值为 .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)已知函数()sin cos f x x a x =+的图象经过点π03⎛⎫- ⎪⎝⎭,. (1)求实数a 的值;(2)设[]2()()2g x f x =-,求函数()g x 的最小正周期与单调递增区间.17.(本小题满分12分)甲,乙,丙三人参加某次招聘会,假设甲能被聘用的概率是25,甲,丙两人同时不能被聘用的概率是625,乙,丙两人同时能被聘用的概率是310,且三人各自能否被聘用相互独立. (1)求乙,丙两人各自能被聘用的概率;(2)设ξ表示甲,乙,丙三人中能被聘用的人数与不能被聘用的人数之差的绝对值,求ξ的分布列与均值(数学期望).18.(本小题满分14分)如图5,在棱长为a 的正方体1111ABCD A B C D -中,点E 是棱1D D 的PEABCD 图4O 1C 1D DE1A 1B4中点,点F 在棱1B B 上,且满足12B F FB =. (1)求证:11EF A C ⊥;(2)在棱1C C 上确定一点G , 使A ,E ,G ,F 四点共面,并求此时1C G 的长;(3)求平面AEF 与平面ABCD 所成二面角的余弦值. 19.(本小题满分14分)已知等差数列{}n a 的首项为10,公差为2,等比数列{}n b 的首项为1,公比为2,*n ∈N .(1)求数列{}n a 与{}n b 的通项公式;(2)设第n 个正方形的边长为{}min ,n n n c a b =,求前n 个正方形的面积之和n S . (注:{}min ,a b 表示a 与b 的最小值.) 20.(本小题满分14分)已知双曲线E :()222104x y a a -=>的中心为原点O ,左,右焦点分别为1F ,2F ,离心率为35,点P 是直线23a x =上任意一点,点Q 在双曲线E 上,且满足220PF QF =.(1)求实数a 的值;(2)证明:直线PQ 与直线OQ 的斜率之积是定值;(3)若点P 的纵坐标为1,过点P 作动直线l 与双曲线右支交于不同两点M ,N ,在线段MN上取异于点M ,N 的点H ,满足PM MHPN HN=,证明点H 恒在一条定直线上. 21.(本小题满分14分)已知函数()()221e x f x x x =-+(其中e 为自然对数的底数). (1)求函数()f x 的单调区间;(2)定义:若函数()h x 在区间[],s t ()s t <上的取值范围为[],s t ,则称区间[],s t 为函数()h x 的“域同区间”.试问函数()f x 在()1,+∞上是否存在“域同区间”?若存在,求出所有符合条件的“域同区间”;若不存在,请说明理由.2014年广州市普通高中毕业班综合测试(一)数学(理科)试题参考答案及评分标准说明:1.参考答案与评分标准给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可C爱迪教育 D 爱迪个性化教育发展中心D Idea Personalized Education Development C 5根据试题主要考查的知识点和能力比照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分.一、选择题:本大题考查基本知识和基本运算.共8小题,每小题,满分40分.题号 1 23 4 5 6 7 8答案 A B A D B C D A二、填空题:本大题考查基本知识和基本运算,体现选择性.共7小题,每小题,满分30分.其中14~15题是选做题,考生只能选做一题.题号 9 10 11 12131415答案23421020112-1-或5- 23三、解答题:本大题共6小题,满分80分. 16.(本小题满分1)(本小题主要考查三角函数图象的周期性、单调性、同角三角函数的基本关系和三角函数倍角公式等等知识,考查化归与转化的数学思想方法,以及运算求解能力)解:(1)因为函数()sin cos f x x a x =+的图象经过点π03⎛⎫- ⎪⎝⎭,,所以03f π⎛⎫-= ⎪⎝⎭. 即ππsin cos 033a ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭. 即302a+=. 解得3a =(2)方法1:由(1)得()sin 3f x x x =.所以2()[()]2g x f x =-()2sin 32x x=+-22sin 23cos 3cos 2x x x x =++-62cos 2x x =+122cos 22x x ⎫=+⎪⎪⎝⎭ 2sin 2cos cos 2sin 66x x ππ⎛⎫=+ ⎪⎝⎭π2sin 26x ⎛⎫=+ ⎪⎝⎭.所以()g x 的最小正周期为22π=π. 因为函数sin y x =的单调递增区间为2,222k k ππ⎡⎤π-π+⎢⎥⎣⎦()k ∈Z , 所以当πππ2π22π262k x k -≤+≤+()k ∈Z 时,函数()g x 单调递增, 即ππππ36k x k -≤≤+()k ∈Z 时,函数()g x 单调递增.所以函数()g x 的单调递增区间为πππ,π36k k ⎡⎤-+⎢⎥⎣⎦()k ∈Z . 方法2:由(1)得()sin f x x x =+2sin cos cos sin 33x x ππ⎛⎫=+ ⎪⎝⎭π2sin 3x ⎛⎫=+ ⎪⎝⎭.所以2()[()]2g x f x =-2π2sin 23x ⎡⎤⎛⎫=+- ⎪⎢⎥⎝⎭⎣⎦2π4sin 23x ⎛⎫=+- ⎪⎝⎭2π2cos 23x ⎛⎫=-+ ⎪⎝⎭分所以函数()g x 的最小正周期为22π=π分 因为函数cos y x =的单调递减区间为[]2,2k k ππ+π()k ∈Z , 所以当22223k x k ππ≤+≤π+π()k ∈Z 时,函数()g x 单调递增.爱迪教育 D 爱迪个性化教育发展中心D Idea Personalized Education Development C 7即ππππ36k x k -≤≤+(k ∈Z )时,函数()g x 单调递增.所以函数()g x 的单调递增区间为πππ,π36k k ⎡⎤-+⎢⎥⎣⎦()k ∈Z .17.(本小题满分1)(本小题主要考查相互独立事件、解方程、随机变量的分布列与均值(数学期望)等知识,考查或然与必然的数学思想方法,以及数据处理能力、运算求解能力和应用意识) 解:(1)记甲,乙,丙各自能被聘用的事件分别为1A ,2A ,3A ,由已知1A ,2A ,3A 相互独立,且满足()()()()()113232,5611,253.10P A P A P A P A P A ⎧=⎪⎪⎪--=⎡⎤⎡⎤⎨⎣⎦⎣⎦⎪⎪=⎪⎩解得()212P A =,()335P A =. 所以乙,丙各自能被聘用的概率分别为12,35. (2)ξ的可能取值为1,3.因为()()()1231233P P A A A P A A A ξ==+()()()()()()123123111P A P A P A P A P A P A =+---⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦213312525525=⨯⨯+⨯⨯625=. 所以()()113P P ξξ==-=61912525=-=. 所以ξ的分布列为所以19613252525E ξ=⨯+⨯=.ξ 1 3P1925625818.(本小题满分1)(本小题主要考查空间线面关系、四点共面、二面角的平面角、空间向量及坐标运算等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力)推理论证法:(1)证明:连结11B D ,BD ,因为四边形1111A B C D 是正方形,所以1111A C B D ⊥. 在正方体1111ABCD A B C D -中,1DD ⊥平面1111A B C D ,11A C ⊂平面1111A B C D ,所以111A C DD ⊥.因为1111B D DD D =,11B D ,1DD ⊂平面11BB D D ,所以11A C ⊥平面11BB D D .因为EF ⊂平面11BB D D ,所以11EF A C ⊥. (2)解:取1C C 的中点H ,连结BH ,则BHAE .在平面11BB C C 中,过点F 作FGBH ,则FGAE .连结EG ,则A ,E ,G ,F 四点共面.因为11122CH C C a ==,11133HG BF C C a ===, 所以1C G 116C C CH HG a =--=.故当1C G 16a =时,A ,E ,G ,F 四点共面.(3)延长EF ,DB ,设EFDB M =,连结AM ,则AM 是平面AEF 与平面ABCD 的交线.过点B 作BN AM ⊥,垂足为N ,连结FN , 因为FB AM ⊥,FB BN B =, 所以AM ⊥平面BNF .因为FN ⊂平面BNF ,所以AM ⊥FN . 所以FNB ∠为平面AEF 与平面ABCD 所成二面角的平面角.因为123132aMB BF MD DE a ===,23=,1D ABCD EF 1A1B1C MN1D ABCD EF 1A1B1C 1DABCDE F 1A1B 1C G H爱迪教育 D 爱迪个性化教育发展中心D Idea Personalized Education Development C 9所以22MB a =.在△ABM 中,AB a =,135ABM ∠=, 所以2222cos135AM AB MB AB MB =+-⨯⨯⨯ ()222222222a aa a ⎛=+-⨯⨯⨯- ⎝⎭213a =. 即13AM a =. 因为11sin13522AM BN AB MB ⨯=⨯⨯, 所以222sin13521321313a a AB MB BN a AMa⨯⨯⨯===.所以2222121371331339FN BF BN a a ⎛⎫⎛⎫=+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭. 所以6cos 7BN FNB FN ∠==.故平面AEF 与平面ABCD 所成二面角的余弦值为67.空间向量法:(1)证明:以点D 为坐标原点,DA ,DC ,1DD 所在的直线分别为x 轴,y 轴,z 轴,建立如图的空间直角坐标系, 则(),0,0A a ,()1,0,A a a ,()10,,C a a ,10,0,2E a ⎛⎫ ⎪⎝⎭,1,,3F a a a ⎛⎫ ⎪⎝⎭,所以()11,,0AC a a =-,1,,6EF a a a ⎛⎫=- ⎪⎝⎭. 因为221100AC EF a a =-++=, 所以11AC EF ⊥.1D ABC D EF 1A1B1C xyz10所以11EF A C ⊥.(2)解:设()0,,G a h ,因为平面11ADD A 平面11BCC B ,平面11ADD A 平面AEGF AE =,平面11BCC B 平面AEGF FG =,所以FGAE .所以存在实数λ,使得FG AE λ=. 因为1,0,2AE a a ⎛⎫=- ⎪⎝⎭,1,0,3FG a h a ⎛⎫=-- ⎪⎝⎭, 所以11,0,,0,32a h a a a λ⎛⎫⎛⎫--=- ⎪ ⎪⎝⎭⎝⎭. 所以1λ=,56h a =. 所以1C G 15166CC CG a a a =-=-=. 故当1C G 16a =时,A ,E ,G ,F 四点共面. (3)解:由(1)知1,0,2AE a a ⎛⎫=- ⎪⎝⎭,10,,3AF a a ⎛⎫= ⎪⎝⎭. 设(),,x y z =n 是平面AEF 的法向量,则0,0.AE AF ⎧=⎪⎨=⎪⎩n n 即10,210.3ax az ay az ⎧-+=⎪⎪⎨⎪+=⎪⎩取6z =,则3x =,2y =-.所以()3,2,6=-n 是平面AEF 的一个法向量. 而()10,0,DD a =是平面ABCD 的一个法向量, 设平面AEF 与平面ABCD 所成的二面角为θ, 则11cos DD DD θ=n n (1)爱迪教育 D 爱迪个性化教育发展中心D Idea Personalized Education Development C 11()()2220302667326a a⨯+⨯-+⨯==+-+⨯. 故平面AEF 与平面ABCD 所成二面角的余弦值为67.第(1)、(2)问用推理论证法,第(3)问用空间向量法: (1)、(2)给分同推理论证法. (3)解:以点D 为坐标原点,DA ,DC ,1DD 所在的直线分别为x 轴,y 轴,z 轴,建立如图的空间直角坐标系, 则(),0,0A a ,10,0,2E a ⎛⎫ ⎪⎝⎭,1,,3F a a a ⎛⎫ ⎪⎝⎭,则1,0,2AE a a ⎛⎫=- ⎪⎝⎭,10,,3AF a a ⎛⎫= ⎪⎝⎭.设(),,x y z =n 是平面AEF 的法向量,则0,0.AE AF ⎧=⎪⎨=⎪⎩nn即10,210.3ax az ay az ⎧-+=⎪⎪⎨⎪+=⎪⎩取6z =,则3x =,2y =-.所以()3,2,6=-n 是平面AEF 的一个法向量. 而()10,0,DD a =是平面ABCD 的一个法向量, 设平面AEF 与平面ABCD 所成的二面角为θ, 则11cos DD DD θ=n n (1)()()2220302667326a a⨯+⨯-+⨯==+-+⨯. 故平面AEF 与平面ABCD 所成二面角的余弦值为67. 19.(本小题满分1)(本小题主要考查等差数列、等比数列、分组求和等知识,考查化归与转化的数学思想方法,以及运算求解能力和创新意识)1D ABC DEF 1A1B1C xyz12解:(1)因为等差数列{}n a 的首项为10,公差为2,所以()1012n a n =+-⨯, 即28n a n =+.因为等比数列{}n b 的首项为1,公比为2,所以112n n b -=⨯, 即12n n b -=.(2)因为110a =,212a =,314a =,416a =,518a =,620a =,11b =,22b =,34b =,48b =,516b =,632b =.易知当5n ≤时,n n a b >.下面证明当6n ≥时,不等式n n b a >成立.方法1:①当6n =时,616232b -==620268a >=⨯+=,不等式显然成立.②假设当n k =()6k ≥时,不等式成立,即1228k k ->+.则有()()()()122222821826218kk k k k k -=⨯>+=++++>++.这说明当1n k =+时,不等式也成立.综合①②可知,不等式对6n ≥的所有整数都成立. 所以当6n ≥时,n n b a >. 方法2:因为当6n ≥时()()()112281128n n n n b a n n ---=-+=+-+()()01211111C C C C 28n n n n n n -----=++++-+()()012321111111C C C C C C 28n n n n n n n n n n ---------≥+++++-+ ()()0121112C C C 28n n n n ---=++-+()()236460n n n n n =--=-+->,所以当6n ≥时,n n b a >.所以{}min ,n n n c a b =12,5,28,5.n n n n -⎧≤=⎨+>⎩爱迪教育 D 爱迪个性化教育发展中心D Idea Personalized Education Development C 13则()22222,5,44, 5.n n n c n n -⎧≤⎪=⎨+>⎪⎩当5n ≤时,2222123n n S c c c c =++++ 2222123n b b b b =++++024222222n -=++++1414n -=-()1413n=-.当5n >时,2222123n n S c c c c =++++()()22222212567n b b b a a a =+++++++()51413=-()()()222464744n ⎡⎤+++++++⎣⎦()()()222341467867165n n n ⎡⎤=+++++++++-⎣⎦ ()()()()2222223414121253267645n n n ⎡⎤=++++-++++++++-⎣⎦()()()()()121653414553264562n n n n n n +++-⎡⎤=+-+⨯+-⎢⎥⎣⎦3242421867933n n n =++-. 综上可知,n S ()32141,5,3424218679, 5.33nn n n n n ⎧-≤⎪⎪=⎨⎪++->⎪⎩20.(本小题满分1)(本小题主要考查直线的斜率、双曲线的方程、直线与圆锥曲线的位置关系等知识,考查数形结合、化归与转化、函数与方程的数学思想方法,以及推理论证能力和运算求解能力) (1)解:设双曲线E 的半焦距为c ,由题意可得22354.c a c a ⎧=⎪⎨⎪=+⎩解得5a =.14(2)证明:由(1)可知,直线2533a x ==,点()23,0F .设点5,3P t ⎛⎫⎪⎝⎭,()00,Q x y , 因为220PF QF =,所以()0053,3,03t x y ⎛⎫----= ⎪⎝⎭. 所以()00433ty x =-. 因为点()00,Q x y 在双曲线E 上,所以2200154x y -=,即()2200455y x =-. 所以20000200005533PQ OQy t y y ty k k x x x x --⋅=⋅=--()()2002004453453553x x x x ---==-.所以直线PQ 与直线OQ 的斜率之积是定值45.(3)证法1:设点(),H x y ,且过点5,13P ⎛⎫⎪⎝⎭的直线l 与双曲线E 的右支交于不同两点()11,M x y ,()22,N x y ,则22114520x y -=,22224520x y -=,即()2211455y x =-,()2222455y x =-. 设PM MH PN HN λ==,则,.PM PN MH HN λλ⎧=⎪⎨=⎪⎩. 即()()1122112255,1,1,33,,.x y x y x x y y x x y y λλ⎧⎛⎫⎛⎫--=--⎪⎪ ⎪⎝⎭⎝⎭⎨⎪--=--⎩整理,得()()()1212121251,31,1,1.x x y y x x x y y y λλλλλλλλ⎧-=-⎪⎪⎪-=-⎨⎪+=+⎪+=+⎪⎩①②③④由①×③,②×④得()()22221222221251,31.x x x y y y λλλλ⎧-=-⎪⎨⎪-=-⎩⑤⑥将()2211455y x =-,()2222455y x =-代入⑥,爱迪教育 D 爱迪个性化教育发展中心D Idea Personalized Education Development C 15得2221224451x x y λλ-=⨯--. ⑦ 将⑤代入⑦,得443y x =-. 所以点H 恒在定直线43120x y --=上.证法2:依题意,直线l 的斜率k 存在. 设直线l 的方程为513y k x ⎛⎫-=- ⎪⎝⎭,由2251,31.54y k x x y ⎧⎛⎫-=- ⎪⎪⎪⎝⎭⎨⎪-=⎪⎩消去y 得()()()22229453053255690k x k k x k k -+---+=. 因为直线l 与双曲线E 的右支交于不同两点()11,M x y ,()22,N x y ,则有()()()()()()()22222122212290053900455690,3053,95425569.954k k k k k k k x x k k k x x k ⎧⎪∆=-+--+>⎪⎪-⎪+=⎨-⎪⎪-+⎪=⎪-⎩设点(),H x y ,由PM MH PN HN =,得112125353x x x x x x --=--. 整理得()()1212635100x x x x x x -+++=.1 将②③代入上式得()()()()()2222150569303553100954954k k x k k x k k -++--+=--.整理得()354150x k x --+=. ④①② ③16因为点H 在直线l 上,所以513y k x ⎛⎫-=- ⎪⎝⎭. ⑤ 联立④⑤消去k 得43120x y --=. 所以点H 恒在定直线43120x y --=上.(本题(3)只要求证明点H 恒在定直线43120x y --=上,无需求出x 或y 的范围.) 21.(本小题满分1)(本小题主要考查函数的单调性、函数的导数、函数的零点等知识,考查数形结合、化归与转化、分类与讨论的数学思想方法,以及运算求解能力、抽象概括能力与创新意识) 解:(1)因为()()221e x f x x x =-+,所以2()(22)e (21)e x x f x x x x '=-+-+()21e xx =-(1)(1)e x x x =+-. 当1x <-或1x >时,()0f x '>,即函数()f x 的单调递增区间为(),1-∞-和()1,+∞. 当11x -<<时,()0f x '<,即函数()f x 的单调递减区间为()1,1-.所以函数()f x 的单调递增区间为(),1-∞-和()1,+∞,单调递减区间为()1,1-. (2)假设函数()f x 在()1,+∞上存在“域同区间”[,](1)s t s t <<,由(1)知函数()f x 在()1,+∞上是增函数,所以(),().f s s f t t =⎧⎨=⎩ 即22(1)e ,(1)e .s ts s t t ⎧-⋅=⎨-⋅=⎩也就是方程2(1)e xx x -=有两个大于1的相异实根. 设2()(1)e (1)xg x x x x =-->,则2()(1)e 1xg x x '=--. 设()h x =2()(1)e 1xg x x '=--,则()()221e x h x x x '=+-.因为在(1,)+∞上有()0h x '>,所以()h x 在()1,+∞上单调递增. 因为()110h =-<,()223e 10h =->,即存在唯一的()01,2x ∈,使得()00h x =.当()01,x x ∈时,()()0h x g x '=<,即函数()g x 在()01,x 上是减函数; 当()0,x x ∈+∞时,()()0h x g x '=>,即函数()g x 在()0,x +∞上是增函数.因为()110g =-<,0()(1)0g x g <<,2(2)e 20g =->,爱迪教育 D 爱迪个性化教育发展中心D Idea Personalized Education Development C 17所以函数()g x 在区间()1,+∞上只有一个零点.这与方程2(1)e xx x -=有两个大于1的相异实根相矛盾,所以假设不成立. 所以函数()f x 在()1,+∞上不存在“域同区间”.。
江门市2014届高三调研测试理科数学试题及答案

图1江门市2014届高三调研测试理科数学一、选择题:本大题共8小题,每小题5分,满分40分.⒈已知集合{}21|<<-=x x A ,{}31|<<=x x B ,则=B A A .) 3 , 1(- B .) 2 , 1 ( C .] 3 , 1[- D .] 2 , 1 [ ⒉若复数 i m m m m )3()65(22-++- 是纯虚数( i 是虚数单位),则实数=m A .2=m B .3=m C .0=m D .2=m 或3=m ⒊已知平面向量)3 , ( -=λa ,)2 , 4( -=b ,若 b a ⊥,则实数=λ A .23-B .23C .6-D .6⒋已知点)2 , 1(A ,)1 , 2(B ,则线段AB 的垂直平分线的方程是A .03=-+y xB .01=+-y xC .0=-y xD .0=+y x ⒌设a 、R b ∈,若0|| <+b a ,则下列不等式中正确的是A .0>-b aB .033>+b aC .022<-b a D .0 <+b a⒍如图1,E 、F 分别是正方体1111D C B A ABCD -中1AD 、C B 1上的动点(不含端点),则四边形FDE B 1的俯视图可能是A .B .C .D .⒎已知函数⎪⎩⎪⎨⎧<-≥-=-,0 , 12,0 ,21)(x x x f x x,则该函数是A .偶函数,且单调递增B .偶函数,且单调递减C .奇函数,且单调递增D .奇函数,且单调递减⒏平面直角坐标系中,抛物线x y 212=与函数x y ln =图象的交点个数为 A .0 B .1 C .2 D .3二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分. (一)必做题(9~13题)⒐3log 2 2log 3(填“>”或“<” ). ⒑在ABC ∆中,3=c ,045=A ,075=B ,则=a .⒒若双曲线的渐近线方程为x y 3±=,它的一个焦点是)0 , 10(,则双曲线方程是 .BCMN1A 1B 1C ⒓若x ,y 满足约束条件⎪⎩⎪⎨⎧≤+≥+≥43430y x y x x ,则y x z -=的最大值是 .⒔若α、β是不重合的平面,a 、b 、c 是互不相同的空间直线,则下列命题中为真命题的是 .(写出所有真命题的序号) ① 若α//a ,α//b ,则b a // ② 若α//c ,α⊥b ,则b c ⊥ ③ 若α⊥c ,β//c ,则βα⊥④ 若α⊂b ,α⊂c 且b a ⊥,c a ⊥,则α⊥a (二)选做题(14、15题,考生只能从中选做一题)⒕直线x y =和抛物线2x y =所围成封闭图形的面积=S . ⒖在数列{}n a 中,11=a ,nn n a a a +=+11(*∈N n ),试归纳出这个数列的通项=n a .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. ⒗(本小题满分12分)已知1)2cos 2sin 3(2cos2)(-+=xx x x f ,R x ∈. ⑴ 求)(x f 的最小正周期;⑵ 设α、)2, 0(πβ∈,2)(=αf ,58)(=βf ,求)(βα+f 的值.⒘(本小题满分13分)如图2,直三棱柱111C B A ABC -中,CB CA ⊥,1==CB CA ,棱21=AA ,M 、N 分别是11B A 、A A 1的中点.⑴ 求证:⊥N C 1平面BCN ;⑵ 求直线C B 1与平面MN C 1所成角θ的正弦值.⒙(本小题满分13分)为配制一种药液,进行了三次稀释,先在体积为V 的桶中盛满纯药液,第一次将桶中药液倒出10升后用水补满,搅拌均匀第二次倒出8升后用水补满,然后第三次倒出10升后用水补满.⑴ 求第一次稀释后桶中药液的含量;⑵ 若第二次稀释后桶中药液含量不超过容积的60%,求V 的取值范围; ⑶ 在第⑵问的条件下,第三次稀释后桶中的药液能否达到容积的50%,为什么?⒚(本小题满分14分)如图3,椭圆Γ的中心在坐标原点O ,过右焦点)0 , 1(F 且垂直于椭圆对称轴的弦MN 的长为3.⑴ 求椭圆Γ的方程;⑵ 直线 l 经过点O 交椭圆Γ于P 、Q 两点,NQ NP =,求直线 l 的方程.⒛(本小题满分14分)已知正项等比数列{}n a (*∈N n ),首项31=a ,前n 项和为n S ,且33a S +、55a S +、44a S +成等差数列.图3⑴ 求数列{}n a 的通项公式; ⑵ 求数列{}n nS 的前n 项和n T .21(本小题满分14分)已知函数)()(b ax e x f x +=,曲线)(x f y =经过点)2 , 0(P ,且在点P 处的切线为l :24+=x y .⑴ 求常数a ,b 的值;⑵ 求证:曲线)(x f y =和直线 l 只有一个公共点;⑶ 是否存在常数k ,使得]1 , 2[--∈x ,)24()(+≥x k x f 恒成立?若存在,求常数k 的取值范围;若不存在,简要说明理由.参考答案一、选择题 BAAC DBCD二、填空题9.> 10.2 11.1922=-y x 12.0 13.②③(对1个3分,错1个2-分) 14.61 15.n 1三、解答题16.解:⑴x x x f cos sin 3)(+=……2分,)6sin(2π+=x ……4分,)(x f 的最小正周期π2=T ……5分⑵因为2)6sin(2=+πα,1)6sin(=+πα,3266ππαπ<+<……6分,所以26ππα=+,3πα=……7分,58)6sin(2=+πβ,54)6sin(=+πβ,3266ππβπ<+<……8分,因为2354<,所以266ππβπ<+<,53)6cos(=+πβ……9分,所以ββππβαβαcos 2)2sin(2)6sin(2)(=+=++=+f ……10分,6sin )6sin(26cos )6cos(2]6)6cos[(2ππβππβππβ+++=-+=……11分,5433+=……12分。
2014年高考理科数学广东卷-答案

所以 = = = = .
【提示】直接由等比数列的性质结合已知得到 ,然后利用对数的运算性质化简后得答案.
【考点】等比数列的性质,数列的前n项和,对数的运算
14.【答案】
【解析】曲线 即 ,故其直角坐标方程为: ,曲线 为 ,则其直角坐标方程为 ,所以两曲线的交点坐标为 .
【解析】由图1可得出样本容量为 .
抽取的高中生近视人数为 ,故选A.
【提示】根据图1可得总体个数,根据抽取比例可得样本容量,计算分层抽样的抽取比例,求得样本中的高中学生数,再利用图2求得样本中抽取的高中学生近视人数.
【考点】频率分布直方图,分层抽样
7.【答案】D
【解析】由 , ,将四条直线放入正方体中,如图所示, , , , 面 ,满足已知条件, 为平面 中的任意一条直线,即可得出结论, 的位置关系不确定.
由①②知,当 时, .
【提示】(Ⅰ)在数列递推式中取 得一个关系式,再把 变为 得另一个关系式,进而可求 ,然后把递推式中n取1,再结合 可求得 .
(Ⅱ)由(Ⅰ)中求得的 的值猜测出数列的一个通项公式,然后利用数学归纳法证明.
【考点】数列的项,数学归纳法求数列的通项公式
20.【答案】(Ⅰ)
(Ⅱ)
【解析】(Ⅰ)可知 ,又 ,
所以 ,
所以 .
(Ⅱ)由(Ⅰ)可知 ,
所以 ,
所以 ,
, .
又 ,
所以 ,
.
【提示】(Ⅰ)由函数 的解析式以及 ,求得 的值.
(Ⅱ)由(Ⅰ)可得 ,根据 ,求得 的值,再由 ,求得 的值,从而求得 的值.
【考点】三角函数求值,同角三角函数的基本关系
17.【答案】
(Ⅰ)由题意可得 =7, =2, =0.28, =0.08.
2014广东省广州市高考数学一模试卷(理科)(含解析)

2014年广东省广州市高考数学一模试卷(理科)一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知i 是虚数单位,若2(i)34i m +=-,则实数m 的值为( ).A .2-B .2±C .D .2【答案】A【解答】解:∵2(i)34i m +=-, ∴222i i 34i m m ++=-, 即22i 134i m m +-=-, ∴22413m m =-⎧⎨-=⎩,解得2m =-,故选A .2.(5分)在ABC △中,角A ,B ,C 所对的边分别为a ,b ,c ,若2C B =,则cb为( ). A .2sin CB .2cos BC .2sin BD .2cos C【答案】B【解答】解:在ABC △中, ∵2C B =,∴sin sin 22sin cos C B B B ==, 即2cos c b B =,则2cos cB b=. 故选B .3.(5分)圆22(1)(2)1x y -+-=关于直线y x =对称的圆的方程为( ).A .22(2)(1)1x y -+-=B .22(1)(2)1x y ++-=C .22(2)(1)1x y ++-=D .22(1)(2)1x y -++=【答案】A【解答】解:∵点(,)P x y 关于直线y x =对称的点为(,)P y x ', ∴(1,2)关于直线y x =对称的点为(2,1),∴圆22(1)(2)1x y -+-=关于直线y x =对称的圆的方程为22(2)(1)1x y -+-=. 故选A .4.(5分)若函数()f x R ,则实数a 的取值范围为( ).A .(2,2)-B .(,2)(2,)-∞-+∞UC .]([,22,)-∞-+∞UD .[]2,2-【答案】D【解答】解:函数()f x R , 则210x ax ++≥恒成立,即240a ∆=-≤,解得22a -≤≤,即实数a 的取值范围是[]2,2-,故选D . 5.(5分)某中学从某次考试成绩中抽取若干名学生的分数,并绘制成如图的频率分布直方图.样本数据分组为[5060),,[60,70),[70,80),[80,90),[90,100].若用分层抽样的方法从样本中抽取分数在[80,100]范围内的数据16个,则其中分数在[90,100]范围内的样本数据有( ).A .5个B .6个C .8个D .10个【答案】B【解答】解:由频率分布直方图知:抽取分数在[80,100]范围内的频率为(0.0250.015)100.4+⨯=, 又在[80,100]范围内的数据有16个,∴样本容量16400.4==个, ∵分数在[90,100]范围内的频率为0.015100.15⨯=, ∴在[90,100]范围内的频数为0.15406⨯=个. 故选B .6.(5分)已知集合{|A x x =∈Z 且3}2x∈-Z ,则集合A 中的元素个数为( ). A .2B .3C .4D .5【答案】C【解答】解:∵{|A x x =∈Z 且{}3}=1,1,3,52x∈--Z , ∴集合A 中的元素有4个. 答案C .7.(5分)设a r ,b r 是两个非零向量,则使||||a b a b ⋅=r r r r成立的一个必要非充分条件是( ).A .a b =r rB .a b r r ⊥C .(0)a b λλ=>r rD .a b r r ∥【答案】D【解答】解:∵a r ,b r 是两个非零向量,则||||a b a b ⋅=r r r r , ∴||||cos ,||||a b a b a b a b ⋅==r r r r r r r r ,∴cos ,1a b =r r,∴,0a b =r r. ∴a b r r ∥. a r ,b r 是两个非零向量,则使||||a b a b ⋅=r r r r成立的一个必要非充分条件是a b r r ∥.故选D . 8.(5分)设a ,b ,m 为整数(0)m >,若a 和b 被m 除得的余数相同,则称a 和b 对模m 同余,记为(mod )a b m ≡.若0122202020202020C C 2C 2C 2a =+⋅+⋅++⋅L ,(mod10)a b ≡,则b 的值可以是( ). A .2011 B .2012 C .2013 D .2014【答案】A【解答】解:∵0122202020202020C C 2C 2C 2a =+⋅+⋅++⋅L ,2020122202020202012312C 2C 2C +==++++L (),∴203a =.∵13个位是3,23个位是9,33个位是7,43个位是1,53个位是3,L ∴203个位是1,若(mod10)a b ≡,则b 的个位也是1.故选A .二、填空题:本大题共5小题,考生作答6小题,每小题5分,满分25分.(一)必做题(9~13题) 9.(5分)若不等式||1x a -<的解集为{}3|1x x <<,则实数a 的值为__________. 【答案】2【解答】解:∵||1x a -<, ∴11x a -<-<, ∴11a x a -<<+,∴不等式||1x a -<的解集为{}1|1x a x a -<<+, ∵不等式||1x a -<的解集为{}3|1x x <<, ∴11a -=且13a +=, 解得:2a =. 故答案为:2.10.(5分)执行如图的程序框图,若输出7S =,则输入*()k k ∈N 的值为__________.【答案】3【解答】解:由程序框图知,程序第一次运行1n =,11021S -=+=; 第二次运行112n =+=,1123S =+=; 第三次运行3n =,121227S =++=. ∵输出7S =,∴程序运行终止时3n =, 又不满足条件n k <时输出S , ∴3k =,故答案为:3. 11.(5分)一个四棱锥的底面为菱形,其三视图如图所示,则这个四棱锥的体积是__________.正主()视图侧左()视图俯视图【答案】4【解答】解:由三视图知几何体为四棱锥,且四棱锥的一条侧棱垂直于底面, 3, ∵底面为菱形,对角线互相垂直平分,∴底面面积124142S =⨯⨯⨯=,∴几何体的体积14343V =⨯⨯=.故答案为:4.12.(5分)设α为锐角,若π3cos 65α⎛⎫+= ⎪⎝⎭,则πsin 12α⎛⎫-= ⎪⎝⎭ __________.【解答】解:∵α为锐角,π3cos 65α⎛⎫+= ⎪⎝⎭为正数,∴π6α+是锐角,π4sin 65α⎛⎫+= ⎪⎝⎭,∴πππsin sin 1264αα⎡⎤⎛⎫⎛⎫-=+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,ππππsin cos cos sin 6464αα⎛⎫⎛⎫=+-+ ⎪ ⎪⎝⎭⎝⎭4355=-=,.13.(5分)在数列{}n a 中,已知11a =,111n n a a ++=-,记n S 为数列{}n a 的前n 项和,则2014S =__________. 【答案】20112-【解答】解:∵11a =,111n n a a ++=-, ∴212a =-,312112a =-=-⎛⎫-+ ⎪⎝⎭,411(2)1a =-=-+,512a =-,L∴数列{}n a 是以3为周期的数列, 又3123131222S a a a =++=--=-,∴20142013201432013201167111222S S a ⎛⎫=+=⨯-+=-+=- ⎪⎝⎭.故答案为:20112-.三、选做题(14~15题,考生只能从中选做一题)(坐标系与参数方程选做题) 14.(5分)在极坐标系中,直线(sin cos )a ρθθ-=与曲线2cos 4sin ρθθ=-相交于A ,B 两点,若||AB =a 的值为__________. 【答案】1-或5-【解答】解:直线(sin cos )a ρθθ-=即0x y a -+=;曲线2cos 4sin ρθθ=-即22cos 4sin ρρθρθ=-,即22 240x y x y ++=-,即22(1)(2)5x y -++=,表示以(1,2)C -设圆心到直线的距离为d ,则d再根据点到直线的距离公式可得d解得1a =-,或5a =-, 故答案为:1-或5-.(几何证明选讲选做题)15.如图,PC 是圆O 的切线,切点为C ,直线PA 与圆O 交于A 、B 两点,APC ∠的平分线分别交弦CA ,CB 于D ,E 两点,已知3PC =,2PB =,则PEPD的值为__________.【答案】2 3【解答】解:作直线CF,连结BF,∴CF PC⊥,∴90PCB BCF∠+∠=︒,∵CF是直径,∴90BCF F∠+∠=︒,∴PCB F∠=∠,∵F A∠=∠,∴PCB A∠=∠,∴PCB PAC△∽△,∴23 PC PBPA PC==,∵PCE PCB A∠=∠=∠,CPE APD∠=∠,∴PCE PAD△∽△,∴23 PE PCPD PA==.故答案为:23.四、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.16.(12分)已知函数()sin cosf x x a x=+的图象经过点π,03⎛⎫-⎪⎝⎭.(1)求实数a的值.(2)设2()()2[]g x f x=-,求函数()g x的最小正周期与单调递增区间.【答案】见解析.【解答】解:(1)∵函数()sin cos f x x a x =+的图象经过点π,03⎛⎫- ⎪⎝⎭,∴π03f ⎛⎫-= ⎪⎝⎭,即ππsin cos 033a ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭,即02a =,解得a(2)由(1)得()sin f x x x =. ∴2()()2[]g x f x =-2(sin )2x x =-22sin cos 3cos 2x x x x =++-2cos2x x +122cos22x x ⎫=+⎪⎪⎝⎭ ππ2sin 2cos cos2sin 66x x ⎛⎫=+ ⎪⎝⎭ π2sin 26x ⎛⎫=+ ⎪⎝⎭.∴函数的最小正周期为2ππ2=. ∵函数sin y x =的单调递增区间为ππ2π,2π()22k k k ⎡⎤-+∈⎢⎥⎣⎦Z ,令πππ2π22π262k x k -++≤≤,k ∈Z ,求得ππππ36k x k -+≤≤,∴函数的单调递增区间为πππ,π()36k k k ⎡⎤-+∈⎢⎥⎣⎦Z .17.(12分)甲,乙,丙三人参加某次招聘会,假设甲能被聘用的概率是25,甲,丙两人同时不能被聘用的概率是625,乙,丙两人同时能被聘用的概率是310,且三人各自能否被聘用相互独立.(1)求乙,丙两人各自能被聘用的概率.(2)设ξ表示甲,乙,丙三人中能被聘用的人数与不能被聘用的人数之差的绝对值,求ξ的分布列与均值(数学期望). 【答案】见解析.【解答】解:(1)记甲,乙,丙各自能被聘用的事件分别为1A ,2A ,3A , 由已知1A ,2A ,3A 相互独立,且满足113232()56[1()][1()]253()()10P A P A P A P A P A ⎧=⎪⎪⎪--=⎨⎪⎪=⎪⎩解得21()2P A =,33()5P A =. ∴乙,丙各自能被聘用的概率分别为12,35. (2)ξ的可能取值为1,3. ∵123123(3)()()P P A A A P ξ==+,123123)))[)][)][)(((1(1(1(]P A P A P A P A P A P A =+---213312525525=⨯⨯+⨯⨯ 625=. ∴619(1)1(3)12525P P ξξ==-==-=. ∴ξ的分布列为∵1963713252525E ξ=⨯+⨯=.18.(14分)如图,在棱长为a 的正方体1111ABCD A B C D -中,点E 是棱1D D 的中点,点F 在棱1B B 上,且满足12B F FB =. (1)求证:11EF AC ⊥.(2)在棱1C C 上确定一点G ,使A ,E ,G ,F 四点共面,并求此时1C G 的长. (3)求平面AEF 与平面ABCD 所成二面角的余弦值.D ABCE F A 1B 1D 1C 1【答案】见解析.【解答】(1)证明:连结11B D ,BD , ∵四边形1111A B C D 是正方形,∴1111B D AC ⊥.在正方体1111ABCD A B C D -中,∵1DD ⊥平面1111A B C D ,11AC ⊂平面1111A B C D , ∴111AC DD ⊥.∵1111B D DD D =I ,11B D ,1DD ⊂平面11BB D D , ∴11AC ⊥平面11BB D D . ∵EF ⊂平面11BB D D , ∴11EF AC ⊥.(2)解:以点D 为坐标原点,以DA ,DC ,1DD 所在的直线分别为x 轴,y 轴,z 轴, 建立如图的空间直角坐标系,则(,0,0)A a ,1,(0,)A a a ,10,(,)C a a ,10,0,2E a ⎛⎫ ⎪⎝⎭,1,,3F a a a ⎛⎫ ⎪⎝⎭,∴11(,,0)AC a a =-u u u u r ,1,,6EF a a a ⎛⎫=- ⎪⎝⎭u u u r . 设(0,,)G a h ,∵平面11ADD A ∥平面11BCC B ,平面11ADD A I 平面AEGF AE =, 平面11BCC B I 平面AEGF FG =,∴存在实数λ,使得FG AE λ=u u u r u u u r. ∵1,0,2AE a a ⎛⎫=- ⎪⎝⎭u u u r ,1,0,3FG a h a ⎛⎫=-- ⎪⎝⎭u u u r ,∴11,0,,0,32a h a a a λ⎛⎫⎛⎫--=- ⎪ ⎪⎝⎭⎝⎭.∴1λ=,56h a =.∴115166C G CC CG a a a =-=-=.∴当116C G a =时,A ,E ,G ,F 四点共面.(3)解:由(1)知1,0,2AE a a ⎛⎫=- ⎪⎝⎭u u u r ,10,,3AF a a ⎛⎫= ⎪⎝⎭u u u r .设(,,)n x y z =r是平面AEF 的法向量,则00n AE n AF ⎧⋅=⎪⎨⋅=⎪⎩r u u u r r u u u r,即102103ax az ay az ⎧-+=⎪⎪⎨⎪+=⎪⎩取6z =,则3x =,2y =-. 所以(3,2,6)n =-r是平面AEF 的一个法向量. 而1(0,0,)DD a =u u u u r是平面ABCD 的一个法向量,设平面AEF 与平面ABCD 所成的二面角为θ,则6cos 7θ==.故平面AEF 与平面PQ 所成二面角的余弦值为67.C 1D 1B 1A 1F EC B AD19.(14分)已知等差数列{}n a 的首项为10,公差为2,等比数列{}n b 的首项为1,公比为2,*n ∈N . (1)求数列{}n a 与{}n b 的通项公式.(2)设第n 个正方形的边长为{}min ,n n n C a b =,求前n 个正方形的面积之和n S .(注:{}min ,a b 表示a 与b 的最小值.) 【答案】见解析.【解答】解:(1)因为等差数列{}n a 的首项为10,公差为2,所以10(1)2n a n =+-⨯,即28n a n =+.因为等比数列{}n b 的首项为1,公比为2,所以112n n b -=⨯,即12n n b -=.(2)因为110a =,212a =,314a =,416a =,518a =,620a =,11b =,22b =,34b =,48b =,516b =,632b =.易知当5n ≤时,n n a b >.下面证明当6n ≥时,不等式n n b a >成立.方法1:①当6n =时,616623220268b a -==>=⨯+=,不等式显然成立.②假设当(6)n k k =≥时,不等式成立,即1228k k ->+.则有12222(28)2(1)8(26)2(1)8k k k k k k -=⨯+=++++>++>.这说明当1n k =+时,不等式也成立.综合①②可知,不等式对6n ≥的所有整数都成立.所以当6n ≥时,n n b a >.方法2:因为当6n ≥时112(28)(11)(28)n n n n b a n n ---=-+=+-+ 01211111(C C C C )(28)n n n n n n -----=++++-+L 012321111111(C C C C C C )(28)n n n n n n n n n n ---------+++++-+≥ 0121112(C C C )(28)n n n n ---=++-+ 236(4)(6)0n n n n n =-=-+->-, 所以当6n ≥时,n n b a >.所以5n ≤时,22222222123123n n nS c c c c b b b b =++++=++++L L 024222222n -=++++L1414n-=-1(41)3n =-. 当5n >时,2222123n nS c c c c =++++L , 22222212567()()n b b b a a a =+++++++L L 52221(41)464)(74()3[(])4n =-+++++++L 2223414678(67)1[(6(5))]n n n =+++++++++-L L222222[()(34141212532(67)64(]5))n n n =++++++++++++--L L L(1)(21)(6)(5)3414553264(5)62n n n n n n +++-⎡⎤=+-+⨯+-⎢⎥⎣⎦3242421867933n n n =++-. 综上可知,321(41),53424218679,533n n n S n n n n ⎧-⎪⎪=⎨⎪++->⎪⎩≤.20.(14分)已知双曲线222:1(0)4x y E a a -=>的中心为原点O ,左,右焦点分别为1F ,2F ,,点P 是直线23a x =上任意一点,点Q 在双曲线E 上,且满足220PF QF ⋅=u u u u r u u u u r . (1)求实数a 的值.(2)证明:直线PQ 与直线OQ 的斜率之积是定值.(3)若点P 的纵坐标为1,过点P 作动直线l 与双曲线右支交于不同两点M ,N ,在线段MN 上取异于点M ,N 的点H ,满足||||||||PM MH PN HN =,证明点H 恒在一条定直线上. 【答案】见解析.【解答】(1)解:设双曲线E 的半焦距为c ,由题意可得224c a c a ⎧=⎪⎨⎪=+⎩,解得a(2)证明:由(1)可知,直线2533a x ==,点2)(3,0F . 设点5,3P t ⎛⎫ ⎪⎝⎭,00)(,Q x y , 因为220PF QF ⋅=u u u u r u u u u r ,所以0053,(3,)03t x y ⎛⎫--⋅--= ⎪⎝⎭, 所以004(3)3ty x =-. 因为点00)(,Q x y 在双曲线E 上,所以2200154x y -=,即22004(5)5y x =-. 所以220000002200000044(5)(3)4535555333PQ OQ x x y t y y ty k k x x x x x x -----⋅=⋅===---. 所以直线PQ 与直线OQ 的斜率之积是定值45. (3)证明:设点(,)H x y ,且过点5,13P ⎛⎫ ⎪⎝⎭的直线l 与双曲线E 的右支交于不同两点11)(,M x y ,22)(,N x y ,则22114520x y -=,22224520x y -=,即22114(5)5y x =-,22224(5)5y x =-. 设||||||||PM MH PN HN λ==,则PM PN MH HNλλ⎧=⎪⎨=⎪⎩u u u u r u u u r u u u u r u u u u r . 即1122112255,1,133(,)(,)x y x y x x y y x x y y λλ⎧⎛⎫⎛⎫--=--⎪ ⎪ ⎪⎝⎭⎝⎭⎨⎪--=--⎩, 整理,得121212125(1)31(1)(1)x x y y x x x y y y λλλλλλλλ⎧-=-⎪⎪⎪-=-⎨⎪+=+⎪+=+⎪⎩①②③④由①×③,②×④得2221222212x x y y λλ⎧-=⎪⎨⎪-⎩将22114(5)5y x =-,22224(5)5y x =-代入⑥, 得2221224451x x y λλ-=⨯--.⑦ 将⑤代入⑦,得443y x =-. 所以点H 恒在定直线43120x y --=上.21.(14分)已知函数2()(21)e x f x x x -=+(其中e 为自然对数的底数). (1)求函数()f x 的单调区间.(2)定义:若函数()h x 在区间[](,)s t s t <上的取值范围为[],s t ,则称区间[],s t 为函数()h x 的“域同区间”.试问函数()f x 在(1,)+∞上是否存在“域同区间”?若存在,求出所有符合条件的“域同区间”;若不存在,请说明理由.【答案】见解析.【解答】解:(1)因为2()(21)e x f x x x -=+,所以22()(22)e (21)e (1)e (1)(1)e x x x x f x x x x x x x '=-++==+---. 当1x <-或1x >时,()0f x '>,即函数()f x 的单调递增区间为(,1)-∞-和(1,)+∞. 当11x -<<时,()0f x '<,即函数()f x 的单调递减区间为(1,1)-. 所以函数()f x 的单调递增区间为(,1)-∞-和(1,)+∞,单调递减区间为(1,1)-. (2)假设函数()f x 在(1,)+∞上存在“域同区间”,1)[](s t s t <<, 由(1)知函数()f x 在(1,)+∞上是增函数,所以()()f s s f t t =⎧⎨=⎩即22(1)e (1)e s t s s t t ⎧-⋅=⎪⎨-⋅=⎪⎩, 也就是方程2(1)e x x x -=有两个大于1的相异实根.设2()(1)e (1)x g x x x x --=>,则2()(1)e 1x g x x -'=-. 设2()()(1)e 1x h x g x x '==--,则2()(21)e x h x x x '=+-. 因为在(1,)+∞上有()0h x '>,所以()h x 在(1,)+∞上单调递增. 因为(1)10h =-<,2(2)3e 10h =->,即存在唯一的0(1,2)x ∈,使得0)(0h x =.当0)(1,x x ∈时,()()0h x g x '=<,即函数()g x 在0(1,)x 上是减函数; 当0(),x x ∈+∞时,()()0h x g x '=>,即函数()g x 在0(),x +∞上是增函数. 因为(1)10g =-<,0)((1)0g x g <<,2(2)e 20g =->, 所以函数()g x 在区间(1,)+∞上只有一个零点.这与方程2(1)e x x x -=有两个大于1的相异实根相矛盾,所以假设不成立. 所以函数()f x 在(1,)+∞上不存在“域同区间”.故答案为:(1)函数()f x 的单调递增区间为(,1)-∞-和(1,)+∞,单调递减区间为(1,1)-. (2)函数()f x 在(1,)+∞上不存在“域同区间”.。
2014广一模(理数)word试题·答案

广州市2014届普通高中毕业班综合测试(一)数学(理科)本试卷共4页,21小题, 满分150分.考试用时120分钟 注意事项:1.答卷前,考生务必用2B 铅笔在“考生号”处填涂考生号。
用黑色字迹钢笔或签字笔将自己所在的市、县/区、学校以及自己的姓名和考生号、试室号、座位号填写在答题卡上。
用2B 铅笔将试卷类型(A )填涂在答题卡相应位置上。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.作答选做题时,请先用2B 铅笔填涂选做题题号对应的信息点,再作答。
漏涂、错涂、多涂的,答案无效。
5.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
参考公式:锥体的体积公式Sh V 31=,其中S 是锥体的底面积,h 是锥体的高. ()()22221211236n n n n ++++++=()*n ∈N . 一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知i 是虚数单位,若()2i 34i m +=-,则实数m 的值为 A .2- B .2± C .2±D .22.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若2C B =,则c b为 A .2sin C B .2cos B C .2sin B D .2cos C3.圆()()22121x y -+-=关于直线y x =对称的圆的方程为A .()()22211x y -+-= B .()()22121x y ++-= C .()()22211x y ++-= D .()()22121x y -++= 4.若函数()21f x x ax =++的定义域为实数集R ,则实数a 的取值范围为A .()2,2-B .()(),22,-∞-+∞C .(][),22,-∞-+∞ D .[]2,2-5.某中学从某次考试成绩中抽取若干名学生的分数,并绘制成如图1的频率分布直方图.样本数据分组为[)50,60,[)60,70,[)70,80,[)80,90,[]90,100.若用分层抽样的方法从样本中抽取分数在[]80,100范围内的数据16个, 则其中分数在[]90,100范围内的样本数据有A .5个B .6个C .8个D .10个 6.已知集合32A x x x ⎧⎫=∈∈⎨⎬-⎩⎭Z Z 且,则集合A 中的元素个数为 A .2 B .3 C .4D .57.设a ,b 是两个非零向量,则使a b =a b 成立的一个必要非充分条件是 A .=a b B .⊥a b C .λ=a b()0λ> D .ab8.设a ,b ,m 为整数(0m >),若a 和b 被m 除得的余数相同,则称a 和b 对模m 同余,记为()mod a b m ≡.若0122202020202020C C 2C 2C 2a =+⋅+⋅++⋅,()mod10a b ≡,则b 的值可以是A .2011B .2012C .2013D .2014二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分. (一)必做题(9~13题)9.若不等式1x a -<的解集为{}13x x <<,则实数a 的值为 .10.执行如图2的程序框图,若输出7S =,则输入k ()*k ∈N 的值为 .11.一个四棱锥的底面为菱形,其三视图如图3所示,则这个四棱锥的体积是 .11 正(主)视图 侧(左)视图图3俯视图452 2图2开始 结束输入k否 是输出S 1n n =+?n k < 0,0n S ==log y x =12n S S -=+图1分数频率/组距50 60 70 80 90 100 0.0100.015 0.020 0.025 0.030 012.设α为锐角,若3cos 65απ⎛⎫+= ⎪⎝⎭,则sin 12απ⎛⎫-= ⎪⎝⎭ .13.在数列{}n a 中,已知11a =,111n n a a +=-+,记n S 为数列{}n a 的前n 项和,则2014S = .(二)选做题(14~15题,考生只能从中选做一题) 14.(坐标系与参数方程选做题)在极坐标系中,直线()sin cos a ρθθ-=与曲线2cos 4sinρθθ=-相交于A ,B 两点,若AB =23,则实数a 的值为 .15.(几何证明选讲选做题)如图4,PC 是圆O 的切线,切点为C ,直线PA 与圆O 交于A ,B 两点,APC ∠的平分线分别交弦CA ,CB 于D ,E两点,已知3PC =,2PB =,则PEPD的值为 .题号 1 23 4 5 67 8答案 A B A D B C D A二、填空题:本大题考查基本知识和基本运算,体现选择性.共7小题,每小题,满分30分.其中14~15题是选做题,考生只能选做一题.题号 9 10 11 12131415答案23421020112-1-或5-23PEABC D 图4O。
2014广州一模高三理科数学答题情况分析
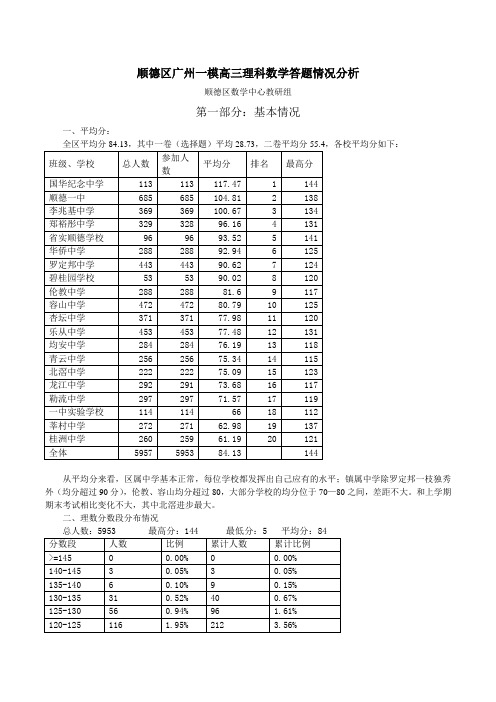
顺德区广州一模高三理科数学答题情况分析顺德区数学中心教研组第一部分:基本情况一、平均分:全区平均分84.13,其中一卷(选择题)平均28.73,二卷平均分55.4,各校平均分如下:班级、学校总人数参加人数平均分排名最高分国华纪念中学113 113 117.47 1 144顺德一中685 685 104.81 2 138李兆基中学369 369 100.67 3 134郑裕彤中学329 328 96.16 4 131省实顺德学校96 96 93.52 5 141华侨中学288 288 92.94 6 125罗定邦中学443 443 90.62 7 124碧桂园学校53 53 90.02 8 120伦教中学288 288 81.6 9 117容山中学472 472 80.79 10 125杏坛中学371 371 77.98 11 120乐从中学453 453 77.48 12 131均安中学284 284 76.19 13 118青云中学256 256 75.34 14 115北滘中学222 222 75.09 15 123龙江中学292 291 73.68 16 117勒流中学297 297 71.57 17 119一中实验学校114 114 66 18 112莘村中学272 271 62.98 19 137桂洲中学260 259 61.19 20 121全体5957 5953 84.13 144从平均分来看,区属中学基本正常,每位学校都发挥出自己应有的水平;镇属中学除罗定邦一枝独秀外(均分超过90分),伦教、容山均分超过80,大部分学校的均分位于70—80之间,差距不大。
和上学期期末考试相比变化不大,其中北滘进步最大。
二、理数分数段分布情况总人数:5953 最高分:144 最低分:5 平均分:84分数段人数比例累计人数累计比例>=145 0 0.00% 0 0.00%140-145 3 0.05% 3 0.05%135-140 6 0.10% 9 0.15%130-135 31 0.52% 40 0.67%125-130 56 0.94% 96 1.61%120-125 116 1.95% 212 3.56%115-120 207 3.48% 419 7.04%110-115 275 4.62% 694 11.66%105-110 415 6.97% 1109 18.63%100-105 496 8.33% 1605 26.96%95-100 585 9.83% 2190 36.79%90-95 552 9.27% 2742 46.06%85-90 489 8.21% 3231 54.28%80-85 527 8.85% 3758 63.13%75-80 399 6.70% 4157 69.83%70-75 365 6.13% 4522 75.96%65-70 316 5.31% 4838 81.27%60-65 250 4.20% 5088 85.47%55-60 177 2.97% 5265 88.44%50-55 158 2.65% 5423 91.10%45-50 133 2.23% 5556 93.33%40-45 101 1.70% 5657 95.03%35-40 92 1.55% 5749 96.57%30-35 63 1.06% 5812 97.63%<30 141 2.37% 5953 100.00%三、全区前十名:姓名班级学校理数名次孙鹏程 1 国华纪念中学144 1高雅玉洁 5 省实顺德学校141 2张逸凡 1 国华纪念中学140 3王健 3 国华纪念中学138 4钟秋宇 3 顺德一中138 5康国强 1 国华纪念中学137 6王鹤燃 1 国华纪念中学137 7罗泳妍12 莘村中学137 8吴文灿 1 国华纪念中学135 9张闳一 1 国华纪念中学134 10 前十名中,国华有7人,一中、省实、莘村各1人第二部分:学生答题情况一、选择题:题号答案平均分得分率选A率% 选B率% 选C率% 选D率%单选1 A 4.77 95.35 95.35 1.62 0.44 2.54 单选2 B 4.37 87.46 4.85 87.46 5.16 2.43 单选3 A 4.67 93.5 93.5 2.48 1.79 2.11 单选4 D 3.44 68.74 5.95 3.15 22.09 68.74 单选5 B 4.83 96.7 0.54 96.7 1.08 1.63 单选6 C 2.68 53.67 22.41 18.86 53.67 4.92单选7 D 2.24 44.73 17.9 8.21 28.99 44.73 单选8A 1.81 36.27 36.27 8.53 23.49 31.31从上表可以看出,选择题中第4、6、7、8得分率较低。
2014年广东省高考数学试卷(理科)答案与解析

2014年广东省高考数学试卷(理科)参考答案与试题解析一、选择题:本小题共8小题,每小题5分,共40分.z===3 3.(5分)(2014•广东)若变量x,y满足约束条件,且z=2x+y的最大值和最小,解得,,解得,4.(5分)(2014•广东)若实数k满足0<k<9,则曲线﹣=1与曲线﹣=1﹣=1﹣=15.(5分)(2014•广东)已知向量=(1,0,﹣1),则下列向量中与成60°夹角的是()解:不妨设向量为.若==,不满足条件..若==.若=,不满足条件..若==6.(5分)(2014•广东)已知某地区中小学学生的近视情况分布如图1和图2所示,为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为(),7.(5分)(2014•广东)若空间中四条两两不同的直线l1,l2,l3,l4,满足l1⊥l2,l2⊥l3,l3⊥l4,8.(5分)(2014•广东)设集合A={(x1,x2,x3,x4,x5)|x i∈{﹣1,0,1},i={1,2,3,+二、填空题:本大题共5小题,考生作答6小题,每小题5分,满分25分.(一)必做题(9~13题)9.(5分)(2014•广东)不等式|x﹣1|+|x+2|≥5的解集为(﹣∞,﹣3]∪[2,+∞).,可得10.(5分)(2014•广东)曲线y=e﹣5x+2在点(0,3)处的切线方程为y=﹣5x+3..11.(5分)(2014•广东)从0,1,2,3,4,5,6,7,8,9中任取七个不同的数,则这七个数的中位数是6的概率为.中任取七个不同的数,有种方法,不同的数即可,有=故答案为:.12.(5分)(2014•广东)在△ABC中,角A,B,C所对应的边分别为a,b,c,已知bcosC+ccosB=2b,则=2.=213.(5分)(2014•广东)若等比数列{a n}的各项均为正数,且a10a11+a9a12=2e5,则lna1+lna2+…lna20=50.=(二)、选做题(14~15题,考生只能从中选作一题)【坐标系与参数方程选做题】14.(5分)(2014•广东)在极坐标系中,曲线C1和C2的方程分别为ρsin2θ=cosθ和ρsinθ=1,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,则曲线C1和C2交点的直角坐标为(1,1).【几何证明选讲选做题】15.(2014•广东)如图,在平行四边形ABCD中,点E在AB上且EB=2AE,AC与DE交于点F,则=9.可得=.∴=∴(三、解答题:本大题共6小题,满分80分,解答须写出文字说明、证明过程或演算步骤. 16.(12分)(2014•广东)已知函数f(x)=Asin(x+),x∈R,且f()=.(1)求A的值;(2)若f(θ)+f(﹣θ)=,θ∈(0,),求f(﹣θ).),求得sin)﹣x+(+)=A=A=sin)sin+=2sin cos= =).(=﹣+==.17.(13分)(2014•广东)随机观测生产某种零件的某工作厂25名工人的日加工零件个数(单位:件),获得数据如下:30,42,41,36,44,40,37,37,25,45,29,43,31,36,49,34,33,43,38,42,32,34,46,39,36.根据上述数据得到样本的频率分布表1212(2)根据上述频率分布表,画出样本频率分布直方图;(3)根据样本频率分布直方图,求在该厂任取4人,至少有1人的日加工零件数落在区间(30,35]的概率.为事件的概率为=,),的概率为.18.(13分)(2014•广东)如图,四边形ABCD为正方形.PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD,交PD于点E.(1)证明:CF⊥平面ADF;(2)求二面角D﹣AF﹣E的余弦值.PD=AF=,,又∴EF=CD=,(,(=,∴,∴=,的一个法向量为(<>=19.(14分)(2014•广东)设数列{a n}的前n项和为S n,满足S n=2na n+1﹣3n2﹣4n,n∈N*,且S3=15.(1)求a1,a2,a3的值;(2)求数列{a n}的通项公式.,,∴20.(14分)(2014•广东)已知椭圆C:+=1(a>b>0)的右焦点为(,0),离心率为.(1)求椭圆C的标准方程;(2)若动点P(x0,y0)为椭圆C外一点,且点P到椭圆C的两条切线相互垂直,求点P 的轨迹方程.)依题意知+++21.(14分)(2014•广东)设函数f(x)=,其中k<﹣2.(1)求函数f(x)的定义域D(用区间表示);(2)讨论函数f(x)在D上的单调性;(3)若k<﹣6,求D上满足条件f(x)>f(1)的x的集合(用区间表示).>x+1>解得﹣<,即﹣1+综上函数的定义域为(﹣)x+1+)﹣或﹣1+﹣1+﹣x+1+)1+1+)∈﹣1+1+)﹣1+。
高三数学一模考试总结分析

高三数学一模考试总结分析高三数学一模考试总结一一、试卷分析作为高三开学后的第一次一模考试,本试卷整体结构及难度分布合理,贴近全国卷试题,着重考查基础知识、基本技能、基本方法(包括基本运算)和数学基本思想,对重点知识作了重点考查,主要检测学生对基本知识的掌握以及解题的一些通性通法。
试题力求创新。
理科和文科试题中有不少新题。
这些题目,虽然素材大都源于教材,但并不是对教材的原题照搬,而是通过提炼、综合、改编新创为另一个全新的题目出现,使考生感到似曾相似但又必须经过自己的独立分析思考才能解答。
二、答卷分析通过本次阅卷的探讨和本人对试卷的分析,学生在答卷中存在的主要问题有一下几点:1、客观题本次考试在考查基础知识的同时,注重考查能力,着重加强对分析分问题和解决问题能力的考查,送分题几乎没有,加大了对知识综合能力与理性思维能力的考察,对于我们这类学生答题比较吃力,客观题得分较低,导致总分低。
2.基础知识不扎实,基本技能和方法掌握不熟练.3.审题不到位,运算能力差,书写不规范.审题不到位在的第18题表现的较为明显。
这是一道概率题,由于审题不到位致使将概率模型搞错、在(Ⅰ)问中学生出现结果重复与遗漏的现象严重导致后面全错,还有不会应用数学语言,表达五花八门。
在考生的试卷中,因审题不到位、运算能力差等原因导致的书写不规范问题到处可见.4.综合能力不够,运用能力欠佳.第21题为例,这道题是导数问题(Ⅰ)求单调区间,(Ⅱ)求恒成立问题(Ⅲ)最值问题"由于学生综合运用能力较弱,致使考生不知如何分类讨论,或考虑问题不全面,导致解题思路受阻。
绝大部分学生几乎白卷。
5.心态不好,应变能力较弱.考试本身的巨大压力,考生信心不足,造成考生情绪紧张,缺乏冷静,不能灵活应变,会而不对、对而不全,甚至会而不得分的情形常可见到三、教学建议后阶段的复习,特别是第二轮复习具有承上启下,知识系统化、条理化的作用,是促进学生素质、能力发展的关键时期,因而对讲练、检测等要求较高,如何才能在最后阶段充分利用有限的时间,取得满意的效果?从这次的检测结果来看:1、研读考纲和说明,明确复习方向认真研读考试大纲和考试说明,关注考试的最新动向,不做无用功,弄清了“不考什么”后,还要弄清“考什么”,做到“有备无患”。
2014年高考广东理科数学试题及答案(word解析版)

2014年高考广东理科数学试题及答案(word解析版)2014年普通高等学校招生全国统一考试(广东卷)数学(理科)一、选择题:本大题共8小题,每小题5分,满分40分,在每小题给出的四个选项中,只有一项是符合题目要求的. (1)【2014年广东,理1,5分】已知集合{1,0,1}M =-,{0,1,2}N =,则M N =U ( ) (A ){1,0,1}- (B ){1,0,1,2}- (C ){1,0,2}- (D ){0,1} 【答案】B【解析】{1,0,1,2}M N =-U ,故选B . (2)【2014年广东,理2,5分】已知复数z 满足(34i)25z +=,则z =( ) (A )34i - (B )34i + (C )34i -- (D )34i -+ 【答案】A【解析】2525(34i)25(34i)=34i 34i (34i)(34i)25z --===-++-,故选A . (3)【2014年广东,理3,5分】若变量,x y 满足约束条件121y xx y z x y y ≤⎧⎪+≤=+⎨⎪≥-⎩且的最大值和最小值分别为M 和m ,则M m -=( ) (A )8 (B )7 (C )6 (D )5 【答案】C 【解析】画出可行域,易知在点(2,1)与(1,1)--处目标函数分别取得最大值3M =,与最小值3m =-,6M m ∴-=,故选C .(4)【2014年广东,理4,5分】若实数k 满足09k <<,则曲线221259x y k-=-与曲线221259x y k -=-的( ) (A )离心率相等 (B )虚半轴长相等 (C )实半轴长相等 (D )焦距相等 【答案】D【解析】09k <<Q ,90k ∴->,250k ->,从而两曲线均为双曲线,又25(9)34(25)9k k k +-=-=-+,两双曲线的焦距相等,故选D .(5)【2014年广东,理5,5分】已知向量()1,0,1a =-,则下列向量中与a 成60︒夹角的是( ) (A )()1,1,0- (B )()1,1,0- (C )()0,1,1- (D )()1,0,1- 【答案】B【解析】2222221210(1)1(1)0=++-⋅+-+,即这两向量的夹角余弦值为12,从而夹角为060,故选A . (6)【2014年广东,理6,5分】已知某地区中小学生人数和近视情况分别如图1和图2所示,为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为( ) (A )200,20 (B )100,20 (C )200,10 (D )100,10 【答案】A【解析】样本容量为(350045002000)2%200++⋅=,抽取的高中生近视人数为:20002%50%20⋅⋅=,故选A .(7)【2014年广东,理7,5分】若空间中四条两两不同的直线1234,,,l l l l ,满足12l l ⊥,23l l ⊥,34l l ⊥则下列结论一定正确的是( )(A )14l l ⊥ (B )14//l l (C )14,l l 既不垂直也不平行 (D )14,l l 的位置关系不确定 【答案】D【解析】平面中的四条直线,14l l ⊥,空间中的四条直线,位置关系不确定,故选D .(8)【2014年广东,理8,5分】设集合(){}12345=,,,,{1,0,1},1,2,3,4,5iA x x x x x x i ∈-=,那么集合A 中满足条件“1234513x x x x x ≤++++≤”的元素个数为( )(A )60 (B )90 (C )120 (D )130 【答案】D【解析】12345x x x x x ++++可取1,2,3,和为1的元素个数为:1125C 10C =;和为2的元素个数为:122255C 40C A +=;和为3的元素个数为:1311225254C C C 80C C +=,故满足条件的元素总的个数为104080130++=,故选D .二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分.(一)必做题(9~13) (9)【2014年广东,理9,5分】不等式125x x -++≥的解集为 .【答案】(][),32,-∞-+∞U【解析】数轴上到1与2-距离之和为5的数为3-和2,故该不等式的解集为:(][),32,-∞-+∞U . (10)【2014年广东,理10,5分】曲线52xy e -=+在点(0,3)处的切线方程为 .【答案】530x y +-=【解析】'55xy e -=-,'5x y =∴=-,∴所求切线方程为35y x -=-,即530x y +-=.(11)【2014年广东,理11】,5分从0,1,2,3,4,5,6,7,8,9中任取七个不同的数,则这七个数的中位数是6的概率为 . 【答案】16【解析】要使6为取出的7个数中的中位数,则取出的数中必有3个不大于6,另外3个不小于6,故所求概率为3671016C C=. (12)【2014年广东,理12,5分】在ABC ∆中,角,,A B C 所对应的边分别为,,a b c ,已知cos cos 2b C c B b +=,则a b = . 【答案】2【解析】解法一:由射影定理知cos cos b C c B a +=,从而2a b =,2ab ∴=. 解法二:由上弦定理得:sin cos sin cos 2sin B C C B B +=,即sin()2sin B C B +=,sin 2sin A B ∴=,即2a b =,2ab ∴=. 解法三:由余弦定理得:222222222a b c a c b b bab ac+-+-⋅+=,即224a ab=,2a b ∴=,即2ab =.(13)【2014年广东,理13,5分】若等比数列{}na 的各项均为正数,且510119122a a a a e +=,则1220ln ln ln a a a +++=L L .【答案】50【解析】1011912a a a a =Q ,51011a a e ∴=,设1220ln ln ln S a a a =+++L ,则20191ln ln ln S a a a =+++L , 51201011220ln 20ln 20ln 100S a a a a e ∴====,50S ∴=.(二)选做题(14-15题,考生只能从中选做一题)(14)【2014年广东,理14,5分】(坐标系与参数方程选做题)在极坐标系中,曲线1C 和2C 的方程分别为2sin cos ρθθ=和sin 1ρθ=,以极点为平面直角坐标系的原点,极轴为x 轴的正半轴,建立平面直角坐标系,则曲线1C 和2C 的交点的直角坐标为 .【答案】(1,1)【解析】1C 即2(sin )cos ρθρθ=,故其直角坐标方程为:2y x =,2C 的直角坐标系方程为:1y =,1C ∴与2C 的交点的直角坐标为(1,1).(15)【2014年广东,理15,5分】(几何证明选讲选做题)如图3,在平行四边形ABCD 中,点E 在AB 上且2EB AE =,AC 与DE 交于点,则CDF AEF ∆=∆的面积的面积. 【答案】9【解析】显然CDF AEF ∆∆:,∴22()()9CDF CDEB AE AEF AEAE∆+===∆的面积的面积.三、解答题:本大题共6题,共80分.解答应写出文字说明,证明过程或演算步骤. (16)【2014年广东,理16,12分】已知函数()sin(),4f x A x x R π=+∈,且53()122f π=. (1)求A 的值;(2)若3()()2f f θθ+-=,(0,)2πθ∈,求3()4f πθ-. 解:(1)5523()sin()sin 1212432f A A ππππ=+==,3323A ∴=⋅=. (2)由(1)得:()3sin()4f x x π=+,()()3sin()3sin()44f f ππθθθθ∴+-=++-+33(sin cos cos sin )3(sin()cos cos()sin )23cos sin 6cos 444442πππππθθθθθθ=++-+-===,6cos θ∴=,(0,)2πθ∈Q ,10sin θ∴=,331030()3sin()3sin()3sin 3444f πππθθπθθ∴-=-+=-==⨯=.(17)【2014年广东,理17,12分】随机观测生产某种零件的某工厂25名工人的日加工零件数(单位:件),获得数据如下:30,42,41,36,44,40,37,37,25,45,29,43,31,36,49,34,33,43,38,42,32,34,46,39,36.根据上述数据得到样本的频率分布表如下:分组 频数 频率 [25,30] 3 0.12 (30,35] 5 0.20 (35,40] 8 0.32 (40,45] 1n 1f (45,50] 2n 2f(1)确定样本频率分布表中121,,n n f 和2f 的值;(2)根据上述频率分布表,画出样本频率分布直方图;(3)根据样本频率分布直方图,求在该厂任取4人,至少有1人的日加工零件数落在区间(]30,35的概率.解:(1)17n =,22n =,170.2825f ==,220.0825f ==. (2)频率分布直方图如下所示:(3)根据频率分布直方图,可得工人们日加工零件数落在区间(]30,35的概率为0.2,设日加工零件数落在区间(]30,35的人数为随机变量ξ,则(4,0.2)B ξ:,故4人中,至少有1人的日加工零件数落在区间(]30,35 的概率为:0441(0.2)(0.8)10.40960.5904C -=-=.(18)【2014年广东,理18,14分】如图4,四边形ABCD 为正方形,PD ⊥平面ABCD ,30DPC ∠︒=,AF PC ⊥于点F ,//FE CD ,交PD 于点E . (1)证明:CF ⊥平面ADF ;(2)求二面角D AF E --的余弦值. 解:(1)PD ⊥平面ABCD ,PD PCD ⊂,∴平面PCD ⊥平面ABCD ,平面PCD I 平面ABCD CD =,AD ⊂平面ABCD ,AD CD ⊥,AD ∴⊥平面PCD ,CF ⊂平面PCD ,CF AD ∴⊥,又AF PC ⊥,CF AF ∴⊥,,AD AF ⊂平面ADF ,AD AF A =I ,CF ∴⊥平面ADF .(2)解法一:过E 作//EG CF 交DF 于G ,CF ⊥Q 平面ADF ,EG ∴⊥平面ADF ,过G 作GH AF ⊥于H ,连EH则EHG ∠为二面角D AF E --的平面角,设2CD =,030DPC ∠=Q ,30CDF ∴∠=,从而1==12CF CD , 4CP =,EF DC Q ∥,DE CFDP CP∴=,即12=223,3DE ∴=,还易求得32EF =,3DF =,从而3332243DE EF EG DF ⋅⋅===,易得19AE =,7AF =,32EF =,19331922747AE EF EH AF ⋅⋅∴===,故22319363()()44747HG =-=,6347257cos 47319GH EHG EH ∴∠==⋅=.解法二:分别以DP ,DC ,DA 为x ,y ,z 轴建立空间直角坐标系,设2DC =,则(0,0,2)A ,(0,2,0)C ,(23,0,0)P ,设CF CP λ=u u u r u u u r ,则(23,22,0)F λλ-,DF CF ⊥u u u r u u u r Q ,可得14λ=,从而33(,0)2F ,易得 3(E ,取面ADF 的一个法向量为11(3,1,0)2n CP ==-u u r u u u r,设面AEF的一个法向量为2(,,)nx y z =u u r, 利用20n AE ⋅=u u r u u u r ,且20n AF ⋅=u u r u u u r ,得2n u u r可以是3),从而二面角的余弦值为121243257||||219n n n n ⋅==⋅⨯u u r u u r u u r u u u r . (19)【2014年广东,理19,14分】设数列{}na 的前n 和为nS ,满足2*1234,n n S na n n n N +=--∈,且315S =. (1)求123,,a a a 的值;(2)求数列{}na 的通项公式.解:(1)211222314127a S a a ==-⨯-⨯=- ①2122331212+=432424()204(15)20a a S a S a a a a =-⨯-⨯=---=---,12+8a a ∴= ②联立①②解得1235a a =⎧⎨=⎩,33121587a S a a ∴=--=-=,综上13a =,25a =,37a =.(2)21234nn Sna n n +=-- ③ ∴当2n ≥时,212(1)3(1)4(1)n n Sn a n n -=----- ④-③④并整理得:1216122n n n n aa n n+-+=+,由(1)猜想21nan =+,以下用数学归纳法证明:(ⅰ)由(1)知,当1n =时,13211a ==⨯+,猜想成立; (ⅱ)假设当n k =时,猜想成立,即21ka k =+,则当1n k =+时,212161211411(21)33232(1)1222222k k k k k k a a k k k k k k k k k+-+--=+=⋅+++=++=+=++,这就是说1n k =+时,猜想也成立,从而对一切n N *∈,21na n =+.(20)【2014年广东,理20,14分】已知椭圆2222:1(0)xy C a b ab+=>>的一个焦点为(5,0)5.(1)求椭圆C 的标准方程;(2)若动点0(,)P x y 为椭圆外一点,且点P 到椭圆C 的两条切线相互垂直,求点P 的轨迹方程.解:(1)5c =,55c e a ==3a ∴=,222954b a c =-=-=,∴椭圆C 的标准方程为:22194x y +=.(2)若一切线垂直x 轴,则另一切线垂直于y 轴,则这样的点P 共4个,它们的坐标分别为(3,2)-±,(3,2)±.若两切线不垂直与坐标轴,设切线方程为()y y k x x -=-,即0()y k x x y =-+,将之代入椭圆方程22194x y+=中并整理得:222(94)18()9()40k x k y kx x y kx ⎡⎤++-+--=⎣⎦,依题意,0∆=,即222200(18)()36()4(94)0k y kx y kx k ⎡⎤----+=⎣⎦,即224()4(94)0y kx k--+=, 2220000(9)240x k x y k y ∴--+-=,Q 两切线相互垂直,121k k∴=-,即2020419y x -=--,220013xy ∴+=,显然(3,2)-±,(3,2)±这四点也满足以上方程,∴点P 的轨迹方程为2213x y +=.(21)【2014年广东,理21,14分】设函数222()(2)2(2)3f x x x k x x k =+++++-2k <-.(1)求函数()f x 的定义域D (用区间表示);(2)讨论()f x 在区间D 上的单调性;(3)若6k <-,求D 上满足条件()(1)f x f >的x 的集合(用区间表示).解:(1)222(2)2(2)30x x k x x k +++++->,则221x x k ++> ① 或 223x x k ++<- ②由①得:2210x x k ++->,144(1)4(2)0k k ∆=--=->(2)k <-Q , ∴方程2210x x k ++-=的解为12k --,∴由2210x x k ++->得12x k <--12x k >--由②得2230x x k +++<,方程2230x x k +++=的判别式244(3)4(2)0k k ∆=-+=-->(2)k <-Q ,∴该方程的解为12k ---,由2230x x k +++<得1212k x k ----<-+--2k <-Q ,121211212k k k k ∴--<-----<-----(,12)(12,12)(12,)D k k k k ∴=-∞--------+---+-+∞U U .(2)设222(2)2(2)30u x x k x x k +++++->, 则3'221()2(2)(22)2(22)2f x u x x k x x -⎡⎤=-⋅⋅++⋅+++⎣⎦ 3222(1)(21)u x x x k -=-+⋅+++, (ⅰ)当(,12)x k ∈-∞--时,10x +<,221110x x k +++>+>,'()0f x ∴>;(ⅱ)当(12,1)x k ∈-----时,10x +<,221310x x k +++<-+<,'()0f x ∴<; (ⅲ)当(1,12)x k ∈--+--时,10x +>,221310x x k +++<-+<,'()0f x ∴>; (ⅳ)当(12,)x k ∈-+-+∞时,10x +>,221110x x k +++>+>,'()0f x ∴<. 综上,()f x 在D 上的单调增区间为:(,12),(1,12)k k -∞-----+--,()f x 在D 上的单调减区间为:(12,1),(12,)k k -----+-+∞.(3)设222(x)(2)2(2)3g x x k x x k =+++++-,由(1)知,当x D ∈时,()0g x >; 又2(1)(3)2(3)3(6)(2)g k k k k =+++-=++,显然,当6k <-时,(1)0g >, 从而不等式()(1)()(1)f x f g x g >⇔<,2222()(1)[(2)2(2)3][(3k)2(3)3]g x g x x k x x k k -=+++++--+++-22222[(2)(3k)]2[(2)(3)](3)(1)(225)x x k x x k k x x x x k =++-++++-+=+-+++,6k <-, 1421212311212142k k k k k k ∴--------<-<<----+--+--(ⅰ)当12x k <--时,(3)(1)0x x +->,∴欲使()(1)f x f >,即()(1)g x g <,亦即22250x x k +++<,即142142k x k ---<<---14212k x k ∴---<---(ⅱ)123k x ---<-时,(3)(1)0x x +->,22225(2)(5)3(5)0x x k x x k k k +++=++++<-++<,此时()(1)g x g <,即()(1)f x f >;(ⅲ)31x -<<时,(3)(1)0x x +-<,22253(5)0x x k k +++<-++<()(1)g x g ∴>不合题意;(ⅳ)112x k <<-+--时,(3)(1)0x x +->,22253(5)0x x k k +++<-++<,()(1)g x g ∴<,不合题意;(ⅴ)12x k >--时,(3)(1)0x x +->,∴欲使()(1)g x g <,则22250x x k +++<,即142142k x k ---<<---,从而12142k x k --<-+--.综上所述,()(1)f x f >的解集为: (()()(142,1212,31,1212,142k k k k k k ----------+-----+--U U U .。
2014届江门市高考模拟考试一模理科数学

1A BCDE1A 1B 1C 1D 2图江门市2014年高考模拟考试数学(理科)本试卷共4页,21小题,满分150分,考试用时120分钟。
参考公式:锥体的体积公式Sh V 31=,其中S 是锥体的底面积,h 是锥体的高. 如果事件A 、B 互斥,那么)()()(B P A P B A P +=+.符合题目要求的.1.在复平面内,复数i z 21+-=( i 是虚数单位)对应的点在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限2.从2、3、5、7这四个质数中任取两个相乘,可以得到不相等的积的个数是( ) A .4 B .5 C .6 D .83.已知函数)(x f 为奇函数,且当0<x 时,x x x f 2)(2+=,则=)1(f ( ) A .1 B .1- C .3 D .3- 4.将甲、乙两个篮球队10场比赛的得分数据整理成如图1所示的茎叶图,由图1可知( )A .甲、乙两队得分的平均数相等B .甲、乙两队得分的中位数相等C .甲、乙两队得分的极差相等D .甲、乙两队得分在) 39 , 30 [分数段的频率相等5.在平面直角坐标系xOy 中,已知) , 1(t -=,)2 , 2(=,若090=∠ABO ,则=t ( ) A .2 B .4 C .5 D .86.已知两条不重合直线1 l 、2l 的斜率分别为1 k 、2k ,则“21//l l ”是“21k k =”成立的( ) A .充分非必要条件 B .必要非充分条件 C .非充分非必要条件 D .充要条件 7.如图2,在正方体1111D C B A ABCD -中,E 是棱1CC 的中点,F 是侧面11BCC B 上的动点,并且//1F A 平面1AED ,则动点F 的轨迹是( )A .圆B .椭圆C .抛物线D .线段8.设函数2sin )(-+=x x x f ,2ln )(-+=x e x g x ,若实数a ,b 满足0)(=a f ,0)(=b g ,则( )A .)(0)(b f ag << B .)(0)(a g b f << C .)()(0b f a g << D .0)()(<<a g b f2二、填空题:本大题共7小题,考生作答6小题,每小题5(一)必做题(9~13题)9.已知命题p :R x ∈∀,0222>++x x .则命题p 的否定p ⌝: . 10.执行如图3的程序框图,输出的=S . 11.定积分=⎰-11|| dx x .12.已知直线 l 过点)1 , 2(A 和) , 1(2m B (R m ∈),则直线 l 斜率的取值范围是 , 倾斜角的取值范围是 .13.某个部件由三个元件如图4方式连接而成,元件A或元件B 正常工作,且元件C 正常工作,则部件正 常工作.若3个元件的次品率均为31,且各个元件 相互独立,那么该部件的次品率为 . (二)选做题(14、15题,考生只能从中选做一题)三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)已知函数16sin(cos 4)(-+=πx x x f ,R x ∈.⑴求)0(f 的值;⑵若将)(x f y =的图象向右平移ϕ(0>ϕ)个单位,所得到的曲线恰好经过坐标原点,求ϕ的最小值.3BD随机询问某大学40名不同性别的大学生在购买食物时是否读营养说明,得到如下列联表: 性别与读营养说明列联表⑴营养说明之间有关系?⑵从被询问的16名不读营养说明的大学生中,随机抽取2名学生,求抽到男生人数ξ的分布列及其均值(即数学期望).(注:))()()(()(22d b c a d c b a bc ad n K ++++-=,其中d c b a n +++=为样本容量.)18.(本小题满分14分)如图6,四棱锥ABCD P -的底面ABCD 是平行四边形,⊥PA 底面ABCD ,3=PA ,2=AD ,4=AB ,060=∠ABC .⑴求证:PC AD ⊥;⑵E 是侧棱PB 上一点,记λ=,是否存在实数λ,使⊥PC 平面ADE ?若存在,求λ的值;若不存在,说明理由. 19.(本小题满分12分)已知数列{}n a 的首项11=a ,*∈∀N n ,nnn a a a +=+221. ⑴求数列{}n a 的通项公式; ⑵求证:*∈∀N n ,312<∑=ni i a .4已知椭圆Γ的焦点为)0 , 1(1-F 、)0 , 1(2F ,点)23, 1(M 在椭圆Γ上. ⑴求椭圆Γ的方程;⑵设双曲线∑:12222=-by a x (0>a ,0>b )的顶点A 、B 都是曲线Γ的顶点,经过双曲线∑的右焦点F 作x 轴的垂线,与∑在第一象限内相交于N ,若直线MN 经过坐标原点O ,求双曲线∑的离心率.21.(本小题满分14分)已知函数)ln ()(2x x a x x f ++=,0>x ,R a ∈是常数.试证明: ⑴R a ∈∀,)12)(1(-+=x a y 是函数)(x f y =的图象的一条切线; ⑵R a ∈∀,存在) , 1(e ∈ξ,使1)1()()(/--=e f e f f ξ.5评分参考一、选择题 BCAA CDDB二、填空题 ⒐ R x ∈∃0(3分),022020≤++x x (0x 写作x 亦可,但要统一,否则只计1处得分;≤写作<扣1分)⒑ 3 ⒒ 1 ⒓ ]1 , (-∞(3分),) , 2(]4 , 0[πππ (1分+1分)⒔2711 ⒕ 22⒖ 15 三、解答题⒗⑴11211416s i n 0co s 4)0(=-⨯⨯=-=πf ……4分(代入1分,三角函数值2分,结果1分) ⑵向右平移ϕ个单位,所得到的曲线为1)6sin()cos(4-+--=πϕϕx x y ……6分曲线经过坐标原点,得01)6sin()cos(4=-+--πϕϕ……7分 化简(和差化积或积化和差),得0)62sin(=-πϕ(或332tan =ϕ)……10分ππϕk =-62,Z k ∈……11分,122ππϕ+=k ,ϕ的最小正值为12πϕ=……12分.(若学生在第⑴问化简函数,则相应的分值仍然计入第⑵问)⒘⑴由表中数据,得635.667.620201624)481216(402>≈⨯⨯⨯⨯-⨯⨯=k ……4分 因此,能在犯错误的概率不超过0.01的前提下,认为性别与读营养说明有关……5分 ⑵ξ的取值为0,1,2……6分2011)0(216212===C C P ξ,52)1(21614112=⨯==C C C P ξ,201)2(21624===C C P ξ……12分 ξ的分布列为……13分ξ的均值为21201252120110=⨯+⨯+⨯=ξE ……14分. ⒙⑴连接AC ,则32cos 222=∠⨯⨯⨯-+=ABC BC AB BC AB AC ……1分(方法一)⊥PA 底面ABCD ,所以AB PA ⊥,AC PA ⊥……2分522=+=AB PA PB ,2122=+=AC PA PC ……3分222BC PC PB +=,所以090=∠PCB ,PC BC ⊥……4分因为BC AD //,所以PC AD ⊥……5分6(方法二)222AC AD CD +=,所以090=∠CAD ,AC AD ⊥……2分⊥PA 底面ABCD ,所以AD PA ⊥……3分因为A AC PA = ,所以⊥AD 平面PAC ……4分 因为⊂PC 平面PAC ,所以PC AD ⊥……5分⑵(方法一)过C 作AB CF ⊥于F ,则⊥CF 平面PAB ……6分 连接PF ,由⑴知⊥PC 平面ADE 当且仅当AE PC ⊥……7分 又AE CF ⊥,所以⊥AE 平面PCF ……8分,PF AE ⊥……9分 依题意,121==BC BF ,所以3=AF ,PA AF =……10分,AE 是PAF ∠的平分线, 从而也是PAB ∠的平分线……11分 在PAE ∆和ABE ∆中,PEA PA PAE PE ∠=∠sin sin ,BEAABBAE BE ∠=∠sin sin ……12分所以43==AB PA BE PE ……13分,73=PB PE ,即所求λ的值为73……14分. (方法二)在平面ABCD 内过点A 作CD AF ⊥,以A 为原点,AF 、AB 、AP 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系……6分则)0 , 0 , 0(A ,)0 , 4 , 0(B ,)3 , 0 , 0(P ……7分,)0 , 3 , 3(C ……8分 设) , , (c b a E ,由λ=得,)3 , 4 , 0()3 , , (-=-λc b a ……9分 解得0=a ,λ4=b ,λ33-=c ……10分由⑴知⊥PC 平面ADE 当且仅当AE PC ⊥……11分,即0=⋅……12分 所以0)33(343)33 , 4 , 0()3 , 3 , 3(=--⨯=-⋅-λλλλ……13分 解得73=λ……14分. (方法三)过E 作BC EF //,交PC 于F ,连接DF ,则平面ADE 即平面ADFE ……6分,由⑴知⊥PC 平面ADE 当且仅当DF PC ⊥……7分由⑴及余弦定理得 211392cos 222⨯=⨯⨯-+=∠PD PC CD PD PC CPD ……9分 所以219cos =∠⨯=CPD PD PF ……12分7321219=⨯=PCPF……13分,又BC EF //,所以73===PC PF PB PE λ……14分.7⒚⑴由nn n a a a +=+221,得21111+=+n n a a ……1分,21111=-+n n a a ……2分所以⎭⎬⎫⎩⎨⎧n a 1是首项11=n a ,公差21=d 的等差数列……3分 212111+=-+=n n a n ……4分,所以*∈∀N n ,12+=n a n ……5分 ⑵(方法一)nn n n n a n 24124)1(42222+<++=+=……6分,222+-=n n ……7分 4>n 时,由以上不等式得 )222()1212()5232()4222()3212(12+-++--++-+-+-<∑=n n n n a ni i……9分 22122212+-+-+=n n ……10分,3<……11分 因为⎭⎬⎫⎩⎨⎧∑=n i i a 12是递增数列,所以*∈∀N n ,312<∑=ni n a ……12分.(方法二))1(4)1(422+<+=n n n a n ……6分,244+-=n n ……7分 2>n 时,由以上不等式得 )144()4434()3424(112212+-++-+-+<+=∑∑==n n a a ni in i i ……9分 14241+-+=n ……10分,3<……11分因为⎭⎬⎫⎩⎨⎧∑=n i i a 12是递增数列,所以*∈∀N n ,312<∑=ni n a ……12分.⒛⑴椭圆Γ的焦距2||2211==F F c ……1分长轴423492||||22211=++=+=MF MF a ……4分 椭圆Γ的短轴3221=b ……5分,所以椭圆Γ的方程为13422=+y x ……6分 ⑵设双曲线∑焦距为c 2,依题意,1||2222=-b FN a c ……7分,a b FN 2||=……8分(方法一)) , (2ab c N ……9分,直线OM 的方程为x y 23=……10分O 、M 、N 共线,所以c a b 232=……11分,即2322=-ac a c ……12分,231=-e e ,02322=--e e ……13分,解得双曲线∑的离心率2=e (21-=e 舍去)……14分.(方法二)依题意,M OF 2∆~OFN ∆……9分,||||||||22OF FN OF M F =……10分 所以acb 223=……11分,即2322=-ac a c ……12分,231=-e e ,02322=--e e ……13分,8解得双曲线∑的离心率2=e (21-=e 舍去)……14分.21.⑴)11(2)(/xa x x f ++=……1分,直线)12)(1(-+=x a y 的斜率)1(2+=a k ……2分,由)1(2)11(2+=++a xa x ,取1=x ……3分22)1(/+=a f ,曲线)(x f y =在点))1( , 1(f 的切线为)1)(22()1(-+=-x a f y , 即)12)(1(-+=x a y ,所以)12)(1(-+=x a y 是曲线)(x f y =的一条切线……4分⑵直接计算知111)1()(-+++=--e aa e e f e f ……5分 设函数1)1(21)1()()()(/--++-=---=e ax a e x e f e f x f x g ……6分 1)1()2(11)1(2----=--+-=e e e a e a a e g ……7分 )1()1(11)(2---=--+-=e e ae e e a e a e e g ……8分 当2)1(->e e a 或2)1(2--<e e a 时,222)1(])1(][)1()2([)()1(-------=e e e e a e e a e g g 0<……10分,因为)(x g y =的图象是一条连续不断的曲线,所以存在) , 1(e ∈ξ,使0)(=ξg ,即) , 1(e ∈ξ,使1)1()()(/--=e f e f f ξ……11分;当22)1(2)1(-≤≤--e e a e e 时,)1(g 、0)(≥e g ,而且)1(g 、)(e g 之中至少一个为正……12分,由均值不等式知,1122)(2--+-≥e e a a x g ,等号当且仅当) , 1(2e ax ∈=时成立,所以)(x g 有最小值1)1(2)1(2112222----+-=--+-=e e a e a e e a a m , 且01)3)(1()]1(2[1)1(2)1(222<---+---=----+-=e e e e a e e a e a m ……13分,此时存在) , 1(e ∈ξ()2 , 1(a ∈ξ或) , 2(e a∈ξ),使0)(=ξg 。
广州市2014届高三年级调研测试理科数学答案

广州市2014届高三年级调研测试 数学(理科)试题参考答案及评分标准说明:1.参考答案及评分标准给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据比照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分.一、选择题:本大题主要考查基本知识和基本运算.共8小题,每小题5分,满分40分.二、填空题:本大题主要考查基本知识和基本运算.本大题共7小题,考生作答6小题,每小题5分,满分30分.其中14~15题是选做题,考生只能选做一题.三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分) 解:(1)在△ABC 中,A B C π++=.………………………………………………………………1分所以coscos22A C Bπ+-=…………………………………………………………………………2分sin23B ==.………………………………………………………………………3分所以2cos 12sin 2BB =-……………………………………………………………………………5分 13=.………………………………………………………………………………………7分(2)因为3a =,b =1cos 3B =, 由余弦定理2222cos b a c ac B =+-,………………………………………………………………9分得2210c c -+=.……………………………………………………………………………………11分 解得1c =. (12)分17.(本小题满分12分) 解:(1)由茎叶图可知,甲城市在2013年9月份随机抽取的15天中的空气质量类别为优或良的天数为5天.…………………………………………………………………………………………………1分所以可估计甲城市在2013年9月份30天的空气质量类别为优或良的天数为10天.…………2分(2)的取值为0,1,2,………………………………………………………………………………3分因为()02510215C C 30C 7P X ===,………………………………………………………………………5分()11510215C C 101C 21P X ===,……………………………………………………………………………7分()20510215C C 22C 21P X ===.…………………………………………………………………………9分所以1所以数学期望.…………………………………………………12分18.(本小题满分14分)(1)证明1:因为BC AB 2=,60ABC ︒∠=,在△ABC 中,由余弦定理可得BC AC 3=.……………………………………………………2分所以222AC BC AB +=.所以BC AC ⊥. (3)分因为AC FB ⊥,BF BC B = ,BF 、BC ⊂平面FBC ,所以⊥AC 平面FBC .………………………………………………………………………………4分证明2:因为60ABC ︒∠=,设BAC α∠=()0120α<<,则120ACB α∠=- .在△ABC 中,由正弦定理,得()sin sin 120BC ABαα=- .…………………………………………1分 因为BC AB 2=,所以()sin 1202sin αα-=.整理得tan 3α=,所以30α= .…………………………………………………………………2分所以BC AC ⊥. (3)分因为AC FB ⊥,BF BC B = ,BF 、BC ⊂平面FBC ,所以⊥AC 平面FBC .………………………………………………………………………………4分……………………10分(2)解法1:由(1)知,⊥AC 平面FBC ,FC ⊂平面FBC ,所以FC AC ⊥.因为平面CDEF 为正方形,所以FC CD ⊥. 因为AC CD C = ,所以⊥FC 平面ABCD .……………………………………………………6分取AB 的中点M ,连结MD ,ME ,因为ABCD 是等腰梯形,且BC AB 2=,60DAM ∠= , 所以MD MA AD ==.所以△MAD 是等边三角形,且ME BF .…………………………7分取AD 的中点N ,连结MN ,NE ,则MN AD ⊥.………8分 因为MN ⊂平面ABCD ,ED FC ,所以ED MN ⊥. 因为AD ED D = ,所以MN ⊥平面ADE . ……………9分 所以MEN ∠为直线BF 与平面ADE 所成角.……………10分 因为NE ⊂平面ADE ,所以MN ⊥NE .…………………11分因为2MN AD =,ME ==,…………………………………………12分在Rt △MNE中,sin MN MEN ME ∠==13分 所以直线BF 与平面ADE14分 解法2:由(1)知,⊥AC 平面FBC ,FC ⊂平面FBC ,所以FC AC ⊥.因为平面CDEF 为正方形,所以FC CD ⊥. 因为AC CD C = ,所以⊥FC 平面ABCD .……………………………………………………6分所以CA ,CB ,CF 两两互相垂直,建立如图的空间直角坐标系xyz C -.………………………7分 因为ABCD 是等腰梯形,且BC AB 2=,60ABC ︒∠= 所以CB CD CF ==.不妨设1BC =,则()0,1,0B ,()0,0,1F,)A,1,02D ⎫-⎪⎪⎝⎭,1,12E ⎫-⎪⎪⎝⎭, 所以()0,1,1BF =-,1,02DA ⎫=⎪⎪⎝⎭ ,()0,0,1DE =.………………………………………9分设平面ADE 的法向量为=()x,y,z n ,则有0,0.DA DE ⎧⋅=⎪⎨⋅=⎪⎩ n n即0,220.y x z +=⎨⎪=⎩ 取1x =,得=n ()1,是平面ADE 的一个法向量.………………………………………11分设直线BF 与平面ADE 所成的角为θ, 则sin cos ,BF BF BF ⋅θ=〈〉===n n n.……………………………13分所以直线BF 与平面ADE 所成角的正弦值为4.………………………………………………14分 19.(本小题满分14分) 解:(1)因为1321nn n a a a +=+,所以111233n n a a +=+.…………………………………………………1分 所以1111113n n a a +⎛⎫-=- ⎪⎝⎭.…………………………………………………………………………3分因为135a =,则11213a -=.…………………………………………………………………………4分所以数列11n a ⎧⎫-⎨⎬⎩⎭是首项为32,公比为31的等比数列.…………………………………………5分(2)由(1)知,112121333n n n a -⎛⎫-=⨯= ⎪⎝⎭,所以332nn n a =+.……………………………………7分假设存在互不相等的正整数m ,s ,t 满足条件, 则有()()()22,111.s m t m t s a a a +=⎧⎪⎨-=--⎪⎩……………………………………………………………………9分由332n n n a =+与()()()2111s m t a a a -=--,得2333111323232s m t s m t ⎛⎫⎛⎫⎛⎫-=-- ⎪ ⎪⎪+++⎝⎭⎝⎭⎝⎭.……………………………………………………10分即232323343m t m t s s ++⨯+⨯=+⨯.……………………………………………………………11分因为2m t s +=,所以3323m t s +=⨯.……………………………………………………………12分因为3323mts +≥=⨯,当且仅当m t =时等号成立,这与m ,s ,t 互不相等矛盾.……………………………………………………………………13分所以不存在互不相等的正整数m ,s ,t 满足条件.……………………………………………14分 20.(本小题满分14分) 解:(1)因为()313f x x ax =-,()221g x bx b =+-, 所以()2f x x a '=-,()2g x bx '=.…………………………………………………………………1分因为曲线()x f y =与()x g y =在它们的交点()c ,1处有相同切线,所以()()11g f =,且()()11g f '='。
2014届高三理科数学江门一模和广州一模考试总结
2014年高三江门一模和广州一模理科数学学科考试质量分析报告2014年03月19日一、试卷分析江门一模和广州一模考试内容是基本上按照高考要求来命题, 其中江门一模注重双基考核, 广州一模注重双基及能力的考核为主。
从考试难度来看, 江门一模试题难度稍微下降, 而广州一模稍微偏难。
两份考题都能以基础知识和基本能力为主, 着重计算能力, 其中也涉及一点难度稍大的题目, 试卷的整体运算量适中, 题目分布的梯度的也合理, 整体难度一易一偏难。
二、成绩分析1. 江门一模成绩分布情况:广州一模成绩分布情况:2. 各层次班分差分布合理:1)江门一模:尖子班分差: 2.56分;重点班分差: 3.4分;普通班分差: 4.02分;复读班分差: 5.32分2)广州一模:尖子班分差: 0.88分;重点班分差: 1.88分;普通班分差: 5.93分;复读班分差: 5.3分3. 各层次学生成绩情况:1)江门一模:平均分:98.45分, 最高分146分, 140分以上人数有11人, 120分以上人数有183人;60分以下人数有67人。
2)广州一模:平均分:91.86分, 最高分140分, 140分以上人数有2人, 107分以上人数有220人;60分以下人数有118人。
三、测试试题中得分较低的试题的统计与分析四、存在的主要问题及对策从两次模考成绩来看, 整体的成绩基本保持稳定。
特别是重点班的数学成绩稳中带升, 但是从广州一模成绩分布情况来看, 中下层生的数学成绩略有下降, 尖子层学生人数还有待提高。
对于存在问题, 我们在下一阶段在教学和课后安排上做如下调整:1)认真抓好课堂教学, 向课堂教学要质量。
争取在课堂中能集中解决学生必须解决的问题, 然后通过课后作业来巩固和提高。
2)加强集体备课, 在备课中集中讨论和挖掘学生集中出现的问题, 在课堂分析和课后通过练习的形式来巩固和提高。
3)利用坐班时间加强各班中、下层生的学法和心理辅导工作, 特别是各课任教师所负责的临界生的辅导工作。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014年高三江门一模和广州一模
理科数学 学科考试质量分析报告
2014年03月19日
一、试卷分析
江门一模和广州一模考试内容是基本上按照高考要求来命题,其中江门一模注重双基考核,广州一模注重双基及能力的考核为主。
从考试难度来看,江门一模试题难度稍微下降,而广州一模稍微偏难。
两份考题都能以基础知识和基本能力为主,着重计算能力,其中也涉及一点难度稍大的题目,试卷的整体运算量适中,题目分布的梯度的也合理,整体难度一易一偏难。
二、成绩分析
1.江门一模成绩分布情况:
理科数学科分析
1162
110
137
156
125
91
65
58
28
21
17
20406080100120
140160180140以上
140~130
130~120
120~110
110~100
100~9090~80
80~70
70~60
60~50
50~4040以下
分数段
人数
广州一模成绩分布情况:
理科数学科分析
2
4
43
124
176175
156
87
44
27
19
22
20406080100120
140160180200140以上
140~130
130~120
120~110
110~100
100~9090~80
80~7070~6060~5050~4040以下
分数段
人数
2.各层次班分差分布合理:
1)江门一模:
尖子班分差:2.56分;重点班分差:3.4分;普通班分差:4.02分;复读班分差:5.32分2)广州一模:
尖子班分差:0.88分;重点班分差:1.88分;普通班分差:5.93分;复读班分差:5.3分3.各层次学生成绩情况:
1)江门一模:平均分:98.45分,最高分146分,140分以上人数有11人,120分以上人数有183人;60分以下人数有67人。
2)广州一模:平均分:91.86分,最高分140分,140分以上人数有2人,107分以上人数有220人;60分以下人数有118人。
三、测试试题中得分较低的试题的统计与分析
1)江门一模情况:
题号试题分数得分率失分原因分析
6 3.23 64.6% 学生对充分必要条件概念的理解不够熟练。
8 3.12 62.4% 学生对函数应用数形结合法运用能力不强。
12 2.39 47.8% 学生对解析几何分类讨论的能力差,还有待提高。
13 2.28 45.6% 学生对概率的知识掌握不好,计算能力差。
19 5.98 42.71
% 学生对数列的知识掌握不好,特别是裂项求和的能力差,基础知识应用能力不强,计算能力差。
21 2 14.29
% 学生对函数、导数综合题的处理能力不强,特别构造函数,分析和计算能力差。
2)广州一模情况:
题号试题分数得分率失分原因分析
6 3.46 69% 学生对集合知识的理解不够熟练。
7 3.28 67% 学生对充分必要条件概念的理解和运用能力不强。
12 3.35 65% 学生对三角变换不熟练,计算能力差,还有待提高。
13 3.18 63.6% 学生对周期数列掌握不好,转变的能力不强,计算能力差。
19 3.68 26.29% 学生对分段数列的知识应用能力不强,计算能力差。
21 2.53 18.07% 学生对函数、导数综合题的处理能力不强,特别构造函数,
分析和计算能力差。
四、存在的主要问题及对策
从两次模考成绩来看,整体的成绩基本保持稳定。
特别是重点班的数学成绩稳中带升,但是从广州一模成绩分布情况来看,中下层生的数学成绩略有下降,尖子层学生人数还有待提高。
对于存在问题,我们在下一阶段在教学和课后安排上做如下调整:
1)认真抓好课堂教学,向课堂教学要质量。
争取在课堂中能集中解决学生必须解决的问题,然后通过课后作业来巩固和提高。
2)加强集体备课,在备课中集中讨论和挖掘学生集中出现的问题,在课堂分析和课后通过练习的形式来巩固和提高。
3)利用坐班时间加强各班中、下层生的学法和心理辅导工作,特别是各课任教师所负责的临界生的辅导工作。
五.后阶段教学的措施
1)认真抓好课堂教学,向课堂教学要质量。
争取在课堂中能集中解决学生必须解决的问题,然后通过课后作业来巩固和提高。
2)加强集体备课,在备课中集中讨论和挖掘学生集中出现的问题,在课堂分析和课后通过练习的形式来巩固和提高。
3)坚强每周三下午40分中的小题练习,提高学生客观题的得分能力。
4)认真落实好数学二轮复习的计划和执行,力争二轮复习有提高。
5)通过测验、作业和限时训练等方式加强学生的书面表达能力的培养,力争把那些非智力的得分也要得到。
6)争取在不同的学习阶段,要求课任教师加强对中、下层生的学法和心理辅导工作。
