欧拉方程的求解教材
教学课件:第八讲-机器人动力学-牛顿-欧拉方程

目录
• 引言 • 牛顿-欧拉方程的原理 • 牛顿-欧拉方程的应用 • 机器人动力学仿真 • 牛顿-欧拉方程的扩展与展望
01 引言
主题简介
01
机器人动力学是研究机器人在运 动过程中力与运动关系的学科。
02
牛顿-欧拉方程是描述机器人关节 运动的数学模型,用于分析机器 人的动态行为。
动态特性分析
动态控制策略
根据动力学模型,设计合适的控制算 法和策略,实现机器人的稳定、快速 和准确的运动控制。
分析机器人在动态环境中的响应特性, 包括稳定性、动态精度和跟踪性能等。
机器人的控制策略
轨迹规划
根据任务需求,规划机器 人的运动轨迹,包括路径 规划、速度规划和加速度 规划等。
控制器设计
基于动力学模型和控制算 法,设计合适的控制器, 实现机器人对给定轨迹的 精确跟踪。
05
总结词:功能模块
06
详细描述:列举仿真软件的功能模块,例如建模模块、求 解器模块、后处理模块等,并简要介绍每个模块的作用。
仿真模型的建立
总结词:建模步骤 总结词:模型精度 总结词:模型验证
详细描述:介绍建立机器人动力学仿真的步骤,包括建 立机器人模型、设置约束和力矩、定义初始状态等。
详细描述:说明建模过程中需要考虑的因素,如模型的 精度、简化程度等,以及如何权衡这些因素。
机器人动力学模型
总结词
描述机器人运动过程中力和运动的数 学模型。
详细描述
机器人动力学模型基于牛顿-欧拉方程, 通过建立力和运动的数学关系,可以 预测机器人的运动轨迹和姿态。该模 型对于机器人的控制和优化设计至关 重要。
03 牛顿-欧拉方程的应用
西工大最优控制课程 第1章 变分法-2-欧拉方程

3 泛函求极值的一般步骤
问题:由 min J ( y) x1 F (x, y(x), y'(x))dx 求 yˆ, J ( yˆ)
y
x0
(1)由EULER方程
d
Fy
dx
(
F y
'
)
0
解出y的通解。
(2)由横截条件求出
F y
'
0
的表达式。
(3)将边值条件代入y的通解与
F y
'
0
求出积分常数,得到 yˆ
当一个端点固定时(假定x0固定)
F y x1 y' x0
Fy'y
x1
Fy'y x0
y(x0 ) 0
Fy'y x1 0Fy' x1 0
y(x0 ) y0
横截条件
F y x1 y' x0
0
当两个端点均可变时
y
y1(x)
y*(x)
δy1
δy0
y2(x)
F y x1 y' x0
Fy'y
x1
x1 0(横截条件)
x0
写成向量形式
t f
t0
(δy)T (Fy
d dx
Fy )dx (δy)T
Fy
x1 x0
0
标量函数F对y的一阶偏导
梯度向量,列向量
向量形式
tf t0
(δy)T (Fy
d dx
Fy )dx (δy)T
Fy
x1 x0
0
n维列向量
泛函极值存在的必要条件:
Fy
d dx
Fy
0
函数极值存在的必要条件
7.9 欧拉方程

7.9 欧拉方程
d 用 D 表示对自变量 t 求导的运算 , dt 上述结果可以写为
xy Dy,
2 d y dy 2 2 x y 2 ( D D ) y D( D 1) y , dt dt
3 2 d y d y dy 3 x y 3 3 2 2 dt dt dt ( D 3 3 D 2 2 D ) y D( D 1)( D 2) y ,
7.9 欧拉方程 一般地, x k y ( k ) D( D 1)( D k 1) y. 将上式代入欧拉方程,则化为以 t 为自变量
的常系数 线性微分方程. 求出这个方程的解后,
. 把 t 换为 ln x 即得到原方程的解 , 注: 转化为常系数线性方程:
D n y b1 D n 1 y bn y f (et )
即 dn y d tn b1 d n 1 y dt
t b y f (e ) n n 1
7.9 欧拉方程 例7.40 求欧拉方程
2 2 x y x y 4 xy 3 x 的通解. 3
解 作变量变换 x e t 或 t ln x, : 原方程化为
7.9 欧拉方程
一、欧拉方程 二、内容小结 三、思考与练习
7.9 欧拉方程
一、欧拉方程
形如
x n y ( n ) p1 x n1 y ( n1 ) pn1 xy pn y f ( x )
的方程(其中 p1 , p2 pn 为常数) 叫欧拉方程.
特点:各项未知函数导数的阶数与乘积因子自 变量的方次数相同.
7.9 欧拉方程
在数学方面他对微积分的两个领域──微分
欧拉方法课件

yi
1 2 h[ f (xi , yi )
f ( xi1 , yi1 )]
隐式措施
这种只用前一步 yi 即可算出 yi1 的公式称为单步法.
显式旳单步法能够逐层求解,简朴以便;
隐式旳单步法需要解具有 yi1 旳方程式,很不以便,
常用迭代法求解。
隐式措施旳迭代求解
梯形措施:
1 yi1 yi 2 h [ f ( xi , yi ) f ( xi1 , yi1 )]
第四步,将差分方程改写为线性方程组旳形式并求 解,解出 yi .
第五步,从理论上研究数值格式旳局部截断误差(即 相容性)、稳定性以及收敛性与整体误差。
第六步,分析数值成果与理论分析是否一致,考察 有无不足及可改善线法)
第一步,对问题(*)旳求解区域作一致网格剖分,
即 yi1 yi h f ( xi , yi ), i 0, 1, n 1.
总旳, yi1 yi h f ( xi , yi ), i 0, 1, n 1.
y0 y( x0 ).
这就是著名旳欧拉(Euler)公式。 以上措施称为欧拉措施或欧拉折线法。
欧拉折线法名称旳由来: yi1 yi h f ( xi , yi ), i 0, 1, n 1.
证:此定理旳证明可在一般旳《常微分方程》教材 上找到,故略。
2.求解问题(*)数值措施旳基本思想
求解问题(*)数值措施旳基本思想是在求解区域 I
上任取 n 1个节点 a x0 x1 x2 xn b ,
在这些节点上采用离散化措施(一般用数值积分、微 分、泰勒公式等)将上述初值问题化成有关离散变量
(xi ,
yi )
yi
h( yi
2xi yi
),
欧拉方程

第六节、欧拉方程
因为变系数的二阶及二阶以上的线性微分方程还 没有一般的解法,所以本节介绍一类特殊的变系数的 线性微分方程——欧拉方程,通过变量替换可以化为 常系数的线性微分方程,因而容易求解. 形如 xny(n)+p1xn-1y(n-1)+…+pn-1xy′+pny=f(x) (6-33n为常数.
代入原方程,得 a=1/3,
即 y =1/3x2,
所以欧拉方程的通解为 y=1/3x2+C1/x+C2x.
谢谢聆听
第六节、欧拉方程
欧拉方程的特点是:方程中各项未知函数导数的阶数与其 乘积因子自变量的幂次相同. 当自变量x>0时,作变量替换x=et,则t=ln x,有
第六节、欧拉方程
如果来用记号D表示对自变量t求导的运算d/dt,则上述结 果可表示为
xy′=Dy,
一般的,有 xky(k)=D(D-1)…(D-k+1)y.(6-34)
当自变量x<0时,作变换x=-et,可得类似结果. 将式(6-34)代入欧拉方程,则方程(6-33)化为以t为自变 量的常系数线性微分方程,求出该方程的解后,回代t=ln x, 即得到原方程的解.
第六节、欧拉方程
【例1】
求欧拉方程x2y″+xy′-y=x2的通解. 解 作变换x=et(设x>0),原方程化为
D(D-1)y+Dy-y=e2t, 即
D2y-y=e2t 或
方程(6-35)所对应的齐次方程为
其特征方程为
r2-1=0,
(6-35) (6-36)
第六节、欧拉方程
特征根为 r1,2=±1,
所以齐次方程(6-36)的通解为 Y=C1e-t+C2et=C1x+C2x.
第十节欧拉方程

作变量变换 x et 或 t ln x,
将自变量换为 t,
dy dy dt 1 dy , dx dt dx x dt
d2y dx 2
1 x2
d2y
dt 2
dy , dt
d3y dx 3
1 x3
d3y
dt 3
3
d2 dt
y
2
2 dy , dt
用 D 表示对自变量 t 求导的运算 d , dt
练习题
求下列欧拉方程的通解: 1.x2 y xy y 0; 2.x2 y 2xy 2 y ln2 x 2 ln x; 3.x2 y 3xy 4 y x x2 ln x.
练习题答案
1.y
C1
C2 x
.
2.y
C1 x
C2 x2
1 2
(ln2
x
ln
x)
1 4
.
3.y
C1
x2
C2
x2
或
d 3 y 2 d 2 y 3 dy 3e2t . dt 3 dt 2 dt
(1)
方程(1)所对应的齐次方程为
d3 dt
y
3
d2 2
dt
y
2
3 dy dt
0,
其特征方程 r 3 2r 2 3r 0,
特征方程的根为 r1 0, r2 1, r3 3.
所以齐次方程的通解为
Y
C1
C2etC3e3t
的常系数 线性微分方程. 求出这个方程的解后,
把 t 换为 ln x,即得到原方程的解.
例 求欧拉方程
x3 y x2 y 4xy 3x2的通解.
解 作变量变换 x et 或 t ln x,
欧拉方程解法课件

一阶线性欧拉方程的解
举例
(y' = 2xy) 的解为 (y = x^2),通过分离变量法得到。
举例
(y' = frac{1}{x}) 的解为 (y = ln x),通过变量代换法得到。
二阶常系数线性欧拉方程的解
举例
(y'' + 4xy = 0) 的解为 (y = c_1x^2 + c_2x^2),通过特征值法得到。
应用示例
对于形如 (frac{partial^2 u}{partial x^2} + frac{partial^2 u}{partial y^2} = f(x,y)) 的偏微分方程,可以 使用有限差分法、有限元法等数值解 法进行求解。
03
欧拉方程的解的性质
解的存在性和唯一性
存在性
对于给定的初值条件和边界条件,欧 拉方程存在一个解。
应用示例
对于形如 (u(x,y) = v(x)w(y)) 的函数,如果满足一定的条件,可以将方程分解为两个独立的常微分方程, 分别求解后再组合得到原方程的解。
积分因子法
01
总结词
通过引入一个积分因子,将偏微分方程转化为全微分方程 ,从而简化求解过程。
02 03
详细描述
积分因子法是一种通过引入一个积分因子来简化偏微分方 程的方法。这种方法适用于具有特定对称性的偏微分方程 ,通过引入积分因子可以将偏微分方程转化为全微分方程 ,从而简化求解过程。
并行计算
将计算任务分解成多个子 任务,利用多核处理器或 分布式计算资源并行处理, 加快计算速度。
THANKS
感谢观看
VS
举例
(y'' - 2y' + y = 0) 的解为 (y = c_1e^x + c_2e^{-x}),通过常数变易法得到。
第十二章 欧拉方程【高等数学+同济大学】

特征方程的根为 r1 0, r2 1, r3 3.
所以齐次方程的通解为
Y
C1
C2etC3e3t
C1
C2 x
C3x3.
设特解为 y be2t bx2 ,
代入原方程,得 b 1 . 2
即 y x2 , 2
所给欧拉方程的通解为
y
C1
C2 x
用 D 表示对自变量 t 求导的运算 d ,
dt 上述结果可以写为
xy Dy,
x2 y d 2 y dy (D2 D) y D(D 1) y, dt 2 dt
x3 y d 3 y 3 d 2 y 2 dy dt 3 dt 2 dt
(D3 3D2 2D) y D(D 1)(D 2) y,
欧拉方程
一、欧拉方程
形如
xn y(n)
p x y n1 (n1) 1
pn1 xy
pn y
f (x)
的方程(其中 p1 , p2 pn为常数) 叫欧拉方程.
特点:各项未知函数导数的阶数与乘积因子自 变量的方次数相同.
解法:欧拉方程是特殊的变系数方程,通过变 量代换可化为常系数微分方程.
一般地, xk y(k) D(D 1)(D k 1) y.
将上式代入欧拉方程,则化为以 t 为自变量
的常系数 线性微分方程. 求出这个方程的解后
把 t 换为 ln x ,即得到原方,程的解.
例 求欧拉方程
x3 y x2 y 4xy 3x2 的通解.
解 作变量变换 x et 或 t ln x,
欧拉公式求解常微分方程数值解培训教材
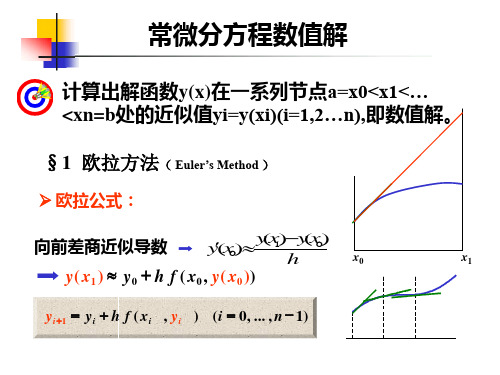
例:用欧拉法解初值问题
y=yxy2(0x0.6)
y(0)=1
取步长 h = 0.2.计算过程保留4位小数.
解:f(x,y)=-y-xy2 , h = 0.2,由欧拉公式得
yk+ 1=yk+h(fxk,yk)=ykhky hkx yk 2 =0.2yk(4xkyk)k(=0,1,2)
故y(0.2)y1=0.2×1(4-0×1)=0.800 0 y(0.4)y2=0.2×0.8×(4-0.2×0.8)=0.614 4 y(0.6)y3=0.2×0.614 4×(4-0.4×0.4613)=0.800 0
Step 2: 将 K2 代入第1式,得到 y i+ 1 = y i+ h1 y ( x i) + 2 [ y ( x i) + p y ( h x i) + O ( h 2 )] = y i+ (1 + 2 ) h y ( x i) + 2 p 2 y h ( x i) + O ( h 3 )
f y ( x, f y ( x,
y) y)
dy dx f (x,
y)
K 2= f(x i+ p,y h i+ p1 h ) K = f(x i,y i)+ px h (x i,y fi)+ p1 h fy (x K i,y i)+ O (h 2 ) = y (x i)+ py h (x i)+ O (h 2 )
例1:用预报-校正公式求解初值问题
y
+y+
y
sinx=
y() =
取步长 h = 0.2,计算 y(1.2), y(1.4)的近似值,计算过程保
欧拉公式PPT课件

在热力学中,欧拉公式被用来描述热量的传递和扩散,以及热力学 系统的状态变化。
电磁学
在电磁学中,欧拉公式可以用来描述电磁场的变化和分布,例如电 势、电场强度等。
在工程领域的应用
01
02
03
控制系统
在控制系统中,欧拉公式 被用来描述系统的稳定性 和性能,以及设计控制器 。
信号处理
在信号处理中,欧拉公式 被用来进行频谱分析和滤 波,以及处理图像和音频 等信号。
总结欧拉公式的要点与贡献
01
02
03
统一了复数域中的指数函数和三 角函数
揭示了复数和实数之间的内在联 系
为解决许多数学问题提供了新的 思路和方法
展望未来在数学、物理等领域的应用前景
在数学领域的应用前景
在物理领域的应用前景
复分析:欧拉公式是复分析中重要的工具之一,可以用于 研究函数的性质和解决某些复杂的积分问题。
CHAPTER 03
欧拉公式的证明
利用泰勒级数展开证明
总结词:直观明了
详细描述:将函数进行泰勒级数展开,得到无限项之和,通过比较级数的各项系数,可以直观地证明 欧拉公式。
利用复数证明
总结词:巧妙简洁
详细描述:利用复数形式的欧拉公式,通过证明复数形式的恒等式,得到欧拉公式的正确性。这种方法需要一定的复数基础 知识。
导数的基本性质包括
和差、积、商、幂函数的导数公式; 常见函数的导数;高阶导数的计算。
积分的基本性质包括
不定积分与定积分的计算;原函数与 微分的概念及其应用;反常积分的计 算。
欧拉公式的推导过程
基于复数的定义和三角函数的定义,通过引入虚数单位i,利用复数的四则运算和 三角函数的性质,推导出欧拉公式e^(ix)=cos(x)+i*sin(x)。
《欧拉方程解法》课件

龙格-库塔方法是另一种常用的数值求解常微分方程的方法,其基本思想是利用 已知的初值和导数值来逼近微分方程的解。
02
龙格-库塔方法的基本步骤是:首先选择一个初始点和初始导数值,然后利用微 分方程、初始条件和初始导数值来计算下一个点和导数值,以此类推,得到一 系列的点和导数值,这些点和导数值就构成了微分方程的近似解。
收敛性分析
随着网格密度的增加,数值解应逐渐接近真实解。
全局误差估计
误差传播
在数值求解过程中,误差会随着 时间和空间的离散化而传播和累 积。全局误差估计需要考虑误差 传播的影响。
收敛速度
全局误差估计还涉及数值解的收 敛速度。理论上,随着时间和空 间的离散化,数值解应逐渐接近 真实解。
误差界
全局误差估计的一个重要目标是 确定数值解的上界和下界,以便 评估其精度和可靠性。
03
欧拉方程的数值解法
欧拉方法
欧拉方法是一种简单的数值求解常微分方程的方法,其基 本思想是利用已知的初值来逼近微分方程的解。
欧拉方法的基本步骤是:首先选择一个初始点,然后利用 微分方程和初始条件来计算下一个点,以此类推,得到一 系列的点,这些点就构成了微分方程的近似解。
欧拉方法的优点是简单易懂,易于实现,但其缺点误差较小,且适用于复杂和非线性的微分方 程,但其缺点是计算量较大,需要更多的计算资源和时间。
04
欧拉方程的稳定性分析
线性稳定性分析
01 线性稳定性分析是研究欧拉方程解的稳定性的基 础方法。
02 通过线性化欧拉方程,可以得到其线性化方程, 进而分析其解的稳定性。
边界问题是指给定微分方 程和某些边界条件,求解 该微分方程的解。
03 方法
使用积分变换、分离变量
高等数学第12章第10节欧拉方程

于是欧拉方程
x n y ( n) p1 x n 1 y ( n 1) pn 1 x y pn y f ( x)
转化为常系数线性方程:
D n y b1D n 1 y bn y f (et )
即 dn y d n 1 y t b1 n 1 bn y f (e ) n dt dt
机动
目录
上页
下页
返回
结束
思考: 如何解下述微分方程
提示: 原方程
直接令
d 记D dt [ D( D 1) p1D p2 ] y f (e t a)
d 记D dt
作业
P319 2 ; 6; 8
第11节 目录 上页 下页 返回 结束
第十节 欧拉方程
欧拉方程
x y
n ( n)
第十二章
p1 x
n 1 ( n 1)
y
pn 1 x y pn y f ( x)
( pk 为常数 )
令 x et , 即 t ln x
常系数线性微分方程
机动 目录 上页 下页 返回 结束
欧拉方程的算子解法:
x n y ( n) p1 x n 1 y ( n 1) pn 1 x y pn y f ( x)
则方程化为
即 特征根:②来自设特解: y A t 2 et , 代入 ② 解得 A = 1, 所求通解为
机动
目录
上页
下页
返回
结束
例3.
解: 由题设得定解问题 ③
④
d 令 x e , 记 D , 则③化为 dt [ D( D 1) D 4] y 5e t
t
( D 2 4) y 5e t
第4章_第7节_欧拉方程

[ ( 1)( n 1) a1 ( 1)( n 2) an1 an ] x
dy dy 即 x Dy dx dt d 2 y d dy d dy dt ( ) ( ) 2 dx dx dt dx dx dx d dy t 1 ( e ) dt dt x
( x et )
d 2 y t dy t 1 d 2 y dy 1 ( 2 e e ) ( 2 ) 2 dt x dt x dt dt
D( D 1)( D 2) y
ny dny n1 y d d dy n x n 1 n1 n n dt dx dt dt D( D 1)( D 2)( D n 1) y
其中 1 , 2 , , n均为实常数.
代入(7.1)式左端,得 dny d n1 y E[ y] L[ y] n b1 n1 bn y dt dt
D( D 1) ( D n 1) y a1 D( D 1) ( D n 2) y an1 Dy an y 0 ( 7.2)
则(7.1)化为:
D( D 1)( D n 1) y a1 D( D 1) ( D n 2) y an1 Dy an y f ( e t )
第四章
§7 欧拉方程
§7
欧拉方程
E[ y] x n y( n) a1 x n1 y( n1) an1 xy an y f ( x ) (7.1)
第七章欧拉方程

I1x ( I 2 I 3 ) y z M x I 2 y ( I 3 I1 )z x M y I ( I I ) M 3 z 1 2 y x z
欧拉动力学方程
I1x I 2 I3 yz M x I3z I1 I 2 xy M z
I 2y I3 I1 zx M y
机械能守恒
1 2 2 2 I1 x I 2 y I 3 z V E 2
(四) 由拉格朗日方程推导欧拉方程
M
R
P
r
O
2.加速度
dv d a r r dt dt
转动加 速度 向轴加 速度
d a r r 2 r dt d a aA r r 2 r dt
例 7-1 B当飞机在空中以定值速度V沿半径为R的水 平圆形轨道C转弯时,求当螺旋桨尖端B与中心A的联 线和沿垂线成θ角时,点的速度及加速度。已知螺旋桨 的长度AB =l,螺旋桨自身旋转的角速度为ω1。 解:这个是一般运动问题
当取惯量主轴为本体坐标系的坐标轴时,全部惯量 积便均为0,于是可以使问题的求解大为简化.
(三).欧拉方程
基本方程
dJ M dt
将坐标系固联于刚体,则
J J xi J y j J z k
但
dJ J xi J y j J z k J dt
为什么?
取惯量主轴为坐标轴,有
这就是由拉格朗日方程推导出的刚体定点运动时的欧拉动力 学方程。
欧拉方程

第七章常微分方程7.12* 欧拉方程数学与统计学院赵小艳1 2 欧拉方程的一般形式1主要内容欧拉方程的解法1 2 欧拉方程的一般形式1主要内容欧拉方程的解法求解: 1 欧拉(Euler)方程的一般形式 ()11111d d d d d d n n n n n n n n x x x t a t a t a x f t t t t----++++=.,,,21均为常数其中n a a a 特点:各项未知函数导数的阶数与乘积因子自变量的乘方次数相同.作变量变换 ,ln t e t ==ττ或t x t x d d d d d d ττ=⎪⎭⎫ ⎝⎛=t x t t x d d d d d d 22 ,1τd d x t =,1222⎪⎪⎭⎫ ⎝⎛-=ττd d d d x x t 代入得到以为自变量的常系数线性微分方程. τ1 2 欧拉方程的一般形式1主要内容欧拉方程的解法例1 求微分方程 02=+-x x t x t 的通解. 解作变量变换 ,ln t e t ==ττ或,1τττd d d d d d d d x t t x t x ==,122222⎪⎪⎭⎫ ⎝⎛-=ττd d d d d d x x t t x 则 代入原方程, 得 该方程的通解为 其特征方程为 ,0122=+-λλ,121==λλ.)(21ττe C C x +=.0222=+-x x x ττd d d d 即得原方程的通解为代换成把,ln t τ.)ln (t C t C x +=2 欧拉(Euler)方程的解法解 令 ,ln t e t ==ττ或代入原方程, 得 .2223τe y y y =+-d d d ,2t x =+原方程变为 .122332=++ty t y t t y t d d d d d d 两端乘以t ,得 .222333t ty t t y t t y t =++d d d d d d 令 则 ,1τττd d d d d d d d y t t y t y ==,122222⎪⎪⎭⎫ ⎝⎛-=ττd d d d d d y y t t y ⎪⎪⎭⎫ ⎝⎛=2233t y t t y d d d d d d ⎪⎪⎭⎫ ⎝⎛+-=τττd d d d d d y y y t 23122333⎪⎪⎭⎫ ⎝⎛--=ττd d d d y y t 2232⎪⎪⎭⎫ ⎝⎛-+2332111ττd d d d 2y t y t t Euler 方程代入原方程, 得 .2223τe y y y =+-d d d 对应齐次方程的特征方程为 ,02223=+-λλλ.1,03,21i ±==λλ对应齐次方程的通解为 ).sin cos (321τττC C e C Y ++=设非齐次方程的特解为 ,τe a y =*则 .1=a 该方程的通解为 .)sin cos (321ττττe C C e C y +++=原方程的通解为].1)2ln(sin )2ln(cos )[2(321++++++=x C x C x C y。
欧拉公式教案完整版

欧拉公式教案完整版介绍欧拉公式是数学中的一个重要定理,描述了复数的指数函数和三角函数之间的关系。
本教案旨在向学生解释欧拉公式的概念和用途,以及展示如何应用欧拉公式进行数学推导。
教学目标在本次课程结束后,学生将能够:- 理解欧拉公式的定义和含义;- 了解欧拉公式在数学中的重要性和应用;- 在数学问题中应用欧拉公式进行计算和推导。
教学内容1. 欧拉公式的定义和含义- 解释欧拉公式的数学表达式:$e^{i \theta} = \cos(\theta) +i\sin(\theta)$;- 解释复数、指数函数和三角函数的概念及其在数学中的作用;- 引导学生理解欧拉公式中的复数单位$i$和角度$\theta$的含义。
2. 欧拉公式在数学中的重要性和应用- 解释欧拉公式在数学中的重要性,尤其在复分析和微积分中的作用;- 展示欧拉公式在三角函数、指数函数和复数运算中的应用;- 提供欧拉公式在解决数学问题中的实际例子,如计算复数的幂、求三角函数的复数幂等。
3. 欧拉公式的应用举例- 通过数学推导和实例演示,展示如何使用欧拉公式解决复数幂、三角函数幂等问题;- 练欧拉公式的应用,包括计算复数的幂、推导三角函数的复数幂等。
教学方法- 通过简明扼要的讲解和示例演示,引导学生理解和掌握欧拉公式的概念;- 提供实际例子和练,帮助学生应用欧拉公式解决数学问题;- 鼓励学生在课堂上积极参与,互相讨论和解答问题。
教学评估- 设计课堂练和作业,测试学生对欧拉公式的理解和应用;- 通过问题解答和示例演示,观察学生在课堂上的表现和参与度。
参考资源- 数学教科书中关于欧拉公式的章节和题;- 在线教学平台和资源,提供欧拉公式的可视化演示和实践练。
结束语本教案旨在将欧拉公式的概念和应用引入学生的数学学习中,帮助他们理解和运用欧拉公式进行数学推导和计算。
通过本次课程,学生将更深入地了解欧拉公式的意义和重要性,并在数学问题中运用欧拉公式发展自己的数学能力。
第九节 欧拉方程

特征根为
例例11 求求方方程程
解 作变换 x = et ,则原方程化为
第九节* 欧拉方程
即 例例22 求求方方程程
的的通通解解. .
的的通通解解. .
亦即解 将方程化为
令 x = et ,则方程化为 特征方程为 r2 – 3r + 2 = 0 , 特征根为 r1 = 1 , r2 = 2,
则 即对应的齐次方程的通解为第九节源自 欧拉方程一、定义 二、解法
第九节* 欧拉方程
一、定义
定义 形如
x n y (n) p1x n1 y (n1) pn1xy pn y f ( x) 的方程(其中 p1 , p2 , … , pn 为常数)称为欧拉方程.
第九节* 欧拉方程 x n y (n) p1x n1 y (n1) pn1xy pn y f ( x)
二、解法
作变换 x = et , 则
类似地可得
第九节* 欧拉方程 如果采用记号 D 表示对 t 求导的运算 计算结果可以写成
那么上述
一般地,有
第九节* 欧拉方程
把它代入欧拉方程,便得一个以 t 为自变量的常系数线 性微分方程. 在求出解后,把 t 换成 ln x 即可得到原方 程的解.
第第九九节节** 欧欧拉拉方方程程
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
欧拉方程的求解1.引言在数学研究领域,我们经常会看到以数学家名字命名的概念、公式、定理等等,让人敬佩跟羡慕.但是,迄今为止,哪位数学家的名字出现得最多呢?他就是数学史上与阿基米德、牛顿、高斯齐名的“四杰”之一,人称“分析学的化身”的盲人数学家欧拉(Leonhard Euler,1707--1783).几乎在每一个数学领域都可以看到他的名字,譬如我们熟悉的“欧拉线”、“欧拉圆”、“欧拉公式”、“欧拉定理”、“欧拉函数”、“欧拉积分”、“欧拉变换”、“欧拉常数”欧拉还是许多数学符号的发明者,例如用π表示圆周率、e 表示自然对数的底、()f x 表示函数、∑表示求和、i 表示虚数单位以欧拉命名的数学名词有很多,本文主要讲解以欧拉命名的方程即“欧拉方程”.在文献[1]中,关于欧拉方程的求解通常采用的是变量变换的方法.变量变换法就是将所求的欧拉方程化为常系数齐次线性微分方程,然后再来求解这个常系数齐次线性微分方程的解,亦即求其形如K y x =的解,进而求得欧拉方程的解.但有些欧拉方程在用变量变换法求解时比较困难.本文在所学的欧拉方程的求解的基础上,对欧拉方程进行了简单的分类,并针对不同阶的欧拉方程的求解给出了不同的定理.最后在每类欧拉方程后面给出了典型的例题加以说明.2.几类欧拉方程的求解定义1 形状为()1(1)110n n n n n n y a x y a xy a y x ---'++++=(1) 的方程称为欧拉方程. (其中1a ,2a ,,1n a -,n a 为常数)2.1二阶齐次欧拉方程的求解(求形如K y x =的解)二阶齐次欧拉方程: 2120x y a xy a y '''++=. (2) (其中1a ,2a 为已知常数)我们注意到,方程(2)的左边y ''、y '和y 的系数都是幂函数(分别是2x 、1a x 和02a x ),且其次依次降低一次.所以根据幂函数求导的性质,我们用幂函数K y x =来尝试,看能否选取适当的常数K ,使得K y x =满足方程(2). 对K y x =求一、二阶导数,并带入方程(2),得212()0K K K K K x a Kx a x -++=或212[(1)]0K K a K a x +-+=,消去K x ,有 212(1)0K a K a +-+=. (3)定义2 以K 为未知数的一元二次方程(3)称为二阶齐次欧拉方程(2)的特征方程.由此可见,只要常数K 满足特征方程(3),则幂函数K y x =就是方程(2)的解.于是,对于方程(2)的通解,我们有如下结论: 定理1 方程(2)的通解为(i) 1112ln K K y c x c x x =+, (12K K =是方程(3)的相等的实根) (ii)1212K K x c x y c +=, (12K K ≠是方程(3)的不等的实根) (iii)12cos(ln )sin(ln )x x c x x y c ααββ+=.(1,2K i αβ=±是方程(3)的一对共轭复根)(其中1c 、2c 为任意常数)证明 (i )若特征方程(3)有两个相等的实根: 12K K =,则11K x y =是方程(2)的解,且设2()u x y =,11()K y x u x =(()u x 为待定函数)也是方程(2)的解(由于21()y u x y =,即1y ,2y 线性无关),将其带入方程(2),得 11122111112[()2]()0K K K x K K u K xu x u a x K u xu a x u ''''-+++++=,约去1K x ,并以u ''、u '、u 为准合并同类项,得22111112(2)[(1)]0x u K a xu K a K a u '''++++-+=.由于1K 是特征方程(3)的二重根, 因此21112(1)0K a K a +-+=或112(1)0K a +-=,于是,得20x u ux '''+=或0xu u '''+=,即 ()0xu ''=, 故 12()ln u x c x c =+. 不妨取()ln u x x =,可得方程(2)的另一个特解12ln K y x x =,所以,方程(2)的通解为1112ln K K y c x c x x =+.(其中1c ,2c 为任意常数)(ii )若特征方程(3)有两个不等的实根: 12K K ≠,则11K x y =,22K y x =是方程(2)的解.又2211()21K K K K y x x y x -==不是常数,即1y ,2y 是线性无关的. 所以,方程(2)的通解为1212K K x c x y c +=.(其中1c ,2c 为任意常数)(iii )若特征方程(3)有一对共轭复根:1,2K i αβ=±(0β≠),则()1i x y αβ+=,()2i y x αβ-=是方程(2)的两个解,利用欧拉公式,有()ln 1(cos(ln )sin(ln ))i i x x x e x x i x y αβαβαββ+===+, ()ln 2(cos(ln )sin(ln ))i i x x x e x x i x y αβαβαββ--===-,显然,12cos(ln )2y y x x αβ+=和12sin(ln )2y y x x iαβ-=是方程(2)的两个线性无关的实函数解.所以,方程(2)的通解为12cos(ln )sin(ln )x x x x y c c ααββ=+.(其中1c ,2c 为任意常数)例1求方程20x y xy y '''-+=的通解. 解 该欧拉方程的特征方程为(1)10K K K --+=,即 2(1)0K -=, 其根为: 121K K ==, 所以原方程的通解为12(ln )y c c x x =+.(其中1c ,2c 为任意常数)例2 求方程280x y xy y '''--=的通解.解 该欧拉方程的特征方程为2(11)80K K +---=,即 2280K K --=, 其根为: 12K =-,24K =, 所以原方程的通解为4122c y c x x=+. (其中1c ,2c 为任意常数)例3 求方程的通解2350x y xy y '''++=. 解 该欧拉方程的特征方程为(1)350K K K -++=,即 2250K K ++=,其根为: 1,212K i =-±, 所以原方程的通解为121[cos(2ln )sin(2ln )]y c x c x x=+.(其中1c ,2c 为任意常数)2.2二阶非齐次欧拉方程的求解(初等积分法)二阶非齐次欧拉方程:212()x y a xy a y f x ++='''. (4) (其中1a ,2a 为已知实常数,()f x 为已知实函数)为了使方程(4)降阶为一阶线性微分方程,不妨设1121a K K =--,212a K K =,(5) 则方程(4)变为212122)(1()K a x y K K xy K y f x +--+=''',即212()()()x xy K y K xy K y f x ---=''', (6)根据韦达定理,由(5)式可知,1K ,2K 是一元二次代数方程212(1)0K a K a +-+= (3) 的两个根.具体求解方法:定理2 若1K ,2K 为方程(2)的两个特征根,则方程(4)的通解为 212111[()]K K K K y x x x f x dx dx ----=⎰⎰. (7)证明 因为1K ,2K 为方程(2)的两个特征根,于是方程(4)等价于方程(6),令 2xy K y p '-=, 代入方程(6)并整理,得1()K f x p x x p =-' 和2K p y y x x'-=, 解之,得方程(4)的通解为212111[()]K K K K y x x x f x dx dx ----=⎰⎰.由定理2知,只需要通过两个不定积分(当(7)式中的积分可积时)即可求得方程(4)的通解.为了方便计算,给出如下更直接的结论.定理3 若1K ,2K 为方程(2)的两个特征根,则(i )当12K K =是方程(2)的相等的实特征根时,方程(4)的通解为11111[ln ()ln ()]K K K x x f x dx x x f x dx y x -----⋅=⎰⎰,(ii )当12K K ≠是方程(2)的互不相等的实特征根时,方程(4)的通解为112211121[()()]K K K K x x f x dx x x f x dx K K y ------=⎰⎰,(iii )当1,2K i αβ=±是方程(2)的共轭复特征根时,方程(4)的通解为111[sin(ln )cos(ln )()cos(ln )sin(ln )()]y x x x x f x dx x x x f x dx αααβββββ----=-⎰⎰证明 (ii )当12K K ≠是方程(2)的互不相等的的实特征根时, 将方程(1)的通解(7)进行分部积分,得21212112212121121111211212112111[()]1[()]1{[()]}1[]()()()K K K K K K K K K K K K K K K K K K K x x x f x dx dxx x f x dx dx K K x x x d x f x dx K K x x K K y x f x dx x f x dx x f x dx -------------------=-===--⎰⎰⎰⎰⎰⎰⎰⎰⎰(8) (iii )当1,2K i αβ=±是方程(2)的共轭复特征根时,122K K i β-=, 再由欧拉公式有1ln [cos(ln )sin(ln )]K i i x x x e x x i x x αβαβαββ+===+,2ln [cos(ln )sin(ln )]K i i x x x e x x i x x αβαβαββ--===-,将其代入(8)式,整理可得方程(4)的通解为111[sin(ln )cos(ln )()cos(ln )sin(ln )()]x x x x f x dx x x x f x dx y αααβββββ-----=⎰⎰(i )的证明和(ii )类似.例1求方程22234ln y xy y x x x x '''-+=+的通解.解 该欧拉方程所对应的齐次方程的特征方程为2440K K -+=, 特征根为 122K K ==, 所以由定理3,原方程的通解为23223222232122223212[ln (ln )ln (ln )]111{ln [(ln )ln ][(ln )(ln )]}23211ln [(ln )(ln )]62x x x x x dx x x x x x dx x x x c x x c x x c x x x x y x x c --+-⋅+++-+-+++===⎰⎰(其中1c ,2c 为任意常数)例2求方程2322x x y xy y x e -+='''的通解. 解 该欧拉方程所对应的齐次方程的特征方程为2320K K -+=,特征根为 12K =,21K =, 所以由定理3,原方程的通解为23323212212()()x x x x x xx x e dx x x x e dxx e c x xe e c c x c x xe y x ---=+---=++=⎰⎰(其中1c ,2c 为任意常数)例3求方程2cos(ln )2xx x y xy y -+='''的通解.解 该欧拉方程所对应的齐次方程的特征方程为2220k k -+=,特征根为 1,21K i =±, 所以由定理3,原方程的通解为212122cos(ln )]cos(ln )cos(ln )11sin(ln )cos(ln )cos(ln ))sin(ln )cos(ln )sin(ln )cos(ln )sin(ln )[sin(ln )]{sin(ln )(ln )cos(ln )[ln(cos(ln )]}[][sin(ln )ln x xx x dx dx x x x dx x dx x x x x c x y x x x x x x x x x x c x x c x c x x x ----+===+++=++⎰⎰⎰⎰cos(ln )ln(cos(ln ))]x x(其中1c ,2c 为任意常数)在定理3中,若令()0f x =,则得到二阶齐次欧拉方程(2)的通解.推论 方程(2)的通解为(i)1112ln K K x c x x y c +=, (12K K =是方程(2)的相等的实特征根) (ii)1212K K x c x y c +=, (12K K ≠是方程(2)的不等的实特征根) (iii)12cos(ln )sin(ln )x x c x x y c ααββ+=.(1,2K i αβ=±是方程(2)的共轭复特征根)(其中1c ,2c 为任意常数)2.3三阶非齐次欧拉方程的求解(常数变易法)三阶非齐次欧拉方程:32123()x y a x y a xy a y f x +++=''''''.(9) (其中1a ,2a ,3a 为常数) (9)对应的齐次方程为321230x y a x y a xy a y +++=''''''. (10) 特征方程为321123(3)(2)0K a K a a K a +-+-++=. (11)定理4 设1K 是方程(11)的根,2K 是方程22122112(31)[3(1)2]0K K a K K K a K a ++-+-++=的根,则(9)的通解为12211211(231)(22){[()]}K K K K a K K a x x x f x dx dx dx y x -++-++-=⎰⎰⎰ . (12)证明 根据条件1K y cx =(c 为任意常数)是方程(10)的解. 设1()K y c x x =是方程(9)的解(其中()c x 是待定的未知数), 将其代入方程(9),整理得1121111112(3)3231111213()(3)()[3(1)2]()[(3)(2)]()()K c x K a x c x K K a K a x c x K a K a a K a x c x xf x ---+-''''''+++-++++-+-++= (13)因为1K 是(11)的根,则321111213(3)(2)0K a K a a K a +-+-++=,于是(13)式化为1(3)121111112()(3)()[3(1)2]()()K c x K a x c x K K a K a x c x x f x -+--''''''+++-++=(14) 这是以()c x '为未知函数的二阶欧拉方程. 设2K 为(14)对应的齐次方程的特征方程21111112(31)[3(1)2]0K K a K K K a K a ++-+-++=,(15) 的根,则221121(23)(2)()[()]K K K a K K c x x x x f x dx dx -+++-'=⎰⎰.从而2211211(23)(22){[()]}()K K K a K K a x x x f x dx dx dx c x -++++-=⎰⎰⎰. 故方程(1)的通解为12211211(231)(22){[()]}K K K K a K K a x x x f x dx dx dx y x -++-++-=⎰⎰⎰.定理5 设1K 是方程(11)的根,2K 是方程(15)的根,则(i )当1K 是方程(11)的单实根,2K 是方程(15)的单实根,则(9)的通解为1212121121(2)1(3)(2)121[()()](32)1K K K K K K a K K a x y x x f x dx x x f x dx dx K K a -++-++++=-++-⎰⎰⎰(ii )当1K 是方程(11)的单实根,2K 是方程(15)的单虚根,则(9)的通解为111(2)(2){[sin(ln )cos(ln )()cos(ln )sin(ln )()]}K K K x x xx f x dx x x x f x dx dxy xαααβββββ-++-++-=⎰⎰⎰(其中11132K a α--=,β=(iii )当1K 是方程(11)的单实根,2K 是方程(15)的重实根,则(9)的通解为121212(2)(2){[ln ()ln ()]}K K K K K K x x x f x dx x x f x dx dx y x -++-++-⋅=⎰⎰⎰,(iv )当1K 是方程(11)的三重实根,方程(15)变为2210K K ++=,有21K =-,则(9)的通解为111(1)(1)1{[ln ()ln ()]}K K K y x x x x f x dx x x f x dx dx -+-+-=-⋅⎰⎰⎰.证明 (i )因为2K 是方程(15)的单实根,得(14)的通解为212121121(2)1(3)(2)31211[()()](32)1()K K K K K a K K a x x f x dx x x f x dx K K a c x -++-++++--++-='⎰⎰则(9)的通解为1212121121(2)1(3)(2)3121[()()](32)1K K K K K K a K K a x y x x f x dx x x f x dx dx K K a -++-++++-=-++-⎰⎰⎰(ii )因为2K 是方程(14)的单虚根,此时方程(15)有一对共轭虚根1,22K =得(14)的通解为11(2)(2)[sin(ln )cos(ln )()cos(ln )sin(ln )()]()K K x x x x f x dx x x x f x dx c x αααβββββ-++-++-='⎰⎰则(9)的通解为111(2)(2){[sin(ln )cos(ln )()cos(ln )sin(ln )()]}K K K x x xx f x dx x x x f x dx dxy xαααβββββ-++-++-=⎰⎰⎰(其中11132K a α--=,β=(iii )因为2K 是方程(15)的重实根,得(9)的通解为121212(2)(2){[ln ()ln ()]}K K K K K K x x x f x dx x x f x dx dx y x -++-++-⋅=⎰⎰⎰.(iv )当1K 是方程(10)的三重实根(1133a K =-),方程(15)变为222210K K ++=,有21K =-,将1133a K =-,21K =-代入(12)式得11(1)11{[()]}K K y x x x x f x dx dx dx -+--=⎰⎰,对上式分部积分得(9)的通解为111(1)(1)1{[ln ()ln ()]}K K K x x x x f x dx x x f x dx dx y -+-+-⋅-⋅=⎰⎰⎰.例1 求三阶欧拉方程32366x y x y xy y x -+-=''''''的通解. 解 原方程对应的齐次方程为323660x y x y xy y -+-='''''',其特征方程为3261160K K K -+-=,解得其特征根为1,2,3,取 11K =, 将11K =,13a =-,26a =,代入方程(15),得2220K K -=,解得21K =或0,利用定理5(i )的通解公式有323212311[]ln 22y x x x dx x dx dx x x c x c x c x --=-=+++⎰⎰⎰. (其中1c ,2c ,3c 为任意常数)例2 求三阶欧拉方程3241313x y x y xy y x ''''''-+-=的通解. 解 原方程对应的齐次方程为32413130x y x y xy y ''''''-+-=,其特征方程为21613()()0K K K -+-=,从而解得特征单实根为11K =,将11K =,14a =-,213a =代入方程(15),得到222250K K -+=,解得 1,2212i K =±. 令212i K =+,则1α=,2β=, 利用定理5(ii )的通解公式有33213{[sin(2ln )cos(2ln )cos(2ln )sin(2ln )]}211ln [sin(2ln )cos(2ln )]816xx x x dx x x x dx dxx x c x c x c x y x ---=+-+=⎰⎰⎰(其中1c ,2c ,3c 为任意常数)2.4 n 阶齐次欧拉方程的求解(求形如K y x =的解)令K y x =是方程(1)的解,将其求导(需要求出y '、y ''(1)n y -、()n y )代入方程(1),并消去K x ,得 1(1)(1)(1)(1)(2)0n n K K K n a K K K n a K a ---++--++++=. (16)定义3 以K 为未知数的一元n 次方程(16)称为n 阶齐次欧拉方程(1)的特征方程.由此可见,如果选取k 是特征方程(16)的根,那么幂函数k y x =就是方程(1)的解.于是,对于方程(1)的通解,我们有如下结论:定理6 方程(1)的通解为112211n n n n y c y c y c y c y --=++++(其中1c ,2c 1n c -,n c 为任意常数),且通解中的每一项都有特征方程(16)的一个根所对应,其对应情况如下表:例1 求方程4(4)3(3)281550x y x y x y xy '''+++=的通解. 解 该欧拉方程的特征方程为(1)(2)(3)8(1)(2)15(1)50K K K K K K K K K K ---+--+-+=,整理,得2(22)0K K K ++=,其根为(ln k d ++120K K ==,3,41K i =-±,所以原方程的通解为3412ln cos(ln )sin(ln )c cy c c x x x x x=+++. (其中1c ,2c ,3c ,4c 为任意常数)例2 求方程(4)(3)432670x y x y x y xy y ++++='''的通解. 解 该欧拉方程的特征方程为(1)(2)(3)6(1)(2)7(1)10K K K K K K K K K K ---+--+-++=,整理,得410K +=,其根为1,2K i =-,3,4K i =(即一对二重共轭复根), 所以原方程的通解为1234cos(ln )sin(ln )ln cos(ln )ln sin(ln )y c x c x c x x c x x =+++. (其中1c ,2c ,3c ,4c 为任意常数)3.结束语从前面的讨论过程来看,和教材中的变量变换法相比,本文中的解决办法更直接、更简单.但需要说明的是,本文中的定理和例题都是在0x >范围内对齐次欧拉方程求解的,如果要在0x <范围内对其求解,则文中的所有ln x 都将变为ln()x -,所得的结果和0x >范围内的结果相似.4.致谢经过这好几个月忙碌的学习跟工作,本次毕业论文的写作已经接近尾声了,但这次毕业论文的写作经历让我感受颇多.首先,自己要有很好的专业知识的储备,这也是写作的基础.其次,自己要有严谨的思维逻辑.再次,自己要善于思考,遇到不懂得问题就要勤于思考,查资料,问老师.最后,自己一定要有坚持不懈的精神.毕业论文的写作是一个长期的过程,在写作过程中我们难免会遇到各种各样的过程,但我们不能因此就放弃,而要做到坚持.要相信“有付出就一定会有所收获”的.在这里首先要感谢我的指导老师胡宏昌教授.胡老师平日里工作繁多,但在我做毕业论文阶段,他都给予了我悉心的指导,细心地纠正论文中的错误并给予指导.如果没有他的大力支持,此次论文的完成将变得非常困难.除了敬佩胡老师的专业水平外,他的治学严谨和科学研究的精神也值得我永远学习,并将积极影响我今后的学习和工作.然后还要感谢大学四年来我的所有的老师跟领导,为我们打下了坚实的专业知识的基础.最后祝各位评审老师身体健康,工作顺利!5、参考文献[1]王高雄,周之铭,朱思铭,王寿松.常微分方程[M].第3版.北京:高等教育出版社,2006:142-144.[2]华东师范大学数学系.数学分析(上)[M].第3版.北京:高等教育出社,1999:87-199.[3]钟玉泉.复变函数论[M].第3版.北京:高等教育出版社,2003:10-11.[4]胡劲松.一类欧拉方程特解的求解.重庆科技学院学报[J],2009,11(2):143-144.[5]胡劲松,郑克龙.常数变易法解二阶欧拉方程.大学数学[J],2005,21(2):116-119.[6]米荣波,沈有建,汪洪波.三阶欧拉方程求解的简化常数变易方法.海南师范大学学报[J],2008,21(3):260-263.[7]胡劲松.齐次欧拉方程的另一种求解方法.重庆工学院学报[J],2004,18(1):4-748.[8]冀弘帅.认识伟大的数学家----欧拉.数学爱好者[J],2006,10:52-53.[9]卓越科学家欧拉.中学生数理化(北师大版)[J],2007,Z2: 101-102.。
