第十八届华杯赛总决赛群答题真题
第十八届华杯赛决赛答案_小高B

第十八届华罗庚金杯少年数学邀请赛决赛试题B参考答案(小学高年级组)一、填空题(每题10 分, 共80分)二、解答下列各题(每题10 分, 共40分, 要求写出简要过程)9.答案:106解答. 图中共有5条最长的水平线段和7条最长的垂直线段, 任意两条水平与任意两条垂直的就构成一个长方形, 一共有2102110)123456()1234(=⨯=+++++⨯+++(个).其中含“*”号有4×15+4×15-4×4=120-16=104 (个).所以不含含“*”号有210-104=106个.10.答案:9解答. 由于三角形AFC的面积和四边形DBEF的面积相等, 可得出三角形AEC 的面积等于三角形BDC的面积. 由BD:DA = 1:2, 得三角形BDC的面积等于三角形ABC面积的13, 即三角形AEC的面积等于三角形ABC面积的13. 那么EC等于BC的13, 得出EC = 6, 进而AD = 6, BD = 3, 最终AB = 9.11.答案:61解答. 设有n 个人, 每人植树x 棵, 则611132013⨯⨯==nx .可以说明:113⨯>n . 若33=n , 则每人植树61棵. 如果5人不参加植树, 则有305棵树, 其余28人每人多植3棵, 才种84棵树, 完不成任务. 可见, 113⨯>n .考虑n = 61. 此时, x = 33. 如果5人不参加植树, 则有165棵树要让56人多植树. 若每人多植2棵, 则56人多植了112256=⨯(棵)树, 完不成植树任务; 若每人多植3棵, 则56人多植了168356=⨯(棵), 完成了植树任务. 所以, n = 61符合要求.12. 答案:59解答.① 观察立体右面的正方体, 标有1个黑点的侧面到标有2个黑点的面, 再到标有4个黑点的面是以逆时针方向围绕这三个面的交点.② 观察中间上面的正方体, 既然从1个黑点到2个黑点, 再到4个黑点是逆时针, 则该正方体标有6个黑点的面的对面标有1个黑点.③ 观察立体左面的正方体, 正方体标有3个黑点的面紧邻标有2个黑点的面, 结合观察立体中间上面的正方体, 可知该正方体中, 标有4个黑点的侧面的对面的黑点有3个, 且底面标有5个黑点. 并且可知, 从1个黑点到2个黑点, 再到3个黑点是顺时针.所以, 四个完全相同的正方体, 黑点为1、2和3的三个侧面顺时针围绕公共顶点, 1对6, 2对5, 3对4. 所以, 立体中右面的正方体紧贴中间正方体的侧面有6个黑点; 立体中左面的正方体紧贴中间正方体的侧面有6个黑点; 立体中间上面的正方体紧邻下方正方体的侧面有5个黑点; 立体中间下面的正方体后面的侧面有2个黑点, 底面有可能是有1个黑点. 所以立体中间下面的正方体紧贴其他3个正方体的3个侧面黑点总数最少是8个.4个正方体黑点总数是84, 3对紧贴的侧面黑点总数最多是25, 所以, 立体的侧面(包括底面)所有黑点的总数最多是59.三、解答下列各题(每题15 分, 共30分, 要求写出详细过程)13.答案:4解答. 用右图代替题目中的12⨯小长方形. 对于拼成的正方形图形, 记过左上顶点的对角线为甲对角线, 另一条对角线为乙对角线.图A首先, 有如下观察:1) 当甲对角线是对称轴时,a)左上角的22⨯小正方形是图A的(1), (2), (3), (4) 中之一;b)右下角的22⨯小正方形是图A的(1), (2), (5), (6) 中之一;c)若右上角的22⨯小正方形是图A的(1), (2), (7), (8) 中的一个, 则左下角的22⨯小正方形分别是图A中的(1), (2), (9), (10);2) 当乙对角线是对称轴时,a)右上角的22⨯小正方形是图A的(1), (2), (7), (8) 中之一;b)左下角的22⨯小正方形是图A的(1), (2), (9), (10) 中之一;c)若左上角的22⨯小正方形是图A中的(1), (2), (3), (4) 之一, 则左下角的22⨯小正方形分别是图A中的(1), (2), (5), (6).根据上述观察, 注意到拼出的正方形中恰有八个星, 再去掉旋转重合的, 得到以下4种图形:14.解答. 记第一种、第二种和第三种分类分别分了i , j , k 类, 每类的盒子数目分别为i a a a ,,,21 , j b b b ,,,21 , k c c c ,,,21 ,令k j i n ++=.1) 因为i a a a ,,,21 , j b b b ,,,21 , k c c c ,,,21 包含了1到30的所有整数, 所以 30≥n . 另一方面,,15534652313030211553212121⨯==⨯=+++≥+++++++++++=⨯ kj i c c c b b b a a a所以 30=++=k j i n , 三种分类各自分类的类数之和是30.2) 不妨设301=a , 记这30个盒子的类为A 类. 因为30=++k j i , 必有14≤j 或14≤k , 不妨设14≤j . A 类的30个盒子分到这不超过14个类中去, 必有一类至少有三个盒子, 这三个盒子里的红球数相同并且黄球数也相同.。
2020年第十八届华杯赛决赛小高年级(A)卷-试题及解析word版

总分第十八届华罗庚金杯少年邀请赛决赛试题A(小学高年级组)(时间2013年4月20日10:00~11:30)一、填空题(每小题10分,共80分)1.计算:19×0.125+281×81-12.5=________.解析:原式=(19+281-100)×0.125=200×0.125=252.农谚‘逢冬数九’讲的是,从冬至之日起,每九天分为一段,依次称之为一九,二九,……,九九,冬至那天是一九的第一天.2012年12月21日是冬至,那么2013年的元旦是________九的第________天.解析:31-21+1+1=12,12÷9=1…3,2013年的元旦是二九的第3天.3.某些整数分别被119977553,,,除后,所得的商化作带分数时,分数部分分别是92725232,,,,则满足条件且大于1的最小整数是________.解析:设整数为A,分别被119977553,,,除后,所得的商分别为A A A A 911795735,,,;)1(911921911)1(7972179)1(5752157)1(3532135-++=-++=-++=-++=A A A A A A A A ,,,显然,当A-1是[3,5,7,9]的时候满足题意。
所以A-1=315,A=316。
4.如右图,在边长为12厘米的正方形ABCD 中,以AB 为底边作腰长为10厘米的等腰三角形PAB .则三角形PAC 的面积等于________平方厘米.解析:过P点做PE⊥AB,由于三角形PAB为等腰三角形,所以AE=EB=6cm。
根据勾股定理:PE 2=102-62=64=82,所以PE=8cm。
S△PAB=12×8÷2=48cm 2,S△PCB=12×6÷2=36cm 2,S△PAC=48+36-12×12÷2=12cm 2。
第18届华杯赛决赛真题答案(小高组a卷)
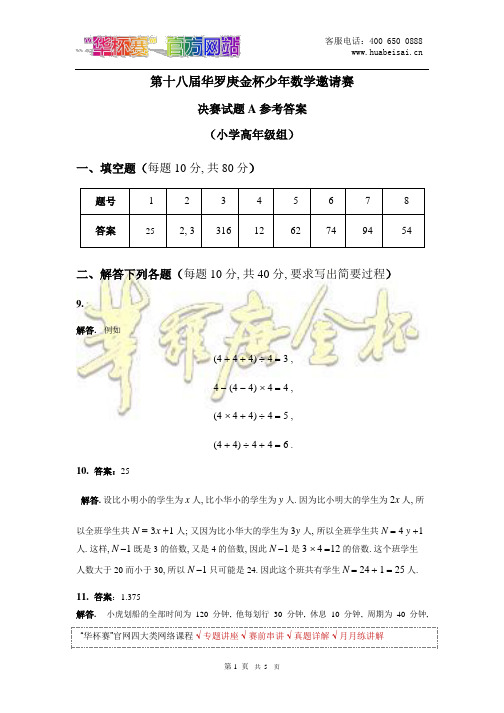
第十八届华罗庚金杯少年数学邀请赛决赛试题 A 参考答案(小学高年级组)一、填空题(每题 10 分, 共 80 分)题号 1 2 3 4 5 6 7 8答案25 2, 3 316 12 62 74 94 54二、解答下列各题(每题 10 分, 共 40 分, 要求写出简要过程)9.解答.例如(4 + 4 + 4) ÷ 4 = 3 ,4 - (4 - 4) ⨯ 4 = 4 ,(4 ⨯ 4 + 4) ÷ 4 = 5 ,(4 + 4) ÷ 4 + 4 = 6 .10.答案:25解答. 设比小明小的学生为x人,比小华小的学生为y人.因为比小明大的学生为2x人,所以全班学生共 N =3x +1人;又因为比小华大的学生为3y人,所以全班学生共N=4y+1人. 这样, N-1既是 3 的倍数, 又是 4 的倍数, 因此N-1是3⨯4=12的倍数. 这个班学生人数大于 20 而小于 30, 所以N-1只可能是 24. 因此这个班共有学生N=24+1=25人.11.答案:1.375解答.小虎划船的全部时间为120分钟,他每划行30分钟,休息10分钟,周期为40分钟, “华杯赛”官网四大类网络课程√专题讲座√赛前串讲√真题详解√月月练讲解所以一共可分为 3 个 30 分钟划行时间段, 有 3 个 10 分钟休息划船时, 顺水的船速与逆水的船速之比为 4.5:1.5=3:1. 因为小虎要把船划到离租船处尽可能远, 他在划船的过程中只能换一次划船的方向, 而且是在尽可能远处. 分两种情况讨论.1)开始向下游划船, 设最远离租船处x千米. 因为回到租船处是逆水, 所以小虎只有 110 分钟可用. 由于划船时顺流速度是逆流速度的 3 倍, 所以用在向下游划船的时间不能超过半小时. 另外两次休息时间只能用在返程, 在休息期间内船向下游漂流了13⨯1.5 , 所以⎛ 1 ⎫x ÷4.5+ x + ⨯1.5⎪ ÷1.5 = 1.5 .3⎝ ⎭整理上式得x +3x +1.5=6.75,4x= 5.25,x =1.3125(千米).2)开始向上游划, 设最远离租船处y千米. 小虎可用 120 分钟, 有两次休息时间用在向上游. 所以⎛ 1 ⎫ ⎛ 1 ⎫y + ⨯1.5⎪ ÷1.5 + y - ⨯1.5⎪ ÷ 4.5 = 1.5 .3 6⎝ ⎭ ⎝ ⎭整理上式得4 y+5 ⨯1.5 = 6.75 , 4 y= 5.5 , y =1.375(千米).6综合 1) 和 2) 的讨论, 小虎的船最多离租船处 1.375 千米.12.答案:不能解答. 设放的最小自然数为a,则放的最大自然数为a+23.于是这24个数的和为A= 12(2a+ 23).假设可能, 设每个正方形边上的数之和为S . 因为共有5个正方形, 这些和的和为5S . 因为每个数在这些和中出现两次, 所以有5S= 2A.“华杯赛”官网四大类网络课程√专题讲座√赛前串讲√真题详解√月月练讲解记最小的 16 个数的和为B , 则B=8(2a+15) . 下面分两种情形讨论:(1)若 B ≤ S ,则S = 2 A = 24 (2a+ 23) ≥ 8(2a+15) , 9.8a+110.4 ≥16a+120 ,5 5不存在自然数 a 使得不等式成立.(2)情形 B > S 也是不可能的,因为此时不可能选择最大正方形边上的16个数使得这16 个数的和等于S .三、解答下列各题(每题 15 分, 共 30 分, 要求写出详细过程)13.答案:5解答. 用右图代替题目中的2⨯1小长方形.因为题目所给的小长方形上下不对称,所以同一个小长方形在拼成的上下对称的正方形中, 不会既在上半部分也在下半部分. 这样, 就可以只考虑上半部分的不同情形.1)相邻的空白格在第一行最左边或最右边. 因为要排除旋转相同的, 所以只考虑相邻空白格在最右边的情况, 有下图所示的 2 种图形,2)相邻的空白格在第一行中间. 去掉旋转重合的, 有下图所示的 3 种图形,所有不同的图形为 5 种.14.答案:6036“华杯赛”官网四大类网络课程√专题讲座√赛前串讲√真题详解√月月练讲解解答. 令n = a1+ a2++ a2010 = b1 + b2 + + b2012 = c1 + c2 ++ c2013 ,其中, 所有的a i数字和相同, 所有的b j数字和相同, 所有的c k数字和相同. 两个自然数数字的和相同, 则它们除以 9 的余数相同, 即a i = 9u i + r, i =1, 2, , 2010,bj = 9v j + s, j =1, 2, , 2012,c k = 9w k + t, k =1, 2, , 2013.则n= 9 ⨯ (u1+u2+ +u2010 ) + 2010⨯r= 9 ⨯ (v1+v2+ +v2012 ) + 2012⨯s (1)= 9 ⨯ (w1+w2+ +w2013 ) + 2013⨯t,由上面的等式可得,9 ⨯ (u1+u2++ u2010 + 223 ⨯ r) + 3r = 9 ⨯ (v1 + v2 ++ v2012 + 223 ⨯ s) + 5 ⨯ s ,(2)9 ⨯ (w1+w2++ w2013 + 223 ⨯ t) + 6 ⨯ t = 9 ⨯ (v1 + v2 ++ v2012 + 223 ⨯ s) + 5 ⨯ s ,(3) 由 (2) 可以得出s是 3 的倍数, 只能是 0, 3 或 6. 下面三种情况讨论:1)s =0.此时,对j=1, 2,, 2012 ,因为b j=9v j的数字和不为零,所以v j≥1. 则n =9⨯(v1+ v2++ v2012 ) ≥ 9 ⨯ 2012 = 18108 .2)s =6.此时“华杯赛”官网四大类网络课程√专题讲座√赛前串讲√真题详解√月月练讲解客服电话:400 650 0888 n =9(v1+ v2++ v2012 ) + 2012 ⨯ 6 ≥ 12072 .3)s =3,此时n= 9(v1+v2+ +v2012 ) + 2012 ⨯ 3 ≥ 6036 .可以取 r =2, t =1.而6036 = 3 + 3 + + 3 = 2 + 2 + + 2 +11 +11 + +112012 个x 个y 个=10 +10 + +10 +1 +1 + +1.=m 个n 个下面计算 x, y 与 m, n,⎧x + y =2010, ⎨ ⎧m + n =2013,⎨⎩10m+n= 6 0 3,6即6036 = 2⨯1786 +11⨯224 =10⨯447 +1566 = 3⨯2012.最终, 满足条件的最小自然数是 6036.“华杯赛”官网四大类网络课程√专题讲座√赛前串讲√真题详解√月月练讲解第 5 页共5页。
2019年第十八届华杯赛决赛小高年级(A)卷-试题及解析word版

第十八届华罗庚金杯少年邀请赛决赛试题A (小学高年级组)(时间2019年4月20日10:00~11:30)一、填空题(每小题 10分, 共80分)1.计算: 19×0.125+281×81-12.5=________. 解析:原式=(19+281-100)×0.125=200×0.125=252.农谚‘逢冬数九’讲的是, 从冬至之日起, 每九天分为一段, 依次称之为一九, 二九, ……, 九九, 冬至那天是一九的第一天. 2019年12月21日是冬至, 那么2019年的元旦是________九的第________天.解析:31-21+1+1=12,12÷9=1…3,2019年的元旦是二九的第3天.3.某些整数分别被119977553,,,除后, 所得的商化作带分数时, 分数部分分别是92725232,,,, 则满足条件且大于1的最小整数是________.解析:设整数为A, 分别被119977553,,,除后, 所得的商分别为A A A A 911795735,,,; )1(911921911)1(7972179)1(5752157)1(3532135-++=-++=-++=-++=A A A A A A A A ,,,显然,当A-1是[3,5,7,9]的时候满足题意。
所以A-1=315,A=316。
4.如右图, 在边长为12厘米的正方形ABCD 中, 以AB 为底边作腰长为10厘米的等腰三角形PAB . 则三角形PAC 的面积等于________平方厘米.解析:过P 点做PE ⊥AB,由于三角形PAB 为等腰三角形,所以AE=EB=6cm 。
根据勾股定理:PE 2=102-62=64=82,所以PE=8cm 。
S △PAB=12×8÷2=48cm 2,S △PCB=12×6÷2=36cm 2,S △PAC=48+36-12×12÷2=12 cm 2。
小学奥数华杯赛试题及答案(第十八届第二期)

小学奥数华杯赛试题及答案(第十八届第二期)教案是教师为顺利而有效地开展教学活动,根据课程标准,教学大纲和教科书要求及学生的实际情况,以课时或课题为单位,对教学内容、教学步骤、教学方法等进行的具体设计和安排的一种实用性教学文书,包括教材简析和学生分析、教学目的、重难点、教学准备、教学过程及练习设计等,下面是由小编为大家整理的范文模板,仅供参考,欢迎大家阅读.这篇关于小学奥数华杯赛试题及答案(第十八届第二期),是小编特地为大家整理的,希望对大家有所帮助!试题一某公司有一项运动——爬楼上班,该公司正好在__大厦_楼办公。
一天编辑箫菲爬楼上班,她数了一下楼梯,每段有_级台阶,每层有2段。
她想我每一步走一级或二级。
那么我到公司走楼梯共有多少种走法呢?亲爱的小朋友你能帮萧菲解决这个难题吗?解析:如果用n表示台阶的级数,an表示某人走到第n级台阶时,所有可能不同的走法,容易得到:①当n=1时,显然只要1种走法,即a1=1。
②当n=2时,可以一步一级走,也可以一步走二级上楼,因此,共有2种不同的走法,即a2=2。
③当n=3时,如果第一步走一级台阶,那么还剩下二级台阶,由②可知有a2=2(种)走法。
如果第一步走二级台阶,那么还剩下一级台阶,由①可知有a1=1(种)走法。
根据加法原理,有a3=a1+a2=1+2=3(种)类推,有:a4=a2+a3=2+3=5(种)a5=a3+a4=3+5=8(种)a6=a4+a5=5+8=_(种)a7=a5+a6=8+_=_(种)a8=a6+a7=_+_=34(种)a9=a7+a8=_+34=55(种)a_=a8+a9=34+55=89(种)a_=a9+a_=55+89=_4(种)a_=a_+a_=89+_4=233(种)a_=a_+a_=_4+233=377(种)a_=a_+a_=233+377=6_(种)一般地,有an=an-1+an-2走一段共有6_种走法。
共有(_-1)_2=34(段)。
第十八届华杯赛总决赛口试

第十八届华罗庚金杯少年数学邀请赛总决赛团体赛 口试(周春荔执笔整理)(上半场)1. (共答题1)汉字“华、杯、赛、成、就、少、年、梦、想”分别代表1~9中不同的数码, 使得算式18=⨯华杯赛成+就+少年+梦+想成立, 那么华杯赛代表的三位数的最大值是多少?【答案】 972 【解答】华杯赛是个被18整除的三位数, 最大为990, 但出现两个9和0, 不合要求. 考虑次大的972. 而972÷18=54. 填法是97218.165834=++⨯++ 所以 华杯赛代表的三位数的最大值是972.2. (群答题1)甲、乙两个花瓶中都放有玫瑰和百合两种花,总计32支. 甲瓶中有三分之一是玫瑰花, 乙瓶中有七分之一是百合花. 问乙瓶中共放有多少支花?【答案】答: 14.【解答】 两瓶有花共32支, 乙瓶花的支数为7的倍数, 只能是7, 14, 21, 28支. 因此甲瓶花的数目对应为25, 18, 11, 5. 而甲瓶花的支数为3的倍数, 只能是18支, 因此乙瓶共有花14支.3. (必答题A1)左下图是一个等腰梯形, 上底和两腰的长度都是2, 下底长度是4; 右下图是一个正六角星形, 面积和等腰梯形的面积相等. 问: 正六角星形的周长是多少?【答案】12【解答】图a中的等腰梯形和图b中的正六角星形面积相等, 都由12个边长为1的正三角形组成, 即可求得正六角星形的周长为12.图a图b4.(必答题A2)将1, 2, 3, 4分别填入下面的方格中, 使得等式□+ 2×□+ 3×□+ 4×□= 22成立, 那么第一个方格填的数与第四个方格填的数之积是多少?【答案】6【解答】设填的数依次是,,,.a b c d由于+++=,23422a b c d又+++=,a b c d10相减得2312.++=b c d因此3 6.22b dc ++= 若,1,3bd =, 33,522b d +=. 因此c 为奇数, 这不可能. 因此只能,2,4.bd = 易知4,d ≠所以只能2,4,d b ==因此, 1,c = 此时只能 3.a = 事实上324314222.+⨯+⨯+⨯=所以3,4,1, 2.a b c d ==== 因此 32 6.a d ⨯=⨯=另解. 已知:23422a b c d +++=.首先, d ≠3, d ≠4. 若d =3, 则1032=++c b a , 但1132≥++c b a , 不合要求. 若d =4, 则,632=++c b a 但,1034332=++≥++c b a 不合要求.若d =1, 则,1832=++c b a 此时, b =3. 当a=2, c =4时, 2320a b c ++=. 当a =4, c =2时, 1632=++c b a , 都不合要求.所以, d =2. 1432=++c b a . 根据奇偶性, 只有a=1, c =3和a=3, c=1两种可能. 当a=1, c =3时, ,1898132=++=++c b a 不合要求; 当a=3, c =1时, 1438332=++=++c b a , 符合要求. 即a =3, d=2. .623=⨯=⨯d a5. (必答题A3)右图的三角形ABC 中, D 、E 分别是所在边的中点, BC = 6 MN , 三角形GMN 的面积等于3平方厘米. 求三角形ABC 的面积.【答案】54平方厘米.【解答】连接AG , 因为D 、E 分别是所在边的中点, 易知△BCG 的面积=△BAG 的面积=△ACG 面积,而△BCG 的面积=6×3=18平方厘米,所以三角形ABC 的面积=18×3=54平方厘米.6. (必答题A4)100以内仅能分解为两个不同质数之积的自然数共有多少个?【答案】30【解答】50以内的的质数2, 3, 5, 7, …, 43, 47共15个, 设分解质因数后为,().a b a b ⨯< 若2,a = 则b 可取由3到47这14个质数; 若 3,a = 则b 可取由5到31这9个质数; 若 5,a = 则b 可取由7到19这5个质数; 若 7,a = 则b 可取由11, 13这2个质数. 若 11a ≥, 1111121100,a b ⨯≥⨯=> 不满足要求.所以满足题设条件的数有14 + 9 + 5 + 2 = 30 (个).7. (必答题A5)梯形 ABCD 中, 腰 AD =10 厘米, 梯形的面积为 70 平方厘米. 则由腰 BC 的中点 M到直线 AD 的距离为多少厘米?【答案】7【解答】过M 作AD 的平行线交AB 于E , 交DC 于F . 由于M 为BC 中点, 相当于△MBE 绕点M 旋转180到△MCF 的位置. 自M 作AB 的垂线, 垂足为H .所以,平行四边形ADFE 的面积 = 梯形ABCD 的面积=70平方厘米.又平行四边形ADFE 的面积 =10AD MH MH ⨯=⨯= 70,所以 7MH =厘米.另解. 连接DM 交AB 的延长线于P ,相当于将△MDC 绕点M 旋转180到△MPB 的位置. 点D , M , P 在一条直线上, 且M 是DP 的中点.△ADP 的面积 = 梯形ABCD 的面积 = 70.连接AM , 自M 作AD 的垂线, 垂足为H . 则△AMD 的面积 =12⨯△ADP 的面积 = 35, 所以 135,2AD MH ⨯⨯= 即11035,2MH ⨯⨯= 所以MH = 7(厘米).8. (必答题A6)某植物园计划在如图所示的 A, B, C, D, E五个地块栽种四种不同颜色的郁金香, 每个地块内的郁金香必须同色. 相邻的(有公共边界的)地块的郁金香不能同色,不相邻的地块可以同色.问共有多少种不同的栽种方案?【答案】72【解答】按A , B , C , D , E 的顺序, 分别有4, 3, 2, 2, 2种颜色可选, 所以不同颜色的着色方案共有4 × 3 × 2 × 2 × 2 = 96 (种).注意到其中包含了只栽种三种颜色的郁金香(例如上图中D 与A 同色, 而E 与B 同色)的方法4×3×2×1=24 (种),因此满足题设要求的不同的栽种方案为962472-=(种).9. (必答题A7)如图所示, 已知△ABC , △ACD ,△ADE , △AEF 都是等腰直角三角形, 若它们的总面积是30平方厘米, 求AB + AD + AF 的长.【答案】14厘米【解答】根据条件容易判定, BAF 共线, 所以 围成的多边形是五边形BCDEF . 作111,,.CC AD DD AF EE AF ⊥⊥⊥设三角形△ABC 面积为,x 则△ACD 的面积为2,x △ADE 的面积为4,x △AEF 的面积为8x . 因此它们的总面积为15x . 由1530,x = 解得 2.x = 而2122AB =, 所以AB =2, AD = 4,. AF = 8, 所以AB + AD + AF = 14厘米.10. (必答题A8)黑板上写有数字1到9. 请你擦掉其中几个数字, 使得剩下的数字的两两乘积中, 个位出现由0到9这十个数字. 你从黑板上最多能擦掉几个数字?【答案】 3【解答】在黑板上应剩下数5. 数1和9可以只由乘积37⨯和19⨯得到, 这意味着, 所有奇数应留下. 还必须有一个偶数, 就是说黑板上剩下的数不少于六个.容易检验, 六个数1, 2, 3, 5, 7, 9 两两的乘积的末位出现由0到9的所有数字. 因此, 从黑板上最多能擦掉3个数字.11.(群答题2)有大、中、小三张圆形纸板, 每次取其中的两个盖在桌面上.如果所有的情况中盖住桌面的最大面积为25, 最小面积为10, 那么大圆纸板的面积为多少?【答案】15【解答】易知,大圆纸板与中圆纸板不重合时盖住的面积最大, 等于25, 是大、中两个圆纸板面积之和, 中圆纸板与小圆纸板完全重合时盖住的面积最小, 此时盖-=.住的面积为中圆纸板的面积, 为10.所以最大的圆纸板面积为25101512.(群答题3)甲乙两人分别在一圆形跑道上的一条直径的两端点, 同时顺时针沿跑道行走, 10分钟后, 甲追及乙. 问至少再过多少时间甲再次追及乙?【答案】20分钟.【解答】因为10分钟的时间甲比乙多走半圈, 再过20分钟甲比乙又多走1圈, 即可追及乙.13.(共答2, 动手操作, 演示)你能用总面积为6的六张不全相等的正方形纸片将111⨯⨯的立方体完全裱糊起来吗? 如果能, 请你演示裱糊的方法; 如果不能, 请说明理由.【答案】能【解答】用六张面积都为1的纸片, 显然可以将111⨯⨯的立方体完全裱糊起来.现在要用总面积为6的六张不全相等的正方形纸片来裱糊111⨯⨯的立方体, 即至少用总面积为6的两种不同大小的正方形纸片来裱糊111⨯⨯的立方体, 考虑到1111=+++++,6222222可以引进相应的例子: 连接111⨯⨯的立方体各界面正方形的两条对角线, 剪出两张边长等于界面正方形的对角线长的大正方形(面积为2)纸片. 其中一张像图a) 那样裱糊在上界面和相邻的每个界面的四分之一(正方形的顶点安放在四个相邻界面的中心). 另一张面积为2的正方形裱糊在下界面以及它每个的侧面的四分之一. 四个剩余的部分的每一个, 可以裱糊面积为12的正方形, 如图b) 所示.14. (必答题B1)在100至200之间有三个连续的自然数, 其中最小的能被3整除, 中间的能被5整除, 最大的能被7整除. 写出这样的三个连续自然数.【答案】159, 160, 161【解答】找中间的那个数, 它能被5整除, 被3除余1, 被7除余6. 先找被5整除被3除余1的最小数是10, 然后每次加[3, 5]=15, 看是否能被7除余6, 找到位于100~200之间的只有10+150=160, 所以这三个数为159、160和161.15. (必答题B2)边长分别为6厘米和8厘米的两张正方形纸板, 放在一个边长为10厘米的大正方形内, 大正方形内未被两张小正方形纸板盖住的部分的面积的最小值是多少平方厘米?【答案】16【解答】易知 2226810+=, 即边长分别为6厘米和8厘米的两张纸板的面积之和恰等于边长为10厘米的大正方形的面积. 只有当两个纸板放在大正方形内重叠的部分面积最小时, 其覆盖的总面积才最大, 这时未被覆盖的总面积为最小. 两个正方形纸板分别在图中的EFGD 与PBMN 的位置时, (两个正方形纸板重叠部分为正方形FHNQ ), 未被覆盖的APQE 与MCGH 的总面积为最小.易知未被覆盖的APQE 与MCGH 的总面积恰等于正方形FHNQ 的面积. 正方形FHNQ 的边长为6 + 8 – 10 = 4厘米, 所以正方形图a) 图 b)FHNQ 的面积为16平方厘米. 也就是大正方形内未被小正方形纸板盖住的部分的面积的最小值是16平方厘米.16. (必答题B3)自然数n 是两个质数的乘积, 它的包含1但不包含n 的所有因数的和等于100. 那么n =?【答案】194【解答】设,n pq =其中p 和q 是不同的质数.根据条件1100,p q ++=因此99.p q += 所以数p 和q 之一是偶数. 设p 是偶质数2, 则2,p =而97.q =即297194.n =⨯=17. (必答题 B4)如图, 三角形ACB 中, 90,ACB ∠= AC =1cm, AB =2cm. 以B 为中心, 将三角形ACB 顺时针旋转, 使得点A 落在边CB 延长线上的A 1点, 此时点C 落在点C 1的位置.设在旋转中边AC 扫过的面积为S , 以B 为中心1为半径的半圆面积为T , 求S 与T 之比.【答案】5:6.【解答】易知1130.ABD A BD ∠=∠=曲边三角形111AC D 的面积= 曲边三角形ACD 的面积.所以边AC 变到A 1C 1所扫过的面积为S =()()2222150524(21)36012BC πππ⨯-⨯=--5.12π= 以B 为中心1为半径的半圆面积T 211.22ππ=⋅= 所以 525.126S T ππ=⨯= 即:5:6.S T = 18. (必答题B5) 非零的自然数n 是25的倍数, 它的数字和也是25的倍数. 那么n 最小是多少?【答案】4975【解答】一个非零的自然数是25的倍数, 这个自然数的末两位数字只可能是00, 25, 50, 75. 而这个自然数的数字和也是25的倍数, 最小数字和为25, 末两位为75时数字和为12, 前面的数字和只能是13, 最少占两位. 即所求的是个4位数75.ab 而13a b +=, a 最小取4, 此时9b =, 所求的自然数最小是4975.19. (必答题B6)如图所示, 6个完全相同的小长方体恰好拼成一个体积等于384立方厘米的长方体, 那么, 一个小长方体所有棱长的总和是多少厘米?【答案】28【解答】设小长方体的长为4k 厘米, 则可知小长方体的宽是2k 厘米, 高是k 厘米, 立即得到: 体积等于384立方厘米的长方体的长和宽相等, 均为4k 厘米, 高是3k 厘米, 体积为33443483848k k k k k ,⨯⨯==⇒=故k = 2. 所以, 1个小长方体所有棱长的总和是564)248(=⨯++(厘米).20. (必答题B7)能够在图中的小圆圈中填入由0到9的所有整数, 使得有三个圆圈的六条线段上的数之和都等于同一个值吗? 请说明理由.【答案】不能【解答】假设, 这是可能的. 设在线段端点的数的和等于A , 在线段中点放的数的和等于B . 而沿每条线段三数的和等于S . 显然, A+B = 0+1+…+9 = 45. 每个端点恰属于三条线段, 而所有中点是不同的. 所以, 顺着全部六条线段的和加在一起, 我们得到 36.A B S += 由此26()645.A S A B S =-+=-但这不可能, 因为2A 是偶数, 而645S -是奇数.得到的矛盾证明了, 要求的放置是不可能的.21. (必答题B8) 有三块长方形钢化玻璃板, 尺寸如图所示.想用这三块玻璃板作侧面, 水泥地平面为底面, 粘合成一个临时的盛水容器, 三块玻璃板不许剪裁和弯曲, 只允许在边缘处粘合, 问容器最多可容多少立方分米的水?【答案】48【解答】根据两边之和大于第三边的要求, 易知这个容器的底面只能是边长为3,4, 5和边长为4, 5, 8的三角形两种情况:(1)底面三角形边长为3, 4, 5. 侧面取最短的高为8;容积为1348482⨯⨯⨯=; (2)底面三角形边长为4, 5, 8., 设引向长为8的边的高为,h 则底面三角形面积18,2h =⨯⨯ 侧面取最短的高为3. 容积11(8)384348.22h =⨯⨯⨯<⨯⨯⨯=所以容器最多可容48立方分米的水.(下半场)22.(群答题4)几位游客上午10: 30进入公园, 沿大道从东门步行走向西门, 在公园大道某处的路标上写着: 距东门2220m , 距西门660m. 然后游客们走到西门出园时间是11: 20. 求游客行走的平均速度是多少(千米/小时)?【答案】3.456【解答】游客行程=2220+660米=2.88千米. 游客共行走了50分钟=56小时, 所以, 游客行走的平均速度为52.88 2.88653.4566÷=⨯÷=(千米/小时).23.(群答题5)能够在图中的圆圈内填入10个数, 使得任意黑三角形顶点的三数之和都等于2012, 而任何白三角形的顶点的三数之和都等于2013吗? 请说明理由.【答案】不能【解答】假设放置了所求的10个数. 设放置在中间六边形的顶点的数为a, b, c, d, e, f, 在它中心的数为p, 则根据条件, 在三个黑三角形顶点的所有数的和为:332012a b c d e f p++++++=⨯. ①同时, 在三个白三角形顶点的所有数的和为:332013a b c d e f p ++++++=⨯. ② 比较①、②得 3201232013,⨯=⨯ 即20122013.=矛盾.另解. 假设放置了所求的10个数. 设放置在中间六边形的顶点的数为a , b , c , d , e , f , 在它中心的数为p , 则根据条件, 任意黑三角形顶点的三数之和都等于2012, 而任何白三角形的顶点的三数之和都等于2013, 易知1,f b =+ 1,d f =+ 1.b d =+三式相加得:3,f d b b f d ++=+++即0=3. 矛盾.24. (共答题3)用一个31角的模版和铅笔为工具,你能在纸上画出一个13的角吗? 说明理由.【答案】能【解答】因为1803311754052713.⨯-⨯=-=画一直线AOB , 取O 为坐标原点. 以射线OA 为角的一边, 在顺时针方向作∠131AOC =, 接着再作16个31的角122334151631.C OC C OC C OC C OC ∠=∠=∠==∠= 得1613.BOC ∠=25. (抢答题1)将九个数码1, 2, 3, 4, 5, 6, 7, 8, 9分成两组, 写成甲、乙两个多位数, 使得甲数恰为乙数的两倍. 请写出三组不同的答案, 每组答案中有一个数的千位是5.【答案】(15384, 7692), (15846, 7923), (15864, 7932)【解答】(1)两个多位数必一个是五位数, 一个是四位数. 且五位数万位是1.(2)已知5在千位上, 若5在四位数的千位, 乘以2之后, 得五位数的万位与千位是10或11(百位进上1时), 由于九个数字中没有0, 且不能重复, 所以5不能出现在四位数的千位. 因此5只能出现在五位数的千位, 这时四位数的千位必为7, 需百位乘2后进一, 得五位数是15abc. 四位数的百位只能是9或8或6.当四位数百位是9时, 有两组解:(15846, 7923); (15864, 7932),当四位数百位是8时, 无解;当四位数百位是6时, 有一组解:(15384, 7692).思维链接. 建议有兴趣的读者可以独立思考解答下面的问题:将九个数码1, 2, 3, 4, 5, 6, 7, 8, 9分成两组, 写成甲、乙两个多位数, 使得甲数恰为乙数的两倍. 请写出各种不同的答案.答案为:(18546, 9273); (18654, 9327); (15846, 7923), (15864, 7932),(15384, 7692); (14658, 7329), (14586, 7293), (14538, 7269);(13458, 6729), (13854, 6927), (13584, 6792).提示:(1)分得的必一个五位数, 一个是四位数, 并且五位数万位是1.(2)5不能在四位数的各个位中, 也不能是五位数的个位.(3)5在五位数的十位或百位, 靠四位数的26, 27, 28, 29乘2后产生五位数十位或百位的5. 5在五位数的千位, 靠79×2=158产生千位的5.(4)四位数的个位或(百位)乘2不进位.按上述要求, 试填即得.26. (抢答题2)将1至2013这2013个自然数依次写下来, 得一多位数123456789101112…201120122013.这个多位数除以9的余数是几?【答案】3【解答】 一个自然数除以9的余数等于这个自然数的各个数位上的数字之和除以9的余数.将0至1999这2000个数分成如下1000组:(0, 1999), (1, 1998), (2, 1997), …, (998, 1001), (999, 1000), 以上每组两数之和都是1999, 且两数相加没有进位, 这样1至1999这1999个自然数的所有数字之和是:(1+9+9+9)×1000=28000.2000~2013这14个自然数各位数字和为28+45+10=83,所以这个多位数除以9的余数就是 (28000+83) 除以9的余数, 得3.27. (抢答题3)如图所示的圆内接正六边形ABCDEF的面积是18平方厘米. 以AB , BD , DE , EA 为直径向外作四个半圆. 问四个月牙形(阴影)面积的和等于多少?【答案】12平方厘米【解答】连接BOE , 知 三角形DBE 为直角三角形. BE右上两个月牙形面积之和等于三角形DBE 的面积, 同理, BE 左下两个月牙形面积之和等于三角形ABE 的面积, 因此, 四个月牙形(阴影)面积的和等于长方形ABDE 的面积. 而容易看出, 长方形ABDE 的面积等于六边形ABCDEF 的面积的2,3等于12平方厘米. 所以四个月牙形(阴影)面积的和等于12平方厘米.28. (抢答题4)今有2013张纸牌, 上面分别写有从1到2013的数字, 问能否将这些纸牌分成三堆, 使各堆牌上的数之和的比为3:2:1吗? 说明理由.【答案】不能【解答】因为2013张牌的数字之和为201310072013220131102320124321⨯=⨯+=++++++ , 如果能分成题中要求的三堆牌, 等于将和数10072013⨯分成相等的6份, 每份都是整数. 也就是10072013⨯应被6整除. 但10072013⨯不被6整除, 矛盾!所以题设的分法是不可能的.29. (抢答题5)棱长为4的立方体支架每条棱上每隔单位长有一个分点与顶点一起共计标出44个点(如图). .至少过这些点中的两个点的不同的直线共有多少条?【答案】838【解答】暂时不考察通过立方体的棱的12条直线. 则a) 通过立方体每个顶点(8个之一), 引 93431⨯+= 条直线(图a ). b) 通过每个“非顶点”(它们是12336⨯=个之一)引113639⨯+=条直线(图b ).因为提到的每条直线计算了两次, 所以直线的总数等于1(8313639)12838.2⨯⨯+⨯+= 另解. 对给出的44个点, 每个点可与其余43个点连接直线, 确定每条直线要2个点, 每条直线对这两个点重复计数了一次, 因此连接的直线总数为44439462⨯=条. 其中在每条棱上的5个点两两连结的直线都是同一条, 多计数了54192⨯-=条, 12条棱上多计数了129108⨯=条. 所以过题设的44个点可确定的不同的直线共计946108838-=条.30. (抢答题6)千位与个位都是偶数码且不被1000整除的四位数共有多少个?【答案】1996【解答】四位数的千位数码依条件可以是2, 4, 6, 8中的任一个, 百位和十位数码可以是十个数码中的任一个, 而个位数码如果不考虑“不被1000整除”的条件, 可以从0, 2, 4, 6, 8这五个数字中任选一个.因此, 千位与个位都是偶数码的四位数共有4101052000⋅⋅⋅=个, 因为其中只有2000, 4000, 6000, 8000被1000整除, 所以千位与个位都是偶数码且不被1000整除的四位数共有200041996-=个.31. (抢答题7)如图, 写有不同的非0自然数的14张卡片数字朝下, 自小到大排成一行. 这些数的和等于170. 去掉最左和最右的两张, 剩下卡片上的数之和等于150.问原来左数第三张卡片写的是什么数?图a 图b【答案】8【解答】去掉最左和最右的两张纸片, 剩下数的和等于150. 表明卡片最小与最大数的和等于20. 因此, 可能是1+19, 2+18, 3+17, 4+16, 5+15, …….-+=<与共14张卡片不如果是4+16及它以后的情形, 卡片数最多为16411314.符. 若是3+17的情况, 而3到17这15个数之和为3+4+5+6+7+8+9+10+11+12+13+14+15+16+17=150,其中14个数不可能等于170.若是2+18的情况, 而2到18共17个数之和等于170. 去掉3个数, 14张卡片之和小于170, 与题设不符.所以只能是1+19的情况., 而由1到19共19个数之和等于190. 去掉和为20的5个数, 才能等于170. 只能去掉2, 3, 4, 5, 6这5个数. 因此原来左数第三张卡片写的是8.数.而在每个顶点写上该顶点所在的三个界面上的数的乘积. 那么八个顶点上写的数之和能是2013吗?如果能, 最初六个界面上写的数之和是多少? 如果不能, 请说明理由.【答案】能, 6个界面上写的数之和是75.【解答】设在立方体相对界面写的正整数分别是:上界面和下界面分别为a 和 b ;左界面和右界面分别为c 和d ;前界面和后界面分别为e 和f .则在各顶点写的数之和为acf adf ace ade bcf bce bdf bde +++++++()()()201331161a b c d e f =+++==⨯⨯,所以在各界面上写的数的和是()()()3116175.a b c d e f +++++=++=33. (共答题4)在纸板上画有一个平行四边形ABCD , P 为形内一点.请用圆规、(无刻度)直尺、铅笔为工具, 画出一个边长分别等于P A 、PB 、PC 和PD 的四边形, 使得该四边形的面积恰是平行四边形面积的一半.【解答】作法如下: 平移PBC ∆到.P AD '∆或平移PAB ∆到P DC '∆即可.易知,△PBC 的面积+△P AD 的面积 = △P AB 的面积+△PCD 的面积 = 12⨯平行四边形ABCD 的面积. 所以平移PBC ∆到P AD '∆(或平移PAB ∆到P DC '∆)即可实现题设要求的作图.。
第18届华杯赛决赛小中组卷及参考答案

第十八届华罗庚金杯少年数学邀请赛决赛(A)卷【小中组】一、填空题(每小题10分,共80分)1.计算:(2014×2014+2012)-2013×2013=________.2.将长方形的纸片ABCD按右图的方式折叠后压平,使三角形DCF落在三角形DEF的位置,顶点E恰落在边AB上.已知∠1=20°,那么∠2是________度.3.鸡兔同笼,共有40个头,兔脚的数目比鸡脚的数目的10倍少8只,那么兔有________只.4.第一次操作将图a左下角的正方形分为四个小正方形,见图b;第二次操作再将图b左下角的小正方形分为四个更小的正方形,见图c;这样继续下去,当完成第六次操作时,得到的图形中共有________个正方形.图a图b图c5.右面的加法竖式中,相同的汉字代表1至9中的相同数字,而不同的汉字代表不同的数字.则竖式中的“数学”所表示的两位数共有________个.6.大小两个正方体积木粘在一起,构成右图所示的立体图形,其中小积木的下底面的四个顶点,恰好是大积木的上底面各边的中点.如果大积木的棱长为2,那么这个立体图形的表面积是________.7.某班学生人数大于20而小于30,其中女同学的人数是男同学的2倍.全班报名参加“华杯赛”的人数是未报名人数的3倍少1人.这个班有学生________名.8.见右图,图形内的数字分别表示所在的矩形或三角形的面积,那么阴影三角形的面积为________.二、简答题(每小题15分,共60分,要求写出简要过程)9.用4个数码4和一些加、减、乘、除号和小括号,写出值分别等于2、3、4、5、6的五个算式.10.右图是U,V,W,X四辆不同类型的汽车每百千米的耗油量.如果每辆车都有50升油,那么这四辆车最多可行驶的路程总计是多少千米?11.某商店卖出一支钢笔的利润是9元,一个小熊玩具的进价为2元.一次,商家采取“买4支钢笔赠送一个小熊玩具”的打包促销,共获利润1922元.问这次促销最多卖出了多少支钢笔?12.编号从1到10的10个白球排成一行,现按照如下方法涂红色:1)涂2个球;2)被涂色的2个球的编号之差大于2,求不同的涂色方法有多少种?第十八届华罗庚金杯少年数学邀请赛决赛(A )卷参考答案【小中组】一、填空题(每小题10分,共80分)1.解析:【知识点】运算律,平方差公式原式6039201240272012)20132014()20132014(20122013201422=+=+-⨯+=+-=2.解析:【知识点】平面几何o 201=∠=∠CDF ,DCF ∠与CDF ∠互余,则o o o 702090=-=∠DFC ,o 70=∠=∠DFC DFE ,o o o o 4070701802=--=∠。
第十八届华杯赛总决赛试题
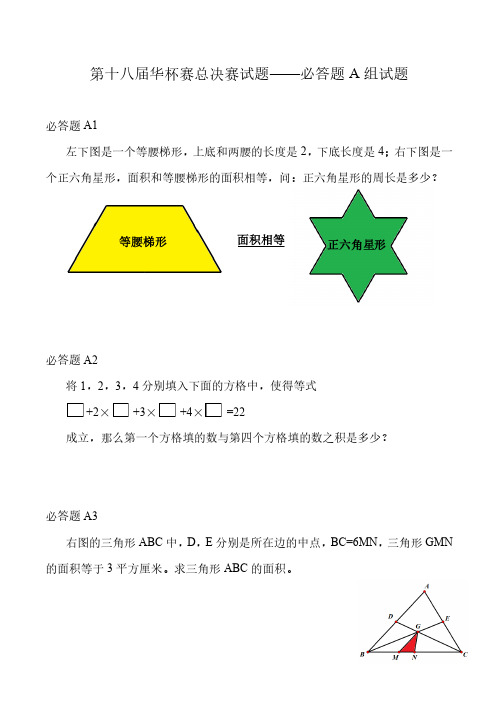
第十八届华杯赛总决赛试题——必答题A 组试题组试题必答题A1 左下图是一个等腰梯形,左下图是一个等腰梯形,上底和两腰的长度是上底和两腰的长度是2,下底长度是4;右下图是一个正六角星形,面积和等腰梯形的面积相等,问:正六角星形的周长是多少?个正六角星形,面积和等腰梯形的面积相等,问:正六角星形的周长是多少?必答题A2 将1,2,3,4分别填入下面的方格中,使得等式分别填入下面的方格中,使得等式+2× +3× +4× =22 成立,那么第一个方格填的数与第四个方格填的数之积是多少?成立,那么第一个方格填的数与第四个方格填的数之积是多少?必答题A3 右图的三角形ABC 中,D ,E 分别是所在边的中点,BC=6MN ,三角形GMN 的面积等于3平方厘米。
求三角形ABC 的面积。
的面积。
等腰梯形正六角星形面积相等,五个地块栽种四种不同颜色不能同色,不相邻的地块可以同色。
问共有多少种不同的栽种方案?E D C B A A黑板上写有数字1到9.请你擦掉其中的几个数字,使得剩下的数字的两两相这十个数字,你从黑板上最多能擦掉几个数字?乘积中,个位出现由0到9这十个数字,你从黑板上最多能擦掉几个数字?第十八届华杯赛总决赛试题——必答题B组试题组试题 必答题B1 在100至200之间有三个连续的自然数,其中最小的能被3整除,中间的能整除。
写出这样的三个连续自然数。
被5整除,最大的能被7整除。
写出这样的三个连续自然数。
必答题B2 边长分别为6厘米和8厘米的两张正方形纸板,放在一个边长为10厘米的大正方形内,大正方形内未被两小正方形纸板盖住的部分的面积最小值是多少平方厘米?厘米?必答题B3 自然数n是两个质数的乘积,它的包含1但不包含n的所有因数的和等于100,那么n=? 必答题B4 如图,三角形ABC中,∠ACB=90°,AC=1cm,AB=2cm.以B为中心,将三角形ACB顺时针旋转,使得点A落在边CB的延长线上A1点,此时点C落在点C1的位置。
18~22届华杯赛【小高组】决赛试题打印版

18~22届华杯赛决赛试题【小高组】目录计算篇 (1)计数篇 (6)几何篇 (16)数论篇 (30)应用题 (40)行程篇 (46)组合篇 (50)第一部分:计算篇1、【第18届华杯赛决赛B A 、卷第1题】 计算:______5.1281281125.019=-⨯+⨯.2、【第18届华杯赛决赛C 卷第1题】计算:______2785111111131322=÷⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+÷⎪⎭⎫ ⎝⎛-⨯.3、【第19届华杯赛决赛D B A 、、卷第5题】 如果54□711○<<成立,则“○”与“□”中可以填入的非零自然数之和最大为______.4、【第19届华杯赛决赛C 卷第1题】 计算:______5213.23.0241225.095.22.3=-⨯++⨯-.5、【第20届华杯赛决赛B 卷第1题】 计算:______2110804.1451848.28586.57=+⨯-⨯+⨯.6、【第20届华杯赛决赛C 卷第1题】 计算:______528.11.03.0441225.175.01=-+⨯++-.7、【第20届华杯赛决赛D 卷第1题】 计算:______8.0195105375.119484=⨯+⨯.8、【第21届华杯赛决赛A 卷第1题】计算:______107143214.2317=÷⎪⎭⎫ ⎝⎛⨯+-.9、【第21届华杯赛决赛B 卷第1题】计算:_____4.213453611753971=-÷⨯⎪⎪⎪⎪⎭⎫ ⎝⎛-.10、【第21届华杯赛决赛B 卷第8题】现有算式:甲数□乙数○1,其中□,○是符号+,-,×,÷中的某两个.李雷对四组甲数、乙数进行了计算,结果见右表,那么,A ○B =______.11、【第21届华杯赛决赛B 卷第9题】 计算:201620152016201420152014201635343201624232201613121+⎪⎭⎫ ⎝⎛++⋅⋅⋅+⎪⎭⎫ ⎝⎛+⋅⋅⋅+++⎪⎭⎫ ⎝⎛+⋅⋅⋅+++⎪⎭⎫ ⎝⎛+⋅⋅⋅++12、【第21届华杯赛决赛C 卷第1题】计算:______525125.022143225.0412=-⨯+-+.13、【第21届华杯赛决赛C 卷第3题】 大于20161且小于20151的真分数有______个.14、【第22届华杯赛决赛A 卷第1题】用][x 表示不超过x 的最大整数,例如3]14.3[=,则⎥⎦⎤⎢⎣⎡⨯+⎥⎦⎤⎢⎣⎡⨯+⎥⎦⎤⎢⎣⎡⨯+⎥⎦⎤⎢⎣⎡⨯+⎥⎦⎤⎢⎣⎡⨯+⎥⎦⎤⎢⎣⎡⨯118201711720171162017115201711420171132017的值为_____.15、【第22届华杯赛决赛A 卷第2题】从4个整数中任意选出3个,求出它们的平均值,然后再求这个平均值和余下1个数的和,这样可以得到4个数:8,12,3210和319,则原来给定的4个整数的和为______.16、【第22届华杯赛决赛B 卷第1题】______2017120161201512017120151514131513131211311=⨯⨯-+⋅⋅⋅+⨯⨯-+⨯⨯-.第二部分:计数篇1、【第18届华杯赛决赛B A 、卷第13题】用八个右图所示的2×1的小长方形可以拼成一个4×4的正方形.若一个拼成的正方形图形经过旋转与另一个拼成的正方形图形相同,则认为两个拼成的正方形相同.问:在所有可能拼成的正方形图形中,上下对称、第一行有两个空白小方格且空白小方格相邻的图形有多少种?2、【第18届华杯赛决赛B 卷第9题】 右图中,不含“*”的长方形有多少个?3、【第18届华杯赛决赛C 卷第3题】 最简单分数b a 满足4151<<b a ,且b 不超过19,那么b a +的最大可能值与最小可能值之积为______.4、【第18届华杯赛决赛C 卷第12题】一次数学竞赛中,参赛各队每题的得分只有0分,3分和5分三种可能.比赛结束时,有三个队的总得分之和为32分.若任何一个队的总得分都可能达到32分,那么这三个队的总得分共有多少种不同的情况?5、【第18届华杯赛决赛C 卷第14题】用八个右图所示的1×2的小长方形可以拼成一个4×4的正方形.若一个拼成的正方形图形经过旋转与另一个拼成的正方形图形相同,则认为两个拼成的正方形相同.问:有几种拼成的正方形图形仅以一条对角线为对称轴?6、【第19届华杯赛决赛D B A 、、卷第3题】从1~8这八个自然数中任取三个数,其中没有连续自然数的取法有______种.7、【第19届华杯赛决赛A 卷第9题】把n 个相同的正方形纸片无重叠地放置在桌面上,拼成至少两层的多层长方形(含正方形)组成的图形,并且每一个上层正方形纸片要有两个顶点各自在某个下层的正方形纸片一边的中点上.下图给出了6=n 时所有的不同放置方法,那么9=n 时有多少种不同放置方法?8、【第19届华杯赛决赛D B 、卷第9题】把n 个相同的正方形纸片无重叠地放置在桌面上,拼成至少两层的多层长方形(含正方形)组成的图形,并且每一个上层正方形纸片要有两个顶点各自在某个下层的正方形纸片一边的中点上.下图给出了6=n 时所有的不同放置方法,那么8=n 时有多少种不同放置方法?9、【第19届华杯赛决赛C卷第7题】1的小正方块堆成一立体,其俯视图如右图所示,问共有用八块棱长为cm种不同的堆法(经旋转能重合的算一种堆法).10、【第19届华杯赛决赛C卷第11题】a、和c.现有5块上面有一颗星、两颗星和三颗星的积木分别见下图的b一颗星,2块两颗星和1块三颗星的积木,如果用若干个这些积木组成一个五颗星的长条,那么一共有多少种不同的摆放方式?(下图d是其中一种摆放方式).(a)(b)(c)(d)11、【第20届华杯赛决赛B卷第5题】贝塔星球有7个国家,每个国家恰有四个友国和两个敌国,没有三个国家两两都是敌国,对于一种这样的星球局势,共可以组成______个两两都是友国的三国联盟.12、【第20届华杯赛决赛B卷第12题】两人进行乒乓球比赛,三局两胜制,每局比赛中,先得11分且对方少于10分者胜,10平后,多得两分者胜,两人的得分总和都是31分,一人赢了第一局且赢得比赛,那么第二局的比分共有多少种可能?13、【第20届华杯赛决赛C卷第2题】将自然数1至8分成两组,使两组的自然数各自之和的差等于16,共有______种不同的分法.14、【第20届华杯赛决赛C卷第5题】如图,3×4的长方形网格纸片,长方形纸片正面是灰色,反面是红色,网格是相同的小正方形,沿网格线将长方形裁剪为两个形状相同的卡片,如果形状和正反面颜色相同,则视为相同类型的卡片,则能裁剪出______种不同类型的卡片.15、【第20届华杯赛决赛D 卷第7题】一次数学竞赛有C B A 、、三题,参赛的39个人中,每人至少答对了一道题,在答对A 的人中,只答对A 的比还答对其他题目的多5人,在没答对A 的人中,答对B 的是答对C 的2倍;又知道只答对A 的等于只答对B 的 与只答对C 的人数之和,那么答对A 的最多有______人.16、【第20届华杯赛决赛D 卷第8题】甲,乙两人进行乒乓球比赛,三局两胜制,每局比赛中,先得11分且对方少于10分者胜,10平后,多得两分者胜,两人的得分总和都是30分,在不计比分先后顺序时,三局的比分共有______种情况.17、【第21届华杯赛决赛A 卷第4题】在9×9的格子纸上,1×1小方格的顶点叫做格点.如右图,三角形ABC 的三个顶点都是格点.若一个格点P 使得三角形PAB 与三角形PAC 的面积相等,就称P 点为“好点”.那么在这张格子纸上共有______个“好点”.18、【第21届华杯赛决赛A 卷第5题】对于任意一个三位数n ,用 表示删掉n 中为0的数位得到的数,例如 102=n 时, 12=那么满足 n <,且 是n 的约数的三位数n 有 ______个.19、【第21届华杯赛决赛A 卷第9题】复活赛上,甲乙二人根据投票结果决出最后一个参加决赛的名额.投票人数 固定,每票必须投给甲乙二人之一.最后,乙的得票数为甲的得票数的2120,甲胜出.但是,若乙得票数至少增加4票,则可胜甲.请计算甲乙所得的票数.20、【第21届华杯赛决赛A 卷第13题】如右图,有一张由四个1×1的小方格组成的凸字形纸片和一张5×6的方格纸.现将凸字形纸片粘到方格纸上,要求凸字形纸片的每个小方格都要与方格纸的某个小方格重合,那么可以粘出多少种不同的图形?(两图形经旋转后相同看作相同图形)21、【第21届华杯赛决赛C 卷第11题】如图,是一个等边三角形,等分为4个小的等边三角形,用红和黄两种颜色涂染它们的顶点,要求每个顶点必须涂色,且只能涂一种颜色.涂完后,如果经过旋转,等边三角形的涂色相同,则认为是相同的涂色,则共有多少种不同的涂法?22、【第22届华杯赛决赛B A 、卷第3题】在3×3的网格中(每个格子是个1×1的正方形)放两枚相同的棋子,每个格子最多放一枚棋子,共有______种不同的摆放方法.(如果两种放法能够由旋转而重合,则把它们视为同一种摆放方法).23、【第22届华杯赛决赛A 卷第5题】某校开设了书法和朗诵两个兴趣小组,已知两个小组都参加的人数是只参加书法小组人数的72,是只参加朗诵小组人数的51,那么书法小组与朗诵小组的人数比是______.24、【第22届华杯赛决赛B A 、卷第8题】如右图,六边形的六个顶点分别标志为F E D C B A 、、、、、.开始的时候“华罗庚金杯赛”六个汉字分别位于F E D C B A 、、、、、顶点处.将六个汉字在顶点处任意摆放,最终结果是每个顶点处仍各有一个汉字,每个字在开始位置的相邻顶点处,则不同的摆放方法共有______种.25、【第22届华杯赛决赛A 卷第10题】某校给学生提供苹果、香蕉和梨三种水果,用作课间加餐.每名学生至少选择一种,也可以多选.统计结果显示:70%的学生选择苹果,40%的学生选了香蕉,30%的学生选了梨.那么三种水果都选的学生数占学生总数至多是百分之几.26、【第22届华杯赛决赛B 卷第4题】小于1000的自然数中,有______个数的数字组成中最多有两个不同的数字.27、【第22届华杯赛决赛B卷第7题】一个两位数,其数字和是它的约数,数字差(较大数减去较小数)也是它的约数,这样的两位数的个数共有______个.28、【第22届华杯赛决赛B卷第11题】从1001,1002,1003,1004,1005,1006,1007,1008,1009中任意选出四个数,使它们的和为偶数,则共有多少种不同的选法.第三部分:几何篇1、【第18届华杯赛决赛A卷第4题】如右图,在边长为12厘米的正方形ABCD中,以AB为底边作腰长为10厘米的等腰三角形PAB.则三角形PAC的面积等于______平方厘米.2、【第18届华杯赛决赛A卷第4题、B卷第6题】两个大小不同的正方体积木粘在一起,构成右图所示的立体图形,其中,小积木的粘贴面的四个顶点分别是大积木的粘贴面各边的一个三等分点.如果大积木的棱长为3,则这个立体图形的表面积为______.3、【第18届华杯赛决赛A卷第8题,B卷第12题】由四个完全相同的正方体堆积成如右图所示的立体,则立体的表面上(包括底面)所有黑点的总数至少是______.4、【第18届华杯赛决赛B 卷第4题】如图所示,Q P 、分别是正方形ABCD 的边AD 和对角线AC 上的点,且4:1:=PD AP ,2:3:=QC AQ ,如果正方形ABCD 的面积为25,那么三角形PBQ 的面积是______.5、【第18届华杯赛决赛B 卷第10题】如右图,三角形ABC 中,BD AD 2=,EC AD =,18=BC ,三角形AFC 的面积和四边形DBEF 的面积相等,那么AB 的长度是多少?6、【第18届华杯赛决赛C 卷第4题】如图所示,Q P 、分别是正方形ABCD 的边AD 和对角线AC 上的点,且3:1:=PD AP ,1:4:=QC AQ ,如果正方形ABCD 的面积为100,那么三角形PBQ 的面积是______.7、【第18届华杯赛决赛C卷第6题】两个较小的正方体积木分别粘在一个大正方体积木的两个面上,构成右图所示的立体图形,其中,每个小积木粘贴面的四个顶点分别是大积木粘贴面各边的一个五等分点.如果三个积木的棱长互不相同且最大的棱长为5,那么这个立体图形的表面积是______.8、【第18届华杯赛决赛C卷第8题】由四个完全相同的正方体堆积成如右图所示的立体,则立体的表面上(包括底面)所有黑点的总数至少是______.9、【第18届华杯赛决赛C卷第9题】右图中,大正方形的周长比小正方形的周长多80厘米,阴影部分的面积为880平方厘米.那么,大正方形的面积是多少平方厘米?10、【第18届华杯赛决赛C 卷第13题】在等腰直角三角形ABC 中,90=∠A 度,1==AC AB ,矩形EHGF 在三 角形ABC 内,且H G 、在边BC 上.求矩形EHGF 的最大面积.11、【第19届华杯赛决赛D B A 、、卷第1题】如右图,边长为12米的正方形池塘的周围是草地,池塘边D C B A 、、、处各有一根木桩,且3===CD BC AB 米.现用长4米的绳子将一头羊拴在其中的某根木桩上.为了使羊在草地上活动区域的面积最大,应将绳子拴在______处的木桩.12、【第19届华杯赛决赛A 卷第4题】如右图所示,网格中每个小正方格的面积都为1平方厘米.小明在网格纸上 画了一匹红鬃烈马的剪影(马的轮廓由小线段组成,小线段的端点在格子点上或在格线上),则这个剪影的面积为______平方厘米.13、【第19届华杯赛决赛A 卷第8题】平面上的五个点E D C B A 、、、、满足:8=AB 厘米,4=BC 厘米, 5=AD 厘米,1=DE 厘米,12=AC 厘米,6=AE 厘米.如果三角形EAB 的面积为24平方厘米,则点A 到CD 的距离等于______厘米.14、【第19届华杯赛决赛A 卷第12题】如右图,在三角形ABC 中,D 为BC 的中点,BF AF 2=,AE CE 3=.连接CF 交DE 于P 点,求DPEP 的值.15、【第19届华杯赛决赛D B 、卷第4题】如右图所示,网格中每个小正方格的面积都为1平方厘米.小明在网格纸上画了一匹红鬃烈马的剪影(马的轮廓由小线段组成,小线段的端点在格子点上或在格线上),则这个剪影的面积为______平方厘米.16、【第19届华杯赛决赛B 卷第8题】平面上的五个点E D C B A 、、、、满足:16=AB 厘米,8=BC 厘米, 10=AD 厘米,2=DE 厘米,24=AC 厘米,12=AE 厘米.如果三角形EAB 的面积为96平方厘米,则点A 到CD 的距离等于______厘米.17、【第19届华杯赛决赛D B 、卷第12题】如右图,在三角形ABC 中,BF AF 2=,AE CE 3=,BD CD 2=.连接CF 交DE 于P 点,求DPEP 的值.18、【第19届华杯赛决赛C 卷第3题】如右图,在直角三角形ABC 中,点F 在AB 上且BF AF 2=,四边形EBCD 是平行四边形,那么EF FD :为______.19、【第19届华杯赛决赛C 卷第4题】右图是由若干块长12厘米、宽4厘米、高2厘米的积木搭成的立体的正视图,上面标出了若干个点.一只蚂蚁从立体的左侧地面经过所标出的点爬到右侧的地面.如果蚂蚁向上爬行的速度为每秒2厘米,向下爬行的速度为每秒3厘米,水平爬行的速度为每秒4厘米,则蚂蚁至少爬行了______秒.20、【第19届华杯赛决赛C 卷第8题】如右图,在三角形ABC 中,BF AF 2=,AE CE 3=,BD CD 4=.连接CF 交DE 于P 点,求DPEP 的值.21、【第19届华杯赛决赛D 卷第8题】长为4的线段AB 上有一动点C ,等腰三角形ACD 和等腰三角形BEC 在过AB 的直线同侧,DC AD =,EB CE =,则线段DE 的长度最小为______.22、【第20届华杯赛决赛B 卷第7题】如图,三角形ABC 的面积为1,3:1:=OB DO ,5:4:=OA EO ,则三角 形DOE 的面积为______.23、【第20届华杯赛决赛B 卷第10题,D 卷第6题】如图,从长、宽、高为15,5,4的长方体中切割走一块长、宽、高为y , 5,x 的长方体(y x 、为整数),余下部分的体积为120,求x 和y 的值.24、【第20届华杯赛决赛B 卷第13题】如图,点M 是平行四边形ABCD 的边CD 上的一点,且2:1:=MC DM ,四边形EBFC 为平行四边形,FM 与BC 交于点G ,若三角形FCG 的面积与三角形MED 的面积之差为13平方厘米,求平行四边形ABCD 的面积?25、【第20届华杯赛决赛C卷第4题】如图,四边形ABCD是边长为11厘米的正方形,G在CD上,四边形CEFG是直角,三角形EDH的是边长为9厘米的正方形,H在AB上,EDH面积是______.26、【第20届华杯赛决赛C卷第6题】一个长方体,棱长都是整数厘米,所有棱长之和是88厘米,问这个长方体总的侧面积最大是______平方厘米.27、【第20届华杯赛决赛C卷第13题】如图,ABCD是平行四边形,F在AD上,三角形AEF的面积是8平方厘米,三角形DEF的面积是12平方厘米,四边形BCDF的面积是72平方厘米,求三角形CDE的面积?28、【第20届华杯赛决赛D 卷第2题】如图,用六个正方形,六个三角形,一个正六边形组成的图案,正方形边 长都是cm 2,这个图案的周长是______.29、【第20届华杯赛决赛D 卷第11题】如图,长方形ABCD 的面积为2m 56,cm 3=BE ,cm 2=DF ,求:三角形AEF 的面积是多少?30、【第20届华杯赛决赛D 卷第13题】如图,ABCD 是平行四边形,MB AM =,CN DN =,FC EF BE ==四边形EFGH 的面积是1,求平行四边形ABCD 的面积.31、【第21届华杯赛决赛A 卷第3题】右图中,5=AB 厘米,85=∠ABC °,45=∠BCA °,20=∠DBC °, 则______=AD 厘米.32、【第21届华杯赛决赛A 卷第10题】如右图,三角形ABC 中,180=AB 厘米,204=AC 厘米,F D 、是AB 上的点,G E 、是AC 上的点,连结FG EF DE CD 、、、,将三角形ABC 分 成面积相等的五个小三角形.则AG AF +为多少厘米?33、【第21届华杯赛决赛B 卷第2题】如右图,30个棱长为1的正方体粘成一个四层的立体,这个立体的表面积等于______.34、【第21届华杯赛决赛B 卷第4题】如右图所示,将一个三角形纸片ABC 折叠,使得点C 落在三角形ABC 所在平面上,折痕为DE .已知74=∠ABE °,70=∠DAB °,20=∠CEB °,那么CDA ∠等于______.35、【第21届华杯赛决赛B 卷第1题】如右图,正方形ABCD 的边长为5,F E 、为正方形外两点,满足4==CF AE ,3==DF BE ,那么______2=EF .36、【第21届华杯赛决赛B 卷第11题】如右图,等腰直角三角形ABC 与等腰直角三角形DEF 之间的面积为20,2=BD ,4=EC ,求三角形ABC 的面积.37、【第21届华杯赛决赛B 卷第13题】如右图,正方形ABCD 的面积为1,M 是CD 边的中点,F E 、是BC 边上的两点,且FC EF BE ==.连接DF AE 、分别交BM 分别于G H 、.求四边形EFGH 的面积.38、【第21届华杯赛决赛卷第5题】如图,AD AB =,21=∠DBC °,39=∠ACB °,则______=∠ABC .39、【第21届华杯赛决赛C 卷第1题】如图,ABCD 是直角梯形,上底2=AD ,下底6=BC ,E 是DC 上一点,三角形ABE 的面积是15.6,三角形AED 的面积是4.8,则梯形ABCD 的面积是______.40、【第22届华杯赛决赛A 卷第6题、B 卷第5题】右图中,三角形ABC 的面积为100平方厘米,三角形ABD 的面积为72平方厘米.M 为CD 边的中点,90=∠MHB °.已知20=AB 厘米.则MH 的长度为______厘米.【几何天地】求阴影面积是正方形面积的几分之几?第四部分:数论篇1、【第18届华杯赛决赛B A 、卷第3题】 某些整数分别被119977553,,,除后,所得的商化作带分数时,分数部分分别是92725232,,,,则满足条件且大于1的最小整数是______.2、【第18届华杯赛决赛A 卷第3题】有一筐苹果,甲班分,每人3个还剩11个;乙班分,每人4个还剩10个;丙班分,每人5个还剩12个.那么这筐苹果至少有______个.3、【第18届华杯赛决赛A 卷第7题】设n 是小于50的自然数,那么使得54+n 和67+n 有大于1的公约数的所有n 的可能值之和为______.4、【第18届华杯赛决赛A 卷第14题】不为零的自然数n 既是2010个数字和相同的自然数之和,也是2012个数 字和相同的自然数之和,还是2013个数字和相同的自然数之和,那么n 最 小是多少?5、【第18届华杯赛决赛B卷第5题】有一箱苹果,甲班分,每人3个还剩10个;乙班分,每人4个还剩11个;丙班分,每人5个还剩12个.那么这箱苹果至少有______个.6、【第18届华杯赛决赛B卷第8题】用“学”和“习”代表两个不同的数字,四位数“学学学学”与“习习习习”的积是一个七位数,且它的个位和百万位数字与“学”所代表的数字相同,那么“学习”所能代表的两位数共有______个.7、【第18届华杯赛决赛B卷第14题】对于155个装有红、黄、蓝三种颜色球的盒子,有三种分类方法:对于每种颜色,将该颜色的球数目相同的盒子归为一类.若从1到30之间所有的自然数都是某种分类中一类的盒子数.1)求三种分类的类数之和?2)说明,可以找到三个盒子,其中至少有两种颜色的球,它们的数目分别相同.8、【第18届华杯赛决赛C卷第5题】四位数abcd与cdab的和为3333,差为693,那么四位数abcd为______.9、【第18届华杯赛决赛C 卷第7题】设c b a 、、分别是0~9中的数字,它们不同时都为0也不同时都为9.将循环小数⋅⋅⋅c b a .0化成最简分数后,分子有______不同情况.10、【第18届华杯赛决赛C 卷第11题】设n 是小于50的自然数,求使得53+n 和45+n 有大于1的公约数的所有n .11、【第19届华杯赛决赛A 卷第2题】在所有是20的倍数的正整数中,不超过2014并且是14的倍数的数之和是______.12、【第19届华杯赛决赛A 卷第13题】从连续自然数1,2,3,…,2014中取出n 个数,使这n 个数满足:任意取其中两个数,不会有一个数是另一个数的5倍.求n 的最大值,并说明理由.13、【第19届华杯赛决赛D B 、卷第2题】在所有是20的倍数的正整数中,不超过3000并且是14的倍数的数之和是______.14、【第19届华杯赛决赛D B 、卷第14题】从连续自然数1,2,3,…,2014中取出n 个数,使这n 个数满足:任意取其中两个数,不会有一个数是另一个数的7倍.求n 的最大值,并说明理由.15、【第19届华杯赛决赛C 卷第5题】设e d c b a 、、、、均是自然数,并且e d c b a <<<<,3005432=++++e d c b a ,则b a +的最大值为______.16、【第19届华杯赛决赛C 卷第10题】 把20142013201420122014220141,,,,⋅⋅⋅中的每个分数都化成最简分数,最后得到的以2014为分母的所有分数的和是多少?17、【第19届华杯赛决赛B 卷第12题】某自然数减去39是一个完全平方数,减去144也是一个完全平方数,求此自然数.18、【第19届华杯赛决赛B 卷第14题】 将每个最简分数m n (其中n m 、为互质的非零自然数)染成红色或蓝色,染色规则如下:1)将1染成红色;2)相差为1的两个数颜色不同;3)不为1的数与其倒数颜色不同.问:20142013和72分别染成什么颜色?19、【第20届华杯赛决赛B 卷第4题】某个三位数是2的倍数,加1是3的倍数,加2是4的倍数,加3是5的倍数,加4是6的倍数,那么这个数最小是______.20、【第20届华杯赛决赛B卷第6题】由四个互不相同的非零数字组成的没有重复数字的所有四位数之和为106656,则这些四位数中最大的是______,最小的是______.21、【第20届华杯赛决赛B卷第8题】三个大于1000的正整数满足:其中任意两个数之和的个位数字都等于第三个数的个位数字,那么3个数之积的末尾3位数有______种可能数值.22、【第20届华杯赛决赛B卷第9题】将1234567891011的某两位的数字交换能否得到一个完全平方数?请说明理由.23、【第20届华杯赛决赛B卷第14题】设“一家之言”,“言扬行举”,“举世皆知”,“知行合一”四个成语中的每个汉字代表11个连续的非零自然数中的一个,相同的汉字代表相同的数,不同的汉字代表不同的数,如果每个成语中四个汉字所代表的数之和都是21,则“行”可以代表的数最大是多少?24、【第20届华杯赛决赛C 卷第7题】5321-=⎥⎦⎤⎢⎣⎡-x x ,这里的[]x 表示不超过x 的最大整数,则______=x .25、【第20届华杯赛决赛C 卷第10题】将2015个分数2016120151413121,,,,,⋅⋅⋅化成小数,共有多少个有限小数?26、【第20届华杯赛决赛C 卷第11题】 b a 、为正整数,小数点后三位经四舍五入后,式子51.175≈+b a ,求 =+b a27、【第20届华杯赛决赛C 卷第12题】 已知原式e aad abcd ⨯=,式中不同字母代表不同的数字,问四位数abcd 的最大值是多少?28、【第20届华杯赛决赛D 卷第5题】由四个非零数字组成的没有重复数字的所有四位数的和为73326,则这些四位数中最大的是______.29、【第20届华杯赛决赛D 卷第9题】两个自然数之和为667,它的最小公倍数除以最大公约数所得的商等于120,求这两个数?30、【第20届华杯赛决赛D 卷第12题】当n 取遍1,2,3,…,2015中的所有的数时,形如33n n 的数中能够被7整除的有多少个?31、【第20届华杯赛决赛D 卷第14题】“虚有其表”,“表里如一”,“一见如故”,“故弄玄虚”四个成语中每个汉字代表11个非零连续自然数中的一个,相同的汉字代表相同的数,不同的汉字代表不同的数,且“表”>“一”>“故”>“如”>“虚”,且 各个成语中四个汉字所代表的数的和都是21,则“弄”可以代表的数最大 是多少?32、【第21届华杯赛决赛B A 、卷第7题】如果832⨯能表示成k 个连续正整数的和,则k 的最大值为______.33、【第21届华杯赛决赛A 卷第14题】设n 是正整数.若从任意n 个非负整数中一定能找到四个不同的数d c b a 、、、使得d c b a --+能被20整除,则n 的最小值是多少?34、【第21届华杯赛决赛B 卷第12题】试找出这样的最大的五位正整数,它不是11的倍数,通过划去它的若干数字也不能得到可被11整除的数.35、【第21届华杯赛决赛C 卷第7题】n 为正整数,形式为12-n 的质数称为梅森数,例如:712,31232=-=-是梅森数.最近,美国学者刷新了最大梅森数,74207281=n ,这个梅森数也是目前已知的最大的质数,它的个位数字是______.36、【第22届华杯赛决赛B A 、卷第12题】 使1523++n n 不为最简分数的三位数n 之和等于多少.37、【第22届华杯赛决赛B 卷第10题】求能被7整除且各位数字均为奇数,各位数字和为2017的最大正整数.第五部分:应用题篇1、【第18届华杯赛决赛A卷第10题】小明与小华同在小六(1)班,该班学生人数介于20和30之间,且每个人的出生日期均不相同.小明说:“本班比我大的人数是比我小的人数的两倍”,小华说:“本班比我大的人数是比我小的人数的三倍”问这个班的有多少名学生?2、【第18届华杯赛决赛B卷第11题】若干人完成了植树2013棵的任务,每人植树的棵数相同.如果有5人不参加植树,其余的人每人多植2棵不能完成任务,而每人多植3棵可以超额完成任务.问:共有多少人参加了植树?3、【第18届华杯赛决赛C卷第10题】某高中根据入学考试成绩确定了录取分数线,录取了四分之一的考生.所有被录取者的成绩平均分比录取分数线高10分,所有没有被录取的平均分比录取分数线低26分,所有考生的平均成绩是70分.求录取分数线是多少?4、【第19届华杯赛决赛A卷第7题】学校组织1511人去郊游,租用42座大巴和25座中巴两种汽车.如果要求恰好每人一座且每座一人,则有______种租车方案.5、【第19届华杯赛决赛A卷第10题】有一杯子装满了浓度为16%的盐水.有大、中、小铁球各一个,它们的体积比为10:4:3.首先将小球沉入盐水杯中,结果盐水溢出10%,取出小球;其次把中球沉入盐水杯中,又将它取出;接着将大球沉入盐水杯中后取出;最后在杯中倒入纯水至杯满为止.此时杯中盐水的浓度是多少?(保留一位小数)B、卷第7题】6、【第19届华杯赛决赛D学校组织482人去郊游,租用42座大巴和20座中巴两种汽车.如果要求每人一座且每座一人,则有______种租车方案.。
第18届华杯赛决赛小高组(A)、(B)卷试题及参考答案

8.用“学”和“习”代表两个不同的数字,四位数“学学学学”与“习习习习”的积是一个七位数,且它的个位和 百万位数字与“学”所代表的数字相同,那么“学习”所能代表的两位数共有_______个.
7.设 n 是小于 50 的自然数,那么使得 4n+5 和 7n+6 有大于 1 的公约数的所有 n 的可能值之和为________. 8.由四个完全相同的正方体堆积成如右图所示的立体,则立体的表面上(包括底面)所有黑点的总数至 少是________.
二、解答下列各题(每题 10 分,共 40 分要求写出简要过程) 9.用四个数字 4 和一些加、减、乘、除号和括号,写出四个分别等于 3,4,5 和 6 的算式.
6.解析:【知识点】立体几何 求出小积木的棱长即可,如图所示:
小积木的棱长是直角三角形的斜边长度,小积木一个面的面积为12 22 5 ,大积木一个面的面积为 32 9 ,立体图形的表面积为: S 9 5 5 5 (9 5) 74 7.解析:【知识点】数论,余数,因数
设 4n 5 和 7n 6 的公约数为 k ,则 (4n 5) k 为整数,(7n 6) k 也为整数,为了作差消去 n ,前者 乘 7,后者乘 4,则[7(4n 5) 4(7n 6)] k 11 k 为整数,因为 k 1,则11 k 为整数时,只能是 k 11, 即 4n 5 和 7n 6 的公约数为 11; 又因为[(7n 6) (4n 5)] 11为整数,则 3n 1 为整数,
第十八届华杯赛决赛小高C试题及详细解答

2013年第十八届华杯赛决赛小高C试题及详细解答说明:试卷及答案由华杯赛官网下载,详细解答由广州启慧教育提供。
广州市决赛使用此卷。
详细解答:一、填空题:1、原式=827551153331138⨯+÷-⨯=827165533838⨯⨯⨯=215(或7.5) 难易程度:☆2、周期问题。
答案是5,92012年12月21到2013年2月3,包含12月21在内,共(31-21+1)+31+3=45天周期为9,45÷9=5,余0,故 五 九的最后一天,即:第 九 天难易程度:☆3、先分别求出a+b 的最大值与最小值:要使a+b 最大,则a 与b 应尽量大,由于b 不超过19,故b 最大为19,由b a 是最简分数,且4151<<b a ,当b=19时,利用商不变性质有:20519204<<a ,故a 最大可为4,因此,a+b 最大可为19+4=23。
同理,可求出a+b 的最小值:由4151<<b a 可得:82102<<b a ,b a 最小可为92,故a 最小可为2,b 最小可为9,a+b 最小可为2+9=11因此,所有的积是:23×11=253难易程度:☆☆4、面积问题。
答案是37.5总体思路是:直接求△PBQ 的面积不容易,转化为用正方形面积减去其他图形的面积。
故需要连接DQ ,把四边形DPQC 转化为二个三角形。
接下来,多次利用同顶点的三角形面积的关系即可求出。
正方形的面积为100,故边长为10(1)、以D 为顶点来看△DQC 与△DQA因为AQ :QC=4:1,所以△QDA 的面积是△QDC 的4倍,所以△DQC 的面积是△ADC 的1/5,而△ADC 的面积是正方形ABCD 的一半,故△DQC 的面积是100÷2÷5=10显然△BCQ 的面积与△DQC 的面积相等,也是10(2)、以Q 为顶点来看△QDP 与△QPA因为AP:PD=1:3,所以△QDP的面积是△QAP 的3倍,所以△QDP的面积是△QDA的3/4,而△QDA的面积是△ACD的面积减去△DQC的面积,也就是50-10=40,故,△QDP的面积为30 (3)、求△ABP的面积:由于AP:PD=1:3,AD=10,因此,AP=2.5,故,△ABP的面积是2.5*10/2=12.5综合以上结论,就可求出△PBQ的面积为:100-10-10-30-12.5=37.5难易程度:☆☆5、和差问题。
2013年第十八届华杯赛决赛中年级(B)卷-试题及解析word版

总分第十八届华罗庚金杯少年邀请赛决赛试题A (小学中年级组)(时间2013年4月20日10:00~11:30) 一、填空题(每小题 10分, 共80分)1.计算: (2014×2014+2012)-2013×2013________.解析:(2014×2014+2012)-2013×2013=(2013+1)×(2013+1)+2013—1-2013×2013=2013×2013+2013+2013+1+2013-1-2013×2013=6039或用平方差公式。
(2014×2014+2012)-2013×2013=20142-20132+2012=2012+2013+2014=6039考试中最直接的方法,死算也OK 。
2.将长方形的纸片ABCD 按右图的方式折叠后压平, 使三角形DCF 落在三角形DEF 的位置, 顶点E 恰落在边AB 上. 已知∠1=20°, 那么∠2是________度.解析:因为翻折,∠CFD=∠E FD=90°-22°=68°∠2=180°-68°-68°=44°3.亮亮上学, 若每分钟行40米, 则8 : 00准时到校; 若每分钟行50米, 则7 : 55到校. 亮亮的家与学校的距离是________米.解析:行程型盈亏问题。
每分钟行40米,刚好够分;若每分钟行50米,则少5×50=250米所以250÷(50-40)=25分钟,亮亮的家与学校的距离是25×40=1000米.法二:六年级可以用。
走同样路程,速度比与时间成反比,速度比为4:5,则时间比为5:4,8:00-7:55=5分钟,则若每分钟行40米,亮亮用时5÷(5-4)×5=25分钟,所以亮亮的家与学校的距离是25×40=1000米.4.第一次操作将图a 左下角的正方形分为四个小正方形, 见图b; 第二次操作再将图b 左下角的小正方形分为四个更小的正方形, 见图c; 这样继续下去, 当完成第五次操作时, 得到的图形中共有________个正方形.解析:找规律。
第18届华杯赛(小学高年级组)试题及讲解

《18届华罗庚金杯少年数学邀请赛小学高年级教程》经典分析P155:初赛模拟测试题(1)6:一副扑克牌54张,将大小王视为0点,A视为1点,J视为11点,Q视为12点,K视为13点,任意抽出若干张,不计花色,如果要求每次抽出的牌中必定有2张牌的点数之和等于14,那么至少要取()牌。
教程答案:29。
我的答案:28因为:54张牌用最坏情况,2张大小王,4组A—6,4×6,再抽一张7,这时最坏情况抽完,然后再抽一张,就可以这些最坏情况的某一张,加起来和等于14点。
所以总共要抽:2+4×6+1+1=28张。
所以最低要取出28张牌。
P159:决赛模拟测试题(1)5:7098能表示成----种若干个(至少两个)连续非零自然数之和。
教程里的答案是12,这个答案和P19页,例1的答案是矛盾的。
而且教程中说这类题要穷举。
我的答案:11【7098=2×3×7×13²,共有(1+1)×(1+1)×(1+1)×(2+1)=12个奇因数,12-1=11】原因,例:把18、27分成两个或两个以上连续正整数之和,共有多少种不同的拆法。
18=2×3²即18=3×6,那么以6为中心,分别向两边扩1个数,和6总共是3个数:5、6、7 又18=9×2,那么以2为中心,分别向两边扩4个数,和6总共是9个数:-2、-1、0、1、2、3、4、5、6,其中在相加过程中-2、-1、0、1、2相抵消,剩余3、4、5、6又18=1×18,这里不能以1为中心,把18-1=17两边平均分,以18为中心的1个数没意义。
所以18=5+6+7=3+4+5+6,有两种不同的拆法在18=2×3²中奇数的个数是2+1=3个,(1,3,6)其中是3个以6为中心的连续数,和6个以3为中心的连续数。
但是1不可以拆分,所以要3-1=2,即只要两种拆法。
第十八届华杯赛决赛答案_初二A

第十八届华罗庚金杯少年数学邀请赛决赛试题A 参考答案(初二组)一、填空(每题 10 分, 共80分)二、解答下列各题(每题 10 分, 共40分, 要求写出简要过程)解答. 例如 74444=++÷, 74444=++÷,74444=÷-+, 74444=-÷, 74444=÷-⨯.9. 答案:61解答. 设成活a 棵, 没有成活b 棵, 未完成植树c 棵. 则⎩⎨⎧=+--=+)2(27113023)1(27125 c b a b a 由(1)可知, a 是奇数, 且54≤a ; 由(2)可知, 47≥a . 下面对 53,51,49,47=a 进行试算, 求得整数解:9,18,47-===c b a ,(不合要求);5.3,13,49-===c b a ,(不合要求);;612851,2,8,51=++=++===c b a c b a 5.7,3,53===c b a ,(不合要求).可见, 植树任务数是61.10. 答案:83 解答. 作BC 边上的高AD , AD 也是A ∠的平分线. AD 交EF 于P . 于是,9030=∠=∠=∠=∠EHB APE BEH EAP设x AE =, 则x AP x EP x EB 23,21,1==-=. 因此, )1(23)1(212321x x x x S FGC EHB AEF --+⨯=∆+∆+∆ []⎥⎦⎤⎢⎣⎡+-=+-=-+=41)21(23)21(23)1(432222x x x x x 由此可见, 当21=x 时, 上述三角形面积和最小, 从而内接矩形EFGH 的面积最大. 此时, 1:=EB AE . 连结ED 和FD , 容易知道,S □EFGH =8323141212121=⨯⨯=⨯⨯⨯=∆AD BC S ABC . 11. 答案:1003解答. 将2013个数分成如下1009组:(2013,35), (2012,36), …, (1025,1023), (1024),(34,30), (33,31), (32), (29,3), (28,4), …, (17,15), (16), (2), (1),其中有1004组中每组都有两个数, 且这两个数之和是2的幂次, 若擦剩下的数的个数大于等于1010, 由抽屉原理知, 必然有一组中两个数都被剩下了, 那么这两数和为2的幂次, 所以擦去1003个数满足题目要求. 如果擦去1004个数, 即剩下1009个数, 我们取这1009组中每一组的较大数, 那么显然这些数的任意两个之和都不是2的幂次, 故不满足题意, 所以最多擦去1003个数.三、解答下列各题(每题 15 分, 共30分, 要求写出详细过程)12. 解答. 连接AK. 先证 AM=CK .CK ACK ACN CD ACD ABD ∆∆==∆∆的面积的面积的面积的面积ABN AMD AM ABD ABD AB∆∆===∆∆的面积的面积的面积的面积. 因为CD=AB ,所以AM=CK . 连接OM ,OK ,ON . 则 △OMA ≌△OKC. 所以 .MOA KOC ∠=∠ 因此180,MOA AOK KOC AOK ∠+∠=∠+∠=所以M ,O ,K 共线,ON 是 △KNM 的中线,所以△ONM 的面积=△OKN 的面积.但△NMB 的面积=△ONM 的面积,△NKC 的面积=△ONK 的面积.所以△ONM 的面积=△OKC 的面积. 因此,三角形NMB 与NKC 等积.13. 87,841,833,81 解答. 若0≤x , 则0878878281][02>+=⎥⎦⎤⎢⎣⎡+++⎥⎦⎤⎢⎣⎡++⎥⎦⎤⎢⎣⎡++≥x x x x x , 矛盾. 所以 0>x .由带余除法,)70(,181]8[88]8[≤≤++=+<≤+=r r q x x r q x .所以818++<≤+r q x r q . 对于70≤≤i , 8188+++<+≤++i r q i x i r q . 当r i -≤7时,即 181≤++i r . 有q i x =⎥⎦⎤⎢⎣⎡+8.当18≥+i r 时,即 r i -≥≥87, 有18+=⎥⎦⎤⎢⎣⎡+q i x . 所以 ].8[8)1()8(87888781][x r q q r q r x r x r x x x =+=++-=⎥⎦⎤⎢⎣⎡+++⎥⎦⎤⎢⎣⎡-++⎥⎦⎤⎢⎣⎡-++⎥⎦⎤⎢⎣⎡++因此 878]8[2+=x x . (*) 因为 ()7}8{]8[7)8(764]8[8222++=+=+=x x x x x ,()8]8[2]8[71]8[]8[87]8[222++=++<≤+x x x x x , 所以 07]8[8]8[2≤+-x x , 08]8[6]8[2<+-x x . 由上面第一个式子得到, 0)7]8)([1]8([≤--x x , 7]8[1≤≤x ;由上面第二个式子得到, 0)3]8)([2]8([>--x x , 2]8[<x 或 4]8[>x . 因此7,6,5,1]8[=x .将]8[x 可以取的四个值分别代入 (*) 式, 解得大于0的x 分别为87,841,833,81.。
18~22届华杯赛决赛小中组试题及解析

第一章 计算篇
1、【第 18 届华杯赛决赛 A、B 卷第 1 题】 计算: (2014 2014 2012) 2013 2013 ______ . 2、【第 18 届华杯赛决赛 A 卷第 8 题】 见右图,图形内的数字分别表示所在的矩形或三角形的面积,那么阴影三角形的 面积为 ______ .
第二章 计数篇
1、【第 18 届华杯赛决赛 A 卷第 12 题】 编号从 1 到 10 的 10 个白球排成一行,现按照如下方法涂红色:1)涂 2 个球;2) 被涂色的 2 个球的编号之差大于 2,求不同的涂色方法有多少种? 2、【第 19 届华杯赛决赛卷第 2 题】 从 1~8 这八个自然数中取三个数,其中有连续自然数的取法有 ______ 种. 3、【第 20 届华杯赛决赛 A 卷第 2 题】 小明有多张面额为 1 元,2 元和 5 元的人民币,他想用其中不多于 10 张的人民 币购买一只价格为 18 元的风筝,要求至少用两种面额的人民币,那么不同的付 款方式有()种. A.3 B.9 C.11 D.8 4、【第 20 届华杯赛决赛 A 卷第 10 题】 妈妈决定假期带小花驾车去 10 个城市旅游,小花查完地图后惊奇地发现:10 个 城市的任意三个城市之间或者都开通了高速公路,或者只有两个城市间没有开通 高速路,那么这 10 个城市间至少开通了 ______ 条高速公路.(注:两个城市间 最多只有一条高速公路) 5、【第 20 届华杯赛决赛 B 卷第 11 题】 如右图所示,有一圆圈填了数字 1,请在空白圆圈内填上 2,3,4,5,6 中的一 个数字,要求无重复数字,且相邻圆圈内的数字的差至少是 2,问共有几种不同 的填法?
华杯赛决赛指导手册
(小学中年级组)
目录
计算篇............................................................................................................................ 1 计数篇............................................................................................................................ 3 几何篇............................................................................................................................ 5 数论篇............................................................................................................................ 9 应用题.......................................................................................................................... 11 行程篇.......................................................................................................................... 13 组合篇.......................................................................................................................... 15
