二维数字滤波器的设计
基于并行神经网络的二维FIR数字滤波器设计

文章 编 号 : 0 02 7 { 0 6 0 .0 2 0 1 0 . 4 2 2 0 )6 0 7 .4
基 于 并 行 神 经 网 络 的 二 维 FI R 数 字 滤 波 器 设 计
王 小华 一龙 . , 英 何 怡 刚 , 十
407; 10 7
( .湖南 大学 电气与信息工程 学院 , 1 湖南 长 沙 4 0 8 ; 10 2
表 明 由该方 法设 计 的二 雏数 字 滤波 器 , 带和 阻 带 范 围波动 小 , 需计算 量 非 常 少 , 定性 通 所 稳
强 . 经 网络 算 法 ; 优化 设计 中 图分 类号 : 13 TP 8 文献 标识 码 : A
3 Deto lcrncadC rmu a o gneig。 . p fEet i n cn mcf nEnier o i n C h iv aUn ,C h .Hua 4 0 0 . lm ) a n n 10 3 Ca i
A src: n w a po c o h eino W —i n i a ( 一 ii — us ep ne( I ier btatA e p rah frted s f Odmes n l 2D)f t i l rso s F R)l a— g t o n e mp e n p aedgtliesspee tdb sdo aal e rl ew rs loi m ( NN hs ii l r i rsne ae naprl l ua n t ok g r h P A)b n lz gtecaa— a ft en a t ya a i h rc yn h
基于Matlab的二维FIR数字滤波器的设计

第22卷 第1期2010年3月 塔 里 木 大 学 学 报Journal of Tari m UniversityVol.22No.1Mar.2010 文章编号:1009-0568(2010)01-0052-06基于Matlab的二维F IR数字滤波器的设计化希耀1 苏博妮1 张燕2(1 塔里木大学信息工程学院,新疆阿拉尔 843300)(2 西北师范大学物理与电子工程学院,甘肃兰州 730070)摘要 数字滤波器设计是数字信号处理的重要组成部分。
文章介绍了基于Matlab编程环境下用窗函数设计法,频率采样法,频率交换法,实现F I R二维数字滤波器的设计,并给出了设计实例仿真。
设计结果表明,利用Matlab软件设计数字滤波器简便、易行。
关键词 Matlab;F I R滤波器;窗函数;频率中文分类号:TP391 文献标识码:AThe D esi gn of2D F I R D i g ita l F ilter Ba sed on M a tl abHua Xiyao1 Su Boni1 Zhang Yan2(1 College of I nf or mati on Engineering,Tari m University,A lar,Xinjiang 843300)(2 College of Physics and Electr onic Engineering,North W est Nor mal University,Lanzhou,Gansu 730070)Abstract The design of digital filter is one of the most i m portant parts in signal p r ocessing.This article intr oduced using window func2 ti on method frequency sa mp ling method and frequency exchange method t o i m p le ment the design of2D F I R digital filter based on M at2 lab p r ogramm ing envir on ment and gave exa mp le of si m ulati on.The result indicates that usingM atlab t o design digital filter is very si m2 p le.Key words Matlab;F I R digital filter;window functi on;frequency 随着信息时代和数字世界的到来,数字信号处理己成为当今一门极其重要的学科和技术领域。
iir 数字滤波器间接设计法 名词解释

数字滤波器是一种对数字信号进行处理的工具,用于去除或减弱信号中的噪音、滤波和频率选择。
数字滤波器间接设计法是一种设计数字滤波器的方法,它通过指定滤波器的频率响应特性,然后利用一些已知的滤波器结构来实现所需的频率响应特性。
在数字滤波器间接设计法中,常用的方法包括脉冲响应不变法、双线性变换法和频率变换法等。
在数字滤波器间接设计法中,常用的方法有:1. 脉冲响应不变法:该方法是通过将模拟滤波器的脉冲响应直接映射到数字滤波器的脉冲响应来实现。
这样做的好处是保持了模拟滤波器的一些重要性质,比如稳定性和线性相位特性。
但是它也存在一些缺点,比如频率响应不稳定,因此在实际应用中需要谨慎选择。
2. 双线性变换法:该方法是通过将模拟滤波器的传输函数进行双线性变换,将其转换成数字滤波器的传输函数。
这种方法的优点是能够保持频率响应的完整性,但是也存在一些局限性,比如需要进行频率归一化,使得频率响应的曲线和模拟滤波器的曲线产生一些偏差。
3. 频率变换法:该方法是通过在频率域上对模拟滤波器进行频率变换,然后从频率域上得到数字滤波器的传输函数。
这种方法的优点是可以直观地理解模拟滤波器和数字滤波器之间的关系,但是也需要考虑到频率变换的误差,需要在设计中加以考虑。
数字滤波器间接设计法是一种常用的数字滤波器设计方法,它允许工程师根据具体的应用需求和特定的滤波器结构选择合适的设计方法。
在实际的工程应用中,需要综合考虑滤波器的性能指标、系统的实时性需求以及硬件成本等方面的因素,来选择最适合的设计方法。
通过灵活运用数字滤波器间接设计法,可以设计出性能稳定、响应准确的数字滤波器,为各种数字信号处理系统提供有效的支持。
数字滤波器是一种可以对数字信号进行处理的工具,可以用于去除或减弱信号中的噪音、滤波和频率选择。
而数字滤波器的设计方法也有很多种,其中间接设计法是一种常用的设计方法之一。
在上文中,我们已经介绍了间接设计法的一些方法,接下来我们将继续探讨数字滤波器间接设计法的特点和应用。
IIR数字滤波器的设计及软件实现

IIR数字滤波器的设计及软件实现IIR数字滤波器(Infinite Impulse Response Digital Filter)是一种常用于信号处理的数字滤波器。
与FIR(Finite Impulse Response)滤波器不同,IIR滤波器的输出取决于过去的输入样本和输出样本。
1.确定滤波器的类型:根据实际应用需求选择低通滤波器、高通滤波器、带通滤波器或带阻滤波器。
2.确定滤波器的阶数:阶数决定了滤波器的频率响应特性的陡峭程度。
一般来说,阶数越高,滤波器的频率响应特性越陡峭。
阶数的选择需要权衡计算复杂度和滤波器性能。
3.设计滤波器的传递函数:传递函数是描述滤波器输入和输出之间关系的数学表达式。
传递函数可以通过频率响应要求来确定。
4.选择滤波器设计方法:针对不同的频率响应要求,可以选择不同的滤波器设计方法,如巴特沃斯方法、切比雪夫方法、椭圆方法等。
5.设计滤波器的参数:根据滤波器的传递函数和设计方法,计算滤波器的系数。
这些系数可以用于实现滤波器。
软件实现的步骤如下:1. 选择合适的软件平台:根据实际需求,选择适合的软件平台,如MATLAB、Python等。
2. 导入相关的滤波器设计库:选择合适的滤波器设计库,如MATLAB的Signal Processing Toolbox、Python的scipy.signal等。
3.使用滤波器设计函数:根据选择的滤波器设计方法,使用相应的函数进行滤波器设计。
这些函数可以根据输入的参数计算出滤波器的系数。
4.实现滤波器:使用得到的滤波器系数,将其用于滤波器的实现。
可以使用滤波器函数对信号进行滤波操作。
5.评估滤波器性能:根据实际应用需求,对滤波器的性能进行评估。
可以通过比较滤波器的输出和期望的输出,或者通过分析滤波器的频率响应特性来评估滤波器的性能。
需要注意的是,IIR数字滤波器的设计和实现过程可能相对复杂,需要一定的信号处理和数学基础。
在实际应用中,可以借助已有的滤波器设计库和工具来简化设计和实现过程。
实验四IIR数字滤波器的设计数字信号处理DSP

实验四IIR数字滤波器的设计数字信号处理DSP
IIR数字滤波器是一种基于无限脉冲响应(Infinite Impulse Response)的数字滤波器。
相比于FIR(有限脉冲响应)滤波器,IIR滤
波器具有更低的复杂度和更快的响应速度,但可能会引入一定的稳定性问题。
设计IIR数字滤波器的一般步骤如下:
1.确定滤波器的规格:包括截止频率、通带增益、阻带衰减等参数。
这些参数将直接影响到滤波器的设计和性能。
2.选择滤波器结构:常见的IIR滤波器结构包括直接型I和II结构、级联型结构、并行型结构等。
选择适当的结构取决于滤波器的性能要求和
计算复杂度。
3. 选择滤波器的类型:根据滤波器的设计规格,可以选择巴特沃斯(Butterworth)、切比雪夫(Chebyshev)、椭圆(Elliptic)等不同类
型的IIR滤波器。
4.滤波器设计:根据所选择的滤波器类型和规格,设计滤波器的传递
函数。
可以借助MATLAB等工具进行数值计算和优化。
5.模拟滤波器转为数字滤波器:将设计好的IIR滤波器转换为数字滤
波器。
可以使用双线性变换等方法来实现。
6.实现滤波器:根据转换后的数字滤波器的差分方程,编写相应的代
码来实现滤波器功能。
7.评估滤波器性能:对设计好的IIR数字滤波器进行性能评估,包括
幅频响应、相频响应、群延迟等指标。
8.优化滤波器性能:根据实际情况,对滤波器的设计参数进行优化,以获得更好的性能。
以上是设计IIR数字滤波器的一般步骤,具体的设计方法和过程还需要根据实际情况进行调整。
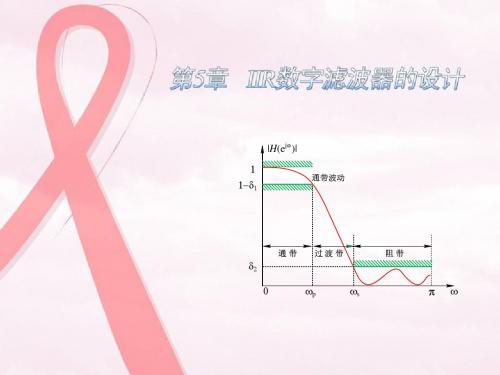
第5章 IIR数字滤波器的设计
10
0.1 p
- 1 (若αp=3dB,ε=1)
2) Ωs,αs →N
s 10lg[ 1 2 (Ws / Wp )2 N ]
100.1 s - 1 l g 2 N 2 l gW s / W p
26
3.由 | Ha ( jW) | 求Ha(s)
6
此时的系统称为有限长单位脉冲响应(FIR,Finite Impulse Response)系统。 反之,h(n)是无限长序列,系统称为无限长单位脉冲响 应(IIR,Infinite Impulse Response)系统。 3.低通、高通、带通、带阻滤波器 从功能上,数字滤波器可分为低通(LP,Low Pass)、高通(HP,High Pass)、带通(BP,Band Pass) 和带阻(BS,Band Stop)四种类型。
9
1.低通滤波器的性能指标
|H(ejw)| 1 1-d1
通带波动
wp ws
均匀过渡
—— 通带截止频率 —— 阻带截止频率 通带
1 - d1 | H (e jω ) | 1
通带 过渡带 阻带
d2 0 wp ws
p
w
阻带 | H (e jω ) | d 2
1 1 p 20lg 20lg 通带(允许的)最大衰减 jwp 1 - d1 | H (e ) |
(1)零极点位置累试 (2)利用模拟滤波器的理论 (3)最优化设计
3.用一个有限精度的算法去实现这个系统函数。
12
数字IIR滤波器设计的具体步骤:
给定数字滤波器的技术指标
w p , w s , p , s (更多)
转换成模拟滤波器的技术指标 W p , W s , p , s (更多) 转换成模拟低通滤波器的技术指标 p , s , p , s 设计模拟低通滤波器G ( p )
IIR数字滤波器的设计流程图

目录目录 0前言 (1)1.1数字滤波器简介 (1)1.2使用数字滤波器的原因 (1)1.3设计的原理和内容 (1)工程概况 (2)正文 (2)3.1 设计的目的和意义 (2)3.2 目标和总体方案 (2)3.3 设计方法和内容 (3)3.4 硬件环境 (3)3.5软件环境 (3)3.6IIR数字滤波器设计思路 (3)3.7 IIR数字滤波器的设计流程图 (3)3.8 IIR数字滤波器设计思路 (4)3.9设计IIR数字滤波器的两种方法 (4)3.10双线性变换法的基本原理 (5)3.11用双线性变换法设计IIR数字滤波器的步骤 (6)3.12程序源代码和运行结果 (6)3.12.1低通滤波器 (6)3.12.3带通滤波器 (10)3.12.4带阻滤波器 (13)3.13结论 (15)3.13.1存在的问题 (15)3.13.2解决方案 (16)致谢 (16)参考文献 (16)前言1.1数字滤波器简介数字滤波器是一种用来过滤时间离散信号的数字系统,通过对抽样数据进行数学处理来达到频域滤波的目的。
可以设计系统的频率响应,让它满足一定的要求,从而对通过该系统的信号的某些特定的频率成分进行过滤,这就是滤波器的基本原理。
如果系统是一个连续系统,则滤波器称为模拟滤波器。
如果系统是一个离散系统,则滤波器称为数字滤波器。
信号通过线性系统后,其输出信号就是输入信号和系统冲激响应的卷积。
从频域分析来看,信号通过线性系统后,输出信号的频谱将是输入信号的频谱与系统传递函数的乘积。
除非为常数,否则输出信号的频谱将不同于输入信号的频谱,某些频率成分较大的模,因此,中这些频率成分将得到加强,而另外一些频率成分的模很小甚至为零,中这部分频率分量将被削弱或消失。
因此,系统的作用相当于对输入信号的频谱进行加权。
1.2使用数字滤波器的原因数字滤波器具有比模拟滤波器更高的精度,甚至能够实现后者在理论上也无法达到的性能。
数字滤波器相比模拟滤波器有更高的信噪比。
四种IIR数字滤波器设计的核心程序(VB-程序)
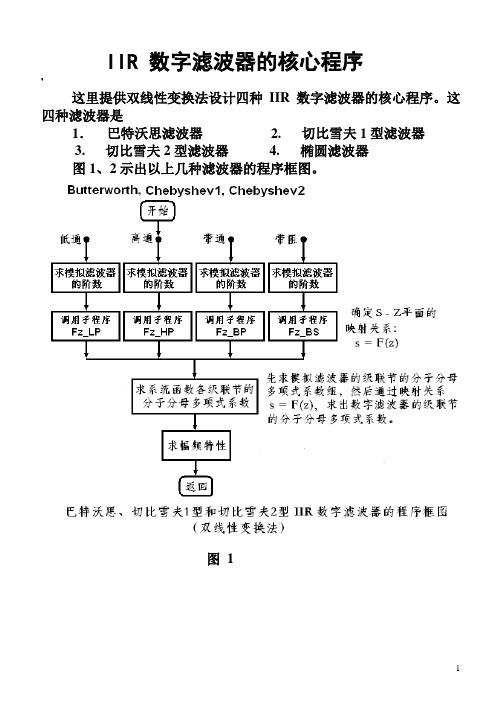
IIR 数字滤波器的核心程序'这里提供双线性变换法设计四种IIR数字滤波器的核心程序。
这四种滤波器是1.巴特沃思滤波器 2. 切比雪夫1型滤波器3. 切比雪夫2型滤波器4. 椭圆滤波器图1、2示出以上几种滤波器的程序框图。
图1图2`' 使用双线性变换法的 Butterworth 型 IIR 数字滤波器设计程序'' 形参说明如下:'' PbType ----------- 输入整型量,滤波器通带类型:' PbType = 0 : 低通滤波器;' PbType = 1 : 高通滤波器;' PbType = 2 : 带通滤波器;' PbType = 3 : 带阻滤波器.' fp1 ----------- 输入双精度量, 低通或高通滤波器的通带边界频率( Hz ); 带通或带阻滤波器的通带低端边‘界频率( Hz ).' fp2 ----------- 输入双精度量, 带通或带阻滤波器的通带低端边界频率( Hz ).' Apass -----------输入双精度量, 通带衰减( dB ).' fs1 ----------- 输入双精度量, 低通或高通滤波器的阻带边界频率( Hz ); 带通或带阻滤波器的阻带高端边‘界频率( Hz ).' fs2 ----------- 输入双精度量, 带通或带阻滤波器的阻带高端边界频率( Hz ).' Astop ----------- 输入双精度量, 阻带衰减( dB ).' fsamp ----------- 输入双精度量, 采样频率( Hz ).' points ----------- 输入整型量, 幅频特性计算点数.' ord ----------- 输入整型量, 滤波器阶数.' NumSec( ) -------- 输出双精度量, 转移函数二阶节的分子多项式系数二维数组.' 元素NumSec( k, i ) 中,' k : 二阶节序号;' i : 多项式系数, i = 0 相应于常数项.' DenSec( ) -------- 输出双精度量转移函数二阶节的分母多项式系数二维数组.' 元素DenSec( k, i ) 中,' k : 二阶节序号;' i : 多项式系数, i = 0 相应于常数项.' NumSec_Z( ) ------ 输出双精度量系统函数二阶节的分子多项式系数二维数组.' 元素NumSec_Z( k, i ) 中,' k : 二阶节序号;' i : 多项式系数, i = 0 相应于常数项.' DenSec_Z( ) ------ 输出双精度量系统函数二阶节的分母多项式系数二维数组.' 元素DenSec_Z( k, i ) 中,' k : 二阶节序号;' i : 多项式系数, i = 0 相应于常数项.' AR( ) ------------ 输出双精度量,滤波器的幅频特性数组.'Sub Butterworth(PbType As Integer, fp1 As Double, fp2 As Double, Apass As Double, fs1 As Double, fs2 As Double, Astop As Double, fsamp As Double, points As Integer, ord As Integer, NumSec() As Double, DenSec() As Double, NumSec_Z() As Double, DenSec_Z() As Double, AR() As Double)Dim i%, j%, k%, ord_t%Dim angle#, emp1#, temp2#, temp3#Dim ratio(0 To 50) As Double''''''''''''''''''''If PbType = 0 Then ' 低通滤波器;wpass = 2# * Pi * fpass / fsamp: wstop = 2# * Pi * fstop / fsamp ' 通带、阻带边界频率omikaP = Tan(wpass / 2#): omikaS = Tan(wstop / 2#)epass = epson(Apass): estop = epson(Astop)' 根据对幅频特性的技术要求,计算模拟滤波器的阶数orde = Ne_B(estop, epass, omikaS, omikaP)ord = Fix(orde) + 1omk0 = omika0(omikaP, epass, ord)' 调用Fz_LP 子程序,将低通模拟滤波器的转移函数变量s 映射为低通数字滤波器的系统函数变量z Call Fz_LP(F1(), F2(), ord_t) 'End If''''''''''''''''''''If PbType = 1 Then ' 高通滤波器;wpass = 2# * Pi * fpass / fsamp: wstop = 2# * Pi * fstop / fsamp ' 通带、阻带边界频率omikaP = 1# / Tan(wpass / 2#): omikaS = 1# / Tan(wstop / 2#)epass = epson(Apass): estop = epson(Astop)' 根据对幅频特性的技术要求,计算模拟滤波器的阶数orde = Ne_B(estop, epass, omikaS, omikaP)ord = Fix(orde) + 1omk0 = omika0(omikaP, epass, ord)' 调用Fz_HP 子程序,将高通模拟滤波器的转移函数变量s 映射为高通数字滤波器的系统函数变量z Call Fz_HP(F1(), F2(), ord_t)End If''''''''''''''''''''If PbType = 2 Then ' 带通滤波器;wp1 = 2# * Pi * fp1 / fsamp: wp2 = 2# * Pi * fp2 / fsamp ' 通带上下边界频率ws1 = 2# * Pi * fs1 / fsamp: ws2 = 2# * Pi * fs2 / fsamp ' 阻带上下边界频率Ci = BpC(wp1, wp2)omikaP = Abs((Ci - Cos(wp2)) / Sin(wp2))omikaS1 = Abs((Ci - Cos(ws1)) / Sin(ws1))omikaS2 = Abs((Ci - Cos(ws2)) / Sin(ws2))If omikaS1 <= omikaS2 ThenomikaS = omikaS1ElseomikaS = omikaS2End Ifepass = epson(Apass): estop = epson(Astop)' 根据对幅频特性的技术要求,计算模拟滤波器的阶数orde = Ne_B(estop, epass, omikaS, omikaP)ord = Fix(orde) + 1omk0 = omika0(omikaP, epass, ord)' 调用Fz_BP 子程序,将带通模拟滤波器的转移函数变量s 映射为带通数字滤波器的系统函数变量z Call Fz_BP(fp1, fp2, fsamp, F1(), F2(), ord_t)End If''''''''''''''''''''If PbType = 3 Then ' 带阻滤波器;wp1 = 2# * Pi * fp1 / fsamp: wp2 = 2# * Pi * fp2 / fsamp ' 通带上下边界频率ws1 = 2# * Pi * fs1 / fsamp: ws2 = 2# * Pi * fs2 / fsamp ' 阻带上下边界频率Ci = BpC(wp1, wp2)omikaP = Abs(Sin(wp2) / (Cos(wp2) - Ci))omikaS1 = Sin(ws1) / (Cos(ws1) - Ci)omikaS2 = Sin(ws2) / (Cos(ws2) - Ci)If Abs(omikaS1) <= Abs(omikaS2) ThenomikaS = Abs(omikaS1)ElseomikaS = Abs(omikaS2)End Ifepass = epson(Apass): estop = epson(Astop)' 根据对幅频特性的技术要求,计算模拟滤波器的阶数orde = Ne_B(estop, epass, omikaS, omikaP)ord = Fix(orde) + 1omk0 = omika0(omikaP, epass, ord)' 调用Fz_BS 子程序,将带阻模拟滤波器的转移函数变量s 映射为带阻数字滤波器的系统函数变量z Call Fz_BS(fp1, fp2, fsamp, F1(), F2(), ord_t)End If''''''''''''''''''''If ord Mod 2 <> 0 Then' 滤波器系统函数的阶数为奇数时,级联节的起始序号为0(序号为0 的级联节是一阶节,其余为‘二阶节)start = 0Else' 滤波器系统函数的阶数为偶数时,级联节的起始序号为1(级联节都是二阶节,没有一阶节)start = 1End IfNR = ord \ 2' 系统函数由一阶、二阶节级联而成,k 是节序号。
iir数字滤波器的设计方法

iir数字滤波器的设计方法IIR数字滤波器的设计方法IIR数字滤波器是一种常用的数字信号处理工具,用于对信号进行滤波和频率域处理。
其设计方法是基于传统的模拟滤波器设计技术,通过将连续时间滤波器转换为离散时间滤波器来实现。
本文将介绍IIR数字滤波器的设计方法和一些常见的实现技巧。
一、IIR数字滤波器的基本原理IIR数字滤波器是一种递归滤波器,其基本原理是将输入信号与滤波器的系数进行加权求和。
其输出信号不仅与当前输入值有关,还与之前的输入和输出值有关,通过不断迭代计算可以得到最终的输出结果。
二、IIR数字滤波器的设计步骤1. 确定滤波器的类型:低通滤波器、高通滤波器、带通滤波器或带阻滤波器。
2. 确定滤波器的阶数:阶数决定了滤波器的陡峭度和性能。
3. 选择滤波器的截止频率或通带范围。
4. 根据所选的滤波器类型和截止频率,设计滤波器的模拟原型。
5. 将模拟原型转换为数字滤波器。
三、IIR数字滤波器的设计方法1. 巴特沃斯滤波器设计方法:- 巴特沃斯滤波器是一种最常用的IIR数字滤波器,具有平坦的通带特性和陡峭的阻带特性。
- 设计方法为先将模拟滤波器转换为数字滤波器,然后通过对模拟滤波器进行归一化来确定截止频率。
2. 阻带衰减设计方法:- 阻带衰减设计方法是一种通过增加滤波器的阶数来提高滤波器阻带衰减特性的方法。
- 通过增加阶数,可以获得更陡峭的阻带特性,但同时也会增加计算复杂度和延迟。
3. 频率变换方法:- 频率变换方法是一种通过对滤波器的频率响应进行变换来设计滤波器的方法。
- 通过对模拟滤波器的频率响应进行变换,可以得到所需的数字滤波器。
四、IIR数字滤波器的实现技巧1. 级联结构:- 将多个一阶或二阶滤波器级联起来,可以得到更高阶的滤波器。
- 级联结构可以灵活地实现各种滤波器类型和阶数的设计。
2. 并联结构:- 将多个滤波器并联起来,可以实现更复杂的频率响应。
- 并联结构可以用于设计带通滤波器和带阻滤波器。
实验五 IIR数字滤波器设计

‘high’为高通滤波器,截止频率wn ‘stop’为带阻滤波器,截止频率wn=[w1,w2] 缺省时为低通或带通滤波器
b,a分别为滤波器传递函数分子和分母的系数向量。
设计一个Butterworth高通数字滤波器,通带边界频率
为300Hz,阻带边界频率为200Hz,通带波纹小于1dB, 阻带衰减大于20dB,采样频率为1000Hz。
例:用直接法设计一个多频带滤波器
已知:f=[0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1];
m=[0,0,1,1,0,0,1,1,0,0,0]
MATLAB程序 N=10; f=0:0.1:1; m=[0,0,1,1,0,0,1,1,0,0,0];
IIR滤波器设计
由于它的脉冲响应序列h(n)是无限长的,称为无限长
冲激响应滤波器。
IIR滤波器的设计根据滤波器某些性能指标要求,设计
滤波器的分子和分母多项式。
设计方法:
模拟滤波器变换法(经典设计法) 直接设计法 参数模型设计法 最大平滑滤波器设计法
IIR设计方法比较
借助模拟filter的设计方法(经典设计法)
实验四 IIR数字滤波器设计
一、实验目的
掌握滤波器的作用、分类。 掌握IIR数字滤波器的原理。
学习数字滤波器的设计方法。
二、实验原理及方法
滤波
是信号处理的一种最基本而重要的技术。利用滤波 从复杂的信号中提取所需要的信号,抑制不需要的部 分。
滤波器
是具有一定传输特性的信号处理装置。
数字滤波器的工作原理
数字滤波器是具有一定传输特性的数字信号处理装置。
它的输入和输出均为离散的数字信号,借助数字器件
实验四IIR数字滤波器设计及软件实现

实验四IIR数字滤波器设计及软件实现IIR数字滤波器是一种重要的信号处理工具,常用于音频处理、图像处理、通信系统等领域。
本实验旨在通过软件实现IIR数字滤波器的设计和使用。
实验目标:1.了解IIR数字滤波器的基本原理和结构。
2. 学会使用Matlab等软件工具进行IIR数字滤波器设计和模拟。
实验步骤:1.确定滤波器的要求:包括滤波器的类型(低通、高通、带通、带阻)、通带和阻带的频率范围、通带和阻带的衰减要求等。
2.根据滤波器的要求选择适合的设计方法:常见的设计方法包括脉冲响应、巴特沃斯、切比雪夫、椭圆等。
3. 使用Matlab等软件工具进行滤波器设计:根据选择的设计方法,使用相应的函数或工具箱进行滤波器的设计。
4.评估滤波器性能:通过频率响应曲线、幅频特性、相频特性等评估滤波器的性能,比如阻带衰减、通带波动等。
5.应用滤波器:将设计好的滤波器应用到实际信号中,观察滤波效果。
6.优化滤波器性能(可选):根据实际应用需求,对滤波器的设计进行调整和优化。
实验注意事项:1.在进行滤波器设计时,要根据实际应用需求选择合适的滤波器类型和设计方法。
2.在评估滤波器性能时,要对设计结果进行全面的分析,包括滤波器的频率响应、幅频特性、相频特性等。
3.在实际应用过程中,可以根据实际需求对设计结果进行优化和调整,以达到更好的滤波效果。
参考资料:1.陈志骏等编著,《信号与系统实验指导书》。
2. Proakis, J. G., & Manolakis, D. G. (1996). Digital signal processing: principles, algorithms, and applications. Pearson Education India.。
实验三IIR数字滤波器设计及软件实现

实验三IIR数字滤波器设计及软件实现IIR数字滤波器是一种常见的数字滤波器类型,它可以实现对信号的频率响应进行调整和改变,常用于信号处理和通信系统中。
本实验将介绍IIR数字滤波器的设计方法和软件实现。
设计一个IIR数字滤波器的一般步骤如下:1.确定滤波器的类型:低通滤波器、高通滤波器、带通滤波器或带阻滤波器。
2.确定滤波器的阶数:阶数决定了滤波器的复杂程度和性能。
3.确定滤波器的截止频率:截止频率决定了滤波器对信号的频率响应的影响。
4.根据滤波器类型和截止频率的要求,选择适当的滤波器设计方法:脉冲响应不变法、双线性变换法等。
5.根据滤波器设计方法,计算出滤波器的系数:系数决定了滤波器的频率响应和性能。
6.实现滤波器的差分方程:将滤波器的系数代入差分方程中,得到滤波器的离散时间域表示。
7. 使用合适的软件工具进行滤波器的软件实现和仿真:可以使用MATLAB、Python等编程语言进行滤波器设计和实现。
在软件实现过程中,通常可以通过以下步骤来实现IIR数字滤波器:1.定义滤波器的参数和输入信号:定义滤波器的类型、阶数、截止频率等参数,并读取输入信号。
2.计算滤波器的系数:根据设计方法和参数,计算滤波器的系数。
3.实现滤波器的差分方程:根据滤波器的差分方程,使用循环结构来实现滤波器的运算。
4.输入信号进入滤波器:将输入信号输入滤波器,进行滤波处理。
5.输出滤波后的信号:获取滤波器的输出结果,并进行处理和显示。
需要注意的是,IIR数字滤波器的设计和实现需要对信号处理和数字滤波器的基本原理有一定的了解,并且需要根据实际需求选择合适的设计方法和参数。
参考资料:2. Zhu, Y., & Buck, J. (2024). VLSI signal processing. John Wiley & Sons.。
10第五章IIR数字滤波器设计

§5 设计IIR数字滤波器的频率变换法
又称为
v 频率变换的两种基本方法
“模拟域频率变换法 ”
法一:从归一化模拟低通原型出发,先在模拟域内经频率
变换成为所需类型的模拟滤波器;然后进行双线性变换,
由S域变换到Z域,而得到所需类型的数字滤波器。
又称为
“数字域频率变换法 ”
去归一化得函 到数 低 Ha: 通 L(s)系 HaL 统 (p)p sc
注意:这里是 模拟低通的, 应该是多少?
由低通到高通的频率转换关系得到模拟高通:
1 HaH (s) HaL( s ) 用双线性变换法得到数字高通:
H
(z)
HaH
(s)
|
s
1 1
z 1 z 1
典型例题
例2:设计一个巴特沃思型数字高通滤波器,通带截止频
可见:模拟滤波器与数字滤波器的响应在对应的频率关 系上发生了“畸变”,也造成了相位的非线性变化,这 是双线性变换法的主要缺点。具体而言,在上刻度为 均匀的频率点映射到上时变成了非均匀的点,而且随 频率增加越来越密。 双线性变换法除了不能用于线性相位滤波器设计外,仍 然是应用最为广泛的设计IIR数字滤波器的方法。
率 p 0.2π弧度,衰减3dB。阻带下边频 =s 0.05π弧
度,阻带衰减 As≥48dB,求数字滤波器的系统函数。
解: ① 频 率p 预 t畸g 变2p求 1 模拟tg 低1通(0 )的.截0 1频1 .3和 2c3阻.4 0带9 7下(7 r 边9 a 频d/ss )
s
tgs
2
112.7062d(/rs)a
反归一化得: H(s)Ha(s/c)
0.203451 (s0.5881)(s4280.5881s408.3459) 18
数字滤波器IIR设计原理指标性能及设计方法

数字滤波器IIR设计原理\指标性能及设计⽅法2019-10-13摘 要在数字信号处理中离不开的是滤波器,其是数字滤波技术的重要研究领域,⽆论是信号获得还是处理都不能离开数字滤波技术,利⽤其消除噪声影响保证信号安全有效的传输,本⽂对数字滤波器IIR设计的原理等进⾏了分析。
关键词数字滤波;IIR技术;设计指标;设计⽅法中图分类号TN713⽂献标识码A⽂章编号1673-9671-(2012)041-0229-011数字滤波器IIR基本设计原理所谓的数字滤波器是⼀种对数字信号进⾏处理的重要功能,对信号进⾏过滤、检测和参数估计等处理,即消除数字信号中的噪声,使得有价值的信号得以保留,数字滤波器应⽤较为⼴泛。
数字滤波和模拟滤波器应⽤中体现出的优势较为明显,精度⾼且稳定,设备的体积⼩使⽤灵活,不要求匹配抗阻就可实现模拟滤波其的特殊滤波功能。
数字滤波器实际上就是⼀个离散系统,从现实的⽹络结构或者单位脉冲相应分类,可以分为⽆限制脉冲相应(IIR)与有限脉冲相应(FIR)两个类型。
其中IIR数字滤波器设计的基本原理如下:从滤波的过程看,就是输⼊与输出的都是数字信号,在经过滤波器的时候利⽤某种运算将改变输⼊信号所含频率的进⾏对⽐与分析,从⽽滤除那些“噪⾳”部分,IIR滤波器的设计原理就是基于模拟滤波器,然后利⽤等价转化为数字滤波器。
其中冲击响应不变法是⼀种较为常见的设计⽅式,流程是:H(s)h(t)h(n)H(z)考虑到传统的滤波器计算量较⼤,滤波特性不易调整,为了解决这个问题⽬前采⽤MATLAB的强⼤数字处理与计算能⼒就解决了设计上计算量较⼤的问题,不仅仅简化了计算量且可以按照设计要求基尼滤波器特性参数调整,更加的灵活。
具体步骤如下:按照⼯程的实际要求确定滤波器的基本指标,如边界频率;阻带最⼩衰减、最⼤衰减等;将数字滤波器的技术指标转换为模拟滤波器指标,常⽤的是脉冲相应不变法;设计模拟滤波器即按照指标选择模拟滤波器的型号,如巴特沃斯或者契⽐雪夫滤波器等;选择合适的变换算法将模拟滤波其转换为数字滤波器;最后利⽤软件或者硬件技术使其运⾏。
IIR数字滤波器设计(Ⅰ)要点

一、实验题目:IIR数字滤波器设计(Ⅰ)二、实验内容:数字滤波器是对数字信号实现滤波的线性时不变系统。
数字滤波实质上是一种运算过程,实现对信号的运算处理。
输入数字信号(数字序列)通过特定的运算转变为输出的数字序列,因此,数字滤波器本质上是一个完成特定运算的数字计算过程,也可以理解为是一台计算机。
描述离散系统输出与输入关系的卷积和差分方程只是给数字信号滤波器提供运算规则,使其按照这个规则完成对输入数据的处理。
时域离散系统的频域特性:,其中、分别是数字滤波器的输出序列和输入序列的频域特性(或称为频谱特性),是数字滤波器的单位取样响应的频谱,又称为数字滤波器的频域响应。
输入序列的频谱经过滤波后,因此,只要按照输入信号频谱的特点和处理信号的目的,适当选择,使得滤波后的满足设计的要求,这就是数字滤波器的滤波原理。
数字滤波器根据其冲激响应函数的时域特性,可分为两种,即无限长冲激响应(IIR)数字滤波器和有限长冲激响应(FIR)数字滤波器。
IIR 数字滤波器的特征是,具有无限持续时间冲激响应,需要用递归模型来实现,其差分方程为:系统函数为:设计IIR滤波器的任务就是寻求一个物理上可实现的系统函数H(z),使其频率响应H(z)满足所希望得到的频域指标,即符合给定的通带截止频率、阻带截止频率、通带衰减系数和阻带衰减系数。
设计一个数字巴特沃斯低通滤波器,设计指标如下:W p=0.2Π, R P=1dBW s=0.3Π, A s=15dB采样时间间隔S。
T1三、实验要求:(1)用单位冲激响应不变变换法进行设计。
(2)给出详细的滤波器设计说明书。
(3)给出经过运行是正确的程序清单并加上详细的注释。
(4)画出所设计滤波器的幅度特性和相位特性。
四.程序与实验说明:1.利用模拟滤波器设计IIR数字滤波器方法(1)根据所给出的数字滤波器性能指标计算出相应的模拟滤波器的设计指标。
(2)根据得出的滤波器性能指标设计出相应的模拟滤波器的系统函数H(S)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
,
, :
)e x
P (一
。 了
、 , :
一 Jo
Zo Z
)
…
》 〔
将对称或 其它 约 束 条件 考 虑 在内时
,
上式 中一些 系数就不都是 独立 了
,
故 J: 式可 写 成
H (。
;,
。
2
)
=
习
£
a
(£ ) 必( 。
`
;
,
。
2
)
向题 成 为利 用 求 E 为 最小 的 条 件
ù子 -
,
计算 a (
一
J
ì
.
ó
一一 十
户
扣
ùù
二
,
。
、
二维递 归 ( n
R
)滤波器
。
二 维 递归 滤 波 器的设 计
,
y
(,
,
)=
E
奋= 一 .
乙
才 =
一
二
“
(k
l)h
。
(m 一k
,
一 l)
上 述诸 信 号 也 可 以 变 换 到 Z 域 来 表 示
H (:
,
,
`
Z
`,
域 变换的 定 义 为
1
一
: 2
)
=
乙 E
.
h
1
:
`:
头`
一
二 1
万=
上 式的 展 开 式 为
h
l:
+ h
+
, 22 :
+
h
13:
+ 盆
几:
42
考
,
)
= 云 (。
,
。
)
w
(m
,
,
拜
)
最 简单 的 二 维 窗 函 数 是矩 形 窗
,
它 的 单 位 冲激 响应为 ,一
`’
,
“
{
一 N (
。
( N
一万《 执 (
卫
其它 时
,
仁 ) 变 换法 将 一 维零 相 移
FI R
滤 波 器 函 数 中 的变 量进 行变 换
便 得 到 二 竺甲 阳移
F
R 滤波器 函 数 I
两 者 各有 所 长
:
。
无论 一 维 和 二 维 滤 波 器
。
其 理 论 都 包 含 用 近似 理 论 求 传 递 函 数
。
,
和 以此
函 数 求 网 络 结 构 两 部分
n R
滤 波器 还 有 稳 定 性 问题
,
但 一 维 的 和 二 维 的 区 别 主 要 由 以 下三
, ;
个 因 素造 成
(1 )
实现 时 只 能 采 用 几 种直 接 形 式
IR
一
1 ) 窗 口法 ( 理想
“
、
二 维 非递 归 ( F
,
万
) 滤波器
,
: 二 维 F I R 滤 波 器 的 设 计 方 法 比 较成熟 现 在列 举三 种
一
,
`
。
F IR
滤 波 器 的 单 位 冲 激 响 应 是无限 的
,
显然 这 是 不 可 能 实 现 的
h ,
h
: : z
3一 z
H(
z ,
,
2 2
)
“
+
h
Z: z :
h
2 2: : z :
+ h
+
Z。: : z
+ 鑫
:
全
:
+
h
3,:
+ 吞3: : 贾
贫
z:
h
。3 :
+ 萝姜
资翌
将 上式 中各 系数 按原 顺 序排 列写 成
h h
L 11
h h
zZ
吞 几 h1 3
璐 幼
吞 h“ 飞 时 J. 肠
21
22
这样
,
就 把高 阶 二 维 滤波 器的 设 计分 解成一 维高 阶 滤 波器 的设计 和 寻 求一 个 低阶 变换 式 的问
题
。
3 ) 等 波动 设 计 法 (
给定 通 带与 阻 带 时
法
。
,
使 滤波器 具 有 最小 通 带 波 动 与 阻 带 波 动 的设 计
:
,
,
称 为 等 波动 设计
设
E
为 误差
,
二 维问题 需 用 大 量 数 据
使 得 计 算很 复 杂
,
(2 )
处 理 多维 系 统 需 用 的 数 学
。
尚不 完善
,
多 数 的多维 多项式 不能分 解 成 一 阶 与 二 阶 的 因 式
( 3 ) 多 维系 统 具 有 更 多 的 自 由
度供 设 计老 选 用
由于 多 维 多项 式不 能分 解
一
’
,
Y
(
e
一` .
’
。
一 ` a , ,
) 二 H (e
一` 。
。 ,
)X (e
一` 。 ,
e一
J
二
、
种
,
动和
。
一 `“
, ,
。一`
“
) 分 别 称 为 空 域 响 应 和 频域 响应
, ,
。
`
武
·
’
:
二
’
二 维 数 字 论 波 器 也 和 一 维 的一 样 分 二 维 非递归 ( I F R ) 滤波 器 与二 维 递 归 ( I I R ) 滤 波 器两
,
如 输人 为 创 。
,
哟
。
,
则 其输 出为 单 位冲
。
)
h (,
,
)
,
= T
, (
,n
,
)]
和 一 淮的 情 况 一 样
应 的 卷积
,
,
二 维线 性 移 不 变 的 输 出 以 m
,
) 是 输入 序 列 城 n
*
*
m
的 与单 位 冲激 的 响
即
y
(饥
。
。
)二
x
(饥
,
。
)
,
h
(跳
,
朴
)
。
或
仿 一 维情 况
,
解决 的 办法 是 以
。
一 定 方 犬割 掉 一 部 分 冲 激 响 应 使 剩余 部 分的 频 响能 接近 理 想 这 相 当 于 以 一 个 窗 函 数 ) 乘 理 想 的 单 位冲 激 响 应 议。
,
n (1
,
蕊
)
,
得到 设 计 时 取 用 的 单 位 冲 激响 应 h ( 。
玛
,
”
)
h (仍
,
I (
。
。
2
) 为理 想 频 响
m
(0
一,
,
H(
。
、
,
:
,
。
:
2
) 为 待求 响应
、
,
,
则
刀二
a x
。 : )
〔
x
}H
,
(。
。
)一 I (。
。
:
)
!
,
厂 是 二 维频 率 面 上 覆盖 通 带及 阻 带 的 区 域
设 所 求 滤波器 是 零相 移
则可 写 出
H (。
:
,
。
:
)
=
乙 乙
(。
.
h
(n
;
,
例如
,
一 维 契 比雪 夫滤 波 器 的 须 响 为
H (。 ) =
乙
a
( 。 ) T [e o
,
。
s
。
〕
。
,
几 〔O 〕表示 契 比 雪夫 多项 式 以 变换 函 数
响
H (拼
,
。
F (“
,
)代替
c。:
便 得 到二 维 F I
R
滤 波器 的频
,
)二
a 。 乙 ( ) T 〔 F (拜
.
,
。
)〕
、
二 维 数 字 滤 波 器 的 设 计
杜
图 象处 理
处理
。
锡
枉
,
,
医 疗诊 断 用 的 C T
,
地 质勘 测 以 及 地 震 信 号 的处理 等
,
都 属于 多 维 数字信号
,
多 维 滤 波 是 多 维 数 字 信 号 处 理 中 的主 要 组 成 部分
.
本 文 将 以 二 维 为例
。
说 明多 维 数 字
,
滤 波 器 设计 的 概 略
左图 是 一 个二 维信号 的 图示
位 取样
,
设 占( m 的 表示 单
即
占( 二
,
柑) ”
,
戏 二
,
几
二 0
,
其它
,
m
,
n
值
,
这样
T
,
设
,
二
(, 则
,
,
。
)与
y
(,
y
) 分另 }代 表 输人 信 号与输 出 信号激源自响应(。,哟
