椭圆形封头卧式容器不同液面高度的容积计算
卧式储罐不同液位下的容积(质量)计算

卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图dhrl il L参数:l:椭圆封头曲面高度( m);l i:椭圆封头直边长度( m);L:卧罐圆柱体部分长度(m);r :卧式储罐半径( d/2,m);d:卧式储罐内径,( m)h:储液液位高度( m);V:卧式储罐总体积( m3);ρ:储液密度( kg/m3)3V h:对应 h 高度卧罐内储液体积( m );椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下。
roh以储罐底部为起点的液高卧式储罐内储液总体积计算公式:V 1 2r Lr 2 arcsin h - rh - r r 2 - h - r 2h 3L r r 2 2 若密度为ρ,则卧式储罐内储液总重量为:m h V h表 1 卧式储罐不同液位下容积(重量)ρr L h V h m h 液体密度储罐半径圆柱体部分长度储液液位高度储液体积储液重量(kg/m3)(m)(m)( m)(m3)( kg)备注:该计算公式推导过程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
rhoh尺以储罐中心为起点的液高(1)椭圆球体部分该椭圆球体符合椭圆球体公式:x2 y2 z21 其中 a=b=r ,则有x2 y2 z2 1a2 b2 c 2 a2 c 2垂直于 y 轴分成无限小微元,任一微元面积为:Syi c (a2 y2 )a当液面高度为h 时,椭圆球体内液氨容积为V1= a S yi dya c ( a 2 y 2 )dy c (a 2 h h 3 2a 3 hh a a 3 3( 2 )直段筒体部分:筒体的纵断面方程为 x 2 y 2 a 2任一微元的面积为 S yj 2 a 2 y 2 dy则筒体部分容积为:hh y 2 dy La 2 (arcsin h h 2 a 2 h 2 V 2S yj L 2 a 2 2 )aa a a 2 (arcsin h ) 2 a 2(3 )卧式储罐储液总体积总容积为 V=V1+V2 ,V= c 2 4h 2 2a 3) + La 2 h h 2 2 2 a (a h3 3 (arcsin a a 2 a h 2 )此公式中液位高度 h 是以储罐内径中心为原点,其中 a=b=r化简后卧式储罐储液总体积为: V12r Lr 2 arcsin h h r 2 - h2 h3L r r 2 2 实例:某热电厂液氨罐尺寸为:储罐体积50m 3,直段筒体长度 L 1=8480mm , 封头直段长度 L 2=40mm (圆柱体部分长度为 (L 1+L 2/2)=8580mm ),筒体半径 R=a=b=1300mm ,封头高度 c=650mmρ V r l L h h 尺 V h m h 误差储液液位高 不同液高下 储罐总 储罐半 封头高计算得到的 液体密度 圆柱体部分 度(中点为 实际标尺 储液体积 储液重量 体积 径 度 体积与实际 3) ) 坐标原点)刻度 3) (kg ) ( kg/m ( 3) ( ) ( ) 长度( m ( ) ( m 储液体积间 m m m m误差1 50 1.3 0.65 8.58 -1.3 0 0.000 0.000 0.00%150 1.3 0.65 8.58 -0.975 0.325 3.619 3.619 150 1.3 0.65 8.58 0 1.3 25.078 25.078 0.31% 150 1.3 0.65 8.58 0.975 2.275 46.537 46.537 1 50 1.3 0.65 8.58 1.3 2.6 50.155 50.155 0.31%若液位高度 h 以卧罐底部为起点,如下图roh则卧式储罐内储液总体积计算公式:V1 2r Lr2 arcsin h - r h - r r 2 - h - r 2 h3L r r 2 2若密度为 ρ,则卧式储罐内储液总重量为:m hV h ρ rL h V h m h 液体密度 储罐半径圆柱体部分长度 储液液位高度 储液体积 储液重量( kg )(kg/m 3) ( m ) ( m ) (m ) (m 3)1 1.3 8.58 1 1.3 8.58 1 1.3 8.58 0.325 3.619 3.6191.3 25.078 25.0782.275 46.537 46.537其它方法如下:第一种方法卧式储罐不同液位下的容积简化计算公卧式储罐内储液总体积计算公式:V h V 2 l ( h r )[ 1 ( h r ) 2 ] L [( h r ) 2 hr h 2 r 2 arcsin( h r )]2 3 r 3 r若密度为ρ,则卧式储罐内储液总重量为:ρV液体密度储罐总体积(kg/m 3)(m3)150150m h V hr l L h V h m h 误差封头高圆柱体不同液高下计储罐半径储液液位高储液体积储液重量算得到的体积度部分长( m)度( m)(m3)( kg)与实际储液体( m)度( m)积间误差0.65 8.58 0 -1.315出现负数,不1.3 复合实际1.3 0.65 8.58 0.3252.276 2.2761 50 1.3 0.65 8.58 1.3 25.000 25.000 0.00%1 50 1.3 0.65 8.58 2.275 47.724 47.7241 50 1.3 0.65 8.58 2.6 51.315 2.63%此方式用到参数较多ρ、V 、r 、l、L 、h。
卧式椭园封头储罐内液体质量与液位高度的对应关系计算

卧式椭园封头储罐内液体质量与液位高度的换算方法
利用电子表格可以计算更复杂的问题,而使计算
变得十分容易,下面是就公司内一个卧式储罐内
储存甲醛成品数量的计算方法。
卧式罐如右图所示:筒体部分长:12.65m ,
内部直径3.0m ,标准椭园封头a/b=2 直边:0cm ;
首先,把整体罐的容积分成两部分计算:即封
头部分的容积V2和筒体部分所对应的容积V1,
再测出液体常温状态下的密度(ρ)然后再代
入液体质量公式:M =ρ×(V1+V2) (1)
(一)筒体部分(如右图所示):
令过圆心的铅直线为x 轴,过圆底边水平切线为y 轴,
罐内液位高度为h ,则圆的方程为:y
2+(x-1.5)2=1.52
图中阴影部分的面积为: ()()()()()⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛-+---=∙=+⎪⎭
⎫ ⎝⎛-+---=--=⎰ππ125.15.15.125.25.15.15.1125.15.15.125.25.15.15.15.15.1222122022h arcSin x h L S
L V h arcSin x h dx
x S h
(二)封头部分:
椭圆水平截面积为:
再将V1与V2代入(1)式,然后用电子表Excel 计算出液位高度每升高1cm 所对应的液体质量,过程十分简便。
愚公2013-4-20 ()[]()π
πππ5625.0125.15.165.125.223202-+-=--=⎰h h dh h V h ()[]2
5.125.22h ab S --==ππ。
卧式储罐不同液位下地容积(高质量)计算
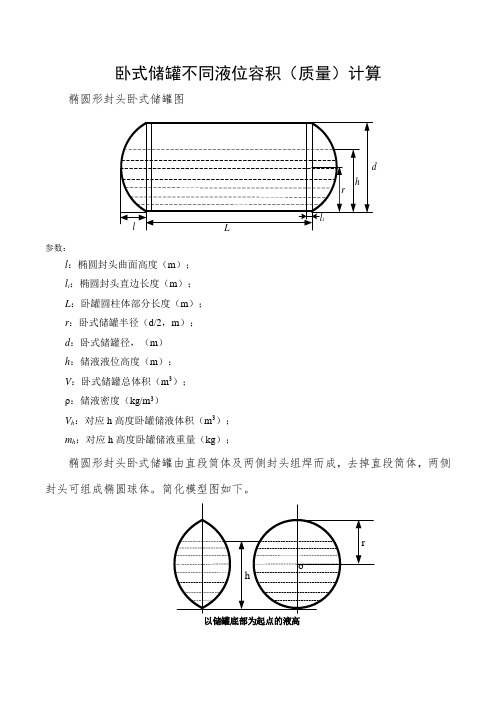
卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图参数:l:椭圆封头曲面高度(m);l i:椭圆封头直边长度(m);L:卧罐圆柱体部分长度(m);r:卧式储罐半径(d/2,m);d:卧式储罐径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);ρ:储液密度(kg/m3)V h:对应h高度卧罐储液体积(m3);m h:对应h高度卧罐储液重量(kg);椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下。
以储罐底部为起点的液高卧式储罐储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐储液总重量为:hh V m ρ=表1 卧式储罐不同液位下容积(重量)该计算公式推导过程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
以储罐中心为起点的液高(1)椭圆球体部分该椭圆球体符合椭圆球体公式:2222221x y z a b c ++= 其中a=b=r ,则有222221x y z a c++= 垂直于y 轴分成无限小微元,任一微元面积为:22()yi cS a y aπ=-当液面高度为h 时,椭圆球体液氨容积为 V1=hyi a S dy -⎰ 22()haca y dy aπ-=-⎰3322()33ch a a h a π=-+ (2)直段筒体部分:筒体的纵断面方程为222x y a +=任一微元的面积为yj S = 则筒体部分容积为:2hyj a V S -=⎰ha L -=⎰2(arcsin )2h La a π=+(arcsin)22h a ππ-≤≤ (3)卧式储罐储液总体积总容积为V=V1+V2,V=23242()33ch a a h a π-++2(arcsin )2h La a π+ 此公式中液位高度h 是以储罐径中心为原点,其中a=b=r 化简后卧式储罐储液总体积为:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2-arcsin 3212222πh r r h r h Lr L r V h若液位高度h 以卧罐底部为起点,如下图则卧式储罐储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐储液总重量为:hh V m ρ=其它方法如下:第一种方法卧式储罐不同液位下的容积简化计算公卧式储罐储液总体积计算公式:)]arcsin(2)[(]3)(1)[(222232rr h r h hr r h L r r h r h l V V h -+--+---+=π若密度为ρ,则卧式储罐储液总重量为:hh V m ρ=此方式用到参数较多ρ、V 、r 、l 、L 、h 。
卧式储罐不同液位下的容积(质量)计算

卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图参数:l:椭圆封头曲面高度(m);l i:椭圆封头直边长度(m);L:卧罐圆柱体部分长度(m);r:卧式储罐半径(d/2,m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);ρ:储液密度(kg/m3)V h:对应h高度卧罐内储液体积(m3);m h:对应h高度卧罐内储液重量(kg);椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下。
以储罐底部为起点的液高卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=表1 卧式储罐不同液位下容积(重量)该计算公式推导过程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
以储罐中心为起点的液高(1)椭圆球体部分该椭圆球体符合椭圆球体公式:2222221x y z a b c ++= 其中a=b=r ,则有222221x y z a c++= 垂直于y 轴分成无限小微元,任一微元面积为:22()yi cS a y aπ=-当液面高度为h 时,椭圆球体内液氨容积为V1=h yi a S dy -⎰ 22()haca y dy aπ-=-⎰3322()33ch a a h a π=-+ (2)直段筒体部分:筒体的纵断面方程为222x y a +=任一微元的面积为yj S = 则筒体部分容积为:2hyj a V S -=⎰ha L -=⎰2(arcsin )2h La a π=+(arcsin)22h a ππ-≤≤ (3)卧式储罐储液总体积总容积为V=V1+V2,V=23242()33ch a a h a π-++2(arcsin )2h La a π+ 此公式中液位高度h 是以储罐内径中心为原点,其中a=b=r 化简后卧式储罐储液总体积为:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2-arcsin 3212222πh r r h r h Lr L r V h若液位高度h 以卧罐底部为起点,如下图则卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=其它方法如下:第一种方法卧式储罐不同液位下的容积简化计算公卧式储罐内储液总体积计算公式:)]arcsin(2)[(]3)(1)[(222232rr h r h hr r h L r r h r h l V V h -+--+---+=π若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=此方式用到参数较多ρ、V 、r 、l 、L 、h 。
椭圆封头卧式储罐相应液位体积计算

椭圆封头卧式储罐相应液位体积计算首先,让我们了解一下椭圆封头卧式储罐的结构特点。
椭圆封头卧式储罐由一个圆筒体和两个椭圆形封头组成。
储罐的长轴长度为2a,短轴长度为2b。
液位高度为h,液位高度H在长轴上的位置为x。
储罐的横截面积可以近似看作一个椭圆形。
首先,我们需要计算椭圆封头卧式储罐的横截面积,然后将其乘以液位高度h,即可得到液位对应的体积。
根据椭圆的性质,椭圆的横截面积可以表示为S=πab。
但是由于液位高度H可能在长轴上的任意位置,所以需要对横截面积进行修正。
储罐的长轴上一般会有一条水平导流槽,导流槽的宽度一般为b/8、当液位高度H小于等于b/8时,导流槽会被液体完全淹没,此时椭圆的横截面积可以近似看作是一个圆形,其半径为b/2、当液位高度H大于b/8时,导流槽会露出水面,此时需要计算椭圆截面的面积。
(1)当H>b/8时,椭圆的横截面面积可以通过使用割线法来进行计算。
割线法的基本原理是通过在椭圆上取两个相距一定角度的点来近似表示此两点之间的弧长。
具体的计算公式如下:
L=2a√[1-(x/a)²]
S=πbL/360
其中L表示椭圆截面上两点之间的弧长,S表示椭圆截面的面积。
(2)当H<=b/8时,椭圆的横截面面积近似为一个圆的面积,可以表示为S=π(b/2)²。
通过使用以上的公式,我们可以计算出椭圆封头卧式储罐中液位高度为H的液体体积。
在实际应用中,我们一般将椭圆封头卧式储罐的液位和体积计算与液位计进行配合使用。
液位计可以根据液体的压力、浮力或者声波等原理来实现对液位的准确测量。
卧式储罐不同液位下的容积计算

卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图d参数:l :椭圆圭寸头曲面高度(m );l i :椭圆圭寸头直边长度(m);L :卧罐圆柱体部分长度(m);r :卧式储罐半径(d/2, m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);P储液密度(kg/m3)V h:对应h高度卧罐内储液体积(m3);m h:对应h高度卧罐内储液重量(kg);椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下卧式储罐内储液总体积计算公式:若密度为p,则卧式储罐内储液总重量为:m h V h表1卧式储罐不同液位下容积(重量)PrLhV hm h液体密度 (kg/m 3)储罐半径 (m )圆柱体部分长度(m )储液液位高度(m )储液体积 (m 3)储液重量 (kg )2r 3LLr 2arcsi4r*r 2rh-r 2以储罐底部为起点的液咼该计算公式推导过程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
(1)椭圆球体部分该椭圆球体符合椭圆球体公式:2 2 2 2 2 2务告务 1 其中a=b=r,则有x 2 务 1 a b c a c垂直于y 轴分成无限小微元,任一微元面积为:S yi —(a 2 y 2)a当液面高度为h 时,椭圆球体内液氨容积为h「3 o 3V1=aS yj dya^(a 2 y 2)dy許2h自(2 )直段筒体部分:筒体的纵断面方程为x 2 y 2 a 2任一微元的面积为S yj 2、.、a 2 y 2dy则筒体部分容积为:L 2 a 2 y 2dy La 2(arcsin 」aahV2aSyj.2 _____________a 2八 2)( arcsin -)2a 2(3)卧式储罐储液总体积总容积为V 二V1+V2 ,232c 2- 4h 2a 2(. h h r .2、V= (a h)+ La (arcsin 2 ; a h ) a 3 3 a a2此公式中液位高度h 是以储罐内径中心为原点,其中a=b=r 化简后卧式储罐储液总体积为:21 三 Lr 2arcsin^ 3L rr 2-h 2r 21 50 1.3 0.65 8.58 0 1.3 25.078 25.0780.31%1 50 1.3 0.65 8.58 0.975 2.275 46.537 46.5371501.30.658.581.32.650.15550.1550.31%若液位高度h 以卧罐底部为起点,如下图/\ A / __________\rf (1)f\ y丿 1 二;o h \ ............. .... J V7\…一j... J■厶■N K A *则卧式储罐内储液总体积计算公式:若密度为p,则卧式储罐内储液总重量为:m hV hprLhV hm h液体密度 储罐半径 圆柱体部分长度储液液位高度储液体积 储液重量(kg )(kg/m 3)(m )(m )(m )(m 3)11.3 8.580.3253.619 3.6192r3LLr 2 arcsi®rh-r r 2h-r 2其它方法如下:第一种方法| PDF.卧式储罐不同液位 下的容积简化计算公卧式储罐内储液总体积计算公式:(hr ) 2--------------- K r2l (h r )[1」 宀]L[( h r)「2hr h 2 r 2 arcsi n( ---------------------------- )]3 rr若密度为p,则卧式储罐内储液总重量为:Vh V此方式用到参数较多P、V、r、l、L、h。
卧式储罐不同液位下的容积(质量)计算

卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图参数:l:椭圆封头曲面高度(m);l i:椭圆封头直边长度(m);L:卧罐圆柱体部分长度(m);r:卧式储罐半径(d/2,m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);ρ:储液密度(kg/m3)V h:对应h高度卧罐内储液体积(m3);m h:对应h高度卧罐内储液重量(kg);椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下。
卧式储罐内储液总体积计算公式:若密度为ρ,则卧式储罐内储液总重量为:表1 卧式储罐不同液位下容积(重量)该计算公式推导过程如下椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体.(1)椭圆球体部分该椭圆球体符合椭圆球体公式:其中a=b=r,则有垂直于y轴分成无限小微元,任一微元面积为:当液面高度为h时,椭圆球体内液氨容积为V1=(2)直段筒体部分:筒体的纵断面方程为任一微元的面积为则筒体部分容积为:(3)卧式储罐储液总体积总容积为V=V1+V2,V=+此公式中液位高度h是以储罐内径中心为原点,其中a=b=r 化简后卧式储罐储液总体积为:若液位高度h以卧罐底部为起点,如下图则卧式储罐内储液总体积计算公式:若密度为ρ,则卧式储罐内储液总重量为:其它方法如下:第一种方法卧式储罐内储液总体积计算公式:若密度为ρ,则卧式储罐内储液总重量为:此方式用到参数较多ρ、V、r、l、L、h。
当液高为0时理论上液体体积应为0,此公式结果为负值,不合逻辑。
第二种方法卧式储罐内储液总体积计算公式:若密度为ρ,则卧式储罐内储液总重量为:此公式是由体积公式推算的,相对误差较大,如储罐中储液在一般高度时,体积间误差偏大。
此外,由于公式中存在分数,液高为0和最大公式不适用。
三种方法对比详见excel表格.。
卧式储罐不同液位下的容积(质量)计算
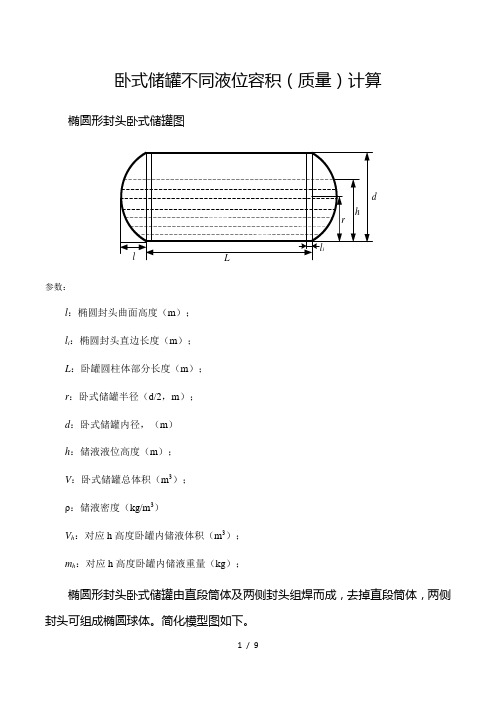
卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图参数:l:椭圆封头曲面高度(m);l i:椭圆封头直边长度(m);L:卧罐圆柱体部分长度(m);r:卧式储罐半径(d/2,m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);ρ:储液密度(kg/m3)V h:对应h高度卧罐内储液体积(m3);m h:对应h高度卧罐内储液重量(kg);椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下。
以储罐底部为起点的液高卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=表1 卧式储罐不同液位下容积(重量)该计算公式推导过程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
以储罐中心为起点的液高(1)椭圆球体部分该椭圆球体符合椭圆球体公式:2222221x y z a b c ++= 其中a=b=r ,则有222221x y z a c++= 垂直于y 轴分成无限小微元,任一微元面积为:22()yi cS a y aπ=-当液面高度为h 时,椭圆球体内液氨容积为 V1=hyi a S dy -⎰ 22()haca y dy aπ-=-⎰3322()33ch a a h a π=-+ (2)直段筒体部分:筒体的纵断面方程为222x y a += 任一微元的面积为yj S = 则筒体部分容积为:2hyj a V S -=⎰ha L -=⎰2(arcsin )2h La a π=+(arcsin)22h a ππ-≤≤ (3)卧式储罐储液总体积总容积为V=V1+V2,V=23242()33ch a a h a π-++2(arcsin )2h La a π+ 此公式中液位高度h 是以储罐内径中心为原点,其中a=b=r 化简后卧式储罐储液总体积为:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2-arcsin 3212222πh r r h r h Lr L r V h若液位高度h 以卧罐底部为起点,如下图则卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=其它方法如下:第一种方法卧式储罐不同液位下的容积简化计算公卧式储罐内储液总体积计算公式:)]arcsin(2)[(]3)(1)[(222232rr h r h hr r h L r r h r h l V V h -+--+---+=π若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=此方式用到参数较多ρ、V 、r 、l 、L 、h 。
卧式储罐不同液位下的容积(质量)计算

卧式储罐分歧液位容积(质量)计算之袁州冬雪创作椭圆形封头卧式储罐图参数:l:椭圆封头曲面高度(m);li:椭圆封头直边长度(m);L:卧罐圆柱体部分长度(m);r:卧式储罐半径(d/2,m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);ρ:储液密度(kg/m3)Vh:对应h高度卧罐内储液体积(m3);mh:对应h高度卧罐内储液重量(kg);椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体.简化模子图如下.卧式储罐内储液总体积计算公式:若密度为ρ,则卧式储罐内储液总重量为:表1 卧式储罐分歧液位下容积(重量)该计算公式推导过程如下椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体.(1)椭圆球体部分该椭圆球体符合椭圆球体公式:其中a=b=r,则有垂直于y轴分成无限小微元,任一微元面积为:当液面高度为h时,椭圆球体内液氨容积为V1=(2)直段筒体部分:筒体的纵断面方程为任一微元的面积为则筒体部分容积为:(3)卧式储罐储液总体积总容积为V=V1+V2,V=+此公式中液位高度h是以储罐内径中心为原点,其中a=b=r化简后卧式储罐储液总体积为:实例:某热电厂液氨罐尺寸为:储罐体积50m3,直段筒体长度若液位高度h以卧罐底部为起点,如下图则卧式储罐内储液总体积计算公式:若密度为ρ,则卧式储罐内储液总重量为:其它方法如下:第一种方法卧式储罐内储液总体积计算公式:若密度为ρ,则卧式储罐内储液总重量为:ρV r l L h Vh mh误差液体密度(kg/m3)储罐总体积(m3)储罐半径(m)封头高度(m)圆柱体部分长度(m)储液液位高度(m)储液体积(m3)储液重量(kg)分歧液高下计算得到的体积与实际储液体积间误差1500出现负数,不复合实际150 2.276 2.27615025.000 25.000 0.00% 15047.724 47.72415051.315 2.63%此方式用到参数较多ρ、V、r、l、L、h.当液高为0时实际上液体体积应为0,此公式成果为负值,分歧逻辑.第二种方法卧式储罐内储液总体积计算公式:若密度为ρ,则卧式储罐内储液总重量为:此公式是由体积公式推算的,相对误差较大,如储罐中储液在一般高度时,体积间误差偏大.此外,由于公式中存在分数,液高为0和最大公式不适用.三种方法对比详见excel表格.。
卧式椭圆形封头贮罐容积的计算
计的零位安装位置比罐底部要高出一定数值,故采用 液位计计数计算液体体积时,要加上零位以下的液体 体积。
图3为不同液位时,实例采用的贮罐所对应液体 体积曲线。
图3 不同液体对应液体体积关系曲线
综上所述,卧式椭圆形封头贮罐在任意液位下的 容积是可以通过相应液位计算出来的。
clear;
clc;
R=1.5;
L=7.08000;
b=0.76400;
H=0:.05:2*R;
x=H- R;
y=- R;
V1=2*L* (x/2.*sqrt (R^2- x.^2)+R^2/2*asin (x./R)
- (y/2.*sqrt (R^2- y.^2) +R^2/2*asin (y./R)));
改良西门子法制备多晶硅工艺过程中[1],需要大 量的容器贮存三氯氢硅及其他液体副产品。容器的数 量较多,体积较大,一般采用卧式椭圆形封头的贮 罐。及时和准确地掌握贮罐的存量及其变化,对于多 晶硅生产过程的物料平衡和动态分析具有重要意义。
本文通过对卧式椭圆形封头贮罐几何结构的分 析,采用分别计算正圆筒部分和椭圆形封头部分任意 液位高度下容积的方法,推导出任意液位高度的容积 计算公式,为多晶硅及其他化工企业中所采用椭圆形 封头贮罐的容积计量提供准确而快捷的方法。
V2=pi*b*H.^2/R.* (R- H/3);
V=V1+V2;
pp=polyfit (H,V,5);
hi=[0,R,2*R]
Vi=polyval (pp,h)i
ph=poly2str (pp,'h)'
卧式储罐不同液位下的容积(质量)计算

卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图参数:l:椭圆封头曲面高度(m);l i:椭圆封头直边长度(m);L:卧罐圆柱体部分长度(m);r:卧式储罐半径(d/2,m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);ρ:储液密度(kg/m3)V h:对应h高度卧罐内储液体积(m3);m h:对应h高度卧罐内储液重量(kg);椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下。
以储罐底部为起点的液高卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=表1 卧式储罐不同液位下容积(重量)该计算公式推导过程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
以储罐中心为起点的液高(1)椭圆球体部分该椭圆球体符合椭圆球体公式:2222221x y z a b c ++= 其中a=b=r ,则有222221x y z a c++= 垂直于y 轴分成无限小微元,任一微元面积为:22()yi cS a y aπ=-当液面高度为h 时,椭圆球体内液氨容积为V1=hyi a S dy -⎰ 22()haca y dy aπ-=-⎰3322()33ch a a h a π=-+ (2)直段筒体部分:筒体的纵断面方程为222x y a +=任一微元的面积为yj S = 则筒体部分容积为:2hyj a V S -=⎰ha L -=⎰2(arcsin )2h La a π=+(arcsin)22h a ππ-≤≤ (3)卧式储罐储液总体积总容积为V=V1+V2,V=23242()33ch a a h a π-++2(arcsin )2h La a π+ 此公式中液位高度h 是以储罐内径中心为原点,其中a=b=r 化简后卧式储罐储液总体积为:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2-arcsin 3212222πh r r h r h Lr L r V h若液位高度h 以卧罐底部为起点,如下图则卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=其它方法如下:第一种方法卧式储罐不同液位下的容积简化计算公卧式储罐内储液总体积计算公式:)]arcsin(2)[(]3)(1)[(222232rr h r h hr r h L r r h r h l V V h -+--+---+=π若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=此方式用到参数较多ρ、V 、r 、l 、L 、h 。
卧式储罐不同液位下的容积(质量)计算

卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图参数:l:椭圆封头曲面高度(m);l i:椭圆封头直边长度(m);L:卧罐圆柱体部分长度(m);r:卧式储罐半径(d/2,m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);ρ:储液密度(kg/m3)V h:对应h高度卧罐内储液体积(m3);m h :对应h 高度卧罐内储液重量(kg );椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下。
以储罐底部为起点的液高卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=表1 卧式储罐不同液位下容积(重量)该计算公式推导过程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
以储罐中心为起点的液高(1)椭圆球体部分该椭圆球体符合椭圆球体公式:2222221x y z a b c ++= 其中a=b=r ,则有222221x y z a c++= 垂直于y 轴分成无限小微元,任一微元面积为:22()yi cS a y aπ=-当液面高度为h 时,椭圆球体内液氨容积为 V1=hyi a S dy -⎰ 22()haca y dy aπ-=-⎰3322()33ch a a h a π=-+ (2)直段筒体部分:筒体的纵断面方程为222x y a +=任一微元的面积为yj S = 则筒体部分容积为:2hyj a V S -=⎰ha L -=⎰2(arcsin )2h La a π=+(arcsin)22h a ππ-≤≤ (3)卧式储罐储液总体积总容积为V=V1+V2,V=23242()33ch a a h a π-++2(arcsin )2h La a π+ 此公式中液位高度h 是以储罐内径中心为原点,其中a=b=r 化简后卧式储罐储液总体积为:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2-arcsin 3212222πh r r h r h Lr L r V h若液位高度h 以卧罐底部为起点,如下图则卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=其它方法如下: 第一种方法卧式储罐不同液位下的容积简化计算公卧式储罐内储液总体积计算公式:)]arcsin(2)[(]3)(1)[(222232rr h r h hr r h L r r h r h l V V h -+--+---+=π若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=此方式用到参数较多ρ、V 、r 、l 、L 、h 。
碟形封头卧式容器不同液面高度的容积计算

碟形封头卧式容器不同液面高度的容积计算
王正秋
【期刊名称】《安装》
【年(卷),期】2000(000)003
【总页数】1页(P43)
【作者】王正秋
【作者单位】
【正文语种】中文
【相关文献】
1.椭圆形封头卧式容器不同液面高度的容积计算 [J], 陈爱丽
2.双椭圆封头或双碟形封头卧式贮罐容积的近似计算 [J], 高振旭
3.各种形状封头的圆筒形卧式容器在不同液面高度时液体体积计算的统一表达式[J], 蒋心亚;宗光
4.椭圆形封头卧式容器容积的计算——根据液面高度计算卧式容器内的物料容积[J], 王宇;陈志军;苏建伟;郭昕
5.各种封头的卧式容器不同液面高度体积计算 [J], 高炳军;苏秀苹
因版权原因,仅展示原文概要,查看原文内容请购买。
椭圆形封头卧式容器不同液面高度的容积计算

椭圆形封头卧式容器不同液面高度的容积计算新疆工学院孟永彪在设计卧式容器时,常常要计算不同液面高度所对应的容积,有时还需列出容积—液位高度对照表或图。
例如,在盛装有毒有害介质的卧式储罐设计中,要根据体积充装系数确定最高液面高度并加以标识。
在一般资料中仅能查到容器的全容积计算公式,而要计算不同液面高度下的容积则需设计者自行推导公式计算。
本文以标准椭圆形封头卧式容器为例介绍不同液面高度下的容积计算方法,并以液化石油气储罐为例编制了QUICK BASIC程序,此法仅供大家参考。
1卧式容器的组成卧式容器是由筒体和两封头组焊而成(如图1),常用的封头为标准椭圆封头。
2卧式容器2.1计算简图及说明计算简图如图2。
L———筒体长度(两封头切线间的距离,含直边段长度)D i———封头及筒体内直径h i———封头曲面深度2.2不同液面高度下封头的容积计算如图2,可假想将卧式容器两端的曲面部分合并,则形成一个完整的椭球面。
2==i ih R c a 122222=++cz a y x )(21222y x a z +-=dxy x a dy h a y a )(2222022+-=⎰⎰--)323(23331a h h a V +-=π其中,a=b=R i因此,椭球面的方程为:推导出: 当容器内的液面高度为h 时(如图3所示)。
封头的容积公式推导:对其积分得从上式可看出,h 变化,V 1也随之变化。
2.3 不同液面高度筒体的容积计算在计算筒体的容积时,忽略尺寸公差及制造误差等因素,可将其断面方程为x 2+y 2=a 2的一圆柱体进行计算,那么如图3所示液面高度的筒体容积为:令:y=acos θ dy=-asin θd θdxdy y x a V s )(2122221+-=⎰⎰dx y x a dy h a y a y a )(2122222222+-=⎰⎰----dy y a L V h a⎰--=2222dy y a L h -=222当 y=-a 时,θ=π;当y=h 时,代入公式积分得:2.4 卧式容器在不同液面高度下的容积通过以上V 1,V 2的计算公式,可计算出卧式容器在不同液面高度下的容积之和V :3 利用QUICK BASIC 语言进行卧式容器的容积计算要计算不同液位高度下的容积以表格、曲线的形式列出是很麻烦的,因此本文利用简便易行的QB 编制程序,当然编程语言可以有多种,本文愿起到抛砖引玉的作用。
卧式储罐不同液位下的容积(质量)计算之欧阳德创编

卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图参数:l:椭圆封头曲面高度(m);li:椭圆封头直边长度(m);L:卧罐圆柱体部分长度(m);r:卧式储罐半径(d/2,m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);ρ:储液密度(kg/m3)Vh:对应h高度卧罐内储液体积(m3);mh:对应h高度卧罐内储液重量(kg);椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下。
卧式储罐内储液总体积计算公式:若密度为ρ,则卧式储罐内储液总重量为:表1 卧式储罐不同液位下容积(重量)备注:该计算公式推导过程如下椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
(1)椭圆球体部分该椭圆球体符合椭圆球体公式:其中a=b=r,则有垂直于y轴分成无限小微元,任一微元面积为:当液面高度为h时,椭圆球体内液氨容积为V1=(2)直段筒体部分:筒体的纵断面方程为任一微元的面积为则筒体部分容积为:(3)卧式储罐储液总体积总容积为V=V1+V2,V=+此公式中液位高度h是以储罐内径中心为原点,其中a=b=r化简后卧式储罐储液总体积为:实例:某热电厂液氨罐尺寸为:储罐体积50m3,直段筒体长度L1=8480mm,封头直段长度L2=40mm (圆柱体部分长度为(L1+L2/2)=8580mm),筒体半径R=a=b=1300mm,封头高度c=650mm150 1.3 0.65 8.58 1.3 2.6 50.155 50.155若液位高度h 以卧罐底部为起点,如下图则卧式储罐内储液总体积计算公式: 若密度为ρ,则卧式储罐内储液总重量为:ρ rLh Vh mh液体密度 (kg/m3)储罐半径(m )圆柱体部分长度(m )储液液位高度(m )储液体积 (m3) 储液重量(kg )1 1.3 8.58 0.325 3.619 3.6191 1.3 8.58 1.3 25.078 25.07811.38.582.27546.53746.537其它方法如下: 第一种方法卧式储罐内储液总体积计算公式:若密度为ρ,则卧式储罐内储液总重量为:此方式用到参数较多ρ、V 、r 、l 、L 、h 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
椭圆形封头卧式容器不同液面高度的容积计算
新疆工学院孟永彪
在设计卧式容器时,常常要计算不同液面高度所对应的容积,有时还需列出容积—液位高度对照表或图。
例如,在盛装有毒有害介质的卧式储罐设计中,要根据体积充装系数确定最高液面高度并加以标识。
在一般资料中仅能查到容器的全容积计算公式,而要计算不同液面高度下的容积则需设计者自行推导公式计算。
本文以标准椭圆形封头卧式容器为例介绍不同液面高度下的容积计算方法,并以液化石油气储罐为例编制了QUICK BASIC程序,此法仅供大家参考。
1卧式容器的组成
卧式容器是由筒体和两封头组焊而成(如图1),常用的封头为标准椭圆封头。
2卧式容器
2.1计算简图及说明
计算简图如图2。
L———筒体长度(两封头切线间的距离,含直边段长度)
D i———封头及筒体内直径
h i———封头曲面深度
2.2不同液面高度下封头的容积计算
如图2,可假想将卧式容器两端的曲面部分合并,则形成一个完整的椭球面。
2==i i
h R c a 122
222=++c
z a y x )(21222y x a z +-=dx
y x a dy h a y a )(2222022+-=⎰⎰--)323(23
331a h h a V +-=π
其中,a=b=R i
因此,椭球面的方程为:
推导出: 当容器内的液面高度为h 时(如图3所示)。
封头的容积公式推导:
对其积分得
从上式可看出,h 变化,V 1也随之变化。
2.3 不同液面高度筒体的容积计算
在计算筒体的容积时,忽略尺寸公差及制造误差等因素,可将其断面方程为
x 2+y 2=a 2的一圆柱体进行计算,那么如图3所示液面高度的筒体容积为:
令:y=acos θ dy=-asin θd θ
dxdy y x a V s )(2122221+-=⎰⎰
dx y x a dy h a y a y a )(2
122222
222+-=⎰⎰----dy y a L V h a
⎰--=2222dy y a L h -=222
当 y=-a 时,θ=π;当y=h 时,代入公式积分得:
2.4 卧式容器在不同液面高度下的容积
通过以上V 1,V 2的计算公式,可计算出卧式容器在不同液面高度下的容积之和V :
3 利用QUICK BASIC 语言进行卧式容器的容积计算
要计算不同液位高度下的容积以表格、曲线的形式列出是很麻烦的,因此本文利用简便易行的QB 编制程序,当然编程语言可以有多种,本文愿起到抛砖引玉的作用。
例如:一台内径与长度任意的液化石油气(以丙烷为主)储罐,再不同特征温度下,根据体积充装系数,得出的最大液位高度;程序中从h=0.1m 开始,每隔1mm 计算一次容积,循环比较,得出最佳值。
5 DIM p(7), H(7),T(7)
8 INPUT "请输入储罐公称容积(立方米):"; GC
10 INPUT "请输入罐体内半径(m):"; R
20 INPUT "请输入罐体(两封头切线间)长度(m):"; L
30 INPUT "请输入最高工作温度下允许充装系数:"; c
40 INPUT "请输入罐体实际全容积(立方米):"; v
60 INPUT "请输入-20℃时丙烷饱和液体的密度(千克/立方米):"; p(1)
70 INPUT "请输入-10℃时丙烷饱和液体的密度(千克/立方米):"; p(2)
80 INPUT "请输入0℃时丙烷饱和液体的密度(千克/立方米):"; p(3)
90 INPUT "请输入10℃时丙烷饱和液体的密度(千克/立方米):"; p(4)
100 INPUT "请输入20℃时丙烷饱和液体的密度(千克/立方米):"; p(5)
110 INPUT "请输入30℃时丙烷饱和液体的密度(千克/立方米):"; p(6)
120 INPUT "请输入45℃时丙烷饱和液体的密度(千克/立方米):"; p(7)
)arccos 1(2
222π+--=a h a h a h La V )arccos 1()323(2223333
21ππ+--++-=+=a h a h a h La a h h a V V V
130 FOR I = 1 TO 7
140 k = c * p(7) / p(I)
145 T(I)=k
150 VK = v * k
160 FOR H = .1 TO R STEP .001
170 v1 = 3.1416 * (R ^ 2 * H - H ^ 3 / 3 + 2 * R ^ 3 / 3) / 2
180 VA = (R ^ 2 - H ^ 2) ^ .5
182 VB = VA / H
183 VC = ATN(VB)
184 VD = H * SQR(1 - H ^ 2 / R ^ 2) / R
185 v2 = L * R ^ 2 * (VD - VC + 3.1416)
210 VH = v1 + v2
220 DH = ABS(VK - VH)
230 IF DH <= .1 GOTO 300
240 NEXT H
300 H(I) = H + R
310 NEXT I
312 LPRINT GC; "立方米液化石油气储罐各工况条件下最高充装液位高度和充装系数" 313 LPRINT
314 LPRINT "-------------------------------------------------------------"
315 LPRINT
316 LPRINT "计算条件"
317 LPRINT
328 LPRINT "储罐公称容积(立方米):"; GC
330 LPRINT "罐体内半径(m):"; R
340 LPRINT "罐体(两封头切线间)长度(m):"; L
350 LPRINT "最高工作温度下允许充装系数:"; c
360 LPRINT "罐体实际全容积(立方米):"; v
370 LPRINT "-20℃时丙烷饱和液体的密度(千克/立方米):"; p(1)
380 LPRINT "-10℃时丙烷饱和液体的密度(千克/立方米):"; p(2)
390 LPRINT "0℃时丙烷饱和液体的密度(千克/立方米):"; p(3)
400 LPRINT "10℃时丙烷饱和液体的密度(千克/立方米):"; p(4)
410 LPRINT "20℃时丙烷饱和液体的密度(千克/立方米):"; p(5)
420 LPRINT "30℃时丙烷饱和液体的密度(千克/立方米):"; p(6)
430 LPRINT "45℃时丙烷饱和液体的密度(千克/立方米):"; p(7)
440 LPRINT
450 LPRINT "--------------------------------------------------------------"
460 LPRINT "计算结果"
470 LPRINT
520 LPRINT " -20℃时最高允许充装液位高度(m) "; H(1);" 最高允许充装系数:";T(1) 530 LPRINT " -10℃时最高允许充装液位高度(m) "; H(2);" 最高允许充装系数:";T(2) 540 LPRINT " 0℃时最高允许充装液位高度(m) "; H(3);" 最高允许充装系数:";T(3) 550 LPRINT " 10℃时最高允许充装液位高度(m) "; H(4);" 最高允许充装系数:";T(4) 560 LPRINT " 20℃时最高允许充装液位高度(m) "; H(5);" 最高允许充装系数:";T(5)
570 LPRINT " 30℃时最高允许充装液位高度(m) "; H(6);" 最高允许充装系数:";T(6) 580 LPRINT " 45℃时最高允许充装液位高度(m) "; H(7);" 最高允许充装系数:";T(7) 590 END。
