β系数、夏普比率与VAR计算

投资学必考公式范文

投资学必考公式范文在投资学中，有一些重要的公式被广泛运用来评估投资项目的风险和回报。

以下是一些必考的投资学公式，它们对于投资决策和资产组合管理都非常有用。

1. Sharpe比率（Sharpe Ratio）Sharpe比率度量了每单位超额收益所承受的单位风险。

它的公式如下：Sharpe Ratio = (R_p - R_f) / σ_p其中，R_p为投资组合的平均回报率，R_f为无风险利率，σ_p为投资组合的标准差。

2. Treynor比率（Treynor Ratio）Treynor比率度量了每单位系统风险所获得的超额回报。

它的公式如下：Treynor Ratio = (R_p - R_f) / β_p其中，R_p为投资组合的平均回报率，R_f为无风险利率，β_p为投资组合的贝塔系数。

3. 市场风险溢价（Market Risk Premium）市场风险溢价表示股票或投资组合的预期收益率与无风险利率之间的差异。

它的公式如下：Market Risk Premium = R_m - R_f其中，R_m为市场的预期回报率，R_f为无风险利率。

4. 计算投资组合的预期回报率（Expected Portfolio Return）计算投资组合的预期回报率可以通过加权所有资产的预期回报率来衡量，其中权重是资产在投资组合中的比例。

5. 计算投资组合的标准差（Portfolio Standard Deviation）计算投资组合的标准差需要考虑资产之间的协方差，公式如下：σ_p = √(w_1^2 * σ_1^2 + w_2^2 * σ_2^2 + ... + 2 * w_1 * w_2 * Cov(1, 2))其中，w_i为资产i在投资组合中的权重，σ_i为资产i的标准差，Cov(1, 2)为资产1和资产2的协方差。

6. 最优投资组合的夏普比率（Optimal Portfolio Sharpe Ratio）寻找最优投资组合的夏普比率需要通过计算不同权重下的夏普比率来确定。

评估基金的八大数据指标

评估基金的八大数据指标投资基金，有时候可以借助一些别人算好的技术指标，来综合分析和判断一只基金的风险与收益，今天我主要讲一讲常见的这几种评判基金的数据指标。

（1）夏普比率：夏普比率=（基金年化收益-年化无风险利率）/基金年化收益的标准差下面通过一个例子来简单地说明什么是夏普比率。

假设有基金A和基金B，基金A的年化收益为20%，标准差为10%，基金B的年化收益为15%，标准差为5%，年平均无风险利率为2%，那么，基金A和基金B的夏普比率分别为1.8和2.6，依据夏普比率，基金B的风险调整收益要高于基金A。

为了更清楚地对此加以解释，可以以无风险利率的水平，融入等量的资金（融资比例为1：1），投资于基金B，那么，基金B的标准差将会扩大1倍，达到与A 相同的水平，但这时基金B的净值增长率则等于28%（即215%－2%），大于基金A。

下面是华安沪深300增强A（000312）的夏普比率：下面是富国沪深300指数增强A（100038）的夏普比率：通过对比我们可以发现：华安沪深300增强A的基金单位风险回报率高，优于富国沪深300指数增强A。

总的来说，夏普比率越大，说明基金的单位风险所获得的风险回报越高。

夏普比率为负时，则该指标没有意义。

（2）贝塔系数：贝塔系数主要用于衡量基金相对于市场波动的变动情况。

贝塔系数越高，说明该基金的风险也越大。

举个实例，如果市场波动为上涨10%，则贝塔系数为1.5的基金要上涨15%左右。

贝塔系数=1，表明基金的价格波动与市场波动一致。

贝塔系数＞1，表明基金的涨跌幅要高于市场涨跌幅。

贝塔系数＜1，表明基金的涨跌幅要低于市场涨跌幅。

下面是华安沪深300增强A（000312）的贝塔系数：下面是富国沪深300指数增强A（100038）的贝塔系数：二者贝塔系数均小于1，而华安沪深300增强A的贝塔系数小于富国沪深300指数增强A的，说明前者的涨跌幅相对于市场波动要比后者小一点，这说明华安沪深300增强A的安全性相对来讲高一点。

excel-β、sharp与VAR计算

日期单位净值信托累计增长率信托净值月增长率上证指数值2008年6月20日 1.00000.00%0.00%2831.74 2008年6月26日 1.00090.09%0.09%2901.85 2008年7月26日 1.00230.23%0.14%2865.10 2008年8月26日 1.00650.65%0.42%2350.08 2008年9月26日0.9928-0.72%-1.36%2293.78 2008年10月26日0.9633-3.67%-2.97%1839.62 2008年11月26日 1.0646 6.46%10.52%1897.88 2008年12月26日 1.106110.61% 3.90%1851.52 2009年1月26日 1.137613.76% 2.85%1990.66 2009年2月26日 1.219721.97%7.22%2121.25 2009年3月26日 1.266726.67% 3.85%2361.70 2009年4月26日 1.298629.86% 2.52%2448.59 2009年5月26日 1.290429.04%-0.63%2588.57 2009年6月26日 1.340634.06% 3.89%2928.21 2009年7月26日 1.402640.26% 4.62%3372.60 2009年8月26日 1.418041.80% 1.10%2967.59 2009年9月26日 1.449544.95% 2.22%2838.84 2009年10月26日 1.495649.56% 3.18%3109.57 2009年11月26日 1.602060.20%7.11%3170.98 2009年12月26日 1.623462.34% 1.34%3141.35 2010年1月26日 1.627362.73%0.24%3019.39 2010年2月26日 1.677367.73% 3.07%3051.94 2010年3月26日 1.655765.57%-1.29%3059.72 2010年4月26日 1.808480.84%9.22%2868.43 2010年5月26日 1.682868.28%-6.95%2625.79 2010年6月26日 1.662066.20%-1.24%2552.82 2010年7月26日 1.654765.47%-0.44%2588.68 2010年8月26日 1.700770.07% 2.78%2603.48 2010年9月26日 1.760176.01% 3.49%2591.55 2010年10月26日 1.837183.71% 4.37%3041.54 2010年11月26日 1.950495.04% 6.17%2871.70 2010年12月26日 1.848384.83%-5.23%2835.16 2010年1月26日 1.756775.67%-4.96%2708.81 2010年2月26日 1.818481.84% 3.51%2878.56Annualized Return25.09%Annualized Benchmark Return-0.30% Positive Month (%)72.73%Semivariance 4.45% Alpha 1.90%Benchmark Max DrawdownAnnualized Volatility13.75%Benchmark monthly returnDownside Volatility 6.46%Benchmark Downside Volatility19.81% Max Drawdown10.19%Benchmark Annualized VolatilitySortino Ratio 3.89Benchmark Sharpe RatioBenchmark Sortino RatioBenchmark Positive Month(%)51.52%指数累计月增长率指数月增长率月无风险利率夏普比率用月收益0.00%0.00%0.34%2.48% 2.48%0.34%-0.25%1.18%-1.27%0.34%-0.20%-17.01%-17.98%0.34%0.08%-19.00%-2.40%0.34%-1.70%-35.04%-19.80%0.30%-3.27%-32.98% 3.17%0.21%10.31%-34.62%-2.44%0.19% 3.71%-29.70%7.51%0.19% 2.66%-25.09% 6.56%0.19%7.03%-16.60%11.34%0.19% 3.67%-13.53% 3.68%0.19% 2.33%-8.59% 5.72%0.19%-0.82%3.41%13.12%0.19% 3.70%19.10%15.18%0.19% 4.44%4.80%-12.01%0.19%0.91%0.25%-4.34%0.19% 2.04%9.81%9.54%0.19% 2.99%11.98% 1.97%0.19% 6.93%10.93%-0.93%0.19% 1.15%6.63%-3.88%0.19%0.05%7.78% 1.08%0.19% 2.89%8.05%0.25%0.19%-1.47%1.30%-6.25%0.19%9.04%-7.27%-8.46%0.19%-7.13%-9.85%-2.78%0.19%-1.42%-8.58% 1.40%0.19%-0.62%-8.06%0.57%0.19% 2.59%-8.48%-0.46%0.19% 3.31%7.41%17.36%0.21% 4.17%1.41%-5.58%0.21% 5.96%0.12%-1.27%0.23%-5.46%-4.34%-4.46%0.23%-5.18%1.65% 6.27%0.23% 3.29%夏普比率Benchmark月收益IR用月收益负月平方增长2.14%-2.39%-1.61% 1.41%0.000330760.0005625100.00%-18.31%18.39%0.000237010.0364082300.00%-2.73% 1.03%0.001102050.00122568-0.01361150.00%-20.09%16.83%0.002430440.04370163-0.04332550.02%2.96%7.35%0000.09%-2.63% 6.34%00.0012588500.00%7.33%-4.67%0000.00%6.37%0.66%0000.00%11.15%-7.48%0000.00%3.49%-1.16%0000.00%5.53%-6.35%0.000670810-0.00631450.00%12.94%-9.23%0000.00%14.99%-10.55%0000.00%-12.19%13.11%7.4063E-050.0171980600.00%-4.52% 6.56%00.0029635400.00%9.35%-6.36%0000.00%1.79% 5.14%0000.00%-1.12% 2.27%3.8779E-050.0004160400.00%-4.07% 4.12%0.000295260.0024877200.00%0.89% 1.99%07.4364E-0800.00%0.07%-1.54%0.001053877.2315E-05-0.01287780.00%-6.44%15.47%00.0054128100.02%-8.64% 1.51%0.007927980.00914755-0.06945370.00%-2.96% 1.54%0.001020540.00150876-0.0818140.48%1.22%-1.84%0.000574940-0.08620630.02%0.39% 2.21%02.8471E-0500.00%-0.64% 3.95%00.0002444600.00%17.16%-12.99%0000.00%-5.79%11.75%00.0044746900.00%-1.50%-3.96%0.005174470.00056535-0.05234820.00%-4.68%-0.50%0.004780980.00309341-0.10190730.27%6.04%-2.75%0000.25%Benchmark负月平方增长相关性0.379216610.00%0.02%3.23%0.06%3.92%0.00%0.06%0.00%0.00%0.00%0.00%0.00%0.00%0.00%1.44%0.19%0.00%0.00%0.01%0.15%0.00%0.00%0.39%0.72%0.08%0.00%0.00%0.00%0.00%0.31%0.02%0.20%。

风险控制指标计算公式及其解读

风险控制指标计算公式及其解读风险控制是现代金融领域中的一个重要概念，它旨在帮助个人和组织在投资和经营活动中降低风险，保护利益。

为了更好地进行风险控制，人们常常使用各种风险控制指标来评估和衡量风险水平。

本文将介绍几个常见的风险控制指标，并详细解读它们的计算公式及含义。

一、价值-at-风险（VaR）VaR是用来衡量潜在损失的风险度量指标。

它通过计算在一定置信水平下的潜在最大损失来评估投资或组织所面临的市场风险。

VaR的计算公式如下：VaR = - [EP - (Z * SD)]其中，EP代表预期回报，Z代表标准正态分布的α分位数，SD代表标准差。

二、条件价值-at-风险（CVaR）CVaR是VaR的一种补充指标，它考虑的是在VaR指标下失去了多少价值。

CVaR计算公式如下：CVaR = EP - [(1/α) * ∫（1- α） * f(x)dx]其中，α代表置信水平，f(x)代表概率密度函数。

三、波动率（Volatility）波动率是衡量资产或投资组合价格波动性的指标。

波动率越高，意味着价格波动性越大，风险也相应增加。

常用的波动率计算方法有历史波动率和隐含波动率。

历史波动率通常使用过去一段时间的价格数据进行计算，其计算公式如下：历史波动率= √（Σ（Ri -R^）^2 / N）其中，Ri代表每期的收益率，R^代表平均收益率，N代表观察期数量。

隐含波动率则是从期权市场中推导出来的，它反映了市场对未来价格波动的预期。

四、夏普比率（Sharpe Ratio）夏普比率是用来衡量投资组合超额收益与承担风险之间的关系。

夏普比率越高，代表单位承担的风险越低，获得的超额回报越高。

夏普比率的计算公式如下：夏普比率 = （Rp - Rf）/ σp其中，Rp代表投资组合的平均收益率，Rf代表无风险收益率，σp 代表投资组合收益率的标准差。

五、贝塔系数（Beta）贝塔系数是一个用来衡量资产相对于市场整体风险的指标。

它可以帮助投资者确定投资组合与市场整体相关性的强弱，从而在风险控制中进行有效的资产配置。

CFAFRM金融分析公式大全

CFAFRM金融分析公式大全1. 期望收益率（Expected Return）：期望收益率=Σ(概率×收益率)2. 预期波动率（Expected Volatility）：预期波动率=√(Σ((概率×(收益率-期望收益率))^2))3. 夏普比率（Sharpe Ratio）：夏普比率=(投资组合的期望年化收益率-无风险收益率)/投资组合的波动率4.温度法宣告证券市场均衡价格：市场均衡价格=Σ(现金流量×温度因子)5. 资本资产定价模型（Capital Asset Pricing Model，CAPM）：期望回报率 = 无风险收益率+ beta × (市场回报率 - 无风险收益率)6. 投资组合的标准差（Standard Deviation）：标准差=√(Σ((权重×收益率)^2))7. 价值-市盈率比（Price-to-Earnings Ratio，P/E Ratio）：P/E Ratio = 市价 / 每股盈利8. 市净率（Price-to-Book Ratio）：市净率=市价/每股净资产9. 黄金交叉与死亡交叉（Golden Cross and Death Cross）：黄金交叉：短期均线上穿长期均线死亡交叉：短期均线下穿长期均线10. RSI相对强弱指标（Relative Strength Index）：RSI=100-(100/(1+(平均上涨收盘价/平均下跌收盘价)))11. 股票的内在价值（Intrinsic Value）：内在价值=Σ((未来现金流/(1+折现率)^n))12. 第一期现金流折现值（Present Value）：第一期现金流折现值=第一期现金流/(1+折现率)13. 直线回归模型的方程（Linear Regression Equation）：y = a + bx14. 杠杆系数（Leverage）：杠杆系数=总债务/资产总额15. 公司的盈利能力（Profitability）：净利润率=净利润/总销售收入毛利率=（总销售收入-成本）/总销售收入净资产收益率=净利润/净资产16. 价值风险度量（Value at Risk，VaR）：VaR=概率×投资组合价值×投资组合的波动率17. 杠杆比率（Leverage Ratio）：杠杆比率=总负债/净值18. 赤字财政（Deficit Finance）：赤字财政=总支出-总收入19. 股票分割和股票的配股（Stock Split and Rights Issue）：股票分割：每股票分割为若干股票，即原来的股份增加了配股：公司向现有股东配售新股票20. 无风险利率（Risk-free Rate）：无风险利率是指在无风险投资的情况下可以获得的回报率，通常以政府债券的利率作为无风险利率。

β系数、夏普比率与VAR计算

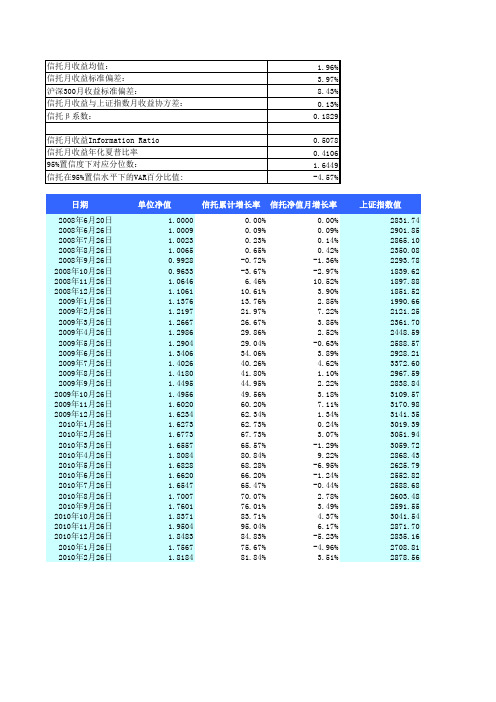
日期单位净值信托累计增长率信托净值月增长率上证指数值2008年6月20日 1.00000.00%0.00%2831.74 2008年6月26日 1.00090.09%0.09%2901.85 2008年7月26日 1.00230.23%0.14%2865.10 2008年8月26日 1.00650.65%0.42%2350.08 2008年9月26日0.9928-0.72%-1.36%2293.78 2008年10月26日0.9633-3.67%-2.97%1839.62 2008年11月26日 1.0646 6.46%10.52%1897.88 2008年12月26日 1.106110.61% 3.90%1851.52 2009年1月26日 1.137613.76% 2.85%1990.66 2009年2月26日 1.219721.97%7.22%2121.25 2009年3月26日 1.266726.67% 3.85%2361.70 2009年4月26日 1.298629.86% 2.52%2448.59 2009年5月26日 1.290429.04%-0.63%2588.57 2009年6月26日 1.340634.06% 3.89%2928.21 2009年7月26日 1.402640.26% 4.62%3372.60 2009年8月26日 1.418041.80% 1.10%2967.59 2009年9月26日 1.449544.95% 2.22%2838.84 2009年10月26日 1.495649.56% 3.18%3109.57 2009年11月26日 1.602060.20%7.11%3170.98 2009年12月26日 1.623462.34% 1.34%3141.35 2010年1月26日 1.627362.73%0.24%3019.39 2010年2月26日 1.677367.73% 3.07%3051.94 2010年3月26日 1.655765.57%-1.29%3059.72 2010年4月26日 1.808480.84%9.22%2868.43 2010年5月26日 1.682868.28%-6.95%2625.79 2010年6月26日 1.662066.20%-1.24%2552.82 2010年7月26日 1.654765.47%-0.44%2588.68 2010年8月26日 1.700770.07% 2.78%2603.48 2010年9月26日 1.760176.01% 3.49%2591.55 2010年10月26日 1.837183.71% 4.37%3041.54 2010年11月26日 1.950495.04% 6.17%2871.70 2010年12月26日 1.848384.83%-5.23%2835.16 2010年1月26日 1.756775.67%-4.96%2708.81 2010年2月26日 1.818481.84% 3.51%2878.56Annualized Return25.09%Annualized Benchmark Return-0.30% Positive Month (%)72.73%Semivariance 4.45% Alpha 1.90%Benchmark Max DrawdownAnnualized Volatility13.75%Benchmark monthly returnDownside Volatility 6.46%Benchmark Downside Volatility19.81% Max Drawdown10.19%Benchmark Annualized VolatilitySortino Ratio 3.89Benchmark Sharpe RatioBenchmark Sortino RatioBenchmark Positive Month(%)51.52%指数累计月增长率指数月增长率月无风险利率夏普比率用月收益0.00%0.00%0.34%2.48% 2.48%0.34%-0.25%1.18%-1.27%0.34%-0.20%-17.01%-17.98%0.34%0.08%-19.00%-2.40%0.34%-1.70%-35.04%-19.80%0.30%-3.27%-32.98% 3.17%0.21%10.31%-34.62%-2.44%0.19% 3.71%-29.70%7.51%0.19% 2.66%-25.09% 6.56%0.19%7.03%-16.60%11.34%0.19% 3.67%-13.53% 3.68%0.19% 2.33%-8.59% 5.72%0.19%-0.82%3.41%13.12%0.19% 3.70%19.10%15.18%0.19% 4.44%4.80%-12.01%0.19%0.91%0.25%-4.34%0.19% 2.04%9.81%9.54%0.19% 2.99%11.98% 1.97%0.19% 6.93%10.93%-0.93%0.19% 1.15%6.63%-3.88%0.19%0.05%7.78% 1.08%0.19% 2.89%8.05%0.25%0.19%-1.47%1.30%-6.25%0.19%9.04%-7.27%-8.46%0.19%-7.13%-9.85%-2.78%0.19%-1.42%-8.58% 1.40%0.19%-0.62%-8.06%0.57%0.19% 2.59%-8.48%-0.46%0.19% 3.31%7.41%17.36%0.21% 4.17%1.41%-5.58%0.21% 5.96%0.12%-1.27%0.23%-5.46%-4.34%-4.46%0.23%-5.18%1.65% 6.27%0.23% 3.29%夏普比率Benchmark月收益IR用月收益负月平方增长2.14%-2.39%-1.61% 1.41%0.000330760.0005625100.00%-18.31%18.39%0.000237010.0364082300.00%-2.73% 1.03%0.001102050.00122568-0.01361150.00%-20.09%16.83%0.002430440.04370163-0.04332550.02%2.96%7.35%0000.09%-2.63% 6.34%00.0012588500.00%7.33%-4.67%0000.00%6.37%0.66%0000.00%11.15%-7.48%0000.00%3.49%-1.16%0000.00%5.53%-6.35%0.000670810-0.00631450.00%12.94%-9.23%0000.00%14.99%-10.55%0000.00%-12.19%13.11%7.4063E-050.0171980600.00%-4.52% 6.56%00.0029635400.00%9.35%-6.36%0000.00%1.79% 5.14%0000.00%-1.12% 2.27%3.8779E-050.0004160400.00%-4.07% 4.12%0.000295260.0024877200.00%0.89% 1.99%07.4364E-0800.00%0.07%-1.54%0.001053877.2315E-05-0.01287780.00%-6.44%15.47%00.0054128100.02%-8.64% 1.51%0.007927980.00914755-0.06945370.00%-2.96% 1.54%0.001020540.00150876-0.0818140.48%1.22%-1.84%0.000574940-0.08620630.02%0.39% 2.21%02.8471E-0500.00%-0.64% 3.95%00.0002444600.00%17.16%-12.99%0000.00%-5.79%11.75%00.0044746900.00%-1.50%-3.96%0.005174470.00056535-0.05234820.00%-4.68%-0.50%0.004780980.00309341-0.10190730.27%6.04%-2.75%0000.25%Benchmark负月平方增长相关性0.379216610.00%0.02%3.23%0.06%3.92%0.00%0.06%0.00%0.00%0.00%0.00%0.00%0.00%0.00%1.44%0.19%0.00%0.00%0.01%0.15%0.00%0.00%0.39%0.72%0.08%0.00%0.00%0.00%0.00%0.31%0.02%0.20%。

投资组合风险度量方法解析

投资组合风险度量方法解析在金融领域中，投资组合的风险度量是评估投资组合潜在风险的关键步骤。

投资组合风险度量旨在帮助投资者评估投资组合的风险水平，并做出相应的投资决策。

本文将介绍一些常见的投资组合风险度量方法。

1. 标准差标准差是一种用来度量投资组合风险的最常见方法。

标准差反映了投资组合收益的波动性，波动性越高，风险越大。

标准差越小，表示投资组合的风险越低。

标准差的计算公式如下：标准差= √(1/n)∑(Ri - Rm)^2其中，n代表投资组合中的资产数量，Ri代表每个资产的收益率，Rm代表投资组合的收益率。

2. VaR（Value at Risk）VaR是衡量投资组合在给定置信水平下的最大可能损失的方法。

VaR可以帮助投资者评估投资组合在特定时间段内的风险水平，并制定相应的风险管理策略。

VaR的计算方法有多种，常用的有历史模拟法、参数法和蒙特卡洛模拟法。

历史模拟法基于历史数据，通过计算历史收益率序列的分布来估计VaR。

参数法利用统计模型来估计投资组合的风险，常见的参数法包括协方差法和极值法。

蒙特卡洛模拟法通过模拟大量的随机路径来估计VaR。

3. CVaR（Conditional Value at Risk）CVaR是对VaR的扩展，它不仅考虑最大可能损失，还对超过VaR 值的损失进行加权。

CVaR能够提供更全面的投资组合风险度量，因为它对投资组合的极端损失更加敏感。

CVaR的计算方法与VaR类似，不同之处在于CVaR需要计算超过VaR值的损失，并对损失进行加权。

CVaR可以帮助投资者更好地理解投资组合的风险分布，制定更科学的风险管理策略。

4. Beta系数Beta系数是一种用来度量投资组合相对于市场（通常指某个大盘指数）的波动性的方法。

Beta系数越高，表示投资组合对市场的波动性越敏感，风险越大。

反之，Beta系数越低，表示投资组合对市场的波动性越不敏感，风险越小。

Beta系数的计算方法是通过回归分析得出的。

夏普指数计算公式

夏普指数计算公式
夏普指数（Sharpe Ratio）是一种测量投资组合中风险和投资回报之间
关系的重要指标。

它最初是由威廉·夏普（William F. Sharpe）于1964
年提出的。

由于它作为一个投资风险收益的度量标准，它有助于分析投资风
险与投资回报之间的关系。

夏普指数可以帮助投资者了解他们正在做投资的
投资组合的收益的长期可持续性，以及投资者所承受的风险水平是否与单位
时间投资所产生的收益水平相当。

夏普指数计算公式是：夏普比率=（投资组合预期收益率-无风险收益率）/投资组合标准差。

然而，在计算夏普指数时需要一些变量，包括投资组合
的预期收益，投资组合的标准差，无风险收益率等。

一般来说，投资组合的
标准差是衡量投资组合波动性的重要参考指标，而无风险收益率可以衡量投
资组合中与市场基准收益相关性。

夏普指数可以用来衡量投资组合的总体风险与收益效用，并帮助投资者
作出投资决策。

根据夏普指数计算的结果，投资者可以知道投资组合所拥有
的回报水平是否合理，同时知道投资组合的风险水平是否可以承受。

因此，夏普指数是衡量投资组合风险和收益的重要指标，它不仅可以指
导投资者如何有效地多种投资组合结构，而且还可以用作衡量投资的过程的
重要参考指标。

总之，夏普指数能够提高投资者投资绩效，促进投资绩效的
创新性，它应该得到更多专业投资者高度重视。

经济学中β系数的计算

计算β系数一、β系数的概念及计算原理1、概念：β系数也称为贝他系数（Beta coefficient），是一种风险指数，用来衡量个别股票或股票基金相对于整个股市的价格波动情况。

β系数是一种评估证券系统性风险的工具，用以度量一种证券或一个投资证券组合相对总体市场的波动性。

投资股市中一个公司，如果其β值为1.1，则意味着股票风险比整个股市场平均风险高10%；相反，如果公司β为0.9，则表示其股票风险比股市场平均风险低10%。

2、理论体系：β系数的计算分为上市公司β系数计算和非上市公司β系数计算两种情况：在被评估企业是上市公司时，可以根据其各期历史收益数据和相应的股票市场综合指数来确定其β系数；当被评估企业不是上市公司时，我们可以寻找相似的上市公司，先得出该上市公司的β系数，然后通过比较和调整来间接计算被评估企业的β系数。

下面的实例讲解了非上市公司β系数的计算方法。

（注：这里所说的“调整”是调整参照公司与被评估对象由于财务杠杆的不同而进行的调整，类似市场比较法中比较因素的修正）3、β系数计算的原理：如果将市场上全部所有股票作为一个资产组合，其市场整体风险收益以市场整体资产组合M收益的方差Var(Rm)表示，任一只股票对系统风险收益的贡献，由这一股票与市场资产组合M收益的协方差Cov(Rm，Ri)表示，则β系数可表示为：β=Cov(Rm，Ri)/ Var(Rm)【知识链接】①方差的概念：样本中各数据与样本平均数的差的平方和的平均数叫做样本方差。

②协方差的概念：在概率论和统计学中，协方差用于衡量两个变量的总体误差。

协方差cov(X,Y)的度量单位是X的协方差乘以Y的协方差。

而取决于协方差的相关性，是一个衡量线性独立的无量纲的数。

方差是协方差的一种特殊情况，即当两个变量是相同的情况。

此外，由于市场整体收益率Y=α+β×(X-参照上市公司的收益率)，通过进行一元线性回归分析，也可以用这一公式计算出β系数。

VaR分析的三种计算方法

VaR分析的三种计算方法VaR度量的三种经典方法1.正态分布法正态分布法计算组合VaR有三种计算方法：A．假设债券组合的对数日收益率服从均值为u，标准差为的正态分布。

则由独立同分布随机变量和的特征知，持有期内组合的对数收益率服从均值为，方差为的正态分布。

通过计算债券组合的收益率分布，估计分布参数，直接计算债券组合的VaR。

若将债券组合看作单一债券，则此种方法也适用于单个债券的VaR计算。

具体步骤为：1、根据成分债券的价格矩阵和对应持仓量矩阵计算债券组合的价格序列，这里价格使用债券的盯市价格（以持仓量计算权重）；2、根据债券组合的价格序列计算对数日收益率；3、根据成分债券的当前价格和当前持仓量计算债券组合的当前价格（以持仓量计算权重）；4、由债券组合的对数收益率序列计算其标准差，作为收益率的波动率；5、计算置信度对应的标准正态分布的分位数；6、计算组合的在置信度下的最大损失金额VaR为：，也称为相对VaR，是指以组合的当前价格为基点考察持有期内组合的价指变化。

其中为持有期；在该置信度下，债券组合绝对VaR为：此值为负，是指以持有期内组合的预期收益率为基点考察持有期内组合的变化，其中u为债券组合的收益率均值。

B．假设债券组合中各成分债券的对数收益率服从多元正态分布，均值为向量U，协方差矩阵为V。

通过计算成分债券的收益率矩阵，估计向量U和协方差矩阵V，进而计算债券组合的VaR.1、计算成分债券的对数收益率矩阵R，每一列表示一种成分债券的收益率序列；2、由成分债券的当前持仓量计算权重向量W（分量和为1）；3、计算收益率矩阵的列均值向量U，计算列均值的加权和，得到债券组合的收益率均值u；计算收益率矩阵的列协方差，得到协方差矩阵V，则债券组合的方差为；4、计算组合在置信度下的最大损失金额为：，也就是相对VaR；债券组合在该置信度下的最差价格为：此值为负，也就是绝对VaR，其中u为组合收益率的均值。

C．根据成分债券的VaR计算组合VaR假设债券组合由n种债券组成，R为这些成分债券的收益率矩阵。

风险系数的计算方法

风险系数的计算方法
风险系数是用来衡量某种风险的大小或者程度的指标。

在金融
领域，风险系数通常用来评估投资组合或者资产的风险水平。

计算
风险系数的方法有多种，下面我将从不同的角度来介绍几种常见的
计算方法。

1. 标准差法，标准差是一种衡量数据分散程度的统计量，计算
投资组合或者资产收益率的标准差可以得到风险系数。

标准差越大，表示投资的波动性越高，风险系数也就越高。

2. Beta系数法，Beta系数是用来衡量一个资产相对于整个市
场的波动性的指标。

计算某个资产的Beta系数可以通过回归分析得到，Beta系数越高，表示该资产的波动性相对于市场更大，风险系
数也就越高。

3. VaR法，Value at Risk（VaR）是一种衡量投资组合或者资
产在一定置信水平下的最大可能损失的方法。

通过计算VaR可以得
到风险系数，通常情况下，VaR越高，风险系数也就越高。

4. 最大回撤法，最大回撤是指投资组合或者资产在某个时期内
从最高点到最低点的损失幅度，计算最大回撤可以得到风险系数。

最大回撤越大，风险系数也就越高。

总的来说，风险系数的计算方法有很多种，每种方法都有其适用的场景和局限性。

在实际应用中，可以根据具体的情况选择合适的方法来计算风险系数，以便更准确地评估风险水平。

希望这些信息能够帮助到你。

证券从业资格必备公式汇总

证券从业资格必备公式汇总在证券市场中，数学和统计学常常被用来解决各种问题和分析市场动态。

证券从业人员需要熟悉并理解一些必备的数学公式，才能更好地理解市场现象，做出明智的投资决策。

本文将汇总一些证券从业资格考试中常见的、必备的数学公式，以供从业人员参考。

一、风险和收益相关公式1. 夏普比率（Sharpe Ratio）夏普比率用于衡量资产或投资组合相对于无风险回报的风险调整收益。

其计算公式为：夏普比率 = (Rp - Rf) / σp其中，Rp为资产或投资组合的预期回报，Rf为无风险回报率，σp 为资产或投资组合的标准差。

2. 资本资产定价模型（Capital Asset Pricing Model）资本资产定价模型用于估算资产或投资组合的预期回报。

其计算公式为：Rp = Rf + βp * (Rm - Rf)其中，Rp为预期回报，Rf为无风险回报率，βp为资产或投资组合的β系数，Rm为市场回报率。

3. 价值加权分析（Discounted Cash Flow）价值加权分析用于估算企业或项目的价值。

其计算公式为：DCF = CF1 / (1 + r)^1 + CF2 / (1 + r)^2 + ... + CFn / (1 + r)^n其中，CF为每年的现金流量，r为折现率，n为现金流量的期数。

二、股票和债券定价相关公式1. 股票定价模型（Gordon Growth Model）股票定价模型用于估算无分红收益的股票价值。

其计算公式为：P0 = D1 / (r - g)其中，P0为股票的现值，D1为未来一年的股票分红，r为股票的期望回报率，g为股票分红增长率。

2. 债券定价模型（Bond Pricing Model）债券定价模型用于估算债券的现值。

其计算公式为：P0 = C / r * (1 - (1 + r)^(-n)) + F / (1 + r)^n其中，P0为债券的现值，C为每年的债券利息，r为债券的收益率，n为债券的期限，F为债券的面值。

夏普比率的计算方法

夏普比率的计算方法
夏普比率呢，它可是个很有用的小玩意儿，能帮咱们衡量投资组合在承担一定风险的情况下，能获得多少额外的收益呢。

那它咋计算呢？其实公式也不是特别复杂啦。

夏普比率等于（投资组合的预期收益率 - 无风险利率）除以投资组合的标准差。

咱先说说这个投资组合的预期收益率哈。

这就像是你对自己投资能赚多少钱的一个小期待。

比如说你买了几只股票组成一个小投资组合，你根据这些股票过去的表现啊，还有对未来市场的一些小判断，估摸出这个组合大概能赚多少百分比，这就是预期收益率啦。

再讲讲无风险利率。

这个就比较稳定啦，像国债的利率就常常被当作无风险利率呢。

为啥呢？因为国债基本上是很安全的，违约风险超级低，所以这个利率就像是一个保底的收益水平。

最后就是投资组合的标准差啦。

这个标准差可有点调皮，它是用来衡量投资组合收益波动情况的。

如果标准差大，就说明这个投资组合的收益一会儿高一会儿低，波动很厉害；要是标准差小呢，就表示收益比较平稳啦。

比如说，你算出你的投资组合预期收益率是15%，无风险利率是3%，投资组合的标准差是5%。

那夏普比率就是（15% - 3%）÷5% = 2.4。

这个2.4就代表了你的投资组合每承担一单位的风险，能获得2.4单位的超额收益呢。

夏普比率计算题讲解

夏普比率计算题讲解
夏普比率是一种用于评估投资组合风险调整后表现的指标。

它综合考虑了投资组合的收益率和风险，通过比较投资组合的超额收益与其风险，来评估投资组合的有效性。

夏普比率的计算公式为：
夏普比率 = (投资组合收益率 - 无风险利率) / 投资组合标准差
其中，投资组合收益率是指投资组合在一定时期内的平均收益率，无风险利率是指与投资组合风险相同的无风险投资的预期收益率，投资组合标准差则代表投资组合的风险水平。

下面我将通过一个简单的例子来解释夏普比率的计算过程。

假设有一个投资组合，在过去一年的平均收益率为10%，标准差为15%。

同时，无风险利率为3%。

夏普比率的计算步骤如下：
1. 计算投资组合的超额收益：投资组合收益率 - 无风险利率 = 10% - 3% = 7%。

2. 计算夏普比率：超额收益 / 投资组合标准差 = 7% / 15% = 。

根据计算结果，该投资组合的夏普比率为，表示在每承受1个标准差的风险下，能够获得个标准差的超额收益。

需要注意的是，夏普比率的大小本身没有意义，只有在与其他组合的比较中才有价值。

因此，投资者在评估不同投资组合时，应该比较它们的夏普比率，以选择具有较高夏普比率的投资组合。

投资策略的关键指标夏普比率和风险收益比

投资策略的关键指标夏普比率和风险收益比夏普比率和风险收益比：投资策略的关键指标在金融投资领域，夏普比率和风险收益比是两个非常重要的指标，用于衡量投资策略的绩效和风险程度。

本文将对夏普比率和风险收益比进行详细介绍，并探讨它们在投资决策中的应用。

1. 夏普比率夏普比率是由诺贝尔经济学奖获得者威廉·夏普（William Sharpe）提出的，用于衡量一个资产或投资组合相对于每单位风险所获得的超额收益。

夏普比率通过比较资产或投资组合的平均收益率与市场无风险利率之差，与标准差（风险）之比来评估投资策略的表现。

夏普比率的计算公式为：夏普比率 = (Rp - Rf) / σp其中，Rp代表投资组合的预期平均收益率，Rf代表市场无风险利率，σp代表投资组合的标准差。

夏普比率越高，代表在承担同样风险的情况下，投资组合获得的超额收益越多。

2. 风险收益比风险收益比是用于衡量投资策略的风险与回报之间关系的指标。

它是投资风险与预期收益的比值，帮助投资者评估投资策略的潜在风险水平和获得的收益是否相符。

风险收益比的计算公式为：风险收益比 = (Rp - Rf) / β其中，Rp代表投资组合的预期收益率，Rf代表市场无风险利率，β代表投资组合的贝塔系数。

风险收益比越高，代表在承担同样风险的情况下，投资组合获得的预期收益越高。

3. 夏普比率与风险收益比的应用夏普比率和风险收益比是投资策略评估中常用的指标，帮助投资者选择风险适度且预期收益良好的投资组合。

首先，夏普比率可以帮助投资者比较不同投资组合之间的表现。

较高的夏普比率意味着在相同风险下，该投资组合获得的超额收益更高，因此更具吸引力。

投资者可以使用夏普比率来评估不同投资策略的绩效，选择表现较好的投资组合。

其次，风险收益比可以帮助投资者衡量投资策略的风险与回报之间的平衡。

通过计算风险收益比，投资者可以知道他们承担的风险与预期收益相比是否合理。

在投资决策过程中，投资者应该寻找具有较高风险收益比的投资组合，以平衡风险与回报。

β系数夏普比率与VAR计算

β系数夏普比率与VAR计算β系数β系数是用来衡量一个资产相对于整个市场的波动性的指标，它反映了该资产与市场的相关性。

具体来说，β系数是一个资产的收益与市场收益之间的相关系数。

β系数的计算公式如下：β = Cov(资产收益, 市场收益) / Var(市场收益)其中，Cov表示相关系数，Var表示方差。

β系数可以是正值也可以是负值，如果β系数大于1，表示该资产比市场更波动；如果β系数小于1，表示该资产比市场波动小；如果β系数等于1，表示该资产的波动与市场波动一致。

夏普比率夏普比率是用来衡量投资组合或资产收益与风险之间的权衡关系。

它是由诺贝尔经济学奖得主威廉·夏普（William F. Sharpe）提出的。

夏普比率的计算公式如下：夏普比率=(资产或组合的期望收益率-无风险利率)/资产或组合的标准差其中，期望收益率表示预期获得的平均收益，无风险利率表示无风险投资的利率，标准差表示投资组合或资产的风险大小。

夏普比率越高，表示单位风险所获得的收益越多，投资效率越高。

VAR，即Value at Risk，是一种用来度量金融风险的方法，它是指在特定的置信水平下，投资组合或资产在一段时间内可能亏损的最大金额。

VAR的计算可以使用不同的方法，其中最常用的是历史模拟法和蒙特卡洛模拟法。

历史模拟法是将过去的一段时间的市场数据作为样本，通过计算样本的标准差来衡量投资组合或资产的风险。

具体来说，历史模拟法计算VAR的步骤如下：1.收集一段时间内的市场数据，例如过去一年的每日收盘价。

2.计算每日收益率，即当日收盘价与前一日收盘价的差异除以前一日收盘价。

这样可以得到一组收益率数据。

3.计算收益率数据的均值和标准差。

均值用来计算预期收益率，标准差用来计算风险。

4.假设投资组合或资产的收益率服从正态分布，根据正态分布的性质，可以计算出在特定的置信水平下VAR的值。

例如，如果置信水平为95%，则VAR表示在一定时间内，投资组合或资产的亏损有95%的概率不超过VAR的金额。

夏普比率-标准差-贝他系数

夏普比率-标准差-贝他系数夏普比率现代投资理论的研究表明,风险的大小在决定组合的表现上具有基础性的作用。

风险调整后的收益率就是一个可以同时对收益与风险加以考虑的综合指标,以期能够排除风险因素对绩效评估的不利影响。

夏普比率就是一个可以同时对收益与风险加以综合考虑的三大经典指标之一。

投资中有一个常规的特点，即投资标的的预期报酬越高，投资人所能忍受的波动风险越高；反之，预期报酬越低，波动风险也越低。

所以理性的投资人选择投资标的与投资组合的主要目的为：在固定所能承受的风险下，追求最大的报酬；或在固定的预期报酬下，追求最低的风险。

·夏普比率计算公式·夏普比率在运用中应该注意的问题夏普比率（Sharpe Ratio），又被称为夏普指数--- 基金绩效评价标准化指标夏普比率概述1990年度诺贝尔经济学奖得主威廉·夏普（William Sharpe）以投资学最重要的理论基础CAPM（CapitalAsset Pricing Model，资本资产定价模式）为出发，发展出名闻遐迩的夏普比率（Sharpe Ratio）又被称为夏普指数，用以衡量金融资产的绩效表现。

威廉·夏普理论的核心思想理性的投资者将选择并持有有效的投资组合，即那些在给定的风险水平下使期望回报最大化的投资组合，或那些在给定期望回报率的水平上使风险最小化的投资组合。

解释起来非常简单，他认为投资者在建立有风险的投资组合时，至少应该要求投资回报达到无风险投资的回报，或者更多。

夏普比率计算公式夏普比率计算公式：=[E(Rp)－Rf]/σp 其中E(Rp)：投资组合预期报酬率Rf：无风险利率σp：投资组合的标准差目的是计算投资组合每承受一单位总风险，会产生多少的超额报酬。

比率依据资本市场线(Capital Market Line,CML)的观念而来，是市场上最常见的衡量比率。

当投资组合的资产皆为风险性资产时，适用夏普比率。

基金表现中的数据中：阿尔法系数（α），贝塔系数（β），R平方

基⾦表现中的数据中：阿尔法系数（α），贝塔系数（β），R平⽅分别代表什么平均回报平均回报为年度化的平均周回报，得出数据未必与过去⼀年实际年度回报相等。

标准差反映计算期内总回报率的波动幅度，即基⾦每周的总回报率相对于平均周回报率的偏差程度，波动越⼤，标准差也越⼤。

夏普⽐率夏普⽐率是衡量基⾦风险调整后收益的指标之⼀，反映了基⾦承担单位风险所获得的超额回报率（ Excess Returns ），即基⾦总回报率⾼于同期⽆风险收益率的部分，⼀般情况下，该⽐率越⾼，基⾦承担单位风险得到的超额回报率越⾼。

阿尔法系数（α）阿尔法系数（α）是基⾦的实际收益和按照β系数计算的期望收益之间的差额。

其计算⽅法如下：超额收益是基⾦的收益减去⽆风险投资收益（在中国为 1 年期银⾏定期存款收益）；期望收益是贝塔系数β和市场收益的乘积，反映基⾦由于市场整体变动⽽获得的收益；超额收益和期望收益的差额即α系数。

贝塔系数（β）贝塔系数衡量基⾦收益相对于业绩评价基准收益的总体波动性，是⼀个相对指标。

β越⾼，意味着基⾦相对于业绩评价基准的波动性越⼤。

β⼤于 1 ，则基⾦的波动性⼤于业绩评价基准的波动性。

反之亦然。

如果β为 1 ，则市场上涨 10 ％，基⾦上涨 10 ％；市场下滑 10 ％，基⾦相应下滑 10 ％。

如果β为 1.1, 市场上涨 10 ％时，基⾦上涨 11%, ；市场下滑 10 ％时，基⾦下滑 11% 。

如果β为 0.9, 市场上涨 10 ％时，基⾦上涨 9% ；市场下滑 10 ％时，基⾦下滑 9% 。

R 平⽅R 平⽅ (R-squared) 是反映业绩基准的变动对基⾦表现的影响，影响程度以 0 ⾄ 100 计。

如果 R 平⽅值等于 100 ，表⽰基⾦回报的变动完全由业绩基准的变动所致；若 R 平⽅值等于 35 ，即 35% 的基⾦回报可归因于业绩基准的变动。

简⾔之， R 平⽅值愈低，由业绩基准变动导致的基⾦业绩的变动便愈少。

quantstats 绩效指标

quantstats 绩效指标QuantStats是一种用于评估和分析投资策略绩效的Python库。

它提供了一系列指标，帮助投资者对其投资组合的表现进行量化评估。

本文将介绍QuantStats库的绩效指标以及如何使用它来评估投资策略的表现。

一、绩效指标的概述QuantStats库提供了多种绩效指标，可以帮助投资者评估其投资策略的盈亏情况、风险水平以及与基准的比较等方面。

以下是QuantStats库中一些常用的绩效指标：1. 年化收益率（Annualized Returns）：衡量投资组合在一年内的平均收益率。

该指标可以帮助投资者了解他们的投资策略是否能够持续地获得正收益。

2. 夏普比率（Sharpe Ratio）：衡量投资组合每承受一单位风险所获得的超额收益。

夏普比率越高，表明投资策略相对于风险的回报越高。

3. 最大回撤（Max Drawdown）：衡量投资组合在特定时间段内的最大损失。

最大回撤越小，表明投资策略的风险水平越低。

4. 胜率（Win Rate）：衡量投资策略获得正收益的比例。

胜率越高，表明投资策略取得成功的概率越大。

5. β系数（Beta）：衡量投资组合相对于基准的波动性。

β系数大于1表示投资组合比基准更波动，小于1表示投资组合比基准更稳定。

6. Alpha系数（Alpha）：衡量投资组合相对于基准的超额收益。

Alpha系数越高，表明投资组合相对于基准的表现越好。

以上只是QuantStats库中的一部分绩效指标，投资者可以根据自己的需求选择合适的绩效指标进行分析。

二、使用QuantStats评估投资策略绩效使用QuantStats库评估投资策略的绩效非常简单。

首先，需要导入QuantStats库：import quantstats as qs然后，通过以下代码可以计算投资策略的绩效指标：# 导入投资组合收益数据returns = ...# 计算绩效指标qs.reports.full(returns)其中，returns是一个包含投资组合每日收益率的Pandas Series对象。

基金投资的关键指标解析AlphaBeta和夏普比率

基金投资的关键指标解析AlphaBeta和夏普比率在证券投资领域中，基金投资是一种常见的方式，它允许个人和机构通过购买股票、债券等资产来获得投资回报。

然而，为了更好地评估基金的业绩，投资者需要了解基金的关键指标。

本文将重点解析基金投资中的两个重要指标：AlphaBeta和夏普比率。

AlphaBeta指标是评估基金在市场上表现的一种度量方式。

Alpha指标衡量了基金相对于市场平均值的超额回报能力，它显示了基金经理的投资技巧和能力。

如果基金的Alpha值为正，说明基金经理的投资策略比市场平均水平更具优势，可以获得超额回报。

相反，如果Alpha 值为负，则意味着基金的表现不如市场平均水平。

Beta指标衡量了基金与市场整体波动的相关性。

如果Beta值为1，意味着基金的波动与市场整体波动一致。

如果Beta值大于1，则表示基金的波动大于市场平均水平，反之则表示基金的波动小于市场平均水平。

夏普比率是基金投资中另一个重要的评估指标。

它将基金的超额回报（即Alpha值）与相对于市场风险的波动性进行比较。

夏普比率越高，意味着基金相对于市场风险获得的回报越高，这被视为投资者偏好的基金选择。

夏普比率的计算公式为：夏普比率 = (基金的年化收益率 - 无风险利率) / 基金的年化波动率。

夏普比率的结果越高，表明基金在承担相同风险的情况下获得的回报越高。

需要注意的是，AlphaBeta和夏普比率虽然是评估基金投资的关键指标，但它们都有一定的局限性。

首先，这些指标是基于历史数据进行分析的，不能保证未来的表现。

其次，AlphaBeta和夏普比率只能提供基金在市场上的综合表现，而不能提供关于基金投资策略和风险分散的详细信息。

因此，在决策投资时，投资者需要综合考虑其他因素，例如基金经理的经验与能力、基金的投资策略、行业和市场前景等。

总结起来，AlphaBeta和夏普比率是基金投资中重要的评估指标，它们能够帮助投资者了解基金的表现和回报能力。