浙江农林大学电容及电容器、静电场的能量、能量密度习题
大学物理练习题 电容 静电场的能量

练习九 电容 静电场的能量一、选择题1. 一孤立金属球,带有电量1.2×10−8C ,当电场强度的大小为3×106V/m 时,空气将被击穿. 若要空气不被击穿,则金属球的半径至少大于(A ) 3.6×10−2m 。
(B ) 6.0×10−6m 。
(C ) 3.6×10−5m 。
(D ) 6.0×10−3m 。
2. 两个半径相同的金属球,一为空心,一为实心,把两者各自孤立时的电容值加以比较,则:(A ) 空心球电容值大。
(B ) 实心球电容值大。
(C ) 两球电容值相等。
(D ) 大小关系无法确定。
3. C 1和C 2两个电容器,其上分别标明200pF (电容量)、500V (耐压值)和300pF 、900V 。
把它们串联起来在两端加上1000V 电压,则(A ) 两者都被击穿。
(B ) 两者都不被击穿。
(C ) C 2被击穿,C 1不被击穿。
(D ) C 1被击穿,C 2不被击穿。
4. 平行板电容器充电后与电源断开,然后在两极板间插入一导体平板,则电容C ,极板间电压V ,极板空间(不含插入的导体板)电场强度E 以及电场的能量W 将(↑表示增大,↓表示减小)(A ) C ↓,U ↑,W ↑,E ↑。
(B ) C ↑,U ↓,W ↓,E 不变。
(C ) C ↑,U ↑,W ↑,E ↑。
(D ) C ↓,U ↓,W ↓,E ↓。
5. 如果某带电体电荷分布的体电荷密度ρ增大为原来的2倍,则电场的能量变为原来的(A ) 2倍。
(B ) 1/2倍。
(C ) 1/4倍。
(D ) 4倍。
6. 一空气平行板电容器,接电源充电后电容器中储存的能量为W 0,在保持电源接通的条件下,在两极间充满相对电容率为εr 的各向同性均匀电介质,则该电容器中储存的能量W 为(A ) W = W 0/εr 。
(B ) W = εr W 0。
(C ) W = (1+εr )W 0。
浙江农林大学电容及电容器静电场的能量能量密度习题

四 计算题1、空气中有一半径为R 的孤立导体球,令无穷远处电势为0,试计算:(1)该导体球的电容;(2)球上所带电荷为Q 时储存的静电能;(3)若空气的击穿场强为Eg ,导体球上能储存的最大电荷值。
答案:4πε0R , Q 2/(8πε0R ), 4πε0R 2E g解:(1)设导体球上带电荷Q ,则导体球的电势为:RQ U 04πε=孤立导体电容:R CQC 04πε==(2)R Q C Q W 02282πε== (3)Eg R Q E ≤=204πε Eg R Q M 204πε=2、一电容器由两个同轴圆筒组成,内筒半径为a ,外筒半径为b ,筒长都是L ,中间充满相对介电常数为r ε的各向同性均匀电介质。
内、外筒分别带有等量异号电荷+Q 和—Q 。
设b-a<<a, L>>b, 可以忽略边缘效应,求:(1) 圆柱形电容器的电容 (填写A 、B 、C 或D ,从下面的选项中选取); (2) 电容器储存的能量 (填写A 、B 、C 或D ,从下面的选项中选取)。
A 、[]02ln(/)r Lb a πεε B 、[]0ln(/)rLb a πεε C 、()20ln 4r Q b a LπεεD 、()20ln 2r Q b a Lπεε答案:A ,C解:由题给条件(b-a )<<a 和L>>b,忽略边缘效应应用高斯定理可求出两筒之间的场强为:E=Q/(20πεr εLr) 两筒间的电势差ab L Q r dr L qU r bar ln 2200επεεπε==⎰电容器的电容[])/ln()2(/0a b L U Q C r επε==电容器储存的能量()a b L Q CU W r ln 421022επε==3、一球形电容器,内球壳半径为R 1 外球壳半径为R 2 两球壳间充满了相对介电常数为r ε的各向同性均匀电介质,设两球壳间电势差为U 12, 求:(1)电容器的电容 ;(2)电容器储存的能量 。
浙江农林大学静电场的高斯定理习题

四、计算题1、 两个无限大的平行平面都均匀带电,电荷的面密度分别为1σ和2σ,试求空间各处场强. 两面间 , 1σ面外 , 2σ面外 . (填写A 、B 、C 或D ,从下面的选项中选取)A 、n E )(21210σσε-=B 、1201()E n σσε=+C 、n E )(21210σσε+-=D 、n E)(21210σσε+=答案:A ,C ,D解: 如图所示,两带电平面均匀带电,电荷面密度分别为1σ与2σ,两面间, n E)(21210σσε-=1σ面外, n E)(21210σσε+-= 2σ面外, n E)(21210σσε+=n:垂直于两平面由1σ面指为2σ面.2、一无限长带电直线,电荷线密度为λ,傍边有长为a , 宽为b 的一矩形平面, 矩形平面中心线与带电直线组成的平面垂直于矩形平面,带电直线与矩形平面的距离为c ,如图,求通过矩形平面电通量的大小. . (填写A 、B 、C 或DA 、()0arctan 22a b c λπε⎡⎤⎣⎦ B 、()0arctan 2a b c λπε⎡⎤⎣⎦ C 、()0arctan 24a b c λπε⎡⎤⎣⎦ D 、()02arctan 2a b c λπε⎡⎤⎣⎦ 答案:Bλ解:取窄条面元adx ds =,该处电场强度为rE 02πελ=过面元的电通量为()220022cos xc acdxadx r s d E d e +=⨯=⋅=Φπελπεθλ ()⎰⎰-+=Φ=Φ2/2/2202b b e e xc acdxd πελ2/2/0arctan 12b b cxc ac -⋅=πελ()[]02arctan πελc b a =3、 如图所示,在x -y 平面内有与y 轴平行、位于x=a / 2和x =-a / 2处的两条“无限长”平行的均匀带电细线,电荷线密度分别为+λ和-λ.求z 轴上任一点的电场强度.. . (填写A 、B 、C 或D ,从下面的选项中选取)A 、()2204a i a z λπε-+B 、()22024a i a z λπε-+ C 、()22024a i a z λπε-+ D 、()22044a i a z λπε-+ 答案:C解:过z 轴上任一点(0 , 0 , z )分别以两条带电细线为轴作单位长度的圆柱形高斯面,如图所示.按高斯定理求出两带电直线分别在该处产生的场强大小为 ()r E 02/ελπ=± 场强方向如图所示. 按场强叠加原理,该处合场强的大小为r a r E E 2/c o s 20⋅π==+ελθ ()22042z a a +π=ελ方向如图所示. 或用矢量表示 ()iz a a E 22042+π-=ελ4、均匀带电球壳内半径6cm ,外半径10cm ,电荷体密度为2×510-C·m -3求距球心5cm 的场强 ,8cm 的场强 ,12cm 的场强 . (填写A 、B 、C 或D ,从下面的选项中选取).A 、43.4810⨯1C N -⋅, 方向沿半径向外 B 、44.1010⨯1C N -⋅ ,沿半径向外C 、44.1010⨯1C N -⋅,方向沿半径向外D 、 0 答案: D, A ,B解: 高斯定理0d ε∑⎰=⋅qS E s,02π4ε∑=q r E当5=r cm 时,0=∑q ,0=E8=r cm 时,∑q 3π4p=3(r )3内r - ∴ ()2023π43π4rr r E ερ内-=41048.3⨯≈1C N -⋅, 方向沿半径向外. 12=r cm 时,3π4∑=ρq -3(外r )内3r ∴ ()420331010.4π43π4⨯≈-=rr r E ερ内外 1C N -⋅ 沿半径向外.5、有两个半径分别为1R 、2R 的同心球壳,带电分别为1Q 、2Q ,试求空间电场分布。
第十章 静电场中的能量精选试卷测试与练习(word解析版)

第十章 静电场中的能量精选试卷测试与练习(word 解析版)一、第十章 静电场中的能量选择题易错题培优(难)1.一均匀带负电的半球壳,球心为O 点,AB 为其对称轴,平面L 垂直AB 把半球壳分为左右两部分,L 与AB 相交于M 点,对称轴AB 上的N 点和M 点关于O 点对称,已知一均匀带电球壳内部任一点的电场强度为零;取无穷远处电势为零,点电荷q 在距离其为r 处的电势为φ=kqr(q 的正负对应φ的正负)。
假设左侧部分在M 点的电场强度为E 1,电势为φ1;右侧部分在M 点的电场强度为E 2,电势为φ2;整个半球壳在M 点的电场强度为E 3,在N 点的电场强度为E 4.下列说法正确的是( )A .若左右两部分的表面积相等,有12E E >,12ϕϕ>B .若左右两部分的表面积相等,有12E E <,12ϕϕ<C .不论左右两部分的表面积是否相等,总有12E E >,34E E =D .只有左右两部分的表面积相等,才有12E E >,34E E = 【答案】C 【解析】 【详解】A 、设想将右侧半球补充完整,右侧半球在M 点的电场强度向右,因完整均匀带电球壳内部任一点的电场强度为零,可推知左侧半球在M 点的电场强度方向向左,根据对称性和矢量叠加原则可知,E 1方向水平向左,E 2方向水平向右,左侧部分在M 点产生的场强比右侧电荷在M 点产生的场强大,E 1>E 2,根据几何关系可知,分割后的右侧部分各点到M 点的距离均大于左侧部分各点到M 点的距离,根据k qrϕ=,且球面带负电,q 为负,得:φ1<φ2,故AB 错误;C 、E 1>E 2与左右两个部分的表面积是否相等无关,完整的均匀带电球壳内部任一点的电场强度为零,根据对称性可知,左右半球壳在M 、N 点的电场强度大小都相等,故左半球壳在M 、N 点的电场强度大小相等,方向相同,故C 正确,D 错误。
2.空间某一静电场的电势φ在x 轴上的分布如图所示,图中曲线关于纵轴对称。
6-(4-5)电容 电容器 静电场的能量和能量密度

R1+ + + R2 +
平行板电 容器电容
第六章 静电场中的导体和电介质
10
物理学
第五版
6-4 电容 电容器
例3 球形电容器的电容 解 设内外球带分别带电 设内外球带分别带电±Q Q ( R1 < r < R2 ) E= 2 4 π ε 0r
v v U = ∫ E ⋅ dl dl
l
Q R2 dr = 4 π ε 0 ∫R1 r 2 Q 1 1 = ( − ) 4 π ε 0 R1 R2
E = E+ + E − λ λ = + 2 π ε 0 x 2 π ε 0 (d − x)
第六章 静电场中的导体和电介质
v E
−λ
o
P
x d −x
d
x
13
物理学
第五版
6-4 电容 电容器
U =
∫
d −R
R
Edx
2R
λ = 2 πε0
∫
d −R
R
1 1 ( + )dx x d−x
+λ
v E
−λ
λ d−R λ d = ln ≈ ln πε0 R πε0 R
第六章 静电场中的导体和电介质
6
B
v v E ⋅ dl
物理学
第五版
6-4 电容 电容器
平行平板电容器 例1 平行平板电容器 σ Q 解 E= = ε 0 ε r ε 0ε r S
U = Ed = Qd
+ + + + + + Q
εr
d
ε 0ε r S
- - - - - - −Q
浙江农林大学物理期末复习题

静电场中的导体和电介质 有介质时的高斯定理一、选择题1、一带正电荷的物体M ,靠近一不带电的金属导体N ,N 的左端感应出负电荷,右端感应出正电荷,若将N 的左端接地,如图所示,则 答案:B(A ) N 上的负电荷入地(B ) N 上的正电荷入地 (C ) N 上的电荷不动(D ) N 上所有电荷都入地分析:选(B )。
导体N 接地表明导体N 为零电势,即与无穷远处等电势,这与导体N 在哪一段接地无关。
3、有一带正电荷的大导体,欲测其附近P 点处的场强,将一电荷量为q 0 (q 0 >0 )的点电荷放在P 点,如图所示,测得它所受的电场力为F .若电荷量q 0不是足够小,则 (A ) F / q 0比P 点处场强的数值大;(B ) F / q 0比P 点处场强的数值小;(C ) F / q 0与P 点处场强的数值相等;(D ) F / q 0与P 点处场强的数值哪个大无法确定.答案:B 分析:选(B )。
q 0电量不是足够小,将影响导体上电荷的分布,近端的电荷在库仑力的作用下原理P 点,因此选B 。
4、有一接地的金属球,用一弹簧吊起,金属球原来不带电.若在它的下方放置一电量为q 的点电荷,则 答案:C(A)只有当q>0时,金属球才下移.(B)只有当q<0时,金属球才下移. (C)无论q 是正是负金属球都下移.(D)无论q 是正是负金属球都不动.分析:选(C )q 不论正负,由于接地,金属球上的出现的感应电荷中只保留与q 异号的电荷,因此在库仑力的作用下,金属球都要下移。
5、把A ,B 两块不带电的导体放在一带正电导体的电场中,如图所示。
设无限远处为电势零点,A 的电势为U A ,B 的电势为U B ,则答案:D(A ) U B >U A ≠0(B ) U B >U A =0(C ) U B =U A (D ) U B < U A 分析:选(D )。
可以根据电场线的分布来判断电势的高低。
(45)电容电容器静电场的能量和能量密度资料

(45)电容电容器静电场的能量和能量密度资料电容器是一种常见的电子元件,它用于存储电荷和电能。
在电容器中,电荷可以在正负极板之间来回流动,从而存储电能。
当电容器上充电或放电时,会产生静电场。
本文将探讨电容器静电场的能量和能量密度。
首先,让我们来了解电容器的电荷和电压之间的关系。
电容器的电荷Q定义为正极板上储存的电荷量。
根据定义,电荷量与电容器电压V之间的关系可以用以下公式表示:Q = CV其中,C为电容器的电容量,单位为法拉(F)。
电压V是正负极板之间的电势差,单位为伏特(V)。
接下来,我们将研究电容器静电场的能量。
在电容器中,电荷Q在电场E中移动时,会产生能量。
电容器的储能量U可以通过以下公式计算:U = 0.5 * C * V^2其中0.5C是电容器的电容量,V是电容器的电压。
可以看出,电容器的能量与电容量和电压的平方成正比。
最后,我们将讨论电容器静电场的能量密度。
能量密度表示单位体积内的能量。
电容器的能量密度u可以通过以下公式计算:u = 0.5 * ε * E^2其中ε是真空中的介电常数,约为8.85419 × 10^(-12)库仑/伏特/米。
E是电容器的电场强度。
通过对这些公式的分析,我们可以得出以下结论:1. 电容器的能量与其电容量和电压的平方成正比。
2. 电容器的能量密度与介电常数和电场强度的平方成正比。
电容器作为常见的电子元件,其存储电能和利用静电场的能力在电路设计和应用中起着重要作用。
理解电容器静电场的能量和能量密度有助于我们更好地设计和应用电容器。
电容器是一种非常常见的电子元件,广泛应用于各个领域,如电子设备、通信系统、能源存储等。
在这些应用中,电容器的重要性不言而喻。
了解电容器静电场的能量和能量密度可以帮助我们更加深入地理解其工作原理和性能。
首先,我们来探讨电容器静电场的能量。
电容器的能量来源于电荷的储存和移动。
当电容器的电压发生变化时,电荷会在正负极板之间来回移动。
浙江农林大学电容及电容器、静电场的能量、能量密度习题

四 计算题1、空气中有一半径为R 的孤立导体球,令无穷远处电势为0,试计算:(1)该导体球的电容;(2)球上所带电荷为Q 时储存的静电能;(3)若空气的击穿场强为Eg ,导体球上能储存的最大电荷值。
答案:4πε0R , Q 2/(8πε0R ), 4πε0R 2E g解:(1)设导体球上带电荷Q ,则导体球的电势为:RQ U 04πε=孤立导体电容:R CQC 04πε==(2)R Q C Q W 02282πε== (3)Eg R Q E ≤=204πε Eg R Q M 204πε=2、一电容器由两个同轴圆筒组成,内筒半径为a ,外筒半径为b ,筒长都是L ,中间充满相对介电常数为r ε的各向同性均匀电介质。
内、外筒分别带有等量异号电荷+Q 和—Q 。
设b-a<<a, L>>b, 可以忽略边缘效应,求:(1) 圆柱形电容器的电容 (填写A 、B 、C 或D ,从下面的选项中选取); (2) 电容器储存的能量 (填写A 、B 、C 或D ,从下面的选项中选取)。
A 、[]02ln(/)r Lb a πεε B 、[]0ln(/)rLb a πεε C 、()20ln 4r Q b a L πεεD 、()20ln 2r Q b a Lπεε答案:A ,C解:由题给条件(b-a )<<a 和L>>b,忽略边缘效应应用高斯定理可求出两筒之间的场强为:E=Q/(20πεr εLr) 两筒间的电势差a b L Q r dr L qU r bar ln 2200επεεπε==⎰电容器的电容[])/ln()2(/0a b L U Q C r επε==电容器储存的能量()a b L Q CU W r ln 421022επε==3、一球形电容器,内球壳半径为R 1 外球壳半径为R 2 两球壳间充满了相对介电常数为r ε的各向同性均匀电介质,设两球壳间电势差为U 12, 求:(1)电容器的电容 ;(2)电容器储存的能量 。
9-4静电场能量、习题
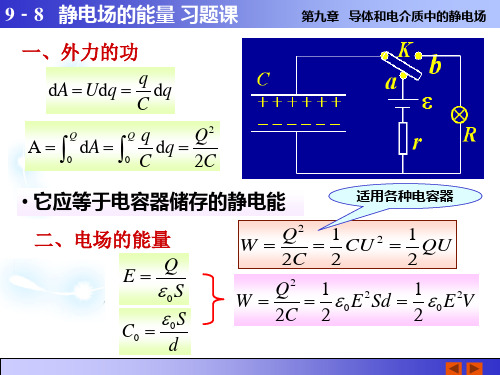
q dA=U q = dq d C
A= ∫ dA= ∫
0 Q Q 0
第九章 导体和电介质中的静电场
q Q2 dq = C 2C
适用各种电容器
• 它应等于电容器储存的静电能 二、电场的能量 Q E= ε0S ε0S C = 0 d
2 Q 1 1 2 W= = C = Q U U 2 C 2 2
9-8 静电场的能量 习题课 -
第九章 导体和电介质中的静电场
v 1.导体静电平衡的充分 导体静电平衡的充分、 1.导体静电平衡的充分、必要条件 E ≡ 0 内 2.导体静电平衡的基本性质 2.导体静电平衡的基本性质 等势体,等势面、电荷分布、场强方向、 等势体,等势面、电荷分布、场强方向、曲率半径与 电荷密度的关系
2
2 0U πε 12 ∴ = λ ln(R / R ) 2 1
λ E1 = 2πε 0 R1
λ E2 = 2πε 0 R2
9-8 静电场的能量 习题课 -
第九章 导体和电介质中的静电场
两电容器的电容之比C 例6 两电容器的电容之比 1 :C2 = 2:3, 求: (1)串联后接到电压一定的电源上充电 电能之比 )串联后接到电压一定的电源上充电,电能之比 (2)并联后充电,电能之比 )并联后充电, (3)上述两种情况下 电容器系统的总电能之比 )上述两种情况下,电容器系统的总电能之比 W =Q2 /(2C ) W1 = C2 = 3 1 串联, 解: (1)串联,电量相等 1 W =Q2 /(2C ) W2 C1 2
Q2 1 1 2 W= = ε 0 E Sd = ε 0 E 2V 2C 2 2
9-8 静电场的能量 习题课 - • 电场的能量密度
静电场的能量 能量密度

C = 4πεo R1 ,
孤立导体球电容。 孤立导体球电容。 ②R2 –R1= d , R2 ≈R1 = R
4πε o R 1 R 2 C = R 2 − R1
C = 4πεo R2 d = ε o S d
平行板电容器电容。 平行板电容器电容。
③
圆柱形电容器
板间电场
R2
R1 l
解:设两极板带电 ± q
Q C= = C 1 + C 2 U
C
22、电容器的串联 、 特点 每个电容器极板所带的电量相等 总电压
Q Q 1 1 U = U 1 + U 2 = + = + Q C1 C 2 C1 C 2 等效电容
C= Q 1 = 1 1 U + C1 C 2
C1
C2
等效
1 1 1 = + C C1 C 2
讨论
C = ∑ Ci
i
并联电容器的电容等于 各个电容器电容的和。 各个电容器电容的和。 串联电容器总电容的倒数 等于各串联电容倒数之和。 等于各串联电容倒数之和。
1 1 =∑ C i Ci
当电容器的耐压能力不被满足时, 当电容器的耐压能力不被满足时,常用串并联 使用来改善。 使用来改善。 串联使用可提高耐压能力 并联使用可以提高容量 电介质的绝缘性能遭到破坏,称为击穿。 电介质的绝缘性能遭到破坏,称为击穿。 击穿 所能承受的不被击穿的最大场强叫做击穿场强或 所能承受的不被击穿的最大场强叫做击穿场强或 击穿场强 介电强度。 介电强度。
球形
柱形
平行板
R1 R2
R1
R2
d
4 4、电容器的作用 、 •在电路中:通交流、隔直流; 在电路中:通交流、隔直流; 在电路中 •与其它元件可以组成振荡器、时间延迟电路等; 与其它元件可以组成振荡器、 与其它元件可以组成振荡器 时间延迟电路等; •储存电能的元件; 储存电能的元件; 储存电能的元件 •真空器件中建立各种电场; 真空器件中建立各种电场; 真空器件中建立各种电场 •各种电子仪器。 各种电子仪器。 各种电子仪器 5 、电容器电容的计算 5、 计算电容的一般步骤为: 计算电容的一般步骤为: •设电容器的两极板带有等量异号电荷; 设电容器的两极板带有等量异号电荷 设电容器的两极板带有等量异号电荷; •求出两极板之间的电场强度的分布; 求出两极板之间的电场强度的分布; 求出两极板之间的电场强度的分布 •计算两极板之间的电势差; 计算两极板之间的电势差; 计算两极板之间的电势差 •根据电容器电容的定义求得电容。 根据电容器电容的定义求得电容。 根据电容器电容的定义求得电容
高中物理第十章静电场中的能量4电容器的电容课后习题含解析3

电容器的电容课后篇巩固提升基础巩固1.如图所示实验中,关于平行板电容器的充、放电,下列说法正确的是()A.开关接1时,平行板电容器充电,且上极板带正电B。
开关接1时,平行板电容器充电,且上极板带负电C.开关接2时,平行板电容器充电,且上极板带正电D.开关接2时,平行板电容器充电,且上极板带负电1时,平行板电容器充电,上极板与电源正极相连而带正电,A对,B错;开关接2时,平行板电容器放电,放电结束后上、下极板均不带电,C、D错误。
2.将电容器两极板的电荷量减半,间距变为原来的4倍,则电容器极板间()A。
电压加倍,电场强度减半B。
电压加倍,电场强度加倍C.电压减半,电场强度减半D。
电压加倍,电场强度不变两板上的带电荷量减半;且间距增加到4d ,则C 减小为原来的14,由公式U=Q Q 可知电压变为原来的2倍,则电场强度E=Q Q 变为原来的12,故电场强度减半,故A 正确,B 、C 、D 错误.3。
如图所示,一平行板电容器充电后与电源断开,这时电容器的电荷量为Q ,P 是电容器内一点,电容器的上极板与大地相连,下列说法正确的是( )A 。
若将电容器的上极板左移一点,则两板间电场强度减小B 。
若将电容器的下极板上移一点,则P 点的电势升高C.若将电容器的下极板上移一点,则两板间电势差增大D 。
若将电容器的下极板上移一点,则两板间电势差减小E=Q Q 、U=Q Q 、C=Q r Q 4πQQ ,可知E=4πQQ Q rQ ,S 减小,E 增大,A 项错误;由E=4πQQ Q rQ 可知d 变化,E 不变,φP 不变,B 项错误;U=Ed ,d 减小,U 减小,C 项错误,D 项正确.4.如图所示,为某一电容器中所带电荷量和两端电压之间的关系图线,若将该电容器两端的电压从40 V 降低到36 V ,对电容器来说正确的是( )A.是充电过程B。
是放电过程C。
该电容器的电容为5×10-2 FD.该电容器的电荷量变化量为0。
11 静电场的能量例题

解
E
2 பைடு நூலகம்ε0r
(R1 r R2)
Eb
2π ε0 R1
Eb 20 R1
U R2 dr ln R2 2 π ε0 R1 r 2 π ε0 R1
-+ l - + R1
-+ -+
R2
_
_
_
_ _
++++++++
_
_
_
单位长度的电场能量
We
1U
2
2
4 π ε0
ln R2 R1
π ε0 Eb2 R12
解少功?
E Q 0 S0
W 12E0 V2
-Q-Q
+Q+Q
A W
1 2
E0
2V
12Q(0dSQ0 2
)2
d
Sd2
d1
d12
21
20S
例2 球形电容器的内、外半径分别为R1和R2 所带电荷为
Q。若在两球壳间充以电容率为的电介质,问此电容器
贮存的电场能量为多少?
-Q
解 E 1 Q 4πε r2
dr Q
ln
R2 R1
dWe dR1
π ε0 Eb2 R1(2 ln
R2 R1
1)
0
R1
R2 e
6.07103 m
r R1
we
1 2
εE2
Q2 32π2 εr4
R2
dWe we dV we 4rd2r
Q2 8πεr2 dr
We
Q2 dWe 8 π ε
2
R2 dr Q ( 1 1 ) r R1 2 8 π ε R1 R2
第十七讲§5.6静电场的能量—习题课

第十七讲 §5.6静电场的能量—习题课 一、电容和电容器1、电容:UqC =是描述孤立导体带电而引起自身电势变化的物理量。
即孤立导体的电容。
2、电容器:BA U U qC -=是描述两个导体组成电容器的电容,二者是相互关联的,即将一个导体放在无限远处就为孤立导体的电容。
二、电容器的储能(电容器的能量):静电场是一个物理场。
此物是否是物质的?其中的一个重要特性就是是否具有能量的特性,即在静电场中移动电荷是需要静电场力做功,这说明静电场是具有能量的。
下面通过对静电场形成能量的过程来说明静电场是具有能量的。
1、带电体的能量:外力做功就等于带电体的能量(电势能)P E W = ①把dq 从∞转移到带电体上,需外力做的微功:()Udq dqU dW U U dq dW A U B B A B ==−−−→−-==∞→0, q Q②把Q 从∞源源不断的转移到带电体上,需外力做的总功:⎰⎰==QUdq dW W 02、电容器的能量:通过电容器储能的过程来推导电容器能量的公式。
①把dq 从A B →上,需外力做的微功:Udq dW = −−→−=UqC dq CqdW =②把Q 从A B →上,需外力做的总功:QU CU C Q dq C q dW W Q21212220=====⎰⎰③电容器的能量:外力所做的总功就等于电容器的能量。
QU CU C Q dq C q dW W Qe 21212220=====⎰⎰可见,外力克服静电力所做的功,就是电容器的带电过程,即非静电能转化为静电能的过程,满足能量守恒定律。
上述三个表达式都非常有用,希望能熟记。
3、静电场的能量 能量密度①电场的能量密度(能量的体密度):单位体积内电场的能量。
()2020221V 2121E Ed d SV CU V W w e e εε==== Sd V = 可见,电能存在于电场之中,电场是电能的携带者,电场的能量是电场物质性的一个重要标志!静电场是物质的,是不以人们的意志为转移,是非精神的。
高中物理第十章静电场中的能量第4节电容器的电容练习含解析必修3

第4节 电容器的电容合格考训练25分钟·满分60分一、选择题(本题共8小题,每题6分,共48分) 1.下列关于电容器的叙述正确的是( D )A .电容器是储存电荷的容器,只有带电的容器才是电容器B .任何两个彼此绝缘且相距很近的物体,就组成了电容器C .电容器所带的电荷量是指每个极板所带电荷量的代数和D .电容器充电过程是将其他形式的能转变成电容器的电能并储存起来,电容器的放电过程是将电容器储存的电能转化为其他形式的能解析:电容器是储存电荷的容器,它里面有无电荷不影响其储存电荷的能力,A 错误;任何两个彼此绝缘而又相距很近的导体组成一个电容器,B 错误;电容器所带的电荷量指任一极板电荷量的绝对值,C 错误;电容器的充、放电伴随能量转化,D 正确。
2.(2019·陕西省南郑中学高二上学期期中)下列关于电容器和电容的说法中,不正确的是( A )A .根据C =Q U可知,电容器的电容与其所带电荷量成正比,跟两板间的电压成反比 B .对于确定的电容器,其所带的电荷量与两板间的电压(小于击穿电压且不为零)成正比 C .无论电容器的电压如何变化(小于击穿电压且不为零),它所带的电荷量与电压比值恒定不变D .电容器的电容是表示电容器容纳电荷本领的物理量,其大小与加在两板上的电压无关 解析:电容的定义式C =Q U是比值法定义,反映电容器本身的性质,C 与U 、Q 无关,不能说电容与其所带电荷量成正比,跟两板间的电压成反比,故A 错误;对于确定的电容器,C 一定,由Q =CU 知,Q 与U 成正比,故B 正确;电容器所带的电荷量与电压比值等于电容,电容与电荷量、电压无关,所以无论电容器的电压如何变化(小于击穿电压且不为零),它所带的电荷量与电压比值恒定不变,故C 正确;电容器的电容是表示电容器容纳电荷本领的物理量,由电容器本身决定,与板间电压无关,故D 正确。
3.传感器是自动控制设备中不可缺少的元件,已经渗透到宇宙开发、环境保护、交通运输以及家庭生活等各种领域。
第十章 静电场中的能量精选试卷练习(Word版 含答案)

第十章 静电场中的能量精选试卷练习(Word 版 含答案)一、第十章 静电场中的能量选择题易错题培优(难)1.两电荷量分别为q 1和q 2的点电荷放在x 轴上的O 、M 两点,两点电荷连线上各点电势φ随x 变化的关系如图所示,其中P 、N 两点的电势为零,NF 段中Q 点电势最高,则( )A .P 点的电场强度大小为零B .q 1和q 2为等量异种电荷C .NQ 间场强方向沿x 轴正方向D .将一负电荷从N 点移到F 点,电势能先减小后增大 【答案】D 【解析】 【详解】A .φ-x 图线的斜率等于电场强度,故可知P 点的电场强度大小不为零,A 错误;B .如果1q 和2q 为等量异种电荷,点连线中垂线是等势面,故连线的中点是零电势点;由于OP PM >,故12q q >,故B 错误;C .沿着电场线的方向,电势降低,由于从N 到Q 电势升高,故是逆着电场线,即NQ 间场强方向沿x 轴正方向;D .由于从N 到F ,电势先增加后减小,将一负电荷从N 点移到F 点,根据公式P E q ϕ=电势能先减小后增大,故D 正确。
故选D 。
【点睛】电势为零处,电场强度不一定为零。
电荷在电场中与电势的乘积为电势能。
电场力做功的正负决定电势能的增加与否。
2.如图所示,在纸面内有一直角三角形ABC ,P 1为AB 的中点, P 2为AP 1的中点,BC =2 cm ,∠A = 30°.纸面内有一匀强电场,电子在A 点的电势能为-5 eV ,在C 点的电势能为19 eV ,在P 2点的电势能为3 eV .下列说法正确的是A .A点的电势为-5 V B .B 点的电势为-19 VC .该电场的电场强度方向由B 点指向A 点D .该电场的电场强度大小为800 V/m 【答案】D 【解析】 【分析】 【详解】 A .由公式pE qϕ=可知,pA A 5eV5V E qeϕ-===- 故A 错误.B .A 到P 2的电势差为2A 5(3)V 8V P U ϕϕ=-=--=B A 4548V 27V U ϕϕ=-=-⨯=-故B 错误.C .A 点到B 点电势均匀降落,设P 1与B 的中点为P 3,该点电势为:3A 3538V 19V P U ϕϕ=-=-⨯=-C p 19eV19V C E qeϕ===-- P 3点与C 为等势点,连接两点的直线为等势线,如图虚线P 3C 所示.由几何关系知,P 3C 与AB 垂直,所以AB 为电场线,又因为电场线方向由电势高指向电势低,所以该电场的电场强度方向是由A 点指向B 点,故C 错误.D .P 3与C 为等势点,该电场的电场强度方向是由A 点指向B 点,所以场强为:28V/cm 800V/m 1U E AP === 故D 正确.3.如图所示,虚线AB 和CD 分别为椭圆的长轴和短轴,相交于O 点,两个等量异号点电荷分别位于椭圆的两个焦点M 、N 上.下列说法中正确的是( )A .O 点的电场强度为零B .A 、B 两点的电场强度相同C .将电荷+q 沿曲线CAD 从C 移到D 的过程中,电势能先减少后增加 D .将电荷+q 沿曲线CBD 从C 移到D 的过程中,电势能先增加后减少 【答案】B 【解析】 【详解】AB.由等量异种电荷的电场线分布情况可知,A 、B 两点的电场强度相同, O 点的电场强度不为零,故A 错误;B 正确;CD. 由等量异种电荷的等势面分布情况可知,A C DB φφφφ>=>正电荷在电势高的地方电势能大,所以将电荷+q 沿曲线CAD 从C 移到D 的过程中,电势能先增大后减少,将电荷+q 沿曲线CBD 从C 移到D 的过程中,电势能先减少后增大,故CD 错误。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四 计算题1、空气中有一半径为R 的孤立导体球,令无穷远处电势为0,试计算:(1)该导体球的电容;(2)球上所带电荷为Q 时储存的静电能;(3)若空气的击穿场强为Eg ,导体球上能储存的最大电荷值。
答案:4πε0R , Q 2/(8πε0R ), 4πε0R 2E g解:(1)设导体球上带电荷Q ,则导体球的电势为:RQ U 04πε=孤立导体电容:R CQC 04πε==(2)R Q C Q W 02282πε== (3)Eg R Q E ≤=204πε Eg R Q M 204πε=2、一电容器由两个同轴圆筒组成,内筒半径为a ,外筒半径为b ,筒长都是L ,中间充满相对介电常数为r ε的各向同性均匀电介质。
内、外筒分别带有等量异号电荷+Q 和—Q 。
设b-a<<a, L>>b, 可以忽略边缘效应,求:(1) 圆柱形电容器的电容 (填写A 、B 、C 或D ,从下面的选项中选取); (2) 电容器储存的能量 (填写A 、B 、C 或D ,从下面的选项中选取)。
A 、[]02ln(/)r Lb a πεε B 、[]0ln(/)rLb a πεε C 、()20ln 4r Q b a LπεεD 、()20ln 2r Q b a Lπεε答案:A ,C解:由题给条件(b-a )<<a 和L>>b, 忽略边缘效应应用高斯定理可求出两筒之间的场强为:E=Q/(20πεr εLr) 两筒间的电势差ab L Q r dr L qU r bar ln 2200επεεπε==⎰电容器的电容[])/ln()2(/0a b L U Q C r επε==电容器储存的能量()a b LQ CU W r ln 421022επε==3、一球形电容器,内球壳半径为R 1 外球壳半径为R 2 两球壳间充满了相对介电常数为r ε的各向同性均匀电介质,设两球壳间电势差为U 12, 求:(1)电容器的电容 ;(2)电容器储存的能量 。
A 、012214r R R R R πεε-B 、012212r R R R R πεε-C 、201212212r R R U R R πεε-D 、20121221r R R U R R πεε-答案:A ,C解: (1) 设内,外球壳分别带电量为+Q,-Q,则两球壳间的电位移大小为 D=Q/(24r π) 场强大小为2004r Q DE r rεπεεε==两球壳间电势差 ⎰⎰=⋅=212120124R R rR R r drQ r d E U επεϖϖ 210122104)()11(4R R R R Q R R Q r rεπεεπε-=--=电容 12210124R R R R U QC r -==επε (2)电场能量 W=1221221021222R R U R R CU r -=επε 4、两根平行“无限长”均匀带电直导线,相距为d ,导线半径都是R(R<<d)。
导线上电荷密度分别为λλ-+和。
试求该导体组单位长度的电容 。
A 、ln[()/]d R R πε- B 、02ln[()/]d R R πε- C 、04ln[()/]d R R πε-D 、8ln[()/]d R R πε-答案:A解:以左边的导线轴线上一点作原点,X 轴通过两导线并垂直于导线,两导线间x 处的场强为)(2200x d x E -+=πελπελ 两导线间的电势差为RR d R d R R R d dxx d x U R d R -=---=-+=⎰-ln )ln (ln 2)11(2000πελπελπελ 设导线长为L 的一段上所带电量为Q ,则有L Q /=λ,故单位长度的电容 5、一空气平行板电容器,两极板面积均为S ,板间距离为d (d 远小于极板线度),在两极板间平行地插入一面积也是S 、厚度为t (<d =的金属片。
试求:(1) 电容C 等于 。
A 、04S d t ε- B 、02()S d t ε- C 、02S d t ε- D 、0Sd tε-答案:D(2) 金属片放在两极板间的位置对电容值有无影响?答案:无影响解:设极板上分别带电量+q 和-q ;金属片与A 板距离为d 1,与B 板距离为d 2;金属片与A 板间的场强为()S q E 01ε=金属片与B 板间的场强为S q E 02ε=金属片内部场强为0='E 两极板间的电势差为 由此得()()t d S U U qC B A -=-=0ε因C 值只与d 、t 有关,与d 1、、d 2无关,故金属片的安放位置对电容值无影响。
6、现有一根单芯电缆,电缆芯的半径为r 1 =15mm ,铅包皮的内半径为r 2 =50mm ,其间充以相对介电常数εr =2.3的各向同性均匀电介质。
求当电缆芯与铅包皮间的电压为U 12=600V 时,长为l=1km 的电缆中储存的静电能是多少? (ε0=8.85×10-12C 2 N -1 m -2)A 、1.9×10-2JB 、1.9×10-3JC 、2.9×10-2JD 、2.9×10-3J 答案:A解:由高斯定理可求得 E=rr επελ02又 ⎰⎰⋅==⋅=2121120012ln 22r r r r r r r r r r dr r r d E U επελεπελ电场能量密度 22122120201)]/[ln(22121rr r U E ED W r r ⋅===εεεε 静电能 ⎰=vwdV W =⎰⋅2121)]/[ln(222122120r r r rdr rr r U πεε =)/ln()]/[ln(122122120r r r r lU r ⋅επε=2122120)]/[ln(r r lU r επε=1.9210-⨯J7、两电容器的电容之比为C 1:C 2=1:2。
(1) 把它们串联后接到电压一定的电源上充电,他们的电能之比是多少? (2) 如果是并联充电,电能之比是多少?(3) 在上述两种情况下电容器系统的总电能之比又是多少?答案:2:1, 1:2, 2:9.解:(1)串联时两电容器中电量相等:W 1=Q 2 / (2C 1),W 2=Q 2 / (2C 2) ∴ W 1 / W 2 = C 2 / C 1 = 2/1 = 2:1 (2)并联时两电容器两端电势差相同:21121U C W =,22221U C W = W 1/W 2=C 1/C 2=1:2(3)串联时电容器系统的总电能:2212122121U C C C C U C W s s +== 并联时电容器系统的总电能:2212)(2121U C C U C W p p +==两者之比:9:2212)(12212221212122121=++=++=+=C C C C C C C C C C C C C C w W P s 8、半径为R 1的导体球,带电荷q ,在它外面同心地罩一金属球壳,其内、外半径分别为R 2 = 2 R 1,R 3 = 3 R 1,今在距球心d = 4 R 1处放一电荷为Q 的点电荷,并将球壳接地(如图所示),试求球壳上感生的总电荷 . A 、-[( 3Q / 4) +q ] B 、-[( 3Q / 2) +q ] C 、-[(Q / 4) +q ] D 、-[( 3Q / 8) +q ] 答案:A解:应用高斯定理可得导体球与球壳间的场强为()304/r r q E επ=ϖϖ (R 1<r <R 2) 设大地电势为零,则导体球心O 点电势为:根据导体静电平衡条件和应用高斯定理可知,球壳内表面上感生电荷应为-q . 设球壳外表面上感生电荷为Q'. 以无穷远处为电势零点,根据电势叠加原理,导体球心O 处电势应为: 假设大地与无穷远处等电势,则上述二种方式所得的O 点电势应相等,由此可得 Q '=-3Q / 4 故导体壳上感生的总电荷应是-[( 3Q / 4) +q ]9、如图所示,一空气平行板电容器,极板面积为S , 两极坂之间距离为d ,其中平行地放有一层厚度为t (t <d )、相对介电常量为r 的各向同性均匀电介质板.略去边缘效应,当在两极板之间加上电势差U 时,试计算该电容器中的电场能量.A 、()2021/1r U S d t εε+-⎡⎤⎣⎦B 、()201/1r U S d t εε+-C 、()2041/1r U S d t εε+-⎡⎤⎣⎦D 、()2081/1r U Sd t εε+-⎡⎤⎣⎦答案:A解:设两极板之间空气中的场强为E 0,电介质中的场强为rE E 0=,则两极板之间的电势差为由此得 ()td UE r 1/10-+=ε电容器中的电场能量为 作法二: ()td SC r 1/10-+=εε10、如题图所示,1C =0.25μF ,2C =0.15μF ,3C =0.20μF .1C 上电压为50V .求:AB U .答案:86V 解: 电容1C 上电量电容2C 与3C 并联3223C C C += 其上电荷123Q Q =∴ 355025231123232⨯===C U C C Q U 11、1C 和2C 两电容器分别标明“200 pF 、500 V”和“300 pF 、900 V”,把它们串联起来后等值电容是多少?如果两端加上1000 V 的电压,是否会击穿? 答案:120 pF, 400 V, 会击穿 解: (1) 1C 与2C 串联后电容 (2)串联后电压比231221==C C U U ,而100021=+U U ∴ 6001=U V ,4002=U V 即电容1C 电压超过耐压值会击穿,然后2C 也击穿.12、将两个电容器1C 和2C 充电到相等的电压U 以后切断电源,再将每一电容器的正极板与另一电容器的负极板相联.试求: (1)每个电容器的最终电荷:C 1 ;C 2 (2)电场能量的损失 .A 、21212()C C C U C C -+ B 、11212()C C C U C C -+C 、212122C C U C C + D 、21212C CU C C +答案:B, A, C解: 如图所示,设联接后两电容器带电分别为1q ,2q则⎪⎪⎩⎪⎪⎨⎧==-=-=+2122112121201021U U U C U C q qU C U C q q q q解得 (1) =1q U C C C C C q U C C C C C 21212221211)(,)(+-=+-(2)电场能量损失13、半径为1R =2.0cm 的导体球,外套有一同心的导体球壳,壳的内、外半径分别为2R =4.0cm 和3R =5.0cm ,当内球带电荷Q =3.0×10-8C 时,求:(1)整个电场储存的能量 ;(2)如果将导体壳接地,计算储存的能量 ; (3)此电容器的电容值 . A 、41.8210J -⨯ B 、41.0110J -⨯C 、124.4910F -⨯D 、104.4910F -⨯ 答案: A, B, C解: 如图,内球带电Q ,外球壳内表面带电Q -,外表面带电Q(1)在1R r <和32R r R <<区域 0=E ϖ在21R r R <<时301π4r rQ E εϖϖ=3R r >时 302π4rrQ E εϖϖ=∴在21R r R <<区域在3R r >区域∴ 总能量 )111(π83210221R R R Q W W W +-=+=ε(2)导体壳接地时,只有21R r R <<时30π4rrQ E εϖϖ=,02=W ∴ 4210211001.1)11(π8-⨯=-==R R Q W W ε J(3)电容器电容 )11/(π422102R R QW C -==ε 一、判断题1、从电容的定义式 可以看出, 电容的大小与极板的带电量成正比,与极板间的电位差成反比。
