SPC统计过程控制与休哈特控制图
统计过程控制

1、统计过程控制(SPC)包含两方面:①利用控制图分析过程的稳定性;②计算过程能力指数,对过程质量进行评价。
主要工具就是控制图。
2、SPC发源于美国。
休哈特《加工产品质量的经济控制》标志着过程控制的开始。
3、统计过程诊断(SPD)是20世纪80年代发展起来的。
4、世界上第一张控制图是美国休哈特在1924年提出来的不合格率(p)控制图5、小概率事件原理:小概率事件在一次实验中几乎不可能发生,若发生判断为异常。
6、控制图是用于监控过程质量是否处于统计控制过程的图7、常规控制图包括中心线、控制限、描点序列。
控制限的作用就是区分偶然波动与异常波动。
8、偶因是过程固有的,始终存在的,对质量的影响微小,但难以除去。
异因不是过程国有的,有时存在,有时不存在,对质量影响打,但不难除去。
9、过程处于统计状态控制时,只有偶因,而无异因产生的变异;点子落在控制限外的概率很小。
10、为控制产品不合格数,可选用的控制图有p图和np图11、为控制产品有瑕疵数,可选用的控制图有c图和u图12、根据5M1E内容,当人、机、料、法、测、环任何一个变动时,控制限需重新制定。
一、常规控制图的分类及应用场合:计数值控制图包括计件值和计点值控制图二、X−R图:(国标规定先作R图)计算步骤:1、取预备数据①取20~25个子组②子组大小一般为4或5,过程稳定性好的话,子组间隔可以扩大。
③同一子组的数据必须在同样的生产条件下取得,故要求在短间隔内来取。
2、计算各个子组的平均是X i和极差R i3、计算样本总均值X̿与平均样本极差R4、计算R图控制限、X控制限,并作图。
5、将子组中的预备数据(R i)在R图中打点,判稳。
若稳进行步骤6;若不稳,除去可查明原因后转入步骤3,即重新计算X̿与R6、将子组中的预备数据(X i)在X图中打点,判稳。
若稳进行步骤;若不稳,除去可查明原因后转入步骤3,即重新计算X̿与R7、计算过程能力指数并检验其是否满足技术要求若过程能力指数满足技术要求,则转入步骤8;若过程能力指数不满足技术要求,则需调整过程直至满足技术要求为止;8、延长X−R的控制线,作控制用控制图,进行日常管理。
SPC1简介及控制图

2
质量管理的第二阶段
统计质量控制阶段(20世纪40年代— 50年代) (1925年)休哈特博士,提出统计过程控制理论; 道奇提出了抽样检查理论;强调用数据说话,开 始将统计学应用于质量管理 特点: 是SPC的初级阶段,主要是运用统计手段分析 研究结果,尚未系统地应用分析工具如柏拉图等。
3
质量管理的第三阶段
课程(控制图 (3)分析手法介绍 (4)过程能力分析
Statistical (统计) Process (过程) Control (控制)
• 以概率统计学为基础,用科学的方法分析数据、 得出结论; ——使用数据分析
• 有输入、输出的一系列活动——分析研究过程
全面品质管理阶段(20世纪60年代—) 20世纪50年代,戴明提出了品质改进理论;朱兰和 费根堡姆提出了全面品质管理理念。全面品质管理 理念在日本取得了巨大的成功,日本70年代的 经济增长很大程度上得益于其产品品质的改善,日 本人称之为品质革命。 特点: 发明了更多的SPC管控工具,强调全员、全过程、 实时监控的品质保证,SPC与体系管理相结合。
( xi x) 2 /( n 1)
i 1 n
数据点
控制线
中心线
SPC控制图的控制限
一个控制图通常有三条线 <1> 中心线(Central line)简称CL线,位置与正态分布 均值重合. <2> 上控制限(Upper Control Limit)简称UCL ,位置在 μ+3δ处. <3> 下控制限(Lower Control limit)简称LCL ,位置在 μ-3δ处.
序号 测量值 序号 测量值 序号 测量值 序号 测量值 1 1495 11 1500 21 1505 31 1499 2 1496 12 1502 22 1498 32 1503 3 1502 13 1504 23 1497 33 1497 4 1504 14 1496 24 1495 34 1504 5 1498 15 1501 25 1511 35 1500 6 1501 16 1503 26 1503 36 1505 7 1503 17 1498 27 1504 37 1499 8 1508 18 1502 28 1505 38 1507 9 1502 19 1495 29 1506 39 1501 10 1497 20 1503 30 1492 40 1506
统计过程控制(SPC)与休哈特控制

统计过程控制(SPC)与休哈特控制图(一)这里介绍SPC,控制图的重要性,控制图原理,判稳及判异准则,休哈特控制图,通用控制图。
第一章统计过程控制(SPC)一、什么是SPCSPC是英文Statistical Process Control的字首简称,即统计过程控制。
SPC就是应用统计技术对过程中的各个阶段进行监控,从而达到改进与保证质量的目的。
SPC强调全过程的预防。
SPC给企业各类人员都带来好处。
对于生产第一线的操作者,可用SPC方法改进他们的工作,对于管理干部,可用SPC方法消除在生产部门与质量管理部门间的传统的矛盾,对于领导干部,可用SPC方法控制产品质量,减少返工与浪费,提高生产率,最终可增加上缴利税。
SPC的特点是:(1)SPC是全系统的,全过程的,要求全员参加,人人有责。
这点与全面质量管理的精神完全一致。
(2) SPC强调用科学方法(主要是统计技术,尤其是控制图理论)来保证全过程的预防。
(3)SPC不仅用于生产过程,而且可用于服务过程和一切管理过程。
二、SPC发展简史过程控制的概念与实施过程监控的方法早在20世纪20年代就由美国的休哈特(W. A.Shewhart)提出。
今天的SPC与当年的休哈特方法并无根本的区别。
在第二次世界大战后期,美国开始将休哈特方法在军工部门推行。
但是,上述统计过程控制方法尚未在美国工业牢固扎根,第二次世界大战就已结束。
战后,美国成为当时工业强大的国家,没有外来竞争力量去迫使美国公司改变传统方法,只存在美国国内的竞争。
由于美国国内各公司都采用相似的方法进行生产,竞争性不够强,于是过程控制方法在1950~1980年这一阶段内,逐渐从美国工业中消失。
反之,战后经济遭受严重破坏的日本在1950年通过休哈特早期的一个同事戴明(W. Ed- wards Deming)博士,将SPC的概念引入日本。
从1950~1980年,经过30年的努力,日本跃居世界质量与生产率的领先地位。
第三章 统计过程控制(SPC)与常规控制图

两个重要的参数:
• µ (mu)--- 位置参数和平均值(mean value) ,表 示 分布的中心位置和期望值 • (sigma) --- 尺度参数,表示分布的分散程度和标 准偏差 (standard deviation),
20字真经 查出异因, 采取措施, 保证消除, 不再出现, 纳入标准。
5. 统计控制状态
任何技术控制都有一个标准作为基准。 统计 过程控制(SPC)的基准是统计控制状态 (State in Statistical Control) 简称控制状态(state in control)或稳态(stable state): 指过程中只有偶因(而无异因)产生 的变异状态。 当过程仅受随机因素影响时,过程处于统计 控制状态(简称受控状态);当过程中存在 系统因素的影响时,过程处于统计失控状态 (简称失控状态)。由于过程波动具有统计 规律性,当过程受控时,过程特性一般服从 稳定的随机分布;而失控时,过程分布将发 生改变。SPC正是利用过程波动的统计规律 性对过程进行分析控制的。 通过对过程不断调整,从理论上讲,控制状 态是可以达到的,虽然质量变异不能完全消 除,应用控制图使得质量变异成为最小的有 效工具。
• 本步骤最困难,最费时。 制订过程控制标准 对过程进行监控 对过程进行诊断并采取措施解决问题
5.推行ISO9000国际标准与推行SPC和 SPD的关系
在ISO9000族标准中运用统计技术的目 的在于:通过对统计技术的适当运用以 解决组织的问题和做出有效决策,提高 管理效率并促进质量管理体系的持续改 进和产品质量的不断提高。推行SPC和 SPD是推行ISO9000国际标准的一项重 要基础工作。
什么是SPC、SPD与SPA?

2. SPD
SPD(Statistical Process Diagnosis)即统计过程诊断,是20世纪80年代由我国质量管理专家张公绪首次提出的。1980年,张公绪提出选控控制图系列。选控图是统计诊断理论的重要工具,奠定了统计诊断理论的基础。1982年,张公绪又提出了“两种质量诊断理论”,突破了传统的休哈特质量控制理论,开辟了质量诊断的新航向。此后,我国又提出“多元逐步诊断理论”和“两种质量多元诊断理论”,解决了多工序、多指标系统的质量控制与质量诊断问题。从此,SPC上升为SPD。SPD是利用统计技术对过程中的各个阶段进行监控与诊断,从而达到缩短诊断异常的时间、以便迅速采取纠正措施、减少损失、降低成本、保证产品质量的目的。 目前,我国依据上述诊断理论已开发出两种诊断软件。一种是依据“两种质量诊断理论”开发的应用软件spcD2000,用于诊断多工序生产线中上工序对下工序的影响;另一种是依据“多元逐步诊断理论”和“两种质量多元诊断理论”开发的多元诊断软件DTTQ2000,用于多因素相关条件下的诊断。而后者同时也考虑了上工序对下工序的影响。
什么是SPC、SPD与SPA?
一、概述
近年来,由于科学技术的迅猛发展,产品的不合格品率迅速降低,如电子产品的不合格率由过去的百分之一、千分之一降低到百万分之一(ppm,10–6),乃至十亿分之一(ppb,10–9)。质量控制方式也由过去的3s控制方式演进为6s控制方式。3s控制方式下的稳定状态不合格品率为2.7×10–3(0.27%),6s控制方式下的稳定状态不合格品率仅为2.0×10–9(10亿分之二),参见图1。(略) 这就是21世纪的超严格质量要求,各种产品都有其相应的超严格质量要求。因此,著名的美国质量管理专家朱兰早在1994年就在美国质量管理学会年会上指出:“21世纪是质量的世纪”。
统计过程控制(SPC)

21
22
1447
1720
1278
1472
2272
2190
1480
1859
1619.25
1810.25
994
718
903
903
2060.6
2060.6
0
0
23
24 25
829
429 1479
1613
312 1529
719
1408 1217
1758
1236 1729
1229.75
846.25 1488.5
SPC(统计过程控制)
根据上海思科统计质量咨询服务有限公司 俞钟行老师讲课整理
内容:
1.SPC(统计过程控制)概述 2.Xbar-R控制图和Xbar-s控制图 3.XmR(即X-RS)控制图 4.分析用控制图和控制用控制图 5.过程能力指数Cp、Cpk 6.过程性能指数Pp、Ppk 7.p控制图(含标准化的应用) 8.控制图判异准则 9.应用和滥用SPC(统计过程控制) 10.测试设备校正(美国“质量”杂志SPC案例2001年) 11.短流程的加工(美国“质量”杂志SPC案例2000年)
n
A3
2 2.659 0 3.267
3 1.954 0 2.568
B3
B4
计算结果(1)
Number 1 2 3 4 5 S 412.8 142.5 494.9 550.9 291.5 Sbar 405.3 405.3 405.3 405.3 405.3 B4Sbar 918.4 918.4 918.4 918.4 918.4 B3Sbar 0 0 0 0 0 Xbarbar 1400.96 1400.96 1400.96 1400.96 1400.96 Xbar+a3Sbar 2060.796172 2060.796172 2060.796172 2060.796172 2060.796172 Xbar-a3Sbar 741.1238285 741.1238285 741.1238285 741.1238285 741.1238285 Xbar 1182.5 1125.5 1435.5 1050.25 1062.25
第三章 控制图

19
3.2 过程波动
3.2 过程波动
3.2 过程波动
过程控制的三种显示型态 过程控制的三种显示型态
(a) 正常型 Frequency LSL=Lower specification limit USL =Upper specification limit (b)共同原因变异 )
(c).特殊原因变异 特殊原因变异
α/2 =0.135
以 X 控制图控制过程前,需决定抽样时间(h)与样本大小(n) 。 故每隔h时间随机抽取n个样本,再将样本统计量 X 描绘控制 图上,即假设检验过程均值是否为 X ,若点出界则表示拒绝H0, 显示过程平均值发生偏差。 H0: µ= X H1: µ ≠ X
3
3.1 统计过程控制
SPC的特点: ——全系统,全过程,全员参加,人人有责。
——强调用科学方法(统计技术,控制图理论) 来保证全过程的预防。 ——不仅用于生产过程,而且可用于服务过程和 一切管理过程。
4
3.1 统计过程控制
SPC发展的三个阶段
SPC——科学地区分生产过程中产品质量的偶然波动和异 常波动,从而对过程的异常及时报警,以便采取措施, 消除异常,恢复过程的稳定。 SPD——统计过程诊断,张公绪提出的选控控制图和两种 质量诊断理论,开辟了统计质量诊断的新方向。 SPA——统计过程调整,过程诊断后要加以措施进行调整 三者之间的关系: 循环不已 不断改进 与时俱进 SPC SPD SPA
Drop to Drop Variation + Wind 油滴之间的变化加上风的作用 Drop to Drop Variation + Wind + the Variation of Steering 油滴之间的变化加上风的作用,以及 方向盘控制的变化 11
统计过程控制

1、统计过程控制(SPC)包含两方面:①利用控制图分析过程的稳定性;②计算过程能力指数,对过程质量进行评价。
主要工具就是控制图。
2、SPC发源于美国。
休哈特《加工产品质量的经济控制》标志着过程控制的开始。
3、统计过程诊断(SPD)是20世纪80年代发展起来的。
4、世界上第一张控制图是美国休哈特在1924年提出来的不合格率(p)控制图5、小概率事件原理:小概率事件在一次实验中几乎不可能发生,若发生判断为异常。
6、控制图是用于监控过程质量是否处于统计控制过程的图7、常规控制图包括中心线、控制限、描点序列。
控制限的作用就是区分偶然波动与异常波动。
8、偶因是过程固有的,始终存在的,对质量的影响微小,但难以除去。
异因不是过程国有的,有时存在,有时不存在,对质量影响打,但不难除去。
9、过程处于统计状态控制时,只有偶因,而无异因产生的变异;点子落在控制限外的概率很小。
10、为控制产品不合格数,可选用的控制图有p图和np图11、为控制产品有瑕疵数,可选用的控制图有c图和u图12、根据5M1E内容,当人、机、料、法、测、环任何一个变动时,控制限需重新制定。
一、常规控制图的分类及应用场合:计数值控制图包括计件值和计点值控制图二、图(国标规定先作R图)计算步骤:1、取预备数据①取20~25个子组②子组大小一般为4或5,过程稳定性好的话,子组间隔可以扩大。
③同一子组的数据必须在同样的生产条件下取得,故要求在短间隔内来取。
2、计算各个子组的平均是和极差3、计算样本总均值与平均样本极差4、计算图控制限、5、将子组中的预备数据()在R图中打点,判稳。
若稳进行步骤6;若不稳,除去可查明原因后转入步骤3,即重新计算与6、将子组中的预备数据()在图中打点,判稳。
若稳进行步骤;若不稳,除去可查明原因后转入步骤3,即重新计算与7、计算过程能力指数并检验其是否满足技术要求若过程能力指数满足技术要求,则转入步骤8;若过程能力指数不满足技术要求,则需调整过程直至满足技术要求为止;8、延长的控制线,作控制用控制图,进行日常管理。
SPC统计过程控制

UCLCLLCLSPC 统计过程控制.SPC 统计过程控制概论产品质量的统计观点认为,过程质量在各种影响因素的制约下,呈现波动(变异性) ,但过程质量的波动并非漫无边际,在一定范围内,过程质量的波动呈现统计规律性。
SPC (Statistical process Control )统计过程控制,就是根据过程质量的统计规律性这一原则, 利用统计技术对过程的各个阶段进行监控,从而达到保证产品质量的目的。
SPC 中的统计技术泛指任何可以应用的数理统计方法。
一般而言,主要是指控制图的应用。
•控制图定义控制图(control chart ),又称管制图、休哈特图。
是美国休哈特博士于1924年发明的。
控制图是区分过程中的异常波动和正常波动,并判断过程是否处于控制状态的一种工具。
三.控制图原理2过程处于统计控制状态时(也即受控状态) ,产品总体的质量特性数据的分布一般服从正态分布,即X~N (卩,6 )(注:卩 --- 过程均值,6 ----- 过程标准差)。
质量特性值落在□土 3 6范围内的概率约为 99.73%,落在□土 3 6以外的概率只有0.27%,因此可用卩土 3 6作为上下控制界限,以质量特性数据是否超越这一上下界限以及数据的排列情况来判 断过程是否处于受控状态,这就是控制图原理若计叫心线为 CL , 上控制限为 UCL 下控制限为LCL ,则有 CL=UCL= 1 +3 6 LCL= i -3 6控制图的基本形式如下图所示四•控制图的种类 1按照用途分(1)分析用控制图分析用控制图主要用来分析:a过程是否处于统计稳态b过程能力是否适宜。
如发现异常(过程失控或过程能力不足) ,则应找出原因,采取措施,使过程达到稳定。
过程处于稳态后,才可将分析用控制图的控制线延长作为控制用控制图。
(2)控制(管理)用控制图。
控制用控制图由分析用控制图转化而来。
它用于使过程保持稳态,预防不合格的产生。
控制用控制图的应用规则:按规定的取样方法获得数据,通过打点观察,控制异常原因的出现一一当点子分布出现异常,说明工序质量不稳定,此时应及时找出原因,消除异常因素,使工序恢复到正常的控制状态。
统计过程控制(SPC)

9.94 9.81 9.85 10.11 10.24 10.17 9.83 10.33 10.39 9.64
10.42 10.13 9.61 10.03 10.60 10.00 9.55 10.15 10.16 9.88
10.30 10.21 10.03 10.15 9.58 10.09 9.87 9.91 9.73 10.02
Mo=1
2 12.67
3.56
练习
数列:12,11,12,13,18,30,24,9 请计算下列统计量:
R
X
Md
Mo
2
数据的收集与整理
群体
行 动
结论
抽样 分析
样本 测 试
数据
每件产品的尺寸与别的都不同
范围
范围
范围
范围
但它们形成一个模型,若稳定,可以描述为一个分布
量具精确度是指测量观察平均值与真实值(基准值) 的差异。 真实值由更精确的测量设备所确定
测量系统变差
量具重复性
量具重复性是由一个操作者采用一种测量 仪器,多次测量同一零件的同一特性时获得的 测量值变差。
测量系统变差
量具再现性
量具再现性是由不同的操作者,采用相同 的测量仪器,测量同一零件的同一特性时测量 平均值的变差。
Statistical Process Control
(统计过程控制)
统计过程控制(SPC)
1、SPC的发展史 2、基本统计概念 3、过程变差 4、控制图 5、过程控制和过程能力
SPC的发展
20世纪20年代,美国休哈特提出; 二战后期,美国将休哈特方法在军工部门推行; 1950~1980,逐渐从美国工业中消失 ;休哈
spc统计过程控制与管制图

SPC统计过程控制与管制图1. 简介SPC〔Statistic Process Control〕是指通过统计方法对生产过程进行过程控制和管制的一种方法。
SPC通过收集和分析过程中的数据,帮助企业发现和解决问题,并实现过程的稳定和改良。
在SPC中,管制图是一种常用的工具,用于判断过程是否处于统计控制之中。
2. 管制图的根本原理管制图是一种时间序列图,通过将样本数据的均值、极差等统计量绘制在图上,以便直观地了解过程的稳定性。
在管制图中,通常会画出上下控制限以及中心线,用于判断过程是否处于统计控制之中。
管制图有多种类型,常用的包括: - 平均数管制图〔Xbar-R图〕:用于监控过程的平均数和极差 - 均值管制图〔X图〕:用于监控过程的平均数 - 极差管制图〔R图〕:用于监控过程的极差 - 标准差管制图〔S图〕:用于监控过程的标准差 - P图:用于监控过程的不良品率 - C 图:用于监控过程的不良品数3. 构建管制图的步骤构建管制图的步骤如下: 1. 收集数据:根据需要监控的指标,收集足够的样本数据。
2. 计算统计量:根据收集到的数据,计算出相应的统计量,如平均数、极差、标准差等。
3. 绘制管制图:根据统计量,绘制出相应的管制图,包括上下控制限和中心线。
4. 分析管制图:通过分析管制图中的数据点是否超出控制限,判断过程是否处于统计控制之中。
5. 做出改良:如果过程处于统计控制之外,需要分析可能的原因并采取相应的改良措施。
4. 管制图的应用管制图广泛应用于制造业和效劳业中的质量管理过程中。
通过使用管制图,企业可以实现以下目标: - 及时发现生产过程中的异常情况,减少不良品率; - 保持生产过程的稳定性,提高生产效率; - 通过长期监控数据,找出改良生产过程的方向。
5. 管制图的本卷须知在使用管制图时,需要注意以下几点: - 样本数据应该具有一定的随机性,否那么可能会影响对过程稳定性的判断。
- 控制限的选择需要根据实际情况进行调整,不同的管制图有不同的选择方法。
统计过程控制(SPC)

解:
于是,过程能力指数为:
过程能力不够充分,从图2发现分布中心μ=0.1968与规范中心M=(TU+TL)/2=0.1720有偏离,应进行调整。调整后,Cp值会有所提高。
单侧规范情况的过程能力指数
01
只有上限要求,而对下限没有要求: 只适用于的范围:
02
只有下限要求,而对上限没有要求: 只适用于的范围:
4
3
6
5
判稳准则的分析 判稳准则的思路
打一个点未出界有两种可能性:
► 过程本来稳定 ► 漏报 (这里由于α小,所以β大),故打一个点子未出界不能立即判稳。
在点子随机排列的情况下,符合下列各点之一判稳:
01
► 连续25个点,界外点数d=0;
02
► 连续35个点,界外点数d<0;
03
► 连续100个点,界外点数d<2。
0.1821
0.1828
0.0086
18
0.1812
0.1585
0.1699
0.168
0.1694
0.0227
19
0.1700
0.1567
0.1694
0.1702
0.1666
0.0135
20
0.1698
0.1664
0.17
0.16
0.1666
0.01
图1
μ’
μ
图2-7 正态曲线随着标准差变化
σ=2.5
σ=1.0
σ=0.4
y
x
不论μ与σ取值为何,产品质量特性值落在[μ-3σ,μ+3σ]范围内的概率为99.73%。 图2-8 正态分布曲线下的面积
控制图

由3σ原理,u图的中心线和控制界限分别为
λ/n和 3 。
n
n2
k
Ci
• λ/n可以用平均单位缺陷数
u
i 1 k
估计,
ni
i 1
CL u
X
Xi
x1
x2
x3 n
xn
式中 X i ——第i个子组的样本平均值
xi ——第i个子组中观测值
n ——子组的大小
各子组样本的极差R的计算公式为
Ri max{ xi} min{ xi}
式中 Ri ——第i个子组的极差
分别为
本例第一组样本的平均值和极差
X1
3.0
4.2
4
3.5
3.8
3.62
1 k
n
k
ni
i 1
不论是Pn控制图还是P控制图,实际 上起控制作用的只是上控制界限、中心 线。因此,实际工作中有的Pn图和P图不 画下控制线。
(三)缺陷数控制图(C控制图)
缺陷数控制图的控制对象是一定单 位(长度、面积、体积)n上面的缺陷 数。
一定单位上的缺陷数c服从泊松分布 P(x),有 P(x) e x
布为N(μ,σ2/n) 按3σ原理,控制界限如下:
的分
CL=μ
UCL 3
n
UCL 3
n
由
x
得
R d2
R
d2
所以有
CL x
UCL x 3 R d2 n
LCL x 3 R d2 n
取
A2
3 d2
n
CL x
统计过程控制(SPC)与常规控制图

SPC发展阶段
SPC迄今已经经历三个阶段﹐ SPC﹑SPD﹑SPA SPC在1920S由休哈特创造的理论 SPD在1982我国张公续教授首创﹐ 目前我国仍然处于领先地位 SPA目前刚刚起步﹐目前尚无实用 性研究成果
SPC
SPD
SPA
2.控制图原理
控制图(Control Chart)是对 过程质量特性值进行测定﹑ 记录﹑评估和监察过程是否 处于控制状态的一种用统计 方法设计的图。
级别
1 2 3 4 5
过程能力的评价参考
过程能力过高(应视具体情况而定) 过程能力充分﹐表示技朮管理能力很好﹐应 继续维持 过程能力较差﹐表示技朮管理能力较勉强﹐ 应设法提升2级 过程能力不足﹐表示技朮管理能力很差﹐应 采取措施立即改善 过程能力严重不足﹐表示应采取紧急措施和 全面检查﹐必要时可停工整顿
R=Xmax-Xmin
令W=R/σ,则E(W)=d2﹐ d2为一与样本量n有关的常量 σ=R/ d2
R=
R1+R2+R3+…+Rn n
总上得到控制线为﹕
式中A2为一与样本量n有关的常量﹐可以从表中查出 X控制图控制线完成
R图的如何控制变异度
μR=R
令W=R/σ,则E(W)=d3﹐ d3为一与样本量n有关的常量
判稳准则
1.
连续25个点子都在控制界限内
2.
3.
连续35个点子至多有1个点子落在控制界限外
连续100个点子至多有2个点子落在控制界限外 α 1=0.0654
不符合上述三原则的概率为﹕
α 2=0.0654 α 3=0.0654
4.控制图判断准则
(a) 连续9点出现在中心线的单侧
SPC中控制图的原理、制作和分析方法

七、X—R图的控制限计算公式 X控制图计算公式
UCLx = μx+3σx = x+A2R CLx = μx=x
LCLx = μx-3σx = x-A2R
13
八、分析用控制图和控制用控制图
二、过程能力指数
过程能力指数(Process Capability Index)简 称PCI或Cp,也可称为工序能力指数。
过程能力一般是通过过程能力指数度量如 下:
Cp
=
规定的公差 过程变异度
=
T 6б
≈
T 6σ
39
式中,公差T=Tu-TL,Tu为公差上限,TL为公 差下限,б为质量特性值的标准差,б为其 估计值,国标GB/T4901-2001可由R/d2(XR控制图)估计。
偶因引起质量的偶然波动,异因引起质量 的异常波动。偶然波动是不可能避免的, 但对质量的影响一般不大。异常波动对质 量的影响大,且采取措施不难消除,故在 过程中异常波动及造成异常波动的原因是 我们注意的对象,一旦发生就应该尽快找 出,并采取措施加以消除。将质量波动区 分为偶然波动与异常波动两类,并分别采 取不同的对策,这是休哈特的贡献。
UCL、CL和CLC统称为控制限,它们是互相平 行的。若控制图中的描点落在控制限之外
或描点在控制限之间的排列不随机,则表
明过程异常。世界上第一张控制图是美国 休哈特(W.A.Shewhart)在1924年提出的不合 格率(P)控制图。
二、控制图的形成
将通常的正态分布图转个90度方向,使自变 量增加方向垂直向上,并将μ、μ+3σ和μ- 3σ分别称为CL、UCL和LCL,这样就得到了 一张控制图。 三、控制图的原理 根据来源的不同,影响质量的原因(因素) 可分为人、机、料、法、测、环六个方面。
统计过程控制与常规控制图

本章主要内容:介绍SPC,控制图的重要
性,控制图的原理,判稳及判异准则,休哈 特控制图,通用控制图,与过程能力指数。
一、SPC
SPC即Statistical Process Control,即统 计过程控制。应用统计计数对过程的各 个阶段进行监控,从而达到保证与改进 质量的目的。SPC强调全过程预防。 SPC的特点:
控制图原理的概率解释
点子超出控制线的事件为小概率事件, 出现小概率事件的几率很小,近似认为 不可能,因此点子出界则判异常。
控制图原理的偶因、异因解释
假定在设计过程中,异因已经被消除, 剩下偶因,则为最小的波动。根据统计 学原理设计出相应的控制界限,当点子 超出界限时即为存在异因。
控制图的预防原则
X R 控制图
X图控制线:
R图控制线
UCLR D4 R CLR R LCLR D3 R
UCL x A R 2 x CLX X LCL X X A2 R
直接打点法
用此法将现场数据直接变化成通用图上 的数据,在现场不需要进行标准变换。 把通用控制图上作出K=-3,-2,-1,0, 1,2,3的七根水平横线,把整个通用图 分成Ⅰ,Ⅱ,…,Ⅷ共八个区域。
八、过程能力与过程能力指数
Process Capability 指过程的加工质量满 足技术要求的能力,是衡量过程加工内 在一致性的。
六、休哈特控制图
常规控制图包括:计量值控制图、计件 值控制图、计点值控制图。其中计件值 控制图和计点值控制图统称为计数值控 制图。 休哈特控制图的设计思想: 点出界判异 点排列不随机判异
统计过程控制休哈特Shewhart控制图

修哈特控制图 – 概述
深圳市共进电子有限公司
休哈特控制图的变量
深圳市共进电子有限公司
_
X 控制图 与 中心极限定理
• 中心极限定理 : • 如果在n个样本中取k个观察,样本x1, x2, . . . , xk将近似
N(x,x)的分布,有:
深圳市共进电子有限公司
k
xi
x
i 1
模块范围
• 产品控制与过程控制 • 识别变化 • 休哈特控制图 • 指标的不稳定性 • 执行控制图
深圳市共进电子有限公司
控制模型产品的质量控制
Raw Material, Components & Sub-Assemblies
Process
Product
Inspection
Fail
Pass
Rework
7 73.995 74.006
深圳市共进电子有限公司
识别变化
Special Variation
Natural Variation under 0 (±30)
Historical Level (0)
Reject Rate
Optimum Level (1)
深圳市共进电子有限公司
Time
Natural Variation under 1 (±31)
• 目标一致 (戴明) • 适应性 (约瑟夫朱兰) • 符合要求 (菲利普克劳士比) • 逆变异 (道格拉斯蒙哥马利)
深圳市共进电子有限公司
识别变化
• 固有的或正常的变化 由于累积的影响,许多小的不可避免的原因在不断的积累 下导致经营过程的唯一机会差异,被认为是“在控制中”
• 特别或分配变化,由于 一)不当调整设计 二)操作员的错误 三)有缺陷的原材料 一个进程中运行存在的分配变化的原因被认为是“失去控 制”
休哈特控制图的介绍
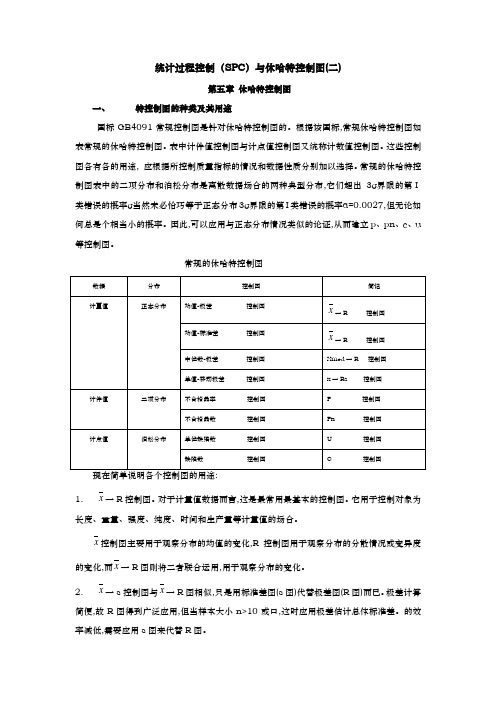
统计过程控制(SPC)与休哈特控制图(二)第五章休哈特控制图一、特控制图的种类及其用途国标GB4091常规控制图是针对休哈特控制图的。
根据该国标,常规休哈特控制图如表常规的休哈特控制图。
表中计件值控制图与计点值控制图又统称计数值控制图。
这些控制图各有各的用途, 应根据所控制质量指标的情况和数据性质分别加以选择。
常规的休哈特控制图表中的二项分布和泊松分布是离散数据场合的两种典型分布,它们超出3σ界限的第Ⅰ类错误的概率σ当然未必恰巧等于正态分布3σ界限的第I类错误的概率α=0.0027,但无论如何总是个相当小的概率。
因此,可以应用与正态分布情况类似的论证,从而建立p、pn、c、u 等控制图。
常规的休哈特控制图1.x一R控制图。
对于计量值数据而言,这是最常用最基本的控制图。
它用于控制对象为长度、重量、强度、纯度、时间和生产量等计量值的场合。
x控制图主要用于观察分布的均值的变化,R控制图用于观察分布的分散情况或变异度的变化,而x一R图则将二者联合运用,用于观察分布的变化。
2.x一s控制图与x一R图相似,只是用标准差图(s图)代替极差图(R图)而已。
极差计算简便,故R图得到广泛应用,但当样本大小n>10或口,这时应用极差估计总体标准差。
的效率减低,需要应用s图来代替R图。
3.XMED一R控制图与x一R图也很相似,只是用中位数图(XMED图)代替均值图(x 图)。
所谓中位数即指在一组按大小顺序排列的数列中居中的数。
例如,在以下数列中2、3、7、13、18,中位数为7。
又如,在以下数列中2、3、7、9、13、18,共有偶数个数据。
这时中位数规定为中间两个数的均值。
在本例即297=8。
由于中位数的计算比均值简单,所以多用于现场需要把测定数据直接记入控制图进行控制的场合,这时为了简便,当然规定为奇数个数据。
4.x一Rs控制图。
多用于下列场合:对每一个产品都进行检验,采用自动化检查和测量的场合;取样费时、昂贵的场合;以及如化工等过程,样品均匀,多抽样也无太大意义的场合。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
统计过程控制(SPC)与休哈特控制图(一)这里介绍SPC,控制图的重要性,控制图原理,判稳及判异准则,休哈特控制图,通用控制图。
第一章统计过程控制(SPC)一、什么是SPCSPC是英文Statistical Process Control的字首简称,即统计过程控制。
SPC就是应用统计技术对过程中的各个阶段进行监控,从而达到改进与保证质量的目的。
SPC强调全过程的预防。
SPC给企业各类人员都带来好处。
对于生产第一线的操作者,可用SPC方法改进他们的工作,对于管理干部,可用SPC方法消除在生产部门与质量管理部门间的传统的矛盾,对于领导干部,可用SPC方法控制产品质量,减少返工与浪费,提高生产率,最终可增加上缴利税。
SPC的特点是:(1)SPC是全系统的,全过程的,要求全员参加,人人有责。
这点与全面质量管理的精神完全一致。
(2) SPC强调用科学方法(主要是统计技术,尤其是控制图理论)来保证全过程的预防。
(3)SPC不仅用于生产过程,而且可用于服务过程和一切管理过程。
二、SPC发展简史过程控制的概念与实施过程监控的方法早在20世纪20年代就由美国的休哈特(W. A.Shewhart)提出。
今天的SPC与当年的休哈特方法并无根本的区别。
在第二次世界大战后期,美国开始将休哈特方法在军工部门推行。
但是,上述统计过程控制方法尚未在美国工业牢固扎根,第二次世界大战就已结束。
战后,美国成为当时工业强大的国家,没有外来竞争力量去迫使美国公司改变传统方法,只存在美国国的竞争。
由于美国国各公司都采用相似的方法进行生产,竞争性不够强,于是过程控制方法在1950~1980年这一阶段,逐渐从美国工业中消失。
反之,战后经济遭受严重破坏的日本在1950年通过休哈特早期的一个同事戴明(W. Ed- wards Deming)博士,将SPC的概念引入日本。
从1950~1980年,经过30年的努力,日本跃居世界质量与生产率的领先地位。
美国著名质量管理专家伯格(Roger W. Berger)教授指出,日本成功的基石之一就是SPC。
在日本强有力的竞争之下,从80年代起,SPC在西方工业国家复兴,并列为高科技制(之一。
例如,加拿大钢铁公司(STELCO)在1988年列出的该公司七大高科技方向如下:(1)连铸,(2) 炉外精炼钢包冶金站,(3) 真空除气,(4) 电镀钵流水线,(5) 电子测量,(6) 高级电子计算机,(7) SPC。
美国从20世纪80年代起开始推行SPC。
美国汽车工业已大规模推行了SPC,如福特汽车公司,通用汽车公司,克莱斯勒汽车公司等,上述美国三大汽车公司在ISO9000的基础上还联合制定了QS9000标准,在与汽车有关的行业中,颇为流行。
美国钢铁工业也大力推行了SPC,如美国LTV钢铁公司,陆钢铁公司,伯利恒钢铁公司等等。
三、什么是SPCD与SPCDA?SPC迄今已经经历了三个发展阶段,即:SPC,SPCD及SPCDA。
1.第一阶段为SPC。
SPC是美国休哈特在20世纪二、三十年代所创造的理论,它能以便人们采取措施,消除异常,恢复过程的稳定。
这就是所科学地区分出生产过程中产品质量的偶然波动与异常波动,从而对过程的异常及时告警,谓统计过程控制。
2.第二个阶段为SPCD。
SPCD是英文Statistical Process Control and Diagnosis的字首简称,即统计过程控制与诊断。
SPC虽然能对过程的异常进行告警,但是它并不能告诉我们是什么异常,发生于何处,即不能进行诊断。
1982年我国公绪首创两种质量诊断理论,突破了传统的美国休哈特质量控制理论,开辟了统计质量诊断的新方向。
从此SPC上升为SPCD,SPCD是SPC 的进一步发展,也是SPC的第二个发展阶段。
1994年公绪教授与其博士生慧英博士提出多元逐步诊断理论,1996年公绪教授又提出两种质量多元诊断理论,解决了多工序、多指标系统的质量控制与诊断问题。
目前SPCD已进入实用性阶段,我国仍然居于领先地位。
3.第三个阶段为SPCDA。
SPCD也是英文Statistical Process Control,Diagnosis and Adjustment 的字首简称,即统计过程控制、诊断与调整。
正如同病人确诊后要进行治疗,过程诊断后自然要加以调整,故SPCDA是SPCD的进一步发展,也是SPC的第三个发展阶段。
这方面国外刚刚起步,他们称之为ASPC(Algorithmic Statistical Process Control,算法的统计过程控制),目前尚无实用性的成果。
公绪教授与他的博士生也正在进行这方面的研究。
四、SPC和SPCD的进行步骤进行SPC和SPCD有下列步骤:步骤1::培训SPC和SPCD。
培训容主要有下列各项:SPC的重要性,正态分布等统计基本知识,质量管理七种工具,其中特别是要对控制图深入学习,两种质量诊断理论,如何制订过程控制网图,如何制订过程控制标准等等。
步骤2:确定关键变量(即关键质量因素)。
具体又分为以下两点:(1)对全厂每道工序都要进行分析(可用因果图),找出对最终产品影响最大的变量,即关键变量(可用排列图)。
如美国LTV钢铁公司共确定了大约20000个关键变量。
(2)找出关键变量后,列出过程控制网图。
所谓过程控制网图即在图中按工艺流程顺序将每道工序的关键变量列出。
步骤3:提出或改进规格标准。
具体又分为以下两点:(1)对步骤2得到的每一个关键变量进行具体分析。
(2)对每个关键变量建立过程控制标准,并填写过程控制标准表。
过程控制标准表本步骤最困难,最费时间,例如制定一个部门或车间的所有关键变量的过程控制标准,大约需要两个多人年(即一个人要工作量年多)。
步骤4:编制控制标准手册,在各部门落实。
将具有立法性质的有关过程控制标准的文件编制成明确易懂、便于操作的手册,使各道工序使用。
如美国LTV公司共编了600本上述手册。
步骤 5:对过程进行统计监控。
主要应用控制图对过程进行监控。
若发现问题,则需对上述控制标准手册进行修订,及反馈到步骤4。
步骤6::对过程进行诊断并采取措施解决问题。
可注意以下几点:(1)可以运用传统的质量管理方法,如七种工具,进行分析。
(2)可以应用诊断理论,如两种质量诊断理论,进行分析和诊断。
(3)在诊断后的纠正过程中有可能引出新的关键质量因素,即反馈到步骤2,3,4 。
推行SPC的效果是显著的。
如美国率LTV公司1985年实施了SPC后,劳动生产率提高了20%以上。
五、宣贯ISO9000国际标准与推行SPC和SPCD的关系ISO9000一1994年新版与1987年初版相比校,有三个强调:(1) 强调“把一切都看成过程",(2) 强调“预防", (3) 强调“统计技术的应用是不可剪裁的"。
其实,这三者是互相联系、密切不可分的。
众所周知,质量管理这门学科有个重要的特点,即对质量管理所提出的原则、方针、目标都要有科学方法和科学措施来加以保证。
例如,强调预防就要应用统计方法(主要是应用SPC 和SPCD)和科学措施来保证它的实现。
这样,后两个强调是紧密联系着的。
其次,SPC即统计过程控制,故第一个强调也与后二者联系起来了。
所以这三个强调是互相联系、密不可分的。
企业推行ISO9000应该注意到这三个强调,在思想上应该明确:SPC和SPCD是推行ISO9000的基础。
第二章控制图原理一、控制图的重要性贯彻预防原则是依靠推行SPC和SPCD来实现的,而居QC七个工具核心地位的控制图是 SPC 和SPCD的重要工具。
1984年日本名古屋工业大学调查了115家日本各行各业的中小型工厂,结果发现平均每家工厂使用137控制图,这个数字对于我们推行SPC和SPCD是有一定的参考意义的。
可以说,工厂中使用控制图的数在某种意义上反映了管理现代化的程度。
二、什么是控制图控制图是对过程质量加以测定、记录从而进行控制管理的一种用科学方法设计的图。
图上有中心线(CL)、上控制界限(UCL)和下控制界限(LCL),并有按时间顺序抽取的样本统计量数值的描点序列,参见控制图示例图。
三、控制图原理的第一种解释假定某车间有部车床车制直径为10mm的机螺丝。
为了了解机螺丝的质量,从车制好的机螺丝中抽出100个,测量并记录其直径数据,如表所示。
机螺丝直径数据(mm)10.24 9.94 10.00 9.99 9.85 9.94 10.42 10.30 10.36 10.0910.21 9.79 9.70 10.04 9.98 9.81 10.13 10.21 9.84 9.5510.01 10.36 9.88 9.22 10.01 9.85 9.61 10.03 10.41 10.1210.15 9.76 10.57 9.76 10.15 10.11 10.03 10.15 10.21 10.059.73 9.82 9.82 10.06 10.42 10.24 10.60 9.58 10.06 9.9810.12 9.97 10.30 10.12 10.14 10.17 10.00 10.09 10.11 9.709.49 9.97 10.18 9.99 9.89 9.83 9.55 9.87 10.19 10.3910.27 10.18 10.01 9.77 9.58 10.33 10.15 9.91 9.67 10.1010.09 10.33 10.06 9.53 9.95 10.39 10.16 9.73 10.15 9.759.79 9.94 10.09 9.97 9.91 9.64 9.88 10.02 9.91 9.54直方高度与该组的频数成正比。
机螺丝直径直方图直方图趋近光滑曲线将各组的频数用数据总和N=100除,就得到各组的频率,它表示机螺丝直径属于各组的可能性大小。
显然,各组频率之和为1。
若以直方面积来表示该组的频率,则所有直方分布曲线正态分布曲线面积总和也为1。
这时,直方的高=直方面积/组距=频率/组距=频数/(N×组距)。
因此,无论纵坐标取为频率或频率/组距,各直方的高都与频数成正比。
故机螺丝直径直方图所示的直方图仍可用,只要再作一条频率纵轴和一条直方面积表示频率的纵轴,见直方图趋近光滑曲线图。
如果数据越多,分组越密,则机螺丝直径直方图的直方图也越趋近一条光滑曲线,如直方图趋近光滑曲线图所示。
在极限情况下得到的光滑曲线即为分布曲线,它反映了产品质量的统计规律,如分布曲线图所示。
在质量特性值为连续值时,最常见的典型分布为正态分布。
例如机螺丝直径直方图中机螺丝直径的分布就是如此,它的特点是中间高、两头低、左右对称并延伸至无限。
正态分布可用两个参数即均值μ和标准差σ来决定。
