USACO月赛(2011)1

合集下载

usaco 试题

usaco 试题USACO试题USACO是美国计算机奥林匹克竞赛的缩写，它是美国学生在计算机科学领域的竞赛之一。

USACO试题涵盖了各种计算机算法和编程知识，并通过解题的方式来测试学生的能力。

本文将介绍USACO试题的背景、难度和一些解题技巧。

一、背景USACO试题由美国计算机奥林匹克竞赛委员会出题，并面向全球学生开放。

该竞赛旨在提高学生在计算机科学领域的技能，并培养他们的创造力和解决问题的能力。

USACO试题通常包括一系列编程问题，要求学生使用特定的编程语言来解决。

学生需要根据问题描述，并编写程序来产生正确的输出结果。

二、难度USACO试题的难度分为四个级别，分别是铜牌（Bronze），银牌（Silver），金牌（Gold）和白金牌（Platinum）。

每个级别的试题都有一定的难度，需要学生具备不同程度的编程和算法能力。

铜牌级别的试题相对较简单，通常涵盖了基本的算法和编程知识。

而白金牌级别的试题则非常复杂，需要学生具备深入的算法和数据结构知识，以及灵活运用编程语言的能力。

三、解题技巧解决USACO试题需要一定的技巧和方法。

以下是一些常用的解题技巧：1. 理解问题：首先，要仔细阅读问题描述，理解问题的要求和限制条件。

只有充分理解问题，才能更好地进行解题分析和编程设计。

2. 分析问题：其次，要对问题进行分析，找出问题的关键点和难点。

可以利用画图、列举样例等方式，深入剖析问题的本质，为后续的解题提供思路和方向。

3. 设计算法：在分析问题的基础上，需要设计合适的算法来解决问题。

根据问题的特点，选择合适的算法策略，如贪心算法、动态规划、搜索等。

同时，要考虑算法的时间复杂度和空间复杂度，尽量保证程序的效率。

4. 编写代码：根据设计的算法，编写相应的代码实现。

要注意代码的规范性和风格，使其易读易懂。

同时，遵循编程语言的语法和规范，确保程序的正确性。

5. 测试和调试：完成代码编写后，需要进行测试和调试，确保程序可以正确地运行。

usaco比赛规则

usaco比赛规则（原创实用版）目录ACO 竞赛简介ACO 竞赛规则3.竞赛报名与参赛方式4.竞赛时间与地点5.竞赛奖项设置6.竞赛备考建议正文【USACO 竞赛简介】USACO（USA Computing Olympiad）是美国计算机奥林匹克竞赛的简称，是一项面向全球高中生的计算机编程竞赛。

该竞赛旨在选拔和培养优秀的计算机科学人才，激发学生对计算机编程的兴趣，提高学生的计算机编程能力。

【USACO 竞赛规则】USACO 竞赛规则分为在线赛和选拔赛两个阶段。

在线赛：在线赛分为月赛、季赛和年赛，每月一次。

参赛选手需要在规定时间内（通常为 4 小时）完成 3-5 道编程题目，每道题目有多个测试点，需要通过所有测试点才能获得满分。

参赛选手可以使用各种编程语言，如 C++、Java、Python 等。

选拔赛：选拔赛分为金级、银级和铜级比赛。

参赛选手需要通过在线赛的选拔，才有资格参加选拔赛。

选拔赛同样分为多个轮次，每个轮次需要完成 3-5 道编程题目。

选拔赛的难度相较于在线赛会有所提高。

【竞赛报名与参赛方式】参赛选手需要首先在 USACO 官方网站上注册账号，然后选择相应的比赛场次进行报名。

报名成功后，参赛选手可以在比赛当天通过官方网站登录系统参加比赛。

【竞赛时间与地点】USACO 竞赛的时间和地点因比赛级别和轮次而异。

在线赛通常在每月的某个周末进行，地点为个人电脑前；选拔赛则通常在各地的指定考场进行，具体时间和地点会在官方网站上公布。

【竞赛奖项设置】USACO 竞赛的奖项分为金、银、铜三个级别。

获得金级比赛奖项的选手将有机会参加更高级别的比赛，如全球信息学奥林匹克竞赛（IOI）。

此外，选拔赛中的成绩也将影响选手的晋级情况。

【竞赛备考建议】对于想要参加 USACO 竞赛的同学，可以提前学习编程语言和算法知识。

在比赛中，合理的时间分配和算法选择至关重要。

另外，多参加模拟赛和在线练习，提高自己的编程能力和应试技巧，也是取得好成绩的关键。

USACO试题精选(第一辑)

USACO试题精选第一辑第1题利润(Profits, USACO 2011 Jan) (3)第2题购买饲料二(Buying Feed II, USACO 2010 Jan) (4)第3题奶牛杂技(Cow Acrobats, USACO 2006 Nov) (5)第4题抓苹果(Apple Catching, USACO 2004 Nov) (6)第5题抢购干草(Hay For Sale, USACO 2008 Dec) (7)第6题建造栅栏(Building A Fence, USACO 2008 Oct) (8)第7题建造道路(Building Roads, USACO 2007 Dec) (9)第8题青铜莲花池(Bronze Lilypad Pond, USACO 2007 Feb) (10)第9题滑雪课程(Ski Lessons, USACO 2009 Open) (11)第10题奶牛飞盘队(Cow Frisbee Team, USACO 2009 Mar) (12)第11题奶牛博览会(Cow Exhibition, USACO 2003 Fall) (13)第12题最近回文(Cheapest Palindrome, USACO 2007 Open) (14)第13题安慰奶牛(Cheering up the Cows, USACO 2008 Nov) (15)第14题玉米迷宫(Corn Maze, USACO 2011 Open) (16)第15题奶牛集会(MooFest, USACO 2004 Open) (17)第16题奶牛文字(Cowlphabet, USACO 2011 Feb) (18)第17题奶牛跨栏(Cow Hurdles, USACO 2007 Nov) (19)第18题工作安排(Work Scheduling, USACO 2009 Open) (20)第19题手机网络(Cell Phone Network, USACO 2008 Jan) (21)第20题提交作业(Turning in Homework, USACO 2004 Open) (22)第21题滑雪缆车(Ski Lift, USACO 2006 Mar) (23)第22题派发巧克力(Chocolate Giving, USACO 2010 Feb) (24)第23题赞助学费(Financial Aid, USACO 2004 Mar) (25)第24题白银莲花池(Silver Lilypad Pond, USACO 2007 Feb) (26)第25题地震(Earthquake, USACO 2001 Open) (27)第26题股票市场(Stock Market, USACO 2009 Feb) (28)第27题奶牛赛车(Cow Cycling, USACO Feb 2002) (29)第28题奶牛观光(Sightseeing Cows, USACO 2007 Dec) (30)第29题道路重建(Rebuilding Roads, USACO Feb 2002) (31)第30题奶牛接力(Cow Relays, USACO 2007 Nov) (32)第31题猜数游戏(Haybale Guessing, USACO 2008 Jan) (33)第32题混乱奶牛(Mixed Up Cows, USACO 2008 Nov) (34)第33题修剪草坪(Mowing the Lawn, USACO 2011 Open) (35)第34题道路翻新(Revamping Trails, USACO 2009 Feb) (36)第35题安排牧场(Corn Fields, USACO 2006 Nov) (37)第36题叠积木(Cube Stacking, USACO 2004 Open) (38)第37题奶牛抗议(Generic Cow Protests, USACO 2011 Feb) (39)第38题洞穴奶牛第一话(Cave Cow 1, USACO 2004 Open) (40)第39题打扫食槽(Cleaning Up, USACO 2009 Mar) (41)第40题购买饲料(Buying Feed, USACO 2010 Nov) (42)第41题土地并购(Land Acquisition, USACO 2008 Mar) (43)第42题干草塔(Tower of Hay, USACO 2009 Open) (44)第43题明星奶牛(Popular Cows, USACO 2003 Fall) (45)第44题电子游戏(Video Game Troubles, USACO 2009 Dec) (46)第45题产奶比赛(Milk Team Select, USACO 2006 Mar) (47)第46题黄金莲花池(Lilypad Pond, USACO 2007 Feb) (48)第47题逢低吸纳(BUY LOW, BUY LOWER, USACO Feb 2002) (49)第48题焊接(Soldering, USACO 2011 Open) (50)第49题旅馆(Hotel, USACO 2008 Feb) (51)第50题道路和航线(Roads and Planes, USACO 2011 Jan) (52)这一辑从USACO月赛中选择了质量很高的50题，是用来训练算法设计和实现的极好素材，如果初学者希望掌握比较扎实的基本功，我建议将这一辑的题目好好研究一下。

usaco竞赛流程

USACO竞赛的流程大致如下：
1.在竞赛开放期间，选手需要进入竞赛页面参与比赛。

点击“Start the Contest!”键即
可开始比赛。

选手的比赛用时就会立即倒计时，且无法暂停。

2.进入题目页面后，选手可以点击标题查看相应题目并提交程序。

对于尚未提交的试题，
封面页会对应显示“Not submitted”。

对于已经提交的试题，封面页会对应显示“Submitted and Graded”。

3.选手需要按要求在自己的编程环境中完成题目，并提交cpp文件。

比赛会在时限过后自
动结束（如已经获得满分，则可以手动提前结束），只需在比赛结束前确保提交过已经完成的题目即可。

4.代码提交后，系统会自动给出评分，如果拿到了满分，系统会提示直接晋级。

如果没有
拿到满分，需要等待官方公布晋级分数线，每场月赛结束后一周内，官方会通过电子邮箱发放参赛选手的程序的评测结果。

成功晋级就可以在下一场月赛中参加更高级别的竞赛，没有成功晋级只能在下一场月赛中继续在原组别中打比赛。

2011年第一次月考

东昌中学2010—2011学年第二学期第一次阶段性检测九年级历史试题时间：70分钟分值：100分命题人：王爱华一．选择题：（每小题1.5分，共60分。

将答案涂在答题卡上。

）1．据报道，安徽发现的繁昌人距今大约有180万年。

如果这一结论确凿的话，可以把中国已知最早人类的历史向前推进A．10万年 B．20万年 C．100万年 D．110万年2.黄河流域是中华文明的发祥地之一，最能体现该地区原始农耕文化成就的应该是A．种植粟 B．种植水稻 C．人工取火 D．住干栏式房子3.中国是世界四大文明古国之一，她的第一个王朝的建立者是A．秦始皇 B．齐桓公 C．启 D．禹4.2010年4月1日起，为期三个月的“国家宝藏——中国国家博物馆典藏珍宝展”在宁波博物馆举行。

其中右图的展品出自中国的A．商周时期 B．隋唐时期C．宋元时期 D．明清时期5.战国时期社会大变革的最主要表现是A．争霸战争频繁 B．铁器、牛耕使用 C．封建制度确立 D．诸子百家争鸣6.读右图，商鞅变法发生在何处？A．① B．②C．③ D．④、7.《论语》是大思想家孔子的语录，宋代宰相赵普有“半部论语治天下”之说。

孔子思想的核心主张是A．“仁”和“礼” B．“因材施教” C．“为政以德” D．“有教无类”8.《大汉天子》是近几年的一部热播电视剧，“大汉天子”为推进我国首次大一统格局做出了重要贡献。

在加强中央对地方的控制方面，他采取的最重要一项措施是A．设司隶校尉 B．实行“推恩令” C．北击匈奴 D.“罢黜百家，独尊儒术”9.汉朝时，派使臣出使大秦，他从长安出发，沿丝绸之路西行，先后要经过的地点是①今新疆境内②河西走廊③西亚④大秦A．①②③④ B．②①③④ C．①②④③ D．②①④③10.中华民族传统文化的瑰宝中医药，越来越受到世界各国的重视和欢迎。

下列人物中，对中国古代医学做出重大贡献的是A．张衡屈原 B．宋应星李时 C．蔡伦张仲景 D．张仲景李时珍11.下列史实，可以通过右图所示著作了解的有①秦始皇统一货币、文字②汉武帝在长安举办太学③宦官蔡伦改进造纸技术④李春设计并主持修建赵州A．①② B．②③ C．①③ D．②④12.电视剧《三国》的热播引起了人们对曹操的关注。

2011年美赛a题

Team #9262Perfect Half-pipe: The Think ofSnowboard CourseAbstractWith the continuous progress and development, People are actively involved in sports and exploring in it continually. Skiing is popular with the majority of sports fans gradually under this condition. Especially，Snowboarding with good view, challenge and the basis of the masses develops rapidly and has become a major Olympic projects. In this paper, how to design and optimize the snowboard course of half pipe is discussed in detail. We strive to get the perfect course so that snowboarders can achieve the best motion state in the established physical conditions. What’s more, it may promote the development of the sport.This problem can be divided into three modules to discuss and solve. For the first problem of the design of half pipe, it can be based on the point of the energy conservation law. The method of functional analysis (Variation principle and Euler differential equation) is used to set up equations, when the secondary cause is ignored and the boundary conditions are taken into consideration. The curve equation is obtained by the above equation, that is, a skilled snowboarder can make the maximum production of “vertical air”.For the second question, athletes’ maximum twist in the air and some other factors need to be taken into account when to optimize the previous model, so that curve can meet the actual game conditions and appraisal requirements as much as possible. Ultimately, a satisfying curve will be got. The third problem is a problem relatively close contact with the actual, which is to setting down a series of tradeoffs that may be required to develop a “practical” course. In this paper, for the formulation of these factors, the main discussions are the thickness of snow on half pipe and the aspect of economy for the construction.After discussing these three aspects, the paper finally summarizes a construction program and evaluation criteria of the course in current conditions. Finally, by evaluating the advantages and disadvantages of the whole model，we put forward the advanced nature of the model, but also point out some limitations of the model.Key words: Snowboard course, Half-pipe,Functional, Euler equation, Fitted curve,Numerical differentiationTable of contentsTable of contents (1)I. Introduction (2)1.1 Half pipe structure (2)1.2 Background problem (3)1.3 Athletes aerials (3)1.4 A ssume (3)II. Models (5)2.1 problem one (5)2.2 P roblem two (11)2.3 Problem three (13)III. Conclusions (14)I V. Future Work (15)V. Model evaluation (15)5.1 Model Advantages (15)5.2 Model disadvantage s (16)VI. References (17)I. IntroductionSnowboarding is a popular pool game with the world of sports. The U-Snowboard’ length is generally 100-140m , U-type with a width of 14-18m,U-type Depth of 3-4.5m.the slope is 14°-18 °. In competition U-athletes Skate within the taxi ramp edge making the use of slide to do all sorts of spins and jumps action. The referees score according to the athletes’ performance as the Vertical air and the difficulty and effectiveness of action. The actions Consist mainly of the leaping grab the board, leaping catch of non-board , rotating leaping upside down and so on.1.1 Half pipe structureHalf pipe structure contains: steel body frame, slide board, steps to help slide and rails.1.2 Background problemIn order to improve the movement of the watch, it can be improved from two aspects: orbit and the athletes themselves. Now according to the problem the orbit can be designed as a curve. on the curve the athletes can get a maximum speed. The design of orbit includes a wide range of content, such as the shape of U-groove design, track gradient, width and length designed to help the design of sliding section, and so on. The rational design of half pipe can be achieved to transform the energy to efficiency power, make the athletes achieve the best performance in the initial state of the air. This paper discusses the rational design of half pipe to these issues.1.3 Athletes aerialsAthletes on the hillside covering with thick snow skill down with the inertia of the platform, jump into the air, and complete a variety of twists or somersault. Rating criteria: vacated, takeoff, height and distance accounted for 20%; body posture and the level of skill accounted for50%; landing 30%. According to the provisions the difficulty of movements are ranged into small, medium and large. The athletes option the actions. However, the ground must have a slope of about 37 ° and 60 cm above the soft snow layer.1.4 AssumeIn order to simplify the model and can come to a feasible solution,making the following assumptions:1• the shape of a snowboard course has a lowest point, the wide and the length of the snowboard course.2• air resistance can be negligible.3• it is assumed that the athletes themselve s have no influence.II. The Description of the ProblemThis problem is a typical engineering design, involving a lot of disciplines, such as advanced mathematics, engineering mathematics, mechanical dynamics and biological dynamics, as well as the relevant provisions of sports competition and judging standards, and so on. According to the requirement of the problem, determine the shape of a snowboard course to maximize the production of “vertical air” by a skilled snowboarder. For this problem, we can use the boundary conditions and site properties (e.g. symmetry) and other requirements to establish functional combining with the variation principle Euler equations. The original equation can be changed into a functional extremum problem.Secondly, we optimize the model boundary and determine the appropriate snowboard course’s slope toe to make the athletes perform maximum twist or do more difficult action.Finally a practical model should meet the requirements of safety, sustainability and economic. According to the high degree of humansecurity, the source of the snow and the topography the model will be optimized more reasonable.II. Models2.1 problem oneAs shown （3.1）A is the lowest point of the snowboard course.From A to B we want to find a curve to make the athletes get the maximum vertical distance above the edge of the snowboard course.Figure 1 Half-pipeSet A as origin of coordinate.Awing of conservation energy and neglecting air resistance, the mathematical function is,f A mgh mv W mv ++=+2202121 (1)Wherev 0 is the initial velocity （m/h ）,v is the velocity towards destination （m/h ）,m is the mass of an athlete (kg),w is the energy which is made by the athlete (J),h is the Vertical height (m),Af is the friction work （J ），According to mechanical analysis ：rv m mg N 2cos =-θ （2）Where θ is the angle the angle between the tangent and the horizontal line, N is the pressure on the object,r is the radius of curvature,According to friction formula ：⎪⎪⎭⎫ ⎝⎛+==r v m mg N f 2cos θμμ （3） To (3) into equation (1), combined with calculus ：⎰⎪⎪⎭⎫ ⎝⎛+++=+s t dl r v m mg mgh mv W mv 02220cos 2121θμ （4） Friction acting A f ：⎰⎰+=⎪⎪⎭⎫ ⎝⎛+=st st f dl r v m mgB dl r v m mg A 02022cos μμθμ （5）Use higher mathematics ：()'''1232y y r += （6）dx y dl 2'1+= （7）According to the nature of the curve, the speed can be assumed to satisfy this expression ：kx e v v 10= （8）Put all these formulas in order and suppose the expression for the functional ：dx y e y mv dl r v m B kx s t ⎰⎰+==∏20222002'1''μμ （9） Set 2220'1''y e y mv F kx +=μ （10）Reference Euler equation ：0'''22=⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎪⎭⎫ ⎝⎛∂∂-∂∂y F dx d y F dx d y F （11） Obtained ：0=∂∂yF （12）()232220'1''''y e y y mv y F kx +-=∂∂μ （13）()212220'1''y e mv y F kx +=∂∂μ （14） To （12）-（14）into equation （11），Obtained ：()()⎪⎪⎪⎭⎫ ⎝⎛+=⎪⎪⎪⎭⎫⎝⎛+-21222022232220'1'1'''y e mv dx d y e y y mv dx d kx kx μμ（15） Integrate it ：()()C y e mv dx d y e y y mv kx kx +⎪⎪⎪⎭⎫⎝⎛+=+-212220232220'1'1'''μμ（16） Simplified ：()()()C y e y ymv y e mv k y e y y mv kx kx kx ++++=+252220232220232220'1'''3'12'1'''μμμ（17） ()'2''12''32y y y k y -+=（18） Suppose ： ()y p dx dy=So ： dy dpp dx dy dy dp dx y d =⋅=22Substituted into the above equation ：()p p p k dy dp p 21232-+= （19）()kdy p dp p p212224=+- （20） Integrate it ： ()⎰⎰=+-kdy p dp p p 212224 （21） Obtained the final results ：02arctan 33313=+-+-c ky p p p （22） For the difficult equation, we obtain numerical solutions by numerical differentiation, and then obtained function equation by numerical fitting method ：Discrete interval [0,8],Wheretake steps ：h = 1.Each point xi, i = 0,1, …… 8.Every interval [x i , x i +1],the boundary conditions ： y (0) = 0, y '(0) = 0.Into the formula （22） for the boundary conditions ：C = 0Put h y y y i i -=+1' into formula （22）：02arctan 33311131=-⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-+++i i i i i i i ky h y y h y y h y yNumerical Solution of each point is obtained in turn：x 0 1 2 3 4 5 6 7 8 y 0 0.0069 0.0094 0.0336 0.1329 0.3669 0.7872 1.4127 4.0382 Functions images and function equation are obtained by numericalfitting on Excel：Figure 2 The results of the numerical solution of the fitting imageAfter fitting the equation：y = 0.0003x6 - 0.0063x5 + 0.0435x4 - 0.1289x3 + 0.1594x2 - 0.0571x -0.0008 （23）Then the entire image can be got by symmetry along the y-axis. This models of problem one can be solved.2.2 Problem twoOn question 2, its main purpose is to improve the model in problemone under the condition of meeting the requirements of other possiblecases. Analyze other possible requirements which include a number ofaspects, such as the maximum twist in the air, players’ safety when they leave the ground and the stability of athletes when they land. Among them, we mainly consider the maximum twist of snowboarder in the air.When players leave the ground, they are only affected by gravity and air resistance. We ignore the players’ adjust ment in the air. After the project flying out of the ground, in order to analyzing simply and thinking clearly, the velocity of the object is divided into lines velocity and angular velocity. Velocity contains components of three different directions: horizontal, vertical and longitudinal. Angular velocity consists of somersault angular velocity and twist angular velocity.Figure 3 Flip velocity analysisAfter athletes flying out of the course, the velocity of longitudinal depends on a rational allocation of their own energy when they ski, so the design of course can not be considered. Vertical speed determines the maximum height with which athletes fly out of the course. So it is therequirement for design of the maximum “vertical air ”. For the horizontal velocity, players’ reaction force when they leave the course should be taken into account. And the horizontal velocity generated by reaction force must satisfy the equation below.x V V ≥' （24）Thus it can ensure that athletes fall back to ground safely after flying out, as the same time, it also meet appreciation, technical and safety requirements. On the problem that athletes reverse in the air, Conservation of energy can be used in the cross section.22222222112121212121212121y x af p y x mv mv w J w J A W m mv ++++=++（25）WhereV is the velocity of each state,Wf is the effective bio-energy an athlete release,J is the moment of inertia under different rotations,Aaf is the energy dissipated by air resistance.By checking the literature, moment of inertia J1 is 1.1(2m kg ⋅) and J2 is84.3(2m kg ⋅ ). Combining with the known data, we get the relationshipof w1, w2,y V . According to the value of V , the relationship of x V and y V will be got. The boundary angle is α.Fromtan∠α= y V/x V∠α=83.30So the boundary angle is 83.302.3 Problem threeIn practice, there are many factors to consider, for example, the thickness of snow covering and the construction of the economy, in addition to shape. The topography should be made the best use of to save project cost. Climate also is a constraint. Snow can be smoother and be used longer when the weather is cold.III. ConclusionsThe basis of this model is snowboarding skilled players can generate the maximum vertical air. Awing of numsolve and fitted the mathematical function is,y = 0.0003x6- 0.0063x5+ 0.0435x4- 0.1289x3+ 0.1594x2- 0.0571x -0.0008h=4(m) x0=8(m)∠α=83.30slope angle ∠θ= 180 （International recommended values）Figure 4 Half-pipeThe ultimate resolution of model takes various factors into account. The model can be applied to other similar improvements similar problems, such as the design of emergency chute.IV. Future WorkAlthough this paper considered a wide variety, but only one purpose getting the best track shape. However, in the actual construction process the aims to be achieved are complex and the design aspects are various. If you want to continue the track design, the following areas to be discussed，1. The run-up route’s height and inclination.2. Design of the best athletes’ running track. In the process you need to consider artistic, challenging and security.3. Design the length of the orbit to make athletes can efficiently complete the 5-8 vacated performances.V. Model evaluation5.1 Model Advantages(1). this model is infusion and the result is intuitive.(2). this paper has Strong theory with calculating the best shape theory.(3). This Problem is close to the real life situation, because of considered comprehensive.5.2 Model DisadvantagesSolving the model is complicated and some factors only have the qualitative analysis and not quantitative discussion.VI. References[1] Jason W. Harding , Kristine Toohey, David T. Martin1, Allan G. Hahn, Daniel A. James . 6/2008. TECHNOLOGY AND HALF-PIPE SNOWBOARD COMPETITION –INSIGHT FROM ELITE-LEVEL JUDGES. ISEA.[2] Wu Wei,Xia Xiujun. 2006. Half-pipe snow-board skiing skill training field in summer Explore and Design. China.[3]Xiao Ningning,Gao Jun.2009. Research of the Technical Characteristics of Half-pipe Snowboarding.China.[4] Building A Zaugg Half-Pipe.America. /resort/pipegroomers/pipe.shtml[5] Olympic Half Pipe Snowboarding ./way_5150384_olympic-half-pipe-snowboardi ng-rules.html[6]The Physics Of Snowboarding./physics-of-snowboard ing.html。

USACO 三月份试题

USACO 三月份试题简体中文版本By xzh************************************华丽的分割线*******************************青铜组问题************************************华丽的分割线*******************************四道题目，编号从11到14************************************华丽的分割线*******************************问题11：极品飞车贝西正在为一场即将到来的大奖赛准备她的赛车。

她希望购买一些部件来提高这辆赛车的性能。

他的赛车质量为M (1 <= M <= 1,000)，加速度为(1 <= F <= 1,000,000)。

在赛车的配件店有N(1 <= N <= 20)个零件，编号分别为1到N。

只要他愿意，贝西可以买任意多个或者任意少个零件。

第P_i个零件增加加速度F_i (1 <= F_i <= 1,000,000)，同时重量为M_i (1 <= M_i <= 1,000)。

根据牛顿第二定律，F=MA，F为加速度，M为质量，A为速度。

为了使她的赛车最大限度的发挥它的加速度的同时减少重量，她应该安装哪些组件？假设一辆赛车，他的初始加速度为1500，初始重量为100，有四种零件可以选择：i F_i M_i1 250 252 150 93 120 54 200 8如果只添加零件2，他的速度将是(1500+150)/(100+9) = 1650/109 = 15.13761。

下面是一个表格，表现了添加或不添加不同的零件后赛车的速度。

（0表示未添加，1表示已添加）部件总和总和1234 F M F/M0000 1500 100 15.00000001 1700 108 15.74070010 1620 105 15.42860011 1820 113 16.10620100 1650 109 15.13760101 1850 117 15.81200110 1770 114 15.52630111 1970 122 16.1475 <-- 最高的F/M1000 1750 125 14.00001001 1950 133 14.66171010 1870 130 14.38461011 2070 138 15.00001100 1900 134 14.17911101 2100 142 14.78871110 2020 139 14.53241111 2220 147 15.1020最终，最佳的方案是选择2，3和4号部件问题名称: boost输入格式：第一行：三个整数：F,M和N从第二行到第N+1行：第I+1行有两个整数：F_i和M_i样例输入：(文件boost.in):1500 100 4250 25150 9120 5200 8输出格式第一到P行：P个贝西应该给他的赛车增加的额外部件的编号，每个一行。

2011年高尔夫重大赛事

2011年高尔夫国内、国外重要赛事
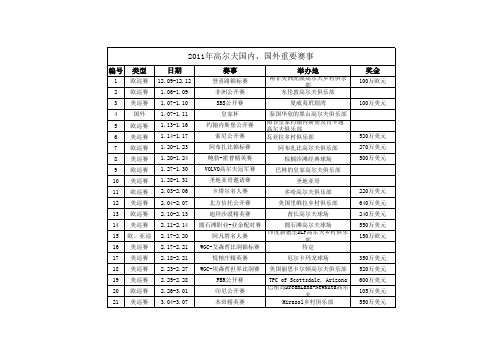
编号
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
类型
欧巡赛欧巡赛美巡赛国外欧巡赛美巡赛欧巡赛美巡赛欧巡赛美巡赛欧巡赛美巡赛欧巡赛美巡赛欧、亚巡美巡赛美巡赛美巡赛美巡赛欧巡赛美巡赛
爱尔兰公开赛绿蔷薇精英赛 WGC-普利司通邀请赛旋石锦标赛英格兰公开赛美国PGA锦标赛捷克公开赛温丹锦标赛尊尼获加锦标赛巴克莱高球赛欧米茄欧洲大师赛德意志银行锦标赛荷兰公开赛宝马锦标赛英国大师赛维旺迪杯法国Canal+公开赛奥地利公开赛巡回锦标赛登喜路林克斯锦标赛科隆韩国公开赛新中国赛事马德里大师赛塞弗杯
4.07-4.10 大满贯、美、欧巡赛欧巡赛美巡赛欧巡赛美巡赛 4.14-4.17 4.15-4.18 4.21-4.24 4.22-4.25 4.28-5.01 4.29-5.02 5.05-5.08 5.05-5.08 5.06-5.09 5.07-5.10 5.12-5.15 5.13-5.16 5.12-5.15
10.13-10.16 10.13-10.16 10.20-10.23 10.27-10.30 11月 11月 11.03-11.06 11.10-11.13 11.17-11.20 11.24-11.27 12.01-12.04 12.08-12.11 12.08-12.11
葡萄牙大师赛美的中国精英赛卡斯特扬大师赛安达卢西亚大师赛澳大利亚公开赛澳大利亚PGA锦标赛 WGC-汇丰冠军赛新加坡公开赛柔佛公开赛欧米茄观澜湖世界杯瑞银香港公开赛迪拜世界高尔夫锦标赛新同一亚洲锦标赛

USACO月赛题解（PDF）

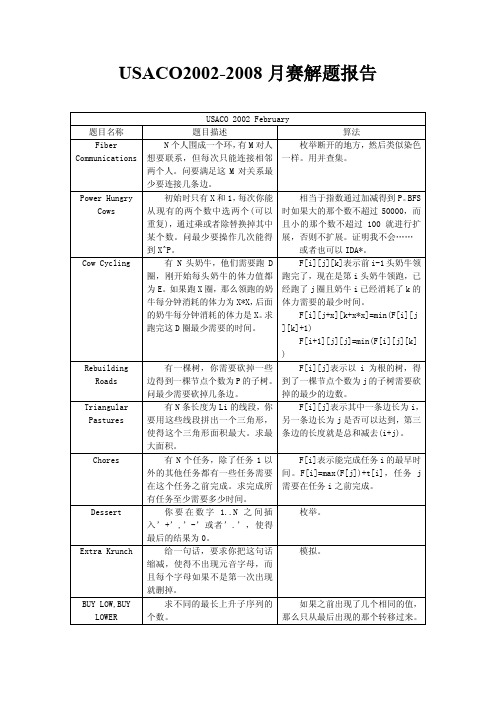
USACO2002-2008月赛解题报告USACO 2002 February题目名称题目描述算法Fiber CommunicationsN个人围成一个环，有M对人想要联系，但每次只能连接相邻两个人。

问要满足这M对关系最少要连接几条边。

枚举断开的地方，然后类似染色一样。

用并查集。

Power HungryCows初始时只有X和1，每次你能从现有的两个数中选两个(可以重复)，通过乘或者除替换掉其中某个数。

问最少要操作几次能得到X^P。

相当于指数通过加减得到P。

BFS时如果大的那个数不超过50000，而且小的那个数不超过100就进行扩展，否则不扩展。

证明我不会……或者也可以IDA*。

Cow Cycling 有N头奶牛，他们需要跑D圈，刚开始每头奶牛的体力值都为E。

如果跑X圈，那么领跑的奶牛每分钟消耗的体力为X*X，后面的奶牛每分钟消耗的体力是X。

求跑完这D圈最少需要的时间。

F[i][j][k]表示前i-1头奶牛领跑完了，现在是第i头奶牛领跑，已经跑了j圈且奶牛i已经消耗了k的体力需要的最少时间。

F[i][j+x][k+x*x]=min(F[i][j ][k]+1)F[i+1][j][j]=min(F[i][j][k] )Rebuilding Roads有一棵树，你需要砍掉一些边得到一棵节点个数为P的子树。

问最少需要砍掉几条边。

F[i][j]表示以i为根的树，得到了一棵节点个数为j的子树需要砍掉的最少的边数。

Triangular Pastures有N条长度为Li的线段，你要用这些线段拼出一个三角形，使得这个三角形面积最大。

求最大面积。

F[i][j]表示其中一条边长为i，另一条边长为j是否可以达到，第三条边的长度就是总和减去(i+j)。

Chores 有N个任务，除了任务1以外的其他任务都有一些任务需要在这个任务之前完成。

求完成所有任务至少需要多少时间。

F[i]表示能完成任务i的最早时间。

F[i]=max(F[j])+t[i]，任务j 需要在任务i之前完成。

2011美赛题目

2011 Contest ProblemsMCM PROBLEMSPROBLEM A: Snowboard CourseDetermine the shape of a snowboard course (currently known as a “halfpipe”) to maximize the production of “vertical air” by a skilled snowboarder."Vertical air" is the maximum vertical distance above the edge of the halfpipe.Tailor the shape to optimize other possible requirements, such as maximum twist in the air.What tradeoffs may be required to develop a “practical” course?MCM-A题中文翻译确定单板滑雪比赛的场地的形状，也叫U池（半管道），使得选手能达到最大的垂直高度。

调整一下其形状，使之可以最优化地满足其他的要求，如在空中最大的旋转。

建一个实用的场地，哪些因素是必须的？PROBLEM B: Repeater CoordinationThe VHF radio spectrum involves line-of-sight transmission and reception. This limitation can be overcome by “repeaters,” which p ick up weak signals, amplify them, and retransmit them on a different frequency. Thus, using a repeater, low-power users (such as mobile stations) can communicate with one another in situations where direct user-to-user contact would not be possible. However, repeaters can interfere with one another unless they are far enough apart or transmit on sufficiently separated frequencies.In addition to geographical separation, the “continuous tone-coded squelch system” (CTCSS), sometimes nicknamed “private line” (PL), technology can be used to mitigate interference problems. This system associates to each repeater a separate subaudible tone that is transmitted by all users who wish to communicate through that repeater. The repeater responds only to received signals with its specific PL tone. With this system, two nearbyrepeaters can share the same frequency pair (for receive and transmit); so more repeaters (and hence more users) can be accommodated in a particular area.For a circular flat area of radius 40 miles radius, determine the minimum number of repeaters necessary to accommodate 1,000 simultaneous users. Assume that the spectrum available is 145 to 148 MHz, the transmitter frequency in a repeater is either 600 kHz above or 600 kHz below the receiver frequency, and there are 54 different PL tones available.How does your solution change if there are 10,000 users?Discuss the case where there might be defects in line-of-sight propagation caused by mountainous areas.MCM-B题中文翻译高频无线电频谱涉及到视线距离之内的传输与接收。

美国2011年物理竞赛决赛答案

2011F=ma Contest25QUESTIONS-75MINUTESINSTRUCTIONSDO NOT OPEN THIS TEST UNTIL YOU ARE TOLD TO BEGIN•Use g=10N/kg throughout this contest.•You may write in this booklet of questions.However,you will not receive any credit for anything written in this booklet.•Your answer to each question must be marked on the optical mark answer sheet.•Select the single answer that provides the best response to each question.Please be sure to use a No.2pencil and completelyﬁll the box corresponding to your choice.If you change an answer,the previous mark must be completely erased.•Correct answers will be awarded one point;incorrect answers will result in a deduction of14point.There isno penalty for leaving an answer blank.•A hand-held calculator may be used.Its memory must be cleared of data and programs.You may use only the basic functions found on a simple scientiﬁc calculator.Calculators may not be shared.Cell phones may not be used during the exam or while the exam papers are present.You may not use any tables,books,or collections of formulas.•This test contains25multiple choice questions.Your answer to each question must be marked on the optical mark answer sheet that accompanies the test.Only the boxes preceded by numbers1through25are to be used on the answer sheet.•All questions are equally weighted,but are not necessarily the same level of diﬃculty.•In order to maintain exam security,do not communicate any information about the questions (or their answers or solutions)on this contest until after February20,2011.•The question booklet and answer sheet will be collected at the end of this exam.You may not use scratch paper.DO NOT OPEN THIS TEST UNTIL YOU ARE TOLD TO BEGIN1.A cyclist travels at a constant speed of 22.0km/hr except for a 20minute stop.The cyclist’s average speed was 17.5km/hr.How far did the cyclist travel?(A)28.5km (B)30.3km (C)31.2km (D)36.5km (E)38.9kmThe correct answer is AQuestions 2to 4refer to the three graphs below which show velocity of three objects as a function of time.Each object is moving only in one dimension.246810−20+2+4v e l o c i t y (m /s )time (s)246810−20+2+4v e l o c i t y (m /s )time (s)246810−20+2+4v e l o c i t y (m /s )time (s)Object I Object II Object III2.Rank the magnitudes of the average acceleration during the ten second interval.(A)I >II >III (B)II >I >III (C)III >II >I (D)I >II =III (E)I =II =III The correct answer is E3.Rank the magnitudes of the maximum velocity achieved during the ten second interval.(A)I >II >III (B)II >I >III (C)III >II >I (D)I >II =III (E)I =II =III The correct answer is D4.Rank the magnitudes of the distance traveled during the ten second interval.(A)I >II >III (B)II >I >III (C)III >II >I (D)I =II >III (E)I =II =III The correct answer is B5.A crude approximation is that the Earth travels in a circular orbit about the Sun at constant speed,at a distanceof150,000,000km from the Sun.Which of the following is the closest for the acceleration of the Earth in this orbit?(A)exactly0m/s2(B)0.006m/s2(C)0.6m/s2(D)6m/s2(E)10m/s2The correct answer is B6.A child is sliding out of control with velocity v c across a frozen lake.He runs head-on into another child,initiallyat rest,with3times the mass of theﬁrst child,who holds on so that the two now slide together.What is the velocity of the couple after the collision?(A)2v c(B)v c(C)v c/2(D)v c/3(E)v c/4The correct answer is E7.An ice skater can rotate about a vertical axis with an angular velocityω0by holding her arms straight out.Shecan then pull in her arms close to her body so that her angular velocity changes to2ω0,without the application of any external torque.What is the ratio of herﬁnal rotational kinetic energy to her initial rotational kinetic energy?(A)√2(B)2(C)2√2(D)4(E)8The correct answer is B8.When a block of wood with a weight of30N is completely submerged under water the buoyant force on the blockof wood from the water is50N.When the block is released itﬂoats at the surface.What fraction of the block will then be visible above the surface of the water when the block isﬂoating?(A)1/15(B)1/5(C)1/3(D)2/5(E)3/5The correct answer is D9.A spring has an equilibrium length of 2.0meters and a spring constant of 10newtons/meter.Alice is pulling on one end of the spring with a force of 3.0newtons.Bob is pulling on the opposite end of the spring with a force of 3.0newtons,in the opposite direction.What is the resulting length of the spring?(A)1.7m (B)2.0m (C)2.3m (D)2.6m (E)8.0mThe correct answer is C10.Which of the following changes will result in an increase in the period of a simple pendulum?(A)Decrease the length of the pendulum (B)Increase the mass of the pendulum(C)Increase the amplitude of the pendulum swing(D)Operate the pendulum in an elevator that is accelerating upward(E)Operate the pendulum in an elevator that is moving downward at constant speed.The correct answer is C11.A large metal cylindrical cup ﬂoats in a rectangular tub half-ﬁlled with water.The tap is placed over the cup andturned on,releasing water at a constant rate.Eventually the cup sinks to the bottom and is completely submerged.Which of the following ﬁve graphs could represent the water level in the sink as a function of time?w a t e r l e v e ltime w a t e r l e v e ltime w a t e r l e v e ltime (A)(B)(C)w a t e r l e v e ltime w a t e r l e v e ltime (D)(E)The correct answer is C12.You are given a large collection of identical heavy balls and lightweight rods.When two balls are placed at the endsof one rod and interact through their mutual gravitational attraction (as is shown on the left),the compressive force in the rod is F .Next,three balls and three rods are placed at the vertexes and edges of an equilateral triangle (as is shown on the right).What is the compressive force in each rod in the latter case?(A)1√3F (B)√32F(C)F(D)√3F (E)2FThe correct answer is C13.The apparatus in the diagram consists of a solid cylinder of radius 1cm attached at the center to two disks ofradius 2cm.It is placed on a surface where it can roll,but will not slip.A thread is wound around the central cylinder.When the thread is pulled at the angle θ=90to the horizontal (directly up),the apparatus rolls to the right.Which below is the largest value of θfor which it will not roll to the right when pulling on the thread?(A)θ=15◦(B)θ=30◦(C)θ=45◦(D)θ=60◦(E)None,the apparatus will always roll to the right The correct answer is D14.You have5diﬀerent strings with weights tied at various point,all hanging from the ceiling,and reaching down totheﬂoor.The string is released at the top,allowing the weights to fall.Which one will create a regular,uniform beating sound as the weights hit theﬂoor?(A)(B)(C)(D)(E)The correct answer is D15.A vertical mass-spring oscillator is displaced2.0cm from equilibrium.The100g mass passes through the equilib-rium point with a speed of0.75m/s.What is the spring constant of the spring?(A)90N/m(B)100N/m(C)110N/m(D)140N/m(E)160N/mThe correct answer is DQuestions16and17refer to the information and diagram below. Jonathan using rope to lift a box with Becky init;the box is hanging oﬀthe side of a bridge,Jonathan is on the top.A rope is hooked up fromthe box and passes aﬁxed railing;Jonathan holdsthe box up by pressing the rope against the rail-ing with a massless,frictionless physics textbook.The static friction coeﬃcient between the rope andrailing isµs;the kinetic friction coeﬃcient betweenthe rope and railing isµk<µs;the mass of the box and Becky combined is M;and the initial height of the bottom of the box above the ground is h. Assume a massless rope.BeckyLoose ropeFloorJonathan, pushesropefixed hardrailingon book against16.What magnitude force does Jonathan need to exert on the physics book to keep the rope from slipping?(A)Mg(B)µk Mg(C)µk Mg/µs(D)(µs+µk)Mg(E)Mg/µsThe correct answer is E17.Jonathan applies a normal force that is just enough to keep the rope from slipping.Becky makes a small jump,barely leaving contact with theﬂoor of the box.Upon landing on the box,the force of the impact causes the rope to start slipping from Jonathan’s hand.At what speed does the box smash into the ground?Assume Jonathan’s normal force does not change.(A)√2gH(µk/µs)(B)√2gH(1−µk/µs)(C)√2gHµk/µs(D)√2gH(1−µk/µs)(E)√2gH(µs−µk)The correct answer is D18.A block of mass m=3.0kg slides down one ramp,and then up a second ramp.The coeﬃcient of kinetic frictionbetween the block and each ramp isµk=0.40.The block begins at a height h1=1.0m above the horizontal.Both ramps are at a30◦incline above the horizontal.To what height above the horizontal does the block rise on the second ramp?(A)0.18m(B)0.52m(C)0.59m(D)0.69m(E)0.71mThe correct answer is AQuestions19and20refer to the following informationA particle of mass2.00kg moves under a force given byF=−(8.00N/m)(xˆi+yˆj)whereˆi andˆj are unit vectors in the x and y directions.The particle is placed at the origin with an initial velocity v=(3.00m/s)ˆi+(4.00m/s)ˆj.19.After how much time will the particleﬁrst return to the origin?(A)0.785s(B)1.26s(C)1.57s(D)2.00s(E)3.14sThe correct answer is C20.What is the maximum distance between the particle and the origin?(A)2.00m(B)2.50m(C)3.50m(D)5.00m(E)7.00mThe correct answer is B21.An engineer is given aﬁxed volume V m of metal with which to construct a spherical pressure vessel.Interestingly,assuming the vessel has thin walls and is always pressurized to near its bursting point,the amount of gas the vessel can contain,n(measured in moles),does not depend on the radius r of the vessel;instead it depends only on V m (measured in m3),the temperature T(measured in K),the ideal gas constant R(measured in J/(K·mol)),and the tensile strength of the metalσ(measured in N/m2).Which of the following gives n in terms of these parameters?(A)n=23V mσRT(B)n=233√V mσRT(C)n=233√V mσ2 RT(D)n=233√V m2σRT(E)n=233V mσ2RTThe correct answer is A22.This graph depicts the torque output of a hypothetical gasoline engine as a function of rotation frequency.Theengine is incapable of running outside of the graphed range.IIIIIIEngine Revolutions per Minute0102030O u t p u t T o r q u e (N m )1,0002,000At what engine RPM (revolutions per minute)does the engine produce maximum power?(A)I(B)At some point between I and II (C)II(D)At some point between II and III (E)IIIThe correct answer is D23.A particle is launched from the surface of a uniform,stationary spherical planet at an angle to the vertical.Theparticle travels in the absence of air resistance and eventually falls back onto the planet.Spaceman Fred describes the path of the particle as a parabola using the laws of projectile motion.Spacewoman Kate recalls from Kepler’s laws that every bound orbit around a point mass is an ellipse (or circle),and that the gravitation due to a uniform sphere is identical to that of a point mass.Which of the following best explains the discrepancy?(A)Because the experiment takes place very close to the surface of the sphere,it is no longer valid to replacethe sphere with a point mass.(B)Because the particle strikes the ground,it is not in orbit of the planet and therefore can follow a non-elliptical path.(C)Kate disregarded the fact that motions around a point mass may also be parabolas or hyperbolas.(D)Kepler’s laws only hold in the limit of large orbits.(E)The path is an ellipse,but is very close to a parabola due to the short length of the ﬂight relative to thedistance from the center of the planet.The correct answer is E24.A turntable is supported on a Teﬂon ring of inner radius R and outer radius R+δ(δ R),as shown in the diagram.To rotate the turntable at a constant rate,power must be supplied to overcome friction.The manufacturer of the turntable wishes to reduce the power required without changing the rotation rate,the weight of the turntable,or the coeﬃcient of friction of the Teﬂon surface.Engineers propose two solutions:increasing the width of the bearing (increasingδ),or increasing the radius(increasing R).What are the eﬀects of these proposed changes?(A)Increasingδhas no signiﬁcant eﬀect on the required power;increasing R increases the required power.(B)Increasingδhas no signiﬁcant eﬀect on the required power;increasing R decreases the required power.(C)Increasingδincreases the required power;increasing R has no signiﬁcant eﬀect on the required power.(D)Increasingδdecreases the required power;increasing R has no signiﬁcant eﬀect on the required power.(E)Neither change has a signiﬁcant eﬀect on the required power.The correct answer is A25.A hollow cylinder with a very thin wall(like a toilet paper tube)and a block are placed at rest at the top of aplane with inclinationθabove the horizontal.The cylinder rolls down the plane without slipping and the block slides down the plane;it is found that both objects reach the bottom of the plane simultaneously.What is the coeﬃcient of kinetic friction between the block and the plane?(A)0tanθ(B)13tanθ(C)12(D)2tanθ3(E)tanθThe correct answer is C。

2011年别克中国高尔夫球俱乐部联赛竞赛总规程

2011年别克中国高尔夫球俱乐部联赛竞赛总规程一、比赛名称2011年别克中国高尔夫球俱乐部联赛二、主办机构中国高尔夫球协会三、推广机构中奥体育产业公司四、冠名赞助商上海通用汽车有限公司别克品牌五、协办单位分区赛、复赛及总决赛举办地所属的省、自治区、直辖市高尔夫球协会（或体育局）；承办比赛的俱乐部/球会。

六、竞赛规则比赛采用由苏格兰圣安德鲁斯皇家古老高尔夫球俱乐部及美国高尔夫球协会联合颁布的2008年版《高尔夫球规则》以及竞赛委员会制定的“比赛条件”和“当地规则”。

七、赛制介绍本年度俱乐部联赛的比赛将采取三个阶段的赛事结构，具体划分如下：第一阶段：六场分区赛（在南、北大区各进行三场）。

第二阶段：两场复赛（在南、北大区各进行一场）。

第三阶段：一场年度总决赛。

八、分区赛、复赛及总决赛的时间安排1、六场分区赛：（1）南一区：4月20日-21日（2）南二区：5月11日-12日（3）南三区：6月1日-2日（4）北一区：7月6日-7日（5）北二区：7月20日-21日（6）北三区：8月3日-4日2、复赛：（1）南方区：6月15日-16日（2）北方区：8月17日-18日3、总决赛：10月27日-29日九、参加各分区赛的区域范围南一区：广东省、海南省南二区：上海市、浙江省、江苏省、安徽省、江西省、福建省南三区：重庆市、云南省、广西自治区、湖南省、四川省、贵州省北一区：河南省、陕西省、山西省、新疆自治区、甘肃省、湖北省、山东省、宁夏自治区、青海省北二区：北京市、河北省北三区：天津市、黑龙江省、吉林省、辽宁省、内蒙古自治区十、参赛资格及条件（一）中国内地拥有18洞球场的高尔夫球俱乐部为基本的参赛单位。

若目前还没有18洞球场的省份中若只有9洞球场的俱乐部也可为参赛单位。

（二）本年度的联赛将分为会员组和专业组（或称公开组，下同）分别进行比赛和排名。

每个参赛的俱乐部既可以组队分别参加会员组和专业组的比赛，也可以单独组队仅参加会员组或者专业组的比赛。

全球CG动画大赛参赛指导

2011年国际动漫节展资讯2011年1月第37届国际法国安古兰漫画艺术节时间：1月27日-1月30日地点：法国安古兰2011年2月美国国际KidScreen儿童荧屏娱乐峰会时间：2月15日-2月18日地点：美国纽约2011年比利时布鲁塞尔国际动画电影节时间：3月4日-3月13日地点：比利时布鲁塞尔2011年第１5届西班牙加泰罗尼亚国际动画电影节时间：2月24日-2月27日地点：西班牙Llotja德莱里达剧院和会议中心2011年第10届TAF东京国际动漫节时间：2011年3月24日-27日地点：日本东京主办方：东京都政府、日本动画协会、东京国际动漫博览会实行委员会2011芝加哥C2E2漫画与娱乐展览会时间：3月18日-3月20日地点：美国芝加哥伊利诺伊州麦考密克广场湖滨中心2011年5月澳大利亚国际动画节时间：5月中旬地点：澳大利亚悉尼沃加沃加雷尔街电影院2011年第18届德国斯图加特国际动画节时间：5月3-8日地点：德国斯图加特2011年5月捷克国际动画节时间：5月中旬地点：捷克共和国特普利采2011年第21届萨格勒布国际动画电影节时间：2011年5月31日-6月5日地点：南斯拉夫萨格勒布2011法国安纳西国际动画节（2011年创建51周年）时间：2011年6月6日至11日地点：法国安纳西2011加拿大班夫电视节时间：2011年6月12-15日地点：班夫2011年6月第11届澳大利亚墨尔本国际动画节时间：6月下旬地点：澳大利亚墨尔本递交作品截止日期：2011年1月19日2011年7月第4届波兰国际动画节时间：7月中旬地点：波兰波兹南2011年第15届韩国国际卡通动漫节 SICAF时间：2011年7月下旬地点：韩国首尔COEX会展中心及乐天影城举行2011年7月美国圣地亚哥动漫展Comic-Con（41周年）时间：2011年7月21日-24日地点：美国圣地亚哥2011年洛杉矶动漫博览会时间：7月1-4日地点：美国洛杉矶2011年8月日本广岛动画节时间：2011年8上旬地点：日本广岛2011年8月伦敦国际动画节时间：8月下旬地点：英国伦敦2011年9月第9届瑞士Fantoche国际动画电影节时间：9月6日-9月11日地点：瑞士巴登2011年第13届富川国际漫画节时间：9月中旬地点：富川动漫信息中心2011年9月第22届欧洲卡通论坛时间：2011年9月13日-9月16日地点：波兰2011第15届年荷兰国际动漫节时间：2011年11月上旬地点：荷兰2011年第35届葡萄牙国际动画电影节时间：11月上旬地点：葡萄牙埃斯皮纽2011美国红树枝国际动画节时间：11月中旬地点：美国路易斯安那州2011第38届国际韩国计算机图形及交互技术国际会议及展览时间：12月中旬地点：韩国首尔2011瑞士卢塞恩国际动画学术会时间：12月，具体待告地点：瑞士卢塞恩全球CG动画大赛参赛指导重点CG赛事参赛精析美国SIGGRAPH盛会法国昂西国际动画节其他国际知名CG天赛巡礼美国安尼奖国际电视包装设计奖美国红树枝国际动画节美国奥斯卡奖Flash发展会议Flash电影节渥太华国际动画节英国国际学生动画＆电脑游戏节英国仲夏广告节英国伦敦国际动画节斯图加特国际动画节莱比锡国际动画节和记录电影节德国柏林短片电影节捷克国际动画电影节荷兰动画电影节萨格勒布国际动画节意大利城堡国际动画片节葡萄牙埃斯平霍国际动画电影节墨尔本国际动画节广岛国际动画节东京国际动画节首尔国际卡通动画节富川国际学生动画节杭州国际动漫节中国（常州）国际动漫艺术周CCGF数字图像中国节北京电影学院动画学院学院奖中国（北京）国际大学生动画节参赛锦囊A.1竞赛参赛流程概述A.2把握制作周期流程图概述分析任务进度安排执行计划后期修改和经验总结资源的合理配置A.3参赛报名表的填写规范英文常用语及国人参赛作品索引B.1参赛中英文索引B.2近年中国动画人海外参赛作品列表（部分）世界五大知名动画节红树枝国际动画节、韩国首尔动画节、法国昂西动画节、加拿大渥太华动画节、希腊雅典动画节其他动画节东京国际动画节中国国际大学生动画节中国动画节/中国国际卡通产业高峰论坛中国杭州国际动画节中国常州国际数码动画节北京国际CG大赛上海国际CG大赛中国动画协会2005成就奖中国电影金鸡奖与华表最佳美术片提名奖加拿大渥太华动画节加拿大OTTAW AINTERNATIONAL2009加拿大渥太华国际动画节海报ANIIATION FESTIV AL 渥太华国际动画节时间：每年九月中旬或下旬地点：渥太华全称：渥太华国际动画节参赛理由四大国际动画电影节之一，比较有个性，最大的特点就是对商业性的作品“不屑一顾”——或者说是不看重，如果你的作品属于实验性质或者其他不带商业气息的片子，而且自信够另类、够特色，不用害怕，就试试这个！赛事简介国际知名的四大动画节之一——渥太华国际动画节一直都在努力随着动画行业的发展而改进，经过漫长的发展岁月，它已经成为一个非常有组织性、各方面成熟完善的大型综合动画盛会，参赛人数逐年增加，而且作品都是非常有个性的精品。

2011年全世界自行车各项赛事的时间表

2011年全世界自行车各项赛事的时间表2011年公路自行车赛程日期赛事比赛地1月18-23日环澳大利亚自行车赛澳大利亚3月6-13日巴黎-尼斯自行车赛法国3月9-15日蒂伦诺-亚德里亚蒂科赛意大利3月19日米兰-圣里诺赛意大利3月21-27日加泰罗尼亚赛西班牙3月27日根特-韦弗尔海姆赛比利时4月3日环弗兰德雷斯赛比利时4月4-9日Vuelta Ciclista al Pais Vasco 西班牙4月10日巴黎-鲁拜克斯赛法国4月17日阿姆斯特尔黄金赛荷兰4月20日拉弗莱舍-瓦隆赛比利时4月24日列日-巴斯托涅-列日赛比利时4月26日-5月1日Tour de Romandie 瑞士5月7-29日环意大利赛意大利6月5-12日多菲纳自由报赛法国6月11-19日环瑞士自行车赛瑞士7月2-24日环法自行车赛法国7月30日圣塞巴斯蒂安赛西班牙7月31日-8月6日环波兰自行车赛波兰8月20日-9月11日环西班牙自行车赛西班牙8月28日普卢艾大奖赛法国9月9日魁北克大奖赛加拿大9月11日蒙特利尔大奖赛加拿大10月15日伦巴第大奖赛意大利2011年场地自行车赛程1月21-23日场地自行车世界杯中国站中国北京3月23-27日场地自行车世锦赛荷兰阿珀尔多伦2011年诺迪维自行车赛事日程及介绍黄山国际山地车节，宏村2011年4月9日☆中国第一个国际山地车马拉松比赛☆业余和专业、国内外车手相聚、互相交流的机会☆赛场设立在风景如画的黄山联合国世界遗产地——宏村和西递☆第一无二的精彩赛道：国家山地车队伍的固定训练场地☆中国山地车专业运动员做客，30分钟电视直播，CCTV-5等电视台现场报道，专题转播☆50公里马拉松比赛，25公里山地车精英挑战赛和团体接力赛中国铁木真国际山地车挑战赛，内蒙古西乌旗2011年7月1-3日☆横过广阔的内蒙古草原，寻找成吉思汗的脚印☆连续3天的184公里山地车分站赛——长距离为精英选手所设，短距离为普通爱好者所设☆住蒙古包、骑蒙古马、吃全烤羊、享受激情澎湃的篝火派对☆挑战体能极限，领略异域风光中国毕克国际山地车节，牙克石2011年9月10日☆世界上最大的山地车比赛——挪威毕克山地车赛的姐妹赛事☆挑战50公里或25公里中国最北的大兴安岭赛道，给选手以终身难忘的经历☆中国毕克国际山地车节与挪威毕克组委会合作，前两名最佳男女中国选手有机会参加挪威毕克山地车节☆比赛赛道设在大兴安岭——中国最大的森林区，原始，壮丽，天然，资源丰富中国瓦腾国际自行车节，云南玉溪2011年10月☆瑞典瓦腾自行车节——世界上最大的锻炼性自行车赛道的姐妹赛事☆骑行环绕神话中的抚仙湖，挑战180公里赛道☆激烈冲刺或以自己的节奏享受骑行在大自然美景中的快感☆在自行车上看五彩的小数民族文化和如诗如画般的人间仙境长城国际自行车嘉年华，北京☆极有挑战性又有趣味的山地车和小轮车比赛在老山奥运自行车赛场进行！☆丰富赛程：业余赛、专业赛、团队接力赛和儿童游乐赛☆杂技表演、音乐和娱乐、饮料和美食！☆带着亲朋好友、家人或同事们参加中国山地车手最喜爱的比赛之一☆首都庆祝自行车运动的无限魅力！上海国际自行车嘉年华，2011年5月☆在中国唯一的方程式赛车场——上海国际赛车场F1赛道上的自行车比赛☆体验F1赛道风驰电掣的速度之战☆为各路爱好者提供的精彩比赛和欢乐节日☆赛事设置：男女个人计时赛、团队接力赛、男女精英赛等通过多年来专业知识，多元文化和实践经验的积累以及与各级政府部门、体育机构长期而紧密地合作，诺迪维为各品牌赛事的商业战略合作伙伴量身制作市场推广、公关以及公司拓展活动的黄金平台。

我校学子荣获2011年美国数学建模竞赛二等奖

我校学子荣获2011年美国数学建模竞赛二等奖4月18日，从数学建模美国赛官网获悉，泉州师院数计学院学生吕珊珊、蔡星孟、隋劼组队获得二等奖(Honorable Mention)。

本次数学建模美国赛于北京时间2月11日上午九点至2月15日九点进行，正值农历新年(初九至十二)，参赛师生克服重重困难，努力拼搏，取得了较好的成绩。

本次竞赛（MCM）的两道赛题分别为“关于滑雪赛道优化设计”、“关于转发器协调配置”，要求在4天时间内，各参赛队（队员不超过3人）需要选择其中一题，利用所学数学知识将实际问题转化成数学问题，进行数学建模，并最终提交论文。

论文的优劣主要依据参赛队在解决实际问题中采用的方法和建立的模型的具体步骤来判断。

该竞赛要求参赛选手具备扎实的数学、计算机和论文写作功底，并且需要高水平的学术英文表达能力。

数学建模美国赛面向全球，通过网络报名，是数学建模领域的国际性权威赛事。

该竞赛以通讯赛的形式举行，每年举办一次。

哈佛大学、麻省理工学院、北京大学、清华大学等国内外名校，每年都会有学生参加各奖项的角逐，是目前大学生各类竞赛中级别最高的一项赛事。

2011年国际大学生数学建模竞赛，吸引了全球高校3000多支队伍参赛。

美国大学生数学建模竞赛包括数学建模竞赛（MCM）和交叉学科数学建模竞赛（ICM）。

该赛事从1985年开始举办，由美国数学及其应用联合会组织，得到美国国家科学基金、美国数学及其应用联合会、美国运筹学及管理科学研究所等单位资助，是当前世界上唯一的国际性学生数学建模竞赛，该赛事一般在每年的2月份举办，设有特等奖（Outstanding Winner / Finalist）、一等奖（Meritorious Winner）、二等奖（Honorable Mentions）和三等奖（Successful Participant）。

2011体育大事件日程表

全国各地
★★★
12日、15日、20日、26日
均有比赛
2月12-13日
柔道
男子世界杯匈牙利站
匈牙利布达佩斯
★★
2月12-13日
柔道
女子世界杯奥地利站
奥地利维也纳
★★
2月12日
滑雪
自由式滑雪世界杯俄罗斯站
莫斯科
★★
2月12-13日
速滑
速度滑冰全能世锦赛
卡尔加里
★★★
2月13日
排球
全国男排联赛甲A
全国各地
WTA
科尔萨尼塔斯杯
波哥大
★★
2月14日-20日
ATP
电信杯
布宜诺斯艾利斯
★★
2月14日-20日
ATP
马赛13公开赛
马赛
★★
2月14日-20日
ATP
摩根基根冠军赛
孟菲斯
★★
2月15日-19日
乒乓球
科威特公开赛
科威特
★★★
2月15-20日
花样滑冰
花滑四大洲赛
中华台北
★★
2月15日-20日
羽毛球
欧洲混合团体锦标赛
3月7日-17日
ATP
巴黎银行赛大师赛
印第安维尔斯
★★★★
3月8-13日
跳水
欧洲跳水锦标赛
意大利都灵
★★
3月8日-13日
羽毛球
全英超级赛
伯明翰
★★★★
3月9日-22日
WTA
巴黎银行公开赛
印第安维尔斯
★★★
3月9-10日
足球
欧冠1/8决赛次回合
待定
★★★★
3月10日-13日