X-R图解析
均值-极差控制图(x-R)

X匀值:是通过每组样本的平均值得出的,然后把每组的平均值相加除以组数,得到总的平均值。
R 匀值:是通过每组两个极端值得到的,就是每组的最大值-最小值,等于每组的极差,再通过每组的极差值来计算总的极差平均值平均极差分布及控制图常数表2 用EXCEL软件绘均值一极差控制图(rR图)2.1 绘图方法2.1.1 EXCEL软件的作用随着计算机技术的不断发展,尤其是计算速度的不断加快,使其在办公领域得以充分应用.一些软件不但能制表,还能绘图,使质量管理工作也上了一个新水平。
近来,笔者尝试用EXCEL 绘均值一极差控制图( R 图),以使质量管理工作更方便、更快捷。
2.1.2 应用示例现以齿条总高为例,用EXCEL软件绘a—R 图.设共有25组数据,样本大小为5,其操作过程如下。
2.1.2.1 打开EXCEL软件中的一个工作薄,选择其中一个工作表.2.1.2.2 在第1行输入表头。
2.1_2.3 在第l列单元格输入样本编号:选定要填充的第1个单元格A2,输入1,A3格输入2,选择A2、A3格将鼠标移到A3格右下角的填充柄上,当鼠标指针变成小黑十字时,按鼠标左键在要填充的区域上拖动(即从A4到A26),松开鼠标左键,填充自动完成。
2.1.2.4 在第2列单元格输入标准值:选定单元格B2,输入2.8,将鼠标移到B2格右下角的填充柄上,当鼠标指针变成小黑十字时,按鼠标左键在B3到B26格上拖动,松开鼠标左键填充自动完成. 2.1.2.5 将收集到的数据输入表中。
2.1.2.6 计算均值:选定H2,选“常用”工具栏中的“粘贴函数"(即厂 ),出现“粘贴函数”对话框,在函数分类栏中选“常用函数”,在函数名栏中选“AV—ERAGE”,点“确定”,在“Number1"栏中输入“C2:G2”,点“确定”,即求得一个均值,选定H2格,点常用工具栏中的“复制”,再选定H3到H26,选“常用”工具栏中的“粘贴”,即求出其余24个均值. 2.1.2.7 计算极差的方法与计算均值大致相同,其公式为:R=max(B2:F2)~min(B2:F2)并将单元格的位置作相应变化。
均值和极差图(X-R)

均值和极差图(X-R)一、收集数据以样本容量恒定的子组形式报告,子组通常包括2-5件连续的产品,并周性期的抽取子组。
注:应制定一个收集数据的计划,将其作为收集、记录及描图的依据。
1. 选择子组大小,频率和数据a)子组大小:一般为5件连续的产品,仅代表单一刀具/冲头/过程流等。
(注:数据仅代表单一刀具、冲头、模具等生产出来的零件,即一个单一的生产流。
)b)子组频率:在适当的时间内收集足够的数据,这样子组才能反映潜在的变化,这些变化原因可能是换班/操作人员更换/材料批次不同等原因引起。
对正在生产的产品进行监测的子组频率可以是每班2次,或一小时一次等。
c)子组数:子组越多,变差越有机会出现。
一般为25组,首次使用管制图选用35 组数据,以便调整。
2. 建立控制图及记录原始数据(见下图)3. 计算每个子组的均值(X)和极差R对每个子组计算:X=(X1+X2+…+Xn)/ nR=Xmax-Xmin式中: X1 ,X2 • • • •为子组内的每个测量值。
n 表示子组的样本容量4. 选择控制图的刻度4-1两个控制图的纵坐标分别用于 X 和 R 的测量值。
4-2刻度选择:对于X 图,坐标上的刻度值的最大值与最小值的差应至少为子组均值(X)的最大值与最小值的差的2倍,对于R图坐标上的刻度值的最大值与最小值的差应为初始阶段所遇到的最大极差(R)的2倍。
注:一个有用的建议是将 R 图的刻度值设置为 X 图刻度值的2倍。
(例如:平均值图上1个刻度代表0.01英寸,则在极差图上1个刻度代表0.02英寸)5. 将均值和极差画到控制图上5-1 X 图和 R 图上的点描好后及时用直线联接,浏览各点是否合理,有无很高或很低的点,并检查计算及画图是否正确。
5-2 确保所画的X 和R点在纵向是对应的。
注:对于还没有计算控制限的初期操作的控制图上应清楚地注明“初始研究”字样。
二、计算控制限首先计算极差的控制限,再计算均值的控制限。
1.计算平均极差(R)及过程均值(X)R=(R1+R2+…+Rk)/ k(K表示子组数量)X =(X1+X2+…+Xk)/ k2.计算控制限计算控制限是为了显示仅存在变差的普通原因时子组的均值和极差的变化和范围。
SPC X-R图 讲义

3-3 计算控制限
3-3-1 计算平均极差(R)及过程均值(X)
R=(R1+R2+„+Rk)/ k(K表示子组数量) X=(X1+X2+„+Xk)/ k 3-3-2 计算控制限 上限 UCLx = X+ A2R (均值) ;UCLR=D4R(极差);
下限 UCLx = X- A2R (均值) ;UCLR=D3R(极差);
4、过程控制分析
4-1 分析极差图上的数据点
4-1-1 超出控制限的点
受控制的过程的极差 UCL
R
LCL
UCL
不受控制的过程的极差(有超过控制限的点)
R
LCL
4、过程控制分析
4-1 分析极差图上的数据点
4-1-2 链 有下列现象之表明过程已改变或出现某种趋势:
• 连续 7点在平均值一侧;
• 连续7点连续上升或下降; a 高于平均极差的链或上升链说明存在下列情况之一或全部: a-1 输出值的分布宽度增加,原因可能是无规律的(例如:设备工作不正常或固定松动)
1、收集 收集数据并画在图上 2、控制 根据过程数据计算实验控制限 识别变差的特殊原因并采取措施 3、分析及改进 确定普通原因变差的大小并采取减小它的措施 重复这三个阶段从而不断改进过程
X-R 均值和极差图
计 量 型 数 据
X-δ 均值和标准差图 X -R 中位值极差图
P chart 不良率管制 图 nP chart 不良数管制 计数 图 型数 C chart 缺点数管制 据 图
1、使用控制图的准备
1)建立适合于实施的环境 a、排除阻碍人员公正的因素 b、提供相应的资源 c、管理者支持 2)定义过程 根据加工过程和上下使用者之间的关系,分析每个阶段的影响因素。 3)确定待控制的特性,应考虑到: 顾客的需求 当前及潜在的问题区域 特性间的相互关系 4)确定测量系统 a、规定检测的人员、环境、方法、数量、频率、设备或量具。 b、确保检测设备或量具本身的准确性和精密性。 5)使不必要的变差最小 确保过程按预定的方式运行 确保输入的材料符合要求 恒定的控制设定值 注:应在过程记录表上记录所有的相关事件,如:刀具更新,新的材料批次等,有利于下一 步的过程分析。
均值极差图(x-r图)分析
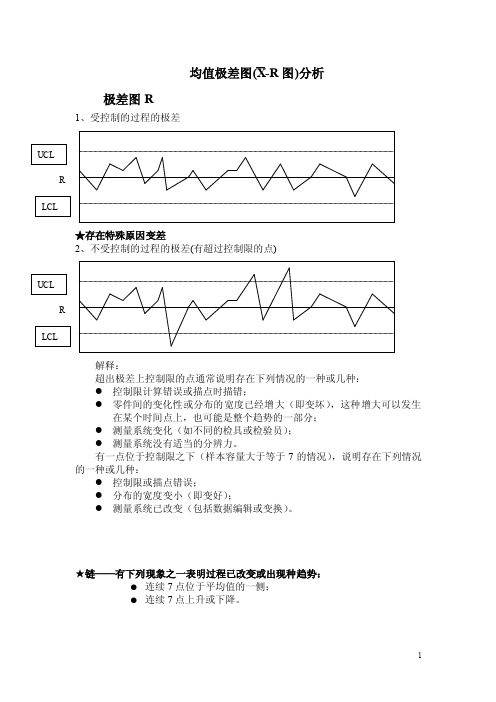
均值极差图(X-R 图)分析极差图R1、受控制的过程的极差★存在特殊原因变差2、不受控制的过程的极差(有超过控制限的点) 解释:超出极差上控制限的点通常说明存在下列情况的一种或几种: ● 控制限计算错误或描点时描错;● 零件间的变化性或分布的宽度已经增大(即变坏),这种增大可以发生在某个时间点上,也可能是整个趋势的一部分; ● 测量系统变化(如不同的检具或检验员); ● 测量系统没有适当的分辨力。
有一点位于控制限之下(样本容量大于等于7的情况),说明存在下列情况的一种或几种:● 控制限或描点错误;● 分布的宽度变小(即变好);● 测量系统已改变(包括数据编辑或变换)。
★链——有下列现象之一表明过程已改变或出现种趋势:● 连续7点位于平均值的一侧; ● 连续7点上升或下降。
(存在高于和低于极差均值的两种链)4、不受控制的过程的极差(存在长的上升链)解释:高于平均极差的链或上升链说明存在下列情况的一种或全部:●输出值的分布宽度增加,其原因可能是无规律的(如设备工作异常或固定松动)或是由于过程中的某个要素变化(如材料变化),是常见问题,需纠正;● 测量系统变化(如不同的检具或检验员);低于平均极差的链或下降链说明存在下列情况的一种或全部:● 输出值的分布宽度减小,这常常是一个好状态,应研究以便推广应用和改进过程;●测量系统改变,这会掩盖过程的真实性的变化。
★其它明显的非随机的图形 5、不受控制的过程的极差 (点离极差均值太近)(点离控制限太近)解释:各点与极差均值R 的距离:一般地,大约2/3的描点应落在控制限的中间1/3的区域内,1/3的描点应落在其外的2/3的区域内。
a )如果显著多于2/3以上的描点落在离极差均值R 很近之处(超过90%的点落在控制限1/3的区域内),说明存在下列情况的一种或全部: ● 控制限计算错误或描点时描错;● 过程或取样方法被分层;每个子组系统化包含了从两个或多个具有完全不同的过程均值的过程流的测量值(如用几根测量轴每一轴测一个数); ● 数据已经过编辑。
X-R控制图应用手册 (2)

X-R控制图操作及应用指南一、X-R控制图定义的目的:1、定义:用于长度、重量、时间、强度、成份等以计量值来管理工程的控制图,利用统计手法,设定控制均值X和极差R的界限,同时利用统计手法判定导致工程质量变异是随机原因,还是异常原因的图表。
2、目的:对公司现场制程的初始能力进行监控,对有规格变异的产品质量特性或过程质量特性值进行动态控制,对配套的各种“零部件”的尺寸进行控制,以判定工程是否处于稳定状态,并依据制定相应的措施纠正异常。
二、X-R控制图操作程序1、X-R控制图编号、规格、参数等填写(填写规范如下)(1)控制图编号:BOM-OF-QC- *** 为工程代号,制程为IP、IQC为I,OQC为O,机加工为J,DC车间控制图在工程代号前加D;(2)部门:工程责任部门或单位(3)工序:X-R控制图控制的工序(4)操作者:工序操作者(4)质量特性:说明控制何种计量特性,如工件长度、工作压力、电机负载转速等(5)工程规范:产品质量特性值或过程特性值设计或规范公差如长度尺寸20+0。
2-0。
1(6)样本容量/频率:抽样测量数据的数量/抽样频次,如5次(件)/每小时,5次/每日等(7)产品型号:受控产品的型号如YDK-60Y-6A电机(9)零件名称:受控产品零件的名称如YDK-60Y-6A电机定子组件(10)测量工具:抽样测量质量或过程特性数据的测量工具,如游标卡尺、深度尺、万能表(11)机器编号:受控工序操作的机器编号(12)控制时段:控制图收集数据的时段,如2002/2/22-2002/2/262、收集数据:(1)合理的子组大小、频率和数据a、在控制时段内,按抽样容量/频率要求,收集产品工序质量或过程特性数据125个或者100个,然后根据抽样时间段连续性,将数据分成25个子组,每个子组由4-5数据组成,每个子组数据是在非常相似的生产条件下生产出来的,并且相互之间不存在着系统的关系,因此,每组之间的变差为普通原因造成的,对于所有的子组的样品应保持恒定。
常规控制图的八种判异准则

准则一:1个点落在A区以外
准则二:连续9点落在中心线同一侧
UCL A
B
X
C
C
B
LCL A
UCL B
XC C B
LCL A
原因:过程平均值变化、计算错误、测量误差、原材 料不合格、设备故障等
原因:主要是过程平均值减小
准则三:连续6点递增或递减
A B XC C B LCL A
原因:工具逐渐磨损、维修逐渐变坏等使得参数随着 时间而变化
准则四:连续14点中相邻点交替上下
UCL B
XC C B
LCL A
原因:主要是数据分层不够,如轮流使用两台设备或 由两位操作人员轮流进行操作
准则五:连续3点中有2点落在中心线同一侧的B区以外
UCL
B
XLeabharlann CCBLCL A
原因:主要是因为过程平均值发生变化
常规控制图(X-R图)的8种判异准则
常规控制图(X-R图)的判异准则有点出界和界内点排列不随机两类
在现场应用的控制图,上下控制限分别位于中心线之上与之下的3σ距离处。为了便于判断控制图是否有异常,将 控制图分为6个区,每个区宽1σ。这6个区的标号分别为A、B、C、C、B、A,两个A区、B区、和C区、都关于中心线
准则六:连续5点中有4点落在中心线同一侧的C区以外 UCL
B XC
C B LCL A
原因:主要是因为过程平均值发生变化
准则七:连续15点落在中心线两侧的C区内
UCL B
XC C B
LCL A
原因:收集的数据虚假或数据分层不够;也可能是过 程质量得到提高
准则八:连续8点落在中心线两侧且无一在C区内
SPC X-R图 讲义

目标值线
预测
时间
范围
如果仅存在变差的普通原因,目标值线随着时间的推移, 过程的输出形成一个稳定的分布并可预测。
变差的普通及特殊原因
特殊原因:是指造成不是始终作用于过程的变差的原因,即当它们 出现时将造成(整个)过程的分布改变。只用特殊原因 被查出且采取措施,否则它们将继续不可预测的影响过程 的输出。 (通常也叫可查明原因)
SPC(Statistical Process Control)
统计制程管制
同心同德 诚信经营 持续创新 追求卓越
细节决定成败 品质成就未来
A 制程控制系统 B 变差的普通及特殊原因 C 局部措施和对系统采取措施 D 过程控制和过程能力 E 过程改进循环及过程控制 F 控制图
工业革命以后, 随着生产力的进一步发展,大规模生 产的形成,如何控制大批量产品质量成为一个突出问题, 单纯依靠事后检验的质量控制方法已不能适应当时经济 发展的要求,必须改进质量管理方式。于是,英、美等 国开始着手研究用统计方法代替事后检验的质量控制方 法。 1924年,美国的休哈特博士提出将3Sigma原理运用 于生产过程当中,并发表了著名的“控制图法”,对过程变 量进行控制,为统计质量管理奠定了理论和方法基础。
注1:R 图和 X 图应分别分析,但可进行比较,了解影响过程的特殊原因。 注2:因为子组极差或子组均值的能力都取决于零件间的变差,因此,首先应分析R图。 4-1 分析极差图上的数据点
4-1-1 超出控制限的点 a 出现一个或多个点超出任何控制限是该点处于失控状态的主要证据,应分析。 b 超出极差上控制限的点通常说明存在下列情况中的一种或几种: b.1 控制限计算错误或描点时描错 b.2 零件间的变化性或分布的宽度已增大(即变坏) b.3 测量系统变化(如:不同的检验员或量具) c 有一点位于控制限之下,说明存在下列情况的一种或多种 c.1 控制限或描点时描错 c.2 分布的宽度变小(变好) c.3 测量系统已改变(包括数据编辑或变换)
X-R控制图操作及应用

• 按上述原则判别定,可能会出现两个误判;
• (1)即冒失者之误:落入控制图的机率为99.97%,也就是 说1000个数据,有3个数据可能逸出控制界外,这是随机原 因,不是异常原因造成的变异。属正常,但误判为异常,此 现象为冒失者之误。用α表示。如α=0.3%。
• (2)迷糊者之误:测量值全部落在控制图中,且无倾向性, 通常也会认为属随机原因变异,而判定为正常。但是,实际 测量数据的分布中心已经偏离了设计规范中心,此时,肯定 存在变异,只是抽样时未碰到而已。这种误判,属迷糊者之 误,用β表示,一般来说, β发生的机率大于α机率。初次 使用SPC手法控制产品质量的QC人员经常会发生α和β两种 情况的误判。
和
作 • 3对于超出控制界限的点采取整改行动。
用 • 4根据样本数据可以对过程性质作出评价
• 5、评定生产/过程性质变化与原来过程状态进行比较。
• 节约成本 • 使标准趋于准确 • 使过程更加稳定 • 使控制规格更加真实 • 减少检验频度 • 减少问题出现的频度 • 改善和提高客户的满意度 • 可靠地测出实际过程能力 • 改善测量结果的准确度 • 改善产品品质 • 减少出货周期时间
• a . 输出值分布宽度减小,这常常是好的状态,应研 究以便推广应用和改进过程。
• b. 测量系统改变,这样会遮掩过程真实性能的变化。
UCLR
R
• C) 明显的非随机有规律变化图形:除了会出现超过 控制界的点或长链之外,数据中还可能出现其他的易 分辨的由于特殊原因造面的图形,属工序质量异常。
UCL
N2 3
4
5
67
8
9
10
d2 1.13 1.69 2.06 2.33 2.53 2.70 2.85 2.97 3.08
SPC-X-R图-讲义(1)

4)确定测量系统 a、规定检测的人员、环境、方法、数量、频率、设备或量具。 b、确保检测设备或量具本身的准确性和精密性。
5)使不必要的变差最小 确保过程按预定的方式运行 确保输入的材料符合要求 恒定的控制设定值
注:应在过程记录表上记录所有的相关事件,如:刀具更新,新的材料批次等,有利于下一 步的过程分析。
R
LCL
4、过程控制分析
4-1 分析极差图上的数据点
4-1-2 链 有下列现象之表明过程已改变或出现某种趋势:
• 连续 7点在平均值一侧; • 连续7点连续上升或下降; a 高于平均极差的链或上升链说明存在下列情况之一或全部:
a-1 输出值的分布宽度增加,原因可能是无规律的(例如:设备工作不正常或固定松动) 或是由于过程中的某要素变化(如使用新的不一致的原材料),这些问题都是常见的 问题,需要纠正;
3、分析及改进 确定普通原因变差的大小并采取减小它的措施
重复这三个阶段从而不断改进过程
X-R 均值和极差图
计 X-δ 均值和标准差图 量
型 数
X -R 中位值极差图
据
X-MR 单值移动极差图
P chart 不良率管制 图
nP chart 不良数管制 计数 图 型数 C chart 缺点数管制 据图
关系等。 b 一般情况,各点与R 的距离:大约2/3的描点应落在控制限的中间1/3的区域内,大约1/3的点落在
其外的2/3的区域。 c 如果显著多余2/3以上的描点落在离 R 很近之处(对于25子组,如果超过90%的点落在控制限的1/3
区域),则应对下列情况的一种或更多进行调查: c-1 控制限或描点已计算错描错 。 c-2 过程或取样方法被分层,每个子组系统化包含了从两个或多个具有完全不同的
均值和极差图 X—R图

均值和极差图(X—R图)在使用X—R图之前,必须作几点适当的准备:·建立适合于实施的环境除非管理者已准备好一个可靠的环境,否则任何统计方法都会失败。
必须排除机构内阻碍人们公正的顾虑。
管理者必须提供资源(人力和物力)来参与和支持改进措施。
·定义过程必须根据过程与其周围的其他操作和上下使用者之间的关系,以及每个阶段的影响因素(人、设备、材料、方法和环境)来理解过程。
因果分析图、过程流程表等技术可以使这些更加直观并且让理解过程的不同方面的人员的经验集中起来。
·确定作图的特性用来确定这些特性的例子为通用公司的《关键特性命名系统》(参见附件H,参考文献24)。
学习的重点应放在那些对过程改进有帮助的特性上[排列图(Pareto)原理的一个应用]。
应适当考虑如下因素:——顾客的需求:包括使用产品和服务作为输入的后续过程顾客和作为最终产品的顾客。
了解这两种顾客的需求,询问他们过程何处需要改进,体现共同合作和理解的精神;——当前的潜在问题区域:考虑存在的浪费或低效能力的证据(如:废品、返工、过长的加班时间、与目标值不符)以及有险情的区域(如:产品或服务的设计或过程中任何元素即将进行的变化)。
这些是改进的机会,需要应用管理企业所涉及的知识;——特性之间的相互关系:为了有效率及有效果地研究应利用特性间的关系。
比如,如果关心的特性很难测量(比如体积),选择一个相关的容易测量的特性(比如重量)。
另外,如果一具项目的几个单独的特性具有相同的变化趋势,可能只用一个特性来画图就足够了。
注意:统计上的相关性不意味着变量之间存在因果关系。
在缺乏现存过程的知识时,可能要设计一个试验来验证这些关系和重要性。
·定义测量系统必须可操作地定义其特性,这样,今天就可以以与昨天意义一样的方式将数据送给所有有关人员。
这包括指明应收集哪些信息,在何处、如何以及在什么条件下收集。
测量设备的本身的准确性和精密性必须是可预测的。
过程扭矩控制X-R图

X2 47.00 47.30 48.30 47.00 47.60 48.40 47.70 47.50 47.00 47.90 47.70 48.20 47.90 47.50 48.00 47.00 47.60 48.10 48.00 47.00 48.00 46.90 47.90 47.50 47.90
控制界限
计算
值
图 形
x
计
算 R
CL
x
UCL x + A2 R
LCL x - A2 R
CL
R
UCL D4 R
LCL
D3 R
47.6952 48.4522 46.9382 1.3120 2.7749 0.0000
过程能力
日期 9/1 9/2 9/3 9/4 9/5 9/6 9/7 9/8 9/9 9/10 9/11 9/12 9/13 9/14 9/15 9/16 9/17 9/18 9/19 9/20 9/21 9/22 9/23 9/24 9/25
车型 品号 品名
49.00
福田U201 后排座椅
Xbar-R(控制图)
过程名称 管理项目
规格
调角器安装
M10螺栓扭矩控制
上 47± 3 下限
限
50 44
测试仪器 测试单位
扭矩搬手 N.m
公司名称 编制日期
测定周期 2014.09.01-2014.09.25 测定人
北汽福田 2014.09.26
付静龙
数据群 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
Xbar-R 系数对照表
n
系 数 表
SPC X-R图 讲义ppt课件

范围
时间
如果仅存在变差的普通原因,目标值线随着时间的推移,
过程的输出形成一个稳定的分布并可预测。
9
持续改进及统计过程控制概述
B 变差的普通及特殊原因
特殊原因:是指造成不是始终作用于过程的变差的原因,即当它们 出现时将造成(整个)过程的分布改变。只用特殊原因 被查出且采取措施,否则它们将继续不可预测的影响过程 的输出。 (通常也叫可查明原因) 目标值线 预测
计量型数据管制图(X-R图)
2、收集数据
以样本容量恒定的子组形式报告,子组通常包括2-5件连续的产品,并周性期的抽取子组。 注:应制定一个收集数据的计划,将其作为收集、记录及描图的依据。
选择子组大小,频率和数据 1)子组大小:一般为5件连续的产品,仅代表单一刀具/冲头/过程流等。
数据仅代表单一刀具、冲头、模具等生产出来的零件,即一个单一的 生产流。 2)子组频率:在适当的时间内收集足够的数据,这样子组才能反映潜在的变化,这 些变化原因可能是换班/操作人员更换/材料批次不同等原因引起。对 正在生产的产品进行监测的子组频率可以是每班2次,或一小时一次等。 3)子 组 数:子组越多,变差越有机会出现。一般为25组,首次使用管制图选用35 组数据,以便调整。
时间
范围 如果存在变差的特殊原因,随着时间的推移,过程的输出不稳定。
10
持续改进及统计过程控制概述
C 局部措施和对系统采取措施 局部措施 通常用来消除变差的特殊原因 通常由与过程直接相关的人员实施 通常可纠正大约15%的过程问题
对系统采取措施 通常用来消除变差的普通原因 几乎总是要求管理措施,以便纠正 大约可纠正85%的过程问题
使用np或p图 否
子组均值是否能很方便地计算? 是
X-R控制图操作及应用

计
算 控
• UCLX= X+A2R X均值上限
制 限
• LCL X= X-A2R X 均值下限
• UCLR=D4R
R极差上限
• LCLR= D3R R极差下限
N3
4
5
6
7
D4 2.57 2.28 2.11 2.00 1.98
D3
*
*
*
*
0.08
A2 1.02 0.73 0.58 0.48 0.42
2002-10
• b. 连续7点上升(后点等于或大于前点)或下降;
• C、中心点一侧出现众多点(11点有10点,14点有12点,17点有14点,20
点有16点)
2002-10
潇湘浪子
第十六页,共30页。
• l 高于平均极差的点链或上升链说明存在下列情况之一或 全部;
• a. 输出值分布宽度增加,其原因可能是无规律的(例如设备不
• (2)部门:工程责任部门或单位
• (3)工序:X-R控制图控制的工序 • (4)操作者:工序操作者 • (4)质量特性:说明控制何种计量特性,如工件长度、工作压力、电机负载转速
等
• (5)工程规范:产品质量特性值或过程特性值设计或规范公差如长度尺寸20+0。2-0。1
2002-10
潇湘浪子
第五页,共30页。
• 以样本平均值X为中心,以X3σ为范围,作成控制
图时,如质量特性值呈现正态分布时(左、右对称),
则测量的数据,就有99.97%机率落在X3σ范围内,
我们可以判定为随机原因的变异,为安定值。当数据 落在界线外侧时,就判定不异常原因时,需要调查。
• 调查方式按下面方法进行:
2002-10
X-R 统计控制图的使用方法(ppt 12页)

Upward/Downward Trends:
Continuous trending on the same direction. These are usually caused by component wear among others.
SPC-advanced training course
SPC-advanced training course
控制图的趋势判断规则
UCL
UCL
LCL
0
10
20
Observation Number
LCL
0
5
10
15
Observation Number
Changes in process means:
These are usually due to the introduction of new operators, machines, procedures, etc. Can also happen because of process improvements.
SPC-advanced training course
控制图失控检验
Test 1. One Point Beyond Zone A
x
UCL A
B C
C
B A
LCL
x
Test 3. Six Points in a Row Steadily
Increasing or Decreasing UCL A
Avg
LCL
U CL
Change in variability
Avg
LCL
解釋控制圖
SPC-advanced training course
SPC_x-r管制图与解析

正確度、精密度
目標值
正確度 精密度
***********
**** ******* ***
優
劣
優
優
劣
劣
劣
優
X-R管制圖製作方法
• 預備數据的調查 先搜集某一期間的數据作為預備數据
步驟1:搜集數据----搜集100個以上的數据,依 測定時間順序,或群体順序排列.
(1)這些數据是最近的數据,并且在技術上可 認為今后的制程不會有多大變化.
管制界限上時,亦視同超出界外的點.
END
步驟3: 記入數据表----把數据記入如表2.1.1 的數据表裡.
步驟4:計算平均值X(4捨5入后,比測定值多求1
位數),求各組的平均值X.
X1+X2+······+Xn
X=
(n:為樣本大小)
n 例如表2.1.1的第1組的平均值為:
48+49+48+50+51
X=
=49.2
5
步驟5:計算全距R 求每組的全距R R=X (最大值) 一X (最小值)
R=
K
例如表2.1.1
3+4+7+6+4+······+8+6+3+4
R=
ቤተ መጻሕፍቲ ባይዱ
=4.7
25
步驟8:計算管制界限 (a) X管制圖
中心線CL=X 上管制界限 UCL=X+A2R 下管制界限 LCL=X–A2R (A2為系數,可由表查得) 例如表2.1.1 因n=5,故查表 得A2=0.577 CL=X=49.74 UCL=X+A2R=52.45 LCL=X-A2R=47.03
