2017年秋季学期新版新人教版八年级数学上学期12.1、全等三角形素材2

合集下载

人教版八年级上册数学教学设计《12.1 全等三角形》

人教版八年级上册数学教学设计《12.1 全等三角形》一. 教材分析《12.1 全等三角形》是人教版八年级上册数学的一个重要章节，主要内容包括全等三角形的概念、全等三角形的性质、全等三角形的判定方法等。

本章通过全等三角形的学习，培养学生对几何图形的认识和理解，提高学生的空间想象力，为后续几何学习打下基础。

二. 学情分析八年级的学生已经掌握了三角形的基本知识，对三角形的性质和判定方法有一定的了解。

但全等三角形作为三角形的一个重要分支，其概念和性质较为抽象，学生理解和掌握全等三角形的难度较大。

因此，在教学过程中，要注重引导学生从实际问题中抽象出全等三角形的概念，并通过大量的实例分析，使学生熟练掌握全等三角形的性质和判定方法。

三. 教学目标1.了解全等三角形的概念，掌握全等三角形的性质和判定方法。

2.培养学生对几何图形的认识和理解，提高学生的空间想象力。

3.培养学生运用全等三角形的知识解决实际问题的能力。

四. 教学重难点1.全等三角形的概念及其性质。

2.全等三角形的判定方法。

3.全等三角形在实际问题中的应用。

五. 教学方法1.采用问题驱动的教学方法，引导学生从实际问题中抽象出全等三角形的概念。

2.通过大量的实例分析，使学生熟练掌握全等三角形的性质和判定方法。

3.运用多媒体辅助教学，提高学生的空间想象力。

4.采用小组合作学习的方式，培养学生的团队合作精神。

六. 教学准备1.准备相关教学课件和教学素材。

2.设计具有代表性的例题和练习题。

3.准备全等三角形的模型或图片，用于直观展示。

七. 教学过程1.导入（5分钟）通过展示一些生活中的实际问题，如拼图、制作模型等，引导学生思考：如何判断两个三角形是否完全相同？从而引出全等三角形的概念。

2.呈现（10分钟）介绍全等三角形的定义、性质和判定方法。

通过PPT展示全等三角形的图形，让学生直观地感受全等三角形的特征。

同时，给出全等三角形的判定方法，如SSS、SAS、ASA、AAS等。

八年级数学上册 12.1《全等三角形》知识讲解全等三角形的概念和性质(提高)素材 (新版)新人教版

全等三角形的概念和性质〔提高〕【学习目标】1．理解全等三角形及其对应边、对应角的概念；能准确识别全等三角形的对应元素.2．掌握全等三角形的性质；会用全等三角形的性质进行简单的推理和计算，解决某些实际问题.【要点梳理】要点一、全等形形状、大小相同的图形放在一起能够完全重合.能够完全重合的两个图形叫做全等形.要点诠释：一个图形经过平移、翻折、旋转后，位置变化了，但形状、大小都没有改变，即平移、翻折、旋转前后的图形全等.两个全等形的周长相等，面积相等.要点二、全等三角形能够完全重合的两个三角形叫全等三角形.要点三、对应顶点，对应边，对应角1. 对应顶点，对应边，对应角定义两个全等三角形重合在一起，重合的顶点叫对应顶点，重合的边叫对应边，重合的角叫对应角.要点诠释：在写两个三角形全等时，通常把对应顶点的字母写在对应位置上，这样容易找出对应边、对应角.如以下列图，△ABC与△DEF全等，记作△ABC≌△DEF，其中点A和点D，点B和点E，点C和点F是对应顶点；AB和DE，BC和EF，AC和DF是对应边；∠A和∠D，∠B和∠E，∠C和∠F是对应角.2. 找对应边、对应角的方法〔1〕全等三角形对应角所对的边是对应边，两个对应角所夹的边是对应边；〔2〕全等三角形对应边所对的角是对应角，两条对应边所夹的角是对应角；〔3〕有公共边的，公共边是对应边；〔4〕有公共角的，公共角是对应角；〔5〕有对顶角的，对顶角一定是对应角；〔6〕两个全等三角形中一对最长的边〔或最大的角〕是对应边〔或角〕，一对最短的边〔或最小的角〕是对应边〔或角〕，等等.要点四、全等三角形的性质全等三角形的对应边相等；全等三角形的对应角相等；要点诠释：全等三角形对应边上的高相等，对应边上的中线相等，周长相等，面积相等.全等三角形的性质是今后研究其它全等图形的重要工具.【典型例题】类型一、全等形和全等三角形的概念1、请观察以下列图中的6组图案，其中是全等形的是__________.【答案】〔1〕〔4〕〔5〕〔6〕；【解析】〔1〕〔5〕是由其中一个图形旋转一定角度得到另一个图形的，〔4〕是将其中一个图形翻折后得到另一个图形的，〔6〕是将其中一个图形旋转180°再平移得到的，〔2〕〔3〕形状相同，但大小不等.【总结升华】是不是全等形，既要看形状是否相同，还要看大小是否相等.举一反三：【变式1】全等三角形又叫做合同三角形，平面内的合同三角形分为真正合同三角形与镜面合同三角形，假设△ABC和△A1B1C1是全等(合同)三角形，点A与点A1对应，点B 与点B1对应，点C与点C1对应，当沿周界A→B→C→A，及A1→B1→C1→A1环绕时，假设运动方向相同，那么称它们是真正合同三角形(如图1)，假设运动方向相反，那么称它们是镜面合同三角形(如图2)，两个真正合同三角形都可以在平面内通过平移或旋转使它们重合，两个镜面合同三角形要重合，那么必须将其中一个翻转180°，以下各组合同三角形中，是镜面合同三角形的是( )【答案】B；提示：抓住关键语句，两个镜面合同三角形要重合，那么必须将其中一个翻转180°，B答案中的两个三角形经过翻转180°就可以重合，应选B；其它三个选项都需要通过平移或旋转使它们重合.类型二、全等三角形的对应边，对应角2、如图，△ABD≌△CDB，假设AB∥CD，那么AB的对应边是〔〕A．DB B. BC C. CD D. AD【答案】C【解析】因为AB∥CD，所以∠CDB＝∠ABD，这两个角为对应角，对应角所对的边为对应边，所以，BC和DA为对应边，所以AB的对应边为CD.【总结升华】公共边是对应边，对应角所对的边是对应边.类型三、全等三角形性质3、如图，将长方形ABCD沿AE折叠，使D点落在BC边上的F点处，如果∠BAF＝60°，那么∠DAE等于〔〕．A.60°B.45°C.30°D.15°【思路点拨】△AFE是由△ADE折叠形成的，由全等三角形的性质，∠FAE＝∠DAE，再由∠BAD＝90°，∠BAF＝60°可以计算出结果.【答案】D；【解析】因为△AFE是由△ADE折叠形成的，所以△AFE≌△ADE，所以∠FAE＝∠DAE，又因为∠BAF＝60°，所以∠FAE＝∠DAE＝90602︒-︒＝15°.【总结升华】折叠所形成的三角形与原三角形是全等的关系，抓住全等三角形对应角相等来解题.举一反三：【变式】如图，在长方形ABCD中，将△BCD沿其对角线BD翻折得到△BED，假设∠1＝35°，那么∠2＝________.【答案】35°；提示：将△BCD沿其对角线BD翻折得到△BED，所以∠2＝∠CBD，又因为AD∥BC，所以∠1＝∠CBD，所以∠2＝35°.4、如图，△ABE和△ADC是△ABC分别沿着AB，AC翻折180°形成的，假设∠1∶∠2∶∠3＝28∶5∶3，∠α的度数是_________.【思路点拨】〔1〕由∠1，∠2，∠3之间的比例关系及利用三角形内角和可求出∠1，∠2，∠3的度数；〔2〕由全等三角形的性质求∠EBC，∠BCD的度数；〔3〕运用外角求∠α的度数.【答案】∠α＝80°【解析】∵∠1∶∠2∶∠3＝28∶5∶3，设∠1＝28x，∠2＝5x，∠3＝3x，∴28x＋5x＋3x＝36x＝180°，x＝5°即∠1＝140°，∠2＝25°，∠3＝15°∵△ABE和△ADC是△ABC分别沿着AB，AC翻折180°形成的，∴△ABE≌△ADC≌△ABC∴∠2＝∠ABE，∠3＝∠ACD∴∠α＝∠EBC＋∠BCD＝2∠2＋2∠3＝50°＋30°＝80°【总结升华】此题涉及到了三角形内角和，外角和定理，并且要运用全等三角形对应角相等的性质来解决问题.见“比例〞设未知数x是比较常用的解题思路.举一反三：【变式】如图，在△ABC中，∠A:∠ABC:∠BCA ＝3:5:10，又△MNC≌△ABC，那么∠BCM：∠BCN等于〔〕A．1:2 B．1:3 C．2:3 D．1:4【答案】D；提示：设∠A＝3x，∠ABC＝5x，∠BCA＝10x，那么3x＋5x＋10x＝18x＝180°，x＝10°. 又因为△MNC≌△ABC，所以∠N＝∠B＝50°，CN＝CB，所以∠N＝∠CBN＝50°，∠ACB＝∠MCN＝100°，∠BCN＝180°－50°－50°＝80°，所以∠BCM：∠BCN＝20°：80°＝1：4.。

2017年秋季学期新版新人教版八年级数学上学期12.2、三角形全等的判定课件94

AB DE BC EF AC DF
∴ △ABC≌△DEF (SSS)
判断两个三角形全等的推理过程，叫做证明三角形全等。
例1、如图，△ABC是一个钢架，AB=AC，AD是连接A与 BC中点D的支架。求证： △ABD≌△ACD 证明：∵D是BC的中点（已知）
A
B
D
ＡＢ＝Ａ′Ｂ′，ＢＣ＝Ｂ′Ｃ′，ＡＣ＝Ａ′Ｃ′， ∠Ａ＝∠ Ａ′， ∠Ｂ＝ ∠Ｂ′， ∠Ｃ＝ ∠Ｃ′，
这六个条件能保证这两个三角形全等吗？
A A′
B
C
B′
C′
只给一个条件
1.只给一条边时； 3㎝ 2.只给一个角时；
45◦ 45◦ 45◦
3㎝
3cm
结论:只有一条边或一个角对应相等的两个三角形不一定全等
12.2 三角形全等的判定
1、什么叫全等三角形？
能够完全重合的两个三角形叫全等三角形． 2、已知△ABC ≌△ DEF，找出其中相等的边与角.
A DBCE NhomakorabeaF
①AB=DE
② BC=EF
③ CA=FD
④ ∠A= ∠D ⑤ ∠B=∠E
⑥ ∠C= ∠F
如果△ ABC和△ A′B′C′满足三条边对应相等，三个角对应相等，即
.
你如能果说给出出有两哪个几条种件可画能三的角情形况，？
①两边； ②一边一角； ③两角。
①如果三角形的两边分别为4cm，6cm 时
4cm
4cm
6cm
6cm
结论:两条边对应相等的两个三角形不一定全等.
②三角形的一个内角为30°,一条边为4cm时
30◦ 4cm
30◦ 4cm

人教版数学八年级上册12.1全等三角形优秀教学案例

（二）讲授新知
1.讲解全等三角形的定义，让学生理解全等三角形的概念。
2.逐步引导学生发现全等三角形的性质和判定方法。
3.通过实例和问题，讲解全等三角形在实际问题中的应用。
四、教学内容与过程
（一）导入新课
1.利用教具和实物，引导学生观察和操作，激发学生对全等三角形的兴趣。
2.结合生活实际，提出与全等三角形相关的问题，引发学生的思考。
3.总结全等三角形的定义和性质，为新课的讲解做好铺垫。
在导入新课时，我会利用教具和实物，引导学生观察和操作，激发学生对全等三角形的兴趣。例如，我会拿出两个完全相同的三角形，让学生通过观察和操作，发现它们的特性。同时，我会结合生活实际，提出与全等三角形相关的问题，引发学生的思考。例如，我会问学生：“你们在生活中有没有遇到过两个完全相同的三角形？”通过这些问题，让学生对全等三角形产生好奇心和兴趣。最后，我会总结全等三角形的定义和性质，为新课的讲解做好铺垫。
三、教学策略
（一）情景创设
1.利用教具和实物，创设直观情境，让学生通过观察和操作，直观地感受全等三角形的特性。
2.结合生活实际，设计一些与全等三角形相关的问题，引导学生发现数学与生活的紧密联系。
3.创设一些具有挑战性的问题情境，激发学生的思维，培养学生的解决问题能力。
在教学过程中，我会利用教具和实物，创设直观情境，让学生通过观察和操作，直观地感受全等三角形的特性。同时，我会结合生活实际，设计一些与全等三角形相关的问题，引导学生发现数学与生活的紧密联系。此外，我还会创设一些具有挑战性的问题情境，激发学生的思维，培养学生的解决问题能力。
（三）小组合作
1.组织学生进行小组合作，培养学生的团队协作精神和沟通能力。
2.设计一些需要小组合作才能完成的任务，让学生在合作中思考、讨论和解决问题。

2017年秋季学期新版新人教版八年级数学上学期12.1、全等三角形课件3

△ABC≌△DEFΒιβλιοθήκη 通过书写格式，我们就能找到
当△ABC≌△DEF时，谁是对应边，谁是对应角呢？
对应边与对应角
A
D
全等三角形性质
B
C
E
F
全等三角形的对应边相等全等三角形的对应角相等
全等三角形对应边相等
全等三角形对应角相等
如图，在△ABC中，∠ACB=90°，△ABC≌△DFC，你能判断DE与AB是
否互相垂直吗？为什么？
解： ∵△ABC≌△DFC， ∴∠D=∠A， ∵∠ACB=90°， ∴∠A+∠B=90°， ∴∠B+∠D=90°， ∴∠BED=90°， ∴DE⊥AB．
专题讨论：有人说如果两个三角形全等，那么它们对应
的角平分线，高也相等，你认为对吗？
全等三角形的性质
A
D
全等三角形的相关定义
B
C
E
F
全等三角形中能够重合的两个顶点叫对应顶点全等三角形中能够重合的两条边叫对应边全等三角形中能够重合的两个角叫对应角比如BC 比如∠ 比如点 A C 与与∠ 与点 EF D F
对应关系
A
F
E 书写要求
B
C
D
书写全等三角形的时候，通常将对应顶点的字母写在对应位置上

人教版初中数学八年级上册第十二章全等三角形

人教版数学八年级上册
12.1 全等三角形/
12.1 全等三角形
导入新知
12.1 全等三角形/
观察这些图片，你能找出形状、大小完全一样的几何图形吗？
导入新知
12.1 全等三角形/
你能再举出生活中的一些类似例子吗？
素养目标
12.1 全等三角形/
3. 初步帮助学生建立平移、翻折、旋转三种图形变化与全等形的关系.
12.1 全等三角形/
观察思考：每组中的两个图形有什么特点？
①
②
③
④
⑤
探究新知
12.1 全等三角形/
归纳总结
全等图形定义：能够完全重合的两个图形叫做全等图形. 全等形性质：如果两个图形全等，它们的形状和大小一定都相等.
探究新知下面哪些图形是全等图形？
12.1 全等三角形/
大小、形状完全相同
课后作业
作业内容
12.1 全等三角形/
教材作业从课后习题中选取自主安排配套练习册练习
2. 熟练掌握全等三角形的性质，并能灵活运用全等三角形的性质解决相应的几何问题.
1. 熟记全等形及全等三角形的概念;能够正确找出全等三角形的对应边、对应角.
探究新知
12.1 全等三角形/
知识点 1 全等图形的定义及性质
下列各组图形的形状与大小有什么特点？
（1）
（2）
（3）
（4）
（5）
探究新知
正确的结论并证明.
解：结论：EF∥NM
其他结论吗？
证明： ∵ △EFG≌△NMH，
∴ ∠E=∠N. ∴ EF∥NM.
巩固练习
12.1 全等三角形/
如图，△ABC ≌△CDA，AB 与CD，BC 与DA 是对应边，

人教版八年级数学上册全等三角形精品课件PPT

•
2、人物作为支撑影片的基本骨架，在影片中发挥着不可替代的作用，也是影片的灵魂，阿甘是影片中的主人公，是支撑起整个故事的重要人物，也是给人最大启示的人物。
•
3、在生命的每一个阶段，阿甘的心中只有一个目标在指引着他，他也只为此而踏实地、不懈地、坚定地奋斗，直到这一目标的完成，又或是新的目标的出现。
•
4、让学生有个整体感知的过程。虽然这节课只教学做好事的部分，但是在研读之前我让学生找出风娃娃做的事情，进行板书，区分好事和坏事，这样让学生能了解课文大概的资料。
•
5、人们都期望自我的生活中能够多一些快乐和顺利，少一些痛苦和挫折。可是命运却似乎总给人以更多的失落、痛苦和挫折。我就经历过许多大大小小的挫折。
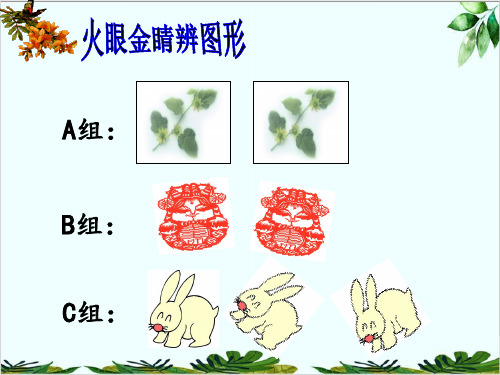
A组： B组： C组：
第十二章全等三角形 12.1 全等三角形
人教版八年级数学上册 12.1 全等三角形课件
1、理解图形全等的概念和特征，能识别全等形； 2、掌握全等三角形的性质，并能进行简单的推理和计算。
人教版八年级数学上册 12.1 全等三角形课件
人教版八年级数学上册 12.1 全等三角形课件
人教版八年级数学上册 12.1 全等三角形课件
找出下面的全等形。
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
解：（1）和（9）、（2）和（8）、（3）和（6）
人教版八年级数学上册 12.1 全等三角形课件
人教版八年级数学上册 12.1 全等三角形课件