培优辅导1 (证明一)

合集下载

音乐培优补差工作计划

音乐培优补差工作计划（实用版）编制人：__________________审核人：__________________审批人：__________________编制单位：__________________编制时间：____年____月____日序言下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!并且，本店铺为大家提供各种类型的实用范文，如工作计划、工作总结、演讲稿、合同范本、心得体会、条据文书、应急预案、教学资料、作文大全、其他范文等等，想了解不同范文格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!Moreover, our store provides various types of practical sample essays for everyone, such as work plans, work summaries, speech drafts, contract templates, personal experiences, policy documents, emergency plans, teaching materials, complete essays, and other sample essays. If you want to learn about different formats and writing methods of sample essays, please stay tuned!音乐培优补差工作计划音乐培优补差工作计划（精选32篇）音乐培优补差工作计划篇1今年所教的是七年级的学生，各班学生对待学习都存在不积极的学习态度，根据实际教学情况，我制定了分层次培优辅差的计划，利用音乐课堂内一定时间，分班分层次进行培优补差。

八年级数学培优辅导讲义竞赛训练导学案分式的运算分式的化简与求值含答案解析

八年级数学培优辅导讲义竞赛训练导学案分式的化简与求值典例剖析【例l 】已知2310a a -+=，则代数式361a a +的值为．（“希望杯”邀请赛试题）解题思路：目前不能求出a 的值，但可以求出13a a+=，需要对所求代数式变形含“1a a +”．【例2】已知一列数1234567,,,,,,,a a a a a a a 且18a =，75832a =，356124234567a a a a a a a a a a a a =====，则5a 为（） A ．648 B ．832 C ．1168 D ．1944（五城市联赛试题）解题思路：引入参数k ，把17a a 用k 的代数式表示，这是解决等比问题的基本思路．【例3】 3(0)x y z a a ++=≠．求222()()()()()()()()()x a y a y a z a z a x a x a y a z a --+--+---+-+-．（宣州竞赛试题）解题思路：观察发现，所求代数式是关于x a y a z a ---、、的代数式，而条件可以拆成x a y a z a ---、、的等式，因此很自然的想到用换元法来简化解题过程．【例4】已知1,2,3,xy yz zxx y y z z x===+++求x 的值．（上海市竞赛试题）解题思路：注意到联立等式得到的方程组是一个复杂的三元一次方程组，考虑取倒数，将方程组化为简单的形式．【例5】不等于0的三个正整数,,a b c 满足1111a b c a b c++=++，求证：,,a b c 中至少有两个互为相反数．解题思路：,,a b c 中至少有两个互为相反数，即要证明()()()0a b b c c a +++=．（北京市竞赛试题）【例6】已知,,a b c 为正整数，满足如下两个条件：①32;a b c ++=②14b c a c a b a b c bc ac ab +-+-+-++= 解题思路：本题熟记勾股定理的公式即可解答．（全国初中数学联赛试题）能力训练1．若a b c d b c d a ===，则a b c d a b c d-+-+-+的值是．（“希望杯”邀请赛试题）2．已知2131xx x =-+，则24291x x x =-+ ．（广东竞赛试题）3．若2221998,1999,2000a x b x c x +=+=++=且24abc =，则111c a b ab bc ac a b c++--- 的值为．（“缙云杯”竞赛试题）4．已知232325x xy y x xy y +-=--，则11x y -= ．5．如果111,1a b b c+=+=，那么1c a +=（）．A ．1B ．2C ．12D ．14（“新世纪杯”竞赛试题）6．设有理数,,a b c 都不为0，且0a b c ++=，则222222222111b c a c a b a b c+++-+-+-的值为（）．A ．正数B ．负数C ．零D ．不能确定7．已知4360,270(0)x y z x y z xyz --=+-=≠，则22222223657x y z x y z++++的值为（）． A ．0 B ．1 C ．2 D ．不能确定8．已知211xx mx =-+，则36331x x m x -+的值为（） A ．1 B ．313m + C ．2132m - D ．2131m + 9．设0a b c ++=，求222222222a b c a bc b ac c ab+++++的值．10．已知111x y z y z x+=+=+其中,,x y z 互不相等，求证2221x y z =．（天津市竞赛试题）11．设,,a b c 满足1111a b c a b c++=++，求证2121212121211111n n n n n n a b c a b c ------++=++．（n 为自然数）（波兰竞赛试题）12．三角形三边长分别为,,a b c ．（1）若a a b cb c b c a ++=+-，求证：这个三角形是等腰三角形；（2）若1111a b c a b c-+=-+，判断这个三角形的形状并证明．13．已知1ax by cz ===，求444444111111111111a b c x y z+++++++++++的值．（“华杯赛”试题）14．解下列方程（组）：（1）18272938x x x x x x x x +++++=+++++；（江苏省竞赛试题）（2）596841922119968x x x x x x x x ----+=+----；（“五羊杯”竞赛试题）（3）111211131114x y z y z x z x y ⎧+=⎪+⎪⎪+=⎨+⎪⎪+=⎪+⎩．（北京市竞赛试题）B 级1．设,,a b c 满足0a b c ++=，0abc >，若a b c x a b c=++， 111111()()()y a b c b c c a a b=+++++，则23x y xy ++= ．2．若0abc ≠，且a b b c c a c a b+++==，则()()()a b b c c a abc +++= ． 3．设,,a b c 均为非零数，且2(),3(),4()ab a b bc b c ac a c =+=+=+，则a b c ++= ．4．已知,,x y z 满足1x y z y z x z y x ++=+++，则222x y z y z x z y x+++++的值为． 5．设,,a b c 是三个互不相同的正数，已知a c c bb a b a-==+，那么有（）． A ．32b c = B ．32a b = C ．2b c = D ．2a b =6．如果0a b c ++=，1114a b c ++=-，那么222111a b c++的值为（）．A ．3B ．8C ．16D ．207．已知2519910x x --=，则代数式42(2)(1)1(1)(2)x x x x -+----的值为（）．A ．1996B ．1997C ．1998D ．199998．若615325x y x y y x y x -==-，则222245623x xy y x xy y-+-+的值为（）． A ．92 B ．94C ．5D ．6 （全国初中数学联赛试题）9．已知非零实数,,a b c 满足0a b c ++=．（1）求证：3333a b c abc ++=；（2）求()()a b b c c a c a bc a b a b b c c a---++++---的值．（北京市竞赛试题）10．已知2410a a ++=，且42321322a ma a ma a++=++．求m 的值．（北京市竞赛试题）11．完成同一件工作，甲单独做所需时间为乙、丙两人合做所需时间的p 倍，乙单独做所需时间为甲、（天津市竞赛试题）12．设222222222,,222b c a a c b b a c A B C bc ac ab+-+-+-===，当3A B C ++=-时，求证：2002200220023A B C ++=．（天津市竞赛试题）13．某商场在一楼和二楼之间安装了一自动扶梯，以均匀的速度向上行驶，一男孩和一女孩同时从自动扶梯上走到二楼（扶梯行驶，两人也走梯）．如果两人上梯的速度都是匀速的，每次只跨1级，且男孩每分钟走动的级数是女孩的2倍．已知男孩走了27级到达扶梯顶部，而女孩走了18级到达顶部．（1）扶梯露在外面的部分有多少级？（2）现扶梯近旁有一从二楼下到一楼的楼梯道，台阶的级数与自动扶梯的级数相等，两人各自到扶梯顶部后按原速度再下楼梯，到楼梯底部再乘自动扶梯上楼（不考虑扶梯与楼梯间的距离）．求男孩第一次追上女孩时走了多少级台阶？（江苏省竞赛试题）专题07 分式的化简求值例1 181提示：3363111aa a a +=+例2 A 提示：7665544332216a a a a a a a a a a a a k •••••==71a a =58328，得k=31±，又25443322151k a a a a a a a a a a =•••= 例3油x+y+z=3a ，得（x-a ）+（y-a ）+（z-a ）=0.设x-a=m ，y-a=n ，z-a=p ，则m+n+p=0，即p=-（m+n ）.原式=222p n m pm np mn ++++=()222p n m n m p mn ++++=()()2222n m n m n m mn ++++-=-21 例4 x=512 提示：由已知条件知xy ≠0，yz ≠0，取倒数，得：⎪⎪⎪⎩⎪⎪⎪⎨⎧+++,31,21,1zx x z zx z y xy y x 即⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=+=+,3111,2111,111x z z y y x ①+②+③，得1211111=++z y x 例5 提示：由已知条件，得()()a bc acb abc bc ac b ab +++++++22=()()[]()c a b a c b a b ++++=()()()0=+++a c c b b a例6 由勾股定理，结论可表示为等式：a=b+c ，①或b=a+c ，②或c=b+a ，③，联立①③，只需证a=16或或b ＝16或c ＝16，即（a －16）（b －16）（c －16）＝0. ④ 展开只需证明0＝abc －16（ab ＋bc ＋ac ）＋162（a ＋b ＋c ）－163＝abc －16（ab ＋bc ＋ac ）＋163 ⑤ 将①平方、移项，有a 2＋b 2＋c 2＝322－2（ab ＋bc ＋ca ），⑥ 又将②移项、通分，有 0＝14－（++b c a bc ＋+c a b ac －＋a b c ab ++）①② ③＝14－（2+ab ac aabc-＋2+bc ab babc-＋2ac bc cabc+-）＝222 8()4()4abc ab bc ac a b cabc-+++++＝28()4[322()]4abc ab bc ac ab bc caabc-+++-++把⑥代入等式中，0＝3 16()164abc ab bc acabc-+++＝23 16()16()164abc ab bc ac a b cabc-+++++-＝(16)(16)(16)4a b cabc---当a－16＝0时，由①有a＝16＝b＋c为斜边的直角三角形.同理，当b＝16或c＝16时，分别有b＝a＋c或c＝b＋a 个直角三角形.A级1. 0或－22. 15∵231x xx-+＝1，∴x＋1x＝4.又∵42291x xx-+＝5，∴24291xx x-+＝153. 184.35. A6. C 提示：b 2＋c 2－a2＝－2bc7.B8. C 提示：取倒数，得x＋1x＝1＋m，原式的倒数＝x3＋31x－m39. 1 提示：2a2＋bc＝2a2＋b（－a－b）＝a2－ab＋a2－b2＝（a－b）（a＋a＋b）＝（a－b）（a－c）10. 提示：由x＋1y＝y＋1z，得x－y＝1z－1y，得zy＝y zx y--11. 提示：参见例5得（a＋b）（b＋c）（a＋c）＝012. （1）∵()a b cbc+＝()b cb c a++-，∴（b＋c）（ab＋ac－a2－bc）＝0.∴（b＋c）（a－b）（c－a）＝0.∵b＋c≠0，∴a＝b或c＝a.∴这个三角形为等腰三角形.（2）∵1a＋1c＝1+a b c-＋1b，∴a cac+＝()a ca b c b+-+∴（a－b＋c）＝ac，∴（a－b）（b－c）＝0, a＝b或b＝c，∴这个三角形为等腰三角形.13. 3 x＝1a，y＝1b，c＝1z，∴411a+＋411x+＝411a+＋4111a+＝1，∴原式＝3.14. （1）x＝－11 2（2）x＝123 14（3）（x，y，z）＝（2310，236，232）提示：原方程组各方程左端通分、方程两边同时取倒数.B级1. 22. －1或8 提示：设a bc+＝b ca+＝c ab+＝k，则k＝－1或2 3.1128354. 0 提示：由xy z+＝1－yz x+－zx y+，得：14＝x－xyz x+－xzx y+5. A6. C7. D 提示：原式＝4(2)(2)(1)(2)x x xx x-+---＝3(2)1x xx-+-＝3261281x x x xx-+-+-＝2(1)5(1)8(1)1x x x x xx---+--＝x2－5x＋88. A 提示：由已知条件得x＝3y9. （1）由a ＋b ＋c ＝0，得a ＋b ＝－c ∴a 3＋b 3＋c 3＝－3ab （a ＋b ）＝3abc（2）∵（a b c -＋b c a -＋c a b -）·ca b-＝1＋22c ab ， ∴同理：（a b c -＋b c a -＋c ab -）·a bc -＝1＋22a bc ，（a b c -＋b c a -＋c a b -）·bc a -＝1＋22b ac ，∴左边＝3＋22c ab ＋22a bc＋22c ab ＝3＋3332()a b c abc ++＝910. ∵a 2＋4a ＋1＝0，∴a 2＋1＝－4a ，①a ≠0. 4232122a ma a ma a++++＝2222(1)(2)2(1)a m a a a ma ++-++＝3.把①代入上式中，222216(2)8a m a a ma +--+＝3，消元得1692)8m m+--+＝3，解得m ＝19.11. 设甲、乙、丙三人单独完成此项工作分别用a 天、b 天、c 天，则,,bc a p b c ac b q a c ab c x a b ⎧=⋅⎪+⎪⎪=⋅⎨+⎪⎪=⋅⎪+⎩即111,111,111p a b c q b a c x c a b ⋅=+⋅=+⋅=+解得x ＝14. 12. 由A ＋B ＋C ＝－3得（2222b c a bc+-＋1）＋222222(1)(1)0.22c a b a b c ac ab +-+-+++=即222222()()()0222b c a c a b a b c bc ac ab+-+-+-++=分解因式，得(b ＋c －a )(a ＋b －c )(a －b ＋c )＝0b ＋c －a ， a ＋b －c ，a －b ＋c 中至少有一个为0，不妨设b ＋c －a ＝0，代入式中， A 2002＋B 2002＋C 2002＝(－1)2002＋12002＋12002＝3．13．（1）设女孩速度x 级/分，电梯速度y 级/分，男孩速度2x 级/分，楼梯S 级，则27271818.S x y S xy -⎧=⎪⎪⎨-⎪=⎪⎩，得13.5271818S S -=-，327418S S -=-，∴S ＝54．（2）设男孩第一次追上女孩时走过扶梯m 编，走过楼梯n 编，则女孩走过扶梯(m －1)编，走过楼梯(n －1)编，男孩上扶梯4x 级/分，女孩上扶梯3x 级/分．545454(1)54(n 1)423m m m x x x x --+=+，即114231m n m n --+=+，得6n ＋m ＝16，m ，n 中必有一个是正整数，且0≤︱m －n ︱≤1．①16m n -=，m 分别取值，则有②m ＝16－6n ，分别取值，则有显然，只有m ＝3，n ＝126满足条件，故男孩所走的数＝3×27＋126×54＝198级． ∴男孩第一次追上女孩时走了198级台阶．。

培优证明

培优证明
XXXX老师任现职以来培优情况：
时间
班别优生名单培养来自施效果2005至2006学年度
初三（7）
韦志强
课后辅导，经常与他讨论、交流学习上的问题。
效果显著，获全国数学竞赛一等奖。
谢国秘
课后辅导，经常与他讨论、交流学习上的问题。
效果显著，获全国数学竞赛二等奖
2006至2007学年度
九（10）
陈文辉
平时多辅导，多交流，增强自信心。
效果显著，获全国数学竞赛一等奖，阳西县中考第三名。
刘星到
平时多辅导，多交流，增强自信心。
效果显著，获全国数学竞赛二等奖
2007至2008学年度
九（9）
敖浩程
课后辅导，多交流，增强自信心。
效果显著，获全国数学竞赛二等奖，阳西县中考第一名。
陈高键
课后辅导，多交流，增强自信心。
效果显著，获全国数学竞赛一等奖。
审核人：
单位（盖章）：
2008年8月5日

人教【数学】培优易错难题一元二次方程辅导专题训练及详细答案

⼈教【数学】培优易错难题⼀元⼆次⽅程辅导专题训练及详细答案⼀、⼀元⼆次⽅程真题与模拟题分类汇编（难题易错题）1．如图，A、B、C、D为矩形的4个顶点，AB＝16cm，BC＝6cm，动点P、Q分别以3cm/s、2cm/s的速度从点A、C同时出发，点Q从点C向点D移动．(1)若点P从点A移动到点B停⽌，点P、Q分别从点A、C同时出发，问经过2s时P、Q 两点之间的距离是多少cm？(2)若点P从点A移动到点B停⽌，点Q随点P的停⽌⽽停⽌移动，点P、Q分别从点A、C 同时出发，问经过多长时间P、Q两点之间的距离是10cm？(3)若点P沿着AB→BC→CD移动，点P、Q分别从点A、C同时出发，点Q从点C移动到点D停⽌时，点P随点Q的停⽌⽽停⽌移动，试探求经过多长时间△PBQ的⾯积为12cm2？【答案】（1）PQ=62cm；（2）85s或245s；（3）经过4秒或6秒△PBQ的⾯积为12cm2．【解析】试题分析：（1）作PE⊥CD于E，表⽰出PQ的长度，利⽤PE2+EQ2=PQ2列出⽅程求解即可；（2）设x秒后，点P和点Q的距离是10cm．在Rt△PEQ中，根据勾股定理列出关于x的⽅程（16-5x）2=64，通过解⽅程即可求得x的值；（3）分类讨论：①当点P在AB上时；②当点P在BC边上；③当点P在CD边上时．试题解析：（1）过点P作PE⊥CD于E．则根据题意，得EQ=16-2×3-2×2=6（cm），PE=AD=6cm；在Rt△PEQ中，根据勾股定理，得PE2+EQ2=PQ2，即36+36=PQ2，∴PQ=62cm；∴经过2s时P、Q两点之间的距离是62cm；（2）设x秒后，点P和点Q的距离是10cm．（16-2x-3x）2+62=102，即（16-5x）2=64，∴16-5x=±8，∴x1=85，x2=245；∴经过85s或245sP、Q两点之间的距离是10cm；（3）连接BQ．设经过ys后△PBQ的⾯积为12cm2．①当0≤y≤163时，则PB=16-3y，∴12PB?BC=12，即12×（16-3y）×6=12，解得y=4；②当163＜x≤223时，BP=3y-AB=3y-16，QC=2y，则1 2BP?CQ=12（3y-16）×2y=12，解得y1=6，y2=-23（舍去）；③223＜x≤8时，QP=CQ-PQ=22-y，则1 2QP?CB=12（22-y）×6=12，解得y=18（舍去）．综上所述，经过4秒或6秒△PBQ的⾯积为 12cm2．考点：⼀元⼆次⽅程的应⽤．2．如图，在△ABC中，AB＝6cm，BC＝7cm，∠ABC＝30°，点P从A点出发，以1cm/s的速度向B点移动，点Q从B点出发，以2cm/s的速度向C点移动．如果P、Q两点同时出发，经过⼏秒后△PBQ的⾯积等于4cm2？【答案】经过2秒后△PBQ的⾯积等于4cm2．【解析】【分析】作出辅助线，过点Q 作QE ⊥PB 于E ，即可得出S △PQB =12×PB×QE ，有P 、Q 点的移动速度，设时间为t 秒时，可以得出PB 、QE 关于t 的表达式，代⼊⾯积公式，即可得出答案．【详解】解：如图，过点Q 作QE ⊥PB 于E ，则∠QEB ＝90°．∵∠ABC ＝30°，∴2QE ＝QB ．∴S △PQB ＝12PBQE ．设经过t 秒后△PBQ 的⾯积等于4cm 2，则PB ＝6﹣t ，QB ＝2t ，QE ＝t ．根据题意，12（6﹣t ）?t ＝4． t 2﹣6t+8＝0．t 2＝2，t 2＝4．当t ＝4时，2t ＝8，8＞7，不合题意舍去，取t ＝2．答：经过2秒后△PBQ 的⾯积等于4cm 2．【点睛】本题考查了⼀元⼆次⽅程的运⽤，注意对所求的值进⾏检验，对于不合适的值舍去．3．已知关于x 的⽅程24832x nx n --=和()223220x n x n -+-+=，是否存在这样的n 值，使第⼀个⽅程的两个实数根的差的平⽅等于第⼆个⽅程的⼀整数根？若存在，请求出这样的n 值；若不存在，请说明理由？【答案】存在，n=0.【解析】【分析】在⽅程①中，由⼀元⼆次⽅程的根与系数的关系，⽤含n 的式⼦表⽰出两个实数根的差的平⽅，把⽅程②分解因式，建⽴⽅程求n ，要注意n 的值要使⽅程②的根是整数.【详解】若存在n 满⾜题意.设x1，x2是⽅程①的两个根，则x 1+x 2=2n ，x 1x 2=324n +-，所以(x 1-x 2)2=4n 2+3n+2，由⽅程②得，(x+n-1)[x-2(n+1)]=0，①若4n 2+3n+2=-n+1，解得n=-12，但1-n=32不是整数，舍. ②若4n 2+3n+2=2(n+2)，解得n=0或n=-14(舍)，综上所述，n=0.4．解⽅程：2332302121x x x x --= ? ?--．【答案】x=15或x=1 【解析】【分析】设321x y x =-，则原⽅程变形为y 2-2y-3=0, 解这个⼀元⼆次⽅程求y ，再求x ．【详解】解：设321x y x =-，则原⽅程变形为y 2-2y-3=0．解这个⽅程，得y 1=-1,y 2=3, ∴3121x x =--或3321x x =-．解得x=15或x=1．经检验：x=15或x=1都是原⽅程的解．∴原⽅程的解是x=15或x=1．【点睛】考查了还原法解分式⽅程，⽤换元法解⼀些复杂的分式⽅程是⽐较简单的⼀种⽅法，根据⽅程特点设出相应未知数，解⽅程能够使问题简单化，注意求出⽅程解后要验根．5．关于x 的⼀元⼆次⽅程()22210x k x k +-+=有两个不等实根1x ，2x . （1）求实数k 的取值范围；（2）若⽅程两实根1x ，2x 满⾜121210x x x x ++-=，求k 的值.【答案】(1) k ＜14;(2) k=0. 【解析】【分析】（1）根据⼀元⼆次⽅程的根的判别式得出△＞0，求出不等式的解集即可；（2）根据根与系数的关系得出x1+x2=-（2k-1）=1-2k，x1?x2=k2，代⼊x1+x2+x1x2-1=0，即可求出k值．【详解】解：（1）∵关于x的⼀元⼆次⽅程x2+（2k-1）x+k2=0有两个不等实根x1，x2，∴△=（2k-1）2-4×1×k2=-4k+1＞0，解得：k＜14，即实数k的取值范围是k＜14；（2）由根与系数的关系得：x1+x2=-（2k-1）=1-2k，x1?x2=k2，∵x1+x2+x1x2-1=0，∴1-2k+k2-1=0，∴k2-2k=0∴k=0或2，∵由（1）知当k=2⽅程没有实数根，∴k=2不合题意，舍去，∴k=0．【点睛】本题考查了解⼀元⼆次⽅程根的判别式和根与系数的关系等知识点，能熟记根的判别式和根与系数的关系的内容是解此题的关键，注意⽤根与系数的关系解题时要考虑根的判别式，以防错解．6．某⽔果店销售某品牌苹果，该苹果每箱的进价是40元，若每箱售价60元，每星期可卖180箱．为了促销，该⽔果店决定降价销售．市场调查反映:若售价每降价1元，每星期可多卖10箱．设该苹果每箱售价x元（40≤x≤60），每星期的销售量为y箱．（1）求y与x之间的函数关系式；（2）当每箱售价为多少元时，每星期的销售利润达到3570元？（3）当每箱售价为多少元时，每星期的销售利润最⼤，最⼤利润多少元?【答案】(1)y=-10x+780；(2) 57；(3)当售价为59元时，利润最⼤，为3610元【解析】【分析】（1）根据售价每降价1元，每星期可多卖10箱,设售价x元,则多销售的数量为60-x,（2）解⼀元⼆次⽅程即可求解,（3）表⽰出最⼤利润将函数变成顶点式即可求解.【详解】解：（1）∵售价每降价1元，每星期可多卖10箱,设该苹果每箱售价x元（40≤x≤60），则y=180+10（60-x）=-10x+780,(40≤x≤60),(2)依题意得：（x-40）(-10x+780)=3570,解得：x=57,∴当每箱售价为57元时，每星期的销售利润达到3570元.（3）设每星期的利润为w，W=（x-40）(-10x+780)=-10（x-59）2+3610,∵-10 0,⼆次函数向下,函数有最⼤值,当x=59时, 利润最⼤，为3610元.【点睛】本题考查了⼆次函数的实际应⽤,中等难度,熟悉⼆次函数的实际应⽤是解题关键.7．已知关于x的⽅程x2﹣2x+m﹣2＝0有两个不相等的实数根．(1)求m的取值范围；(2)如果m为正整数，且该⽅程的根都是整数，求m的值．【答案】(1)m＜3；(2)m＝2．【解析】【分析】（1）根据题意得出△＞0，代⼊求出即可；（2）求出m=1或2，代⼊后求出⽅程的解，即可得出答案．【详解】（1）∵⽅程有两个不相等的实数根．∴△＝4﹣4(m﹣2)＞0．∴m＜3；（2）∵m＜3 且 m为正整数，∴m＝1或2．当 m＝1时，原⽅程为 x2﹣2x﹣1＝0．它的根不是整数，不符合题意，舍去；当 m＝2时，原⽅程为 x2﹣2x＝0．∴x(x﹣2)＝0．∴x1＝0，x2＝2．符合题意．综上所述，m＝2．【点睛】本题考查了根的判别式和解⼀元⼆次⽅程，能根据题意求出m的值和m的范围是解此题的关键．8．已知关于x的⽅程（x-3）(x-2)-p2=0.（1）求证：⽆论p取何值时，⽅程总有两个不相等的实数根；（2）设⽅程两实数根分别为x1、x2，且满⾜x12+x22=3 x1x2，求实数p的值.【答案】（1）详见解析；（2）p=±1.【解析】【分析】（1）先把⽅程化成⼀般形式，再计算根的判别式，判定△＞0，即可得到总有两个不相等的实数根；（2）根据⼀元⼆次⽅程根与系数的关系可得两根和与两根积，再把2212123x x x x +=变形，化成和与乘积的形式，代⼊计算，得到⼀个关于p 的⼀元⼆次⽅程，解⽅程即可求解．【详解】证明：（1）（x ﹣3）（x ﹣2）﹣p 2=0，x 2﹣5x+6﹣p 2=0，△=（﹣5）2﹣4×1×（6﹣p 2）=25﹣24+4p 2=1+4p 2，∵⽆论p 取何值时，总有4p 2≥0，∴1+4p 2＞0，∴⽆论p 取何值时，⽅程总有两个不相等的实数根；（2）x 1+x 2=5，x 1x 2=6﹣p 2，∵2212123x x x x +=，∴（x 1+x 2）2﹣2x 1x 2=3x 1x 2，∴52=5（6﹣p 2），∴p=±1．考点：根的判别式；根与系数的关系．9．⼭西特产专卖店销售核桃，其进价为每千克40元，按每千克60元出售，平均每天可售出100千克，后来经过市场调查发现，单价每降低2元，则平均每天的销售可增加20千克，若该专卖店销售这种核桃要想平均每天获利2240元，请回答：（1）每千克核桃应降价多少元？（2）在平均每天获利不变的情况下，为尽可能让利于顾客，赢得市场，该店应按原售价的⼏折出售？【答案】（1）4元或6元；（2）九折.【解析】【详解】解：（1）设每千克核桃应降价x 元.根据题意，得（60﹣x ﹣40）（100+x 2×20）=2240，化简，得 x 2﹣10x+24=0，解得x 1=4，x 2=6.答：每千克核桃应降价4元或6元.（2）由（1）可知每千克核桃可降价4元或6元.∵要尽可能让利于顾客，∴每千克核桃应降价6元. 此时，售价为：60﹣6=54（元），54100%=90%60. 答：该店应按原售价的九折出售.10．如图，在△ABC中，∠B＝90°，AB＝6 cm，BC＝8 cm，若点P从点A沿AB边向B点以1 cm/s的速度移动，点Q从B点沿BC边向点C以2 cm/s的速度移动，两点同时出发．(1)问⼏秒后，△PBQ的⾯积为8cm2？(2)出发⼏秒后，线段PQ的长为42cm ?(3)△PBQ的⾯积能否为10 cm2？若能，求出时间；若不能，请说明理由．【答案】(1) 2或4秒2 cm；(3)见解析.【解析】【分析】（1）由题意，可设P、Q经过t秒，使△PBQ的⾯积为8cm2，则PB=6-t，BQ=2t，根据三⾓形⾯积的计算公式，S△PBQ=12BP×BQ，列出表达式，解答出即可；（2）设经过x秒后线段PQ的长为2cm，依题意得AP=x，BP=6-x，BQ=2x，利⽤勾股定理列⽅程求解；（3）将△PBQ的⾯积表⽰出来，根据△=b2-4ac来判断．【详解】(1)设P，Q经过t秒时，△PBQ的⾯积为8 cm2，则PB＝6－t，BQ＝2t，∵∠B＝90°，∴12(6－t)× 2t＝8，解得t1＝2，t2＝4，∴当P，Q经过2或4秒时，△PBQ的⾯积为8 cm2；(2)设x秒后，PQ＝2 cm，由题意，得(6－x)2＋4x2＝32，解得x1＝25，x2＝2，故经过25秒或2秒后，线段PQ的长为2 cm；(3)设经过y秒，△PBQ的⾯积等于10 cm2，S△PBQ＝12×(6－y)× 2y＝10，即y2－6y＋10＝0，∵Δ＝b2－4ac＝36－4× 10＝－4＜ 0，∴△PBQ的⾯积不会等于10 cm2.【点睛】本题考查了⼀元⼆次⽅程的应⽤，熟练的掌握⼀元⼆次⽅程的应⽤是本题解题的关键.。

学校培优辅差工作计划(6篇)

学校培优辅差工作计划为全面提高学生的综合素质，构建和谐校园，进一步规范我校全体学生的学习行为，进一步完善全体学生的学习习惯，使后进生尽快克服自卑心理，树立学习的信心和勇气，在全校形成"赶、帮、超"浓厚的学习氛围，使每位教师的后进生转化工作更扎实有效，现结合我校的实际情况，制定本方案。

一、工作目标后进生转化工作是提升学生综合素质、提高学生整体成绩的有效途径，也是教学工作的长期抓手和永恒主题。

通过扎实的培优辅差工作，使全体学生意识到学习的重要性，针对不同的学生因材施教，基础不扎实成绩不稳定的临界生和学习缺乏信心的后____%学困生的不同需求。

学科任课教师（指导师）要了解不同层次学生的思想、生活及学习状况，通过个体谈话、个别辅导、家访等方式，关心学生、走近学生、帮助学生，让不同层次的学生确立不同的学习目标，树立信心，切实有效地做好后进生转化工作。

二、指导对象后进生对象：班主任结合本班学业成绩后____%学生的德育、日常行规等综合表现，确立本班总人数的____%为辅差对象，但辅差名单不得在班级公布，需个别谈话明确帮扶计划。

此类学生基础不扎实，学习缺乏兴趣，对所学的内容消化不良，辅差工作的重点是要帮助他们疏导心理、树立信心。

班主任需了解学生的兴趣特长和现有的师生关系，并以此为突破口，帮助确定一位任课老师为指导师，进行辅差结对指导。

三、具体措施班主任根据本班学生总人数，确定后____%的辅差对象的人数及名单，联系合适的任课老师为指导师，并告知结对的师生双方，同时将结对的名单上传学校各指导师根据结对学生的学习情况，制定具体有效的学年补差计划，按要求将所结对学生的补差计划于每学年第一学期期末前上交教务处，并按计划有序进行学年结对指导。

班主任及各指导师要经常与家长取得联系，及时交流反馈学生的学习、生活情况，力争家长最大的配合与支持。

指导师要深入了解后____%学困生现行的学习方法、当下的思想状态，给予正确的引导，使其朝正确的方向发展。

学而思初二数学上册培优辅导讲义(人教版)

第1讲与相交有关概念及平行线的判定考点·方法·破译1．了解在平面内，两条直线的两种位置关系：相交与平行.2．掌握对顶角、邻补角、垂直、平行、内错角、中旁内角的定义，并能用图形或几何符号表示它们.3．掌握直线平行的条件，并能根据直线平行的条件说明两条直线的位置关系. 经典·考题·赏析【例1】如图，三条直线AB 、CD 、EF 相交于点O ，一共构成哪几对对顶角？一共构成哪几对邻补角？【解法指导】⑴对顶角和邻补角是两条直线所形成的图角.⑵对顶角：有一个公共顶点，并且一个角的两边是另一个角的两边的反向延长线.⑶邻补角：两个角有一条公共边，另一边互为反向延长线.有6对对顶角. 12对邻补角.【变式题组】01．如右图所示，直线AB 、CD 、EF 相交于P 、Q 、R ，则：⑴∠ARC 的对顶角是 . 邻补角是 .⑵中有几对对顶角，几对邻补角？02．当两条直线相交于一点时，共有2对对顶角；当三条直线相交于一点时，共有6对对顶角；当四条直线相交于一点时，共有12对对顶角. 问：当有100条直线相交于一点时共有对顶角.【例２】如图所示，点O 是直线AB 上一点，OE 、OF 分别平分∠BOC 、 ∠AOC ．⑴求∠EOF 的度数；⑵写出∠BOE 的余角及补角.【解法指导】解这类求角大小的问题，要根据所涉及的角的定义，以及各角的数量关系，把它们转化为代数式从而求解；【解】⑴∵OE 、OF 平分∠BOC 、∠AOC ∴∠EOC ＝21∠BOC ，∠FOC ＝21∠AOC ∴∠EOF ＝∠EOC ＋∠FOC ＝21∠BOC ＋21∠AOC ＝()AOC BOC ∠+∠21又∵∠BOC ＋∠AOC ＝180° ∴∠EOF ＝21×180°＝90° ⑵∠BOE 的余角是：∠COF 、∠AOF ；∠BOE 的补角是：∠AOE.【变式题组】 01．如图，已知直线AB 、CD 相交于点O ，OA 平分∠EOC ，且∠EOC＝100°，则∠BOD 的度数是（） A ．20° B ． 40° C ．50° D ．80°02．（杭州）已知∠1＝∠2＝∠3＝62°，则∠4＝ .【例３】如图，直线l1、l2相交于点O ，A 、B 分别是l1、l2上的点，试用三角尺完成下列作图：⑴经过点A 画直线l2的垂线.⑵画出表示点B 到直线l1的垂线段.【解法指导】垂线是一条直线，A B C D E F A B C DEF PQ R A BCE F E A ACD O （第1题图） 1 4 3 2（第2题图）2垂线段是一条线段. 【变式题组】01．P 为直线l 外一点，A 、B 、C 是直线l 上三点，且PA ＝4cm ，PB ＝5cm ，PC ＝6cm ，则点P 到直线l 的距离为（） A ．4cm B ． 5cm C ．不大于4cm D ．不小于6cm02 如图，一辆汽车在直线形的公路AB 上由A 向B 行驶，M 、N 为位于公路两侧的村庄；⑴设汽车行驶到路AB 上点P 的位置时距离村庄M 最近.行驶到AB 上点Q 的位置时，距离村庄N 最近，请在图中的公路上分别画出点P 、Q 的位置.⑵当汽车从A 出发向B 行驶的过程中，在的路上距离M 村越来越近..在的路上距离村庄N 越来越近，而距离村庄Ｍ越来越远.【例４】如图，直线AB 、CD 相交于点O ，OE ⊥CD ，OF ⊥AB ，∠DOF ＝65°，求∠BOE 和∠AOC 的度数.【解法指导】图形的定义现可以作为判定图形的依据，也可以作为该图形具备的性质，由图可得：∠AOF ＝90°，OF ⊥AB ．【变式题组】01．如图，若EO ⊥AB 于O ，直线CD 过点O ，∠EOD ︰∠EOB ＝1︰3，求∠AOC 、∠AOE 的度数.02．如图，O 为直线AB 上一点，∠BOC ＝3∠AOC ，OC 平分∠AOD ． ⑴求∠AOC 的度数；⑵试说明OD 与AB 的位置关系.03．如图，已知AB ⊥BC 于B ，DB ⊥EB 于B ，并且∠CBE ︰∠ABD ＝1︰2，请作出∠CBE 的对顶角，并求其度数.【例５】如图，指出下列各组角是哪两条直线被哪一条直线所截而得到的，并说出它们的名称： ∠1和∠2：∠1和∠3：∠1和∠6：∠2和∠6： F B AO CD EAEB ACDO A BA E DCF EBAD 1 4 2 3 6 5∠2和∠4： ∠3和∠5： ∠3和∠4：【解法指导】正确辩认同位角、内错角、同旁内角的思路是：首先弄清所判断的是哪两个角，其次是找到这两个角公共边所在的直线即截线，其余两条边所在的直线就是被截的两条直线，最后确定它们的名称.【变式题组】 01．如图，平行直线AB 、CD 与相交直线EF ，GH 相交，图中的同旁内角共有（） A ．4对 B ． 8对 C ．12对 D ．16对 02．如图，找出图中标出的各角的同位角、内错角和同旁内角.03．如图，按各组角的位置判断错误的是（） A ．∠1和∠2是同旁内角 B ．∠3和∠4是内错角 C ．∠5和∠6是同旁内角 D ．∠5和∠7是同旁内角【例６】如图，根据下列条件，可推得哪两条直线平行？并说明理由• ⑴∠CBD ＝∠ADB ； ⑵∠BCD ＋∠ADC ＝180° ⑶∠ACD ＝∠BAC 【解法指导】图中有即即有同旁内角，有“ ”即有内错角. 【解法指导】⑴由∠CBD ＝∠ADB ，可推得AD ∥BC ；根据内错角相等，两直线平行.⑵由∠BCD ＋∠ADC ＝180°，可推得AD ∥BC ；根据同旁内角互补，两直线平行. ⑶由∠ACD ＝∠BAC 可推得AB ∥DC ；根据内错角相等，两直线平行. 【变式题组】 01．如图，推理填空.⑴∵∠A ＝∠ （已知） ∴AC ∥ED （） ⑵∵∠C ＝∠ （已知）∴AC ∥ED （）⑶∵∠A ＝∠ （已知） ∴AB ∥DF （）02．如图，AD 平分∠BAC ，EF 平分∠DEC ，且∠1＝∠2，试说明DE 与AB 的位置关系.解：∵AD 是∠BAC 的平分线（已知）∴∠BAC ＝2∠1（角平分线定义）又∵EF 平分∠DEC （已知） A BDC HＧ E F 7 1 5 6 84 1 2 乙丙 3 23 4 5 61 23 4甲1 A BC 2 3 45 67 A B CDO A BD E FA E12∴ （）又∵∠1＝∠2（已知） ∴ （） ∴AB ∥DE （） 03．如图，已知AE 平分∠CAB ，CE 平分∠ACD ．∠CAE ＋∠ACE ＝90°，求证：AB ∥CD ． 04．如图，已知∠ABC ＝∠ACB ，BE 平分∠ABC ，CD 平分∠ACB ，∠EBF ＝∠EFB ，求证：CD ∥EF. 【例７】如图⑴，平面内有六条两两不平行的直线，试证：在所有的交角中，至少有一个角小于31°.【解法指导】如图⑵，我们可以将所有的直线移动后，使它们相交于同一点，此时的图形为图⑵. 证明：假设图⑵中的12个角中的每一个角都不小于31° 则12×31°＝372°＞360°这与一周角等于360°矛盾所以这12个角中至少有一个角小于31° 【变式题组】 01．平面内有18条两两不平行的直线，试证：在所有的交角中至少有一个角小于11°.02．在同一平面内有2010条直线a1,a2,…，a2010,如果a1⊥a2,a2∥a3，a3⊥a4，a4∥a5……那么a1与a2010的位置关系是 . 03．已知n （n ＞2）个点P1，P2，P3…Pn.在同一平面内没有任何三点在同一直线上，设Sn 表示过这几个点中的任意两个点所作的所有直线的条数，显然：S2＝1，S3＝3，S4＝6，∴S5＝10…则Sn ＝ . 演练巩固·反馈提高01．如图，∠EAC ＝∠ADB ＝90°.下列说法正确的是（） A ．α的余角只有∠B B ．α的邻补角是∠DACC ．∠ACF 是α的余角D ．α与∠ACF 互补 A BC D E A BC D E F l 1 l 2 l 3 l 4 l 5 l 6l 1 l 2 l 3l 4 l 5 l 6 A EA B EMα A02．如图，已知直线AB、CD被直线EF所截，则∠EMB的同位角为（）A．∠AMF B．∠BMF C．∠ENC D．∠END03．下列语句中正确的是（）A．在同一平面内，一条直线只有一条垂线B．过直线上一点的直线只有一条C．过直线上一点且垂直于这条直线的直线有且只有一条D．垂线段就是点到直线的距离04．如图，∠BAC＝90°，AD⊥BC于D，则下列结论中，正确的个数有（）①AB⊥AC ②AD与AC互相垂直③点C到AB的垂线段是线段AB ④线段AB 的长度是点B到AC的距离⑤垂线段BA是点B到AC的距离⑥AD＞BD A．0 B． 2 C．4 D．605．点A、B、C是直线l上的三点，点P是直线l外一点，且PA＝4cm，PB＝5cm，PC＝6cm，则点P到直线l的距离是（）A．4cm B．5cm C．小于4cm D．不大于4cm06．将一副直角三角板按图所示的方法旋转（直角顶点重合），则∠AOB＋∠DOC ＝.07．如图，矩形ABCD沿EF对折，且∠DEF＝72°，则∠AEG＝. 08．在同一平面内，若直线a1∥a2,a2⊥a3,a3∥a4,…则a1 a10.（a1与a10不重合）09．如图所示，直线a、b被直线c所截，现给出下列四个条件：①∠1＝∠5，②∠1＝∠7，③∠2＋∠3＝180°，④∠4＝∠7，其中能判断a∥b的条件的序号是.10．在同一平面内两条直线的位置关系有.11．如图，已知BE平分∠ABD，DE平分∠CDB，且∠E＝∠ABE＋∠EDC．试说明AB∥CD？12．如图，已知BE平分∠ABC，CF平分∠BCD，∠1＝∠2，那么直线AB与CD的位置关系如何？13．如图，推理填空：⑴∵∠A＝（已知）∴AC∥ED（）⑵∵∠2＝（已知）∴AC∥ED（）⑶∵∠A＋＝180°（已知）∴AB∥FD．14．如图，请你填上一个适当的条件使AD∥BC．ABCDOAB CDEFGHabc第6题图第7题图第9题图123 4567 81AC DEBAC DE12AB CDEF第14题图培优升级·奥赛检测01．平面图上互不重合的三条直线的交点的个数是（）A ．1，3B ．0，1，3C ．0，2，3D ．0，1，2，302．平面上有10条直线，其中4条是互相平行的，那么这10条直线最多能把平面分成（）部分. A ．60 B ． 55 C ．50 D ．45 03．平面上有六个点，每两点都连成一条直线，问除了原来的6个点之外，这些直线最多还有（）个交点. A ．35 B ． 40 C ．45 D ．5504．如图，图上有6个点，作两两连线时，圆内最多有__________________交点. 05．如图是某施工队一张破损的图纸，已知a 、b 是一个角的两边，现在要在图纸上画一条与这个角的平分线平行的直线，请你帮助这个施工队画出这条平行线，并证明你的正确性.06．平面上三条直线相互间的交点的个数是（）A ．3B ．1或3C ．1或2或3D ．不一定是1，2，3 07．请你在平面上画出6条直线（没有三条共点）使得它们中的每条直线都恰好与另三条直线相交，并简单说明画法？08．平面上有10条直线，无任何三条交于一点，要使它们出现31个交点，怎么安排才能办到？09．如图，在一个正方体的2个面上画了两条对角线AB 、AC ，那么两条对角线的夹角等于（）A ．60°B ． 75°C ．90°D ．135°10．在同一平面内有9条直线如何安排才能满足下面的两个条件？a b AB C⑴任意两条直线都有交点；⑵总共有29个交点.第13讲平行线的性质及其应用考点·方法·破译1．掌握平行线的性质，正确理解平行线的判定与性质定理之间的区别和联系；2．初步了解命题，命题的构成，真假命题、定理；3．灵活运用平行线的判定和性质解决角的计算与证明，确定两直线的位置关系，感受转化思想在解决数学问题中的灵活应用.经典·考题·赏析【例１】如图，四边形ABCD中，AB∥CD，BC∥AD度数.【解法指导】两条直线平行，同位角相等；两条直线平行，内错角相等；两条直线平行，同旁内角互补.平行线的性质是推导角关系的重要依据之一，必须正确识别图形的特征，看清截线，识别角的关系式关键.【解】：∵AB∥CD BC∥AD∴∠A＋∠B＝180°∠B＋∠C＝180°(两条直线平行，同旁内角互补)∴∠A＝∠C ∵∠A＝38°∴∠C＝38°【变式题组】01．如图，已知AD∥BC，点E在BD的延长线上，若∠ADE＝155°，则∠DBC的度数为（）A．155°B．50°C．45°D．25°1＝55°，∠2＝65°，则∠3为（）A．50°B．55°C．60°D．65°03．如图，已知FC∥AB∥DE，∠α：∠D：∠B＝2: 3: 4, 试求∠α、∠D、∠B的度数.【例２】如图，已知AB∥CD∥EF，GC⊥CF，∠B＝60°，∠EFC＝45°，求∠BCG的度数.【解法指导】平行线的性质与对顶角、邻补角、垂直和角平分线相结合，可求各种位置的角的度数，但注意看清角的位置.【解】∵AB∥CD∥EF ∴∠B＝∠BCD ∠F＝∠FCD(两条直线平行，内错角相等)又∵∠B＝60°∠EFC＝45°∴∠BCD＝60°∠FCD＝45°又∵GC⊥CF ∴∠GCF＝90°（垂直定理）∴∠GCD＝90°－45°＝45°∴∠BCG＝60°－45°＝15°【变式题组】EAFGDCB01．如图，已知AF ∥BC, 且AF 平分∠EAB ，∠B ＝48°，则∠C 的的度数＝_______________02.如图,已知∠ABC ＋∠ACB ＝120°，BO 、CO 分别∠ABC 、∠ACB ，DE 过点O 与BC 平行，则∠BOC ＝___________03．如图，已知AB ∥ MP ∥CD, MN 平分∠AMD ，∠A ＝40°，∠D ＝50°，求∠NMP 的度数.【例３】如图，已知∠1＝∠2，∠C ＝∠D ．求证：∠A ＝∠F. 【解法指导】因果转化，综合运用.逆向思维：要证明∠A ＝∠F ，即要证明DF ∥AC ．要证明DF ∥AC, 即要证明∠D ＋∠DBC ＝180°，即：∠C ＋∠DBC ＝180°；要证明∠C ＋∠DBC ＝180°即要证明DB ∥EC ．要证明DB ∥EC 即要证明∠1＝∠3.证明：∵∠1＝∠2，∠2＝∠3（对顶角相等）所以∠1＝∠3 ∴DB ∥EC （同位角相等•两直线平行）∴∠DBC ＋∠C ＝180°（两直线平行，同旁内角互补）∵∠C ＝∠D ∴∠DBC ＋∠D ＝180° ∴DF ∥AC （同旁内角，互补两直线平行）∴∠A ＝∠F （两直线平行，内错角相等）【变式题组】01．如图，已知AC ∥FG ，∠1＝∠2，求证：DE ∥FG02．如图，已知∠1＋∠2＝180°，∠3＝∠B ．求证：∠AED ＝∠ACB03．如图，两平面镜α、β的夹角θ，入射光线AO 平行于β入射到α上，经两次反射后的出射光线O′B 平行于α，则角θ等于_________.【例４】如图，已知EG ⊥BC ，AD ⊥BC ，∠1＝∠3. 求证：AD 平分∠BAC ．【解法指导】抓住题中给出的条件的目的，仔细分析条件给我们带来的结论，对于不能直接直接得出结论的条件，要准确把握住这些条件的意图.（题目中的： ∠1＝∠3）证明：∵EG ⊥BC ，AD ⊥BC ∴∠EGC ＝∠ADC ＝90° （垂直定义）∴EG ∥AD （同位角相等，两条直线平行）∵∠1＝∠3 ∴∠3＝∠BAD （两条直线平行，内错角相等）ABCDOE FAEBC （第1题图）（第2题图） BA MC D N P （第3题图）DE F2GB 3C A 1D 2E F （第1题图） A2 CF 3 E D1B（第2题图） 31ABG D CEDA2 E1 B C B F E AC D ∴AD 平分∠BAC （角平分线定义）【变式题组】01．如图，若AE ⊥BC 于E ，∠1＝∠2，求证：DC ⊥BC ．02．如图，在△ABC 中，CE ⊥AB 于E,DF ⊥AB 于F, AC ∥ED ，CE 平分∠ACB ．求证：∠EDF ＝∠BDF.3．已知如图，AB ∥CD ，∠B ＝40°，CN 是∠BCE 的平分线. CM ⊥CN ，求：∠BCM 的度数.【例５】已知，如图，AB ∥EF ，求证：∠ABC ＋∠BCF ＋∠CFE ＝360° 【解法指导】从考虑360°这个特殊角入手展开联想，分析类比，联想周角.构造两个“平角”或构造两组“互补”的角.过点C 作CD ∥AB 即把已知条件AB ∥EF 联系起来，这是关键.【证明】：过点C 作CD ∥AB ∵CD ∥AB ∴∠1＋∠ABC＝180°(两直线平行，同旁内角互补) 又∵AB ∥EF ，∴CD ∥EF （平行于同一条直线的两直线平行） ∴∠2＋∠CFE ＝180°(两直线平行，同旁内角互补) ∴∠ABC ＋∠1＋∠2＋∠CFE ＝180°＋180°＝360° 即∠ABC ＋∠BCF ＋∠CFE ＝360° 【变式题组】01．如图，已知，AB ∥CD ，分别探究下面四个图形中∠APC 和∠PAB 、∠PCD 的关系，请你从所得四个关系中选出任意一个，说明你探究的结论的正确性. 结论：⑴____________________________ ⑵____________________________⑶____________________________ ⑷____________________________BAPCAC CDAAPCBDPBPD BD ⑴⑵⑶⑷A DMCN EB F E D 2 1 AB Cα β P B C D A∠P ＝α＋βF γ Dα β E B C A FD EBC A AA ′ lB ′C ′【例６】如图，已知，AB ∥CD ，则∠α、∠β、∠γ、∠ψ之间的关系是 ∠α＋∠γ＋∠ψ－∠β＝180° 【解法指导】基本图形善于从复杂的图形中找到基本图形，运用基本图形的规律打开思路【解】过点E 作EH ∥AB ．过点F 作FG∥AB ． ∵直线平行，内错角相等）又∵FG ∥AB ∴EH∥FG （平行于同一条直线的两直线平行）∴∠2＝∠3 又∵AB ∥CD ∴FG ∥CD ∴∠ψ＋∠4＝180°＋∠3＋∠4－ψ－∠1－∠2＝∠4＋ψ＝180° 【变式题组】01．如图， AB ∥EF ，∠C ＝90°，则∠α、∠β、∠γA ． ∠β＝∠α＋∠γ B ．∠β＋∠α＋∠γ＝180° C ． ∠α＋∠β－∠γ＝90° D ．∠β＋∠γ－∠α＝90°02．如图，已知，AB ∥CD ，∠ABE 和∠CDE 的平分线相交于点F ，∠E ＝140°，求∠BFD 的度数.【例７】如图，平移三角形ABC ，设点A 移动到点A/，画出平移后的三角形A/B/C/.【解法指导】抓住平移作图的“四部曲”——定，找，移，连. ⑴定：确定平移的方向和距离. ⑵找：找出图形的关键点. ⑶移：过关键点作平行且相等的线段，得到关键点的对应点. ⑷连: 按原图形顺次连接对应点.的平行线l ③在l 截取BB/＝AA/,则点B/C 的对应点C/.连接A/B/，B/C/，C/A/就21cm ，作出平移后的图形. 三角形ABC 中，∠C ＝90°, BC ＝4，AC ＝4，现将△ABC 沿CB 方向平移到△A/B/C/的位置，若平移距离为3, 求△ABC与△A/B/C/的重叠部分的面积. 03．原来是重叠的两个直角三角形，将其中一个三角形沿着BC 方向平移BE 的距离，就得到此图形，求阴影部分的面积.（单位：厘米）BB / AA / C C /演练巩固反馈提高 01．如图，由A 测B 得方向是（） A ．南偏东30° B ．南偏东60° C ．北偏西30° D ．北偏西60° 02平行；④平行于同一条直线的两直线垂直.其中的真命题的有（） A ．1个 B ．2个 C ．3个 D ．4个 03．一个学员在广场上练习驾驶汽车，两次拐弯后，行驶的方向与原来的方向相同，两次拐弯的角度可能是（） A ．第一次向左拐30°，第二次向右拐30° B ．第一次向右拐50°，第二次向左拐130° C ．第一次向左拐50°，第二次向右拐130° D ．第一次向左拐60°，第二次向左拐120° 04．下列命题中，正确的是（） A ．对顶角相等 B ．同位角相等 C ．内错角相等 D ．同旁内角互补 05．学习了平行线后，小敏想出过直线外一点画这条直线的平行线的新方法，是通过折一张半透明的纸得到的[如图⑴—⑷]） .C ．③④D ．①④ A 地测得B 地的走向是南B 两地要同时开工，若干天后，公路准确对接，则B 地所修公路的走向应该是（） A ．北偏东52° B ．南偏东52° C ．西偏北52° D ．北偏西38° 07．下列几种运动中属于平移的有（） ①水平运输带上的砖的运动；②笔直的高诉公路上行驶的汽车的运动（忽略车轮的转动）；③升降机上下做机械运动；④足球场上足球的运动. A ．1种 B ．2种 C ．3种 D ．4种 08．如图，网格中的房子图案正好处于网格右下角的位置.平移这个图案，使它正好位于左上角的位置（不能出格）150°120°DBCE 湖09．观察图，哪个图是由图⑴平移而得到的（）10．如图，AD∥BC，AB∥CD，AE⊥BC，现将△ABE进行平移. 平移方向为射线AD的方向. 平移距离为线段BC的长，则平移得到的三角形是图中（）图的阴影部分.11．判断下列命题是真命题还是假命题，如果是假命题，举出一个反例.⑴对顶角是相等的角；⑵相等的角是对顶角；⑶两个锐角的和是钝角；⑷同旁内角互补，两直线平行.12．把下列命题改写成“如果……那么……”的形式，并指出命题的真假.⑴互补的角是邻补角；⑵两个锐角的和是锐角；⑶直角都相等.13．如图，在湖边修一条公路.如果第一个拐弯处∠A＝120°，第二个拐弯处∠B ＝150°，第三个拐弯处∠C，这时道路CE恰好和道路AD平行，问∠C是多少度？并说明理由.14．如图，一条河流两岸是平行的，当小船行驶到河中E点时，与两岸码头B、D成64°角. 当小船行驶到河中F点时，看B点和D点的视线FB、FD恰好有∠1＝∠2，∠3＝∠4的关系. 你能说出此时点F与码头B、D所形成的角∠BFD的DEAB CE DB CE D AB CED AB CEDA B C4 P 23 1A BEF CD15．如图，AB ∥CD ，∠1＝∠2，试说明∠E 和∠F 的关系.培优升级·奥赛检测01．如图，等边△ABC 各边都被分成五等分，这样在△ABC 内能与△DEF 完成重合的小三角形共有25个，那么在△ABC 内由△DEF 平移得到的三角形共有（）个02．如图，一足球运动员在球场上点A 处看到足球从B 点沿着BO 方向匀速滚来，运动员立即从A 处以匀速直线奔跑前去拦截足球.若足球滚动的速度与该运动员奔跑的速度相同，请标出运动员的平移方向及最快能截住足球的位置.（运动员奔跑于足球滚动视为点的平移）A3向右平移1个单位得到B1B2B3，得到封闭图形A1A2 A3B3B2B1 [即阴影部分如图⑵];⑴在图⑶中，请你类似地画出一条有两个折点的直线，同样的向右平移1个单位，从而得到1个封闭图形，并画出阴影.⑵请你分别写出上述三个阴影部分的面积S1＝________, S2＝________, S3＝________.⑶联想与探究：如图⑷，在一矩形草地上，有一条弯曲的柏油小路（小路在任何地方的水平宽度都是1个单位），请你猜想空白部分草地面积是多少？05．一位模型赛车手遥控一辆赛车，先前进一半，然后原地逆时针旋转α°（0°＜⑶ ⑷ ... AF E B A C GD α°＜180°），被称为一次操作，若5次后发现赛车回到出发点，则α°角为（） A ．720° B ．108°或144° C ．144° D ．720°或144° 06．两条直线a 、b 互相平行，直线a 上顺次有10个点A1、A2、…、A10，直线b 上顺次有10个点B1、B2、…、B9，将a 上每一点与b 上每一点相连可得线段.若没有三条线段相交于同一点，则这些选段的交点个数是（） A ．90 B ．1620 C ．6480 D ．200607．如图，已知AB ∥CD ，∠B ＝100°，EF 平分∠BEC ，EG ⊥EF. 求∠BEG 和∠DEG.08．如图，AB ∥CD ，∠BAE ＝30°，∠DCE ＝60°，EF 、EG 三等分∠AEC ．问：EF 与EG 中有没有与AB 平行的直线？为什么？09．如图，已知直线CB ∥OA ，∠C ＝∠OAB ＝100°，E 、F 在CB 上，且满足∠FOB ＝∠AOB ，OE 平分∠COF. ⑴求∠EOB 的度数；⑵若平行移动AB ，那么∠OBC ：∠OFC 的值是否随之发生变化？若变化，找出变化规律；若不变，求出这个比值.⑶在平行移动AB 的过程中，是否存在某种情况，使∠OEC ＝∠OBA ？若存在，求出其度数；若不存在，说明理由.10．平面上有5条直线，其中任意两条都不平行，那么在这5条直线两两相交所成的角中，至少有一个角不超过36°,请说明理由.11．如图，正方形ABCD 的边长为5,把它的对角线AC 分成n 段，以每一小段为对角线作小正方形，这n 个小正方形的周长之和为多少？12．如图将面积为a2的小正方形和面积为b2的大正方形放在一起，用添补法如何求出阴影部分面积？FEB AC GD 100° FE BAC O ABCD第06讲实数考点·方法·破译 1．平方根与立方根：若2x ＝a(a ≥0)则x 叫做a 的平方根，记为：a 的平方根为xa 的平方根为xa 的算术平方根．若x3＝a ，则x 叫做a 的立方根．记为：a 的立方根为x2．无限不循环小数叫做无理数，有理数和无理数统称实数．实数与数轴上的点一一对应．任何有理数都可以表示为分数pq （p 、q 是两个互质的整数，且q ≠0）的形式． 3非负数：实数的绝对值，实数的偶次幂，非负数的算术平方根（或偶次方根）都是非负数．即a>0，2na ≥0（n 为正整数）0(a ≥0) ．经典·考题·赏析【例1】若2m －4与3m －1是同一个数的平方根，求m 的值．【解法指导】一个正数的平方根有两个，并且这两个数互为相反数．∵2m −4与3m−l 是同一个数的平方根，∴2m−4 ＋3m−l ＝0，5m ＝5，m ＝l ．【变式题组】01．一个数的立方根与它的算术平方根相等，则这个数是____． 02．已知mm 的平方根是____． 03____．04．如图，有一个数值转化器，当输入的x 为64时，输出的y 是____．【例2】（全国竞赛）已知非零实数a 、b 满足24242a b a -+++=，则a ＋b 等于( ) A ．－1 B ． 0 C ．1 D ．2有意义，∵a 、b 为非零实数，∴b2>0∴a －3≥0 a≥3∵24242a b a -+++=∴24242a b a -++=，∴20b ++=．∴()22030b a b +=⎧⎪⎨-=⎪⎩，∴32a b =⎧⎨=-⎩，故选C ．【变式题组】0l3b +＝0成立，则ab ＝____．02()230b -=，则a b 的平方根是____．03．（天津）若x 、y为实数，且20x +=，则2009x y ⎛⎫⎪⎝⎭的值为（）A ．1B ．－1C ．2D ．－204．已知x1x π-的值是( )A ．11π-B ．11π+C ．11π- D ．无法确定【例3】若a 、b都为有理效，且满足1a b -+=+a ＋b 的平方根．【解法指导】任何两个有理数的和、差、积、商（除数不为0）还是有理数，但两个无理数的和、差、积、商（除数不为0）不一定是无理数．∵1a b -+=+∴1a b -=⎧⎪=1a b -=⎧⎪=，∴1312a b =⎧⎨=⎩， a ＋b ＝12 ＋13＝25．∴a ＋b的平方根为：5==±．【变式题组】01．（西安市竞赛题）已知m 、n2）m ＋(3－)n ＋7＝0求m 、n ．02．（希望杯试题）设x 、y 都是有理数，且满足方程（123π+）x ＋（132π+）y−4−π＝0，则x−y ＝____．【例4】若a2的整数部分，b−1是9的平方根，且a b b a-=-，求a＋b 的值．【解法指导】−2＝整数部分＋小数部分．整数部分估算可得2−2 −2−4．∵a ＝2，b−1＝±3 ，∴b ＝－2或4 ∵a b b a-=-．∴a<b ，∴a ＝2， b ＝4，即a ＋b ＝6．【变式题组】01．若3a ，的小数部分是b ，则a ＋b 的值为____． 02a ，小数部分为ba ）·b ＝____．演练巩固反馈提高0l ．下列说法正确的是( )A ．－2是(－2)2的算术平方根B ．3是－9的算术平方根C ． 16的平方根是±4D ．27的立方根是±302．设3a =-，b ＝－2，52c =-，则a 、b 、c 的大小关系是( ) A ．a<b<c B ．a<c<b C ． b<a<c D ．c<a<b03．下列各组数中，互为相反数的是( ) A ．－9与81的平方根 B ．4与364- C ．4与364 D ．3与904．在实数1.414，2-，0.1•5•，5−16，π，3.1•4•，83125中无理数有( )A ．2个B ．3个C ．4个D ． 5个05．实数a 、b 在数轴上表示的位置如图所示，则( ) A ．b>a B ．a b>C ．－a ＜bD ．－b>a06．现有四个无理数5，6，7，8，其中在2＋1与3＋1之间的有( ) A ． 1个 B ．2个 C ． 3个 D ．4个 07．设m 是9的平方根，n ＝()23．则m ，n 的关系是( )A. m ＝±nB.m ＝n C .m ＝－n D.m n≠08．（烟台）如图，数轴上 A 、B 两点表示的数分别为－1和3，点B 关于点A 的对称点C ，则点C 所表示的数为( )A ．－23-B ．－13-C ．－2 ＋3D ．l ＋309．点A 在数轴上和原点相距5个单位，点B 在数轴上和原点相距3个单位，且点B 在点A 左边，则A 、B 之间的距离为____．10．用计算器探索：已知按一定规律排列的一组数：1，12，13…，119，120．如果从中选出若干个数，使它的和大于3，那么至少要选____个数． 11．对于任意不相等的两个数a 、b ，定义一种运算※如下：a ※b ＝a ba b +-，如3※2＝3232+-＝5．那么12.※4＝____．12．（长沙中考题）已知a 、b 为两个连续整数，且a<7 <b ，则a ＋b ＝____．13．对实数a 、b ，定义运算“*”，如下a*b ＝()()22a b a b ab a b ⎧⎪⎨⎪⎩≥<，已知3*m ＝36，则实数m ＝____．14．设a 是大于1的实数．若a ，23a +，213a +在数轴上对应的点分别是A 、B 、C，则三点在数轴上从左自右的顺序是____．15.如图，直径为1的圆与数轴有唯一的公共点P ．点P表示的实数为－1．如果该圆沿数轴正方向滚动一周后与数轴的公共点为P′，那么点P′所表示的数是____．16．已知整数x、y满足x＋2y＝50，求x、y．17．已知2a−1的平方根是±3，3a＋b−1的算术平方根是4，求a＋b＋1的立方根．18．小颖同学在电脑上做扇形滚动的游戏，如图有一圆心角为60°，半径为1个单位长的扇形放置在数轴上，当扇形在数轴上做无滑动的滚动时，当B点恰好落在数轴上时，(1)求此时B点所对的数；(2)求圆心O移动的路程．19．若b＝315a-＋153a-＋3l，且a＋11的算术平方根为m，4b＋1的立方根为n，求（mn−2）(3mn ＋4)的平方根与立方根．20．若x、y为实数，且（x−y＋1）2与533x y--互为相反数，求22x y+的值．培优升级奥赛检测01．（荆州市八年级数学联赛试题）一个正数x的两个平方根分别是a＋1与a−3，则a值为( )A．2 B．－1 C．1 D．002．（黄冈竞赛）代数式x＋1x-＋2x-的最小值是( )A．0 B．1＋2C．1 D．203．代数式53x+−2的最小值为____．04．设a、b为有理数，且a、b满足等式a2＋3b＋则a＋b＝____．05．若a b-＝1，且3a＝4b，则在数轴上表示a、b两数对应点的距离为____．06．已知实数a满足2009a a-=，则a− 20092＝_______．m满足关系式199y x=--，试确定m的值．08．（全国联赛）若a、b满足5b＝7，S＝3b，求S的取值范围．09．（北京市初二年级竞赛试题）已知0<a<1，并且123303030a a a⎡⎤⎡⎤⎡⎤+++++⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦2830a⎡⎤+++⎢⎥⎣⎦2930a⎡⎤++⎢⎥⎣⎦18=，求[10a]的值[其中[x]表示不超过x的最大整数] ．10．（北京竞赛试题）已知实数a、b、x、y满足y＋21a=-，231x y b-=--，求22x y a b+++的值．第14讲平面直角坐标系（一）考点．方法．破译1．认识有序数对，认识平面直角坐标系．2．了解点与坐标的对应关系．3．会根据点的坐标特点，求图形的面积．经典．考题．赏析【例1】在坐标平面内描出下列各点的位置．A(2，1)，B(1，2)，C(－1，2)，D(－2，－1)，E(0，3)，F(－3，0)【解法指导】从点的坐标的意义去思考，在描点时要注意点的坐标的有序性．【变式题组】01．第三象限的点P(x，y)，满足|x|＝5,2x＋|y|＝1，则点P得坐标是_____________．02．在平面直角坐标系中，如果m.n＞０，那么（m, |n|）一定在____________象限.03．指出下列各点所在的象限或坐标轴．A(－3，0)，B(－2，－13)，C(2，12)，D(0,3)，E(π－3.14，3.14－π)【例2】若点P(a，b)在第四象限，则点Q(―a，b―1)在（）A．第一象限B．第二象限C．第三象限D．第四象限【解法指导】∵P(a，b)在第四象限，∴a＞0，b＜0，∴－a＜0, b－１＜0,故选C．【变式题组】01．若点G(a，2－a)是第二象限的点，则a的取值范围是（）A．a＜0 B．a＜2 C．0＜a＜2 B．a＜0或a＞2 02．如果点P(3x－２，２－x)在第四象限，则x的取值范围是____________．03．若点P(x，y)满足xy＞0，则点P在第______________象限．04．已知点P(2a－8，2－a)是第三象限的整点，则该点的坐标为___________．【例３】已知A点与点B(－3，4)关于x轴对称，求点A关于y轴对称的点的坐标．【解法指导】关于x轴对称的点的坐标的特点：横坐标(x)相等，纵坐标(y)互为相反数，关于y轴对称的点的坐标特点：横坐标互为相反数，纵坐标(y)相等．【变式题组】01．P(－1，3)关于x轴对称的点的坐标为____________．02．P(3，－2)关于y轴对称的点的坐标为____________．03．P(a，b)关于原点对称的点的坐标为____________．04．点A(－3，2m－１) 关于原点对称的点在第四象限，则m的取值范围是____________．05．如果点Ｍ(a＋b，ab)在第二象限内，那么点N(a，b) 关于y轴对称的点在第______象限．【例４】P(3，－4)，则点P到x轴的距离是____________．【解法指导】P(x，y)到x轴的距离是| y|，到y轴的距离是|x|．则P到轴的距离是|－4|＝4【变式题组】01．已知点P(3，5)，Q(6，－５)，则点P、Q到x 轴的距离分别是_________，__________．P到y轴的距离是点Q到y轴的距离的________倍．02．若x轴上的点Ｐ到y轴的距离是3，则P点的坐标是__________．03．如果点B(m＋1，3m－5) 到x轴的距离与它到y轴的距离相等，求m的值．04．若点(5－a，a－3)在一、三象限的角平分线上，求a的值．05．已知两点A(－3，m)，B(n，4)，AB∥x轴，求m的值，并确定n的取值范围．【例５】如图，平面直角坐标系中有A、B两点．(1)它们的坐标分别是___________，___________；(2)以A、B为相邻两个顶点的正方形的边长为_________；(3)求正方形的其他两个顶点C、D的坐标．【解法指导】平行x轴的直线上两点之间的距离是：两个点的横坐标的差得绝对值，平行y轴的直线上两点之间的距离是：两个点的纵坐标的差得绝对值．即：A(x1，y1)，B(x2，y2)，若AB∥x轴，则|AB|＝|x1－x2|；若AB∥y，则|AB|＝|y1－y2|，则(1)A(2，2)，B(2，－1)；(2)3；(3)C(5，2)，D(5，－1)或C(－1，2)，D(－1，－1)．【变式题组】01．如图，四边形ACBD是平行四边形，且AD∥x轴，说明，A、D两点的___________坐标相等，请你依据图形写出A、B、C、D四点的坐标分别是_________、_________、____________、____________．02．已知：A(0，4)，B(－3，0)，C(3，0)要画出平行四边形ABCD，请根据A、B、C三点的坐标，写出第四个顶点D的坐标，你的答案是唯一的吗？03．已知：A(0，4)，B(0，－1)，在坐标平面内求作一点，使△ABC的面积为5，请写出点C的坐标规律．【例6】平面直角坐标系，已知点A(－3，－2)，B(0，3)，C(－3，2)，求△ABC 的面积．【解法指导】(1)三角形的面积＝12×底×高．。

培优补差工作计划具体措施8篇

培优补差工作计划具体措施8篇培优补差工作方案详细措施8篇培优补差工作方案如何写？培优补差就是要兼顾全班每一个同学、不让一个同学落下的教学方式，它对于提高班级教学成果具有非常重要的作用和意义。

下面是我给大家带来的培优补差工作方案详细措施，期望能够帮到你哟!培优补差工作方案详细措施篇1今年，我担当七年级202、204班数学课，从这个班的整体状况来看，同学的数学成果比较差，有的同学甚至基本的代数式的运算都不会。

因此，后进生的转化的任务相当艰难。

本学年，我预备从以下几个方面做起：一、确立指导思想。

以老师特殊的爱奉献给特殊的同学。

“帮同学一把，带他们一同上路”。

对差生高看一眼，厚爱三分，以最大限度的急躁和恒心补出成效。

二、差生缘由分析及实行措施。

（查找根源，发觉造成学习困难的缘由有生理因素，也有心理因素，但更多的是同学自身缘由。

）1、志向性障碍：学习无目的性、无乐观性和主动性，对自己抱自暴自弃的态度。

2、情感性障碍：缺乏乐观的学习动机，随着时间的推移，学问欠帐日益增加，成果每况愈下，久而久之成为学习困难同学。

3、不良的学习习惯：学习困难同学通常没有良好的学习习惯，他们一般贪玩，上课留意力不集中，上课不听讲，练习不完成，作业不能独立完成,甚至抄袭作业。

依据以上这些状况要做好后进生的思想工作。

一些同学脑子也很聪慧，但是由于意识不到学习的重要性，对学习好像一点爱好都没有，再加上平常紧急不起来，这样日久天长，基础学问变渐渐拉了下来，从而变成后进生;对于这部分同学，我预备从三个方面做好同学思想工作，其一，多传输一些名人事迹，特殊是从他们过去那种困难的环境入手，告知他们学习机会的来之不易;其二，提高课堂教学技能，尽量把课堂讲得的生动些，以提高他们的学习爱好;其三，尽量多从生活中取材，以让同学意识到，学习并不是没有用，而是用途很大，因此来提高他们的学习乐观性;通过这三项，来转化他们的学习态度，使他们从消极的学习态度转化为乐观的学习态度。

【数学】培优一元二次方程辅导专题训练附答案解析

一、一元二次方程真题与模拟题分类汇编（难题易错题）1．关于x 的方程x 2﹣2（k ﹣1）x +k 2＝0有两个实数根x 1、x 2．（1）求k 的取值范围；（2）若x 1+x 2＝1﹣x 1x 2，求k 的值．【答案】（1）12k ≤；（2）3k = 【解析】试题分析：（1）方程有两个实数根，可得240b ac ∆=-≥，代入可解出k 的取值范围；（2）由韦达定理可知，()2121221,x x k x x k +=-=，列出等式，可得出k 的值．试题解析：(1)∵Δ＝4(k －1)2－4k 2≥0，∴－8k ＋4≥0，∴k ≤12； (2)∵x 1＋x 2＝2(k －1)，x 1x 2＝k 2，∴2(k －1)＝1－k 2，∴k 1＝1，k 2＝－3.∵k ≤12，∴k ＝－3.2．解下列方程：（1）x 2﹣3x=1．（2）12（y+2）2﹣6=0．【答案】(1)12313313,22x x +-== ;(2)12223,223y y =-+=-- 【解析】试题分析：（1）利用公式法求解即可；（2）利用直接开方法解即可；试题解析：解：（1）将原方程化为一般式，得x 2﹣3x ﹣1=0，∵b 2﹣4ac=13＞0∴． ∴12313313,22x x +-==．（2）（y+2）2=12， ∴或，∴12223,223y y =-+=--3．已知为正整数，二次方程的两根为，求下式的值：【答案】【解析】由韦达定理，有，．于是，对正整数，有原式=4．解下列方程：(1)2x2－4x－1＝0(配方法)；(2)(x＋1)2＝6x＋6.【答案】(1)x1＝1＋62x2＝1－621＝－1，x2＝5.【解析】试题分析：（1）根据配方法解一元二次方程的方法，先移项，再加减一次项系数一半的平方，完成配方，再根据直接开平方法解方程即可；（2）根据因式分解法，先移项，再提公因式即可把方程化为ab=0的形式，然后求解即可.试题解析：(1)由题可得，x2－2x＝12，∴x2－2x＋1＝32.∴(x－1)2＝32.∴x－1＝32±6 2.∴x1＝1＋62，x2＝1－62.(2)由题可得，(x＋1)2－6(x＋1)＝0，∴(x＋1)(x＋1－6)＝0.∴x＋1＝0或x＋1－6＝0.∴x1＝－1，x2＝5.5．已知两条线段长分别是一元二次方程28120x x-+=的两根，（1）解方程求两条线段的长。

初二-第01讲-三角形的证明(培优)-教案

学科教师辅导讲义学员编号：年级：八年级(下) 课时数：3学员姓名：辅导科目：数学学科教师：授课主题第01讲-三角形的证明授课类型T同步课堂P实战演练S归纳总结教学目标①掌握等腰三角形、直角三角形的概念与性质；②掌握线段的垂直平分线与角平分线的性质与定理；③掌握各种思想的运用。

授课日期及时段T（Textbook-Based）——同步课堂一、知识梳理1、等腰三角形的性质定理（1）两角分别相等且其中一组等角的对边相等的两个三角形全等。

（AAS）（2）等腰三角形的两底角相等。

即等边对等角。

（3）推论：等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合。

即三线合一。

（4）等边三角形的三个内角都相等，并且每个角都等于60°。

体系搭建2、等腰三角形的判定定理（1）有两条边相等的三角形是等腰三角形。

（2）有两个角相等的三角形是等腰三角形。

即等角对等边。

（3）三个角都相等的三角形是等边三角形。

（4）有一个角等于60°的等腰三角形是等边三角形。

3、在直角三角形中，如果有一个锐角等于30°，那么它所对的直角边等于斜边的一半。

4、直角三角形的性质和判定方法定理：直角三角形的两个锐角互余。

定理：有两个角互余的三角形是直角三角形。

5、勾股定理：勾股定理：直角三角形两条直角边的平方和等于斜边的平方。

6、勾股定理的逆定理：如果三角形两边的平方和等于第三边的平方，那么这个三角形是直角三角形。

7、逆命题、逆定理互逆命题：在两个命题中，如果一个命题的条件和结论分别是另一个命题的结论和条件，那么这两个命题称为互逆命题，其中一个命题称为另一个命题的逆命题。

互逆定理：如果一个定理的逆命题经过证明是真命题，那么它也是一个定理，其中一个定理称为另一个定理的逆命题。

8、斜边、直角边定理定理：斜边和一条直角边分别相等的两个直角三角形全等。

简述为“斜边、直角边定理”或“HL”定理。

9、线段垂直平分线的性质定理：定理：线段垂直平分线上的点到这条线段两个端点的距离相等。

培优证明

效果显著，获全国数学竞赛三等奖。
冯洁容
平时多辅导，多交流，
增强自信心。
效果显著，考上市重点中学。
2001至2002学年度
初三（3）
黄业结
学习上多交流，课后
多辅导。
效果显著，考上市重点中学。
黎基凡
学习上多交流，课后
多辅导。
效果显著，获全国数学联赛一等奖。
2002至2003学年度
初三（2）
张明新
平时多辅导，多交流，增强自信心。
周宏彪
平时多辅导，多交流，
增强自信心。
效果显著。获学校数学竞赛一等奖。
陈木许
平时多辅导，多交流，
增强自信心。。
效果显著。获学校数学竞赛一等奖。
单位（盖章）
审核人签名：
2008年8月5日
效果显著，考上市重点中学。。
林小丽
平时多辅导，多交流，增强自信心。
效果显著，中考成绩优异。。
2003至2004学年度
初一（1）
钟宏艺
课后辅导，经常与他交流学习上的问题。
效果显著，获全县数学竞赛一等奖。
黄土福
课后辅导，经常与他交流学习上的问题。
效果显著，获全县数学竞赛二等奖。
2004至2005学年度
初二（2）
培优证明
XXXX老师任现职以来培优情况：
时间
班别
优生名单
培养措施
效果
1999至2000学年度
初三（3）
林庆
课后辅导，经常与他讨论、交流学习上的问题。
效果显著，获全国流学习上的问题。
效果显著，是阳西县中考状元。
2000至2001学年度
初三（1）
冯理
平时多辅导，多交流，增强自信心。

初中培优补差工作计划（通用15篇）

初中培优补差工作计划（通用15篇）初中培优补差工作计划（通用15篇）时间流逝得如此之快，又迎来了一个全新的起点，为此需要好好地写一份计划了。

你所接触过的计划都是什么样子的呢？以下是小编收集整理的初中培优补差工作计划，欢迎阅读，希望大家能够喜欢。

初中培优补差工作计划1一、培优补差对象二、主要措施1。

课外辅导，利用课余时间，组织学生加以辅导训练。

2。

采用一优生带一差生的一帮一行动。

3。

请优生介绍学习经验，差生加以学习。

4。

课堂上创造机会，用优生学习思维、方法来影响差生。

5。

对差生实施多做多练措施，优生适当增加题目难度。

6、根据学生的个体差异，安排不同的作业。

6。

采用激励机制，对差生的每一点进步都给予肯定，并鼓励其继续进取，在优生中树立榜样，给机会表现，调动他们的学习积极性和成功感。

7。

充分了解差生现行学习方法，给予正确引导，朝正确方向发展，保证差生改善目前学习差的状况，提高学习成绩。

8。

重视中等成绩学生，保持其成绩稳定和提高。

我一定努力把这项工作制定的措施落到实处，抓好落实，充分发挥各种积极因素，一定要把此项工作做好，争取做出好的成绩。

初中培优补差工作计划2本期我又一次担任七年级语文课教学，由于他们是新生，大多数来源于村小，知识面比较狭窄，语文素养较差，学习方法也比较死板，因此，为了在本学期中有效的提高成绩，使学生在语文素养上有明显的提高，特制定以下培优转差计划。

一、指导思想：提高优生的自主和自觉学习能力，进一步巩固并提高中等生的学习成绩，帮助差生取得适当进步，让差生在教师的辅导和优生的帮助下，逐步提高学习成绩，并培养较好的学习习惯，形成基本能力。

培辅计划要落到实处，发掘并培养一批尖子，挖掘他们的潜能，从培养能力入手，训练良好学习习惯，从而形成较扎实基础，并能协助老师进行辅差活动，提高整个班级的素养和成绩。

二、现状分析我所教的一、5班共有学生68人，从开学两星期的学习情况及知识技能掌握情况看，大部分学生学习基础不够扎实，学习不够灵活，知识面比较狭窄，学习习惯很差，优生不优，差生很差，学习的目的不够明确，有少数学生的态度也不够端正，书写较潦草，，因此本学期除在教学过程中要注重学生的个体差异外，我准备在提高学生学习兴趣上下功夫，通过培优辅差的方式使优秀学生得到更好的发展，潜能生得到较大进步。

重点高中提前招生培优专题--二次函数(附详细解析)

重点高中提前招生培优专题－－二次函数1、已知二次函数2y ax bx c =++（其中a 是正整数）的图像经过点(1,4)A -与点(2,1)B ，并且与x 轴有两个不同的交点，求b c +的最大值.2、在直角坐标系中，抛物线223(0)4y x mx m m =+->与x 轴交于A 、B 两点，若A 、B 两点到原点的距离分别为OA 、OB ，且满足1123OB OA -=，求m 的值．3、已知抛物线2()y ax a c x c =-++（其中0a ≠）不经过第二象限．（1）判断这条抛物线的顶点00(,)A x y 所在的象限，并说明理由；（2）若经过这条抛物线顶点00(,)A x y 的直线y x k =-+与抛物线的另一个交点为(,)a c B c a +-，求抛物线的解析式．4、已知点A 、B 的坐标分别为(1,0)A 、(2,0)B ，若二次函数2(3)3y x a x =+-+的图像与线段AB 恰有一个交点，求a 的取值范围．5、已知关于正整数n 的二次式2y n an =+（a 为实常数）．若当且仅当5n =时，y 有最小值，求实数a 的取值范围．6、已知2()6f x x ax a =+-，()y f x =的图像与x 轴有两个不同的交点1(,0)x 、2(,0)x ，且1212383(1)(1)(16)(16)a a x x a x a x -=-++----，求a 的值．7、已知二次函数2(3)y x m x m =---，求所有的m 值，使得此二次函数图像与x 轴的两个交点不可能都落在x 轴的正半轴上．8、设有二次函数2()f x x bx c =++与x 轴交于两点A 、B ，现有直线1y x =-过其中一交点且与抛物线交于另一点C ，又若3ABC S =△，求抛物线的方程．9、已知二次函数2()y ax bx c a b =++<的图象恒不在x 轴下方，且a b cm b a++<-恒成立，求实数m 的取值范围．10、已知方程20x bx c ++=有两个实数根s 、t ，并且2s <，2t <．证明：（1）4c <；（2）4b c <+．11、设m 、n 为正整数，且2m ≠，如果对一切实数t ，二次函数2(3)3y x mt x mt =+--的图象与x 轴的两个交点间的距离不小于2t n +，求m 、n 的值．12、设m 、n 为正整数，且2m ≠，二次函数2(3)3y x mt x mt =+--的图象与x 轴的两个交点间的距离为1d ，二次函数2(2)2y x t n x nt =-+-+的图象与x 轴的两个交点间的距离为2d ．如果12d d ≥对一切实数t 恒成立，求m 、n 的值．13、已知函数2211()962()33f x x ax a a x =---+-≤≤有最大值3-，求实数a 的值.14、设a 、b 是实常数，当是取任意实数时，函数2222(1)2()3y k k x a k x k ak b =++-++++的图象与x 轴都交于点(1,0)A ．（1）求a 、b 的值；（2）若函数图象与x 轴的另一交点为B ，当k 变化时，求AB 的最大值．15、当a 取遍0到5的所有实教时，求满足3(38)b a a =-的整数b 的个数．16、在坐标平面上，纵坐标与横坐标都是整数的点称为整点．试在二次函数2910105x x y =-+的图象上找出满足y x ≤的所有整点(,)x y ，并说明理由．17、坐标平面上，横坐标与纵坐标都是整数的点(,)x y 称为整点，如果将二次函数23984y x x =-+-与x 轴所围成的封闭图形涂成红色，求在此红色区域内部及其边界上的整点的个数．18、已知点M 、N 的坐标分别为(0,1)M 、(0,1)N ，点P 是抛物线214y x =上一个动点．（1）判断以点P 为圆心，PM 为半径的圆与直线1y =-的位置关系；（2）设直线PM 与抛物线214y x =的另一个交点为Q ，连结NP 、NQ ，求证：PNM QNM ∠=∠．19、已知抛物线21:34C y x x =--+和抛物线22:34C y x x =--相交于A 、B 两点，P 是在抛物线1C 上且位于A 和B 之间的一点，Q 是在抛物线2C 上且位于A 和B 之间的一点．（1）求线段AB 的长；（2）当PQ y ∥轴时，求PQ 长度的最大值．20、设a 是正整数．如果二次函数22(223)107y x a x a =+++-和反比例函数113ay x-=的图象有公共整点（横坐标和纵坐标都是整数的点），求a 的值和对应的公共整点．21、m 是什么实数时，方程245x x m -+=有四个互不相等的实数根？22、如果满足2||61610x x a ---=的实数x 恰有6个，求实数a 的值．23、已知01k <<，试确定关于x 的方程21x kx k -=+的解的个数．24、求使方程1223x x x c ---+-=恰好有两个解的所有实数c ．25、设2()f x x px q =++，p 、q 为实数．若()f x 在11x -≤≤时的最大值为M ，求M 的最小值．《二次函数》竞赛辅导材料（一）参考答案1、已知二次函数2y ax bx c =++（其中a 是正整数）的图像经过点(1,4)A -与点(2,1)B ，并且与x 轴有两个不同的交点，求b c +的最大值.解析由于二次函数的图像过点(1,4)A -、(2,1)B ，所以 4,421,a b c a b c -+=⎧⎨++=⎩ 解得1,32.b a c a =--⎧⎨=-⎩因为二次函数图像与x 轴有两个不同的交点，所以240b ac =->△，2(1)4(32)0a a a ---->，即(91)(1)0a a -->，由于a 是正整数，故1a >．所以2a ≥．又因为324b c a +=-+≤-，且当2a =，3b =-，1c =-时，，满足题意，故b c +的最大值为4-．2、在直角坐标系中，抛物线223(0)4y x mx m m =+->与x 轴交于A 、B 两点，若A 、B 两点到原点的距离分别为OA 、OB ，且满足1123OB OA -=，求m 的值．解析设方程22304x mx m +-=的两根分别为1x 、2x ，且12x x <，则有120x x m +=-<，212304x x m =-<．所以10x <，20x >，由1123OB OA -=，可知OA OB >，又0m >，所以，抛物线的对称轴在y 轴的左侧，于是11OA x x ==-，2OB x =．所以 211123x x +=， 121223x x x x +=，故 22334m m -=-．解得2m =．3、已知抛物线2()y ax a c x c =-++（其中0a ≠）不经过第二象限．（1）判断这条抛物线的顶点00(,)A x y 所在的象限，并说明理由；（2）若经过这条抛物线顶点00(,)A x y 的直线y x k =-+与抛物线的另一个交点为(,)a c B c a+-，求抛物线的解析式．解析（1）因为若0a >，则抛物线开口向上，于是抛物线一定经过第二象限，所以当抛物线2()y ax a c x c =-++的图像不经过第二象限时，必有0a <．又当0x =时，y c =，即抛物线与y 轴的交点为(0,)c ．因为抛物线不经过第二象限，所以0c ≤．于是002a c x a+=>，2204()()044ac a c a c y a a-+--==>，所以顶点00(,)A x y 在第一象限．（2）由于点(,)a cB c a+-在抛物线，所以2()()a c a c c a a c c a a++-=-+⋅+，所以0c =．于是点B 的坐标为（1，0），点A 的坐标为1(,)24a-．由于点B 在直线y x k=-+上，所以01k =-+，所以1k =．又由于直线1y x =-+经过点1(,)24a A -，所以1142a -=-+，所以2a =-．抛物线的解析式为222y x x =-+．4、已知点A 、B 的坐标分别为(1,0)A 、(2,0)B ，若二次函数2(3)3y x a x =+-+的图像与线段AB 恰有一个交点，求a 的取值范围．解析设2()(3)3f x x a x =+-+，由(1)(2)0f f <，得112a -<<-；由(1)0f =，得1a =-，此时11x =，23x =，符合题意；由(2)0f =，得12a =-，此时12x =，232x =，不符合题意．令2(3)30x a x +-+=，由判别式0=△，得3a =±当3a =+12x x ==3a =-12x x =综上所述，a 的取值范围是112a -≤<-或者3a ==-5、已知关于正整数n 的二次式2y n an =+（a 为实常数）．若当且仅当5n =时，y 有最小值，求实数a 的取值范围．解析由于对于实数x ，有222()24a a y x ax x =+=+-，其图像对称轴为2ax =-．当x 可以取正整数n 时，且当且仅当5n =使得y 有最小值．于是必有对称轴2ax =-在4x =与6x =之间，且偏于5x =，即 115222a -<--<，得119a -<<-．所以，a 的取值范围是119a -<<-．6、已知2()6f x x ax a =+-，()y f x =的图像与x 轴有两个不同的交点1(,0)x 、2(,0)x ，且1212383(1)(1)(16)(16)a a x x a x a x -=-++----，求a 的值．解析首先，由23640a a =+>△，得0a >或19a <-．由题意，可设212()6()()f x x ax a x x x x =+-=--，则 12(1)(1)(1)17x x f a ++=-=-， 12(16)(16)(16)17a x a x f a a ----=-=-，所以 38317a a a-=--，解得12a =，或者0a =（舍去）．故12a =． 7、已知二次函数2(3)y x m x m =---，求所有的m 值，使得此二次函数图像与x 轴的两个交点不可能都落在x 轴的正半轴上．解析根据题意，问题可转化为求当方程 2(3)0x m x m ---=的两根中至少有一根为非正数时m 的值．因为此方程根的判别式为22(3)4()(1)80m m m =---=-+>△，所以此方程必有两实根，即函数2(3)y x m x m =---与x 轴必有两个焦点．运用方程根与系数的关系得方程的两根1x 、2x 满足 123x x m +=-，12x x m =-当0m >时，120x x m =-<，则方程有且只有一个根的负数；当0m ≤时，120x x m =-≥，但1230x x m +=-<，则1x 、2x 均为非正数．所以，满足要求的m 为一切实数．评注在处理有关二次函数问题时，常常转化为二次方程根的问题予以解决．反过来，在处理有关二次方程根的问题时，常常转化为二次函数及其图像的问题加以解决．二次函数与二次方程“相得益彰”，它们是相通的．8、设有二次函数2()f x x bx c =++与x 轴交于两点A 、B ，现有直线1y x =-过其中一交点且与抛物线交于另一点C ，又若3ABC S =△，求抛物线的方程．解析由已知条件知，其中一交点(1,0)A ．A 为二次函数图像上的点．如图所示．故01b c =++，且AB 即为方程20x br c ++=的两根之差的绝对值．12AB x x =-ABC △的高为点C 的纵坐标的绝对值．解方程组2,1.y x bx c y x ⎧=++⎪⎨=-⎪⎩①② 由②知1x y =+代入①，得2(1)10y b y b c ++++++=．而10b c ++=，故此方程即2(1)0y b y ++=，得点C 的纵坐标为(1)y b =-+．由于3ABC S =△，故132b +=．解方程组10,1 3.2b c b ++=⎧⎪⎨+=⎪⎩得41,3 2.b b c c =-=⎧⎧⎨⎨==-⎩⎩或所以，抛物线的方程为243y x x =-+或22y x x =+-．9、已知二次函数2()y ax bx c a b =++<的图象恒不在x 轴下方，且a b cm b a++<-恒成立，求实数m 的取值范围．解析由题设知，20y ax bx c =++≥恒成立，所以， 0a >，且240b ac -≤．记1bt a=>，则 222244444444()4()44a b c a ab ac a ab b t t b a a b a a b a t ++++++++=≥=---- 191((1)6)(66)3414t t =-++≥+=-，当且仅当4t =，即4b a =，24b ac =时，不等式等号成立，从而a b cb a++-的最小值为3，于是，m 的取值范围是3m <．10、已知方程20x bx c ++=有两个实数根s 、t ，并且2s <，2t <．证明：（1）4c <；（2）4b c <+．解析（1）由韦达定理知 4c st s t ==<．（2）设2()f x x bx c =++，则()y f x =的图象是开口向上的抛物线，且与x 轴的两交点在2-与2之间，所以(2)0f ±>，即 420b c ++>， 420b c -+>，所以 24b c ±<+， 24b c <+ 故 24b b c ≤<+评注利用二次函数的图象来研究二次方程的根以及系数之间的关系，是一种行之有效的方法．11、设m 、n 为正整数，且2m ≠，如果对一切实数t ，二次函数2(3)3y x mt x mt =+--的图象与x 轴的两个交点间的距离不小于2t n +，求m 、n 的值．解析因为一元二次方程2(3)30x mt x mt +--=的两根分别为mt 和3-，所以二次函数2(3)3y x mt x mt =+--的图象与x 轴的两个交点间的距离为3mt +．由题意，32mt t n +≥+，即22(3)(2)mt t n +≥+，即222(4)(64)90m t m n t n -+-+-≥由题意知，240m -≠，且上式对一切实数t 恒成立，所以 222240,(64)4(4)(9)0,m m n m n ⎧->⎪⎨=----≤⎪⎩△ 22,4(6)0,m mn >⎧⇒⎨-≤⎩2,6,m mn >⎧⇒⎨=⎩所以3,2,m n =⎧⎨=⎩或6,1.m n =⎧⎨=⎩12、设m 、n 为正整数，且2m ≠，二次函数2(3)3y x mt x mt =+--的图象与x 轴的两个交点间的距离为1d ，二次函数2(2)2y x t n x nt =-+-+的图象与x 轴的两个交点间的距离为2d ．如果12d d ≥对一切实数t 恒成立，求m 、n 的值．解析因为一元二次方程2(3)30x mt x mt +--=的两根分别为mt 和3-，所以13d mt =+；一元二次方程2(2)20x t n x nt -+-+=的两根分别为2t 和n -，所以22d t n =+．所以，12d d ≥32mt t n ⇔+≥+ 22(3)(2)mt t n ⇔+≥+222(4)(64)9m t m n t n ⇔-+-+- 0≥． ①由题意知，240m -≠，且①式对一切实数t 恒成立，所以 222240,(64)4(4)(90),m m n m n ⎧->⎪⎨=----≤⎪⎩△ 22,4(6)0,m mn >⎧⇒⎨-≤⎩3,2,m n =⎧⇒⎨=⎩ 所以3,2,m n =⎧⎨=⎩或6,1.m n =⎧⎨=⎩'13、已知函数2211()962()33f x x ax a a x =---+-≤≤有最大值3-，求实数a 的值.解析因为2()9()23a f x x a =-++，1133x -≤≤，它的对称轴是直线3a x =-，于是必须根据值3a x =-是否在1133x -≤≤的范围内分三种情况讨论．（1）若133a -<-，即1a >时，11()()33f x x -≤≤随着x 的增加而减少．这时，()f x 的最大值1()3f -，即241a a -+-．由2413a a -+-=-得2a =1a >，故2a =（2）若11333a -≤-≤，即11a -≤≤时，11()()33f x x -≤≤的最大值为()3af -，即2a ．由23a =-得32a =-，这与11a -≤≤矛盾．（3）若133a ->，即1a <-时，11()()33f x x -≤≤随着x 增加而增加，这时()f x 的最大值是1()3f ，即21a --．由213a --=-，得a =a =1a <-，故a =综上所述，满足题意的a 为2 14、设a 、b 是实常数，当是取任意实数时，函数2222(1)2()3y k k x a k x k ak b =++-++++的图象与x 轴都交于点(1,0)A ．（1）求a 、b 的值；（2）若函数图象与x 轴的另一交点为B ，当k 变化时，求AB 的最大值．解析（1）由题设知，点(1,0)A 在函数的图象上，所以222(1)2()30k k a k k ak b ++-++++=， 2(1)(12)0a k b a -++-=．上面这个关于k 的一次方程有无穷多个解，所以210,120.a b a -=⎧⎨+-=⎩解得1a =，1b =．（2）由（1）知，1a =，1b =，这时函数为 2222(1)2(1)31y k k x k x k k =++-++++．设点2(,0)B x ，则21AB x =-．由韦达定理知2223111k k x k k ++⋅=++， 2222(1)(3)(1)0x k x k x -+-+-=，所以2222(3)4(1)0x x =---≥△，2513x -≤≤，所以 22213x -≤-≤，所以 212x -≤．又当1k =-时，21x =-，此时，212x -=．所以，AB 的最大值为2．15、当a 取遍0到5的所有实教时，求满足 3(38)b a a =-的整数b 的个数．解析由题设等式，得228416()339b a a a =-=--．它的图象是以416(,)39-为顶点，开口向上的抛物线，当05a ≤≤时，b 在43a =处取最小值169-，在5a =处取最大值40352533-=．所以 163593b -≤≤，所以1b =-，0，1，2，…，10，11．满足题设条件的整数b 共有13个．16、在坐标平面上，纵坐标与横坐标都是整数的点称为整点．试在二次函数2910105x x y =-+的图象上找出满足y x ≤的所有整点(,)x y ，并说明理由．解析由题意得2910105x x y x =-+≤，即有 21810x x x -+≤． ①当0x ≥时，式①化为 211180x x -+≤，得 29x ≤≤2．又210220(2)(1)20y x x x x =--+=-++，则满足x 及y 均是整数的有2r =，2y =；4x =，3y =；7r =，6y =；9x =，9y =．当x 0<时，式①化为 29180x x ++≤，得63x -≤≤-．则满足x 及y 均是整数的有3x =-，3y =；6x =-，6y =．所以满足题中要求的整点是(3,3)-、(6,6)-、(2,2)、(4,3)、(7,6)、99（，）．17、坐标平面上，横坐标与纵坐标都是整数的点(,)x y 称为整点，如果将二次函数23984y x x =-+-与x 轴所围成的封闭图形涂成红色，求在此红色区域内部及其边界上的整点的个数．解析 313()()22y x x =---与x 轴有两个交点3(,0)2M 和13(,0)2N ，x 轴上在32x =与132x =之间共有5个整数：2、 3、 4、 5、6．将函数改写为225(4)4y x =--+．当2x =，有94y =，满足904y ≤≤的整数有0、1、2，共3个；当3x =，有214y =等，满足2104y ≤≤等的整数有0，1，…．5．共6个；当5x =，有254y =，满足2504y ≤≤的整数有0，1，…，6，共7个；当5x =，有214y =等，满足2104y ≤≤的整数有0，1，…，5，共6个；当6x =，有94y =-，满足904y ≤≤的整数有0、1、2，共3个．共得25个整点，18、已知点M 、N 的坐标分别为(0,1)M 、(0,1)N ，点P 是抛物线214y x =上一个动点．（1）判断以点P 为圆心，PM 为半径的圆与直线1y =-的位置关系；（2）设直线PM 与抛物线214y x =的另一个交点为Q ，连结NP 、NQ ，求证：PNM QNM ∠=∠．解析（1）设点P 的坐标为2001(,)x x ，则20114PM x ==+，而点P 到直线1y =-的距离为 220011(1)144x x --=+．所以，以点P 为圆心，PM 为半径的圆与直线1y =-相切．（2）过点P 、Q 分别作直线1y =-的垂线，垂足分别为H 、R ，由（1）知，PH PM =，同理可得，QM QR =．因为，PH 、MN 、QR 都垂直于直线1y =-，所以，PH MN QR ∥∥，于是QM MPRN NH =，于是 QR PHRN HN=，所以，Rt Rt PHN QRN △∽△，于是HNP RNQ ∠=∠，从而PNM QNM ∠=∠．19、已知抛物线21:34C y x x =--+和抛物线22:34C y x x =--相交于A 、B 两点，P 是在抛物线1C 上且位于A 和B 之间的一点，Q 是在抛物线2C 上且位于A 和B 之间的一点．（1）求线段AB 的长；（2）当PQ y ∥轴时，求PQ 长度的最大值．解析（1）解方程组2234,34,y x x y x x ⎧=--+⎪⎨=--⎪⎩ 得112,6,x y =-⎧⎨=⎩222,6,x y =⎧⎨=-⎩ 所以，点A 、B 的坐标分别是(2,6)A -、(2,6)B -，于是AB（2）当PQ y ∥轴时，可设点P 、Q 的坐标分别为2(,34)P t t t --+、2(,34)Q t t t --， 22t -<<，于是 22(4)8PQ t =-≤，当0t =时等号成立．故PQ 的长的最大值为8．20、设a 是正整数．如果二次函数22(223)107y x a x a =+++-和反比例函数113ay x-=的图象有公共整点（横坐标和纵坐标都是整数的点），求a 的值和对应的公共整点．解析联立方程组22(223)107,113,y x a x a ay x ⎧=+++-⎪⎨-=⎪⎩消去y 得21132(223)107ax a x a x-+++-=，即322(223)(107)3110x a x a x a +++-+-=，分解因式得2(21)(12)1130x x a x a ⎡⎤-+++-=⎣⎦．①如果两个函数的图象有公共整点，则方程①必有整数根，从而关于x 的一元二次方程2(12)1130x a x a +++-=② 必有整数根，所以一元二次方程②的判别式△应该是一个完全平方数，而 2(12)4(113)a a =+--△2236100(18)224a a a =++=+-．所以2(18)224a +-应该是一个完全平方数，设22(18)224a k +-=（其中k 为非负整数），则22(18)224a k +-=．即(18)(18)224a k a k +++-=．显然18a k ++与18a k +-的奇偶性相同，且1818a k ++≥，而2241122564288=⨯=⨯=⨯，所以18112,182,a k a k ++=⎧⎨+-=⎩或1856,184,a k a k ++=⎧⎨+-=⎩或1828,188,a k a k ++=⎧⎨+-=⎩ 解得39,55,a k =⎧⎨=⎩或12,26,a k =⎧⎨=⎩或0,0.a k =⎧⎨=⎩而a 是正整数，所以只可能39,55,a k =⎧⎨=⎩或12,26.a k =⎧⎨=⎩当39a =时，方程②即2511060x x +-=，它的两根分别为2和53-，易求得两个函数的图象有公共整点(2,53)-和(53,2)-．当12a =时，方程②即224250x x +-=，它的两根分别为1和25-，易求得两个函数的图象有公共整点（1，-25）和（-25．1）．21、m 是什么实数时，方程245x x m -+=有四个互不相等的实数根？解析1 将原方程变形为 2441x x m -+=-．令2441y x x m =-+=-，则244y x x =-+22(2),0(2),0x x x x ⎧+<⎪=⎨-≥⎪⎩当时当时它的图象如图，而1y m =-是一条与x 轴平行的直线．原方程有四个互不相等的实根，即直线应与曲线有四个不同的交点，由图象可知，当014m <-<，即15m <<时，直线与曲线有四个不同的交点，所以，当15m <<时，方程245x x m -+=有四个互不相等的实数根．解析2 原方程变形为 2(2)1x m -=-所以21)x x -=≥，2x =12x =22x =32x =-，42x =-要使这4个数互不相等，必须10m -≠，且20，即15m <<． 22、如果满足2||61610x x a ---=的实数x 恰有6个，求实数a 的值．解析本题先分段讨论脱去绝对号，再研究a 为何值时方程有6个实根，由于绝对号内套绝对号，则相当繁琐．注意到方程的实根个数就是函数 2||61610y x x =---的图象与直线y-a 的公共点的个数，因此只要设法画出函数 2||61610y x x =--- 的图象．为了作出函数2616y x x =--的图象，我们分两步，先作出函数2616y x x =--，即2(3)25y x =--的图象（图（1）中的实线）．接着将上述图象向下移动10个单位，并将x 轴下方的部分改成它关于z 轴对称的图形，这样就得到函数2||61610y x x =---图象（图（2））．于是，由图应知与T 轴平行的直线中只有直线10y =与该函数图象有6个公共点．故10a =．23、已知01k <<，试确定关于x 的方程21x kx k -=+的解的个数．解析先画出函数21y x =-，即21y x =-的图象，再画直线(01)y kx k k =+<<（如图）．注意到该直线经过定点(1,0)-，且在y 轴上的截距k 满足01k <<．(1)(2)易见，直线(01)y kx k k =+<<与函数21y x =-图象的公共点有3个，故原方程有3个解．24、求使方程1223x x x c ---+-=恰好有两个解的所有实数c ．解析先作出1223y x x x =---+-的图象．由1223y x x x =---+-25,13,227,232 5.3x x x x x x x -+<⎧⎪≤<⎪=⎨-+≤≤⎪⎪-≤⎩当时当1时当时当时可得图象如图所示：从图中可知，当且仅当13c <<或3c >时，y c =的图象与1223y x x x =---+-有两个不同的交点．所以，所求的c 为13c <<或3c >．评注本题解答所用的方法是“数形结合法”，通过函数的图象，可以“直观”地解决问题．本题也可以通过分类讨论的方法解决，请读者自己试一试．25、设2()f x x px q =++，p 、q 为实数．若()f x 在11x -≤≤时的最大值为M ，求M 的最小值．解析当实数p 、q 在实数范围内变化时，()f x 在11x -≤≤时的最小值M 当然也在变化，要求在M 的这种变化中能达到的最小值．先借助绝对值不等式求出M 的下界．然后构造一个例子证实这个下界能够达到，从而判定这个下界即是所求的M 的最小值．按M 的定义，2(1)1M f p q≥-=-+，(1)1M f p q≥=++，(0)M f q≥=．于是，4112M p q p q q ≥-+++++(1)(1)22p q p q q≥-++++-=，所以，12M≥．若取0p=，12q=-，则21()2f x x=-．212y x=-的图象如图所示，此时12M=．所以，M的最小值是12．。

八年级陪优讲义第一讲：如何做几何证明题

二、菱形
（1）把一组邻边相等的平行四边形叫做菱形 .
（2）定理 1:菱形的四条边都相等
（3）菱形的对角线互相垂直，并且每条对角线平分一组对角
.
（4）菱形的面积等于菱形的对角线相乘除以
2
（5）菱形判定定理 1：四边都相等的四边形是菱形
（6）菱形判定定理 2：对角线互相垂直的平行四边形是菱形。
三、正方形
平行四边形具有的是：矩形具有的是：菱形具有的是：正方形具有的是：
【巩固】
1、下列说法中错误．．的是（
）
A.四个角相等的四边形是矩形
B.四条边相等的四边形是正方形
C . 对角线相等的菱形是正方形
D .对角线互相垂直的矩形是正方形
2、如果一个四边形的两条对角线互相平分，互相垂直且相等，那么这个四边形是
第三讲：平行四边形（二）
【知识梳理】
由平行四边形的结构知，平行四边形可以分解为一些全等的三角形，并且包含着平行线
的有关性质，因此，平行四边形是全等三角形知识和平行线性质的有机结合，
平行四边形包
括矩形、菱形、正方形。另一方面，平行四边形有许多很好的性质，使得构造平行四边形成
为解几何题的有力工具。
⊥AG 于点 F. (1) 求证： DE －BF ＝ EF ．
(2) 当点 G 为 BC 边中点时，试探究线段 EF 与 GF 之间的数量关系，并说明理由．
(3) 若点 G 为 CB 延长线上一点，其余条件不变．请你在图②中画出图形，写出此时 BF 、 EF 之间的数量关系（不需要证明）．
DE 、
【例题精讲】
【例 1】四边形四条边的长分别为 m、n、p、q ，且满足 m2 n 2 p 2 q 2 2mn 2 pq ，

学而思初二数学(上册)培优辅导讲义(人版)

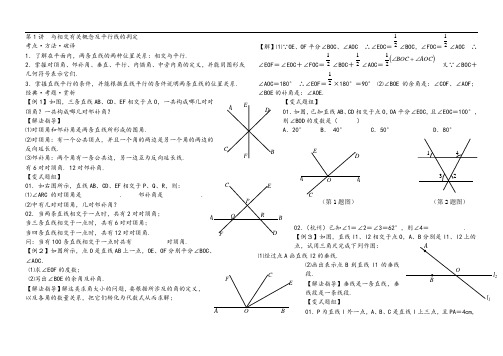
第1讲与相交有关概念及平行线的判定考点·方法·破译1．了解在平面内，两条直线的两种位置关系：相交与平行.2．掌握对顶角、邻补角、垂直、平行、内错角、中旁内角的定义，并能用图形或几何符号表示它们.3．掌握直线平行的条件，并能根据直线平行的条件说明两条直线的位置关系. 经典·考题·赏析【例1】如图，三条直线AB 、CD 、EF 相交于点O ，一共构成哪几对对顶角？一共构成哪几对邻补角？【解法指导】⑴对顶角和邻补角是两条直线所形成的图角.⑵对顶角：有一个公共顶点，并且一个角的两边是另一个角的两边的反向延长线.⑶邻补角：两个角有一条公共边，另一边互为反向延长线.有6对对顶角. 12对邻补角. 【变式题组】01．如右图所示，直线AB 、CD 、EF 相交于P 、Q 、R ，则：⑴∠ARC 的对顶角是 . 邻补角是 .⑵中有几对对顶角，几对邻补角？02．当两条直线相交于一点时，共有2对对顶角；当三条直线相交于一点时，共有6对对顶角；当四条直线相交于一点时，共有12对对顶角. 问：当有100条直线相交于一点时共有对顶角.【例２】如图所示，点O 是直线AB 上一点，OE 、OF 分别平分∠BOC 、 ∠AOC ．⑴求∠EOF 的度数；⑵写出∠BOE 的余角及补角.【解法指导】解这类求角大小的问题，要根据所涉及的角的定义，以及各角的数量关系，把它们转化为代数式从而求解；【解】⑴∵OE 、OF 平分∠BOC 、∠AOC ∴∠EOC ＝21∠BOC ，∠FOC ＝21∠AOC ∴∠EOF ＝∠EOC ＋∠FOC ＝21∠BOC ＋21∠AOC ＝()AOC BOC ∠+∠21又∵∠BOC ＋∠AOC ＝180° ∴∠EOF ＝21×180°＝90° ⑵∠BOE 的余角是：∠COF 、∠AOF ；∠BOE 的补角是：∠AOE.【变式题组】 01．如图，已知直线AB 、CD 相交于点O ，OA 平分∠EOC ，且∠EOC ＝100°，则∠BOD 的度数是（）A ．20°B ． 40°C ．50°D ．80°02．（杭州）已知∠1＝∠2＝∠3＝62°，则∠4＝ .【例３】如图，直线l1、l2相交于点O ，A 、B 分别是l1、l2上的点，试用三角尺完成下列作图： ⑴经过点A 画直线l2的垂线.⑵画出表示点B 到直线l1的垂线段. 【解法指导】垂线是一条直线，垂线段是一条线段.【变式题组】01．P 为直线l 外一点，A 、B 、C 是直线l 上三点，且PA ＝4cm ，A B C D E F A B C DEF PQ R AB CE F OE A ACD O （第1题图） 1 4 3 2 （第2题图）l 2PB ＝5cm ，PC ＝6cm ，则点P 到直线l 的距离为（） A ．4cm B ． 5cm C ．不大于4cm D ．不小于6cm02 如图，一辆汽车在直线形的公路AB 上由A 向B 行驶，M 、N 为位于公路两侧的村庄；⑴设汽车行驶到路AB 上点P 的位置时距离村庄M 最近.行驶到AB 上点Q 的位置时，距离村庄N 最近，请在图中的公路上分别画出点P 、Q 的位置.⑵当汽车从A 出发向B 行驶的过程中，在的路上距离M 村越来越近..在的路上距离村庄N 越来越近，而距离村庄Ｍ越来越远.【例４】如图，直线AB 、CD 相交于点O ，OE ⊥CD ，OF ⊥AB ，∠DOF ＝65°，求∠BOE 和∠AOC 的度数.【解法指导】图形的定义现可以作为判定图形的依据，也可以作为该图形具备的性质，由图可得：∠AOF ＝90°，OF ⊥AB ．【变式题组】01．如图，若EO ⊥AB 于O ，直线CD 过点O ，∠EOD ︰∠EOB ＝1︰3，求∠AOC 、∠AOE 的度数.02．如图，O 为直线AB 上一点，∠BOC ＝3∠AOC ，OC 平分∠AOD ． ⑴求∠AOC 的度数；⑵试说明OD 与AB 的位置关系.03．如图，已知AB ⊥BC 于B ，DB ⊥EB 于B ，并且∠CBE ︰∠ABD ＝1︰2，请作出∠CBE 的对顶角，并求其度数.【例５】如图，指出下列各组角是哪两条直线被哪一条直线所截而得到的，并说出它们的名称： ∠1和∠2：∠1和∠3：∠1和∠6：∠2和∠6：∠2和∠4：∠3和∠5： ∠3和∠4：【解法指导】正确辩认同位角、内错角、同旁内角的思路是：首先F B AO CD EC DA EOB ACDO A BA E DCF EBAD 1 4 2 3 6 5弄清所判断的是哪两个角，其次是找到这两个角公共边所在的直线即截线，其余两条边所在的直线就是被截的两条直线，最后确定它们的名称.【变式题组】 01．如图，平行直线AB 、CD 与相交直线EF ，GH 相交，图中的同旁内角共有（） A ．4对 B ． 8对 C ．12对 D ．16对 02．如图，找出图中标出的各角的同位角、内错角和同旁内角. 03．如图，按各组角的位置判断错误的是（） A ．∠1和∠2是同旁内角 B ．∠3和∠4是内错角 C ．∠5和∠6是同旁内角 D ．∠5和∠7是同旁内角【例６】如图，根据下列条件，可推得哪两条直线平行？并说明理由• ⑴∠CBD ＝∠ADB ； ⑵∠BCD ＋∠ADC ＝180° ⑶∠ACD ＝∠BAC 【解法指导】图中有即即有同旁内角，有“ ”即有内错角. 【解法指导】⑴由∠CBD ＝∠ADB ，可推得AD ∥BC ；根据内错角相等，两直线平行. ⑵由∠BCD ＋∠ADC ＝180°，可推得AD ∥BC ；根据同旁内角互补，两直线平行.⑶由∠ACD ＝∠BAC 可推得AB ∥DC ；根据内错角相等，两直线平行.【变式题组】01．如图，推理填空.⑴∵∠A ＝∠ （已知） ∴AC ∥ED （） ⑵∵∠C ＝∠ （已知）∴AC ∥ED （）⑶∵∠A ＝∠ （已知） ∴AB ∥DF （）02．如图，AD 平分∠BAC ，EF 平分∠DEC ，且∠1＝∠2，试说明DE 与AB 的位置关系. 解：∵AD 是∠BAC 的平分线（已知）∴∠BAC ＝2∠1（角平分线定义）又∵EF 平分∠DEC （已知） ∴ （）又∵∠1＝∠2（已知）∴ （）∴AB ∥DE （） 03．如图，已知AE 平分∠CAB ，CE 平分∠ACD ．∠CAE ＋∠ACE ＝90°，求证：AB ∥CD ．A BDC HＧ E F 7 1 5 6 8 4 1 2 乙丙 3 23 4 56 1 2 3 4甲 1 AB C 2 3 4 5 6 7 A B C D O A B D E F CABE A B CD EF1 204．如图，已知∠ABC ＝∠ACB ，BE 平分∠ABC ，CD 平分∠ACB ，∠EBF ＝∠EFB ，求证：CD ∥EF.【例７】如图⑴，平面内有六条两两不平行的直线，试证：在所有的交角中，至少有一个角小于31°.【解法指导】如图⑵，我们可以将所有的直线移动后，使它们相交于同一点，此时的图形为图⑵.证明：假设图⑵中的12个角中的每一个角都不小于31°则12×31°＝372°＞360°这与一周角等于360°矛盾所以这12个角中至少有一个角小于31°【变式题组】01．平面内有18条两两不平行的直线，试证：在所有的交角中至少有一个角小于11°.02．在同一平面内有2010条直线a1,a2,…，a2010,如果a1⊥a2,a2∥a3，a3⊥a4，a4∥a5……那么a1与a2010的位置关系是 . 03．已知n （n ＞2）个点P1，P2，P3…Pn.在同一平面内没有任何三点在同一直线上，设Sn 表示过这几个点中的任意两个点所作的所有直线的条数，显然：S2＝1，S3＝3，S4＝6，∴S5＝10…则Sn ＝ . 演练巩固·反馈提高 01．如图，∠EAC ＝∠ADB ＝90°.下列说法正确的是（）A ．α的余角只有∠B B ．α的邻补角是∠DAC C ．∠ACF 是α的余角D ．α与∠ACF 互补02．如图，已知直线AB 、CD 被直线EF 所截，则∠EMB 的同位角为（）A ．∠AMFB ．∠BMFC ．∠ENCD ．∠END03．下列语句中正确的是（）A ．在同一平面内，一条直线只有一条垂线B ．过直线上一点的直线只有一条C ．过直线上一点且垂直于这条直线的直线有且只有一条D ．垂线段就是点到直线的距离04．如图，∠BAC ＝90°，AD ⊥BC 于D ，则下列结论中，正确的个数有（）①AB ⊥AC ②AD 与AC 互相垂直 ③点C 到AB 的垂线段是线段AB ④线段AB 的长度A B C D E Fl 1l 2 l 3 l 4 l 5 l 6图⑴ l 1 l 2 l 3l 4 l 5 l 6 图⑵ A EB C F D A B C DFEMN α 第1题图第2题图AB D C第4题图是点B到AC的距离⑤垂线段BA是点B到AC的距离⑥AD＞BDA．0 B． 2 C．4 D．605．点A、B、C是直线l上的三点，点P是直线l外一点，且PA＝4cm，PB＝5cm，PC＝6cm，则点P到直线l的距离是（）A．4cm B．5cm C．小于4cm D．不大于4cm06．将一副直角三角板按图所示的方法旋转（直角顶点重合），则∠AOB＋∠DOC ＝ .07．如图，矩形ABCD沿EF对折，且∠DEF＝72°，则∠AEG＝ . 08．在同一平面内，若直线a1∥a2,a2⊥a3,a3∥a4,…则a1 a10.（a1与a10不重合）09．如图所示，直线a、b被直线c所截，现给出下列四个条件：①∠1＝∠5，②∠1＝∠7，③∠2＋∠3＝180°，④∠4＝∠7，其中能判断a∥b的条件的序号是 .10．在同一平面内两条直线的位置关系有 .11．如图，已知BE平分∠ABD，DE平分∠CDB，且∠E＝∠ABE＋∠EDC．试说明AB ∥CD？12．如图，已知BE平分∠ABC，CF平分∠BCD，∠1＝∠2，那么直线AB与CD的位置关系如何？13．如图，推理填空：⑴∵∠A＝（已知）∴AC∥ED（）⑵∵∠2＝（已知）∴AC∥ED（）⑶∵∠A＋＝180°（已知）∴AB∥FD．14．如图，请你填上一个适当的条件使AD∥BC．ABCDOAB CDEFGHabc第6题图第7题图第9题图123 4567 81AC DEBAC DE12AB CDEF第14题图培优升级·奥赛检测 01．平面图上互不重合的三条直线的交点的个数是（） A ．1，3 B ．0，1，3 C ．0，2，3 D ．0，1，2，3 02．平面上有10条直线，其中4条是互相平行的，那么这10条直线最多能把平面分成（）部分. A ．60 B ． 55 C ．50 D ．45 03．平面上有六个点，每两点都连成一条直线，问除了原来的6个点之外，这些直线最多还有（）个交点. A ．35 B ． 40 C ．45 D ．55 04．如图，图上有6个点，作两两连线时，圆内最多有__________________交点. 05．如图是某施工队一张破损的图纸，已知a 、b 是一个角的两边，现在要在图纸上画一条与这个角的平分线平行的直线，请你帮助这个施工队画出这条平行线，并证明你的正确性. 06．平面上三条直线相互间的交点的个数是（） A ．3 B ．1或3 C ．1或2或3 D ．不一定是1，2，3 07．请你在平面上画出6条直线（没有三条共点）使得它们中的每条直线都恰好与另三条直线相交，并简单说明画法？ 08．平面上有10条直线，无任何三条交于一点，要使它们出现31个交点，怎么安排才能办到？ 09．如图，在一个正方体的2个面上画了两条对角线AB 、AC ，那么两条对角线的夹角等于（） A ．60° B ． 75° C ．90° D ．135° 10．在同一平面内有9条直线如何安排才能满足下面的两个条件？ ⑴任意两条直线都有交点；⑵总共有29个交点. 第13讲平行线的性质及其应用考点·方法·破译 1．掌握平行线的性质，正确理解平行线的判定与性质定理之间的区别和联系； 2．初步了解命题，命题的构成，真假命题、定理； 3．灵活运用平行线的判定和性质解决角的计算与证明，确定两直线的位置关系，感受转化思想在解决数学问题中的灵活应用.经典·考题·赏析【例１】如图，四边形ABCD 中，AB ∥CD ， BC ∥AD ，∠A C 的度数. 【解法指导】两条直线平行，同位角相等；两条直线平行，内错角相等；两条直线平行，同旁内角互补. 平行线的性质是推导角关系的重要依据之一，必须正确识别图形的特征，看清截a b AB C线，识别角的关系式关键.【解】：∵AB∥CD BC∥AD∴∠A＋∠B＝180° ∠B＋∠C＝180°(两条直线平行，同旁内角互补)∴∠A＝∠C ∵∠A＝38°∴∠C＝38°【变式题组】01．如图，已知AD∥BC，点E在BD的延长线上，若∠ADE＝155°，则∠DBC的度数为（）A．155°B．50°C．45°D．25°02．（安徽）如图，直线l1 ∥ l2,∠1＝55°，∠2＝65°，则∠3为（）A． 50° B． 55° C． 60° D．65°03．如图，已知FC∥AB∥DE，∠α：∠D：∠B＝2: 3: 4, 试求∠α、∠D、∠B的度数.【例２】如图，已知AB∥CD∥EF，GC⊥CF，∠B＝60°，∠EFC＝45°，求∠BCG的度数.【解法指导】平行线的性质与对顶角、邻补角、垂直和角平分线相结合，可求各种位置的角的度数，但注意看清角的位置.【解】∵AB∥CD∥EF ∴∠B＝∠BCD ∠F＝∠FCD(两条直线平行，内错角相等)又∵∠B＝60° ∠EFC＝45° ∴∠BCD＝60° ∠FCD＝45° 又∵GC⊥CF∴∠GCF＝90°（垂直定理）∴∠GCD＝90°－45°＝45° ∴∠BCG＝60°－45°＝15°【变式题组】01．如图，已知AF∥BC, 且AF平分∠EAB，∠B＝48°，则∠C的的度数＝_______________02.如图,已知∠ABC＋∠ACB＝120°，BO、CO分别∠ABC、∠ACB，DE过点O与BC平行，则∠BOC＝___________03．如图，已知AB∥ MP∥CD, MN平分∠AMD，∠A＝40°，∠D＝50°，求∠NMP的度数.【例３】如图，已知∠1＝∠2，∠C＝∠D．求证：∠A＝∠F.【解法指导】因果转化，综合运用.逆向思维：要证明∠A＝∠F，即要证明DF∥AC．要证明DF∥AC, 即要证明∠D＋∠DBC＝180°，即：∠C＋∠DBC＝180°；要证明∠C＋∠DBC＝180°即要证明DB∥EC．要证明DB∥EC即要证明∠1＝∠3.AB CD O EFAEB C（第1题图）（第2题图）AGBBAMCDNP（第3题图）D A 2 E1 B C B F EA C D 证明：∵∠1＝∠2，∠2＝∠3（对顶角相等）所以∠1＝∠3 ∴DB ∥EC （同位角相等•两直线平行）∴∠DBC ＋∠C ＝180°（两直线平行，同旁内角互补）∵∠C ＝∠D ∴∠DBC ＋∠D ＝180° ∴DF ∥AC （同旁内角，互补两直线平行）∴∠A ＝∠F （两直线平行，内错角相等）【变式题组】 01．如图，已知AC ∥FG ，∠1＝∠2，求证：DE ∥FG02．如图，已知∠1＋∠2＝180°，∠3＝∠B ．求证：∠AED ＝∠ACB03．如图，两平面镜α、β的夹角θ，入射光线AO 平行于β入射到α上，经两次反射后的出射光线O′B 平行于α，则角θ等于_________.【例４】如图，已知EG ⊥BC ，AD ⊥BC ，∠1＝∠3. 求证：AD 平分∠BAC ．【解法指导】抓住题中给出的条件的目的，仔细分析条件给我们带来的结论，对于不能直接直接得出结论的条件，要准确把握住这些条件的意图.（题目中的：∠1＝∠3）证明：∵EG ⊥BC ，AD ⊥BC ∴∠EGC ＝∠ADC ＝90° （垂直定义）∴EG ∥AD （同位角相等，两条直线平行） ∵∠1＝∠3 ∴∠3＝∠BAD （两条直线平行，内错角相等） ∴AD 平分∠BAC （角平分线定义）【变式题组】 01．如图，若AE ⊥BC 于E ，∠1＝∠2，求证：DC ⊥BC ．02．如图，在△ABC 中，CE ⊥AB 于E,DF ⊥AB 于F, AC ∥ED ，CE 平分∠ACB ．求证：∠EDF ＝∠BDF. AB ∥CD ，∠B ＝40°，CN 是∠BCE 的平分线. CM ⊥CN ，求：∠BCMA D M CN E B C DA B E F1 32 GB 3C A 1D 2EF （第1题图） A2 CF 3 E D1 B（第2题图） 31AEα β P B C D A∠P ＝α＋β3 21 γ 4ψ D α βE B C AFH F γ Dα β E B C AF D E BC A AA ′l B ′C ′【例５】已知，如图，AB ∥EF ，求证：∠ABC ＋∠BCF ＋∠CFE ＝360° 【解法指导】从考虑360°这个特殊角入手展开联想，分析类比，联想周角.构造两个“平角”或构造两组“互补”的角. 过点C 作CD ∥AB 即把已知条件AB ∥EF 联系起来，这是关键. 【证明】：过点C 作CD ∥AB ∵CD ∥AB ∴∠1＋∠ABC ＝180° (两直线平行，同旁内角互补) 又∵AB ∥EF ，∴CD ∥EF （平行于同一条直线的两直线平行） ∴∠2＋∠CFE ＝180°(两直线平行，同旁内角互补) ∴∠ABC ＋∠1＋∠2＋∠CFE ＝180°＋180°＝360° 即∠ABC ＋∠BCF ＋∠CFE ＝360° 【变式题组】 01．如图，已知，AB ∥CD ，分别探究下面四个图形中∠APC 和∠PAB 、∠PCD 的关系，请你从所得四个关系中选出任意一个，说明你探究的结论的正确性. 结论：⑴____________________________ ⑵____________________________ ⑶____________________________ ⑷____________________________【例６】如图，已知，AB ∥CD ，则∠α、∠β、∠γ、∠ψ之间的关系是 ∠α＋∠γ＋∠ψ－∠β＝180° 【解法指导】基本图形善于从复杂的图形中找到基本图形，运用基本图形的规律打开思路. 【解】过点E 作EH ∥AB ．过点F 作FG ∥AB ． ∵AB ∥EH ∴∠α＝∠1（两直线平行，内错角相等）又∵FG ∥AB ∴EH ∥FG （平行于同一条直线的两直线平行）∴∠2＝∠3 又∵AB ∥CD ∴FG ∥CD （平行于同一条直线的两直线平行）∴∠ψ＋∠4＝180°（两直线平行，同旁内角互补）∴∠α＋∠γ＋∠ψ－∠β＝∠1＋∠3＋∠4－ψ－∠1－∠2＝∠4＋ψ＝180° 【变式题组】01．如图， AB ∥EF ，∠C ＝90°，则∠α、∠β、∠γ的关系是（）A ． ∠β＝∠α＋∠γB ．∠β＋∠α＋∠γ＝180°C ． ∠α＋∠β－∠γ＝90°D ．∠β＋∠γ－∠α＝90° 02．如图，已知，AB ∥CD ，∠ABE 和∠CDE 的平分线相交于点F ，∠E ＝140°，求∠BFD 的度数.【例７】如图，平移三角形ABC ，设点A 移动到点A/，画出平移后的三角形A/B/C/. 【解法指导】抓住平移作图的“四部曲”——定，找，移，连. ⑴定：确定平移的方向和距离. ⑵找：找出图形的关键点. ⑶移：过关键点作平行且相等的线段，得到关键点的对应点. ⑷连: 按原图形顺次连接对应点.BAP C A C C DA A P CB D PB PD B D ⑴ ⑵ ⑶ ⑷ FE D 2 1AB CA北【解】①连接AA/ ②过点B 作AA/的平行线l ③在l 截取BB/＝AA/,则点B/就是的B 对应点，用同样的方法作出点C 的对应点C/.连接A/B/，B/C/，C/A/就得到平移后的三角形A/B/C/. 【变式题组】01．如图，把四边形ABCD 按箭头所指的方向平移21cm ，作出平移后的图形.02．如图,角形ABC 中，∠C ＝90°, BC＝4，AC ＝4，现将△ABC 沿CB 方向平移到△A/B/C/的位置，若平移距离为3, 求△ABC 与△A/B/C/的重叠部分的面积.03．原来是重叠的两个直角三角形，将其中一个三角形沿着BC 方向平移BE 的距离，就得到此图形，求阴影部分的面积.（单位：厘米）演练巩固反馈提高01．如图，由A 测B 得方向是（）A ．南偏东30°B ．南偏东60°C ．北偏西30°D ．北偏西60°02．命题：①对顶角相等；②相等的角是对顶角；③垂直于同一条直线的两直线平行；④平行于同一条直线的两直线垂直.其中的真命题的有（） A ．1个 B ．2个 C ．3个 D ．4个03．一个学员在广场上练习驾驶汽车，两次拐弯后，行驶的方向与原来的方向相同，两次拐弯的角度可能是（）A ．第一次向左拐30°，第二次向右拐30°B ．第一次向右拐50°，第二次向左拐130°C ．第一次向左拐50°，第二次向右拐130°D ．第一次向左拐60°，第二次向左拐120°04．下列命题中，正确的是（）A ．对顶角相等B ．同位角相等C ．内错角相等D ．同旁内角互补05．学习了平行线后，小敏想出过直线外一点画这条直线的平行线的新方法，是通过折一张半透明的纸得到的[如图⑴—⑷]从图中可知，小敏画平行线的依据有（）①两直线平行，同位角相等；②两直线平行，内错角相等；③同位角相等，两直线平行；④内错角相等，两直线平行.A ．①②B ．②③C ．③④D ．①④06．在A 、B 两座工厂之间要修建一条笔直的公路，从A 地测得B 地的走向是南偏B B /AA /CC /东52°.现A、B两地要同时开工，若干天后，公路准确对接，则B地所修公路的走向应该是（）A．北偏东52° B．南偏东52° C．西偏北52°D．北偏西38°07．下列几种运动中属于平移的有（）①水平运输带上的砖的运动；②笔直的高诉公路上行驶的汽车的运动（忽略车轮的转动）；③升降机上下做机械运动；④足球场上足球的运动.A．1种B．2种C．3种D．4种08．如图，网格中的房子图案正好处于网格右下角的位置.平移这个图案，使它正好位于左上角的位置（不能出格）09．观察图，哪个图是由图⑴平移而得到的（）10．如图，AD∥BC，AB∥CD，AE⊥BC，现将△ABE进行平移. 平移方向为射线AD 的方向. 平移距离为线段BC的长，则平移得到的三角形是图中（）图的阴影部分. 11．判断下列命题是真命题还是假命题，如果是假命题，举出一个反例.⑴对顶角是相等的角；⑵相等的角是对顶角；⑶两个锐角的和是钝角；⑷同旁内角互补，两直线平行.12．把下列命题改写成“如果……那么……”的形式，并指出命题的真假.⑴互补的角是邻补角；⑵两个锐角的和是锐角；⑶直角都相等.13．如图，在湖边修一条公路.如果第一个拐弯处∠A＝120°，第二个拐弯处∠B＝150°，第三个拐弯处∠C，这时道路CE恰好和道路AD平行，问∠C是多少度？并说明理由.DAB CEDB CED AB CED AB CEA B C15．如图，AB∥CD，∠1＝∠2，试说明∠E和∠F的关系.培优升级·奥赛检测01．如图，等边△ABC各边都被分成五等分，这样在从而得到1个封闭图形，并画出阴影.⑵请你分别写出上述三个阴影部分的面积S1＝________, S2＝________, S3＝________.1个单位），请你猜想空白部分草地面积是F EB A 多少？ 05．一位模型赛车手遥控一辆赛车，先前进一半，然后原地逆时针旋转α°（0°＜α°＜180°），被称为一次操作，若5次后发现赛车回到出发点，则α°角为（） A ．720° B ．108°或144°C ．144°D ．720°或144° 06．两条直线a 、b 互相平行，直线a 上顺次有10个点A1、A2、…、A10，直线b 上顺次有10个点B1、B2、…、B9，将a 上每一点与b 上每一点相连可得线段.若没有三条线段相交于同一点，则这些选段的交点个数是（） A ．90 B ．1620 C ．6480 D ．2006 07．如图，已知AB ∥CD ，∠B ＝100°，EF 平分∠BEC ，EG ⊥EF. 求∠BEG 和∠DEG. 08．如图，AB ∥CD ，∠BAE ＝30°，∠DCE ＝60°，EF 、EG 三等分∠AEC ．问：EF 与EG 中有没有与AB 09．如图，已知直线CB ∥OA ，∠C ＝∠OAB ＝100°，E 、F 在CB 上，且满足∠FOB ＝∠AOB ，OE 平分∠COF. ⑴求∠EOB 的度数； ⑵若平行移动AB ，那么∠OBC ：∠OFC 的值是否随之发生变化？若变化，找出变化规律；若不变，求出这个比值. ⑶在平行移动AB 的过程中，是否存在某种情况，使∠OEC ＝∠OBA ？若存在，求出其度数；若不存在，说明理由.10．平面上有5条直线，其中任意两条都不平行，那么在这5条直线两两相交所成的角中，至少有一个角不超过36°,请说明理由.11．如图，正方形ABCD 的边长为5,把它的对角线AC 分成n 段，以每一小段为对角线作小正方形，这n 个小正方形的周长之和为多少？FE B AC GD 100°F E BAC O A12．如图将面积为a2的小正方形和面积为b2的大正方形放在一起，用添补法如何求出阴影部分面积？第06讲实数考点·方法·破译 1．平方根与立方根：若2x ＝a(a ≥0)则x 叫做a 的平方根，记为：a的平方根为x a 的平方根为x叫做a 的算术平方根．若x3＝a ，则x 叫做a 的立方根．记为：a 的立方根为x2．无限不循环小数叫做无理数，有理数和无理数统称实数．实数与数轴上的点一一对应．任何有理数都可以表示为分数pq （p 、q 是两个互质的整数，且q ≠0）的形式． 3非负数：实数的绝对值，实数的偶次幂，非负数的算术平方根（或偶次方根）都是非负数．即a>0，2na ≥0（n 为正整数）0(a ≥0) ．经典·考题·赏析【例1】若2m －4与3m －1是同一个数的平方根，求m 的值．【解法指导】一个正数的平方根有两个，并且这两个数互为相反数．∵2m −4与3m −l 是同一个数的平方根，∴2m −4 ＋3m −l ＝0，5m ＝5，m ＝l．【变式题组】01．一个数的立方根与它的算术平方根相等，则这个数是____． 02．已知m的最大整数，则m 的平方根是____． 03____．04．如图，有一个数值转化器，当输入的x 为64时，输出的y 是____．【例2】（全国竞赛）已知非零实数a 、b 满足24242a b a -+++=，则a ＋b 等于( ) A ．－1 B ． 0 C ．1 D ．2 有意义，∵a 、b 为非零实数，∴b2>0∴a －3≥0 a≥3 ∵24242a b a -+++=∴24242a b a -++=，∴20b ++=．∴()22030b a b +=⎧⎪⎨-=⎪⎩，∴32a b =⎧⎨=-⎩，故选C ．【变式题组】0l3b+＝0成立，则ab＝____．02()230b-=，则ab的平方根是____．03．（天津）若x、y为实数，且20x+=，则2009xy⎛⎫⎪⎝⎭的值为（）A．1 B．－1 C．2 D．－204．已知x1xπ-的值是( )A．11π-B．11π+C．11π-D．无法确定【例3】若a、b都为有理效，且满足1a b-+=+a＋b的平方根．【解法指导】任何两个有理数的和、差、积、商（除数不为0）还是有理数，但两个无理数的和、差、积、商（除数不为0）不一定是无理数．∵1 a b-+=+∴1a b-=⎧⎪=1a b-=⎧⎪=，∴1312ab=⎧⎨=⎩，a ＋b＝12 ＋13＝25．∴a＋b的平方根为：5==±．【变式题组】01．（西安市竞赛题）已知m、n2）m＋(3－＋7＝0求m、n．02．（希望杯试题）设x、y都是有理数，且满足方程（123π+）x＋（132π+）y−4−π＝0，则x−y＝____．【例4】若a2的整数部分，b−1是9的平方根，且a b b a-=-，求a＋b的值．−2＝整数部分＋小数部分．整数部分估算可得2，−2 −2−4．∵a＝2，b−1＝±3 ，∴b＝－2或4∵a b b a-=-．∴a<b ，∴a＝2， b＝4，即a＋b＝6．【变式题组】01．若3a，3−b，则a＋b的值为____．02a，小数部分为ba）·b＝____．演练巩固反馈提高0l．下列说法正确的是( )A ．－2是(－2)2的算术平方根B ．3是－9的算术平方根C ． 16的平方根是±4D ．27的立方根是±302．设3a =-，b ＝－2，52c =-，则a 、b 、c 的大小关系是( )A ．a<b<cB ．a<c<bC ． b<a<cD ．c<a<b 03．下列各组数中，互为相反数的是( )A ．－9与81的平方根B ．4与 364- C ．4与364 D ．3与904．在实数1.414，2-，0.1•5•，5−16，π，3.1•4•，83125中无理数有( )A ．2个B ．3个C ．4个D ． 5个05．实数a 、b 在数轴上表示的位置如图所示，则( ) A ．b>a B ．a b>C ．－a ＜bD ．－b>a06．现有四个无理数5，6，7，8，其中在2＋1与3＋1之间的有( ) A ． 1个 B ．2个 C ． 3个 D ．4个 07．设m 是9的平方根，n ＝()23．则m ，n 的关系是( )A. m ＝±nB.m ＝n C .m ＝－n D.m n≠08．（烟台）如图，数轴上 A 、B 两点表示的数分别为－1和3，点B 关于点A的对称点C ，则点C 所表示的数为( )A ．－23-B ．－13-C ．－2 ＋3D ．l ＋309．点A 在数轴上和原点相距5个单位，点B 在数轴上和原点相距3个单位，且点B 在点A 左边，则A 、B 之间的距离为____．10．用计算器探索：已知按一定规律排列的一组数：1，12，13…，119，120．如果从中选出若干个数，使它的和大于3，那么至少要选____个数． 11．对于任意不相等的两个数a 、b ，定义一种运算※如下：a ※b ＝a ba b +-，如3※2＝3232+-＝5．那么12.※4＝____．12．（长沙中考题）已知a 、b 为两个连续整数，且a<7 <b ，则a ＋b ＝____．13．对实数a 、b ，定义运算“*”，如下a*b ＝()()22a b a b ab a b ⎧⎪⎨⎪⎩≥<，已知3*m ＝36，则实数m ＝____．14．设a 是大于1的实数．若a ，23a +，213a +在数轴上对应的点分别是A 、B 、C，则三点在数轴上从左自右的顺序是____．15.如图，直径为1的圆与数轴有唯一的公共点P．点P表示的实数为－1．如果该圆沿数轴正方向滚动一周后与数轴的公共点为P′，那么点P′所表示的数是____．16．已知整数x、y满足x＋2y＝50，求x、y．17．已知2a−1的平方根是±3，3a＋b−1的算术平方根是4，求a＋b＋1的立方根．18．小颖同学在电脑上做扇形滚动的游戏，如图有一圆心角为60°，半径为1个单位长的扇形放置在数轴上，当扇形在数轴上做无滑动的滚动时，当B点恰好落在数轴上时，(1)求此时B点所对的数；(2)求圆心O移动的路程．19．若b＝315a-＋153a-＋3l，且a＋11的算术平方根为m，4b＋1的立方根为n，求（mn−2）(3mn ＋4)的平方根与立方根．20．若x、y为实数，且（x−y＋1）2与533x y--互为相反数，求22x y+的值．培优升级奥赛检测01．（荆州市八年级数学联赛试题）一个正数x的两个平方根分别是a＋1与a−3，则a值为( )A． 2 B．－1 C． 1 D． 002．（黄冈竞赛）代数式x＋1x-＋2x-的最小值是( )A．0 B． 1＋2 C．1 D． 203．代数式53x+−2的最小值为____．04．设a、b为有理数，且a、b满足等式a2＋3b＋b3＝21−53，则a＋b＝____． 05．若a b-＝1，且3a＝4b，则在数轴上表示a 、b 两数对应点的距离为____．06．已知实数a满足2009a a-=，则a − 20092＝_______．m 满足关系式199y x =--，试确定m的值．08．（全国联赛）若a 、b 满足5b＝7，S ＝3b，求S 的取值范围．09．（北京市初二年级竞赛试题）已知0<a<1，并且123303030a a a ⎡⎤⎡⎤⎡⎤+++++⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦2830a ⎡⎤+++⎢⎥⎣⎦2930a ⎡⎤++⎢⎥⎣⎦18=，求[10a]的值[其中[x]表示不超过x 的最大整数] ．10．（北京竞赛试题）已知实数a 、b 、x 、y 满足y ＋21a =-，231x y b -=--，求22x ya b +++的值．第14讲平面直角坐标系（一）考点．方法．破译1．认识有序数对，认识平面直角坐标系．2．了解点与坐标的对应关系．3．会根据点的坐标特点，求图形的面积．经典．考题．赏析【例1】在坐标平面内描出下列各点的位置．A(2，1)，B(1，2)，C(－1，2)，D(－2，－1)，E(0，3)，F(－3，0) 【解法指导】从点的坐标的意义去思考，在描点时要注意点的坐标的有序性．【变式题组】01．第三象限的点P(x，y)，满足|x|＝5,2x＋|y|＝1，则点P得坐标是-_____________．02．在平面直角坐标系中，如果m.n＞０，那么（m, |n|）一定在____________象限.03．指出下列各点所在的象限或坐标轴．A(－3，0)，B(－2，－13)，C(2，12)，D(0,3)，E(π－3.14，3.14－π)【例2】若点P(a，b)在第四象限，则点Q(―a，b―1)在（）A．第一象限 B．第二象限 C．第三象限 D．第四象限【解法指导】∵P(a，b)在第四象限，∴a＞0，b＜0，∴－a＜0, b－１＜0,故选C．【变式题组】01．若点G(a，2－a)是第二象限的点，则a的取值范围是（）A．a＜0 B．a＜2 C．0＜a＜2 B．a＜0或a＞2 02．如果点P(3x－２，２－x)在第四象限，则x的取值范围是____________．03．若点P(x，y)满足xy＞0，则点P在第______________象限．04．已知点P(2a－8，2－a)是第三象限的整点，则该点的坐标为___________．【例３】已知A点与点B(－3，4)关于x轴对称，求点A关于y轴对称的点的坐标．【解法指导】关于x轴对称的点的坐标的特点：横坐标(x)相等，纵坐标(y)互为相反数，关于y轴对称的点的坐标特点：横坐标互为相反数，纵坐标(y)相等．【变式题组】01．P(－1，3)关于x轴对称的点的坐标为____________．02．P(3，－2)关于y轴对称的点的坐标为____________．03．P(a，b)关于原点对称的点的坐标为____________．04．点A(－3，2m－１) 关于原点对称的点在第四象限，则m的取值范围是____________．05．如果点Ｍ(a＋b，ab)在第二象限内，那么点N(a，b) 关于y轴对称的点在第______象限．【例４】P(3，－4)，则点P到x轴的距离是____________．【解法指导】P(x，y)到x轴的距离是| y|，到y轴的距离是|x|．则P到轴的距离是|－4|＝4【变式题组】01．已知点P(3，5)，Q(6，－５)，则点P、Q到x 轴的距离分别是_________，__________．P到y轴的距离是点Q到y轴的距离的________倍．02．若x轴上的点Ｐ到y轴的距离是3，则P点的坐标是__________．03．如果点B(m＋1，3m－5) 到x轴的距离与它到y轴的距离相等，求m的值．04．若点(5－a，a－3)在一、三象限的角平分线上，求a的值．05．已知两点A(－3，m)，B(n，4)，AB∥x轴，求m的值，并确定n的取值范围．【例５】如图，平面直角坐标系中有A、B两点．(1)它们的坐标分别是___________，___________；(2)以A、B为相邻两个顶点的正方形的边长为_________；(3)求正方形的其他两个顶点C、D的坐标．【解法指导】平行x轴的直线上两点之间的距离是：两个点的横坐标的差得绝对值，平行y轴的直线上两点之间的距离是：两个点的纵坐标的差得绝对值．即：A(x1，y1)，B(x2，y2)，若AB∥x轴，则|AB|＝|x1－x2|；若AB∥y，则|AB|＝|y1－y2|，则(1)A(2，2)，B(2，－1)；(2)3；(3)C(5，2)，D(5，－1)或C(－1，2)，D(－1，－1)．【变式题组】01．如图，四边形ACBD是平行四边形，且AD∥x轴，说明，A、D两点的___________坐标相等，请你依据图形写出A、B、C、D四点的坐标分别是_________、_________、____________、____________．02．已知：A(0，4)，B(－3，0)，C(3，0)要画出平行四边形ABCD，请根据A、B、C三点的坐标，写出第四个顶点D的坐标，你的答案是唯一的吗？03．已知：A(0，4)，B(0，－1)，在坐标平面内求作一点，使△ABC的面积为5，请写出点C的坐标规律．【例6】平面直角坐标系，已知点A(－3，－2)，B(0，3)，C(－3，2)，求△ABC 的面积．【解法指导】(1)三角形的面积＝12×底×高．(2)通过三角形的顶点做平行于坐标轴的平行线将不规则的图形割补成规则图形，然后计算其面积．则Ｓ△ABC＝Ｓ△ABD＝Ｓ△BCD＝12·3·5－12·3·1＝6．【变式题组】01．在平面直角坐标系中，已知△ABC三个顶点的坐标分别为A(―3，―1)，B(1，3)，C(2，－3)，△ABC的面积．02．如图，已知A(－4，0)，B(－2，2)，C,0，－1)，D(1，0)，求四边形ABDC 的面积．03．已知：A(－3，0)，B(3，0)，C(－2，2)，若D点在y轴上，且点A、B、C、D四点所组成的四边形的面积为15，求D点的坐标．【例7】如图所示，在平面直角坐标系中，横、纵坐标都为整数的点称为整点．请你观察图中正方形A1B1C1D1、A2B2C2D2……每个正方形四条边上的整点的个数，推算出正方形A10B10C10D10四条边上的整点共有__________个．【解法指导】寻找规律，每个正方形四条边上的整点个数为S＝8n，所以S10＝8×10＝80个．【变式题组】01．如图所示，在平面直角坐标系中，第一次将△OAB变换成△OA1B1，第二次将△OA1B1变换成△OA2B2，第三次将△OA2B2变成△OA3B3．已知：A(1，2)， A1(2，2)，A2(4，2)，A3(8，2)，B(2，0)，B1(4，0)，B2(8，0)，B3(16，0)．(1)观察每次变换前后的三角形有何变化？找出规律，按此规律再将三角形△OA3B3变换成△OA4B4，则A4的坐标是____________，B4的坐标是_____________；(2)若按(1)题找到的规律将△OAB进行n次变换，得到三角形△OAnBn，推测An的坐标是_____________，Bn的坐标是_____________．【解法指导】由AA1A2A3、BB1B2B3的坐标可知，每变换一次，顶点A的横坐标乘以2，纵坐标不变，顶点B的横坐标乘以2，纵坐标不变．如图，已知A1(1，0)，A2(1，1)，A3(－1，1)，A4(－1，－1)，A5(2，－1)…则点A2010的坐标为_______________．演练巩固反馈提高01．若点A(－2，n)在x轴上，则点B(n－1，n＋1)在( )A．第一象限B．第二象限C．第三象限 D．第四象限02．若点M(a＋2，3－2a)在y轴上，则点M的坐标是( )A．(－2，7) B．(0，3) C．(0，7) D．(7，0)03．如果点A(a，b)，则点B(－a＋1，3b－5)关于原点的对称点是( ) A．第一象限B．第二象限C．第三象限 D．第四象限04．下列数据不能确定物体位置的是( )A．六楼6号 B．北偏西400 C．文昌大道10号 D．北纬260，东经135005．在坐标平面内有一点P(a，b)，若ab＝0，则P点的位置是( )A．原点 B．x轴上 C．y轴上 D．坐标轴上06．已知点P(a，b)到x轴的距离为2，到y轴的距离为5，且|a－b |＝b－a，则点P的坐标是_______________．。

培优补差工作的方法和措施_

培优补差工作的方法和措施一.思想方面的培优补差。

1．做好学生的思想工作，经常和学生谈心，关心他们，关爱他们，让学生觉得老师是重视他们的，激发他们学习的积极性。

了解学生们的学习态度、学习习惯、学习方法等。

从而根据学生的思想心态进行相应的辅导。

2．定期与学生家长、班主任联系，进一步了解学生的家庭、生活、思想、课堂等各方面的情况。

二.有效培优补差措施。

利用课余时间和晚自习，对各种情况的同学进行辅导、提高，“因材施教、对症下药”，根据学生的素质采取相应的方法辅导。

具体方法如下：1．课上差生板演，中等生订正，优等生解决难题。

2．安排座位时坚持“好差同桌”结为学习对子。

即“兵教兵”。

3．课堂练习分成三个层次：第一层“必做题”—基础题，第二层：“选做题”—中等题，第三层“思考题”--拓广题。

满足不同层次学生的需要。

4．培优补差过程必须优化备课，功在课前，效在课上，成果巩固在课后培优。

培优补差尽可能“耗费最少的必要时间和必要精力”。

备好学生、备好教材、备好练习，才能上好课，才能保证培优补差的效果。

要精编习题、习题教学要有四度。

习题设计（或选编习题）要有梯度，紧扣重点、难点、疑点和热点，面向大多数学生，符合学生的认知规律，有利于巩固“双基”，有利于启发学生思维；习题讲评要增加信息程度，围绕重点，增加强度，引到学生高度注意，有利于学生学会解答；解答习题要有多角度，一题多解，一题多变，多题一解，扩展思路，培养学生思维的灵活性，培养学生思维的广阔性和变通性；解题训练要讲精度，精选构思巧妙，新颖灵活的典型题，有代表性和针对性的题，练不在数量而在质量，训练要有多样化。

5．每周进行一次测试—“周考”，每月进行一次“月考”，建立学生学习档案。

三.在培优补差中注意几点：1、不歧视学习有困难的学生，不纵容优秀的学生，一视同仁。

2、根据优差生的实际情况制定学习方案，比如优秀生可以给他们一定难度的题目让他们进行练习，学困生则根据他们的程度给与相应的题目进行练习和讲解，已达到循序渐进的目的。

七年级数学尖子生培优竞赛专题辅导专题15 几何证明

专题15 几何证明专题解读】几何证明题的一般结构由已知条件和求证目标两部分组成.解答几何证明题的一般步骤如下：审题，寻找证明的思路，书写证明过程，最终实现求证目标.几何证明是初中数学学习的重要组成部分，也是学好初中数学的重要一环.要学好几何证明，不但需要我们具有扎实的基础、科学的方法、良好的数学学习习惯，还需要具有敢于尝试、不怕挫折的勇气，更需要有吃苦耐劳、持之以恒的精神.思维索引】例1.△ABC中，三个内角的平分线交于点O，过点O作∠ODC=∠AOC，交边BC于点D.B图1 图2（1）如图1，求∠BOD的度数；（2）如图2，作∠ABC外角∠ABE的平分线交CO的延长线于点F.①求证：BF∥OD；②若∠F=50°，求∠BAC的度数；③若∠F=∠ABC=40°，将△BOD绕点O顺时针旋转一定角度后得△B'OD'（0°<<360°），B'D'所在直线与FC平行，请直接写出所有符合条件的旋转角度的值.例2.如图1，直线MN 与直线AB 、CD 分别交于点E 、F ，∠1与∠2互补. （1）试判断直线AB 与直线CD 的位置关系，并说明理由；（2）如图2，∠BEF 与∠EFD 的角平分线交于点P ，EP 与CD 交于点G ，点H 是MN 上一点，且 GH EG ，求证：PF /∥GH ；（3）如图3，在（2）的条件下，连接PH ，K 是GH 上一点使∠PHK =∠HPK ，作PQ 平分∠EPK ，问∠HPQ 的大小是否发生变化？若不变，请求出其值；若变化，说明理由.CA图1 图2 图3例3.在△ABC中，∠BAC=100°，∠ABC=∠ACB，点D在直线BC上运动（不与点B、C重合），点E 在射线AC上运动，且∠ADE=∠AED，设∠DAC=n.（1）如图①，当点D在边BC上时，且n=36°，则∠BAD=_______，∠CDE=______；（2）如图②，当点D运动到点B的左侧时，其他条件不变，请猜想∠BAD和∠CDE的数量关系，并说明理由；（3）当点D运动到点C的右侧时，其他条件不变，∠BAD和∠CDE还满足（2）中的数量关系吗？请画出图形，并说明理由.BD①②③素养提升1.如图，AB CD ，∠1=58°，FG 平分∠EFD ，则∠FGB 的度数等于（） A .122°B .151°C .116°D .97°CA（第1题）（第2题）（第3题）2.如图，直线l ∥m ，将含有45°角的三角形板ABC 的直角顶点C 放在直线m 上.若∠1=25°，则∠2的度数为（） A .20°B .35°C .44°D .67°3.如图，在正方形网格中，每个小方格都是边长为1的小正方形，点A 、B 是方格纸中的两个格点（网格线的交点称格点），在这个7×7的方格纸中，找出格点C ，使△ABC 的面积为3，则满足条件的格点C 的个数是（） A .2个B .4个C .5个D .6个4.如图，将一副三角板和一张对边平行的纸条按下列方式摆放，两个三角板的一直角边重合，含30°角的直角三角板的斜边与纸条一边重合，含45°角的三角板的一个顶点在纸条的另一边上，则图中∠1的度数是（） A .15°B .22.5°C .30°D .45°5.如图，AB ∥CD ，OE 平分∠BOC ，,OFOE OP CD ，∠ABO =，则下列结论：①∠BOE =1902；②OF 平分∠BOD ；③∠POE =∠BOF ；④∠POB =2∠DOF ，其中不正确的个数有（） A .1个B .2个C .3个D .4个CDA（第4题）（第5题）（第6题）6.如图，长方形ABCD 中，AB =4cm ，BC =3cm ，点E 是CD 的中点，动点P 从A 点出发，以每秒1cm 的速度沿A →B →C →E 运动，最终到达点E .若点P 运动的时间为x 秒，那么当x =_______时，△APE 的面积等于5.7.各边长度都是整数、最大边长为8的三角形共有_______个.8．如图，点A 、C 、F 、B 在同一直线上，CD 平分∠ECB ，FG //CD ．若∠ECA 为a ，则∠GFB 为．GDEB C DPC NEMABP 8P 7P 6P 5P 4P 3P 2P 1（第8题）（第9题）（第10题）9．如图，∠ABC =∠ACB ，BD 、CD 、BE 分别平分△ABC 的内角∠ABC 、外角∠ACP 、外角∠MBC ．以下结论：①AD //BC ；②DB ⊥BE ：③∠BDC +∠ABC =90°；④∠A +2∠BEC =180°；⑤DB 平分∠ADC ．其中正确的结论有：（填序号）．10．如图，若平面内有点P 1、P 2、P 3、P 4、P 5、P 6、P 7、P 8，连接P 1P 3、P 2P 4、P 3P 5、P 4P 6、P 5P 7、P 6P 8、P 7P 1、P 8P 2，则∠P 1+∠P 2+∠P 3+∠P 4+∠P 5+∠P 6+∠P 7+∠P 8的度数是．11．在△ABC 中，∠ACB =90°，BD 是△ABC 的角平分线，P 是射线AC 上任意一点（不与A 、D 、C 三点重合），过点P 作PQ ⊥AB ，垂足为Q ，交直线BD 于E ．（1）如图1，当点P 在线段AC 上时，说明∠PDE =∠PED ．（2）作∠CPO 的角平分线交直线AB 于点F ，则PF 与BD 有怎样的位置关系？画出图形并说明理由．图 1 图 2CBAE DQP CBA12．探究与发现：如图1，在△ABC 中，∠B =∠C =45°，点D 在BC 边上，点E 在AC 边上，且∠ADE =∠AED ，连接DE ．（1）当∠BAD =60°时，求∠CDE 的度数；（2）当点D 在BC （点B 、C 除外）边上运动时，试探究∠BAD 与∠CDE 的数量关系；（3）深入探究：如图2，若∠B =∠C ，但∠C ≠45°，其它条件不变，试继续探究∠BAD 与∠CDE 的数量关系．图 1 图 2ABCDE EDCBA13．如图，AC⊥CB，垂足为C点，AC=CB=8cm，点Q是AC的中点，动点P由B点出发，沿射线BC 方向匀速移动．点P的运动速度为2cm/s．设动点P运动的时间为t s．为方便说明，我们分别记三角形ABC 面积为S，三角形PCQ的面积为S1，三角形P AQ的面积为S2，三角形ABP的面积为S3．（1）S3= cm2（用含t的代数式表示）；（2）当点P运动几秒，S1=1S，说明理由；4（3）请你探索是否存在某一时刻，使得S1=S2=S3？若存在，求出t值；若不存在，说明理由．AQC B14．某课题研究小组就图形面积问题进行专题研究，他们发现如下结论：（1）有一条边对应相等的两个三角形面积之比等于这条边上的对应高之比；（2）有一个角对应相等的两个三角形面积之比等于夹这个角的两边乘积之比；……现请你继续对下面问题进行探究，探究过程可直接应用上述结论．（S表示面积）问题1：如图1，现有一块三角形纸板ABC，P1、P2三等分边AB，R1、R2三等分边AC．经探究知四边，请证明．形P1P2R2R1的面积恰为△ABC的面积的13问题2：若有另一块三角形纸板，可将其与问题1中的拼合成四边形ABCD，如图2，Q1、Q2三等分边DC．请探究四边形P1Q1Q2P2的面积与四边形ABCD的面积之间的关系．问题3：如图3，P1，P2，P3，P4五等分边AB，Q1，Q2，Q3，Q4五等分边DC．若S四边形ABCD=1，求四边形P2Q2Q3P3的面积.问题4：如图4，P1，P2，P3四等分边AB，Q1，Q2，Q3四等分边DC，P1Q1，P2Q2，P3Q3将四边形ABCD 分成四个部分，面积分别为S1，S₂，S3，S4．请直接写出含有S1，S₂，S3，S4的一个等式．专题15几何证明思维索引】例1．(1)∠BOD ＝90°； (2)．①略 ②∠BAC ＝2∠F ＝100° ③x ＝30°，210° 例2．略例3．(1)64°，32° (2)∠BAD ＝2∠CDE (3)∠BAD ＝2∠CDE 素养提升】1．B ； 2．A ； 3．C ； 4．A ； 5．A ； 6．103或5；7．20；8．90°－2α：9．①②③④；10．720°； 11．(1)略； (2)当P 在线段AC 上时，此时PF ∥BD ，当P 在线段AC 的延长线上时，PF ⊥BD ； 12．(1)30°； (2)∠EDC ＝12∠BAD ； (3)∠EDC ＝12∠BAD ； 13．(1)8t ； (2)当点P 运动2秒或6秒时，S 1＝14； (3)当43t =时，S 1＝S 2＝S 3； 14．(1) 122113ABC P P R R S S =△四边形； (2) 11223ABCD PQ Q P S S =四边形四边形； (3) 22331155P Q Q P ABCD S S ==四边形四边形； (4)S 2＋S 3＝S 1＋S 4．。

语文培优补差总结

语文培优补差总结语文培优补差总结1不知不觉在忙碌而充实的工作中，我们即将结束本学期的教育教学工作。

从我班的基本情况来看，学生的语文总体来说还是不错的，可是也有少部分学生在语文学习上遇到了一些困难。

因此，针对我班学生学习活动中的一些具体表现，如不爱学习、学习习惯不好以及学习过程常出现错误等情况，我在开学初便有针对性地制定了我班语文培优补差计划，并争取在日常的语文教育教学中认真实施落实到位。

经过一个学期的努力，我班在培优补差工作中取得了一定的效果，现将培优补差工作情况总结如下。

一、基本情况：我所带的三（7）班共有73名学生，根据他们上学期的学习情况、知识技能掌握情况以及成绩跟踪分析，大部分学生学习积极性高，学习目的明确，上课认真，各科作业能按时按量完成，且质量较好。

优等生有周博源、陈予萱、阳昶、陈雨鑫、陈冬梅、陈裔兴等，但也有少部分学生，如李彦儒、陈紫岩、赖奕含、林书环、王林等，他们基础知识薄弱，学习态度欠端正，书写较潦草，作业有时不能及时完成。

因此，本学期我除了在教学过程中充分注重学生的个体差异外，还在提高学生学习兴趣上苦下功夫，通过培优辅差的方式使优秀学生得到了更好的发展，使学困生得到了较大的进步。

二、工作目标：1、认真挑选好培优补差的对象。

2、通过培优补差，使学生能充分认识到学习的重要性。

3、带动全班同学的学习积极性，形成良好的学习氛围。

4、有针对性地认真做好学生每周至少2次的辅导工作。

5、让优生掌握正确学习方法，培养良好素质和创新意识。

6、做好学困生的转化工作，消除他们的自卑心理，让学困生体会到成功的喜悦。

三、具体措施：（一）培优措施我认为只有扎实做好培优工作，才会让优生更优，差生不差。

对于优良学生在时间上把好关，课堂内他们能吃饱，但不会吃好，因此给予“精科”，也就是精心挑选一些拔高题，题型要多种多样，这样能给他们新鲜感，然后通过各种形式的活动来提高他们的学习积极性，从而逐步提高优良学生的学习成绩。

培优辅导1 (证明一)

音乐培优补差工作计划

八年级数学培优辅导讲义竞赛训练导学案 分式的运算 分式的化简与求值 含答案解析

培 优 证 明

人教【数学】培优易错难题一元二次方程辅导专题训练及详细答案

学校培优辅差工作计划(6篇)

学而思初二数学上册培优辅导讲义(人教版)

培优补差工作计划具体措施8篇

【数学】培优一元二次方程辅导专题训练附答案解析

初二-第01讲-三角形的证明(培优)-教案

培优证明

初中培优补差工作计划（通用15篇）

重点高中提前招生培优专题--二次函数(附详细解析)

八年级陪优讲义第一讲：如何做几何证明题

学而思初二数学(上册)培优辅导讲义(人版)

培优补差工作的方法和措施_

七年级数学尖子生培优竞赛专题辅导专题15 几何证明

语文培优补差总结

八年级数学培优辅导讲义竞赛训练导学案分式的运算分式的化简与求值含答案解析

培优证明