期末复习测试题一

合集下载

国家开放大学《道路工程》期末复习模拟测试题1-3

国家开放大学《道路工程》期末复习模拟测试题模拟测试1一、选择题1.高速公路和具干线功能的一级公路，设计交通量预测年限是（）A.10年B.15年C.20年D.25年答案：20年2.路面结构总变形中土基的变形约占（）。

A.70%以上B.70％以下C.50%左右D.50％以下答案：70%以上3.路基中心高度与边坡高度（）。

A.相同B.不同C.无关D.两者接近答案：不同4.不含或含很少细料的颗粒类混合料（）。

A.密实度高B.透水性好C.易冰冻D.易压实答案：透水性好5.沥青玛蹄脂碎石混合料的矿料级配为（）。

A.连续级配B.开级配C.密级配D.间断级配答案：间断级配6.应用弹性层状体系理论分析计算沥青路面时将其视做（）。

A.非线性的弹粘塑性体B.线性弹性体C.粘一塑性体D.非线性体答案：线性弹性体D.180天答案：90天8.具集散功能的一级公路以及二、三级公路的设计个预测年限是（）A.10年B.15年C.20年D.25年答案：15年9.水泥砼路面应力分析时，将砼板下由基层，垫层及土基组成的体系视为（）。

A.多层弹性体B.弹塑性体C.弹一粘一塑性体D.弹性地基答案：弹性地基10.从路基的实际工作状态，确定对其上、中、下不同层位的压实度要求（）。

A.上、中层应高些B.上、下层应高些C.中、下层应高些D.上层高些答案：上、下层应高些11.石灰剂量对石灰土强度的影响表现为（）。

A.随剂量增加强度增加B.随剂量增加强度减小C.存在最佳剂量D.两者无关答案：存在最佳剂量12.中间带与中央分隔带的关系是（）A.中间带与中央分隔带相等B.中间带为中央分隔带与两侧路缘带之和C.中央分隔带为中间带与两侧路缘带之和D.中间带为中央分隔带与一侧路缘带之和答案：中间带为中央分隔带与两侧路缘带之和13.道路中线竖向剖开再行展开在立面上的投影叫做（）。

A.道路剖面B.道路纵断面C.道路立面D.道路平面答案：道路纵断面D.过山桥答案：隧道15.在平面设计中曲率半径是变化的曲线是（）。

2020年统编版语文六年级下册期末测试题一(含答案)(一)共3篇

2020年小学语文期末复习检测模拟试卷1一、读句子，看拼音，写词语。

（5分）春节到了，各家都准备包jiǎo zi（），走在大街上，有各类小tān fàn （），彼此见面的第一句话都是zhù hè（）新年好。

在家里，要chèdǐ（）打扫一遍卫生，每个人要贡献自己的力量，此后就是不停地niàn dao （）着家人的归来。

二、找出下列词语中的错别字并改正。

（4分）信手粘来戛然而止弃而不舍见微知著名记在心皆然不同三、根据拼音用汉字写出古诗词的后一句。

（4分）四、给句子中加点的词语选择正确的解释。

（填序号）（3分）徘徊：①在一个地方来回地走；②比喻犹豫不决；③比喻事物在某个范围内来回浮动、起伏。

1.她徘徊了许久还是无法做出一个明确的决定。

（）2.这个广每月的产值一直在三百万元左右徘徊。

（）3.只有徘徊罢了，只有匆匆罢了。

（）五、补全词语并选词填空。

（6分）万不（）（）（）（）不同（）（）倒柜阳光（）（）（）（）四海司空（）（）1.不到（），我是不会这样做的。

2.窗外（），鸟语花香，一片生机盎然的景象。

3.大街上的车辆比往日少多了，平常（）的堵车现象今日踪影全无。

六、写出下列句子运用的修辞手法。

（5分）（）1.到年底，蒜泡得色如翡翠，酷也有了些辣味，色味双美，使人忍不住要多吃几个饺子。

（）2.在八千多日的匆匆里，除徘徊外，又剩些什么呢？（）3.太阳他有脚啊，轻轻悄悄地挪移了，我也茫茫然跟着旋转。

（）4.过了二十三，大家就更忙了，春节眨眼就到了啊。

（）5.在逃去如飞的日子里，在千门万户的世界里的我能做什么呢？只有徘徊罢了，只有匆匆罢了。

七、按要求写句子。

（8分）1.刚刚读过的那些字仍然停留在原地。

（缩句）2.八千多日子已经从我手中溜去，像针尖上一滴水滴在大海里，我的日子滴在时间的流里，没有声音，也没有影子。

（仿照该句的修辞手法写句子）3.“不要多嘴！”法官怒气冲冲．．．．的，又拿起他面前那块木板狠狠地拍了几下。

人教版小学数学五年级下册期末总复习三套测试题附答案

期末测试卷(一)一、认真审题，填一填。

(第3题6分，第4题3分，其余每小题2分，共25分)1．有10个机器零件，其中9个质量合格，另有1个稍重，不合格。

如果用天平称，至少称( )次能保证找出这个不合格的零件来。

2．把一个棱长是12 cm 的正方体铁块铸造成一个长是18 cm ，宽是12 cm 的长方体，这个长方体的高是( )cm ，表面积是( )cm 2。

3．在( )里填上合适的数。

0.85 m 3＝( )cm 3 4 L ＝( )mL 150 dm 3＝( )m 3 47 mL ＝(——)L 59秒＝(——)分 31 cm ＝(——)dm4．9÷( )＝()25＝21（）＝35 5．用数字卡片2345可以组成最大的带分数是( )，最小的带分数是( )。

6．在89、121、132、480、157、783中，是3的倍数的是( )。

7．甲数＝3×5×7，乙数＝5×3×11，甲、乙两数的最大公因数是( )，最小公倍数是( )。

8．把8吨煤平均分给5户居民，每户居民分得总吨数的(——)，每户居民分得(——)吨。

9．一个长方体，长是8 cm ，宽和高都是质数，它们的和等于长方体的长，这个长方体的体积是( )。

10．右图要保持从上面看到的图形不变，最多可以拿掉()个小正方体。

二、仔细推敲，选一选。

(将正确答案的序号填在括号里)(每小题1分，共8分)1．“龟兔赛跑”讲述了这样的故事：领先的兔子看着慢慢爬行的乌龟，骄傲起来，睡了一觉。

当它醒来时发现乌龟快到终点了，于是急忙追赶，但为时已晚，乌龟还是先到达了终点。

用s1、s2分别表示乌龟和兔子所行的路程，t为时间，下面图()与故事情节相吻合。

2．在分数818－x中，x不能等于()。

A．9B．6C．3D．18 3．用丝带捆扎一种礼品盒(如右图)，接头处长30 cm，要捆扎这种礼品盒至少需要准备()cm的丝带比较合理。

九年级数学第一学期期末考试综合复习测试题(含答案)

九年级数学第一学期期末考试综合复习测试题（含答案）一．选择题（共10小题，每小题3分，共30分） 1．2022的相反数是( )A ．2022B ．2022-C ．12022D ．2022± 2．若代数式3125m x y -与822m nx y +-是同类项，则( )A ．73m =，83n =-B ．3m =，4n =C ．73m =，4n =- D ．3m =，4n =-3．下列四组线段中，能组成直角三角形的是( ) A ．1a =，3b =，3c = B ．2a =，3b =，4c = C ．2a =，4b =，5c =D ．3a =，4b =，5c = 4．如图所示，直线//a b ，231∠=︒，28A ∠=︒，则1(∠= )A ．61︒B ．60︒C ．59︒D ．58︒5．下列关于事件发生可能性的表述，正确的是( )A ．“在地面向上抛石子后落在地上”是随机事件B ．掷两枚硬币，朝上面是一正面一反面的概率为13C ．在同批次10000件产品中抽取100件发现有5件次品，则这批产品中大约有500件左右的次品D ．彩票的中奖率为10%，则买100张彩票必有10张中奖6．某校10名学生参加课外实践活动的时间分别为：3，3，6，4，3，7，5，7，4，9（单位：小时），这组数据的众数和中位数分别为( ) A ．9和7 B ．3和3 C ．3和4.5 D ．3和5 7．一个正多边形的每一个内角都是150︒，则它的边数为( ) A ．6 B ．9 C ．12 D ．158．若不等式组841x x x m +<-⎧⎨>⎩的解集是3x >，则m 的取值范围是( )A ．3m <B ．3mC ．3m >D ．3m9．已知关于x 的一元二次方程22(21)0x m x m --+=有实数根，则m 的取值范围是( ) A ．14m 且0m ≠ B ．14m C ．14m < D ．14m >10．如图1，一个扇形纸片的圆心角为90︒，半径为6．如图2，将这张扇形纸片折叠，使点A 与点O 恰好重合，折痕为CD ，图中阴影为重合部分，则阴影部分的面积为( )A ．9632π-B ．693π-C ．91232π-D ．94π二．填空题（共5小题，每小题3分，共15分） 11．将数据2022万用科学记数法表示为．12．已知当3x =时，代数式35ax bx +-的值为20，则当3x =-时，代数式35ax bx +-的值是．13．将抛物线229y x x =-+-向左平移2个单位，再向上平移1个单位后，得到的抛物线的解析式为．14．已知ABC ∆中，点O 是ABC ∆的外心，140BOC ∠=︒，那么BAC ∠的度数为．15．如图，在正方形ABCD 中，顶点(5,0)A -，(5,10)C ，点F 是BC 的中点，CD 与y 轴交于点E ，AF 与BE 交于点G ，将正方形ABCD 绕点O 顺时针旋转，每次旋转90︒，则第2023次旋转结束时，点G 的坐标为．三．解答题（一）（共3小题，每小题8分，共24分） 16．计算（1）2()(2)x y x y x +--；（2）2219(1)244a a a a --÷--+．17．如图，90ACB ∠=︒，AC AD =．（1）过点D 作AB 的垂线DE 交BC 与点E ，连接AE ．（尺规作图，并保留作图痕迹）（2）如果8BD =，10BE =，求BC 的长．18．如图，在四边形ABCD 中，AC 与BD 交于点O ，BE AC ⊥，DF AC ⊥，垂足分别为点E ，F ，且BE DF =，ABD BDC ∠=∠．求证：四边形ABCD 是平行四边形．四．解答题（二）（共3小题，每小题9分，共27分） 19．阳光中学为了丰富学生的课余生活，计划购买围棋和中国象棋供棋类兴趣小组活动使用，若购买3副围棋和5副中国象棋需要98元；若购买1副围棋和2副中国象棋需要36元．（1）求每副围棋和每副中国象棋各多少元；（2）阳光中学决定购买围棋和中国象棋共40副，总费用不超过538元，且围棋的副数不低于象棋的副数，问阳光中学有几种购买方案；（3）请求出最省钱的方案需要多少钱？20．我市某中学举行“中国梦⋅我的梦”的演讲比赛，赛后整理参赛学生的成绩，将学生的成绩分为A，B，C，D四个等级，并将结果绘制成如图所示的条形统计图和扇形统计图，但均不完整，请你根据统计图解答下列问题．（1）参加比赛的学生人数共有名，在扇形统计图中，表示“D等级”的扇形的圆心角为度，图中m的值为；（2）补全条形统计图；（3）组委会决定从本次比赛中获得A等级的学生中，选出两名去参加市中学生演讲比赛，已知A等级中男生只有1名，请用画树状图或列表的方法求出所选学生恰是一男一女的概率．21．22．某网店专售一款新型钢笔，其成本为20元/支，销售中发现，该商品每天的销售量y与销售单价x（元/支）之间存在如下关系：10400y x=-+，自武汉爆发了“新型冠状病毒”疫情该网店店主决定从每天获得的利润中抽出200元捐赠给武汉，同时又让顾客得到实惠，当销售单价定位多少元时，捐款后每天剩余利润为550元？五．解答题（三）（共2小题，每小题12分，共24分）22．如图，以点O为圆心，AB长为直径作圆，在O上取一点C，延长AB至点D，连接DC，过点A作O的切线交DC的延长线于点E，且DCB DAC∠=∠．（1）求证：CD是O的切线；（2）若6AD=，2:3BC CA=，求AE的长．23．如图，在平面直角坐标系中，直线33y x =--与x 轴交于点A ，与y 轴交于点C ．抛物线2y x bx c =++经过A 、C 两点，且与x 轴交于另一点B （点B 在点A 右侧）．（1）求抛物线的解析式；（2）若点M 是线段BC 上一动点，过点M 的直线ED 平行y 轴交x 轴于点D ，交抛物线于点E ，求ME 长的最大值及此时点M 的坐标；（3）在（2）的条件下：当ME 取得最大值时，在x 轴上是否存在这样的点P ，使得以点M 、点B 、点P 为顶点的三角形是等腰三角形？若存在，请直接写出所有点P 的坐标；若不存在，请说明理由．答案一．选择题1． B ．2． D ．3． D ．4． C ．5． C ．6． C ．7． C ．8． B ．9． B ．10． C ．二．填空题11． 72.02210⨯．12． 30-．13． 228y x x =---．14． 70︒或110︒．15． (4,3)-．三．解答题16．解：（1）2()(2)x y x y x +--22222x xy y xy x =++-- 2y =；（2）2219(1)244a a a a --÷--+ 23(3)(3)2(2)a a a a a ---+=÷-- 23(2)2(3)(3)a a a a a --=⋅---+ 23a a -=--． 17．解：（1）如图所示即为所求作的图形．（2）ED 垂直AB ， 90ADE EDB ∴∠=∠=︒，在Rt BDE ∆中，22221086DE BE BD =-=-=，在Rt ADE ∆和Rt ACE ∆中， AC ADAE AE =⎧⎨=⎩， Rt ADE Rt ACE(HL)∴∆≅∆， 6EC ED ∴==， 16BC BE EC ∴=+=．18．证明：ABD BDC ∠=∠， //AB CD ∴．BAE DCF ∴∠=∠．在ABE ∆与CDF ∆中， 90BAE DCF AEB CFD BE DF ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩． ()ABE CDF AAS ∴∆≅∆． AB CD ∴=．∴四边形ABCD 是平行四边形．19．解：（1）设每副围棋x 元，每副中国象棋y 元，根据题意得：3598236x y x y +=⎧⎨+=⎩，∴1610x y =⎧⎨=⎩，∴每副围棋16元，每副中国象棋10元；（2）设购买围棋z 副，则购买象棋(40)z -副，根据题意得：1610(40)538m m +-，40m z -，2023m ∴，m 可以取20、21、22、23则有：方案一：购买围棋20副，购买中国象棋20副方案二：购买围棋21副，购买中国象棋19副方案：购买围棋22副，购买中国象棋18副方案四：购买围棋23副，购买中国象棋17副由4种方案；（3）由上一问可知共有四种方案：方案一：购买围棋20副，购买中国象棋20副；方案二：购买围棋21副，购买中国象棋19副；方案三：购买围棋22副，购买中国象棋18副；方案四：购买围棋23副，购买中国象棋17副；方案一需要20162010520x x +=；方案二需要21161910526x x +=；方案三需要22161810532x x +=；方案四需要23161710538x x +=；所以最省钱是方案一，需要520元．20．（1）解：根据题意得：总人数为：315%20÷=（人)，表示“D 等级”的扇形的圆心角为43607220⨯︒=︒；C等级所占的百分比为8100%40% 20⨯=，所以40m=，故答案为：20，72，40．（2）解：等级B的人数为20(384)5-++=（人)，补全统计图，如图所示：（3）解：根据题意，列出表格，如下：男女1女2男女1、男女2、男女1男、女1女2、女1女2男、女2女1、女2共有6种等可能结果，其中恰是一男一女的有4种，所以恰是一男一女的概率为42 63 =．21．解：由题意可得(20)(10400)200550x x--+-=解得125x=，235x=因为要让顾客得到实惠，所以25x=答：当销售单价定为25元时，捐款后每天剩余利润为550元．22．（1）证明：连接OC，OE，如图，AB为直径，90ACB∴∠=︒，即190BCO∠+∠=︒，又DCB CAD∠=∠，1CAD∠=∠，1DCB∴∠=∠，90DCB BCO ∴∠+∠=︒，即90DCO ∠=︒， CD ∴是O 的切线；（2）解：EC ，EA 为O 的切线， EC EA ∴=，AE AD ⊥， OC OA =， OE AC ∴⊥，90BAC EAC ∴∠+∠=︒，90AEO EAC ∠+∠=︒， BAC AEO ∴∠=∠， tan tan BAC AEO ∴∠=∠，∴23BC AO AC AE ==， Rt DCO Rt DAE ∆∆∽，∴23CD OC OA DA AE AE ===， 2643CD ∴=⨯=，在Rt DAE ∆中，设AE x =，222(4)6x x ∴+=+，解得52x =．即AE 的长为52．23．解：（1）直线33y x =--与x 轴、y 轴分别交于点A 、C ， (1,0)A ∴-，(0,3)C -抛物线2y x bx c =++经过点(1,0)A -，(0,3)C -， ∴103b c c -+=⎧⎨=-⎩，解得23b c =-⎧⎨=-⎩，∴抛物线的解析式为223y x x =--．（2）设(E x ，223)(03)x x x --<<，则(,3)M x x -， 222393(23)3()24ME x x x x x x ∴=----=-+=--+，∴当32x =时，94ME =最大，此时3(2M ，3)2-．（3）存在．如图3，由（2）得，当ME 最大时，则3(2D ，0)，3(2M ，3)2-，32DO DB DM ∴===； 90BDM ∠=︒，223332()()222OM BM ∴==+=．点1P 、2P 、3P 、4P 在x 轴上，当点1P 与原点O 重合时，则1322PM BM ==，1(0,0)P ；当2322BP BM ==时，则232632322OP -=-=， 2632(2P -∴，0)；当点3P 与点D 重合时，则3332P M P B ==，33(2P ，0)；当4322BP BM ==时，则432632322OP +=+=， 4632(2P +∴，0)．综上所述，1(0,0)P ，2632(2P -，0)，33(2P ，0)，4632(2P +，0)．。

期末复习综合测试题(1)-【新教材】人教A版(2019)高中数学必修第一册

模块一测试题一一．选择题（共10小题）1．设集合2{|10}A x x =-=，则( ) A ．A ∅∈B ．1A ∈C ．{1}A -∈D ．{1-，1}A ∈2．命题“[1x ∀∈，2]，220x a -”为真命题的一个充分不必要条件是( ) A ．1a <B ．2aC ．3aD ．4a3．若命题“[1x ∀∈，4]时，240x x m --≠”是假命题，则m 的取值范围( ) A ．[4-，3]-B ．(,4)-∞-C ．[4-，)+∞D ．[4-，0]4．已知函数22()4(0)f x x ax a a =-+>的两个零点分别为1x ，2x ，则1212ax x x x ++的最小值为( ) A ．8B ．6C ．4D ．25．已知动点(,)a b 的轨迹为直线:124x yl +=在第一象限内的部分，则ab 的最大值为( ) A ．1 B ．2 C．D ．46．设函数()f x 的图象与2x a y +=的图象关于直线y x =-对称，若2020m n +=，(2)(2)2m n f f -+-=，则(a = ) A ．1011 B ．1009C ．1009-D ．1011-7．已知(2πθ∈-，0)，且3cos2cos()02πθθ++=，则sin()(4πθ+= ) ABCD8．已知函数()sin()cos()(06f x x x πωϕωϕω=++++>，0)3πϕ-<<，若点11(12π，0)为函数()f x 的对称中心，直线6x π=为函数()f x 的对称轴，并且函数()f x 在区间4(3π，3)2π上单调，则(2)(f ωϕ= )A ．1-B ．3C ．12 D ．12-二．多选题（共4小题）9．设集合{|4}x M y y e ==-+，{|[(2)(3)]}N x y lg x x ==+-，则下列关系正确的是( )A ．R RM N ⊆B ．N M ⊆C ．M N =∅D ．RN M ⊆10．《几何原本》中的几何代数法（以几何方法研究代数问题）成为了后世数学家处理问题的重要依据，通过这一原理，很多代数的公理或定理都能够通过图形实现证明．如图，在AB 上取一点C ，使得AC a =，BC b =，过点C 作CD AB ⊥交以AB 为直径，O 为圆心的半圆周于点D ，连接OD ．下面不能由OD CD 直接证明的不等式为( )A (0,0)2a baba b +>> B 2(0,0)ababa b a b>>+C ．222(0,0)a bab a b +>>D ．22(0,0)22a b a b a b ++>> 11．已知定义在R 上的函数()f x 满足()()0f x f x -+=，且当0x 时，2()2f x x x =+，则可作为方程()(1)f x f x =-实根的有( )A 13-- B ．12C 13-+D 33+ 12．给出下列四个结论，其中正确的结论是( ) A ．sin()sin παα+=-成立的条件是角α是锐角B ．若1cos()()3n n Z πα-=∈，则1cos 3α=C ．若()2Z πα≠∈，则1tan()2tan παα-+=D ．若sin cos 1αα+=，则sin cos 1n n αα+= 三．填空题（共4小题）13．对于正数a ，a a a 可以用有理数指数幂的形式表示为．14．若函数12|1|log (1),1021,0x x x y x m---<⎧⎪=⎨⎪-⎩的值域为[1-，1]，则实数m 的取值范围为．15．已知22log log 16sincos1212a b ππ+=⋅，则a b +的最小值为．16．用I M 表示函数sin y x =在闭区间I 上的最大值．若正数a 满足[0,][,2]2a a a M M ，则a 的最大值为．四．解答题（共8小题）17．某居民小区欲在一块空地上建一面积为21200m 的矩形停车场，停车场的四周留有人行通道，设计要求停车场外侧南北的人行通道宽3m ，东西的人行通道宽4m ，如图所示（图中单位：)m ，问如何设计停车场的边长，才能使人行通道占地面积最小？最小面积是多少？18．已知a ，(0,)b ∈+∞，且24a 2b =．（Ⅰ）求21a b+的最小值；（Ⅱ）若存在a ，(0,)b ∈+∞，使得不等式21|1|3x a b-++成立，求实数x 的取值范围．19．已知函数212log (1)&0()log (1)&0x x f x x x +⎧⎪=⎨-<⎪⎩．（1）判断函数()y f x =的奇偶性；（2）对任意的实数1x 、2x ，且120x x +>，求证：12()()0f x f x +>；（3）若关于x 的方程23[()]()04f x af x a +-+-=有两个不相等的正根，求实数a 取值范围．20．已知函数()sin (cos )f x x x x =+．（1）求()3f π的值及函数()f x 的单调增区间；（2）若[12x π∀∈，]2π，不等式()2m f x m <<+恒成立，求实数m 的取值集合．21．已知函数()sin()(0f x A x B A ωϕ=++>，0ω>，||)2πϕ<在一个周期内的最高点和最低点分别为(2,1)，(8,3)-．（1）求函数()f x 的表达式；（2）求函数()f x 在区间[0，6]的最大值和最小值；（3）将()y f x =图象上的点的横坐标变为原来的6tπ倍(0)t >，纵坐标不变，再向上平移1个单位得到()y g x =的图象．若函数()y g x =在[0，]π内恰有4个零点，求t 的取值范围．22．已知函数()4cos sin()1()6f x x x x R π=-+∈，将函数()y f x =的图象向左平移6π个单位，得到函数()y g x =的图象．（1）求()3f π的值；（2）求函数()y g x =的解析式；（3）若0()2x f =0()g x ．模块一测试题一参考答案与试题解析一．选择题（共10小题）1．设集合2{|10}A x x =-=，则( ) A ．A ∅∈B ．1A ∈C ．{1}A -∈D ．{1-，1}A ∈【分析】根据题意，用列举法表示集合A ，据此判断各选项，即可得答案．【解答】解：根据题意，2{|10}{1A x x =-==-，1}，对于A ，A ∅⊆，A 错误，对于B ，1A ∈，B 正确，对于C ，{1}A -⊆，C 错误，对于D ，{1-，1}A =，D 错误，故选：B ．【点评】本题考查元素与集合的关系，涉及集合的表示方法，属于基础题． 2．命题“[1x ∀∈，2]，220x a -”为真命题的一个充分不必要条件是( ) A ．1a <B ．2aC ．3aD ．4a【分析】求出函数恒成立的充要条件，根据集合的包含关系判断即可．【解答】解：若[1x ∀∈，2]，220x a -恒成立，则2(2)2min a x =，故命题“[1x ∀∈，2]，220x a -”为真命题的充要条件是2a ，而(-∞，1)(⊆-∞，2]，故命题“[1x ∀∈，2]，220x a -”为真命题的一个充分不必要条件是1a <，故选：A ．【点评】本题考查了充分必要条件，考查集合的包含关系以及函数恒成立问题，是一道基础题．3．若命题“[1x ∀∈，4]时，240x x m --≠”是假命题，则m 的取值范围( ) A ．[4-，3]-B ．(,4)-∞-C ．[4-，)+∞D ．[4-，0]【分析】根据全称命题是假命题，得到命题的否定是真命题，利用参数分离法进行求解即可．【解答】解：若命题“[1x ∀∈，4]时，240x x m --≠”是假命题，则命题“[1x ∃∈，4]时，240x x m --=”是真命题则24m x x =-，设22()4(2)4f x x x x =-=--，当14x 时，4()0f x - 则40m -，故选：D ．【点评】本题主要考查命题真假的应用，利用全称命题的否定是特称命题转化为特称命题是解决本题的关键．难度中等．4．已知函数22()4(0)f x x ax a a =-+>的两个零点分别为1x ，2x ，则1212ax x x x ++的最小值为( )A ．8B ．6C ．4D ．2【分析】由韦达定理求出124x x a +=，212x x a =，再根据基本不等式的性质求出代数式的最小值即可．【解答】解：由题意得：124x x a +=，212x x a =，故1212114244a x x a a x x a a ++=+⋅=，当且仅当12a =时“=”成立，故选：C ．【点评】本题考查了二次函数的性质，考查基本不等式的性质，是一道基础题． 5．已知动点(,)a b 的轨迹为直线:124x yl +=在第一象限内的部分，则ab 的最大值为( ) A ．1 B ．2 C ．D ．4【分析】直接利用基本不等式的应用求出结果．【解答】解：动点(,)a b 的轨迹为直线:124x yl +=在第一象限内的部分，所以124a b+=，由基本不等式122424a b a b=+，解得2ab ，当且仅当1242a b ==时，等号成立，故ab 的最大值为2．故选：B ．【点评】本题考查的知识要点：基本不等号式的应用，主要考查学生的运算能力和转换能力及思维能力，属于基础题．6．设函数()f x 的图象与2x a y +=的图象关于直线y x =-对称，若2020m n +=，(2)(2)2m n f f -+-=，则(a = ) A ．1011B ．1009C ．1009-D ．1011-【分析】在函数()y f x =的图象上取点(,)x y ，则关于直线y x =-对称点为(,)y x --，代入2x a y +=，结合题目条件可得答案．【解答】解：因为函数()y f x =的图象与2x a y +=的图象关于直线y x =-对称，令(2)m f p -=，(2)n f q -=，则2p q +=；故(p -，2)m ，(q -，2)n 在2x a y +=的图象上，所以22m p a -+=，22n q a -+=，即m p an q a =-+⎧⎨=-+⎩，两式相加得()2m n p q a +=-++，所以2202022022a m n p q =+++=+=，解得1011a =，故选：A ．【点评】本题考查图象的对称性，考查学生分析解决问题的能力，属于中档题． 7．已知(2πθ∈-，0)，且3cos2cos()02πθθ++=，则sin()(4πθ+= )A B C D 【分析】由已知结合二倍角公式可先求sin θ，进而可求cos θ，然后结合两角和的正弦公式可求．【解答】解：因为(2πθ∈-，0)，且3cos2cos()02πθθ++=，所以cos2sin 0θθ+=，即22sin sin 10θθ-++=，解得，sin 1θ=（舍)或1sin 2θ=-，所以cos θ=则sin()cos )4πθθθ+=+=故选：A ．【点评】本题主要考查了诱导公式，同角平方关系，和差角公式在三角求值中的应用，属于基础题．8．已知函数()sin()cos()(06f x x x πωϕωϕω=++++>，0)3πϕ-<<，若点11(12π，0)为函数()f x 的对称中心，直线6x π=为函数()f x 的对称轴，并且函数()f x 在区间4(3π，3)2π上单调，则(2)(f ωϕ= )A ．1- BC ．12 D ．12-【分析】利用两角和差和辅助角公式化简函数函数()sin()cos()sin()63f x x x x ππωϕωϕωϕ=++++=++，再利用三角函数的单调性、周期性和对称性可得2(21)3ω=+，N ∈．66l ππϕωπ=-+，I Z ∈．又因为03πϕ-<<，且06ω<．解得解得：26ωπϕ=⎧⎪⎨=-⎪⎩，即4(33ππϕ++，3)(3236πππωϕπ++=-，3)6ππ+符合单调性条件，所以函数()sin(2)6f x x π=+，即可得21(2)()32f f πωϕ=-=．【解答】解：函数()sin()cos()sin()63f x x x x ππωϕωϕωϕ=++++=++，并且函数()f x 在区间4(3π，3)2π上单调，因此62T ππω=，所以06ω<．又因为点11(12π，0)为函数()f x 的对称中心，直线6x π=为函数()f x 的对称轴，因此113126442T Tπππ-==+，N ∈，所以2321T ππω==+，解得2(21)3ω=+，N ∈．将6x π=代入函数()f x 时函数有最值，即632m πππωϕπ++=+，m Z ∈，即66m ππϕωπ=-+，m Z ∈．又因为03πϕ-<<，且06ω<．解得：26ωπϕ=⎧⎪⎨=-⎪⎩，即4(33ππϕ++，3)(3236πππωϕπ++=-，3)6ππ+符合单调性条件，所以函数()sin(2)6f x x π=+，则21(2)()32f f πωϕ=-=，故选：C ．【点评】本题考查三角函数的图象与性质、三角恒等变换、二倍角公式，考查推理论证能力和运算求解能力，考查逻辑推理、直观想象、数学运算核心素养．二．多选题（共4小题）9．设集合{|4}x M y y e ==-+，{|[(2)(3)]}N x y lg x x ==+-，则下列关系正确的是( )A ．R RM N ⊆B ．N M ⊆C ．M N =∅D ．RN M ⊆【分析】由指数函数的性质求出函数的值域即集合A ，由对数函数的性质即真数大于0，解一元二次不等式得到集合B ，判断两个集合的关系，结合选项可得正确答案．【解答】解：集合{|4}{|4}(,4)x M y y e y y ==-+=<=-∞，集合{|[(2)(3)]}{|(2)(3)0}{|(2)(3)0}(2N x y lg x x x x x x x x ==+-=+->=+-<=-，3)，N M ∴⊆，即RM RN C C ⊆，故选：AB ．【点评】本题考查了集合间的关系，以及指数函数和对数函数的性质，属于基础题． 10．《几何原本》中的几何代数法（以几何方法研究代数问题）成为了后世数学家处理问题的重要依据，通过这一原理，很多代数的公理或定理都能够通过图形实现证明．如图，在AB 上取一点C ，使得AC a =，BC b =，过点C 作CD AB ⊥交以AB 为直径，O 为圆心的半圆周于点D ，连接OD ．下面不能由OD CD 直接证明的不等式为( )A ．(0,0)2a baba b +>> B ．2(0,0)ababa b a b>>+C ．222(0,0)a bab a b +>>D ．22(0,0)22a b a b a b ++>> 【分析】由题意得，1()2OD a b =+，然后结合射影定理可得，2CD AC BC ab =⋅=，从而可判断．【解答】解：因为AC a =，BC b =，所以1()2OD a b =+，由题意得，90ADB ∠=︒，由射影定理可得，2CD AC BC ab =⋅=，由OD CD ，得1()2a b ab +，当且仅当a b =时取等号，A 正确，B ，C ，D 不正确．故选：BCD ．【点评】本题主要考查了直角三角形的射影定理，属于基础题．11．已知定义在R 上的函数()f x 满足()()0f x f x -+=，且当0x 时，2()2f x x x =+，则可作为方程()(1)f x f x =-实根的有( )AB ．12CD【分析】由已知求得函数解析式，得到(1)f x -，进一步写出分段函数()()(1)g x f x f x =--，求解方程()0g x =得答案．【解答】解：()()0f x f x -+=，()f x ∴为定义在R 上的奇函数，当0x 时，2()2f x x x =+，设0x >，则0x -<，得2()2()f x x x f x -=-=-，即2()2f x x x =-+．222,0()2,0x x x f x x x x ⎧+∴=⎨-+>⎩，则221,1(1)2,1x x f x x x x ⎧-+<-=⎨-+⎩，令22263,1()()(1)21,01221,0x x x g x f x f x x x x x x ⎧-+-⎪=--=-<<⎨⎪+-⎩，当()0g x =时，解得x =或12x =或x =．故选：ABD ．【点评】本题考查函数的奇偶性的应用，考查函数与方程思想，考查逻辑思维能力与运算求解能力，是中档题．12．给出下列四个结论，其中正确的结论是( )A ．sin()sin παα+=-成立的条件是角α是锐角B ．若1cos()()3n n Z πα-=∈，则1cos 3α=C ．若()2Z πα≠∈，则1tan()2tan παα-+=D ．若sin cos 1αα+=，则sin cos 1n n αα+=【分析】由诱导公式二即可判断A ；分类讨论，利用诱导公式即可判断B ；利用同角三角函数基本关系式即可判断C ；将已知等式两边平方，可得sin 0α=，或cos 0α=，分类讨论即可判断D ．【解答】解：由诱导公式二，可得R α∈时，sin()sin παα+=-，故A 错误；当2n =，Z ∈时，cos()cos()cos n πααα-=-=，此时1cos 3α=，当21n =+，Z ∈时，cos()cos[(21)]cos()cos n παπαπαα-=+-=-=-，此时1cos 3α=-，故B 错误；若2πα≠，Z ∈，则sin()cos 12tan()2sin tan cos()2παπααπααα++===--+，故C 正确；将sin cos 1αα+=，两边平方，可得sin cos 0αα=，所以sin 0α=，或cos 0α=，若sin 0α=，则cos 1α=，此时22sin cos 1αα+=；若cos 0α=，则sin 1α=，此时22sin cos 1αα+=，故sin cos 1n n αα+=，故D 正确．故选：CD ．【点评】本题主要考查了诱导公式，同角三角函数基本关系式的应用，考查了函数思想和分类讨论思想，属于中档题．三．填空题（共4小题）13．对于正数a可以用有理数指数幂的形式表示为 78a ．【分析】根据指数幂的运算法则即可求出．【解答】解：原式7111311317182222224242(())(())()()a a a a a a a a a =⋅==⋅==．故答案为：78a ．【点评】本题考查了指数幂的运算法则，属于基础题．14．若函数12|1|log (1),1021,0x x x y x m---<⎧⎪=⎨⎪-⎩的值域为[1-，1]，则实数m 的取值范围为 [1，2] ．【分析】可求出10x -<时，10y -<，然后根据原函数的值域为[1-，1]可得出0x m 时，0|1|1x -，01y ，这样即可求出m 的范围．【解答】解：10x -<时，112x <-，121(1)0log x --<，且原函数的值域为[1-，1]，0x m ∴时，0|1|1x -，即02x ， 12m ∴，m ∴的取值范围为：[1，2]．故答案为：[1，2]．【点评】本题考查了对数函数和指数函数的单调性，函数值域的定义及求法，考查了计算能力，属于中档题．15．已知22log log 16sincos1212a b ππ+=⋅，则a b +的最小值为 8 ．【分析】由已知结合对数的运算性质及二倍角公式进行化简可求ab ，然后结合基本不等式即可求解．【解答】解：因为22log log 16sincos8sin412126a b πππ+=⋅==，所以2log 4ab =，故16ab =，则28a b ab +=，当且仅当4a b ==时取等号，a b +的最小值8．故答案为：8．【点评】本题主要考查了对数的运算性质，二倍角公式及基本不等式，属于基础题． 16．用I M 表示函数sin y x =在闭区间I 上的最大值．若正数a 满足[0,][,2]2a a a M M ，则a 的最大值为98π．．【分析】分a 在不同区间进行讨论，得出符合条件的a 取值范围，即可求得a 的最大值．【解答】解：当[0a ∈，]2π时，2[0a ∈，]π，[0,]sin a M a =，[,2]1a a M =，由[0,][,2]2a a a M M ，得sin 2a，此时不成立；当[2a π∈，]π时，2[a π∈，2]π，[0,]1a M =，[,2]sin a a M a =，由[0,][,2]2a a a M M ，得12sin a ，即2sin a ，所以34a ππ；当[a π∈，3]2π时，2[2a π∈，3]π，[0,]1a M =，[,2]sin 2a a M a =或1，由[0,][,2]2a a a M M ，得12sin 2a ，即2sin 2a且222a ππ+，解得98a ππ；当3[2a π∈，)+∞时，2[3a π∈，)+∞，[0,]1a M =，[,2]1a a M =，不合题意．综上，a 得最大值为98π．故答案为：98π．【点评】本题主要考查三角函数的最值的求法，考查分类讨论的数学思想，考查计算能力，属于中档题．四．解答题（共8小题）17．某居民小区欲在一块空地上建一面积为21200m的矩形停车场，停车场的四周留有人行通道，设计要求停车场外侧南北的人行通道宽3m，东西的人行通道宽4m，如图所示（图中单位：)m，问如何设计停车场的边长，才能使人行通道占地面积最小？最小面积是多少？【分析】设矩形车场南北侧边长为xm，则其东西侧边长为1200mx，人行道占地面积为12007200(6)(8)1200848S x xx x=++-=++，然后结合基本不等式即可求解．【解答】解：设矩形车场南北侧边长为xm，则其东西侧边长为1200mx，人行道占地面积为120072007200(6)(8)1200848284896S x x xx x x=++-=++⋅=，当且仅当72008xx=，即30()x m=时取等号，296()minS m=，此时120040()mx=，所以矩形停车场的南北侧边长为30m，则其东西侧边长为40m，才能使人行通道占地面积最小，最小面积是2528m．【点评】本题主要考查了基本不等式在实际问题中的应用，体现了转化思想的应用．18．已知a，(0,)b∈+∞，且24a2b=．（Ⅰ）求21a b+的最小值；（Ⅱ）若存在a，(0,)b∈+∞，使得不等式21|1|3xa b-++成立，求实数x的取值范围．【分析】()I由已知结合指数的运算性质可得，21a b+=，然后结合2121()(2)a ba b a b+=++，展开后利用基本不等式可求，()II 存在a ，(0,)b ∈+∞，使得21|1|3x a b-++成立，则结合()I 得|1|34x -+成立，解不等式可求．【解答】解：因为a ，(0,)b ∈+∞，且24a 222b a b +==，所以21a b +=，212144()()(2)4428b a b I a b a b a b a b a +=++=+++=，当且仅当4b a a b =且21a b +=，即14b =，12a =时取等号，故21a b+的最小值8， ()II 由21()I a b+的最小值4，又存在a ，(0,)b ∈+∞，使得21|1|3x a b-++成立，所以|1|34x -+>，所以|1|1x ->，解得，2x >或0x <，故x 的范围{|2x x >或0}x <．【点评】本题主要考查了利用基本不等式求解最值及不等式的存在性问题与最值的相互转化关系的应用，属于中档题．19．已知函数212log (1)&0()log (1)&0x x f x x x +⎧⎪=⎨-<⎪⎩．（1）判断函数()y f x =的奇偶性；（2）对任意的实数1x 、2x ，且120x x +>，求证：12()()0f x f x +>；（3）若关于x 的方程23[()]()04f x af x a +-+-=有两个不相等的正根，求实数a 取值范围．【分析】（1）利用函数奇偶性的定义判断函数的奇偶性；（2）证明函数2log (1)y x =+在[0，)+∞上是严格增函数，结合函数的奇偶性可得12(1)y log x =-在(,0)-∞上也是严格增函数，从而()y f x =在R 上是严格增函数，由120x x +>，即可证明12()()0f x f x +>；（3）由（1）知，()y f x =是R 上的奇函数，故原方程可化为23[()]()04f x af x a -+-=，把原方程有两个不等正根转化为关于a 的不等式组求解．【解答】解：（1）2(0)log (10)0f =+=．当0x >时，0x -<，有122()[1()](1)()f x log x log x f x -=--=-+=-，即()()f x f x -=-．当0x <时，0x ->，有212()[1()](1)()f x log x log x f x -=+-=--=-，即()()f x f x -=-．综上，函数()f x 是R 上的奇函数；证明：（2）函数2log y x =是(0,)+∞上的严格增函数，函数1u x =+在R 上也是严格增函数，故函数2log (1)y x =+在[0，)+∞上是严格增函数．由（1）知，函数()y f x =在R 上为奇函数，由奇函数的单调性可知，12(1)y log x =-在(,0)-∞上也是严格增函数，从而()y f x =在R 上是严格增函数．由120x x +>，得12x x >-，122()()()f x f x f x ∴>-=-，即12()()0f x f x +>；解：（3）由（1）知，()y f x =是R 上的奇函数，故原方程可化为23[()]()04f x af x a -+-=．令()f x t =，则当0x >时，()0t f x =>，于是，原方程有两个不等正根等价于：关于t 的方程23()04t at a -+-=有两个不等的正根．即234()04034a a a a ⎧=-->⎪⎪>⎨⎪⎪->⎩⇔1,3034a a a a ⎧⎪⎪>⎨⎪⎪>⎩或⇔314a <<或3a >．因此，实数a 的取值范围是3(4，1)(3⋃，)+∞．【点评】本题考查函数奇偶性的判定及应用，考查函数的单调性，考查函数零点与方程根的关系，考查化归与转化思想，是中档题．20．已知函数()sin (cos )f x x x x =+．（1）求()3f π的值及函数()f x 的单调增区间；（2）若[12x π∀∈，]2π，不等式()2m f x m <<+恒成立，求实数m 的取值集合．【分析】（1）利用三角函数恒等变换的应用化简函数解析式，代入计算可求()3f π的值，结合正弦函数的单调性列出不等式解出单调区间；（2）求出()f x 在[12π，]2π上的值域，根据题意列出不等式组即可解出m 的范围．【解答】解：（1）211cos2()sin (cos )sin cos sin 2sin(2)223x f x x x x x x x x x π-====-，()sin(2)sin 3333f ππππ∴=⨯-==，令222232x πππππ-+-+，解得51212xππππ-++，Z ∈．()f x ∴的单调递增区间是[12ππ-+，5]12ππ+，Z ∈．（2）[12x π∈，]2π，可得2[36x ππ-∈-，2]3π，∴当232x ππ-=时，()f x 取得最大值1，当236x ππ-=-时，()f x 取得最小值12-． ()2m f x m <<+恒成立，∴1221m m ⎧<-⎪⎨⎪+>⎩，解得112m -<<-．∴实数m 的取值范围是1(2-，1)-．【点评】本题考查了三角函数的恒等变换，三角函数的单调性，三角函数的值域，考查了转化思想和函数思想，属于中档题．21．已知函数()sin()(0f x A x B A ωϕ=++>，0ω>，||)2πϕ<在一个周期内的最高点和最低点分别为(2,1)，(8,3)-．（1）求函数()f x 的表达式；（2）求函数()f x 在区间[0，6]的最大值和最小值；（3）将()y f x =图象上的点的横坐标变为原来的6tπ倍(0)t >，纵坐标不变，再向上平移1个单位得到()y g x =的图象．若函数()y g x =在[0，]π内恰有4个零点，求t 的取值范围．【分析】（1）由最值求出A 、B ，由周期求ω，由五点法作图求出ϕ的值，可得函数的解析式．（2）由题意利用正弦函数的定义域和值域，得出结论．（3）利用函数sin()y A x ωϕ=+的图象变换规律，求得()g x 的解析式，再利用正弦函数的性值，求得t 的取值范围．【解答】解：（1）由题意可得，1A B +=，3A B -+=-，故2A =，1B =-．12822πω⋅=-，6πω∴=．根据五点法作图，262ππϕ⨯+=，6πϕ∴=，()2sin()166f x x ππ=+-．（2）[0x ∈，6]，∴7[]6666x ππππ+∈，故当662x πππ+=时，()f x 取得最大值为211-=；当7666x πππ+=时，()f x 取得最小值为12()122⨯--=-．（3）将()y f x =图象上的点的横坐标变为原来的6t π倍(0)t >，纵坐标不变，可得62sin()12sin()1666t y x tx ππππ=⨯+-=+-的图象；再向上平移1个单位得到()2sin()6y g x tx π==+的图象．当[0x ∈，]π，[66tx ππ+∈，]6t ππ+，若函数()y g x =在[0，]π内恰有4个零点，则456t ππππ+<，求得232966t <．【点评】本题主要考查由函数sin()y A x ωϕ=+的部分图象求解析式，由函数的图象的顶点坐标求出A ，由周期求出ω，由五点法作图求出ϕ的值，函数sin()y A x ωϕ=+的图象变换规律，正弦函数的图象和性质，属于中档题．22．已知函数()4cos sin()1()6f x x x x R π=-+∈，将函数()y f x =的图象向左平移6π个单位，得到函数()y g x =的图象．（1）求()3f π的值；（2）求函数()yg x =的解析式；（3）若0()2x f =0()g x ．【分析】（1）由题意利用三角恒等变换化简()f x 的解析式，可得()3f π的值．（2）由题意利用函数sin()y A x ωϕ=+的图象变换规律，得出结论．（3）由题意求得0sin()6x π-的值，再利用诱导公式、二倍角公式，求得0()g x 的值．【解答】解：（1）函数2()4cos sin()1cos 2cos 12cos22sin(2)66f x x x x x x x x x ππ=-+=-+=-=-，故()2sin 232f ππ==．（2）将函数()2sin(2)6y f x x π==- 的图象向左平移6π个单位，得到函数()2sin(2)6y g x x π==+的图象，（3）若00()2sin()26x f x π==-，则0sin()6x π-= 000()2sin(2)2cos(2)2cos(63g x x x ππ∴=+=-=2002)2[12sin ()]36x x ππ-=⨯-- 32[12]14=-⨯=-．【点评】本题主要考查三角恒等变换，函数sin()y A x ωϕ=+的图象变换规律，属于中档题．。

人教版七年级数学下册期末测试题及复习资料详解共五套

李庄人教版七年级数学下学期末模拟试题（一）一、选择题：(本大题共10个小题，每小题3分，共30分) 1．若m ＞－1，则下列各式中错误的．．．是（） A ．6m ＞－6 B ．－5m ＜－5 C ．1＞0 D ．1－m ＜2 2.下列各式中,正确的是( )16±4 B.±164 C 327- 3 2(4)- 4 3．已知a ＞b ＞0，那么下列不等式组中无解．．的是（） A ． B ． C ． D ．4．一辆汽车在马路上行驶，两次拐弯后，仍在原来的方向上平行行驶，那么两个拐弯的角度可能为（）(A) 先右转50°，后右转40° (B) 先右转50°，后左转40° (C) 先右转50°，后左转130° (D) 先右转50°，后左转50° 5．解为的方程组是（） A. B. C. D.6．如图，在△中，∠500，∠800，平分∠，平分∠，则∠的大小是（） A ．1000 B ．1100 C ．1150 D ．1200PCBA 小刚小军小华(1) (2) (3)7．四条线段的长分别为3，4，5，7，则它们首尾相连可以组成不同的三角形的个数是（） A ．4 B ．3 C ．2 D ．1 8．在各个内角都相等的多边形中，一个外角等于一个内角的12，则这个多边形的边数是（） A ．5 B ．6 C ．7 D ．89．如图，△A 1B 1C 1是由△沿方向平移了长度的一半得到的，若△的面积为20 cm 2，则四边形A 11的面积为（）A ．10 cm 2B ．12 c m 2C ．15 cm 2D ．17 cm 210.课间操时,小华、小军、小刚的位置如图1,小华对小刚说,假如我的位置用(•0,0)表示,小军的位置用(2,1)表示,那么你的位置可以表示成( )A.(5,4)B.(4,5)C.(3,4)D.(4,3)二、填空题：本大题共8个小题，每小题3分，共24分，把答案干脆填在答题卷的横线上． 11.49的平方根是,算术平方根是8的立方根是. 12.不等式59≤3(1)的解集是.13.假如点P(a,2)在第二象限,那么点Q(-3)在.14.如图3所示,在铁路旁边有一李庄,现要建一火车站,•为C 1A 1ABB 1CD了使李庄人乘火车最便利(即间隔最近),请你在铁路旁选一点来建火车站(位置已选好),说明理由.15.从A 沿北偏东60°的方向行驶到B,再从B 沿南偏西20°的方向行驶到C,•则∠度.16.如图∥,∠100°平分∠,则∠.17．给出下列正多边形：① 正三角形；② 正方形；③ 正六边形；④ 正八边形．用上述正多边形中的一种可以辅满地面的是．(将全部答案的序号都填上) 18.若│x 2-25则.三、解答题：本大题共7个小题，共46分，解答题应写出文字说明、证明过程或演算步骤． 19．解不等式组：,并把解集在数轴上表示出来．20．解方程组：2313424()3(2)17x y x y x y ⎧-=⎪⎨⎪--+=⎩21.如图, ∥ , 平分∠,你能确定∠B 及∠C 的数量关系吗?请说明理由。

六年级下册英语试题- 期末测试湘少版(含答案)

2019年湘少版英语六年级下册期末复习测评卷（一）一、选出每组中不同类的一项.( )1. A. took B.have C.saw( )2. A. sun B.Earth C.water( )3. A. tired B.happy C.close( )4. A. spring B.season C.summer( )5. A. English B.Canada C.New Zealand二、根据图片及汉语提示写短语.1．____________（看电影） 2．___________（去购物）3．__________（一块肉） 4．_______________（吃健康的食物）三、用所给单词的适当形式填空.1．I like_____(play) games.2. Peter is_____(tall) than Dick.3. We should _____(do) exercise every day.4. Tom and Tim are______(talk) about the film.5. Anne ______(take) pictures of her party last Sunday.四、单项选择.( )1. Mr Li______ exercise every day.A. doB. didC. does( )2. Listening to music is good ______ us.A. forB. toC.in( )3. Mr Tang is good ______ drawing.A.inB. atC. on( )4.Peter was very______in the film.A. interestB. interestingC. interested( )5. The Earth looks like a _____ in space.A. earB. sunC. ball( )6.I can't do it.It is too_____ .A. easyB. difficultyC. difficult五、判断图片与句子是(√)否(×)相符.( )1. They are going shopping.( )2. He is planting a tree.( )3. There are many stars in the sky.( )4. He took many pictures.( )5. She likes playing the piano.六、给问句选择相应的答语.( )1. How old is Jack?A. I'm 12 years old.B.He is 11 years old.( )2. What did she want to do?A. She wanted to dance.B. She wants to play the piano.( )3. What are we going to do at weekends?A. I'm going to go shopping.B. We are going to see a film.( )4. What does he have for lunch？A. He has vegetables,fruit and chicken.B．He has lunch at 11:30.( )5. Where are you going today?A. I'm going to paint a picture.B. I'm going to the beach.七、连词成句我最棒.1. go the Shall today to we park (?)___________________________________________________________ 2. can home at a We have rest (.)___________________________________________________________ 3.looks space this Our in Earth like (.)___________________________________________________________ 4.can place the Trees beautiful make (.)___________________________________________________________ 5.stand one to Anne on wanted foot (.)___________________________________________________________ 八 .阅读短文 ,选择正确的答案 .Last Sunday,Peter went swimming in a lake. The weather was fine. There were many people by the lake. A little boy was playing by the lake,too. Suddenly,the boy fell into the lake. He was too little to swim. Then a strong man jumped into the lake and swam to that boy. He brought the boy back to the bank (岸边). The boy's parents were very grateful(感激的 ) to the strong man.( )1. When did Peter go swimming in a lake?A. Today.B. Last Sunday.C. Last Saturday.( )2. What was the boy doing at first?A. Crying.B. Playing.C. Singing.( )3. Who jumped into the lake to save(救 ) the boy?A. A strong man.B. The boy's parents.C. Peter.( )4. Can the boy swim?A. Yes.B. No.C. We don't know.( )5. Who were grateful to the strong man?A. The boy and Peter.B. People by the lake.C. The boy's parents.期末复习测评卷（一）一、1．B 2．C 3．C 4．B 5．A二、1．watch a movie2．go shopping3．a piece of meat4．eat healthy food三、1. playing/to play 2.taller 3.do 4．talking 5．took四、1．C 2．A 3．B 4．C 5．C 6．C五、1．√ 2．× 3．× 4．× 5．√六、1．B 2．A 3．B 4．A 5．B七、1. Shall we go to the park today?2. We can have a rest at home.3. Our Earth looks like this in space.4. Trees can make the place beautiful.5. Anne wanted to stand on one foot.八、1．B 2．B 3．A 4．B 5．C金钟一小2018—2019学年度第二学期达标检测（1）六年级英语（湘少版）试题听力部分（30分）一、听录音，判断下列图片与你所听内容是（T）否（F）相符（5分）（）（）（）（）（）二、听录音，选择正确的答案。

七年级生物上册期末考试复习测试题(含答案)1

七年级生物上册期末考试复习测试题（含答案）（范围：第三单元1、2章时间：60分钟满分：100分）一、选择题（本大题共30小题，每小题2分，共60分。

在每小题列出的四个选项中，只有一个选项最符合题意要求）1.下列植物类群都具有输导组织的一组是A.藻类植物、苔藓植物、蕨类植物B.藻类植物、蕨类植物、裸子植物C.苔藓植物、蕨类植物、被子植物D.蕨类植物、裸子植物、被子植物2.以下几种生物在广东省很常见，其中没有根、茎、叶分化的是A.紫菜B.葫芦藓C.肾蕨D.苏铁3.温暖多雨地区的森林中，树干或阴湿的小路上，常常能看到一层毛茸茸的“绿毯”，根据所学知识判断，毛茸茸的“绿毯”主要是A.藻类植物B.苔藓植物C.蕨类植物D.种子植物4.鱼缸长期不换水，缸的内壁上就会长出绿膜。

这些绿膜所属的植物类群是A.藻类植物B.苔藓植物C.蕨类植物D.种子植物5.叶既是吸收水分和无机盐的主要器官又是光合作用的主要场所的植物是A.葫芦藓B.海带C.卷柏D.花生6.小明想收集一些植物的种子用于兴趣小组的研究，以下植物中无法产生种子的是A.苏铁B.无花果C.水绵D.木棉7.下列古诗句中描绘裸子植物的是A.西湖春色归，春水绿于染B.苔痕上阶绿，草色入帘青C.墙角数枝梅，凌寒独自开D.亭亭山上松，瑟瑟谷中风8.藻类、苔藓和蕨类植物都不具有的器官是A.根B.茎C.叶D.花9.浮萍是一种漂浮在水面上的水生植物，叶近圆形，叶背面垂生丝状根，果实近陀螺状。

根据这些特征分析，浮萍属于A.藻类植物B.苔藓植物C.被子植物D.裸子植物10.图3-1-4中圆圈表示各生物的特征，重合部分表示它们之间的共同特征，下列观点正确的是图3-1-4A.F可以表示有果实B.Q可以表示有种子C.E可以表示绿色开花植物D.P可以表示种子中有胚乳11.面粉是由小麦种子磨成的，花生油是从花生种子中榨取出来的。

面粉和花生油分别来自种子中的A.胚芽和子叶B.胚乳和子叶C.胚根和胚轴D.子叶和胚乳12.如图为玉米种子结构示意图，新植物的幼体是A.①②③④B.①②③⑤C.①②③D.③④⑤⑥13.泡在水中的种子不易萌发，主要原因是A.缺少阳光B.缺少空气C.温度太低D.淀粉不溶于水14.“天街小雨润如酥，草色遥看近却无。

人教版七年级语文上册诗歌鉴赏期末复习测试题试题1

人教版七年级语文上册诗歌鉴赏期末复习测试题试题1一、七年级语文上册诗歌鉴赏1．阅读下面的诗歌，回答问题。

次北固山下（唐）王湾客路青山外，行舟绿水前。

潮平两岸阔，风正一帆悬。

海日生残夜，江春入旧年。

乡书何处达？归雁洛阳边。

（1）本诗表达了诗人________的情感。

（2）明代胡应麟在《诗薮·内编》里说，本诗颈联“形容景物，妙绝千古”。

你能从炼字上说说它妙在哪里吗？2．阅读下面的古诗，回答问题。

东栏梨花苏轼梨花淡白柳深青，柳絮飞时花满城。

惆怅东栏一株雪①，人生看得几清明。

【注释】①雪：指梨花（1）除了以“雪”比喻梨花，诗人还用了________、________词语来描写梨花。

（2）诗人借雪白的梨花抒发了________的感慨。

3．阅读（十一月四日风雨大作》，按要求回答问题。

十一月四日风雨大作陆游僵卧孤村不自哀，尚思为国戌轮台。

夜阑卧听风吹雨，铁马冰河入梦来。

（1）诗中僵与孤，写出了诗人当时怎样的处境？它们在诗中有什么作用？（2）本诗表达了作者怎样的愿望？4．阅读刘禹锡《秋词》，完成问题秋词刘禹锡自古逢秋悲寂寥，我言秋日胜春朝。

晴空一鹤排云上，便引诗情到碧霄。

注：此诗是作者被贬朗州时的作品。

（1）前人写诗填词讲究炼字，谈谈诗歌第三句“晴空一鹤排云上”中“排”字的表达作用。

（2）全诗表达了诗人怎样的人生态度?你认为诗人眼中秋日胜春朝的理由是什么?5．诗歌鉴赏（甲）西洲曲南北朝乐府民歌海水梦悠悠，君愁我亦愁。

南风知我意，吹梦到西洲。

（乙）闻王昌龄左迁龙标遥有此寄唐·李白杨花落尽子规啼，闻到龙标过五溪。

我寄愁心与明月，随君直到夜郎西。

（1）（甲）（乙）两首诗所写的季节分别是________、________。

（2）请结合知识卡片，分析两首诗是如何表达诗人的离愁别绪。

6．阅读下面这首古诗，完成后边题目。

十一月四日风雨大作僵卧孤村不自哀，尚思为国戍轮台。

夜阑卧听风吹雨，铁马冰河入梦来。

（1）这首诗的作者是南宋时期伟大的爱国主义诗人________。

2021年高一上学期期末复习测试(一)物理试题含答案

2021年高一上学期期末复习测试（一）物理试题含答案一、选择题（本题共10小题，每小题4分，共40分．1-8题为单选，9、10题为不定项，少选得2分，错选或多选不得分。

）1．以下情景中，带下划线的物体可看成质点的是 ( ) A．裁判员在跳水比赛中给跳水运动员评分B．在国际大赛中，乒乓球运动员王浩准备接对手发出的旋转球C．研究“天宫一号”飞行姿态D．计算火车从大杨树到北京的运行时间2.下列说法中表示时刻的是（）A．停车8分B．第3S末C．第3S内D．前3s3.下列物理量中属于标量的是 ( )A．速率B．速度C．位移D．加速度4.下列说法错误的是（）A．速率是瞬时速度的大小B．曲线运动中位移大小小于路程C．在800m跑比赛中，不同跑道的运动员跑完全程的位移和路程都相同D．汽车收费标准1.20元/公里中的公里说的是路程5.以下说法不可能存在的是（）A．物体运动的加速度等于0，而速度不等于0B．物体加速度方向向东，而速度方向向西C．物体运动的速度等于0，而加速度不等于0D．速度变化率很大，加速度却很小6.一汽车在平直的公路上以做匀速直线运动，刹车后，汽车以大小为的加速度做匀减速直线运动，有关说法正确的是（）A. 刹车后经8s汽车通过的位移为32mB. 刹车后经6s汽车通过的速度为4m/sC.刹车到静止所经过的时间为5sD.刹车过程中的平均速度为15m/s7.一辆汽车向南行驶了300m，接着又向东行驶了400m，汽车行驶的位移大小为（）A.700mB.500mC.300mD.400m8.在忽略空气阻力的情况下，让一轻一重两石块从同一高度处同时自由下落，则（）A.下落过程两者加速度相同B．重的石块下落得快、轻的石块下落得慢C．它们在前1 s内、前2 s内、前3s内的位移之比为1:2:3D．从赤道到两极他们下落的加速度大小不变9.下列图像中描述的属于匀速直线运动的是（）10. 一个质点，初速度大小为8 m/s ，经过2 s ，速度大小变为10m/s ，则物体在这段时间内的平均加速度可能为（） A ．6 m/s 2 B ．9m/s 2 C. 2m/s 2 D. 1m/s 2二、填空题（每空2分，共24分）11.火车机车原来的速度是36km/h,在一段下坡路上加速度为0.2 m/s 2。

七年级语文第一学期期末考试复习测试题(含答案)

七年级语文第一学期期末考试复习测试题（含答案）（全卷满分120分，考试时间150分）第Ⅰ卷（选择题，共33分）本卷共11小题，每小题3分。

每小题都给出A、B、C、D四个选项，其中只有一项正确，请考生用2B铅笔在答题卡上将选定的答案选项涂黑。

一、（15分）阅读下面诗歌，完成第1题观沧海曹操东临碣石，以观沧海。

水何澹澹，山岛竦峙。

树木丛生，百草丰茂。

秋风萧瑟，洪波涌起。

日月之行，若出其中；星汉灿烂，若出其里。

幸甚至哉，歌以咏志。

1.下面对这首诗的理解，不恰当的一项是（3分）A.曹操字孟德，东汉末期的政治家、军事家和诗人。

这首诗是他在征战乌桓胜利的归途中，登上碣石山，面对波涛汹涌的大海，看到如此宏伟的景象而写下的。

B.海面浩淼，水波澹澹，映入眼帘的是岛上的树木一丛丛生长着，百草丰盛繁茂；在萧瑟的秋风中，大海汹涌起伏；太阳和月亮不停运转，都好像是大海吐纳的；天上的云河，星光灿烂，它们都好像出自于大海广阔的胸间。

C. 这首诗描写海水荡漾，山岛竦峙，是动态描写；描写百草树木丛生，是静态描写。

显示了大海的辽阔和宏伟气象。

D.这首诗抒发了诗人宏伟的政治抱负和建功立业的雄心壮志，对前途充满信心的乐观气度和精神。

阅读下面两篇文言文，完成2—4题【甲】诫子书夫君子之行，静以修身，俭以养德。

非淡泊无以明志，非宁静无以致远。

夫学须静也，才须学也，非学无以广才，非志无以成学。

淫慢则不能励精，险躁则不能治性。

年与时驰，意与日去，遂成枯落，多不接世，悲守穷庐，将复何及！【乙】《论语十二章》节选子曰：“学而时习之，不亦说乎？有朋自远方来，不亦乐乎？人不知而不愠，不亦君子乎？”《学而》曾子曰：“吾日三省吾身：为人谋而不忠乎？与朋友交而不信乎？传不习乎？”子曰：“吾十有五而志于学，三十而立，四十而不惑，五十而知天命，六十而耳顺，七十而从心所欲，不逾矩。

”子曰：“温故而知新，可以为师矣。

”子曰：“学而不思则罔，思而不学则殆。

”2.下面加点词的解释，不正确的一项是（3分）A. 非淡泊．．无以明志。

高一数学上册期末复习题及详细解答

高一数学期末复习测试题一姓名: 班级:一、选择题: 本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、若),1,3(),2,1(-==b a 则=-b a 2 （）A 、 )3,5(B 、 )1,5(C 、 )3,1(-D 、 )3,5(-- 2．在单位圆中，面积为1的扇形所对的圆心角为（）弧度。

A 、 1B 、 2C 、3 D. 43、如图是函数f (x)sin(x )=+ϕ一个周期内的图像，则ϕ可能等于（） A 、 56π B 、C 、 6π- D 、6π 4．化简结果是（）A B 、 C 、-5、已知函数f (x)sin(x )cos(x )=+ϕ++ϕ为奇函数，则ϕ的一个取值为（） A 、0 B 、2πC 、4π- D 、π6.把函数742++=x x y 的图像按向量a 经过一次平移以后得到2x y =的图像，则a 是A 、 )3,2(-B 、 )3,2(-C 、 )3,2(--D 、 )3,2(7.设),6,2(),3,4(21--P P 且P 在21P P 的延长线上，=则点P 的坐标是A 、)15,8(-B 、 (0,3)C 、)415,21(- D 、)23,1( 8.函数44f (x)sin(x)sin(x)ππ=+-是（）A 、周期为2π的奇函数B 、周期为2π的偶函数C 、周期为π的奇函数D 、周期为π的偶函数 9. 若为则ABC AB BC AB ∆=+•,02（）A 、直角三角形B 、钝角三角形C 、锐角三角形D 、等腰直角三角形 10.稳定房价是我国今年实施宏观调控的重点，国家最近出台的一系列政策已对各地的房地产市场产生了影响，温州市某房地产介绍所对本市一楼群在今年的房价作了统计与预测：发现每个季度的平均单价y （每平方面积的价格，单位为元）与第x 季度之间近似满足：y 500sin(x )9500(0)=ω+ϕ+ω>，已知第一、二季度平均单价如右表所示：则此楼群在第三季度的平均单价大约是（）元A 、 10000B 、 9500C 、9000D 、8500二、填空题：本大题共6小题，每小题4分，满分24分.把答案填在题中横线上. 11、已知113a (,2sin ),b (cos ,),a 322=α=α且∥b ，则锐角α的值为； 12、m,n a 2m a n,|a |=⊥=设是两个单位向量，向量-n ，则； 13、函数y cos 2x 4cos x,x [,]32ππ=-∈-的值域是； 14、在三角形ABC 中，设a =AB ，b =AC ，点D 在线段BC 上，且DC BD 3=，则AD 用b ,a 表示为；15、已知偶函数f (x)2sin(x )(0,0)=ω+ϕω><ϕ<π的最小正周期是π，则f(x)的单调递减区间为； 16、下列命题：①若c a c b b a =⋅=⋅，则 ②若a 与b 是共线向量，b 与c 是共线向量，则a 与c 是共线向量：-=+，则0=⋅b a ④若a 与b 是单位向量，则1=⋅b a 其中真命题的序号为。

人教版小学四年级下册数学期末复习测试练习试题试卷含答案

期末复习试卷一、填空题。

（20分）1、用“四舍五入法”求出一个数的近似数是7万,这个数最大是（_____）,最小是（____）。

2、（____）减去176得239；185加上（____），得数是530．3、1块长方形菜园占地面积是100平方米，（________）块这样的菜园占地面积是1公顷。

4、4.96×2.4的积精确到十分位约是()，精确到百分位约是()。

5、有一个数，十位和百分位都是8，个位和十分位都是0，这个数写作（_____），读作（_______）。

6、9.0968保留一位小数是（____）,保留两位小数是（____）,保留整数是（____）。

7、若三角形的一个角是104°，另两个角是（_____）°和（____）°时，它是等腰三角形。

若一个等腰三角形的两条边长分别是7cm和14cm，那么它的周长是（_____）cm。

8、用简便方法计算376＋592＋24，要先算（_____），这是根据（_____）律。

9、被除数乘6，要使商不变，除数应___，除数除以9，要使商不变，被除数应___．10、一个等腰三角形两条边长分别是2cm和5cm，则三角形的周长是（____）cm。

二、选择题（把正确答案前面的序号填在（）里）（10分）1、小明画了两条直线，这两条直线都和同一条直线垂直，这两条直线（）A．互相平行B．互相垂直C．相交2、一批本子分发给六（1）班的学生，平均每人分到12本，若只分给女生，平均每人分到20本，若只分给男生，平均每人分到（）本。

A．32B．28C．30D．353、鸡兔同笼，共有30个头，94只脚，则笼中兔有()只。

A．13B．17C．124、如图表示两个游泳池的长、宽以及池内的人数，比较两池的拥挤程度，结果是（）A．甲池比较拥挤B．乙池比较拥挤C．比不出谁拥挤5、边长是300米的正方形花圃，占地面积是9（）。

A．平方米B．公顷C．平方千米三、判断题：对的在（）里画“√”，错的画“×”。

人教版数学五年级上册期末真题试卷1(含答案)

人教版五上期末复习测试卷（一）2.（1）（2）根据，直接写出下面各式的得数．3.制作一套校服需要布料，现在制衣厂还有同样的布料，则可以制作套这样的校服．4.依据下图列出的方程是．5.图书角有本书，借出本，还剩下本，当时，还剩本书．6.街道上有大、小两种混凝土圆球（如下图），这些圆球是为了防止车辆停泊而设置的，每一个圆球都被牢固的固定在地面上的某一点，相邻两个圆球固定点之间相距米，在相邻两个大圆球之间放置了个小圆球，相邻两个大圆球固定点之间的距离是米．7.王叔叔骑车到离家千米的郊外游玩，他骑车的速度是千米/时，估一估，小时他到达目的地．（填“能”或“不能”）．8.下图是由两个等腰直角三角形和一个正方形拼成的一个大三角形，正方形的边长是，大三角形的面积是．1.（1）（2）在横线填上“”、””或“”．9.下面是某楼房一层到二层的楼梯示意图．每级台阶高米．总长度米总高度米10.约翰和父母来中国旅游，花了元人民币买了一个纪念品，折合成美元是美元．美元换人民币元美元换港币元港元换人民币元日元换人民币元11.1.2.3.4.5.判断对错．一个数除以，商一定大于这个数．（）两个面积相等的三角形一定可以拼成一个平行四边形．（）的倍比少，用方程表示是．（）将一个平行四边形框架拉成长方形，它的周长不变，面积变大．（）两个完全一样的三角形，不可能拼成一个正方形．（）12.A.个一B.个C.个D.个观察右边除法算式，方框内的数表示（）．13.A.B.C.D.将、、、按从大到小的顺序排列，排在第二位的是（）．14.平行四边形如图所示，计算其面积的正确算式是（）．A. B. C. D.15.A.黄球B.篮球C.红球D.白球在一个纸箱里装有个红球，个篮球，个黄球和个白球，它们的形状、大小、质量完全相同．欢欢从箱子中任意摸出一个球，拿到（）的可能性最大．16.A. B. C. D.如下图所示，不规则图形的面积大约是（）平方厘米．（每个小正方形的面积是平方厘米）．17.（1）（2）笔算．18.（1）（2）计算下面各题．．．19.（1）（2）（3）解方程．20.按要求画图并填空．（1）（2）在右图方格纸中（每小格代表平方厘米），先画一个面积是平方厘米的平行四边形，再用数对表示格顶点的位置分别是：（，）、（，）、（，）、（，）．请你再画出与平行四边形面积相等的三角形，这个三角形的底是厘米，高是厘米．21.计算下面图形中阴影部分的面积．厘米厘米厘米厘米22.研究表明，体育运动可以适当提高人体的肺活量，一名游泳运动员的肺活量可以达到普通小学生肺活量的倍．23.下面是张阿姨去便利超市的购物小票，不小心撕掉了一部分．24.假日里同学们一起去游乐园玩儿，儿童票每张元，元最多能买几张儿童票呢？25.少年宫合唱团共有学生人，其中男生人数是女生人数的倍，合唱团中男生、女生各有多少人？（用方程解答）26.A 套餐 78元/月包含：免费通话80分钟、免费使用8G 上网流量．B 套餐 128元/月包含：免费通话150分钟、免费使用20G 上网流量．两种套餐收费补充说明通话时间超出套餐部分按0.20元/分钟收费．上网流量超出套餐部分按5元/G 进行收费．免收短信费．（1）（2）电信公司推出两种手机套餐服务．李叔叔每月的通话时间大约是分钟，使用上网流量，他选择哪种套餐比较便宜？每月大约花费多少元？王阿姨购买了套餐，她月份共缴费元，其中使用上网流量，王阿姨这个月的通话时间是多少分钟？27.甲乙两车分别从、两地同时出发相向而行，乙车每小时行千米，乙车速度是甲车速度的倍，经过小时相遇．、两地相距多少千米？28.（1）（2）李大爷用米长的篱笆，在靠墙的地方围了一块梯形菜地（如图）．米梯形菜地的面积是多少平方米?如果用这些篱笆靠墙改围成一块长为米的长方形菜地，菜地的面积会增加多少平方米？人教版五上期末复习测试卷（一）(详解)2.（1）（2）（1）（2）【答案】（1）（2）【解析】【踩分点】根据，直接写出下面各式的得数．因为相比于小数点向左移动了位，相比于小数点也向左移动了位，所以的小数点要向左移动两位，即﹒由，得，被除数小数点向左移动位，除数小数点向左移动位，则商的小数点向右移动位，最终结果为．3.【答案】制作一套校服需要布料，现在制衣厂还有同样的布料，则可以制作套这样的校服．1.（1）（2）（1）（2）【答案】（1）（2）【解析】【踩分点】在横线填上“”、””或“”．一个数乘一个小于的数，积小于这个数本身，一个数除以一个小于的数，商大于这个数本身．【解析】【踩分点】制作一套校服需要米的布料，现在制衣厂有米同样的布料，那么可以制作套这样的校服．但是需要采用去尾法的方法舍掉整数后面的数字．因为剩余的布料无法再做出一套这样的校服，所以最多可以做套这样的校服．4.【答案】【解析】【踩分点】依据下图列出的方程是．从图中可知，左右两边的重量是相等的，所以左边三个物体的总重量为千克，故列方程为：，即，故答案为：．5.【答案】【解析】【踩分点】图书角有本书，借出本，还剩下本，当时，还剩本书．;剩下的本数（本），把代入算式为：（本）．6.【答案】【解析】街道上有大、小两种混凝土圆球（如下图），这些圆球是为了防止车辆停泊而设置的，每一个圆球都被牢固的固定在地面上的某一点，相邻两个圆球固定点之间相距米，在相邻两个大圆球之间放置了个小圆球，相邻两个大圆球固定点之间的距离是米．因为两个大圆球之间放了个小圆球，所以两个大圆球之间的距离就是个米，（米）．【踩分点】7.【答案】【解析】【踩分点】王叔叔骑车到离家千米的郊外游玩，他骑车的速度是千米/时，估一估，小时他到达目的地．（填“能”或“不能”）．不能（千米），．8.【答案】【解析】【踩分点】下图是由两个等腰直角三角形和一个正方形拼成的一个大三角形，正方形的边长是，大三角形的面积是．因为正方形的边长是，所以等腰直角三角形的两个直角边都是，所以大三角形的面积．9.【答案】【解析】【踩分点】下面是某楼房一层到二层的楼梯示意图．每级台阶高米．总长度米总高度米（米）．10.约翰和父母来中国旅游，花了元人民币买了一个纪念品，折合成美元是美元．【答案】【解析】【踩分点】美元换人民币元美元换港币元港元换人民币元日元换人民币元（美元）．11.1.2.3.4.5.【答案】1 ：2 ：3 ：4 ：5 ：【解析】判断对错．一个数除以，商一定大于这个数．（）两个面积相等的三角形一定可以拼成一个平行四边形．（）的倍比少，用方程表示是．（）将一个平行四边形框架拉成长方形，它的周长不变，面积变大．（）两个完全一样的三角形，不可能拼成一个正方形．（）×××✓×零除以任何非零的数都为零，所以一个数除以，商一定大于这个数的说法是错误的．故答案为：错误．例如：底边长为，高为和底边长为，高为的两个三角形，面积相等，但是不能拼成平行四边形．面积相等的两个三角形一定能拼成平行四边形，说法错误．故答案为：错误．的倍比少，即，说法错误．故答案为：错误．平行四边形活动框架拉成长方形之后，每条边的长度不变，所以周长不变；平行四边形活动框架拉成长方形之后，长方形的宽大于平行四边形的高，长方形的长等于原来平行四边形的底，所以长方形的面积比平行四边形的面积大，说法正确．故答案为：正确．要拼成一个长方形，需要两个完全一样的等腰直角三角形，以斜边为公共边来拼．如图：故：原题说法错误．12.A.个一B.个C.个D.个【答案】【解析】观察右边除法算式，方框内的数表示（）．C 方框中的表示，，所以方框中的表示个．故选．13.A.B.C.D.【答案】【解析】将、、、按从大到小的顺序排列，排在第二位的是（）．D 14.A.B. C. D.【答案】【解析】平行四边形如图所示，计算其面积的正确算式是（）．B 解：或，答：这个平行四边形的面积是．15.A.黄球B.篮球C.红球D.白球在一个纸箱里装有个红球，个篮球，个黄球和个白球，它们的形状、大小、质量完全相同．欢欢从箱子中任意摸出一个球，拿到（）的可能性最大．【答案】【解析】C红球的个数最多，可能性最大．16.A.B. C. D.【答案】【解析】如下图所示，不规则图形的面积大约是（）平方厘米．（每个小正方形的面积是平方厘米）．C数图中所占的格子数有个大格子和个半格子，所以面积为：（平方厘米）．故选．17.（1）（2）（1）（2）【答案】（1）（2）【解析】笔算．．3.5×2.7414024579.590．【踩分点】4.22·510·5.150518.（1）（2）（1）（2）【答案】（1）（2）【解析】【踩分点】计算下面各题．．．．．．．19.（1）（2）（3）（1）（2）【答案】解方程．．．（3）（1）（2）（3）【解析】【踩分点】．，，．，，，．，，，，．20.（1）（2）（1）（2）【答案】按要求画图并填空．在右图方格纸中（每小格代表平方厘米），先画一个面积是平方厘米的平行四边形，再用数对表示格顶点的位置分别是：（，）、（，）、（，）、（，）．请你再画出与平行四边形面积相等的三角形，这个三角形的底是厘米，高是厘米．; ; ; ;; ; ;;（1）（2）【解析】【踩分点】方格纸的边长为厘米，；（答案正确即可，图正确即可），三角形的底为厘米，高是厘米；或底为厘米，高是厘米．（选其中一个填入即可，图正确即可）21.【答案】【解析】【踩分点】计算下面图形中阴影部分的面积．厘米厘米厘米厘米．小正方形里阴影部分三角形的面积是，大正方形里三角形的面积是，．22.研究表明，体育运动可以适当提高人体的肺活量，一名游泳运动员的肺活量可以达到普通小学生肺活量的倍．【答案】【解析】【踩分点】毫升．（毫升）．23.【答案】【解析】【踩分点】下面是张阿姨去便利超市的购物小票，不小心撕掉了一部分．元．（元），（元）．24.【答案】【解析】【踩分点】假日里同学们一起去游乐园玩儿，儿童票每张元，元最多能买几张儿童票呢？张．（张）（元）．答：元最多购买张儿童票．25.【答案】【解析】少年宫合唱团共有学生人，其中男生人数是女生人数的倍，合唱团中男生、女生各有多少人？（用方程解答）男生人，女生人．设：合唱团女生人数为，则男生人数为人，（人）．【踩分点】26.A 套餐 78元/月包含：免费通话80分钟、免费使用8G 上网流量．B 套餐 128元/月包含：免费通话150分钟、免费使用20G 上网流量．两种套餐收费补充说明通话时间超出套餐部分按0.20元/分钟收费．上网流量超出套餐部分按5元/G 进行收费．免收短信费．（1）（2）（1）（2）【答案】（1）（2）【解析】【踩分点】电信公司推出两种手机套餐服务．李叔叔每月的通话时间大约是分钟，使用上网流量，他选择哪种套餐比较便宜？每月大约花费多少元？王阿姨购买了套餐，她月份共缴费元，其中使用上网流量，王阿姨这个月的通话时间是多少分钟？使用套餐便宜，元．分钟．如果使用套餐：，（G ），（元），（元），如果使用套餐，，需要花费元，，使用套餐便宜．，（元），（分），（分）．27.【答案】【解析】【踩分点】甲乙两车分别从、两地同时出发相向而行，乙车每小时行千米，乙车速度是甲车速度的倍，经过小时相遇．、两地相距多少千米？千米．（千米）．答：、两地相距千米．28.李大爷用米长的篱笆，在靠墙的地方围了一块梯形菜地（如图）．（1）（2）（1）（2）【答案】（1）（2）【解析】【踩分点】米梯形菜地的面积是多少平方米?如果用这些篱笆靠墙改围成一块长为米的长方形菜地，菜地的面积会增加多少平方米？梯形菜地的面积平方米．菜地的面积会增加平方米．根据题意，可用篱笆的长减去梯形的高米计算出梯形上底与下底的和，然后再利用梯形的面积（上底下底）高进行计算即可得到答案．（平方米），答：梯形菜地的面积平方米．已知篱笆的长，减去长方形菜地的长米，就是长方形的两个宽，再除以即可得到长方形菜地的宽，利用长方形的面积长宽即可解决．长方形菜地的宽为：（米），（平方米）；答：菜地的面积会增加平方米．。

专题11.1 期末综合复习测试(专项练习1)-2020-2021学年七年级数学下(华东师大版)

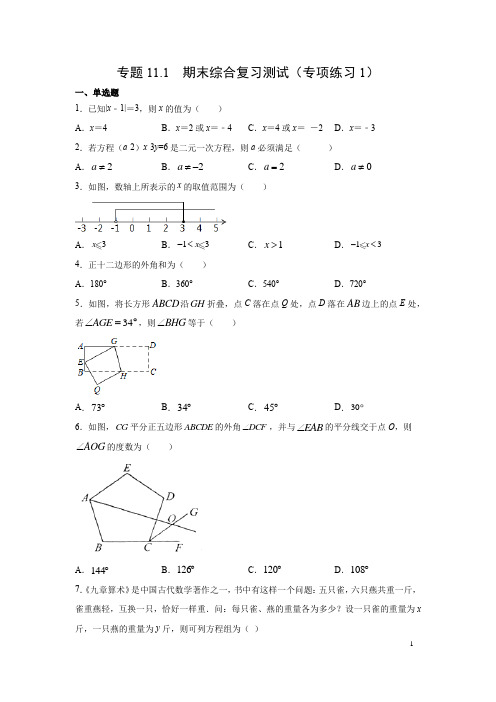
专题11.1 期末综合复习测试（专项练习1）一、单选题1．已知|x ﹣1|＝3，则x 的值为（）A ．x ＝4B ．x ＝2或x ＝﹣4C ．x ＝4或x ＝－2D ．x ＝﹣3 2．若方程（a -2）x -3y =6是二元一次方程，则a 必须满足（）A ．2a ≠B ．2a ≠-C ．2a =D ．0a ≠ 3．如图，数轴上所表示的x 的取值范围为（）A ．3xB ．13x -<C ．1x >D ．13x -< 4．正十二边形的外角和为（）A ．180°B ．360°C ．540°D ．720° 5．如图，将长方形ABCD 沿GH 折叠，点C 落在点Q 处，点D 落在AB 边上的点E 处，若34AGE ∠=︒，则BHG ∠等于（）A ．73︒B ．34︒C ．45︒D ．30 6．如图，CG 平分正五边形ABCDE 的外角DCF ∠，并与EAB ∠的平分线交于点O ，则AOG ∠的度数为（）A ．144︒B ．126︒C ．120︒D ．108︒ 7．《九章算术》是中国古代数学著作之一，书中有这样一个问题：五只雀，六只燕共重一斤，雀重燕轻，互换一只，恰好一样重．问：每只雀、燕的重量各为多少？设一只雀的重量为x 斤，一只燕的重量为y 斤，则可列方程组为（）A．56156x yx y y x+=⎧⎨-=-⎩B．65156x yx y y x+=⎧⎨+=+⎩C．56145x yx y y x+=⎧⎨+=+⎩D．65145x yx y y x+=⎧⎨-=-⎩8．解方程21(6)2(6)33x x-=--时，最简便的方法是先（）A．去分母B．去括号C．移项D．化分数为小数9．如图，在Rt△ACB中，△BAC＝90°，AD△BC，垂足为D，△ABD与△ADB’关于直线AD 对称，点B的对称点是点B’，若△B’AC＝14°，则△B的度数为（）A．38°B．48°C．50°D．52°10．如图，直角三角形ABC的顶点A在直线m上，分别度量：△△1，△2，△C；△△2，△3，△B；△△3，△4，△C；△△1，△2，△3，可判断直线m与直线n是否平行的是（）A．△B．△C．△D．△二、填空题11．如图是一个由两个相同的大正方形（甲），一个小正方形（乙）和两个相同的直角三角形（丙）无缝拼接而成的六边形，已知这个六边形的面积为272cm，则图中阴影部分面积为________2cm．12．古代一歌谣：栖树一群鸦，鸦树不知数：三个坐一棵，五个地上落；五个坐一棵，闲了一棵树．请你动脑筋，鸦树各几何？若设乌鸦有x 只，树有y 棵，由题意可列方程组________． 13．若不等式组531x x x m+<-⎧⎨>⎩的解集是3x >，则m 的取值范围是_________．14．如图，将分别含有30°、45°角的一副三角板重叠，使直角顶点重合，若两斜边相交构成的一个角为60°，则图中角α的度数为_____度．15．如图，将直角三角形ABC 沿BC 方向平移3.5cm 得到三角形DEF ．如果6cm 2cm AB DH ==，，那么图中阴影部分的面积为__________2cm ．16．如图，在ABC ∆中，已知点D 、E 、F 分别为BC 、AD 、CE 的中点，且21ABC S cm ∆=，则BEF S ∆=______2cm .17．如图，在ABC ∆中，EF BC ∥，ACG ∠是ABC ∆的外角，BAC ∠的平分线交BC 于点D ，记ADC α∠=，ACG β∠=，AEF γ∠=，则：α、β、γ三者间的数量关系式是______.18．若|x+y ﹣7|+（3x+y ﹣17）2=0，则x ﹣2y=________ ．19．如图，在△ABC 中，△ACB =90°，△B =30°，CD 为AB 边上的高，E 是AB 上一点，且CE =BE .（1）写出图中所有的等腰三角形：______________________________（2）写出图中所有的等边三角形：______________________________（3）若DE =2cm ，则AB =______cm ,AC =______cm .20．将长为2，宽为a 的长方形纸片（1＜a ＜2）如图那样折一下，剪下一个边长等于长方形的宽度的正方形（称为第一次操作）；再把剩下的长方形如图那样折一下，剪下一个边长等于此时长方形宽度的正方形（称为第二次操作）；如此反复操作下去．若第3次操作后，剩下的长方形恰好是正方形，则a 的值为_____．21．钱塘江汛期即将来临，防汛指挥部在一危险地带两岸各安置了一探照灯，便于夜间查看江水及两岸河堤的情况．如图，灯A 射线自AM 顺时针旋转至AN 便立即回转，灯B 射线自BP 顺时针旋转至BQ 便立即回转，两灯不停交叉照射巡视．若灯A 转动的速度是a ︒/秒，灯B 转动的速度是b ︒/秒，且,a b 满足2|3|(4)0a b a b -++-=．假定这一带长江两岸河堤是平行的，即//PQ MN ，且45BAN ∠=︒．（1）2+a b =_____．（2）如图，两灯同时转动，在灯A 射线到达AN 之前，若射出的光束交于点C ，过C 作CD AC ⊥交PQ 于点D ，则在转动过程中，BAC ∠与BCD ∠的数量关系_________． 22．如图，A B C D E ∠+∠+∠+∠+∠=________° ．23．如图，在钝角ABC 中，60,2,6A AB AC ︒∠===，点M 是ABC 内一动点，则点M 到ABC 的三个顶点的距离之和的最小值是_____．三、解答题24．（1）求二元一次方程3423x y +=的正整数解；（2）已知m 是正整数，且方程组210320mx y x y +=⎧⎨-=⎩有整数解（x y ，均为整数）求m 的值．25．防疫期间，某公司购买A B 、两种不同品牌的免洗洗手液，若购买A 种10件，B 种5件，共需130元；若购A 种5件，B 种10件，共需140元．（1）A B 、两种洗手液每件各多少元？（2）若购买A B 、两种洗手液共100件，且总费用不超过900元，则A 种洗手液至少需要购买多少件？26．（1）如图（1），DE∥AB ，求证：三角形ABC 的三个内角（即A ∠、B 、ACB ∠）之和等于180︒；（2）如图（2），求证：AGF AEF F ∠=∠+∠；（3）如图（3），//AB CD ，119CDE ∠=︒，GF 交DEB ∠的平分线EF 于点F ，150AGF ∠=︒，求F ∠．27．如图，D ，E 分别是△ABC 的边AB ，AC 上的点，把△ADE 沿DE 折叠，使点A 落在四边形BCED 所在的平面上，点A 的对应点为A '，已知△B=80°，△C=70°．（1）求△A 的度数；（2）在图△，图△，图△中，写出△1，△2的数量关系，并选择一种情况说明理由．28．如图△，已知线段AB ，CD 相交于点O ，连接AD ，CB ，我们把形如图△的图形称之为“8字形”．如图△，在图△的条件下，△DAB 和△BCD 的角平分线AP 和CP 相交于点P ，并且与CD，AB分别相交于点M，N，试解答下列问题：(1)在图△中，请直接写出△A，△B，△C，△D之间的数量关系；(2)在图△中，若△D＝40°，△B＝36°，试求△P的度数；(3)如果图△中△D和△B为任意角时，其他条件不变，试问△P与△D，△B之间存在着怎样的数量关系(直接写出结论即可)．参考答案1．C【分析】根据绝对值的意义求解．解：△|x﹣1|＝3，△x﹣1＝±3，解得：x＝4或x＝－2故选：C．【点拨】本题考查绝对值的意义及解一元一次方程，理解概念正确计算是解题关键．2．A【分析】根据等式中含有两个未知数，且未知数的次数是一次的方程是二元一次方程，可得答案．解：方程（a-2）x-3y=6是二元一次方程，△a-2≠0，△a≠2，故选：A．【点拨】本题考查了二元一次方程，注意未知数的系数不能为0．3．B【分析】若边界点含于解集为实心点，不含于解集即为空心点，根据数轴确定出x的范围即可．解：根据数轴得：x＞-1，x≤3，△x的取值范围为：-1＜x≤3，故选：B．【点拨】此题考查了在数轴上表示不等式的解集，熟练掌握运算法则是解本题的关键．4．B【分析】根据多边形的外角和定理求解．解：正十二边形的外角和的度数为360°．故选：B．【点拨】本题考查多边形的外角和，熟练掌握多边形外角和定理是解题关键．5．A【分析】由折叠可得，1732DGH EGH DGE ∠=∠=∠=︒，再根据//AD BC ，即可得到73BHG DGH ∠=∠=︒．解：34AGE ∠=︒，146DGE ∴∠=︒，由折叠可得，1732DGH EGH DGE ∠=∠=∠=︒， //AD BC ，73BHG DGH ∴∠=∠=︒．故选：A ．【点拨】本题主要考查了平行线的性质，解题时注意：两直线平行，内错角相等． 6．B【分析】根据正五边形的性质分别解得正五边形的每个内角、每个外角的度数，结合角平分线的性质得到36DCG ∠=︒，54OAB ∠=︒，接着由四边形的内角和为360°解得54AOC ∠=︒，最后由邻补角定义解题即可．解：CG 平分正五边形ABCDE 的外角DCF ∠，DCG GCF ∴∠=∠ AO 平分EAB ∠，EAO OAB ∴∠=∠，正五边形ABCDE 中，(52)180360108,7255ABC DCF -⨯︒︒∴∠==︒∠==︒ 11723622DCG DCF ∴∠=∠=⨯︒=︒，111085422OAB EAB ∠=∠=⨯︒=︒ 5410810836306OAB ABC BCD DCG ∴∠+∠+∠+∠=︒+︒+︒+︒=︒36030654AOC ∴∠=︒-︒=︒18054126AOG ∴∠=︒-︒=︒，故选：B ．【点拨】本题考查正多边形的内角和与外角和，涉及角平分线的性质等知识，是重要考点，难度较易，掌握相关知识是解题关键．7．C【分析】根据题意，可以列出相应的方程组，从而可以解答本题．解：由题意可得：56145x y x y y x+=⎧⎨+=+⎩，故选：C ．【点拨】本题考查由实际问题抽象出二元一次方程组，解答本题的关键是明确题意，列出相应的方程组．8．C【分析】由于x -6的系数分母相同，所以可以把（x -6）看作一个整体，先移项，再合并（x -6）项．解：由方程的形式可得最简便的方法是先移项，故选C ．【点拨】本题考查的是解一元一次方程，熟知解一元一次方程的一般步骤是解答此题的关键．9．D【分析】由对称的性质得=BAD B AD '∠∠，根据△BAC ＝90°可得38BAD ∠=︒，再根据直角三角形两锐角关系求解即可．解：△△ABD 与△ADB’关于直线AD 对称，△=BAD B AD '∠∠△△BAC ＝90°，△B’AC ＝14°△90BAD B AD B AC ∠+∠+'∠='︒△38BAD ∠=︒△903852B ∠=︒-︒=︒故选D ．【点拨】本题考查了轴对称的性质以及直角三角形两锐角关系，掌握轴对称的性质是本题的关键．10．B【分析】根据平行线的性质、以及三角形外角的性质依次判断即可．解：A ．度量：△△1，△2，△C ，不能判断直线m 与直线n 是否平行，不合题意； B ．度量：△△2，△3，△B ，可得△4的度数，结合△2的度数，即可判断直线m 与直线n 是否平行，符合题意；C．度量：△△3，△4，△C不能判断直线m与直线n是否平行，不合题意；D．度量：△△1，△2，△3，不能判断直线m与直线n是否平行，不合题意；故选：B．【点拨】本题主要考查了平行线的判定，三角形外角的性质．熟练掌握平行线的判定定理，并能正确识图是解题关键．11．24【分析】设大正方形（甲）的边长为x，一个小正方形（乙）的边长为y，根据这个六边形的面积为72，列方程即可得到结论．解：设大正方形（甲）的边长为x，一个小正方形（乙）的边长为y，△这个六边形的面积为72，△2x2+y2+2×12（x+y）（x-y）=72，△3x2=72，△x2=24，△两个相同的大正方形（甲）的面积=24×2=48，△图中阴影部分面积为72-48=24，故答案为：24．【点拨】本题考查了三角形的面积，正方形的面积，正确的识别图形是解题的关键．12．531 5xyxy-⎧=⎪⎪⎨⎪=-⎪⎩【分析】根据“三个坐一棵，五个地上落；五个坐一棵，闲了一棵树”，即可得出关于x，y 的二元一次方程组，此题得解．解：设乌鸦有x只，树有y棵，由题意可列方程组：5315xyxy-⎧=⎪⎪⎨⎪=-⎪⎩，故答案为：5315xyxy-⎧=⎪⎪⎨⎪=-⎪⎩．【点拨】本题考查了由实际问题抽象出二元一次方程组，找准等量关系，正确列出二元一次方程组是解题的关键．13．3m【分析】分别求出每一个不等式的解集，根据不等式组的解集结合口诀：同大取大、同小取小、大小小大中间找、大大小小无解了可得答案．解：x+5＜3x-1，得：x＞3，△不等式组的解集是x＞3，△m≤3，故答案为：m≤3．【点拨】本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．14．45【分析】根据三角形内角和求出△GFE，再根据三角形外角性质求出△α即可．解：△△C＝△B＝45°，△E＝30°，△EGF＝60°，△△GFE＝180°﹣△E﹣△EGF＝180°﹣30°﹣60°＝90°，△△GFE＝△C+△α，△△α＝△GFE﹣△C＝90°﹣45°＝45°．故答案为：45．【点拨】本题主要考查三角形内角和定理与三角形外角性质，熟练掌握基本性质是解题关键．15．17.5【分析】利用平移的性质得到BE=3.5，DE=AB=6，再根据面积的和差得到阴影部分的面积=S梯形ABEH，然后利用梯形的面积公式计算即可．解：△直角三角形ABC沿着BC方向平移3.5cm得到直角三角形DEF，△BE=3.5，DE=AB=6，△EH=6-2=4，S△ABC=S△DEF，△阴影部分的面积=S梯形ABEH=12（HE+AB）×BE=12×（4+6）×3.5=17.5（cm2）．故答案为：17.5．【点拨】本题考查了平移的性质：把一个图形整体沿某一直线方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同；新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点．连接各组对应点的线段平行且相等．16．14. 【解析】【分析】由于D 、E 、F 分别为BC 、AD 、CE 的中点，可判断出AD 、BE 、CE 、BF 为△ABC 、△ABD 、△ACD 、△BEC 的中线，根据中线的性质可知将相应三角形分成面积相等的两部分，据此即可解答．【详解】△由于D 、E 、F 分别为BC 、AD 、CE 的中点，△ABE ∆、DBE ∆、DCE ∆、AEC ∆的面积相等，21122BEC ABC S S cm ∆∆==. 211112224BEF BEC S S cm ∆∆==⨯=. 解法2：△D 是BC 的中点，△ABD ADC S S ∆∆=（等底等高的三角形面积相等），△E 是AD 的中点，△ABE BDE S S ∆∆=，ACE CDE S S ∆∆=（等底等高的三角形面积相等），△ABE DBE DCE AEC S S S S ∆∆∆∆===， △21122BEC ABC S S cm ∆∆==. △F 是CE 的中点，△BEF BCE S S ∆∆=， △211112224BEF BEC S S cm ∆∆==⨯=. 故答案为：14. 【点拨】此题考查了三角形的面积，根据三角形中线将三角形的面积分成相等的两部分解答．17．2αβγ∠=∠+∠.【解析】【分析】根据两直线平行，同位角相等可得△γ=△B ，然后根据三角形的一个外角等于与它不相邻的两个内角的和表示出△α、△β，再根据角平分线的定义可得△BAD=△CAD ，然后整理即可得解．【详解】△EF BC ∥，△B γ∠=∠，由三角形的外角性质得，B BAD BAD αγ∠=∠+∠=∠+∠，CAD βα∠=∠+∠，△AD 是BAC ∠的平分线，△BAD CAD ∠=∠，△αβγα∠-∠=∠-∠，△2αβγ∠=∠+∠.故答案为：2αβγ∠=∠+∠.【点拨】本题考查了平行线的性质，角平分线的定义，三角形的一个外角等于与它不相邻的两个内角的和的性质，熟记各性质是解题的关键．18．1【解析】【分析】先根据非负数的性质求出x 、y 的值，再代入代数式进行计算即可．【详解】△|x+y -7|+（3x+y -17）2=0，△703170x y x y +-⎧⎨+-⎩＝＝，解得52x y ⎧⎨⎩＝＝， △x -2y=5-4=1．故答案为1．【点拨】本题考查的是非负数的性质，熟知当几个数或式的偶次方或绝对值相加和为0时，则其中的每一项都必须等于0是解答此题的关键．19．△ACE ，△BCE △ACE 8 4【解析】根据题意，在△ABC 中，△△ACB ＝90°，△B ＝30°，△△A ＝60°，△CE ＝BE ，△△EBC 为等腰三角形；△B ＝△ECB ＝30°，△△BEC ＝120°，△△AEC ＝60°，△△AEC 是等边三角形．△CD 为AB 边上的高，DE =2cm ，△AE=4cm ，△AC=AE=4cm ，△△ACB ＝90°，△B ＝30°，△AB=2AC=8cm.故答案为：(1) △EBC ，△AEC ； (2) △AEC ；（3）8，4.20．35或34【分析】根据题意易得第二次操作后，剩下的长方形的两边长分别为1a -与21a -，则可分△当121a a ->-时，△当121a a -<-时，然后根据题意可进行列方程求解．解：由题意得第二次操作后，剩下的长方形的两边长分别为1a -与21a -，则有： △当121a a ->-时，根据题意得：()12121a a a ---=-，解得：35a =，经检验35a =满足题意； △当121a a -<-时，根据题意得：()()2111a a a ---=-，解得：34a =，经检验34a =满足题意；综上所述：第3次操作后，剩下的长方形恰好是正方形，则a 的值为35或34；故答案为35或34．【点拨】本题主要考查一元一次方程的应用，熟练掌握一元一次方程的应用及分类讨论思想是解题的关键．21．5 2△BAC=3△BCD【分析】（1）利用非负数的性质解决问题即可．（2）由参数t表示△BAC，△BCD即可判断．解：（1）△|a-3b|+（a+b-4）2=0．又△|a-3b|≥0，（a+b-4）2≥0．△a-3b=0，a+b-4=0，解得：a=3，b=1，△a+2b=5；（2）设A灯转动时间为t秒，△△CAN=180°-3t，△△BAC=45°-（180°-3t）=3t-135°，又△PQ△MN，△△BCA=△CBD+△CAN=t+180°-3t=180°-2t，△△ACD=90°，△△BCD=90°-△BCA=90°-（180°-2t）=2t-90°，△△BAC：△BCD=3：2，即2△BAC=3△BCD．【点拨】本题主要考查了解二元一次方程组，平行线的判定与性质，以及角的和差关系的运用，解决问题的关键是理解题意，属于中考常考题型．22．180【分析】连接AB，可知△C+△D=△CAB+△DBA，进而根据三角形内角和求出A B C D E∠+∠+∠+∠+∠的值．解：连接AB，△△C+△D+△DFC=△CAB+△DBA+△AFB，△DFC=△AFB，△△C+△D=△CAB+△DBA，CAE DBE C D E CAE DBE CAB DBA E ∠+∠+∠+∠+∠=∠+∠+∠+∠+∠， =EAB ABE E ∠+∠+∠，=180°故答案为：180．【点拨】本题考查了三角形内角和，解题关键是恰当的连接辅助线，把所求的角转化为同一个三角形的内角．23．【分析】在三角形内任取一点，将ACM △逆时针旋转60︒，确定线段之和的最小值，后用勾股定理求解即可.【详解】如图（1）所示，在ABC 内取一点，连接,,MA MB MC ，将ACM △逆时针旋转60︒，得到AC M ''，连接,MM BC ''，由旋转性可得：,60,60ACM AC M MAM CAC '''︒'︒≅∠==，,,CM C M AM AM AC AC ''''∴===，MAM '∴为等边三角形，即有AM MM '=，BM AM CM BM MM C M BC '''∴++=++，BM AM CM ∴++的最小值为BC '，且6060120BAC BAC CAC ''︒︒︒∠=+∠=+=，△在BAC '中，如图（2）所示，过B 作AC '的垂线交C A '延长线于点E ，120BAC '︒∠=，180********BAE BAC ︒'︒︒︒∴∠=-∠=-=，又BE AE ⊥，△在Rt ABE △中，ABE ∠180BAE BEA ︒=-∠-1806090︒︒︒=--30︒=，112122AE AB ∴==⨯=，由勾股定理得：BE == 617C E AC AE AC AE ''∴=+=+=+=，△在Rt BC E '中，由勾股定理得：BC '====BM AM CM ∴++的最小值为故答案为：【点拨】本题考查了三线段和的最小值，旋转，等边三角形的判定与性质，勾股定理，熟练运用旋转思想确定线段之和的最小值线段，并用勾股定理求解是解题的关键.24．（1）15x y =⎧⎨=⎩，52x y =⎧⎨=⎩；（2）2 【分析】（1）把y 看做已知数求出x ，即可确定出正整数解；（2）利用加减消元法易得x 、y 的值，由x 、y 均为整数可解得m 的值．解：（1）由已知得：2343y x -=，要使x ，y 都是正整数，当y =5时，x =1，当y =4时，x =73，不符合，当y =3时，x =113，不符合，当y =2时，x =5，当y =1时，x =193，不符合，则二元一次方程3423x y +=的正整数解为：15x y =⎧⎨=⎩，52x y =⎧⎨=⎩；（2）210320mx y x y +=⎧⎨-=⎩①②， △+△得：（3+m ）x =10，即x =103m +，代入△得：y =153m+， △方程的解x 、y 均为整数，△3+m 既能被10整除也能被15整除，即3+m =5，解得m =2．【点拨】本题考查了二元一次方程组的解法，解二元一次方程，解二元一次方程组有加减法和代入法两种，一般选用加减法解二元一次方程组较简单．25．（1）A 种洗手液每件8元，B 种洗手液每件各10元；（2）50件【分析】（1）设A 种洗手液每件x 元，B 种洗手液每件各y 元，根据题意列出二元一次方程组，解方程组即可求解；（2）设A 种洗手液购买m 件，根据题意列出不等式，从中找到最小整数解即可．【详解】解：（1）设A 种洗手液每件x 元，B 种洗手液每件各y 元，根据题意得105130510140x y x y +=⎧⎨+=⎩解得：810x y =⎧⎨=⎩ 答：A 种洗手液每件8元，B 种洗手液每件各10元；（2）设A 种洗手液购买m 件，则B 种洗手液购买()100m -件，根据题意可得()810100900m m +-≤，解得：50m ≥．答：A 种洗手液至少需要购买50件．【点拨】本题主要考查二元一次方程组和不等式，读懂题意列出方程组及不等式是关键． 26．（1）证明见解析；（2）证明见解析；（3）△F =29.5°．【分析】（1）因为平角为180°，若能运用平行线的性质，将三角形三个内角集中到同一顶点，并得到一个平角，问题即可解决；（2）根据平角的定义和三角形的内角和定理即可得到结论；（3）根据平行线的性质得到△DEB =119°，△AED =61°，由角平分线的性质得到△DEF =59.5°，根据三角形的外角的性质即可得到结论．【详解】解：（1）如图1所示，在△ABC 中，△DE △AB ，△△B =△1，△A =△2（内错角相等）．△△1+△BCA +△2=180°，△△A +△B +△ACB =180°．即三角形的内角和为180°；（2）△△AGF+△FGE=180°，由（2）知，△GEF+△F+△FGE=180°，△△AGF=△AEF+△F；（3）△AB△CD，△CDE=119°，△△DEB=119°，△AED=61°，△GF交△DEB的平分线EF于点F，△△DEF=59.5°，△△AEF=120.5°，△△AGF=150°，△△AGF=△AEF+△F，△△F=150°-120.5°=29.5°．【点拨】本题考查了平行线的性质，三角形的内角和定理，三角形的外角的性质，熟练掌握平行线的性质定理是解题的关键．27．（1）△A=30°；（2）△1－△2=2△A，△1+△2=2△A，△2－△1=2△A，证明见解析【分析】（1）根据三角形内角和即可求解；'交于H，根据外角性质及折叠性质得到△AHD=△A+△2，再利用外（2）图△中AC与A D角性质得到△1=△A+△AHD，然后进行代换即可得到结论；图△中根据平角及折叠的性质可得到△1+△2+2(△AED+△ADE)=360°，再根据三角形内角和得到△AED+△ADE=180°－△A，从而进行代换计算即可得到结果；图△中AB与A E'交于M，根据外角性质及折叠性质得到△AME=△A+△1，再利用外角性质得到△2=△A+△AME，然后进行代换即可得到结论．【详解】解：（1）△△A+△B+△C=180°，△B=80°，△C=70°，△△A=180°－80°－70°=30°；（2）数量关系分别为：△1－△2=2△A，△1+△2=2△A，△2－△1=2△A，理由如下：'交于H，图△：如图，AC与A D△△AHD=A '∠+△2，A '∠=△A ，△△AHD=△A+△2，△△1=△A+△AHD ，△△1=△A+△A+△2，△△1－△2=2△A ；图△：由折叠可知，AED A ED '∠=∠，ADE A DE '∠=∠，△2180AED A ED '∠+∠+∠=︒，1180ADE A DE '∠+∠+∠=︒，△()122360AED ADE ∠+∠+∠+∠=︒，又△△A+△AED+△ADE=180°，△△AED+△ADE=180°－△A ，△△1+△2+2(180°－△A)=360°，即△1+△2－2△A=0，△△1+△2=2△A ；图△：如图，AB 与A E '交于M ，△△AME=A '∠+△1，A '∠=△A ，△△AME=△A+△1，△△2=△A+△AME ，△△2=△A+△A+△1，△△2－△1=2△A ．【点拨】本题考查了探究角之间的数量关系，熟练掌握折叠的性质，三角形内角和，外角性质等知识是解题的关键．28．（1）△A +△D =△B +△C ；（2）38°；（3）2△P =△B +△D【分析】（1）利用三角形的内角和定理表示出AOD ∠与BOC ∠，再根据对顶角相等可得AOD BOC ∠=∠，然后整理即可得解；（2）根据（1）的关系式求出OCB OAD ∠-∠，再根据角平分线的定义求出DAM PCM ∠-∠，然后利用“8字形”的关系式列式整理即可得解；（3）根据“8字形”用B 、D ∠表示出OCB OAD ∠-∠，再用D ∠、P ∠表示出DAM PCM ∠-∠，然后根据角平分线的定义可得1()2DAM PCM OCB OAD ∠-∠=∠-∠，然后整理即可得证．解：（1）在AOD △中，180AOD A D ∠=︒-∠-∠，在BOC 中，180BOC B C ∠=︒-∠-∠，AOD BOC ∠=∠（对顶角相等），180180A D B C ∴︒-∠-∠=︒-∠-∠，A DBC ∴∠+∠=∠+∠；（2）40D ∠=︒，36B ∠=︒，4036OAD OCB ∴∠+︒=∠+︒，4OCB OAD ∴∠-∠=︒， AP 、CP 分别是DAB ∠和BCD ∠的角平分线，12DAM OAD ∴∠=∠，12PCM OCB ∠=∠，又DAM D PCM P ∠+∠=∠+∠，1()382P DAM D PCM OAD OCB D ∴∠=∠+∠-∠=∠-∠+∠=︒；（3）根据“8字形”数量关系，OAD D OCB B ∠+∠=∠+∠，DAM D PCM P ∠+∠=∠+∠，所以，OCB OAD D B ∠-∠=∠-∠，PCM DAM D P ∠-∠=∠-∠， AP 、CP 分别是DAB ∠和BCD ∠的角平分线，12DAM OAD ∴∠=∠，12PCM OCB ∠=∠， ∴1()2D B D P ∠-∠=∠-∠，整理得，2P B D ∠=∠+∠．【点拨】本题考查了三角形内角和定理，角平分线的定义，多边形的内角和定理，对顶角相等的性质，整体思想的利用是解题的关键．。

语文七年级上册期末高分突破讲练复习(部编版)期末测试(一)(解析版)

期末测试（一）一．选择题（共10小题）1．下面一段话的顺序已被打乱，将其还原，顺序正确的一项是（）①坐着，躺着，打两个滚，踢几脚球，赛几趟跑，捉几回迷藏。

②园子里，田野里，瞧去，一大片一大片满是的。

③风轻悄悄的，草软绵绵的。

④小草偷偷地从土里钻出来，嫩嫩的，绿绿的。

A．①②③④B．④③②①C．④②①③D．③④②①【分析】此题考查了句子的排序。

【解答】文段写人的活动和人的感觉反衬出春草勃发给人带来的欢乐，表现春草的可爱。

正确的语序是：④②①③。

故选：C。

2．阅读下面的文字，回答问题。

忽然到了晚间，水银柱降下来，黎明提前敲着窗户，你睁眼一看，屋顶、树枝、街道，都已经盖上柔软的雪被，地上的光亮比天上还亮。

这雨的精灵，雨的公主，给南国城市和田野带来异常的蜜情，是它送给人们一年中最后的一份礼物。

下列表述有误的一项是（）A．“屋顶”树枝”“街道”是名词。

B．“晚间”“忽然”不全是名词。

C．画线句子运用了比喻和拟人的修辞手法。

D．“柔软”“蜜情”是名词。

【分析】本题考查学生对词性和修辞的辨析能力。

结合词性和修辞的相关知识解答即可。

【解答】ABC.正确。

D.有误。

“柔软”是形容词。

故选：D。

3．下列对病句的修改不正确的一项是（）A．珠算“申遗”成功后，不少网友认为，珠算是我国古代的重大发明，是中华民族智慧的结晶，应该加以发扬和传承。

（将“发扬”与“传承”互换位置）B．昆虫学家法布尔把科学和文学巧妙地结合起来，用生动形象的语言为我们刻画了一个绚丽多姿的昆虫世界。

（把“刻画”改为“描绘”）C．我国自行设计的北斗卫星导航系统具有覆盖范围广、受地面影响小、定位准确及时，在抗震救灾中大显身手。

（在“准确及时”后加上“的特点”）D．《标准汉语》的主要读者是为英语国家中的中国留学生子女及汉语爱好者编写的一套汉语学习材料。

（删去“为”）【分析】本题考查对病句的辨析与修改能力。

病句的病因有很多，主要有成分残缺、语序不当、不合逻辑、句式杂糅等。