选3-5-1

合集下载

与名师对话2022 新高考专题总复习 2-1-3-5

请简要概括汤显祖读书为文的特点。(3分) 答：_________________________________________________ _____________________________________________________
第8页
与名师对话·系列丛书
(新)高考总复习•语文•课标版
夜，读书声还朗朗不停。家人笑话他：“老博士还用得着读书吗？”他说：“我
读我的书，不问是不是博士。”不久以太常博士的身份转任南京祠部郎。部里虽
然没有什么事，但是汤公任职认真谨慎，他认为北京南京两个政府任用亲信而堵
塞了进谏的渠道，就上书直言这件事，被贬谪为广东徐闻县尉。过了很长时间，
转任遂昌县令。又因为矿税的事情有很多谬误，和计吏一起到京的那天，就向吏
第14页
与名师对话·系列丛书
(新)高考总复习•语文•课标版
[解析] 题干说“韩信死后，萧何得到皇帝封赏，众人祝贺”，根据对文章 “言”的理解，找到事件出现的信息区域“未罢，淮阴侯谋反关中，吕后用萧何计，诛淮阴侯。上已闻淮阴侯诛，使使拜丞相何为相国，益封五千户，令卒五百人一都尉为相国卫”；“为什么召平却为萧何担忧”，借助内容理解，“分析召平担忧的原因”。
第13页
与名师对话·系列丛书
(新)高考总复习•语文•课标版
身随我，多者两三人；今萧何举宗数十人皆随我，功不可忘也。”群臣皆莫敢言。汉十一年，陈豨反，高祖自将，至邯郸。未罢，淮阴侯谋反关中，吕后用萧何计，诛淮阴侯。上已闻淮阴侯诛，使使拜丞相何为相国，益封五千户，令卒五百人一都尉为相国卫。诸君皆贺，召平独吊。召平谓相国曰：“祸自此始矣。愿君让封勿受，悉以家私财佐军，则上心说。”相国从其计，高帝乃大喜。
[解析] 汤显祖读书为文的情况主要在第③④段。第③段“掷书万卷……不问博士与不博士也”，说明汤公读书的目的不为功名，乐此不疲。第④段“公于书……不讹只字”，说明汤公读书面广，又有专攻。“于诗若文……青莲少陵氏”，说明他读书的效果。“公又以其……声振寥廓”，说明他不但创作戏剧的水平超过元代作家，还与侍从一起演唱，创演合一。根据以上“读书为文”的信息，用精练的语言分条概括出即可。

当代中国政治制度机考题库3-1-5

当代中国政治制度-3_0001试卷总分：100 测试时间：180单项选择题多项选择题判断题简答题论述题一、单项选择题（共 15 道试题，共 15 分。

）1. 香港特别行政区行政长官任职的年龄要求是\（）A. 年满二十周岁B. 年满三十周岁C. 年满四十周岁D. 年满四十五周岁2. 自治县（旗）可以设立在一般行政地方，也可以设立在民族自治地方。

设立自治县最多的省是（）A. 黑龙江B. 青海C. 云南D. 四川3. 在全国人民代表大会闭会期间，决定部长、委员会主任、审计长、秘书长人选的是（）。

A. 中共中央政治局B. 中共中央书记处C. 全国人大常委会D. 国务院总理4. 地方性法规与国家部门规章之间对同一事项的规定不一致，不能确定如何适用时，如果国务院认为应当适用部门规章的，应当由( )。

A. 全国人大裁决B. 地方同级人大裁决C. 全国人大常委会裁决D. 国务院裁决5. 中国少数民族中，有文字的民族有（）。

A. 20个B. 21个C. 22个D. 23个6. 省、自治区、直辖市政府财政部门所编制和汇编的本级年度总预算草案，经本级政府审定后，报财政部的时间是（）A. 当年12月30日前B. 下一年1月10日前C. 下一年1月30日前D. 下一年2月15日前7. 我国政府机构数量众多、规模庞大，其中地级市、行署一般有（）A. 29-30个左右B. 30-40个左右C. 40-50个左右D. 50-60个左右8. 国家主席、副主席连选连任不得超过（）A. 不得超过10年B. 不得超过15年C. 不得超过20年D. 无限制9. 我国的省作为一级政区的行政地位基本成形于（）A. 唐代B. 宋代C. 元代D. 明代10. 我国目前地方政府的层级设置最多有（）A. 二级B. 三级C. 四级D. 五级11. 在我国所授予的勋章和称号中，具有最高荣誉等级者的授予人是( )。

A. 中共中央总书记B. 全国人大委员长C. 国务院总理D. 国家主席12. 国务院总理办公会议( )。

省考行测模考数量关系试题练习模拟含解析

省考行测模考数量关系试题解析数字推理（1）2048，512，128，32，8，（）A.1B.2C.4D.6【解析】等比数列，8÷4=2，选B（2）5，8，14，26，50，（）A.76B.98C.100D.150【解析】相邻两项作差得3、6、12、24、（48）为等比数列，50+48=98，选B（3）322，44，117，550，335，（）A.551B.280C.907D.606【解析】每个数的数字和分别为7、8、9、10、11、（12），选D（4）2，19/8，2.75，25/8，（）A、7/8B、7/2C、4.5D、5.4【解析】分别转化为16/8、19/8、22/8、25/8、（28/8=7/2），选B（5）8，4，14，10，24，12，30，18，36，（）A.20B.22C.24D.26【解析】两个一组，每组之和12、24、36、48、（60）为等差数列，60-36=24，选C （6）136542，33654，7365，1236，723，（）A.103B.102C.106D.105【解析】首尾相加作为下一项的首位、其余部分不动，7+3=10，选B（8）4，4，5，8，13，22，（）A.39B.29C.59D.49【解析】相邻两项作差得0、1、3、5、9、（17），再作差得1、2、2、4、8为递推积数列，22+17=39，选A（9）0，1，1，4，25，（）A.832B.824C.841D.817【解析】（第一项+第二项）2=第三项，依次类推，（4+25）2=841，选C（10）2+√3，3-√3，5，8-√3，13-√3，（）A.21-2√3B.21-√3C.5+2√2D.1+2√2【解析】递推和数列，（8-√3）+（13-√3）=21-2√3，选A（11）1，2，3，5，8，12，20，28，（），（）A.35B.37C.48D.64【解析】两个一组，（1、2）（3、5）（8、12）（20、28）（48、64），每组之和为下一组的第一个数，每组之差1、2、4、8、16为等比数列，选CD（12）（），4，1，2，5，3，9，11，（）A.0B.4C.8D.12【解析】以5为对称点，2+3=5、1+9=10、4+11=15、（8）+（12）=20，选CD（13）（），3，9，45，315，（）A、1.5B、2C、2478D、3465【解析】相邻两项作商得2、3、5、7、11为连续质数列，3÷2=1.5、315×11=3465，选（14）（），22，54，74，130，158，（）A.8B.10C.212D.238【解析】分别转化为（32+1=10）、52-3、72+5、92-7、112+9、132-11、（152+13=238），选BD（15）3，5，18，59，195，（），（）A.644B.734C.1827D.2127【解析】第一项+（第二项×3）=第三项，依次类推，59+（195×3）=644、195+（644×3）=2127，选AD（18）1/3，5/6，13/12，5/4，（）A.11/6B.7/4C.5D.11/8【解析】相邻两项作差得1/2、1/4、1/6、（1/8），（5/4）+（1/8）=11/8，选D（19）2，4，8，24，88，（）A.663B.636C.664D.646【解析】第一项2+第二项=第三项，依次类推，242+88=664，选C（20）3，10，24，65，（）A.167B.168C.169D.170【解析】分别转化为22-1、32+1、52-1、82+1、（132-1=168），选B数学运算（1）甲、乙两个仓库均放满货物，甲仓库货物比乙仓库少1/6。

五年级下册数学第一单元试卷(共9篇)

五年级下册数学第一单元试卷〔共9篇〕篇1：五年级下册数学第一单元试卷一、仔细看题，认真填空(18%)1、在14-x=8，7×5=35，x÷0.9=1.8，4x，79”、“篇2：五年级下册数学第一单元试卷一、填一填。

(23分) 假如一个图形沿着一条直线对折，两侧的图形可以完全重合，这样的图形就叫( )图形，那条直线就是( )。

正方形有( )条对称轴。

长方形有( )条对称轴。

平行四边形( )轴对称图形。

这些现象哪些是“平移”现象，哪些是“旋转”现象：(1)张叔叔在笔直的公路上开车，方向盘的运动是( )现象。

(2)升国旗时，国旗的升降运动是( )现象。

(3)妈妈用拖布擦地，是( )现象。

(4)自行车的车轮转了一圈又一圈是( )现象。

4、移一移，说一说。

(1)向( )平移了( )格。

(2)向( )平移了( )格。

(3)向( )平移了( )格。

5.(1)指针从A开场，( )旋转( )°会转到B;指针从C开场，( )旋转( )°，会转到D。

指针从B开场，逆时针旋转90°会转到( )。

指针从D开场，逆时针旋转90°，会转到( )。

(2)从10：00到10：15，分针旋转了( )°;从1：30到1：50，分针旋转了( )°。

二、动手操作。

(14分)1.图形①是以点( )为中心旋转的;图形②是以点( )为中心旋转的;图形③是以点( )为中心旋转的。

2、(1)图形1绕A点( )旋转90。

到图形2。

(2)图形2绕A点( )旋转90。

到图形3。

(3)图形4绕A点顺时针旋转( )到图形2。

(4)图形3绕A点顺时针旋转( )到图形1。

三、画出以下图形的对称轴。

(20分)四、请画出对称图形的另一半。

(15分)五请按照给出的对称轴画出第一个图形的对称图形，第二个图形请向上挪动3格。

(6分)六、(1)画出以下图经过平移或旋转的图形。

(15分)(1).利用平移变换设计美丽的图案。

【章节讲义】第一单元《混合运算》—2021-2022学年数学三年级上册章节复习精讲精练

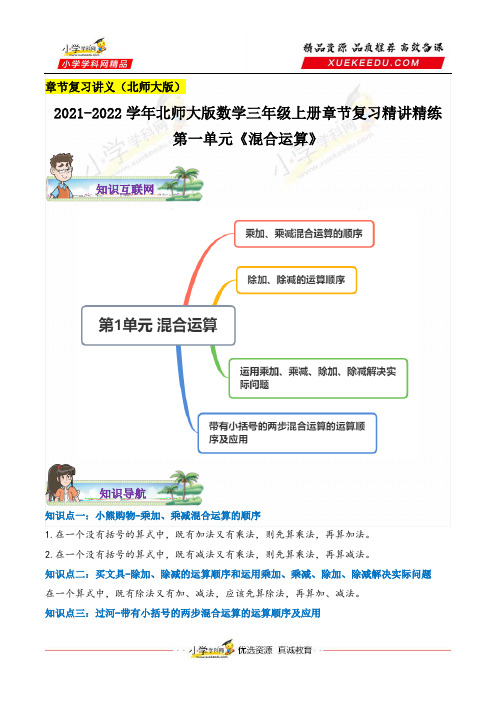
章节复习讲义（北师大版）2021-2022学年北师大版数学三年级上册章节复习精讲精练第一单元《混合运算》知识互联网知识导航知识点一：小熊购物-乘加、乘减混合运算的顺序1.在一个没有括号的算式中，既有加法又有乘法，则先算乘法，再算加法。

2.在一个没有括号的算式中，既有减法又有乘法，则先算乘法，再算减法。

知识点二：买文具-除加、除减的运算顺序和运用乘加、乘减、除加、除减解决实际问题在一个算式中，既有除法又有加、减法，应该先算除法，再算加、减法。

知识点三：过河-带有小括号的两步混合运算的运算顺序及应用1.解决问题时要认真分析题意，如果要先算加、减法，再算乘、除法，就要用小括号来帮忙。

2.在含有小括号的算式中，计算时要先算小括号里面的，再算小括号外面的。

夯实基础一、精挑细选（共5题；每题2分，共10分）1．(本题2分)（2021·辽宁三年级课时练习）不能先算除法的算式是（）。

A．48÷6＋42 B．45＋30÷5C．27÷（51－48）2．(本题2分)（2021·辽宁）一群兔子到森林公园玩，其中灰兔19只，白兔17只，如果它们都住大房子，需要几间？（）A．2 B．4 C．5 D．63．(本题2分)（2021·辽宁）每千克梨比每千克苹果便宜（）元？A．2 B ．4 C．6 D．84．(本题2分)（2021·辽宁）水果店有30筐苹果，每筐5千克，第一天卖出45千克，第二天卖出苹果10筐。

第二天比第一天多卖出几筐苹果？正确的列式是（）。

A．10－45÷5B．10×5－4 C．30－10÷55．(本题2分)（2020·辽宁）某机械厂制造一种机器，平均每台用1.69吨钢材。

通过技术革新，每台节约0.26吨钢材，原来制造50台机器用的钢材，现在可以制造多少台？（保留整数）正确列式是( ) A ．1.69×50÷(1.69－0.26) B ．1.69×50÷0.26 C ．1.69×50÷1.69－0.26D ．0.26×50÷(1.69－0.26)二、仔细想，认真填（共11题；共18分）6．(本题1分)（2021·辽宁三年级课时练习）平安停车场停了3排小汽车，每排有6辆；大汽车停了9辆。

国考行测数字推理每日一练

【例题】1.5，3，7.5（原文是7又2分之1），22.5（原文是22又2分之1），（）A.60B.78.25（原文是78又4分之1）C.78.75D.80【例题】2，2，3，6，15，( ) A、25 B、36 C、45 D、49【例题】5，6，19，17，( )，-55 A. 15 B. 344 C. 343 D. 11【例题】2，21，( )，91，147 A. 40 B. 49 C. 45 D. 60【例题】-1/7，1/7，1/8，-1/4，-1/9，1/3，1/10，( )A. -2/5B. 2/5C. 1/12D. 5/8【解析】选C，后项除以前项=>2、2.5、3、3.5 等差。

【解析】选C。

2/2=1 3/2=1.5 6/3=2 15/6=2.5 45/15=3。

其中，1， 1.5， 2， 2.5， 3 等差。

【解析】选B，第一项的平方减去第二项等于第三项。

【解析】选B，21=2(第一项)×10+1，49=2×24+1，91=2×45+1，147=2×73+1，其中10、24、45、73 二级等差。

【解析】选A，分三组=>-1/7，1/7； 1/8，-1/4； -1/9，1/3； 1/10，( -2/5 )，每组后项除以前项=>-1，-2，-3，-4 等差。

2012年国考行测数字推理每日一练（2）【例题】63，26，7，0，-1，-2，-9，（）A、-18B、-20C、-26D、-28【例题】5，12 ,24，36，52，( ), A.58 B.62 C.68 D.72【例题】1，3, 15，( ), A.46 B.48 C.255 D.256【例题】3/7，5/8，5/9，8/11，7/11，( )A.11/14B.10/13C.15/17D.11/12【例题】1，2，2， 3，3，4，5，5，( ) A.4 B.6 C.5 D.0【解析】选D，63=43-1，26=33-1，7=23-1，0=13-1，-1=03-1，-2=(-1)3-1，-9=(-2)3-1 -28=(-3)3-1。

物理化学5-1 相律

单组分系统两相平衡时： f 1
T、P之间的关系。
一、物态转变方程式 1、克拉佩龙方程式在T、P下，纯物质以α 和β 两相平衡共存，则当 T→T+dT 则 P→P+dP

,即 G

G m m
为保持两相的平衡,则由热力学基本方程：
G m dG m G m dG m dG m dG m S mdT V mdP S mdT V mdP
对于气体，无论何种不同气体都能无限均匀混合，因此只有一相。对于液体，纯液体和真溶液都只是一相; 多种液体混合时，根据溶解程度可分为一相，二相或三相共存。对于固体，纯固体为一相，一般体系中，多一种固体便多一个相，即使两种固体物质细小弥散的相互掺合，仍为两相，只有这些物质以原子（或分子）状态相互混合成固溶体，才是均相体系。
H m dP H 0 dT T Vm dP 汽 V 0 0 dT dP 水 V 0 0 dT dP 汽 V 0 0 dT
2、OA、OB、OC把图分为三个单相区：g，l，s。f = 1-1+2 = 2
即有T、P两个自由度，T、P在一定范围内可独立变化，而不影响该相的单独存在。
fus H 0
水 fusVm 0 dT 0, P , T dP
Vm ( g ) ? Vm (l )或Vm (s)
RT Vm Vm ( g ) P
(理想气体) dP vap H P 2
dP Hm dT T Vm
反应了T、P之间的关系：
会溶温度的高低反映了一对液体间的互溶能力，可以用来选择合适的萃取剂。
二、杠杆规则
杠杆规则：由相图可知一定条件下，系统中含有哪些相，及各相的成分。还可知两共存相的相对量。

中考数学5年真题(2019-2023)专题汇总解析—二次根式

中考数学5年真题（2019-2023）专题汇总解析—二次根式考点1二次根式一、单选题1．（2023）A．25与30之间B．30与35之间C．35与40之间D．40与45之间【答案】D【详解】解∶∵160020232025<<．即4045<，40与45之间．故选D．【点睛】本题主要考查了估算无理数的大小，正确估算无理数的取值范围是解题关键．2．（2023年江苏省无锡市中考数学真题）实数9的算术平方根是（）A．3B．3±C．19D．9-【答案】A【分析】根据算术平方根的定义即可求出结果．3=，故选：A．【点睛】本题考查了平方根和算术平方根的定义．注意一个正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根．3．（2023年重庆市中考数学真题（A卷）的值应在（）A ．7和8之间B ．8和9之间C ．9和10之间D ．10和11之间【答案】B【分析】先计算二次根式的混合运算，再估算结果的大小即可判断．=4=+∵2 2.5<<，∴45<<，∴849<+<，故选：B ．【点睛】此题考查了二次根式的混合运算，无理数的估算，正确掌握二次根式的混合运算法则是解题的关键．4．（2019·广东·的结果是()A ．4-B ．4C ．4±D ．2【答案】B【分析】根据算术平方根的定义进行求解即可.，故选B.【点睛】本题考查了算术平方根，熟练掌握算术平方根的定义是解题的关键.5．（2020·广西贵港·在实数范围内有意义，则实数x 的取值范围是（）A ．1x <-B ．1x ≥-C ．0x ≥D ．1x ≥【答案】B【分析】根据二次根式的被开方数为非负数即可得出的取值范围．∴x＋1≥0∴x≥﹣1故选：B【点睛】本题考查了二次根式有意义的条件，解答本题的关键是掌握二次根式有意义：被开方数为非负数．6．（2020·山东聊城·÷）．A．1B．53C．5D．9【答案】A【分析】利用二次根式的乘除法则计算即可得到结果．÷==1=，故选：A．【点睛】本题主要考查了二次根式的乘除法，熟练掌握运算法则是解题的关键．7．（2023年辽宁省大连市中考数学真题）下列计算正确的是（）A．0=B．+=C=D)26=-【答案】D【分析】根据零指数幂，二次根式的加法以及二次根式的性质，二次根式的混合运算进行计算即可求解．【详解】解：A.)1=，故该选项不正确，不符合题意；B.=C.=D.)26=-，故该选项正确，符合题意；故选：D ．【点睛】本题考查了零指数幂，二次根式的加法以及二次根式的性质，二次根式的混合运算，熟练掌握二次根式的运算法则是解题的关键．8．（2021·广东·统考中考真题）若0a =，则ab =（）AB ．92C ．D ．9【答案】B【分析】根据一个实数的绝对值非负，一个非负实数的算术平方根非负，且其和为零，则它们都为零，从而可求得a 、b 的值，从而可求得ab 的值．【详解】∵0a ≥0≥，且0a =∴0a =0==即0a =，且320a b -=∴a =b∴92ab ==故选：B ．【点睛】本题考查了绝对值和算术平方根的非负性，一般地，几个非负数的和为零，则这几个非负数都为零．9．（2022·河北·统考中考真题）下列正确的是（）A23=+B 23=⨯CD 0.7=【答案】B【分析】根据二次根式的性质判断即可．【详解】解：23=≠+，故错误；=⨯，故正确；23=≠≠，故错误；0.7故选：B．【点睛】本题主要考查二次根式的性质，掌握二次根式的性质是解题的关键．10．（2023()A．点P B．点Q C．点R D．点S【答案】B<<【详解】解：∵479<<，<<23Q，故选：B．11．（2023年河北省中考数学真题）若a b===（）A．2B．4C D【答案】A【分析】把a b【详解】解：∵a b==2==，故选：A．【点睛】本题考查了求二次根式的值，掌握二次根式的乘方和乘除运算是解题的关键．12．（2019·四川资阳·统考中考真题）设x=x的取值范围是（）A．23x<<B．34x<<C．45x<<D．无法确定【答案】B【分析】根据无理数的估计解答即可．【详解】解：∵91516<<，∴34<<，故选B．【点睛】此题考查估算无理数的大小，关键是根据无理数的估计解答．13．（2021·广东·统考中考真题）设6a，小数部分为b，则(2a b+的值是（）A．6B．C．12D．【答案】A的整数部分可确定a的值，进而确定b的值，然后将a与b的值代入计算即可得到所求代数式的值．【详解】∵34<<，∴263<<，∴62a=，∴小数部分624b==∴(((22244416106a b+=⨯+-=+-=-=．故选：A．【点睛】本题考查了二次根式的运算，正确确定6a与小数部分b的值是解题关键．二、填空题14．（2019·江苏苏州·x的取值范围为.【答案】6x≥【分析】根据根式有意义的条件，得到不等式，解出不等式即可.-60x≥，解出得到6x≥.【点睛】本题考查根式有意义的条件，能够得到不等式是解题关键.15．（2020·广西·=．【分析】利用二次根式的性质化简，再相减．==【点睛】本题考查了二次根式的减法，解题的关键是掌握二次根式的化简及性质．16．（2021·天津·统考中考真题）计算1)的结果等于．【答案】9【分析】根据二次根式的混合运算法则结合平方差公式计算即可．【详解】21)19=-=．故答案为9．【点睛】本题考查二次根式的混合运算．掌握二次根式的混合运算法则是解答本题的关键．17．（2023年湖北省武汉市数学真题）写出一个小于4的正无理数是．【分析】根据无理数估算的方法求解即可．<4<．．【点睛】本题主要考查了无理数的估算，准确计算是解题的关键．18．（2023x 的取值范围是．【答案】13x ≥-【分析】根据二次根式有意义的条件得到130x +≥，解不等式即可得到答案．∴130x +≥，解得13x ≥-，故答案为：13x ≥-【点睛】此题考查了二次根式有意义的条件，熟知被开方式为非负数是解题的关键．19．（2019·河南·12--=＝．【答案】112【分析】本题涉及二次根式化简、负整数指数幂两个考点．针对每个考点分别进行计算，然后根据实数的运算法则求得计算结果．12--122=-112=．故答案为11 2．【点睛】本题考查实数的综合运算能力，是各地中考题中常见的计算题型．解决此类题目的关键是熟练掌握负整数指数幂、二次根式等考点的运算．20．（2021·安徽·统考中考真题）埃及胡夫金字塔是古代世界建筑奇迹之一，其底面是正方形，侧面是全等的等腰三角形，1-，它介于整数n和1n+之间，则n的值是．【答案】11即可完成求解．2.236≈；1 1.236≈；因为1.236介于整数1和2之间，所以1n=;故答案为：1．分即可；该题题干前半部分涉及到数学文化，后半部分为解题的要点，考查了学生的读题、审题等能力．21．（20231+=．【答案】3【分析】根据求一个数的立方根，有理数的加法即可求解．1+=213+=，故答案为：3．【点睛】本题考查了求一个数的立方根，熟练掌握立方根的定义是解题的关键．22．（2023年上海市中考数学真题）已知关于x2=，则x=【答案】18【分析】根据二次根式的性质，等式两边平方，解方程即可．【详解】解：根据题意得，140x -≥，即14x ≥，2=，等式两边分别平方，144x -=移项，18x =，符合题意，故答案为：18．【点睛】本题主要考查二次根式与方程的综合，掌握含二次根式的方程的解法是解题的关键．23．（2023年黑龙江省绥化市中考数学真题）若式子x有意义，则x 的取值范围是．【答案】5x ≥-且0x ≠/0x ≠且5x ≥-【分析】根据分母不为零，二次根式的被开方数是非负数，列出不等式计算即可．【详解】∵式子∴50x +≥且0x ≠，∴5x ≥-且0x ≠，故答案为：5x ≥-且0x ≠．【点睛】本题考查了分母不为零，二次根式的被开方数是非负数，熟练掌握二次根式和分式有意义的条件是解题的关键．24．（2023年黑龙江省齐齐哈尔市中考数学真题）在函数12y x +-中，自变量x 的取值范围是．【答案】1x >且2x ≠【分析】根据分式有意义的条件，二次根式有意义的条件得出10,20x x ->-≠，即可求解．【详解】解：依题意，10,20x x ->-≠∴1x >且2x ≠，故答案为：1x >且2x ≠．【点睛】本题考查了求函数自变量的取值范围，熟练掌握分式有意义的条件，二次根式有意义的条件是解题的关键．三、解答题25．（2019·福建·统考中考真题）先化简，再求值：(x －1)÷(x －21xx-),其中x【答案】1x x -，1+2【分析】先化简分式，然后将x 的值代入计算即可．【详解】解：原式＝（x−1）÷221x x x-+()()211xx x =-⋅-1x x =-当x ＋1时，12=+【点睛】本题考查了分式的化简求值，熟练掌握分式混合运算法则是解题的关键．26．（2022·福建·统考中考真题）先化简，再求值：2111aa a -⎛⎫+÷ ⎪⎝⎭，其中1a =．【答案】11a -．【分析】根据分式的混合运算法则化简，再将a 的值代入化简之后的式子即可求出答案．【详解】解：原式()()111a a a a a+-+=÷()()111a a a a a +=⋅+-11a =-．当1a =时，原式2=．【点睛】本题考查了分式的化简求值，熟练掌握运算法则是解题的关键．27．（2023年安徽中考数学真题）先化简，再求值：2211x x x +++，其中1x =．【答案】1x +【分析】先根据分式的性质化简，最后将字母的值代入求解．【详解】解：2211x x x +++()211x x +=+1x =+，当1x =-时，∴原式11+=．【点睛】本题考查了分式化简求值，解题关键是熟练运用分式运算法则进行求解．28．（20232133-⎛⎫- ⎪⎝⎭【答案】6-【分析】根据立方根、负整数指数幂及二次根式的运算可进行求解．【详解】解：原式2293=-+6=-．【点睛】本题主要考查立方根、负整数指数幂及二次根式的运算，熟练掌握立方根、负整数指数幂及二次根式的运算是解题的关键．29．（2023年吉林省长春市中考数学真题）先化简．再求值：2(1)(1)a a a ++-，其中3a =．【答案】31a +1+【分析】根据完全平方公式以及单项式乘以单项式进行化简，然后将字母的值代入进行计算即可求解．【详解】解：2(1)(1)a a a ++-2221a a a a =+++-31a =+当a =311==【点睛】本题考查了整式乘法的化简求值，实数的混合运算，熟练掌握完全平方公式以及单项式乘以单项式的运算法则是解题的关键．30．（2023年内蒙古通辽市中考数学真题）计算：21tan 453-⎛⎫+︒-⎪⎝⎭【答案】0【分析】根据负整数次幂、特殊角的三角函数值、算术平方根化简，然后在计算即可．【详解】解：21tan 453-⎛⎫+︒-⎪⎝⎭9110=+-，0=．【点睛】本题主要考查了负整数次幂、特殊角的三角函数值、算术平方根等知识点，掌握基本的运算法则是解答本题的关键．31．（2019·河南·统考中考真题）先化简，再求值：22121244x x x x x x +-⎛⎫-÷ ⎪--+⎝⎭，其中x =【答案】3x【分析】先根据分式的混合运算顺序和运算法则化简原式，再将x 的值代入计算可得．【详解】解：原式212(2)22(2)x x x x x x x +--⎛⎫=-÷ ⎪---⎝⎭322x x x-=⋅-3x=，当x ===．【点睛】本题主要考查分式的化简求值，解题的关键是熟练掌握分式的混合运算顺序和运算法则．32．（2023年辽宁省营口市中考数学真题）先化简，再求值：524223m m m m-⎛⎫++⋅⎪--⎝⎭，其中tan 45m =︒．【答案】26--m ，原式16=-【分析】先根据分式的混合计算法则化简，然后根据特殊角三角函数值和二次根式的性质求出m 的值，最后代值计算即可．【详解】解：524223m m m m-⎛⎫++⋅⎪--⎝⎭()22245223m m m m m-⎛⎫-=-⋅⎪---⎝⎭()222923m m m m--=⋅--()()()332223m m m m m+--=⋅--()23m =-+26m =--，∵tan 45m =︒，∴415m =+=，∴原式25610616=-⨯-=--=-．【点睛】本题主要考查了分式的化简求值，求特殊角三角函数值，化简二次根式等等，正确计算是解题的关键．33．（2023·重庆九龙坡·的值应在（）A ．2和3之间B ．3和4之间C ．4和5之间D ．5和6之间【答案】A【分析】根据二次根式的乘法进行计算，以及估算无理数的大小的方法解答即可．=6=∵91416<<，∴34<，∴43-<<-，∴263<<，故选：A ．【点睛】本题考查了估算无理数的大小和二次根式的运算．解题的关键是掌握二次根式的运算方法，以及估算无理数的大小的方法．34．（2023·辽宁丹东·统考二模）在函数y =x 的取值范围是（）A ．12x -<≤B ．21x -<≤C ．12x ≤≤D ．12x <≤【答案】D【分析】根据函数有意义的条件得到2010x x -≥⎧⎨->⎩,解不等式组即可得到自变量x 的取值范围．【详解】解：由题意得2010x x -≥⎧⎨->⎩，解不等式组得12x <≤，故选：D ．【点睛】此题考查了自变量的取值范围，熟练掌握二次根式和分式有意义的条件是解题的关键．35．（2023·安徽蚌埠·统考三模）下列运算正确的是（）A 3=B ．()3328a a -=-C =D ．112235+=【答案】B【分析】根据二次根式的性质，积的乘方法则，二次根式的加法运算法则，有理数的加法运算法则依次判断即可得出答案．【详解】解：A 333==B ．()3328a a -=-，故此选项符合题意；CD ．11522365+=≠，故此选项不符合题意．故选：B ．【点睛】本题考查二次根式的性质，积的乘方法则，二次根式的加法运算法则，有理数的加法运算法则．掌握相应的运算法则和性质是解题的关键．36．（2023·河北沧州·校考模拟预测）下列运算中，正确的是（）．A3=±B 2=C 2=D 8=-【答案】C【分析】利用二次根式的化简的法则对各项进行运算即可．【详解】解答：解：A 3=，故A 不符合题意；B 2=-，故B 不符合题意；C 2=，故C 符合题意；D 8=，故D 不符合题意；故选：C ．【点睛】本题主要考查二次根式的化简，解答的关键是对相应的运算法则的掌握．37．（2023·四川泸州·四川省泸县第一中学校考三模）实数2的平方根为（）A ．2B ．2±C D ．【答案】D【分析】利用平方根的定义求解即可．【详解】∵2的平方根是．故选D ．【点睛】此题主要考查了平方根的定义，注意一个正数的平方根有2个，它们互为相反数．38．（2023·西南大学附中校考三模）估计(3-）A ．0和1之间B ．2和3之间C ．3和4之间D ．4和5之间【答案】A【分析】由题意知(34-，由1.4 1.5=<<=，可得4.2 4.5<<，0.240.5<<，然后判断作答即可．【详解】解：(34-⨯，∵1.4 1.5=<<=，∴4.2 4.5<<，∴0.240.5<<，∴估算(3-0和1之间，故选：A ．39．（2023·河北石家庄·校联考一模）下列计算正确的是（）A =B1=-C =D 23=【答案】C【分析】根据二次根式加法、二次根式减法、二次根式乘法、二次根式除法分别进行判断即可．【详解】解：AB 0-=，故选项错误，不符合题意；C =D 1=，故选项错误，不符合题意．故选：C ．【点睛】此题考查了二次根式的加法、减法、乘法、除法，熟练掌握运算法则是解题的关键．40．（2023·江苏无锡·校考二模）函数y x的取值范围是（）A ．5x ≥-B ．5x ≤-C ．5x ≥D ．5x ≤【答案】C【详解】试题分析：求函数自变量的取值范围，就是求函数解析式有意义的条件，根据二次根式被开方数x 50x 5-≥⇒≥.故选C.考点：1.函数自变量的取值范围；2.二次根式有意义的条件.41．（2023·湖南长沙·校联考二模）4的算术平方根是（）A ．2B ．2±C ．8D ．16【答案】A【分析】如果一个数x 的平方等于(0)a a ≥，那么这个数x 叫做a 的平方根，可以表示为平方根叫做a 的算术平方根．正数的算术平方根是正数，0的算术平方根是0，负数没有算术平方根．【详解】解：42=，故选：A ．【点睛】本题考查算术平方根的定义，明确平方根与算术平方根的区别与联系是本题的关键．42．（2023·重庆九龙坡·重庆市育才中学校考一模）x）A ．0B ．2C ．3D ．5【答案】D【分析】根据二次根式有意义的条件进行求解即可．∴40x -≥，即4x ≥，∴四个选项中只有D 选项中的5符合题意，故选：D ．【点睛】本题主要考查了二次根式有意义的条件，熟知二次根式有意义的条件是被开方数大于等于零是解题的关键．43．（2023·甘肃平凉·的结果是．【答案】2【分析】根据二次根式的性质进行化简即可．2=．故答案为：2．()()(0000a a a a a a ⎧⎪===⎨⎪-⎩＞）＜．44．（2021·黑龙江大庆·=【答案】4【分析】先算4(2)-，再开根即可．==4=故答案是：4．【点睛】本题考查了求一个数的4次方和对一个实数开根号，解题的关键是：掌握相关的运算法则．45．（2023·广东茂名·校考一模）已知实数x，y |4|0y -=，则1x y -=⎛⎫⎪⎝⎭．【答案】2【分析】根据算术平方根的非负性，绝对值的非负性得出24x y ==，，进而根据负整数指数幂进行计算即可求解．40y -=0≥，40y -≥，∴20x -=，40y -=，∴24x y ==，，∴11112422x y ---⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭===．故答案为：2．【点睛】本题主要考查了算术平方根和绝对值的非负性、负整数次幂等知识点，根据非负性正确求得x 、y 的值是解答本题的关键．46．（2023·福建福州·校考二模）已知2a =2b =22a b ab -的值等于．【答案】【分析】先求出a b -=1ab =，再由()22a b ab ab a b -=-进行求解即可．【详解】解：∵2a =2b =∴22a b -=++=((22431ab =+⨯-=-=，∴22a b ab -()ab a b =-1=⨯=故答案为：【点睛】本题主要考查了二次根式的混合运算、求代数式的值，正确得到a b -=1ab =是解题的关键47．（2023·山东聊城·x 的取值范围是．【答案】12x ≥【分析】根据二次根式有意义的条件可得210x -≥，即可．【详解】解：由题意得：210x -≥，解得：12x ≥，故答案为：12x ≥．【点睛】此题主要考查了二次根式有意义的条件，关键是掌握二次根式中的被开方数是非负数．48．（2023·安徽滁州·校考模拟预测）计算)11-的结果等于．【答案】22【分析】直接利用平方差公式进行简便运算即可．【详解】解：)2211123122=-=-=，故答案为：22【点睛】本题考查的是二次根式的乘法运算，熟练的利用平方差公式进行简便运算是解本题的关键．49．（2023·陕西西安·校考模拟预测）－64的立方根是．【答案】-4【分析】直接利用立方根的意义，一个数的立方等于a ，则a 的立方根是这个数进行求解．【详解】解：根据立方根的意义，一个数的立方等于a ，则a 的立方根是这个数，可知-64的立方根为-4．故答案为：-4．【点睛】本题考查了立方根，解题的关键是掌握一个数的立方等于a ，则a 的立方根是这个数．50．（2023·云南昭通·x 的取值范围是．【答案】x＞8【分析】由分式的分母不等于零和二次根式的被开方数是非负数得到x﹣8＞0．【详解】解：由题意，得x﹣8＞0，解得x＞8．故答案是：x＞8．【点睛】考查了分式有意义的条件和二次根式有意义的条件，注意，二次根式在分母上，所以不能取到0．51．（2023·四川泸州·四川省泸县第一中学校考三模）函数y=x的取值范围是．【答案】x>3【分析】求函数自变量的取值范围，就是求函数解析式有意义的条件，根据二次根式被开方数必须是非负数和分式分母不为0的条件.x30x3x>3x30x3-≥≥⎧⎧⇒⇒⎨⎨-≠≠⎩⎩．52．（2023·河南洛阳·统考一模）计算：22-=．【答案】74-【分析】先计算22-，再算减法．【详解】解：原式17244=-=-．故答案为：74-．【点睛】本题考查了实数的计算，掌握负整数指数幂、二次根式的化简是解决本题的关键．53．（2023·安徽蚌埠·统考三模）计算：212022--=．【答案】2023【分析】根据有理数的乘方，二次根根式的性质，化简绝对值进行计算即可求解．【详解】解：212022--=122022-++2023=，故答案为：2023．【点睛】本题考查了有理数的乘方，二次根根式的性质，化简绝对值，正确的计算是解题的关键．54．（2022·新疆·x的取值范围是．【答案】x≥3【分析】直接利用二次根式有意义的条件得到关于x的不等式，解不等式即可得答案.【详解】由题意可得：x—3≥0，解得：x≥3，故答案为：x≥3【点睛】本题考查了二次根式有意义的条件，熟练掌握二次根式的被开方数是非负数是解题的关键.55．（2023·黑龙江哈尔滨·统考三模）计算=．【答案】【分析】先根据二次根式的性质化简，然后根据二次根式的加减法则求解即可．【详解】解：=-2=-=故答案为：【点睛】本题主要考查了二次根式的性质、二次根式的加减运算等知识点，灵活运用二次根式的的性质化简是解题的关键．x的取值范围是．56．（2023·云南昆明·一模）要使式子3有意义，x≥【答案】5【分析】二次根式中的被开方数是非负数，依此即可求解．x-≥，【详解】解：依题意有：50x≥．解得5x≥．故答案为：5【点睛】本题考查了二次根式有意义的条件，关键是熟悉二次根式中的被开方数是非负数的知识点．57．（云南省丽江市华坪县2020-2021=．【答案】6【分析】利用二次根式的乘法法则进行求解即可．==．6故答案为：6．【点睛】本题考查了二次根式的乘法，熟练掌握二次根式的乘法法则和二次根式的性质是解题的关键．58．（2023·山西·模拟预测）计算：=．【答案】【分析】先化简二次根式，再根据二次根式的加减计算法则求解即可．【详解】解：3=⨯=+=故答案为：【点睛】本题主要考查了二次根式的加减计算，二次根式的化简，正确计算是解题的关键．59．（2023·重庆沙坪坝·重庆八中校考模拟预测）如果2y=+，那么yx的值是．【答案】225【分析】根据二次根式有意义的条件，求出,x y的值，进而求出y x的值即可．【详解】解：∵2y=，∴150,150x x -≥-≥，∴15150x x -=-=，∴15,2x y ==，∴215225y x ==；故答案为：225．【点睛】本题考查二次根式有意义的条件，代数式求值．熟练掌握二次根式的被开方数是非负数，是解题的关键．60．（江西省崇仁县第二中学2016-2017学年八年级上学期第二次月考数学试题）计算:=【答案】61．（2015年初中毕业升学考试（山东滨州卷）数学（带解析））计算的结果为．【答案】﹣1【分析】此题用平方差公式计算即可.【详解】22=-23=-1=-62．（2023·黑龙江哈尔滨·=．【答案】3【分析】根据二次根式的化简方法和运算法则进行计算．【详解】解：原式33==【点睛】本题考查二次根式的计算，在化简二次根式的基础上再把同类二次根式合并．63．（福建省永春县第一中学2017【分析】根据二次根式乘法，加减法运算法则计算即可．【详解】解：原式＝【点睛】本题考查了二次根式的混合运算，熟练掌握二次根式的化简方法是解题的关键．64．（2023·广东茂名·校考一模）先化简，再求值：2121211x x x x +⎛⎫÷+ ⎪-+-⎝⎭其中1x +．【答案】11x -；2【分析】先通分算括号内的，把除化为乘，再约分，化简后将x 的值代入计算．【详解】解：212(1)211x x x x +÷+-+-211(1)1x x x x ++=÷--211(1)1x x x x +-=⋅-+11x =-，当1x =+时，原式=2=．【点睛】本题考查了分式化简求值，掌握分式的基本性质，将分式通分和约分进行化简是关键．65．（2023·四川泸州·011+()3-23－【答案】【分析】根据实数的混合运算法则即可求解．011+()3-23－=(1+32-=1+32-+【点睛】此题主要考查实数的运算，解题的关键是熟知实数的性质及运算法则．66．（2023·安徽六安·1+【分析】先计算算术平方根．化简绝对值，求解立方根，再合并即可．1+=+-413=【点睛】本题考查是算术平方根的含义，化简绝对值，求解立方根，实数的混合运算，掌握“算术平方根与立方根的含义”是解本题的关键．67．（2022·新疆·统考中考真题）计算：20-+(2)|(3【分析】分别计算有理数的乘方、绝对值、二次根式及零指数幂，再进行加减即可．【详解】解：原式451=++=【点睛】本题考查有理数的乘方，绝对值和二次根式的化简及零指数幂的性质，属于基础题，正确运算是=．解题的关键．要熟练掌握：任何一个不等于零的数的零次幂都等于1a。

3-5年职业规划(精选10篇)

3-5年职业规划随着社会的发展和竞争的加剧，职场人员的规划也越来越在意起来。

职业规划是指对职业发展的关注、思考和安排，是各位同学在职业生涯中必须要进行的重要工作。

在此，笔者提出3-5年职业规划的设想，以供参考。

1. 建立职业目标首先应该建立一个明确的职业目标，按照这个目标去规划和安排职业生涯的发展。

目标的设立应当具有可行性和切实性，同时要注意设定目标的时间限制。

在进行目标的设立时，同学们可以参考即将走向的行业和自身的特长和优势。

2. 学习技能和知识在现代社会中，技术和知识是一个人能否在职场上获得成功的关键。

同学们在职业规划中需要时刻保持自身的学习热情，提高自身的技能水平和知识储备。

在职场中，了解最新的发展趋势和技术方法，将会是同学们不断前进和成功的关键。

3. 扩展社交圈"熟人"在职场中的重要性不可忽视。

建立良好的人脉关系，在职业规划中具有非常重要的作用。

在职场中，可以通过多参与一些行业活动、参加职业俱乐部或者社交网络，认识更多的人，获得更多的发展机会和资源。

4. 探究及早思考职场走向除了进行对已有职业领域的深入思考，同学们同样需要关注新的职业领域。

现代社会发展速度之快，职业领域也在不断扩大和更新，寻找新的领域，及早布局，将有望在未来取得成功。

5.提升自身的关键能力职场成功需要具备一定的关键能力，比如领导力、沟通能力、组织能力等等。

同学们在职业规划中应该注重提升这些能力，进行自我反思和定位，同时也需要不断地探究和试错。

6. 坚持自信和决心即便在职业规划中有了明确的目标和计划，在职场中也难免遇到各种考验和挫折。

这个时候，拥有自信和决心是非常重要的。

同学们应该坚信自己能够成功，为职业目标而奋斗。

总之，职业规划是一个长期的过程，需要不断地思考和努力。

在此，笔者强烈建议同学们在日常生活中多关注职场和行业动态，并向身边成功人士寻求建议和指导。

希望大家能够在职业规划中持续前进，最终达成自己的职业目标。

一年级下册数学思维训练第二课堂教案

一年级下册数学思维训练第二课堂教案第一讲找规律画图形教学目标我们在认识图形、数图形、按规律填数的基础上来学习按规律填图。

对于一组按一定的变化规律排列起来的图形，我们通过对图形大小、图形的颜色，图形的排列及图形所处的位置等方面的仔细观察，找出其中变化规律，并正确地画出所要填的图。

例题与思维【例题】找规律在空格处填图形。

【思路点拨】：仔细观察所给的第一、三行，可以发现，每行的第二个图形平移到第一个图形中就变成了第三个图形。

因此可以推断，第二行空格处应填图形“×”。

【解法】：空格处应填图形“×”。

思考与练习1.请你根据前面几幅的规律接着画。

2.摆一摆，画一画，一个横线上画一个图形。

（1）☆○☆○☆○☆（2）◆◆◆◇◆◆◆◇◆（3）▲△▲△△▲△△△3.根据前面几幅图的规律，接着画。

4.后面2个方框里应该怎么画？请你试一试。

○○○○○○○○○○○○○○○△△△△△△5. 下面的4组图形中，哪一组的排列规律与其它3组不同？在（）里打“√”。

（）（）（）（）第二讲找规律填数教学目标根据已知数的排列规律，进行合理地分析、推理，找出不知道的数，使所填写的数字符合一定的要求，这类问题通常称为找规律填数。

【例题】根据前面几个数的排列规律，在（）里填上合适的数。

（1）1、3、5、7、（）、（）13 。

（2）20、17、（）、（）、8、（）。

（3）1、2、4、5、7、8、10、（）、（）。

【思路点拨】第（1）组数的排列规律是：后一个数比它前面的一个数多2 。

第（2）组数的排列规律是：后一个数比它前面的一个数少3 。

第（3）组数的排列规律是：第一个数增加1是第二个数，第二个数增加2是第三个数，第三个数增加1是第四个数，第四个数增加2是第五个数，即从前往后增加数的规律依次是1，2，1，2…… 【解法】（1）1、3、5、7、9、11、13 。

（2）20、17、14、11、8、5 。

七年级数学上册第一单元测试题人教版3篇

七年级数学上册第一单元测试题人教版3篇篇一：人教版初一数学上册第一章有理数单元测试题及答案有理数单元测试题满分100分时间60分一、选择题（本题共有10个小题，每小题都有A、B、C、D四个选项，请你把你认为适当的选项前的代号填入题后的括号中，每题2分，共20分）1、下列说法正确的是（）A整数就是正整数和负整数B负整数的相反数就是非负整数C有理数中不是负数就是正数D零是自然数，但不是正整数2、下列各对数中，数值相等的是（）A －27与(－2)7B －32与(－3)2C －3×23与－32×2D ―(―3)2与―(―2)33、在－5，－9，－3.5，－0.01，－2，－212各数中，最大的数是（）A.－12B.－9C.－0.01D.－54、如果一个数的平方与这个数的差等于0，那么这个数只能是（）A. 0B.－1C.1D. 0或15、绝对值大于或等于1，而小于4的所有的正整数的和是（）A. 8B. 7C. 6D. 56、计算：(－2)100+(－2)101的是（）A. 2100B.－1C.－2D.－21007、比－7.1大，而比1小的整数的个数是（）A. 6B. 7C. 8D. 98、2003年5月19日，国家邮政局特别发行万众一心，抗击“非典”邮票，收入全部捐赠给卫生部门用以支持抗击“非典”斗争，其邮票发行为12050000枚，用科学记数法表示正确的是( )A．1.205×107 B．1.20×108 C．1.21×107 D．1.205×1049、下列代数式中，值一定是正数的是( )A．x2 B.|－x+1| C.(－x)2+2 D.－x2+110、已知8.622＝74.30，若x2＝0.7430，则x的值等于（）A. 86. 2B. 862C. ±0.862D. ±86211、一幢大楼地面上有12层，还有地下室2层，如果把地面上的第一层作为基准，记为0，规定向上为正，那么习惯上将2楼记为；地下第一层记作；数－2的实际意义为，数＋9的实际意义为。

高中物理教科版选修3-5教学案：第一章第1节碰撞 Word版含答案

第1节碰__撞( 对应学生用书页码P1 )一、碰撞现象1、碰撞做相对运动的两个( 或几个)物体相遇而发生相互作用，运动状态发生改变的过程。

2、碰撞特点( 1 )时间特点:在碰撞过程中，相互作用时间很短。

( 2 )相互作用力特点:在碰撞过程中，相互作用力远远大于外力。

( 3 )位移特点:在碰撞过程中，物体发生速度突变时，位移极小，可认为物体在碰撞前后仍在同一位置。

试列举几种常见的碰撞过程。

提示:棒球运动中，击球过程；子弹射中靶子的过程；重物坠地过程等。

二、用气垫导轨探究碰撞中动能的变化1、实验器材气垫导轨，数字计时器、滑块和光电门，挡光条和弹簧片等。

2、探究过程( 1 )滑块质量的测量仪器:天平。

( 2 )滑块速度的测量仪器:挡光条及光电门。

( 3 )数据记录及分析，碰撞前、后动能的计算。

三、碰撞的分类1、按碰撞过程中机械能是否损失分为:( 1 )弹性碰撞:碰撞过程中动能不变，即碰撞前后系统的总动能相等，E k1＋E k2＝E k1′＋E k2′。

( 2 )非弹性碰撞:碰撞过程中有动能损失，即动能不守恒，碰撞后系统的总动能小于碰撞前系统的总动能。

E k1′＋E k2′＜E k1＋E k2。

( 3 )完全非弹性碰撞:碰撞后两物体黏合在一起，具有相同的速度，这种碰撞动能损失最大。

2、按碰撞前后，物体的运动方向是否沿同一条直线可分为: ( 1 )对心碰撞( 正碰 ):碰撞前后，物体的运动方向沿同一条直线。

( 2 )非对心碰撞( 斜碰 ):碰撞前后，物体的运动方向不在同一直线上。

( 高中阶段只研究正碰 )。

( 对应学生用书页码P1 )探究一维碰撞中的不变量1.探究方案方案一:利用气垫导轨实现一维碰撞 ( 1 )质量的测量:用天平测量。

( 2 )速度的测量:v ＝Δx Δt ，式中Δx 为滑块( 挡光片 )的宽度，Δt 为数字计时器显示的滑块( 挡光片 )经过光电门的时间。

( 3 )各种碰撞情景的实现:利用弹簧片、细绳、弹性碰撞架、胶布、撞针、橡皮泥设计各种类型的碰撞，利用滑块上加重物的方法改变碰撞物体的质量。

高中物理新教材的使用体会--选择性必修1、2、3教材

高中物理新教材的使用体会--选择性必修1、2、3教材摘要：本文从新、旧教材的对比变化，及使用过程中的体会讨论如何更好地使用新教材以适应新高考的要求。

关键词：新教材变化新高考一、新教材的变化总体变化：①选择性必修教材相对旧教材知识章节编排顺序上变化较大②各章节知识优化组合，删去了难度较大或非主干内容，增加了必做实验③减少了每个章节的节数，增加了每一节的知识内容（每一节内容都很饱满）④部分知识内容由正文转为拓展性学习内容或以习题形式呈现，有的甚至用简单的旁批代替(一)选择性必修教材相对旧教材知识章节编排顺序上变化较大1、选修3-1的绝大部分内容放在必修3教材中；2、选修3-1、3-2、3-4、3-5的部分内容放在必修3中最后一章；3、《电磁波》由选修3-4调整编排在选择性必修2中；4、《动量》由选修3-5调整编排在选择性必修1中；5、选修3-3《热学》和选修3-5近代物理部分合并为选择性必修3；6、选修3-4《相对论简介》精减内容后放在必修2第七章第5节。

(二)各章节知识优化组合，删去了难度较大或非主干内容，增加了必做实验删除的难度较大或非主干内容：《电路》删除了简单逻辑门电路；《电磁感应》删除反电动势内容；《交变电流》删除互感器内容；《电磁波》删除电磁波与信息化社会；《气体》删除了饱和汽和饱和汽压、物态变化中的能量交换；《机械波》删除了惠更斯原理等内容；《光》删除了光的颜色和色散、液晶显示、全息照相等内容；《相对论》保留了狭义相对论的时空观，删除了广义相对论及其他内容；《波粒二象性》删除了概率波、不确定性关系；《原子核》删除了探测射线的方法；原子核中质子与中子的比例；增加的必做实验：1、用单摆测量重力加速度2、探究影响感应电流方向的因素3、探究变压器原、副线圈电压与匝数的关系4、用油膜法估测油酸分子的大小5、探究等温情况下一定质量气体压强与体积的关系(三)减少了每个章节的节数，增加了每一节的知识内容（每一节内容都很饱满）1、《电磁感应》由7节压缩为5节内容：旧教材1~2节合并为一节内容放在必修3第十三章；旧教材第5节拆分为二，“动生电动势”放在《法拉第电磁感应定律》那一节，“感生电场”放在《涡流》那一节；2、《传感器》由4节压缩为3节内容：旧教材2~3节合并为1节；3、《电磁波》由5节压缩为4节内容：删除旧教材电磁波与信息化社会1节；4、《机械波》由7节压缩为5节内容：旧教材第2、3节《波动图像》和《波长、频率、波速》合并为1节内容；第4、5节合并为1节《波的反射、折射和衍射》；5、《光》由8节压缩为6节内容：旧教材“薄膜干涉”和“双缝干涉”合并为《光的干涉》1节内容；激光和光的偏振合为1节；6、《热学》由19节压缩为13节内容：旧教材第一章1、2、3节实验单独称为1节，其他内容合并为1节，第三章功和内能、热和内能2节合并为1节，热力学第二定律的微观解释与热力学第二定律合并为1节，删除饱和汽和饱和汽压、物态变化中的能量交换2节，能源与可持续性发展1节放在必修3第十二章；7、《原子结构和波粒二象性》由9节压缩为5节内容：删除了概率波和不确定性关系2节内容，电子的发现和核式结构合并为1节，氢原子光谱和玻尔原子模型合并为1节；8、《原子核》由8节压缩为5节内容：删除了探测射线的方法1节；放射性的应用与防护与放射性元素的衰变合并为1节；核裂变和核聚变合并为1节。

2022-2023学年北京市海淀区七年级上册数学期中专项提升模拟(卷一卷二)含解析

2022-2023学年北京市海淀区七年级上册数学期中专项提升模拟（卷一）一、选一选（本大题共10小题，每小题3分，共30分）1. －5的相反数是()A. B. C. 5 D. -515-152. 在数：3.14159，1.010010001…，7.56，π，中，无理数的个数有（）227A .1个B. 2个C. 3个D. 4个3. 下列各式符合代数式书写规范的是　( )A. B. a×3 C. 3x-1个D. 2nb a124. 下列代数式中，单项式共有（）a ，　2ab ，，x+y ，x 2+y 2，　1，3x 2312ab cA. 2个B. 3个C. 4个D. 5个5. 下面计算正确的是（）A. 6a -5a ＝1 B. a ＋2a 2＝3a 2C. -（a -b ）＝-a ＋bD. 2（a ＋b ）＝2a ＋b6. 用代数式表示“m 的3倍与n 的差的平方”，正确的是（）A.B.C. D.()23m n -()23m n -23m n-()23m n -7. 对有理数a 、b ，规定运算如下：a※b=a +ab ，则﹣2※3的值为（）A. 8B. 6C. 4D. 28. 甲、乙两班共有98人，若从甲班调3人到乙班，那么两班人数正好相等．设甲班原有人数是x 人，可列出方程（）A. 98+x ＝x ﹣3 B. 98﹣x ＝x ﹣3C. （98﹣x ）+3＝xD. （98﹣x ）+3＝x ﹣39.如图是计算机程序计算，若开始输入x=则输出的结果是（）12-A. 11B. -11C. 12D. -1210. 某小朋友用手指按如图所示的规则练习数数，数到2017时对应的手指是（）（各手指对应依次为大拇指、食指、中指、无名指、小拇指）A. 大拇指B. 食指C. 中指D. 无名指二、填空题（本大题共8小题，每空2分，共24分）11. ﹣2的值是_____，﹣3的倒数是_____．12. 比较大小（用“＜”或“＞”填空）：﹣_____　；　|　8|_____　（　3）．233413. 单项式﹣的系数是_____次数是_____．32x yπ14. 已知关于x 的方程ax +4=1﹣2x 的解为x=3，则a=_____．15. 若单项式2x 2m ﹣3y 与﹣8x 3y n ﹣1是同类项，则m=_____；n=_____．16. 若，则代数式的值为______.2212x x --=2247x x --17. 若关于x 、y 的多项式3x |m|y 2+（m　2）x 2y﹣4是四次三项式，则m 的值为_____．18. 将正整数从1开始，按如图所表示的规律排列．规定图中第m 行、第n 列的位置记作（m ，n ），如正整数8的位置是（2，3），则正整数137的位置记作_____．三、解答题（本大题共9小题，共56分）19. 计算：（1）﹣10﹣（﹣16）+（　24）（2）（）×（　20 ）111245+-（3）　14+（　2）2　6×（）1231-20. 化简下列各式：（1）2a 2b ﹣3ab ﹣14a 2b +4ab（2）5（x +y ）﹣4（3x ﹣2y ）+3（2x ﹣y ）21. 解方程：（1）4﹣x=3（2﹣x）（2）．121146x x -+-=22. 有理数、、在数轴上的位置如图：a b c (1)判断正负，用“>”或“<”填空：－c 0，＋0，c －0.b a b a (2)化简：| b －c|＋|＋b|－|c －a|a 23. 已知：A ＝2a 2＋3ab －2a －1，B ＝－a 2＋ab ＋1（1）当a ＝－1，b ＝2时，求A +2B 的值；（2）若（1）中的代数式的值与a 的取值无关，求b 的值．24. 问题背景：小红同学在学习过程中遇到这样一道计算题“计算4×3.142　4×3.14×3.28+3.282”，他觉得太麻烦，估计应该有可以简化计算的方法，就去请教崔老师．崔老师说：你完成下面的问题后就可能知道该如何简化计算啦！获取新知：请你和小红一起完成崔老师提供的问题：（1）填写下表：x=　1，y=1x=1，y=0x=3，y=2x=1，y=1x=5，y=3A=2x　y 32417B=4x 2　4xy+y 294（2）观察表格，你发现A 与B 有什么关系？解决问题：（3）请上述的有关信息，计算4×3.142　4×3.14×3.28+3.282．25. 定义一种新运算：观察下列各式：1⊙3=1×4+3=73⊙（　1）=3×4　1=115⊙4=5×4+4=244⊙（　3）=4×4　3=13（1）请你想一想：a⊙b= ；（2）若a≠b，那么a⊙b b⊙a（填入“=”或“≠”）（3）若a⊙（﹣2b）=4，则2a﹣b= ；请计算（a﹣b）⊙（2a+b）的值．26. 小明的妈妈在某玩具厂工作，厂里规定每个工人每周要生产某种玩具140个，平均每天生产20个，但由于种种原因，实际每天生产量与计划量相比有出入．下表是小明妈妈某周的生产情况（超产记为正、减产记为负）：星期一二三四五六日增减产值+10　12　4+8　1+60（1）根据记录的数据可知小明妈妈星期三生产玩具个；（2）根据记录的数据可知小明妈妈本周实际生产玩具个；（3）该厂实行“每日计件工资制”，每生产一个玩具可得工资5元，若超额完成任务，则超过部分每个另奖3元；少生产一个则倒扣3元，那么小明妈妈这一周的工资总额是多少元？（4）若将上面第（3）问中“实行每日计件工资制”改为“实行每周计件工资制”，其他条件没有变，在此方式下小明妈妈这一周的工资与按日计件的工资哪一个更多？请说明理由．27. 如图所示，在数轴上A点表示数a，B点表示数b，且a、b满足|2a+6|+|b　9|=0（1）点A表示的数为，点B表示的数为；（2）若点A与点C之间的距离表示为AC，点B与点C之间的距离表示为BC，请在点A、点B 之间的数轴上找一点C，使BC=2AC，则C点表示的数为；（3）在（2）的条件下，若一动点P从点A出发，以3个单位长度/秒速度由A向B运动；同一时刻，另一动点Q从点C出发，以1个单位长度/秒速度由C向B运动，终点都为B点．当一点到达终点时，这点就停止运动，而另一点则继续运动，直至两点都到达终点时才结束整个运动过程．设点Q运动时间为t秒．请用含t的代数式表示：点P到点A的距离PA= ，点Q到点B的距离QB= ；点P与点Q之间的距离 PQ= ．2022-2023学年北京市海淀区七年级上册数学期中专项提升模拟（卷一）一、选一选（本大题共10小题，每小题3分，共30分）1. －5的相反数是()A. B. C. 5 D. -515-15【正确答案】C【分析】根据相反数的定义解答即可．【详解】-5的相反数是5．故选C ．本题考查了相反数，熟记相反数的定义：只有符号没有同的两个数互为相反数是关键．2. 在数：3.14159，1.010010001…，7.56，π，中，无理数的个数有（）227A. 1个 B. 2个C. 3个D. 4个【正确答案】B【详解】根据无理数的定义“无限没有循环小数叫做无理数”分析可知，上述各数中，属于无理数的有：两个.1.010010001π 、故选B.3. 下列各式符合代数式书写规范的是　( )A. B. a×3 C. 3x-1个D. 2nb a12【正确答案】A【分析】根据书写规则，分数没有能为带分数，没有能出现除号，乘号通常简写成“•”或者省略没有写，单位名称前面的代数式没有是单项式要加括号，对各项的代数式进行判定，即可求出答案．【详解】解：根据代数式的书写规范要求,选项B 中3应写在a 前,即写成3a,选项C 中3x-1应加括号,即(3x-1)个,选项D 中2应写成,即写成n,125252故B,C,D 均错误，故选A.此题考查了代数式的书写．注意代数式的书写要求：（1）在代数式中出现的乘号，通常简写成“•”或者省略没有写；（2）数字与字母相乘时，数字要写在字母的前面；（3）在代数式中出现的除法运算，一般按照分数的写法来写．带分数要写成假分数的形式．4. 下列代数式中，单项式共有（）a ，　2ab ，，x+y ，x 2+y 2，　1，3x 2312ab cA. 2个B. 3个C. 4个D. 5个【正确答案】C【详解】根据单项式的定义：“表示数与字母乘积的式子叫做单项式，特别的，单独的一个数和字母也是单项式”分析可知，上述各式中，属于单项式的有：共计2312 1 2a ab ab c 、、、--4个.故选C.5. 下面计算正确的是（）A. 6a -5a ＝1 B. a ＋2a 2＝3a 2C. -（a -b ）＝-a ＋bD. 2（a ＋b ）＝2a ＋b 【正确答案】C【详解】解：A ．6a ﹣5a =a ，故此选项错误，没有符合题意；B ．a 与没有是同类项，没有能合并，故此选项错误，没有符合题意；22a C ．﹣（a ﹣b ）=﹣a +b ，故此选项正确，符合题意；D ．2（a +b ）=2a +2b ，故此选项错误，没有符合题意；故选C ．6. 用代数式表示“m 的3倍与n 的差的平方”，正确的是（）A.B.C. D.()23m n -()23m n -23m n-()23m n -【正确答案】A【详解】解：∵m 的3倍为，3m ∴m 的3倍与n 的差为，3m n -∴m 的3倍与n 的差的平方为．()23m n -故选：A本题主要考查了列代数式，明确题意，准确得到数量关系是解题的关键．7. 对有理数a 、b ，规定运算如下：a※b=a +ab ，则﹣2※3的值为（）A. 8B. 6C. 4D. 2【正确答案】A【详解】∵a※b=a+ab ，∴　2※3=-2+（-2）×3=-2+（-6）=-8.故选A.8. 甲、乙两班共有98人，若从甲班调3人到乙班，那么两班人数正好相等．设甲班原有人数是x 人，可列出方程（）A. 98+x ＝x ﹣3 B. 98﹣x ＝x ﹣3C. （98﹣x ）+3＝xD. （98﹣x ）+3＝x ﹣3【正确答案】D【分析】直接根据两班人数正好相等列方程即可．【详解】解：设甲班原有人数是x 人，（98﹣x ）+3＝x ﹣3．故选：D ．此题主要考查根据等量关系列方程，解题的关键是找出等量关系．9. 如图是计算机程序计算，若开始输入x=则输出的结果是（）12-A. 11B. -11C. 12D. -12【正确答案】B【详解】由题意可得：当输入时，12x =-∵，14(1)152-⨯--=->-∴需将-1转回输入端，∵当时，，1x =-14(1)35-⨯--=->-∴需将-3转回输入端，∵当时，，3x =-34(1)115-⨯--=-<-∴可将-11输出，即输出结果是：-11.故选B.点睛：解这类按“程序”计算的问题时，当计算结果没有符合“输出”条件时，需将计算结果返回到“输入端”作为下计算的“输入”数据，直到计算结果符合“输出”条件时，停止运算，输出结果.10. 某小朋友用手指按如图所示的规则练习数数，数到2017时对应的手指是（）（各手指对应依次为大拇指、食指、中指、无名指、小拇指）A. 大拇指B. 食指C. 中指D. 无名指【正确答案】A【详解】观察、分析可知，按题意数数从大拇指到小拇指，再从小拇指到大拇指，数字增加了8，即数字在大拇指上出现的周期为8，∵2017÷8=252……1，∴数到2017时，对应的手指是大拇指.故选A.二、填空题（本大题共8小题，每空2分，共24分）11. ﹣2的值是_____，﹣3的倒数是_____．【正确答案】①. 2，②. -12【分析】根据当a 是正有理数时，a 的值是它本身a ；乘积是1的两数互为倒数进行计算即可．根据乘积为1的两个数互为倒数，可得一个数的倒数．【详解】解： -4的值是4； -2的倒数是-.12（1）此题主要考查了倒数和值，关键是掌握倒数定义和值的性质．（2）本题考查了倒数，分子分母交换位置是求一个数的倒数的关键．12. 比较大小（用“＜”或“＞”填空）：﹣_____　；　|　8|_____　（　3）．2334【正确答案】①. ＞②. ＜【详解】（1）∵，，且，2283312-==3394412-==981212>∴；2334->-（2）∵，，且，88--=-(3)3--=83-<∴.8(3)--<--故答案为（1）>；（2）<.13. 单项式﹣的系数是_____次数是_____．32x yπ【正确答案】①.②. 42π-【详解】单项式的系数是，次数是4.32x yπ-2π-故；4.2π-在本题中，圆周率要看作常数，而没有能作为字母因数.π14. 已知关于x 的方程ax +4=1﹣2x 的解为x=3，则a=_____．【正确答案】-3【详解】∵关于的方程的解为，x 412ax x +=-3x =∴，解得.34123a +=-⨯3a =-故答案为-3.15. 若单项式2x 2m ﹣3y 与﹣8x 3y n ﹣1是同类项，则m=_____；n=_____．【正确答案】①. 3②. 2【详解】∵单项式与是同类项，232m x y -318n x y --∴ ，解得： .23311m n -=⎧⎨-=⎩32m n =⎧⎨=⎩故答案为（1）3；（2）2.16. 若，则代数式的值为______.2212x x --=2247x x --【正确答案】-1.【分析】直接将已知变形，进而代入原式求出答案．【详解】∵x 2-2x-1=2，∴x 2-2x=3，∴代数式2x 2-4x-7=2（x 2-2x ）-7=2×3-7=-1．故-1．此题主要考查了代数式求值，正确将原式变形是解题关键．17. 若关于x 、y 的多项式3x |m|y 2+（m　2）x 2y﹣4是四次三项式，则m 的值为_____．【正确答案】-2【详解】∵关于的多项式是四次三项式，x y 、223(2)4mx y m x y +--∴ ，解得：m=-2.220m m ⎧=⎨-≠⎩故答案为-2.点睛：本题是考查多项式的次数与项数的问题，需注意“m ”的取值需同时满足两个条件：（1）多项式的项：的次数是4；（2）第二项；的系数的值没有能为0.23mx y 2(2)m x y -(2)m -18. 将正整数从1开始，按如图所表示的规律排列．规定图中第m 行、第n 列的位置记作（m ，n ），如正整数8的位置是（2，3），则正整数137的位置记作_____．【正确答案】（12，8）【详解】试题分析：根据题意可得：正整数137的位置为（12，8）．考点：规律题三、解答题（本大题共9小题，共56分）19. 计算：（1）﹣10﹣（﹣16）+（　24）（2）（）×（　20 ）111245+-（3）　14+（　2）2　6×（）1231-【正确答案】（1）　18；（2）　11；（3）2．【详解】试题分析：（1）先把减法统一为加法，再按有理数的加法法则计算即可；（2）先用乘法分配律将括号去掉，再按有理数的乘法法则计算即可；（3）先确定好运算顺序，再按有理数相关运算的法则计算即可.试题解析：（1）原式=　10+16　24=　10　8=　18；（2）原式=　10　5+4=　11；（3）原式=　1+4　3+2=2．20. 化简下列各式：（1）2a 2b ﹣3ab ﹣14a 2b +4ab（2）5（x +y ）﹣4（3x ﹣2y ）+3（2x ﹣y ）【正确答案】（1）﹣12a 2b +ab ；（2）﹣x +10y ．【分析】（1）直接合并同类项即可；（2）先去括号，再合并同类项即可.【详解】（1）原式=﹣12a 2b +ab ；（2）原式=5x +5y ﹣12x +8y +6x ﹣3y =﹣x +10y ．21. 解方程：（1）4﹣x=3（2﹣x）（2）．121146x x -+-=【正确答案】（1）x=1；（2）x=　17．【详解】试题分析：按解一元方程的一般步骤解答即可.试题解析：（1）去括号，得：4　x=6　3x ，移项，得：﹣x+3x=6　4，合并同类项，得：2x=2，系数化为1，得：x=1；（2）去分母，得：3（x　1）　12=2（2x+1），去括号，得：3x　3　12=4x+2，移项，得：3x　4x=2+3+12，合并同类项，得：﹣x=17，系数化为1，得：x=　17．22. 有理数、、在数轴上的位置如图：a b c (1)判断正负，用“>”或“<”填空：－c 0，＋0，c －0.b a b a (2)化简：| b －c|＋|＋b|－|c －a|a 【正确答案】（1）<,<, >;（2）-2b【分析】（1）根据数轴得出a<0<b<c ，|b|<|a|<|c|，即可求出答案；（2）去掉值符号，合并同类项即可．【详解】(1)∵从数轴可知：a<0<b<c ，|b|<|a|<|c|，∴b−c<0，a+b<0，c−a>0，(2)∵b−c<0，a+b<0，c−a>0，∴|b−c|+|a+b|−|c−a|=c−b+(−a−b)−(c−a)=c−b−a−b−c+a=−2b.此题考查数轴、值、整式的加减，解题关键在于数轴判断值的大小.23. 已知：A ＝2a 2＋3ab －2a －1，B ＝－a 2＋ab ＋1（1）当a ＝－1，b ＝2时，求A +2B 的值；（2）若（1）中的代数式的值与a 的取值无关，求b 的值．【正确答案】（1）5ab ﹣2a +1，﹣7；（2）b =．25【分析】（1）先将A =2a 2+3ab ﹣2a ﹣1，B =﹣a 2+ab +1代入A +2B 并化简，再将a =﹣1，b =2代入化简后的式子计算即可；（2）把（1）中所得式子看着关于“a ”的代数式，则由题意可知，式子中字母a 的系数之和为0，由此可得关于字母b 的方程，解方程即可求得b 的值.【详解】（1）∵A =2a 2+3ab ﹣2a ﹣1，B =﹣a 2+ab +1，∴A +2B =2a 2+3ab ﹣2a ﹣1+2（﹣a 2+ab +1）=2a 2+3ab ﹣2a ﹣1﹣2a 2+2ab +2=5ab ﹣2a +1．∴当a =﹣1，b =2时，A +2B =﹣10+2+1=﹣7．（2）∵A +2B =5ab ﹣2a +1=（5b ﹣2）a +1，且代数式的值与a 的取值无关，∴5b ﹣2=0，∴b =．2524. 问题背景：小红同学在学习过程中遇到这样一道计算题“计算4×3.142　4×3.14×3.28+3.282”，他觉得太麻烦，估计应该有可以简化计算的方法，就去请教崔老师．崔老师说：你完成下面的问题后就可能知道该如何简化计算啦！获取新知：请你和小红一起完成崔老师提供的问题：（1）填写下表：x=　1，y=1x=1，y=0x=3，y=2x=1，y=1x=5，y=3A=2x　y 32417B=4x 2　4xy+y 294（2）观察表格，你发现A 与B 有什么关系？解决问题：（3）请上述的有关信息，计算4×3.142　4×3.14×3.28+3.282．【正确答案】（1）16，1，49；（2）B=A 2；（3）9．【详解】试题分析：（1）将所给“”的值代入B 中计算即可得到对应的值，再填入表格即可；x y 、（2）观察、分析表格中的数据可得：B 的值等于A 的值的平方；（3）观察、分析可知，式子中的3.14相当于A 、B 中的，而3.28相当于A 、B 中的，由此即x y 可得到原式的值=（2×3.14-3.28）2=9.试题解析：（1）当x=3，y=2时，B=4x 2　4xy+y 2=4×32　4×3×2+22=16；当x=1，y=1时，B=4x 2　4xy+y 2=4×12　4×1×1+12=1；当x=5，y=3时，B=4x 2　4xy+y 2=4×52　4×5×3+32=49．填入表格如下：x=　1，y=1x=1，y=0x=3，y=2x=1，y=1x=5，y=3A=2x　y 32417B=4x 2　4xy+y 294　16　　1 　49 （2）观察、分析表格中的数据可得：B=A 2；（3）4×3.142　4×3.14×3.28+3.282=（2×3.14　3.28）2=9．25. 定义一种新运算：观察下列各式：1⊙3=1×4+3=73⊙（　1）=3×4　1=115⊙4=5×4+4=244⊙（　3）=4×4　3=13（1）请你想一想：a ⊙b= ；（2）若a ≠b ，那么a ⊙b b ⊙a （填入“=”或“≠”）（3）若a ⊙（﹣2b）=4，则2a﹣b= ；请计算（a﹣b）⊙（2a+b ）的值．【正确答案】（1）4a+b ；（2）≠；（3）2；6．【详解】试题分析：（1）观察、分析所给各式可知：；4a b a b =+ （2）根据（1）中所得结论把a ⊙ b 和b ⊙ a 转为用普通代数式表达的形式，并列式表达出二者的差，可得出它们的差没有等于0，由此即可得到“”的结论；a b ¹a b b a ≠ （3）根据（1）中所得结论，把所给式子转化为普通代数式表达，再化简即可.试题解析：（1）观察、分析题目中的式子可得：a ⊙ b=4a+b ，故答案为4a+b ；（2）∵a ⊙ b=4a+b ，b ⊙ a=4b+a ，∴（a ⊙b ）　（b ⊙ a ）=（4a+b ）　（4b+a ）=4a+b　4b　a =3a-3b ，∵a≠b ，∴3a-3b≠0，∴（a ⊙b ）≠（b ⊙ a ），故答案为≠；（3）①∵a ⊙ b=4a+b ，∴a ⊙（　2b ）=4a+（　2b ）=4a　2b ，又∵a ⊙（　2b ）=4， ∴ 4=4a　2b ，∴2a　b=2，故答案为2；②∵a ⊙ b=4a+b ，∴（a　b ）⊙（2a+b ）=4（a　b ）+（2a+b ）=4a　4b+2a+b =6a　3b =3（2a　b ），又∵2a　b=2，∴原式=3×2=6．26. 小明的妈妈在某玩具厂工作，厂里规定每个工人每周要生产某种玩具140个，平均每天生产20个，但由于种种原因，实际每天生产量与计划量相比有出入．下表是小明妈妈某周的生产情况（超产记为正、减产记为负）：星期一二三四五六日增减产值+10　12　4+8　1+60（1）根据记录的数据可知小明妈妈星期三生产玩具个；（2）根据记录的数据可知小明妈妈本周实际生产玩具个；（3）该厂实行“每日计件工资制”，每生产一个玩具可得工资5元，若超额完成任务，则超过部分每个另奖3元；少生产一个则倒扣3元，那么小明妈妈这一周的工资总额是多少元？（4）若将上面第（3）问中“实行每日计件工资制”改为“实行每周计件工资制”，其他条件没有变，在此方式下小明妈妈这一周的工资与按日计件的工资哪一个更多？请说明理由．【正确答案】（1）16；（2）147；（3）小明妈妈这一周的工资总额是756元；（4）小明妈妈这一周的工资与按日计件的工资一样多．【详解】试题分析：（1）由题意可知，星期三比计划减产4个，由此可得星期三的产量为20-4=16（个）；（2）先将表格中的增减产值相加，再把所得的“和”同140相加，所得结果即为小明妈妈这周实际生产玩具的个数；（3）根据（2）中计算结果表中所给数据按题意列式计算即可；（4）按题意（2）中所得数据列式计算出按“周计件工资制”小明妈妈这周的工资收入，并和（3）中所得结果比较即可得到结论.试题解析：（1）由表格中的数据可知：小明妈妈星期三生产玩具：20　4=16（个）；（2）由题意可得：（+10）+（　12）+（　4）+（+8）+（　1）+（+6）+0=10　12　4+8　1+6=7，∴小明妈妈这周共生产玩具：140+7=147（个）；（3）由题意可得：147×5+（10+8+6）×3+（12+4+1）×（　3）=735+24×3+17×（　3）=735+72　51=756（元）．即小明妈妈这一周的工资总额是756元；（4）由题意可知，按周计件工资制，小明妈妈这周的工资为：147×5+7×3=735+21=756（元）．∴小明妈妈这一周的工资与按日计件的工资一样多．27. 如图所示，在数轴上A 点表示数a ，B 点表示数b ，且a 、b 满足|2a+6|+|b　9|=0（1）点A 表示的数为，点B 表示的数为；（2）若点A 与点C 之间的距离表示为AC ，点B 与点C 之间的距离表示为BC ，请在点A 、点B 之间的数轴上找一点C ，使BC=2AC ，则C 点表示的数为；（3）在（2）的条件下，若一动点P 从点A 出发，以3个单位长度/秒速度由A 向B 运动；同一时刻，另一动点Q 从点C 出发，以1个单位长度/秒速度由C 向B 运动，终点都为B 点．当一点到达终点时，这点就停止运动，而另一点则继续运动，直至两点都到达终点时才结束整个运动过程．设点Q 运动时间为t 秒．请用含t 的代数式表示：点P 到点A 的距离PA= ，点Q 到点B 的距离QB= ；点P 与点Q 之间的距离 PQ= ．【正确答案】（1）　3， 9；（2）1；（3）；8　t （0≤t≤8）；.()()3041248t t t ⎧≤≤⎪⎨<≤⎪⎩()()()42022424848t t t t t t ⎧-≤≤⎪-<≤⎨⎪-<≤⎩【详解】试题分析：（1）由|2a+6|+|b　9|=0“任何一个代数式的值都是非负数”和“两个非负数的和为0，则这两个数都为0”即可求出a 、b 的值；（2）由（1）中的结果可知，AB=12，BC=2AC 即可解得BC=8，再OB=9即可得到OC=1，且点C 在原点的右边，由此即可得到点C 表示的数为1；（3）由题意AB=12，BC=8可知，点P 的运动时间为4秒，点Q 的运动时间为8秒；由此可得点P 到A 的距离需分和两种情况讨论：点Q 到B 的距离为：8-t ；由于在第04t ≤≤48t <≤2秒时，点P 与点Q 重合，第4秒时，点P 得到达终点，因此点P 到点Q 的距离需分，及三种情况讨论.02t ≤≤24t <≤48t <≤试题解析：（1）∵|2a+6|+|b　9|=0∴2a+6=0，b　9=0，解得a=　3，b=9，∴点A 表示的数为﹣3，点B 表示的数为9；（2）AB=9　（　3）=12，∵BC=2AC ，∴BC=8，AC=4，∴OC=1，∴C 点表示的数为1；（3）由题意可得：①点P 到点A 的距离PA =；()()3041248t t t ⎧≤≤⎪⎨<≤⎪⎩②点Q 到点B 的距离QB=8　t （0≤t≤8）；③当0≤t≤2时，点P 与点Q 之间的距离 PQ=t+4﹣3t=4﹣2t ，当2＜t≤4时，点P 与点Q 之间的距离 PQ=3t　t　4=2t　4，当4＜t≤8时，点P 与点Q 之间的距离 PQ=8　t ．即PQ =．()()()42022424848t t t t t t ⎧-≤≤⎪-<≤⎨⎪-<≤⎩点睛：（1）任何代数式的值都是非负数；（2）两个非负数的和为0，则这两个数都为0；（3）在本题第3小题用含“t ”的式子表达P 、Q 间的距离PQ 时，需注意两个动点运动的最长时间为8秒，而点P 在第2秒时追上点Q ，在第4秒时点P 到达终点B 停止运动，点Q 在第8秒时到达终点B ，因此需分三个时间段，即：分别进行讨论.02 24 48t t t ≤≤<≤<≤，，2022-2023学年北京市海淀区七年级上册数学期中专项提升模拟（卷二）一、选一选（本大题共10小题，每小题4分，满分40分）1. 计算的结果是（）()23-+A. B. 1C. 5D. 1-5-2. 下列几何体的截面一定是圆的是（）A. 圆柱B. 圆锥C. 球D. 正方体3. 一种面粉的质量标识为“”千克，则下列面粉中合格的有（）250.25±A .B. C. D. 25.3025.5124.8024.704. 在数轴上标识4与-3的两个点之间的距离是（）A. -1B. 1C. -7D. 75. 下列图形中，没有是三棱柱的表面展开图的是（）A. B. C. D.6. 下列说确的是（）A. 两个数的和一定大于每一个加数B. 互为相反数的两个数的和等于零C. 若两数之和为正，则这两个数都是正数D. 若|a|=|b|，则a=b7. 值小于3的所有整数之和是（）A. OB. 3C. -3D. 68. 一个几何体从上面看是圆，从左面和正面看是长方形，则该几何体是（）A. 正方体B. 圆锥C. 圆柱D. 球9. 若有理数x ，y 满足|x|=1.|y|=2，且x+y 为正数，则x+y 等于（）A. 1B. 2C. 3D. 1或310. 如图，将直角三角形绕其斜边旋转一周，得到的几何体为（）A. B. C. D.二、填空题（本大题共4小题，每小题5分，满分20分）11. ﹣1的相反数是_____．12. 小志家冰箱的冷冻室的温度为-6℃，调高4℃后的温度为____________.13. 由两个长方体组合而成的一个立体图形，从两个没有同的方向看得到的形状图如图所示，根据图中所标尺寸（单位：mm ）可知这两个长方体的体积之和是____________mm 3.14. 将若干个正方体小方块堆放在一起，形成一个几何体，分别从正面看和从上面看，得到的图形如图所示，则这对小方块共有____________块.三、（本大题共2小题，每小题8分，满分16分）15. 计算：；()121223--+-+-16. 计算.10.53 2.757.54⎛⎫---+-⎪⎝⎭四、（本大题共2小题，每小题8分，满分16分）17. 如图所示是一个正方体纸盒的展开图，按虚线折成正方体后，若使相对面上的两数互为相反数，试写出A、B、C分别表示的数.18. 画数轴表示下列有理数，并用“<”连接各数.-2.5；0；4；-1；0.4.五、（本大题共2小题，每小题10分，满分20分）19. 实数a，b，c在数轴上的位置如图所示.（1）比较大小：|a|与|b|.（2）化简：|c|-|a|+|-b|+|-a|.20.如图所示是一个正方体骰子的表面展开图，将其折叠成正方体骰子，请根据要求回答问题：（1）若1点在上面，3点在左面，则几点在前面？（2）若3点在下面，则几点在上面？六、（本题满分12分）21. 如图所示是某几何体的三种形状图.（1）说出这个几何体的名称.（2）若从正面看到的形状图是长为15cm，宽为4cm的长方形，从左面看到的形状图是宽为3cm的长方形，从上面看到的形状图是最长的边长为5cm，求这个几何体的侧面积（没有包括上下底面）.七、（本题满分12分）22. 某水果店香蕉，前未卖完的香蕉会有部分由于没有新鲜而损耗，未损耗的水果第二天继续，当天结束时，若库存较前减少，则记为负数，若库存较前增加，则记为正数.10月1日至10月5日的经营情况如下表：日期10月1日10月2日10月3日10月4日10月5日购进（千克）5545505050库存变化（千克）4-2-82-3损耗（千克）141221（1）10月3日卖出香蕉千克.（2）问卖出香蕉至多的是哪？（3）这五天经营结束后，库存是增加了还是减少了？变化了多少？八、（本题满分14分）23. 如图，半径为1个单位的圆片上有一点Q与数轴上的原点重合（提示：圆的周长C=2πr，本题中π的取值为3.14）（1）把圆片沿数轴向右滚动1周，点Q到达数轴上点A的位置，则点A表示的数是．（2）圆片在数轴上向右滚动的周数记为正数，圆片在数轴上向左滚动的周数记为负数，依次运动的情况记录如下：+2，-1，-5，+4，+3，-2.①第几次滚动后，Q点距离原点最近？第几次滚动后，Q点距离原点最远？②当圆片结束运动后，Q 点运动的路程共有多少？此时点Q 所表示的数是多少？2022-2023学年北京市海淀区七年级上册数学期中专项提升模拟（卷二）一、选一选（本大题共10小题，每小题4分，满分40分）1. 计算的结果是（）()23-+A. B. 1C. 5D. 1-5-【正确答案】B【分析】直接利用有理数的加法法则计算得出答案．【详解】解：．(2)31-+=故选：．B 此题主要考查了有理数的加法法则，正确掌握相关运算法则是解题关键．2. 下列几何体的截面一定是圆的是（）A. 圆柱 B. 圆锥C. 球D. 正方体【正确答案】B【详解】求体的截面一定是圆.所以选C.3. 一种面粉的质量标识为“”千克，则下列面粉中合格的有（）250.25±A. B. C. D. 25.3025.5124.8024.70【正确答案】C【分析】根据一种面粉的质量标识为“25±0.25千克”，可以求出合格面粉的质量的取值范围，从而可以解答本题．【详解】解：说明合格范围为千克千克之间，250.25±24.75~25.25则C 正确．本题考查正数和负数，解题的关键是明确正负数在题目中的实际意义．4. 在数轴上标识4与-3的两个点之间的距离是（）A. -1B. 1C. -7D. 7【正确答案】D【详解】4-(-3)=7.所以选D.5. 下列图形中，没有是三棱柱的表面展开图的是（）A. B. C. D.【正确答案】D【详解】利用棱柱及其表面展开图的特点解题．解：A、B、C中间三个长方形能围成三棱柱的侧面，上、下两个三角形围成三棱柱的上、下两底面，故均能围成三棱柱，均是三棱柱的表面展开图．D围成三棱柱时，两个三角形重合为同一底面，而另一底面没有．故D没有能围成三棱柱．故选D．6. 下列说确的是（）A. 两个数的和一定大于每一个加数B. 互为相反数的两个数的和等于零C. 若两数之和为正，则这两个数都是正数D. 若|a|=|b|，则a=b【正确答案】B【详解】选项A. 1+（-2）=1.A错误.选项B. 互为相反数的两个数的和等于零,正确.选项C. 1+（-2）=1,C错误.选项 D. 若|a|=|b|，则a=b.D错误.所以选B.7. 值小于3的所有整数之和是（）A. OB. 3C. -3D. 6【正确答案】A【详解】1+2+3+0-1-2-3=0,所以选A.8. 一个几何体从上面看是圆，从左面和正面看是长方形，则该几何体是（）A.正方体B. 圆锥C. 圆柱D. 球【正确答案】C【详解】这个图象是圆柱体.所以选C.9. 若有理数x，y满足|x|=1.|y|=2，且x+y为正数，则x+y等于（）A. 1B. 2C. 3D. 1或3【正确答案】D【详解】因为|x|=1.|y|=2，1±2±所以x=,y=,所以x+y=3或者1.所以选D.10. 如图，将直角三角形绕其斜边旋转一周，得到的几何体为（）A. B. C. D.【正确答案】D【分析】已知图形，将图中的三角形绕其斜边旋转一周，所得到的几何体应该是两个底面重合的圆锥，且下面的圆锥的高大于上面圆锥的高；再根据各选项，选出其从正面看所得到的图形，问题即可得解.【详解】因为由题意可知：旋转一周所得的几何体是两个底等相连的圆锥，所以该几何的主视图是两个底边相等的等腰三角形相连.故选D.本题考查了旋转的性质，解题的关键是判断出旋转后得到的图形.二、填空题（本大题共4小题，每小题5分，满分20分）11. ﹣1的相反数是_____．【正确答案】1【分析】根据相反数的定义可得出答案．【详解】根据相反数的定义，得﹣1的相反数是1．本题考查了相反数的意义，一个数的相反数就是在这个数前面添上“-”号；一个正数的相反数是负数，一个负数的相反数是正数，0的相反数是0．12. 小志家冰箱的冷冻室的温度为-6℃，调高4℃后的温度为____________.【正确答案】-2℃【详解】-6+4=-2°C.13. 由两个长方体组合而成的一个立体图形，从两个没有同的方向看得到的形状图如图所示，根据图中所标尺寸（单位：mm ）可知这两个长方体的体积之和是____________mm 3.【正确答案】128【详解】下面的长方体：2．6896⨯⨯=上面的长方体：432．42⨯⨯=两个长方体的体积之和：96+32=128，故128．14. 将若干个正方体小方块堆放在一起，形成一个几何体，分别从正面看和从上面看，得到的图形如图所示，则这对小方块共有____________块.【正确答案】4或5【详解】如图方块有4或5块.三、（本大题共2小题，每小题8分，满分16分）15. 计算：；()121223--+-+-【正确答案】176-【详解】试题分析：利用值直接计算.试题解析：原式=-1+216+=.176-16. 计算.10.53 2.757.54⎛⎫---+-⎪⎝⎭【正确答案】-2【详解】试题分析：把分数化成小数，直接计算.试题解析：原式=-0.5+（3.25+2.75）-7.5=6-8=-2.点睛：熟练掌握常用分数和小数的互化：，，，，10.52=10.254=10.25=10.1258= ,10.110=,,.20.45=30.65=340.3750.885==，四、（本大题共2小题，每小题8分，满分16分）17. 如图所示是一个正方体纸盒的展开图，按虚线折成正方体后，若使相对面上的两数互为相反数，试写出A 、B 、C 分别表示的数.【正确答案】-5，π，32【详解】试题分析：由相反数的定义和正方体各面的位置关系可得.试题解析：A ，B ，C 分别表示-5，π，.3218. 画数轴表示下列有理数，并用“<”连接各数.-2.5；0；4；-1；0.4.【正确答案】图形见解析【详解】试题分析：把每个数标到数轴上.试题解析：如图所示-2.50<-1<0<0.4<4.五、（本大题共2小题，每小题10分，满分20分）19. 实数a ，b ，c 在数轴上的位置如图所示.（1）比较大小：|a|与|b|.（2）化简：|c|-|a|+|-b|+|-a|.。

健康管理实务练习题(附参考答案)

健康管理实务练习题（附参考答案）一、单选题（共90题，每题1分，共90分）1.不属于肥胖症和伴有并发症患者肥胖干预策略的是A、进行健康教育B、重点预防其肥胖程度进一步加重，预防出现与肥胖相关的并发症C、进行选择性干预D、对已出现并发症的患者进行疾病管理E、争取家属配合正确答案：C2.健康管理在我国兴起与快速发展的原因不包括A、我国民众健康物质文化和精神需求增加B、国民物质与精神生活不断改善与提高C、我国健康管理理论与技术已成熟和完善D、国际健康产业和健康管理行业的发展E、中国改革开放以来社会经济持续发展正确答案：C3.现代社会中身体活动不足是造成多种慢性病流行增加的原因。

糖尿病合并糖尿病足的患者在进行身体活动时应注意的事项不包括A、运动初期随身携带糖果B、建议跳高、跑步等运动方式C、运动量和强度安排要循序渐进D、每天运动前应检查足部E、运动时选择合适的鞋子正确答案：B4.吴女士，46岁，汉族，文职人员。

身高155cm，体重68kg，血压165/88mmHg，腰围82cm。

工作压力大，经常加班，喜爱喝可乐及吃零食，很少参加体育运动。

其父母健在，均患有高血压病。

吴女士可改变性行为是A、身高B、运动不足C、高血压家族史D、年龄E、性别正确答案：B5.实现初级卫生保健的关键是A、高能特效药物B、现代化的医学设备C、适宜的卫生技术D、高精尖的医疗设备E、社会经济的高度发展正确答案：C6.关于肥胖的概念，最合适的描述是A、是由多因素引起的脂肪细胞体积增大、数量增多，导致体脂占体重的比例增高的慢性代谢性疾病B、体重指数（BMI）成年人≥28kg/m2C、体重指数（BMI）成年人≥24kg/m2且&lt；28kg/m2D、腰围成年男性≥85cm，成年女性≥80cmE、体重超过了所对应的正常标准正确答案：A7.健康风险评估一般需要按照基本的步骤来进行，其中的跟踪指导随访以及效果评估对保证健康管理的效果至关重要，请根据掌握的知识回答下列问题。