二进制转BCD码

八位二进制码转化为BCD码及余三码、BCD码转化余三码

河南科技大学课程设计说明书课程名称 EDA技术题目八位二进制转化为BCD码及余三码、BCD码转化为余三码学院车辆与动力工程学院班级学生姓名指导教师日期2012年7月14号八位二进制码转化为BCD码及余三码、BCD码转化余三码摘要八位二进制数转化为BCD码和余三码的转换在计算机语言中起到了非常重要的作用，通过这次的课程设计让我们更好地掌握二进制数转化为BCD 码和余三码。

二进制转化为余三码不能直接转化，只能通过BCD码为中介进而转化成余三码。

余三码（余3码）是由8421BCD码加上0011形成的一种无权码，由于它的每个字符编码比相应的8421BCD码多3，故称为余三码。

BCD码的一种。

余三码是一种对9的自补代码，因而可给运算带来方便。

其次，在将两个余三码表示的十进制数相加时，能正确产生进位信号，但对“和”必须修正。

修正的方法是：如果有进位，则结果加3；如果无进位，则结果减3。

如，（526）10进制=（0101 0010 0110）8421BCD码=（1000 0101 1001）余3码EDA技术打破了软件和硬件间的壁垒，使计算机的软件技术与硬件实现、设计效率与产品性能合二为一，它代表了电子设计技术和应用技术的发展方向。

VHDL主要用于描述数字系统的接口，结构和功能，它的语法简单易懂，移植性好。

本设计采用VHDL，Altera公司的Quartus II软件仿真，来实现八位二进制到BCD和BCD到余三码的转换。

由于八位二进制的最大范围是0~255，而八位BCD码的范围是0~99，故在转换时输入信号只能取99以内的数。

关键词：八位二进制、BCD码、余三码、VHDL目录第一章绪论 (1)§1.1 课程设计题目 (1)§1.2 设计目的 (2)§1.3 课程设计要求 (2)第二章EDA、VHDL简介 (3)§2.1 EDA简介 (3)§2.2 VHDL简介 (3)第三章设计过程 (5)§3.1设计规划 (5)§3.2各个模块设计及原理图 (5)§3.2.1八位二进制码转化为八位BCD码 (5)§3.2.2八位BCD码转化为八位余三码 (6)§3.2.3八位二进制码转化为8位余三码 (7)第四章系统仿真 (9)§4.1八位二进制码转化为八位BCD码仿真及分析 (9)§4．2八位BCD码转化为八位余三码仿真及分析 (9)§4.3八位二进制码转化为八位余三码仿真及分析 (10)第五章总结 (11)参考文献 (12)第一章绪论随着计算机科学与技术突飞猛进地发展，用数字电路进行信号处理的优势也更加突出，自20世纪70年代开始，这种用数字电路处理模拟信号的所谓“数字化”浪潮已经席卷了电子技术几乎所有的应用领域EDA是电子设计自动化（Electronic Design Automation）的缩写，在20世纪90年代初从计算机辅助设计（CAD）、计算机辅助制造（CAM）、计算机辅助测试（CAT）和计算机辅助工程（CAE）的概念发展而来的。

verilog实现任意位二进制转换BCD

verilog实现任意位二进制转换BCD一直感觉这是个很简单的问题，直到突然自己连BCD都不太清楚的时候，才发现这没有看起来那么简单，这里介绍里任意位二进制转为BCD的verilog代码，这个转换方法也可以用在C上面，此为原创，转载请注明，谢谢。

基础知识：BCD：BCD码又称为8421码，意义：之所以有时候需要将binary转换为BCD，一般是用在本科的实验中，为了将binary显示在数码管中，当然还有很多应用，只是目前我还没有用到。

转换算法：左移加3法移位加3法的具体原理，在网上感觉也没有人能够说的清楚，以后找到书籍再说吧。

下面解释下左移加三算法。

这里以8bit二进制数FF做例子。

该算法的操作为上图。

下面对上图的操作进行详细的解释：由于8bit的二进制最大为FF，转换为十进制为255。

所以需要使用三个BCD码来表示所有的8bit二进制数。

上图的hundreds表示百位的BCD，tens表示十位的BCD，Units表示个位的BCD。

算法的操作为一直将binary数据左移，移出的数据按顺序存在hundreds，tens，Units。

例如上面的shift1，shift2，shift3操作后，Units变为了0111，至于为何在shift3后进行add3操作，是因为在算法中每一次左移，都要对hundreds，tens和Units进行判断，如果hundreds，tens和Units里面的值大于或等于5，就将hundreds，tens和Units自加3.所以shift3后，Units里面为0111，表示为7，此时不能左移，而是对Units加三操作，所以Units的值从0111变为了1010.值得注意的是，只要hundreds，tens和Units中任意一个的值大于或等于5（0101），就要先进行一次自加三的操作，然后才能继续左移，后面的操作同上。

注意2：n位的binary就需要进行n次左移注意3：最后一次左移不需要进行add3操作注意4: 亲自推导16位的，和24位的binary转换，结果正确，所以该算法适用于任意位binarytoBCD，当然这种论断没有足够的理论依据。

二进制与BCD码转换资料

16位二进制数转换成BCD码的的快速算法－51单片机2010-02-18 00:43在做而论道上篇博文中，回答了一个16位二进制数转换成BCD码的问题，给出了一个网上广泛流传的经典转换程序。

程序可见：/%D7%F6%B6%F8%C2%DB%B5%C0/blog/item/6154551f93ba561440341732. html中的HEX2BCD子程序。

.说它经典，不仅是因为它已经流传已久，重要的是它的编程思路十分清晰，十分易于延伸推广。

做而论道曾经利用它的思路，很容易的编写出了48位二进制数变换成16位BCD码的程序。

但是这个程序有个明显的缺点，就是执行时间太长，转换16位二进制数，就必须循环16遍，转换48位二进制数，就必须循环48遍。

上述的HEX2BCD子程序，虽然长度仅仅为26字节，执行时间却要用331个机器周期。

.单片机系统多半是用于各种类型的控制场合，很多时候都是需要“争分夺秒”的，在低功耗系统设计中，也必须考虑因为运算时间长而增加系统耗电量的问题。

为了提高整机运行的速度，在多年前，做而论道就另外编写了一个转换程序，程序的长度为81字节，执行时间是81个机器周期，（这两个数字怎么这么巧！）执行时间仅仅是经典程序的1/4！.近来，在网上发现了一个链接：/news/Article/uc/uc8051/200803/4751.html，也对这个经典转换程序进行了改进，话是说了不少，只是没有实质性的东西。

这篇文章提到的程序，一直也没有找到，也难辩真假。

这篇文章好像是选自某个著名杂志，但是在术语的使用上，有着明显的漏洞，不像是专业人员的手笔。

比如说文中提到的：“使用51条指令代码，但执行这段程序却要耗费312个指令周期”，就是败笔。

51条指令代码，真不知道说的是什么，指令周期是因各种机型和指令而异的，也不能表示确切的时间。

.下面说说做而论道的编程思路。

;-----------------------------------------------------------------------;已知16位二进制整数n以b15~b0表示，取值范围为0~65535。

汇编语言16位二进制转bcd码 8086

题目：深度探讨汇编语言下16位二进制转BCD码的实现方法在计算机科学与技术领域中，汇编语言是一种底层的编程语言，适用于对硬件进行直接控制和优化。

而16位二进制转BCD码正是其中一个常见的应用场景。

在本文中，我们将深入探讨在8086汇编语言下实现16位二进制转BCD码的方法，并分析其原理和实现步骤。

1. 汇编语言简介汇编语言是一种低级语言，与机器语言一一对应，因此可以直接操作计算机硬件。

相比高级语言，如C语言和Java，汇编语言执行效率更高，并且能够精确地控制硬件资源。

在8086汇编语言中，我们可以直接操作寄存器和内存，实现对16位二进制数据的处理。

2. 16位二进制转BCD码的原理BCD码是一种二进制编码方式，用4位二进制数表示一位十进制数。

16位二进制数转BCD码的核心思想就是将每一位二进制数转换为对应的BCD码。

在8086汇编语言中，我们可以通过多次除以10和取余数来完成这一转换过程，具体步骤如下：1) 将16位二进制数存放在两个8位寄存器中；2) 用除法指令将两个8位寄存器中的内容转换为对应的BCD码；3) 将转换后的BCD码存放在指定的内存单元中。

3. 实现方法及步骤下面我们将详细介绍实现16位二进制转BCD码的具体步骤，以帮助读者更好地理解和掌握这一转换方法。

步骤1：准备工作在开始之前，我们需要先准备好16位二进制数和相应的寄存器、内存单元等资源。

在8086汇编语言中，我们可以使用DW（定义字）指令定义16位二进制数，使用MOV（将数据从一个位置转移到另一个位置）指令将数据加载到寄存器中。

步骤2：除法运算接下来，我们需要使用DIV（无符号数除法）指令将16位二进制数转换为BCD码。

通过多次除以10和取余数的运算，我们可以得到每一位二进制数对应的BCD码。

步骤3：存储结果我们将转换后的BCD码存放在指定的内存单元中，以便后续的处理和使用。

4. 总结及个人观点总体来说，在8086汇编语言下实现16位二进制转BCD码的过程相对复杂，需要进行多次除法运算和数据转移。

二进制,十进制,十六进制,ASCII,BCD码的转换,单片机

1.在片内RAM 30H单元有-个8位二进制数，将其转换成压缩BCD码，存于片内RAM 41H（高位）40H（低位）中。

方法：2^8=256,所以8位二进制A<=256,A/100商是百位数，存放到41h单元，余数再除以10，再得商是10位数,高低位互换，) ORG 0100HSTART:MOV A,30H ;取来8位二进制数MOV B,#100DIV AB ;除以100MOV 41H,A ;商是百位数，存放到41h单元MOV A,B ;取回余数MOV B,#10DIV AB ;再除以10SWAP A ;商是10位数,高低位互换ORL A,BMOV 40H,A ;将十位数与个位位数存入40hSJMP $END2.一个字节（8位）BCD码转换为二进制数（方法：先将高半字节乘以10，再加上低半字节）设待转换的BCD码存放于R2中DTOB:MOV A,R2ANL A,#0F0HSWAP AMOV B,#0AHMUL ABMOV R3,AMOV A,R2ANL A,#0FHADD A,R3RET3.二进制数转换为ASCII码设(30H)=4BH,将高4位的ASCII码放在31H单元,低4位的ASCII码放在32H单元,程序具有通用性,向入口参数30H存入任何数,都能将其变成相应的ISCII 码.ORG 0000HLJMP MAINORG 0030HMAIN:MOV SP,#60HMOV 30H,#4BHMOV R2,30HMOV A,R2ANL A,#0FHCJNE A,#0AH,NEQNEQ: JC LOOPADD A,#37HJMP LOOP3LOOP:ADD A,#30HLOOP3:MOV 31H,AMOV A,R2SWAP AANL A,#0FHCJNE A,#0AH,NE1NE1: JC LOOP1ADD A,#37HJMP LOOP4LOOP1:ADD A,#30HLOOP4:MOV 32H,AA1: SJMP A1END4.已知R0的低半个字节为一个四位的二进制数，要求将其转换为ASCAII码后送回R0中。

16位二进制转换为BCD码的C51汇编程序

MOV A,@R1
SWAP A
ANL 36H,#0F0H
MOV A,36H
SWAP A
MOV 30H,A
RET
XIANSHI:MOV DPTR,#TAB
DE: MOV R6,#0FFH
DJNZ R6,$
DJNZ R7,DE
RET
TAB:DB 3FH,05H,5BH,4FH,65H,6EH,7EH,07H,7FH,6FH
DB 0BFH,85H,0DBH,0CFH,0E5H,0EEH,0FEH,87H,0FFH,0EFH
UBCD: MOV A,34H
CJNE A,#00H,WUWEI
MOV R1,#35H
MOV R0,#36H
MOV A,#00H
XCHD A,@R0
AJMP RETURN
JIA: CLR C
MOV A,36H
ADDC A,#56H
DA A
MOV 36H,A
MOV A,35H
16位二进制转BCD码的程序算法及51汇编实现：
n=b15~b0
n=[b15~b8]*256+[b7~b0]
=[b15~b12]*4096+[b11~b0]
,高四位[b15~b12]取值范围为0~15，代表了4096的个数
n=[b15~b12]*4000+{[b15~b12]*(100-4)+[b11~b0]}
[b6~b0]中减去2*y
就有：
n=n=4*x(千位）+(x+y)(百位）+3*y(十位）+[b6~b0]-2*y
由此，就可以明确由高9位[b15~b7]变换出来十进制的各个位的数值，可能大于9，到最后整理一下即可。

74ls48的功能级原理

74ls48的功能级原理
74LS48是一种数字集成电路，具有四位二进制BCD编码器功能。

BCD编码器将4位的二进制数转换为BCD码，BCD码用4位二进制数表示十进制数字0-9。

74LS48的功能原理如下：
1. 数据输入：74LS48有四个输入引脚（A, B, C 和D），输入为4位二进制数。

2. BCD编码：根据输入的4位二进制数，74LS48会将其转换为对应的BCD码。

BCD码共有四位，每位用一个输出引脚（a, b, c 和d）表示。

3. 数据输出：74LS48的BCD码输出通过四个共阳极七段数码管（使用a, b, c 和d引脚）显示。

每个引脚对应一个数码管的一段，通过控制某一段的高低电平，来实现显示0-9的数字。

4. 输入使能控制：74LS48还拥有一个输入使能引脚（G），通过使能引脚控制，可以选择是否使能BCD编码器的工作。

当使能为低电平时，BCD编码器将停止工作，数码管显示为空。

5. 码无效检测：在74LS48中，如果输入的二进制数超出了0-9的范围，并且使能为高电平，则显示“E”。

这个功能可以用来检测输入的二进制数是否有效。

总结：74LS48是一种用于将4位二进制数转换为BCD码的编码器，通过控制四个七段数码管的高低电平，实现在数码管上显示对应的十进制数字。

八位二进制码转化为BCD码及余三码、BCD码转化余三码

河南科技大学课程设计说明书课程名称 EDA技术题目八位二进制转化为BCD码及余三码、BCD码转化为余三码学院车辆与动力工程学院班级学生姓名指导教师日期2012年7月14号八位二进制码转化为BCD码及余三码、BCD码转化余三码摘要八位二进制数转化为BCD码和余三码的转换在计算机语言中起到了非常重要的作用，通过这次的课程设计让我们更好地掌握二进制数转化为BCD 码和余三码。

二进制转化为余三码不能直接转化，只能通过BCD码为中介进而转化成余三码。

余三码（余3码）是由8421BCD码加上0011形成的一种无权码，由于它的每个字符编码比相应的8421BCD码多3，故称为余三码。

BCD码的一种。

余三码是一种对9的自补代码，因而可给运算带来方便。

其次，在将两个余三码表示的十进制数相加时，能正确产生进位信号，但对“和”必须修正。

修正的方法是：如果有进位，则结果加3；如果无进位，则结果减3。

如，（526）10进制=（0101 0010 0110）8421BCD码=（1000 0101 1001）余3码EDA技术打破了软件和硬件间的壁垒，使计算机的软件技术与硬件实现、设计效率与产品性能合二为一，它代表了电子设计技术和应用技术的发展方向。

VHDL主要用于描述数字系统的接口，结构和功能，它的语法简单易懂，移植性好。

本设计采用VHDL，Altera公司的Quartus II软件仿真，来实现八位二进制到BCD和BCD到余三码的转换。

由于八位二进制的最大范围是0~255，而八位BCD码的范围是0~99，故在转换时输入信号只能取99以内的数。

关键词：八位二进制、BCD码、余三码、VHDL目录第一章绪论 (1)§1.1 课程设计题目 (1)§1.2 设计目的 (2)§1.3 课程设计要求 (2)第二章EDA、VHDL简介 (3)§2.1 EDA简介 (3)§2.2 VHDL简介 (3)第三章设计过程 (5)§3.1设计规划 (5)§3.2各个模块设计及原理图 (5)§3.2.1八位二进制码转化为八位BCD码 (5)§3.2.2八位BCD码转化为八位余三码 (6)§3.2.3八位二进制码转化为8位余三码 (7)第四章系统仿真 (9)§4.1八位二进制码转化为八位BCD码仿真及分析 (9)§4．2八位BCD码转化为八位余三码仿真及分析 (9)§4.3八位二进制码转化为八位余三码仿真及分析 (10)第五章总结 (11)参考文献 (12)第一章绪论随着计算机科学与技术突飞猛进地发展，用数字电路进行信号处理的优势也更加突出，自20世纪70年代开始，这种用数字电路处理模拟信号的所谓“数字化”浪潮已经席卷了电子技术几乎所有的应用领域EDA是电子设计自动化（Electronic Design Automation）的缩写，在20世纪90年代初从计算机辅助设计（CAD）、计算机辅助制造（CAM）、计算机辅助测试（CAT）和计算机辅助工程（CAE）的概念发展而来的。

二进制转化bcd

二进制码转BCD码在单片机里面，如：显示个温度值，这时，要取一个数的个位、十位、百位，可以用/和 %（求商和求余）来解决。

但是，在FPGA里面用求商和求余将会非常消耗资源，这样就必须用到二进制转BCD码了，这里介绍一种简单的加3移位算法。

注：B代表二进制，D代表十进制，0x代表十六进制，BCD为BCD 码,下同。

1、加3移位法以二进制数（0000_101 Xn）B＝（10+Xn）D为例，串行输入三位后，（0101）B＝5（D）左移一位后：（0000_101Xn）B＝（10+Xn）D如果（0000_101Xn）B直接输出显示为：当Xn＝0时，0000_1010＝0x0A。

此为错误的BCD码。

采用加3移位法，修正移位结果：串行输入三位后，结果大于4（0101）B＝5（D）加3：（0101）B+（0011）B＝（1000）B --十进制表示：5+3＝8 再左移一位后：（1000Xn）B＝（0001_000Xn）BCD对应十进制显示：1 Xn每四位BCD码对应一位十进制数，即：（10+Xn）D，转换成功注：Xn为下一位串行输入的二进制数。

2、设计思路这里一共需要四个模块：计数器、移位器、加法器、寄存器输出。

分别设计好之后，用状态机控制它们，就完成了。

3、仿真结果注：图中clk为时钟,en为高电平使能，rst为高电平复位，data_in为输入的12位二进制码，以十进制的形式显示在时序图；qout为输出的16位BCD码，以十六进制的形式显示在时序图，17个时钟上升沿可完成转换任务。

4、综合结果5、难点分析要搞懂这个加3移位算法，必须要按照8位二进制（11101011）转BCD过程图，自己手动推导一下，才容易理解。

此算法的难点在于，需要把输入的二进制数，按照每四个bit来划分为一个单元（所以输入的二进制数，位宽必须是4的倍数），然后，每个单元都要同时判断是否大于4，大于就要加3，否则不加.理解了这个算法之后，那么BCD转二进制就非常容易了，减3移位即可，减3可以用补码来解决。

BCD与binary的转换算法

BCD（binary-coded decimal）码亦称二进制码十进制数。

是用二进制编码的十进制代码。

在硬件电路中BCD码与二进制码的转换很常见。

在用硬件描述语言设计电路之前要先了解转换算法。

BCD to binary：一个很容易想到的思路是把BCD码转换为十进制数，然后再把十进制数转换为二进制数。

但这样会浪费硬件资源，其实BCD码和二进制数有着更简洁或者说更直接的关系。

比如十进制数458的BCD码是0100_0101_1000，二进制码是111001010 。

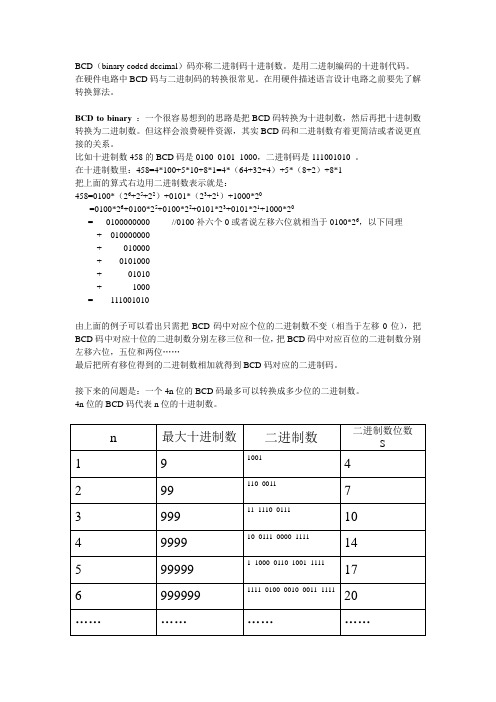
在十进制数里：458=4*100+5*10+8*1=4*（64+32+4）+5*（8+2）+8*1把上面的算式右边用二进制数表示就是：458=0100*（26+25+22）+0101*（23+21）+1000*20=0100*26+0100*25+0100*22+0101*23+0101*21+1000*20= 010******* //0100补六个0或者说左移六位就相当于0100*26，以下同理+ 010000000+ 010000+ 0101000+ 01010+ 1000= 111001010由上面的例子可以看出只需把BCD码中对应个位的二进制数不变（相当于左移0位），把BCD码中对应十位的二进制数分别左移三位和一位，把BCD码中对应百位的二进制数分别左移六位，五位和两位……最后把所有移位得到的二进制数相加就得到BCD码对应的二进制码。

接下来的问题是：一个4n位的BCD码最多可以转换成多少位的二进制数。

4n位的BCD码代表n位的十进制数。

n 最大十进制数二进制数二进制数位数S1 9 1001 42 99 110_0011 73 999 11_1110_0111 104 9999 10_0111_0000_1111 145 99999 1_1000_0110_1001_1111 176 999999 1111_0100_0010_0011_1111 20 ……………………由上表可以看出S可以由N的数学表达式给出。

汇编程序设计—二进制码转换为BCD码

汇编程序设计—二进制码转换为BCD码
一、算法原理
BCD（Binary Coded Decimal）码是把十进制数据以二进制的方式进
行编码，每四位二进制数字表示一个十进制的数字，比如数字“7”用二
进制表示为“0111”，把“0111”放在一起就是十进制数“7”的BCD码。

1）对任意两个BCD码，可以按位相加，得到结果，其运算规则如下：（1）如果两个BCD码都是规范的BCD码，其相加结果也是BCD码；
（2）如果两个BCD码的相加结果不是正确的BCD码，则可以在最高
位1的位置添加1，使之成为BCD码，另一个BCD位置上也添加1，然后
最低位置上的1被移位，最终结果也是BCD码。

2）工程实现
该BCD码转换程序主要由二进制转换为BCD码的过程组成，根据算法
原理，实现程序如下：
1.首先把输入的二进制码按4位1组进行分组，得到分组后的二进制数，如果分组后的高位不足4位，则用0补足，得到规范的二进制码；
2.对二进制码进行转换，将2进制码转换成BCD码，得到相应的BCD 码；
3.对于每组BCD码，检查它是否是正确的BCD码，如果不是则需要添
加1；
4.最后将BCD码拼接起来，就是最终的BCD码结果。

二、汇编代码
MOV AL, offset BinaryCode ; 把二进制码移到AL中MOVCL,4;CL设置为4。

八位二进制——BCD码转换器

实验报告：8位二进制-BCD码转换器姓名：学号：指导教师：一．实验目的了解二进制-BCD码转换器实现原理，掌握移位加3算法，熟悉Verilog编程中模块复用模式。

二．实验任务1.掌握用移位加三算法实现二进制-BCD码转换器的设计；2.设计Verilog实验程序；3.生成比特流文件，将文件下载到开发板中进行硬件验证。

三．实验设备1.计算机（安装Xilinx ISE 10.1软件平台）；2.NEXYS2 FPGA开发板一套（带USB-MIniUSB下载线）四．实验原理设计任意数目输入的二进制-BCD码转换器的方法就是采用移位加三算法（Shift and Add 3 Algorithm）。

此方法包含以下4个步骤：1）把二进制左移1位；2）如果共移了8位，那么BCD数就在百位、十位和个位列；3）如果在BCD列中，任何一个二进制数是5或者比5更大，那么就在BCD列的数值加上3；4）回到步骤1）。

其工作过程如图1所示：图1. 一个8位的二进制数转换成BCD码的步骤五．实验内容在Xilinx ISE 10.1上完成8位二进制-BCD码转换器设计，输入设计文件，仿真后，生成二进制码流文件下载到FPGA开发板上进行验证；1）依照实验1的方式，在Xilinx ISE 10.1中新建一个工程example02；2）在工程管理区任意位置单击鼠标右键，在弹出的快捷菜单中选择“New Source”命令，弹出新建源代码对话框，这里我们选择“Verilog Module”类型，输入Verilog文件名“binbcd8.v”,完整代码如下：module binbcd8(input [7:0] b,output reg [9:0] p);reg [17:0] z;integer i;always @(*)beginfor (i=0;i<=17;i=i+1)z[i]=0;z[10:3]=b;repeat(5) //重复5次beginif (z[11:8]>4)z[11:8]=z[11:8]+3;if (z[15:12]>4)z[15:12]=z[15:12]+3;z[17:1]=z[16:0];endp=z[17:8];endendmodule3）设计相应的7段显示管程序，将相应的十进制数在开发板的显示管上显示出来。

⼆进制转BCD码应⽤：⽤fpga实现对数码管显⽰，以前通常的⽅法是进⾏整除和取余进⾏运算，但是fpga并不擅长乘法除法运算，所以可以⽤BCD码来转换。

BCD码：通俗的可以理解为⽤四位⼆进制数表⽰⼀位⼗进制数字。

例如，256就可以⽤bcd码表⽰为：0010_1001_0110因此在数码管显⽰中，也就是把256各位分出来，就可以⽤bcd码来表⽰，下⾯说⼀种⼆进制转换bcd码的⽅法。

加3移位法：bcd码中只有0~9⼗进制数，但是在四位⼆进制中是16进制进1，因此在移位过程中要对⼆进制进⾏判断，当在移位之后的状态Qn+1⼤于9，要对Qn加6才可以。

例如1000移位⼤于9加6为0001_0110,对应bcd码中的16。

我们也可以在移位之前进⾏判断，如果移位之前的Qn数据⼤于4，说明Qn+1会溢出，所以可以+3再进⾏移位，例如1000⼤于4,加3为1011然后再进⾏移位0001_0110,16和刚才结果是⼀样的。

简单的说，判断的⽬的是防⽌下⼀次移位，发⽣数据溢出的情况思路：代码可以总结为三个部分：移位，加⼆进制数，判断（最后⼀次不需要判断）例如15 --- 1111（1）移位 0000_0000 加 0000_0001 判断 0000_0001（2）移位 0000_0010 加 0000_0011 判断 0000_0011（3）移位 0000_0110 加 0000_0111 判断 0000_1010（4）移位 0001_0100 加 0001_0101/*********************************功能：实现对6位⼗进制数以内的bcd码转换time: 2017/4/29vision:1.0*********************************/`define data_in_num 19`define data_bcd_num 23module pro_bcd(clk,rst_n,data_in,data_bcd);input clk;input rst_n;input [`data_in_num :0] data_in;output [`data_bcd_num:0] data_bcd;reg [`data_bcd_num:0] data_bcd_r;reg [1:0] state;reg [5:0] shift_cnt;always @(posedge clk or negedge rst_n)if(!rst_n)begindata_bcd_r <= 0;state <= 0;shift_cnt <= 0;endelsecase(state)2'd0:beginshift_cnt <= 0;data_bcd_r <= 0;state <= state + 1;end2'd1:begin //移位if(shift_cnt < `data_in_num + 1)begindata_bcd_r <= data_bcd_r<<1;shift_cnt <= shift_cnt + 1;state <= state + 1;endelsestate <= 0;end2'd2:begin //相加data_bcd_r <= data_bcd_r + data_in[`data_in_num + 1 - shift_cnt];state <= state + 1;end2'd3:begin //判断if(data_bcd_r[3:0] > 4 ) //1data_bcd_r <= data_bcd_r + 3;if(data_bcd_r[7:4]>4) //2data_bcd_r[7:4] <= data_bcd_r[7:4] + 3;if(data_bcd_r[11:8]>4) //3data_bcd_r[11:8] <= data_bcd_r[11:8] + 3;if(data_bcd_r[15:12]>4) //4data_bcd_r[15:12] <= data_bcd_r[15:12] + 3;if(data_bcd_r[19:16]>4) //5data_bcd_r[19:16] <= data_bcd_r[19:16] + 3;if(data_bcd_r[`data_bcd_num:20]>4) //6data_bcd_r[`data_bcd_num:20] <= data_bcd_r[`data_bcd_num:20] + 3;state <= 1;enddefault:state <= 0;endcaseassign data_bcd = (state == 3)&&(shift_cnt == `data_in_num + 1) ? data_bcd_r : data_bcd; endmodule。

二进制转化为8421bcd码

二进制转化为8421bcd码
二进制转化为8421BCD码是一种将二进制数转换为BCD码的方法。

BCD码是一种十进制数系统的二进制表示形式，即每个十进制数位用一个4位二进制数表示。

8421BCD码是BCD码中最常用的一种，根据位权原理，每个4位二进制数的位权依次为8、4、2、1。

因此，将一个二进制数转化为8421BCD码，需要将每个二进制数位分别转化为4位二进制数，并分别赋予对应的位权。

具体转换过程如下：
1. 将原二进制数从右往左按位分组，每组分别为4位二进制数。

如果最高位不足4位，则在左侧补0，直至凑成4位二进制数。

2. 对于每个4位二进制数，按照8421BCD码的位权原则，将其转化为对应的十进制数。

即，将每个二进制数位与对应的位权相乘，再将结果相加，得到该4位二进制数所表示的十进制数。

3. 将每个4位二进制数转化为对应的十进制数后，将它们按从左往右的顺序排列，得到最终的8421BCD码。

例如，将二进制数1101101011转化为8421BCD码的过程如下： 1. 将二进制数从右往左每4位分组，得到：
1101 1010 11
2. 将每个4位二进制数转化为对应的十进制数，得到：
1101 -> 13
1010 -> 10
0011 -> 3
3. 将每个十进制数按从左往右的顺序排列，得到最终的8421BCD码：
13 10 3
因此，1101101011的8421BCD码为13103。

利用verilog将二进制码转换为十进制BCD码

利用verilog将二进制码转换为十进制BCD码下面我自己加了注释小序：先说一个bear 的亲身体会，bear 在做一些fpga 小设计时经常会用到数据显示功能，比如数字时钟，数字频率计，温度计，跑表等等，往往我们会选用 led 数码管来做显示，因为它驱动起来比lcd 液晶要简单的很多，我们知道fpga 中寄存器在定义和储存的数据都是采用二进制的格式，而fpga 输出给数码管做显示的数据必须是十进制的格式，之前bear 经常会选择把一个寄存器的个位和十位分开定义，比如在做数字时钟时，就会把时，分，秒的各位和十位都分别定义成一个变量，无疑这种方法会增加代码的复杂度，所以考虑需要一个专门把二进制的数据转换成十进制BCD码的模块，在网上有一些，但是好像都不太完整，所以bear花了一下午写了一个，亲测效果不错，希望对朋友们有所帮助下面开始正文。

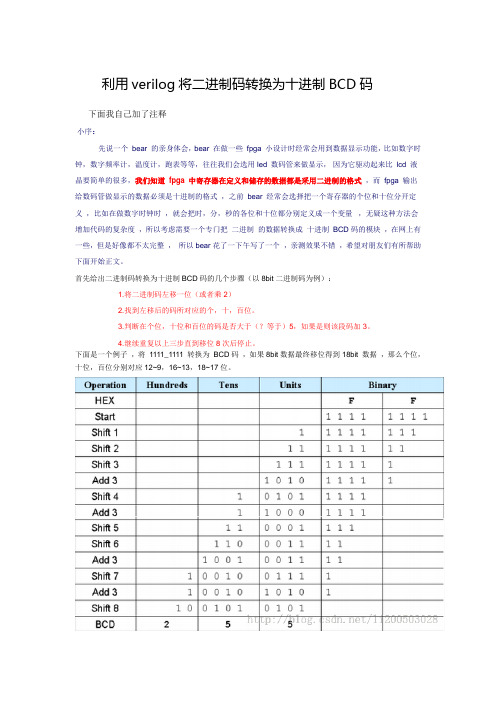
首先给出二进制码转换为十进制BCD码的几个步骤（以8bit二进制码为例）：1.将二进制码左移一位（或者乘2）2.找到左移后的码所对应的个，十，百位。

3.判断在个位，十位和百位的码是否大于（？等于）5，如果是则该段码加3。

4.继续重复以上三步直到移位8次后停止。

下面是一个例子，将1111_1111 转换为BCD码，如果8bit数据最终移位得到18bit 数据，那么个位，十位，百位分别对应12~9，16~13，18~17位。

之前写的代码在转换完之后没有对count清零，所以在仿真时候需要用rst_n清零，感谢博友onlytime417的提示，经过修改之后可以对不同的输入值连续转换，而不需要rst_n的复位，下面是修改后的代码以及仿真结果，（该转换模块已经在实际项目中应用）。

CODE:module bin_dec(clk,bin,rst_n,one,ten,hun,count,shift_reg );input [7:0] bin;input clk,rst_n;output [3:0] one,ten;output [3:0] count;output [1:0] hun;output [17:0]shift_reg;reg [3:0] one,ten;reg [1:0] hun;reg [3:0] count;reg [17:0]shift_reg=18'b000000000000000000;//全部位数，包括hun,ten,one,bin////////////////////// 计数部分////////////////////////always @ ( posedge clk or negedge rst_n )beginif( !rst_n )count<=0;else if (count==9)count<=0;elsecount<=count+1;end////////////////////// 二进制转换为十进制///////////////////判断四种情况，1：个位和十位都大于52：只有一个大于53：都不大于5always @ (posedge clk or negedge rst_n )beginif (!rst_n)shift_reg=0;else if (count==0)shift_reg={10'b0000000000,bin};else if ( count<=8) //实现8次移位操作if(shift_reg[11:8]>=5) //判断个位是否>5，如果是则+3 beginif(shift_reg[15:12]>=5) //判断十位是否>5，如果是则+3 beginshift_reg[15:12]=shift_reg[15:12]+2'b11;shift_reg[11:8]=shift_reg[11:8]+2'b11;shift_reg=shift_reg<<1; //对个位和十位操作结束后，整体左移endelsebeginshift_reg[15:12]=shift_reg[15:12];shift_reg[11:8]=shift_reg[11:8]+2'b11;//个位加3shift_reg=shift_reg<<1;endendelsebeginif(shift_reg[15:12]>=5) //十位>=5beginshift_reg[15:12]=shift_reg[15:12]+2'b11;shift_reg[11:8]=shift_reg[11:8];shift_reg=shift_reg<<1;endelsebeginshift_reg[15:12]=shift_reg[15:12];shift_reg[11:8]=shift_reg[11:8];shift_reg=shift_reg<<1;endendendend/////////////////输出赋值//////////////////////////always @ ( posedge clk or negedge rst_n )if ( !rst_n )beginone<=0;ten<=0;hun<=0;endelse if (count==9) //此时8次移位全部完成，将对应的值分别赋给个,十,百位beginone<=shift_reg[11:8];ten<=shift_reg[15:12];hun<=shift_reg[17:16];endendendmodule。

数字电路-二进制转BCD码

数字电路-⼆进制转BCD码
BCD码实际上就是将原本的⼗进制数的每⼀位⽤⼀个4位⼆进制数表⽰，每⼀位0-9。

⼆进制4位能够表达的数字范围是0-15。

由此可见BCD码的⼀段与普通四位⼆进制来表⽰⼗进制位有6的进制差。

所以这就是⼆进制转化为BCD码的关键所在。

下⾯来讲讲主要步骤：
先预估⼗进制数的位数，预先给BCD码分好段，此时的BCD码为空⽆任何数据
接着讲原本的⼆进制数的最⾼位⼀端从BCD码的最低位端插⼊，也可以看作是将⼆进制数与BCD码同时左移每次将⼆进制的头砍掉补到BCD码最后，但个⼈觉得逐位插⼊更加形象~
关键来啦，之前提到过BCD码每⼀个四位⼆进制（表⽰⼗进制的⼀位）存储范围是0-9，⽽原本的⼆进制四位的存储范围是0-15，所以⼆进制在逐位后端插⼊BCD码时，若BCD码的某⼀段（四位⼆进制）>9 则我们⼿动给该段+6强⾏使其进位满⾜BCD码的存储范围的要求--简单的说就是⼀直同时左移，某⼀段>9就+6。

这⾥可以进⾏优化，就是常⽤的+3（+011）左移法，即在左移之前先判断本段是否>4（>0100），若⼤于则左移之后必然会超过9，所以在左移之前先在该段+3（+011），那么左移之后就已经实现了进位啦。

就这么⼀直将⼆进制逐位从底端插⼊（左移），同时保持每段的范围在0-9内最终就能得到BCD码聊。

单片机二进制BCD码转换实验程序流程图

二进制BCD码转换一、实验目的1.掌握简单的数值转换算法2.基本了解数值的各种表达方法二、实验说明单片机中的数值有各种表达方式，这是单片机的基础。

掌握各种数制之间的转换是一种基本功。

我们将给定的一字节二进制数，转换成二十进制（BCD）码。

将累加器A的值拆为三个BCD码，并存入RESULT开始的三个单元，例程A赋值#123。

三、实验内容及步骤1.安装好仿真器，用串行数据通信线连接计算机与仿真器，把仿真头插到模块的单片机插座中，打开模块电源，插上仿真器电源插头（USB线）。

2.启动PC机，打开KEIL软件，软件设置为模拟调试状态。

在所建的Project文件中添加TH2.ASM源程序进行编译，编译无误后，全速运行程序，打开数据窗口(DATA) （在MEMORY#3中输入D:30H 回车），点击暂停按钮，观察地址30H、31H、32H的数据变化，30H更新为01，31H更新为02，32H更新为03。

用键盘输入改变地址30H、31H、32H的值，点击复位按钮后，可再次运行程序，观察其实验效果。

修改源程序中给累加器A的赋值，重复实验，观察实验效果。

3.打开CPU窗口，选择单步或跟踪执行方式运行程序，观察CPU窗口各寄存器的变化，可以看到程序执行的过程，加深对实验的了解。

四、流程图及源程序（见光盘中的程序文件夹）1.源程序RESULT EQU 30HORG 0000HLJMP STARTBINTOBCD：MOV B，#100DIV ABMOV RESULT，A ；除以100得百位数MOV A，BMOV B，#10DIV ABMOV RESULT+1，A ；余数除以10得十位数MOV RESULT+2，B ；余数为个位数RETSTART：MOV SP，#40HMOV A，#123CALL BINTOBCDLJMP $END2.流程图。