平面直角坐标系复习讲义
平面直角坐标系复习课件

坐标系命名
通常把横轴称为x轴,纵轴称为y轴 ,垂直于x轴的轴称为z轴。
坐标系方向
x轴正向为东,x轴负向为西;y轴正 向为北,y轴负向为南;z轴正向为 上,z轴负向为下。
坐标系中的基本元素
原点
坐标系的原点O称为原点。
坐标轴
x轴和y轴构成了平面直角坐标系的两个坐 标轴。
象限
单位长度
在坐标系中,我们把第一象限到第四象限 按照逆时针方向依次称为第一象限、第二 象限、第三象限和第四象限。
面积。
解决几何问题
利用平面直角坐标系,可以解决 各种几何问题,如求角度、证明
相等、求长度等。
平面直角坐标系在实际问题中的应用案例
天气预报
通过使用平面直角坐标系,天气预报员可以分析 和预测天气的变化趋势。
地图绘制
在地图绘制中,平面直角坐标系被广泛使用,以 便准确地表示地理信息。
航空航天领域
在航空航天领域,平面直角坐标系被用于导航、 飞行路线规划以及空间探索等。
THANKS FOR WATCHING
感谢您的观看
直线方程
描述一条直线的方程通常 形式为y=kx+b,其中k和 b是常数,x和y是变量。
曲线方程
描述一个曲线的方程通常 形式为f(x,y)=0,其中f是 函数,x和y是变量。
方程的图形表示
方程在平面直角坐标系中 的图形表示了满足方程的 点的集合。
平面直角坐标系中的点与方程的关系
点的坐标满足方程
平面直角坐标系中任意一点的坐标都满足相应的方程。
答案解析
在平面直角坐标系中,任何一个点都 可以用一对有序数对来表示其在x轴 和y轴上的坐标。
综合题
总结词 详细描述 示例题目 答案解析
中考复习 平面直角坐标系基础知识详解

平面直角坐标系目录一、平面直角坐标系二、坐标方法的简单应用三、《平面直角坐标系》全章复习与巩固一、平面直角坐标系基础知识讲解+基本典型例题解析【学习目标】1.理解平面直角坐标系概念,能正确画出平面直角坐标系.2.能在平面直角坐标系中,根据坐标确定点,以及由点求出坐标,掌握点的坐标的特征.3.由数轴到平面直角坐标系,渗透类比的数学思想.【要点梳理】要点一、有序数对定义:把有顺序的两个数a与b组成的数对,叫做有序数对,记作(a,b).要点诠释:有序,即两个数的位置不能随意交换,(a,b)与(b,a)顺序不同,含义就不同,如电影院的座位是6排7号,可以写成(6,7)的形式,而(7,6)则表示7排6号.要点二、平面直角坐标系与点的坐标的概念1. 平面直角坐标系在平面内画两条互相垂直、原点重合的数轴就组成平面直角坐标系.水平的数轴称为x 轴或横轴,习惯上取向右为正方向;竖直的数轴称为y轴或纵轴,取向上方向为正方向,两坐标轴的交点为平面直角坐标系的原点(如图1).要点诠释:平面直角坐标系是由两条互相垂直且有公共原点的数轴组成的.2. 点的坐标平面内任意一点P,过点P分别向x轴、y轴作垂线,垂足在x轴、y轴上对应的数a,b 分别叫做点P的横坐标、纵坐标,有序数对(a,b)叫做点P的坐标,记作:P(a,b),如图2.要点诠释:(1)表示点的坐标时,约定横坐标写在前,纵坐标写在后,中间用“,”隔开.(2)点P(a,b)中,|a|表示点到y轴的距离;|b|表示点到x轴的距离.(3) 对于坐标平面内任意一点都有唯一的一对有序数对(x,y)和它对应,反过来对于任意一对有序数对,在坐标平面内都有唯一的一点与它对应,也就是说,坐标平面内的点与有序数对是一一对应的.要点三、坐标平面1. 象限建立了平面直角坐标系以后,坐标平面就被两条坐标轴分成如图所示的Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分,分别叫做第一象限、第二象限、第三象限和第四象限,如下图.要点诠释:(1)坐标轴x轴与y轴上的点(包括原点)不属于任何象限.(2)按方位来说:第一象限在坐标平面的右上方,第二象限在左上方,第三象限在左下方,第四象限在右下方.2. 坐标平面的结构坐标平面内的点可以划分为六个区域:x轴,y轴、第一象限、第二象限、第三象限、第四象限. 这六个区域中,除了x轴与y轴有一个公共点(原点)外,其他区域之间均没有公共点.要点四、点坐标的特征1.各个象限内和坐标轴上点的坐标符号规律要点诠释:(1)对于坐标平面内任意一个点,不在这四个象限内,就在坐标轴上.(2)坐标轴上点的坐标特征:x轴上的点的纵坐标为0;y轴上的点的横坐标为0.(3)根据点的坐标的符号情况可以判断点在坐标平面上的大概位置;反之,根据点在坐标平面上的位置也可以判断点的坐标的符号情况.2.象限的角平分线上点坐标的特征第一、三象限角平分线上点的横、纵坐标相等,可表示为(a,a);第二、四象限角平分线上点的横、纵坐标互为相反数,可表示为(a,-a).3.关于坐标轴对称的点的坐标特征P(a,b)关于x轴对称的点的坐标为 (a,-b);P(a,b)关于y轴对称的点的坐标为 (-a,b);P(a,b)关于原点对称的点的坐标为 (-a,-b).4.平行于坐标轴的直线上的点平行于x轴的直线上的点的纵坐标相同;平行于y轴的直线上的点的横坐标相同.【基本典型例题】(1)类型一、有序数对1.如果将一张“13排10号”的电影票简记为(13,10),那么(10,13)表示的电影票是排号.【思路点拨】在平面上,一个数据不能确定平面上点的位置.须用有序数对来表示平面内点的位置.【答案】10,13.【解析】由条件可知:前面的数表示排数,后面的数表示号数.【总结升华】在表示时,先要“约定”顺序,一旦顺序“约定”,两个数的位置就不能随意交换,(a,b)与(b,a)顺序不同,含义就不同.类型二、平面直角坐标系与点的坐标的概念2.如图,写出点A、B、C、D各点的坐标.【思路点拨】要确定点的坐标,要先确定点所在的象限,再看点到坐标轴的距离.【答案与解析】解:由点A向x轴作垂线,得A点的横坐标是2,再由点A向y轴作垂线,得A点的纵坐标是3,则点A的坐标是(2,3),同理可得点B、C、D的坐标.所以,各点的坐标:A(2,3),B(3,2),C(-2,1),D(-1,-2).【总结升华】平面直角坐标系内任意一点到x轴的距离是这点纵坐标的绝对值,到y轴的距离是这点横坐标的绝对值.举一反三:【变式】在平面直角坐标系中,如果点A既在x轴的上方,又在y轴的左边,且距离x轴,y轴分别为5个单位长度和4个单位长度,那么点A的坐标为( ).A.(5,-4) B.(4,-5) C.(-5,4) D.(-4,5)【答案】D.3.在平面直角坐标系中,描出下列各点A(4,3),B(-2,3),C(-4,1),D(2,-2).【答案与解析】解:因为点A的坐标是(4,3),所以先在x轴上找到坐标是4的点M,再在y轴上找到坐标是3的点N.然后由点M作x轴的垂线,由点N作y轴的垂线,过两条垂线的交点就是点A,同理可描出点B、C、D.所以,点A、B、C、D在直角坐标系的位置如图所示.【总结升华】对于坐标平面内任意一点,都有唯一的一对有序数对和它对应;对于任意一对有序数对,在坐标平面内都有唯一的一点与它对应,也就是说,坐标平面内的点与有序实数对是一一对应的.举一反三:【变式】在平面直角坐标系中,O为坐标原点,已知:A(3,2),B(5,0),则△AOB的面积为.【答案】5.类型三、坐标平面及点的特征4.(2014春•夏津县校级期中)根据要求解答下列问题:设M(a,b)为平面直角坐标系中的点.(1)当a>0,b<0时,点M位于第几象限?(2)当ab>0时,点M位于第几象限?(3)当a为任意实数,且b<0时,点M位于何处?【思路点拨】(1)利用第四象限点的坐标性质得出答案;(2)利用第二、四象限点的坐标性质得出答案;(3)利用第三、四象限和纵轴点的坐标性质得出答案.【答案与解析】解:∵M(a,b)为平面直角坐标系中的点.(1)当a>0,b<0时,点M位于第四象限;(2)当ab>0时,即a,b同号,故点M位于第一、三象限;(3)当a为任意实数,且b<0时,点M位于第三、四象限和纵轴的负半轴.【总结升华】本题考查点的坐标的确定,正确掌握各象限对应坐标的符号是解题关键.举一反三:【变式】(2015•威海)若点A(a+1,b﹣2)在第二象限,则点B(﹣a,b+1)在()A.第一象限B.第二象限C.第三象限D.第四象限【答案】解:由A(a+1,b﹣2)在第二象限,得a+1<0,b﹣2>0.解得a<﹣1,b>2.由不等式的性质,得﹣a>1,b+1>3,点B(﹣a,b+1)在第一象限,故选:A.5.(2016春•宜阳县期中)已知点P(2m+4,m﹣1).试分别根据下列条件,求出点P的坐标.(1)点P的纵坐标比横坐标大3;(2)点P在过A(2,﹣3)点,且与x轴平行的直线上.【思路点拨】(1)根据横纵坐标的大小关系得出m﹣1﹣(2m+4)=3,即可得出m的值,进而得出P点坐标;(2)根据平行于x轴点的坐标性质得出m﹣1=﹣3,进而得出m的值,进而得出P点坐标.【答案与解析】解:(1)∵点P(2m+4,m﹣1),点P的纵坐标比横坐标大3,∴m﹣1﹣(2m+4)=3,解得:m=﹣8,∴2m+4=﹣12,m﹣1=﹣9,∴点P的坐标为:(﹣12,﹣9);(2)∵点P在过A(2,﹣3)点,且与x轴平行的直线上,∴m﹣1=﹣3,解得:m=﹣2,∴2m+4=0,∴P点坐标为:(0,﹣3).【总结升华】此题主要考查了坐标与图形的性质,根据已知得出关于m的等式是解题关键.举一反三:【变式】在直角坐标系中,点P(x,y)在第二象限且P到x轴,y轴的距离分别为2,5,则P 的坐标是_________;若去掉点P在第二象限这个条件,那么P的坐标是________.【答案】(-5,2);(5,2),(-5,2),(5,-2),(-5,-2).【基本典型例题】(2)类型一、有序数对表示位置1.如图是小刚的一张笑脸,他对妹妹说:如果我用(0,2)表示左眼,用(2,2)表示右眼,那么嘴的位置可以表示成().A.(1,0) B.(-1,0) C.(-1,1) D.(1,-1)【思路点拨】由(0,2)表示左眼,用(2,2)表示右眼,可以确定平面直角坐标系中x 轴与y轴的位置,从而可以确定嘴的位置.【答案】A.【解析】解:根据(0,2)表示左眼,用(2,2)表示右眼,可得嘴的坐标是(1,0),故答案为A.【总结升华】此题考查了坐标确定位置,由已知条件正确确定坐标轴的位置是解决本题的关键.类型二、平面直角坐标系与点的坐标的概念2.有一个长方形ABCD,长为5,宽为3,先建立一个平面直角坐标系,在此坐标系下求出A,B,C,D各点的坐标.【答案与解析】解:本题答案不唯一,现列举三种解法.解法一:以点A为坐标原点,边AB所在的直线为x轴,边AD所在直线为y轴,建立平面直角坐标系,如图(1):A(0,0),B(5,0),C(5,3), D (0,3).解法二:以边AB的中点为坐标原点,边AB所在的直线为x轴,AB的中点和CD的中点所在的直线为y轴,建立平面直角坐标系,如图(2):A(﹣2.5,0),B(2.5,0),C(2.5,3), D (-2.5,3).解法三:以两组对边中点所在直线为x轴、y轴,建立平面直角坐标系,如图(3):A(﹣2.5,-1.5),B(2.5,-1.5),C(2.5,1.5), D (-2.5,1.5).【总结升华】在不同平面直角坐标系中,长方形顶点坐标不同,说明位置的相对性与绝对性,即只要原点、x轴和y轴确定,每一个点的位置也确定,而一旦原点或x轴、y轴改变,每一个点的位置也相对应地改变.举一反三:【变式】如图所示,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),……,则点A2008的坐标为________.【答案】(-502,-502).3.平面直角坐标系中,已知△ABC 三个顶点的坐标分别是A (-3,-1),B (1,3),C (2,-3).求△ABC 的面积.【思路点拨】三角形的三边都不与坐标轴平行,根据平面直角坐标系的特点,可以将三角形的面积转化为梯形或长方形的面积减去多余的直角三角形的面积,即可求得此三角形的面积.【答案与解析】解:如图所示,过点A 、C 分别作平行于y 轴的直线与过B 点平行于x 轴的直线交于点D 、E ,则四边形ACED 为梯形,根据点A (-3,-1)、B (1,3)、C (2,-3)可求得AD =4,CE =6,DB =4,BE =1,DE =5,所以△ABC 的面积为:. 【总结升华】点的坐标能体现点到坐标轴的距离,解决平面直角坐标系中的三角形面积问题,就是要充分利用这一点,将不规则图形转化为规则图形,再利用相关图形的面积计算公式求解.类型三、坐标平面及点的特征111()222ABC S AD CE DE AD DB CE BE =+--g g g △111(46)5446114222=+⨯-⨯⨯-⨯⨯=4.(2016春•沂水县期中)已知点P(a﹣2,2a+8),分别根据下列条件求出点P的坐标.(1)点P在x轴上;(2)点P在y轴上;(3)点Q的坐标为(1,5),直线PQ∥y轴;(4)点P到x轴、y轴的距离相等.【思路点拨】根据点的坐标特征一一求解.【答案与解析】解:(1)∵点P(a﹣2,2a+8),在x轴上,∴2a+8=0,解得:a=﹣4,故a﹣2=﹣4﹣2=﹣6,则P(﹣6,0);(2))∵点P(a﹣2,2a+8),在y轴上,∴a﹣2=0,解得:a=2,故2a+8=2×2+8=12,则P(0,12);(3)∵点Q的坐标为(1,5),直线PQ∥y轴;,∴a﹣2=1,解得:a=3,故2a+8=14,则P(1,14);(4)∵点P到x轴、y轴的距离相等,∴a﹣2=2a+8或a﹣2+2a+8=0,解得:a1=﹣10,a2=﹣2,故当a=﹣10则:a﹣2=﹣12,2a+8=﹣12,则P(﹣12,﹣12);故当a=﹣2则:a﹣2=﹣4,2a+8=4,则P(﹣4,4).综上所述:P(﹣12,﹣12),(﹣4,4).【总结升华】此题主要考查了点的坐标性质,包括坐标轴上的点的坐标特征,平行于坐标轴的点的特征,以及到坐标轴的距离相等的点的特征,考察很全面.举一反三:【变式】若点C(x,y)满足x+y<0,xy>0,则点C在第_____象限.【答案】三.5.一个正方形的一边上的两个顶点O、A的坐标为O(0,0),A(4,0),则另外两个顶点的坐标是什么.【思路点拨】有点的坐标说明已有确定的平面直角坐标系,但正方形的另两个顶点位置不确定,所以应按不同位置分类去求.【答案与解析】解:不妨设另外两个顶点为B、C,因为OABC是正方形,所以OC=BA=BC=OA=4.且OC∥AB,OA∥BC,则:(1)当顶点B在第一象限时,如图所示,显然B点坐标为(4,4),C点坐标为(0,4).(2)当顶点B在第四象限时,如图所示,显然B点坐标为(4,-4),C点坐标为(0,-4).【总结升华】在解答这类问题时,我们千万不要忽略了分类讨论而导致错误.举一反三:【变式】(2015•济南)在平面直角坐标系中有三个点A(1,﹣1)、B(﹣1,﹣1)、C(0,1),点P(0,2)关于A的对称点为P1,P1关于B的对称点P2,P2关于C的对称点为P3,按此规律继续以A、B、C为对称中心重复前面的操作,依次得到P4,P5,P6,…,则点P2015的坐标是()A.(0,0)B.(0,2)C.(2,﹣4)D.(﹣4,2)【答案】A.二、坐标方法的简单应用基础知识讲解+基本典型例题解析【学习目标】1.能建立适当的平面直角坐标系描述物体的位置.2. 能在同一坐标系中,感受图形变换后点的坐标的变化.【要点梳理】要点一、用坐标表示地理位置根据已知条件,建立适当的平面直角坐标系,是确定点的位置的必经过程,只有建立了适当的直角坐标系,点的位置才能得以确定,才能使数与形有机地结合在一起.利用平面直角坐标系绘制区域内一些地点分布情况的过程:(1)建立坐标系,选择一个适当的参照点为原点,确定x轴,y轴的正方向;(2)根据具体问题确定适当的比例尺,在坐标轴上标出单位长度;(3)在坐标平面内画出这些点,写出各点的坐标和各个地点的名称.要点诠释:(1)建立坐标系的关键是确定原点和坐标轴的位置,我们一般选择那些使点的位置比较容易确定的方法,例如借助于图形的某边所在直线为坐标轴等,而建立平面直角坐标系的方法是不唯一的.所建立的平面直角坐标系也不同,得到的点的坐标不同.(2)应注意比例尺和坐标轴上的单位长度的确定.要点二、用坐标表示平移1.点的平移:在平面直角坐标系中,将点(x,y)向右或向左平移a个单位长度,可以得到对应点(x+a,y)或(x-a,y);将点(x,y)向上或向下平移b个单位长度,可以得到对应点(x,y+b)或(x,y-b).要点诠释:(1)在坐标系内,左右平移的点的坐标规律:右加左减;(2)在坐标系内,上下平移的点的坐标规律:上加下减;(3)在坐标系内,平移的点的坐标规律:沿x轴平移纵坐标不变,沿y轴平移横坐标不变.2.图形的平移:在平面直角坐标系内,如果把一个图形各个点的横坐标都加上(或减去)一个正数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;如果把它各个点的纵坐标都加上(或减去)一个正数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度.要点诠释:(1)平移是图形的整体位置的移动,图形上各点都发生相同性质的变化,因此图形的平移问题可以转化为点的平移问题来解决.(2)平移只改变图形的位置,图形的大小和形状不发生变化.【基本典型例题】(1)类型一、用坐标表示地理位置1.(2015春•建昌县期末)课间操时,小聪、小慧、小敏的位置如图所示,小聪对小慧说,如果我的位置用(1,1)表示,小敏的位置用(7,7)表示,那么你的位置可以表示成()A.(5,4)B.(4,4)C.(3,4)D.(4,3)【答案】B.【解析】解:如图,小慧的位置可表示为(4,4).【总结升华】本题考查了坐标确定位置:平面坐标系中的点与有序实数对一一对应;记住平面内特殊位置的点的坐标特征.2.如图所示,在一次敌我双方交战中,我军先头部队在距敌方据点A处200米的B 处遇到敌方火力阻击,为了尽快扫除障碍,使我军驻C处的后续大部队顺利前进,先头部队请求大部队炮火支援.如果你就在先头部队中,你能表述出敌方据点的准确位置吗?【思路点拨】建立适当的直角坐标系,把A、B、C三点的位置用坐标表示出来.【答案与解析】解:如图所示,以B点为坐标原点,正东方向为x轴的正方向,正北方向为y轴正方向,建立平面直角坐标系,A、B、C各点的位置为A(-200,0)、B(0,0)、C(800,-600).若以A为坐标原点,正东方向为x轴的正方向,正北方向为y轴正方向,建立平面直角坐标系,A、B、C各点的位置为A(0,0)、B(200,0)、C(1000,-600).若以C为坐标原点,正东方向为x轴的正方向,正北方向为y轴正方向,建立平面直角坐标系,A、B、C各点的位置为A(-1000,600)、B(-800,600)、C(0,0).【总结升华】对于本题,选取的坐标原点不同,各个据点的坐标也不同,不论是哪个点表示原点,都要让人一听一看就清楚所描述的位置.当然,就本题而言,选择B点为坐标原点更贴切一些.举一反三:【变式】如图所示是某市市区几个旅游景点的示意图(图中每个小正方形的边长都为1个单位长度),请以某景点为坐标原点,画出直角坐标系,并用坐标表示下列景点的位置.光岳楼________,金风广场________,动物园________.【答案】本题的答案不唯一,现给出三种答案:(1)如果以山峡会馆为坐标原点,水平方向为横轴,取向右方向为正方向,竖直方向为纵轴,取竖直向上方向为正方向,则光岳楼的位置是(-3,1),金风广场的位置是1 5,2⎛⎫--⎪⎝⎭,动物园的位置是(4,4);(2)如果以光岳楼为坐标原点,水平方向为横轴,取向右方向为正方向,竖直方向为纵轴,取竖直向上方向为正方向,则光岳楼的位置是(0,0),金风广场的位置是12,12⎛⎫--⎪⎝⎭,动物园的位置是(7,3);(3)若以动物园为坐标原点,水平方向为横轴.取向右方向为正方向,竖直方向为纵轴,取竖直向上方向为正方向,则光岳楼(-7,-3),金风广场19,42⎛⎫--⎪⎝⎭,动物园(0,0).类型二、用坐标表示平移3.(2016•徐州模拟)在平面直角坐标系中,将点A向左平移1个单位长度,再向下平移4个单位长度得点B,点B的坐标是(2,﹣2),则A点的坐标是.【思路点拨】首先设点A的坐标是(x,y),根据平移方法可得A的对应点坐标为(x﹣1,y﹣4),进而可得x﹣1=2,y﹣4=﹣2,然后可得x、y的值,从而可得答案.【答案】(3,2).【解析】解:设点A的坐标是(x,y),∵将点A向左平移1个单位长度,再向下平移4个单位长度得点B,可得B的对应点坐标为(x﹣1,y﹣4),∵得到点B的坐标是(2,﹣2),∴x﹣1=2,y﹣4=﹣2,∴x=3,y=2,∴A的坐标是(3,2).【总结升华】左右平移的单位数是平移后点的横坐标减去平移前对应点的横坐标,上下平移的单位数是平移后点的纵坐标减去对应平移前点的纵坐标.举一反三:【变式1】已知:两点A(-4,2)、B(-2,-6),(1)线段AB的中点C坐标是;(2)若将线段AB沿x轴向右平移5个单位,得到线段A1B1,则A1点的坐标是 ,B1点的坐标是.(3)若将线段AB沿y轴向下平移3个单位,得到线段A2B2,则A2点的坐标是 ,B2点的坐标是.【答案】(1)(-3, -2); (2)(1,2),(3,-6); (3)(-4,-1),(-2,-9).【变式2】(2015•甘南州)将点A(2,1)向上平移3个单位长度得到点B的坐标是.【答案】(2,4).解:原来点的横坐标是2,纵坐标是1,向上平移3个单位长度得到新点的横坐标不变,纵坐标为1+3=4.即该坐标为(2,4).4.如图所示的直角坐标系中,△ABC的顶点坐标分别是A(0,0),B(6,0),C(5,5).(1)求△ABC的面积;(2)如果将△ABC向上平移1个单位长度,得△A1B1C1,再向右平移2个单位长度,得到△A2B2C2,试求A2、B2、C2的坐标;(3)△A2B2C2与△ABC的大小、形状有什么关系.【思路点拨】 (1)已知AB=6,故只要求得C到x轴距离即可.(2)在平面直角坐标系中,将图形向右(或左)平移a个单位长度,那么图形的点(x,y)向右(或向左)平移a个单位长度,可得对应点(x+a,y)或(x-a,y),将图形向上(或向下)平移b个单位长度,可得到对应点(x,y+b)或(x,y-b).(3)可根据平移的性质进行分析和判断.【答案与解析】解:(1)点C到x轴的距离为5,所以11651522ABCS AB h==⨯⨯=g△;(2)根据题意求出三角形A2B2C2各顶点的坐标为A2(2,1),B2(8,1),C2(7,6);(3)连接A2B2C2三点可以看出△A2B2C2与△ABC的大小、形状相等或相同.【总结升华】平移只改变图形的位置,不改变图形的形状和大小.举一反三:【变式】如图,三角形DEF经过平移后得到三角形ABC,则点D坐标为,点E的坐标为.【答案】D(2,2),E(3,-2).【基本典型例题】(2)类型一、用坐标表示地理位置1.小明写信给他的朋友介绍学校的有关情况:校门正北方100米处是教学楼,从校门向东50米,再向北50米是科教楼,从校门向西100米,再向北150米是宿舍楼……请画出适当的平面直角坐标系表示校门、教学楼、科技楼、宿舍楼的位置,并写出这四个点的坐标.【思路点拨】选取校门所在的位置为原点,并以正东,正北方向为x轴、y轴的正方向,可以容易地写出三个建筑物的坐标.否则就较复杂.【答案与解析】解:(1)平面直角坐标系及学校的建筑物位置如图所示,比例尺为1:10000.(2)校门的坐标为(0,0);教学楼的坐标为(0,100);科技楼的坐标是(50,50);宿舍楼的坐标为(-100,150).【总结升华】选取的坐标原点不同,各个据点的坐标也不同,不论是哪个点表示原点,都要让人一听一看就清楚所描述的位置.举一反三:【变式】一个探险家在日记上记录了宝藏的位置,从海岛的一块大圆石O出发,向东1000m,向北1000m,向西500m,再向南750m,到达点P,即为宝藏的位置.(1)画出坐标系确定宝藏的位置;(2)确定点P的坐标.【答案】解:根据数据的特点,选择250作为单位长度,以大圆石O为原点,建立平面直角坐标系.(1)如图,中心带有箭头的线是行动路线,点P的位置如图所示.(2)点P的坐标是(500,250)2.如图是一所学校的平面示意图,已知国旗杆的坐标为(-1,1),写出其他几个建筑物位置的坐标.若国旗杆的坐标为(3,1),则其他几个建筑物位置的坐标是否发生改变?若改变,请写出坐标,若不改变,请说明理由.【答案与解析】解:当国旗杆的坐标是(-1,1)时,校门的坐标是(-4,1),实验楼的坐标是(2,-2),教学楼的坐标是(2,1),图书馆的坐标是(1,4);若国旗杆的坐标是(3,1),则校门的坐标是(0,1),实验楼的坐标是(6,-2),教学楼的坐标是(6,1),图书馆的坐标是(5,4).【总结升华】根据已知点确定平面直角坐标系,进一步求得要求点的坐标.举一反三:【变式】(2016春•石家庄期末)如图,是象棋棋盘的一部分.若位于点(1,﹣2)上,位于点(3,﹣2)上,则位于点上.【答案】(﹣2,1).解:∵位于点(1,﹣2)上,位于点(3,﹣2)上,∴位于点(﹣2,1)上.类型二、用坐标表示平移3.(2015春•文安县期末)如如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).(1)写出点A、B的坐标:A(,)、B(,)(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,则A′B′C′的三个顶点坐标分别是A′(,)、B′(,)、C′(,).(3)△ABC的面积为.【思路点拨】(1)A在第四象限,横坐标为正,纵坐标为负;B的第一象限,横纵坐标均为正;(2)让三个点的横坐标减2,纵坐标加1即为平移后的坐标;(3)△ABC的面积等于边长为3,4的长方形的面积减去2个边长为1,3和一个边长为2,4的直角三角形的面积,把相关数值代入即可求解.【答案与解析】解:(1)写出点A、B的坐标:A(2,﹣1)、B(4,3)(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,则A′B′C′的三个顶点坐标分别是A′(0,0)、B′(2,4)、C′(﹣1,3).(3)△ABC的面积=3×4﹣2××1×3﹣×2×4=5.【总结升华】用到的知识点为:左右移动改变点的横坐标,左减,右加;上下移动改变点的纵坐标,下减,上加;格点中的三角形的面积通常用长方形的面积减去若干直角三角形的面积表示.举一反三:【变式】已知三角形ABC 三个顶点的坐标为A(-2,3),B(-4,-1),C(2,0).三角形ABC 中任意一点P(x 0,y 0)经平移后对应点为P 1(x 0+5,y 0+3).将三角形ABC 作同样的平移得到三角形A 1B 1C 1:(1)求A 1B 1C 1的坐标.(2)求三角形ABC 和△A 1B 1C 1的面积大小. 【答案】 解:(1)A 1(3,6),B 1(1,2),C 1(7,3).(2)ABC A B C S S '''=△△11124246143222=-⨯⨯-⨯⨯-⨯⨯=24-4-3-6=11. 类型三、综合应用4.在A 市北300km 处有B 市,以A 市为原点,东西方向的直线为x 轴,南北方向的直线为y 轴,并以50km 为1个单位建立平面直角坐标系.根据气象台预报,今年7号台风中心位置现在C (10,6)处,并以40千米/时的速度自东向西移动,台风影响范围半径为200km ,问经几小时后,B 市将受到台风影响?并画出示意图.【思路点拨】当台风中心移动到据B点200千米时,B市将受到台风影响,从而求出台风中心的移动距离,除以速度,即可求出所需时间.【答案与解析】解:∵台风影响范围半径为200km,∴当台风中心移动到点(4,6)时,B市将受到台风的影响.所用的时间为:50×(10-4)÷40=7.5(小时).所以经过7.5小时后,B市将受到台风的影响.(注:图中的单位1表示50km)【总结升华】考查类比点的坐标解决实际问题的能力和阅读理解能力.解决此类问题需要先确定原点的位置,再求未知点的位置.或者直接利用坐标系中的移动法则“右加左减,上加下减”来确定坐标.举一反三:【变式】一长方形住宅小区长400m,宽300m,以长方形的对角线的交点为原点,过原点和较长边平行的直线为x轴,和较短边平行的直线为y轴,并取50m为1个单位.住宅小区内和附近有5处违章建筑,它们分别是A(3,3.5),B(-2,2),C(0,3.5),D(-3,2),E(-4,4).在坐标系中标出这些违章建筑位置,并说明哪些在小区内,哪些不在小区内.【答案】在小区内的违章建筑有B、D;不在小区内的违章建筑有A、E、C.三、《平面直角坐标》全章复习与巩固【学习目标】1. 理解平面直角坐标系及象限的概念,并会在坐标系中根据点的坐标描出点的位置、由点的位置写出它的坐标;2. 掌握用坐标系表示物体位置的方法及在物体平移变化前后点坐标的变化;3. 通过学习平面直角坐标系的基础知识,逐步理解平面内的点与有序实数对之间的一一对应关系,进而培养数形结合的数学思想.。
平面直角坐标系复习讲义(知识点+典型例题)

D、第四象限.
【例 3】点 P(m,1)在第二象限内,则点 Q(-m,0)在( )
A.x 轴正半轴上 B.x 轴负半轴上 C.y 轴正半轴上 D.y 轴负半轴上
【例 4】(1)在平面直角坐标系内,已知点(1-2a,a-2)在第三象限的角平分线上,则 a= ,点的坐标为
。
(2)当 b=______时,点 B(-3,|b-1|)在第二、四象限角平分线上.
电量为 8 千瓦时,则应交电费 4.4 元;④若所交电费为 2.75 元,则用电量为 6 千瓦时,其中正确的有( )
A.4 个 B.3 个 C.2 个 D.1 个
【例 7】小明骑自行车上学,开始以正常速度匀速行驶,途中自行车出了故障,他只好停下来修车.车修好后,因怕
耽误上课,故加快速度继续匀速行驶赶往学校.如图是行驶路程 S(米)与时间 t(分)的函数图象,那么符合小明骑
D. .
11、星期天,小明从家里出发到图书馆去看书,再回到家.他离家的距离 y(千米)与时间 t(分钟)的关系如图所示.根 据图象回答下列问题:
2
2
巩固练习
5
1、下列 各曲线中表示 y 是 x 的函数的是( )
A.
B.
C.
D.
2、下列平面直角坐标系中的图象,不能表示 y 是 x 的函数的是( )
A.
B.
C.
D.
3、下列四个选项中,不是 y 关于 x 的函数的是( )
A.|y|=x﹣1 B.y=
C.y=2x﹣7 D.y=x2
4、下列四个关系式:(1)y=x;(2) y x2 ;(3) y x3 ;(4) y x ,其中 y 不是 x 的函数的是( )
.
【例 8】在坐标系内,点 P(2,-2)和点 Q(2,4)之间的距离等于
平面直角坐标系复习(知识点)

位置与坐标一、知识要点回顾(一)基础知识知识点1.生活中位置确定的方法① 行列定位法:用,表示位置;② 极坐标定位法(方向定位法):用,表示位置;③ 经纬网定位法:用,表示位置;④ 区域定位法:用,表示位置;知识点2.有序数对:有序数对是指______的两个数组成的数对,它的表示形式是(a,b ).注意:(1)a 与b 要用逗号分开,以示它们是两个独立有序的数,又要用括号“包装”起来,表示它们是一个整体;(2)若a≠b 则(a,b)与(b,a)表示两个不同的有序数对;(3)在直角坐标系中,有序数对(a,b )表示点的坐标,a,b 依次表示横坐标、纵坐标.知识点3.平面直角坐标系的意义:在平面内,两条具有公共原点、并且的数轴所构成的图形叫做平面直角坐标系,其中水平的数轴叫做______或_______,向______方向为正方向,竖直的数轴叫做______或_______,向______方向为正方向,横轴与纵轴的交点叫做平面直角坐标系的______,平面直角坐标系的两条数轴把坐标平面分成四个象限,这两条数轴的正方向的所夹的象限叫做第______象限,其它三个象限按逆时针方向依次叫做第______、______、______象限,坐标轴不属于任何象限;注意:(1)组成平面直角坐标系的四个要素:①在同一平面内;②两条数轴;③互相垂直;④有公共原点.(2)两个规定:①正方向的规定:横轴取向右为正方向,纵轴取向上为正方向;②两条数轴单位长度规定:一般情况下,横轴与纵轴单位长度相同,为了实际需要有时横轴与纵轴单位长度可以不同. 知识点4根据坐标描点(1)在平面直角坐标系内描点的方法:① 先在横轴上找到点的横坐标对应的点,过该点作横轴的;② 再在纵轴上找到点的纵坐标对应的点,过该点作纵轴的;③ 两垂线的交点就是所要描出的点。
(2)在直角坐标系中,对于平面上的任意一点,都有唯一的一个有序实数对(即点的坐标)与之对应;反过来,对于任意一个有序实数对,在平面内都有的一点与它对应。
平面直角坐标系--专题 讲义

平面直角坐标系-位置认识1.小义同学给如图建立平面直角坐标系,使医院的坐标为(0,0),火车站的坐标为(2,2).(1)写出体育场、文化馆、超市、宾馆、市场的坐标;(2)在图中标出小义家(3,﹣1),小锐家(﹣1,﹣1)和学校(﹣1,1)的位置.(3)小义从家途径小锐家到学校最近的路是个单位长度.平面直角坐标系-密码组合1.如图是一组密码的一部分,为了保密,许多情况下可采用不同的密码,请你运用所学的知识找到破译密码的“钥匙”.目前,已破译出“今天考试”的真实意思是“努力发挥”,若“今”所处的位置是(x,y),你找到的密码钥匙是(,),破译“正做数学”的真实意思是“”.平面直角坐标系-诗词调整1.如图,我们从唐代诗人韩愈的《早春呈水部张十八员外》和刘禹锡的《浪淘沙•其一》中各选取一句整齐排列放在平面直角坐标系中,“浪”的坐标是(1,1).(1)“曲”和“酥”的坐标依次是和.(2)将第2行与第3行对调,再将第4列与第7列对调,“河”由开始的坐标最终变换为.(3)“雨”开始的坐标是,使它的坐标变换到(5,3),应该哪两行对调,同时哪两列对调?1.如图是一个平面直角坐标系.(1)请在图中描出以下6个点:A(0,2)、B(4,2)、C(3,4)A′(﹣4,﹣4)、B'(0,﹣4)、C′(﹣1,﹣2)(2)分别顺次连接A、B、C和A′、B'、C',得到三角形ABC和三角形A′B′C′;(3)观察所画的图形,判断三角形A′B′C′能否由三角形ABC平移得到,如果能,请说出三角形A′B′C′是由三角形ABC怎样平移得到的;如果不能,说明理由.1.如图,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B 与点E,点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说对应点的坐标有哪些特征;(2)若点P(a+3,4﹣b)与点Q(2a,2b﹣3)也是通过上述变换得到的对应点,求a、b的值.平面直角坐标系-面积求解1.△ABC与△A'B'C'在平面直角坐标系中的位置如图.(1)分别写出下列各点的坐标:A';B';C';(2)说明△A'B'C'由△ABC经过怎样的平移得到?.(3)若点P(a,b)是△ABC内部一点,则平移后△A'B'C'内的对应点P'的坐标为;(4)求△ABC的面积.1.已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.(1)写出A′、B′、C′的坐标;(2)求出△ABC的面积;(3)点P在y轴上,且△BCP与△ABC的面积相等,求点P的坐标.1.如图,在平面直角坐标系中,点A(﹣3b,0)为x轴负半轴上一点,点B(0,4b)为y轴正半轴上一点,其中b满足方程3(b+1)=6.(1)求点A,B的坐标;(2)点C为y轴负半轴上一点,且△ABC的面积为12,求点C的坐标;1.已知点P(a﹣2,2a+8),分别根据下列条件求出点P的坐标.(1)点P在x轴上;(2)点P在y轴上;(3)点Q的坐标为(1,5),直线PQ∥y轴;(4)点P到x轴、y轴的距离相等.1.已知,点P(2m﹣6,m+2).(1)若点P在y轴上,P点的坐标为;(2)若点P的纵坐标比横坐标大6,求点P在第几象限?(3)若点P和点Q都在过A(2,3)点且与x轴平行的直线上,PQ=3,求Q点的坐标.平面直角坐标系-文字叙述求解3 1.已知在平面直角坐标系中有一点M(2m﹣1,m﹣3).(1)当点M到y轴的距离为1时,求点M的坐标;(2)当点M到x轴的距离为2时,求点M的坐标.1.在平面直角坐标系中,已知点M(m,2m+3).(1)若点M在x轴上,求m的值;(2)若点M在第二象限内,求m的取值范围;(3)若点M在第一、三象限的角平分线上,求m的值.1.已知点P(3m﹣6,m+1),试分别根据下列条件,求出点P的坐标.(1)点P在y轴上;(2)点P在x轴上;(3)点P的纵坐标比横坐标大5;(4)点P在过点A(﹣1,2),且与x轴平行的直线上.1.如图所示,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|a+2|+=0,点C的坐标为(0,3).(1)求a,b的值及SABC;△(2)若点M在x轴上,且SACM=S△ABC,试求点M的坐标.△1.如图,A(﹣1,0),C(1,4),点B在x轴上,且AB=3.(1)求点B的坐标;(2)求△ABC的面积;(3)在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由.1.如图在直角坐标系中,已知A(0,a),B(b,0)C(3,c)三点,若a,b,c满足关系式:|a﹣2|+(b﹣3)2+=0.(1)求a,b,c的值.(2)求四边形AOBC的面积.(3)是否存在点P(x,﹣x),使△AOP的面积为四边形AOBC 的面积的两倍?若存在,求出点P的坐标,若不存在,请说明理由.1.已知:如图,△ABC的三个顶点位置分别是A(1,0)、B(﹣2,3)、C(﹣3,0).(1)求△ABC的面积是多少?(2)若点A、C的位置不变,当点P在y轴上时,且SACP=2S△ABC,△求点P的坐标?(3)若点B、C的位置不变,当点Q在x轴上时,且SBCQ=2S△ABC△求点Q的坐标?1.已知点A(a,0)和B(0,b)满足(a﹣4)2+|b﹣6|=0,分别过点A、B作x轴、y轴的垂线交于点C,如图所示,点P从原点出发,以每秒1个单位长度的速度沿着O﹣B﹣C﹣A﹣O的路线移动.(1)写出A、B、C三点的坐标;A,B,C;(2)点P在运动过程中,当△OAP的面积为6时,求点P的坐标;(3)当P运动14秒时,连接O、P两点,将线段OP向上平移h个单位(h>0),得到O'P',若O'P'将四边形OACB的面积分成相等的两部分,求h的值.1.如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式|a﹣2|+(b﹣3)2=0,(c﹣4)2≤0(1)求a、b、c的值;(2)如果在第二象限内有一点P(m,),请用含m的式子表示四边形ABOP的面积;(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标,若不存在,请说明理由.1.在平面直角坐标系中,O为坐标原点,过点A(8,6)分别作x轴、y轴的平行线,交y轴于点B,交x轴于点C,点P是从点B出发,沿B→A→C以2个单位长度/秒的速度向终点C运动的一个动点,运动时间为t(秒).(1)直接写出点B和点C的坐标B(,)、C(,);(2)当点P运动时,用含t的式子表示线段AP的长,并写出t的取值范围;(3)点D(2,0),连接PD、AD,在(2)条件下是否存在这样的t值,使SAPD=S四边形ABOC,若存在,请求出t值,若不存在,请说明理由.△1.如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向依次平移,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A2022的坐标为.2.在平面直角坐标系中,点A1(1,0),A2(2,3),A3(3,8),A4(4,15),…,用你发现的规律确定点A n的坐标为.1.如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位长度,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,-1),P5(2,-1),P6(2,0)…,则P2020的坐标是2.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(﹣1,1),第2次接着运动到点(﹣2,0),第3次接着运动到点(﹣3,2),…,按这样的运动规律,经过第2022次运动后,动点P的坐标是1.点A在y轴正半轴上,OA=a,点B位于第二象限,且点B到两坐标轴的距离均为b,其中a、b满足b=++4.(1)a=,b=;(2)点C在x轴的负半轴上,射线CD∥AB.①如图1,过C作射线CE交y轴于点E,使∠DCE=3∠ECO,过A作射线AF交CE于点F,使∠BAF=3∠OAF,求∠AFE的度数;1.如图,在平面直角坐标系中,点O(0,0),A(0,a),C(b,0)满足+|b﹣2|=0.(1)直接写出A、C两点的坐标.(2)如图2,点G是第二象限上的点,连OG,且OG∥AC,点F是线段AC上一点,满足∠AOG=∠AOF.点E是射线OA上一动点,连CE交直线OF于点H,当点E在射线OA上运动的过程中,请确定∠OHC,∠ACE 和∠OEC的数量关系,并说明理由.平面直角坐标---动点和面积压轴1.如图,在平面直角坐标系中,点O(0,0),A(0,a),C(b,0)满足+|b﹣2|=0.(1)直接写出A、C两点的坐标.(2)如图1,已知坐标轴上有两动点P、Q同时从O点出发,P点沿x轴正方向以2个单位长度每秒的速度匀速移动,Q点以1个单位长度每秒的速度沿y轴正方向移动,点D(1,2)为线段AC上一点,设运动时间为t(t>0)秒.问:是否存在这样的t,使SDPC=S三角形DQO,若存在,请求出t的值;三角形若不存在,请说明理由.。
平面直角坐标系复习讲义
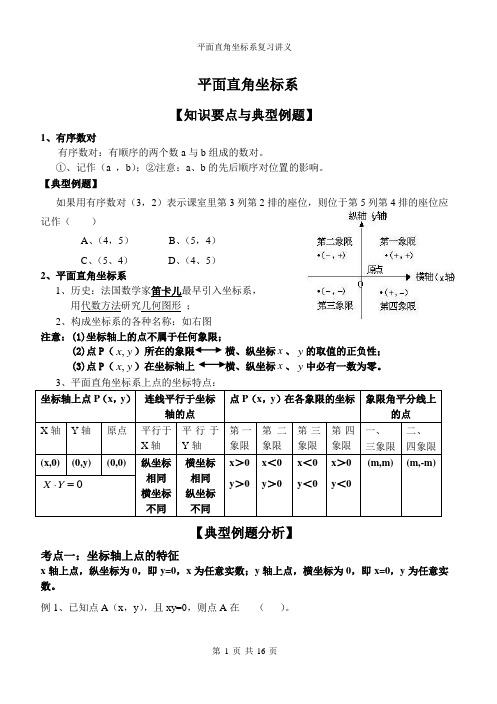
平面直角坐标系【知识要点与典型例题】1、有序数对有序数对:有顺序的两个数a与b组成的数对。
①、记作(a ,b);②注意:a、b的先后顺序对位置的影响。
【典型例题】如果用有序数对(3,2)表示课室里第3列第2排的座位,则位于第5列第4排的座位应记作()A、(4,5)B、(5,4)C、(5、4)D、(4、5)2、平面直角坐标系1、历史:法国数学家笛卡儿最早引入坐标系,用代数方法研究几何图形;2、构成坐标系的各种名称:如右图注意:(1)坐标轴上的点不属于任何象限;(2)点P(yx,)所在的象限横、纵坐标x、y的取值的正负性;(3)点P(yx,)在坐标轴上横、纵坐标x、y中必有一数为零。
3、平面直角坐标系上点的坐标特点:坐标轴上点P(x,y)连线平行于坐标轴的点点P(x,y)在各象限的坐标象限角平分线上的点X轴Y轴原点平行于X轴平行于Y轴第一象限第二象限第三象限第四象限一、二、三象限四象限(x,0) (0,y) (0,0) 纵坐标相同横坐标不同横坐标相同纵坐标不同x>0 x<0 x<0 x>0 (m,m) (m,-m)=⋅YX y>0 y>0 y<0 y<0【典型例题分析】考点一:坐标轴上点的特征x轴上点,纵坐标为0,即y=0,x为任意实数;y轴上点,横坐标为0,即x=0,y为任意实数。
例1、已知点A(x,y),且xy=0,则点A在()。
A.原点B.x 轴上C.y 轴上D.x 轴或y 轴上例2、已知点P (x ,y ),且x y 0+=,则点B 在 ( )。
A.原点B.x 轴的正半轴或负半轴C.y 轴的正半轴或负半轴上D.在坐标轴上,但不在原点练习:1、已知点A (-3,2m+3)在x 轴上,点B (n-4,4)在y 轴上,则点C (m ,n )在 ( )A.第一象限B.第二象限C.第三象限D.第四象限2、如果点B (x -1,x +3)在y 轴上,那么x= ( )A.1B.-1C.3D.-33、点P (m +3, m +1)在直角坐标系的x 轴上,则点P 坐标为 ( )A .(0,-2)B .( 2,0)C .( 4,0)D .(0,-4) 考点二:各个象限内点的特征各象限中的点的坐标特征:平面内一点P (x ,y ),如位于第一象限,则x>0,y>0;如位于第二象限,则x<0,y>0;如位于第三象限,则x<0,y<0;如位于第四象限,则x>0,y<0。
平面直角坐标系复习课件

详细描述:设点P1(x1, y1),点 P2(x2, y2),则它们之间的距离 d可由以下公式计算:d = sqrt[(x2-x1)² + (y2-y1)²]。
通过以上的基本运算,我们可 以进一步理解和掌握平面直角 坐标系中的基本概念和性质。
03
平面直角坐标系中的曲线与方 程
曲线的方程
01
02
03
抛物线运动方程
描述一个质点的抛物线运动可以用平面直角坐标系中的一条抛物线来表示,如质点从原点 出发,沿斜向上方向抛出,且在t时刻到达点(t,2t^2),则该质点的坐标为(t,2t^2)。
圆周运动方程
描述一个质点的圆周运动可以用平面直角坐标系中的一个圆来表示,如质点从原点出发, 沿圆形轨迹运动,且在t时刻到达点(2cos(t),2sin(t)),则该质点的坐标为(2cos(t),2sin(t)) 。
一一对应关系
每个坐标点都对应一个唯一的实 数对(x, y),反之亦然。
坐标表示法
在坐标系中,通常用(x, y)表示一 个点的位置。
02
平面直角坐标系中的基本运算
点的加减法
总结词
点的加减法是指将点的坐标进行相应的加或减,得到新的点的坐标。
详细描述
设点P1(x1, y1),点P2(x2, y2),则点P1加到点P2得到的点为(x1+x2, y1+y2)。 同样地,点P1减去点P2得到的点为(x1-x2, y1-y2)。
市场均衡
在市场均衡状态下,需求量等于供给量,市场达到平衡状态。这种现象可以通过平面直角坐标系中的交 点来表示,如需求曲线和供给曲线交于一点,该点的横坐标表示市场均衡时的价格水平。
06
复习题与巩固练习
基本概念的复习题
平面直角坐标系复习讲义教师用

12章 平面直角坐标系的复习讲义一、平面直角坐标系相关概念1、有序数对:有顺序的两个数a 与b 组成的数对,叫做有序数对,记作(x 0,y 0). 点在y 轴右边,则x 0>0;在y 轴上,则x 0=0;在y 轴左边,则x 0<0。
点在x 轴上方,则y 0>0;在x 轴上,则y 0=0;在y 轴下边,则 y 0<0。
坐标原点坐标为(0,0);P (a ,b )到x 轴的距离为纵坐标的绝对值b ,到y 轴的距离为横坐标的绝对值a 。
2、平面直角坐标系及其有关的概念(1)平面直角坐标系:在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系,如图1.(2)坐标轴:在平面直角坐标系中,水平的数轴称为x 轴或横轴,习惯上取向右为正方向;竖直的数轴称为y 轴或纵轴,取向上方向为正方向;两坐标轴的交点为平面直角坐标系的原点. (3)象限:如图1,坐标平面被两条坐标轴分成Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分,分别叫做第一象限、第二象限、第三象限和第四象限. 值得的注意是:坐标轴上的点不属于任何象限.3.点的坐标①已知点的位置确定点的坐标:对于平面内任意一点P如图2,过点P 分别向x 轴、y 轴作垂线,垂足在x 轴、y 轴上对应的数a ,b 分别叫做点P 的横坐标、纵坐标,有序实数对(a ,b )叫做点P 的坐标.②已知点的坐标确定点的位置已知平面直角坐标系内一点的坐标,如P (-3,1),只需在x 轴上找出表示-3的点,再在y 轴上找出表示1的点,过这两点分别作x 轴和y 轴的垂线,两垂线的交点就是点P.二、点的坐标的特征:(1)各个象限内的点的坐标特征:第一、二、三、四象限内的点的坐标符号分别是(+,+)、(-,+)、(-,-)、(+,-)。
反之也成立。
例1、如果点c(x,y)在第三象限,︱x+1︳=2,︱y -2︳=3.则点c 的坐标为——分析:因为c(x,y)在第三象限,所以x ﹤0,y ﹤0.︱x+1︳=2,有x+1=2或-2,解得x=1或-3 ︱Y -2︳=3,有y -2=3或-3,解得y=5或-1所以x=-3,y= -1.故点c 的坐标为(-3,-1)(2)坐标轴上的点的坐标特征:x 轴上的点表示为(x,0), 当在x 轴正半轴上x 为正,当在x 轴负半轴上x 为负;y 轴上的点表示为(0,y), 当在y 轴正半轴上y 为正,当在x 轴负半轴上y 为负;坐标原点的坐标表示为(0,0).反之,如果某点的坐标为(x,0),则它必在x 轴上,如果某点的坐标为(0,y),则它必在y 轴上, 如果某点的坐标为(0,0),则它必是坐标原点。
第7讲 《平面直角坐标系》复习讲义

《平面直角坐标系》复习讲义第一部分 知识导航知识点1:平面直角坐标系的相关概念(1)有序数对:用“9排7号”、“第1列第5排”这样含有两个数的表达方式来表示一个确定的位置,其中两个数各表示不同的含义,我们把这种有 的两个数组成的数对,叫做有序数对.(2)平面直角坐标系:在平面内画两条互相 、原点 的 ,组成平面直角坐标系.水平面的数轴称为 轴或 轴,习惯上取向右为 方向;竖直的数轴称为 轴或 轴,取 方向为正方向;两坐标轴的交点为平面直角坐标系的 . 知识点2:坐标轴上点的坐标特征 (1)x 轴上点的纵坐标为 . (2)y 轴上点的横坐标为 . (3)原点坐标为 . 知识点3:各象限点的坐标特征(1)点),(y x P 在第 象限(00>,>y x )(2)点),(y x P 在第二象限(x 0,0>y )(3)点),(y x P 在第三象限( )(4)点),(y x P 在第四象限( )知识点4:各象限角平分线上点的坐标特征(1)第一、三象限角平分线上点的横、纵坐标 .(2)第二、四象限角平分线上点的横、纵坐标 . 知识点4:对称点的坐标特征(1)),(y x P 关于x 轴对称的点的坐标为 .(2)),(y x P 关于y 轴对称的点的坐标为 .(3)),(y x P 关于原点对称的点的坐标为 .知识点5:平面内点到x 、y 轴及原点的距离在平面直角坐标系中,已知点P ),(b a ,则点P 到x 轴的距离为 ;点P 到y 轴的距离为 ;点P 到原点O 的距离为 PO . 知识点6:点平移的坐标特征(1)将点),(y x P 向右或向左平移a 个单位,得到对应点的坐标为1p 是( )或( ).如将点A (-4,3)向左平移2个单位得到点的坐标为 .(2)将点),(y x P 向上或向下平移b 个单位,得到对应点的坐标为2p 是( )或( ).如将点A (1,2)向下平移3个单位得到点的坐标为 .(3)将点),(y x P 向右或向左平移a 个单位,再向上或向下平移b 个单位,得到对应点的坐标3p 是( )或( ),记为:左加右减, . 知识点7:确定物质位置的方法A)平面直角坐标法 B)方向角和距离定位法第三部分 考点突破考点一:平面直角坐标系内点的坐标特征1.若点P (a ,a -2)在第四象限,则a 的取值范围是( )A .-2<a <0B .0<a <2C .a >2D .a <02.已知点),(m P 0在y 轴的负半轴上,则点M (1,+--m m )在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限3.在平面直角坐标系中,如果mn >0,那么点(m ,|n |)一定在( )A .第一象限或第二象限B .第一象限或第三象限C .第二象限或第四象限D .第三象限或第四象限3.如图,所有正方形的中心均在坐标原点,且各边与x 轴或y 轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A 1,A 2,A 3,A 4,…表示,则顶点A 55的坐标是( ) (A)(13,13) (B)(―13,―13) (C)(14,14) (D)(-14,-14) 考点二:对称点的坐标的特征4.点P (1,2)关于x 轴的对称点P 1的坐标是______点P (1,2)关于y 轴的对称点P 2的坐标,点P (1,2)关于原点O 的对称点P 3的坐标是_______,点P (1,2)关于直线y=-x 的对称点P 4的坐标是_______考点三:图形的变换与坐标5.在如图所示的方格纸中,把每个小正方形的顶点称为“格点”,以格点为顶点的三角形叫做“格点三角形”.根据图形,解决下面的问题:(1)请描述图中的格点△A′B′C′是由格点△ABC通过哪些变换方式得到的(2)若以直线a,b为坐标轴建立平面直角坐标系后,点C的坐标为(-3,1),请写出格点△DEF各顶点的坐标,并求出△DEF的面积.6.在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).(1)请在如图所示的网格平面内作出平面直角坐标系;(2)请作出△ABC关于y轴对称的△A′B′C′;(3)写出点B′的坐标.7.如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A (0,1),B (-1,1),C (-1,3).(1)画出△ABC 关于x 轴对称的△A 1B 1C 1,并写出点C 1的坐标;(2)画出△ABC 绕原点O 顺时针方向旋转90°后得到的△A 2B 2C 2,并写出点C 2的坐标; (3)将△A 2B 2C 2平移得到△A 3B 3C 3,使点A 2的对应点是A 3,点B 2的对应点是B 3,点C 2的对应点是C 3(4,-1),在坐标系中画出△A 3B 3C 3,并写出点A 3,B 3的坐标.考点4:与平面直角坐标系有关的问题8.菱形OABC 在平面直角坐标系中的位置如图所示,若OA=2, AOC=45,则B 点的坐标是( )(A) (22,2) (B) (22,2)(C) (22,2) (D) (22,2)9.如图,OABC 是一张放在平面直角坐标系中的矩形纸片,O 为原点,点A 在x 轴的正半轴上,点C 在y 轴的正半轴上,OA =10,OC =8,在OC 边上取一点D ,将纸片沿AD 翻折,使点O 落在BC 边上的点E 处,求D ,E 两点的坐标.ABCOyx第四部分《平面直角坐标系》过关测试一、选择题(共6题,每小题4分,共24分)1.在平面直角坐标系中,点P(-1,3)位于()A. 第一象限B.第二象限C. 第三象限D. 第四象限2.在平面直角坐标系中,将点P(-2,3)沿x轴方向向右平移3个单位得到点Q,则点Q的坐标是()A.(-2,6)B.(-2,0)C.(-5,3)D.(1,3)3.在平面直角坐标系中,点A(2,3)与点B关于x轴对称,则点B的坐标为()A.(3,2) B.(-2,-3) C.(-2,3) D.(2,-3)4.若点A的坐标为(6,3),O为坐标原点,将OA绕点O按顺时针方向旋转900得到OA',则点A'的坐标为()A.(3,-6)B.(-3,6)C.(-3,-6)D.(3,6)5.在一次“寻宝”游戏中,“寻宝”人找到了如图所标示的两个标志点A()3,2、B()1,4,A、B 两点到“宝藏”点的距离都是10,则“宝藏”点的坐标是A.()0,1B.()4,5C.()0,1或()4,5D.()1,0或()5,4 6.如图,在平面直角坐标系中,正方形ABCD的顶点A、C分别在y轴、x轴上,以AB为弦的⊙M与x轴相切.若点A的坐标为(0,8),则圆心M的坐(5题图)yxMOCB A标为( )A.(-4,5)B.(-5,4)C.(5,-4)D.(4,-5) 二、填空题(共4题,每题5分,共29分)7.点P(3,a)关于y 轴的对称点1P 的坐标是(b ,2),则ab= .8.若点P (x,y )的坐标满足x+y=xy ,则称点P 为“和谐点”。
《平面直角坐标系》复习讲义

第一部分 知识导航知识点1:平面直角坐标系的相关概念(1)有序数对:用“9排7号”、“第1列第5排”这样含有两个数的表达方式来表示一个确定的位置,其中两个数各表示不同的含义,我们把这种有 的两个数组成的数对,叫做有序数对.(2)平面直角坐标系:在平面内画两条互相 、原点 的 ,组成平面直角坐标系.水平面的数轴称为 轴或 轴,习惯上取向右为 方向;竖直的数轴称为 轴或 轴,取 方向为正方向;两坐标轴的交点为平面直角坐标系的 .知识点2:坐标轴上点的坐标特征(1)x 轴上点的纵坐标为 .(2)y 轴上点的横坐标为 .(3)原点坐标为 .知识点3:各象限点的坐标特征(1)点),(y x P 在第 象限(00>,>y x )(2)点),(y x P 在第二象限(x 0,0>y )(3)点),(y x P 在第三象限( )(4)点),(y x P 在第四象限( )知识点4:各象限角平分线上点的坐标特征(1)第一、三象限角平分线上点的横、纵坐标 .(2)第二、四象限角平分线上点的横、纵坐标 .知识点4:对称点的坐标特征(1)),(y x P 关于x 轴对称的点的坐标为 .(2)),(y x P 关于y 轴对称的点的坐标为 .(3)),(y x P 关于原点对称的点的坐标为 .知识点5:平面内点到x 、y 轴及原点的距离在平面直角坐标系中,已知点P ),(b a ,则点P 到x 轴的距离为 ;点P 到y 轴的距离为 ;点P 到原点O 的距离为=PO .知识点6:点平移的坐标特征(1)将点),(y x P 向右或向左平移a 个单位,得到对应点的坐标为1p 是( )或( ).如将点A (-4,3)向左平移2个单位得到点的坐标为 .(2)将点),(y x P 向上或向下平移b 个单位,得到对应点的坐标为2p 是( )或( ).如将点A (1,2)向下平移3个单位得到点的坐标为 .(3)将点),(y x P 向右或向左平移a 个单位,再向上或向下平移b 个单位,得到对应点的坐标3p 是( )或( ),记为:左加右减, .知识点7:确定物质位置的方法A)平面直角坐标法B)方向角和距离定位法第三部分 考点突破考点一:平面直角坐标系内点的坐标特征1.若点P (a ,a -2)在第四象限,则a 的取值范围是( )A .-2<a <0B .0<a <2C .a >2D .a <02.已知点),(m P 0在y 轴的负半轴上,则点M (1,+--m m )在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限3.在平面直角坐标系中,如果mn >0,那么点(m ,|n |)一定在( )A.第一象限或第二象限 B.第一象限或第三象限C.第二象限或第四象限 D.第三象限或第四象限3.如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1,A2,A3,A4,…表示,则顶点A55的坐标是()(A)(13,13) (B)(―13,―13)(C)(14,14) (D)(-14,-14)考点二:对称点的坐标的特征4.点P(1,2)关于x轴的对称点P1的坐标是______点P(1,2)关于y轴的对称点P2的坐标,点P(1,2)关于原点O的对称点P3的坐标是_______,点P(1,2)关于直线y=-x的对称点P4的坐标是_______考点三:图形的变换与坐标5.在如图所示的方格纸中,把每个小正方形的顶点称为“格点”,以格点为顶点的三角形叫做“格点三角形”.根据图形,解决下面的问题:(1)请描述图中的格点△A′B′C′是由格点△ABC通过哪些变换方式得到的?(2)若以直线a,b为坐标轴建立平面直角坐标系后,点C的坐标为(-3,1),请写出格点△DEF各顶点的坐标,并求出△DEF的面积.6.在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).(1)请在如图所示的网格平面内作出平面直角坐标系;(2)请作出△ABC关于y轴对称的△A′B′C′;(3)写出点B′的坐标.7.如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(0,1),B(-1,1),C (-1,3).(1)画出△ABC关于x轴对称的△A1B1C1,并写出点C1的坐标;(2)画出△ABC绕原点O顺时针方向旋转90°后得到的△A2B2C2,并写出点C2的坐标;(3)将△A2B2C2平移得到△A3B3C3,使点A2的对应点是A3,点B2的对应点是B3,点C2的对应点是C3(4,-1),在坐标系中画出△A3B3C3,并写出点A3,B3的坐标.考点4:与平面直角坐标系有关的问题8.菱形OABC在平面直角坐标系中的位置如图所示,若OA=2是()(A) (2?,) (B) (2?,)(C) (?2?,) (D) (?2?,)9.如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标.第四部分《平面直角坐标系》过关测试一、选择题(共6题,每小题4分,共24分)1.在平面直角坐标系中,点P(-1,3)位于()A. 第一象限B.第二象限C. 第三象限D. 第四象限2.在平面直角坐标系中,将点P(-2,3)沿x轴方向向右平移3个单位得到点Q,则点Q的坐标是()A.(-2,6)B.(-2,0)C.(-5,3)D.(1,3)3.在平面直角坐标系中,点A(2,3)与点B关于x轴对称,则点B的坐标为( )A.(3,2) B.(-2,-3) C.(-2,3) D.(2,-3)4.若点A的坐标为(6,3),O为坐标原点,将OA绕点O按顺时针方向旋转900得到OA',则点A'的坐标为()A.(3,-6)B.(-3,6)C.(-3,-6)D.(3,6)5.在一次“寻宝”游戏中,“寻宝”人找到了如图所标示的两个标志点A()3,2、B()1,4,A、B两点到“宝藏”点的距离都是10,则“宝藏”点的坐标是A.()0,1B.()4,5C.()0,1或()4,5D.()1,0或()5,4(5题图)6.如图,在平面直角坐标系中,正方形ABCD的顶点A、C分别在y轴、x轴上,以AB为弦的⊙M与x轴相切.若点A的坐标为(0,8),则圆心M的坐标为( )A.(-4,5)B.(-5,4)C.(5,-4)D.(4,-5)二、填空题(共4题,每题5分,共29分)7.点P(3,a)关于y 轴的对称点1P 的坐标是(b ,2),则ab= .8.若点P (x,y )的坐标满足x+y=xy ,则称点P 为“和谐点”。
(学生~提高)《平面直角坐标系》全章复习与巩固 知识讲解
《平面直角坐标系》全章复习与巩固(提高)知识讲解【学习目标】1. 理解平面直角坐标系及象限的概念,并会在坐标系中根据点的坐标描出点的位置、由点的位置写出它的坐标;2. 掌握用坐标系表示物体位置的方法及在物体平移变化前后点坐标的变化;3. 通过学习平面直角坐标系的基础知识,逐步理解平面内的点与有序实数对之间的一一对应关系,进而培养数形结合的数学思想.【知识网络】【要点梳理】要点一、有序数对把一对数按某种特定意义,规定了顺序并放在一起就形成了有序数对,人们在生产生活中经常以有序数对为工具表达一个确定的意思,如某人记录某个月不确定周期的零散收入,可用(13,2000), (17,190), (21,330)…,表示,其中前一数表示日期,后一数表示收入,但更多的人们还是用它来进行空间定位,如:(4,5),(20,12),(13,2),…,用来表示电影院的座位,其中前一数表示排数,后一数表示座位号.要点二、平面直角坐标系在平面内画两条互相垂直、原点重合的数轴就组成平面直角坐标系,如下图:要点诠释:(1)坐标平面内的点可以划分为六个区域:x轴,y轴、第一象限、第二象限、第三象限、第四象限,这六个区域中,除了x轴与y轴有一个公共点(原点)外,其他区域之间均没有公共点.(2)在平面上建立平面直角坐标系后,坐标平面上的点与有序数对(x,y)之间建立了一一对应关系,这样就将‘形’与‘数’联系起来,从而实现了代数问题与几何问题的转化. (3)要熟记坐标系中一些特殊点的坐标及特征:① x轴上的点纵坐标为零;y轴上的点横坐标为零.②平行于x轴直线上的点横坐标不相等,纵坐标相等;平行于y轴直线上的点横坐标相等,纵坐标不相等.③关于x轴对称的点横坐标相等,纵坐标互为相反数;关于y轴对称的点纵坐标相等,横坐标互为相反数;关于原点对称的点横、纵坐标分别互为相反数.④象限角平分线上的点的坐标特征:一、三象限角平分线上的点横、纵坐标相等;二、四象限角平分线上的点横、纵坐标互为相反数.注:反之亦成立.(4)理解坐标系中用坐标表示距离的方法和结论:①坐标平面内点P(x,y)到x轴的距离为|y|,到y轴的距离为|x|.② x轴上两点A(x1,0)、B(x2,0)的距离为AB=|x1 - x2|;y轴上两点C(0,y1)、D(0,y2)的距离为CD=|y1 - y2|.③平行于x轴的直线上两点A(x1,y)、B(x2,y)的距离为AB=|x1 - x2|;平行于y轴的直线上两点C(x,y1)、D(x,y2)的距离为CD=|y1 - y2|.(5)利用坐标系求一些知道关键点坐标的几何图形的面积:切割、拼补要点三、坐标方法的简单应用1.用坐标表示地理位置(1)建立坐标系,选择一个适当的参照点为原点,确定x轴、y轴的正方向;(2)根据具体问题确定适当的比例尺,在坐标轴上标出单位长度;(3)在坐标平面内画出这些点,写出各点的坐标和各个地点的名称.要点诠释:(1)我们习惯选取向东、向北分别为x轴、y轴的正方向,建立坐标系的关键是确定原点的位置.(2)确定比例尺是画平面示意图的重要环节,要结合比例尺来确定坐标轴上的单位长度.2.用坐标表示平移(1)点的平移点的平移引起坐标的变化规律:在平面直角坐标中,将点(x,y)向右(或左)平移a个单位长度,可以得到对应点(x+a,y)(或(x-a,y));将点(x,y)向上(或下)平移b个单位长度,可以得到对应点(x,y+b)(或(x,y-b)).要点诠释:上述结论反之亦成立,即点的坐标的上述变化引起的点的平移变换.(2)图形的平移在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;如果把它各个点的纵坐标都加(或减去)一个正数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度.要点诠释:平移是图形的整体运动,某一个点的坐标发生变化,其他点的坐标也进行了相应的变化,反过来点的坐标发生了相应的变化,也就意味着点的位置也发生了变化,其变化规律遵循:“右加左减,纵不变;上加下减,横不变”.【典型例题】类型一、有序数对1.如图所示,用点A(3,1)表示放置3个胡萝卜、1棵青菜,用点B(2,3)表示放置2个胡萝卜,3棵青菜.(1)请你写出点C、D、E、F所表示的意义;(2)若一只兔子从点A到达点B(顺着方格线走),有以下几条路线可以选择:①A→C→D→B;②A→E→D→B;③A→E→F→B,问走哪条路吃到的胡萝卜最多?走哪条路吃到的青菜最多?类型二、平面直角坐标系2. (1)若点(5-a,a-3)在第一、三象限的角平分线上,求a的值.(2)已知两点A(-3,m),B(n,4),若AB∥x轴,求m的值,并确定n的范围.(3)点P到x轴和y轴的距离分别是3和4,求P点的坐标.举一反三:【变式】已知,点P(-m,m-1),试根据下列条件:(1)若点P在过A(2,-4),且与x轴平行的直线上,则m= ,点P的坐标为.(2)若点P在过A(2,-4),且与y轴平行的直线上,则m= ,点P的坐标为.3.如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3,依此类推,已知A(1,3),A1(2,3),A2(4,3),A3(8,3)…B(2,0),B1(4,0),B2(8,0),B3(16,0)…①观察每次变化后的三角形,找出规律,按此规律再将△OA3B3变换成△OA4B4,则A4的坐标为,B4的坐标为.②若按上述规律,将三角OAB进行n次变换,得三角形△OA n B n,比较每次变换三角形顶点的变化规律,探索顶点A n的坐标为,顶点B n的坐标为.举一反三:【变式】某校数学课外小组,在坐标纸上为学校的一块空地设计植树方案如下:第k棵树种植在(,)k k kP x y处,其中x1=1,y1=1,当k ≥2时,111215,5512,55kkk kk kx xk ky y--⎧⎛--⎫⎡⎤⎡⎤=+--⎪ ⎪⎢⎥⎢⎥⎪⎣⎦⎣⎦⎝⎭⎨--⎡⎤⎡⎤⎪=+-⎢⎥⎢⎥⎪⎣⎦⎣⎦⎩[a]表示非负实数a的整数部分,例如[2.6]=2,[0.2]=0.按此方案,第2009棵树种植点的坐标为( ).A.(5,2009) B.(6,2010) C.(3,401) D.(4,402)类型三、坐标方法的简单应用4.如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式|a﹣2|+(b﹣3)2=0,(c﹣4)2≤0(1)求a、b、c的值;(2)如果在第二象限内有一点P(m,),请用含m的式子表示四边形ABOP的面积;(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标,若不存在,请说明理由.举一反三:【变式】 如图,已知火车站的坐标为(2,1),文化宫的坐标为(﹣1,2).(1)请你根据题目条件,画出平面直角坐标系;(2)写出体育馆、市场、超市、宾馆的坐标;(3)请将原点O ,宾馆C 和文化宫B ,看作三点用线段连起来,将得△OBC,然后将此三角形向下平移3个单位长度,画出平移后的△O 1B 1C 1,并求出其面积.5. 如图所示,在直角坐标平面内,线段AB 垂直于y 轴,垂足为B ,且AB =2,如果将线段AB 沿y 轴翻折,点A 落在C 处,那么C 的横坐标是_______.类型四、综合应用6.(1)对数轴上的点P 进行如下操作:先把点P 表示的数乘以13,再把所得数对应的点向右平移1个单位,得到点P 的对应点P '.点A B ,在数轴上,对线段AB 上的每个点进行上述操作后得到线段A B '',其中点A B ,的对应点分别为A B '',.如图1,若点A 表示的数是3-,则点A '表示的数是 ;若点B '表示的数是2,则点B 表示的数是 ;已知线段AB 上的点E 经过上述操作后得到的对应点E '与点E 重合,则点E 表示的数是 ;(2)如图2,在平面直角坐标系xOy 中,对正方形ABCD 及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘以同一种实数a ,将得到的点先向右平移m 个单位,再向上平移n 个单位(00m n >>,),得到正方形A B C D ''''及其内部的点,其中点A B ,的对应点分别为A B '',.已知正方形ABCD 内部的一个点F 经过上述操作后得到的对应点F '与点F 重合,求点F 的坐标.举一反三:【变式】 把点P 1(m ,n)向右平移3个单位长度再向下平移2个单位长度到一个位置P 2后坐标为P 2 (a ,b),则m ,n ,a ,b 之间存在的关系是________________.。
平面直角坐标系讲义

平面直角坐标系知识梳理1.有序数对:我们把这种有顺序的两个数a与b组成的数队,叫做________。
2.平面直角坐标系:我们可以在平面内画两条________、________的数轴,组成____________。
水平的数轴称为x轴或____,习惯上取____为正方向;竖直的数轴称为y轴或____,取____方向为正方向;两坐标轴的交战为平面直角坐标系的____。
3.象限:坐标轴上的点不属于任何象限第一象限:x>0,y>0 第二象限:x<0,y>0第三象限:x<0,y<0 第四象限:x>0,y<0横坐标轴上的点:(x,0)纵坐标轴上的点:_______4.距离问题:点(x,y)距x轴的距离为y的绝对值,距y轴的距离为x的______。
坐标轴上两点间距离:点A(x1,0)点B(x2,0),则AB距离为 x1-x2的绝对值;点A(0,y1)点B(0,y2),则AB距离为 y1-y2的绝对值。
5.绝对值相等的代数问题:a与b的绝对值相等,可推出a=b或者________。
6.角平分线问题:若点(x,y)在一、三象限角平分线上,则x=y若点(x,y)在二、四象限角平分线上,则______7.对称问题:一点关于x轴对称,则x同y反;关于y轴对称,则y同x反;8.平移:在平面直角坐标系中,将点(x,y)向右平移a个单位长度,可以得到对应点(x+a,y);向左平移a个单位长度,可以得到对应点________;向上平移b个单位长度,可以得到对应点(x,y+b);向下平移b个单位长度,可以得到对应点________。
经典例题1.有序数对【例1】电影院中“2排5号”记作(2,5),则(10,18)的意义为_______________ 练1.根据下列条件,能确定位置的有哪些?①座位是2排4号;②某城市在东经118°,北纬39°;③家住前进路20号;④甲地距乙地20km ;⑤沉船距A 港50km2.平面直角坐标系相关概念【例2】写出图中A 、B 、C 、D 、E 、F 、O 各点坐标,并说明个点在哪个象限练2.下列各点中,在第二象限的点是( )A. (2,3)B. (2,-3)C. (-2,-3)D. (-2,3) B. 练3.已知点M (,)在第二象限,则的值是 。
第七章《平面直角坐标系》复习讲义

面积;
(3)若 B(x1,y1)、C(x2,y2)为平面直角坐标系内任意的两点,O、B、C 三点不在同一条直线上.请你探 索(1)中的结论是否仍然成立?若不成立,用含 x1、x2、y1、y2 的代数式表示△OBC 的面积.
5 / 10
拓展延伸
1.如果│3x 3││x 3y 2│ 0 ,那么点 P(x,y)在第几象限?点 Q(x+1,y-1)在坐标平面 内的什么位置?
点为平面直角坐标系的原点.
坐标:平面内的点用一个有序数对来表示. 已知点(0,-2),(-3,0),(0,4),(-3,
3
原点 O 的坐标为(0,0);x 轴上的点的纵 1),其中在 x 轴上的点的个数是( )
坐标为 0;y 轴上的点的横坐标为 0.
A.0
B.1 C.2 D.3
坐标平面被两条坐标轴分成 I,II,III,IV 在平面直角坐标系中,点(3,-4)在( )
坐标.
ቤተ መጻሕፍቲ ባይዱ2 / 10
利用平面直角坐标系绘制区域内一些地点分布情况平面图的过程如下: 1.建立坐标系,选择一个适当的参照点为原点,确定 x 轴、y 轴的正方向; 2.根据具体问题确定单位长度; 3.在坐标平面内画出这些点,写出各点的坐标和各个地点的名称.
重点题型 2
【用坐标表示平移】
例题 2:(10 贺州)已知△ABC 在平面直角坐标系中的位置如图所示.将△ABC 向右平移 6 个单位长度,再向下
5.将点(0,1)向右平移 2 个单位后,所得点的坐标为
.
6.在平面直角坐标系中,将三角形各点的纵坐标都减去 3,横坐标保持不变,所得图形与原图
形相比向
平移了
个单位.
7.已知点 A(n,-2)在 y 轴上,则点 B(n+1,n-1)在( )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7-6 第六章平面直角坐标系复习讲义姓名:第一部分:本章知识点归纳:一、本章的主要知识点(一)有序数对:有顺序的两个数a与b组成的数对,记作(a ,b);注意:a、b的先后顺序对位置的影响。
(二)平面直角坐标系1、历史:法国数学家笛卡儿最早引入坐标系,用代数方法研究几何图形;2、构成坐标系的各种名称;3、各种特殊点的坐标特点。
(三)坐标方法的简单应用1、用坐标表示地理位置;2、用坐标表示平移。
二、平行于坐标轴的直线的点的坐标特点:平行于x轴(或横轴)的直线上的点的纵坐标相同;平行于y轴(或纵轴)的直线上的点的横坐标相同。
三、各象限的角平分线上的点的坐标特点:第一、三象限角平分线上的点的横纵坐标相同;第二、四象限角平分线上的点的横纵坐标相反。
四、与坐标轴、原点对称的点的坐标特点:关于x轴对称的点的横坐标相同,纵坐标互为相反数关于y轴对称的点的纵坐标相同,横坐标互为相反数关于原点对称的点的横坐标、纵坐标都互为相反数五、特殊位置点的特殊坐标:点p ( x , y )到x轴的距离为_______,到y轴的距离为_______。
六、利用平面直角坐标系绘制区域内一些点分布情况平面图过程如下:•建立坐标系,选择一个适当的参照点为原点,确定x轴、y轴的正方向;•根据具体问题确定适当的比例尺,在坐标轴上标出单位长度;•在坐标平面内画出这些点,写出各点的坐标和各个地点的名称。
◆知识讲解O1 A 1A 2A 3 A 4 A 5A 6A 7 A 8 A 9A 1A 1A 1A 1xy①坐标平面内的点与有序实数对一一对应;②点P (a ,b )到x 轴的距离为│b │,•到y 轴距离为│a③各象限内点的坐标的符号特征:P (a ,b ),P •在第一象限⇔a>0且b>0,P 在第二象限⇔a<0,b>0,P 在第三象限⇔a<0,b<0,P 在第四象限⇔a>0,b<0; ④点P (a ,b ):若点P 在x 轴上⇔a 为任意实数,b=0;P 在y 轴上⇔a=0,b 为任意实数;P 在一,三象限坐标轴夹角平分线上⇔a=0; P 在二,四象限坐标轴夹角平分线上⇔a=-b ;⑤A (x 1,y 1),B (x 1,y 2):A ,B 关于x 轴对称⇔x 1=x 2,y 1=-y 2; A 、B 关于的y 轴对称⇔x 1=-x 2,y 1=y 2;A ,B 关于原点对称⇔x 1=-x 2,y 1=-y 2;AB ∥x 轴⇔y 1=y 2且x 1≠x 2; AB ∥y 轴⇔x 1=x 2且y 1≠y 2(A ,B 表示两个不同的点).◆例题解析例1(2011贵州贵阳,24,10分) 【阅读】在平面直角坐标系中,以任意两点P (x 1,y 1)、Q (x 2,y 2)为端点的线段中点坐标为(x 1 +x 22,y 1 +y 22).【运用】(1)如图,矩形ONEF 的对角线交于点M ,ON 、OF 分别在x 轴和y 轴上,O 为坐标原点,点E 的坐标为(4,3),则点M 的坐标为______; (2)在直角坐标系中,有A (-1,2),B (3,1),C (1,4)三点,另有一点D 与点A 、B 、C 构成平行四边形的顶点,求点D 的坐标.(6分)(第24题图)例2如图所示,在直角坐标系中,点A ,B 的坐标分别是(0,6),(-8,0),求Rt △ABO 的内心的坐标. 三、解答题1.(2011安徽,18,8分)在平面直角坐标系中,一蚂蚁从原点O 出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位.其行走路线如下图所示.(1)填写下列各点的坐标:A 4(,),A 8(,),A 12(,);(2)写出点A 4n 的坐标(n 是正整数);(3)指出蚂蚁从点A 100到点A 101的移动方向.2.(2011贵州贵阳,24,10分) 【阅读】在平面直角坐标系中,以任意两点P (x 1,y 1)、Q (x 2,y 2)为端点的线段中点坐标为(x 1 +x 22,y 1 +y 22).【运用】(1)如图,矩形ONEF 的对角线交于点M ,ON 、OF 分别在x 轴和y 轴上,O 为坐标原点,点E 的坐标为(4,3),则点M 的坐标为______;(2)在直角坐标系中,有A (-1,2),B (3,1),C (1,4)三点,另有一点D 与点A 、B 、C 构成平行四边形的顶点,求点D 的坐标.(第24题图)3.(2011湖南永州,19,6分)在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC 的顶点A ,C 的坐标分别为(4-,5),(1-,3).⑴请在如图所示的网格平面内作出平面直角坐标系;⑵请作出△ABC 关于y 轴对称的△A′B′C′;⑶写出点B′的坐标.2013年中考数学专题复习第十一讲:平面直角坐标系与函数【基础知识回顾】 一、平面直角坐标系:1、定义:具有 的两条 的数轴组成平面直角坐标系,两条数轴分别称 轴 轴或 轴 轴,这两系数轴把一个坐标平面分成的四个部分,我们称作是四个2、有序数对:在一个坐标平面内的任意一个点可以用一对 来表示,如A (a .b ),(a .b )即为点A 的 其中a 是该点的 坐标,b 是该点的 坐标平面内的点和有序数对具有 的关系。
3、各象限内点的特点:平面内点的坐标特征① P (a .b ):第一象限 第二象限 第三象限 第四象限 X 轴上 Y 轴上 ②对称点:P 对称点③特殊位置点的特点:P (a .b )若在一、三象限角的平分线上,则 若在二、四象限角的平分线上,则④对坐标轴的距离:P (a .b )到x 轴的距离 到y 轴的距离 到原点的距离 ⑤坐标平面 内点 的 平移:将点P (a .b )向左右平移h 个点位,对应点坐标为 或 向上(下)平移K 个点位,对应点坐标为 或【名师提醒:坐标平面内点的坐标所具备的特征必须结合坐标平面去理解和记忆,不可生硬死记一些结论】 二、确信位置常用的方法:一、一般由两种:1、 平面直角坐标系中的有序数时 2、 方位角与距离 三、函数的有关概念:1、常量与变量:在某一变化过程中,始终保持 的量叫做常量,数值发生 的量叫做变量【名师提醒:常量与变量是相对的,在一个变化过程中,用一个量在不同情况下可以是常量,也可以是变量,要根据问题的条件来确定】 2、函数:⑴、函数的概念:一般的在某个 过程中如果有两个变量x 、y 对于x 德每一个确定的值,y 都有 的值与之对应,我们就成x 是 y 是x 的 ⑵、自变量的取值范围:主要有两种情况:①、解析或有意义的条件,常见分式和二次根式两种情况②、实际问题有意义的条件:必须符合实际问题的背景⑶、函数的表示方法:通常有三种表示函数的方法:①、法②、法③、法⑷、函数的同象:对于一个函数,把自变象x和函数y的每对对应值作为点的与在平面内描出相应的点,组成这些点的图形叫做这个函数的同象【名师提醒:1、在确定自变量取值范围时要注意分式和二次根式同时存在,应保证两者都有意义,即被开数应同时分母应2、函数的三种表示方法应根据实际需要选择,有时需同时使用几种方法3、函数同象是在自变量取值范围内无限个点组成的图形,同象上任意一点的坐标是解析式方程的一个解,反之满足解析式方程的每一个解都在函数同象上】【重点考点例析】考点一:平面直角坐标系中点的特征例1 (2012•扬州)在平面直角坐标系中,点P(m,m-2)在第一象限内,则m的取值范围是.对应训练1.(2012•怀化)在平面直角坐标系中,点(-3,3)所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限考点二:平面直角坐标系例2 (2012•济南)如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2012次相遇地点的坐标是()A.(2,0)B.(﹣1,1)C.(﹣2,1)D.(﹣1,﹣1)对应训练2.(2012•莆田)如图,在平面直角坐标系中,A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2).把一条长为2012个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A﹣B﹣C﹣D﹣A﹣…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是()A.(1,﹣1)B.(﹣1,1)C.(﹣1,﹣2)D.(1,﹣2)考点三:函数的概念及函数自变量的取值范围=中,自变量x的取值范围是.例3 (2012•凉山州)在函数yx对应训练y=中自变量x的取值范围是()3.(2012•衡阳)函数考点四:函数图象的运用例4 (2012•鸡西)一天晚饭后,小明陪妈妈从家里出去散步,如图描述了他们散步过程中离家的距离S(米)与散步时间t(分)之间的函数关系,下面的描述符合他们散步情景的是()A.从家出发,到了一家书店,看了一会儿书就回家了B.从家出发,到了一家书店,看了一会儿书,继续向前走了一段,然后回家了C.从家出发,一直散步(没有停留),然后回家了D.从家出发,散了一会儿步,到了一家书店,看了一会儿书,继续向前走了一段,18分钟后开始返回例5 (2012•铁岭)如图,ABCD的边长为8,面积为32,四个全等的小平行四边形对称中心分别在ABCD的顶点上,它们的各边与ABCD的各边分别平行,且与ABCD相似.若小平行四边形的一边长为x,且0<x≤8,阴影部分的面积的和为y,则y与x之间的函数关系的大致图象是()A.B.C.D.对应训练4.(2012•绥化)甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程s(米)与时间t(分钟)之间的函数关系图象如图所示,请你根据图象判断,下列说法正确的是()A.甲队率先到达终点B.甲队比乙队多走了200米路程C.乙队比甲队少用0.2分钟D.比赛中两队从出发到2.2秒时间段,乙队的速度比甲队的速度快5.(2012•绥化)如图,点A、B、C、D为⊙O的四等分点,动点P从圆心O出发,沿OC-CD-DO的路线做匀速运动,设运动的时间为t秒,∠APB的度数为y度,则下列图象中表示y(度)与t(秒)之间函数关系最恰当的是()A.B.C.D.2013平面直角坐标系与点的坐标真题一、选择题1.(2013贵州安顺,3,3分)将点A(-2,-3)向右平移3个单位长度得到点B,则点B所处的象限是()A.第一象限B.第二象限C.第三象限D.第四象限2.(2013山东德州,12,3分)如图,动点P从(0,3)出发,沿所示的方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2013次碰到矩形的边时,点P 的坐标为A、(1,4)B、(5,0)C、(6,4)D、(8,3)3.(2013山东日照,6,3分)如果点P(2x+6,x-4)在平面直角坐标系的第四象限内,那么x的取值范围在数轴上可表示为()4.(2013广东湛江,6,4分)在平面直角坐标系中,点A(2,-3)在()象限A.一B.二C.三D.四5.(2013湖北荆门,10,3分)在平面直角坐标系中,线段OP的两个端点坐标分别为O(0,0),P(4,3),将线段OP绕点O逆时针旋转90°到OP′位置,则点P′的坐标为( )A.(3,4) B.(-4,3) C.(-3,4) D.(4,-3)6.(2013深圳,7,3分)在平面直角坐标系中,点(20,)P a -与点(,13)Q b 关于原点对称,则a b +的值为A .33B .33-C .7-D .77. (2013湖南邵阳,8,3分)图(二)是我市几个旅游景点的大致位置示意图.如果用(0,0)表示新宁崀山的位置,用(1,5)表示隆回花瑶的位置,那么城步南山的位置可以表示为( )A .(2,1)B .(0,1)C .(-2,-1)D .(-2,1)8 (湖南株洲,9,3分)在平面直角坐标系中,点P (1,2)位于第 象限.10.(2013广西钦州,12,3分)定义:直线l 1与l 2相交于点O ,对于平面内任意一点M ,点M 到直线l 1、l 2的距离分别为p 、q ,则称有序实数对(p ,q )是点M 的“距离坐标”,根据上述定义,“距离坐标”是(1,2)的点的个数是( )11.(2013贵州安顺,3,3分)将点A (﹣2,﹣3)向右平移3个单位长度得到点B ,则点B 所处的象限是( )A .第一象限B .第二象限C .第三象限D .第四象限12.(2013湖北孝感,9,3分)在平面直角坐标系中,已知点E (﹣4,2),F (﹣2,﹣2),以原点O 为位似中心,相似比为,把△EFO 缩小,则点E 的对应点E ′的坐标是( )13.(2013湖北宜昌,15,3分)如图,点A ,B ,C ,D 的坐标分别是(1,7),(1,1),(4,1),(6,1),以C ,D ,E 为顶点的三角形与△ABC 相似,则点E 的坐标不可能是( )14. .([2013湖南邵阳,8,3分] 图(二)是我市几个旅游景点的大致位置示意图.如果用(0,0)表示 新宁崀山的位置,用(1,5)表示隆回花瑶的位置,那么城步南山的位置可以表示为( ) A .(2,1) B .(0,1) C .(-2,-1) D .(-2,1)15.(2013·泰安,11,3分)在如图所示的单位正方形网格中,△ABC 经过平移后得到△A1B 1C 1,已知在AC 上一点P (2.4,2)平移后的对应点为P 1,点P 1绕点O 逆时针 旋转180°,得到对应点P 2,则P 2点的坐标为( )A .(1.4,-1)B .(1.5,2)C .(1.6,1)D .(2.4,1)16.(2013•东营,6,3分)若定义:(,)(,)f a b a b =-, (,)(,)g m n m n =-,例如(1,2)(1,2)f =-,(4,5)(4,5)g --=-,则((2,3))g f -=( )A .(2,3)-B .(2,3)-C .(2,3)D .(2,3)--17.(2013·济宁,8,3分)如图,在直角坐标系中,点A 、B 的坐标分别为(1,4)和(3,0),点C 是y 轴上的一个动点,且A 、B 、C 三点不在同一条直线上,当△ABC 的周长最小时,点C 的坐标是( ) A .(0,0)B .(0,1)C .(0,2)D .(0,3)18.(2013四川乐山,6,3分)如图,在直角坐标系中,P 是第一象限内的点,其坐标是(3,m ),且OP 与x 轴正半轴的夹角α的正切值是43,则sin α的值是【 】A .45B .54C .35D .5319.(2013四川遂宁,7,4分)将点A (3,2)沿x 轴向左平移4个单位长度得到点A ′,点A ′关于y 轴对称的点的坐标是( )二、填空题1.(2013江苏苏州,17,3分)如图,在平面直角坐标系中,四边形OABC 是边长为2的正方形,顶点A ,C 分别在x ,y 轴的正半轴上.点Q 在对角线OB 上,且OQ =OC ,连接CQ 并延长CQ 交边AB 于点P ,则点P 的坐标为( , ).2. (2013四川雅安,17,3分)在平面直角坐标系中,已知点A (-5,0),B (5,0),点C 在坐标轴上,且AC +BC =6,写出满足条件的所有点C 的坐标________.3.(2013兰州,19,4分)如图,在直角坐标系中,已知点A (﹣3,0)、B (0,4),对△OAB 连续作旋转变换,依次得到△1、△2、△3、△4…,则△2013的直角顶点的坐标为 .4.(2013贵州安顺,17,4分)如图,在平面直角坐标系中,将线段AB 绕点A 按逆时针方向旋转90°后,得到线段AB ′,则点B ′的坐标为 .5.(2013陕西,13,3分)请从以下两个小题中任选一个....作答,若多选,则按所选的第一题计分. A .在平面直角坐标第中,线段AB 的两个端点的坐标分别为)3,1(),1,2(B A -,将线段AB 经过平移后得到线段//B A ,若点A 的对应点为)2,3(/A ,则点B 的对应点/B 的坐标是 .6.(2013贵州省黔东南州,11,4分)平面直角坐标系中,点A (2,0)关于y 轴对称的点A ′的坐标为 . 三、 解答题1. (2013福建福州,19,12分)如图,在平面直角坐标系xOy 中,点A 的坐标为(-2,0),等边三角形AOC 经过平移或轴对称或旋转都可以得到△OBD .(1)△AOC 沿x 轴向右平移得到△OBD ,则平移的距离是__________个单位长度;△AOC 与△BOD 关于直线对称,则对称轴是__________;△AOC 绕原点O 顺时针旋转得到△DOB ,则旋转角度可以是__________度;(2)连结AD ,交OC 于点E ,求∠AEO 的度数。
