2019版高考物理通用版二轮复习专题检测:(二十一) 技法专题——10法速解物理选择题 Word版含解析
2019版高考物理通用版二轮复习讲义第二部分 第二板块 第3讲 技法专题——3步稳解物理计算题

基第 3 讲| 技法专题——3步稳解物理计算题物理计算题历来是高考拉分题,试题综合性强,涉及物理过程较多,所给物理情境较复杂,物理模型较模糊或隐蔽,运用的物理规律也较多,对考生的挖掘隐含条件的能力、 本过程的分析能力、思维推理能力、基本运算能力等要求很高。
为了在物理计算题上得到理想的分值,应做到细心审题、大胆拆题、规范答题。
一、细心审题——做到“一读、二思、三析”1.读题“读题”是从题目中获取信息的最直接方法,一定要全面、细心,读题时不要急于求解,对题中关键的词语要多加思考,明白其含义,对特殊字、句、条件要用着重号加以标注;要重点看清题目中括号内的附加条件及题目给出的图形及图像等。
2.思题“思题”就是默读试题,是物理信息内化的过程,它能解决漏看、错看等问题。
边读题边思索、边联想,以弄清题目中所涉及的现象和过程,排除干扰因素,充分挖掘隐含条件。
3.析题“析题”就是在“思题”获取一定信息的基础上,调动大脑中所储存的相关知识,准确、全面、快速思考,要对研究对象的各阶段变化进行剖析,建立起清晰的物理情景,确定每一个过程对应的物理模型、规律及各过程间的联系。
[例 1] 下暴雨时,有时会发生山体滑坡或泥石流等地质灾害。
某地有一倾角为 θ=37°(sin 37°=0.6)的山坡 C ,上面有一质量为 m 的石板B ,其上下表面与斜坡平行;B 上有一碎石堆 A (含有大量泥土),A 和 B均处于静止状态,如图所示。
假设某次暴雨中,A 浸透雨水后总质量也为 m (可视为质量不变的滑块),在极短时间内,A 、B 间的动摩擦因数 μ13减小为8,B 、C 间的动摩擦因数 μ2 减小为 0.5,A 、B 开始运动,此时刻为计时起点;在第2 s 末,B 的上表面突然变为光滑,μ2 保持不变。
已知 A 开始运动时,A 离 B 下边缘的距离l =27 m ,C 足够长,设最大静摩擦力等于滑动摩擦力。
取重力加速度大小 g =10 m/s 2。
高中物理总复习 15种快速解题技巧
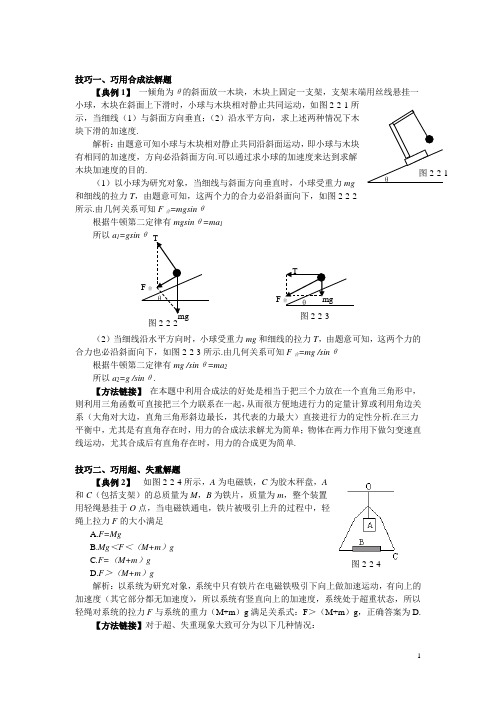
技巧一、巧用合成法解题【典例1】 一倾角为θ的斜面放一木块,木块上固定一支架,支架末端用丝线悬挂一小球,木块在斜面上下滑时,小球与木块相对静止共同运动,如图2-2-1所示,当细线(1)与斜面方向垂直;(2)沿水平方向,求上述两种情况下木块下滑的加速度.解析:由题意可知小球与木块相对静止共同沿斜面运动,即小球与木块有相同的加速度,方向必沿斜面方向.可以通过求小球的加速度来达到求解木块加速度的目的. (1)以小球为研究对象,当细线与斜面方向垂直时,小球受重力mg和细线的拉力T ,由题意可知,这两个力的合力必沿斜面向下,如图2-2-2所示.由几何关系可知F 合=mgsin θ根据牛顿第二定律有mgsin θ=ma 1所以a 1=gsin θ(2)当细线沿水平方向时,小球受重力mg 和细线的拉力T ,由题意可知,这两个力的合力也必沿斜面向下,如图2-2-3所示.由几何关系可知F 合=mg /sin θ根据牛顿第二定律有mg /sin θ=ma 2所以a 2=g /sin θ.【方法链接】 在本题中利用合成法的好处是相当于把三个力放在一个直角三角形中,则利用三角函数可直接把三个力联系在一起,从而很方便地进行力的定量计算或利用角边关系(大角对大边,直角三角形斜边最长,其代表的力最大)直接进行力的定性分析.在三力平衡中,尤其是有直角存在时,用力的合成法求解尤为简单;物体在两力作用下做匀变速直线运动,尤其合成后有直角存在时,用力的合成更为简单.技巧二、巧用超、失重解题【典例2】 如图2-2-4所示,A 为电磁铁,C 为胶木秤盘,A和C (包括支架)的总质量为M ,B 为铁片,质量为m ,整个装置用轻绳悬挂于O 点,当电磁铁通电,铁片被吸引上升的过程中,轻绳上拉力F 的大小满足A.F=MgB.Mg <F <(M+m )gC .F=(M+m )g D.F >(M+m )g解析:以系统为研究对象,系统中只有铁片在电磁铁吸引下向上做加速运动,有向上的加速度(其它部分都无加速度),所以系统有竖直向上的加速度,系统处于超重状态,所以轻绳对系统的拉力F 与系统的重力(M+m )g 满足关系式:F >(M+m )g ,正确答案为D.【方法链接】对于超、失重现象大致可分为以下几种情况:θ 图2-2-1 θ mg TF 合 图2-2-2 θ mgF 合 T 图2-2-3 图2-2-4(1)如单个物体或系统中的某个物体具有竖直向上(下)的加速度时,物体或系统处于超(失)重状态.(2)如单个物体或系统中的某个物体的加速度不是竖直向上(下),但有竖直向上(下)的加速度分量,则物体或系统也处于超(失)重状态,与物体水平方向上的加速度无关.在选择题当中,尤其是在定性判断系统重力与支持面的压力或系统重力与绳子拉力大小关系时,用超、失重规律可方便快速的求解.技巧三、巧用碰撞规律解题【典例3】 在电场强度为E 的匀强电场中,有一条与电场线平行的几何线,如图2-2-5虚线所示.几何线上有两个可视为质点的静止小球A 和B.两小球的质量均为m ,A 球带电量+Q ,B 球不带电.开始时两球相距L ,释放A 球,A 球在电场力的作用下沿直线运动,并与B 发生正碰,碰撞中A 、B 两球的总动能无损失.设在每次碰撞中,A 、B 两球间无电量转换,且不考虑重力及两球间的万有引力.求(1)A 球经多长时间与B 球发生第一次碰撞. (2)第二次碰撞前,A 、B 两球的速率各为多少? (3)从开始到第三次相碰,电场力对A 球所做的功. 解析:(1)设A 经时间t 与B 球第一次碰撞,根据运动学规律有L=at 2/2A 球只受电场力,根据牛顿第二定律有QE=ma∴(2)设第一次碰前A 球的速度为V A ,根据运动学规律有V A 2=2aL碰后B 球以速度V A 作匀速运动,而A 球做初速度为零的匀加速运动,设两者再次相碰前A 球速度为V A1,B 球速度为V B .则满足关系式V B = V A1/2= V A∴V B = V A =V A1=2 V A =2(3)第二次碰后,A 球以初速度V B 作匀加速运动,B 球以速度V A1作匀速运动,直到两者第三次相碰.设两者第三次相碰前A 球速度为V A2,B 球速度为V B1.则满足关系式V B1= V A1=(V B + V A2)/2∴V B1=2 V A ;V A2=3 V A第一次碰前A 球走过的距离为L ,根据运动学公式V A 2=2aL设第二次碰前A 球走过的距离为S 1,根据运动学公式V A12=2aS 1∴S 1=4L设第三次碰前A 球走过的距离为S 2,有关系式V A22-V A12=2aS 2∴S 2=8L即从开始到第三次相碰,A 球走过的路程为S=13L此过程中电场力对A 球所做的功为W=QES=13 QEL .【技巧点拨】 利用质量相等的两物体碰撞的规律考生可很容易判断出各球发生相互作用前后的运动规律,开始时B 球静止,A 球在电场力作用下向右作匀加速直线运动,当运m m L B A 图2-2-5图2-2-6 动距离L 时与B 球发生相碰.两者相碰过程是弹性碰撞,碰后两球速度互换,B 球以某一初速度向右作匀速直线运动,A 球向右作初速度为零的匀加速运动.当A 追上B 时两者第二次发生碰撞,碰后两者仍交换速度,依此类推.技巧四、巧用阻碍规律解题【典例4】 如图2-2-6所示,小灯泡正常发光,现将一与螺线管等长的软铁棒沿管的轴线迅速插入螺线管内,小灯泡的亮度如何变化A 、不变B 、变亮C 、变暗D 、不能确定解析:将软铁棒插入过程中,线圈中的磁通量增大,感应电流的效果要阻碍磁通量的增大,所以感应电流的方向与线圈中原电流方向相反,以阻碍 磁通量的增大,所以小灯泡变暗,C 答案正确.【方法链接】 楞次定律“效果阻碍原因”的几种常见形式.(1)就磁通量而言:感应电流的磁场总是阻碍引起感应电流的磁通量(原磁通量)的变化.即当原磁通量增加时,感应电流的磁场方向与原磁场方向相反;当原磁通量减少时,感应电流的磁场方向与原磁场方向相同,简称口诀“增反减同”.(2)就相对运动而言:感应电流的效果阻碍所有的相对运动,简称口诀“来拒去留”,从运动效果上看,也可形象的表述为“敌进我退,敌逃我追”.(3)就闭合电路的面积而言:致使电路的面积有收缩或扩张的趋势.收缩或扩张是为了阻碍电路磁通量的变化.若穿过闭合电路的磁感线都为同一方向,则磁通量增大时,面积有收缩趋势;磁通量减少时,面积有扩张趋势.简称口诀“增缩减扩”.若穿过回路的磁感线有两个相反的方向,则以上结论不一定成立,应根据实际情况灵活应用,总之要阻碍磁通量的变化.(4)就电流而言:感应电流阻碍原电流的变化,即原电流增大时,感应电流与原电流反向;原电流减小时,感应电流与原电流同向,简称口诀“增反减同”.技巧五、巧用整体法解题【典例5】 如图2-2-7所示,光滑水平面上放置质量分别为m 和2m 的四个木块,其中两个质量为m 的木块间用一不可伸长的轻绳相连,木块间的最大静摩擦力是μmg .现用水平拉力F 拉其中一个质量为2 m 的木块,使四个木块以同一加速度运动,则轻绳对m 的最大拉力为A 、5mg 3μB 、4mg 3μC 、2mg 3μ D 、mg 3μ解析:以上面2个木块和左边的质量为2m 的木块整体为研究对象,根据牛顿第二定律有μmg=4ma再以左边两木块整体为研究对象,根据牛顿第二定律有T=3ma∴T=4mg 3μ B 答案正确. 【技巧点拨】 当系统内各物体有相同加速度时(一起处于静止状态或一起加速)或题意要求计算系统的外力时,巧妙选取整体(或部分整体)为研究对象可使解题更为简单快捷.技巧六、巧用几何关系解题图2-2-7图2-2-9 图2-2-10 图2-2-11 【典例6】 如图2-2-8所示,在真空区域内,有宽度为L 的匀强磁场,磁感应强度为B ,磁场方向垂直纸面向里,MN 、PQ 是磁场的边界.质量为m ,带电量为-q 的粒子,先后两次沿着与MN 夹角为θ(0<θ<90º)的方向垂直磁感线射入匀强磁场B 中,第一次,粒子是经电压U 1加速后射入磁场,粒子刚好没能从PQ 边界射出磁场.第二次粒子是经电压U 2加速后射入磁场,粒子则刚好垂直PQ 射出磁场.不计重力的影响,粒子加速前速度认为是零,求:(1)为使粒子经电压U 2加速射入磁场后沿直线运动,直至射出PQ 边界,可在磁场区域加一匀强电场,求该电场的场强大小和方向.(2)加速电压12U U 的值. 解析:(1)如图答2-2-9所示,经电压2U 加速后以速度2v 射入磁场,粒子刚好垂直PQ 射出磁场,根据几何关系可确定粒子在磁场中做匀速圆周运动的圆心在PQ 边界线的O 点,半径2R 与磁场宽L 的关系式为2cos L R θ=又因为22mv R Bq =所以2cos BqL v m θ= 加匀强电场后,粒子在磁场中沿直线运动射出PQ 边界的条件为Eq =Bq 2v ,电场力的方向与磁场力的方向相反. 所以2cos B qL E m θ=,方向垂直磁场方向斜向右下,与磁场边界夹角为2παθ=-,如图答2-2-10所示.(2)经电压1U 加速后粒子射入磁场后刚好不能从PQ 边界射出磁场,表明在磁场中做匀速圆周运动的轨迹与PQ 边界相切,要确定粒子做匀速圆周运动的圆心O 的位置,如图答2-2-11所示,圆半径1R 与L 的关系式为:111cos ,1cos L L R R R θθ=+=+ 又11mv R Bq= 所以1(1cos )BqL v m θ=+ 根据动能定理有21112U q mv =,22212U q mv =, 所以22112222cos (1cos )U v U v θθ=+. 【方法链接】 解决带电粒子在匀强磁场中匀速圆周运动问题,关键是确定圆心的位置,正确画出粒子运动的草图,利用几何关系结合运动规律求解.技巧七:巧用可逆原理解题【典例7】 某同学在测定玻璃折射率时得到了多组入射角i 与折射角r ,并作出了sini 与sinr 的图象如图2-2-12所示.则下列说法正确的是 A . 实验时,光线是由空气射入玻璃 B . 实验时,光线是由玻璃射入空气C . 利用sini /sinr 可求得玻璃的折射率D . 该玻璃的折射率为1.5解析:由图象可知入射角的正弦值小于折射角的正弦值.根据折射定律可知光线是从光密介质射向光疏介质,即由玻璃射向空气,B 答案正确;根据折射定律n=sini /sinr 可求得介质的折射率,但一定要注意此公式一定要满足光线从空气射向介质,而本题中光线是由玻璃射入空气,所以不能直接利用sini /sinr 求介质的折射率,根据光路可逆原理,当光线反转时,其传播路径不变,即光从空气中以入射角r 射到该玻璃界面上时,折射后的折射角一定为i ,根据折射定律可得玻璃的折射率n= sinr / sini=1.5(这里要注意很容易错选C ),C 错误,D 正确.正确答案为B 、D.【方法链接】 在光的反射或折射现象中,光路具有可逆性.即当光线的传播方向反转时,它的传播路径不变.在机械运动中,若没有摩擦阻力、流体的粘滞阻力等耗散力做功时,机械运动具有可逆性.如物体的匀减速直线运动可看作反向的加速度不变的匀加速运动.方法八:巧用等效法解题【典例8】 如图2-2-13所示,已知回旋加速器中,D 形盒内匀强磁场的磁感应强度B =1.5T ,盒的半径R =60 cm ,两盒间隙d =1.0 cm ,盒间电压U =2.0×104 V ,今将α粒子从近于间隙中心某点向D 形盒内以近似于零的初速度垂直B 的方向射入,求粒子在加速器内运行的总时间.解析:带电粒子在回旋加速器转第一周,经两次加速,速度为v 1,则根据动能定理得:0.1 0.2 sinrsini0.3 0.4 0.5 0.2 0.1 0.40.3 0.5 图2-2-122qU =21mv 12 设运转n 周后,速度为v ,则:n 2qU =21 mv 2 由牛顿第二定律有qvB =m Rv 2粒子在磁场中的总时间:t B =nT =n ·qB m π2=qmU R q B 4222·qB m π2 =UB R 22π 粒子在电场中运动就可视作初速度为零的匀加速直线运动,由公式:t E =a v v t 0-,且v 0=0,v t = ,a =dmqU 得:t E =UBRd 故:t =t B +t E =U BR (2R π+d )=4.5×10-5×(0.94+0.01) s =4.3×10-5s.【技巧点拨】 粒子在间隙处电场中每次运动时间不相等,且粒子多次经过间隙处电场,如果分段计算,每一次粒子经过间隙处电场的时间,很显然将十分繁琐.我们注意到粒子离开间隙处电场进入匀强磁场区域到再次进入电场的速率不变,且粒子每在电场中加速度大小相等,所以可将各段间隙等效“衔接”起来,把粒子断断续续在电场中的加速运动等效成初速度为零的匀加速直线运动.技巧九:巧用对称法解题【典例9】 一根自由长度为10 cm 的轻弹簧,下端固定,上端连一个质量为m 的物块P ,在P 上放一个质量也是m 的物块Q.系统静止后,弹簧长度为6 cm ,如图2-2-14所示.如果迅速向上移去Q ,物块P 将在竖直方向做简谐运动,此后弹簧的最大长度为A .8 cmB .9 cmC .10 cmD .11 cm 解析:移去Q 后,P 做简谐运动的平衡位置处弹簧长度8 cm ,由题意可知刚移去Q 时P 物体所处的位置为P 做简谐运动的最大位移处.即P 做简谐运动的振幅为2 cm.当物体P 向上再次运动到速度为零时弹簧有最大长度,此时P 所处的位置为另一最大位移处,根据简谐运动的对称性可知此时弹簧的长度 为10 cm ,C 正确.【方法链接】在高中物理模型中,有很多运动模型有对称性,如(类)竖直上抛运动的对称性,简谐运动中的对称性,电路中的对称性,带电粒子在匀强磁场中匀速圆周运动中几何关系的对称性.方法十:巧用假设法解题假设法是解决物理问题的一种常见方法,其基本思路为假设结论正确,经过正确的逻辑推理,看最终的推理结果是否与已知条件相矛盾或是否与物理实际情境相矛盾来判断假设是否成立.【典例10】如图2-2-15,abc 是光滑的轨道,其中图2-2-14 P Q 6cmdd 21 ab 是水平的,bc 为与ab 相切的位于竖直平面内的半圆,半径R =0.3m.质量m =0.2kg 的小球A 静止在轨道上,另一质量M=0.6kg ,速度V 0=5.5m/s 的小球B 与小球A 正碰.已知相碰后小球A 经过半圆的最高点C ,落到轨道上距b 为L = 处,重力加速度g =10m/s 2,试通过分析计算判断小球B 是否能沿着半圆轨道到达C 点.解析 :A 、B 组成的系统在碰撞前后动量守恒,碰后A 、B 运动的过程中只有重力做功,机械能守恒,设碰后A 、B 的速度分别为V 1、V 2,由动量守恒定律得M V 0=M V 2+m V 1A 上升到圆周最高点C 做平抛运动,设A 在C 点的速度为V C ,则A 的运动满足关系式2R=gt 2/2 V C t=LA 从b 上升到c 的过程中,由机械能守恒定律得(以ab 所在的水平面为零势面,以下同)m V 12/2= m V C 2/2+2mgR∴V 1=6 m/s ,V 2=3.5 m/s方法1:假设B 球刚好能上升到C 点,则B 球在C 点的速度V C '应满足关系式Mg=M V C '2/R所以V C '=1.73 m/s则B 球在水平轨道b 点应该有的速度为(设为V b )由机械能守恒定律得M V b 2/2=M V C '2/2+2MgR则由V b 与V 2的大小关系可确定B 能否上升到C 点若V 2≥V b ,B 能上升到C 点若V 2<V b ,B 不能上升到C 点代入数据得V b =3.9 m/s >V 2 =3.5 m/s ,所以B 不能上升到C 点.【方法链接】 假设法在物理中有着很广泛的应用,凡是利用直接分析法很难得到结论的问题,用假设法来判断不失为一种较好的方法,如判断摩擦力时经常用到假设法,确定物体的运动性质时经常用到假设法.技巧十一、巧用图像法解题【典例11】 部队集合后开发沿直线前进,已知部队前进的速度与到出发点的距离成反比,当部队行进到距出发点距离为d 1的A位置时速度为V 1,求(1)部队行进到距出发点距离为d 2的B 位置时速度为V 2是多大? (2)部队从A 位置到B 位置所用的时间t 为多大.解析:(1)已知部队前进的速度与到出发点的距离成反比,即有公式V =k/d (d 为部队距出发点的距离,V 为部队在此位置的瞬时速度),根据题意有V 1=k / d 1 V 2=k / d 2 ∴ V 2=d 1 V 1 / d 2. (2)部队行进的速度V 与到出发点的距离d 满足关系式d =k/V ,即d -图象是一条过原点的倾斜直线,如图2-2-16所示,由题意已知,部队从A 位置到B 位置所用的时间t 即为图中斜线图形(直角梯形)的面积.由数学知识可知t =(d 1 + d 2)(1/V 2-1/V 1)/2∴t =(d 22-d 12)/2 d 1 V 1【方法链接】1.此题中部队行进时速度的变化即不是匀速运动,也不是匀变速运动,很图2-2-16V 图2-2-18难直接用运动学规律进行求解,而应用图象求解则使问题得到简化.2.考生可用类比的方法来确定图象与横轴所围面积的物理意义.v-t图象中,图线与横轴围成图形的面积表示物体在该段时间内发生的位移(有公式S =v t ,S 与v t 的单位均为m );F -S 图象中,图线与横轴围成图形的面积表示F 在该段位移S 对物体所做的功(有公式W =FS ,W 与FS 的单位均为J ).而上述图象中t =d ×1/V (t 与d ×1/V 的单位均为s ),所以可判断出该图线与横轴围成图形的面积表示部队从出发点到此位置所用的时间.技巧十二、巧用极限法解题【典例12】 如图2-2-17所示,轻绳的一端系在质量为m的物体上,另一端系在一个轻质圆环上,圆环套在粗糙水平杆MN上,现用水平力F 拉绳上一点,使物体处于图中实线位置,然后改变F 的大小使其缓慢下降到图中虚线位置,圆环仍在原来的位置不动,则在这一过程中,水平拉力F 、环与杆的摩擦力F 摩和环对杆的压力F N 的变化情况是A.F 逐渐增大,F 摩保持不变,F N 逐渐增大B.F 逐渐增大,F 摩逐渐增大,F N 保持不变C.F 逐渐减小,F 摩逐渐增大,F N 逐渐减小D.F 逐渐减小,F 摩逐渐减小,F N 保持不变解析:在物体缓慢下降过程中,细绳与竖直方向的夹角θ不断减小,可把这种减小状态推到无限小,即细绳与竖直方向的夹角θ=0;此时系统仍处于平衡状态,由平衡条件可知,当θ=0时,F=0,F 摩 =0.所以可得出结论:在物体缓慢下降过程中,F 逐渐减小,F 摩也随之减小,D 答案正确. 【方法链接】 极限法就是运用极限思维,把所涉及的变量在不超出变量取值范围的条件下,使某些量的变化抽象成无限大或无限小去思考解决实际问题的一种解题方法,在一些特殊问题当中如能巧妙的应用此方法,可使解题过程变得简捷.方法十三、巧用转换思想解题【典例13】 如图2-2-18所示,电池的内阻可以忽略不计,电压表和可变电阻器R 串联接成通路,如果可变电阻器R 的值减为原来的1/3时,电压表的读数由U 0增加到2U 0,则下列说法中正确的是A .流过可变电阻器R 的电流增大为原来的2倍B .可变电阻器R 消耗的电功率增加为原来的4倍C .可变电阻器两端的电压减小为原来的2/3D .若可变电阻器R 的阻值减小到零,那么电压表的示数变为4U 0确 解析: 在做该题时,大多数学生认为研究对象应选可变电阻器,因为四个选项中都问的是有关R的问题;但R 的电阻、电压、电流均变,判断不出各量的定量变化,从而走入思维的误区.若灵活地转换研究对象,会出现“柳暗花明”的意境;分析电压表,其电阻为定值,当它的读数由U 0增加到2U 0时,通过它的电流一定变为原来的2倍,而R 与电压表串联,故选项A 正确.再利用P =I 2R 和U =IR ,R 消耗的功率P ′=(2I )2R/3=4P/3;R 后来两端的电压U =2IR/3,不难看出C 对B 错.又因电池内阻不计,R 与电压表的电压之和为U 总,当R 减小到零时,电压表的示数也为总电压U总;很轻松地列出U 总=IR +U 0=2 IR/3+2U 0,解得U 总=4U 0,故D 也对.图2-2—17图2-2-22 2-2-19【方法链接】 常见的转换方法有研究对象的转换、时间角度的转换、空间角度的转换、物理模型的转换,本例题就是应用研究对象的转换思想巧妙改变问题的思考角度,从而达到使问题简化的目的.技巧十四、巧用结论解题【典例14】如图2-2-19所示,如图所示,质量为3m 的木板静止放在光滑的水平面上,木板左端固定着一根轻弹簧.质量为m 的木块(可视为质点),它从木板右端以未知速度V 0开始沿木板向左滑行,最终回到木板右端刚好未从木板上滑出.若在小木块压缩弹簧的过程中,弹簧具有的最大弹性势能为E P ,小木块与木板间的动摩擦因数大小保持不变,求: (1)木块的未知速度V 0(2)以木块与木板为系统,上述过程中系统损失的机械能解析:系统在运动过程中受到的合外力为零,所以系统动量定恒,当弹簧压缩量最大时,系统有相同的速度,设为V ,根据动量守恒定律有m V 0=(m+3m )V木块向左运动的过程中除了压缩弹簧之外,系统中相互作用的滑动摩擦力对系统做负功导致系统的内能增大,根据能的转化和守恒定律有m V 02/2-(m+3m )V 2/2=E P +μmgL (μ为木块与木板间的动摩擦因数,L 为木块相对木板走过的长度)由题意知木块最终回到木板右端时刚好未从木板上滑出,即木块与木板最终有相同的速度由动量守恒定律可知最终速度也是V.整个过程中只有系统内相互作用的滑动摩擦力做功(弹簧总功为零),根据能量守恒定律有m V 02/2-(m+3m )V 2/2=2μmgL∴有 , E P =μmgL故系统损失的机械能为2 E P .【误点警示】根据能的转化和守恒定律,系统克服滑动摩擦力所做的总功等于系统机械能损失,损失的机械能转化为系统的内能,所以有f 滑L 相对路程=△E (△E 为系统损失的机械能).在应用公式解题时,一定要注意公式成立所满足的条件.当系统中只有相互作用的滑动摩擦力对系统做功引起系统机械能损失(其它力不做功或做功不改变系统机械能)时,公式f 滑L 相对路程=△E 才成立.如果系统中除了相互作用的滑动摩擦力做功还有其它力对系统做功而改变系统机械能,则公式f 滑L 相对路程=△E 不再成立,即系统因克服系统内相互作用的滑动摩擦力所产生的内能不一定等于系统机械能的损失.所以同学们在应用结论解题时一定要注意公式成立的条件是否满足,否则很容易造成错误.方法十五、巧用排除法解题【典例15】 如图2-2-22所示,由粗细均匀的电阻丝制成的边长为L 的正方形线框abcd ,其总电阻为R .现使线框以水平向右的速度v匀速穿过一宽度为2L 、磁感应强度为B 的匀强磁场区域,整个过程中ab 、cd 两边始终保持与磁场边界平行.令线框的cd 边刚好与磁场左边界重合时开始计时(t =0),电流沿abcda 流动的方向为正,U o =BLv .在下图中线框中a 、b 两点间电势差U ab 随线框cd 边的位移x 变化的图像正确的是下图中的x x解析:当线框向右穿过磁场的过程中,由右手定则可判断出总是a点的电势高于b点电势,即U ab>0,所以A、C、D错误,只有B项正确.【方法链接】考生可以比较题设选项的不同之外,而略去相同之处,便可得到正确答案,或者考生能判断出某三个选项是错误的,就没必要对另外一个选项做出判断而应直接把其作为正确答案.对本例题,考生只需判断出三个过程中(进磁场过程、全部进入磁场过程、出磁场过程)中a、b两点电势的高低便可选择出正确答案,而没有必要对各种情况下a、b 两点电势大小规律做出判断.。
2019届全国高考物理复习精选测试(二)(解析版)

2019届全国高考物理复习精选测试(二)★祝考试顺利★注意事项:1、答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B铅笔将答题卡上试卷类型A后的方框涂黑。
2、选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3、填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4、选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B铅笔涂黑。
答案写在答题卡上对应的答题区域内,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
5、考试结束后,请将本试题卷和答题卡一并上交。
一、选择题1、小陈在地面上从玩具枪中竖直向上射出初速度为v0的塑料小球,若小球运动过程中受到的空气阻力与其速率成正比,小球运动的速率随时间变化的规律如图所示,t1时刻到达最高点,再落回地面,落地速率为v1,下列说法中正确的是()A.小球在上升过程中的加速度小于下降过程中的加速度B.小球上升过程中的平均速度大于C.小球下降过程中的平均速度大于D.小球下降过程中加速度越来越大【答案】C2、(2018湖北省宜昌金东方高级中学月考)水平面上有质量相等的a、b两物体,水平推力F1、F2分别作用在a、b上.各作用一段时间后撤去推力,物体将继续运动一段时间后停下来.撤去推力时两物体速度相等,它们运动的v﹣t图象如图所示,图中AB∥CD,整个过程中()A. 水平推力F1、F2的大小相等B. a、b与水平面间的动摩擦因数相等C. a的平均速度大于b的平均速度D. 水平推力F1、F2所做的功可能相等【答案】B3、(2018山东省青岛市城阳区期中)如图所示,A、B、C、D是水平面内同一直线上的四点,且AB=BC=CD,在A点正上方的O点以水平抛出一小球,刚好落在C点,小球运动的轨迹与OD的连线交于E点,不计空气阻力,下列说法正确的是()A. 小球经过E点与落在C点的水平位移之比是2:3B. 小球经过E点与落在C点的水平位移之比是3:4C. 小球经过E点与落在C点时重力做功的比为5:9D. 小球经过E点与落在C点时重力做功的比为7:16【答案】A4、从塔顶以相同速率抛出A、B、C三小球,A球竖直上抛,B球平抛,C球竖直下抛。
2019届高考物理二轮复习专项2题型3三大技巧破解计算题课件(36张)(全国通用)

⑥求乙球过 D 点的速度 vD′的范围? 建模: 竖直面内圆周运动模型(B→D 过程) 规律:动能定理 -mg·2R-qE·2R=12mvD′2-12mvm2
⑦求小球落点到 B 点的距离范围? 建模: 类平抛运动 规律: 水平方向匀速运动__x′=vD′t
[典例 2] 如图 2,ABD 为竖直平面内的光滑绝缘轨道,其中 AB 段是水平 的,BD 段为半径 R=0.2 m 的半圆,两段轨道相切于 B 点,整个轨道处在竖直 向下的匀强电场中,场强大小 E=5.0×103V/m.一不带电的绝缘小球甲,以速度 v0 沿水平轨道向右运动,与静止在 B 点带正电的小球乙发生弹性碰撞.已知甲、 乙两球的质量均为 m=1.0×10-2kg,乙所带电荷量 q=2.0×10-5C,g 取 10 m/s2.(水平轨道足够长,甲、乙两球可视为质点,整个运动过程无电荷转移)求:
3.必要演算、明确结果 (1)演算时一般要从列出的一系列方程,推导出结果的计算式,然后代入数据并写出结果(要 注意简洁,千万不要在卷面上书写许多化简、数值运算式). (2)计算结果的有效数字位数应根据题意确定,一般应与题目中所列的数据的有效数字位数 相近,若有特殊要求,应按要求确定. (3)计算结果是数据的要带单位(最好采用国际单位),是字母符号的不用带单位. (4)字母式的答案中所用字母都必须使用题干中所给的字母,不能包含未知量,且一些已知 的物理量也不能代入数据. (5)题中要求解的物理量应有明确的答案(尽量写在显眼处),待求量是矢量的必须说明其方 向. (6)若在解答过程中进行了研究对象转换,则必须交代转换依据,对题目所求要有明确的回 应,不能答非所问.
④
(2)设碰撞后甲、乙的速度分别为 v 甲、v 乙 根据动量守恒有:
高考数学二轮复习专题11 离心率问题速解(精讲精练)(解析版)

专题11离心率问题速解【命题规律】求椭圆或双曲线的离心率、与双曲线的渐近线有关的问题,多以选择、填空题的形式考查,难度中等.【核心考点目录】核心考点一:顶角为直角的焦点三角形求解离心率的取值范围问题核心考点二:焦点三角形顶角范围与离心率核心考点三:共焦点的椭圆与双曲线问题核心考点四:椭圆与双曲线的4a 通径体核心考点五:椭圆与双曲线的4a 直角体核心考点六:椭圆与双曲线的等腰三角形问题核心考点七:双曲线的4a 底边等腰三角形核心考点八:焦点到渐近线距离为b核心考点九:焦点到渐近线垂线构造的直角三角形核心考点十:以两焦点为直径的圆与渐近线相交问题核心考点十一:渐近线平行线与面积问题【真题回归】1.(2022·全国·统考高考真题)椭圆2222:1(0)x y C a b a b+=>>的左顶点为A ,点P ,Q 均在C上,且关于y 轴对称.若直线,AP AQ 的斜率之积为14,则C 的离心率为()A2B.2C .12D .13【答案】A【解析】[方法一]:设而不求设()11,P x y ,则()11,Q x y -则由14AP AQk k ⋅=得:21112211114AP AQ y y y k k x a x a x a ⋅=⋅==+-+-+,由2211221x y a b +=,得()2221212b a x y a -=,所以()2221222114b a x ax a -=-+,即2214b a =,所以椭圆C 的离心率c e a = A.[方法二]:第三定义设右端点为B ,连接PB ,由椭圆的对称性知:PB AQk k =-故14AP AQ PA AQ k k k k ⋅=⋅-=-,由椭圆第三定义得:22PA AQb k k a⋅=-,故2214b a =所以椭圆C 的离心率c e a = A.2.(2021·天津·统考高考真题)已知双曲线22221(0,0)x y a b a b-=>>的右焦点与抛物线22(0)y px p =>的焦点重合,抛物线的准线交双曲线于A ,B 两点,交双曲线的渐近线于C 、D 两点,若|CD AB .则双曲线的离心率为()A BC .2D .3【答案】A【解析】设双曲线22221(0,0)x y a b a b-=>>与抛物线22(0)y px p =>的公共焦点为(),0c ,则抛物线22(0)y px p =>的准线为x c =-,令x c =-,则22221c y a b -=,解得2b y a =±,所以22b AB a=,又因为双曲线的渐近线方程为b y x a =±,所以2bcCD a=,所以2bc a =c =,所以222212a c b c =-=,所以双曲线的离心率ce a==故选:A.3.(2021·全国·统考高考真题)设B 是椭圆2222:1(0)x y C a b a b+=>>的上顶点,若C 上的任意一点P 都满足||2PB b ≤,则C 的离心率的取值范围是()A .⎫⎪⎪⎣⎭B .1,12⎡⎫⎪⎢⎣⎭C .⎛ ⎝⎦D .10,2⎛⎤⎥⎝⎦【答案】C【解析】设()00,P x y ,由()0,B b ,因为2200221x y a b+=,222a b c =+,所以()()2223422222220000022221y c b b PB x y b a y b y a b b b c c ⎛⎫⎛⎫=+-=-+-=-++++ ⎪ ⎪⎝⎭⎝⎭,因为0b y b -≤≤,当32bb c-≤-,即22b c ≥时,22max 4PB b =,即max 2PB b =,符合题意,由22b c ≥可得222a c ≥,即0e <≤;当32b b c ->-,即22b c <时,42222max b PB a b c=++,即422224b a b b c ++≤,化简得,()2220c b -≤,显然该不等式不成立.故选:C .4.(多选题)(2022·全国·统考高考真题)双曲线C 的两个焦点为12,F F ,以C 的实轴为直径的圆记为D ,过1F 作D 的切线与C 交于M ,N 两点,且123cos 5F NF ∠=,则C 的离心率为()A B .32C .2D .2【答案】AC【解析】[方法一]:几何法,双曲线定义的应用情况一M 、N 在双曲线的同一支,依题意不妨设双曲线焦点在x 轴,设过1F 作圆D 的切线切点为B ,所以1OB F N ⊥,因为123cos 05F NF ∠=>,所以N 在双曲线的左支,OB a =,1OF c =,1FB b =,设12F NF α∠=,由即3cos 5α=,则4sin 5α=,235NA NF 22a a ==,21NF NF 2a-=532222a a b a ⎛⎫--= ⎪⎝⎭,2b e a =∴=,选A 情况二若M 、N 在双曲线的两支,因为123cos 05F NF ∠=>,所以N 在双曲线的右支,所以OB a =,1OF c =,1FB b =,设12F NF α∠=,由123cos 5F NF ∠=,即3cos 5α=,则4sin 5α=,235NA NF 22a a ==,12NF NF 2a -=352222a b a a +-=,所以23b a =,即32b a =,所以双曲线的离心率2c e a ==选C[方法二]:答案回代法A e =选项特值双曲线())22121,F ,F 4x y -=∴,过1F 且与圆相切的一条直线为(y 2x =+,两交点都在左支,N ⎛∴ ⎝,2112NF 5,NF 1,FF ∴===则123cos 5F NF ∠=,C e =选项特值双曲线())2212x y 1,F ,F 49-=∴,过1F 且与圆相切的一条直线为(2y x 3=,两交点在左右两支,N 在右支,N ∴,2112NF 5,NF 9,FF ∴===则123cos 5F NF ∠=,[方法三]:依题意不妨设双曲线焦点在x 轴,设过1F 作圆D 的切线切点为G ,若,M N 分别在左右支,因为1OG NF ⊥,且123cos 05F NF ∠=>,所以N 在双曲线的右支,又OG a =,1OF c =,1GF b =,设12F NF α∠=,21F F N β∠=,在12F NF △中,有()212sin sin sin NF NF cβαβα==+,故()122sin NF NF cαββα-=+-即()sin sin sin a c αββα=+-,所以sin cos cos sin sin sin a cαβαββα=+-,而3cos 5α=,sin a c β=,cos b c β=,故4sin 5α=,代入整理得到23b a =,即32b a =,所以双曲线的离心率c e a ==若,M N 均在左支上,同理有()212sin sin sin NF NF c βαβα==+,其中β为钝角,故cos bcβ=-,故()212sin sin sin NF NF c βαβα-=-+即sin sin cos cos sin sin a cβαβαβα=--,代入3cos 5α=,sin a c β=,4sin 5α=,整理得到:1424a b a =+,故2a b =,故2e ==,故选:AC.5.(2022·全国·统考高考真题)已知椭圆2222:1(0)x y C a b a b+=>>,C 的上顶点为A ,两个焦点为1F ,2F ,离心率为12.过1F 且垂直于2AF 的直线与C 交于D ,E 两点,||6DE =,则ADE V 的周长是________________.【答案】13【解析】∵椭圆的离心率为12c e a ==,∴2a c =,∴22223b a c c =-=,∴椭圆的方程为222222213412043x y x y c c c+=+-=,即,不妨设左焦点为1F ,右焦点为2F ,如图所示,∵222AF a OF c a c ===,,,∴23AF O π∠=,∴12AF F △为正三角形,∵过1F 且垂直于2AF 的直线与C 交于D ,E 两点,DE 为线段2AF 的垂直平分线,∴直线DE 的斜率为3,斜率直线DE 的方程:x c -,代入椭圆方程22234120x y c +-=,整理化简得到:221390y c --=,判别式()22224139616c c ∆=+⨯⨯=⨯⨯,∴122264613cDE y =-=⨯⨯⨯⨯=,∴138c =,得1324a c ==,∵DE 为线段2AF 的垂直平分线,根据对称性,22AD DF AE EF ==,,∴ADE V 的周长等于2F DE △的周长,利用椭圆的定义得到2F DE △周长为22221121222413DF EF DE DF EF DF EF DF DF EF EF a a a ++=+++=+++=+==.故答案为:13.6.(2022·浙江·统考高考真题)已知双曲线22221(0,0)x y a b a b-=>>的左焦点为F ,过F 且斜率为4ba的直线交双曲线于点()11,A x y ,交双曲线的渐近线于点()22,B x y 且120x x <<.若||3||FB FA =,则双曲线的离心率是_________.【解析】过F 且斜率为4ba 的直线:()4b AB y xc a =+,渐近线2:b l y x a=,联立()4b y x c a b y xa ⎧=+⎪⎪⎨⎪=⎪⎩,得,33c bc B a ⎛⎫ ⎪⎝⎭,由||3||FB FA =,得5,,99c bc A a ⎛⎫- ⎪⎝⎭而点A 在双曲线上,于是2222222518181c b c a a b -=,解得:228124c a =,所以离心率e 4=.故答案为:4.7.(2022·全国·统考高考真题)记双曲线2222:1(0,0)x y C a b a b-=>>的离心率为e ,写出满足条件“直线2y x =与C 无公共点”的e 的一个值______________.【答案】2(满足1e <≤【解析】2222:1(0,0)x y C a b a b -=>>,所以C 的渐近线方程为b y x a =±,结合渐近线的特点,只需02b a <≤,即224b a≤,可满足条件“直线2y x =与C 无公共点”所以==c e a 又因为1e >,所以1e <≤故答案为:2(满足1e <≤皆可)【方法技巧与总结】求离心率范围的方法一、建立不等式法:1、利用曲线的范围建立不等关系.2、利用线段长度的大小建立不等关系.12,F F 为椭圆22221(0)x y a b a b +=>>的左、右焦点,P 为椭圆上的任意一点,[]1,PF a c a c ∈-+;12,F F 为双曲线22221(0,0)x y a b a b-=>>的左、右焦点,P 为双曲线上的任一点,1PF c a ≥-.3、利用角度长度的大小建立不等关系.12,F F 为椭圆22221x y a b +=的左、右焦点,P 为椭圆上的动点,若12F PF θ∠=,则椭圆离心率e 的取值范围为sin12e θ≤<.4、利用题目不等关系建立不等关系.5、利用判别式建立不等关系.6、利用与双曲线渐近线的斜率比较建立不等关系.7、利用基本不等式,建立不等关系.【核心考点】核心考点一:顶角为直角的焦点三角形求解离心率的取值范围问题【典型例题】例1.(2022·全国·高二专题练习)已知椭圆()222210x y a b a b +=>>上一点A 关于原点的对称点为点B ,F 为其右焦点,若AF BF ⊥,设ABF α∠=,且,124ππα⎛⎫∈ ⎪⎝⎭,则该椭圆的离心率e 的取值范围是()A .12,23⎛⎫ ⎪⎝⎭B .2⎝⎭C .,23⎛ ⎝⎭D .23⎫⎪⎪⎝⎭【答案】B【解析】由题意椭圆22221x y a b+=()00a b >>,上一点A 关于原点的对称点为点B ,F 为其右焦点,设左焦点为N ,连接AN ,BN ,因为AF ⊥BF ,所以四边形AFBN 为长方形.根据椭圆的定义:2AF AN a +=,由题∠ABF =α,则∠ANF =α,所以22cos 2sin a c c αα+=,利用2112sin cos 4c e a πααα===+⎛⎫+ ⎪⎝⎭,∵,124ππα⎛⎫∈ ⎪⎝⎭,∴342πππα<+<14πα<⎛⎫+ ⎪⎝⎭,即椭圆离心率e 的取值范围是23⎛⎫⎪ ⎪⎝⎭,故选B .例2.(2022春·辽宁葫芦岛·高二统考期中)已知点12F F ,分别是椭圆22221(0)x ya b a b+=>>的左、右焦点,点P 12PF F ∆是直角三角形的动点P 恰好有6个,则该椭圆的离心率为()A .12BC.2D【答案】C【解析】由题意知,椭圆的最大张角为090,所以b c =,所以a =,所以c e a ===,故应选C .例3.(2022秋·安徽·高二校联考开学考试)若P 是以1F ,2F 为焦点的椭圆22221(0)x y a b a b +=>>上的一点,且120PF PF ⋅= ,125tan 12PF F ∠=,则此椭圆的离心率为()AB .1517C .1315D .1317【答案】D【解析】因为120PF PF ⋅=,所以12PF PF ⊥,在12Rt PF F 中,设25PF m =(0m >),则112PF m =,1213F F m ==,所以213c m =,12217a PF PF m =+=,所以213217c e a ==.故选:D.核心考点二:焦点三角形顶角范围与离心率【典型例题】例4.(2022春·福建漳州·高二校联考期中)已知椭圆2222:1x y C a b+=(0a b >>),椭圆的左、右焦点分别为1F ,2F ,P 是椭圆C 上的任意一点,且满足120PF PF ⋅>,则椭圆C 的离心率e 的取值范围是()A .10,2⎛⎫ ⎪⎝⎭B .2⎛⎫ ⎪ ⎪⎝⎭C .122⎛⎫⎪ ⎪⎝⎭D .,12⎛⎫⎪ ⎪⎝⎭【答案】B【解析】由已知得1(,0)F c -,2(,0)F c ,设()00,P x y ,则()100,PF c x y =--- ,()200,PF c x y =--,因为120PF PF ⋅> ,所以()()0000,,0c x y c x y ---⋅-->,即222000c x y -++>,即22200x y c +>,因为点P 是椭圆上的任意一点,所以2200x y +表示椭圆上的点到原点的距离的平方,因为()22200minx y b +=,所以22b c >,所以222a c c ->,即2212c a <,所以2c e a ⎛⎫=∈ ⎪ ⎪⎝⎭,故选:B .例5.(2022春·北京·高二人大附中校考期末)已知椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为12,F F ,若C 上存在一点P ,使得12120F PF ︒∠=,且12F PF △,则C 的离心率的取值范围是()A .⎛ ⎝⎦B .110,12⎛⎫⎪⎝⎭C .311212⎫⎪⎢⎣⎭D .11,112⎛⎫⎪⎝⎭【答案】C【解析】设12||2=F F c ,12F PF △内切圆的半径为r .因为12||+||2PF PF a =,所以()22212121212||||||2||||(1cos1204|||)|F F PF PF PF PF a PF PF ︒=+-+=-,则212||||4PF PF b =.由等面积法可得)22211(22)4sin12022a c rb ac ︒+=⨯⨯=-,整理得)r a c =-,又12r a >故1112c a <.又12120F PF ︒∠=,所以16900F PO ︒∠≤≤则c a ≥11212e ≤<.故选:C例6.(2022春·新疆乌鲁木齐·高二乌市八中校考阶段练习)已知1F ,2F 是椭圆()222210x y a b a b+=>>的两个焦点,若存在点P 为椭圆上一点,使得1260F PF ∠=︒,则椭圆离心率e 的取值范围是().A .,12⎫⎪⎪⎣⎭B .2⎛⎫⎪ ⎪⎝⎭C .1,12⎡⎫⎪⎢⎣⎭D .122⎡⎫⎢⎣⎭【答案】C 【解析】如图,当动点P 在椭圆长轴端点处沿椭圆弧向短轴端点运动时,P 对两个焦点的张角12F PF ∠渐渐增大,当且仅当P 点位于短轴端点0P 处时,张角12F PF ∠达到最大值.由此可得:存在点P 为椭圆上一点,使得1260F PF ∠=︒,012P F F ∴△中,10260F P F ∠≥︒,可得02Rt P OF △中,0230OP F ∠≥︒,所以02P O ,即b ≤,其中c =2223a c c ∴-≤,可得224a c ≤,即2214c a ≥椭圆离心率ce a=,且0a c >>112e ∴≤<故选:C例7.(2022春·吉林辽源·高三辽源市第五中学校校考期中)已知椭圆22221(0)x y a b a b+=>>上一点A 关于原点的对称点为B ,F 为其右焦点,若AF BF ⊥,设ABF α∠=,且ππ[,]64α∈,则该椭圆离心率e 的最大值为___________.1-【解析】已知椭圆22221(0)x y a b a b+=>>上一点A 关于原点的对称点为点B 、F 为其右焦点,设椭圆的左焦点为N ,连接,,,AF AN BF BN ,所以四边形AFBN为长方形,根据椭圆的定义2AF AN a +=,且ABF α∠=,则ANF α∠=,所以22cos 2sin a c c αα=+,又由离心率的公式得211π2sin cos )4c e a ααα==++,由ππ[,]64α∈,则5πππ1242α≤+≤,所以112)π4α≤≤+1-.1例8.(2022春·黑龙江佳木斯·高二建三江分局第一中学校考期中)已知椭圆22221(0)x y a b a b +=>>上一点A 关于原点的对称点为点B ,F 为其右焦点,若AF BF ⊥,设ABF α∠=,且,63ππα⎡⎤∈⎢⎣⎦,则该椭圆的离心率e 的取值范围是___________.【答案】2,312⎡⎤-⎢⎥⎣⎦【解析】椭圆上点A 关于原点的对称点为点B ,F 为其右焦点,设左焦点为1F ,连接11AF AF BF BF ,,,,则四边形1AFF B 为矩形.根据椭圆的定义:12AF AF a ABF α+=∠=,,则1BAF α∠=.∴1||2c sin ||2cos 22cos 2AF AF c a c c sin αααα=⋅=⋅=⋅+⋅,,椭圆的离心率2112sin cos 2sin 4c e a πααα===+⎛⎫+ ⎪⎝⎭,64ππα⎡⎤∈⎢⎥⎣⎦,∴51242πππα≤+≤,则2(31)sin 144πα+⎛⎫≤+≤ ⎪⎝⎭,∴213122sin()4πα≤≤-+,∴椭圆离心率e 的取值范围2312⎡⎤-⎢⎥⎣⎦,.故答案为:2312⎡⎤-⎢⎥⎣⎦,例9.(2022·高二单元测试)椭圆2222:1(0)x y C a b a b +=>>上一点A 关于原点的对称点为B ,F 为其右焦点,若AF BF ⊥,设ABF θ∠=,且5,412ππθ⎡⎤∈⎢⎥⎣⎦,则该椭圆离心率的取值范围为________.【答案】2623⎢⎣⎦【解析】记椭圆C 的左焦点为F ',连AF ',BF ',由椭圆的对称性和性质知BF AF '=,2AF B AFB π∠∠==',由2AF BF a +=,可得2cos 2sin 2c c a θθ+=,得11sin cos 4c e a πθθθ===+⎛⎫+ ⎪⎝⎭,由5,412ππθ⎡⎤∈⎢⎥⎣⎦,可得2,423πππθ⎛⎫⎡⎤+∈ ⎪⎢⎥⎝⎭⎣⎦sin 14πθ⎛⎫≤+≤ ⎪⎝⎭,所以23e ≤≤.故答案为:2⎢⎣⎦.核心考点三:共焦点的椭圆与双曲线问题【典型例题】例10.(2022春·江苏苏州·高二江苏省苏州第十中学校校考阶段练习)已知椭圆和双曲线有共同的焦点12,,,F F P Q 分别是它们在第一象限和第三象限的交点,且260QF P ∠=,记椭圆和双曲线的离心率分别为12,e e ,则221231e e +等于_______.【答案】4【解析】设椭圆长半轴长为1a ,双曲线实半轴长为2a ,()1,0F c -,()2,0F c ,P 为两曲线在第一象限的交点,Q 为两曲线在第三象限的交点.由椭圆和双曲线定义知:1212+=PF PF a ,1222-=PF PF a ,112PF a a ∴=+,212=-PF a a ,由椭圆和双曲线对称性可知:四边形12PF QF 为平行四边形,260QF P ∠= ,12120F PF ∴∠= ,222121212122cos F F PF PF PF PF F PF ∴=+-∠,即()()()()22222121212121243c a a a a a a a a a a =++-++-=+,22122222123314a a e e c c∴+=+=.故答案为:4.例11.(2022春·山东青岛·高二统考期末)已知椭圆1C 和双曲线2C 有共同的焦点1F ,2F ,P 是它们的一个交点,且1223F PF π∠=,记椭圆1C 和双曲线2C 的离心率分别为1e ,2e ,则2212484w e e =+的最小值为()A .24B .37C .49D .52【答案】C【解析】设椭圆的长半轴长为1a ,双曲线的实半轴长2a ,焦距2c ,则1212+=PF PF a ,1222-=PF PF a ,解得112=+PF a a ,212=-PF a a,如图在△F1PF2中,根据余弦定理可得:()()()22212121222cos3F F PF PF PF PF π=+-⋅,整理得2221243c a a =+,即2212314e e +=,所以()2222222112122222121231213148448437494e e w e e e e e e e e ⎛⎫=+=⨯+⨯+=++≥ ⎪⎝⎭,当且仅当1242e e ==时,取等号.故选:C.例12.(2022春·广西·高三校联考阶段练习)已知椭圆和双曲线有共同的焦点1F ,2F ,P 是它们的一个交点,且12π3F PF ∠=,记椭圆和双曲线的离心率分别为1e ,2e ,则12e e ⋅的最小值为()A2B .34CD .3【答案】A【解析】如图,设椭圆的长半轴为1a ,双曲线的实半轴长为2a ,则根据椭圆及双曲线的定义:1211222,2PF PF a PF PF a +=-=,所以112212,PF a a PF a a =+=-,设122F F c =,因为12π3F PF ∠=,则在12PF F △中,由余弦定理得:22212121212π4()()2()()cos3c a a a a a a a a =++--+-,化简得:2221234a a c +=,即2212134e e +=,从而有2212134e e =+≥整理得12e e ⋅≥=(当且仅当122e e =时等号成立)故选:A.例13.(2022春·辽宁沈阳·高二沈阳市第三十一中学校考阶段练习)已知椭圆和双曲线有共同的焦点1F ,2F ,P 是它们的一个交点,且123F PF π∠=,记椭圆和双曲线的离心率分别为1e ,2e ,则当121e e 取最大值时,1e ,2e 的值分别是()A2,2B .12C.3D.4【答案】A【解析】不妨设椭圆与双曲线的标准方程分别为:()222210x y a b a b+=>>,c =2222111x y a b -=,c =设1PF m =,2PF n =.m n >.则2m n a +=,12m n a -=,∴1m a a =+,1n a a =-.因为123F PF π∠=,所以()22221cos322m n c mnπ+-==,即()()()()22211114a a a a c a a a a ++--=+-.∴2221340a a c +-=,∴2221314e e +=,∴4≥,则121e e ≤12e =2e =时取等号.故选:A .例14.(2022·河南洛阳·校联考模拟预测)已知椭圆1C :()222210x y a b a b +=>>和双曲线2C :()222210,0x y m n m n-=>>有共同的焦点1F ,2F ,P 是它们在第一象限的交点,当1260F PF ∠=︒时,1C 与2C 的离心率互为倒数,则双曲线2C 的离心率是()ABC .2D【答案】B【解析】设1C ,2C 的离心率分别为1e ,2e ,焦距为2c ,因为122PF PF a +=,122PF PF m -=,所以1PF a m =+,2PF a m =-,由余弦定理,得222121212122cos F F PF PF PF PF F PF =+-⋅∠,即()()()()22242cos 60c a m a m a m a m =++--+-︒,化简,得22243c a m =+,两边同除以2c ,得2212134e e =+.又121e e =,所以222234=+e e .又21e >,所以2e =.故选:B核心考点四:椭圆与双曲线的4a 通径体【典型例题】例15.(2022·广西南宁·南宁市第八中学校考一模)已知椭圆()222210x y a b a b+=>>的左、右焦点分别为12,F F ,过1F 且与x 轴垂直的直线交椭圆于,A B 两点,直线2AF 与椭圆的另一个交点为C ,若222=AF F C ,则椭圆的离心率为()ABCD【答案】A【解析】过点C 作CD x ⊥轴于D ,则122~ AF F CDF ,由222=AF F C ,则122||2||=F F F D ,12AF CD =,所以点22,2⎛⎫⎪⎝⎭b C c a ,由点C 在椭圆上,所以有222222(2)1b ac a b ⎛⎫⎪⎝⎭+=,即225c a =,所以e ==c a 故选:A.例16.(2022·全国·高三专题练习)已知椭圆22221(0)x y C a b a b+=>>:的左、右焦点分别为1F ,2F ,过2F 直线与椭圆C 交于M ,N 两点,设线段1NF 的中点D ,若10MD NF ⋅=,且12//MF DF,则椭圆C 的离心率为()A .13BC .12D【答案】B【解析】因为10MD NF ⋅=,所以1MD NF ⊥,又D 是1NF 中点,所以1MF MN =,因为12//MF DF,所以2F 是MN 中点,则22MF NF =,因此MN x ⊥轴,设2MF m =,则12MF m =,1232MF MF m a +==,23a m =,在12MF F △中,由勾股定理得22242(((2)33m m c +=,变形可得3c e a ==.故选:B .例17.(2022春·云南·高三校联考阶段练习)已知双曲线2222:1(0,0)x y C a b a b-=>>的左、右焦点为1F ,2F ,过1F 且垂直于x 轴的直线交C 于M ,N 两点,若22MF NF ⊥,则C 的离心率为()A 1+B .2CD【答案】A【解析】由题可得:MN x c =-,代入双曲线2222:1(0,0)x y C a b a b -=>>,解得2b y a=±,又22MF NF ⊥,∴112F M F F =,即22bc a=,222c a ac ∴-=,2210e e ∴--=,1e ∴=1e > ,1e ∴.故选:A例18.(2022春·江苏宿迁·高三校考阶段练习)如图,已知A ,B ,C 是双曲线22221(0,0)x y a b a b -=>>上的三个点,AB 经过原点O ,AC 经过右焦距F ,若BF AC ⊥且2CF FA =,则该双曲线的离心率等于_____.【答案】3【解析】若E 是左焦点,连接,,AE BE EC ,设||BF m =,||AF n =,∴由双曲线的对称性且BF AC ⊥知:AEBF 是矩形,则||AE m =,||BE n =,又2CF FA =,即||2FC n =,则||2||22EC a FC a n =+=+,∴在Rt EAC △中,222||||||AE AC EC +=,即22294()m n a n +=+,而2m n a -=,∴23an =,83a m =,∵在Rt EAF V 中,2224m n c +=,即226849a c =,可得3e =..核心考点五:椭圆与双曲线的4a 直角体【典型例题】例19.(2022春·福建福州·高二福建省福州格致中学校考阶段练习)已知1F ,2F 是双曲线()2222:10,0x y E a b a b-=>>的左、右焦点,过1F l ,l 分别交y 轴和双曲线右支于点M ,P ,且212F F PM F M -=uuu u r uuu r uuuu r,则E 的离心率为______.【答案】2【解析】因为212F F PM F M -=uuu u r uuu r uuuu r ,所以1MF PM =uuu r uuu r,即M 为1PF 的中点.又O 为1F 2F 的中点,所以OM 为中位线.所以2//OM PF ,即2PF x ⊥轴.因为直线l 过1F 122F F c =,所以212PF F ==,11224PF F F c ==.由双曲线的定义可得:122PF PF a -=,即42c a -=,解得:2c a ==心率为2e =故答案为:2例20.(2022·全国·高三专题练习)如图所示,双曲线C :()222210,0x y a b a b-=>>的左、右焦点分别为1F 、2F ,过1F 的直线与双曲线C 的两条渐近线分别交于A 、B 两点,A 是1F B 的中点,且12F B F B ⊥,则双曲线C 的离心率e =()AB .2CD1【答案】B【解析】 A 是1F B 的中点,AO ∴为△12F F B 的中位线,12F B F B ⊥,所以1OA F B ⊥,所以1OB F O c ==.设1(B x ,1)y ,2(A x ,2)y ,点B 在渐近线by x a=上,∴2221111x y c b y x a ⎧+=⎪⎪⎨⎪=⎪⎩,得11x a y b =⎧⎨=⎩.又A 为1F B 的中点,∴2222c a x b y -+⎧=⎪⎪⎨⎪=⎪⎩,A 在渐近线by x a=-上,∴22b b a c a -=-⋅,得2c a =,则双曲线的离心率2c e a==.故选:B例21.(2022·天津·统考一模)设12,F F 分别是双曲线22221(0,0)x y a b a b -=>>的左、右焦点,O 为坐标原点,过左焦点1F 作直线1F P 与圆222x y a +=切于点E ,与双曲线右支交于点P ,且满足()112OE OP OF =+,OE =()A .221612x y -=B .22169x y -=C .22136x y -=D .221312x y -=【答案】D【解析】∵E 为圆222x y a +=上的点,OE a ∴==()112OE OP OF =+,∴E 是1PF 的中点,又O 是12F F 的中点,222PF OE a ∴===,且2//PF OE ,又12124PF PF a PF a -==∴==1PF 是圆的切线,121,OE PF PF PF ∴⊥∴⊥,又222222212122460,15,12F F c c PF PF c b c a =∴=+=∴=∴=-=,,∴双曲线方程为221312x y -=.故选:D例22.(2022·四川广元·统考三模)设1F ,2F 分别是椭圆2222:1(0)x y E a b a b+=>>的左、右焦点,过2F 的直线交椭圆于A ,B 两点,且120AF AF ⋅= ,222AF F B =,则椭圆E 的离心率为()A .23B .34C D 【答案】C【解析】因为222AF F B =,不妨令()22220B AF F m m ==>,过2F 的直线交椭圆于A ,B 两点,由椭圆的定义可得,122AF AF a +=,122BF BF a +=,则12BF a m =-,122AF a m =-,又120AF AF ⋅=,所以12AF AF ⊥,则12AF F △和1AF B △都是直角三角形,则22211AF AB BF +=,即()()2222292a m m a m -+=-,解得3a m =,所以143AF a =,223AF a =,又122F F c =,2221212AF AF F F +=,所以222164499a a c +=,因此2259c a =,所以椭圆E 的离心率为c a =故选:C.例23.(2022春·江西抚州·高二江西省临川第二中学校考阶段练习)如图,已知1F ,2F 为双曲线E :22221(0,0)x y a b a b-=>>的左、右焦点,过点1F ,2F 分别作直线1l ,2l 交双曲线E 于A ,B ,C ,D 四点,使得四边形ABCD 为平行四边形,且以AD 为直径的圆过1F ,11DF AF =,则双曲线E 的离心率为()A BC .52D .2【答案】D【解析】设11DF AF x ==,则22DF x a =-,由双曲线的对称性和平行四边形的对称性可知:21CF AF x ==,连接1CF ,则有1222CF CF x a =+=+,2222DC DF CF x a=+=-由于1F 在以AD 为直径的圆周上,11DF AF ∴⊥,∵ABCD 为平行四边形,//AB CD ,1DF DC ∴⊥,在直角三角形1CDF 中,22211CF DF CD =+,()()222222x a x x a +=+-,解得:3x a =,123,DF a DF a ==;在直角三角形12F F D 中,2221212DF DF F F +=,()()22232a a c +=,得2252a c =,c e a =,故选:D.核心考点六:椭圆与双曲线的等腰三角形问题【典型例题】例24.(2022春·陕西西安·高二期末)设1F ,2F 是椭圆E :()222210x y a b a b+=>>的左、右焦点,过点()2,0F c 且倾斜角为60°的直线l 与直线2a x c=相交于点P ,若12PF F △为等腰三角形,则椭圆E 的离心率e 的值是()A2B .13C.3D.2【答案】A【解析】直线l的方程为)y x c =-,由)2y x c a x c ⎧=-⎪⎨=⎪⎩解得2y c =,则2a P c ⎛ ⎝⎭,由于12PF F △为等腰三角形,所以21cos 6022a c c c -︒==,222212,,22c c a c a a ===.故选:A例25.(2022·全国·高三专题练习)已知双曲线22221x y a b-=的左焦点为1F ,过1F 作一倾斜角为15 的直线交双曲线右支于P 点,且满足1POF △(O 为原点)为等腰三角形,则该双曲线离心率e 为()A.e =B .2e =C.e =D.12e =【答案】C【解析】记右焦点为2F ,由题意知,1215PF F ∠=,且1POF △为等腰三角形,则只能是1OF OP =,所以212230POF PF F ∠∠==,OP c =,所以直线OP的方程为y x =,由2222331y x x y a b ⎧=⎪⎪⎨⎪-=⎪⎩,得2222222222333P Pa b x b a a b y b a ⎧=⎪⎪-⎨⎪=⎪-⎩所以222222222333a b a b c b a b a+=--,整理,得42243840c a c a -+=,即423840e e -+=,解得22e =或23(舍去),所以2e =.故选:C .例26.(2022·河南鹤壁·鹤壁高中校考模拟预测)已知12F F 、是椭圆22221(0)x y a b a b+=>>的左、右焦点,点P 为抛物线28(0)y ax a =->准线上一点,若12F PF △是底角为15︒的等腰三角形,则椭圆的离心率为()A .31-B .21-C .312-D .212-【答案】A【解析】如图,抛物线的准线与x 轴的交点为M因为12,F F 是椭圆22221(0)x y a b a b+=>>的左、右焦点,所以12(,0),(,0)F c F c -抛物线28(0)y ax a =->准线为:直线2x a =,所以(2,0)M a 因为12F PF △是底角为15︒的等腰三角形,则1212==15PF F F PF ∠∠︒则22122=30,==2PF M F F PF c ∠︒则222223cos ===22F M a c PF M PF c -∠,整理得:2=(3+1)a c 所以离心率23131c e a==+.故答案为:A.例27.(2022·全国·高三专题练习)已知椭圆2222:1(0)x y C a b a b+=>>的左右焦点为12,F F ,若椭圆C 上恰好有6个不同的点P ,使得12F F P 为等腰三角形,则椭圆C 的离心率的取值范围是()A .111,,1322⎛⎫⎛⎫⋃ ⎪ ⎪⎝⎭⎝⎭B .110,,132⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭C .1,13⎛⎫ ⎪⎝⎭D .1,12⎛⎫ ⎪⎝⎭【答案】A【解析】法一:显然,P 是短轴端点时,12PF PF =,满足12F F P 为等腰三角形,因此由对称性,还有四个点在四个象限内各有一个,设(,)P x y 是第一象限内使得12F F P 为等腰三角形的点,若112PF F F =,则222212x y a b c ⎧+=⎪=,又222a b c =+,消去y 整理得:222224240c x a cx a c a +-+=,解得22a ac x c --=(舍去)或22a acx c -+=,由0x a <<得220a aca c-+<<,所以112c a <<,即112e <<,若212PF F F =,则222212x y a b c ⎧+=⎪=,又222a b c =+,消去y 整理得:222224240c x a cx a c a --+=,解得22a ac x c -=或22a ac x c +=,22a aca c +>舍去.所以220a aca c-<<,所以1132c a <<,即1132e <<,12e =时,2a c =,12PF F △是等边三角形,P 只能是短轴端点,只有2个,不合题意.综上,e 的范围是111(,)(,1)322⋃.法二:①当点P 与短轴的顶点重合时,12F F P 构成以12F F 为底边的等腰三角形,此种情况有2个满足条件的12F F P ;②当12F F P 构成以12F F 为一腰的等腰三角形时,根据椭圆的对称性,只要在第一象限内的椭圆上恰好有一点P 满足12F F P 为等腰三角形即可,则1122PF F F c ==或2122PF F F c ==当12PF c =时,则2c a >,即12c e a =>,则112e <<,当22PF c =时,则有22c a c c a>-⎧⎨<⎩,则1132e <<,综上所述,椭圆的离心率取值范围是111,,1322⎛⎫⎛⎫⋃ ⎪ ⎪⎝⎭⎝⎭.故选:A.核心考点七:双曲线的4a 底边等腰三角形【典型例题】例28.(2022·全国·高三专题练习)已知1F ,2F 是双曲线2222:1(0,0)x y C a b a b-=>>的左,右焦点,过点1F作斜率为2的直线l 与双曲线的左,右两支分别交于M ,N 两点,以2F 为圆心的圆过M ,N ,则双曲线C 的离心率为()ABC .2D【答案】B【解析】取MN 中点A ,连AF 2,由已知令22||||MF NF m ==,则2AF MN ⊥,如图:因点M ,N 为双曲线左右两支上的点,由双曲线定义得12||||22MF MF a m a =-=-,12||||22NF NF a m a =+=+,则11||||||4,||2MN NF MF a MA a =-==,令双曲线半焦距为c ,12Rt AF F △中,12||,||AF m AF =2Rt AMF中,2||AF=22222m a c =+,因直线l的斜率为2,即12tan 2AF F ∠=,而2121||tan ||AF AF F AF ∠=,即21||||AF AF =,2221||1||2AF AF =,于是有2222221222c a c a -=+,c =,==c e a ,所以双曲线C故选:B例29.(2022·全国·高三专题练习)设双曲线2222:1(0,0)x y C a b a b -=>>的左、右焦点分别为12,F F ,过点1Fl 与双曲线C 的左、右两支分别交于,M N 两点,且()220F M F N MN +⋅=,则双曲线C 的离心率为()ABCD .2【答案】A【解析】如图,设D 为MN 的中点,连接2F D .易知2222F M F N F D +=,所以()22220F M F N MN F D MN +⋅=⋅= ,所以2F D MN ⊥.因为D 为MN 的中点,所以22F M F N =.设22F M F N t ==,因为212MF MF a -=,所以12MF t a =-.因为122NF NF a -=,所以12NF t a =+.所以114MN NF MF a =-=.因为D 是MN 的中点,11F D F M MD =+,所以12,MD ND a F D t ===.在Rt 12F F D中,2F D =;在Rt 2MF D中,2F D ==22222t a c =+.所以21F D F D t ===因为直线l所以2121tan F D DF F F D ∠===,所以2222221,23c a c a a c -==+,c =,所以离心率为ca=故选:A核心考点八:焦点到渐近线距离为b 【典型例题】例30.(2022·全国·模拟预测)设1F ,2F 分别是双曲线C :()222210,0x ya b a b-=>>的左、右焦点,O 为坐标原点,过右焦点2F 作双曲线的一条渐近线的垂线,垂足为A .若12212AF F S OF =△,则双曲线C 的离心率为()AB .2C D 【答案】D【解析】根据对称性,不妨取双曲线C 的一条渐近线的方程为by x a=,即0bx ay -=,点()2,0F c b =.因为2OF c =,所以AO a =,所以122124422AF F AOF S S ab ab ==⨯=△△.由题意知2222ab c a b ==+,所以a b =,离心率e ==,故选:D.例31.(2022·全国·高三专题练习)设1F ,2F 是双曲线2222:1(0,0)x yC a b a b-=>>的左、右焦点,O 是坐标原点.过2F 作C 的一条渐近线的垂线,垂足为P .若1||||PF OP ,则C 的离心率为()AB .2CD【答案】B【解析】不妨设双曲线的一条渐近线方程为b y x a=,则2b c a PF b ⨯==,2OF c =,PO a ∴=,1|||PF OP ==在2Rt POF △中,222cos PF b PF O OF c∠==, 在12Rt PF F 中,22221212212cos 2PF F F PF b PF O PF F F c∠+-==,b c=,即224c a =,e=2,故选:B .例32.(2022·全国·高三专题练习)设1F ,2F 是双曲线2222:1(0,0)x y C a b u b -=>>的左、右焦点,O 是坐标原点.过2F 作C 的一条渐近线的垂线,垂足为P,若1PF ,则C 的离心率为()A.B .2CD【答案】C【解析】双曲线2222:1(0,0)x y C a b a b -=>>的渐近线为b y x a =±,焦点()2,0F c 到直线b y x a=的距离d b ==,所以2PF b =,由勾股定理得OP a =,所以2cos a POF c ∠=,在1POF △中,()122cos cos cos aPOF POF POF cπ∠=-∠=-∠=-,因为1PF 由余弦定理可得22211112cos PF OP OF OP OF POF =+-⋅∠,即)2222a a c ac c ⎛⎫=+-- ⎪⎝⎭,即222a c =,所以离心率c e a ==故选:C例33.(多选题)(2022秋·广东·高二校联考阶段练习)过双曲线2222:1x y C a b-=(0a >,0b >)的右焦点F 引C 的一条渐近线的垂线,垂足为A ,交另一条渐近线于点B .若FB AF λ=,23λ≤≤,则C 的离心率可以是()A B C .2D .2【答案】BC【解析】右焦点(c,0)F ,设一渐近线OA 的方程为b y x a=,则另一渐近线OB 的方程为b y x a=-,由FA 与OA 垂直可得FA 的方程为()a y x c b=--,联立方程2222()b y x a c a ax a a b c y x c b ⎧=⎪⎪⇒==⎨+⎪=--⎪⎩,可得A 的横坐标为2a c,联立方程()2222222b y x a c ca ax a a b a c y x c b ⎧=-⎪⎪⇒==⎨--⎪=--⎪⎩可得B 的横坐标为2222ca a c-.因为FB AF λ= ,所以()2222222222()22c c a ca a c a c c a c c a c cλλ---=-⇒=⨯--,可得2222222c e a c e λ==--,因为23λ≤≤,所以22322e e ≤-≤,即22222340432*******2e e e e e e ⎧-≥⎪⎪-⇒≤≤⇒≤⎨-⎪≤⎪-⎩,BC 满足题意,AD 不合题意,故选:BC.核心考点九:焦点到渐近线垂线构造的直角三角形【典型例题】例34.(2022·陕西西安·西安中学校考模拟预测)已知双曲线:C 22221(0,0)x y a b a b-=>>的左、右焦点分别为12,F F ,过2F 作双曲线C 的一条渐近线的垂线l ,垂足为H ,直线l 与双曲线C 的左支交于E 点,且H 恰为线段2EF 的中点,则双曲线C 的离心率为()ABC .2D【答案】D【解析】连结1EF ,因为点,O H 分别为12F F 和2EF 的中点,所以1//OH EF ,且12EF EF ⊥设点()2,0F c 到一条渐近线by x a=的距离d b ==,所以22EF b =,又212EF EF a -=,所以122EF b a =-,12Rt EF F 中,满足()2222244b a b c -+=,整理为:2b a =,双曲线的离心率ce a===故选:D例35.(2022秋·安徽·高二校联考期中)已知双曲线22221(0,0)x y a b a b-=>>的左右焦点分别为1F ,2F ,以1OF 为直径的圆与双曲线的一条渐近线交于点M (异于坐标原点O ),若线段1MF 交双曲线于点P ,且2//MF OP 则该双曲线的离心率为()ABCD【答案】A【解析】不妨设渐近线的方程为by x a=-,因为2//MF OP ,O 为12F F 的中点,所以P 为1MF 的中点,将直线OM ,1MF 的方程联立()b y x aa y x cb ⎧=-⎪⎪⎨⎪=+⎪⎩,可得2,a ab M c c ⎛⎫- ⎪⎝⎭,又()1,0F c -,所以2,22a c cab P c ⎛⎫⎛⎫-+-⎪ ⎪⎝⎭⎪ ⎪ ⎪⎝⎭即22,22a c ab P c c ⎛⎫+- ⎪⎝⎭,又P 点在双曲线上,所以()2222222144c ac a a c+-=,解得c a =故选:A.例36.(2022·全国·高三专题练习)已知双曲线2222:1(0,0)x y E a b a b-=>>的左焦点为1F ,过点1F 的直线与两条渐近线的交点分别为M N 、两点(点1F 位于点M 与点N 之间),且112MF F N =,又过点1F 作1F P OM ⊥于P (点O 为坐标原点),且||||ON OP =,则双曲线E 的离心率e =()ABCD .62【答案】C【解析】不妨设M 在第二象限,N在第三象限,如下图所示:因为ON OP =,11F OP F ON ∠=∠,所以11F OP F ON ≅ ,所以1190F PO F NO ∠=∠=︒,11F P F N =,又()1:,,0OM bl y x F c a=--,所以11F F N b ==,所以ON OP a ==,所以1122MF F N b ==,因为113tan ,tan tan 2b b F OP MON F OP a a∠=∠=∠=,所以22231bba b a a =-,所以222222113b c a e a a -==-=,所以e =故选:C.例37.(2022·全国·统考模拟预测)设F 是双曲线22221(0)x y b a a b-=>>的一个焦点,过F 作双曲线的一条渐近线的垂线,与两条渐近线分别交于,P Q 两点.若2FP FQ =,则双曲线的离心率为()A BC .2D .5【答案】C【解析】不妨设(,0)F c -,过F 作双曲线一条渐近线的垂线方程为()ay x c b=+,与b y x a =-联立可得2a x c =-;与b y x a =联立可得222a cx b a=-,∵2FP FQ = ,∴22222a ca c cb ac ⎛⎫+=-+ ⎪-⎝⎭,整理得,22222c b a =-,即224c a =,∵1e >,∴2e =.故选:C .核心考点十:以两焦点为直径的圆与渐近线相交问题【典型例题】例38.(2022春·四川宜宾·高二四川省宜宾市第四中学校校考阶段练习)已知F 是双曲线2222:1(0,0)x y C a b a b-=>>的右焦点,O 为坐标原点,过F 的直线与C 的两条渐近线的交点分别为,M N ,若0OM MF ⋅= ,||MN b =,则C 的离心率为________.【答案】2【解析】因为0OM MF ⋅= ,所以OM MF ⊥,即⊥OM MF所以MF 为点(),0F c 到渐近线0bx ay -=的距离,bcMF b c===,所以MF MN b ==,可得点M 为NF 的中点,又因为⊥OM MF ,所以ON OF c ==,所以222OM c b a =-=,设双曲线的左焦点为1F ,1F ON θ∠=,(),N x y 则()tan tan tan b FON FON aθπ=-∠=-∠=,因为222c a b =+,所以cos a c θ=,sin b cθ=所以cos a x ON c a c θ=-=-⋅=-,sin by ON c b cθ==⋅=,所以(),N a b -,因为M 为NF 中点,所以,22a M c b -⎛⎫⎪⎝⎭,222222c a b OMa -⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭,将222b c a =-代入整理可得:()22224c a c a a -+-=即222240c ac a --=,所以220e e --=,可得()()210e e -+=,解得:2e =或1e =-(舍),故答案为:2例39.(2022·山西运城·统考模拟预测)已知双曲线E :()222210,0x y a b a b-=>>的左焦点为1F ,过点1F 的直线与两条渐近线的交点分别为M ,N 两点(点1F 位于点M 与点N 之间),且13MN F N =,又过点1F 作1F P OM ⊥于P (点О为坐标原点),且ON OP =,则双曲线E 的离心率e 为__________.【解析】双曲线E :()222210,0x y a b a b-=>>的渐近线方程为b y x a =±,如图所示,设11,b M x x a ⎛⎫- ⎪⎝⎭,22,b N x x a ⎛⎫⎪⎝⎭,()1,0F c -,。
通用版2019版高考物理二轮复习第二部分第一板块第8讲技法专题__10法速解物理选择题讲义含解析20190411264

技法专题——10法速解物理选择题理综全国卷中,物理8道选择题分单选和多选,主要考查对物理概念、物理现象、物理过程和物理规律的认识、判断、辨析、理解和应用等,具有信息量大、知识覆盖面广、干扰性强、命题灵活性强、层次丰富、能考查学生的多种能力等特点。
要想迅速、准确地解答物理选择题,不但要熟练掌握和应用物理学的基本概念和规律,还要学会一些非常规巧解妙招,针对题目特性“有的放矢”,达到快速解题的目的。
技法1 直接判断法通过观察题目中所给出的条件,根据所学知识和规律推出结果,直接判断,确定正确的选项。
直接判断法适用于推理过程较简单的题目,这类题目主要考查学生对物理知识的记忆和理解程度,如考查物理学史和物理常识的试题等。
[应用体验] [多选]下列说法中正确的是( )A .电荷在某处不受电场力的作用,则该处电场强度为零B .一小段通电导线在某处不受磁场力作用,则该处磁感应强度一定为零C .电场强度的大小等于把一个试探电荷放在该点时受到的电场力与试探电荷本身电荷量的比值D .磁感应强度的大小等于把一小段通电导线放在该点时受到的磁场力与该小段导线长度和电流乘积的比值[解析] 电场对放入其中的电荷有力的作用,磁场对通电导线有力的作用的条件是:磁场方向和电流方向不平行,A 正确,B 错误;根据电场强度的定义式E =F q 可知,C 正确;磁感应强度B =F IL中,I 和B 的方向必须垂直,D 错误。
[答案] AC技法2 比较排除法运用排除法解题时,对于完全肯定或完全否定的判断,可通过举反例的方式排除;对于相互矛盾或者相互排斥的选项,则最多只有一个是正确的,要学会从不同方面或不同角度思考与推敲,将不符合题意的选项一一排除,最终留下的就是符合题意的选项。
[应用体验] 如图所示,以MN 、PQ 为边界的区域内存在垂直纸面向里的匀强磁场,磁场宽为2L ,高为L 的正三角形闭合金属框由粗细均匀的电阻丝围成,在外力作用下由图示位置被水平向右匀速拉过磁场区域,ab 边始终与MN平行,取逆时针方向为电流的正方向。
高考物理二轮复习讲义:解题方法专题——微元法、整体与隔离

微元法本专题主要讲解利用微元法解决动力学问题、变力做功问题、电场和电磁感应等问题,主要分为时间微元和位移微元两大类。
微元法在近几年高考中考查频率较高,出现了分值高、难度较大的计算题。
微元法是一种非常有效的解题方法,将研究对象或研究过程分解为众多细小的“微元”,分析这些“微元”,进行必要的数学推理或物理思想处理,能够有效的简化复杂的物理问题。
考查学生的分析推理能力,应用数学方法解决物理问题能力。
时间微元微元思想是中学物理中的重要思想。
所谓微元思想,是将研究对象或者物理过程分割成无限多个无限小的部分,先取出其中任意部分进行研究,再从局部到整体综合起来加以考虑的科学思维方法。
如图所示,两根平行的金属导轨MN和PQ放在水平面上,左端连接阻值为R的电阻。
导轨间距为L,电阻不计。
导轨处在竖直向上的匀强磁场中,匀强磁场的磁感应强度为B。
一根质量为m、阻值为r的金属棒放置在水平导轨上。
现给金属棒一个瞬时冲量,使其获得一个水平向右的初速度v0后沿导轨运动。
设金属棒运动过程中始终与导轨垂直且接触良好,导轨足够长,不计一切摩擦。
求:(1)金属棒的速度为v时受到的安培力是多大?(2)金属棒向右运动的最大距离是多少?物理学研究问题一般从最简单的理想情况入手,由简入繁,逐渐贴近实际。
在研究真实的向上抛出的物体运动时,我们可以先从不受阻力入手,再从受恒定阻力研究,最后研究接近真实的、阻力变化的运动情形。
现将一个质量为m的小球以速度v0竖直向上抛出,重力加速度为g。
(1)若忽略空气阻力对小球运动的影响,求物体经过多长时间回到抛出点;(2)若空气阻力大小与小球速度大小成正比,已知小球经t时间上升到最高点,再经一段时间匀速经过抛出点时,速度大小为v1,求小球抛出后瞬间的加速度和上升的最大高度。
涉及时间微元问题的一般解题步骤:(1)本方法一般用来处理变加速直线运动的情况且物体所受的变力与速度成正比。
(2)找微元:对于这类变速运动,通常选取极短的一段时间∆t,在这段极短的时间内可认为物体的受力、速度等物理量不变。
2019年高考物理二轮复习 习题(一)十大技法破解选择题

一、选择题快速练选择题在高考中属于保分题目,只有“选择题多拿分,高考才能得高分”,在平时的训练中,针对选择题要做到两个方面:一是练准度:高考中遗憾的不是难题做不出来,而是简单题和中档题做错以及平时会做的题目没做对,平时训练一定要重视选择题的正答率。
二是练速度:提高选择题的答题速度,能为攻克后面的解答题赢得充足时间。
解答选择题时除了掌握直接判断和定量计算等常规方法外,还要学会一些非常规巧解妙招,针对题目特性“不择手段”,达到快速解题的目的。
(一)十大技法破解选择题技法1 直接判断法通过观察题目中所给出的条件,根据所学知识和规律推出结果,直接判断,确定正确的选项。
直接判断法适用于推理过程较简单的题目,这类题目主要考查学生对物理知识的记忆和理解程度,如考查物理学史和物理常识的试题等。
例1在物理学发展的过程中,许多物理学家的科学研究推动了人类文明的进程。
在对以下几位物理学家所做科学贡献的叙述中,正确的说法是( )A.英国物理学家牛顿用实验的方法测出了引力常量GB.第谷接受了哥白尼日心说的观点,并根据开普勒对行星运动观察记录的数据,应用严密的数学运算和椭圆轨道假说,得出了开普勒行星运动定律C.亚里士多德认为两个从同一高度自由落下的物体,重物体与轻物体下落一样快D.胡克认为只有在一定的条件下,弹簧的弹力才与弹簧的形变量成正比答案 D解析牛顿提出了万有引力定律及引力常量的概念,但没能测出G的数值,G的数值是由卡文迪许通过实验得出的,故A错误。
开普勒接受了哥白尼日心说的观点,并根据第谷对行星运动观察记录的数据,应用严密的数学运算和椭圆轨道假说,得出了开普勒行星运动定律,故B错误。
亚里士多德认为两个从同一高度自由落下的物体,重物体比轻物体下落得快,故C错误。
胡克认为只有在一定的条件下,弹簧的弹力才与弹簧的形变量成正比,故D正确。
点评物理学史是考试内容之一,熟记牛顿、伽利略、卡文迪许、库仑、法拉第等物理学家的成就,直接作出判断。
高考物理二轮专题复习 素能提升 211 10法妙解突破选择题(含解析)新人教版

【优化探究】2015高考物理二轮专题复习 素能提升 2-1-1 10法妙解突破选择题(含解析)新人教版1.(多选)如图所示,杂技演员站在一块被他踩成斜面的木板上处于静止状态.关于斜面对演员的作用力,下面说法正确的是( )A .木板对人可能有摩擦力作用,也可能没有摩擦力作用B .木板对人一定有摩擦力作用C .木板对人的弹力方向一定竖直向上D .木板对人的作用力方向一定竖直向上解析:人在斜面上静止,必然受到静摩擦力作用,A 错误,B 正确;木板对人的作用力是摩擦力与支持力的合力,根据二力平衡,木板对人的作用力与重力大小相等,方向相反,C 错误,D 正确.答案:BD2.惯性制导系统已广泛应用于弹道式导弹工程中,这个系统的重要元件之一是加速度计.加速度计构造原理的示意图如图所示:沿导弹长度方向安装的固定光滑杆上套一质量为m 的滑块,滑块两侧分别与劲度系数均为k 的弹簧相连;两弹簧的另一端与固定壁相连.滑块原来静止,弹簧处于自然长度.滑块上有指针,可通过标尺测出滑块的位移,然后通过控制系统进行制导.设某段时间内导弹沿水平方向运动,指针向左偏离0点的距离为s ,则这段时间内导弹的加速度( )A .方向向左,大小为ks/mB .方向向右,大小为ks/mC .方向向左,大小为2ks/mD .方向向右,大小为2ks/m解析:滑块静止时,两弹簧均处于自然长度,当滑块相对0向左移的距离为s ,则右边弹簧伸长了s ,左边弹簧压缩了s ,两个弹力的合力F 合=2ks ,则F 合=2ks =ma ,所以a =2ks m ,方向向右,正确选项为D.答案:D3.如图所示,一辆小车在拉力F 作用下,在水平地面上做匀速直线运动,小车上有一木块(木块在小车上不滑动).此时,木块的受力情况是(不计空气阻力)( )A .受重力和支持力作用B .受重力、支持力和向右的摩擦力C .受重力、支持力和向左的摩擦力D .以上说法均不正确解析:显而易见,木块受到重力和支持力的作用,而且它们是一对平衡力,到底受不受摩擦力呢?假设木块受水平向右(或向左)的摩擦力,而木块在水平方向不再受到其他力的作用,则木块在水平方向受力不平衡,而物体只有在不受力或受平衡力作用时,才能保持匀速直线运动状态或静止状态.因此,正确答案是A.答案:A4.(多选)如图所示,三个物块A 、B 、C 叠放在光滑的斜面上,用方向与斜面平行的拉力F 作用在B 上,使三个物块一起沿斜面向上匀速运动.设物块C 对A 的摩擦力为FfA ,对B 的摩擦力为FfB ,下列说法正确的是( )A .FfA 与FfB 方向相同B .FfA 与FfB 方向相反C .FfA<FfBD .FfA>FfB解析:A 相对C 有向下滑的趋势,C 对A 的摩擦力FfA 沿斜面向上,B 相对于C 有沿斜面向上滑的趋势,C 对B 的摩擦力FfB 沿斜面向下,B 正确,A 错误;由平衡条件得FfA =mAgsin θ,FfB =(mA +mC)gsin θ,故FfA<FfB ,C 正确,D 错误.答案:BC5.如图所示,一根轻质弹簧上端固定,下端挂一质量为m0的平盘,盘中有一物体,质量为m.当盘静止时,弹簧的长度比其自然长度伸长了L.今向下拉盘使弹簧再伸长ΔL 后停止,然后松手放开.设弹簧总处在弹性限度以内,则刚松开手时盘对物体的支持力等于( )A .(1+ΔL L )mgB .(1+ΔL L )(m +m0)gC.ΔL L mgD.ΔL L (m +m0)g解析:此题可以以盘内物体为研究对象进行受力分析,根据牛顿第二定律列出一个式子,然后再以整体为研究对象进行受力分析,根据牛顿第二定律再列一个式子和根据平衡位置的平衡条件联立求解,求解过程较麻烦.若采用假设法,本题将变得非常简单.假设题中所给条件ΔL =0,其意义是没有将盘往下拉,则松手放开,弹簧长度不会变化,盘仍静止,盘对物体的支持力的大小应为mg ,将ΔL =0代入四个选项中,只有A 能得到mg ,由上述分析可知,此题答案应为A.答案:A6.(多选)如图所示,在水平地面上的A点以速度v1与地面成θ角射出一弹丸,恰好以速度v2垂直穿入竖直壁上的小孔B,下列说法正确的是(不计空气阻力)()A.在B点以与v2大小相等的速度,与v2方向相反射出弹丸,它必定落在地面上的A点B.在B点以与v1大小相等的速度,与v2方向相反射出弹丸,它必定落在地面上的A点C.在B点以与v1大小相等的速度,与v2方向相反射出弹丸,它必定落在地面上A点的左侧D.在B点以与v1大小相等的速度,与v2方向相反射出弹丸,它必定落在地面上A点的右侧解析:以速度v1与地面成θ角射出一弹丸,恰好以速度v2垂直穿入竖直壁上的小孔B,说明弹丸在B点的竖直速度为零,v2=v1cos θ,根据对称性“逆向思维”:在B点以与v2大小相等方向相反的速度射出弹丸,它必落在地面上的A点,A正确;在B点以与v1大小相等的速度,与v2方向相反射出弹丸,由于v1>v2,弹丸在空中运动的时间不变,所以它必定落在地面上A 点的左侧,C正确,B、D错误.答案:AC7.如图所示,一不可伸长的轻质细绳跨过定滑轮后,两端分别悬挂质量为m1和m2的物体A 和B.若滑轮有一定大小,质量为m且分布均匀,滑轮转动时与绳之间无相对滑动,不计滑轮与轴之间的摩擦.设细绳对A和B的拉力大小分别为FT1和FT2,已知下列四个关于FT1的表达式中有一个是正确的.请你根据所学的物理知识,通过一定的分析,判断正确的表达式是()A.FT1=m+2m2m1gm+2m1+m2B.FT1=m+2m1m2gm+4m1+m2C.FT1=m+4m2m1gm+2m1+m2D.FT1=m+4m1m2gm+4m1+m2解析:设滑轮的质量为零,即看成轻滑轮,若物体B的质量较大,由整体法可得加速度a=m2-m1m1+m2g,隔离物体A,由牛顿第二定律可得FT1=2m1m2m1+m2g,应用“极限推理法”,将m=0代入四个选项分别对照,可得C正确.答案:C8.如图所示,轻细绳的一端系在质量为m的物体上,另一端系在一个轻质圆环上,圆环套在粗糙水平杆MN上,现用水平力F拉绳上一点,使物体处于图中实线位置,此时细绳与竖直方向的夹角为θ,然后改变F的大小使物体缓慢下降到图中虚线位置,圆环仍在原来的位置不动,则在这一过程中,水平拉力F、环与杆的摩擦力Ff和环对杆的压力FN的变化情况是()A.F逐渐增大,Ff保持不变,FN逐渐增大B.F逐渐增大,Ff逐渐增大,FN保持不变C.F逐渐减小,Ff逐渐增大,FN逐渐减小D.F逐渐减小,Ff逐渐减小,FN保持不变解析:在物体缓慢下降的过程中,细绳与竖直方向的夹角θ不断减小,可把这种θ减小状态推到无限小,即细绳与竖直方向的夹角θ=0,此时系统仍处于平衡状态,由平衡条件可知,当θ=0时,F=0,Ff=0,所以可得出结论:在物体缓慢下降过程中,F逐渐减小,Ff也随之减小,D正确.答案:D9.如图所示,由粗细均匀的电阻丝制成的边长为L的正方形线框abcd,其总电阻为R,现使线框以水平向右的速度v匀速穿过一宽度为2L,磁感应强度为B的匀强磁场区域,整个过程中ab、cd两边始终保持与磁场边界平行,令线框的cd边刚好与磁场左边界重合时开始计时(t =0),电流沿abcda流动的方向为正,U0=BLv,在下图中线框中a、b两点间电势差Uab随线框cd边的位移x变化的图象正确的是图中的()解析:在线框向右穿过磁场的过程中,由右手定则可判断出总是a点的电势高于b点电势,即Uab>0,A、C、D错误,B正确.答案:B10.(多选)如图甲所示,理想变压器的原线圈匝数n1=350匝,副线圈匝数n2=70匝,电阻R =20 Ω,○V是理想交流电压表,原线圈加上如图乙所示的交变电流,则下列说法正确的是()A .加在原线圈上的交流电压瞬时值的表达式为u =202sin(50πt) VB .原线圈电流的有效值为0.04 AC .在t =0.01 s 时,电压表的示数为零D .电阻R 上消耗的电功率为0.8 W解析:由图乙知交变电流的周期是0.02 s ,频率是50 Hz ,交流电压的瞬时值表达式为u =Umsinωt =202sin(100πt) V ,A 错误;根据U1U2=n1n2,副线圈电压的有效值U2=4 V ,输出功率P =U22R=0.8 W ,输入功率等于输出功率,根据P =U1I1可得,原线圈电流的有效值为I1=0.04 A ,B 、D 正确;电压表的读数是R 两端电压的有效值,大小始终为4 V ,C 错误.答案:BD11.(多选)如图所示,站在汽车上的人用手推车的力为F ,脚对车向后的摩擦力为Ff ,下列说法正确的是( )A .当车匀速运动时,F 和Ff 对车做功的代数和为零B .当车加速运动时,F 和Ff 对车做功的代数和为负功C .当车减速运动时,F 和Ff 对车做功的代数和为正功D .不管车做何种运动,F 和Ff 的总功和总功率都为零解析:不少学生在做此题时,认为研究对象很显然应选汽车,因为四个选项中都涉及到F 和Ff 对汽车做功问题,但很快走进死胡同,原因是汽车在水平方向共受四个力:牵引力、地面对它的摩擦力、人对它的摩擦力Ff 和人对它的推力F ,因前两个力比较不出大小,故也无法比较后两者大小,因而也就无法比较二力的功.若转换一下研究对象,则会变难为易.对人进行受力分析,人在水平方向只受两个力:车对人向后的作用力F′,车对人向前的摩擦力Ff′,这两个力恰好是F 、Ff 的反作用力.根据人和汽车的运动状态,即可确定出F 、Ff 的大小,当车匀速运动,人也匀速,F′=Ff′,F =Ff ,又因二者的位移相等,故F 做的正功等于Ff 做的负功,A 正确;当车加速时,人也加速,有F′<Ff′,F <Ff ,故Ff 做的负功大于F 做的正功,B 正确;同理可得C 正确,D 错误.答案:ABC12.如图所示,在光滑的水平面上有一质量为M 、倾角为θ的光滑斜面体,它的斜面上有一质量为m 的物块沿斜面下滑.关于物块下滑过程中对斜面压力大小的解答,有如下四个表达式.要判断这四个表达式是否合理,你可以不必进行复杂的计算,而根据所学的物理知识和物理方法进行分析,从而判断解的合理性或正确性.根据你的判断,下述表达式中可能正确的( )A.Mmgsin θM -msin2θB.Mmgsin θM +msin2θC.Mmgcos θM -msin2θD.Mmgcos θM +msin2θ解析:θ角的大小可取任意值,当θ=0时,压力为mg ,A 、B 错误;物块对斜面的压力肯定非负,而当m ≫M 时,C 有可能为负,C 错误,D 正确.答案:D13.如图所示为一个内、外半径分别为R1和R2的圆环状均匀带电平面,其单位面积所带电荷量为σ.取环面中心O 为原点,以垂直于环面的轴线为x 轴.设轴上任意点P 到O 点的距离为x ,P 点电场强度的大小为E.下面给出E 的四个表达式(式中k 为静电力常量),其中只有一个是合理的.你可能不会求解此处的场强E ,但是你可以通过一定的物理分析,对下列表达式的合理性做出判断.根据你的判断,E 的合理表达式应为( )A .E =2πkσ(R1x2+R21-R2x2+R22)x B .E =2πkσ(1x2+R21-1x2+R22)x C .E =2πkσ(R1x2+R21+R2x2+R22)x D .E =2πkσ(1x2+R21+1x2+R22)x 解析:场强的单位为N/C ,k 为静电力常量,单位为N·m2/C2,σ为单位面积所带电荷量,单位为C/m2,则2πkσ表达式的单位即为N/C ,故各表达式中其它部分应无单位,故可知A 、C 肯定错误;当x =0时,此时要求的场强为O 点的场强,由对称性可知EO =0.当x→∞时E→0,而D 项中E→4πkσ,故D 项错误,所以正确选项只能为B.答案:B14.迄今发现的二百余颗太阳系外行星大多不适宜人类居住,绕恒星“Gliese581”运行的行星“Gl -58lc”却很值得我们期待.该行星的温度在0 ℃到40 ℃之间,质量是地球的6倍,直径是地球的1.5倍,公转周期为13个地球日.“Gliese581”的质量是太阳质量的0.31倍.设该行星与地球均视为质量分布均匀的球体,绕其中心天体做匀速圆周运动,则( ) A .在该行星和地球上发射卫星的第一宇宙速度相同B .如果人到了该行星,其体重是地球上的223倍C .该行星与“Gliese581”的距离是日地距离的 13365倍D .由于该行星公转速率比地球大,地球上的米尺如果被带上该行星,其长度一定会变短 解析:根据万有引力定律、牛顿第二定律和星球对卫星的万有引力提供卫星绕星球表面做匀速圆周运动的向心力可得GMm R2=m v2R ,解得v =GM R ,又根据所给已知量可得,在“Gl -581c”行星上发射人造卫星的第一宇宙速度是在地球上发射人造卫星的第一宇宙速度的2倍,故A 选项错误;由于在星球表面附近(忽略星球的自转)星球对物体的重力等于星球对物体的万有引力,即mg =GMm R2,又根据所给已知量可得,在“Gl -581c”行星上人的体重是在地球上的223倍,故B 选项正确;根据万有引力提供行星做匀速圆周运动的向心力可得GMm r2=m(2πT )2r ,又根据所给数据可得,“Gl-581c”行星与“Gliese581”恒星的距离是日地距离的352.39133 225倍,故C选项错误;虽然“Gl-581c”行星的公转速率大于地球的公转速率,但其速率远小于光速,“尺缩效应”可以忽略,此外,即使其速率接近光速,还要看米尺在行星上怎么放置,如果是垂直速度方向放置,米尺的长度不变,尺的缩短效应只有在沿速度方向才有,故D选项错误.答案:B。
2019高考物理二轮复习专题检测:(六) 掌握“两定律、一速度”破解天体运动问题 Word版含解析

专题检测(六) 掌握“两定律、一速度”,破解天体运动问题1.(2018·全国卷Ⅲ)为了探测引力波,“天琴计划”预计发射地球卫星P ,其轨道半径约为地球半径的16倍;另一地球卫星Q 的轨道半径约为地球半径的4倍。
P 与Q 的周期之比约为( )A .2∶1B .4∶1C .8∶1D .16∶1解析:选C 由G Mm r 2=mr 4π2T 2得r 3T 2=GM 4π2⎝⎛⎭⎫或根据开普勒第三定律r 3T 2=k ,则两卫星周期之比为T P T Q = ⎝⎛⎭⎫r P r Q 3= ⎝⎛⎭⎫1643=8,故C 正确。
2.(2018·北京高考)若想检验“使月球绕地球运动的力”与“使苹果落地的力”遵循同样的规律,在已知月地距离约为地球半径60倍的情况下,需要验证( )A .地球吸引月球的力约为地球吸引苹果的力的1602B .月球公转的加速度约为苹果落向地面加速度的1602 C .自由落体在月球表面的加速度约为地球表面的16D .苹果在月球表面受到的引力约为在地球表面的160解析:选B 若想检验“使月球绕地球运动的力”与“使苹果落地的力”遵循同样的规律——万有引力定律,则应满足G Mm r2=ma ,因此加速度a 与距离r 的二次方成反比,B 对。
3.(2018·江苏高考)我国高分系列卫星的高分辨对地观察能力不断提高。
今年5月9日发射的“高分五号”轨道高度约为705 km ,之前已运行的“高分四号”轨道高度约为36 000 km ,它们都绕地球做圆周运动。
与“高分四号”相比,下列物理量中“高分五号”较小的是( )A .周期B .角速度C .线速度D .向心加速度解析:选A “高分五号”的运动半径小于“高分四号”的运动半径,即r 五<r 四。
由万有引力提供向心力得GMm r 2=mr 4π2T2=mrω2=m v 2r =ma 。
T = 4π2r 3GM ∝r 3,T 五<T 四,故A 正确;ω=GM r 3∝1r 3,ω五>ω四,故B 错误;v = GMr ∝1r ,v 五>v 四,故C 错误; a =GM r 2∝1r 2,a 五>a 四,故D 错误。
2019版高考物理二轮复习 第二部分 一、“九法”巧解选择题 选择题专项练2

选择题专项练(二)(本题共8小题,每小题6分。
在每小题给出的四个选项中,第14~18题只有一项符合题目要求,第19~21题有多项符合题目要求。
全部选对的得6分,选对但不全的得3分,有选错的得0分) 14.(2018全国Ⅰ卷)高铁列车在启动阶段的运动可看作初速度为零的匀加速直线运动。
在启动阶段,列车的动能()A.与它所经历的时间成正比B.与它的位移成正比C.与它的速度成正比D.与它的动量成正比15.(2018河南驻马店二质检)甲、乙两辆汽车沿同一平直路面行驶,其v-t图象如图所示,下列对汽车运动状态的描述正确的是()A.在第20 s末,甲、乙两车相遇B.若乙车在前,则可能相遇两次C.在第10 s末,乙车改变运动方向D.在第10 s末,甲、乙两车相距150 m16.(2018山东青岛二模)如图所示,水平面上A、B两物块的接触面水平,二者叠放在一起在作用于B上的水平恒定拉力F的作用下沿地面向右做匀速运动,某时刻撤去力F后,二者仍不发生相对滑动,关于撤去力F前后下列说法正确的是()A.撤去力F之前A受到3个力作用B.撤去力F之前B受到4个力作用C.撤去力F前后,A的受力情况不变D.A、B间的动摩擦因数μ1不小于B与地面间的动摩擦因数μ217.(2018江苏卷)从地面竖直向上抛出一只小球,小球运动一段时间后落回地面。
忽略空气阻力,该过程中小球的动能E k与时间t的关系图象是()18.(2018北京卷)根据高中所学知识可知,做自由落体运动的小球,将落在正下方位置。
但实际上,赤道上方200 m处无初速下落的小球将落在正下方位置偏东约6 cm处。
这一现象可解释为,除重力外,由于地球自转,下落过程小球还受到一个水平向东的“力”,该“力”与竖直方向的速度大小成正比。
现将小球从赤道地面竖直上抛,考虑对称性,上升过程该“力”水平向西,则小球()A.到最高点时,水平方向的加速度和速度均为零B.到最高点时,水平方向的加速度和速度均不为零C.落地点在抛出点东侧D.落地点在抛出点西侧19.(2018江苏南京、盐城一模)电荷量为Q1和Q2的两点电荷分别固定在x轴上的O、C两点,规定无穷远处电势为零,x轴上各点电势随x的变化关系如图所示。
2019版高考物理二轮复习 第二部分 一、“九法”巧解选择题 选择题专项练1

选择题专项练(一)(本题共8小题,每小题6分。
在每小题给出的四个选项中,第14~18题只有一项符合题目要求,第19~21题有多项符合题目要求。
全部选对的得6分,选对但不全的得3分,有选错的得0分) 14.(2018山西太原三模)在研究光电效应的实验中。
保持P的位置不变,用单色光a照射阴极K,电流计G的指针不发生偏转;改用另一频率的单色光b照射K,电流计的指针发生偏转。
那么()A.增加a的强度一定能使电流计的指针发生偏转B.用b照射时通过电流计的电流由d到cC.只增加b的强度一定能使通过电流计的电流增大D.a的波长一定小于b的波长15.(2018河南中原名校四模)如图所示为甲、乙两质点做直线运动的v-t图象,若两质点从同一地点出发,到t1时刻相遇,则下列说法正确的是()A.v1=8 m/sB.v2=12 m/sC.t1=(3+) sD.0~t1时间内,甲、乙相距的最大距离为3 m16.(2018江苏卷)我国高分系列卫星的高分辨对地观察能力不断提高。
今年5月9日发射的“高分五号”轨道高度约为705 km,之前已运行的“高分四号”轨道高度约为36 000 km,它们都绕地球做圆周运动。
与“高分四号”相比,下列物理量中“高分五号”较小的是()A.周期B.角速度C.线速度D.向心加速度17.(2018北京卷)某空间存在匀强磁场和匀强电场。
一个带电粒子(不计重力)以一定初速度射入该空间后,做匀速直线运动;若仅撤除电场,则该粒子做匀速圆周运动。
下列因素与完成上述两类运动无关的是()A.磁场和电场的方向B.磁场和电场的强弱C.粒子的电性和电荷量D.粒子入射时的速度18.(2018天津部分区期末)如图所示,E、F、G、H为矩形ABCD各边的中点,O为EG、HF的交点,AB边的长度为d。
E、G两点各固定一等量正点电荷,另一电荷量为Q的负电荷置于H点时,F点处的电场强度恰好为零。
若将H点的负电荷移到O点,则F点处电场强度的大小和方向为(静电力常量为k)()A.,方向向右B.,方向向左C.,方向向右D.,方向向左19.(2018江西师范大学附中三模)如图所示,abcd为一边长为l的正方形导线框,导线框位于光滑水平面内,其右侧为一匀强磁场区域,磁场的边界与线框的cd边平行,磁场区域的宽度为2l,磁感应强度为B,方向竖直向下。
2019全国二卷物理及答案

2019年普通高等学校招生全国统一考试(全国II 卷) 理科综合二、选择题:本题共8小题,每小题6分。
在每小题给出的四个选项中,第14~17题只有一项符合题目要求,第18~21题有多项符合题目要求。
全部选对的得6分,选对但不全的得3分,有选错的得0分。
14.2019年1月,我国嫦娥四号探测器成功在月球背面软着陆,在探测器“奔向”月球的过程中,用h 表示探测器与地球表面的距离,F 表示它所受的地球引力,能够描F 随h 变化关系的图像是15.太阳内部核反应的主要模式之一是质子-质子循坏,循环的结果可表示为1401214H He+2e+2v →,已知11H 和42He 的质量分别为P 1.0078u m =和 4.0026u m α=,1u=931MeV/c 2,c 为光速。
在4个11H 转变成1个42He 的过程中,释放的能量约为A .8 MeVB .16 MeVC .26 MeVD .52 MeV16.物块在轻绳的拉动下沿倾角为30°的固定斜面向上匀速运动,轻绳与斜面平行。
已知物块与斜面之间的动摩擦因数为33,重力加速度取10m/s 2。
若轻绳能承受的最大张力为1 500 N ,则物块的质量最大为 A .150kgB .1003kgC .200 kgD .2003kg17.如图,边长为l 的正方形abcd 内存在匀强磁场,磁感应强度大小为B ,方向垂直于纸面(abcd 所在平面)向外。
ab 边中点有一电子发源O ,可向磁场内沿垂直于ab 边的方向发射电子。
已知电子的比荷为k 。
则从a 、d 两点射出的电子的速度大小分别为A .14kBl ,54kBlB .14kBl ,54kBlC .12kBl ,54kBlD .12kBl ,54kBl18.从地面竖直向上抛出一物体,其机械能E总等于动能E k与重力势能E p之和。
取地面为重力势能零点,该物体的E总和E p随它离开地面的高度h的变化如图所示。
2019高考物理二轮(十一月)课外优选(10)(含解析)

亲爱的同学:这份试卷将再次记录你的自信、沉着、智慧和收获,我们一直投给你信任的目光……2019高考物理二轮(十一月)课外优选(10)李仕才一、选择题1、(2018·河北承德市月考)图示是某质点运动的速度图象,由图象得到的正确结果是( )A .0~1 s 内的平均速度是2 m/sB .0~2 s 内的位移大小是3 mC .0~1 s 内的加速度大于2~4 s 内的加速度D .0~1 s 内的运动方向与2~4 s 内的运动方向相反解析:根据v -t 图象可知,质点在0~1 s 内的位移x 1=1 m ,平均速度v 1=x 1t 1=1 m/s,1~2 s 内的位移x 2=2 m,0~2 s 内的位移x =x 1+x 2=3 m ,A 错误、B 正确.0~1 s 内的加速度a 1=2 m/s 2,2~4 s 内的加速度a 2=-1 m/s 2,负号表示a 2和v 方向相反,故a 1>a 2,C 正确.0~1 s 内与2~4 s 内的速度均为正值,表示物体都沿正方向运动,D 错误.选B 、C. 答案:BC2、如图所示,轻绳的一端固定在O 点,另一端系一质量为m 的小球(可视为质点).当小球在竖直平面内沿逆时针方向做圆周运动时,通过传感器测得轻绳拉力F T 、轻绳与竖直线OP 的夹角θ满足关系式F T =a +bcos θ,式中a 、b 为常数.若不计空气阻力,则当地的重力加速度为( )A.b 2mB.2bm C.3b m D.b 3m解析:当小球运动到最低点时,θ=0,拉力最大,F T1=a +b ,F T1=mg +mv 21L ;当小球运动到最高点时,θ=180°,拉力最小,F T2=a -b ,F T2=-mg +mv 22L;由动能定理有mg·2L=12mv 21-12mv 22,联立解得g =b3m,选项D 正确. 答案:D3、(2018·陕西省咸阳市高考模拟考试)如图所示,一根跨过一固定的水平光滑细杆的轻绳两端拴有两个小球,球a 置于水平地面上,球b 被拉到与细杆同一水平的位置.把绳拉直后,由静止释放球b ,当球b 摆到O 点正下方时,球a 对地面的压力大小为其重力的13,已知图中Ob 段的长度小于Oa 段的长度,不计空气阻力.则( )A .球b 下摆过程中处于失重状态B .球b 下摆过程中向心加速度变小C .当球b 摆到O 点正下方时,球b 所受的向心力为球a 重力的49D .两球质量之比m a :m b =:2解析:球b 下摆过程中加速度方向向上,处于超重状态,速度逐渐增大,向心加速度逐渐增大,选项A 、B 错误.设Ob 段长度为L ,对球b 下摆过程,由机械能守恒定律,有m b gL =12m b v 2,在球b 下摆到O 点正下方时,由牛顿第二定律,有F -m b g =m b v 2L ,联立解得F =3m b g.对球a ,设地面支持力为F N ,则F N =13m a g.由平衡条件,F N +F =m a g ,联立解得m a :m b =:2,选项D 正确.球b 所受向心力为F b =m b v 2L =2m b g =49m a g ,选项C 正确.答案:CD4、如图所示,水平放置的平行板电容器的两板间有一竖直向上的匀强电场,下板接地,两板间距离为10 cm ,A 点距下板3 cm ,B 点距上板3 cm.质量m =0.01 kg 、电荷量q =+10-3C 的小球能够在A 点保持静止.现将小球移到匀强电场之外.g =10 m/s 2,下列说法正确的是( )A .上板的电势比下板低10 VB.A点的电势为3 VC.电荷量为-10-3 C的带负电的点电荷在A点的电势能为3×10-3 JD.将电荷量为-10-3C的带负电的点电荷从A点移到B点,电场力对该点电荷做功4×10-3 J解析:首先根据小球能够在A点保持平衡得mg=Eq,可求出E=100 N/C,方向为从下到上.在匀强电场中,有U=Ed,得U下上=10 V,下板电势比上板高10 V,故A选项正确,同理可得A点的电势为φA=-3 V,故B选项错误;电荷量为-10-3C的带负电的点电荷在A点的电势能为E pA=φA q′=3×10-3 J,所以C选项正确;将电荷量为-10-3 C的带负电的点电荷从A点移到B点,电场力对该点电荷做功W=Eq′d AB=-4×10-3 J,故D选项错误.答案:AC5、在研究自感现象的实验中,用两个完全相同的灯泡A、B与自感系数很大的线圈L和定值电阻R组成如图所示的电路(线圈的直流电阻可忽略,电源的内阻不能忽略),关于这个实验下面说法中正确的是( )A.闭合开关的瞬间,A、B一起亮,然后A熄灭B.闭合开关的瞬间,B比A先亮,然后B逐渐变暗C.闭合开关,待电路稳定后断开开关,B逐渐变暗,A闪亮一下然后逐渐变暗D.闭合开关,待电路稳定后断开开关,A、B灯中的电流方向均为从左向右解析:闭合开关的瞬间,线圈中产生很大的自感电动势,阻碍电流的通过,故B立即亮,A逐渐变亮.随着A中的电流逐渐变大,流过电源的电流也逐渐变大,路端电压逐渐变小,故B逐渐变暗,A错误、B正确;电路稳定后断开开关,线圈相当于电源,对A、B供电,回路中的电流在原来通过A的电流的基础上逐渐变小,故A逐渐变暗,B闪亮一下然后逐渐变暗,C错误;断开开关后,线圈中的自感电流从左向右,A灯中电流从左向右,B灯中电流从右向左,故D错误.答案:B6、(2018·广西重点高中高三一模)如图所示,理想变压器原、副线圈的匝数比为:1,a、b端接入一正弦式交流电源.L1、L2为两只规格均为“22 V 6 W”的灯泡,两电表为理想交流电表.当滑动变阻器的滑片P处于中间位置时,两灯泡恰好都正常发光.下列说法正确的是( )A .电流表示数为0.27 AB .电压表示数为44 VC .滑片P 向下移动时,灯泡L 2将变暗D .滑片P 向上移动时,灯泡L 1将变暗 解析:由于原、副线圈匝数比为:1,则原、副线圈电流比为:2,因两灯泡正常发光,所以原线圈电流为311 A ,则副线圈电流为611A =0.55 A ,A 错.原、副线圈两端电压比为:1,副线圈两端电压为22 V ,所以原线圈两端电压为44 V ,B 对.滑片P 向下移动时,副线圈电路的电阻变小,电流变大,则原线圈电路中电流也变大,即通过灯泡L 2的电流变大,灯泡L 2可能变亮或烧毁,C 错.滑片P 向上移动时,通过灯泡L 2的电流变小,原线圈两端电压变大,则副线圈两端电压也变大,灯泡L 1可能变亮或烧毁,D 错. 答案:B二、非选择题1、(2018·江西赣州期末)如图所示,固定的水平光滑金属导轨,间距为L ,左端接有阻值为R 的电阻,处在方向竖直向下,磁感应强度为B 的匀强磁场中.质量为m 、电阻为R/2的导体棒与固定弹簧相连,放在导轨上,导轨的电阻不计.初始时刻,弹簧恰处于自然长度,导体棒具有水平向右的初速度v 0.沿导轨往复运动的过程中,导体棒始终与导轨垂直并保持良好接触.求:(1)求初始时刻导体棒受到的安培力;(2)若导体棒从初始时刻到速度第一次为零时,弹簧的弹性势能为E p ,则这一过程中安培力所做的功W 1和整个回路产生的焦耳热Q 分别为多少;(3)从导体棒开始运动直到最终静止的过程中,电阻R 上产生的焦耳热Q 1. 解析:(1)初始时刻导体棒切割磁感线产生的感应电动势E =BLv 0,感应电流I =ER +R 2,导体棒受到的安培力F =ILB ,联立解得F =2B 2L 2v 03R,方向水平向左.(2)导体棒从初始时刻到速度第一次为零的过程中,由动能定理有W 1-E p =0-12mv 20,得安培力所做的功W 1=E p -12mv 20,整个回路产生的焦耳热Q =12mv 20-E p .(3)棒最终静止于初始位置,则电阻R 上产生的焦耳热Q 1=23Q 总=23×12mv 20=13mv 20.答案:(1)2B 2L 2v 03R ,方向水平向左 (2)E p -12mv 20 12mv 20-E p (3)13mv 2。
2019届高考物理二轮阶段性效果检测 21 Word版含答案

一、选择题(本大题共7小题,每小题8分,共56分。
多选题已在题号后标出,选不全得4分)1.如图是一种升降电梯的示意图,A 为载人箱,B 为平衡重物,它们的质量均为M,上下均有跨过滑轮的钢索系住,在电动机的牵引下使电梯上下运动。
如果电梯中乘客的质量为m,匀速上升的速度为v,电梯即将到顶层前关闭电动机,依靠惯性上升h 高度后停止,在不计空气和摩擦阻力的情况下,重力加速度为g,下列说法正确的是( )A.关闭电动机后,乘客处于超重状态B.关闭电动机后,乘客处于失重状态C.由于A 、B 质量相等,故关闭电动机后,乘客的加速度大小为gD.关闭电动机后,电梯上升的高度h 一定小于2v 2g2.如图所示,两个质量相同的物体A 和B 紧靠在一起放在光滑水平桌面上,如果它们分别受到水平推力F 1和F 2,且F 1>F 2,则A 施于B 的作用力的大小为( )A.F 1B.F 2C.12(F 1+F 2) D.12(F 1-F 2) 3.(多选)(2018·河西区模拟)如图甲所示,一个物体放在光滑的水平地面上。
在t=0时刻,物体在水平力F 作用下由静止开始做直线运动。
在0到t 0时间内物体的加速度a 随时间t 的变化规律如图乙所示。
则( )A.在0到t 0时间内,力F 大小恒定B.在0到t 0时间内,物体的位移逐渐变大C.在0到t 0时间内,物体的速度逐渐变大D.在0到t 0时间内,物体的速度逐渐变小4.(多选)(2018·上饶模拟)如图所示,小车的质量为M,人的质量为m,人用恒力F 拉绳,若人与车保持相对静止,且地面为光滑的,不计滑轮与绳的质量,则车对人的摩擦力可能是( )A.0B.m MFm M-+,方向向右C.m MFm M-+,方向向左D.M mFm M-+,方向向右5.(2018•乐山模拟)如图所示,不计绳的质量及绳与滑轮的摩擦,物体A的质量为M,水平面光滑。
当在绳B端挂一质量为m的物体时,物体A的加速度为a1;当在绳B端施以F=mg的竖直向下的拉力作用时,A的加速度为a2,则a1与a2的大小关系是( )A.a1=a2B.a1>a2C.a1<a2D.无法确定6.(2018·九江模拟)如图所示,n个质量均为m的相同木块并排放在水平地面上,当木块1受到水平恒力F而向右加速运动时,木块3对木块4的作用力为( )A.FB.若地面光滑,为F;若地面不光滑,小于FC.若地面光滑,为(1-3n)F;若地面不光滑,小于(1-3n)FD.不论地面是否光滑,均为(1-3n)F7.(2018·华东师大附中模拟)一质量为m的铝球用细线悬挂静止在足够深的油槽中(如图甲),某时刻剪断细线,铝球开始在油槽中下沉,通过传感器得到铝球的加速度随下沉速度变化的图像如图乙所示,已知重力加速度为g,根据上述信息,下列说法正确的是( )A.铝球下沉的速度越来越大B.开始释放时,铝球加速度a0=gC.铝球下沉过程所受到油的阻力00ma vf vD.铝球下沉过程机械能的减少等于克服油阻力所做功二、计算题(本大题共3小题,共44分。
高考物理全程备考二轮课件:2.1.8-10法速解物理选择题ppt课件(含答案)

[解析] 本题中既有金属杆切割磁感线又有磁场变化,为此 可进行模型转换,转换为磁场不变的金属杆切割磁感线与面积不 变的变化磁场的叠加,令金属杆的加速度为 a,经时间 t,金属 杆与初始位置的距离为 x=12at2,此时金属杆的速度 v=at,所以 回路中的感应电动势 E=BLv+ΔΔBt S=ktLv+kLx,而回路的总电 阻 R=2xr0,所以金属杆所受安培力为 F=BIL=BLER=3k22rL0 2t, C 正确。
B 错误;根据电场强度的定义式 E=Fq可知,C 正确;磁感应强
度 B=IFL中,I 和 B 的方向必须垂直,D 错误。
[答案] AC
技法 2 比较排除法
运用排除法解题时,对于完全肯定或完全否定的判断, 可通过举反例的方式排除;对于相互矛盾或者相互排斥的选 项,则最多只有一个是正确的,要学会从不同方面或不同角 度思考与推敲,将不符合题意的选项一一排除,最终留下的 就是符合题意的选项。
技法 1 直接判断法
通过观察题目中所给出的条件,根据所学知识和规律推出 结果,直接判断,确定正确的选项。直接判断法适用于推理过 程较简单的题目,这类题目主要考查学生对物理知识的记忆和 理解程度,如考查物理学史和物理常识的试题等。
[应用体验] [多选]下列说法中正确的是
()
A.电荷在某处不受电场力的作用,则该处电场强度为零
A.
3 3gR 2
B.
3gR 2
3gR
C.
2
3gR
D.
3
忍别人所不能忍受的痛,吃别人所不能吃的苦,是为了收获别人得不到的收获!加油!!!忍别人所不能忍受的痛,吃别人所不能吃的苦,是为了收获别人得不到的收获!加油!!!忍别人所不能忍受的痛,吃别人所不能吃的苦,是为了收获别人得不到的收获!加油!!! 保持健康心态,勇敢面对中考;合理饮食,合理睡眠;预祝金榜题名,万事如意!保持健康心态,勇敢面对中考;合理饮食,合理睡眠;预祝金榜题名,万事如意!加油!!!专业1
(通用版)2019版高考物理第8讲技法专题——10法速解物理选择题讲义(含解析)

技法专题——10法速解物理选择题理综全国卷中,物理8道选择题分单选和多选,主要考查对物理概念、物理现象、物理过程和物理规律的认识、判断、辨析、理解和应用等,具有信息量大、知识覆盖面广、干扰性强、命题灵活性强、层次丰富、能考查学生的多种能力等特点。
要想迅速、准确地解答物理选择题,不但要熟练掌握和应用物理学的基本概念和规律,还要学会一些非常规巧解妙招,针对题目特性“有的放矢”,达到快速解题的目的。
技法1 直接判断法通过观察题目中所给出的条件,根据所学知识和规律推出结果,直接判断,确定正确的选项。
直接判断法适用于推理过程较简单的题目,这类题目主要考查学生对物理知识的记忆和理解程度,如考查物理学史和物理常识的试题等。
[应用体验] [多选]下列说法中正确的是( )A .电荷在某处不受电场力的作用,则该处电场强度为零B .一小段通电导线在某处不受磁场力作用,则该处磁感应强度一定为零C .电场强度的大小等于把一个试探电荷放在该点时受到的电场力与试探电荷本身电荷量的比值D .磁感应强度的大小等于把一小段通电导线放在该点时受到的磁场力与该小段导线长度和电流乘积的比值[解析] 电场对放入其中的电荷有力的作用,磁场对通电导线有力的作用的条件是:磁场方向和电流方向不平行,A 正确,B 错误;根据电场强度的定义式E =F q 可知,C 正确;磁感应强度B =F IL中,I 和B 的方向必须垂直,D 错误。
[答案] AC技法2 比较排除法运用排除法解题时,对于完全肯定或完全否定的判断,可通过举反例的方式排除;对于相互矛盾或者相互排斥的选项,则最多只有一个是正确的,要学会从不同方面或不同角度思考与推敲,将不符合题意的选项一一排除,最终留下的就是符合题意的选项。
[应用体验] 如图所示,以MN 、PQ 为边界的区域内存在垂直纸面向里的匀强磁场,磁场宽为2L ,高为L 的正三角形闭合金属框由粗细均匀的电阻丝围成,在外力作用下由图示位置被水平向右匀速拉过磁场区域,ab 边始终与MN平行,取逆时针方向为电流的正方向。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题检测(二十一) 技法专题——10法速解物理选择题1.如图所示,在一粗糙的水平面上有两个质量分别为m 1和m 2的木块1和2,用原长为l 、劲度系数为k 的轻弹簧连接起来,两木块与地面间的动摩擦因数均为μ。
现用一水平力(未画出)向右拉木块2,当两木块一起匀速运动时,两木块间的距离为( )A .l +μm 1g kB .l +μ(m 1+m 2)g kC .l +μm 2g kD .l +μm 1m 2g k (m 1+m 2) 解析:选A 由题意知,弹簧对木块1的拉力与木块1所受的摩擦力平衡,当m 1的质量越小时摩擦力越小,弹簧的拉力也越小。
当m 1的值等于零时(极限),不论m 2多大,弹簧的伸长量都为零,说明弹簧的伸长量与m 2无关,故选A 项。
2.[多选]一物体在粗糙水平面上以某一初速度做匀减速直线运动直到停止,已知此物体在最初5 s 内的平均速度为3.3 m/s ,且在最初5 s 内和最后5 s 内经过的路程之比为11∶5,则下列说法中正确的是( )A .物体一共运动了8 sB .物体做匀减速直线运动的加速度大小为0.6 m/s 2C .物体运动的初速度大小为6 m/sD .物体运动过程中的平均速度为256m/s 解析:选AB 设物体做匀减速直线运动的加速度大小为a ,运动总时间为t 。
把物体的运动视为反向的初速度为零的匀加速直线运动,则物体最后5 s 内的位移为x 2=12a ×52=12.5a ,最初5 s 内的位移为x 1=12at 2-12a (t -5)2=5at -12.5a ,由题意知x 1∶x 2=11∶5,联立解得t =8 s ,A 正确;物体最初5 s 内的位移为x 1=3.3×5 m =16.5 m ,即5at -12.5a =16.5,解得a =0.6 m/s 2,B 正确;由v =at 知物体运动的初速度大小为v =0.6×8 m/s =4.8 m/s ,C 错误;由平均速度定义知,运动过程中的平均速度为v =v +02=12×0.6×8 m/s = 2.4 m/s ,D 错误。
3.竖直上抛物体的初速度大小与返回抛出点时速度大小的比值为k ,物体返回抛出点时速度大小为v ,若在运动过程中空气阻力大小不变,重力加速度为g ,则物体从抛出到返回抛出点所经历的时间为( )A.(k 2-1)v (k 2+1)gB.(k 2+1)v (k 2-1)gC.(k +1)(k 2+1)v 2kgD.(k 2-1)2v 2kg解析:选C 取k =1,说明物体运动过程中所受空气阻力为零,则物体从抛出到返回抛出点所经历的时间为2v g ,代入后只有C 满足。
4.如图所示电路中,R 1=4 Ω,R 2=6 Ω,电源内阻不可忽略。
闭合开关S 1,当开关S 2闭合时,电流表A 的示数为3 A 。
则当S 2断开时,电流表示数可能为( )A .3.2 AB .2.1 AC .1.2 AD .0.8 A解析:选B S 2断开后,总电阻变大,电流变小,排除A 项;S 2断开前路端电压是U =IR 1=3×4 V =12 V ,S 2断开后路端电压增大,则电流大于I ′=U R 1+R 2=124+6A =1.2 A ,排除C 、D 两项,故可得正确选项为B 。
5.12根长直导线并排构成长为l 的直导线带ab ,P 1、P 2是位于ab 所在直线上的两点,位置如图所示,P 1到导线带左端的距离等于P 2到导线带右端的距离,所有长直导线中均通有大小相等、方向垂直纸面向外的恒定电流,ab 上所有直导线产生的磁场在P 1处的合磁感应强度大小为B 1,在P 2处的合磁感应强度大小为B 2,若仅将右边6根直导线移走,则P 2处的磁感应强度大小为( )A.B 22B .B 2-B 1C .B 1-B 22D .B 1+B 22解析:选B 由于所有直导线中的电流一样,将直导线一分为二,由右手螺旋定则及对称性知,左边6根直导线电流在P 1处产生的磁场互相抵消,所有直导线电流在P 1处产生的磁场,仅相当于右边6根直导线电流在P 1处产生的磁场,磁感应强度大小为B 1,方向垂直ab 向下;由对称性知,右边6根直导线电流在P 2处产生的磁场的磁感应强度大小为B 1,方向垂直ab 向上,而所有直导线的电流在P 2处产生的磁场的磁感应强度大小为B 2,方向垂直ab 向上,所以将右边6根直导线移走后,由磁场的叠加原理知,左边6根直导线电流在P 2处产生的磁场的磁感应强度大小为B 2-B 1,B 选项正确。
6.如图所示,在边长为a 的正方形区域内,有以对角线为边界、垂直于纸面的两个匀强磁场,磁感应强度大小相等、方向相反,纸面内一边长为a 的正方形导线框沿x 轴匀速穿过磁场区域,t =0时刻恰好开始进入磁场区域,以顺时针方向为导线框中电流的正方向,选项图中能够正确表示电流与位移关系的是( )解析:选B 在x ∈(0,a )时,导线框右边框切割磁感线产生感应电流,电流大小i =B (a -x )v -Bx v R =B v (a -2x )R ,其中x ∈⎝⎛⎭⎫0,a 2时,导线框中感应电流方向为顺时针;x =a 2时,导线框中感应电流为零;x ∈⎝⎛⎭⎫a 2,a 时,导线框中感应电流方向为逆时针。
在x ∈(a,2a )时,导线框左边框切割磁感线产生感应电流,感应电流大小i =B [a -(x -a )]v -B (x -a )v R=B v (3a -2x )R ,其中x ∈⎝⎛⎭⎫a ,32a 时,导线框中感应电流方向为逆时针;x =32a 时,导线框中感应电流为零;x ∈⎝⎛⎭⎫32a ,2a 时,导线框中感应电流方向为顺时针,所以B 正确,A 、C 、D错误。
7.[多选]如图所示,电源的内阻可以忽略不计,电压表(内阻不能忽略)和可变电阻R 串联在电路中。
如果可变电阻R 的阻值减为原来的13,电压表的读数由U 0增加到2U 0,则下列说法正确的是( ) A .流过可变电阻R 的电流增大为原来的2倍B .可变电阻R 消耗的电功率增大为原来的4倍C .可变电阻R 两端的电压减小为原来的23D .若可变电阻R 的阻值减小到零,那么电压表的示数变为4U 0解析:选ACD 电压表阻值一定,当它的读数由U 0增加到2U 0时,通过它的电流一定变为原来的2倍,而R 与电压表串联,A 正确;根据P =UI 和U =IR ,可知R 的阻值减为原来的13后,R 消耗的功率P ′=(2I )2R 3=43P ,R 两端的电压U =23IR ,C 正确,B 错误;又因电源内阻不计,R 与电压表两端的电压之和为E ,当R 的阻值减小到零时,电压表示数为E ,其值为E =IR +U 0=23IR +2U 0,解得E =4U 0,D 正确。
8.如图所示,水平放置的金属板间有匀强电场,一带正电的粒子以水平速度v 0从M 点射入匀强电场,穿过电场后,从N 点以速度v 射出,粒子重力不计,则以下判断正确的是( )A .如果让粒子从M 点以速率v 沿水平方向射入,则粒子从N 点射出时的速率为v 0B .如果让粒子从N 点以速度-v 射入,则粒子从M 点射出时的速度为-v 0C .如果让粒子从M 点以速率v 沿水平方向射入,则粒子能到达N 点D .如果让粒子从N 点以速率v 0沿-v 方向射入,则粒子从M 点射出时的速率为v 且沿-v 0方向解析:选B 粒子在电场力作用下做类平抛运动,初速度v 0与末速度v 的水平分量相等,可知A 、C 、D 错误;当粒子从N 点以速度-v 射入电场中时,粒子在水平方向上做匀速运动,而在竖直方向上做匀减速运动,与题述运动过程互为可逆运动,可知B 正确。
9.如图所示,AB 为电荷均匀分布、带电荷量为+Q 的细棒,C 为AB 棒附近的一点,CB 垂直于AB 。
AB 棒上电荷形成的电场中C 点的电势为φ0,φ0可以等效成AB 棒上某点P 处、带电荷量为+Q 的点电荷所形成的电场在C 点的电势,设PC 的距离为r ,由点电荷电势的知识可知φ0=k Q r。
若某点处在多个点电荷形成的电场中,则电势为每一个点电荷在该点所产生的电势的代数和。
根据题中提供的知识与方法,我们可将AB 棒均分成两段,并看成两个点电荷,可以求得AC 连线中点C ′处的电势为( )A .φ0 B.2φ0 C .2φ0 D .4φ0解析:选C AB 棒带电均匀,由对称性可知,其等效点电荷P 点即AB 棒的中点,如图所示,已知PC =r ,将AB 棒均分成两段,设左半段的中点为E ,其电荷量为12Q ,由图可知C ′E 的长度为12r ,故其在C ′的电势为φ=k 12Q 12r =k Q r =φ0,同理,右半段在C ′产生的电势也为φ0,根据题意可知其代数和为2φ0,故选项C 正确。
10.[多选]水平地面上有两个固定的、高度相同的粗糙斜面甲和乙,底边长分别为L 1、L 2,且L 1<L 2,如图所示。
两个完全相同的滑块A 、B (可视为质点)与两个斜面间的动摩擦因数相同,将滑块A 、B 分别从甲、乙两个斜面的顶端同时由静止开始释放,取地面所在的水平面为参考平面,则()A .两个滑块从顶端到底端的运动过程中,由于克服摩擦而产生的热量一定相同B .滑块A 到达底端时的动能一定比滑块B 到达底端时的动能大C .两个滑块从顶端运动到底端的过程中,滑块A 所受重力做功的平均功率比滑块B 大D .两个滑块加速下滑的过程中,到达同一高度时,机械能可能相同解析:选BC 根据二级结论:动摩擦因数处处相同的斜面和水平面(如图1、2),物体克服摩擦力做功(生热)均为W =μmgs ,结合动能定理、功率的定义及功能关系,可以快速判定A 、D 错误,B 、C 正确。
11.[多选]如图所示,两个可视为质点的相同木块A 和B 放在水平转盘上,且木块A 、B 与转盘中心在同一条水平直线上,木块A 、B 用长为L 的轻绳连接,木块与转盘之间的最大静摩擦力均为各自重力的k 倍。
整个装置能绕通过转盘中心的竖直转轴O 1O 2转动,A 在距离转轴L 处。
开始时,轻绳恰好伸直但无弹力。
现让转盘从静止开始转动,使角速度ω缓慢增大,以下说法正确的是( )A .当ω>2kg 3L 时,A 、B 相对于转盘会滑动 B .当ω>kg 2L 时,轻绳一定有弹力 C .当ω在 kg 2L <ω< 2kg 3L范围内增大时,B 所受摩擦力变大 D .当ω在0<ω< 2kg 3L范围内增大时,A 所受摩擦力一直变大 解析:选ABD 当A 、B 所受静摩擦力均达到最大值时,A 、B 恰好不相对转盘滑动,设A 、B 质量均为m ,则2kmg =mω2L +mω2·2L ,解得ω= 2kg 3L,A 项正确;当B 所受静摩擦力达到最大值后,轻绳开始有弹力,此时有kmg =mω2·2L ,解得ω=kg 2L ,B 项正确;当 kg 2L <ω< 2kg 3L时,随着角速度的增大,轻绳弹力不断增大,B 所受静摩擦力一直保持最大静摩擦力不变,C 项错误;当0<ω≤ kg 2L时,A 所受静摩擦力F f 提供向心力,即F f =mω2L ,静摩擦力随角速度的增大而增大;当kg 2L <ω< 2kg 3L 时,以A 、B 整体为研究对象,F f +kmg =mω2L +mω2·2L ,可知A 所受静摩擦力随角速度的增大而增大,D 项正确。
