湖北省物理专题十二动量和动量守恒定律复习题无答案新人教版7
动量和动量守恒定律(解释版)--高一物理下学期期末真题分类汇编(新高考)

动量和动量守恒定律一、单选题1(22-23高一下·内蒙古赤峰·期末)蹦极是一项非常刺激的体育运动。
如图所示,质量m=50kg的人身系弹性绳自高空自由下落,弹性绳绷直后在下降过程经过a点的速度大小为12m/s,落到最低点c后反弹至b点的速度大小为9m/s。
人从a→c→b共用时3s,在此过程中弹性绳对人的平均作用力为()A.350NB.450NC.550ND.850N【答案】D【详解】取向上为正,根据动量定理有t=mvb-m(-va)F合解得=350NF合其中=T-mgF合则T=850N故选D。
2(22-23高一下·北京海淀·期末)如图所示,甲、乙两人静止在水平冰面上,甲推乙后,两人向相反方向沿直线做减速运动。
已知甲的质量小于乙的质量,两人与冰面间的动摩擦因数相同,两人之间的相互作用力远大于地面的摩擦力。
下列说法正确的是()A.甲推乙的过程中,甲和乙的机械能守恒B.乙停止运动前任意时刻,甲的速度总是小于乙的速度C.减速过程中,地面摩擦力对甲做的功等于对乙做的功D.减速过程中,地面摩擦力对甲的冲量等于对乙的冲量【详解】A.甲、乙两人静止在水平冰面上,重力势能一定,开始动能为0,甲推乙后,两者动能增大,即甲推乙的过程中,甲和乙的机械能增大,故A错误;B.甲推乙过程,由于两人之间的相互作用力远大于地面的摩擦力,则有m甲v甲-m乙v乙=0由于甲的质量小于乙的质量,则有v 甲>v乙两人与冰面间的动摩擦因数相同,即减速过程的加速度大小相等,可知乙停止运动前任意时刻,甲的速度总是大于乙的速度,故B错误;C.减速过程中,根据W f=0-12mv02=0-12pv0根据上述,两人互推过程,动量大小相等,甲的速度大于乙的速度,则地面摩擦力对甲做的功大于对乙做的功,故C错误;D.根据I f=0-mv0根据上述,两人互推过程,动量大小相等,则减速过程中,地面摩擦力对甲的冲量大小等于对乙的冲量,故D正确。
物理动量守恒定律专题练习(及答案)含解析

物理动量守恒定律专题练习(及答案)含解析一、高考物理精讲专题动量守恒定律1.水平放置长为L=4.5m 的传送带顺时针转动,速度为v =3m/s ,质量为m 2=3kg 的小球被长为1l m =的轻质细线悬挂在O 点,球的左边缘恰于传送带右端B 对齐;质量为m 1=1kg 的物块自传送带上的左端A 点以初速度v 0=5m/s 的速度水平向右运动,运动至B 点与球m 2发生碰撞,在极短的时间内以碰撞前速率的12反弹,小球向右摆动一个小角度即被取走。
已知物块与传送带间的滑动摩擦因数为μ=0.1,取重力加速度210m/s g =。
求:(1)碰撞后瞬间,小球受到的拉力是多大?(2)物块在传送带上运动的整个过程中,与传送带间摩擦而产生的内能是多少? 【答案】(1)42N (2)13.5J 【解析】 【详解】解:设滑块m1与小球碰撞前一直做匀减速运动,根据动能定理:221111011=22m gL m v m v μ--解之可得:1=4m/s v 因为1v v <,说明假设合理滑块与小球碰撞,由动量守恒定律:21111221=+2m v m v m v - 解之得:2=2m/s v碰后,对小球,根据牛顿第二定律:2222m v F m g l-=小球受到的拉力:42N F =(2)设滑块与小球碰撞前的运动时间为1t ,则()01112L v v t =+ 解之得:11s t =在这过程中,传送带运行距离为:113S vt m == 滑块与传送带的相对路程为:11 1.5X L X m ∆=-=设滑块与小球碰撞后不能回到传送带左端,向左运动最大时间为2t 则根据动量定理:121112m gt m v μ⎛⎫-=-⋅⎪⎝⎭解之得:22s t =滑块向左运动最大位移:121122m x v t ⎛⎫=⋅⋅ ⎪⎝⎭=2m 因为m x L <,说明假设成立,即滑块最终从传送带的右端离开传送带 再考虑到滑块与小球碰后的速度112v <v , 说明滑块与小球碰后在传送带上的总时间为22t在滑块与传送带碰撞后的时间内,传送带与滑块间的相对路程22212X vt m ∆==因此,整个过程中,因摩擦而产生的内能是()112Q m g x x μ=∆+∆=13.5J2.如图:竖直面内固定的绝缘轨道abc ,由半径R =3 m 的光滑圆弧段bc 与长l =1.5 m 的粗糙水平段ab 在b 点相切而构成,O 点是圆弧段的圆心,Oc 与Ob 的夹角θ=37°;过f 点的竖直虚线左侧有方向竖直向上、场强大小E =10 N/C 的匀强电场,Ocb 的外侧有一长度足够长、宽度d =1.6 m 的矩形区域efgh ,ef 与Oc 交于c 点,ecf 与水平向右的方向所成的夹角为β(53°≤β≤147°),矩形区域内有方向水平向里的匀强磁场.质量m 2=3×10-3 kg 、电荷量q =3×l0-3 C 的带正电小物体Q 静止在圆弧轨道上b 点,质量m 1=1.5×10-3 kg 的不带电小物体P 从轨道右端a 以v 0=8 m/s 的水平速度向左运动,P 、Q 碰撞时间极短,碰后P 以1 m/s 的速度水平向右弹回.已知P 与ab 间的动摩擦因数μ=0.5,A 、B 均可视为质点,Q 的电荷量始终不变,忽略空气阻力,sin37°=0.6,cos37°=0.8,重力加速度大小g =10 m/s 2.求:(1)碰后瞬间,圆弧轨道对物体Q 的弹力大小F N ;(2)当β=53°时,物体Q 刚好不从gh 边穿出磁场,求区域efgh 内所加磁场的磁感应强度大小B 1;(3)当区域efgh 内所加磁场的磁感应强度为B 2=2T 时,要让物体Q 从gh 边穿出磁场且在磁场中运动的时间最长,求此最长时间t 及对应的β值.【答案】(1)24.610N F N -=⨯ (2)1 1.25B T = (3)127s 360t π=,001290143ββ==和【解析】 【详解】解:(1)设P 碰撞前后的速度分别为1v 和1v ',Q 碰后的速度为2v 从a 到b ,对P ,由动能定理得:221011111-22m gl m v m v μ=- 解得:17m/s v =碰撞过程中,对P ,Q 系统:由动量守恒定律:111122m v m v m v '=+取向左为正方向,由题意11m/s v =-', 解得:24m/s v =b 点:对Q ,由牛顿第二定律得:2222N v F m g m R-=解得:24.610N N F -=⨯(2)设Q 在c 点的速度为c v ,在b 到c 点,由机械能守恒定律:22222211(1cos )22c m gR m v m v θ-+=解得:2m/s c v =进入磁场后:Q 所受电场力22310N F qE m g -==⨯= ,Q 在磁场做匀速率圆周运动由牛顿第二定律得:2211c c m v qv B r =Q 刚好不从gh 边穿出磁场,由几何关系:1 1.6m r d == 解得:1 1.25T B = (3)当所加磁场22T B =,2221m cm v r qB == 要让Q 从gh 边穿出磁场且在磁场中运动的时间最长,则Q 在磁场中运动轨迹对应的圆心角最大,则当gh 边或ef 边与圆轨迹相切,轨迹如图所示:设最大圆心角为α,由几何关系得:22cos(180)dr r α-︒-= 解得:127α=︒ 运动周期:222m T qB π=则Q 在磁场中运动的最长时间:222127127•s 360360360m t T qB παπ===︒此时对应的β角:190β=︒和2143β=︒3.如图所示,两块相同平板P 1、P 2置于光滑水平面上,质量均为m 。
物理动量守恒定律练习题及答案.docx

物理动量守恒定律练习题及答案一、高考物理精讲专题动量守恒定律1. 如图,足够大的光滑水平面上固定着一竖直挡板,挡板前L 处静止着质量 m 1=1kg 的小球 A ,质量 m 2=2kg 的小球 B 以速度 v 0 运动,与小球 A 正碰.两小球可看作质点,小球与小球及小球与挡板的碰撞时间忽略不计,且碰撞中均没有机械能损失.求(1)第 1 次碰撞后两小球的速度;(2)两小球第 2 次碰撞与第 1 次碰撞之间的时间; (3)两小球发生第 3 次碰撞时的位置与挡板的距离.【答案】 (1) 4 v 1v 方向均与 v 0 相同 (2)6L 9L(3) 35v 03【解析】 【分析】(1)第一次发生碰撞,动量守恒,机械能守恒; (2)小球 A 与挡板碰后反弹,发生第2 次碰撞,分析好位移关系即可求解;( 3)第 2 次碰撞过程中,动量守恒,机械能守恒,从而找出第三次碰撞前的初始条件,分析第 2 次碰后的速度关系,位移关系即可求解. 【详解】( 1)设第 1 次碰撞后小球 A 的速度为 v 1 ,小球 B 的速度为 v 2 ,根据动量守恒定律和机械 能守恒定律 : m 2 v 0 m 1v 1 m 2v 21m 2 v 021m 1v 121m 2v 222 22整理得: v 12m 2 v 0 , v 2m 2m 1v 0m 1 m 2m 1 m 2解得 v 14v 0 , v 21v 0 ,方向均与 v 0 相同.33(2)设经过时间 t 两小球发生第 2 次碰撞,小球 A 、 B 的路程分别为 x 1 、 x 2 ,则有x 1 v 1t , x 2 v 2t由几何关系知:x 1 x 2 2L6L整理得: t5v 0(3)两小球第2 次碰撞时的位置与挡板的距离:x L x 23 L5以向左为正方向,第 2 次碰前 A 的速度v A4v 0 ,B 的速度为 v B1v 0 ,如图所示.3 3碰后A 的速度 v A ,B 的速度 v B .根据 量守恒定律和机械能守恒定律,有m 1v A m 2v B m 1v Am 2v B ;1m 1v A 2 1m 2 v B 21m 1v A21m 2v B 222 2 2整理得: v A(m 1 m 2 ) v A2m 2vB, v B(m 2 m 1 )v B 2m 1v Am 1 m 2 m 1 m 2解得: v A8v 0 , v B7v 099第 2 次碰后t 生第 3 次碰撞,碰撞 的位置与 板相距x ,x x v B t ,x x v At整理得: x9L2. 冰球运 甲的 量80.0kg 。
动量守恒定律练习题及答案

一、选择题(每小题中至少有一个选项是正确的)1.在下列几种现象中,动量守恒的有( )A .原来静止在光滑水平面上的车,从水平方向跳上一个人,人车为一系统B .运动员将铅球从肩窝开始加速推出,以运动员和球为一系统C .从高空自由落下的重物落在静止于地面上的车厢中,以重物和车厢为一系统D .光滑水平面上放一斜面,斜面光滑,一个物体沿斜面滑下,以重物和斜面为一系统2.两物体组成的系统总动量守恒,这个系统中( )A .一个物体增加的速度等于另一个物体减少的速度B .一物体受的冲量与另一物体所受冲量相同C .两个物体的动量变化总是大小相等,方向相反D .系统总动量的变化为零3.砂子总质量为M 的小车,在光滑水平地面上匀速运动,速度为v 0,在行驶途中有质量为m 的砂子从车上漏掉,砂子漏掉后小车的速度应为 ( ) A .v 0 B .m M Mv -0 A .m M mv -0 A .M v m M 0)(-4.A 、B 两个相互作用的物体,在相互作用的过程中合外力为0,则下述说法中正确的是( )A .A 的动量变大,B 的动量一定变大 B .A 的动量变大,B 的动量一定变小C .A 与B 的动量变化相等D .A 与B 受到的冲量大小相等5.把一支枪水平固定在小车上,小车放在光滑的水平地面上,枪发射子弹时,关于枪、子弹、车的下列说法正确的有( )A. 枪和子弹组成的系统动量守恒B.枪和车组成的系统动量守恒C .枪、弹、车组成的系统动量守恒D .若忽略不计弹和枪筒之间的摩擦,枪、车组成的系统动量守恒6.两球相向运动,发生正碰,碰撞后两球均静止,于是可以判定,在碰撞以前( )A .两球的质量相等B .两球的速度大小相同C .两球的动量大小相等D .以上都不能断定7.一只小船静止在水面上,一个人从小船的一端走到另一端,不计水的阻力,以下说法正确的是( )A .人在小船上行走,人对船的冲量比船对人的冲量小,所以人向前运动得快,小船后退得慢B .人在小船上行走时,人的质量比船的质量小,它们受到的冲量大小是一样的,所以人向前运动得快,船后退得慢C .当人停止走动时,因为小船惯性大,所以小船要继续后退D .当人停止走动时,因为总动量守恒,所以小船也停止后退8.如图所示,在光滑水平面上有一静止的小车,用线系一小球,将球拉开后放开,球放开时小车保持静止状态,当小球落下以后与固定在小车上的油泥沾在一起,则从此以后,关于小车的运动状态是 ( )A .静止不动B .向右运动C .向左运动D .无法判断*9.木块a 和b 用一根轻弹簧连接起来,放在光滑水平面上,a 紧靠在墙壁上,在b 上施加向左的水平力使弹簧压缩,如图所示,当撤去外力后,下列说法中正确的是( )A .a 尚未离开墙壁前,a 和b 系统的动量守恒B .a 尚未离开墙壁前,a 与b 系统的动量不守恒C .a 离开墙后,a 、b 系统动量守恒D .a 离开墙后,a 、b 系统动量不守恒*10.向空中发射一物体.不计空气阻力,当物体的速度恰好沿水平方向时,物体炸裂为a,b 两块.若质量较大的a 块的速度方向仍沿原来的方向则 ( )A .b 的速度方向一定与原速度方向相反B .从炸裂到落地这段时间里,a 飞行的水平距离一定比b 的大C .a ,b 一定同时到达地面D .炸裂的过程中,a 、b 中受到的爆炸力的冲量大小一定相等二、填空题11.质量分别为m 1、m 2的两物体在光滑水平面上碰撞 , 碰撞前两物体的速度分别为V 1、V 2,当两物体发生碰撞后速度分别为V 1/ 、V 2/。
物理:《动量与动量守恒定律》课件-(复习专题)

一、动量定理的应用 练习1:一个质量为0.18kg的垒球, 以25 m/s的水平速度飞向球棒,被球棒 打击后,反向水平飞回,速度的大小为 45 m/s,设球棒与垒球的作用时间为 0.01 s,求球棒对垒球的平均作用力有 多大?
练习2:质量1kg的铁球从沙坑上方由静 止释放,下落1s落到沙子表面上,又 经过0.2s,铁球在沙子内静止不动。 假定沙子对铁球的阻力大小恒定不变, 求铁球在沙坑里运动时沙子对铁球的 阻力。(g=10m/s2)
v0
m2
练习3:如图示:质量为M的滑槽静止在光滑的水平面 滑槽的AB部分是半径为R的1/4的光滑圆弧,BC部分是 水平面,将质量为m 的小滑块从滑槽的A点静止释放,沿 圆弧面滑下,并最终停在水平部分BC之间的D点,则D A. 滑块m从A滑到B的过程,物体与滑块组成的系统动 量守恒、 机械能守恒
2m gR v2 ( M m) M
2
练习2:如图所示,光滑水平面上质量为m1=2kg 的物块以v0=2m/s的初速冲向质量为m2=6kg静止 的光滑圆弧面斜劈体。求: (1)物块m1滑到最高点位置时,二者的速度; (2)物块m1从圆弧面滑下后,二者速度; (3)若m1= m2,物块m1从圆弧面滑下后,二者速 度。
B. 滑块滑到B点时,速度大小等于 2 gR C. 滑块从B运动到D的过程,系统的动量和机械能都 不守恒 A
D. 滑块滑到D点时,物体的 速度等于0
B D C
; /q2532273645/mine/ 时时计划群
gvh95hyc
泛着银子般的亮光、活泼泼流过去。小道童蹲下去喝口水,岸边有锯齿边缘的小草,给他手上拉了小小一道血口子,他点了点 那片绿叶子,决定不跟他计较,半立起身子,搔搔头皮,自言自语埋怨:“霞姐好没道理,这道髻挽得裳儿好紧。”便把短簪、 发带都抽开,一头青丝摇将下来,与宝音发质一般无二,还更细柔些。又抚着胸道:“这也箍得裳儿好紧。”竟探手入怀,把 一条布带子也松开,胸脯也像吹了气似的涨起来。她身姿娇小如鸟儿,胸脯倒比小鸟的胸丰满得多。深青的草穗,在浓碧的穗 鞘里摇晃。一条六寸长的虎头鱼从细浪里甩个尾巴钻上来,又要一头扎下去,裳儿哪肯放过,吐气开手,长臂一抓,抓住了, 那鱼挣扎扭动个不住,鳞片滑溜溜的,就指望滑出去,裳儿五指如钉,抓进鱼身里,笑斥:“你想回哪儿去?”那鱼吃痛,抖 颤不已。裳儿同情道:“还是给你个痛快罢!”右手五指仍钩着鱼身不放,左手食指扎进鱼腮中间,一拉,把肚皮都划开,连 鱼泡带肝肠都一把拉出来,不曾捏碎了苦胆,全甩在一边,道:“这下了帐了?”鱼已不能大动作,但鱼鳍仍在颤动。裳儿嗔 道:“你们鱼儿总是这般作势,连下了油锅还能跳起来,我可没法子了,只当你已经死了罢。”便在溪中大石块上找了个好位 置盘膝坐下,将鱼摆在面前,谢过三清,以短簪作刀,将鱼腹两边嫩肉都片下来,去了大刺,笑道:“幸亏把芋大娘的淡酱油 偷出来。”便袖中出一装丹药用的小瓷瓶,瓶里丹药早没了,装了谢府厨房里芋大娘自酿的好酱油,点在嫩肉上头,也不炙烤, 就这么生啖,且啖且夸赞,一时腹肉食毕,连鱼头中好物色也挑罢吮尽了,剩下一条鱼脊、一条鱼尾肉,小刺多,裳儿不耐烦 再吃,都丢回溪里,抹抹嘴,心满意足继续取路往山上回去。一路阴阴的古木参天、娇娇的雀鸟啭鸣,快近山顶,裳儿转过一 条小道,便见山石益奇、林木益秀,分叶蹬岧,眼前一亮,是一座极大的观院,台阶雪白,花开得无边无际,有女孩子们赤着 脚、端着烛台和果碟走来走去,都披着淡紫色的纱衣,耳旁垂下长长的明月珰。第四十八章 毓秀垂钟附眉刀(5)裳儿开开心 心奔过去,正待同那些女孩子们打招呼,有一个大姑娘跑出来,十八九的年纪,瓜子脸儿,戴个道冠,把水绿的袖子挽起来: “裳儿!”那些女孩子们向裳儿作个眼色,一半同情、一半幸灾乐祸,哄然散去。裳儿吸进一口气,认命的上前行礼道:“取 霞姐姐!”取霞冷笑:“去了恁多时光!这丫头又祸害了哪条生灵回来?”裳儿奇道:“咦,怎么又被霞姐姐看出来?”取霞 摇头道:“一口腥气不说,指缝间鲜血还在。”裳儿就笑着低头剔指甲里的鱼血。取霞问道:“没有动火,又是生吃的?什么 时候偷了我的芥辣酱去?”一边动手
《动量守恒定律》测试题(含答案)
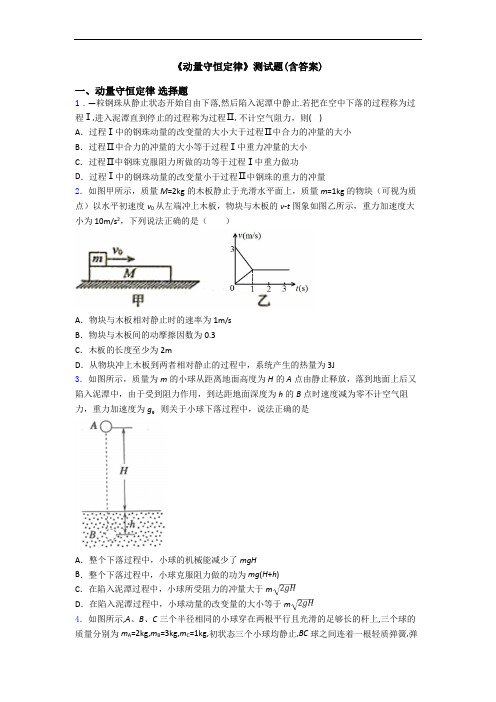
《动量守恒定律》测试题(含答案)一、动量守恒定律选择题1.—粒钢珠从静止状态开始自由下落,然后陷入泥潭中静止.若把在空中下落的过程称为过程Ⅰ,进入泥潭直到停止的过程称为过程Ⅱ, 不计空气阻力,则( )A.过程Ⅰ中的钢珠动量的改变量的大小大于过程Ⅱ中合力的冲量的大小B.过程Ⅱ中合力的冲量的大小等于过程Ⅰ中重力冲量的大小C.过程Ⅱ中钢珠克服阻力所做的功等于过程Ⅰ中重力做功D.过程Ⅰ中的钢珠动量的改变量小于过程Ⅱ中钢珠的重力的冲量2.如图甲所示,质量M=2kg的木板静止于光滑水平面上,质量m=1kg的物块(可视为质点)以水平初速度v0从左端冲上木板,物块与木板的v-t图象如图乙所示,重力加速度大小为10m/s2,下列说法正确的是()A.物块与木板相对静止时的速率为1m/sB.物块与木板间的动摩擦因数为0.3C.木板的长度至少为2mD.从物块冲上木板到两者相对静止的过程中,系统产生的热量为3J3.如图所示,质量为m的小球从距离地面高度为H的A点由静止释放,落到地面上后又陷入泥潭中,由于受到阻力作用,到达距地面深度为h的B点时速度减为零不计空气阻力,重力加速度为g。
则关于小球下落过程中,说法正确的是A.整个下落过程中,小球的机械能减少了mgHB.整个下落过程中,小球克服阻力做的功为mg(H+h)C.在陷入泥潭过程中,小球所受阻力的冲量大于mD.在陷入泥潭过程中,小球动量的改变量的大小等于m4.如图所示,A、B、C三个半径相同的小球穿在两根平行且光滑的足够长的杆上,三个球的质量分别为m A=2kg,m B=3kg,m C=1kg,初状态三个小球均静止,BC球之间连着一根轻质弹簧,弹簣处于原长状态.现给A 一个向左的初速度v 0=10m/s,A 、B 碰后A 球的速度变为向右,大小为2m/s ,下列说法正确的是A .球A 和B 碰撞是弹性碰撞B .球A 和B 碰后,球B 的最小速度可为0C .球A 和B 碰后,弹簧的最大弹性势能可以达到96JD .球A 和B 碰后,弹簧恢复原长时球C 的速度可能为12m/s5.一物体在外力的作用下从静止开始做直线运动,合外力方向不变,大小随时间的变化如图所示.设该物体在0t 和02t 时刻相对于出发点的位移分别是1x 和2x ,速度分别是1v 和2v ,合外力从开始至o t 时刻做的功是1W ,从0t 至02t 时刻做的功是2W ,则A .215x x =,213v v =B .1221,95x x v v ==C .2121,58x x W W ==D .2121,39v v W W ==6.A 、B 两球沿同一直线运动并发生正碰,如图所示为两球碰撞前后的位移—时间(x-t)图像,图中a 、b 分别为A 、B 两球碰撞前的图线,c 为碰撞后两球共同运动的图线.若A 球的质量2A m kg =,则由图可知下列结论正确的是( )A .A 、B 两球碰撞前的总动量为3 kg·m/sB .碰撞过程A 对B 的冲量为-4 N·sC .碰撞前后A 的动量变化为4kg·m/sD .碰撞过程A 、B 两球组成的系统损失的机械能为10 J7.如图所示,将质量为M 1、半径为R 且内壁光滑的半圆槽置于光滑水平面上,左侧靠竖直墙壁,右侧靠一质量为M 2的物块.今让一质量为m 的小球自左侧槽口A 的正上方h 高处从静止开始下落,与半圆槽相切自A 点进入槽内,则以下结论中正确的是( )A .小球在槽内运动的全过程中,小球与半圆槽在水平方向动量守恒B .小球在槽内运动的B 至C 过程中,小球、半圆槽和物块组成的系统水平方向动量守恒 C .小球离开C 点以后,将做竖直上抛运动D .小球从A 点经最低点向右侧最高点运动的过程中,小球、半圆槽和物块组成的系统机械能守恒8.如图所示,光滑水平面上有一质量为m =1kg 的小车,小车右端固定一水平轻质弹簧,弹簧左端连接一质量为m 0=1kg 的物块,物块与上表面光滑的小车一起以v 0=5m/s 的速度向右匀速运动,与静止在光滑水平面上、质量为M =4kg 的小球发生弹性正碰,若碰撞时间极短,弹簧始终在弹性限度内.则( )A .碰撞结束时,小车的速度为3m/s ,速度方向向左B .从碰后瞬间到弹簧最短的过程,弹簧弹力对小车的冲量大小为4N·sC .小车的最小速度为1m/sD .在小车速度为1m/s 时,弹簧的弹性势能有最大值9.A 、B 两球沿同一直线运动并发生正碰,如图所示为两球碰撞前后的位移—时间(x-t)图像,图中a 、b 分别为A 、B 两球碰撞前的图线,c 为碰撞后两球共同运动的图线.若A 球的质量2A m kg ,则由图可知下列结论正确的是( )A .A 、B 两球碰撞前的总动量为3 kg·m/sB .碰撞过程A 对B 的冲量为-4 N·sC .碰撞前后A 的动量变化为4kg·m/sD .碰撞过程A 、B 两球组成的系统损失的机械能为10 J10.如图所示,足够长的光滑水平面上有一质量为2kg 的木板B ,质量为1kg 的木块C 叠放在B 的右端点,B 、C 均处于静止状态且B 、C 之间的动摩擦因数为μ = 0.1。
第三章 动量定理 动量守恒定律(习题)

第三章 动量定理及动量守恒定律(习题)3.5.1质量为2kg 的质点的运动学方程为 j ˆ)1t 3t 3(i ˆ)1t 6(r 22+++-=(t 为时间,单位为s ;长度单位为m).求证质点受恒力而运动,并求力的方向大小。
解,j ˆ)3t 6(i ˆt 12v ++= j ˆ6i ˆ12a +=jˆ12i ˆ24a m F +==(恒量)12257.262412tg )N (83.261224F ==θ=+=-3.5.2质量为m 的质点在oxy 平面内运动,质点的运动学方程为ωω+ω=b,a, ,j ˆt sin b i ˆt cos a r为正常数,证明作用于质点的合力总指向原点。
解, ,j ˆt cos b i ˆt sin a v ωω+ωω-= r,j ˆt sin b i ˆt cos a a 22 ω-=ωω-ωω-= r m a m F ω-==3.5.3在脱粒机中往往装有振动鱼鳞筛,一方面由筛孔漏出谷粒,一方面逐出秸杆,筛面微微倾斜,是为了从较底的一边将秸杆逐出,因角度很小,可近似看作水平,筛面与谷粒发生相对运动才可能将谷粒筛出,若谷粒与筛面静摩擦系数为0.4,问筛沿水平方向的加速度至少多大才能使谷物和筛面发生相对运动。
解答,以谷筛为参照系,发生相对运动的条件是,g a ,mg f a m 000μ≥'μ=≥'a ' 最小值为)s /m (92.38.94.0g a 20=⨯=μ='以地面为参照系:解答,静摩擦力使谷粒产生最大加速度为,mg ma 0max μ= ,g a 0max μ=发生相对运动的条件是筛的加速度g a a0max μ=≥',a '最小值为)s /m (92.38.94.0g a20=⨯=μ='3.5.4桌面上叠放着两块木板,质量各为,m ,m 21如图所示。
2m 和桌面间的摩擦系数为2μ,1m 和2m 间的静摩擦系数为1μ。
高考物理《动量守恒定律》真题练习含答案

高考物理《动量守恒定律》真题练习含答案1.[2024·全国甲卷](多选)蹦床运动中,体重为60 kg的运动员在t=0时刚好落到蹦床上,对蹦床作用力大小F与时间t的关系如图所示.假设运动过程中运动员身体始终保持竖直,在其不与蹦床接触时蹦床水平.忽略空气阻力,重力加速度大小取10 m/s2.下列说法正确的是()A.t=0.15 s时,运动员的重力势能最大B.t=0.30 s时,运动员的速度大小为10 m/sC.t=1.00 s时,运动员恰好运动到最大高度处D.运动员每次与蹦床接触到离开过程中对蹦床的平均作用力大小为4 600 N答案:BD解析:根据牛顿第三定律结合题图可知,t=0.15 s时,蹦床对运动员的弹力最大,蹦床的形变量最大,此时运动员处于最低点,运动员的重力势能最小,故A错误;根据题图可知运动员从t=0.30 s离开蹦床到t=2.3 s再次落到蹦床上经历的时间为2 s,根据竖直上抛运动的对称性可知,运动员上升时间为1 s,则在t=1.3 s时,运动员恰好运动到最大高度处,t=0.30 s时运动员的速度大小v=10×1 m/s=10 m/s,故B正确,C错误;同理可知运动员落到蹦床时的速度大小为10 m/s,以竖直向上为正方向,根据动量定理F·Δt-mg·Δt=mv-(-mv),其中Δt=0.3 s,代入数据可得F=4 600 N,根据牛顿第三定律可知运动员每次与蹦床接触到离开过程中对蹦床的平均作用力大小为4 600 N,故D正确.故选BD.2.[2022·山东卷]我国多次成功使用“冷发射”技术发射长征十一号系列运载火箭.如图所示,发射仓内的高压气体先将火箭竖直向上推出,火箭速度接近零时再点火飞向太空.从火箭开始运动到点火的过程中()A.火箭的加速度为零时,动能最大B.高压气体释放的能量全部转化为火箭的动能C.高压气体对火箭推力的冲量等于火箭动量的增加量D.高压气体的推力和空气阻力对火箭做功之和等于火箭动能的增加量答案:A解析:从火箭开始运动到点火的过程中,火箭先加速运动后减速运动,当加速度为零时,动能最大,A项正确;高压气体释放的能量转化为火箭的动能和重力势能及火箭与空气间因摩擦产生的热量,B项错误;根据动量定理可得高压气体对火箭的推力F、火箭自身的重力mg和空气阻力f的冲量矢量和等于火箭动量的变化量,C项错误;根据动能定理可得高压气体对火箭的推力F、火箭自身的重力mg和空气阻力f对火箭做的功之和等于火箭动能的变化量,D项错误.3.[2022·湖南卷]1932年,查德威克用未知射线轰击氢核,发现这种射线是由质量与质子大致相等的中性粒子(即中子)组成.如图,中子以速度v0分别碰撞静止的氢核和氮核,碰撞后氢核和氮核的速度分别为v1和v2.设碰撞为弹性正碰,不考虑相对论效应,下列说法正确的是()A.碰撞后氮核的动量比氢核的小B.碰撞后氮核的动能比氢核的小C.v2大于v1D.v2大于v0答案:B解析:设中子质量为m0,被碰粒子质量为m,碰后中子速度为v′0,被碰粒子速度为v,二者发生弹性正碰,由动量守恒定律和能量守恒定律有m 0v 0=m 0v ′0+m v ,12 m 0v 20 =12m 0v ′20 +12 m v 2,解得v ′0=m 0-m m 0+m v 0,v =2m 0m 0+mv 0,因为当被碰粒子分别为氢核(m 0)和氮核(14m 0)时,有v 1=v 0,v 2=215 v 0,故C 、D 项错误;碰撞后氮核的动量为p 氮=14m 0·v 2=2815m 0v 0,氢核的动量为p 氢=m 0·v 1=m 0v 0,p 氮>p 氢,故A 错误;碰撞后氮核的动能为E k 氮=12·14m 0v 22 =28225 m 0v 20 ,氢核的动能为E k 氢=12 ·m 0·v 21 =12m 0v 20 ,E k 氮<E k 氢,故B 正确. 4.[2021·全国乙卷]如图,光滑水平地面上有一小车,一轻弹簧的一端与车厢的挡板相连,另一端与滑块相连,滑块与车厢的水平底板间有摩擦.用力向右推动车厢使弹簧压缩,撤去推力时滑块在车厢底板上有相对滑动.在地面参考系(可视为惯性系)中,从撤去推力开始,小车、弹簧和滑块组成的系统( )A .动量守恒,机械能守恒B .动量守恒,机械能不守恒C .动量不守恒,机械能守恒D .动量不守恒,机械能不守恒答案:B解析:撤去推力后,小车、弹簧和滑块组成的系统所受合外力为零,满足系统动量守恒的条件,故系统动量守恒;由于撤去推力时滑块在车厢底板上有相对滑动,存在摩擦力做功的情况,故系统机械能不守恒,所以选项B 正确.5.[2023·新课标卷](多选)使甲、乙两条形磁铁隔开一段距离,静止于水平桌面上,甲的N 极正对着乙的S 极,甲的质量大于乙的质量,两者与桌面之间的动摩擦因数相等.现同时释放甲和乙,在它们相互接近过程中的任一时刻( )A .甲的速度大小比乙的大B .甲的动量大小比乙的小C .甲的动量大小与乙的相等D .甲和乙的动量之和不为零答案:BD解析:对甲、乙两条形磁铁分别做受力分析,如图所示对于整个系统,由于μm 甲g >μm 乙g ,合力方向向左,合冲量方向向左,所以合动量方向向左,甲的动量大小比乙的小,m 甲v 甲<m 乙v 乙,又m 甲>m 乙,故v 甲<v 乙,B 、D 正确,A 、C 错误.故选BD.6.[2021·全国乙卷](多选)水平桌面上,一质量为m 的物体在水平恒力F 拉动下从静止开始运动.物体通过的路程等于s 0时,速度的大小为v 0,此时撤去F ,物体继续滑行2s 0的路程后停止运动.重力加速度大小为g .则( )A .在此过程中F 所做的功为12m v 20 B .在此过程中F 的冲量大小等于32m v 0 C .物体与桌面间的动摩擦因数等于v 20 4s 0gD .F 的大小等于物体所受滑动摩擦力大小的2倍答案:BC解析:设物体与桌面间的动摩擦因数为μ,根据功的定义,可知在此过程中,F 做的功为W F =Fs 0=12m v 20 +μmgs 0,选项A 错误;物体通过路程s 0时,速度大小为v 0,撤去F 后,由牛顿第二定律有μmg =ma 2,根据匀变速直线运动规律有v 20 =2a 2·2s 0,联立解得μ=v 20 4s 0g ,选项C 正确;水平桌面上质量为m 的物体在恒力F 作用下从静止开始做匀加速直线运动,有F -μmg =ma 1,又v 20 =2a 1s 0,可得a 1=2a 2,可得F =3μmg ,即F 的大小等于物体所受滑动摩擦力大小的3倍,选项D 错误;对F 作用下物体运动的过程,由动量定理有Ft -μmgt=m v 0,联立解得F 的冲量大小为I F =Ft =32m v 0,选项B 正确.。
(完整版)动量守恒定律综合专题练习与解答

动量守恒定律综合专题练习与解答1.如图所示,光滑水平面上有一带半径为R 的1/4光滑圆弧轨道的滑块,其质量为2m ,一质量为m 的小球以速度v 0沿水平面滑上轨道,并从轨道上端飞出,求 ⑴小球上升的到离水平面的最大高度H 是多少?⑵小球离开轨道的瞬间,轨道的加速度大小a 是多少?解答:⑴小球到达最高点时,球与轨道在水平方向有相同的速度,设为v 。
由于小球和滑块组成的系统在水平方向不受外力作用,故系统在水平方向动量守恒,由根据动量守恒定律有 ()02mv m m v =+ 由机械能守恒有22201112222mv mv m v mgh =+⋅⋅+ 联立上述方程可得 203v h g=⑵小球离开轨道的瞬间,轨道的圆心没有竖直方向的速度,小球相对于轨道圆心在竖直方向的速度大小为小球的竖直分速度,设为v 竖。
水平方向的速度和轨道速度相同。
由运动的可逆性知道 ()2v g h R =-竖在轨道最高点,弹力提供做向心力,则有22022()23v mv m N m g h R mg R R R==⋅-=-竖由运动定律可得,小球对轨道的水平弹力大小为20223mv N'mg R=-由运动定律得轨道的加速度为 2023v N'a g m R==-2.如图所示,abc 是光滑的轨道,其中ab 是水平的,bc 为与ab 相切的、位于竖直平面内的半圆,半径R =0.30m ,质量m =0.20kg 的小球A 静止在轨道上,另一质量M =0.60kg ,速度v 0=5.5m/s 的小球B 与小球A 正碰。
已知相碰后小球A 经过半圆的最高点c 落到轨道上距b 点为L =42R 处,重力加速度g =10m/s 2,求 ⑴碰撞结束时,小球A 和B 的速度大小。
⑵试论证小球B 是否能沿着半圆轨道到达c 点。
解答:设A 球过C 点时的速度为v A ,平抛后的飞行时间为t ,则242122A R v t R gt⎧=⋅⎪⎨=⎪⎩ 解得2226m/s A v gR ==设碰撞结束后,小球A 、B 的速度分别为v 1和v 2。
专项练习(7)动量守恒定律(解析版)

2021届高考物理二轮复习易错题型专项练习(7)动量守恒定律一.选择题1.(2021•湖北模拟)如图所示,曲面体P静止于光滑水平面上,物块Q自P的上端静止释放。
Q与P的接触面光滑,Q在P上运动的过程中,下列说法正确的是()A.P对Q做功为零B.P和Q之间相互作用力做功之和为零C.P和Q构成的系统机械能守恒、动量守恒D.P和Q构成的系统机械能不守恒、动量守恒【答案】B【解答】A、Q在P上运动过程,P对Q有弹力且在力的方向上Q有位移,则P对Q做功不为零,故A 错误;BCD、Q在P上运动过程,P和Q构成的系统只有重力做功,系统机械能守恒,P、Q之间的弹力做功和必为零;系统在水平方向所受合外力为零,系统在水平方向动量守恒,但系统在竖直方向所受合外力不为零,系统在竖直方向动量不守恒,系统动量不守恒,故B正确,CD错误。
故选:B。
2.(2021•河北模拟)如图,一小船以1.0m/s的速度匀速前行,站在船上的人竖直向上抛出一小球,小球上升的最大高度为0.45m。
当小球再次落入手中时,小船前进的距离为(假定抛接小球时人手的高度不变,不计空气阻力,g取10m/s2)()A.0.3m B.0.6m C.0.9m D.1.2m【答案】B【解答】竖直向上抛出小球过程,小球与小船组成的系统在水平方向所受合外力为零,系统在水平方向动量守恒,由动量守恒定律可知,竖直向上抛出小球后小球与小船在水平方向的速度不变,小球与小船在水平方向都做匀速直线运动;设小球抛出后在竖直方向上升的时间为t,小球上升高度h=代入数据解得:t=0.3s从抛出小球到小球再从落入手中过程的时间t′=2t=2×0.3s=0.6s在此时间内小船在水平方向做匀速直线运动,小船前进的距离:x=vt′=1.0×0.6m=0.6m,故B正确,ACD错误。
故选:B。
3.(2021•山东模拟)放射性原子核X静止于匀强磁场中,某时刻衰变为两个粒子A和B,衰变后A和B 的运动速度与磁场垂直。
动量守恒定律练习题(含答案)

动量守恒定律复习测试题1.如图所示,质量为M的小船在静止水面上以速率v0向右匀速行驶,一质量为m 的救生员站在船尾,相对小船静止.若救生员以相对水面速率v水平向左跃入水中,则救生员跃出后小船的速率为()A.v0+mM v B.v0-m M vC.v0+mM(v0+v) D.v0+mM(v0-v)2.在2010年温哥华冬奥会上,首次参赛的中国女子冰壶队喜获铜牌,如图13-1-8为中国队员投掷冰壶的镜头.在某次投掷中,冰壶运动一段时间后以0.4 m/s 的速度与对方的静止冰壶发生正碰,碰后对方的冰壶以0.3 m/s的速度向前滑行.若两冰壶质量相等,规定向前运动的方向为正方向,则碰后中国队冰壶获得的速度为()A.0.1 m/s B.-0.1 m/sC.0.7 m/s D.-0.7 m/s3.如图所示,光滑水平面上有大小相同的A、B两球在同一直线上运动.两球质量关系为m B=2m A,规定向右为正方向,A、B两球的动量均为6 kg·m/s,运动中两球发生碰撞,碰撞后A球的动量增量为-4 kg·m/s,则()A.左方是A球,碰撞后A、B两球速度大小之比为2∶5B.左方是A球,碰撞后A、B两球速度大小之比为1∶10C.右方是A球,碰撞后A、B两球速度大小之比为2∶5D.右方是A球,碰撞后A、B两球速度大小之比为1∶104.如图所示,轻质弹簧的一端固定在墙上,另一端与质量为m的物体A相连,A放在光滑水平面上,有一质量与A相同的物体B,从高h处由静止开始沿光滑曲面滑下,与A相碰后一起将弹簧压缩,弹簧复原过程中某时刻B与A分开且沿原曲面上升.下列说法正确的是()A .弹簧被压缩时所具有的最大弹性势能为mghB .弹簧被压缩时所具有的最大弹性势能为mgh 2C .B 能达到的最大高度为h 2D .B 能达到的最大高度为h5.如图,大小相同的摆球a 和b 的质量分别为m 和3m ,摆长相同,并排悬挂,平衡时两球刚好接触.现将摆球a 向左拉开一小角度后释放,若两球的碰撞是弹性的,下列判断正确的是( )A .第一次碰撞后的瞬间,两球的速度大小相等B .第一次碰撞后的瞬间,两球的动量大小相等C .第一次碰撞后,两球的最大摆角不相同D .发生第二次碰撞时,两球在各自的平衡位置6.如图所示,光滑水平直轨道上有三个滑块A 、B 、C ,质量分别为m A =m C =2m ,m B =m ,A 、B 用细绳连接,中间有一压缩的轻弹簧(弹簧与滑块不拴接).开始时A 、B 以共同速度v 0运动,C 静止.某时刻细绳突然断开,A 、B 被弹开,然后B 又与C 发生碰撞并粘在一起,最终三滑块速度恰好相同.求B 与C 碰撞前B 的速度.7.如图所示,光滑水平桌面上有长L =2 m 的挡板C ,质量m C =5 kg ,在其正中央并排放着两个小滑块A 和B ,m A =1 kg ,m B =3 kg ,开始时三个物体都静止.在A 、B 间放有少量塑胶炸药,爆炸后A 以6 m/s 速度水平向左运动,A 、B 中任意一块与挡板C 碰撞后,都粘在一起,不计摩擦和碰撞时间,求:(1)当两滑块A 、B 都与挡板C 碰撞后,C 的速度是多大;(2)A 、C 碰撞过程中损失的机械能.8.如图所示,在光滑水平面上有质量均为m 的两辆小车A 和B ,A 车上表面光滑水平,其上表面左端有一质量为M 的小物块C (可看做质点).B 车上表面是一个光滑的14圆弧槽,圆弧槽底端的切线与A 的上表面相平.现在A 和C 以共同速度v 0冲向静止的B 车,A 、B 碰后粘合在一起,之后物块C 滑离A ,恰好能到达B 的圆弧槽的最高点.已知M =2m ,v 0=4 m/s ,取g =10 m/s 2.求圆弧槽的半径R .动量守恒复习题答案1.如图所示,质量为M的小船在静止水面上以速率v0向右匀速行驶,一质量为m 的救生员站在船尾,相对小船静止.若救生员以相对水面速率v 水平向左跃入水中,则救生员跃出后小船的速率为()A.v0+mM v B.v0-m M vC.v0+mM(v0+v) D.v0+mM(v0-v)【解析】小船和救生员组成的系统满足动量守恒:(M+m)v0=m·(-v)+Mv′解得v′=v0+mM(v0+v)故C项正确,A、B、D三项均错.【答案】 C2.在2010年温哥华冬奥会上,首次参赛的中国女子冰壶队喜获铜牌,如图13-1-8为中国队员投掷冰壶的镜头.在某次投掷中,冰壶运动一段时间后以0.4 m/s的速度与对方的静止冰壶发生正碰,碰后对方的冰壶以0.3 m/s的速度向前滑行.若两冰壶质量相等,规定向前运动的方向为正方向,则碰后中国队冰壶获得的速度为() A.0.1 m/s B.-0.1 m/sC.0.7 m/s D.-0.7 m/s【解析】设冰壶质量为m,碰后中国队冰壶速度为v x,由动量守恒定律得mv0=mv+mv x解得v x=0.1 m/s,故选项A正确.【答案】 A3.如图所示,光滑水平面上有大小相同的A、B两球在同一直线上运动.两球质量关系为m B=2m A,规定向右为正方向,A、B两球的动量均为6 kg·m/s,运动中两球发生碰撞,碰撞后A球的动量增量为-4 kg·m/s,则()A .左方是A 球,碰撞后A 、B 两球速度大小之比为2∶5B .左方是A 球,碰撞后A 、B 两球速度大小之比为1∶10C .右方是A 球,碰撞后A 、B 两球速度大小之比为2∶5D .右方是A 球,碰撞后A 、B 两球速度大小之比为1∶10【解析】 由m B =2m A ,p A =p B 知碰前v B <v A若左为A 球,设碰后二者速度分别为v ′A 、v ′B由题意知p ′A =m A v ′A =2 kg·m/sp ′B =m B v ′B =10 kg·m/s 由以上各式得v ′A v ′B =25,故正确选项为A. 若右为A 球,由于碰前动量都为6 kg·m/s ,即都向右运动,两球不可能相碰.【答案】 A4.如图所示,轻质弹簧的一端固定在墙上,另一端与质量为m 的物体A 相连,A 放在光滑水平面上,有一质量与A 相同的物体B ,从高h 处由静止开始沿光滑曲面滑下,与A 相碰后一起将弹簧压缩,弹簧复原过程中某时刻B 与A 分开且沿原曲面上升.下列说法正确的是( )A .弹簧被压缩时所具有的最大弹性势能为mghB .弹簧被压缩时所具有的最大弹性势能为mgh 2C .B 能达到的最大高度为h 2D .B 能达到的最大高度为h【解析】 根据机械能守恒定律可得B 刚到达水平地面的速度v 0=2gh ,根据动量守恒定律可得A 与B 碰撞后的速度为v =12v 0,所以弹簧被压缩时所具有的最大弹性势能为E pm =12·2mv 2=12mgh ,即A 错,B 正确;当弹簧再次恢复原长时,A 与B 将分开,B 以v 的速度沿斜面上滑,根据机械能守恒定律可得mgh ′=12mv 2,B 能达到的最大高度为h /4,即D 错误.【答案】 B5.如图,大小相同的摆球a 和b 的质量分别为m 和3m ,摆长相同,并排悬挂,平衡时两球刚好接触.现将摆球a 向左拉开一小角度后释放,若两球的碰撞是弹性的,下列判断正确的是( )A .第一次碰撞后的瞬间,两球的速度大小相等B .第一次碰撞后的瞬间,两球的动量大小相等C .第一次碰撞后,两球的最大摆角不相同D .发生第二次碰撞时,两球在各自的平衡位置【解析】 弹性碰撞遵守能量守恒和动量守恒,设第一次碰撞前,a 的速度为v ,第一次碰撞后a 的速度为v 1、b 的速度为v 2,根据动量守恒,得mv =mv 1+3mv 2① 根据能量守恒,得:12mv 2=12mv 21+12×3mv 22② ①②联立得:v 1=-12v ,v 2=12v ,故A 选项正确;第一次碰撞后瞬间,a 的动量大小为12mv ,b 的动量大小为32mv ,故B 选项错误;由于第一次碰撞后瞬间的速度大小相等,根据机械能守恒可知,两球的最大摆角相等,C 选项错误;由于摆长相同,两球的振动周期相等,所以第二次碰撞时,两球在各自的平衡位置,D 选项正确.【答案】 AD6.如图所示,光滑水平直轨道上有三个滑块A 、B 、C ,质量分别为m A =m C =2m ,m B =m ,A 、B 用细绳连接,中间有一压缩的轻弹簧(弹簧与滑块不拴接).开始时A 、B 以共同速度v 0运动,C 静止.某时刻细绳突然断开,A 、B 被弹开,然后B 又与C 发生碰撞并粘在一起,最终三滑块速度恰好相同.求B 与C 碰撞前B 的速度.【解析】 设共同速度为v ,球A 与B 分开后,B 的速度为v B ,由动量守恒定律(m A +m B )v 0=m A v +m B v B ①m B v B =(m B +m C )v ②联立①②式,得B 与C 碰撞前B 的速度v B =95v 0.7.如图所示,光滑水平桌面上有长L =2 m 的挡板C ,质量m C =5 kg ,在其正中央并排放着两个小滑块A 和B ,m A =1 kg ,m B =3 kg ,开始时三个物体都静止.在A 、B 间放有少量塑胶炸药,爆炸后A 以6 m/s 速度水平向左运动,A 、B 中任意一块与挡板C 碰撞后,都粘在一起,不计摩擦和碰撞时间,求:(1)当两滑块A 、B 都与挡板C 碰撞后,C 的速度是多大;(2)A 、C 碰撞过程中损失的机械能.【解析】 (1)A 、B 、C 系统动量守恒0=(m A +m B +m C )v C , v C =0.(2)炸药爆炸时A 、B 系统动量守恒m A v A =m B v B解得:v B =2 m/s A 、C 碰撞前后系统动量守恒m A v A =(m A +m C )v v =1 m/sΔE =12m A v 2A -12(m A +m C )v 2=15 J.8.如图所示,在光滑水平面上有质量均为m 的两辆小车A 和B ,A 车上表面光滑水平,其上表面左端有一质量为M 的小物块C (可看做质点).B 车上表面是一个光滑的14圆弧槽,圆弧槽底端的切线与A 的上表面相平.现在A 和C 以共同速度v 0冲向静止的B 车,A 、B 碰后粘合在一起,之后物块C 滑离A ,恰好能到达B 的圆弧槽的最高点.已知M =2m ,v 0=4 m/s ,取g =10 m/s 2.求圆弧槽半径R .【解析】 设A 、B 碰后的共同速度为v 1,C 到达最高点时A 、B 、C 的共同速度为v 2,A 、B 碰撞过程动量守恒:mv 0=2mv 1C 冲上圆弧最高点过程系统动量守恒:Mv 0+2mv 1=(M +2m )v 2机械能守恒:12Mv 20+2×12mv 21=12(M +2m )v 22+MgR 联立以上三式解得:R =v 2016g代入数据得:R =0.1 m。
动量守恒定律试题(含答案)

动量守恒定律试题(含答案)一、动量守恒定律 选择题1.四个水球可以挡住一颗子弹!如图所示,是央视《国家地理》频道的实验示意图,直径相同(约30cm 左右)的4个装满水的薄皮气球水平固定排列,子弹射入水球中并沿水平线做匀变速直线运动,恰好能穿出第4个水球,气球薄皮对子弹的阻力忽略不计。
以下判断正确的是( )A .子弹在每个水球中的速度变化相同B .每个水球对子弹做的功不同C .每个水球对子弹的冲量相同D .子弹穿出第3个水球的瞬时速度与全程的平均速度相等 2.如图所示,用长为L 的细线悬挂一质量为M 的小木块,木块处于静止状态.一质量为m 、速度为v 0的子弹自左向右水平射穿木块后,速度变为v .已知重力加速度为g ,则A .子弹刚穿出木块时,木块的速度为0()m v v M - B .子弹穿过木块的过程中,子弹与木块组成的系统机械能守恒C .子弹穿过木块的过程中,子弹与木块组成的系统动量守恒D .木块上升的最大高度为2202mv mv Mg- 3.如图,在光滑的水平面上有一个长为L 的木板,小物块b 静止在木板的正中间,小物块a 以某一初速度0v 从左侧滑上木板。
已知物块a 、b 与木板间的摩擦因数分别为a μ、b μ,木块与木板质量均为m ,a 、b 之间的碰撞无机械能损失,滑动摩擦力等于最大静摩擦力。
下列说法正确的是( )A .若没有物块从木板上滑下,则无论0v 多大整个过程摩擦生热均为2013mvB .若22ab a μμμ<≤,则无论0v 多大,a 都不会从木板上滑落C .若032a v gL μ≤ab 一定不相碰D .若2b a μμ>,则a 可能从木板左端滑落4.如图所示,长木板A 放在光滑的水平面上,质量为m =4kg 的小物体B 以水平速度v 0=2m/s 滑上原来静止的长木板A 的表面,由于A 、B 间存在摩擦,之后A 、B 速度随时间变化情况如图乙所示,取g=10m/s 2,则下列说法正确的是( )A .木板A 获得的动能为2JB .系统损失的机械能为2JC .A 、B 间的动摩擦因数为0.1D .木板A 的最小长度为2m5.平静水面上停着一只小船,船头站立着一个人,船的质量是人的质量的8倍.从某时刻起,人向船尾走去,走到船中部时他突然停止走动.不计水对船的阻力,下列说法正确的是( )A .人在船上走动过程中,人的动能是船的动能的8倍B .人在船上走动过程中,人的位移是船的位移的9倍C .人走动时,它相对水面的速度大于小船相对水面的速度D .人突然停止走动后,船由于惯性还会继续运动一小段时间6.如图所示,两个小球A 、B 在光滑水平地面上相向运动,它们的质量分别为m A =4kg ,m B =2kg ,速度分别是v A =3m/s (设为正方向),v B =-3m/s .则它们发生正碰后,速度的可能值分别为( )A .v A ′=1 m/s ,vB ′=1 m/sB .v A ′=4 m/s ,v B ′=-5 m/sC .v A ′=2 m/s ,v B ′=-1 m/sD .v A ′=-1 m/s ,v B ′=-5 m/s7.如图所示,左图为大型游乐设施跳楼机,右图为其结构简图.跳楼机由静止从a 自由下落到b ,再从b 开始以恒力制动竖直下落到c 停下.已知跳楼机和游客的总质量为m ,ab 高度差为2h ,bc 高度差为h ,重力加速度为g .则A .从a 到b 与从b 到c 的运动时间之比为2:1B .从a 到b ,跳楼机座椅对游客的作用力与游客的重力大小相等C .从a 到b ,跳楼机和游客总重力的冲量大小为m ghD .从b 到c ,跳楼机受到制动力的大小等于2mg8.如图所示,小车质量为M ,小车顶端为半径为R 的四分之一光滑圆弧,质量为m 的小球从圆弧顶端由静止释放,对此运动过程的分析,下列说法中正确的是(g 为当地重力加速度)( )A .若地面粗糙且小车能够静止不动,则地面对小车的静摩擦力最大为mgB .若地面粗糙且小车能够静止不动,则地面对小车的静摩擦力最大为32mg C .若地面光滑,当小球滑到圆弧最低点时,小车速度为2()gR m M M m + D .若地面光滑,当小球滑到圆弧最低点时,小车速度为2()gR Mm M m + 9.如图,质量为m 的小木块从高为h 的质量为M 的光滑斜面体顶端滑下,斜面体倾角为θ,放在光滑水平面上,m 由斜面体顶端滑至底端的过程中,下列说法正确的是A .M 、m 组成的系统动量守恒B .M 移动的位移为()tan mh M m θ+ C .m 对M 做功为222cos ()(sin )Mm gh M m M m θθ++ D .m 对M 做功为222sin ()(cos )Mm gh M m M m θθ++ 10.如图所示,A 、B 、C 是三级台阶的端点位置,每一级台阶的水平宽度是相同的,其竖直高度分别为h 1、h 2、h 3,将三个相同的小球分别从A 、B 、C 三点以相同的速度v 0水平抛出,最终都能到达A 的下一级台阶的端点P 处,不计空气阻力。
物理动量守恒定律专题练习(及答案)含解析

①求弹簧恢复原长时乙的速度大小; ②若乙与挡板 P 碰撞反弹后,不能再与弹簧发生碰撞.求挡板 P 对乙的冲量的最大值. 【答案】v 乙=6m/s. I=8N 【解析】 【详解】 (1)当弹簧恢复原长时,设甲乙的速度分别为 和 ,对两滑块及弹簧组成的系统,设向 左的方向为正方向,由动量守恒定律可得:
又知
(2 分)
因为子弹在射穿第一块钢板的动能损失为 ΔE 损 1=f·d=
mv
2 0
(1
分),
由能量守恒得:
1 2
mv
2 1
+
1 2
mV
2 1
=
1 2
mv
2 0
-ΔE
损 1(2
分)
且考虑到 v1 必须大于 V1,
解得:v1= ( 1 3 ) v0 26
设子弹射入第二块钢板并留在其中后两者的共同速度为 V2,
物理动量守恒定律专题练习(及答案)含解析
一、高考物理精讲专题动量守恒定律
1.在图所示足够长的光滑水平面上,用质量分别为 3kg 和 1kg 的甲、乙两滑块,将仅与甲 拴接的轻弹簧压紧后处于静止状态.乙的右侧有一挡板 P.现将两滑块由静止释放,当弹簧 恢复原长时,甲的速度大小为 2m/s,此时乙尚未与 P 相撞.
(1)求物块 M 碰撞后的速度大小; (2)若平台表面与物块 M 间的动摩擦因数 μ=0.5,物块 M 与小球的初始距离为 x1=1.3 m, 求物块 M 在 P 处的初速度大小. 【答案】(1)3.0m/s(2)7.0m/s 【解析】 试题分析:(1)碰后物块 M 做平抛运动,设其平抛运动的初速度为 V
6.如图所示,光滑平行金属导轨的水平部分处于竖直向下的 B=4T 的匀磁场中,两导轨间 距 L=0.5m,导轨足够长金属棒 a 和 b 的质量都为 m=1kg,电阻 Ra Rb 1 .b 棒静止于轨 道水平部分,现将 a 棒从 h=80cm 高处自静止沿弧形轨道下滑,通过 C 点进入轨道的水平 部分,已知两棒在运动过程中始终保持与导轨垂直,且两棒始终不相碰.求 a、b 两棒的最 终速度大小以及整个过程中 b 棒中产生的焦耳热(已知重力加速度 g 取 10m/s2)
人教版高中物理《动量》精选典型习题集(含答案)

人教版高中物理《动量》精选练习题1. 一个运动的物体,受到恒定摩擦力而减速至静止,若其位移为s,速度为v,加速度为a,动量为p,则在下列图象中能正确描述这一运动过程的图象是( )2.从同一高度由静止落下的玻璃杯,掉在水泥地上易碎,掉在棉花上不易碎,这是因为玻璃杯掉在棉花上时( )A.受到冲量小B.受到作用力小C.动量改变量小D.动量变化率小3. 关于动量、冲量,下列说法正确的是( )A.物体动量越大,表明它受到的冲量越大B.物体受到合外力的冲量等于它的动量的变化量C.物体的速度大小没有变化,则它受到的冲量大小等于零D.物体动量的方向就是它受到的冲量的方向4.物体在恒力F作用下做直线运动,在时间△t1内速度由0增至v,在时间△t2内速度由2v增至3v,设F在时间△t1内冲量为I1,在时间△t2内冲量为I2,则有( )A.I1=I2B.I1<I2C.△t1=△t2D.△t1<△t25.质量为m的小球A,在光滑水平面上以速度v与质量为2m的静止小球B发生正碰后,A球的速率变为原来的,则B球碰后的速率可能是( )A. B. C. D.6.一个质量为2kg的物体在光滑水平面上,有一个大小为5N的水平外力作用其上后,持续10s立即等值反向作用,在经过10s时有( )A.物体正好回到出发点B.物体速度恰为零C.物体动量为100kg·m/sD.20s内物体动量改变量为零7.质量为m的物体,在水平面上以加速度a从静止开始运动,所受阻力是f,经过时间为t,它的速度是v,在此过程中物体所受合外力的冲量是( )A. B.mv C.mat D.8.如图所示,两个小球在光滑水平面上,沿同一直线运动,已知m1=2kg,m2=4kg,m1以2m/s的速度向右运动,m2以8m/s的速度向左运动,两球相碰后,m1以10m/s的速度向左运动,由此可知( )A.相碰后m2的速度大小为2m/s,方向向右B.相碰后m2的速度大小为2m/s,方向向左C.在相碰过程中,m2的动量改变大小是24kg·m/s,方向向右D.在相碰过程中,m1的冲量大小为24N·s,方向向左9.两个物体质量分别为mA 、mB,mA>mB,速度分别为vA、vB,当它们以大小相等的动量做方向相反的相互碰撞后,下列哪种情况是可能的( ) A.两物体都沿vA方向运动B.两物体都沿vB方向运动C.一个物体静止,而另一个物体向某方向运动D.两物体各自被弹回10.放在光滑水平面上质量不等的两物体,质量分别为M1和M2,用细线连接这两物体,且夹紧一根轻质弹簧,然后将细线烧断,则对两物体运动的叙述,正确的有( )A.两物体离开弹簧时速率有v1:v2xbj=M1:M2B.两物体离开弹簧时动量大小有p1:p2=M1:M2C.两物体离开弹簧前受力大小有F1:F2=M1:M2D.在任意时刻两物体动量大小相等二、填空题11.质置为m的物体,在倾角为θ的光滑斜面上由静止开始下滑,经过时间t,物体的速度为v1,在这段时间内,重力对物体的冲量为______,支持力的冲量大小为______,合外力对物体的冲量大小为______.12.物体A、B的质量之比为mA :mB=4:1,使它们以相同的初速度沿水平地面滑行,若它们受到的阻力相等,那么它们停下来所用的时间之比为tA :tB=______,若两物体与地面的动摩擦因数相同,那么它们停下来所用的时间之比为tA :tB=______13.以30m/s的速度竖直向上抛出一物体,经2s达到最高点,则空气阻力和重力之比为______.(g取10m/s2)14.一质量为1.0kg的小球静止在光滑水平面上,另一质量为0.5kg的小球以2m/s的速度和静止的小球发生碰撞,碰后以0.2mAs的速度被反弹,仍在原来的直线上运动,碰后两球的总动量是______kg·m/s,原来静止的小球获得的速度大小为______m/s.15.质量为1kg的小球从离地面5m高处自由落下,碰地后反弹的高度为0.8m,碰地的时间为0.05s.设竖直向上速度为正方向,则碰撞过程中,小球动量的增量为______kg·m/s,小球对地的平均作用力为______,方向______三、计算题:16.质量为1kg的钢球静止在光滑水平面上,一颗质量为50g的子弹以1000m/s的速率水平碰撞到钢球上后,又以800m/s的速率反向弹回,则碰后钢球的速度大小等于多少?17.质量为60kg的人,不慎从高空支架上跌落,由于弹性安全带的保护,使他悬挂在空中,已知安全带长5m,缓冲时间是1.2s,求安全带受到的平均冲力大小是多少?18.某人在一只静止的小船上练习射击,船、人连同枪(不包括子弹)及靶的总质量为M,枪内装有n颗子弹,每颗子弹的质量均为m,枪口到靶的距离为L,子弹水平射出枪口对于地的速度为v,在发射后一颗子弹时,前一颗子弹已射人靶中,在发射完n颗子弹时,小船后退的距离等于多少?19.动摩擦因数为0.1的水平面上,放有距离9.5m的两个物体A和B,质量分别为m=2kg,A=1kg,如图所示,现给A一个冲量使A以10m/s的初速度向静止的B运动当A与B发生碰mB撞后,A仍沿原方向运动,且A从开始运动到停止共经历6s,求碰撞后B经多长时间停止运动?20.如图所示,有A、B两质量均为M的小车,在光滑水平面上以相同的速度如在同一直线上相对运动,A车上有一质量为m的人至少要以多大的速度(对地)从A车跳到B车上,才能避免两车的相撞?21.如图所示,水平地面上O点正上方H高处以速度v水平抛出一个物体,当物体下落时,物体爆裂成质量相等的两块,两块同时落到地面,其中一块落在O点,不计空气阻力,求另一块的落地点距O点的距离.22.在光滑水平地面上放有一质量为M带光滑弧形槽的小车,—个质量为m的小铁块以速度v 沿水平槽口滑去,如图所示,求:(1)铁块能滑至弧形槽内的最大高度H (设m不会从左端滑离M).(2)铁块到最大高度时,小车的速度大小.(3)当铁块从右端脱离小车时,铁块和小车的速度分别是多少?23.如图所示,在光滑的水平面上停放着一辆质量为2m平板车C,在车上的左端放有一质量为m的小木块B,在小车的左边紧靠着一个固定在竖直平面内、半径为r的14光滑圆形轨道,轨道底端的切线水平且与小车的上表面相平。
湖北省宜昌市高中物理专题十二动量和动量守恒定律复习题无解答新人教版

十二、动量和动量守恒定律1.放在水平面上的物体,用水平推力F推它t秒,物体始终不动,则在这t秒内,关于合力的冲量与摩擦力冲量的大小,下列说法正确的是( )A.合力的冲量及摩擦力的冲量均为0B.合力的冲量及摩擦力的冲量均为FtC.合力的冲量为0,摩擦力的冲量为FtD.合力的冲量为Ft,摩擦力的冲量为02.物体在恒定的合力作用下做直线运动,在时间t1内动能由零增大到E1,在时间t2内动能由E1增加到2E1,设合力在时间t1内做的功为W1,冲量为I1,在时间t2内做的功是W2,冲量为I2,则( )A.I1<I2,W1=W2B.I1>I2,W1=W2C.I1>I2,W1<W2D.I1=I2,W1<W23.质量是60 kg的建筑工人,不慎从高空跌下,由于弹性安全带的保护,他被悬挂起来。
已知安全带的缓冲时间是1.2 s,安全带长5 m,取g=10 m/s2,则安全带所受的平均冲力的大小为( )A.500 N B.600 N C.1 100 N D.100 N4.如图所示,甲木块的质量为m1,以v的速度沿光滑水平地面向前运动,正前方有一静止的、质量为m2的乙木块,乙上连有一轻质弹簧。
甲木块与弹簧接触后( )A.甲木块的动量守恒B.乙木块的动量守恒C.甲、乙两木块所组成系统的动量守恒D.甲、乙两木块所组成系统的动能守恒5.如图所示,质量为m的人立于平板车上,人与车的总质量为M,人与车以速度v1在光滑水平面上向东运动。
当此人相对于车以速度v2竖直跳起时,车向东的速度大小为( )A.Mv1-Mv2M-mB.Mv1M-mC.Mv1+Mv2M-mD.v16.如图所示,一质量M=3.0 kg的长方形木板B放在光滑水平地面上,在其右端放一个质量m=1.0 kg的小木块A。
给A和B以大小均为4.0 m/s,方向相反的初速度,使A开始向左运动,B开始向右运动,A始终没有滑离B板。
在小木块A做加速运动的时间内,木板速度大小可能是( )A.1.8 m/s B.2.4 m/sC.2.8 m/s D.3.0 m/s7.在光滑水平桌面上停放着两辆玩具小车A、B,其质量之比m A∶m B=1∶2,两车用一根轻质细线缚住,中间夹着被压缩的轻弹簧,当烧断细线,轻弹簧将两车弹开,A车与B车( )A.动量大小之比为1∶2 B.动量大小之比为1∶1C.速度大小之比为1∶2 D.速度大小之比为1∶18.“爆竹声中一岁除,春风送暖入屠苏”,爆竹声响是辞旧迎新的标志,是喜庆心情的流露。
动量-动量守恒定律专题练习(含答案)

动量 动量守恒定律一、动量和冲量1、关于物体的动量和动能,下列说法中正确的是:A 、一物体的动量不变,其动能一定不变B 、一物体的动能不变,其动量一定不变C 、两物体的动量相等,其动能一定相等D 、两物体的动能相等,其动量一定相等2、两个具有相等动量的物体A 、B ,质量分别为m A 和m B ,且m A >m B ,比较它们的动能,则:A 、B 的动能较大 B 、A 的动能较大C 、动能相等D 、不能确定3、恒力F 作用在质量为m 的物体上,如图所示,由于地面对物体的摩擦力较大,没有被拉动,则经时间t ,下列说法正确的是:A 、拉力F 对物体的冲量大小为零;B 、拉力F 对物体的冲量大小为Ft ;C 、拉力F 对物体的冲量大小是Ftcosθ;D 、合力对物体的冲量大小为零。
4、如图所示,PQS 是固定于竖直平面内的光滑的14圆周轨道,圆心O 在S 的正上方,在O 和P 两点各有一质量为m 的小物块a 和b ,从同一时刻开始,a 自由下落,b 沿圆弧下滑。
以下说法正确的是A 、a 比b 先到达S ,它们在S 点的动量不相等B 、a 与b 同时到达S ,它们在S 点的动量不相等C 、a 比b 先到达S ,它们在S 点的动量相等D 、b 比a 先到达S ,它们在S 点的动量不相等 二、动量守恒定律 1、一炮艇总质量为M ,以速度v 0匀速行驶,从船上以相对海岸的水平速度v 沿前进方向射出一质量为m 的炮弹,发射炮弹后艇的速度为v /,若不计水的阻力,则下列各关系式中正确的是 。
A 、'0()Mv M m v mv =-+B 、'00()()Mv M m v m v v =-++C 、''0()()Mv M m v m v v =-++D 、'0Mv Mv mv =+2、在高速公路上发生一起交通事故,一辆质量为1500kg 向南行驶的长途客车迎面撞上了一辆质量为3000kg 向北行驶的卡车,碰后两车接在一起,并向南滑行了一段距离后停止。
新高考物理复习专题七动量守恒定律练习含答案

专题七动量守恒定律五年高考考点过关练考点一动量、冲量和动量定理1.(2021湖南,2,4分)物体的运动状态可用位置x和动量p描述,称为相,对应p⁃x图像中的一个点。
物体运动状态的变化可用p⁃x图像中的一条曲线来描述,称为相轨迹。
假如一质点沿x轴正方向做初速度为零的匀加速直线运动,则对应的相轨迹可能是()A B C D答案D2.(2022重庆,4,4分)在测试汽车的安全气囊对驾乘人员头部防护作用的实验中,某小组得到了假人头部所受安全气囊的作用力随时间变化的曲线(如图)。
从碰撞开始到碰撞结束过程中,若假人头部只受到安全气囊的作用,则由曲线可知,假人头部()A.速度的变化量等于曲线与横轴围成的面积B.动量大小先增大后减小C.动能变化正比于曲线与横轴围成的面积D.加速度大小先增大后减小答案D3.(2023新课标,19,6分)(多选)使甲、乙两条形磁铁隔开一段距离,静止于水平桌面上,甲的N极正对着乙的S极,甲的质量大于乙的质量,两者与桌面之间的动摩擦因数相等。
现同时释放甲和乙,在它们相互接近过程中的任一时刻()A.甲的速度大小比乙的大B.甲的动量大小比乙的小C.甲的动量大小与乙的相等D.甲和乙的动量之和不为零答案BD4.(2023天津,5,5分)质量为m的列车以速度v匀速行驶,突然以大小为F的力制动刹车直到列车停止,整个过程中列车还受到大小恒为f的阻力,下列说法正确的是()A.减速运动过程的加速度大小a=FmB.力F的冲量大小为mvC.刹车距离为mv22(F+f)D.匀速行驶时功率为(f+F)v答案C5.(2023福建,7,6分)(多选)甲、乙两辆完全相同的小车均由静止沿同一方向出发做直线运动。
以出发时刻为计时零点,甲车的速度⁃时间图像如图(a)所示,乙车所受合力⁃时间图像如图(b)所示。
则()A.0~2 s内,甲车的加速度大小逐渐增大B.乙车在t=2 s和t=6 s时的速度相同C.2~6 s内,甲、乙两车的位移不同D.t=8 s时,甲、乙两车的动能不同答案BC6.(2021北京,10,3分)如图所示,圆盘在水平面内以角速度ω绕中心轴匀速转动,圆盘上距轴r处的P点有一质量为m的小物体随圆盘一起转动。
高中物理《动量定理、动量守恒专项复习》练习题(人教版,精心总结有答案)

高中物理《动量定理、动量守恒专项复习》练习题例 1.如图所示,三辆完全相同的平板小车a b c 、、成一直线排列,静止在光滑水平面上.已知c 车上有一小孩跳到b 车上,接着又立即从b 车跳到a 车上.小孩跳离c 车和b 车时对地水平速度相同.他跳到a 车上相对a 车保持静止.此后( )A .a b 、两车运动速率相等B .a c 、两车运动速率相等C .三辆车的速率关系c a b v v v >>D .a c 、两车运动方向相同例2.小球1追碰小球2,碰撞前两球的动量分别为15kg m/s p =⋅,27kg m/s p =⋅,正碰后小球2的动量210kg m/s p =⋅,两球的质量关系可能是( )A .21m m =B .212m m =C .214m m =D .216m m =例3.如图所示,长2m 的木板Q 静止在某水平面上,0t =时刻,可视为质点的小物块P 以水平向右的某一初速度从Q 的左端向右滑行.P Q 、的速度-时间图象见图,其中,a b 分别是0~1s 内P Q 、的速度-时间图线,c 是1~2s 内P Q 、共同的速度-时间图线.已知P Q 、的质量均是1kg ,g 取210m/s .则以下判断正确的是( )A .在0~2s 内,木板Q 下表面与水平面之间有摩擦力B .在0~2s 内,摩擦力对Q 的冲量是2N s ⋅C .P Q 、之间的动摩擦因数为0.1D .P 相对Q 静止的位置在Q 木板的最右端例 4.将质量为m 的铅球以大小为0v ,沿仰角为θ的方向抛入一个装着砂子的总质量为M 的静止砂车中,如图所示,设车与地面间的摩擦可忽略,则球落入砂车后,车的速度例5.质量为M 的斜面体B 置于光滑的水平地面上,斜面体底边长为b,在其斜面上放有一质量为m 的与斜面体相似的物块,其上边长为a ,且与水平面平行.系统处于静止状态,如下图所示.在物块A 从B 的顶端下滑到接触地面的过程中,斜面体B 后退的距离为( )A .m M mb + B . m M Mb + C .a b m -)( D .a b M -)(例 6.如图所示,AB 为一光滑水平横杆,杆上套一质量为M 的小圆环,环上系一长为L 质量不计的细绳,绳的另一端拴一质量为m 的小球,现将绳拉直,且与AB 平行,由静止释放小球,则当线绳与AB 成 角时,圆环移动的距离是例7.如图所示,一轻质弹簧两端各连接一质量均为的滑块和,两滑块都置于光滑水平面上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学习资料汇编
十二、动量和动量守恒定律
1.放在水平面上的物体,用水平推力F推它t秒,物体始终不动,则在这t秒内,关于合力的冲量与摩擦力冲量的大小,下列说法正确的是( )
A.合力的冲量及摩擦力的冲量均为0
B.合力的冲量及摩擦力的冲量均为Ft
C.合力的冲量为0,摩擦力的冲量为Ft
D.合力的冲量为Ft,摩擦力的冲量为0
2.物体在恒定的合力作用下做直线运动,在时间t1内动能由零增大到E1,在时间t2内动能由E1增加到2E1,设合力在时间t1内做的功为W1,冲量为I1,在时间t2内做的功是W2,冲量为I2,则( )
A.I1<I2,W1=W2B.I1>I2,W1=W2
C.I1>I2,W1<W2D.I1=I2,W1<W2
3.质量是60 kg的建筑工人,不慎从高空跌下,由于弹性安全带的保护,他被悬挂起来。
已知安全带的缓冲时间是1.2 s,安全带长5 m,取g=10 m/s2,则安全带所受的平均冲力的大小为( )
A.500 N B.600 N C.1 100 N D.100 N
4.如图所示,甲木块的质量为m1,以v的速度沿光滑水平地面向前运动,正前方有一静止的、质量为m2的乙木块,乙上连有一轻质弹簧。
甲木块与弹簧接触后( )
A.甲木块的动量守恒
B.乙木块的动量守恒
C.甲、乙两木块所组成系统的动量守恒
D.甲、乙两木块所组成系统的动能守恒
5.如图所示,质量为m的人立于平板车上,人与车的总质量为M,人与车以速度v1在光滑水平面上向东运动。
当此人相对于车以速度v2竖直跳起时,车向东的速度大小为( )
A.Mv1-Mv2
M-m
B.
Mv1
M-m
C.Mv1+Mv2
M-m
D.v1
6.如图所示,一质量M=3.0 kg的长方形木板B放在光滑水平地面上,在其右端放一个质量m=1.0 kg的小木块A。
给A和B以大小均为4.0 m/s,方向相反的初速度,使A开始向左运动,B开始向右运动,A始终没有滑离B板。
在小木块A做加速运动的时间内,木板速度大小可能是( )
A.1.8 m/s B.2.4 m/s
C.2.8 m/s D.3.0 m/s
7.在光滑水平桌面上停放着两辆玩具小车A、B,其质量之比m A∶m B=1∶2,两车用一根轻质细线缚住,中间夹着被压缩的轻弹簧,当烧断细线,轻弹簧将两车弹开,A车与B车( )
A.动量大小之比为1∶2 B.动量大小之比为1∶1
C.速度大小之比为1∶2 D.速度大小之比为1∶1
8.“爆竹声中一岁除,春风送暖入屠苏”,爆竹声响是辞旧迎新的标志,是喜庆心情的流露。
有一个质量为3m的爆竹斜向上抛出,到达最高点时速度大小为v0、方向水平向东,在最高点爆炸成质量不等的两块,其中一块质量为2m,速度大小为v,方向水平向东;
则另一块的速度为( )
A.3v0-v B.2v0-3v C.3v0-2v D.2v0+v
9.如图所示,光滑圆形管道固定在竖直面内,直径略小于管道内径可视为质点的小球A、B 质量分别为m A、m B,A球从管道最高处由静止开始沿管道下滑,与静止于管道最低处的B
球相碰,碰后A、B球均能刚好到达与管道圆心O等高处,关于两小球质量比值m A
m B
的说法
正确的是( )
A.m A
m B
=2+1 B.
m A
m B
=2-1 C.
m A
m B
=1 D.
m A
m B
= 2
10.牛顿的《自然哲学的数学原理》中记载,A、B两个玻璃球相碰,碰撞后的分离速度和它们碰撞前的接近速度之比总量约为15∶16,分离速度是指碰撞后B对A的速度,接近速度是指碰撞前A对B的速度。
若上述过程是质量为2m的玻璃球A以速度v0碰撞质量为m的静止玻璃球B,且为对心碰撞,求碰撞后A、B的速度大小。
11.如图所示,竖直平面内的四分之一圆弧轨道下端与水平桌面相切,小滑块A和B分别静止在圆弧轨道的最高点和最低点。
现将A无初速释放,A与B碰撞后结合为一个整体,并沿桌面滑动。
已知圆弧轨道光滑,半径R=0.2 m;A和B的质量相等;A和B整体与桌面之间的动摩擦因数μ=0.2。
取重力加速度g=10 m/s2。
求:
(1)碰撞前瞬间A的速率v;
(2)碰撞后瞬间A和B整体的速率v′;
(3)A和B整体在桌面上滑动的距离l。
12.如图所示。
质量M=2 kg的足够长的小平板车静止在光滑水平面上,车的一端静止着质量为M A=2 kg的物体A(可视为质点)。
一个质量为m=20 g的子弹以500 m/s的水平速度射穿A后,速度变为100 m/s,最后物体A静止在车上。
若物体A与小车间的动摩擦因数μ=0.5(g取10 m/s2)。
(1)平板车最后的速度是多大?
(2)全过程损失的机械能为多少?
(3)A在平板车上滑行的时间为多少?
敬请批评指正。
