Role of the Coulomb and the vector-isovector $rho$ potentials in the isospin asymmetry of n
同一直线上三个点电荷的平衡问题

同一直线上三个点电荷的平衡问题英文回答:The problem of balancing three point charges on a line is an interesting one. Let's consider a scenario where we have three charges, Q1, Q2, and Q3, placed on a line. The goal is to find the positions of these charges such that the net force on each charge is zero, resulting in a state of equilibrium.To solve this problem, we can start by analyzing the forces acting on each charge. According to Coulomb's Law, the force between two point charges is directlyproportional to the product of their magnitudes and inversely proportional to the square of the distance between them. Therefore, the force between Q1 and Q2 can be represented as F12 = k(Q1Q2/r12^2), where k is the electrostatic constant and r12 is the distance between Q1 and Q2. Similarly, the forces between Q1 and Q3 and between Q2 and Q3 can be represented as F13 = k(Q1Q3/r13^2) and F23= k(Q2Q3/r23^2), respectively.In order to achieve equilibrium, the net force on each charge must be zero. This means that the vector sum of the forces acting on each charge should add up to zero. Mathematically, this can be represented as F1 + F2 + F3 = 0, where F1, F2, and F3 are the forces acting on Q1, Q2, andQ3, respectively.Now, let's consider a specific example to better understand this concept. Suppose we have three charges, Q1= +2C, Q2 = -3C, and Q3 = +4C, placed on a line. We want to find the positions of these charges such that they are in equilibrium.By applying the equations mentioned earlier, we can calculate the forces between each pair of charges. Let'ssay the distance between Q1 and Q2 is 2 meters, thedistance between Q1 and Q3 is 4 meters, and the distance between Q2 and Q3 is 3 meters. Using Coulomb's Law, we can calculate the forces as F12 = 9k, F13 = 1k, and F23 = 16k, where k is a constant.To achieve equilibrium, the vector sum of these forces must be zero. Therefore, we need to find positions for the charges where the magnitudes and directions of the forces balance out. In this example, we can place Q1 at the origin, Q2 at 2 meters to the left of Q1, and Q3 at 1 meter to the right of Q1. This arrangement ensures that the forcescancel each other out, resulting in a state of equilibrium.中文回答:三个点电荷在一条直线上达到平衡的问题是一个有趣的问题。
coulomb定律

coulomb定律Coulomb's Law is a fundamental principle in physics that describes the force between two charged objects. It states that the force between two charged objects is directly proportional to the product of their charges and inversely proportional to the square of the distance between them.The formula for Coulomb's Law is:F = k * (q1 * q2) / r^2where F is the force between the two charges, q1 and q2 are the magnitudes of the charges, r is the distance between the charges, and k is the electrostatic constant.Coulomb's Law is based on the concept of electric charge, which is a fundamental property of matter. There are two types of electric charge: positive and negative. Like charges repel each other, while opposite charges attract each other. Coulomb's Law quantifies this force of attraction or repulsion.The electrostatic constant, denoted by k, is a proportionality constant that depends on the medium through which the charges are interacting. In a vacuum, the value of k is approximately 9 x 10^9 Nm^2/C^2.Coulomb's Law can be used to calculate the force between two charged objects at a specific distance. By knowing the charges and the distance between them, one can determine the strength of the force. The force is a vector quantity, which means it has both magnitude and direction. The direction of the force is along the line connecting the charges.Coulomb's Law has numerous applications in various fields, including physics, engineering, and everyday life. It is used to study the behavior of electric charges, design electrical circuits, analyze the forces between particles in atoms, and understand the properties of materials. The law also plays a crucial role in the field of electrostatics, which deals with the behavior of stationary electric charges.One example of Coulomb's Law in action is the attraction between the positively charged nucleus and negatively charged electrons in an atom. The force of attraction holds the electrons in orbit around the nucleus, maintaining the stability of the atom. Without Coulomb's Law, the structure of matter as we know it would not exist.In conclusion, Coulomb's Law is a fundamental principle in physics that describes the force between two charged objects. It provides a quantitative relationship between the charges and the distance between them. The law has wide-ranging applications and is essential for understanding the behavior of electric charges.。
The role of the hippocampus in solving the Morris water maze

Communicated by Mikhail Tsodyks The Role of the Hippocampus in Solvingthe Morris Water MazeA.David RedishDavid S.TouretzkyComputer Science Department and Center for the Neural Basis of Cognition, Carnegie Mellon University,Pittsburgh,P A15213-3891,U.S.A.We suggest that the hippocampus plays two roles that allow rodents to solve the hidden-platform water maze:self-localization and route replay.When an animal explores an environment such as the water maze,the combination of placefields and correlational(Hebbian)long-term poten-tiation produces a weight matrix in the CA3recurrent collaterals such that cells with overlapping placefields are more strongly interconnected than cells with nonoverlappingfields.When combined with global inhi-bition,this forms an attractor with coherent representations of position as stable states.When biased by local view information,this allows the animal to determine its position relative to the goal when it returns to the environment.We call this self-localization.When an animal traces specific routes within an environment,the weights in the CA3recurrent collaterals become asymmetric.We show that this stores these routes in the recurrent collaterals.When primed with noise in the absence of sensory input,a coherent representation of position still forms in the CA3population,but then that representation drifts,retracing a route.We show that these two mechanisms can coexist and form a basis for memory consolidation,explaining the anterograde and limited retrograde amnesia seen following hippocampal lesions.1Amnesia Following Hippocampal LesionsHippocampal lesions in humans produce devastating impairments in declar-ative memory(memories of specific items,events,or episodes)(Scoville &Milner,1957;Squire&Zola-Morgan,1988;Cohen&Eichenbaum,1993; Zola-Morgan&Squire,1993).Although these patients perform immediate recall tasks normally,they are strongly impaired at times greater than a few minutes.In addition to the anterograde amnesia,these amnesias extend backward in time to recently before the occurrence of the lesion,but they leave early memories intact(Squire&Zola-Morgan,1988).Similar results have been seen in nonhuman primates with hippocampal lesions(Squire& Zola-Morgan,1988;Zola-Morgan&Squire,1993).Neural Computation10,73–111(1998)c 1997Massachusetts Institute of Technology74 A.David Redish and David S.TouretzkyThe theory proposed to explain these data is that the hippocampus serves as a temporary store for memory(Marr,1969;Buzs´a ki,1989;Cohen& Eichenbaum,1993;McClelland,McNaughton,&O’Reilly,1995).However, no models of hippocampal function in specific memory tasks exist;all pub-lished models of declarative memory demonstrate storage and retrieval of arbitrary binary vectors(Marr,1971;Rolls,1989;Gluck&Myers,1993;Al-varez&Squire,1994;Hasselmo&Schnell,1994;O’Reilly&McClelland, 1994;Levy,1996;Rolls,1996).Although these theories can address general principles involved in memory,they cannot address the role of the hip-pocampus in specific tasks.This makes it difficult to compare their results to real experiments or to generate testable predictions from them.Anterograde and limited retrograde amnesias after hippocampal lesion are also seen in rats tested in the Morris water maze(Sutherland&Hoesing, 1993).The Morris water maze consists of a submerged platform placed somewhere within a pool of water made opaque with milk or chalk(Mor-ris,Garrud,Rawlins,&O’Keefe,1982).When placed in this pool,rats try to find a way out;they initially swim randomly until theyfind the platform and climb out.Normal rats quickly learn the location of the platform:if the platform is removed,the rats search at the place where the platform had been(Morris et al.,1982).Rats with hippocampal lesions cannot learn this task(Morris et al.,1982;Morris,Schenk,Tweedie,&Jarrard,1990;McDon-ald&White,1994).If the rats are trained on the taskfirst and then given a hippocampal lesion1week later,they show profound deficits;however,the same lesion12weeks after training produces much smaller deficits(Suther-land&Hoesing,1993).Here,then,is a specific amnesia result that can be modeled in detail.2Modeling Memory in the Morris Water MazeWe suggest that rats trained on the Morris water maze use two different mechanisms tofind the hidden platform,one locale based and one route based.The two mechanisms can be subdivided intofive steps,thefirst two of which are locale based and the last three route based.Thesefive steps occur in order(we address possible ways to sidestep this in section4.2):1.Exploration.The animal familiarizes itself with the environment.2.Self-localization.Upon reentry into the environment,the animal mustdetermine its location relative to the platform.From this information, it can determine the direction it needs to swim in order to reach the platform.3.Route learning.When the animal travels along a specific path,routesare stored in the recurrent connections of hippocampal area CA3.4.Replay of routes during sleep.During sleep,the recent routes are replayedbecause,when primed with noise,the hippocampal formation settlesThe Role of the Hippocampus75 to a stable representation of a location,which then drifts along the routes stored in the CA3recurrent connections.McNaughton,Skaggs, and Wilson(Wilson&McNaughton,1994;Skaggs&McNaughton, 1996)have reported data supporting this hypothesis:simultaneous ex-tracellular recordings from hippocampal pyramidal cells have shown that cells tend tofire in the same sequence during slow-wave sleep as they did during recent experience in an environment.We discuss this and its implications for the theory in section2.4.5.Consolidation.The“dreamed”routes are transferred to long-term stor-age by a slowly learning cortical network.Anterograde amnesia occurs because long-term memory requires a hip-pocampus in order to learn the routes.Retrograde amnesia occurs when long-term memory has not been completely trained at the time the hip-pocampus is lesioned.Once the routes have been stored in long-term mem-ory,the animal can solve the task without a hippocampus.Our previous work laid out a theory of the role of the hippocampus in navigation(Touretzky&Redish,1996;Redish&Touretzky,1997)(see Figure1).The key components of the expanded theory presented here are as follows:•Path integration occurs via a loop including the superficial layers of the entorhinal cortex(ECs),the subiculum(Sub),and the parasubiculum (PaS).1•Sensory cues(called the local view,but not solely visual)enter the hippocampal formation from high-level sensory association areas,re-ferred to here as HLS.•The path integration and local view representations arefirst combined in ECs,but any conflicts are resolved by the recurrent connections in CA3.•On reentry into a familiar environment,competitive dynamics in the hippocampus allows the system to settle to a coherent place code even with ambiguous sensory cues.2This coherent code resets the path inte-grator so that multiple experiences of the same environment are com-patible with each other.•During sleep,recurrent connections within the hippocampus force a coherent code to form from noise,but due to asymmetric connection strengths produced during training,the represented location precesses 1Path integration is the ability to return to a starting point,even after a long,circuitous path,using only idiothetic cues(Mittelstaedt&Mittelstaedt,1980;Gallistel,1990;Etienne, 1992).2The place code is coherent if all neural activities are consistent with a representation of the same location in space.76 A.David Redish and David S.TouretzkyThe Role of the Hippocampus77 two modes.During motion,in the presence of ACh,the hippocampal EEG shows a7–12Hz rhythm called theta;during rest and slow-wave sleep,in the absence of ACh,the hippocampal EEG shows irregular activity,called LIA(large-amplitude irregular activity),characterized by short-duration sharp waves(Vanderwolf,1971).We now proceed to detail how our theory accounts for each of thefive steps discussed above,reviewing the data supporting the theory and sim-ulation results demonstrating each point.Additional simulation details are given in appendix A.2.1Exploration:Learning the Cognitive Graph.We begin by showing that the combination of random exploration and correlational(Hebbian) learning produces a weight matrix in the CA3recurrent connections that is appropriate for the competitive dynamics needed for self-localization.Fol-lowing Muller,Kubie,and Saypoff(1991),we call this connection function the cognitive graph:the synaptic efficacies between place cells are inversely related to the distance between the centers of their placefields.As the animal wanders around the environment,cells with nearby place fields are more likely to be coactive than cells with well-separatedfields. Combined with correlational long-term potentiation(LTP),in which the synaptic efficacy is increased when both cells are simultaneously active, after a session of wandering around an environment,the intrahippocampal connections will be inversely proportional to the distance between place field centers(Muller et al.,1991).LTP has been shown extensively in the recurrent connections in CA3and in the Schaffer collaterals connecting CA3 to CA1(see Landfield&Deadwyler,1988).Also supporting this theory are data showing the effect of ACh:while suppressing neuronal transmission in intrahippocampal synapses,ACh en-hances LTP in them(Hasselmo&Schnell,1994).We make the simplifying assumption that ACh shuts off the CA3recurrent connections completely. Experiments in hippocampal slices show that it diminishes synaptic efficacy across the Schaffer collaterals by approximately90percent,while diminish-ing the efficacy of the perforant path(inputs from ECs)by only approxi-mately45percent(Hasselmo&Schnell,1994).ACh presumably is present during theta mode,while the animal is moving about the environment.Dis-ruption of ACh has been found to shift the hippocampus out of theta,while cholinergic agonists shift the hippocampus into theta mode(Huerta&Lis-man,1993).LTP produced by hippocampal stimulation during theta or at intervals corresponding to the theta frequency is much stronger than similar stimulation during nontheta(LIA)(Larson,Wong,&Lynch,1986;Larson &Lynch,1989;Greenstein,Pavlides,&Winson,1988;Pavlides,Greenstein, Grudman,&Winson,1988;Huerta&Lisman,1993).Simulations.The network used to demonstrate the generation of the cognitive graph consisted of a limited version of the total model presented78 A.David Redish and David S.Touretzky in Figure1.It included HLS,PI,HD,ECs,and CA3/1components.Specific neuronal model details are given in appendix A.The HD component consisted of a1D(circular)neural array.At every time step,the currently represented value was calculated by a directional mean,the represented value was updated by the angular velocity,and then a new(idealized)HD representation was generated.This allowed us to simulate the neural interactions between the head direction and other rep-resentations without the computational time required to simulate the ac-tual head direction update mechanism.We have previously shown that a postsubiculum-anterior thalamic nuclei head direction model can track real angular velocity sequences accurately(Redish,Elga,&Touretzky,1996). The PI simulation was similar but used a two-dimensional(2D)(toroidal) neural sheet.We also simulated the HLS component as a bump on a2D neural sheet(as in Samsonovich&McNaughton,in press)and assumed that at every point in the environment,the position of the animal was correctly represented by the population.We did this because it is not clear what aspects of the environment are included in the local view;any set of spatial information about landmarks sufficient to localize the animal to a point will do.For some experiments,such as those described in section2.2,there was more than one peak in the local view representation.This allowed us to ask questions about the ability of the system to handle ambiguous inputs without having to build a complicated,speculative model of the visual system of the rodent.The EC’s population was also simulated as a2D neural sheet receiving input from the HLS and PI components.Because we do not separately simulate CA3and CA1,we refer to the combined simulated population as CA3/1but refer to CA3and CA1in our discussions of the theory proper.The CA3/1population consisted of a2D neural sheet connected to the PI representation by one-to-one connections.A sparse random connection pattern works just as well,but by using a one-to-one pattern,we know the center of the placefield for each CA3neuron.According to our theory,every time an animal enters an environment,it self-localizes as best it can by a sharp wave(LIA mode).We do not measure EEG in our simulations,but the self-localization sequence begins with a high proportion of the CA3cells active at low levels,and settles to a small number of highly active cells within approximately100ms(see section2.2). We believe this corresponds to a single sharp wave(Buzs´a ki,1989).We thus begin exploration byfirst placing the simulated animal at a random location and triggering a100-ms sharp wave.Since this is a novel environment,there are no stored associations in the intrahippocampal con-nections,and the sharp wave serves only to reset the path integrator to a random point.This random location becomes the reference point for the en-vironment,and the origin for the path integrator coordinate system.The an-imal then explores the environment by wandering randomly,during which LTP occurs in the intrahippocampal connections.The Role of the Hippocampus79Figure2:Route traveled by simulated rodent while exploring a100-cm diameter circular environment for5minutes.Dots indicate position sampled every10 seconds.Gray area denotes arena.Two effects must occur for the animal to have familiarized itself with the environment.First,a mapping from local views(in HLS)to path inte-grator coordinates(in ECs)must be learned.Second,because local views may be ambiguous,the cognitive graph must be learned in the recurrent connections of CA3.We show that the appropriate connection function appears within thefirst minutes of exploration.Figure2shows the track of the simulated animal wandering over the environment during the5minutes of exploration.The animal has clearly covered the entire environment.Figure3shows a scatter plot of the learned synaptic weights as a function of the distance between each pair of units in the CA3/1population.The synaptic efficacy between two cells is,on average,inversely related to the distance between the centers of their placefields.A similar plot of HLS-to-ECs synapse strengths would show that local view representations(in HLS)have been associated with path integrator coordinates(in ECs).Although the connection function appears quickly in our simulations,we used very large learning rates in order to minimize computation time.We do not know whether more realistic learning rates would allow the function to be acquired so quickly.If they did,the random trajectories shown by80 A.David Redish and David S.TouretzkyFigure3:Scatter plot of learned synaptic weights as a function of distance be-tween pairs of units.Distance is in cm.Line indicates the mean.animalsfirst placed in the water maze(with no knowledge of the goal location)would be sufficient to“explore”the environment.2.2Self-Localization and Place Field Stability.In order to navigate within a familiar environment,an animal must use a consistent representa-tion of position from session to session.Although visual cues can serve to inform the animal of its initial position,if they are ambiguous,there must be a mechanism to settle on a consistent representation of location.We be-lieve intrinsic competitive dynamics force the hippocampus to settle on a coherent code.These dynamics can serve as a disambiguation mechanism and can reproduce the search pattern that gerbils make when faced with ambiguous local cues(Touretzky&Redish,1996).We suggest that the competitive dynamics realized in the rodent pro-ceeds thusly:subiculum,parasubiculum,hipppocampus,and entorhinal cortex are initially noisy;sensory cues in HLS passed through ECs into the hippocampus proper bias the randomfiring rates with candidate locations. The recurrent connections in CA3allow one of these candidate locations to win out,forming a coherent place code in hippocampus.The connec-tions between CA1and subiculum reset the path integrator to the correct representation of the animal’s location in path integrator coordinates.This happens in the course of a single sharp wave during LIA.In our simulations, the place code in CA3/1is coherent within50to100ms.Figure4shows the first70ms of a simulated sharp wave.The Role of the Hippocampus81Figure4:Starting from random noise,a coherent place code forms in less than 50ms.Plot showsfiring rates of CA3/1place cells.Cells are laid out in a2D sheet with their locations in the sheet corresponding to the centers of their place fields in the environment.Intensity values have been interpolated for clarity. White indicates highfiring rate,black low.82 A.David Redish and David S.TouretzkyDuring a sharpwave,place cells do not show normal placefields;many cells are simultaneously active(many more than would normally be active during theta)(Buzs´a ki,1989).Because ACh is not present,synaptic efficacy between CA3cells is presumably at full strength,allowing the system to settle from an initially noisy state to a coherent representation of the ani-mal’s location.Once this representation is coherent,the path integrator(in subiculum,receiving strong connections from CA1)is driven by the now co-herent representation of location in CA1and is effectively reset.The animal can now navigate around the environment.Simulations.The network used to demonstrate self-localization used a similar architecture to that set out in section2.1.The2D neural sheets were enlarged to20×20,and the hippocampal simulation was more detailed.We simulated the CA3/1population as two pools,one excitatory and one in-hibitory(labeled CAE and CAI,respectively,in appendix A).The excitatory neurons were interconnected within and between pools by an idealization of the connection function learned in section2.1(a gaussian with a standard deviation of20cm).We had to use an idealization because our networks are small relative to those in the actual rodent brain.Inhibitory CA3/1neurons were broadly connected to both the excitatory and inhibitory pools.Essen-tially,this connection structure corresponds to local excitation and global inhibition.We measured the ability of this self-localization process to handle ambi-guities in the local view by locking three bumps into the HLS representation. This simulates three“candidate positions”in the local view.This ambigu-ous local view representation is resolved in the CA3/1representation intoa coherent representation of position similar to that shown in Figure4.2.3Route Learning.Given a representation of the animal’s current loca-tion in the environment and a representation of the current goal,the animal should be able to calculate the direction to take to reach the goal.The nu-cleus accumbens receives information about current needs and desires from the amygdala(Davis,Rainnie,&Cassell,1994)and information about cur-rent location via the fornix(Witter,Ostendorf,&Groenwegen,1990)and is optimally situated to perform this function.This function of the nucleus accumbens wasfirst suggested by Mogenson(1984),and a model showing its feasibility has been presented by Brown and Sharp(1995).(See Redish and Touretzky(1997)for a review.)There are three neurophysiological effects that allow the hippocampus to store routes as the animal travels.First,the postsynaptic potential(PSP) has a nonzero time constant.As an animal travels from the placefield of one neuron(say,a)to another(say,that of neuron b),neuron a continues to have an effect on thefiring rate of neuron b,but when the animal was in placefield a,neuron b did not have an effect on neuron a.Second,imagine the animal at an instant along the route taken,passingThe Role of the Hippocampus83 through a placefield centered slightly off the route.This cell will have a firing rate somewhere between its maximum and minimumfiring rates. Cells with placefields closer to the animal’s position will have higherfiring rates,and cells with placefields farther will have lower rates.This means that the output connection function from the neuron in question will be biased asymmetrically toward the path traveled.Finally,as the animal moves through the placefield,the timing of the spikesfired by that cell precesses with respect to the theta rhythm:cells behind the animalfire early in the cycle,while cells ahead of the animal fire late in the cycle(O’Keefe&Recce,1993;Skaggs,1995;Skaggs&Mc-Naughton,1996;Skaggs,McNaughton,Wilson,&Barnes,1996).Thus the represented position sweeps across the actual position from back to front with each theta cycle.When combined with the biophysical time course of LTP,this phase precession will also favor connections pointing along routes to a goal(Blum&Abbott,1996).Simulations.The route-learning simulation consisted of the same net-work as used in section2.2,with the addition of a new hippocampal mode. The simulation parameters as described in section2.2correspond to LIA mode,while the simulation parameters used for the route-learning simula-tion correspond to theta mode(see appendix A).We do not explicitly model the nucleus accumbens.Instead we compare the subicular representation at the goal and the current subicular represe-nation,and then simulate travel in a straight line until the animal reaches either the goal or a wall.Figure5shows the paths traveled to reach the goal from the four cardinal points.These are the four routes that will be stored in the CA3/1population.We model the asymmetric nature of LTP by making the learning rule dependent on the synaptic drive of the presynaptic neuron and thefiring rate of the postsynaptic neuron(see equation A.4).The synaptic drive S i of neuron i is the effect of that neuron on all the neurons on which it synapses divided by the synaptic weight over each synapse(Pinto,Brumberg,Simons, &Ermentrout,1996;see appendix A).It can be understood as a model of the postsynaptic potential or as a decaying memory of recentfiring rates shown by neuron i,with a decay time constant ofτi.We do not model phase precession as an emergent result of a complex process;instead we assume that phase precession exists and show that, when combined with the asymmetric temporal nature of LTP,routes are stored in the recurrent connections of the hippocampus.In order to produce phase precession,we derive the preferred phase of each CA3neuron using the approximation in Figure6.We then define thefiring rate of each neuron at time t asF i(t)=e−(˜θi(t)−θ(t))2/ρ2·ˆF i(t),(2.1)84 A.David Redish and David S.TouretzkyFigure5:Four routes to the goal location.In order to demonstrate the accuracy of the simulation,the direction to the goal was determined by comparing the representation in subiculum with the prior subicular representations of the goal location.Lines indicate trajectories taken by the simulated animal to reach the goal(indicated by small circle).An x has been drawn at the initial location of the animal in each position.These routes are stored in the CA3/1structure via LTP.Gray area denotes arena.where˜θi(t)is the preferred phase of neuron i,θ(t)is the current phase of the theta rhythm,ρis a constant,andˆF i(t)is the peakfiring rate at θ(t)=˜θ(t).We assume a theta rhythm with a frequency of7Hz,soθ(t)=(7·360◦sec ·t)mod360◦.ˆF i(t)is determined by equation A.2(see appendix A).This makes the representation of position sweep from behind the animal to in front of it with each theta cycle as it does in the real animal(O’Keefe &Recce,1993;Skaggs et al.,1996).We do not claim this as a model of how phase precession is actually generated in the rodent hippocampus,only that it produces a phase precession effect so that routes can be stored in the CA3 recurrent connections.These effects combine to store routes in the recurrent connections of CA3. They produce a vectorfield pointing toward the path and then leading to the goal.Figure7shows the routes stored by an animal traversing the four paths in Figure5.The Role of the Hippocampus85Figure6:How we simulated phase precession.Let L(t)be a ray originating at the simulated rodent’s current position(as represented by the pyramidal cells in CA3),pointing in the direction of its current heading(as represented by the cells in postsubiculum).Let P i(t)be a vector from the represented position of the rodent to the center of the placefield of place cell i,and D i(t)be the projectionof P i(t)onto L(t).Then the preferred phase of neuron i,˜θi(t)is proportional to D i(t):˜θi(t)=K·D i(t),where K is a scale factor chosen to be small enough that the phase precession will not wrap around(K=1.2deg/cm in our simulations). Thus,cells with placefields behind the represented position(in CA3)fire earlier in the theta cycle,and cells ahead of the represented positionfire later.We do not claim this as a model of how phase precession is actually generated in the rodent brain,only that it produces a phase precession effect so that routes can be stored in the CA3recurrent connections.2.4Replay of Routes During Sleep.When there is sensory input into the hippocampus and the hippocampus is in LIA mode(i.e.,the animal is awake and looking around but not moving),sensory cues enter the system via HLS and ECs,and those CA3cells that are consistent with the current local view will be more active than those that are not.This biases CA3to settle to a place code consistent with the local view and thus can serve as a self-localization procedure.On the other hand,when there is no sensory input,this bias will be absent,but due to the recurrent connections in CA3,the hippocampus will still settle into a coherent activity pattern.Due to the asymmetric connections that were stored when the animal traversed the routes to the goal,the place86 A.David Redish and David S.TouretzkyFigure7:Vectorfield of routes to a goal stored in the recurrent connections of the model CA3.For each cell j,we calculated the center of mass of the output connection weights,and plotted an arrow from the placefield center toward the center of mass.Length of arrow corresponds to linearly scaled distance to center of mass of the output connection weights.code will precess along one of these remembered routes.The bias provided by the sensory input should be enough to keep the system from precessing when awake,but in the absence of sensory input(during sleep),there is nothing to stop the precession.During sleep,when sharp waves occur without sensory input,we expect to see replay of routes.This is shown in Figure8.Given an initial noisy state,a coherent code forms within half a second,and then over the next few seconds,it drifts along a remembered route.Data supporting a replay of recent experience in hippocampus during sleep werefirst seen by Pavlides and Winson(1989).They showed that cells with recently visited placefields were more active during REM sleep than other cells whose placefields had not been recently visited.Wilson andThe Role of the Hippocampus87Figure8:Replay of routes during LIA without sensory input.A coherent code forms quickly and then slowly drifts to the goal over the subsequent few seconds. McNaughton(1994)showed that during slow-wave sleep(SWS),cells that showed correlatedfiring during a session in an environment(because their placefields overlapped)also showed a stronger correlation during sleep immediately after the session.Skaggs and McNaughton(1996)explicitly examined the temporal nature of replay during sharp waves in slow-wave sleep.They defined the temporal bias B ij between two cells i and j to be the difference between the integrated cross-correlation for the200ms after each spike of cell j and the integrated cross-correlation for the200ms before each spike of cell j.Thus,if cell i generallyfires after cell j rather than before,B ij will be greater than0.。
跃迁偶极矩
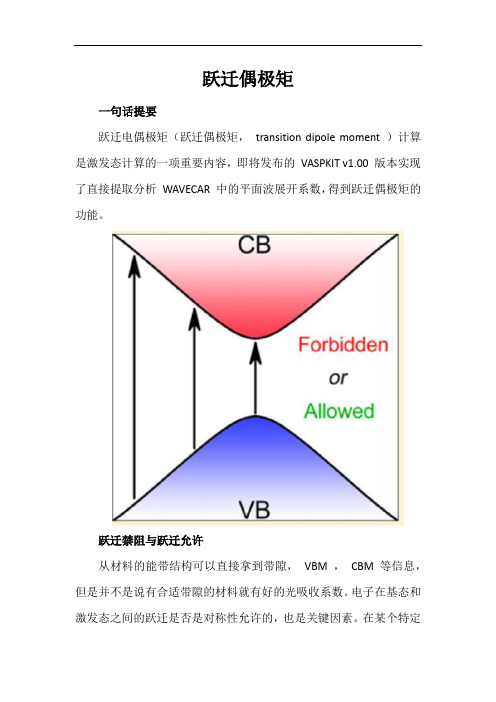
跃迁偶极矩一句话提要跃迁电偶极矩(跃迁偶极矩,transition dipole moment )计算是激发态计算的一项重要内容,即将发布的VASPKIT v1.00 版本实现了直接提取分析WAVECAR 中的平面波展开系数,得到跃迁偶极矩的功能。
跃迁禁阻与跃迁允许从材料的能带结构可以直接拿到带隙,VBM ,CBM 等信息,但是并不是说有合适带隙的材料就有好的光吸收系数。
电子在基态和激发态之间的跃迁是否是对称性允许的,也是关键因素。
在某个特定的K 点,假设基态电子波函数为|i> ,末态为|j> ,则两个态之间的跃迁电偶极矩为<i|-r |j> 。
r 是坐标矢量,负号是因为电子带负电荷。
有了跃迁偶极矩,可以进一步对其平方计算振子强度和荧光寿命等信息。
实例分析(双钙钛矿)比如Cs2AgInCl6 这种双钙钛矿材料。
虽然展现出较独特的白光发光特性,但其价带顶和导带底具有相同的宇称,存在跃迁禁阻;同时其中的电子和空穴的波函数分布差异极大,导致重叠面积小,降低辐射复合概率;两个因素导致其荧光产率极低(< 0.1% ),不具备应用价值。
通过替换掺杂,可以破坏该材料在直接带隙位置的对称性禁阻( parity-forbidden transition ),从而大大提高其光吸收效率。
例如,下述两篇文章都用到该思路,并且计算了其参杂以后的跃迁电偶极矩变化。
文献案例JPCL,跃迁偶极矩计算第一篇文章(J. Phys. Chem. Lett. 2017, 8, 2999−3007 )用Bi 替换掉Ag ,本来Cs2AgInCl6 在Gamma 点是(Gamma3 态到Gamma1 态)禁阻跃迁,但是把Ag 换成Bi ,在直接带隙位置变成了(Gamma1 态到Gamma4 态)。
进一步计算跃迁电偶极矩,发现原本在Gamma 点为0 ,Bi 替换以后变成了最大值。
▲J. Phys. Chem. Lett. 2017, 8, 2999−3007.▲Cs2AgInCl6 与Cs2InBiCl6 的跃迁偶极矩对比用VASPKIT ( v1.00 ) 计算得到的结果,VB -> CB 的跃迁偶极矩的平方和文献结果完全一样,只是单位不同。
常用物理英语单词

常用物理英语单词absolute acceleration 绝对加速度absolute motion 绝对运动absolute velocity 绝对速度accelerated motion 加速运动acceleration of gravity 重力加速度acceleration 加速度accelerometer 加速度计acting force 作用力active force 主动力angle of friction 摩擦角angle of nutation 章动角angle of precession 进动角angle of rotation 自转角angular acceleration 角加速度angular displacement 角位移angular motion 角[向]运动angular velocity vector 角速度矢[量]angular velocity 角速度areal velocity 掠面速度又称“扇形速度(sector velocity)”arm of couple 力偶臂attraction force 吸引力Atwood machine 阿特伍德机average velocity,mean velocity 平均速度axial acceleration 轴向加速度axial vector 轴矢[量]ballistic curve 弹道ballistic pendulum 弹道摆ballistics 弹道学base point 基点bearing 轴承binormal acceleration 副法向加速度bounce 反弹center of force 力心center of gravity 重心center of mass 质心center of moment 矩心center of parallel force system 平行力系中心center of percussion 撞击中心center of reduction 简化中心又称“约化中心”。
Role of Regularization in Quantum Corrections to the Scalar-Tensor Theories of Gravity

a rXiv:g r-qc/9616v14Oct1996Role of Regularization in Quantum Corrections to the Scalar-Tensor Theories of Gravity Yasunori Fujii ∗Nihon Fukushi University,Handa,475Japan and ICRR,University of Tokyo,Tanashi,Tokyo,188Japan Abstract We show that regularizing divergent integrals is crucially important when applied to the loop diagrams corresponding to quantum cor-rections to the coupling of the “gravitational”scalar field due to the interaction among matter fields.We use the method of continuous spacetime dimensions to demonstrate that WEP is a robust property of the Brans-Dicke theory beyond the classical level,hence correct-ing our previous assertion of the contrary.The same technique can be used to yield the violation of WEP when applied to the scale-invariant theory,thus providing another reason for expecting fifth-force-type phenomena.In our previous paper [1]we argued that a type of quantum correction to the Brans-Dicke (BD)theory [2]results in a rather large effect of violating composition-independence of the scalar-matter coupling.It was claimed that pre-cision tests of WEP constrain the parameter ωmuch more strongly than thosederived from the solar-system experiments.Subsequently,however,we came to realize that the effect is an artifact of our neglect of “regularizing”basically divergent integrals,thus re-establishing WEP as a robust property of the theory beyond the classical level.The revised analysis to be presented here is essentially revisiting the lesson which was learned in such historic issues as self-stress [3]and trace anomaly [4].It seems,however,that the same care might be crucially important in studying other quantum effects to some of the matter-gravity interaction.For this reason we try to explain essential ingredients of the discussion briefly but in a somewhat self-contained manner,hence allowing minimum overlapping with Ref.[1].According to the “lesson,”the fact that an integral which is divergent judged from power-counting turns out to be finite does not necessarily mean that noregularization procedure is required[5].We use the method of continuous space-time dimensions which is particularly convenient when gauge invariance is to be observed.We start with the Lagrangian†L=√2ξφ2R−1−g2(D/−←D/)+m ψ,(3) L A=−1−g gµνgρσ∂µAρ∂νAσ+···,(4) whereDµ=∂µ+ieAµ+···,(5) while we use the Feynman gauge,ignoring gravitationally higher-order terms.In order that the standard technique of quantum electrodynamics can be applied we move to a conformal frame(Einstein frame)in which no nonminimal coupling is present.For a conformal transformation withgµν=Ω−2g∗µν,(6) whereΩ= ξφ2 1/(N−2),(7) wefindR=Ω2[R∗+2(N−1)2∗f−(N−1)(N−2)(∇∗µf)(∇µ∗f)],(8) wheref=lnΩ.(9) The scalarfieldσwhich is canonical in E-frame is related to the originalφbyφ=ξ−1/2eβσ,(10)where‡β−1= N−2+ξ−1.(11) Notice thatβis in fact multiplied by√ν−1βσ ,(12) withν≡N/2.The kinetic part ofψcan be made canonical by introducingψ∗byψ=Ω(N−1)/2ψ∗,andψ∗.(13) The mass term is then transformed to−me−βσ/(ν−1)ψ∗γµψ∗A∗µσn with n=1,2,3,···.In practice we are concerned with n=1only.In this sense we follow two approaches either computing the trace of the energy-momentum tensor or evaluating the linearσcouplings directly.Wefirst obtain the energy-momentum tensor in E-frame:T∗µν=−2−g∗∂L∗m22g∗µνgκλ∗gρσ∗∂κA∗ρ∂λA∗σ,(17)hence giving−T∗=me−βσ/(ν−1)G0σ,though possibly entirely different physics may be expected in general.We now compute the matrix elements of T∗betweenG0.We are concerned also with the limit of zero4-momentum transferred toσ.In what follows we suppress the symbol∗to simplify the notation.At the tree-level in4dimensions we have an obvious result:−T0=m§Thisϕis in factφin the original notation in[2].it is most convenient to work with the self-energy diagrams(c1)and(c2)in Fig. 2forψand Aµ,respectively,and the corresponding functions:Σ(m,ip/)=−i α(m+ik/)(k−p)2γµ,(23)Πµν(k)=−i αm+ip/γν1∂mΣ(m,ip/) ip/=−m.(27)We include the contributions from diagrams(a1′)and(a1′′).Strictly speaking we must have added the left-right symmetric diagrams,but thefinal result should remain the same according to the spirit of wave-function renormalization.In this way we arrive at a simple result:−<T>(a)ψ=m dA(m)4π3m dx d N k N+x(2−N)(k2+a2)n =i1Γ(ν) a2 ν−n+m−2Γ(m−2+ν)Γ(n−m+2−ν) 4πmΓ(2−ν) dx(a2)ν−2(N+x(2−N)).(32)We substitute this into(28)obtaining−<T>(a)ψ=A+αdm(N+x(2−N))α=A−Γ(3−ν)2m dx(4−2x)4π3α=A−m(2−ν)Γ(2−ν) dx(4−2x)2π3α=Πµν(k),(38)∂mwhere we use(26)withC(k2,m2)=α∂m k2=0,(41) wherem ∂C∂m2=2m2αdm22x(1−x) =2m22αm2+x(1−x)k2k2=0−→−4α3π,(42)which would indicate an effective termL′=−2α4FµνFµνσ,(43)in the Lagrangian,obviously a non-T coupling ofσ.However,we now consider the diagram(b2)arising from the second term of (18).In the same way as in obtaining(28)wefind−(ν−2)2k213π(2−ν)Γ(2−ν)=2αnonminimal coupling)between the scalarfield and the spin-0part of the metric field that endorses composition-independence.Mathematically,the contributions from the second term of(18)are precisely what is known as the“trace anomaly.”¶[4]This may sound a little confusing, however,because the same terms in our discussion act to remove the composition-dependent terms which might be also called“anomaly”because they would break the property expected to hold classically.On the other hand,the occurrence of“self-stress,”hence violating Lorentz covariance of an energy-momentum vector of the one-particle state,is related closely to the emergence of composition-dependence due to thefirst term of(18); the extra term in(33)has been simply identified with T i i as part of Tµµ.The same success in solving the problem by means of Pauli-Villars regulators[3,5]is enjoyed also by appealing to the method of continuous dimensions.We reinforce our conclusion by evaluating the1-loop correction to the linear σcoupling without invoking the trace of the energy-momentum tensor explicitly.We evaluate the same diagrams as(a1),(a1′),(a1′′)and(a2).Instead of(b1) and(b2),however,we consider the diagrams(d1)and(d2)in Fig.3,which arise from the term in(16)linear inσ.In effect we replace e in the diagrams(c1)and (c2)in Fig.2by(ν−2)βσ.(46)We removeβσin accordance with the fact that the linear term in(14)is mβσ, thus simply multiply2(ν−2)with A and C,where the factor2implies that we have the contributions from both vertices.For theψterm,this is found to be the same as(36),whereas the Aµterm gives the same term as(45),reproducing the same result obtained from T∗.Before closing the paper we add an interesting discussion on the same role of regularization in the“scale-invariant theory”which is similar to but somewhat different from BD theory,serving as a basis of expecting afinite-range gravity due to a dilaton[7].Suppose we replace(3)by−√ψ 1¶As one of the striking examples,wefind that(45)emerges hence giving nonzero<T>µνeven if m=0.This is justified if we letν→2in(39)and(40)before setting k2=0.toL′=−√ν−1βσ.(50)dmThe same contribution J3from(e3)isJ3=2β(ν−2)A.(51) Using(32)we compute6αJ=J1,2+J3=−βSee Ref.[8],for example,for a review of the phenomenological status of the“fifth force.”The same analysis can be applied to the photonfield as well.The diagrams to be included are(a2)(multiplied by(ν−2))in Fig.1and(d2)in Fig.3.These are now added together rather than as alternative contributions leading to the same result in BD theory.We thus have twice the non-trace coupling shown in (43).The parameters will be constrained by the phenomenological analyses in the same way as in Ref.[1],but taking thefinite force-range into account.References1.Y.Fujii,Mod.Phys.Lett.A9(1994)3685.2.C.Brans and R.H.Dicke,Phys.Rev.124(1961)925.3.A.Pais and S.T.Epstein,Rev.Mod.Phys.21(1949)445;J.M.Jauchand F.Rohrlich,The Theory of Photons and Electrons,Addison-Wesley, Cambridge,1954.4.M.S.Chanowitz and J.Ellis,Phys.Lett.40B(1972)397.5.See also,Y.Fujii and Y.Takahashi,Lecture Notes in Physics39,Mathemat-ical Problems in Theoretical Physics,ed.H.Araki,p.261,Springer-Verlag, Berlin,1975.6.Y.Fujii,Brans-Dicke cosmology corrected for a quantum effect due to thescalar-matter coupling,gr-qc/9609044.7.Y.Fujii,Int.J.Mod.Phys.A6(1991)3505,and papers cited therein.8.E.Fischbach and C.Talmadge,Nature,356(1992)207.(a1")(a2)X X(b2)(b1)A T A T (a1’)(a1)Figure 1:Diagramsof 1-loop correctionto the σ-matter coupling.The ×’s in (a’s)indicate the mass insertion,first term of (18)(e −βσdropped),while those in (b’s)are for the second term coming from the photon off4dimensions.(c2)(c1)Figure 2:Self-energy diagrams.(d2)(d1)X X β(ν−2)β(ν−2)Figure 3:Diagrams off4dimensions.At each vertex of (c1)and (c2)now marked by ×,β(ν−2)is multiplied.(e3)(e2)(e1)Figure 4:Diagrams for ψin the scale-invariant theory.β(ν−2)is multiplied at ×’s.。
Uncoupling the Perron eigenvector problem

A1i . . . Ai−1,i A ∗i = Ai+1,i . . . . Aki
That is, Ai∗ is the ith row of blocks with Aii removed and A∗i is the ith column of blocks with Aii removed. The Perron complement of Aii in A is defined to be the matrix Pii = Aii + Ai∗ (ρI − Ai )−1 A∗i .
m
Aπ = ρπ,
π > 0,
i=1
πi = 1.
For relatively small values of m , this is not a difficult problem to solve using adaptations of standard techniques for solving systems of linear equations. However, there exist many applications for which m is too large to be comfortably handled by standard methods. For large scale problems, it is only natural to attempt to somehow uncouple the original matrix A into two or more smaller matrices — say P1 , P2 , · · · , Pk — of order r1 , r2 , · · · , rk , respectively, where
机器人机械手外文文献

A Nonlinear Disturbance Observer forRobotic ManipulatorsWen-Hua Chen,Member,IEEE,Donald J.Ballance,Member,IEEE,Peter J.Gawthrop,Senior Member,IEEE,and John O’Reilly,Senior Member,IEEEAbstract—A new nonlinear disturbance observer(NDO) for robotic manipulators is derived in this paper.The global exponential stability of the proposed disturbance observer(DO) is guaranteed by selecting design parameters,which depend on the maximum velocity and physical parameters of robotic manipulators.This new observer overcomes the disadvantages of existing DO’s,which are designed or analyzed by linear system techniques.It can be applied in robotic manipulators for various purposes such as friction compensation,independent joint control, sensorless torque control,and fault diagnosis.The performance of the proposed observer is demonstrated by the friction estimation and compensation for a two-link robotic manipulator.Both simulation and experimental results show the NDO works well. Index Terms—Friction,nonlinear estimation,observers,robots.I.I NTRODUCTIOND ISTURBANCE observers(DO’s)have been used inrobotic manipulator control for a long time.In general, the main objective of the use of DO’s is to deduce external unknown or uncertain disturbance torques without the use of an additional sensor.The use of DO’s in robotic manipulators can be divided into the following categories.1)Independent joint control is widely used in industrialrobots where a multilink manipulator is divided into several independent links with linear dynamics.The per-formance of these kind of controllers can be improved by the use of a DO.This is accomplished by considering the coupling torques from other links as an unknown external disturbance and using a DO to estimate and compensate for it[1].This technique has also been extended to deal with parameter variations and unmodeled dynamics whereby it improves the robustness of robots[2];2)Friction is a common phenomenon in mechanical sys-tems and plays an important role in system performance.Many friction models and compensation methods have been proposed[3].One of the most promising methodsManuscript received December22,1998;revised March23,2000.Abstract published on the Internet April21,2000.An earlier version of this paper was presented at the38th IEEE Control and Decision Conference,Phoenix,AZ, December7–10,1999.This work was supported by the U.K.Engineering and Physical Sciences Research Council under Grant GR/L62665.W.-H.Chen and J.O’Reilly are with the Centre for Systems and Control, Department of Electronics and Electrical Engineering,University of Glasgow, Glasgow G128QQ,U.K.(e-mail:w.chen@).D.J.Ballance and P.J.Gawthrop are with the Centre for Systems and Control, Department of Mechanical Engineering,University of Glasgow,Glasgow G12 8QQ,U.K.(e-mail:D.Ballance@).Publisher Item Identifier S0278-0046(00)06805-2.is observer-based control where a DO is used to estimate friction[4];3)DO’s have been used in robotic manipulators for forcefeedback and hybrid position/force control where the DO works as a torque sensor[5]–[7].In this case,it is sup-posed that the friction and other dynamics are well mod-eled and compensated for.The use of a DO,rather than several torque sensors(for each link,at least one torque sensor is required),simplifies the structure of the system, reduces the cost,and improves the reliability.With this technique,sensorless torque control can be implemented[5]–[7].4)Robotic manipulators work in a dynamic highly uncertainenvironment.In this application,DO’s provide signals for monitoring and trajectory planning rather than for control.For example,in robotic assembly when the component is misinserted,the reaction torque/force is greatly increased and could damage the robotic manipulator.A DO can es-timate the reaction torque online and transmit this infor-mation to the monitoring or planning level.Chan[8]usesa DO in electronic component assembly,while Ohishi andOhde[9]give an example of the use of a DO in collision. Although the DO technique has been widely used in robotic manipulator control for various purposes,in almost all cases, the analysis or design is based on linearized models or using linear system techniques.Since a multilink robotic manipulator is a highly nonlinear and coupled system,the validity of using linear analysis and synthesis techniques may be doubtful.Many important properties of existing DO’s have not been established, e.g.,unbiased estimation or even global stability.There are, however,some recent results using nonlinear disturbance ob-servers(NDO’s).A variable structure DO has been proposed [10]and a nonlinear observer for a special kind of friction,i.e., Coulomb friction,has been proposed by Friedland and Park [11].This nonlinear observer is designed based on the model of Coulomb friction,and the global convergence ability has been shown.It has been further modified and implemented on robotic manipulators by Tafazoli et al.[12].However,a specific model of friction will not be used in this paper,and the whole design is based on the DO concept.That is,similar to other unknown torques,the friction is considered as a disturbance on the control torque.It should be stressed that the DO rather than a velocity ob-server of a manipulator is considered in this paper.A velocity observer has been considered by many authors.Bona and Indri have compared and implemented several linear and nonlinear velocity observers on a robotic manipulator[13].0278–0046/00$10.00©2000IEEEAn NDO for multilink robotic manipulators will be presented in this paper.By carefully selecting the observer gain function,it will be shown that global convergence is guaranteed.This result is based on Lyapunov theory.II.P ROBLEM F ORMULATION AND A B ASIC O BSERVER A.Problem FormulationFor the sake of simplicity,a two-link robotic manipulator is considered in this paper.The main idea is readily extended to the more general case.The model of a two-link robotic manipulator can be representedbyis either the torque orforce.has different meaningsin different observer applications.For example,it can be fric-tion in friction compensation,reaction torque or force in forcecontrol,and unmodeled dynamics in independent joint control.Since a general observer will be derived in this paper,all of themare considered as“disturbances.”When the first-order dynamicsof dc motors are included in the abovemodel,is the disturbancevoltage in this case.The objective of this paper is to design an observer suchthat the estimation yielded by the observer exponentiallyapproaches thedisturbance,,and(2)a DO is proposedas,it is reasonable to supposethat(4)which implies that the disturbance varies slowly relative to theobserver dynamics.However,it will be illustrated by simulationand experiment that the observer developed in this paper canalso track some fast time-varying disturbances.Define the observererror(6)That is,the observer error is governedby.III.NDOThe acceleration signal is not available in many robotic ma-nipulators,and it is also difficult to construct the accelerationsignal from the velocity signal by differentiation due to mea-surement noise.However,although the observer(3)is not prac-tical to implement,it provides a basis for the further nonlinearobserver design.A.Modified ObserverDefine an auxiliary variablevector(12)and(14)The estimation approaches thedisturbance(15)where are inertial parameters,which dependon the masses of the links,motors and tip load,and the lengthsof the links.Theorem:For the two-link robotic manipulator(1),when thefunction(16)and(17)where denotes the maximum velocity of the second link,then the observer(12)and(13)is globally asymptotically stable.Proof:Since(19)since and and,therefore,invertible.From(15),(20)where,a Lyapunov func-tion candidate for the observer(12)and(13)can be chosenas(23)Differentiating the Lyapunov function with respect totimeandif(25)Thatis,(26)Since)is then globally asymptotically stable.From the Theorem,the stability of the observer depends onthe maximum velocity of the second link and other physicalparameters.By choosing the designparameteris givenby(28)Let.It then follows from(24)that,the desired exponential conver-gence rate can be achieved.IV.S IMULATION AND E XPERIMENTAL R ESULTSThe proposed NDO is tested in this section.As stated in Sec-tion I,the NDO can be used in robotic manipulators for variouspurposes.In what follows,the NDO is designed as a frictionobserver.That is,the NDO is used to estimate the friction fora two-link robotic manipulator.The reason for designing a fric-tion observer here is that friction varies rapidly,even discontin-uously.It is a challenging task in observer design.The simula-tion and experiment are based on a two-link manipulator withFig.1.Structure of the revised friction model.dc motor actuators.The dynamic model of the manipulator in-cluding the first-order dc motor dynamics is governed by(1)and is detailed in[15].A.Friction SimulationThe friction considered is Coulomb and Viscous friction, givenbyNNis given by(30),is asmall positive scalar,and,thefriction.Whenthe velocity is greater than this,the second term in the above ex-pression vanishes and thefrictionis chosenas0.001.The frictions given by these two models are almost in-distinguishable.However,experience has shown that using therevised model greatly improves the computational efficiency forsimulation.B.Simulation ResultsA controller is designed by computed torque control wherethe disturbance is not taken into account.When square-wavecommand references are given for first and second links,respec-tively,the velocity and friction histories are shown in Figs.3and4.It can be seen that the friction varies very rapidly with the ve-locity.A friction observer is designed by the NDO technique de-veloped in this paper.The designparameterFig.4.Second link velocity and friction time histories.Fig.5.First-link friction estimated by the friction observer.C.Experimental ResultsThe proposed NDO is implemented on a two-link robotic ma-nipulator in the laboratory.The experimental results for a com-puted torque controller with and without the NDO are com-pared.The control structure,which combines a computed torque controller with the NDO,is shown in Fig.7,where the effect of the friction is compensated for by the outputs of the NDO viafeedforward.With the NDO,the parameterFig.9.Experimental results with DO:estimatedfriction.Fig.10.Experimental results with DO:velocity.Fig.11.Experimental results with DO:motor voltages.V .C ONCLUSIONThis paper has presented a procedure for the design of an NDO for robotic manipulators.Following the procedure presented in this paper,a condition for convergence was established.The speed of the convergence can be specified by the design parameters.The proposed observer was tested by simulation and experiment.Even though the theory is developed for constant disturbances,it was shown that,for a rapid time-varying signal like friction,the observer exhibits satisfactory performance.By feedforward compensation of the estimated friction yielded by the DO,the performance,in particular,the steady-state performance,was significantly improved.The NDO proposed in this paper can also be applied in independent joint control,sensorless torque control,and fault diagnosis in robotics.A CKNOWLEDGMENTThe authors greatly appreciate the comments and discussion by Dr.J.J.Gribble pertaining to the earlier version of this paper.R EFERENCES[1]K.S.Eom,I.H.Suh,and W.K.Chung,“Disturbance observer basedpath tracking control of robot manipulator considering torque satura-tion,”in Proc.Int.Advanced Robot.Conf.,1997,pp.651–657.[2] B.K.Kim,W.K.Chung,and Y .Youm,“Robust learning control forrobot manipulator based on disturbance observers,”in Proc.IEEE Ind.Electron.Conf.,1996,pp.1276–1282.[3]H.Olsson,K.J.Åström,C.C.de Wit,M.Gafvert,and P.Lischinsky,“Friction models and friction compensation,”Eur.J.Control ,vol.4,no.3,pp.176–195,1998.[4]G.Zhang and J.Furusho,“Control of robot arms using joint torque sen-sors,”IEEE Control Syst.Mag.,vol.18,no.1,pp.48–55,1998.[5]S.Komada and K.Ohnishi,“Force feedback control of robot manipu-lator by the acceleration tracing orientation method,”IEEE Trans.Ind.Electron.,vol.37,pp.6–12,Feb.1990.[6]S.Komada,K.Nomura,M.Ishida,and T.Hori,“Robust force controlbased on compensation for parameter variations of dynamic environ-ment,”IEEE Trans.Ind.Electron.,vol.40,pp.89–95,Feb.1993.[7]T.Murakami,F.Yu,and K.Ohnishi,“Torque sensorless control in mul-tidegree-of-freedom manipulator,”IEEE Trans.Ind.Electron.,vol.40,pp.259–265,Apr.1993.[8]S.P.Chan,“A disturbance observer for robot manipulators with appli-cation to electronic components assembly,”IEEE Trans.Ind.Electron.,vol.42,pp.487–493,Oct.1995.[9]K.Ohishi and H.Ohde,“Collision and force control for robot manip-ulator without force sensor,”in Proc.IEEE Ind.Electron.Conf.,1994,pp.766–771.[10]H.N.Lin and Y .Kuroe,“Decoupling control of robot manipulators byusing variable structure disturbance observer,”in Proc.IEEE Ind.Elec-tron.Conf.,1995,pp.1266–1271.[11] B.Friedl and Y .J.Park,“On adaptive friction compensation,”IEEETrans.Automat.Contr.,vol.37,pp.1609–1612,Oct.1992.[12]S.Tafazoli,C.W.de Silva,and wrence,“Tracking control of anelectrohydraulic manipulator in the presence of friction,”IEEE Trans.Contr.Syst.Tech.,vol.6,pp.401–411,May 1998.[13] B.Bona and M.Indri,“Analysis and implementation of observersfor robotic manipulators,”in Proc.IEEE Int.Conf.Robot.Automat.,Leuven,Belgium,1998,pp.3006–3011.[14]P.J.Gawthrop and L.P.S.Smith,Metamodeling:Bond Graphs andDynamic Systems .New York:Prentice-Hall,1996.[15]W.-H.Chen,D.J.Ballance,and P.J.Gawthrop,“Nonlinear generalizedpredictive control and optimal dynamic inversion control,”in Proc.14th IFAC World Congr.,vol.E,Beijing,China,1999,pp.415–420.[16] D.Karnopp,“Computer simulation of strick-stip friction in mechanicaldynamic systems,”ASME J.Dynam.Syst.,Meas.,Contr.,vol.107,pp.100–103,1985.Wen-Hua Chen(M’00)received the M.Sc.and Ph.D.degrees from Northeast University,Shengyang,China,in1989and1991,respectively.From1991to1997,he was a Lecturer in the De-partment of Automatic Control,Nanjing Universityof Aeronautics and Astronautics.He then held a re-search position in the Centre for Systems and Con-trol,Department of Mechanical Engineering,Univer-sity of Glasgow,Glasgow,U.K.He is currently a Lec-turer at the Centre for Systems and Control,Depart-ment of Electronics and Electrical Engineering,Uni-versity of Glasgow.His research interests include robust control,nonlinear con-trol and their application in mechatronics,and aerospaceengineering.Donald J.Ballance(M’91)received the D.Phil.de-gree in control engineering from the University ofOxford,Oxford,U.K.,in1989.Since then,he has been at the Centre for Systemsand Control,Department of Mechanical Engi-neering,University of Glasgow,Glasgow,U.K.,initially as a Research Assistant and currently asa Senior Lecturer.His research interests includemodeling and analysis of systems using bond graphs,quantitative feedback theory and the effect of pa-rameter uncertainty on control system performance,nonlinear control,and the practical application of thesetechniques.Peter J.Gawthrop(M’82–SM’94)was born inSeascale,Cumberland,U.K.,in1952.He receivedthe B.A.(first class honors),D.Phil.and M.A.de-grees in engineering science from Oxford University,Oxford,U.K.,in1973,1977,and1979,respectively.Following a period as a Research Assistant withthe Department of Engineering Science,Oxford Uni-versity,he became a W.W.Spooner Research Fellowat the New College,Oxford.He then moved to theUniversity of Sussex,initially as a Lecturer,and thenas a Reader in control engineering.Since1987,he hasheld the Wylie Chair of Control Engineering in the Department of MechanicalEngineering,Glasgow University,Glasgow,U.K.He was involved in foundingthe Centre for Systems and Control,which is a cross-departmental researchgrouping at Glasgow University.His research interests include self-tuning con-trol,continuous-time system identification,and system modeling,particularlyusing bond graphs in the context of partially known systems.He is also inter-ested in applying control techniques to a number of areas,including process con-trol,robotics,aerospace systems,and anaesthesia.He has authored and co-au-thored approximately120conference and journal papers and three books inthese areas.He was an associate editor of Automatica and an honorary editorof the Proceeding of the IEE,and serves on the editorial boards of a numberof journals,including the IMechE Journal of Systems and Control,Journal ofProcess Control,IMA Journal of Mathematical Control and Information,theInternational Journal of Adaptive Control and Signal processing,and the Euro-pean Journal of Control.Dr.Gawthrop was the recipient of the1994Honeywell International Medalpresented by the Institute of Measurement andControlJohn O’Reilly(M’82–SM’00)received the B.Sc.,Ph.D.,and D.Sc.degrees in engineering fromQueen’s University,Belfast,Belfast,NorthernIreland,in1972,1976,and1985,respectively.He is currently a Professor of control engineeringat the Centre for Systems and Control,Departmentof Electronics and Electrical Engineering,Universityof Glasgow,Glasgow,U.K.He is currently a VisitingErskine Fellow in the Department of Electrical andElectronic Engineering,University of Canterbury,Canterbury,New Zealand.His main research inter-ests are centered on integrated and nonlinear control,with particular applicationto aerospace and deregulated power systems.He is also a Consultant Editorfor the International Journal of Control.Dr.O’Reilly was the recipient of a U.K.Royal Academy of Engineering Fore-sight Award.。
Evans ’ Rules for Sketching the Root Locus

We will compute the closed-loop poles as explicit functions of K . In general, this is a tedious, and uninformative exercise, but for this simple system it serves to illustrate how closed-loop poles vary as the gain K is varied. The closed-loop transfer function is Hd (s) = The closed-loop poles are obtained from 0 = 1+ K s(s + 2) = s2 + 2s + K.
we first recall some facts about complex numbers. First, a complex number can be represented in polar form, for example z = reiθ where r is the radial distance from the origin to the point z and θ is the angle to z measured counter-clockwise from the positive real axis. Consider the complex function C (s) = (s − z1 ) · · · (s − zm ) . (s − p1 ) · · · (s − pn )
yd
+
-
F d
u
P
y
Figure 1: One degree of freedom closed-loop control structure. Consider the simple feedback control system shown in Figure 1. The closed-loop transfer function is Hd (s) = Closed-loop poles are values of s for which 1 + P (s)Fd (s) = 0. Since P (s)Fd (s) is a function of a complex variable, the equation P (s)Fd (s) = −1 can be expressed in terms of the magnitude and phase of P (s)Fd (s): |P (s)Fd (s)| = 1 and ∠P (s)Fd (s) = (2k + 1)π k = 0, ±1, ±2, . . . P (s)Fd (s) y (s) = . yd (s) 1 + P (s)Fd (s)
Wave-particleduality

1. Wave Particle Dualitya. Write the relationship for the kinetic energy and momentum for particle moving at speeds much slower than the speed of light.b. Find the wavelength of an electron in an x -ray machine having a kinetic energy 10 keV.c. Write the relationship for the kinetic energy and momentum for a particle moving at speeds which are on the order of the speed of light.d. Write the relationship for the kinetic energy and momentum for a photon.e . The maximum energy of an x -ray photon produced by a 10 keV electron is 10 keV. Find the wavelength of such an x -ray photon.2. Schroedinger’s EquationA completely free beam of electrons is moving in the +x direction with a kinetic energy of 10 keV. a. Write the Schroedinger equation for a particle moving in the x direction. b. Show that the wave function in a. is a solution to the Schroedinger equation.3. Schroedinger’s EquationAn electron is confined to move freely in a one dimensional box of length L =1.0 nm having infinite potential walls.a. Write the space part wave function for the ground state, and draw it in the upper left provided axes.b. Write the space part probability density and draw it in the lower left provided axes.c. Draw the wave function and probability density for the same situation but for the case where the height of the potential walls is finite.d. Which state, a. or c., has the lower energy. Explain in one sentence.4. In momentum space (k -space) the separation of states is given by Δk x =Δk y =Δk z =π/L .a. Find the number of states in a volume V =L 3 with momentum less than k and kinetic energy less than E .b. Find the Fermi energy for neutrons in a neutron star having 5×1057neutrons with radius 10 km.c. Find the total zero-point kinetic energy of the neutrons at temperature T =0 K.ψx ψxP x P x1. R elativityA s tar i s e mitting l ight i n t he p ositive x d irection. T he w avelength o f t he l ight i s 400 n m.a. (5 p t) W hat i s t he p eriod Δt i n n s o f o ne o scillation o f l ight i n t he s tar’s f ixed reference f rame.Assuming t he w ave t urns o n a t t=0b. (5 p t) H ow f ar d oes i t g o i n t =100 n s i n t he s tar’s f ixed f rame?c. (5 p t) W rite t he 4-‐vector f or t he s pace-‐time p osition a fter a t ime 100 n s.d. (5 p t) O btain t he s pace-‐time i nvariant i nterval t hat t he l ight t ravels i n 100 n s. Suppose t he s tar m oves a way f rom t he e arth i n t he p ositive x d irection w ith a v elocity 0.8c.e. (5 p t) W hat i s t he p eriod Δ′t i n n s o f o ne o scillation o f l ight i n t he e arth’s m oving r eference f rame?f. (5 p t) H ow f ar d oes t he l ight t ravel a fter o ne o scillation a s s een b y t he e arth.f. (5 p t) W rite t he 4-‐vector f or t he s pace-‐time p osition a fter a t ime ′t corresponding t o one o scillation a s s een f rom t he e arth’s r eference f rame.g. (5 p t) O btain t he s pace-‐time i nvariant i nterval i n t he e arth’s f rame t hat t he l ight travels i n 100 n s2.) B ohr m odel.According t o t he B ohr m odel o f t he h ydrogen a tom, a n e lectron i n t he g round s tateorbits a t a r adius o f a bout 0.5 A o. S uppose t he e lectron i s r eplaced b y a m uon( mµc2=105 MeV) t o f orm a m uonic a tom.a. (10 p t) W hat i s t he r adius o f o rbit f or t he m uonic a tom i n i ts g round s tate?b. (10 p t) W hat a re t he e nergies o f t he g round a nd f irst a nd f irst e xcited s tates?c. (10 p t) W hat i s t he w avelength c orresponding t o t he t ransition b etween t he f irst exciteds tate a nd t he g round s tate?3.)Schroedinger e quation.A s imple h armonic o scillator (SHO) h as a m ass m a nd s pring c onstant K. T he p otential e nergy is 1/2Kx2.a. (10 p t) W rite t he S chroedinger e quation f or t he s pace p art o f t he S HO.b. (10 p t) T he w ave f unction f or t he g round s tate h as t he f orm Ae bx2. B y d irects ubstitution s how t his i s a s olution, a nd t hereby f inding t he c onstant b i n t erms o f m a nd Kc. (10 p t) W rite t he p robability d istribution f or t he g round s tate, a nd c arefullyg raph i t.d. (10 p t) W rite a n i ntegral w hichwould b e u sed t o o btain t he n ormalizing c onstantA.You d o n ot n eed t o s olve t his i ntegral)4.)Schroedinger E q. i n 3 d imensions.Consider a t hree d imensional c ubic p otential w ell w ith r igid (infinite) w alls, h avingsides o f d imension L x = L y = L z = L=0.1 n m.a. (5 p t) W rite t he S chroedinger e quation f or a p article w ithin t he w ell.b. (5 p t) W rite t he q uantum c onditions o n k x , k y a nd k z.c. (5 p t) O btain t he q uantum c ondition o n t he w ave n umber k2.d. (5 p t) O btain t he q uantum c ondition o n t he a llowed e nergies E.e. (5 p t) W rite t he g round s tate s olution Ψ(x,y,z)to t he S chroedingere quationf or a p article w ithin t he w ell.f. (5 p t) W rite t he p robability d ensity f or a p article w ithin t he w ell i n t he g roundstate.g. (5 p t) O btain t he n umerical r esult o n t he a llowed e nergies E i n u nits o f e V.h. (5 p t) O btain t he n umber o f e lectrons w hich c an b e a ccommodated a t e ach o ft he l owest 3 e nergy l evels. T ake i nto a ccount t hat d ifferent c ombinations o fq uantum n umbers c an h ave t he s ame e nergy, a nd t hat t wo e lectrons,c orresponding t o s pin u p a nd d own c an f it i ntoe ach c ombination of s patialq uantum n umbers.2006 Exam. 21. A b aby s eal i n t he p acific o cean h as a b ody t emperature o f 310 K. I f t he m ean temperature o f t he w ater i s 287 K a t w hat r ate w ill t he s eal l ose e nergy b y r adiating p hotons? (σ=5.7×10−8 W⋅m-2⋅K-4)2. W ave p article d uality.Compare t he w avelength a nd f requency o f a p hoton a nd e lectron, e ach w ith k ineticenergy 10 K eV.3. B ohr m odel.a. U se t he B ohr m odel o f t he a tom t o e stimate t he e nergy l evels o f p ositronium, i n w hich a n electron o rbits a p ositron.b. T he i onization e nergy (binding e nergy) o f a n e lectron i n h ydrogen i s 13.6 e V.What i s t he i onization e nergy o f p ositronium?4. P article i n a b ox.Approximate a n a tomic n ucleus a s a n i nfinite c ubical b ox o f s ide L=2 f m, w here1 f m = 10-‐15 m, i n w hich t he n ucleons m ove f reely.a. O btain a n e xpression f or t he w avelength o f t he g round, o r l owest l ying e nergy s tate.b. W hat i s t he k inetic e nergy o f a n eutron i n t he g round s tate o f t his a tom. T he r estenergy o f a n eutron i s m c2=939 M eV.5. S imple h armonic o scillator.A n a pproximate r epresentation o f t he i nteraction b etween t wo a toms i n a d iatomicm olecule i s a s pring l ike f orce F=-Kx w ith o scillator f requency ω=. T ake t he f orcec onstant t o b e 8×103 e V/nm2 = 1000 N/m, a nd t he m ass of e ach a tom a round t o b e5×10−27kg(mc2=4.69 G eV). T he w ave f unction f or t he g round s tate o f a s imple h armonic o scillatori s ψ0(x)=mωπ⎛⎝⎜⎞⎠⎟1/4e−mω2x2.a. W hat i s t he e nergy o f t he g round s tate?b. F ind t he w ave f unction i n m omentum s pace b y p erforming a F ourier t ransformation.6. D ensity o f s tates a nd F ermi e nergy.a. F ind t he a verage e nergy o f a n e lectron i n a w hite d warf s tar o f r adius 10,000 k mcontaining 2×1057 n ucleons, h alf o f w hich a re p rotons. T he d ensity o f s tates d istribution i sdNdE=E1/2.b. F rom t he r esults i n p art a, c omment o n w hether i t i s a pproporiate t o u se n on-‐relativistickinematics.Other p roblems f rom p revious e xams:1. A f ree e lectron h as k inetic e nergy 1000 e V. I t m oves i n t he x-y p lane i n a d irection w hichmakes a n a ngle 30 d eg. r elative t o t he x a xis.a. F ind i ts m omentum p, w avelength λ a nd w ave n umber k.b. W rite t he w ave f unction Ψ(x,y,z,t) i n s ymbols (not n umerical v alues) i n C artesiancoordinates.c. W rite t he p robability d ensity P(x,y,z).d. W hat c an y ou s ay a bout t he u ncertainty i n t he e lectron’s p osition.Approximate a n ucleus c onsisting o f f ree n ucleons i n a s pherical r igid w all p otential w ith radius R=4 f m. F or t he i sotope 17O:a. W hat a re t he q uantum n umbers o f e ach o f t he n eutrons a nd p rotons?b. W hat a re t he e nergies o f e ach o f t he n eutrons a nd p rotons i n t he i sotope 17O?2. a. W rite t he w ave f unction f or a f ree p article m oving i n 3-‐dimensional C artesiancoordinates.b. T he r elativistic v ersion o f t he S chroedinger e quation i s c alled t he K lein-‐Gordon e quation.Using E2=p2c2+m2c4, c onstruct t he K lein-‐Gordon e quation b y e xpressing t he e nergy a nd momentum i n t erms o f d ifferential o perators.c. S how t hat t he w ave f unction i n p art a. i s a s olution t o t he K lein-‐Gordon w ave f unction t hatwas c onstructed i n p art c.3.) C onsider a n e lectron w hich m oves f reely i n a 2 d imensional i nfinite s quare w ell o f s ide a . a. W rite t he S chroedinger e quation f or t his c ase. b. W hat a re t he a llowed v alues o fk x and k yc. W hat a re t he a llowed e nergy l evels?d. I f a =10Angstroms, w hat i s t he l owest e nergy.e. W rite t he w ave f unction f or t his s tate.4.) T he t hree p rimary t erms w hich d etermine t he b inding e nergy o f a n ucleusare v olume , s urface a nd C oulomb , E V , E S , E C e nergies.a. W hat i s t he R a nd Z d ependence o f e ach, w here R i s t he n uclear r adius a nd Z t he a tomic number.Also i ndicate t he s ign o f e ach. i E V ∝ii E S ∝iii E C ∝b. W hat i s t he A a nd Z d ependence o f e ach, w here A i s t he n umber o f n ucleons. A lso i ndicate the s ign o f e ach. i E V /A ∝ii E S /A ∝iii E C /A ∝c. D raw t he m agnitude o f e ach a s a f unction o f A , a s w ell a s t he s um o f e ach. B e s ure t o c learly fill i n t he e nergy s cale i n t he v ertical a xis a nd t he n umber o f n ucleons i n the h orizontal a xis a t t he p osition o f t he t ic m arks.5.) I n t he b lank s paces p rovided i n t he t able, f ill i n t he p roperties o f t he p article s hown, a s w ell a s t he energy s cales a nd q uark m akeup w here a ppropriate.6.Draw a g raph f or t he s hape o f t he n ucleon-‐nucleon a ttractive p otential e nergy, i ndicating the a pproximate r ange a nd d epth.particl e Charge Rest m ass energy Units o f energy QuarkFlavor c ontent p +1 .93 GeV uud nπ−.139 π+ e 0.511 ν γ W 89 g7. a . 92238U c aptures a n eutron, f ollowed b y a symmetric f ission i nto 2 u nbound n eutrons a nd3892Sr a nd 54140Xe . O btain t he d ifference i n t he b inding e nergy b etween t he i nitial 92238U and t he f inal 3892Sr a nd 54140Xe n uclides, a nd t herefore t he e nergy r eleased.b . C alculate t he k inetic e nergyd ue t o t he e lectrostatic r epulsion b etween t he 3892Sr a nd 54140Xe w hen t hey a re s till t ouching, a nd s how t hat i t i s t he s ame o rder a s y our a nswerin p art a . a bove. (note:r =r 0A 1/3with r 0≈1.2fm.)8.Fill i n t he t able b elow:9. a . T he m ajor s ource o f e nergy p roduction i n t he s un i s t he p roton-‐proton c ycle. Trace t he s teps o f t he p -p c ycle a s w e d iscussed i n c lass.b . I f t he f inal r esult i s t he f usion o f 4 p rotons i nto 4He ,c alculate t he t otal e nergy r eleased in t he c ycle.10. D raw a F eynman d iagram f or e ach o f t he f ollowing p rocesses, a nd i dentify t he e xchanged quantum:a. e - +µ+♑e - +µ+via t he e lectromagnetic i nteraction. b. e - +µ+♑e + +µ- v ia t he w eak i nteraction.c. u +u →s +s v ia t he s trong i nteraction.6. F rom t he i nformation o n s pin, b aryon n umber a nd s trangeness g iven i n t he t ablebelow, f ill i n t he q uark f lavor c ontent a nd d ecay i nteraction o f e ach o f t he f ollowing h adrons.Decay interact we。
A SHORT SURVEY OF NONCOMMUTATIVE GEOMETRY

(C) The proof that Mod is a complete invariant and that all virtual subgroups are obtained. The module of a factor M was first defined ([1]) as a closed subgroup of R∗ + by the equality Spec(∆ϕ ) ⊂ R+ , (3) S (M ) =
∼
(2)
which is a virtual closed subgroup of R∗ + in the sense of G. Mackey, i.e. an ergodic ∗ action of R+ . The classification involves three independent parts, (A) The definition of the invariant Mod(M ) for arbitrary factors. (B) The equivalence of all possible notions of approximate finite dimensionality. 2
Abstract We give a survey of selected topics in noncommutative geometry, with some emphasis on those directly related to physics, including our recent work with Dirk Kreimer on renormalization and the Riemann-Hilbert problem. We discuss at length two issues. The first is the relevance of the paradigm of geometric space, based on spectral considerations, which is central in the theory. As a simple illustration of the spectral formulation of geometry in the ordinary commutative case, we give a polynomial equation for geometries on the four dimensional sphere with fixed volume. The equation involves an idempotent e, playing the role of the instanton, and the Dirac operator D. It expresses the gamma five matrix as the pairing between the operator theoretic chern characters of e and D. It is of degree five in the idempotent and four in the Dirac operator which only appears through its commutant with the idempotent. It determines both the sphere and all its metrics with fixed volume form. We also show using the noncommutative analogue of the Polyakov action, how to obtain the noncommutative metric (in spectral form) on the noncommutative tori from the formal naive metric. We conclude on some questions related to string theory.
2 role of anthocyanins in plant defence

2Role of Anthocyanins in Plant DefenceAbstract. In addition to their well-documented beneficial effects on plant physiological processes, anthocyanins have also been proposed to function in a diverse array of plant/animal interactions. These include the attraction of pollinators and frugivores, as well as the repellence of herbivores and parasites. The optical properties of anthocyanins may serve as visual signals to potential herbivores, indicating a strong metabolic investment in toxic or unpalatable chemicals. Anthocyanins have also been implicated in the camouflage of plant parts against their backgrounds, in the undermining of insect crypsis, and in the mimicry of defensive structures. These hypotheses have in recent years attracted strong theoretical support and increasing experimental evidence. We emphasize that both the defensive and the physiological functions of anthocyanins may operate in plants simultaneously.2.1 IntroductionIn their natural environments, plants run the risk of multiple attacks by many different species of herbivores and pathogens. Phytophagous species feature in all major groups of vertebrates; mammals and birds are undoubtedly the most injurious to plants, but reptiles, amphibians, and fish also inflict damage (Schulze et al. 2002). Invertebrates, too, have the potential to devastate plant communities. In a collection of German woodlands, for example, Reichelt and Wilmanns (1973) identified numerous species of leaf chewers, excavators, leaf miners, bark borers, wood borers, sap suckers, bud and shoot eaters, root eaters, and seedling eaters. Some herbivores feed preferentially at the canopy, others focus on lower branches or seedlings; some parasitize the sugars and nitrogen flowing through leaf veins, others will eat the lamina tissues surrounding the veins; some cause the plants to develop galls in which the animals live and feed, yet others employ chemical signals to redirect the flow of plant nutrients in their direction (Karban and Baldwin 1997). Little wonder, therefore, that plants have evolved elaborate strategies of avoidance and/or a sophisticated armoury of morphological devices to counteract herbivore attacks. Chemical weaponry, too, is known to play a significant role in plant defence. A vast K. Gould et al. (eds.), Anthocyanins , DOI: 10.1007/978-0-387-77335-3_2,© Springer Science+Business Media, LLC 2009Simcha Lev-Yadun 1 and Kevin S. Gould 21 Department of Biology Education, Faculty of Science and Science Education, University of Haifa, Oranim, Tivon 36006, Israel, levyadun@research.haifa.ac.il2 School of Biological Sciences, Victoria University of Wellington, P.O. Box 600, Wellington, New Zealand, kevin.gould@22 S. Lev-Yadun, K.S. Gouldassortment of secondary metabolites has been demonstrated to act as antifeedants, toxins, warning signals, or precursors to physical defence systems (Bennett and Wallsgrove 1994; Harborne 1997). Among them are the phenolics, a large group of structurally diverse compounds that includes terpenoids, cinnamic acids, catechols, coumarins, tannins, as well as certain flavonoids such as the anthocyanins, the subject of this chapter.There are several different ways anthocyanins might assist plants in their defence against other organisms. These include both direct roles as chemical repellents and more indirect roles as visual signals. In common with other flavonoids, certain anthocyanins have demonstrable antiviral, antibacterial, and fungicidal activities (Konczak and Zhang 2004; Wrolstad 2004, and references therein). They have the potential, therefore, to protect plants from infections by pathogenic microorganisms. In general, however, the antimicrobial activities of anthocyanins are appreciably less effective than those of other phenolic compounds, such as key flavonols and hydroxycinnamic acids that are also likely to be present in the shoot (Padmavati et al. 1997; Werlein et al. 2005). Moreover, anthocyanins have not been found to be toxic to any higher animal species (Lee et al. 1987). Aphid survival rates, for example, are unaffected by anthocyanins in their diet (Costa-Arbulú et al. 2001). Thus, direct chemical defence is unlikely to be a major function of these pigments in plants. There is, in contrast, strong theoretical support and growing empirical evidence for a role of anthocyanins in the defence from “visually oriented” herbivores. This discussion focuses largely on the defensive roles of anthocyanins as visual cues, though some of these mechanisms also involve associated chemical or mechanical components such as poisons and thorns.Although it is generally accepted that the colours of flowers and fruits enhance reproductive success by facilitating communication between plants, their pollinators, and seed-dispersers (Ridley 1930; Faegri and van der Pijl 1979; Willson and Whelan 1990; Weiss 1995; Schaefer et al. 2004), there is no a priori reason to assume that flower, fruit and leaf colours cannot also serve in defence from herbivory. This is achievable if the colours (i) undermine an herbivorous invertebrate’s camouflage, (ii) are aposematic, (iii) mimic an unpalatable plant or animal, or (iv) serve in plant camouflage (see Hinton 1973; Givnish 1990; Cole and Cole 2005; Lev-Yadun 2006). Of course, anthocyanins are not the only class of pigments that might contribute to defence in these ways. In several species, leaf variegation caused by pigments unrelated to anthocyanins has been shown to correlate to reduced herbivory (Cahn and Harper 1976; Smith 1986). Such examples may, however, help to understand the principles that operate when anthocyanins serve in defence. Moreover, it has long been recognised that the non-photosynthetic plant pigments have the potential to serve more than one function concurrently (Gould et al. 2002; Lev-Yadun et al. 2002, 2004; Schaefer and Wilkinson 2004; Lev-Yadun 2006). The UV-absorbing dearomatized isoprenylated phloroglucinols, for example, serve a defensive role in the stamens and ovaries of Hypericum calycinum, but an attractive role in the petals of the same species (Gronquist et al. 2001). Thus, the various functional hypotheses concerning pigmentation in leaves and other plant parts need not contrast or exclude any other functional explanation for specific types of plant colouration, and those traits, such as colouration, that might have more than one type of benefit, may beRole of Anthocyanins in Plant Defence23 selected for by several agents. Indeed, Armbruster (2002) suggested that plants for which anthocyanins are deployed in the defence of vegetative organs would be the more likely also to use anthocyanins to attract pollinators and seed dispersers. Combinations of traits that simultaneously enhance both pollination and defence would likely confer a disproportionate fitness advantage (Herrera et al. 2002). Such synergistic gains may act for a quicker and more common evolution of the red plant organ colour trait.2.2 HypothesesHypotheses for an anti-herbivory function of anthocyanic plant organs include:(i)aposematism (conspicuous colouration serving to parry predators) inpoisonous fruits and seeds (Cook et al. 1971; Harborne 1982; Williamson1982), flowers (Hinton 1973), and thorns (Lev-Yadun 2001, 2003a, 2003b,2006);(ii)mimicry of dead or senescing foliage (Stone 1979; Juniper 1994), of thorns and spines (Lev-Yadun 2003a), and of ants, aphids, and poisonouscaterpillars (Lev-Yadun and Inbar 2002);(iii)camouflage of seeds against the background of the soil substrate (Saracino et al. 1997, 2004), and of variegated foliage in forest understory herbs(Givnish 1990);(iv)the undermining of herbivorous insect crypsis by leaf variegation (Lev-Yadun et al. 2004; Lev-Yadun 2006);(v)attraction of herbivores to young, colourful leaves, diverting them from the more costly older leaves (Lüttge 1997); and(vi)signalling to insects by red autumn leaves that the trees are well defended (Archetti 2000; Hamilton and Brown 2001; Schaefer and Rolshausen 2006). Each of these hypotheses is discussed in detail below.2.3 Reluctance to Accept Hypotheses on Defensive Colouration Prior to the year 2000, much of the published information on defensive plant colouration, including anthocyanin-based ones, had been largely anecdotal. As Harper (1977) commented in his seminal book about the possibility of defensive colouration operating in plants, botanists have been surprisingly reluctant to accept ideas that are commonplace for zoologists. The relative scarcity of papers on defensive colouration in botany as compared to those in zoology was highlighted in the annotated bibliography on mimicry and aposematism by Komárek (1998). It should be appreciated, however, that that it has taken zoologists more than a century to understand the defensive role and the genetic mechanisms of pigmentation in animals (Hoekstra 2006); the effort needed to achieve the same progress in botany24 S. Lev-Yadun, K.S. Gouldwould surely not be smaller. Thus, our explanations for the role of pigments in plant defences remain imperfect. Notwithstanding the difficulties involved in providing concrete evidence for plant defensive colouration, it has therefore been extremely encouraging to note a recent wave of interest in this area, particularly in relation to foliar anthocyanins.2.4 Colour Vision in AnimalsA frequent criticism of the anti-herbivory hypotheses for foliar anthocyanins is that herbivorous insects may lack ocular receptors for red light. Insects have up to five kinds of photoreceptors sensitive to different regions of the visible and UV spectrum (Kelber 2001; Kelber et al. 2003). Butterflies of the genera Papilio and Pieris have arguably the most sophisticated colour vision system of the insects studied so far, including a red receptor maximally sensitive around 610 nm (Arikawa et al. 1987; Shimohigashi and Tominaga 1991). However, most of the insects that have been examined to date – including the phytophagous aphid Myzus persica e – possess only three types of photoreceptors, maximally sensitive to green, blue, and ultraviolet light, respectively (Briscoe and Chittka 2001; Kirchner et al. 2005). In the absence of a red light receptor, it could be argued that insects would be unable to perceive the visual cue presented by anthocyanins.There is nevertheless good evidence that red is recognised by insects. Döring and Chittka (2007) recently summarised the results from 38 studies in which the behavioural responses to red or green stimuli were compared in aphid species. In 28 of those studies, the aphids had been observed to move preferentially towards the green stimulus, and in only one of the reports had aphids not demonstrated a colour preference. In the remaining studies, the experimenters had varied the shade of the green stimulus, and found that insects moved preferentially towards whichever stimulus was the brighter, red or green. It is likely, therefore, that both chromatic (wavelength related) and achromatic (intensity related) information is involved, as is known also to be used by frugivorous birds (Schaefer et al. 2006). There are insufficient data to state with confidence whether aphids tend to avoid red light or, instead, are simply more attracted to green than to red light. Only one publication has addressed this issue, albeit indirectly: in a “no-choice” experiment, Nottingham et al. (1991) recorded positive phototaxis towards red targets by the bird cherry aphid Rhopalosiphum padi. Although response rates were very low, that experiment suggested that the insects were not innately repelled by red objects.Detail of the mechanism by which insects lacking a red photoreceptor perceive red colours remains to be resolved. A colour opponency mechanism has been proposed, which may explain colour discrimination in certain aphid species (Döring and Chittka 2007). This requires negative excitation in the blue and UV, and positive excitation in the green waveband. It is unclear, however, how such a mechanism might facilitate perception of anthocyanic leaves which, compared to green leaves, typically reflect smaller quantities of both green light (Neill and Gould 1999) and UV radiation (Lee and Lowry 1980). It may simply be that red leaves are less attractive to insect herbivores because the excitation of their green receptor isRole of Anthocyanins in Plant Defence25 lower than when excited by green leaves (Thomas Döring, personal communication). Contrasts in colour and/or brightness between red leaves and the visual background are likely also to be important (Dafni et al. 1997).2.5 Anthocyanins and Other Red PigmentsAnthocyanins usually appear red in leaf cells, but depending on their chemical nature and concentration, the vacuolar pH, and interactions with other pigments, they can result in pink, purple, blue, orange, brown, and even black leaf colours (Schwinn and Davies 2004; Andersen and Jordheim 2006; Hatier and Gould 2007). Many of the published articles on plant defensive colouration have assumed red foliage to be the outcome of the production of anthocyanins, this despite the fact that other pigments – carotenoids, apocarotenoids, betalains, condensed tannins, quinones and phytomelanins – can also contribute to plant vermilion (Davies 2004). There is, moreover, a dearth of systematic information on the full complement of pigments in all plant organs at all developmental stages. This lack of data precludes detailed taxon-wide comparisons of the involvement of anthocyanin, or indeed any pigment, in plant defence. Clearly, if only visible cues (hue, lightness, and colour saturation) are involved in defence, the chemical nature of a pigment would be unimportant to a herbivore; red warnings would be similarly effective irrespective of whether they were generated by anthocyanins, carotenoids, or betalains. If, on the other hand, the efficacy of the warning relied on a combination of attributes, for example the reflection of red light plus the presence of a toxic or olfactory phenolic derived from an offshoot in the anthocyanin biosynthetic pathway, then the pigment type could be critical.2.6 Olfactory SignalsAn important, if not critical issue is whether or not olfactory signals are involved along with the visual ones. From studies of deceptive pollination, wherein insects are lured to flowers but receive no sugar reward, we know that signalling to animals can involve a combination of both visual and olfactory components (Dafni 1984; Ayasse et al. 2000; Schiestl et al. 2000); there are good reasons to think that the same may be true in the defence of vegetative organs (Pichersky and Gershenzon 2002). The identification of olfactory volatiles is achievable using modern laboratory equipment (e.g., Jürgens 2004; Jürgens et al. 2002, 2003; Pichersky and Dudareva 2007), but such procedures are difficult to accomplish in the field. It is, in addition, very difficult to identify the specific molecules that deter specific herbivores from among the many volatile molecules that plants omit, and there is the possibility that deterrence operates only if several molecules are sensed simultaneously. The fact that not all animals respond similarly to any chemical signal or cue, should also be considered.26 S. Lev-Yadun, K.S. Gould2.7 Aposematic ColourationAposematic colouration, a well-known phenomenon in animals, has until recently been given little attention in plants. Often, a brightly-coloured animal (red, orange, yellow, white with black markings, or combinations of these colours) is dangerous or unpalatable to predators – a trait that confers a selective advantage because predators learn to associate the colouration with unpleasant qualities (Cott 1940; Edmunds 1974; Gittleman and Harvey 1980; Harvey and Paxton 1981; Wiklund and Järvi 1982; Ruxton et al. 2004). Although several authors had noted a similar association between conspicuous colouration and toxicity in plants (Cook et al. 1971; Hinton 1973; Harper 1977; Wiens 1978; Rothschild 1980; Harborne 1982; Williamson 1982; Knight and Siegfried 1983; Smith 1986; Lee et al. 1987; Coley and Aide 1989; Givnish 1990; Tuomi and Augner 1993), only in the past decade have the scope and significance of this phenomenon been appreciated. Indeed, the possibility of aposematic colouration was discounted in some of these earlier studies (Knight and Siegfried 1983; Smith 1986; Lee et al. 1987; Coley and Aide 1989). A related phenomenon, olfactory aposematism in poisonous plants, has also been proposed (e.g., Eisner and Grant 1981; Harborne 1982; Launchbaugh and Provenza 1993; Provenza et al. 2000) although this has received scant attention.2.7.1 Poisonous PlantsThe first detailed hypothesis for a possible defence from herbivory attributable to red colouration (and other colours) was published by Hinton (1973), who proposed that colourful poisonous flowers should be considered aposematic, and that they probably have mimics. His review about deception in nature was published in a book about illusion; this was not a biological book, but rather dealt with art. His hypothesis was briefly referred to by Rothschild (1980) in her discussion on the roles of carotenoids, but otherwise did not stir botanists or ecologists to pursue this issue. Indeed, Harper (1977), who had written the comment about botanists being reluctant to accept things that were commonplace for zoologists, omitted to explain why zoologists who dealt with animal aposematism, and who were also involved in research on plant-animal interactions, had not recognized how common are these phenomena in plants. Harborne (1982) proposed that the brightly coloured, purple-black berries of the deadly Atropa belladonna warn grazing mammals of the danger to consume them. Williamson (1982) also proposed that brightly coloured (red, or red and black) seeds lacking an arillate or fleshy reward (e.g. Erythrina, Ormosia, and Abrus) might be aposematically coloured to warn seed eaters of their toxicity. These hypotheses were written only as short paragraphs within long reviews, however, and there has been no further effort to study the function of their colouration.2.7.2 Thorny PlantsIn English there are three terms for pointed plant organs: spines (modified leaves), thorns (modified branches), and prickles (comprising cortical tissues, e.g. in roses). For the purposes of this discussion, we refer to plants as “thorny” if they produce anyRole of Anthocyanins in Plant Defence 27of the three types of sharp appendages. Thorny appendages provide mechanical protection against herbivory (Janzen and Martin 1982; Janzen 1986; Myers and Bazely 1991; Grubb 1992; Rebollo et al. 2002) because they can wound mouths, digestive systems (Janzen and Martin 1982; Janzen 1986), and other body parts of herbivores. They might also inject pathogenic bacteria into herbivores (Halpern et al. 2007). Thus, once herbivores learn to identify thorns – and their bright colours and associated markings should help in their recognition – they can avoid harmful plants displaying them.The flora of countries such as Israel, which has a millennia-long history of large-scale grazing, clearly and “sharply” indicates the ecological benefit of being thorny when grazing pressure is high. A continuous blanket of spiny shrubs such as Sarcopoterium spinosum , as well as many types of thistles, covers large tracts of the land. The thorns effectively impede the rate at which an herbivore feeds within the canopy of the individual plant, and this presents an overall considerable advantage to such plants over non-defended ones. Spiny plants, such as Echinops sp. (Asteraceae), which normally grow as individuals or in small groups, sometimes become the most common perennial plant over many acres in heavily grazed lands. The same is true for many other taxa.Fig. 2.1 Thorns and their mimics. (A) Anthocyanic thorns on a rose stem. (B) Red mucron at the apex of a leaf of Limonium angustifolium . (C) Red fruit of Erodium laciniatum . See Plate 1 for colour version of these photographsThousands of thorny species have colourful or otherwise conspicuous markings (e.g. Fig. 2.1A), many of which can be considered to be aposematic (Lev-Yadun 2001). We will not discuss this common phenomenon in the thorniest taxon – the Cactaceae – since they lack anthocyanins, and use betalains instead (Stafford 1994). Lev-Yadun (2001) categorised two types of thorn ornamentation, which are typical of many thorny plant species: (i) colourful thorns, and (ii) white spots, or white and colourful stripes, in leaves and stems associated with the thorns. Both types have been recorded for approximately 2,000 species originating from several continents in both the Old and New World (Lev-Yadun 2001, 2003a, 2003b, 2006; Rubino andMcCarthy 2004; Halpern et al. 2007; Lev-Yadun unpublished). It has been proposed28 S. Lev-Yadun, K.S. Gouldthat the pigmentation in thorns and associated organs (in many cases resulting from anthocyanins) are cases of vegetal aposematic colouration, analogous to such colouration of poisonous animals, that serves to communicate between plants and herbivores (Lev-Yadun 2001, 2003a, 2003b, 2006; Lev-Yadun and Ne`eman 2004; Rubino and McCarthy 2004; Ruxton et al. 2004; Speed and Ruxton 2005; Halpern et al. 2007). Interestingly, spiny animals also show the same phenomenon (Inbar and Lev-Yadun 2005; Speed and Ruxton 2005).Colourful thorns are especially common in the genera Agave, Aloe and Euphorbia. Agave species can have two types of thorns in their leaves: spines at the leaf apex, and/or teeth along the leaf margins (Lev-Yadun 2001). In addition, many Agave species also have colourful stripes running along the margins that enhance spine and tooth visibility. The spines and the teeth along the margins of the leaves are brown, reddish, gray, black, white, or yellow; these colours are known to serve in aposematism. The same phenomenon is true for Aloe species for which the colourful thorns can be white, red, black, or yellow, and for thorny African Euphorbia species, many of which have colourful thorns or colourful markings associated with thorns along the ribs of the stems (Lev-Yadun 2001). Anthocyanins are known to contribute to the markings in Agave and Euphorbia, though the carotenoid rhodoxanthin is involved in leaf colouration in Aloe. Colourful thorns advertise their defensive quality directly, unlike poisonous aposematic organisms in which the poison is advertised indirectly (Ruxton et al. 2004; Speed and Ruxton 2005).Since the colouration and markings of thorns in plants are so widespread, they are probably neither a neutral nor a random phenomenon. Lev-Yadun (2001) proposed that, like aposematic colouration in animals, the conspicuousness of thorns would be of adaptive value since herbivorous animals would remember the signal, and subsequently tend to avoid tasting such plants. Annual and perennial plants usually survive damage caused by herbivores (Williamson 1982; Crawley 1983; Ohgushi 2005), so an herbivore reacting to aposematic colouration would be of direct benefit to the individual plant, which would probably suffer fewer repeated attacks. Hence, as with animals (Sillén-Tullberg and Bryant 1983), there is no need to propose kin/group selection, or altruism, as the evolutionary drive for the spread of this character. Indeed, there are several probable reasons for the quick and easy route to aposematism in plants in general. Thorny or poisonous plants are already well-defended, even without aposematic colouration. Plants recover much better than most animals from herbivore (predator) damage (Crawley 1983; Ohgushi 2005). Thus, the original thorny, aposematic mutant would have had a good chance of survival and producing offspring, even despite the risks associated with being conspicuous to herbivores and being partly eaten. Furthermore, an herbivore might pass over an aposematic individual and eat its non-aposematic neighbour, thereby reducing the competition between the aposematic and neighbouring plants. A recent hypothesis proposed that since thorns harbour many types of pathogenic microbes, their aposematism serves to signal both about their biological risks as well as the mechanical ones (Halpern et al. 2007). It is possible, therefore, that the evolution and spread of aposematism progressed even more swiftly in plants than in animals.Role of Anthocyanins in Plant Defence 292.8 Defensive MimicryDefensive mimicry is said to occur if a plant gains protection against herbivory by resembling a noxious or unpalatable model species. Williamson (1982) proposed that because plants are sessile organisms, mimicry is less likely to be successful in plants than in animals; plant mimics are less likely to be mistaken for their models than are the mobile animal mimics. Moreover, because plants that have been partially eaten by herbivores can often regenerate new organs, defensive mimicry would in theory provide less advantage to plants than animals. In contrast, Augner and Bernays (1998) studied the theoretical conditions for an evolutionary stable equilibrium of defended, signalling plants and of plants mimicking these signals. Their model showed that mimicry of plant defence signals could well be a common occurrence; even imperfect mimics had the potential to invade a population of defended model plants. Theoretically, natural selection would allow the success of even imperfect mimics (Edmunds 2000). Wiens (1978) estimated that about 5% of the land plants are mimetic, listing various types of protective plant mimicry. Several types of anthocyanin-related defensive mimicry have been proposed, especially in recent years, and these are discussed below.2.8.1 Mimicry of Dead LeavesAn interesting hypothesis in relation to anthocyanins was published in a brief note by Stone (1979), who proposed that young leaves of understory palms mimic old or dead leaves. He observed that the combination of chlorophylls and anthocyanins in the developing leaves of several species produced a dull brown colour which “strikingly mimics the drab color of dying or withered dead leaves”. The leaves, moreover, showed no evidence of browsing damage, possibly because they appeared unpalatable to potential herbivores.Juniper (1994) suggested a similar explanation for the abundant red, brown and even blue flushes of young leaves in tropical trees and shrubs from the families Annonaceae, Fabaceae subfam. Caesalpinioideae, Guttiferae, Lauraceae, Meliaceae, Rutaceae, and Sapindaceae. It was postulated that to a phytophagous insect, such leaves would appear dull, like advanced senescent foliage. “If you do not look like a normal leaf … if you do not feel like a leaf to a palpating insect, because you are soggy; if you do not have the posture of a proper leaf, i.e. you are hanging down like wet facial tissue; if you do not smell like a leaf because you have no photosynthesis and, if on the first suck or bite, you do not taste like a leaf because you have no sugars … you might escape being eaten” (Juniper 1994).micry (Pasteur 1982). The idea seems 1994; Dominy et al. 2002; Gould 2004; Karageorgou and Manetas 2006; Lev-Yadun 2006; Manetas 2006) although there is little in the way of supporting experimental data. As is the case for many of these anthocyanin defence hypotheses, the chemical nature of the pigments in many such red leaves has not been tested, the anatomical location of the pigmentation is not always known, and possible physiological roles of the colouration are unclear. Young foliage that acquires a protective advantage by resembling older, non-green leaves would be an example of cryptic mi to have been generally accepted (Juniper。
《物理双语教学课件》Chapter 17 Electric Potential 电势

1. Newton’s law for the gravitational force and Coulomb’s lawfor the electrostatic force are mathematically identical. Thus the general feature we have discussed for the gravitational force should apply to the electrostatic force.2. In particular, we can infer that the electrostatic force is aconservative force . Thus when that force acts between two or more charged particles within a system of particles, we can assign an electric potential energy U to the system.3. Moreover, If the system changes its configuration from aninitial state i to a different final state f, the electrostatic force does work W on the particles. The resulting change U in thepotential energy of the system is U = U U = W . As withf iother conservative forces, the work done by the electrostatic force is path independent.4. For convenience, we usually take the reference configurationof a system of charged particles to be that in which the particles are all infinitely separated from each other. And we usually set the corresponding reference potential energy to be zero.17.2 Electric Potential1. The potential energy of a charged particle in an electric field depends on the magnitude of the charge. However, the potential energy per unit charge has a unique value at any point in the electric field. Thus the potential energy per unit charge, which can be symbolized as U/q, is independent of the charge q of the particle and is characteristic only as the electric field we are investigating. The potential energy per unit charge at a point in an electric field is called the electric potential V(or simply the potential) at that point . Thus V = U Electricpotential is a scalar, not a vector.2. The electric potential difference V between any two points i and f in an electric field is equal to the difference in potential energy per unit charge between the two point : V = V f V i = q U = q W. The potential difference between two point is thus the negative of the work done by the electrostaticforce per unit charge that move from one point to the other .3. The SI unit for electric potential is the joule per coulomb. This combination occurs so often that a special unit, the volt (abbreviated V) is used to represent it.4. One electron-volt (eV) is the energy equal to the workq .required to move a single elementary charge e through a.potential difference of exactly one volt, so 1eV 1.60 1019 J 17.3 Equi-potential Surfaces1. Adjacent points that have the same electric potential form anequipotential surface, which can be either an imaginary surface or a real, physical surface. No net work W is done on a charged particle by anelectric field when theparticle moves betweentwo points i and f on thesame equipotential surface. See the Figure.2. Figure shows the electric field lines and cross sections ofequipotential surface for several cases. We can find that equipotential surfaces are always perpendicular to electric field lines and thus to E which is always tangent to these lines.17.4 Calculating the Potential from the Field1. We can calculate the potential difference between any twopoints i and f in an electric field if we know the field vectorat all positions along any path connecting those points.2. Consider an arbitraryelectric field, representedby the field lines in theright figure, and a positivetest charge q that moves along the path shown from point ito point f. The differential work done on the particle by theelectrostatic force during a displacement is Thus the total work done on the particle by dW = F . ds = q E . ds .the fields is theintegration of the differential work done on the charge for all the differential displacement along the path. W = q ϕf . d.i Therefore, V V = W = ϕ f . d.f i q i3. If we choose the potential V at point i to be zero, theniV = ϕf . d, in which we have drooped the subscript f. It gives ius the potential V at any point f in the electric field relative to the zero potential at point i.4. Potential due to a point charge: V = 1 q .4几r5. Potential due to a group of point charges: We can find the netpotential at a point due to a group of point charges to sum up the potential resulting from each charge at the given point . V = n V =1 n q i . Here q is the value of the ith charge, and i 4χ r ii =1 0 i =1 ir is the radial distance of the given point from the ith charge. i6. Potential due to an electric dipole : (1) V = 1 p cos 9 . (2)4χ r 2Induced dipole moment: Many molecules such as water(Seeing right figure) have permanentelectric dipole moments. In othermolecules (nonpolar molecules) andin every atom, the centers of thepositive and negative charges coincide and thus no dipole moment is set up. However, if we place an atom or nonpolar molecule in an external electric field, the field distorts the electron orbits and separates the centers of positive and negative charge and sets up a dipole moment that points in the direction of the field. This dipole moment p said to be induced by the field, and the atom or molecule is said to be polarized by the field. When the field is moved, the induced dipole moment and thepolarization disappear. See the figure.7. Potential due to a continuous charge distribution :V = ϕ dV = ϕ 1 dq . Here the integral is to be taken over the4 r 0entire charge distribution. (1) lines of charge; (2)Charged disk.1. The component of E in any direction is the negative of the rate of change of the electric potential with distance in that direction . Ex = ?V ?x ; E y = ?V ?y ; E z = ?V ?z.1. The electric potential energy of a system of fixed point-charges is equal to the work that must be done by external agent to assemble the system, bringing each charge in from an infinite distance .1. An excess charge placed on anisolated conductor will distributeitself on the surface of that conductorso that all points of theconductor-whether on the surface or inside-come to the same potential. This is true regardless of whether the conductor has an internal cavity.2. If an isolated conductor is placed in an external electric field,as in the right figure, all points of the conductor still come toa single potential regardless of whether the conductor has anexcess charge.。
Coulomb interaction in a quantum dot

a rX iv:c ond-ma t/98531v3[c ond-m at.m trl-sci ]3Sep1998Coulomb interaction in a quantum dot Lin-Wang Wang National Renewable Energy Laboratory,Golden,CO 80401Abstract One approximation is made to describe a M+1electron many-body wavefunc-tion by a M electron many-body wavefunction and a single electron wavefunc-tion.Under this approximation,we have derived the Coulomb energy which relates the exciton energy E exc in a quantum dot with the quasiparticle band gap (defined as the difference between the ionization energy and the electron affinity),and the Coulomb energy which relates E exc with the single particle eigen values.We found that these two Coulomb energies are different.We have compared our results with the formulae used in different groups,which are proposed either ad hov ,or from the classical electrostatic point of view.We found important difference between our results and the classical formu-lae.Finally,under the above approximation,we provided an effective single particle Hamiltonian,which gives the quasiparticle band structure in a bulk system.Keywords:quantum dot,screening,Coulomb interaction.73.20.Dx,78.20.Ci,78.66.DbTypeset using REVT E XI.IntroductionThe screened Coulomb interaction in a bulk semiconductor between an excited electron and a hole has been studied theoretically30years ago[1,2]from many body point of views. As a result of such theoretical analysis,the screening of the Coulomb interaction can be expressed using the dielectric response function of the bulk system.Recently,nanometer scalefinite system has attracted a lot of research interests[3].The confined excited electrons and holes within thefinite systems have enhanced Coulomb interactions comparing to the bulk material[4].However,there are different opinions about how to screen the Coulomb interactions in various cases.While the screening of the Coulomb interaction is clear when the electron is outside the nanostructure,it becomes clouded from a classical point of view when it enters the nanostructure.One problem is that the classical dielectric screening effects can already been partially represented by the single particle eigen energies.Thus combining the classical electrostatic model with the single particle Hamiltonian does not always provide a clear picture free from ambiguities.The more rigorous approach is to derive the single particle effective Hamiltonian and the screened Coulomb interaction from the many body Hamiltonian.However,the Feyman diagram technique used in the bulk study thirty years ago can not be directly applied to thefinite system without complicated modifications of the Green’s functions according to the new quantum dot boundary conditions.In this article,we will present a derivation of the screened electron-hole Coulomb interaction in a nanosystem started from a many body Hamiltonian.Instead of basing on the Green’s functions,our derivation is based on many particle wavefunctions.We will restrict ourselves to the cases that the excited electrons and holes are strongly confined by a0dimension nanostructure (quantum dot).That means,the correlation between the excited electron and the hole can be ignored[5,6]One of the earlier works on the quantum dot Coulomb interaction and its screening effects is given by L.E.Brus[7].Using a classical model of the dielectric screening and a single particle Hamiltonian,Brus derived the change of electron affinity of a quantum dot (spherical,with radius R)relative to the bulk system:E N−E N+1=E bulk aff−ǫe−12m∗e R2under an effective mass model of electron effective mass m∗e.12R¯P′.(2) Hereǫh is the single hole confinement energy,which equalsπ2R¯P′.(3)Here,we have used the fact that the bulk band gap E bulkgequals the difference between bulkionization energy E bulkion and the bulk electron affinity E bulkaff.In this paper,we discuss onlythe cases where the quantum dot is surrounded by vacuum.Then if the dielectric constant of the quantum dotǫis much larger than1,we have(following Ref.[8]):1ǫ)1ǫR(ǫ−1E exc=E bulk+ǫe+ǫh−1.8ǫR(ǫ−1grepresents the direct Coulomb integral between the electron charge and hole ǫRcharge,screened byǫ,using the effective mass wavefunctions.The last term in Eq(5)is said to be the time averaged instantaneous dielectric energy while the classical particle moves around inside the quantum paring Eq(3)to Eq(5),with the help of Eq(4),we haveE exc=E qp g−1.8ǫ)1is used(in the effective mass limit):ǫRE exc=E qp g−1.8To settle the dispute between Eq(7)and Eq(6),and to test the other classical formulae [e.g,Eq(5)],it will be very useful to derive the above relationships from many body Hamil-tonians.This will be provided in the rest of this paper.We found out that Eq(6)is correct instead of Eq(7),and Eq(5)is correct after deleting its last term.II.The basic FormalismIn this section,we will derive our basic formula to be used in later sections.This formula is based on an approximation that the many-body wavefunctionΦM+1of a M+1electron system can be separated into one single particle wavefunctionψ[i.e,ψv(top of valence band state)orψc(bottom of conduction band state)]and the rest of the M particle wavefunction ΦM.More specifically,we have:ΦM+1(x1,x2,...,x M,x M+1)≡|ΦMψ>≡1M+1[ΦM(x1,x2,...,x M)ψ(x M+1)−ΦM(x M+1,x2,...,x M)ψ(x1)...−ΦM(x1,x2,...,x M+1)ψ(x M)].(8) Here,we have used|ΦMψ>to denote the break down of the total wavefunctionΦM+1 intoΦM andψ.x≡(r,σ),and r is the three dimensional Cartesian coordinate,andσis the spin index.Note that through the definition of Eq(8),ΦM+1(x1,x2,...,x M,x M+1) is antisymmetric,providedΦM is antisymmetric.In general,ΦM(x1,x2,...,x M)can be represented by a linear combination of different electron configurations(i.e,single slater determinates from a single particle orthogonal basis set includingψ).Any slater determinate which consists ofψwill be eliminated in Eq(8)by the antisymmetry operation.Thus,it does not lose any generacity(in terms of variational degree of freedom forΦM+1)to exclude the single particle orbitalψfrom the configurations ofΦM(x1,x2,...,x M).In another word, we can restrictΦM(x1,x2,...,x M)to be orthogonal toψ(x),i.e,ΦM(x1,x2,...,x M)ψ∗(x1)d3x1=0.(9)This orthogonal condition is also called strong orthogonal condition[12,13].Notice that, since we have not restrict any degree of freedom inΦM+1of Eq(8)by introducing Eq(9), Eq(9)should not be considered as an additional approximation.The approximation,if any,has already been made in Eq(8).By using Eq(8),we have neglected the correlation between the single particle stateψand the rest of the systemΦM.This is one approximate way to define an quasiparticle wavefunctionψ(x1)out of a many particle system.The approximation of Eq(8)has been called group function approximation[12,13],and has been used to study the effects(e.g,screening)of one group to another group.Thus,it is natural here to use it to describe the Coulomb screening effects of the background system(ΦM) to the quasiparticle(and exciton)system(ψ).Note that,Eq(8)goes beyond Hartree-Fock [14]approximation by retaining correlations withinΦM.Since our focus is to study the dielectric screening of the Coulomb interaction,which can already be described by Hartree Fock approximation,we expect Eq(8)to be adequate to represent the main physics of interest here.Similar approximations of Eq(8)has been used in the derivation of Extended Koopmans’Theorem by Day,Smith,and Garrod[15],by Morrell,Parr and Levy[16],and by Kent,etal[17].In Eq(8),one gets the wavefunctionΦM+1of the M+1electron system by adding one electronψto the M electron wavefunctionΦM.Similary,one can get the M electron system wavefunctionΦM by elminatingψ(x1)from the M+1electron wavefunction ΦM+1:ΦM(x1,x2,...,x M)= ψ∗(x M+1)ΦM+1(x1,x2,...,x M,x M+1)d3x M+1.(10) Using the orthogonal condition Eq(9),one can derive Eq(10)from Eq(8).Equation(10)is also used in the derivation of the Extended Koopmans’Theorem[15–17].To appreciate the approximation embodied in Eq(8),we can take a look at the density matrix of the M+1system.Under Eqs(8)and(9),ρM+1(x,x′)=ψ(x)ψ∗(x′)+ρM(x,x′), hereρM+1andρM are the density matrix of the M+1and M electron systems respectively. Besides,following the orthogonal condition of Eq(9), ρM(x,x′)ψ(x′)d3x′=0.As a result,ψ(x)is a natural orbital ofρM+1with an occupation number of1.As well known[17],the occupation numbers of the natural orbitals are usually less than1,thus the Eq(8)is definitely an approximation.However,this approximation is similar to the approximations which use one single particle wavefunction to represent a quasiparticle in a many-body system.These include:the Hartree-Fock theory[14],empirical pseudopotential theory[11],the Kohn-Sham representation of the density functional theory[20]and in some extent the GW theory[18]. To include the correlation betweenψandΦM in Eq(8),one has to add in Eq(8)other configurations|Φ′Mψ′>.However,if the quasiparticle is represented by a unique single particle wavefunctionψ,thenψ′must beψ.As a result,|ΦMψ>+|Φ′Mψ′>=|Φ′′Mψ>, whereΦ′′M=ΦM+Φ′M,and Eq(8)remains unchanged.The Hamiltonian for the M+1particle system can be written asH M+1=−1|r i−r j|.(11)Using Eq(11)and Eq(8),we can evaluate<ΦM+1|H M+1|ΦM+1>.After some algebras,it can be expressed as<ΦM+1|H M+1|ΦM+1>=Eψ+<ΦM|H M|ΦM>+ ρM(r)Vψcoul(r)d3r− Vψex(x,x′)¯ρM(x,x′)d3xd3x′,(12) where H M is just the H M+1of Eq(11),but change the M+1to M.Eψis defined asEψ= ψ(x) −1|r−r′||ψ(x′)|2d3x′,(14)ρM(r)is the total charge density ofΦM,ρM(r)=M σ |ΦM((r,σ),x2,...x M)|2d3x2...d3x M,(15) Vψex(x,x′)is the exchange nonlocal potential due toψ,e2Vψex(x,x′)=band single particle stateψv is unoccupied).Then the Coulomb energy which connects E qp g (≡E N+1+E N−1−2E N)with E exc isE coul≡E exc−E qp g=(E∗N−E N−1)−(E N+1−E N),(18) where,E N−1and E N+1are the ground state energies of N-1and N+1electron systems. Note that in E∗N,E N,E N−1and E N+1systems,the ionic potential V ion(r)in Eq(11)is the same.The difference is the electron ing the approach outlined in the previous section,we will approximate the wavefunctions of E∗N,E N,E N−1and E N+1systems as|Φc N−1ψc>,|Φ0N>,|Φ0N−1>and|Φc Nψc>ing the orthogonal conditions of Eq(9),and applying it equally to all the systems in Eq(18),we haveΦc N−1,Φ0N,Φ0N−1and Φc N all orthogonal toψc[Eq(9),replacingψbyψc,andΦM by these four wavefunctions]. In addition,Φc N−1andΦ0N−1should be orthogonal toψv[Eq(9),replacingψbyψv],so that a hole exists in these systems.Notice that,we have used the superscription“0”to indicate that the corresponding wavefunctionΦ0M is a minimum energy variational solution of<Φ0M|H M|Φ0M>.Similarly,the superscription“c”indicates that the corresponding wavefunctionΦc M is the variational solution of Eq(12)under the perturbation ofψc[through Vψc coul and Vψc ex].Notice that,only in the strong confinement quantum dot size region[5],we can writeΦ∗N as|Φc N−1ψc>through Eq(8).In this size region,the electron and the hole are not correlated.As a result,we don’t have to writeΦ∗N as a summation of configurations |Φc N−1ψc>with different electron(ψc)and hole(ψv)wavefunctions.After the definitions of the wavefunctions,we can replace E∗N,E N,E N−1and E N+1by<Φc N−1ψc|H N|Φc N−1ψc>, <Φ0N|H N|Φ0N>,<Φ0N−1|H N−1|Φ0N−1>and<Φc Nψc|H N+1|Φc Nψc>,ing Eq(12),we have:E∗N−E N−1=Eψc+<Φc N−1|H N−1|Φc N−1>−<Φ0N−1|H N−1|Φ0N−1>+ ρc N−1(r)Vψc coul(r)d3r− ¯ρc N−1(x,x′)Vψc ex(x,x′)d3xd3x′,(19)andE N+1−E N=Eψc+<Φc N|H N|Φc N>−<Φ0N|H N|Φ0N>+ ρc N(r)Vψc coul(r)d3r− ¯ρc N(x,x′)Vψc ex(x,x′)d3xd3x′.(20) The changes fromΦ0N−1,Φ0N toΦc N−1,Φc N can be described infirst order by perturbation theory,under the external perturbation potentials Vψc coul(r)and Vψc ex in Eq(12).For a N-1 electron system,the energy changes from<Φ0N−1|H N−1|Φ0N−1>to<Φc N−1|H N−1|Φc N−1> in response to these perturbative potentials.The amplitude of this energy change is in the same order of the Coulomb interaction of the perturbation charge(ψ2c)with the re-sponse charge of the system(which is also in the order ofψ2c).In other words,∆E N−1≡<Φc N−1|H N−1|Φc N−1>−<Φ0N−1|H N−1|Φ0N−1>scales as1,instead of N.This is also evident from Eq(19).Note that E∗N−E N−1scales as1.At the right hand side of Eq(19),combining the Eψc term defined in Eq(13)with the ρc N−1(r)Vψc coul(r)d3r− ¯ρc N−1(x,x′)Vψc ex(x,x′)d3xd3x′term,one gets an energy similar to that of the Hartree Fock single particle eigen energy. Thus,this combined term also scales as1.As a result,the∆E N−1scales as1.The same is true for∆E N≡<Φc N|H N|Φc N>−<Φ0N|H N|Φ0N>.The difference between ∆E N−1and∆E N is the difference between N-1and N electron system,which should scale as∆E N/N∝1/N.Thus,this difference is negligible comparing to the Coulomb energy E coul which we are calculating.As a result,subtract Eq(20)from Eq(19),we haveE coul= [ρc N−1(r)−ρc N(r)]Vψc coul(r)d3r¯ρc N−1(x,x′)−ρc N(x,x′) Vψc ex(x,x′)d3xd3x′.(21)−Further more,following the same perturbation argument,we haveρc N(r)−ρ0N(r)≃ρc N−1(r)−ρ0N−1(r)and¯ρc N(x,x′)−¯ρ0N(x,x′)≃¯ρc N−1(x,x′)−¯ρ0N−1(x,x′).Again,the approximation has an relative error∝1/N,thus negligible.Then,we can change Eq(21)toE coul= [ρ0N−1(r)−ρ0N(r)]Vψc coul(r)d3r− ¯ρ0N−1(x,x′)−¯ρ0N(x,x′) Vψc ex(x,x′)d3xd3x′.(22)This is our central result.Notice that,ρ0N−1(r)is the total electron charge density of a N-1 electron system(containing one hole),andρ0N(r)is the total electron charge density of a N electron neutral system.Thus,ρsrc v(r)≡ρ0N−1(r)−ρ0N(r)is the screened hole charge(the bare hole charge plus the response screening charge)in the quantum dot.Note thatρsrc v(r)d3r=−1.(23) Thus,if we ignore the exchange interaction in Eq(22)(which is usually much smaller than the Hartree interaction),and express Vψc coul(r)using Eq(14),we haveE exc=E qp g+ ρsrc v(r1)ρc(r2)ρv(r)for r<Rǫ1=−(1−that,the dielectric constantǫis not derived here,unlike in the case of bulk exciton screening [2].This,of course,doesn’t mean that we have no screening in our formalism.The dielectric screening of the Coulomb interaction is enclosed inρsrc v of Eq(24)in our formula.We just didn’t derive the detail screening function in our formula(i.e,how to calculateρsrc v fromρv by a detailǫmodel).That is not the focus of our current study.In the cases of Eqs(6)and (7),the simple response model of Eq(25)is assumed.It is in this context,ǫis used here, and Eq(6)is found to be correct.IV.Coulomb energy associated with the single particle eigenvaluesHad proved Eq(6),now we like to test Eq(5).What important here is to define an effective single particle Hamiltonian,for whichǫe andǫv are its conduction band minimum and valence band maximum eigen energies.Let’s start from the definition of the exciton energy:E exc=E∗N−E N.Now,we will rewrite the N particle ground state wavefunction Φ0N of E N as|Φv N−1ψv>,withΦv N−1being orthogonal to bothψv andψing Eq(12),E N can be written as:E N−Eψv=<Φv N−1|H N−1|Φv N−1>+ ρv N−1(r)Vψv coul(r)d3r− ¯ρv N−1(x,x′)Vψv ex(x,x′)d3xd3x′.(26) Here,Eψv is evaluated from Eq(13).Similarly,like before,the exciton wavefunction can be expressed as|Φc N−1ψc>,withΦc N−1being orthogonal toψv andψc.Then,E∗N can be written as:E∗N−Eψc=<Φc N−1|H N−1|Φc N−1>+ ρc N−1(r)Vψc coul(r)d3r− ¯ρc N−1(x,x′)Vψc ex(x,x′)d3xd3x′.(27) Comparing Eq(27)with Eq(26),wefind that we can obtainΦc N−1fromΦv N−1by applying potentials Vψc coul−Vψv coul and Vψc ex−Vψv ex into Eq(26).More specifically we can defineE(β)≡<ΦβN−1|Hβeff|ΦβN−1>=<ΦβN−1|H N−1+[(1−β)Vψv coul+βVψc coul]−[(1−β)Vψv ex+βVψc ex]|ΦβN−1>.(28) In Eq(28),ΦβN−1is defined as the minimum energy variational solution of the Hamiltonian Hβeff,while subjected to orthogonal condition Eq(9)toψc andψing Eq(26)and Eq(27), we have E(β=0)=E N−Eψv and E(β=1)=E∗N−Eψc.Now,using the“adiabatic integration technique”,we haveE(β=1)=E(β=0)+ 10∂E(β)∂ΦβN−1∂β|Hβeff|ΦβN−1>=<ΦβN−1|Hβeff|∂β|ΦβN−1>dβ=E(β=0)+ 10 ρβN−1(r) Vψc coul(r)− Vψv coul(r) d3r¯ρβN−1(x,x′) Vψc ex(x,x′)− Vψv ex(x,x′) d3xd3x′ dβ.(31)−ρβN−1and¯ρβN−1are the density and density matrix of the N-1electron system under the perturbation ofβ[Vψc coul−Vψv coul]andβ[Vψc ex−Vψv ex](the nonperturbated values areρv N−1and ¯ρv N−1).These perturbative potentials are due to charge densityβ[|ψc(x)|2−|ψv(x)|2]and density matrixβ[ψc(x)ψ∗c(x′)−ψv(x)ψ∗v(x′)].Here,we will only consider cases where a phenomenological macroscopic dielectric constantǫcan be used to describe the response of the N-1electron system to these perturbative charges.These perturbative charges can be considered as external to the N-1electron system.Thus,under this phenomenological description,the N-1electron charges can be expressed as1ρβN−1(r)=ρv N−1(r)+β(ǫ−1)[ψc(x)ψ∗c(x′)−ψv(x)ψ∗v(x′)](33) Note that,ρβN−1(r)= σρβN−1[(r,σ),(r,σ)],thus the dielectric constantǫused to describe the response ofρβN−1(r)[Eq(32)]and¯ρβN−1(x,x′)[Eq(33)]must be the same.Also notice that,the dielectric constantǫused in Eqs(32),(33)is consistent with the conventional def-inition ofǫ,and there is no surface response charge as in Eq(25)because the net charge of σ[|ψc(r,σ)|2−|ψv(r,σ)|2]is zero.Now,substitute Eqs(32)-(33)into Eq(31),carry out the βintegration,we have:E∗N−Eψc=E N−Eψv+ ρv N−1(r)+1ǫ−1) σ[|ψc(r,σ)|2−|ψv(r,σ)|2] [Vψc coul(r)−Vψv coul(r)]d3r+ ¯ρv N−1(x,x′)+1ǫ−1)[ψc(x)ψ∗c(x′)−ψv(x)ψ∗v(x′)] [Vψc ex(x,x′)−Vψv ex(x,x′)]d3xd3x′.(34) Note thatρ0N(r)=ρv N−1(r)+ σ|ψv(r,σ)|2and¯ρ0N(x,x′)=¯ρv N−1(x,x′)+ψv(x)ψ∗v(x′),where ρ0N(r)and¯ρ0N(x,x′)are the neutral system N electron ground state charge density and density ing this relations,and E exc=E∗N−E N,we can derive from Eq(34)that:ρ0N(r)[Vψc coul(r)−Vψv coul(r)]d3r− ¯ρ0N(x,x′)[Vψc ex(x,x′)−Vψv ex(x,x′)]d3xd3x′E exc=Eψc−Eψv+−1|r−r′|d3xd3x′+1|r−r′|d3xd3x′(35) Similar to Eqs(14)and(16),we can now define Coulomb and exchange potentials due to the N electron ground state charge densityρ0N(r)and density matrix¯ρ0N(x,x′):V N coul(r)= 1|r−r′|¯ρ0N(x,x′)(37)Then,we can defined a effective single particle Hamiltonian H s:ǫψ≡<ψ|H s|ψ>=ψ∗(x) δ(x−x′)[−1|ψv(x)|2|ψc(x′)|2ǫψc(x)ψv(x)ψ∗c(x′)ψ∗v(x′)ǫΦM.The difference is that,here,the sameΦN is used for bothψv andψc.This H s can be compared with the conventional single particle Hamiltonians e.g,EPM[11],local density approximation(LDA)[20],quasi-particle GW calculation[18]and Hartree-Fock equation[14].H s is almost the same as the Hartree-Fock equation,but that the uncorrelated HF exchange potential V N ex,HF(x,x′)=1ǫ(R)) 1there is a well know LDA error for the band gap energy,this error exists in both(E N+1+ E N−1−2E N)and(ǫc−ǫv),thus should be cancelled.As a result,Eq(40)should still be valid for LDA calculations.In Fig.1,the quantity(E N+1+E N−1−2E N)−(ǫc−ǫv)is plotted as a function of1/R..The agreement is quite good.Here,ǫ(R)is a This quantity is compared with(1−1Rfunction of the quantum dot radius R.This function is calculated in Ref.[21],and can be expressed asǫ(R)=1+(11.4−1)/(1+(α/R)l).Here,we have usedǫ(R)which corresponds to the total polarizibility of the quantum dot(ǫs in Ref.[21]),i.e,α=4.25˚A and l=1.25.Of course,the agreement of Eq(40)depends on how good is the phenomenological macroscopic description of the quantum dot screening[Eq(25)].There is no reason to believe that Eq(25) is exact for a small quantum dot.After considered all these uncertainties,the agreement in Fig.1is quite good.Notice that,the LDA Kohn-Sham single particle band gapǫc−ǫv is almost the same (within0.1eV)as the single particle band gap calculated from empirical pseudopotential after a0.68eV band gap correction is added to LDA result.This can be confirmed by taken the data from Ref.[10]and Ref.[11].It has also been confirmed separately by Delley etal in Ref.[22].Then,using the good agreement between LDA(E N+1+E N−1−2E N)−(ǫc−ǫv) and(1−1/ǫ(R))/R as shown in Fig.1,we know that the exciton energy E exc calculated from LDA quasiparticle energy through Eq(6)[plus0.68eV correction],should be the same asE exc calculated from empirical pseudopotential single particle eigen values through Eq(40)[11].VI.ConclusionsOne approximation[Eq(8)]to the many-body wavefunction is presented.This approx-imation allows us to define a single particle wavefunction in a many-body system.This approximation is more accurate than the Hartree-Fock Slater determinate for the many-body wavefunction.Under this approximation,we have derived the Coulomb energy needed to relate the quasiparticle energy E qp g to the exciton energy E exc(=the optical transition energy)[Eqs(22),(24)].In the limit where the phenomenological description of the dielectric screening is valid,we found that the correct formula for this Coulomb energy is Eq(6),not Eq(7).We also derived the Coulomb energy which relates the single particle eigen values with the E exc[Eq(39)].We found that the classical instantaneous dielectric energy in the last term of Eq(5)does not exist in our currently derived formula[Eq(39)].Under the assumption of Eqs(32)-(33),we found that the exchange interaction in Eq(39)is screened as for the Hartree ing Eq(24)and Eq(39)respectively,we found that the optical transition energy obtained from the LDA E qp g(plus the LDA band gap correction), is almost the same as the result obtained from the EPM single particle eigen values.Thus, the conclusion made in Ref.[10],that EPM misses the change of selfenergy with size R,is incorrect.Finally,we presented an effective single particle Hamiltonian H s[Eq(38)],which under the assumption of Eq(8),provides the band structure of a bulk system.Further testing of Eq(38)is needed.I thank my colleagues A.Zunger,A.William,A.Franceschetti and R.Needs for useful discussions.This work was supported by the Office of Energy Research,Material Science Division,U.S.Department of Energy,under Grant No.DE-AC02-83CH10093.REFERENCES[1]Y.Abe,Y.Osaka,And A.Morita,J.Phy.Soc.Japan17,1576(1962).[2]L.J.Sham and T.M.Rice,Phys.Rev.144,708(1966).[3]A.Zunger,MRS Bulletin,23,no.2(1998).[4]R.C.Ashoori,Nature,379,413(1996).[5]A.D.Yoffe,Adv.Phys.42,173(1993).[6]T.Takagahara,K.Takeda,Phys.Rev.B46,15578(1992).The exciton binding energycalculated in this paper including the correlation effects between the excited electron and the hole is very close to the Coulomb energy−1.8/ǫR.[7]L.E.Brus,J.Chem.Phys.79,5566(1983).[8]G.Allan,C.Delerue,nnoo,and E.Martin,Phys.Rev.B,52,11982(1995).[9]L.E.Brus,J.Chem.Phys.80,4403(1984).[10]S.Ogut.J.R.Chelikowsky,and S.G.Louie,Phys.Rev.Lett.79,1770(1997).[11]L.W.Wang and A.Zunger,J.Phys.Chem.98,2158(1994).[12]R.G.Parr,F.O.Ellison and P.G.Lykos,J.Chem.Phys.24,1106(1956).[13]R.McWeeny and B.T.Sutcliffe,Methods of Molecular Quantum Mechanics,(Londonand New York,Academic press,1969);or,R.McWeeny,Methods of Molecular Quantum Mechanics,second edition,(London,San Diego,Academic press,1989).[14]See for example:N.W.Ashroft and N.D.Mermin,Solid State Physics,page332,(Saun-ders College,Philadelphia,PA,1976).[15]O.W.Day,D.W.Smith and C.Garrod,Int.J.Quantum Chem.Symp.8,501(1974).[16]M.M.Morrell,R.G.Parr,and M.Levy,J.Chem.Phys.62,549(1975).[17]P.R.C.Kent,R.Q.Hood,M.D.Towler,R.J.Needs,and G.Rajagopal,Phys.Rev.B(inpress).[18]M.S.Hybertsen and S.G.Louie,Phys.Rev.B47,5390(1986).[19]L.C.Andreani,F.Bassani and A.Quattropani,L.Nuovo Cimento,10,1473(1988);K.Cho,Solid State Commun.33,911(1980);K.Ehara and K.Cho,Solid State Commun.44,453(1982).[20]W.Kohn and L.J.Sham,Phys.Rev.140,A1133(1965).[21]L.W.Wang and A.Zunger,Phys.Rev.Lett.73,1039(1994).[22]B.Delley and E.F.Steigmeier,Appl.Phys.Lett.67,2370(1995).FIGURESFIG.1.The LDA calculated(E N+1+E N−1−2E N)−(ǫc−ǫv)compared with the surface polarization Coulomb interaction(1−1/ǫ(R))/R.21A (-1)1/R E N +1E +N -1-E N 2)((-εc -εv )(e V ): (1-ε(R))11R E N+1E +N-1-E N 2)((-εc -εv )00.511.522.500.050.10.150.2: calc.Fig.1, Wang, etal。
电气工程专业英语试卷及参考答案

《电气工程专业英语》试卷一、根据英文单词,写出中文意义(20X0.5=10,共10分)alternator 交流发电机automation 自动控制,自动操作bandwidth 带宽,频带宽度built-in 内置的,固定的,嵌入的capacitance 容量,电容charge 负荷,电荷,费用,充电coil 线圈converter 转换器,变换器diode 二极管impedance 阻抗,全电阻insulator 绝缘体semiconductor 半导体sensor 传感器suppression 抑制switch 开关,电闸threshold 临界值vacuum 真空,空间vector 向量,矢量waveform 波形ammeter 电表二、根据中文意义,写出英文单词(20X0.5=10,共10分)n.近似值,接近,走近Approximationn.能力,性能,容量Capabilityv.补偿,偿还Compensaten.损耗Depletionadj.微分的Differentialn.打扰,干扰Disturbancen.以太网Ethernetn.频率, 周率Frequencyadj.不相容的, 矛盾的n.隔绝, 绝缘adj.瞬间的, 刹那间的Momentaryn.极性Polarityn.转发器,中继器Repeatern.排斥Repusionn.阻力,电阻,阻抗Resistancevt.模拟,模仿Simulaten.晶体管Transistorn.传感器,发送器,传递器n.阀n.波长三、根据英文词组,写出中文意义(30X0.5=15,共15分)between…and在……之间on the other hand 另一方面take advantage of 利用negative charge 负电荷electric field 电场free electron 自由电子current flow 电流sine wave 正弦波Root-Mean-Square 均方根(值)series circuit 串联电路voltage drop 电压降parallel circuit 并联电路compound circuit s复合电路parallel branch 并联分支decimal system 十进制系统programmable controller 可编程控制器truth table 真值表carbon brus 碳刷permanent magnet 永久磁铁armature field 电枢场magnetic lines 磁力线proportional system 比例系统 sampling period 采样周期 analog signal 模拟信号 baud rate 波特 discrete input 开关量输入 limit switch 限位开关 proximity switch 接近开关 industrial bus 工业总线 voltage difference电压差四、根据英文缩写,写出英文完整形式及中文意思(10X2=20,共20分)PLC PPI CNC EIA RF FCCCMOS VLSI CEMF五、根据下列方框中所给的词填空(5X1=5,共5分)Resistance in a material arises from the collision of electrons with the atoms and with each other as they move. The ___ 1、 collisions ___ produce heat, increasing the temperature of the material. Consider the ordinary toaster. Current flows through the ___2、wires ___ of the power cord and through the toaster's filament (the glowing wire you see inside). The same current must flow in the power cord as flows through the filament. The cord has very little ___ 3、resistance ___, while the filament has considerably more. Since the filament has a much higher resistance than the cord, it ___ 4、produces ___ much more heat. That's as it should be. Y ou want the heat for your toast, but you do not want the power cord getting ___ 5、hot ___! The standard incandescent light bulb is another example. The filament inthe light bulb glows white hot (hence, the word "incandescent") to produce light and a lot of heat as well. But, the low-resistance power cord stays cool.六、根据下列短文回答问题,回答请使用英文。
机器学习预测校级计算教学平台作业运行时间研究

第 22卷第 11期2023年 11月Vol.22 No.11Nov.2023软件导刊Software Guide机器学习预测校级计算教学平台作业运行时间研究于潇雪1,韦建文1,张战炳1,高亦沁1,林新华1,周云2,周衍晓2(1.上海交通大学网络信息中心,上海 200240;2.上海擎云物联网股份有限公司,上海 200070)摘要:机器学习方法在预测作业运行时间中被广泛采用,但在实际使用中,算例数据收集、预测方法选择、作业特征提取、小样本数据预测准确度提升等,仍是亟待解决的问题。
以上海交通大学校级计算教学平台使用负载中占比相当大的高斯应用为例,基于SLURM作业调度系统的前后处理机制设计了高斯算例收集系统,评估了不同机器学习方法结合不同特征采集方式对于预测作业运行时间的适用性。
最终,在5 314个样本数据集上,基于决策树和深度神经网络结合Text-CNN提取特征及加入库伦矩阵F范数的方法分别获得71.87%和84.93%的准确度,优于传统支持向量机方法;在仅有118个样本的小数据集上,使用迁移学习方法复用预训练参数分别获得65.2%和63.3%的准确度,优于从零开始训练的方法;使用Text-CNN能够避免one-hot编码导致的稀疏矩阵特征且拓展性更强;引入库伦矩阵F范数对提高准确度发挥了重要作用。
关键词:机器学习;计算教学平台;作业调度系统;运行时间;高斯应用DOI:10.11907/rjdk.231905开放科学(资源服务)标识码(OSID):中图分类号:TP391 文献标识码:A文章编号:1672-7800(2023)011-0104-06Study on Predicting Job Runtime of Computational Learning Platform viaMachine LearningYU Xiaoxue1, WEI Jianwen1, ZHANG Zhanbing1, GAO Yiqin1, LIN Xinhua1, ZHOU Yun2, ZHOU Yanxiao2(work and Information Center, Shanghai Jiao Tong University, Shanghai 200240, China;2.Shanghai Qingyun Internet of Things Co., Ltd., Shanghai 200070, China)Abstract:Machine learning approaches are widely adopted in job runtime prediction tasks. However, how to collect data, the choice of ML methods,tricks to use in training,plus how to improve accuracy on small data sets are obstacles for real use. This paper implements a SLURM-based job collection system for Gaussian, one of the most popular scientific applications on computational learning platform. Multiple ML and feature extraction methods are evaluated. Experiments show that, on a data set containing 5 314 samples, the methods based on deci‑sion tree and deep neural network combined with feature extracted by Text-CNN and F-norm of coulomb matrix obtained 71.87% and 84.93% accuracy respectively, surpassing traditional linear regression and support vector machine methods. On two small data sets with only 118 sam‑ples, the transfer migration learning method which reuses the pre-training parameters, achieves 65.2% and 63.3% accuracy, surpassing that of training from. Using Text-CNN can avoid sparse matrix caused by one-hot encoding and achieve a higher scalability. Besides, the F-norm of the Coulomb matrix played an important role in improving the accuracy.Key Words:machine learning; computational learning platform; job scheduling systems; job runtime; Gaussian application0 引言当今数字时代,计算对各领域发挥着颠覆性作用。
库洛米英文句子

库洛米英文句子Coulomb's Law: The Fundamental Principle of Electrostatic InteractionsThe study of electricity and magnetism is a fundamental aspect of physics, and at the heart of this field lies the concept of electrostatic interactions. One of the most important principles governing these interactions is Coulomb's law, named after the French physicist Charles-Augustin de Coulomb. This law, which was formulated in the late 18th century, provides a quantitative description of the force between two stationary electric charges.According to Coulomb's law, the force between two point charges is directly proportional to the product of the charges and inversely proportional to the square of the distance between them. Mathematically, this can be expressed as:F = k * (q1 * q2) / r^2where F is the force between the two charges, q1 and q2 are the magnitudes of the charges, r is the distance between them, and k is a constant known as the Coulomb constant, which has a value ofapproximately 8.99 × 10^9 N⋅m^2/C^2.The direction of the force is along the line connecting the two charges, and the force is attractive if the charges have opposite signs (i.e., one is positive and the other is negative) and repulsive if the charges have the same sign (both positive or both negative).One of the key implications of Coulomb's law is that the force between two charges decreases rapidly with increasing distance. This means that the influence of a charge on its surroundings diminishes rapidly as the distance from the charge increases. This property of electrostatic interactions has important consequences in various areas of physics, from the behavior of charged particles in electric fields to the stability of atomic and molecular structures.Coulomb's law also provides a foundation for understanding the concept of electric field, which is a vector field that describes the force experienced by a test charge placed at a particular location in space. The electric field at a point is defined as the force per unit charge experienced by a hypothetical positive test charge placed at that point. The electric field due to a point charge can be calculated using Coulomb's law, and the resulting expression is:E = k * q / r^2where E is the electric field, q is the charge, and r is the distance from the charge.The concept of electric field is particularly useful in understanding the behavior of charged particles in electric fields, as well as in the analysis of electric circuits and the propagation of electromagnetic waves.Coulomb's law has also found numerous applications in various fields of science and technology. In chemistry, it is used to understand the interactions between charged atoms and molecules, which are crucial in the formation of ionic and polar covalent bonds. In astrophysics, it is used to study the behavior of charged particles in the solar system and the dynamics of charged particles in the Earth's magnetosphere.Furthermore, Coulomb's law is the foundation for the development of more advanced theories in electromagnetism, such as Maxwell's equations, which describe the fundamental laws governing the behavior of electric and magnetic fields and their interactions.In conclusion, Coulomb's law is a fundamental principle in the study of electrostatic interactions, providing a quantitative description of the force between two stationary electric charges. This law has had a profound impact on our understanding of the behavior of chargedparticles and the nature of electric and magnetic fields, and it continues to be a cornerstone of modern physics and its applications in various fields of science and technology.。
有关库仑定律的英语作文

有关库仑定律的英语作文Coulomb's Law。
Coulomb's Law, named after the French physicistCharles-Augustin de Coulomb, describes the force between two electrically charged objects. The law states that the force between two point charges is directly proportional to the product of their charges and inversely proportional to the square of the distance between their centers. Mathematically, Coulomb's Law is expressed as F = k |q1 q2| / r^2, where F is the force between the charges, q1 and q2 are the magnitudes of the charges, r is the distance between the charges, and k is Coulomb's constant.Coulomb's Law is fundamental to the study ofelectricity and magnetism, and it has many practical applications in the fields of engineering, physics, and chemistry. For example, it is used to calculate the force between the protons and electrons in an atom, the force between the plates of a capacitor, and the force betweenthe poles of a magnet.One of the most important applications of Coulomb's Law is in the design and operation of electrical circuits. Engineers and technicians use the law to calculate theforce between the positive and negative charges in acircuit, which allows them to predict and control the flowof electricity. This is essential for the development of electronic devices and power systems.In addition to its practical applications, Coulomb'sLaw has also played a crucial role in the development ofour understanding of the natural world. By studying the forces between charged particles, scientists have been able to uncover the fundamental laws of electromagnetism and develop new technologies that have revolutionized our lives.Overall, Coulomb's Law is a fundamental principle of physics that has had a profound impact on our understanding of electricity and magnetism. Its practical applicationsand contributions to scientific knowledge make it an essential concept for students and professionals in thefields of science and engineering.In conclusion, Coulomb's Law is a fundamental principle of physics that describes the force between electrically charged objects. It has many practical applications in engineering, physics, and chemistry, and it has played a crucial role in the development of our understanding of the natural world. Its importance cannot be overstated, and it continues to be a foundational concept in the study of electricity and magnetism.。
Coulomb blockade effects in driven electron transport

a r X i v :c o n d -m a t /0606457v 2 [c o n d -m a t .m e s -h a l l ] 19 A p r 2007EPJ manuscript No.(will be inserted by the editor)Coulomb repulsion effects in driven electron transportFranz J.Kaiser,Peter H¨a nggi,and Sigmund KohlerInstitut f¨u r Physik,Universit¨a t Augsburg,Universit¨a tsstraße 1,D-86135Augsburg,Germany19April 2007Abstract.We study numerically the influence of strong Coulomb repulsion on the current through molec-ular wires that are driven by external electromagnetic fields.The molecule is described by a tight-bindingmodel whose first and last site is coupled to a respective lead.The leads are eliminated within a pertur-bation theory yielding a master equation for the wire.The decomposition into a Floquet basis enables an efficient treatment of the driving field.For the electronic excitations in bridged molecular wires,we find that strong Coulomb repulsion significantly sharpens resonance peaks which broaden again with increasing temperature.By contrast,it has only a small influence on effects like non-adiabatic electron pumping and coherent current suppression.PACS.05.60.Gg Quantum transport –85.65.+h Molecular electronic devices –72.40.+w Photoconduction and photovoltaic effects –73.63.-b Electronic transport in mesoscopic or nanoscale materials and structures1IntroductionRecent experiments on the conductance of single organic molecules opened a new direction in mesoscopic trans-port [1–3].Of particular interest is thereby the influence of electronic and vibronic excitations of the molecules which leave their fingerprints in the resulting current-voltage characteristics.At low temperatures,these effects become more pronounced [4].Much of our knowledge about excita-tions of molecules is based on spectroscopy,i.e.the optical response to light.In the context of molecular conduction,it has been proposed to study as well the signatures of such excitations in the transport quantifiers like the cur-rent [5–7]and its fluctuations [8].Such experiments are at present attempted,but clearcut evidence for the proposed effects is still missing because the irradiation also causes unwanted thermal effects in the contacts,which in today’s setups seem to dominate.One possibility to protect the contacts against the radiation is using the evanescent light at the tip of a near-field optical microscope.Coupled quantum dots represent a setup with proper-ties similar to those of molecular wires [9,10],albeit at dif-ferent length and energy scales.As compared to molecular wires,they are more stable and tunable,but have the dis-advantage that only a few dots can be coupled coherently.The transport properties of these “artificial molecules”can be significantly modified by microwaves [10].It has for example been demonstrated experimentally that res-onant excitations between the levels of double quantum dots result in the so-called photon-assisted transport,i.e.a significant enhancement of the dc current [11,12].In addition to photon-assisted transport [13],other less intuitive phenomena have been predicted in this context.For example the so-called coherent suppression of tun-nelling in a double-well potential due to a time-dependent dipole force can also be found in ac driven transport through coupled quantum dots:For characteristic ratios between the amplitude and the frequency of the driving,it has been predicted that the dc current [14–16]and the shot noise [17]will be suppressed.A further prominent effect is adiabatic electron pumping,which is the generation of a dc current by means of a periodic variation of the con-ductor parameters in the absence of any net bias [18–21].It has been proposed [22,23]and experimentally demon-strated [10,11]that pumping is more effective at internal resonances,i.e.,beyond the adiabatic limit where,in addi-tion,the pump current possesses a surprisingly low noise level [24].Periodically time-dependent quantum systems can be described very efficiently within a Floquet theory which originally has been derived for driven closed quantum sys-tems [25]and later been generalised to dissipative quan-tum systems [26,27].Furthermore,it is possible to derive Floquet theories for the description of transport through mesoscopic conductors which are connected to external leads.For cases in which electron-electron interactions do not play any role,one can derive a Floquet scatter-ing theory that provides exact expressions for the cur-rent [17,28]and its noise [8,17].Treating the coupling between the conductor and the leads perturbatively,one can obtain a master equation for the reduced density oper-ator of the wire.This enables a rather efficient treatment of time-dependent transport after decomposing the wire density operator into a Floquet basis.Then it is possi-ble to study relatively large driven conductors [29]and to include also electron-electron [30]and electron-phonon interactions [31].If the time-dependent field consists of2Franz J.Kaiser et al.:Coulomb repulsion effects in driven electron transportFig. 1.Bridged molecular wire model consisting of N=5sites with internal tunnelling matrix elements∆and effectivewire-lead coupling strengthsΓL/R.one or a few laser pulses,it is possible to obtain the den-sity operator by propagating the Liouville-von Neumannequation[32].In this work,we derive in Sections2and3a Flo-quet master equation formalism that captures situationsin which strong Coulomb repulsion restricts the excesscharge residing on the conductor to a single electron.Forlater reference,we adapt in Section4our approach tothe case of spinless electrons and non-interacting elec-trons.We then investigate in Section5the role of strongCoulomb repulsion for photon-assisted transport throughbridged molecular wires,non-adiabatic electron pumping,and coherent current suppression.2The wire-lead modelThe system of the driven wire,the leads,and the couplingbetween the molecule and the leads,as sketched in Fig.1,is described by the HamiltonianH(t)=H wire(t)+H leads+H wire-leads.(1)The wire is modelled within a tight-binding description bythe molecular orbitals|n ,n=1,...,N,so thatH wire(t)= n,n′,s H nn′(t)c†ns c n′s+U[H wire(t)+H leads,ρ(t)](8)1−Franz J.Kaiser et al.:Coulomb repulsion effects in driven electron transport3 Here thefirst term corresponds to the coherent dynam-ics of both the wire electrons and the lead electrons,whilethe second term describes resonant electron tunnelling be-tween the leads and the wire.The tilde denotes operatorsin the interaction picture with respect to the molecule andthe lead Hamiltonian without the molecule-lead coupling,X(t,t′)=U†0(t,t′)X U0(t,t′),where U0is the propagatorwithout the coupling.The net(incoming minus outgoing)electrical current through the left contact is given by mi-nus the time-derivative of the electron number in the leftlead multiplied by the electron charge−e.From Eq.(8)follows for the current in the wide-band limit the expres-sionI L(t)=e tr[˙ρ(t)N L]=−e ΓLd t |ϕα(t) =ǫα|ϕα(t) ,(12)whose solution allows one to construct via Slater deter-minants many-particle Floquet states.In analogy to thequasimomenta in Bloch theory for spatially periodic po-tentials,the quasienergiesǫαcome in classesǫα,k=ǫα+k Ω,k∈Z,(13)of which all members represent the same physical solutionof the Schr¨o dinger equation.Thus we can restrict ourselvesto states within one Brillouin zone like for example0≤ǫα< Ω.For the computation of the current it is convenient tohave an explicit expression for the interaction picture rep-resentation of the wire operators.It can be obtained fromthe(fermionic)Floquet creation and annihilation opera-tors[36]defined via the transformationcαs(t)= n ϕα(t)|n c ns.(14)The inverse transformationc ns= α n|ϕα(t) cαs(t)(15)follows from the mutual orthogonality and the complete-ness of the Floquet states at equal times[27].Note thatthe right-hand side of Eq.(15)becomes time independentafter the summation.The Floquet annihilation operator(14)has the inter-action picture representation˜cαs(t,t′)=U†0(t,t′)cαs(t)U0(t,t′)(16)=e−i(ǫα+UN wire)(t−t′)/ cαs(t′),(17)with the important feature that the time difference t−t′enters only via the exponential prefactor.This will allowus to evaluate theτ-integration of the master equation(8)after a Floquet decomposition.Relation(17)can easily beshown by computing the time derivative with respect to twhich by use of the Floquet equation(12)becomesd(ǫα+UN wire)˜cαs(t,t′).(18)Together with the initial condition˜cα(t′,t′)=cα(t′)fol-lows relation(17).Note that the time evolution inducedby H wire(t)conserves the number of electrons on the wire.3.2.2Master equation and current formulaIn order to make use of the Floquet ansatz,we decomposethe master equation(8)and the current formula(9)intothe Floquet basis derived in the last subsection.For that4Franz J.Kaiser et al.:Coulomb repulsion effects in driven electron transport purpose we use the fact that we arefinally interested inthe current at asymptotically large times in the limit of alarge interaction U.The latter has the consequence thatonly wire states with at most one excess electron play arole,so that the density operatorρwire can be decomposedinto the2N+1dimensional basis{|0 ,c†αs(t)|0 },where|0 denotes the wire state in the absence of excess electronsand s=↑,↓.Moreover,it can be shown that at large times,the density operator of the wire becomes diagonal in theelectron number N wire.Therefore a proper ansatz readsρwire(t)=|0 ρ00(t) 0|+ α,β,s,s′c†αs|0 ραs,βs′(t) 0|cβs′.(19)Note that we keep terms withα=β,which means that wework beyond a rotating-wave approximation.Indeed in anon-equilibrium situation,the off-diagonal density matrixelementsραβwill not vanish and neglecting them mightlead to artefacts[8,37].In the context of molecular wires,such a treatment of strong Coulomb repulsion by a re-striction to at most one excess electron has recently alsobeen applied to incoherent[38–40]as well as to coherenttransport[41].By inserting the decomposition(19)into the masterequation(8),we obtain an equation of motion for the ma-trix elementsραs,βs′= 0|cαsρwire c†βs′|0 .We evaluate thetrace over the lead states and compute the matrix element0|cαs(t)...c†βs′(t)|0 .Thereby we neglect the two-particleterms which are of the structure c†αs c†βs |0 0|cβs cαs.For-mally,these terms drop out in the limit of strong Cou-lomb repulsion because they are accompanied by a rapidly oscillating phase factor exp(−i UN wireτ/ ).Then theτ-integration results in a factor f L(ǫα,k+U)which vanishes in the limit of large U.Since the total Hamiltonian(1)is diagonal in the spin index s,wefind that the density ma-trix elementsραs,βs′are spin-independent as well so that after a transient stageρα↑,β↑(t)=ρα↓,β↓(t)≡ραβ(t)(20)andρα↑,β↓=0.Moreover,at large times,the density op-erator(19)will acquire the time periodicity of the driving field[8]and,thus,can be decomposed into the Fourier seriesραβ(t)= k e−i kΩtραβ,k(21)andρ00(t)accordingly.After some algebra,we arrive at a set of N2coupled equations of motion forραβ(t)which in Fourier represen-tation readi(ǫα−ǫβ−k Ω)ραβ,k=ΓL2 α′,k′,k′′ ϕα,k′+k′′|1 1|ϕα′,k+k′′ ρα′β,k′¯f L(ǫα′,k+k′′)−ΓLRe α,k β,k′ ϕβ,k′+k|1 1|ϕα,k ραβ,k′¯f L(ǫα,k)− k′ ϕα,k′+k|1 1|ϕα,k ρ00,k′f L(ǫα,k) .(24) Physically,the second contribution of the current formula (24)describes the tunnelling of an electron from the left lead to the wire and,thus,is proportional toρ00f L which denotes the probability that a lead state is occupied while the wire is empty.Thefirst terms corresponds to the re-versed process namely the tunnelling on an electron from site|1 to the left lead.The results of this section allow us the numerical com-putation of the dc current through a driven conductor in the the following way:First,we solve the quasienergy equation(12)which provides the coefficients ϕα,k|n .Next, we solve the master equation(22)and insert the solution into the current formula(24).4Separating interaction and spinIn order to determine the role of a strong interaction, we shall compare below our results to the non-interacting case.Moreover,a particular consequence of strong Cou-lomb repulsion is the mutual blocking of different spin channels.This motivates us to also compare to the case of spinless electrons which is physically realised by spin po-larisation.In this section,we adapt our master equation approach to these situations.Franz J.Kaiser et al.:Coulomb repulsion effects in driven electron transport5 4.1Spinless electronsIn order to describe spinless electrons,we drop in the ini-tial Hamiltonian all spin indices.Physically,this limit isrealised by a sufficiently strong magneticfield that po-larises all electrons contributing to the transport.By thesame calculation as in Section3,we then obtain for thecurrent also the expression(24)but without the prefactor2.The factor2is also no longer present in the normalisa-tion condition(23)which now readstrρwire(t)=ρ00(t)+ αραα(t)=1.(25)4.2Non-interacting electronsIn the absence of interactions,U=0,each spin degree offreedom can be treated separately.Still one has to considerfor each spin projection up to N electrons so that therelevant Hilbert space has the dimension2N.Therefore,it is more efficient to consider the single-particle densitymatrixRαβ(t)= c†αs(t)cβs(t) t=R∗βα(t)= k e−i kΩt Rαβ,k,(26)which is of dimension N2and nevertheless contains allrelevant information.The Fourier decomposition in thelast expression uses the fact that,at asymptotically largetimes,Rαβ(t)becomes time-periodic.We express the time derivative of Rαβ(t)with the mas-ter equation(8)and insert for˜cα(t,t−τ)the Floquetrepresentation(18).After some algebra,we obtain for theFourier coefficients Rαβ,k the equationi(ǫα−ǫβ+k Ω)Rαβ,k=ΓLα,k Reβ,k′ϕβ,k′+k|1 1|ϕα,k Rαβ,k′−| 1|ϕα,k |2f L(ǫα,k) .(28)For a detailed derivation see Ref.[36].5Interplay of dipole radiation and CoulombrepulsionIn our model Hamiltonian(1)we have already specifiedthe interaction,the lead Hamiltonian,and the wire-leadcoupling.By contrast,for the Hamiltonian of the drivenwire,we have thus far only assumed that the externalfieldis periodic in time.In the following we focus on modelswhere the single-particle dynamics is determined by theN-site tight-binding HamiltonianH nn′(t)=−∆N−1n=1(|n n+1|+|n+1 n|)+Nn=1{E n+Ax n cos(Ωt)}|n n|.(29)Neighbouring sites are coupled by a tunnel matrix element∆.The onsite energies E n are modulated by a harmon-ically time-dependent dipole force,where the amplitudeA is given by the electricalfield amplitude multiplied bythe electron charge and the distance between neighbour-ing sites.x n=16Franz J.Kaiser et al.:Coulomb repulsion effects in driven electron transportU =∞spinless00.10.2I [10−3e Γ/¯h ]89101112Ω[∆/¯h ]∞U =,spinless U =0,Fig.2.Photon-assisted current in a bridged molecular wirewith length N =8and height E B =10∆.Leads with a chemi-cal potential difference eV =5∆couple to the wire with an ef-fective strength Γ=0.1∆.The driving amplitude is A =0.3∆.For U =∞,the current for spinless electrons coincides with the one for real electrons.a factor 2.The electron dynamics within the wire,how-ever,is described by the coherent first term of the master equation (8)which is spin-independent.Consequently,we expect that the spin only plays a minor role whenever the tunnelling from the donor to the acceptor becomes the bottleneck for the electrons.This is indeed the case for the transport across a barrier considered here.As compared to the non-interacting case,one notices that strong Coulomb repulsion modifies the shape of the peaks:They become slightly higher and much sharper.This effect is more pronounced for large wires.A closer look at the resonance peaks for wires with up to N =10sites (not shown)indicates that the resonance widths scale roughly like 1/N .This is possibly caused by the fact that the Coulomb repulsion reduces the number of available (many-particle)wire states and,thus,the number of decay channels.This relates to the observation made in Ref.[41],namely that Coulomb repulsion can improve quantum co-herence and thereby enhance the current.Since quantum coherence is also temperature depen-dent,it is natural to ask whether the resonance peaks become sharper for lower temperatures.Figure 3shows the width of the central peak of Fig.2as a function of the temperature.While in the non-interacting case,the peak widths are essentially temperature independent,the sit-uation changes for strong Coulomb repulsion:There one finds that with an increasing temperature,the peaks be-come roughly twice as broad once the temperature exceeds T =∆/k B .We attribute this behaviour to the reduced coherence for thermal energies that are larger than the tunnelling matrix element.5.2Non-adiabatic electron pumpingAnother well studied phenomenon in driven transport is coherent electron pumping,i.e.,the creation of a non-vanishing dc current by ac fields in the absence of any net bias.For adiabatically slow driving,this effect exists onlyU =∞U =0,spinless00.050.10.15F W H M [∆/¯h ]0.0010.010.1110100T [∆/k B ]Fig.3.Temperature dependence of the widths of the reso-nance peaks at Ω≈9.71∆/ .The graph shows the full widths at half of the maximum.All other parameters are as in Fig.2.For U =∞,the values for spinless electrons and real electrons coincide.Fig.4.Tight-binding model for two coupled quantum dots in pump configuration,i.e.in the absence of a bias voltage but with an internal bias E 2−E 1=0which breaks reflection symmetry.in the absence of time-reversal symmetry [18–20].Beyond the adiabatic regime,this is no longer the case:For fast,time-periodic driving fields,it can be shown that the rele-vant symmetry is the so-called generalized parity which is defined as the invariance under spatial reflection in com-bination with a time shift by half a driving period [8].Non-adiabatic electron pumping is particularly interesting because at internal resonances of the central system the pump current can assume rather large values [10,22,35],while at the same time the current noise is remarkably low [24].For studying the influence of strong Coulomb repulsion on non-adiabatic electron pumping,we consider the setup sketched in Fig.4.Of particular interest is the parameter regime with large internal bias and intermediate dot-lead coupling because in this regime,the current-to-noise ratio is most favourable [24].The currents obtained for the three considered approaches are shown in Fig.5.Again we find that the spin degree of freedom is not of major influence,which indicates that the transport is governed by internal excitations;cf.the discussion in the preceeding subsection.The influence of the Coulomb repulsion is a modifica-tion of the current peak height up to 5%.This means that interactions are here much less important than for photon-assisted transport:The reason for this is that for our pump configuration,one energy level lies below the Fermi energyFranz J.Kaiser et al.:Coulomb repulsion effects in driven electron transport 700.10.20.3I [e Γ/¯h ]1234567Ω[∆/¯h ]U =∞U =∞,spinless U =0,spinlessFig.5.Pump current for strong Coulomb repulsion and fornon-interacting electrons as a function of the frequency.The dot levels with energies E 1=−2.5∆and E 2=2.5∆are couple to the leads with strength Γ=0.3∆.The driving amplitude is A =3.7∆and the temperature k B T =0.005∆.while the other lies well above.Thus in equilibrium for a sufficiently small dot-lead coupling,the left site is occu-pied while the right site is empty,whatever the interaction strength.Thus,the double dot is populated with only one electron so that interactions become irrelevant.Unless the driving amplitude is huge,this occupation is altered only slightly.Consequently interactions do not modify the cur-rent significantly.We emphasise that for strong dot-lead coupling Γand finite interaction U ,these arguments no longer hold true.5.3Coherent current controlAn intriguing example of quantum control is the so-called coherent destruction of tunnelling in a double-well po-tential by a suitable driving field [43],which can be ex-plained within a rotating-wave approximation:In the driv-ing dominated regime,the tunnel matrix element is es-sentially replaced by an effective tunnel matrix element ∆eff=J 0(A/ Ω),where J 0is the zeroth order Bessel function of the first kind and A the driving amplitude [44,45].Related effects have been predicted for driven tight-binding lattices [46].For driven transport between two leads,the corresponding situation has been investi-gated only recently:It has been found that driving fields that suppress tunnelling in a closed driven system,also suppress the current through the corresponding open sys-tem [14,47].A setup in which this coherent current suppression can be studied is sketched in Fig.6.It is characterized by the fact that all internal levels lie within the voltage window,i.e.below one chemical potential and above the other.For this system,strong interaction has already a significant influence on the current in the absence of any driving field [41]:For U =0,the system is half filled,which means it is populated by N/2electron,and the current is independent of N .By contrast for U =∞,the stationary population is N/(N +1)and the current becomes I ∝1/(N +1).Fig.6.Triple quantum dot configuration for coherent current control:A large bias voltage and the unbiased dot levels with E n =0ensure optimal transport in the absence of the driving.N =5N =300.20.40.6I [e Γ/¯h ]5101520253035A [∆]U =∞U =∞,spinless U =0,spinless00.20.40.6I [e Γ/¯h ]U =∞U =∞,spinless U =0,spinlessFig.7.Coherent current suppression as a function of the driv-ing amplitude A for a wire that consists of N =3sites.The applied voltage is eV =50∆,the driving frequency Ω=5∆,and the wire-lead coupling Γ=0.5∆.Figure 7shows the influence of Coulomb repulsion on the current suppression studied in Ref.[17].Independent of the interaction,one finds that the current almost van-ishes whenever the ratio A/ Ωmatches a zero of the Bessel function J 0.If the driving amplitude is far from the values for which the current is suppressed,we observe the behaviour found for the static situation,namely that Cou-lomb repulsion reduces the current by a factor 1/(N +1)for spinless electrons [41].If one considers the spin,this factor becomes 2/(2N +1).In the vicinity of the current suppressions,by contrast,the influence of both the inclu-sion of the spin and the interaction is less pronounced.In this regime,the effective tunnel matrix element ∆effis small,so that tunnelling along the wire happens at a low rate.This again indicates that whenever the transport is limited by the dynamics within the wire,the influence of interaction is rather small.8Franz J.Kaiser et al.:Coulomb repulsion effects in driven electron transport6ConclusionsWe studied the influence of strong interaction on the trans-port properties of ac-driven coherent conductors.In par-ticular,we compared the strongly interacting case with the opposite extreme of non-interacting electrons.Moreover, we worked out the relevance of the spin degree of free-dom for weak wire-lead coupling.In our studies,we con-sidered three archetypical effects,namely photon-assisted tunnelling through bridged molecular wires,non-adiabatic electron pumping,and coherent current suppression.The most significant effect is found for photon-assisted tunnelling where Coulomb repulsion renders the resonance linewidths much sharper.Thus unfortunately,interactions might contribute to the difficulties in photon-assited tun-nelling experiments with molecular wires.By contrast, Coulomb repulsion is not too relevant for electron pump-ing in double quantum dots.For coherent current suppres-sion,the same holds true only for parameters for which the current is already significantly reduced.Outside this region,onefinds that Coulomb repulsion reduces the cur-rent essentially in the same way as in the absence of driv-ing.The two extreme cases of zero and very strong interac-tion do not necessarily allow a simple interpolation.Thus, it is desireable to extend the present studies tofinite values of the interaction strength,which requires the generalisa-tion of our formalism to at least a second excess electron. Moreover,the dc current is certainly not the only relevant quantity for the characterisation of the electron transport. Investigating the influence of Coulomb repulsion on,e.g., the current noise would complement the picture drawn above.We thank M.Strass and A.Nitzan for interesting discussions. This work has been supported by Deutsche Forschungsgemein-schaft through SFB484and SPP1243.One of us(FJK)ac-knowledges funding by Bayerisches Staatsministerium f¨u r Wis-senschaft,Forschung und Kunst through Elitenetzwerk Bay-ern.References1.M.A.Reed,C.Zhou,C.J.Muller,T.P.Burgin,and J.M.Tour,Science278,252(1997).2.X.D.Cui et al.,Science294,571(2001).3.J.Reichert,R.Ochs, D.Beckmann,H. B.Weber,M.Mayor,and H.von L¨o hneysen,Phys.Rev.Lett.88,176804 (2002).4.J.Reichert,H. B.Weber,M.Mayor,and H.vonL¨o hneysen,Appl.Phys.Lett.82,4137(2003).5.S.Kohler,J.Lehmann,S.Camalet,and P.H¨a nggi,IsraelJ.Chem.42,135(2002).6. A.Keller,O.Atabek,M.Ratner,and V.Mujica,J.Phys.B35,4981(2002).7. A.Tikhonov,R.D.Coalson,and Y.Dahnovsky,J.Chem.Phys.117,567(2002).8.S.Kohler,J.Lehmann,and P.H¨a nggi,Phys.Rep.406,379(2005).9.R.H.Blick,R.J.Haug,J.Weis,D.Pfannkuche,K.vonKlitzing,and K.Eberl,Phys.Rev.B53,7899(1996). 10.W.G.van der Wiel,S.De Franceschi,J.M.Elzerman,T.Fujisawa,S.Tarucha,and L.P.Kouwenhoven,Rev.Mod.Phys.75,1(2003).11.T.H.Oosterkamp et al.,Nature395,873(1998).12.W.G.van der Wiel,T.Fujisawa,T.H.Oosterkamp,and L.P.Kouwenhoven,Physica B(Amsterdam)272,31 (1999).13.G.Platero and R.Aguado,Phys.Rep.395,1(2004).14.J.Lehmann,S.Camalet,S.Kohler,and P.H¨a nggi,Chem.Phys.Lett.368,282(2003).15. F.Grossmann,Phys.Rev.B70,113306(2004).16.S.Welack,M.Schreiber,and U.Kleinekath¨o fer,J.Chem.Phys.124,044712(2006).17.S.Camalet,J.Lehmann,S.Kohler,and P.H¨a nggi,Phys.Rev.Lett.90,210602(2003);S.Camalet,et al.,Phys.Rev.B70,155326(2004).18.P.W.Brouwer,Phys.Rev.B58,R10135(1998).19. B.L.Altshuler and L.I.Glazman,Science283,1864(1999).20.M.Switkes,C.M.Marcus,K.Campman,and A.C.Gos-sard,Science283,1905(1999).21. B.Wang,J.Wang,and H.Guo,Phys.Rev.B65,073306(2002).22. C.A.Stafford and N.S.Wingreen,Phys.Rev.Lett.76,1916(1996).23.M.Wagner and F.Sols,Phys.Rev.Lett.83,4377(1999).24.M.Strass,P.H¨a nggi,and S.Kohler,Phys.Rev.Lett.95,130601(2005).25.J.H.Shirley,Phys.Rev.138,B979(1965).26.S.Kohler,T.Dittrich,and P.H¨a nggi,Phys.Rev.E55,300(1997).27.M.Grifoni and P.H¨a nggi,Phys.Rep.304,229(1998).28.M.Moskalets and M.B¨u ttiker,Phys.Rev.B66,205320(2002).29.J.Lehmann,S.Kohler,P.H¨a nggi,and A.Nitzan,Phys.Rev.Lett.88,228305(2002).30. C.Bruder and H.Schoeller,Phys.Rev.Lett.72,1076(1994).31.J.Lehmann,S.Kohler,V.May,and P.H¨a nggi,J.Chem.Phys.121,2278(2004).32.U.Kleinekath¨o fer,G.Li,S.Welack,and M.Schreiber,Europhys.Lett.75,139(2006).33.Yu.V.Nazarov,Physica B189,57(1993).34.S.A.Gurvitz and Ya.S.Prager,Phys.Rev.B53,15932(1996).35.P.Brune,C.Bruder,and H.Schoeller,Phys.Rev.B56,4730(1997).36.J.Lehmann,S.Kohler,P.H¨a nggi,and A.Nitzan,J.Chem.Phys.118,3283(2003).37.T.Novotn´y,Europhys.Lett.59,648(2002).38. E.G.Petrov and P.H¨a nggi,Phys.Rev.Lett.86,2862(2001).39. E.G.Petrov,V.May,and P.H¨a nggi,Chem.Phys.281,211(2002).40.J.Lehmann,G.-L.Ingold,and P.H¨a nggi,Chem.Phys.281,199(2002).41. F.J.Kaiser,M.Strass,S.Kohler,and P.H¨a nggi,Chem.Phys.322,193(2006).42. A.Nitzan,Annu.Rev.Phys.Chem.52,681(2001).43. F.Grossmann,T.Dittrich,P.Jung,and P.H¨a nggi,Phys.Rev.Lett.67,516(1991).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
arXiv:nucl-th/0301063v2 2RODUCTION
Pseudospin was introduced in the late 1960s [1, 2] to account for the quasidegeneracy of single-nucleon states with quantum numbers (n, ℓ, j = ℓ + 1/2) and (n − 1, ℓ + 2, j = ℓ + 3/2) where n, ℓ, and j are the radial, the orbital, and the total angular momentum quantum numbers, respectively. These levels have the same “pseudo-orbital” angular ˜ = ℓ + 1, and “pseudospin” quantum number, s momentum quantum number, ℓ ˜ = 1/2. The pseudospin symmetry has been analyzed in nonrelativistic models by several works [3, 4, 5]. The subject was revived in recent years when Ginocchio [6] presented a relativistic interpretation for this symmetry showing that the ˜ is the orbital quantum number of the lower component of the Dirac spinor for spherical potentials. quantum number ℓ ˜ is a good quantum number in a relativistic theory for the nucleon with scalar S and vector Moreover, he showed that ℓ V potentials with opposite signs and the same magnitude, i.e., Σ = S + V = 0. Actually, this condition can be relaxed to demand that only the derivative of Σ is zero [7], but, if Σ goes to zero at infinity, both conditions are equivalent. These findings are in agreement with the nuclear phenomenology obtained in relativistic mean field (RMF) theories, in view of the fact that the scalar and vector potentials in RMF for the nucleus [8, 9, 10, 11], although large, cancel each other to a great extent, giving a relatively small negative value for Σ on the nucleon mass scale [12]. The structure of the radial nodes occurring in pseudospin levels as well as the nuclei wave function for them were also explained in recent works [13, 14, 15]. Unfortunately, because in the nonrelativistic reduction of the Dirac equation Σ acts as the binding potential, it cannot be set to zero in nuclei, since in that case there would not be any bound state. So the question remains how the pseudospin symmetry is realized in nuclei, namely how some levels of pseudospin partners become degenerate or near degenerate. A partial answer to this question has been given in two previous works [16, 17], in which were shown that, using Woods-Saxon potentials, this degeneracy not only depends on the value of the depth of the Σ potential but also on its characteristic extension (radius) and its surface steepness (diffusivity). Furthermore, using an energy decomposition based on a Schr¨ odinger-like equation for the radial lower component of the Dirac spinor, it was shown that the near-degeneracy of some pseudospin doublets arises from a cancellation between the terms in that decomposition, and that the pseudospin-orbit term is in general bigger than the splitting itself. This agreed with the findings of Refs. [18, 19] in which the pseudospin-orbit coupling was shown to be a nonperturbative quantity. The conclusion was that pseudospin symmetry in nuclei has a dynamical character. The systematics found in Refs. [16, 17] for the pseudospin dependence on the shape of the nuclear mean fields allowed the explanation for the difference between the energy splittings of proton and neutron pseudospin partners. This was done by revealing the influence of the ρ potential Vρ , which appears in RMF theories, on pseudospin-orbit interaction, favoring pseudospin symmetry for neutron levels as is found experimentally. However, the role of the Coulomb potential VCoul for the proton splittings, which has the opposite sign of Vρ , was not considered. A previous study of the isospin dependence of the pseudospin symmetry was done in Ref. [20] for the Zr and Sn isotopes, where it was shown that the pseudospin symmetry becomes better for exotic nuclei with a highly diffuse potential.
P. Alberto
Departamento de F´ ısica and Centro de F´ ısica Computacional, Universidade de Coimbra, P-3004-516 Coimbra, Portugal (Dated: February 8, 2008) We investigate the role of the Coulomb and the vector-isovector ρ potentials in the asymmetry of the neutron and proton pseudospin splittings in nuclei. To this end, we solve the Dirac equation for the nucleons using central vector and scalar potentials with Woods-Saxon shape and Z and N − Z dependent Coulomb and ρ potentials added to the vector potential. We study the effect of these potentials on the energy splittings of proton and neutron pseudospin partners along a Sn isotopic chain. We use an energy decomposition proposed in a previous work to assess the effect of a pseudospin-orbit potential on those splittings. We conclude that the effect of the Coulomb potential is quite small and the ρ potential gives the main contribution to the observed isospin asymmetry of the pseudospin splittings. This isospin asymmetry results from a cancellation of the various energy terms and cannot be attributed only to the pseudospin-orbit term, confirming the dynamical character of this symmetry pointed out in previous works.
